图1 小鼠几何模型
Fig.1 Proposed geometric model for mouse
摘要 该文研究了两种常见亥姆霍兹线圈产生磁场的均匀性，并根据装置线圈所产生磁场作用下的生物组织治疗温度分布分析了磁场均匀性对治疗效果的影响。其中，文中的磁纳米粒子（MNPs）以磁流体形式注射进肿瘤区域并假定以注射点为中心呈现高斯分布。该文在多种约束条件下应用改进粒子群算法优化了磁场的频率和强度、磁纳米粒子粒径，以及磁纳米粒子体积分数等参数，而涉及的约束条件包括治疗最高安全温度、治疗磁场安全范围上限、MNPs粒径范围，以及MNPs产热有效条件等。同时，该文以累积等效分钟数来评估圆形和正方形亥姆霍兹线圈及理想磁场在不同血液灌注率下的细胞热损伤程度。研究结果表明，正方形亥姆霍兹线圈相比于圆形线圈能产生更大范围的匀强磁场，这使其磁热疗效果更接近于理想磁场情况。同时，考虑温度依赖的血液灌注率相比定值情况具有更高的治疗温度。
关键词：磁热疗 粒子群优化算法 亥姆霍兹线圈 血液灌注率 磁场 温度场
磁热疗因其具有低副作用和微创性等优势特征，故而在近年来被广泛关注和深入研究[1-2]。磁纳米粒子（Magnetic Nanoparticles, MNPs）以磁流体的形式注射进肿瘤区域后，在交变磁场的作用下将肿瘤区域的治疗温度加热至42～46℃。癌细胞在该治疗温度范围内会因热敏感性发生热消融，而健康组织则不会受损[3-4]。磁热疗治疗温度取决于诸多因素，而MNPs产热则是其中重要的决定因素之一。MNPs的产热在粒径较小时可通过Rosensweig理论来描述，其又进一步取决于外加交变磁场属性、生物组织属性及含有MNPs的磁流体属性等影响因素[5]。为尽可能地减小副作用，理想的磁热疗应是在控制最高安全治疗温度（46℃）的同时还应尽可能减少进入体内的MNPs数量，即减少剂量或降低体积分数[6]。此外，治疗装置磁场及MNPs分布的均匀性也是影响治疗效果的重要因素。
尽管以往的报道在磁热疗的不同领域均做了较大的贡献，然而基于磁场装置的磁热疗优化研究仍缺少足够的关注。现有研究通常假定治疗磁场强度在肿瘤区域为定值[7-8]，即假设治疗磁场在肿瘤区域为理想匀强磁场，而实际装置所产生的磁场通常为非均匀分布。治疗磁场的不均匀将导致治疗温度分布的不理想并最终影响治疗效果，故装置磁场均匀度的优化是磁热疗过程中不可忽略的重要环节。文献[9]通过修改线圈结构并在线圈端部增加磁通集中器环后，有效地增加了线圈装置磁场的均匀性。不足的是，该研究并未进一步深入将结果应用于磁热疗的后续治疗温度及治疗效果等研究。进一步地，亥姆霍兹线圈可作为磁热疗的磁场发生装置，圆形及正方形是最为常见的两种亥姆霍兹线圈的形状。文献[10-11]均基于圆形亥姆霍兹线圈磁场研究了给定生物组织模型的磁热疗温度分布，但均未对磁场的不均匀性进行分析。同时，两者的模型均假定磁流体为均匀分布的核形式，而实际上磁流体注射进生物组织后应呈现以注射点为中心的类高斯函数分布形式[12]。文献[13]则是基于正方形亥姆霍兹线圈磁场进行研究，其也存在上述两篇基于圆形亥姆霍兹线圈磁场的文献所存在的问题。此外，以往报道也较少基于治疗安全温度来优化MNPs的产热，进而最终优化磁场和MNPs属性等。事实上，磁热疗在保证热疗效果的前提下，期望MNPs浓度或MNPs数量越小越好，而此前大多研究使用典型值并未考虑优化问题[14-16]。为此，文献[17]在考虑了最高安全温度46℃的前提下首先获取了MNPs的产热临界值，并基于该值对磁场或MNPs属性进行相应的优化，尽管该方法能实现对磁场和部分MNPs属性的优化，然而并未优化MNPs体积分数也未考虑磁场治疗安全系数Hf（磁场强度×频率）的上限值[18]。此外，文献[19]将上限安全温度与最高治疗温度之间的差值设定为目标函数，采用Nelder-Mead算法对磁热疗进行优化并获得MNPs的最佳耗散功率，并基于此耗散功率分析了磁场特性及MNPs特性所需的取值。但是，该文献并未针对MNPs的体积分数问题进行优化，也未考虑磁热疗中存在的各种约束问题。同时，文献[17, 19]的治疗磁场并非实际线圈所产生，而仅简单地假定为理想磁场并且均匀作用于生物组织内。
本文研究了两种不同亥姆霍兹线圈装置产生的磁热疗所需治疗磁场，并分析了线圈磁场内不同位置对生物组织治疗温度分布的影响，讨论了不同血液灌注率下不同磁场对治疗评价指标的影响。此外，本研究基于改进粒子群优化算法对磁热疗中MNPs产热进行优化，以得到多个约束下所需注射点体积分数的最小值和此时相应的MNPs半径、磁场强度和频率等。其中，本文所研究的磁场包括正方形和圆形亥姆霍兹线圈磁场及理想均匀磁场，考虑的血液灌注率则有定值及温度依赖的血液灌注率，而对治疗效果则采用治疗温度与43℃下的累计等效分钟值来评估。此外，本文磁场和温度场偏微分方程均采用有限元方式进行求解，同时两个不同物理场之间采用顺序耦合方式进行关联。
1.1.1 生物组织模型
本文仿照实际小鼠轮廓建立了一个三维的小鼠模型来评估磁热疗过程中肿瘤、肿瘤所在的健康生物组织以及小鼠的治疗温度分布和癌细胞损伤情况。此模型忽略了小鼠的四肢和复杂的小鼠具体生物结构，而主要聚焦于小鼠体内肿瘤和其所在的健康组织，剩余部分简化为皮肤，这在保证结果准确性的同时很大程度上简化了分析和计算的过程。小鼠几何模型如图1所示，三维小鼠模型头部长4.5cm，头部最大直径为4cm，体长11.5cm，躯干最大直径为6cm；肿瘤组织和健康组织则设定为两个不同半径的同心球，分别为0.8cm和1.5cm。此外，为便于分析，本文将所提模型的几何坐标系原点O(0, 0, 0)设置在两个同心球的中心位置。
图1 小鼠几何模型
Fig.1 Proposed geometric model for mouse
1.1.2 亥姆霍兹线圈模型
本文提出两种常见的亥姆霍兹线圈，分别为圆形亥姆霍兹线圈和正方形亥姆霍兹线圈，用于产生磁热疗所需的交变磁场，并比较在所产生磁场下磁热疗过程中的治疗温度及组织热损伤的差异。亥姆霍兹线圈由两个完全相同的线圈组成，它们沿着相同的轴线间隔一定的距离对称地放置。两个线圈形状相同、匝数相同，且在不同时刻均携带有同方向、同大小的电流。若两个线圈的特征有所不同或者没有沿着轴线完全对齐放置，亥姆霍兹线圈将无法产生良好的均匀磁场[20]。亥姆霍兹线圈的两个线圈间距的合理设定可使得产生的均匀磁场范围最优，其中圆形亥姆霍兹线圈两线圈间隔距离应为线圈直径的1/2，而正方形亥姆霍兹线圈两线圈间隔距离应为线圈边长的0.544 5倍[21]。
本文基于小鼠模型的躯干尺寸对亥姆霍兹线圈做以下设定可使得磁场匀强范围最大：圆形亥姆霍兹线圈的线圈直径为22cm，两线圈间距为11cm；正方形亥姆霍兹线圈的线圈边长为22cm，两线圈间距为12cm。基于小鼠模型和最优亥姆霍兹线圈尺寸的三维模型如图2所示，其中图2a为圆形线圈，图2b为正方形线圈。
图2 基于小鼠模型和最优亥姆霍兹线圈尺寸的三维模型
Fig.2 Optimal three-dimensional models for Helmholtz coil considering the proposed mouse model
1.2.1 亥姆霍兹线圈磁场模型
交变电流通过亥姆霍兹线圈的两个线圈后将会产生交变磁场。根据麦克斯韦理论，广义安培定律可以以微分形式表示为[22-23]
（1）
其中
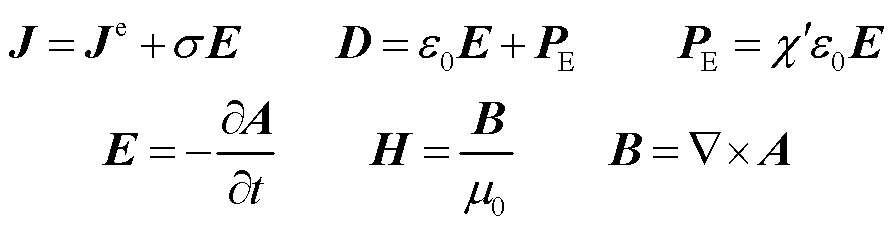
式中，J为电流密度；σ为电导率，σ=1.46×107S/m；
为外部电流引起的电流密度；E为感生电场强度；D为电位移矢量；ε0为真空介电常数，ε0= 8.85×10-12F/m；PE为极化强度[24]；
为介质材料磁化率，本文模型不考虑介质材料，故极化强度为0；H为磁场强度；μ0为真空磁导率，μ0=4π×10-7H/m；B为磁感应强度；A为磁矢势。综合以上分析，可得到基于磁矢势A的偏微分方程为
（2）
式（2）的磁矢势在给定初始条件和边界条件后，可通过有限元方法求解得到。接着，亥姆霍兹线圈产生的磁场强度可根据关系式
和
进一步求解得到。
1.2.2 磁纳米粒子的产热模型
磁热疗是将含有MNPs的磁流体注入肿瘤区域内，而后在外加交变磁场的作用下产热，使肿瘤区域温度升高至42～46℃，并最终导致癌细胞凋亡。磁流体中所有MNPs产热值
可通过体积分数和单位体积MNPs耗散功率
进行关联，即[19]
（3）
式中，
(x, y, z)为生物组织内不同位置处的MNPs的体积分数，其由磁流体的注射部位和性质等诸多因素决定，其与磁流体的浓度C的关系为C=(x, y, z)
，为磁纳米粒子密度。然而，目前还没有一个通用的模型来对整体的体积分数进行描述，而均匀分布或高斯分布是目前最常用的表达方式。相比而言，后者更接近实际情况[12]，故本文使用高斯分布来描述肿瘤区域整体的粒子体积分数，即MNPs在肿瘤内的分布呈高斯分布，则(x, y, z)表达式为
（4）
式中，max为体积分数的最大值，位于磁纳米流体注射处；(x0, y0, z0)为磁纳米流体注射处的坐标，本文设置其为(0, 0, 0)，即肿瘤中心处；
为MNPs空间分布的方差，其值设为15。
单位体积MNPs的耗散功率
在粒径较小时可用Rosensweig理论[5]来描述，该理论只考虑弛豫行为引起的功率耗散，包括Néel弛豫和Brownian弛豫[25]。单位体积MNPs耗散功率可表示为
（5）
其中
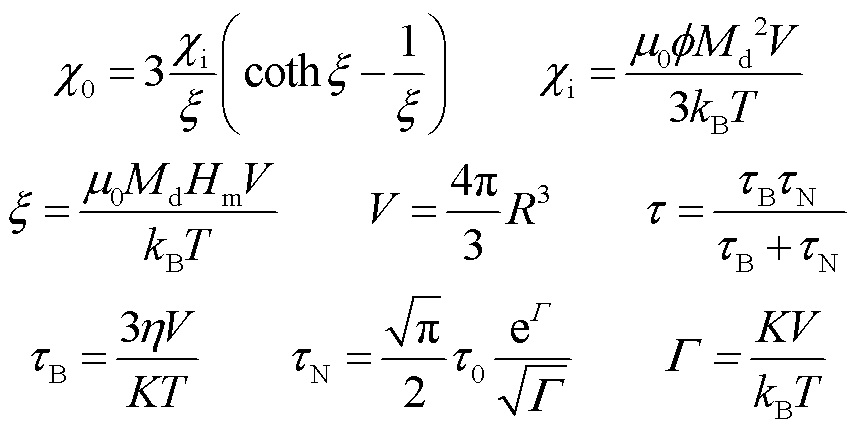
式中，f为交变磁场频率；
为磁场强度峰值；
为平衡磁化率；
为初始磁化率；
为磁畴磁化强度；V为MNPs的体积；R为MNPs的半径；kB为玻耳兹曼常数，kB=1.380 6×10-23J/K；τ为弛豫时间；
为Brownian弛豫时间；
为Néel弛豫时间；
和
为参数；
、K、
分别为载液粘度系数、各向异性常数、平均弛豫时间常数；T为治疗温度。
1.2.3 生物传热模型
生物组织在磁热疗过程中的治疗温度分布可以根据求解传热方程进行估计[26]，本研究中采用的传热方程是改进pennes生物传热方程[27]。该方程是在经典pennes生物传热方程的基础上引入一个系数来补偿水介质和细胞内介质之间的误差而提出的[28-30]，可表示为
（6）
式中，i的取值为0, 1, 2，分别代表健康组织、肿瘤、皮肤；
、
、
、
、
、
分别为对应组织（健康组织、肿瘤、皮肤）的密度、比热容、治疗温度、导热系数、代谢产热和血液灌注率；
、
、
分别为血液的密度、比热容、温度；
为所有注射进肿瘤组织的MNPs在外加交变磁场作用下所产生的总热值；α为补偿系数，α=0.55，用于补偿溶液为水的理论模型和溶液为生物组织中的组织液的实际情况间的差异[27]。
1.2.4 细胞热损伤模型
肿瘤细胞在磁热疗温度达到42～46℃范围时会因热损伤而最终凋亡，因此细胞热损伤程度可以用于评估磁热疗的效果。细胞热损伤程度通常可使用阿累尼乌斯模型或CEM43来进行评估[29, 31-32]。CEM43是指生物组织中某一点在43℃时的累计等效分钟值，其相比于阿累尼乌斯模型能够更加直观地反映出细胞损伤的程度大小。因此，本研究使用CEM43来进行细胞热损伤程度评估，其表达式为[32]
（7）
式中，t为治疗时间；T(x, y, z, t)为生物组织(x, y, z)位置处t时刻的治疗温度，其值由式（6）计算得到；参数
可表示为
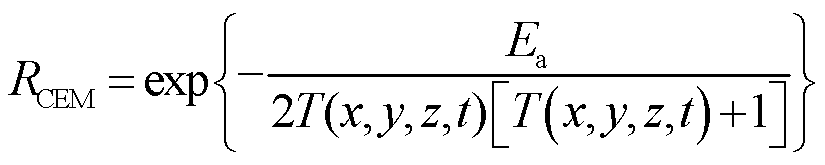（8）
式中，
为活化能。式（8）可被概括为：当治疗温度大于43℃时，其值为0.5；治疗温度小于43℃时，其值为0.25[33]。计算式（7）即可对细胞热损伤程度进行评估，其值越大损伤程度越大。
粒子群优化算法是一种随机搜索算法，其模拟鸟群随机搜索食物的行为，通过不断地迭代搜索找到连续非线性函数所需的最优解，已在工程和科学研究中被广泛应用[34-36]。磁纳米热疗的治疗效果取决于治疗过程中的温度，而治疗温度的主要影响因素之一便是MNPs总产热值。MNPs总产热值与许多因素有关，包括MNPs的体积分数、注射点、磁场强度和频率，以及MNPs粒径等。本文设定磁纳米流体在肿瘤内的浓度呈高斯分布，且以注射点为中心向外逐渐减小。出于安全性考虑，磁热疗的理想情况应该是：在保证磁热疗效果的情况下所需的MNPs体积分数或相同体积分数所需的磁纳米流体剂量越小越好。由式（3）和式（5），可得到基于磁场和MNPs属性的注射点体积分数的非线性表达式为
（9）
其中
式中，
为达到磁热疗所需上限安全温度的最大产热值，即磁流体注射点处的产热值。因此，本文在确认治疗1.1.1节中所述小鼠模型所需的注射点产热值后，采用改进粒子群优化算法以磁纳米流体注射点体积分数表达式（即式（9））为被优化函数，期望得到达到磁热疗上限安全温度所需的注射点体积分数最小值，以及此时相应的MNPs粒径、磁场强度和频率。
此外，本文所提出的改进粒子群算法的约束条件如下：
（1）出于治疗安全考虑，磁场频率范围设置为100～500kHz，磁场强度范围设置为0～50kA/m，同时外加交变磁场还应满足
A·m-1·s-1[18]。
（2）本文MNPs的产热由Rosensweig理论描述，故需满足线性响应理论的有效条件：
[37]。
（3）Rosensweig理论描述具有超顺磁性的MNPs的产热，故应满足
[37]。
（4）MNPs半径范围设置为1～10nm。
本文基于以上的约束条件设计了一种改进的粒子群优化算法，算法流程如图3所示。
图3 改进粒子群优化算法流程
Fig.3 Flow chart of the improved particle swarm optimization algorithm
此外，该优化算法还对其他相关参数做如下设置：①文献[38]指出传统粒子群优化算法设置的种群规模较小，因此本文设置优化算法的种群规模为100；②自我学习因子和全局学习因子均设置为2；③惯性权重设置为递减线性惯性权重，最大权重值为0.9，最小权重值为0.4；④迭代次数设置为300次。本文通过所提优化算法的计算，便可获得所需注射点体积分数最小值及相应的MNPs半径、磁场强度和频率。
本节总结了本文研究过程中所需要的所有参数值，其中MNPs的相关特性参数见表1[5, 39]。本文所采用的是迄今为止研究和使用最为广泛的Fe3O4-MNPs，该种MNPs具有生物相容性并被美国食品药品监督管理局（Food and Drug Administration, FDA）批准用于人体治疗和试验[40]，而小鼠模型的生物组织特性参数见表2[39, 41]。
表1 MNPs特性参数
Tab.1 MNPs parameters
参数数值 /(kA/m)446 /[kg/(m·s)]2.35×10-3 /(kJ/m3)30 /s10-9 /(kg/m3)5 180 /[J/(kg·K)]670 /[W/(m·K)]40
表2 生物组织特性参数
Tab.2 Bio-tissue parameters
参数皮肤健康组织肿瘤血液 /(kg/m3)1 0001 0791 0501 050 /[J/(kg·K)]3 7703 5403 7503 750 /[W/(m·K)]0.30.520.590.59 /(W/m3)368.114 414684.2—
需要注意的是，肿瘤组织的特性参数还应考虑注入MNPs的影响，而注入MNPs后的肿瘤组织特性参数变化可通过式（10）来描述[15]。
（10）
式中，
、
、
分别为注入MNPs后的肿瘤密度、比热容和导热系数；
、
、
分别为肿瘤本身的密度、比热容和导热系数；
、
、
分别为MNPs的密度、比热容和导热系数。
值得一提的是，生物组织的血液灌注率会受到治疗过程中变化的温度影响，但以往不少研究为了降低建模难度而采用了传统的定值血液灌注率[8,15]。本文为了使研究结果更接近实际情况，故采用随温度变化的生物组织血液灌注率，如式（11）和式（12）所示[42]。
（11）
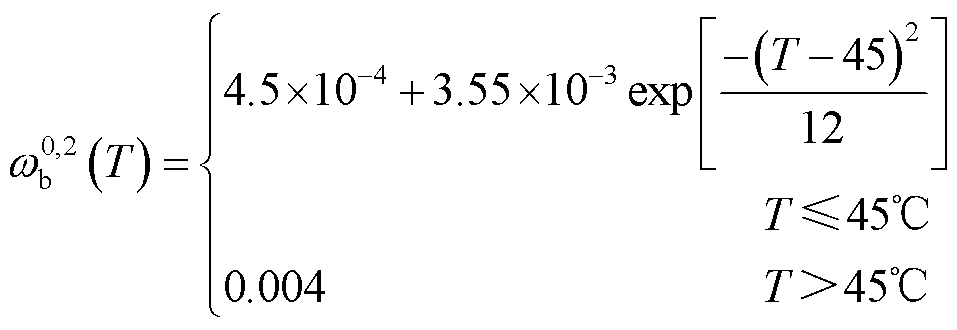（12）
式中，
为健康组织和皮肤的血液灌注率；
为肿瘤的血液灌注率。
除了血液灌注率，生物组织的导热系数也应是治疗温度的函数，随着治疗温度的变化而变化[43]，表示为
（13）
式中，为表2中所示的定值导热系数。
小鼠和周围环境的热通量密度为[44]
（14）
式中，
为热通量密度；
为环境温度，设置为25℃；h为表面传热系数，其值为6W/(m2∙K)[45]。
此外，磁热疗开始前小鼠模型内各生物组织的初始温度均设定为正常体温37℃。
粒子群算法对磁热疗参数进行优化前，需确认最高治疗温度达到46℃所需的MNPs最大产热值（磁流体注射点MNPs产热值）。本研究根据式（6）应用有限元分析软件预测治疗温度分布，并使用二分法对所需的磁流体注射点产热值进行估计。二分法估计过程见表3，注射点产热值的估计区间设置为（2×104～50×104）W/m3，最后求得治疗温度达到46℃时所需的磁流体注射点处产热值为38.9×104W/m3。
表3 二分法估计过程
Tab.3 Dichotomy estimation process
产热值区间/(W/m3)头部结果/℃尾部结果/℃中间结果值/℃ (2×104, 50×104)38.647.843.6 (26×104, 50×104)43.647.845.8 (38×104, 50×104)45.847.846.8 (38×104, 44×104)45.846.846.3 (38×104, 41×104)45.746.346.1 (38.7×104, 39.1×104)45.9646.0346.00
磁流体注射点处产热值通过二分法估计确定后，便可将其应用于带约束的改进粒子群优化算法。优化后的结果为：磁纳米流体注射点体积分数为0.009 96，磁场强度为50kA/m，磁场频率为100kHz，MNPs半径为7.005nm。可以看出，优化后的磁场及MNPs属性均在磁热疗所需范围内，然而磁热疗的体积分数值目前尚无完整有效的临床报道。尽管如此，文献[5,12]中分别指定了两个不同的常规磁热疗体积分数值，分别为0.071和0.033。由此可知，本文优化后体积分数值明显小于以上两篇报道所提，故其在一定程度上可以认为是合理的。算法收敛曲线如图4所示，优化算法在50次迭代后各参数和目标函数的值便基本稳定不再改变。
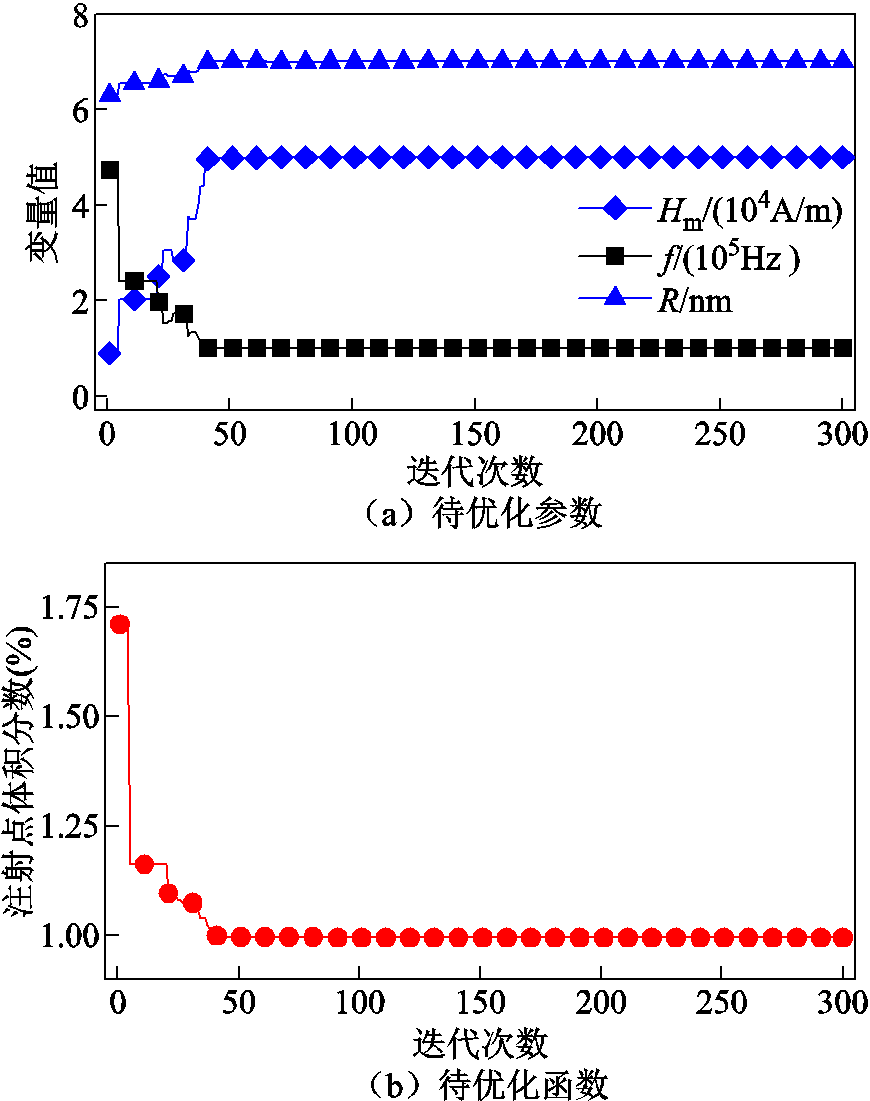
图4 算法收敛曲线
Fig.4 Convergence curves for the proposed algorithm
本研究考虑了两种常见的亥姆霍兹线圈，即传统的圆形线圈和能够产生更大范围匀强磁场的正方形线圈，用于产生磁热疗所需的交变磁场，线圈模型如图2所示。磁场的均匀度将会影响磁热疗效果。为了比较不同线圈产生磁场的均匀度，本文设定两个线圈中心位置的磁场强度均等于3.1节的优化算法结果（50kA/m），故可得到相同线圈匝数（1 000匝）下不同线圈通过的电流值分别为：圆形线圈7.80A和正方形线圈8.68A。值得一提的是，本文计算得到的线圈电流和匝数都较大，因此实际应用中应考虑通过水冷等方案对装置线圈进行合理散热降温，以保证装置能正常工作。正方形亥姆霍兹线圈产生磁场过中心点的xOy平面磁场强度如图5a所示。图5a中为获得较好的显示效果，设定磁场强度大于75kA/m区域等效为75kA/m，因该区域仅存在于线圈附近故不影响本文的研究。当线圈中心磁场一致时，两种线圈产生的磁场分布仅存在较小的差异。图5b展示了两种不同线圈产生磁场强度的差值，可以看出两者在中心位置一致，但在偏移线圈中心一定距离后，两者均不保持匀强且圆形亥姆霍兹线圈的变化程度更大。需注意的是，图中有颜色的区域磁场强度差值范围为-10～10kA/m，超出此范围则显示为黑色和灰色。这两种颜色是由于两种线圈间隔不同，而线圈附近的磁场非常大而导致的。
图5 亥姆霍兹线圈磁场
Fig.5 Magnetic field for Helmholtz coils
为比较两种线圈在均匀度上的差异，本文提出了两种用于评估不同线圈磁场均匀程度的方法，分别为非均匀性系数法和有效体积百分比法。非均匀性系数的定义为
，其值越小均匀性越高，其中
和
分别为区域内磁场强度的最大值和最小值，
为磁场强度的平均值；有效体积百分比的定义为
，其值越大均匀性越高，其中Heff和Veff分别代表49～51kA/m范围的磁场强度和相应的体积。应用两种方法计算可得到圆形亥姆霍兹线圈磁场的非均匀性值为1.565，有效体积百分比为52.21%；正方形亥姆霍兹线圈磁场的非均匀性值为1.087，有效体积百分比为57.21%。由此表明，正方形亥姆霍兹线圈磁场的匀强范围相比圆形线圈更优。
磁场分布确定后，肿瘤区域的治疗温度分布将可通过有限元方法对传热方程求解获得。由3.2节分析可知，两种线圈在中心处的磁场分布十分相近，也均接近理想匀强磁场，故两者对相同目标的治疗温度分布也应相近，特别是肿瘤位于线圈中心时。肿瘤和线圈中心重合时的小鼠模型治疗温度分布的过中心点xOy平面图如图6所示。由图6可见，肿瘤中心温度为46℃，且治疗温度从中心向边缘逐渐降低，除肿瘤及其所在的健康组织外，生物组织的治疗温度基本均小于40℃。治疗温度大于42℃时将对癌细胞造成损伤，但并不影响健康组织，故本文后续如无特别说明，均展示肿瘤及其所在健康组织周围的治疗温度分布。
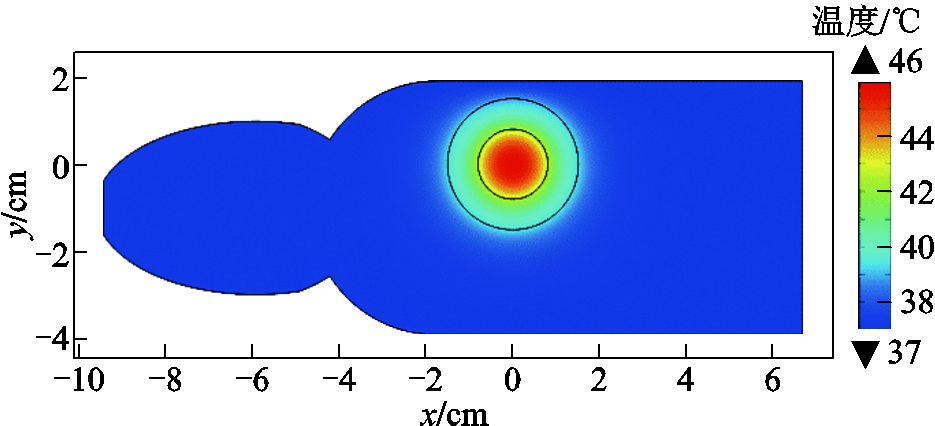
图6 肿瘤位于线圈中心时的治疗温度分布
Fig.6 Treatment temperature distribution when the tumor is located in Helmholtz coil center
尽管肿瘤部位和亥姆霍兹线圈中心重合可使得肿瘤区域磁场均匀程度最优且治疗效果也最佳，但实际应用中，肿瘤部位往往会偏离线圈中心，且肿瘤形状也可能不规则。当肿瘤中心偏移线圈均匀磁场范围时，磁场的差异会导致治疗温度分布的差异，并最终体现在治疗效果上。此外，正方形亥姆霍兹线圈产生的磁场比传统圆形线圈产生的磁场匀强范围更大，故当肿瘤偏移线圈中心情况相同时，正方形线圈产生的磁场可使治疗效果更优，同时允许肿瘤位置有着更大程度的偏移。为了进行更有效的对比，图7a展示了肿瘤向z轴正半轴偏移3cm后再沿着x轴负半轴偏移时治疗温度最大值变化的曲线；而图7b则为肿瘤向y轴正半轴偏移3cm后再沿着x轴负半轴偏移时治疗温度最大值变化的曲线。由图7可知，两种线圈磁场的治疗温度最大值均随着偏移量的增大逐渐偏移46℃，且圆形线圈偏离46℃的程度比正方形线圈更大。
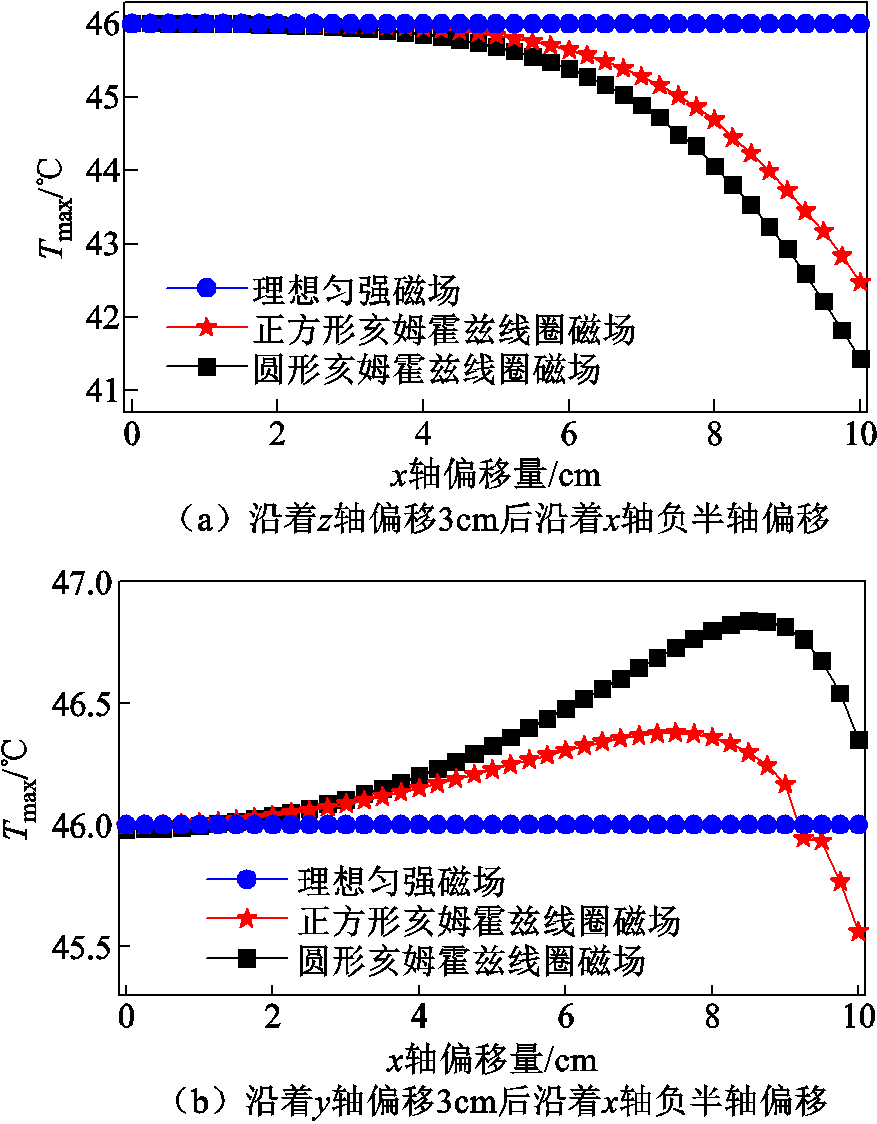
图7 治疗温度最大值随肿瘤偏移变化的曲线
Fig.7 Curves for maximum treatment temperature with tumor deviation
亥姆霍兹线圈在中心区域磁场趋于均匀分布，导致其所产生的治疗温度最大值与理想磁场的结果基本一致。然而，当肿瘤区域偏离线圈中心时，不同磁场下的治疗温度分布差异将因远离中心位置而越加明显。图8a展示了肿瘤中心由原点向x轴负半轴偏移6cm并向z轴正半轴偏移3cm后，正方形亥姆霍兹线圈磁场作用下生物组织的治疗温度分布。此时的最大值45.6℃相比肿瘤位于线圈中心位置的结果下降了0.4℃，而圆形亥姆霍兹线圈磁场作用下的治疗温度分布与图8a也有一定的差异，两者的治疗温度分布差如图8b所示。
图8 肿瘤中心沿x负半轴偏移6cm并沿z正半轴偏移3cm后的治疗温度分布
Fig.8 Treatment temperature distribution with a tumor center location away from 3cm of positive z-axis after shifting 6cm along negative x-axis
由图8可见，两种不同线圈磁场下的治疗温度分布差异主要体现在肿瘤区域内，因此对治疗效果会造成明显影响。总的来说，尽管正方形和圆形亥姆霍兹线圈中心位置的磁场对治疗温度影响不明显，但在偏离中心的其他位置对治疗温度的影响还是存在较大差异。
除了线圈磁场差异对治疗温度分析的影响外，不同血液灌注率的设定也是影响磁热疗效果的主要因素之一。血液灌注率的值越大，意味着生物组织内血液流动越加活跃，将导致治疗区域内温度下降越为明显。此外，以往较多研究为了简化模型而设定血液灌注率为定值，而实际上其应受治疗温度的影响。本文为了使计算结果更接近真实情况，故而均考虑温度依赖的血液灌注率。尽管如此，本文依然描述了肿瘤位于亥姆霍兹线圈中心时两种不同血液灌注率下治疗温度分布的差异，结果如图9所示。其中，图9a为考虑温度依赖的血液灌注率的情况，图9b则为两种不同情况下的温度分布差异。可以看出，小鼠模型在考虑温度依赖的血液灌注率时，最大温度相比定值的情况上升了约0.66℃，其主要差异发生在肿瘤组织的边缘位置。也就是说，考虑温度依赖的血液灌注率在实际应用中能获得更高的治疗温度，这在肿瘤和健康组织交界处尤为明显。
图9 肿瘤位于线圈中心时不同血液灌注率下的治疗温度分布差异
Fig.9 Treatment temperature difference considering two blood perfusion rates with a tumor center location
治疗温度分布通过传热方程确定后，细胞热损伤程度CEM43则可通过式（7）和式（8）描述得到，而CEM43值越大表明损伤程度越高。沿x负半轴偏移6cm并沿z正半轴偏移3cm后的三种磁场情况下考虑不同血液灌注率的CEM43最大值如图10所示。由图10可知，理想匀强磁场相比两种线圈磁场具有最大的CEM43值，而正方形线圈磁场的最大值则大于圆形线圈。此外，所有温度依赖血液灌注率下的CEM43值均较定值血液灌注率略高。可以看出，不同情况下的细胞热损伤程度最大值与治疗温度分布趋势大体一致，因此实际应用中可考虑优先使用正方形亥姆霍兹线圈，而进行数学建模时应尽量考虑温度依赖的血液灌注率。
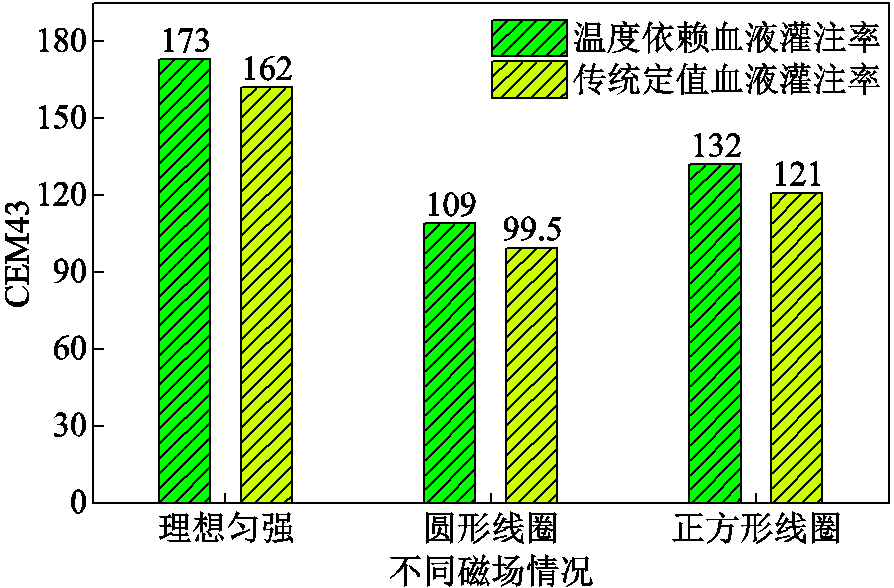
图10 不同情况的CEM43最大值
Fig.10 CEM43 maximum value in different cases
本研究以治疗温度与43℃下的累积等效分钟数为指标，比较了两种不同亥姆霍兹线圈磁场和理想匀强磁场下的磁热疗治疗效果。治疗所需的磁场强度和频率、MNPs粒径及磁流体注射点体积分数等通过利用带约束的粒子群算法，并以最小化注射点体积分数为目标进行优化后获得。研究结果表明，正方形线圈产生磁场的匀强范围优于圆形线圈，也更接近于理想磁场情况。因此，当肿瘤精确放置在亥姆霍兹线圈中心时，三种磁场的磁热疗效果几乎一致；但随着肿瘤位置的偏移，正方形亥姆霍兹线圈因其较大的匀强范围能获得相较于圆形线圈更好的治疗结果。同时，本文提出对磁场和MNPs属性的优化方法，不仅可以满足最高治疗安全温度及磁场安全标准，也能保证注射进体内的MNPs粒子数量最少。此外，温度依赖的血液灌注率相比传统定值更符合实际情况，同时在相同治疗条件下也具有更高的总体治疗温度分布。
参考文献
[1] Jose J, Kumar R, Harilal S, et al. Magnetic nanoparticles for hyperthermia in cancer treatment: an emerging tool[J]. Environmental Science and Pollution Research International, 2020, 27(16): 19214-19225.
[2] Raouf I, Khalid S, Khan A, et al. A review on numerical modeling for magnetic nanoparticle hyperthermia: progress and challenges[J]. Journal of Thermal Biology, 2020, 91: 102644.
[3] Gangwar A, Varghese S S, Meena S S, et al. Fe3C nanoparticles for magnetic hyperthermia application[J]. Journal of Magnetism and Magnetic Materials, 2019, 481: 251-256.
[4] Shaw S K, Biswas A, Gangwar A, et al. Synthesis of exchange coupled nanoflowers for efficient magnetic hyperthermia[J]. Journal of Magnetism and Magnetic Materials, 2019, 484: 437-444.
[5] Rosensweig R E. Heating magnetic fluid with alternating magnetic field[J]. Journal of Magnetism and Magnetic Materials, 2002, 252: 370-374.
[6] 闫孝姮, 李政兴, 潘也, 等. 相同极性永磁体对感应式磁声磁粒子浓度成像过程影响的仿真[J]. 电工技术学报, 2022, 37(8): 1926-1937. Yan Xiaoheng, Li Zhengxing, Pan Ye, et al. Simulation of the influence of permanent magnets of the same polarity on the magneto-acoustic concentration tomography of magnetic nanoparticles with magnetic induction process[J]. Transactions of China Electrotechnical Society, 2022, 37(8): 1926-1937.
[7] Singh G, Kumar N, Avti P K. Computational evaluation of effectiveness for intratumoral injection strategies in magnetic nanoparticle assisted thermotherapy[J]. International Journal of Heat and Mass Transfer, 2020, 148: 119129.
[8] Suleman M, Riaz S. 3D in silico study of magnetic fluid hyperthermia of breast tumor using Fe3O4 magnetic nanoparticles[J]. Journal of Thermal Biology, 2020, 91: 102635.
[9] Bordelon D E, Goldstein R C, Nemkov V S, et al. Modified solenoid coil that efficiently produces high amplitude AC magnetic fields with enhanced uniformity for biomedical applications[J]. IEEE Transactions on Magnetics, 2012, 48(1): 47-52.
[10] Wu Lei, Cheng Jingjing, Liu Wenzhong, et al. Numerical analysis of electromagnetically induced heating and bioheat transfer for magnetic fluid hyperthermia[J]. IEEE Transactions on Magnetics, 2015, 51(2): 1-4.
[11] 蔡忠祥, 逯迈. 磁感应热疗作用于胆管癌模型热场分布的研究[J]. 生物医学工程学杂志, 2021, 38(3): 528-538, 548. Cai Zhongxiang, Lu Mai. Study on the thermal field distribution of cholangiocarcinoma model by magnetic fluid hyperthermia[J]. Journal of Biomedical Engineering, 2021, 38(3): 528-538, 548.
[12] Salloum M, Ma R H, Weeks D, et al. Controlling nanoparticle delivery in magnetic nanoparticle hyperthermia for cancer treatment: experimental study in agarose gel[J]. International Journal of Hyperthermia, 2008, 24(4): 337-345.
[13] Rast L, Harrison J G. Computational modeling of electromagnetically induced heating of magnetic nanoparticle materials for hyperthermic cancer treatment[J]. PIERS Online, 2010, 6(7): 690-694.
[14] Liu K C, Cheng P J. Numerical analysis of power dissipation requirement in magnetic hyperthermia problems[J]. Journal of Thermal Biology, 2019, 86: 102430.
[15] Astefanoaei I, Dumitru I, Chiriac H, et al. Thermofluid analysis in magnetic hyperthermia using low Curie temperature particles[J]. IEEE Transactions on Magnetics, 2016, 52(7): 1-5.
[16] 汤云东, 苏航, 弗莱施C.C.鲁道夫, 等. 考虑质量扩散的瘤内磁流体分布对磁热疗影响研究[J]. 仪器仪表学报, 2021, 42(12): 146-156. Tang Yundong, Su Hang, Flesch R C C, et al. Effect of intratumoral nanofluid distribution on magnetic hyperthermia considering mass diffusion[J]. Chinese Journal of Scientific Instrument, 2021, 42(12): 146-156.
[17] Tang Yundong, Flesch R C C, Jin Tao. Numerical analysis of temperature field improvement with nanoparticles designed to achieve critical power dissipation in magnetic hyperthermia[J]. Journal of Applied Physics, 2017, 122(3): 034702.
[18] Hergt R, Dutz S. Magnetic particle hyperthermia—biophysical limitations of a visionary tumour therapy[J]. Journal of Magnetism and Magnetic Materials, 2007, 311(1): 187-192.
[19] Tang Yundong, Su Hang, Flesch R C C, et al. An optimization method for magnetic hyperthermia considering Nelder-Mead algorithm[J]. Journal of Magnetism and Magnetic Materials, 2022, 545: 168730.
[20] Beiranvand R. Analyzing the uniformity of the generated magnetic field by a practical one-dimensional Helmholtz coils system[J]. Review of Scientific Instruments, 2013, 84(7): 075109.
[21] Piergentili F, Candini G P, Zannoni M. Design, manufacturing, and test of a real-time, three-axis magnetic field simulator[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2): 1369-1379.
[22] 胡亚楠, 包家立, 朱金俊, 等. 纳秒电脉冲对肝脏组织不可逆电穿孔消融区分布的时域有限差分法仿真[J]. 电工技术学报, 2021, 36(18): 3841-3850. Hu Yanan, Bao Jiali, Zhu Jinjun, et al. The finite difference time domain simulation of the distribution of irreversible electroporation ablation area in liver tissue by nanosecond electrical pulse[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3841-3850.
[23] 张改杰, 阮江军, 刘守豹, 等. 固体C型电枢几何结构优化设计[J]. 电气技术, 2010(增刊1): 19-23. Zhang Gaijie, Ruan Jiangjun, Liu Shoubao, et al. The optimization design of geometric structure for the solid C-shaped armature[J]. Electrical Engineering, 2010(S1): 19-23.
[24] 王昊月, 李成榕, 王伟, 等. 高压频域介电谱诊断XLPE电缆局部绝缘老化缺陷的研究[J]. 电工技术学报, 2022, 37(6): 1542-1553. Wang Haoyue, Li Chengrong, Wang Wei, et al. Local aging diagnosis of XLPE cables using high voltage frequency domain dielectric spectroscopy[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1542-1553.
[25] Ondeck C L, Habib A H, Ohodnicki P, et al. Theory of magnetic fluid heating with an alternating magnetic field with temperature dependent materials properties for self-regulated heating[J]. Journal of Applied Physics, 2009, 105(7): 07B324.
[26] 刘士利, 罗英楠, 刘宗烨, 等. 基于电磁-热耦合原理的三芯铠装电缆在低频输电方式下的损耗特性研究[J]. 电工技术学报, 2021, 36(22): 4829-4836. Liu Shili, Luo Yingnan, Liu Zongye, et al. Study on loss characteristics of three core armored cable under low-frequency transmission mode based on electromagnetic, thermal coupling principle[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4829-4836.
[27] Tang Yundong, Jin Tao, Flesch R C C. Numerical temperature analysis of magnetic hyperthermia considering nanoparticle clustering and blood vessels[J]. IEEE Transactions on Magnetics, 2017, 53(10): 1-6.
[28] Pennes H H. Analysis of tissue and arterial blood temperatures in the resting human forearm[J]. Journal of Applied Physiology, 1948, 1(2): 93-122.
[29] 米彦, 彭文成, 芮少琴, 等. 高频纳秒脉冲串作用下皮肤肿瘤热效应的多参数有限元仿真与实验[J]. 电工技术学报, 2017, 32(22): 264-274. Mi Yan, Peng Wencheng, Rui Shaoqin, et al. Thermal effects in skin tumor exposed to high-frequency nanosecond pulse bursts: multi-parametric finite element simulation and experiment[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 264-274.
[30] 赵军, 李乃良, 王磊, 等. 电动汽车无线充电系统对人体及体内植入器件电磁安全研究[J]. 电工技术学报, 2018, 33(增刊1): 26-33. Zhao Jun, Li Nailiang, Wang Lei, et al. An electromagnetic safety study about human body and body implanted device in electric vehicle wireless charging system[J]. Transactions of China Electrotechnical Society, 2018, 33(S1): 26-33.
[31] Pearce J A. Models for thermal damage in tissues: processes and applications[J]. Critical Reviews in Biomedical Engineering, 2010, 38(1): 1-20.
[32] MacLellan C J, Fuentes D, Prabhu S, et al. A methodology for thermal dose model parameter development using perioperative MRI[J]. International Journal of Hyperthermia, 2018, 34(6): 687-696.
[33] Pearce J A. Comparative analysis of mathematical models of cell death and thermal damage processes[J]. International Journal of Hyperthermia, 2013, 29(4): 262-280.
[34] 赖纪东, 谢天月, 苏建徽, 等. 基于粒子群优化算法的孤岛微电网电压不平衡补偿协调控制[J]. 电力系统自动化, 2020, 44(16): 121-129. Lai Jidong, Xie Tianyue, Su Jianhui, et al. Coordinated control of voltage unbalance compensation in islanded microgrid based on particle swarm optimization algorithm[J]. Automation of Electric Power Systems, 2020, 44(16): 121-129.
[35] Iqbal A, Singh G K. PSO based controlled six-phase grid connected induction generator for wind energy generation[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(1): 41-49.
[36] 李青兰, 吴琛, 陈磊, 等. 抑制频率振荡的电力系统稳定器参数优化[J]. 电力系统自动化, 2020, 44(7): 93-99. Li Qinglan, Wu Chen, Chen Lei, et al. Parameter optimization of power system stabilizer for suppressing frequency oscillation[J]. Automation of Electric Power Systems, 2020, 44(7): 93-99.
[37] Delavari H H, Madaah Hosseini H R, Wolff M. Modeling of self-controlling hyperthermia based on nickel alloy ferrofluids: proposition of new nanoparticles[J]. Journal of Magnetism and Magnetic Materials, 2013, 335: 59-63.
[38] Piotrowski A P, Napiorkowski J J, Piotrowska A E. Population size in particle swarm optimization[J]. Swarm and Evolutionary Computation, 2020, 58: 100718.
[39] Wang Q, Deng Z S, Liu J. Theoretical evaluations of magnetic nanoparticle-enhanced heating on tumor embedded with large blood vessels during hyperthermia[J]. Journal of Nanoparticle Research, 2012, 14(7): 974.
[40] Khandhar A P, Ferguson R M, Krishnan K M. Monodispersed magnetite nanoparticles optimized for magnetic fluid hyperthermia: implications in biological systems[J]. Journal of Applied Physics, 2011, 109(7): 07B310.
[41] Kandala S K, Sharma A, Mirpour S, et al. Validation of a coupled electromagnetic and thermal model for estimating temperatures during magnetic nanoparticle hyperthermia[J]. International Journal of Hyper-thermia, 2021, 38(1): 611-622.
[42] Rodrigues H F, Capistrano G, Mello F M, et al. Precise determination of the heat delivery during in vivo magnetic nanoparticle hyperthermia with infrared thermography[J]. Physics in Medicine and Biology, 2017, 62(10): 4062-4082.
[43] Balasubramaniam T A, Bowman H F. Thermal conductivity and thermal diffusivity of biomaterials: a simultaneous measurement technique[J]. Journal of Biomechanical Engineering, 1977, 99(3): 148-154.
[44] 纽春萍, 矫璐璐, 王小华, 等. 基于多场耦合的环保型GIS热特性分析[J]. 电工技术学报, 2020, 35(17): 3765-3772. Niu Chunping, Jiao Lulu, Wang Xiaohua, et al. Thermal characteristics analysis of environmentally friendly GIS based on multi-field coupling[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3765-3772.
[45] Candeo A, Dughiero F. Numerical FEM models for the planning of magnetic induction hyperthermia treatments with nanoparticles[J]. IEEE Transactions on Magnetics, 2009, 45(3): 1658-1661.
Abstract The treatment magnetic field usually presents an inhomogeneous distribution inside a real therapeutic equipment during magnetic hyperthermia, which will ultimately affect the treatment effects due to its unsatisfactory distribution of treatment temperature inside tumor region. However, previous literature has paid less attention to optimize the uniformity for magnetic field device and also to investigate its influences on the treatment effect during magnetic hyperthermia. Furthermore, the magnetic nanoparticles (MNPs) concentration under the same magnetic fluid dose is expected to have a value as small as possible in order to reduce the effect of the MNPs residual inside bio-tissue, which however was also rarely reported by the existing researches.
This article investigates the therapeutic magnetic field for circular and square Helmholtz coil devices, analyzes the influence of magnetic field uniformity on the therapeutic effect by evaluating the temperature distribution of biological tissue due to the applied magnetic field, and also discusses the influence of different magnetic fields on the cumulative equivalent heating minutes at 43℃ under two different blood perfusion rates. In addition, this study proposes an improved particle swarm optimization algorithm considering several constraints in order to obtain the minimum volume fraction of MNPs at the injection point and the corresponding optimized properties for MNPs radius and magnetic field at this time. The proposed constraints involved in this study consist of the maximum safe temperature for treatment, the safe upper limit of treatment magnetic field, the size range of MNPs, and the effective conditions for MNPs heat generation. The partial differential equations involved magnetic field and temperature field are solved using finite element method for the proposed Helmholtz coil devices and a three-dimensional mouse model, respectively. The MNPs inside the proposed tumor region are assumed to have a Gaussian distribution centered on the injection point. Simulation results demonstrate that the final optimization results considering the proposed method meet the requirements of proposed constraints, which are 0.009 96 for the volume fraction of MNPs at the injection point, 50kA/m for the magnetic field intensity, 100kHz for the magnetic field frequency, and 7.005nm for the radius of MNPs during therapy. Both circular and square Helmholtz coils can generate a uniform magnetic field near the coil center while tend to have an inhomogeneous distribution away from the coil center. In comparison, the square Helmholtz coil presents a better uniformity in magnetic field distribution away from the coil center with respect to the circular one. This characteristic is also mirrored in the treatment temperature distribution and ultimately the treatment effect. In addition, the case considering the temperature-dependent blood perfusion rate presents a higher cumulative equivalent heating minutes at 43℃ than the case considering a constant one under the three different magnetic fields.
The following conclusions can be drawn from the simulation analysis: (1) The circular Helmholtz coils can have a better performance in the magnetic field uniformity with respect to the square Helmholtz coil, and this characteristic is also true for the treatment temperature distribution and the treatment effect during magnetic hyperthermia. (2) The proposed method based on the improved particle swarm optimization algorithm can not only meet the safe criterions of maximum treatment temperature and the magnetic field but also obtain a far less volume fraction of MNPs than the classical value. (3) Temperature-dependent blood perfusion rate can result in an overall higher treatment temperature distribution and thermal damage for malignant tissue with respect to a constant one in the same therapeutic condition.
keywords：Magnetic hyperthermia, particle swarm optimization algorithm, Helmholtz coil, blood perfusion rate, magnetic field, temperature field
国家自然科学基金（62071124）和福建省自然科学基金（2020J01464）资助项目。
收稿日期 2022-05-17
改稿日期 2022-06-23
DOI: 10.19595/j.cnki.1000-6753.tces.220866
中图分类号：TM154.1；R730.5
汤云东 男，1981年生，博士，副研究员，研究方向为生物医学电子信息技术及相关交叉学科。E-mail：tangyundong@fzu.edu.cn（通信作者）
丁宇彬 男，2000年生，硕士研究生，研究方向为生物医学电子信息技术。E-mail：221120102@fzu.edu.cn
（编辑 李冰）