0 引言
传统的发射方式利用高压气体推动负载,气体发生机构的结构、时序等要素固化,工作时按照预设的参数运行,发射过程是开环的,无法根据负载状态进行实时精准调节,因此难以满足越发增长的多样化发射的需求。电磁发射具有可控性好、安全性高、隐蔽性强等优点。电磁发射通过位置检测或者无位置算法,能够得到负载的运动状态,作为反馈信息进行位置闭环控制,在控制性能上对传统化学能发射方式构成代差,将逐渐替代传统化学能发射方式。
地面电磁发射装置的阻力主要是非线性的滑动摩擦力和气动阻力,在中低速范围内阻力较小,因此通常将地面发射系统简化为线性系统。本文研究的集成式液压平衡电磁发射系统,流体阻力大,且与流速呈强非线性关系,附加发射质量在负载出管过程中不断增大,系统动力学模型复杂,不能将系统简化为线性系统。
将电磁发射技术用于水下武器发射,使得内弹道的闭环调节成为可能,但要实现内弹道的高性能控制还需要匹配合适的控制算法。本文从发射装置的非线性动力学建模和控制算法设计两方面着手,开展了水下电磁发射控制策略的研究。
水下电磁发射系统的非线性主要源自三个方面:①直管内稳定流体与管道摩擦产生的层流压力沿程损失;②流体经过阀门、弯管时,由于截面和方向的急剧变化,产生的紊流压力局部损失;③液体压缩与膨胀引起的压力变化。文献[1]针对层流和紊流两种状态,分析了直管内压力损失和管道局部压力损失的计算特点。文献[2]利用“场路结合”的方法建立了循环管路系统的水动力模型,利用计算流体动力学(Computational Fluid Dynamics,CFD)计算了层流和紊流的压力损失系数。采用参数拟合的方法建立水动力模型,但不是从数学上推导运动与压力的关系。文献[3-4]建立了气动水压平衡式水下武器发射系统的数学模型,将水缸、发射水柜和发射管视为三个压力均匀的工作腔,忽略非线性特性,在活塞组件、武器及流体间建立了线性关系。
目前,线性系统理论针对分析线性系统的稳定性、可控可观性以及优化控制等问题,给出了完整全面的理论框架。弱非线性系统可采用线性系统理论进行分析,强非线性系统则需采用非线性系统理论分析。由于非线性特征形式多样,还没有普适的分析方法,需要具体问题具体分析,通过多种算法的复合来达到满意的效果[5-7]。文献[8-9]提出一种反馈线性化与滑模控制结合的策略,用于抑制风电并网的次同步振荡,文献[8]采用等速趋近律和饱和函数结合的滑模控制律减小抖振,文献[9]选取线性切换函数和指数趋近律提高系统对参数摄动和外界干扰的鲁棒性。文献[10]采用反馈线性化控制方法,将电机模型线性化为独立的电流子系统和线速度子系统,设计了动态滑模控制器,降低了反馈线性化控制对直线电机数学模型的依赖性。文献[11]针对参数不确定的非线性电液伺服系统,提出一种积分滑模自适应控制策略。在滑模控制中引入积分控制项,消除了传统滑模变结构控制需要被跟踪信号导数已知的假设。文献[12]提出一种感应电机非线性积分滑模电流控制器,设计了非线性积分滑模面,将滑模面的信息引入幂次趋近律,在削弱系统抖振的同时,实现了定子电流误差在有限时间内收敛。文献[13]针对水轮发电机组水门调节的大惯性非线性模型,采用二阶扩张状态观测器进行动态反馈线性化,采用极点配置的理论设计预期动力学方程的方法,可以获得与精确反馈线性化方法相近的动态特性,具有更强的鲁棒性。文献[14]将高超声速飞行器高度非线性的数学模型进行反馈线性化,采用滑模控制器提高飞行器纵向运动的鲁棒性。文献[15]综述了导弹控制系统中的非线性理论研究和应用情况,重点介绍了动态逆系统方法和滑模控制。文献[16]指出伪线性复合控制策略能有效改善流体动力机械控制系统的动态性能,对潜艇驱动、导弹发射器控制规律的设计具有参考价值。文献[17]采用输入输出反馈线性化的方法,对自主水下航行器的俯仰角和深度分别进行控制。文献[18]采用高阶滑模控制策略避免抖振效应,与局部线性化的比例微分控制进行了对比,结果表明,高阶滑模控制响应更快、鲁棒性更强。文献[19]提出一种定结构滑模控制器与扩展滑模扰动观测器相结合的复合式滑模位置控制方法。文献[20]提出了基于反馈线性化控制与最优化控制的复合控制方法,抑制了直线电机的推力波动,使伺服平台满足高精度轮廓加工的要求。文献[21]采用二阶滑模控制和递归径向基神经网络相结合的方法来提高永磁直线同步电机的位置跟踪控制性能。文献[22]提出一种基于自适应模糊神经网络时变滑模控制方法,将时变滑模面引入传统滑模控制器中,并将其与模糊神经网络相结合。
本文根据液压平衡电磁发射装置的原理和结构,首先推导了系统的非线性动力学解析方程,掌握了系统非线性特性的具体形式;然后通过状态反馈线性化,将系统转换为伪线性系统;在控制方式的选择上,目前各式新型智能算法研究方兴未艾,但具体使用还需考虑多方面因素,尤其是在高风险的水下发射场景更需谨慎。本文从实际应用出发,以经典的比例积分微分(Proportion Integration Differentiation,PID)和滑模控制为基础,分别采用“反馈线性化+PID”和“反馈线性化+滑模”的复合控制策略对发射过程进行控制,并与经典的线性PID 控制进行对比。仿真和试验结果表明,单纯的PID 控制有明显的滞后误差,结合推力前馈可以加快动态响应;反馈线性化结合PID 或滑模控制的复合控制策略,跟踪误差小、抗干扰能力强、适应性好。
1 集成式液压平衡电磁发射原理
集成式液压平衡电磁发射装置原理如图 1 所示,由圆筒型直线电机动子和定子、电动阀、发射筒、负载组成,动子充当活塞,定子充当水缸,发射筒充当发射管。发射时电动阀打开,直线电机通电产生电磁力,动子向下运动推水,水经过电动阀进入发射管内推动负载加速。图中变量的定义见表1。
表1 变量说明Ⅰ
Tab.1 Variables declaration Ⅰ


图1 水下发射装置原理
Fig.1 Schematic of the underwater launcher
图2 为系统的位置闭环控制原理,控制器生成内弹道参考轨迹,根据位置偏差调节电机出力,使动子跟踪参考轨迹,实现位置闭环发射,位置闭环调节是实现高性能内弹道控制的关键。

图2 发射系统控制原理
Fig.2 Control schematic diagram of launch system
2 液压平衡发射系统的非线性动力学建模
2.1 负载受力方程
负载受到头部和尾部静压阻力、重力和头部动压阻力,其表达式为
式中,Cm 为负载头部阻力系数;ρ 为水的密度。
2.2 负载到活塞的全压平衡方程
负载尾部到活塞压水面的压力平衡方程为
式(2)中压力损失由五部分构成,有
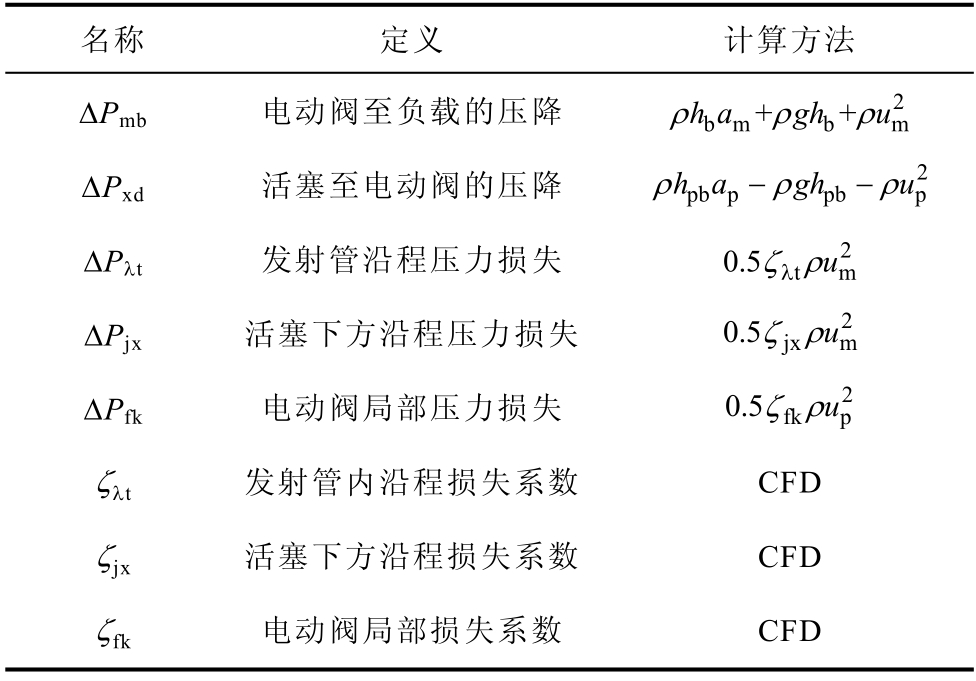
压力损失的定义和计算方法见表2。
表2 变量说明Ⅱ
Tab.2 Variables declaration Ⅱ
2.3 外界到活塞的全压平衡方程
外界到活塞上表面的压力平衡方程为
压力损失的定义和计算方法见表3。
表3 变量说明Ⅲ
Tab.3 Variables declaration Ⅲ

表2 和表3 中的ΔPmb、ΔPxd、ΔPhs 为建立非线性水动力模型的关键环节,其推导过程见附录。
2.4 动子受力方程
动子受到电磁力、活塞上下表面压差力、重力,其表达式为
2.5 非线性水动力方程推导
将式(2)减去式(4),得到

由式(1)可得
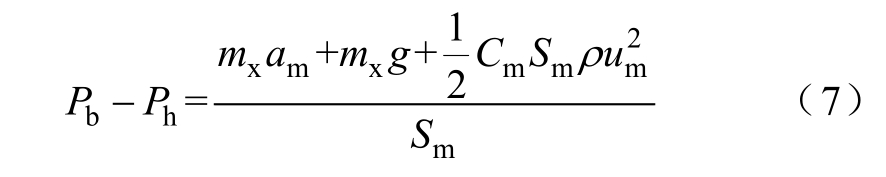
将式(7)代入式(6),整理可得

将式(8)代入式(5),整理可得

式中,ζ 为集总损失系数,是发射系统所有的流体损失;ζ jx、ζ js、ζ jk为活塞侧的参数;C m、ζλt、ζ fk为负载侧的参数。本文中传动比为k=4.27,![]()
![]() 。系数k2 意味着负载侧向活塞侧折算,这说明流体损失主要产生在流速更高的负载侧流道,体现了变截面压水发射系统的基本规律。
。系数k2 意味着负载侧向活塞侧折算,这说明流体损失主要产生在流速更高的负载侧流道,体现了变截面压水发射系统的基本规律。
集总损失系数是水动力解析方程的核心参数,通过实测各处损失系数来计算集总损失系数面临的两大困难:一是传感器难以布置,二是传感器的存在改变了流道。因此通常采用CFD 的方法计算损失系数,见附录。
基于上文开展的工作,本文提出根据式(11),利用外部易测量的推力、动子和负载的速度,直接计算集总损失系数,即

集总损失系数曲线如图3 所示。损失系数是主要由结构决定的固有参数,图3 中曲线首先迅速下降,然后快速恢复并趋于稳定,最终稳定在55。前期曲线变化的原因是此时速度较低,速度项处于分母的位置,因此计算误差较大。至此,本文得到了发射系统的非线性水动力解析模型和损失系数的取值,可以继续开展控制算法设计。

图3 集总损失系数曲线
Fig.3 Curve of lumped loss coefficient
3 非线性系统的反馈线性化控制
式(11)中的![]() 两项体现了系统的非线性,非线性系统不存在传递函数,因此无法运用线性系统理论分析,下文对比了两种策略:
两项体现了系统的非线性,非线性系统不存在传递函数,因此无法运用线性系统理论分析,下文对比了两种策略:
(1)将系统看成是线性定常系统,采用经典PID进行控制。
(2)将系统线性化,比如局部线性化或者状态反馈线性化。局部线性化不适合电磁发射系统这种非周期瞬态工作方式的系统。状态反馈线性化通过数学手段可将非线性系统变换为n 阶积分伪线性系统,要求系统必须是解析的,式(11)已经给出了解析表达式,因此具备了实施反馈线性化的条件。
下文采取三类方法对水下电磁发射系统进行位置闭环调节:①前馈线性化与PID 复合控制;②反馈线性化与PID 复合控制;③反馈线性化与滑模复合控制。
3.1 前馈线性化+PID 复合控制
经典PID 控制的速度轨迹如图4 所示,增益越大响应越快,也越不稳定。电磁发射的过程短,要求轨迹曲线既稳又快,对于非线性系统仅采用PID控制难以兼顾稳定性和快速性。

图4 速度跟踪曲线
Fig.4 Speed tracking curves
采用推力前馈可以在不改变系统稳定性的前提下加快动态响应,控制结构如图5 所示。

图5 前馈+反馈控制示意图
Fig.5 Feedforward plus feedback control diagram
既然2.5 节已经得到了水动力解析方程,那么式(11)就可用作前馈力的计算式。前馈力和总推力的对比如图6 所示,可见二者差别小,前馈精度高。

图6 前馈力和总推力对比
Fig.6 Feedforward force versus total thrust
假设系统的输出状态完美跟踪了参考轨迹,那么基于参考轨迹计算的前馈力,与下文“反馈线性化”基于输出状态计算的补偿量作用类似,均是对非线性部分的对消,因此本文将利用式(11)进行推力前馈的方法称为“前馈线性化”。
3.2 反馈线性化+PID 复合控制
反馈线性化与其他非线性控制方法相比,不依赖系统运动的求解或稳定性分析,只需要研究反馈结构,从而使得非线性系统的控制变得简单,反馈结构的推导过程如下:

式(11)简化为
令经过反馈线性化变换后的伪线性系统为2 阶积分系统,输入为φ,即 =φ,代入式(12),解得反馈控制律为
=φ,代入式(12),解得反馈控制律为
根据式(13)绘出伪线性系统的结构,如图7所示。

图7 伪线性系统的结构
Fig.7 Structure of pseudo-linear system
对伪线性系统采用PID 控制器进行调节,闭环传递函数为
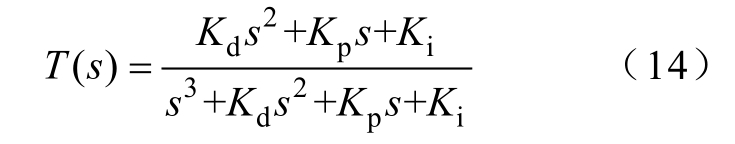
式中,Kp、Ki、Kd 分别为比例系数、积分系数、微分系数。
参照典型的三阶系统,PID 参数选取为

式中,ζ 按照工程经验取0.707;wn 为位置环的截止频率,取值为6。
3.3 反馈线性化+滑模复合控制
反馈线性化对参数不确定性和外界扰动较敏感,滑模控制的鲁棒性强,可以弥补反馈线性化的不足。取x1=xp,x2=up,u=F,将式(11)写成状态方程的形式为

式中,d1、d2 为扰动。式(16)中输出y 与输入u没有直接联系,对y 连续求两次微分可得

定义误差e=yd-y,yd 为参考位置,滑模函数 s=c1 e + 。定义Lyapunov 函数V=0.5s2。
。定义Lyapunov 函数V=0.5s2。
在趋近律的选择上,本文采用指数趋近律与等速趋近律结合,有
指数趋近律的初始趋近速度快,能缩短趋近时间,但不能保证在有限时间内到达切换面,因此还要增加等速趋近律保证有限时间到达切换面。
对Lyapunov 函数求导得到
设计控制律为
代入式(22)可得
因为 为负半定,所以系统是渐近稳定的。推力指令的计算式为
为负半定,所以系统是渐近稳定的。推力指令的计算式为
4 控制效果对比
基于图1 所示的装置原理,研制了一套水下电磁发射试验装置,主要包括:推力200 t 的圆筒型直线电机集成发射装置、50 MV·A 逆变装置、30 MW锂电池储能装置,发射装置安装在水下40 m 处。
4.1 典型发射轨迹控制效果对比
典型发射轨迹的对比如图8 所示。为便于阅读,图中用PID1 代表“无前馈的PID”,用PID2 代表“前馈线性化+PID”,用 FBL(反馈线性化,Feedback Linearization)代表“反馈线性化+PID”,用 SMC(滑模控制,Sliding Mode Control)代表“反馈线性化+滑模”。

图8 发射轨迹跟踪曲线
Fig.8 Launch trajectory tracking curves
表4 给出了轨迹跟踪误差的量化指标,“峰峰值比”代表误差峰峰值与目标值的比值,反映了轨迹的最大波动程度;“终点值比”代表误差终点值与目标值的比值,反映了发射轨迹终点的控制精度;平方误差积分准则(Integral Square Error,ISE)和时间乘绝对误差积分准则(Integral Time Absolute Error,ITAE)均反映发射过程的轨迹波动水平,ITAE降低了初始误差的权重。从表4 可知,除PID1 之外的三种控制方法误差均较小,说明前馈线性化和反馈线性化均能有效地改善控制性能,其中SMC 的综合表现最好。
表4 发射轨迹跟踪性能
Tab.4 Launch trajectory tracking performance

4.2 异常条件下的控制效果对比
由于发射装置与外界连通,可能有异物侵入电磁活塞间隙导致阻力突然增大。本节模拟这种异常情况以考察控制算法的调节能力,设置异物卡在冲程0.7 m 处,导致阻力突增50 t。
突加阻力时的轨迹跟踪曲线如图9 所示,与图8 相比,PID2、FBL、SMC 的误差都有增大,PID1 的速度误差反而略有减小,这不过是突增的阻力正好阻止了PID1 的速度过冲。PID1、PID2 的速度曲线有轻微振荡,FBL 和SMC 的速度曲线则无振荡,说明反馈线性化的稳定性更强。PID2 和FBL 的误差接近,SMC 的误差略大。突加阻力时轨迹跟踪性能见表5。表5 中的量化指标与图9 一致,FBL 的综合表现最好。


图9 突加阻力时的轨迹跟踪曲线
Fig9 Trajectory tracking curves with impact load
表5 突加阻力时轨迹跟踪性能
Tab.5 Tracking performance with impact load

4.3 强扰动条件下的控制效果对比
发射装置在使用过程中受到多种不利因素的影响,比如干湿交替环境下的腐蚀十分严重,使得活塞的表面粗糙度不均匀;活塞密封件的磨损和老化现象;在水压作用下装置的直线度发生变化,活塞运动存在偏心现象;装置固有模态引起的周期性振动等,这些因素均会对发射过程的控制构成扰动。本节采用标准正态分布的随机信号模拟随机扰动,采用52 Hz 的正弦信号模拟固有模态振动,强度设置为最大推力的10 %,以考察强扰动条件下控制算法的鲁棒性。
强扰动时的轨迹跟踪曲线如图10 所示,与图8相比,误差曲线的趋势没有变化,但速度曲线均有轻微的振荡,其中SMC 的振荡程度最轻,体现了滑模控制鲁棒性好的特点。对比表6 和表4 可知,量化指标的变化也很小,说明三种控制方法均能在强扰动条件下进行有效控制。


图10 强扰动时的轨迹跟踪曲线
Fig.10 Trajectory tracking curves with strong disturbance
表6 强扰动时轨迹跟踪性能
Tab.6 Tracking performance with strong disturbance

4.4 变轨迹条件下的控制效果对比
电磁发射的高可控性使变轨迹发射成为可能,是实现通用动力发射的基础,控制算法应满足变轨迹发射的要求。本节在末速度不变的前提下,减小参考轨迹的峰值过载和加加速度,以满足过载敏感型负载的发射要求。
图11 为新发射轨迹的控制效果对比,PID1 的误差最大,PID2 和FBL 的误差接近,SMC 的误差略大,表7 中的量化指标与图11 一致。
表7 不同轨迹的跟踪性能
Tab.7 Tracking performance of different trajectory


图11 新发射轨迹跟踪曲线
Fig.11 Tracking curves of different trajectory
与图8 相比,PID1 滞后程度减轻,因为新轨迹的变化率降低了,PID2 和FBL 的指标基本持平,SMC 的指标略降,总体上前馈线性化和反馈线性化的适应性均较好。
4.5 小结
上文分析了四种控制方法在典型工况、异常工况、强扰动工况、变轨迹工况下的控制效果。没有推力前馈的PID 控制,响应慢、误差大,与其他三种方式存在较大差距;“前馈线性化+PID”根据预设的参考轨迹计算前馈力,前馈力是确定的,安全性高,在异常工况下前馈精度下降通过PID 补偿,总体性能没有明显降低;“反馈线性化+PID”和“滑模+PID”的指标相当,但是滑模控制存在抖振现象,推力的瞬变会产生噪声,破坏载具的声学隐身。综合考虑各方面因素,“反馈线性化+PID”最契合水下电磁发射的要求。
5 结论
本文为了解决集成式液压平衡电磁发射系统的控制难题,推导了系统的非线性动力学方程,采用线性化的策略设计复合控制方法。仿真和试验结果表明:三种线性化复合控制方法在典型工况下、异常工况下、强扰动工况下、变轨迹工况下的控制效果良好,出口速度和位置误差均小于±2 %,其中以“反馈线性化+PID”的综合效果最好。
本文在对象建模和控制算法上充分地考虑了非线性因素,建模方法适用于水压平衡式发射系统,控制算法概念清晰、通用性强,为类似发射系统的分析和控制提供了参考。实现了水下电磁发射内弹道的高性能控制,有利于提升负载的发射安全性和后续动作的可靠性,具有较高的应用价值。
附 录
1.变体积舱段压降通用计算方法
以ΔPmb 的推导为例,给出变体积舱段的压降通用计算方法。负载下端至电动阀的圆柱体区域如附图1 所示,高度为h,面积为S。

附图1 负载下方区域示意图
App.Fig.1 Trajectory tracking curve with strong disturbance
由动量守恒定理得到该区域水体的动力学方程为

随着负载向上运动,水体的质量增大,有
式中,Vmb为负载尾部水体的体积。
同时假设水只有垂直方向的运动,流速和负载速度相同,因此有
水体所受合力包括压力和重力,即
因此得到压强差方程为
式中,![]() 。ΔPxd、ΔPhs 的计算方法可以类推。
。ΔPxd、ΔPhs 的计算方法可以类推。
2.损失系数的CFD 计算方法
发射过程中电动阀处的流速、流向、压强剧烈变化,是影响发射效率的关键环节。以电动阀损失系数的计算为例,给出损失系数的CFD 计算方法。
电动阀损失系数计算模型如附图2 所示,绿色平面为进流边界,设置为速度进口,表征动子运动速度,红色平面为出流边界,黄色部分表示电动阀开口。

附图2 电动阀损失系数计算模型
App.Fig.2 Computing model of loss coefficient for valve
建立进流面和出流面之间的伯努利方程为
式中,p1、p2分别为进流面和出流面的平均静压;u1、u2分别为进流面和出流面的平均流速;ζ 为电磁阀损失系数;ux为流经电磁阀的平均流速。
附图3 为压强与流速分布,代入压强和流速,可解得电磁阀的损失系数为


附图3 压强与流速分布
App.Fig.3 Pressure and flow rate distribution
[1] 马宪亭.流体传动中的压力损失分析与计算[J].流体传动与控制,2010(4): 50-51,60.
Ma Xianting.The analysis and calculation of the pressure loss in the transmission fluid system[J].Fluid Power Transmission &Control,2010(4): 50-51,60.
[2] 黄垂兵,许金,杨琼方,等.水下发射循环管路系统水动力性能的仿真分析与验证[J].海军工程大学学报,2019,31(2): 26-31,43.
Huang Chuibing,Xu Jin,Yang Qiongfang,et al.Simulation analysis and verification of hydrodynamic performance of underwater launch cycle pipeline system[J].Journal of Naval University of Engineering,2019,31(2): 26-31,43.
[3] 程广涛,孔岩峰,张振山.液压平衡式水下武器发射系统仿真分析[J].兵工学报,2009,30(7): 915-919.
Cheng Guangtao,Kong Yanfeng,Zhang Zhenshan.Simulation and analysis of hydraulic and balanceable underwater weapon launching system[J].Acta Armamentarii,2009,30(7): 915-919.
[4] 张孝芳,王树宗,练永庆.气动水压式水下武器发射系统建模与仿真[J].系统仿真学报,2009,21(10):3092-3095.
Zhang Xiaofang,Wang Shuzong,Lian Yongqing.Modeling and simulation of pneumatic and hydraulic underwater weapon launching system[J].Journal of System Simulation,2009,21(10): 3092-3095.
[5] 胡寿松.自动控制原理[M].6 版.北京: 科学出版社,2013.
[6] Hassan K K.Nonlinear system[M].Beijing: Publishing House of Electronics Industry,2005.
[7] 刘金琨.滑模变结构控制 MATLAB 仿真: 基本理论与设计方法[M].3 版.北京: 清华大学出版社,2015.
[8] 邵冰冰,赵书强,高本锋,等.基于反馈线性化滑模控制的直驱风电场经柔直并网系统次同步振荡抑制策略[J].中国电机工程学报,2021,41(9):3090-3106.
Shao Bingbing,Zhao Shuqiang,Gao Benfeng,et al.Sub-synchronous oscillation mitigation strategy of direct-drive wind farms via VSC-HVDC system based on feedback linearization sliding mode control[J].Proceedings of the CSEE,2021,41(9): 3090-3106.
[9] 李鹏瀚,王杰,吴飞.双馈风电机组次同步控制相互作用的反馈线性化滑模变结构抑制[J].电工技术学报,2019,34(17): 3661-3671.
Li Penghan,Wang Jie,Wu Fei.Sub-synchronous control interaction mitigation for DFIGs by sliding mode control strategy based on feedback linearization[J].Transactions of China Electrotechnical Society,2019,34(17): 3661-3671.
[10] 张康,王丽梅.基于反馈线性化的永磁直线同步电机自适应动态滑模控制[J].电工技术学报,2021,36(19): 4016-4024.
Zhang Kang,Wang Limei.Adaptive dynamic sliding mode control of permanent magnet linear synchronous motor based on feedback linearization[J].Transactions of China Electrotechnical Society,2021,36(19): 4016-4024.
[11] 管成,朱善安.电液伺服系统的积分滑模自适应控制[J].电工技术学报,2005,20(4): 52-57.
Guan Cheng,Zhu Shan'an.Integral sliding mode adaptive control for electro-hydraulic servo system[J].Transactions of China Electrotechnical Society,2005,20(4): 52-57.
[12] 王勃,王天擎,于泳,等.感应电机电流环非线性积分滑模控制策略[J].电工技术学报,2021,36(10):2039-2048.
Wang Bo,Wang Tianqing,Yu Yong,et al.Nonlinear integral sliding mode control strategy for current loop of induction motor drives[J].Transactions of China Electrotechnical Society,2021,36(10): 2039-2048.
[13] 孙立明,姜学智,李东海,等.水轮机水门非线性控制器设计[J].电力系统自动化,2003,27(16):45-49.
Sun Liming,Jiang Xuezhi,Li Donghai,et al.Design of nonlinear control for hydroturbine governor[J].Automation of Electric Power Systems,2003,27(16):45-49.
[14] 王倩.高超声速飞行器飞行控制系统设计方法与仿真研究[D].上海: 复旦大学,2011.
[15] 宋闯,魏毅寅.非线性系统理论在导弹控制中的应用研究进展与展望[J].战术导弹技术,2003(6):48-53.
Song Chuang,Wei Yiyin.Development and forecast of study on nonlinear system theory application to missile control[J].Tactical Missile Technology,2003(6): 48-53.
[16] 方红庆,沈祖诒.非线性非最小相位系统伪线性复合控制[J].南京理工大学学报(自然科学版),2005,29(1): 85-89.
Fang Hongqing,Shen Zuyi.Pseudo-linearization hybrid control strategy for nonlinear and non-minimumphase control systems[J].Journal of Nanjing University of Science and Technology,2005,29(1): 85-89.
[17] Cao Jian,Su Yumin.Input-output linearization design for dive-plane control of AUV[C]//Proceedings of 2011 International Conference on Electronic &Mechanical Engineering and Information Technology,Harbin,China,2011: 2439-2442.
[18] Salgado-Jimenez T,Jouvencel B.Using a high order sliding modes for diving control a torpedo autonomous underwater vehicle[C]//Oceans 2003.Celebrating the Past … Teaming Toward the Future,San Diego,CA,USA,2004,2: 934-939.
[19] 武志涛,李帅,程万胜.基于扩展滑模扰动观测器的永磁直线同步电机定结构滑模位置跟踪控制[J].电工技术学报,2022,37(10): 2503-2512.
Wu Zhitao,Li Shuai,Cheng Wansheng.Fixed structure sliding mode position tracking control for permanent magnet linear synchronous motor based on extended sliding mode disturbance observer[J].Transactions of China Electrotechnical Society,2022,37(10): 2503-2512.
[20] 武志涛,徐建英.基于反馈线性化的直线电动机伺服平台轨迹跟踪控制研究[J].电工技术学报,2015,30(13): 143-149.
Wu Zhitao,Xu Jianying.Trajectory tracking control for the linear motor servo platform based on feedback linearization[J].Transactions of China Electrotechnical Society,2015,30(13): 143-149.
[21] 王天鹤,赵希梅,金鸿雁.基于递归径向基神经网络的永磁直线同步电机智能二阶滑模控制[J].电工技术学报,2021,36(6): 1229-1237.
Wang Tianhe,Zhao Ximei,Jin Hongyan.Intelligent second-order sliding mode control based on recurrent radial basis function neural network for permanent magnet linear synchronous motor[J].Transactions of China Electrotechnical Society,2021,36(6): 1229-1237.
[22] 魏惠芳,王丽梅.永磁直线同步电机自适应模糊神经网络时变滑模控制[J].电工技术学报,2022,37(4): 861-869.
Wei Huifang,Wang Limei.Adaptive fuzzy neural network time-varying sliding mode control for permanent magnet linear synchronous motor[J].Transactions of China Electrotechnical Society,2022,37(4):861-869.