0 引言
铁镓合金(Galfenol)作为一种新型磁致伸缩功能材料,在低外加磁场下可表现出较大(250×10-6~300×10-6)的磁致伸缩量,且具有良好的机械加工性能,在换能器、传感器、精密机械控制和机械传动机构等高技术领域具有重要应用前景[1-3]。其中,以铁镓合金棒为核心驱动元件制成的磁致伸缩水声换能器作为水下声呐系统中重要的电-机械-声能量转换器件,通常需要棒材工作在几千赫兹的高频范围内[4],因此有必要准确测量和分析该频段下铁镓合金棒材的磁特性,才能为此类高频大功率磁致伸缩器件的结构优化、模型研究以及性能调控等方面提供理论指导和实验数据支持[5-6]。
文献[7-9]设计了不同的铁镓合金磁特性测试装置,对棒状铁镓合金材料的磁致伸缩效应、逆磁致伸缩效应进行静态、准静态和动态测量,但是测试处于静态或几十赫兹以内的低频段内,难以适用于研究磁致伸缩材料的高频磁特性。文献[10]采用AMH-1M-S 动态磁特性测试仪对环形片状TbDyFe小样品进行了高频条件下动态磁特性测试,得出样品在励磁频率为10 kHz 时不同温度下的一系列动态磁滞回线,分析了变温条件下样品的高频磁特性和损耗特性,但该实验过程中样品内部磁通密度数值始终较低(B≤0.07 T),没有进一步研究在高频且高磁通密度条件下棒状磁致伸缩材料的动态磁特性。文献[11]为了得到电机柱状定子的铁心损耗数值,从环形取向性硅钢片小样品出发,建立样品损耗模型并提取相关系数,经有限元法处理得到柱状定子铁心损耗,但该方法在高频、高磁通密度条件下求得的柱状定子铁心损耗计算值较实际数据误差过大(在频率为1 kHz、磁通密度为0.9 T 条件下,铁损计算误差达24 %)。目前,在高频、高磁通密度条件下对于棒状磁致伸缩材料的动态磁特性测试研究较少。
当频率达1 kHz 以上时,要使磁致伸缩材料内部获得数值较高的磁通密度变得十分困难。一方面,随着频率的升高,导磁回路铁心损耗剧增,带来的等效电阻阻值也随之增加;另一方面,由于励磁线圈的趋肤效应以及相邻导体邻近效应的影响,线圈本身阻抗也将变得相当大,使得在输入电压一定时,线圈中励磁电流的幅值不断下降,产生的高频磁场也迅速减小;此外,由于磁致伸缩材料磁导率较小,在低外加磁场环境下,其内部磁通密度也很低。
为解决上述问题,本文基于电磁场理论设计了一种铁镓合金棒材的高频高磁通密度磁特性测试装置。首先,根据电磁损耗理论选取高频导磁材料以降低铁心损耗,并采用参数化扫描的方法调整导磁体尺寸参数,为验证优化方案可行性,在此基础上,依据麦克斯韦方程组建立棒材内部磁场强度的微分方程,利用多物理场有限元计算软件Comsol 对棒材上磁场大小与分布情况进行建模计算;然后,以提高电磁转化效率为目标,选择受高频趋肤效应和邻近效应影响小的励磁线圈线材设计装置的电路部分,并依据串联谐振原理进行阻抗匹配;最后,制作了磁特性测试样机,在高频高磁通密度条件下(其中1 kHz 下磁通密度幅值最高可达0.89 T,9 kHz下磁通密度幅值最高可达0.26 T)对棒状铁镓合金样品进行动态磁特性测试,验证了设计理论的可行性,对高频大功率磁致伸缩换能器件的优化设计具有重要指导意义。
1 磁特性测试装置磁路设计
1.1 高频导磁材料选择
磁特性测试装置主体结构采用如图1 所示的左右对称窗式结构,由导磁回路、极头、被测棒材和两个并联的励磁线圈共同构成,上下自由调整的极头可适应不同长度样品的测试需求,且极头的横截面尺寸大于被测试棒材的横截面积以保证加载在棒材上的磁场尽可能地均匀。由于测试装置工作于高频激励条件下,为减小磁回路铁心损耗,需要选择合适的高频导磁材料。
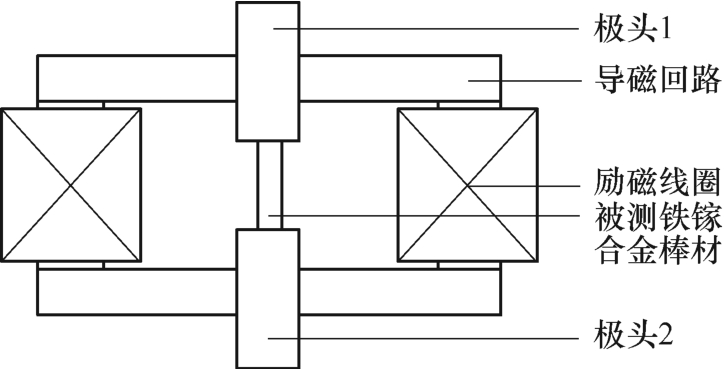
图1 磁路部分结构
Fig.1 Structure of the magnetic circuit
由改进的Steinmetz 公式[12]可知,导磁体铁心损耗Pc 可表示为
式中,Fw.c 为磁通波形系数;α、β 为与材料有关的常数;fd 为加载在导磁体上的磁场频率;Bd 为导磁体内部磁通密度。就典型的磁心材料:硅钢片、铁氧体、纳米晶材料、非晶材料,表1 分别给出其在PWM 方波激励下的Steinmetz 系数。
表1 磁性材料Steinmetz 系数
Tab.1 Steinmetz coefficients of magnetic material
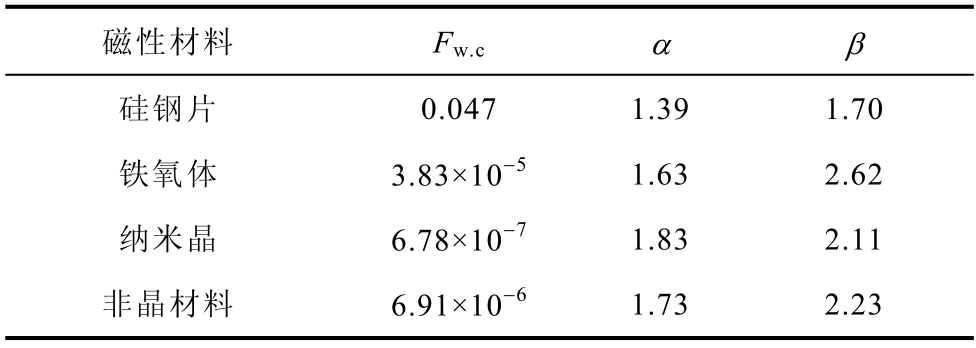
由表1 数据和式(1)计算可知,相较于铁氧体、纳米晶、非晶材料磁心,当频率升高达1 kHz 以上时,传统的硅钢片由于铁心损耗过大,已不适用于充当导磁材料;纳米晶材料高频损耗虽小但带材过薄且脆性大,加工装配困难;非晶材料磁致伸缩应变较大,高频下噪声问题不容忽视;铁氧体材料在高频率、宽频带内具有以下优势:电阻率高,涡流损耗小,不必加工成薄片,磁致伸缩系数小,不易产生噪声问题,且有较高的磁导率[13]。故本设计选用铁氧体作为导磁材料。
1.2 磁路结构参数优化
对于励磁线圈产生的磁场与磁路总磁通Φ 之间的关系为
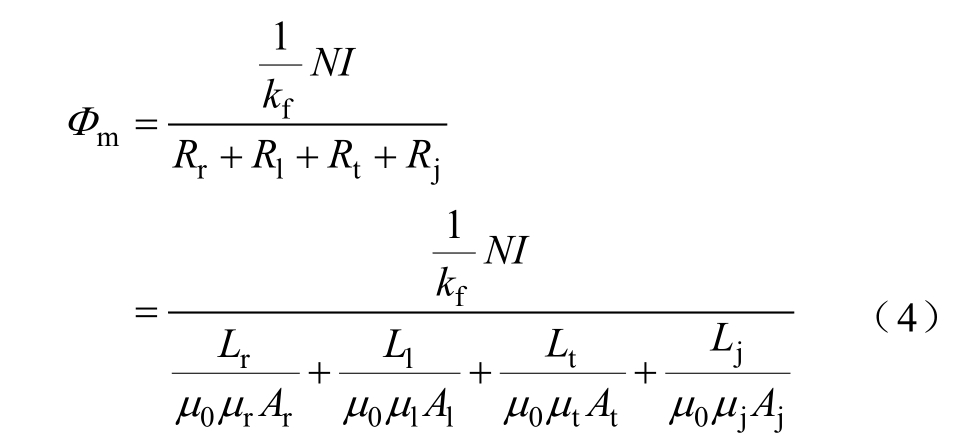
式中,N 为励磁线圈匝数;I 为励磁线圈中电流有效值;Φ 为磁路总磁通;R 为磁路总磁阻。将磁路简化,得到磁路模型如图2 所示,图中,NI 表示线圈磁动势,Rr、Rl、Rt、Rj 分别表示铁镓合金棒、左右导磁体、上下导磁体、极头的等效磁阻。
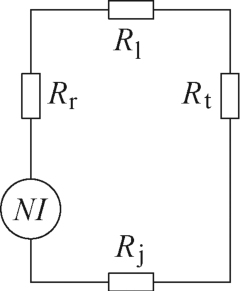
图2 磁路模型
Fig.2 Magnetic circuit model
其中
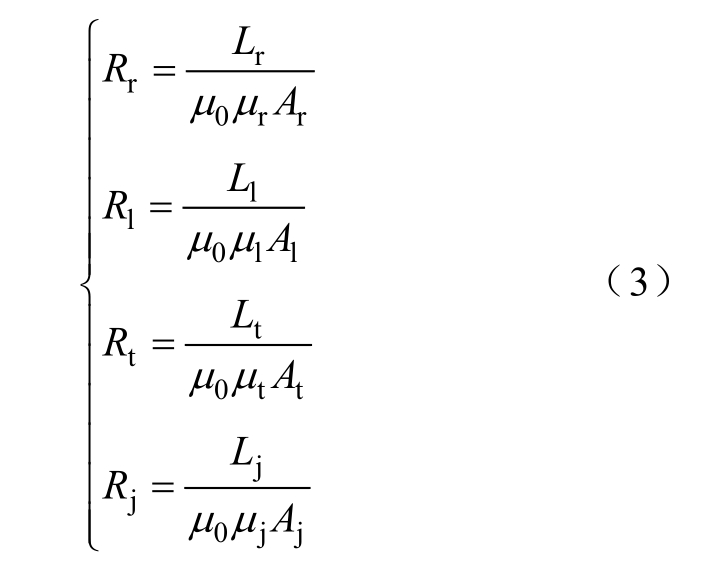
式中,μ0 为真空磁导率;μr、μl、μt、μj,Ar、Al、At、Aj,Lr、Ll、Lt、Lj 分别为铁镓合金棒、左右导磁体、上下导磁体、极头的相对磁导率,等效截面积和有效长度。由于铁镓合金磁导率相对较低,因此在实际的磁路中应考虑漏磁。定义kf 为励磁线圈的漏磁系数,由磁路欧姆定律可得
由式(4)可知,磁回路的结构形式、导磁体材料特性与尺寸参数等均会对主磁通Φm 产生影响,在磁路结构和材料类型确定的前提下,为使被测棒材内部磁场分布更加均匀,需要调整导磁体的相关尺寸。沿棒材轴线按一定步长取n 个点,定义磁场均匀度K 为
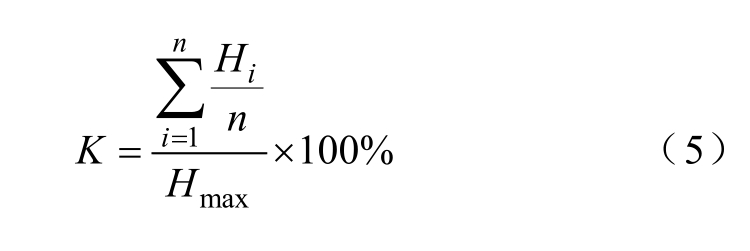
式中,Hi 为棒材上第i 个点的磁场强度;Hmax 为棒材上磁场强度最大值。
在磁回路实际尺寸满足应用的基础上,对可调整的导磁体尺寸参数(长、宽、高等)进行参数化扫描,每次只改变一个参数,其他参数不变,以此为顺序找到每个可调尺寸的最佳参数值进行建模计算,比较每次结果的磁场均匀度,选出磁场分布最均匀的方案。图3 为最优参数求解流程,图3 中,X 为欲调整的尺寸参数,Xmax 为根据实际条件设定的参数值上限,Xmin 为使K 最接近100 %的最优参数值。

图3 最优参数求解流程
Fig.3 Flow chart of optimal parameter solution
1.3 优化结构的磁场三维有限元分析
为验证采用参数化扫描的方法优化导磁体尺寸参数的可行性,建立柱面坐标系如图4 所示,对铁镓合金棒材内部磁场进行分析,设r、θ、z 分别对应的单位向量为er、eθ、ez[14]。
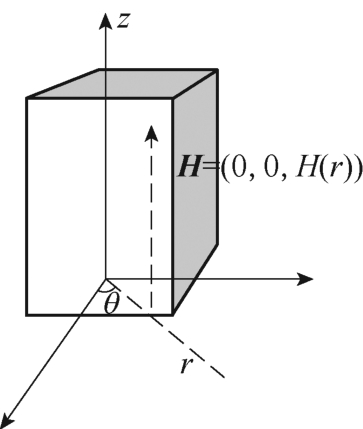
图4 柱面坐标系
Fig.4 Cylindrical coordinate system
在铁镓合金棒材高频磁特性测试装置的模型搭建过程中,为了建模和计算方便,作出如下假设:
1)励磁电流以一定角频率随时间呈时谐(余弦或正弦)变化,以此为场源产生的电磁场也以同样角频率时谐变化,即为时谐电磁场。
2)在此主要为考虑趋肤效应对磁场强度分布的影响,在ez 方向上视为磁场强度恒定,又因铁镓合金棒材结构对称,磁场强度大小与θ 无关,铁镓合金棒材上的磁场强度只是坐标 r 的函数,即:H=(0,0,H(r))。
3)由于在励磁电流附近,比该频率的电磁波在真空中的波长小得多的区域内,可忽略电磁场的推迟效应,故将棒材内部磁场看作似稳电磁场。
根据假设,磁场H 的旋度为
对式(6)两端取旋度,有
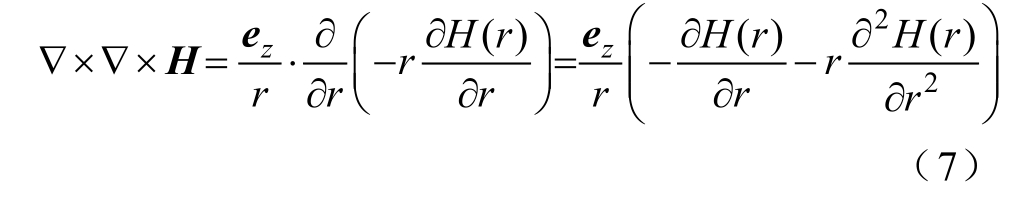
在似稳电磁场中,复数形式的麦克斯韦方程组为

式中,E 为电场强度;B 为磁通密度;J 为电流密度;D 为电位移;ρ 为电荷密度。对式(8)中第一个等式两边取旋度并将第二个等式代入,可得

式中,σ 为铁镓合金电导率,结合式(7)和式(9),可建立微分方程
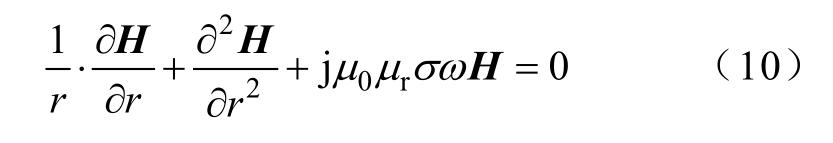
式(10)给出了关于磁致伸缩棒材内部磁场强度的微分方程,可用于求解模型中磁场强度数值及分布。
为进一步考虑z 方向上磁场强度变化,利用多物理场有限元计算软件Comsol,采用1.2 节中确定的测试装置三维结构模型尺寸参数并进行仿真计算,可较准确地得出被测铁镓合金棒材内部磁场强度大小和分布情况,如图5 所示。完整的剖分网格包含107 317 个域单元、15 325 个边界元。
图5 优化结构三维有限元网格模型
Fig.5 Mesh model of the optimized prototype
图6 为1 kHz 激励下被测铁镓合金棒材外表面、中心截面磁场强度分布云图,由此可见,棒材外表面和中心截面磁场强度大小相近,可通过霍尔元件测试棒材表面磁场强度进而确定内部磁场强度值。图7 为沿长度方向上棒材外表面轴线和中心轴线磁场强度分布折线,以5 mm 为步长取5 个点,由式(5)计算得出,棒材外表面轴线、中心轴线磁场均匀度分别为80.15 %、84.72 %。可见,利用参数化扫描的方法调整导磁体尺寸参数后,确实可使铁镓合金棒材内部获得均匀度较高的磁场,初步验证了优化方法的可行性。
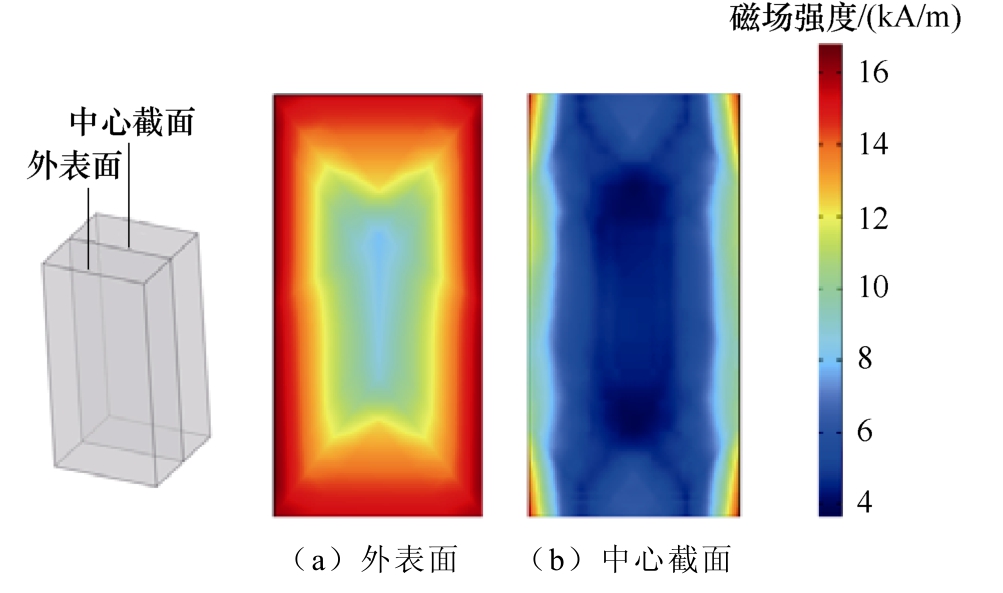
图6 磁场强度分布云图
Fig.6 Cloud diagram of magnetic field intensity distribution

图7 棒轴向磁场强度分布折线
Fig.7 Line chart of axial magnetic field distribution
2 磁特性测试装置电路设计
2.1 励磁线圈线材选择
励磁线圈是磁特性测试装置的电路部分,当线圈内通入高频励磁电流时,由于趋肤效应和邻近效应的影响,使线圈的交流电阻值随着频率的升高而增加,从而导致线圈损耗变大,因此需要选择适用于高频条件下的励磁线圈线材。
图8 为在利兹线、普通圆导线内通以频率为10 kHz、有效值为1 A 的电流后导体截面电流密度分布云图,如图8 所示,利兹线采用多条金属导线相互缠绕的方法,使得导体内电流能够比较均匀的分布,降低高频条件下趋肤效应带来的影响。
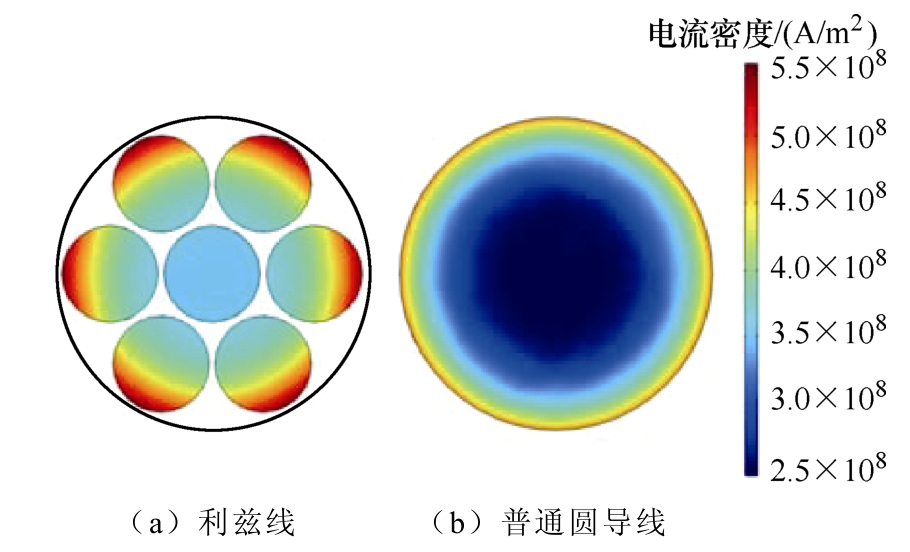
图8 导体中电流密度分布
Fig.8 Current density in conductors
对于高频条件下的邻近效应,利兹线通过扭转结构使导体受磁场影响的部位交叉换位,以此来消除这个磁场效应。利兹线三维示意图如图9 所示。利兹线的特殊结构使一根导线在扭转一个圆周(θ =2π)之后回到初始点,外磁场对该导线的影响方向会随之改变,从而在一个节距λ 内消除外磁场影响。

图9 利兹线三维示意图
Fig.9 Three dimensional schematic diagram of Leeds line
通过以上分析,相较于普通圆导线,利兹线可明显缓解高频激励条件下趋肤效应和临近效应的影响,以减小线圈交流电阻值,降低电路损耗,故本设计采用利兹线绕制励磁线圈。励磁线圈尺寸如图10 所示。
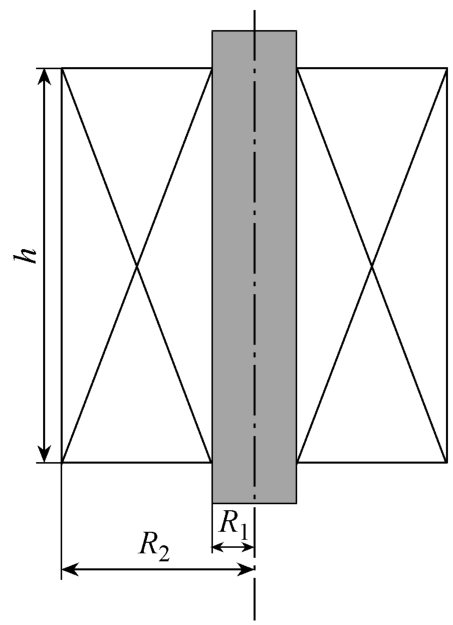
图10 励磁线圈尺寸
Fig.10 Size of exciting coil
2.2 励磁线圈参数设计
为进一步降低励磁线圈电阻损耗,提高电磁转化效率,需要对励磁线圈内径R1、外径R2、高度h等几何参数进行优化设计。
励磁线圈中轴线处的磁场强度Hz 可表示为

式中,N 为励磁线圈匝数;I 为励磁线圈电流有效值。
励磁线圈的电阻损耗p 为
式中,ρd 为导体电阻率;γ 为励磁线圈几何因子。
几何因子γ 为
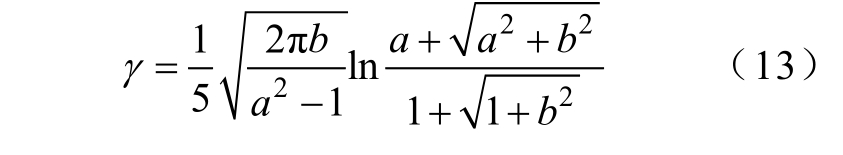
由式(12)可知,励磁线圈几何因子γ 越大,电阻损耗越小,根据式(13),利用Matlab 软件求解出γ 的等值线如图11 所示。

图11 励磁线圈几何因子γ 等值线
Fig.11 Contour map of the geometry of the electromagnetic coil γ
由图11 可知,γ 的最大值约为0.179,此时a≈2,b≈3。此时励磁线圈电阻损耗最小,电磁转换效率最高。
2.3 励磁线圈阻抗匹配
带磁心的励磁线圈中通入正弦交流电时,磁心中会产生正弦交变的磁场,随着通入电流频率的增加,线圈等效阻抗增大,导致励磁电流的幅值不断减小,产生的交变磁场也会不断减小。此外,由于铁镓合金棒材磁导率较低,因此难以保证其内部获得较高的磁通密度幅值。为了在高频励磁电流激励下,励磁线圈仍然能产生较大的磁场,根据串联谐振原理设计阻抗匹配模块,抵消电路中的感抗分量,使励磁电流保持较大幅值以产生较大的交变磁场,进而提高铁镓合金内部磁通密度幅值。
根据机电类比的方法,建立如图12a 所示的该装置并联等效电路[15],图中,Rw 为线圈损耗等效电阻,Rc 为导磁体铁心损耗等效电阻,L 为线圈电感,C 为寄生电容。
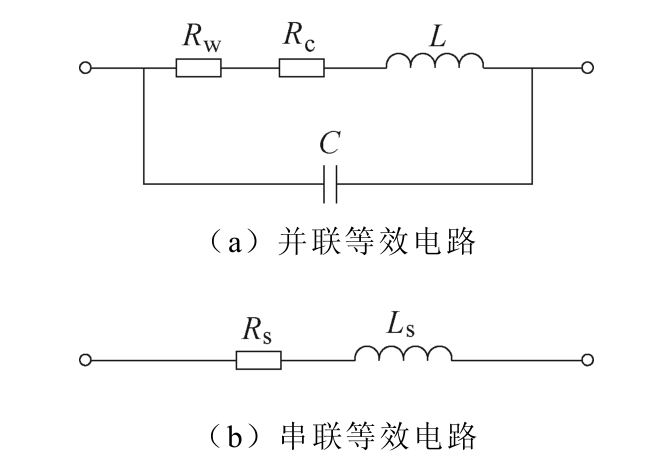
图12 装置等效电路
Fig.12 Equivalent circuit model of device
高频条件下,利兹线的交流电阻Rw 表达式[16]为
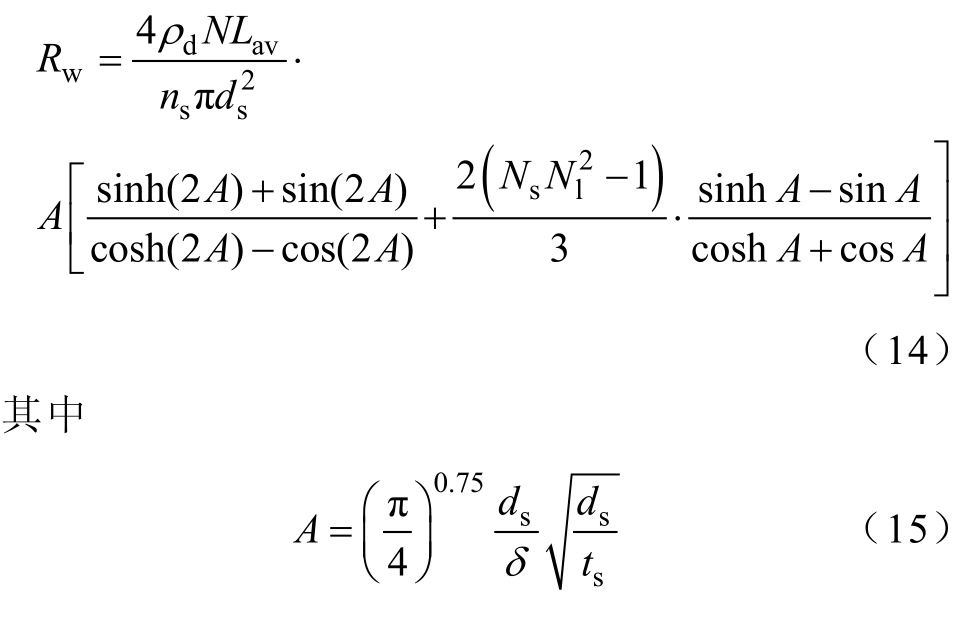
式中,ds 为每股导线直径;ts 为相邻两股中心点间距;δ 为导体趋肤深度;Lav 为平均每匝利兹线长度;Ns 为每根利兹线内导体股数;Nl 为线圈层数。
导磁体铁心损耗等效电阻Rc 可表示为[17]
式中,e、k 为比例系数;ƒ 为励磁线圈中电流频率;μ0 为真空磁导率;μe 为磁心材料相对磁导率;Ae 为磁心材料截面积;le 为磁路长度。
在图12b 所示的串联等效电路中,Rs 为
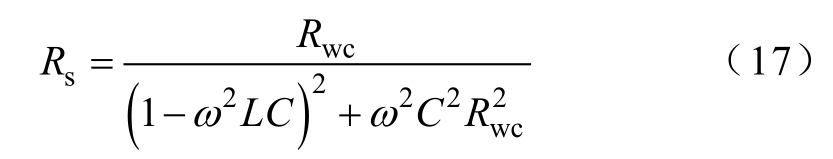
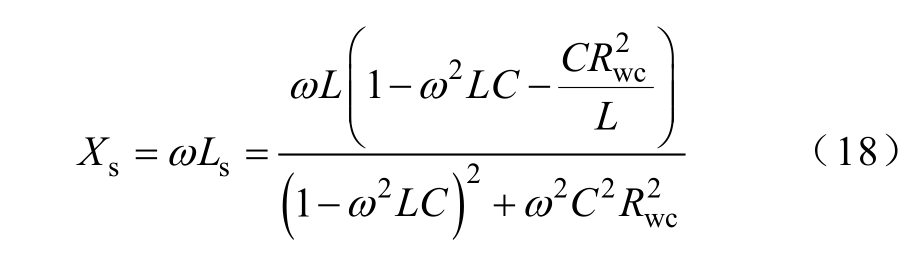
式中,Rwc=Rw+Rc。
根据串联谐振原理,在棒材高频磁特性测试装置等效电路中串接一个随频率可调的电容Cj,保证等效电路在不同测试频率下均处于串联谐振状态,此时电回路中等效阻抗最小,外电源输出电压一定时,励磁线圈中的电流最大,计算可得串接的电容值为

至此,完成了对棒状铁镓合金材料高频高磁通密度磁特性测试装置的设计。首先在第1 节通过式(1)计算导磁体高频损耗以确定装置磁路材料,并根据图3 算法调整导磁体尺寸参数,再利用式(6)~式(10)分析被测铁镓合金棒上的磁场分布,在多物理场有限元计算软件Comsol 中建立三维有限元模型验证优化方案的可行性;然后在第2 节分析高频趋肤效应和邻近效应对导体的影响以选定励磁线圈线材,根据式(11)~式(13)优化励磁线圈结构;最后通过式(14)~式(19)计算得出相应的匹配电路数据。
3 实验平台搭建
为验证以上设计方法的可行性,制作了棒状铁镓合金高频磁特性测试装置样机并搭建了实验平台,对棒状铁镓合金样品进行了不同磁通密度幅值和不同驱动频率条件下的实验测试,首先选定一个被测试铁镓合金棒,其尺寸参数为:采用叠堆结构,叠片厚度为1 mm,高为20 mm,棒横截面尺寸为10 mm×10 mm。根据上文导磁体尺寸参数调整和励磁线圈结构的优化结果,磁特性测试样机主要参数见表2。
表2 磁特性测试装置主要参数
Tab.2 Relevant parameters of magnetic characteristic testing device

本实验测试系统的测试原理如图13 所示,它由四部分构成:磁场施加部分、信号检测部分、数据采集部分和数据处理部分,图14 为测试系统的实物。
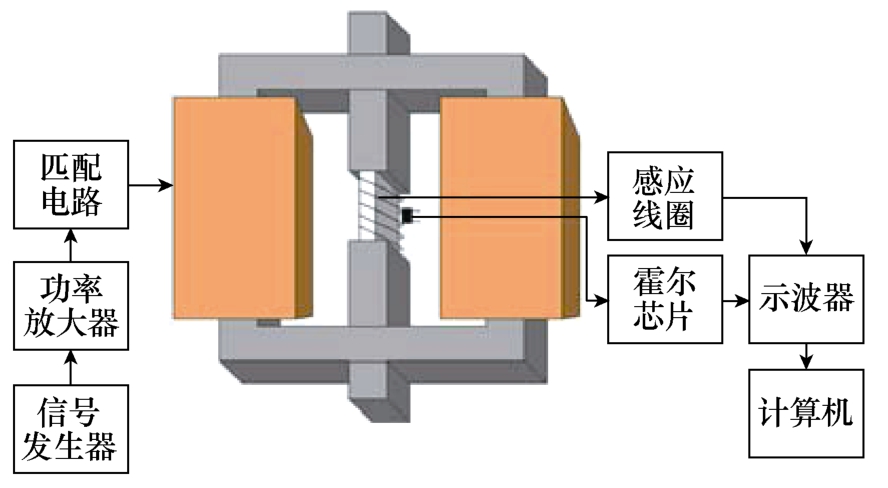
图13 磁特性测量原理
Fig.13 Schematic diagram of measurement system

图14 磁特性测试系统实物
Fig.14 Real picture of testing system
磁场施加部分包括:信号发生器、功率放大器、导磁回路、励磁线圈和匹配电容。功率放大器将信号发生器产生的高频正弦信号放大,功放输出端经匹配电容接在励磁线圈两端,在励磁线圈内部通入高频励磁电流以产生高频交变磁场,高频磁场经导磁回路加载到被测铁镓合金棒材上。
信号检测部分包括:感应线圈和霍尔芯片。采用A1321LUA 型霍尔芯片采集铁镓棒上的磁场强度H,该芯片可以测量10-7~10 T 范围内的恒定磁场,也可测量频率为1 Hz~100 MHz、磁通密度达5 T的交变磁场[18]。由霍尔效应可知
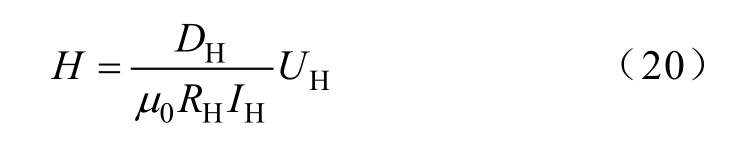
式中,DH 为霍尔芯片厚度;RH 为霍尔系数;IH 为流过霍尔芯片的电流瞬时值;UH 为霍尔芯片感应电动势瞬时值。
铁镓合金棒材内部的磁通密度B 由固定线圈法测量,即在棒状样品上绕制一定匝数的感应线圈。当棒状样品外加磁场发生变化时,穿过感应线圈的磁通量则会相应改变,通过电磁感应定律得
式中,Φg 为穿过感应线圈的磁通量;Ng 为感应线圈匝数;S 为铁镓棒的横截面积;e 为感应线圈电压瞬时值。
对式(21)两边同时积分得
数据采集部分由示波器完成,示波器分别采集霍尔芯片、感应线圈实时输出电压波形和电压瞬时值数据并保存为电子文件。
计算机作为数据处理部分,将采集到的数据转化为txt 文件或excel 文件保存后,通过调用Matlab程序即可绘制H-t 图、B-t 图和B-H 曲线。
4 测试结果及分析
铁镓合金材料的饱和磁通密度约在1.5~1.6 T,磁化曲线膝点的磁通密度值约在0.7~1.2 T(随工作频率和预应力等的不同而变化)。为提升磁致伸缩换能器等大功率磁致伸缩器件的工作性能,铁镓合金应工作在磁化曲线膝点以内的线性区域,当外加压应力0 MPa 时最佳线性区段为1~3 kA/m,6 MPa时为7~9 kA/m[19]。图15 为利用所设计的高频磁特性测试装置测得的当驱动频率为1 kHz、最大磁通密度分别为0.04、0.25、0.50、0.62、0.89 T 时的一组动态磁滞回线。该图中动态磁滞回线为一组同心曲线,测得的矫顽力分别为156、313、620、951、1 560 A/m,剩磁分别为0.019、0.038、0.076、0.094、0.108 T,随着磁通密度增加,曲线拉伸变宽变高。通过调节信号发生器输出信号幅值,所设计的磁特性测试装置在1 kHz 频率下可为铁镓合金棒材提供高达0.89 T 的磁通密度。此外,由于采取了适用于高频条件的导磁材料和绕组线材,有效降低了电路中等效电阻,并添加阻抗匹配模块,抵消电路中的感抗分量,使得在电压一定时,电路中有较高的励磁电流以产生较大磁场,相应的磁场强度最高可达11 kA/m,可完成膝点以下常用线性工作区域内棒材的动态磁特性测试。
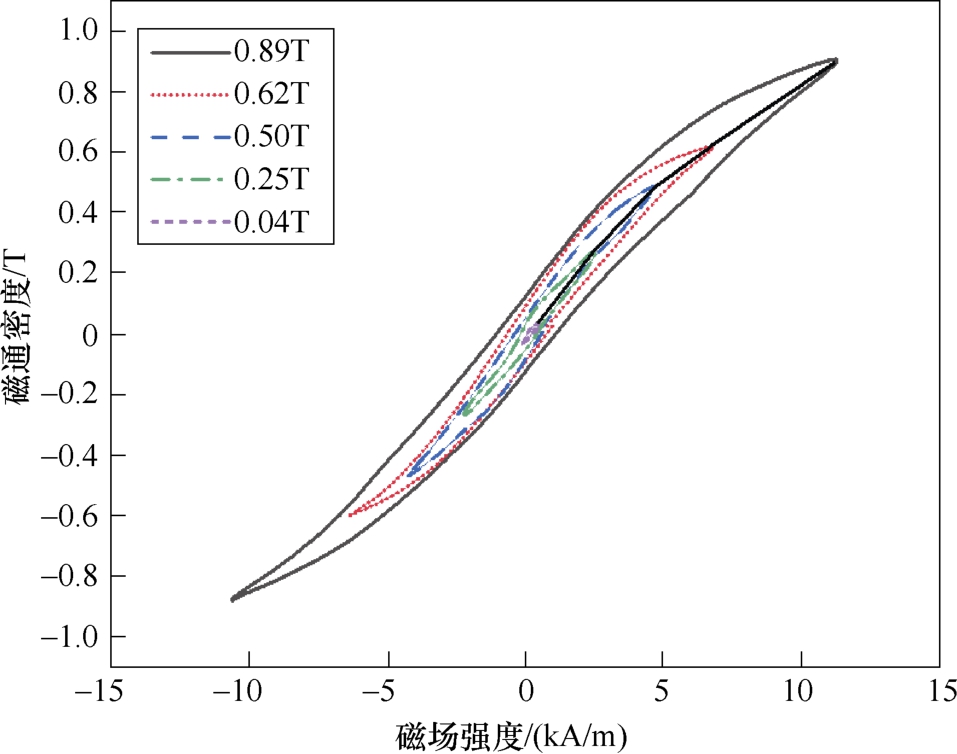
图15 1 kHz 频率下不同磁通密度的动态磁滞回线
Fig.15 Dynamic hysteresis curves at different magnetic induction intensities (f=1 kHz)
随着频率的升高,电路中导磁体铁心损耗和线圈的趋肤效应和邻近效应带来的等效电阻增加,使励磁电流减小,产生的磁场随之降低,当测试频率高达 9 kHz,此时棒材内磁通密度幅值可调至0.26 T。为方便对比,通过改变信号发生器输出信号频率和匹配电容参数值,在最大磁通密度为0.26 T、驱动磁场频率分别为1、3、5、7、9 kHz 条件下,测得的该铁镓棒材的一组动态磁滞回线如图16 所示。可见,随着频率的升高,矫顽力分别为243、437、531、564、728 A/m,剩磁通约为0.031、0.057、0.069、0.075、0.089 T,磁滞回线随着频率的增加横向变宽,曲线的斜率不断变小,这一变化趋势与国外报道的铁镓合金片状小样品的磁特性变化趋势一致[20]。

图16 磁通密度幅值为0.26 T 时不同频率的动态磁滞回线
Fig.16 Dynamic hysteresis curves at different frequencies(Bm=0.26 T)
大量的实验测试结果表明,所设计的棒状铁镓合金高频磁特性测试装置可为磁致伸缩棒在励磁频率高达9 kHz 时提供最高数值为0.26 T 的磁通密度;在10 kHz 以上的测试频段内仍能保证棒材内部获得最高约0.2 T 的磁通密度;当频率为1 kHz 时,最高可测磁通密度可达0.89 T;在频率小于1 kHz 条件下,棒材内部最大磁通密度数值可提高到1 T 以上;在准静态或静态条件下,可测磁通密度的范围将进一步扩大,棒材内可获得的最高磁通密度数值随着测试频率的降低而升高。此外,通过调节上、下极头,该装置还可适用于不同尺寸铁镓合金棒材高频磁特性测试,具有普适性。
5 结论
针对以往铁镓合金棒材磁特性测试装置磁路损耗大、电阻抗高,难以使棒材内部获得均匀且数值较高的磁通密度的问题,本文基于电磁场理论设计了一种棒状铁镓合金高频磁特性测试装置。首先,根据电磁损耗机理选择高频磁心材料,并采用参数化扫描的方法调整导磁体尺寸参数,依据麦克斯韦方程组建立被测铁镓合金棒材内部磁场强度的微分方程,利用多物理场有限元计算软件Comsol 构建测试装置三维有限元模型,仿真计算棒材上磁场强度大小与分布情况,验证了参数优化的可行性;然后,为提高电磁转化效率,降低电路损耗,选择合适的线材设计励磁线圈并依据串联谐振原理进行阻抗匹配;最后,搭建磁特性测试平台,进行实验测量。实验结果表明:所设计的高频磁特性测试装置可在千赫兹频率范围内为铁镓合金棒材动态磁特性测试提供较高的磁通密度,且操作简单、稳定可靠。为高频大功率磁致伸缩换能器件的优化设计提供重要参考。
[1] 杜杲娴,杨鑫,韦艳飞,等.稀土超磁致伸缩棒材特性测试平台优化与实验研究[J].电工技术学报,2021,36(18): 3867-3875.
Du Gaoxian,Yang Xin,Wei Yanfei,et al.Optimization and experimental research on the test platform of rare-earth gaint magnetostrictive rod characteristics[J].Transactions of China Electrotechnical Society,2021,36(18): 3867-3875.
[2] Zhang Zilong.Tailoring the magnetic properties of galfenol film grown on single-crystal diamond[J].Journal of Alloys and Compounds,2021,858: 157683.
[3] 翁玲,李薇娜,曹晓宁,等.环形Fe-Ga 合金动态磁导率和损耗分析[J].电工技术学报,2019,34(3):459-465.
Weng Ling,Li Weina,Cao Xiaoning,et al.Analysis of dynamic permeability and energy loss of ringshaped Fe-Ga alloy[J].Transactions of China Electrotechnical Society,2019,34(3): 459-465.
[4] Pan Yaozong,Mo Xiping,Li Yingming,et al.A magnetostrictive underwater transducer directly driven by iron-gallium alloy (Galfenol) without bias magnetic field[C]//OCEANS 2015-MTS/IEEE Washington.Washington,DC,USA,2015: 1-4.
[5] Weng Ling,Zhao Qing,Sun Ying,et al.Dynamic experiments of strain and magnetic field for galfenol rod and its modeling[J].IEEE Transactions on Applied Superconductivity,2016,26(4): 0600605.
[6] Scheidler J J,Asnani V M,Dapino M J.Frequencydependent,dynamic sensing properties of polycrystalline Galfenol (Fe81.6Ga18.4)[J].Journal of Applied Physics,2016,119(24): 244902.
[7] 翁玲,罗柠,张露予,等.Fe-Ga 合金磁特性测试装置的设计与实验[J].电工技术学报,2015,30(2):237-241.
Weng Ling,Luo Ning,Zhang Luyu,et al.Design and experiment of a testing device for Fe-Ga magnetic properties[J].Transactions of China Electrotechnical Society,2015,30(2): 237-241.
[8] 李波,李鹏辉,舒亮,等.磁特性测试系统的优化与两种磁性材料的对比[J].机械设计与研究,2016,32(3): 129-133.
Li Bo,Li Penghui,Shu Liang,et al.Optimal design of magnetic testing system and the comparative research of two magnetic materials[J].Machine Design &Research,2016,32(3): 129-133.
[9] 翁玲,曹晓宁,梁淑智,等.棒状铁镓合金磁滞特性和功耗特性分析[J].农业机械学报,2018,49(2):411-418.
Weng Ling,Cao Xiaoning,Liang Shuzhi,et al.Analysis of hysteresis and power consumption characteristics of Fe-Ga rod alloy[J].Transactions of the Chinese Society for Agricultural Machinery,2018,49(2): 411-418.
[10] 黄文美,夏志玉,郭萍萍,等.变温条件下TbDyFe合金高频磁特性和损耗特性分析[J].电工技术学报,2022,37(1): 133-140.
Huang Wenmei,Xia Zhiyu,Guo Pingping,et al.Analysis of high frequency magnetic properties and loss characteristics of TbDyFe alloy under variable temperature[J].Transactions of China Electrotechnical Society,2022,37(1): 133-140.
[11] Chen Junquan,Wang Dong,Jiang Yapeng,et al.Examination of temperature-dependent iron loss models using a stator core[J].IEEE Transactions on Magnetics,2018,54(11): 1-7.
[12] Du Yu,Baek S,Bhattacharya S,et al.High-voltage high-frequency transformer design for a 7.2kV to 120V/240V 20kVA solid state transformer[C]//IECON 2010-36th Annual Conference on IEEE Industrial Electronics Society,Glendale,AZ,USA,2010: 493-498.
[13] Ahmad M K,Ali M S,Majid A,et al.Comparison and analysis of core materials for high frequency (1MHz)planar transformers[C]//2018 International Conference on Computing,Mathematics and Engineering Technologies (iCoMET),Sukkur,Pakistan,2018: 1-5.
[14] 陈绍林,刘淑英.轴对称场涡流的数值计算方法[J].东北大学学报(自然科学版),2003(2): 125-127.
Chen Shaolin,Liu Shuying.Numerical method for eddy current in axis-symmetrical fields[J].Journal of Northeastern University (Natural Science),2003(2):125-127.
[15] Kazimierczuk M K,Sancineto G,Grandi G,et al.High-frequency small-signal model of ferrite core inductors[J].IEEE Transactions on Magnetics,1999,35(5): 4185-4191.
[16] Patel R,Premkumar S,Ambade A,et al.AC resistance calculation of Litz wire and its modeling with FEMM[C]//2016 IEEE International Conference on Recent Trends in Electronics,Information &Communication Technology,Bangalore,India,2016: 692-696.
[17] Bartoli M,Reatti A,Kazimierczuk M K.Modelling iron-powder inductors at high frequencies[C]//Proceedings of 1994 IEEE Industry Applications Society Annual Meeting,Denver,CO,USA,1994:1225-1232.
[18] Sibilska-Mroziewicz A,Czubaj S,Ładyżyńska-Kozdraś E,et al.The use of Hall effect sensors in magnetic levitation systems[J].Applied Mechanics and Materials,2016,817: 271-278.
[19] 翁玲,梁淑智,王博文,等.考虑预应力的双励磁线圈铁镓换能器输出特性[J].电工技术学报,2019,34(23): 4859-4869.
Weng Ling,Liang Shuzhi,Wang Bowen,et al.Output characteristics of double-excited coil Fe-Ga transducer considering pre-stress[J].Transactions of China Electrotechnical Society,2019,34(23): 4859-4869.
[20] Grossinger R,Mehboob N,Suess D,et al.An eddycurrent model describing the frequency dependence of the coercivity of polycrystalline galfenol[J].IEEE Transactions on Magnetics,2012,48(11): 3076-3079.