0 引言
近年来，随着大功率、高压、超高压输电网的发展，根据电网负荷的变化而自动、快速、准确地进行无功功率调节十分重要，可控式并联电抗器因其调节能力强而广泛应用于其中，但在实际运行中会出现很严重的振动噪声问题[1-4]。严重的振动噪声不仅影响附近居民的生活，也会造成紧固件松动、影响电抗器的使用寿命等问题。目前，电抗器振动问题被广泛关注，其研究具有现实意义。
许多学者对电抗器振动问题展开了广泛研究。文献[5]考虑了硅钢片磁化与磁致伸缩特性的各向异性，分析了电磁应力对铁心振动的影响。文献[6-8]测量了谐波与直流偏磁条件下硅钢片的磁特性，为进一步分析电抗器振动问题提供基础。文献[9]基于历史声振数据对电抗器运行状态进行评估。
在实际工作时，电抗器铁心会受到螺杆与夹件施加的静态压紧力作用，也会受到动态的磁致伸缩力与麦克斯韦力共同作用，动静态力均会对硅钢片磁特性产生影响，从而进一步影响电抗器铁心电磁振动特性。文献[10]通过制作的测试仪测量了单轴应力下硅钢片的交变磁化特性，得出单轴应力不仅影响磁滞回线的形状，也影响磁导率和损耗特性的结论。文献[11]提出一种基于磁通密度线圈与磁感应强度线圈结合的测量结构，在二维旋转磁化的过程中测量了压应力与磁化性能的关系。文献[12]测量了直流偏磁叠加应力情况下硅钢片的磁特性，分析了磁致伸缩应力与麦克斯韦应力对电抗器振动特性的影响。文献[13-15]利用测得的机械应力下磁特性曲线计算了电抗器不同位置的振动情况。文献[16]研究了夹紧力对非晶合金材料的磁特性以及铁心振动特性的影响，结果表明，非晶合金磁致伸缩效应随夹紧力非线性变化，且非晶合金铁心在沿着夹紧力方向随夹紧力增加振动减弱显著。文献[17]通过施加螺杆压紧力的方法抑制电抗器振动，结果表明，适当的预紧力有减振效果，当预紧力过大时，减振效果很差。
过去的研究均未考虑动态力对硅钢片磁特性及铁心振动的影响，也没有考虑动静态力共同作用的影响。因此，本文测量硅钢片在动静态力共同作用下的磁特性，建立电抗器电磁场-机械场双向耦合模型，分析电抗器电磁振动特，进行电抗器振动测量实验，对比实验结果与理论分析结果，研究动静态力对电抗器振动影响规律。
1 动静态力条件下硅钢片磁特性测量
电抗器铁心电磁振动仿真计算时，硅钢片磁特性数据对计算结果的准确性有直接影响。本次实验采用爱泼斯坦方圈测量系统，该测量系统由25 cm标准爱泼斯坦方圈、AFG1022 型信号发生器、Model-MB500VI 型功率放大器、Model-50 型激振器、220V 调压器、LC1004 型动态信号采集卡等组成。本次实验中选用32 片硅钢片作为试样，采用双搭接接头的方式。该系统测量硅钢片磁化特性的工作原理为：在交变磁场的作用下，硅钢片被磁化，通过改变二次电压的数值以调节磁感应强度，同时采集一次电流的数值来计算磁场强度，进而得到样片的磁化曲线。磁致伸缩应变由动态信号采集卡、应变片和电桥测量与采集。当硅钢片产生磁致伸缩应变时，应变片受应力弯曲，其阻值发生变化，通过转换电路将阻值的变化转换为电压的变化，从而实现磁致伸缩应变的测量。本次实验中测量了顺磁化方向的磁致伸缩应变大小，其余两个方向的磁致伸缩应变大小取该方向磁致伸缩应变数值的一半。硅钢片磁特性曲线测量平台如图1 所示。
图1 磁特性曲线测量平台
Fig.1 Magnetic characteristic curve measurement platform
试件的一侧通过紧固螺杆固定，静态压紧力由另一侧施压螺杆施加，施加的压紧力大小由压力显示屏显示。动态力由信号发生器、功率放大器、激振器向样片施加，动态力的合理模拟是本次实验重点。电抗器铁心振动可认为由动态的磁致伸缩力与麦克斯韦力共同激励，因此在工频交流电条件下动态力的变化趋势为频率100 Hz 的正弦曲线。在实验中由信号发生器输出频率100 Hz 的正弦信号，该信号经功率放大器放大后输入激振器，此时激振器的输出便为正弦变化的激振力。方圈右侧设置螺杆起紧固作用，动态激励在左侧施加，通过磁铁将激振器输出顶杆接头与硅钢片紧密连接，通过调节激振力的大小使待测样品的振动情况与不同压紧力条件下铁心振动情况一致，激振力的大小可通过调节功率放大器供给的电流瞬时值来改变。
图2 所示为同时考虑静态压紧力与动态振动力条件下硅钢片磁化曲线。从图2 中可以看出，静态压紧力的施加使硅钢片磁化曲线右移，这是由于压紧力的施加使硅钢片内部磁畴偏转更困难，随着压紧力的增大，硅钢片工作点逐渐向右偏移，饱和磁感应强度逐渐下降。当考虑动态力的影响时，动态力的施加会使硅钢片内部磁畴偏转更活跃，硅钢片工作点向左偏移，硅钢片会更易被磁化，饱和磁感应强度升高，但随着压紧力的增大，动态力对硅钢片磁化特性的影响逐渐变小。
图2 硅钢片磁化曲线
Fig.2 Magnetization curves of silicon steel sheet
图3 所示为不同磁通密度、不同工况下的硅钢片磁致伸缩特性测量曲线。施加的电压激励为50 Hz，在正弦电压的一个周期内，磁致伸缩特性曲线出现两个峰值，其周期近似为100 Hz，随着磁通密度的增大，磁致伸缩现象加剧。以磁通密度1.6 T时不同工况下测量曲线为例，分析可知，当考虑静态应力的影响时，静态应力的施加使硅钢片内部磁畴偏转更困难，因此考虑静态应力时磁致伸缩效应减弱。当考虑动静态力共同作用的影响时，其磁致伸缩效应进一步减弱，这是因为施加的动态力为100 Hz 变化的力，这会引起一部分磁畴活跃，此时由磁致伸缩效应引起的磁畴偏转较少，因此考虑动静态力共同作用时磁致伸缩效应会减弱很多。
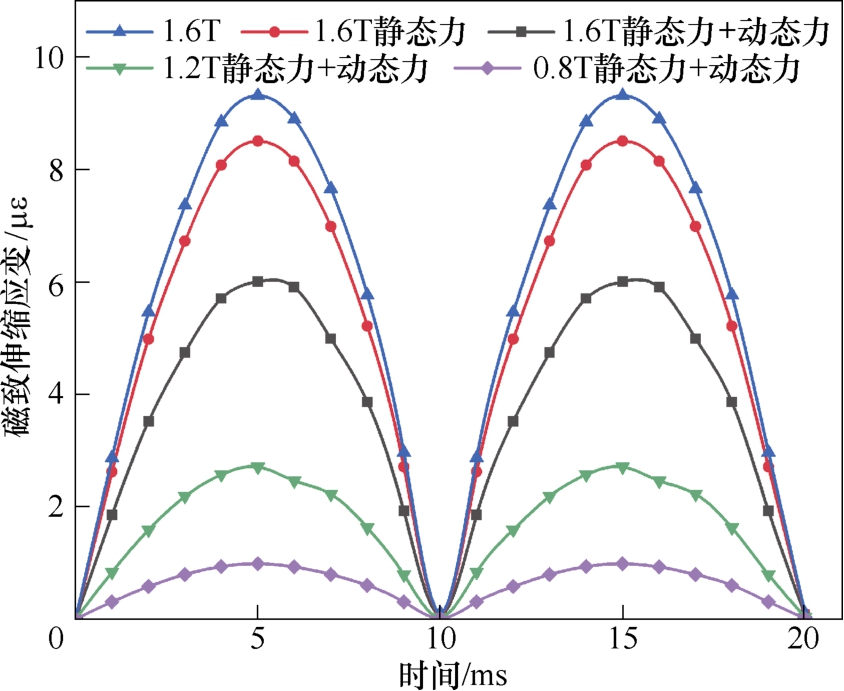
图3 硅钢片磁致伸缩曲线
Fig.3 Magnetostrictive curves of silicon steel sheet
图4 所示为考虑动静态力共同作用影响时不同时间下的单值磁致伸缩插值曲线。在后文的电抗器电磁振动计算中，并非采用单一的磁致伸缩峰值插值曲线，在每个时间步的计算中使用对应的磁致伸缩单值插值曲线，一方面更符合实际工况；另一方面可以更方便地在不同时间下根据动静态力更新磁特性曲线，使计算结果更加精确。
图4 不同时间下磁致伸缩单值插值曲线
Fig.4 Magnetostrictive single-valued interpolation curves at different times
根据磁致伸缩特性测量结果，磁致伸缩系数d可看作为随时间变化的量，其可写为
式中，ω 为基波角频率；n 为谐波次数；Nh 为计算中截断谐波的次数；df,n 为d(t)的第n 次谐波分量。
综上所述，静态压紧力与动态振动力均会影响硅钢片磁特性，进一步对电抗器铁心电磁振动产生影响，因此在对电抗器进行电磁振动计算时应考虑这部分影响。
2 电磁场-机械双向耦合模型
2.1 磁致伸缩效应
磁致伸缩效应是电抗器振动的原因之一。磁致伸缩效应仅在磁场施加时产生，去掉磁场后，磁致伸缩效应消失。因此可应用弹性力学的关系等效磁致伸缩应力，三维弹性体的应力应变关系可写为
式中，σms为等效磁致伸缩应力矩阵；ε 为磁致伸缩应变矩阵；D 为弹性张量矩阵，可写为
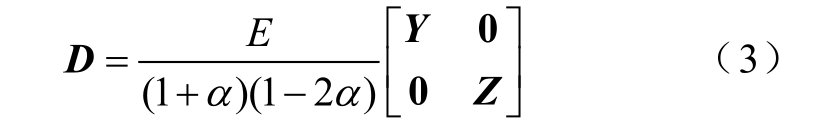
式中，E 为材料杨氏模量；α 为材料泊松比；Y 与Z分别为
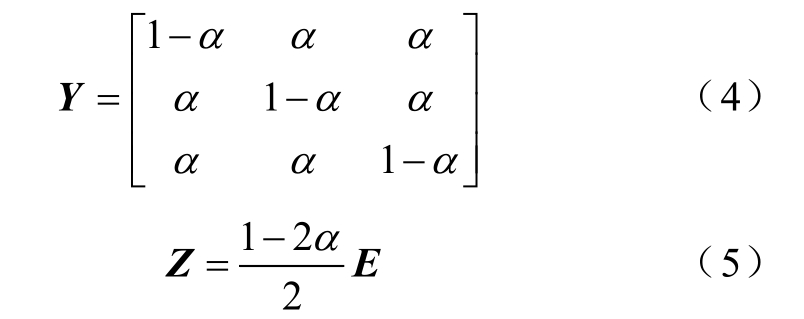
式中，E 为三阶单位矩阵。根据虚位移原理，可将单元节点的磁致伸缩力等效为
式中，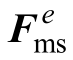
为节点单元的等效磁致伸缩力； K e为单元e 的机械刚度矩阵； x e为单元的位移。由磁致伸缩引起的单元e 的位移等于单元中心到节点的距离与磁致伸缩应变的乘积。
2.2 麦克斯韦力
带气隙结构的电抗器，在气隙区域存在麦克斯韦力，麦克斯韦应力张量是一个多重方向性的张量，麦克斯韦力Fmw 可由应力张量T 的面积分计算。
式中，Bx、By、Bz 分别为磁通密度在x、y、z 方向上的分量；Hx、Hy、Hz 分别为磁场强度在x、y、z方向上的分量；nx、ny、nz 为方向矢量。
铁心内部麦克斯韦电磁力随时间周期性变化，当考虑静态压紧力与动态力对硅钢片磁化特性的影响时，硅钢片磁化特性的变化会对麦克斯韦力的计算产生影响。
2.3 电磁场-机械双向耦合模型
考虑动静态力共同影响时，电抗器系统能量包含磁场能、电流位能、应变能、磁弹性能、磁边界上的位能、外力位能、磁致伸缩力位能与麦克斯韦力位能，其能量泛函可写为
式中，Ω1、Ω2 分别为机械场和磁场的分析域；Γ1、Γ2 分别为机械场Ω1 和磁场Ω2 的边界；A 为矢量磁位；B 为磁通密度；H 为磁场强度；J 为电流密度；u 为位移矢量；fΓ 为外表面力密度；fΩ 为外体积力密度。
由于A、B、H、J、u、Fms、Fmw 这些变量是时间性的周期变量，因此可由复数形式表示为
式中，Af,n、Bf,n、Hf,n、Jf,n、uf,n、Fmsf,n、Fmwf,n 分别为A(t)、B(t)、H(t)、J(t)、u(t)、Fms(t)、Fmw(t)的第n 次谐波分量。
在三维对称场中只存在第一类边界条件，因此磁边界上的位能为零，将能量泛函中各项按直角坐标系展开，磁场能为
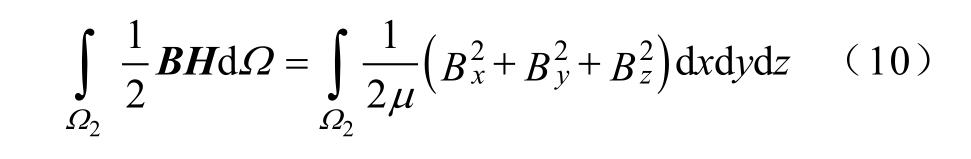
电流位能为
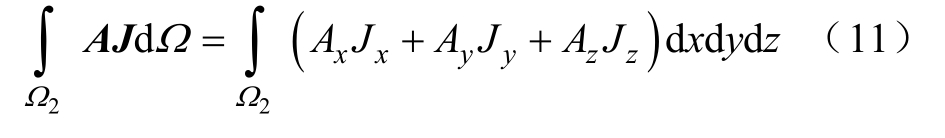
应变能为
磁弹性能为
静态力位能为
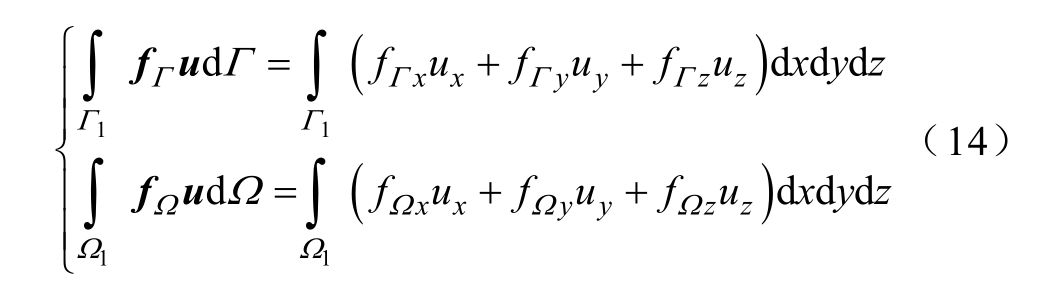
磁致伸缩力位能与麦克斯韦力位能可写为
在对三维轴对称场离散时，采用四面体单元，以磁场离散为例，设四面体四个顶点对应的磁矢位函数AK、AM、AN、AL，则四面体单元内任意一点磁矢位函数均可由线性插值函数逼近，可写为
式中，V 为四面体单元体积，位移场离散同理。为了进行单元变分计算，将能量泛函定义到单元区域内，即
，e 为单元总数，由于磁矢位与位移矢量均已离散到各个节点上，因此能量泛函I 可写为关于磁矢位A 和位移矢量u 的函数，将泛函变分问题转换为多元函数求极值问题，能量泛函I 对每一个节点上磁矢位分量与位移矢量分量的偏导数都为零，可表示为
可将方程写成矩阵形式为
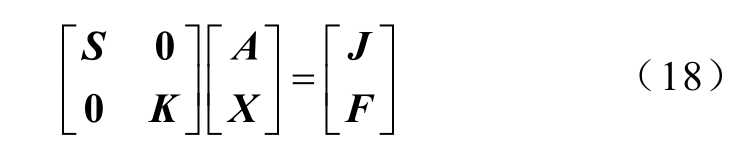
式中，S 为电磁刚度矩阵；K 为机械刚度矩阵；S与K 中的每一个元素都是常数，可看作与时间无关的线性项；X 为位移矢量矩阵；F 为由外体积力、外表面力、磁致伸缩力、麦克斯韦力组成的列矩阵。
图5 所示为并联电抗器电磁机械场双向耦合计算流程，在每个时间步下选用对应的磁特性曲线，对建立的铁心模型进行电磁振动计算。考虑动静态力共同作用对硅钢片磁特性的影响时，根据不同的实际工况更新硅钢片磁特性曲线重新进行计算，当两次迭代的计算结果小于设定误差时，模型收敛满足条件，输出计算结果。
图5 并联电抗器双向耦合计算流程
Fig.5 Flow chart of two-way coupling calculation of shunt reactor
3 仿真与实验分析
根据建立的电抗器电磁场-机械场耦合模型，可对电抗器铁心进行电磁振动计算，仿真中并联电抗器铁心尺寸为190 mm×170 mm×40 mm，3 个铁心柱宽为40 mm，关于中线对称开有两个宽35 mm 窗口，窗口高度为90 mm，每个铁心柱中间开有2 mm 的气隙，气隙处填充环氧树脂垫块。左右两侧为交流绕组，交流绕组匝数为200 匝，中间为直流控制绕组，直流绕组匝数500 匝，并联电抗器铁心模型如图6所示。计算中，将铁心分为两部分，受到静态压紧力与动态振动力影响的铁轭部分和仅受到动态振动力影响的铁心柱部分，分别在铁轭部分与铁心柱部分取测点A、B。
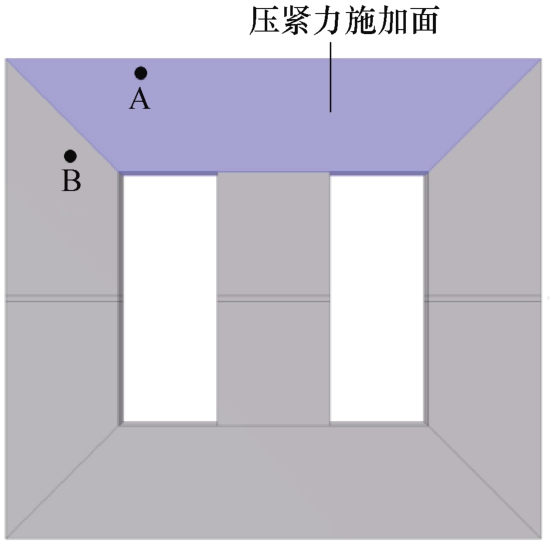
图6 并联电抗器铁心模型
Fig.6 Shunt reactor core model
3.1 磁场、应力分析
根据测量的磁特性曲线，利用仿真软件对并联电抗器进行电磁振动计算，t=0.005 s 时刻电抗器铁心磁通密度、应力分布如图7 所示。
由图7 分析可知，铁心中间直流柱磁通密度较小，两侧交流柱磁通密度较大，铁心拐角处为磁通密度集中分布区。由于设置了底部约束，因此应力集中分布于下铁轭处，铁心拐角处同样出现应力集中分布区。
图7 铁心磁通密度、应力分布
Fig.7 Core magnetic density distribution
电抗器铁心振动可近似认为由磁致伸缩应力与麦克斯韦应力共同激励，首先定量计算磁致伸缩应力与麦克斯韦应力，进一步分析其对振动的影响，测点B 应力曲线如图8 所示。分析可知，磁致伸缩应力与麦克斯韦应力均为100 Hz 变化的正弦曲线。对于并联电抗器，磁致伸缩应力数值较麦克斯韦应力数值小很多，因此并联电抗器铁心振动主要由麦克斯韦应力引起。总应力的数值小于麦克斯韦应力，这是由于铁心材料硅钢片的磁致伸缩效应是正效应，而铁心饼间麦克斯韦力可看作电磁吸力，其方向在空间上与磁致伸缩效应相反，二者有一定的“相消”作用，因此总应力的数值会较麦克斯韦应力的数值小，磁致伸缩应力与麦克斯韦应力在空间上呈一定的电角度，二者并不是直接相减的关系。
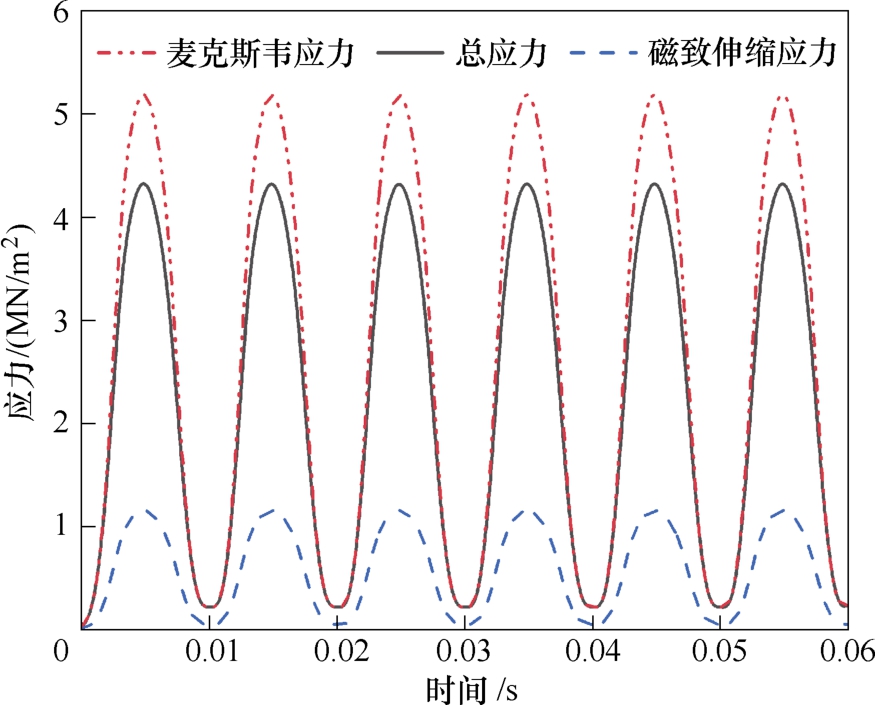
图8 测点B 应力曲线
Fig.8 Stress curves of measuring point B
由于麦克斯韦应力是并联电抗器振动的主要原因，当考虑动静态力共同作用对硅钢片磁特性的影响时，变化的磁特性影响了麦克斯韦应力的分布，从而影响了铁心应力分布，进一步影响了铁心振动情况。
为了更直观地分析动静态力对铁心磁通密度、应力分布的影响，对两代表性测点A、B 进行分析，结果如图9 所示。对于铁轭处测点A，其同时受到压紧力与动态力作用，随着压紧力的增加，磁通密度计算值减小。由于该部分直接受到外部施加压紧力的影响，因此应力的计算值会随施加压紧力的增大而增大。考虑动态力对硅钢片磁特性的影响时，硅钢片磁化工作点左移，饱和磁感应强度增大，因此磁通密度、应力的计算值有所增大，随着压紧力的增大，动态力对硅钢片磁特性的影响逐渐减小，其对磁通密度、应力计算值的影响也逐渐减小。对于铁心柱处测点B，其不直接受到压紧力的作用，但压紧力的施加对铁心整体的磁通密度、应力分布均有影响，磁通密度、应力的计算受压紧力的影响基本呈线性变化。外部施加压紧力相同条件下，考虑动态力对硅钢片磁特性的影响时铁心饱和程度较高，测点B 磁通密度、应力的计算值也有所增大。对于高磁通密度区测点B，其磁通密度、应力计算数值受动态力影响较大，根据第1 节磁化曲线测量的结果可知，动态力对硅钢片磁化特性的影响主要集中于0.9 T 以上的高磁通密度区，因此在铁心高磁通密度区的数值计算结果会受动态力影响较大。
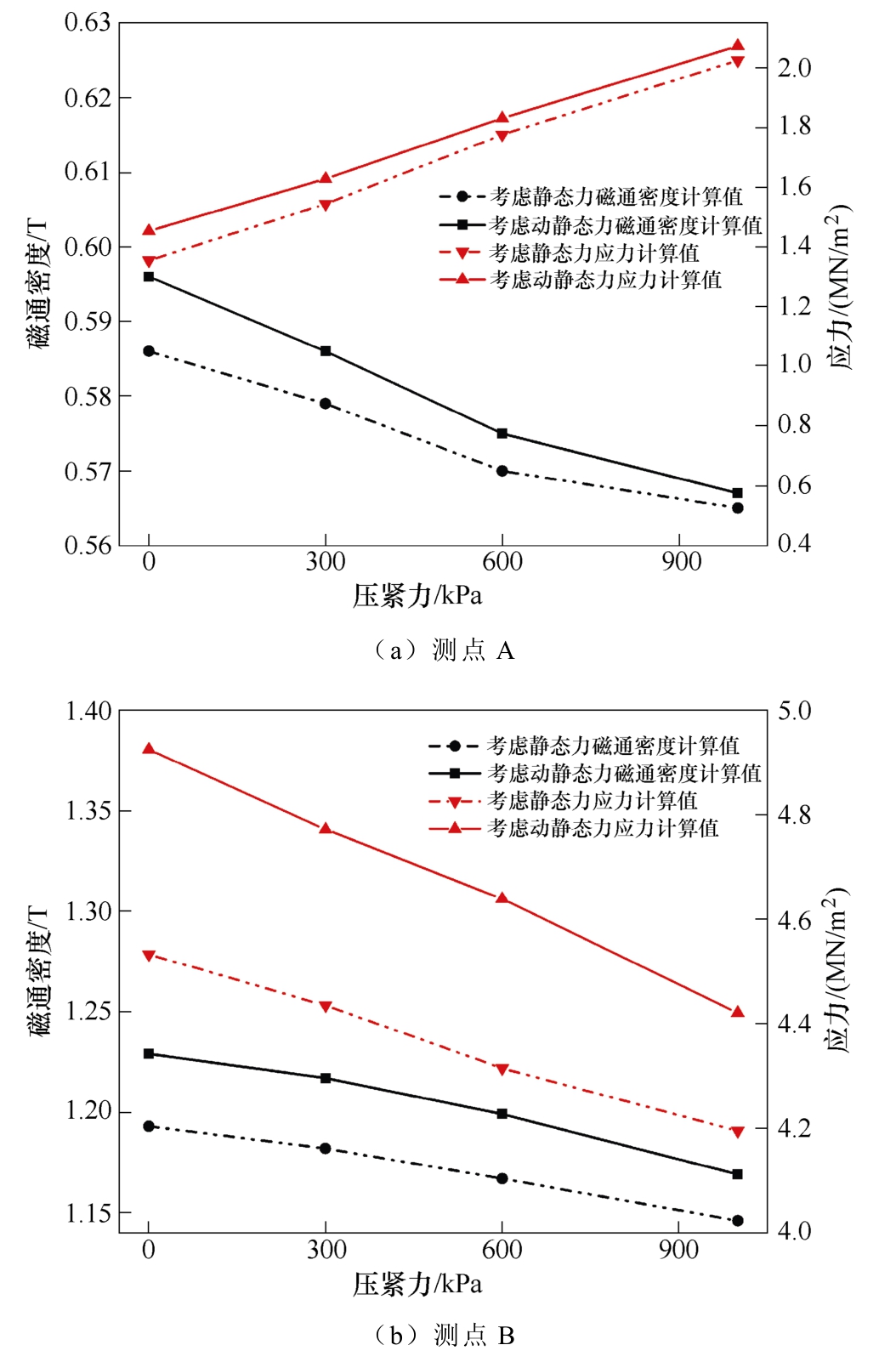
图9 磁通密度、应力比较
Fig.9 Magnetic density and stress comparison
3.2 振动分析
采用第2 节建立的耦合模型进行计算，如图10所示为测点A、B 的加速度曲线，分析可知，各方向加速度曲线均为100 Hz 变化的正弦曲线。对于测点A，压紧力沿着y 轴方向施加，其应对y 方向加速度计算数值影响较大，但y 方向加速度计算数值较小，其对电抗器振动影响不大，因此仅考虑压紧力对x、z 方向振动的影响，随着压紧力的增加，x、z 方向加速度数值不同程度地下降。对于测点B，其位于铁心拐角处高磁通密度区，因此振动情况较测点A 剧烈。
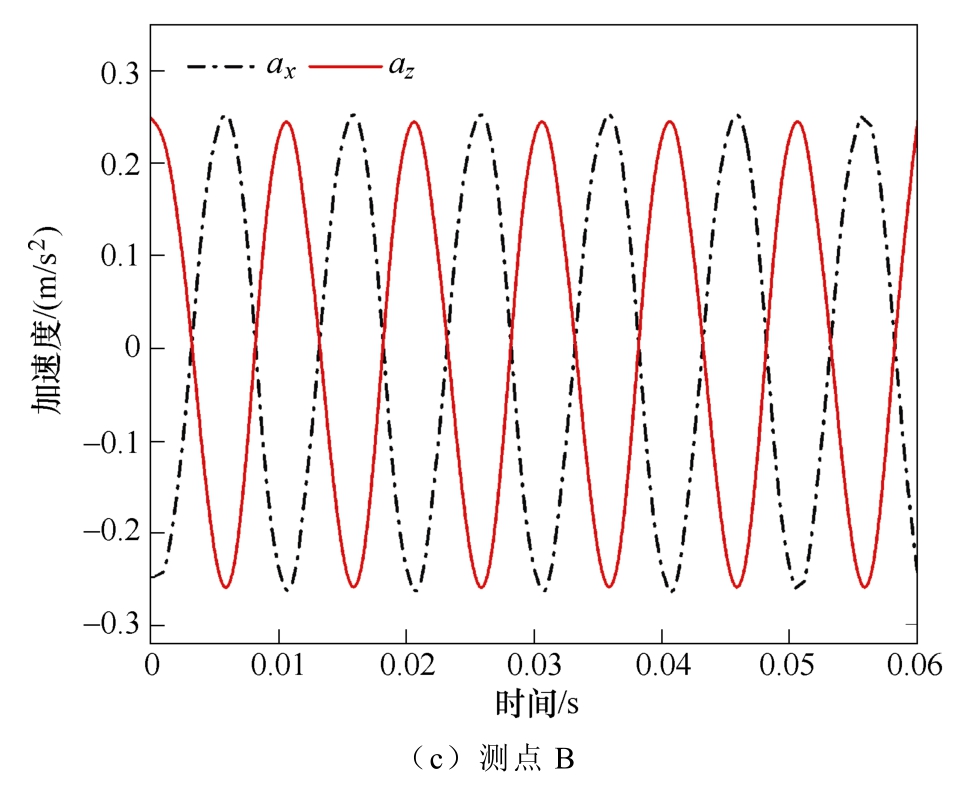
图10 不同测点加速度曲线
Fig.10 Acceleration curves of different measuring points
3.3 实验验证
为了对仿真模型进行验证，对并联电抗器进行不同压紧力下振动特性实验。振动实验测量系统由220V 调压器、PC、并联电抗器、加速度传感器、Squadriga_II 振动测试仪组成。调压器输出工频交流电，加速度传感器通过蜜蜡粘至测点，测量的振动信号通过振动测试仪传至 PC，测量平台如图11 所示。
图11 振动测量系统
Fig.11 Vibration measurement system
测点A 实验加速度曲线如图12 所示。从图中可以看出，实验与仿真存在误差，产生误差的原因可归结为以下几个方面：①在仿真过程中对电抗器设置为底部约束，但是在实际实验过程中，电抗器很难实现效果很好的底部约束效果；②实验中外界环境的干扰与其他设备的运行也会使实验结果出现误差；③仿真过程中仅采用硅钢片的磁测量数据，不能很好地模拟叠片铁心的效果。由图12 可知，y方向加速度数值较小，其对铁心振动影响不大，随着压紧力的增加，x、z 方向加速度幅值不同程度下降。总体来说，实验值与仿真值波形趋势一致，幅值存在一定的误差，但误差也在接受范围内，证明了建模的合理性，也证明了理论分析的正确性。
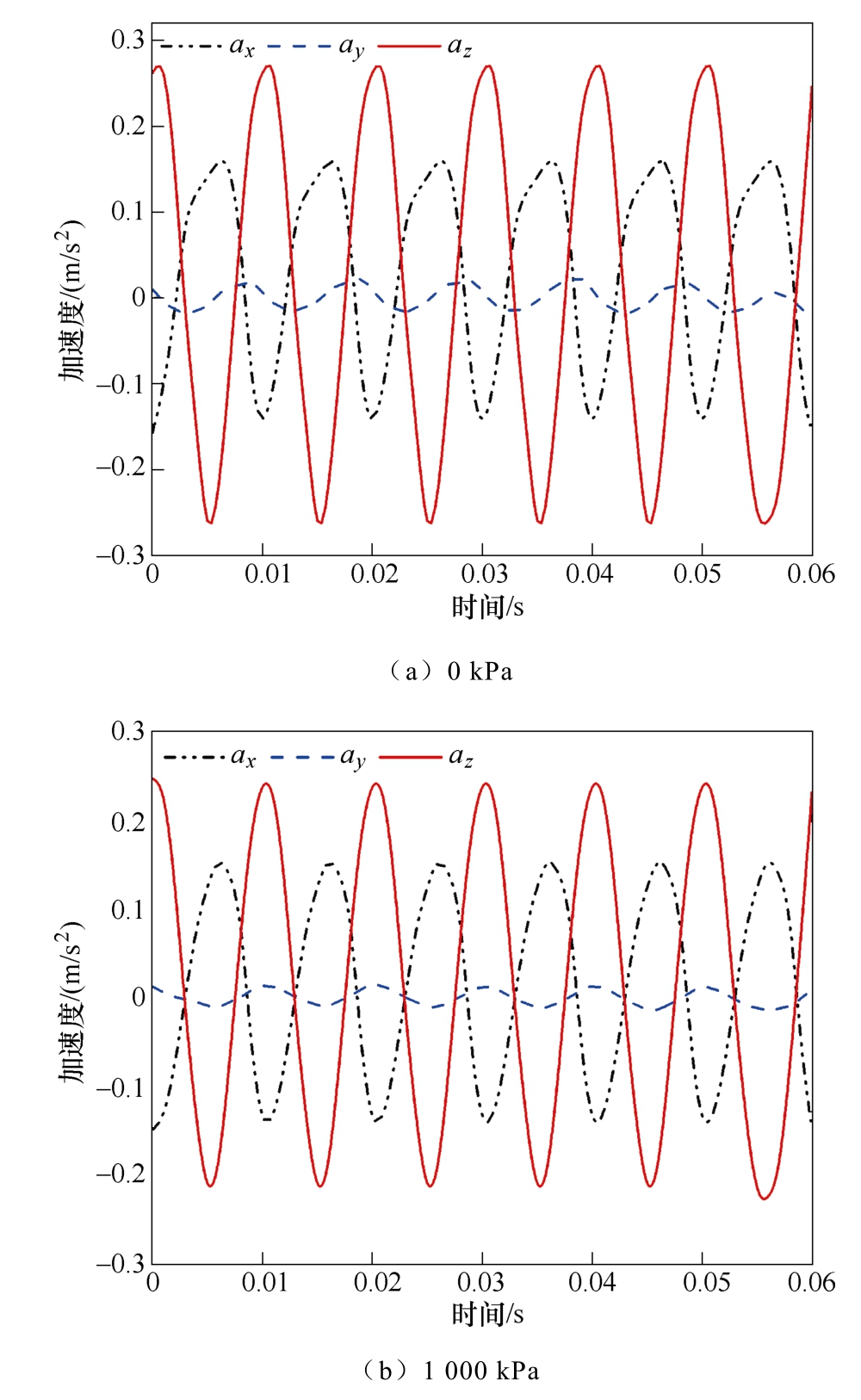
图12 测点A 实验加速度曲线
Fig.12 Experimental acceleration curves of measuring point A
为了更直观地分析考虑动静态力对铁心振动的影响，采用加速度峰峰值表征铁心振动情况，将实验测量的数据与仿真计算的数据进行对比，得到的结果见表1。
由表1 数据分析可知，静态压紧力对x 方向加速度影响较小，z 方向加速度影响较大。图13 所示为不同条件下加速度计算值对比，当仅考虑静态压紧力的影响时，加速度计算值随压紧力的增加而减小。当考虑动静态力共同作用对硅钢片磁特性影响时，加速度计算数值较仅考虑压紧力时有所增大。动态力影响硅钢片磁致伸缩效应，使其数值下降很多，但由3.1 节分析可知，磁致伸缩应力对电抗器振动影响较小，麦克斯韦力是并联电抗器振动的主要原因，因此动态力对硅钢片磁化特性的影响才是影响电抗器振动的关键因素，动态力使硅钢片饱和磁感应强度升高，变化的磁特性影响了麦克斯韦力的计算，在机械场计算中又将麦克斯韦力作为激励施加，因此改变了振动计算的结果。无压紧力时动态力对加速度计算数值影响较大，随着压紧力的增加，动态力对加速度计算影响程度下降。当考虑动静态力共同作用对硅钢片磁特性的影响时，其振动计算精度高于仅考虑静态力影响时振动计算精度，证明了考虑动静态力共同作用时电抗器建模的合理性与精准性。
表1 实验与仿真加速度峰峰值对比
Tab.1 Experiment and simulation acceleration peak-to-peak comparison
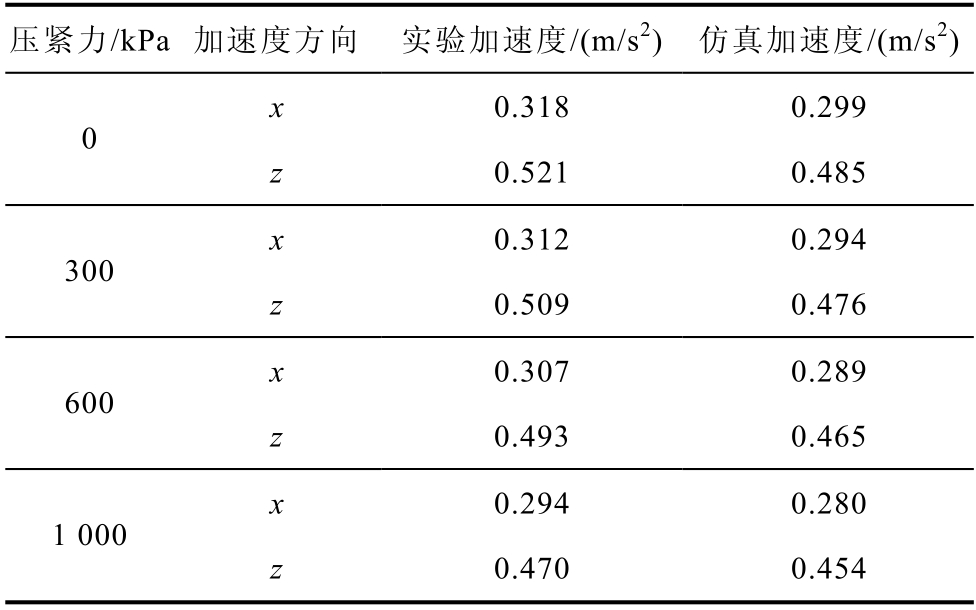
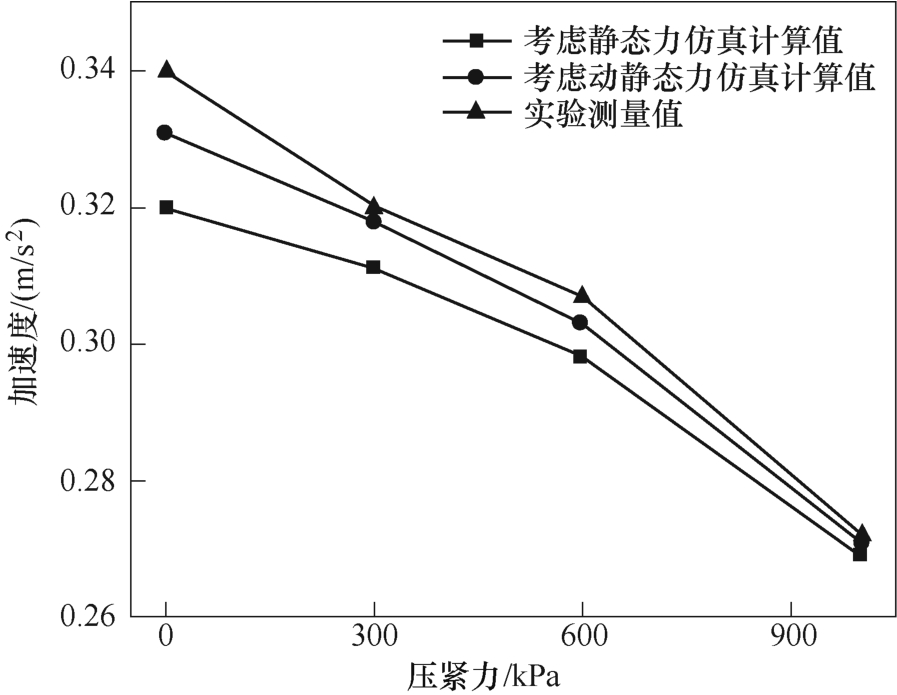
图13 加速度对比
Fig.13 Acceleration comparison chart
为了进一步对电抗器振动情况进行分析，将加速度曲线转换成频谱图，结果如图14 所示。
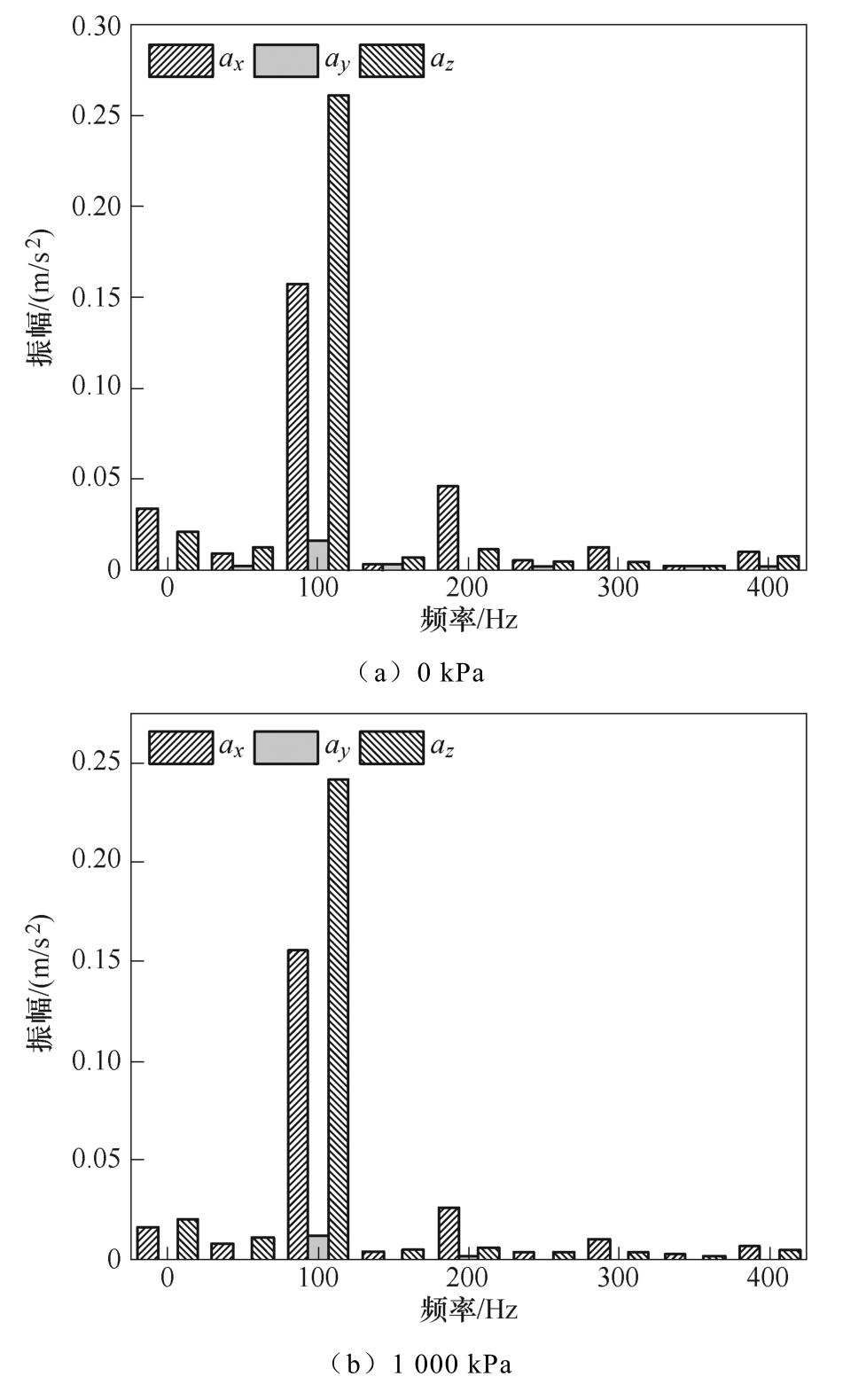
图14 测点A 实验加速度频谱图
Fig.14 Acceleration spectrogram of measuring point A
由图14 的频谱图分析可知，压紧力的施加仅影响加速度各频率分量的幅值，并不在振动中产生新的谐波分量。工频交流电条件下，100 Hz 分量占振动信号的主要分量，这是由于铁心的磁致伸缩效应与铁心饼间的麦克斯韦力是铁心振动的主要原因，并联电抗器工作于工频下，麦克斯韦力与磁通密度的二次方成正比，磁致伸缩效应基本正比于磁通密度的二次方，因此此时电抗器的振动主频率为100 Hz，其余振动分量分布于100 Hz 的整数倍。这也验证了第1 节在考虑动、静态力共同作用的硅钢片磁特性实验中施加频率100 Hz 动态激励的正确性。
4 结论
本文在考虑动静态力共同作用对硅钢片磁特性影响的基础上，建立并联电抗器电磁场-机械场双向耦合模型，分析电抗器铁心电磁振动特性，通过仿真与实验相结合，分析结果如下：
1）搭建硅钢片磁特性测量平台，测量了考虑动静态力共同作用下硅钢片的磁化特性与磁致伸缩特性。仅考虑静态压紧力影响时，磁导率减小，磁致伸缩效应减弱；考虑动静态力共同影响时，磁导率较仅考虑静态压紧力影响时增大，磁致伸缩效应进一步减弱。
2）建立并联电抗器电磁场-机械场双向耦合模型，对并联电抗器铁心进行电磁振动计算，分析了动静态应力对电抗器铁心电磁振动的影响。
3）搭建振动测量实验平台，对考虑动静态力共同作用影响的并联电抗器电磁场-机械场双向耦合模型进行实验验证，实验结果表明，加速度的波形与幅值误差均在合理的范围内，考虑动静态力共同作用的影响时振动计算误差更小，证明了建模的正确性与精准性，其可为电抗器振动问题进一步研究提供理论指导。
[1] 郑涛,赵彦杰.超/特高压可控并联电抗器关键技术综述[J].电力系统自动化,2014,38(7): 127-135.
Zheng Tao,Zhao Yanjie.Overview of key techniques of EHV/UHV controllable shunt reactor[J].Automation of Electric Power Systems,2014,38(7): 127-135.
[2] 张鹏宁,李琳,程志光,等.并联电抗器与变压器模型铁心振动仿真与试验对比[J].电工技术学报,2018,33(22): 5273-5281.
Zhang Pengning,Li Lin,Cheng Zhiguang,et al.Vibration simulation and experiment comparison of shunt reactor and transformer model core[J].Transactions of China Electrotechnical Society,2018,33(22):5273-5281.
[3] 王革鹏,金文德,曾向阳,等.特高压并联电抗器铁心振动的分析与控制研究[J].电工技术学报,2022,37(9): 2190-2198.
Wang Gepeng,Jin Wende,Zeng Xiangyang,et al.Analysis and control research on core vibration of UHV shunt reactor[J].Transactions of China Electrotechnical Society,2022,37(9): 2190-2198.
[4] 伍文科,杜林林,秦敬伟,等.干式铁芯电抗器设备振动控制措施研究[J].噪声与振动控制,2022,42(2): 214-218,246.
Wu Wenke,Du Linlin,Qin Jingwei,et al.Research on vibration control measures of dry-type reactor equipment[J].Noise and Vibration Control,2022,42(2): 214-218,246.
[5] Zhang Pengning,Li Lin,Cheng Zhiguang,et al.Study on vibration of iron core of transformer and reactor based on maxwell stress and anisotropic magnetostriction[J].IEEE Transactions on Magnetics,2019,55(2): 1-5.
[6] 赵小军,王瑞,杜振斌,等.交直流混合激励下取向硅钢片磁滞及损耗特性模拟方法[J].电工技术学报,2021,36(13): 2791-2800.Zhao Xiaojun,Wang Rui,Du Zhenbin,et al.
Hysteretic and loss modeling of grain oriented silicon steel lamination under AC-DC hybrid magnetization[J].Transactions of China Electrotechnical Society,2021,36(13): 2791-2800.
[7] 李冰,王泽忠,刘海波,等.直流偏磁下 500kV 单相变压器振动噪声的试验研究[J].电工技术学报,2021,36(13): 2801-2811.
Li Bing,Wang Zezhong,Liu Haibo,et al.Experiment on vibro-acoustic characteristic of 500kV singlephase transformer under DC-bias[J].Transactions of China Electrotechnical Society,2021,36(13): 2801-2811.
[8] 张长庚,田亚坤,李永建,等.谐波及直流偏磁下变压器叠片式磁屏蔽杂散损耗模拟与验证[J].电工技术学报,2022,37(15): 3733-3742.
Zhang Changgeng,Tian Yakun,Li Yongjian,et al.Modeling and validation of stray-field loss in laminated magnetic shield of transformer under harmonics and DC bias[J].Transactions of China Electrotechnical Society,2022,37(15): 3733-3742.
[9] 高树国,汲胜昌,孟令明,等.基于在线监测系统与声振特征预测模型的高压并联电抗器运行状态评估方法[J].电工技术学报,2022,37(9): 2179-2189.
Gao Shuguo,Ji Shengchang,Meng Lingming,et al.Operation state evaluation method of high-voltage shunt reactor based on on-line monitoring system and vibro-acoustic characteristic prediction model[J].Transactions of China Electrotechnical Society,2022,37(9): 2179-2189.
[10] Dou Yu,Li Yongjian,Zhang Changgeng,et al.Effects of uniaxial stress along different directions on alternating magnetic properties of silicon steel sheets[J].IEEE Transactions on Magnetics,2020,56(3): 1-4.
[11] Ding Xiaofeng,Ren Suping,Xiong Yanwen,et al.2-D magnetic properties measurement system for electrical steel sheets considering laminated direction mechanical stress[J].IEEE Transactions on Magnetics,2017,53(10): 1-11.
[12] Ben Tong,Yang Qingxin,Yan Rongge,et al.Magnetically controlled saturable reactor core vibration under practical working conditions[J].IEEE Transactions on Magnetics,2017,53(6): 1-4.
[13] 闫荣格,郜玉香,贲彤,等.考虑实际工况下串联铁心电抗器的振动研究[J].电气传动,2019,49(1):78-82.
Yan Rongge,Gao Yuxiang,Ben Tong,et al.Research on vibration of series iron-core reactors under the practical working conditions[J].Electric Drive,2019,49(1): 78-82.
[14] 闫荣格,谷浩伟,张晓杰,等.拉紧螺杆对并联电抗器的振动影响分析[J].电工电能新技术,2021,40(3): 39-45.
Yan Rongge,Gu Haowei,Zhang Xiaojie,et al.Analysis of vibration effect of tightening screw on shunt reactor[J].Advanced Technology of Electrical Engineering and Energy,2021,40(3): 39-45.
[15] 张会燕,王昱皓,张俊杰,等.压应力对硅钢片磁特性的影响研究[J].河北工业大学学报,2021,50(4): 10-16.
Zhang Huiyan,Wang Yuhao,Zhang Junjie,et al.Study on the effect of compressive stress on magnetic properties of silicon steel sheets[J].Journal of Hebei University of Technology,2021,50(4): 10-16.
[16] 祝丽花,石永恒,杨庆新.夹紧力对非晶合金磁特性及铁芯振动的影响研究[J].中国电机工程学报,2020,40(24): 8155-8164,8252.
Zhu Lihua,Shi Yongheng,Yang Qingxin.Effect of clamping force on magnetic properties and core vibration of amorphous alloys[J].Proceedings of the CSEE,2020,40(24): 8155-8164,8252.
[17] 常晨,刘兰荣,卢美林,等.并联电抗器等效模型的振动噪声特性试验研究[J].电气技术,2019,20(2): 37-41,47.
Chang Chen,Liu Lanrong,Lu Meilin,et al.Investigates the characteristics of vibration and noisebased on the equivalent model to shunt reactor[J].Electrical Engineering,2019,20(2): 37-41,47.