0 引言
大型干式空心电抗器(Dry-type Air core Reactors,DAR)(以下简称空心电抗器)具有线性度高、损耗小、参数稳定、电阻小等优点,在高压、特高压电力系统中得到了广泛应用[1-5]。然而,随着空心电抗器的电压等级和尺寸逐渐增加,其向周围空间产生的强烈的磁场(以下简称为空间磁场)均已不可忽视[6-11]。例如,变电站的变压器、气体绝缘全封闭组合电器(Gas Insulated Switchgear,GIS)等大型电气设备以及接地网中的铁磁材料均可能因为空心电抗器的空间磁场产生涡流和环流,从而导致铁心损耗增加、温度升高、保护误动作、接地网过热失效等严重后果[12-16]。此外,随着人们环保意识的增强,大型空心电抗器对周边环境的电磁污染问题亦逐渐受到关注。因此,研究空心电抗器的空间磁场分布和磁场预测显得尤为重要。
虽然通过实地测量能够准确直观地测量电抗器的空间磁场分布,但是仍需投入大量的人力物力,且无法在电抗器建造完成前进行测量。有必要建立空心电抗器缩比模型,开展空间磁场的预测研究,为大型电抗器的设计和制造提供理论和技术依据。
目前,已有两种基于相似理论的电抗器简化模型用于空间磁场分布的预测,即缩比模型和简化缩比模型。确定简化规则之后,这两种模型均可以方便地测量两种电抗器任意方向的磁感应强度,这对设计阶段提前预测电抗器的空间磁场分布具有重要意义。
对于缩比模型,在推导了空心电抗器的相似原理后,通过几何相似度展开可以得到其电参数和空间磁场分布[17-18]。但是,在试验室中,实际缠绕多封装多层干式空心电控器的缩比模型仍然是一件复杂而费时的事情。所以,建立一种结构更简单且能较准确预测空间磁场的试验模型,即空心电抗器简化缩比模型,显得尤为必要。
简化缩比模型仅由数个同轴线圈沿轴向叠加组成,克服了制作缩比模型过于费时的缺点。Q.Yu等建立了SINGLE 模型、3FIXED 模型和FLEXIBLE模型三种不同的简化缩比模型,并计算了5 个典型方向的磁通密度[19-20]。为了使简化缩比模型在各个典型方向上的磁感应强度尽可能接近原始电抗器,需对简化缩比模型的结构参数进行优化。邹亮等[21]提出了空心电抗器的三环简化缩比模型,该模型可有效减少磁场预测过程的工作量,然而三环简化模型仍然存在可调自由度低、径向磁场误差较大的问题。因此,有必要在此基础上提高简化缩比模型的磁场预测的参数调节自由度和预测精度。
考虑到适当增加简化缩比模型中线圈的数量是提高磁场预测精度的有效方法,本文在三环简化缩比模型的研究基础上,提出一种匝数和位置均可调节的五环简化缩比模型,并分析得到了空心电抗器简化缩比模型的最优结构。首先,根据Biot-Savart定律推导原始模型和简化缩比模型的数学表达式,并计算典型方向上的磁感应强度;其次,探究线圈间距和匝数对简化缩比模型磁场分布的影响,并基于最小二乘法的仿真结果,获取简化缩比模型的最优结构参数;最后,基于搭建的空心电抗器简化缩比模型磁场测量平台,验证所提最优简化缩比模型的有效性。
1 空心电抗器的简化缩比模型
空心电抗器的多包封结构可以用单包封结构等效,所以选择单包封结构作为原始模型[22]。单包封电抗器的原模型如图 1 所示,选取中心轴向遍历(Axial Traverse Center,ATC)、轴向遍历(Axial Traverse Side,ATS)、ATC 方向和ATS 方向之间的轴向遍历(Axial Traverse,Halfway between ATC and ATS,ATH)、底部径向遍历(Lateral Traverse Bottom,LTB)、中心径向遍历(Lateral Traverse Center,LTC)、LTB 方向和 LTC 方向之间的径向遍历(Lateral Traverse,Halfway between LTB and LTC,LTH),缩写为ATC、ATS、ATH、LTB、LTC、LTH 的6 个典型方向来表示空心电抗器整个空间的磁场分布情况。原模型的结构参数见表1。
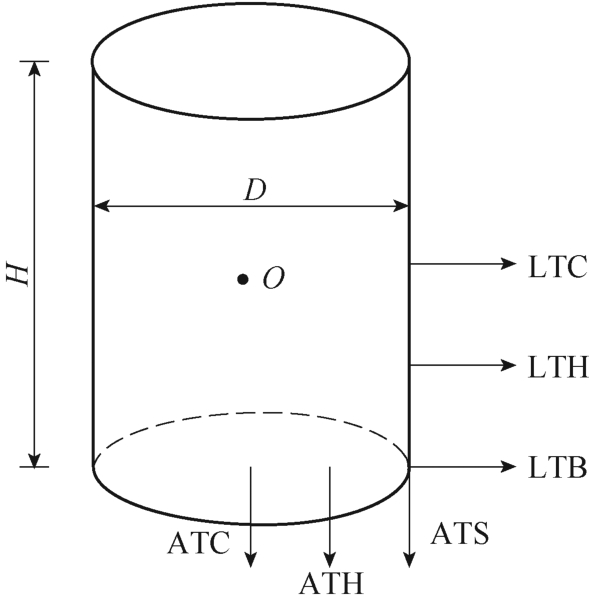
图1 单包封电抗器的原模型
Fig.1 Original model of a single package DAR
表1 原模型参数
Tab.1 The parameters of original model

单包封电抗器的三环和五环简化缩比模型如图2 所示。图2a 所示为图1 中原模型对应的三环简化缩比模型,它是由3 个同轴线圈沿轴向叠加组成的。2 号线圈位于中心位置,匝数为n1;1 号和3 号线圈的匝数为n2,到中心的距离为s。三环简化模型的总匝数N=n1+2n2,三环简化缩比模型的结构参数见表2,其中2 号线圈的匝数p1、1 号和3 号线圈的匝数p2、1 号和3 号线圈到中心的距离s 为可调参数,该3 个参数确定之后就得到了对应的三环简化模型。图2b 为图1 中原模型对应的五环简化缩比模型,是由5 个同轴线圈沿轴向叠加组成的。3 号线圈位于中心位置,匝数为n1;2 号和4 号线圈到中心的距离为a2,匝数为n2;1 号和5 号线圈到中心的距离为a1,匝数为n3。五环简化模型的总匝数N=n1+2n2+2n3,且遵循等安匝原则。五环简化缩比模型的结构参数见表3,其中3 号线圈的匝数n1、2号和4 号线圈的匝数n2、1 号和5 号线圈的匝数n3、1 号和5 号线圈到中心的距离a1、2 号和4 号线圈到中心的距离a2 为可调参数,该5 个参数确定之后就得到了对应的五环简化模型。
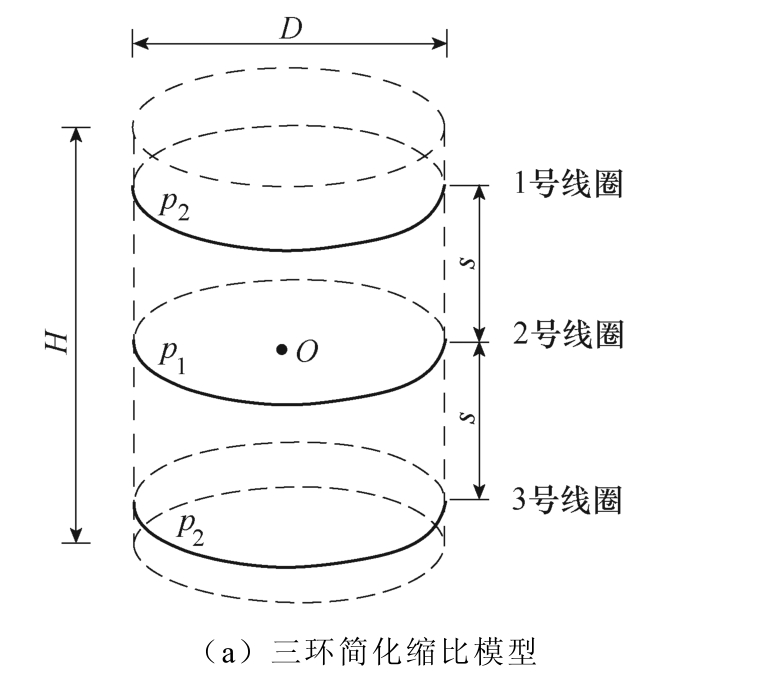
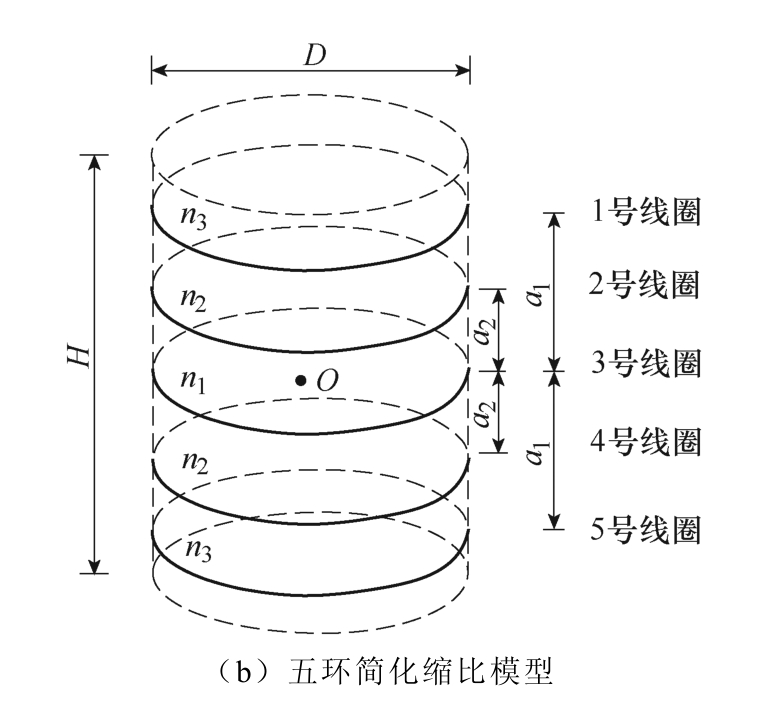
图2 单包封电抗器的三环和五环简化缩比模型
Fig.2 Three-loop and five-loop simplified scaling model of a single package DAR
表2 三环简化缩比模型参数
Tab.2 The parameters of three-loop simplified model

表3 五环简化缩比模型参数
Tab.3 The parameters of five-loop simplified model

相比于三环简化缩比模型,五环简化缩比模型增加了线圈的数目,这使得两两线圈之间的间距缩小,从而减小了漏磁;同时,在五环简化缩比模型中可以调整n2、n3、a1、a2 这4 个参数,相比于三环简化缩比模型的p2 和s 这两个可调参数而言有更高的自由度,这样可以达到提高预测精度的目的。
λ、μ 为三环简化模型的结构参数,η1、η2、ρ1、ρ2 为五环简化模型的结构参数,表达式分别为
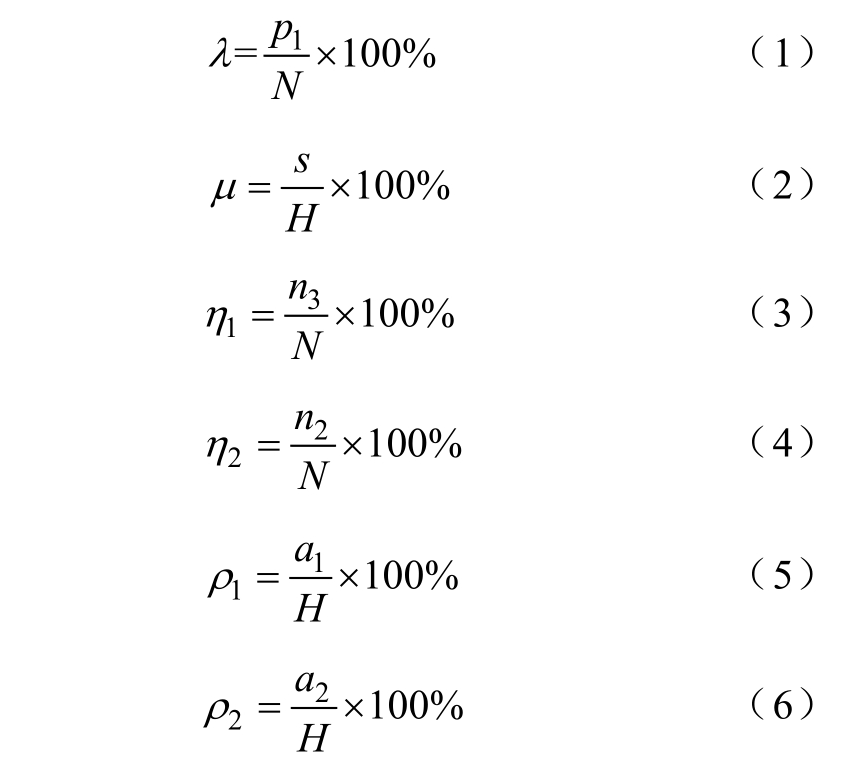
2 空间磁场分布的计算
单载流回路的空间磁场分布计算如图3 所示,在平面xOy 中,假设载流回路是半径为R 的圆环,坐标原点在圆心的位置,P 为空间中一点。

图3 单载流回路的空间磁场分布计算
Fig.3 Calculation of the spatial magnetic field distribution of the single current-carrying loop
根据Biot-Savart 定律推导得到P 点磁感应强度的表达式为

其中
式中,dl 为源电流的微小线元素;μ0 为真空磁导率;I 为电流;R 为载流回路的半径;x、y、z 为P 点在三维直角坐标系中的坐标值;θ 为载流电流元与 x轴夹角;i、j、k 分别为与x 轴、y 轴、z 轴方向相同的单位向量。
载流回路在空间中产生的磁感应强度分量为

2.1 原模型的空间磁场分布计算
以原模型底平面为xOy 平面、中心轴为z 轴、底面中心O 为原点建立空间直角坐标系。忽略绕组节距角的影响,根据叠加定理可以得到原模型的空间磁场分布。空间中任一点P(x,y,z)的磁感应强度为

式中,原模型的线圈位置均采用线圈匝数与导线直径的乘积表示;W 为导线的线径;l 为原模型中的各匝线圈的编号,即最下面的一匝线圈编号为0,线圈编号向上依次增加,最上面一匝线圈的编号即为N-1。lW 为原模型中某一匝线圈的z 坐标。
2.2 简化缩比模型的空间磁场分布计算
简化缩比模型由若干个同轴线圈轴向叠加组成,其坐标系与原模型保持一致。同轴线圈的线径为W,导线中的电流为I。三环简化模型与五环简化模型的计算公式类似,以五环简化模型为例,5个线圈的匝数为 n=[n3 n2 n1 n2 n3],位置分别为 。忽略绕组节距角的影响,五环简化缩比模型的空间磁场分布可以根据叠加定理得到。空间中点P(x,y,z)的磁感应强度为
。忽略绕组节距角的影响,五环简化缩比模型的空间磁场分布可以根据叠加定理得到。空间中点P(x,y,z)的磁感应强度为
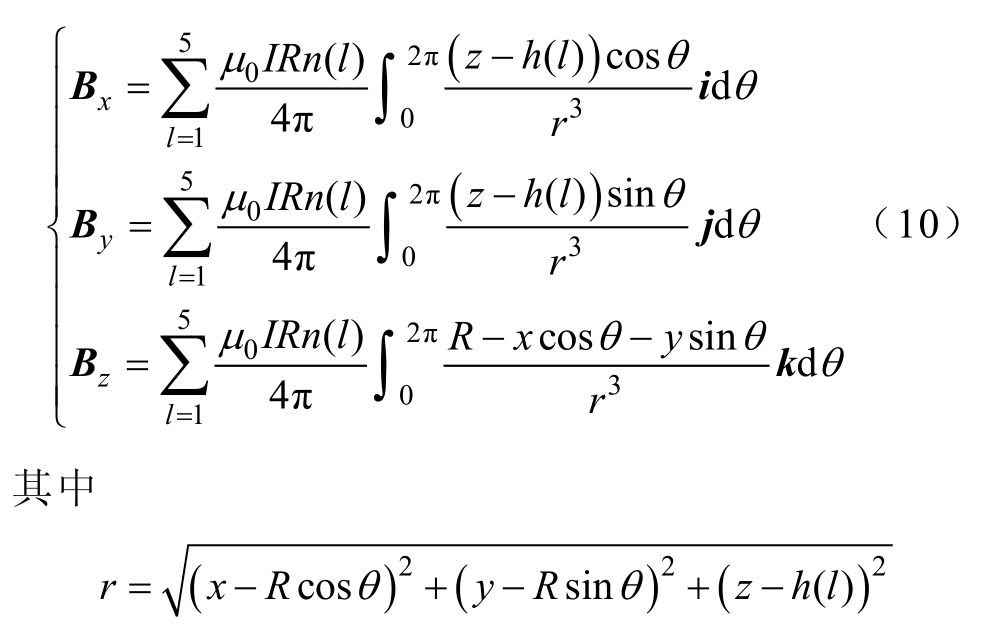
3 空心电抗器最优简化缩比模型计算
研究过程中,先保持各个线圈的匝数不变,仅调整线圈位置,得到匝数相等位置可调的三环和五环简化缩比模型;在此基础上,研究线圈匝数和位置同时调整时对应的三环和五环简化缩比模型。
设置电抗器原模型的底面直径为124 mm,导线线径为0.6 mm,电抗器原模型的高径比H/D 的变化范围为1~2,即高度为120~240 mm,模型中通入1.5 A 的工频电流。原模型认为是紧密绕制的,所以不考虑匝间节距角的影响,为便于计算,共选择20 套模型作为研究对象,每两个模型匝数差为10。为保证简化缩比模型的准确性,设置简化缩比模型的匝数与原模型相等,且简化模型中电流符合等安匝原则,因此,简化缩比模型中也通入 1.5 A的工频电流,且简化缩比模型的线径、底面直径和高度都与原模型一致。
由Maxwell 方程推导可得涡流损耗计算式为
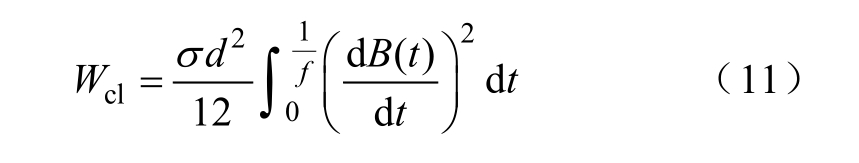
式中,σ 为铁磁材料电导率;d 为铁磁材料叠片厚度;f 为磁化频率;B(t)为瞬时磁通密度。在工频电流的激励下,铁磁材料内部涡流较小[23],趋肤效应可以忽略不计,且为了简化分析计算,μT 级的背景磁场的干扰也忽略不计。
3.1 线圈匝数不变,调节线圈位置
首先,在五环简化模型中保持各个线圈的匝数均为N/5,调整线圈的位置,研究五环简化模型中a1、a2 的变化对于空间磁场分布的影响。
N=300 的原模型6 个典型方向的磁感应强度如图4 所示。ATC 曲线与ATH 曲线相似,LTC 曲线与LTH 曲线相似。随着测量点远离电抗器,磁感应强度逐渐减小趋于一致,即ATC 和ATS,LTC 和LTB 分别可以代表这两个方向之间的所有方向。由于空心电抗器在径向和轴向上都是对称的,因此ATC、ATS、LTC 和LTB 4 个方向可以代表反应器模型的所有空间方向。
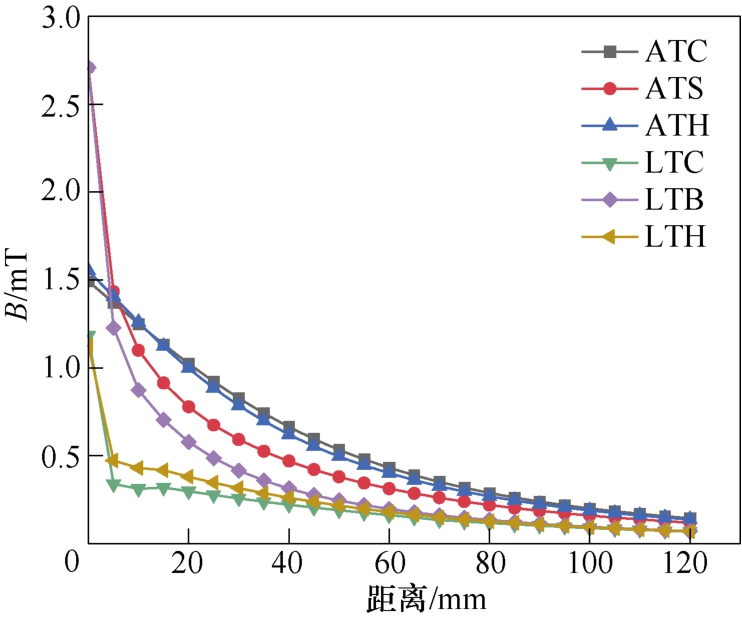
图4 原模型在6 个典型方向上的磁感应强度分布
Fig.4 Magnetic induction intensity in the six typical directions of the original model
通过最小二乘法计算空间中各点磁感应强度误差的二次方和,误差二次方和最小时对应的结构即为最优五环简化缩比模型。对于空间中一点P(x,y,z),磁感应强度的误差可以表示为
式中,![]() 为原模型磁感应强度的模值;
为原模型磁感应强度的模值;![]() 为五环简化缩比模型磁感应强度的模值。
为五环简化缩比模型磁感应强度的模值。
以ATC 方向为例,在点(0,0,0)到点(0,0,-D)之间设置50 个等间距的测量点。计算每个点对应的磁感应强度误差之后,列出二次方损失函数的表达式为

通过搜索最小的QATC,就可以确定在ATC 方向上的最优五环简化缩比模型。为了求得整体的最优结构,需要求出4 个方向上Q 值之和的最小值。约束条件为
式中,参照ATC 方向的二次方损失函数计算,QATS、QLTC、QLTB 分别为ATS、LTC、LTB 方向上的二次方损失函数。
选择N=300 的原模型进行验证,其最优模型对应的Q=1.317 2×10-7,结构参数为a1=75 mm,a2=33.6 mm。原模型和五环简化模型的磁感应强度在4个典型方向上的分布如图5 所示。可以看出,五环简化缩比模型在ATC、ATS 和LTB 方向上可以很好地模拟原模型的磁感应强度,但是LTC 方向的近场区域则与原模型有明显不同。这是五环简化缩比模型和原模型结构不同导致的,由于原模型是紧密缠绕的螺线管,所以磁场主要分布在模型内部。然而,简化后的模型仅由5 个独立线圈组成,线圈之间的间隙导致近场区域在LTC 方向上存在较大的漏磁,从而导致空间磁场分布在LTC 方向上存在差异。经计算,该方向在0~H/5 距离范围内误差较大。在实际应用中,由于大型一次设备一般距离电抗器较远,可不考虑近场区域等效误差的影响。
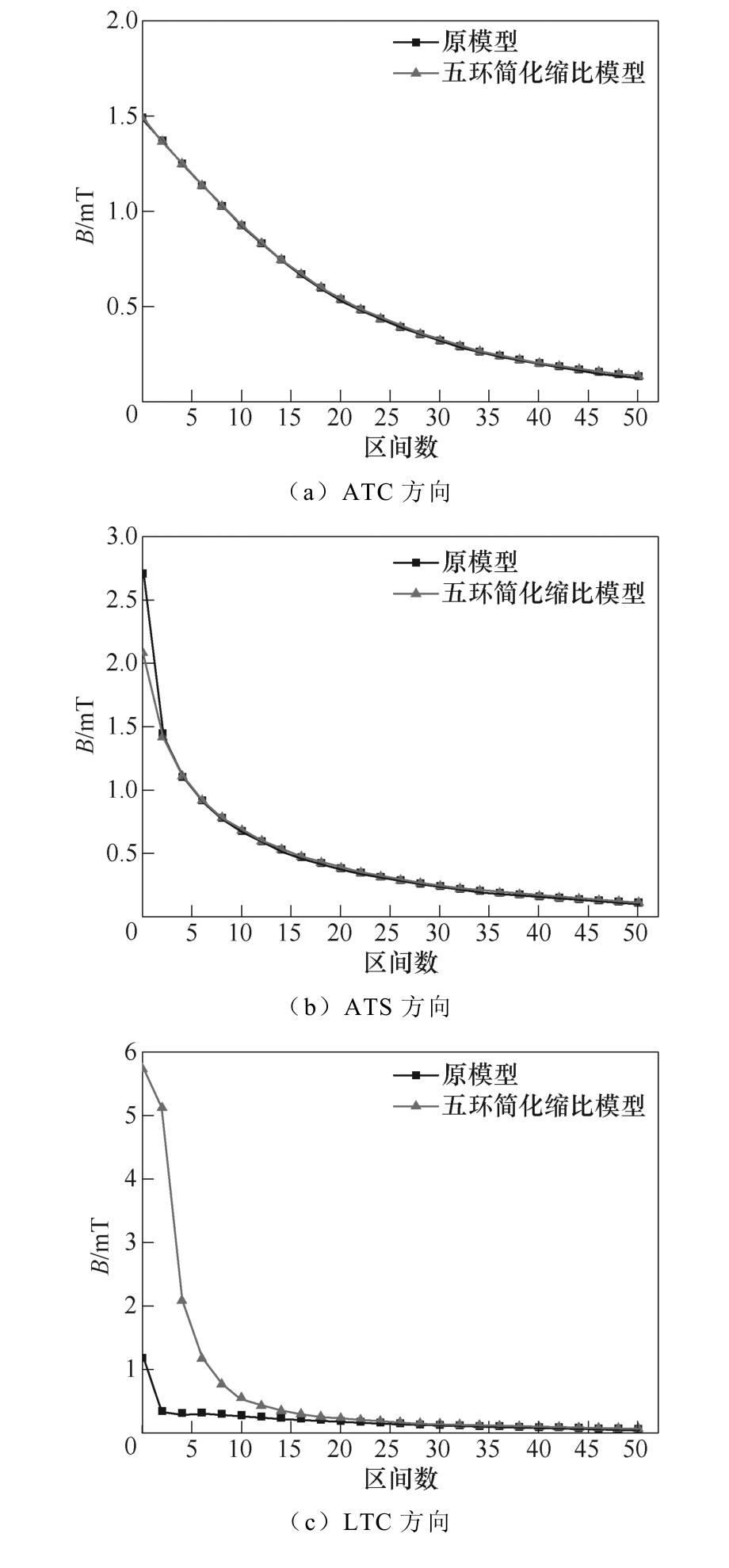

图5 原模型和最优五环简化模型在4 个典型方向上的磁感应强度比较
Fig.5 Magnetic induction intensity of the original model and the optimal simplified model in four typical directions
最优简化模型结构和原模型结构的关系如图6所示。图6a 和图6b 说明最优五环简化缩比模型中a1、a2 与原模型中H 呈正相关关系。由图6c 和图6d 可知,最优五环简化缩比模型中的ρ1 随着原模型高径比H/D 的增加而增大,而ρ2 则呈现相反的变化趋势,这种关系可以用拟合公式表示为
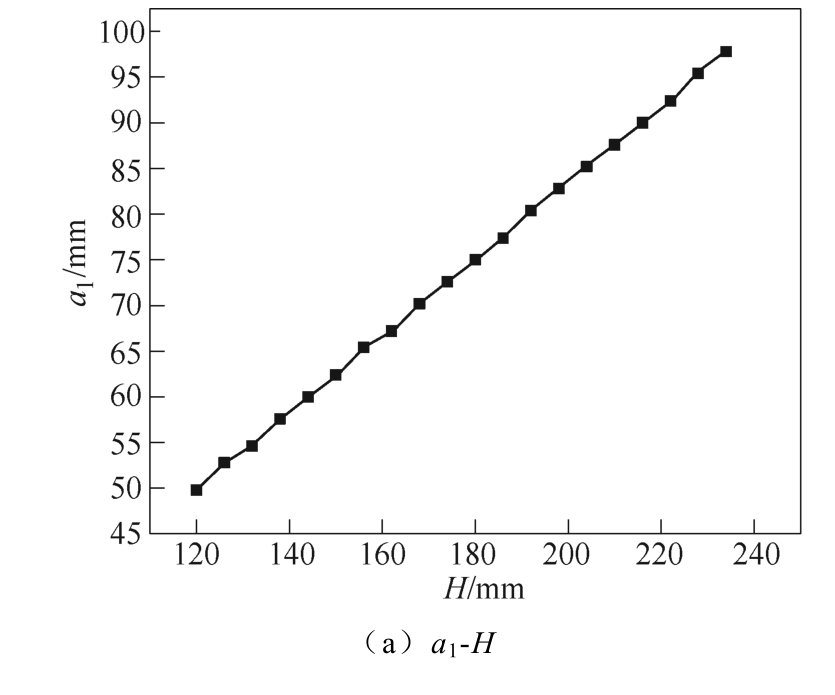

图6 最优简化模型结构和原模型结构的关系
Fig.6 Relationship between optimal simplified model structure and original model structure
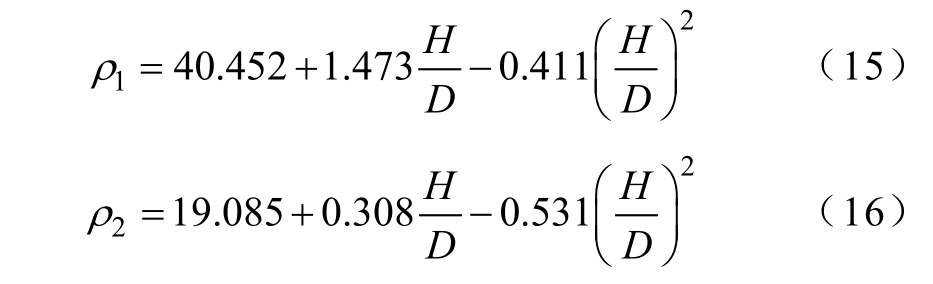
式(15)和式(16)描述了五环简化模型结构参数ρ1、ρ2 和原模型结构参数H/D 的对应关系,说明任何结构的空心电抗器均可用以上公式计算出最优的五环简化缩比模型。
同理可得,在三环简化模型中,保持3 个线圈的匝数均为N/3,调整线圈的位置,得到其相对位置百分数μ 的表达式为
下面对两种模型的计算误差进行对比。
方均根误差(RMSE)的定义为

式中,yi 为实际值;fi 为预测值。利用RMSE 作为预测两种简化缩比模型等效精度的标准,其值越小,表示预测精度越高。RMSE、MAPE、R2 如图7 所示。由图7a 可知,随着原模型高径比H/D 的增大,两种简化缩比模型的RMSE 也增大。
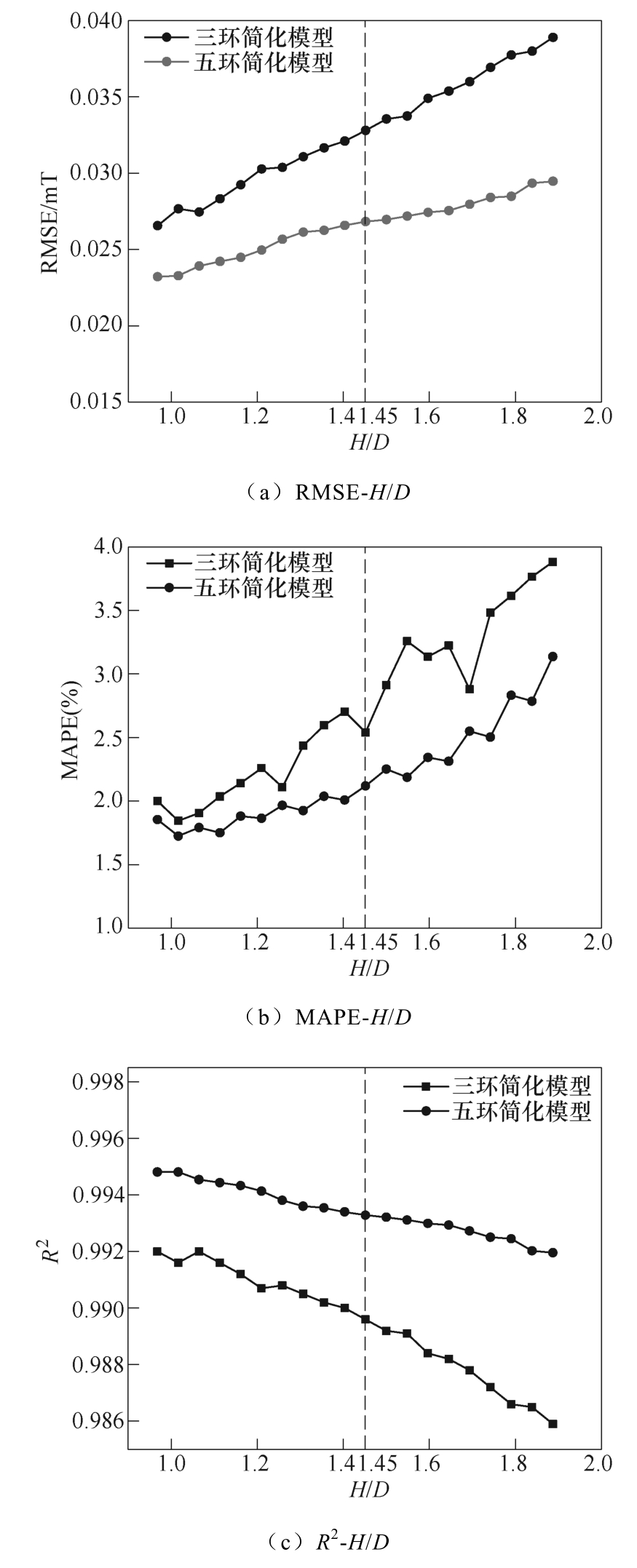
图7 RMSE、MAPE、R2
Fig.7 RMSE, MAPE and R2
平均绝对百分比误差(MAPE)的定义为

MAPE 为描述预测方法准确性的测量统计量。由图7b 可知,随着原模型H/D 的增加,两种简化缩比模型对应的MAPE 也在逐渐增大,MAPE 与RMSE 的变化趋势一致。当H/D 的值在1~2 之间时,两种最优简化缩比模型的MAPE 在1.8 %~4 %之间。
决定系数 R2 是预测值与实际值相关性密切程度的定量指标,其数值越大表示预测值与实际值相关性越密切,表达式为
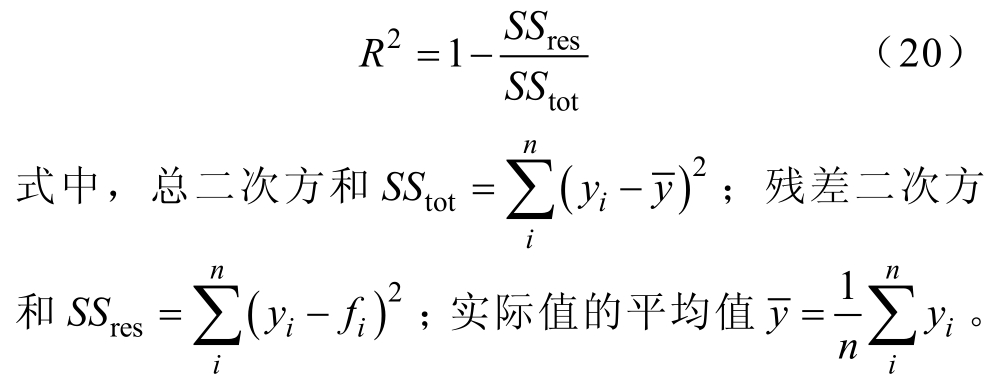
由图7c 可知,两种最优简化缩比模型的R2 随着H/D 的增大而减小。
对比图7 中两种模型的各项指标,可以发现,针对不同结构的电抗器原模型五环简化模型的RMSE 和MAPE 均小于三环简化模型,而R2 均大于三环简化模型,当原模型的高径比H/D 为1.45 时,五环简化模型的RMSE 和MAPE 分别比三环简化模型降低18 %和17 %,说明了五环简化模型比三环简化模型有更高的预测精度。当原模型的高度一定时,五环简化模型中两两线圈之间的距离明显小于三环简化模型,线圈之间的联系更加紧密,因此漏磁减小,五环简化缩比模型的fi 就更接近于真实值,所以五环简化缩比模型的预测精度相对更高。
3.2 线圈的匝数和位置均可调
仿真过程中,3 号线圈的匝数变化范围为1<n1<N-8,则另外4 个线圈的匝数满足n2+n3=(N-n1)/2。图8 为线圈高度发生变化时,五环简化缩比模型中1 号线圈和5 号线圈匝数和位置的关系,以H 为z轴,不同的颜色表示电抗器原模型的不同高度,范围为120~240 mm。可以看出,原模型尺寸一定时,五环简化模型中1 号和5 号线圈的匝数和中心距呈负相关的关系。图中黑色曲线上的点坐标(a1, n3,H)的含义是:当原模型的高度为H 时,最优五环简化缩比模型中1 号和5 号线圈的匝数为n3,且到中心点的距离为a1。

图8 随着H 的变化,a1 和n3 之间的关系
Fig.8 Relationship between a1 and n3 as H varies
图9 描述了当原模型的高径比H/D 发生变化时对应的最优五环简化缩比模型参数ρ1和η1的变化趋势,随着H/D 的增大,ρ1 逐渐增大,而η1 逐渐减小,它们之间的关系用拟合公式可以表示为
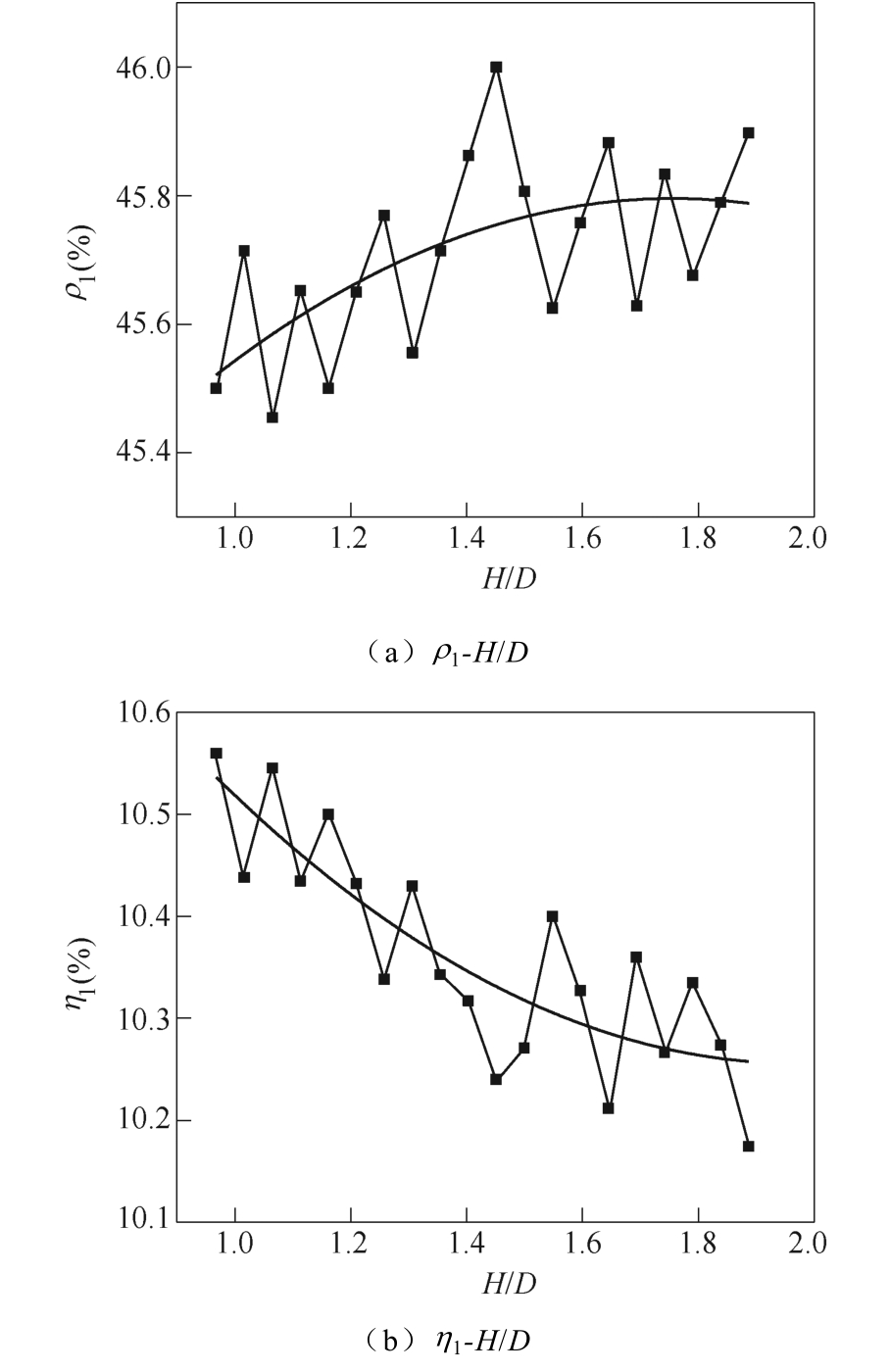
图9 ρ1、η1 与H/D 的关系
Fig.9 Relationship between ρ1,η1 and H/D

图10 为线圈高度发生变化时,五环简化缩比模型中2 号线圈和4 号线圈匝数和位置的关系,以H为z 轴,不同的颜色表示不同尺寸的电抗器原模型。可以看出,原模型尺寸一定时,五环简化模型中2号和4 号线圈的匝数和中心距呈负相关的关系。图中黑色曲线上的点坐标(a2,n2,H)的含义是:当原模型的高度为H 时,最优五环简化缩比模型中2 号和4 号线圈的匝数为n2,且到中心点的距离为a2。

图10 随着H 的变化,a2 和n2 之间的关系
Fig.10 Relationship between a2 and n2 as H varies
图11 描述了当原模型的高径比H/D 发生变化时对应的最优五环简化缩比模型参数ρ2和η2的变化趋势,随着H/D 的增大,ρ2 逐渐增大,而η2 逐渐减小,它们之间的关系用拟合公式可以表示为

图11 ρ2、η2 与H/D 的关系
Fig.11 Relationship between ρ2,η2 and H/D
同理可得,在三环简化模型中,2 号线圈的匝数p1 的变化范围是1~N-2,1 号和3 号线圈的匝数p2=(N-p1)/2。在此基础上调整线圈的位置,得出三环最优简化模型相对位置百分数μ 和相对匝数百分数λ 的表达式分别为

RMSE、MAPE、R2 如图12 所示,两种简化模型的RMSE 和MAPE 都随着H/D 的增加逐渐增加,R2 随着H/D 的增加逐渐减小,但幅度都明显小于3.1 节中只调整线圈位置的情况,当H/D=1.45 时,匝数和位置均可调的五环简化模型对应的RMSE 比仅可调整位置时减小了29 %。由于结构的限制,缩比模型在ATC 和ATS 方向上的磁感应强度总是略小于原模型,当线圈匝数不变时只能通过使1、2、4、5 号线圈远离中心的方式弥补误差,但是这种方式会导致LTC 方向上磁感应强度的减小,使得磁场预测精度下降;如果线圈的匝数可调,可以实现在1、2、4、5 号线圈远离中心的同时适当增加3 号线圈的匝数,以达到使ATC、ATS、LTC、LTB 4 个方向的误差同时减小的目的,这就是提高简化缩比模型参数自由度的优势。


图12 RMSE、MAPE、R2
Fig.12 RMSE,MAPE and R2
通过对比图12 中两种简化缩比模型的各项指标发现,当H/D=1.45 时,线圈匝数和位置均可调整的五环简化模型在RMSE 和MAPE 两项指标上比三环简化模型分别减小40 %和21 %,相比三环简化模型而言,这种模型明显减小了两两线圈之间的漏磁,相比线圈位置可调的五环简化模型,可以同时减小4 个方向的磁场等效误差,因此在文中提及的几种简化缩比模型中是精度最高的。
4 试验验证
在试验室中绕制了电抗器的原模型和两种简化缩比模型。单包封电抗器的原模型和两种简化缩比模型如图13 所示。如图13a 所示,原模型是高度为180 mm 的紧密绕制螺线管,高径比H/D 仍然采用1.45,原模型其他参数与第3 节中设置相同。鉴于试验条件,同时调整多个线圈的匝数会增大试验误差,因此本文中仅采用调整线圈位置的方式制作简化缩比模型,并测量各个模型的空间磁场分布。

图13 单包封电抗器的原模型和两种简化缩比模型
Fig.13 Original model and 2 simplified model of a single package reactor
为便于试验,三环和五环简化缩比模型均设置为几个等匝线圈同轴排列,如图13b、图13c 所示,四种参数的三环简化缩比模型的结构参数如下:μ =40 %,μ =35 %,μ =30 %,μ =25 %;四种参数的五环简化缩比模型的结构参数如下:ρ1=40 %、ρ2=30 %,ρ1=40 %、ρ2=20 %,ρ1=30 %、ρ2=20 %,ρ1=30 %、ρ2=10 %。
原模型的磁场测量示意图如图14 所示。频率f =50 Hz 的交流电源提供原型号所需的电流;万用表是用来测量电路中的电流的;采用分辨率为0.01 μT的特斯拉计测量磁感应强度的标量值,背景磁场的磁感应强度为0.03 μT。LTC 方向的磁感应强度小于0.2 mT,在测量过程中受测量误差的影响较大。磁感应强度在ATC 和ATS 方向上的分布曲线非常相似,为简化试验流程,只选择其中一个代表原模型和简化模型在轴向上的磁场分布情况。综上所述,试验过程中选择ATC 和LTB 两个方向进行磁感应强度标量值的测量。为便于描述试验过程中测量点的位置,文中采用了坐标的形式如图15a 和图15b所示,图中x 轴表示LTB 方向,测量范围为6~16 cm,y 轴表示ATC 方向,测量范围为0~10 cm,两个方向上测量点之间的间距均为1 cm。试验中测量点的位置示意图如图15 所示,在LTB 和ATC 两个方向上都每间隔1 cm 选取10 个测量点。
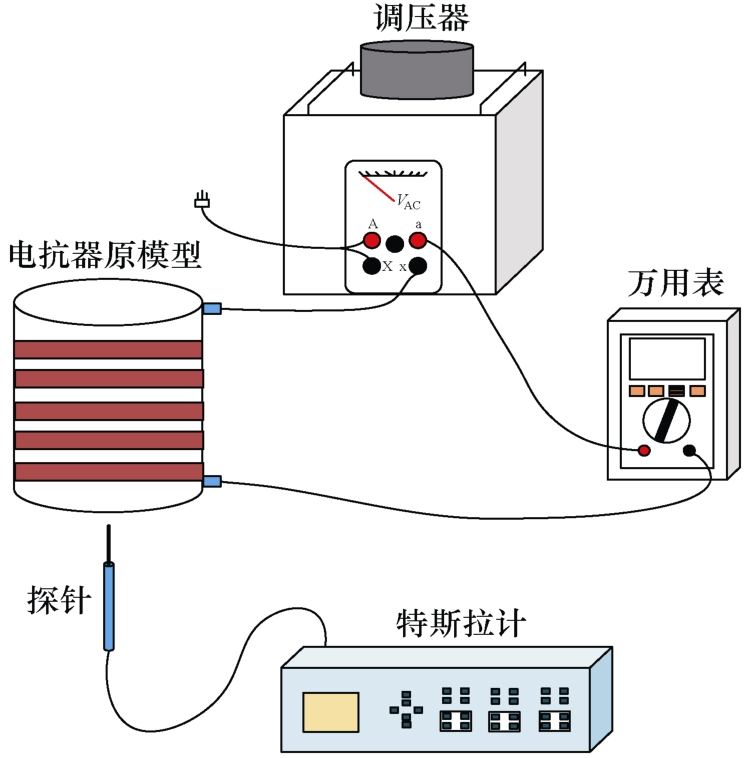
图14 五环简化模型ATC 方向的磁场测量示意图
Fig.14 Schematic diagram of the magnetic field measurement in the ATC direction of the five-loop simplified model
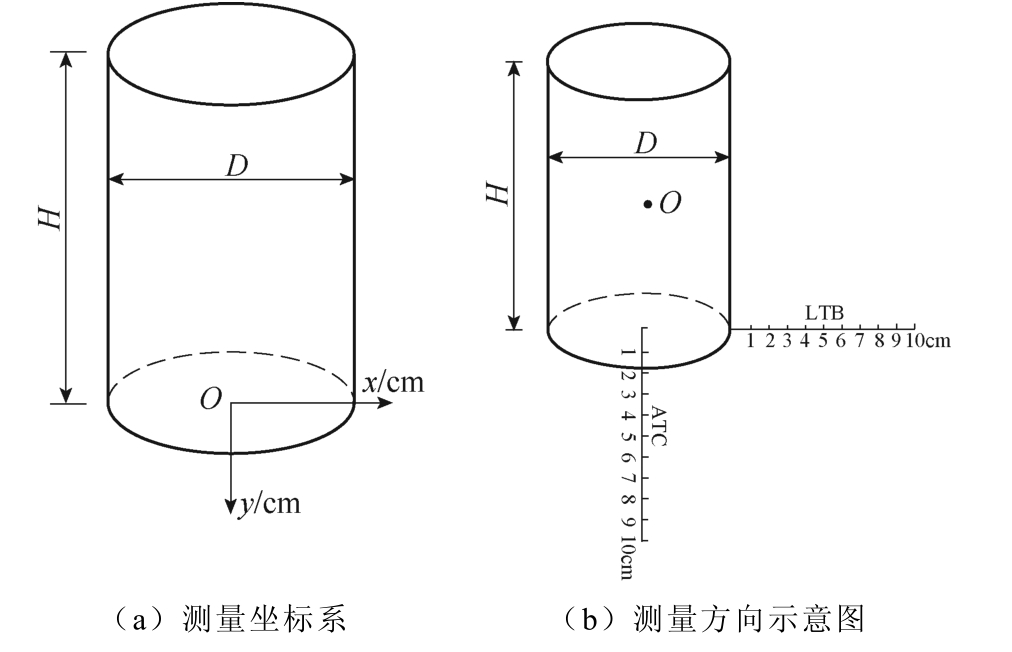
图15 试验中具体测量点的位置示意图
Fig.15 The position diagram of the specific measuring points in the experiment
对四种参数的五环简化缩比模型和原模型在ATC 和LTB 方向的磁感应强度进行10 次测量,得到在不同测量点处的磁感应强度数值,计算得到10个数据集的均值和标准差。图16 为原模型和四种简化缩比模型空间磁场分布的测量结果,可以看出,当结构参数为ρ1=40 %,ρ2=20 %时,简化缩比模型在两个方向上的磁感应强度与原模型最为相似。四种五环简化缩比模型的统计参数见表4,由式(14)和式(15)可知,当H/D=1.45 时,最优简化模型的结构参数是ρ1=41.72 %,ρ2=18.41 %,从表4 可以看出,结构参数为ρ1=40 %,ρ2=20 %的简化缩比模型的RMSE 和MAPE 均为最小值。因此,可以认为该模型是试验中的最优简化模型。
表4 四种五环简化模型的统计参数
Tab.4 Statistical parameters of the four five-loop simplified models
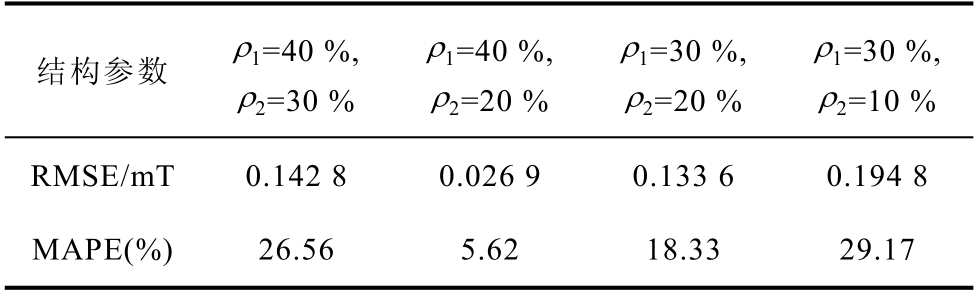

图16 原模型和四种简化模型在两个方向上的空间磁场分布测量结果
Fig.16 Spatial magnetic field distributionmeasurement results of the four simplified models and the original model in two directions
三环简化缩比模型在ATC 和LTB 两个方向上磁场分布测量的试验结果如图17 所示。可以看出,当μ =35 %时,三环简化模型的空间磁场分布情况与原模型相似度最高。四种三环简化缩比模型的统计参数见表5,可以看出,结构参数μ =35 %时,三环简化缩比模型的RMSE 和MAPE 均为最小值,且通过式(16)可知,该种情况下的最优结构参数μ =36 %,因此可以认为μ =35 %是该试验中的最优结构参数。
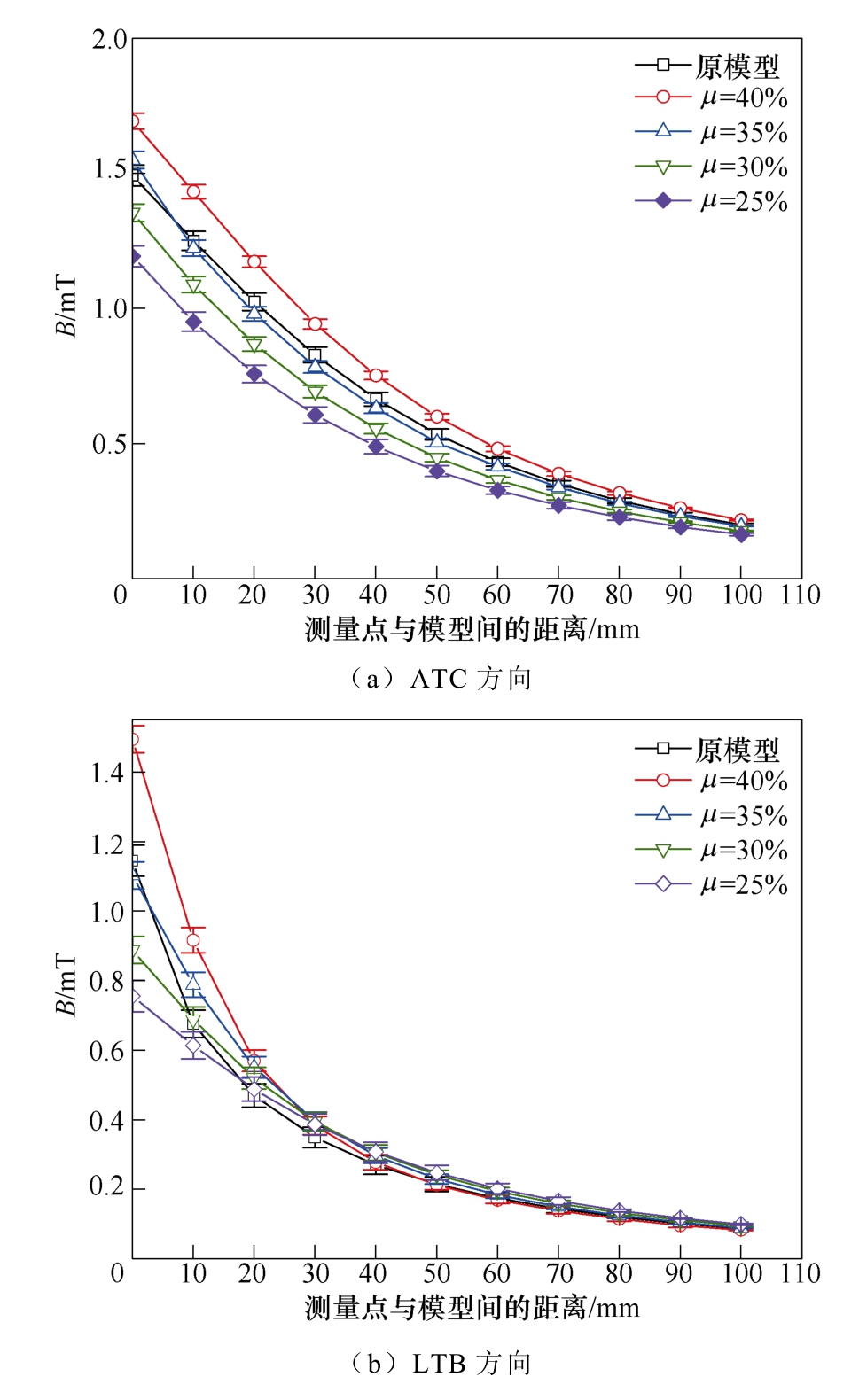
图17 原模型和四种三环简化模型在两个方向上的空间磁场分布测量结果
Fig.17 Spatial magnetic field distribution measurement results of the four three-loop simplified models and the original model in two directions
对比表4 和表5 中的统计参数可以发现,五环简化缩比模型最优结构参数对应的RMSE 和MAPE分别比三环简化缩比模型降低了21 %和22 %,因此证明了五环简化模型相比于三环简化模型在磁场预测方面有着更高的预测精度。
表5 四种三环简化模型的统计参数
Tab.5 Statistical parameters of the four three-loop simplified models

5 现场试验
为验证本文提出的五环简化缩比模型等效效果优于三环简化缩比模型,采用了如图18 所示的某换流站中±660 kV 平波电抗器进行空间磁场分布的测量试验。该平波电抗器的参数为:双极额定容量为4 000 MW,额定电压为±660 kV,额定电流为3 030 A,单台额定电感值为75 mH,测试时为双极满负荷运行。极母平波电抗器安装在绝缘支柱上,本体底部距地面13.4 m。测试时环境温度20 ℃,相对湿度48 %,海拔23 m,北风2 级,无降雨。

图18 ±660 kV 换流站极母线平波电抗器
Fig.18 ±660 kV flat-wave reactor of converter station pole bus
测试区域为38 m×14 m。建立如图19 所示坐标系,每隔1 m 设置一个采样点,距电抗器较远处采样间隔适当增大。根据高压直流换流站电磁环境的相关行业标准,测量点对地高度为1.5 m。测试时使用米尺和三脚架对采样点进行定位。试验过程中,使用GMR50 手持高精度弱磁场高斯计进行测试。GMR50 分辨率为0.1 μT,磁场测量范围0~4.5 mT,频率响应范围为DC~100 Hz,能够满足测试需要,且体积小、便于携带、操作简便。
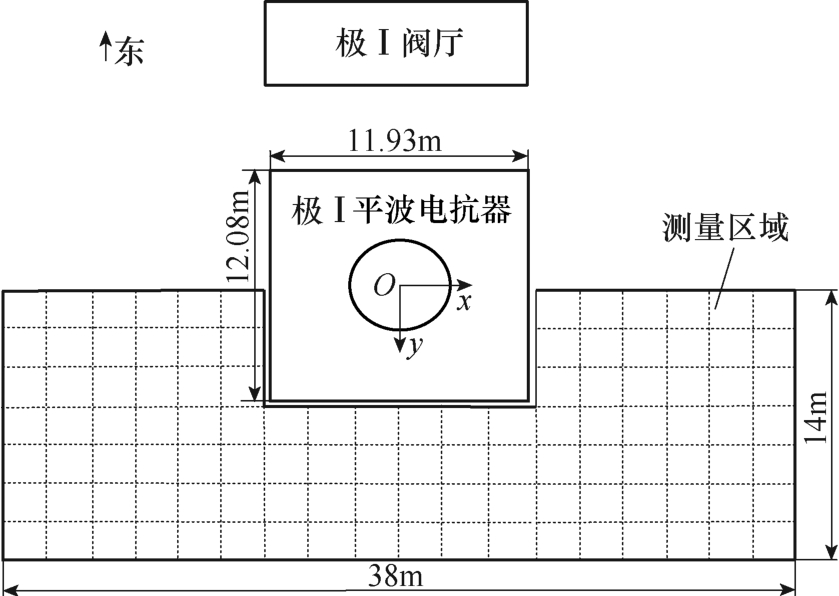
图19 测量区域
Fig.19 Survey area
试验过程中平波电抗器磁场测量示意图如图20 所示,两种简化缩比模型空间磁场测量的示意图分别如图21a 和图21b 所示。从图20 中可以看出,平波电抗器的高径比H/D 约为1,将H/D=1 代入式(21)~式(23)并设置简化缩比模型的高度为0.124 m,可得三环简化缩比模型的参数s=9.7 cm,p1=80,p2=63,五环简化缩比模型中 a1=5.6 cm,a2=3.8 cm,n1=70,n2=46,n3=22。

图20 平波电抗器磁场测量示意图
Fig.20 Schematic diagram of magnetic field measurement for flat wave reactor
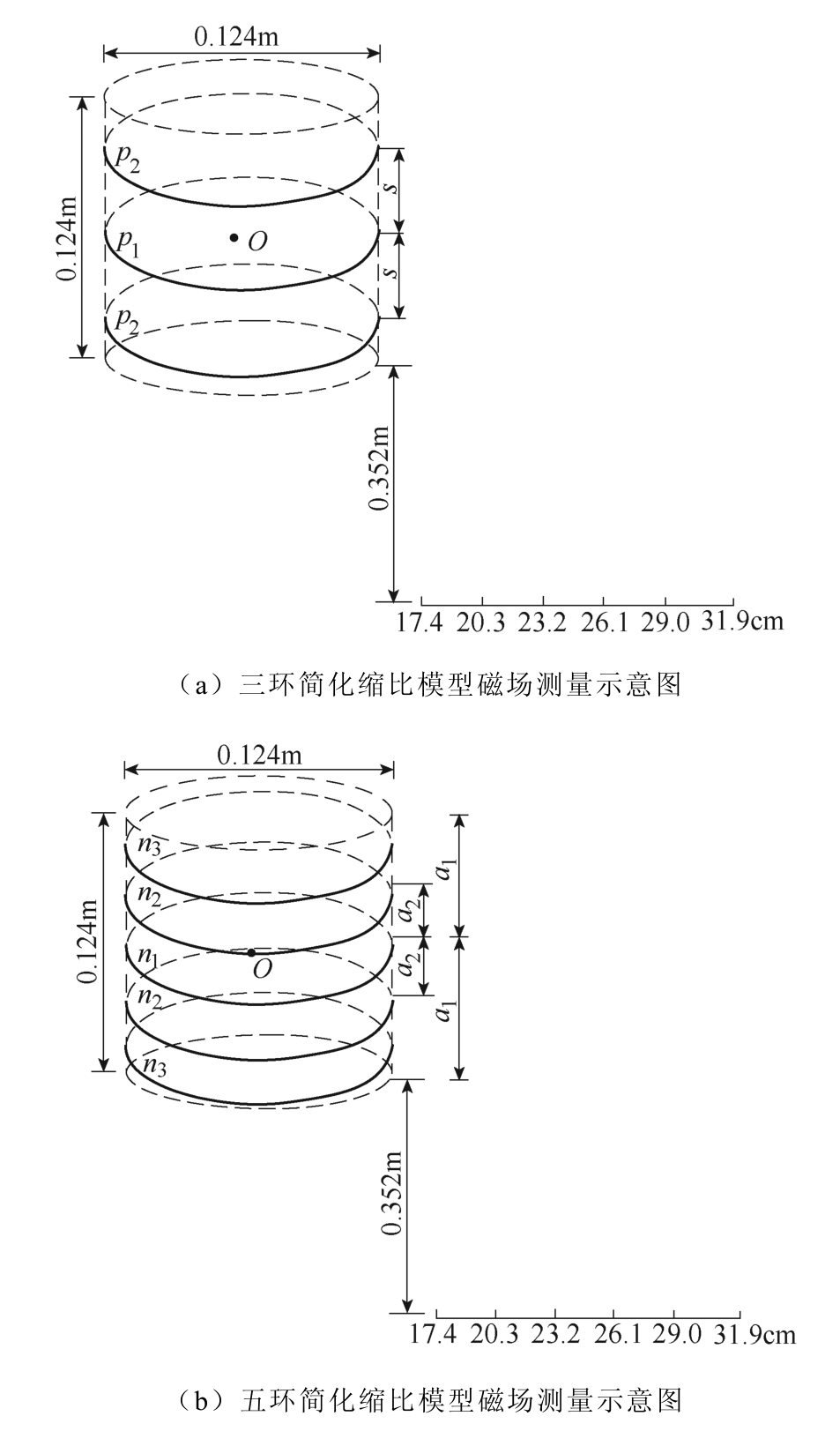
图21 简化缩比模型磁场测量示意图
Fig.21 Schematic diagram of magnetic field measurement for simplified scaling model
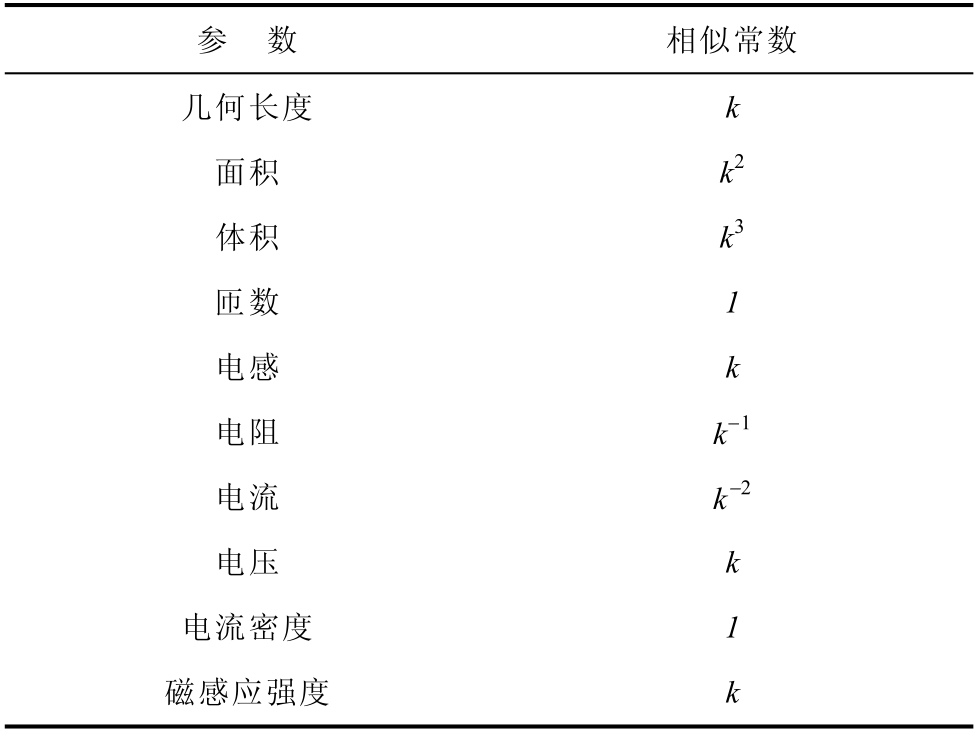
文献[24]中推导了空心电抗器的缩比准则见表6,表中展示了干式空心电抗器和简化缩比模型在电气量和非电气量上的比例关系。本文中将简化缩比模型的高度定为0.124 m,因此表中k 的取值约为34。现场中对平波电抗器的磁感应强度进行测量时测量点位于电抗器下方11.92 m 的平面上,且测量点间距为1 m,通过缩比准则的转换,对简化缩比模型进行磁感应强度的测量时,测量点应位于模型下方0.352 m 的平面上,且两测量点间距为2.9 cm。
表6 空心电抗器的缩比准则
Tab.6 Scaling criterion for hollow reactor
试验过程中对每一个测量点磁感应强度均测量10 次,最后取平均值进行统计。对简化缩比模型的磁感应强度进行缩比准则转换之后绘制了实际平波电抗器和两种简化缩比模型的空间磁场分布情况如图22 所示,可以看出,三环简化缩比模型与五环简化缩比模型对于平波电抗器的空间磁场分布都有较好的模拟效果。两种模型的统计参数见表7,可以看出,五环简化缩比模型的RMSE 和MAPE 两项参数均优于三环简化缩比模型,现场试验的数据也证明了五环简化缩比模型具有良好的空间磁场等效效果。

图22 三种情况下的空间磁场分布对比
Fig.22 Comparison of spatial magnetic field distribution under three conditions
表7 两种模型的统计参数
Tab.7 Statistical parameters of two models

6 结论
本文提出了干式空心电抗器的五环简化缩比模型,通过计算五环和三环简化模型各个典型方向上的空间磁场分布确定了不同结构原模型对应的两种最优简化模型的最优结构参数函数表达式,最终得出以下结论:
1)在LTC 方向,简化缩比模型在近场区域的磁感应强度远小于原模型,这种差异是线圈间隙中的漏磁造成的,在仿真计算的过程中需要去除LTC方向上的近场区域。
2)当线圈匝数不变只调整位置时,五环简化模型中两两线圈之间的距离明显小于三环简化模型,线圈之间的联系更加紧密,因此漏磁减小。原模型的高径比H/D=1.45 时,五环简化模型的RMSE 和MAPE 分别比三环简化模型降低18 %和17 %,而R2 则升高了4 %,3 个指标均说明了五环简化模型比三环简化模型有更高的预测精度。
3)当线圈的匝数和位置均可调时,五环简化缩比模型充分体现了参数调整自由度高的优势,减小了线圈间漏磁,也同时减小了4 个监测方向上等效误差。线圈位置和匝数均可调的五环简化模型对应的RMSE 和MAPE 相比三环简化模型分别降低了40 %和21 %,是本文中最准确的等效模型。
4)制作了ρ1=40 %、ρ2=30 %,ρ1=40 %、ρ2=20 %,ρ1=30 %、ρ2=20 %,ρ1=30 %、ρ2=10 %四种结构的五环简化模型和μ =40 %,μ =35 %,μ =30 %,μ =25 %四种结构的三环简化模型,结果表明,ρ1=40 %、ρ2=20 %和μ =35 %分别是最优的五环和三环简化模型参数,且五环简化缩比模型最优结构参数对应的RMSE 和MAPE 分别比三环简化缩比模型降低了21 %和22 %,试验结果证明了五环简化模型比三环简化模型有更高的精度。
5)针对某换流站中的平波电抗器,分别建立的其对应的五环简化缩比模型和三环简化缩比模型,测量了距地面1.5 m 处的磁感应强度,结果表明,五环简化缩比模型的RMSE 和MAPE 分别比三环简化缩比模型降低了38.7 %和4.9 %,证明了五环简化模型可以等效实际空心电抗器的空间磁场分布,且等效效果优于三环简化缩比模型。
[1] Wang Yu,Chen Xiaoyue,Pan Zhuohong,et al.Theoretical and experimental evaluation of the temperature distribution in a dry type air core smoothing reactor of HVDC station[J].Energies,2017,10(5):623.
[2] 汪泉弟,张艳,李永明,等.干式空心电抗器周围工频磁场分布[J].电工技术学报,2009,24(1): 8-13.
Wang Quandi,Zhang Yan,Li Yongming,et al.The power frequency magnetic field distribution around dry-type air-core reactor[J].Transactions of China Electrotechnical Society,2009,24(1): 8-13.
[3] 姜志鹏,周辉,宋俊燕,等.干式空心电抗器温度场计算与试验分析[J].电工技术学报,2017,32(3):218-224.
Jiang Zhipeng,Zhou Hui,Song Junyan,et al.Temperature field calculation and experimental analysis of dry-type air-core reactor[J].Transactions of China Electrotechnical Society,2017,32(3): 218-224.
[4] 宋晗,邹亮,张秀群,等.基于空间磁场分布的干式空心电抗器匝间短路检测方法[J].电工技术学报,2019,34(增刊1): 105-117.
Song Han,Zou Liang,Zhang Xiuqun,et al.Inter-turn short-circuit detection of dry-type air-core reactor based on spatial magnetic field distribution[J].Transactions of China Electrotechnical Society,2019,34(S1): 105-117.
[5] 高树国,汲胜昌,孟令明,等.基于在线监测系统与声振特征预测模型的高压并联电抗器运行状态评估方法[J].电工技术学报,2022,37(9): 2179-2189.
Gao Shuguo,Ji Shengchang,Meng Lingming,et al.Operation state evaluation method of high-voltage shunt reactor based on on-line monitoring system and vibro-acoustic characteristic prediction model[J].Transactions of China Electrotechnical Society,2022,37(9): 2179-2189.
[6] Lin Dingsheng,Zhou Ping,Fu Weinong,et al.A dynamic core loss model for soft ferromagnetic and power ferrite materials in transient finite element analysis[J].IEEE Transactions on Magnetics,2004,40(2): 1318-1321.
[7] 王革鹏,金文德,曾向阳,等.特高压并联电抗器铁心振动的分析与控制研究[J].电工技术学报,2022,37(9): 2190-2198.
Wang Gepeng,Jin Wende,Zeng Xiangyang,et al.Analysis and control research on core vibration of UHV shunt reactor[J].Transactions of China Electrotechnical Society,2022,37(9): 2190-2198.
[8] Cook R D,Malkus D S,Plesha M E,et al.Concepts and applications of finite element analysis[M].River Street: John Wiley &Sons,2007.
[9] 郑涛,刘校销.磁控式并联电抗器容量调节暂态过程及其对匝间保护的影响[J].电工技术学报,2021,36(5): 1052-1063.
Zheng Tao,Liu Xiaoxiao.Power regulation transient process of magnetically controlled shunt reactor and its impact on protection against turn-to-turn faults[J].Transactions of China Electrotechnical Society,2021,36(5): 1052-1063.
[10] 毛启武,曾庆赣.空心与铁心电抗器工频磁场测量与分析[J].高电压技术,2003,29(4): 49-50.
Mao Qiwu,Zeng Qinggan.Measurement and analysis of power frequency magnetic of air-core and iron-core reactors field[J].High Voltage Engineering,2003,29(4): 49-50.
[11] 袁发庭,吕凯,刘健犇,等.基于电磁-热-结构多物理场耦合的铁心电抗器线圈结构优化方法[J].电工技术学报,2022,37(24): 6431-6441.
Yuan Fating,Lü Kai,Liu Jianben,et al.Coil structures optimization method of iron core reactor based on electromagnetic-thermal-structure multiphysical field coupling[J].Transactions of China Electrotechnical Society,2022,37(24): 6431-6441.
[12] Binns K J,Lawrenson P J.Analysis and computation of electric and magnetic field problems: pergamon international library of science,technology,engineering and social studies[M].2nd ed.Amsterdam,The Netherlands: Elsevier,2013.
[13] 张鹏宁,李琳,聂京凯,等.考虑铁心磁致伸缩与绕组受力的高压并联电抗器振动研究[J].电工技术学报,2018,33(13): 3130-3139.
Zhang Pengning,Li Lin,Nie Jingkai,et al.Study on the vibration of high voltage shunt reactor considering of magnetostriction and winding force[J].Transactions of China Electrotechnical Society,2018,33(13):3130-3139.
[14] 聂洪岩,魏新劳,姚远航,等.热老化对干式空心电力电抗器匝间绝缘操作过电压耐受特性的影响[J].电工技术学报,2020,35(24): 5096-5104.
Nie Hongyan,Wei Xinlao,Yao Yuanhang,et al.Effect of thermal aging on the characteristic to withstand switching overvoltage of interturn insulation of dry-type air core power reactor[J].Transactions of China Electrotechnical Society,2020,35(24): 5096-5104.
[15] Yan Xiuke,Dai Zhongbin,Yu Cunzhan,et al.Research on magnetic field and temperature field of air core power reactor[C]//2011 International Conference on Electrical Machines and Systems,Beijing,China,2011: 1-4.
[16] de Abreu Silveira C,da Costa C A,da Costa E Silva R,et al.Electromagnetic environment measurement under steady-state conditions in utility substations[C]//2006 IEEE/PES Transmission &Distribution Conference and Exposition,Caracas,Venezuela,2007:1-6.
[17] Xu Gan,Zou Liang,Zhang Li,et al.Investigation on small-scale experiments of magnetic field around air-core reactors[J].Applied Mechanics and Materials,2014,521: 389-393.
[18] 邹亮,宫攀,张黎,等.干式空心电抗器空间磁场缩比试验与模型简化[J].高电压技术,2014,40(6):1675-1682.
Zou Liang,Gong Pan,Zhang Li,et al.Small-scale experiment and model simplification of space magnetic fields around air-core reactors[J].High Voltage Engineering,2014,40(6): 1675-1682.
[19] Yu Q,Sebo S A.Calculation accuracy of the planar filament current loop stack model of large air-core reactor coils[J].IEEE Transactions on Magnetics,1997,33(5): 3313-3315.
[20] Yu Q,Sebo S A.Simplified magnetic field modeling and calculation of large air-core reactor coils[J].IEEE Transactions on Magnetics,1996,32(5): 4281-4283.
[21] Han Zhiyun,Zou Liang,Song Han,et al.Study on optimal structure of three-loop simplified scaling model for dry-type air-core reactors[J].IEEE Access,2018,6: 48259-48267.
[22] 杜淑文,宋春燕,祝春捷,等.10kV 空心电抗器周围工频磁场的简化计算及影响范围[J].高压电器,2006,42(3): 179-182.
Du Shuwen,Song Chunyan,Zhu Chunjie,et al.Simplified calculation and coverage of power frequency magnetic field around 10kV air-core reactors[J].High Voltage Apparatus,2006,42(3): 179-182.
[23] 陈彬,秦小彬,万妮娜,等.基于 R-L 型分数阶导数与损耗统计理论的铁磁材料高频损耗计算方法[J].电工技术学报,2022,37(2): 299-310.
Chen Bin,Qin Xiaobin,Wan Nina,et al.Calculation method of high-frequency loss of ferromagnetic materials based on R-L type fractional derivative and loss statistical theory[J].Transactions of China Electrotechnical Society,2022,37(2): 299-310.
[24] 徐干.基于缩比简化的干式空心电抗器空间磁场分析与预测[D].济南: 山东大学,2016.