0 引言
近年来，随着微电子机械系统[1]和微放电等离子体[2]的广泛应用，研究在强电场作用下微米间隙的绝缘特性及放电机制，对微结构的绝缘性能评价与微放电等离子体的产生具有重要的意义。现有的微米尺度击穿理论认为，微米尺度气隙中阴极表面的场致电子发射和二次电子发射过程将直接影响其击穿特性及物理机制，因此阴极在微米气隙击穿中起到关键作用[3]。一方面，阴极处发生的场致电子发射效应是微米尺度气隙击穿的主要机制，影响场发射效应的因素将最终影响击穿特性和物理过程；另一方面，阴极表面的二次电子发射γ 过程亦是微米尺度击穿的重要过程，在不同阴极条件下二次电子发射电流密度将会不同，从而在一定程度上影响间隙内载流子密度，最终影响击穿过程[4]。因此，深入探索阴极在微米气隙击穿过程中的作用，进一步认识和理解微米尺度击穿特性和击穿机理对微米尺度的绝缘性能评价和放电等离子体应用具有重要的理论和应用价值。
对于不同阴极条件下微米尺度气隙击穿的研究，国内外学者通过实验与数值计算均取得了一定的进展。实验研究方面，英国赫瑞瓦特大学的J.M.Torres[5-6]、美国南卡罗来纳大学的T.S.Sudarshan[7]、美国迈拓公司的A.Wallash 等[8]使用不同材料制成的电极展开实验，结果表明，在较高二次发射系数和场发射系数电极材料下击穿电压将会降低，由于阴极表面更易产生电子，击穿Vb-d 曲线将向左下方移动。美国普渡大学的R.S.Brayfield 等[9]使用具有不同表面粗糙度的电极进行实验研究，发现击穿电压将随表面粗糙度减小而增大，并且击穿在阴极表面产生的圆形烧蚀凹坑，将会影响击穿距离进而影响击穿特性。数值计算方面，清华大学孙钧等[10]利用有限元方法对阴极表面微米量级微凸起的场增强因子进行了计算，拟合得到了阴极凸起处场增强因子的经验表达式和变化规律。密歇根州立大学的付洋洋等[11-12]向阴极引入单个或多个凸起，详细分析计算了凸起自身的性质结构以及数量等对于击穿过程及其阈值的影响，并进一步研究分析阴极表面存在多个凸起时的尺度效应。另有大量针对阴极表面状况的研究成果表明，电极表面状况反映了局部电场畸变程度，局部毛刺或粗糙部分将会导致局部场发射增强，击穿起始点易出现在阴极局部电场畸变较严重的位置[13-17]。然而，受电极制备工艺限制，使用不同尺寸、形貌电极进行的实验研究仍有待完善。而对于数值计算，现阶段的研究多为一维模型，即局限于板-板电极，电极形貌的不同在一维模型中难以体现，同时阴极条件多通过引入微凸起加以改变，而阴极的其他条件（针阴极曲率半径等）对击穿特性影响的研究鲜有涉及，故亟须通过二维或三维模型对不同阴极在击穿中发挥的作用进行更系统、深入的研究，探明不同阴极条件下发生微米尺度气隙击穿时的电场分布、电流特性以及粒子分布情况。
本文建立了微米尺度气隙（气隙距离d=5 μm）击穿的二维物理模型，基于粒子模拟/蒙特卡洛碰撞（Particle in Cell/Monte Carlo Collision,PIC/MCC）方法分别仿真研究了阴极不同曲率半径R0（1,3,5,7,10 μm）条件下微米尺度的击穿特性，得到了击穿发展过程中气隙内电场分布特性、电流变化特性及带电粒子的空间分布特性，定量分析了场致电子发射等机制在击穿过程中的贡献程度，并结合实验研究结果对不同阴极条件下的气隙击穿特性与不同击穿机制的变化规律展开了讨论。
1 微米尺度气体击穿实验系统与仿真二维物理模型
1.1 微米尺度气体击穿实验系统
本文对文献[18]中的实验系统进行调整，所搭建的微米尺度气体击穿实验系统如图1a 所示，该系统中，由HB-Z502-20A 型直流高压电源、Tektronix AFG3102C 函数发生器，纳秒方波发生器（高速开关）构成纳秒脉冲发生器，输出一个上升沿为100 ns、平顶宽度为500 ns，且幅值可调的高压脉冲信号，作为测试电极两端的输入电压；由Pearson 6585 脉冲电流传感器、Tektronix P5100 无源高压探头和LecroyWaveSurfer 104MXS-B 示波器构成电学测试单元，采集放电电压与电流信号；由光学减振平台、压电测微头位移控制器、Olympus BX51M 型光学显微镜组成光学标定单元，实现对实验所用电极及其间隙的高精度调节和标定。其中压电测微头位移控制器调节范围为1～25 μm，最小步长为1 μm。光学显微镜的最高放大倍数为1 000 倍。利用电化学腐蚀法制备出具有不同曲率半径的钨针电极，建立图1b 所示的针-板电极结构（该图像为光学显微镜下拍摄所得）。基于上述实验系统，调节电极间距至5 μm，在电极两端施加电压，由于所施加的电压为一个宽度为500 ns 的方波信号，方波宽度已经远大于击穿持续时间，当击穿发生在方波的平顶区时，则其与直流电压下的击穿无异。在施加方波电压后，若通过示波器观察到电极两端电压在脉冲激励施加过程中突然下降，电极间出现A 级的电流，且电压的突变发生在方波平顶区，则此时所施加电压幅值为击穿电压，同时记录击穿电流幅值。
图1 实验与仿真中的针-板电极
Fig.1 Needle-plate electrodes in experiments and simulations
1.2 二维物理模型及参数设置
本文针对微米间隙击穿所进行的仿真计算使用美国Tech-X 公司的Vsim Composer 软件实现，它是一款包含了电磁场、粒子和等离子体物理的模拟软件。仿真中通过几何模型H 函数对阴极和阳极进行几何建模，根据实验所用的针-板电极结构，建立了微米尺度气隙击穿的二维物理模型，如图1c 所示。其中阴极曲率半径R0=1～10 μm，阳极为板电极，间隙宽度d=5 μm。通过静电场yeeStaticEmField 模型对计算区域内电场进行模拟，仿真过程中设置阴极电势为0 V，模拟实验中阴极接地，阳极施加一个恒定电压，模拟实验中击穿瞬态电极两端电压。计算区域在设置时需考虑到尽可能实现对主要碰撞与反应区域的覆盖，同时又需要尽量节约计算成本。结合文献[19]中所获得的5 μm间隙击穿图像实验结果，放电集中发生在电极尖端5～10 μm 范围内，综合考虑计算的准确性与高效性两个方面，将电场计算区域设置为LX=40 μm，LY=20 μm，如图1c 中黑色长方形区域所示。粒子碰撞区域LX 设置为40 μm，LY 根据阴极曲率半径设置为5.5～20 μm，如图1b中长方形区域所示，当带电粒子运动出上述边界时，则认为其运动过远无法对电场或碰撞造成影响。
本文模拟1 atm（1 atm=101 325 Pa）大气环境，设置氮气分子数密度为2.0×1025 个/m3，氧气分子数密度为5.0×1024 个/m3。通过设置不同粒子电荷和质量定义的粒子有电子、氧气分子、氮气分子、氮正离子（N2+）、氧正离子（O2+）和氧负离子（O2-）。同时由于间隙内存在少量自由移动电子，所以预设每个网格中存在一个电子。
在该尺度击穿时发生的物理过程包括场致电子发射、二次电子发射、电子与背景气体间蒙特卡洛碰撞等。仿真中通过Fowler-Nordheim 方程（F-N方程）增加一个明确的场发射源的方法引入场发射效应，以fieldEmitterVelGen 模块实现，由于实验所用针阴极材质为钨，因而设置功函数参数 work_function=4.5 eV；而场增强系数在不同条件下取值区别较大，本文根据实验所得扫描电子显微镜（Scanning Electron Microscope,SEM）图像中电极表面形貌平整度，选定场增强系数beta_FN=100。根据仿真中电场分布、设置的场增强因子、电极功函数等参数大小生成粒子发射速度、方向和权重。二次电子发射模块在仿真中即为入射粒子被边界吸收、再从边界吸收点释放出若干次生电子的过程，在本文中以ParticleSource 粒子产生模块单独定义二次电子段落，模拟了氮正离子（N2+）、氧正离子（O2+）和电子在预设二次电子系数和入射能量下碰撞阴极表面并沿表面法线方向产生二次电子的过程。发生的蒙特卡洛碰撞具体包括电子（包括电离出来的二次电子）和背景气体中的中性氮气分子、氧气分子之间的弹性碰撞、激发、电离以及电子附着在O2 上形成氧负离子（O2-）等过程，此外还包括离子与氮、氧等中性原子之间的电荷交换碰撞与动量交换等物理过程。不同物理过程及反应式见表1，其中部分反应式两端的粒子种类基本相同，但其反应截面与反应率会存在差别，不同反应的具体相关数据可由参考文献[20-21]获得。
表1 不同物理过程及反应式
Tab.1 Different physical processes and reaction equations
除上述几个物理过程外，仿真中还以能量动量守恒为原则设置了粒子合并，分别设置了电子、氮离子、氧离子和氧负离子的合并阈值为10，即每个网格中的粒子数超过10 个就会进行合并，宏粒子的最大权重为1.0×1010，即如果宏粒子代表的物理粒子数达到1.0×1010 个就不再进行合并。
仿真区域的网格尺寸与时间步长的设置遵循以下原则：①仿真区域的网格尺寸不能超过等离子体的德拜长度；②一个时间步长dt 内，粒子的运动距离不会超过一个网格的尺寸。其中德拜长度λD 定义[22]为
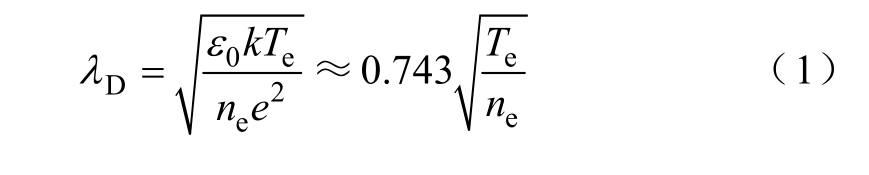
式中，ε0 为真空介电常数；k 为玻耳兹曼常数；e 为电子电荷量；Te 为等离子体电子温度；ne 为等离子体电子密度。式（1）中一般情况下的气体放电中电子的密度能达到1016/m3[22]，根据式（1）可以估算出其德拜长度大于0.13 μm，同时在对不同网格尺寸下仿真结果进行分析后，综合计算成本与仿真结果准确性两方面考虑，在整个计算区域内采用均匀剖分网格方法，设置基本网格单元为矩形网格，网格数量为 900×900，网格单元尺寸为 0.044 μm×0.022 μm，该尺寸远小于物理模型中的最小曲率半径（1 μm）以及最小间隙距离（5 μm），因此计算精度能够得以保证。
时间步长dt 应满足条件
式中，Δx、Δy 为网格尺寸参数；vemax 为电子可达到的最大速度，而电子速度ve 则通过式（3）计算得到。
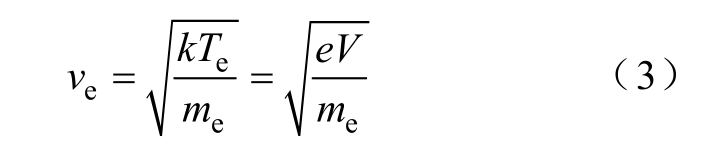
式中，me 为电子质量；V 为电压。由式（2）和式（3）可以估算得到dt 应小于3.0×10-13 s，并且dt 设置越小计算越准确，但同时计算量也会越大，因此仿真中设置dt =1.0×10-14 s。
2 结果与分析
2.1 气隙内电场分布特性
本文利用电化学腐蚀法制备得到曲率半径为1～10 μm 的钨针电极，基于第1 节中所述实验系统与方法得到了不同针阴极曲率半径下针-板电极气隙击穿电压，实验结果如图2 黑色曲线所示。可以发现，击穿电压Vb 随阴极曲率半径增加而增大，当阴极曲率R0 从1 μm 增加至10 μm 时，间隙的击穿电压增加37.4 %，同时Vb-R0 的斜率亦随曲率半径增大逐渐减小。
图2 针-板电极间的电场分布特性
Fig.2 Electric field distribution characteristics between needle-plate electrodes
气隙击穿电压与其内部电场分布有着极为密切的关系，为进一步理解上述实验现象，开展了不同阴极曲率半径下气隙内的电场分布特性的仿真研究。以阴极曲率半径R0=3 μm 为例，施加电压Vapply为实验所得到的击穿阈值电压，其电场分布情况如图2 所示，可以看到针电极表面电场发生畸变，越靠近针尖处电场强度越大，针尖处最大电场强度高达2.338×108 V/m，而向针电极两侧电场迅速减小，电场计算区域的边缘电场强度仅为5.5×107 V/m，仅为最高电场强度值的23.5 %。
由于阴极处的局部电场大小将在很大程度上影响场发射电流[23]，为了描述不同阴极曲率半径下电场不均匀程度，引入场增强因子β，其定义为
式中，Emax 为间隙内电场强度最大值，为电场畸变最严重处电场强度大小；Eavg 为间隙内电场强度平均值；β 越大表示电场分布越不均匀。使用不同曲率半径针阴极时场增强因子、对应的仿真得到的击穿电压、实验得到的击穿电压如图3 中曲线所示。图3 中实验与仿真的结果有着较好的对应关系，从一定程度上能够反映本文所用二维模型的准确性。仿真结果显示，场增强因子β 随着曲率半径增加而减小，当阴极曲率从1 μm 增加至10 μm 时，场增强因子从2.50 减小至1.65，并且β-R0 曲线的斜率逐渐减小。
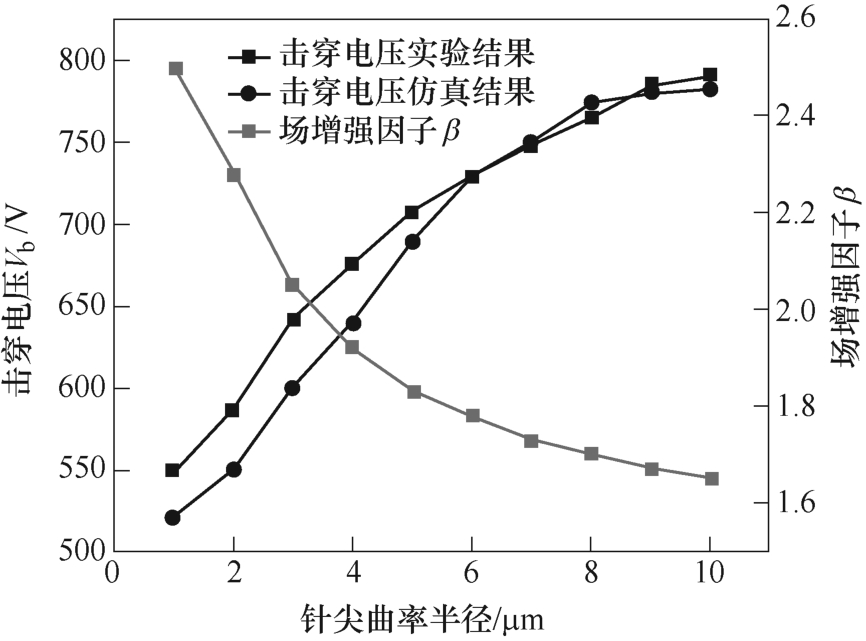
图3 不同阴极曲率半径的击穿电压与场增强因子变化规律
Fig.3 The variation of breakdown voltage and field enhancement factor with different cathode curvature radius
结合实验与仿真结果分析可以发现，当曲率半径较小时，阴极处局部电场强度较大，电场畸变程度较高，此时场发射阈值电压降低，在较低的电压下即可达到较高的发射电流，因此击穿电压较低。随着曲率半径增大，电场不均匀度降低，阴极表面局部电场畸变减小，场发射阈值电压增大，需要施加更大的电压才可使场发射产生足够多的电子，因此击穿电压逐渐升高。同时，Vb-R0 与β -R0 曲线斜率的变化也具有一定的对应关系，随着阴极曲率半径增大，电场畸变程度降低，且在曲率半径较大时，其对电场的影响逐渐变小，因而场发射过程受 R0的影响程度亦会逐渐减弱，最终导致Vb-R0 曲线斜率的降低。
2.2 击穿过程中电流变化特性
数值模拟中击穿时刻是电子碰撞产生和被阳极吸收的平衡过程的结果，阳极电流、间隙内带电粒子密度、电场畸变程度等参数均可作为击穿判据，而单一参量作为判据时，若改变参数，则会影响判断结果，导致判据可能不再适用。为了进一步提高对击穿时刻判断的准确性，本文综合多参数进行击穿时刻的判断[7,24-25]。本文中击穿时刻主要基于阳极电流峰值并综合击穿过程中电场强度以及场发射电流等物理量进行综合判定。以曲率半径为 5 μm的针阴极与板电极间隙击穿为例，基于第1 节中所建立的二维物理模型，用PIC/MCC 方法分析击穿过程中的电场特性，在完成仿真计算后，可直接在Visim 软件中对间隙内的电场分布、电流值、粒子分布等参数进行读取。在得到了不同时刻的间隙内电场强度最大值Emax、场发射电流IFN 以及阳极电流Ianode 后，将其绘制为如图4 中所示的Emax、Ianode、IFN 三条曲线，对Emax、IFN 求一次导，得到其斜率变化曲线
。从0 时刻开始，间隙内的最大电场强度Emax 大幅增加，特别是在22～27 ps 间，电场强度 Emax 随时间的变化速率
维持在较高水平，此阶段内，局部电场明显增强，电场畸变严重。在这一过程中，由于局部电场强度的升高，场发射过程也逐渐加剧，场发射电流IFN 持续增长，在24 ps 时刻，其增长速率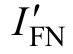
达到峰值，此时场发射电流增长最快，场致电子发射效应急剧增加。阳极电流 Ianode 在击穿发展过程中亦持续增长，在25.5 ps 左右时达到峰值，此时间隙内电流密度最大、反应最为剧烈，此时可视为击穿发生的时刻，该时刻过后，阳极电流开始逐渐下降。综上所述，击穿时刻的判定以阳极电流峰值作为主要参考，辅以Emax 及其曲线斜率
及其曲线斜率
等参数，进一步明确击穿过程并验证本研究中以阳极电流峰值作为击穿时刻的合理性。
图4 击穿过程中电场强度、阳极电流与场发射电流变化规律
Fig.4 Variation of electric field intensity,anode current and field emission current during breakdown process
图5 所示为当阴极具有不同曲率半径时，击穿时刻t 与击穿电流幅值的实验和仿真结果，其中击穿电流的实验数据通过Pearson6585 电流传感器采集获得。对比发现，施加相同电压时仿真得到的击穿电流随阴极曲率半径增加而增加，这与实验得到的结果基本一致。由于场致发射是该尺度下气隙击穿的重要机制，为进一步理解上述电流变化特性，将仿真结果中的场发射电流与阳极电流进行对比如图5 和图6 所示，以R0=5 μm 时为例，当t =25 ps时场发射电流为1.098×107，阳极吸收电流为1.070×107，此时场发射电流约为阳极电流的97.4 %，说明此时场发射机制占主导地位，即在该间隙下场发射电流对阳极电流起主要贡献[26]。场发射电流随曲率半径增加而增加，当R0=10 μm 时场发射电流约为R0=1 μm 时的4 倍，与阳极吸收电流差异吻合，说明曲率半径通过影响场发射电流大小进而影响击穿电流大小，曲率半径越大，场发射电流越大，因此阳极电流越大。在2.1 小节的分析中可以发现，当阴极曲率半径减小时，会导致局部电场强度大幅增加，从而加剧场发射过程。而图6 的结果显示，当阴极曲率半径增大时，场发射电流亦会增大，这说明气隙内的电场畸变程度并非影响场发射电流大小的唯一因素，对于此问题的讨论将在2.3 节中展开。
图5 不同阴极曲率半径下电流与击穿时刻变化规律
Fig.5 Variation of current and breakdown time with different radius of cathode curvature
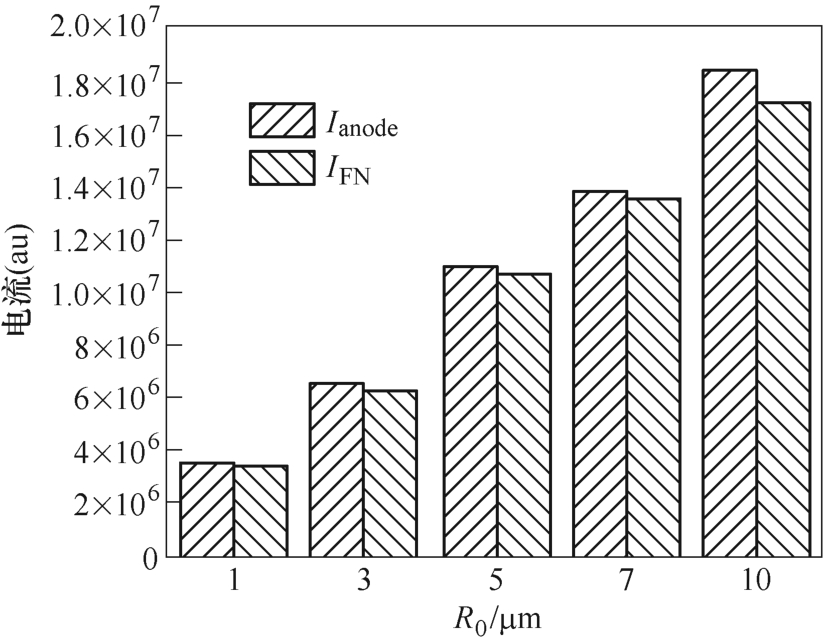
图6 不同阴极曲率半径击穿时刻场发射电流与阳极电流对比
Fig.6 Comparison of field emission current and anode current with different radius of curvature of cathode
图5 中通过多参数综合分析得到的击穿时间t亦随R0 的增大出现了较大的变化，当R0=1 μm 时t =22.4 ps，当R0=10 μm 时t =30.6 ps，增幅达33.6 %。分析认为出现击穿时间的变化是由于带电粒子在间隙内受不同强度电场力的作用，速度不同导致的。对于较小的曲率阴极而言，阴极表面发射的大量电子将在不均匀电场下被加速并具有更高的动能，运动至阳极所需时间更短，同时更高动能的电子将会在间隙内发生更为剧烈的碰撞电离，产生更多的正离子，使得间隙内电场更强，这将更进一步加速击穿过程。
2.3 击穿过程中带电粒子空间分布特性
图7a～图 7c 为仿真得到的针阴极曲率半径R0=1,5,7 μm 时间隙内电子密度分布特性。可以看到对于不同曲率半径阴极，击穿时刻电子在阴极处都较为集中，向阳极过渡电子密度逐渐减小，出现阴极侧面粒子集中现象，针阴极中心处电子密度较低。图7d～图7f 显示在击穿时刻，阴极尖端场强明显弱于尖端两侧，这样的电场分布形成的原因在于间隙内的空间电荷效应，当阴极为针电极时，由于较大的场增强因子，其发射电子能力较强，进而导致针尖处的电子密度更大，空间电荷作用更强，这将会削弱阴极尖端附近的电场，同时也将导致阴极表面场发射受暂态过程中电场作用而减弱，使得场发射的过程受到抑制，最终出现针阴极中心处电子密度较低的现象。图7g～图7i 所示为实验得到的不同曲率半径、间隙距离为5 μm 时的击穿放电图像。可以看到，不同曲率半径下的击穿放电形貌与仿真得到的电子密度和电场强度分布特性基本一致，且阴极表面放电区域面积与曲率半径呈正相关特性（与图8 中的仿真结果相一致）。值得注意的是，主要的区别在于实验得到的击穿放电图像并没有出现仿真结果中的阴极尖端中心处的电子密度和电场强度减弱区，原因在于仿真结果是计算得到的某一击穿时刻的特性分布图，而实验结果为整个微米间隙击穿过程的光学成像图，是击穿起始、发展、贯通直至放电结束整个过程的累积成像，因此导致了两者之间的差异，而这也说明数值计算在研究微米、纳米尺度击穿瞬态过程中的重要作用。
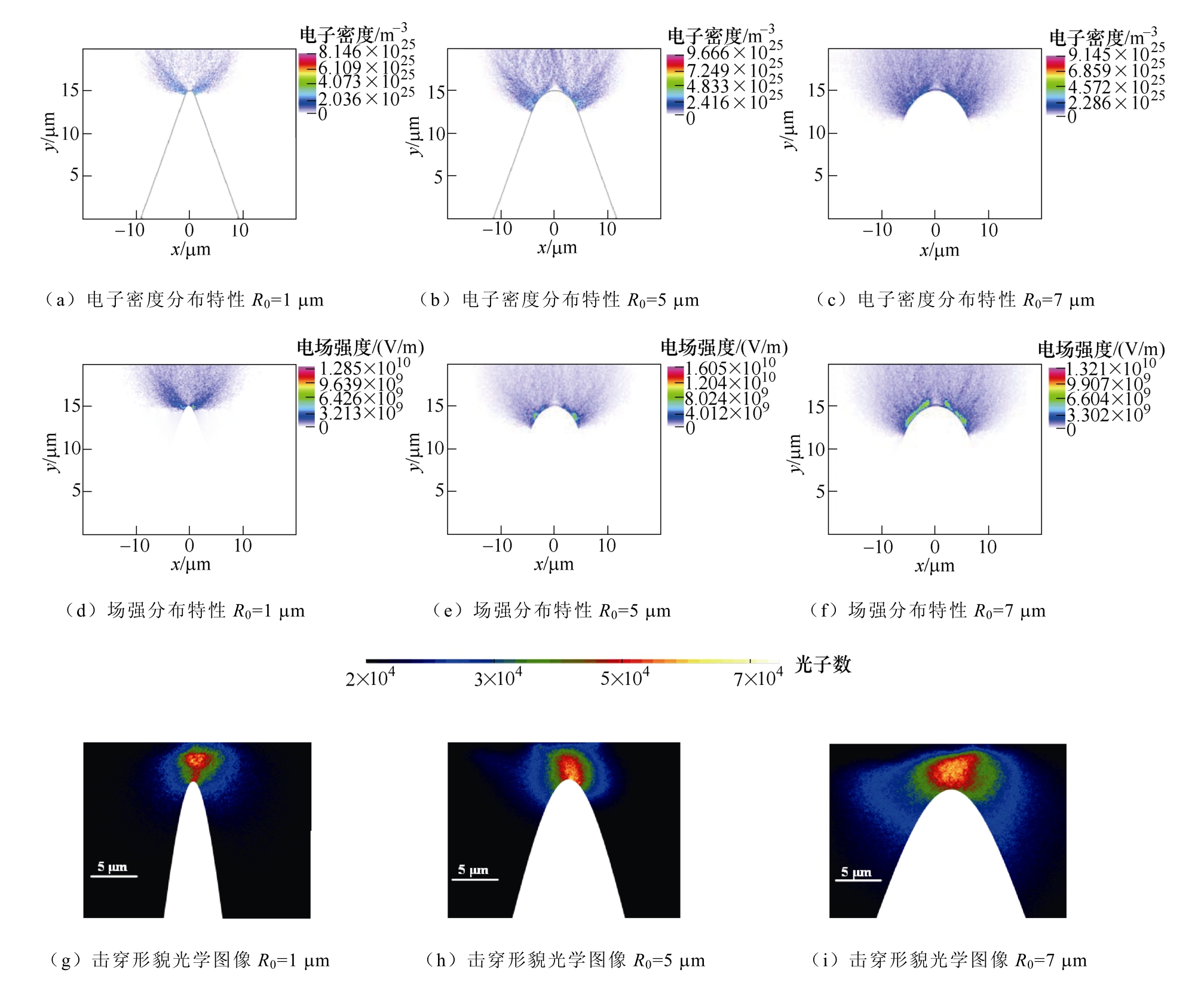
图7 不同阴极曲率半径下的电子密度、电场强度分布特性的仿真结果与间隙击穿形貌的实验结果
Fig.7 Simulation results of spatial distribution of electron and electric field,and the experimental results of breakdown morphology with different radius of cathode curvature
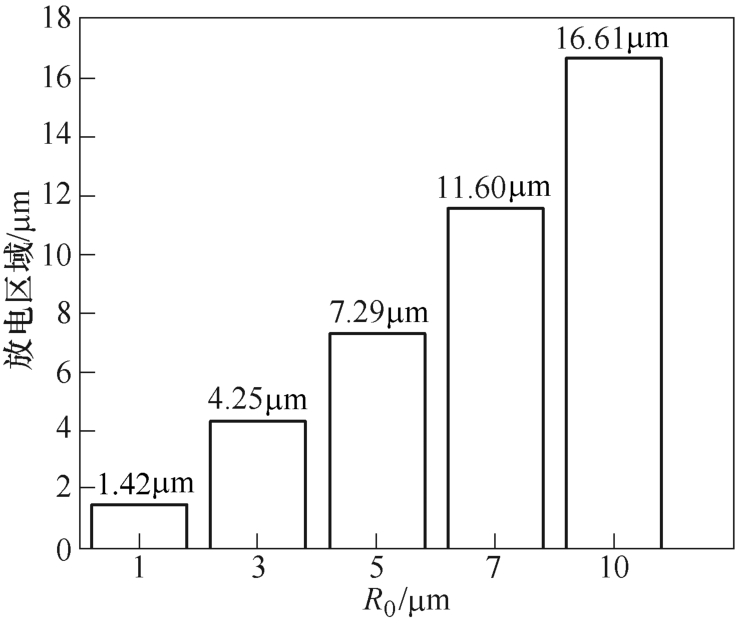
图8 不同曲率针阴极下阴极放电面积变化
Fig.8 Variation of cathode discharge area with different radius of cathode curvature
图8 所示为不同曲率半径阴极击穿时阴极表面放电区域大小，基于本文所建立的二维物理模型，此处选取阴极上的电子发射区域两边界点的直线距离对放电区域进行表征。对比放电通道起始区域发现，阴极表面放电起始区域面积随曲率半径增加而增加。对于R0=1 μm 阴极，阴极发射的有效区域约为1.42 μm，对于R0=7 μm 阴极，阴极发射的有效区域增加到约8.2 倍，约为11.6 μm；对比阳极电子吸收面积发现，阳极电子吸收面积也随阴极曲率半径增加而增加，由此说明击穿通道宽度随曲率半径增加而增加。由此可见，阴极曲率半径会影响阴极表面电子发射的有效面积、阳极电子吸收面积及电通道面积，这将直接导致曲率半径较大阴极下场发射电流大，从而导致阳极吸收电流大，并且更宽的放电通道意味着更剧烈的碰撞电离，因此击穿电流将随曲率半径增大而增大。
3 结论
本文利用微米尺度放电二维粒子仿真计算并结合实验结果，研究了不同阴极曲率半径对于微米尺度击穿特性的影响规律，研究结果表明：
1）在5 μm 间隙内，针阴极表面电场强度达到了2×108 V/m 以上，场发射电流占阳极电流95 %以上，此时场发射电流对击穿的贡献极大，其将在气隙击穿过程中成为主要击穿机制之一。
2）阴极尖端附近会出现明显的电场畸变并产生最大电场强度，且随着针尖曲率半径的减小，电场的畸变程度增加，在较低的电压下即可产生较大场发射电流，因此击穿电压随着阴极曲率半径的减小而逐渐减小，并且电场畸变程度增加将使得在相同电压下间隙内带电粒子动能增加，加速击穿，使得击穿时间亦随着针尖曲率半径减小而减小。
3）对间隙内电子空间分布特性的研究发现，场发射的有效面积随曲率半径的增加而增大，这将直接导致场发射电流的增大，同时放电通道宽度的增大将引起气隙内更为剧烈的碰撞电离，最终导致击穿电流随阴极曲率半径增加而增加。
[1] Lyshevski S E.MEMS and NEMS-systems,devices,and structures[J].IEEE Electrical Insulation Magazine,2004,20(4): 46.
[2] Go D B,Venkattraman A.Microscale gas breakdown:ion-enhanced field emission and the modified Paschen's curve[J].Journal of Physics D: Applied Physics,2014,47(50): 503001.
[3] 成永红,孟国栋,董承业.微纳尺度电气击穿特性和放电规律研究综述[J].电工技术学报,2017,32(2): 13-23.
Cheng Yonghong,Meng Guodong,Dong Chengye.Review on the breakdown characteristics and discharge behaviorsat the micro &nano scale[J].Transactions of China Electrotechnical Society,2017,32(2): 13-23.
[4] 孟国栋,折俊艺,应琪,等.微米尺度气体击穿的数值模拟研究进展[J].电工技术学报,2022,37(15):3857-3875.
Meng Guodong,She Junyi,Ying Qi,et al.Research progress on numerical simulation of gas breakdown at microscale[J].Transactions of China Electrotechnical Society,2022,37(15): 3857-3875.
[5] Torres J M,Dhariwal R S.Electric field breakdown at micrometer separations in air and vacuum[J].Microsystem Technologies,1999,6(1): 6-10.
[6] Torres J M,Dhariwal R S.Electric field breakdown at micrometer separations[J].Nanotechnology,1999,10(1): 102-107.
[7] Ma Xianyun,Sudarshan T S.High field breakdown characteristics of micrometric gaps in vacuum[J]//Journal of Vacuum Science &Technology,B.Microelectronics and Nanometer Structures: Processing,Measurement and Phenomena,1998,16(2): 745-748.
[8] Wallash A,Levit L.Electrical breakdown and ESD phenomena for devices with nanometer-to-micron gaps[J].Proceedings of SPIE-The International Society for Optical Engineering,2003,4980: 87-96.
[9] Brayfield R S,Fairbanks A J,Loveless A M,et al.The impact of cathode surface roughness and multiple breakdown events on microscale gas breakdown at atmospheric pressure[J].Journal of Applied Physics,2019,125(20): 203302.
[10] 孙钧,刘国治,林郁正,等.阴极金属微凸起电场增强因子数值模拟[J].强激光与粒子束,2005,17(8): 1183-1186.
Sun Jun,Liu Guozhi,Lin Yuzheng,et al.Numerical simulation of electric field enhancement factor of metallic microprotrusion[J].High Power Laser and Particle Beams,2005,17(8): 1183-1186.
[11] Fu Yangyang,Krek J,Zhang Peng,et al.Gas breakdown in microgaps with a surface protrusion on the electrode[J].IEEE Transactions on Plasma Science,2019,47(5): 2011-2019.
[12] Fu Yangyang,Zhang Peng,Verboncoeur J P,et al.Electrical breakdown from macro to micro/nano scales: a tutorial and a review of the state of the art[J].Plasma Research Express,2020,2(1): 013001.
[13] 董克亮,孙岩洲,刘绪光.微间距气体放电的实验研究与分析[J].高压电器,2019,55(5): 29-34.
Dong Keliang,Sun Yanzhou,Liu Xuguang.Experimental study and analysis of gas discharge with micro-gap[J].High Voltage Apparatus,2019,55(5):29-34.
[14] Radmilović-Radjenović M,Matejčik,Klas M,et al.The role of the field emission effect in direct-current argon discharges for the gaps ranging from 1 to 100μm[J].Journal of Physics D: Applied Physics,2013,46(1): 015302.
[15] Venkattraman A.Cathode fall model and currentvoltage characteristics of field emission driven direct current microplasmas[J].Physics of Plasmas,2013,20(11): 113505.
[16] 孙志,付琳清,高鑫,等.基于原子力显微镜的微间隙空气放电研究[J].电工技术学报,2018,33(23):5616-5624.
Sun Zhi,Fu Linqing,Gao Xin,et al. Research of discharge in micro-gap based on atomic force microscope[J].Transactions of China Electrotechnical Society,2018,33(23): 5616-5624.
[17] Klas M,Matejčik Š,Radjenović B,et al.The breakdown voltage characteristics and the secondary electron production in direct current hydrogen discharges for the gaps ranging from 1μm to 100μm[J].Physics Letters A,2012,376(10/11): 1048-1052.
[18] Meng Guodong,Ying Qi,Loveless A M,et al.Spatiotemporal dynamics of pulsed gas breakdown in microgaps[J].Physics of Plasmas,2019,26(1):014506.
[19] Meng Guodong,Gao Xinyu,Loveless A M,et al.Demonstration of field emission driven microscale gas breakdown for pulsed voltages using in situ optical imaging[J].Physics of Plasmas,2018,25(8):082116.
[20] 郑殿春.气体放电数值仿真方法[M].北京: 科学出版社,2016.
[21] Phelps A V,Pitchford L C.Anisotropic scattering of electrons by N2 and its effect on electron transport[J].Physical Review A,General Physics,1985,31(5):2932-2949.
[22] Raĭzer I P.Gas discharge physics[M].Berlin:Springer-Verlag,1991.
[23] Fowler R H,Nordheim L.Electron emission in intense electric fields[J].Proceedings of The Royal Society a Mathematical Physical and Engineering Science,1928,119(781): 173-81.
[24] Fu Yangyang,Zhang Peng,Krek J,et al.Gas breakdown and its scaling law in microgaps with multiple concentric cathode protrusions[J].Applied Physics Letters,2019,114(1): 014102.
[25] Gao Xinyu,Meng Guodong,Wang Kejing,et al.Numerical simulation of gas breakdown in microgaps based on PIC/MCC method[C]//2018 IEEE 2nd International Conference on Dielectrics,Budapest,Hungary,2018: 1-4.
[26] Semnani A,Venkattraman A,Alexeenko A A,et al.Prebreakdown evaluation of gas discharge mechanisms in microgaps[J].Applied Physics Letters,2013,102(17):174102.