图1 DCCB与CR-DCCB拓扑结构
Fig.1 Topology diagram of DCCB and CR-DCCB
摘要 直流断路器是中压直流配电系统的重要设备。为满足大容量高速分断的迫切需求,该文提出一种基于耦合电抗器的阻容型混合直流断路器拓扑结构并分析了其工作过程,将耦合电抗器一、二次绕组分别串联于主支路和真空开关支路实现加速电弧电流转移,阻容元件串联于固态开关支路以便限制故障电流。通过Matlab/Simulink构建了基于耦合电抗器的阻容型混合直流断路器仿真模型,仿真分析了耦合电抗器和阻容元件参数对电流转移时间、限流效果、整机开断时间的影响规律,并进行了小电流开断的初步实验验证。研究表明:耦合电抗器一、二次绕组分别为300μH、50μH,阻容元件参数为0.1Ω、50μF,电流转移时间由1.5ms缩短至0.5ms,截断电流峰值降低了47.1%,整机关断时间缩短了1.9ms,初步验证了新拓扑结构在限流和快速开断方面的可行性,为研制高性能混合直流断路器提供参考依据。
关键词:中压混合式直流断路器 直流开断 电流转移 耦合电抗器
直流断路器作为中压配电系统控制和保护的重要设备,是构建柔性直流电网的关键设备[1-2]。中压柔性配电、直流牵引等系统对大容量快速分断的直流断路器需求迫切[3]。
直流断路器主要包括机械式直流断路器、固态直流断路器和混合式直流断路器[4-5]。混合式直流断路器综合了机械开关通流能力强和固态开关动作速度快的优点,是中压直流断路器的主要发展趋势。高压混合式直流断路器无法通过自然换相实现电流由机械开关向固态开关的转移,需借助辅助开关或耦合负压等措施实现强迫转移。在中低压小电流领域国内外开展较多研究。ABB公司基于集成门极换流晶闸管(Integrated Gate-Commutated Thyristor, IGCT)和快速机械开关设计了1.5kV/4kA混合式直流断路器,利用真空电弧电压实现4.5kA电流转移[6]。意大利的L. Novello等将IGCT与快速机械开关结合,利用IGCT的串并联技术研制出1kV/10kA混合式直流断路器的原理样机[7]。上述开断过程中故障电流由机械开关向固态开关转移主要由电弧弧压的自然换相实现,但随着故障电流的增加(>10kA),自然换相时间拖尾甚至换相失败。为实现大容量开断,清华大学基于耦合负压电路加速电流转移,研制了10kV多端口混合式直流断路器。文献[8]提出在断路时限流电感快速旁路方法,可降低直流断路器(DC Circuit Breaker, DCCB)在切断故障电流过程中的能量耗散。文献[9]研究机械式直流断路器弧后电流测量原理,得出换相频率和恢复电压对弧后电流的影响规律。文献[10]研究三种不同超导限流直流开断技术,并完成了10kV/10kA超导限流强迫过零直流电流开断实验。文献[11]中采用耦合电感辅助电流转移的断路器拓扑结构,该结构在正常运行时电能损耗低、能够有效限制故障电流且加速电流转移过程。文献[12]提出了一种新型快速响应直流限流器,加速了开断过程,同时该限流器能全程自适应动作,无需触发控制装置,响应直接迅速。文献[13]提出了一种阻容型限流式直流断路器拓扑,可实现稳态低电抗和暂态高限流电抗的灵活切换,同时起到限流作用。文献[14]研究了熄弧后真空断路器恢复电压变化规律,并通过仿真与实验进行对比分析,验证改进真空断路器弧后电磁暂态建模精确性。上述研究在加速电流转移和故障电流方面取得了一定进展[15-19],但围绕耦合电抗器和阻容限流之间协同工作过程及其对加速电流转移、限流效果等特性研究较少。
在前期城市轨道交通混合式直流断路器电流转移判据和整机开断性能研究基础上[20-21],本文提出了一种基于耦合电抗器的阻容型混合直流断路器拓扑结构,采用耦合电抗器加速电流转移,阻容元件限制故障电流峰值。搭建基于耦合电抗器的阻容型混合直流断路器模型,研究不同阶段耦合电抗器参数对电流转移、故障限流等作用过程,得到了耦合电抗器参数和阻容参数对电流转移和截断电流峰值的影响规律,确定了相关参数的取值,并进行了初步验证。
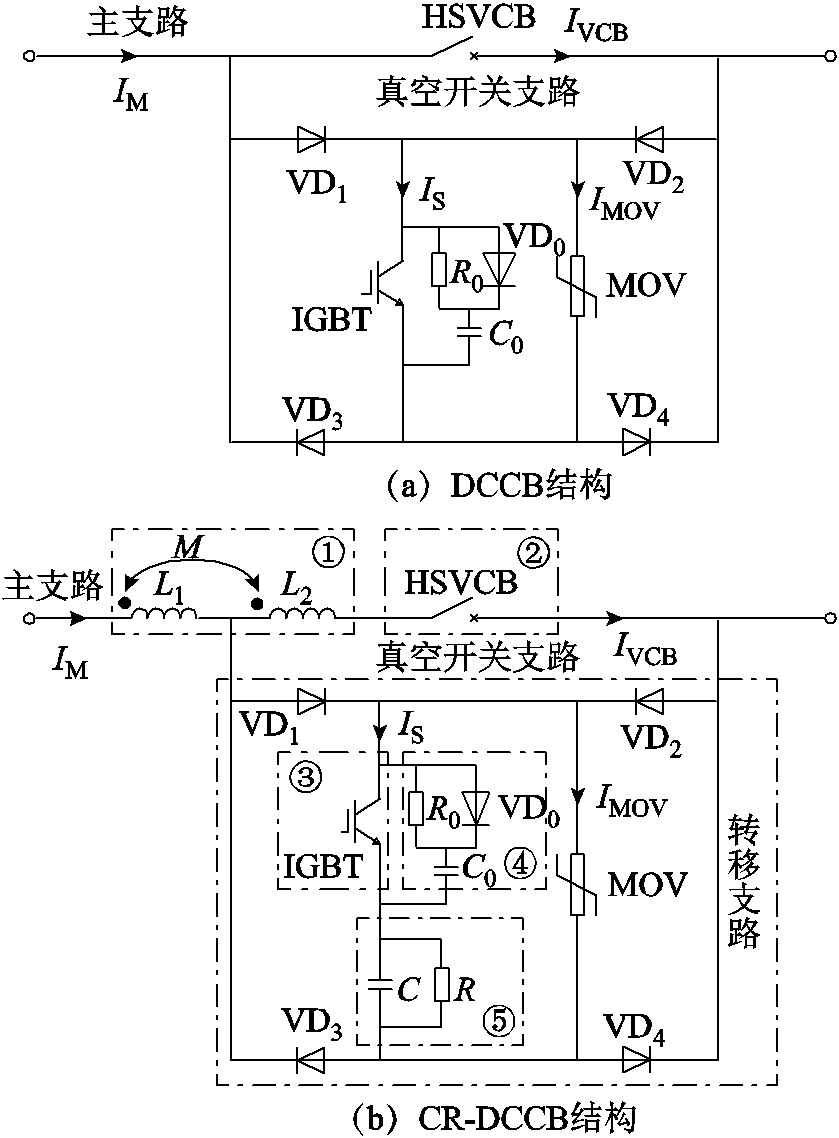
传统混合式直流断路器拓扑结构和基于耦合电抗器的阻容型混合直流断路器(Resistance-Capacitance Hybrid DC Circuit Breaker with Coupled Reactor, CR-DCCB)拓扑结构如图1所示。CR-DCCB相较于DCCB增加了耦合电抗器和阻容限流元件,其中耦合电抗器①的一、二次绕组分别串联于主支路和真空开关支路,IGBT③和缓冲电路④构成固态开关支路,阻容元件⑤串联于上述固态开关支路,VD1、VD2、VD3、VD4构成桥式电路,可实现故障电流的双向开断,MOV作为耗能支路。其中IM为主支路电流、IVCB为真空开关电流、IS为固态开关支路电流、IMOV为MOV支路电流。

图1 DCCB与CR-DCCB拓扑结构
Fig.1 Topology diagram of DCCB and CR-DCCB
在故障发生时,耦合电抗器作为限流电抗器在一定程度上可限制故障电流,待检测到故障后固态开关合闸,快速真空开关接收分闸命令。由于快速真空开关存在一定的分闸时间(一般为0.5~2ms),触头仍然处于闭合状态,此阶段由于耦合电抗器二次侧电感和互感的阻碍作用,强迫真空开关支路电流向固态开关支路转移。在上述转移过程后期或者转移完成后,真空开关触头分离。在故障电流完全转移到固态开关支路后,阻容元件可以实现限制故障电流,降低系统故障电流峰值进而减小了固体开关开断电流需求,可以在一定程度减少IGBTs并联数量和容量,降低整机成本。CR-DCCB和DCCB的电流由真空开关向固态开关支路的转移过程不同,DCCB是依靠真空开关弧压,转移起点时刻是触头分离时刻,而CR-DCCB依靠的是耦合电抗器,转移起点是检测到故障且固态开关导通时刻,即CR-DCCB电流转移过程早于DCCB。
CR-DCCB和DCCB的开断过程波形分别如图2a和图2b所示,其中UMOV为断路器端电压。DCCB在开断电流大于10kA时,由于真空电弧弧压较低(一般为20~40V),真空开关触头分离后,电流开始由真空开关向固态开关支路转移,自然换相过程可达几ms以上甚至换相失败,同时无限流效果,故障电流发展到较高水平,对固态开关开断容量需求较高。而CR-DCCB在故障发生(1ms时)后,耦合电抗器可以起到一定的限流作用。故障检测单元在2ms时检测到故障,同时向固态开关发出合闸命令,向快速真空开关发出分闸命令,固态开关微秒级实现合闸导通,快速真空开关分闸需要0.5~2ms,此时触头仍然处于闭合状态。耦合电抗器二次绕组和互感的阻碍作用强迫电流由真空开关支路向固态开关支路转移,而不是依靠弧压实现电流转移(具体分析见第2节t2~t3阶段分析),此转移过程可以控制在1ms之内。而真空开关触头分离时刻是在上述转移过程后期或转移完成后,真空开关属于无弧或少弧操作,电气寿命可更长。而传统DCCB是依靠真空开关弧压实现的自然换相。待转移完成后固态开关承担主电流,耦合电抗器一次绕组和阻容元件可以限制故障电流峰值,故障电流由DCCB的15.3kA降低至CR-DCCB的8.1kA,避雷器耗能时间也缩短。综上所述,由于耦合电抗器可大幅加速电流转移过程,而阻容元件在电流转移到固态开关支路后限制其电流峰值,在正常通流过程中不会额外增加通态损耗。
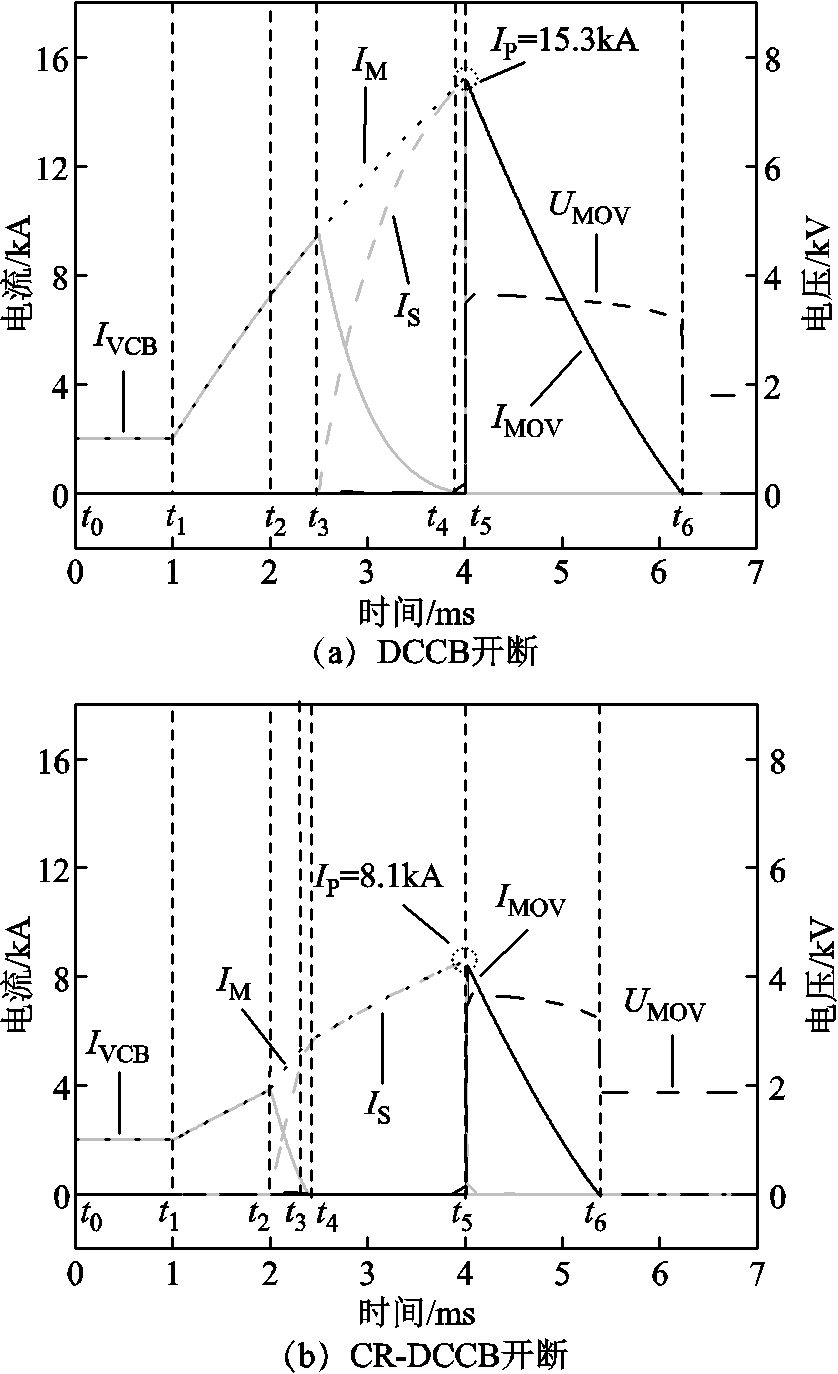
图2 DCCD和CR-DCCB开断过程对比
Fig.2 Comparison diagram of the DCCB and CR-DCCB
下面以正向故障开断为例,不同阶段电流路径示意图如图3所示。图中uN为系统电压,RS、LS分别为等效线路电阻和电感,Rload、Lload分别为等效负载电阻和电感。
1)正常通流阶段(t0 ~ t1)
系统正常通流阶段时,系统额定电流i0表示为
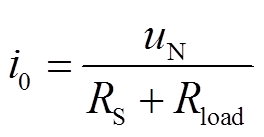 (1)
(1)
2)故障检测阶段(t1 ~ t2)
短路故障发生后,故障电流迅速增加,耦合电抗器可以起到一定的限流作用,耦合电抗器和系统电抗共同决定电流上升率,即
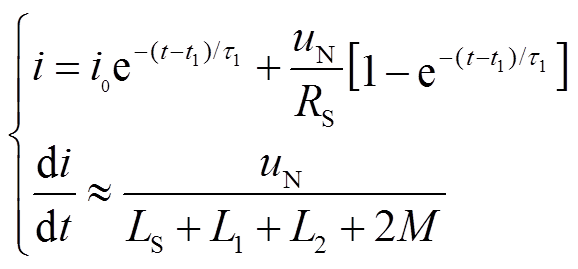 (2)
(2)
式中,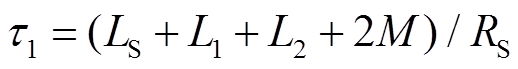 ;L1为一次电感;L2为二次电感;M为互感。
;L1为一次电感;L2为二次电感;M为互感。
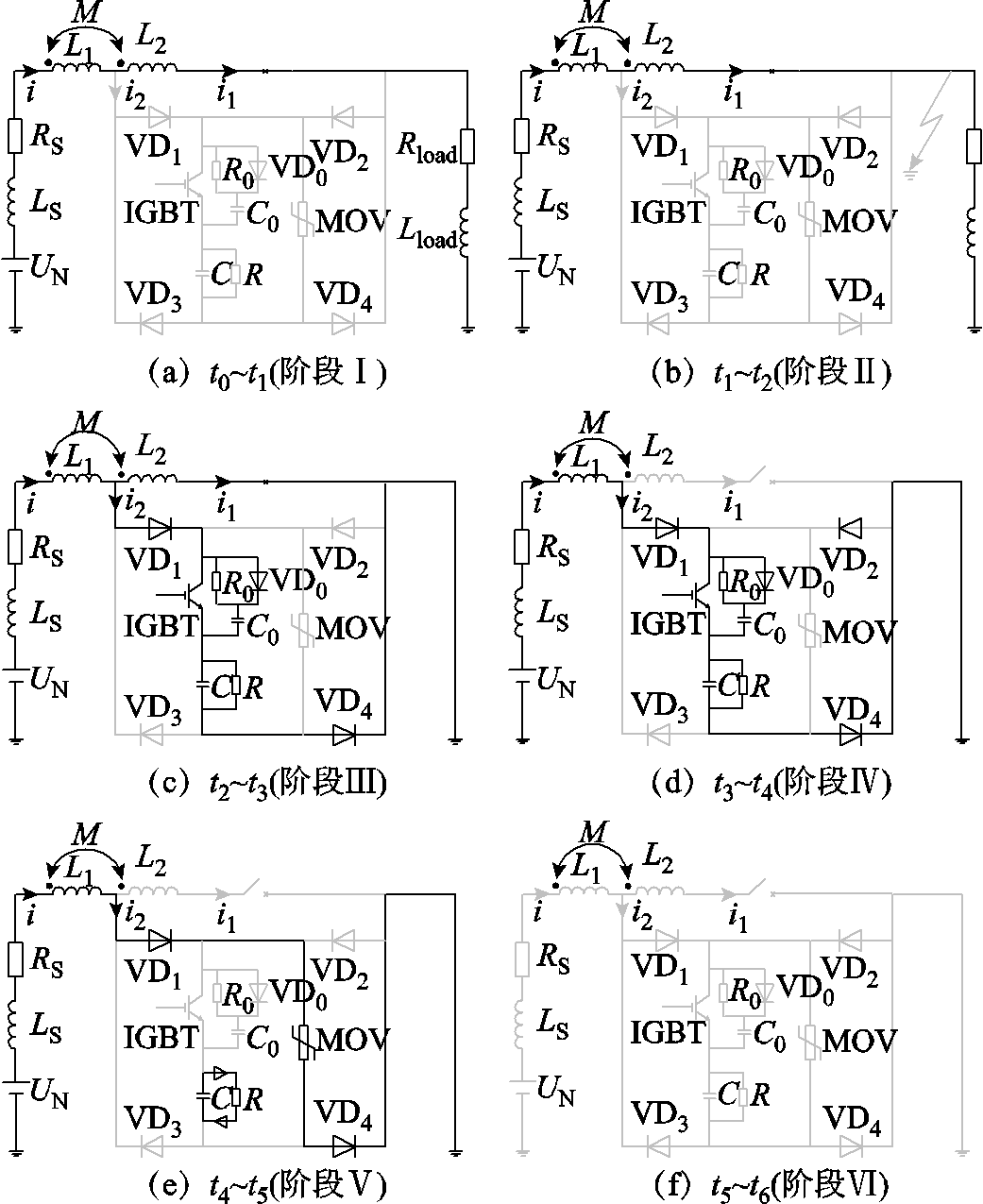
图3 不同阶段电流路径示意图
Fig.3 Schematic diagram of current path at different stages
3)电流转移阶段(t2 ~ t3)
检测到故障后,同时向固态开关发出导通命令和快速真空开关分闸命令,固态开关微秒级实现合闸导通,快速真空开关分闸需要0.5~2ms。此时触头仍然处于闭合状态,由于耦合电抗器的作用电流开始从由真空开关转移至固态开关。根据电流KCL定律和耦合原理,此阶段CR-DCCB满足
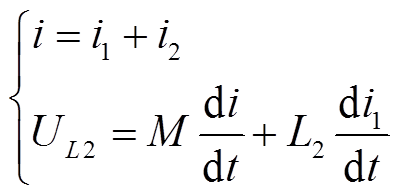 (3)
(3)
式中,UL2为二次绕组L2的压降;i、i1、i2分别为主支路电流、真空开关支路和固态开关支路电流。由于电流转移阶段固态开关支路导通压降较小[11],与之并联的耦合电抗器二次侧和真空开关支路电压较低,可将UL2≈0,进而得到
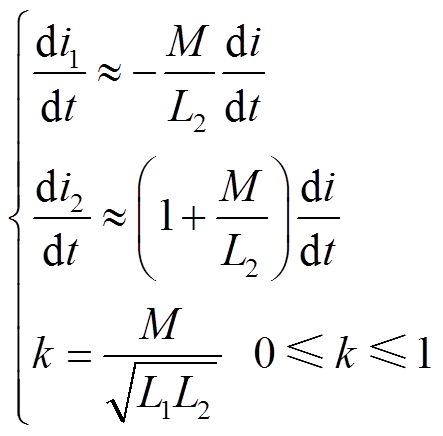 (4)
(4)
式中,k为一、二次绕组耦合系数。
为研究耦合系数对电流转移影响,此阶段假设阻容取值较小,因此对转移过程影响较小。将耦合电抗器进行等效化简,由式(4)可知
 (5)
(5)
耦合系数一般取0.85~0.95,再次取k≈1,进而简化得到
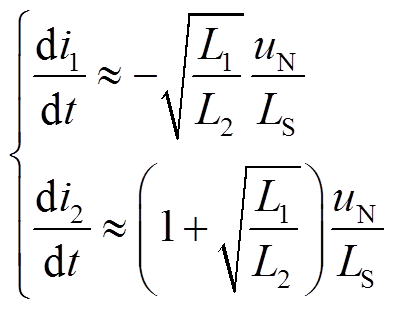 (6)
(6)
由式(6)可知,当耦合电抗器一、二次电感比值较大时,真空开关支路电流下降率较大,固态开关支路电流上升率较大,说明耦合电抗器可以实现加速电流转移,且一、二次电感比值越大,转移越快。
4)真空开关触头分闸阶段(t3 ~ t4)
在上述转移过程(t2 ~ t3)中,快速真空开关由于其固有的分闸时间,触头仍然处于闭合状态。在电流转移的后期或转移完成后,真空开关触头分离。触头分离是在转移完成后还是后期主要取决于转移时间和分闸时间的大小。如果分闸时间大于转移时间,则真空开关触头分离不产生电弧。当分闸时间小于转移时间,则真空开关在转移过程后期电流较小的阶段拉弧,即产生小电流电弧。因此CR-DCCB中真空开关属于无弧或少弧分断。
5)真空开关介质恢复阶段(t4 ~ t5)
真空开关电弧在t4时刻熄灭,介质强度开始恢复,主电流完全由固态开关支路承担,该阶段电流路径如图3c所示,t2时刻电容电压为零,根据以上条件可列写
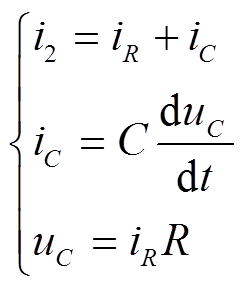 (7)
(7)
根据式(7)计算得到固态开关支路瞬态电流表达式见式(8),阻容元件的电容参数主要用于限制暂态电压,而稳态电流主要由电阻进行限流。
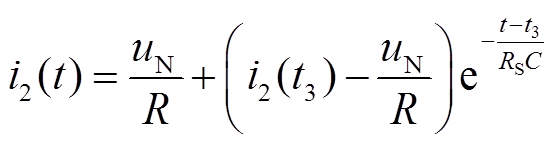 (8)
(8)
6)避雷器泄能阶段(t5 ~ t6)
IGBT关断后,系统残余能量由MOV耗散,避雷器吸能主要因素为系统电感和线路电流大小。根据文献[22]取γ为0.438,因此避雷器吸收的能量EMOV为
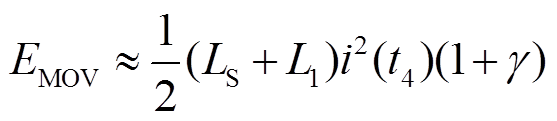 (9)
(9)
CR-DCCB模型包括真空开关模型、避雷器、固态开关和外电路模型等,其中真空开关模型是其重点建模部分,其他模型可采用电路模型进行参数设置。
3.1.1 真空开关模型
真空电弧模型包括燃弧和介质恢复阶段模型。在燃弧过程中电弧电压与电流大小、燃弧时间都有一定的关系,一般稳定在20V。电弧电压燃弧过程主要分为三个阶段:起弧阶段、稳定燃烧阶段、电弧熄灭阶段。弧后介质恢复过程通常采用真空电弧连续过渡模型[23],该模型的具体数学模型为
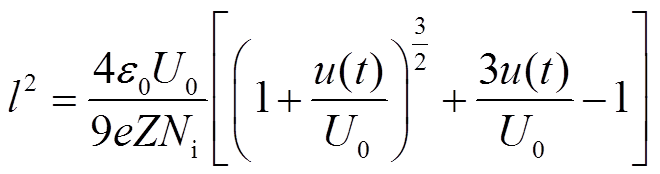 (10)
(10)
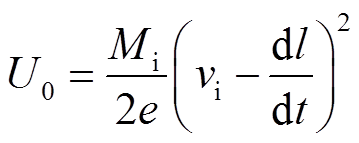 (11)
(11)
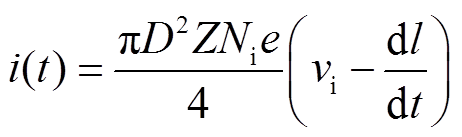 (12)
(12)
式中,ε0为真空介电常数;l为新阴极和等离子体之间正离子鞘层厚度;U0为鞘层电位;e为电子电荷量;Z为离子所带平均电荷数;Ni为鞘层边缘离子密度;u(t)为极间电压;Mi为金属离子质量;vi为离子运动速度;dl/dt为鞘层发展速度;i(t)为鞘层发展开始后的弧后电流;D为电极直径。计算时除了设定常数外,还需给定Z、vi、D等初始值,并用式(13)、式(14)计算鞘层边缘离子密度及初始值[24]。
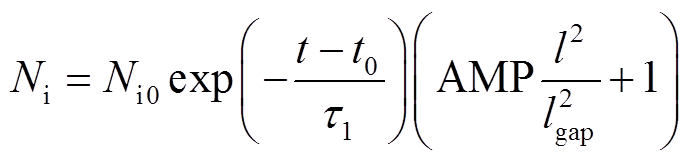 (13)
(13)
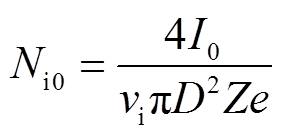 (14)
(14)
式中,lgap为真空间隙距离;AMP为控制两电极间离子空间电荷分布系数;τ1为离子扩散时间常数。
3.1.2 其他参数设置
建立CR-DCCB的仿真模型,与DCCB相比在相同的参数条件下,增加耦合电抗器和阻容元件,IGBT型号为TIM1500ESM33-PSA011单管模块,仿真系统参数见表1。
表1 仿真参数
Tab.1 Simulation parameters

系统参数数值 系统电压/V线路电阻/Ω线路电感/μH负载电阻/Ω负载电感/μH耦合电感L1, L2/μH耦合系数固态开关支路杂散电感/μH固态开关支路杂散电阻/mΩ固态开关通态压降/V阻容元件R/Ω, C/μF避雷器保护电压/V1 8000.033000.874 500300, 500.981.212.70.1, 503 600
3.1.3 仿真模型
直流电压源设置为1 800V,用于模拟城市轨道直流供电系统。1ms时系统发生故障,2ms时检测到故障并向固态开关发出合闸命令和快速真空开关分闸命令,在2.5ms时快速真空开关触头分离,4ms时IGBT关断,避雷器吸收残余能量,完成整体开断。总体仿真模型如图4所示。
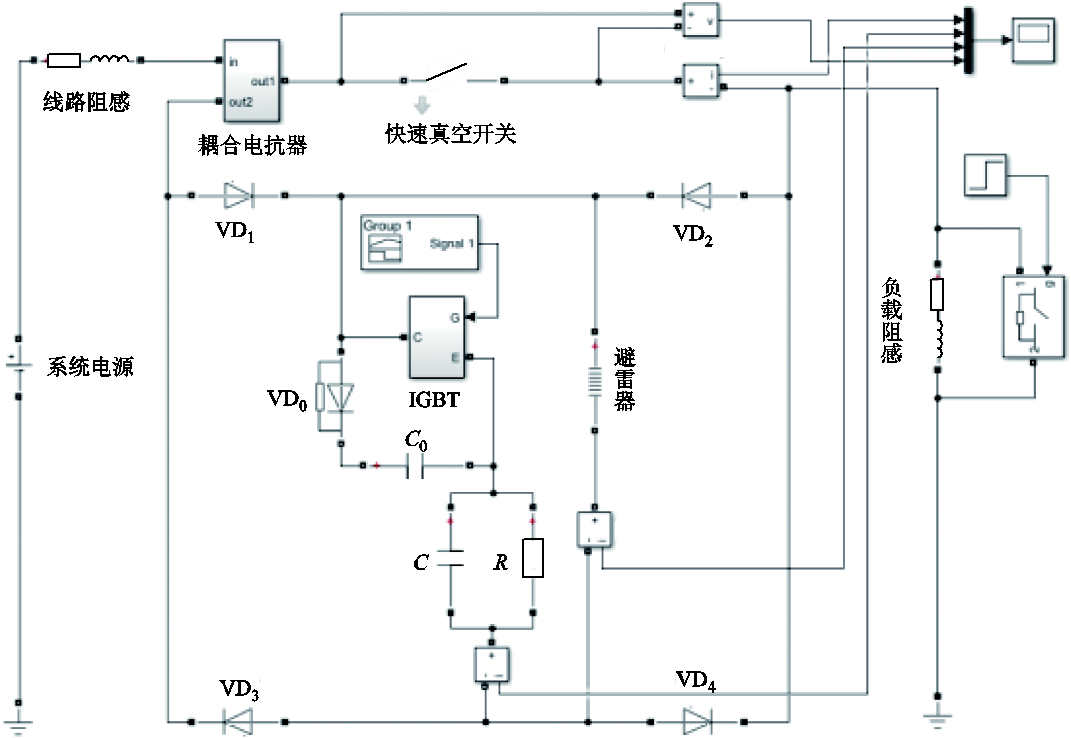
图4 仿真模型
Fig.4 The simulation model
3.2.1 耦合电抗器参数影响
当耦合电抗器一、二次绕组(L1、L2)为50μH、100μH、150μH、200μH、250μH、300μH,k值分别取0.6~1时,得到耦合系数k对阶段Ⅲ转移时间的影响如图5所示。随着耦合系数k的增加,转移时间随之减小,因此,在实际情况中应使两绕组的耦合系数k接近1,即达到全耦合。
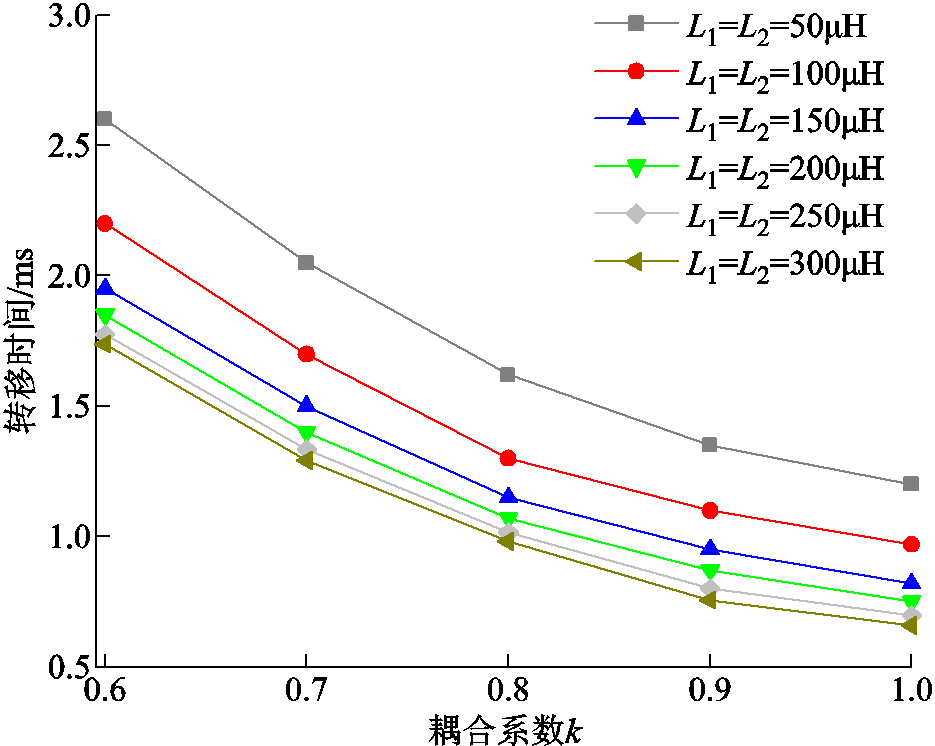
图5 耦合系数k对阶段Ⅲ转移时间的影响
Fig.5 The influence of coupling coefficient k on the phase Ⅲcommutation time
由以上仿真结果,耦合系数选取0.98,为探究L1/L2比值对转移时间影响规律,取L2的电感值为50μH,L1的取值分别为50~300μH,研究L1/L2的比值n对转移时间的影响如图6所示。可以看出随着n的增加,转移时间随之减少,当一次绕组取300μH,二次绕组取50μH时,转移时间为0.38ms,但如果二次绕组取更小时,转移时间基本保持不变。因此,实际工程中可选取较大的一、二次电感比值以便加快电流转移过程。
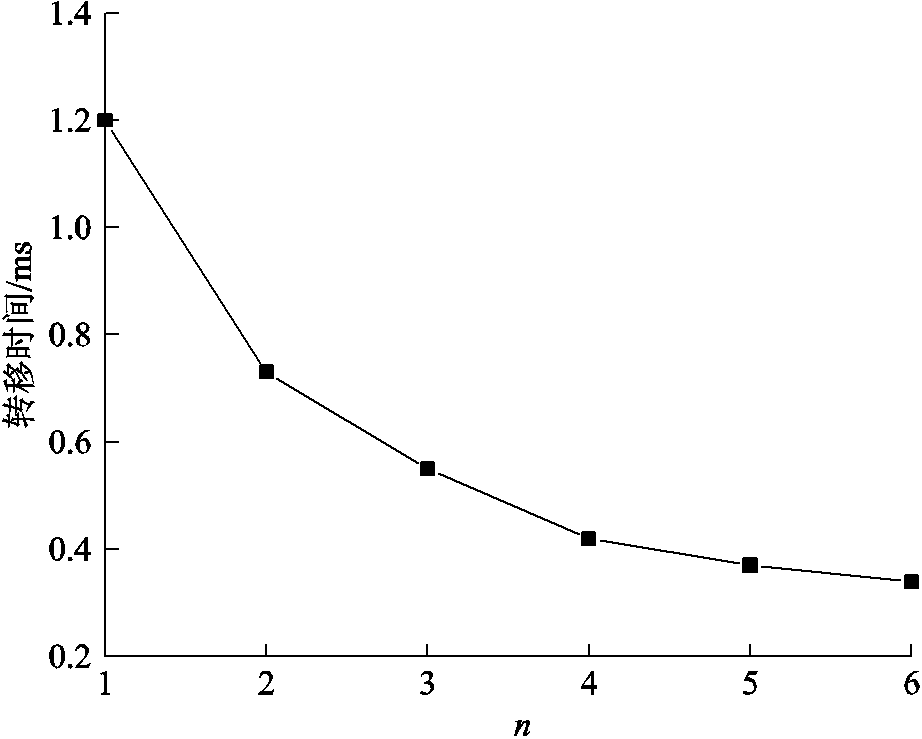
图6 一、二次电感比值对转移时间的影响
Fig.6 The influence of the ratio of primary and secondary winding to commutation time
3.2.2 阻容元件参数影响
由以上仿真可知,耦合电抗器参数选取如下:耦合系数k为0.98,一、二次绕组L1、L2分别为300μH、50μH。阻容元件参数对电流峰值及转移时间的影响如图7所示,电容参数对截断电流峰值IP影响较小,但随着电容从0增加到50μF,转移时间可以大幅减小。在相同的电容参数下,随着电阻的增加,截断电流峰值减小,转移时间增加,说明电阻可以有效限制固态开关支路电流峰值,但也影响电流转移,综合考虑阻容元件参数既能限制截断电流峰值,对电流转移时间影响程度又最小,因此阻容元件参数电容为50μF,电阻为0.1Ω。
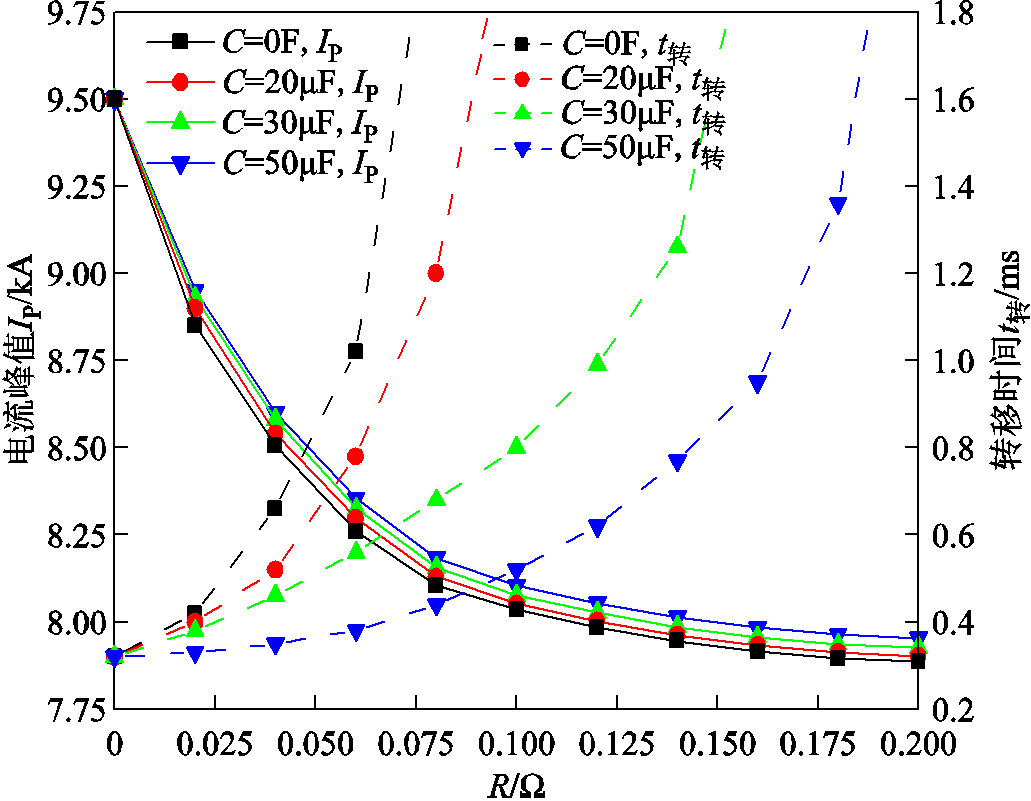
图7 阻容参数对电流峰值及转移时间的影响
Fig.7 Influence of the RC parameters on the current peak value and commutation time
由于系统电感能量需要避雷器耗散,本文提出的CR-DCCB和传统的DCCB的避雷器吸收能量对比如图8所示。CR-DCCB可将避雷器耗能由51.5kJ降至28.7kJ,大幅缩短避雷器耗能时间,进而减少整机开断时间。
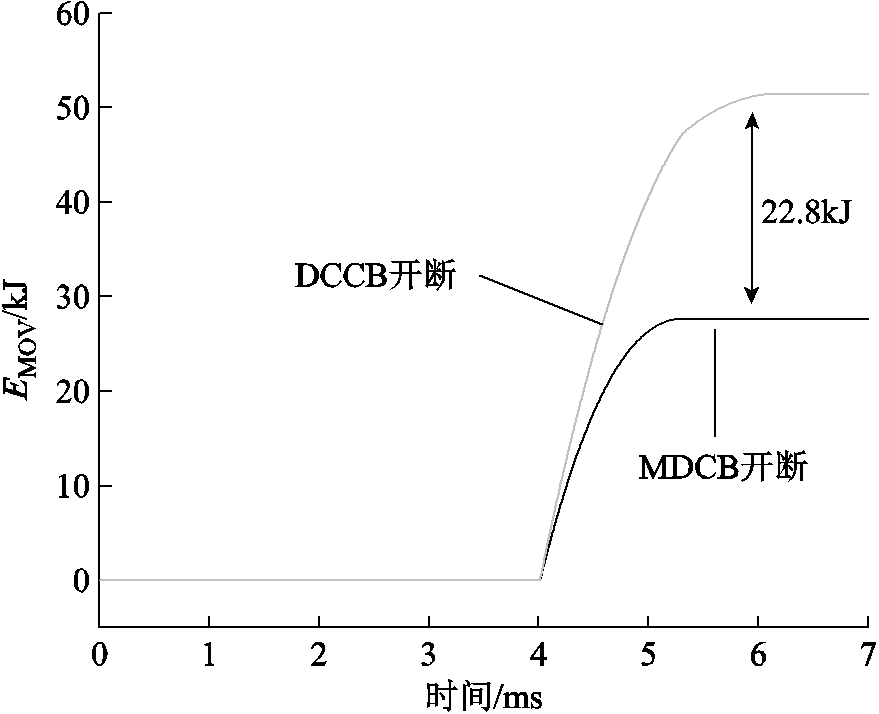
图8 避雷器吸收能量
Fig.8 Energy dissipation waveforms of arrester
CR-DCCB和DCCB整机开断波形如图9所示。CR-DCCB开断可以将截断电流峰值从15.3kA降至8.1kA,避雷器耗能时间从2.2ms降至1.3ms,整机开断时间缩短了1.9ms。
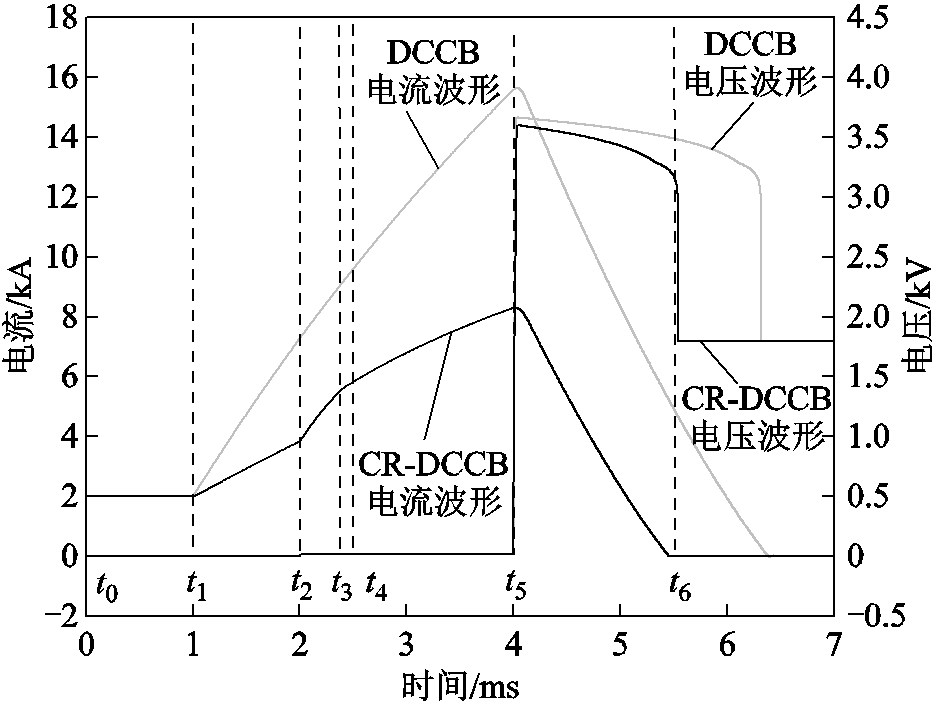
图9 CR-DCCB和DCCB整机开断波形
Fig.9 Breaking waveforms of the CR-DCCB and DCCB
3.2.3 系统电感参数影响
为探究系统电抗参数对转移时间的影响,研究了系统电感从250~900µH变化时,转移时间的变化,具体如图10所示。随着系统电感的减小,转移时间逐渐减小,这与式(6)中系统电感对转移过程影响的理论分析一致。
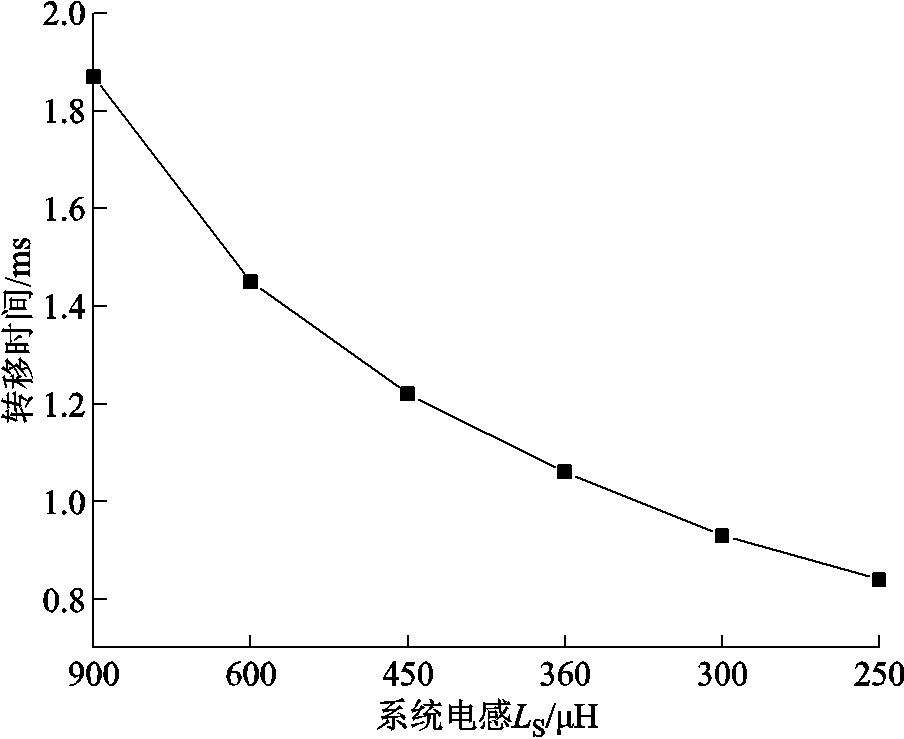
图10 系统电感对转移时间的影响
Fig.10 Influence of the system inductance on commutation time
综上所述,耦合电抗器设计应选一、二次绕组电感量比值相对较大且耦合系数高,同时耦合电抗器电感与系统电感相当时可同时起到较好的限流和加速电流转移效果。阻容元件中电阻可起到较好的限制固态开关支路电流的效果,但不易过大,一般选取0.1Ω,电容可以较好地起到加速转移效果,综合经济和性能要求可选取50μF以内。
为验证CR-DCCB拓扑结构理论分析结果的有效性,搭建了CR-DCCB实验电路如图11所示。电容器组和电感串联放电产生低频振荡电路用于模拟直流故障电流,晶闸管负责引入故障电流,其中VD为保护二极管,防止电容反向充电。CR-DCCB结构主要包括耦合电抗器、真空开关、IGBT模块、阻容元件、避雷器。耦合电抗器一、二次绕组采用同轴绕线以尽可能增加一、二次耦合系数。经测量得一次绕组电感为137μH,二次绕组电感为24.5μH,耦合系数为0.84,阻容值分别为0.01Ω、10μF。
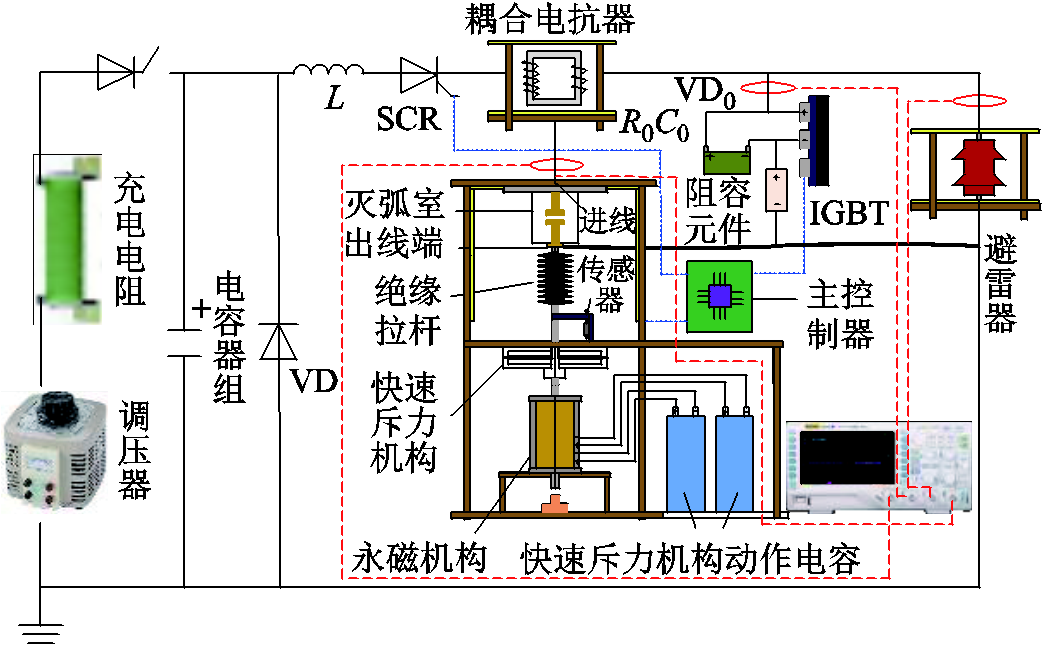
图11 实验电路
Fig.11 The experimental circuit
4.2.1 DCCB和CR-DCCB开断对比分析
实验开断波形如图12所示。从图12a可以看出固态开关截断电流峰值为1 980A,电流转移时间约为283μs,避雷器耗能时间为186μs。图12b为CR-DCCB开断波形,在同等条件下,可以看出固态开关截断电流峰值被限制至950A,电流转移时间缩短至约204μs,避雷器耗能时间约为124μs。初步验证了基于耦合电抗器的阻容型混合直流断路器拓扑可加速电流转移过程、降低避雷器耗能时间,进而减小整机开断时间。
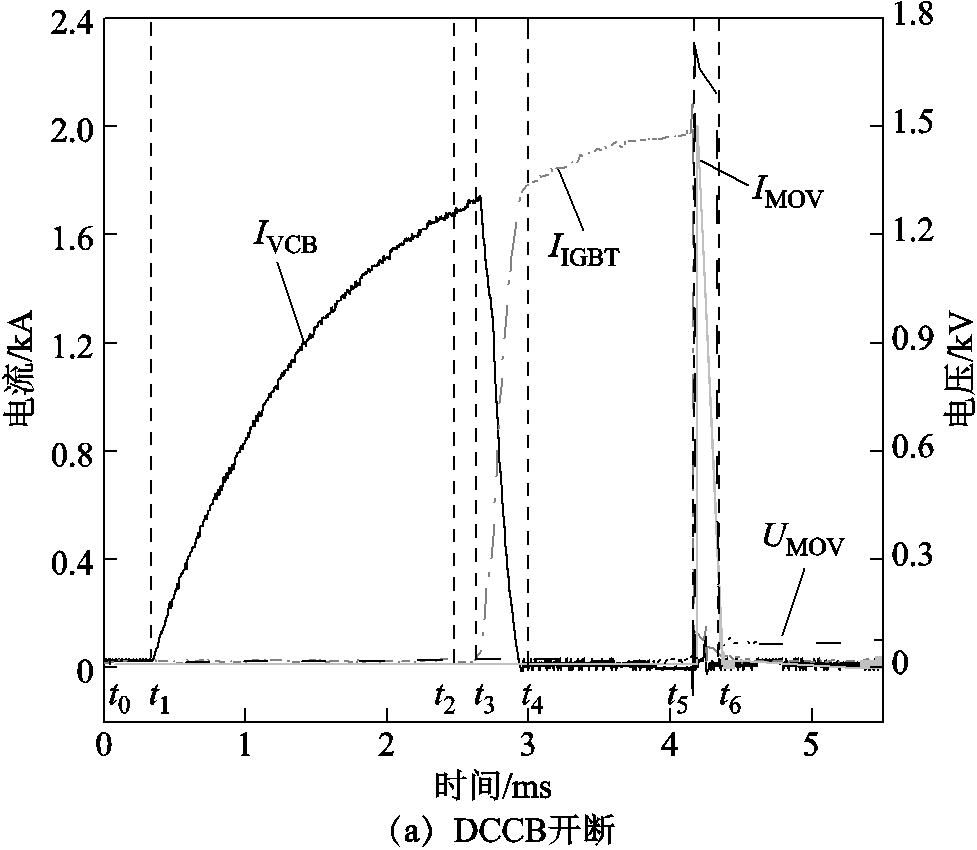
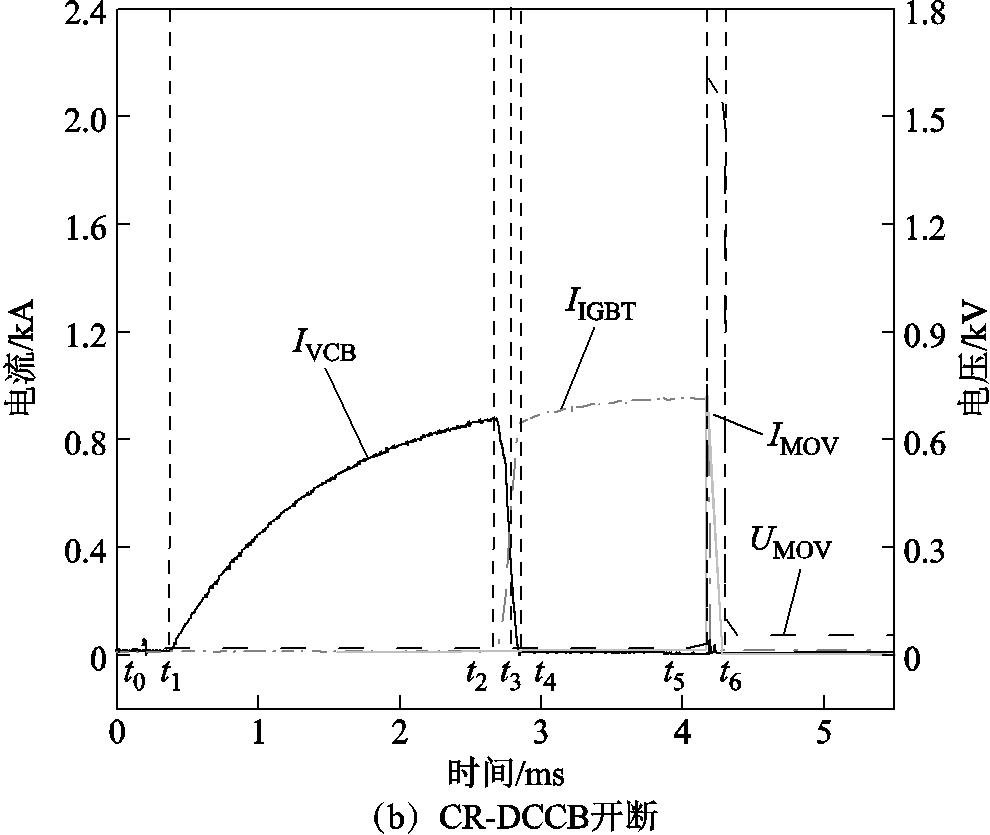
图12 实验开断波形
Fig.12 Experimental breaking waveforms
4.2.2 耦合电抗器一、二次变比对电流转移特性影响
为进一步探究耦合电抗器参数对电流转移特性的影响,进行了耦合电抗器一、二次变比对电流转移特性影响的实验和仿真对比研究。在二次绕组为12.8µH时,改变L1/L2比值从5~18,测试得到一、二次绕组变比对电流转移过程的影响如图13所示,随着变比的增加,电流转移时间减小,仿真与实验规律基本一致。实验中在变比大于10时,电流转移时间变化不明显是由于耦合电抗器存在磁饱和,因此在设计耦合电抗器时需要重视磁饱和影响。
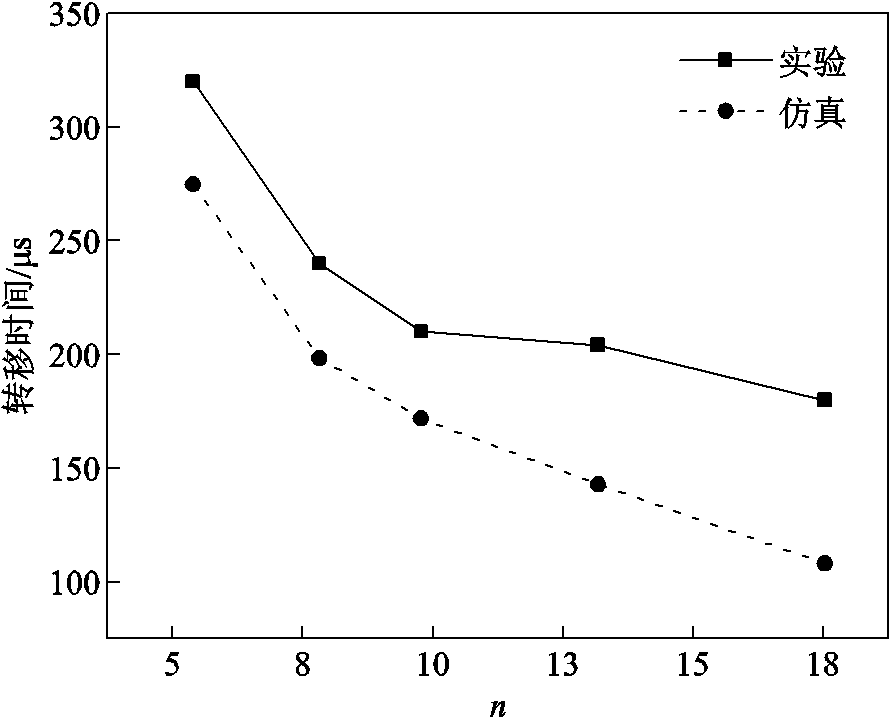
图13 耦合电抗器变比对电流转移时间影响
Fig.13 Influence of L1/L2 on current commutation time
1)本文提出一种耦合电抗器的阻容型混合直流断路器拓扑结构,理论分析得到耦合电抗器和阻容元件参数对电流峰值、电流转移速度、避雷器耗能等影响规律。
2)仿真分析了耦合电抗器一、二次绕组取值分别为300μH、50μH,阻容元件取值为0.1Ω、50μF时,电流转移时间从1.5ms缩短至0.5ms,故障电流峰值可降低47.1%,整机关断时间可缩短1.9ms,该拓扑结构可加速电流转移和实现故障限流。
3)搭建实验电路进行初步验证,实验结果表明所提出CR-DCCB拓扑结构能够实现抑制故障电流、加速电流转移、缩短避雷器清除故障电流时间。初步验证了该拓扑结构的可行性和有效性,为后续样机的研制提供了参考依据。
参考文献
[1] 吴翊, 荣命哲, 钟建英, 等. 中高压直流开断技术[J]. 高电压技术, 2018, 44(2): 337-346.
Wu Yi, Rong Mingzhe, Zhong Jianying, et al. Medium and high voltage DC breaking technology[J]. High Voltage Engineering, 2018, 44(2): 337-346.
[2] 秦涛涛, 董恩源, 刘贵新, 等. 真空直流开断固有介质恢复强度研究[J]. 中国电机工程学报, 2016, 36(5): 1453-1459.
Qin Taotao, Dong Enyuan, Liu Guixin, et al. Free recovery of dielectric strength after DC interruption in vacuum[J]. Proceedings of the CSEE, 2016, 36(5): 1453-1459.
[3] 程显, 杨培远, 葛国伟, 等. 基于真空与SF6气体串联间隙的新型高压直流断路器介质恢复特性[J]. 高电压技术, 2019, 45(8): 2393-2402.
Cheng Xian, Yang Peiyuan, Ge Guowei, et al. Dielectric recovery characteristics of serial vacuum and SF6 gaps in novel HVDC circuit breakers[J]. High Voltage Engineering, 2019, 45(8): 2393-2402.
[4] 张梓莹, 梁德世, 蔡淼中, 等. 机械式高压直流真空断路器换流参数研究[J]. 电工技术学报, 2020, 35(12): 2554-2561.
Zhang Ziying, Liang Deshi, Cai Miaozhong, et al. Research on commutation parameters of mechanical HVDC vacuum circuit breaker[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2554-2561.
[5] 邓二平, 应晓亮, 张传云, 等. 新型通用混合型直流断路器用IGBT测试平台及测试分析[J]. 电工技术学报, 2020, 35(2): 300-309.
Deng Erping, Ying Xiaoliang, Zhang Chuanyun, et al. Novel general-purpose IGBT test platform for hybrid DC circuit breakers and analysis[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 300-309.
[6] Meyer J M, Rufer A. A DC hybrid circuit breaker with ultra-fast contact opening and integrated gate-commutated thyristors (IGCTs)[J]. IEEE Transactions on Power Delivery, 2006, 21(2): 646-651.
[7] Novello L, Baldo F, Ferro A, et al. Development and testing of a 10-kA hybrid mechanical–static DC circuit breaker[J]. IEEE Transactions on Applied Super-conductivity, 2011, 21(6): 3621-3627.
[8] 韩乃峥, 贾秀芳, 赵西贝, 等. 一种新型混合式直流故障限流器拓扑[J]. 中国电机工程学报, 2019, 39(6): 1647-1658, 1861.
Han Naizheng, Jia Xiufang, Zhao Xibei, et al. A novel hybrid DC fault current limiter topology[J]. Proceedings of the CSEE, 2019, 39(6): 1647-1658, 1861.
[9] 程显, 徐鹏飞, 葛国伟, 等. 机械式真空直流断路器弧后电流测量研究[J]. 电工技术学报, 2021, 36(16): 3516-3524.
Cheng Xian, Xu Pengfei, Ge Guowei, et al. Research on measurement of post-arc current of mechanical vacuum DC circuit breaker[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3516-3524.
[10] 王建华, 项彬, 杨騉, 等. 超导限流直流开断技术研究[J]. 电工技术学报, 2019, 34(20): 4196-4207.
Wang Jianhua, Xiang Bin, Yang Kun, et al. Superconducting fault current limiting DC current interrupting technology[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4196-4207.
[11] Pei Xiaoze, Smith A C, Cwikowski O, et al. Hybrid DC circuit breaker with coupled inductor for automatic current commutation[J]. International Journal of Electrical Power & Energy Systems, 2020, 120: 106004.
[12] 袁佳歆, 陈鹤冲, 陈凡, 等. 一种快速响应直流限流器拓扑结构与参数设计[J]. 电工技术学报, 2021, 36(8): 1646-1657.
Yuan Jiaxin, Chen Hechong, Chen Fan, et al. Topology and parameter design of a fast response DC current limiter[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1646-1657.
[13] 许建中, 张继元, 李帅, 等. 一种阻容型限流式直流断路器拓扑及其在直流电网中的应用[J]. 中国电机工程学报, 2020, 40(8): 2618-2628.
Xu Jianzhong, Zhang Jiyuan, Li Shuai, et al. A resistor-capacitor type current-limiting high voltage DC circuit breaker and its application in DC grid[J]. Proceedings of the CSEE, 2020, 40(8): 2618-2628.
[14] 李博, 包涌泉, 彭振东, 等. 基于改进型直流真空断路器弧后暂态仿真及介质恢复特性分析[J]. 电工技术学报, 2021, 36(8): 1752-1760.
Li Bo, Bao Yongquan, Peng Zhendong, et al. Post-arc transient simulation and dielectric recovery analysis based on improved DC vacuum circuit breaker[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1752-1760.
[15] Lazzari R, Piegari L. Design and implementation of LVDC hybrid circuit breaker[J]. IEEE Transactions on Power Electronics, 2019, 34(8): 7369-7380.
[16] 葛国伟, 程显, 王华清, 等. 低压混合式直流断路器中真空电弧电流转移判据[J]. 电工技术学报, 2019, 34(19): 4038-4047.
Ge Guowei, Cheng Xian, Wang Huaqing, et al. Investigation on the vacuum arc current commutation criteria of the low voltage DC hybrid circuit breaker[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 4038-4047.
[17] 秦涛涛, 张颖, 董恩源, 等. 真空直流强迫过零开断过充特性[J]. 高电压技术, 2020, 46(8): 2663-2669.
Qin Taotao, Zhang Ying, Dong Enyuan, et al. Overcharge characteristics in vacuum DC forced current-zero interruption[J]. High Voltage Engineering, 2020, 46(8): 2663-2669.
[18] Pei Xiaoze, Cwikowski O, Smith A C, et al. Design and experimental tests of a superconducting hybrid DC circuit breaker[J]. IEEE Transactions on Applied Superconductivity, 2018, 28(3): 1-5.
[19] 葛国伟, 程显, 张鹏浩, 等. 多断口真空开关电弧磁场调控需求与机理[J]. 电工技术学报, 2018, 33(21): 5007-5014.
Ge Guowei, Cheng Xian, Zhang Penghao, et al. Mechanism and demand of the magnetic arc control in multi-break VCBs[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 5007-5014.
[20] 程显, 王华清, 葛国伟, 等. 城市轨道交通1800 V高速混合式直流断路器研制[J]. 电力自动化设备, 2020, 40(1): 212-218.
Cheng Xian, Wang Huaqing, Ge Guowei, et al. Research and design of 1800 V high-speed hybrid DC circuit breaker for urban rail transit system[J]. Electric Power Automation Equipment, 2020, 40(1): 212-218.
[21] 王华清, 程显, 葛国伟, 等. 中压混合式直流断路器真空短间隙介质恢复特性[J]. 电网技术, 2020, 44(1): 377-384.
Wang Huaqing, Cheng Xian, Ge Guowei, et al. Investigation on dielectric recovery performance of short vacuum gap in medium-voltage hybrid DC circuit breakers[J]. Power System Technology, 2020, 44(1): 377-384.
[22] 潘垣, 陈立学, 袁召, 等. 针对直流电网故障的限流与限能技术研究[J]. 中国电机工程学报, 2020, 40(6): 2006-2016.
Pan Yuan, Chen Lixue, Yuan Zhao, et al. Research on current limiting and energy limiting technology for DC power grid fault[J]. Proceedings of the CSEE, 2020, 40(6): 2006-2016.
[23] Andrews J G, Varey R H. Sheath growth in a low pressure plasma[J]. The Physics of Fluids, 1971, 14(2): 339-343.
[24] Huang Chongyang, Liu Xiaoming, Chen Hai, et al. Investigation of arc characteristics of a DC vacuum circuit breaker with double-break under asynchronous interrupting[J]. IEEE Transactions on Plasma Science, 2019, 47(8): 3533-3539.
Abstract DC circuit breaker is an important equipment for the control and protection of urban rail transit system. Its on-off reliability directly affects the operation safety of DC traction power supply system. In order to meet the urgent needs of large capacity high-speed segmentation and current limiting capacity. A resistance-capacitance hybrid DC circuit breaker with coupled reactor (CR-DCCB) is proposed. The primary and secondary windings of the coupled reactor are connected in series with the main branch and the vacuum switch branch, respectively. The structure can accelerate the current transfer process, and the resistive-capacitive elements are connected in series with the solid-state switch branch to limit the fault current peak. To verify the feasibility and effectiveness of the topology. First, the theoretical analysis of the coupling coefficient of coupling reactor and the primary and secondary winding inductance value of the influence of fault current transfer process and the influence of the peak value of fault current resistance capacity components, by improving the coupling coefficient and the primary and secondary winding inductance ratio to shorten the current transfer time, increase the resistance capacity components can limit the fault current peak value. Different from the traditional hybrid DC circuit breaker transfer principle, when the contacts are not separated, the current transfer can be realized by coupling reactor in the early stage. Since the contact separation time of the vacuum switch is in the late stage of the current transfer process, the vacuum switch belongs to less arc or no arc breaking, which can prolong its electrical life. Then, the CR-DCCB simulation model was established in Matlab/Simulink simulation software, and the influence law of coupling reactor parameters and resistance-capacitive elements parameters on current transfer process, current limiting effect and turn-off time of the whole machine was simulated and analyzed, and the optimal parameters of coupling reactor and resistance-capacitive elements were initially determined. Finally, based on the experimental platform of the research group, the experimental circuit under small current was built, and the preliminary experimental verification was carried out. The simulation results were compared and analyzed with the experimental results, and the reasons for the error between simulation and experiment were obtained. The simulation results show that when the inductance of the primary and secondary winding of the coupled reactor is set as 300μH and 50μH, and the resistance and capacitance elements are set as 0.1Ω and 50μF, the current transfer time can be shortened from 1.5ms to 0.5ms, the peak fault current is reduced by 47.1%, and the turn-off time is shortened by 1.9ms. The experimental results show that the current transfer time is shortened from 204μs to 124μs, and the peak fault current is reduced from 1 980A to 950A. Simulation results and experimental results are consistent rule, both verified the current transfer time as the primary and secondary winding inductance ratio increases with the shortened, but when the ratio is more than 10, current transfer time change is not obvious, because the problem of magnetic saturation, therefore when designing the coupling reactor need to attach importance to the influence of magnetic saturation, The conclusion of this paper provides a reference for the subsequent prototype development.
keywords:Medium voltage hybrid DC circuit breaker, DC breaking, current commutation, coupling reactor
DOI:10.19595/j.cnki.1000-6753.tces.211395
中图分类号:TM561
国家自然科学基金项目(51977195,52107170)、河南省重大科技专项(221100240500)、河南省优秀青年科学基金项目(202300410370)、河南省高校科技创新人才(21HASTIT022)资助。
收稿日期 2021-09-03
改稿日期 2021-11-04
程 显 男,1982年生,教授,博士生导师,研究方向为高压电器及高电压新技术,重点研究混合断路器技术、多断口真空开关技术。E-mail:chengxian@zzu.edu.cn
葛国伟 男,1987年生,博士,讲师,研究方向为智能化高压电器及高电压新技术,重点研究多断口真空开关技术、真空电弧动态恢复特性。E-mail:ggw@zzu.edu.cn(通信作者)
(编辑 赫蕾)