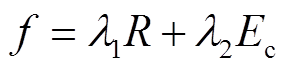（1）
摘要 线间潮流控制器（IPFC）拥有强大的潮流调控能力，可为解决大规模新能源接入背景下的潮流调控问题提供全新的解决方案。该文提出一种计及风电出力不确定性的含IPFC电力系统安全约束经济调度方法，首先基于MARKOV链生成风电出力场景，构建相应概率风险指标以描述系统安全性，并给出了兼顾经济性与安全性的优化目标函数；然后，在充分考虑双回线结构IPFC控制特性的情况下建立了故障前后电力系统的等式/不等式约束；最后，针对所建立的强非线性安全约束经济调度优化模型，设计了基于粒子群算法的计算构架并实现了模型的求解。基于江苏电网的算例分析表明，利用该文方法获得的策略比基于传统方法获得的策略能更好地满足潮流安全约束，且准确地计及了IPFC的控制特性，具有较高的应用价值。
关键词：线间潮流控制器（IPFC） 双回线控制特性 风电场景 经济调度
在“碳达峰、碳中和”目标提出的背景下，清洁能源将迎来更加持续、高速的发展，我国电力系统深度脱碳已成为必经之路。随着大规模风电不断接入，电力系统安全、特别是潮流安全问题，受到广泛关注。柔性交流输电系统（Flexible AC Transmission System, FACTS）是基于电力电子、控制与通信等方面的综合技术[1-4]。FACTS可在不改变网架结构的基础上，迅速地调控电网的线路参数，与其他设备一起优化电网潮流，以提高电网的安全性和经济性[5-6]。
线间潮流控制器（Interline Power Flow Controller, IPFC）是功能强大的综合型FACTS设备之一。与统一潮流控制器（Unified Power Flow Controller, UPFC）不同的是，IPFC串联于多条线路，可以解决负荷密集型受端电网输电廊道稀缺、潮流分布不均导致的断面输电能力受限等一系列输电难题[7-10]。在含FACTS设备的安全约束经济调度方面，文献[11-12]提出新型算法，解决了含UPFC系统在突发故障后的潮流越限问题。文献[13]将FACTS引入潮流优化问题中，在保证安全约束的前提下提高了系统的经济性。文献[14]考虑了N-1突发情况，以系统最大负载能力为目标确定了输电系统中UPFC的安装站址和容量。以上文献采用的UPFC模型均隐含假设UPFC注入电压在偶发事件前后保持不变。而在实际运行中，UPFC通常在毫秒级[15]时间内快速调整注入电压，使受控线路潮流在突发事件发生后保持不变。模型假设与实际操作的不一致不可避免地会带来误差，导致调度决策不当。在某些情况下，这种调度决策甚至会威胁系统安全，如线路潮流越限。IPFC也存在相同的问题。并且，国内关于IPFC的优化调度研究刚刚起步[16-18]，目前的研究都没有考虑风电接入对系统安全的影响。而风电的接入会带来潮流的大规模转移，部分潮流可能会越限[19-20]。另外，现有研究采用的IPFC模型都是单回线的IPFC模型，而国内220kV及以上电压等级的输电线路往往采用并联双回线路的结构，单回线IPFC模型应用在双回线路的工程场景下很可能不够准确，无法反映IPFC所控线路断开一回线后的控制特性，大大影响了模型的实用性和准确性。
上述研究存在两方面不足：①在研究含IPFC的安全约束经济调度问题时，故障前后默认IPFC注入电压不变，没有准确地计及IPFC的控制特性。且上述文献都采用单回线的IPFC模型，出于安全性考虑，国内220kV及以上电压等级的输电线路往往采用并联双回线路的结构。因此，采用IPFC单回线模型得到的优化结果在工程实践方面并不严谨。②目前关于IPFC的优化调度问题都没有考虑风电接入对系统的影响。而随着风电并网的比例不断提高，风电出力会带来大规模的潮流转移，很可能导致线路潮流越限。同时，风电对潮流的影响也具有不确定性，需要考虑不同的风电出力场景[21]。
针对以上两个问题，本文提出一种计及风电场景和双回线IPFC控制特性的经济调度方法。首先构建概率风险指标，给出了兼顾经济性与安全性的优化目标函数，并建立了描述双回线IPFC控制特性的约束；由于所建立的安全约束经济调度优化模型呈现强非线性，本文进一步设计了基于粒子群算法的计算构架并实现了模型的求解。基于江苏电网的算例分析表明，与未计及双回线IPFC控制特性的经济调度策略进行对比，本文方法可以准确地计及IPFC所控线路断开一回线后的控制特性；又与未考虑风电场景时的经济调度策略对比，验证了在风电场景下，用本文方法得到的经济调度策略能够更好地满足潮流安全约束，具有一定的工程应用价值；另外还分析了经济性指标对优化调度结果的影响，验证了本文提出的经济调度方法可以在保证一定的系统潮流安全裕度的前提下，提升系统调度的经济性。
为兼顾系统的安全性与经济性，本文设立目标函数为
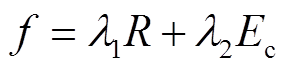（1）
式中，f为本文经济调度优化模型的总目标函数；R为安全性目标函数；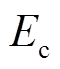
为经济性目标函数；l1、l2分别为安全性目标函数和经济性目标函数对应的权重系数。
1）安全性目标函数
本文在高比例风电注入的背景下进行研究，使用传统的确定性分析方法无法全面评估未来风电出力随机场景下的潮流安全。为此，本文引入了风险指标，将其与本文所分析的风电场景相匹配。风险指标[22]的定义为
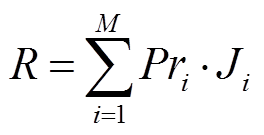（2）
式中，R为风险指标，也是本文的安全性目标函数；M为随机场景的总个数；Pri为第i个场景发生的概率；Ji为第i个场景发生时对应后果的严重度。为描述风电场景的概率分布，本文采用MARKOV链进行建模。MARKOV链具有方法简单、计算速度快、精度高等优点[23]。
本文重点关注潮流，以期充分调动IPFC的控制潜力，解决风电大规模接入背景下潮流分布不均引起的热稳定安全问题。为了使优化策略满足潮流的N-1安全约束，本文引入发生N-1故障[24-25]时重载线路的负载率之和来描述第i个场景发生时对应的严重度Ji，即
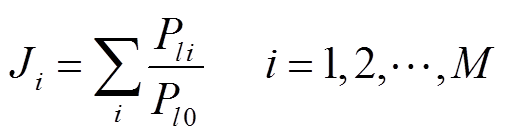（3）
式中，li为第i个场景下的重载线路；Pli为重载线路li在第i个场景下的有功潮流；Pl0为线路l的有功容量（重载率取(Pli/Pl0)≥0.8）。
2）经济性目标子函数
除了IPFC参与调节外，还可选择一些发电机参与最优潮流调节。本文将发电机出力成本作为考察系统经济性的指标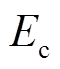，有
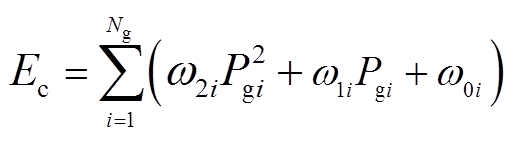（4）
式中，ω2i、ω1i、ω0i为第i台发电机的发电成本系数[26]；Pgi为第i台发电机的有功出力；Ng为系统参与优化调节的发电机总数。
综上所述，本文所提计及风电场景和双回线IPFC控制特性的电力系统经济调度优化模型的目标函数可表示为
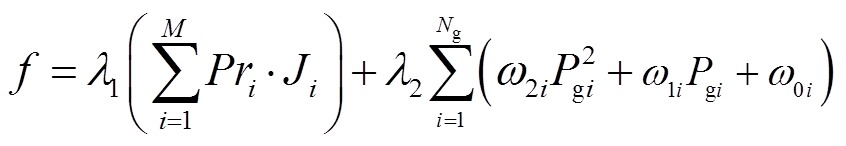（5）
（6）
式中，Pg为所有参与优化调度的发电机的有功出力，Pg=[Pg1, Pg2,
, 
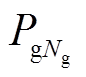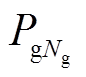]，为第Ng个发电机的有功出力；Vg为所有参与优化调度的发电机节点的电压幅值，Vg=[Vg1, Vg2,, 
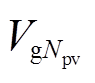]，Npv为参与优化调节的PV节点个数；P1ref、Q1ref、P2ref、Q2ref、Viref即为IPFC的控制目标。
IPFC可以灵活控制潮流，但引入其的同时会增加新的约束条件，包括IPFC运行约束和N-1故障后考虑其控制特性的约束。为方便后续描述，本节先给出双回线IPFC的拓扑结构和等效电路，如图1和图2所示。
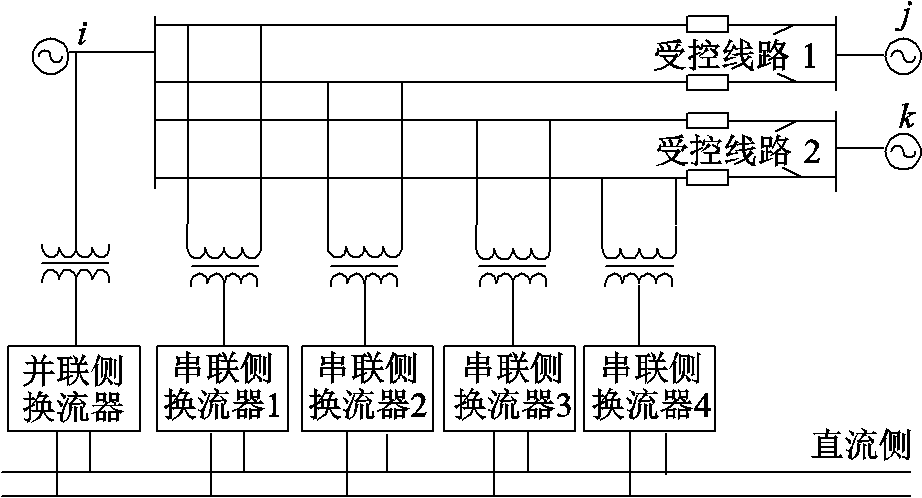
图1 双回线IPFC拓扑结构
Fig.1 Topology diagram of IPFC for double-circuit
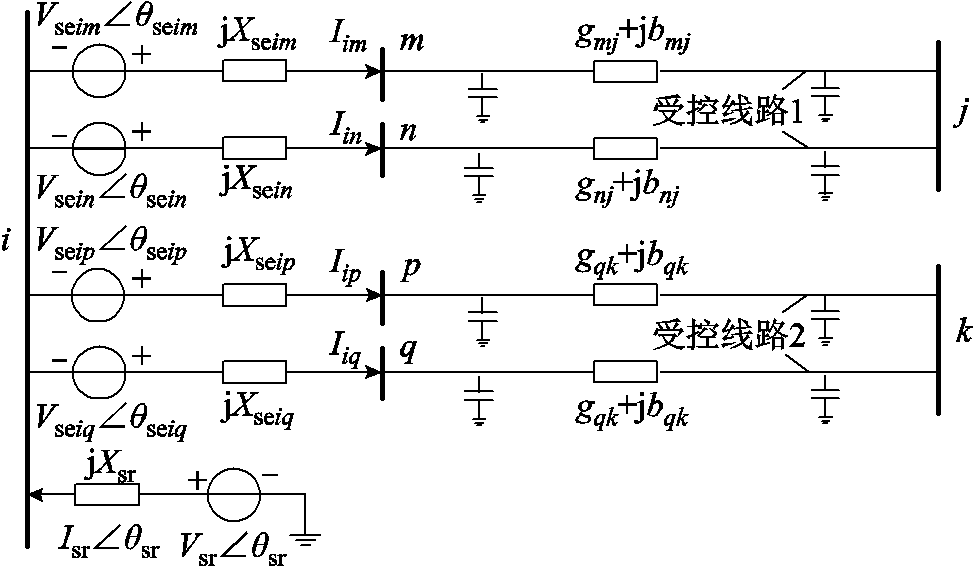
图2 双回线IPFC等效电路
Fig.2 Equivalent circuit diagram of IPFC for double-circuit
图2中,为方便后续模型推导，添加m, n, p, q作为附加虚拟节点，记h∈{m, n, p, q}。IPFC所在的受控线路1和受控线路2均为双回线线路，受控线路1对应线路im、in，受控线路2对应线路ip, iq。Vseih为四回线路串联换流器输出电压的幅值，qseih为四回线路串联换流器输出电压的相位，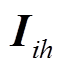
为四回线路串联换流器流过的电流向量，Isr∠θsr为并联侧换流器流过的电流向量；Xseih为线路串联耦合换流器等效阻抗；gmj、gnj、bmj、bnj分别为线路mj、nj的等效电导、电纳，gpk、gqk、bpk、bqk分别为线路pk、qk的等效电导、电纳。Vsr∠θsr、Xsr分别为并联侧换流器的输出电压和等效电抗。带有并联侧换流器的IPFC可将公共节点i的电压维持在恒定值Viref[27-28]，而i节点的有功注入功率可以通过IPFC自身的有功功率平衡计算获得，因此在进行潮流计算时，将节点i设置为PV节点[29-31]，节点m、n、p、q设置为PQ节点。
双回线IPFC运行需要满足一定的功率平衡约束。根据传统功率注入模型，IPFC串联侧附加虚拟节点m、n、p、q的注入功率表示为
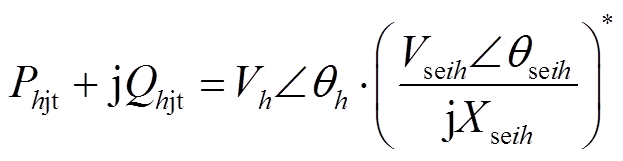（7）
式中，Vh为附加虚拟节点的电压幅值；θh为附加虚拟节点的电压相位；*表示共轭值。
节点i的注入功率可表示为
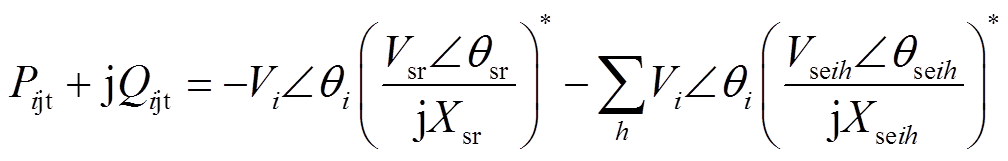（8）
式中，Vi为节点i的电压幅值；θi为节点i的电压相角。
忽略自身损耗，IPFC满足所有换流器有功守恒，即
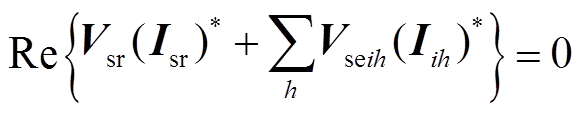（9）
式中，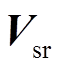
、
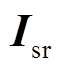分别为并联侧换流器对应的电压向量和电流向量；
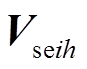为四回线路串联换流器的输出电压向量。
由于实际运行中IPFC通常工作在恒功率控制模式下，本文建立正常运行情况和N-1故障情况下描述IPFC恒功率控制特性的相关约束。当IPFC正常工作时，其控制特性可以表示为
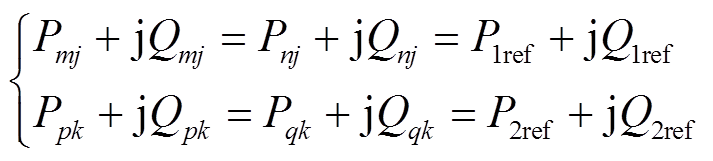（10）
式中，Pmj+jQmj为线路mj的潮流；Pnj+jQnj为线路nj的潮流；Ppk+jQpk为线路pk的潮流；Pqk+jQqk为线路qk的潮流；P1ref+jQ1ref为受控线路1的目标潮流；P2ref+jQ2ref为受控线路2的目标潮流。
当发生N-1故障时，设置如下的IPFC控制策略。分两种情况：
1）N-1故障发生在双回线IPFC的任一串联侧，则该故障侧其中一回线的换流器失去控制作用，而另一回线的换流器仍可发挥控制作用。以线路nj发生N-1故障为例，此时IPFC的等效拓扑如图3所示。
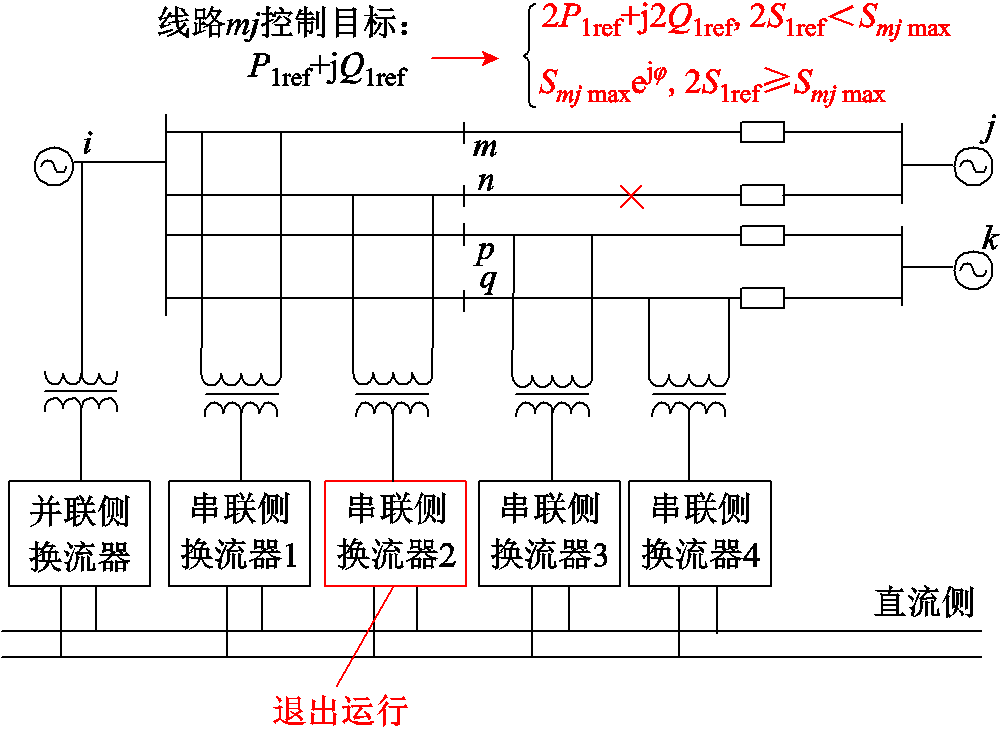
图3 N-1故障发生在IPFC任一串联侧时IPFC拓扑结构
Fig.3 Topology diagram of IPFC when N-1 fault occurs on either serial side of IPFC
对于故障侧（即受控线路1），原双回线的控制目标为2(P1ref+jQ1ref)，为保持该线路传输功率的变化在故障前后尽量小，将故障侧剩下一回线的控制目标设为原来的两倍，若潮流越限则设定为该回线路的最大额定容量；而对于非故障侧，保持IPFC非故障侧的控制目标不变即可。以线路nj发生N-1故障为例进行说明，数学表达为
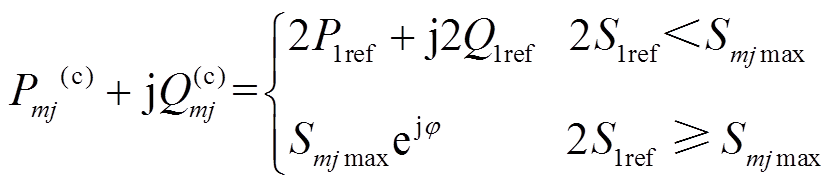（11）
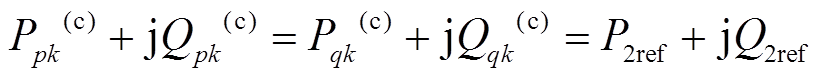（12）
式中，S1ref=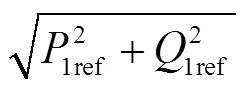
；(·)(c)表示系统发生故障后的各变量；Smjmax为线路mj的容量；j为线路mj的功率因数。
2）N-1故障发生在非IPFC串联侧。此时，IPFC的等效拓扑与图1一致，故障前后IPFC所控线路潮流保持不变。数学表达为
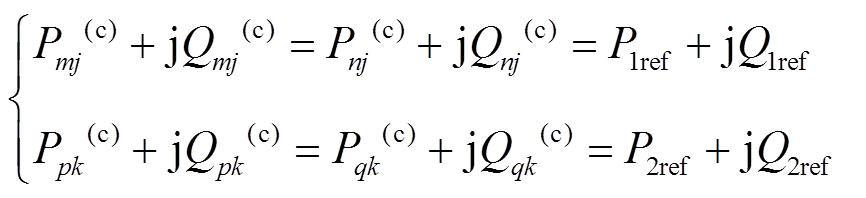（13）
IPFC并联侧采用恒定电压调节方式，保持故障前后并联侧母线电压不变且等于其电压目标值，有
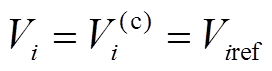（14）
式中，Vi为并联侧母线i的电压；Viref为并联侧母线i电压的目标值。
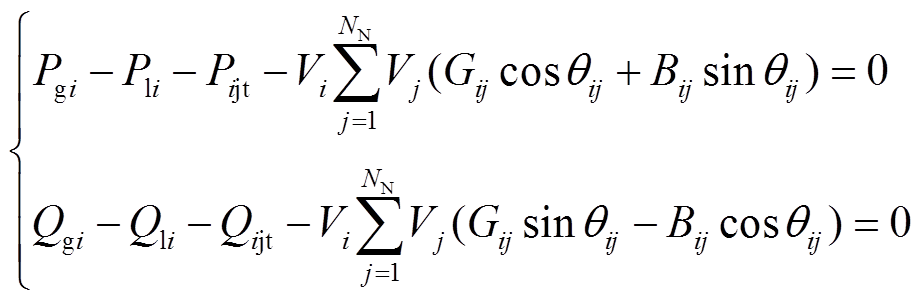（15）
定义N为系统所有节点集合（含附加注入节点），NN为节点总个数，i, j∈N；Pgi和Qgi为并联于节点i的可调发电机有功和无功出力；Pli、Qli分别为节点i的有功和无功负荷；Gij、Bij为线路ij的导纳；θij为节点i, j之间的相位差。
当i为与IPFC注入功率有关的节点（公共节点和附加虚拟节点）时，Pijt、Qijt为相应的注入功率值；当i为系统中其他节点时，Pijt=0, Qijt=0。
需要满足的不等式约束包括
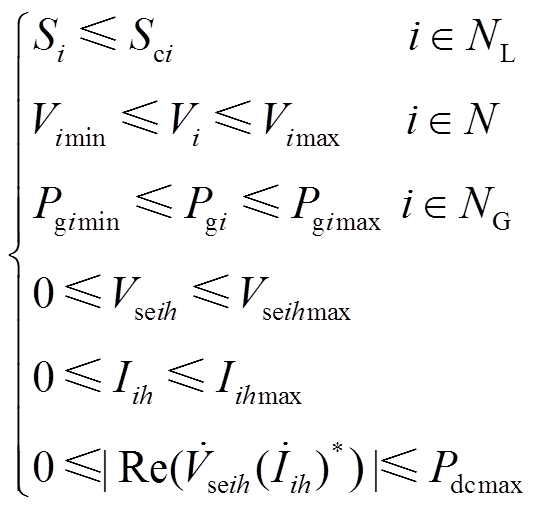（16）
式中，NL为系统所有线路的集合；NG为系统所有参与优化调节的发电机节点的集合；Sci为该线路能够承受的热稳定极限容量；Vimin、Vimax分别为节点电压的下限值和上限值；Pgimin、Pgimax分别为发电机出力的下限值和上限值；Pdcmax、Vseihmax、Iihmax分别为换流器交互有功功率最大值、输出电压幅值和电流幅值的上限值。
N-1故障下的潮流平衡约束为
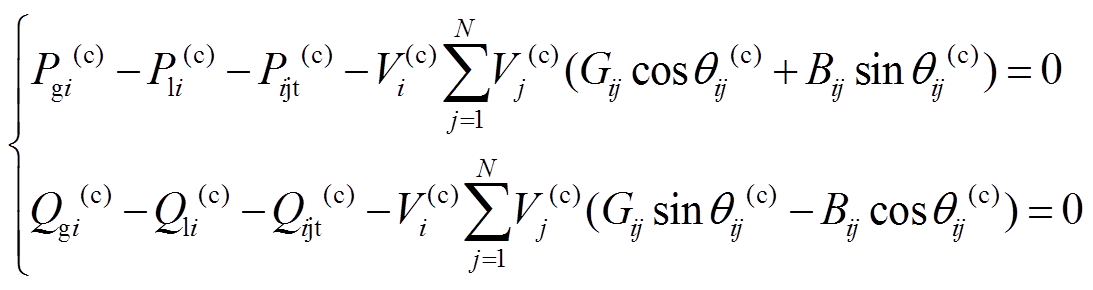（17）
本文希望调度策略被应用后系统满足N-1安全约束，故N-1故障前后发电机出力计划不变，需满足
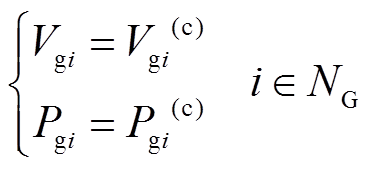（18）
需要满足的不等式约束包括
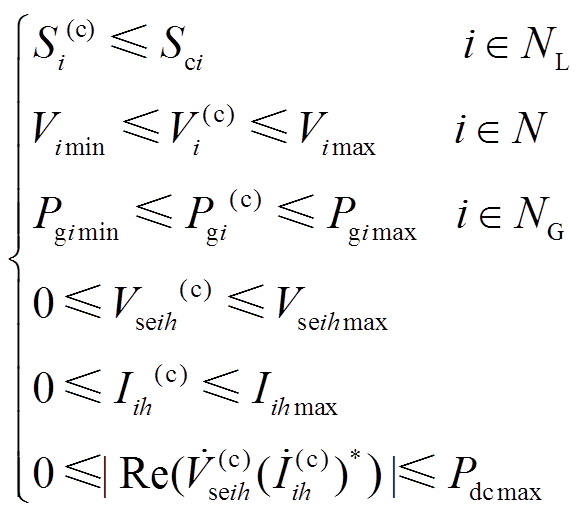（19）
由于第1节所提优化模型的非线性，本节设计了基于粒子群算法[32]的计算结构并实现了模型的求解。在该计算结构中，用罚函数处理不等式约束式（16）、式（19），以潮流计算保证等式约束式（15）、式（17）。
首先，推导含双回线IPFC的潮流计算迭代方法。IPFC正常运行情况下，双回线IPFC的潮流计算迭代方法可参考单回线IPFC的潮流计算迭代方法推导出。在图2所示的等效电路中，当两条受控线路有功、无功目标值为P1ref、Q1ref及P2ref、Q2ref时，如果第k次迭代后满足
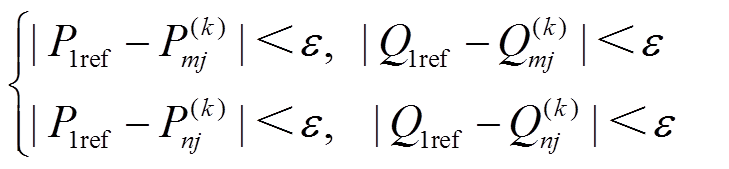（20）
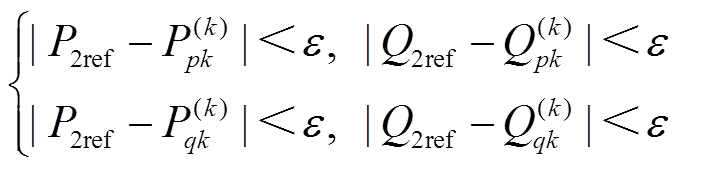（21）
则说明目标线路潮流已收敛至目标值，且系统潮流收敛；否则就需要对IPFC控制参数Vseih,qseih进行修正。以节点i的电压方向为参考方向，对IPFC注入线路的电压Vseih∠qseih进行正交分解，有功分量为Vseihx∠θseihx,无功分量为Vseihy∠θseihy。再将Vseihx, Vseihy看作待求变量，可解得Vseihx, Vseihy为
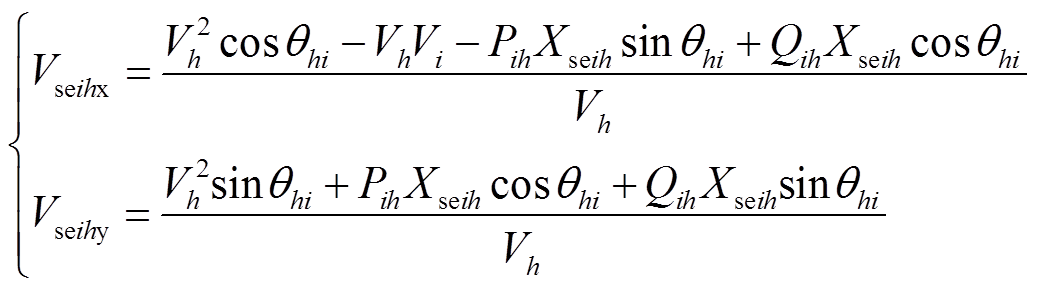（22）
基于第k次潮流计算迭代结果，推导出的迭代公式为
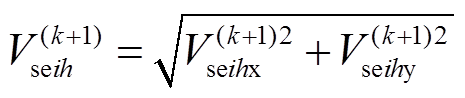（23）
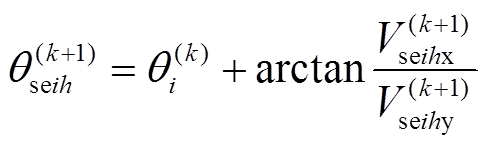（24）
在本文设计的基于粒子群算法的计算结构中，设粒子为一多维向量x，在本文设计的基于粒子群算法的计算结构中，设粒子为一多维向量x，x=[Pg1, Pg2,
, 
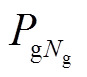, Vg1, Vg2,, 
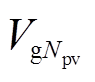, P1ref, Q1ref, P2ref, Q2ref, Viref]。其中，Ng为系统参与优化调节的发电机总数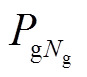，为第Ng个发电机的有功和无功出力。Npv为参与优化调节的PV节点总数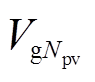，为第Npv个PV节点的电压幅值。x的分量P1ref、Q1ref、P2ref、Q2ref、Viref即为IPFC的控制目标。
当系统发生N-1故障时，分两种情况：
（1）N-1故障发生在IPFC非串联侧。故障前后IPFC所控线路潮流保持不变。向量x的IPFC控制目标分量设置如式（13），潮流迭代方法遵循式（20）～式（24）。
（2）N-1故障发生在双回线IPFC的任一串联侧。该故障侧其中一回线的换流器失去控制作用，而另一回线的换流器仍可发挥控制作用。应将向量x的IPFC控制目标分量设置如式（11）、式（12），潮流计算迭代方法遵循式（20）～式（24）。
通过上述的潮流计算迭代方法保证粒子满足潮流方程式（15）和式（17）成立，通过在目标函数中增加罚函数处理不等式约束式（16）和式（19），从而可得到一组粒子对应的总目标函数。不断更新粒子速度和位置，经过多次迭代后可求得最优解，即最优控制方案。基于粒子群优化算法（Particle Swarm Optimization, PSO）的求解流程如图4所示。将考虑IPFC控制特性的潮流计算迭代方法看作一个子模块：当系统有N-1故障发生时，通过子模块计算后，若潮流收敛则说明粒子可满足等式约束式（17），否则不满足，需增加惩罚项。
本文采用江苏省2020年500kV规划网架数据（拓扑图见附图1）及2019年江苏电网风电出力系数数据（采样间隔为5min），对比分析了本文所提方法得到的策略、未考虑IPFC控制特性和未考虑风电场景所得的策略应用于江苏电网时电网的潮流安全情况，另外还分析了经济性指标对优化调度结果的影响。
由于盐城和南通的年风力发电量占江苏电网的60%以上，本文将风电接入点放在盐城和南通两个节点上。由于不同季节风电出力呈现明显不同的规律，本文的历史运行数据采用盐城、南通春季的风电出力数据，时间跨度为2019年1月1日～2019年3月31日，调度周期为15min。选取风电出力系数较高的1月3日00:15为当前时刻，预测下一个调度周期的风电出力情况。生成场景的方法采用基于风电出力波动量的MARKOV链，具体方法见文献[33]。00:30时各场景的概率分布见表1。
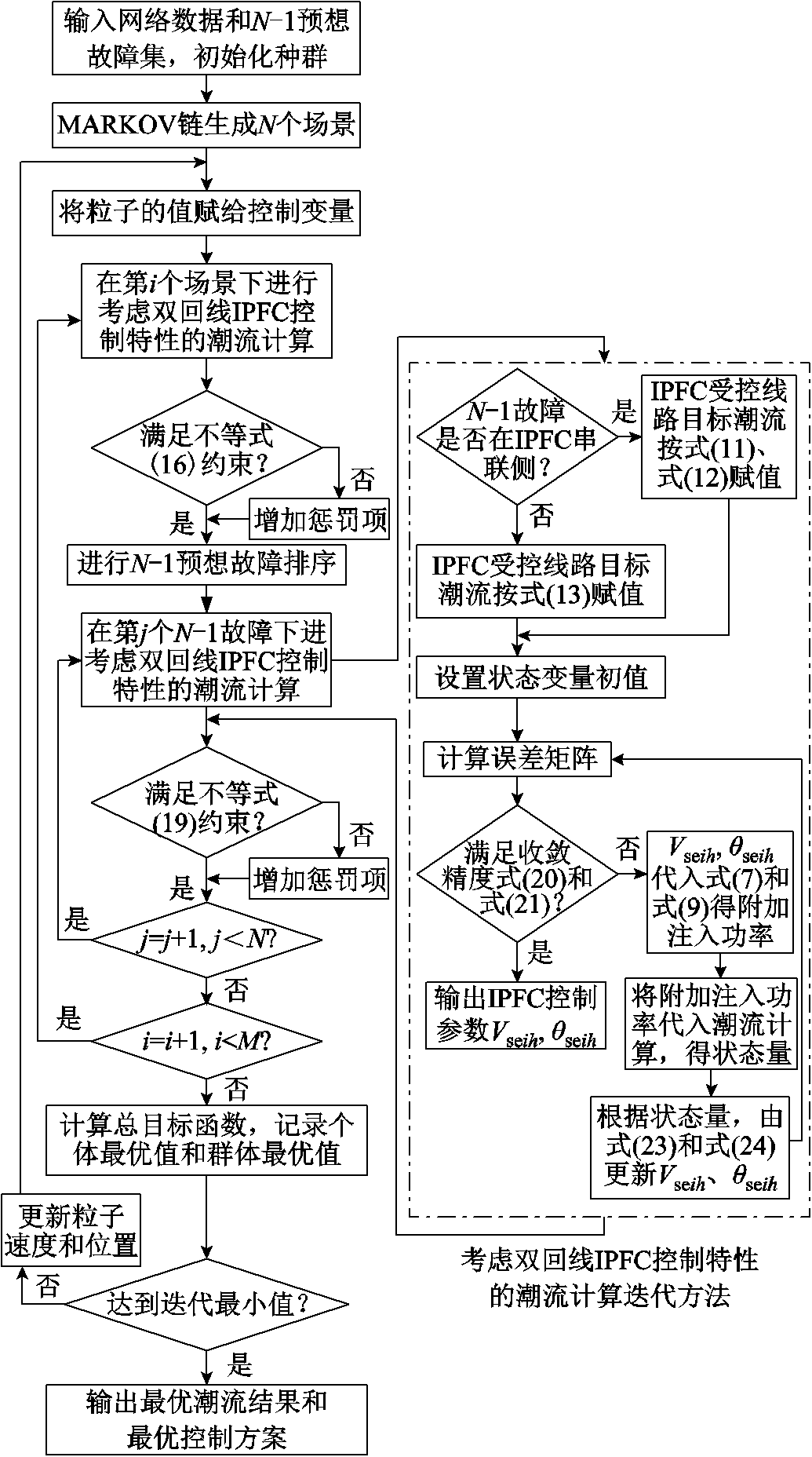
图4 计及风电场景和双回线IPFC控制特性的电力系统经济调度优化模型求解算法流程
Fig.4 Flow chart of solving algorithm for economic dispatch optimization model of power system considering wind power scenarios and control characteristics of IPFC for double-circuit
为了充分发挥IPFC的线间潮流调控能力，将双回线结构的IPFC安装在风电接入点附近、且潮流分布严重不均的两条线路上。本文的受控线路1为重载线路泰州-泰兴，受控线路2为轻载线路泰兴-胜利。预想故障集（见附表1）IPFC附近各线路的N-1断路故障。应用PSO算法进行算例求解，PSO参数设置如下：惯性因子w取0.729，加速因子c1、c2均取1.496 2，最大迭代次数取100次，粒子群总数取100个。IPFC参数为：Xseim=Xsein=Xseip=Xseiq= 0.04(pu)。所得的最优解即为最优经济调度策略。粒子群迭代收敛曲线和最优经济调度策略见附图2和附表2。
表1 风电场景的概率分布
Tab.1 Probability distribution of wind power scenarios
场景概率场景概率 10.014 3110.214 3 20.014 3120.085 7 30.014 3130.157 1 40.014 3140.100 0 50.042 9150.014 3 60.014 3160.042 9 70.042 9170.014 3 80.042 9180.014 3 90.028 6190.014 3 100.100 0200.014 3
3.2.1 有无考虑双回线IPFC控制特性的电力系统经济调度对比仿真
传统的含IPFC安全约束经济调度模型[11-14]假设IPFC的等效注入电压保持不变。然而实际运行中IPFC通常工作在恒功率控制模式下，为了保持受控线路传输功率不发生变化，会动态调整IPFC的等效注入电压，故而传统模型的假设是不成立的，这可能会导致基于传统模型获得的调度策略不安全。另外，传统方法往往没有考虑N-1故障发生在IPFC所控线路的情况，如果IPFC本身或其所控线路发生故障，基于传统方法获得的调度策略很可能导致线路潮流越限的情况。
为了揭示传统经济调度方法的潜在风险，说明本文所提经济调度方法在实际运行中的安全可靠，本节在实际江苏电网中对如下两个调度策略进行对比仿真。①将本文所提出的经济调度方法应用于实际电网或者某个算例场景，具体的优化调度模型的最优解即为相应的最优调度策略，也即包括发电机的出力、IPFC的控制参考值、PV节点的电压等的调度策略，简称为“基于本文方法获得的调度策略”；②由传统优化调度方法获得的调度策略，也同理可得，简称为“基于传统方法获得的调度策略”。
本文采用2020年江苏电网500kV网架和2019年夏季高峰潮流数据，IPFC安装在泰州-泰兴、泰兴-胜利（即线路43、169）上。首先在江苏电网算例中求解出两个策略，接着在如下两个考虑非IPFC所控线路和IPFC所控线路发生故障的场景下进行对比仿真，结果如下。
1）N-1故障发生在非IPFC所控线路
图5为线路147发生故障时，系统在下一个调度周期分别采用上述两种调度策略得到的潮流分布情况。可以看出，采用基于传统方法获得的调度策略时，线路33和线路50均超载；而采用基于本文方法获得的调度策略时，系统没有出现过载线路。这说明基于传统方法获得的调度策略在应用于江苏电网时，可能存在不满足潮流的N-1安全约束的情况。而本文提出的经济调度方法获得的调度策略合理地考虑了IPFC的控制特性，并可以保证系统的潮流安全。
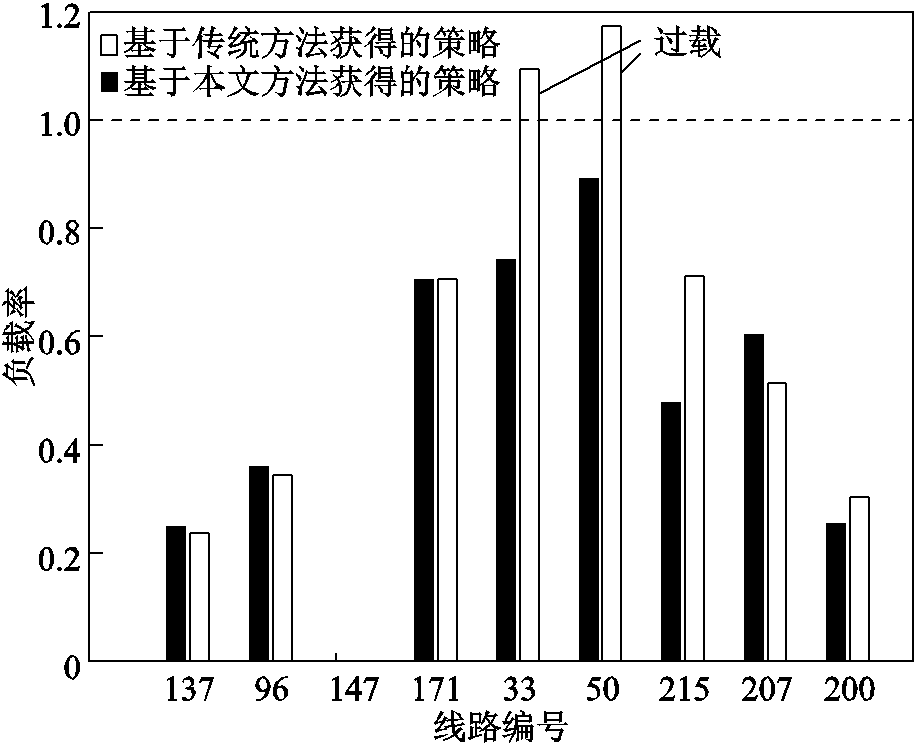
图5 两种调度策略在线路147故障时系统的潮流分布情况
Fig.5 Power flow distribution of two strategies in case of line 147 failure
2）N-1故障发生在IPFC所控线路
在电网实际运行时，IPFC所控线路存在发生故障的风险，可能导致IPFC失去调控潮流的作用，致使潮流越限，因此有必要校验IPFC所控线路发生故障时系统潮流的N-1安全约束。两种调度策略在IPFC所控线路43发生故障后，系统的潮流分布情况如图6所示。
从图6中可以看出，IPFC所控线路43发生故障后，基于传统方法获得的调度策略由于没有计及N-1故障发生在IPFC所控线路的情况，导致IPFC附近线路44、50发生潮流过载。而采用基于本文方法获得的调度策略计算的线路潮流无过载。由此可见，基于本文提出的经济调度方法获得的调度策略，不仅可以在非IPFC所控线路故障时满足系统N-1安全校核，还可以在IPFC所控线路故障时满足系统N-1安全校核，很好地保证了系统的潮流安全，提升系统的N-1静态安全性。
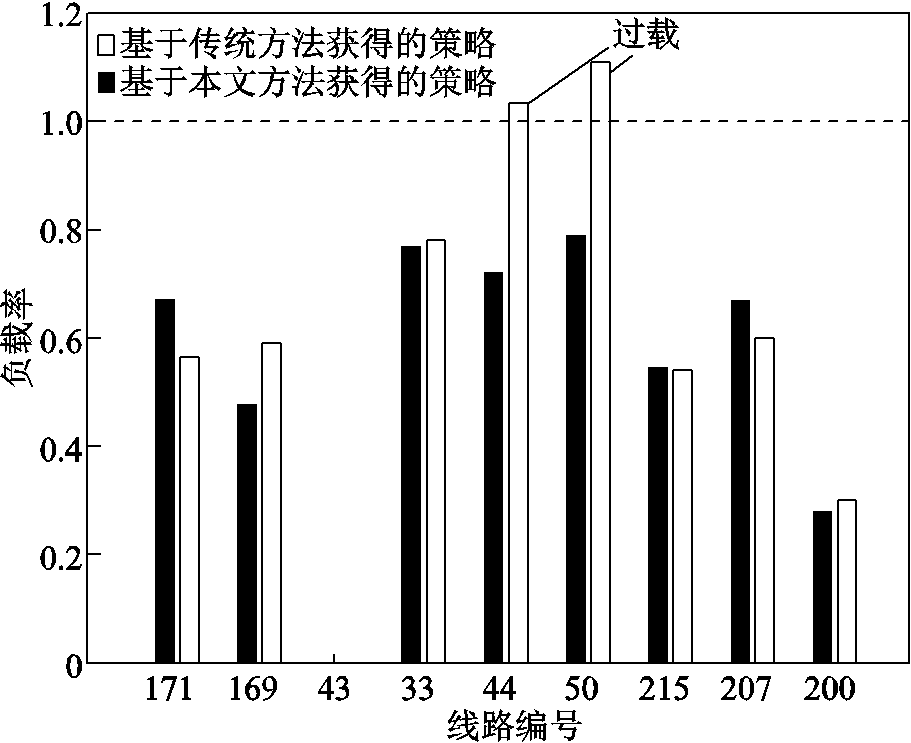
图6 两种调度策略在IPFC所控线路N-1故障后系统的潮流分布情况
Fig.6 Power flow distribution after N-1 contingency of IPFC-controlled line with two dispatching policies
3.2.2 有无考虑风电场景的含IPFC电力系统经济调度对比仿真
在未考虑风电场景的经济调度优化中，风电的出力为常数，因此可看成是单一场景的含IPFC电力系统经济调度优化。本文以3.1节生成场景中场景6的风电出力作为风电场的输入，求解出单场景优化所得调度策略。接着，在所有风电不确定场景下分别应用了单场景优化得到的调度策略和本文方法得到的调度策略，并对所有的线路逐一进行N-1校核。限于篇幅，本文仅展示部分场景在N-1故障时的线路过载情况及临近线路的负载率对比，如表2和图7所示。
表2 部分风电场景下系统发生严重N-1故障时两种策略对应的线路过载情况
Tab.2 The line overload condition corresponding to the two strategies when serious N-1 contingencies occur in some wind power scenarios
场景故障线路编号单场景优化所得策略本文优化方法所得策略 466线路210, 212过载无线路过载 158线路45过载无线路过载 943线路44, 50过载无线路过载 66线路210, 212过载无线路过载 212线路66, 210过载无线路过载
（续）
场景故障线路编号单场景优化所得策略本文优化方法所得策略 1543线路50过载无线路过载 66线路210过载无线路过载 158线路44, 45过载无线路过载 1643线路44, 50过载无线路过载 170线路74, 75过载无线路过载 20158线路128, 129过载无线路过载 643无线路过载无线路过载
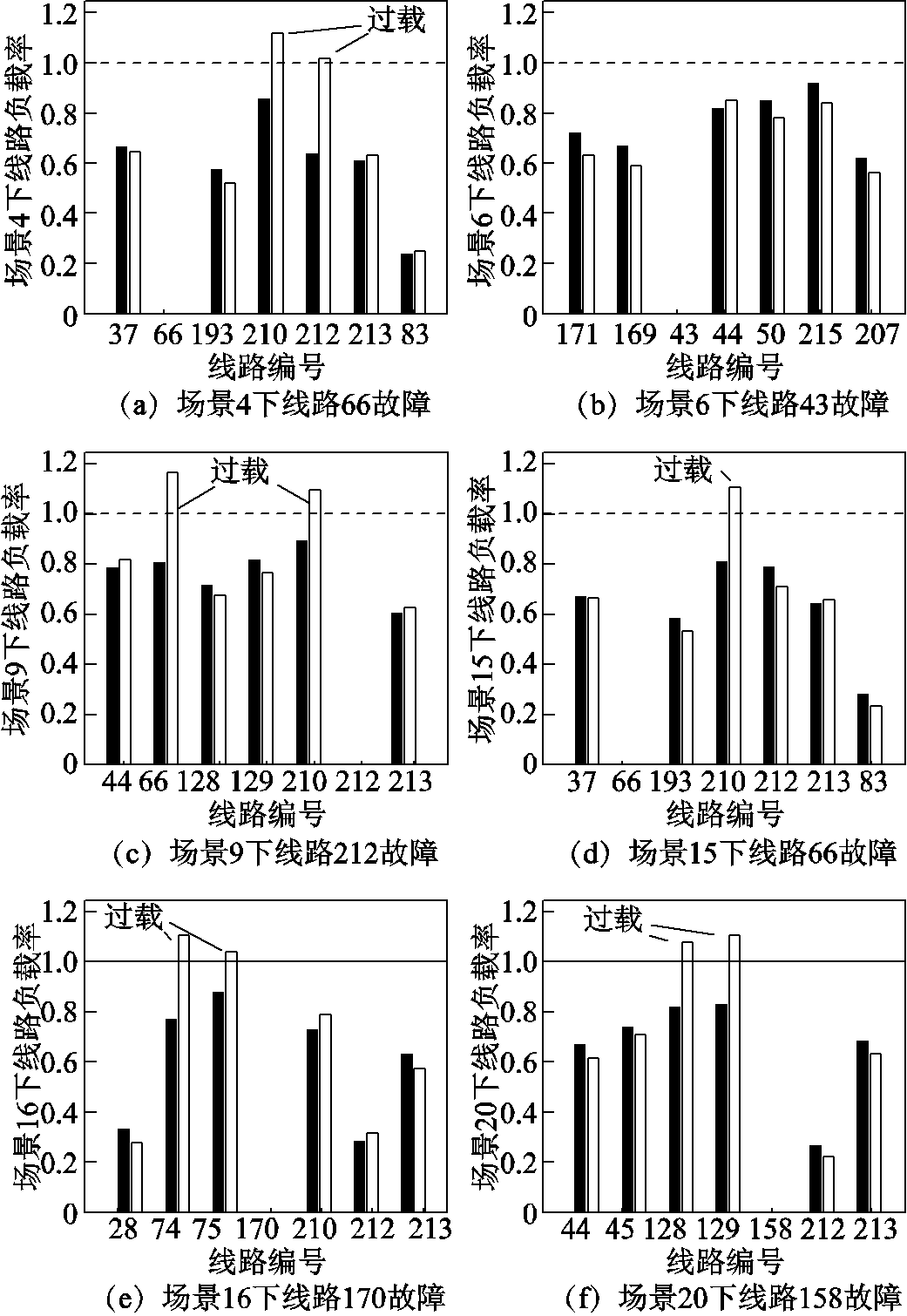
图7 部分风电场景下系统发生最严重N-1故障时两种策略对应的潮流结果对比
Fig.7 Comparison of power flow results corresponding to the two strategies when the most serious N-1 contingency occurs in some wind power scenarios
由表2和图7可知，在场景6下各线路潮流均满足N-1安全约束，这是由于单场景优化是在场景6下进行的；而在场景4、9、15、16、20下，均有线路会在系统N-1故障时发生潮流越限。这说明由单场景优化得到的调度策略不能应对实际运行中可能出现的所有风电预测场景，在实际使用时有一定风险。在大规模风电接入的背景下，考虑风电场景的调度策略在潮流安全方面明显优于单场景调度策略。
3.2.3 经济性指标对优化调度结果影响的分析
在本文所提的经济调度方法中，经济性指标和安全性指标同时参与了优化。为分析经济性指标对经济调度结果的影响，在江苏电网算例中求解出仅以安全性指标为目标函数的调度策略和本文所提综合考虑安全性和经济性指标的调度策略。应用这两种调度策略最终得到的经济性和安全性指标见表3。
表3 仅优化安全性指标和本文优化方法所得结果对比
Tab.3 Comparison of the results of only the optimized safety index and the optimization method in this paper
目标函数值经济性指标安全性指标 仅优化安全性指标42.5750.62 本文优化方法35.3356.35
由表3可以看出，与本文优化经济和安全性指标获得的调度策略相比，仅优化安全性指标获得的调度策略在系统安全性方面更好，但是发电机的出力成本高了近20%。这说明安全性要求的提高改变了考虑发电机出力成本的机组出力计划，导致系统的运行成本大幅升高，运行的经济性变差。而本文提出的经济调度方法可以在保证一定的系统潮流安全裕度的前提下，提升系统调度的经济性。
本文提出了一种计及风电场景的含IPFC电力系统经济调度方法。构建概率风险指标，给出兼顾经济性与安全性的优化目标函数，并建立描述双回线IPFC控制特性的约束。由于所建立的安全约束经济调度优化模型呈现强非线性，本文进一步设计了基于粒子群算法的计算构架并实现了模型的求解。最后，将本文所建立的模型用实际的江苏省2020年500kV规划网架和风电出力数据进行验证，将本文方法所得策略与未计及双回线IPFC控制特性的策略进行对比，验证了本文方法可以准确地计及IPFC所控线路断开一回线后的控制特性，更好地保证系统的潮流安全；又与仅考虑单场景得到方案进行对比，结果表明在风电场景下，用本文方法得到的控制策略能够比未考虑风电场景时的控制策略更好地满足潮流安全约束，具有一定的工程应用价值。另外本文还分析了经济性指标对优化调度结果的影响，验证了本文提出的经济调度方法可以在保证一定的系统潮流安全裕度的前提下，提升系统调度的经济性。
附表1 预想故障集
App.Tab.1 Expected fault set
预想故障线路 高港-泰兴泰兴-胜利高港-南通南通-胜利 东洲-新丰东洲-如东如东-仲洋仲洋-凤城 胜利-三官殿三官殿-东洲三官殿-新丰凤城-泰州 泰州-泰兴
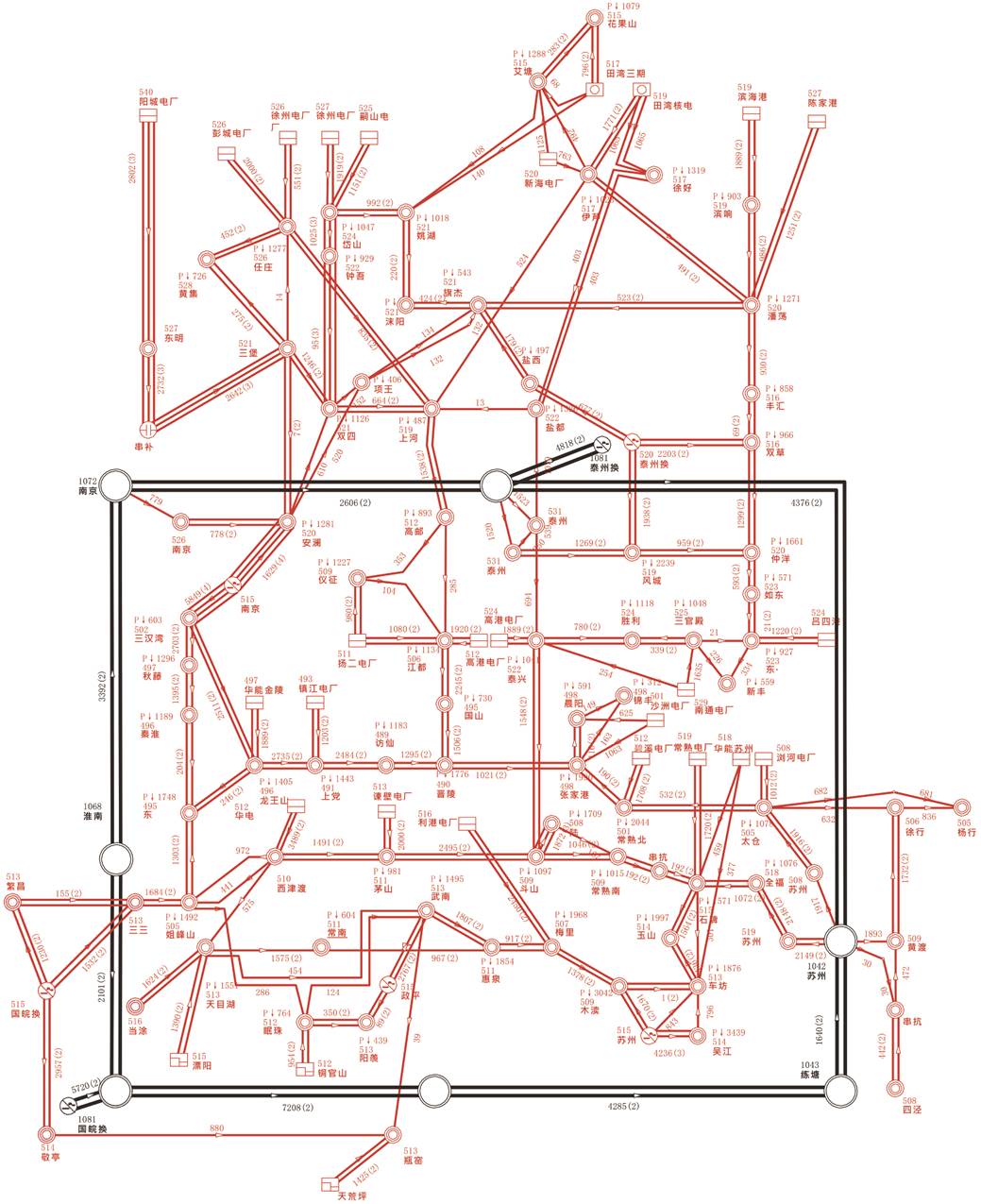
附图1 江苏省2020年500kV规划网架
App.Fig.1 The 500kV planning grid of Jiangsu Province in 2020
附图2 计及风电场景的含IPFC经济调度优化模型PSO收敛曲线
App.Fig.2 The PSO convergence curve of IPFC economic dispatching optimal model considering wind power scenario
附表2 最优经济调度策略
App.Tab.2 Optimal economic dispatching strategy (pu)
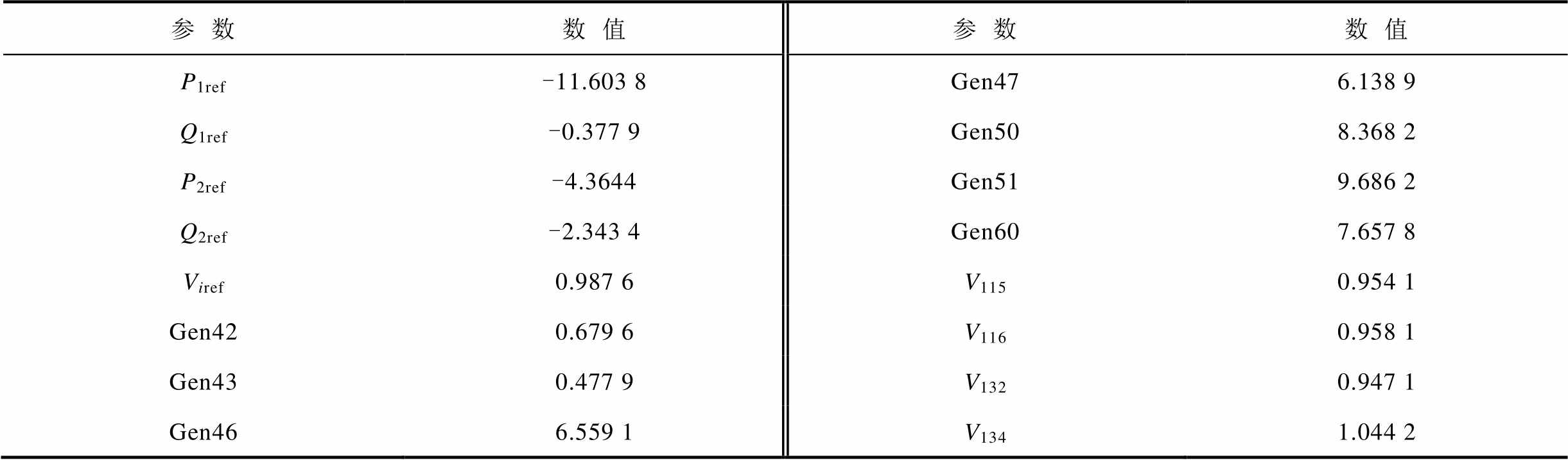
参数数值参数数值 P1ref-11.603 8Gen476.138 9 Q1ref-0.377 9Gen508.368 2 P2ref-4.3644 Gen519.686 2 Q2ref-2.343 4Gen607.657 8 Viref0.987 6V1150.954 1 Gen420.679 6V1160.958 1 Gen430.477 9V1320.947 1 Gen466.559 1V1341.044 2
注：Gen42为最优经济调度策略中42号发电机的有功出力；V115示最优经济调度策略中参与优化调度的115号节点的电压幅值。
参考文献
[1] Liu Pengcheng, Wang Zheng, Wei Sanmin, et al. Recent developments of modulation and control for high-power current-source-converters fed electric machine systems[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(3): 215-226.
[2] Zhu Rongwu, Andresen M, Langwasser M, et al. Smart transformer/large flexible transformer[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(4): 264-274.
[3] 薛翼程, 王国腾, 张哲任, 等. MMC-HVDC接入对同步发电机阻尼转矩的影响机理分析[J]. 电力系统自动化, 2022, 46(9): 99-108.
Xue Yicheng, Wang Guoteng, Zhang Zheren, et al. Mechanism analysis of influence of MMC-HVDC integration on damping torque of synchronous generators[J]. Automation of Electric Power Systems, 2022, 46(9): 99-108.
[4] 韩建, 李幸, 罗德荣, 等. 基于双级矩阵变换器的统一潮流控制器并联侧无功扩展[J]. 电工技术学报, 2020, 35(7): 1498-1508.
Han Jian, Li Xing, Luo Derong, et al. Extending the reactive power range of shunt side for unified power flow controllers based on indirect matrix converters[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1498-1508.
[5] Palma-Behnke R, Vargas L S, Perez J R, et al. OPF with SVC and UPFC modeling for longitudinal systems[J]. IEEE Transactions on Power Systems, 2004, 19(4): 1742-1753.
[6] Wu Xi, Zhou Zhengyu, Liu Gang, et al. Preventive security-constrained optimal power flow considering UPFC control modes[J]. Energies, 2017, 10(8): 1199.
[7] 李国庆, 宋莉, 李筱婧. 计及FACTS装置的可用输电能力计算[J]. 中国电机工程学报, 2009, 29(19): 36-42.
Li Guoqing, Song Li, Li Xiaojing. Available transfer capability calculation considering FACTS controllers[J]. Proceedings of the CSEE, 2009, 29(19): 36-42.
[8] Zhang Y, Zhang Y, Chen C. A novel power injection model of IPFC for power flow analysis inclusive of practical constraints[J]. IEEE Transactions on Power Systems, 2006, 21(4): 1550-1556.
[9] Jiang Xia, Chow J H, Edris A A, et al. Transfer path stability enhancement by voltage-sourced converter-based FACTS controllers[J]. IEEE Transactions on Power Delivery, 2010, 25(2): 1019-1025.
[10] Hingorani N, Gyuyi L. Combined compensators: unified power flow controller (UPFC) and interline power flow controller (IPFC)[M]. New York: IEEE Press, 2009.
[11] Rostami M, Lotfifard S. Optimal remedial actions in power systems considering wind farm grid codes and UPFC[J]. IEEE Transactions on Industrial Informatics, 2020, 16(12): 7264-7274.
[12] Sreejith S, Simon S P, Selvan M P. Analysis of FACTS devices on security constrained unit commitment problem[J]. International Journal of Electrical Power & Energy Systems, 2015, 66: 280-293.
[13] Khodaei A, Shahidehpour M. Security-constrained transmission switching with voltage constraints[J]. International Journal of Electrical Power & Energy Systems, 2012, 35(1): 74-82.
[14] Naveen Kumar G, Surya Kalavathi M. Cat swarm optimization for optimal placement of multiple UPFC's in voltage stability enhancement under contingency[J]. International Journal of Electrical Power & Energy Systems, 2014, 57: 97-104.
[15] Eremia M, Liu C C, Edris A A. Advanced solutions in power systems[M]. New York: IEEE Press, 2016.
[16] Rao B S, Vaisakh K. Multi-objective adaptive clonal selection algorithm for solving optimal power flow considering multi-type FACTS devices and load uncertainty[J]. Applied Soft Computing, 2014, 23: 286-297.
[17] Mishra A, Venkata Nagesh Kumar G. Congestion management of deregulated power systems by optimal setting of interline power flow controller using gravitational search algorithm[J]. Journal of Electrical Systems and Information Technology, 2017, 4(1): 198-212.
[18] 吴熙, 王亮, 陈曦, 等. 计及线间潮流控制器的电力系统潮流优化[J]. 电网技术, 2019, 43(11): 4125-4134.
Wu Xi, Wang Liang, Chen Xi, et al. Optimal power flow considering interline power flow controller[J]. Power System Technology, 2019, 43(11): 4125-4134.
[19] 麻秀范, 王戈, 朱思嘉, 等. 计及风电消纳与发电集团利益的日前协调优化调度[J]. 电工技术学报, 2021, 36(3): 579-587.
Ma Xiufan, Wang Ge, Zhu Sijia, et al. Coordinated day-ahead optimal dispatch considering wind power consumption and the benefits of power generation group[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 579-587.
[20] 周博, 艾小猛, 方家琨, 等. 计及超分辨率风电出力不确定性的连续时间鲁棒机组组合[J]. 电工技术学报, 2021, 36(7): 1456-1467.
Zhou Bo, Ai Xiaomeng, Fang Jiakun, et al. Continuous-time modeling based robust unit commitment considering beyond-the-resolution wind power uncertainty[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1456-1467.
[21] 张大波, 朱志鹏, 连帅. 考虑发电计划的电网阻塞疏导UPFC配置研究[J]. 电气技术, 2018, 19(6): 14-19.
Zhang Dabo, Zhu Zhipeng, Lian Shuai. Allocation schemes research of UPFC based on relieving power blockage considering the power generation schedule[J]. Electrical Engineering, 2018, 19(6): 14-19.
[22] Ni M, McCalley J D, Vittal V, et al. Online risk-based security assessment[J]. IEEE Power Engineering Review, 2002, 22(11): 59.
[23] 朱晨曦, 张焰, 严正, 等. 采用改进马尔科夫链蒙特卡洛法的风电功率序列建模[J]. 电工技术学报, 2020, 35(3): 577-589.
Zhu Chenxi, Zhang Yan, Yan Zheng, et al. A wind power time series modeling method based on the improved Markov chain Monte Carlo method[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 577-589.
[24] 杨林, 蔡晖, 汪惟源, 等. 500kV统一潮流控制器在苏州南部电网的工程应用[J]. 中国电力, 2018, 51(2): 47-53.
Yang Lin, Cai Hui, Wang Weiyuan, et al. Application of 500kV UPFC in Suzhou southern power grid[J]. Electric Power, 2018, 51(2): 47-53.
[25] 祁万春, 杨林, 宋鹏程, 等. 南京西环网UPFC示范工程系统级控制策略研究[J]. 电网技术, 2016, 40(1): 92-96.
Qi Wanchun, Yang Lin, Song Pengcheng, et al. UPFC system control strategy research in Nanjing western power grid[J]. Power System Technology, 2016, 40(1): 92-96.
[26] 夏鹏, 刘文颖, 蔡万通, 等. 基于风电离散化概率序列的机会约束规划优化调度方法[J]. 电工技术学报, 2018, 33(21): 5069-5079.
Xia Peng, Liu Wenying, Cai Wantong, et al. Optimal scheduling method of chance constrained programming based on discrete wind power probability sequences[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 5069-5079.
[27] Eremia M, Liu C C, Edris A A. Advanced solutions in power systems: HVDC, FACTS, and Artificial Intelligence[M]. New York: John Wiley & Sons, 2017.
[28] 朱梓荣, 李群, 卫志农, 等. 含新型统一潮流控制器的电力系统安全校正模型[J]. 电力系统自动化, 2019, 43(2): 58-66.
Zhu Zirong, Li Qun, Wei Zhinong, et al. Security correction model of power system with novel unified power flow controller[J]. Automation of Electric Power Systems, 2019, 43(2): 58-66.
[29] 罗玉春, 王毅, 闪鑫, 等. 调控系统中统一潮流控制器稳态建模的实现[J]. 电力系统保护与控制, 2022, 50(1): 148-157.
Luo Yuchun, Wang Yi, Shan Xin, et al. Realization of steady state modeling of unified power flow controller in a control system[J]. Power System Protection and Control, 2022, 50(1): 148-157.
[30] Galvani S, Hagh M T, Sharifian M B B, et al. Multiobjective predictability-based optimal placement and parameters setting of UPFC in wind power included power systems[J]. IEEE Transactions on Industrial Informatics, 2019, 15(2): 878-888.
[31] Zhang X P. Modelling of the interline power flow controller and the generalised unified power flow controller in Newton power flow[J]. IEE Proceedings-Generation, Transmission and Distribution, 2003, 150(3): 268.
[32] 金义雄, 程浩忠, 严健勇, 等. 改进粒子群算法及其在输电网规划中的应用[J]. 中国电机工程学报, 2005, 25(4): 46-50, 70.
Jin Yixiong, Cheng Haozhong, Yan Jianyong, et al. Improved particle swarm optimization method and its application in power transmission network planning[J]. Proceedings of the CSEE, 2005, 25(4): 46-50, 70.
[33] Sun Jingwen, Yun Zhihao, Liang Jun, et al. Wind power forecasting based on a Markov chain model of variation[C]//2015 12th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD), Zhangjiajie, China, 2016: 778-782.
Abstract Interline power flow controller (IPFC) proposed is a device with powerful power flow control ability, which provides a new method for power flow control under the increasing integration of large-scale renewable energy. In this paper, a security-constrained economic dispatching method for the power system with IPFC considering wind power uncertainty is proposed. Compared with the conventional method, the proposed method accurately considers the control characteristics of IPFC and can guarantee the security requirement under N-1 contingencies.
Firstly, the optimization objective function considering both economy and security is expressed as Equ. (1) in this paper. The wind power output scenarios are predicted based on MARKOV chain, and the security objective function is expressed risk index R, which can be expressed by Equ. (2) in this paper.
Furthermore, with full consideration of the control characteristics of IPFC with the double-circuit structure, the equality/inequality constraints of the power system before and after contingencies are established:
1) N-1 contingency occurs on either series side of the IPFC of the double-circuit line. At this time, the converter of the primary line on the fault side loses its control while the converter of the other primary line can still play control functions. Take the N-1 contingency on line nj is taken as an example. At this time, the mathematical expression of control characteristics are Equ.(11) and Equ.(12) in this paper.
2) N-1 contingency occurs on the non-IPFC series side. At this time, the power flow of the line controlled by IPFC remains unchanged before and after the fault. The mathematical expression is Equ. (13) in this paper.
Finally, an improved particle swarm optimization algorithm is designed to solve the proposed optimization model with strong nonlinear constraints. In this structure, inequality constraints are treated by penalty function and equality constraints are guaranteed by power flow calculation. The particle velocity and position are constantly updated, and the optimal solution can be obtained after several iterations, that is, the optimal control scheme. The flow chart based on PSO is shown in Fig.4 in this paper.
With the strategy obtained by the proposed method and the strategy without considering the IPFC control characteristics, the power flow in the Jiangsu power grid is compared, as shown in Fig.5 and Fig.6 respectively. It can be seen that the line load rate under the strategy obtained by the proposed method meets the security requirement whether the contingency occurs on the line controlled by IPFC or not. It indicates that the strategy obtained by the proposed method can meet the security requirement under N-1 contingencies and improve the static security of the system.
The two dispatching strategies obtained by single scenario optimization and the optimization method in this paper are respectively applied to all wind power uncertainty scenarios. The comparison results of the line overload condition of two strategies when serious N-1 contingencies occur in some wind power scenarios are shown in Tab.2 in this paper. Under the background of large-scale wind power integration, the dispatching strategy considering the wind power scenario can satisfy the security constraints of power flow while the single-scenario dispatching strategy cannot.
keywords：Interline power flow controller (IPFC), control characteristics for double-circuit, wind power scenario, economic dispatch
DOI:10.19595/j.cnki.1000-6753.tces.211809
中图分类号：TM732
国家自然科学基金项目（52177075）、江苏省自然科学基金项目（BK20221466）、国网江苏省电力有限公司科技项目“基于线间潮流控制的新型FACTS装置协调规划技术与系统级运行控制策略研究”（J2021015）资助。
收稿日期 2021-11-10
改稿日期 2022-08-06
吴 熙 男，1987年生，副教授，研究方向为电力系统优化。E-mail：wuxi@seu.edu.cn（通信作者）
陆 瑶 女，1998年生，硕士研究生，研究方向为电力系统优化。E-mail：luyao006@seu.edu.cn
（编辑 赫蕾）