 线电压带动异步电动机;RAM系统由笼型异步电动机经过飞轮质量块拖动隐极发电机,产生
线电压带动异步电动机;RAM系统由笼型异步电动机经过飞轮质量块拖动隐极发电机,产生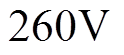 线电压供给下游负荷。RAM系统出口母线经半桥整流,给控制棒驱动机构各类工作线圈供电。
线电压供给下游负荷。RAM系统出口母线经半桥整流,给控制棒驱动机构各类工作线圈供电。摘要 核电站控制棒电源(简称棒控电源)是控制棒驱动机构的唯一供电系统,确保该系统的安全可靠运行对提高核电站安全性具有重大意义。实际运行的棒控电源系统中发电机的失磁保护判据原理简单,现场发生了多起失磁保护失配事件,且棒控电源系统中发电机的运行状态不同于常规并网发电机;为了有效解决失磁保护失配问题,需对棒控电源系统中发电机的失磁故障进行重新解析。首先,根据转差率和功角特点将失磁发展历程划分为等功角阶段、异步运行阶段和周期异步运行阶段;其次,以发电机等效电路及相量图为基础,以q轴电动势为切入点,结合发电机基本方程,由各阶段q轴电动势的变化解析得到各电气量稳态表达式;最后,通过实际机组的失磁实验数据以及基于PSCAD平台的失磁故障仿真,全面验证了解析结果的正确性。该文给出的失磁故障解析过程为棒控电源系统发电机失磁保护方案的制定奠定了理论基础。
关键词:核电站控制棒电源系统 发电机失磁 故障解析 故障分段
核电站控制棒驱动机构电源系统(简称棒控电源)是控制棒驱动机构唯一的电源系统,棒控电源系统采取百分百冗余配置方案,由两列参数及保护配置完全相同的电动机-发电机组构成,正常工作时两列机组并列运行[1]。完整的棒控电源系统结构如图1所示,分为上游供电部分、旋转异步电机(Rotating Asynchronous Machine, RAM)系统及下游负荷部分。上游供电部分由核电站主发电机经分裂变压器和降压变压器产生 线电压带动异步电动机;RAM系统由笼型异步电动机经过飞轮质量块拖动隐极发电机,产生
线电压带动异步电动机;RAM系统由笼型异步电动机经过飞轮质量块拖动隐极发电机,产生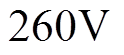 线电压供给下游负荷。RAM系统出口母线经半桥整流,给控制棒驱动机构各类工作线圈供电。
线电压供给下游负荷。RAM系统出口母线经半桥整流,给控制棒驱动机构各类工作线圈供电。
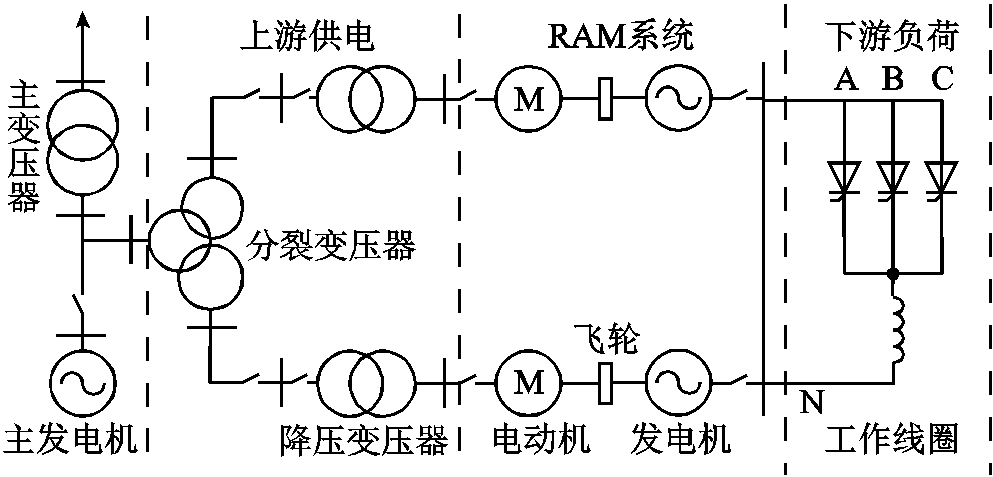
图1 完整棒控电源系统结构图
Fig.1 Complete structure of control rod power system
由于对RAM系统发电机的失磁过程认识不清,工程实际中仅采用简单的转子低电流作为保护判据,导致现场发生多起保护失去选择性而误动的事件。如2019年11月14日,某百万kW级核电站并列运行的RAM系统中一列机组因故障导致失磁,进而造成正常列过电流。由于当前采用的转子低电流判据适用性存在问题,使得正常列过电流保护动作将正常列切除,故障列失磁保护动作将故障列切除,两列系统全部失效,控制棒线圈失电落棒导致反应堆停堆,给核电站造成了巨大的经济损失。
同步发电机失去励磁是发电机励磁回路常见的故障,发电机失磁不仅会影响自身安全,还可能会危及整个系统的稳定运行[2-6]。现有的失磁故障特征分析主要针对并网发电机。并网发电机发生失磁后,伴随着失磁程度的加深,主要有发电机无功功率反向、系统电压降低、定子过电流及转子过热等特点,且发电机以低转差率联网运行,输出一定的有功功率[7-11]。
目前对并网发电机失磁研究,主要分为定性和定量分析两方面。定性分析的技术路线为根据发电机失磁后的运行状态将整个失磁历程分为等有功阶段、异步运行阶段和稳态异步运行阶段,并阐述了各阶段电气量变化规律;其中,文献[3,7,12]基于Matlab对单机无穷大系统进行失磁仿真,并按阶段对电气量变化规律进行了说明。定量分析主流技术路线为通过建立发电机数学模型,将失磁故障特征量化为方程,代入发电机数学模型求解,进而得到定转子侧各电气量的时域表达式[13-16]。
针对发电机模型,文献[17]给出了四种发电机失磁异步运行的数学模型,包含传统的Park模型、计及实心转子涡流的定参数模型、计及实心转子涡流的d轴三绕组变参数模型和计及实心转子涡流的d轴两绕组变参数模型,并通过失磁仿真,得出后两种模型精度更高的结论。此外,文献[18-19]从气隙磁通密度谐波变化、转子端部漏抗变化及涡流损耗计算角度出发考量发电机失磁后的动态特性,并通过建立有限元模型求解,验证了方法的有效性。
现有针对并网发电机失磁过程的研究并不适用于RAM系统发电机,原因在于RAM系统发电机与并网发电机存在两方面的差异:一是RAM系统发电机不具有调速器,电动机输出机械功率取决于发电机电磁功率。但该系统具有惯性质量很大的飞轮,飞轮的作用是在失去上游供电的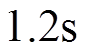 内,拖动发电机输出不低于
内,拖动发电机输出不低于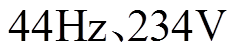 的电能。在失磁故障发生瞬间,机组转速不突变。二是RAM系统经出口母线直接连至负荷,而非无穷大电网,机端电压和频率不恒定。因此,需要单独展开对RAM系统发电机失磁过程的解析工作。
的电能。在失磁故障发生瞬间,机组转速不突变。二是RAM系统经出口母线直接连至负荷,而非无穷大电网,机端电压和频率不恒定。因此,需要单独展开对RAM系统发电机失磁过程的解析工作。
明确失磁故障特征是制定保护方案的基础,因此对失磁过程的解析很关键。针对RAM系统发电机失磁故障解析,本文基于合理的假设,由其等效电路与发电机数学模型,得到q轴电动势的一般表达式;按照发电机失磁后转差率及功角特点,将失磁发展历程分为等功角阶段、异步运行阶段及周期异步运行阶段;根据各阶段q轴电动势表达式推导得到各电气量的解析表达式,之后通过实际机组失磁实验数据和失磁仿真全面验证了解析结果的正确性。本文对RAM系统发电机失磁故障的解析为失磁保护方案的制定奠定了理论基础。
为了突出RAM发电机失磁过程的主要规律,本文忽略次要因素,进行以下假设:
(1)认为RAM机组具有足够的无功支撑能力。当对列具有足够的无功供给能力,且忽略发电机磁饱和,则认为母线出口电压在故障发展过程中保持不变。
(2)忽略定、转子间漏磁及阻尼绕组引起的次暂态过程。针对RAM系统失磁的研究最终要落实到保护优化上,侧重于失磁后各电气量稳态时的规律,因此忽略定转子漏磁及阻尼绕组引起的次暂态变化过程。
RAM系统采取百分百冗余配置,并列运行的两列机组参数及保护配置完全相同,单列机组便可充分满足下游负荷需求。忽略发电机定子电阻及漏抗,单列RAM机组等效电路如图2所示。图2中,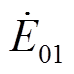 为发电机空载电动势;
为发电机空载电动势;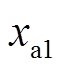 为电枢反应电抗;
为电枢反应电抗;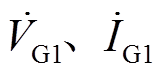 分别为机端电压、电流;
分别为机端电压、电流;![]() 分别为发电机输出有功功率及无功功率;
分别为发电机输出有功功率及无功功率;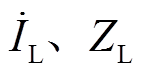 分别为负荷电流和阻抗。
分别为负荷电流和阻抗。
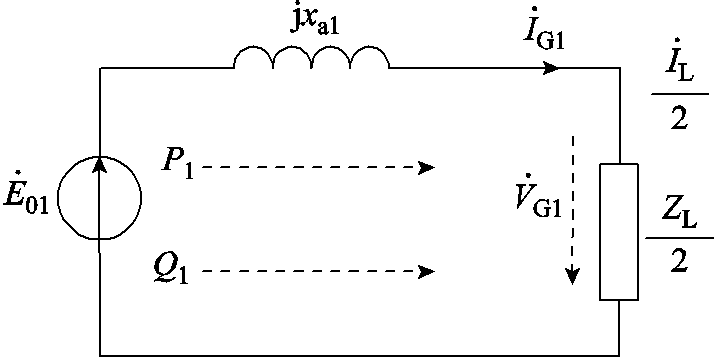
图2 单列RAM机组等效电路
Fig.2 Equivalent circuit of single RAM unit
RAM系统隐极同步发电机数学模型稳态等效电路模型如图3所示,其相量图如图4所示[20]。图中,![]() 为d轴、q轴同步电抗;
为d轴、q轴同步电抗;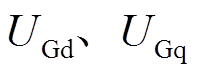 和
和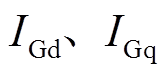 分别为机端电压电流d、q轴分量;
分别为机端电压电流d、q轴分量;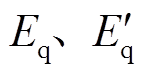 分别为q轴电动势稳态值和暂态值;
分别为q轴电动势稳态值和暂态值;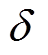 为发电机功角,
为发电机功角,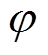 为发电机功率因数角。
为发电机功率因数角。
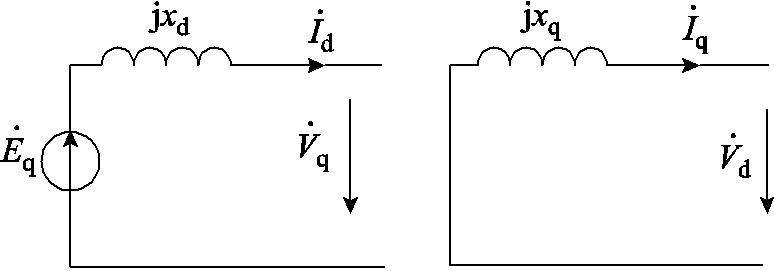
图3 RAM隐极发电机稳态运行dq轴等效电路
Fig.3 The dqaxis equivalent circuit of RAM generator steady state
根据图4所示相量图可以得到稳态时机端电流表达式为
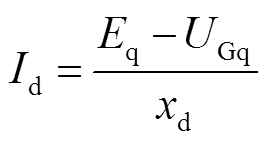 (1)
(1)
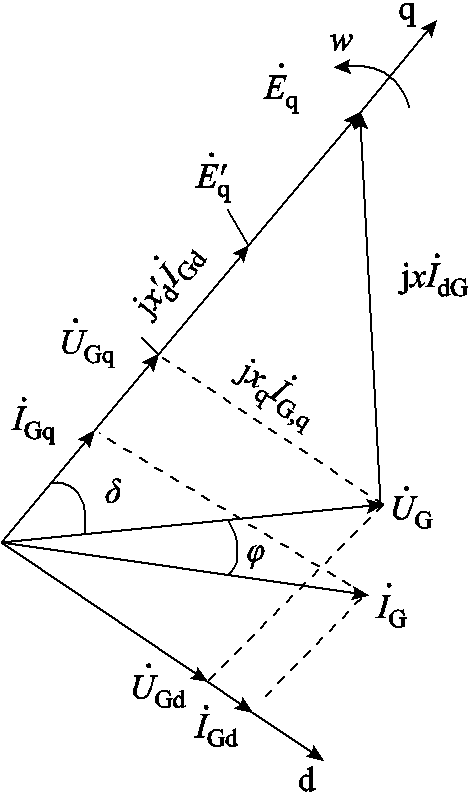
图4 RAM隐极发电机运行相量图
Fig.4 Phasse diagram of RAM non-salient pole generator
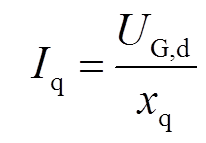 (2)
(2)
输出有功功率及无功功率分别为
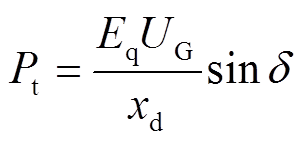 (3)
(3)
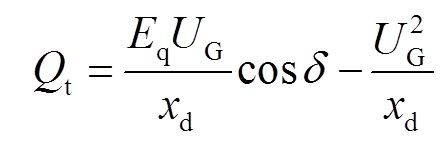 (4)
(4)
发电机转子运动方程为
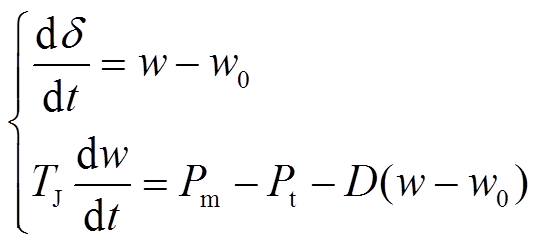 (5)
(5)
式中, 为原动机输出机械功率;
为原动机输出机械功率;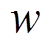 为电气角速度;D为无量纲的阻尼系数;TJ为发电机组惯性时间常数。
为电气角速度;D为无量纲的阻尼系数;TJ为发电机组惯性时间常数。
发电机任意时刻都有转子方程式(6)成立。
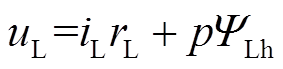 (6)
(6)
式中,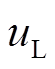 为施加在发电机转子上的励磁电压;
为施加在发电机转子上的励磁电压;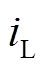 为发电机励磁绕组中的电流;
为发电机励磁绕组中的电流;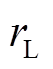 为励磁绕组电阻;
为励磁绕组电阻;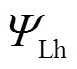 为励磁绕组上的合成磁链;p为微分算子。
为励磁绕组上的合成磁链;p为微分算子。
将式(6)两边同除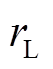 ,并乘以电枢反应电抗
,并乘以电枢反应电抗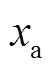 ,可得[21]
,可得[21]
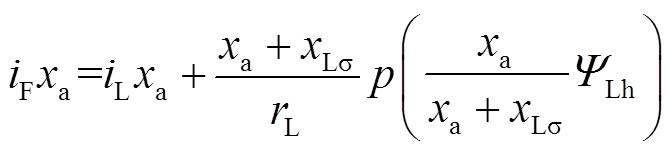 (7)
(7)
式中,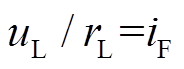 ;
;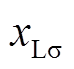 为励磁线圈漏抗。又有[21]
为励磁线圈漏抗。又有[21]
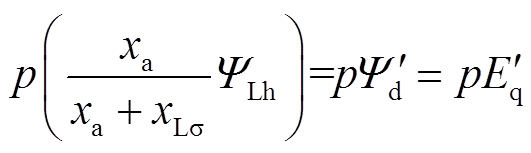 (8)
(8)
将式(8)代入式(7)中,结合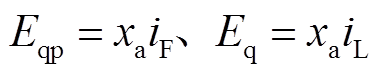 ,则有
,则有
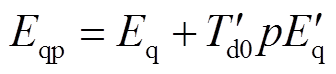 (9)
(9)
式中,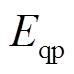 为励磁机供给的励磁电流
为励磁机供给的励磁电流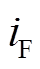 所引起的纵轴同步电动势;
所引起的纵轴同步电动势;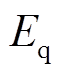 为励磁绕组电流
为励磁绕组电流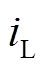 引起的纵轴同步电势;
引起的纵轴同步电势;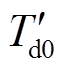 为纵轴瞬变开路时间常数,
为纵轴瞬变开路时间常数,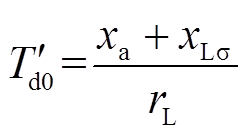 。
。
由图4发电机相量图可知有
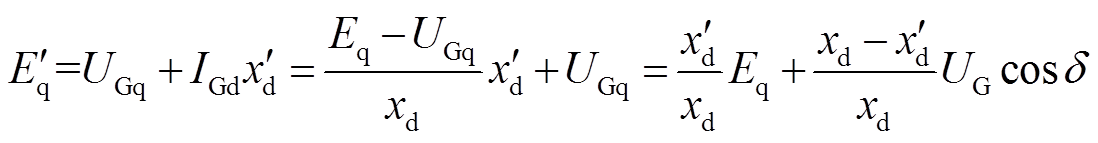 (10)
(10)
式中,各量均采用瞬时值,在发电机失磁后,RAM机组有足够的无功功率支撑使得机端电压保持不变,则有
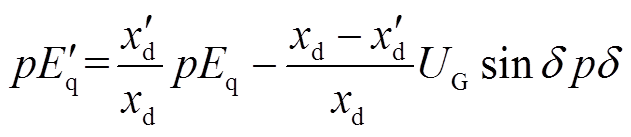 (11)
(11)
将式(11)代入式(9)有
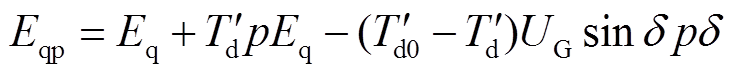 (12)
(12)
式中,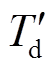 为纵轴瞬变短路时间常数[22],
为纵轴瞬变短路时间常数[22],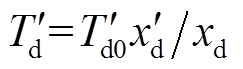 。式(12)由基于隐极发电机的磁链方程和转子回路方程推得,其在失磁后的任一时刻都是成立的。
。式(12)由基于隐极发电机的磁链方程和转子回路方程推得,其在失磁后的任一时刻都是成立的。
正常运行时两列RAM机组转速相同,RAM发电机直连至出口母线,则失磁后故障列功角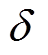 代表q轴电动势与母线电压
代表q轴电动势与母线电压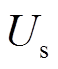 夹角,而母线电压、频率为正常列机端电压、频率,因此故障列功角变化量
夹角,而母线电压、频率为正常列机端电压、频率,因此故障列功角变化量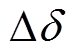 实质上反映了两列机组的转速差在时间维度上的累积。
实质上反映了两列机组的转速差在时间维度上的累积。
根据发电机失磁后的功角及转差率特点,可将RAM发电机失磁发展历程划分为等功角阶段、异步运行阶段和周期异步运行阶段三个阶段,如图5所示。
等功角阶段:原动机输出机械功率不能突变,发电机输出有功减小,由式(5)可得,故障列转子有加速趋势,正常列机组有减速趋势;而电动机与发电机同轴连接一惯性质量大的飞轮,因此转速不能突变,所以功角在失磁初始阶段不变,称之为等功角阶段。RAM系统发生失磁导致故障列q轴电动势衰减,由式(1)和式(2)可知,输出电流和有功功率减小,无功功率减小乃至反向。正常列机组通过增加励磁来增加无功功率输出,输出有功功率、无功功率及电流增加。此阶段故障列发电机基本可视为同步运行。
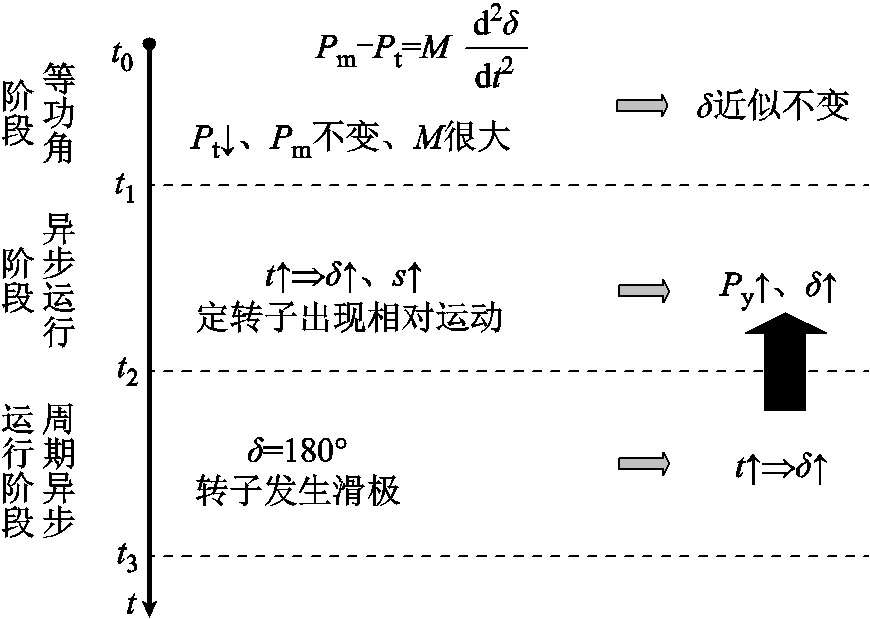
图5 RAM发电机失磁发展历程分段
Fig.5 Segmentation of the development process of RAM generator loss of field
异步运行阶段:随着失磁程度加深,机组转速突破飞轮限制出现缓慢变化。故障列功角和转差率开始增加,与正常机组不同步,进入异步运行阶段。故障机组定转子之间出现相对运动,在转子上产生感应电势,减缓了励磁的衰减;随着转差率及功角增大,发电机输出异步有功功率及从对列吸收无功功率增大;反向无功的增大及定子上的感应电动势使得定子电流增加。在此阶段中,正常列机组仍然基本为同步运行。
周期异步运行阶段:在无外界条件干预的情况下,故障列功角逐渐增加到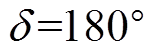 ,即出现了滑极现象,象征着故障机组进入周期异步运行阶段。此时转子上感应电动势、电流反向,进而使得各电气量产生相应的波动,直至出现下一次滑极,各电气量重复异步运行阶段的变化规律。随着转子滑极的不断发生,各电气量呈现周期性变化。在此阶段中,正常列仍基本为同步运行。
,即出现了滑极现象,象征着故障机组进入周期异步运行阶段。此时转子上感应电动势、电流反向,进而使得各电气量产生相应的波动,直至出现下一次滑极,各电气量重复异步运行阶段的变化规律。随着转子滑极的不断发生,各电气量呈现周期性变化。在此阶段中,正常列仍基本为同步运行。
发电机发生失磁,导致q轴电动势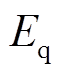 衰减,进而引起各电气量变化;其中有功功率的变化又导致机电暂态过程的发生[23],使得失磁过程变得更加复杂。本文采用的失磁故障解析技术路线为:按照RAM机组失磁过程的分段方法,以q轴电动势
衰减,进而引起各电气量变化;其中有功功率的变化又导致机电暂态过程的发生[23],使得失磁过程变得更加复杂。本文采用的失磁故障解析技术路线为:按照RAM机组失磁过程的分段方法,以q轴电动势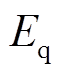 为切入点,分析各阶段内
为切入点,分析各阶段内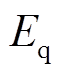 的变化规律,再通过各电气量与
的变化规律,再通过各电气量与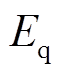 之间的关系得到各阶段内的解析表达式。以RAM系统突然失去励磁电压为例给出解析过程。
之间的关系得到各阶段内的解析表达式。以RAM系统突然失去励磁电压为例给出解析过程。
1)等功角阶段
此阶段功角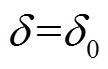 ,即
,即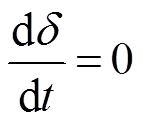 ,代入式(12)中,则有
,代入式(12)中,则有
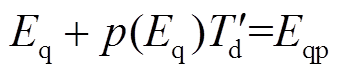 (13)
(13)
对式(13)进行积分求解,结合初始条件,有
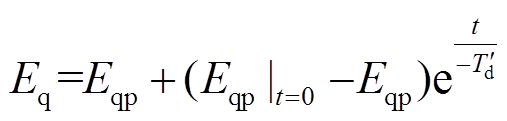 (14)
(14)
式中,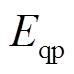 为发电机发生部分失磁后,励磁机继续向发电机提供的励磁电流所产生的q轴电动势。又因为完全短路失磁,有
为发电机发生部分失磁后,励磁机继续向发电机提供的励磁电流所产生的q轴电动势。又因为完全短路失磁,有 ,代入可得等功角阶段q轴电动势变化规律为
,代入可得等功角阶段q轴电动势变化规律为
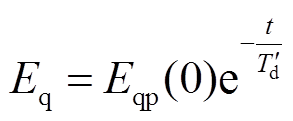 (15)
(15)
式中,![]() 为失磁故障发生前的稳态q轴电动势。
为失磁故障发生前的稳态q轴电动势。
根据式(1)~式(4)可得此阶段故障机组输出有功、无功及电流为
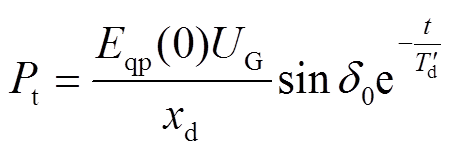 (16)
(16)
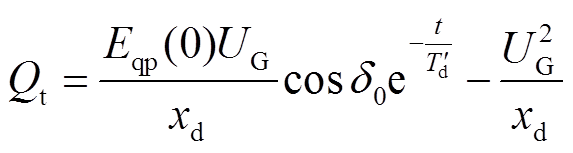 (17)
(17)
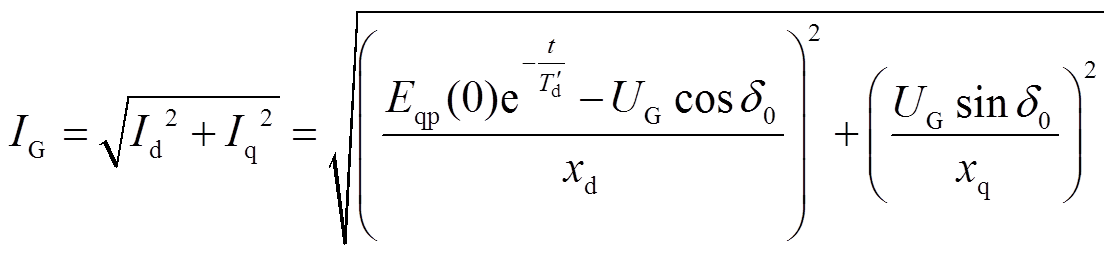 (18)
(18)
由式(18)可知,等功角阶段,故障机组![]() 与q轴电动势衰减规律一致,而
与q轴电动势衰减规律一致,而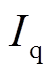 与励磁无关,
与励磁无关,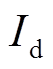 随着q轴电动势
随着q轴电动势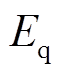 衰减而衰减,且
衰减而衰减,且 衰减速度快于q轴电动势。
衰减速度快于q轴电动势。
2)异步运行阶段
此阶段中故障机组功角及转差率缓慢增大,定转子出现相对运动,转子上产生感应电动势减缓q轴电动势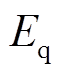 的衰减,因此有
的衰减,因此有
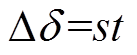 (19)
(19)
式中,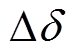 为异步运行阶段故障机组功角变化量;s为故障机组转差率。将式(19)代入式(12)中有
为异步运行阶段故障机组功角变化量;s为故障机组转差率。将式(19)代入式(12)中有
 (20)
(20)
对式(20)进行求解得
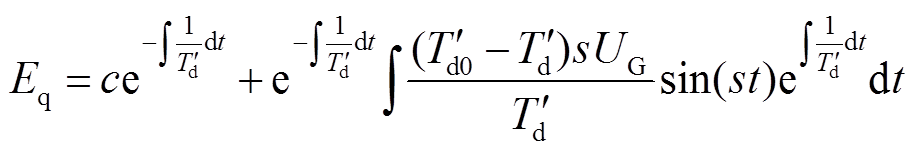 (21)
(21)
而实际RAM系统中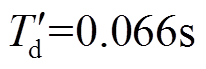 ,
,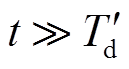 ,所以
,所以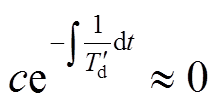 ,进而可得此阶段q轴电动势表达式为
,进而可得此阶段q轴电动势表达式为
 (22)
(22)
由于故障机组定子电压仍是对称三相交流电,因此产生的磁场为圆形旋转磁场,转子相对于定子磁场的转速为-sw(w为正常机组转速),进而在转子侧各绕组中感应出频率为sf(f为正常机组频率)的单相电流。此电流产生的功率是发电机异步运行输出有功的主要成分。
将式(22)代入式(3)中,可得纵轴方向励磁绕组磁通与定子磁场作用产生的异步有功功率为
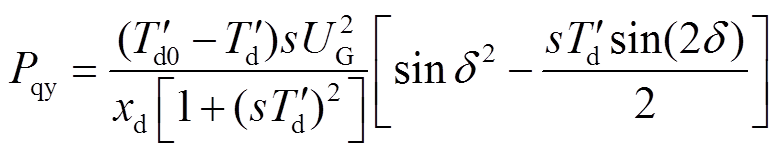 (23)
(23)
又因为 ,且RAM机组发电机转子对称度较高,因此在横轴方向产生的有功功率与纵轴方向相等;当转差率s平均值不变时,可得异步有功功率平均值为
,且RAM机组发电机转子对称度较高,因此在横轴方向产生的有功功率与纵轴方向相等;当转差率s平均值不变时,可得异步有功功率平均值为
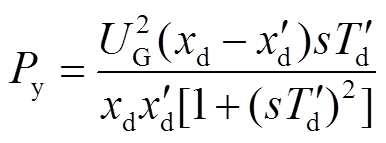 (24)
(24)
同理可得此阶段输出无功功率平均值为
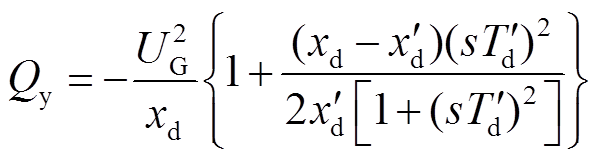 (25)
(25)
定子电流变化规律可由有功功率、无功功率及机端电压求出,即
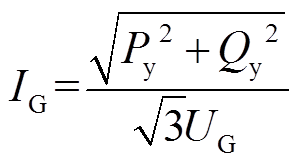 (26)
(26)
3)周期异步运行阶段
进入此阶段的标志是故障机组功角 180°,即转子发生滑极。在无外界条件干预情况下,转子会不断发生滑极现象,转子滑极导致转子上感应电流反向,进而使得各电气量发生波动。随着转子重复滑极,各电气量重复异步运行阶段的变化规律。
180°,即转子发生滑极。在无外界条件干预情况下,转子会不断发生滑极现象,转子滑极导致转子上感应电流反向,进而使得各电气量发生波动。随着转子重复滑极,各电气量重复异步运行阶段的变化规律。
电动机参数见表1,发电机参数见表2。
表1 电动机参数
Tab.1 Motor parameters

参数数值 额定功率/kW135 额定电压/V380 额定转速/(r/min)1 485 功率因数0.89 转动惯量/(kg×m2)3.5
表2 发电机参数
Tab.2 Generator parameters

参数数值参数数值 容量/(kV×A)400额定励磁电流(pu)0.8 额定功率/kW100纵轴瞬变短路时间常数/s0.066 额定电压/V260直轴同步电抗(pu)1.96 额定转速/(r/min)1 500交轴同步电抗(pu)1.96
RAM系统电动机、飞轮、发电机同轴连接,且电动机无调速器。建模时将飞轮转动惯量等效进电动机惯量中,M-G机组耦合原理如图6所示。电动机运行在转矩控制模式,发电机运行在转速控制模式。将电动机-发电机视为一个面向负荷的整体,由机组整体与负荷实现功率与转矩的平衡;在机组内部,发电机将对应负荷条件下所需的电磁功率传递给电动机,由电动机实现相应功率下的转速要求,并将此转速传递至发电机,使两者运行在同一转速。

图6 M-G机组耦合原理
Fig.6 The coupling principle of M-G unit
由于PSCAD中发电机和电动机模型的转矩输入输出采取标幺值,该标幺值均以各自的额定转矩作为基准值。而系统中的电动机和发电机的额定转矩不同,本文将发电机额定电磁转矩与电动机额定电磁转矩之比定义为转矩耦合系数k,由该系数来实现两者转矩的匹配。
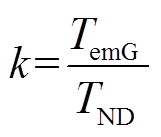 (27)
(27)
式中,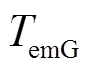 为发电机额定电磁转矩(N
为发电机额定电磁转矩(N m);
m);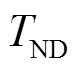 为电动机额定转矩(N
为电动机额定转矩(N m)。
m)。
由于发电机电枢绕组电阻很小,忽略电枢绕组上产生的损耗,有
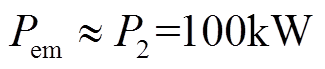 (28)
(28)
式中, 为发电机电磁功率;
为发电机电磁功率;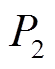 为发电机输出的三相电功率。
为发电机输出的三相电功率。
发电机额定电磁转矩为
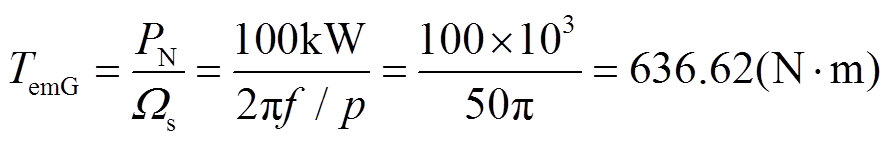 (29)
(29)
式中,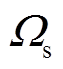 为机械角速度。
为机械角速度。
电动机额定转矩计算公式为
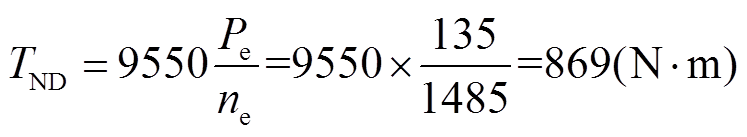 (30)
(30)
因此由式(27)可得转矩耦合系数为
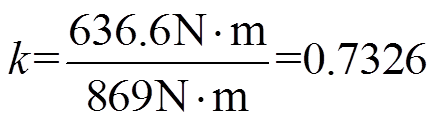 (31)
(31)
为验证本文失磁过程解析工作的准确性,对某核电站的棒控电源系统进行了部分失磁实验。失磁故障前两列机组负载水平为P =22kW、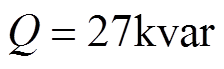 ,部分失磁发生后的1.2s内,失磁列机组的励磁电流从0.8(pu)减小至0.2(pu)。
,部分失磁发生后的1.2s内,失磁列机组的励磁电流从0.8(pu)减小至0.2(pu)。
将两机组机端电压a相、机端电流a相及励磁电流原始录波数据进行导出,并经标幺化处理。失磁列机组电压电流波形如图7a所示,用标号1来表示正常列机组电压电流波形如图8a所示,用标号2来表示。同时为验证仿真模型的正确性,在模型中模拟本次失磁故障,仿真条件同实验条件,在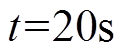 发生失磁,失磁故障的持续时间为1.2s。失磁列机组和正常列机组电压电流仿真波形如图7b及图8b所示。
发生失磁,失磁故障的持续时间为1.2s。失磁列机组和正常列机组电压电流仿真波形如图7b及图8b所示。
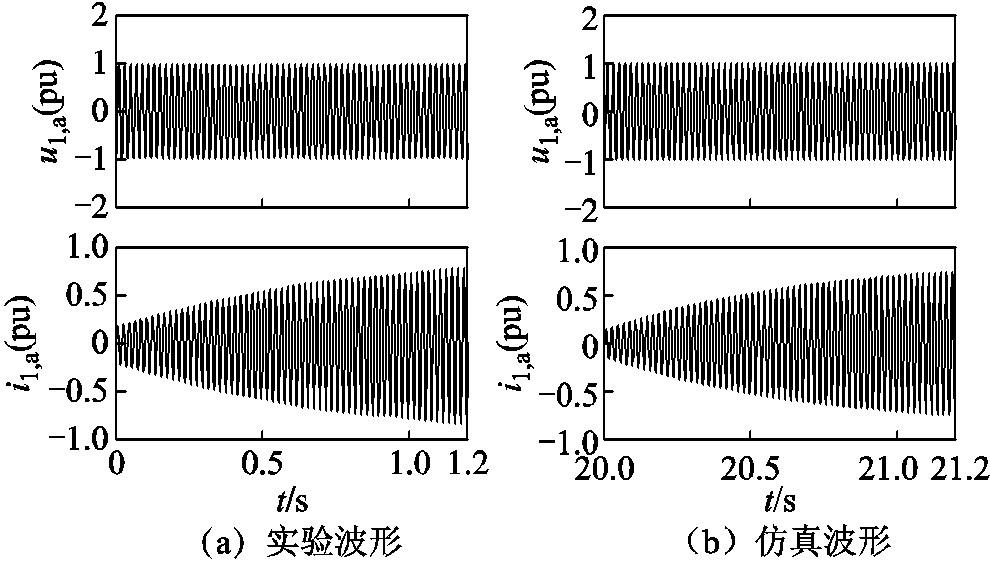
图7 失磁机组波形对比
Fig.7 Comparison of LOF unit waveforms

图8 正常机组波形对比
Fig.8 Comparison of normal unit waveforms
两机组励磁电流实际录波值与仿真值对比如图9所示。为便于对比,已将仿真波形时间与录波时间对齐。
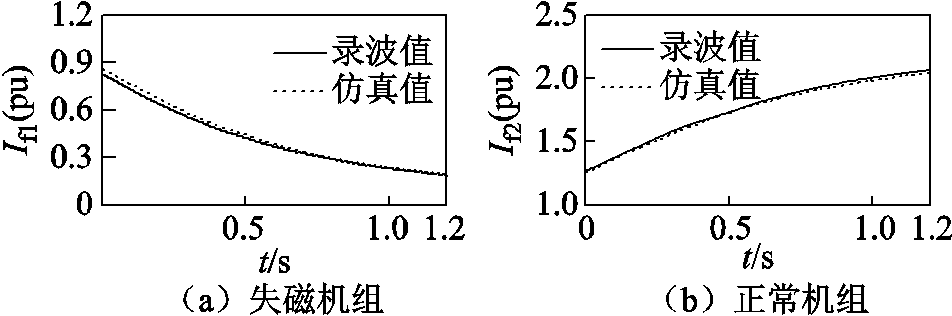
图9 励磁电流仿真值与录波值对比
Fig.9 Comparison between simulated and recorded values of excitation current
由图9可知,在失磁后的1.2s内,随着失磁列机组励磁电流从0.8(pu)降至0.2(pu),正常列机组的励磁电流从1.2(pu)升高至2.1(pu);由图7及图8可知,整个失磁过程中机端电压稳定在1(pu);失磁机组因从对列吸取无功功率,导致机端电流增大,而正常机组增发无功功率导致机端电流增大。
由图7~图9可知,仿真模型中的机端电压、电流和励磁电流变化情况与原始录波数据基本吻合,进一步验证了模型的正确性。因此,仿真模型可以正确模拟出实际机组中各电气量变化过程,对于实验过程中无法测取的发电机功角和转差率以及更多工况和时间尺度的数据可采用仿真值进行分析。失磁过程中功角及转差率的仿真波形如图10所示。
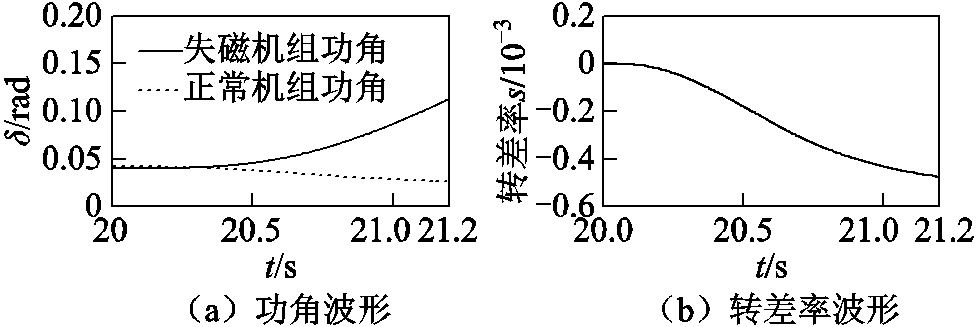
图10 功角及转差率波形
Fig.10 Power angle and turndown rate waveforms
机组发生失磁后,由于惯性存在导致两机组转速不突变。由图10可知,转差率和功角在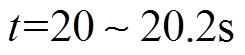 内基本不变,即失磁机组进入等功角阶段,等功角阶段持续时间约为0.2s。
内基本不变,即失磁机组进入等功角阶段,等功角阶段持续时间约为0.2s。
本文所推导出的等功角阶段q轴电动势变化规律如式(15)所示,则由本次失磁实验及对图9a中曲线进行拟合可得失磁机组q轴电动势变化规律为
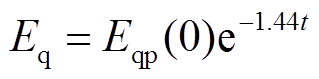 (32)
(32)
由式(16)和式(17)可知,失磁机组输出有功功率和无功功率分别为
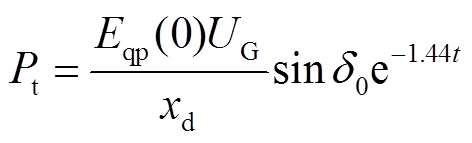 (33)
(33)
 (34)
(34)
经由式(33)和式(34)计算得到的功率解析值与实际仿真值对比如图11所示。
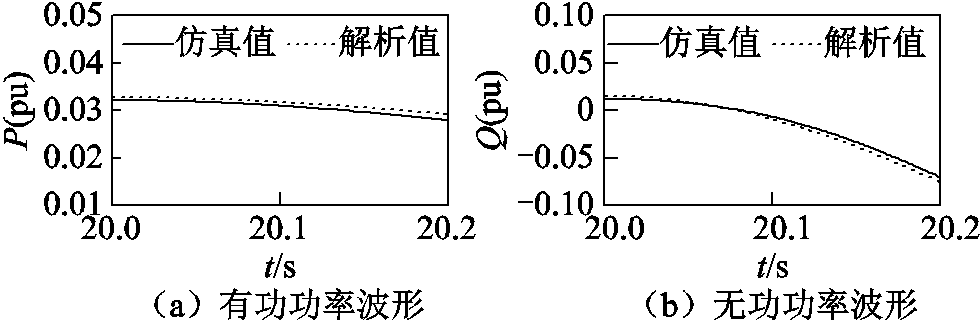
图11 失磁机组功率仿真值与解析值对比
Fig.11 Comparison of simulated and analyzed values of power of LOF units
由图11对比结果可知,等功角阶段解析结果与仿真结果相吻合,验证了解析过程的正确性。随着失磁程度加深,功角及转差增大,机组进入异步运行阶段,即失磁机组相对正常机组异步运行。而本次实验出于安全考虑,只进行了较短时间内轻负载水平下发生部分失磁的实验,因此实验数据无法对异步运行阶段及周期异步运行阶段进行验证。
为了进一步全面且深入地了解RAM机组失磁过程,采用实验验证过的仿真模型进行双机并列运行、满载水平下完全失磁的故障仿真。令总仿真时长为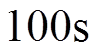 ,在
,在 时一列RAM机组失去励磁电压[24],用下标1代表故障机组,下标2代表正常机组,得到各阶段电气量波形。
时一列RAM机组失去励磁电压[24],用下标1代表故障机组,下标2代表正常机组,得到各阶段电气量波形。
3.3.1 等功角阶段
由图12功角波形可知,在失磁后的初始阶段内,功角及转速近似不变,即两列机组处于等功角阶段,该阶段时长为: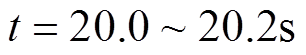 。用励磁电流
。用励磁电流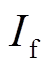 表征同步电动势
表征同步电动势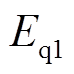 的变化,发电机
的变化,发电机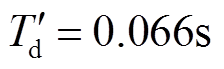 ,由式(15)做出励磁电流理论衰减曲线,如图12b所示,其余各电气量波形如图13所示。
,由式(15)做出励磁电流理论衰减曲线,如图12b所示,其余各电气量波形如图13所示。

图12 等功角阶段功角及励磁电流波形
Fig.12 The power angle and excitation current waveforms of equal power angle stage
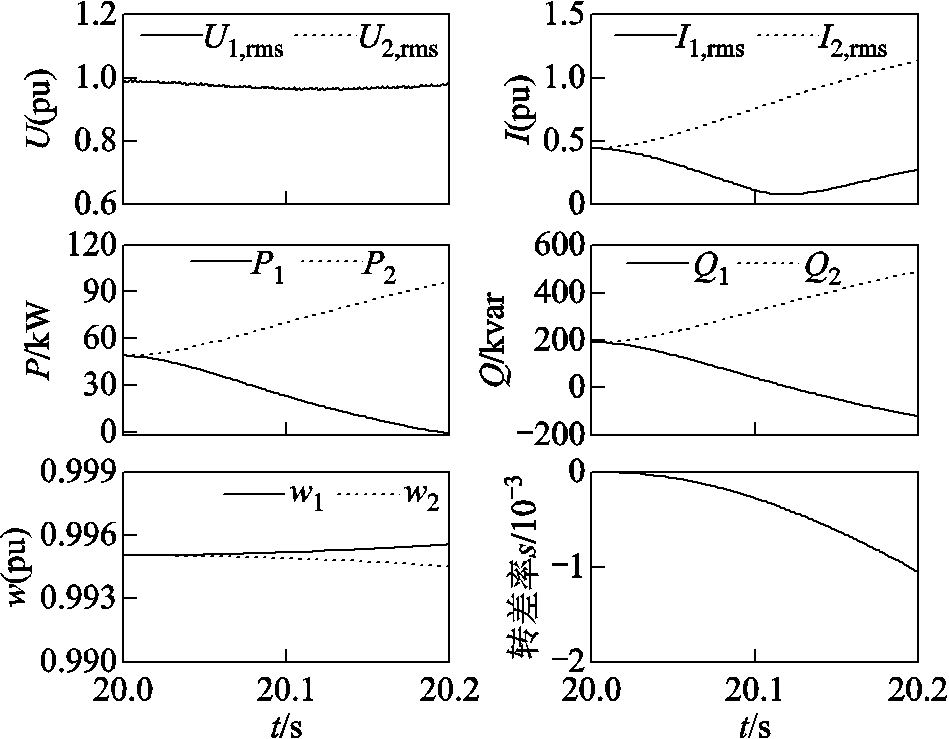
图13 等功角阶段其余各电气量波形
Fig.13 Electrical waveforms of equal power angle stage
由图12b可知,实际励磁电流失磁后的衰减规律与理论一致,均呈指数规律变化。之所以实际衰减值高于理论值,是因为在等功角阶段,两列机组功角仍出现了较小差别,进而在转子绕组上产生感应电动势,减缓了励磁电流的衰减。
故障机组发生失磁,需要从相邻机组吸取无功来维持自身磁场,而正常列有足够的无功支撑能力,因此可以维持出口母线电压在整个失磁阶段内维持不变。
由式(16)和式(17)可知,故障机组在等功角阶段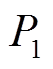 、
、 的衰减与q轴电动势
的衰减与q轴电动势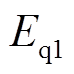 衰减规律相同。
衰减规律相同。 随着
随着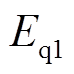 的衰减很快过零变负;励磁衰减和反向无功电流双重作用使得
的衰减很快过零变负;励磁衰减和反向无功电流双重作用使得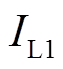 下降,且由式(18)可知,
下降,且由式(18)可知,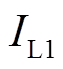 衰减规律快于
衰减规律快于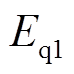 ,结果与图13相符。RAM2列增加励磁来增加无功功率输出,因此
,结果与图13相符。RAM2列增加励磁来增加无功功率输出,因此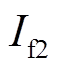 、
、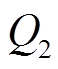 增加,无功电流使得
增加,无功电流使得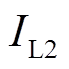 增加,同样由式(16)可知,励磁增加使得
增加,同样由式(16)可知,励磁增加使得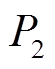 增加。
增加。
3.3.2 异步运行阶段
此阶段出现的明显标志为两列机组的转速出现差别,该阶段时间对应: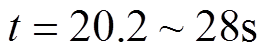 。波形如图14所示。
。波形如图14所示。
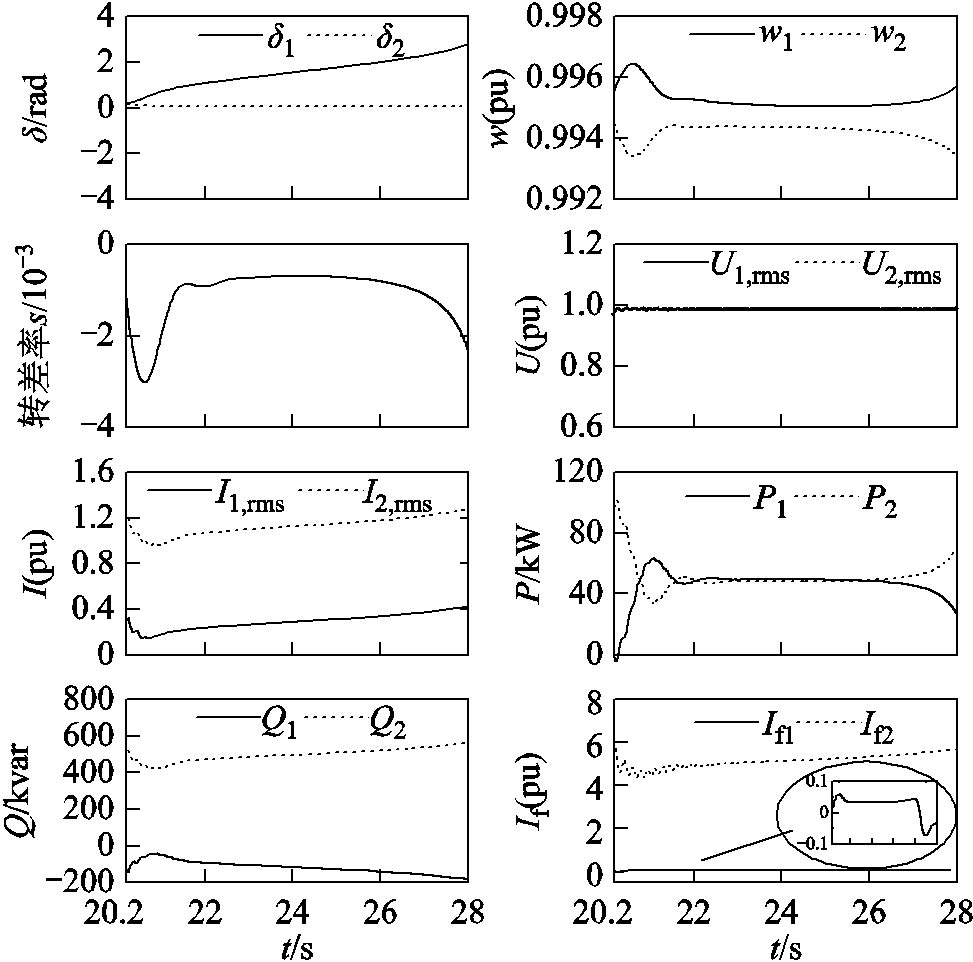
图14 异步运行阶段各电气量波形
Fig.14 Electrical waveforms of asynchronous operation stage
由等功角阶段分析可知,故障列发电机输出有功功率下降,进而原动机输出机械功率下降,则有转速w1升高;同理可得,正常列转速w2下降;进而使得功角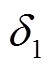 及转差率s开始显著增加。
及转差率s开始显著增加。
功角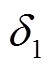 增加,意味着故障列发电机定转子出现相对运动,使得定转子上分别出现感应电动势。反映在转子上感应出频率为sf的单相交流电流,励磁电流
增加,意味着故障列发电机定转子出现相对运动,使得定转子上分别出现感应电动势。反映在转子上感应出频率为sf的单相交流电流,励磁电流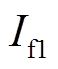 回升。功角初始值
回升。功角初始值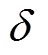 =9°,在
=9°,在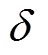 <90°之前,随着功角及励磁增大,
<90°之前,随着功角及励磁增大,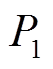 升高并恢复至失磁前有功功率水平;
升高并恢复至失磁前有功功率水平; 升高使得正常机组励磁减小,即
升高使得正常机组励磁减小,即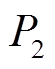 、
、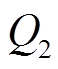 、
、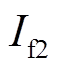 、
、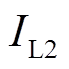 下降。感应电动势反映在定子上体现为发电机输出电流
下降。感应电动势反映在定子上体现为发电机输出电流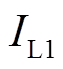 回升。
回升。
由于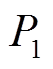 升高、
升高、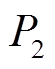 下降,由机组耦合原理可知,原动机转速
下降,由机组耦合原理可知,原动机转速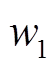 下降、
下降、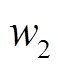 升高,但此时仍有
升高,但此时仍有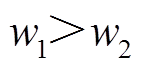 。故障列吸收无功功率
。故障列吸收无功功率 随着转差增大而增大。由式(24)可知,此时输出有功功率及端电压不变,则电流
随着转差增大而增大。由式(24)可知,此时输出有功功率及端电压不变,则电流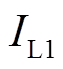 跟随无功变化,且由图14可知,两者变化规律一致。正常列继续增加励磁来增加无功输出,即
跟随无功变化,且由图14可知,两者变化规律一致。正常列继续增加励磁来增加无功输出,即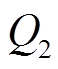 、
、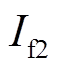 、
、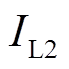 升高。
升高。
当 ,由式(23)可知,
,由式(23)可知,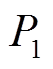 随着功角增大而减小,
随着功角增大而减小,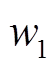 升高,
升高, 反向增大。同理可知,正常列增加励磁使得
反向增大。同理可知,正常列增加励磁使得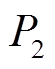 增加,
增加,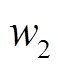 减小。
减小。
3.3.3 周期异步运行阶段
随着故障列机组发电机功角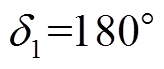 ,即出现滑极现象,进入周期异步运行阶段,此阶段波形如图15所示。
,即出现滑极现象,进入周期异步运行阶段,此阶段波形如图15所示。
发电机转子上的感应电动势反向,经历一次换向过程,进而导致有功、无功、电流、转差率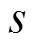 、原动机转速
、原动机转速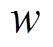 重复上述异步运行阶段的规律做周期性变化。由功角变化周期可知,出现滑极的频率约为8s一次,因此上述各电气量及转速、转差率的变化周期约为
重复上述异步运行阶段的规律做周期性变化。由功角变化周期可知,出现滑极的频率约为8s一次,因此上述各电气量及转速、转差率的变化周期约为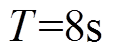 。
。
图15 周期异步运行阶段各电气量波形
Fig.15 Electrical waveform of periodic asynchronous operation stage
将上述RAM系统发电机失磁过程与并网发电机失磁过程进行对比总结,见表3。
表3 失磁过程总结
Tab.3 Summary of demagnetization process

RAM发电机失磁过程并网发电机失磁过程 等功角阶段P、Q、I随励磁减小衰减;U不变等有功阶段 P基本不变;Q随励磁减小而衰减;U减小 异步运行阶段P随δ及励磁增大恢复故障前大小;Q先随励磁正向恢复,后随转差增大而反向增大;I与Q变化一致;U不变临界异步运行阶段 P振荡衰减,逐渐趋于0;Q减小至反向; 周期异步运行阶段转子周期性滑极,重复上述变化异步运行阶段 P恢复至失磁前水平;Q反向;随转子滑极,重复上述变化
由表3明显得知,RAM系统发电机的失磁过程与并网发电机有显著差异。
本文以核电站RAM系统为研究对象,对RAM发电机失磁故障特征展开了定性分析和定量解析。定性分析为根据失磁后功角及转差率特点,将整个失磁发展历程分为等功角阶段、异步运行阶段和周期异步运行阶段。定量分析为根据各阶段q轴电动势的变化,解析得到各阶段电气量一般表达式,并通过失磁实验录波数据和失磁仿真全面验证了解析结果的正确性。上述失磁故障解析工作为制定失磁保护方案及提高核电站的安全稳定运行提供了依据。本文并未对RAM系统失磁保护方案进行讨论,需要进一步研究。
参考文献
[1] 俞高伟, 周蕴花, 沈志华, 等. 核电站控制棒驱动机构电源系统[J]. 发电设备, 2012, 26(4): 278-281.
Yu Gaowei, Zhou Yunhua, Shen Zhihua, et al. Power system for control rod drive mechanism of nuclear power plants[J]. Power Equipment, 2012, 26(4): 278-281.
[2] 郝亮亮, 李佳慧, 段贤稳, 等. 核电多相环形无刷励磁机转子绕组短路故障特征分析[J]. 电工技术学报, 2020, 35(6): 1251-1261.
Hao Liangliang, Li Jiahui, Duan Xianwen, et al. Characteristic analysis of short-circuit fault in rotor winding of nuclear power multi-phase annular brushless exciter[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1251-1261.
[3] 薛磊, 陈远志, 寇水潮, 等. 660 MW汽轮发电机失磁后稳态异步运行过程分析[J]. 电力系统保护与控制, 2019, 47(11): 181-187.
Xue Lei, Chen Yuanzhi, Kou Shuichao, et al. Analysis of stable asynchronous running of 660 MW turbine generator for loss of excitation[J]. Power System Protection and Control, 2019, 47(11): 181-187.
[4] 郑作伟, 郑玉平, 潘书燕, 等. 调相机失磁保护励磁电压判据性能分析与改进[J]. 电力系统自动化, 2020, 44(10): 174-179.
Zheng Zuowei, Zheng Yuping, Pan Shuyan, et al. Performance analysis and improvement of excitation voltage criterion for loss of excitation protection of condenser[J]. Automation of Electric Power Systems, 2020, 44(10): 174-179.
[5] 郭智琳, 郝亮亮, 曹虹, 等. 基于励磁电流差异的调相机失磁保护方案[J]. 电力自动化设备, 2021, 41(12): 178-186.
Guo Zhilin, Hao Liangliang, Cao Hong, et al. Excitation loss protection scheme based on excitation current difference for synchronous condenser[J]. Electric Power Automation Equipment, 2021, 41(12): 178-186.
[6] 田代宗, 孙宇光, 王善铭, 等. 多相整流永磁同步发电机绕组内部相间短路的故障分析[J]. 电工技术学报, 2020, 35(6): 1262-1271.
Tian Daizong, Sun Yuguang, Wang Shanming, et al. Analysis of stator internal phase-to-phase short-circuit in the multiphase permanent magnet synchronous generator with rectifier load system[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1262-1271.
[7] 樊波, 牛天林, 薛钧义. 基于MATLAB的发电机失磁故障仿真研究[J]. 电气技术, 2007, 8(2): 60-63.
Fan Bo, Niu Tianlin, Xue Junyi. The simulation research of generator loss-of-excitation faults based on MATLAB[J]. Electrical Engineering, 2007, 8(2): 60-63.
[8] 王道元, 徐余法, 梁旭彪, 等. 百万千瓦汽轮发电机失磁异步特性研究[J]. 电气自动化, 2015, 37(6): 18-20.
Wang Daoyuan, Xu Yufa, Liang Xubiao, et al. A research on the asynchronous characteristics of loss of excitation of the 1 000 MW turbo-generator[J]. Electrical Automation, 2015, 37(6): 18-20.
[9] Hasani A, Haghjoo F, da Silva F M F, et al. A current-based differential technique to detect loss of field in synchronous generators[J]. IEEE Transactions on Power Delivery, 2020, 35(2): 514-522.
[10] Das A, Dhar S, Royburman S, et al. The efficacy of generator protection under sudden loss of excitation using offset-type MHO-relay[J]. Journal of the Institution of Engineers (India): Series B, 2017, 98(1): 115-120.
[11] 马波涛, 姚缨英. 汽轮发电机失磁过程分析[J]. 机电工程, 2008, 25(9): 21-24.
Ma Botao, Yao Yingying. Analysis of dynamic processes for turbo-generator[J]. Mechanical & Electrical Engineering Magazine, 2008, 25(9): 21-24.
[12] 周卫巍. 基于PSCAD的AP1000核电厂发电机失磁故障仿真研究[J]. 电气应用, 2013, 32(13): 31-33, 93.
Zhou Weiwei. Study on simulation of generator loss of excitation in AP1000 nuclear power plant based on PSCAD[J]. Electrotechnical Application, 2013, 32(13): 31-33, 93.
[13] 王维俭侯炳蕴. 大型机组继电保护理论基础[M]. 北京: 水利电力出版社, 1982.
[14] Maity A, Bhattacharya K, Sanyal A N. Asynchronous operation of synchronous generators under field failure[C]//2014 First International Conference on Automation, Control, Energy and Systems (ACES), Adisaptagram, India, 2014, 1-6.
[15] 陈光. 大型发电机失磁故障仿真及其保护研究[D]. 北京: 华北电力大学(北京), 2008.
[16] Shen Yubo, Zhang Hongda, Lan Sen, et al. Analysis of XLPE asynchronized synchronous generator under loss of excitation[C]//2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 2019: 1-5.
[17] 郭可忠, 赵军. 汽轮发电机失磁异步运行数学模型的比较[J]. 电网技术, 1999, 23(8): 13-16.
Guo Kezhong, Zhao Jun. Comparison of mathematic model of turbogenerator's asynchronous operation during loss of field[J]. Power System Technology, 1999, 23(8): 13-16.
[18] 梁艳萍, 陆永平, 朱宽宁, 戈宝军. 汽轮发电机失磁异步运行时转子端部漏磁参数与涡流损耗的分析计算[J]. 中国电机工程学报, 2004, 24(11): 112-115.
Liang Yanping, Lu Yongping, Zhu Kuanning, et al. Calculation of leakage reactance and eddy current losses in the rotor end region of large turbogenerator at asynchronous operation[J]. Proceedings of the CSEE, 2004, 24(11): 112-115.
[19] 吕艳玲, 戈宝军, 陶大军, 等. 超高压发电机失磁异步运行磁场分析[J]. 中国电机工程学报, 2012, 32(6): 170-175.
Lü Yanling, Ge Baojun, Tao Dajun, et al. Analysis on magnetic field of extra high voltage generators asynchronously operated under loss-of-field condition[J]. Proceedings of the CSEE, 2012, 32(6): 170-175.
[20] 王瑾, 李岩, 贾建国, 等. 反电动势和凸极率对高效永磁同步磁阻电机稳态特性影响分析[J]. 电工技术学报, 2020, 35(22): 4688-4698.
Wang Jin, Li Yan, Jia Jianguo, et al. Analysis of the influence of back-EMF and saliency ratio on steady-state characteristics of a high efficiency permanent magnet synchronous reluctance motor[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4688-4698.
[21] 姚晴林. 同步发电机失磁及其保护[M]. 北京: 机械工业出版社, 1981.
[22] 吕智勇, 王东, 林楠, 等. 高速交错磁极混合励磁发电机直流侧短路电流分析计算[J]. 电工技术学报, 2020, 35(11): 2396-2405.
Lü Zhiyong, Wang Dong, Lin Nan, et al. Analysis and calculation of DC side short-circuit current of high-speed staggered pole hybrid excitation generator[J]. Transactions of China Electrotechnical Society, 2020, 35(11): 2396-2405.
[23] 霍承祥, 高磊, 吴剑超, 等. 励磁系统动态增益对凸极发电机暂态稳定的影响[J]. 电力系统自动化, 2020, 44(21): 58-63.
Huo Chengxiang, Gao Lei, Wu Jianchao, et al. Effect of dynamic gain of excitation system on transient stability of salient pole generator[J]. Automation of Electric Power Systems, 2020, 44(21): 58-63.
[24] 孙文涛, 刘涤尘, 赵洁, 等. 大型压水堆核电机组失磁动态特性及机理研究[J]. 中国电机工程学报, 2014, 34(10): 1538-1545.
Sun Wentao, Liu Dichen, Zhao Jie, et al. Study on dynamic characteristics and mechanism of the loss of excitation of large-scale pressurized water reactor nuclear power plant[J]. Proceedings of the CSEE, 2014, 34(10): 1538-1545.
Abstract Nuclear power plant control rod power is the only power supply system of control rod drive mechanism, to ensure the safe and reliable operation of this system is of great significance to improve the safety of nuclear power plants. The principle of loss of field protection is simple, and many mismatch events of loss of field(LOF) protection have occurred on site; the operation state of the control rod power system generator is different from that of the conventional grid-connected generator; In order to effectively solve the loss of field protection mismatch problem, this paper has carried out the qualitative analysis and quantitative analysis of the loss of field fault of the generator in control rod power system.
Firstly, it is assumed that the RAM unit has sufficient reactive power support capacity and ignores the magnetic leakage between stator and rotor and the sub transient process caused by damping winding, and the general expression of longitudinal potential is obtained on the basis of the equivalent circuit of RAM system and the mathematical model of generator. Since the variation quantity of power angle of fault-unit essentially reflects the accumulation of the speed difference between two units in time dimension, the loss of field development process is divided into equal power angle phase, asynchronous operation phase and periodic asynchronous operation phase according to the slip rate and power angle characteristics. Fault-unit generator can be regarded as synchronous operation in equal power angle phase, while normal-unit generator can be regarded as synchronous operation in asynchronous operation phase and periodic asynchronous operation phase.
After that, according to the segmentation method of the loss of field process of RAM units and taking the longitudinal potential as the starting point, the analytical expressions of electrical quantities in each phase are obtained from the longitudinal potential variation law in each stage and the basic equation of generator. The specific analytical process is given by taking the sudden complete loss of field voltage of RAM system as an example.
In order to fully verify the correctness of the analytical results of loss of field, experimental verification and simulation verification are carried out respectively.
Through the experimental data of partial loss of field in an actual nuclear power plant under light load level and combined with correct simulation model, the actual simulation values of active power and reactive power of the field loss unit are compared with the theoretical analysis values and the results are found to be very consistent, which verifies the correctness of analytical results of equal power angle phase after loss of field.
Furthermore, the simulation model verified by the experiment is used to simulate the fault of complete loss of field under two-generator parallel operation and full load level, and the simulation parameter settings are that total simulation duration is 100s and one RAM unit loses field voltage at 20s. The results show that, the variation of electrical quantities in each phase is consistent with theoretical analysis, and the loss of field process of RAM system generator is significantly different from that of grid-connected generator.
The analytical process of loss of field fault lays a theoretical foundation for the formulation of generator loss of field protection plan of the control rod power system.
keywords:Nuclear power plant control rod power system, generator loss of field, fault analysis, fault block
DOI:10.19595/j.cnki.1000-6753.tces.211667
中图分类号:TM341
中广核集团公司科技项目(3100077013)和中央高校基本科研业务费项目(2020JBM070)资助。
收稿日期 2021-10-20
改稿日期 2022-01-20
肖项涛 男,1996年生,硕士,研究方向为电力系统主设备故障分析及保护。E-mail:19121511@bjtu.edu.cn
郝亮亮 男,1985年生,副教授,博士生导师,研究方向为电力系统主设备故障分析及保护、直流输电控制与保护、励磁控制。E-mail:llhao@bjtu.edu.cn(通信作者)
(编辑 郭丽军)