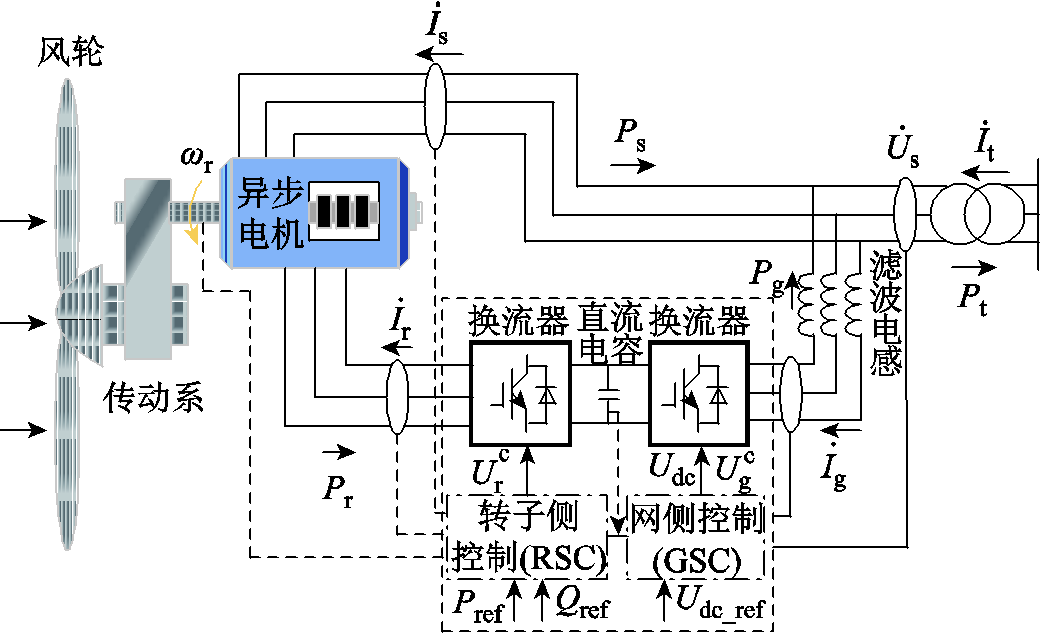
图1 双馈风力发电机结构
Fig.1 DFIG structure diagram
摘要 基于相量测量单元(PMU)的风力发电机动态状态估计能够为风电场能量管理系统提供实时可靠的数据基础。然而,目前多数风电场不具备为每台风机都安装PMU的量测条件,且动态状态估计易受不良数据及扰动的影响。针对上述问题,提出一种考虑风电场量测相关性的双馈风机鲁棒动态状态估计方法。在用最少数量的PMU实现风电场所有节点可观的基础上,提出基于PMU量测空间相关性和风机动态模型时间相关性的冗余量测集构造方法,进而利用加权最小绝对值鲁棒估计得到所有风机的机端电气量,并滤除不良数据。考虑到扰动时状态预报值不准确,提出了基于过程噪声尺度因子的鲁棒滤波方法,在扰动时降低不准确预报值的权重。仿真表明,所提方法对量测配置要求低,并能准确估计风电场内单台风机的动态状态。
关键词:双馈风机 动态状态估计 量测相关性 最小绝对值估计 鲁棒容积卡尔曼滤波
在落实“碳达峰、碳中和”目标的大背景下,风电的开发利用必然会更加受到重视。然而风电具有强间歇性、随机波动性和低可调度性的特点[1],风电场侧能量管理系统(Energy Management System, EMS)可抑制风电波动对电网的影响,提高风电利用率[2]。相量测量单元(Phasor Measurement Unit, PMU)能够实现快速同步量测,使动态状态估计(Dynamic State Estimation, DSE)成为可能[3]。DSE能在量测系统主站提高量测数据质量,并通过卡尔曼滤波的预报-滤波框架实时估计风机等动态元件的运行状态,进而用于风电场优化控制等EMS高级应用[4],对风电场全状态感知具有重要意义。
双馈式风力发电机组(Doubly-Fed Induction Generator, DFIG)因其良好的经济性和运行特性成为风电场主力机型之一,本文选择其作为风电场DSE的研究对象。目前DFIG动态状态估计的相关文献[5-7]大多使用风电场等值模型,然后利用风电场并网点处的同步相量量测对该等效模型进行DSE。文献[5]假设DFIG等值模型的换流器输出电压可量测并作为DSE的输入,这对于等效模型难以实现。文献[6-7]用包括换流器控制系统在内的DFIG详细模型作为风电场等效模型,然而该等效模型控制器参数的准确获取是一个棘手问题。随着新能源占比的提高及测量技术的发展,已有针对风机等新能源电源的PMU,如新能源场站同步测量装置(Synchronized Measurement Device for Renewables, SMD-R)[8]等,与现有输电网PMU相比,其测量频带更宽,上传速率更快,可安装在风电场内部,基于此,可对风场内的单台风机进行DSE。然而,单台DFIG的DSE需要其机端电气量作为状态估计器的输入和量测,但风电场内风机数量众多,目前每台DFIG都装有PMU的量测配置并未普及,DFIG本身的量测也只用于本地控制且非同步相量量测,因此存在DSE量测要求难以满足的问题。
常用非线性卡尔曼滤波方法包括扩展卡尔曼滤波[9]、无迹卡尔曼滤波[7]、容积卡尔曼滤波(Cubature Kalman Filter, CKF)[10]及粒子滤波[11],其中容积卡尔曼滤波无截断误差,不需选择任何参数且算法效率和精度较高,因此本文基于CKF对DFIG进行状态估计。然而,在电力系统实际运行中,由于缺乏校准、硬件故障或脉冲噪声等原因,PMU会出现不良数据,上述方法易受不良数据的影响。文献[12]利用残差检测和迭代排除的方式辨识并滤除量测中的不良数据。文献[13-14]基于新息异常来调整量测噪声方差阵,进而抑制量测不良数据的影响。但上述方法未考虑同样由PMU量测得来的估计器输入也有可能存在不良数据的问题。此外,卡尔曼滤波需要根据前一时刻状态估计值进行状态预报,但 DFIG容量小且采用电力电子装置控制,扰动后状态变化迅速[15],因此扰动时的状态预报值可能存在较大偏差,进而影响状态估计结果。
针对上述问题,本文提出一种考虑风电场量测相关性的DFIG鲁棒动态状态估计方法。首先,考虑到风电场本身可视为一个小型辐射状电网,基于风电场的拓扑特点对PMU进行最优配置,并结合DFIG时间维度的动态模型约束信息构造冗余量测集。其次,基于该冗余量测集和加权最小绝对值(Weighted Least Absolute Value, WLAV)估计得到所有DFIG的机端电气量,并利用扰动和不良数据的判别以及WLAV方法的鲁棒性滤除DSE输入和量测中的不良数据。然后,在扰动时引入过程噪声尺度因子调整过程噪声方差阵,从而降低预报值对状态估计结果的影响。最后,搭建DFIG风电场仿真模型,验证所提方法的有效性。
DFIG动态模型由风轮及传动系、异步电机、转子侧和网侧换流器及其控制器、直流电容以及滤波电感等部分组成,其具体结构如图1所示。本文使用DFIG的相量模型,采用电动机惯例,所有电流相量以流入DFIG为正方向。
风轮及传动系统的单质块模型为

图1 双馈风力发电机结构
Fig.1 DFIG structure diagram
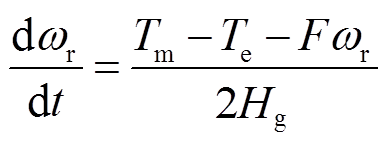 (1)
(1)
式中,ωr为转子转速;Tm为风轮输出的机械转矩,与风速Vwind有关;Te为电磁转矩;F为摩擦系数;Hg为轴系等效惯性时间常数。
电机定子磁通ψds、ψqs及转子磁通ψdr、ψqr的动态变化为
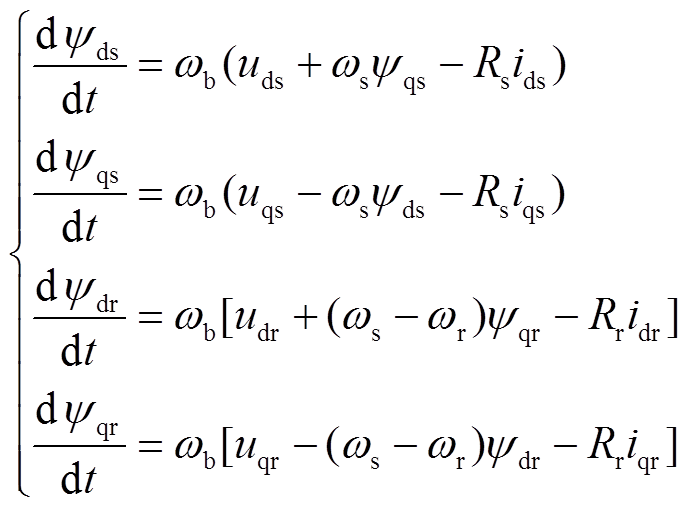 (2)
(2)
式中,ωb为角速度基准值;ωs为同步转速标幺值;Rs和Rr分别为定子和转子的电阻;下标s表示定子侧电气量;下标r表示转子侧电气量;uds、uqs分别为DFIG机端电压的d、q轴分量,其作为DSE的输入将DFIG与外部网络解耦;ids、iqs分别为DFIG 定子电流的d、q轴分量;udr、uqr分别为DFIG 转子电压的d、q轴分量;idr、iqr分别为DFIG 转子电流的d、q轴分量。
DFIG的转子侧换流器主要控制DFIG输出的有功功率和无功功率,网侧换流器负责保持直流电容电压稳定,其控制指令由PI控制器给出,对应的积分环节状态变量用x1~x7表示,其控制框图及x1~x7的具体定义见附录。此外,直流电容和滤波电感的动态方程为
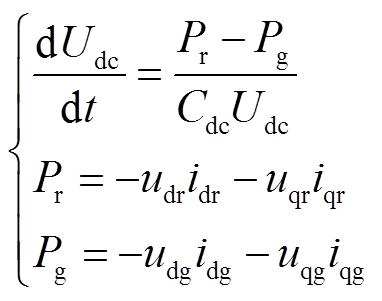 (3)
(3)
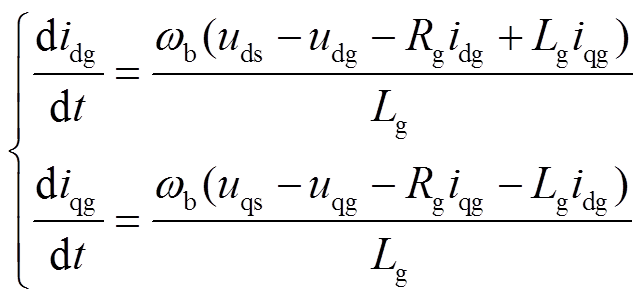 (4)
(4)
式中,Udc为直流电容电压;Pr和Pg分别为换流器转子侧和网侧功率;Cdc为直流电容;下标g表示换流器网侧电气量;udg、uqg分别为换流器网侧电压的d、q轴分量;idg、iqg分别为换流器网侧电流的d、q轴分量;Rg和Lg分别为滤波电感的电阻和电抗。式(1)~式(4)组成DSE的状态转换方程f(x)。
对于量测方程,结合DFIG状态估计的能观性需求及PMU可提供的量测量,选择DFIG机端电流idt、iqt以及发电机输出功率Pt、Qt作为量测量,则每台DFIG动态状态估计的量测方程h(x)为
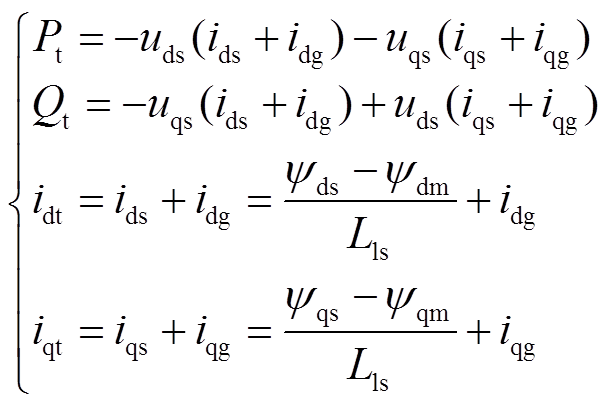 (5)
(5)
式中,idt、iqt分别为DFIG机端电流相量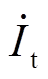 的d轴、q轴分量;Lls为定子绕组漏感;
的d轴、q轴分量;Lls为定子绕组漏感;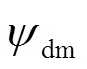 、
、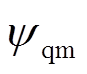 分别为主磁通d、q轴分量。对于上述量测量,需在每台DFIG机端安装PMU以获取这些电气量,对风场量测配置要求较高。
分别为主磁通d、q轴分量。对于上述量测量,需在每台DFIG机端安装PMU以获取这些电气量,对风场量测配置要求较高。
将上述DFIG连续动态模型离散化[16],并写为一般状态空间形式,有
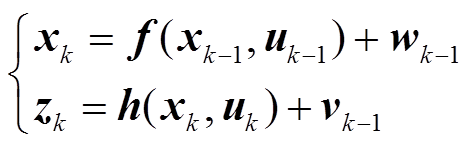 (6)
(6)
式中,f为系统方程; w为系统过程噪声,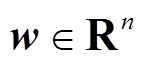 ,其方差阵为
,其方差阵为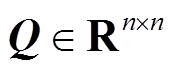 ,n为状态向量维数;h为量测方程;v为量测噪声,
,n为状态向量维数;h为量测方程;v为量测噪声,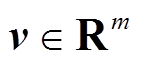 ,其方差阵为
,其方差阵为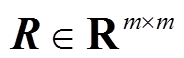 ,m为量测向量维数;下标k为所处时刻;状态向量x、输入向量u及量测向量z分别为
,m为量测向量维数;下标k为所处时刻;状态向量x、输入向量u及量测向量z分别为
 (7)
(7)
基于上述离散状态空间模型,即可利用CKF算法对DFIG的动态状态进行估计。
CKF包括预报步和滤波步。在k时刻的预报步中,首先生成容积采样点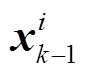 ,即
,即
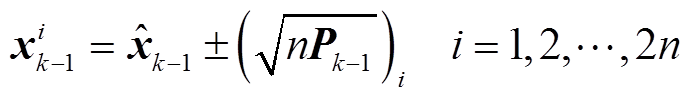 (8)
(8)
式中,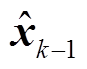 和Pk-1分别为k-1时刻状态估计向量和误差协方差阵;
和Pk-1分别为k-1时刻状态估计向量和误差协方差阵;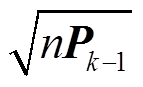 为nPk-1的二次方根矩阵。然后将容积点代入式(6)的DFIG离散动态方程得到
为nPk-1的二次方根矩阵。然后将容积点代入式(6)的DFIG离散动态方程得到 ,进而得到状态预报向量xk|k-1及其对应的协方差矩阵Pk|k-1为
,进而得到状态预报向量xk|k-1及其对应的协方差矩阵Pk|k-1为
![]() (9)
(9)
xk|k-1的准确性对DSE结果有较大影响。在上述过程中可能导致xk|k-1产生较大偏差的原因有:①DFIG机端电压被视为输入,以将DFIG与外部网络解耦,然而由PMU量测得到的机端电压中可能存在不良数据,进而使xk|k-1不准确;②由式(9)可知,xk|k-1由k-1时刻的状态和输入计算得到,由于扰动无法预测,若在[k-1, k]这一时间段内发生扰动,DFIG的迅速响应会使其状态迅速变化,导致xk|k-1与实际值存在较大偏差。
在滤波步中,根据xk|k-1和量测方程计算量测预报容积点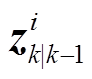 ,并加权计算得到量测预报向量zk|k-1为
,并加权计算得到量测预报向量zk|k-1为
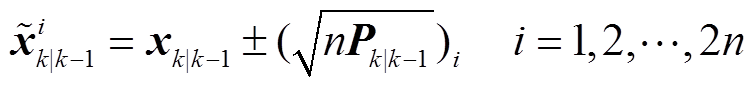 (12)
(12)
进一步地,计算量测预报误差协方差阵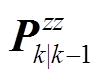 、交叉协方差矩阵
、交叉协方差矩阵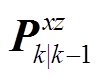 及增益矩阵Kk分别为
及增益矩阵Kk分别为
![]() (14)
(14)
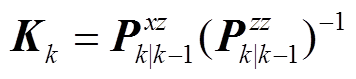 (15)
(15)
最后利用Kk和新息ek = zk-zk|k-1修正状态预报向量,得到k时刻状态估计向量 和估计协方差矩阵Pk为
和估计协方差矩阵Pk为
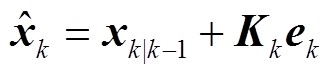 (16)
(16)
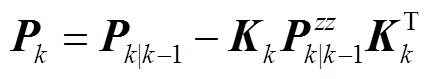 (17)
(17)
可知量测预报向量zk|k-1和PMU量测向量zk中的不良数据会导致ek异常,进而影响状态估计结果。由式(12)可知,zk|k-1中的异常值主要来自xk|k-1及uk,而zk的不良数据主要来自PMU量测过程。
基于新息ek的量测不良数据处理方法[14]在假设输入向量u和状态预报值xk|k-1准确的基础上处理量测z中的不良数据。然而,由上述分析可知,PMU的量测不良数据对输入向量u及量测向量z都有影响,且扰动会使基于前一时刻状态计算得到的xk|k-1不能及时跟随实际状态的变化,这些情况都会引起新息ek变大。因此仅基于ek异常判定量测z中存在不良数据会导致对正常量测值的误判。
针对风电场内量测配置不足的问题,本节通过PMU最优配置和量测空间相关性实现所有节点可观,并利用DFIG动态状态的时间相关性构造冗余量测集,为准确估计所有DFIG的机端电气量提供量测基础。
风电场典型拓扑如图2所示,图中的放射型连接是风电场集电系统的主要连接方式[17],具有结构简单经济、运行方便的特点。从量测配置的角度看,风电场的放射状结构与配电网结构[18]类似,含有较多的零注入节点和叶子节点(只与一个节点相连的节点,如风机箱变的低压侧),因此可将量测配置问题转换为0-1型整数线性规划问题。
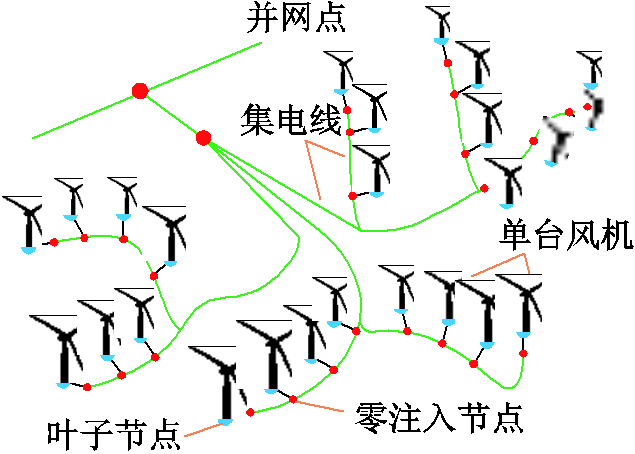
图2 风电场典型拓扑
Fig.2 Typical topologies of wind farms
假设风电场共有N个节点,则目标函数为
式中,i为节点编号; X为PMU放置的情况,X = [X1 X2  XN],Xi = 1表示该节点配置PMU,Xi=0表示不配置。进一步地,该整数规划问题的约束可表示为
XN],Xi = 1表示该节点配置PMU,Xi=0表示不配置。进一步地,该整数规划问题的约束可表示为
1)如果某节点配置PMU,则认为与其相连的节点可观测,如式(19)中Oi表达式的前半部分所示。
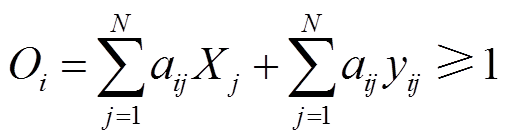 (19)
(19)
![]() (20)
(20)
式中,Oi为节点i被观察到的次数,要求每个节点可观则需Oi≥1;aij为节点关联矩阵的元素;yij为零注入节点j影响的二元辅助变量,yij=1表示节点i可根据基尔霍夫电流定律由零注入节点j及其相连节点观测。
2)零注入约束。假设某个零注入节点及其相连节点共p+1个,若其中任意p个节点可观,则节点p+1也可观[19],反映此特征的约束如式(19)和式(21)所示。
 (21)
(21)
由于只有一个节点可从零注入节点及其相连节点的可观性中受益,因此yij要满足式(21)。
3)叶子节点约束。在叶子节点安装PMU只能使叶子节点及其相连节点共两个节点可观,而若在其相连节点安装PMU则可能使两个以上的节点可观,因此不在叶子节点iL安装PMU,即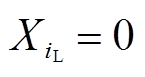 。
。
求解上述整数规划问题,即可得到以使用最少数量的PMU实现所有节点可观为目标的配置方案。
风电场内的DFIG彼此存在电气联系,故不同节点的PMU量测具有空间相关性。对于配置了PMU的节点i,其节点电压相量及与其相连支路的电流相量可测,且与各节点电压相量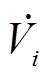 存在如式(22)和式(23)所示的线性关系。
存在如式(22)和式(23)所示的线性关系。
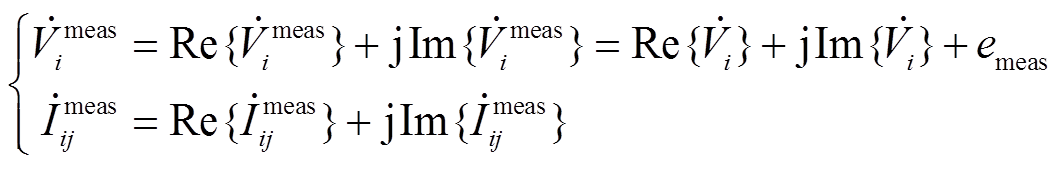 (22)
(22)
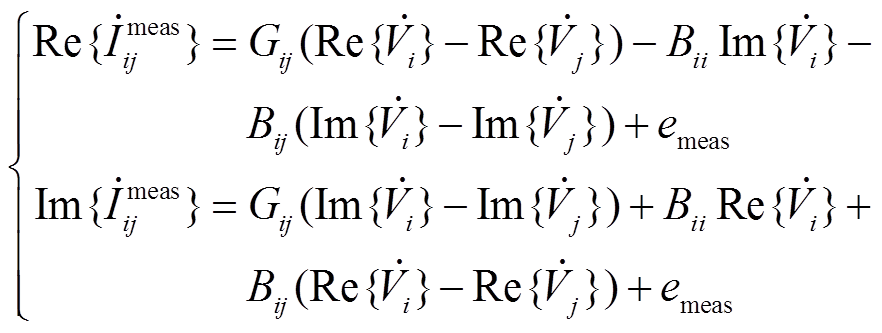 (23)
(23)
式中,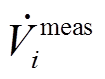 为节点i的电压测量值;
为节点i的电压测量值;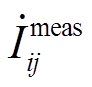 为支路i-j的电流测量值;
为支路i-j的电流测量值;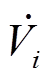 为节点i电压相量真实值;Gij+jBij为支路i-j的串联导纳;Bii为节点i的并联电纳;emeas为测量误差;
为节点i电压相量真实值;Gij+jBij为支路i-j的串联导纳;Bii为节点i的并联电纳;emeas为测量误差;![]() 、
、![]() 分别为相量
分别为相量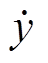 的实部和虚部。
的实部和虚部。
根据基尔霍夫电流定律,与零注入节点iZIB相连的p条支路的电流之和为零,故定义虚拟量测为
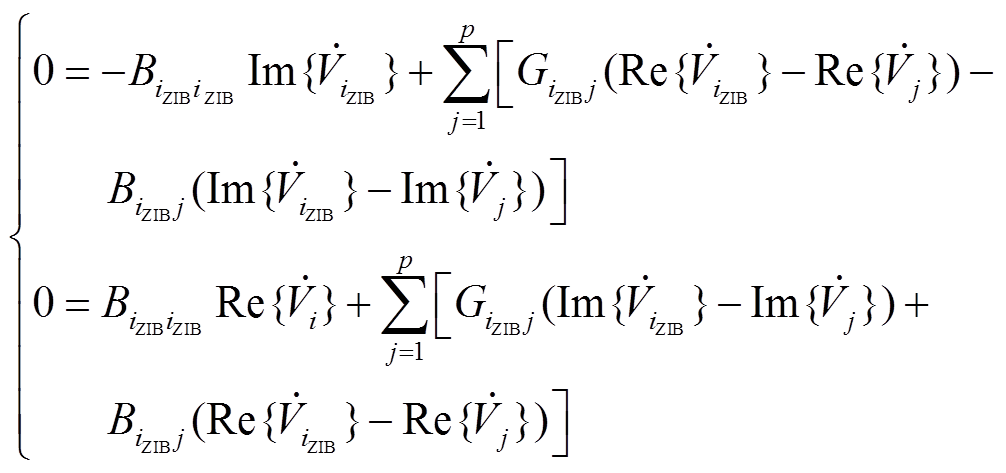 (24)
(24)
状态估计需要利用量测冗余来提高估计准确性,而仅包含上述PMU量测和零注入虚拟量测的量测集冗余度较低。DFIG动态模型包含其状态随时间变化的规律,因此状态具有时间相关性,可用于提高量测冗余。在得到各DFIG的状态预报值之后,计算其各自输出电流 的预报值,并作为虚拟量测参与风电场DFIG机端电气量估计。
的预报值,并作为虚拟量测参与风电场DFIG机端电气量估计。 与x的关系如式(25)所示,将其表示为
与x的关系如式(25)所示,将其表示为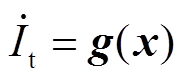 ,即
,即
![]() (25)
(25)
在利用式(9)得到 后,机端电流预报值
后,机端电流预报值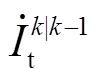 及对应的协方差矩阵可表示为
及对应的协方差矩阵可表示为
基于上述分析,可用于估计所有DFIG机端电气量的冗余量测集,包括PMU节点的电压相量{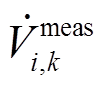 }、支路电流相量{
}、支路电流相量{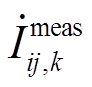 }以及零注入节点的虚拟量测{0}等反映风电场空间拓扑约束的量测信息,还有反映DFIG动态模型约束的DFIG机端电流相量虚拟量测{
}以及零注入节点的虚拟量测{0}等反映风电场空间拓扑约束的量测信息,还有反映DFIG动态模型约束的DFIG机端电流相量虚拟量测{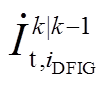 }等。将上述量测用zi,k = zRe i,k+ jzIm i,k,i=1, 2,
}等。将上述量测用zi,k = zRe i,k+ jzIm i,k,i=1, 2, , M表示,然后写作2M维向量
, M表示,然后写作2M维向量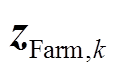 ,有
,有
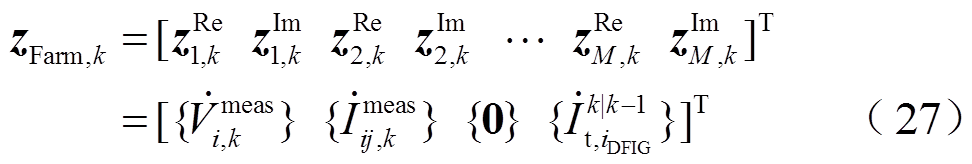
量测向量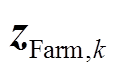 对应的误差方差矩阵
对应的误差方差矩阵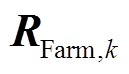 为
为
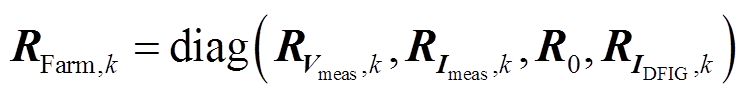 (28)
(28)
式中,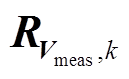 和
和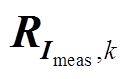 分别为节点电压和支路电流量测误差方差;R0为零注入电流虚拟量测的误差方差,选择较小正数;
分别为节点电压和支路电流量测误差方差;R0为零注入电流虚拟量测的误差方差,选择较小正数;![]() 为DFIG机端电流虚拟量测的误差方差,其值为diag(
为DFIG机端电流虚拟量测的误差方差,其值为diag(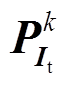 );各元素均为对角矩阵。
);各元素均为对角矩阵。
输入向量u及量测向量z中的不良数据都会导致新息ek异常,难以在DSE执行过程中对二者进行区分。针对该问题,在前述冗余量测集的基础上,本节通过基于WLAV的鲁棒方法来估计所有DFIG机端电气量,在DSE之前滤除PMU量测不良数据。
量测不良数据严重偏离真实值,而扰动也会导致由xk|k-1计算得到的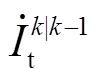 产生较大偏差,所以二者都会影响DFIG机端电气量的估计结果,需分别进行处理,同时二者行为相似,都会造成量测量突变[20]。因此有必要对扰动和量测不良数据进行判别。
产生较大偏差,所以二者都会影响DFIG机端电气量的估计结果,需分别进行处理,同时二者行为相似,都会造成量测量突变[20]。因此有必要对扰动和量测不良数据进行判别。
风电场内各DFIG机组间的电气联系较紧密,因此正常运行或扰动发生时各PMU的量测变化相似;当某台PMU量测存在不良数据时,其他PMU出现类似行为的概率很小,即不良数据的空间相关性差。由此,本文对每台PMU的量测数据进行突变检测,如果多台PMU检测到突变,则认为是扰动数据;如果只有一台PMU有突变,则认为该台PMU产生了不良数据。
正常运行时,PMU测量信号相邻量测点的变化很小,因此对PMU测量结果作差值绝对值运算,可认为其结果只包含噪声信号;而当扰动发生或存在不良数据时,相邻量测点的变化较大,则差值绝对值信号中将包含有噪声与突变信号。因此,通过差值绝对值可以检测突变,但需确定一个阈值,要求其既能滤除噪声影响,也能准确检测扰动或不良数据。考虑到固定阈值的适应性较差,文献[21]提出了一种适用于电能质量扰动检测的自适应阈值,本文将其扩展至相量量测信号,如式(29)所示。
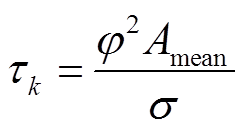 (29)
(29)
式中,τk为k时刻阈值;φ为量测噪声统计标准差;Amean为窗长内的量测幅值信号均值;σ为差值绝对值信号的方差。
![]() (30)
(30)
式中,L为窗长;Ai为原始量测幅值信号;ΔAi为差值绝对值;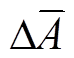 为ΔAk-L+2,
为ΔAk-L+2, ,ΔAk均值,其定义为
,ΔAk均值,其定义为
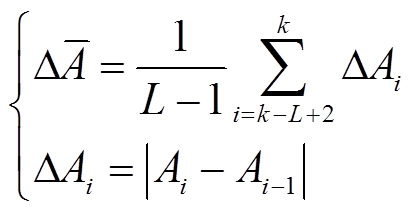 (32)
(32)
正常情况下量测中的噪声稳定,σ只与噪声有关,故其保持在较小范围,进而阈值τk较大,差值绝对值不会超过阈值的范围,即判别无突变;当出现扰动或存在不良数据时,差值绝对值增加,同时方差σ也会迅速增大,导致阈值减小,差值绝对值就会超出阈值线,即该台PMU检测到突变,若多台PMU同时检测到突变,则认为扰动发生,否则为不良数据。
当判定为扰动时,式(28)中的![]() 修改为
修改为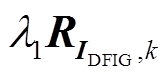 ,正常运行时调整系数
,正常运行时调整系数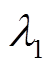 =1,检测到扰动后,由于
=1,检测到扰动后,由于![]() 一般小于1,将
一般小于1,将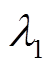 增大为
增大为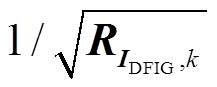 ,以降低不准确的
,以降低不准确的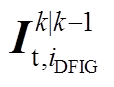 对估计结果的影响。当判定存在不良数据时,将式(28)中该PMU量测对应的
对估计结果的影响。当判定存在不良数据时,将式(28)中该PMU量测对应的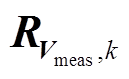 和
和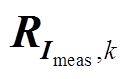 都乘以调整系数
都乘以调整系数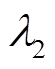 ,相比于扰动数据,量测不良数据严重偏离正常值,因此
,相比于扰动数据,量测不良数据严重偏离正常值,因此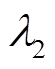 应设置为较大正数以大幅降低其权重。
应设置为较大正数以大幅降低其权重。
将N个节点的电压相量表示为2N维向量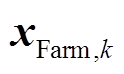 ,即
,即
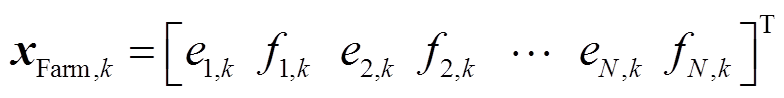 (33)
(33)
式中,![]() 为
为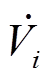 的直角坐标形式。因为
的直角坐标形式。因为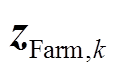 由相量量测组成,故将式(22)~式(24)的量测方程写为线性形式,有
由相量量测组成,故将式(22)~式(24)的量测方程写为线性形式,有
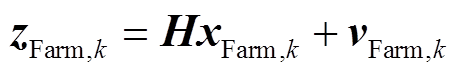 (34)
(34)
式中,H为2M×2N维量测雅可比矩阵;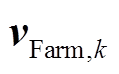 为量测噪声,协方差矩阵
为量测噪声,协方差矩阵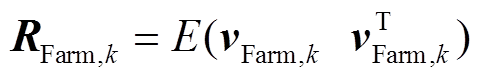 。
。
为进一步降低量测不良数据和扰动的影响,在前述降低权重的基础上,采用具有良好抗差性能的WLAV[22]对DFIG机端电气量进行估计,目标函数为
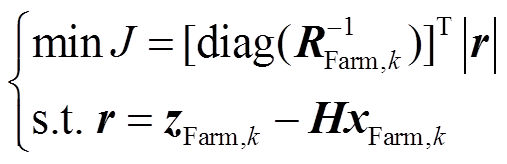 (35)
(35)
式中,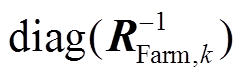 为
为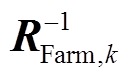 对角元素组成的列向量。
对角元素组成的列向量。
该问题可转换为常规的线性规划问题[22],然后利用成熟的线性规划软件即可求解。本文使用Matlab的linprog函数求解得到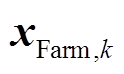 。根据
。根据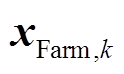 即可计算出所有DFIG的机端电气量,包括各DFIG的机端电压、机端电流及输出功率。由冗余量测集估计机端电气量的过程可知,本文所提方法是在CKF的预报-滤波框架中插入了机端电气量估计步骤,因此滤波步所需的量测信息要在CKF预报步之后得到。
即可计算出所有DFIG的机端电气量,包括各DFIG的机端电压、机端电流及输出功率。由冗余量测集估计机端电气量的过程可知,本文所提方法是在CKF的预报-滤波框架中插入了机端电气量估计步骤,因此滤波步所需的量测信息要在CKF预报步之后得到。
扰动发生时基于扰动前状态计算得到的状态预报值xk|k-1不能及时反映实际状态变化,由于已经通过DFIG机端电气量鲁棒估计滤除了输入向量u及量测向量z中的不良数据,因此当新息ek异常时,可认为是由xk|k-1偏离真实值导致的,基于此对CKF进行改进。
状态预报值xk|k-1异常时将导致过程误差方差阵Q与实际值不符,从而使不正确的xk|k-1在最终状态估计结果中占有较大权重,故引入过程噪声尺度因子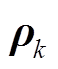 对Q进行在线调整。将式(10)改为
对Q进行在线调整。将式(10)改为
由式(6)可知,过程噪声估计值应满足
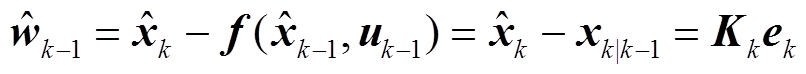 (37)
(37)
则其协方差矩阵估计值可表示为
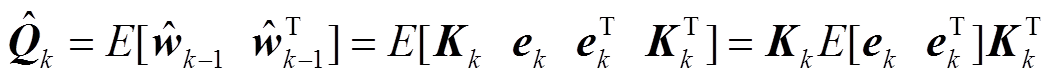 (38)
(38)
式中,Kk为滤波增益矩阵,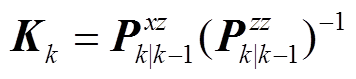 。可知
。可知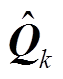 与新息ek的协方差阵相关:正常情况下ek较小,CKF实际使用的
与新息ek的协方差阵相关:正常情况下ek较小,CKF实际使用的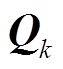 与其估计值
与其估计值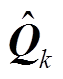 接近;当扰动导致ek和
接近;当扰动导致ek和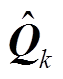 增大时,CKF的
增大时,CKF的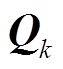 固定不变,此时
固定不变,此时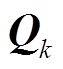 与估计值不符。由此,
与估计值不符。由此,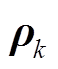 引入后应使过程噪声方差阵与实际过程噪声重新匹配,即满足
引入后应使过程噪声方差阵与实际过程噪声重新匹配,即满足
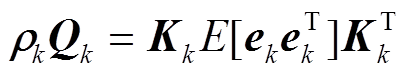 (39)
(39)
基于式(39)可确定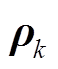 。首先利用开窗估计法计算新息实时协方差
。首先利用开窗估计法计算新息实时协方差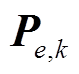 为
为
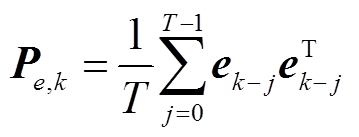 (40)
(40)
式中,T为开窗估计法的窗长。为了保持过程噪声方差阵的正定性,将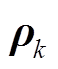 定义为对角阵,即
定义为对角阵,即
 (41)
(41)
式中,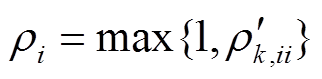 ,
,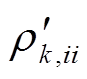 为式(42)中
为式(42)中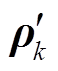 的第i个对角元素。
的第i个对角元素。
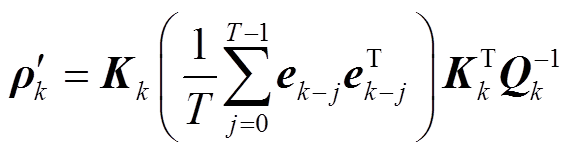 (42)
(42)
在确定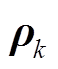 后,按照式(36)即可重新确定Pk|k-1。
后,按照式(36)即可重新确定Pk|k-1。
为方便实施,图3给出了考虑风电场量测相关性的DFIG鲁棒动态状态估计流程。本文所提算法具体步骤总结如下:
1)初始化:输入参数;利用式(18)~式(21)对风电场PMU进行最优配置;设定初始时刻状态值x0、误差协方差矩阵P0,令k=1。
2)预报步:在k时刻,利用式(8)~式(10)计算状态预报向量xk|k-1及其协方差矩阵Pk|k-1;基于式(25)、式(26)计算DFIG机端电流虚拟量测。
3)机端电气量估计:利用式(27)、式(28)构造冗余量测集;基于式(29)~式(32)对扰动和不良数据进行判别,并根据判定结果确定量测集各元素的权重;利用式(33)~式(35)估计所有DFIG机端电气量。
4)滤波步:判定存在扰动时,利用式(36)~式(42)重新确定Pk|k-1;利用式(11)~式(17)计算状态估计值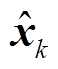 及其协方差矩阵Pk。
及其协方差矩阵Pk。
5)令k=k+1,返回步骤2),进行下一次迭代。
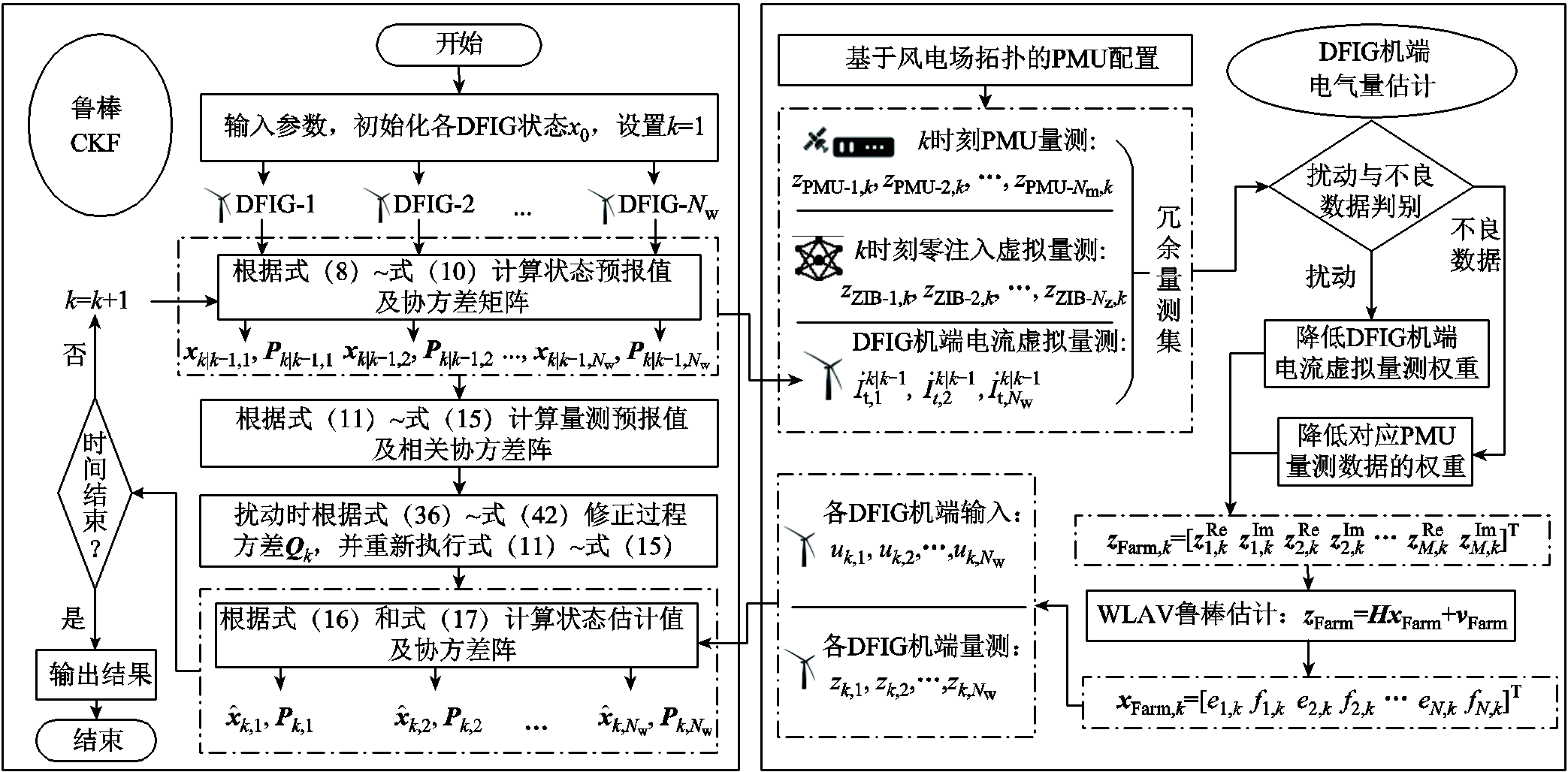
图3 本文所提方法流程
Fig.3 Flow chart of the proposed method
5.1.1 量测布点及仿真设置
在Matlab/Simulink中构建了如图4a所示的风电场,DFIG使用Simulink内置的相量模型,采用一机组一箱变的接线方式,16台1.5MW双馈风机通过4条集电线路连接至风电场主变压器,DFIG和风电场的具体参数见附表1。
按照2.1节量测配置方法,输入上述风电场的拓扑信息,生成节点关联矩阵G,并按以下步骤求解。
1)输入目标函数系数矩阵f1。

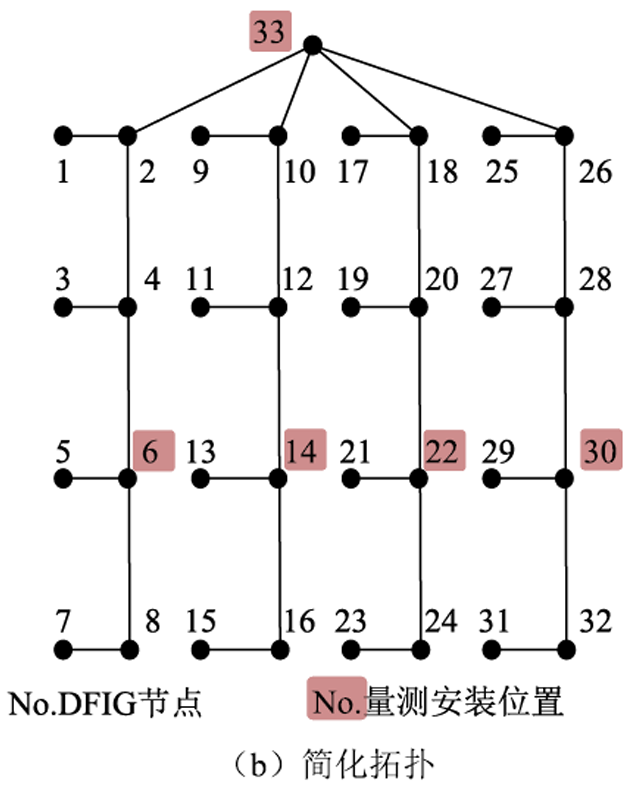
图4 含16台DFIG风电场拓扑和量测配置
Fig.4 The topology of the wind farm with 16 DFIGs and measurement configuration
表1 算例1中PMU布点方案详细信息
Tab.1 Detailed information of PMU placements in case 1

系统节点数ZIB数叶子节点数PMU数量PMU配置节点 含16台DFIG风电场33171656, 14, 22, 30, 33
2)根据零注入节点约束和叶子节点约束,设置相关不等式约束AineqX≤bineq、等式约束AeqX=beq中的系数矩阵Aineq、Aeq和约束向量bineq、beq。
3)X各元素取0或1,故上限Ub=1、下限Lb=0。
4)利用Matlab中intlinprog函数求解,[X, minf1(X)] = intlinprog(f1, Aineq, bineq, Aeq, beq, Lb, Ub)。
所得PMU配置方案如图4b所示,详细信息见表1。以最左侧集电线路为例,在节点6安装PMU,可使节点4、5、8可观测,由于流过支路8-6的电流等于支路7-8的电流,故节点7也可观测;在节点33安装PMU,可使节点2可观测,由于节点2、4为零注入节点,由零注入节点约束可知节点1、3也可观测,故这一条集电线路的节点都可观,其他集电线路的分析类似。由上述分析可知,由于考虑了风电场内节点间的电气联系,在该风电场每条集电线路配置1台PMU即可实现该风电场内所有节点可观测。结合2.2节基于DFIG动态模型所得到的机端电流相量虚拟量测,如图4a中(蓝色)箭头所示,即可得到用于估计风场内所有DFIG机端电气量的冗余量测集合。
仿真开始时风电场DFIG运行在稳定状态,在2s时主变压器低压侧发生三相短路故障,500ms后故障清除,仿真时间持续10s,采样间隔0.01s。将时域仿真数据作为真实值,在真实值基础上添加高斯噪声作为量测。根据PMU量测的相关标准[23],量测误差最大不超过幅值的0.2%,因此设本文PMU的量测噪声服从高斯分布N(0, σ2),其中标准差σ=0.1%,进而CKF的量测协方差矩阵R设定为10-6Im×m,I表示单位矩阵。对于CKF的过程协方差矩阵Q,其主要反映模型和参数误差的影响。根据风电机组建模的相关标准[24]可知,风电机组在投入运行之前都需经过建模验证和参数校验,故本文将Q也设为10-6In×n;零注入虚拟量测对应的误差方差设为10-10;量测方差调整系数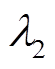 设置为106。此外,定义如式(43)所示的方均根误差(Root-Mean-Square Error, RMSE)作为状态估计误差评价指标。
设置为106。此外,定义如式(43)所示的方均根误差(Root-Mean-Square Error, RMSE)作为状态估计误差评价指标。
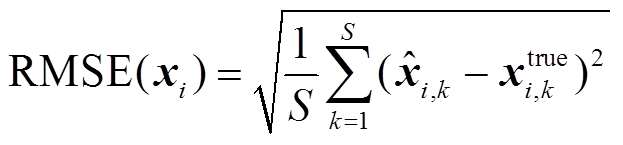 (43)
(43)
式中,S为总的采样点个数;xi,k为k时刻第i个状态的估计值;xtrue i,k为k时刻第i个状态的真值。
5.1.2 DFIG机端电气量的估计准确性评价
基于风电场时空维度信息和WLAV来估计所有DFIG的机端电气量,能够降低量测需求并滤除不良数据,本节对此进行仿真验证。
1)量测正常
在正常量测情况下,设置不同幅度的电压降落和量测噪声,测试突变检测的准确性。三相短路的过渡电阻分别设置为1Ω和5Ω,对应风场并网点(Point of Common Coupling, PCC)电压幅值分别跌落65%和15%,并分别添加1%和0.1%的量测噪声,检测结果如图5所示。
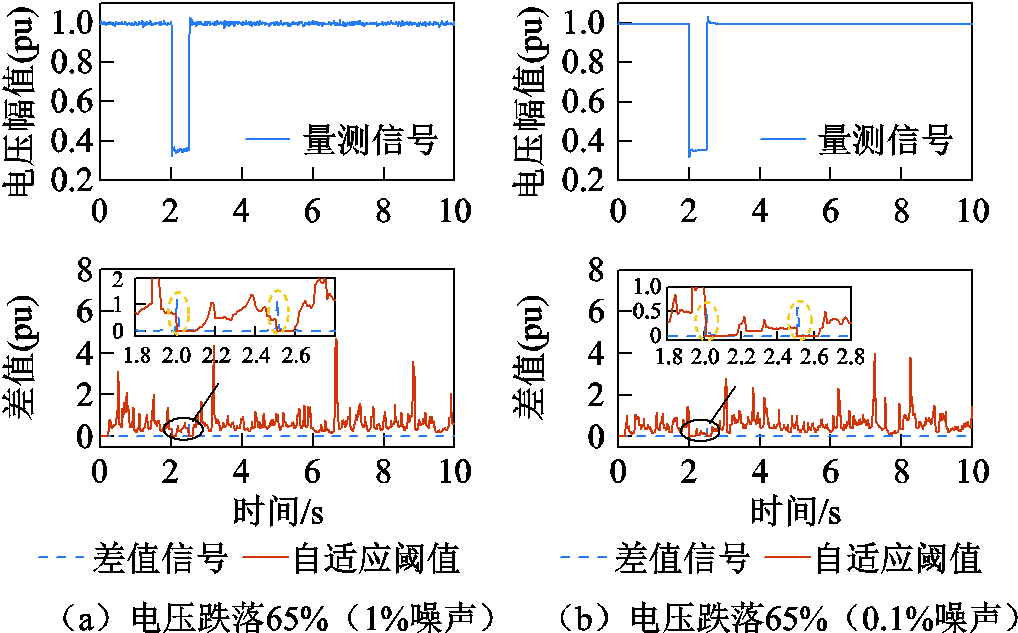
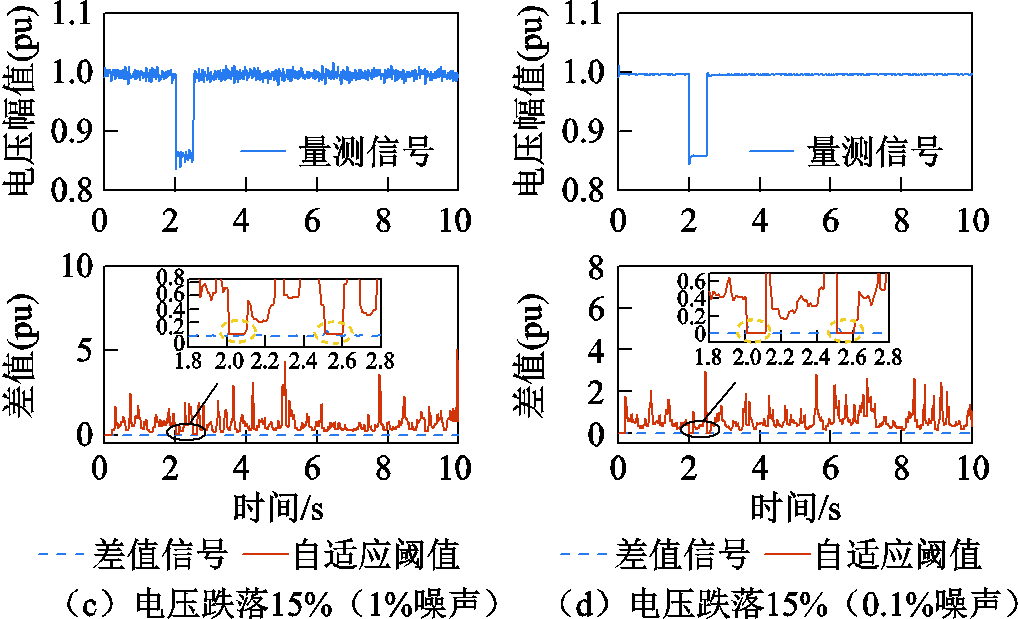
图5 不同情况下的突变检测结果
Fig.5 Mutation detection results under different conditions
由图5可知,对于不同幅度电压降落和噪声的影响,正常运行时差值信号在阈值以下,发生扰动时差值信号的方差变大,阈值能够自适应减小,而差值信号则会上升并超过阈值,即能够准确检测到扰动导致的突变,且对不同情况的适应性较强。
在上述情况下,风电场内的PMU均检测到突变,因此判定有扰动,故降低所有DFIG机端电流虚拟量测在机端电气量估计中的权重。PCC电压跌落65%时,节点3所连接DFIG的机端电流虚拟量测和估计值如图6所示,该节点未安装PMU。由于扰动无法预测,扰动发生后DFIG机端电流预报值存在偏差;通过增大其对应的量测方差后,估计值更倾向于风电场内的PMU量测值,因此能够准确跟踪实际值的变化。
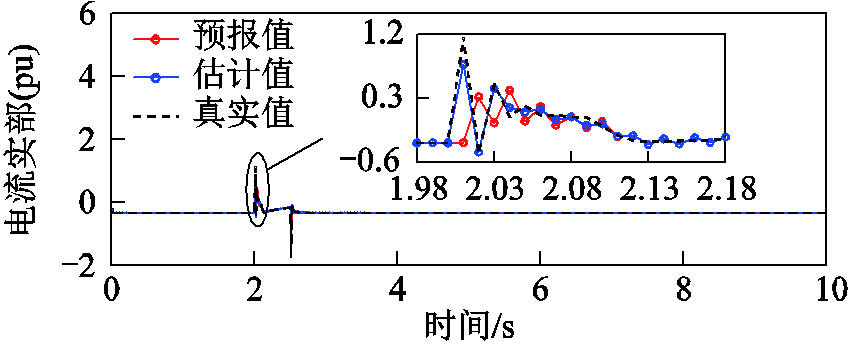
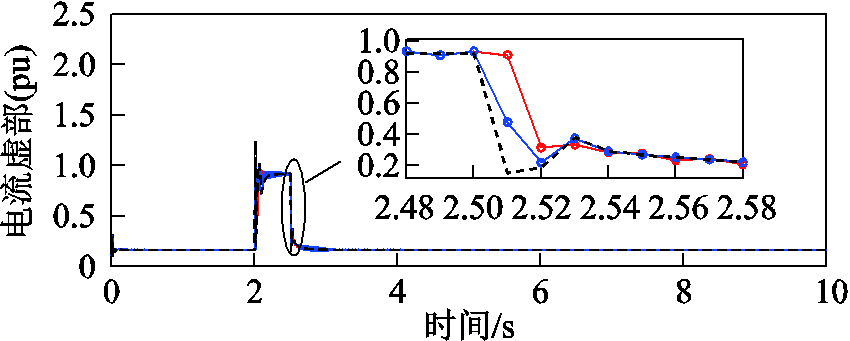
图6 节点3电流相量预报值与估计值的比较
Fig.6 The predicted and estimated current phasor at bus 3
为验证DFIG机端电流虚拟量测对提高估计结果精度的有效性,设置三组量测集:5.1.1节配置方案中PMU测得的电压电流相量构成量测集1;量测集1和所有DFIG机端电流虚拟量测构成量测集2;假设所有DFIG机端都安装PMU这一理想情况,其测得的电压电流相量构成量测集3。图7比较了这三组量测集下节点3电压的估计结果,可知量测集1的估计结果虽能跟踪电压变化趋势,但存在较大误差,这是由于5.1.1节的量测配置方案只保证系统可观,但量测冗余度低;量测集2的估计结果误差与量测集3接近,说明利用DFIG机端电流虚拟量测确实可以提高估计结果精度。
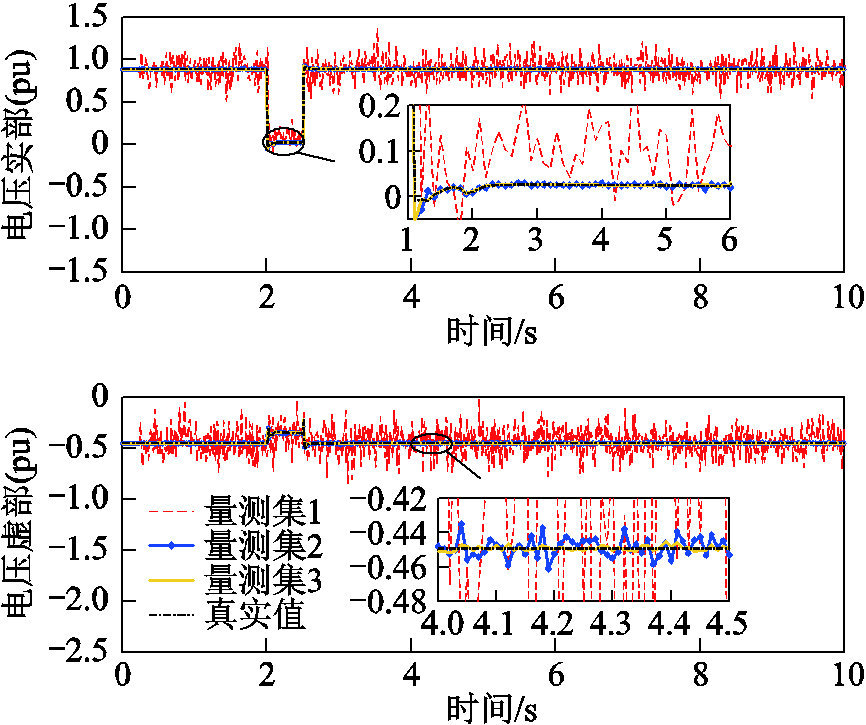
图7 节点3电压估计值的比较
Fig.7 Comparison of the estimated voltage phasor at bus 3
表2进一步对比了三组量测集的PMU数量、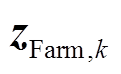 的维数以及风电场所有DFIG机端电压和电流相量估计结果的RMSE均值。可知将DFIG机端电流预报值作为虚拟量测,使得
的维数以及风电场所有DFIG机端电压和电流相量估计结果的RMSE均值。可知将DFIG机端电流预报值作为虚拟量测,使得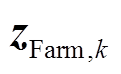 维数由34提高至50,与量测集3相接近,即在不增加量测装置的同时有效提高了量测冗余,故与只使用PMU量测的量测集1相比,其RMSE均值大大降低,且与量测集3在同一水平。
维数由34提高至50,与量测集3相接近,即在不增加量测装置的同时有效提高了量测冗余,故与只使用PMU量测的量测集1相比,其RMSE均值大大降低,且与量测集3在同一水平。
表2 不同量测集估计结果RMSE的比较
Tab.2 Comparison of RMSE of different measurement sets

量测集PMU数量维数机端电压RMSE均值机端电流RMSE均值 15342.511×10-11.742×10-1 25509.015×10-36.965×10-3 317535.083×10-34.758×10-3
2)量测存在不良数据
在PCC电压幅值跌落65%时,4.0~4.3s在安装有PMU的节点6电压量测幅值中加入10%的随机不良数据。PCC和节点6的电压量测幅值及突变检测结果如图8所示,可以看出,在2.0s和2.5s时,PCC和节点6电压幅值的差值信号上升,自适应阈值下降,即都检测到了突变;在4.0~4.3s时,系统不存在扰动,图8a中PCC电压幅值的差值信号远小于自适应阈值,而节点6的电压幅值存在不良数据,导致图8b中的差值信号超过了阈值,即检测到突变。所有PMU的检测结果见表3,“√”表示检测到突变,可知在2.0s和2.5s时所有PMU都检测到了扰动,因此判定扰动发生;而在4.0~4.3s只有节点6的PMU检测到扰动,因此判定其存在量测不良数据,进而减小其量测数据的权重。
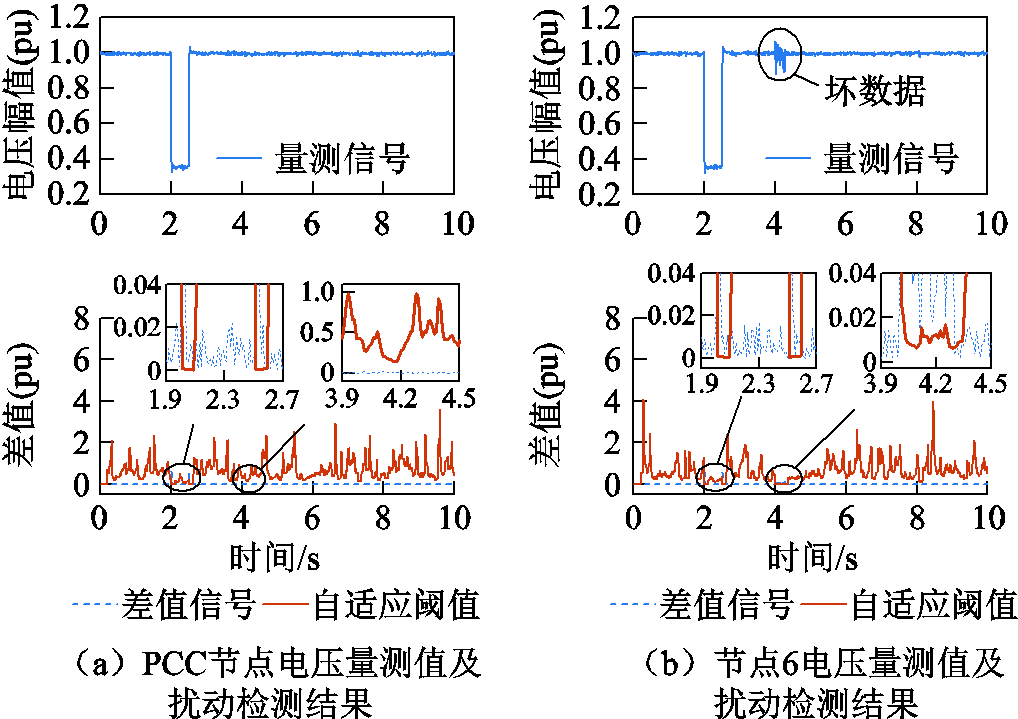
图8 PCC和节点6的突变检测结果
Fig.8 Mutation detection results at PCC and bus 6
表3 扰动与不良数据判别结果
Tab.3 Judgement results of disturbance and bad data

时间/sPMU 1(PCC节点)PMU 2(节点6)PMU 3PMU 4PMU 5判定结果 2√√√√√扰动 2.5√√√√√扰动 4.0~4.3×√×××PMU 1不良数据
在节点6电压量测幅值存在不良数据时,节点6和节点3的电压相量实部估计值如图9所示,为了突出WLAV对量测不良数据的鲁棒性,选择WLS作为对比。可以看出,对于安装了PMU的节点6,WLAV和WLS能够有效降低PMU的量测误差;在扰动或量测存在不良数据时,WLAV的估计值依然准确;而WLS的估计结果误差相比量测值小,但仍大于WLAV。对于未安装PMU的节点3,其节点电压实部的WLS估计结果受扰动和节点6 的PMU不良数据的影响,而WLAV的估计结果较准确,表现出了较强的鲁棒性。
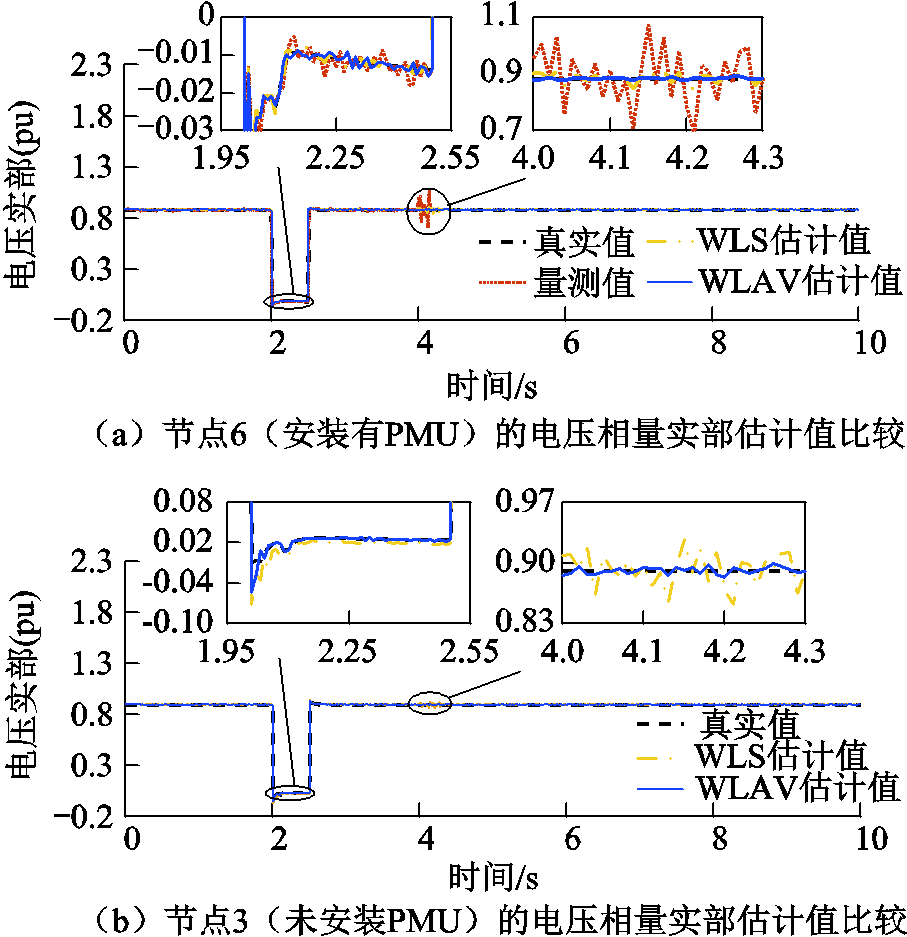
图9 量测存在不良数据时节点6和节点3的电压估计结果
Fig.9 Estimated voltages of bus 6 and 3 when bad data exists in the measurements
5.1.3 DFIG鲁棒动态状态估计的准确性评价
本文所提方法通过DFIG机端电气量鲁棒估计,滤除输入向量u和量测向量z中的不良数据,进而引入过程噪声尺度因子抑制扰动影响,故该方法对输入和量测不良数据及扰动同时具有鲁棒性。本节通过仿真测试其对DFIG动态状态估计的准确性,并选择经典CKF作为对比算法1。文献[14]中只基于新息处理量测不良数据的鲁棒CKF作为对比算法2,文献[25]中基于噪声估值器的滤波算法作为对比算法3。
以节点5所连接的DFIG为研究对象,在2.0~2.5s设置三相短路故障,PCC电压幅值跌落65%;在4.0~4.2s对式(7)量测向量z中的输出有功功率Pt加入10%的随机不良数据;在6.0~6.2s对式(7)量测向量z中的输出有功功率Pt及输入向量u的节点电压幅值都加入10%的随机不良数据,四种方法部分状态的估计结果如图10所示。由图10可知,在2.0 s发生故障时,由于本文算法基于过程噪声尺度因子修正过程噪声,估计结果较准确;而其他对比方法的估计值存在一定偏差,其中对比算法1和2本身不对扰动时不准确的预报值做处理,而对比算法3对Q的估计值在下一时刻才起作用,导致k时刻预报值xk|k-1的误差协方差矩阵与实际不匹配,因此无法处理扰动时状态的大幅变化。在4.0~4.2s只有量测存在不良数据时,本文算法和对比算法2能够滤除量测不良数据的影响,而CKF和对比算法3的估计结果误差较大;在6.0~6.2s,由于量测与输入同时存在不良数据,只有本文算法能够基于DFIG机端电气量鲁棒估计同时处理这两种不良数据,估计结果与真实值基本吻合,其他三种方法的估计结果都出现了较大误差。其中,对比算法2利用新息的异常来检测并抑制不良数据,但无法处理输入和量测同时存在不良数据的情况。
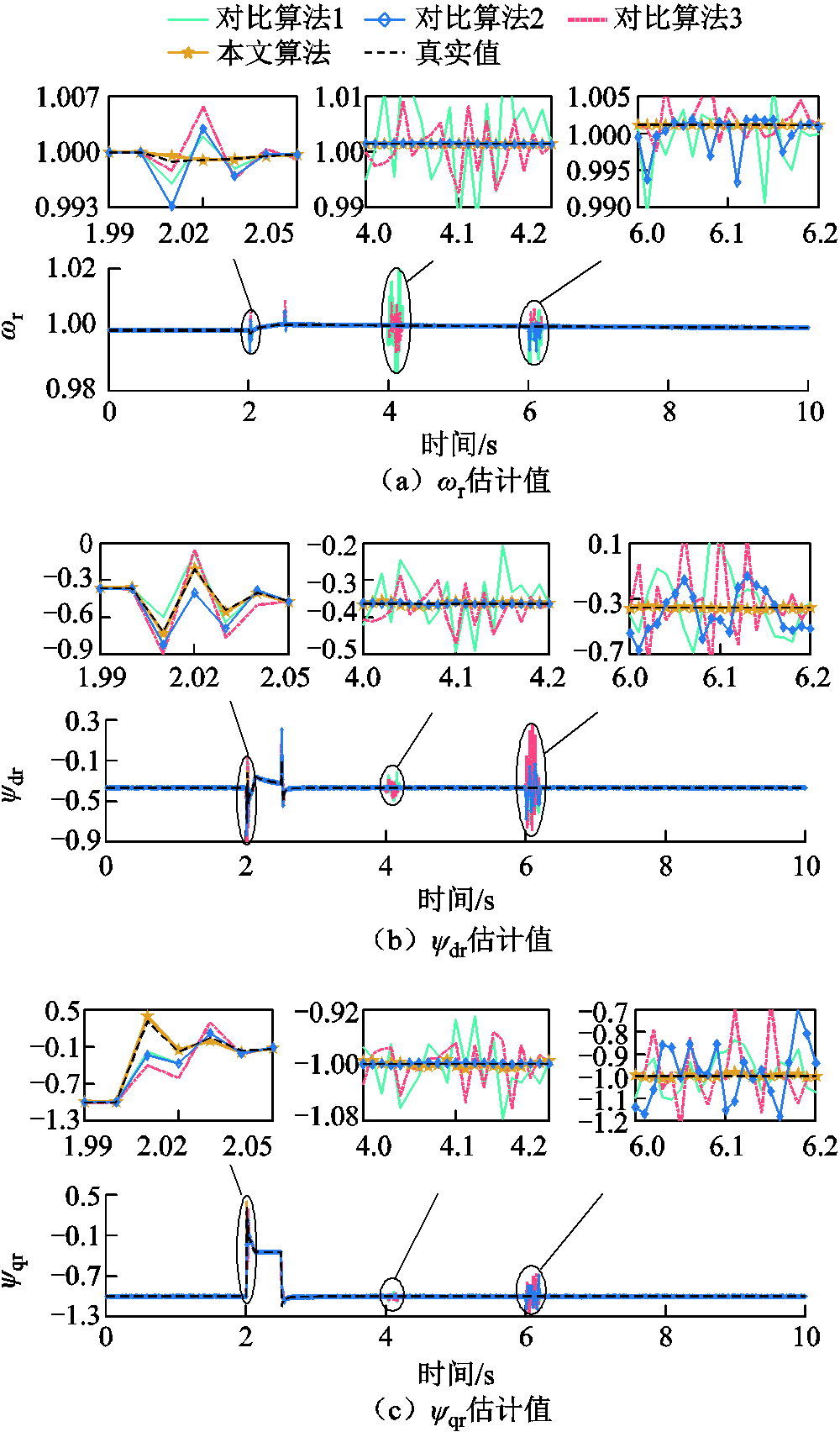
图10 不同方法ωr、ψds与ψqs的估计结果对比
Fig.10 Comparison of ωr、ψds and ψqs of different methods
图11对比了四种方法状态估计值的RMSE。由于控制器中间变量x1~x7无实际物理意义,只统计了前8个状态的RMSE,可知本文所提算法的RMSE最小,表明该方法能够有效处理扰动的影响,并且输入和量测都存在不良数据时,也具有较高的鲁棒性。
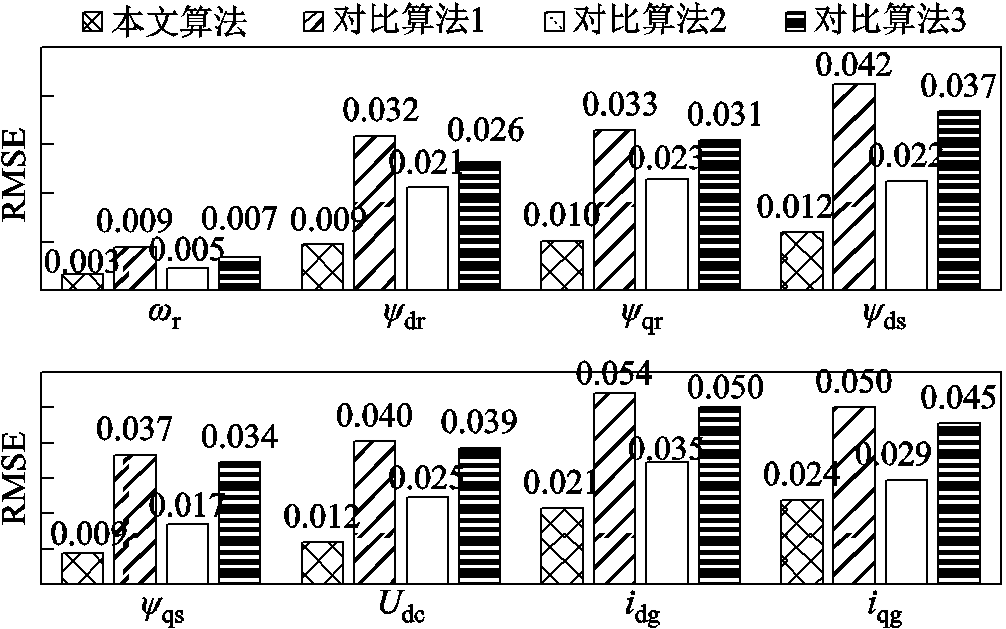
图11 DFIG状态估计结果的RMSE比较
Fig.11 Comparison of the RMSE of estimated DFIG states
此外,经多次测试后取平均,四种方法的单步计算时间见表4。由于考虑了风电场内的量测相关性,本文所提算法计算效率低于其他方法,但仍然能够满足实时性需求(PMU数据间隔10ms)。
表4 单步计算时间比较
Tab.4 Comparison of single step computation time

方法本文算法对比算法1对比算法2对比算法3 单步时间/ms7.5213.2865.9736.562
为测试本文所提方法的适用性,以某实际风场[26]为研究对象进行算例分析。该算例中包含了两个相同的风场,以模拟多风场协调的实际场景。每个风场中,32台1.5MW双馈风机通过集电线路连接至风电场主变,如图12a所示。
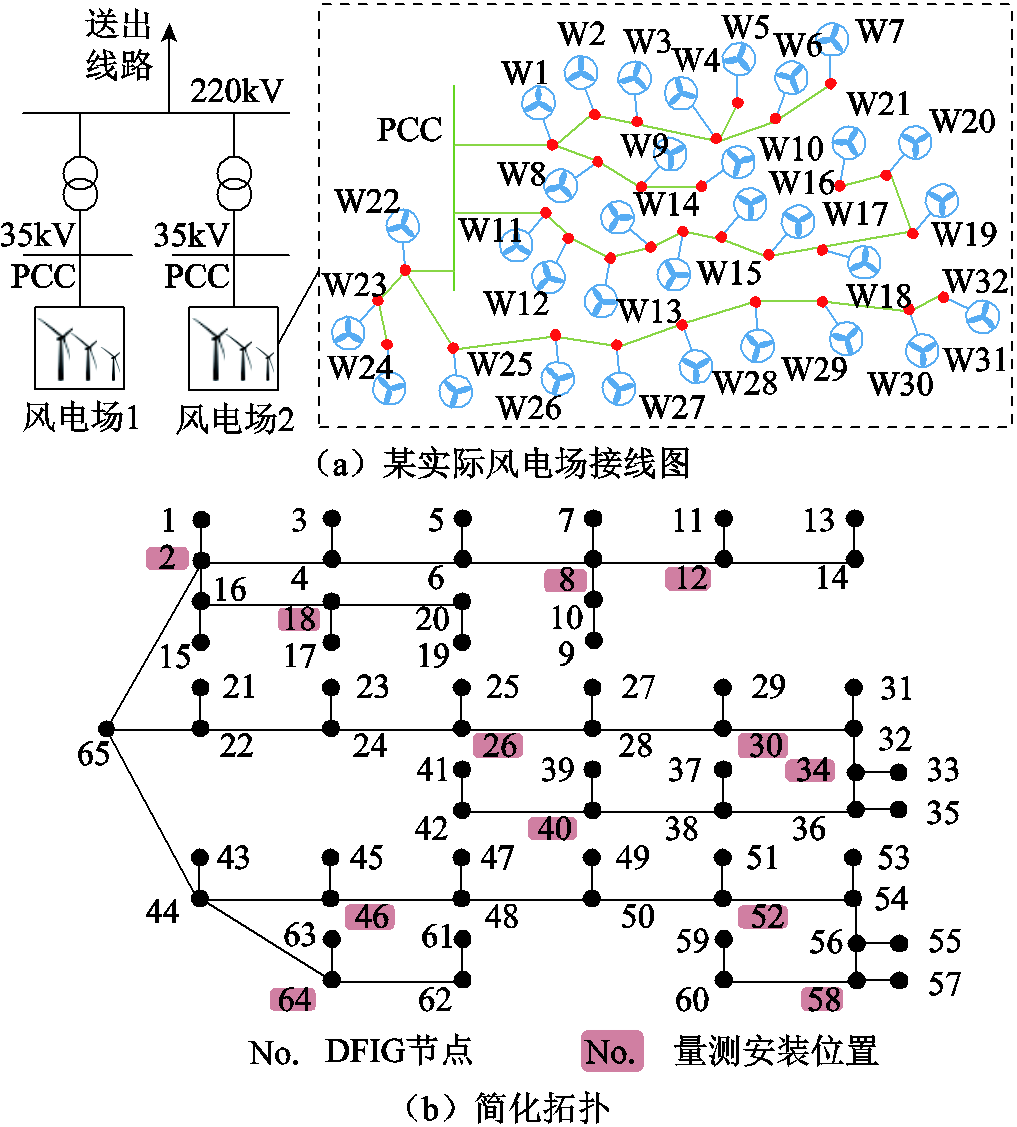
图12 某实际风电场拓扑和量测配置
Fig.12 The topology of the an actual wind farm and measurement configuration
按照5.1.1节的PMU优化配置步骤,得到风电场2的布点方案如图12b和表5所示,风电场1的配置与风电场2相同。可知,对于有32台DFIG和65个节点的风电场,用12台PMU可实现所有节点可观测。
表5 算例2中PMU布点方案详细信息
Tab.5 Detailed information of PMU placements in case 2

系统节点数ZIB数叶子节点数PMU数量PMU配置节点 某实际风场653332122, 8, 12, 18, 26, 30, 34, 40, 46, 52, 58, 64
仿真开始时系统运行在稳定状态,2s时220kV侧发生三相短路故障,PCC电压幅值跌落65%,500ms后故障清除,仿真时间持续10 s,采样间隔0.01s,其他参数设置与算例1相同。设置与5.1.2节相同的三组量测集,其对应的风电场所有DFIG机端电压和电流相量估计结果的RMSE均值见表6。可知,本文所提方法对应的量测集2的RMSE较小,且与理想量测集3接近。因此,在较大规模风电场中,将DFIG机端电流预报值作为虚拟量测同样能够有效提高量测冗余,并提高机端电气量估计准确性。
表6 不同量测集估计结果RMSE的比较
Tab.6 Comparison of RMSE of different measurement sets

量测集PMU数量维数机端电压RMSE均值机端电流RMSE均值 112821.863×10-11.187×10-1 2121147.259×10-34.268×10-3 3321026.013×10-34.226×10-3
利用冗余量测集估计得到所有DFIG机端电气量后,即可对单台DFIG状态进行估计。上述场景下,所有DFIG状态的RMSE均值见表7,可知整体估计结果的平均误差较小,证明所提方法在较大规模风场以及多风场协调场景下也具有较好的适用性。
表7 所有DFIG状态估计结果的RMSE均值
Tab.7 Mean RMSE of all DFIGs

状态ωrψdrψqrψdsψqsUdcidgiqg RMSE均值/10-20.211.341.150.971.021.551.882.37
进一步地,以风电场2中的双馈风机W1为研究对象,对有功功率Pt和节点电压幅值的量测值分别加入不良数据,以模拟量测和输入不良数据,具体参数与5.1.3节相同。然后,利用5.1.3节四种方法对风机W1的状态进行估计,估计结果的RMSE见表8。可知,本文所提方法对应的RMSE最小,即在实际风电场算例中,该方法也具有较好的鲁棒性。
表8 不同方法风机W1状态估计结果的RMSE
Tab.8 Comparison of RMSE of W1 with different methods

状态ωrψdrψqrψdsψqsUdcidgiqg 本文方法/10-20.211.531.651.370.822.072.312.11 算法1/10-20.824.143.795.644.845.155.976.10 算法2/10-20.532.423.253.042.641.952.653.43 算法3/10-20.741.932.833.534.043.824.733.94
为克服风电场量测不足及DSE易受不良数据和扰动影响的问题,本文提出一种考虑风电场量测相关性的DFIG鲁棒动态状态估计方法,并通过仿真算例验证了该方法的有效性,得出以下结论:
1)风电场可视为一个小型辐射状电网,利用PMU最优配置及量测空间相关性可实现所有节点可观,进而利用DFIG状态的时间相关性可在量测不冗余时构造冗余量测集。对于仿真中有16台和32台DFIG的风电场,分别需要5台和12台PMU就可实现对所有节点状态的准确估计。
2)在冗余量测集的基础上,利用PMU量测的空间相关性可有效区分扰动和不良数据,并通过WLAV鲁棒方法来估计所有DFIG的机端电气量。仿真结果表明其能在DSE之前滤除PMU量测不良数据对输入向量u及量测向量z的影响,解决了难以在DSE执行过程中对二者进行区分的问题。
3)针对扰动发生时DFIG状态预报值不准确的问题,引入过程噪声尺度因子,在扰动时降低预报值权重。仿真结果表明其能有效提高扰动时CKF估计结果的准确性。
1. DFIG转子侧和网侧变流器及其控制系统
由于变流器的时间常数是秒级,忽略其调制过程,即变流控制器输出的参考电压直接作为异步电机的励磁电压和换流器网侧电压,其控制框图如附图1所示。
正文中的x1~x7表示换流器控制框图中7个PI环节的积分状态变量,用ki1~ki7表示积分系数,kp1~kp7表示比例系数。
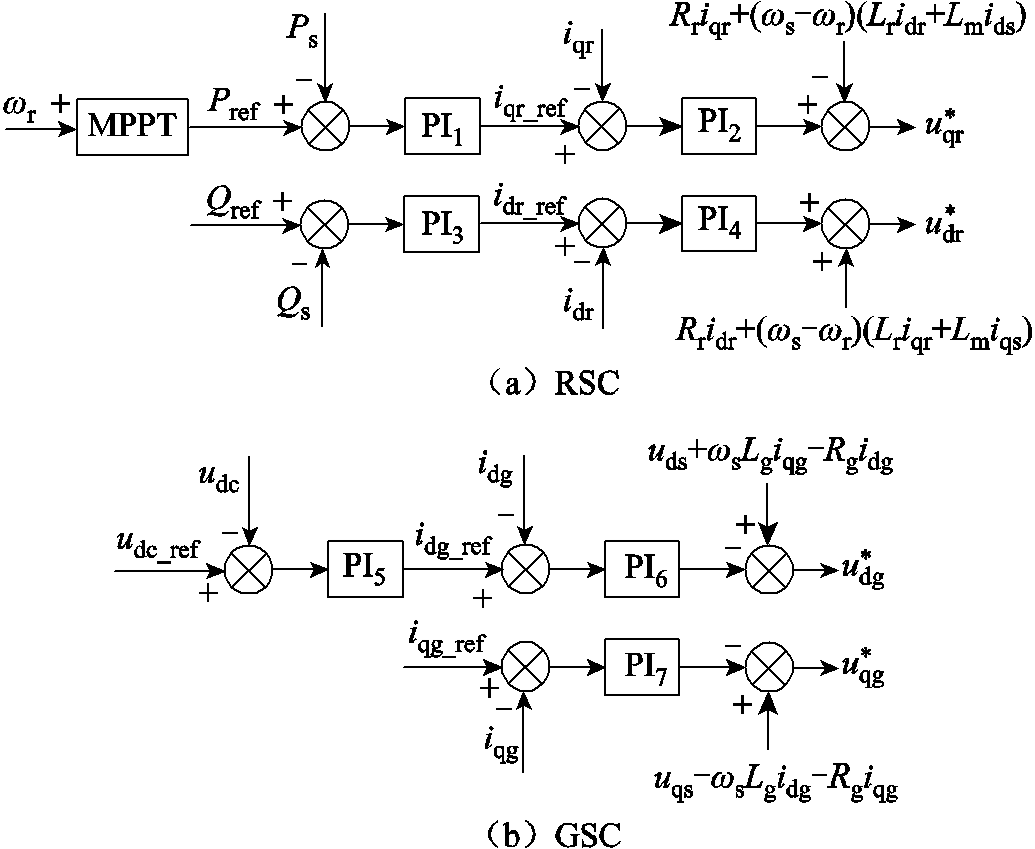
附图1 换流器控制框图
App.Fig.1 Converter control block diagram
积分环节的具体表达式为
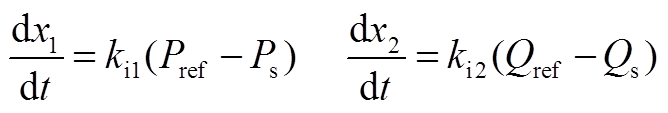 (A1)
(A1)
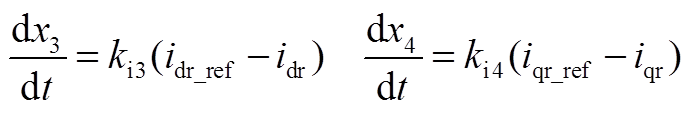 (A2)
(A2)
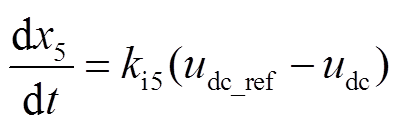 (A3)
(A3)
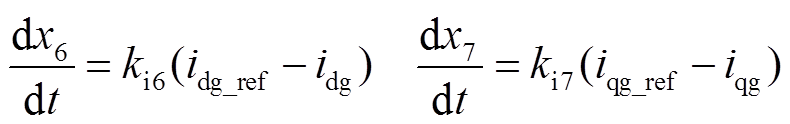 (A4)
(A4)
2. DFIG和风电场参数
附表1 DFIG和风电场参数
App.Tab.1 The parameters of DFIG and wind farm
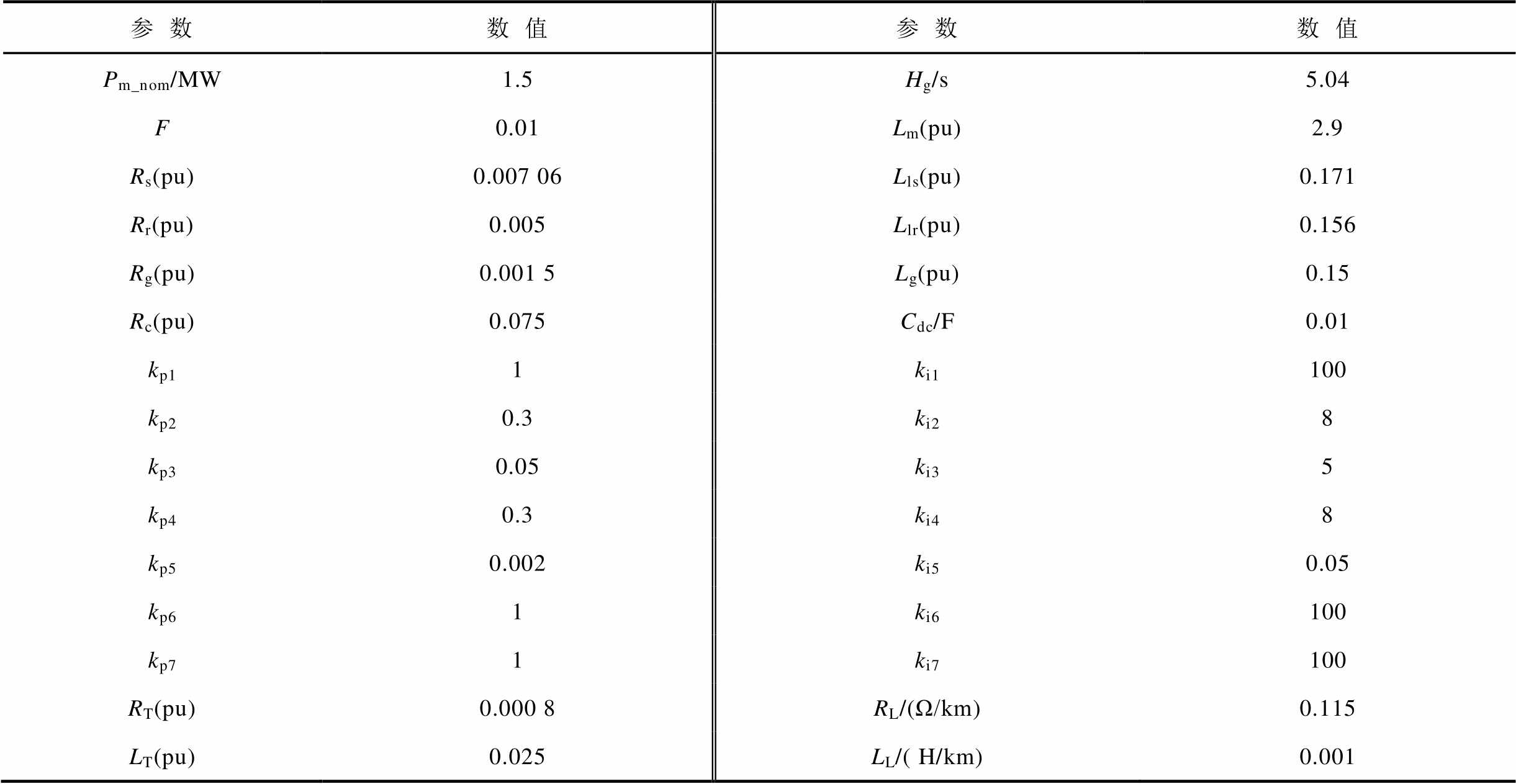
参数数值参数数值 Pm_nom/MW1.5Hg/s5.04 F0.01Lm(pu)2.9 Rs(pu)0.007 06Lls(pu)0.171 Rr(pu)0.005Llr(pu)0.156 Rg(pu)0.001 5Lg(pu)0.15 Rc(pu)0.075Cdc/F0.01 kp11ki1100 kp20.3ki28 kp30.05ki35 kp40.3ki48 kp50.002ki50.05 kp61ki6100 kp71ki7100 RT(pu)0.000 8RL/(Ω/km)0.115 LT(pu)0.025LL/( H/km)0.001
参考文献
[1] 周博, 艾小猛, 方家琨, 等. 计及超分辨率风电出力不确定性的连续时间鲁棒机组组合[J]. 电工技术学报, 2021, 36(7): 1456-1467.
Zhou Bo, Ai Xiaomeng, Fang Jiakun, et al. Continuous-time modeling based robust unit commitment considering beyond-the-resolution wind power uncertainty[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1456-1467.
[2] 陈昌松, 段善旭, 殷进军, 等. 基于发电预测的分布式发电能量管理系统[J]. 电工技术学报, 2010, 25(3): 150-156.
Chen Changsong, Duan Shanxu, Yin Jinjun, et al. Energy management system of distributed generation based on power forecasting[J]. Transactions of China Electrotechnical Society, 2010, 25(3): 150-156.
[3] Zhao Junbo, Gómez-Expósito A, Netto M, et al. Power system dynamic state estimation: motivations, definitions, methodologies, and future work[J]. IEEE Transactions on Power Systems, 2019, 34(4): 3188-3198.
[4] 贾宁, 王彬, 孙宏斌, 等. 基于全景精细化模型的风电场能量管理系统研制及应用[J]. 电力系统保护与控制, 2016, 44(14): 61-68.
Jia Ning, Wang Bin, Sun Hongbin, et al. Development and application of panoramic fine modeling based wind farm energy management system[J]. Power System Protection and Control, 2016, 44(14): 61-68.
[5] 王彤, 高明阳, 黄世楼, 等. 基于自适应容积卡尔曼滤波的双馈风力发电机动态状态估计[J]. 电网技术, 2021, 45(5): 1837-1845.
Wang Tong, Gao Mingyang, Huang Shilou, et al. Dynamic state estimation for doubly fed induction generator wind turbine based on adaptive cubature Kalman filter[J]. Power System Technology, 2021, 45(5): 1837-1845.
[6] Yu Shenglong, Fernando T, Iu H H C, et al. Realization of state-estimation-based DFIG wind turbine control design in hybrid power systems using stochastic filtering approaches[J]. IEEE Transactions on Industrial Informatics, 2016, 12(3): 1084-1092.
[7] Yu Shenglong, Emami K, Fernando T, et al. State estimation of doubly fed induction generator wind turbine in complex power systems[J]. IEEE Transactions on Power Systems, 2016, 31(6): 4935-4944.
[8] Liu Hao, Bi Tianshu, Xu Sudi, et al. A full-view synchronized measurement system for the renewables, controls, loads, and waveforms of power-electronics-enabled power distribution grids[J]. IEEE Transactions on Smart Grid, 2022, 13(5): 3879-3890.
[9] 巫春玲, 胡雯博, 孟锦豪, 等. 基于最大相关熵扩展卡尔曼滤波算法的锂离子电池荷电状态估计[J]. 电工技术学报, 2021, 36(24): 5165-5175.
Wu Chunling, Hu Wenbo, Meng Jinhao, et al. State of charge estimation of lithium-ion batteries based on maximum correlation-entropy criterion extended Kalman filtering algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5165-5175.
[10] Anagnostou G, Kunjumuhammed L P, Pal B C. Dynamic state estimation for wind turbine models with unknown wind velocity[J]. IEEE Transactions on Power Systems, 2019, 34(5): 3879-3890.
[11] 焦自权, 范兴明, 张鑫, 等. 基于改进粒子滤波算法的锂离子电池状态跟踪与剩余使用寿命预测方法[J]. 电工技术学报, 2020, 35(18): 3979-3993.
Jiao Ziquan, Fan Xingming, Zhang Xin, et al. State tracking and remaining useful life predictive method of Li-ion battery based on improved particle filter algorithm[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3979-3993.
[12] 马安安, 江全元, 熊鸿韬, 等. 考虑量测坏数据的发电机动态状态估计方法[J]. 电力系统自动化, 2017, 41(14): 140-146.
Ma Anan, Jiang Quanyuan, Xiong Hongtao, et al. Dynamic state estimation method for generator considering measurement of bad data[J]. Automation of Electric Power Systems, 2017, 41(14): 140-146.
[13] 毕天姝, 陈亮, 薛安成, 等. 基于鲁棒容积卡尔曼滤波器的发电机动态状态估计[J]. 电工技术学报, 2016, 31(4): 163-169.
Bi Tianshu, Chen Liang, Xue Ancheng, et al. Dynamic state estimator for synchronous machines based on robust cubature Kalman filter[J]. Transactions of China Electrotechnical Society, 2016, 31(4): 163-169.
[14] 刘朋成, 项中明, 江全元, 等. 基于鲁棒容积卡尔曼滤波的同步发电机实时动态状态估计方法[J]. 电网技术, 2019, 43(8): 2860-2868.
Liu Pengcheng, Xiang Zhongming, Jiang Quanyuan, et al. Real-time dynamic state estimation for synchronous machines based on robust CKF[J]. Power System Technology, 2019, 43(8): 2860-2868.
[15] 魏博, 邵冲, 张柏林, 等. 基于下垂特性的风电场参与电网快速频率调整实测分析[J]. 电气技术, 2020, 21(6): 39-44, 62.
Wei Bo, Shao Chong, Zhang Bolin, et al. Actual measurement and analysis of wind power plant participating in power grid fast frequency regulation base on droop characteristic[J]. Electrical Engineering, 2020, 21(6): 39-44, 62.
[16] Simon D. Optimal state estimation[M]. Hoboken: Wiley, 2006.
[17] 李龙源, 付瑞清, 吕晓琴, 等. 接入弱电网的同型机直驱风电场单机等值建模[J]. 电工技术学报,2022: 1-14.
Li Longyuan, Fu Ruiqing, Lü Xiaoqin, et al. Single machine equivalent modeling of weak grid connected wind farm with same type PMSGs [J]. Transactions of China Electrotechnical Society, 2022: 1-14.
[18] Chen Xuebing, Wei Feng, Cao Shuyu, et al. PMU placement for measurement redundancy distribution considering zero injection bus and contingencies[J]. IEEE Systems Journal, 2020, 14(4): 5396-5406.
[19] Ghosh S, Isbeih Y J, Azman S K, et al. Optimal PMU allocation strategy for completely observable networkswith enhanced transient stability characteristics[J]. IEEETransactions on Power Delivery, 2022, 37(5): 4086-4102.
[20] 刘灏, 朱世佳, 毕天姝. 基于局部离群因子的PMU连续坏数据检测方法[J]. 电力系统自动化, 2022, 46(1): 25-32.
Liu Hao, Zhu Shijia, Bi Tianshu. Continuous bad data detection method for PMU based on local outlier factor[J]. Automation of Electric Power Systems, 2022, 46(1): 25-32.
[21] 杨晓梅, 罗月婉, 肖先勇, 等. 基于自适应阈值和奇异值分解的电能质量扰动检测新方法[J]. 电网技术, 2018, 42(7): 2286-2294.
Yang Xiaomei, Luo Yuewan, Xiao Xianyong, et al. A new detection approach of power quality disturbances based on adaptive threshold and singular value decomposition[J]. Power System Technology, 2018, 42(7): 2286-2294.
[22] Rouhani A, Abur A. Linear phasor estimator assisted dynamic state estimation[J]. IEEE Transactions on Smart Grid, 2018, 9(1): 211-219.
[23] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB/T 26862—2011 电力系统同步相量测量装置检测规范[S]. 北京: 中国标准出版社, 2011.
[24] 国家电网公司. Q/GDW 11491-2015 风电机组建模验证及参数校验导则[S]. 北京,2016.
[25] 赵洪山, 田甜. 基于自适应无迹卡尔曼滤波的电力系统动态状态估计[J]. 电网技术, 2014, 38(1): 188-192.
Zhao Hongshan, Tian Tian. Dynamic state estimation for power system based on an adaptive unscented Kalman filter[J]. Power System Technology, 2014, 38(1): 188-192.
[26] 韩佶, 苗世洪, 李力行, 等. 基于多视角迁移学习的风场内机群划分及等值风场参数综合优化[J]. 中国电机工程学报, 2020, 40(15): 4866-4881.
Han Ji, Miao Shihong, Li Lixing, et al. Wind turbines clustering in wind farm based on multi-view transfer learning and synthetic optimization of parameters in equivalent wind farm[J]. Proceedings of the CSEE, 2020, 40(15): 4866-4881.
Abstract Wind power is characterized by strong intermittency, random fluctuating and low schedulability. Dynamic state estimation (DSE) of doubly-fed induction generators (DFIGs) based on phasor measurement unit (PMU) can provide reliable data basis for wind farm energy management system, which helps to suppress the influence of wind power fluctuation on power grid. However, DSE of a single DFIG needs input its terminal measurements, but currently it is not common for wind farms (WFs) configuring PMUs for each wind turbine. Besides, DSE based on the prediction-filtering framework of Kalman filter is susceptible to bad measurement data and disturbances. To address these issues, this paper proposes a robust DSE method of DFIG considering the measurement correlation in WFs.
Firstly, considering that a WF can be considered as a small radial grid, its topological characteristics are leveraged to obtain the optimal installation locations of PMUs. And the time-dimension constraint information of DFIG dynamic model is included to construct the redundant measurement set. Secondly, the terminal electrical quantities of all DFIGs are estimated by weighted least absolute value (WLAV) estimation method based on the redundant measurement set. This way, the bad data in the DSE inputs and measurements can be filtered out by WLAV after distinguishing disturbances and bad measurement data. Finally, when the innovation of cubature Kalman filter is abnormal, it can be considered that the prediction vector deviates from the true value. The process noise covariance matrix is then adjusted by introducing a process noise scale factor, which can reduce the influence of the predicted values on the final estimation results. Thus, this integrated method has low requirements for measurement configuration and can deal with disturbances and bad data in the DSE inputs and measurements simultaneously.
Simulation results on a WF with 16 DFIGs show that, only 5 PMUs are needed to make all buses of the WF observable, and the dimension of the measurement set increases from 34 to 50 by incorporating the predicted terminal currents of all DFIGs as virtual measurements. As the measurement redundancy increases, the root-mean-square error (RMSE) of the estimated DFIG terminal electrical quantities reduces from 0.251 to 0.009 which is close to the RMSE of the ideal measurement set. Besides, based on the spatial correlation of the PMU measurements at the different buses, the voltage drop disturbance at the point of common coupling and bad measurement data at Bus 6 are correctly detected and discriminated. And when bad measurement data and disturbances exist, the mean RMSE of the dynamic states estimated by the proposed method is lower than other comparison methods. For example, the RMSE of rotor speed drops from 0.009 to 0.003. Simulation is also carried out on an actual wind farm in a certain area to verify the performance of the proposed method for large scale wind farms, and the results demonstrate its good generalization ability.
The following conclusions can be drawn from the simulation analysis: ① With the optimal configuration of PMUs and the spatial correlation of phasor measurements, all wind farm buses can be observed with a small number of PMUs. The temporal correlation of DFIG dynamic states can be leveraged to construct the redundant measurement to improve the estimation accuracy. ② The spatial correlation of PMU measurements can be used to effectively distinguish disturbances and bad measurement data. And the robust WLAV method is used to estimate the terminal electrical quantities of all DFIGs. It can also filter out the influence of PMU bad data on input vector and measurement vector of DSE, which is difficult to cope with during the DSE execution. ③The process noise scale factor introduced to reduce the weight of prediction value is able to deal with the inaccurate predicted states of DFIG when a disturbance occurs.
Keywords:Doubly-fed induction generator, dynamic state estimation, measurement correlation, minimum absolute value, robust cubature Kalman filter
DOI:10.19595/j.cnki.1000-6753.tces.221468
中图分类号:TM614
国家自然科学基金资助项目(51725702)。
收稿日期 2022-07-29
改稿日期 2022-10-12
朱茂林 男,1996年生,博士研究生,研究方向为电力系统动态状态估计。E-mail:mlzhu@ncepu.edu.cn
刘 灏 男,1985年生,副教授,研究方向为广域同步相量测量技术。E-mail:hliu@ncepu.edu.cn(通信作者)
(编辑 赫蕾)