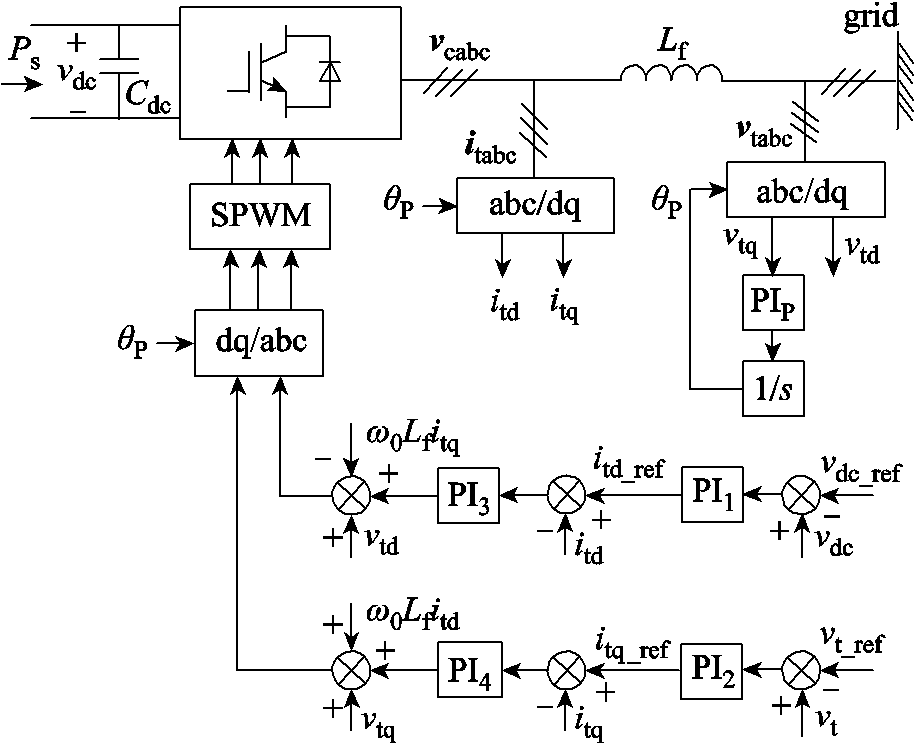
图1 直驱风机模型
Fig.1 Direct-drive PMSG model
摘要 目前直驱风电场并弱电网稳定性研究中，风电场普遍采用单机等值，然而对于单机等值的前提条件缺少相关理论支撑。该文基于解析分析提出直驱风电场单机等值的前提条件；给出直驱风电场满足单机等值的判据；基于风电场各风机参数、出力和集电线路接线完全相同的基础假设，建立直驱风电场状态空间模型；应用矩阵相似变换理论解析分析其状态矩阵的特征根和特征向量；根据判据对单机等值进行论证。进一步地，在比基础假设更加宽泛的条件下，基于蒙特卡洛法仿真研究了同型机直驱风电场单机等值建模的有效性。为单机等值建模的应用提供了一定的理论支撑。
关键词：同型机直驱风电场 弱电网 单机等值建模 前提条件 判据
光伏、风电等新能源多经过电力电子变换器接入电网，在接入弱电网时可能会出现宽频范围内不稳定的振荡。因此，在以新能源为主的新型电力系统中，确保新能源并弱电网的稳定运行具有重要意义[1]。
直驱风机采用电压源变换器（Voltage Source Converter, VSC）接入电网，在并弱电网时出现宽频带振荡的主要原因是其逆变器控制与弱电网的交互作用，根据时间尺度可分为慢交互稳定性问题（10Hz左右）和快交互稳定性问题（100Hz左右及以上）[2]。本文主要研究慢交互稳定性问题。研究表明，直驱风机的锁相环（Phase Locked Loop, PLL）、直流电压控制（DC Voltage Control, DVC）、交流电压控制（AC Voltage Control, AVC）与其相关性较大，而电流控制、甚至于开关控制则由于时间尺度小而基本与之无关[2-3]。当前针对直驱风机并弱电网的稳定性分析工作开展较多，并得到了许多有价值的结论[4-13]。
在研究大规模直驱风电场并弱电网系统的稳定性问题时，建立所有机组的模型会带来工作量大、计算维数灾等问题，需要对其进行等值。现有针对风电场并网系统问题的研究大多以单机无穷大系统为背景，多机系统通常仅考虑相同控制参数、同种类型风电机组的情况[14]。在研究中，通常假设风电场为理想系统，即各机组的参数、出力等均完全相同，且经对称的集电线路接入电网，进而基于此假设将风电场等效为单机模型[5,14]。
在假设风电场为理想系统的前提条件下，文献[15-16]将风机与电网接口处的电流放大n倍，得到等效风电场模型，相当于直接修改了系统的状态矩阵；文献[17]则将风机出线阻抗乘以n，得到系统的等效模型。上述研究均将风电场等效为2个子系统，并没有论证单机等值是否可行。基于参数聚合的单机等值方法简单明了、易于操作，在风电场等值研究中应用广泛，以前多用于动态仿真研究[18-20]，近年来也有学者将其应用于次同步振荡分析[21-22]，但当前该方法的准确性多基于算例进行说明，缺少理论论证。
另外，实际风电场并不是一个理想系统，大部分风电场中仅风机参数相同（即同型机），各机出力和接入的集电线路均不同。此时风电场是否还能进行单机等值仍需要进一步研究。文献[23]考虑了风电场内的集电线路，但假设各机出力完全相同。
本文的研究思路为，先分析总结直驱风电场能否采用单机等值的判据，根据此判据来论证特殊和一般直驱风电场单机等值的准确性。在风电场为理想系统的前提条件下，采用理论推导的方式进行分析：首先，根据现有研究中对单机等值建模的假设条件，建立相应详细风电场并网模型，分别从系统的振荡特性和等值模型特征根两方面入手，判断此时单机等值是否满足判据。进一步将基础假设条件放松，采用蒙特卡洛仿真的形式对更加宽泛的前提条件下的同型机直驱风电场进行研究，判断单机等值是否依然满足要求。
在应用于小扰动稳定分析时，等值模型准确性的判断标准为等值模型能否保留详细模型的弱阻尼（或负阻尼）特征根（下文称为关键特征根）。除此之外，根据直驱风机并弱电网的振荡特性和风电场等值建模的目的，直驱风电场能否采用单机等值建模还需考虑另外两个要求：①系统必须至多只有一对关键特征根；②电网侧必须参与系统关键特征根。要求①与直驱风机并弱电网系统的振荡特性有关。现有研究表明，在单台直驱风机并网系统中，关键特征根的数量与电网强度有关：当电网足够弱时，系统有1对关键特征根；而当电网比较弱但没有足够弱时，系统所有特征根都较强，关键特征根数量为0[4-5,7]。因此，为了确保单机等值模型不会漏掉弱阻尼（或负阻尼）特征根，要求风电场并弱电网系统的关键特征根不能大于1对；为了兼顾电网没有足够弱的情况，允许系统的关键特征根数量为0。要求②与风电场等值建模的目的有关。一般而言，建立等值模型的目的是分析风电场与电网之间的相互作用[5,14]，从而将风电场内部的相互作用忽略。因此，如果电网不参与某一振荡模式，那么在等值模型中保留该模式则没有意义。
综上分析，本文提出接入弱电网的直驱风电场是否满足单机等值的三条判据如下：①系统至多只有一对关键特征根；②电网侧状态变量有参与该振荡模式；③单机等值模型和详细模型的关键特征根相等（若系统无弱阻尼或负阻尼特征根，则要求最弱的特征根相等）。当前在直驱风电场并弱电网系统的稳定性研究中，大部分学者均直接采用单机等值模型，而未加以判别单机等值是否可用。
本文先通过分析详细风电场的振荡特性，判断是否满足前两条判据；再进一步对比等值模型和详细模型的关键特征根来判断是否满足第三条判据。
由于直驱风机的次同步振荡主要与网侧变流器及其控制相关，因此本文采用的直驱风机模型忽略其机侧部分并将其等值为功率源，仅考虑网侧变流器及其控制部分，并根据大部分研究与风机实际情况[4-7]将其建模为如图1所示的两电平VSC。建立风机的线性化模型，包括PLL（2阶）、DVC（2阶）、AVC（1阶）、电流控制（4阶）。
图1 直驱风机模型
Fig.1 Direct-drive PMSG model
已有文献推导出直驱风机小信号模型[6-7]，本文不再赘述，此处只给出其状态空间形式的模型，即
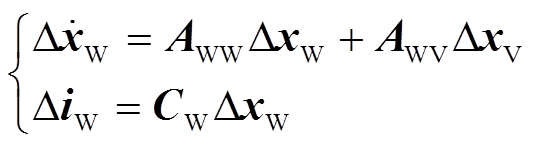（1）
式中，ΔxV为由风机机端电压组成的输入变量，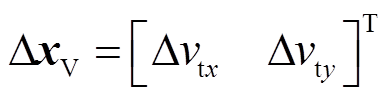
；ΔiW为由风机输出电流组成的输出变量，
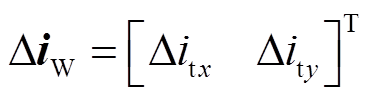；ΔxW为风机的状态变量，
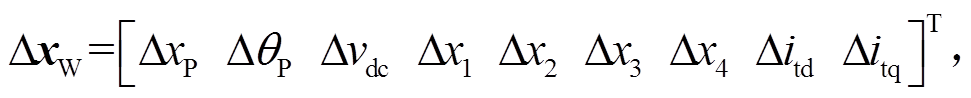ΔxP和ΔθP分别为PLL的状态变量和输出相角，Δvdc为直流电压，Δx1为DVC的状态变量，Δx2为AVC的状态变量，Δx3和Δx4分别为d轴和q轴电流控制的状态变量，Δitd和Δitq分别为d轴和q轴电流；矩阵AWW、AWV、CW分别为状态矩阵（9×9阶）、输入矩阵（9×2阶）、输出矩阵（2×9阶）。
在现有研究中常用单机等值模型对风电场进行建模，常将风电场假设为理想情况，即各风机的参数和出力完全相同，且集电线路接线对称[5,14]。本节基于该基础假设建立相应详细风电场并网模型。
假设风电场有n台机经公共母线接入电网，如图2所示。其中各机接线对称，即Lt1=Lt2=…=Ltn=Lt，机端母线上的接地电容Ct1=Ct2=…=Ctn=Ct；为了在建模时让各支路的电流互相独立[24]，电容Ct和Cg均为一极小值。
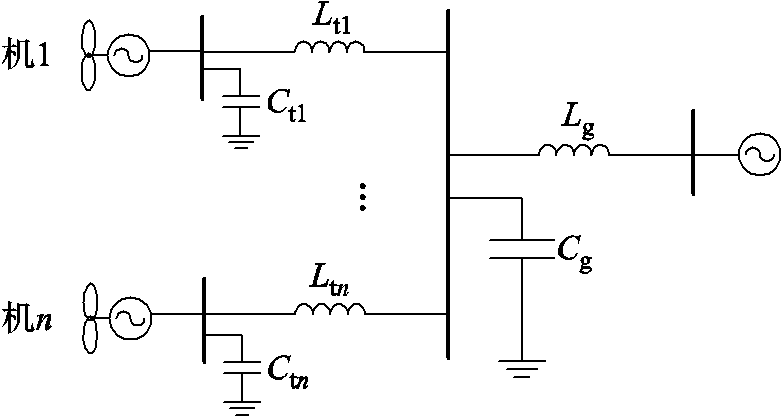
图2 系统接线图
Fig.2 System connection diagram
针对如图2所示的风电场，建立系统的状态空间模型为
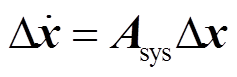（2）
其中
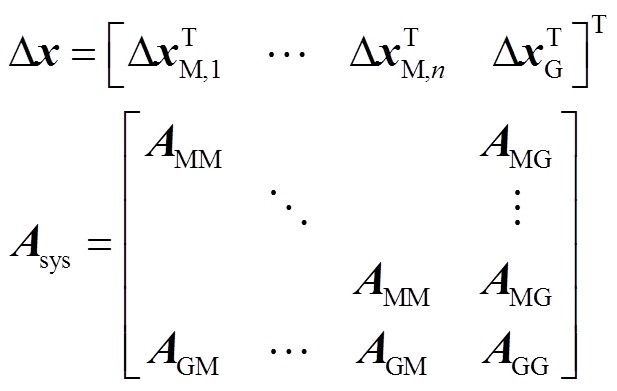
式中，下标M和G分别为风机侧和电网侧的状态变量；n为风机编号；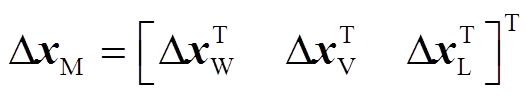
，由风机状态变量ΔxW、机端母线的电压
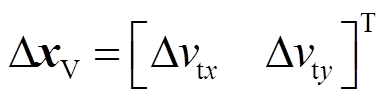和机端线路的电流（即电感Lt的电流）
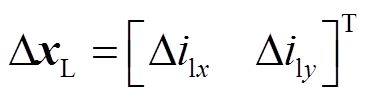组成；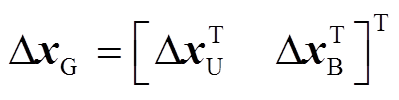
，由公共母线电压
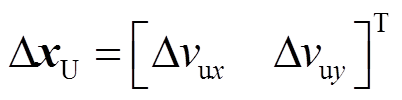和输电线路电流（即电感Lg的电流）
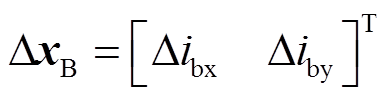组成；状态矩阵Asys各子块及其各元素说明见附录。
本节将研究直驱风电场在基础假设的前提条件下接入弱电网时的振荡特性，分析其是否满足单机等值的前两个判据。
对式（2）中状态矩阵Asys进行相似变换，得
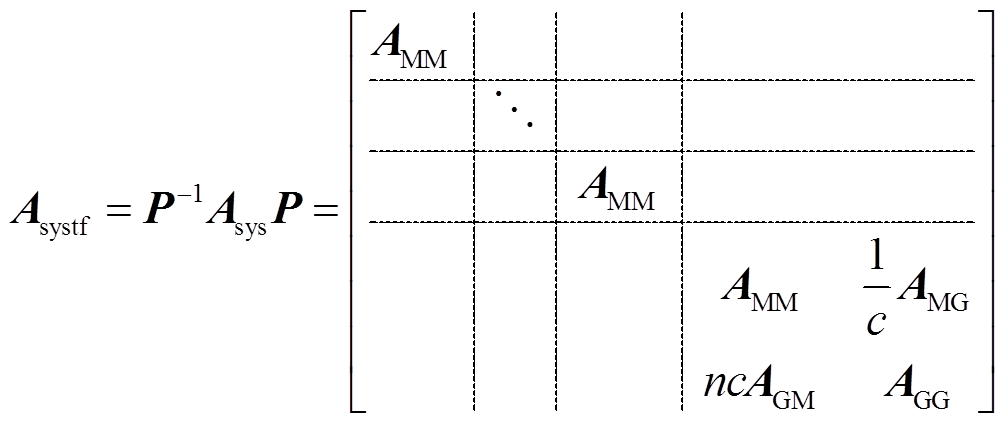（3）
其中
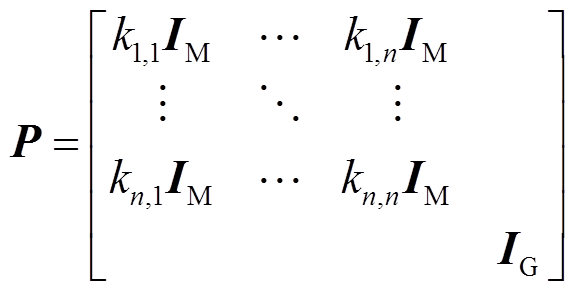（4）
式中，P为实变换矩阵；
且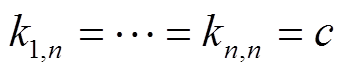
，c为非0常数；IM、IG分别为与AMM和AGG同阶的单位矩阵。
将矩阵Asystf按式（3）进行分块，显然左上角的前n-1个方阵与右下角的方阵互相独立。
设矩阵Asystf的特征根和右特征向量分别为Λ和Φ，也都分为n个子块，形式为
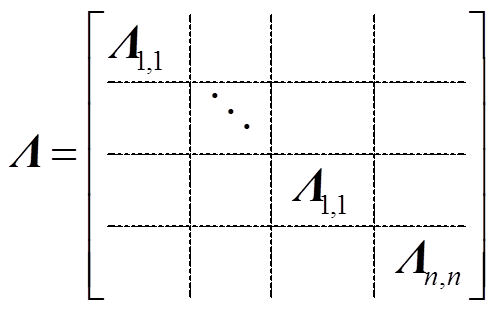（5）
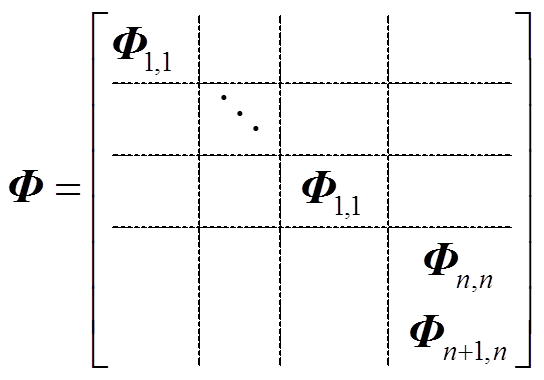（6）
则系统的状态矩阵Asys的特征根和右特征向量分别为Λ和Γ，即
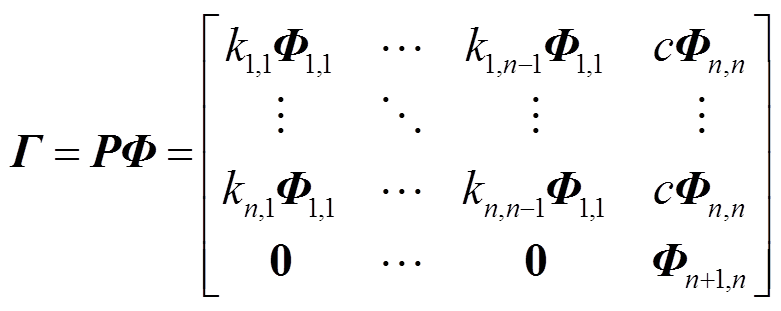（7）
物理上会将一对共轭复根称为一个振荡模式，将其相应的右特征向量称为振荡模态，系统的右特征向量反映了在状态变量上观察相应振荡模式的相对幅值和相位，其模值越大，则可观性越强[24]。
从特征根来看（见式（5）），系统有n-1组重特征根Λ1,1和1组非重特征根Λn,n，分别对应于式（3）中矩阵Asystf的n个子块。
从振荡模态来看，系统的1组非重特征根对应的右特征向量（式（7）的最后一列）有如下特点：①前n行相同，均为cΦn,n，这表明各机侧状态变量的模态相同；②第n+1行不为0，表明该模式在风机侧和电网侧均可观。类比于轴系扭振，本文将该模式称为共模。
系统的n-1组重特征根对应的右特征向量（式（7）的前n-1列）有如下特点：①n-1组特征向量之间线性无关[25]，各特征向量之间的线性组合依然为其特征向量；②第n+1行为0，且前n行之和为0，表明该模式在电网侧不可观，表现为各机之间互相振荡。类比于轴系扭振，本文将该模式称为异模。特别地，当n=2时，特征向量如式（8），两机的异模模态恰好相位相反。
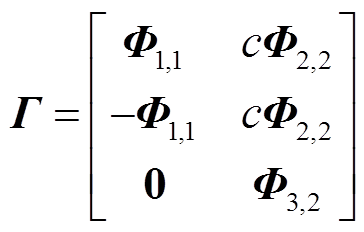（8）
本节主要研究何种扰动能激发系统的共模和异模。
考虑输入变量后，系统状态方程变为
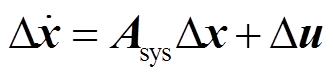（9）
式中， Du为输入变量，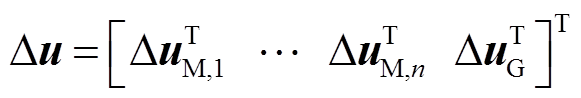
，
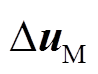为各风机侧输入变量，
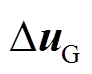为电网侧输入变量。
可求得其状态变量在复频域下的解如式（10），第1项为异模的响应，第2、3项为共模的响应。
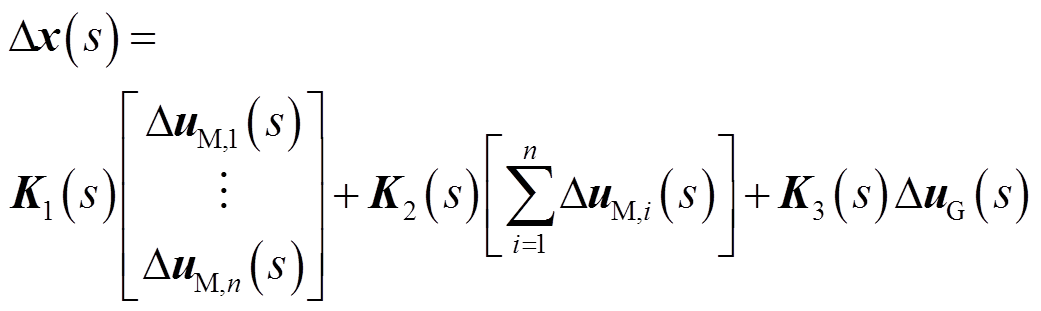（10）
式中
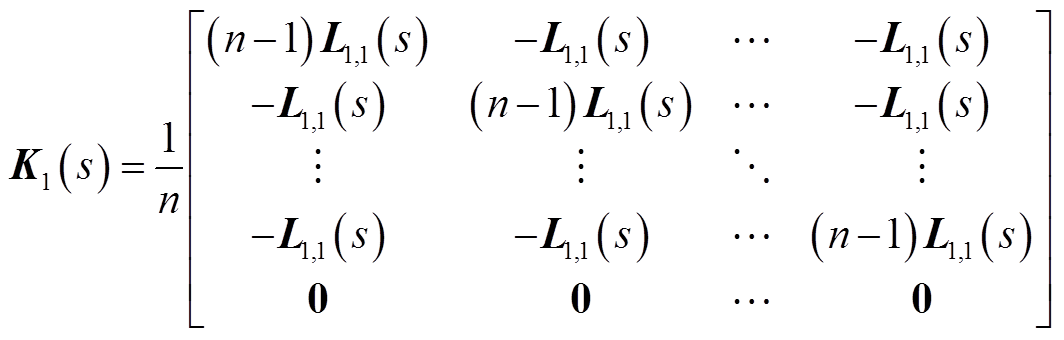
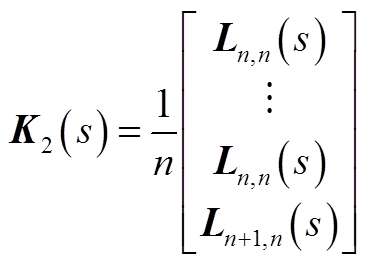
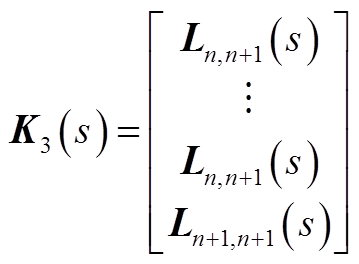
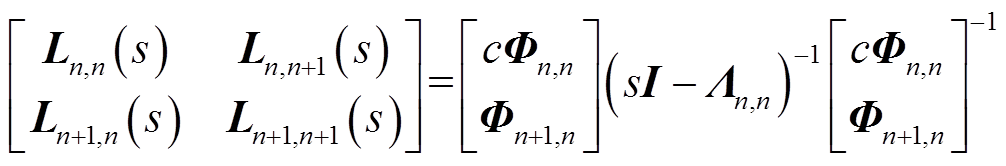
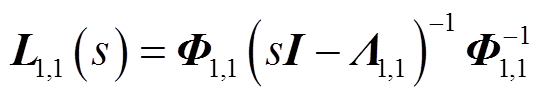
式中，I为与Λ同阶单位阵。
先看异模的响应。尽管变换矩阵P有无数种取法，各机异模模态也有无数种情况，但各机异模的响应是唯一的，且只有各风机侧的扰动可以激发异模。但当各风机侧扰动对称，即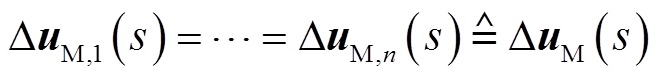
时，异模仍无法被激发，此时响应为
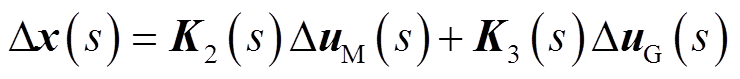（11）
再看共模的响应。由于K2(s)和K3(s)的前n行完全相同，所以各机的共模响应完全相同。从表达式可以看出，风机侧扰动和电网侧扰动均可以激发共模模式。但是，当扰动位于风机侧、且各扰动互相抵消时，即
，系统的共模模式不会被激发。
通常情况下，风机侧扰动不对称，也不互相抵消，即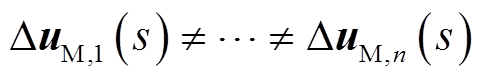
且
。因此，风机侧扰动会同时激发共模和异模，而电网侧扰动只会激发共模。换言之，无论扰动位于哪一侧，共模都会被激发，而异模只会被风机侧扰动激发。
根据式（3）可知，矩阵Asystf可以分为n个独立的子块，因此该系统可以等效为n个互相独立的子系统。
针对前n-1个相同的子块AMM，观察其构成可以发现，其等效系统如图3所示，为原系统（见图2）中各机对称的部分。
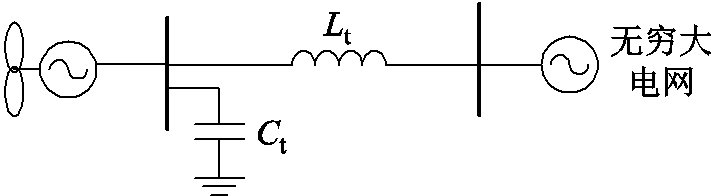
图3 前n-1个相同子块的等效系统
Fig.3 The equivalent system of n-1 repeated blocks
针对第n个子块，令c=1，将其取出，记为
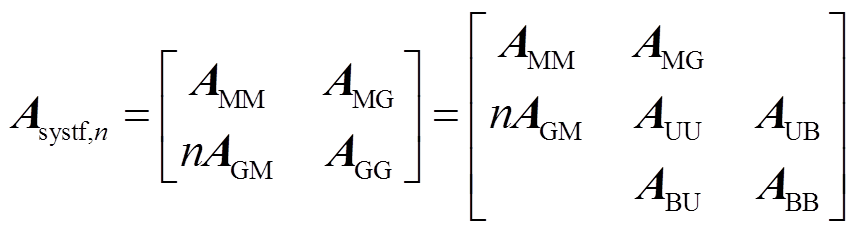（12）
将其进行相似变换，得
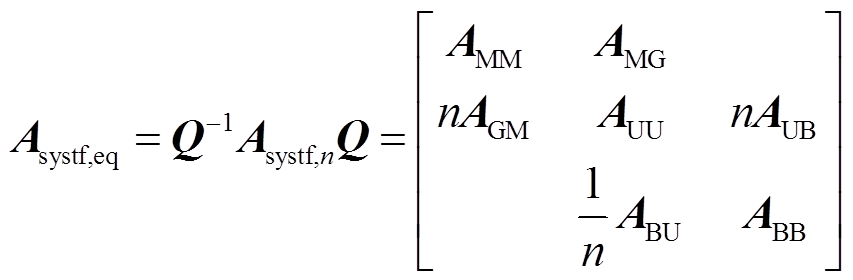（13）
式中，Q为实变换矩阵，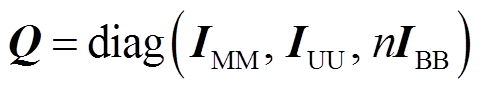
；I为单位矩阵，阶数与Asystf,n中相同下标的子块相同。
显然，矩阵Asystf,n和Asystf,eq相似，二者有相同的特征根。
以Asystf,eq为状态矩阵的系统如图4a所示，相应地等效参数为
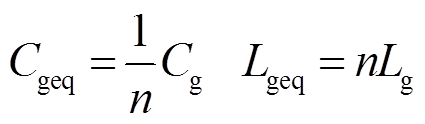（14）
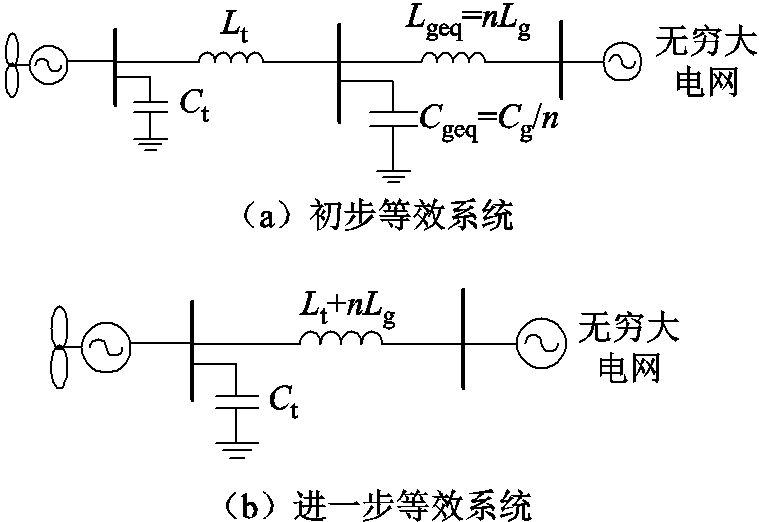
图4 第n个子块的等效系统
Fig.4 The equivalent system of nth blocks
前文所述，母线对地电容为一极小值，是为了使所有连接母线的线路状态变量之间互相独立而引入，对系统的特征根基本没影响。因此，系统进一步等效成如图4b的形式。需要注意的是，只有接入无穷大电网时，第n个子块的等效系统才成立，否则电网的各设备也需要进行等效。
综上所述，当各机接入无穷大电网时，系统可以等效为n个单机系统：其中1个为单机接入阻抗为Lt+nLg的无穷大电网，该系统特征根对应1组共模；剩余n-1个为单机接入阻抗为Lt的无穷大电网，该系统特征根对应n-1组异模。
进而有如下结论：保持阻抗Lt+nLg不变而单独改变Lt或Lg的值，系统的共模不变。在保持阻抗Lt+nLg不变的前提下，随着公共线路的阻抗Lg减小，系统异模逐渐靠近共模；当各机完全解耦（即Lg=0）时，系统异模与共模重合；当各机完全耦合（即Lt=0）时，系统异模与各机自身模式重合。
大量研究表明，在基于锁相环控制的电力电子设备并网的稳定问题中，电网越强稳定性越高[1-2,26]。本文所研究的直驱风机并网系统在参数正常的情况下也得到这样的结论。根据前文所得到的子系统可知，共模对应的电网阻抗Lt+nLg永远大于异模对应的电网阻抗Lt，故而共模的稳定性永远比异模的稳定性更差，即在复平面上最弱的共模永远比最弱的异模更靠右。因此，在研究中只需关注共模即可，特别是共模中最弱的那个模式，只要共模稳定，系统必然稳定。
综上所述，系统最弱的模式一定是共模，关键特征根至多只有1对，即最弱的共模模式；电网侧只对共模有较大参与度，且任意侧的扰动都会激发共模。可以看出，在基础假设的前提条件下，接入弱电网的直驱风电场满足单机等值的前两个判据，在等值时只需保证共模相同即可。
本节将研究直驱风电场在基础假设的前提条件下，是否满足单机等值的第③个判据，即关键特征根是否相等。
对风电场进行单机等值后，风电场接线图如图5所示。
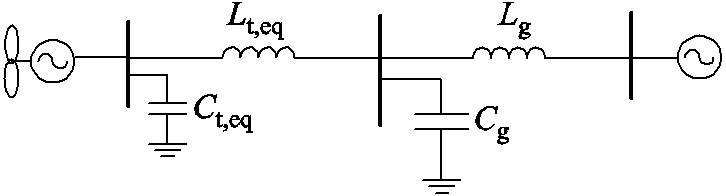
图5 单机等值后的风电场接线图
Fig.5 Single machine equivalent wind farm connection diagram
基于聚合的方式[18-22]得到等值风电场的各参数是一种常用方法，稳态参数和动态参数分别为
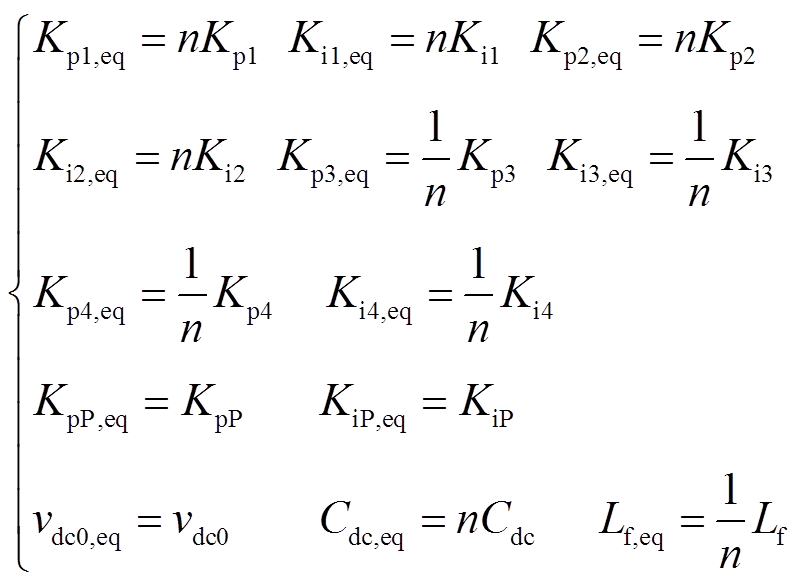（15）
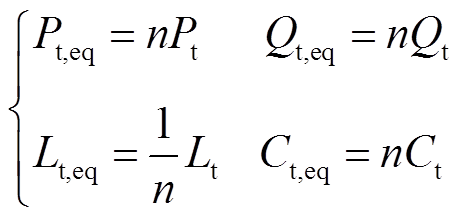（16）
式中，Kp1和Ki1为直流电压控制的PI参数；Kp2和Ki2为交流电压控制的PI参数；Cdc为直流电容；Kp3、Ki3、Kp4、Ki4分别为d轴和q轴电流控制的PI参数；Lf为滤波电感；KpP和KiP为锁相环的PI参数；vdc0为直流电容电压；Pt、Qt分别为有功功率和无功功率；Lt、Ct分别为线路电感和母线对地电容；下标eq表示等值机。
将等值机参数代入其状态空间方程，得到其状态空间模型为
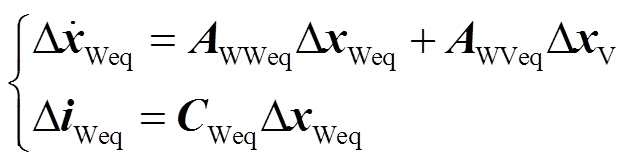（17）
式中，ΔxWeq、ΔxV、ΔiWeq分别为等值机的状态变量、由机端电压组成的输入变量、由输出电流组成的输出变量；矩阵AWWeq、AWVeq、CWeq分别为状态矩阵、输入矩阵、输出矩阵。
令
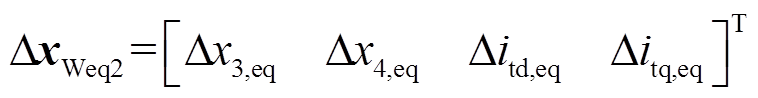
则式（17）中的状态矩阵、输入矩阵、输出矩阵可分别写为
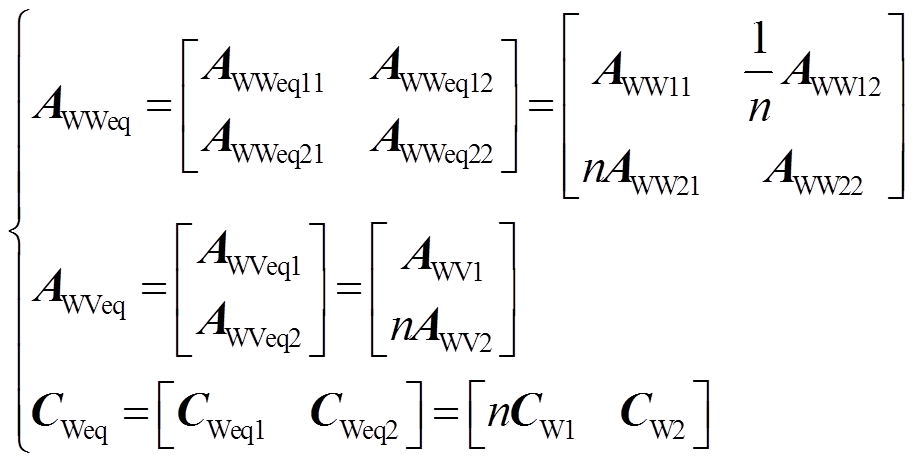（18）
针对图5所示的单机等值的风电场，其系统的状态空间模型为
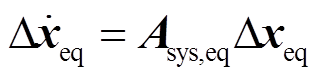（19）
其中
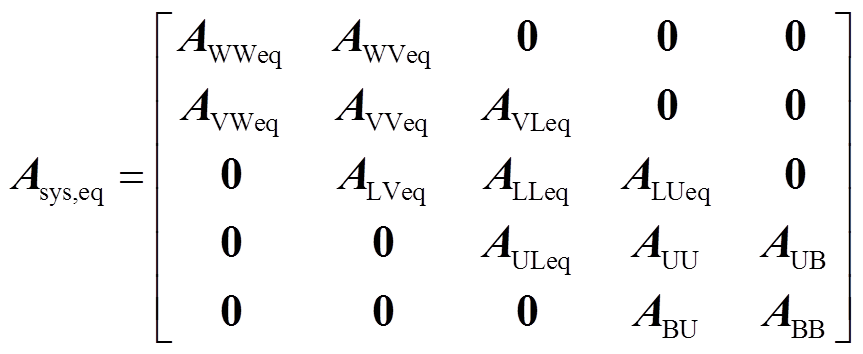
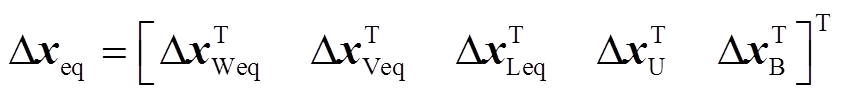
根据前文，风机与机端母线电压之间的互矩阵在等值前后的关系为
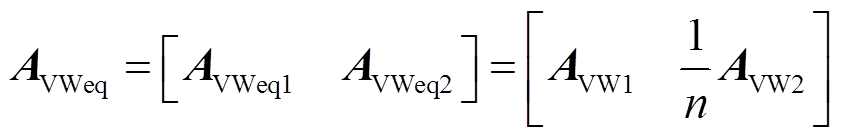（20）
因此，单机等值系统的状态矩阵可写为
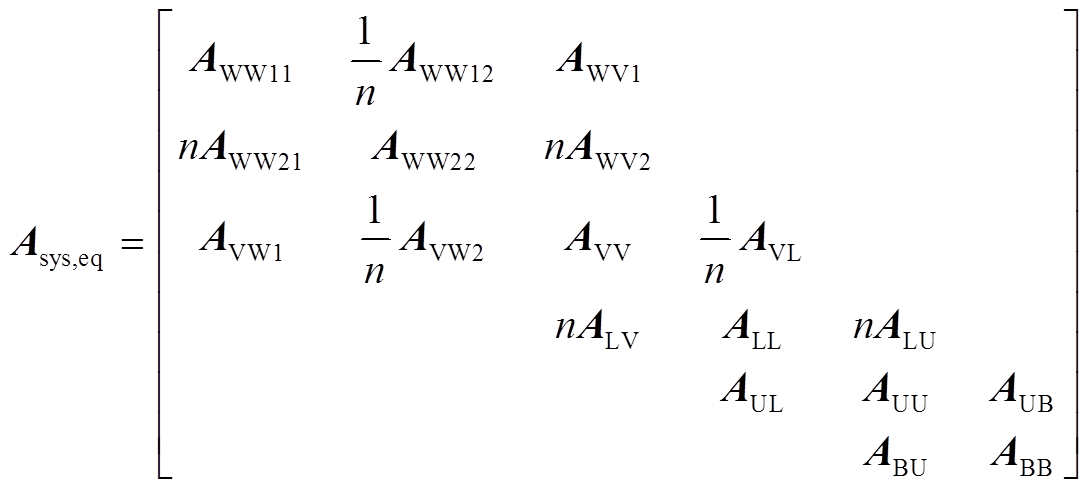（21）
令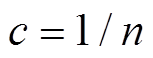
，将式（3）的第n个子块取出，记为
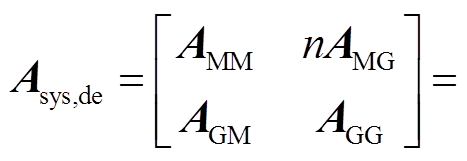
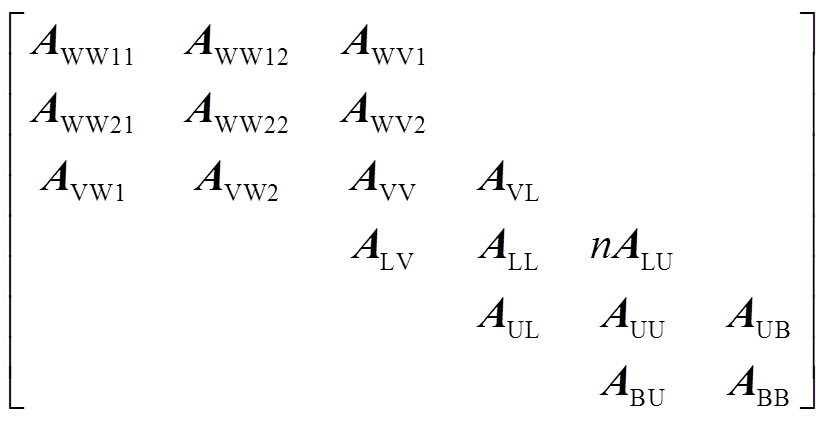（22）
矩阵Asys,de的特征根即为详细风电场并网系统的共模。
根据矩阵Asys,eq和Asys,de的形式，可知
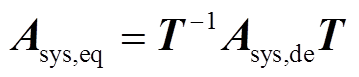（23）
其中
式中，T为实变换矩阵；I为单位阵，阶数与Asys,de中相同下标的子块相同。
由式（23）可知，矩阵Asys,de和Asys,eq相似，故二者有相同的特征根[25]。
因此，等值模型的特征根与详细模型的共模完全相同，等值模型可以准确表征详细风电场的振荡特性。此时，在基础假设的前提条件下，直驱风电场满足单机等值的第三个判据。
系统包括三台直驱风机，采用如图2所示的接线形式，主要电路参数见附录。
采用特征根分析法对该系统进行分析，系统在次同步范围内的特征根如图6所示。需注意的是，图6中圆点处为两个相同的根，在图上重叠在一起。分析可知，共模均为非重特征根，即λ1,2和λ7,8；异模均为两重特征根，即λ3,4,5,6和λ9,10,11,12。
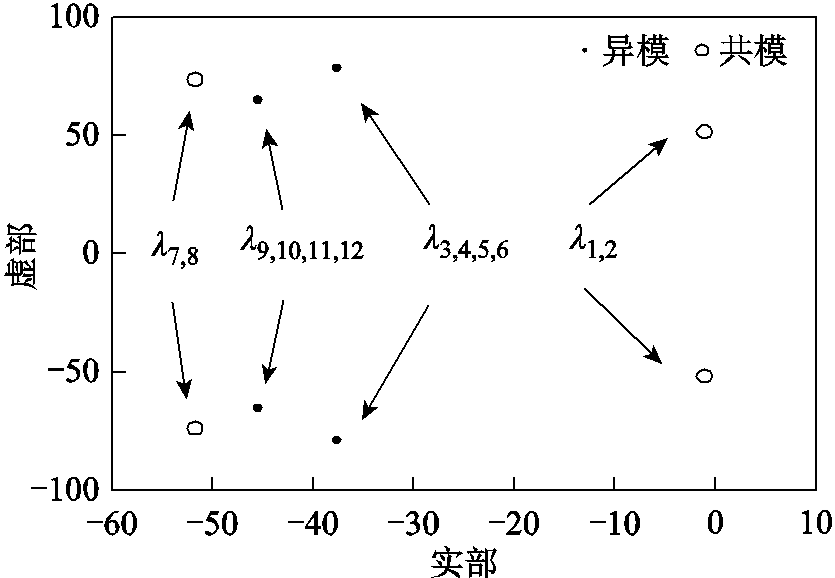
图6 系统振荡模式
Fig.6 Oscillation modes of the system
分别给出共模λ1,2和异模λ3,4,5,6的振荡模态图如图7所示，每个箭头为该状态变量对相应振荡模式的右特征向量，根据前文所述，右特征向量幅值越大则可观性越大。在异模的振荡模态中可以看出，电网侧状态变量的右特征向量均为0，即电网侧状态变量对异模完全不可观；而非0的右特征向量均属于风机侧状态变量，故风机侧状态变量对异模有较大可观性。因此，只有风机会参与异模的振荡。而在共模的振荡模态中可以看出，风机侧和电网侧状态变量的右特征向量均不为0，二者均对共模可观，风机和电网均会参与共模的振荡。
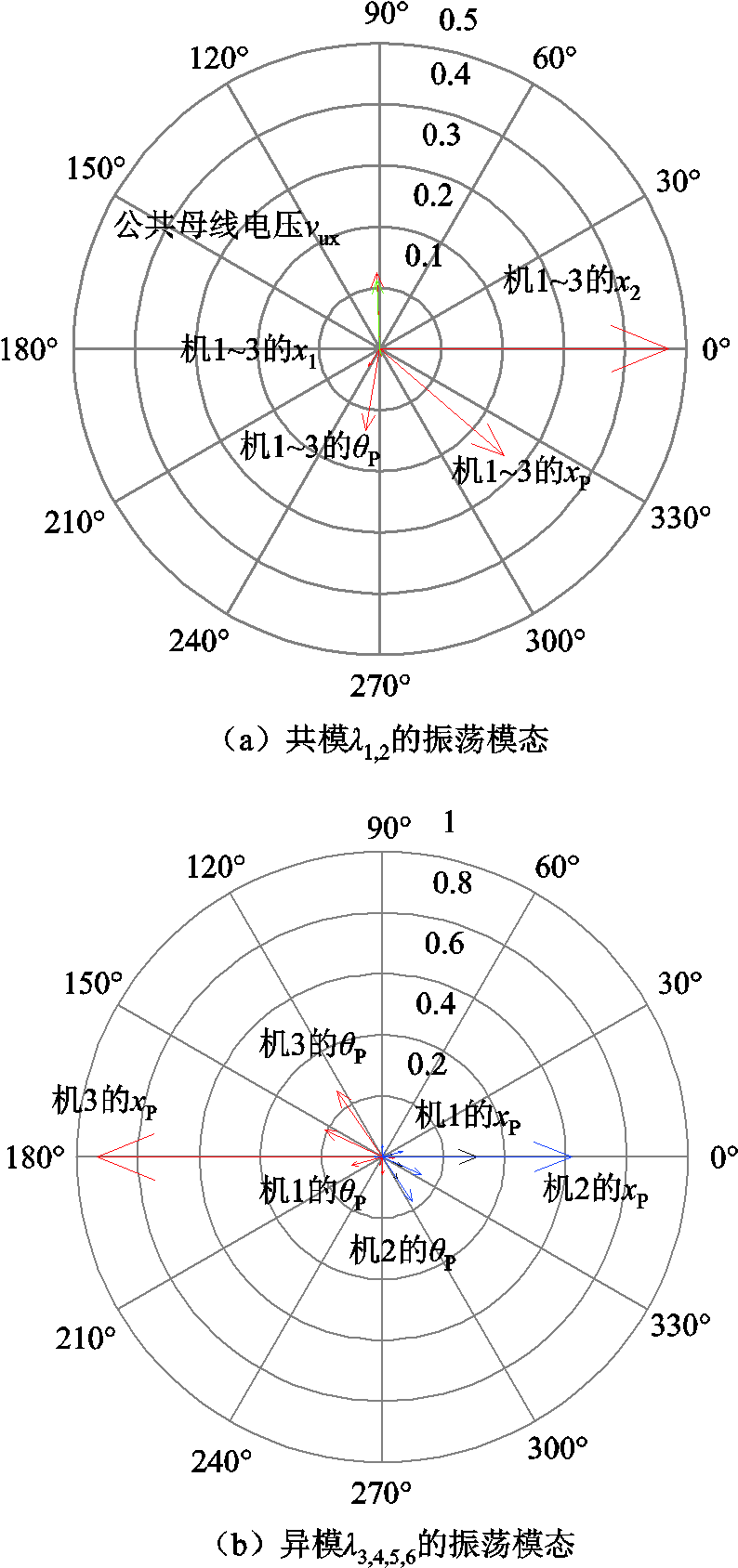
图7 系统共模和异模的振荡模态
Fig.7 Mode shapes of in-phase and anti-phase modes of the system
保持Lg+3Lt不变，逐渐减小Lg，得到系统特征根的变化轨迹如图8所示，系统的共模保持不变，异模则逐渐向共模靠拢，直到Lg=0时二者重合（图8中最后一组特征根）。可以看出，共模中最弱的模式λ1,2就是系统最弱的模式。
从算例中可以看出，系统只有一对关键特征根，即共模λ1,2，而且电网侧对其有较高参与度，满足了单机等值的前两个判据，可以进行单机等值。
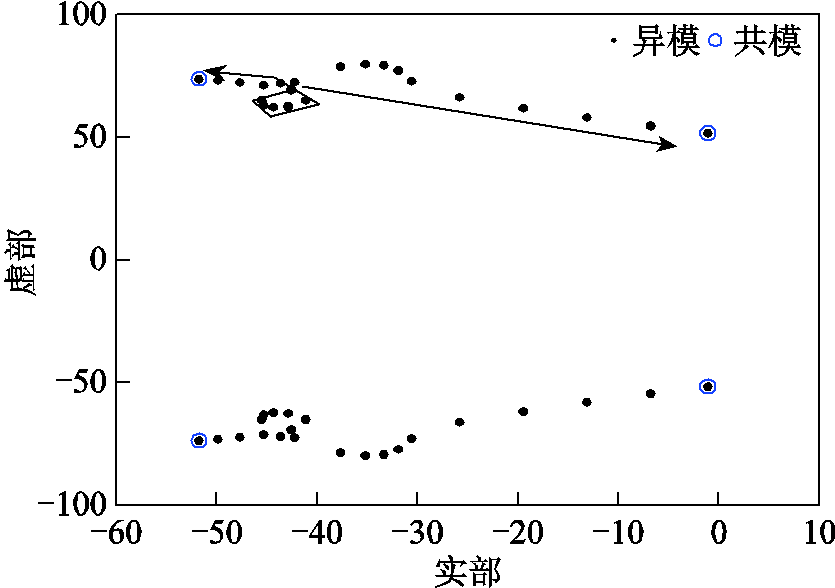
图8 随Lg变小特征根轨迹
Fig.8 Eigenvalue trajectories with Lg gets smaller
采用和5.1节相同的三机系统，分别得到详细模型和等值模型，二者的振荡模式如图9所示。与图6对照可知，等值模型的特征根与详细模型的共模完全重合，能准确反映系统的最弱振荡模式。满足了单机等值的第三个判据。
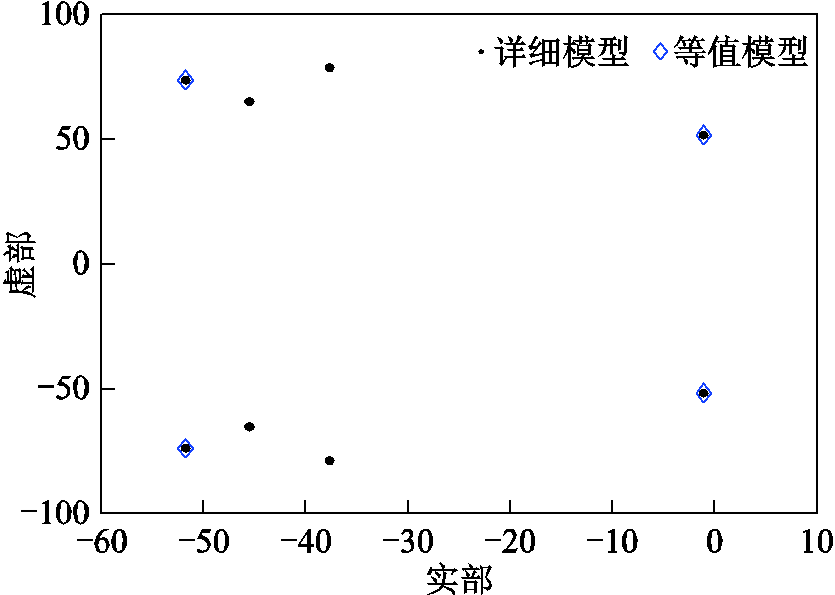
图9 振荡模式比较
Fig.9 Oscillation mode comparison
除了基于小信号模型的验证之外，本节同样在在PSCAD上基于电磁暂态的时域仿真进行了验证。通过设置扰动以激发出系统振荡模式，然后观察等值前后的时域仿真曲线是否具有较高的吻合度，以此来判断等值效果。
仿真采用与图9相同的三机系统，以电网电压跌落的小扰动形式来激发系统振荡模式[21-22]，具体为：在0.1s时电网母线电压由690V跌落5%，持续0.02s后恢复。仿真曲线如图10所示，无论从风电场功率还是风机直流电压，均可以看出等值模型与详细模型均比较接近，等值模型能反映系统的振荡模式。
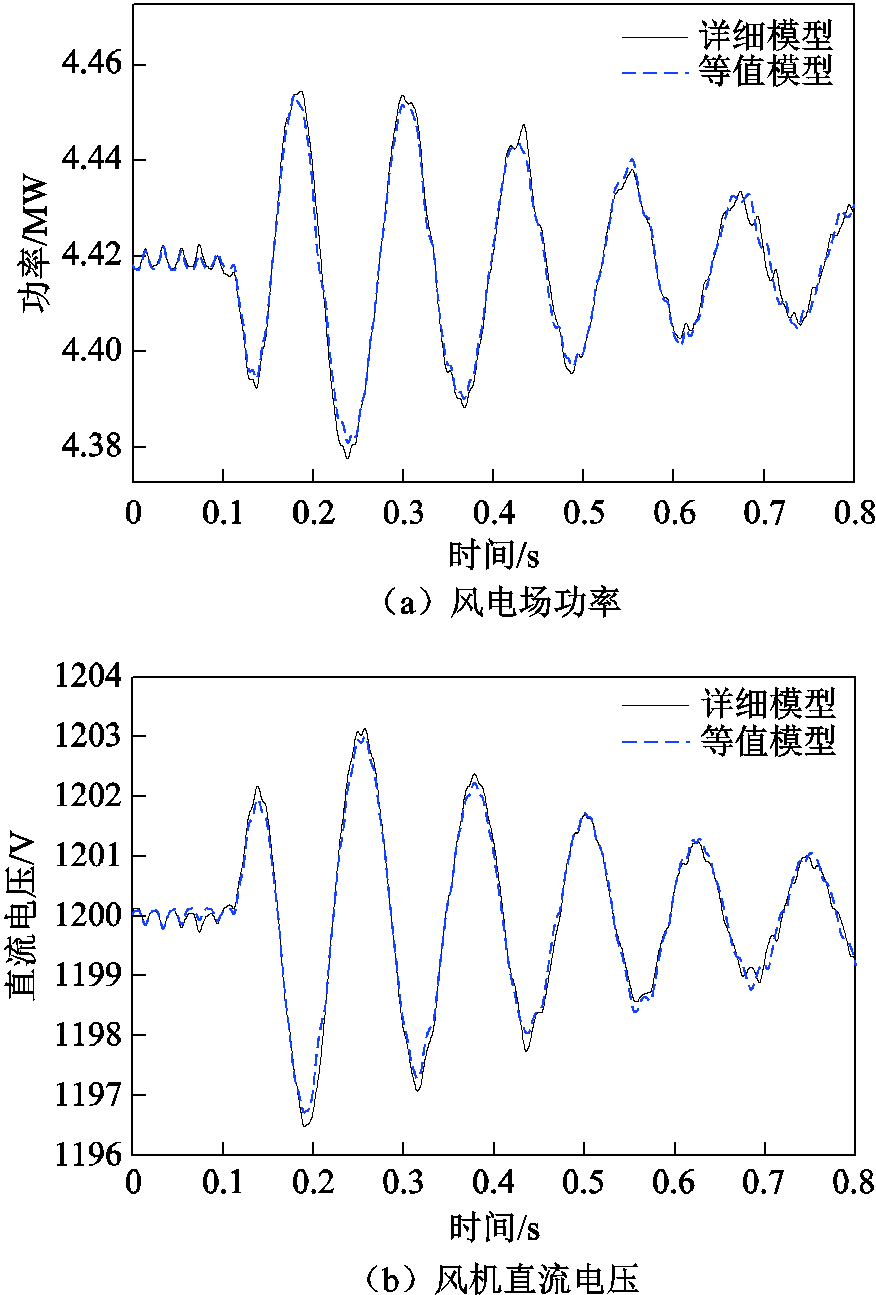
图10 时域仿真曲线比较
Fig.10 Time domain simulation curves comparison
大部分实际风电场中的风机仅参数相同（即同型机），出力和接入的集电线路均不同，为非理想系统，难以通过解析的方法进行分析。因此，本节利用蒙特卡洛仿真的方法来研究更加宽泛条件下的一般同型机直驱风电场，重点分析在各风机参数相同、出力和集电线路接线均不同的前提条件下，直驱风电场是否满足单机等值的三个判据。
根据前文对理想系统振荡特性的分析可知，n机系统存在1组共模和n-1组异模，电网只参与系统共模模式。本节即研究系统是否与理想系统有类似的振荡性质，以确定其是否满足单机等值的前两个判据。
6.1.1 振荡模式分析
本节以一个实际风电场为对象进行研究，其中含n=66台机，有6条集电线路将各机汇流，然后风电场接入一个弱电网。风电场内集电系统参数采用实际参数，而风机的参数和出力均随机生成，包括各机的出力、DVC的带宽和阻尼、PLL的带宽和阻尼、AVC的PI控制参数，各参数的上、下限见表1。共生成N=2 000组样本，每个样本中，各机的参数相同，但出力不同。
表1 各风机参数上下限
Tab.1 Upper and lower limits of PMSG parameters
参数下限上限 PLL带宽/Hz1040 PLL阻尼0.300.80 DVC带宽/Hz525 DVC阻尼0.300.80 AVC比例系数/S0.220 AVC积分系数/(S/s)8800 出力/MW0.0751.5
计算各样本的特征根。对每个样本的特征根进行聚类分析，发现每个样本都会分成两个只有1对特征根的群和两个有65对特征根的群，分别对应了共模和异模。而且在每个样本中，最弱特征根总是为共模。一个典型的特征根分布如图11所示，可以看出，系统包含1组共模和65组异模，且关键特征根为共模中最弱的模式，与前文中理想系统的分析一致。此时，风电场满足单机等值的第一个判据。
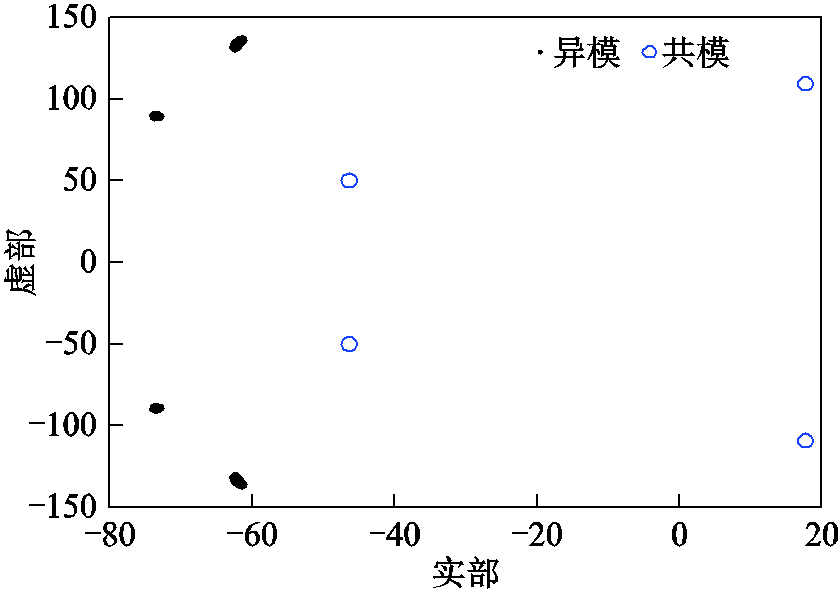
图11 一种典型的特征根分布
Fig.11 A typical eigenvalues scatter diagram
6.1.2 电网参与程度分析
基于参与因子，定义风电场或电网对特征根的相对参与度，分别为风电场或电网内所有状态变量对特征根的参与因子之和在全部状态变量的参与因子之和中的占比[27]，即
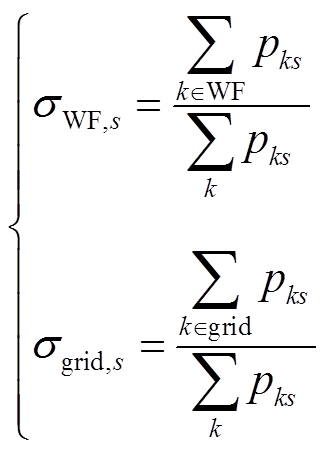（24）
式中，σWF,s和σgrid,s分别为风电场和电网对第s个特征根的相对参与度；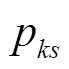
为系统第k个状态变量对第s个特征根的参与因子。
计算电网和风电场分别对共模和异模的参与度，对6.1.1节所有样本进行统计分析，风电场和电网相对参与的平均值见表2。可以看出，电网只对共模有较高参与度，而几乎不参与异模。此时，风电场满足单机等值的第二个判据。
表2 风电场和电网相对参与的平均值
Tab.2 Average values of relative participations of wind farm and grid
风电场相对参与度电网相对参与度 共模0.860 840.139 16 异模0.999 980.000 02
上述仿真设置中系统运行在很弱的工况下，使得大部分样本为小扰动失稳状态，因此，本文也研究了直驱风电场并弱电网系统在稳定运行时的振荡特性。同样采用蒙特卡洛仿真的方法进行研究，抽样、计算和分析与前文类似，不同之处在于各样本均处于稳定运行状态。分析结果表明，系统包含1组共模和65组异模，电网只对共模有较高参与度。结论与前述分析一致。
综上所述，更加宽泛条件下的一般同型机风电场中，其接入弱电网时的振荡特性与理想系统相似：系统拥有1组共模和n-1组异模，系统最弱的振荡模式是共模中最弱的模式；关键特征根至多只有1对，即最弱的共模模式；电网侧只对共模有较大参与度，几乎完全不参与异模，即电网对关键特征根有较大参与度。
可以看出，一般的同型机直驱风电场也满足单机等值的前两个判据，在等值时只需保证关键特征根相同即可。
6.2.1 基于蒙特卡洛方法的分析
等值准确性的判断标准为等值前后系统关键特征根能否保持一致。单机等值模型中风机的动态参数如式（15）所示，等值机的出力为各机之和，等值集电网络采用恒电压差的方法进行等值，具体可见文献[20]。
本节依然采用蒙特卡洛方法进行研究，针对6.1.1节中抽样的N=2 000组样本，分别进行单机等值，然后分别计算详细模型和等值模型的特征根，并比较关键特征根的误差。其中一组典型的样本的振荡模式如图12所示，可以看出，等值模型与详细模型的共模基本重合。
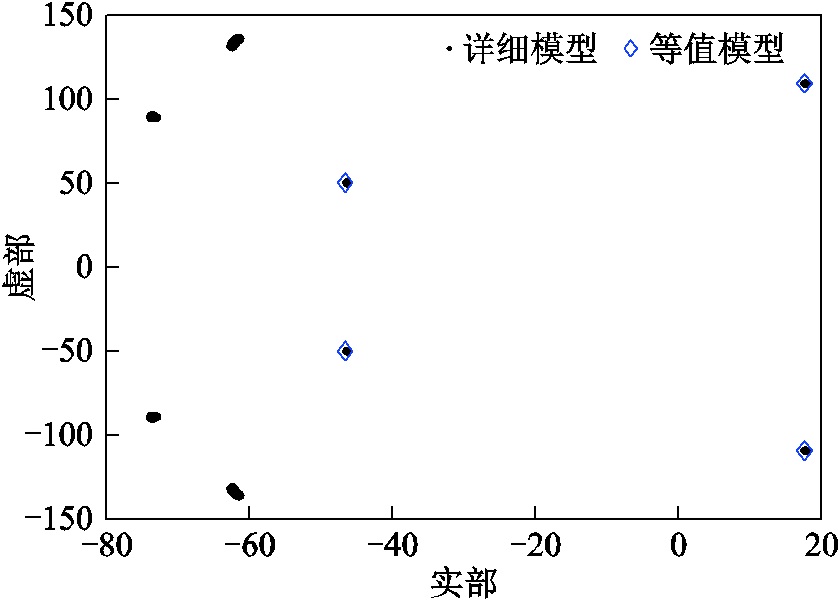
图12 振荡模式比较
Fig.12 Oscillation mode comparison
统计所有样本的关键特征根误差，其分布直方图如图13所示。可以看出，实部的误差主要在-1～0.5之间，虚部的误差主要在-0.5～1之间，误差均很小，基于参数聚合的单机等值模型可以用来表征详细模型。
图13 单机等值模型的关键特征根误差分布直方图
Fig.13 Histogram of critical eigenvalue error of single machine equivalent model
等值模型与详细模型的关键特征根之间的实部、虚部、频率、阻尼、幅值和临界特征根的误差统计信息见表3。可以发现，几个指标的误差比较小，在可接受范围内。
表3 关键特征根误差比较
Tab.3 Comparison of critical eigenvalues error
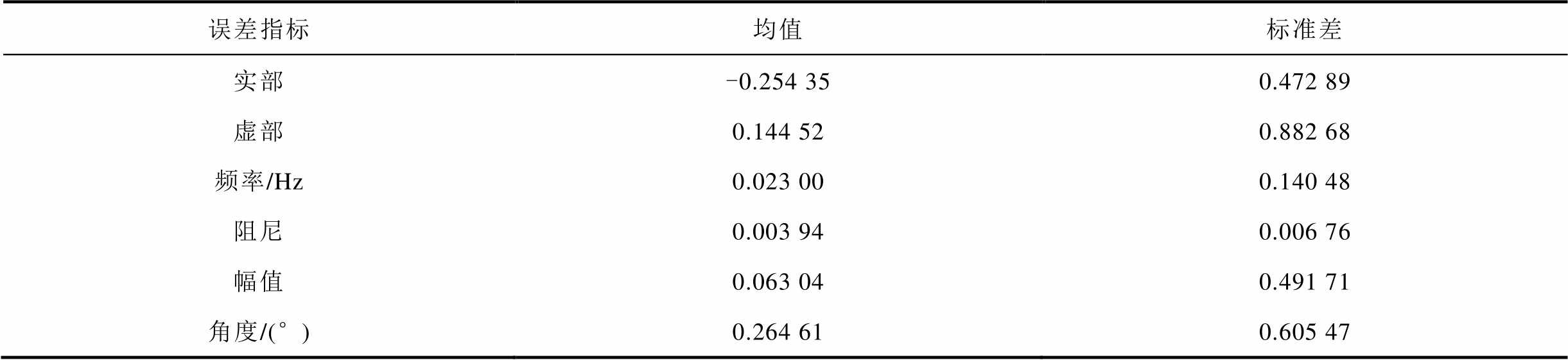
误差指标均值标准差 实部-0.254 350.472 89 虚部0.144 520.882 68 频率/Hz0.023 000.140 48 阻尼0.003 940.006 76 幅值0.063 040.491 71 角度/(°)0.264 610.605 47
综上所述，尽管等值模型和详细模型的关键特征根不相等，但二者之间误差很小，可以接受。因此，单机等值尽管不严格满足第三条判据，但依然有效。
6.2.2 基于电磁暂态时域仿真的分析
除了基于小信号模型的验证之外，本节同样在在PSCAD上基于电磁暂态的时域仿真进行了验证。由于规模限制，难以仿真66机系统，此处采用一个不对称的三机系统进行验证，各机之间只有参数相同，系统主要电路参数见附录。依然采用电网电压跌落的小扰动形式来激发系统振荡模式，形式为：在0.1s时电网母线电压由690V跌落5%，持续0.02s后恢复。仿真曲线如图14所示，无论从风电场功率还是风机直流电压，均可以看出等值模型与详细模型均相差不大，等值模型可以反映系统的振荡模式。
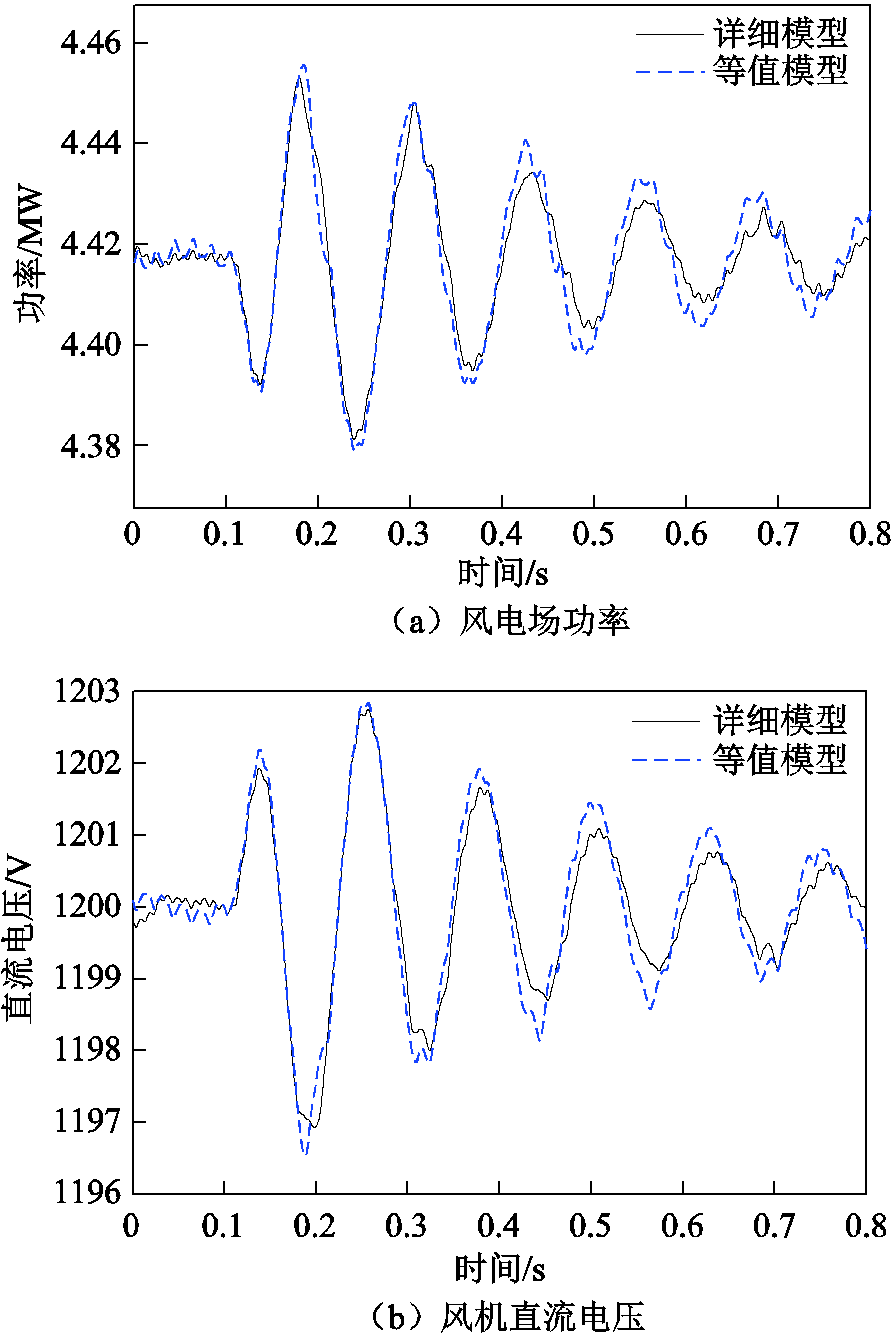
图14 时域仿真曲线比较
Fig.14 Time domain simulation curves comparison
本文分别基于解析分析和蒙特卡洛仿真，研究了接入弱电网的同型机直驱风电场单机等值建模的前提条件和准确性，得到如下结论：
1）分析提出了直驱风电场满足单机等值建模的判据，即系统至多只有一对弱阻尼（或负阻尼）特征根，且单机等值模型和详细模型的该特征根相等，电网侧状态变量有参与该振荡模式。
2）通过对状态空间方程中状态矩阵的解析分析表明：系统最弱的振荡模式是共模中最弱的模式；电网侧和风机侧均会参与共模振荡模式，两侧的扰动都会将其激发；异模振荡模式只有风机侧参与，只会被风机侧扰动激发。
3）直驱风电场单机等值成立的前提是各风机参数、出力和集电线路接线完全相同。此时，系统只有一对弱阻尼（或负阻尼）特征根，且在单机等值模型和详细模型中相等，电网侧有较大参与度。因此，单机等值模型可以完全准确地描述风电场的振荡特性。
4）基于蒙特卡洛仿真，进一步研究了当风电场各风机参数相同、但出力和集电线路接线不同时直驱风电场单机等值的有效性。结果表明，此时系统只有一对弱阻尼（或负阻尼）特征根，电网侧有较大参与度。虽然单机等值模型和详细模型的该特征根不相等，但是特征根很接近。因此，单机等值方法仍然具有较高的准确性。
1.状态矩阵Asys
式（2）中矩阵Asys的各子块为
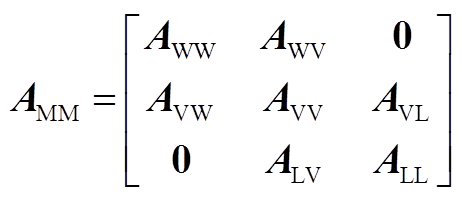
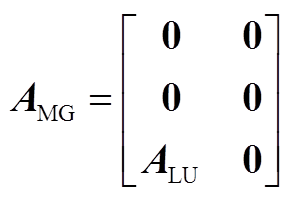
其中各元素定义如下。
矩阵AWW为9阶方阵，其非零元素为
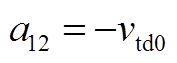
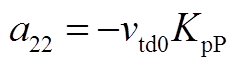
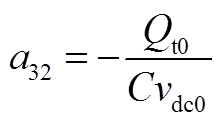
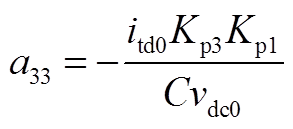
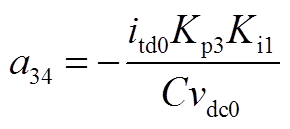
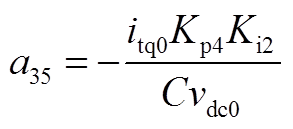
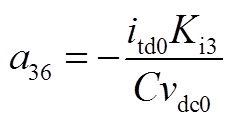
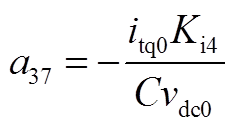
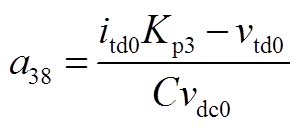
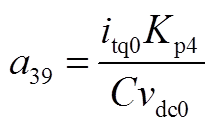
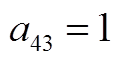
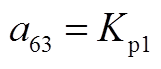
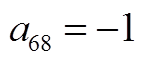
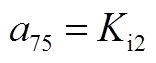
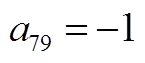
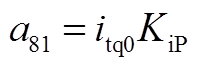
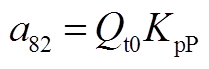
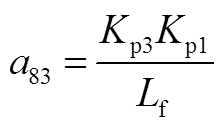
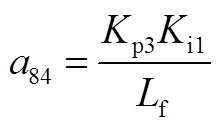
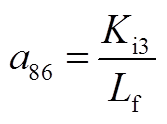
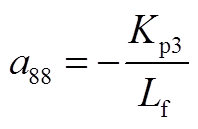
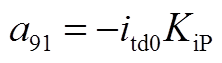
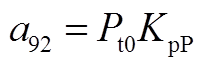
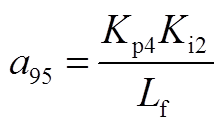
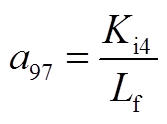
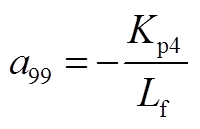
矩阵AWV为9×2阶矩阵，其非零元素为
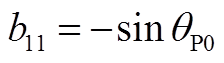
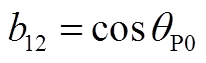
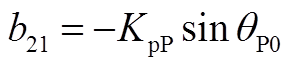
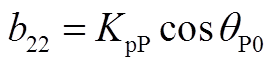
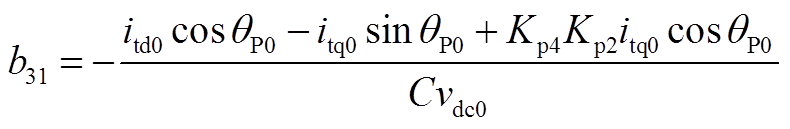
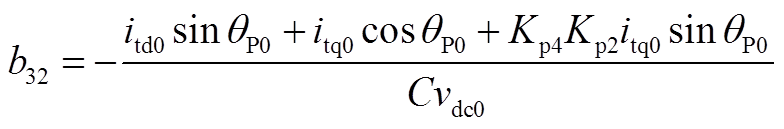
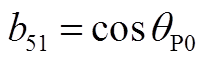
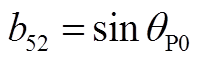
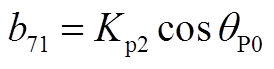
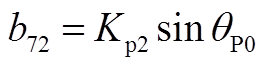
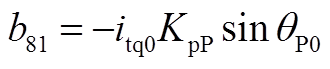
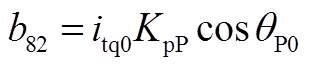
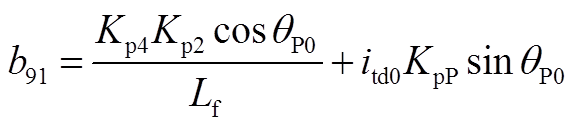
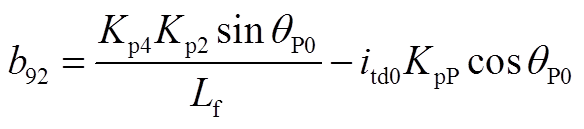
矩阵AVW为2×9阶矩阵，其非零元素为
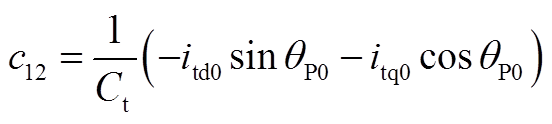
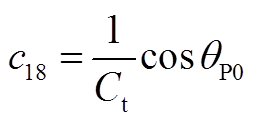
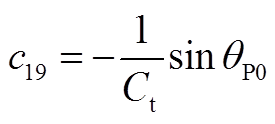
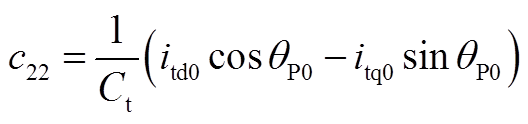
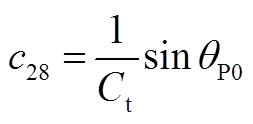
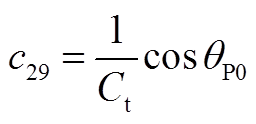
其他矩阵为
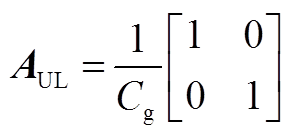
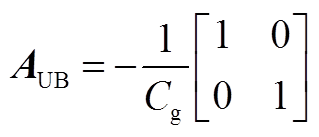
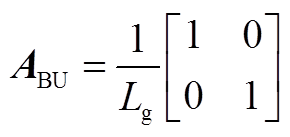
2.算例中主要电路参数
第5节三机系统电路参数如下。
详细模型：Lg=2.25mH，Lt1=Lt2=Lt3=0.075 77mH，Pt1=Pt2=Pt3=1.5MW，无穷大电网电压690V。
等值模型：Lg=2.25mH，Lt,eq=0.025 26mH，Pt,eq=4.5MW，无穷大电网电压690V。
第6节三机系统电路参数如下。
详细模型：Lg=2.25mH，Lt1=0.075 77mH，Lt2=0.074 26mH，Lt3=0.072 74mH，Pt1=1.5MW，Pt2=1.25MW，Pt3=1.75MW，无穷大电网电压690V。
等值模型：Lg=2.25mH，Lt,eq=0.024 72mH，Pt,eq=4.5MW，无穷大电网电压690V。
参考文献
[1] 马宁宁, 谢小荣, 贺静波, 等. 高比例新能源和电力电子设备电力系统的宽频振荡研究综述[J]. 中国电机工程学报, 2020, 40(15): 4720-4732.
Ma Ningning, Xie Xiaorong, He Jingbo, et al. Review of wide-band oscillation in renewable and power electronics highly integrated power systems[J]. Proceedings of the CSEE, 2020, 40(15): 4720-4732.
[2] Hatziargyriou N, Milanovic J V, Rahmann C, et al. Definition and classification of power system stability revisited & extended[J]. IEEE Transactions on Power Systems, 2021, 36(4): 3271-3281.
[3] 袁小明, 程时杰, 胡家兵. 电力电子化电力系统多尺度电压功角动态稳定问题[J]. 中国电机工程学报, 2016, 36(19): 5145-5154.
Yuan Xiaoming, Cheng Shijie, Hu Jiabing. Multi-time scale voltage and power angle dynamics in power electronics dominated large power systems[J]. Proceedings of the CSEE, 2016, 36(19): 5145-5154.
[4] Wang Dong, Liang Liang, Shi Lei, et al. Analysis of modal resonance between PLL and DC-link voltage control in weak-grid tied VSCs[J]. IEEE Transactions on Power Systems, 2019, 34(2): 1127-1138.
[5] Liu Huakun, Xie Xiaorong, He Jingbo, et al. Subsynchronous interaction between direct-drive PMSG based wind farms and weak AC networks[J]. IEEE Transactions on Power Systems, 2017, 32(6): 4708-4720.
[6] 宋瑞华, 郭剑波, 李柏青, 等. 基于输入导纳的直驱风电次同步振荡机理与特性分析[J]. 中国电机工程学报, 2017, 37(16): 4662-4670.
Song Ruihua, Guo Jianbo, Li Baiqing, et al. Mechanism and characteristics of subsynchronous oscillation in direct-drive wind power generation system based on input-admittance analysis[J]. Proceedings of the CSEE, 2017, 37(16): 4662-4670.
[7] Huang Yunhui, Yuan Xiaoming, Hu Jiabing, et al. Modeling of VSC connected to weak grid for stability analysis of DC-link voltage control[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2015, 3(4): 1193-1204.
[8] 薛安成, 王子哲, 付潇宇, 等. 基于非光滑分叉的直驱风机次同步振荡机理分析[J]. 电力系统自动化, 2020, 44(7): 87-92.
Xue Ancheng, Wang Zizhe, Fu Xiaoyu, et al. Mechanism analysis of subsynchronous oscillation in direct-driven wind turbine based on non-smooth bifurcation[J]. Automation of Electric Power Systems, 2020, 44(7): 87-92.
[9] 曾锋, 李崇涛, 舒进, 等. 基于阻抗法的稳定性判据论证及其适用性分析[J]. 电力系统自动化, 2021, 45(8): 146-154.
Zeng Feng, Li Chongtao, Shu Jin, et al. Demonstration of stability criterion based on impedance method and analysis on its applicability[J]. Automation of Electric Power Systems, 2021, 45(8): 146-154.
[10] 涂春鸣, 高家元, 李庆, 等. 具有复数滤波器结构锁相环的并网逆变器对弱电网的适应性研究[J]. 电工技术学报, 2020, 35(12): 2632-2642.
Tu Chunming, Gao Jiayuan, Li Qing, et al. Research on adaptability of grid-connected inverter with complex coefficient-filter structure phase locked loop to weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2632-2642.
[11] 胡鹏, 艾欣, 肖仕武, 等. 静止无功发生器序阻抗建模及对次同步振荡影响因素的分析[J]. 电工技术学报, 2020, 35(17): 3703-3713.
Hu Peng, Ai Xin, Xiao Shiwu, et al. Sequence impedance of static var generator and analysis of influencing factors on subsynchronous oscillation[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3703-3713.
[12] 陈剑, 杜文娟, 王海风. 采用深度迁移学习定位含直驱风机次同步振荡源机组的方法[J]. 电工技术学报, 2021, 36(1): 179-190.
Chen Jian, Du Wenjuan, Wang Haifeng. A method of locating the power system subsynchronous oscillation source unit with grid-connected PMSG using deep transfer learning[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 179-190.
[13] 涂春鸣, 高家元, 赵晋斌, 等. 弱电网下具有定稳定裕度的并网逆变器阻抗重塑分析与设计[J]. 电工技术学报, 2020, 35(6): 1327-1335.
Tu Chunming, Gao Jiayuan, Zhao Jinbin, et al. Analysis and design of grid-connected inverter impedance remodeling with fixed stability margin in weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1327-1335.
[14] 王伟胜, 张冲, 何国庆, 等. 大规模风电场并网系统次同步振荡研究综述[J]. 电网技术, 2017, 41(4): 1050-1060.
Wang Weisheng, Zhang Chong, He Guoqing, et al. Overview of research on subsynchronous oscillations in large-scale wind farm integrated system[J]. Power System Technology, 2017, 41(4): 1050-1060.
[15] Yan Gangui, Wang Dan, Jia Qi, et al. Equivalent modeling of DFIG-based wind farms for sub-synchronous resonance analysis[J]. Energies, 2020, 13(20): 5426.
[16] 邵冰冰, 赵书强, 高本锋. 基于相似变换理论的直驱风电场经柔直并网系统次同步振荡简化模型[J]. 中国电机工程学报, 2020, 40(15): 4780-4791.
Shao Bingbing, Zhao Shuqiang, Gao Benfeng. Simplified model for studying the sub-synchronous oscillation of direct-drive wind farms via VSC-HVDC system based on similar transformation theory[J]. Proceedings of the CSEE, 2020, 40(15): 4780-4791.
[17] Du Wenjuan, Dong Wenkai, Wang Haifeng, et al. Dynamic aggregation of same wind turbine generators in parallel connection for studying oscillation stability of a wind farm[J]. IEEE Transactions on Power Systems, 2019, 34(6): 4694-4705.
[18] 杨晓波, 岳程燕, 谢海莲. 用于电磁暂态仿真分析的永磁同步发电机风电场模型聚合方法[J]. 电网技术, 2011, 35(2): 115-120．
Yang Xiaobo, Yue Chengyan, Xie Hailian. An aggregation method of permanent magnet synchronous generators wind farm model for electromagnetic transient simulation analysis[J]. Power System Technology, 2011, 35(2): 115-120.
[19] Liu Hongzhi, Chen Zhe. Aggregated modelling for wind farms for power system transient stability studies[C]//2012 Asia-Pacific Power and Energy Engineering Conference (APPEEC), Shanghai, 2012: 1-6.
[20] 苏勋文. 风电场动态等值建模方法研究[D]. 保定:华北电力大学, 2010.
[21] Liao Shuhan, Huang Meng, Zha Xiaoming, et al. Emulation of multi-inverter integrated weak grid via interaction-preserved aggregation[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(4): 4153-4164.
[22] Zheng Zetian, An Zhi, Shen Chen. Evaluation method for equivalent models of PMSG-based wind farms considering randomness[J]. IEEE Transactions on Sustainable Energy, 2019, 10(3): 1565-1574.
[23] 董文凯, 杜文娟, 王海风. 用于风电场小干扰稳定性检验的降阶模式计算方法[J]. 电工技术学报, 2021, 36(7): 1468-1479.
Dong Wenkai, Du Wenjuan, Wang Haifeng. Reduced-order modal computation method for small-signal stability examination of a wind farm[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1468-1479.
[24] 倪以信, 陈寿孙, 张宝霖. 动态电力系统的理论和分析[M]. 北京: 清华大学出版社, 2002.
[25] 史荣昌, 魏丰. 矩阵分析[M]. 3版. 北京: 北京理工大学出版社, 2010.
[26] 辛焕海, 董炜, 袁小明, 等. 电力电子多馈入电力系统的广义短路比[J]. 中国电机工程学报, 2016, 36(22): 6013-6027.
Xin Huanhai, Dong Wei, Yuan Xiaoming, et al. Generalized short circuit ratio for multi power electronic based devices infeed to power systems[J]. Proceedings of the CSEE, 2016, 36(22): 6013-6027.
[27] Beerten J, D’Arco S, Suul J A. Identification and small-signal analysis of interaction modes in VSC MTDC systems[J]. IEEE Transactions on Power Delivery, 2016, 31(2): 888-897.
Abstract In the current studies on stability of weak grid connected permanent magnet synchronous generator(PMSGs) wind farm, single machine equivalence is generally used for wind farm, and it is usually assumed that the wind farm is an ideal system, that is, the parameters, outputs and collector lines of all PMSGs are identical. However, there is still a lack of related theoretical support for the prerequisites of single machine equivalent modeling for PMSGs wind farm. In addition, in the actual wind farm, only the parameters of PMSGs are identical (that is, the same type), the outputs and collector lines of PMSGs are different, which is a nonideal system. Whether the single machine equivalent modeling is effective remains to be studied. In response to the problems, this paper presents the criterions for the PMSGs wind farm to meet the single machine equivalence and proposes the prerequisites of single machine equivalent modeling. It provides a certain theoretical support for the application of single machine equivalence.
Firstly, three criterions are proposed to determine whether the PMSGs wind farm can be equivalent to a single machine model. There is at most one pair of critical eigenvalues in the system (i.e. weak damping or negative damping eigenvalues). The grid side state variables must participate in this oscillation mode. The critical eigenvalues of single machine equivalent model and detailed model are equal.
Secondly, the oscillation characteristics and single machine equivalent modeling of the ideal system are studied analytically and theoretically. The state space model of weak grid connected PMSGs wind farm is established. The eigenvalues and eigenvectors of the state matrix are analytically analyzed using the matrix similarity transformation theory. It shows that there are one set of in-phase modes and n-1 sets of anti-phase modes in an ideal system with n PMSGs. The in-phase modes can be excited by both machine and grid sides, while the anti-phase modes can be only excited by machine sides. The weakest oscillation mode must be the in-phase mode under normal conditions. The single machine equivalent model of PMSGs wind farm is obtained based on the aggregation method. The theoretically analysis results show that the eigenvalues of equivalent model are equal to the in-phase mode of detailed model. Therefore, the single machine equivalence of PMSGs wind farm meets the three criterions. The single machine equivalent model can accurately represent the oscillation characteristics of detailed wind farms.
Furthermore, in nonideal system, the Monte Carlo method is used to analyze the oscillation characteristics and single machine equivalent modeling. A total of 2000 groups of samples are generated randomly, where only the parameters of PMSGs are identical in every sample. The cluster analysis of eigenvalues calculated in each sample shows that the distribution of eigenvalues is similar to that in ideal system. There is at most one pair of critical eigenvalues, which meets the first criterion. The relative participation on in-phase modes and anti-phase modes shows that, the grid side only has a high participation on in-phase modes, while nearly no participation on anti-phase modes, which satisfies the second criterion. The comparison of critical eigenvalues between single machine equivalent model and detailed model shows that the errors are very small. Although they do not strictly meet the third criterion, the two critical eigenvalues are approximately equal. Therefore, the single machine equivalence is still effective.
The time-domain simulation results show that the responses of single machine equivalent model are close to that of detailed model. The single machine equivalent model can reflect the oscillation mode, and has high accuracy.
The following conclusions can be drawn: 1) The three criterions are proposed to determine whether the PMSGs wind farm can be equivalent to a single machine model. 2) The prerequisites of single machine equivalent modeling for PMSGs wind farm are the parameters, outputs and collector lines of all PMSGs are identical, which are theoretically proved. 3) The single machine equivalence is still effective, where only the parameters of PMSGs are identical, and the outputs and collector lines are different.
keywords： Wind farm with same type permanent magnet synchronous generator(PMSGs), weak grid, single machine equivalent modeling, prerequisites, criterions
Doi:10.19595/j.cnki.1000-6753.tces.211555
中图分类号：TM712
四川省科技计划应用基础研究重点项目资助（2020YJ0252）。
收稿日期 2021-09-29
改稿日期 2021-12-09
李龙源 男，1993年生，博士研究生，研究方向为含新能源的电力系统稳定性分析、风电建模。E-mail：lilongyuan2012@163.com
王晓茹 女，1962年生，博士，教授，博士生导师, 研究方向为电力系统稳定性分析与控制。E-mail：xrwang@home.swjtu.edu.cn（通信作者）
（编辑 赫蕾）