
图1 兆瓦级永磁直驱风力发电机结构
Fig.1 Structure diagram of megawatt permanent magnet direct drive generator
摘要 该文开展了负载工况下永磁直驱发电机气隙磁场研究。基于精确域求解和保角变换,计算考虑齿槽效应的气隙磁场标量磁势;采用离散线电流元,定量模拟发电机定转子局部出现的磁饱和现象;基于考虑几何尺寸的定转子非线性磁阻计算方法,建立包含发电机定转子结构以及气隙长度的等效磁路,给出相应的迭代求解流程。以实际在役兆瓦级永磁直驱风力发电机为对象,计算考虑齿槽效应的气隙磁场分布,分析了空载和负载工况下磁饱和效应对气隙磁场分布曲线波形和谐波成分的影响,并与有限元计算结果对比,验证了所提出的分析模型和求解方法的有效性。
关键词:永磁直驱发电机 气隙磁场 等效磁路 负载工况 磁饱和 齿槽效应 非线性磁阻
由于低速性能好、发电效率高、维护成本低、运行可靠等突出优点,兆瓦级永磁直驱风力发电机是大型陆上及海上风力发电的理想选择[1-3]。在永磁直驱风力发电机性能分析与优化设计中,准确高效地获得气隙磁场分布是重要前提。
尽管有限元法普适性强、计算精度高,但建模和计算时间较长[4];而计算量小、速度快且物理概念清晰的解析法仍然受到学者的广泛关注。由于定子开槽导致气隙磁通密度发生畸变,谐波成分增加,所以基于解析法准确计算气隙磁通密度变得困难。通过经验系数的修正,采用传统磁路法可获得考虑齿槽效应的气隙磁通密度最大值[5]。因定子槽形、定转子轭部尺寸和形状等参数的影响,修正系数难以准确得到,致使考虑齿槽效应的传统磁路法计算精度不高[6]。子域法[7-9]将电机域划分为气隙、永磁体和齿槽三个子域,通过交界条件建立各个子域的拉普拉斯方程或泊松方程的联系,进而采用解析法求解。基于保角变换,将齿槽等不规则域变换为规则求解域,利用子域法的解析结果可获得气隙磁场分布[10-11]。与传统磁路法相比,基于保角变换的解析法计算精度较高。但上述方法均难以考虑因铁磁材料非线性引起的磁饱和效应,因而具有局限性[6]。
磁饱和导致定子齿端部的相对磁导率降低。F.R.Alam和K. Abbaszadeh[12-13]提出一种改进的保角变换,通过增加定子齿槽开口宽度模拟磁饱和效应。因经验饱和因子的引入,使得该方法的精度不易保证。基于磁路基尔霍夫定律的等效磁路法[14],是一种用于电机定量分析的方法,可考虑磁饱和效应。但是与有限元法相比,其网格划分较粗略,虽然计算效率较高,但精度较差。经过S.D.Sudhoff等[15]的不断改进,等效磁路法的计算精度已有很大提升,且可计及电机精细几何尺寸、三维空间磁场等复杂因素的影响。目前,等效磁路法已广泛用于多种形式的永磁电机稳态和瞬态磁场分析中,取得很好的效果。很多学者结合保角变换和等效磁路法,研究了考虑饱和与否对表面永磁电机气隙磁场分布的影响[6,16-21]。但这些研究主要针对空载工况,针对负载工况的研究则较少[22]。与空载相比,负载工况下的气隙磁场变化更为明显,谐波成分更为复杂,磁饱和效应更为显著。
因此,本文开展负载工况下永磁直驱发电机气隙磁场研究。基于精确域求解和保角变换,计算考虑齿槽效应的气隙磁场标量磁势;采用离散线电流元,定量模拟发电机定转子局部出现的磁饱和现象;基于考虑几何尺寸的定转子非线性磁阻计算方法,建立包含发电机定转子结构以及气隙长度的等效磁路,给出相应的迭代求解框架。以实际在役兆瓦级永磁直驱风力发电机为对象,计算考虑齿槽效应的气隙磁场分布,并与有限元计算结果对比,验证所提出的分析模型和求解方法。在此基础上,分析了空载和负载工况下磁饱和效应对气隙磁场分布曲线波形和谐波成分的影响。
典型兆瓦级永磁直驱风力发电机结构如图1所示,为外转子结构。径向磁化的永磁体,粘贴于转子内径。磁极对数为p,齿槽数为Qs。2倍磁极对数与齿槽数的最大公约数为Ng=gcd(2p,Qs)。考虑结构周期性并忽略局部细节尺寸(如定/转子磁轭的散热结构),建立永磁发电机对称分析模型,如图2所示。其中所考虑的永磁体个数为2p/Ng,齿槽数为Qs/Ng。

图1 兆瓦级永磁直驱风力发电机结构
Fig.1 Structure diagram of megawatt permanent magnet direct drive generator
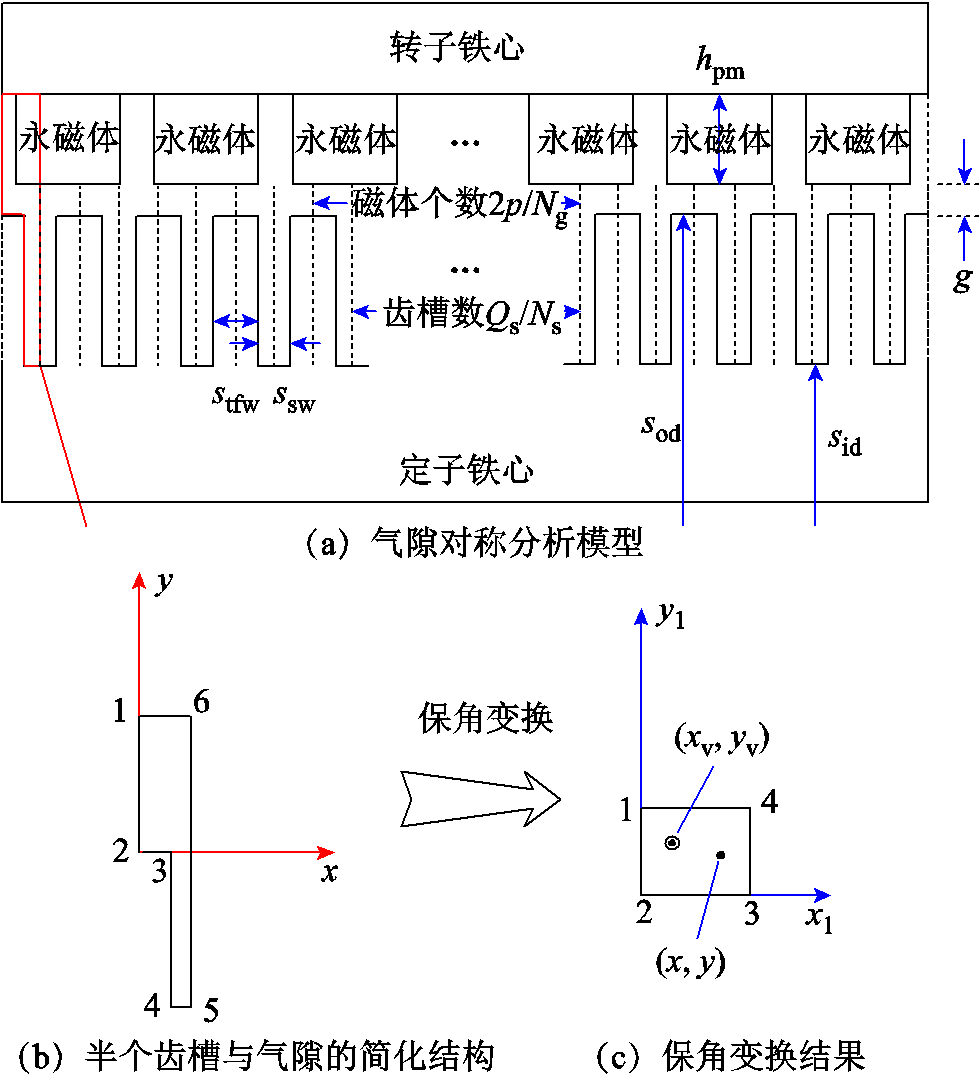
图2 永磁发电机气隙磁场分析
Fig.2 Air gap magnetic field analysis of permanent magnet generator
暂不计入永磁体和负载绕组对标量磁势的影响。为了提高计算效率,仅分析定子齿邻近半个齿槽与气隙的简化结构,如图2b所示。其余气隙和齿槽区域的解,通过“镜像对称”的方式获得。对于图2b所示的气隙结构,在物理坐标系(O-x-y)下,需要6个顶点来定义。各个顶点的坐标(xi, yi)为
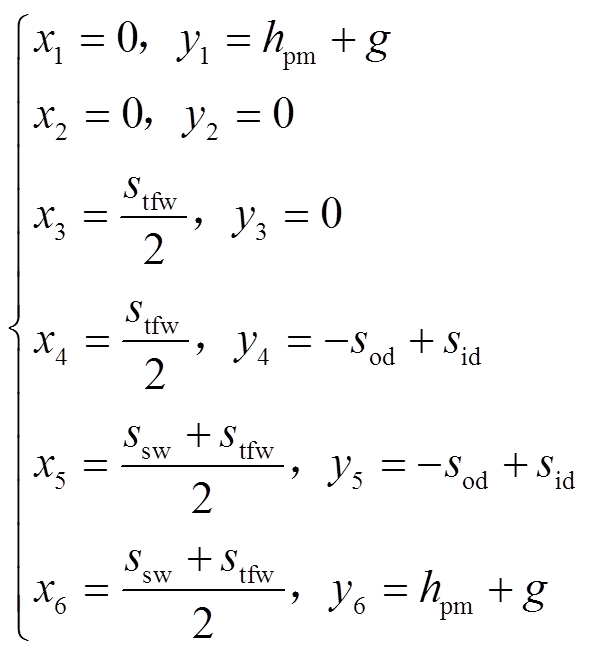 (1)
(1)
式中,sod、sid分别为定子外径和内径;stfw、ssw分别为定子齿宽度和齿槽宽度;hpm为永磁体厚度;g为气隙长度,如图2a所示。
基于保角变换,可将原物理平面上复杂几何域映射成像平面上的单位矩形平面、半无限平面等。多数情况下,难以获得保角变换的解析解,需借助数值方法。本文利用Matlab中的Schwarz–Christoffel保角变换工具包[11],将包含齿槽的气隙区域变换为规则的矩形区域,如图2c所示。矩形的上下两边(1-4和2-3)分别为转子和定子铁心(磁导率可近似为无穷大),而1-2和3-4则为气隙边界。若该矩形区域存在一个离散电流元I,坐标为(xv, yv)。任意一点(x, y)的标量磁势可表示为
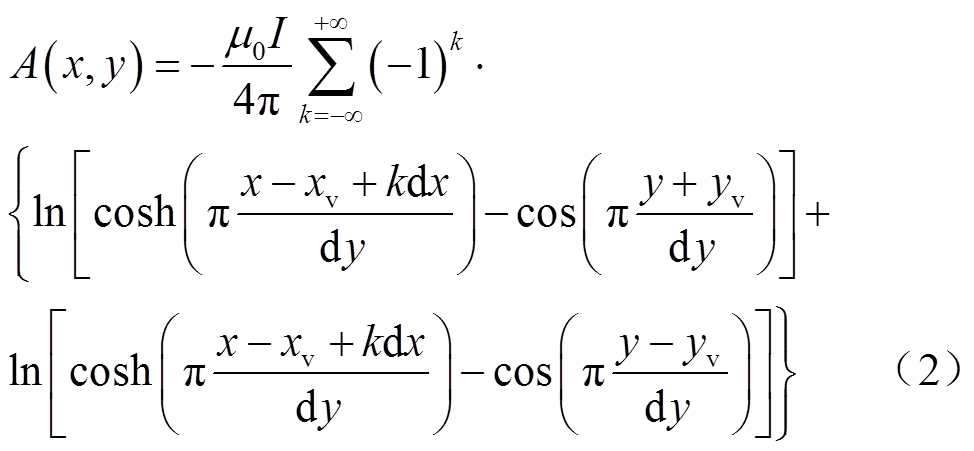
式中,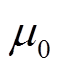 为真空磁导率;dx、dy分别为保角变换后矩形区域的长度、宽度值。若存在多个离散电流元,可分别利用式(2)计算后线性叠加即可得到总的标量磁势。
为真空磁导率;dx、dy分别为保角变换后矩形区域的长度、宽度值。若存在多个离散电流元,可分别利用式(2)计算后线性叠加即可得到总的标量磁势。
对于径向磁化的永磁体,其磁场可通过磁体两侧的电流片模拟。电流片可用Nmms个线电流元离散。在这种情况下,单个电流元的幅值为
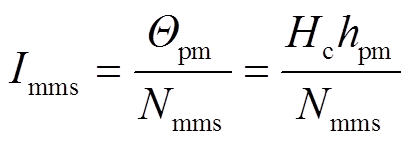 (3)
(3)
式中,Θpm为永磁体的磁动势;Hc为永磁体的矫顽力。将所分析的永磁体分别采用离散电流元进行等效,离散线电流元模拟永磁体、绕组以及定转子饱和效应如图3所示。类似地,采用离散线电流元模拟负载绕组的作用,表示为Iwi(i=1,2, , Qs/Ng)。
, Qs/Ng)。
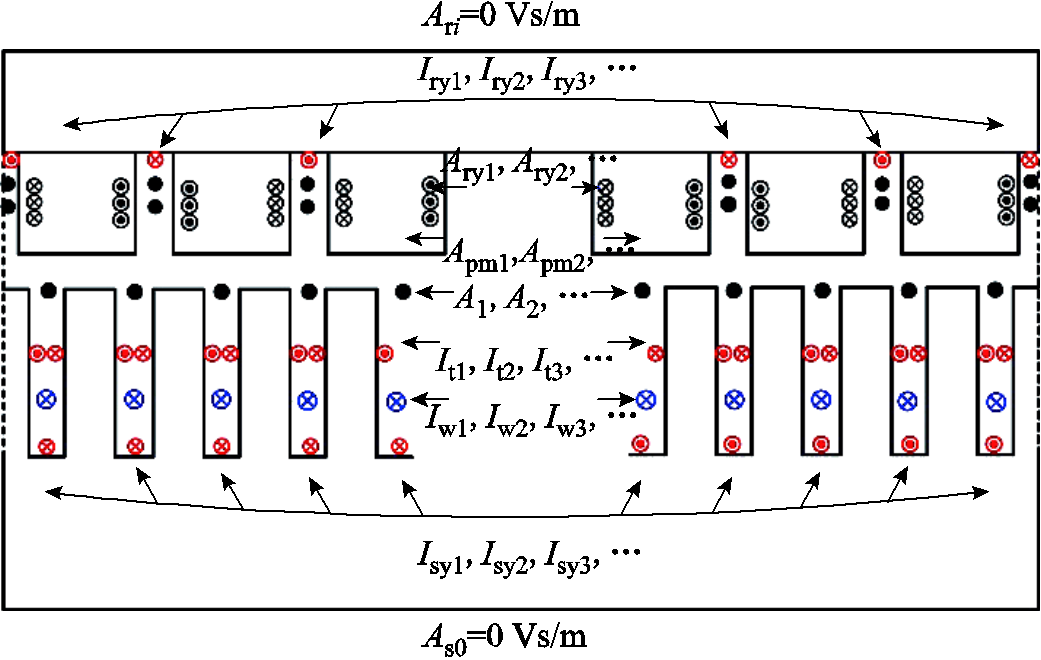
图3 离散线电流元模拟永磁体、绕组以及定转子饱和效应
Fig.3 Simulation of permanent magnet, winding and saturation effects in stator and rotor by discrete line current element
为了计入定子齿端部、定子铁心和转子铁心的非线性饱和效应,并考虑永磁体磁导率大于1的问题,采用虚拟离散线电流元,并通过迭代求解等效磁路模型的方式得到准确的气隙磁场分布。如图3所示,在定子齿、定子铁心以及转子铁心处的增加虚拟线电流,分别表示为Iti、Isyi(i=1,2, , Qs/Ng)和Iryi(i=1,2,
, Qs/Ng)和Iryi(i=1,2, ,2p/Ng)。为避免数值计算奇异问题,通常将这些线电流的位置设定在接近图2b所示区域的边界(如0.1mm处)。基于保角变换,可将这些线电流以及永磁体线电流的位置转换至规则的矩形区域内,进而根据式(2),得到气隙磁势Ai(i=1,2,
,2p/Ng)。为避免数值计算奇异问题,通常将这些线电流的位置设定在接近图2b所示区域的边界(如0.1mm处)。基于保角变换,可将这些线电流以及永磁体线电流的位置转换至规则的矩形区域内,进而根据式(2),得到气隙磁势Ai(i=1,2, , Qs/Ng),永磁体磁势Apmi(i=1,2,
, Qs/Ng),永磁体磁势Apmi(i=1,2, , 2p/Ng+1)及转子磁势Aryi(i=1,2,
, 2p/Ng+1)及转子磁势Aryi(i=1,2, , 2p/Ng),如图3所示。
, 2p/Ng),如图3所示。
建立如图4所示的永磁直驱发电机等效磁路模型。ΦTi、Φsyi、Φryj(i=1,2, , Qs/Ng,j=1,2,
, Qs/Ng,j=1,2, , 2p/Ng)分别表示定子齿、定子磁轭和转子磁轭的磁通量源。以定子铁心以及转子铁心内部的磁势为参考点,即图3中As0=0Vs/m和Ari=0Vs/m处,依据保角变换得到的标量磁势,可计算上述磁通量源为
, 2p/Ng)分别表示定子齿、定子磁轭和转子磁轭的磁通量源。以定子铁心以及转子铁心内部的磁势为参考点,即图3中As0=0Vs/m和Ari=0Vs/m处,依据保角变换得到的标量磁势,可计算上述磁通量源为
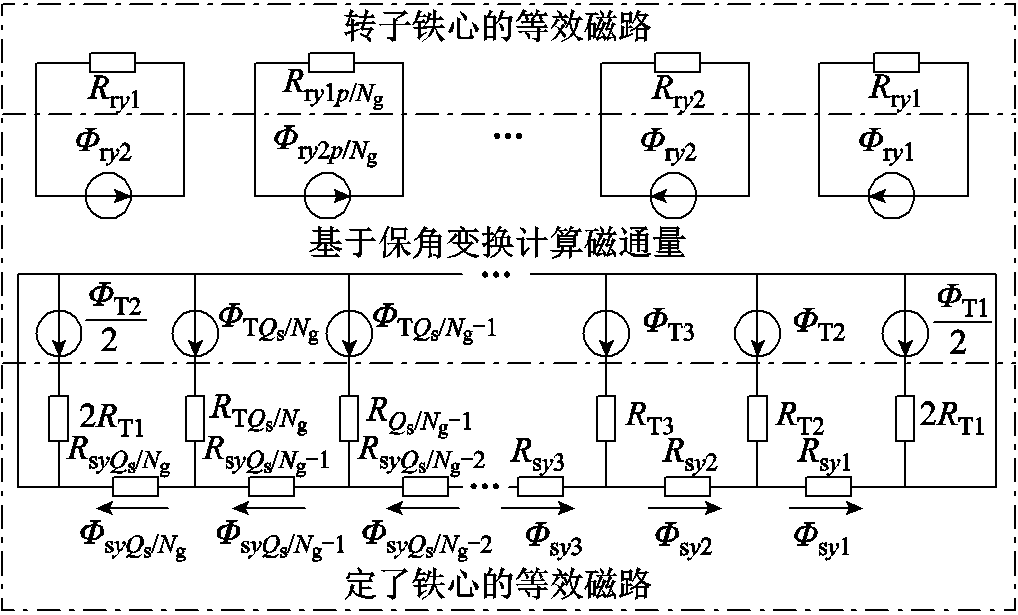
图4 永磁直驱发电机等效磁路模型
Fig.4 Magnetic equivalent circuit model of permanent magnet direct drive generator
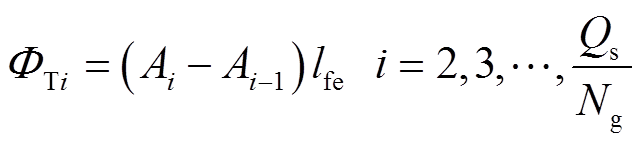 (4)
(4)
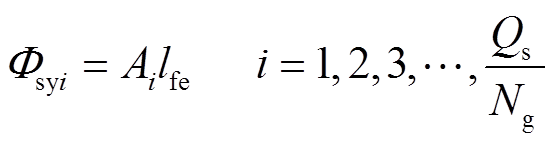 (5)
(5)
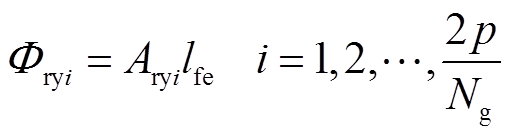 (6)
(6)
式中,lfe为电机轴向长度。对于第1个定子齿,注意到边界条件为第Qs/Ng+1个齿的右半部分的磁势大小相等,但与第1个齿的左半部分的磁势符号相反,则有
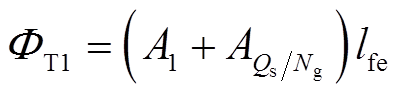 (7)
(7)
用于模拟磁阻非线性的线电流与穿过铁心磁阻的磁动势相同,可从等效磁路模型中获得。在已知磁通量的前提下,定子齿线电流可以计算为
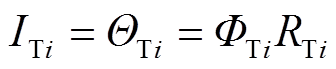 (8)
(8)
式中,RTi为定子齿的非线性磁阻,如图4所示。根据磁阻的定义,本研究所关注的定子磁阻可表示为
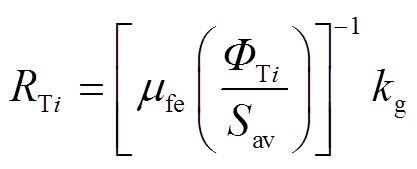 (9)
(9)
其中
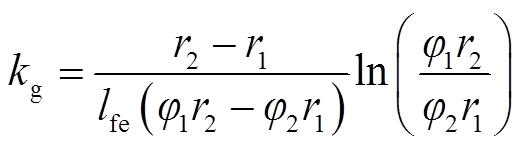 (10)
(10)
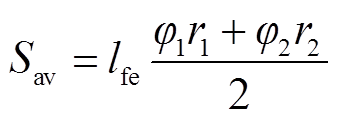 (11)
(11)
式中,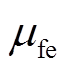 为定子铁心磁导率,与磁感应强度ΦTi /Sav有关;几何参数
为定子铁心磁导率,与磁感应强度ΦTi /Sav有关;几何参数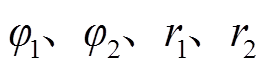 如图5中所示。
如图5中所示。
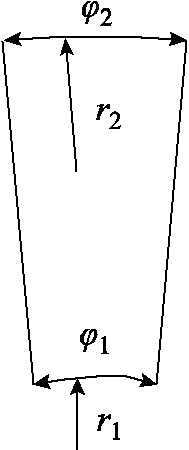
图5 定子齿磁阻计算尺寸
Fig.5 Calculation of stator tooth reluctance
定子铁心的线电流可表示为
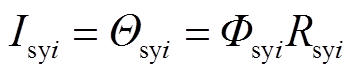 (12)
(12)
其中非线性定子轭部磁阻为
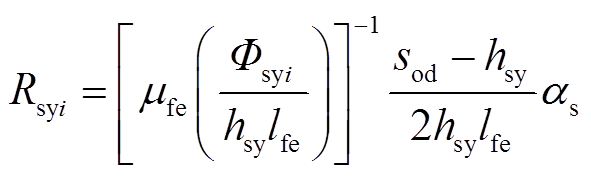 (13)
(13)
式中,hsy和αs分别为定子轭部高度和齿槽节圆跨度。显然,定子轭部磁阻与磁感应强度也是非线性关系。类似地,转子轭部的线电流为
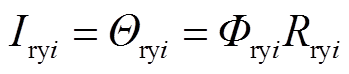 (14)
(14)
式中,Rryi为转子轭部的非线性磁阻,其表达式为
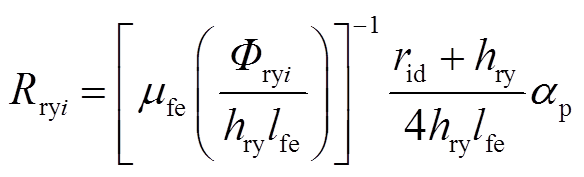 (15)
(15)
式中,hry和αp分别为转子轭部高度和节圆跨度。
在保角变换中,将原本永磁体的位置也采用空气模拟。因永磁体磁导率大于1,这样处理将带来一定的误差。需将永磁体的磁动势进行迭代修正,即乘以ΔRpmi(i=1,2, , 2p/Ng)。由此,使得线电流增加ΔIpmi,其表达式为
, 2p/Ng)。由此,使得线电流增加ΔIpmi,其表达式为
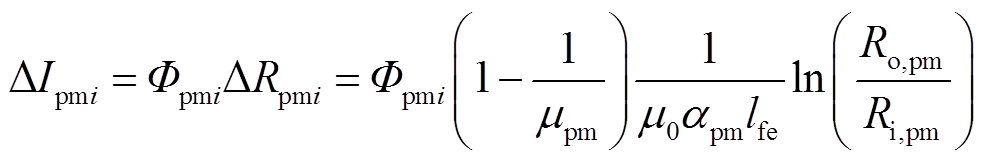 (16)
(16)
式中,αpm为弧形永磁体的跨度;Ro,pm、Ri,pm分别为永磁铁的内径和外径;Φpmi为流经永磁体的磁通量,有
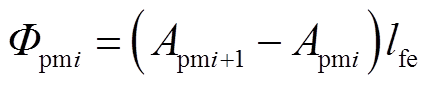 (17)
(17)
因此,在新的迭代计算步中,需将永磁体模拟线电流更新为
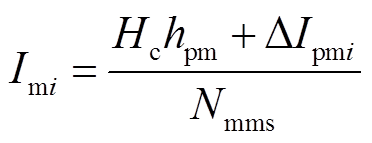 (18)
(18)
基于保角变换与等效磁路法的永磁直驱发电机气隙磁场计算流程如图6所示,步骤如下。
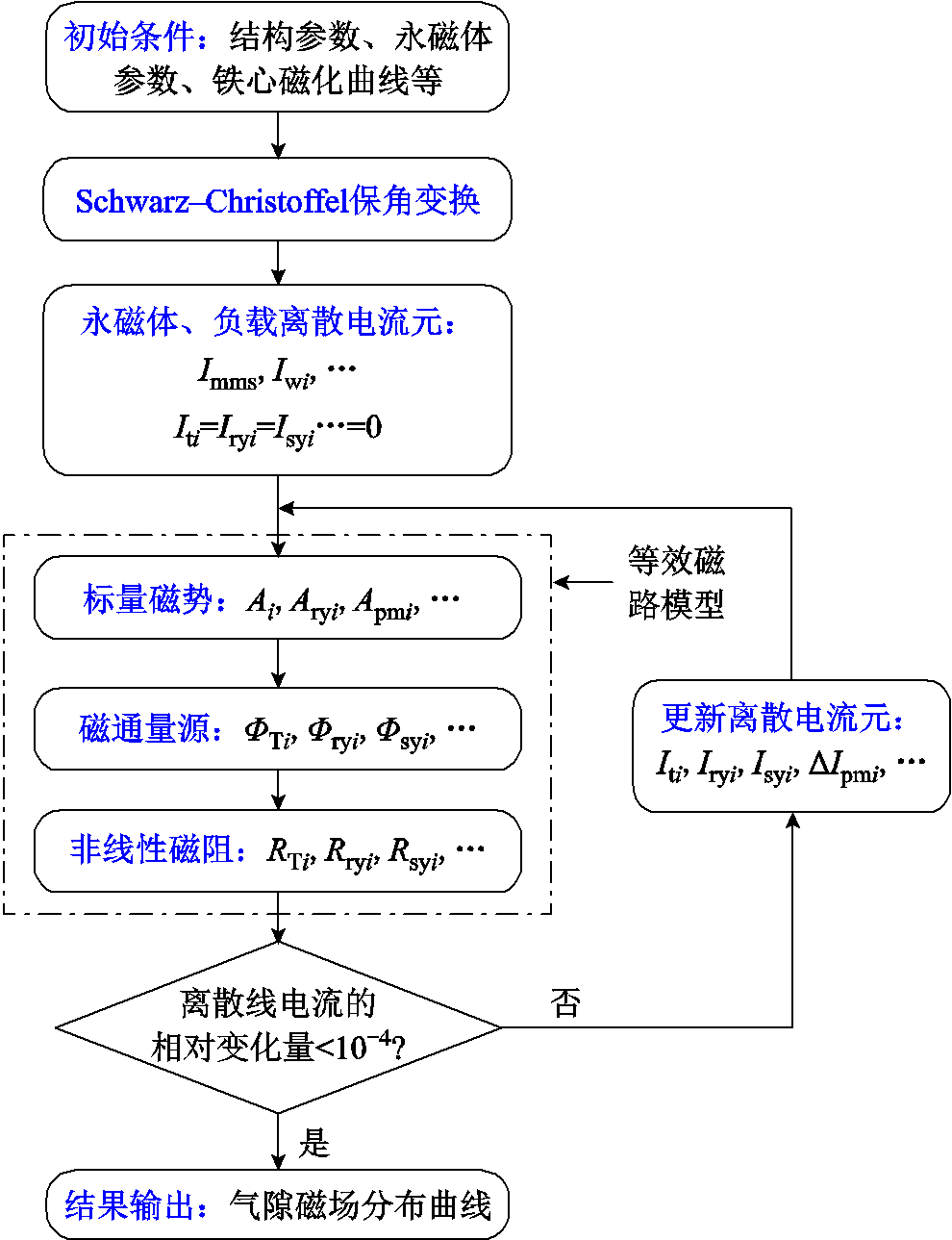
图6 永磁直驱发电机气隙磁场求解流程
Fig.6 Air gap magnetic field solution process of permanent magnet direct drive generator
(1)在给定的初始条件下(包括结构参数、永磁体参数、铁心磁化曲线等),开展Schwarz-Christoffel保角变换,将包含齿槽的气隙区域变换至规则的矩形区域。
(2)采用离散线电流元模拟永磁体和负载绕组作用,包括Imms、Iwi,以及定子齿端部、定子铁心和转子铁心的磁饱和效应,包括Iti、Isyi、Iryi。
(3)计算规则矩形区域内的标量磁势,包括Ai、Apmi、Aryi等;构建等效磁路模型,计算磁通量源(ΦTi、Φsyi、Φryj等),确定转/定子非线性磁阻(RTi、Rsyi、Rryi),得到更新后的用于模拟饱和效应的离散线电流元(Iti、Isyi、Iryi),以及用于修正永磁体磁动势的线电流ΔIpmi。
若更新后的离散线电流元与前次结果相比,相对变化量大于给定的阈值(比如1×10-4),重复步骤(3);否则,停止迭代,输出气隙磁场分布结果。需要说明的是,空载时离散线电流元的初值可设置为零,即Iti = Isyi = Iryi = 0;负载时,由于磁饱和效应较为突出,可将空载时的离散线电流值作为初值进行迭代,以提高收敛速度。
以金风1.5MW永磁直驱发电机为研究对象。极对数p=44,齿槽数Qs=576,主要结构尺寸可参考文献[4]。永磁体的矫顽力Hc=1 018kA/m,相对反冲磁导率为1.031 8。通常仅可获得定/转子硅钢片相对磁导率随磁感应强度变化的离散点。为了便于分析计算,需对其进行拟合。根据C. Heida和P. Regtien[23]的研究,可选择拟合函数为
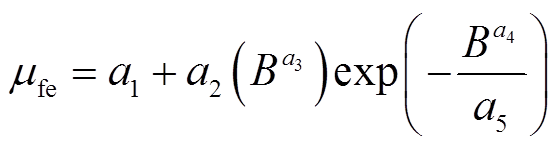 (19)
(19)
式中,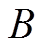 为磁感应强度;
为磁感应强度;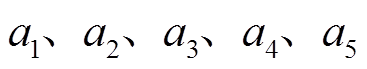 为拟合系数。依据相对磁导率数据,采用式(19)进行拟合,得到硅钢片的相对磁导率结果如图7所示。拟合系数的具体值见表1,拟合置信度为95%。
为拟合系数。依据相对磁导率数据,采用式(19)进行拟合,得到硅钢片的相对磁导率结果如图7所示。拟合系数的具体值见表1,拟合置信度为95%。
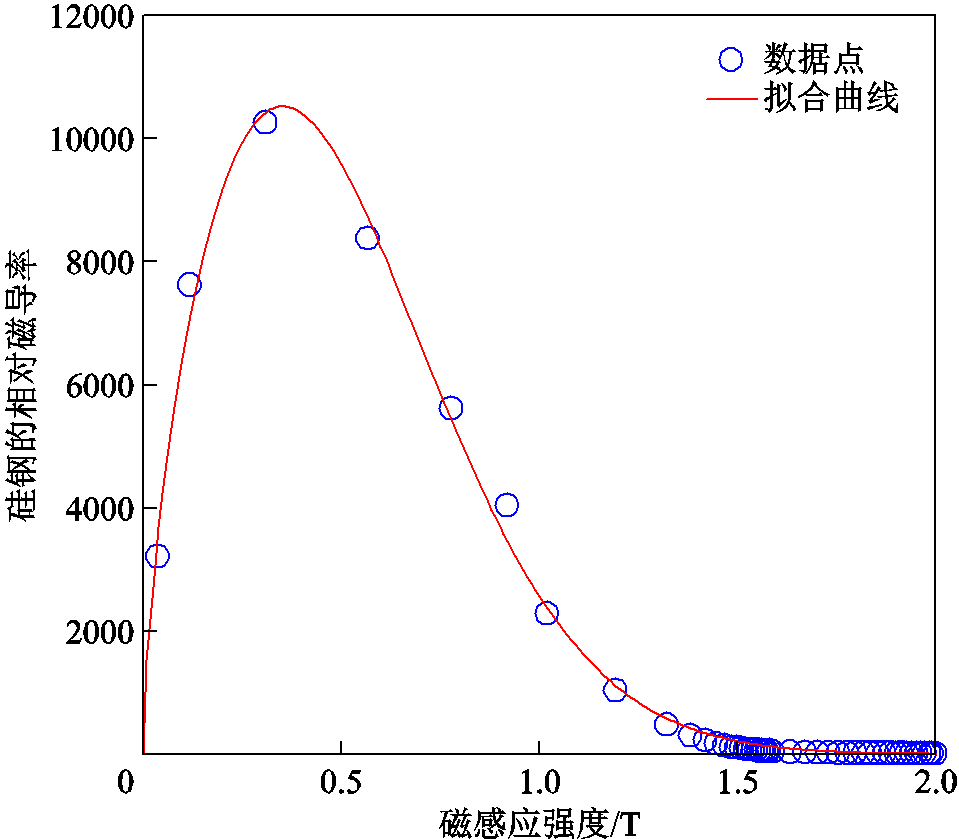
图7 硅钢片的相对磁导率及其拟合结果
Fig.7 Relative permeability of silicon steel sheet and its fitting results
表1 硅钢片相对磁导率拟合系数结果
Tab.1 Fitting coefficient results of relative permeability of silicon steel sheet

参数数值 a10.002 406 a228 730 a30.636 7 a41.879 a50.414 3
构建永磁直驱发电机的电磁有限元模型,如图8所示。以1/2气隙长度处为例,空载条件下本文结果与有限元结果的对比如图9所示。以空载时气隙最大磁感应强度为尺度,对图中结果做了无量纲化处理。由于2倍磁极对数与齿槽数的最大公约数为Ng=8,计算时截取72槽与11块永磁体所对应的扇区(45°)进行计算。从波形上看,本文结果与有限元结果基本保持一致。最大磁感应强度出现在永磁体(非齿槽开口处)。由于齿槽的存在,使得气隙磁感应强度出现波动。从幅值上看,本文所得到的最大气隙磁感应强度值稍低于有限元结果。上述对比验证了本文模型的正确性。

图8 有限元模型
Fig.8 The finite element model
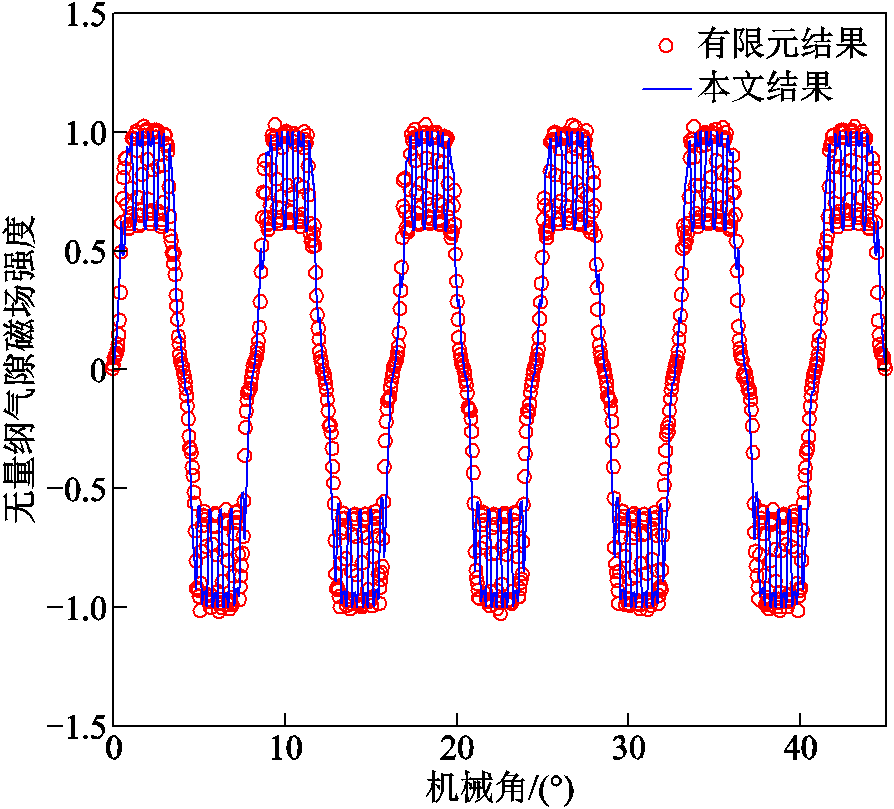
图9 空载条件下本文结果与有限元结果的对比(1/2气隙长度处)
Fig.9 Comparison between the present and finite element results under no-load condition at 1/2 air gap length
考虑定/转子铁心磁饱和效应、永磁体磁导率大于1等因素,重新计算了空载下气隙磁感应强度结果,如图10所示。图中结果也做了无量纲化处理,尺度为空载气隙最大磁感应强度。考虑饱和效应与否,二者差别很小(不超过0.5%),表明空载条件下定/转子铁心的磁饱和效应较弱,可忽略不计。气隙磁感应强度的谐波次数和幅值如图11所示。可以看出,基波频率及其奇数倍频(fc, 3fc, 7fc, 9fc)的幅值较为明显。此外,齿槽频率与基波频率的组合成分也可观察到,即fs±fc。
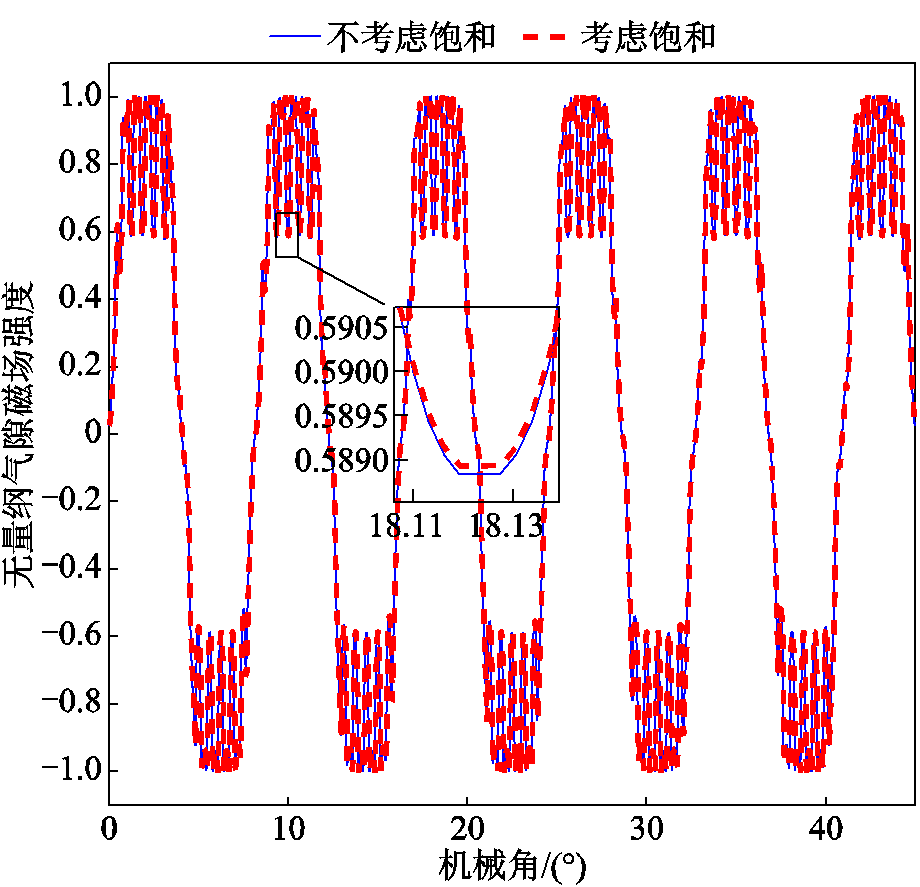
图10 空载条件下考虑饱和和不考虑饱和时气隙磁感应强度分布
Fig.10 Distribution of magnetic field intensity in air gap with and without saturation under no-load condition
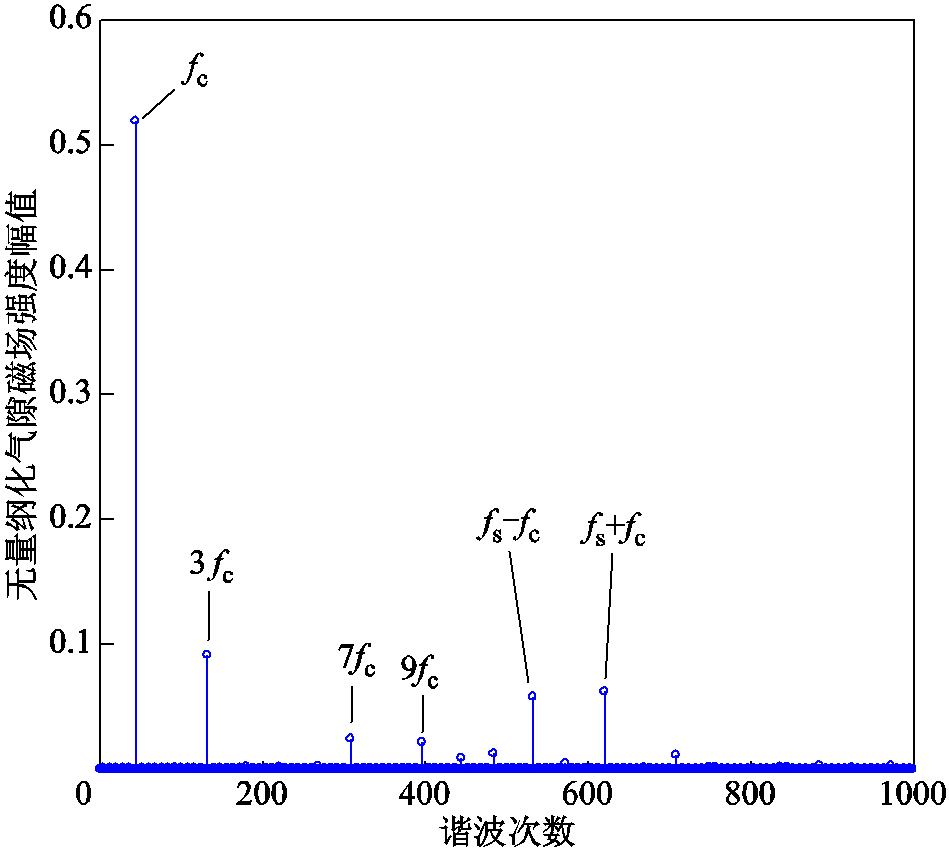
图11 空载气隙磁感应强度谐波幅值
Fig.11 Harmonic amplitudes of no-load air gap magnetic field intensity
对于本研究的永磁直驱发电机,共有两套三相绕组。第1套,标记为1U1, 1V1, 1W1,相位差为120°;第2套,标记为2U1, 2V1, 2W1,相位差120°。两套绕组的相位差为27.5°,联结方式为2Y。已知额定电流的有效值为642A,并联支路数为8。每个齿槽含有上、下两层绕组,匝数为10。根据绕组联结方式,可确定特定时刻(例如t=0),上下两层绕组的电流值分布,如图12所示。以电流最大值(642A×1.414×8/10=1134.7A)为尺度,对图12中结果进行了无量纲处理。
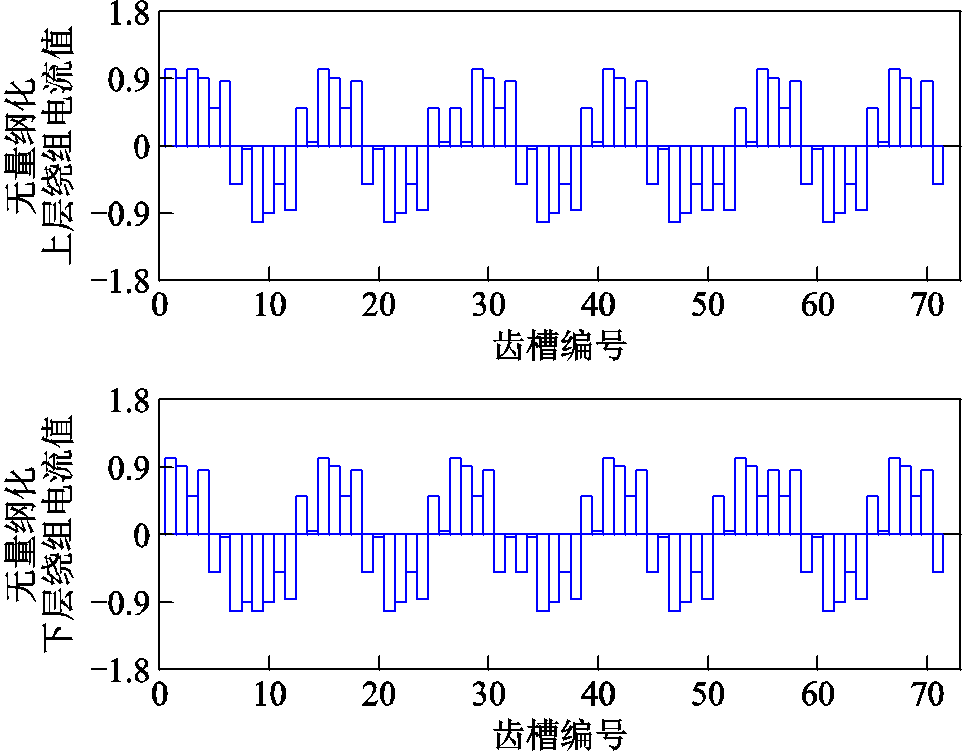
图12 特定时刻上下两层绕组的电流值分布
Fig.12 Current distributions of upper and lower windings at a specific time
负载工况下考虑磁饱和与否气隙磁感应强度分布结果如图13所示。图中结果也做了无量纲化处理,尺度为空载气隙最大磁感应强度。与空载时的结果相比,气隙磁感应强度的变化幅值明显增大,最大相对磁感应强度已超过1.4。磁饱和效应的影响也显著增强,考虑饱和后气隙磁感应强度与不考虑饱和时的结果相差可达15%以上。由于负载绕组的引入,使得气隙磁场的变化变得剧烈,在定子齿端部、定子铁心和转子铁心出现了不同程度的磁饱和现象。负载气隙磁感应强度的谐波次数和幅值如图14所示。谐波次数与空载时的情况基本一致,包括基波频率及其奇数倍频,以及齿槽频率与基波频率的组合成分。幅值要高于空载时的结果,尤其负载时基波频率fc的幅值已接近0.6。此外,在基波频率附近,考虑绕组负载后,出现了幅值相对较低的谐波阶次,如图14所示。
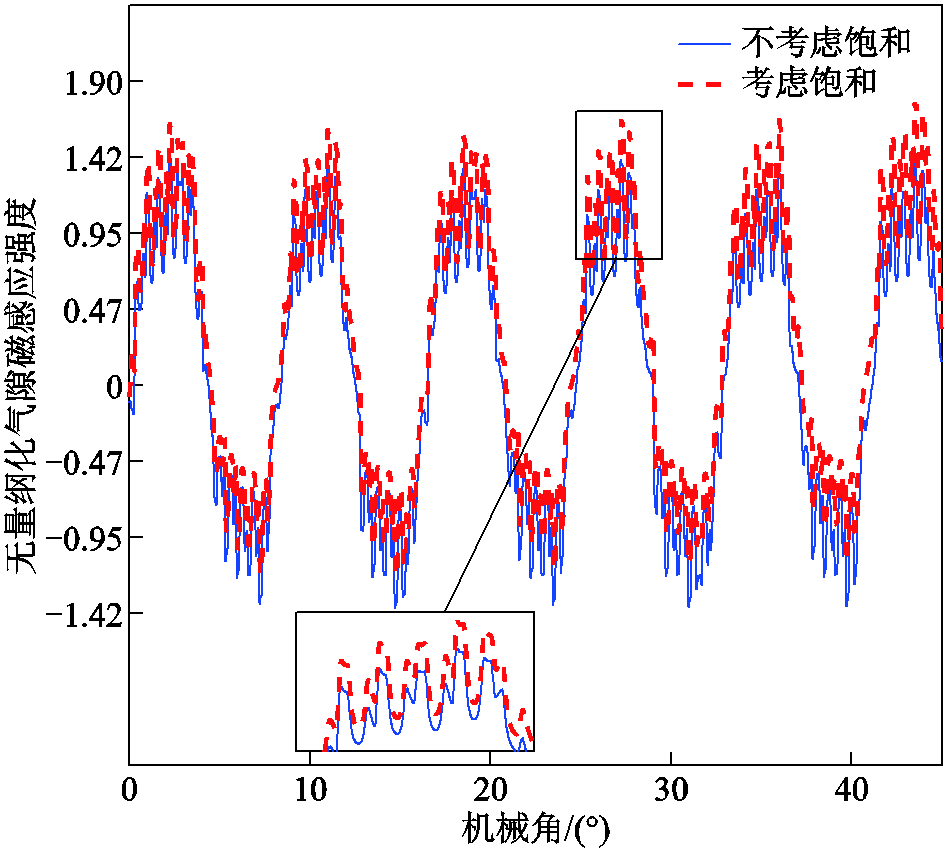
图13 负载条件下考虑饱和和不考虑饱和时气隙磁感应强度分布
Fig.13 Distribution of magnetic field intensity in air gap with and without saturation under load condition
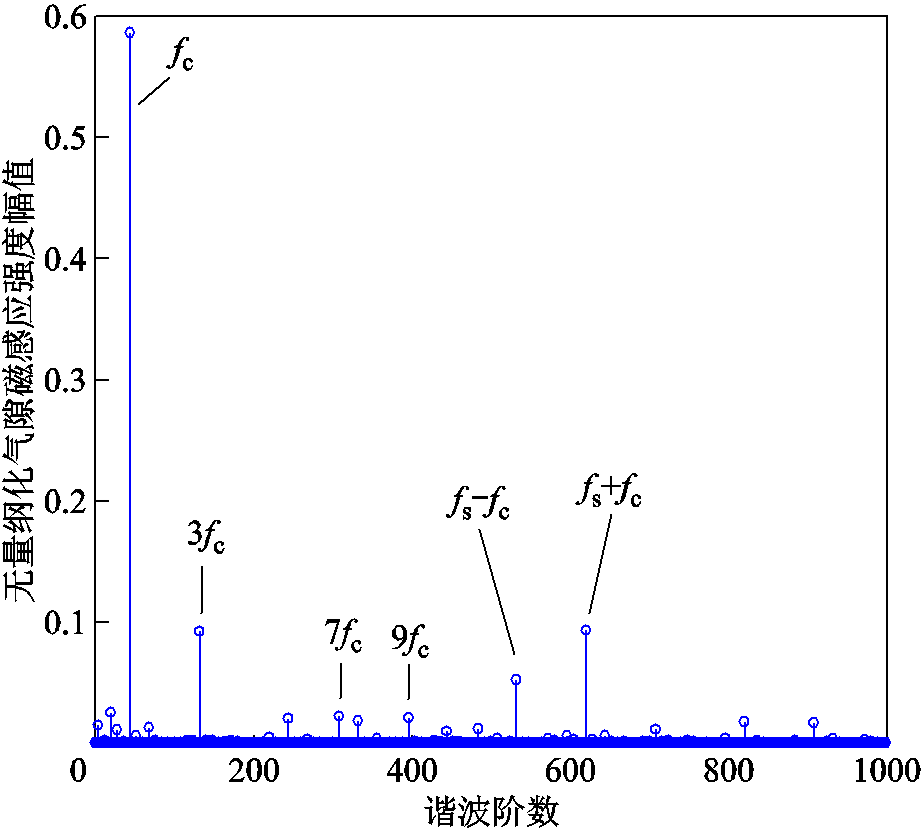
图14 负载气隙磁感应强度谐波幅值
Fig.14 Harmonic amplitudes of air gap magnetic field intensity under load condition
基于保角变换和等效磁路模型,开展了空载和负载工况下永磁直驱发电机气隙磁场研究。以实际在役兆瓦级永磁直驱发电机为对象,获得了考虑齿槽效应的气隙磁场分布,并与有限元计算结果对比,验证了所提出分析模型和求解方法的有效性。主要结论如下:
1)空载时考虑饱和效应与否气隙磁感应强度基本不变,表明空载条件下定/转子铁心的磁饱和效应较弱,可忽略不计。谐波成分包括基波频率及其奇数倍频、齿槽频率与基波频率的组合成分。
2)负载时考虑饱和后气隙磁感应强度与不考虑饱和时的结果相差可达15%以上,表明磁饱和效应的影响显著增强。与空载时的结果相比,气隙磁感应强度的变化幅值明显增大。谐波成分与空载时的情况基本一致,但幅值要高于空载时的结果,尤其是基波频率的幅值增长最为明显。
本文所提出的分析模型和求解方法,为兆瓦级永磁直驱风力发电机磁固耦合分析和性能优化设计提供重要的前提条件。
参考文献
[1] 王凤翔. 永磁电机在风力发电系统中的应用及其发展趋向[J]. 电工技术学报, 2012, 27(3): 12-24.
Wang Fengxiang. Application and development tendency of PM machines in wind power generation system[J]. Transactions of China Electrotechnical Society, 2012, 27(3): 12-24.
[2] 高剑, 黄守道, 张文娟, 等. 基于变流器控制策略的直驱永磁风力发电机优化设计[J]. 电工技术学报, 2013, 28(7): 103-109.
Gao Jian, Huang Shoudao, Zhang Wenjuan, et al. Optimal design for permanent magnet wind power generators based on converter controlling algorithm[J]. Transactions of China Electrotechnical Society, 2013, 28(7): 103-109.
[3] 许水清, 陶松兵, 何怡刚, 等. 基于相电流瞬时频率估计的永磁直驱风电变流器开路故障诊断[J]. 电工技术学报, 2022, 37(2): 433-444.
Xu Shuiqing, Tao Songbing, He Yigang, et al. Open-circuit fault diagnosis for back-to-back converter of PMSG wind generation system based on estimated instantaneous frequency of phase current[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 433-444.
[4] 何山, 王维庆, 张新燕, 等. 基于有限元方法的大型永磁直驱同步风力发电机电磁场计算[J]. 电网技术, 2010, 34(3): 157-161.
He Shan, Wang Weiqing, Zhang Xinyan, et al. Electromagnetic field calculation of high capacity direct-driven permanent magnet synchronous wind power generator based on finite element method[J]. Power System Technology, 2010, 34(3): 157-161.
[5] 唐任远. 现代永磁电机: 理论与设计[M]. 北京: 机械工业出版社, 2016.
[6] 庞古才, 邓智泉, 张忠明. 基于改进广义磁路法的表贴式永磁电机空载气隙磁场解析计算[J]. 电工技术学报, 2019, 34(22): 4623-4633.
Pang Gucai, Deng Zhiquan, Zhang Zhongming. Analytical calculation of no-load air gap magnetic field in surface-mounted permanent magnet motor based on improved generalized magnetic circuit method[J]. Transactions of China Electrotechnical Society, 2019, 34(22): 4623-4633.
[7] 范坚坚, 吴建华. 极间隔断Halbach型磁钢的永磁同步电机气隙磁场解析计算及参数分析[J]. 电工技术学报, 2010, 25(12): 40-47.
Fan Jianjian, Wu Jianhua. Analytical calculation and parameter analysis of air-gap magnetic field distribution in permanent magnet synchronous motor with partition-between-poles Halbach magnet[J]. Transactions of China Electrotechnical Society, 2010, 25(12): 40-47.
[8] 章跃进, 李春江, 屠关镇, 等. 面贴式永磁力矩电机气隙主磁场解析数值分析法[J]. 电工技术学报, 2011, 26(9): 13-17.
Zhang Yuejin, Li Chunjiang, Tu Guanzhen, et al. Analytical method for air-gap main magnetic field computation of surface mounted permanent magnet torque motors[J]. Transactions of China Electrotechnical Society, 2011, 26(9): 13-17.
[9] 李节宝, 井立兵, 周晓燕, 等. 表贴式永磁无刷电机直接解析计算方法[J]. 电工技术学报, 2012, 27(11): 83-88.
Li Jiebao, Jing Libing, Zhou Xiaoyan, et al. Exact analytical method for surface-mounted permanent-magnet brushless motors[J]. Transactions of China Electrotechnical Society, 2012, 27(11): 83-88.
[10] Zarko D, Ban D, Lipo T A. Analytical calculation of magnetic field distribution in the slotted air gap of a surface permanent-magnet motor using complex relative air-gap permeance[J]. IEEE Transactions on Magnetics, 2006, 42(7): 1828-1837.
[11] O'Connell T C, Krein P T. A schwarz–christoffel-based analytical method for electric machine field analysis[J]. IEEE Transactions on Energy Conversion, 2009, 24(3): 565-577.
[12] Alam F R, Abbaszadeh K. Magnetic field analysis in eccentric surface-mounted permanent-magnet motors using an improved conformal mapping method[J]. IEEETransactions on Energy Conversion, 2016, 31(1): 333-344.
[13] Abbaszadeh K, Alam F R. On-load field component separation in surface-mounted permanent-magnet motors using an improved conformal mapping method[J]. IEEE Transactions on Magnetics, 2016, 52(2): 1-12.
[14] Ostović V. Dynamics of Saturated Electric Machines[M]. New York: Springer, 1989.
[15] Sudhoff S D, Kuhn B T, Corzine K A, et al. Magnetic equivalent circuit modeling of induction motors[J]. IEEE Transactions on Energy Conversion, 2007, 22(2): 259-270.
[16] Lim D K, Yi K P, Woo D K, et al. Analysis and design of a multi-layered and multi-segmented interior permanent magnet motor by using an analytic method[J]. IEEE Transactions on Magnetics, 2014, 50(6): 1-8.
[17] 程明, 文宏辉, 曾煜, 等. 电机气隙磁场调制行为及其转矩分析[J]. 电工技术学报, 2020, 35(5): 921-930.
Cheng Ming, Wen Honghui, Zeng Yu, et al. Analysis of airgap field modulation behavior and torque component in electric machines[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 921-930.
[18] 戈宝军, 毛博, 林鹏, 等. 无刷双馈电机转子偏心对气隙磁场的影响[J]. 电工技术学报, 2020, 35(3): 502-508.
Ge Baojun, Mao Bo, Lin Peng, et al. Effect of rotor eccentricity fault on air gap magnetic field in brushless doubly-fed machine[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 502-508.
[19] 尧磊, 秦雪飞, 蔡顺, 等. 内置式永磁电机转子硅钢片叠装错位对气隙磁场的影响[J]. 电工技术学报, 2021, 36(5): 1096-1100.
Yao Lei, Qin Xuefei, Cai Shun, et al. Influence of rotor lamination stacking misalignment on airgap field in interior permanent magnet motors[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 1096-1100.
[20] 高锋阳, 齐晓东, 李晓峰, 等. 不等宽不等厚Halbach部分分段永磁同步电机电磁性能解析计算与优化分析[J]. 电工技术学报, 2022, 37(6): 1398-1414.
Gao Fengyang, Qi Xiaodong, Li Xiaofeng, et al. Analytical calculation and optimization analysis of electromagnetic performance of Halbach partially-segmented permanent magnet synchronous motors with unequal width and thickness[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1398-1414.
[21] Hanic A, Zarko D, Hanic Z. A novel method for no-load magnetic field analysis of saturated surface permanent-magnet machines using conformal mappingand magnetic equivalent circuits[J]. IEEE Transactions on Energy Conversion, 2016, 31(2): 740-749.
[22] Hanic A, Zarko D, Kuhinek D, et al. On-load analysis of saturated surface permanent magnet machines using conformal mapping and magnetic equivalent circuits[J]. IEEE Transactions on Energy Conversion, 2018, 33(3): 915-924.
[23] Heida C, Regtien P. Estimation of permeability for magnetic flux leakage modeling[C]//10th IMEKO TC7 International Symposium on Advances of Measurement Science, Saint-Petersburg, 2004: 321-326.
Abstract Owing to its outstanding advantages such as good low-speed performance, high power generation efficiency, low maintenance cost and reliable operation, megawatt permanent magnet direct drive wind turbine is an ideal choice for large-scale onshore and offshore wind power generation. In the performance analysis and optimal design of permanent magnet direct drive wind turbines, accurate and efficient air gap magnetic field distribution is an important premise.
In this paper, the air gap magnetic field of permanent magnet direct drive generator under load condition is studied. Based on the exact domain solution and conformal mapping, the scalar magnetic potential of the air gap magnetic field considering the cogging effect is calculated. Discrete line current element is used to quantitatively simulate the local magnetic saturation of generator stator and rotor. Based on the calculation method of the nonlinear reluctance of the stator and rotor considering the geometric size, the magnetic equivalent circuit model including the structure of the stator and rotor and the length of the air gap is established, and the corresponding iterative solution process is presented. Taking the actual megawatt permanent magnet direct drive generator in service as an example, the air gap magnetic field distribution considering the cogging effect is calculated, and the influence of magnetic saturation effect on the air gap magnetic field distribution curve waveform and harmonic components under no-load and load conditions is analyzed. The proposed analysis model and solution method are verified by comparing with the finite element results.
Under the no-load condition, the air gap magnetic field intensity is basically unchanged whether the saturation effect is considered or not. The harmonic component includes the fundamental frequency and its odd frequency multiples, and the combination of the tooth slot frequency and the fundamental frequency. Under the load condition, the relative difference between the magnetic field intensity with and without saturation effects can exceed 15%, indicating that the influence of magnetic saturation effect is significantly enhanced and cannot be ignored in the load condition. Compared with the result in the no-load condition, the variation amplitude of the air gap magnetic field intensity increases obviously. The harmonic component is basically the same as that in no-load condition, but the amplitude is higher than that in no-load condition, especially for the increase of the amplitude of fundamental wave frequency.
The analysis model and solution method proposed in this paper provide important preconditions for the magneto-solid coupling analysis and performance optimization design of megawatt permanent magnet direct drive wind turbines.
Keywords: Permanent magnet direct drive generator, air gap magnetic field, magnetic equivalent circuit, load condition, magnetic saturation, cogging effect, nonlinear reluctance
DOI:10.19595/j.cnki.1000-6753.tces.210769
中图分类号:TM351
国家自然科学基金资助项目(11872222)。
收稿日期 2021-05-27
改稿日期 2021-10-22
张志弘 男,1982年生,工程师,研究方向为永磁直驱风电机组动力学、发电机磁固耦合分析。E-mail:zhangzhihong@goldwind.com.cn
韩勤锴 男,1982年生,博士,副教授,研究方向为旋转机械动力学、永磁直驱电机磁固耦合分析。E-mail:hanqinkai@mail.tsinghua.edu.cn(通信作者)
(编辑 赫蕾)