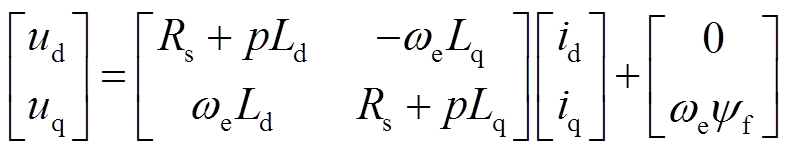（1）
摘要 高频方波信号注入法已广泛运用于内置式永磁同步电机（IPMSM）无位置传感器低速控制中，该方法可以避免使用滤波器且明显提高系统带宽。然而，在轻载或空载等基波较小时，当逆变器的死区效应使高频电流响应出现畸变，此时逆变器的非线性将会严重影响高频注入法的位置估算精度。针对上述问题，该文重点分析逆变器非线性对IPMSM高频方波注入法的影响，提出一种新型高频纹波电流提取和补偿方法，有效降低死区的影响，提高注入电压的效率，抑制逆变器非线性引起的位置角度误差。通过仿真和实验结果证明，与传统方法相比，该方法可以在注入相同电压幅值的情况下有效降低位置估算误差，验证了所提出方法的可行性和有效性。
关键词：永磁同步电机 无传感器控制 高频方波注入 逆变器非线性 纹波电流补偿
内置式永磁同步电机（Interior Permanent Magnet Synchronous Motor,IPMSM）具有功率密度高、效率高、调速范围宽和噪声低的优点，广泛应用于电动汽车、压缩机、风力发电等领域。在永磁同步电机的典型控制策略中，需要实时获取转子的位置信息以进行高精度控制。位置传感器的使用增加了系统成本和复杂度，在一些特殊场合也不适合安装机械式传感器。因此，为提高电机系统的可靠性和轻便性，对永磁同步电机的无传感器控制的研究具有重要意义[1-4]。
近年来，学者们对无传感器控制进行了大量的研究和探索，主要可以分为反电动势法和高频信号注入法。反电动势法主要通过检测电机反电动势，利用电机模型对转子位置信息进行观测[5-6]，而在低速甚至零速时，电机的反电动势较小，信噪比较低，位置估算精度会严重下降，因此这种方法一般多用于中高速的位置估算。高频信号注入法将高频信号注入到电机绕组中，通过对高频响应信号的提取和处理可以得到低速或零速下的转子位置信息[7-10]。文献[11]提出了一种旋转正弦电压注入方法，在静止坐标系下注入高频旋转电压矢量，该方法会引起q轴电流波动进而引起转矩脉动。文献[12]提出了脉振正弦电压注入方法，注入电压频率为载波频率的1/10左右，该方法需要使用低通滤波器进行电流的分离，而低通滤波器的引入将降低系统的带宽。文献[13]提出基于高频方波信号注入的无传感器控制方法，d轴注入频率为开关频率一半的高频方波，让速度和位置控制的带宽提高了5倍。高频注入方法的无传感器控制中，高频电压信号的注入会减小逆变器的电压利用率。当减小注入高频电压时，逆变器非线性的影响将不能忽略，尤其是在空载和轻载工况下，其可能导致转子位置估计误差，影响系统的稳定性[14]。
为了抑制逆变器非线性在高频信号注入法中的影响，文献[15]提出一种注入信号幅值自适应的方法，通过变化的注入电压幅值抑制逆变器非线性造成的高频电压矢量信号畸变，但该方法不能在整个控制过程中有效减小注入电压的幅值。文献[16]针对高频脉振正弦信号注入，提出了一种补偿零电流钳位的方法，但该方法提出的补偿模型不适合注入频率更高的方波。文献[17]通过改变注入方波在载波周期不同阶段的幅值，实时调节纹波电流，使得响应的高频电流更接近真实情况，从而抑制逆变器非线性的影响，但该方法计算量较大，实现较为复杂。
针对现有高频注入方法的相关问题，在分析高频方波注入的IPMSM位置估算策略基础上，本文重点分析逆变器非线性对IPMSM高频方波注入法的影响，提出一种新型高频纹波电流提取和补偿方法，抑制逆变器非线性引起的位置角度误差。最后，通过Matlab/Simulink仿真和10kW功率的样机实验，验证了提出方法的正确性和有效性，在母线电压10%的注入幅值下，可以将观测的位置误差减小20%以上。
IPMSM在同步旋转坐标系下的电压方程为
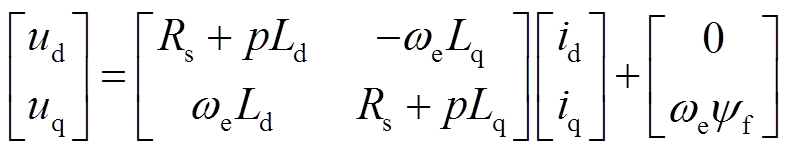（1）
式中，ud、uq和id、iq分别为d、q轴电压和电流；Rs为定子电阻；ψf为永磁体磁链；Ld、Lq分别为d、q轴电感；ωe为电机转子电角速度；p为微分算子。
基于逆变器脉冲宽度调制控制方式，可以方便地生成方波电压。对于采用矢量控制方法，通常在载波底部对称地采样相电流，避免在电流信号上产生较大电流纹波，方波电压频率fh一般选为载波频率fpwm的一半。
由于高频方波电压注入用在低速和零速的速度范围，注入电压频率fh远大于电机旋转的基波频率fe，定子电阻压降、旋转电压和反电动势的影响可以忽略不计。因此，高频信号注入下的电压方程可以简化为
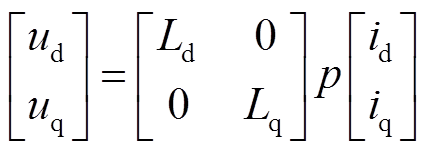（2）
在同步旋转坐标系下注入的高频方波电压为
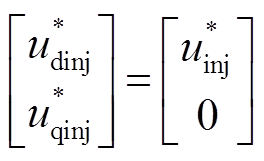（3）
其中
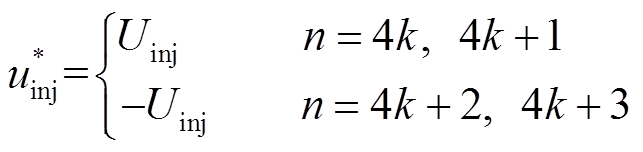
式中，Uinj为注入电压幅值。
由于实际与估算的同步旋转坐标系之间存在一定的角度误差，所以在实际转子坐标系中由注入高频信号产生的电流响应差值为
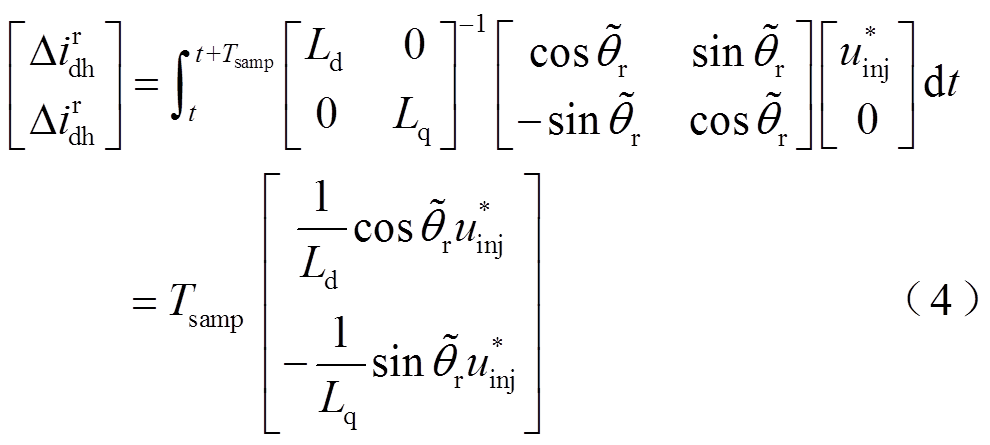
式中，Δir dh、Δir qh分别为实际同步旋转坐标系下的d、q轴高频纹波电流；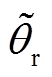
为实际轴系角度
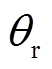与估算轴系角度
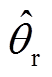之间的位置误差；Tsamp为采样周期。
将式（4）变换回到估算的旋转坐标系得到
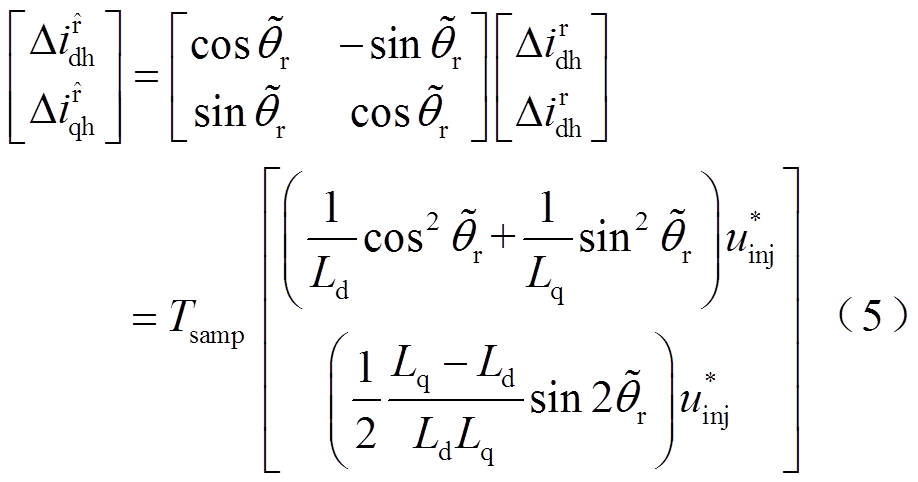
式中，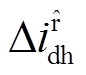
、
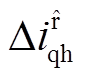分别为估算同步旋转坐标系下的d、q轴高频纹波电流。
为了有效提取d、q轴电流中高频纹波电流分量，需要将高频纹波电流从包含基波分量的电流中分离，以q轴为例，其基本结构如图1所示。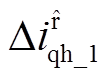
和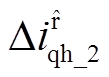
分别为最新两次采样的d、q轴电流差值；将两次差值再作差得到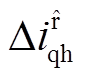，取注入电压符号后可提取到当前注入周期下的高频纹波电流分量
。
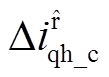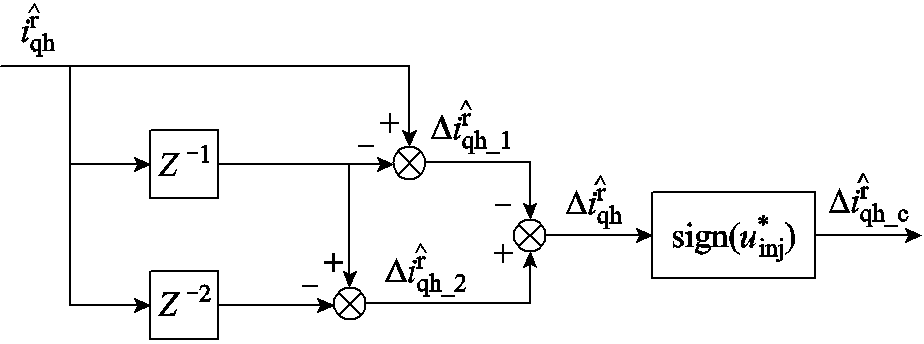
图1 同步旋转坐标系下高频纹波电流提取
Fig.1 High-frequency ripple current extraction in synchronous rotating coordinate system
通过提取q轴电流中的高频纹波电流，得到关于位置误差的数学表达式，当误差角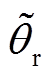
很小时，有
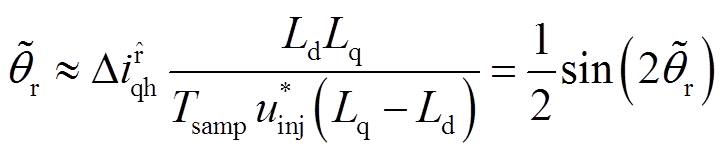（6）
由此，估算同步旋转坐标系下的位置信息可以由图2所示的位置跟踪观测器来解调出位置和速度信息。
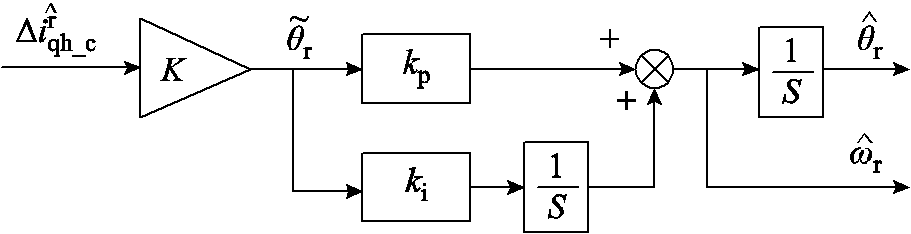
图2 位置和速度观测器
Fig.2 Position and velocity observer
高频方波电压的注入会产生额外的噪声，降低逆变器的电压裕度和系统效率。减小注入电压的幅值可以降低其造成的负面影响，但也使位置观测的误差更大。
当电机基波电流较大时，高频电流响应承载在基波电流之上，此时死区对于高频电流造成影响的占比较小，高频电流的畸变不明显；当电机运行在轻载或空载等低速工况下，基波电流的幅值相比高频电流分量非常小，电机的相电流方向主要由注入电压决定。相邻两次电流采样的电流方向随高频电压注入的正负发生变化，三相的电流也以注入高频方波电压频率反复穿越零点。此时，逆变器非线性对三相高频电流响应造成了严重的畸变，从而影响了位置观测的精度。
逆变器的非线性主要是由死区时间和管压降造成的，其中，管压降的影响相对较小。当电流流经半导体器件时，在功率管内部会产生压降，包括管压降和二极管压降，可以近似表示为
（7）
式中，vDrop为一个周期总的管压降；Ts为载波周期；vD1、vD2和TD1、TD2分别为功率管压降和二极管压降与其对应的时间，且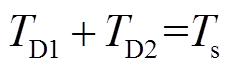
。
对于高频方波注入而言，注入的电压幅值都远大于vDrop的幅值，且管压降是整个载波周期都存在的，在vD1和vD2相差不大时，可以认为管压降的影响只是略微降低高频注入电压的幅值。所以，本文将忽略管压降对逆变器非线性的影响，重点对死区影响展开分析。
假设电流不存在断续情况，且忽略器件开关和关断的时间。三相逆变器任意相桥臂x在电流方向不同时的拓扑结构示意图如图3所示。
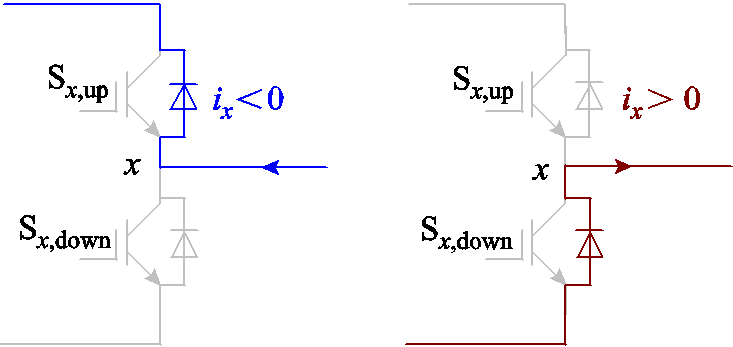
图3 单相桥臂续流示意图
Fig.3 Schematic diagram of single-phase bridge arm freewheeling
图4为上下桥臂在有无死区情况下的驱动信号示意图。vxn为以母线电压中点n为参考的x相电压输出，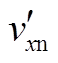
和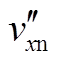
分别为不同电流方向时以母线电压中点n为参考的x相电压输出。从图中可以看出，存在死区时，相电流的流向会引起不同效果的电压失真。
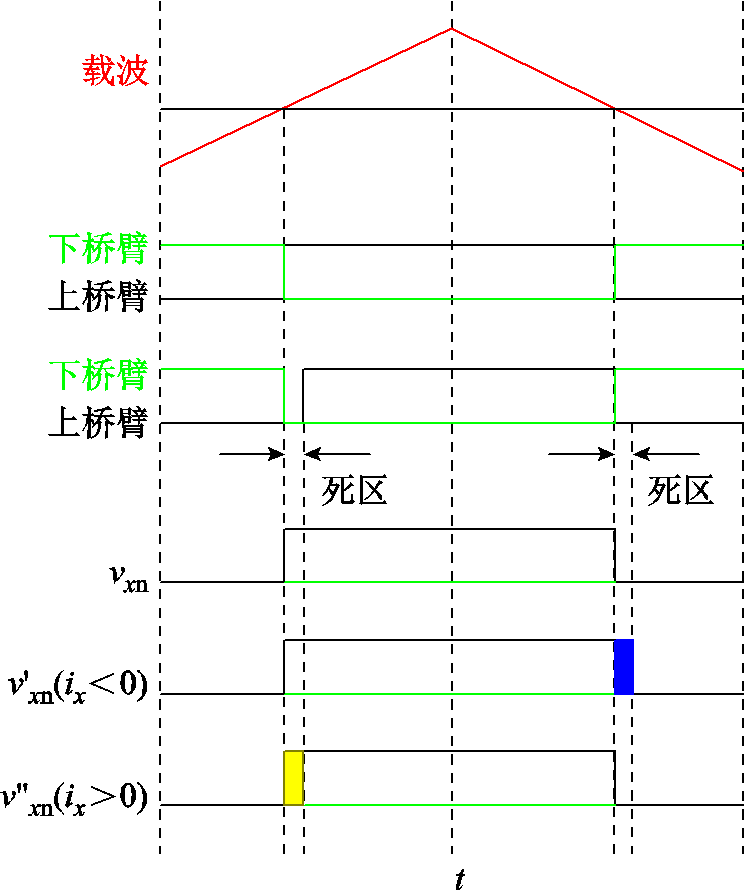
图4 上下桥臂死区分析
Fig.4 Dead time analysis of upper and lower bridge arms
在死区时间内，相电流不流经开关器件，而是由二极管续流。当相电流小于零时（电流流出电机），上桥臂的二极管导通；当相电流大于零时（电流流入电机），下桥臂的二极管导通。此时，死区时间内二极管导通特性引起的电压误差为
（8）
式中，vx_dead为死区时引起的电压误差；Tdead为死区时间；Vdc为母线电压。
死区对位置观测精度的影响主要是输出三相电压误差对采样的三相电流造成了畸变。以空载运行工况为例，本文分别对相电流在有无死区情况下进行分析。
图5为在空载时，向d轴注入2Ts周期的等幅正负交替的方波电压后的电流响应波形，PWMA、PWMB和PWMC均为高电平有效导通，深色黑线条为上桥臂的导通信号，浅色细线条为下桥臂的导通信号。
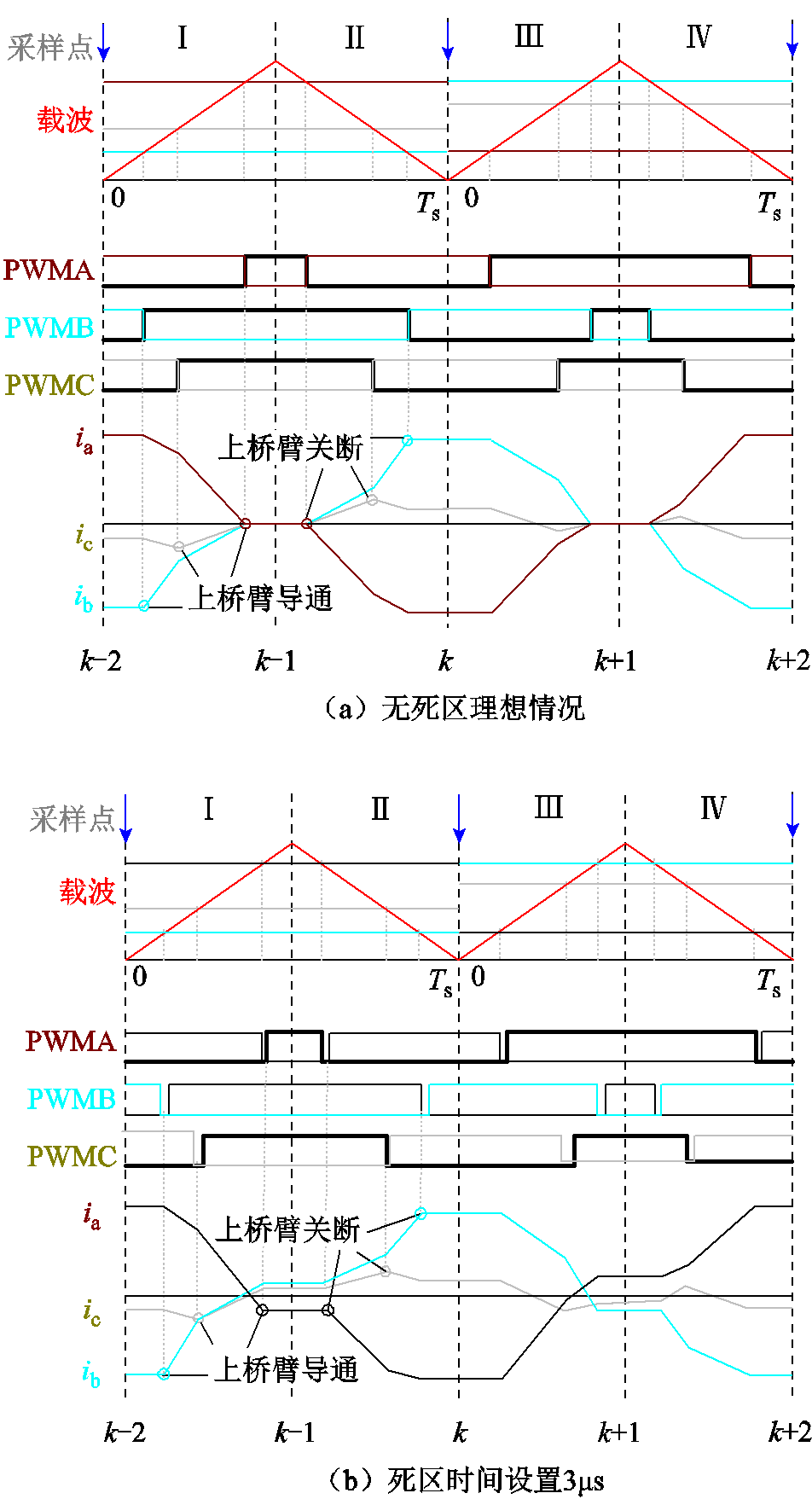
图5 三相电流响应波形
Fig.5 Response waveform of three-phase current
由图5a分析可知，在没有死区时，电流响应主要可分为三相电流中两相为正（imid＞0，imid为三相中更接近于0的相电流）或者两相为负（imid＜0）的情况。但无论哪种情况，在一个载波周期中的零矢量时间点，即载波的初始时刻和载波的中点时刻，电流幅值为高频电流的最大值或为载波中点时刻等于零的值。一个载波周期后，每一相的高频电流幅值不变，方向相反。
如图5b，在有死区时，分别讨论以上两种情况。当三相电流两相为负（imid＜0），即图中的Ⅰ、Ⅱ阶段，ib、ic小于零，由式（7）可知，Ⅰ阶段的导通和Ⅱ阶段的关断将由上桥臂二极管续流，该相电压不受死区的影响。对于ia而言，在该相导通时刻电流已从正变为负，此时也不受死区影响。但在关断时，由于电流为负，关断时下桥臂二极管续流，母线电压导通时间缩短，即此时受到了死区的影响。同理，当三相电流两相为正（imid＞0）时，ib、ic在导通时电流已从正变为负，将不会受到死区影响，而关断时导通时间缩短受到死区影响。
通过上述分析可知，在有死区情况下，高频注入电压在两种情况下的载波周期前半个周期（Ⅰ、Ⅲ）导通时间均大于后半个周期（Ⅱ、Ⅳ），使得电流的过零点左移，从而使载波中点三相电流值均不为零。
尽管相电流在前半个周期受死区的影响较小，但由于过零点位置的偏移，也会使整个周期的采样值存在误差。从2.2节分析可知，由于受死区的影响，电流相应波形在后半个载波周期有一定的削减。取A相电流采样分析，响应波形与采样波形如图6所示，ia和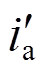
分别为无死区和有死区影响的A相电流。可以看出，尽管注入电压只在后半个周期有削减，但其导致了整个周期相电流的幅值衰减。对采样的相电流而言，死区造成了与注入高频电压正负同向的误差ierr_samp。
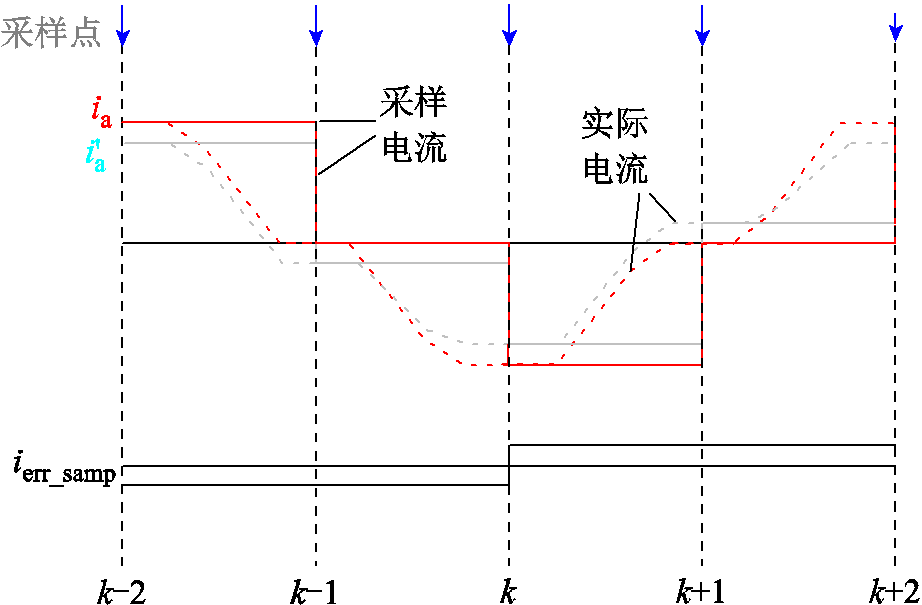
图6 A相电流响应波形与采样波形
Fig.6 Phase A current response waveform and sampling waveform
相电流误差幅值与相电流大小成正比关系，且与注入电压的正负sign(u* inj)同向。因为在d轴注入的是等幅值高频方波，设三相电流的误差值为
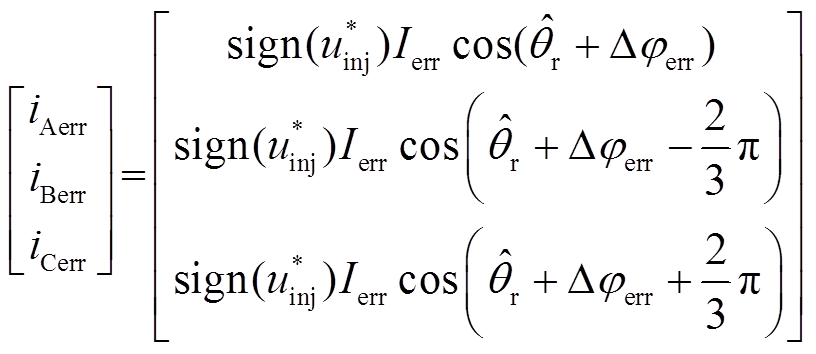（9）
式中，Ierr为注入高频电压后的相电流误差幅值；Δφerr为由于采样精度和精度延时等相关因素引起的不可以避免的注入与实际的偏差角；“Δ”代表不同状况时会引起不同的变化，尤其在基波电流换向时有较为明显的周期性波动。
基于坐标变换理论，将三相误差电流变换至正交旋转坐标系为
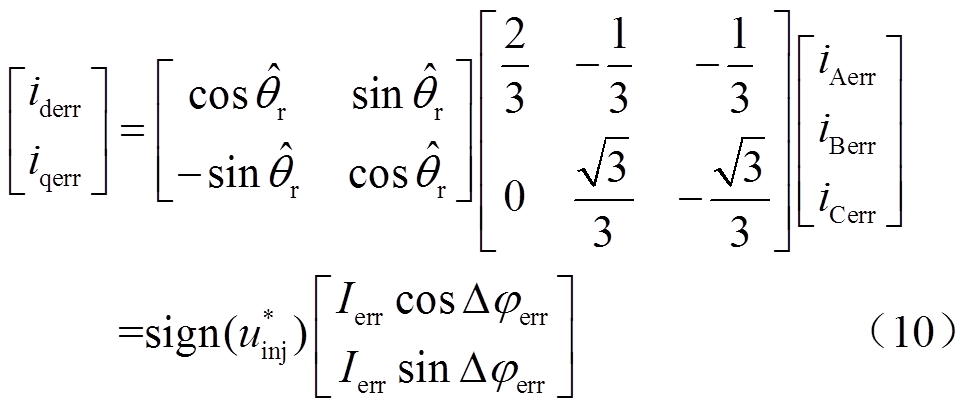
将误差项式（10）代入式（6）中，得到
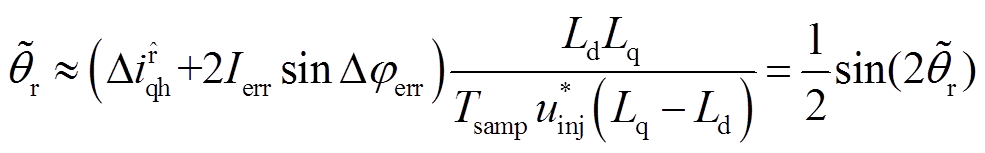（11）
根据式（11），由死区造成的三相电流的畸变在采样之后将会加入包含Ierr和Δφerr的误差耦合项，会给最后的位置信息计算带来额外误差。
由于死区的存在，会对三相电流造成畸变，从而影响观测角度的精度。传统的高频电流提取方法是基于同步旋转坐标系下进行的。根据2.3节分析知，由于三相电流畸变，导致在同步旋转坐标系下提取的高频电流产生误差。因此，本文提出一种在自然坐标轴系下基波电流的提取与高频电流的修正策略，以减小低速空载情况下由死区产生的位置观测误差。
高频方波注入法中，各个轴系的高频电流ih都是承载在基波电流if之上，由图5可知，在没有死区的情况下，载波中点的三相高频电流为零。由于高频电压的注入频率远大于基波的频率，所以可以近似认为相邻两个载波周期内基波电流不变，载波中点的电流可以认为是基波电流，即
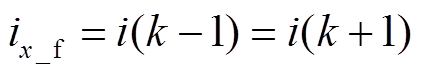（12）
在有死区的情况下，载波中点的采样值会出现偏差，但由于注入电压正负交替，死区影响也只存在于后半周期，使得相邻周期的偏差值一正一负。结合电流波形在正负注入阶段的对称性，基波电流可以认为是相邻两次载波中点的采样值取平均，如式（13）所示。
（13）
通过基波电流与高频电流在自然坐标轴系进行有效分离，将其坐标变换至同步旋转坐标系，得到不含高频分量的d-q轴电流，如图7所示，由此可减少相邻注入电压耦合对矢量控制的影响。图中iAsamp、iBsamp和iCsamp分别为三相采样电流；iabc_f、iabc_h、idq_f和idq_h分别为自然坐标系下和正交旋转坐标系下的基波和高频电流；iabc_ch为补偿后的相电流。
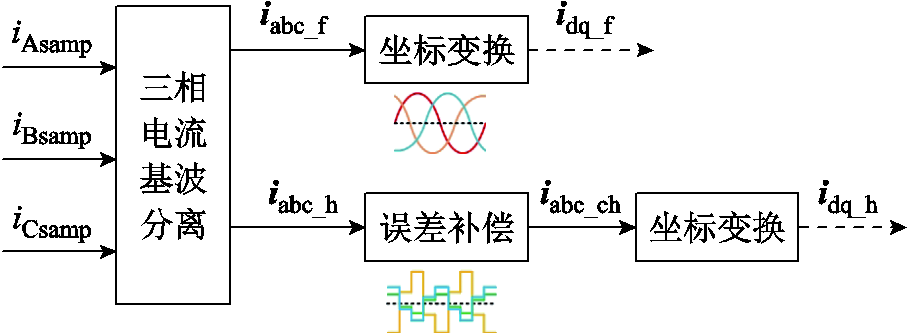
图7 三相电流分离示意图
Fig.7 Schematic diagram of three-phase current separation
分离出基波电流后，将其与原始采样电流相减可以得到三相高频纹波电流ix_h，即
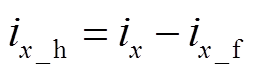（14）
从2.2节分析可知，由于死区造成了高频电流的畸变，使采样出的高频电流的幅值变小。为了修正已经分离出的高频电流ix_h的畸变，本文提出了一种三相高频电流的补偿方法。尽管高频电流的幅值Ix_h变小，但由于死区对前半个载波周期的采样电流没有影响，因此认为前半个载波周期的电流增量Δisamp1没有受到改变，如图8所示。但这会使得电流过零点左移，以致电流上移，从而产生电流误差ierr_samp。由于此时该高频电流中已经不含基波电流，所以电流误差ierr_samp的大小可以由载波中点的采样值获取。而后半个载波周期由于死区的影响，电流增量Δisamp2将减小。同理根据对称性，Δisamp3可以认为没有受到改变。载波后期的误差大小也可以由下一周期载波中点的采样值获取。
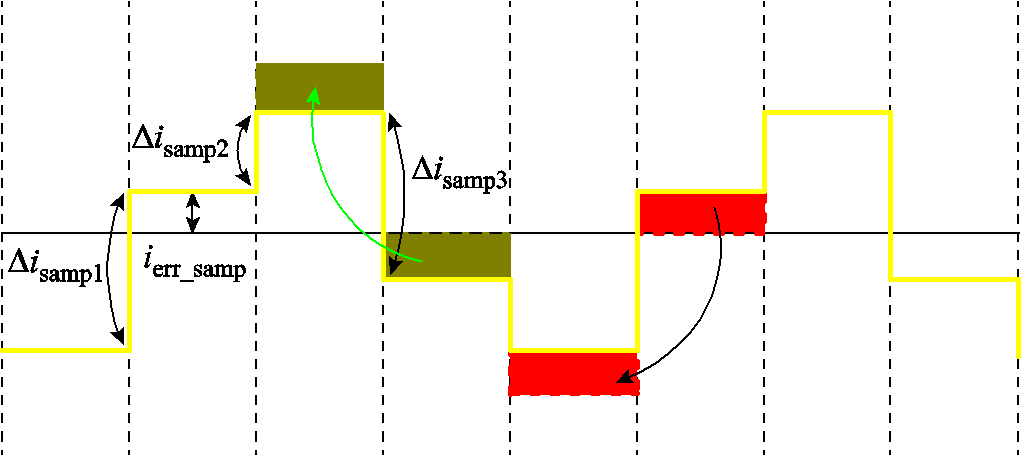
图8 相电流分析与补偿示意图
Fig.8 Schematic diagram of phase current analysis and compensation
对于提取的高频电流，将载波中点的采样值作为实时更新的电流误差ierr_samp，每两个采样周期（一个载波周期）更新一次，同时实时补偿给电流的正负阶段的幅值，使采样电流更接近没有死区影响的幅值。该方法将有效减小电流畸变带来的转子位置观测误差。
在式（11）中，由于Δφerr为三相电流耦合的相位扰动误差变量，无法实时地获取和补偿。但是通过对ierr_samp的提取和利用，补偿采样电流幅值后，可以有效地减小Ierr的大小，从而抑制死区对位置观测产生的影响。
结合改进的三相采样电流的基波提取与高频电流的补偿方法，本文提出的高频纹波电流补偿的改进无传感器控制策略的控制框图如图9所示。图中iabc_err为补偿的误差电流。
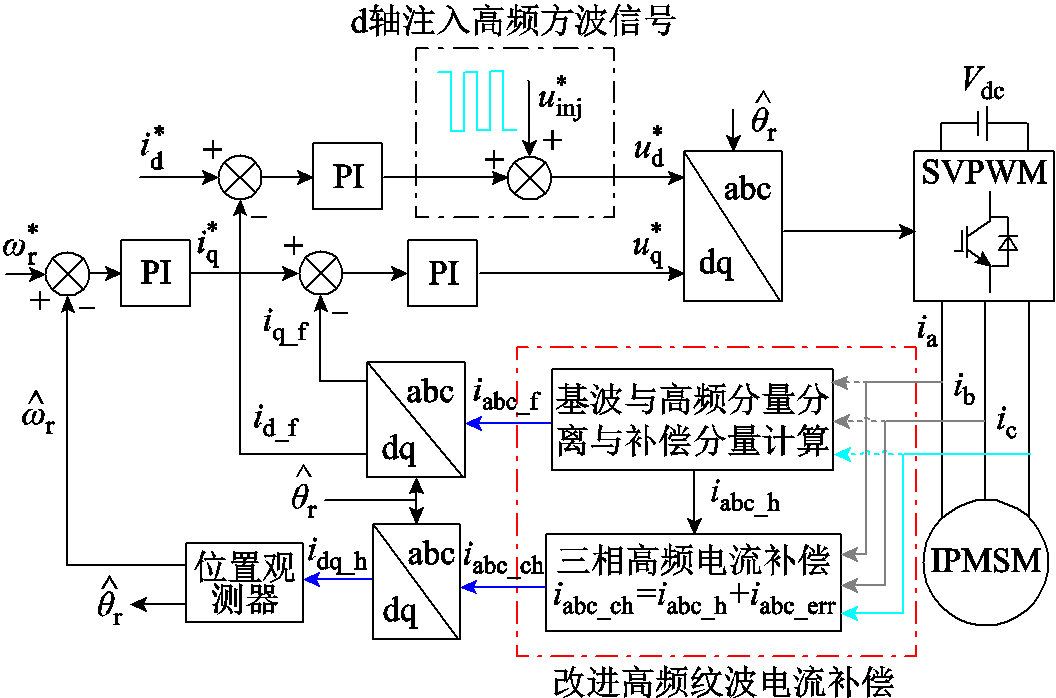
图9 改进无传感器优化方法的控制框图
Fig.9 Improved overall block diagram of sensorless optimization method
本文使用Matlab/Simulink对所提策略进行仿真实验。仿真与实验的电机采取相同参数，见表1。高频方波电压注入幅值选为15V，载波频率为10kHz，高频注入方波频率为5kHz，死区时间设置为3ms。
表1 内置式永磁同步电机样机参数
Tab.1 Test IPMSM characteristics
参数数值 电压/V96 线电流/A100 电阻/Ω0.005 6 极对数3 直轴电感/mH0.079 1 交轴电感/mH0.174 9 反电动势系数/(V∙s)0.024 7
为了验证本文提出的基波分离方法，进行了空载和负载下的基波分离实验。电机转速从0加速到100r/min，前0.5s为空载，在0.5s时刻，负载从0N∙m增加到10N∙m。
图10为三相电流iabc的采样波形和分离出的基波电流ia_f、ib_f、ic_f和高频电流ia_h、ib_h、ic_h波形。可以看出，在空载阶段，基波电流基本为零，采样的三相电流主要由高频纹波电流构成；在负载阶段，基波电流增大，高频电流承载于基波电流之上，按本文提出方法，成功地将基波电流提取出，高频电流的幅值和空载阶段保持一致。
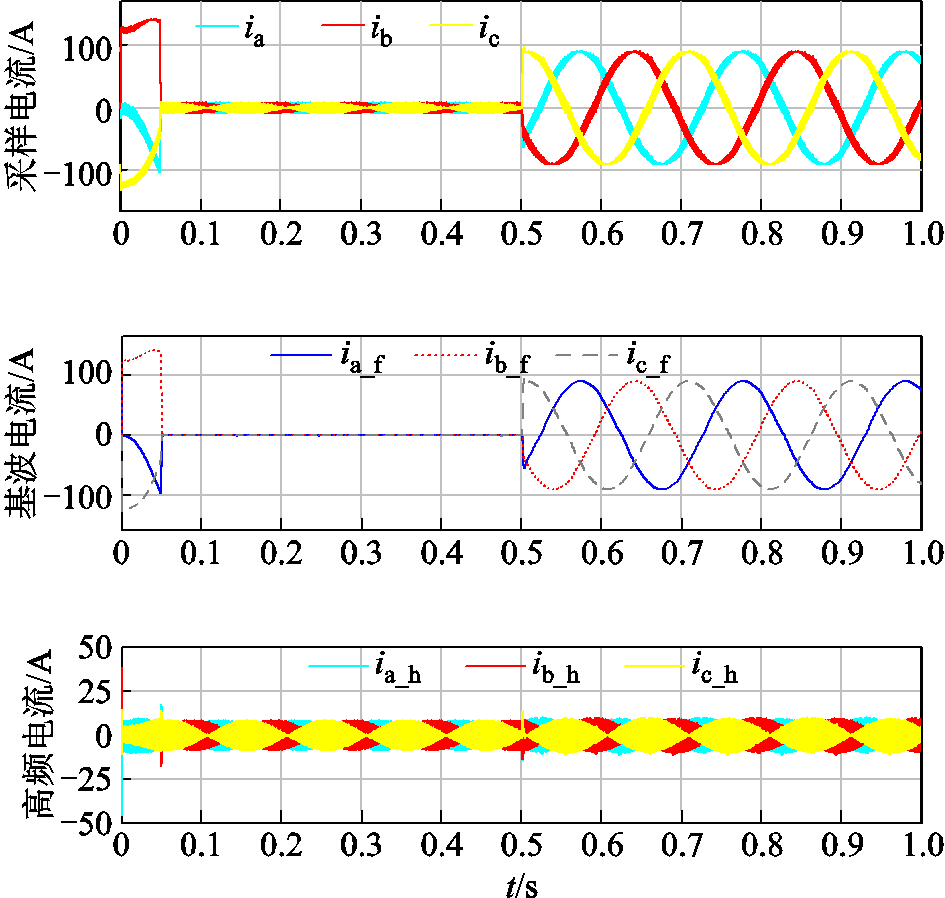
图10 三相电流与分离后的电流
Fig.10 Three-phase current and separated current
同步旋转坐标系下误差电流如图11所示。可以看出，在空载阶段，由于死区影响，d、q轴下高频纹波电流的误差值都比较大，且d、q轴的误差电流呈耦合趋势；在负载阶段，高频电流所占比例下降，死区影响也相应减小，高频纹波电流的误差幅值也大幅减小。值得注意的是，在相电流的换向阶段，由于基波电流的过零，出现零电流钳位现象，此时也会对高频纹波电流产生较大的误差值，也是式（9）中Δφerr变化的原因之一，所以本文重点讨论空载和轻载的死区影响。
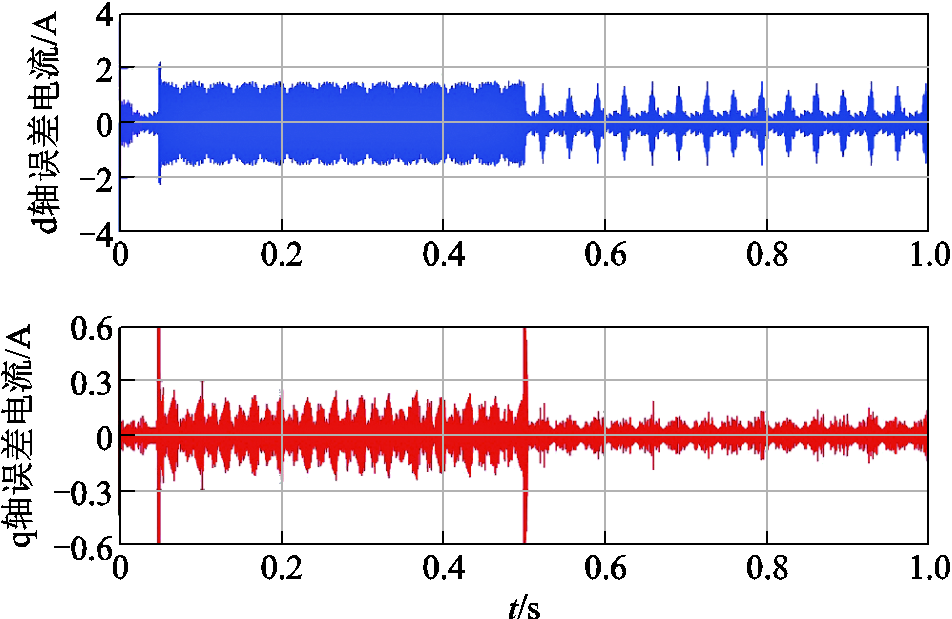
图11 同步旋转坐标系下误差电流
Fig.11 Error current in synchronous rotating coordinate system
图12为A相分离出的高频纹波电流ia_h和经过本文所提方法补偿后的电流ia_ch。可以看出，在空载阶段，补偿后的高频电流幅值明显大于原始高频电流，且该补偿幅值随着电流的幅值动态调整；在负载阶段，由于死区影响相应减小，补偿后的高频电流也基本与原始高频电流重合。
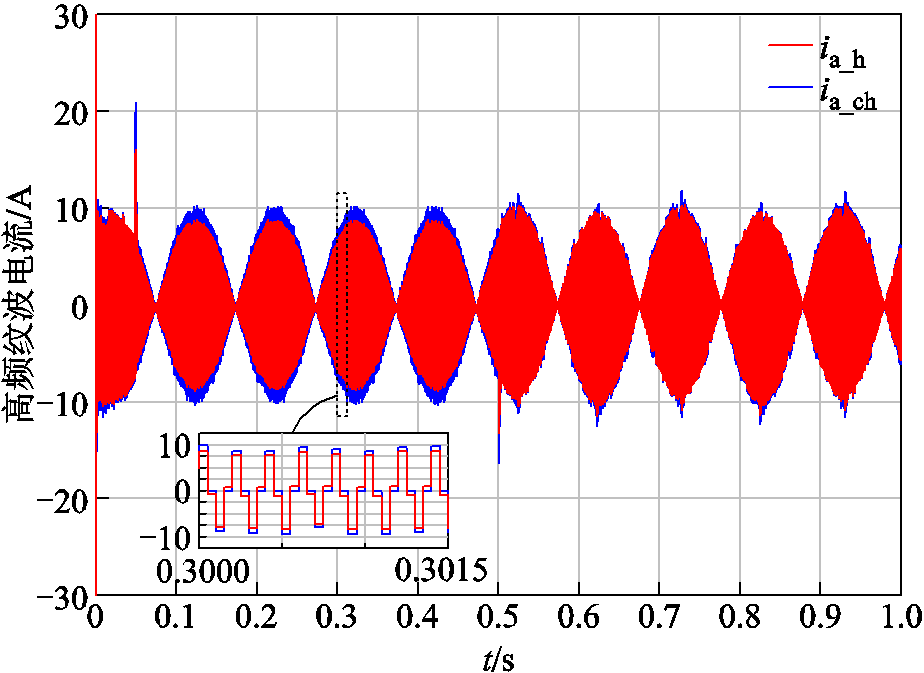
图12 A相高频纹波电流与补偿后的电流
Fig.12 Phase A high frequency ripple current and compensated current
图13为仿真得到的转子位置及其观测误差的波形。图13a和图13b分别为传统高频方波注入在无、有死区下的角度和角度误差波形，图13c为使用改进三相高频电流提取和补偿方法后的波形。可以看出，在没有死区时，全程的角度误差波动都不大；有死区时，轻载的时候，改进方法位置角度跟踪得更加精确，角度误差从±1.8°减小到±0.5°；在负载时，两种方法下的角度误差区别不大。由仿真可以看出，本文所提方法在轻载和空载时对逆变器非线性造成的位置观测误差有明显的抑制作用。
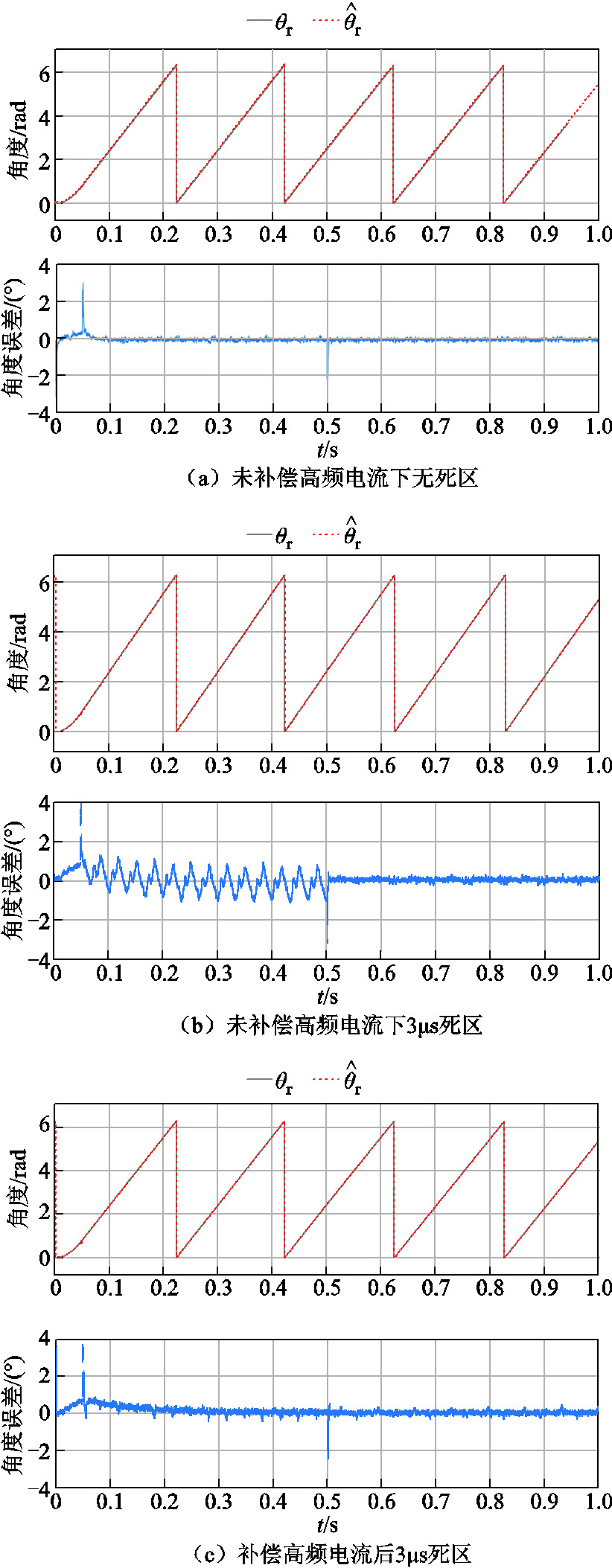
图13 转子位置及其观测误差
Fig.13 Rotor position and its observation error
电机驱动系统实验在如图14所示的IPMSM系统实验平台上进行，电机参数见表1。实验采用德州仪器公司的TMS320F2812作为主控制器，英飞凌的IPM模块作为驱动，采用旋转变压器来获取真实角度位置和转速信息。实验中PWM开关频率及采样频率均为10kHz，改进方法采样频率为20kHz，d轴高频方波电压注入频率为5kHz，死区时间设置为3.5μs。
图14 内置式永磁同步电机驱动系统实验平台
Fig.14 IPMSM drive system testing bed
图15为注入高频方波下的三相高频纹波电流的波形。与2.2节所分析的情况一致，由于死区的影响，在载波中点的三相纹波电流均不为零。而载波前期不受死区影响，电流的变化幅度（Δi2）明显大于载波后期（Δi1）。所以只要能合理提取到三相高频电流，便可以有效补偿轻载和空载时的高频电流畸变。
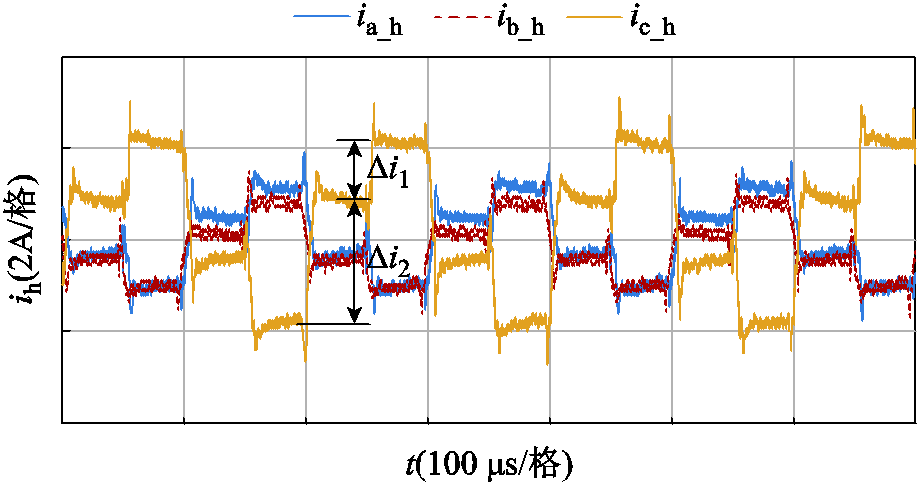
图15 三相高频纹波电流
Fig.15 Three-phase high frequency ripple current
为了验证本文所提方法的正确性，图16a为电机转速从80～100r/min、空载情况下，基于id=0的矢量控制下无位置传感器控制的传统高频方波注入法的实验波形，此时注入d轴电压为9.6V（母线电压10%）。可以看出此时的位置估算误差的波动超过了±17°，估算误差RMS（方均根值）为9.32°。图16b为进行三相高频电流补偿后的相同工况下的实验波形，此时的位置估算误差的波动约为±13°，误差RMS为5.28°，减小的位置误差约为23.5%。
图17a为传统方法下，注入d轴电压为9.6V时，50r/min正反转实验波形，此时的位置估算误差的波动约为±16°，误差RMS为9.34°。图17b为进行三相高频电流补偿后的相同工况下的实验波形，此时的位置估算误差的波动约为±12°，误差RMS为4.94°，减小的位置误差约为25.0%。
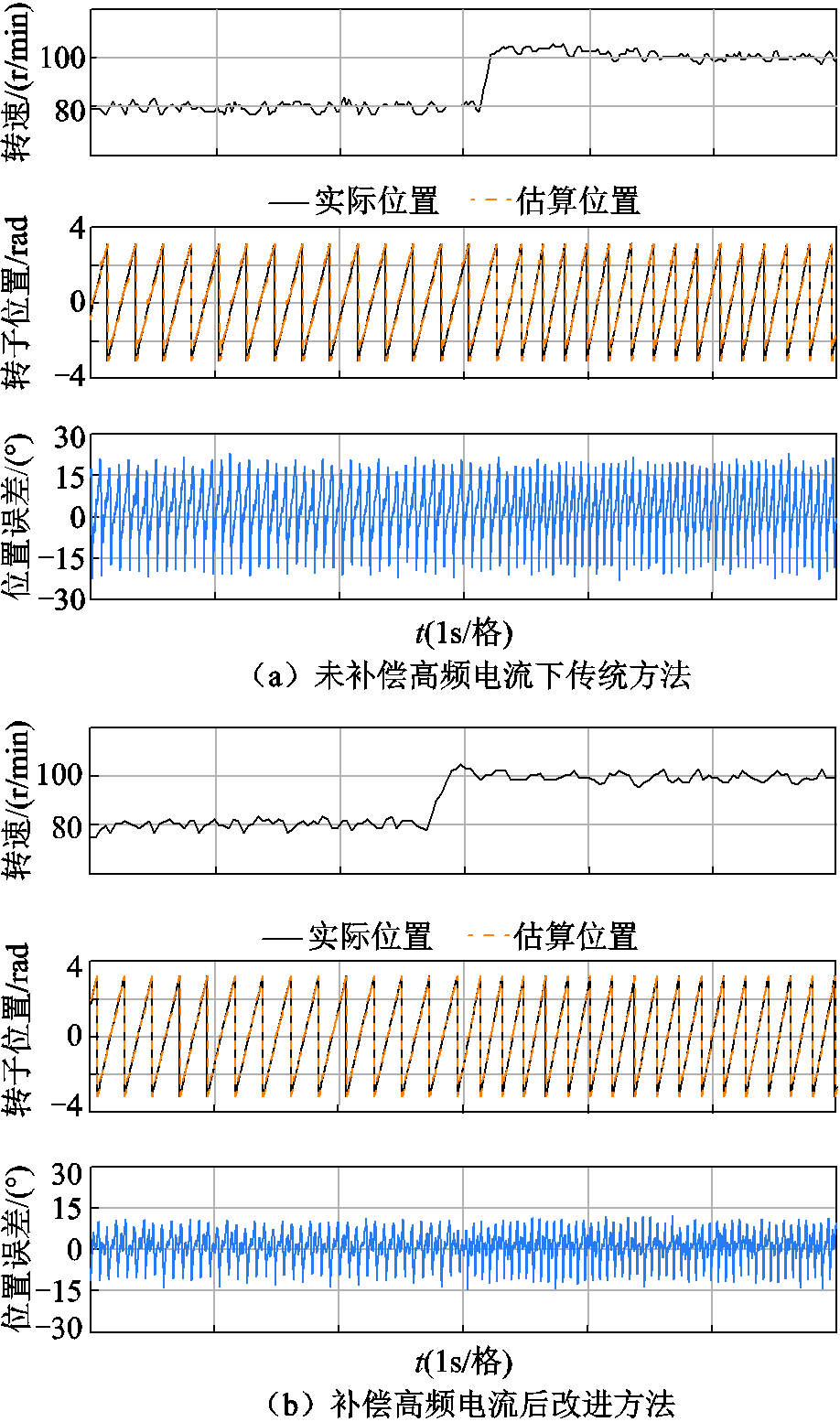
图16 转速突变转子位置及其观测误差
Fig.16 Rotor position and its observation error with sudden change in speed
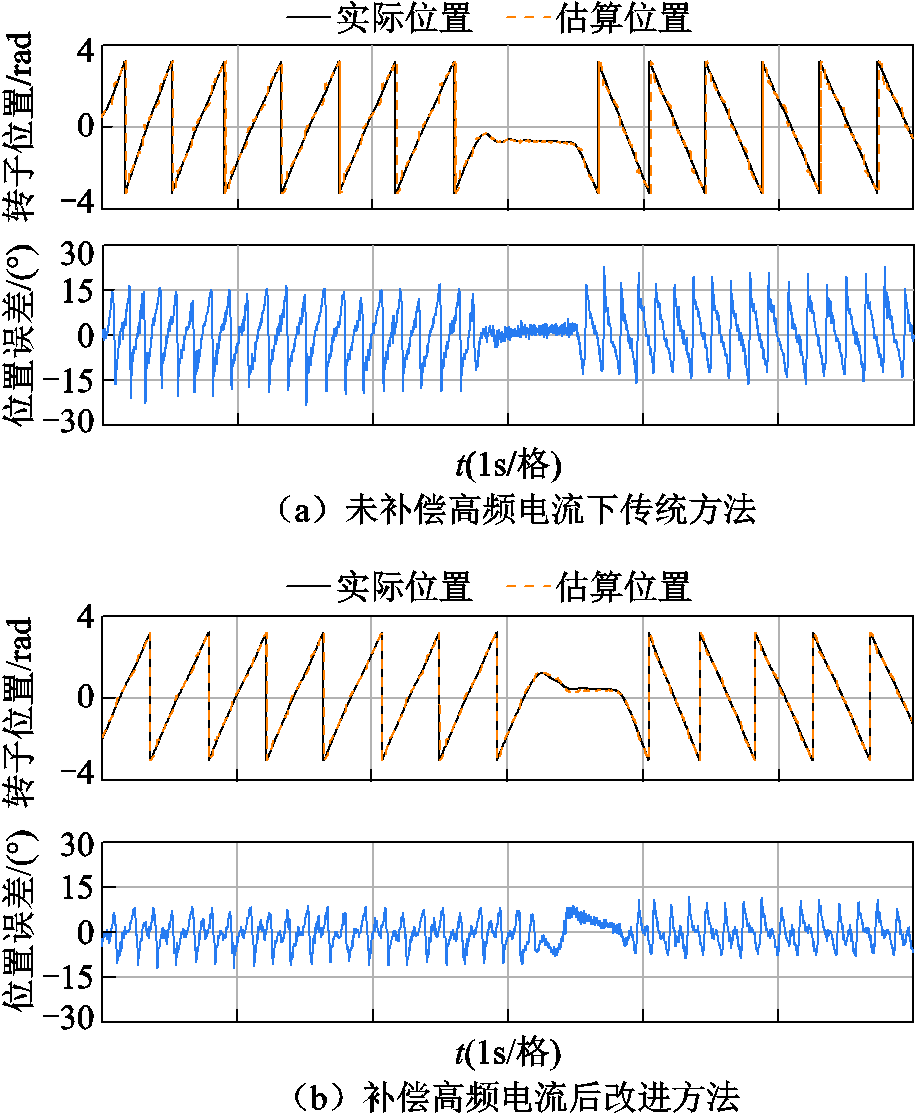
图17 正反转转子位置及其观测误差
Fig.17 Rotor position and its observation error under forward and reverse rotation
可以看出，在基波电流较小时，本文提出的方法可以在相同的注入电压幅值下有效减小无传感器观测转子位置角度误差，提高位置观测的精度。
由于死区影响，在相电流过零时会使观测转子位置有较大误差，空载时主要以高频电流的包络线过零点呈现。在传统方法下，位置误差波形由于高频电流畸变不对称而只呈现三次脉动；而改进方法中，高频电流包络线会更加对称，所以一个周期有呈现六次脉动的趋势。
图18为注入d轴电压为9.6V时，空载情况下的不同速度的位置误差对比波形。可以看出，在所提出方法下，不同转速时均对位置误差观测有较好的效果。
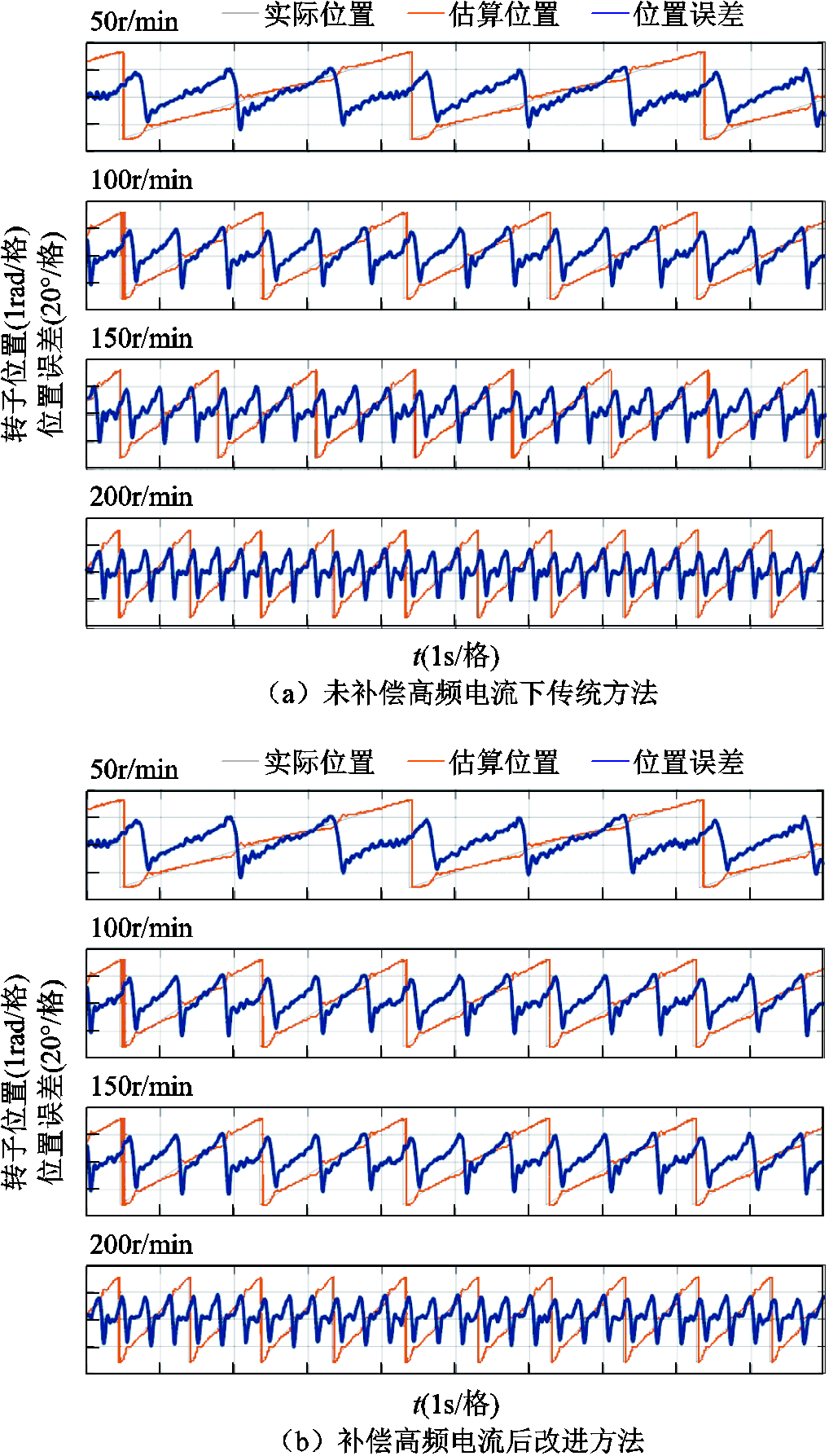
图18 不同转速转子位置及其观测误差
Fig.18 Rotor position and its error at different speeds
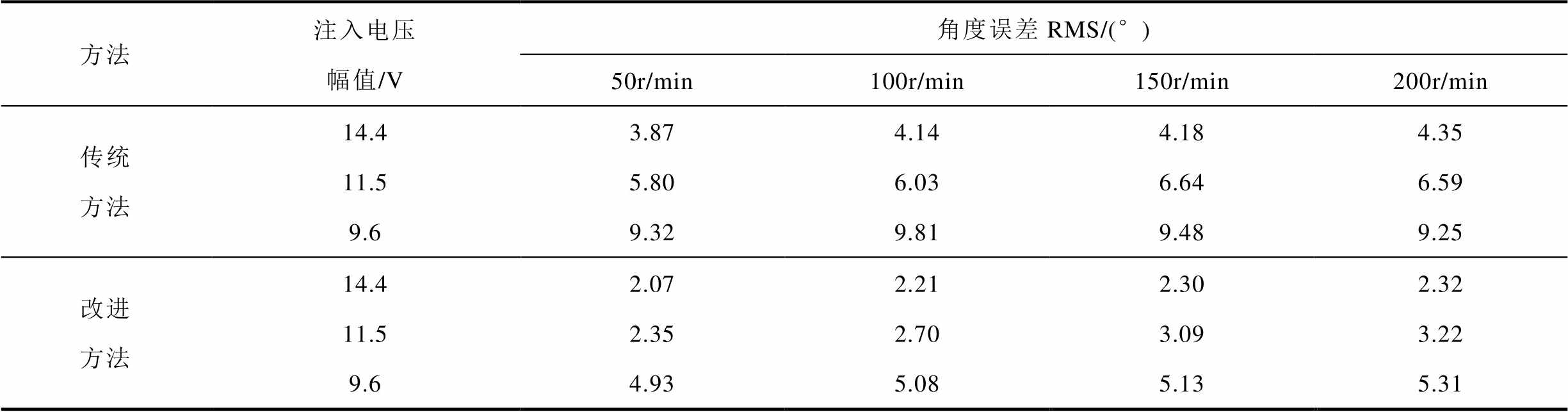
两种方法分别在不同注入电压和工况下的实验对比见表2。在注入电压提升后，两种方法的观测精度都大幅提高，在逐渐降低注入幅值后，本文所提方法将有更高的观测精度。同时，随着转速的增加，每个基波电流周期的注入高频方波数量减小，误差也成略微增大的趋势。
表2 实验结果比较
Tab.2 Comparison of experimental results
方法注入电压幅值/V角度误差RMS/(°) 50r/min100r/min150r/min200r/min 传统方法14.43.874.144.184.35 11.5 5.806.036.646.59 9.6 9.329.819.489.25 改进方法14.4 2.072.212.302.32 11.5 2.352.703.093.22 9.6 4.935.085.135.31
图19为注入d轴电压为9.6V时，100r/min下用磁粉制动器加载5N∙m和10N∙m的位置误差和q轴电流的对比波形。从对比图中可以看出，随着负载的提升，q轴电流加大，逆变器非线性对位置观测的影响均显著减小，两种方法下的位置误差大小均减至±5°以内，而补偿纹波电流的改进方法在空载阶段的位置误差与负载阶段大小基本一致。由于磁场饱和与交叉耦合效应，位置误差曲线随电流增大整体偏离零点，本文在此不做详细讨论。
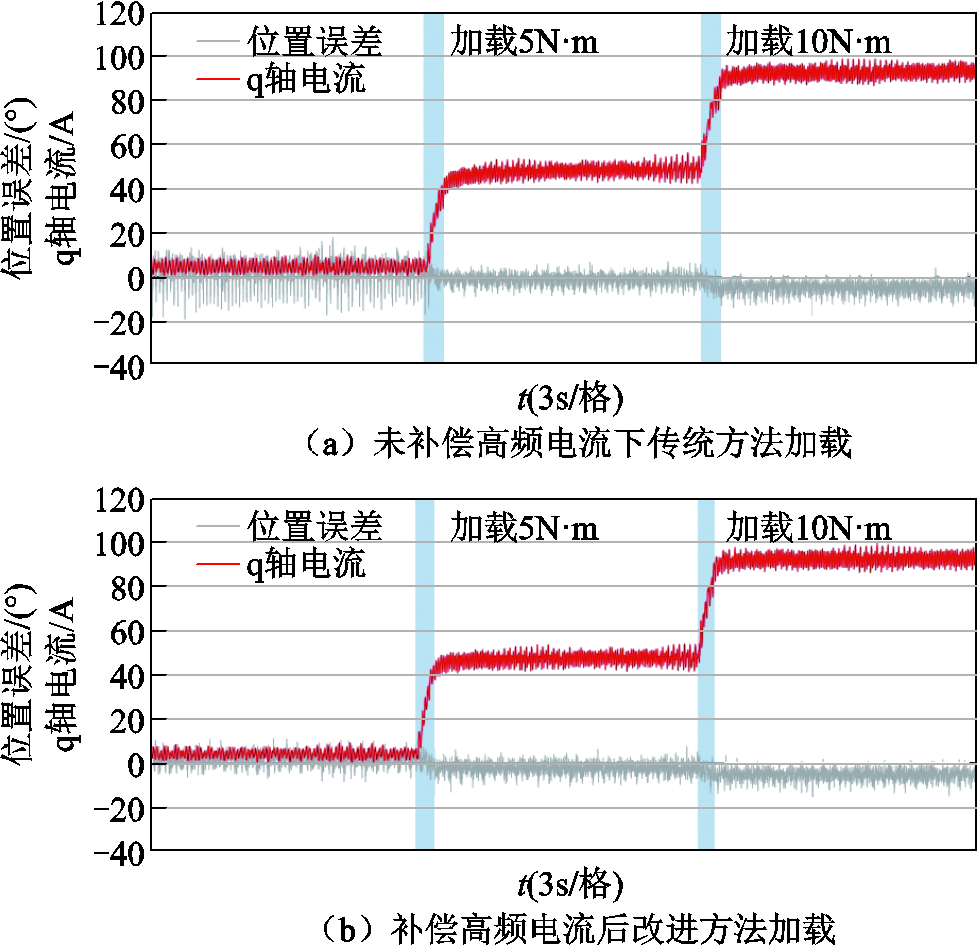
图19 加载时位置观测误差和q轴电流
Fig.19 Position observation error and q-axis current during loading
当持续降低注入d轴方波电压幅值至2.4V（母线电压2.5%）时，高频方波注入法下的位置观测已经被逆变器非线性等因素严重影响。图20为该电压注入下转速100r/min的对比实验波形。此时两种方法下的位置误差均已接近50°，而传统方法下的速度波动更为剧烈，运行一段时间后，锁相环中位置观测发散，导致电机失控，甚至反转。
图20 极限注入电压幅值下的电机运行情况
Fig.20 Motor operation under extremely low injection voltage amplitude
本文针对高频方波信号注入的无传感器控制方法，提出了一种新型补偿高频纹波电流畸变的方法来抑制逆变器非线性对位置观测的影响，主要研究成果如下：
1）本文分析了逆变器的非线性在高频方波信号注入法中对电流造成的畸变，并分析其对位置观测造成的误差。
2）本文针对空载情况下载波周期的不同阶段对三相电流造成畸变的不同，采用直接在自然坐标系进行高频电流的提取。根据死区对电流影响的特征，进行三相高频电流的补偿，再将补偿后的电流变换到正交旋转坐标系进行位置角度的估算，并进行了仿真验证。
3）实验结果表明，与传统方法相比，该方法在母线电压10%的注入幅值下，可以将位置估计误差减小20%以上，无传感器控制系统的动态性能和位置估计性能得到显著改善。该方法可以在不改变注入方式的情况下，有效减小注入电压幅值，提高母线电压利用率。
参考文献
[1] Kwon Y C, Sul S K, Baloch N A, et al. Improved design of IPMSM for sensorless drive with absolute rotor position estimation capability[J]. IEEE Transactions on Industry Applications, 2016, 52(2): 1441-1451.
[2] 刘计龙, 肖飞, 沈洋, 等. 永磁同步电机无位置传感器控制技术研究综述[J]. 电工技术学报, 2017, 32(16): 76-88.
Liu Jilong, Xiao Fei, Shen Yang, et al. Position-sensorless control technology of permanent-magnet synchronous motor-a review[J]. Transactions of China Electrotechnical Society, 2017, 32(16): 76-88.
[3] Sul S K, Kwon Y C, Lee Y. Sensorless control of IPMSM for last 10 years and next 5 years[J]. CES Transactions on Electrical Machines and Systems, 2017, 1(2): 91-99.
[4] 李垣江, 董鑫, 魏海峰, 等. 表贴式永磁同步电机转速环复合PI无位置传感器控制[J]. 电工技术学报, 2020, 35(10): 2119-2129.
Li Yuanjiang, Dong Xin, Wei Haifeng, et al. Sensorless compound PI control for surface permanent magnet synchronous motor speed regulation system[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2119-2129.
[5] 姜燕, 李博文, 吴轩, 等. 基于比例谐振滤波的改进永磁同步电机转子位置观测器[J]. 电工技术学报, 2020, 35(17): 3619-3630.
Jiang Yan, Li Bowen, Wu Xuan, et al. An improved rotor position observer for permanent magnet synchronous motors based on proportional resonant filtering[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3619-3630.
[6] Yin Zhonggang, Gao Fengtao, Zhang Yanqing, et al. A review of nonlinear Kalman filter appling to sensorless control for AC motor drives[J]. CES Transactions on Electrical Machines and Systems, 2019, 3(4): 351-362.
[7] 杜博超, 崔淑梅, 宋立伟, 等. 一种基于变频电流信号的IPMSM无位置传感器高频注入电流噪声抑制方法[J]. 电工技术学报, 2020, 35(18): 3830-3837.
Du Bochao, Cui Shumei, Song Liwei, et al. A variable frequency current injection sensorless control strategy of IPMSM for audible noise reduction[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3830-3837.
[8] Kim S, Ha J I, Sul S K. PWM switching frequency signal injection sensorless method in IPMSM[C]// 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 2011: 3021-3028.
[9] 张国强, 王高林, 徐殿国. 基于无滤波器方波信号注入的永磁同步电机初始位置检测方法[J]. 电工技术学报, 2017, 32(13): 162-168.
Zhang Guoqiang, Wang Gaolin, Xu Dianguo. Filterless Square-wave injection based initial position detection for permanent magnet synchronous machines[J]. Transactions of China Electrotechnical Society, 2017, 32(13): 162-168.
[10] 于安博, 刘利, 阚志忠, 等. 高频脉振信号注入永磁同步电机无滤波器初始位置辨识方法[J]. 电工技术学报, 2021, 36(4): 801-809.
Yu Anbo, Liu Li, Kan Zhizhong, et al. Initial position identification of PMSM with filterless high frequency pulse signal injection method[J]. Transactions of China Electrotechnical Society, 2021, 36(4): 801-809.
[11] 刘善宏, 杨淑英, 李浩源, 等. 基于旋转坐标系解调的内置式永磁同步电机旋转高频注入法位置观测[J]. 电工技术学报, 2020, 35(4): 708-716.
Liu Shanhong, Yang Shuying, Li Haoyuan, et al. Rotating high frequency signal injection based on interior permanent magnet synchronous motor rotor position estimation with the demodulation implementedon the synchronous reference frame[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 708-716.
[12] 刘颖, 周波, 冯瑛, 等. 基于脉振高频电流注入SPMSM低速无位置传感器控制[J]. 电工技术学报, 2012, 27(7): 139-145.
Liu Ying, Zhou Bo, Feng Ying, et al. Sensorless control of SPMSM based on high frequency current signal injection in the direct axis at low and zero speed[J]. Transactions of China Electrotechnical Society, 2012, 27(7): 139-145.
[13] Yoon Y D, Sul S K, Morimoto S, et al. High-bandwidth sensorless algorithm for AC machines based on square-wave-type voltage injection[J]. IEEE Transactions on Industry Applications, 2011, 47(3): 1361-1370.
[14] Guerrero J M, Leetmaa M, Briz F, et al. Inverter nonlinearity effects in high-frequency signal-injection-based sensorless control methods[J]. IEEE Transactions on Industry Applications, 2005, 41(2): 618-626.
[15] Kim D, Kwon Y C, Sul S K, et al. Suppression of injection voltage disturbance for high frequency square-wave injection sensorless drive with regulation of induced High Frequency Current ripple[C]//2014 International Power Electronics Conference (IPEC-Hiroshima 2014 - ECCE ASIA), Hiroshima, Japan, 2014: 925-932.
[16] Choi C H, Seok J K. Compensation of zero-current clamping effects in high-frequency-signal-injection-based sensorless PM motor drives[J]. IEEE Transactions on Industry Applications, 2007, 43(5): 1258-1265.
[17] 邓国发, 王辉, 吴轩, 等. 一种可抑制逆变器非线性影响的永磁同步电机无位置传感器控制策略[J]. 中国电机工程学报, 2018, 38(24): 7381-7390, 7464.
Deng Guofa, Wang Hui, Wu Xuan, et al. A sensorless control strategy of permanent magnet synchronous motor for suppressing nonlinear effects of inverter[J]. Proceedings of the CSEE, 2018, 38(24): 7381-7390, 7464.
Abstract High frequency square wave injection method can avoid the use of filters and improve the system bandwidth. However, when the fundamental wave is small such as light load or no load situation, when the dead time effect of the inverter distorts the high frequency current, the dead time in the inverter nonlinearity will affect the position estimation accuracy of the high frequency injection method. To address these issues, this paper analyzes the influence of inverter nonlinearity on high frequency square wave injection method, and then proposes a new method of high frequency ripple current extraction and compensation. This method can separate and compensate three-phase current from the natural coordinate system, can effectively reduce the influence of dead time, improve the efficiency of injection voltage, and suppress the position angle error caused by inverter nonlinearity.
When the fundamental current of the motor is large, the high-frequency current response is carried above the fundamental current, the dead time has little influence on the high frequency current, and the current distortion is not obvious; When the motor operates at low speed conditions such as light load or no load, the inverter nonlinearity will cause serious distortion to the three-phase high frequency current response, which will affect the accuracy of position observation, because the high frequency current is the dominant component compared with the fundamental current. The existence of dead time, the three-phase current will be distorted, the high frequency current extracted in synchronous rotating coordinate system will produce errors. Therefore, this paper proposes a strategy of extracting fundamental current and modifying high frequency current in natural coordinate system to reduce the position observation error caused by dead time under low speed and no load conditions. Firstly, according to the symmetry of the current waveform in the positive and negative injection phase, the fundamental current can be considered as the sampling average of the midpoint in two adjacent carriers. The fundamental current and high frequency current are separated in the natural coordinate system and transformed into synchronous rotating coordinate system. Then, for the extracted high frequency current, the sampling value of the carrier midpoint is taken as the current error updated every two sampling periods, and the amplitude of the positive and negative phases of the current is compensated in real time, so that the sampling current is closer to the amplitude without dead time effect, reducing the rotor position observation error caused by current distortion.
Finally, the method is verified by simulation and experiment. The method without compensation is compared with the compensation method proposed in this paper, and the position error is observed at different speeds and under different loads. The fluctuation of position error under heavy load is small, while it is large under no load situation. The proposed method reduces the error RMS value by 23.5%～25.0% while the injection voltage is 9.6V.
The experimental results show that compared with the traditional method, this method can reduce the position estimation error by more than 20% at 10% of the bus voltage injection amplitude, and the dynamic performance and position estimation performance of the sensorless control system are significantly improved. This method can effectively reduce the amplitude of injection voltage and improve the utilization of bus voltage without changing the injection mode.
keywords：Permanent magnet synchronous motor, sensorless control, high frequency square-wave injection, inverter nonlinearity, ripple current compensation
DOI:10.19595/j.cnki.1000-6753.tces.211231
中图分类号：TM351
国防科技工业核动力技术创新中心资助项目（HDLCXZX-2021-ZH-016）。
收稿日期 2021-08-09
改稿日期 2022-02-17
徐奇伟 男，1983年生，副教授，博士生导师，研究方向为特种电机设计与控制，电动汽车电驱动系统，混合动力的控制与仿真。E-mail：xuqw@cqu.edu.cn（通信作者）
熊德鑫 男，1996年生，硕士，研究方向为永磁同步电机控制技术。E-mail：joesonxiong@cqu.edu.cn
（编辑 赫蕾）