
图1 金属微粒飞萤现象
Fig.1 Firefly phenomenon of particles
摘要 直流气体绝缘开关与输电管道(GIS/GIL)中线形微粒存在特殊的飞萤运动行为,即未碰撞地电极而反向运动或在高压电极表面悬浮运动,是影响直流GIS/GIL绝缘性能的关键因素之一。为厘清微粒飞萤运动物理机制,搭建了微粒飞萤运动观测与荷电量测试平台,获得了不同电压下线形微粒的运动与荷电特性。研究表明,线形微粒附近空间电荷导致微粒荷电量的极性变化,是产生飞萤运动的关键诱因,电极表面线形微粒的电晕起始电压是导致微粒荷电量极性改变的临界电压。进一步,基于直流棒板间隙的光电离模型计算了电极表面线形微粒的起晕电压,由测量结果拟合得到纳入起晕电压影响的微粒荷电量表达式,并结合电荷端部集中特性建立了线形微粒的荷电运动模型,由此提出飞萤运动的临界起始判据,实现了线形微粒飞萤运动的动态模拟。计算获得100kV直流GIL样机中不同尺寸微粒的飞萤起始电场强度,对于0.5MPa的SF6气体环境,直径0.2mm、长度5mm线形微粒的负极性飞萤起始电场强度为2.78MV/m,正极性飞萤起始电场强度为4.93MV/m。该研究在抑制微粒飞萤运动方面为直流GIL的主绝缘设计提供了参考依据。
关键词:直流气体绝缘输电管道(GIL) 线形微粒 飞萤机制 临界起始电场强度
在气体绝缘设备的生产、运输、组装、运行等阶段的机械碰撞、设备振动以及热伸缩摩擦,会不可避免地产生金属微粒,这些金属微粒在电场力的作用下,克服重力进行运动,并在气体绝缘设备中产生局部不均匀电场,从而危害气体绝缘设备的绝缘性能[1-3]。
长期以来,国内外学者定量研究了交直流电压下规则形状微粒,特别是球形微粒的带电机理、受力类型以及运动特性[4-8]。相较于交流电压下微粒集中于地电极附近的运动,直流电场中微粒表现为电极间往复运动形式,特别是线形、片状等微粒存在特殊运动——“飞萤现象”,即微粒未碰撞地电极而反向或在高压电极表面悬浮运动,如图1所示[9-10]。飞萤微粒长时间运动于高压电极表面等高场强区域,甚至沿高压电极运动并吸附在绝缘子表面,显著降低气固组合绝缘耐电强度,而陷阱、覆膜等微粒抑制措施往往设置或涂覆于地电极表面,难以实现对飞萤微粒的有效抑制[11-12]。因此,厘清气体绝缘设备中金属微粒飞萤运动机制,提出飞萤运动起始判据,对提升气体绝缘设备绝缘性能具有重要的实际意义与工程价值。

图1 金属微粒飞萤现象
Fig.1 Firefly phenomenon of particles
国内外研究人员通过将金属微粒假设为一个点电荷来计算其所受电场力,实现了球形微粒运动轨迹的模拟[13-14]。而线形、片状及不规则形状微粒的电荷集中于微粒端部,在非均匀电场中的电场梯度力已不能忽略,不能将其简化为点电荷来分析,M. Wohlmuth认为长度10mm的颗粒,其电场梯度力是库仑力的10%[15]。西安交通大学张乔根教授团队的研究认为,飞萤现象与SF6气体中空间电荷的分布密切相关,微粒在空间发生局部放电,产生大量空间电荷严重影响微粒在空间的飞行行为[16]。P. Wenger等进一步分析了微粒飞萤运动与局部放电特高频信号间的关联关系,发现高压电极表面悬浮运动飞萤微粒的典型特高频脉冲包络线呈V形[17]。
综上所述,现有的微粒运动分析模型,将微粒模拟为点电荷,难以分析电荷集中于端部的飞萤运动微粒。此外,国内外学者定性分析了直流电压下微粒的飞萤运动行为,认为飞萤运动与微粒局部放电产生的空间电荷密切相关。但微粒飞萤运动过程的受力特性尚不明晰,其物理机制及定量判据仍有待进一步研究,这也是本文研究工作的主要目的。
鉴于上述问题,本文搭建了SF6中金属微粒飞萤运动观测与荷电量测试平台,探究了微粒飞萤的运动与荷电特征,考虑微粒荷电特征与空间电荷分布,揭示了微粒飞萤运动的物理机制,建立了考虑电晕放电与端部电荷集中特性的微粒荷电运动模型,提出了飞萤运动的临界起始判据,获得了直流气体绝缘输电管道(Gas Insulated Transmission Line, GIL)中不同尺寸微粒的飞萤起始场强。
为便于观测金属微粒飞萤运动规律与特性,本文搭建了如图2所示的平板电极实验平台,将电极使用塑料螺栓固定于有机玻璃间,并置于开设观察窗的方形密闭腔体中,直流电压通过套管接入,平板电极极间距20mm,可通过塑料螺栓进行调节,电极直径为200mm。为说明平板电极电场强度的大小,与导体半径45mm、外壳内径120mm的100kV直流GIL电场强度做对比。同轴圆柱电极的外壳内表面电场强度与导体表面电场强度可分别由式(1)和式(2)计算,平板电极极间电场强度由式(3)计算。平板电极外施电压17kV时,与GIL外壳内表面电场强度一致;外施电压45kV时与导体表面电场强度一致。
![]() (2)
(2)
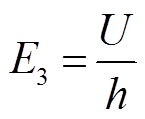 (3)
(3)
式中,E1、E2为同轴圆柱电极表面电场强度;U为外施电压;R1、R2分别为导体半径与外壳内径;E3为平板电极表面电场强度;h为平板电极极间距。

图2 金属微粒飞萤运动实验平台
Fig.2 Observation platform of firefly particles
实验平台同时具有微粒荷电量测试功能。平板电极悬空置于有机玻璃漏斗型腔体中,漏斗底部布置有带法拉第杯的库仑计,腔体侧壁与平板电极平行处安装风扇。风扇可将平板电极中运动的微粒吹入漏斗形腔体中,微粒沿漏斗落入法拉第杯,通过库仑计可测得金属微粒的荷电量。同时采用高速相机观测金属微粒的运动,并使用强光LED对高速相机进行补光,获得微粒落入法拉第杯前的运动状态与位置。微粒吹落过程中微粒与玻璃接触会损失部分电荷,为纠正测量误差,对未启举的电荷量测量值与理论值进行比对,获得了荷电测量修正系数,系数值为1.13,库仑计测量值乘以修正系数即为微粒实际荷电量。
金属微粒采用不同尺寸的铝丝,实验前将金属微粒、电极板用乙醇浸润的丝绸擦拭,待乙醇挥发后将微粒置于下极板中央,对金属密闭腔体抽真空后充入纯SF6气体。快速升压至指定电压后,通过高速相机记录微粒运动特征。
以直径d=0.3mm、长度l=4mm的线形微粒为例,对其施加一系列电压,获得了不同电压下线形微粒的运动特性。
不同负极性直流电压下微粒运动状态如图3所示。当外施电压为-15kV时,微粒启举并加速向高压电极运动,与高压电极碰撞后,加速向地电极运动,并在电极间往复反弹,如图3a所示;外施电压提升至-25kV时,微粒仍在电极间往复反弹,但微粒与高压电极碰撞后向地电极运动时呈现减速运动特征,如图3b所示;而提升电压至-35kV时,微粒未碰撞地电极而反向运动,并在高压电极表面悬浮运动,即飞萤现象,如图3c所示。根据运动行为的差异,飞萤微粒呈现两种不同的运动形态,分别为悬浮飞萤与跳跃飞萤。悬浮飞萤指微粒两端围绕质心旋转,形成具有旋转轴的双锥体,同时在电极表面以低于1mm的幅值跳动,是飞萤运动的稳定状态,微粒在该状态保持数秒至数分钟。跳跃飞萤指微粒在电极表面以大于1mm的幅值进行跳动,但未碰撞地电极,是飞萤运动的过渡状态。微粒在跳跃数次后转为悬浮飞萤或在电极间往复运动。

图3 不同负极性直流电压下微粒运动状态
Fig.3 Wire particle motion state under different negative DC voltage
不同正极性直流电压下微粒运动状态如图4所示。与负极性电压相似,外施电压为+15kV时,微粒启举并在电极间往复反弹。相较于负极性电压,外施电压提升至+35kV后,微粒并未在高压电极表面进行悬浮运动,而在地电极表面呈双锥体运动,并以微小幅值跳动,即竖立现象,如图4b所示。电压提升至+45kV时,微粒首先表现为竖立运动模式,在某一时刻打破稳定的竖立运动行为,呈现如图4c的飞萤运动。

图4 不同正极性直流电压下微粒运动状态
Fig.4 Wire particle motion state under different positive DC voltages
为获得飞萤微粒的荷电特性,对不同尺寸微粒碰撞高压极板后的荷电量进行测试,随电压变化的微粒荷电量如图5所示。负极性电压下,微粒碰撞高压极板后初始荷电量为负极性,微粒荷电量随电压升高而增加,在电压达到临界值后,微粒荷电状态极性改变,携带正极性电荷,而荷电量极性改变的微粒均呈现了飞萤运动状态,如图5a所示。正极性电压下也出现了微粒荷电极性改变的现象,如图5b所示,在电压达到临界值,碰撞高压极板后微粒的荷电从正极性变为负极性,且微粒呈现飞萤运动状态。相较于负极性电压,正极性下微粒荷电极性变化的电压临界值更高。

图5 高压极板表面碰撞反弹微粒荷电量
Fig.5 Charges of rebound particles on high voltage plate surface
线形微粒在直流电压下的飞萤现象源于微粒荷电量极性变化。飞萤运动机理如图6所示。当微粒运动至负极板时,微粒通过传导带电获得负极性电荷,在库仑力Fq与重力G的共同作用下与负极板分离,如图6右部所示。线形微粒端部会形成极不均匀电场,场强较大时会产生大量的带电粒子,其中正离子向负极板运动,电子被SF6分子俘获形成负离子并向正极板运动,形成如图6右部所示的空间电荷分布。微粒离开负极板后处于正离子积聚区域,微粒吸附这些游离的正离子,导致微粒的荷电量甚至荷电极性改变。
如图6左部,微粒荷电极性改变后,库仑力Fq方向将指向高压电极,若此时库仑力足以克服重力G与气体阻力Fv,微粒将获得向高压电极的运动加速度;同时,微粒在运动至地电极前,竖直方向合力的做功大于微粒碰撞反弹后的动能,微粒将向负极板运动。即满足式(4)时,微粒呈现飞萤运动现象。
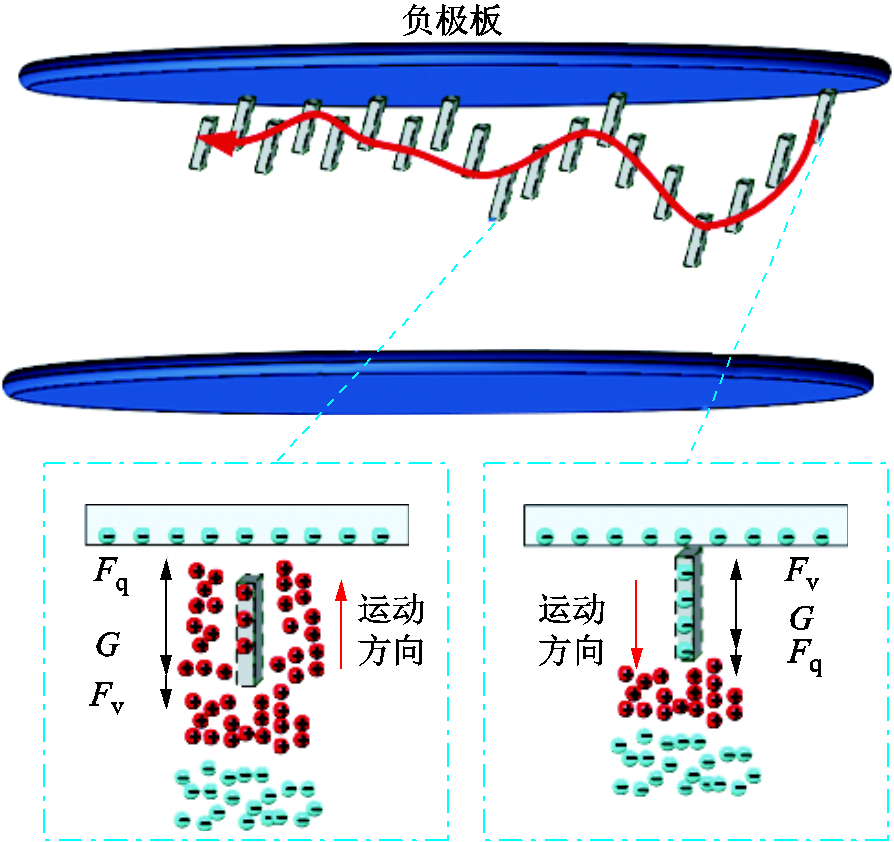
图6 飞萤运动机理
Fig.6 Mechanism of firefly
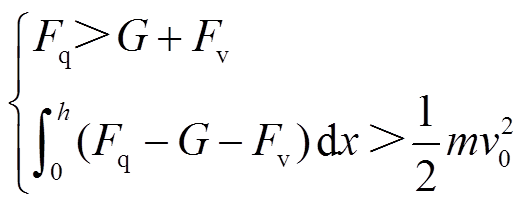 (4)
(4)
式中,h为电极间距离;m为微粒质量;v0为微粒碰撞负极板后的反弹速度。
外施电压为正极性时,负极板位于下方,微粒在库仑力与重力的共同作用下启举运动。外施电压达到临界值后,负极板表面微粒端部形成正离子积聚区域,微粒离开负极板时吸附游离的正离子,导致微粒荷电量甚至极性发生改变。微粒荷电极性改变后,库仑力与重力方向均指向负极板,此时微粒表现为竖立现象。正极性电压下,这种平衡状态被打破时,微粒将重新启举并在极板间往复运动。微粒运动至正极板时,若达到正极性下微粒荷电极性改变的临界电压,并满足式(4),微粒表现为正极性下的飞萤运动。
对于微粒荷电量极性改变的临界电压,在微粒起始电晕前,微粒附近会产生正负离子对,但由于不能形成自持放电,正负离子对数量级较低,不足以对微粒荷电量产生显著影响;而起始电晕后,微粒附近将持续产生大量的带电粒子,微粒离开负极板后,足以改变微粒的荷电极性。因此认为电晕起始电压即微粒荷电极性改变的临界电压。
正极性电压下微粒同样会呈现飞萤运动行为,直流下的飞萤运动具有极性效应,即正极性飞萤电压高于负极性飞萤电压。从起始电晕的角度分析,微粒在高压电极表面时,微粒端部形成极不均匀电场,正极性起晕电压高于负极性起晕电压,因此正极性下飞萤临界起始电压相较于负极性更高,微粒飞萤现象更容易发生在负极性电压下。
从起始电晕的角度进一步分析,微粒的曲率半径越小时,端部电场强度不均匀程度越大,外施电压较低时即可达到起晕电压,飞萤起始电压也随之变化,在微粒曲率半径较小或电场强度较大时,更容易出现飞萤现象。除微粒尺寸外,气体环境也决定了飞萤的起始条件,相较于空气,SF6环境中放电难以发展,且气压越大起晕电压越高,微粒的飞萤临界起始电压就越高。
综上所述,线形微粒电晕放电产生的空间电荷导致微粒荷电量变化甚至改变荷电极性,是产生飞萤运动的关键诱因。根据这一特征,不仅是线形微粒,片状、螺旋状等具有低曲率半径尖端的微粒,也会在尖端产生类似的空间电荷并改变微粒荷电极性,而文献[10, 17]通过实验观测到了片状微粒和螺旋微粒的飞萤运动。
根据第1节分析,线形微粒放电导致微粒荷电量的变化是微粒飞萤的主要原因,为模拟线形微粒飞萤运动获得飞萤临界起始判据,本节首先基于棒板间隙直流起晕电压的光电离模型计算了电极表面线形微粒的起晕电压,进而结合测量结果拟合了考虑起晕电压的线形微粒荷电量的表达式,最后考虑线形微粒荷电的端部集中特性,建立了线形微粒荷电运动模型。通过该模型,实现了线形微粒飞萤运动的动态模拟,并获得了直流GIL中不同尺寸微粒的飞萤起始电场强度。
线形微粒飞萤或站立于电极表面时,微粒端部形成极不均匀电场,因而可采用棒板间隙起晕电压光电离模型来分析电极表面微粒的电晕起始电压。
外施直流电压时,微粒端部附近电场强度超过临界值时,自由电子与气体分子发生碰撞引起初始电子崩,电子崩发展过程中产生的光子引发光电离产生光电子,进一步形成二次电子崩。根据Nasser判据,二次电子崩崩头电子数不小于初始电子崩崩头电子数时,电晕起始。
对于正极性电晕,初始电子崩由电场强度临界区向微粒端部发展,到达临界区的光电离产生至少一个光电子,正电晕得以自持,如式(5)所示;对于负极性电晕,初始电子崩从微粒端部向电场强度临界区发展,到达微粒端部的光电离产生至少一个光电子时,负电晕得以自持,如式(6)所示[18]。
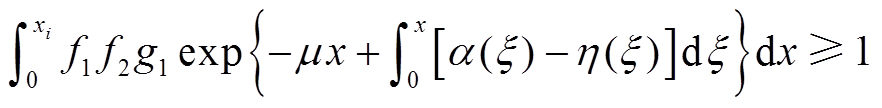 (5)
(5)
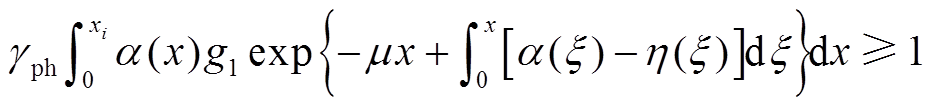 (6)
(6)
式中,xi为场强临界区与微粒端部的距离;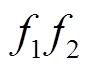 为气体的光电子发射系数;g1为面积因数;m 为气体的光子吸收系数;a 为碰撞电离系数;h为吸附系数;
为气体的光电子发射系数;g1为面积因数;m 为气体的光子吸收系数;a 为碰撞电离系数;h为吸附系数;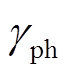 为阴极光电子发射系数,参数取值见附录。
为阴极光电子发射系数,参数取值见附录。
根据上述光电离模型,计算了第1节中平板电极下不同微粒的电晕起始电压,如图7所示。直径0.2mm、长度5mm微粒的负极性电晕起始电压为22kV,结合图5的荷电量测试结果,达到电极表面微粒的电晕起始电压后,碰撞反弹离开电极的微粒荷电极性发生变化,微粒呈现飞萤运动。一定程度上证明了电晕起始电压为线形微粒荷电量极性改变的临界电压。
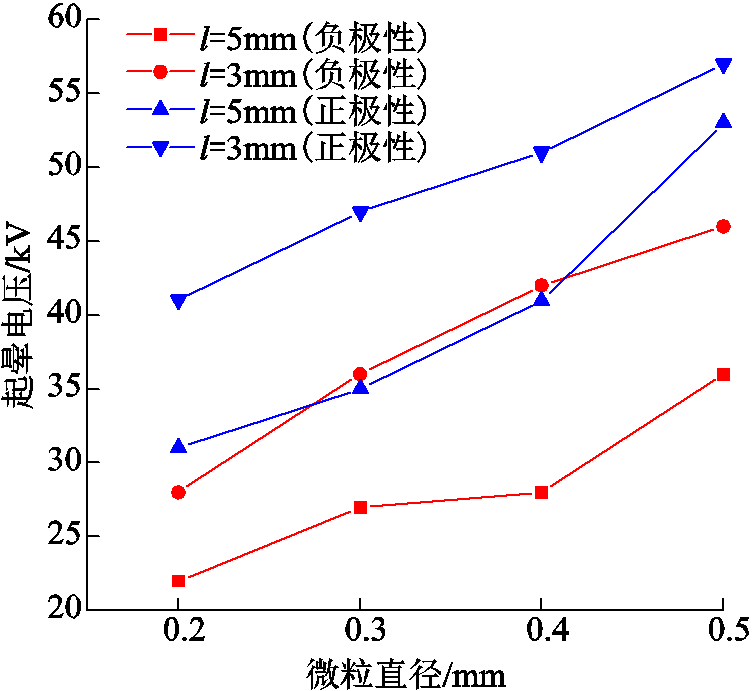
图7 平板电极下不同微粒的电晕起始电压
Fig.7 Corona onset voltage of different particles at plate electrode
如图5所示,达到电极表面线形微粒的电晕起始电压后,微粒总荷电量与起晕电压相关。为此,本节提出了考虑起晕电压的线形微粒荷电量计算方法。
未达到微粒起晕电压时,与不考虑电晕放电的微粒荷电量相同,站立于电极表面的线形微粒所带电荷q可表示为[19]
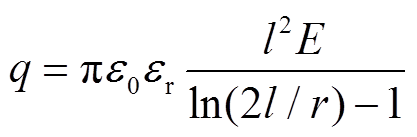 (7)
(7)
式中,e0为真空介电常数;er为气体介质相对介电常数;l为微粒长度;E为电极表面电场强度; r为微粒半径。
达到起晕电压后,根据微粒电荷测量结果与起晕电压计算值,微粒荷电量可拟合为
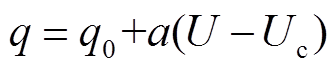 (8)
(8)
式中,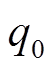 、a为与微粒尺寸相关的系数;Uc为起晕电压。
、a为与微粒尺寸相关的系数;Uc为起晕电压。
线形微粒的运动行为相较于球形微粒更加复杂,为实现飞萤运动的动态模拟,本节引入荷电量集中系数k表示微粒两端荷电量的不均匀程度,并考虑线形微粒运动的旋转特性,建立了线形微粒的动力学模型。
线形微粒受力模型如图8所示。考虑微粒荷电的端部集中特性后,库仑力Fqh和Fql分别作用于微粒的两端,包含了线形微粒在不均匀场中的电场梯度力。库仑力可以分解为沿半径方向和长度方向的作用力,沿半径方向的作用力与微粒长度一半的乘积作为转矩,改变微粒的旋转角度;沿长度方向的作用力与重力、气体阻力共同改变微粒的位置。微粒具体受力表达式如下。
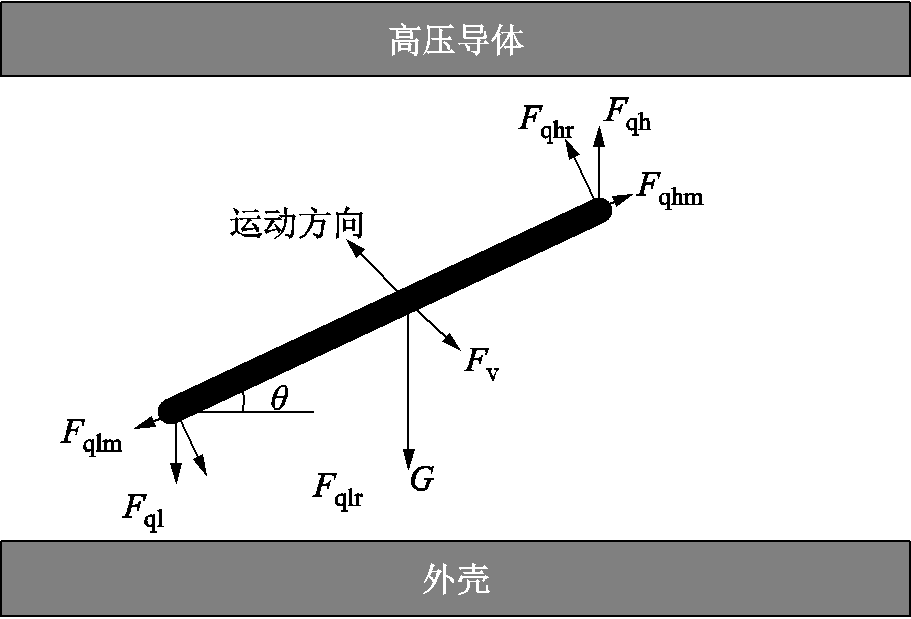
图8 线形微粒受力模型
Fig.8 Force acting on the wire particle
微粒荷电总量为q,电荷量较大一端的荷电量为kq,另一侧荷电量则为(1-k)q,荷电量集中系数k取值见附录。微粒所受库仑力为
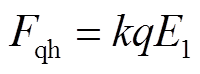 (9)
(9)
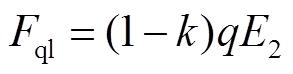 (10)
(10)
式中,E1和E2分别为微粒两端的电场强度。
微粒所受重力为
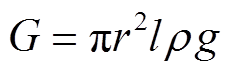 (11)
(11)
式中,r为金属微粒密度;g为重力加速度。
微粒转动惯量为
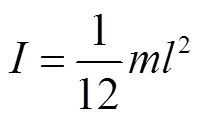 (12)
(12)
所受气体阻力为
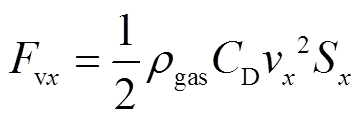 (13)
(13)
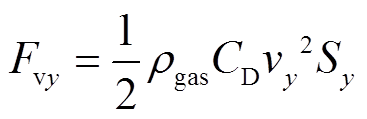 (14)
(14)
式中,rgas为气体密度;CD为阻力系数;vx、vy分别为微粒横向和纵向运动速度;Sx、Sy分别为微粒在纵向和横向平面上的投影面积。
微粒在直角坐标系下非碰撞时刻运动方程为
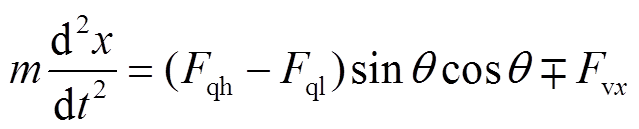 (15)
(15)
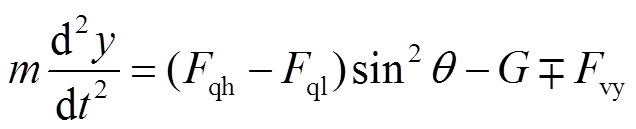 (16)
(16)
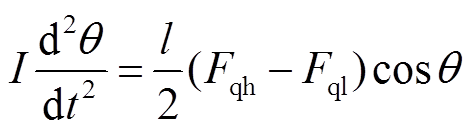 (17)
(17)
式中,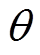 为微粒倾角。
为微粒倾角。
微粒与电极碰撞时,考虑碰撞能量损耗系数e,取v为微粒碰撞电极前的速度,微粒与电极碰撞后的速度为
根据式(15)~式(17),微粒除平动外,还围绕质心转动。随外施电压增大,微粒两端所受库仑力增加,轴向和纵向运动加速度随之增大,微粒平动更加剧烈;同时,微粒的转动角速度增大,微粒的转动也更加剧烈,飞萤微粒的摆动幅度更大。除外施电压,微粒运动特性也与自身尺寸相关,在微粒倾角q与外施电压一定时,随着微粒半径减小或长度增加,微粒平动加速度增大;而转动角加速度受微粒长度影响较小,随微粒半径减小而增大。
根据1.3节分析,外施电压大于微粒起晕电压后,微粒碰撞高压电极后会携带与高压导体极性相反的电荷。若库仑力足以克服重力与气体阻力,且微粒在运动至地电极前,竖直方向合力的做功大于微粒碰撞反弹后的动能,微粒将向负极板运动,即呈现飞萤现象。因此,根据SF6中线形微粒起晕电压计算方法与线形微粒的动力学模型,微粒飞萤临界起始判据可表示为
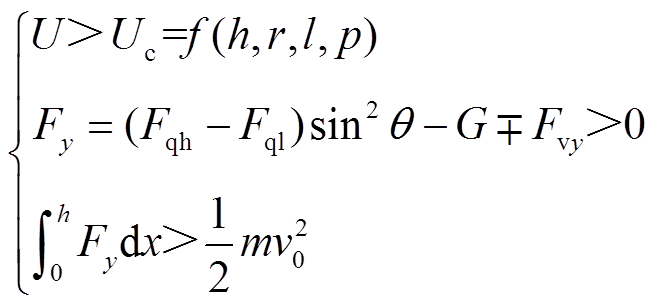 (19)
(19)
式中,p为气体压强;Fy为微粒从高压电极向地电极运动时所受竖直方向合力;v0为微粒碰撞离开高压电极的速度。
根据上述线形微粒荷电动力学模型,采取COMSOL与Matlab联用方法,对直流气体绝缘设备中线形微粒运动轨迹进行仿真计算。参考实际交流设备尺寸建立GIL模型,导体半径45mm,外壳内径120mm。GIL右端设置绝缘子,微粒放置于外壳底部距离绝缘子50cm处。实际气体绝缘设备中,仅有少数微粒能飞萤运动,这些微粒虽数量少,但尺寸较大,沿高压电极运动至绝缘子后,对气体绝缘设备的绝缘危害更大。因此本文在仿真计算中仅假设存在一个微粒,对飞萤运动进行分析。
外施电压150kV时,直径d=0.2mm、长度l=5mm微粒的运动行为模拟如图9a所示,图9a中虚线为微粒轨迹,实线表示微粒位置与旋转角度,从图中可以看出微粒在启举后呈现飞萤现象,微粒沿高压电极向绝缘子运动。在相同电压下,直径d=0.2mm、长度l=3mm微粒的运动轨迹如图9b所示,此时微粒在极间往复运动,未出现飞萤现象。

图9 线形微粒运动模拟
Fig.9 Simulation of wire particles’ motion
对于不同电压等级或尺寸的气体绝缘设备,飞萤起始电场强度更具有参考性,因此本文基于对100kV GIL样机中微粒运动计算,探讨直流GIL中的飞萤临界起始电场强度。
负极性电压下,0.5MPa的SF6气体环境中不同尺寸微粒的飞萤起始电场强度如图10所示,可以看出,随着微粒长度增加或半径减小,飞萤起始电场强度呈减小趋势。根据图4a微粒荷电测试结果,随着电压升高,微粒荷电极性改变,而荷电极性改变的微粒均呈现了飞萤运动状态。随着微粒长度增加或半径减小,荷电极性发生改变的临界电压,即飞萤现象的临界电压呈减小趋势。因此,负极性下飞萤起始电场强度随微粒尺寸的变化规律仿真结果与实验观测结果一致。
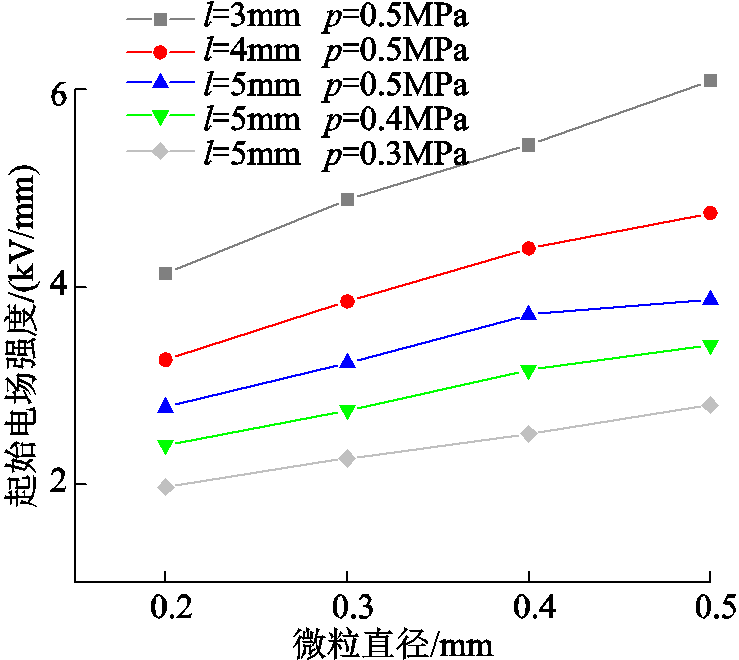
图10 负极性下不同尺寸与气压下微粒飞萤起始电场强度
Fig.10 Onset electric field intensity of firefly with different particle sizes and gas pressures at negative DC voltage
长度5mm线形微粒的负极性飞萤起始电场强度随气压变化规律如图10所示,随着气压升高,微粒飞萤起始场强增大。其原因在于,随着气压升高,SF6有效碰撞电离系数减小,微粒电晕起始电压增大,更难以产生足以改变微粒荷电极性的空间电荷。以直径0.2mm、长度5mm线形微粒为参考,为避免负直流电压下的飞萤现象,0.5MPa SF6气体环境的GIL高压导体表面场强应低于2.78kV/mm。
为验证仿真计算的有效性,在导体半径45mm,外壳内径120mm的真型GIL样机中布置直径0.2mm、长度5mm的线形微粒,观测并记录不同气压下线形微粒是否出现飞萤现象。飞萤起始电场强度实验验证如图11所示。图11中,导体表面电场强度为2.6kV/mm(120kV)时,0.3MPa和0.4MPa、SF6气压下微粒出现飞萤现象;而导体表面电场强度为时2.2kV/mm(100kV),仅0.3MPa、SF6气压下微粒出现飞萤现象。实验结果符合微粒飞萤起始场强的预测。
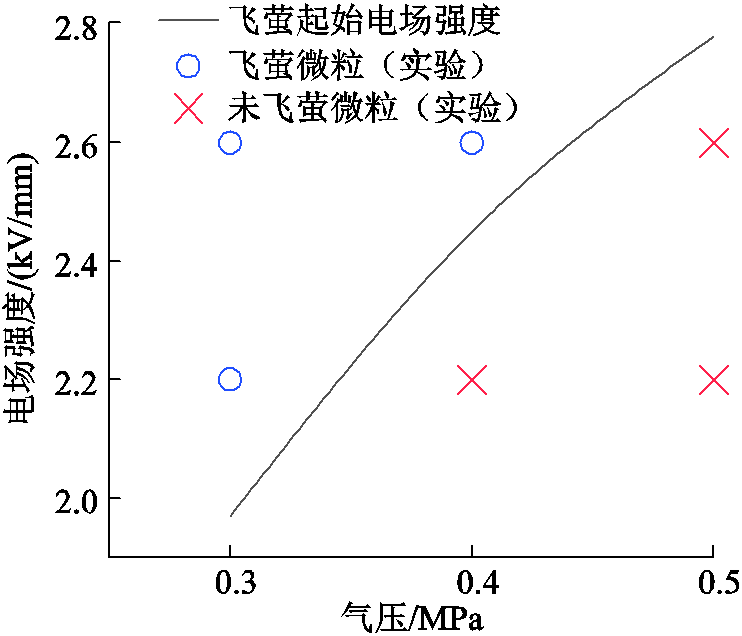
图11 飞萤起始电场强度实验验证
Fig.11 Experimental verification of firefly onset electric field intensity
正极性电压下微粒飞萤起始场强如图12所示。与负极性飞萤相似,随着微粒长度增加、半径减小或气压降低,正极性飞萤起始电场强度呈减小趋势。以直径0.2mm、长度5mm线形微粒为参考,为避免正直流电压下的飞萤现象,0.5MPa SF6气体环境的GIL高压导体表面电场强度应低于4.93kV/mm。

图12 正极性电压下微粒飞萤起始电场强度
Fig.12 Onset electric field intensity of firefly at positive DC voltage
正极性电压下,线形微粒在直流GIL同轴圆柱电极中的运动行为与平板电极中有所不同,达到飞萤起始电压时,微粒启举后直接向高压电极运动而未出现竖立现象,在运动至高压电极后呈现飞萤运动。正极性电压下的竖立现象与负极性电压下的飞萤现象本质上是相同的,均源于负极板附近电晕放电导致的微粒荷电极性变化。在GIL设计中,为达到绝缘设计要求,高压导体表面电场强度一般为外壳表面电场强度的2.1~3.9倍,本文模型中该比例为2.7。以长度5mm线形微粒为例,外施电压300kV时,地电极表面电场强度为2.54kV/mm,未达到竖立现象所需电场强度,而高压电极表面电场强度为6.79kV/mm,大于正极性飞萤起始电场强度。正极性GIL电极表面电场强度与飞萤起始电场强度对比如图13所示。因此,在正极性GIL中,微粒呈现飞萤运动行为而非竖立行为。
为验证正极性GIL中微粒飞萤运动行为,搭建了同轴圆柱电极缩比模型,导体半径20mm、外壳内径60mm,导体表面电场强度为外壳表面电场强度的3倍。将缩比模型置于方形密闭腔体后,在缩比模型中放置了直径0.2mm,长度4mm的线形微粒,充入SF6气体,观测了正极性电压下线形微粒的运动行为。正极性GIL中飞萤运动如图14所示。图14中可以看到,随外施电压增加,微粒均未出现竖立行为,当电压升高至92kV时,微粒出现正极性飞萤运动。
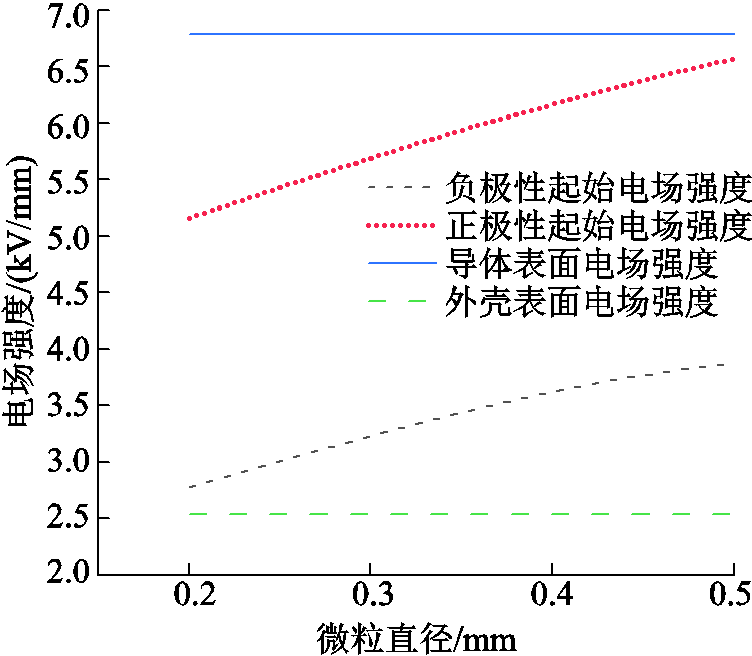
图13 正极性GIL电极表面电场强度与飞萤起始电场强度对比
Fig.13 Comparison of firefly onset electric field intensity with the surface field intensity in positive DC GIL
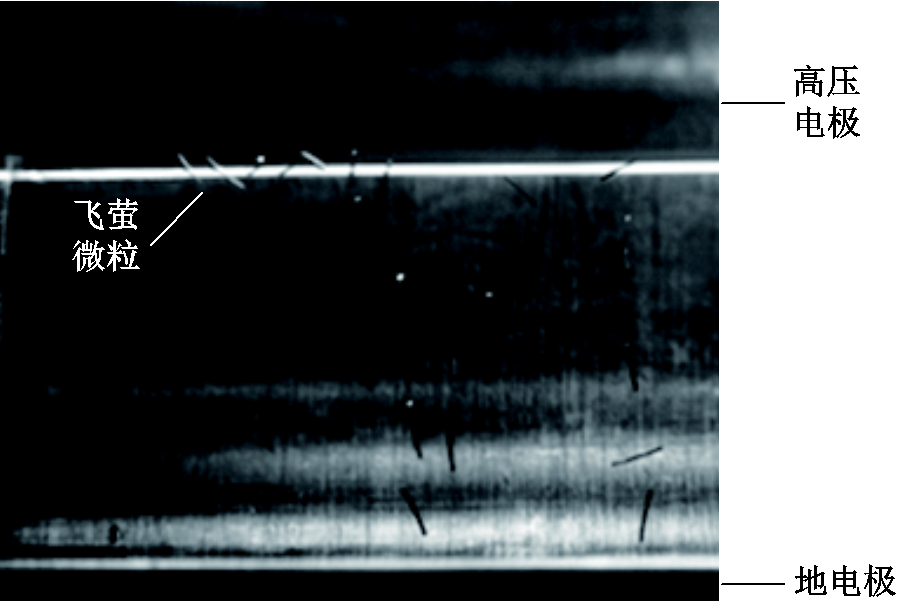
图14 正极性GIL中飞萤运动
Fig.14 Firefly movement in positive GIL
1)通过实验测试和物理建模,揭示了直流电压下线形微粒的飞萤运动机制。利用搭建的微粒飞萤运动观测与荷电量测试平台,探究了不同电压下线形微粒的运动与荷电特性。实验结果表明,线形微粒放电产生的空间电荷导致微粒荷电极性变化,是微粒飞萤运动的关键诱因;电晕起始电压为微粒荷电量极性改变的临界电压;该机制也适用于片状、螺旋状等具有低曲率半径尖端的微粒。
2)建立了GIL中线形微粒荷电运动模型,实现了飞萤运动的动态模拟。基于直流棒板间隙光电离模型计算了电极表面线形微粒的起晕电压,结合测试结果拟合了纳入起晕电压的线形微粒荷电量表达式,并考虑线形微粒电荷的端部集中特性,建立了线形微粒荷电运动模型,实现了线形微粒旋转过程与飞萤运动的模拟。
3)获得了正、负极性直流GIL中不同线形微粒的飞萤临界起始电场强度。通过线形微粒荷电运动模型,计算了直流GIL中不同尺寸微粒的飞萤起始电场强度,并在真型GIL中验证了计算结果的有效性。结果表明,随着微粒长度增加、半径减小或气压降低,正负极性飞萤起始电场强度均呈减小趋势。其中,0.5MPa、SF6的100kVGIL内,直径0.2mm、长度5mm线形微粒,负极性飞萤起始电场强度为2.78kV/mm,正极性飞萤起始电场强度为4.93 kV/mm。
4)提出的飞萤运动临界起始电场强度计算方法适用于不同电压等级的直流GIL,为直流GIL的主绝缘设计以及飞萤抑制技术提供了有效依据。此外,模型中尚未考虑电晕放电离子风对微粒运动的影响,以及多微粒情况下的飞萤运动特性,未来将开展进一步研究以提升模型计算精度与工程应用价值。
式(5)式(6)中系数取值为[20]: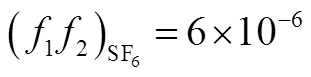 ,
,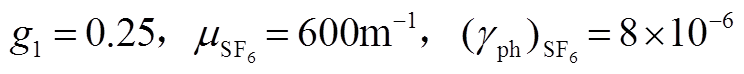 。对于碰撞电离系数与吸附系数[21]
。对于碰撞电离系数与吸附系数[21]
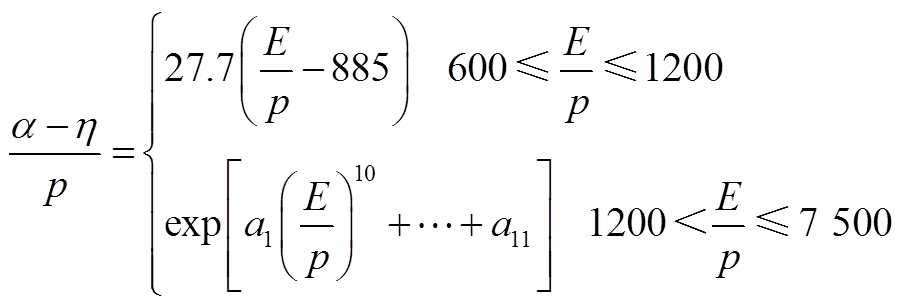 (A1)
(A1)
其中
a1=-0.212 90´10-25 a2=0.132 19´10-21 a3=-0.361 57´10-18,
a4=0.572 76´10-15 a5=-0.132 19´10-12 a6=0.393 08´10-9
a7=-0.179 50´10-6 a8=0.545 25´10-4 a9=-0.105 42´10-1
a10=0.117 61´101 a11=-0.566 92´102
式中,a 和h 的单位均为cm-1,E的单位为kV/cm,p的单位为MPa。
荷电量集中系数取值为[22]
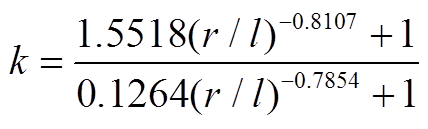 (A2)
(A2)
参考文献
[1] 胡琦, 李庆民, 刘智鹏, 等. 基于表层梯度电导调控的直流三支柱绝缘子界面电场优化方法[J]. 电工技术学报, 2022, 37(7): 1856-1865.
Hu Qi, Li Qingmin, Liu Zhipeng, et al. Interfacial electric field optimization of DC tri-post insulator based on gradient surface conductance regulation[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1856-1865.
[2] 程涵, 魏威, Bilallqbal Ayubi, 等. 直流GIL中线形金属微粒电动力学行为研究[J]. 电工技术学报, 2021, 36(24): 5283-5293.
Cheng Han, Wei Wei, Ayubi B, et al. Study on the electrodynamic behavior of linear metal particles in DC gas insulated transmission line[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5283-5293.
[3] 张连根, 路士杰, 李成榕, 等. GIS中线形和球形金属微粒的运动行为和危害性[J]. 电工技术学报, 2019, 34(20): 4217-4225.
Zhang Liangen, Lu Shijie, Li Chengrong, et al. Motor behavior and hazard of spherical and linear particle in gas insulated switchgear[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4217-4225.
[4] Wang Jian, Li Qingmin, Liu Sihua, et al. Experimental studies of the air gap breakdown triggered by a free conducting particle in DC uniform field[C]//2016 IEEE International Conference on Dielectrics (ICD), Montpellier, France, 2016, 2: 1147-1150.
[5] 李杰, 李晓昂, 吕玉芳, 等. 正弦振动激励下GIS内自由金属微粒运动特性[J]. 电工技术学报, 2021, 36(21): 4580-4589, 4597.
Li Jie, Li Xiaoang, Lü Yufang, et al. Motion characteristics of free metal particles in GIS under sinusoidal vibration[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4580-4589, 4597.
[6] Khan Y, Sakai K I, Lee E K, et al. Motion behavior and deactivation method of free-conducting particle around spacer between diverging conducting plates under DC voltage in atmospheric air[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2003, 10(3): 444-457.
[7] Techaumnat B, Huynh V Q, Hidaka K. Numerical analysis and experiments on the electromechanical behavior of wired-shape conducting particles[J]. IEEE Transactions on Magnetics, 2018, 54(3): 1-5.
[8] 王健, 李庆民, 李伯涛, 等. 直流GIL中自由线形金属微粒的运动与放电特性[J]. 中国电机工程学报, 2016, 36(17): 4793-4800.
Wang Jian, Li Qingmin, Li Botao, et al. Motion and discharge behavior of the free conducting wire-type particle within DC GIL[J]. Proceedings of the CSEE, 2016, 36(17): 4793-4800.
[9] Cooke C M, Wootton R E, Cookson A H. Influence of particles on AC and DC electrical performance of gas insulated systems at extra-high-voltage[J]. IEEE Transactions on Power Apparatus and Systems, 1977, 96(3): 768-777.
[10] 魏威. 直流GIL电极表面纳米复合薄膜对放电及微粒的综合抑制机理研究[D]. 济南: 山东大学, 2020.
[11] Hama H, Okabe S. Factors dominating dielectric performance of real-size gas insulated system and their measures by dielectric coatings in SF6 and potential gases[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2013, 20(5): 1737-1748.
[12] 常亚楠, 王健, 李庆民, 等. 交直流气体绝缘管道输电装备微粒污染治理措施研究进展[J]. 高压电器, 2021, 57(10): 91-100, 110.
Chang Yanan, Wang Jian, Li Qingmin, et al. Research progress of particle contamination suppression measures in AC and DC gas-insulated transmission equipment[J]. High Voltage Apparatus, 2021, 57(10): 91-100, 110.
[13] 孙秋芹, 罗宸江, 王峰, 等. 直流GIL导体表面金属颗粒跳跃运动特性研究[J]. 电工技术学报, 2018, 33(22): 5206-5216.
Sun Qiuqin, Luo Chenjiang, Wang Feng, et al. Jumping characteristics of metal particle on the surface of DC gas insulated transmission line conductor[J]. Transactions of China Electrotechnical Society, 2018, 33(22): 5206-5216.
[14] Sakai K, Labrado Abella D, Suehiro J, et al. Charging and behavior of a spherically conducting particle on a dielectrically coated electrode in the presence of electrical gradient force in atmospheric air[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2002, 9(4): 577-588.
[15] Wohlmuth M. Motion and discharges of free metallic particles[C] //8th International Symposium on High Voltage Engineering, Yokohama, 1993: 115-119.
[16] 张乔根, 游浩洋, 马径坦, 等. 直流电压下SF6中自由线形导电微粒运动特性[J]. 高电压技术, 2018, 44(3): 696-703.
Zhang Qiaogen, You Haoyang, Ma Jingtan, et al. Motion behavior of free conducting wire-type particles in SF6 gas under DC voltage[J]. High Voltage Engineering, 2018, 44(3): 696-703.
[17] Wenger P, Beltle M, Tenbohlen S, et al. Combined characterization of free-moving particles in HVDC-GIS using UHF PD, high-speed imaging, and pulse-sequence analysis[J]. IEEE Transactions on Power Delivery, 2019, 34(4): 1540-1548.
[18] Abdel-Salam M, Weiss P, Lieske B. Discharges in air from point electrodes in the presence of dielectric plates-experimental results[J]. IEEE Transactions on Electrical Insulation, 1992, 27(2): 309-319.
[19] Khan Y, Oda A, Okabe S, et al. Wire particle motion behavior and breakdown characteristics around different shaped spacers within diverging air gap [J]. IEEJ Transactions on Power and Energy,2003, 123(11): 1288-1295.
[21] Parekh H, Srivastava K D. Effect of avalanche space charge field on the calculation of corona onset voltage[J]. IEEE Transactions on Electrical Insulation, 1979, EI-14(4): 181-192.
[22] Natsuume D, Inami K, Hama H, et al. Development of numerical computational model for metallic wire particles' behavior in GIS for the estimation of the partial discharge-free allowable maximum flight height[J]. IEEJ Transactions on Power and Energy, 2004, 124(4): 634-642.
Abstract In the DC gas-insulated switchgear and transmission lines (GIS/GIL), wire particles may exhibit a special firefly motion, namely, reverse motion without colliding with the ground electrode or suspended motion on the surface of the high-voltage electrode, which case is one of the principal factors affecting the insulation performance of the DC GIS/GIL.
To clarify the physical mechanism of the firefly motion, a test platform was established to observe the firefly movement and measure the particle charge amount. The motion and charge characteristics of the wire particles at different voltage levels showed that, the polarity change of the particle charge due to the space charge near the wire particles was the key influential factor of the firefly movement, while the corona onset voltage of the wire particles on the electrode surface tended to be the critical voltage for the polarity change of the particle charge, as shown in Fig.1. The mechanism is applicable to the flake or spiral particles with low curvature radius, which generate similar space charge at the tip and change the charged polarity, leading to the firefly.
Further, based on the photoionization model of the DC rod-plate gap corona, the corona onset voltage of the wire particles on the electrode surface was calculated, and the mathematical expression of the wire particle charge considering the corona voltage was fitted together with the measurement results. The charged wire particle motion model was thereby established considering the end concentration characteristics of the charge. Based on the proposed critical starting criterion of firefly, dynamic simulation of the linear particle flying motion was implemented as to obtain the onset electric field strength of firefly particles of different sizes in DC GIL.
Then, the onset electric field strength of firefly particles with different sizes in DC GIL was calculated based on the charged wire particle motion model, as shown in Fig.2, and the validity of the calculation results is verified in real GIL. The obtained results indicated that, with the particle length increase, the particle radius decrease or the pressure decrease, the onset electric field strength of firefly particles decreased under positive and negative DC voltage. The onset field strength of a wire particle with 0.2mm diameter and 5 mm length in a 100kV GIL under 0.5MPa SF6 environment was 2.78MV/m for negative DC voltage and 4.93 MV/m for positive DC voltage.
This study was based on the experiment in 110kV GIS, even though the particle motion characteristics at different voltage are numerically different from those at 110kV, the calculation method of particle motion characteristics are the same for different voltages. Therefore, the proposed research is suitable for DC GIL with different voltage levels, presents useful reference for DC GIL insulation design from the firefly particle suppression point of view.
keywords:DC gas insulated transmission line(GIL), wire particle, firefly mechanism, onset electric field strength
DOI: 10.19595/j.cnki.1000-6753.tces.220432
中图分类号:TM851
国家自然科学基金资助项目(51737005,51929701,52127812)。
收稿日期 2022-03-26
改稿日期 2022-04-26
常亚楠 男,1994年生,博士研究生,研究方向为GIL金属微粒运动与抑制。E-mail:changyanan9662@163.com
李庆民 男,1968年生,教授,博士生导师,研究方向为高电压与绝缘技术、放电物理。E-mail:lqmeee@ncepu.edu.cn(通信作者)
(编辑 郭丽军)