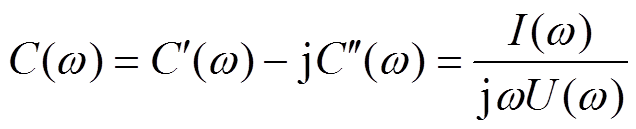 (1)
(1)
摘要 扩展德拜模型参数的准确辨识对油纸绝缘设备状态诊断具有重要意义。针对目前扩展模型参数辨识方法存在的不足,该文首次提出频谱解构法实现扩展德拜模型的精准辨识。首先,引入Kramers-Kronig变换对频域介电谱进行解耦,获取绝缘电阻谱线、几何电容谱线及弛豫极化谱线,并利用最小二乘法确定绝缘电阻和几何电容参数。然后,提出频谱微分法对极化复电容实部微分谱线进行逐次分解,根据微分谱线峰值点数和剩余谱线最大峰值点坐标求解极化等效电路参数,从而构建完整、精准的油纸绝缘扩展德拜等效电路模型。最后,通过仿真和实例验证了该方法辨识油纸绝缘扩展德拜模型参数的准确性。该文可为频域介电谱法开展油纸绝缘内部弛豫特性研究提供可靠的物理模型。
关键词:油纸绝缘 频域介电谱 扩展德拜模型 参数辨识 频谱解构法
在推进“双碳”目标实现的过程中,为确保电力设备安全可靠运行,诊断评估延长设备寿命已成为未来电网发展趋势。研究表明,油纸绝缘劣化是引起电力设备故障的重要原因。因此有效的油纸绝缘状态诊断方法是保障落实“双碳”目标、维护设备稳定运行的重要抓手[1]。建立油纸绝缘系统等效模型并进行参数分析是诊断油纸绝缘状态的有效方法。众多研究结果表明,扩展德拜模型参数能有效反映油纸绝缘状态:绝缘电阻Rg与油纸绝缘的电导率相关[2];几何电容Cg与油纸之间的界面极化附加电容相关[3],绝缘劣化,则Rg减小,Cg增大;极化支路数n与绝缘介质内的极化支路数相关,随着绝缘老化程度加深,介质内老化产物的数量增加,形成多个具有不同时间常数的极化支路,则极化支路数增加[4];极化支路电阻Rpi和极化支路电容Cpi反映绝缘的受潮程度,微水含量增加,Rpi减小,Cpi增大[5];此外,由扩展德拜模型参数推导得到的如最大时间常数τmax、平均时间常数τav和弛豫最小法谱线Lτmin等诸多特征量均能有效诊断油纸绝缘状态[6]。根据以上特征量准确诊断油纸绝缘状态的关键和前提在于模型参数的准确辨识,因此,深入研究扩展德拜模型参数辨识方法有着重要意义。
扩展德拜模型参数辨识方法按照测量数据的不同分为:基于回复电压数据、基于极化/去极化电流数据以及基于频域介电谱的参数辨识方法。文献[7]基于回复电压极化谱建立扩展德拜模型参数方程组,利用粒子群智能优化算法进行参数辨识,此方法具有公式推导简单和曲线拟合度高的优点,但仅以曲线拟合效果判断极化支路数缺乏理论依据,且粒子寻优得到模型参数存在随机性;文献[8-10]分别基于回复电压数据、极化电流数据和去极化电流数据,利用微分谱线的峰值点确定极化支路数,并通过对子谱线末端随机取点的方式计算得到扩展德拜极化支路参数,提高了极化支路数辨识结果的可信度,但是末端取点存在一定的人为因素,选点不同则极化支路参数辨识结果也会发生变化。文献[11]提出了去极化电流二阶微分解谱法,提高极化支路数和极化支路参数辨识结果的可靠性,然而在本质上没有解决末端取点导致参数辨识结果不唯一的问题。文献[12-13]利用去极化电流数据,分别通过三次微分解析法以及稳定图和状态空间模型融合算法求解极化等效电路参数,其辨识结果具有唯一确定的优点,然而无法求解扩展德拜模型中几何等效支路参数。频域介电谱蕴含丰富的绝缘信息,文献[5,14]融合遗传算法与L-M算法求解扩展德拜模型参数,然而油纸绝缘频域响应数据的实部和虚部相差较大,制定目标函数的权值系数存在人为因素,且参数辨识结果具有随机性。文献[15]对复介电常数虚部进行微分并分析了1~4阶微分谱线的峰值点特性,提出根据4阶微分谱线峰值点数判断极化支路数,然而虚部微分公式复杂,且包含了电导的贡献,无法进一步计算扩展德拜模型其他参数。综上所述,目前尚未有能够完整且确定扩展模型参数的辨识方法。
针对以上不足,本文基于油纸绝缘频域介电谱数据,结合Kramers-Kronig(K-K)变换和微分解谱法,首次提出频谱解构法实现扩展德拜模型参数的辨识。首先,引入K-K变换对频域介电谱进行解耦,得到绝缘电阻谱线、几何电容谱线以及弛豫极化谱线,并通过最小二乘法计算绝缘电阻和几何电容参数;然后提出频谱微分法对极化复电容实部微分谱线进行逐次分解,根据微分谱线峰值点数和剩余谱线最大峰值点坐标求解极化等效电路参数,最终构建完整、精准的油纸绝缘扩展德拜等效电路模型。该方法利用绝缘电阻和几何电容的频域特性,通过数值计算确定绝缘电阻和几何电容参数;再由实部微分子谱线的叠加特性和最大峰值点的唯一性,确定了极化支路数和极化支路参数,避免了智能优化算法和末端选点法的随机性,进而真正实现完整的油纸绝缘扩展德拜模型参数辨识。
交变电场下的绝缘介质响应过程包括电导过程和极化过程,随着电场频率的不同,介质内部发生不同程度的电导和极化响应[16],因此材料中输出电流的相位和幅度也会发生变化。复电容是关于电流和电压的函数,因此常用来反映宏观水平上电荷的传导和极化,表示为
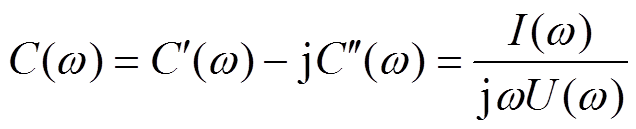 (1)
(1)
式中,I(ω)和U(ω)是响应复电流和施加的复电压,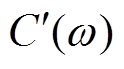 和
和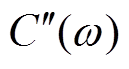 是复电容C(ω)的实部和虚部,分别反映了介电响应过程中电荷的储存和能量的损耗。测量电介质介电响应的过程即测量电介质复电容的过程。此外,复电容还可以用复极化率
是复电容C(ω)的实部和虚部,分别反映了介电响应过程中电荷的储存和能量的损耗。测量电介质介电响应的过程即测量电介质复电容的过程。此外,复电容还可以用复极化率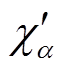 和
和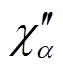 表示为[17]
表示为[17]
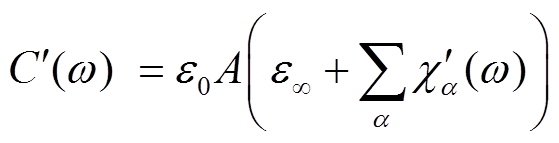 (2)
(2)
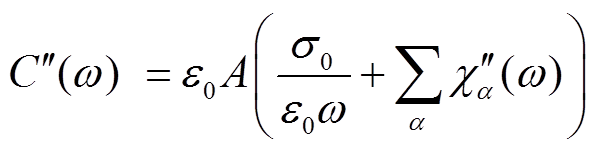 (3)
(3)
式中,ε0为真空介电常数;A为仅和介质样品结构大小相关的形状系数;ε∞为无穷频率相对介电常数,σ0为电导率;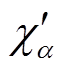 和
和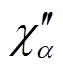 分别为单一弛豫过程复极化率
分别为单一弛豫过程复极化率 的实部和虚部。
的实部和虚部。
电介质复极化率定义为交变电场下介质的响应函数f(t)的傅里叶变换,表达式为[18]
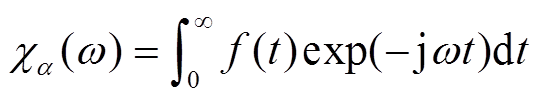 (4)
(4)
式中,响应函数f(t)描述的是电介质中参与弛豫极化的微观粒子在交变电场的作用下的滞后过程。从式(4)可以看出,复极化率的实部和虚部是由同一个介质的响应函数分离出来的,因此它们之间有不可切割的联系,二者互为Hilbert变换,且满足Kramers-Kronig(K-K)关系。在因果律成立的前提下,K-K关系可以表示为[17]
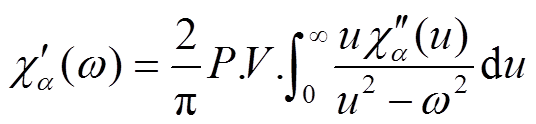 (5)
(5)
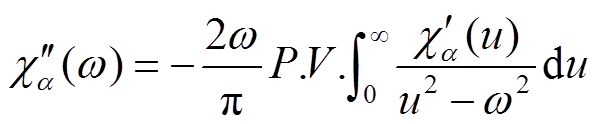 (6)
(6)
式中,P.V.表示柯西主值积分。从式(5)和式(6)可以看出,已知复极化率实部(虚部),则可以利用K-K关系计算得到复极化率虚部(实部),该计算过程即Kramers-Kronig(K-K)变换。
德拜假设电介质中产生弛豫过程的微观粒子仅有偶极子,并且偶极子之间没有相互作用,得到单一弛豫过程的复极化率表达式为[19]
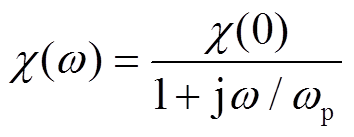 (7)
(7)
式中,χ(0)为电介质在静电场下的极化强度幅值;ωp为介质的特征频率,为弛豫时间的倒数。
设油纸绝缘复合介质中有N个不同弛豫时间的弛豫过程,每个弛豫过程对应的特征频率为ωpi,根据式(2)、式(3)和式(7),可得到油纸绝缘扩展德拜模型等效电路如图1所示[5]。
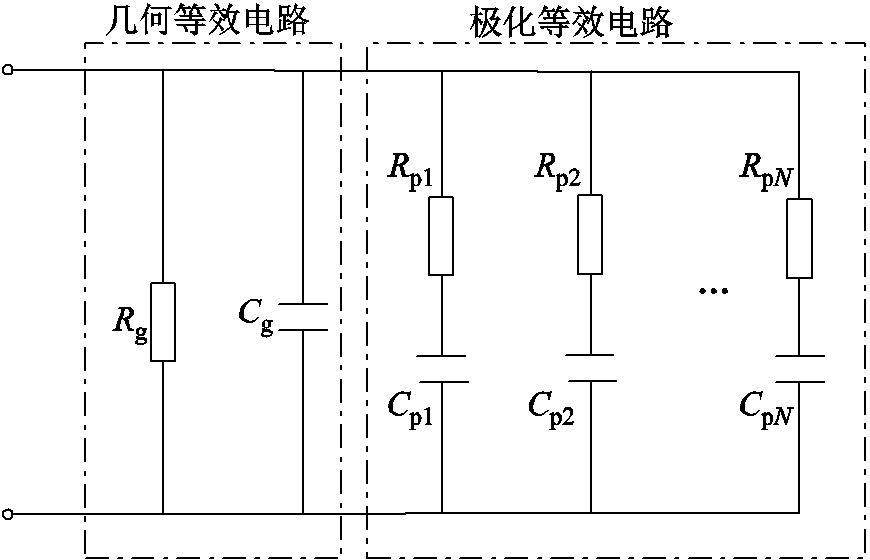
图1 油纸绝缘扩展德拜模型等效电路
Fig.1 Equivalent circuit of extended Debye model for oil paper insulation
在图1中,扩展德拜模型等效电路包括几何等效电路和由N条极化支路构成的极化等效电路两部分组成。几何等效电路中绝缘电阻Rg=σ0A反映了油纸绝缘系统的电导情况;几何电容Cg=ε0Aε∞表示测量频率范围内不发生弥散现象的电容总和[19];极化等效电路中极化支路电容Cpi=ε0Aχpi(0)表示第i条极化支路的复电容幅值;极化支路电阻Rpi=τpi/ Cpi,反映了第i条极化支路的能量损耗;τpi表示第i条极化支路弛豫时间常数,数值为特征频率ωpi的倒数。
由图1可得扩展德拜模型的导纳Y为
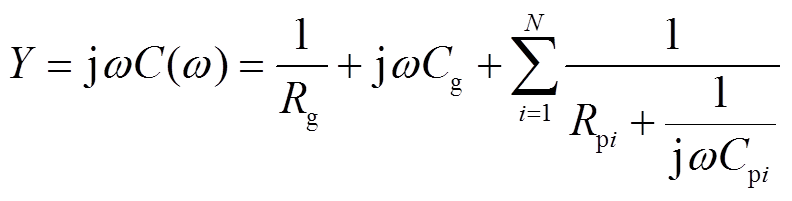 (8)
(8)
对式(8)进行变换,得到复电容C(ω)为
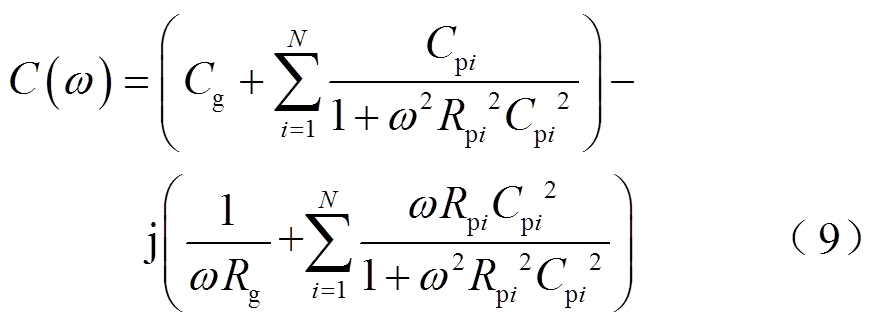
由式(9)可得,复电容实部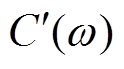 和复电容虚部
和复电容虚部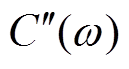 分别表示为
分别表示为
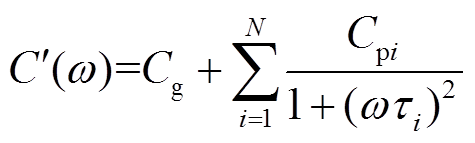 (10)
(10)
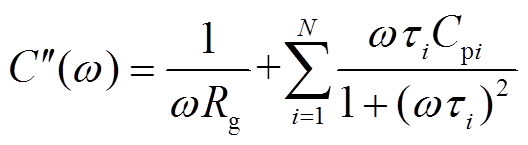 (11)
(11)
由式(10)和式(11)可以看出,复电容实部由几何电容和N条极化等效支路的贡献耦合而成,复电容虚部由绝缘电阻和N条极化等效支路的贡献耦合而成,因此根据测量复电容谱线实现扩展德拜模型唯一参数辨识的难点在于:①测量复电容谱线包含了绝缘电阻、几何电容和极化过程的信息,如何剔除绝缘电阻和几何电容的贡献并提取仅含有极化等效电路贡献的弛豫极化谱线;②解耦得到的弛豫极化谱线中含有多条极化支路的贡献,如何判断极化支路数并实现极化支路参数的完整辨识。下文将详述以上问题的解决方法以及基于频域介电谱的扩展德拜模型参数辨识流程。
实际频域介电谱(Frequencg Domain Spectroscopy, FDS)法测量得到的复电容实部中一定包含几何电容的贡献,复电容虚部低频部分一定包含绝缘电阻的贡献[17],根据复电容和复极化率的换算关系,结合式(5)和式(6)可得到测量复电容实部和虚部的关系为
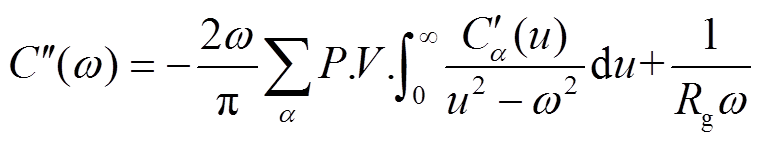 (13)
(13)
式中,Cα=ε0Aχα表示单一极化支路复电容,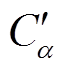 、
、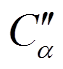 为
为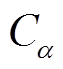 的实部和虚部。
的实部和虚部。
由式(12)和式(13)可知,测量复电容的实部和虚部一定不满足K-K关系,即复电容的实部和虚部彼此之间并不能通过K-K变换计算获得。由于绝缘电阻仅对复电容虚部有贡献,且经过K-K变换后得到的复电容实部结果为0;几何电容仅对复电容实部有贡献,且经过K-K变换后得到的复电容虚部结果为0。因此测量复电容实部进行K-K变换计算获得的复电容虚部与测量复电容虚部相差的部分即绝缘电阻的贡献;测量复电容虚部进行K-K变换计算获得的复电容实部与测量复电容实部相差的部分即几何电容的贡献。因此得到绝缘电阻和几何电容的复电容谱线的表达式为
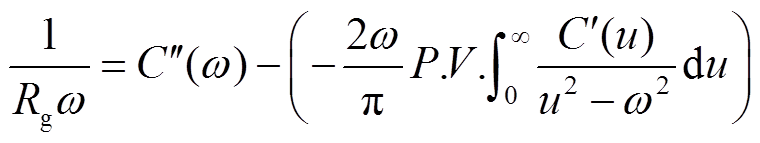 (14)
(14)
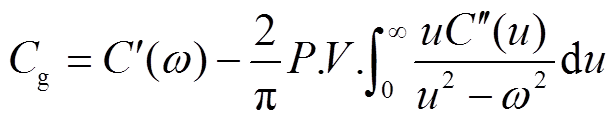 (15)
(15)
在双对数坐标系下,绝缘电阻谱线呈现为斜率为-1的直线。因此用最小二乘直线对绝缘电阻谱线进行拟合,根据拟合直线的纵截距即可计算得到绝缘电阻Rg。几何电容谱线在双对数坐标系呈现为斜率为0的直线,因此用最小二乘直线对无穷频率电容谱线进行拟合,根据拟合直线的纵截距即可计算得到几何电容Cg。将测量复电容谱线减去绝缘电阻和几何电容的贡献后即得到弛豫极化谱线。
以上分析表明,通过K-K变换即可实现绝缘电阻、几何电容、弛豫极化谱线的解耦分析,并确定绝缘电阻和几何电容参数。
由式(10)和式(11)可得剔除绝缘电阻和几何电容的贡献后的极化等效电路复电容(简称极化复电容)实部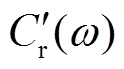 和虚部
和虚部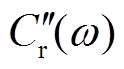 表达式为
表达式为
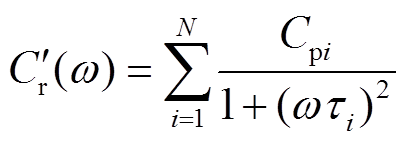 (16)
(16)
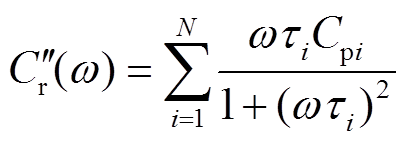 (17)
(17)
由式(16)和式(17)可知,极化复电容是由N个不同时间常数极化支路的介电响应过程组成。为准确判断弛豫极化谱线中含有的极化支路数N,且将本文提出的实部微分方法与文献[15]的虚部微分方法进行比较,分别对式(16)和式(17)进行坐标变换和微分处理。令ω=ex,对x进行一次微分,得到极化复电容实部一次微分谱线的表达式为
 (18)
(18)
式中,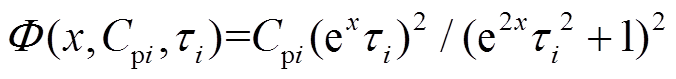 表示第i条极化复电容实部微分子谱线,其特征是具有单一峰值点(ln1/τi,1/4Cpi),两侧的曲线逐渐衰减至0。
表示第i条极化复电容实部微分子谱线,其特征是具有单一峰值点(ln1/τi,1/4Cpi),两侧的曲线逐渐衰减至0。
极化复电容虚部一次微分谱线的表达式为
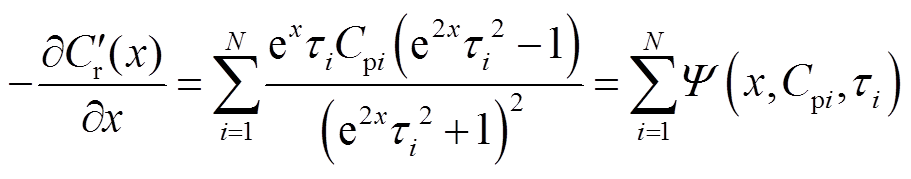 (19)
(19)
式中,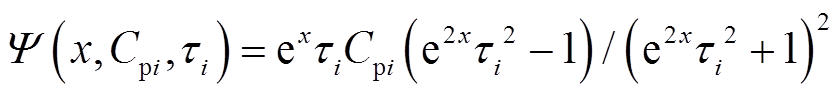 表示第i条极化复电容虚部微分子谱线,当x→-∞时,
表示第i条极化复电容虚部微分子谱线,当x→-∞时,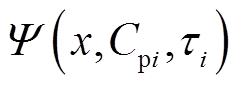 →0。
→0。
为了研究多条极化支路叠加后的极化复电容微分谱线特性,现以3个不同弛豫时间常数极化支路叠加而成的复电容谱线为例进行分析,如图2和图3所示,各极化支路的极化电容和时间常数分别为Cp1=3,Cp2=2,Cp3=1pF;τ1=1s,τ2=0.1s,τ3=0.01s。
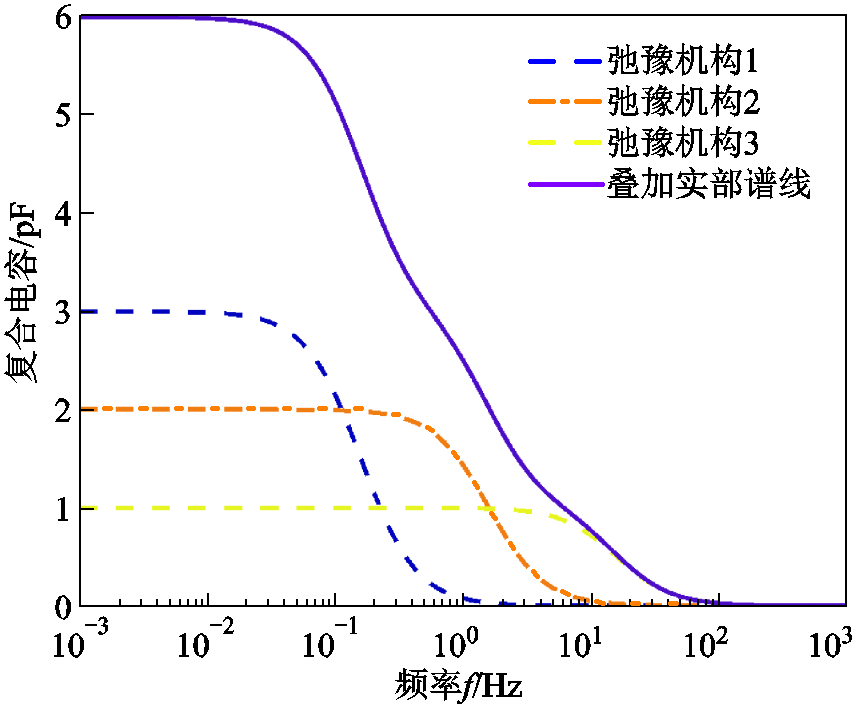
图2 复电容实部叠加谱线
Fig.2 Real part of superposition spectral line of complex capacitance

图3 复电容虚部叠加谱线
Fig.3 Imaginary part of superposition spectral line of complex capacitance
由图2和图3可知,叠加后的复电容虚部出现弛豫峰相互覆盖的情况,复电容实部中多个阶梯叠加成一个坡度较缓的阶梯,因此不能通过虚部的弛豫峰数以及实部的阶梯数来准确判断极化支路数。
为了准确判断极化支路数,本文对复电容实部曲线进行一次微分,并计算各个极化支路的微分子谱线,如图4所示。
由图4可以看出,经过一次微分后得到的复电容实部微分谱线的单调性相较于复电容实部叠加曲线有了质的变化。其原因在于每个极化支路产生的复电容实部贡献经过微分后,由原本的阶梯特征谱线改变为具有单一峰值点的弛豫峰谱线,因此根据复电容实部微分谱线即可以清晰地判断极化支路数。进一步观察图4中子谱线峰值点与微分谱线峰值点的对应关系,可以发现极化支路1的子谱线峰值点与微分谱线峰值点基本重合,极化支路2、3的微分子谱线的峰值点与微分谱线的峰值点的重合程度次之,且存在向右侧偏移的现象。这是由于极化支路1的极化电容数值最大,在微分子谱线上表现为子谱线峰值点能真实准确地反映在叠加后的微分谱线上,受其他极化支路的影响几乎可以忽略;而极化支路2、3的极化电容数值较小,因此受到相邻子谱线的影响,微分子谱线的峰值点反映在叠加后的微分谱线上产生了一定偏移。
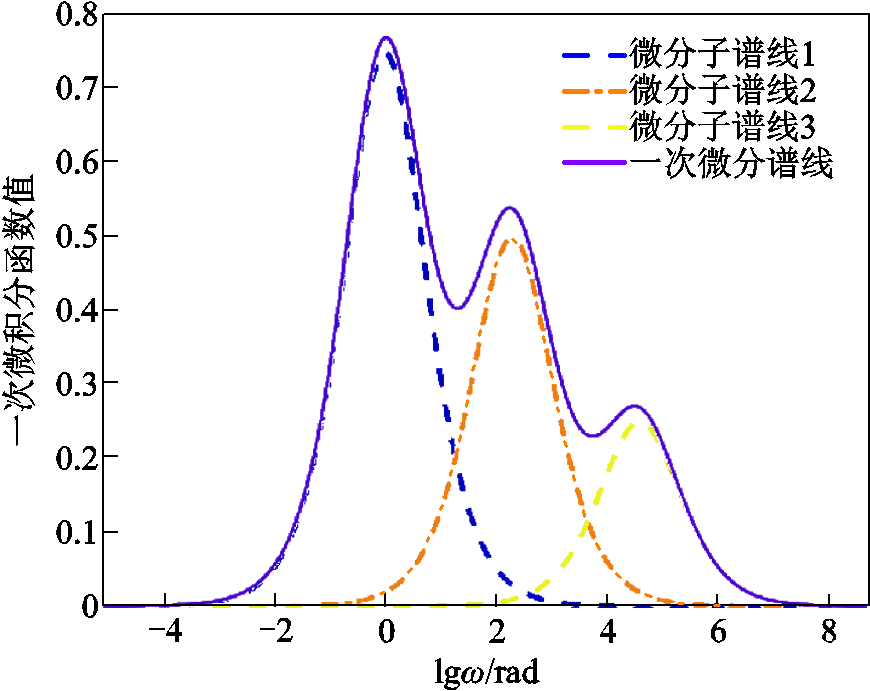
图4 复电容实部一次微分谱线及其子谱线
Fig.4 First order differential spectral line and its sub spectral line of real part of complex capacitance
通过以上分析对比,可总结得到极化等效电路的复电容实部微分谱线以及微分子谱线具有以下特性:
1)极化等效支路复电容实部微分谱线由多个具有单峰值的子谱线叠加而成,相较于复电容虚部谱线,复电容实部微分谱线各峰值点更为明显,且不存在波谷和峰值点相互叠加的现象,因此,可靠性更高,可作为极化支路数的判据。
2)最大极化电容极化支路的实部微分子谱线峰值点与叠加后的微分谱线的峰值点基本重合,较小极化电容极化支路的实部微分子谱线峰值点与对应的微分谱线的峰值点存在一定的覆盖和偏移现象。
3)各复电容实部微分子谱线的峰值点坐标为(ln(1/τi), Cpi/4),根据复电容实部微分谱线的最大峰值点(xm,ym),可以求解最大极化电容的极化支路参数极化电容Cpim以及弛豫时间常数τim,再将后者除以前者便可计算出极化电阻Rpim,即
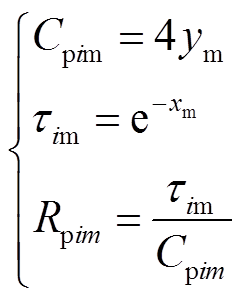 (20)
(20)
通过以上对微分谱线特性的分析,可知根据复电容实部微分谱线的最大峰值点坐标便可求得最大极化电容极化支路的极化电容、弛豫时间常数和极化电阻;从当前复电容实部微分谱线中减去最大极化电容极化支路的贡献
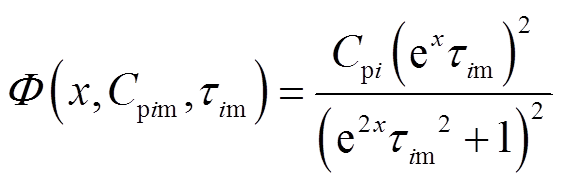 (21)
(21)
得到剩余谱线,再从剩余曲线末端的峰值点坐标值,求出第二大极化电容极化支路参数,依此类推直到最后一个峰值点,即完成极化等效电路参数辨识。
结合2.1节和2.2节对于几何等效电路和极化等效电路的参数辨识方法研究,可得到基于频谱解构法的扩展德拜模型参数辨识步骤如下:
(1)对油纸绝缘样品进行FDS测量,获得复电容数据。分别对测量复电容实部和虚部进行K-K变换,得到计算复电容实部和虚部。
(2)将测量复电容实部减去计算复电容实部,得到几何电容谱线;将测量复电容虚部减去计算复电容虚部,得到绝缘电阻谱线;剩余谱线为极化复电容谱线。
(3)分别以最小二乘直线拟合几何电容谱线和绝缘电阻谱线,根据纵截距计算几何电容参数和绝缘电阻参数;对极化等效电路复电容实部谱线求一次微分,并乘以-1/2,得到极化等效电路复电容实部微分谱线。微分谱线峰值点数即极化支路数N。
(4)从实部微分谱线得到最大峰值点坐标值(xm,ym),并根据式(20)计算最大极化电容极化支路参数极化电容Cpim、弛豫时间常数τim和极化电阻Rpim。
(5)从实部微分谱线减去最大极化电容极化支路子谱线,得到剩余微分曲线。
(6)判断已求解的弛豫机构数是否小于N,若小于则返回第(4)步,从剩余微分曲线得到最大峰值点坐标值,求出对应最大极化电容极化支路参数极化电容Cpim-1、弛豫时间常数τim-1和极化电阻Rpim-1,依此类推,直到求解完各极化支路参数,得到扩展德拜模型参数完整辨识结果。
得到基于频谱解构法的扩展德拜模型唯一参数辨识流程图,如图5所示。
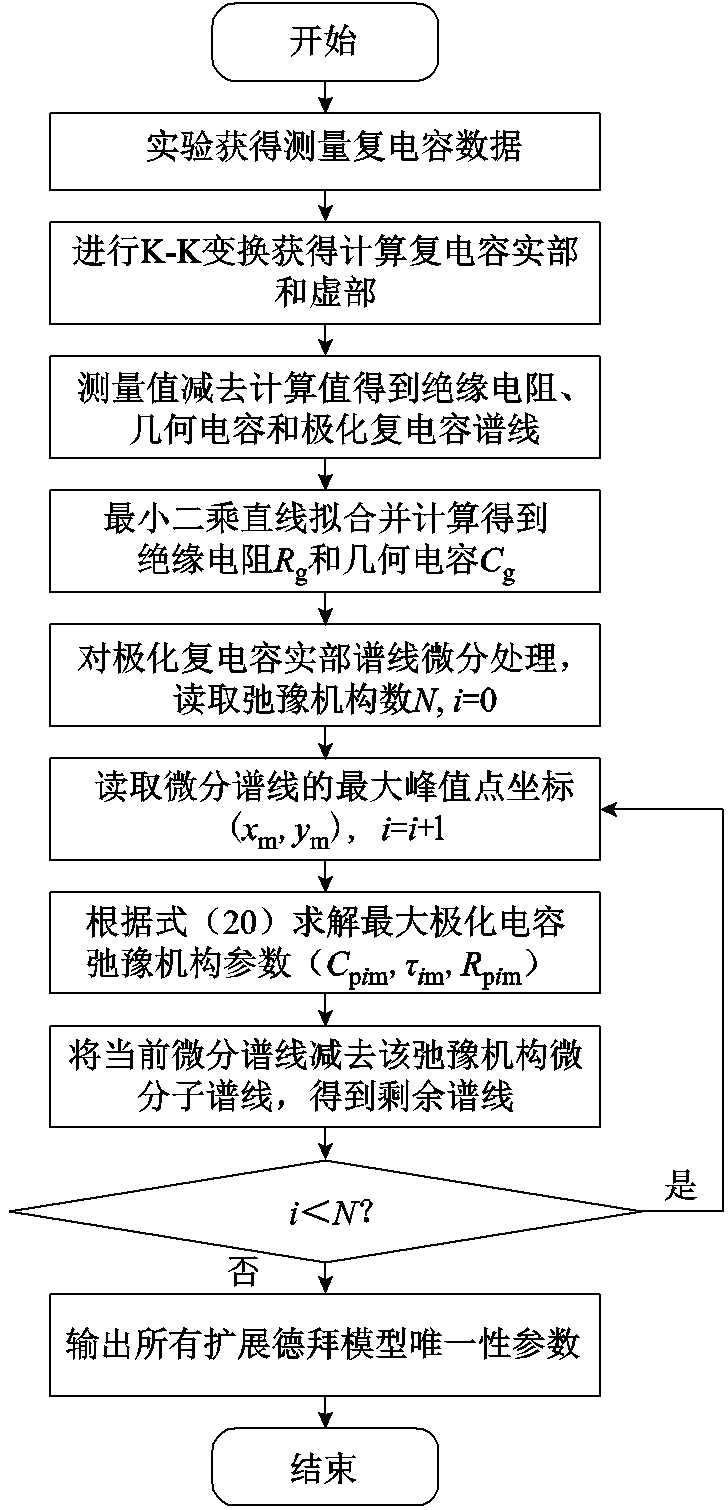
图5 扩展德拜模型参数辨识流程图
Fig.5 Flow chart of parameter identification for extended Debye model
为了验证上述参数辨识方法的有效性和准确性,现随机选取文献[14]基于FDS实测数据辨识得到的具有6条极化支路的扩展德拜等效模型,模型参数数值见表1。
表1 仿真扩展德拜模型参数数值
Tab.1 Simulating extended Debye model parameter settings
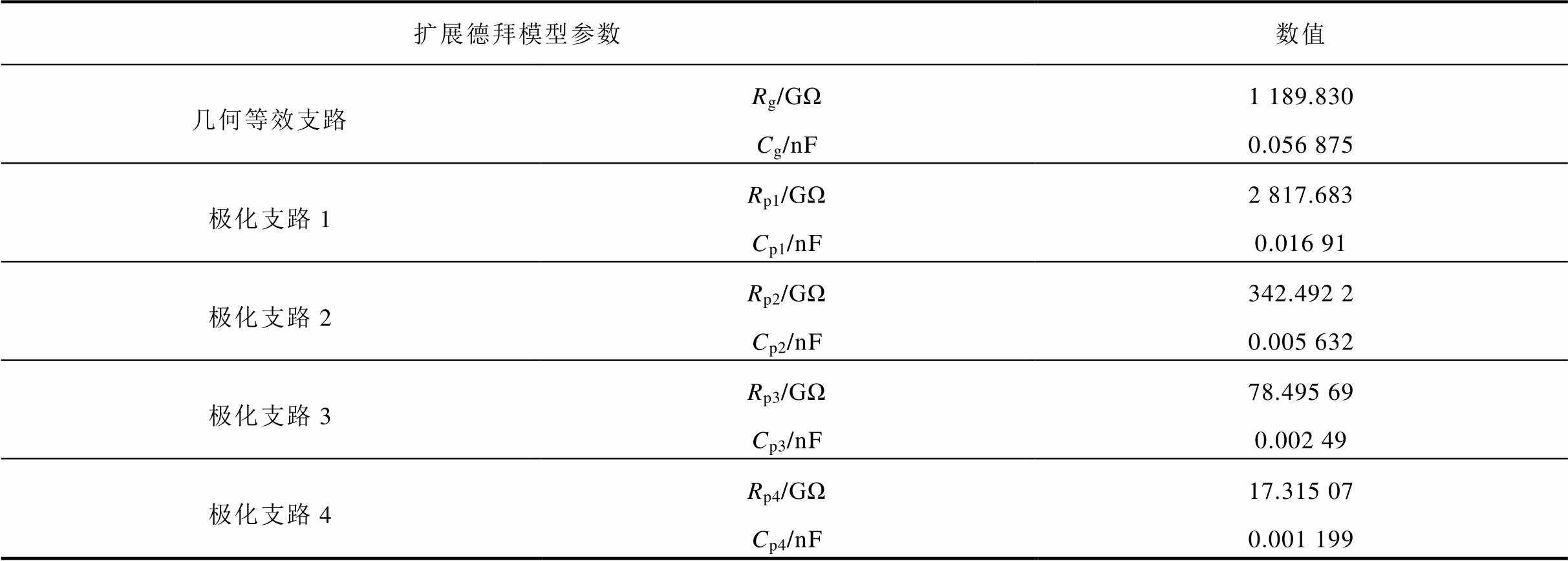
扩展德拜模型参数数值 几何等效支路Rg/GΩ1 189.830 Cg/nF0.056 875 极化支路1Rp1/GΩ2 817.683 Cp1/nF0.016 91 极化支路2Rp2/GΩ342.492 2 Cp2/nF0.005 632 极化支路3Rp3/GΩ78.495 69 Cp3/nF0.002 49 极化支路4Rp4/GΩ17.315 07 Cp4/nF0.001 199
(续)

扩展德拜模型参数数值 极化支路5Rp5/GΩ2.010 289 Cp5/nF0.001 018 极化支路6Rp6/GΩ0.166 3 Cp6/nF0.001 357
根据以上模型参数,结合式(10)和式(11)计算仿真得到复电容谱线,如图6所示。

图6 仿真复电容实部和虚部
Fig.6 The real and imaginary parts of a simulating complex capacitor
利用K-K变换分别对复电容实部和虚部谱线进行解耦,获得绝缘电阻谱线和几何电容谱线,并以最小二乘直线拟合,得到仿真复电容实部、虚部解耦如图7所示,拟合公式和几何等效电路参数计算结果见表2。
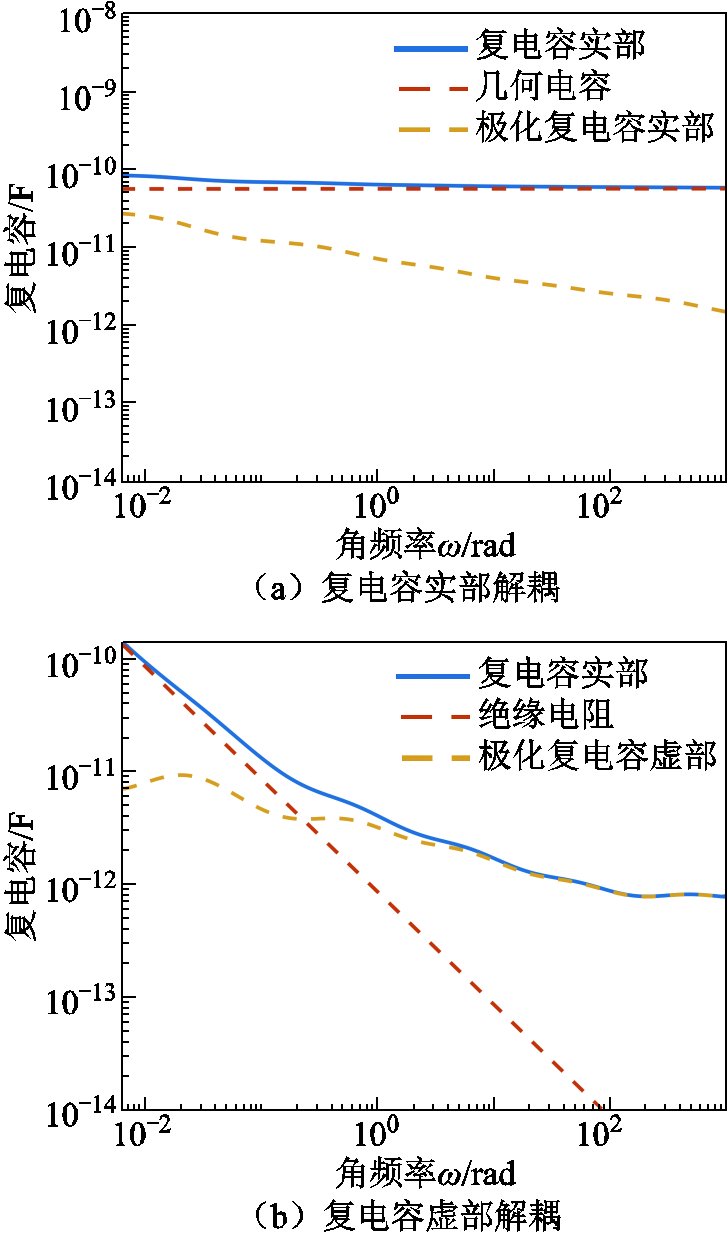
图7 仿真复电容谱线解耦
Fig.7 Decoupling simulated complex capacitance
表2 直线拟合公式和参数辨识结果
Tab.2 Linear fitting formula and parameter identification results

参数拟合公式计算值 Rg/GΩlny=-0.9968lnω-27.80531 190.359 1 Cg/nFlny=0.0007lnω-23.59630.056 529
根据图7a的极化复电容实部谱线,进一步计算扩展德拜模型的极化等效电路参数。按照式(18)对极化复电容实部进行微分,得到极化复电容实部微分谱线,并将峰值点以竖线标记,如图8所示。
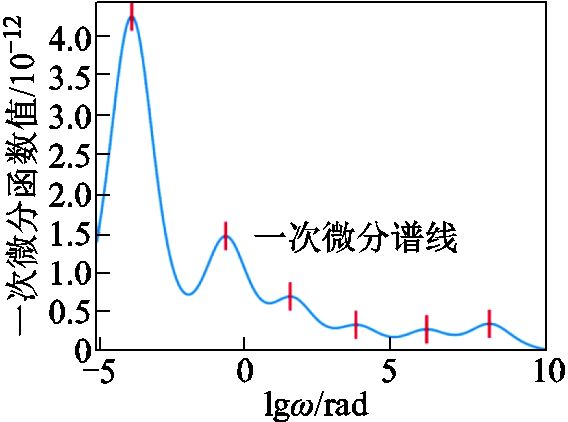
图8 极化复电容实部一次微分谱线
Fig.8 First order differential spectrum of real part of polarized complex capacitance
由图8中可以清晰地看出,一次微分谱线有6个峰值点,因此可以判断该谱线包含了6条极化支路数。设图8的一次微分谱线为当前剩余谱线,按照图5流程求解各极化支路参数。图9为极化复电容实部微分谱线的解谱过程。图10所示解谱后剩余微分谱线。表3所示为各峰值点坐标。
根据表3所计算得到的结果,由式(20)便可计算出各极化支路参数,将计算结果与设定值进行对比,见表4。
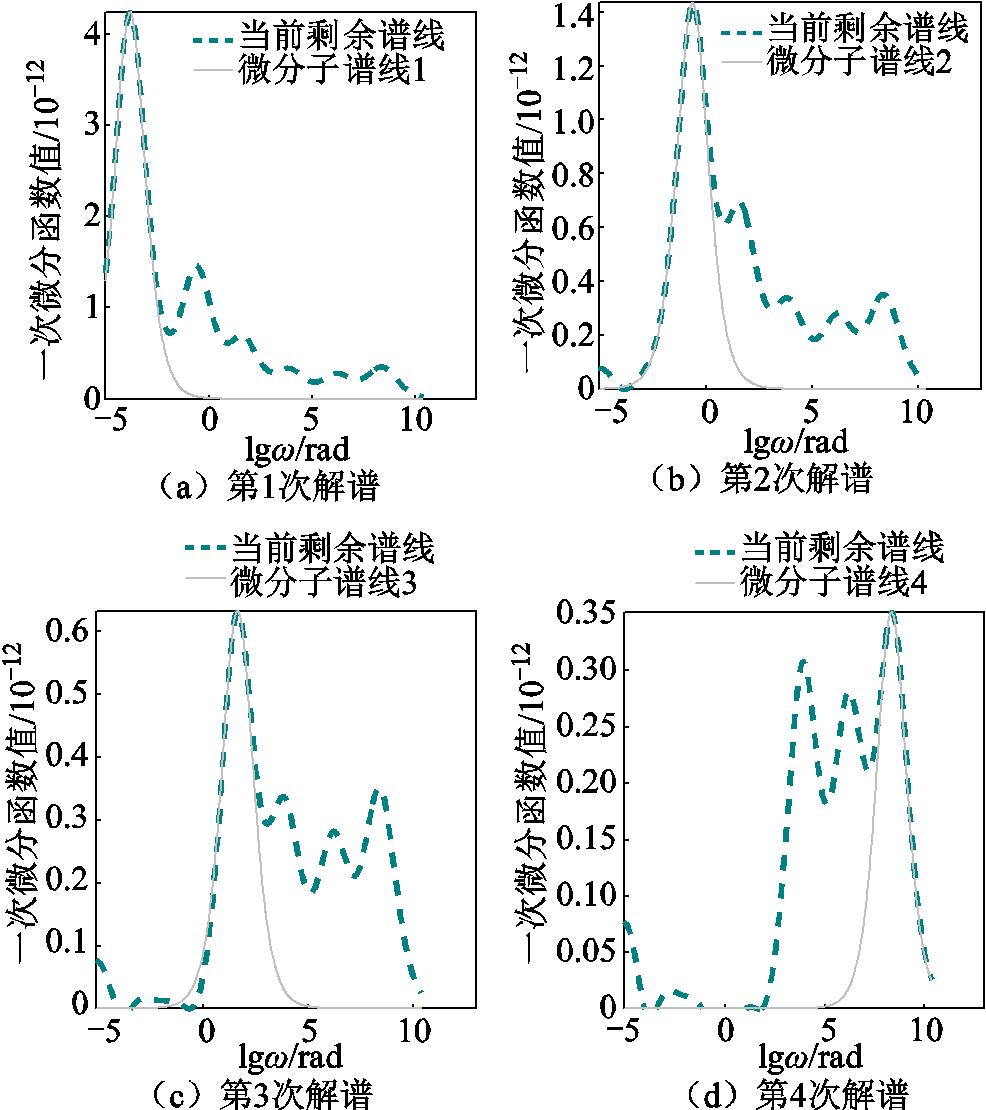
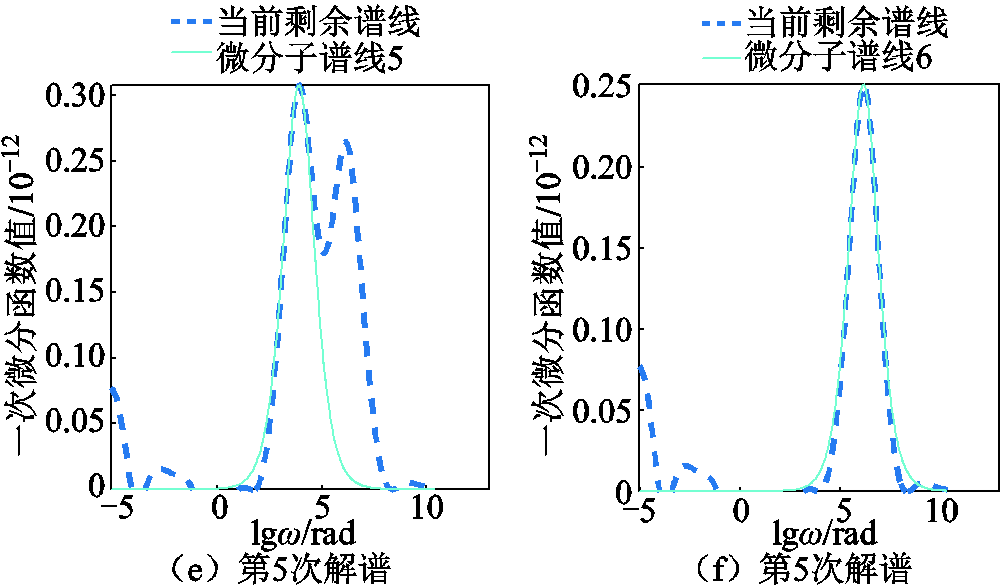
图9 极化复电容实部微分谱线解谱过程
Fig.9 Spectral decomposition of polarized complex capacitance real differential lines
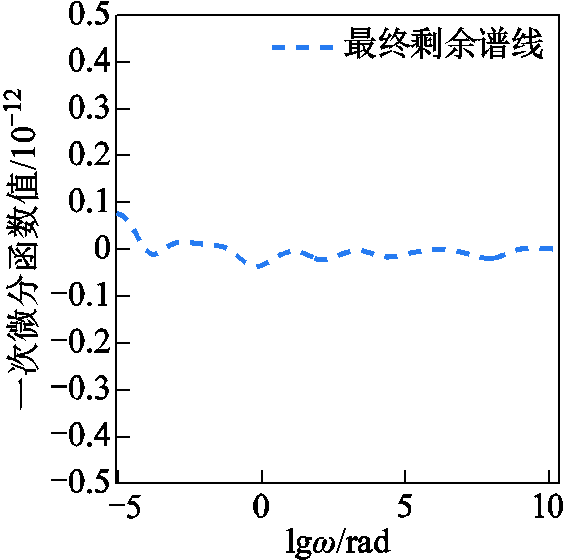
图10 最终剩余谱线
Fig.10 Final residual lines
表3 逐次解谱获得的最大峰值点坐标
Tab.3 Coordinates of maximum peak point obtained by successive spectrum resolution
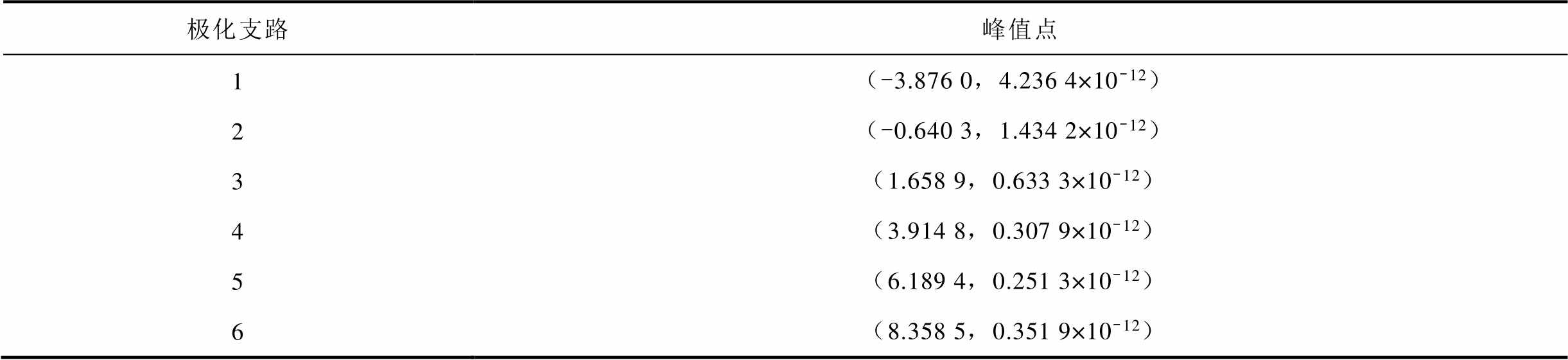
极化支路峰值点 1(-3.876 0,4.236 4×10-12) 2(-0.640 3,1.434 2×10-12) 3(1.658 9,0.633 3×10-12) 4(3.914 8,0.307 9×10-12) 5(6.189 4,0.251 3×10-12) 6(8.358 5,0.351 9×10-12)
为直观比较计算值和模型值的差异程度,定义为

从表4可以看出,频谱微分法求解的扩展德拜模型参数与仿真模型参数相对比,最高相对误差不超过7%。
根据求解得到绝缘电阻、几何电容以及极化等效电路参数,按照式(10)和式(11)得到计算复电容实部和计算复电容虚部,将其与仿真模型的复电容实部和虚部谱线进行对比,如图11所示。可以看出,计算复电容和模型复电容谱线具有较高的一致性。
表4 扩展德拜模型参数求解结果与误差
Tab.4 Solution results and errors of extended Debye model parameters
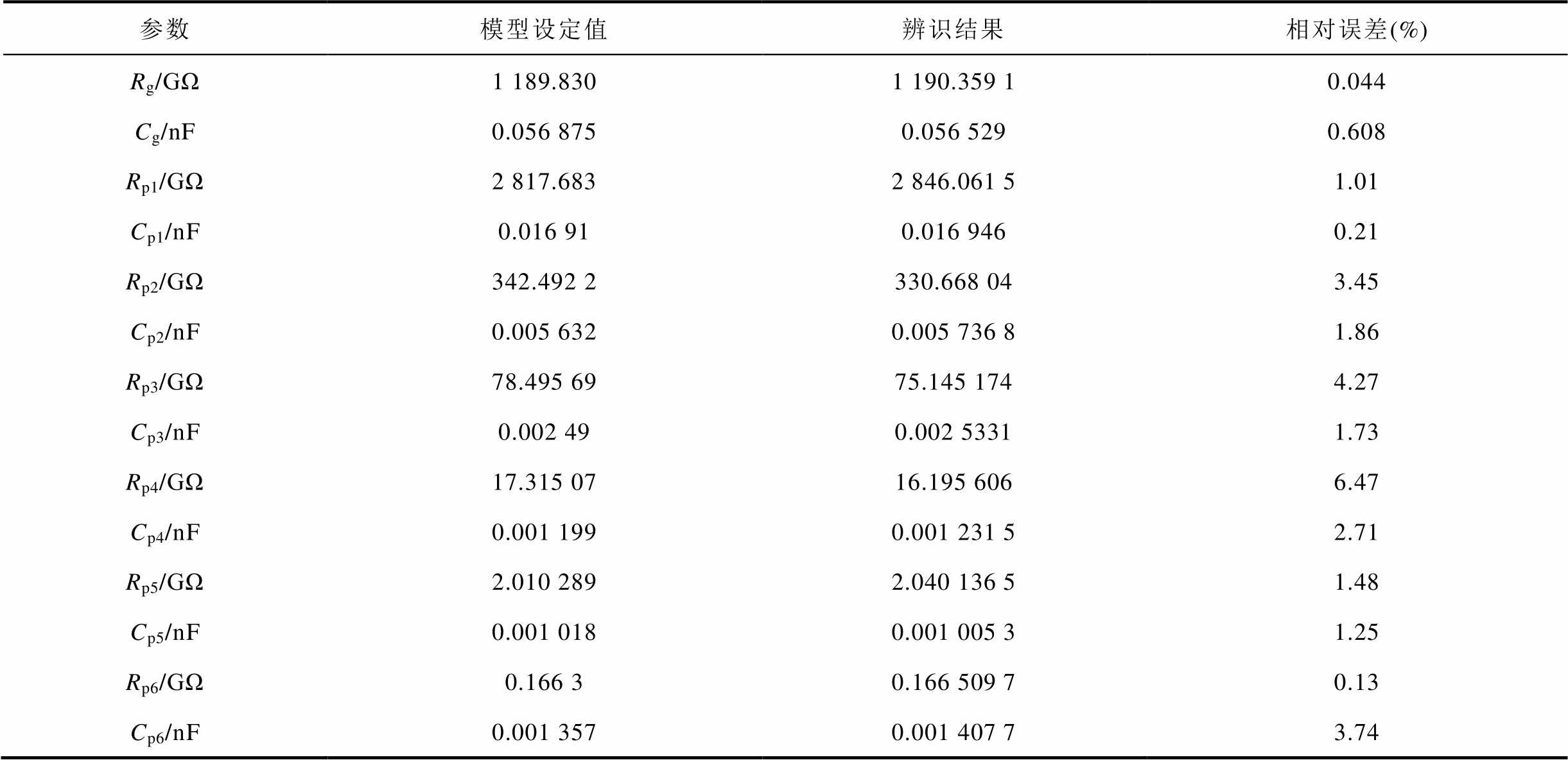
参数模型设定值辨识结果相对误差(%) Rg/GΩ1 189.8301 190.359 10.044 Cg/nF0.056 8750.056 5290.608 Rp1/GΩ2 817.6832 846.061 51.01 Cp1/nF0.016 910.016 9460.21 Rp2/GΩ342.492 2330.668 043.45 Cp2/nF0.005 6320.005 736 81.86 Rp3/GΩ78.495 6975.145 1744.27 Cp3/nF0.002 490.002 53311.73 Rp4/GΩ17.315 0716.195 6066.47 Cp4/nF0.001 1990.001 231 52.71 Rp5/GΩ2.010 2892.040 136 51.48 Cp5/nF0.001 0180.001 005 31.25 Rp6/GΩ0.166 30.166 509 70.13 Cp6/nF0.001 3570.001 407 73.74
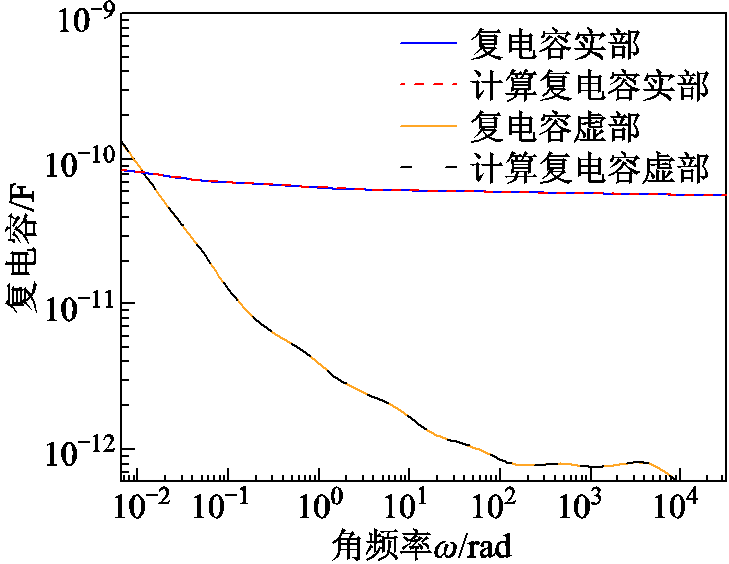
图11 复电容实部和虚部拟合曲线
Fig.11 Fitting curves for real and imaginary parts of complex capacitance
本节以一台油浸式自耦调压器(型号为TSJA30/0.5)的实测数据为例,进一步验证本文提出的参数辨识方法应用于现场油纸绝缘系统的扩展德拜模型建模的可行性和准确性。首先利用DIRANA介电响应分析仪采集该调压器的频域介电谱数据,采样点设置在10-3~103Hz之间,电压输出峰值为200V。然后根据图6所示步骤对测量介电谱进行分解,辨识得到扩展德拜模型唯一参数,见表5。最后根据计算得到的模型重构频域介电谱,并与测量频域介电谱进行对比,如图12所示。
由图12可以看出,计算复电容实部和虚部与测量谱线在低频段吻合情况良好。由于10rad处存在复杂夹层界面极化,计算复电容实部在10rad处相较于测量复电容实部以及计算复电容高频处相较于测量复电容虚部有些许误差。而总体来说计算谱线和测量谱线吻合情况较好且趋势一致,因此验证了本文提出的方法应用于现场实测数据的可行性和准确性。
表5 TSJA30/0.5扩展德拜模型参数辨识结果
Tab.5 TSJA30/0.5 extended Debye model parameter identification results
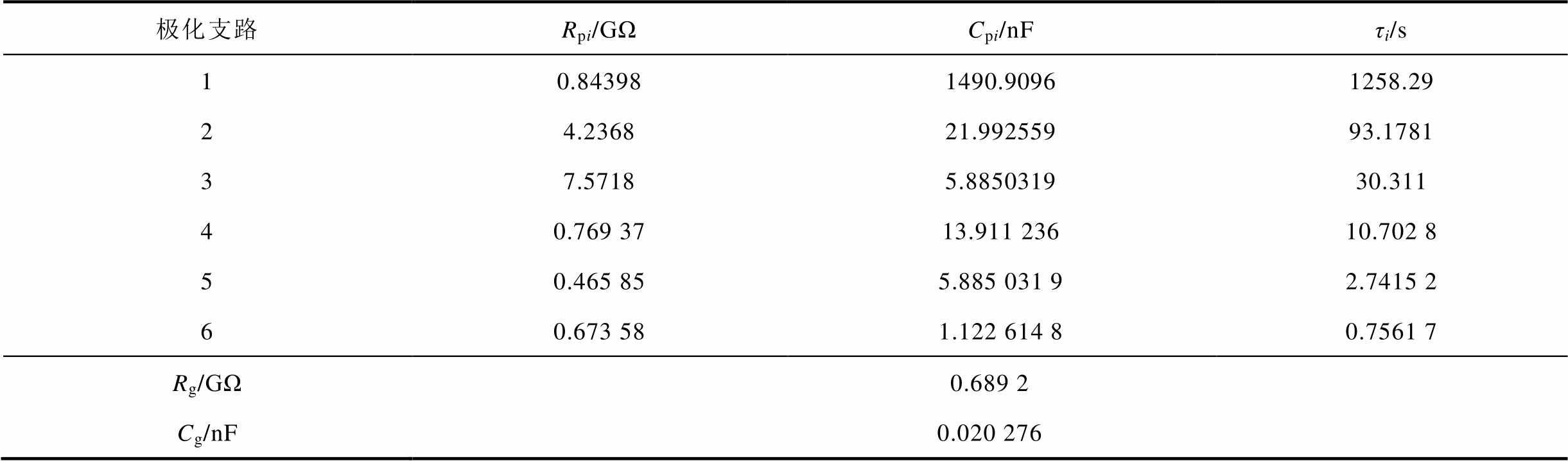
极化支路Rpi/GΩCpi/nFτi/s 10.843981490.90961258.29 24.236821.992559 93.1781 37.57185.885031930.311 40.769 3713.911 23610.702 8 50.465 855.885 031 92.7415 2 60.673 581.122 614 80.7561 7 Rg/GΩ0.689 2 Cg/nF0.020 276
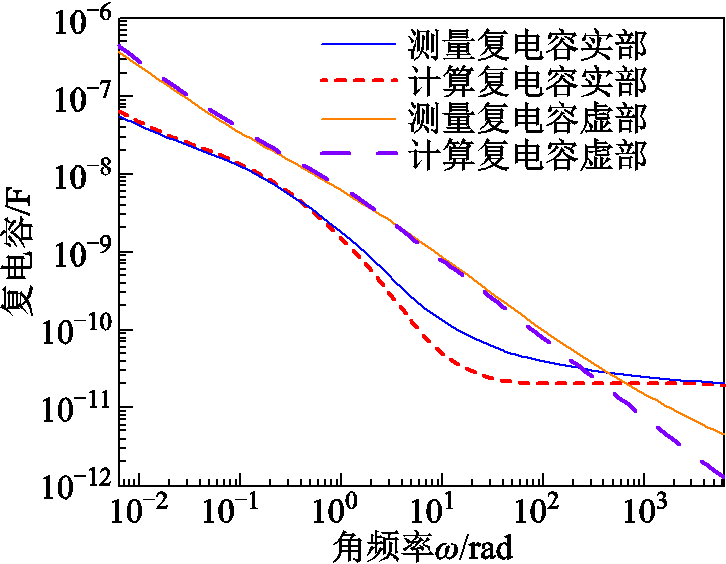
图12 测量复电容和计算复电容谱线对比
Fig.12 Comparison of spectrum lines of complex capacitance measured and calculated
本文针对目前扩展德拜模型参数辨识方法,支路数不确定、辨识结果随机性等问题。将K-K变换与微分解谱法相结合,提出了一种新的参数辨识方法,即频谱解构法。本方法具有充分的理论和公式基础,依据数值计算辨识得到的参数结果具有确定性的特点。通过对仿真和实验数据的分析,得到如下结论:
1)通过K-K变换可实现频域介电谱中绝缘电阻、几何电容、弛豫极化谱线的解耦,并可以完整确定绝缘电阻和几何电容参数。
2)由极化复电容实部微分谱线的峰值点数可清晰判断扩展德拜模型的极化支路数;利用频谱微分法逐次解谱可以辨识得到各极化支路参数,避免了智能优化算法求解方程组以及末端选点的随机性。
3)本文提出的频谱解构法可以完整地实现油纸绝缘扩展德拜模型参数的辨识,因此在获取油纸绝缘系统频域介电谱后可以建立确定的扩展德拜模型,为油纸绝缘设备状态诊断提供可靠的依据。
参考文献
[1] 林朝明, 叶荣, 吴国兰. 油纸绝缘混合极化的频域谱模型及参数辨识[J]. 仪器仪表学报, 2019, 40(4): 172-178.
Lin Chaoming, Ye Rong, Wu Guolan. Frequency domain spectrum model and parameter identification of oil-paper insulation mixed polarization[J]. Chinese Journal of Scientific Instrument, 2019, 40(4): 172-178.
[2] 谢松, 邹阳, 蔡金锭. 基于模糊粗糙集的变压器油纸绝缘状态评估[J]. 仪器仪表学报, 2017, 38(1): 190-197.
Xie Song, Zou Yang, Cai Jinding. Assessment of transformer oil-paper insulation status with fuzzy rough set[J]. Chinese Journal of Scientific Instrument, 2017, 38(1): 190-197.
[3] 张大宁, 刘孝为, 詹江杨, 等. 变压器油纸绝缘频域介电谱的虚部分析[J]. 电工技术学报, 2019, 34(4): 847-854.
Zhang Daning, Liu Xiaowei, Zhan Jiangyang, et al. Analysis of imaginary part of frequency domain spectroscopy for oil-paper insulation transformer[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 847-854.
[4] 黄云程, 蔡金锭. 油纸绝缘系统回复电压函数建模及拓扑结构辨识[J]. 电力自动化设备, 2016, 36(3): 149-153.
Huang Yuncheng, Cai Jinding. Return voltage function modeling and topology recognition of oil-paper insulation system[J]. Electric Power Automation Equipment, 2016, 36(3): 149-153.
[5] 杨峰, 唐超, 周渠, 等. 基于等效电路的油纸绝缘系统受潮状态分析[J]. 电工技术学报, 2020, 35(21): 4586-4596.
Yang Feng, Tang Chao, Zhou Qu, et al. Analyzing the moisture state of oil-paper insulation system using an equivalent circuital model[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4586-4596.
[6] 刘庆珍, 张晓燕, 蔡金锭. 油纸绝缘弛豫法谱线特征量提取及老化诊断[J]. 电机与控制学报, 2020, 24(5): 124-134.
Liu Qingzhen, Zhang Xiaoyan, Cai Jinding. Relaxation spectrum characteristic parameters extraction and aging diagnosis for oil-paper insulation[J]. Electric Machines and Control, 2020, 24(5): 124-134.
[7] 李安娜, 蔡金锭. 油纸绝缘系统混联等效电路及参数辨识的研究[J]. 仪器仪表学报, 2014, 35(9): 2130-2136.
Li Anna, Cai Jinding. Study on parallel-series equivalent circuit and parameters identification of oil-paper insulation system[J]. Chinese Journal of Scientific Instrument, 2014, 35(9): 2130-2136.
[8] 蔡金锭, 刘永清, 蔡嘉. 油纸绝缘变压器极化等效电路分析及其老化评估[J]. 电工技术学报, 2016, 31(15): 204-212.
Cai Jinding, Liu Yongqing, Cai Jia. Analysis of equivalent circuit of oil-paper insulation transformer relaxation response and aging evaluation[J]. Transactions of China Electrotechnical Society, 2016, 31(15): 204-212.
[9] 蔡锋, 江修波, 蔡金锭. 应用极化电流辨识油纸绝缘系统等值电路参数[J]. 高压电器, 2016, 52(8): 64-70.
Cai Feng, Jiang Xiubo, Cai Jinding. Extended Debye equivalent circuit parameter identification based on polarization current[J]. High Voltage Apparatus, 2016, 52(8): 64-70.
[10] 蔡金锭, 严欣, 蔡嘉. 去极化电流微分法在求解变压器极化等效电路参数中的应用[J]. 高电压技术, 2016, 42(10): 3172-3177.
Cai Jinding, Yan Xin, Cai Jia. Application of differential depolarization current method for solving equivalent polarization circuit parameters of transformer[J]. High Voltage Engineering, 2016, 42(10): 3172-3177.
[11] 蔡金锭, 曾静岚. 基于二次时域微分解析法的油纸绝缘介质响应参数辨识[J]. 高电压技术, 2017, 43(6): 1937-1942.
Cai Jinding, Zeng Jinglan. Parameter identification for dielectric response of oil-paper insulation based on second time-differential analysis[J]. High Voltage Engineering, 2017, 43(6): 1937-1942.
[12] 叶荣, 蔡金锭. 油纸绝缘极化等效电路的时域介电谱三次微分解析法[J]. 仪器仪表学报, 2018, 39(6): 112-119.
Ye Rong, Cai Jinding. Analytic method of cubic differential in time domain dielectric spectroscopy for oil-paper insulation polarization equivalent circuit[J]. Chinese Journal of Scientific Instrument, 2018, 39(6): 112-119.
[13] 饶显杰, 周凯, 谢敏, 等. 稳定图法在极化等效电路参数辨识中的应用[J]. 电工技术学报, 2020, 35(10): 2248-2256.
Rao Xianjie, Zhou Kai, Xie Min, et al. Application of stabilization diagram method for solving polarization equivalent circuit parameters[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2248-2256.
[14] 杜林, 杨峰, 蔚超, 等. 基于频域介电谱的油纸绝缘宽频等效模型参数辨识研究[J]. 电工技术学报, 2018, 33(5): 1158-1166.
Du Lin, Yang Feng, Wei Chao, et al. Parameter identification of the wide-band model of oil-impregnated paper insulation using frequency domain spectroscopy[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 1158-1166.
[15] Olmi R, Bittelli M. Dielectric data analysis: recovering hidden relaxations by fourth-order derivative spectroscopy[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2015, 22(6): 3334-3340.
[16] 雷清泉, 刘关宇. 如何理解工程电介质中极化与电导两个基本物理过程及其测量的科学原理与方法[J]. 中国电机工程学报, 2018, 38(23): 6769-6789, 7113.
Lei Qingquan, Liu Guanyu. How to understand the two basic physical processes of polarization and conductance in engineering dielectrics and scientific principles and methods of their measurement[J]. Proceedings of the CSEE, 2018, 38(23): 6769-6789, 7113.
[17] 高岩峰, 卢毅, 梁曦东, 等. Kramers-Kronig变换在介电响应分析中的数值计算方法、意义及应用[J]. 中国电机工程学报, 2020, 40(1): 318-329, 398.
Gao Yanfeng, Lu Yi, Liang Xidong, et al. Numerical computational method, application and significance of the Kramers-Kronig transform in the analysis of dielectric response[J]. Proceedings of the CSEE, 2020, 40(1): 318-329, 398.
[18] 赵孔双. 介电谱方法及应用[M]. 北京: 化学工业出版社, 2008.
[19] 高岩峰, 梁曦东, Chalashkanov N M, 等. 等效电路模型分析介电响应的方法、意义及应用[J]. 中国电机工程学报, 2018, 38(1): 300-308, 368.
Gao Yanfeng, Liang Xidong, Chalashkanov N M, et al. Application and significance of the equivalent circuit method in the analysis of dielectric response[J]. Proceedings of the CSEE, 2018, 38(1): 300-308, 368.
Abstract As a classical topological circuit model, the extended Debye model is of great significance for the condition diagnosis of oil paper insulation equipment. Aiming at the uncertain branches and the random identification results of the current extended Debye model. This paper based on the branch characteristics of the model, combining the real and imaginary parts relation of repolarization rate with spectrum differentiation method, proposing a spectrum decomposition method to realize the complete identification of the extended Debye model.
Undering the external electric field, the dielectric relaxation process will cover the conductivity loss, and the coupling and superposition of the internal multiple polarization maps make uncertainly to the polarization identification. It obscures the number of branches’s determination of the equivalent model, and makes the identification of model parameters difficult. In order to solve those problems, firstly, the frequency domain dielectric spectrum is decoupled based on Kramers-Kronig transform. Since the resistance and infinite capacitance terms calculated result is 0, the real and imaginary parts of the complex capacitance calculated by K-K relationship only contain relaxation polarization components. Therefore it can realize the separation of the geometric branch and the polarization branch of the extended Debye model, and can also complete the quantitative extraction of the insulation resistance, the geometric capacitance and the relaxation polarization spectrum line. Then, using the spectral characteristics of resistance and capacitance, the unique parameters of insulation resistance and geometric capacitance can be determined by the least square method. Next, according to the spectrum differentiation method, the first-order differentiation of the real part of the polarization complex capacitance is carried out. Because the single relaxation polarization real part is a ladder, the differential spectrum line has a relaxation peak . The number of relaxation mechanisms can be confirmed by the number of peak points of differential spectral lines, and the unique polarization equivalent circuit parameters can be solved by using the uniqueness of peak points. Finally, the feasibility of this method is verified by existing model parameters and examples: the identification error of insulation resistance and geometric capacitance parameters is less than 1%, the polarization equivalent circuit error is less than 7%. In general, the calculated and measured spectral lines are in good agreement and the trend is consistent. The spectral deconstruction method can provide a reliable physical model for the study of the internal relaxation characteristics of oil paper insulation.
Through simulation and case analysis, the following conclusions can be drawn: ①the conductance and relaxation processes can be accurately separated by K-K transformation, and the insulation resistance and geometric capacitance parameters can be determined. ②The number of polarization branches of the extended Debye model can be clearly determined by the peak number of the real part differential spectral line of the polarization complex capacitance; The parameters of each polarization branch can be identified by using the spectrum differentiation method to solve the spectrum step by step. ③The spectrum deconstruction method proposed in this paper can completely identify the parameters of oil paper insulation extended Debye model, and the results are unique within a certain accuracy range.
Keywords: Oil paper insulation, frequency domain dielectric spectrum, extended Debye model, parameter identification, spectrum deconstruction method
DOI:10.19595/j.cnki.1000-6753.tces.220963
中图分类号:TH183; TM411
新能源装备检测福建省高等学校重点实验室(XNY202102)、国家自然科学基金(51977039)和福建省自然科学基金(2019J01248)资助项目。
收稿日期 2022-05-31
改稿日期 2022-08-24
邹 阳 男,1980年生,博士,副教授,研究方向为电气系统智能化故障诊断。E-mail:24001744@qq.com
林锦煌 男,1997年生,硕士研究生,研究方向为电气系统智能化故障诊断。E-mail:944701176@qq.com(通信作者)
(编辑 郭丽军)