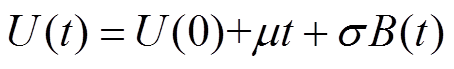（1）
摘要 该文针对机器学习、随机过程、贝叶斯滤波算法等剩余寿命（RUL）预测模型存在的不足，融合热应力作用下电机绝缘加速寿命数据和现场监测数据，结合随机过程和支持向量机模型，提出了基于拓展卡尔曼滤波的电机绝缘寿命预测模型。以剩余击穿电压为状态变量，基于Wiener过程建立了卡尔曼滤波模型的状态方程；以最大局部放电量的加速退化数据及现场监测数据为依据构建卡尔曼滤波模型的观测方程；为解决卡尔曼滤波模型由于无法获取新的监测信息而导致的预测精度不足问题，采用支持向量机建立了最大局部放电量预测模型。最后，针对电机主绝缘用6650聚酰亚胺，基于290℃、300℃、310℃、320℃下的加速退化数据构建状态方程，结合240℃下试样的局部放电数据构建观测方程，并以240℃下60h的试样实测老化数据为基准对模型进行了验证，证明了所提出模型在提高剩余寿命预测精度方面的有效性。
关键词：电机绝缘寿命预测 Wiener过程 拓展卡尔曼滤波 支持向量机
电气化交通、高性能伺服系统的高效轻量化发展需求对电机功率密度提出了更高要求，同时也给电机可靠性带来了巨大挑战。绝缘系统是电机的心脏，是电机可靠性的最关键的环节，超过1/3的电机事故是由于电机绝缘故障引起的[1]。根据IEEE工业应用协会（IEEE Industry Application Society）关于电机可靠性的一次调查结果显示，电机故障的平均故障时间为几十到上百小时，非计划停机将严重威胁电机运行安全性并造成巨大经济损失。因此，对电机绝缘状态进行监测，结合历史退化数据等信息对其进行寿命预测并实现故障预警，对提高电机运行可靠性和安全性具有重要的工程意义[2]。
在工程上，常通过非破坏性的宏观表征对电机绝缘状态进行评估[3-7]。数据驱动的唯象寿命模型是电机绝缘剩余寿命（Remaining Useful Life, RUL）预测的主流方法。众多学者应用机器学习算法、随机过程、卡尔曼滤波算法等方法建立了剩余寿命预测模型，以解决数据驱动的寿命预测问题，并取得了一定进展[8-11]。比如，于永进等基于鲸鱼优化算法和长短期记忆网络对绝缘纸剩余寿命进行预测，为换流变压器绝缘系统安全稳定运行提供了有力保障[12]；熊大顺等提出了一种基于Wiener过程的电机剩余寿命预测方法，得到了剩余寿命的概率密度函数及可靠度函数[13]；刘帼巾等对高可靠性、长寿命的电子式漏电断路器建立基于Wiener过程的剩余寿命预测模型，并对其进行了可靠性预测[14]；刘芳等提出一种完全数据驱动的基于改进扩展卡尔曼滤波算法的动力电池全生命周期荷电状态估计方法[15]。但是机器学习算法只能获得剩余寿命的点估计值，无法获得预测值的置信度评价；电机是典型的长寿命高可靠性产品，基于随机过程的RUL预测模型难以获取充足的故障数据以保证寿命预测精度，且无法体现单个样本的个体特征；卡尔曼滤波算法在长时寿命预测中难以解决协方差矩阵的更新问题，导致预测精度下降。
氧化反应引起的化学键断裂是电机绝缘失效的主要原因，温度升高加快氧化反应速率进而加速绝缘老化[16]，在宏观层面常表现为绝缘电阻、绝缘电容、介质损耗角正切值、最大局部放电量以及剩余击穿电压等宏观电气参数的变化。剩余击穿电压是评估电机绝缘寿命最直观的依据，电机主绝缘失效判断以其剩余击穿电压值是否小于标准规定的阈值为准则，IEC 60034—18—1及IEC 60034—18—32关于旋转电机成型绝缘结构的电评定标准中规定了剩余击穿电压失效阈值为(2US+1)kV，其中US为额定电压。因此，可以通过监测电机绝缘剩余击穿电压来进行电机绝缘寿命预测。但由于剩余击穿电压测量是破坏性试验，导致在工程上难以直接进行测量[17]。因此，采用绝缘电阻、绝缘电容、介质损耗角正切值、最大局部放电量等非破坏性电气参数间接估计电机绝缘剩余击穿电压是工程上广泛采用的电机绝缘寿命预测方法[16]。
本文面向以热老化为主要故障模式的电机主绝缘RUL预测问题。针对上述主流RUL预测模型存在的不足，融合热应力作用下电机绝缘加速寿命数据和现场监测数据，结合随机过程和支持向量机（Support Vector Machine, SVM）模型，提出了基于拓展卡尔曼滤波的电机绝缘寿命预测模型。采用Arrhenius模型作为加速模型，基于Wiener过程构架了热应力水平与Wiener模型中漂移系数和扩散系数的映射关系，以剩余击穿电压为状态变量，建立了实际工况下基于加速退化数据的电机绝缘寿命预测模型，并将其作为卡尔曼滤波模型的状态方程；以局部放电量的加速退化数据及现场监测数据为依据构建了卡尔曼滤波模型的观测方程；为解决卡尔曼滤波模型在寿命预测中由于无法获取新的监测信息、协方差矩阵无法更新而导致的预测精度不足的问题，采用支持向量机建立了最大局部放电量预测模型。最后，针对电机常用的6650聚酰亚胺薄膜材料，基于290℃、300℃、310℃、320℃下的加速退化数据构建状态方程，结合240℃下材料试样的局部放电数据构建观测方程，并以240℃下60h的试样实测老化数据为基准对模型进行了验证，通过与随机过程模型和卡尔曼滤波模型的预测结果对比，验证了所提出模型在提高剩余寿命预测精度方面的有效性及工程应用价值。
本文利用Wiener过程描述电机绝缘剩余击穿电压的退化轨迹。Wiener过程可用于描述由大量微小损失累积而导致的产品退化过程，由于其数学友好特性在退化数据建模中得到广泛应用[18]。
根据Wiener过程模型，剩余击穿电压损失值U(t)可表示为[18]
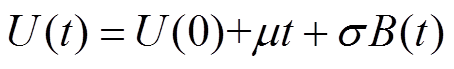（1）
式中，U(t)为t时刻剩余击穿电压损失值；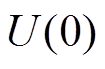
为初始剩余击穿电压损失值，通常假设U(0)=0；μ为漂移系数，用于描述个体退化速率差异；B(t)为一个用于表征退化过程随机性的标准布朗运动；σ为扩散系数，描述了材料、环境等不确定性因素及制造过程波动等随机因素对产品性能的影响。t～t+
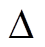t时间段内的击穿电压损失值的增量ΔU(t)满足正态分布[19]，即
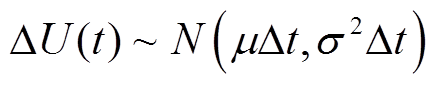（2）
其概率密度函数为
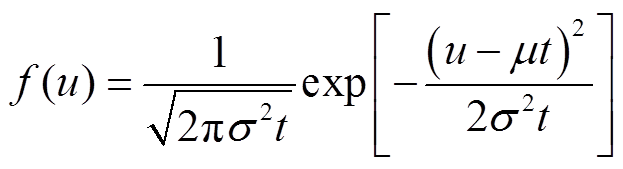（3）
设Fq(tq)和Fh(th)分别为产品在Tq和Th温度下的寿命累积分布函数，当满足
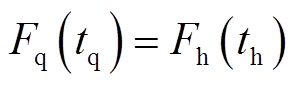（4）
可将Tq相对于Th的加速因子定义为
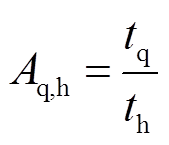（5）
根据加速因子不变原则[20]，可推导出
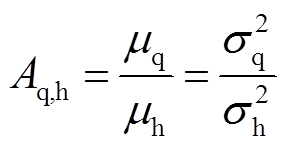（6）
热应力作用下，利用Arrhenius方程描述Wiener过程中的漂移系数、扩散系数与热应力水平之间的映射关系。在加速热应力 Ti(i=q, h)下的扩散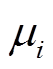系数
与漂移系数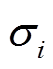
可分别表示为
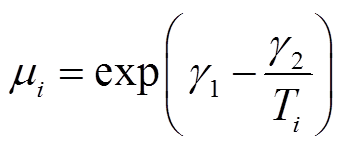（7）
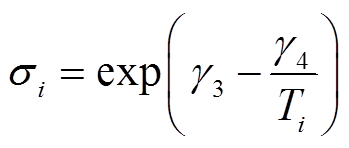（8）
式中，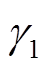
～
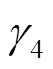为待定参数。为了满足
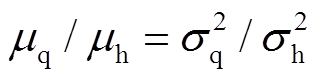，可得到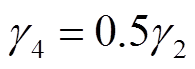
。因此，建立加速退化模型为
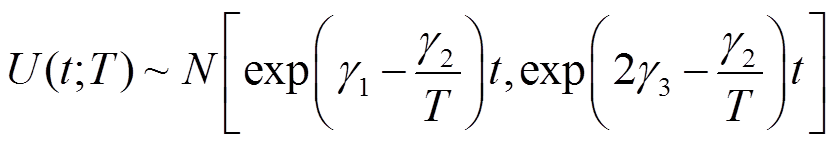（9）
式中，U(t; T)为热应力T作用下的剩余击穿电压损失值。在热应力T作用下，任意k时刻的剩余击穿电压Uk可表示为
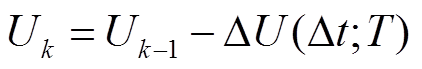（10）
式中，ΔU(Δt; T)为Δt时间段剩余击穿电压退化量，即
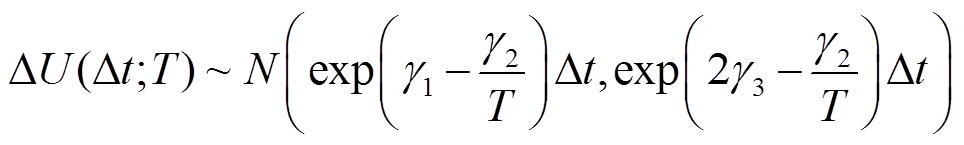（11）
将ΔU(Δt; T)用Wiener过程的数学表达式展开，即可得到剩余击穿电压状态方程为
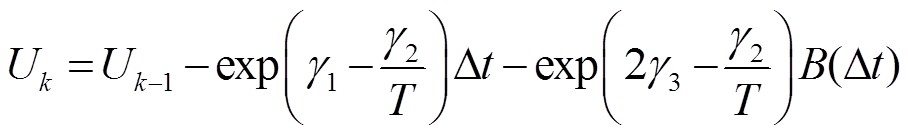（12）
本文采用的融合了最大局部放电量、介质损耗、绝缘电阻值和电容值等多状态数据的击穿电压估计方程[21]为
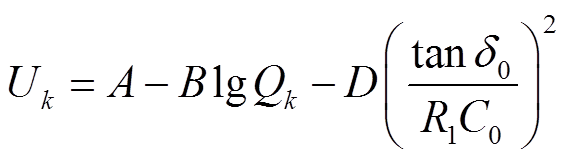（13）
式中，Qk为最大局部放电量；C0为绝缘电容；R1为绝缘电阻；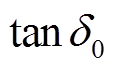
为介质损耗角正切值；A、B、D为待定系数。C0、R1和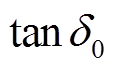采用离线定期检测的方法进行更新；局部放电量由于受绝缘状态变化影响较为明显，采用离线、在线融合数据。由于C0、R1和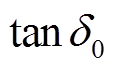在检测周期内变化缓慢，为了简化模型，本文假设一个检测周期内的C0、R1和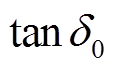为定值。以最大局部放电量作为观测变量，可以得到其观测方程为
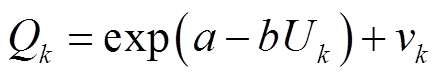（14）
式中，a、b为待定参数，可通过加速退化试验数据进行估计；vk为观测噪声，vk ～ N(0, V)，V为其噪声方差。
卡尔曼滤波算法迭代过程中需要实时更新协方差矩阵，但在长时寿命预测中缺乏合适的手段对协方差矩阵进行有效的更新，这是应用卡尔曼滤波模型进行寿命预测时需首要解决的问题。本文采用支持向量机模型，将时间作为输入变量，最大局部放电量作为输出变量，通过加速因子折算，将加速退化数据及现场数据共同作为训练集，对任意时刻Qk的真值作出预测，以此实现协方差矩阵的更新。
为了建立观测方程，将最大局部放电量数据以退化时间进行分类，即将输入变量和输出变量分别设为退化时间和最大局部放电量。若训练样本为
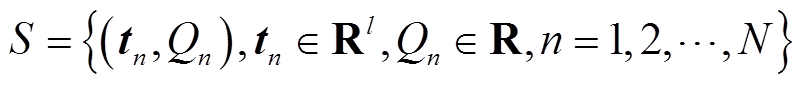（15）
式中，tn为l维输入变量（l≥1）；Qn为与tn对应的输出变量；N为训练样本数。
当Q与t为线性关系时，得到
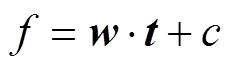（16）
式中，f为对应输出变量Q的回归函数；wÎRl，为权值矢量；cÎR，为待定参数；w·t表示w与t的点积。
w与c可通过如下优化问题求得。
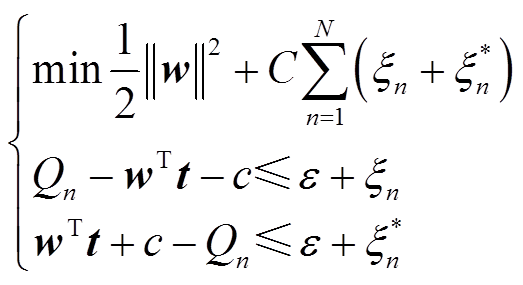（17）
式中，ε和C分别为不敏感因子和惩罚因子；ξn和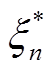
为松弛因子。通过引入拉格朗日乘子a和
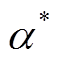。式（17）可转换为凸二次优化问题[22]，即
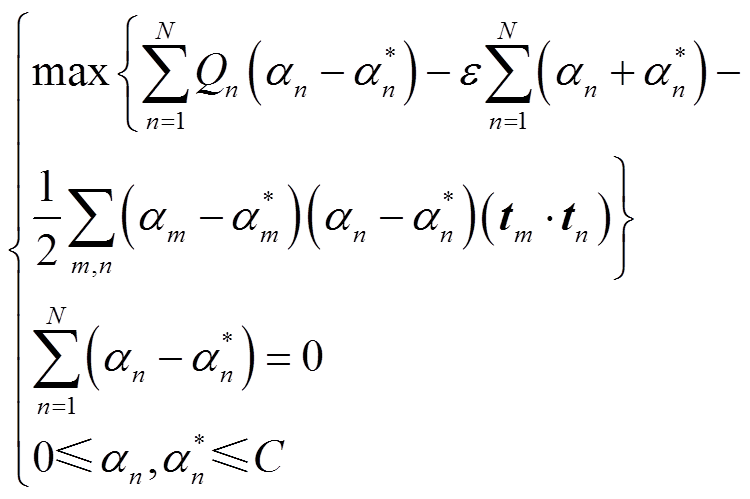（18）
设式（18）的解为
和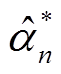
，则可得其对偶问题式（17）的解为
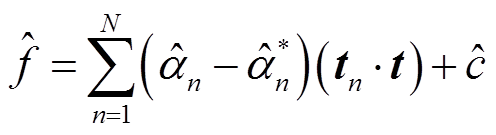（19）
其中
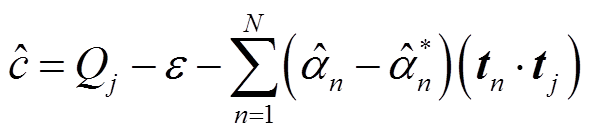（20）
式中，Qj需满足对应的αj Î[0, C]。
当t与Q为非线性关系时，可通过满足Mercer条件的核函数将该非线性问题转为更高维度的线性问题。此时只需将式（19）中的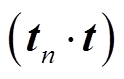
替换为核函数K(tn, t)，则回归函数为
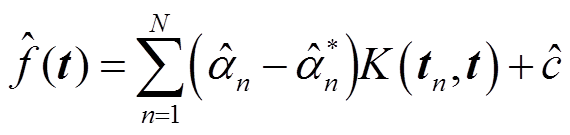（21）
本文取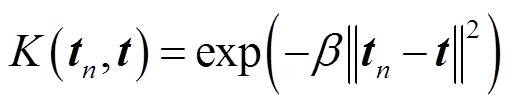
，β为核函数参数。给定训练样本S、惩罚因子C及核函数参数
对SVM模型精度和外推能力有很大影响，采用K-fold交叉验证法[23]来确定最优(C,β)组合。本文采用10-fold交叉验证法，在二维空间优化(C, β)，得到最优参数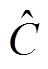
=16.02，
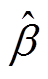=3.28。
综上所述，将时间作为输入变量，最大局部放电量作为输出变量，可通过SVM模型预测任意时刻最大局部放电量观测值，式（16）的观测方程进而可更新为
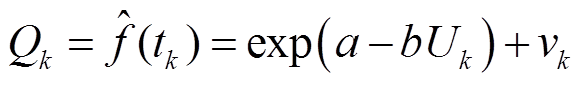（22）
式（22）即为所建卡尔曼滤波寿命预测模型的最大局部放电量观测方程。
结合式（12）、式（22）构建卡尔曼滤波模型得到
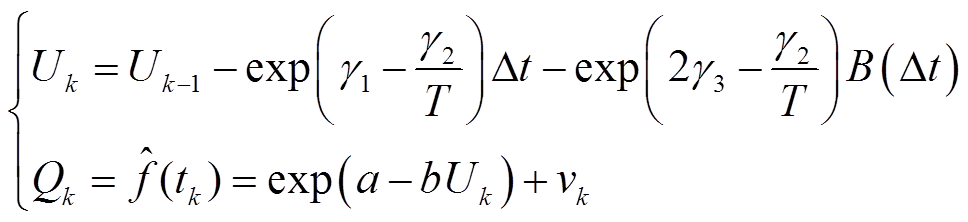（23）
构建状态空间模型后，整体迭代计算过程包含状态估计与状态更新两个步骤。
（1）状态估计：通过上一时刻的剩余击穿电压预测结果以及状态转移方程进行当前时刻剩余击穿电压的估计。
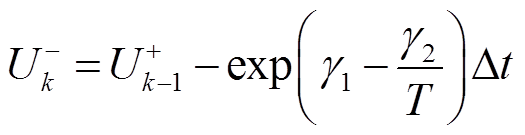（24）
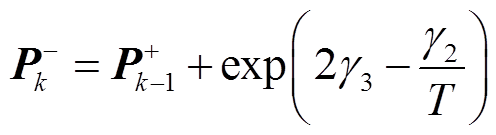（25）
式中，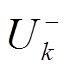
为k时刻的状态估计值；
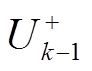为上一时刻的状态更新值；
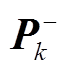为k时刻系统状态协方差矩阵的估计值；
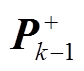为k-1时刻系统状态协方差矩阵的更新值。
（2）状态更新：首先将观测方程h进行Taylor展开，并利用其一阶部分进行非线性方程的线性化近似，可得
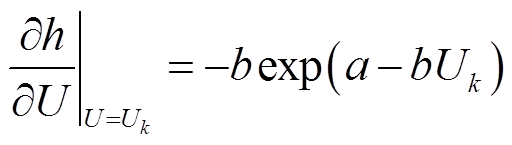（26）
因此，观测矩阵为
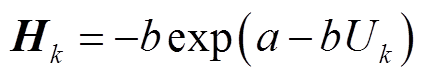（27）
通过状态估计后，可以得到当前时刻的估计值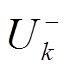，将该估计值代入观测方程便可得到观测值的估计值。将观测值的估计值与观测值真值进行比较得到测量余差，并通过相应的计算步骤得到最优卡尔曼增益，对状态估计值进行基于最小方差原则下的状态更新，得到最终的状态预测结果。具体更新步骤如下：
最大局部放电量估计值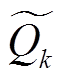
为
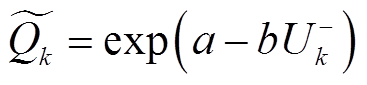（28）
测量余差协方差[24]为
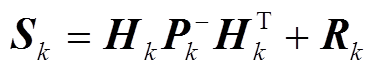（29）
式中，Rk为测量噪声协方差。
卡尔曼增益[24]为
（30）
状态更新为
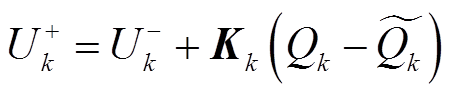（31）
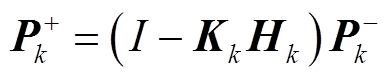（32）
式中，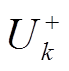
为k时刻状态更新值；
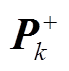为k时刻系统状态协方差矩阵的更新值；
为支持向量机预测的k时刻最大局部放电量真实值。
模型迭代流程如图1所示。可以看到，本文所建卡尔曼滤波模型解决了协方差矩阵更新问题，实现了模型迭代，能够对电机的隐藏状态量剩余击穿电压进行观测。
本文通过设计加速退化试验所获取的加速退化数据对参数进行拟合。在不同热应力水平下对产品进行恒应力加速退化试验。设Tk为第k个加速温度，tijk为Tk下第j个样品的第i次测量时间，每次对绝缘材料的最大局部放电量与剩余击穿电压进行检测。Uijk为剩余击穿电压退化测量值，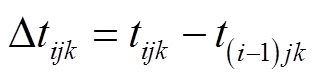
为时间增量，
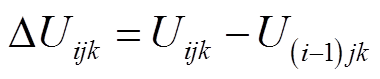为退化增量。其中，i为一定温度下，每个样品的测量次数，
；j为一定温度下的样品数量，
；k为试验中设置的热应力水平数量，
。
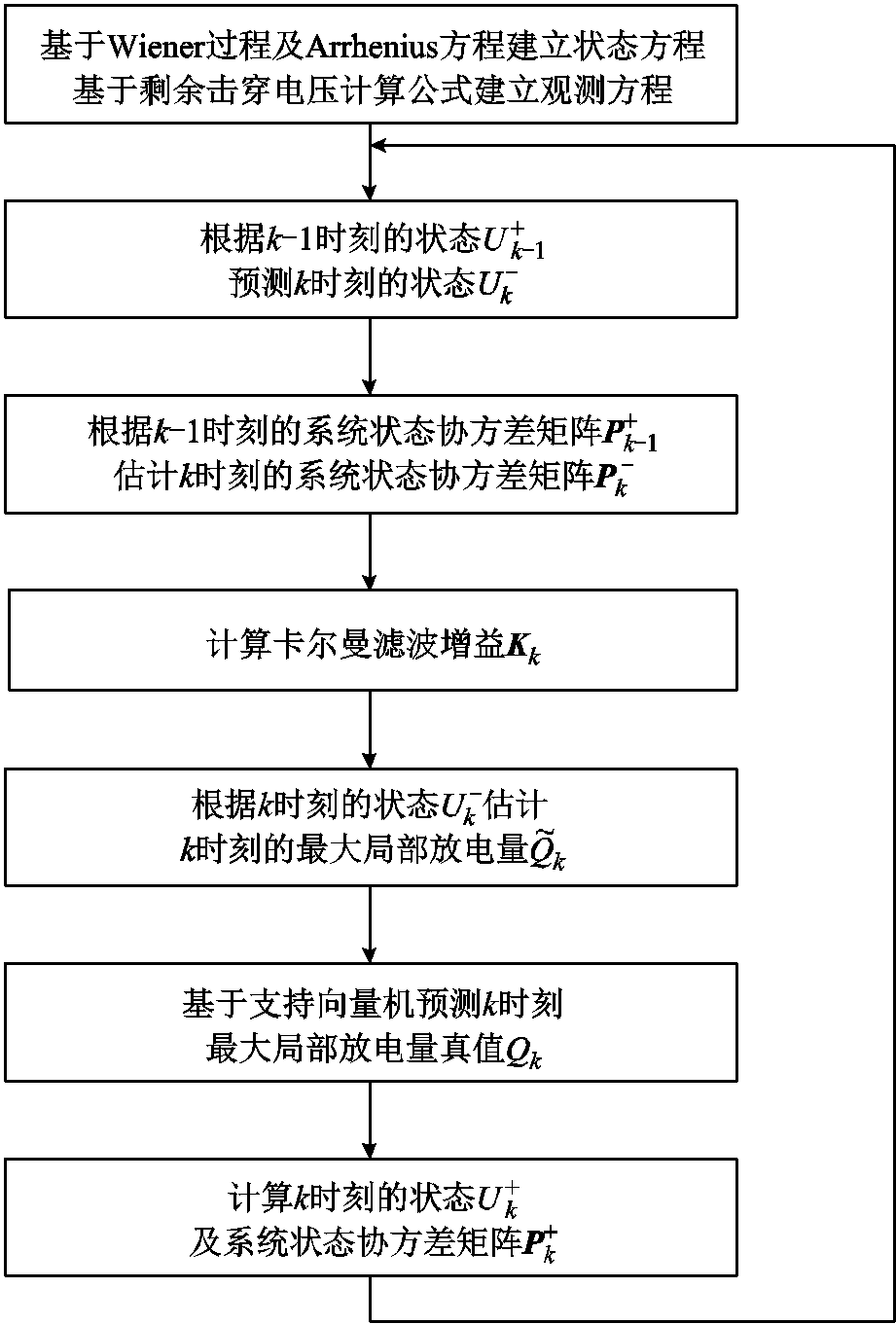
图1 模型迭代流程
Fig.1 The flow chart of model iteration
根据Wiener加速退化模型的独立增量特性，可建立似然函数[19]
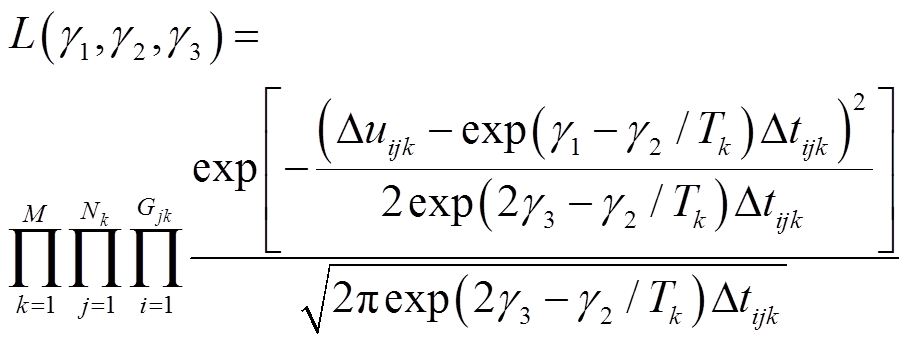（33）
本文借助Matlab软件中的fminsearch函数自动利用非线性优化方法预设的参数初值为起点迭代寻优，来获取极大似然估计值。建立Matlab函数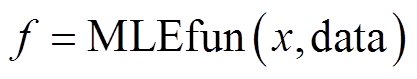
，令x = x(1), x(2), x(3)分别对应未知参数γ1, γ2,γ3，data为所有样品的加速退化数据，f为函数MLEfun(·)的输出；在函数MLEfun(·)内实现对数似然函数求和
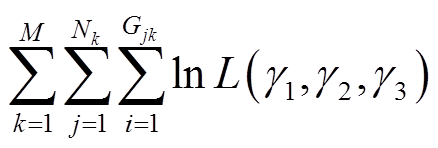，令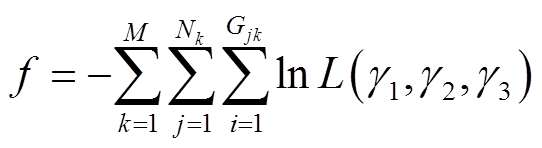
，则可将求极大值的问题转换为求极小值问题。
为获取合适的参数初值，本文利用最小二乘法确定参数初值。利用式（34）所示似然函数求取Wiener退化模型在各加速热应力Tk下的参数估计值。
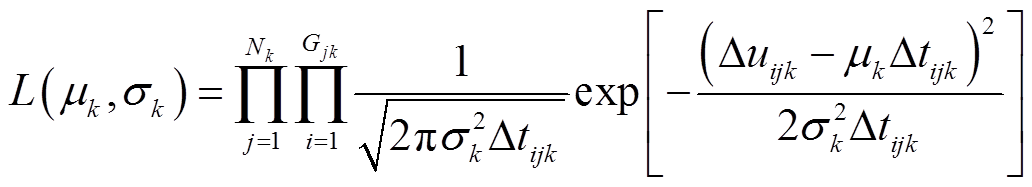（34）
得到参数估计值向量为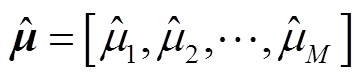
，
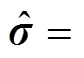
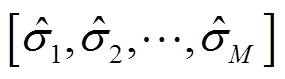。根据式（7）和式（8）可得
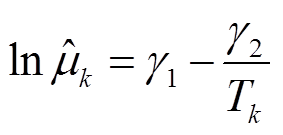（35）
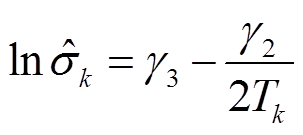（36）
建立矩阵方程
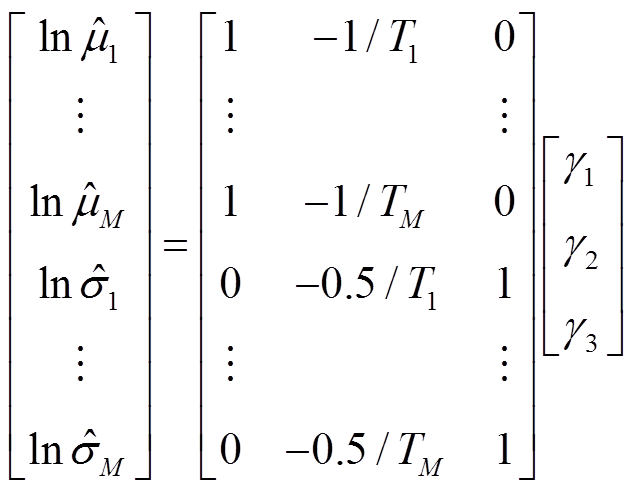（37）
可解得最小二乘估计参数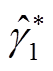
、
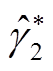和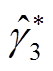
，并以此作为初值求解极大似然估计值。
同样地，以加速退化实验数据为数据集，根据最小二乘原理，记
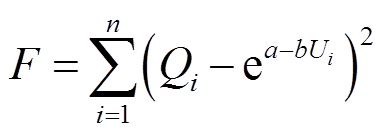（38）
式中，n为试验样本数量。令
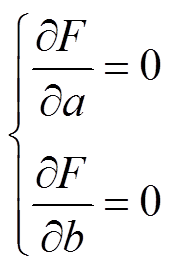（39）
求解方程即可得到观测方程中a和b的估计值。
本文以聚酰亚胺6650薄膜绝缘材料为试验对象，设计了加速退化试验，对所提出模型的精度进行了验证。
依据国家标准GB/T 13542.6—2006《电气绝缘用薄膜第6部分：电气绝缘用聚酰亚胺薄膜》[25]，本文以厚度为0.25mm的聚酰亚胺6650薄膜为研究对象，分为四组，每组10个样品，在不影响聚酰亚胺老化机理，保持退化规律一致的前提下，本文参考了其他学者对聚酰亚胺的加速老化研究[26-28]，综合考虑老化时间及试验成本，选取了290℃、300℃、310℃、320℃四个老化温度进行加速退化试验。定期检测绝缘材料试样的绝缘电阻、绝缘电容、介质损耗角正切值、最大局部放电量以及剩余击穿电压五个不同的参数，并进行统计分析，避免试验操作等带来的随机误差。最后将所得数据绘制成老化曲线，分析绝缘电阻、介质损耗特性、局部放电量及剩余击穿电压的老化规律，验证四个绝缘参数与绝缘性能之间的相关性。
同时，在240℃下测试不同老化时间点的剩余击穿电压，对所建模型进行试验验证。将已经在310℃下老化100h，处于性能退化阶段的聚酰亚胺薄膜在240℃下加速老化60h，记录其剩余击穿电压数据，并作为模型验证数据用于4.3节中的模型精度验证。
采用体积电阻电阻率测试仪，并依据国家标准GB/T 13542.2—2009《电气绝缘用薄膜第2部分：试验方法》[29]在200℃下测量绝缘电阻。
采用IDX300介损测试仪，依据国家标准GB/T 13542.2—2009《电气绝缘用薄膜第2部分：试验方法》开展试验，记录50Hz下材料的介质损耗及电容数据。
采用局部放电监测系统，以耦合电容为传感器监测局部放电信号。监测系统符合国家标准GB/T 7354—2003《局部放电测量》[30]。局部放电监测系统原理如图2所示，其中Cx为试品电容，Zm为测量阻抗，Ck为耦合电容，Z为接在电源与测量回路间的低通滤波器。
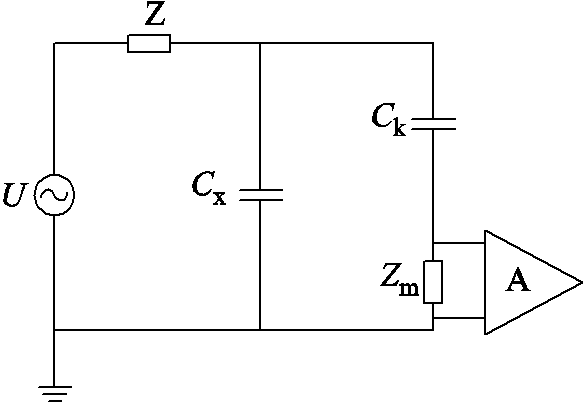
图2 局部放电监测系统原理
Fig.2 Schematic diagram of partial discharge monitoring system
试验电压U经Z施加于试品Cx，测量回路由Ck与Zm串联而成，并与Cx并联成并联测量回路。试品上的局部放电脉冲经Ck耦合到Zm上，经放大器A输送至测量仪器。
参照国家标准GB/T 1408.2—2006《绝缘材料电气强度试验方法第2部分：对应用直流电压试验的附加要求》[31]，测试环境为室温。为了防止沿面闪络，将试样放置在硅油中进行测试，选取上电极为直径25mm的柱电极，升压速率为1kV/s，直至试样击穿，记录试验数据。
绝缘电阻、绝缘电容、介质损耗角正切值与最大局部放电量的试验结果分别如图3～图6所示。试验结果表明，绝缘电容、介质损耗角正切值及最大局部放电量随老化时间的延长基本呈现上升趋势；而绝缘电阻随老化时间的延长基本呈下降趋势。由于瞬间加载直流电压，电荷由电极注入后，绝缘内部空间电荷重新分布需要一定时间才能达到稳定，这一过程被称为“吸收”现象。“吸收”现象会导致测量绝缘电阻时，阻值在一开始会随时间增加逐渐增加，最后达到稳定[32]。试验初期由于对“吸收”现象认识不足，导致绝缘电阻测试时间不足，引起了290℃下绝缘电阻出现了初期增大的现象。在后续试验中延长了试验时间，消除了“吸收”现象带来的误差。试验结果整体说明了模型所选参数与聚酰亚胺薄膜老化程度有着良好的相关性。
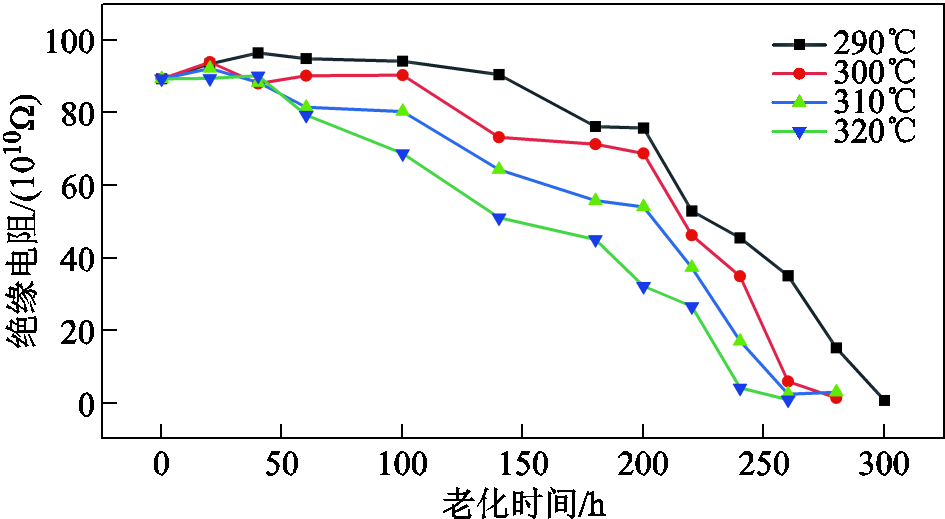
图3 绝缘电阻退化曲线
Fig.3 Insulation resistance degradation curve
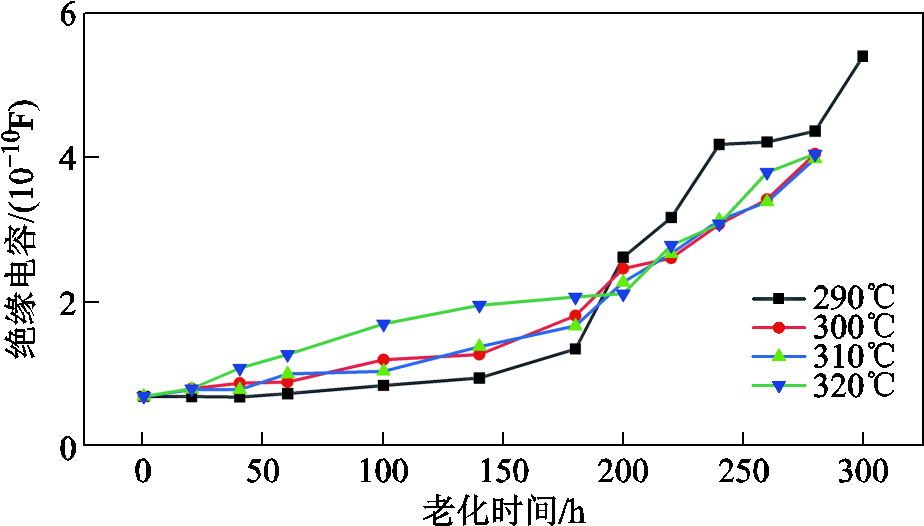
图4 绝缘电容退化曲线
Fig.4 Insulation capacitance degradation curve
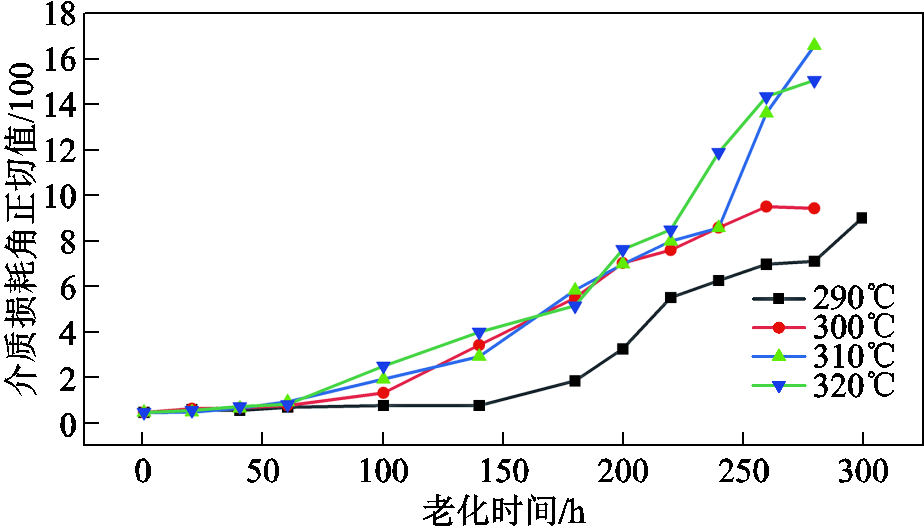
图5 介质损耗角正切值退化曲线
Fig.5 Dielectric loss tangent degradation curve
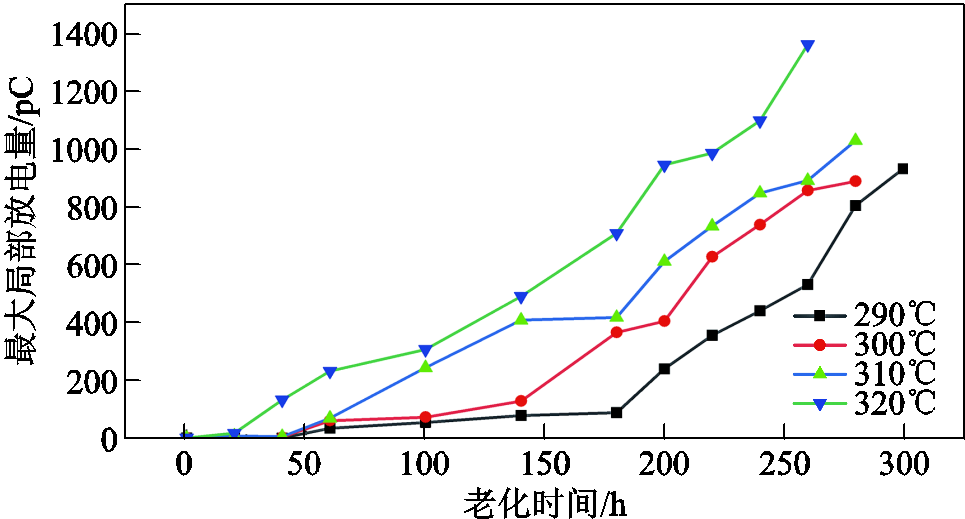
图6 最大局部放电量退化曲线
Fig.6 Maximum partial discharge degradation curve
剩余击穿电压退化曲线如图7所示。从图7可以看到，剩余击穿电压与聚酰亚胺薄膜老化程度有着极强的相关性，随着老化时间的延长，剩余击穿电压基本呈现线性下降的趋势；而在老化时间一定的情况下，随着老化温度的升高，剩余击穿电压下降程度明显提高。加速退化试验结果一定程度上验证了本文所建模型参数选择的合理性。
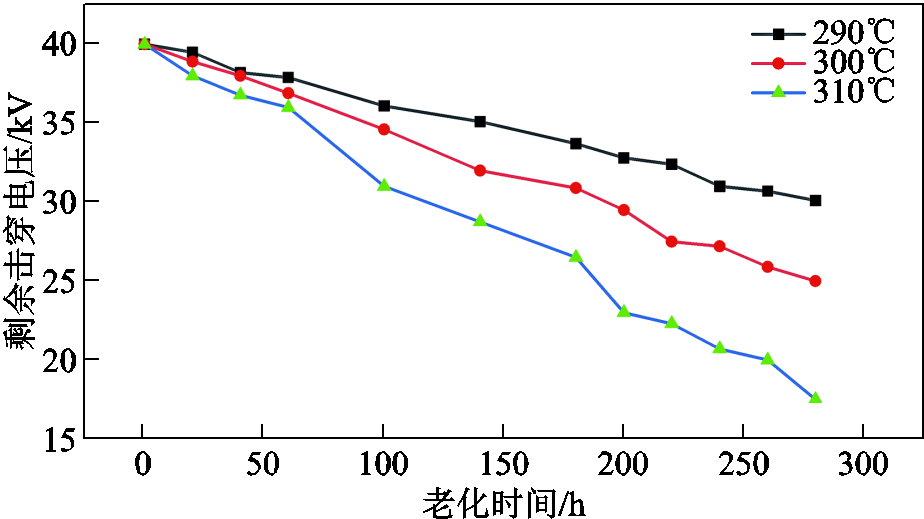
图7 剩余击穿电压退化曲线
Fig.7 Residual breakdown voltage degradation curve
结合试验得到的不同温度下剩余击穿电压加速退化数据以及现场退化数据，通过3.2节所推导的极大似然估计法对状态方程中的γ1, γ2, γ3进行拟合。拟合结果为
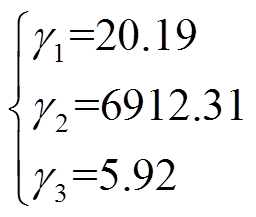（40）
状态方程即为
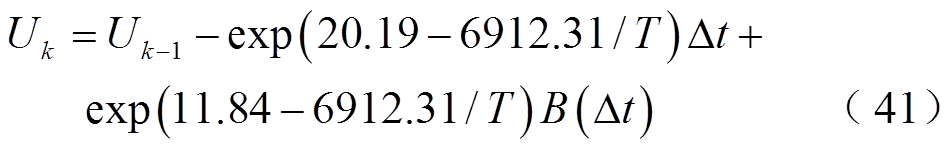
同样地，结合加速退化数据，可以对第二观测方程式（22）中的a, b进行拟合，拟合结果为
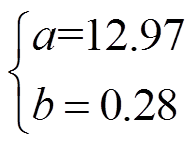（42）
则观测方程为
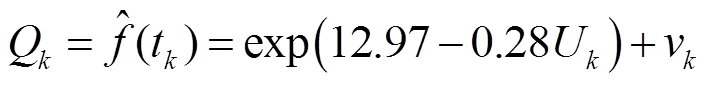（43）
为验证支持向量机对最大局部放电量真值的跟踪效果，本文以290℃的加速退化数据为依据，对支持向量机模型进行了验证，跟踪效果如图8所示。
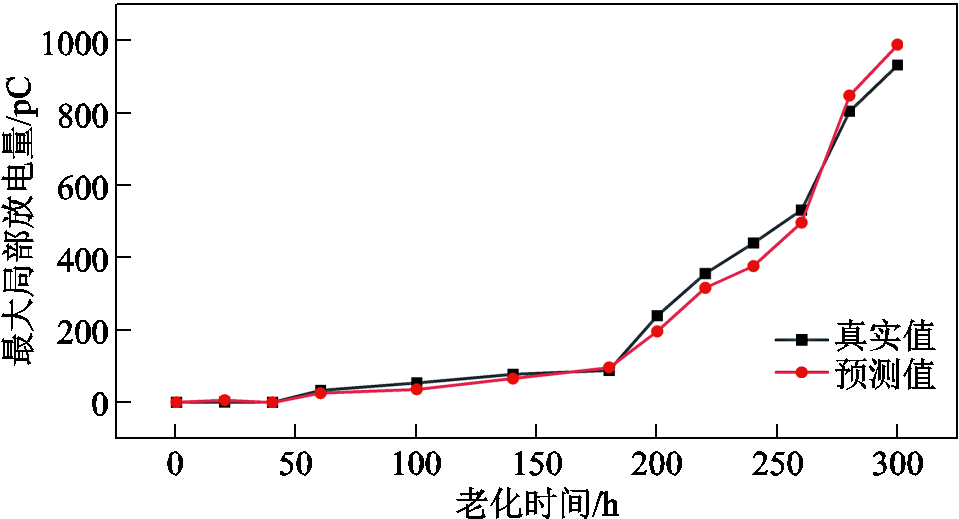
图8 最大局部放电量预测值与实际值对比
Fig.8 Comparison between the predicted value of the maximum partial discharge and the actual value
从图8可以看出，支持向量机模型对最大局部放电量的预测误差在8%以内，考虑到试验过程中随机因素引起的测量误差约为3%，本文所建模型可以较好地对最大局部放电量进行预测。
基于支持向量机对最大局部放电量准确的跟踪效果，即可实现本文所建卡尔曼滤波模型对剩余击穿电压的预测。同样地，以240℃的剩余击穿电压试验数据为依据，对寿命预测模型的可靠性进行验证，并给出了置信水平为0.95的上下限曲线。预测效果如图9所示，预测误差在4%之内。
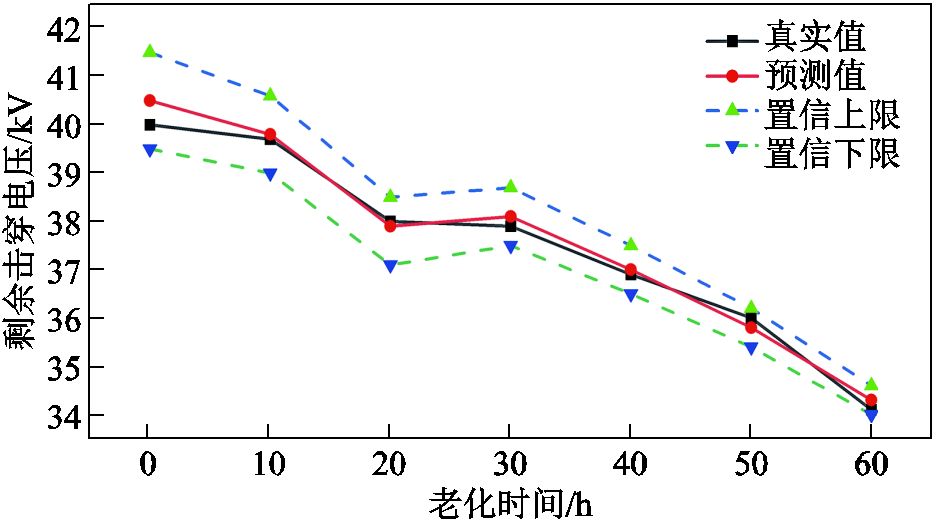
图9 剩余击穿电压预测值与实际值对比
Fig.9 Comparison of predicted value of residual breakdown voltage with actual value
在此基础上进一步比较了Wiener过程模型与本文所建卡尔曼滤波模型的优劣，预测精度对比如图10所示。从图10可以看出，融合了现场数据的卡尔曼滤波模型预测精度较Wiener过程模型有了明显的提升。
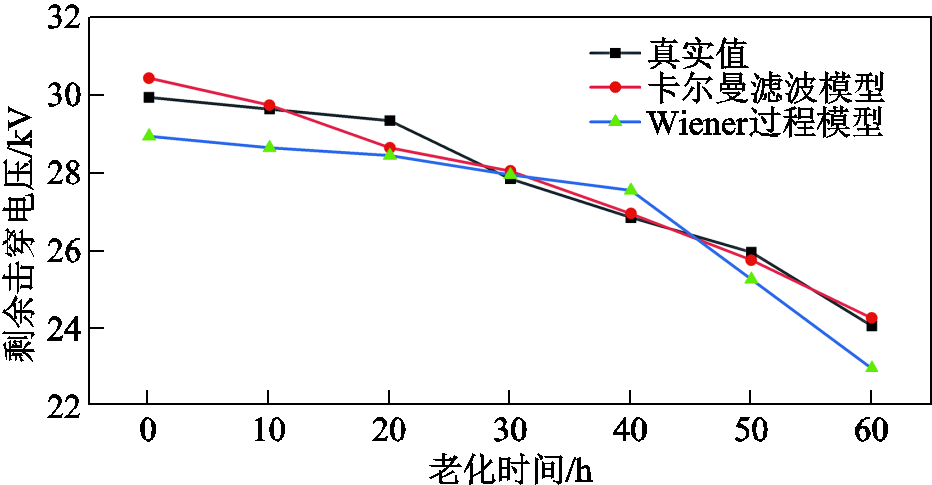
图10 预测精度对比
Fig.10 Comparison of prediction accuracy
本文提出了一种基于支持向量机与非线性卡尔曼滤波的电机绝缘寿命预测模型。该模型具有以下特点：①利用SVM模型对第一观测方程进行了修正，解决了卡尔曼滤波模型协方差矩阵的更新问题；②模型关注绝缘寿命的统计特性，在一定置信区间内给出寿命预测结果；③融合了加速退化数据及现场退化数据，最大限度地保证了退化信息的完整性。
通过聚酰亚胺薄膜的实例分析，可以得出以下结论：①SVM模型可以有效预测最大局部放电量真实值，建立第二观测方程；②本文提出的寿命预测模型可以有效预测聚酰亚胺薄膜的剩余寿命；③置信水平为0.95的剩余寿命置信区间基本包含真实剩余寿命，有效弥补了模型可能存在的误差。
因此，本文提出的方法可以为制定合理的设备维护策略提供参考，为解决工程中的类似问题提供借鉴。
参考文献
[1] 郑大勇, 张品佳. 交流电机定子绝缘故障诊断与在线监测技术综述[J]. 中国电机工程学报, 2019, 39(2): 395-406, 637.
Zheng Dayong, Zhang Pinjia. A review of fault diagnosis and online condition monitoring of stator insulation in AC electrical machine[J]. Proceedings of the CSEE, 2019, 39(2): 395-406, 637.
[2] 高俊国, 孟睿潇, 胡海涛, 等. 电机定子绝缘老化寿命预测研究进展[J]. 电工技术学报, 2020, 35(14): 3065-3074.
Gao Junguo, Meng Ruixiao, Hu Haitao, et al. Research progress on prediction of aging life of motor stator insulation[J]. Transactions of China Electrotechnical Society, 2020, 35(14): 3065-3074.
[3] 李福兴. 大型发电机定子绝缘诊断和剩余寿命预测[J]. 华东电力, 2004, 32(2): 54-56.
[4] Shinkarenko G V. Determination of the dielectric characteristics of electric equipment insulation in the presence of utility-frequency interference currents[J]. Power Technology and Engineering, 2016, 50(3): 341-346.
[5] Terase H, Hirabayashi S, Hasegawa T, et al. A new AC current testing method for non-destructive insulation tests[J]. IEEE Transactions on Power Apparatus and Systems, 1980, PAS-99(4): 1557-1566.
[6] Kimura K, Kaneda Y, Itoh K. A new approach to breakdown voltage and nondestructive parameters of micaceous insulation systems[C]// Proceedings of the 3rd International Conference on Properties and Applications of Dielectric Materials, Tokyo, Japan, 1991: 769-772.
[7] 胡波, 梁智明, 漆临生, 等. 电极系统对电机定子线棒绝缘介质损耗的影响[J]. 电气技术, 2011, 12(1): 13-17.
Hu Bo, Liang Zhiming, Qi Linsheng, et al. Study on effects of electrode system on dissipation factor of insulation of stator bar in rotating machine[J]. Electrical Engineering, 2011, 12(1): 13-17.
[8] 徐佳宁, 倪裕隆, 朱春波. 基于改进支持向量回归的锂电池剩余寿命预测[J]. 电工技术学报, 2021, 36(17): 3693-3704.
Xu Jianing, Ni Yulong, Zhu Chunbo. Remaining useful life prediction for lithium-ion batteries based on improved support vector regression[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3693-3704.
[9] 黄凯, 丁恒, 郭永芳, 等. 基于数据预处理和长短期记忆神经网络的锂离子电池寿命预测[J]. 电工技术学报, 2022, 37(15): 3753-3766.
Huang Kai, Ding Heng, Guo Yongfang, et al. Prediction of remaining useful life of lithium-ion battery based on adaptive data preprocessing and long short-term memory network[J]. Transactions of China Electrotechnical Society, 2022, 37(15): 3753-3766.
[10] 王义军, 左雪. 锂离子电池荷电状态估算方法及其应用场景综述[J]. 电力系统自动化, 2022, 46(14): 193-207.
Wang Yijun, Zuo Xue. Review on estimation methods for state of charge of lithium-ion battery and their application scenarios[J]. Automation of Electric Power Systems, 2022, 46(14): 193-207.
[11] 曲正伟, 董一兵, 王云静, 等. 用于电力系统动态状态估计的改进鲁棒无迹卡尔曼滤波算法[J]. 电力系统自动化, 2018, 42(10): 87-92.
Qu Zhengwei, Dong Yibing, Wang Yunjing, et al. Improved robust unscented Kalman filtering algorithm for dynamic state estimation of power systems[J]. Automation of Electric Power Systems, 2018, 42(10): 87-92.
[12] 于永进, 姜雅男, 李长云. 基于鲸鱼优化-长短期记忆网络模型的机-热老化绝缘纸剩余寿命预测方法[J]. 电工技术学报, 2022, 37(12): 3162-3171.
Yu Yongjin, Jiang Yanan, Li Changyun. Prediction method of insulation paper remaining life with mechanical-thermal synergy based on whale optimization algorithm-long-short term memory model[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3162-3171.
[13] 熊大顺, 李颖晖, 朱喜华, 等. 基于EMD的随机Wiener过程电机剩余寿命预测方法[J]. 微电机, 2013, 46(11): 14-17.
Xiong Dashun, Li Yinghui, Zhu Xihua, et al. Random Wiener process residual life prediction method for motor based on EMD[J]. Micromotors, 2013, 46(11): 14-17.
[14] 刘帼巾, 李想, 王泽, 等. 基于Wiener过程电子式漏电断路器的剩余寿命预测[J]. 电工技术学报, 2022, 37(2): 528-536.
Liu Guojin, Li Xiang, Wang Ze, et al. Remaining life prediction of electronic residual current circuit breaker based on Wiener process[J]. Transactions of China Electrotechnical Society, 2022, 37(2): 528-536.
[15] 刘芳, 马杰, 苏卫星, 等. 基于自适应回归扩展卡尔曼滤波的电动汽车动力电池全生命周期的荷电状态估算方法[J]. 电工技术学报, 2020, 35(4): 698-707.
Liu Fang, Ma Jie, Su Weixing, et al. State of charge estimation method of electric vehicle power battery life cycle based on auto regression extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 698-707.
[16] Stone G C, Culbert I, Boulter E A, et al. Electrical insulation for rotating machines-design, evaluation, aging, testing, and repair[M]. 2nd ed. Piscataway: Wiley-IEEE Press, 2014.
[17] Stone G C, Sedding H G, Lloyd B A, et al. The ability of diagnostic tests to estimate the remaining life of stator insulation[J]. IEEE Transactions on Energy Conversion, 1988, 3(4): 833-841.
[18] Pang Zhenan, Si Xiaosheng, Hu Changhua, et al. A Bayesian inference for remaining useful life estimation by fusing accelerated degradation data and condition monitoring data[J]. Reliability Engineering & System Safety, 2021, 208: 107341.
[19] 王浩伟. 加速退化数据建模与统计分析方法及工程应用[M]. 北京: 科学出版社, 2019.
[20] 王浩伟, 周源, 滕飞, 等. 基于加速因子不变原则的加速退化试验优化设计[J]. 机械工程学报, 2018, 54(18): 212-219.
Wang Haowei, Zhou Yuan, Teng Fei, et al. Optimal design of accelerated degradation test based on acceleration factor constant principle[J]. Journal of Mechanical Engineering, 2018, 54(18): 212-219.
[21] 马宏忠. 电机状态监测与故障诊断[M]. 北京: 机械工业出版社, 2008.
[22] 吴崇明, 王晓丹, 白冬婴, 等. 利用KKT条件与类边界包向量的SVM增量学习算法[J]. 计算机工程与设计, 2010, 31(8): 1792-1794, 1798.
Wu Chongming, Wang Xiaodan, Bai Dongying, et al. Fast SVM incremental learning algorithm using KKT conditions and between-class convex hull vectors[J]. Computer Engineering and Design, 2010, 31(8): 1792-1794, 1798.
[23] 刘学艺, 李平, 郜传厚. 极限学习机的快速留一交叉验证算法[J]. 上海交通大学学报, 2011, 45(8): 1140-1145.
Liu Xueyi, Li Ping, Gao Chuanhou. Fast leave-one-out cross-validation algorithm for extreme learning machine[J]. Journal of Shanghai Jiao Tong University, 2011, 45(8): 1140-1145.
[24] 李明干, 孙健利, 刘沛. 基于卡尔曼滤波的电力系统短期负荷预测[J]. 继电器, 2004, 32(4): 9-12.
Li Minggan, Sun Jianli, Liu Pei. Short-term load forecast of power system based on Kalman filter[J]. Relay, 2004, 32(4): 9-12.
[25] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB/T 13542.6—2006 电气绝缘用薄膜第6部分：电气绝缘用聚酰亚胺薄膜[S]. 北京: 中国标准出版社, 2006.
[26] 周远翔, 莫雅俊, 刘慧芳, 等. 加速热老化下聚酰亚胺材料力学性能和寿命模型研究[J]. 绝缘材料, 2017, 50(7): 31-35.
Zhou Yuanxiang, Mo Yajun, Liu Huifang, et al. Mechanical properties and life model of polyimide materials under accelerated thermal ageing[J]. Insulating Materials, 2017, 50(7): 31-35.
[27] 赵延召, 陈红生, 朱菲菲, 等. 聚酰亚胺薄膜热老化特性试验与分析[J]. 机械研究与应用, 2015, 28(1): 91-93.
Zhao Yanzhao, Chen Hongsheng, Zhu Feifei, et al. Experimental analysis on thermal aging characteristics of polyimide film[J]. Mechanical Research ＆ Application, 2015, 28(1): 91-93.
[28] 莫雅俊, 张灵, 周远翔, 等. 基于理化分析的热老化聚酰亚胺薄膜的电导特性[J]. 高电压技术, 2019, 45(4): 1241-1248.
Mo Yajun, Zhang Ling, Zhou Yuanxiang, et al. Conduction Current characteristics of thermally aged polyimide films based on physico-chemical analysis[J]. High Voltage Engineering, 2019, 45(4): 1241-1248.
[29] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB/T 13542.2—2009 电气绝缘用薄膜第2部分：试验方法[S]. 北京: 中国标准出版社, 2009.
[30] 国家质量监督检验检疫总局. GB/T 7354—2003 局部放电测量[S]. 北京: 中国标准出版社, 2003.
[31] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB/T 1408.2—2016 绝缘材料电气强度试验方法第2部分：对应用直流电压试验的附加要求[S]. 北京: 中国标准出版社, 2016.
[32] 朱德恒, 严璋. 高电压绝缘[M]. 北京: 清华大学出版社, 1992.
Abstract Insulation system is the weakest part of motor reliability. Monitoring its condition and realizing accurate remaining life prediction is an effective means to ensure the reliability and safety of motor operation. Aiming at the disadvantages of mainstream remaining useful life (RUL) prediction models, including machining learning model, stochastic process model and stochastic filtering model, a motor insulation RUL prediction model based on accelerating degradation data and field state monitoring data under thermal stress, which combines extended Kalman filtering (EKF) with support vector machine(SVM) model and stochastic process model, is proposed.This model is mainly oriented to the RUL prediction problem of motor main insulation with thermal aging as the main failure mode.First, the Arrhenius model is used as the acceleration model, and the mapping relationship between the thermal stress level and the Wiener model drift coefficient and diffusion coefficient is constructed based on the Wiener process.Taking the residual breakdown voltage as the state variable, a prediction model of motor insulation life based on accelerated degradation data under actual working conditions is established, and it is used as the state equation of the Kalman filter model.Secondly, the expression of the maximum partial discharge is deduced by the breakdown voltage estimation equation, and the observation equation of the Kalman filter model is constructed based on the accelerated degradation data of the maximum partial discharge and on-site monitoring data;Then, in order to solve the problem of insufficient prediction accuracy caused by the inability to obtain new monitoring information and the inability to update the covariance matrix of the EKF model in life prediction,this paper takes time as the input variable and the maximum partial discharge as the input variable. Based on the support vector machine, a prediction model of the maximum partial discharge is established to realize the continuous update of the covariance matrix.Finally, for the 6650 polyimide film commonly used in motors, an accelerated degradation test is designed, and the test data of insulation resistance, insulation capacitance, dielectric loss tangent, maximum partial discharge and residual breakdown voltage with aging time are recorded.Based on the accelerated degradation data at 290℃, 300℃, 310℃, and 320℃, the maximum likelihood estimation method is used to construct the state equation. The observation equation was constructed by fusing the accelerated degradation data and the partial discharge data of the material sample at 240℃. The model was verified based on the measured aging data of the sample at 240 °C for 60 hours. The results showed that the model prediction error was within 4%.Then, the prediction accuracy of the EKF model and the stochastic process model were compared, and the comparison results showed that the prediction accuracy of the Kalman filter model was higher, which verifies the effectiveness and engineering application value of the proposed model in improving the remaining life prediction accuracy.
keywords：Motor insulation life prediction, Wiener process, extended Kalman filter, support vector machine
DOI:10.19595/j.cnki.1000-6753.tces.221227
中图分类号：TM306
国家自然科学基金项目（51977192）和宁波市第一批重大科技攻关暨“揭榜挂帅”项目（20211ZDYF020218）资助。
收稿日期 2022-06-28
改稿日期 2022-08-04
张 健 男，1980年生，副教授，硕士生导师，研究方向为永磁电机、电机状态监测与智能化故障诊断、面向大数据的装备健康管理等。E-mail：jian_zhang_zju@zju.edu.cn
田 杰 男，1989年生，博士，研究方向为电力变换装备。E-mail：tianjie_eee_126@126.com（通信作者）
（编辑 李冰）