图1 高频局部放电测试平台
Fig.1 High frequency partial discharge test platform
摘要 局部放电是导致高频电力变压器中聚酰亚胺（PI）绝缘劣化的重要原因。为研究高频电压下聚酰亚胺局部放电机理，探索温度、频率因素对局部放电特性的影响，建立了高频局部放电测试平台。针对使用脉冲电流传感器采集局部放电信号容易受噪声干扰的问题，采用变分模态分解（VMD）对局部放电原始信号进行去噪。其中，针对VMD难以自适应选取分解参数的问题，使用平衡优化器（EO）算法获得最优模态分解个数K与惩罚因子α。实验获取了25～100℃四个温度点与10～50kHz五个频率点下的聚酰亚胺局部放电情况，并分析其变化规律。实验结果表明，温度越大放电起始电压越小，而频率与局部放电起始电压无关；最大放电幅值、总放电幅值和单周波平均放电次数与温度、频率呈正相关；频率越高，温度对局部放电特征量的影响越大，而温度越高，频率对局部放电特征量的影响也更为显著，两者呈现一种耦合促进关系。
关键词：局部放电 平衡优化器 变分模态分解 温度 频率 聚酰亚胺
当前能源与电力系统的发展呈现出可再生分布式电源大量接入、大型交-直流电网互联以及电力电子装备广泛应用等新的特征。电力电子变压器（Power Electronic Transformer, PET）是一种新型电力输变电装备，因其两侧电压、电流可控，可任意调节功率因数，改善电能质量的特点，具有非常广阔的应用前景[1]。高频电力变压器（High Frequency Power Transformer, HFPT）是PET的核心组件，负责实现电压等级变换。聚酰亚胺（Polyimide, PI）具有良好的耐高温、耐辐射特性及优异的介电性能，被广泛地应用在HFPT的匝间绝缘和对地绝缘中。聚酰亚胺在HFPT中的工作环境非常恶劣，通常需要承受10kHz以上的高频电压[2]；同时，高频电压下趋肤效应、邻近效应更为显著，铁耗、铜耗、介质损耗、开关损耗远大于工频情况，使HFPT正常工作温升远大于普通变压器[3-4]，由此带来的电-热耦合应力导致的局部放电（Partial Discharge, PD）是致使材料绝缘失效的主要因素。
由于局部放电检测通常处于复杂的电磁环境下，实际采集到的局部放电信号包含着大量的混合噪声，影响检测效果[5]。目前采用的去噪方法中，小波变换可以用来滤除实验信号中的高斯白噪声，但小波变换难以选择合适的小波基函数和分解层数[5-6]；经验模态分解（Empirical Mode Decomposition, EMD）算法则存在严重的模态混叠和端点效应[7]；而变分模态分解（Variational Mode Decomposition, VMD）通过引入变分模型，构造约束模型寻优的方式将原始信号分解为多个单分量模态[8]，可以有效地避免EMD方法中的模态混叠现象，但其惩罚因子和分解个数必须事先确定，这两个参数选取不当将严重影响VMD算法的分解效果。本文采用改进的VMD算法分解PD信号，利用平衡优化器（Equilibrium Optimizer, EO）算法优化分解个数K与惩罚因子α，并以峭度准则确定有效分量，对重构信号使用小波阈值去噪进一步去除残留的白噪声。该去噪方法能有效地抑制PD信号中的混合噪声，保留PD信号的完整性，有利于局部放电后续的研究。
研究表明，温度、频率等影响因子对绝缘的局部放电有很大影响。刘思华等发现电源频率更高时，局部放电起始电压显著降低，放电相位更宽，而单位周期内的平均放电幅值与放电次数先增后降，在20kHz达到极大值[9]。A. Cavallini等研究发现，局部放电幅值随频率的增加而减小[10]。徐跃等研究了1～10kHz下的聚酰亚胺薄膜局部放电，发现频率增加导致放电残余电荷不易扩散，放电次数增多，高频情况下，温度升高使得局部放电显著增强[11]。韩帅等模拟了固态变压器中高频正弦电压下聚酰亚胺绝缘的局部放电，发现随着温度升高，最大放电幅值、平均放电幅值与放电次数都显著增大[12]。罗杨等研究了连续方波脉冲下的聚酰亚胺局部放电特性，发现随着实验温度增加，放电幅值与放电次数均会减小[13]。现有研究成果均是在不同高频电压参数下对绝缘材料高频放电特性进行的分析与表征，学者们针对温度、频率对绝缘材料高频放电特性的影响给出了不同甚至截然相反的结论。因此，针对温度、频率及二者间可能存在的耦合协同作用对局部放电的影响机理仍需深入研究。本文设计了高频电-热联合局部放电测试平台，实验研究了25～100℃四个温度点与10～50kHz五个频率点下的聚酰亚胺局部放电情况，使用EO-VMD去噪算法进行数据处理后，统计了局部放电起始电压（Partial Discharge Inception Voltage, PDIV）、最大放电幅值、放电次数等特征量，分析了温度、频率及二者的耦合协同作用对高频电应力下聚酰亚胺局部放电的影响机理。
选择杜邦公司的75μm聚酰亚胺薄膜作为试样。高频局部放电测试平台如图1所示。其中，高频高压电源可以输出峰-峰值为0～20kV、频率为5～50kHz的高频正弦电压，通过调频单元档位可实现频率的连续可调。由于球-板电极之间存在稍不均匀电场，兼有法向和切向电场分量，选择球-板电极模拟HFPT中PI所承受的实际电场，其尺寸参考国际标准IEC 60243—1:2013《绝缘材料电气强度试验方法 第一部分：工频下试验》，其中，球电极直径为20mm，板电极厚为10mm、直径为75mm。基于高频电应力下PD信号宽频带、低幅值的特点，选择测量带宽10kHz～100MHz的ETS—93686型脉冲电流传感器采集PD信号。采用泰克MDO3024四通道示波器同时采集高频正弦信号和局部放电信号，并将实时采集的数据上传到计算机中保存。
图1 高频局部放电测试平台
Fig.1 High frequency partial discharge test platform
选择25℃、50℃、75℃、100℃四个温度点与10kHz、20kHz、30kHz、40kHz、50kHz五个频率点进行实验。首先，设定恒温老化箱加热温度，升温至设定值后在该温度稳定持续30min。参考工频下局部放电短时快速升压方法，选取200V/s作为升压速度，在不同温度、频率条件下施加电压至初次产生重复性放电脉冲，观察并记录此时电压幅值即局部放电起始电压。实验发现，同一温度不同频率下的PDIV大致相同，室温下10～50kHz实验中PDIV均为1.30kV左右。不同温度下PDIV略有差异，总体随温度增大而降低。不同温度、频率条件下局放起始电压见表1。
表1 不同温度、频率条件下局部放电起始电压
Tab.1 PDIV under different temperatures and frequencies
温度/℃PDIV/kV 10kHz30kHz50kHz 251.32±0.21.33±0.11.29±0.2 501.30±0.11.28±0.11.27±0.1 751.28±0.21.28±0.21.26±0.1 1001.22±0.21.25±0.21.24±0.1
选择PDIV的1.5～2倍作为不同实验条件下的局部放电测试电压[14]，保持每次实验在2.5kV恒电压条件下进行，每个实验条件下重复进行五组实验。使用上述PD数据采集存储系统记录局部放电的幅值与相位。为避免电极在高温下发生氧化或熔融产生表面杂质，影响电极表面光滑度并对实验结果产生影响，放电实验后应使用酒精擦拭电极表面[15]。
实验过程中，脉冲电流传感器所测得数据中会存在大量噪声信号，包括外部空间电磁干扰、测量仪器电源线引入电磁干扰、接地线干扰等，因此直接使用原始数据无法准确获得局部放电的特征量，而使用EO-VMD与小波阈值函数联合的去噪算法可以实现对局部放电信号的良好滤波效果。
VMD是一种非递归、准正交的自适应模态分解算法，它需要构建一个变分模式分解模型，在模型框架中不断迭代，获得使各模态分量估计带宽之和最小的最优解[16]，最后将原始信号分解为一系列有限带宽的本征模态函数（Band-limited Intrinsic Mode Function, BIMF）。各模态分量彼此相互独立，有效抑制了EMD算法存在的模态混叠现象。
VMD将输入信号f(t)分解为K个模态函数ui(t)，i=1, 2,…, K。构建的约束变分模型为
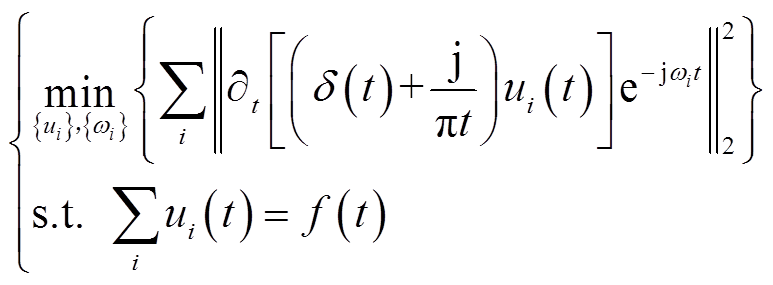（1）
式中，ωi为各固有模态分量对应的中心频率；δ(t)为单位脉冲函数。
在模型框架中求解式（1）的最优解，引入拉格朗日乘法算子λ(t)使约束变分问题转化为非约束变分问题，则扩展的拉格朗日表达式为
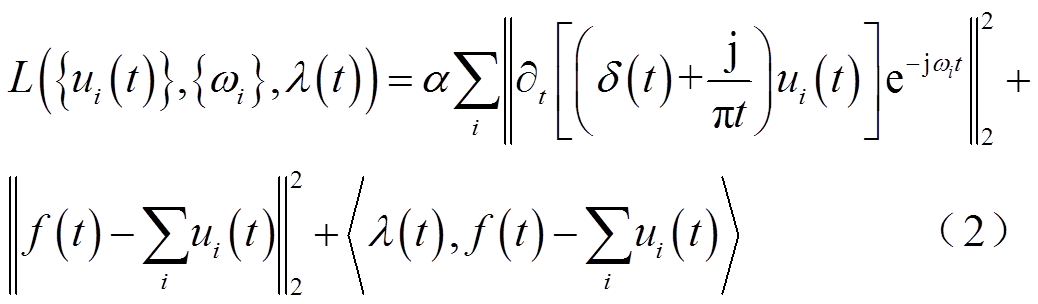
式中，α为惩罚因子，保证噪声条件下信号的重构精度；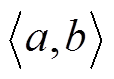
为变量a与b求内积。
使用交替方向乘子算法（Alternate Direction Meth-odof Multipliers, ADMM）迭代求取增广拉格朗日函数的“鞍点”，即为原约束变分问题的最优解。
平衡优化器是一种基于质量平衡方程启发的优化算法，即控制体积内输入、输出和产生的质量守恒[17]。首先根据预设的粒子数和维数在搜索空间中随机均匀构造初始种群，即
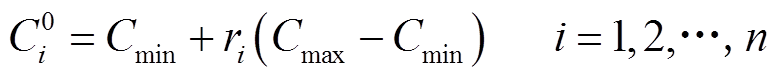（3）
式中，Cmin和Cmax分别为待优化变量的最小值和最大值；ri为[0, 1]之间的随机数；n为种群数。
然后基于粒子适应度函数的排序确定平衡候选解。平衡池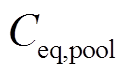
中的前四项为当前迭代中适应度值前四位的粒子，有助于提高全局搜索能力；第五项为前四项的算术平均值，有助于提高局部开发能力，即
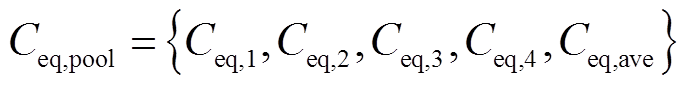（4）
指数项系数F用于平衡算法的探索和开发。其中，时间t定义为迭代函数，随着迭代次数的增加而减少。产生率G通过改进开发阶段提供精确解。
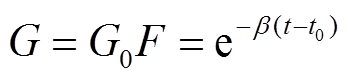（5）
其中
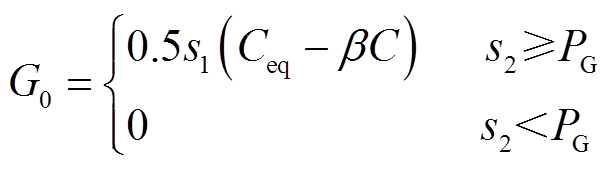（6）
式中，s1, s2, β为[0, 1]之间的随机数；PG为产生概率，用于控制探索和开发能力，在PG=0.5时，探索和开发能力达到平衡；G0为初值，受产生概率PG控制；C为使用产生项更新状态的粒子；Ceq为平衡池Ceq,pool中随机一项。
经过对质量平衡方程的改进与抽象处理，EO算法的更新规则为
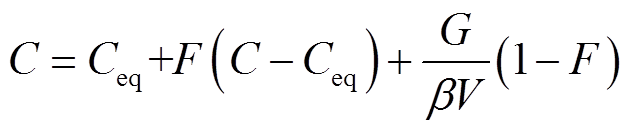（7）
式中，V为单位体积。
VMD算法分解效果受分解个数K和惩罚因子α的影响。K选取不当时，会出现过分解和欠分解；惩罚因子α影响VMD分解得到的BIMF的带宽。因此，需根据PD信号特点合理选择分解参数。为了更好地保留PD脉冲信号，去除干扰信号，使用EO算法优化不同实验条件下的惩罚因子。
在寻优过程中，EO的适应度函数需要能充分体现PD信号在VMD分解下的特点，通过对比适应度函数值的大小进行浓度更新。若获得的本征模态函数（Intrinsic Mode Function, IMF）分量中含有大量噪声，此时该分量稀疏性较弱，包络熵较大；若IMF分量中主要包含放电脉冲信号，此时该分量稀疏性较强，包络熵较小。因此，包络熵越小说明分量包含的PD放电信号越多，也说明信号分解得更充分[18]，本文使用最小包络熵作为EO算法的目标函数。
由于不同温度、频率下的局部放电信号可能具有不同特点，多次实验下环境噪声干扰也有较大差异，因此需要使用EO算法对每一组实验数据进行VMD的参数优化。具体优化流程如下：
初始化EO算法参数，随机生成n个初始粒子，其中VMD分解个数K为1～10之间的整数，惩罚因子α范围为100～7 000；以初始粒子进行VMD分解，获得最小包络熵作为适应度值；评价适应度值，选出最优四项与四者算数平均值作为候选解，构建平衡池；进行浓度更新，判断是否达到最大迭代次数；最终获得VMD分解最优参数K与α。联合EO-VMD与小波阈值函数的去噪流程如图2所示。
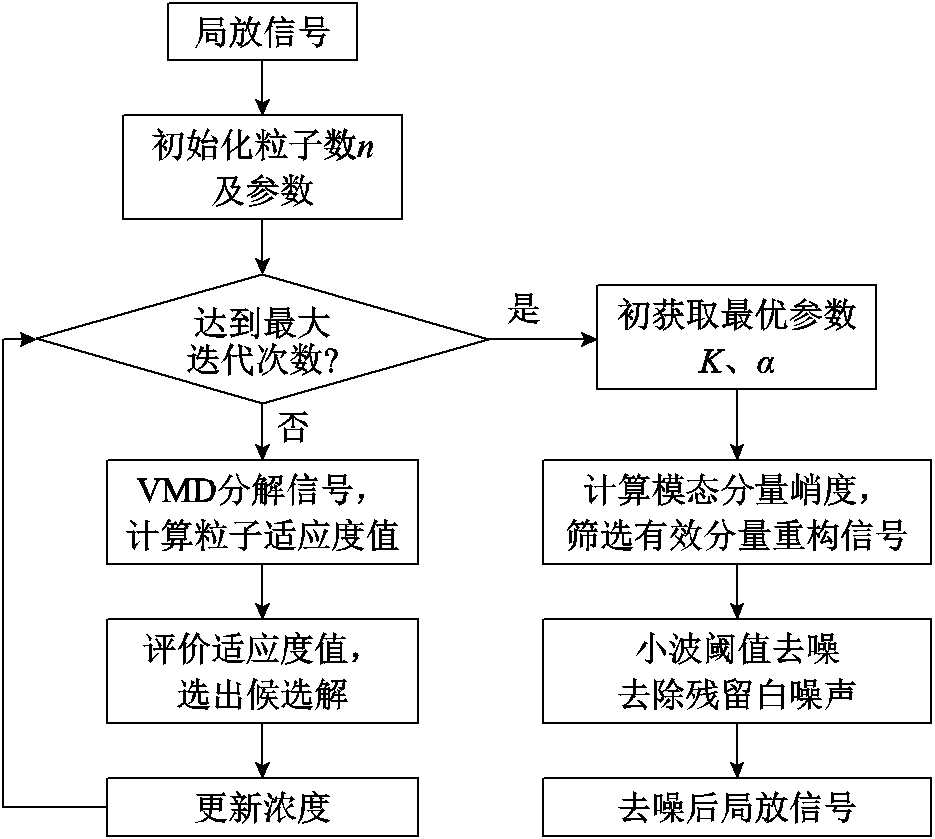
图2 联合EO-VMD与小波阈值函数的去噪流程
Fig.2 Denoising process combining EO-VMD and wavelet threshold function
对VMD分解后的模态分量进行信号重构，重构前需要舍弃噪声较多而放电信息较少的分量。峭度Q可以反映波形的尖峰度[8]，因此分量的选取依据峭度准则，其计算方法为
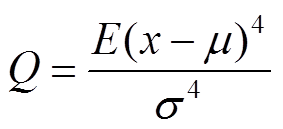（8）
式中，μ为信号幅值的算术平均值；E(x-μ)4为四阶数学期望；σ为标准差。由于PD信号是一种瞬时、突变的信号，其峭度值往往远大于3。因此，舍弃峭度值小于3的分量以去除窄带干扰信号，依据剩余分量进行放电信号重构。由于白噪声时域幅值较小，选取的有效分量中仍有白噪声残留，为更好地保留PD信号特征，本文采用小波阈值去噪进一步去除重构信号中的残留噪声。
通过搭建的高频局部放电实验平台获取局部放电信号，以恒温箱温度为25℃、电源频率为50kHz、幅值为2.5kV的实验数据为例，其原始信号波形和经小波去噪的信号波形分别如图3和图4所示。可以看出，实验噪声并非单纯的高斯白噪声，仅对实验数据进行小波阈值去噪的情况并不理想。
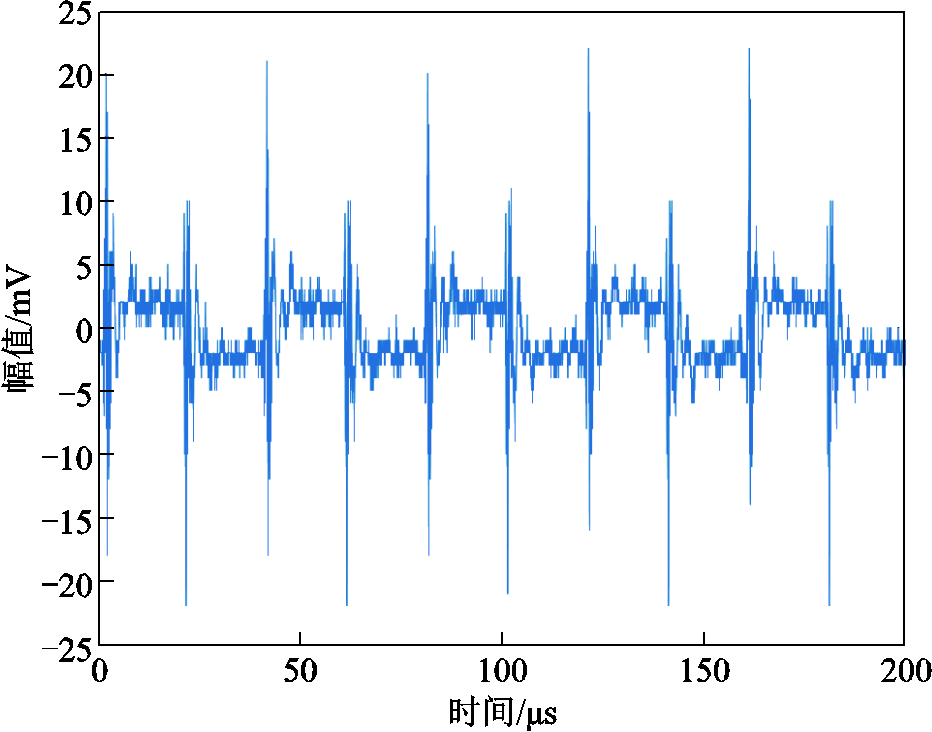
图3 局部放电原始信号
Fig.3 Original partial discharge signal
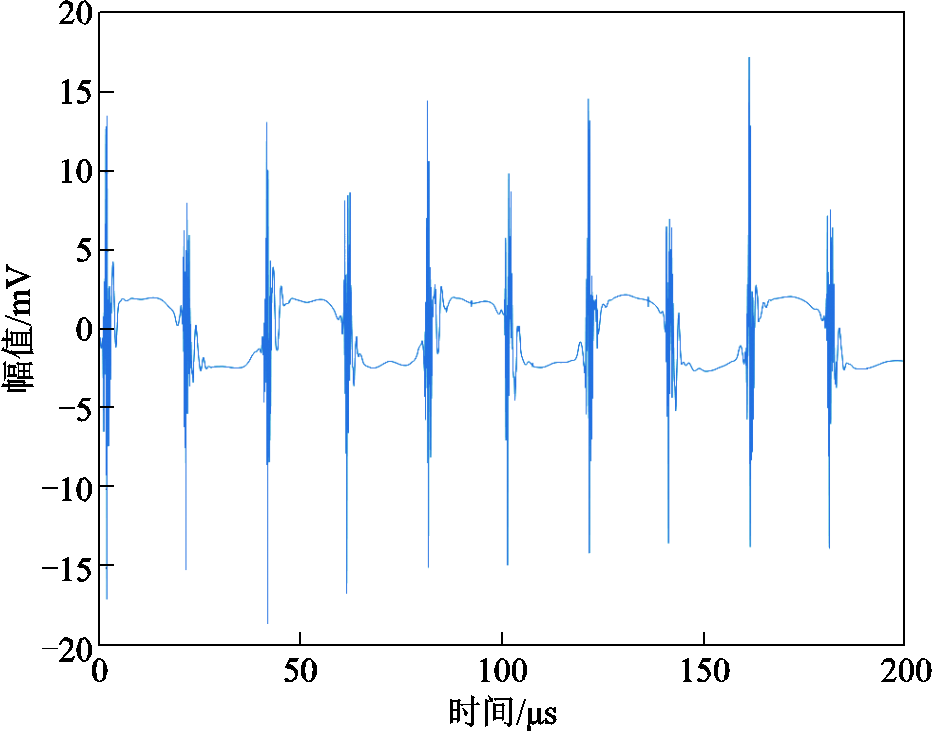
图4 小波去噪后局部放电信号
Fig.4 Partial discharge signal after wavelet denoising
使用EO-VMD算法对局部放电信号的去噪过程如下：设定EO算法中粒子数为20，最大迭代次数为50，获取该组实验数据下VMD算法最优参数。优化得到的最优惩罚因子α取值为4 976，分解个数K取值为5，此时信号最小包络熵为0.926 9。分解后的五个模态分量如图5所示。
计算VMD分解后的各IMF分量的峭度值，其结果见表2。由表2可知，IMF2、IMF3的峭度值远大于其余三个模态。由于通常选择峭度值大于3的分量为有效分量，此时剔除的噪声分量仅有IMF1，而IMF4、IMF5则包含了大量白噪声与部分放电分量。因此，提取IMF2、IMF3、IMF4、IMF5进行信号重构，重构后的信号如图6所示。由图6可见，信号重构后仍有白噪声残留。
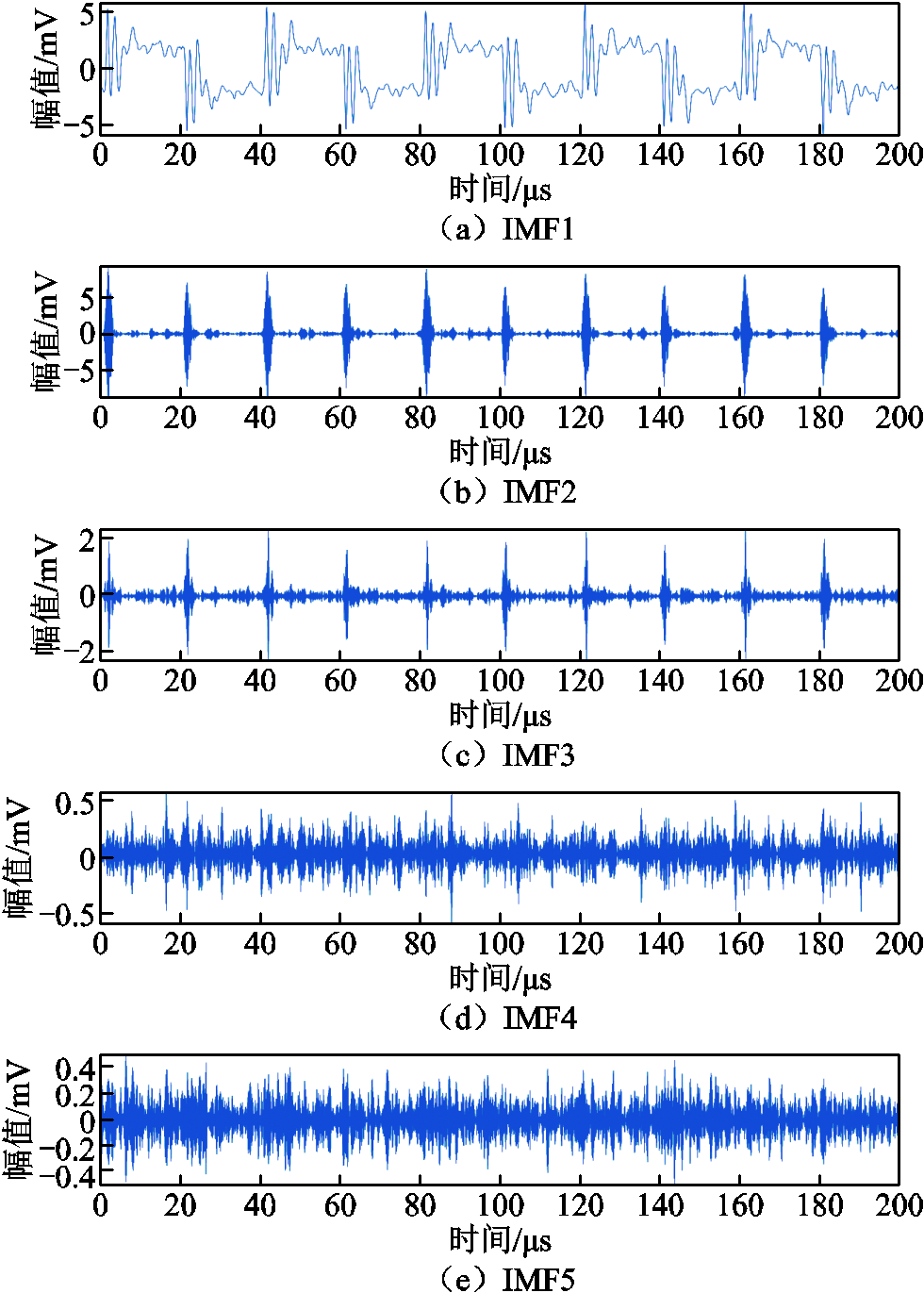
图5 VMD分解模态分量
Fig.5 VMD decomposes modal components
表2 各模态分量峭度值
Tab.2 Kurtosis value of each modal component
模态分量IMF1IMF2IMF3IMF4IMF5 峭度1.869 20.50127.3833.7553.195
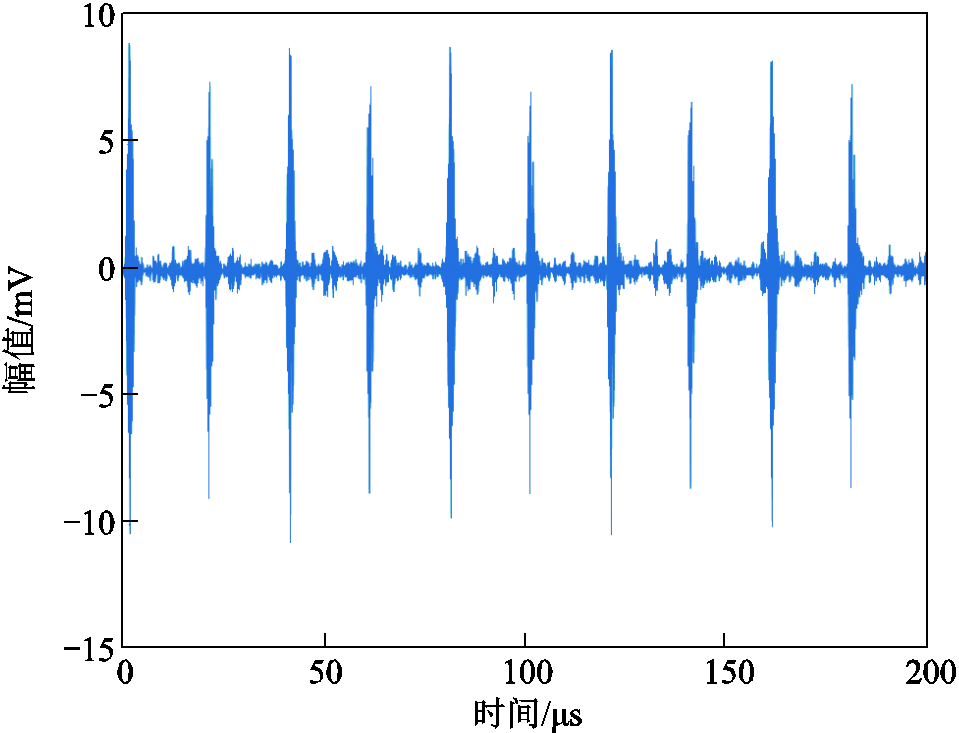
图6 重构信号
Fig.6 Reconstructed signal
为了去除残留高斯白噪声的干扰，调用Matlab中自带的sym8小波基函数对重构信号进行八层分解去噪，最终得到的去噪后的局部放电信号如图7所示。
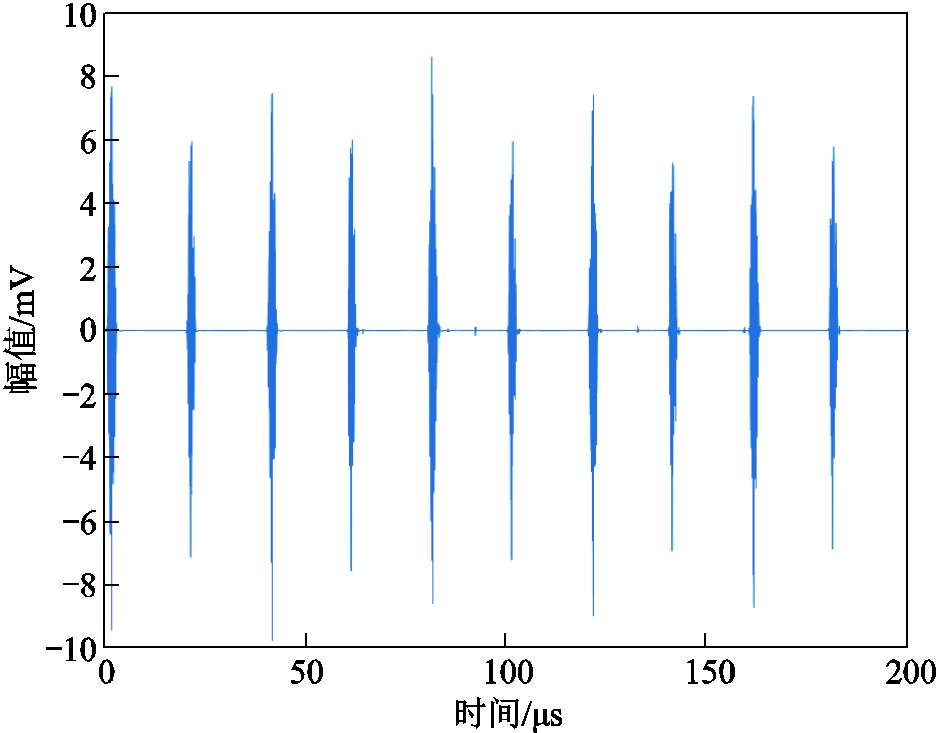
图7 去噪后最终得到的局部放电信号
Fig.7 Final partial discharge signal after denoising
对比图4与图7的波形可以看出，EO-VMD与小波阈值函数相结合的去噪方式可以滤除大部分的实验噪声。
保持幅值2.5kV不变，进行25～100℃，10～50kHz下的局部放电实验，绘制局部放电相位分布（Phase Resolved Partial Discharge, PRPD）谱图。温度一定时，不同频率下的局部放电形态如图8所示。其中，放电点的相对密集程度由点的不同颜色表征，红色代表该谱图中的放电最密区域，深蓝色代表放电最稀疏区域。
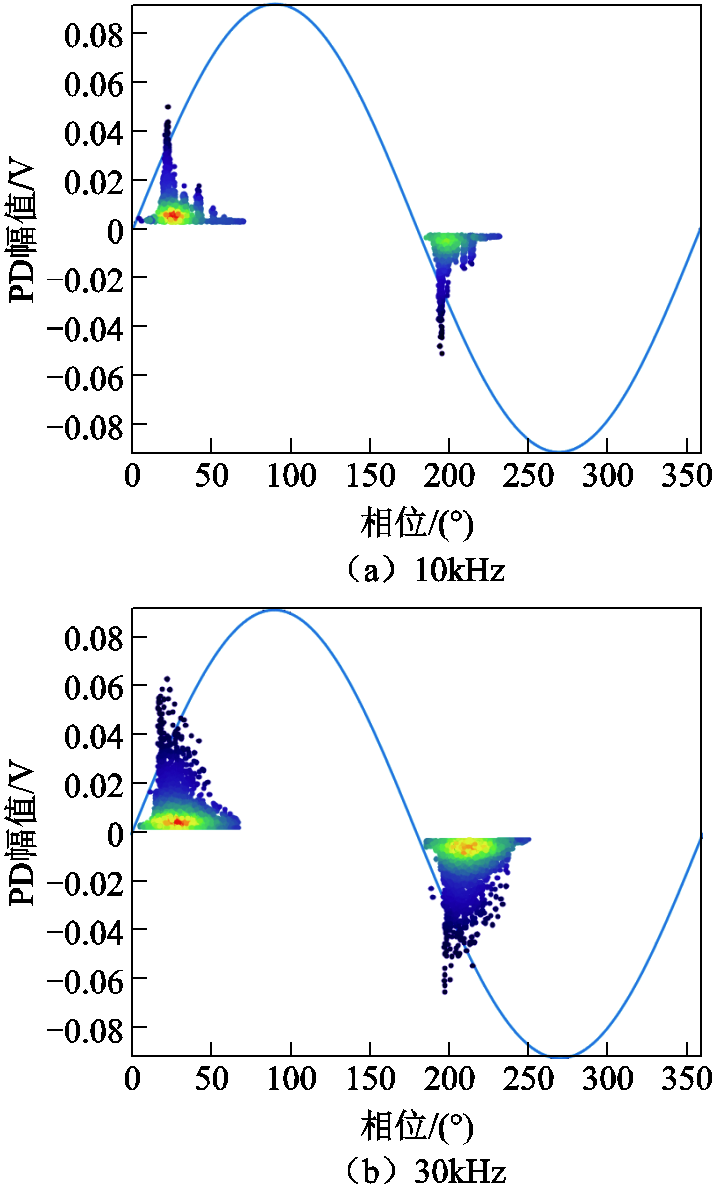
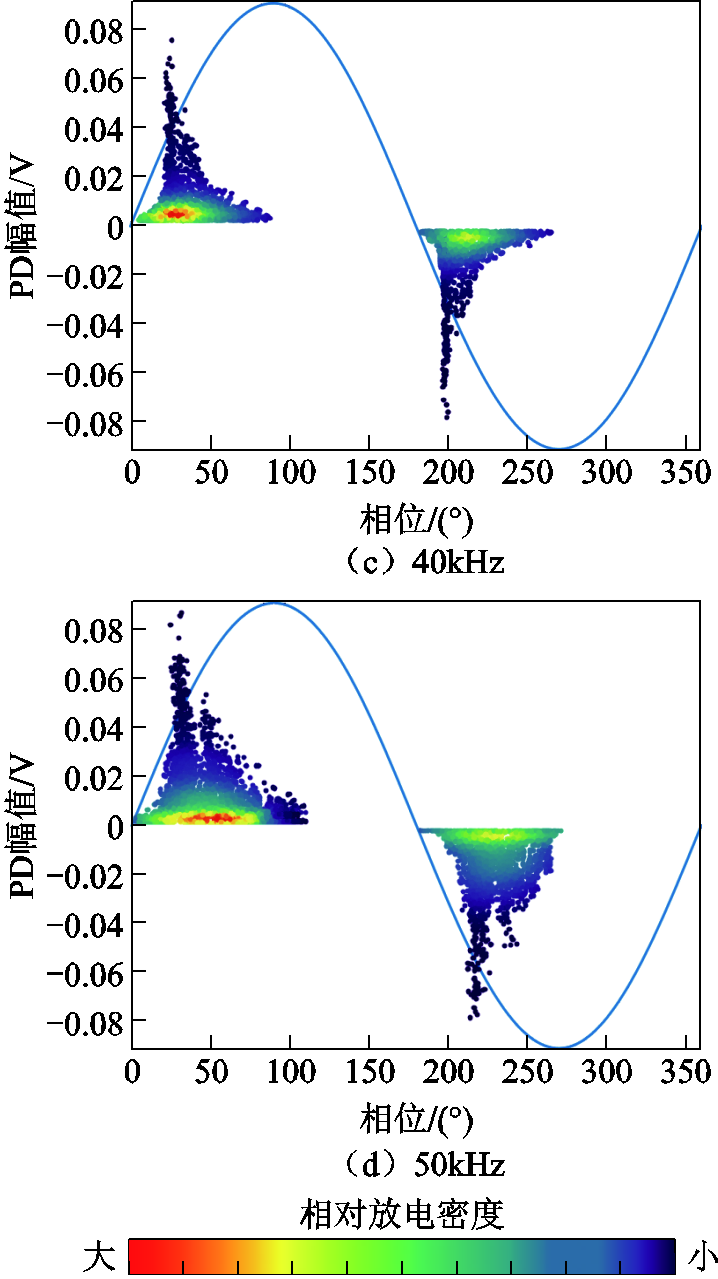
图8 100℃下局部放电特性
Fig.8 Partial discharge characteristics at 100℃
可以看出，随着频率增大，放电现象越来越剧烈，最大放电幅值与总放电次数均呈上升趋势。单周波中，局部放电现象主要集中于正/负半波的上升沿，下降沿与峰值处只存在少量放电。低频条件下，放电出现“分簇”形态，即出现多个不同峰值的放电簇；频率升高，放电相位增大，且放电“分簇”现象减弱。所有频率段的放电均存在“分层”现象，即大量小幅值的放电分布在较宽的相位区间中，而幅值较高的放电则集中在较小的相位区间内；频率较低时，放电的分层现象比频率高时更为明显，且放电相位的分布与高频率下相比更为集中。
频率为30kHz时，不同温度下的局部放电形态如图9所示。可以看出，温度对局部放电形态的影响与频率类似，低温条件下，放电相位分布较为集中且出现“分簇”形态；随着温度不断上升，放电幅值逐渐增大，放电次数增多且呈现弥散状，但放电区间仍主要处于正负半轴上升沿。此时，放电的“分簇”与“分层”现象逐渐削弱。
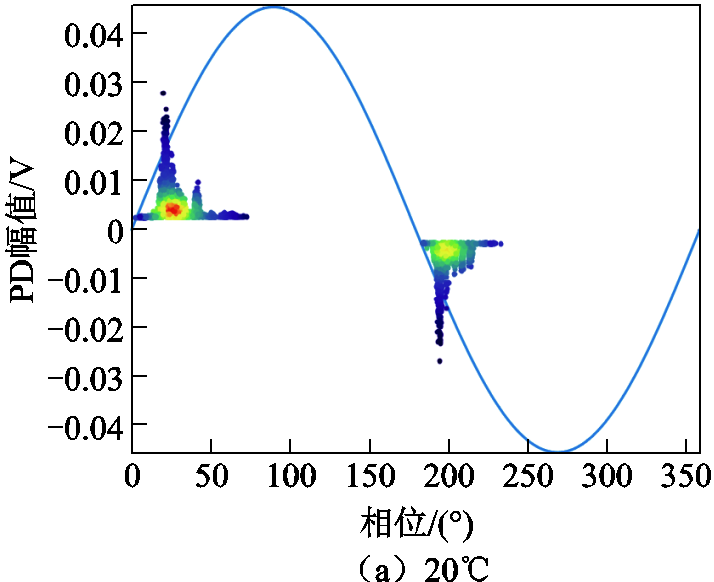
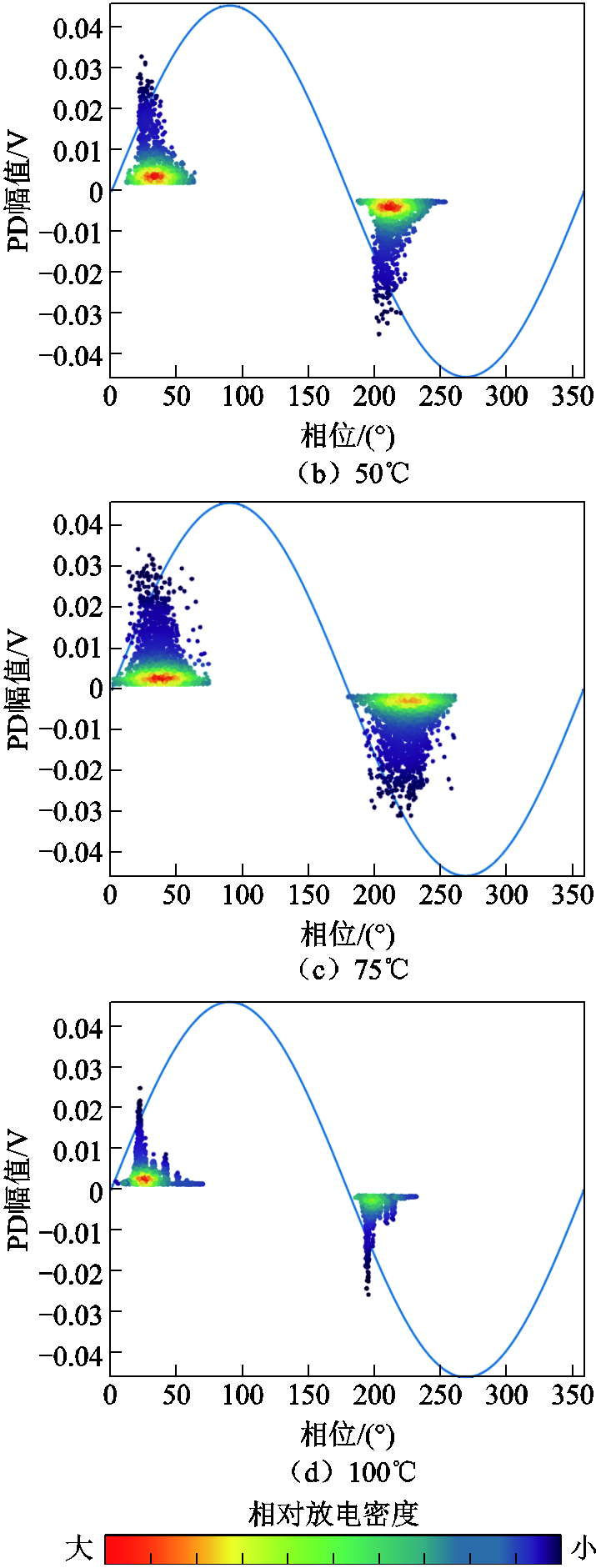
图9 30kHz下局部放电特性
Fig.9 Partial discharge characteristics at 30kHz
统计25～100℃、10～50kHz下的局部放电特征量，不同温度下频率对最大放电幅值的影响如图10所示。分析可知，最大放电幅值随温度升高而增大，且高频下温度对最大放电幅值的影响更为显著，50kHz下温度与最大放电幅值接近线性关系。总体而言，最大放电幅值随频率增大而增大；不同温度下，10～50kHz频段内最大放电幅值上升量大致相同，均为35mV左右；温度达到100℃时，频率对最大放电幅值的影响接近线性关系，如图10所示。
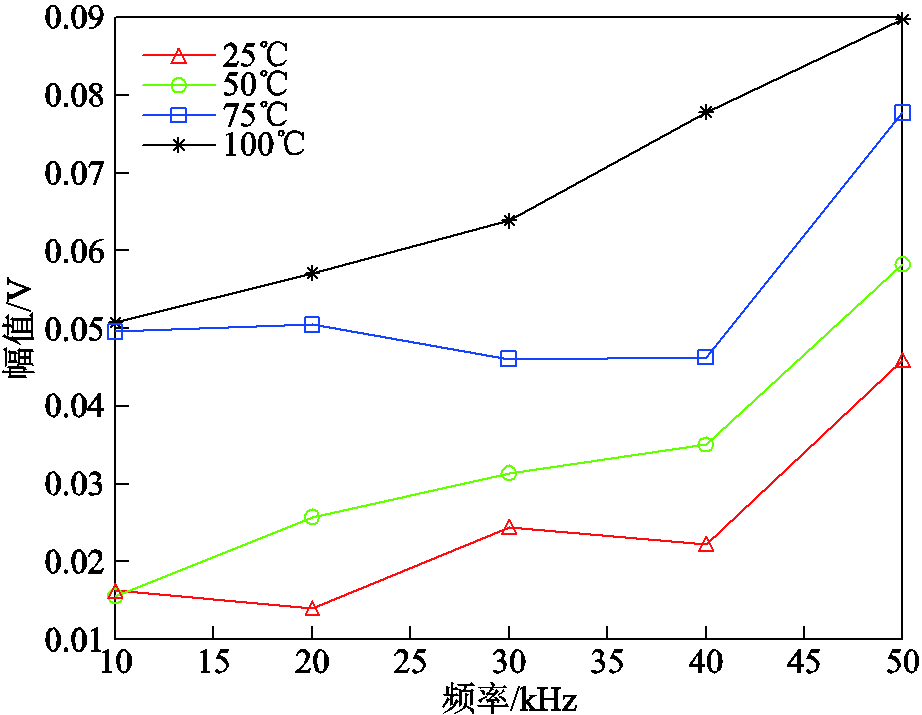
图10 不同温度下频率对最大放电幅值的影响
Fig.10 Influence of frequency on maximum discharge amplitude at different temperatures
不同温度下频率对单周波平均放电次数的影响如图11所示。可以发现，单周波平均放电次数随温度升高而增大，但10kHz和20kHz情况下，温度升高对平均放电次数的增加不明显；30～50kHz时，温度对平均放电次数的影响显著增强，与文献[11]在1kHz下规律一致，分析认为是实验用聚酰亚胺薄膜厚度不同造成的差异。随频率升高，不同温度下局部放电的平均放电次数均呈上升趋势；温度越高则频率对平均放电次数的影响越大，曲线越陡峭，100℃时50kHz下的平均放电次数是10kHz下的15.2倍。总体上，不同频率下平均放电次数随温度增大而增加；高频下温度对平均放电次数的影响大于低频情况。
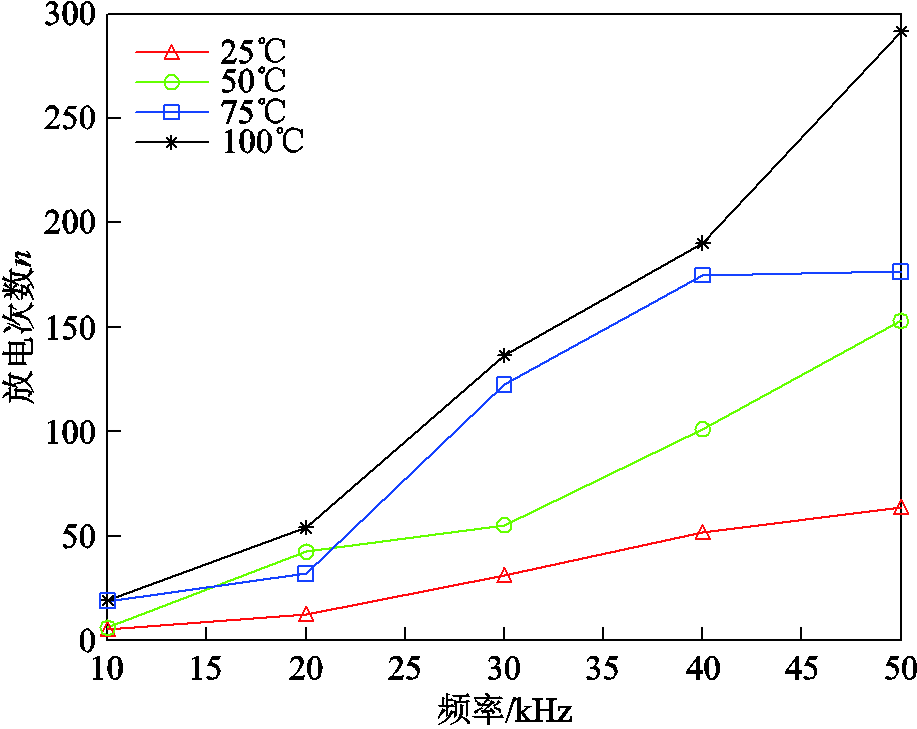
图11 不同温度下频率对单周波平均放电次数的影响
Fig.11 Influence of frequency on average discharge times of single cycle at different temperatures
不同温度下频率对总放电幅值和平均放电幅值的影响分别如图12和图13所示，其变化规律与放电次数类似。总放电幅值随温度升高而增大，且频率越大温度影响越显著：总放电幅值随频率增大而增大；在低温下，总放电幅值-频率曲线较为平缓，在100℃时急剧上升。而对于平均放电幅值，高温、高频条件下放电“分层”现象削弱，导致大量较低幅值的放电点弥散在较宽的相位区间中，使得平均幅值没有呈现较明显的规律性，但总体而言，温度上升时平均放电幅值呈增大趋势，如图13所示。频率对平均放电幅值的影响规律与文献[9]部分一致，其试样处理温度为80℃，观测得到的20kHz平均放电幅值拐点与图13中75℃时的拐点一致。然而由于文献[9]并没有使用其他温度进行实验，其实验频率也只包含10kHz、20kHz、30kHz，因此并未体现出图13中其他曲线的变化规律。
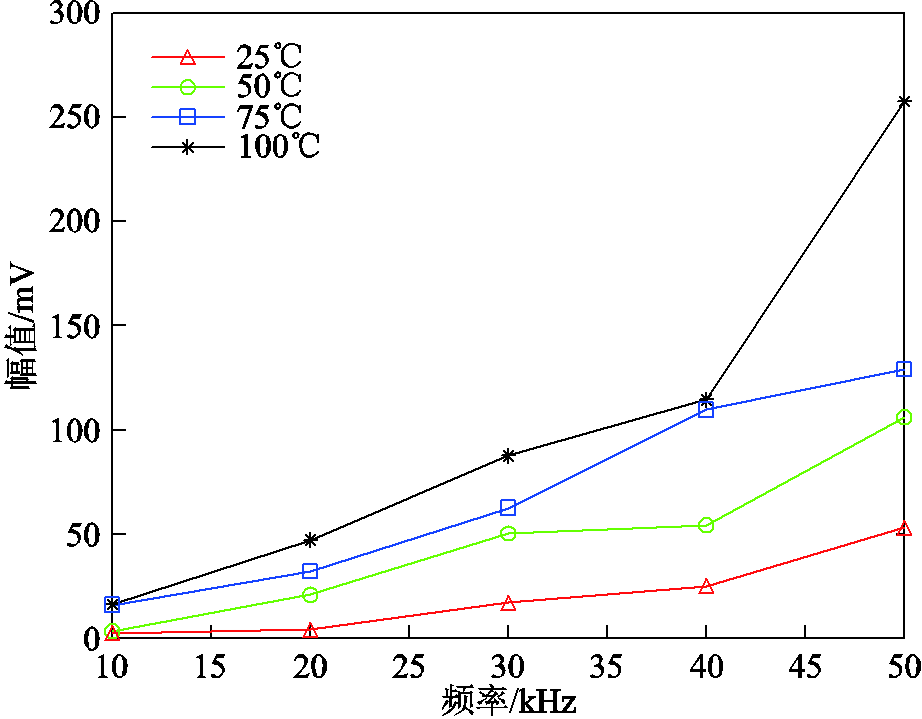
图12 不同温度下频率对总放电幅值的影响
Fig.12 Influence of frequency on total discharge amplitude at different temperatures
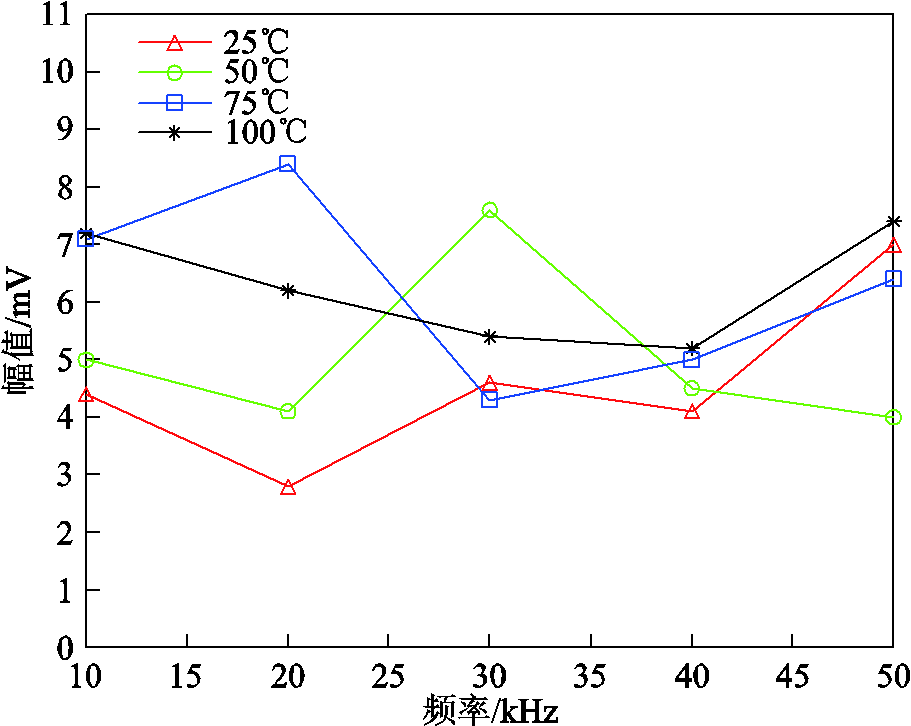
图13 不同温度下频率对平均放电幅值的影响
Fig.13 Influence of frequency on average discharge amplitude at different temperatures
从放电的各个特征量来看，温度升高与频率增大均会导致高频正弦电压下的局部放电更为剧烈。高频下温度对局部放电特征量的影响较低频情况更为明显，而高温下频率对局部放电特征量的影响也显著大于低温情况，两者呈现一种耦合促进关系。但其中，平均放电幅值受放电形态改变的影响，随着频率升高并未呈现明显变化，仅随温度升高有大致上升趋势。
气固绝缘中，由于介电常数的差异，气隙上的电场强度远大于聚酰亚胺薄膜上的电场强度；又因为空气的击穿场强远大于聚酰亚胺薄膜的击穿场强，局部放电主要发生在球形电极与聚酰亚胺薄膜接触表面的气隙。为便于分析频率、温度及二者的耦合协同作用对高频电应力下聚酰亚胺局部放电的影响机理，将球-板电极间的稍不均匀电场假设为均匀电场，使用微等效电路模型并联构成整个放电气隙，如图14所示[12,19]。图中，C1、R1分别为聚酰亚胺绝缘等效电容和电阻，C2、R2分别为气隙等效电容和电阻，R3为等离子体电阻，R4为绝缘介质表面电阻。
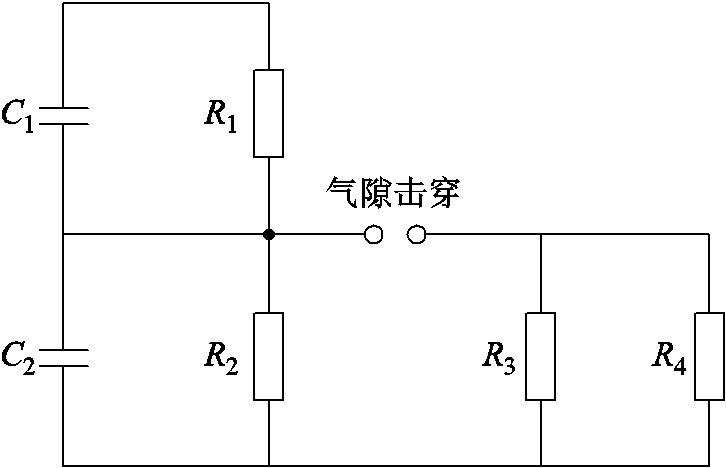
图14 放电气隙微等效电路模型
Fig.14 Discharge air gap micro equivalent circuit model
气隙击穿时，大量电离产生的异极性电荷被球电极吸收，剩余的大量同极性电荷附着在聚酰亚胺薄膜表层，形成表面电荷。此时气隙表面电荷产生的电场将严重影响电荷的积聚和耗散现象，其耗散规律[20]为
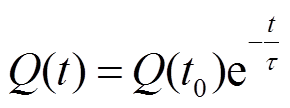（9）
式中，Q(t0)为放电发生后的表面电荷数量；τ为电荷消散的时间常数，τ越小则电荷耗散速度越快，表示为
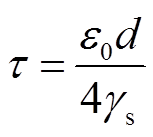（10）
式中，ε0为真空介电常数；d为气隙尺寸；γs为聚酰亚胺薄膜的表面电导率。等待有效电子出现时间与有效电子激发概率P有关[21]，表示为
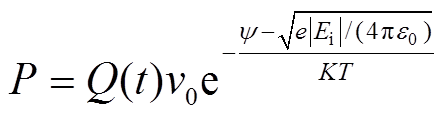（11）
式中，v0为光电离常数；ψ为脱陷功函数；K为玻耳兹曼常数；T为温度；e为基本电荷；Ei为瞬时场强。
反映至微等效电路中，气隙电容、电阻将并联等离子体电阻R3与绝缘介质表面电阻R4。此时，气隙电压U2可以表示为
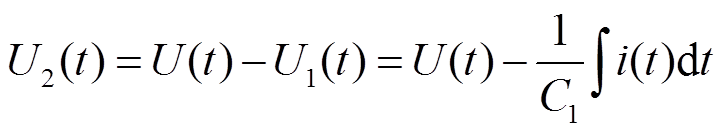（12）
式中，U为球-板电极上的外加电压；U1为绝缘介质上的电压；i为流过绝缘等效电阻R1的电流。
3.3.1 放电“分簇”现象产生机理分析
随着气隙电压U2不断上升，当气隙电场强度到达击穿场强时，气隙发生击穿。此时，由于等离子体电阻R3、绝缘介质表面电阻R4的存在，C1中的残留电荷持续衰减，但由于外施电压的高频特性，部分注入的空间电荷留驻在聚酰亚胺非晶区的深层陷阱中，电荷耗散速度小于电荷注入速度[21]，使得介质电压U1仍维持在较大值。当外施电压U过零时，残留的介质电压U1作用在气隙上，一旦使得气隙电场强度大于空气击穿场强，就可以使得气隙发生反向击穿，因此在电源电压极小时便产生放电簇。但由于实际气隙为稍不均匀电场，残留的介质电压U1往往只能使得部分电场强度较高的区域反向击穿；对于较弱场强区域，需要外施电压过零后的进一步增大使得电场强度大于介质击穿场强才能发生击穿，因此产生有一定相位间隔的放电“分簇”现象，如图8a所示。图8a中，第一簇放电相位集中分布在电压极性反转后10°～30°之间，第二簇放电则集中分布于极性反转后35°～45°之间，且幅值明显小于第一簇放电。
3.3.2 放电“分簇”现象随温度、频率变化机理分析
由于频率增大对介质表面电导率无影响，电荷消散时间常数τ也基本不变。而随着外施电压频率升高，电压下降速度与电荷耗散速度差距增大，导致电压过零时残留的表面电荷较低频情况更多，介质残留电场强度更大。因此，频率增大时表面电荷增多，由式（11）可知，有效电子出现概率增大，反向放电现象更容易发生。且由于电源电压周期减小，该放电簇在相位谱图中延展更大，放电相位更宽。同时，由于残留介质电压增大，更多的弱场强区域无需等待外施电压增大也会发生反向击穿，使得低频情况下出现的第二簇放电更早到来。因此，两簇放电在高频情况下往往重合，导致放电“分簇”现象消失，如图8所示。
而随着温度升高，介质表面电导率增大[12]，反映至微等效电路中即绝缘介质表面电阻R4减小，使得气隙放电电流增大，放电微粒在材料表面的转移速度加快。这会导致切向的放电分量增大，放电向弱电场强度区域发展，也会导致放电“分簇”现象消失，如图9所示。
3.3.3 放电“分层”现象随温度、频率变化机理分析
由于实际气隙为稍不均匀电场，强、弱电场强度区域放电幅值具有较大差异，由此产生了放电“分层”现象。温度升高时，载流子具有更高能量，更容易克服电极金属的逸出功，因此会发射更多的热电子，气隙的空间电荷注入量增多[22]；同时，由于温升带来的表面电导率增大，放电向切向发展，两者共同加强了弱电场区域的电场强度。这使得弱电场区域也出现一些大幅值的放电，因此“分层”现象减弱，如图9所示。
瞬时增加的电场会诱发电子崩，频率增大时，单位时间内电压极性翻转次数增加，电子崩产生放电的电离数也呈正比例上升，同样也会带来更大的累积破坏作用。因此，频率提高与温度增加同样会增大气隙的切向电场，使得放电向弱电场区发展，同样会使得“分层”现象减弱，如图8所示。
3.3.4 局部放电起始电压机理分析
同样是由于稍不均匀电场的特点，气隙的初次放电一定发生于球电极与介质接触点附近的强电场强度区域。此时电场主要为法向分量，切向场强较小且对初次放电影响可以忽略。随温度升高，绝缘介质的体电导率下降，且由式（11）可知，温度增大时有效电子激发概率增大，因此温度升高降低了局部放电起始电压。而由于初次放电前并无空间电荷的留驻现象，初次击穿电压几乎完全取决于外施电压幅值，而与电荷耗散速度和外施电压频率无关[23]，如表1中的结果所示。
3.3.5 局部放电特征量机理分析
温度升高和频率增大均会导致放电幅值、放电次数增加。首先，温度升高时介质体电导率增大，而体电导率与放电重复率成正比[20]，最终使得绝缘的局部放电次数增加。另外，频率的提高会提高单位时间内空间电荷注入-抽出的次数，幅值不变时，频率增大也将导致电压上升率提高，并由于等效电容的存在而产生更大的位移电流。较大的位移电流使电极与绝缘介质的局部温升严重，进一步提高单位时间局部放电量和放电次数。温度、频率提高均会导致热电离更剧烈，生成的热电子增多；材料受到热电子反复冲击，带来的极化效应、疲劳效应进一步加强，引起更大的介质损耗，同时导致介质温度上升，进一步增大了热电离剧烈程度。因此，高频下温度对局部放电特征量的影响更大，而高温下频率对局部放电特征量的影响也更为显著，两者呈现出一种耦合促进关系。
本文搭建了高频正弦电压下聚酰亚胺气固绝缘实验平台，通过25～100℃四个温度点与10～50kHz五个频率点下的局部放电实验数据，获取了温度、频率对聚酰亚胺局部放电的影响规律，得到以下结论：
1）通过EO算法实现了针对不同温度、频率下局部放电信号的VMD参数优化，进行了局部放电信号的自适应去噪处理。
2）温度、频率与局部放电的特征量，如最大放电幅值、总放电幅值与放电次数均呈正相关；同时随温度升高或频率增大，放电的“分簇”与“分层”现象逐渐减弱。温度越高，频率对局部放电特征量的影响越大；频率越高，温度对局部放电特征量的影响也越大，两者呈耦合促进关系。
3）分析了温-频协同作用的影响机理。高频高温时气固界面的切向电场增强，放电向弱场强区域发展，因此放电的“分簇”与“分层”现象逐渐减弱。频率升高会导致单位时间内空间电荷注入-抽出的次数上升，位移电流增大而局部温升增大；温度升高会导致载流子更容易克服逸出功，造成更多的热电子发射。因此，在高频正弦电压下，温度与频率两者对局部放电呈现一种耦合促进关系。
参考文献
[1] 涂春鸣, 黄红, 兰征, 等. 微电网中电力电子变压器与储能的协调控制策略[J]. 电工技术学报, 2019, 34(12): 2627-2636.
Tu Chunming, Huang Hong, Lan Zheng, et al. Coordinated control strategy of power electronic transformer and energy storage in microgrid[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2627-2636.
[2] 高范强, 李子欣, 李耀华, 等. 面向交直流混合配电应用的10kV-3MV·A四端口电力电子变压器[J]. 电工技术学报, 2021, 36(16): 3331-3341.
Gao Fanqiang, Li Zixin, Li Yaohua, et al. 10kV-3MV·A four-port power electronic transformer for AC-DC hybrid power distribution applications[J]. Transactions of China Electrotechnical Society, 2021, 36(16): 3331-3341.
[3] Qin Hengsi, Kimball J W. Solid-state transformer architecture using AC–AC dual-active-bridge converter[J]. IEEE Transactions on Industrial Electronics, 2013, 60(9): 3720-3730.
[4] Le Besnerais J, Fasquelle A, Hecquet M, et al. Multiphysics modeling: electro-vibro-acoustics and heat transfer of PWM-fed induction machines[J]. IEEE Transactions on Industrial Electronics, 2010, 57(4): 1279-1287.
[5] 马星河, 张登奎. 基于改进经验小波变换的高压电缆局部放电噪声抑制研究[J]. 电工技术学报, 2021, 36(增刊1): 353-361.
Ma Xinghe, Zhang Dengkui. Research on suppression of partial discharge noise of high voltage cable based on improved empirical wavelet transform[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 353-361.
[6] 李文华, 姜惠, 赵正元, 等. 基于波形匹配端点延拓法优化的经验模态分解算法在铁路继电器参数降噪上的应用[J]. 电工技术学报, 2022, 37(10): 2656-2664.
Li Wenhua, Jiang Hui, Zhao Zhengyuan, et al. Application of empirical mode decomposition algorithm based on waveform matching endpoint continuation method in noise reduction of railway relay parameters[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2656-2664.
[7] 李睿彧, 刘飞, 梁霖, 等. 基于参数优化变分模态分解的交流变频电机转子断条故障识别方法[J]. 电工技术学报, 2021, 36(18): 3922-3933.
Li Ruiyu, Liu Fei, Liang Lin, et al. Fault identification of broken rotor bars for the variable frequency AC motor based on parameter optimized variational mode decomposition[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3922-3933.
[8] 刘冲, 马立修, 潘金凤, 等. 联合VMD与改进小波阈值的局放信号去噪[J]. 现代电子技术, 2021, 44(21): 45-50.
Liu Chong, Ma Lixiu, Pan Jinfeng, et al. PD signal denoising based on VMD and improved wavelet threshold[J]. Modern Electronics Technique, 2021, 44(21): 45-50.
[9] 刘思华, 王健, 刘涛, 等. 高频电压下油纸绝缘系统的局部放电及产气特性研究[J]. 高压电器, 2018, 54(2): 121-127.
Liu Sihua, Wang Jian, Liu Tao, et al. Research on partial discharge and gas production characteristics of oil-paper insulation system under high frequency voltage[J]. High Voltage Apparatus, 2018, 54(2): 121-127.
[10] Cavallini A, Montanari G C. Effect of supply voltage frequency on testing of insulation system[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2006, 13(1): 111-121.
[11] 徐跃, 邓小军. 不同频率和温度的电晕放电对聚酰亚胺薄膜的损伤特性研究[J]. 绝缘材料, 2014, 47(1): 85-88.
Xu Yue, Deng Xiaojun. Study on the effect of corona discharge on the damage mechanism of polyimide film under different frequency and temperature[J]. Insulating Materials, 2014, 47(1): 85-88.
[12] 韩帅, 李庆民, 刘伟杰, 等. 温-频耦合效应对高频固态变压器绝缘局部放电特性的影响[J]. 电工技术学报, 2015, 30(2): 204-210.
Han Shuai, Li Qingmin, Liu Weijie, et al. Impacts of coupled temperature-frequency effects on partial discharge characteristics of high frequency solid state transformer insulation[J]. Transactions of China Electrotechnical Society, 2015, 30(2): 204-210.
[13] 罗杨, 吴广宁, 王鹏, 等. 连续方波脉冲电压下温度对聚酰亚胺薄膜局部放电特性的影响[J]. 中国电机工程学报, 2012, 32(19): 154-160, 199.
Luo Yang, Wu Guangning, Wang Peng, et al. Effect of temperature on partial discharge properties of polyimide film under continuous square impulse voltage[J]. Proceedings of the CSEE, 2012, 32(19): 154-160, 199.
[14] 刁常晋, 程养春, 邓春, 等. 阶梯升压试验和恒定电压试验中油纸绝缘局部放电发展规律的对比[J]. 高电压技术, 2013, 39(2): 365-373.
Diao Changjin, Cheng Yangchun, Deng Chun, et al. Contrast of the developing regularity of partial discharge of oil-paper insulation using step-stress test and constant-stress test[J]. High Voltage Engineering, 2013, 39(2): 365-373.
[15] 罗杨. 局部放电对聚酰亚胺薄膜的损伤特性及材料改性研究[D]. 成都: 西南交通大学, 2014.
[16] 肖洒, 陈波, 沈道贤, 等. 改进VMD和阈值算法在局部放电去噪中的应用[J]. 电子测量与仪器学报, 2021, 35(11): 206-214.
Xiao Sa, Chen Bo, Shen Daoxian, et al. Application of improved VMD and threshold algorithm in partial discharge denoising[J]. Journal of Electronic Measurement and Instrumentation, 2021, 35(11): 206-214.
[17] 杨蕾, 李胜男, 黄伟, 等. 基于平衡优化器的含高比例风光新能源电网无功优化[J]. 电力系统及其自动化学报, 2021, 33(4): 32-39.
Yang Lei, Li Shengnan, Huang Wei, et al. Reactive power optimization of power grid with high-penetration wind and solar renewable energies based on equilibrium optimizer[J]. Proceedings of the CSU-EPSA, 2021, 33(4): 32-39.
[18] 魏才懿, 杨军, 马建桥. 参数优化VMD对变压器声音信号的故障诊断[J]. 兰州交通大学学报, 2021, 40(4): 49-58.
Wei Caiyi, Yang Jun, Ma Jianqiao. Fault diagnosis of transformer sound signal by parameter optimization VMD[J]. Journal of Lanzhou Jiaotong University, 2021, 40(4): 49-58.
[19] 潘俊, 方志. 多脉冲均匀介质阻挡放电特性的仿真及实验研究[J]. 高电压技术, 2012, 38(5): 1132-1140.
Pan Jun, Fang Zhi. Simulation and experimental studies on discharge characteristics of multiple pulse homogeneous dielectric barrier discharge[J]. High Voltage Engineering, 2012, 38(5): 1132-1140.
[20] 张开放, 张黎, 赵彤, 等. 高频正弦电应力对气-固绝缘局部放电的影响[J]. 高电压技术, 2019, 45(12): 3879-3888.
Zhang Kaifang, Zhang Li, Zhao Tong, et al. Influence of high frequency sinusoidal electrical stress on partial discharge of gas-solid insulation[J]. High Voltage Engineering, 2019, 45(12): 3879-3888.
[21] 邢轩, 赵庆昕, 王志清, 等. 电压频率和环境湿度对聚酰亚胺薄膜局部放电特性的影响[J]. 绝缘材料, 2020, 53(1): 35-40.
Xing Xuan, Zhao Qingxin, Wang Zhiqing, et al. Effect of voltage frequency and ambient humidity on partial discharge characteristics of polyimide films[J]. Insulating Materials, 2020, 53(1): 35-40.
[22] 钟力生, 李盛涛, 徐传骧. 工程电介质物理与介电现象[M]. 西安: 西安交通大学出版社, 2013.
[23] Fabiani D, Montanari G C, Cavallini A, et al. Relation between space charge accumulation and partial discharge activity in enameled wires under PWM-like voltage waveforms[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2004, 11(3): 393-405.
Abstract Partial discharge (PD) is a significant reason for the deterioration of polyimide (PI) insulation in high-frequency power transformers (HFPT). In order to study the partial discharge mechanism of polyimide under high-frequency voltage and explore the influence of temperature and frequency on the partial discharge characteristics, a high frequency partial discharge test platform was established. Spherical plate electrode was selected to simulate the actual electric field distribution of polyimide in HFPT, and ETS-93686 high-frequency pulse current sensor was used to collect PD signal. Teck MDO3024 oscilloscope was used to simultaneously collect high-frequency sinusoidal signal and partial discharge signal.
Four temperatures (25℃, 50℃, 75℃, 100℃) and five frequencies (10kHz, 20kHz, 30kHz, 40kHz, 50kHz) were selected for the experiment. The partial discharge inception voltage (PDIV) was recorded at a boosting speed of 200V/s. The test selected 1.5～2 times of PDIV as the partial discharge test voltage, which means keeping each experiment at a constant voltage of 2.5kV.
There are a lot of noise signals in the data measured by the pulse current sensor. Because it is difficult to adaptively select decomposition parameters of variational mode decomposition (VMD), equilibrium optimizer (EO) algorithm was used to obtain the optimal number of modal decomposition K and the penalty factor α. First, initialized the parameters of the EO algorithm and generated n initial particles randomly. Limited K to an integer ranging from 1 to 10, and constrained the penalty factor α ranging from 100 to 7 000. Second, decomposed the initial particles by VMD, and obtained the minimum envelope entropy as the fitness value. Evaluated the fitness value, then selected the best four terms and the arithmetic mean value of these four terms as candidate solutions to build a balance pool. Updated the concentration to determine whether the maximum number of iterations has been reached. Finally, the optimal parameter K and α of VMD decomposition was obtained. The result of experimental data denoising shows that the EO-VMD algorithm proposed in this paper can remove the experimental noise very well.
The experimental results show that temperature and frequency have positive correlation with the characteristic quantity of partial discharge, such as the maximum discharge amplitude, the total discharge amplitude and the discharge times. At the same time, with the increase of temperature or frequency, the phenomenon of "clustering" and "delamination" of discharge decreases gradually. The influence of frequency on the characteristic quantity of PD is greater at high temperature, while the influence of temperature is greater at high frequency. These two variables have a coupling promoting relationship. In this paper, the mechanism of temperature-frequency synergy is analyzed. At high frequency and high temperature, the tangential electric field at the gas-solid interface increases, and the discharge develops to the weak electric field region. Therefore, the phenomenon of "clustering" and "delamination" of the discharge gradually weakens. High frequency will lead to the increasing times of space charge injection and extraction per unit time, which means the increase of displacement current and local temperature. High temperature will make it easier for carriers to overcome the work function and cause more hot electron emission. Therefore, under high-frequency sinusoidal voltage, temperature and frequency have a coupling promoting relationship to partial discharge.
keywords：Partial discharge, equilibrium optimizer, variational mode decomposition, temperature, frequency, polyimide
DOI:10.19595/j.cnki.1000-6753.tces.221258
中图分类号：TM855
国家自然科学基金资助项目（52077127, 51929701）。
收稿日期 2022-06-29
改稿日期 2022-07-29
徐黄宽 男，1997年生，硕士研究生，研究方向为高频高压绝缘放电。E-mail：sduxhk@163.com
张 黎 男，1979年生，副教授，博士生导师，研究方向为高电压与绝缘技术、电力系统电磁兼容。E-mail：zhleee@sdu.edu.cn（通信作者）
（编辑 李冰）