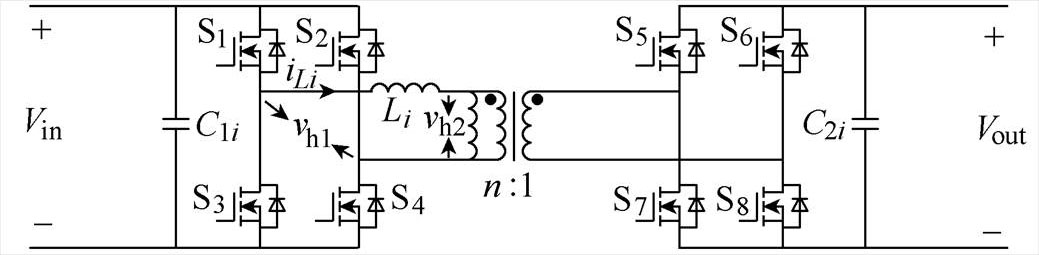
图1 DAB单模块拓扑结构
Fig.1 Topology of single module DAB converter
摘要 单模块双有源全桥DC-DC变换器,可通过最优移相策略来保证电流有效值最优。然而,当多模块并联运行时,由于模块间电气量无法完全匹配一致,不同模块间的电流有效值特性将有所差异,导致传统的均功率控制无法做到总效率最优。基于此,该文提出一种基于遗传算法的多模块输入并联输出并联(IPOP)双有源全桥DC-DC变换器总电流有效值优化策略。首先,该文结合遗传算法对单模块双有源全桥变换器的电流有效值特性进行分析与优化,该算法集成了单、双、三重移相控制的优势,同时可自然实现三种移相策略的无缝过渡。其次,针对输入输出并联的多模块变换器系统,提出一种基于离线计算在线查表,总电感电流有效值最优的控制策略。不同于传统的均功率控制方法,该策略可根据模块间辅助电感的差异化对总功率进行优化分配,以实现系统的总电感电流有效值最优。最后,搭建一台基于碳化硅器件的8 kW/100 kHz三模块并联样机对优化控制策略进行验证,实验表明,基于优化控制策略,样机峰值效率可达98.8 %,与传统均功率控制策略进行对比,在降压和升压工况下,平均效率分别提升了1.2 %和0.84 %,验证了该文所提控制策略的有效性。
关键词:双有源全桥变换器 输入并联输出并联 遗传算法 功率分配 电感电流有效值
近年来,随着化石能源的消耗,以及环境问题的日益突出,新能源发电、电动汽车、储能技术已经成为电力行业的研究重点[1-2]。其中,DC-DC变换器作为电力电子系统中的重要组成部分,是充电桩、储能系统、直流微电网中的关键部件[3-4]。
目前,已经有多种DC-DC变换器拓扑被提出,双有源全桥(Dual Active Bridge, DAB)变换器是DC-DC变换器的热门研究拓扑之一,其集成了输入输出端电气隔离、高电压增益、较宽负载范围内实现全体开关器件零电压开通(Zero Voltage Switching, ZVS)等优点[5]。通过控制各个开关桥臂之间的移相,即可实现能量的双向流动。
移相控制是DAB变换器常用的控制方法。目前,已有多个单模块DAB移相控制方法被提出,包括单重移相(Single Phase Shift, SPS)控制[6]、双重移相(Double Phase Shift, DPS)控制[7]、扩展移相(Extended Phase Shift, EPS)控制[8]和三重移相(Triple Phase Shift, TPS)控制[9]。TPS控制有三个控制自由度,SPS、DPS和EPS控制都是TPS控制的特殊形式,TPS控制已广泛应用于DAB的控制中。TPS控制通过控制三个移相,能让DAB变换器在同一输出功率下实现不同的软开关、电流应力和电感电流有效值特性。文献[5]提出了一种利用TPS控制扩大零电压开通范围的方法。文献[10]基于TPS控制,优化了变换器的电流应力。文献[11]利用TPS控制对变换器的电感电流有效值进行优化。以上的优化目标中,电感电流有效值与开关器件的导通损耗、辅助电感铜损、变压器铜损都有重要关系,因此,电感电流有效值是影响单模块DAB变换器效率的重要指标。现有的对单模块DAB的优化方法大多需要复杂的数学分析,在DAB变换器需要在不同工作模态之间进行切换时或是面对多约束多目标优化问题时,较难分析出结果。多个模块协同控制的场景,传统的数学分析方法也会变得更加复杂。
在大功率充电桩、储能系统等对DC-DC变换器的功率和耐压指标要求较高的应用场景中,受制于开关器件、继电器、接插件等硬件设备的载流能力,单变换器模块无法实现指定功率输出。对于DAB变换器,其输入输出端口均为电压源特性,多模块运行时也可保证单模块功率解耦运行,因此,大功率运行场景中DAB变换器也得到了广泛运用。针对多模块连接方式,可分为输入并联输出并联(Input Parallel and Output Parallel, IPOP)、输入串联输出并联(Input Series and Output Parallel, ISOP)、输入并联输出串联(Input Parallel and Output Series, IPOS)、输入串联输出串联(Input Series and Output Series, ISOS)等方式[12]。
对变换器进行模块化组合可有效提高系统整体的耐压水平、额定功率。理想情况下,各个独立模块均是按同一标准进行生产,但由于生产工艺,以及产品的不断更新换代等原因,各个模块的参数,如辅助电感、变压器电压比、开关器件的内阻、滤波电压等参数均有差异。这些差异将会导致变换器实际工作时模块间电压分配不均、各模块输出功率不均衡等问题,大大增加独立模块的故障概率。近年来,多种多模块DAB变换器的控制方法被提出,文献[13]提出了一种增加均流环作为反馈的三环均流控制方法。文献[14]提出了一种根据采样信息和PI反馈对下一周期的移相角进行补偿的控制方法,实现各个模块的功率均衡。以上控制策略的核心思想均是让各个模块均分变换器的总功率并实现各个模块的输入输出电压相等,消除独立模块参数差异带来的功率、电压不均衡等问题。
然而,由于模块间的参数差异,尤其是电感参数的差异,根据DAB变换器的运行特性,让每一个独立模块均分总功率,并不一定能使整个变换器系统效率以及各项指标达到最优。该差异导致的效率降低在重载工况会尤为明显。
现有的DAB效率优化算法大多只针对单个模块,一般基于某个优化目标,从时域[11]、频域[15]角度获得控制量的显性表达式数值解。然而,考虑到n并联运行时,若采用三重移相控制,将会产生3n个控制变量,根据实时工况求解3n个最优值将会给芯片带来极大的运算量。人工智能技术的发展为解决这一问题提供了新的思路,目前粒子群优化(Particle Swarm Optimization, PSO)算法和遗传算法(Genetic Algorithm, GA)已被用于DAB变换器的优化控制中[16-18],文献[16, 18]分别利用粒子群优化算法对DAB的移相角进行计算,对电感电流有效值和电流应力进行优化。GA相比于PSO,不容易掉入局部最优解中,文献[17]利用GA对单模块DAB的零电压开关范围和电流应力进行优化。以上的人工智能算法能够避免繁杂的分段化公式计算,一次运行便可得到全域最优解。同时,由于DAB功率模块在制作完成后,其硬件参数为一定值,使用智能算法计算得到所有运行工况的最优移相角,再通过查表的方式嵌入控制器中,可有效地减少实时计算类的控制算法带来的额外运算量,提升系统计算速度。
针对上述提到的单模块DAB变换器以及多模块DAB变换器系统效率优化的关键问题,本文基于GA以IPOP模块化连接的双有源全桥变换器为基本拓扑展开研究。对于独立模块,本文基于三重移相控制,采用GA对其电感电流有效值进行优化,保证独立模块的电感电流有效值最优。同时对于整个系统,本文提出了一种考虑模块间电感差异因素,保证总输出功率一定的情况下,实现多模块功率差异化分配的控制策略。本文研究如何根据各个独立模块的等效电感参数差异来对总功率进行分配,从而实现变换器系统总输出功率一定的情况下,总电感电流有效值最小。
综上所述,本文首先分析DAB变换器三重移相控制下的工作模式,利用GA计算建立单模块电感电流有效值优化模型。其次基于单模块的电感电流有效值优化模型,以变换器系统总电感电流有效值最小为优化目标,利用GA和多项式拟合相结合的方法,构建了一种多模块功率分配控制策略,并实现了IPOP多模块DAB变换器总电感电流有效值最小。然后搭建了多模块IPOP运行样机,对控制策略进行了验证,并与其他控制策略进行了对比分析。最后对本文的理论以及实验分析进行总结,并提出结论。
在分析多个模块并联的整体特性之前,先对单个模块的控制进行分析。以第i个模块为例,DAB单模块拓扑结构如图1所示。
图1中,Vin为模块输入电压,Vout为模块输出电压,C1i为第i个模块的输入支撑电容,C2i为第i个模块的输出支撑电容,Li为折算到一次侧的辅助电感和变压器漏感之和,后文提到的辅助电感,均是指辅助电感与变压器漏感之和,iLi为流过第i个模块的电感电流,Sx(x=1~8)为开关管,vh1为一次侧两桥臂中点间的电压,vh2为变压器折算到一次侧的电压,每个模块变压器的一次侧与二次侧的变压器匝数比均为n。定义输出电压增益M=nVout/Vin。

图1 DAB单模块拓扑结构
Fig.1 Topology of single module DAB converter
三重移相控制是通过控制DAB各个桥臂开关管之间的移相角来对功率传输进行控制,为了分析方便,图2给出了三重移相控制波形。
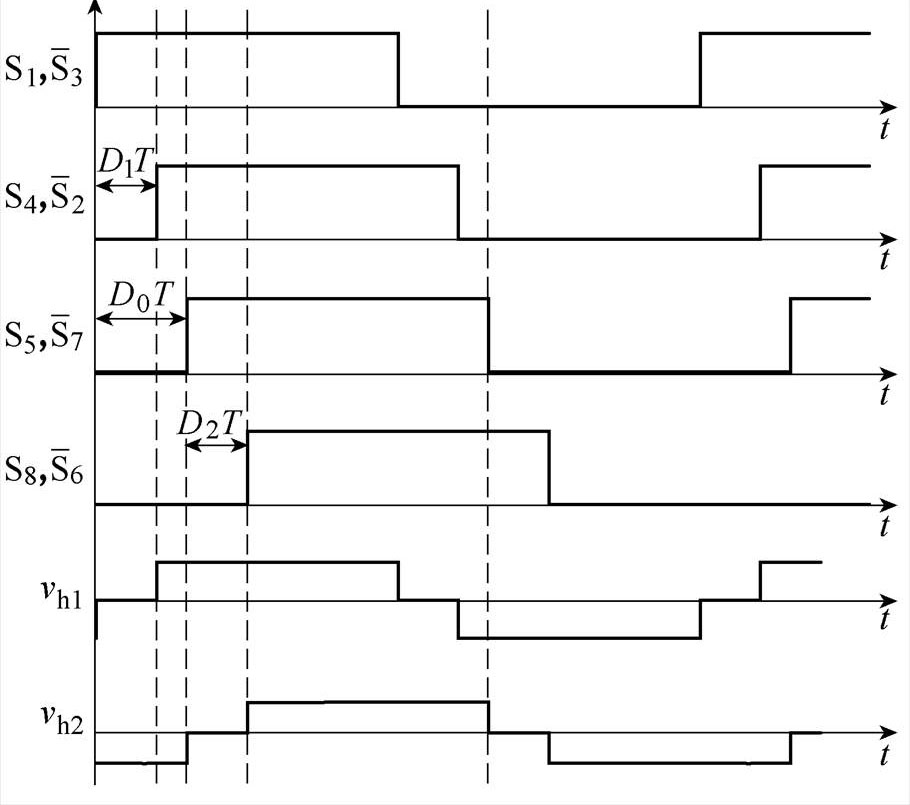
图2 三重移相控制波形
Fig.2 Operation waveforms of TPS control
图2中,D1为开关管S1与S4之间的移相比,D0为S1和S5之间的移相比,D2为开关管S5和S8之间的移相比,T为半个开关周期,T=1/(2fs),fs为变换器的开关频率。
根据变压器一次、二次侧方波之间的位置关系,DAB的三重移相一共可以分为8个工作模式,为了提高DAB工作效率,变换器一般工作在如图3所示的四种工作模式中,这四种模式一次、二次侧高低电平电压重合度较高,具备较高的效率特性[18]。定义第i个模块的电感电流有效值二次方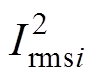 以及传输功率Pi分别为
以及传输功率Pi分别为
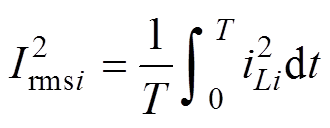 (1)
(1)
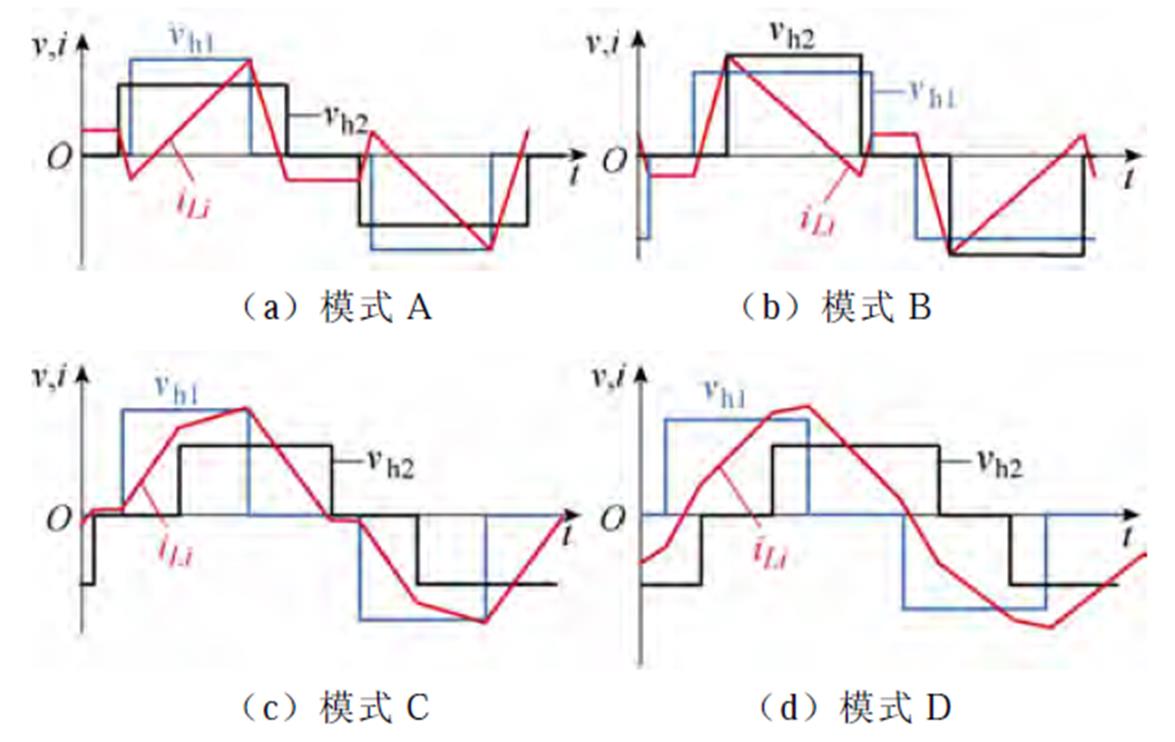
图3 DAB典型工作模式波形
Fig.3 Typical modulation modes waveforms of DAB converter
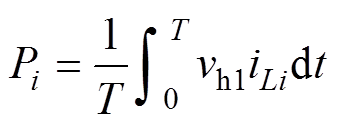 (2)
(2)
结合各个移相角的定义以及不同工作模态的开关时序,推导计算得到四种工作模式下电感电流有效值和输出功率公式见表1,表中,Pbase=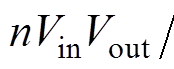
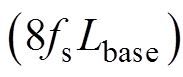 ,a=
,a=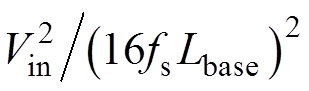 ,b=
,b= ,g=
,g=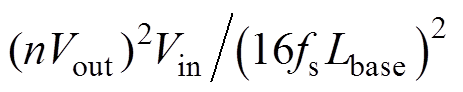 ,其中,Pbase为单模块的峰值输出功率,Lbase为单模块辅助电感的设计参数。
,其中,Pbase为单模块的峰值输出功率,Lbase为单模块辅助电感的设计参数。
由于在TPS控制中,实现指定功率输出具有无穷多个移相角组合,因此需要结合算法找到使得电感电流有效值最小的最优组合。根据1.1节中电感电流有效值和输出功率模型,可以通过拉格朗日乘法等最优化数学方法求解最优移相角[11]。但由于在时域视角下,DAB的常用的工作模式分为四种,每种模式具备不同的工作运行特性,最后得到的是分段化的数值解。
以上数学分析方法虽然可以在一定约束条件下求得三重移相控制下的以电感电流有效值为最优化目标的移相组合,但分析计算过程较为繁琐和复杂,在遇到多变量和非线性的约束时(如DAB中需要兼顾多种模式切换、软开关问题的约束)可能无法求出数值解。利用智能优化算法,可以通过多次迭代计算、利用适应度函数评价来简化优化过程,约束条件的改变可以加入罚函数来进行调整。GA是一个将最优化问题模拟成自然选择的过程,根据适应度函数,对最优化结果进行搜索,相比于PSO算法等其他智能算法,通过调整GA的初始参数,可以有效避开局部最优化结果。下面将对GA在单模块的三重移相控制中的优化进行分析。
表1 TPS控制不同工作模式下输出功率和电感电流有效值二次方公式
Tab.1 Output power and inductor RMS current square equations in different operation modes under TPS control

工作模式移相角约束输出功率电感电流有效值 模式A 模式B 模式C 模式D
DAB变换器中的电感电流有效值优化可视为传统的优化模型问题,其优化目标函数及其约束条件为
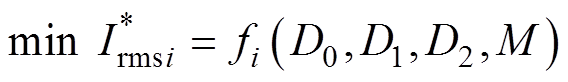 (3)
(3)
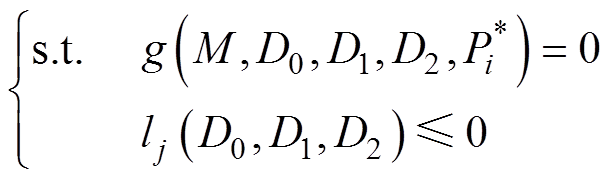 (4)
(4)
式中,M为电压增益;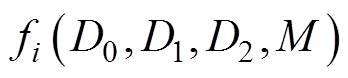 为模块i电感电流有效值标幺化表达式,不同工作模式下计算公式为表1计算后再进行标幺化;
为模块i电感电流有效值标幺化表达式,不同工作模式下计算公式为表1计算后再进行标幺化;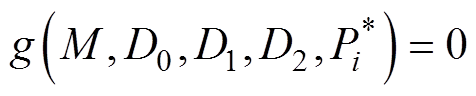 为传输功率的约束;
为传输功率的约束;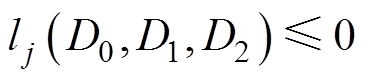 为工作模式j下的移相角约束。根据表1中单个模块的输出功率、电压增益与三个移相之间的关系,在给定参考功率、电压增益以及D0和D1时,可以推出D2表达式为
为工作模式j下的移相角约束。根据表1中单个模块的输出功率、电压增益与三个移相之间的关系,在给定参考功率、电压增益以及D0和D1时,可以推出D2表达式为
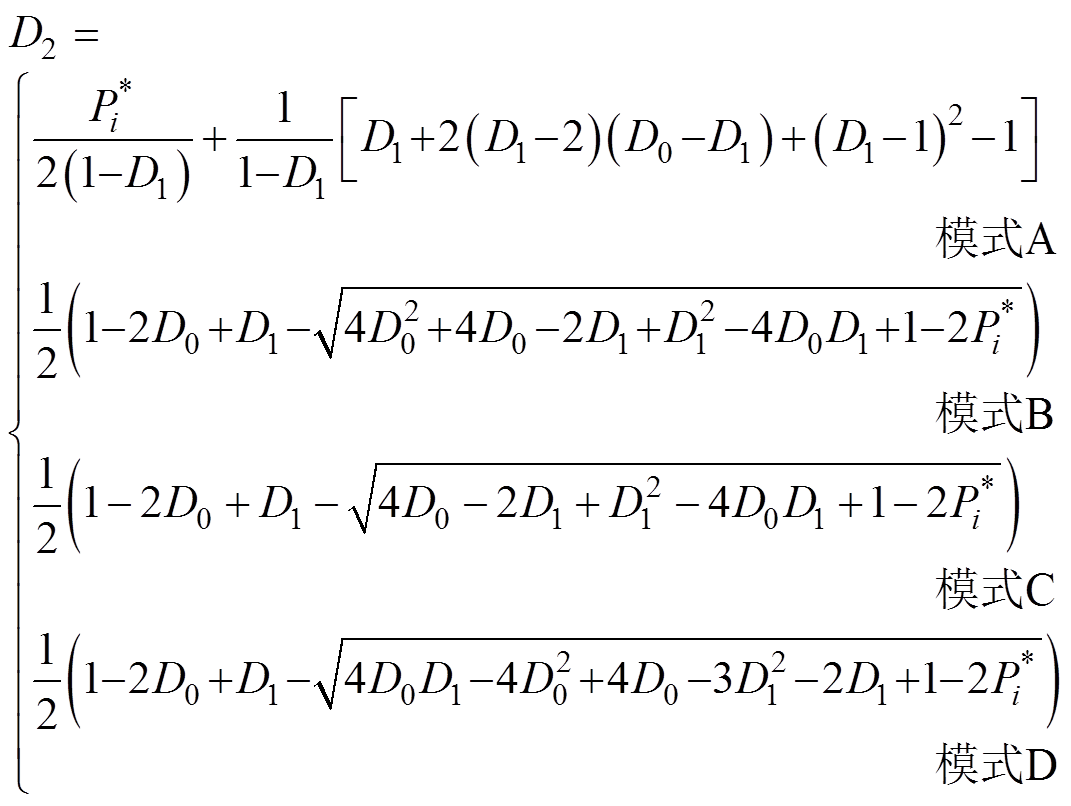 (5)
(5)
式中, 为模块i的输出功率标幺值,
为模块i的输出功率标幺值, =
= 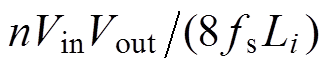 。
。
由表1中的公式可知,单模块电感电流有效值优化涉及5个自由变量,且不同工作模式下的电感电流有效值计算公式也不相同,优化的计算量大、分析复杂。下面将用GA进行优化计算。
GA的具体流程包括编码、解码、遗传运算、适应度计算、评价等,初始化参数见表2。
表2 单模块优化GA初始参数
Tab.2 Initial parameters of genetic algorithm for single module optimization

参 数数 值 种群数量20 进化代数120 交配概率0.5 变异概率0.3
GA的计算流程如下所示:
(1)对GA参数进行初始化,获取种群内各个个体的初始参数D0和D1。
(2)根据式(5)计算各个个体该功率和电压增益下不同工作模式时的D2。
(3)根据表1中的公式计算各个不同工作模式下的电感电流有效值,并判断最优工作模式。
(4)根据式(3)计算种群适应度,并计算个体被复制的概率。
(5)对个体移相组合参数进行编码,根据设定的参数对种群进行复制、交配、基因变异操作,操作过后进行解码,得到新种群的D0和D1。
(6)用本轮迭代的适应度与最优适应度比较,取较优结果更新最优适应度和最优解。
(7)判断迭代次数是否超出设定值,若超出则结束运算,否则回到步骤(3)。
以升降压增益M=1.25和M=0.8为例,GA的移相角随功率的变化如图4所示。从图中可以看出,三个移相角随着功率的变化都能平滑地变化。
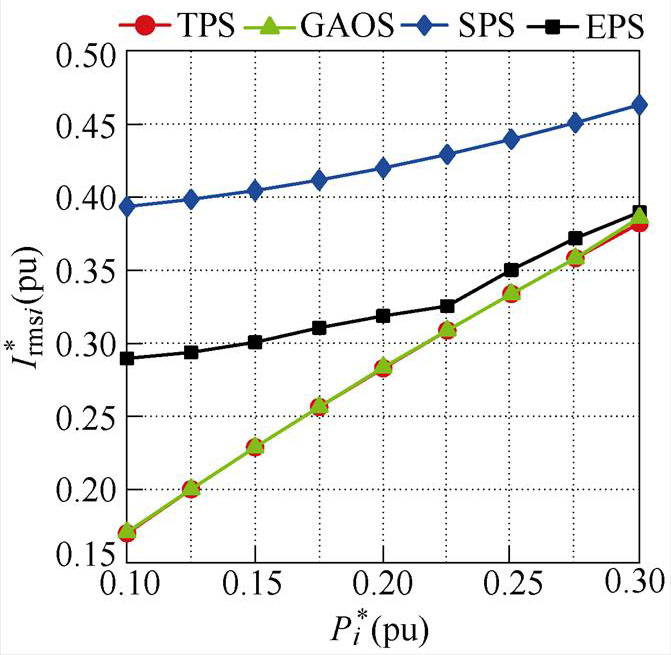
图5展示了升压和降压工况下,不同控制方式电感电流有效值随功率变化的关系曲线。可以看出,本文提出的基于遗传算法的优化控制策略(Genetic Algorithm Optimal Strategy, GAOS)相比于SPS[6]、EPS[8],在电压增益和功率标幺值相同的情况下电感电流有效值都是最小的。随着负载的增加,GAOS的优化移相角逐渐与EPS和SPS相同,在重载工况下三种控制策略的电感电流有效值趋于相等,而在轻载的情况下,GAOS控制策略的优势非常明显。GAOS与通过拉格朗日乘法优化的理论最优TPS[11]几乎重叠,可以认为通过GA可达到通过数学最优化分析相似的效果。
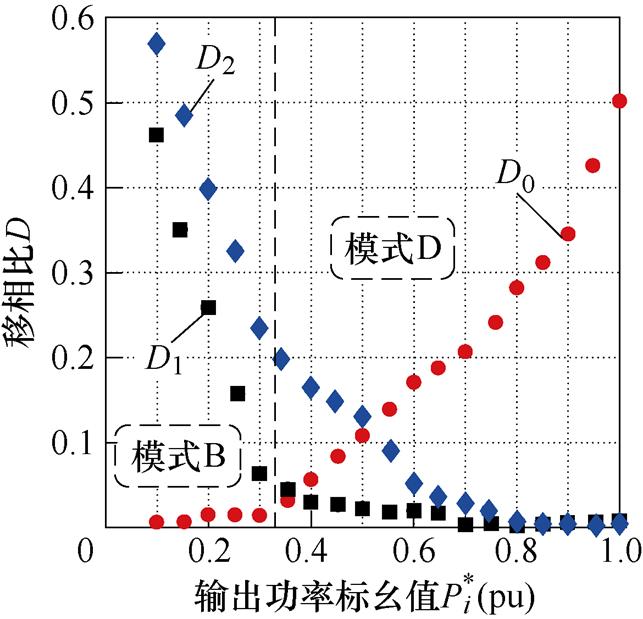
(a)M=1.25
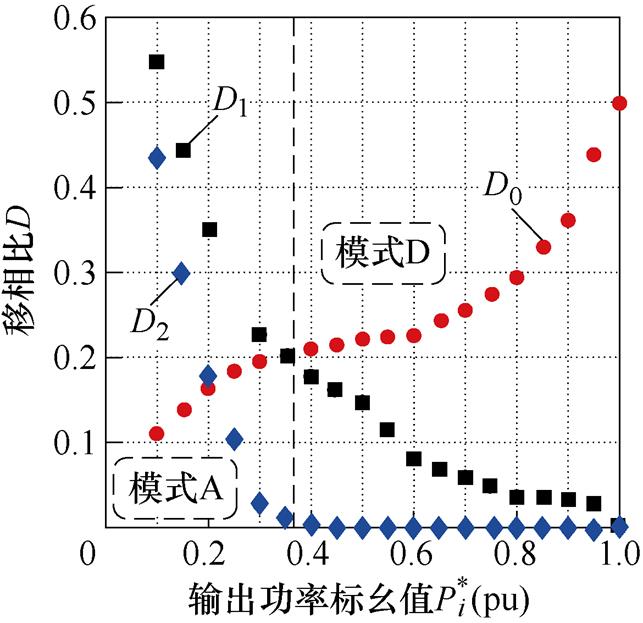
(b)M=0.8
图4 遗传算法优化移相比结果
Fig.4 Results of optimal phase shift based on genetic algorithm
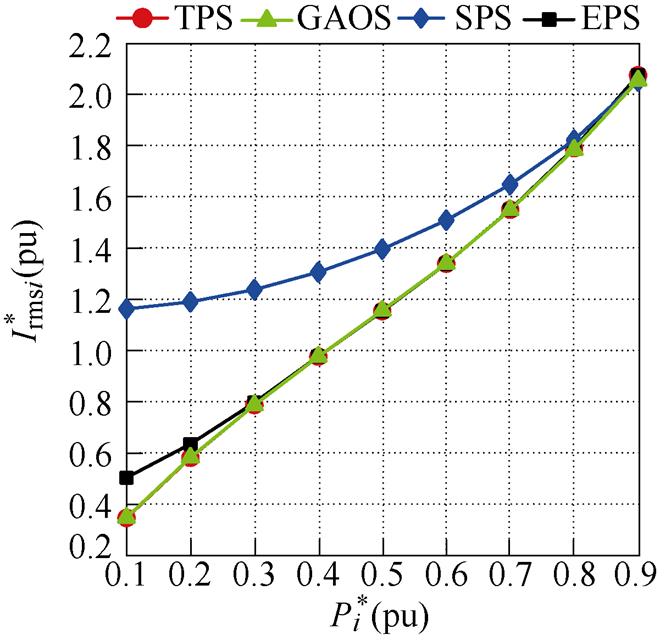
(a)M=0.5,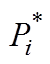 =0.1~0.9
=0.1~0.9
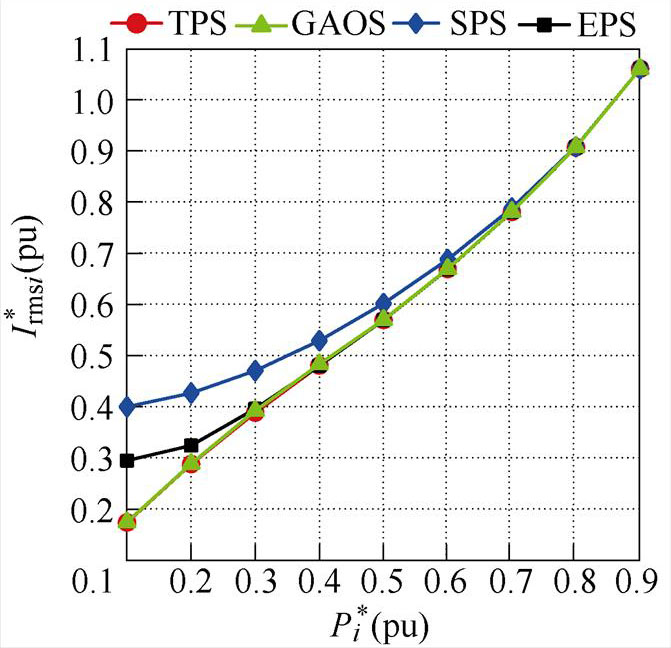
(b)M=1.5,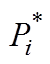 =0.1~0.9
=0.1~0.9
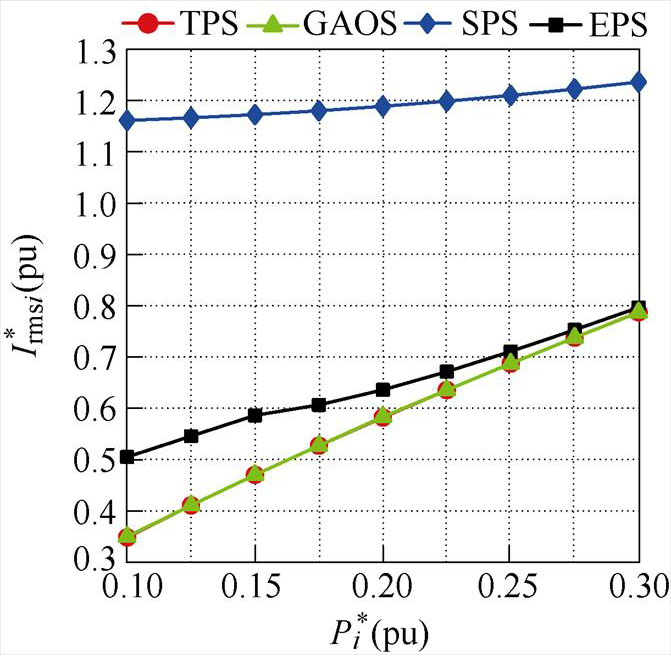
(c)M=0.5,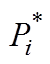 =0.1~0.3
=0.1~0.3
(d)M=1.5,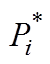 =0.1~0.3
=0.1~0.3
图5 不同控制策略单模块电感电流有效值对比
Fig.5 Comparison of auxiliary inductor RMS current of single module in different control strategies
图6给出了单模块运行的优化控制框图。图中,mode表示模块的运行模式。首先,在系统运行前,需要将GA的计算结果存储在单片机中。针对系统功率控制,单个模块的参考功率独立于其他模块,通过检测该模块实际输出功率,与给定功率做差,经过PI控制器后得出该模块的移相比D0,根据PI参数、给定功率以及对输入输出电压采样计算后的电压增益对D1进行在线查表,得到D1和D0后根据式(5)计算出D2,得出优化移相组合。
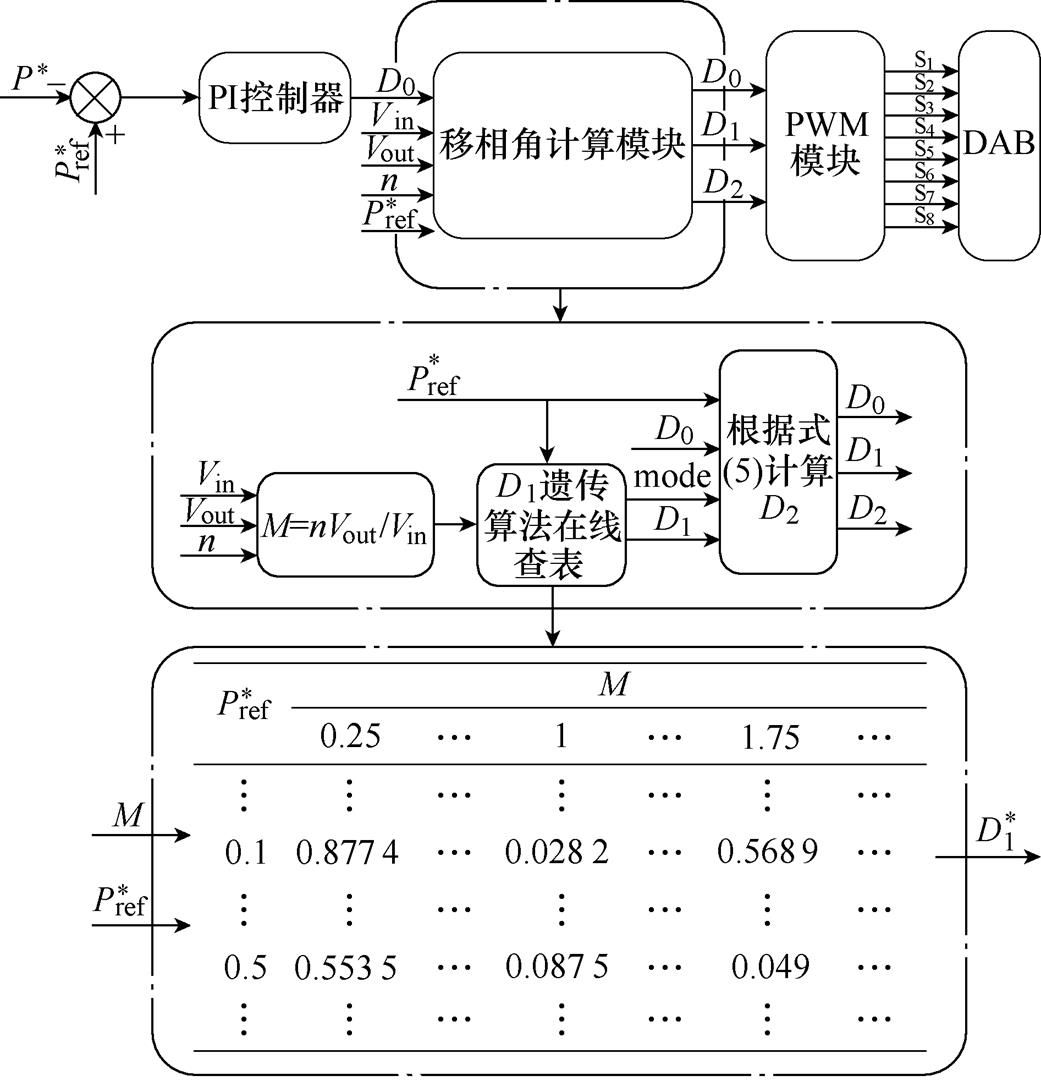
图6 单模块优化策略控制框图
Fig.6 Block diagram of the proposed control strategy for single module
IPOP连接方式的DAB变换器无需进行均压控制,仅结合DAB本身的电流源特性进行输出电流控制即可实现模块均功率运行,因此该连接方式在中低压大功率直流充电场合得到了广泛应用[12]。多模块IPOP的双有源全桥拓扑如图7所示。图7中,h为并联模块的总数。
变换器的总输出功率Ptotal为
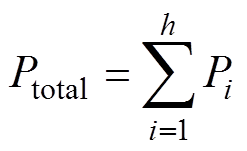 (6)
(6)
总电流有效值Irms为
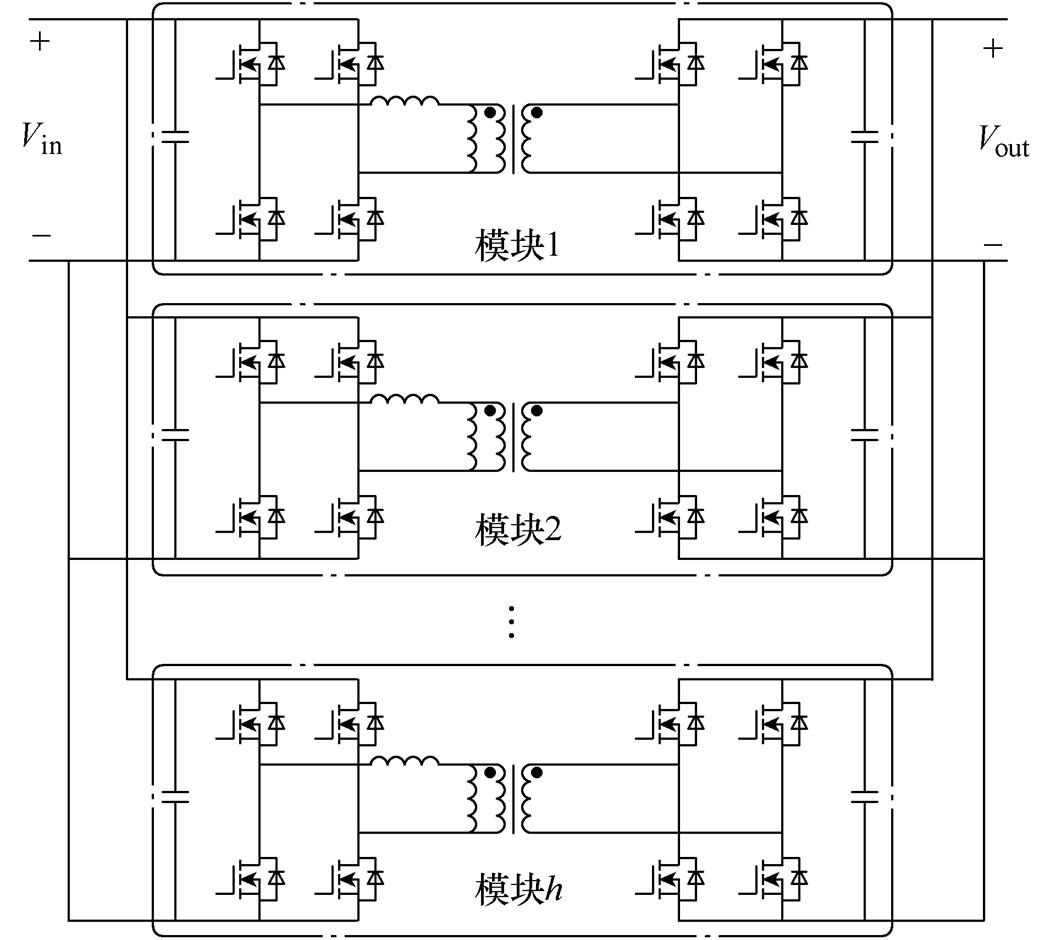
图7 多模块IPOP双有源全桥拓扑
Fig.7 Topology of IPOP connected DAB converters
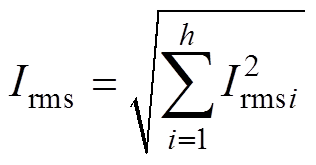 (7)
(7)
式中,Irmsi为第i个模块的电感电流有效值。
传统的多模块DAB变换器系统中,为保证各模块的安全与稳定运行,模块间一般采用平均输出电流[19]和平均功率[20]的控制方式。传统均功率控制策略的基本框图如图8所示,即让每一个模块的参考输出功率为系统总参考功率的1/h,模块内采用优化移相策略进行优化。
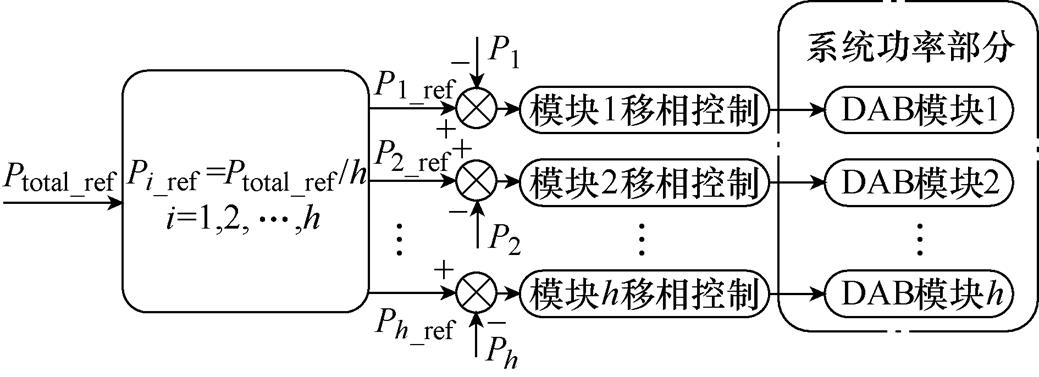
图8 传统均功率控制策略框图
Fig.8 Block diagram of traditional power balancing control strategy
均功率控制策略的目标是让每一个独立模块输出相同的功率,同时承担相同的损耗。然而,在电感参数不匹配的多DAB模块中采用均功率控制会导致部分模块的电感电流有效值过大,进而相应地增大导通损耗。虽然其他模块相应的电感电流有效值较低,但变换器的总导通损耗并非最优值,将会导致变换器的总效率无法达到最优。
考虑到储能电感与变换器电流有效值特性密切相关,而电流有效值特性关乎整个系统运行效率,本节提出一种根据系统中各模块辅助电感差异而进行功率差异化分配的控制策略,该策略以变换器总电流有效值最小为目标,保证实现指定总功率的情况下,根据每个并联模块的辅助电感的大小来合理分配参考功率,实现总电流有效值最优。
模块间的辅助电感的误差通过误差比进行表示,第i个模块辅助电感的误差比ki可以表示为
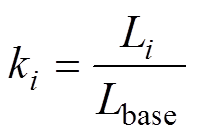 (8)
(8)
为了分析方便,需要对参数进行标幺化,功率和电流的基值取为Pbase=nV1V2/(8fsLbase)和Ibase= nV2/(8fsLbase)。定义模块i的输出功率标幺值和电感电流有效值标幺值分别为
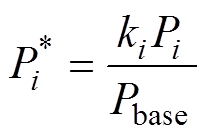 (9)
(9)
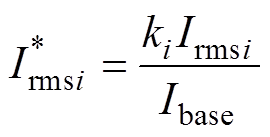 (10)
(10)
首先需要分析模块间辅助电感之间的差异对电感电流有效值的影响。基于第2节的单模块TPS优化控制算法,以及表1中电感电流有效值公式,计算并做出电感差异比分别为k1=0.8,k2=1.0,k3=1.2的电感电流有效值随功率变化的曲线,为了方便对比分析,电感电流有效值以及输出功率的标幺值均以k=1.0的情况作为基值。
不同电感差异比下电感电流有效值对比如图9所示。从图9可以看出,无论DAB工作在升压还是降压模式中,轻载时相同输出功率情况下电感误差比小的模块电感电流有效值最大,而电感误差比大的模块电感电流有效值最小。相同功率下负载较重时,电感误差比大的模块电感电流有效值最大,并且差异更加明显。基于以上规律,在多模块并联的DAB变换器中,可以在总负载功率较轻时,让电感误差比大的模块分担更多的负载,在总负载功率较重时,让电感误差比小的模块带更多的负载。在输出功率一定的情况下,各个模块需要分配多少功率,从而使变换器的总电流有效值最小,需要进行优化分析,下面将分析GA的优化过程。
首先,需要测量独立模块的辅助电感的真实值,计算出独立模块的电感误差比,然后根据各个模块的辅助电感的误差比,利用GA,计算各个模块最佳功率分配比。定义模块功率分配比mi表示为
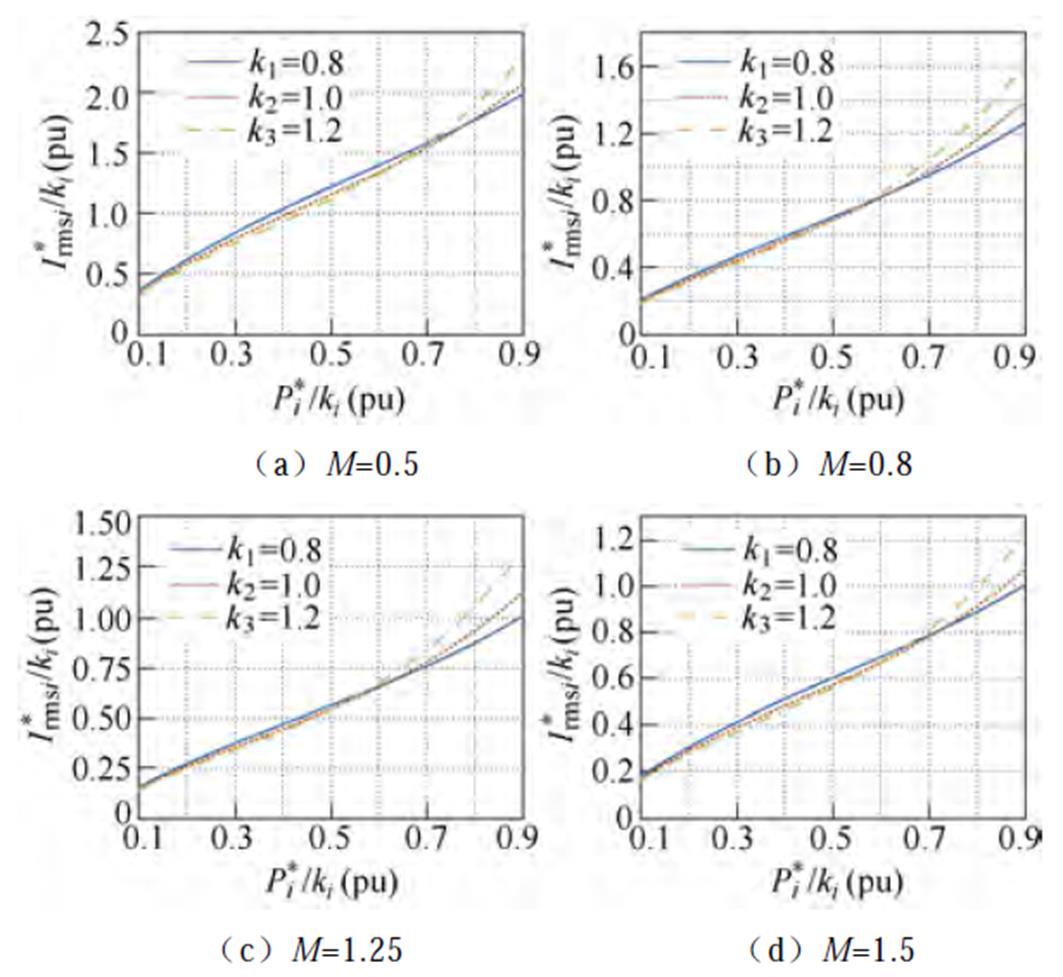
图9 不同电感差异比下电感电流有效值对比
Fig.9 Comparison of inductor RMS current in different inductance variance ratio
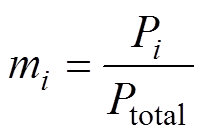 (11)
(11)
由于每个模块的输出功率相加需要等于总功率,则需要满足
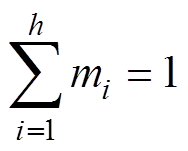 (12)
(12)
同时,每一个模块自身有功率上限,独立模块分配到的功率不能高于其功率上限,第i个模块功率上限的表达式为
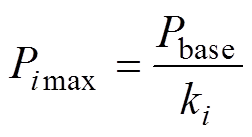 (13)
(13)
独立模块根据分配到的功率,结合第2节所述的三重移相控制方法进行电感电流有效值最优化,从而可并行实现变换器的总有效值优化以及独立模块内部有效值优化。
多模块IPOP总有效值优化的数学模型表示为
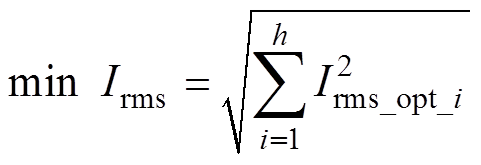 (14)
(14)
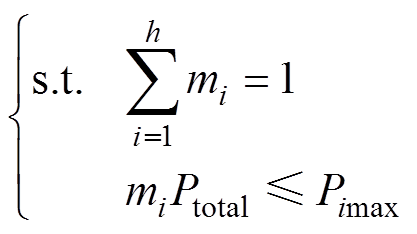 (15)
(15)
式中,Irms_opt_i为模块i分配到相应的功率后结合GAOS得到的电感电流有效值。多模块GA的初始参数见表3,多模块的总电流有效值优化的GA运算流程与第2节所述的单模块TPS优化的GA运算流程相似,区别在于种群个体为每个模块的功率分配比,适应度函数为总电感电流有效值二次方。
表3 总电感电流有效值优化GA初始参数
Tab.3 Initial parameters of genetic algorithm for single module optimization

参 数数 值 种群数量100 进化代数250 交配概率0.5 变异概率0.3
以三模块DAB并联的变换器优化为例,假设三个模块的电感误差比分别为k1=0.8,k2=1.0,k3= 1.2。图10为电压增益为M=1.5时,多个功率点的迭代过程示意图,可以看到,250步的迭代步数可以使得适应度优化达到饱和。利用GA计算得出的模块1和模块3的功率占比如图11所示。
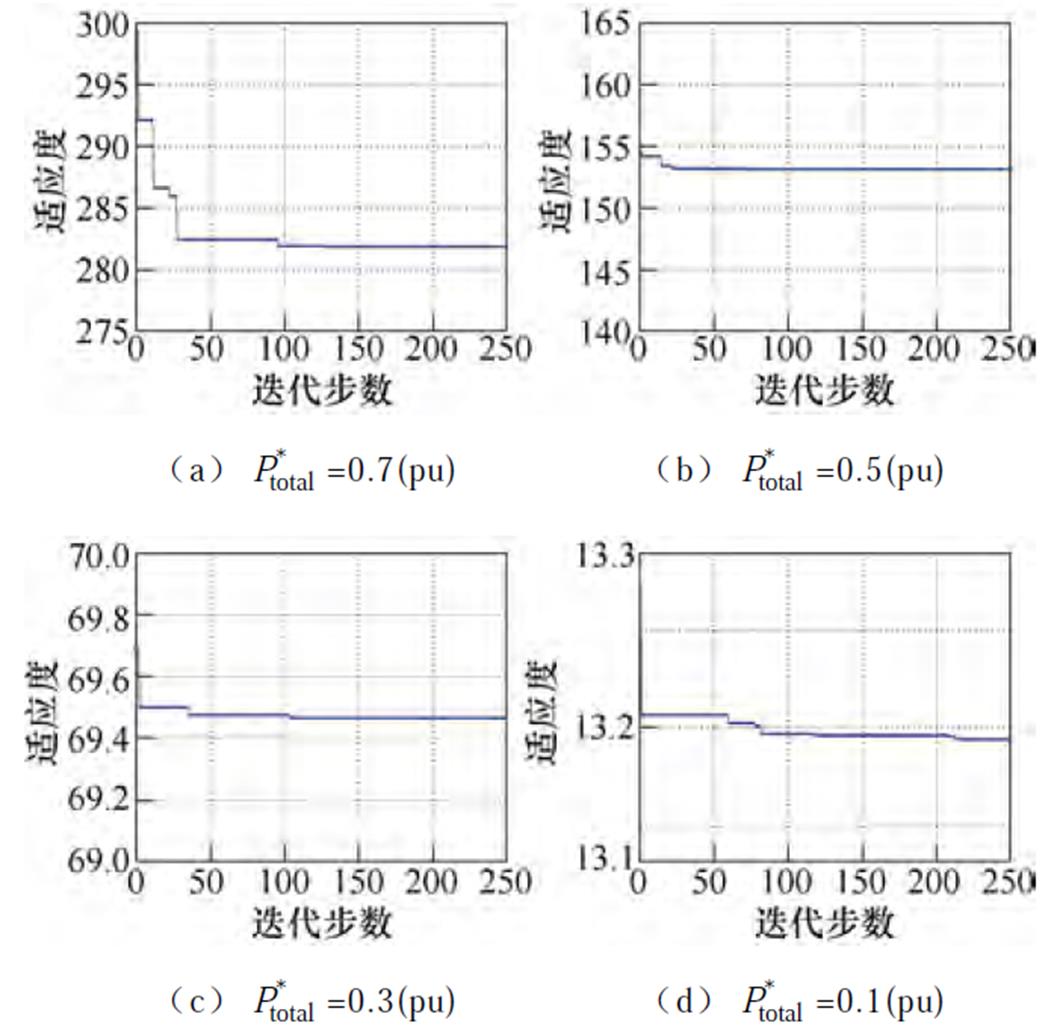
图10 M=1.5各输出功率迭代过程适应度变化
Fig.10 The change of fitness value during iterations with different output power when M=1.5
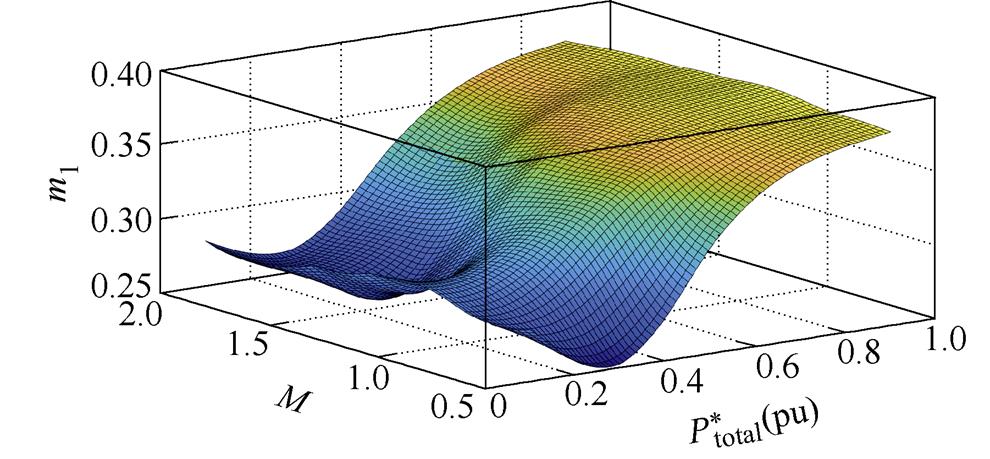
(a)k1=0.8三维图
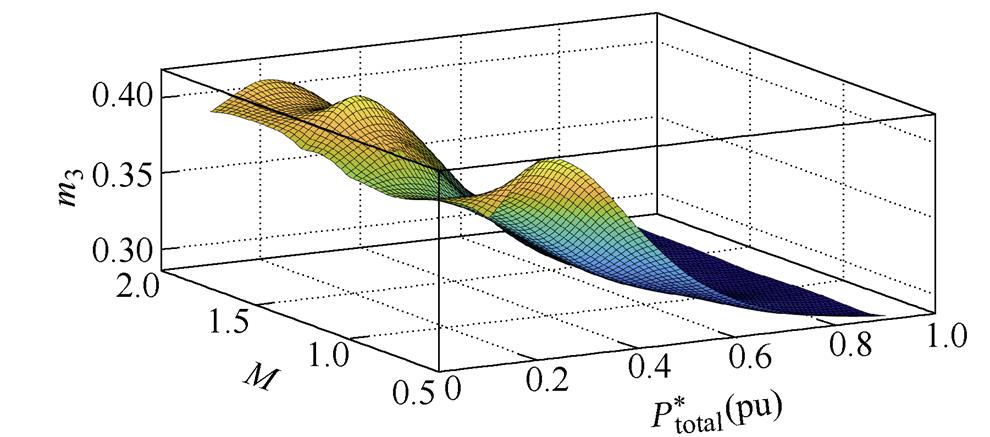
(b)k3=1.2三维图
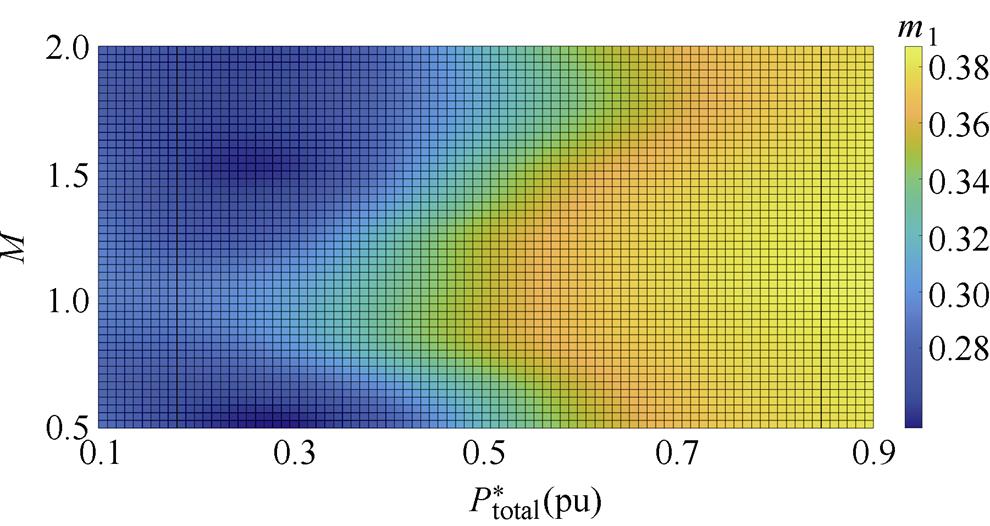
(c)k1=0.8俯视图
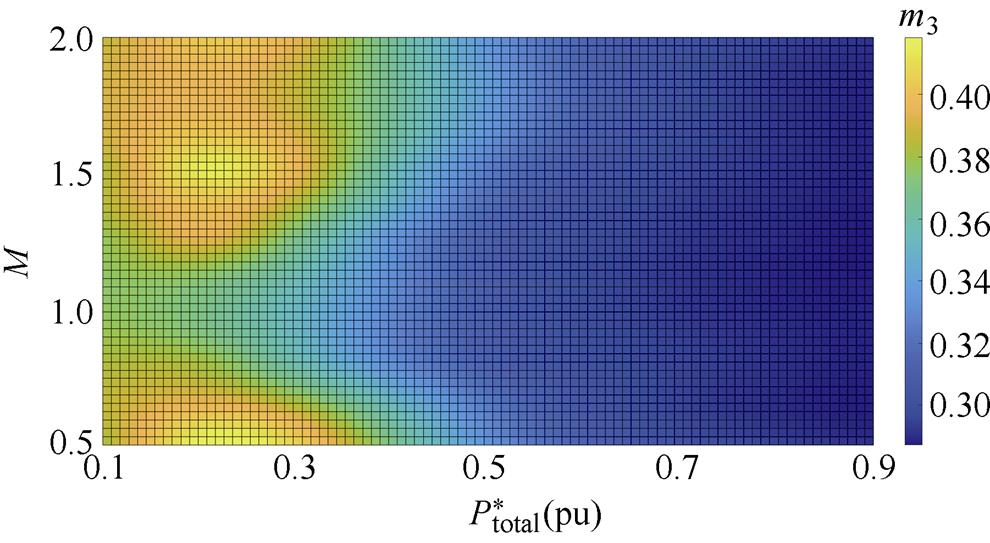
(d)k3=1.2俯视图
图11 功率分配比在多种增益及功率下的变化三维图像
Fig.11 3D graph of power distribution ratio in full power range and voltage gain
模块2分配的功率占比就是总功率减去模块1和模块3所分配的功率,三维图中x轴代表电压增益,y轴代表总功率标幺值,总功率标幺值定义为
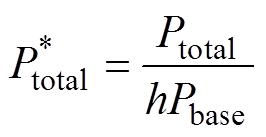 (16)
(16)
从三维图可以看出,各个模块在各种电压增益下的功率分配比均是平滑变化的,没有出现参数突变的情况。
图12为三个模块在各个电压增益下的功率分配比对比。可以看出,在各个电压增益下,通过优化算法得到的三个模块的功率分配随着总功率的变化趋势相似,均是在负载较轻的时候,模块3负载比最大,而模块1的负载比最小,负载较重时,模块1的负载比最大,模块3的负载比最小。也就是说,在变换器总输出功率较小的时候,应该让辅助电感较大的模块带更大的负载,让辅助电感较小的模块带更小的负载,而总输出功率较大时,应该让辅助电感更小的模块带更多的负载,从而实现总电感电流有效值最小。
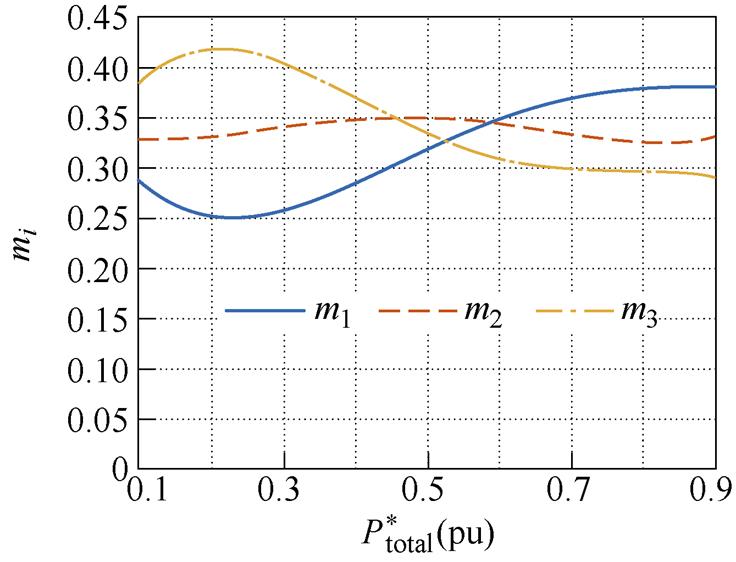
(a)M=0.5
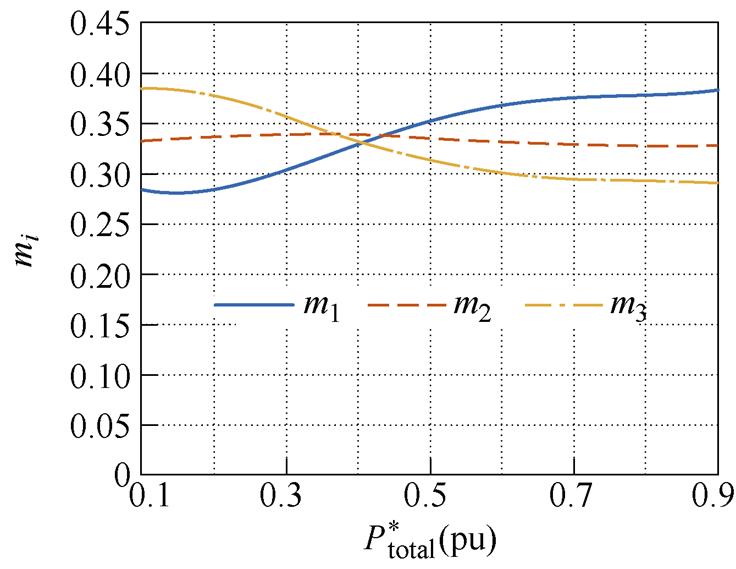
(b)M=0.8
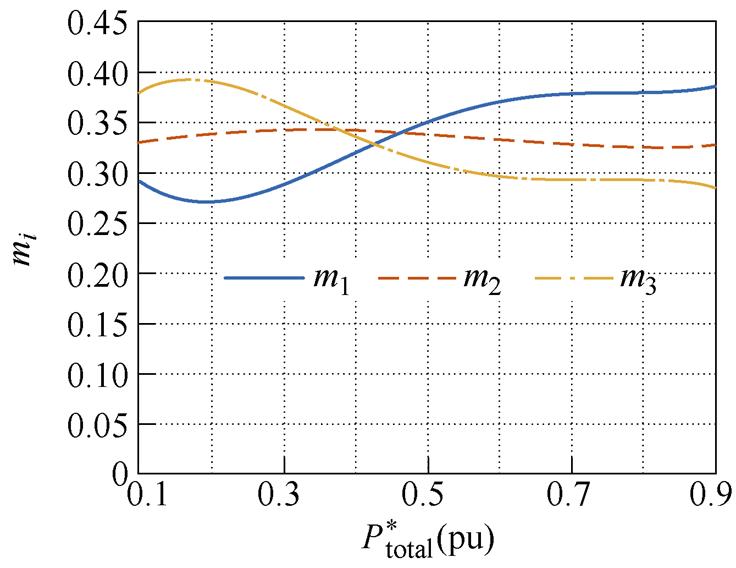
(c)M=1.25
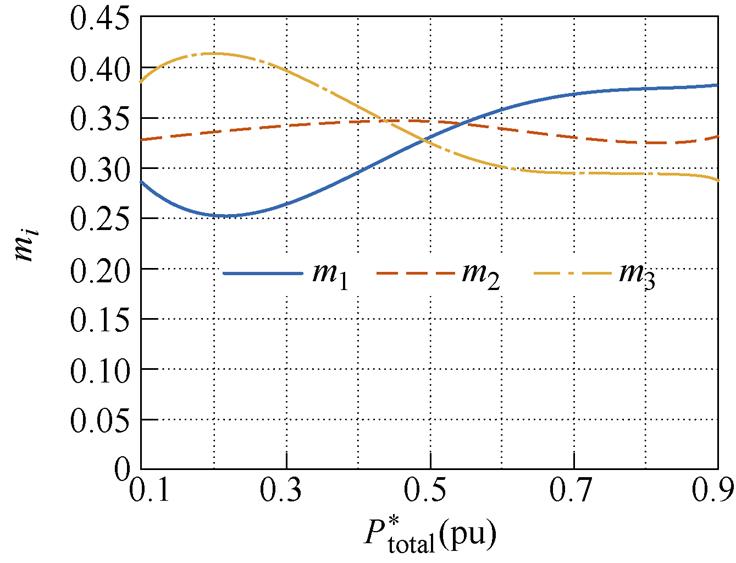
(d)M=1.5
图12 功率分配比在不同增益及功率下的变化对比
Fig.12 The change of power distribution in different power range and voltage gain
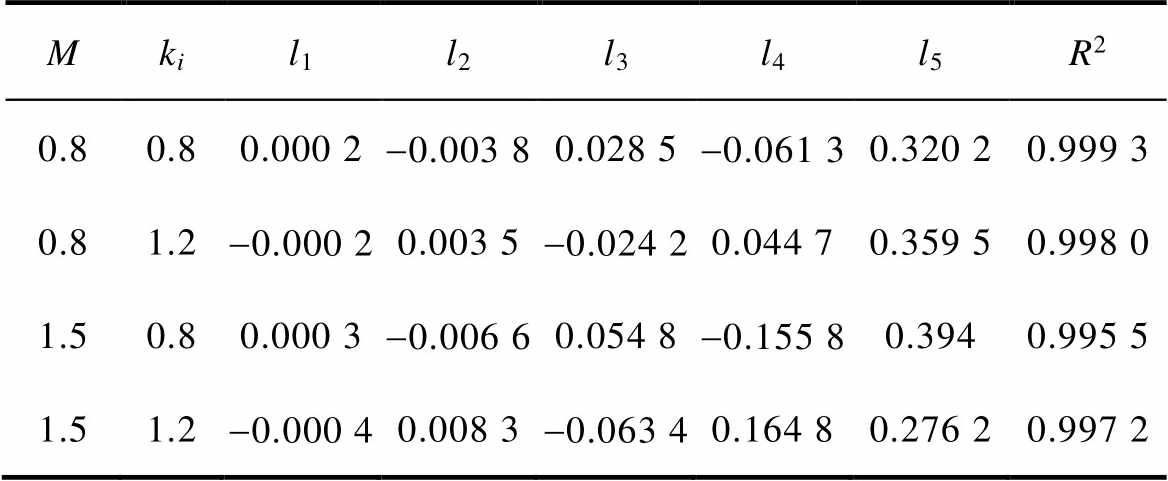
对于多模块DAB变换器的功率分配优化控制,也采用离线计算在线查表的方法,为了减小数字电源中央控制芯片的存储负担,这里使用结合公式拟合的查表控制方法。根据图11中模块1和模块3在各个电压增益情况下的功率占比随总功率标幺值变化的趋势,对数据采用多项式拟合的方法,利用R2作为拟合优度的判定条件。拟合和R2的具体结果见表4。
表4 拟合结果
Tab.4 Results of polynomial
Mkil1l2l3l4l5R2 0.80.80.000 2-0.003 80.028 5-0.061 30.320 20.999 3 0.81.2-0.000 20.003 5-0.024 20.044 70.359 50.998 0 1.50.80.000 3-0.006 60.054 8-0.155 80.3940.995 5 1.51.2-0.000 40.008 3-0.063 40.164 80.276 20.997 2
从表4中可以看出,在升压和降压工况下,四次多项式的拟合公式与实际数据的R2均大于0.99,可以认为模块1和模块3的功率占比随总功率的变化呈四次方函数关系。四次方函数的系数与增益有关,即满足
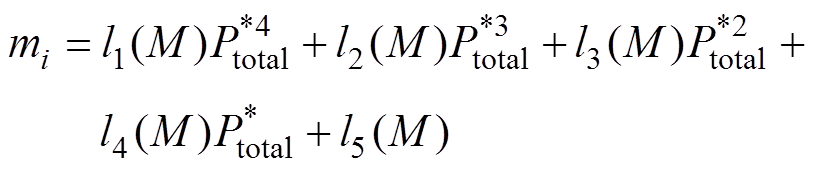 (17)
(17)
将上述分析方法扩展到多个模块。对于多个DAB模块并联的DC-DC变换器,通过GA优化得出各电压增益下各个模块随总功率变化的功率分配比。选出所有模块中电感值处于中间的模块,设该模块为模块h。对电感误差比大于和小于模块h的模块,用多项式对功率分配比与总功率标幺值之间的关系进行拟合,拟合后单模块得到的系数在不同增益下不同。将这些系数存储在数字电源的单片机中,控制中根据电压比来对这些系数进行查表,代入到这些公式,再计算出相应的功率分配比。则对于模块1, 2,…, h-1,其功率分配比为
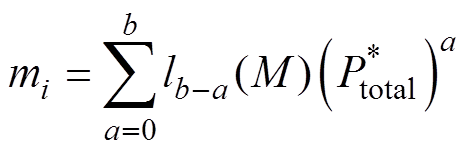 (18)
(18)
模块h的功率分配比为
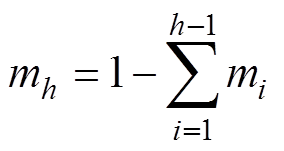 (19)
(19)
为了减小单片机的计算量,拟合多项式的最高次数b应取让拟合优度R2>0.99的最小值,b随着并联模块的增加逐渐增加。
根据以上的分析,下面提出一种IPOP多模块DAB变换器的控制方法,基本控制框图如图13所示。该控制方法的流程如下:
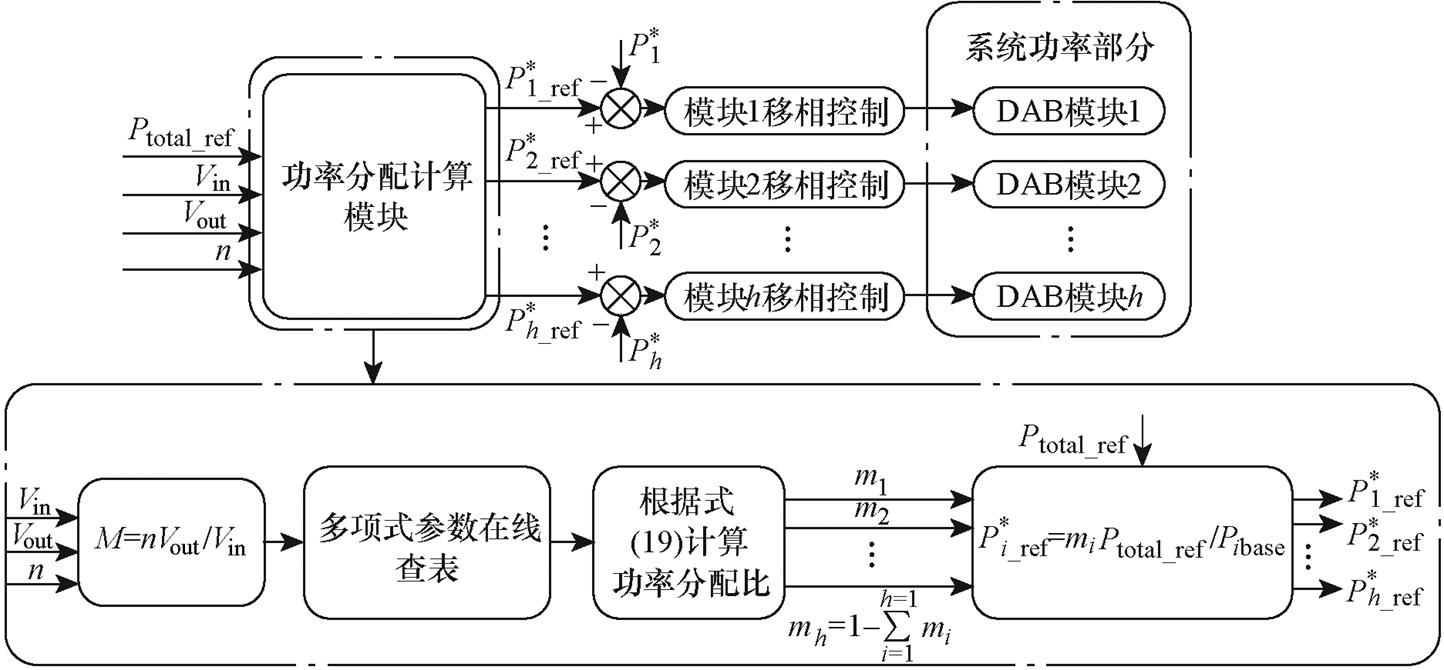
图13 多模块功率分配优化控制策略框图
Fig.13 Block diagram of multi modules optimal power distribution control strategy
(1)将拟合多项式各次系数根据电压增益储存在单模块的单片机中。
(2)采集输出电压和输入电压,计算电压增益。
(3)模块1, 2, 3,…, h-1根据电压增益,通过式(18)计算功率分配比。模块h根据式(19)计算功率分配比。
(4)各模块根据功率分配比得到本模块的功率参考值,根据第2节所述的单模块优化控制方法进行控制。
为了验证本文提出的IPOP多模块DAB总电流有效值优化控制策略,设计搭建了3模块并联的DAB实验平台,每个独立模块均采用STM32G474作为中央控制芯片,模块间采用CAN通信。多模块双有源全桥实验样机如图14所示。样机的参数见表5。

图14 多模块双有源全桥实验样机
Fig.14 Prototype of multi module DAB converter
表5 样机参数
Tab.5 Parameter of Prototype
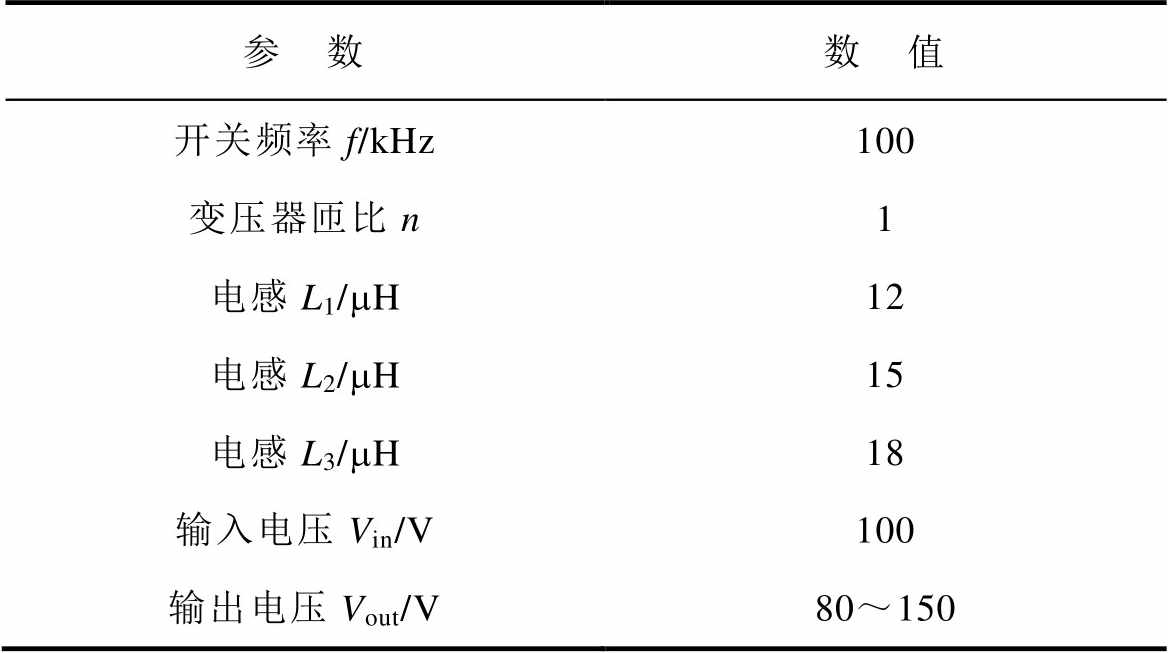
参 数数 值 开关频率f/kHz100 变压器匝比n1 电感L1/mH12 电感L2/mH15 电感L3/mH18 输入电压Vin/V100 输出电压Vout/V80~150
为了对比本文的各模块功率差异控制方法的优化效果,需将本文提出的控制策略与其他控制策略进行对比分析。对比的控制为文献[20]提出的功率均衡控制策略。实验主要包括三个部分:第一部分为不同电压增益和负载下对本文所提的控制策略的验证;第二部分为本文所提的优化控制策略与功率均衡控制策略的总电流有效值和效率特性进行对比;第三部分为优化控制算法的动态性能验证实验。
升压工况下设置输入电压为100 V,输出电压为150 V,总输出功率分别在低功率点(381 W),中功率点(1 127 W),高功率点(2 702 W)下各模块的实验波形如图15所示。根据波形,三种负载条件下,各个模块的三个移相角均不相同,承担的功率也不相同。优化控制策略根据各个模块的辅助电感的差异将总输出功率分配给各个模块,样机中各个模块输入输出电压相等,但输出功率不同,在功率较小的时候,模块1的输出功率最小,模块3的输出功率最大;总输出功率较大时,模块3的输出功率最小,模块1的输出功率最大。
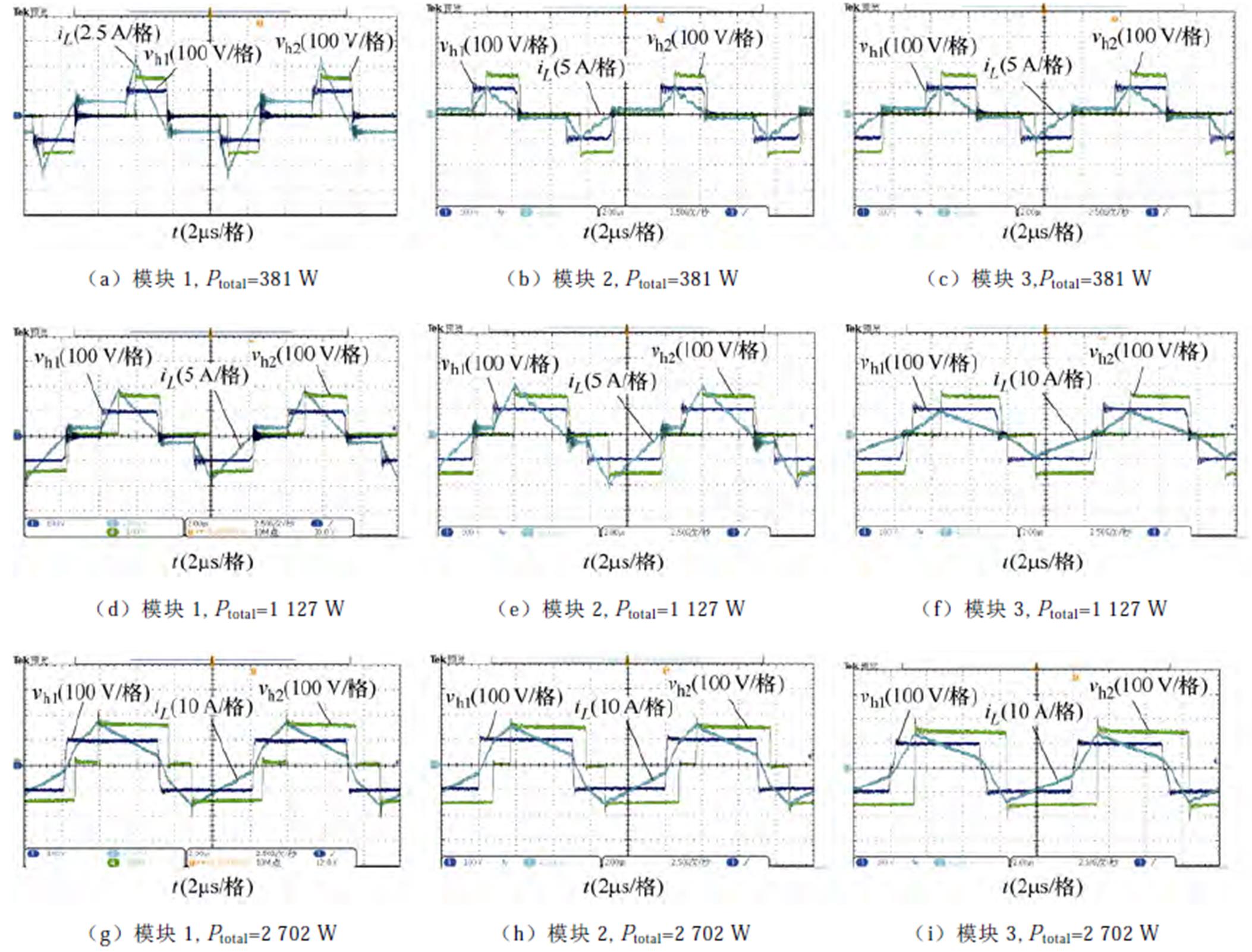
图15 Vin=100 V, Vout=150 V时,不同总输出功率下的实验波形
Fig.15 Experimental waveforms for Vin=100 V, Vout=150 V with different Ptotal
图16为输入电压100 V,输出电压80 V,三个模块分别在总输出功率为低功率点(207 W),中功率点(803 W),高功率点(1 404 W)下的实验波形。由图16可得,在降压模式下,各个模块也是根据辅助电感的差异来对总输出功率进行差异化分配,在相同总输出功率的情况下,不同模块的移相角不同,所承担的输出功率也不同。在总输出功率较大时模块1在所有模块中承担最多功率,而在轻载的情况下,模块3承担最多的功率。
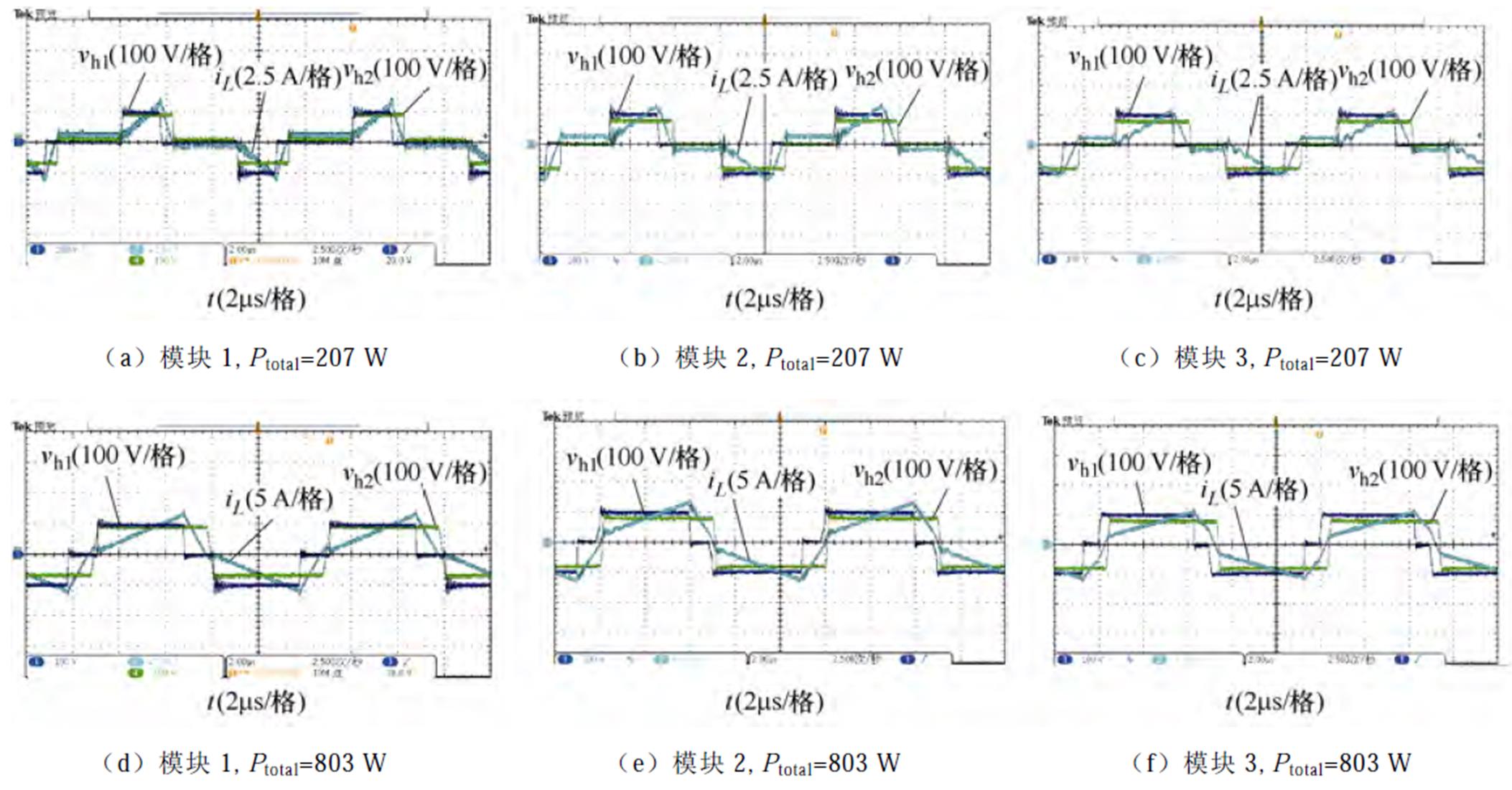
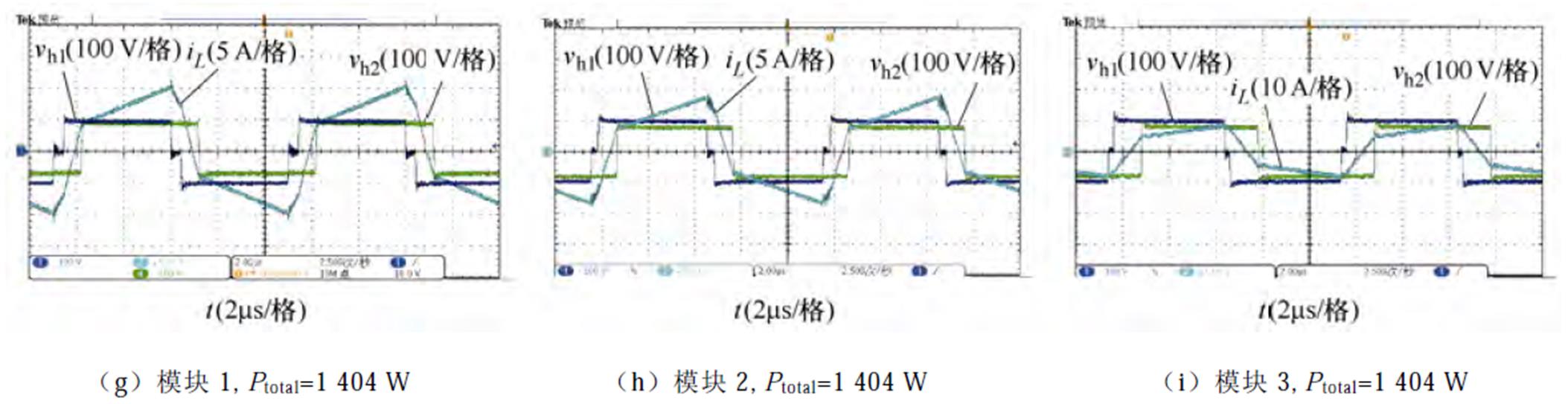
图16 Vin=100 V, Vout=80 V时,不同总输出功率下的实验波形
Fig.16 Experimental waveforms for Vin=100 V, Vout=80 V with different Ptotal
图17展示了本文提出的优化方法相比于均功率控制的优化方法的系统总有效值对比曲线,从图17中可以看出,无论工作在升压模式还是降压模式,本文提出的优化算法均能使系统的总电感电流有效值小于功率算法,并且随着总功率的提升,总电感电流有效值的差异性增大。
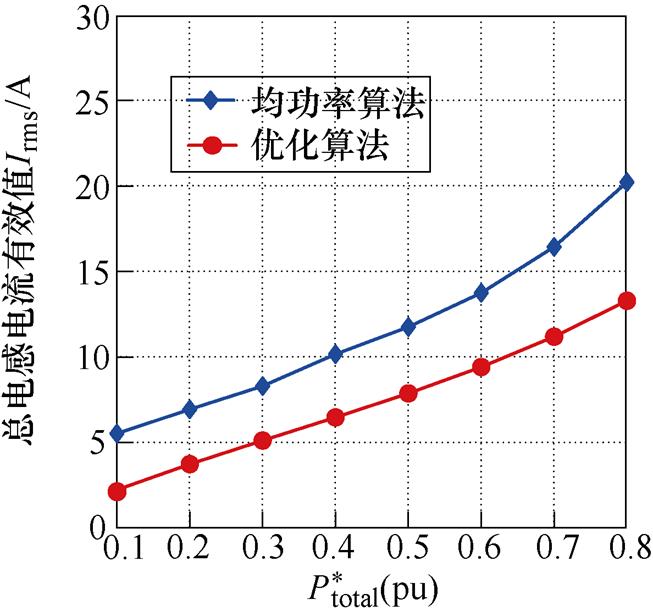
(a)Vin=100 V, Vout=80 V
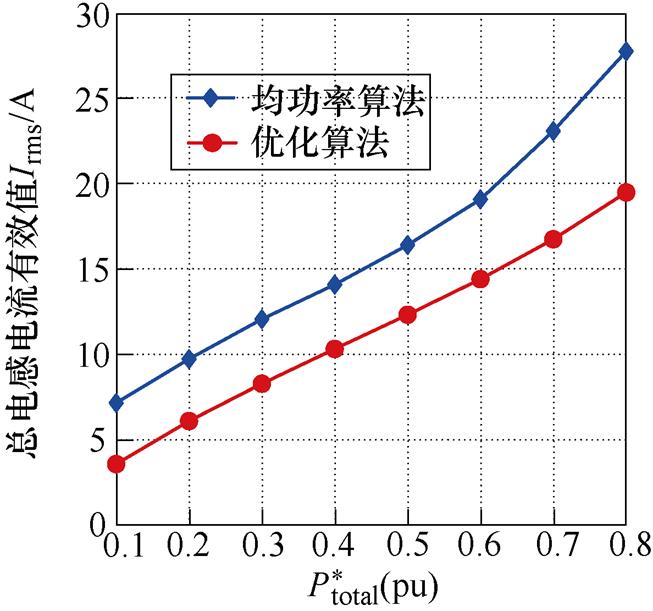
(b)Vin=100 V, Vout=150 V
图17 总电流有效值对比
Fig.17 Comparison of the root-mean-square total current
图18为本文提出的优化算法和均功率算法之间的效率对比,由于优化算法有效降低系统的总电感电流有效值,从而降低了系统的总导通损耗,使得系统的总效率得以提高。对于系统的整体效率,降压工况下,平均效率提升大约1.2 %;升压工况下,平均效率大约提升0.84 %,而优化算法的峰值效率最高能达98.8 %。
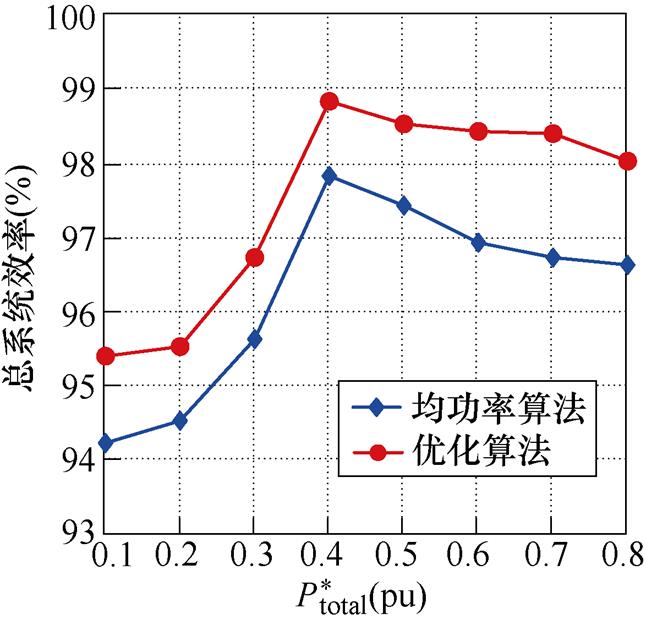
(a)Vin=100 V, Vout=80 V
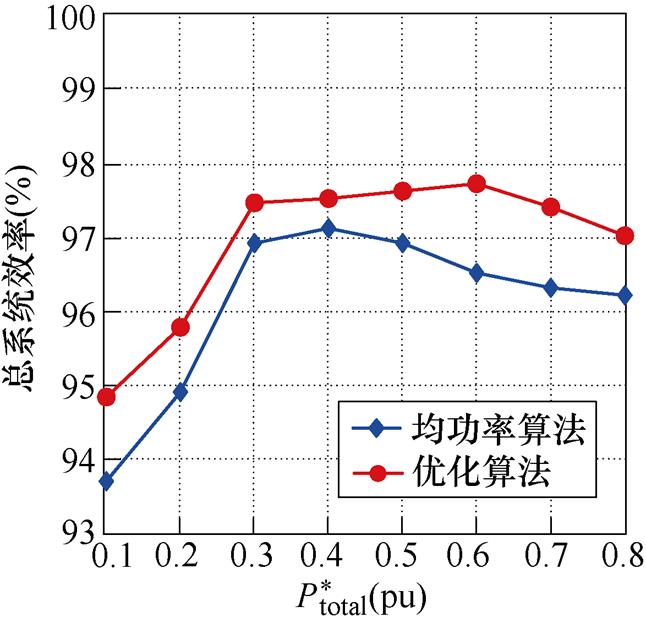
(b)Vin=100 V, Vout=150 V
图18 本算法与均功率算法在升降压工况下的效率对比
Fig.18 Efficiency comparsion between the proposed control strategy and power balance strategy in buck-boost mode
从实验的分析结果可以看出,本文提出的控制策略,无论对于升压工况还是降压工况,均是在总输出功率较轻时,让等效电感较大的模块承担更多的功率,在总输出功率较重时,让等效电感更小的模块承担更多的功率,从而实现在IPOP的多模块DAB变换器总输出功率一定的情况下,总电流有效值最小,进而使得系统的总效率上升。
变换器系统在工作过程中,会出现总输出参考功率突变的情况,各个独立模块需要迅速调整到差异化分配的功率,变换器系统的总输出功率才能实现快速响应。为验证优化算法的动态性能,进行了系统参考功率突变的动态性能测试。
图19a为输入电压100 V,输出电压150 V时总输出参考功率从700 W到3 000 W来回切换的实验波形。图19b为输入电压100 V,输出电压80 V时总输出参考功率从450 W到1 400 W来回切换的实验波形。图中,ioi为模块i的输出电流。
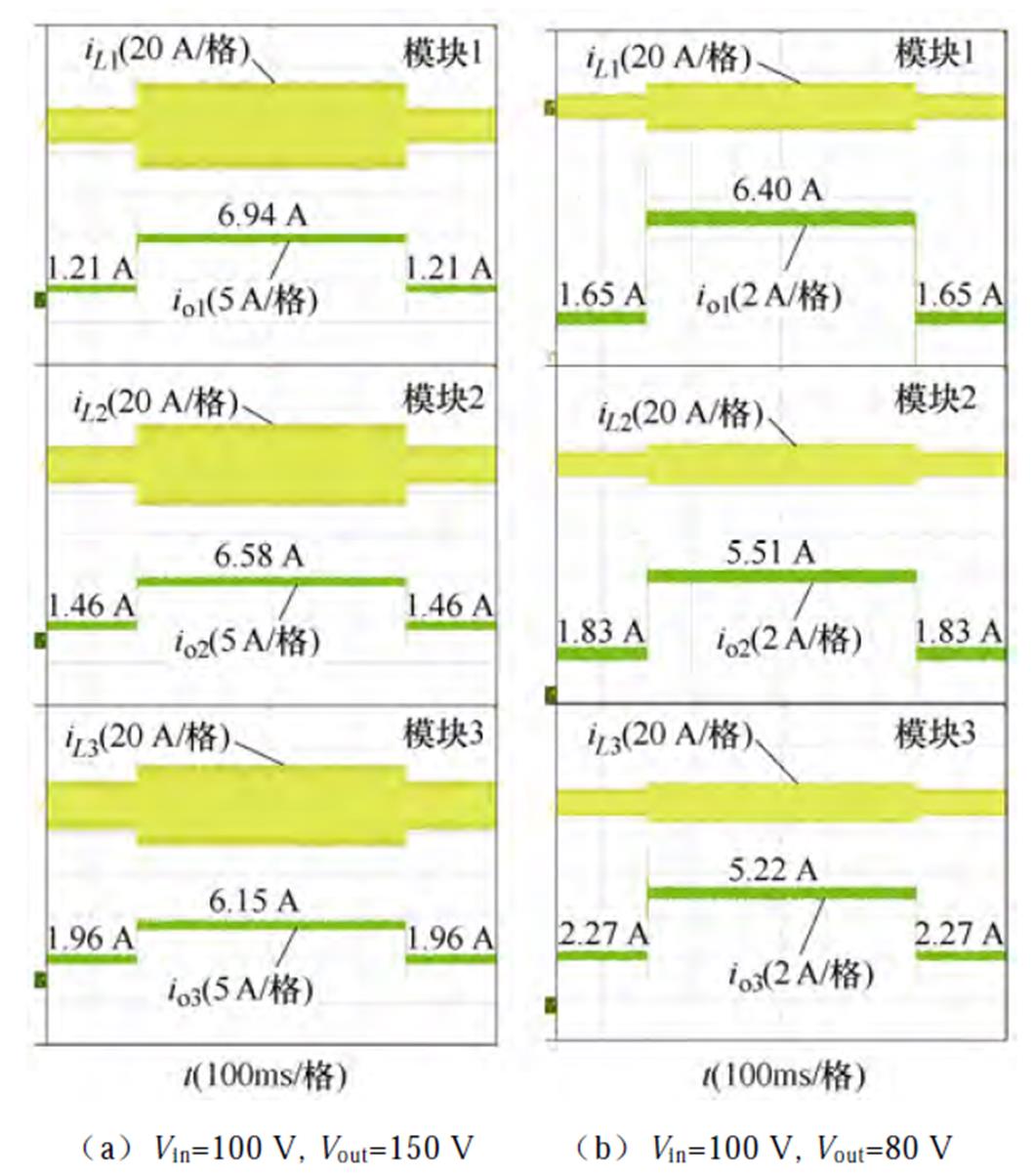
图19 总参考功率突变时三模块电流波形
Fig.19 Current waveforms of each module when Ptotal_ref step up and step down
从波形可以看出,当输出总参考功率发生变化时,各个模块能迅速调整到本模块所分配到的功率,调整时间约为2 ms。
本文针对多模块IPOP的双有源全桥变换器系统,分析了每个模块的电感电流有效值与移相角的关系,通过GA,先对单个模块一定功率下的电感电流进行优化,并且从模块间的电感参数差异出发,提出了一种系统总功率一定的情况下让不同参数的模块分别承担不同功率的控制策略。并搭建了以STM32G474作为主控芯片的三模块并联的样机对控制方法进行验证,理论分析与实验表明:
1)本控制策略在总输出功率一定的情况下,让不同模块承担不同的功率能满足总输出功率要求,并且系统能够稳定运行。
2)对于单个模块,本优化策略能有效降低模块内电感电流有效值,优化效果在轻载到中载时相比于传统控制策略较为明显,并且数学分析的复杂性得以降低。
3)对于整个变换器系统,功率差异控制策略相比于传统的多模块均功率控制策略,无论是在升压还是降压的工况下,均能有效降低IPOP系统总电感电流有效值,并且随着输出功率的增加,相比于均功率控制策略的电感电流有效值减小的更多。功率差异控制算法使得整个系统的效率得以提高,峰值效率可达98.8 %,降压工况下,平均效率提升约1.2 %,升压工况下,平均效率提升约0.84 %。
参考文献
[1] 李厚基, 刘明, 杨煜志, 等. 基于E类逆变电路的宽负载范围软开关无线充电补偿网络研究[J]. 中国电机工程学报, 2022, 42(20): 7375-7387.
Li Houji, Liu Ming, Yang Yuzhi, et al. Research on wide load range soft switching wireless charging compensation network based on class E inverter circuit[J]. Proceedings of the CSEE, 2022, 42(20): 7375-7387.
[2] 黄珺, 付亚楠, 吕晓飞, 等. 基于无功优化的三端口双向DC-DC变换器控制策略[J]. 电工技术学报, 2022, 37(8): 2086-2096.
Huang Jun, Fu Yanan, Lü Xiaofei, et al. Control strategy of three-port bidirectional DC-DC converter based on reactive power optimization[J]. Transactions of China Electrotechnical Society, 2022, 37(8): 2086- 2096.
[3] 何绍民, 杨欢, 王海兵, 等. 电动汽车功率控制单元软件数字化设计研究综述及展望[J]. 电工技术学报, 2021, 36(24): 5101-5114.
He Shaomin, Yang Huan, Wang Haibing, et al. Review and prospect of software digital design for electric vehicle power control unit[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5101- 5114.
[4] 王议锋, 陈晨, 陈博, 等. 一种基于串联输入并联输出型LLC的噪声抑制磁集成方法[J]. 电工技术学报, 2022, 37(9): 2319-2328.
Wang Yifeng, Chen Chen, Chen Bo, et al. A magnetic integrated method for noise suppression based on input series output parallel LLC[J]. Transactions of China Electrotechnical Society, 2022, 37(9): 2319- 2328.
[5] Gong Linxiao, Jin Xinyu, Xu Junzhong et al. A dynamic ZVS-guaranteed and seamless-mode- transi- tion modulation scheme for the DAB converter that maximizes the ZVS range and lowers the inductor RMS current[J]. IEEE Transactions on Power Elec- tronics, 2022, 37(11): 13119-13134.
[6] De Doncker R W, Divan D M, Kheraluwala M H. A three-phase soft-switched high power density DC/DC converter for high power applications[C]//IEEE Indu- stry Applications Society Annual Meeting, Pittsburgh, PA, 2002, 1: 796-805.
[7] Bai Hua, Mi C. Eliminate reactive power and increase system efficiency of isolated bidirectional dual- active-bridge DC-DC converters using novel dual- phase-shift control[J]. IEEE Transactions on Power Electronics, 2008, 23(6): 2905-2914.
[8] Zhao Biao, Yu Qingguang, Sun Weixin. Extended- phase-shift control of isolated bidirectional DC-DC converter for power distribution in microgrid[J]. IEEE Transactions on Power Electronics, 2012, 27(11): 4667-4680.
[9] Wu Kuiyuan, De Silva C W, Dunford W G. Stability analysis of isolated bidirectional dual active full- bridge DC-DC converter with triple phase-shift control[J]. IEEE Transactions on Power Electronics, 2012, 27(4): 2007-2017.
[10] 王仁龙, 杨庆新, 操孙鹏, 等. 一种优化电流应力的双有源桥式DC-DC变换器双重移相调制策略[J]. 电工技术学报, 2021, 36(增刊1): 274-282.
Wang Renlong, Yang Qingxin, Cao Sunpeng, et al. An optimized dual phase shift modulation strategy for dual active bridge DC-DC converter[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 274-282.
[11] Tong Anping, Hang Lijun, Li Guojie, et al. Modeling and analysis of a dual-active-bridge-isolated bidire- ctional DC/DC converter to minimize RMS current with whole operating range[J]. IEEE Transactions on Power Electronics, 2018, 33(6): 5302-5316.
[12] 孙志峰, 肖岚, 王勤. 输出并联型双有源全桥变换器控制技术研究综述[J]. 中国电机工程学报, 2021, 41(5): 1811-1831.
Sun Zhifeng, Xiao Lan, Wang Qin. Review research on control technology of output parallel dual-active- bridge-converters[J]. Proceedings of the CSEE, 2021, 41(5): 1811-1831.
[13] 章涛, 阮新波. 输入串联输出并联全桥变换器的均压均流的一种方法[J]. 中国电机工程学报, 2005, 25(24): 47-50.
Zhang Tao, Ruan Xinbo. A method to voltage sharing and current sharing for input-series output-parallel full-bridge converter[J]. Proceedings of the CSEE, 2005, 25(24): 47-50.
[14] 武明义, 侯聂, 宋文胜, 等. 独立输入并联输出全桥隔离DC-DC变换器直接功率平衡控制[J]. 中国电机工程学报, 2018, 38(5): 1329-1337.
Wu Mingyi, Hou Nie, Song Wensheng, et al. Direct power balance control scheme of the input- independent-output-parallel operated full-bridge isolated DC-DC converters[J]. Proceedings of the CSEE, 2018, 38(5): 1329-1337.
[15] Shah S S, Bhattacharya S. A simple unified model for generic operation of dual active bridge converter[J]. IEEE Transactions on Industrial Electronics, 2019, 66(5): 3486-3495.
[16] Zhou Lu, Gao Yihan, Ma Hao, et al. Wide-load range multiobjective efficiency optimization produces closed-form control solutions for dual active bridge converter[J]. IEEE Transactions on Power Electronics, 2021, 36(8): 8612-8616.
[17] Li Jia, Luo Quanming, Mou Di, et al. A hybrid five-variable modulation scheme for dual-active- bridge converter with minimal RMS current[J]. IEEE Transactions on Industrial Electronics, 2022, 69(1): 336-346.
[18] Hebala O M, Aboushady A A, Ahmed K H, et al. Generic closed-loop controller for power regulation in dual active bridge DC-DC converter with current stress minimization[J]. IEEE Transactions on Indu- strial Electronics, 2019, 66(6): 4468-4478.
[19] Lin C S, Chen C L. Single-wire current-share paralleling of current-mode-controlled DC power supplies[J]. IEEE Transactions on Industrial Elec- tronics, 2000, 47(4): 780-786.
[20] 安峰, 王嵩, 杨柯欣. 输入串联输出并联双有源全桥DC-DC变换器多模块优化功率平衡控制方法[J]. 电工技术学报, 2018, 33(16): 3732-3742.
An Feng, Wang Song, Yang Kexin. Multi-module optimized power balance control scheme of the input-series-output-parallel operated dual-active- bridge DC-DC converters[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3732-3742.
Total Root Mean Square Current Optimization of IPOP Dual Active Bridge DC-DC Converter Based on Genetic Algorithm
Abstract The dual active bridge (DAB) converter is one of the most popular DC-DC topologies due to its galvanic isolation between input and output, wide voltage gain, and zero-voltage-switching (ZVS) operation in a wide load range. For a single module dual active bridge (DAB) converter, minimum root mean square current can be achieved using an optimized phase shift control strategy. However, for multi-module parallel operation systems, virtually identical electrical characteristics for each module are difficult to achieve, making the power balance control strategy unable to achieve general optimum efficiency. Therefore, this paper proposes a power difference control strategy for the input parallel and output parallel (IPOP) DAB converter system. By analyzing the difference of auxiliary inductors of each module, a differential power distribution ratio is set, which minimizes the root mean square current of the system.
Firstly, an optimized triple-phase shift control strategy for a single-module DAB converter is analyzed. An optimized triple-phase shift is calculated by introducing a genetic algorithm, which minimizes the root mean square inductor current. Secondly, based on a single-module optimized control strategy, the different RMS inductor current for each module with a differential auxiliary inductor in the IPOP DAB converter system is illustrated. Thirdly, an optimal model to minimize total RMS current for the IPOP DAB converter system is constructed. The optimal results of the model are carried out by a genetic algorithm. Finally, based on the calculation results, an optimal control strategy for the IPOP DAB converter system is proposed. Unlike the traditional strategy that ensure power balancing between modules, the differential power distribution ratio for each module is set based on the difference of auxiliary inductors in the proposed control strategy to minimize the root mean square (RMS) current of the system.
To verify the theoretical analysis, an experimental prototype with three parallel modules based on SIC devices of 8 kW/100 kHz is built. Herein, two conditions are considered: the input voltage of 100 V and output voltage of 80 V, and the input voltage of 100 V and output voltage of 150 V. According to theoretical analysis, when the total load is small, the power distribution ratio for the module with a smaller auxiliary inductor is lower. Moreover, the module with a larger auxiliary inductor distributes larger power. On the contrary, when the total load is large, the module with a larger auxiliary inductor distributes smaller power, and a larger power distribution ratio is set to the module with a smaller auxiliary inductor. The experiment verified the theory of differential power distribution in the whole load range.
Based on theoretical analysis and experimental results, the following conclusions are drawn. (1) The proposed control strategy distributes different power to modules with different auxiliary inductors to meet the total output power requirements, and the system can operate stably under various load conditions. (2) For a single module DAB converter, the optimization strategy can effectively reduce the RMS inductor current. Compared with the traditional control strategy, the optimization effect is more apparent when the load is light and medium, and the complexity of mathematical analysis is reduced. (3) The peak efficiency of the prototype is 98.8 %. The average efficiency is improved by 1.2 % in Buck mode and 0.84 % in Boost mode compared with the traditional power balancing strategy, which verifies the proposed control strategy.
keywords:Dual active bridge converter, input parallel output parallel, genetic algorithm, power distribution, inductor root mean square current
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.221788
收稿日期 2022-09-21
改稿日期 2022-12-26
江凌峰 男,1998年生,硕士研究生,研究方向为DC-DC变换器。E-mail: lingfengjiang@sjtu.edu.cn
王 勇 男,1975年生,教授,博士生导师,研究方向为电力电子新能源。E-mail: wangyong75@sjtu.edu.cn(通信作者)
(编辑 陈 诚)