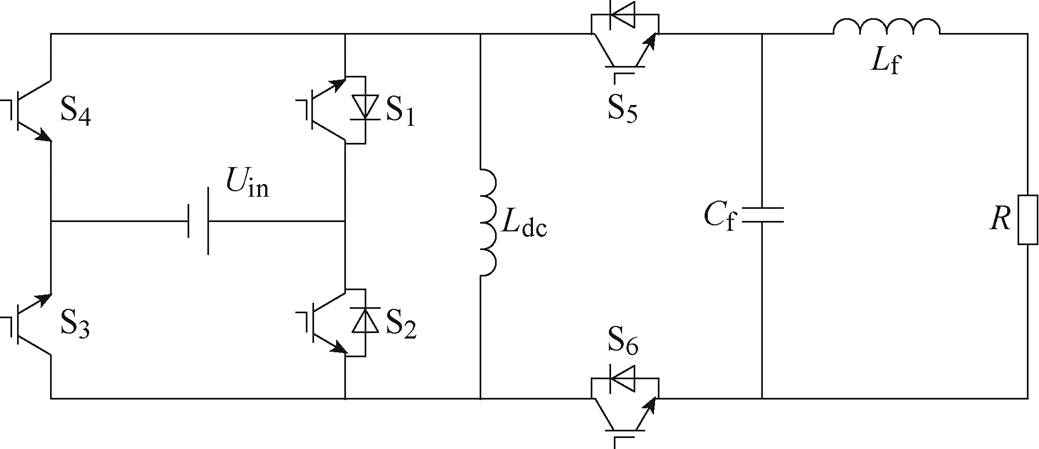
图1 单级单相无电解电容Buck-Boost逆变器拓扑结构
Fig.1 Single-stage single-phase Buck-Boost inverter without electrolytic capacitor
摘要 该文给出一种无电解电容的单级单相Buck-Boost逆变器。该逆变器可以灵活地实现升降压以适应宽输入范围的直流侧电压；仅用一个工作于正负半周的低值直流储能电感而无需电解电容和大电感，开关器件和无源器件数目少，因而降低了成本和体积，提高了可靠性、使用寿命和功率密度；通过改变储能电感电流方向实现极性反转，控制方式十分简洁，非常适用于中小功率光伏系统。该文详述了Buck-Boost逆变器的工作原理、升降压能力及调制策略，并在此基础上，完成该逆变器升降压、扰动以及并网控制的仿真和实验，结果良好且与理论分析相契合。
关键词：电力电子 无电解电容 单级单相非隔离 Buck-Boost 光伏逆变器
社会的飞速发展加剧了能源与环境、气候的矛盾，发展高效可持续、绿色清洁的新能源俨然成为了新时代发展的重要方向[1-2]。而我国广袤的地域决定了太阳光辐射产生的能量丰富，加之其利用时清洁无污染、运营成本低，因而太阳能应用前景极为广阔[3]。在时代发展要求与“双碳”目标提出的双重驱动下，我国起步较早的光伏产业脱颖而出，在新时代能源转换革命中被普遍看好[4]。
逆变器作为光伏系统的核心，其内部结构以及外部环境条件均对系统的可靠性有决定性影响。为避免不确定因素对光伏系统输出造成波动，进而引发功率输出不稳定[5]，当今比较主流的解决方式就是采用具备升降压能力的逆变器，以灵活应对输入电压宽范围的波动[6-8]。目前，具备升降压能力的逆变器可分为隔离型和非隔离型。工频隔离型逆变器噪声大、体积十分笨重；高频隔离型逆变器产生高频噪声、器件数目多、功率密度低、成本高；另外，隔离型逆变器具有噪声、体积和成本等难以克服的固有劣势[9-11]。非隔离型逆变器则可极大程度地解决上述问题，避免了隔离型变压器造成的能量传输损耗，进而提高了功率密度。但常见的多级逆变器往往结构复杂，导致安装繁琐、器件多、质量大、成本高、效率低，并且中间级大多需要电解电容[12-14]，进一步降低了系统的使用寿命和可靠性。因此，具有升降压能力的无电解电容单级非隔离逆变器才是较全面的满足光伏发电系统要求的拓扑结构。
利用基本斩波电路构造逆变器拓扑结构，是一种通用的做法。Buck-Boost变换器仅需一个中间电感，无中间电容，是所有具备升降压能力的基本斩波电路中最简洁的，因此选择以Buck-Boost电路为基础的单级单相非隔离型逆变器。将基本斩波电路扩展为逆变器的方法分为两种：双变换器组合法、斩波器与桥式逆变器级联法。采用这两种方法，构造出了多种单相单级Buck-Boost逆变器。
双变换器组合法，是将两个Buck-Boost逆变器通过串并联组合构成逆变器。文献[15]给出了一种输入并联型Buck-Boost逆变器，只用了4个开关管，高频工作时不存在桥臂直通，但该电路使用了两个大电解电容使系统的可靠性和寿命降低。文献[16]给出输入串联型Buck-Boost逆变器对滤波电容进行了合并，而输入侧仍需要两个电解电容，其均压控制也比较复杂。文献[17]给出了一种差模Buck-Boost逆变器，其适用场合广泛，谐波失真度在线性化方案下降低，但其器件复用率低，开关管使用较多。文献[18]中单相非隔离Buck-Boost逆变器功率器件复用率很高，但开关器件偏多、成本高。
斩波器与桥式逆变器级联法是将Buck-Boost变换器与H桥逆变器进行级联并省去中间滤波电容，构成了单级单相逆变器，H桥逆变器的参与使此类逆变器控制方式灵活。文献[19]所提拓扑仅使用了一个储能电感，但利用了5个二极管保证电流单向流通，增加了系统损耗与造价。文献[20]在拓扑前侧增加耦合电感，电压增益高、开关损耗小、工作不受干扰，但工作原理复杂、控制不便，电感器件使用较多造成了体积大、功率密度低。
在级联式单级单相Buck-Boost逆变器的基础上，将Buck-Boost变换器与H桥逆变器中的开关器件和无源器件进行混合复用，形成了集成式单级单相Buck-Boost逆变器。文献[21]给出了一种单级双电感Buck-Boost逆变器，利用倍流电感使之具备高电压增益，可很好地满足光伏系统需要，但使用器件总数多、系统冗杂，不符合小型化和轻量化的发展趋势。文献[22]中拓扑均采用较少的功率器件，但是使用了两个储能电感。文献[23]提出的Buck- Boost集成式升压逆变器使用了电解电容，且仅能升压。文献[24]给出的拓扑为双电源电路，结构繁琐、劣势明显。
通过以上对单级单相非隔离型Buck-Boost逆变器拓扑现状分析，目前需要解决的问题包括：升降压能力、电解电容、单电源输入、拓扑器件数目、器件复用率以及拓扑和控制的整体简洁性等，而已有的拓扑构造大多顾此失彼。本文取长补短，综合兼顾，提出了一种无电解电容的单级单相Buck- Boost逆变器。该逆变器的拓扑既可满足升降压要求，也不需要电解电容，仅需一个低值电感作为储能元件，功率器件及无源器件少，整体结构简洁紧凑、质量轻，器件复用率高，工作模式以及控制方式简单，非常适用于中小功率光伏发电系统。本文首先介绍该逆变器的拓扑结构和工作原理，然后推导其稳态电压增益并分析其开关应力，最终给出仿真与实验结果验证理论分析的正确性。
本文所提出的无电解电容的单级单相Buck- Boost逆变器的拓扑结构如图1所示，以可升降压且结构最简洁的Buck-Boost变换器为构造基础，与可灵活控制的开关管前置组合并复用器件。该拓扑可以看成三个部分：由电源与开关管S1～S4组成的电源及极性反转部分；由电感Ldc与开关管S5、S6组成的能量传递部分以及由CL滤波器与负载组成的交流侧部分。该拓扑可以通过在直流电源两侧的开关管改变储能电感Ldc上的电流方向，并且使用S5、S6两个开关管配合Ldc向负载侧释放能量。
图1 单级单相无电解电容Buck-Boost逆变器拓扑结构
Fig.1 Single-stage single-phase Buck-Boost inverter without electrolytic capacitor
该拓扑结构继承了Buck-Boost电路的工作特性，既可升压也可降压，适用于直流侧电压宽范围变化的光伏发电系统。电路包括6个IGBT开关管（S3和S4选用逆阻型IGBT，其他均为双向IGBT），1个直流电感，1个CL滤波器，单直流输入电源（光伏电池板），输出侧接入负载或并入电网。
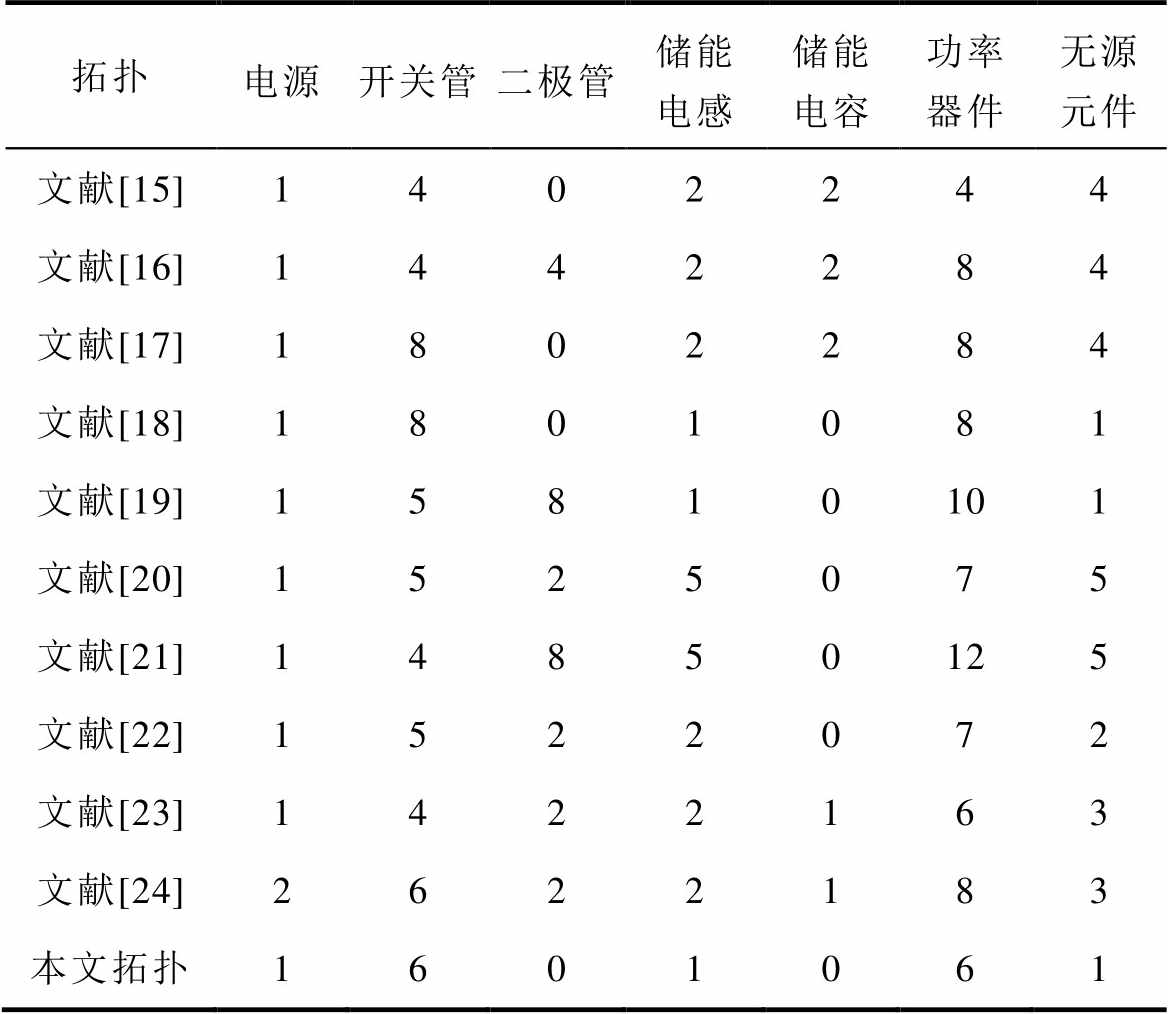
表1给出了本文所提拓扑与引言所提拓扑中功率器件（开关管和二极管）以及无源元件（储能电感和储能电容）数目上的对比，滤波器部分不计。通过表1对单级单相非隔离Buck-Boost逆变器对比结果，可以明显地看出，本文所提拓扑是无源器件数目最少，同时功率器件数目也不多的拓扑，整体结构简洁、紧凑，尽可能地减小体积、质量以及成本，有利于提高系统运行的可靠性、使用寿命及功率密度。
表1 引言中拓扑与本文拓扑器件数目对比
Tab.1 Comparison of the number of topological devices between the introduction and this paper
拓扑电源开关管二极管储能电感储能电容功率器件无源元件 文献[15]1402244 文献[16]1442284 文献[17]1802284 文献[18]1801081 文献[19]15810101 文献[20]1525075 文献[21]14850125 文献[22]1522072 文献[23]1422163 文献[24]2622183 本文拓扑1601061
按中间电感电流断续与否，该逆变器可工作于电流连续模式和电流断续模式；共有六种工作模态（运行模态Ⅰ～Ⅵ）。设运行模态Ⅰ、Ⅱ、Ⅴ为正半周，Ⅲ、Ⅳ、Ⅵ为负半周，则正负半周工作模式均为Buck-Boost变换器运行模式，断续运行模式的六种运行模态如图2所示。
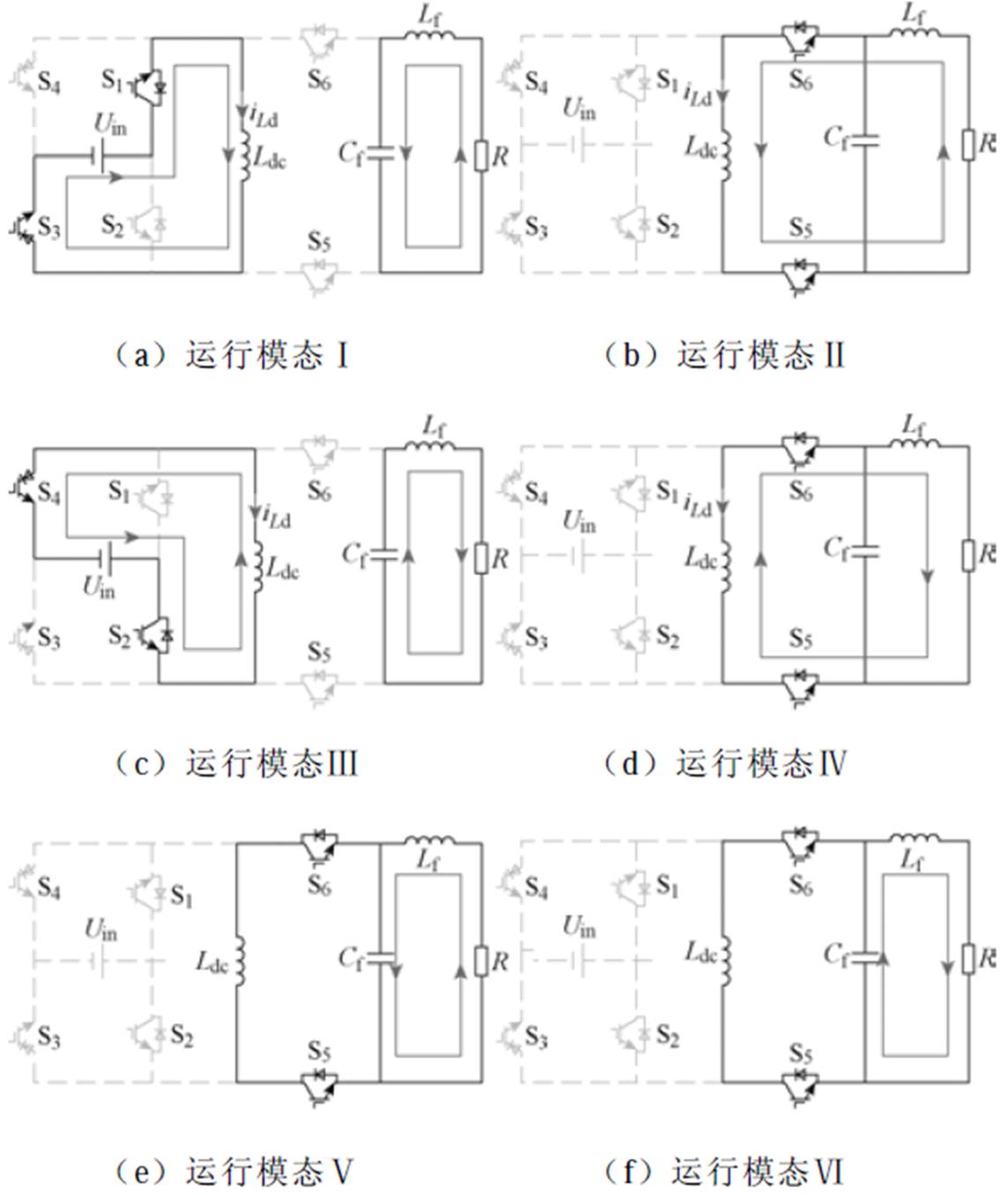
图2 断续运行模式的六种运行模态
Fig.2 Six operation modes of intermittent mode operation
（1）运行模态Ⅰ：如图2a所示，功率开关管S1、S3开通，其他开关管关断。电源Uin经开关S1和S3顺时针向直流电感Ldc充电，该电感储能，经过的电流iLd呈斜直线上升；滤波电容Cf经过滤波电感Lf为负载R逆时针方向供电。
（2）运行模态Ⅱ：如图2b所示，开关管S5开通，其他开关管关断。电感Ldc中储存的能量经过开关管S5、滤波电感Lf以及S6中反向并联的二极管为负载R逆时针方向供电，直流储能电感释放 能量。
（3）运行模态Ⅲ：如图2c所示，功率开关管S2、S4开通，其他开关管关断。电源经开关S2和S4逆时针向直流电感Ldc充电，该电感储能；滤波电容Cf经过滤波电感Lf为负载R顺时针方向供电。
（4）运行模态Ⅳ：如图2d所示，开关管S6开通，其他开关管关断。电感Ldc中储存的能量经过开关管S6、滤波电感Lf以及S5中反向并联的二极管为负载R顺时针方向供电，直流储能电感释放 能量。
（5）运行模态Ⅴ：如图2e所示，6个IGBT全部关断。滤波电容Cf经过滤波电感Lf为负载R逆时针方向供电。
（6）运行模态Ⅵ：如图2f所示，6个IGBT全部断开。滤波电容Cf经过滤波电感Lf为负载R顺时针方向供电。
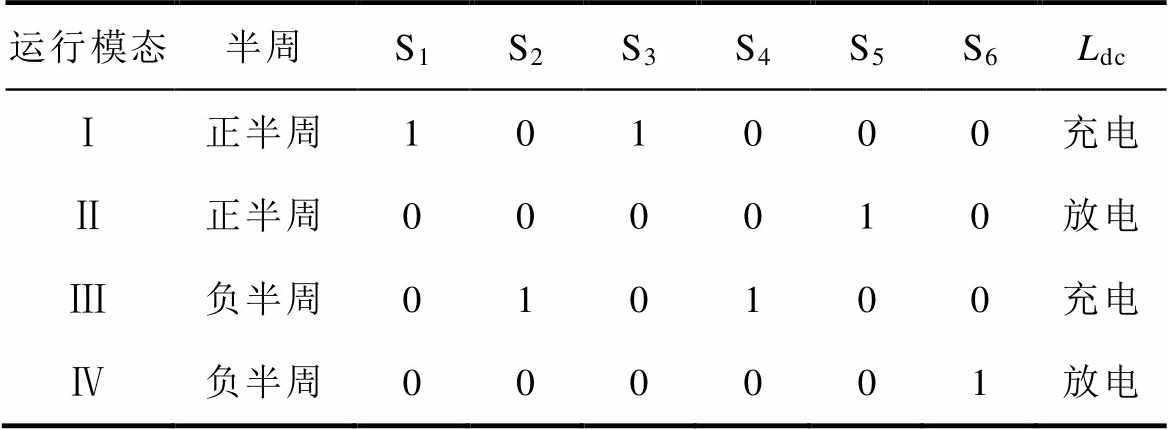
图2中，运行模态Ⅰ～Ⅳ为该逆变器工作在连续模式下的运行模态。断续模式则为Ⅴ和Ⅵ两个运行模态。6个功率开关通断情况对应电感Ldc的充放电状态见表2。
表2 电感Ldc充放电情况
Tab.2 Inductor Ldc charge and discharge situation
运行模态半周S1S2S3S4S5S6Ldc Ⅰ正半周101000充电 Ⅱ正半周000010放电 Ⅲ负半周010100充电 Ⅳ负半周000001放电
注：“1”表示开通；“0”表示关断。
至此，可以看出，本文所提拓扑在开关管的选型上比较合理，原因如下：以正半周工作模态Ⅰ为例，电源通过S1、S3开关管为直流电感Ldc充电，如果S4是具有反并联二极管的双向IGBT，由于S3在正半周一直开通，因此正半周一直存在S4-S3反并联二极管-Ldc-S4逆时针回路，直流电感Ldc将无法完成充电释能过程。虽然该过程中同样有S2-Ldc- S1反并联二极管-S2逆时针回路，但S2在正半周是高频驱动下开断的，因此该回路并非一直存在于正半周，直流电感Ldc是可以完成充电储能释能过程的。故前侧H桥中带有反并联二极管的开关管必须以高频驱动。因此，S1、S2也可以采用逆阻型IGBT，但是为了尽可能地降低成本，采用常规IGBT开关是考虑原理及成本后的最佳选型方式，且逆阻型IGBT无反向二极管损耗，双向IGBT（S5和S6）中的反向二极管也得到了充分利用。
在断续模式下，中间电感取值可以取更小，有利于降低体积和成本，本文只分析断续模式的工作情况。由于H桥前置在电源侧，开关切换高频驱动信号时叠流（造成短路）与死区（无放电回路）均不合适，故本逆变器采用简单的单极性正弦脉宽调制（Sine Pulse Width Modulation, SPWM）技术，实际应用性好。SPWM原理下驱动示意图如图3所示，S3、S4、S5和S6工频工作，S1和S2半高频工作。
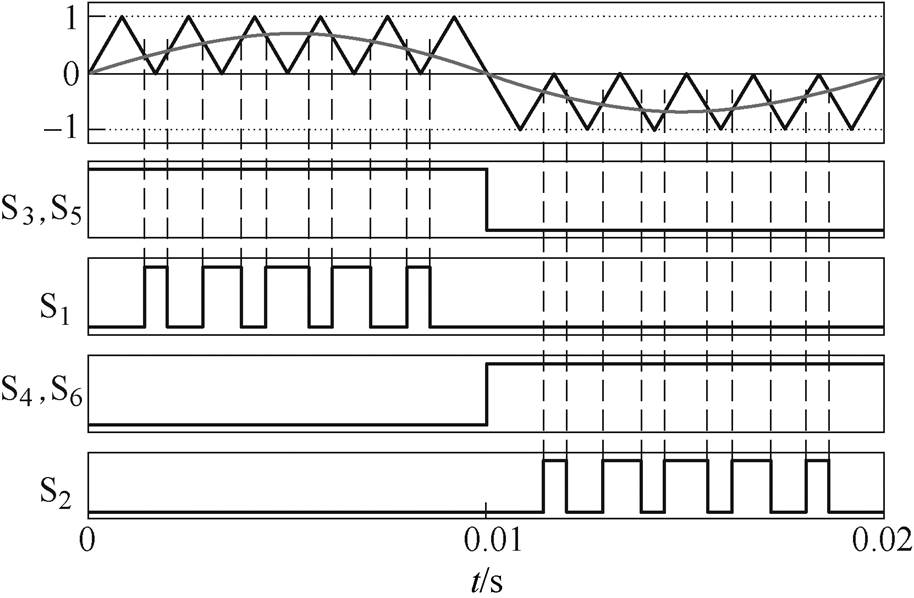
图3 SPWM原理下驱动示意图
Fig.3 Schematic diagram of driving under SPWM principle
Buck-Boost变换器运行在断续状态时，输出uo与输入Uin的比值为
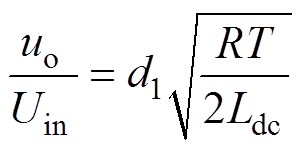（1）
式中，T为逆变器工作时的开关周期；d1为占空比，即高频导通时间与T的比；R为负载电阻；Ldc为直流储能电感。
本文提出的新型单级Buck-Boost逆变器的增益仍可按式（1）进行推导。在单极性SPWM方式下，d1=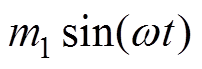
，代入式（1）即可得到
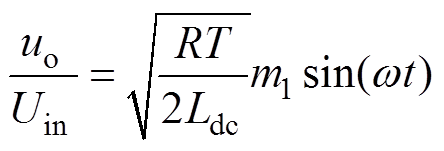（2）
根据式（2）可以得出，直流输入和逆变器输出之间的关系是由多种因素决定的，包括调制度m1、直流储能电感值Ldc、开关工作周期T、阻值R。而后三者是可以经过设计计算选取的，这样根据式（2）就可以确定，输出与输入的比值与调制度m1成正比，根据m1的取值可以确定该Buck-Boost逆变器的升降压情况，显然在断续模式下，该逆变器同时具备升压和降压能力的。根据相关计算，断续模式下，电阻R=50 W，T=0.000 05 s，直流电感Ldc=0.25 mH，将该参数代入可以得出升降压情况见表3。
电压增益三维图如图4所示。图4中，在负载R=50 W 为固定值时，图4a表示开关频率fs=20 kHz时，不同电压直流电感与占空比下的电压增益三维图，图4b表示直流电感Ldc=0.25 mH时，不同电压、开关频率与占空比下的电压增益三维图。虽然该逆变器的电压增益为本文仿真及实验中的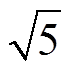
倍，但是本逆变器拓扑的电压增益不限于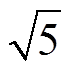倍。通过调整相关参数可以提高增益，即：电压增益随着开关频率和直流电感增大而减小，随着负载和占空比增大而增大；另外，也可以通过提升频率来尽可能地减小电感体积，具体可如图4所示。
表3 升降压情况
Tab.3 Analysis of voltage up and down
调制度m1取值升降压情况 m1=0.447平压 m1＞0.447升压 m1＜0.447降压
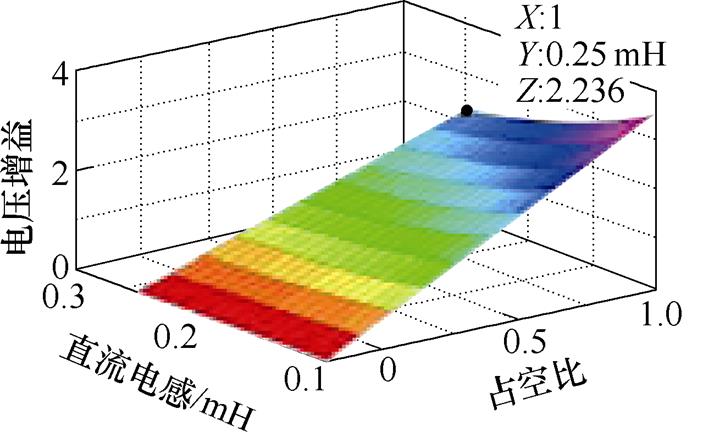
（a）增益与占空比、电感的关系
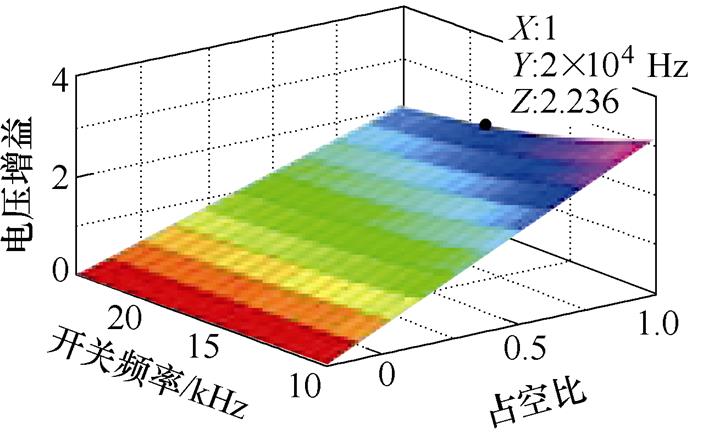
（b）增益与占空比、频率的关系
图4 电压增益三维图
Fig.4 Three dimensional diagram of voltage gain
由于S2、S4和S6 3个开关管的开断动作与S1、S3和S5 3个开关管是正负半周对称的，所以仅分析S2、S4、S6开关管应力即可，故不再对S1、S3、S5开关管做单独分析。同样地，以相同工况下，承受应力更大的断续模式为例进行分析。
首先，由电路拓扑结构可知，逆变器中的开关管应力基本保留了Buck-Boost直流变换器的特性。对开关管电压应力分析，只需要观察开关管在整个工作周期中所承受的最大电压即可。设Uo为输出电压（电网电压）峰值，当逆变器工作在断续模式，S2在其关断且与输入和输出侧均有通路时承受电压最大，既承受直流电源电压又承受交流输出电压，S4反向承受的输出电压峰值Uo最大，S6承受的最大电压与S2一致，即Uin+Uo。
同样地，分析开关管的电流应力，只需考虑整个工作周期中通过的最大电流即可。因对应开关管开通时与直流电感形成了串联回路，所以通过开关管电流的最大值均为通过直流电感的电流峰值。在断续模式下该逆变器功率器件承受的最大电流Im为
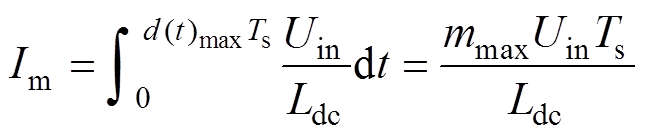（3）
式中，mmax为一个工频周期内占空比最大值。
对各个功率开关管电压应力以及电流应力的分析见表4。
表4 功率开关管应力
Tab.4 Power switch stress
功率开关管电压应力电流应力 S1, S2, S5, S6Uin+UoIm S3, S4UoIm
直流电感Ldc可表示为
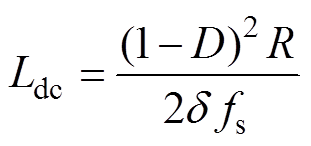（4）
式中，D为斩波电路的占空比；d 为储能电感电流的脉动参数；fs为开关动作频率。
若要逆变器工作在断续模式，令d=1，正常工况时负载电阻R=50 W，开关动作频率fs=20 kHz。占空比按照输出电压峰值和输入电压保持一致，即既不升压也不降压，令占空比D=0.5。将以上各参数代入式（4），得到直流电感Ldc=0.31 mH，即在Ldc选取低于该值时，电路运行于断续状态，实际取值Ldc=0.25 mH。
本文所提单级单相Buck-Boost逆变器属于电流型逆变器，故采用CL滤波器，在纯阻性负载与并网情况下均适用。作为二阶滤波器，CL滤波器继承了L、LC、LCL三种滤波器优势的同时，避免了其劣势，且参数结构易于设计，结构中的电感也可较好地抵御电网造成的电流冲击。
滤波电容Cf和滤波电感Lf满足的传递函数的表达式为
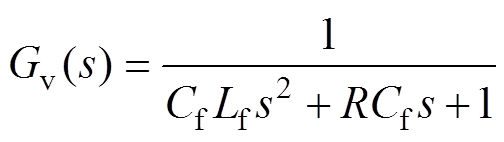（5）
为尽可能地消除高频谐波分量，保留输出基波分量。转折频率f1、开关频率fs以及基波频率f0的设计原则为
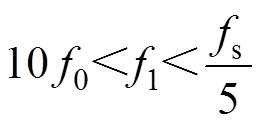（6）
为尽量增大滤波电容以更好地将谐波滤除的同时，不会造成无功功率增加，令x =0.707，系统开关频率fs=20 kHz，转折频率f1=2 kHz时，计算得滤波电容Cf=2.25 μF，根据型号选择耐压为630 V，容值为2.2 μF的聚丙烯（CBB）电容，计算滤波电感Lf =2.8 mH，实际选择Lf =3 mH。
根据逆变器的拓扑结构可以得出，未经过滤波处理的电流Ih(s)到经过滤波处理的电流Io(s)的传递函数恰恰就是式（5）所得出的CL滤波器传递函数，从而可以得到电流Ih(s)到输出电压Uo(s)的传递函数G(s)为
（7）
由功率守恒定律可知，逆变器的输入功率和输出功率是一致的，进而可以得到直流储能电感电流平均值为
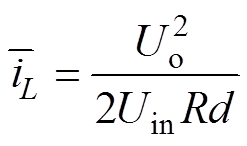（8）
式中，d为一个开关周期内的平均占空比。
根据储能电感充放电原理，可以得到经过CL滤波器滤波之前的输出电流ih的平均值为
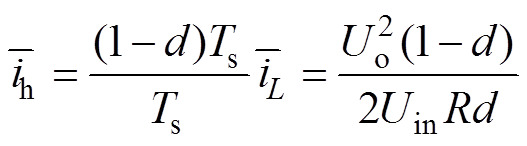（9）
本文主要针对逆变器系统运行在断续模式时建模，即在传统单极性SPWM控制下进行数学建模分析。假设在一个开关周期内储能电感放电时间为d2Ts，从而可以得到在(d1+d2)Ts时间段内电感电流的平均值为
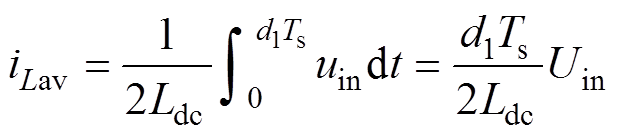（10）
根据一个开关周期内直流电感的充放电原理，容易得到ih在该周期内的平均值为
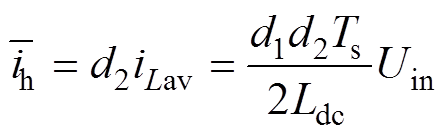（11）
在单极性SPWM策略下
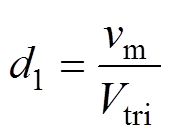（12）
式中，vm为调制波；Vtri为三角载波幅值。
逆变器系统工作在断续模式时有
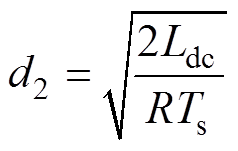（13）
将式（12）和式（13）代入式（11），经过化简可得
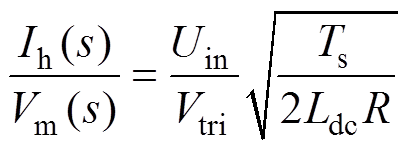（14）
因此，调制器输入至CL滤波器输入的传递函数为
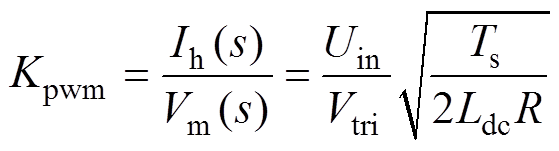（15）
联立式（7）和式（15）可得到调制器输入至逆变器输出的传递函数为
（16）
式（16）传递函数的矫正前伯德图如图5所示。由幅频特性可见，系统以-40 dB/dec的斜率穿越0 dB线。由相频特性可见，系统的相位裕度仅为25.6 °，系统的稳定性较差，需要加入调节器进行 校正。
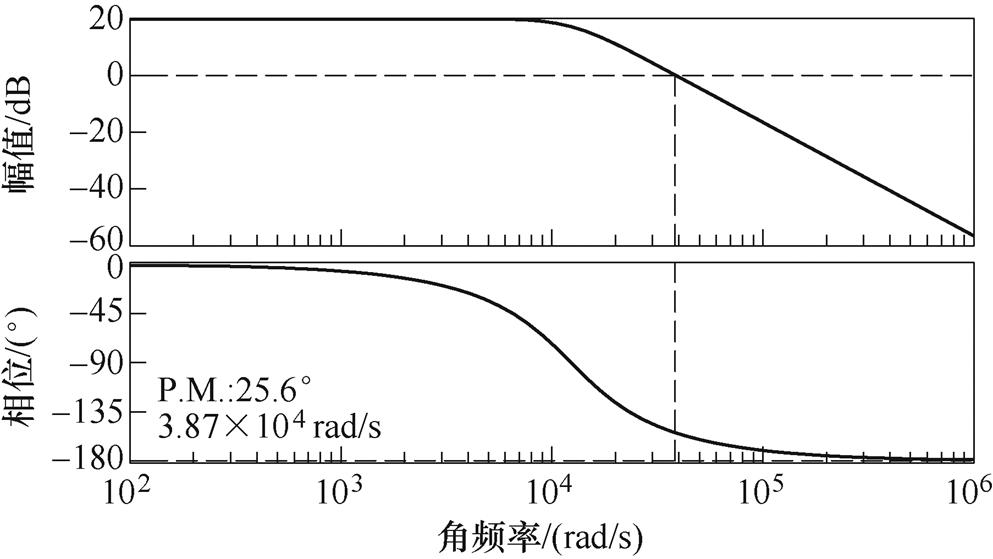
图5 矫正前伯德图
Fig.5 Bode diagram of system before adjustment
为了实现对正弦信号的无静差跟踪，根据内模原理，若控制回路中包含与给定信号相同的环节，即可实现对给定信号的无静差跟踪。本文采用单电流闭环调节器，PR调节器传递函数为
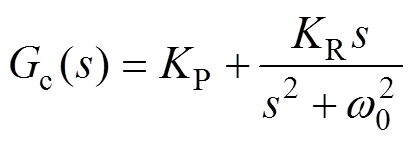（17）
式中，KP、KR分别为PR调节器的比例、谐振参数；w0为基波角频率。
在远离基频的频域上，PR调节器与PI调节器传递函数相同，频率特性基本相同。控制系统中影响动态性能的频域段满足远离基频段的条件，因此按照PI调节器设计方式。将零点设为转折频率点，令穿越频率wc=wn/10，并在穿越频率处，令传递函数的增益为1，可以得到
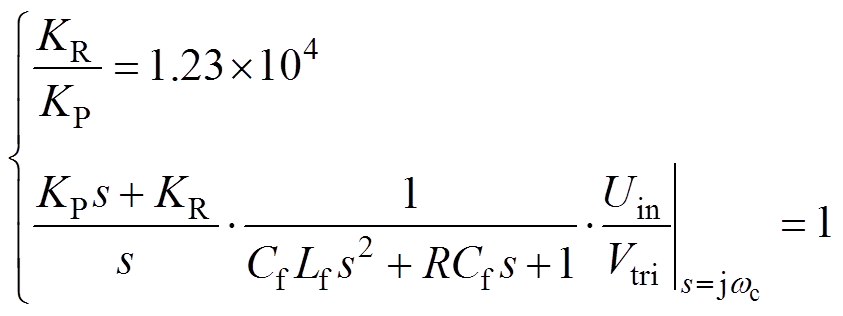（18）
经计算可得PR调节器参数为：KP=0.000 3，KR= 3.7。
加入PR调节器矫正后系统的伯德图如图6所示，可见系统以-40 dB/dec的斜率穿越0 dB线，相位裕度为88.1 °，系统稳定性大大提高。穿越频率wc=333 rad/s，系统的快速性较好。并且在高频段以-40 dB/dec的斜率衰减，因此系统抗高频噪声干扰的能力较强。
图6 矫正后伯德图
Fig.6 Bode diagram of system after adjustment
为验证理论分析正确性以及拓扑运行性能，本节进行了相应的仿真分析，以下结果均直接从闭环系统开始，为保证仿真波形清晰，对电流进行了一定倍数的扩大，电路相关参数见表5。
闭环升降压仿真结果如图7所示，图7a与图7b输出电压幅值311 V，图7a输入电压440 V，图7b输入电压220 V，均跟随给定，适应宽范围输入电压，能够实现正弦度良好的升降压逆变。
表5 器件参数（仿真、实验）
Tab.5 Device parameters (simulation and experiment)
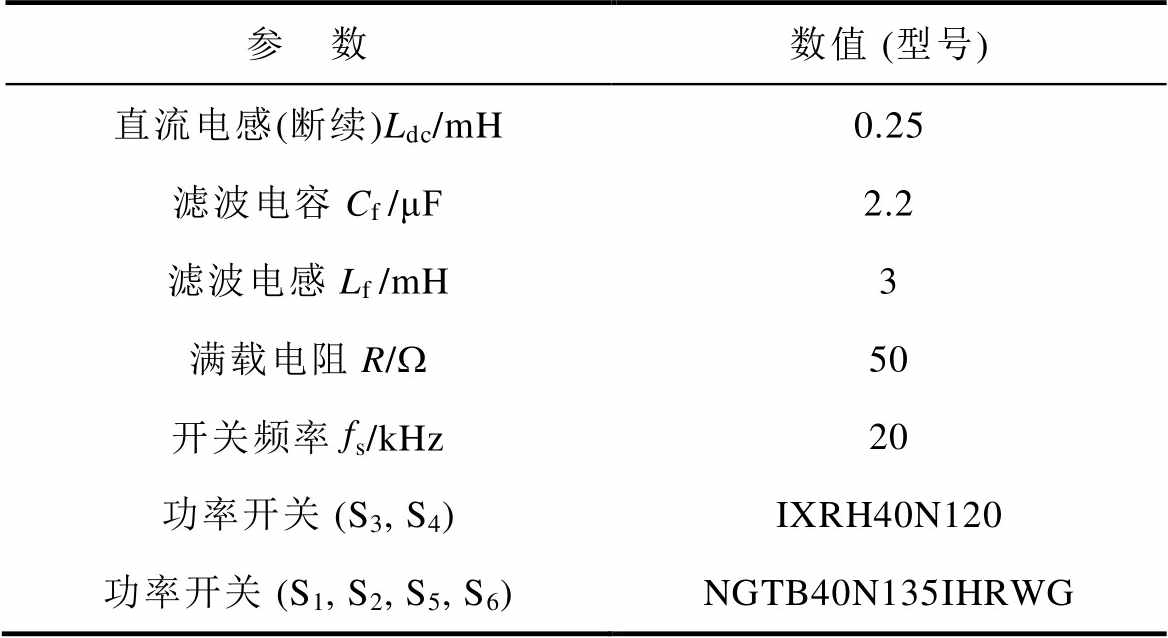
参 数数值 (型号) 直流电感(断续)Ldc/mH0.25 滤波电容Cf /μF2.2 滤波电感Lf /mH3 满载电阻R/W50 开关频率fs/kHz20 功率开关 (S3, S4)IXRH40N120 功率开关 (S1, S2, S5, S6)NGTB40N135IHRWG
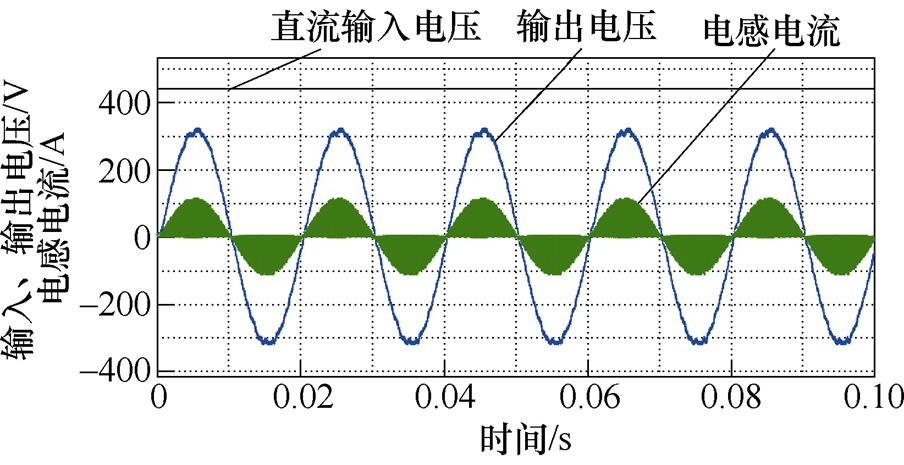
（a）降压
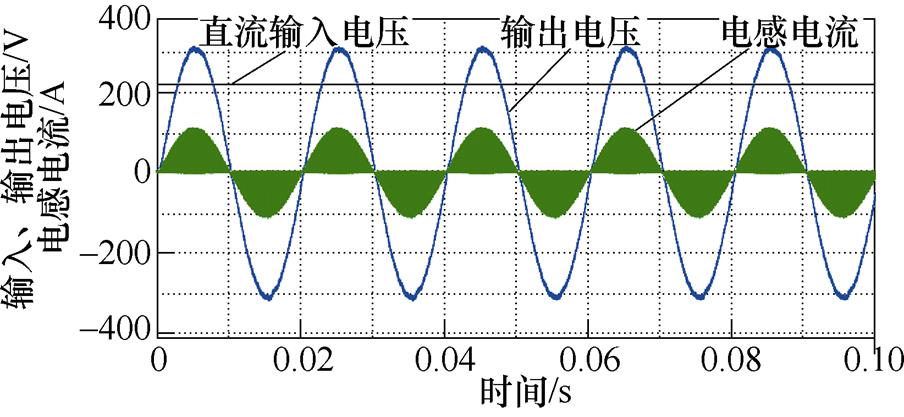
（b）升压
图7 闭环仿真结果分析
Fig.7 Closed-loop simulation results and analysis
满载工况下，半载切换满载以及满载切换半载的仿真结果分别如图8a和图8c所示，满载时电阻负载50 W，半载时电阻负载100 W。半载切满载后输出电流加倍，满载切半载输出电流减半，输出电压稳定跟随311 V给定，基本没有波动，切载过程平滑迅速，系统具备良好的抵抗负载扰动能力。
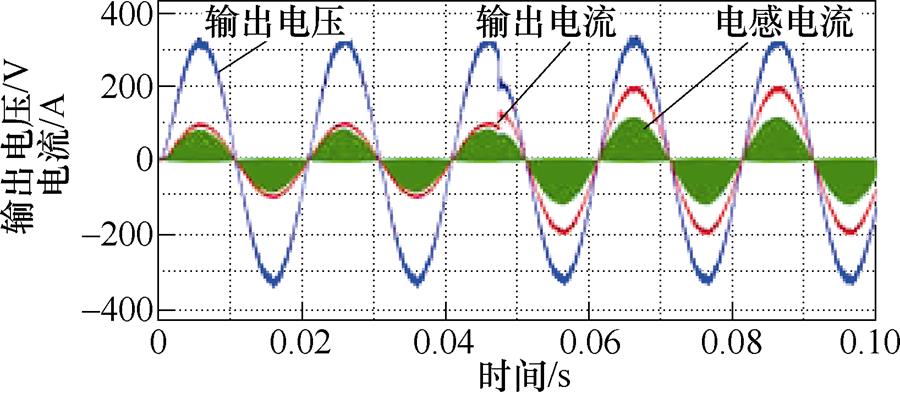
（a）半载切满载
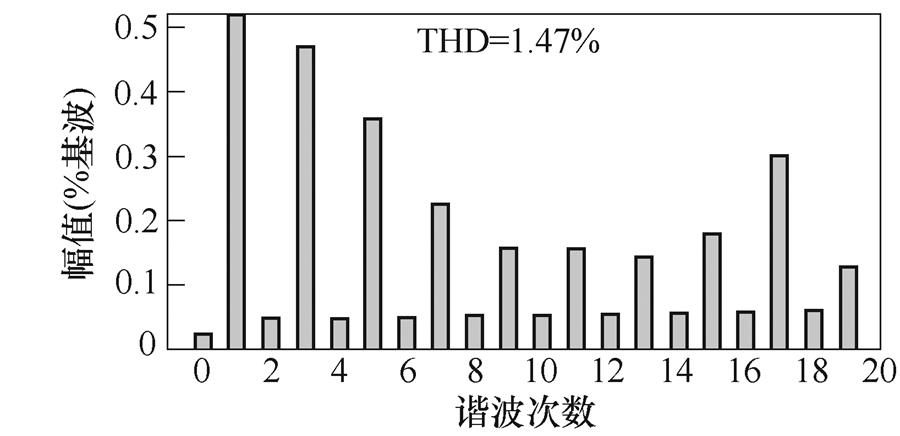
（b）切满载后输出FFT
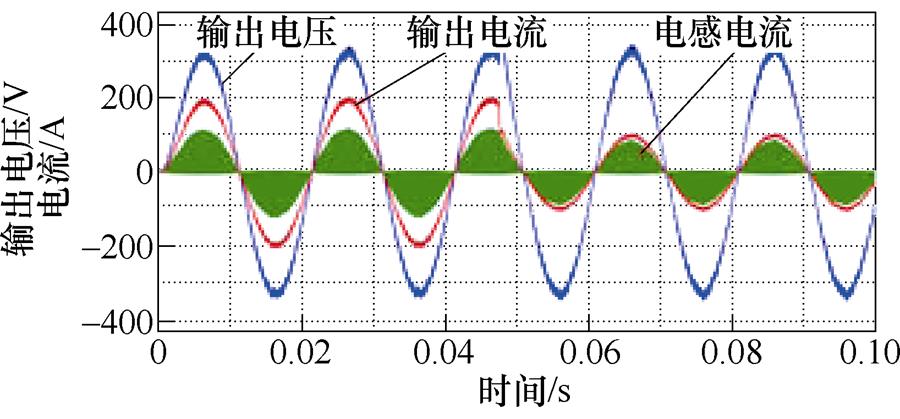
（c）满载切半载
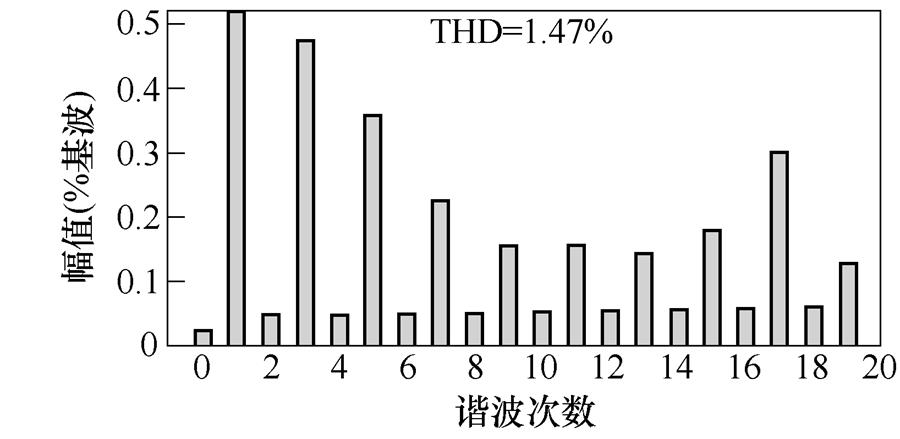
（d）切半载后输出FFT
图8 负载扰动仿真结果
Fig.8 Load disturbance simulation results
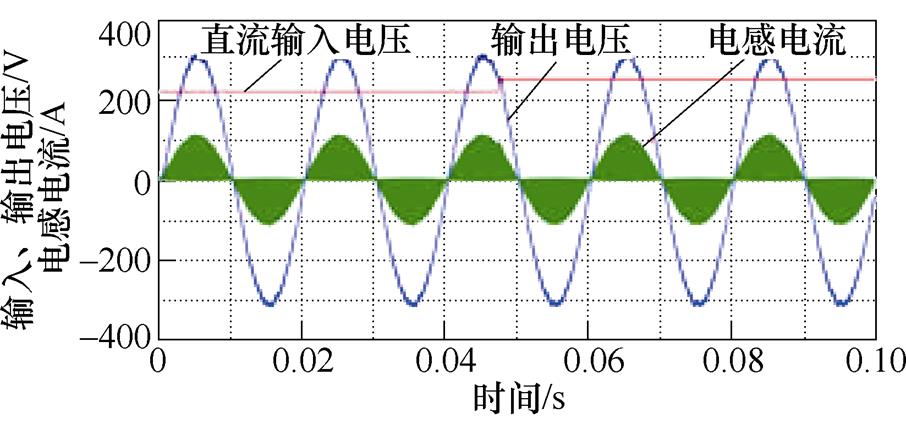
对逆变器的输入扰动仿真结果如图9所示，图9a和图9c分别表示降压工况以及升压工况下的输入扰动仿真。输入扰动分别为250 V降至220 V以及220 V升至250 V，逆变输出峰值分别为160 V和311 V，在输入扰动后输出波形无明显波动，逆变输出跟随给定，效果良好，逆变器具备良好的抗输入扰动性能。
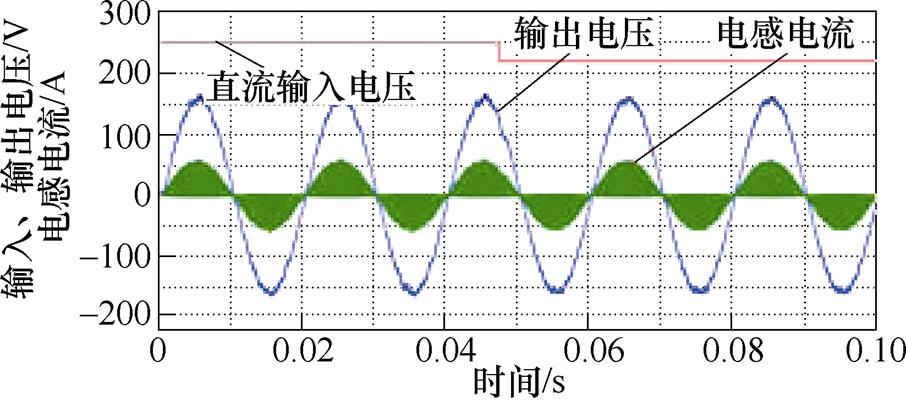
（a）降压输入扰动
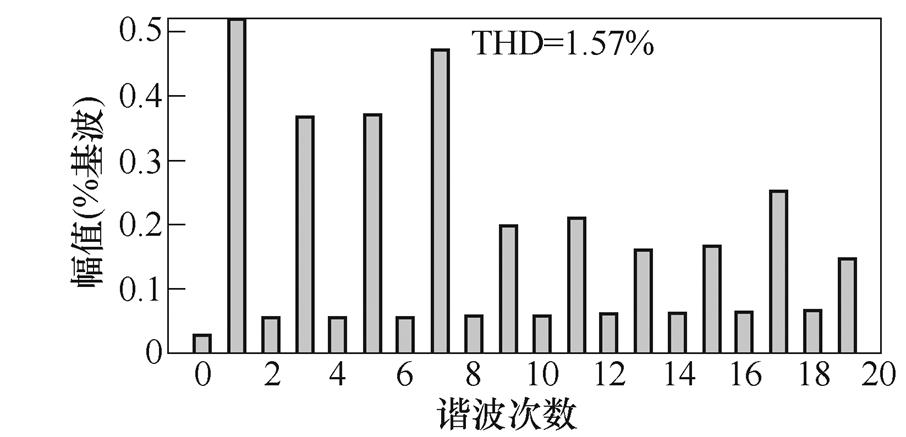
（b）降压输入扰动后输出FFT
（c）升压输入扰动
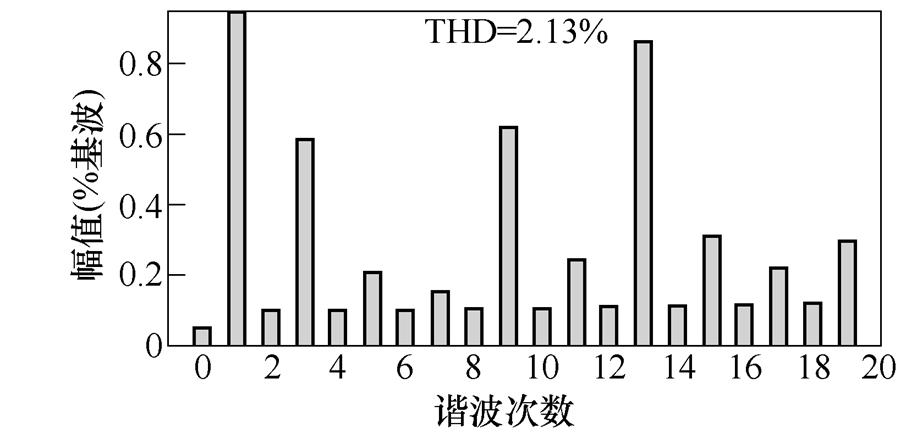
（d）升压输入扰动后输出FFT
图9 输入扰动仿真结果
Fig.9 Input disturbance simulation results
电网电压并不是理想的正弦波输出，为了在仿真中使得并网电压更加契合实际情况，尽量模拟出较符合的效果，是在仿真的并网电压中注入了总谐波畸变率（Total Harmonic Distortion, THD）近10 %的谐波，由以下仿真中的并网波形可以看出，电网波形有较明显的畸变。
图10为对电路进行的并网仿真波形分析，直流输入为220 V，升压并网电压幅值为311 V，降压为160 V，并网电流为5 A。并网电流的THD满足标准，仿真初步验证该逆变器具备很好的并网运行能力。
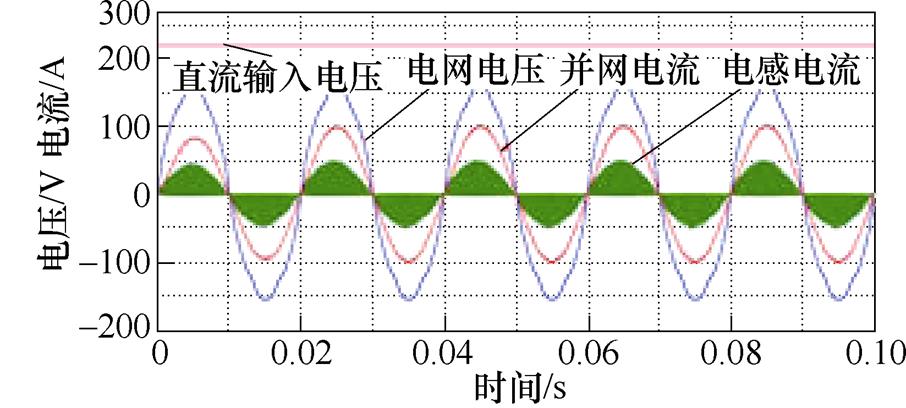
（a）降压并网波形
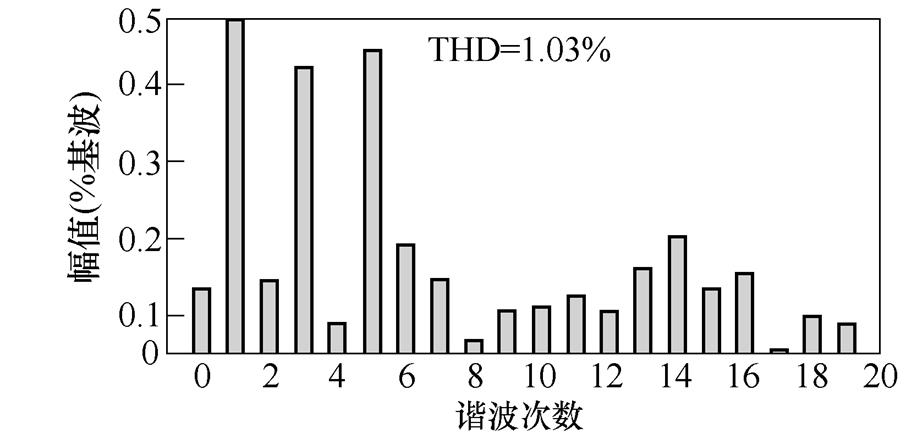
（b）降压并网电流FFT
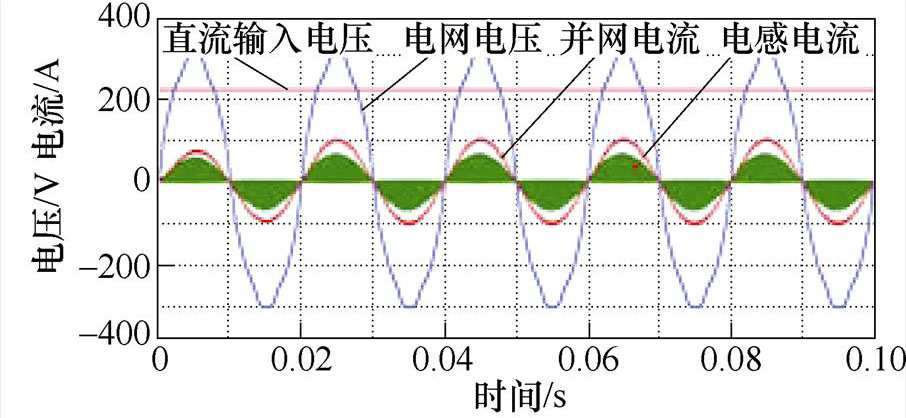
（c）升压并网波形
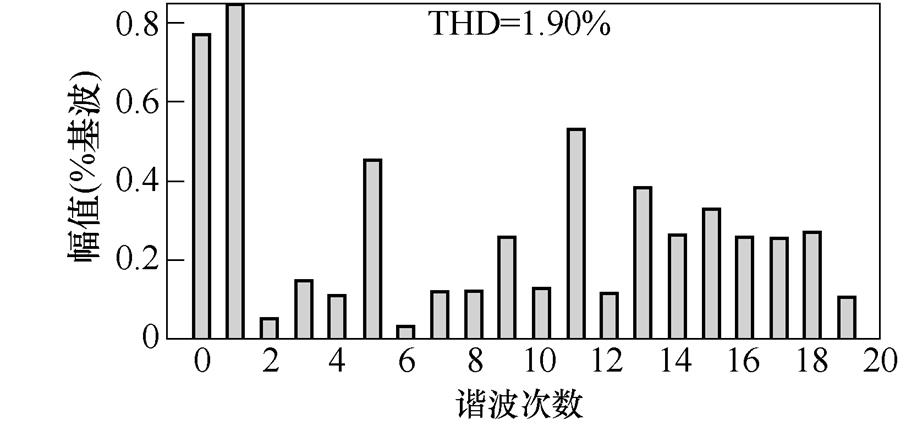
（d）升压并网电流FFT
图10 并网仿真结果
Fig.10 Grid connected simulation results
仿真参数条件为输入220 V直流电压，输出峰值311 V的交流电压。图11a为器件电压应力波形。S2、S4、S6的开关管应力按第3节理论分析分别为531 V、311 V和531 V，与仿真结果基本相符合。留有一定裕度，S1、S2、S5和S6开关管应力按照600 V，S3和S4按350 V设计。图11b为器件电流应力波形，与理论分析一致，6个开关管的电流应力均为40 A，作为开关管电流承受能力的选型依据。
（a）电压应力
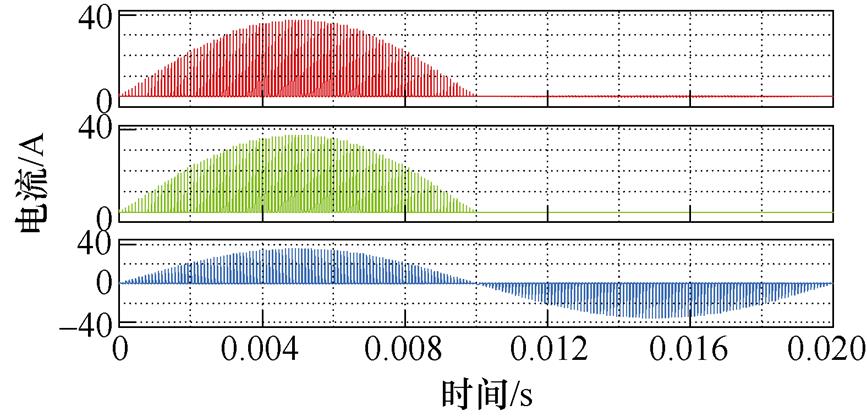
（b）电流应力
图11 开关应力仿真结果
Fig.11 Switch stress simulation results
实验平台如图12所示。本实验为基本原理型实验，在结构设计和热设计方面并未优化考虑，不是十分紧凑，实验取值参数与仿真取值参数是相同的，下面不再赘述。
图12 实验平台
Fig.12 Experimental platform
闭环实验结果如图13所示。图13a和图13b分别为逆变器工作在440 V→311 V降压、220 V→311 V升压逆变器下的实验波形，经过谐波分析，其输出电压的THD均在5 %以内，实验进一步验证了逆变器具备良好的升降压能力，闭环系统参数良好。
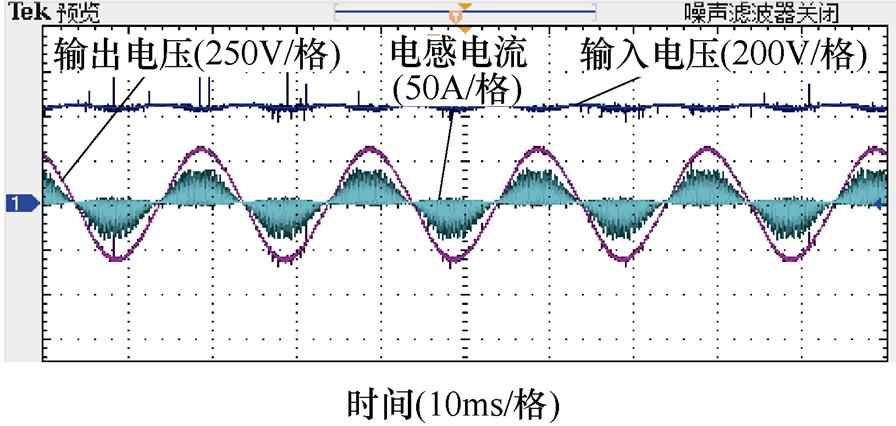
（a）降压实验波形
（b）升压实验波形
图13 闭环实验结果
Fig.13 Closed loop experimental results
负载扰动实验结果如图14所示。图14a和图14c分别为满载情况下，和仿真分析相对应的半载切满载以及满载切半载的负载扰动实验波形。由实验结果可知，负载扰动前后输出跟随给定，THD满足要求，进一步证明了该逆变器系统具备十分良好的抗负载扰动的能力。
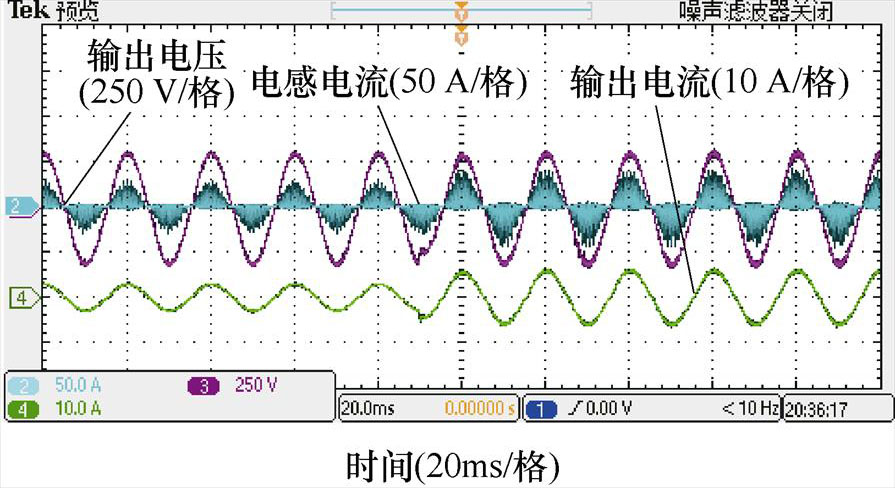
（a）半载切满载
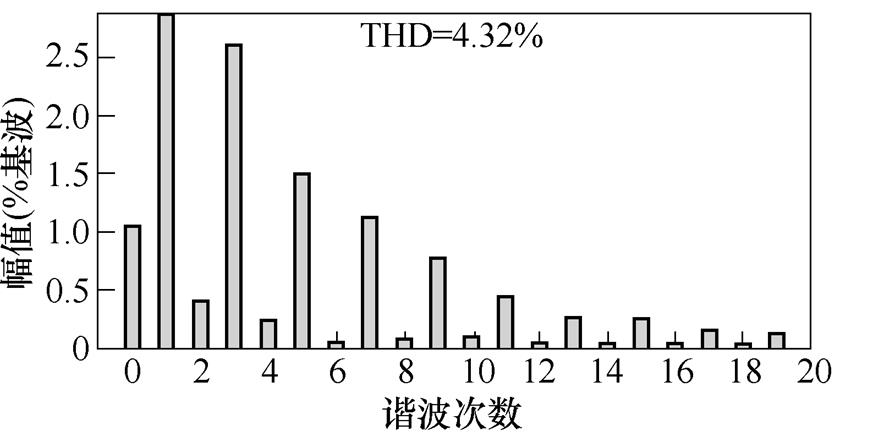
（b）切满载后输出FFT
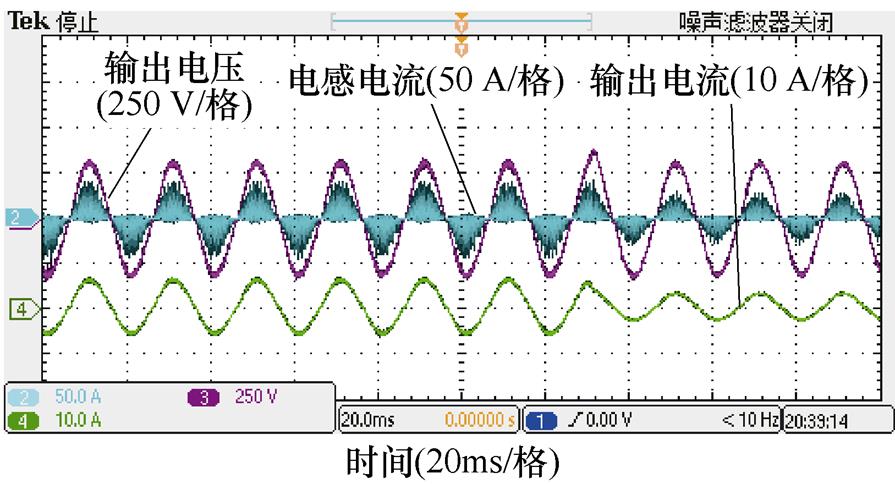
（c）满载切半载
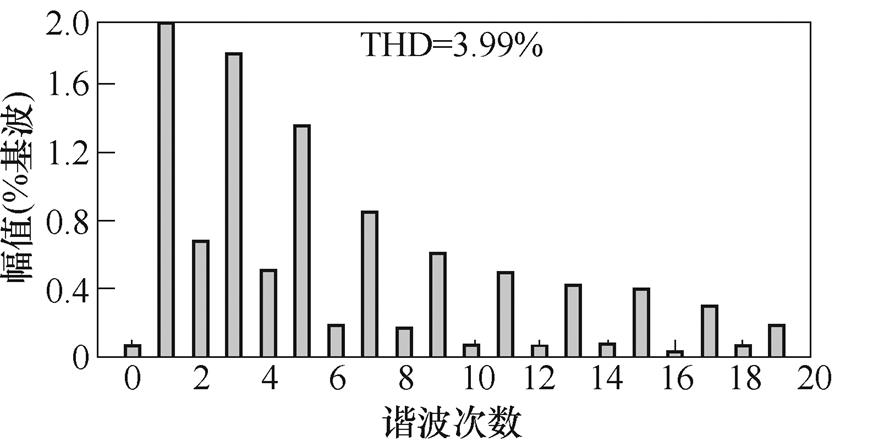
（d）切半载后输出FFT
图14 负载扰动实验结果
Fig.14 Load disturbance experimental results
输入扰动实验结果如图15所示。图15a和图15c分别为与仿真分析相对应的降压输入扰动和升压输入扰动实验波形。由实验结果，THD满足要求，扰动前后的输出波形正弦度良好，且扰动后没有明显波动，进一步验证了该系统具备十分良好的抗输入扰动的能力。
上述可编程电源做的输入扰动是有一定斜率的，故在此加入了如图16所示对输出电压给定阶跃扰动的实验波形。降压时，输入电压为220 V，输出峰值由200 V突变至160 V；升压时，输入电压为220 V，输出峰值由270 V突变至311 V，可以看出，输入阶跃扰动后波形能够很快恢复稳定，扰动过后THD满足要求，从侧面证明了系统是可以抵抗阶跃扰动的。
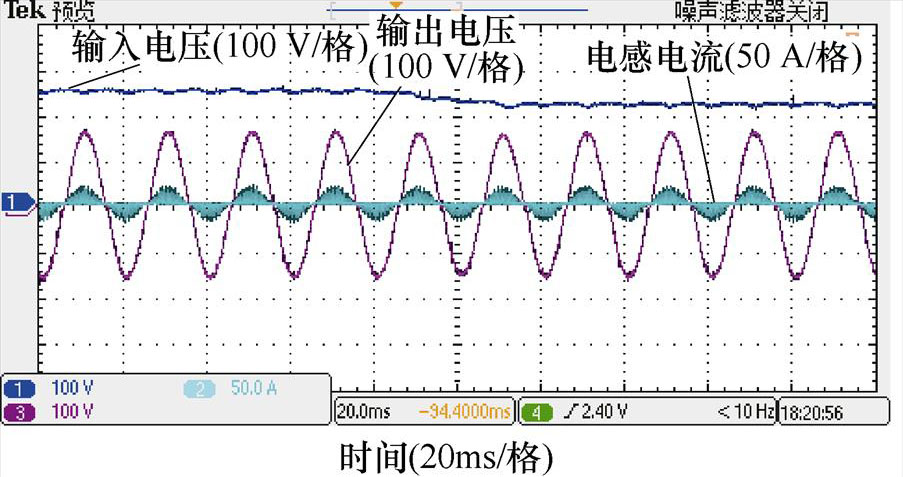
（a）降压输入扰动
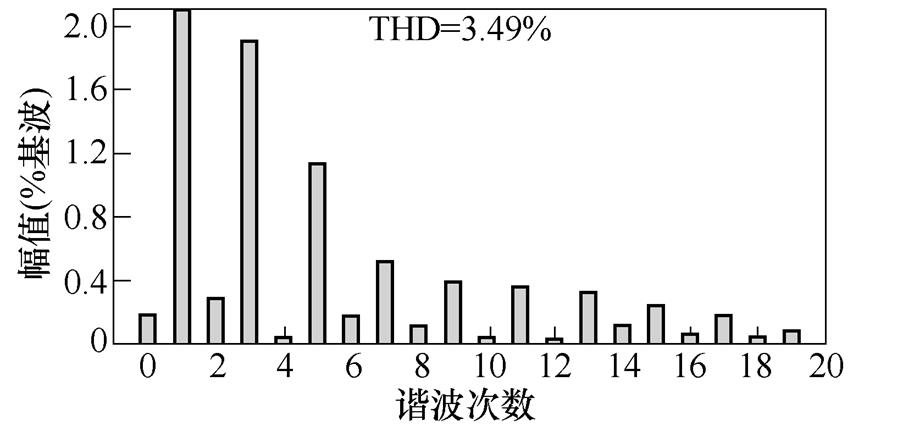
（b）降压输入扰动后输出FFT
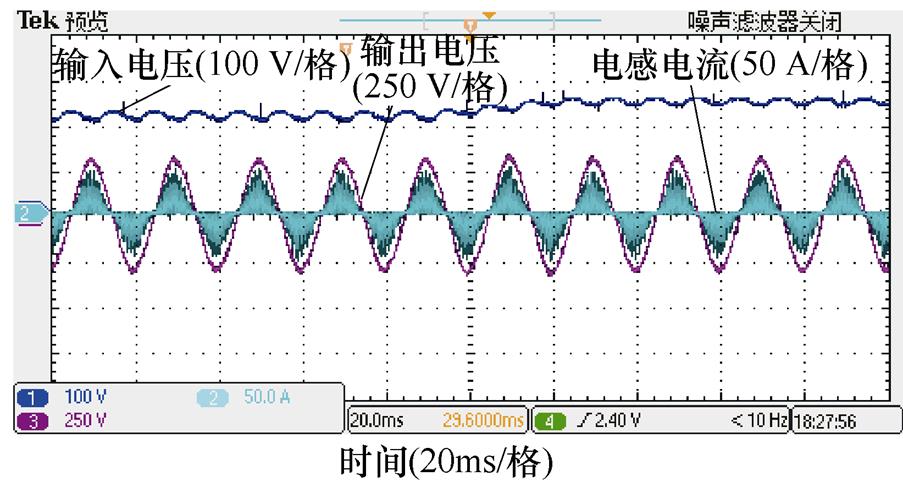
（c）升压输入扰动
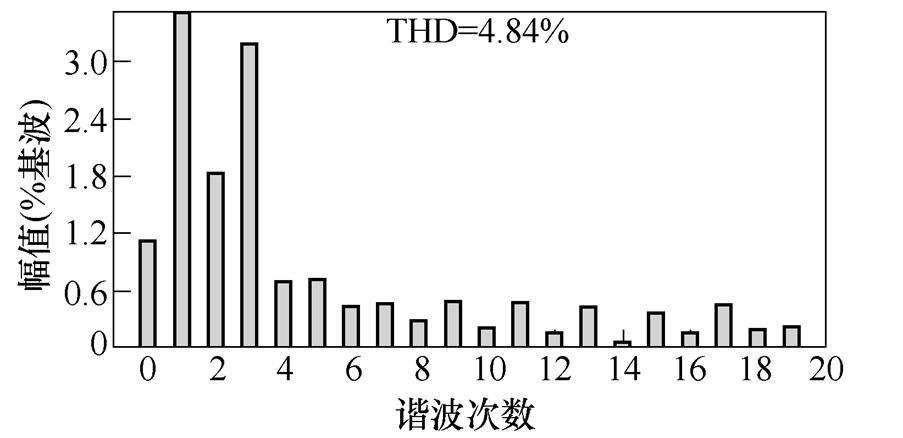
（d）升压输入扰动后输出FFT
图15 输入扰动实验结果
Fig.15 Input disturbance experimental results
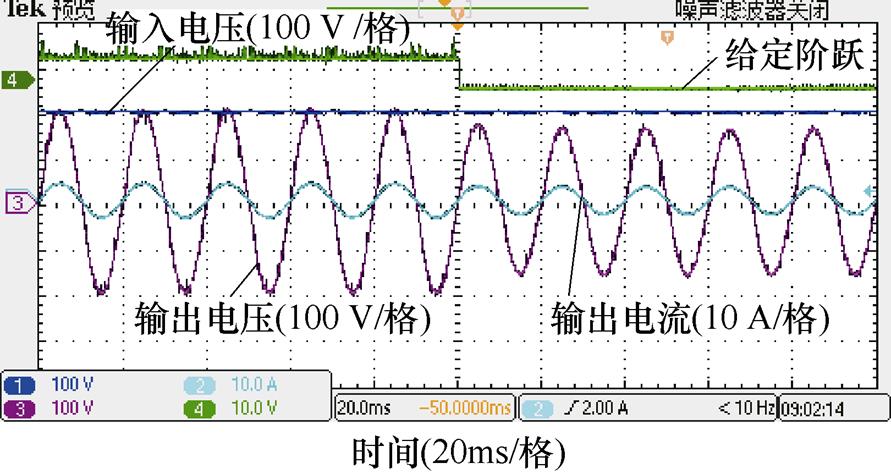
（a）降压给定扰动
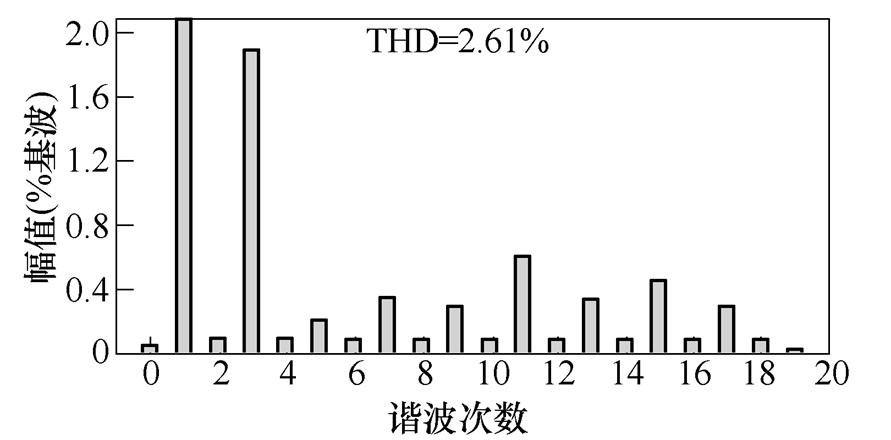
（b）降压给定扰动后输出FFT
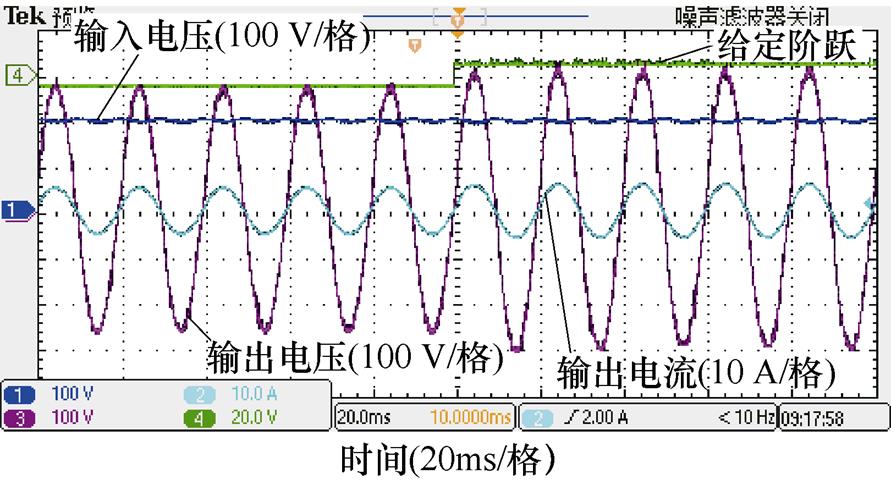
（c）升压给定扰动
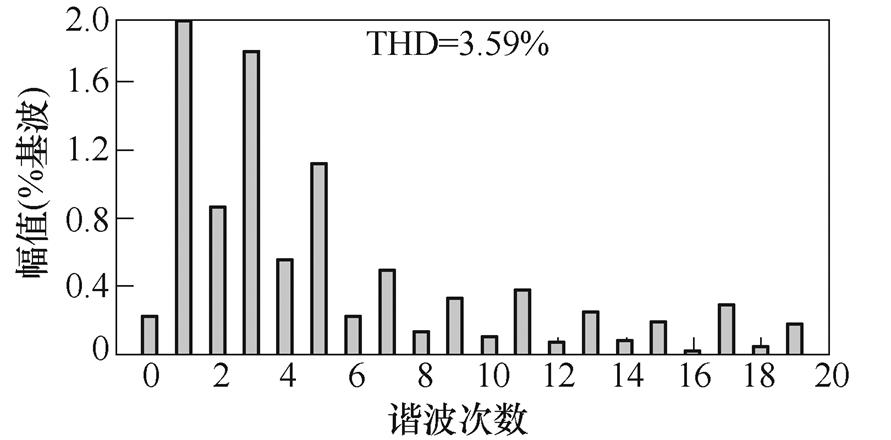
（d）升压给定扰动后输出FFT
图16 输出扰动实验结果
Fig.16 Output given disturbance experimental results
图17列出了降压及升压并网实验结果及THD分析，并网电流和电网电压同频同相，且谐波总含量均在5 %以内，满足相关标准。实验结果表明，该逆变器具备良好的升降压并网能力，具备光伏系统应用条件。
由实验波形的THD分析可以看出，存在一定偶数次谐波，其产生主要可归结为三个方面：①控制中驱动为互补的，故存在一定不对称，难以完全消除偶数次谐波；②检测误差；③实际电路并非理想的，故存在一定的偶次谐波。但在仿真及实验波形的谐波中可以明显看出，占主导部分的仍然是奇数次谐波，偶数次谐波含量低于2 %，是满足相关标准的。故可通过相应闭环控制引入抵抗不平衡方案以及尽可能地提升设备精度，优化电路设计，来对其进行抑制。
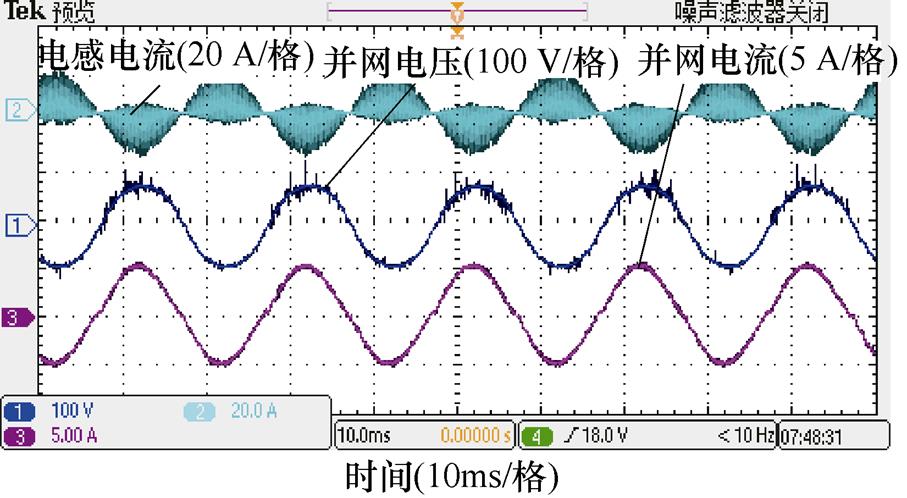
（a）降压并网波形
（b）降压并网电流FFT
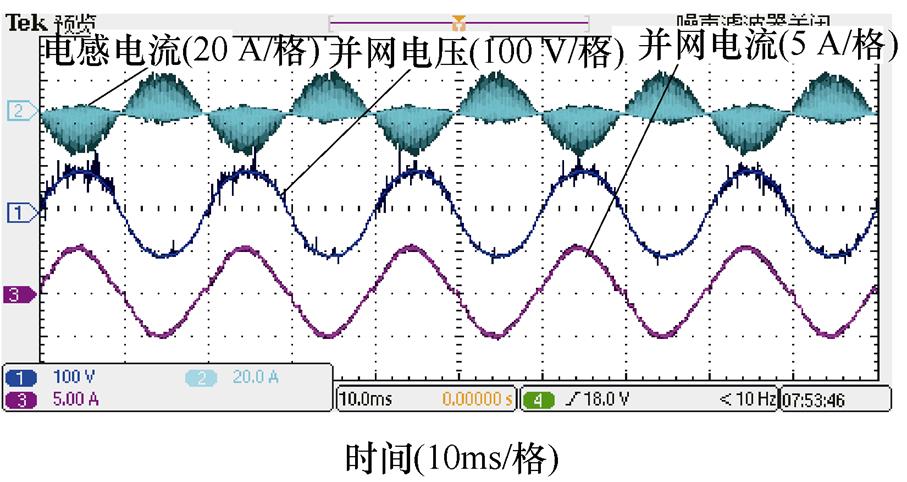
（c）升压并网波形
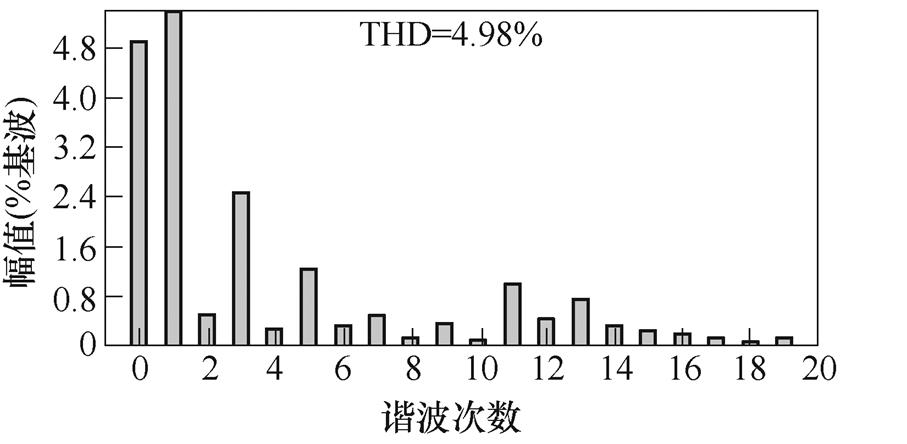
（d）升压并网电流FFT
图17 并网实验结果
Fig.17 Grid connected experimental results
本文给出了一种无电解电容的单级单相Buck- Boost逆变器，该逆变器无电解电容的使用，可以灵活地实现均衡的升降压，整体结构简洁，使用的无源器件和功率器件少，利于降低系统的体积及造价，提升功率密度。
本文先后对该逆变器的工作原理、升降压能力进行了分析，最后通过仿真以及实验验证了理论分析，具体可总结以下几点：
1）本文所提逆变器拓扑整体结构简洁，功率器件和无源器件使用少，仅一个直流电感工作于正负半周进行储能与释能，利用率高。开关管的选型兼项了拓扑工作原理和造价，普通IGBT的反向并联二极管也得到充分利用，器件浪费率及损耗率降低。
2）该逆变器为单相单级非隔离型升降压光伏逆变器，无需使用电解电容，相比于多级式和隔离型逆变器，其结构简单，有利于系统效率提升，并可通过改变调制比大小灵活控制其实现均衡升降压逆变，可很好地适应直流输入宽范围变化。
3）前置H桥结构下，利用简洁的控制方式即可在采用低感值直流电感情况下使得逆变输出正弦度良好，有利于控制体积和成本，相对提升功率密度，而巧妙的工频开断、高频工作方式使得控制中无需高频死区对输出造成畸变影响，系统具备十分良好的抗扰能力。
参考文献
[1] 王立乔, 李占一, 刘乐, 等. 一种无电解电容单级Buck-Boost逆变器[J]. 电工技术学报, 2019, 34(20): 4295-4305.
Wang Liqiao, Li Zhanyi, Liu Le, et al. A single-stage Buck-Boost inverter with non-electrolytic capacitor[J]. Transactions of China Electrotechnical Society, 2019, 34(20): 4295-4305.
[2] Nath U K, Sen Ruma. A comparative review on renewable energy application, difficulties and future prospect[C]//2021 Innovations in Energy Management and Renewable Resources(52042), Kolkata, India, 2021: 1-5.
[3] 喜琍. 太阳能发展前景与应用[J]. 科技风, 2021(21): 7-8.
Xi Li. Development prospect and application of solar energy[J]. Technology Wind, 2021(21): 7-8.
[4] 舟丹. 我国光伏产业发展历程[J]. 中外能源, 2021, 26(11): 33.
Zhou Dan. Development course of photovoltaic industry in China[J]. Sino-Global Energy, 2021, 26(11): 33.
[5] 李程. 太阳能光伏发电并网技术的应用[J]. 产业科技创新, 2019, 1(27): 63-64.
Li Cheng. Application of grid connection technology of solar photovoltaic power generation[J]. Industrial Scientific and Technological Innovation, 2019, 1(27): 63-64.
[6] 王立乔, 韩胥静, 李占一, 等. 一种新型飞跨电容型Zeta多电平逆变器[J]. 电工技术学报, 2022, 37(1): 254-265.
Wang Liqiao, Han Xujing, Li Zhanyi, et al. A novel flying-capacitor zeta multi-level inverter[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(1): 254-265.
[7] 陈思哲, 徐梦然, 范元亮, 等. 一种基于开关电容的九电平逆变器[J]. 电工技术学报, 2022, 37(4): 931-941.
Chen Sizhe, Xu Mengran, Fan Yuanliang, et al. A nine-level inverter based on switched-capacitor[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 931-941.
[8] 王要强, 李娜, 赵朝阳, 等. 一种新型多电平逆变器及其模块化分析[J]. 电工技术学报, 2022, 37(18): 4676-4687.
Wang Yaoqiang, Li Na, Zhao Zhaoyang, et al. A new type of multilevel inverter and its modular analysis[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4676-4687.
[9] 江加辉, 陈道炼, 佘敏. 准单级隔离Buck-Boost型多输入逆变器[J]. 电工技术学报, 2018, 33(18): 4323-4334.
Jiang Jiahui, Chen Daolian, She Min. Quasi single- stage isolated Buck-Boost mode multi-input inver- ter[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 4323-4334.
[10] Saeidabadi S, Ashraf Gandomi A, Sabahi M. Two new transformer-based isolated seven-level inverters[C]// 2017 8th Power Electronics, Drive Systems & Tech- nologies Conference (PEDSTC), Mashhad, Iran, 2017: 195-200.
[11] Fang Xupeng, Wang Song, Wang Xiaoli. New high- frequency isolated quasi-Z-source inverter[C]//2020 Chinese Automation Congress (CAC), Shanghai, China, 2021: 85-89.
[12] 代云中, 张荣飞, 谢开汶, 等. 非隔离型级联双降压并网逆变器及其漏电流抑制[J]. 高电压技术, 2020, 46(7): 2434-2445.
Dai Yunzhong, Zhang Rongfei, Xie Kaiwen, et al. Analysis of non isolated cascaded dual-buck grid con- nected inverter and its leakage current suppression[J]. High Voltage Engineering, 2020, 46(7): 2434-2445.
[13] Zhu Yingfeng, Guo Shengnan, Chen Lingying, et al. A novel hybrid cascaded multilevel inverter[C]//2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 2018: 1-5.
[14] Singh G, Garg V K. THD analysis of cascaded H-bridge multi-level inverter[C]//2017 4th Inter- national Conference on Signal Processing, Computing and Control (ISPCC), Solan, India, 2018: 229-234.
[15] Cuk S, Middlebrook R D. Advances in switched-mode power conversion part Ⅰ[J]. IEEE Transactions on Industrial Electronics, 1983, 30(1): 10-19.
[16] 洪峰. 双降压式半桥逆变器及输出并联型组合变换器研究[D]. 南京: 南京航空航天大学, 2008.
[17] Correa A M P, Lazzarin T B, Barbi I. New topology for a single-phase Buck-Boost inverter[C]//2018 IEEE Applied Power Electronics Conference and Expo- sition (APEC), San Antonio, TX, 2018: 2550-2554.
[18] Nattymol Y J, Shanavas T N. Power quality analysis of single-phase transformer-less Buck-Boost inverter for compressor load[C]//2019 IEEE International Conference on Intelligent Techniques in Control, Optimization and Signal Processing (INCOS), Tamilnadu, India, 2020: 1-4.
[19] 任佳丽. 单相非隔离型Buck-Boost逆变器[D]. 秦皇岛: 燕山大学, 2015.
[20] Sreekanth T, Lakshminarasamma N, Mishra M K. Coupled inductor-based single-stage high gain DC- AC Buck-Boost inverter[C]//in IET Power Electronics, 2016: 1590-1599.
[21] 高申昊, 陈超波. 单级双电感Buck-Boost逆变器的研究[J]. 电子设计工程, 2017, 25(12): 109-114.
Gao Shenhao, Chen Chaobo. Research on single-stage double inductor Buck-Boost inverter[J]. Electronic Design Engineering, 2017, 25(12): 109-114.
[22] Melo F C, Garcia L S, Buiatti G M, et al. Novel transformeless single-stage 4-switches Buck-Boost inverter[C]//2013 Twenty-Eighth Annual IEEE AppliedPower Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 2013: 2811-2816.
[23] 胡茂, 秦岭, 陈瑞祥, 等. 基于单极倍频SPWM调制的单相Buck-Boost集成式升压逆变器研究[J]. 中国电机工程学报, 2017, 37(13): 3863-3873.
Hu Mao, Qin Ling, Chen Ruixiang, et al. Research on single-phase Buck-Boost integrated step-up inverter with monoploe frequency doubling SPWM modu- lation[J]. Proceedings of the CSEE, 2017, 37(13): 3863-3873.
[24] Najiya Nesrin A K, Sukanya M, Joseph K D. Switched dual input Buck-Boost inverter for continuous power operation with single stage con- version[C]//2020 International Conference on Power Electronics and Renewable Energy Applications (PEREA), Kannur, India, 2021: 1-6.
Abstract The existing single-stage, single-phase non-isolated inverters need to solve the following problems: buck and boost voltage capability, electrolytic capacitors, single-supply inputs, the number of topology devices, device multiplexing rate, and the overall simplicity of topology and control, while most of the existing solutions can not take into account all problems.
This paper proposes a simple and compact inverter. Its topology can meet the requirements of the Buck-Boost voltage without electrolytic capacitors. It only needs a low-value inductor as an energy storage component, and fewer power and passive devices. The proposed inverter is lightweight, has a high device reuse rate, and has simple working and control modes, suitable for small and medium-power photovoltaic power generation systems. The circuit consists of 6 IGBT switches (S1～S6, S3, and S4 with inverse resistance IGBT, the others are bidirectional IGBTs), 1 DC inductor, 1 AC filter capacitor, 1 AC filter inductor, and a single DC input power supply (photovoltaic panel). The output side is connected to the load or merged into the grid. After consulting a large number of domestic and foreign literature, it is found that the inverter proposed in this paper has superiority in structure.
This paper provides a theoretical analysis of the circuit. The circuit has six operating modes when the energy storage inductor Ldc current is interrupted. The operating modes Ⅰ, Ⅱ, and Ⅴ are positive half-cycles, and Ⅲ, Ⅳ, and Ⅵ are negative half-cycles. Due to the special structure of the H-bridge front on the input power side, unipolar SPWM modulation is used, in which S3, S4, S5, and S6 power frequencies work, and S1 and S2 semi-high frequencies work. In this paper, the inverter has a good Buck-Boost capability, and the voltage gain is related to the duty cycle, DC inductance, and switching frequency. The maximum voltage stress of switches S1, S2, S5, and S6 is Uin+Uo, the maximum voltage stress of switches S3 and S4 is Uo, and the maximum current stress of all switches is Im. The parameters of the energy storage inductor and the filter in the circuit are designed separately, the energy storage inductor Ldc=0.25 mH, the filter capacitor is 2.2 mF, and the filter inductor is 3 mH.
According to the theoretical, simulation, and experimental results, it can be concluded that the overall structure of the inverter proposed in this paper is simple, the power devices and passive devices are used less, and only one DC inductor works in positive and negative half weeks for energy storage and release, and the utilization rate is high. In the overall principle and cost of the switch selection, full use of the IGBT reverse diode reduces the device waste rate and loss rate. Compared with multi-stage and isolated inverters, the proposed inverter can improve efficiency, and is flexibly controlled by changing the modulation ratio to achieve a balanced Buck-Boost inverter, which can be well adapted to the wide range of DC input changes. Under the front-facing H-bridge structure, a simple control mode can make the inverter output sinusoidal degree good for low DC inductance, control volume, and cost while improving the power density. Clever power frequency breaking, high-frequency working mode makes the control not need a high-frequency dead zone to distort the output, which has excellent anti-disturbance ability.
keywords：Power electronics, non-electrolytic capacitor, single-stage single-phase non-isolated, Buck- Boost, photovoltaic inverter
中图分类号：TM464
DOI: 10.19595/j.cnki.1000-6753.tces.221883
国家自然科学基金（51677162）和河北省自然科学基金（E2017203235）资助项目。
收稿日期 2022-10-07
改稿日期 2022-11-23
王立乔 男，1974年生，博士，教授，研究方向高频功率变换、脉冲调制理论、大功率变流技术、可再生能源发电及分布式发电系统。E-mail: brent@ysu.edu.cn（通信作者）
陈建医 男，1995年生，硕士，研究方向为中小容量电流型并网逆变器的轻量化。E-mail: 2982288707@qq.com
（编辑 陈 诚）