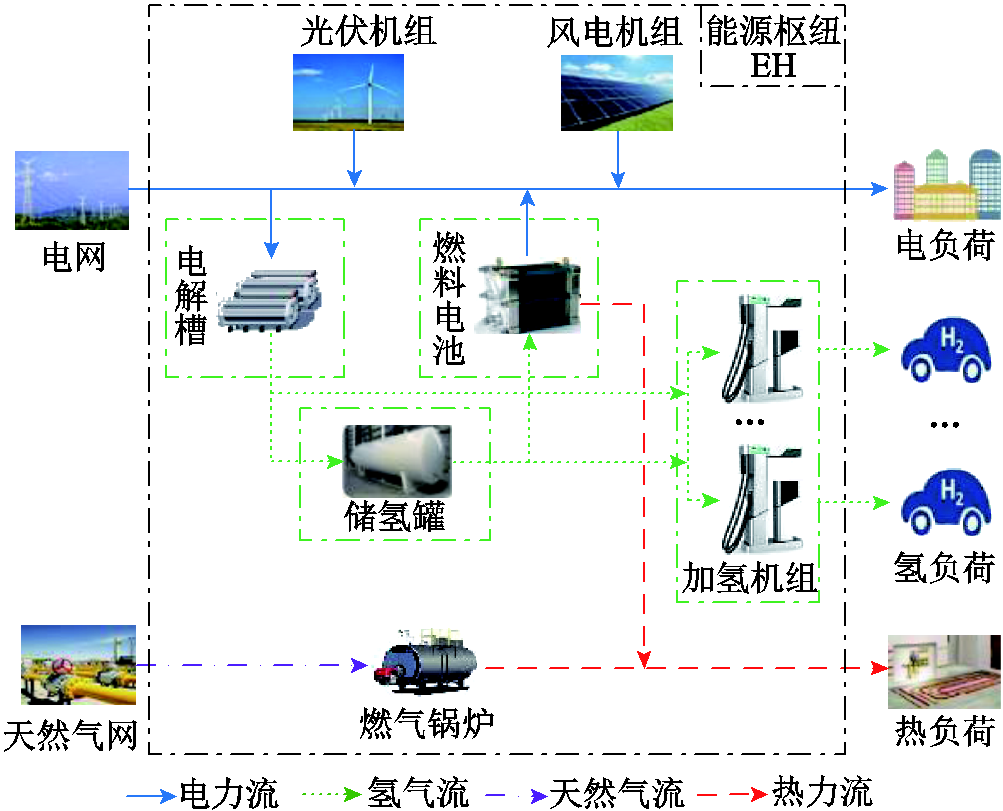
图1 EH-RIESs典型结构
Fig.1 The typical structural diagram of EH-RIESs
摘要 针对现有电氢区域综合能源系统(EH-RIESs)可靠性评估方法未能充分考虑氢能设备故障机理及其多状态运行特性、缺乏供氢可靠性水平量化评估指标及方法等问题,该文提出基于氢能设备多状态模型的EH-RIESs可靠性评估方法。首先,剖析了氢能设备运行特性与故障机理,建立了考虑降额运行状态的碱性电解槽多状态可靠性评估模型、计及热电联产模式的燃料电池多状态可靠性评估模型及加氢机组的多状态可靠性评估模型,为准确模拟EH-RIESs运行状态奠定了坚实基础;其次,以弃风光成本和异质能源负荷削减成本之和最小为目标,建立考虑电氢异质能量系统耦合的最优负荷削减模型;然后,从供氢可靠性水平、设备对氢负荷缺供能量的贡献程度及系统经济损失等方面,构建了供氢可靠性评估指标体系;最后,结合氢能设备多状态模型和马尔科夫链蒙特卡洛法,建立了EH-RIESs可靠性评估方法,实现了对EH-RIESs内氢能等异质能源供给可靠性水平的准确量化。采用两个不同规模的EH-RIESs进行仿真分析,验证了该文所提模型及评估方法的有效性和适应性。
关键词:电氢区域综合能源系统 电解槽 燃料电池 马尔科夫链蒙特卡洛 供氢可靠性
“碳达峰、碳中和”战略目标下[1],电力能源系统实现绿色低碳转型迫在眉睫。电氢区域综合能源系统(Electricity-Hydrogen Regional Integrated Energy Systems, EH-RIESs)能够充分发挥氢能系统零碳、灵活、高效运行等优势,被认为是实现电力能源系统绿色低碳转型的关键路径[2-4]。
EH-RIESs可靠性评估方法是EH-RIESs规划理论的关键组成部分,可为EH-RIESs规划、建设等提供科学的理论支撑与决策依据,有效指导氢能有序、健康发展。因此,EH-RIESs可靠性评估方法具有重要的理论研究价值和工程应用前景。
氢能设备故障机理复杂,且电、氢、热等异质能源系统之间存在强耦合关系,如何构建氢能设备可靠性模型,准确量化氢能等异质能源的供给可靠性成为EH-RIESs可靠性评估方法亟待解决的关键难题,然而相关研究较为匮乏。接下来,从氢能设备可靠性模型和EH-RIESs可靠性评估两个关键方面进行研究现状述评。
1)氢能设备可靠性模型
氢能系统包含制氢、储氢、用氢、加氢等环节,涉及电解槽、储氢罐、燃料电池、加氢机等关键设备。文献[5]建立了电解槽和储氢罐的正常-停运两状态模型。然而电解槽的供氢能力与辅助元件的工作状态密切相关[6],两状态模型显然无法准确刻画电解槽的实际运行工况。文献[7-8]分析了燃料电池发电系统内各辅助元件的失效影响机理,建立了发电模式下的燃料电池多状态模型。燃料电池发电效率仅为30%~50%左右,热电联产模式能够大幅提高能源利用效率[9-10],但目前尚缺少热电联产模式下的燃料电池可靠性模型。针对氢气分配的最后环节,文献[11]对加氢站内的维护和故障统计数据进行了分析,但并未建立加氢机组的可靠性模型。
2)EH-RIESs可靠性评估
文献[12]针对光伏-热-燃料电池集成系统内各组件的故障严重性、故障发生概率和可检测性等,制定了评价标准以评估各组件的风险等级,但无法计算负荷供电可靠性等指标,难以反映系统的可靠供能水平。文献[13]基于序贯蒙特卡洛模拟建立了含氢能孤岛交直流微电网的可靠性评估方法,但仅采用常规供电可靠性评估指标论证了氢能系统对提高微电网可靠性水平的积极作用。可见,目前尚缺乏有效的EH-RIESs可靠性评估方法及供氢可靠性评估指标体系,无法量化氢负荷供给可靠性水平,难以确定影响供氢可靠性的关键因素。
针对上述问题,本文提出了基于氢能设备多状态模型的EH-RIESs可靠性评估方法,主要贡献如下:
(1)揭示换热器管程故障对制氢效率的影响机理,建立了考虑降额运行状态的碱性电解槽多状态模型。基于燃料电池组件故障与热电转换效率关系分析,建立了考虑热电联产模式的燃料电池多状态模型。建立加氢机组的多状态模型,为准确评估EH-RIESs内氢能等异质能源供给可靠性水平奠定理论基础。
(2)提出考虑电氢异质能量系统耦合的最优负荷削减模型。从氢负荷缺供能量、设备供氢贡献度等方面建立了供氢可靠性评估指标体系。建立基于马尔科夫链蒙特卡洛(Markov Chain Monte Carlo, MCMC)模拟的EH-RIESs可靠性评估方法,有效地量化EH-RIESs内异质能源的供给可靠性水平,挖掘影响供氢可靠性的关键因素,为系统规划建设等提供科学合理的决策依据。
EH-RIESs典型结构如图1所示,通过能源枢纽(Energy Hub, EH)中能源的生产、转换及存储设备将电、氢、气、热等异质能量系统紧密耦合。

图1 EH-RIESs典型结构
Fig.1 The typical structural diagram of EH-RIESs
外部电网和新能源场站提供电能以保障电力负荷和电解槽用电需求的可靠供应。在风光出力较大或用电低谷时期,电解槽可利用富余电力制取氢气,满足燃料电池汽车等的用氢需求,或由储氢罐进行存储。在风光出力较低或用电高峰时期,可由储氢罐和燃料电池分别供给氢负荷和用电负荷。可见,氢能系统能够有效地提高综合能源系统的运行灵活性,促进新能源消纳,避免电、氢负荷削减,可靠供能水平大幅提升。
燃气锅炉将天然气转换为热能,是主要的热源。处于热电联产模式下的燃料电池可作为辅助热源,满足用热需求。当天然气管网或燃气锅炉发生故障时,燃料电池能够将储氢设备的氢气持续转换为电能和热能,有效弥补热量缺额,提高系统供热可靠性水平。
本节深入分析了氢能设备的运行特性与故障机理,建立考虑降额运行状态的碱性电解槽多状态可靠性评估模型、考虑热电联产模式的质子交换膜燃料电池多状态可靠性评估模型,以及加氢机组的多状态可靠性评估模型,并给出了储氢罐的两状态可靠性评估模型。
目前,碱性电解槽技术最为成熟,得到了广泛应用[14],其设备结构如图2所示。水在电解池中被电解;电解产生的氢气和氧气伴随着部分碱液分别进入氢气和氧气分离装置;离开分离器后,剩下的碱液经换热器冷却,并通过循环水泵被送回电解池。该过程中消耗的碱液可通过分离器得到及时补充[15-16]。
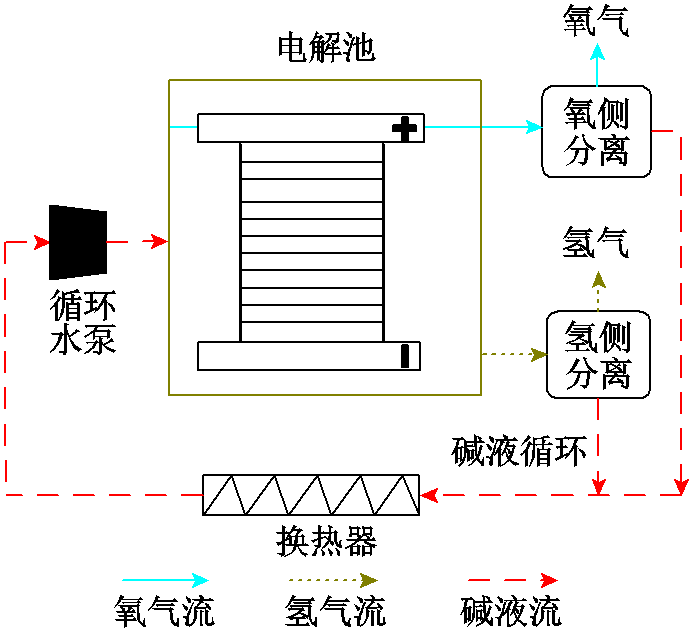
图2 碱性电解槽结构
Fig.2 The structural diagram of alkaline electrolyzer
根据经验系数拟合方法[17],可得到单个电解池t时刻运行电压Uel,t与电流Iel,t之间的函数关系,有
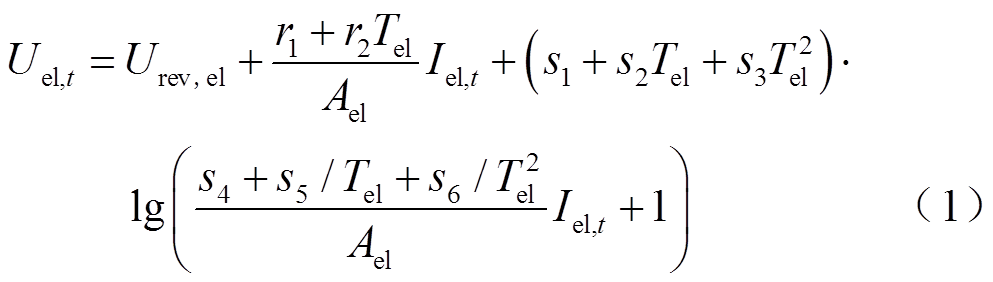
式中,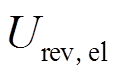 为电解池可逆电压;r1、r2分别为碱液的欧姆电阻和热阻参数;Tel为电解池温度;Ael为电解池的有效反应面积;s1~s6为拟合得到的电极过电压系数。
为电解池可逆电压;r1、r2分别为碱液的欧姆电阻和热阻参数;Tel为电解池温度;Ael为电解池的有效反应面积;s1~s6为拟合得到的电极过电压系数。
一个碱性电解槽由数个电解池串并联构成。基于串并联电压电流公式和法拉第定律可计算其t时刻的耗电功率PEL,t(kW)和产氢量mEL,t(N·m3)分别[18]为
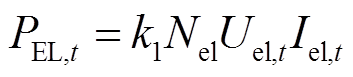 (2)
(2)
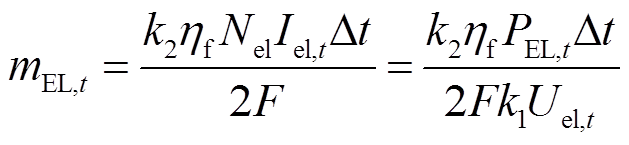 (3)
(3)
式中,k1、k2为单位转换系数;Nel为电解池数量;ηf为法拉第效率;Dt为单位时间间隔;F为法拉第常数,代表每摩尔电子所携带的电荷。
由图2可知,当所有元件均未发生故障时,电解槽处于正常运行状态。除电解池发生故障会导致设备停运外,气体分离装置发生故障时将导致气体纯度、温度等不满足安全运行需求[6],循环水泵发生故障时将导致电解槽无法获取碱液制取氢气[12]。因此,当上述元件(记为组件1)发生故障时,电解槽设备将进入故障停运状态。当换热器管程(记为组件2)发生故障,即管程破裂时,碱液由管程泄漏至壳程并与冷却水混合,导致电解槽中的碱液浓度降低[6]。当碱液浓度小于等于常规配置浓度时,其浓度与电导率呈正相关[19],因此碱液的电导率将会降低,即欧姆电阻增加。由式(1)可知,电解槽电压将随之升高。由式(2)和式(3)可知,若此时产氢量mEL,t不变,电解槽耗电功率PEL,t将会增加,即制氢效率降低,电解槽进入降额运行状态。
以组件2发生故障后,碱液浓度降低导致其电导率降低50%为例,根据式(1)~式(3)模拟得到碱性电解槽在正常运行和降额运行状态下的制氢曲线,如图3所示。可见,在降额运行状态下,电解槽的产氢能力及耗电特性与正常运行状态截然不同。
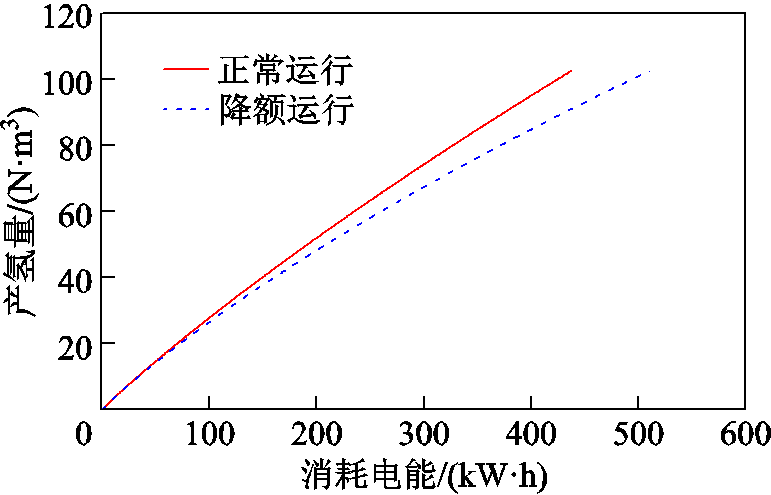
图3 不同运行状态下碱性电解槽制氢曲线
Fig.3 Hydrogen production curves of alkaline electrolyzer under different operating states
本文假设在抽样时间间隔Dt内仅有一个组件的状态发生改变,并根据碱性电解槽的故障机理分析,建立碱性电解槽的多状态Markov模型,如图4所示。图中,λel,i、μel,i均为碱性电解槽多状态间的转移率,i=1, 2;“1U、2D”分别表示组件1处于工作状态、组件2处于故障状态。
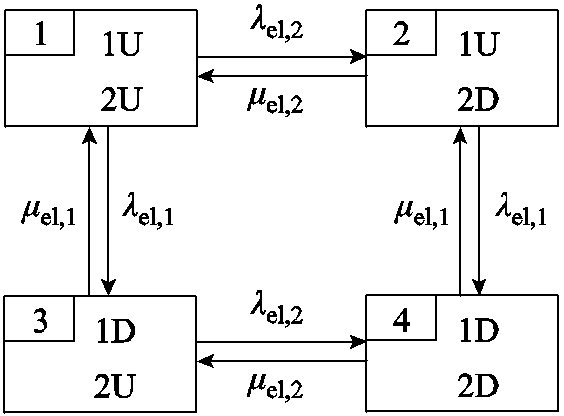
图4 碱性电解槽的多状态Markov模型
Fig.4 Multi-state Markov model of alkaline electrolyzer
根据图4可划分碱性电解槽的运行状态,见表1。定义碱性电解槽t时刻的运行状态变量为sEL,t,sEL,t=1,2,3,4;fSEL,t(PEL,t)表示碱性电解槽处于状态sEL,t下产氢量mEL,t与耗电功率PEL,t之间的函数关系,可根据式(1)~式(3)得到。
表1 碱性电解槽的运行状态
Tab.1 Operation status of alkaline electrolyzer

运行状态组件编号运行模型 12 正常运行(1)UUmEL,t=f1(PEL,t) 降额运行(2)UDmEL,t=f2(PEL,t) 故障停运(3,4)D—mEL,t= f3(PEL,t)= f4(PEL,t)=0
根据图4建立碱性电解槽的状态转移概率矩阵P,如式(4)所示。矩阵中各元素表示各状态间的转移概率。假设t时刻碱性电解槽处于状态k(即sEL,t=k,k∈{1, 2, 3, 4})。基于MCMC[20]产生随机数x∈[0,1],根据式(5)即可判断碱性电解槽在t+1时刻的运行状态sEL,t+1。
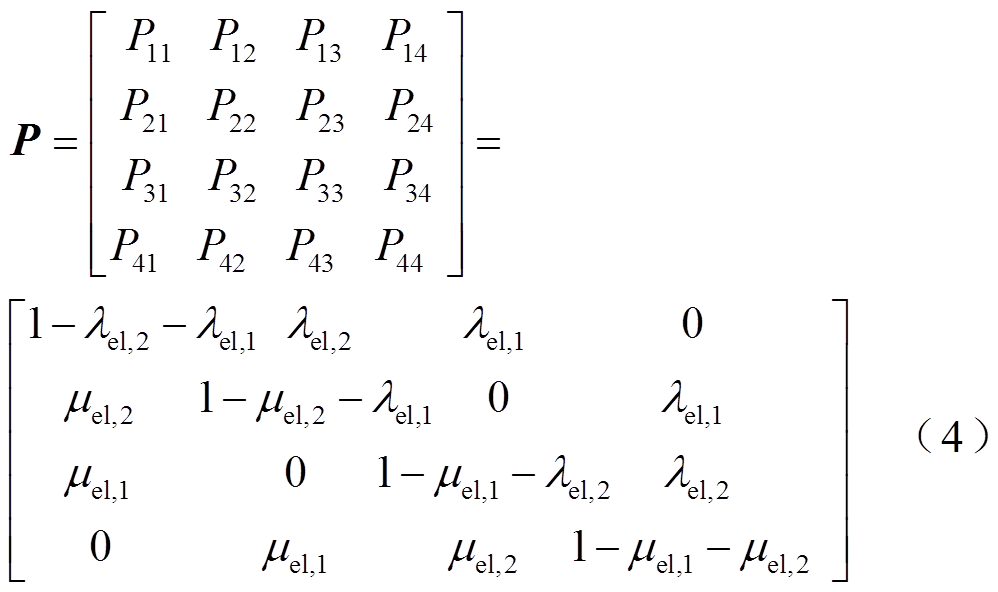
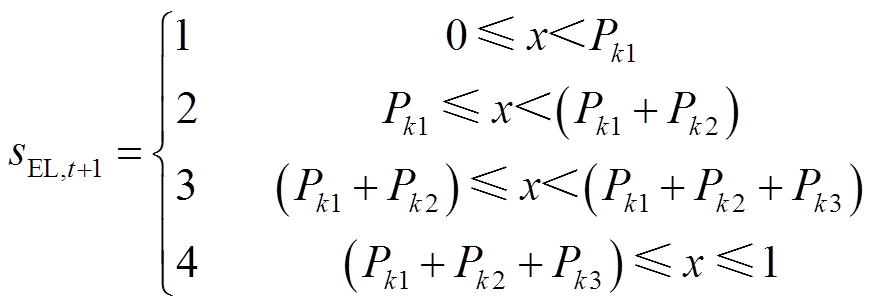 (5)
(5)
通过重复随机抽样,即可获得模拟周期内碱性电解槽各时刻的状态。其余设备的状态模拟过程与碱性电解槽类似,下文不再赘述。
质子交换膜燃料电池具有工作温度低、灵活调节能力强等优点[14],发展前景良好,其设备结构如图5所示[8]。在阳极和阴极处分别供应氢气和氧气,电解质将电离子从阳极输送到阴极产生电能。热电联产模式下,通过冷却水循环系统排出热量,经换热器送至热网,实现能量的有效利用[10]。
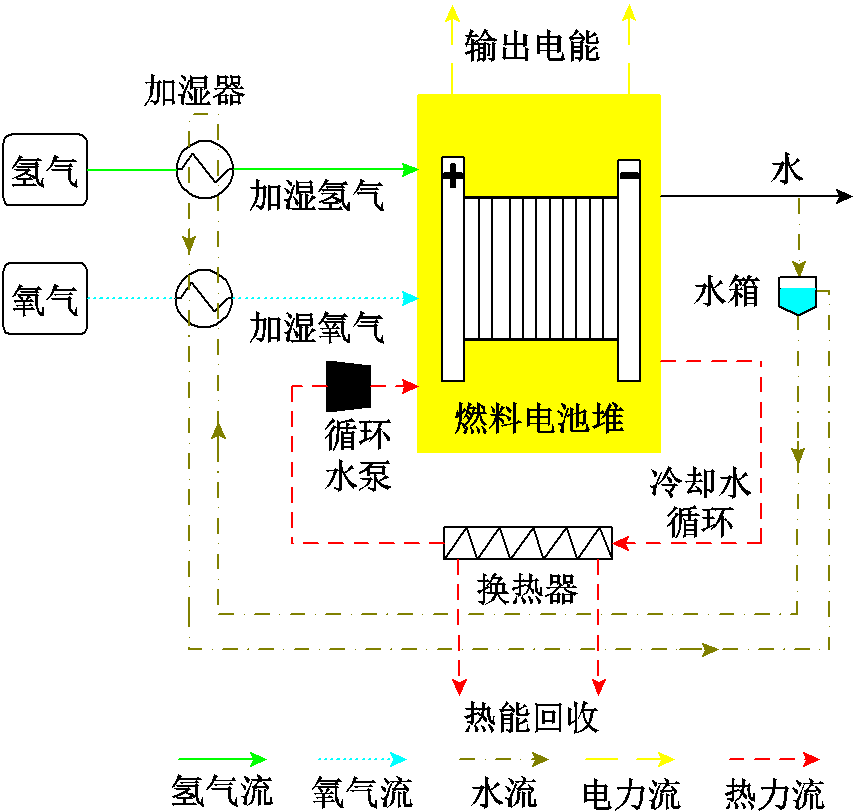
图5 质子交换膜燃料电池设备结构
Fig.5 The structural diagram of proton exchange membrane fuel cell
在实际应用中,由于活化极化、欧姆极化和浓度差极化等过程存在电压损耗,质子交换膜燃料电池输出电压无法达到理想值。考虑上述电压损耗,可得到单个电堆t时刻运行电压Ufc,t与电流Ifc,t的函数关系[8]为
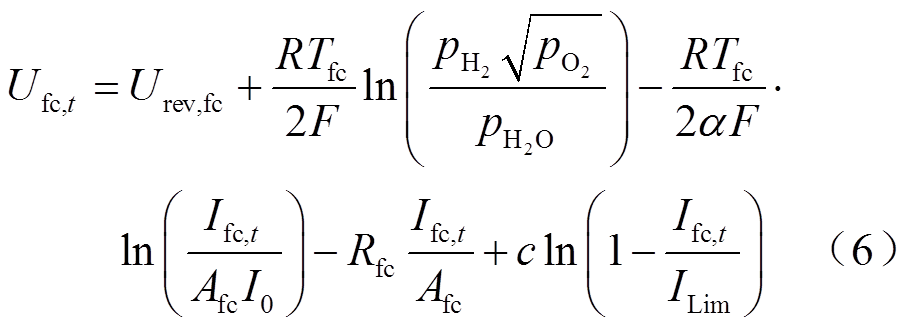
式中,Urev,fc为电堆可逆电压;R为理想气体常数;Tfc为电堆运行温度;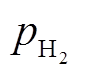 、
、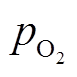 和
和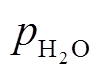 分别为氢气分压、氧气分压和水蒸气分压;α为电极的电荷转移系数;Afc为电堆的有效反应面积;I0为电堆的交换电流;Rfc为质子交换膜的内部电阻;c为浓度差过电压的经验系数;ILim为电堆的电流限值。
分别为氢气分压、氧气分压和水蒸气分压;α为电极的电荷转移系数;Afc为电堆的有效反应面积;I0为电堆的交换电流;Rfc为质子交换膜的内部电阻;c为浓度差过电压的经验系数;ILim为电堆的电流限值。
一个质子交换膜燃料电池由数个电堆串并联构成。基于法拉第定律可计算得到t时刻燃料电池的耗氢量mFC,t(N·m3),如式(7)所示;基于串并联电压电流公式可计算得到t时刻燃料电池的产电功率PFC,t(kW),如式(8)所示[18]。此外,因电压损耗的存在,燃料电池运行过程中有相当部分的能量并未转换为电能,而是以热能形式释放。t时刻燃料电池的产热功率HFC,t(kW)可由式(9)计算得到[21]。
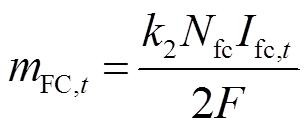 (7)
(7)
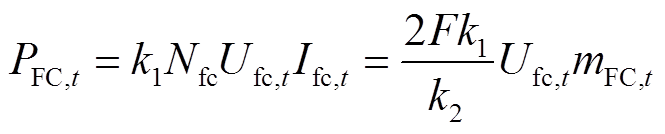 (8)
(8)
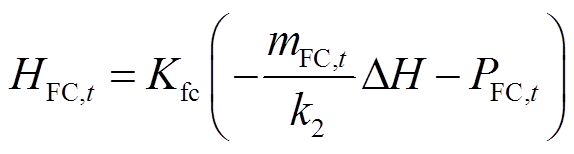 (9)
(9)
式中,Nfc为串并联的电堆数量;Kfc为燃料电池的热回收利用系数;DH为氢气的摩尔热值。
由图5可知,当所有组件均未发生故障时,燃料电池处于正常运行状态,氢气消耗量和产电产热功率可由式(7)~式(9)确定。除燃料电池堆发生故障会导致设备停运外,当氧气供应装置发生故障时,电池堆中氧气分压可能低于安全阈值,造成质子交换膜故障,燃料电池必须紧急停机[8]。因此,当上述元件(记为组件1)发生故障时,燃料电池设备将进入故障停运状态。当冷却循环装置(记为组件2)发生故障导致循环冷却液流量不足时,会造成燃料电池堆工作温度升高。根据式(6)可知,电池活化过电压和欧姆过电压随之增加,燃料电池总输出电压将会降低[8]。由式(8)可知,在耗氢量不变的情况下,燃料电池的输出电功率也将降低,并进入降额运行状态。当加湿装置(记为组件3)发生故障时,质子交换膜因气体加湿不足变得干燥,质子膜的内部欧姆电阻将会增加[8],根据式(6)可知,电池电压随之降低,进而减少输出的电功率,并进入降额运行状态。当氢气供应装置(记为组件4)产生机械磨损或控制部分发生故障时,将导致燃料电池的氢气利用量减少[8],根据式(8)和式(9)可知,其输出电功率和热功率均降低,并进入降额运行状态。在不同的降额运行状态下,燃料电池的产热功率仍可根据式(9)进行计算。
根据燃料电池的故障机理分析,本节建立了热电联产模式下的燃料电池多状态Markov模型,如图6所示。图中,λfc,j、μfc,j均为燃料电池多状态间的转移率j=1, 2, 3, 4;“1U、2D、3U、4D”分别表示组件1、3处于工作状态,组件2、4处于故障状态。
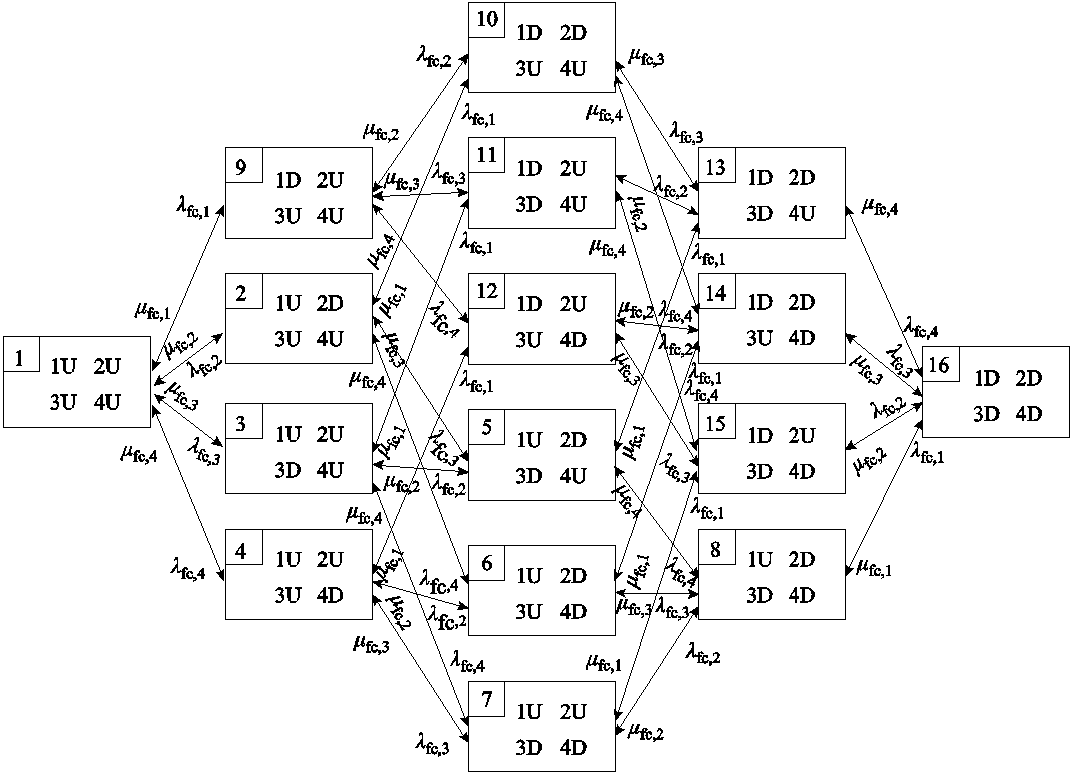
图6 热电联产燃料电池的多状态Markov模型
Fig.6 Multi-state Markov model of fuel cell in cogeneration mode
根据图6及燃料电池热电联产模式下的运行特性,可划分燃料电池的运行状态,见表2。定义燃料电池t时刻的运行状态变量为sFC,t,sFC,t=1,2, ,16;RPSFC,t为燃料电池处于状态sFC,t下产电功率的降额系数[8];g(mFC,t)为正常运行状态下产电功率PFC,t与耗氢量mFC,t的函数关系,即式(8);h(mFC,t, PFC,t)为产热功率HFC,t与耗氢量mFC,t和产电功率PFC,t的函数关系,即式(9)。
,16;RPSFC,t为燃料电池处于状态sFC,t下产电功率的降额系数[8];g(mFC,t)为正常运行状态下产电功率PFC,t与耗氢量mFC,t的函数关系,即式(8);h(mFC,t, PFC,t)为产热功率HFC,t与耗氢量mFC,t和产电功率PFC,t的函数关系,即式(9)。
表2 热电联产燃料电池的运行状态
Tab.2 Operation status of fuel cell in cogeneration mode

运行状态组件编号运行模型 1234 正常运行 (1)UUUUPFC,t=(1-RP1)g(mFC,t)= g(mFC,t);HFC,t= h(mFC,t, PFC,t)
(续)
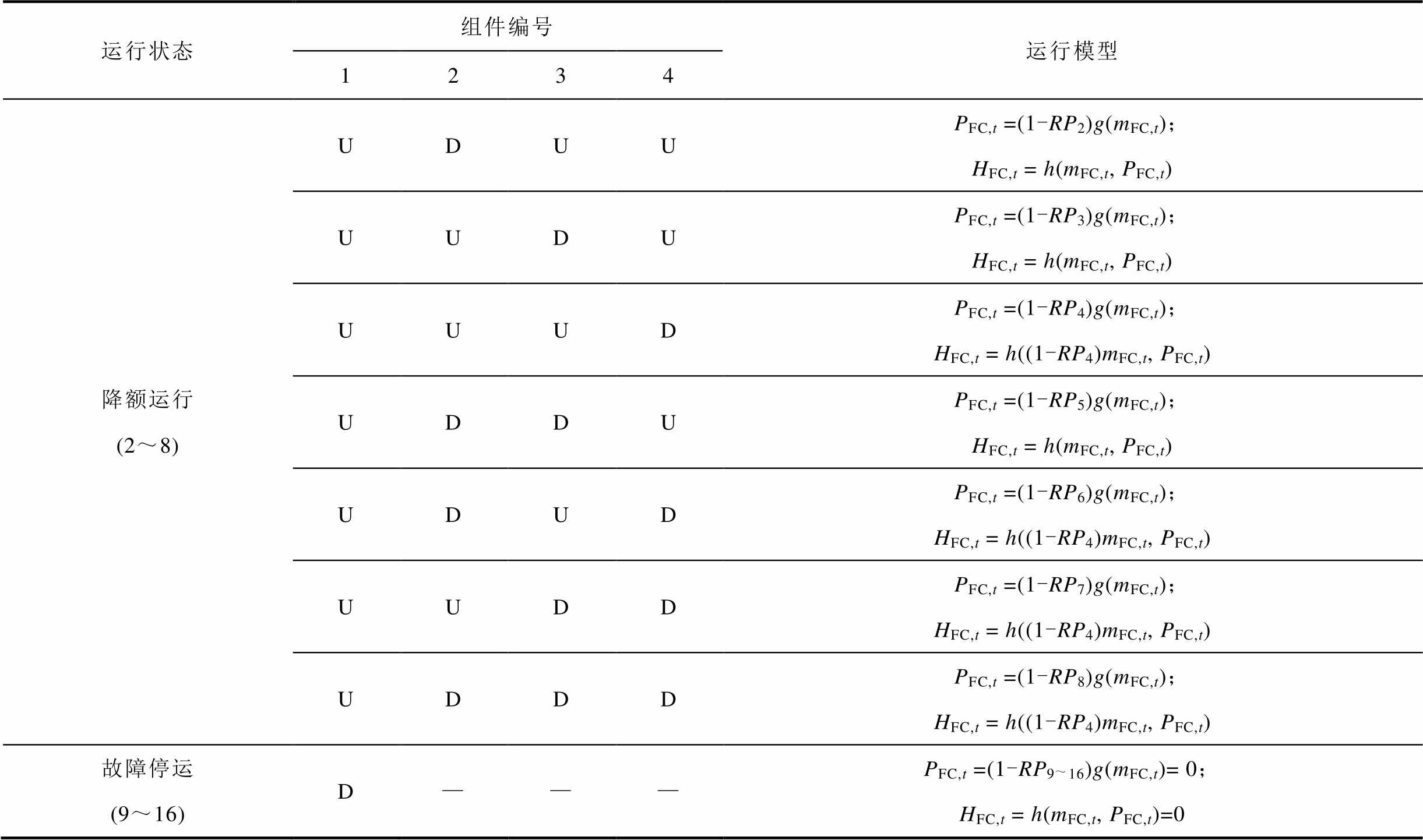
运行状态组件编号运行模型 1234 降额运行 (2~8)UDUUPFC,t=(1-RP2)g(mFC,t);HFC,t= h(mFC,t, PFC,t) UUDUPFC,t=(1-RP3)g(mFC,t);HFC,t= h(mFC,t, PFC,t) UUUDPFC,t=(1-RP4)g(mFC,t);HFC,t= h((1-RP4)mFC,t, PFC,t) UDDUPFC,t=(1-RP5)g(mFC,t);HFC,t= h(mFC,t, PFC,t) UDUDPFC,t=(1-RP6)g(mFC,t);HFC,t= h((1-RP4)mFC,t, PFC,t) UUDDPFC,t=(1-RP7)g(mFC,t);HFC,t= h((1-RP4)mFC,t, PFC,t) UDDDPFC,t=(1-RP8)g(mFC,t);HFC,t= h((1-RP4)mFC,t, PFC,t) 故障停运(9~16)D———PFC,t=(1-RP9~16)g(mFC,t)=0;HFC,t= h(mFC,t, PFC,t)=0
加氢站通常由数台加氢机共同提供加氢服务。为保障加氢过程的安全性,单位时间内每台加氢机的充氢流量有一定的限制[22],本节将其定义为单台加氢机的可用容量cDP。以NDP台加氢机为例,建立加氢机组的多状态Markov模型,如图7a所示。图中,λdp、μdp为加氢机组多状态间的转移率;“1U、2D”分别表示第1台加氢机处于工作状态、第2台加氢机处于故障状态。
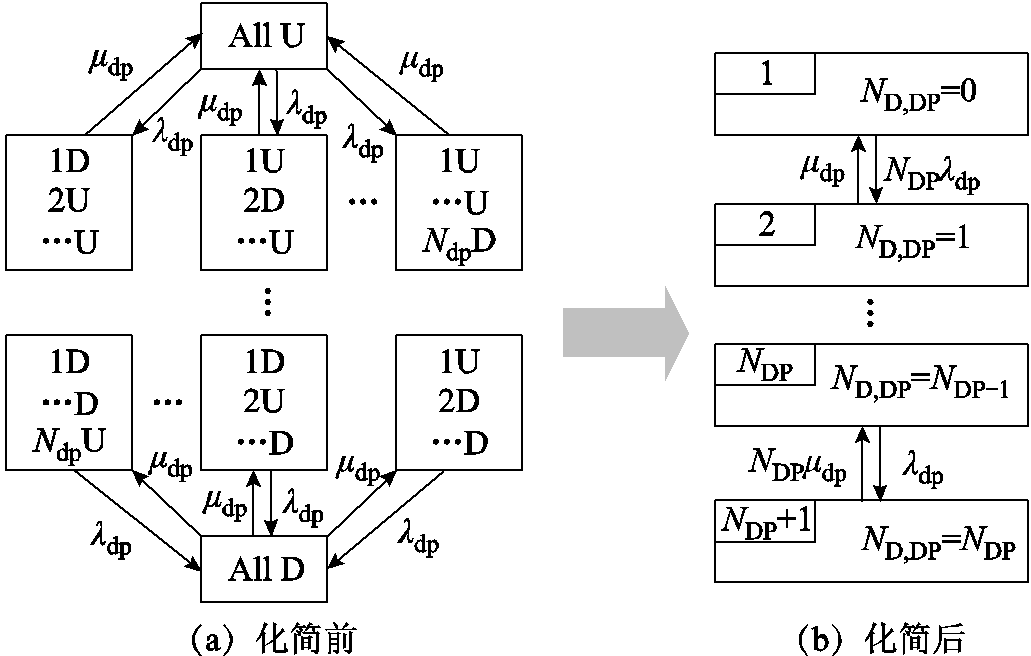
图7 加氢机组的多状态Markov模型
Fig.7 Multi-state Markov model of hydrogen dispenser units
将图7a中加氢机故障数量相同的状态进行合并化简[23],如图7b所示。图中,ND,DP为故障加氢机的数量。根据图7b的划分得到加氢机组的运行状态,见表3。表3中,CDP,t为t时刻加氢机组的总可用容量。
表3 加氢机组的运行状态
Tab.3 Operation status of hydrogen dispenser units

运行状态故障加氢机数量ND,DP/台运行模型 正常运行(1)0CDP,t=cDPNDP 降额运行 (2~NDP)1CDP,t=cDP(NDP-1) NDP-1CDP,t=cDP 故障停运(NDP+1)NDPCDP,t=0
储氢罐主要用于存储和释放氢气。本文采用经典的两状态模型[13]模拟储氢罐的运行状态,如图8所示,λht、μht为储氢罐两状态间的转移率。
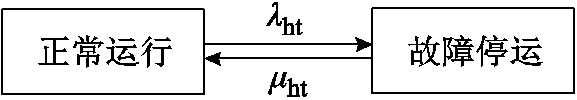
图8 储氢罐的两状态Markov模型
Fig.8 Two-state Markov model of hydrogen storage tank
以弃风弃光惩罚成本和氢能等异质能源负荷削减惩罚成本之和最小为目标,综合考虑异质能量流约束和氢能设备运行约束等,建立考虑电氢异质能量系统耦合的最优负荷削减模型,以模拟故障状态下系统运行状态及氢能等负荷的缺供量。
为保障新能源高效消纳和氢能等负荷的可靠供给,以弃风、弃光惩罚成本、异质能源负荷削减惩罚成本之和最小为目标函数f,有
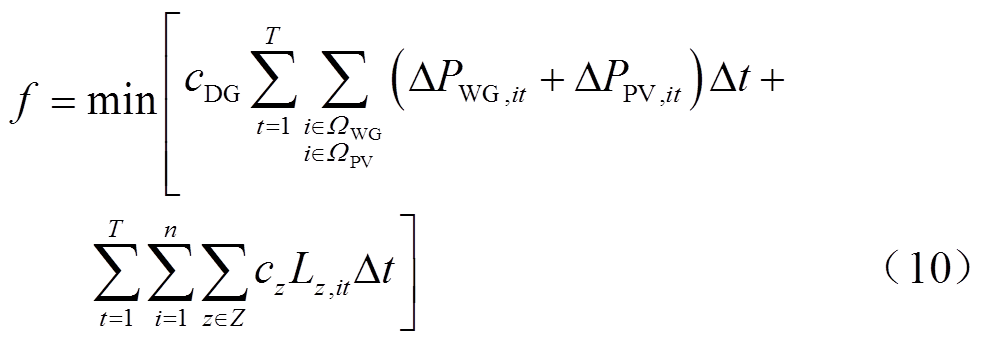
式中,cDG为弃风、弃光的单位惩罚成本;ΩWG、ΩPV分别为风、光机组并网节点集合;DPWG,it、DPPV,it分别为弃风弃光功率;T为调度周期;n为节点数;Z为EH-RIESs供给负荷类型集合,包括电、氢、热负荷;cz为第z类负荷的单位削减惩罚成本;Lz,it为第z类负荷的削减功率;下标i、t分别为节点与时刻。
本文采用线性化的DistFlow公式[24]模拟配电网潮流约束,其余异质能量流约束包括电、氢、热能量平衡约束、异质能源负荷削减约束和EH交互功率约束。
3.2.1 电功率平衡约束
在EH中,来自配电网、风光机组和燃料电池的电能将供给电解槽和电力负荷用电,即
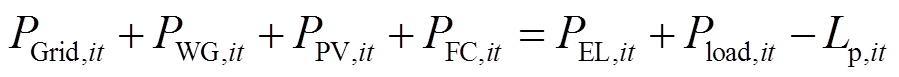 (11)
(11)
式中,PGrid,it为EH与电网交互的有功功率;PWG,it、PPV,it分别为风光机组实际输出的有功功率;PFC,it、PEL,it分别为燃料电池输出的有功功率和电解槽消耗的有功功率;Pload,it、Lp,it分别为有功负荷和负荷削减功率。
3.2.2 氢气平衡约束
在EH中,加氢机组接收来自电解槽与储氢罐提供的氢气,如式(12)所示;加氢机组输出的氢气供给EH内的氢负荷需求,如式(13)所示。
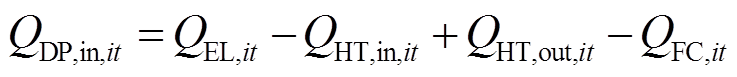 (12)
(12)
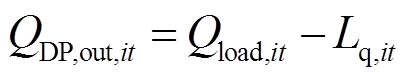 (13)
(13)
式中,QDP,in,it、QDP,out,it分别为加氢机组输入、输出的氢气量;QEL,it、QFC,it分别为电解槽产氢量和燃料电池耗氢量;QHT,in,it、QHT,out,it分别为储氢罐的充氢量和放氢量;Qload,it、Lq,it分别为氢负荷的需求量和削减量。
3.2.3 热功率平衡约束
在EH中,由燃气锅炉产热与燃料电池产热共同满足EH内的热负荷需求,即
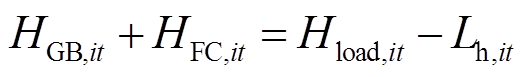 (14)
(14)
式中,HGB,it为燃气锅炉产热功率;HFC,it为燃料电池产热功率;Hload,it、Lh,it分别为热负荷需求功率和削减功率。
3.2.4 异质能源负荷削减约束
异质能源负荷削减约束用以保证t时刻节点i的电、氢、热负荷削减量不得大于负荷需求功率。电、氢、热负荷削减约束分别为
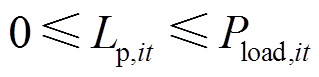 (15)
(15)
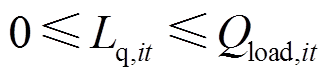 (16)
(16)
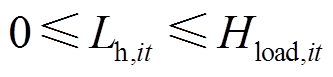 (17)
(17)
3.2.5 EH交互功率约束
EH与电网和天然气网的交互功率受变压器和燃气管道等设备的容量限制。为此,建立EH与电网和天然气网的交互功率约束,分别为
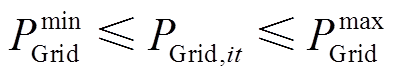 (18)
(18)
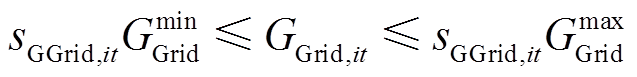 (19)
(19)
式中,PmaxGrid、PminGrid分别为EH与电网交互功率的上、下限;GGrid,it为EH与天然气网的交互功率;sGGrid,it为天然气网等效元件的运行状态变量,1表示正常运行状态,0表示故障停运状态;GmaxGrid、GminGrid分别为EH与天然气网交互功率的上、下限。
基于氢能设备的故障机理分析及其可靠性评估模型,分别建立碱性电解槽、储氢罐、质子交换膜燃料电池与加氢机组的运行约束模型。
3.3.1 碱性电解槽运行约束
基于第2.1节中建立的碱性电解槽多状态模型,其在不同运行状态下的产氢量可通过式(20)计算得到;式(21)表示当碱性电解槽启动时,其耗电功率应在安全运行范围内;式(22)表示碱性电解槽处于正常运行或降额运行状态时可选择是否启停,而处于故障停运状态时则必须停机。
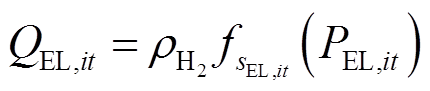 (20)
(20)
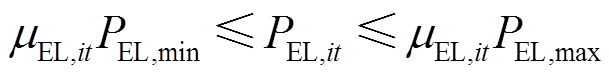 (21)
(21)
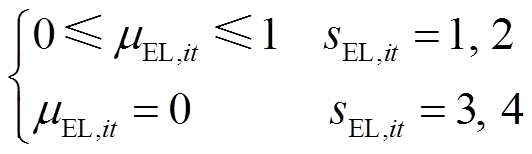 (22)
(22)
式中,ρH2为氢气的标准密度[kg/(N·m3)];μEL,it为电解槽的启停状态变量,1表示启动状态,0表示停机状态;PEL,max和PEL,min分别为电解槽耗电功率的上、下限。
3.3.2 储氢罐运行约束
储氢罐在某时刻的储氢状态与上一时刻的储氢状态和该时刻充/放的氢气量相关,如式(23)所示;式(24)、式(25)分别表示储氢罐的充/放氢量应在安全运行范围内;式(26)表示储氢罐的储氢状态应在安全运行范围内;式(27)限制了调度周期始末时刻储氢罐的储氢状态相同,便于下一周期调度;式(28)和式(29)表示在正常运行状态下,储氢罐同一时刻只能选择充氢或放氢操作,若储氢罐发生故障则不能充氢或放氢[25-26]。
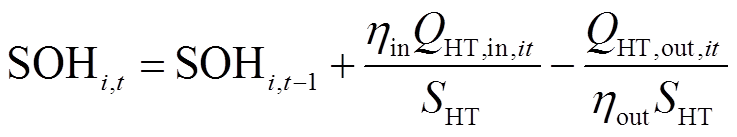 (23)
(23)
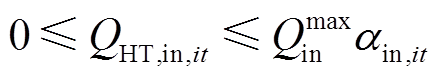 (24)
(24)
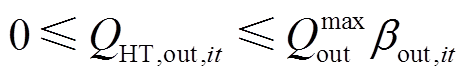 (25)
(25)
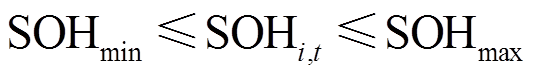 (26)
(26)
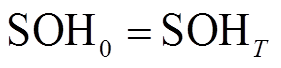 (27)
(27)
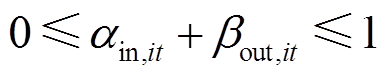 (28)
(28)
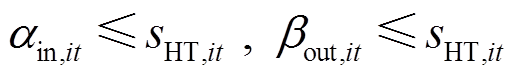 (29)
(29)
式中,SOHi,t、SOHi,t-1分别为t时刻和t-1时刻储氢罐的储氢状态,即当前时刻储氢量与储氢罐容量之比;ηin、ηout分别为储氢罐的充/放氢效率;SHT为储氢罐容量;αin,it、βout,it分别为储氢罐充氢和放氢的状态变量,0表示无氢气充/放,1表示有氢气充/放;Qmaxin、Qmaxout分别为储氢罐充、放氢量的上限;SOHmax、SOHmin分别为储氢罐储氢状态的上、下限;SOH0、SOHT分别为调度周期内初始时刻、末尾时刻储氢罐的储氢状态;sHT,it为储氢罐的运行状态变量,1表示正常运行状态,0表示故障停运状态。
3.3.3 质子交换膜燃料电池运行约束
基于第2.2节中建立的考虑热电联产的燃料电池多状态模型,其消耗的氢气量可由式(30)计算得到,不同运行状态下燃料电池的产电功率与产热功率可分别通过式(31)、式(32)计算得到;式(33)、式(34)分别表示当燃料电池启动时,其产电功率和消耗氢气量应在安全运行范围内;式(35)表示燃料电池处于正常运行或降额运行状态时可选择是否启停,而处于故障停运状态时则必须停机。
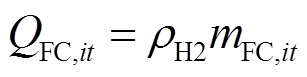 (30)
(30)
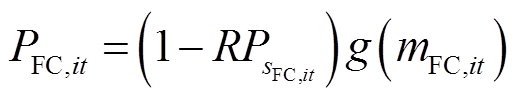 (31)
(31)
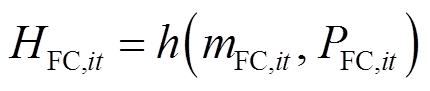 (32)
(32)
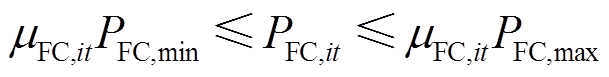 (33)
(33)
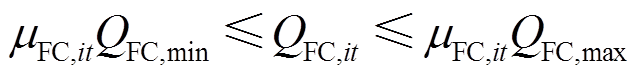 (34)
(34)
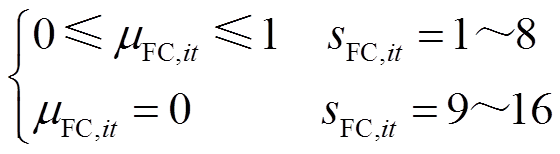 (35)
(35)
式中,μFC,it为燃料电池的启停状态变量,1表示启动状态,0表示停机状态;PFC,max、PFC,min分别为燃料电池产电功率的上、下限;QFC,max、QFC,min分别为燃料电池耗氢量的上、下限。
3.3.4 加氢机组运行约束
考虑加氢过程中的能量损失,如式(36)所示;基于第2.3节建立的加氢机组多状态模型可知,由加氢机组提供的氢气量应当不超过当前时刻所有未故障加氢机的总可用容量,如式(37)所示。
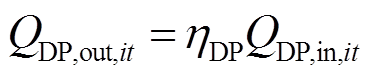 (36)
(36)
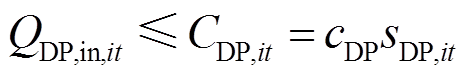 (37)
(37)
式中,ηDP为加氢效率;sDP,it为未故障的加氢机数量。
此外,电力线路、风光机组和燃气锅炉等设备均基于经典的两状态可靠性评估模型建立其运行约束模型[24,27],此处不再赘述。
可见,本节建立的最优负荷削减模型属于典型的非线性混合整数规划问题。采用分段线性化方法[28]将非线性约束式(20)和式(31)进行线性化处理,从而将该最优负荷削减模型转换为混合整数线性规划问题,并采用Gurobi商业软件进行求解。
电、热等系统的供能可靠性指标已较为成熟,但目前仍缺少供氢能力的可靠性评估指标。为此,本节构建了供氢可靠性评估指标体系,量化评估氢负荷的可靠供给程度。
1)氢负荷削减概率(Loss of Hydrogen Load Probability, LOHLP)为
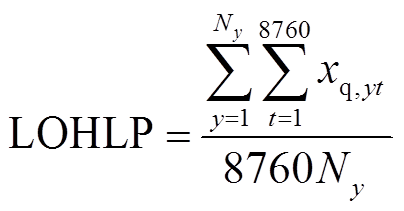 (38)
(38)
式中,xq,yt为第y年t时刻系统氢负荷的削减状态变量,1表示有氢负荷削减,0表示无氢负荷削减;Ny为模拟年限。
2)氢负荷削减时间期望(Loss of Hydrogen Load Expectation, LOHLE)为
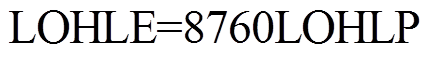 (39)
(39)
3)氢负荷缺供能量期望(Expected Hydrogen Not Supply, EHNS)
利用模拟周期内氢负荷削减量总和与模拟年限的比值,表示年氢负荷缺供能量期望值。
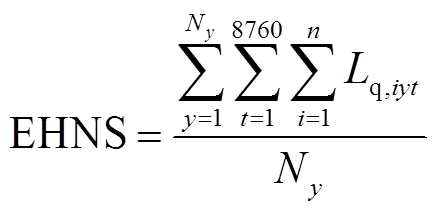 (40)
(40)
式中,Lq,iyt为第y年t时刻节点i处EH的氢负荷削减量。
4)设备供氢贡献度(Hydrogen Supply Contribution of Equipment, HSCOE)
利用某一设备随机故障造成的氢负荷缺供能量期望与总氢负荷缺供能量期望的比例,反映该设备对供氢可靠性的影响程度。
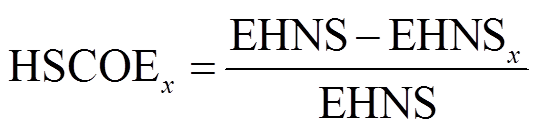 (41)
(41)
式中,HSCOEx为设备x对氢负荷缺供能量期望的贡献度指标;EHNSx为考虑仅设备x完全正常运行情况下的氢负荷缺供能量期望。
5)缺供能量综合损失CENS为
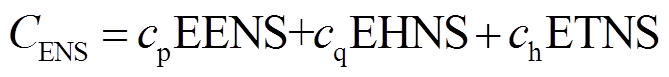 (42)
(42)
式中,cp、cq、ch分别为电、氢、热负荷的单位削减惩罚成本;EENS、ETNS分别为电负荷和热负荷的缺供能量期望。
本文基于MCMC模拟[20],建立了考虑氢能设备等时序状态转移过程的可靠性评估方法,具体计算步骤如下所示:
(1)输入EH-RIESs及其设备参数等数据,初始化各类型设备状态,设定最大仿真年限Ny,max及缺供能量期望的最小方差系数εmin。
(2)基于氢能设备的多状态模型及其他设备的可靠性模型,通过MCMC模拟抽样得到仿真年限内每小时的系统状态。
(3)初始化模拟天数d =1和模拟年数Ny =1。
(4)获取第d天每个时段的系统状态,求解最优负荷削减模型,得到第d天每个时段的负荷削减状态和最优负荷削减量。
(5)若d>365,转向步骤(6);否则,令d =d+1,转向步骤4)。
(6)计算第Ny年的系统可靠性评估指标,并令Ny = Ny +1。
(7)若Ny>Ny,max,或缺供能量期望方差系数ε<εmin,转向步骤(8);否则令d =1,转向步骤(4)。
(8)输出电、氢等异质能源供给可靠性评估指标。
本节基于IEEE 14节点配电网[29]和52节点实际配电网分别构建了EH-RIES-A和EH-RIES-B两个系统进行仿真分析。首先针对EH-RIES-A测试系统,采用不同的氢能设备可靠性模型进行可靠性评估,以说明本文所提氢能设备多状态模型和EH-RIESs可靠性评估方法的优势。然后,针对EH-RIES-B测试系统进行仿真分析,以验证本文所提模型与可靠性评估方法对不同EH-RIESs的适应性。两个系统的网架结构分别如图9、图10所示,系统中EH的配置方案分别见附表1、附表2,并采用我国中部地区某风光场站实测数据及文献[25]中负荷曲线模拟源荷时序特性。
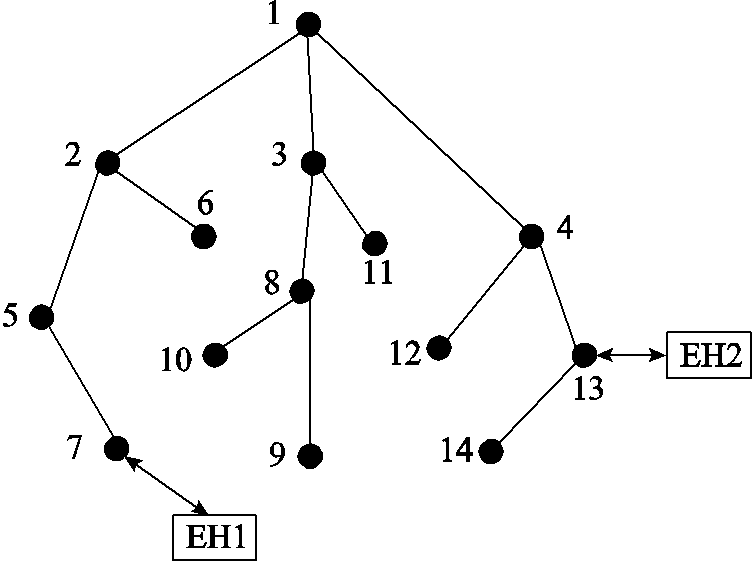
图9 基于IEEE 14节点配电网的EH-RIES-A
Fig.9 The EH-RIES-A based on IEEE 14-bus distribution network
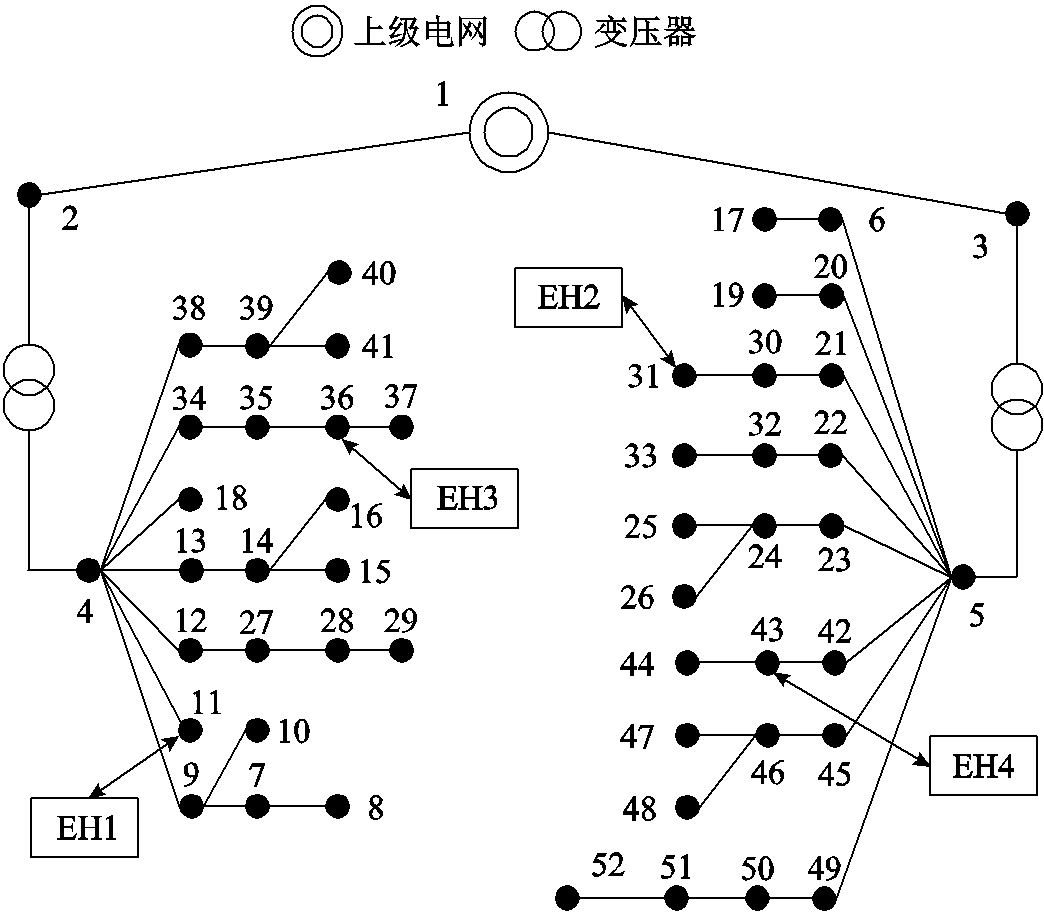
图10 基于52节点配电网的EH-RIES-B
Fig.10 The EH-RIES-B based on 52-bus distribution network
电解槽与燃料电池运行模型的参数详见文献[8,17-18],其安全运行范围为额定功率的20%~100%[30],其余设备运行参数见表4[25-26,31]。各类型设备的可靠性参数见表5[8,11,13,26,32]。电、热负荷的单位削减惩罚成本分别设置为50元/(kW·h)、40元/(kW·h)[26]。考虑到碱性电解槽制氢的平均能耗约为4.5 kW·h/m3[33],本文按电负荷削减惩罚成本设置氢负荷的单位削减惩罚成本为2 500元/kg。
表4 设备运行参数
Tab.4 Equipment parameters

设备类型运行参数数值 燃气锅炉产热效率ηGB0.90 储氢罐充放氢效率ηin、ηout0.95 初始储氢状态SOH00.5 储氢状态上下限SOHmax,SOHmin0.9,0.2 加氢机加氢效率ηDP0.96
表5 设备可靠性参数
Tab.5 Reliability parameters of equipment
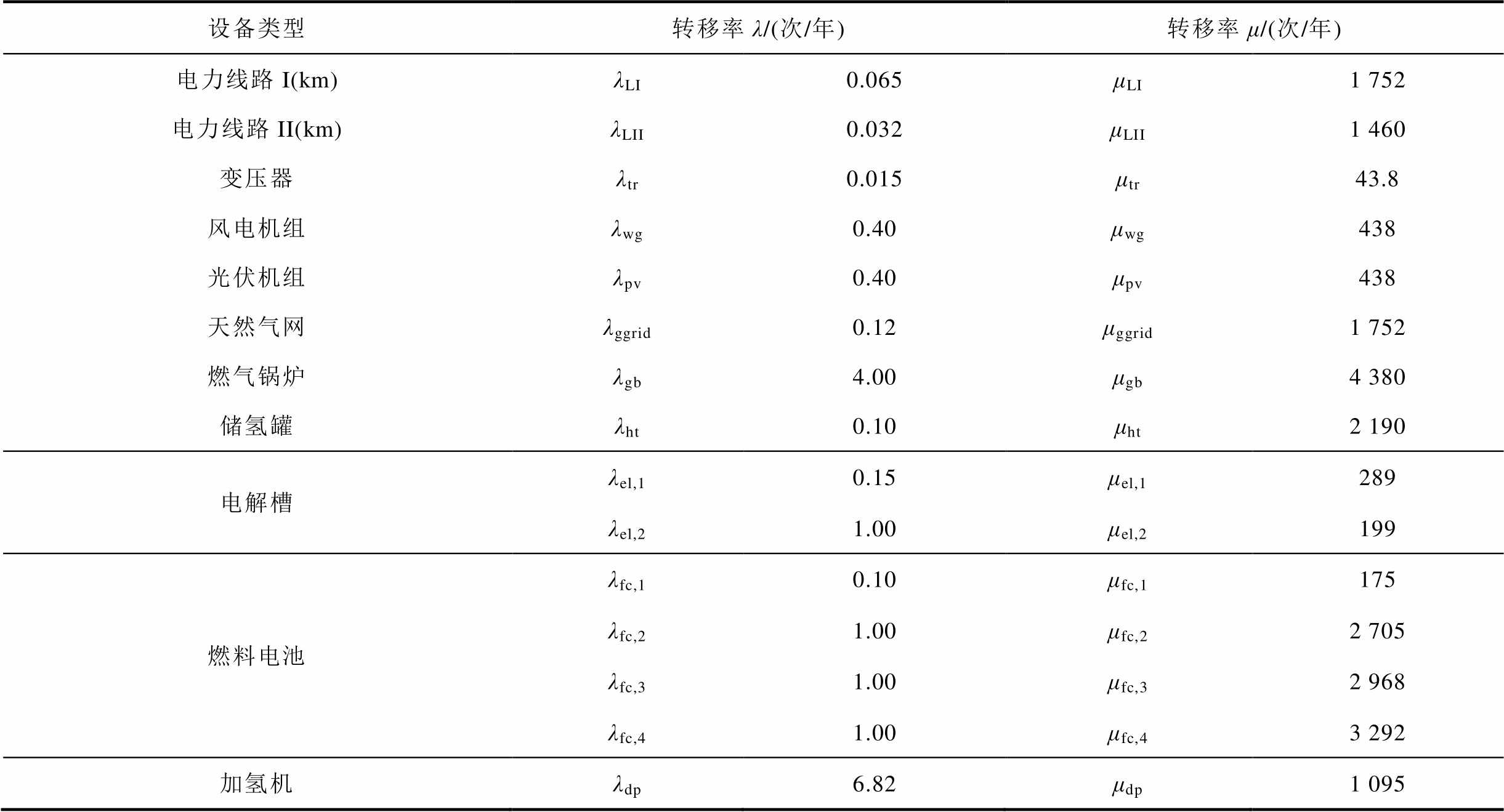
设备类型转移率λ/(次/年)转移率μ/(次/年) 电力线路I(km)λLI0.065μLI1 752 电力线路II(km)λLII0.032μLII1 460 变压器λtr0.015μtr43.8 风电机组λwg0.40μwg438 光伏机组λpv0.40μpv438 天然气网λggrid0.12μggrid1 752 燃气锅炉λgb4.00μgb4 380 储氢罐λht0.10μht2 190 电解槽λel,10.15μel,1289 λel,21.00μel,2199 燃料电池λfc,10.10μfc,1175 λfc,21.00μfc,22 705 λfc,31.00μfc,32 968 λfc,41.00μfc,43 292 加氢机λdp6.82μdp1 095
5.2.1 系统可靠性分析
针对EH-RIES-A,采用如下四种方法进行仿真分析,以说明本文所提加氢机组、碱性电解槽的多状态模型和热电联产燃料电池多状态模型的优势。
方法1:采用加氢机组的两状态模型[34],文献[13]中的碱性电解槽两状态模型和文献[8]中发电模式下的燃料电池多状态模型。
方法2:采用本文所提的加氢机组多状态模型,文献[13]中的碱性电解槽两状态模型和文献[8]中发电模式下的燃料电池多状态模型。
方法3:采用本文所提加氢机组和碱性电解槽的多状态模型,以及文献[8]中发电模式下的燃料电池多状态模型。
方法4:采用本文方法,即加氢机组和碱性电解槽的多状态模型,以及考虑热电联产模式的燃料电池多状态模型。
四种方法计算得到EH-RIES-A的可靠性评估指标见表6。LOELP、LOELE、EENS分别为电负荷的削减概率、削减时间期望和缺供能量期望;LOTLP、LOTLE、ETNS分别为热负荷的削减概率、削减时间期望和缺供能量期望。
表6 EH-RIES-A的可靠性评估指标
Tab.6 Reliability evaluation indexes of EH-RIES-A
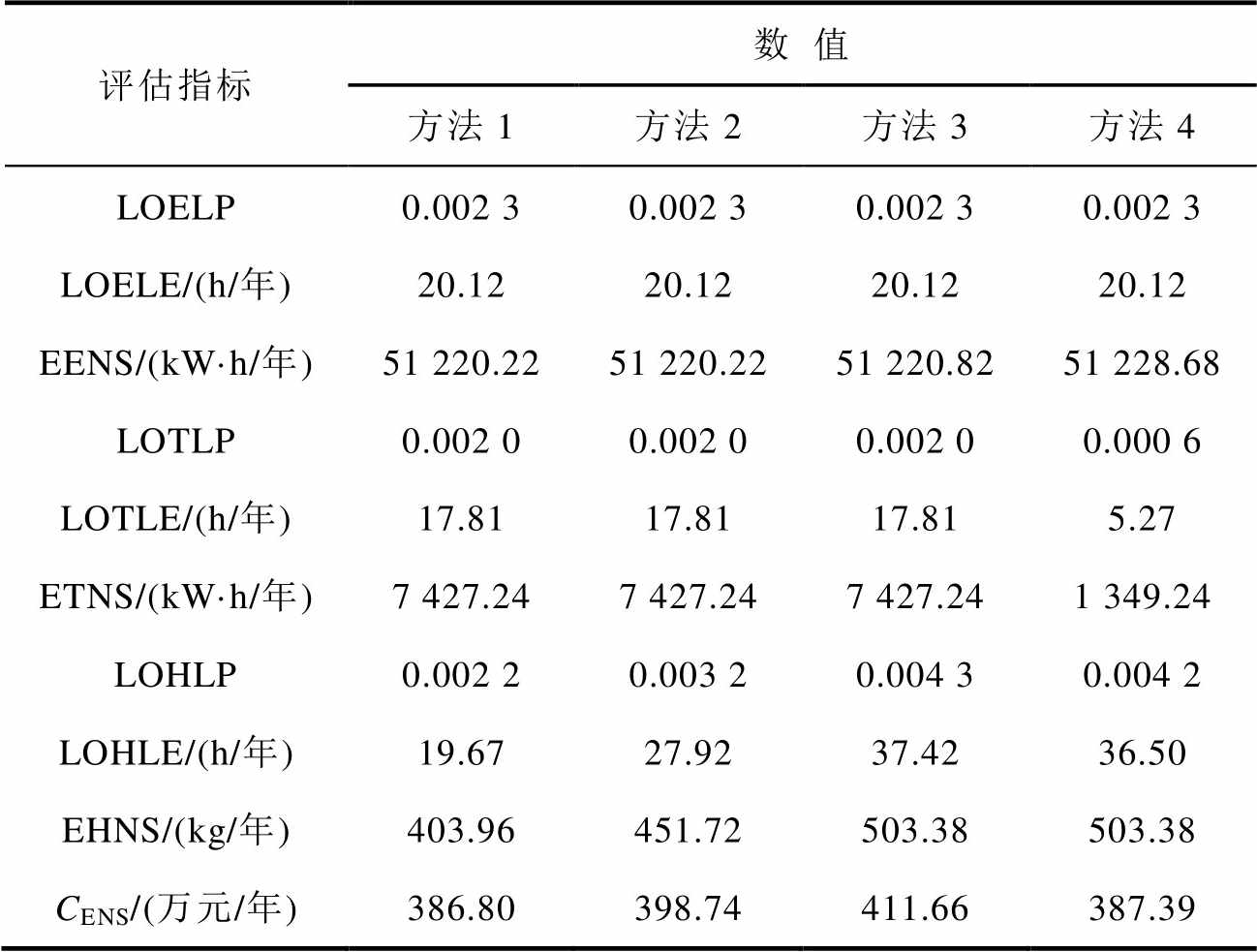
评估指标数值 方法1方法2方法3方法4 LOELP0.002 30.002 30.002 30.002 3 LOELE/(h/年)20.1220.1220.1220.12 EENS/(kW·h/年)51 220.2251 220.2251 220.8251 228.68 LOTLP0.002 00.002 00.002 00.000 6 LOTLE/(h/年)17.8117.8117.815.27 ETNS/(kW·h/年)7 427.247 427.247 427.241 349.24 LOHLP0.002 20.003 20.004 30.004 2 LOHLE/(h/年)19.6727.9237.4236.50 EHNS/(kg/年)403.96451.72503.38503.38 CENS/(万元/年)386.80398.74411.66387.39
从表6可见,方法2的LOHLP相比方法1增加了45.45%(0.001 0),LOHLE增加了41.94%(8.25 h/年),EHNS和CENS相比方法1也分别增加了11.82%(47.76 kg/年)和3.09%(11.94 万元/年)。这是因为方法1仅考虑加氢机组全部正常运行或全部故障停运的状态,而方法2能够充分考虑加氢机组的多状态运行特性。
从表6可知,方法3与方法2中电、热负荷的可靠性水平相同,但方法3考虑了碱性电解槽的降额运行状态,其氢负荷供给可靠性水平劣于方法2。以秋季典型日为例,当碱性电解槽处于降额运行状态(sEL=2)时,EH-RIES-A中EH2的电、氢能量平衡分别如图11a、图11b所示。与正常运行状态相比,处于降额运行状态下的碱性电解槽将消耗更多的电能,但受EH与电网交互功率的限制,碱性电解槽的制氢量不能满足全部的氢负荷需求。在设定的单位氢负荷削减惩罚成本下,考虑到制-储-加氢等过程中的效率损失,系统会优先削减氢负荷以保障电负荷的可靠供给,减少弃能损失。因此,与方法2相比,方法3的氢负荷削减概率LOHLP增加了34.38%(0.001 1),氢负荷削减时间期望LOHLE增加了34.03%(9.50 h/年),氢负荷缺供能量期望EHNS和系统缺供能量综合损失CENS分别增加了11.44%(51.66 kg/年)和3.24%(12.92 万元/年)。上述分析表明,若不考虑加氢机组和碱性电解槽的降额运行状态,均会过高地估计供氢可靠性水平。

图11 sEL=2时EH2的电、氢能量平衡
Fig.11 Electricity and hydrogen energy balance of EH2 when sEL=2
与方法3相比,方法4的电、氢负荷可靠性指标未发生较大变化,但方法4的热负荷削减概率LOTLP降低了70.00%(0.001 4),热负荷削减时间期望LOTLE减少了70.41%(12.54 h/年),热负荷缺供能量ETNS和系统缺供能量综合损失CENS分别减少了81.83% (6 078.00 kW·h/年)和5.90%(24.27 万元/年),供热可靠性水平大幅提升。以秋季典型日燃气锅炉发生故障为例,在燃料电池不同运行模式下,EH2的热负荷削减量如图12所示。可见,在燃料电池发电模式(即方法3)下,燃气锅炉是热负荷唯一供给来源,发生故障时热负荷被削减;当燃料电池采用热电联产模式(即方法4)且处于正常运行状态(sFC=1)或降额运行状态(如sFC=2,3,4)时,能够有效降低部分时段内的热负荷削减量,提高供热可靠性水平。
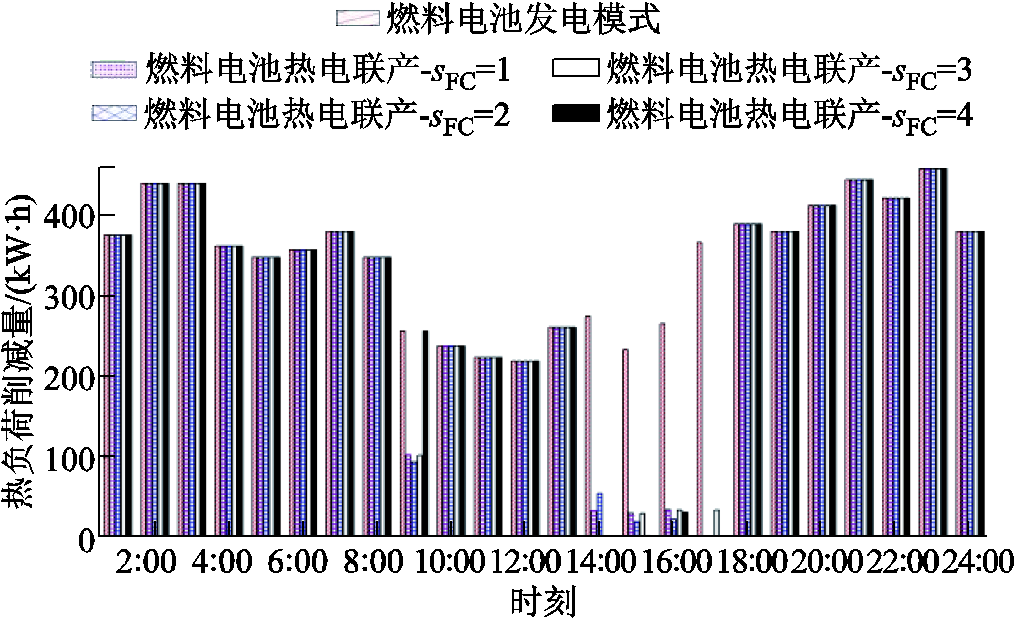
图12 不同燃料电池运行模式下EH2的热负荷削减量
Fig.12 Heat load shedding of EH2 under different operation modes of fuel cell
综上所述,本文所提加氢机组和碱性电解槽的多状态模型能够充分考虑其降额运行状态造成的氢负荷削减,避免过高地估计供氢可靠性水平;所提燃料电池多状态模型能够充分考虑燃料电池热电联产模式对供热可靠性的贡献,避免过低地估计供热可靠性水平。
5.2.2 设备供氢贡献度指标分析
为了明晰影响氢能供给可靠性的关键因素,为EH-RIESs的规划建设等提供科学合理的决策依据,本节基于5.2.1节所提方法4与式(41)计算得到各类设备的供氢贡献度指标,如图13所示。
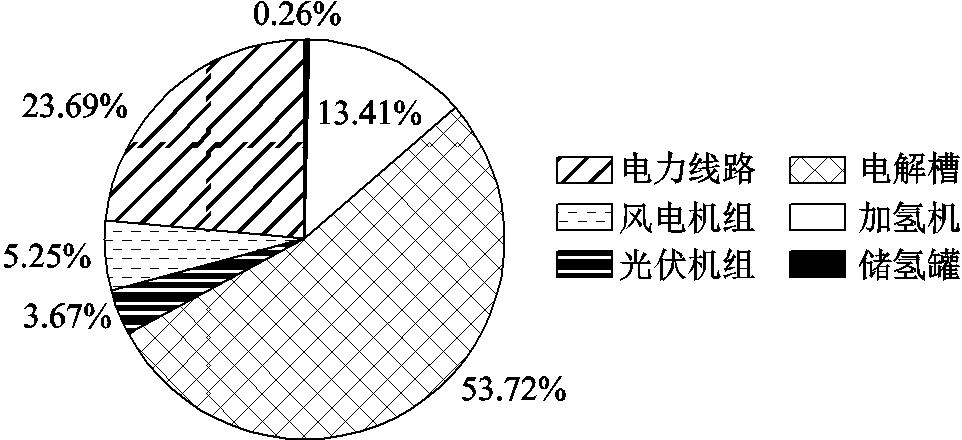
图13 设备供氢贡献度指标
Fig.13 Hydrogen supply contribution index of equipment
由图13可见,EH-RIESs中天然气网与燃气锅炉等热能设备随机故障对氢负荷缺供能量期望没有影响。由于EH中氢气唯一的生产设备为电解槽,电力设备的随机故障会导致电解槽缺乏电能制氢,从而导致氢负荷的供应不足。由图13可见,电力线路和风光机组随机故障对系统氢负荷缺供能量期望的贡献度之和达到了32.61%。
作为系统中唯一的制氢设备,电解槽的降额运行状态和故障停运状态均会造成较大的氢能供应缺额,其供氢贡献度指标高达53.72%。虽然EH1和EH2中均有两台加氢机互为备用,但单台加氢机的故障率较高,其随机故障对氢负荷缺供能量期望的贡献度有13.41%。当储氢罐发生故障时,电解槽难以实时满足故障时段内的高峰氢负荷需求,但储氢罐的故障率较低且替换时间短,所以对氢负荷缺供能量期望的影响较小,仅为0.26%。
上述仿真结果说明电力设备和电解槽是影响供氢可靠性的关键因素,在EH-RIESs未来的规划建设中可通过提供此类设备的备用或进行设备扩容等方法提升供氢可靠性水平。
5.2.3 氢负荷削减惩罚成本影响分析
根据5.2.1节的分析可知,当单位氢负荷削减惩罚成本cq为2 500元/kg时,系统优先选择削减氢负荷以保障电负荷的可靠供给,从而减少总弃能损失。为分析cq对系统缺供能量综合损失CENS的影响,以2 500元/kg为基值,采用方法4评估不同cq下的CENS,计算结果如图14所示。

图14 不同单位氢负荷削减惩罚成本的缺供能量综合损失
Fig.14 Comprehensive loss of energy not supply under different penalty costs of unit hydrogen load shedding
从图14可以看出,cq不影响热负荷削减量。当cq低于基值时,若发生电力线路等设备故障,系统尽可能选择削减氢负荷以减少电负荷的削减,从而降低总的负荷削减惩罚成本。随着cq逐步降低,电负荷可靠性水平略有提升,CENS不断下降。当cq高于基值时,在电解槽处于降额运行状态等情况下,系统尽可能选择削减电负荷以保障供氢可靠性,从而降低总的负荷削减惩罚成本。随着cq逐步增加,电负荷可靠性水平逐步降低,CENS也在不断增加。
为进一步验证本文模型及评估方法的适应性,采用第5.2.1节设置的四种方法分别对EH-RIES-B进行可靠性评估,仿真结果见表7。
表7 EH-RIES-B的可靠性评估指标
Tab.7 Reliability evaluation indexes of EH-RIES-B

评估指标数值 方法1方法2方法3方法4 LOELP0.001 20.001 20.001 20.001 2 LOELE/(h/年)10.4810.4810.4810.48 EENS/(kW·h/年)165 561.89165 559.28165 563.83165 574.03 LOTLP0.003 80.003 80.003 80.001 1 LOTLE/(h/年)33.5933.5933.599.90 ETNS/(kW·h/年)13 783.6813 783.6813 783.682 617.32 LOHLP0.010 20.014 60.016 50.016 4 LOHLE/(h/年)89.51128.01144.67143.85 EHNS/(kg/年)1 648.661 937.432 042.132 042.42 CENS/(万元/年)1 295.111 367.291 393.491 348.94
由表7可见,与方法1相比,考虑加氢机组的多状态模型后,方法2的氢负荷缺供能量期望EHNS和系统缺供能量综合损失CENS分别增加了17.52%(288.77 kg/年)和5.57%(72.18万元/年)。与方法2相比,考虑碱性电解槽的降额运行状态后,方法3的氢负荷缺供能量期望EHNS和系统缺供能量综合损失CENS分别增加了5.40%(104.70 kg/年)和1.92%(26.20万元/年)。与方法3相比,考虑燃料电池的热电联产模式后,方法4的热负荷缺供能量期望ETNS和系统缺供能量综合损失CENS分别减少了81.01%(11 166.36 kW·h/年)和3.20%(44.55万元/年),热负荷可靠性水平得到大幅提升。综上所述,本节的仿真结论与5.2.1节一致。
本文建立了碱性电解槽、热电联产燃料电池和加氢机组的多状态模型,提出供氢可靠性评估指标体系及EH-RIESs可靠性评估方法,用两个测试系统验证了本文模型及方法的有效性和适应性,并得出如下结论:
1)忽略加氢机组和碱性电解槽的降额运行状态,均会过高地估计供氢可靠性水平。考虑热电联产模式的燃料电池多状态模型,能够有效地弥补供热设备故障后的热能缺额,有助于准确评估EH-RIESs的供热可靠性水平。
2)本文提出的供氢评估指标体系和EH-RIESs可靠性评估方法,能够量化系统供氢可靠性水平、经济损失以及设备故障对氢负荷缺供能量的贡献程度,可为系统规划建设等提供关键的决策支撑。
3)随着单位氢负荷削减惩罚成本的增加,氢负荷可靠性水平随之提升,但电负荷可靠性水平却逐步降低。合理设定氢负荷削减惩罚成本,对平衡系统的供能可靠性及经济运行水平至关重要。
附 录
附表1 EH-RIES-A的EH配置方案
App.Tab.1 EH Configuration scheme of EH-RIES-A
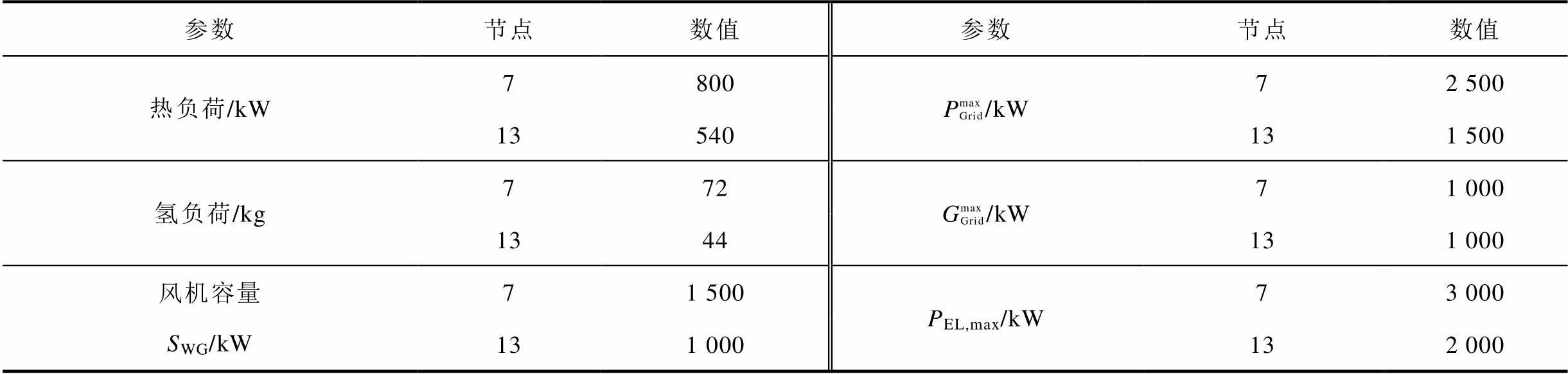
参数节点数值参数节点数值 热负荷/kW7800PmaxGrid/kW72 500 13540131 500 氢负荷/kg772GmaxGrid/kW71 000 1344131 000 风机容量SWG/kW71 500PEL,max/kW73 000 131 000132 000
(续)
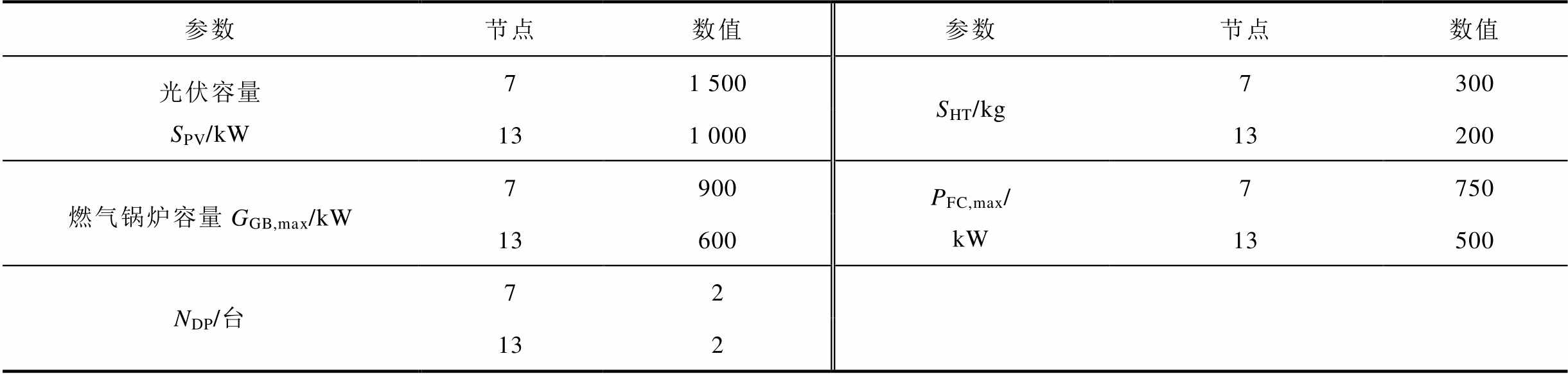
参数节点数值参数节点数值 光伏容量SPV/kW71 500SHT/kg7300 131 00013200 燃气锅炉容量GGB,max/kW7900PFC,max/ kW7750 1360013500 NDP/台72 132
附表2 EH-RIES-B的EH配置方案
App.Tab.2 EH configuration scheme of EH-RIES-B

参数节点数值参数节点数值 热负荷/kW11800112 500 31270311 000 36540361 500 431 070433 000 氢负荷/kg1170111 000 3126311 000 3643361 000 4385432 000 SWG/kW111 500PEL,max/kW113 000 31500311 000 361 000362 000 432 000434 000 SPV/kW111 500SHT/kg11300 3150031100 361 00036200 432 00043400 GGB,max/kW11900PFC,max/kW11750 3150031250 3660036500 431 500431 000 NDP/台112 311 362 432
参考文献
[1] 习近平. 继往开来, 开启全球应对气候变化新征程[EB/OL]. 人民网, [2020-12-14]. http://env.people. com.cn/n1/2020/1214/c1010-31965084.html.
[2] 潘光胜, 顾伟, 张会岩, 等. 面向高比例可再生能源消纳的电氢能源系统[J]. 电力系统自动化, 2020, 44(23): 1-10.
Pan Guangsheng, Gu Wei, Zhang Huiyan, et al. Electricity and hydrogen energy system towards accomodation of high proportion of renewable energy[J]. Automation of Electric Power Systems, 2020, 44(23): 1-10.
[3] Bartolucci L, Cordiner S, Mulone V, et al. Hydrogen based multi energy systems: assessment of the marginal utility of increasing hydrogen penetration on system performances[J]. International Journal of Hydrogen Energy, 2021, 46(78): 38588-38602.
[4] 任洲洋, 罗潇, 覃惠玲, 等. 考虑储氢物理特性的含氢区域综合能源系统中长期优化运行[J]. 电网技术, 2022, 46(9): 3324-3333.
Ren Zhouyang, Luo Xiao, Qin Huiling, et al. Mid/long-term optimal operation of regional integrated energy systems considering hydrogen physical characteristics[J]. Power System Technology, 2022, 46(9): 3324-3333.
[5] Johnston D L, Johnson B K. Comparison of reliability indices with the effect of protection failure for an electrical to hydrogen distribution system[C]//41st North American Power Symposium, Starkville, MS, USA, 2010: 1-5.
[6] 李亚东. 风光互补联合发电制氢系统的安全性分析与研究[D]. 邯郸: 河北工程大学, 2016.
[7] Lee S, Zhou Dao, Wang Huai. Reliablity assessment of fuel cell system-a framework for quantitative approach[C]//2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 2017: 1-5.
[8] Tanrioven M, Alam M S. Impact of load management on reliability assessment of grid independent PEM fuel cell power plants[J]. Journal of Power Sources, 2006, 157(1): 401-410.
[9] Assaf J, Shabani B. Experimental study of a novel hybrid solar-thermal/PV-hydrogen system: towards 100% renewable heat and power supply to standalone applications[J]. Energy, 2018, 157: 862-876.
[10] 随权, 马啸, 魏繁荣, 等. 计及燃料电池热-电综合利用的能源网日前调度优化策略[J]. 中国电机工程学报, 2019, 39(6): 1603-1613, 1857.
Sui Quan, Ma Xiao, Wei Fanrong, et al. Day-ahead dispatching optimization strategy for energy network considering fuel cell thermal-electric comprehensive utilization[J]. Proceedings of the CSEE, 2019, 39(6): 1603-1613, 1857.
[11] Kurtz J, Sprik S, Peters M, et al. Retail hydrogen station reliability status and advances[J]. Reliability Engineering & System Safety, 2020: 106823.
[12] Ogbonnaya C, Abeykoon C, Nasser A, et al. Engineering risk assessment of photovoltaic-thermal-fuel cell system using classical failure modes, effects and criticality analyses[J]. Cleaner Environmental Systems, 2021, 2: 100021.
[13] 岳大为, 袁行行, 赵文体, 等. 含电-氢系统的孤岛型交直流混合微电网可靠性评估[J]. 高电压技术, 2021, 47(11): 4002-4012.
Yue Dawei, Yuan Hanghang, Zhao Wenti, et al. Reliability evaluation of islanded AC/DC hybrid microgrid with electricity-hydrogen system[J]. High Voltage Engineering, 2021, 47(11): 4002-4012.
[14] 裴煜. 含氢能的冷热电联供微能源网运行优化[D]. 太原: 太原理工大学, 2020.
[15] Diéguez P M, Ursúa A, Sanchis P, et al. Thermal performance of a commercial alkaline water electrolyzer: experimental study and mathematical modeling[J]. International Journal of Hydrogen Energy, 2008, 33(24): 7338-7354.
[16] Li Jiarong, Lin Jin, Song Yonghua, et al. Operation optimization of power to hydrogen and heat (P2HH) in ADN coordinated with the district heating network[J]. IEEE Transactions on Sustainable Energy, 2019, 10(4): 1672-1683.
[17] Abdelkafi A, Krichen L. Energy management optimization of a hybrid power production unit based renewable energies[J]. International Journal of Electrical Power & Energy Systems, 2014, 62: 1-9.
[18] 余娟, 时权妍, 杨知方, 等. 考虑电解水与甲烷化运行特性的电转气系统日前调度方法[J]. 电力系统自动化, 2019, 43(18): 18-25.
Yu Juan, Shi Quanyan, Yang Zhifang, et al. Day-ahead scheduling method of power-to-gas system considering operation characteristics of water electrolysis and methanation[J]. Automation of Electric Power Systems, 2019, 43(18): 18-25.
[19] 孙涛. 金属杂质离子对电解水的影响[D]. 长沙: 湖南大学, 2011.
[20] Chao Huawei, Hu Bo, Xie Kaigui, et al. A sequential MCMC model for reliability evaluation of offshore wind farms considering severe weather conditions[J]. IEEE Access, 2019, 7: 132552-132562.
[21] 裴煜, 宋天昊, 袁铁江, 等. 计及燃料电池热电联供的区域综合能源系统经济运行[J]. 电力系统及其自动化学报, 2021, 33(2): 142-150.
Pei Yu, Song Tianhao, Yuan Tiejiang, et al. Economic operation of regional integrated energy system considering combined heating and power generation with fuel cell[J]. Proceedings of the CSU-EPSA, 2021, 33(2): 142-150.
[22] 中华人民共和国住房和城乡建设部. 加氢站技术规范: GB 50516—2010[S]. 北京: 中国计划出版社, 2021.
[23] Tang Yi, Zhao Yuan, Li Wenyuan, et al. Incorporating compressor station multiple failure modes in risk evaluation of electricity-gas integrated energy systems[J/OL]. CSEE Journal of Power and Energy Systems, 2021, DOI: 10.17775/CSEEJPES.2020.05850.
[24] 郁琛, 李尚轩, 谢云云, 等. 考虑交通网与配电网信息融合的台风后配电网抢修策略优化[J]. 电力系统自动化, 2022, 46(4): 15-24.
Yu Chen, Li Shangxuan, Xie Yunyun, et al. Optimization of post-typhoon rush repair strategy for distribution network considering information integration of traffic network and distribution network[J]. Automation of Electric Power Systems, 2022, 46(4): 15-24.
[25] 李健强, 余光正, 汤波, 等. 考虑风光利用率和含氢能流的多能流综合能源系统规划[J]. 电力系统保护与控制, 2021, 49(14): 11-20.
Li Jianqiang, Yu Guangzheng, Tang Bo, et al. Multi-energy flow integrated energy system planning considering wind and solar utilization and containing hydrogen energy flow[J]. Power System Protection and Control, 2021, 49(14): 11-20.
[26] 路红池, 谢开贵, 王学斌, 等. 计及多能存储和综合需求响应的多能源系统可靠性评估[J]. 电力自动化设备, 2019, 39(8): 72-78.
Lu Hongchi, Xie Kaigui, Wang Xuebin, et al. Reliability assessment of multi-energy system considering multi-storage and integrated demand response[J]. Electric Power Automation Equipment, 2019, 39(8): 72-78.
[27] 倪伟, 吕林, 向月, 等. 基于马尔可夫过程蒙特卡洛法的综合能源系统可靠性评估[J]. 电网技术, 2020, 44(1): 150-158.
Ni Wei, Lü Lin, Xiang Yue, et al. Reliability evaluation of integrated energy system based on Markov process Monte Carlo method[J]. Power System Technology, 2020, 44(1): 150-158.
[28] 姜云鹏, 任洲洋, 李秋燕, 等. 考虑多灵活性资源协调调度的配电网新能源消纳策略[J]. 电工技术学报, 2022, 37(7): 1820-1835.
Jiang Yunpeng, Ren Zhouyang, Li Qiuyan, et al. An accommodation strategy for renewable energy in distribution network considering coordinated dispatching of multi-flexible resources[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1820-1835.
[29] Chen Lijuan, Deng Zhenli, Xu Xiaohui. Two-stage dynamic reactive power dispatch strategy in distribution network considering the reactive power regulation of distributed generations[J]. IEEE Transactions on Power Systems, 2019, 34(2): 1021-1032.
[30] 沈小军, 聂聪颖, 吕洪. 计及电热特性的离网型风电制氢碱性电解槽阵列优化控制策略[J]. 电工技术学报, 2021, 36(3): 463-472.
Shen Xiaojun, Nie Congying, Lü Hong. Coordination control strategy of wind power-hydrogen alkaline electrolyzer bank considering electrothermal characteristics[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 463-472.
[31] 滕云, 闫佳佳, 回茜, 等. “无废”电–氢充能服务区多源微网优化运行模型[J]. 中国电机工程学报, 2021, 41(6): 2074-2088.
Teng Yun, Yan Jiajia, Hui Qian, et al. Optimization operation model of “zero-waste” electricity-hydrogen charging service area multi-energy microgrid[J]. Proceedings of the CSEE, 2021, 41(6): 2074-2088.
[32] 林毓军, 苗世洪, 尹斌鑫, 等. 基于改进协同演化算法的综合能源系统经济性与可靠性优化规划[J]. 电力自动化设备, 2021, 41(9): 173-181.
Lin Yujun, Miao Shihong, Yin Binxin, et al. Optimal planning for economy and reliability of integrated energy system based on improved co-evolution algorithm[J]. Electric Power Automation Equipment, 2021, 41(9): 173-181.
[33] 张红, 袁铁江, 谭捷, 等. 面向统一能源系统的氢能规划框架[J]. 中国电机工程学报, 2022, 42(1): 83-94.
Zhang Hong, Yuan Tiejiang, Tan Jie, et al. Hydrogen energy system planning framework for unified energy system[J]. Proceedings of the CSEE, 2022, 42(1): 83-94.
[34] 史清芳, 徐习东, 赵宇明. 电力电子设备对直流配电网可靠性影响[J]. 电网技术, 2016, 40(3): 725-732.
Shi Qingfang, Xu Xidong, Zhao Yuming. Effects of power electronic devices on DC distribution reliability[J]. Power System Technology, 2016, 40(3): 725-732.
Abstract Electricity-hydrogen regional integrated energy systems (EH-RIESs) are considered as one of the key paths to realize the green and low-carbon transformation of power and energy systems. However, the fault mechanism of hydrogen energy equipment hasn’t been considered by the existing reliability evaluation methods of EH-RIESs, as well as the multi-state characteristics of hydrogen energy equipment. There is no efficient reliability evaluation indexes and methods to quantify the reliability level of hydrogen supply. It means the reasonable decision-making basis for the planning and construction of EH-RIESs cannot be provided. A reliability evaluation method of EH-RIESs based on the multi-state models of hydrogen energy equipment is proposed in this paper. By accurately simulating the operation states of EH-RIESs, the reliability levels of heterogeneous energy supply are effectively quantified.
Firstly, the operation characteristics and fault mechanisms of hydrogen energy equipment are analyzed. A multi-state reliability model of alkaline electrolyzers considering de-rated operation state, a multi-state reliability model of fuel cells considering cogeneration mode and a multi-state reliability model of hydrogen dispenser units are established, which provide the basic models for the operation state simulation of EH-RIESs. Secondly, an optimal load shedding model considering the coupling relationship of electricity-hydrogen heterogeneous energy systems is established to minimize the wind power and photovoltaic power curtailment costs and heterogeneous energy load reduction costs. Then, an evaluation index system of hydrogen supply reliability is constructed from the aspects of hydrogen supply reliability level, the contribution of equipment to expected hydrogen not supply and system economic loss. Finally, based on the multi-state models of hydrogen energy equipment and a Markov Chain Monte Carlo method, a reliability evaluation method is developed for EH-RIESs to quantify the reliability levels of heterogeneous energy supply.
Two EH-RIESs with different scales were used to validate the effectiveness and the advantages of the proposed method. The simulation results show that after considering the de-rated operation state of hydrogenation dispenser units, the expected hydrogen not supply (EHNS) of two EH-RIESs increases by 11.82% and 17.52%, respectively. After considering the de-rated operation state of alkaline electrolyzers, the EHNS of two EH-RIESs increase by 11.44% and 5.40%, respectively. After considering the cogeneration mode of fuel cells, the expected thermal energy not supply of two EH-RIESs decrease by 81.83% and 81.01%, respectively. The hydrogen supply contribution index of electrical equipment and electrolyzers in the first EH-RIES reach 32.61% and 53.72%, respectively, which are the key factors affecting the reliability levels of hydrogen supply. In addition, with the increase of penalty cost of unit hydrogen load shedding, the economic loss of the first EH-RIES caused by electricity shortage is gradually increasing, and the comprehensive loss of energy not supply is also increasing.
The following conclusions can be drawn from the simulation results. (1) The hydrogen supply reliability levels of EH-RIESs will be overestimated if the de-rated states of alkaline electrolyzers and hydrogen dispenser units are ignored. The proposed multi-state model of fuel cells considering the cogeneration mode is helpful to accurately evaluate the thermal energy supply reliability levels of EH-RIESs. (2) The proposed reliability evaluation index system and evaluation method of EH-RIESs can quantify the hydrogen supply reliability level, economic loss and the contribution of equipment failures to the hydrogen energy shortage. (3) With the increase of penalty cost of unit hydrogen load shedding, the reliability level of hydrogen supply is improved, but the reliability level of electricity supply is gradually reduced. A reasonable penalty cost of unit hydrogen load shedding is essential to balance the energy supply reliability and economic levels of systems.
keywords:Electricity-hydrogen regional integrated energy systems, electrolyzer, fuel cell, Markov Chain Monte Carlo, hydrogen supply reliability
中图分类号:TM732
DOI:10.19595/j.cnki.1000-6753.tces.221459
国家自然科学基金资助项目(52277080)。
收稿日期 2022-07-28
改稿日期 2022-11-10
任洲洋 男,1986年生,副教授,博士生导师,研究方向为电力能源系统低碳运行及规划、人工智能等。E-mail:rzhouyang1108@163.com(通信作者)
王 皓 男,1998年生,硕士研究生,研究方向为配电网运行与规划、电氢区域综合能源系统可靠性评估等。E-mail:wh19980913@163.com
(编辑 赫 蕾)