图1 本级线路盲区故障下的一、二次波过程
Fig.1 The primary and secondary travelling waves processes under internal non-detection zone faults
摘要 针对现有的交流电网相继速动保护判据的可靠性能受限于运行工况与系统参数，以及其无法耐受较高过渡电阻的难题，该文首先研究了本级线路盲区故障与下级线路故障时由对端断路器开断产生的二次振荡波过程的差异性，并基于行波模量网络分析了特定故障工况下的特殊波过程；然后，提出了基于数学形态学梯度算法的振荡波头极性辨识判据以及特殊故障工况下的辅助判据，以形成全新的相继速动保护判据；最后，基于PSCAD仿真平台验证了所提保护判据的有效性、灵敏性与可靠性，其适用于三相/单相跳闸方式、适应于所有故障类型、不受系统运行工况与系统参数影响，同时耐受过渡电阻能力高达300 Ω。
关键词：相继速动 二次振荡波 数学形态学梯度 盲区故障 行波模量网络
目前高压/超高压输电线路主要以纵联差动保护作为主保护，但如工频量距离、突变量距离等单端就地化保护，作为与纵联差动保护互相补充的保护功能，在电网安全运行中发挥着不可或缺的重要作用[1-3]。出于动作选择性与可靠性考虑，单端就地化保护均难以覆盖被保护线路全长，即存在保护“盲区”，其通常为本地保护范围内的高阻故障区域以及本级线路保护整定范围外的所有区域。
为了使得单端就地化保护在不借助通信通道的前提下实现线路的全范围保护，就需要具有基于本地信息的盲区故障保护判据，即相继速动保护判据。为此，业界学者前期研究提出了诸多成果，其主要包括以下几个方面：
（1）利用线路对端三相跳闸后健全相电流变化特征，实现本地相继速动跳闸[4-5]。该判据的动作前提为距离Ⅱ段元件正确动作且健全相在对侧跳闸后变为仅存在电容电流，但其只适用于110 kV及以下的三相跳闸系统和不对称故障，且当线路处于空载时，保护判据存在误动的可能。
（2）预计并等待对侧断路器在近区故障情况下的最长动作时间后，本侧保护再次判断故障是否仍然存在，从而确定是否加速本地保护动作[6-7]。该判据利用延时判据与故障判据实现相继速动功能，其适用于三相/单相跳闸系统以及所有故障类型，但在未知对侧断路器动作信号的前提下，仅仅利用预计延时去加速本地保护，存在越级跳闸的可能性。同时，其故障判据为判断故障后电流与电压分量的变化程度，在稍高阻值故障下判据的灵敏性和可靠性便严重下降。
（3）利用对侧断路器跳闸后产生的负序/零序电流的二次变化量来加速本侧断路器相继速动[8-10]。该判据的动作前提仍为距离Ⅱ段元件动作且负序/零序分量产生突变，其适用于三相/单相跳闸系统，但仅适用于不对称故障工况，同时其可靠程度与保护背侧系统的参数息息相关。此外，随着新型电力系统发展下新能源场站的广泛接入[11]，电网故障后换流器控制策略的改变可能也会带来序分量变化。例如，光伏场站中换流器的负序抑制策略可能在故障后数十毫秒才得以稳定[12]，而负零序网络间耦合紧密，由此将导致负序/零序分量在上述控制策略切换未稳定期间持续产生变化，进而对相继速动判据的可靠动作造成不利影响。
综上所述，现有的相继速动判据的可靠性能受限于运行工况及系统参数，并且距离Ⅱ段元件[4-5, 8-10]和故障判据[6-7]的抗过渡电阻能力均较为有限，由此也必将导致上述相继速动判据不能耐受较高的过渡电阻。针对前述保护领域仍然存在的技术挑战，文献[13]针对多端直流线路分析了直流断路器在快速开断后产生的异于故障行波的二次波过程，并基于此设计了直流线路保护加速判据。受其启发，实际上，交流线路在对端断路器断开后同样会产生二次波过程[14-15]，本级线路断路器断开后该二次波将在本级线路故障点处依据过渡电阻大小产生不尽相同的折反射过程，而在下级线路断路器断开后该二次波将在本级线路上传输而不经过下级线路故障点。因此，若能够有效区分本级线路保护盲区范围内与下级线路故障下的不同二次振荡波过程，并对其进行准确提取与辨识，则有望据此构造全新的相继速动保护判据。
根据上述研究思路，本文首先，研究了交流线路本级线路盲区故障与下级线路故障时二次波过程的差异性，并基于行波模量网络分析了特定故障工况下的特殊波过程；然后，提出基于波头极性辨识的二次振荡波识别判据及特殊故障工况下的辅助判据，据此构建了全新的交流线路相继速动保护判据；最后，基于PSCAD仿真平台验证了所提保护判据的有效性、灵敏性与可靠性。
在本级线路保护盲区及下级线路故障发生后，本地保护处将先后感受到故障产生的一次波过程，以及对端本级或下级线路断路器断开所产生的二次波过程。本节主要分析上述本级线路保护盲区故障和下级线路故障时二次波过程的差异性，以及特定故障工况下波过程的特殊性。
在本级线路保护盲区发生故障时，本地侧的距离Ⅰ段保护或其他欠范围式保护无法动作，而对端保护因距离故障点较近，其断路器将先于本地侧可靠跳开，从而形成二次波过程。此类工况下的一、二次波过程如图1所示，图中，R0、R1和R2分别为本级线路本侧断路器、本级线路对端断路器和下级线路出口断路器。
当对端本级线路断路器R1断开后，将产生二次波过程，本地侧保护感受到的由对端断路器开断产生的二次波时刻为
图1 本级线路盲区故障下的一、二次波过程
Fig.1 The primary and secondary travelling waves processes under internal non-detection zone faults
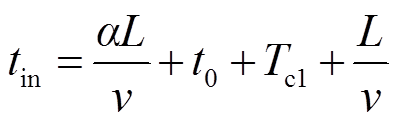（1）
式中，α为故障点与对端保护之间的距离占本级线路长度的比例；L为本级线路长度；v为线模行波的传播速度，本文选取1模电流行波作为研究对象；t0为对端保护动作时间；Tc1为R1的开断时间。
由后文1.3节可知，行波在故障点的折射系数处于0～1之间，因此故障点反射波将会改变其极性。而当对端本级线路断路器R1开断后，二次波在故障点的反射波将在对端断路器处发生全反射，行波极性保持不变。所以本地保护侧将感受到二次波在故障点与对端断路器之间的振荡波过程，且波头极性将以正负、负正、正负极性顺序先后交替出现，因此本地保护侧在tin以后感受到的本级线路盲区故障下的二次波振荡周期为
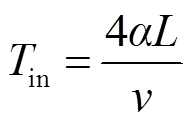（2）
值得注意的是，由故障产生的一次波过程也会在故障点与对端母线之间形成振荡波过程。但考虑到交流输电线路及波阻抗不连续处的衰减作用，一次振荡波的能量耗散过程大约在20 ms以下，而对端保护动作时间t0和断路器开断时间Tc之和一般至少在30 ms以上，因此一次与二次振荡波过程在时间尺度上并不会发生重叠。
在下级线路故障下，本地侧的距离Ⅱ段等保护因延时无法快速动作，而对端下级线路距离Ⅰ段等保护将无延时迅速切除故障，其下级线路断路器R2将先于本地侧跳开，从而形成二次波过程。此类工况下的一、二次波过程如图2所示。
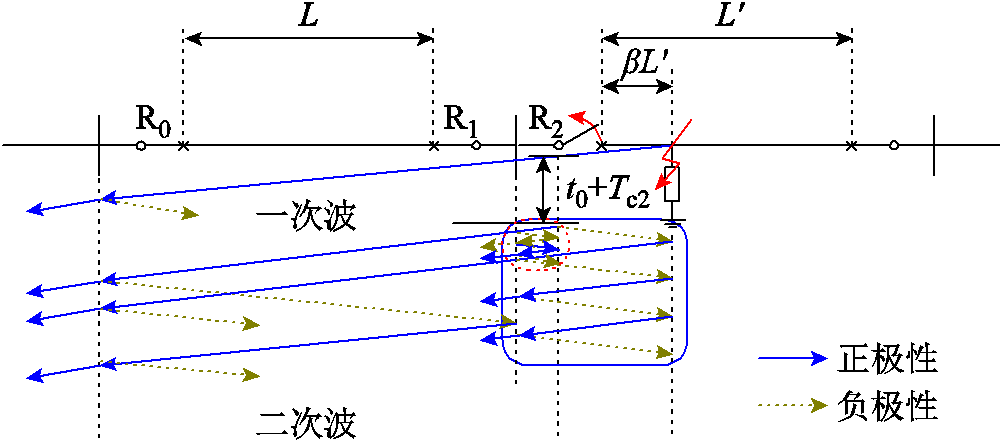
图2 下级线路故障下的一、二次波过程
Fig.2 The primary and secondary travelling waves processes under external faults
当对端下级线路断路器R2断开后，将产生二次波过程，本地侧保护感受到的由对端断路器产生的二次波时刻为
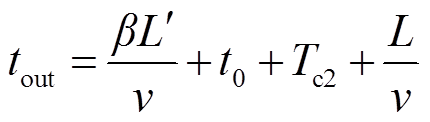（3）
式中，β为故障点与对端保护之间的距离占下级线路长度的比例；L'为下级线路长度；Tc2为R2的开断时间。
对端断路器R2开断后，将在对端母线与对端断路器之间形成类似于图2红虚线框所示的振荡波过程。然而由于对端断路器与对端母线之间的距离仅为几十米，因此该振荡波的振荡频率很高，同时其将在高频振荡中快速衰减，故而在当前工程采样条件下暂无法对该振荡波进行有效识别。因此，在对端断路器开断后，本地保护侧所能感受的是以线路全长为振荡周期的振荡波过程。由于本级线路通常存在多条下级线路，以及母线对地杂散电容也会对行波折反射造成影响，因此二次波一般在对端母线处并非发生全反射，本地保护侧将感受到二次波波头极性以正负、正负极性顺序先后交替出现，故而本地保护侧在tout以后感受到的下级线路故障下二次波在本级线路全长上传输的振荡周期为
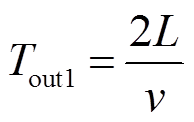（4）
但是，当发生区外单相接地故障时，下级线路的断路器仅单相跳开，故障相产生的二次波可能在故障点发生交叉反射，进而将在对端母线与下级故障点之间的非故障相上形成类似于图2实线框所示的振荡波过程。该振荡过程也可能被本地保护侧所感受到，且二次波波头极性同样以正负、正负极性顺序先后交替出现，故而本地保护侧在tout以后还可能感受到的下级线路故障下二次波在对端母线与下级故障点之间传输的振荡周期为
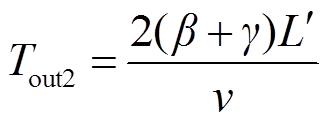（5）
式中，γ为下级断路器与对端母线之间的距离占下级线路长度的比例，该值几乎可以忽略。
由式（1）和式（3）可知，在本地侧保护感受到的一、二次波过程至少相差保护动作时间与断路器开断时间，因此一、二次波之间不会相互影响。此外，由式（2）、式（4）和式（5）可知，本级线路盲区故障与下级线路故障下的二次波过程在行波极性与振荡周期上存在显著的差异，故而能够以此设计相应的保护判据实现本级线路盲区故障与下级线路故障的有效区分。
当对端断路器开断后，输电线路上存储的电磁能量将从故障稳态向断路器开断后新的稳态跃迁，由此造成电场和磁场能量的突变，形成二次振荡波过程。对于下级线路故障产生的振荡波而言，其始终能够被本地保护侧检测到；对于本级线路盲区故障产生的振荡波而言，其能否被有效检测需分析故障点的折反射系数。现将根据行波模量网络[16]分析不同故障类型下的振荡波传输过程。
为了消除相间耦合影响，一般通过相模转换将相量转换成模量，常用的凯伦贝尔模变换矩阵为
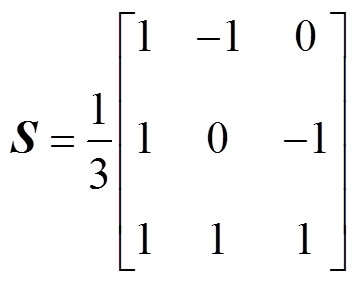（6）
记故障处的三相电压和电流分别为um和im，其中m分别为A相、B相或C相。以A相为故障参考相，根据不同故障类型的三相边界条件，由式（6）计算得到其模量网络的边界条件见表1。表中，u1、u2、u0分别为故障点1模、2模、0模电压分量；i1、i2、i0分别为故障点1模、2模、0模电流分量；zf为故障阻抗。
根据表1可绘制不同故障类型下的行波模量网络如图3所示，图中，Z1、Z2、Z0分别为1模、2模、0模特性阻抗，1模行波在AB相间传输，2模行波在AC相间传输，0模行波在ABC相与大地之间传输。
表1 不同故障类型下的模量边界条件
Tab.1 The Modulus boundary conditions for different fault types
故障类型三相边界条件模量边界条件 单相接地 两相接地 相间故障 三相接地
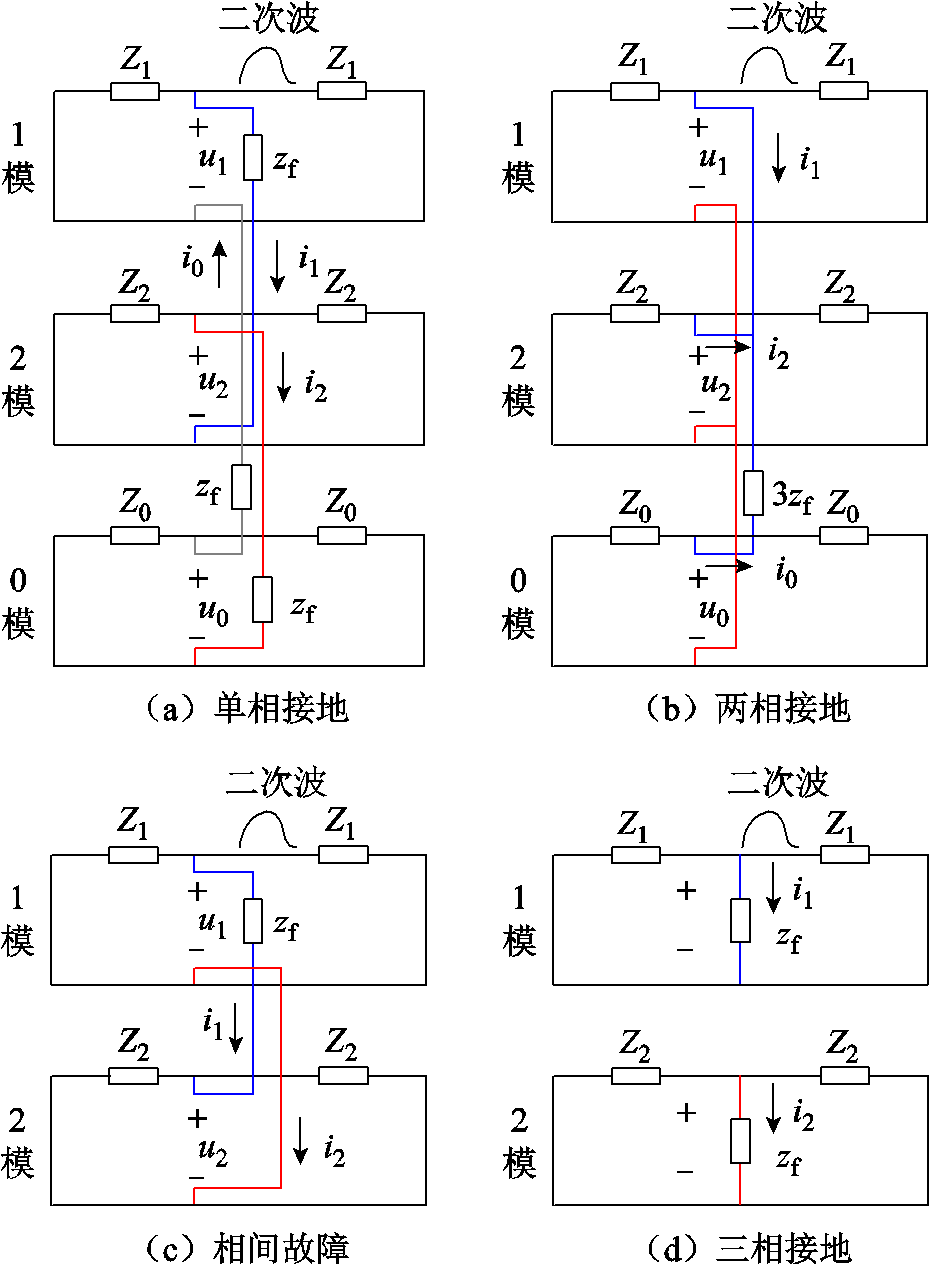
图3 不同故障类型下的行波模量网络
Fig.3 The modulus equivalent circuits under different fault types
根据彼得逊等效法则，可将初始二次波在故障点的折射系数统一表示为
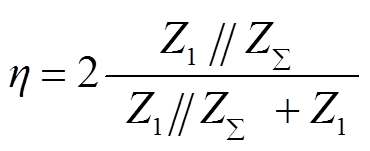（7）
式中，η为折射系数；ZΣ为故障阻抗zf与除1模网络外其余模量网络特性阻抗的等效阻抗。
分析图3和式（7）可得以下结论：
（1）在单相接地故障与两相接地故障下，无论故障阻抗zf的大小，折射系数η始终满足0＜η＜1，因此本地保护侧始终能够检测到振荡波过程。
（2）在相间故障下，当故障阻抗zf为0时（金属性故障），由于Z1与Z2近似相等，可认为1模网络与2模网络之间同样相等，此时折射系数η为0.5。由于三相故障电流不可能同时过零，因而三相断路器不可能同时被开断。从最先开断相来看，故障开断只存在两种类型，即单相依次开断和两相同时开断，后者只有在两相短路时才有可能发生[14-15]。假若单相依次开断，则本地保护侧能够检测到式（2）所示的振荡波过程；假若两相同时开断，则1模行波与2模行波近似相等，其在故障点的交叉反射将使得各模量网络中的反射波与入射波近乎抵消，二次波将在故障处仅产生折射现象，故而在相间金属性故障工况下，本地保护侧所感受到的振荡波过程将以线路全长为振荡周期。
（3）在三相接地故障下，当故障阻抗zf为0时（金属性故障），故障点直接接地。因此，此时等效阻抗ZΣ近似为0，折射系数η近似为0，二次波将在故障处发生全反射，保护安装处将无法检测到振荡波过程。
（4）对于相间与三相非金属性故障而言，因故障阻抗zf不为0，二次波在故障点的折射系数η始终满足0＜η＜1，因此本地保护侧始终能够检测到振荡波过程。
综上所述，对于本级线路保护盲区内的绝大多数故障工况，本地保护侧始终能够检测到故障点与对端断路器之间的振荡波过程。但对于相间金属性故障工况，本地保护侧所感受到的振荡波过程将可能以线路全长为振荡周期；对于三相金属性故障，由于金属性接地使得故障点两侧的系统被完全电气隔离，本地保护侧将始终无法感受到对侧断路器动作产生的二次振荡波。后文仿真结果验证了上述分析的正确性。
鉴于工程实际中电流互感器优良的高频传变特性，本文选取电流线模行波分量作为研究对象，以计算其二次振荡波头极性的改变次数，亦即检测振荡波上升沿、下降沿的突变边缘。针对该问题，现有研究通常采用较为成熟的数学形态学梯度（Mathematical Morphology Gradient, MMG）算法来解决。其中，文献[17]提出了一种能够同时反映波形边缘及突变方向的改进MMG算法，其计算公式为
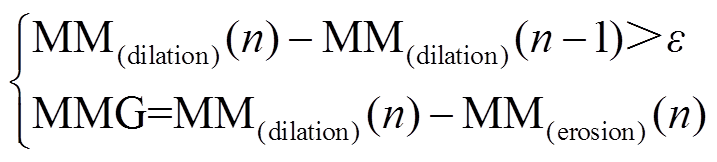（8）
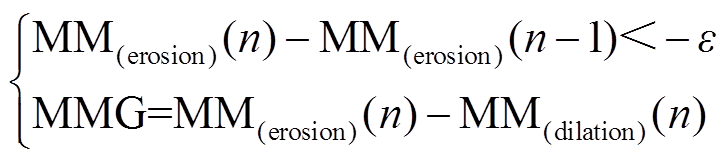（9）
式中，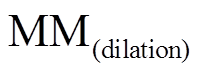
为原波形经膨胀算法处理后的结果；
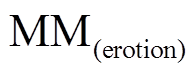为原波形经腐蚀算法处理后的结果；n为采样点数；MMG为算法输出结果，当式（8）、式（9）均不满足时，输出0；ε为阈值，兼具噪声滤除功能。由于二次振荡行波分量的幅值大小与故障工况相关，故障工况越严重，故障后电流突变量越大，二次振荡波幅值越大；故障工况越轻微，故障后电流突变量越小，二次振荡波幅值越小。因此ε的设定宜采用自适应门槛，本文以故障后电流突变量最大值与比例系数的乘积作为阈值，其计算公式为
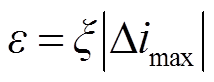（10）
式中，Δimax为电流突变量的最大值；ξ为比例系数，根据后文仿真结果总结，本文可取为0.01，工程应用中可根据实际效果适时调整。
记线路末端盲区范围占本级线路长度的比例为αmax，则由式（2）可知，本级线路盲区故障下的最大振荡周期Tmax为
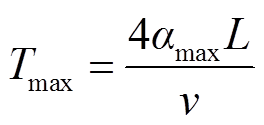（11）
目前高压/超高压输电工程配置的单端保护方案主要为工频变化量距离保护和距离保护。其中，工频变化量距离保护主要为快速保护线路出口近区故障，而距离保护Ⅰ段的保护范围最大可为本线路全长的80%～85% [18]。因此在分析中，可暂假定αmax的最大取值为20%。与式（4）对比可知，此时最大振荡周期Tmax仍然小于下级线路故障下振荡周期的一半，所以能够以保护窗长实现本级线路盲区与下级线路故障的有效区分，但无法可靠应对式（5）所示故障场景。为此，还需从二次振荡波的极性进行辨识。应注意到，在最大振荡周期Tmax时间内，对于本级线路盲区故障，本地保护侧一般能够感受MMG极值按照正负、负正、正负极性顺序先后交替出现，其极值数量为4次及以上；而对于下级线路故障，理论上本地保护侧只能够感受MMG极值按照正负、正负极性顺序先后交替产生的次数为2次及以上。为更好地保证动作可靠性，保护判据的设计需保留合适的裕度，故而二次振荡波识别判据中的保护计算时间窗长Tpro与波头极性计数N判据可分别确定为
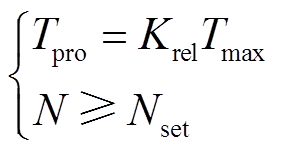（12）
式中，Krel为可靠系数，本文取值为1.1；N为保护时间窗长内按照正负、负正、正负极性顺序先后交替出现的MMG极值数量；Nset为计算阈值，本文取值为4。
根据以上分析可知，二次振荡波波头的极性变化顺序是区分区内外故障的关键，而保护时间窗长Tpro的作用相对较小。由理论分析推导和后文仿真结果可知，只要式（12）中的Tpro小于式（4）中的Tout1，本文所提的相继速动判据即可正确有效动作。由此推导可得，理论上αmax的最大取值可高达45.45%。但必须注意到，当故障发生在保护范围末端时，αmax越大，则所提判据的灵敏性、速动性与可靠性就越低，因此，本文假定αmax的最大取值为20%能够有效保证所提判据具备较优异的动作性能。如若传统距离保护方案因受新能源电源馈出短路电流特性影响而导致其可靠保护范围大幅缩短，则所提相继速动判据在该应用场景下的动作性能将会下降，此时可考虑与其余相继速动判据协同配合，共同保障输电系统的安稳运行。
式（12）所示的二次振荡波识别判据能够可靠应对相间非金属性故障，但可能在识别相间金属性故障时失效。由1.3节分析可知，对于相间金属性故障工况，本地保护侧所感受到的振荡波过程将可能与下级线路故障下产生的振荡波过程一致。值得注意的是，当MMG检测到行波波形突变后，则可认为对端断路器发生了动作，若此时距离Ⅱ段阻抗元件检测到故障仍然存在，则可认为是对端本级线路断路器跳开，本地侧保护执行相继速动；若此时距离Ⅱ段阻抗元件检测到故障已消除，则可认为是对端下级线路断路器跳开，本地侧保护可靠闭锁。且由于是金属性故障，所以距离Ⅱ段阻抗元件此时的灵敏性与可靠性最高。因此，当式（12）失效后，需再经辅助判据判断，以有效识别相间金属性故障，其计算公式为
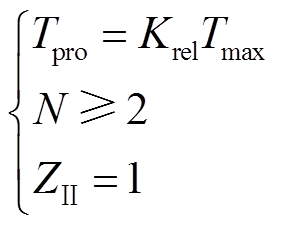（13）
式中，ZⅡ为距离Ⅱ段阻抗元件动作信号，当故障存在时输出1，当故障消除时输出0，在保护时间窗长Tpro内持续输出1则可认为故障仍然存在。
式（12）所示的二次振荡波识别判据能够可靠应对三相非金属性故障，但将在三相金属性故障时失效。由1.3节分析可知，对于三相金属性故障，由于金属性接地使得故障点两侧的系统被完全电气隔离，本地保护侧将始终无法感受到对侧断路器的动作信号。为此，本文现提出以下两类可行方案：
1）主动式方案。
由于仅根据被动故障信息已无法实现相继速动功能，故可考虑基于辅助设备主动注入特征信号以实现三相金属性故障的有效辨识。在特征信号注入方面，现有研究成果丰硕，例如，文献[19]提出可利用统一潮流控制器实现主动注入式故障测距；文献[20]针对交直流混联系统提出了基于模块化多电平换流器的注入式自适应重合闸方案。此外，新能源发电系统的逆变器模块同样具备强大的特征信号调制能力。
因此效仿上述研究思路，当对端保护装置判定发生三相故障时，约定对端母线所连接的辅助装置立即向系统注入特征信号，当本地保护侧能够接收到特征信号时，意味着故障类型为非金属性，故依据式（12）即可实现相继速动功能；当本地保护侧在特定时间窗长内始终无法接收到特征信号时，意味着故障类型为金属性，故在保护时间窗长结束后即可跳开本侧断路器。上述保护思路可表示为
（14）
式中，S为本地保护侧针对特征信号的动作信号，当接收到特征信号时输出1，当未接收到特征信号时输出0。
从理论分析而言，基于上述思路，对端本级断路器未跳开时本地侧始终能够接收到特征信号，而其跳开时则特征信号中断也能实现相继速动功能，然而在故障情况下持续注入特征信号可能会进一步劣化电能质量与系统稳定性。因此本文仅针对三相故障进行短时注入，其余故障仍然采用前述二次振荡波识别判据，实现本地侧保护加速。由于特征信号的注入方案不一而足，且该内容并非本文重点，因此借鉴相关文献方案实现式（14）所述功能即可实现三相金属性故障的有效辨识。结合式（12）～式（14），本文所提的相继速动判据能够覆盖所有盲区范围和各类故障工况。
2）被动式方案。
式（14）所需的辅助装置成为了限制上述主动式方案推广应用的主要原因，当一般性的母线系统并不具备注入特征信号的能力时，式（14）将失效。考虑到相继速动模块属于线路继电保护方案的辅助判据，因此当发生三相金属性故障，即式（14）失效时，本地保护侧严格依照传统阶段式时间配合动作，不再执行相继速动功能。但应该指出的是，输电线路发生三相金属性故障的概率很小，也即本文所提方法出现保护失效的概率相对较低。
本文所提的相继速动判据逻辑框图如图4所示。其中，鉴于传统距离保护方案因受新能源电源馈出短路电流特性影响而导致其可靠保护范围可能大幅缩短，本文将距离保护Ⅰ段保护方案和文献[21]所提的单端暂态量边界欠范围式保护方案共同作为Ⅰ段主保护，并仍然暂假定其保护盲区为线路末端20%的长度范围。此外，距离Ⅱ段方案仍为传统形式，其与距离Ⅰ段方案之间的阶梯式时间配合为300 ms。本文所提的相继速动保护原理流程详述如下：
（1）在保护安装处采集本地侧的电压与电流信息，当正向故障判据启动后，由文献[22]所提方案执行故障选相，并由Ⅰ段主保护判断故障是否发生于保护范围内，若判断为本级线路故障，则保护动作，否则保护闭锁。而后，为躲开故障产生的行波信号的影响，并为二次波的到达留有一定的时间裕度，本文从故障发生后20～300 ms之间以保护时间窗长Tpro持续滑动并识别二次振荡波过程。
（2）若根据选相结果判定为发生不对称接地故障，当式（12）成立时，可认为故障发生于保护盲区范围内，本地侧Ⅱ段保护立即动作。
（3）若根据选相结果判定为发生相间故障，当式（12）或式（13）成立时，可认为故障发生于保护盲区范围内，本地侧Ⅱ段保护立即动作。
（4）若根据选相结果判定为发生三相故障且对端母线系统具备式（14）所述条件时，在故障发生后立即注入特征信号。当本地保护侧在特定时间窗长内始终无法接收到特征信号时，可认为于保护盲区范围内发生三相金属性故障，本地侧保护立即动作；当本地保护侧能够接收到特征信号时，则仍然以保护时间窗长Tpro持续滑动，并判断二次振荡波过程，当式（12）成立时，本地侧Ⅱ段保护立即动作。
（5）若根据选相结果判定为发生三相故障但系统并不具备式（14）所述条件时，则当式（12）成立时，本地侧Ⅱ段保护立即动作，否则保护持续闭锁。
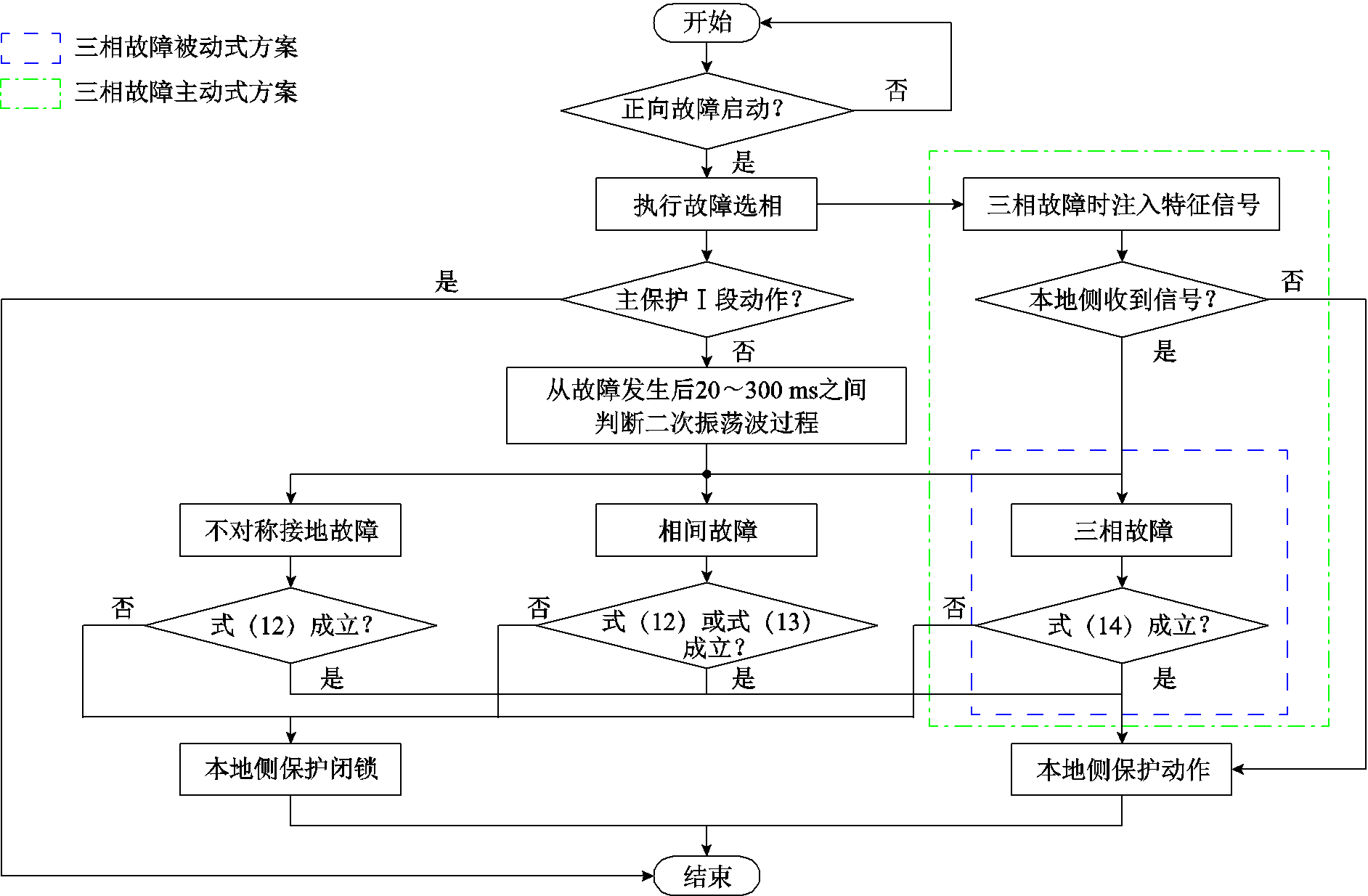
图4 相继速动判据逻辑框图
Fig.4 The flowchart of the fast sequential action principle
基于PSCAD/EMTDC仿真软件平台搭建如图5所示的220 kV高压输电线路，其中，输电线路结构参数详见附图1；新能源场站由多台光伏电源组成，其采用PQ控制策略，并配置负序抑制及低电压穿越等故障控制模块[23]，送出功率为90+j20 MV·A；两处负荷消耗功率均为200+j100 MV·A；变压器电压比均为35 kV/220 kV；线路L1、L2、L3、L4、L5的长度分别为200、200、150、150、30 km；线路L3和L4之间连接有统一潮流控制器（Unified Power Flow Controller, UPFC）[19]。
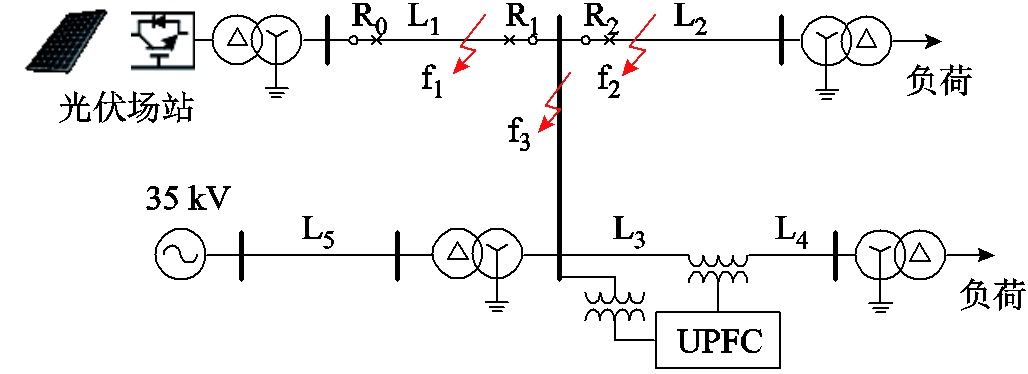
图5 220 kV新能源输电系统
Fig.5 HV transmission system with new energy of 220 kV
假定故障发生时刻为2 s，采样频率为200 kHz。220 kV线路上线模行波波速为2.96×105 km/s，线路L1保护盲区为线路末端20%的长度范围，则由式（11）、式（12）计算可得，保护时间窗长Tpro为0.59 ms。现主要考察R0处保护检测点的动作性能。
现于线路L1上f1处设置不同的故障类型，其距离R1处20 km，考虑过渡电阻Rf分别为0 Ω和300 Ω，其中相间短路时主要为电弧电阻，初期阻值较小，故最多仅考虑20 Ω过渡电阻。考虑相间金属性短路时断路器两相同时开断，此时R0处保护检测点所感受到的电流线模行波分量i1以及相继速动判据动作情况如图6所示。分析图6可得以下结论：
（1）对于单相接地故障、两相接地故障及相间非金属性故障、三相非金属性故障，本地保护侧能够感受到MMG极值按照正负、负正、正负极性顺序先后交替出现，其周期约为0.28 ms，计算可得行波传输路程大约为80 km，即本级线路盲区故障时二次振荡波在故障点与对端断路器之间形成来回振荡过程，并以该路程的4倍为一个振荡周期，与式（2）分析结果一致。在保护时间窗长Tpro内保护检测点能够感受到MMG极值按上述规律先后交替产生的次数远超过4次，满足式（12）所示的相继速动判据，因此可认为故障发生于保护盲区范围内，本地侧距离Ⅱ段保护立即动作。此时相继速动判据的耐受过渡电阻能力高达300 Ω。
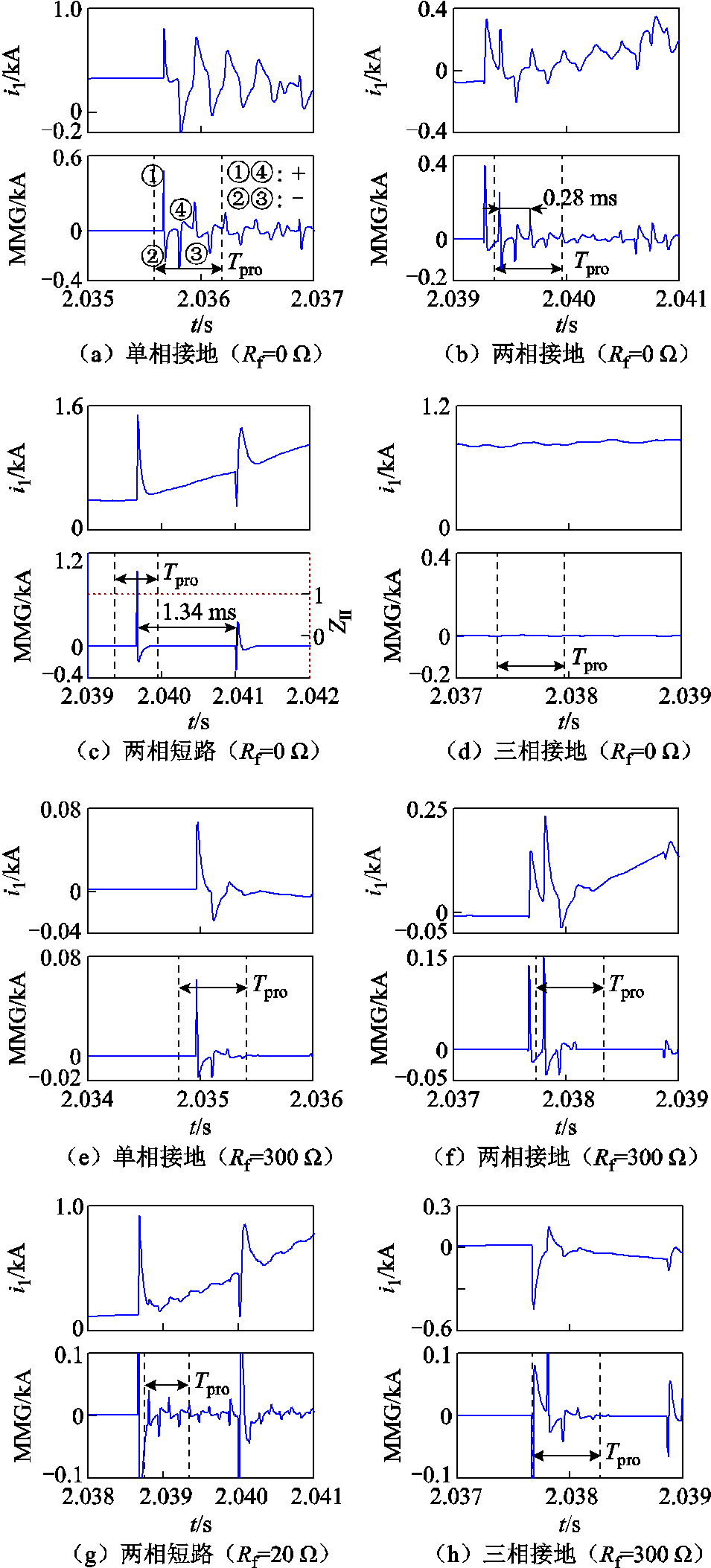
图6 本级线路盲区故障下判据动作情况
Fig.6 The criterion action results under internal non-detection zone fault
（2）如图6c所示，对于相间金属性故障，此时保护检测点先后感受到的行波波头相差大约1.34 ms，计算可得行波传输路程大约为400 km，即此时二次振荡波以线路全长形成来回振荡过程，因此在保护时间窗长内保护检测点能够感受到MMG正负极值先后交替产生的次数仅为2次，不满足式（12）所示的判据。但当MMG检测到行波波形突变后，则可认为对端断路器发生了动作，且此时距离Ⅱ段阻抗元件检测到故障仍然存在，即满足式（13）所示的辅助判据，因此可认为故障发生于保护盲区范围内，本地侧距离Ⅱ段保护立即动作。
（3）如图6d所示，针对三相金属性故障，在对端断路器断开后本地保护侧完全无法感知到二次振荡波过程，式（12）、式（13）将无法在三相金属性故障下可靠动作。依据文献[19]指导原则，约定图5中所连接的UPFC在故障后立即向系统中注入频率75 Hz、幅值0.2IN的特征电流信号，其中IN为系统正常运行时的额定电流，本仿真算例中为0.1 kA，注入时长仅为20 ms，并约定R0处端保护检测点的特征信号检测阈值为2 A，此时故障电流傅里叶频谱分析结果如图7所示。
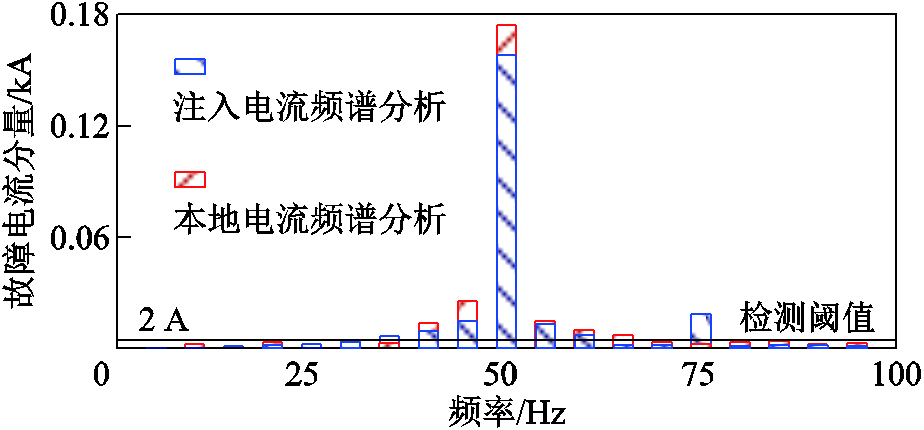
图7 故障电流傅里叶频谱分析结果
Fig.7 The FFT analysis results of fault current
图7展示了故障发生后20 ms内对端设备的注入电流与本地保护侧所采集故障电流的傅里叶频谱分析结果。可见，对端设备成功地向系统中注入了频率75 Hz、幅值20 A的特征电流信号。但是由于特征电流直接在金属性故障点流入大地中，本地保护侧所采集故障电流中的特征电流成分远小于检测阈值2 A，即满足式（14）所示的辅助判据。因此可认为故障发生于保护盲区范围内，本地侧距离Ⅱ段保护立即动作。
由于特征信号的注入方式并非本文重点，如何设计合理且有效的注入方案有待后续开展详细的研究。如若对端母线处在三相故障情况下并不具备上述注入特征信号的能力，则本地保护侧严格依照传统阶段式时间配合动作，不再执行相继速动功能。
现于线路L2上f2处设置金属性单相接地故障与三相金属性接地故障，其距离R2处10 km，此时R0处保护检测点所感受到的电流线模行波分量i1以及相继速动判据动作情况如图8所示。分析图8可得以下结论：
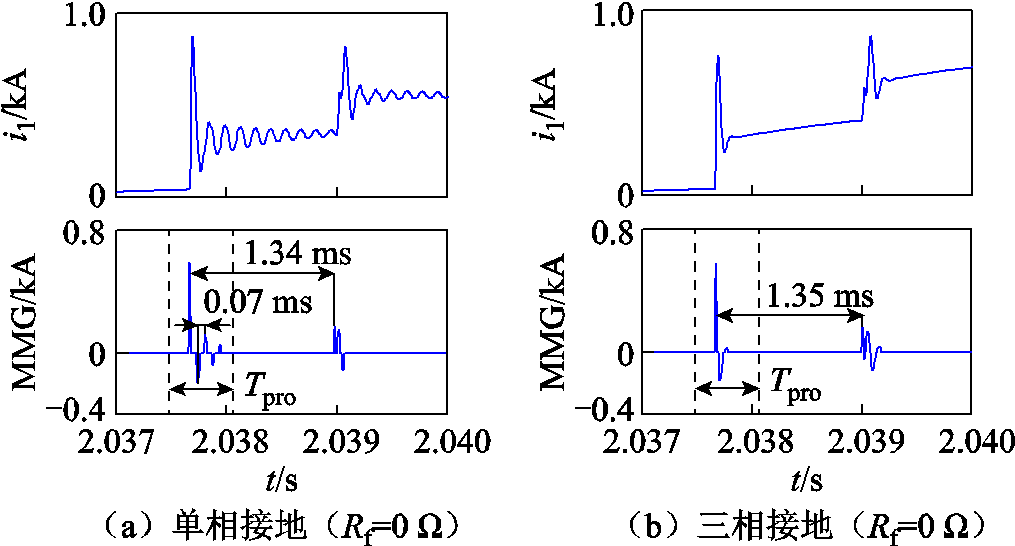
图8 下级线路故障下判据动作情况
Fig.8 The criterion action results under external fault
（1）如图8a所示，针对单相接地故障，R2断路器单相开断。此时本地保护侧除了能感受到二次波在线路全长上传输的振荡周期外，还能感受到二次波在R2和f2之间传输的振荡周期，其周期约为0.07 ms。计算可得行波传输路程大约为20 km，即以R2和f2之间路程的2倍为一个振荡周期。因此在保护时间窗长Tpro内保护检测点能够感受到MMG极值次数远超过4次，但因二次波波头极性以正负、正负顺序变化，不满足式（12）所示的相继速动判据，因此可认为故障发生于故障盲区外，本地侧距离Ⅱ段保护闭锁不动作。
（2）如图8b所示，针对三相接地故障，R2断路器三相开断，此时本地保护侧能感受到二次波在线路全长上传输的振荡周期，且二次波波头极性以正负、正负顺序变化，不满足式（12）所示的相继速动判据。因此可认为故障发生于下级线路，本地侧距离Ⅱ段保护闭锁不动作。
3.3.1 对噪声干扰的适应性
现于线路L1上f1处和线路L2上f2处设置两相接地故障，其距离R1和R2处均为15 km，考虑过渡电阻Rf为0 Ω。在考虑高斯白噪声的情况下，R0处保护检测点所感受到的电流线模行波分量i1及相继速动判据动作情况如图9所示。
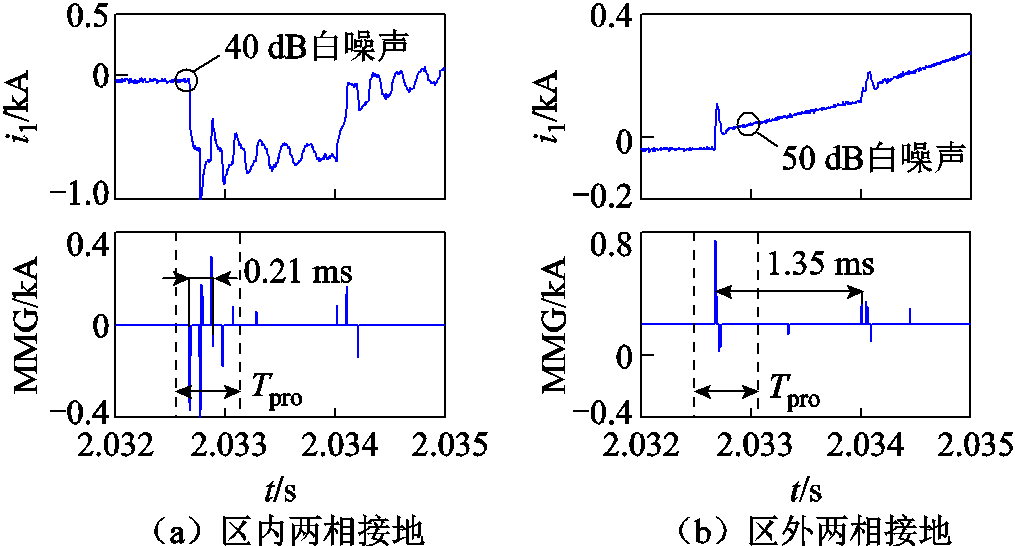
图9 保护判据对噪声干扰的适应性分析
Fig.9 The adaptability analysis of criterion to noises
由图9可知，由于式（10）所示的阈值具备一定的噪声滤除功能，本文所提判据在40 dB白噪声的区内故障下，以及在50 dB白噪声的区外故障下尚且能够可靠工作。但若遭遇噪声强度进一步增大的极端场景，则保护判据存在拒/误动的可能性。为了应对噪声干扰，可考虑先采用硬件屏蔽及软件滤波等环节对行波信号进行有效去噪，以充分提高本文所提保护判据的动作可靠性。
3.3.2 对线路盲区范围的适应性
现于线路L1上f1处设置单相接地故障，考虑过渡电阻Rf为0 Ω，当线路盲区范围αmax=30%时，f1距离R1处为60 km，计算得保护时间窗长为0.88 ms；当线路盲区范围αmax=50%时，f1距离R1处为100 km，计算得保护时间窗长为1.47 ms。在上述两类工况下，R0处保护检测点所感受到的电流线模行波分量i1及相继速动判据动作情况如图10所示。
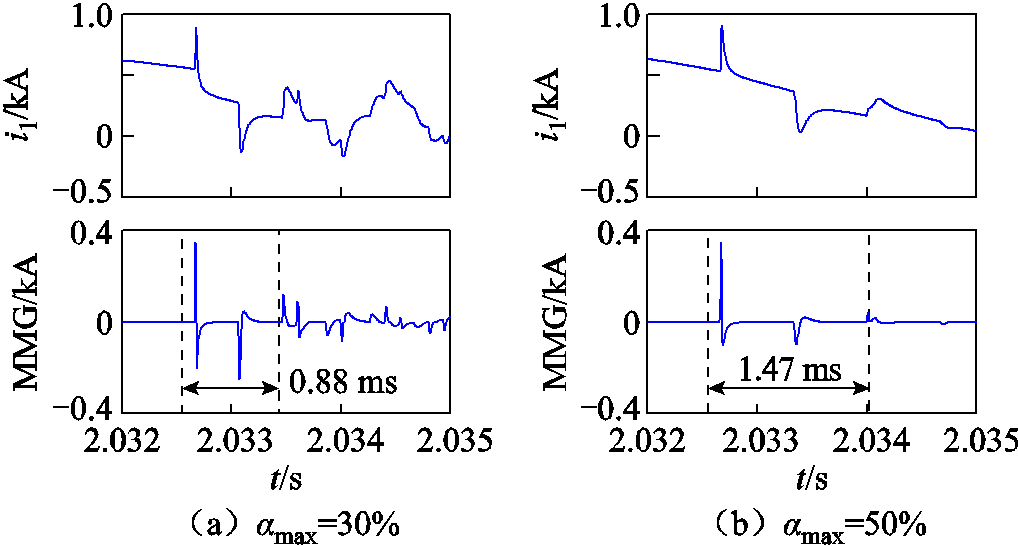
图10 保护判据对线路盲区范围的适应性分析
Fig.10 The adaptability analysis of criterion to the scope of the non-detection zone
由图10可知，不论αmax如何变化，本地保护侧均能感受到二次波波头极性以正负、负正、正负顺序变化，但当线路盲区范围αmax=50%时，1.47 ms的保护时间窗长已超过区外故障时1.35 ms的保护窗长。由此将导致只能凭借波头极性变换顺序区分区内、外故障。当受噪声干扰影响时易使得所提判据拒/误动的概率大大提升，在丢失了保护时间窗长Tpro的辅助作用后，相继速动判据的可靠性严重降低。此外，当αmax变大时，二次波的振荡周期变长，行波能量耗散程度变大，MMG极性幅值降低，导致保护速动性和灵敏性下降。因此，本文假定αmax的最大取值为20%能够有效保证所提判据具备较优异的动作性能。
3.3.3 对线路空载运行的适应性
设置新能源场站因夜间环境而不向外馈出功率，此时线路L1处于空载运行状态。现于线路L1上f1处设置带20 Ω过渡电阻的相间故障，其距离R1处25 km，此时R0处保护检测点所感受到的电流线模行波分量i1及相继速动判据动作情况如图11所示。
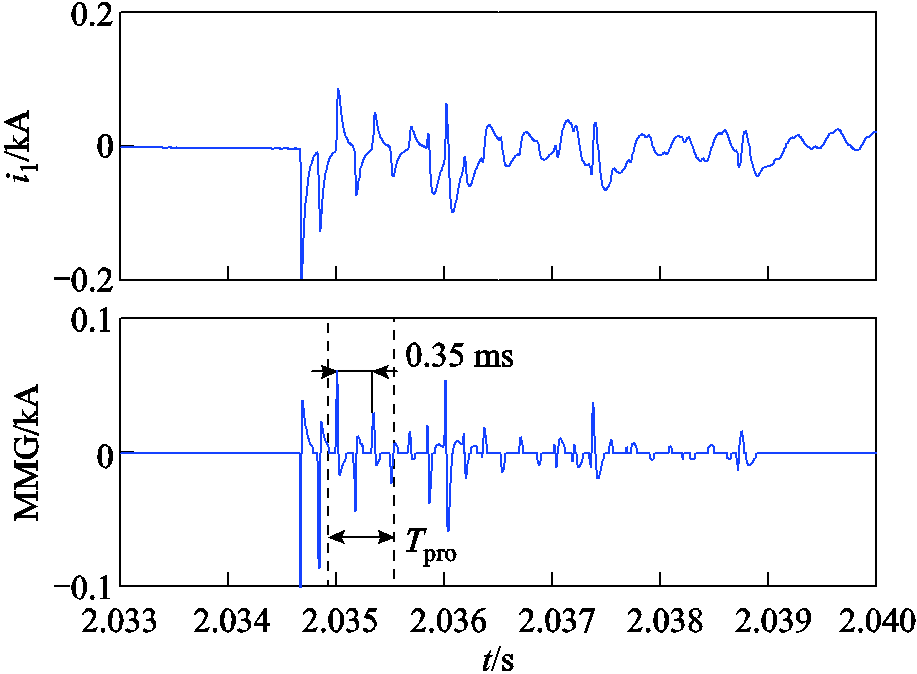
图11 保护判据对线路空载运行的适应性分析
Fig.11 The adaptability analysis of criterion to unloaded lines
由图11可知，当线路空载运行时，对端断路器断开后仍然能够产生十分显著的二次振荡波过程，这是因为线路空载运行时输电线路上依然存储有沿线分布的电磁能量，由此证明了本文所提相继速动判据的动作性能与系统运行方式无关。
3.3.4 对35 kV三相跳闸系统的适应性
220 kV及以上的系统在单相接地故障时采用单相跳闸方式，在其余故障时采用三相跳闸方式；110 kV及以下的系统仅采用三相跳闸方式。现于图5中35 kV线路L5上设置带50 Ω过渡电阻的单相接地故障，其距离变压器处母线4 km（35 kV电源侧主保护本级线路盲区故障范围内），此时变压器侧线路断路器三相跳闸，该线路线模行波波速为2.98×105 km/s，保护时间窗长Tpro为0.089 ms，则此时35 kV电源侧线路保护检测点所感受到的电流线模行波分量i1及相继速动判据动作情况如图12所示。
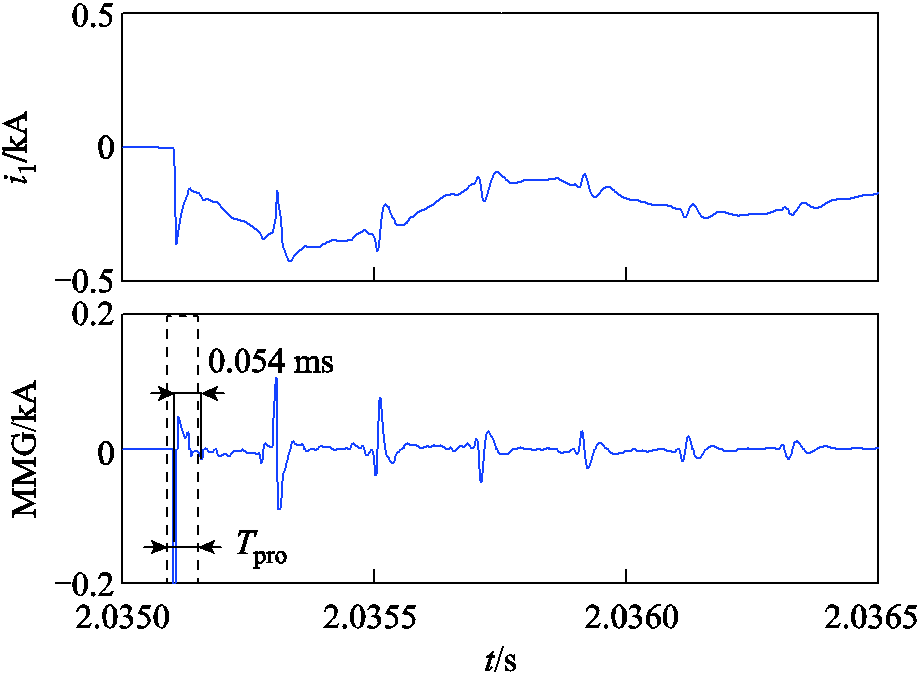
图12 保护判据对断路器跳开方式的适应性分析
Fig.12 The adaptability analysis of criterion to the tripping modes of the circuit breaker
由图12可知，此时35 kV电源侧线路保护检测点同样能够感受到MMG极值按照正负、负正、正负极性顺序先后交替出现的二次振荡波过程。因此，本文在第1节所分析的二次振荡波传输特性与断路器的跳开方式无关，其能够同时适用于不同电压等级的输电系统。但是，对于相间以及三相金属性故障而言，其在不同电压等级下均属于特殊故障类型，仍然需要辅以相应的辅助判据，以实现相继速动功能。
由于时间分辨率的限制，以及实际工程中无法无限制地提高采样频率，当故障位置极度靠近对端母线时，二次波过程振荡频率过高，本地保护侧因受采样定理制约而将无法感受到振荡波过程。由式（2）振荡周期公式推导可知，采样频率与保护判据动作死区的关系为
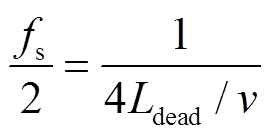（15）
式中，fs为采样频率；Ldead为保护判据动作死区。
当采样频率为200 kHz时，根据式（15）计算可得，保护判据动作死区为线路末端743 m范围内，即对于线路L1而言，若故障位置位于线路末端99.63%～100%范围内时，本地保护侧将无法感知到振荡波过程而导致判据拒动。当采样频率分别为100 kHz、500 kHz、1 MHz时，保护判据动作死区分别为线路末端1 485、297、149 m范围内，即采样频率越高，所提相继速动判据的动作死区越小。现于线路L1上f1处设置带10 Ω过渡电阻的相间故障，其距离R1处0.5 km（保护判据动作死区内），此时R0处保护检测点所感受到的电流线模行波分量i1及相继速动判据动作情况如图13所示。
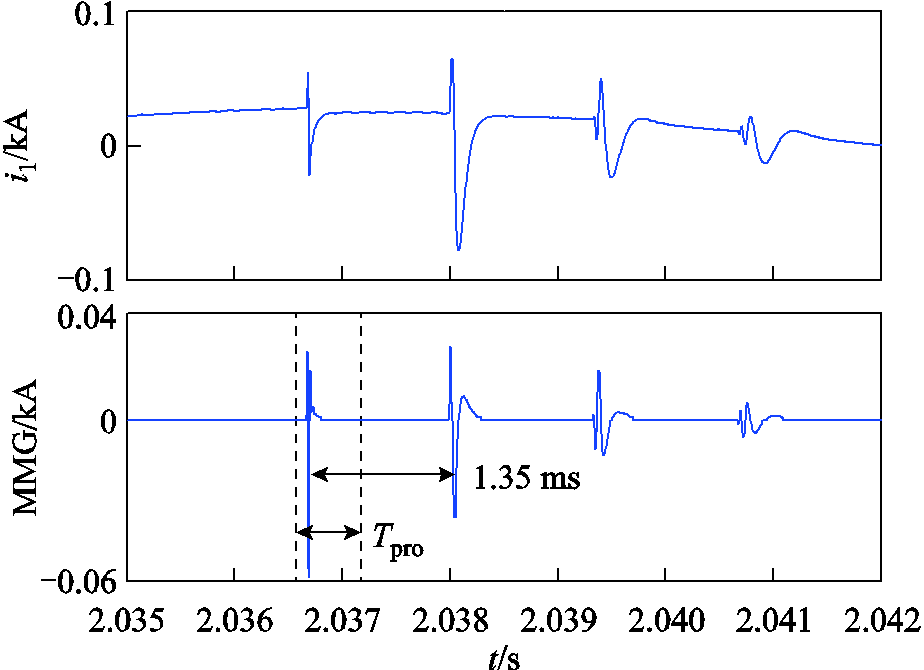
图13 本级线路动作死区判据动作情况
Fig.13 The criterion action result under dead zone faults
由图13可知，此时本地保护侧无法量测到故障点与对端断路器之间的二次振荡波，但仍能感受到以线路全长为振荡周期的振荡波过程，因此不满足式（12）所示的判据，相继速动保护将拒动。但是注意到，当故障位置位于式（12）不能反应的、范围极小的动作死区内时，本地保护侧仍能感受到以线路全长为振荡周期的振荡波过程，因此同样可考虑利用判据式（13）进行故障判别，即以距离Ⅱ段阻抗元件判断故障是否仍然存在，由此即可进一步改善保护的动作性能。但考虑到阻抗元件对过渡电阻的耐受能力十分有限，因此当发生位于本级线路保护判据动作死区内的高阻故障时，式（13）判据仍会拒动。针对位于相继速动判据动作死区范围内的高阻故障难题，有待后续开展深入研究。
现将本文所提的基于二次振荡波过程的相继速动判据与现有的相继速动判据进行对比，其性能比较结果见表2。
表2 本文所提判据与现有保护判据的性能比较
Tab.2 The performance comparisons between the proposed criterion and the conventional protection criterions
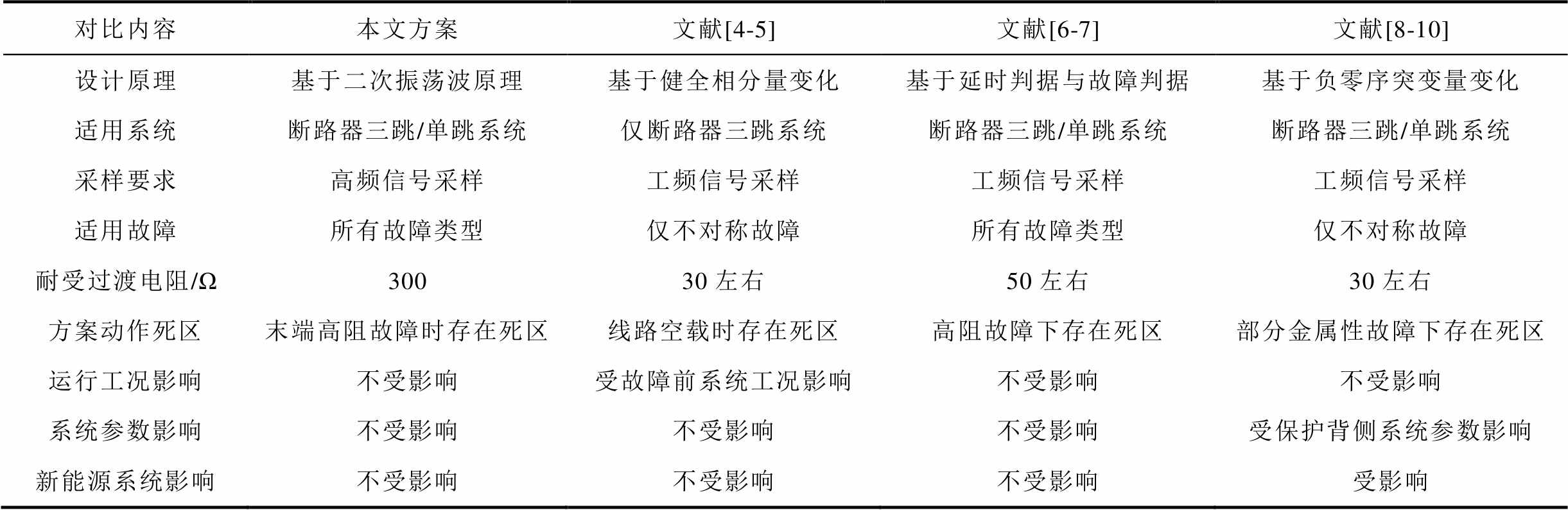
对比内容本文方案文献[4-5]文献[6-7]文献[8-10] 设计原理基于二次振荡波原理基于健全相分量变化基于延时判据与故障判据基于负零序突变量变化 适用系统断路器三跳/单跳系统仅断路器三跳系统断路器三跳/单跳系统断路器三跳/单跳系统 采样要求高频信号采样工频信号采样工频信号采样工频信号采样 适用故障所有故障类型仅不对称故障所有故障类型仅不对称故障 耐受过渡电阻/Ω30030左右50左右30左右 方案动作死区末端高阻故障时存在死区线路空载时存在死区高阻故障下存在死区部分金属性故障下存在死区 运行工况影响不受影响受故障前系统工况影响不受影响不受影响 系统参数影响不受影响不受影响不受影响受保护背侧系统参数影响 新能源系统影响不受影响不受影响不受影响受影响
分析表2可知，本文所提的相继速动判据相比现有判据的优势在于适应三相/单相跳闸系统，不受运行工况及系统参数影响，耐受过渡电阻能力强，特别是本文判据的设计原理为基于输电线路固有特性的二次振荡波过程，其与新能源场站的电源控制特性无关，因此该判据能够可靠承担起新型电力系统下的相继速动职能。但与此同时，本文判据所需的高频采样条件也对实际保护硬件设备提出了客观需求。
在细致分析断路器开断产生的二次振荡波传输机理的基础上，本文提出一种基于二次振荡波过程的交流电网全新相继速动判据，得到以下结论：
1）本文所提判据适用于三相/单相跳闸系统和所有故障类型，不受运行工况与系统参数影响，同时耐受过渡电阻能力高达300 Ω。
2）当母线系统并不具备注入特征信号的能力时，本地保护侧在三相金属性故障下将不再执行相继速动功能，该难题有待后续开展深入研究。
3）采样频率越高，本文所提相继速动判据的动作死区越小。本文针对保护判据动作死区提出了初步的解决方案，但暂时无法有效应对动作死区内的高阻故障工况。
附 录
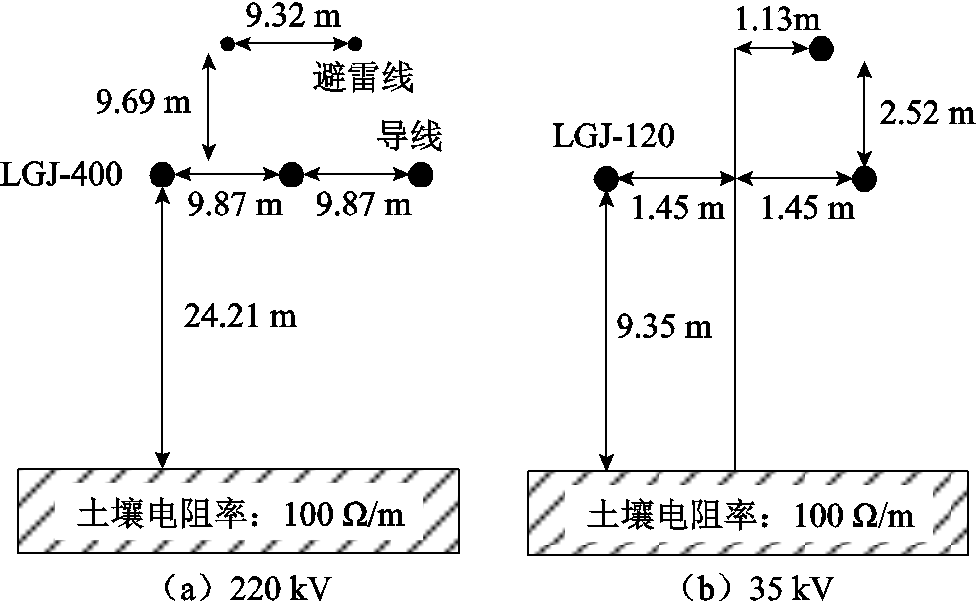
附图1 输电线路结构参数
App.Fig.1 The transmission line configuration parameters
·避雷线 ●导线
参考文献
[1] 束洪春, 刘力滔, 唐玉涛, 等. 基于行波暂态能量的半波长输电线路高灵敏增强型纵联保护方案[J]. 电工技术学报, 2022, 37(24): 6372-6387.
Shu Hongchun, Liu Litao, Tang Yutao, et al. Highly sensitive enhanced pilot protection scheme for half-wavelength transmission lines based on traveling wave transient energy[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6372-6387.
[2] 金瑞, 林湘宁, 时伯年. 基于测量阻抗轨迹的接地距离保护自适应整定方法[J]. 电力系统自动化, 2022, 46(14): 185-192.
Jin Rui, Lin Xiangning, Shi Bonian. Adaptive setting method of grounding distance protection based on measured impedance trajectory[J]. Automation of Electric Power Systems, 2022, 46(14): 185-192.
[3] 李宝伟, 石欣, 王志伟, 等. 基于罗氏线圈电流互感器的等传变距离保护[J]. 电工技术学报, 2023, 38(5): 1353-1362.
Li Baowei, Shi Xin, Wang Zhiwei, et al. Distance relay based on rogowski coil current transformer by using instantaneous value after equal transfer processes[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1353-1362.
[4] 黄烜, 张安琪, 周培钰. 基于不同运行方式的不对称相继速动功能投退策略的研究[J]. 广西电力, 2021, 44(2): 79-86.
Huang Xuan, Zhang Anqi, Zhou Peiyu. Research on switching strategy of asymmetric successive quick-acting function based on different operation modes[J]. Guangxi Electric Power, 2021, 44(2): 79-86.
[5] 刘少波. 具有全线相继速动功能的110kV线路微机距离保护装置研究[D]. 武汉: 华中科技大学, 2008.
[6] 甘忠, 董新洲, 薄志谦. 输电线路自适应无通道保护(一) 故障分析与保护原理[J]. 电力系统自动化, 2002, 26(7): 33-37.
Gan Zhong, Dong Xinzhou, Bo Zhiqian. Adaptive non-communication protection for transmission lines part one: fault analysis and protection principle[J]. Automation of Electric Power Systems, 2002, 26(7): 33-37.
[7] 甘忠, 董新洲, 薄志谦. 输电线路自适应无通道保护(二): 构成方案与仿真试验[J]. 电力系统自动化, 2002, 26(8): 29-32, 68.
Gan Zhong, Dong Xinzhou, Bo Zhiqian. Adaptive non-communication protection for transmission lines part two: scheme and simulation[J]. Automation of Electric Power Systems, 2002, 26(8): 29-32, 68.
[8] Liu Pei, Chen Deshu, Peng Hua, et al. Analysis of an accelerated trip scheme for faults in the second zone of protection of a transmission line[J]. IEEE Transactions on Power Delivery, 1990, 5(1): 72-78.
[9] 侯喆, 张艳霞, 戴剑锋. 基于小波理论的全线相继速动保护方案[J]. 电力系统自动化, 2003, 27(9): 54-57.
Hou Zhe, Zhang Yanxia, Dai Jianfeng. Accelerated trip scheme for the whole transmission line based on wavelet transform[J]. Automation of Electric Power Systems, 2003, 27(9): 54-57.
[10] 施慎行, 董新洲, 刘建政, 等. 配电线路无通道保护研究[J]. 电力系统自动化, 2001, 25(6): 31-34.
Shi Shenxing, Dong Xinzhou, Liu Jianzheng, et al. Non- communication protection for power linesin distribution system[J]. Automation of Electric Power Systems, 2001, 25(6): 31-34.
[11] 亢丽君, 王蓓蓓, 薛必克, 等. 计及爬坡场景覆盖的高比例新能源电网平衡策略研究[J]. 电工技术学报, 2022, 37(13): 3275-3288.
Kang Lijun, Wang Beibei, Xue Bike, et al. Research on the balance strategy for power grid with high proportion renewable energy considering the ramping scenario coverage[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3275-3288.
[12] 晁晨栩, 郑晓冬, 高飘, 等. 针对光伏场站送出线路不对称短路故障的自适应距离保护原理[J]. 中国电机工程学报, 2022, 42(18): 6681-6693.
Chao Chenxu, Zheng Xiaodong, Gao Piao, et al. Adaptive distance protection principle for asymmetric short circuit fault of photovoltaic station transmission line[J]. Proceedings of the CSEE, 2022, 42(18): 6681-6693.
[13] Lin Xiangning, Zheng Yuchao, Tong Ning, et al. Fast mutual-speed-up protection adaptive to dead-zone grounding-fault identification for VSC-MTDC[J]. IEEE Transactions on Power Delivery, 2021, 36(6): 3393-3403.
[14] 陈平, 葛耀中, 索南加乐, 等. 输电线路故障开断暂态行波的传播特性研究[J]. 中国电机工程学报, 2000, 20(7): 75-78.
Chen Ping, Ge Yaozhong, Suonan Jiale, et al. Study on propagation characteristics of fault switching-off induced transient travelling waves on transmission lines[J]. Proceedings of the CSEE, 2000, 20(7): 75-78.
[15] 陈平, 葛耀中, 徐丙垠. 利用故障线路分闸暂态行波的故障测距研究[J]. 电力系统自动化, 2004, 28(1): 53-58.
Chen Ping, Ge Yaozhong, Xu Bingyin. Research on fault location using fault tripping induced travelling waves[J]. Automation of Electric Power Systems, 2004, 28(1): 53-58.
[16] 季涛. 基于暂态行波的配电线路故障测距研究[D]. 济南: 山东大学, 2006.
[17] Namdari F, Salehi M. High-speed protection scheme based on initial current traveling wave for transmission lines employing mathematical morphology[J]. IEEE Transactions on Power Delivery, 2017, 32(1): 246-253.
[18] 张保会, 尹项根. 电力系统继电保护[M]. 北京: 中国电力出版社, 2022.
[19] 郑涛, 王赟鹏, 马家璇, 等. 适用于UPFC接入线路的主动注入式故障测距方法[J]. 电力自动化设备, 2022, 42(6): 138-145.
Zheng Tao, Wang Yunpeng, Ma Jiaxuan, et al. Fault locating method based on active injection for transmission lines equipped with UPFC[J]. Electric Power Automation Equipment, 2022, 42(6): 138-145.
[20] Wang Ting, Song Guobing, Hussain K S T. Adaptive AC autoreclosing scheme in MMC-based hybrid AC/DC transmission[J]. IET Generation, Transmission & Distribution, 2019, 13(19): 4464-4471.
[21] 哈恒旭, 张保会, 吕志来, 等. 超高压输电线单端暂态量保护的新原理探讨[J]. 电工技术学报, 2001, 16(6): 65-69, 94.
Ha Hengxu, Zhang Baohui, Lü Zhilai, et al. A study of non-unit transient protection principle for EHV transmission lines[J]. Transactions of China Electrotechnical Society, 2001, 16(6): 65-69, 94.
[22] 陈双, 何正友, 李小鹏. 基于行波固有频率的特高压输电线路故障选相[J]. 电网技术, 2011, 35(6): 15-21.
Chen Shuang, He Zhengyou, Li Xiaopeng. Faulty phase selection for UHV transmission lines based on natural frequencies of traveling waves[J]. Power System Technology, 2011, 35(6): 15-21.
[23] 杜磊, 赵涛, 冯之健, 等. 单相短路故障条件下级联模块中压光伏发电系统的有功功率回流抑制[J]. 电工技术学报, 2022, 37(20): 5201-5213.
Du Lei, Zhao Tao, Feng Zhijian, et al. Suppression of active power backflow in cascaded module medium voltage photovoltaic power generation system under single-phase short circuit fault condition[J]. Transactions of China Electrotechnical Society, 2022, 37(20): 5201-5213.
The Fast Sequential Action Principle for AC Power Grid Based on the Secondary Travelling Waves Processes
Abstract Currently, high-voltage/ultra-high-voltage transmission lines mainly adopt unit protections as their main protection. However, considering communication failure, transmission time delay, and expensive construction cost for unit protections, non-unit protections, such as impedance relays, as complementary protection functions with the unit protections, play an indispensable role in the safe operation of the power grid. Due to protection selectivity and reliability, it is difficult for non-unit protections to cover the full length of the protected line. That is, there is a protection non-detection zone, usually the high-resistance zone within the protection scope, and all zones outside the protection scope of the protected line.
In order to accelerate the fault clearing in the non-detection zone, non-unit protections must realize reliable identification of non-detection zone faults, namely, the fast sequential action principle. Therefore, many scholars have presented many achievements in early research. However, the performance of the existing fast sequential action principle is limited by operating conditions and system parameters, and they cannot withstand high fault resistance. Therefore, constructing a novel fast sequential action principle to overcome the above problems is urgent.
This paper presents a novel fast sequential action principle based on the secondary oscillating traveling waves generated by remote circuit breaker operation. Firstly, the differences in the secondary oscillating traveling waves process under the internal non-detection zone and external faults are studied using the Bewley lattice diagram. The secondary oscillating traveling waves under different fault locations exhibit significant differences in oscillatory period and wave front polarity. Secondly, the local relay can always detect the secondary oscillating traveling waves generated by faults on the adjacent line. However, for the secondary oscillating traveling waves generated by internal fault, whether it can be effectively detected needs to analyze the reflection and refraction coefficient of the fault point. Therefore, the propagation processes of secondary oscillating traveling waves under different fault types are investigated based on the modulus equivalent circuit. And the special traveling waves processes under BC and ABC metallic faults are discussed. Afterward, the identification criterion of oscillating traveling waves’ polarity based on the mathematical morphology gradient algorithm is proposed, which can deal with the most fault conditions in the non-detection zone. Otherwise, the additional criterion for BC metallic fault is constructed based on the Zone-2 impedance relay. For ABC metallic fault, an active scheme based on the signal injection and a passive scheme based on blocking fast sequential action principle are proposed, respectively.
Finally, based on the PSCAD simulation platform, the proposed protection criterion’s effectiveness, sensitivity, and reliability are verified through extensive simulation cases. The criterion adaptability to noises, the scope of the non-detection zone, the unloaded lines, and the tripping modes of the circuit breaker are analyzed. Compared with the existing schemes, the proposed approach is suitable for three-pole/single-pole tripping and all fault types, unaffected by operating conditions and system parameters, and can endure fault resistance up to 300 Ω.However, due to the sampling frequency having an upper limit, the oscillating frequency of secondary traveling waves processes is too high to be detected when the fault is extremely close to the opposite bus. In other words, there is a dead zone for the proposed fast sequential action principle. Although the preliminary solution is proposed based on the Zone-2 impedance relay, it can still not effectively cope with the high resistance fault in the dead zone, which is worth further studying.
keywords：Fast sequential action principle, the secondary oscillating traveling waves, mathematical morphology gradient, non-detection zone fault, traveling waves modulus equivalent circuit
中图分类号：TM773
DOI:10.19595/j.cnki.1000-6753.tces.221731
国家重点研发计划资助项目（2021YFB2401000）。
收稿日期 2022-09-13
改稿日期 2023-03-26
吴宇奇 男, 1997年生, 博士研究生, 研究方向新型电力系统保护与控制。E-mail：798893267@qq.com
黎 钊 男, 1998年生, 硕士研究生, 研究方向为新型电力系统保护与控制。E-mail：M202071511@hust.edu.cn（通信作者）
（编辑 赫 蕾）