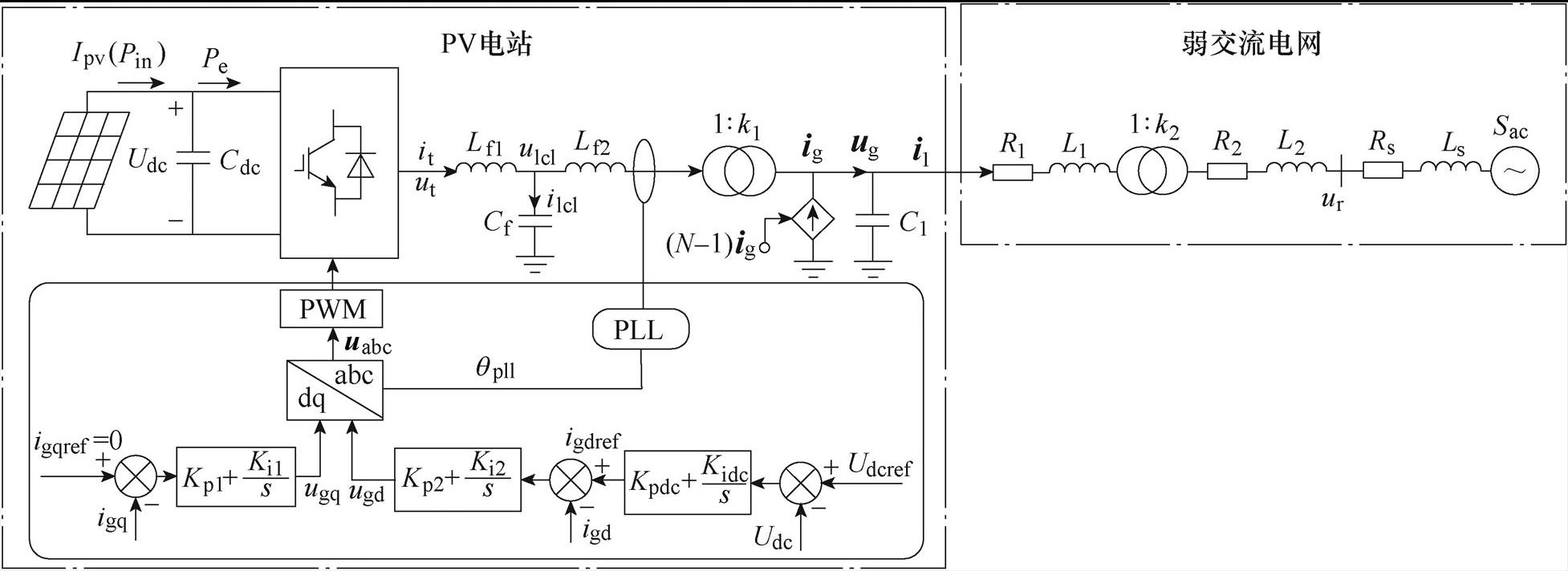
图1 PV并入弱交流电网系统结构
Fig.1 Schematic diagram of the PV plant integrated to weak AC grid system
摘要 大规模光伏发电经长距离输电线路并入主网时,光伏电站和弱交流电网的交互作用可能使光伏并网系统面临次同步振荡(SSO)的威胁,但目前针对系统内部次同步交互作用的相关研究较少。针对上述问题,该文首先将阻尼转矩法推广到锁相环(PLL)振荡模态,并推导了光伏并网系统的线性化闭环传递函数框图。然后,基于闭环传递函数框图,揭示了PLL主导的SSO模式下系统阻尼构成和光伏电站与弱交流电网间动态交互过程。最后,借鉴等效阻尼系数量化评估了次同步交互作用的阻尼特性。结果表明,光伏并入弱交流电网系统存在PLL主导的SSO风险;光伏电站与弱交流电网的次同步交互作用向光伏并网系统提供负阻尼,是系统SSO的主导因素;增加PLL比例系数、交流电网强度、光伏电站光照强度或温度,减小PLL积分系数或光伏容量,能够增加次同步交互作用的阻尼贡献,提高光伏并网系统稳定性。时域仿真验证了理论分析结果的正确性。
关键词:光伏电站 次同步振荡 次同步交互作用 阻尼转矩法 锁相环
近年来,我国光伏(Photovoltaic, PV)发电新增装机容量不断增加[1],已明确到2030年,风电和太阳能发电总装机容量将达到12亿kW以上,PV发电具有广阔的发展前景[2-4]。其中,我国西北省份太阳能发电量优势明显[5],是PV基地的主力区域。然而,大规模PV电站通过远距离输电并入电网时,系统可能存在次同步振荡(Subsynchronous Oscilla- tion, SSO)风险,严重威胁新能源并网系统的稳定运行。
2015年,我国新疆哈密直驱风电场发生多起SSO事故[6],风电场和弱交流电网间次同步交互作用是造成风机并网系统SSO的主要原因之一[7-10]。PV与风机的逆变器控制策略较为相似,并网接口具有较高的一致性,两者表现出相似的涉网特性[11]。因此,PV电站与弱交流电网间次同步交互作用同样存在引起PV并网系统SSO的风险。然而,鲜有文献针对PV并网系统中次同步交互作用的机理特性展开研究。文献[12]研究了PV并网逆变器与串补线路的交互作用对PV经串补并网系统稳定性的影响。文献[13]建立了PV并网系统小信号模型,分析了PV电站参数和电网强度对系统SSO模态的影响。文献[14]指出PV电站与弱交流电网在次同步频域交点处的相位裕度不足,PV并入弱交流电网存在SSO风险。现有研究主要对PV并网系统的SSO发生机理展开分析,但系统内部次同步交互作用的阻尼特性及影响因素尚不清楚。因此,有必要对PV电站与弱交流电网间次同步交互作用展开相关分析,弥补当前PV并网系统SSO研究的不足。
目前,主流的SSO交互作用的分析方法主要有特征值法、开环模态谐振分析法和阻抗分析法。特征值法能够分析得到系统不同SSO模态的参与变量和相关子系统[13, 15];开环模式谐振分析法则能够从开环模态耦合的角度揭示子系统之间的动态交互作用[16-17]。然而,基于状态空间模型的特征值法和开环模态谐振分析法作为一种数学分析方法,分析过程物理意义不明确。基于频域的阻抗分析法则能够从阻抗外特性角度解释子系统间交互作用机 理[18-19],但其缺乏交互作用阻尼特性的量化评估指标。鉴于现有方法的局限性,亟须从新的角度对PV电站与弱交流电网间次同步交互作用进行研究。
相比于特征值法和阻抗分析法等方法,阻尼转矩法(Damping Torque Analysis, DTA)能够通过阻尼系数定量评估子系统间交互作用对同步机轴系稳定性的影响[20]。已有文献通过将风机换流站的直流电容动态过程建模为类似于DTA中的同步机转子运动方程,分析了风力发电系统直流电容振荡模态的稳定性[21-23]。然而,DTA在PV并网系统SSO模态的稳定性分析的适用性尚不清楚。并且,当研究机网间交互作用的阻尼特性时,新能源并网系统更关注锁相环(Phase-Locked Loop, PLL)动态特性造成的失稳[24-26]。
因此,针对PV并入弱交流电网系统中PLL主导的弱阻尼SSO模式(下文简称SSO模式),本文将DTA推广到PLL动态方程,分析SSO模式下PV电站与弱交流电网间次同步交互作用的机理特性。为了便于分析,本文推导了PV并网系统闭环传递函数框图,并将反映系统SSO模式阻尼的闭环扰动传递路径定义为阻尼路径。通过分析系统SSO模式阻尼路径,揭示子系统间耦合关系和交互作用路径,以及交互作用路径影响系统SSO模式阻尼的动态过程。然后,通过传递函数推导,分离得到反映次同步交互作用的阻尼路径,并借鉴等效阻尼系数[20]量化评估次同步交互作用的SSO模式阻尼。因此,本文方法实现了次同步交互作用阻尼特性的定量分析,有利于新能源并网系统的局部阻尼精准调控,提高系统稳定性。
本文首先将DTA推广到PLL动态方程,实现了DTA在PV并网系统SSO模式的扩展和稳定性分析。其次,基于PV并网系统线性化闭环传递函数框图,从内部扰动传递角度揭示了PV电站与弱交流电网间的耦合关系和交互作用路径,并分析了交互作用路径影响SSO模式阻尼的动态过程。然后,通过阻尼路径分离实现次同步交互作用阻尼贡献的量化评估。最后,分析了PLL控制参数、PV容量、交流电网强度、PV电站光照强度和温度对次同步交互作用阻尼特性的影响。
PV并入弱交流电网系统结构如图1所示。图1中参数及相关变量定义如下:Cdc为PV电站直流电容,Cf、Lf1、Lf2分别为滤波器电容、电感,R1、R2、L1、L2、C1分别为线路电阻、电感、电容,Rs、Ls分别为电网等值阻抗;ipv、Udc、Pin、Pe分别为PV阵列输出电流、直流电容电压、PV阵列输出功率和网侧换流器输入功率,ut(it)、ulcl(ilcl)、ug(ig)分别为网侧换流器端电压(电流)、LCL滤波器电容电压(电流)和网侧电压(电流),il、ur分别为输电线路电流和电网电压。为便于研究PV电站与弱交流电网间次同步交互作用,本文将研究系统分为PV电站和弱交流电网两个子系统。

图1 PV并入弱交流电网系统结构
Fig.1 Schematic diagram of the PV plant integrated to weak AC grid system
PV电站子系统中,PV阵列经网侧换流器和滤波器输出电能,通过一级升压变压器并入35 kV汇集线。研究表明,当新能源并网系统发生SSO时,新能源场站作为一个整体与电网进行动态交互[15],基于新能源场站聚合模型得到的交互作用分析结果,对实际工程仍具有重要的参考价值[27-28]。故本文采用聚合等值模型来分析PV电站整体与弱交流电网间次同步交互作用。PV电站由150个1.4 MW的PV阵列聚合而成,光照强度和温度均采用标准工况下参数;网侧换流器基于电网电压定向的矢量控制,采用外环定直流电压、内环定电流的双闭环解耦控制策略;此外,PV电站采用LCL滤波器以抑制高频谐波,降低注入电网的谐波电流分量。PV电站具体参数见附表1。
弱交流电网子系统包含输电线路和受端交流系统两部分,其等效阻抗由35 kV线路阻抗Z1、二级升压变压器ZT、345 kV线路阻抗Z2及交流系统阻抗Zs组成,弱交流电网具体参数见附表2。交流电网强度由PV并网系统短路比(Short Circuit Ratio, SCR)确定,即
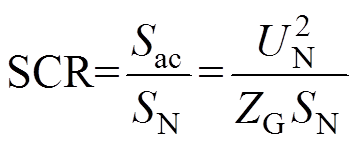 (1)
(1)
式中,Sac和SN分别为交流系统短路容量和PV电站额定功率;UN为系统额定电压;ZG为弱交流电网等效阻抗,ZG=Z1+Z2+ZT+Zs。
当PV电站远距离并网时,线路阻抗增大,ZG增大,SCR变小,电网强度降低。通过计算可得,本文所研究的PV并网系统SCR在2~3之间(SCR= 2.5),属于弱交流电网范畴。
本节将DTA中同步机转子方程推广到PLL动态方程,分析PV并网系统PLL振荡模态的稳定性,并结合阻尼转矩的物理意义,分析PV电站与弱交流电网间次同步交互作用的机理特性。
DTA中经典同步机转子的线性化动态方程为
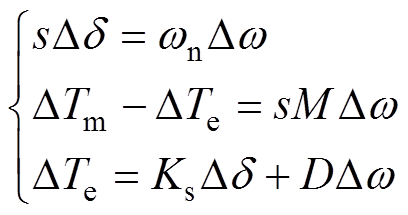 (2)
(2)
式中,M为惯性时间常数;Ks和D分别为同步系数和阻尼系数;Dd 为功角增量;Dw 为角速度增量;wn为同步角速度;DTm和DTe分别为机械转矩增量和电磁转矩增量。当转速产生偏差时,阻尼系数D的作用为形成阻尼转矩[29],抑制同步机轴系振荡,同步系数Ks则主要反映振荡频率。
下文通过传递函数推导将PLL的动态过程表示为类似于式(2)的形式,实现DTA在PV并网系统PLL振荡模态的应用和稳定性分析。其中,本文线性化传递函数方程中变量与图1中变量意义相同,D 表示增量,下标d、q和x、y表示变量在相应坐标系下的对应分量,下标0表示稳态值。
图2给出了PV电站PLL的结构原理框图,PLL的线性化方程可表示为
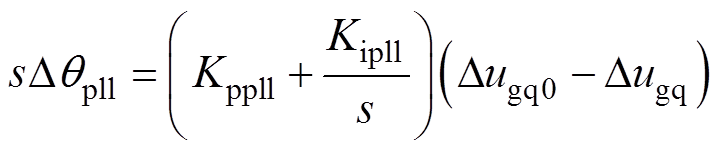 (3)
(3)
式中,Dugq为网侧电压q轴分量的增量;Dqpll为PLL输出角的增量。
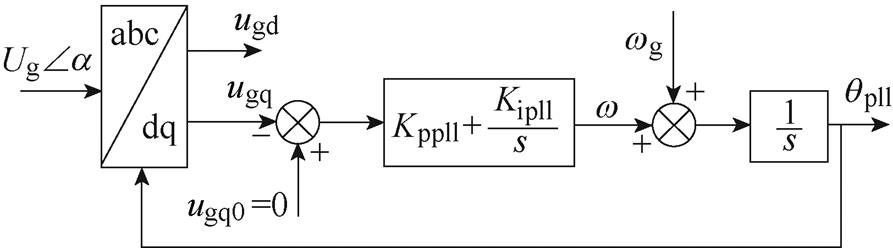
图2 PLL结构原理框图
Fig.2 Schematic diagram of the structure of PLL
令DTgq=(sKppll+Kipll)Dugq,式(3)可简写为
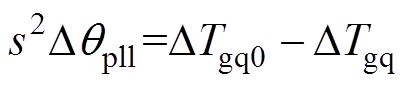 (4)
(4)
在PV并网系统中,当PLL的变量满足Dugq= Gpll(s)Dqpll,得到DTgq的表达式为
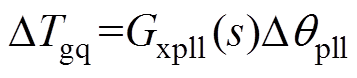 (5)
(5)
式中,Gxpll(s)=Gpll(s)(sKppll+Kipll)。将算子s=jw 代入Gxpll(s),得到Gxpll(s)的频域响应Gxpll(jw)。并且,Gxpll(jw)能够表示为实部和虚部的组合,即
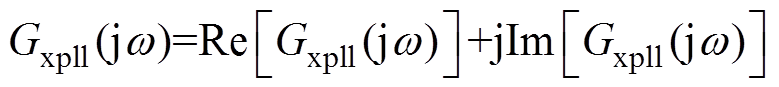 (6)
(6)
将式(6)代入式(5),得到DTgq的频域表达式为
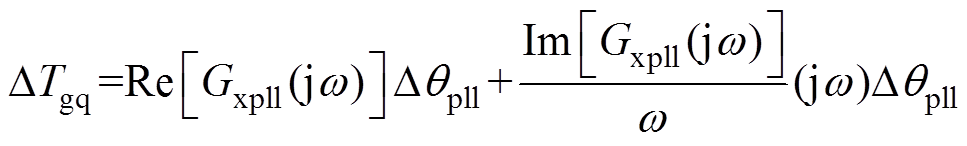 (7)
(7)
联立式(4)和式(7),得到了类似于式(2)的动态方程,即
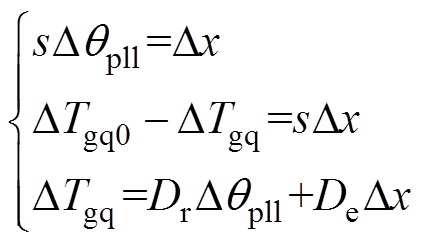 (8)
(8)
式中,De和Dr分别为SSO模式下相应的阻尼系数和同步系数。
因此,系统PLL动态具有类似于同步机转子的小干扰稳定性,如图3所示。参考DTA中相应系数的概念,SSO模式阻尼系数De和同步系数Dr的频域表达式分别为Im[Gxpll(jw)]/w 和Re[Gxpll(jw)]。当DTgq0=Dugq0=0时,式(8)可表示成一个二阶微分方程,其特征值为
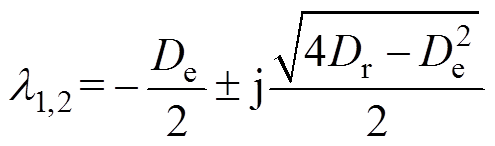 (9)
(9)
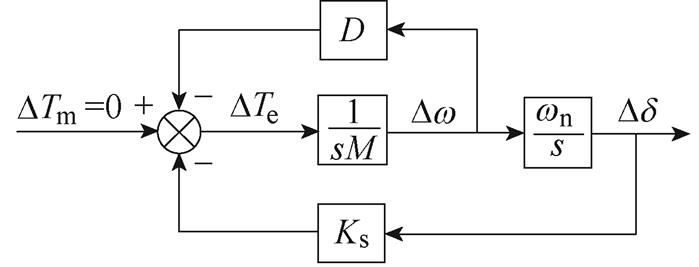
(a)同步机转子动态方程框图
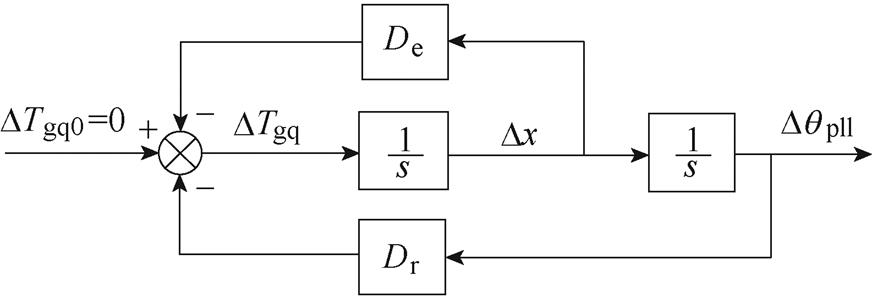
(b)PLL动态方程框图
图3 DTA动态方程的应用
Fig.3 Application of DTA dynamic equation
根据DTA中阻尼系数稳定判据,De可作为SSO模式阻尼的评估指标[23],判断系统稳定性。由式(9)特征值得到,当De<0时,电力系统或研究对象表现出负阻尼特性,可能导致系统SSO模式失稳。De越小,系统稳定性越差。
由De的表达式可得,SSO模式阻尼受PLL控制参数和Gpll(s)的影响。对应于本文PV并网系统,Gpll(s)刻画了PV电站与弱交流电网的复频域特性。通过分析Gpll(s)具体扰动传递过程,能够揭示系统阻尼构成和次同步交互作用机理。本文将反映系统SSO模式阻尼的扰动传递路径定义为阻尼路径,基于阻尼路径分析PV并网系统PLL振荡模态下次同步交互作用的机理特性。
系统闭环传递函数框图是基于阻尼路径进行次同步交互作用分析的基础,下一节推导PV并入弱交流电网系统的详细闭环传递函数框图,直观地展示系统的扰动传递过程和阻尼路径。
基于模块化建模[30]的方法,本节根据PV电站和弱交流电网子系统的各模块线性化传递函数方程,推导了PV并入弱交流电网系统的线性化模型,并得到相应详细的闭环传递函数框图。通过对比线性化模型与基于PSCAD/EMTDC的电磁暂态模型的阶跃响应,验证线性化模型及其闭环传递函数框图的有效性。
PV电站的动态模型包含PV阵列、直流电容、逆变器、LCL滤波器、PLL、线路电容和变压器。PV电站的开环传递函数框图推导过程如下。
本文研究SSO模式是由PV电站PLL主导的,其线性化传递函数方程为
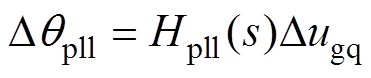 (10)
(10)
式中,Hpll(s)为PLL的开环传递函数,其具体表达式见附录式(A1)。
PV阵列、直流电容和网侧换流器的线性化传递函数方程分别如式(11)~式(13)所示。
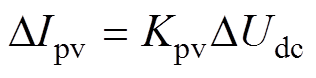 (11)
(11)
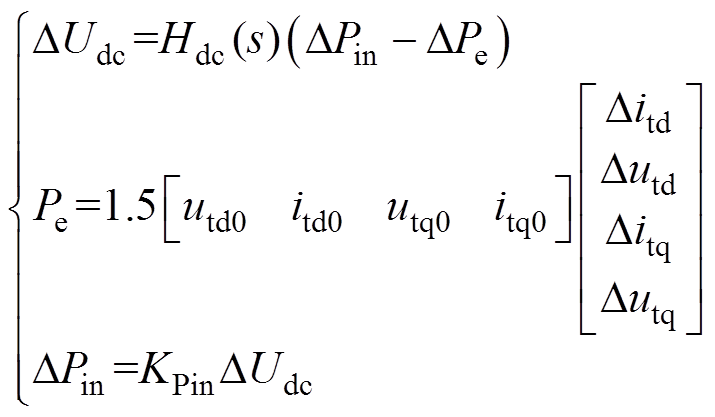 (12)
(12)
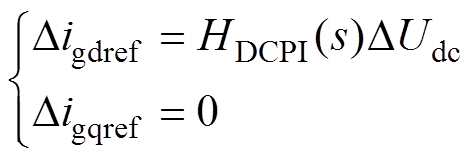 (13)
(13)
式中,Kpv、KPin分别为光伏阵列输出电流和输出有功功率的表达式;Hdc(s)、HDCPI(s)分别为直流电容环节、直流电压控制外环的开环传递函数,其具体表达式均已在附录式(A1)中给出。
其中,网侧换流器采用双闭环解耦控制策略,并且,直流电压控制外环的带宽通常是电流控制内环带宽的1/10。因此,可认为电流控制内环中网侧电流的实际值能够瞬时跟踪其指令值[31],即Digd= Digdref,Digq=Digqref。逆变器的功率因数通常设置为1[32],即igqref=0,满足Digq=Digqref=0。
LCL滤波器和线路并联电容的线性化传递函数方程分别为
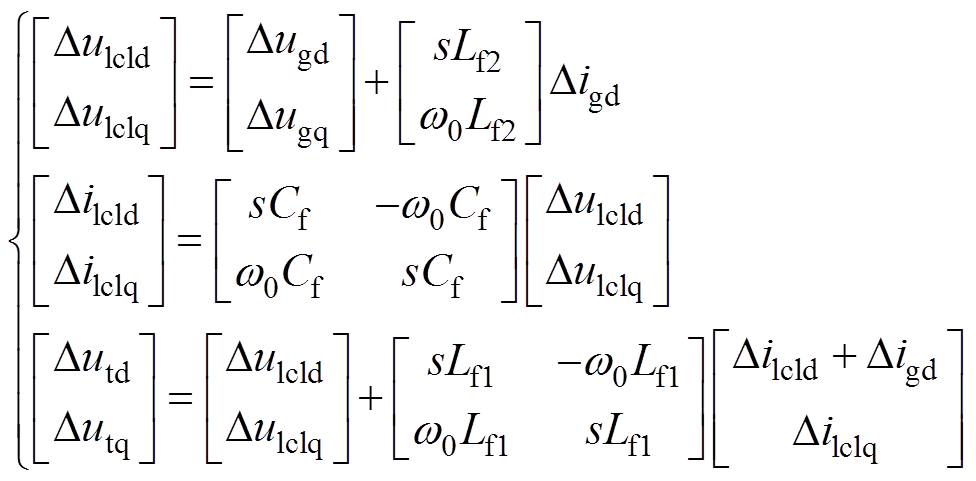 (14)
(14)
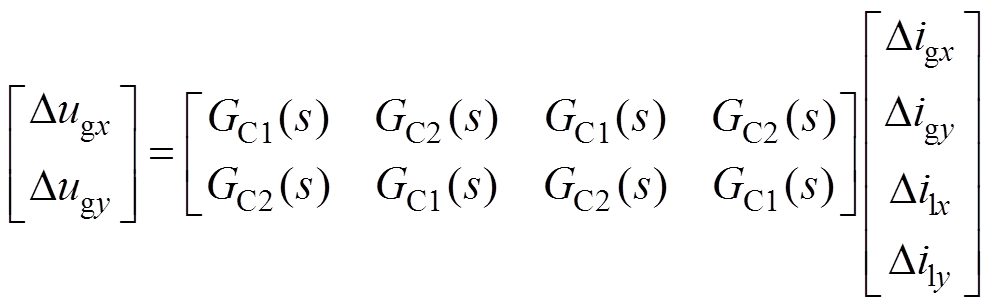 (15)
(15)
式中,GC(s)分别为线路并联电容在xy坐标系下的开环传递函数矩阵,其具体表达式见附录式(A2)。并且,根据式(14),可得到LCL滤波器的开环传递函数框图,如附图1所示。
网侧电压电流在dq坐标系与xy坐标系间的转换关系分别为
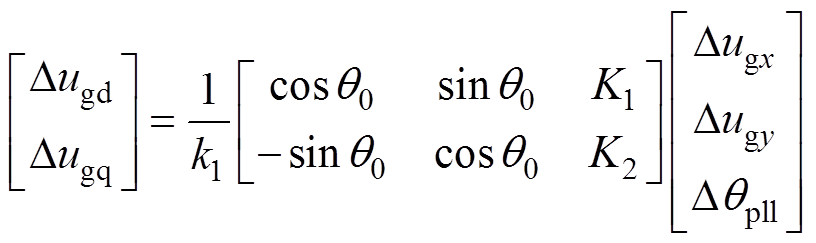 (16)
(16)
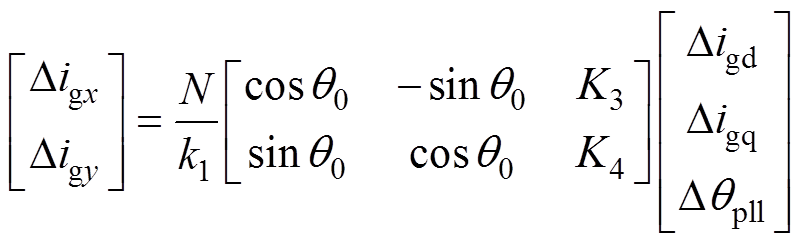 (17)
(17)
式中,N为PV阵列数;k1为一级升压变压器电压比;K1~K4为坐标变换的线性化表达式,其具体表达式见附录式(A3)。
联立式(10)和式(16),得
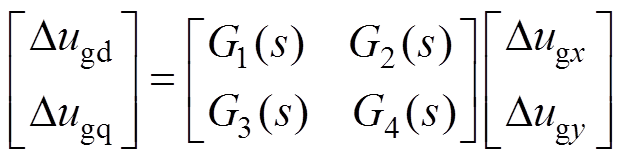 (18)
(18)
式中,G(s)为网侧电压Dug从xy坐标系到dq坐标系的开环传递函数矩阵,其具体表达式见附录式(A4)。
联立式(15)、式(17),消去中间变量Dig(x,y)得
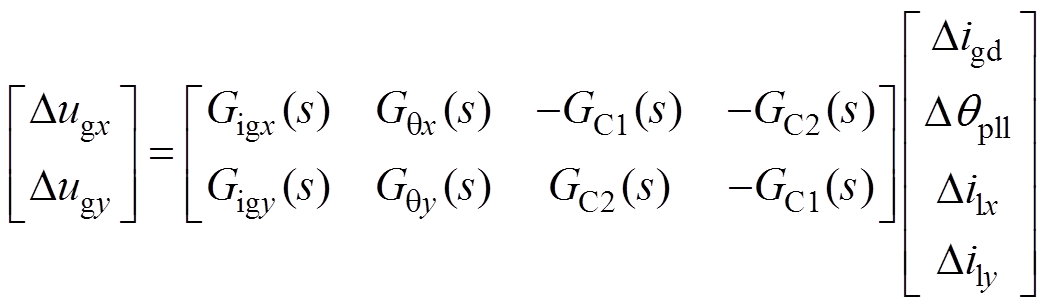 (19)
(19)
式中,GC(s)具体表达式与式(15)一致,Gig(s)、Gq(s)分别为网侧电流Digd、PLL输出角Dqpll到网侧电压xy轴分量Dug(x,y)的开环传递函数矩阵,其具体表达式见附录式(A5)。
根据式(10)、式(12)~式(14)和式(18)、式(19),得到PV电站的开环传递函数框图,如图4所示。图4说明PV电站的线性化模型以Dil(x,y)为输入、Dug(x,y)为输出,框图内扰动变量的传递体现了次同步扰动在PV电站中各个模块间动态传递过程。
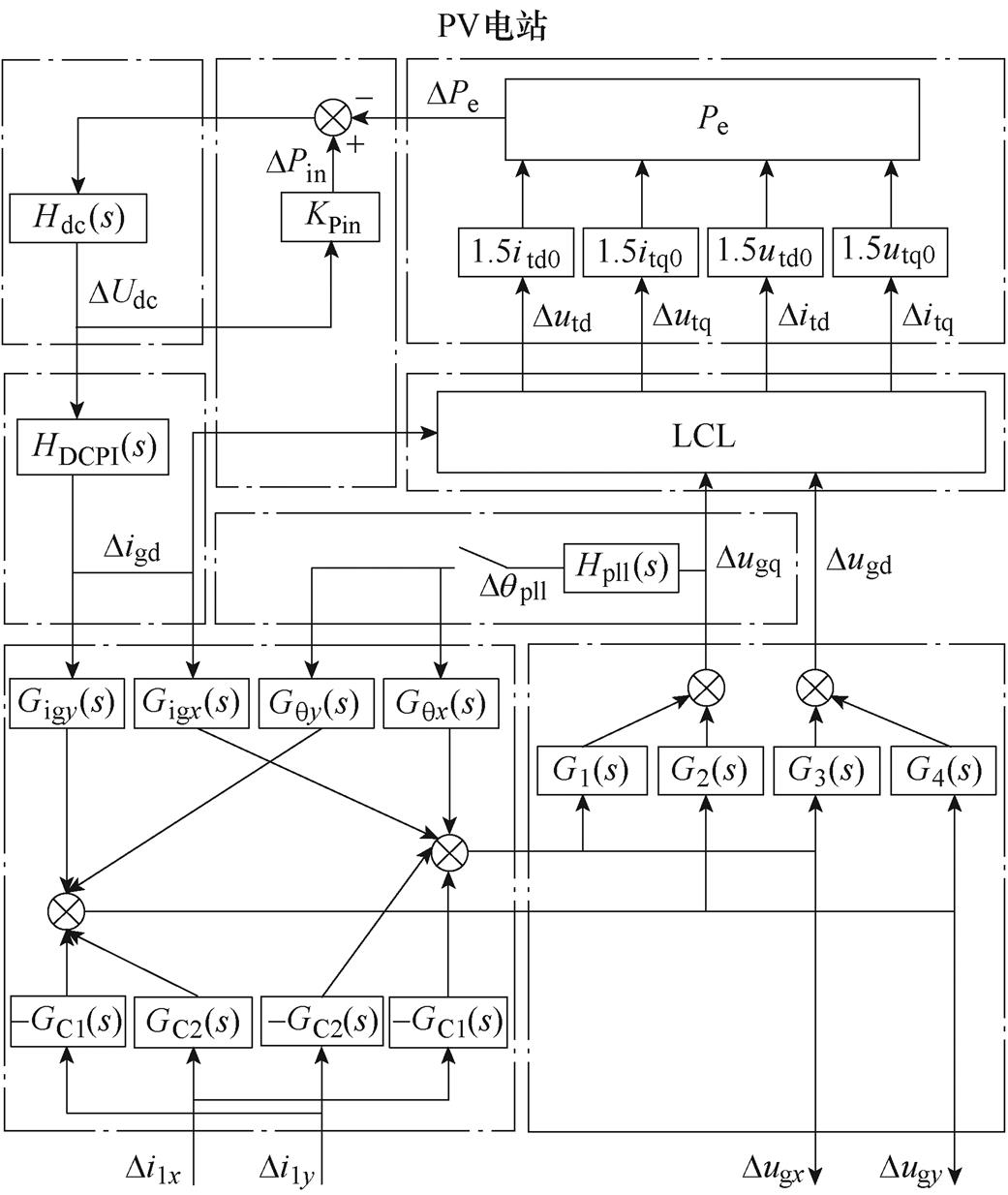
图4 PV电站传递函数框图
Fig.4 Transfer function block diagram of PV plant
弱交流电网子系统由输电线路和受端交流系统构成,通过求取弱交流电网等效阻抗,得到其线性化传递函数方程为
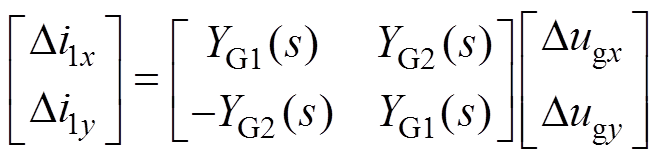 (20)
(20)
式中,YG(s)为弱交流电网子系统网侧电压xy轴分量Dug(x,y)到线路电流Dil(x,y)的开环传递函数矩阵,其具体表达式见附录式(A6)。
由式(20)得到弱交流电网的开环传递函数框图,如图5所示。图5说明弱交流电网的线性化模型以Dug(x,y)为输入、Dil(x,y)为输出,体现了弱交流电网导纳对次同步扰动的影响。
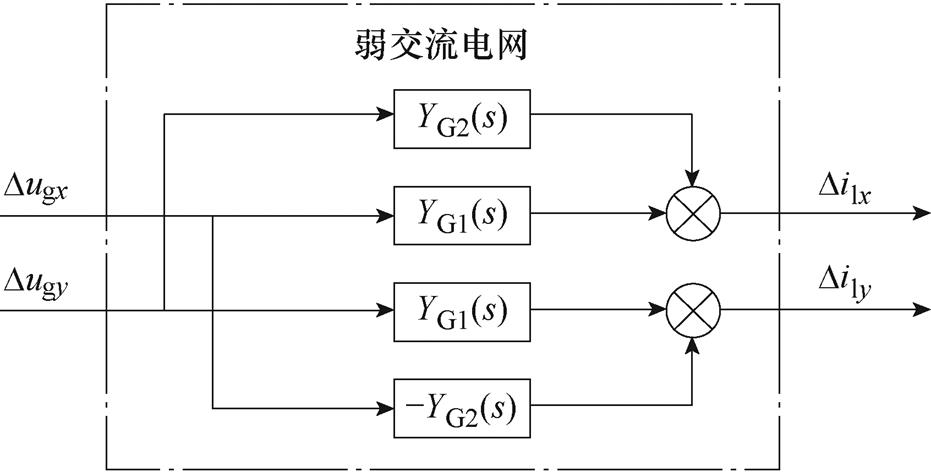
图5 弱交流电网传递函数框图
Fig.5 Transfer function block diagram of weak AC grid
连接子系统模型的输入输出端口,得到PV并网系统线性化模型及其详细闭环传递函数框图,对比线性化模型与基于PSCAD/EMTDC的电磁暂态模型的阶跃响应来验证其有效性。系统参数及运行工况如第1节所述,3.0 s时PV电站直流电容电压参考值Udcref由0.965 kV阶跃为1.015 kV,其他参数维持不变。图6a~图6d分别给出PV阵列输出电流Ipv、直流电容电压Udc、网侧电流d轴分量Igd、网侧电压q轴分量ugq在两种模型下的阶跃响应波形对比。
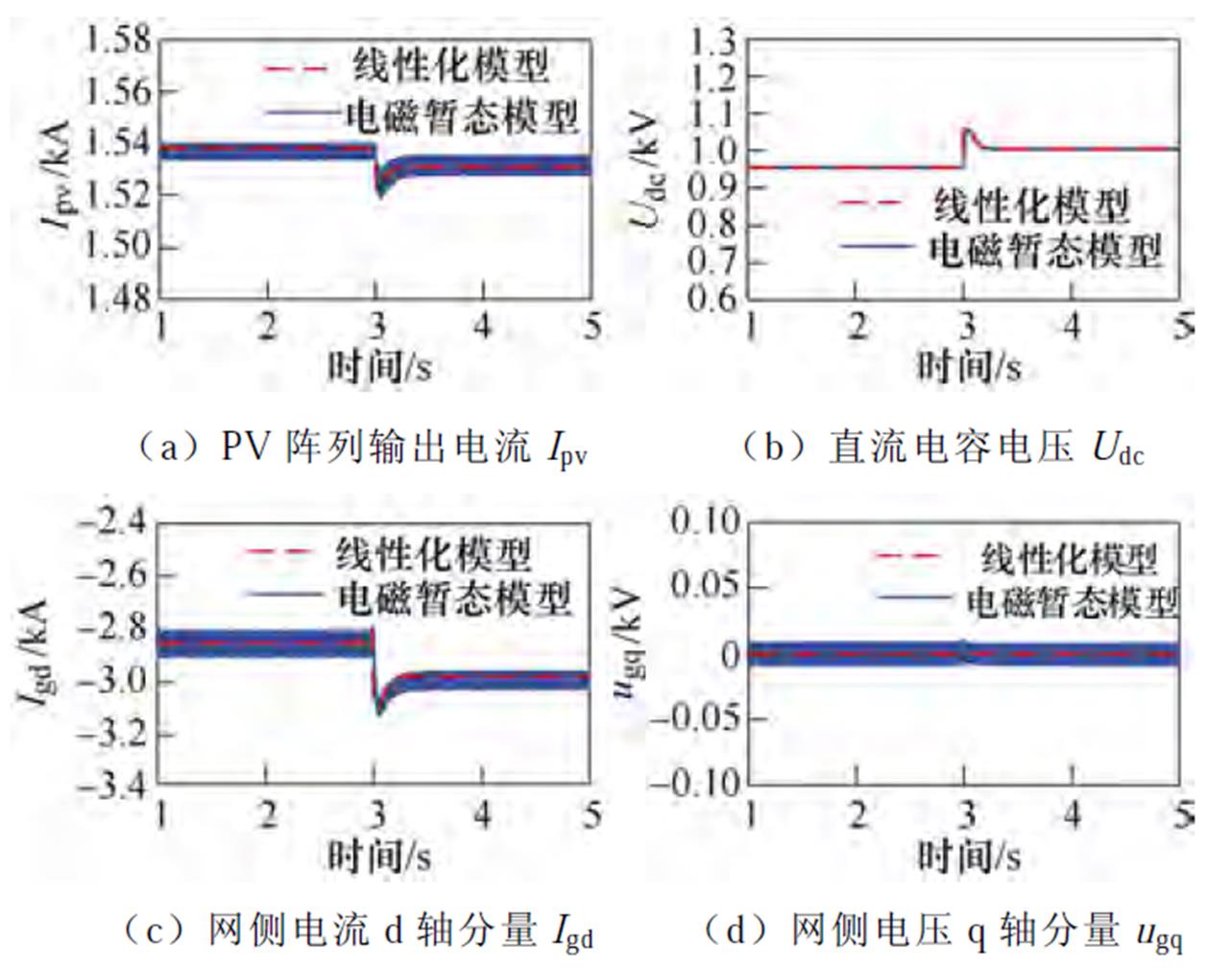
图6 阶跃响应波形
Fig.6 Step response waveforms
由图6a~图6d可得,线性化模型与电磁暂态模型的阶跃响应特性基本一致,验证了线性化模型及相应闭环传递函数框图的有效性。
本节以PLL振荡模态为例,基于系统闭环传递函数框图,从内部扰动传递的角度分析PV电站与弱交流电网间次同步交互作用路径和交互作用路径影响SSO模式阻尼的动态过程。并且,通过等效阻尼系数量化评估系统PV并网系统中次同步交互作用的阻尼特性。
为了直观地反映SSO模式下PV电站与弱交流电网间动态交互过程,本节将保留PLL和并网点电压电流变量,通过对其他环节的动态方程进行联立、合并,简化PV并网系统的闭环传递函数框图。
由图4可得,PV电站网侧电流Digd可表示为
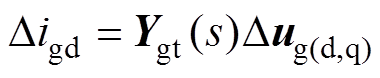 (21)
(21)
式中,Ygt(s)为PV电站从网侧电压dq轴分量Dug(d,q)到网侧电流Digd的开环传递函数矩阵(包含PV阵列、直流电容、逆变器以及LCL滤波器模块)。
PV电站网侧电压xy轴分量Dug(x,y)可表示为
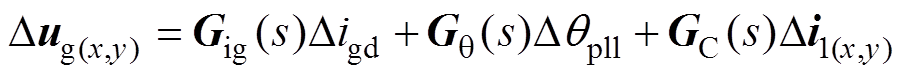 (22)
(22)
网侧电压Dug满足坐标变换关系
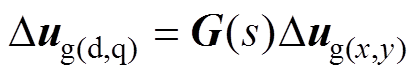 (23)
(23)
由图5可得,弱交流电网的线性化传递函数方程可简写为
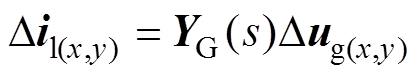 (24)
(24)
为反映PV电站与弱交流电网间变量联系,联立式(23)和式(24),得
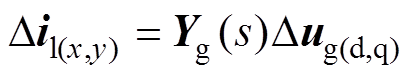 (25)
(25)
式中,Yg(s)=YG(s)G-1(s)为弱交流电网系统网侧电压dq轴分量Dug(d,q)到线路电流Dil(x,y)的开环传递函数矩阵。
式(21)~式(23)表征PV电站子系统中各变量间的开环传递函数关系,式(25)表征弱交流电网子系统输入量与输出量间的开环传递函数关系,连接PV电站和弱交流电网的输入输出端口,得到PV并网系统的简化闭环传递函数框图,如图7所示。图7体现了扰动在PV电站各个模块和弱交流电网导纳的动态传递过程,箭头表示扰动传递的方向。并且,在PLL主导的SSO模式下,阻尼路径可具体表示为次同步频率扰动围绕PLL形成的闭环扰动传递路径,如图7中实线闭环DP。
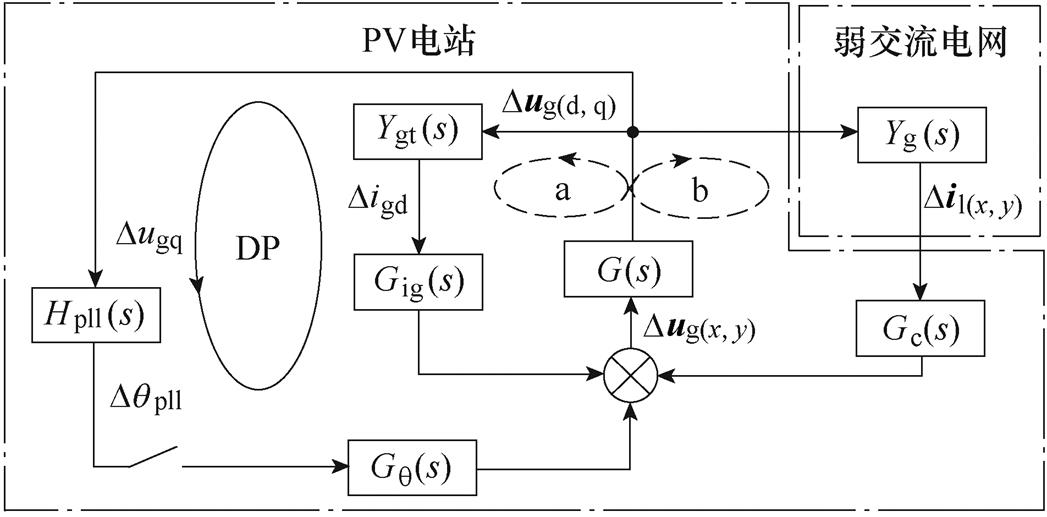
图7 系统闭环传递函数框图
Fig.7 System closed-loop transfer function block diagram
阻尼路径DP表明SSO模式下次同步扰动从Dqpll出发,经过网侧电压Dug后返回到Dqpll。并且,阻尼路径DP内部包含两个闭环回路,如图7中虚线闭环a和b。闭环a反映了PV电站各模块对网侧电压扰动Dug的影响;闭环b反映了弱交流电网导纳也将影响网侧电压扰动Dug。闭环a与闭环b之间的具体耦合关系如下:网侧电压扰动Dug通过PV电站各个模块传递后导致网侧电流扰动Digd;同时,网侧电压扰动Dug通过弱交流电网导纳导致线路电流扰动Dil;最后,网侧电流扰动Digd和线路电流扰动Dil在并网点再次产生网侧电压扰动Dug。综上所述,PV电站与弱交流电网的电流扰动Digd和Dil与网侧电压扰动Dug在并网点相互驱动,将形成次同步交互作用路径。对于PV并入弱交流电网系统,次同步交互作用路径循环产生的网侧电压扰动Dug与原始扰动电压叠加,将逐步增大并网系统网侧电压波动,影响PLL输出特性,从而导致PV电站和电网振荡。
因此,次同步交互作用路径与PLL形成的闭环阻尼路径将影响SSO模式阻尼,阻尼路径DP受到PV电站本身参数及其与弱交流电网次同步交互作用的影响。并且,已有文献指出PV并网系统的SSO问题主要是由PV电站与弱交流电网在次同步频域的交互作用导致的[15],有必要针对系统内部次同步交互作用的阻尼特性展开分析。
为了量化分析PV并网系统中次同步交互作用的阻尼特性,本节基于系统闭环传递函数框图进行阻尼路径分离,将系统总的阻尼路径DP分解为PV电站阻尼路径和次同步交互作用阻尼路径,分别定义为自阻尼路径DP1和交互阻尼路径DP2,并得到了单输入单输出(Single Input and Single Output, SISO)的系统闭环传递函数模型。具体步骤如下:
(1)分离自阻尼路径DP1。将式(21)和式(23)代入式(22),消去中间变量Digd,通过Dθpll和Dil(x, y)表示网侧电压Dug(x, y),如式(26),得到反映PV电站阻尼贡献的自阻尼路径DP1,如图8a所示。
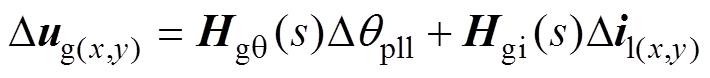 (26)
(26)
其中
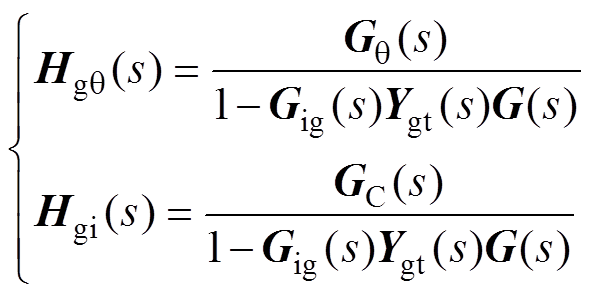 (27)
(27)
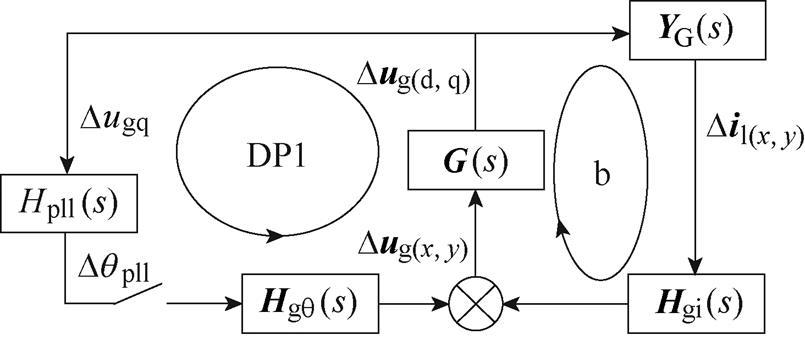
(2)分离交互阻尼路径DP2。将式(26)代入式(24),通过Dqpll表示线路电流Dil(x,y),如式(28),实现闭环回路b与自阻尼路径DP1的分离,得到反映次同步交互作用阻尼贡献的交互阻尼路径DP2,如图8b所示。
(a)步骤1
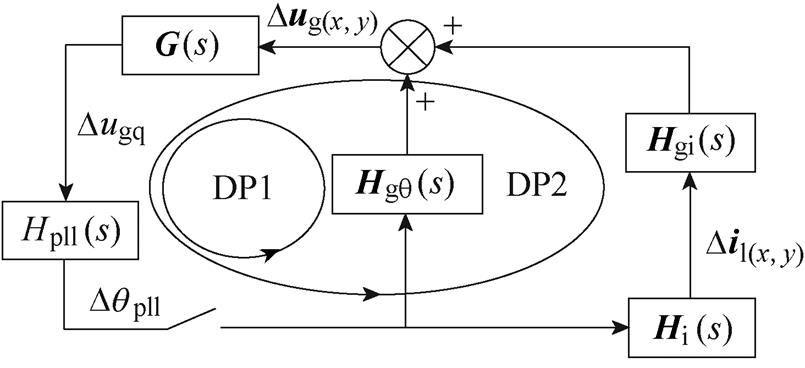
(b)步骤2
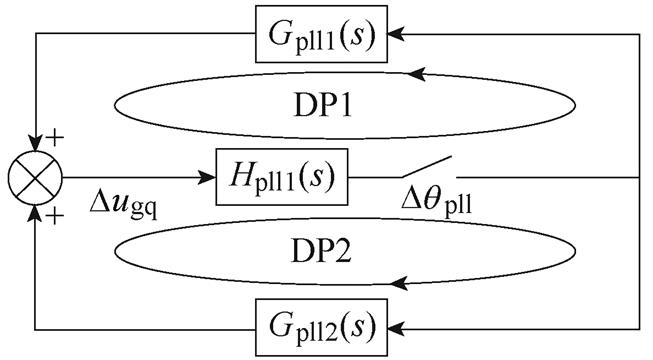
(c)步骤3
图8 阻尼路径分离推导
Fig.8 Derivation of damping path separation
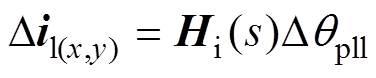 (28)
(28)
其中
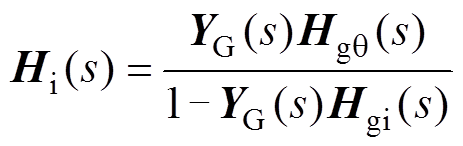 (29)
(29)
(3)求取阻尼路径传递函数。消去图8b的中间变量Dil(x,y)和Dug(x,y),分别得到阻尼路径DP1和DP2从Dqpll到Dugq的传递函数Gpll1(s)和Gpll2(s),具体表达式见式(30),此时,系统SISO闭环传递函数模型如图8c所示。
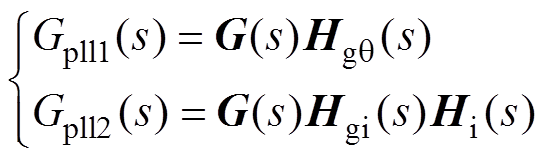 (30)
(30)
通过阻尼路径分离,系统总的阻尼路径DP分解为自阻尼路径DP1和交互阻尼路径DP2,并得到以PLL动态方程为反馈路径的SISO闭环传递函数模型,为阻尼路径的量化分析奠定基础。
依照第2节阻尼系数定义,De=Im[Gxpll(jw)]/w,Gxpll(s)=Gplli(s)(sKppll+Kipll),即可根据PLL控制参数和从∆θpll至∆ugq的传递函数Gpll(s)来计算阻尼路径相应的阻尼系数。因此,根据阻尼路径分离的结果,将Gpll1(s)和Gpll2(s)具体表达式代入阻尼系数求取公式,就能得到反映自阻尼路径DP1和交互阻尼路径DP2阻尼特性的阻尼系数De1和De2,即
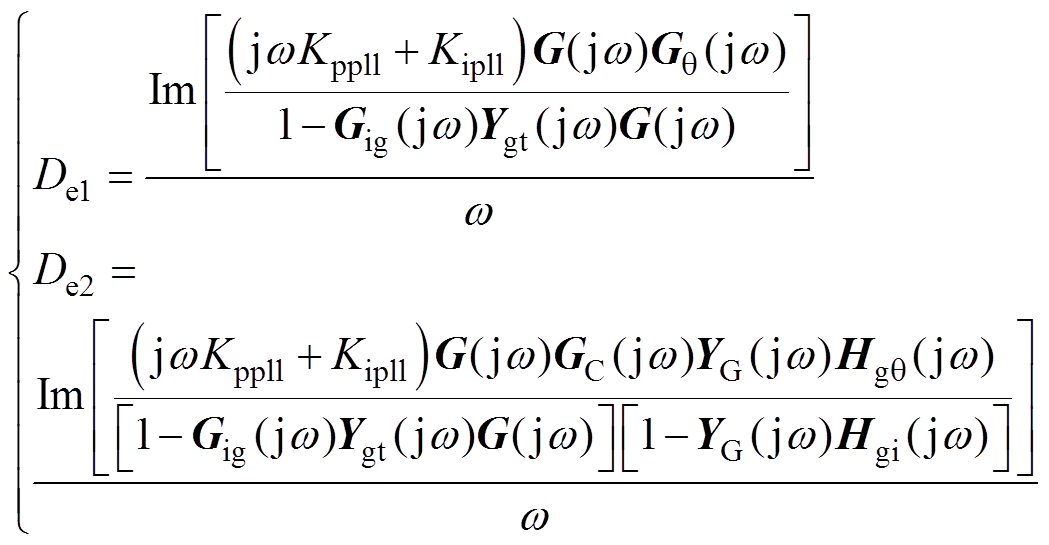 (31)
(31)
式中,De1具体表达式仅与PV电站各模块传递函数相关,表示自阻尼路径DP1的SSO模式阻尼贡献,称为自阻尼系数,当De1<0时,PV电站本身表现为负阻尼特性,PV电站并入无穷大电网会发生振荡;De2具体表达式与PV电站和电网阻抗传递函数均相关,表示交互阻尼路径DP2的SSO模式阻尼贡献,称为交互阻尼系数,当De2<0时,交互作用表现为负阻尼特性,向系统提供负阻尼,降低系统稳定性。由于PV并入弱交流电网系统总的阻尼路径由DP1和DP2构成,因此,系统总的阻尼系数De=De1+De2,当De<0时,PV并入弱交流电网系统表现为负阻尼特性,系统会发生振荡。
本节基于阻尼路径分离结果量化分析了PV电站与弱交流电网间次同步交互作用的阻尼特性。本文将PLL的比例系数Kpllp和积分系数Kplli分别从950和1 900改为95和19 000,以激发SSO,其他参数与附录表1和表2所示一致。基于阻尼路径分离得到自阻尼系数De1、交互阻尼系数De2以及系统总的阻尼系数De的频率特性曲线,如图9所示。
由图9可得:自阻尼系数De1在0~50 Hz均为正值,自阻尼路径DP1向PV并网系统提供正阻尼,PV电站并入无穷大电网系统具有较高稳定性,不易振荡。交互阻尼系数De2在11 Hz之后变为负值,交互阻尼路径DP2向PV并入弱交流电网系统提供负阻尼,尤其13~21 Hz提供较大负阻尼,增加了系统SSO风险。系统总的阻尼系数De=De1+De2,且De在13~21 Hz的次同步频率范围内变为负值,说明受到PV电站与弱交流电网间次同步交互作用的影响,PV并入弱交流电网系统会发生SSO。
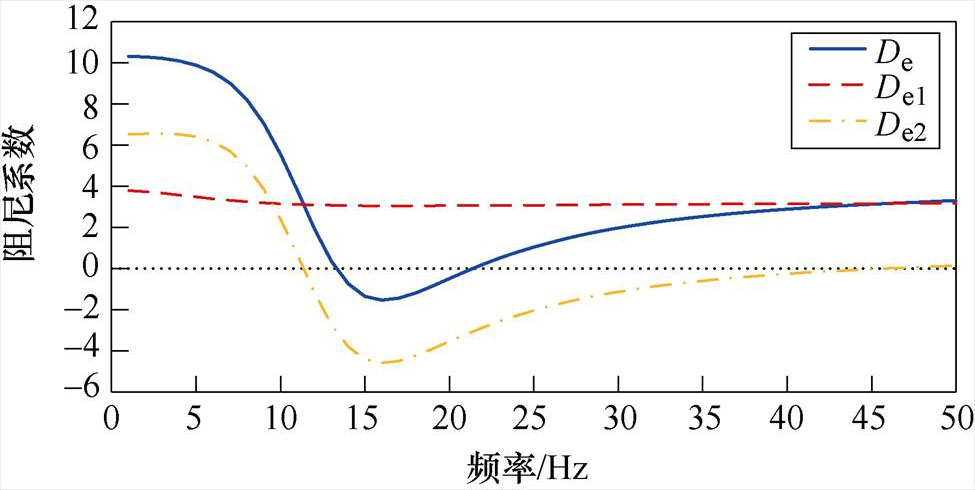
图9 阻尼系数频率特性曲线
Fig.9 Frequency characteristic curves of damping coefficient
基于PSCAD/EMTDC对上述理论分析结果进行电磁暂态仿真验证,并通过设置受端交流系统阻抗参数,得到两种工况。工况1:设置交流系统阻抗参数与附表2一致,模拟PV并入弱交流电网系统,对应系统总的阻尼系数De;工况2:将交流系统阻抗设置为0,模拟PV并入无穷大电网系统,对应自阻尼系数De1。在3 s时,将两种工况下PV电站PLL的比例系数Kpllp和积分系数Kplli按照上述理论分析分别调整为95和19 000,得到PV电站网侧电压的q轴分量ugq的时域仿真波形及频谱分析结果,如图10所示。
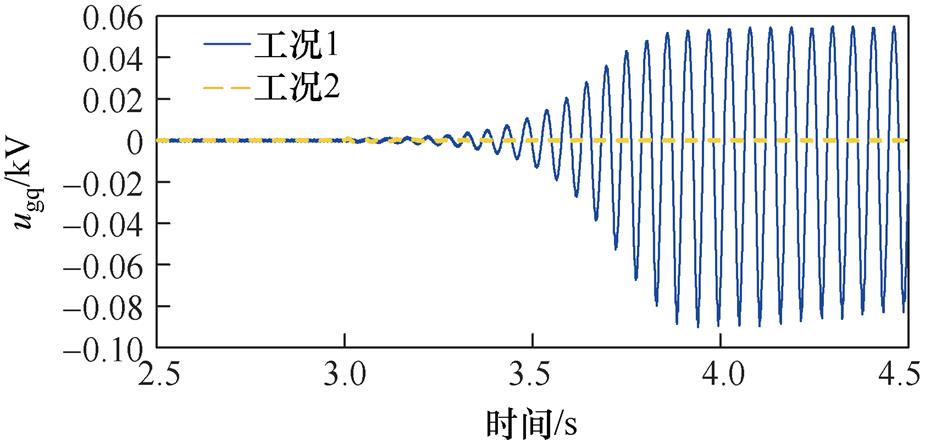
(a)网侧电压ugq波形
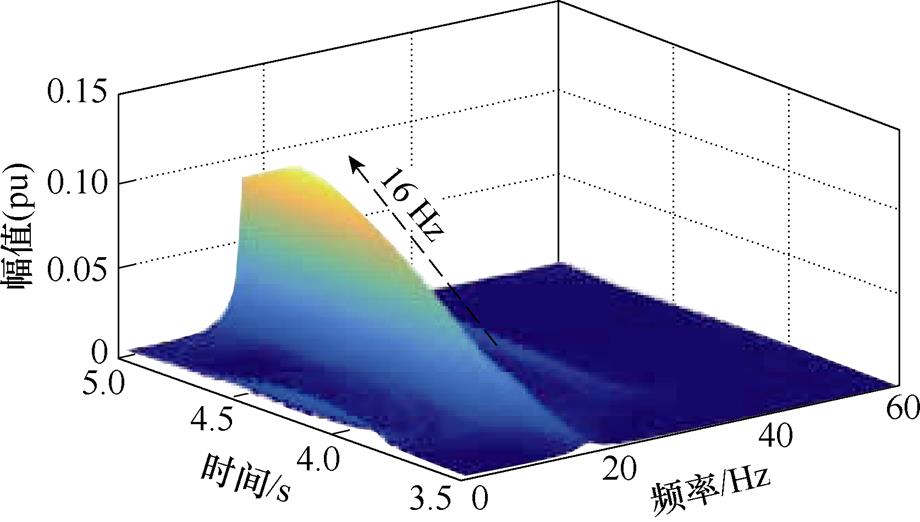
(b)FFT分析结果
图10 网侧电压ugq波形及频谱分析结果
Fig.10 Waveforms and FFT analysis result of ugq
由图10可得:在改变PLL的控制参数后,工况2系统能够保持稳定,与De1在0~50 Hz大于0相符;但工况1系统发生了振荡,且ugq的振荡频率主要为16 Hz,与De在SSO频域小于0相符。两种工况下系统不同的稳定性说明在SSO模式下,PV电站与弱交流电网间次同步交互作用向系统提供负阻尼,导致PV并入弱交流电网系统呈现负阻尼特性,与De2在SSO频域小于0的理论分析相符。
上述分析证明了阻尼路径分离结果的有效性,并得到SSO模式下,虽然PV电站自阻尼路径DP1向系统提供正阻尼,但由于交互阻尼路径DP2向系统提供了负阻尼,PV并入弱交流电网系统可能会发生振荡。值得注意的是,本文分析方法也适用于PV并网系统其他振荡模态下次同步交互作用阻尼特性的分析。
根据阻尼路径分离结果可得,PV并入弱交流电网系统阻尼受到自阻尼路径和交互作用路径的影响,且交互阻尼路径对系统稳定性影响较大。然而,现有文献大多直接分析系统总的阻尼特性,对次同步交互作用阻尼特性的研究较少。因此,针对SSO模式下PV电站与弱交流电网间次同步交互作用的阻尼特性,本节分析了PLL控制参数、PV容量、交流电网强度、PV电站光照强度和温度对自阻尼路径和交互阻尼路径阻尼贡献的影响,并得到系统阻尼特性变化的主导路径。
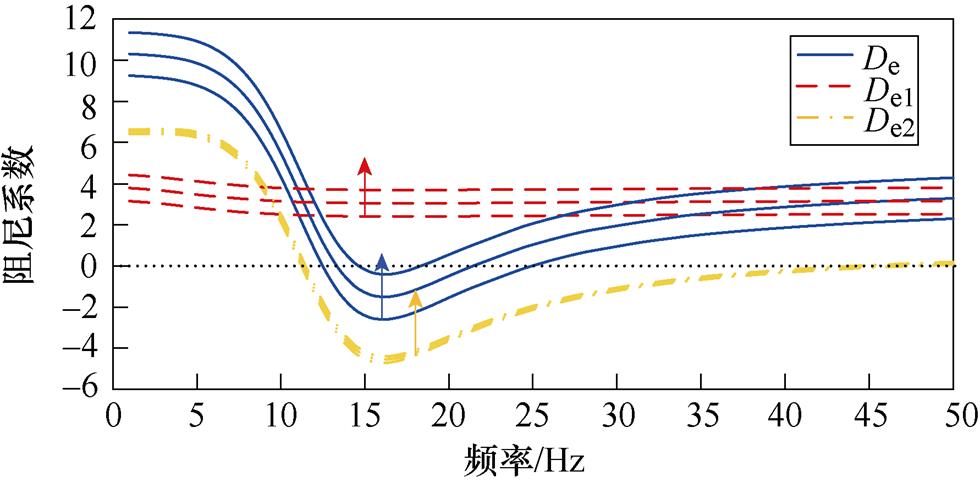
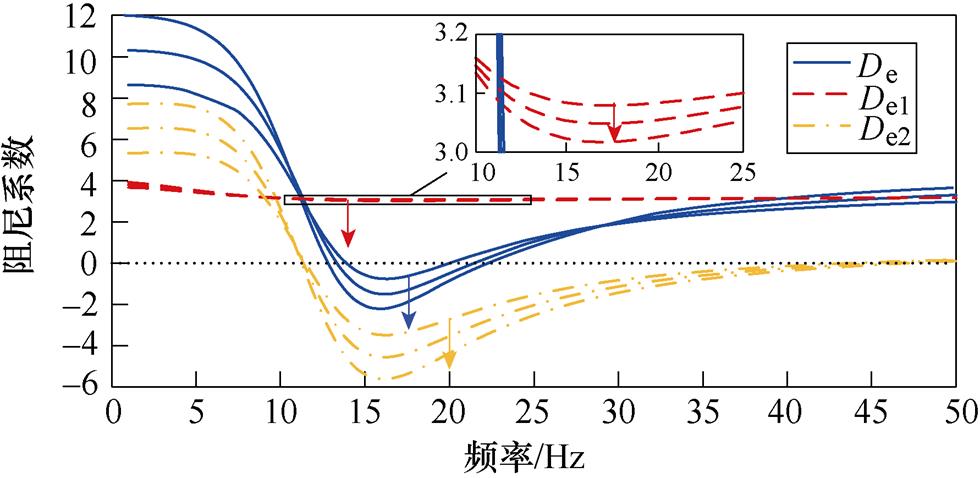
将PV电站中PLL的Kppll和Kipll分别设置为95和19 000,以激发SSO。分别改变PV电站PLL控制参数,得到De、De1和De2的频率特性曲线,如图11所示。在图11a中,PLL的比例系数Kppll分别为76、95和114,在图11b中,PLL的积分系数Kipll分别为15 200、19 000和22 800。箭头表示阻尼系数随参数增加而变化的方向,后文不再赘述。
由图11a可得:在SSO频率附近,随着Kppll的增加,De、De1和De2均上移,但De2变化不明显。结果表明,随着Kppll的增加,自阻尼路径的阻尼贡献增大,PV电站保持正阻尼特性;交互阻尼路径的阻尼贡献略微增大;PV并入弱交流电网系统的阻尼将增加,且自阻尼路径阻尼贡献增大是系统阻尼特性变化的主导因素。
(a)比例系数
(b)积分系数
图11 PLL控制参数的影响
Fig.11 Influence of PLL control parameters
由图11b可得:在SSO频率附近,随着Kipll的增加,De、De1和De2均下移,但De1变化不明显。结果表明,随着Kipll的增加,自阻尼路径的阻尼贡献略微减小,PV电站保持正阻尼特性;交互阻尼路径提供的阻尼贡献同样减小;PV并入弱交流电网系统的阻尼将减小,且交互阻尼路径阻尼贡献减小是系统阻尼特性变化的主导因素。
为验证PLL控制参数对系统稳定性的影响,在3.0 s时分别改变PLL的控制参数,得到PV并入弱交流电网系统中ugq的时域仿真波形,分别如图12a和图12b所示。
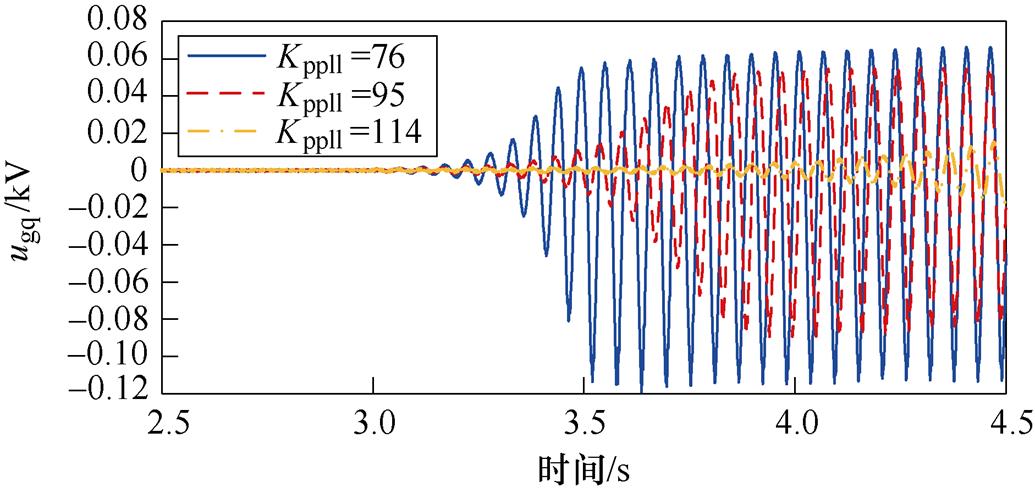
(a)比例系数
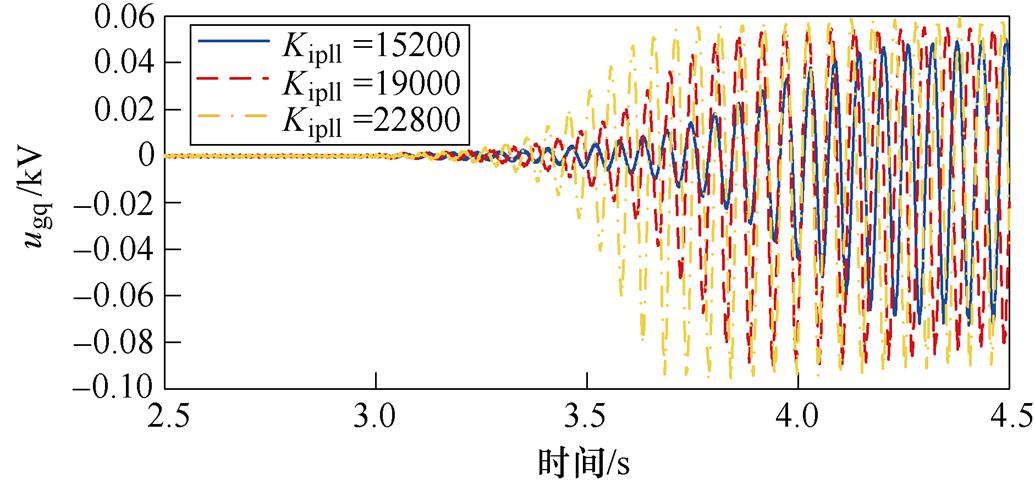
(b)积分系数
图12 ugq波形(PLL控制参数变化)
Fig.12 Waveforms of ugq (PLL control parameters change)
从图12可以看出,随着Kppll的增加,ugq的振幅减小,系统SSO模式阻尼逐渐增加;随着Kipll的增加,ugq的振幅增加,系统SSO模式阻尼逐渐减小。时域仿真结果与理论分析一致。
将PV电站中PLL的Kppll和Kipll分别设置为95和19 000,以激发SSO。当PV容量分别为154、182和210 MW时,得到De、De1和De2的频率特性曲线,如图13所示。
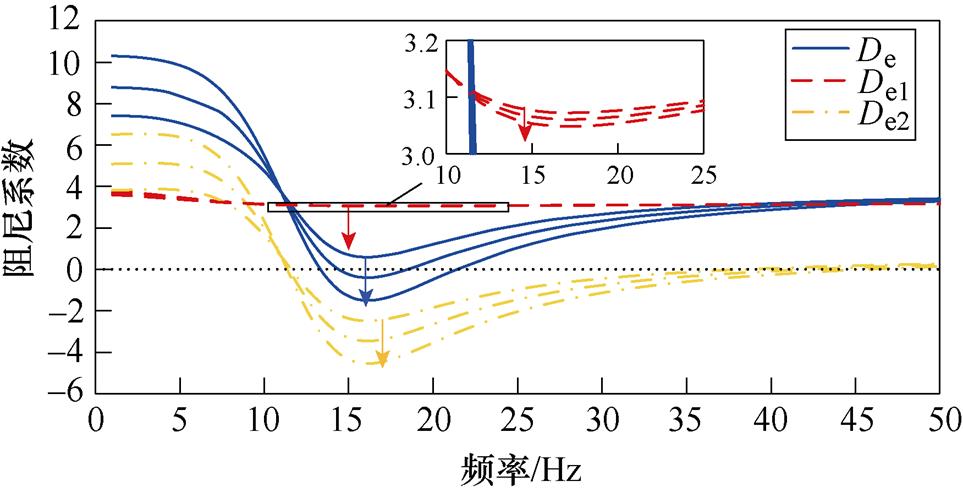
图13 PV容量的影响
Fig.13 Influence of PV capacity
由图13可得:在SSO频率附近,随着PV容量的增加,De、De1和De2均下移,但De1变化不明显。结果表明,随着PV容量的增加,自阻尼路径的阻尼贡献略微减小,PV电站保持正阻尼特性;交互阻尼路径的阻尼贡献减小;PV并入弱交流电网系统的阻尼将减小,且交互阻尼路径阻尼贡献减小是系统阻尼特性变化的主导因素。另外,当PV容量为154 MW时,系统表现为正阻尼特性。
为验证PV容量对系统稳定性的影响,在3.0 s时改变PV容量,得到PV并入弱交流电网系统中ugq的时域仿真波形,如图14所示。
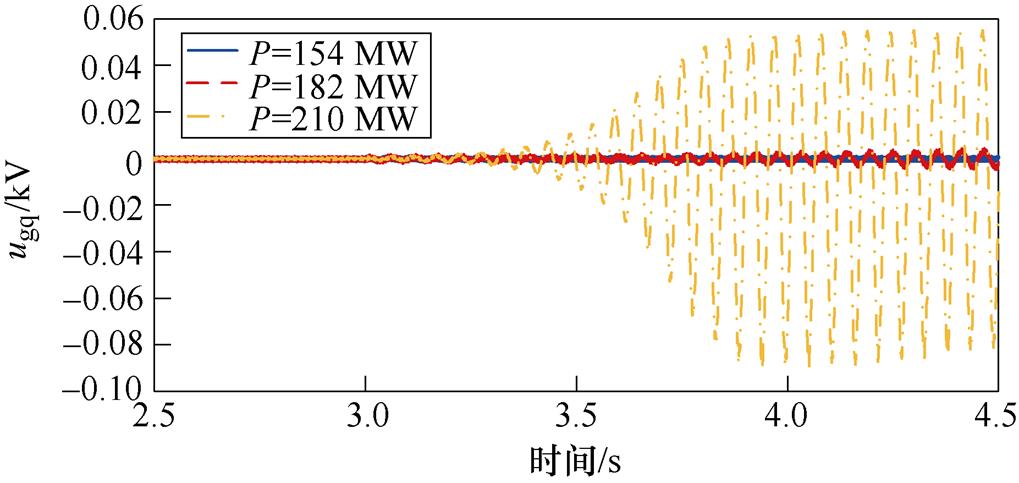
图14 ugq波形(PV容量变化)
Fig.14 Waveforms of ugq (PV capacity changes)
由图14可得:当PV容量为154 MW时,系统不发生振荡。随着PV容量的增加,ugq发生振荡且振幅增大,系统SSO模式阻尼逐渐减小。时域仿真结果与理论分析一致。
将PV电站中PLL的Kppll和Kipll分别设置为95和19 000,以激发SSO。改变弱交流电网等效阻抗,模拟PV并入弱交流电网系统时不同交流电网强度的影响。通过SCR反映交流电网强度,当SCR分别为2.0、2.5和3.0时,得到De、De1和De2的频率特性曲线,如图15所示。
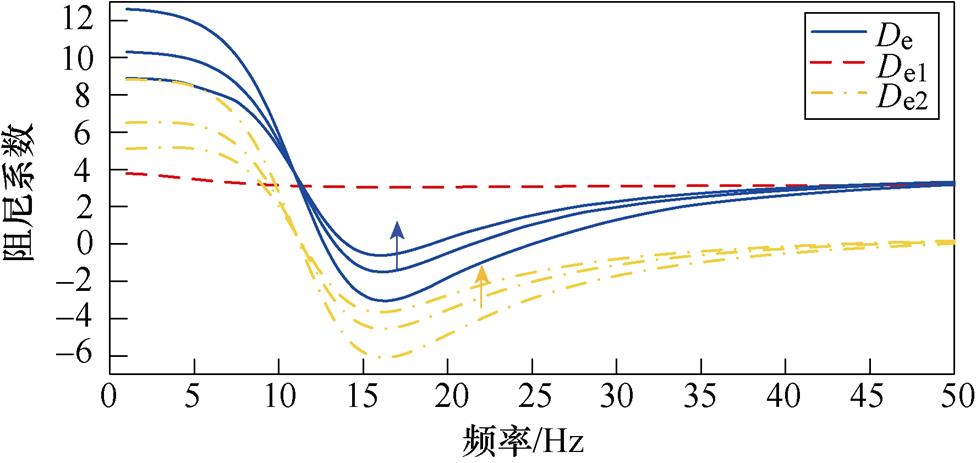
图15 SCR的影响
Fig.15 Influence of SCR
由图15可得:在SSO频率附近,随着SCR的增加,De和De2上移,De1不随SCR变化而移动。结果表明,随着SCR的增加,仅与PV电站参数相关的自阻尼路径阻尼贡献不变,PV电站保持正阻尼特性;交互阻尼路径的阻尼贡献增大;PV并入弱交流电网系统的阻尼将增加,且交互阻尼路径阻尼贡献增大是系统阻尼特性变化的主导因素。
为验证SCR对系统稳定性的影响,在3.0 s时改变SCR,得到PV并入弱交流电网系统中ugq的时域仿真波形,如图16所示。
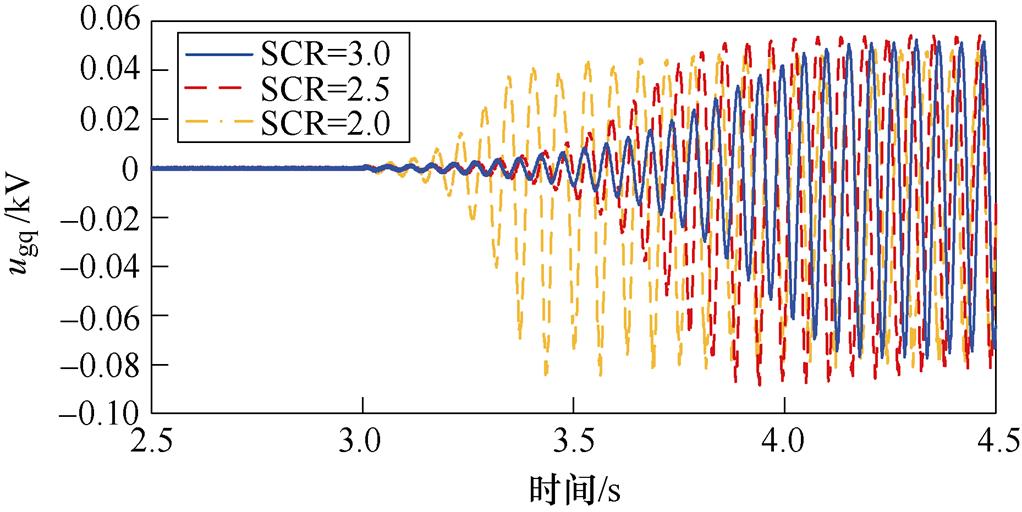
图16 ugq波形(SCR变化)
Fig.16 Waveforms of ugq (SCR changes)
由图16可得:随着交流电网强度的增强,ugq的振荡程度减弱,系统SSO模式阻尼逐渐增加,且在一定的弱交流电网强度范围内,系统都会发生SSO。时域仿真结果与理论分析一致。
将PV电站中PLL的Kppll和Kipll分别设置为95和19 000,以激发SSO。当PV电站光照强度分别为975、1 000和1 025 W/m2时,得到De、De1和De2的频率特性曲线,如图17所示。
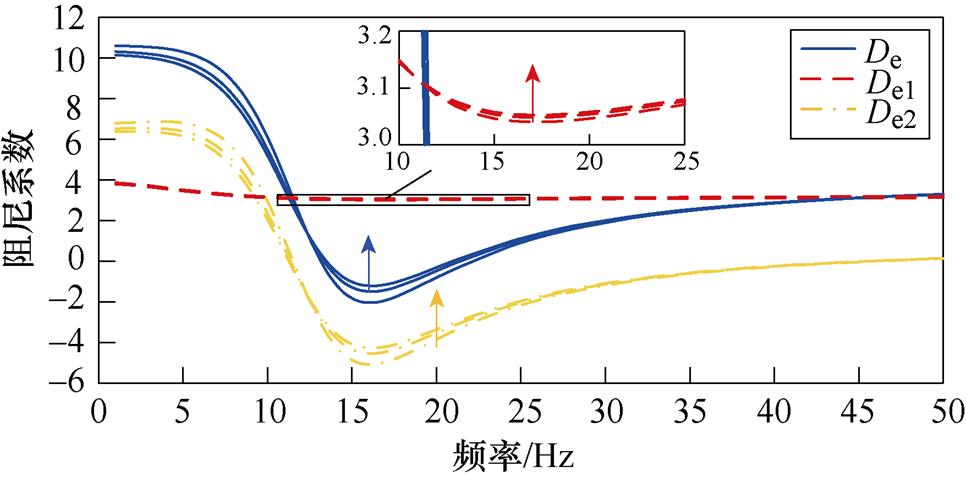
图17 光照强度的影响
Fig.17 Influence of irradiance
由图17可得:在SSO频率附近,随着光照强度的增加,De、De1和De2均上移,但De1变化不明显。结果表明,在标准工况附近,随着光照强度的增加,自阻尼路径的阻尼贡献略微增大,PV电站保持正阻尼特性;交互阻尼路径的阻尼贡献增大;PV并入弱交流电网系统的阻尼将增大,且交互阻尼路径阻尼贡献增大是系统阻尼特性变化的主导因素。
为验证PV电站光照强度对系统稳定性的影响,在3.0 s时改变光照强度,得到PV并入弱交流电网系统中ugq的时域仿真波形,如图18所示。
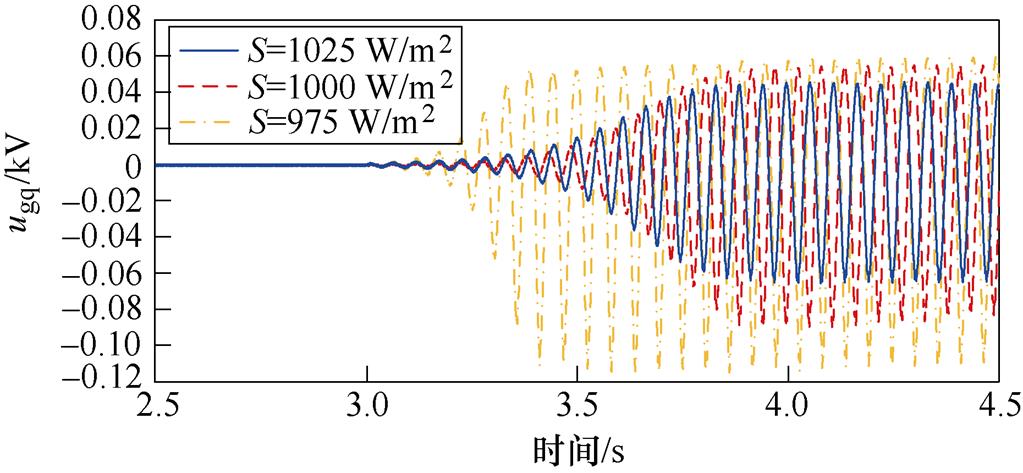
图18 ugq波形(光照强度变化)
Fig.18 Waveforms of ugq (irradiance changes)
由图18可得:在一定范围内,随着PV电站光照强度的增加,ugq振幅减小,系统SSO模式阻尼逐渐增大。时域仿真结果与理论分析一致。值得注意的是,当算例偏离标准工况较大,系统原本的稳定工作点同样会发生振荡。
将PV电站中PLL的Kppll和Kipll分别设置为95和19 000,以激发SSO。当PV电站温度分别为15、20和25℃时,得到De、De1和De2的频率特性曲线,如图19所示。
由图19可得:在SSO频率附近,随着PV电站温度的增加,De、De1和De2均上移,但De1变化不明显。结果表明,随着温度的增加,自阻尼路径的阻尼贡献略微增大,PV电站保持正阻尼特性;交互阻尼路径的阻尼贡献增大;PV并入弱交流电网系统的阻尼将增大,且交互阻尼路径阻尼贡献增大是系统阻尼特性变化的主导因素。
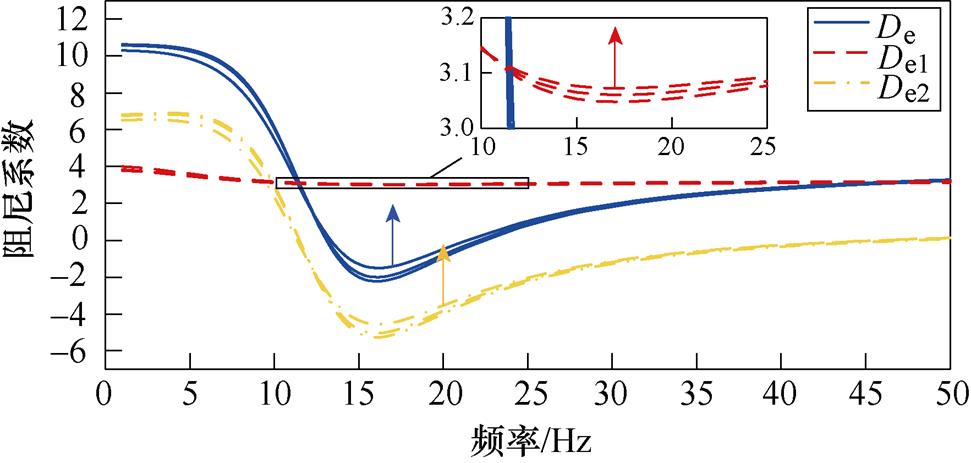
图19 温度的影响
Fig.19 Influence of temperature
为验证PV电站温度对系统稳定性的影响,在3.0 s时改变温度,得到PV并入弱交流电网系统中ugq的时域仿真波形,如图20所示。
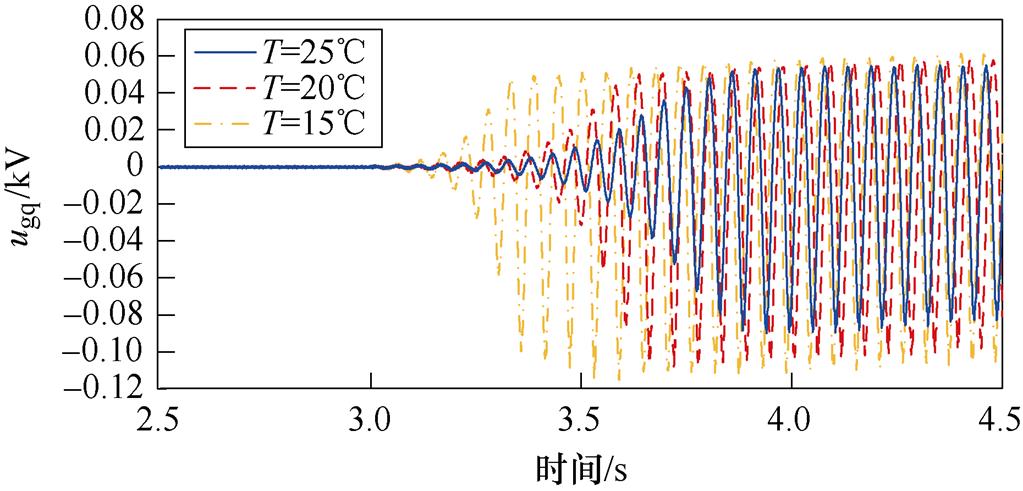
图20 ugq波形(温度变化)
Fig.20 Waveforms of ugq (temperature changes)
由图20可得:在一定范围内,随着PV电站温度的增加,ugq振荡程度减小,系统SSO模式阻尼逐渐增大。时域仿真结果与理论分析一致。
上述研究结论表明:对于PV并入弱交流电网系统,PLL比例系数主要通过改变PV电站阻尼贡献影响系统阻尼特性,PLL积分系数、PV容量、交流电网强度、PV电站光照强度和温度则对PV电站阻尼贡献的影响较小,主要是通过改变PV电站与弱交流电网间次同步交互作用阻尼贡献影响系统阻尼特性。考虑到PV电站与弱交流电网间次同步交互作用是PV并入弱交流电网系统SSO的主导因素,通过优化后者参数能够较好地保持PV电站原本的阻尼特性,提高PV并入弱交流电网系统稳定性,实现了PV并网系统阻尼的精准调控。
本文基于阻尼转矩法在PLL振荡模态的扩展,分析了PV电站与弱交流电网间次同步交互作用路径,揭示了交互作用路径影响系统SSO模式阻尼的动态过程,并量化评估了次同步交互作用的阻尼特性。主要研究结论如下:
1)PV并入弱交流电网系统存在PLL主导的SSO风险。PV电站与弱交流电网的电流扰动和网侧电压扰动在并网点相互驱动,形成次同步交互作用路径,且交互作用路径将通过PLL形成阻尼路径,影响系统SSO模式阻尼。
2)通过系统阻尼路径分离,能够量化评估PV电站和次同步交互作用的SSO模式阻尼贡献。次同步交互作用向系统提供负阻尼,是PV并入弱交流电网系统SSO的主导因素。
3)在一定范围内,PLL比例系数、交流电网强度、PV电站光照强度或温度增大时,次同步交互作用及PV并网系统SSO模式阻尼增加;而PLL积分系数或PV容量增大时,次同步交互作用及PV并网系统SSO模式阻尼减小。
4)针对次同步交互作用的负阻尼特性合理设计系统参数,能够有效增加PV并入弱交流电网系统SSO模式阻尼,同时较好地保持PV电站原本的阻尼特性,对实际工程具有一定的指导意义。
附 录
1. 仿真系统参数说明
附表1 PV电站主要参数
App.Tab.1 Main parameters of PV plant
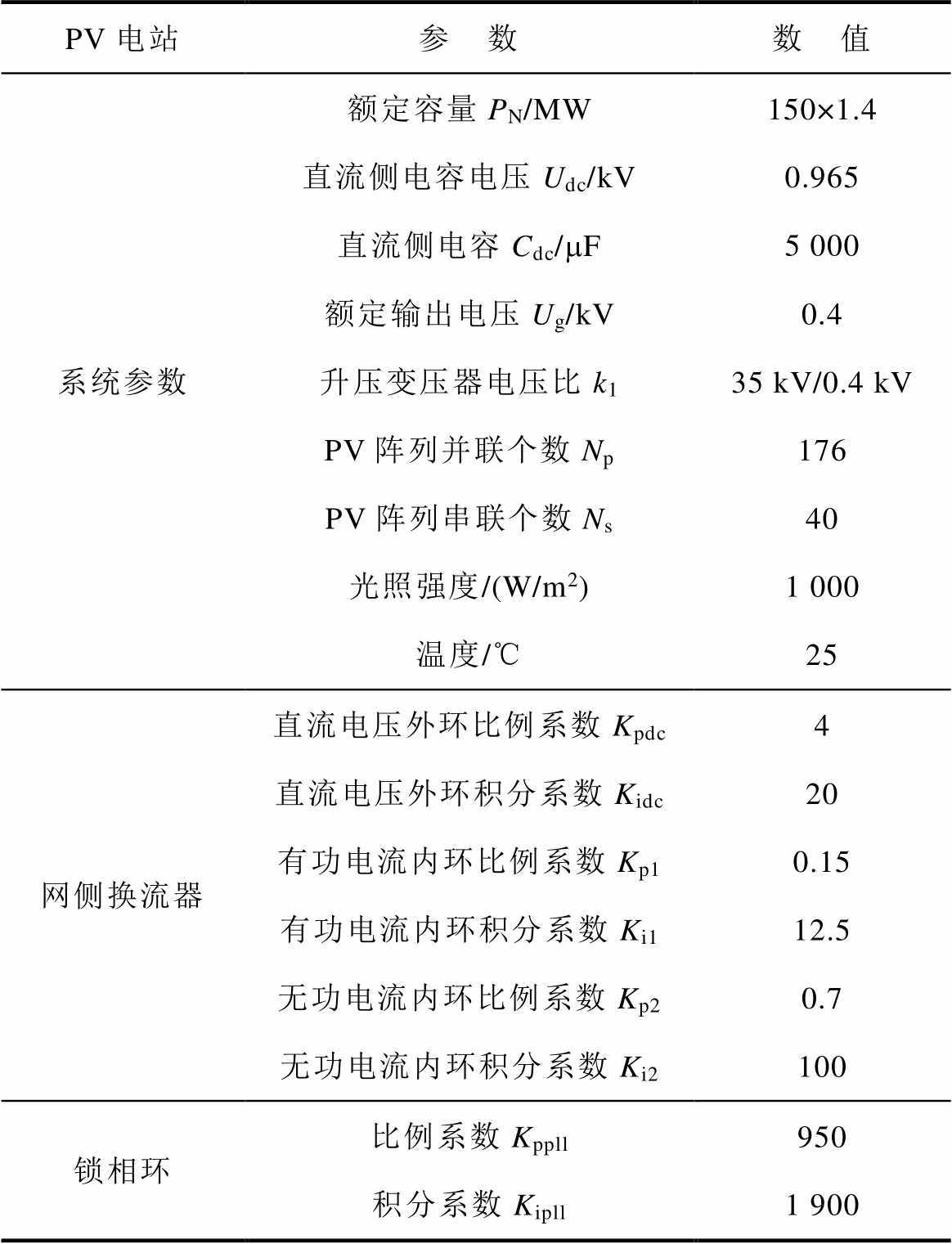
PV电站参 数数 值 系统参数额定容量PN/MW150×1.4 直流侧电容电压Udc/kV0.965 直流侧电容Cdc/mF5 000 额定输出电压Ug/kV0.4 升压变压器电压比k135 kV/0.4 kV PV阵列并联个数Np176 PV阵列串联个数Ns40 光照强度/(W/m2)1 000 温度/℃25 网侧换流器直流电压外环比例系数Kpdc4 直流电压外环积分系数Kidc20 有功电流内环比例系数Kp10.15 有功电流内环积分系数Ki112.5 无功电流内环比例系数Kp20.7 无功电流内环积分系数Ki2100 锁相环比例系数Kppll950 积分系数Kipll1 900
附表2 弱交流电网主要参数
App.Tab.2 Main parameters of the weak AC grid
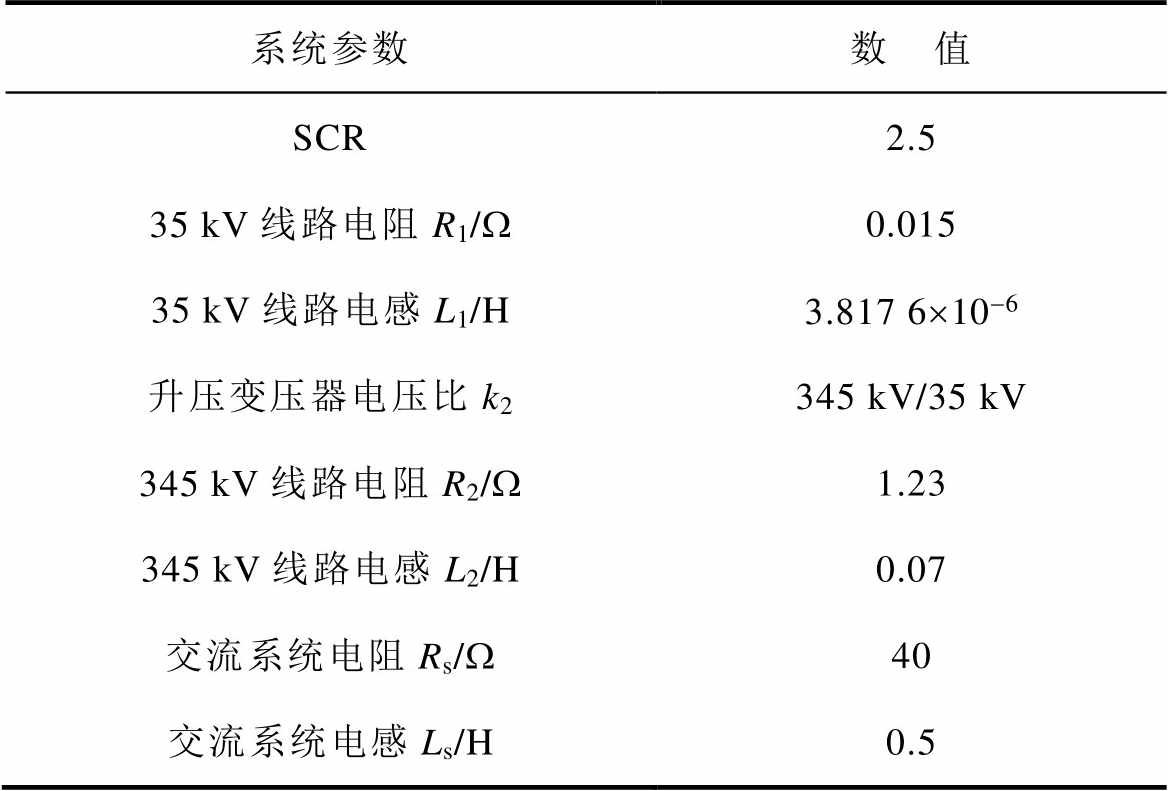
系统参数数 值 SCR2.5 35 kV线路电阻R1/W0.015 35 kV线路电感L1/H3.817 6´10-6 升压变压器电压比k2345 kV/35 kV 345 kV线路电阻R2/W1.23 345 kV线路电感L2/H0.07 交流系统电阻Rs/W40 交流系统电感Ls/H0.5
2. 系统传递函数模型
式(10)~式(13)中传递函数具体表达式为
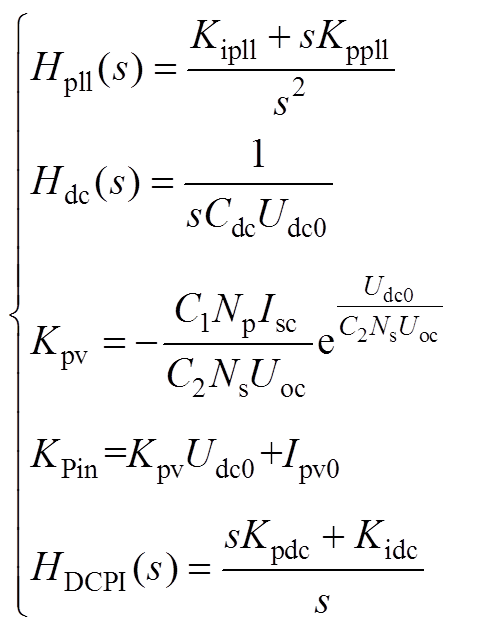 (A1)
(A1)
式中,Isc、Uoc分别为标准测试条件下PV阵列的短路电流、开路电压,均由生产厂家提供;系数C1、C2可由厂家参数求得。
根据式(14),LCL滤波器传递函数框图如附图1所示。图中,网侧换流器电流Ditd=Digd+Dilcld、Ditq=Digq。
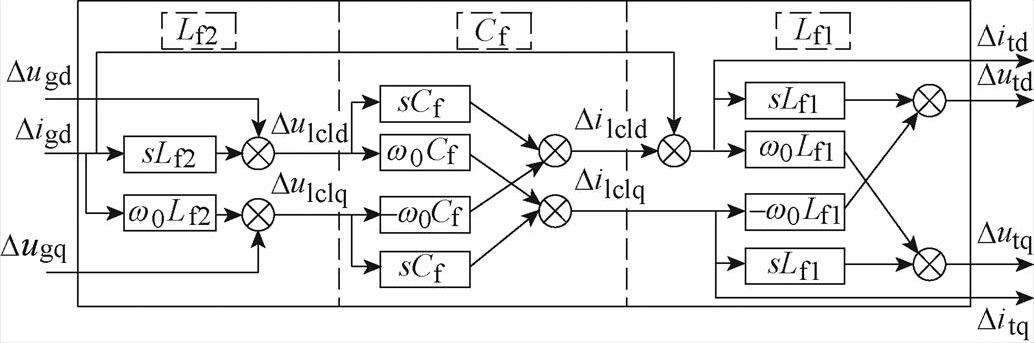
附图1 LCL滤波器传递函数框图
App.Fig.1 Transfer function block diagram of LCL filter
式(15)中传递函数具体表达式为
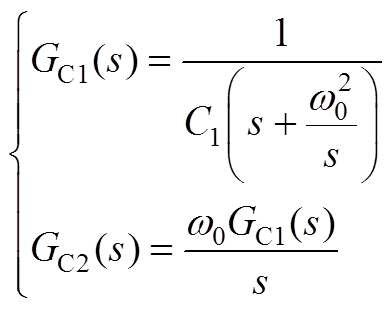 (A2)
(A2)
式(16)和式(17)中坐标变换传递函数表达式为
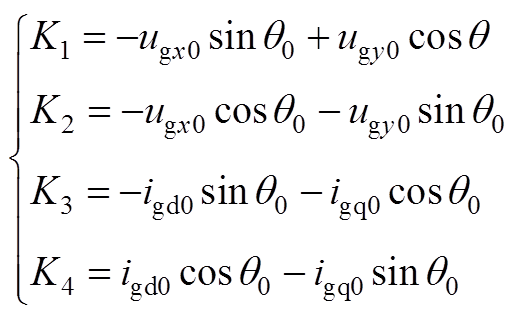 (A3)
(A3)
式(18)中传递函数具体表达式为
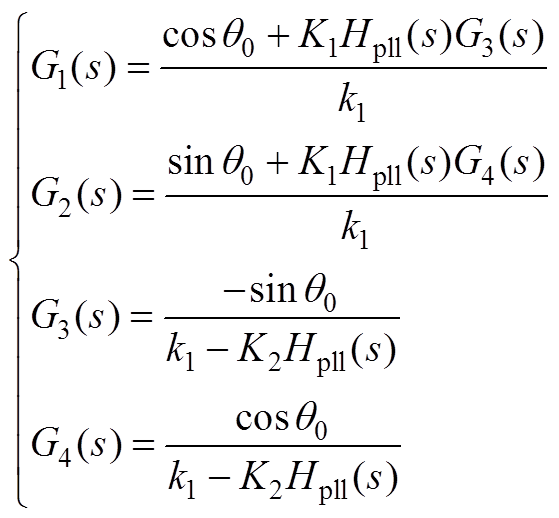 (A4)
(A4)
式(19)中传递函数具体表达式为
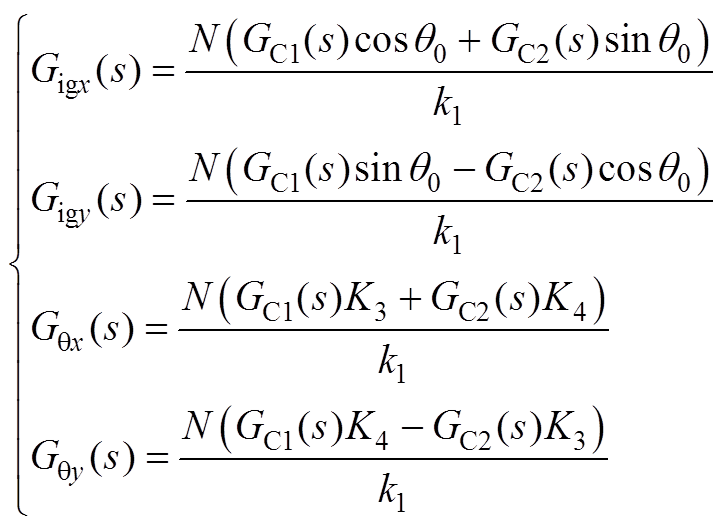 (A5)
(A5)
弱交流电网中式(20)的传递函数具体表达式为
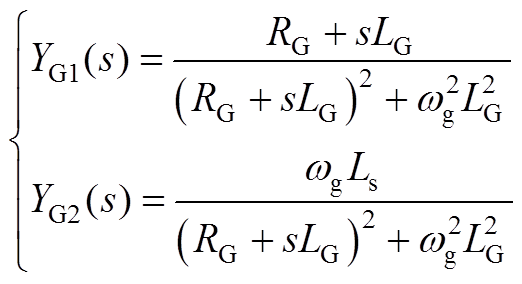 (A6)
(A6)
式中,LG、RG分别为弱交流电网的等效电感和等效电阻,其表达式如式(A7)所示。
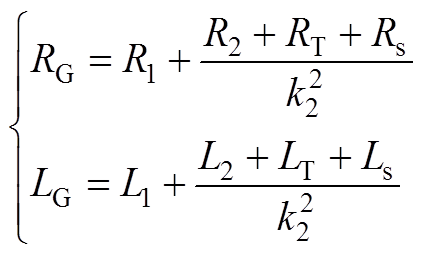 (A7)
(A7)
式中,k2为二级升压变压器电压比。
参考文献
[1] 国家能源局. 2021年光伏发电建设运行情况[EB/OL]. [2022-03-09].http://www.nea.gov.cn/2022-03/09/c_ 1310508114.htm.
[2] 郑超, 王士元, 张波琦, 等. 光伏高渗透电网动态频率特性及应对措施[J]. 电网技术, 2019, 43(11): 4064-4073.
Zheng Chao, Wang Shiyuan, Zhang Boqi, et al. Dynamic frequency characteristics and counter- measures of power grid with highly penetrated photovoltaics[J]. Power System Technology, 2019, 43(11): 4064-4073.
[3] 张金平, 汪宁渤, 黄蓉, 等. 高渗透率光伏参与电力系统调频研究综述[J]. 电力系统保护与控制, 2019, 47(15): 179-186.
Zhang Jinping, Wang Ningbo, Huang Rong, et al. Survey on frequency regulation technology of power grid by high-penetration photovoltaic[J]. Power System Protection and Control, 2019, 47(15): 179- 186.
[4] 蔡纪鹤, 李蓓, 张永春. 基于SVPWM的光伏无功控制研究[J]. 电工技术学报, 2016, 31(24): 233-239.
Cai Jihe, Li Bei, Zhang Yongchun. Research on photovoltaic reactive power control based on SVPWM[J]. Transactions of China Electrotechnical Society, 2016, 31(24): 233-239.
[5] 商皓钰, 刘天琪, 卜涛, 等. 计及风电与光伏并网的电力系统运行风险评估[J]. 现代电力, 2020, 37(4): 358-367.
Shang Haoyu, Liu Tianqi, Bu Tao, et al. Operational risk assessment of power system considering wind power and photovoltaic grid connection[J]. Modern Electric Power, 2020, 37(4): 358-367.
[6] 张剑云. 哈密并网风电场次同步振荡的机理研究[J]. 中国电机工程学报, 2018, 38(18): 5447-5460.
Zhang Jianyun. Research on the mechanism of subsynchronous oscillations of wind farms in Hami[J]. Proceedings of the CSEE, 2018, 38(18): 5447-5460.
[7] 薛安成, 付潇宇, 乔登科, 等. 风电参与的电力系统次同步振荡机理研究综述和展望[J]. 电力自动化设备, 2020, 40(9): 118-128.
Xue Ancheng, Fu Xiaoyu, Qiao Dengke, et al. Review and prospect of research on sub-synchronous oscillation mechanism for power system with wind power participation[J]. Electric Power Automation Equipment, 2020, 40(9): 118-128.
[8] 张天翼, 王海风. 风电并入弱交流系统引发次同步振荡的研究方法综述[J]. 电力系统保护与控制, 2021, 49(16): 177-187.
Zhang Tianyi, Wang Haifeng. Research methods for subsynchronous oscillation induced by wind power under weak AC system: a review[J]. Power System Protection and Control, 2021, 49(16): 177-187.
[9] 谢小荣, 刘华坤, 贺静波, 等. 直驱风机风电场与交流电网相互作用引发次同步振荡的机理与特性分析[J]. 中国电机工程学报, 2016, 36(9): 2366- 2372.
Xie Xiaorong, Liu Huakun, He Jingbo, et al. Mechanism and characteristics of subsynchronous oscillation caused by the interaction between full- converter wind turbines and AC systems[J]. Pro- ceedings of the CSEE, 2016, 36(9): 2366-2372.
[10] Liu Huakun, Xie Xiaorong, He Jingbo, et al. Subsynchronous interaction between direct-drive PMSG based wind farms and weak AC networks[J]. IEEE Transactions on Power Systems, 2017, 32(6): 4708-4720.
[11] Li Chun. Unstable operation of photovoltaic inverter from field experiences[J]. IEEE Transactions on Power Delivery, 2018, 33(2): 1013-1015.
[12] 陈武晖, 杨彦霁, 谢永胜, 等. 大规模光伏发电经串补并网系统次同步振荡机制[J]. 电网技术, 2021, 45(12): 4711-4721.
Chen Wuhui, Yang Yanji, Xie Yongsheng, et al. SSO mechanism of large-scale PV generation connected to series-compensated power system[J]. Power System Technology, 2021, 45(12): 4711-4721.
[13] 高本锋, 姚磊, 李忍, 等. 大规模光伏电站并网的振荡模式分析[J]. 电力自动化设备, 2017, 37(8): 123-130.
Gao Benfeng, Yao Lei, Li Ren, et al. Analysis on oscillation modes of large-scale grid-connected PV power plant[J]. Electric Power Automation Equip- ment, 2017, 37(8): 123-130.
[14] 赵书强, 李忍, 高本锋, 等. 光伏并入弱交流电网次同步振荡机理与特性分析[J]. 中国电机工程学报, 2018, 38(24): 7215-7225, 7448.
Zhao Shuqiang, Li Ren, Gao Benfeng, et al. Analysis of mechanism and characteristics in sub synchronous oscillation between PV and weak AC networks[J]. Proceedings of the CSEE, 2018, 38(24): 7215-7225, 7448.
[15] 赵书强, 高瑞鑫, 邵冰冰, 等. 多光伏发电单元并入弱交流电网系统的站内/站网次同步振荡特性分析[J]. 电力建设, 2021, 42(12): 49-58.
Zhao Shuqiang, Gao Ruixin, Shao Bingbing, et al. Inside-plant and plant-grid sub-synchronous oscilla- tion characteristics analysis of multiple PV generation units connected to a weak AC power grid[J]. Electric Power Construction, 2021, 42(12): 49-58.
[16] Du Wenjuan, Fu Qiang, Wang Haifeng. Method of open-loop modal analysis for examining the subsyn- chronous interactions introduced by VSC control in an MTDC/AC system[J]. IEEE Transactions on Power Delivery, 2018, 33(2): 840-850.
[17] 甄自竞, 杜文娟, 王海风. 近似强模式谐振下高压直流输电系统引起的次同步振荡仿真研究[J]. 中国电机工程学报, 2019, 39(7): 1976-1985.
Zhen Zijing, Du Wenjuan, Wang Haifeng. The simulation study on SSOs caused by the HVDC under the condition of near strong modal resonance[J]. Proceedings of the CSEE, 2019, 39(7): 1976-1985.
[18] 杨明, 周林, 张东霞, 等. 考虑电网阻抗影响的大型光伏电站并网稳定性分析[J]. 电工技术学报, 2013, 28(9): 214-223.
Yang Ming, Zhou Lin, Zhang Dongxia, et al. Stability analysis of large-scale photovoltaic power plants for the effect of grid impedance[J]. Transactions of China Electrotechnical Society, 2013, 28(9): 214-223.
[19] 陈新, 张旸, 王赟程. 基于阻抗分析法研究光伏并网逆变器与电网的动态交互影响[J]. 中国电机工程学报, 2014, 34(27): 4559-4567.
Chen Xin, Zhang Yang, Wang Yuncheng. A study of dynamic interaction between PV grid-connected inverters and grid based on the impedance analysis method[J]. Proceedings of the CSEE, 2014, 34(27): 4559-4567.
[20] 张美清, 袁小明, 胡家兵. 基于自稳/致稳性的路径级数展开方法及其在含多样化电力电子装备电力系统稳定性分析中的应用[J]. 中国电机工程学报, 2021, 41(5): 1637-1655.
Zhang Meiqing, Yuan Xiaoming, Hu Jiabing. Path series expansion method based on self-/en-stabilizing properties and its application in the stability analysis of power systems with diversified power electronic devices[J]. Proceedings of the CSEE, 2021, 41(5): 1637-1655.
[21] Huang Yunhui, Yuan Xiaoming, Hu Jiabing, et al. DC-bus voltage control stability affected by AC-bus voltage control in VSCs connected to weak AC grids[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(2): 445-458.
[22] Yuan Hao, Yuan Xiaoming, Hu Jiabing. Modeling of grid-connected VSCs for power system small-signal stability analysis in DC-link voltage control times- cale[J]. IEEE Transactions on Power Systems, 2017, 32(5): 3981-3991.
[23] 高本锋, 刘毅, 李蕴红, 等. 直驱风电场与LCC- HVDC次同步交互作用的扰动传递路径及阻尼特性分析[J]. 中国电机工程学报, 2021, 41(5): 1713- 1729.
Gao Benfeng, Liu Yi, Li Yunhong, et al. Analysis on disturbance transfer path and damping characteristics of sub-synchronous interaction between D-PMSG- based wind farm and LCC-HVDC[J]. Proceedings of the CSEE, 2021, 41(5): 1713-1729.
[24] Du W, Wang X, Wang H. Sub-synchronous inter- actions caused by the PLL in the grid-connected PMSG for the wind power generation[J]. International Journal of Electrical Power & Energy Systems, 2018, 98: 331-341.
[25] 高本锋, 姚磊, 李忍. 弱电网下锁相环对大型光伏电站振荡模式的影响[J]. 太阳能学报, 2017, 38(12): 3302-3310.
Gao Benfeng, Yao Lei, Li Ren. Influence of phase- locked loop on oscillation modes of large-scale PV power plant in weak grid[J]. Acta Energiae Solaris Sinica, 2017, 38(12): 3302-3310.
[26] 刘巨, 姚伟, 文劲宇. 考虑PLL和接入电网强度影响的双馈风机小干扰稳定性分析与控制[J]. 中国电机工程学报, 2017, 37(11): 3162-3173, 3371.
Liu Ju, Yao Wei, Wen Jinyu. Small signal stability analysis and control of double-fed induction generator considering influence of PLL and power grid strength[J]. Proceedings of the CSEE, 2017, 37(11): 3162-3173, 3371.
[27] 韩平平, 林子豪, 夏雨, 等. 大型光伏电站等值建模综述[J]. 电力系统及其自动化学报, 2019, 31(4): 39-47.
Han Pingping, Lin Zihao, Xia Yu, et al. Review on equivalent modeling of large-scale photovoltaic power plant[J]. Proceedings of the CSU-EPSA, 2019, 31(4): 39-47.
[28] 董文凯, 任必兴, 王海风, 等. 适用于系统次同步振荡分析的风电场等值建模方法综述[J]. 电力工程技术, 2022, 41(4): 33-43.
Dong Wenkai, Ren Bixing, Wang Haifeng, et al. Small-signal equivalent modeling methods of the wind farm and its application in sub-synchronous oscillations analysis of gird-connected wind power systems[J]. Electric Power Engineering Technology, 2022, 41(4): 33-43.
[29] 黄云辉, 翟雪冰, 刘栋, 等. 弱电网下风力发电机组并网变流器直流电压稳定性机理分析[J]. 高电压技术, 2017, 43(9): 3127-3136.
Huang Yunhui, Zhai Xuebing, Liu Dong, et al. Stability analysis on DC-link voltage of wind turbine grid-connected converter as integrated to weak grid[J]. High Voltage Engineering, 2017, 43(9): 3127-3136.
[30] 赵书强, 李忍, 高本锋, 等. 适用于多源系统次同步振荡分析的图形化建模方法[J]. 电工技术学报, 2017, 32(14): 184-193, 228.
Zhao Shuqiang, Li Ren, Gao Benfeng, et al. A graphical modeling method applied for multi-sources system subsynchronous oscillation analysis[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(14): 184-193, 228.
[31] 徐衍会, 曹宇平. 直驱风机网侧换流器引发次/超同步振荡机理研究[J]. 电网技术, 2018, 42(5): 1556- 1564.
Xu Yanhui, Cao Yuping. Research on mechanism of sub/sup-synchronous oscillation caused by GSC con- troller of direct-drive permanent magnetic syn- chronous generator[J]. Power System Technology, 2018, 42(5): 1556-1564.
[32] 赵伟然, 汪海蛟, 李光辉, 等. 分布式光伏并网电压和功率因数协调控制策略[J]. 电力工程技术, 2017, 36(6): 20-26.
Zhao Weiran, Wang Haijiao, Li Guanghui, et al. Voltage and power factor coordination control for distributed photovoltaic integration[J]. Electric Power Engineering Technology, 2017, 36(6): 20-26.
Analysis of Path and Damping Characteristics of Subsynchronous Interaction Between Photovoltaic Plant and Weak AC Grid
Abstract When a large-scale photovoltaic (PV) plant is integrated into the AC grid through long transmission lines, the interaction between the PV plant and weak AC grid may make the integration face the threat of subsynchronous oscillation (SSO). However, the mechanism of the subsynchronous interaction between the PV plant and weak AC grid are unclear, and quantifying the damping characteristics of the subsynchronous interaction is difficult by the existing analysis methods. Therefore, this paper proposes a damping torque method extended to the dynamic equation of phase-locked loop (PLL) to analyze the subsynchronous interaction between the PV plant and weak AC grid.
Firstly, the damping torque method is extended to the PLL dynamic equation to analyze the stability of the PV plant integrated into the weak AC grid system in the SSO mode dominated by PLL. Secondly, the linearization model of the PV plant integration and its corresponding closed-loop transfer function block diagram are derived. Based on the closed-loop transfer function diagram, the coupling relationship and interaction path between the PV plant and weak AC grid are revealed from the perspective of internal disturbance transfer, and the dynamic process of the interaction path affecting SSO mode damping is analyzed. Thirdly, through transfer function derivation, the damping path reflecting the subsynchronous interaction is separated, and the equivalent damping coefficient is used to quantify the SSO mode damping of the subsynchronous interaction. Finally, the influences of PLL control parameters, PV capacity, AC grid strength, PV plant intensity, and temperature on the damping characteristics of subsynchronous interaction are analyzed.
The mechanism analysis shows that the PV plant-weak AC grid current disturbance and the grid-side voltage disturbance drive each other at the point of common coupling, forming the subsynchronous interaction path. Then, the subsynchronous interaction path will form a closed-loop damping path through the PLL in the SSO mode dominated by PLL, affecting the system SSO mode damping. Therefore, the damping contribution of the PV plant and subsynchronous interaction are quantitatively evaluated through the damping path separation. The results show that the PV plant and the subsynchronous interaction provide positive damping and negative damping to the system, respectively, resulting in the SSO of the PV plant integrated into the weak AC grid system. In addition, the subsynchronous interaction damping can be decreased by increasing the PLL proportion coefficient, AC grid strength, PV plant intensity or temperature, or decreasing the PLL integration coefficient or PV capacity, thereby improving the stability of the PV plant integrated to weak AC grid system.
The following conclusions can be drawn from the theoretical analysis: (1) The subsynchronous interaction between the PV plant and weak AC grid will form the damping path through the PLL, affecting the SSO mode damping of the system. There is the SSO risk dominated by PLL in the PV plant integration. (2) The subsynchronous interaction provides negative damping to the system, which is the dominant factor for the SSO of the PV plant integration. (3) Reasonable design of system parameters according to the negative damping characteristics of subsynchronous interaction can effectively increase the SSO mode damping and better maintain the original positive damping characteristics of the PV plant.
keywords:Photovoltaic plant, subsynchronous oscillation, subsynchronous interaction, damping torque method, phase-locked loop
中图分类号:TM712
DOI: 10.19595/j.cnki.1000-6753.tces.221776
国家重点研发计划资助项目“响应驱动的大电网稳定性智能增强分析与控制技术”(2021YFB2400800)。
收稿日期 2022-09-18
改稿日期 2022-10-26
高本锋 男,1981年生,副教授,研究方向为高压直流输电和电力系统次同步振荡。E-mail: gaobenfeng@126.com
邓鹏程 男,1998年生,硕士,研究方向为新能源并网系统次同步振荡分析。E-mail: 1533202670@qq.com(通信作者)
(编辑 郭丽军)