表1 电动汽车用感应电机参数
Tab.1 The parameters of induction motor for electric vehicles
参 数数 值 额定电压/V72 额定功率/kW12.5 峰值功率/kW30 转速范围/(r/min)0～6 000 极对数2 定子外径/mm188 定子槽数36 转子外径/mm108.6 转子内径/mm38 转子槽数42 铁心长度/mm180 定子内径/mm110
摘要 死区、管压降等非线性因素会在逆变器的输出电压中注入低次谐波，从而引起定子电流发生5次与7次谐波畸变并增加转矩脉动。同时，由于电动汽车用感应电机的固有频率较低，当电机中高速运行时，定子电流的低次谐波频率与电机固有频率重合，从而产生低频共振。针对上述问题，该文首先对感应电机固有频率的仿真与测试方法展开研究，确定电机的固有频率范围。然后在对死区与管压降所引起谐波畸变特性进行分析的基础上，提出在转子磁链定向后的两相旋转坐标系（dq坐标系）下矢量控制系统中电流内环加入可衰减6次谐波的谐振控制器，并针对谐振控制器参数的设计方法展开研究。最后建立仿真模型与实验平台，结合电流快速傅里叶变换（FFT）分析结果与功率谱密度以及振动实验数据，并与其他前馈补偿方法进行对比，证明通过对dq坐标系下6次谐波的抑制，可有效降低定子电流的5次与7次谐波以及固有频率处电机的振动功率，同时说明该文的理论分析与所提的dq坐标系下6次谐波抑制方法是正确且可行的。
关键词：感应电机 低频共振 低次谐波 控制策略 死区
发展电动汽车是解决能源与环境问题，实现“碳达峰、碳中和”目标的有效手段[1]。然而，电动汽车的电机驱动系统存在严重的振动与噪声问题[2-3]。首先，在调制过程中，逆变器输出电压在开关频率及其整数倍频处的较窄频段中存在丰富的高次谐波，不仅产生强烈的电磁干扰，还会给电机带来严重的电磁振动与噪声，降低电机寿命，容易让用户感觉不适[4-5]。针对以上问题，国内外学者提出用变载波频率调制代替传统固定载波频率调制。包括随机载波频率[6-7]与周期载波频率等调制策略[8]，在总谐波能量不变的前提下，以上方法能够将开关频率及其倍频附近分布的特征谐波频谱分散至更宽的频段内，对因调制引起的电机高频噪声具有良好抑制效果。
当定子电流存在与电机固有频率重合的谐波时，就会引发电机共振[4-5]。在理想情况下，逆变器线电压与定子电流仅存在基波与开关频率及其倍数频率附近分布的边带谐波，并不包含其他低次谐波[9]。但是，逆变器中开关管的导通压降、缓冲电容以及在调制过程为防止桥臂直通而加入的死区时间等非线性因素会导致电机定子电流发生低次谐波畸变[10]，加之电动汽车用感应电机的固有频率低，且电机运行速域宽，调制过程所产生的低次谐波难免会与电机的固有频率重合，从而发生低频共振[5]。文献[11]通过选择合理的槽配合，以削弱与电磁振动相关的电磁力波，降低感应电机（Induction Motor, IM）在固有频率处的振动峰值。除了电机本体优化设计，减小因死区与管压降引起的电流低次谐波畸变是削弱电机低频共振的必要手段。基于脉冲时间补偿是最为传统且常用的低次谐波抑制方法，即根据定子电流极性将死区与管压降引起的电压误差转换为一个开关周期内的脉冲宽度调制（Pulse Width Modulation, PWM）并进行补偿，但是该方法的补偿效果有限[12]，尤其是零电流钳位现象依然明显。文献[13]提出一种无死区调制方法，上下桥臂的开关信号不再保持互补，而是根据电流极性，仅有一路发生动作，另一路保持关断状态，依靠体二极管完成续流，从而避免了因死区加入而产生电流谐波，但是该方案存在电流过零时极性判断不准确的问题，零电流钳位效应较为明显。为此文献[9]提出一种反向补偿法，促使电流提前过零，但是电流低次谐波畸变情况依然较为严重。文献[14]提出在电压给定信号进行平均电压误差前馈补偿，能够降低次谐波畸变，但是抑制效果有限，且依赖于电流极性的采样精度。由于死区、管压降等非线性因素所产生的电流谐波主要为5次与7次，文献[15]提出一种基于PI控制器的5、7次谐波抑制策略，该方案需要通过坐标变换分别将定子电流的5、7次谐波映射为直流量，再利用4个PI控制器得到5、7次谐波dq坐标系下电流补偿量，但是该方法实现过程较为复杂。文献[16]在进行控制系统建模时将非线性误差，通过合理配置PI控制器参数实现对低次谐波引起扰动作用的抑制，但是该方案会降低控制系统的动态响应速度。文献[17]提出一种考虑死区的特定低次谐波消除策略，并给出了死区时间设计的经验公式，但是该方案未考虑管压降引起的谐波畸变。文献[5]提出一种基于带通滤波器的固有频率范围内的电流频谱整形控制策略，但是未考虑滤波器参数的优化设计。文献[18]将逆变器的非线性电压误差视为扰动量，并分解为考虑缓冲电容下由死区时间引起的电压误差以及由导通压降引起的电压误差。针对两种电压误差分别提出了相应的前馈补偿量计算方法。
本文针对减小电机低频共振的定子电流低次谐波抑制方法展开研究，首先对电机低频固有频率进行仿真与实验测试；然后对低次谐波特性进行分析，在此基础上对矢量控制进行改进，提出在dq坐标系下的电流内环中引入6次谐振控制器，并给出控制器参数设计的理论依据；最后分别通过仿真与实验对所提方法及其理论分析的可行性与正确性进行验证。
首先对本文所研究电动汽车用感应电机进行模态分析，其参数见表1。然后在SoildWorks等比例绘制电机三维模型，导入至有限元软件Ansys/ Workbench进行模态分析，并在不施加任何约束的前提下，对各阶振型和固有频率进行求解。在4 kHz以内得到容易产生共振的两个二阶模态和两个三阶模态，如图1所示。
表1 电动汽车用感应电机参数
Tab.1 The parameters of induction motor for electric vehicles
参 数数 值 额定电压/V72 额定功率/kW12.5 峰值功率/kW30 转速范围/(r/min)0～6 000 极对数2 定子外径/mm188 定子槽数36 转子外径/mm108.6 转子内径/mm38 转子槽数42 铁心长度/mm180 定子内径/mm110
图1 电机模态分析振形
Fig.1 Mode shape of the modal analysis for motor
采用单点激振力锤锤击法进行电机的模态实验，测量电机的固有频率。采用带有传感器的钢质力锤产生宽频带激励，用加速传感器吸附在电机上测量激励响应信号，用信号分析仪采样与存储激励信号和响应信号，并将数据传送至上位机数据处理软件，得到电机的模态数据，电机模态实验示意图如图2所示。
进行多次测试，得到垂直方向的电机频率响应曲线，如图3所示。频率响应曲线中的峰值点所对应的频率为电机的固有频率，与有限元仿真结果相同，共包含两个二阶固有频率和两个三阶固有频率。
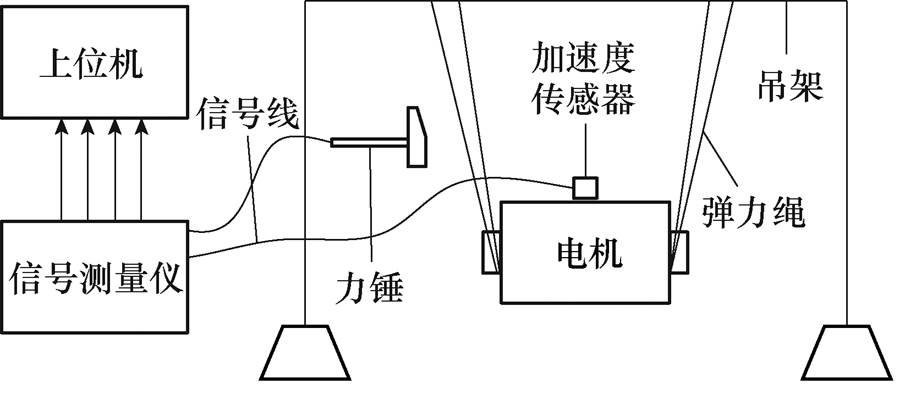
图2 电机模态实验示意图
Fig.2 Schematic of motor modal experiment
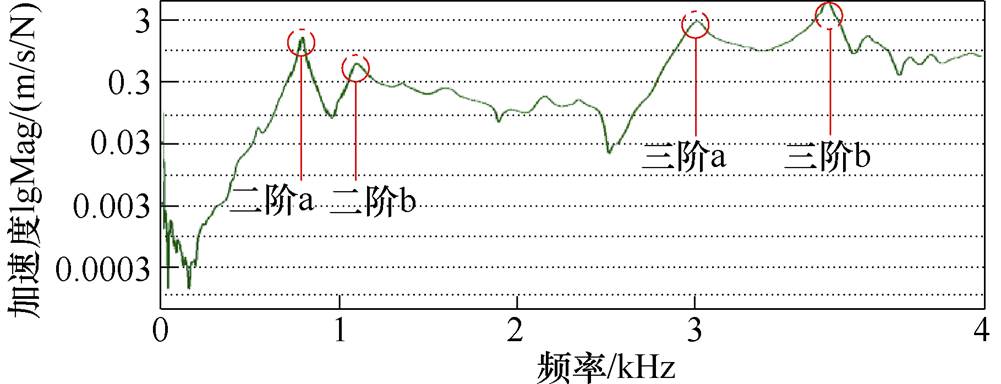
图3 电机模态实验下的频率响应曲线
Fig.3 Frequency response curve under motor modal experiment
固有频率的仿真与实验结果见表2，两者误差较小，证明固有频率的仿真与实验测试方法的正确性。
表2 固有频率的仿真与实验结果
Tab.2 Simulation and experimental results of motor natural frequency
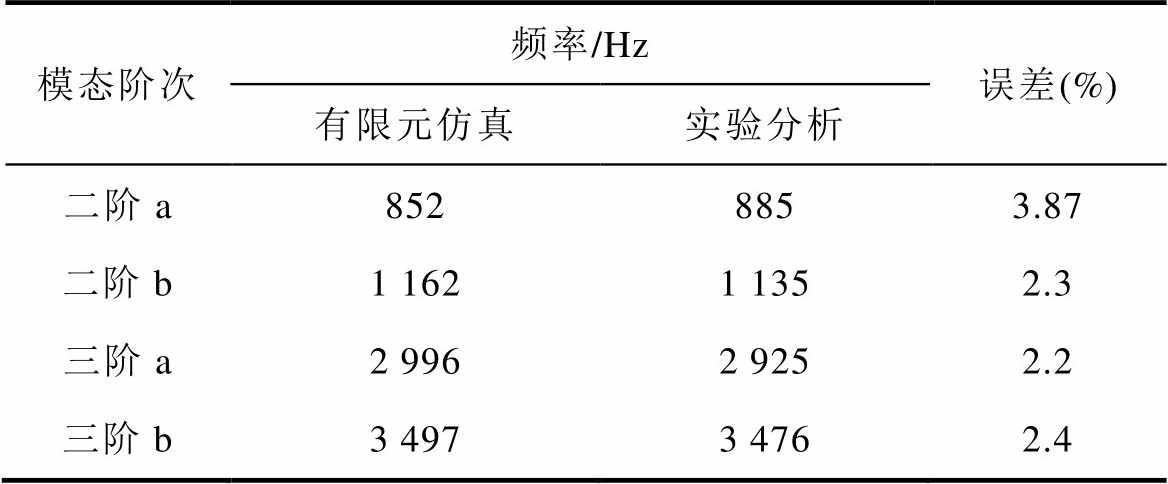
模态阶次频率/Hz误差(%) 有限元仿真实验分析 二阶a8528853.87 二阶b1 1621 1352.3 三阶a2 9962 9252.2 三阶b3 4973 4762.4
三相电压源型感应电机驱动系统拓扑结构如图4所示。
在理想情况下，采用空间矢量脉宽调制（Space Vector PWM, SVPWM）策略的线电压仅含有基波与开关频率与倍数频率附近的高次谐波，其谐波分布如图5a所示，此时定子电流的低次谐波分布如图5b所示，低次谐波含量很低。而当加入死区后，定子电流的低次谐波分布如图5c所示，与图5a相比，5次与7次谐波显著增加，考虑开关管与体二极管导通压降情况下的电流谐波分布如图5d所示，5次与7次谐波又进一步增加。低次谐波不仅会增加转矩脉动，恶化电机的动力性能，尤其在转速大于4 000 r/min的情况下，低次谐波将会与电机的二阶固有频率发生重合，从而引发低频共振。
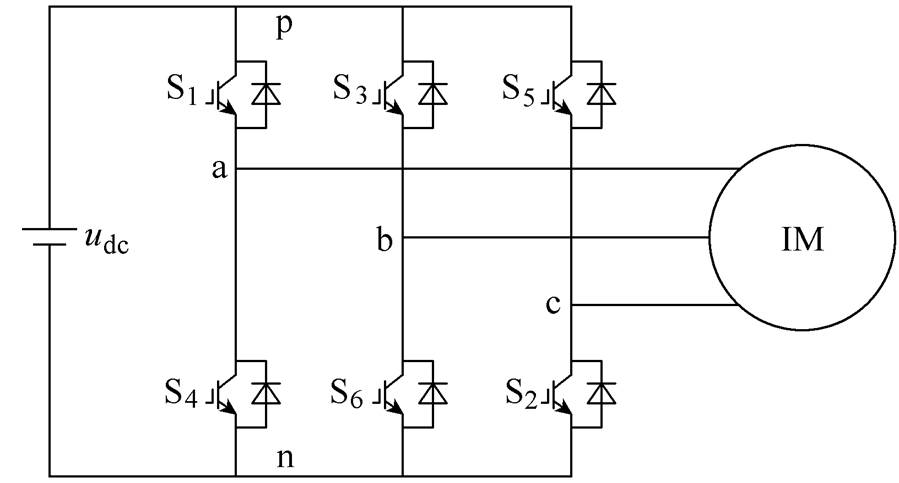
图4 电压源型电机驱动系统拓扑结构
Fig.4 Topology of IM fed by voltage source inverter
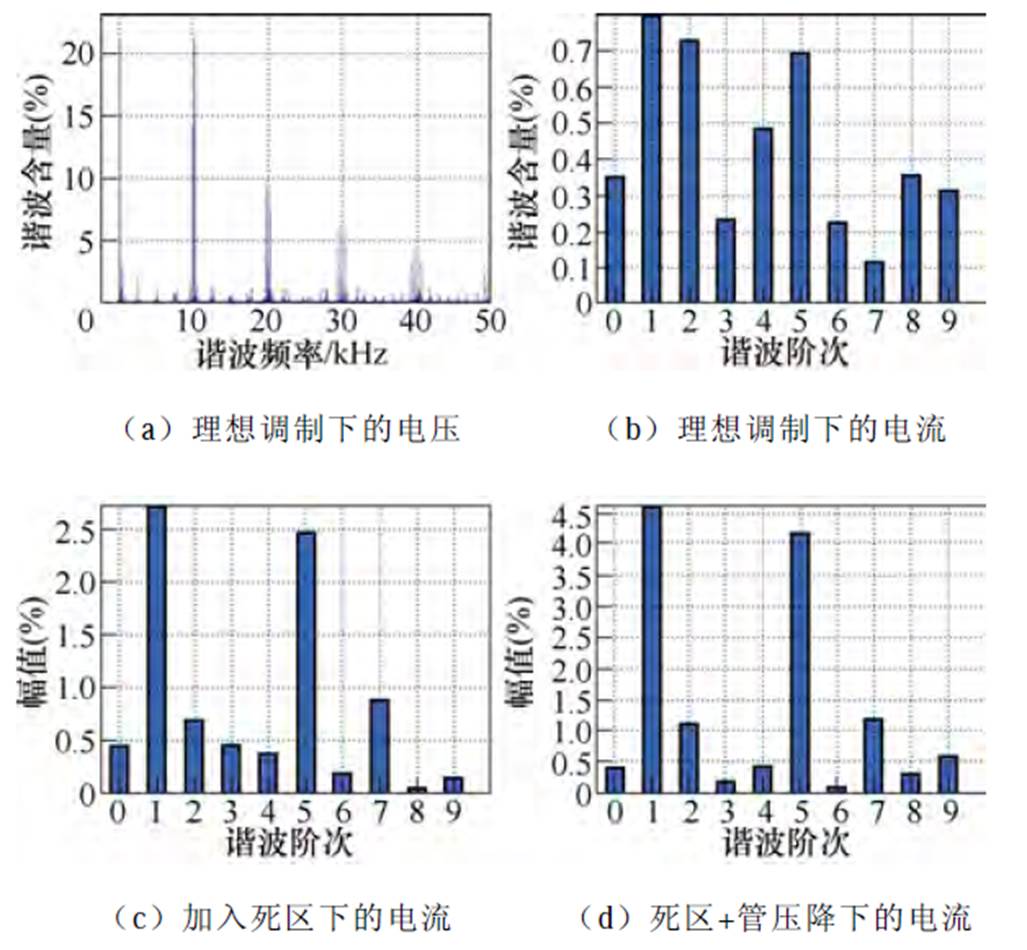
图5 不同情况下的谐波分布
Fig.5 Harmonic distribution under different conditions
定义三相定子电流5次谐波分量表达式为
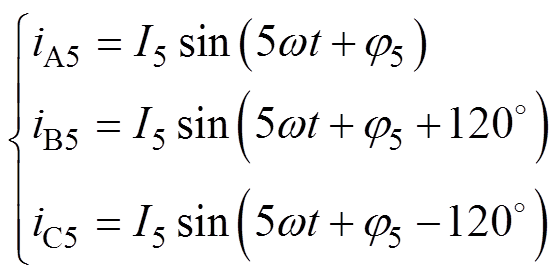（1）
式中，iA5、iB5、iC5分别为A、B、C三相定子电流的5次谐波分量；I5为5次谐波幅值；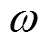
为基波角频率；
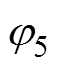为5次谐波的相位。三相5次谐波的时序为负序。对其进行基于转子磁链定向的坐标变换后，得到两相旋转坐标系（dq坐标系）下5次电流谐波分量表达式为
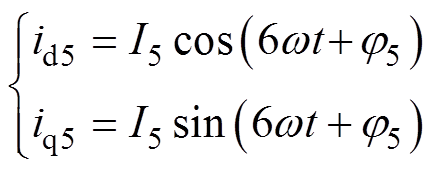（2）
三相7次谐波分量的时序为正序，定义其表达式为
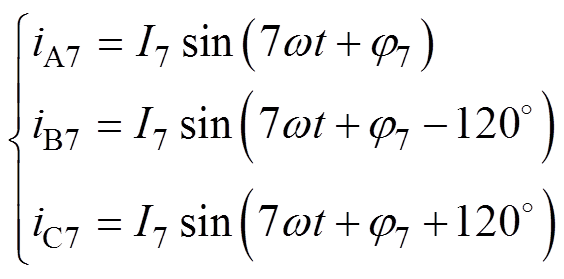（3）
式中，I7与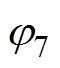
分别为7次谐波的幅值与相位。对其进行基于转子磁链定向的坐标变换后，dq坐标系下7次电流谐波分量表达式为
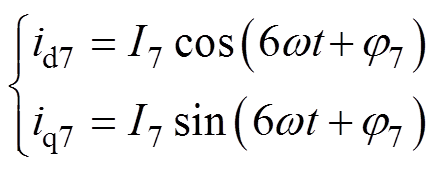（4）
图6为考虑死区与管压降情况下dq坐标系下定子电流id、iq的低次谐波分布示意图。可以看出dq坐标系下5次与7次电流谐波的频率均为6次，与式（2）和式（4）的结果是一致的。因此，降低dq坐标系下电流的6次谐波与减小三相定子电流的5、7次谐波是等效的。
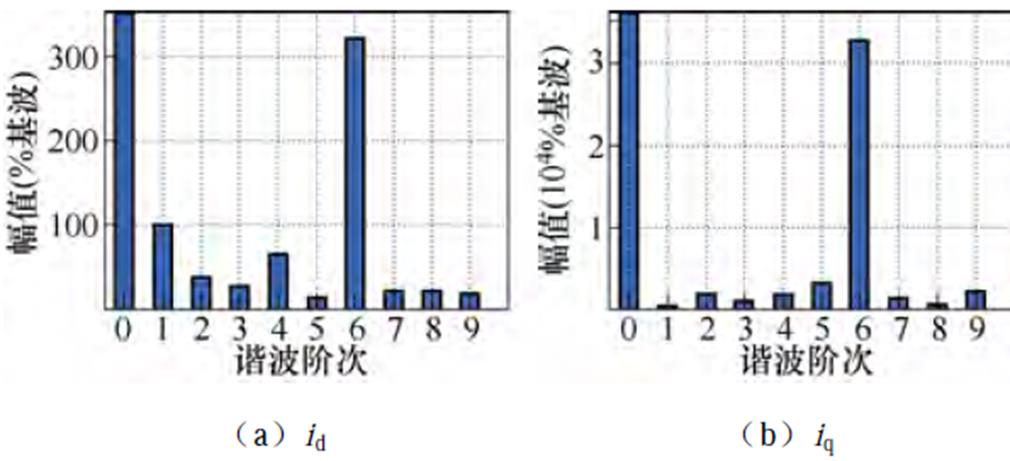
图6 dq坐标系下定子电流的低次谐波分布
Fig.6 Low-order harmonic distribution of id and iq
为减小id、iq中的6次谐波含量，本文提出在电流环的控制器中加入6次谐波谐振控制器，其表达式为
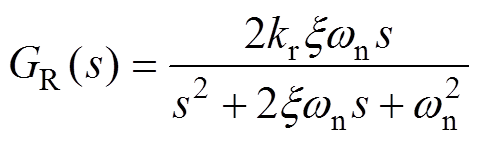（5）
式中，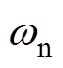
为谐振频率，设置为6次谐波频率；
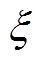为阻尼比；kr为谐振控制器的系数。忽略dq坐标系交叉耦合的影响，电流内环的控制环路结构如图7所示。
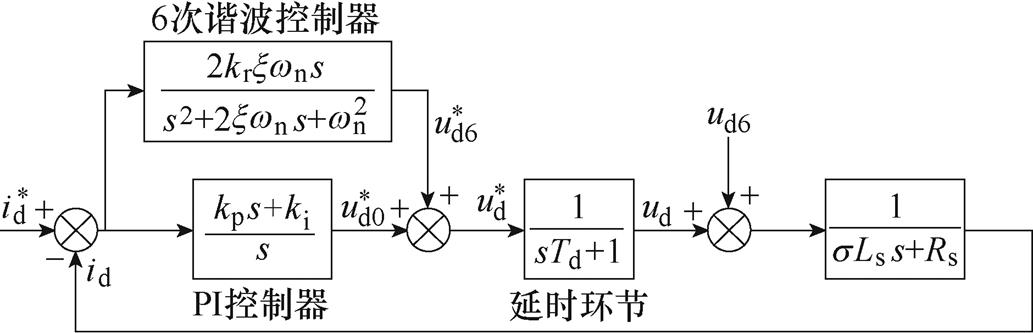
图7 引入6次谐波谐振控制器的电流内环结构
Fig.7 Inner current loop structure with sixth harmonic resonance controller
图7中，Td为开关周期，本文取100 ms，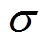
为漏磁系数，Ls为定子等效电感，Rs为定子电阻。采用零极点对消的原则配置PI控制器的参数kp与ki，并期望电流内环的带宽为开关频率的1/10，即1 kHz，PI控制器的参数设置为
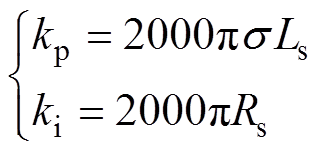（6）
在不加入6次谐波控制器的情况下，电流内环的开环传递函数Gi_ol(s)为
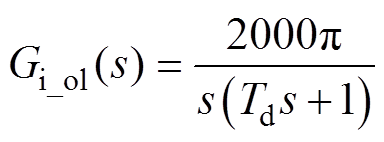（7）
电流的闭环传递函数Gi_cl(s)表达式为
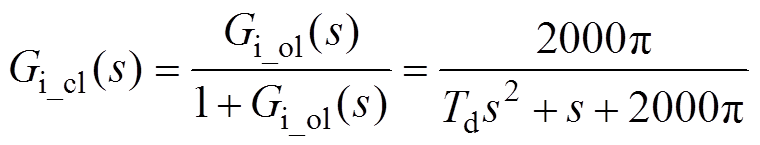（8）
其幅频特性曲线如图8a所示。将死区与管压降在dq坐标系产生的6次谐波畸变视为扰动量ud6，ud6到id的传递函数Gu_i(s)的表达式为
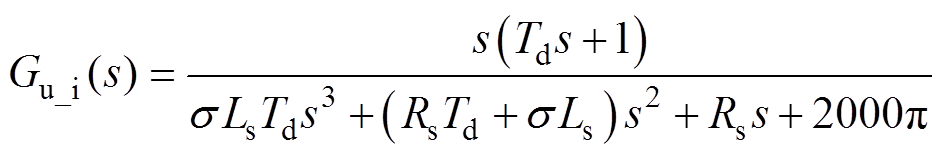（9）
Gu_i(s)的幅频特性曲线如图8b所示，可以明显看出，在70 Hz～1.8 kHz范围内的Gu_i(s)增益在0 dB以上，说明常规PI控制器不具备抑制该频段内电压非线性引起定子电流低次谐波畸变的能力。
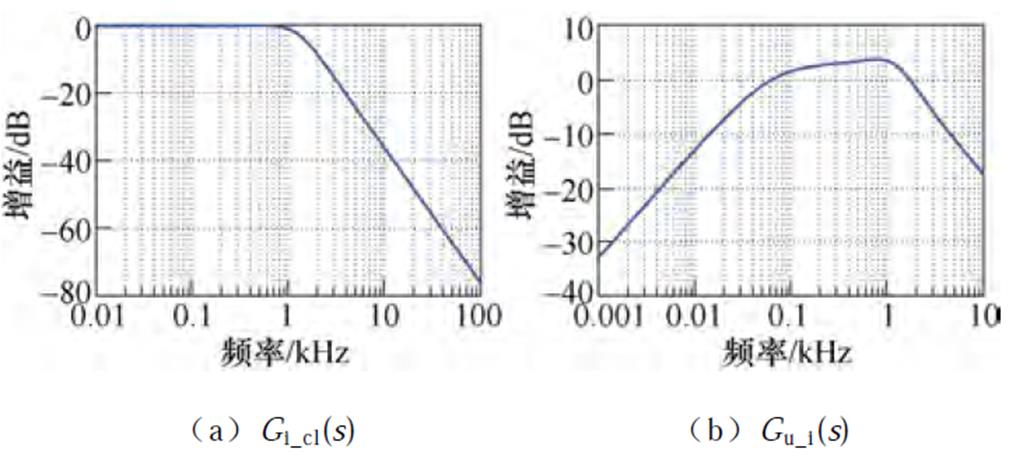
图8 电流内环与电压扰动传递函数的幅频特性曲线
Fig.8 Bode diagram of Gi_cl(s) and Gu_i(s)
当基频为170 Hz时，5次与7次谐波频率分别为850 Hz和1 190 Hz，与电机的二阶固有频率重合，谐波过大时将会发生共振。令6次谐波控制器中自然频率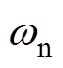=2 240p rad/s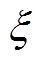，=0.5，绘制不同kr取值下开环传递函数Gi_ol(s)的幅频特性曲线，如图9所示。可以看出，6次谐波控制器的加入，对Gi_ol(s)的低频特性不产生影响，但是随着kr的增加，在1 000 Hz处的增益明显增加，截止频率也同样增加，但是相位裕度随之减小，可能导致系统不稳定。为了进一步分析kr对系统稳定性的影响，绘制kr从1增加至4情况下闭环传递函数Gi_cl(s)的极点分布，如图10所示。随着kr增加，系统的一对共轭极点向右移动，当kr＞3.5时，Gi_cl(s)出现右半平面极点，导致系统处于不稳定状态。为了从理论上证明6次谐波控制器对6次谐波的抑制效果，绘制kr从1增加至3情况下电压扰动传递函数Gu_i(s)的幅频特性曲线，如图11所示。由于控制器的加入，6次谐波处及其周边频段的幅值增益下降至0 dB以下，随着kr的增加，抑制效果越明显。尽管出现了另一个尖峰，但是dq坐标系下逆变器输出电压在该尖峰所处频率范围并不存在谐波，因此不会引起额外的谐波畸变。但是应尽量满足Gu_i(s)的截止频率小于12次谐波频率，以防止增加定子电流的11次与13次谐波。
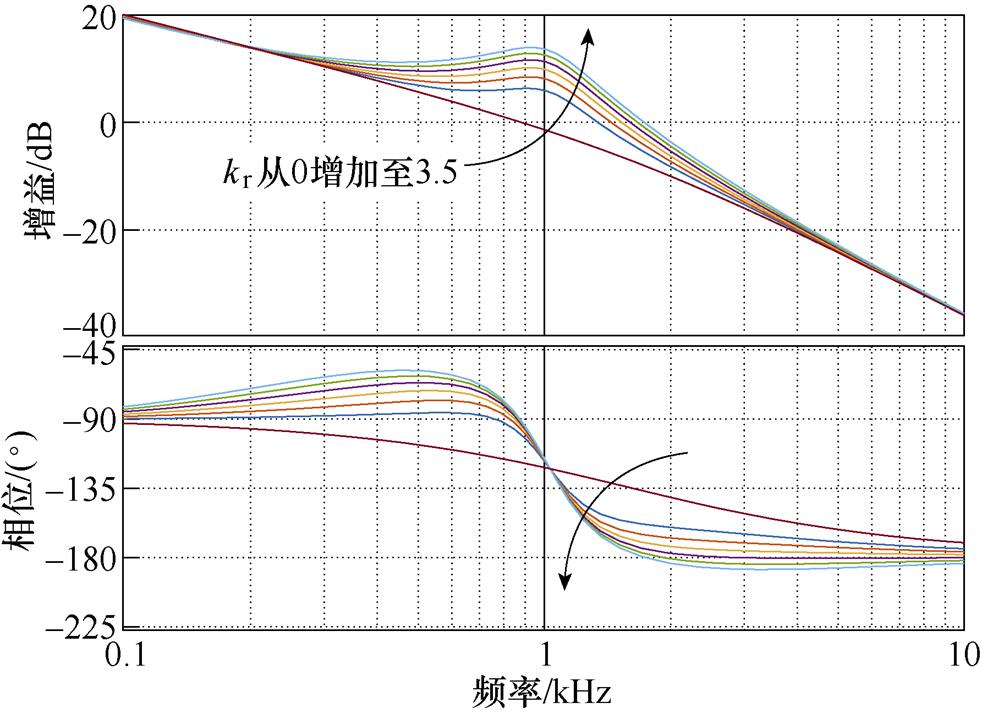
图9 不同kr取值下电流开环传递函数的幅频特性曲线
Fig.9 Bode diagram of Gi_ol(s) under different kr
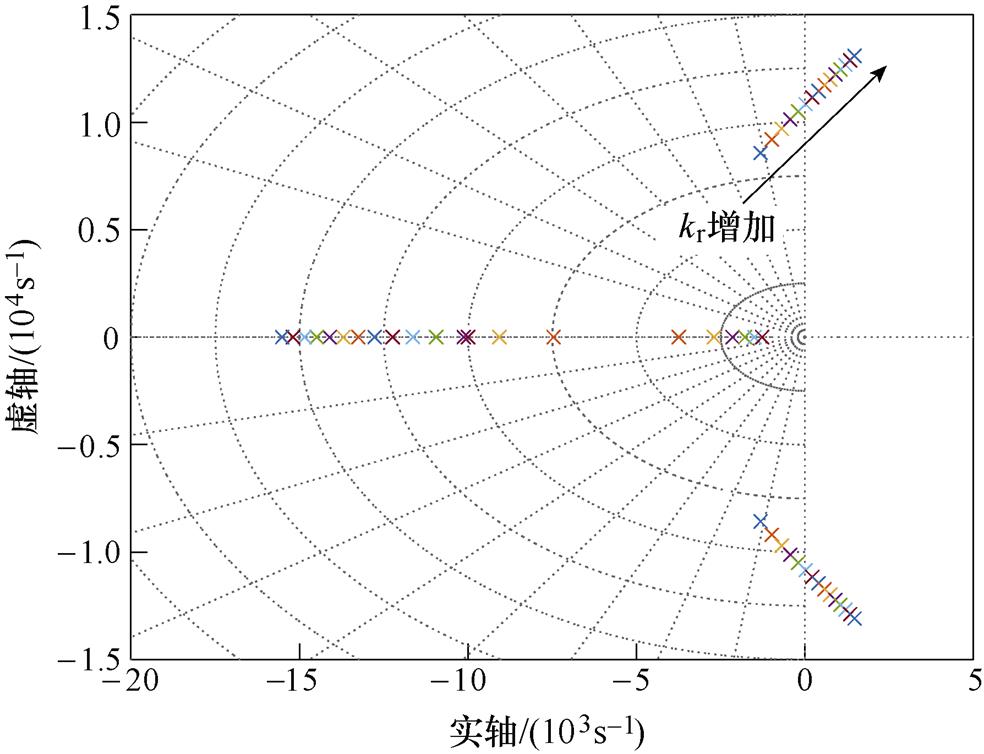
图10 不同kr取值下电流闭环传递函数的极点分布
Fig.10 Poles distribution of Gi_cl(s) under different kr
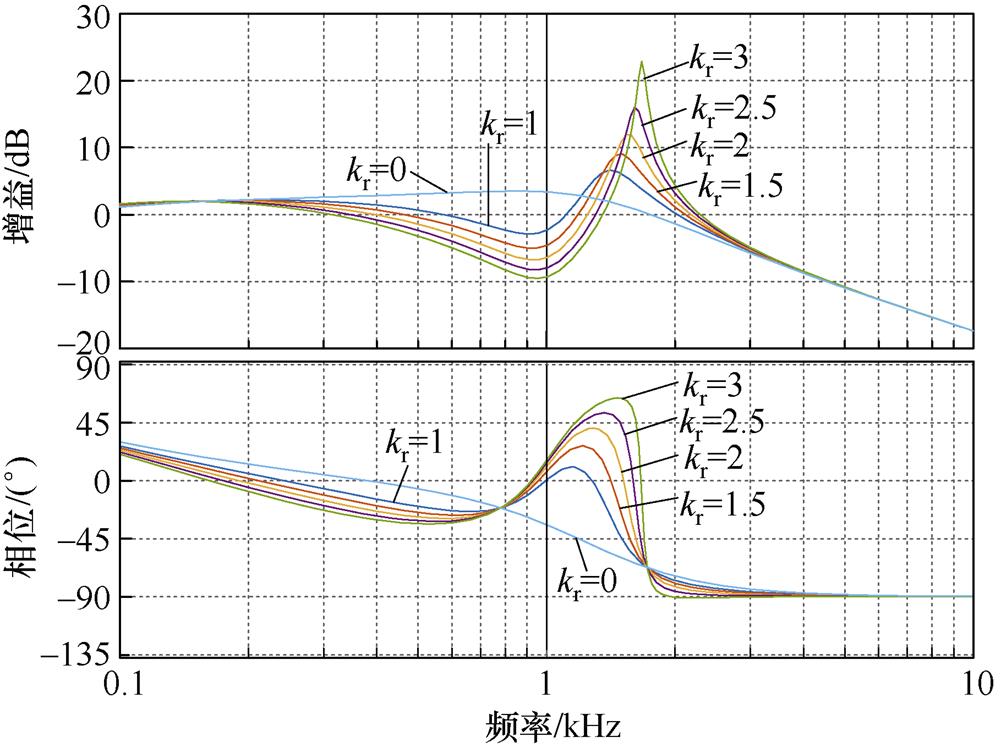
图11 不同kr取值下Gu_i(s)的幅频特性曲线
Fig.11 Bode diagram of Gu_i(s) under different kr
综上所述，6次谐波控制器的谐振频率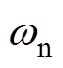设置为6次谐波角频率，kr则依据闭环传递函数极点分布与电压扰动传递函数幅频特性曲线进行配置，在满足电流内环稳定性与Gu_i(s)的截止频率低于2倍谐振频率的条件下进行选择。
首先结合仿真与理论分析对本文所提方法的优越性进行验证与说明。在Matlab的Simulink平台分别构建了传统基于脉冲时间补偿模型、文献[18]提出的逆变器非线性前馈补偿模型以及本文所提6次谐波控制器模型，对电机固有频率处的低次谐波抑制效果进行仿真与比较。仿真模型中感应电机与逆变器参数见表3，开关频率与采样频率均为10 kHz，kr设置为2.5。在电机转速给定为5 000 r/min，负载4 N·m的工况下进行仿真，设置死区时间为2 ms，传统基于脉冲时间补偿模型、逆变器非线性前馈补偿模型以及本文所提6次谐波控制器模型的仿真结果分别如图12～图14所示。
表3 电机与逆变器参数
Tab.3 Parameters of IM and inverter
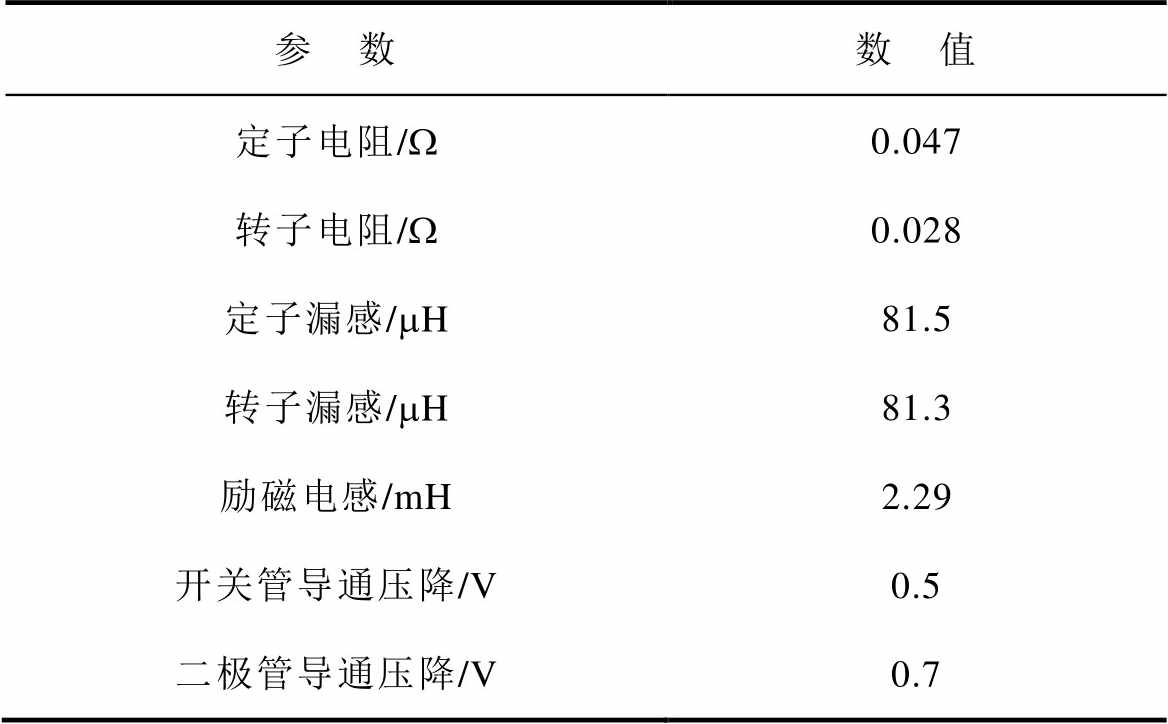
参 数数 值 定子电阻/W0.047 转子电阻/W0.028 定子漏感/mH81.5 转子漏感/mH81.3 励磁电感/mH2.29 开关管导通压降/V0.5 二极管导通压降/V0.7
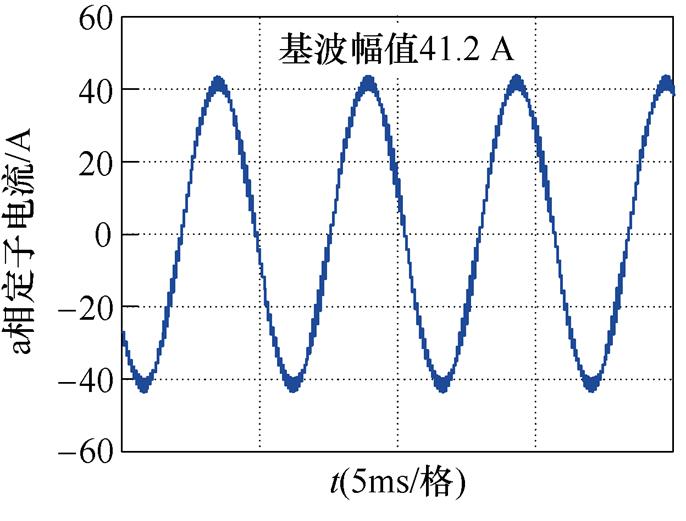
（a）定子电流波形
（b）谐波分析结果
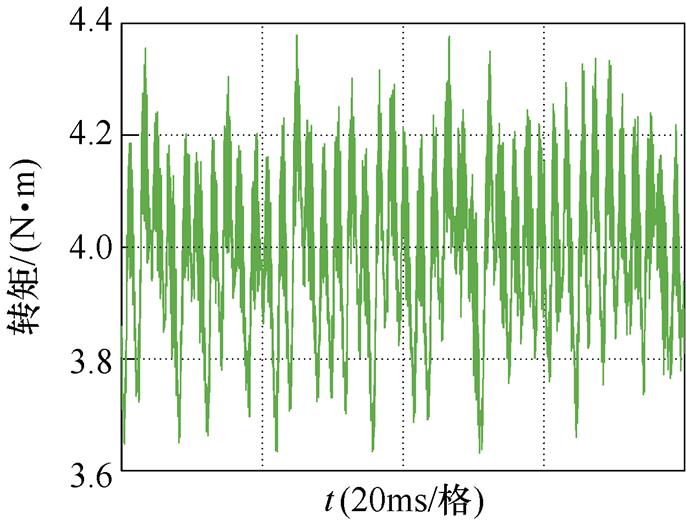
（c）转矩波形
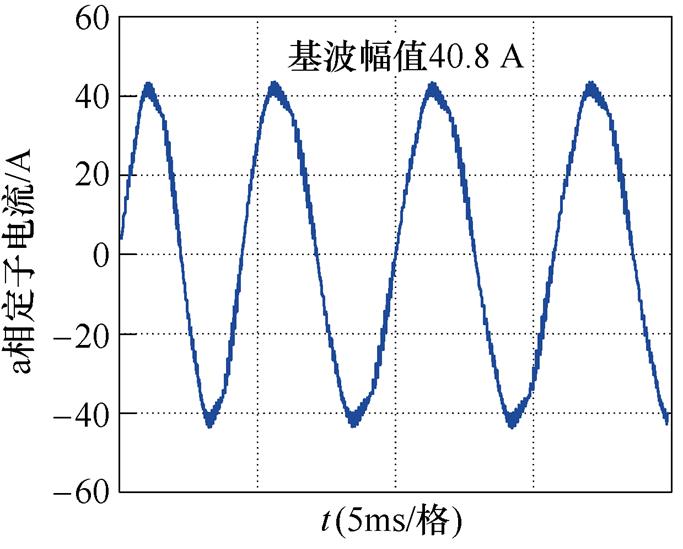
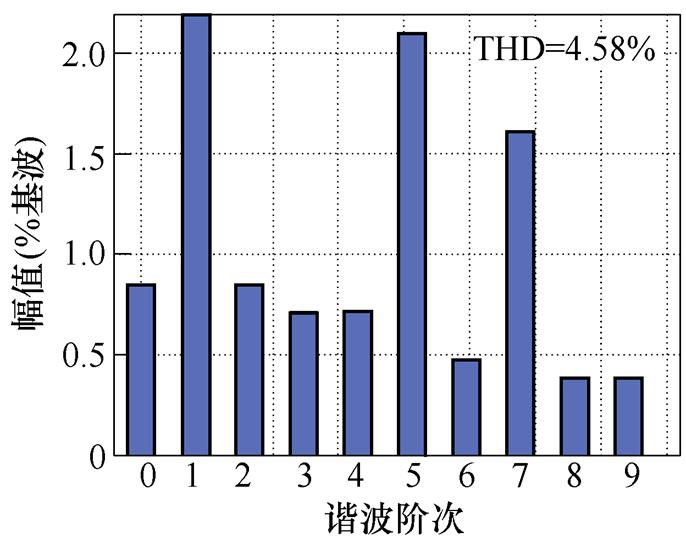
图12 基于脉冲时间补偿下的仿真波形
Fig.12 Simulation waveforms under compensation of the duration of pulse
此时基波电流频率为169.5 Hz，定子电流5次谐波频率为847.5 Hz，定子电流7次谐波频率为1 186.5 Hz，与电机的两个二阶固有频率比较接近。其中传统基于脉冲时间补偿策略下的总谐波畸变率（Total Harmonic Distortion, THD）与转矩脉动高于其他两种方法，5次谐波占比为2.1%，7次谐波占比为1.6%，对低次谐波的抑制效果最差。接下来结合图15从理论上对基于脉冲时间补偿策略的缺陷进行说明。图15a中，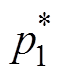
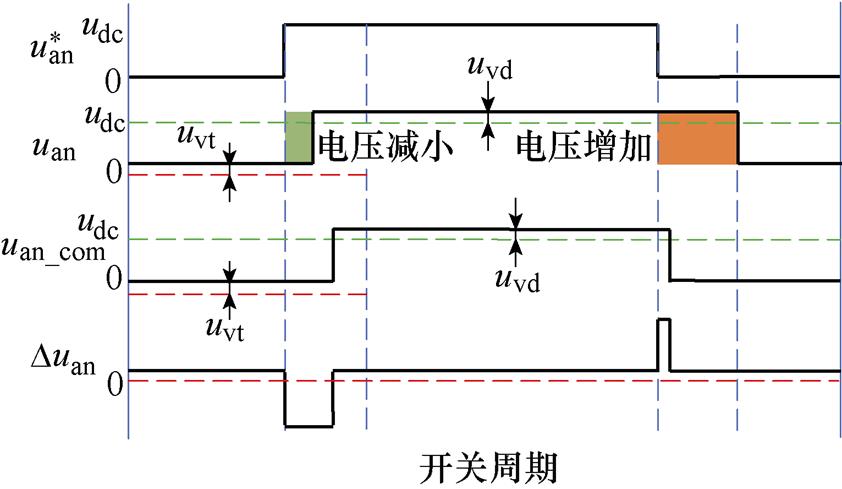
与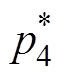
分别为逆变器a相上、下桥臂的理想开关信号，p1与p4为考虑死区时间td、开通延时时间ton、关断延时时间toff下的实际开关信号。在考虑功率器件导通压降uvt、反并联二极管压降uvd的前提下，一个开关周期内逆变器a相输出电压uan如图15b与图15c中所示。尽管采用脉冲时间补偿方法可以在理论上实现一个开关周期内平均电压误差为零，但是经过补偿后的逆变器实际输出电压uan_com与SVPWM出的理想输出电压
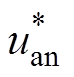之间误差Duan存在直流偏移与两个脉冲，必然会产生一定的低次谐波畸变，因此传统脉冲时间补偿方法对由死区、管压降引起的低次谐波畸变抑制作用有限。另外，开通延时、关断延时、管压降会随着电流与温度等工作情况发生变化，采用离线的脉冲时间补偿方法无法做到精确补偿。
（a）定子电流波形
（b）谐波分析结果
（c）转矩波形
图13 逆变器非线性前馈补偿下的仿真波形
Fig.13 Simulation waveforms under inverter nonlinearity feedforward compensation
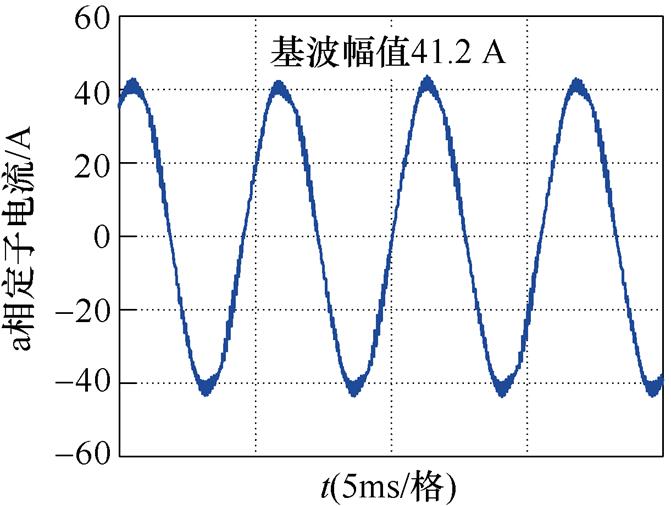
（a）定子电流波形
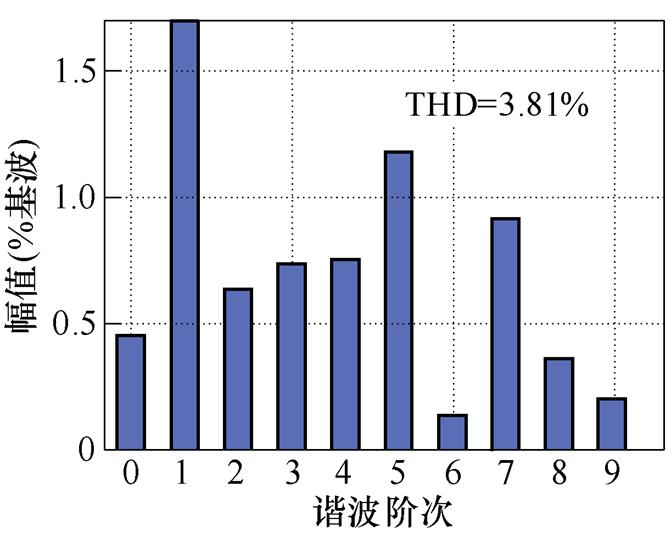
（b）谐波分析结果
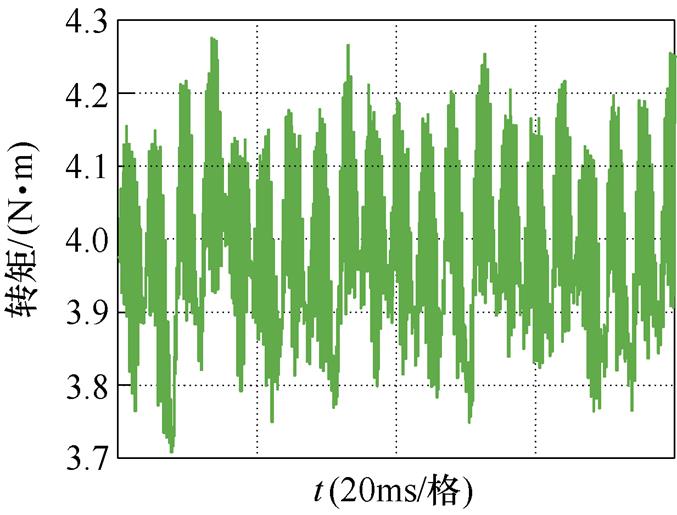
（c）转矩波形
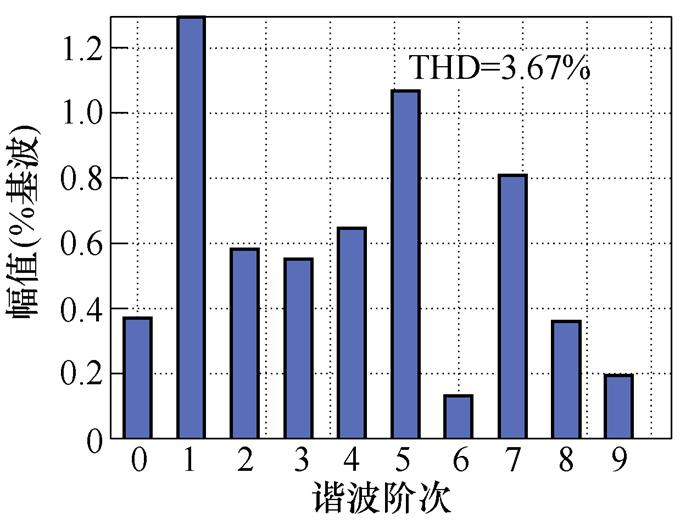
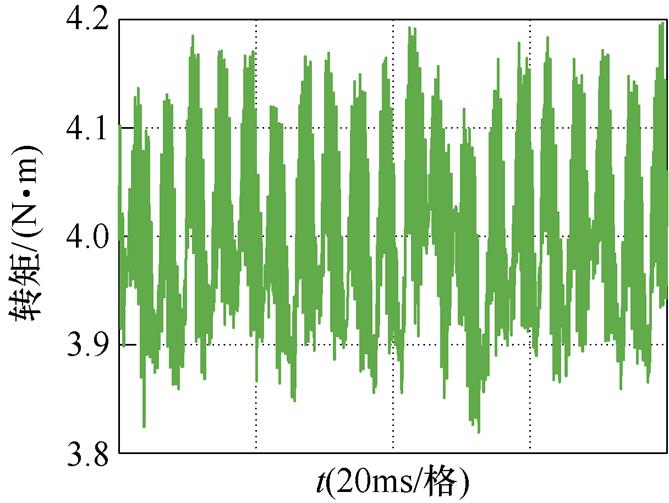
图14 采用6次谐波控制器的仿真波形
Fig.14 Simulation waveforms under control of 6th harmonic
文献[18]提出的逆变器非线性前馈补偿策略则考虑了死区阶段缓冲电容的影响，并将死区与管压降引起的电压误差在给定值上进行补偿，与脉冲时间补偿相比，低次谐波抑制效果有所提高。其中，定子电流5次谐波占比为1.2%，7次谐波占比为0.9%。转矩脉动范围±0.3 N·m。而在dq坐标系的电流内环加入本文所提出的6次谐波控制器之后，THD下降至3.67%，其中5次谐波与7次谐波均显著减小，分别为1.07%和0.8%，转矩脉动范围也减小至3.8～4.2 N·m之间，仿真结果证明了本文所提出的6次谐波控制器及其参数设计方法是有效可行的。
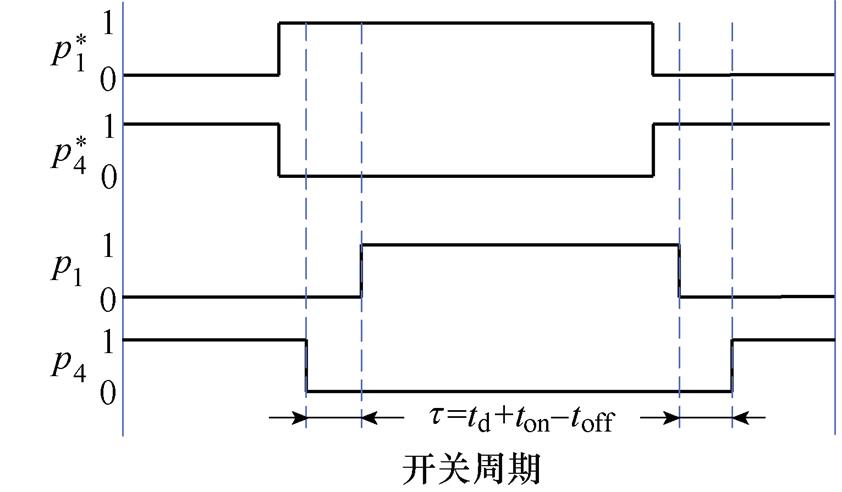
（a）开关信号
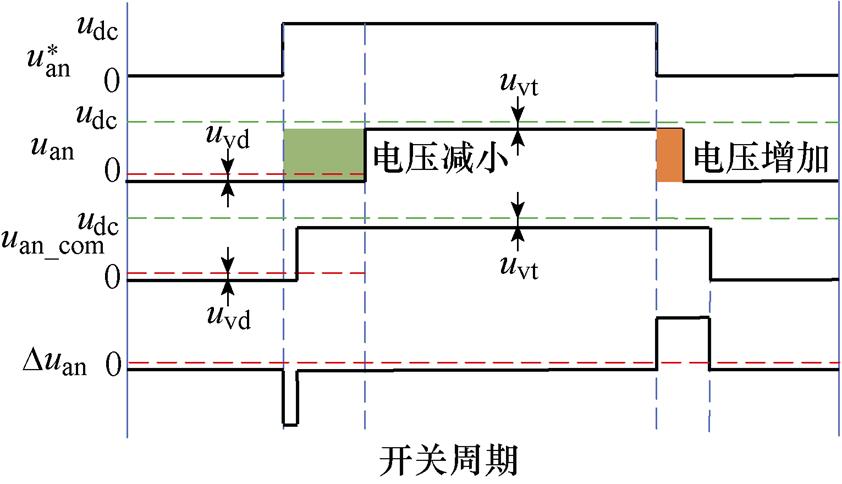
（b）ia＞0情况下的输出电压
（c）ia＜0情况下的输出电压
图15 传统脉冲时间补偿方法的示意图
Fig.15 The diagram for the compensation method of the duration of pulse
为了对本文所提方法的有效性进行进一步验证，搭建了如图16所示的电机对拖实验平台。采用TMS320F28069进行数据处理，采用非接触式传感器MLX91205采样电机定子电流，开关频率与采样频率均为10 kHz，电机参数与仿真一致。在四种不同工况下，对本文所提方法进行实验验证，并与传统基于脉冲时间补偿以及文献[18]提出的逆变器非线性前馈补偿进行比较。
图16 电机对拖实验平台
Fig.16 Experiment platform of IM drag
（1）工况1（低速500 r/min，额定负载4 N·m）：传统脉冲时间补偿方法、逆变器非线性前馈补偿方法与本文所提6次谐波控制的实验结果分别如图17～图19所示。此时定子电流基波频率为26.3 Hz，6次谐波控制器中谐振频率wn设置为991.5 rad/s，由于电流过零点附近所持续的开关周期较多，零电流钳位效应较为严重。脉冲时间补偿下定子电流THD为4.82%，转矩脉动为±0.4 N·m，5次谐波占比为1.74%，7次谐波占比为1.79%。
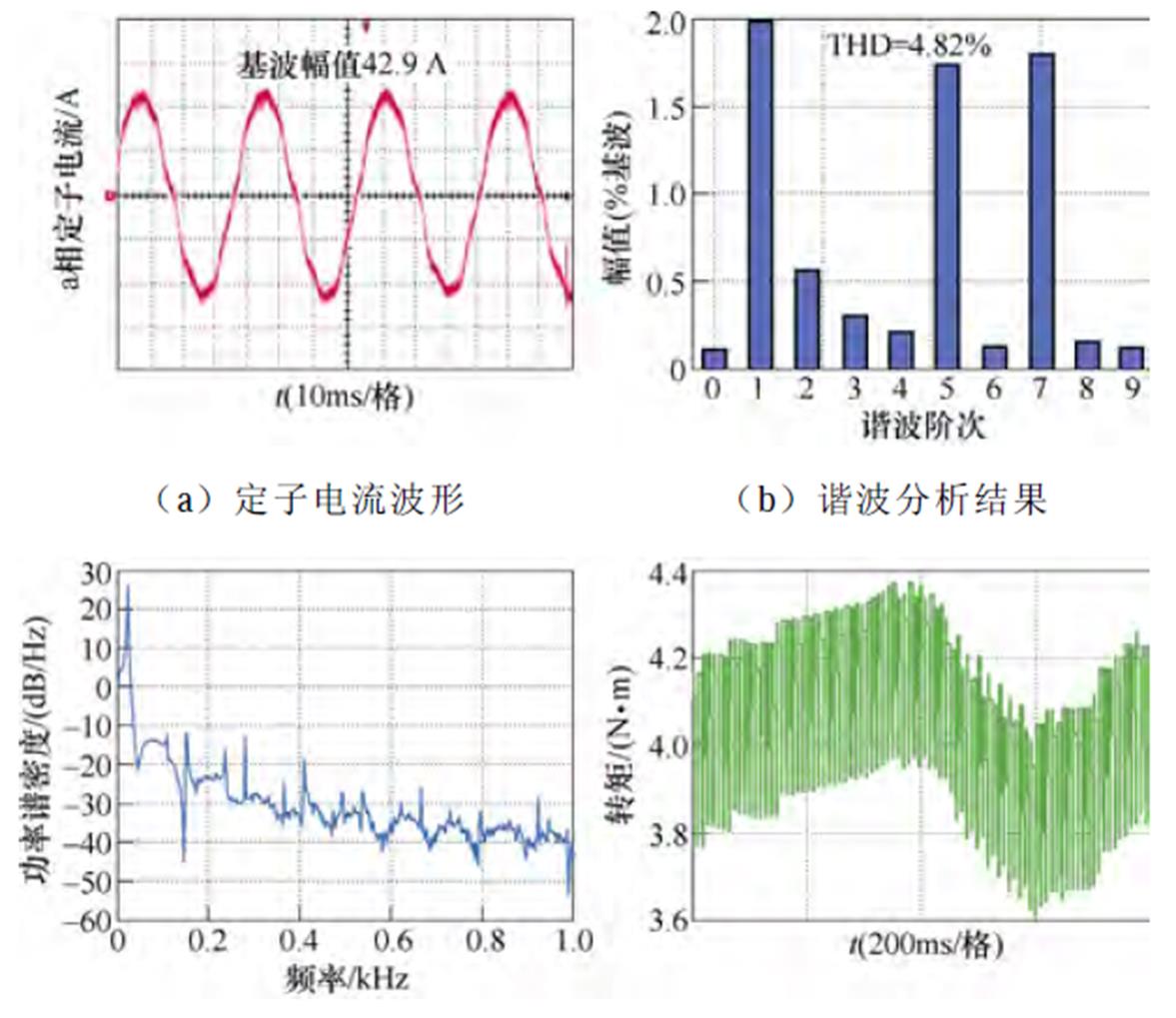
图17 500 r/min，4 N·m工况下基于脉冲时间补偿策略的实验波形
Fig.17 Experimental waveforms under compensation of the pulse duration when IM operates at 500 r/min and 4 N·m
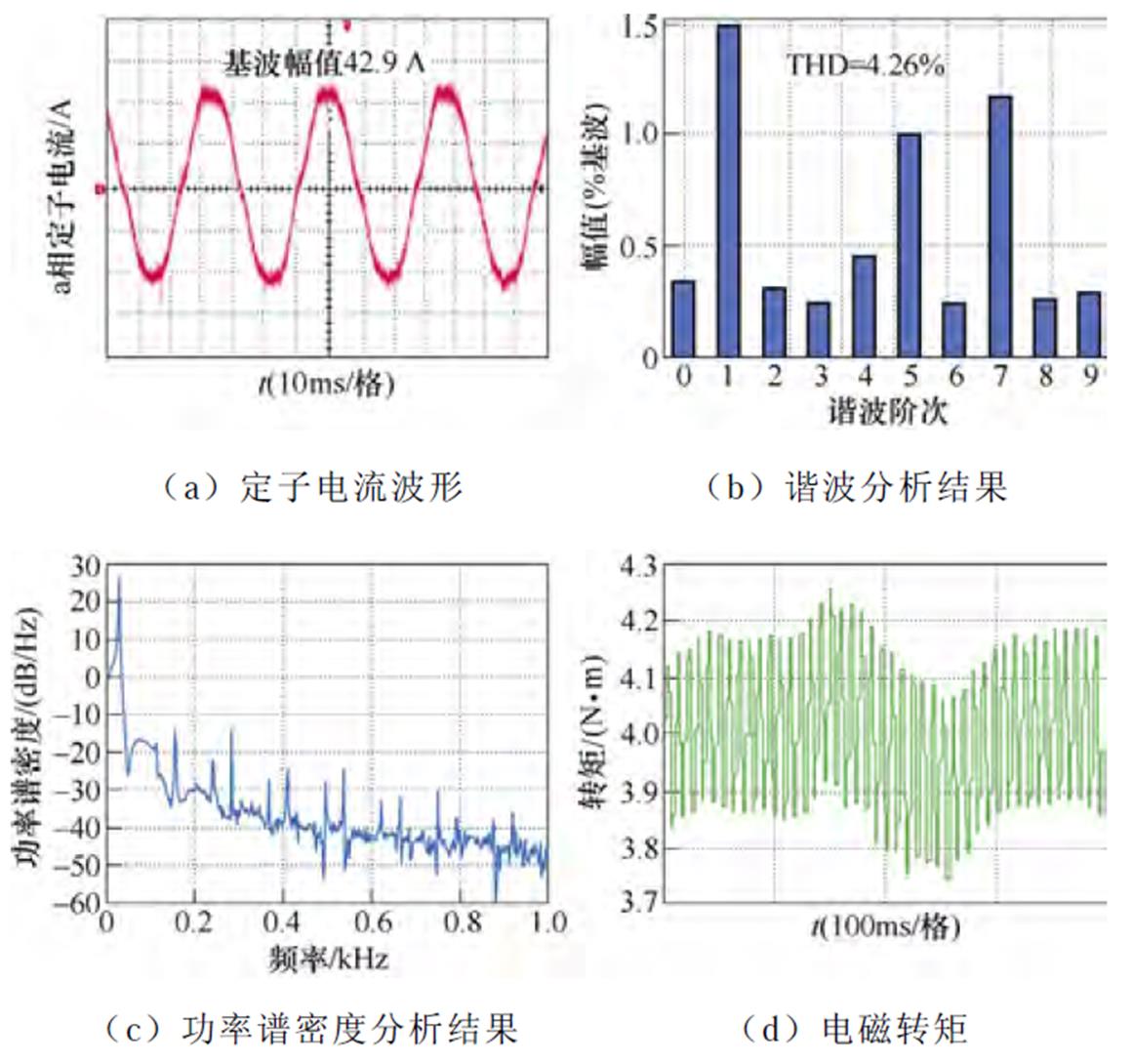
图18 500 r/min，4 N·m工况下逆变器非线性前馈补偿策略的实验波形
Fig.18 Experimental waveforms under inverter nonlinearity feedforward compensation when IM operates at 500 r/min and 4 N·m
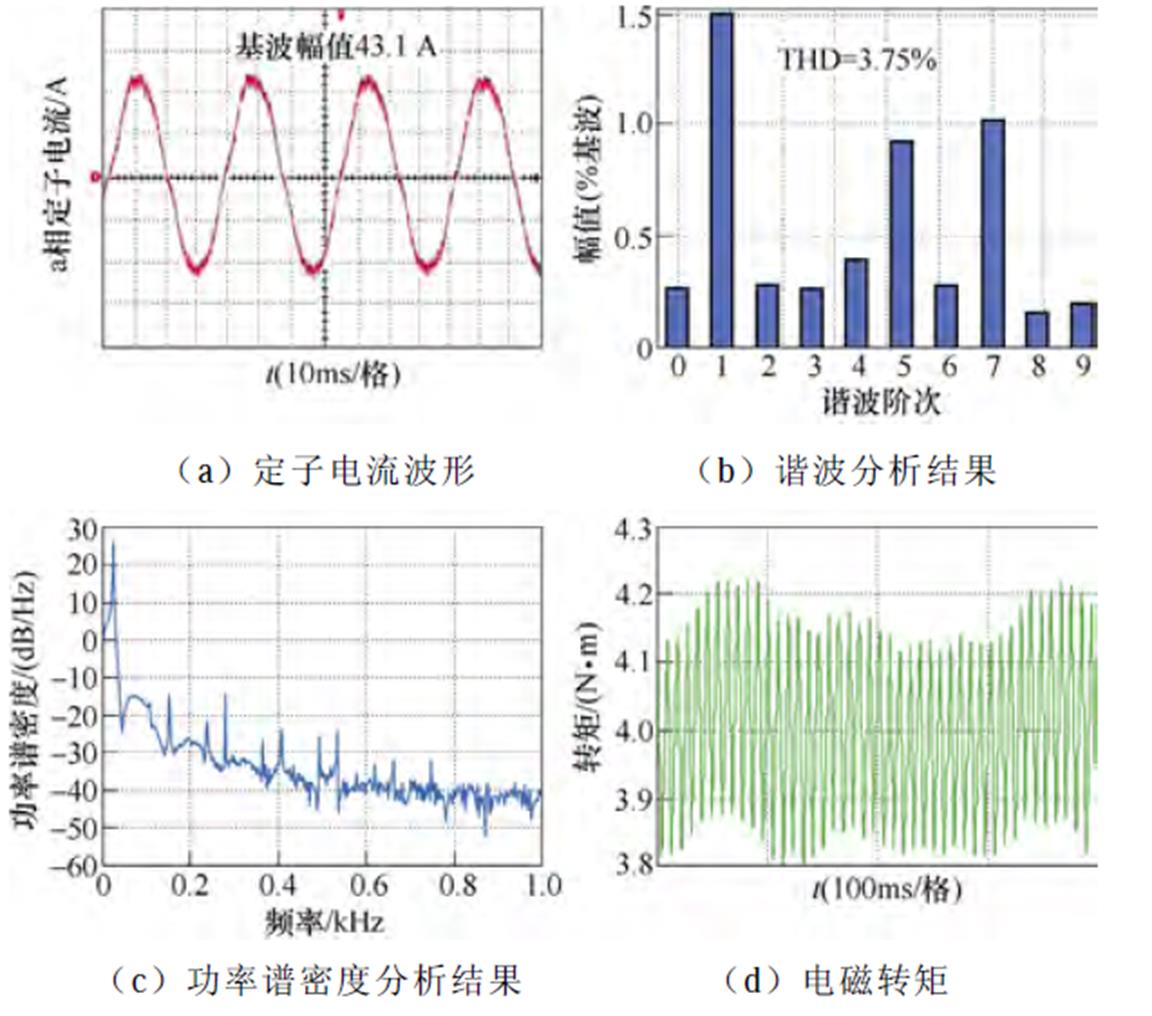
图19 500 r/min，4 N·m工况下采用6次谐波控制器的实验波形
Fig.19 Experimental waveforms under control of 6th harmonic when IM operates at 500 r/min and 4 N·m
文献[18]提出的逆变器非线性电压前馈补偿策略将电压误差分解为由导通压降引起的电压误差Duan_cond与死区阶段形成的电压误差Duan_dt，其计算模型为
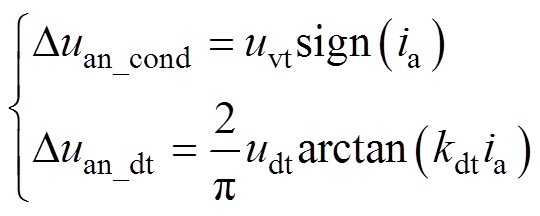（10）
式样，uvt为导通压降，随温度变化不大，uvt可根据数据手册设置为常数；udt为因死区时间引起的电压误差；kdt与缓冲电容参数有关。udt、kdt均需要通过多次实验测试得到。最后将Duan_cond与Duan_dt叠加至指令电压。由图18可以看出，采用逆变器非线性电压前馈补偿方法后，定子电流的THD为4.26%，转矩脉动为±0.25 N·m，5次谐波占比为1.01%，7次谐波占比为1.19%。而采用本文所提6次谐波控制策略后，定子电流的THD降低至3.75%，转矩脉动为±0.2 N·m，5次谐波占比为0.92%，7次谐波占比为1.03%。尽管文献[18]提出的逆变器非线性电压前馈补偿策略与传统脉冲时间补偿方法相比，能够提高电压补偿量的精度，但是两者本质均属于离线前馈补偿策略，对低次谐波的抑制效果有限。而本文所提出的6次谐波控制器本质属于一种反馈控制方法，当dq轴系下定子电压的6次谐波在定子电流中产生6次谐波分量时，谐波控制器会自适应输出相应幅值与频率的给定电压，能够抵消dq轴系下定子电压的6次谐波分量。另外，当开通延时、关断延时、管压降等非线性因素发生变化时，与离线前馈补偿方法相比，6次谐波控制器可以自适应调整六倍频给定电压的幅值与相位，具有良好的抗扰动性。
（2）工况2（额定转速3 000 r/min，额定负载4 N·m）：传统脉冲时间补偿方法、逆变器非线性前馈补偿方法与本文所提6次谐波控制的实验结果分别如图20～图22所示。定子电流基波频率为111.6 Hz，6次谐波控制器中自然频率wn设置为4 222 rad/s，脉冲时间补偿下，定子电流THD为4.20%，转矩脉动为±0.3 N·m，5次谐波占比为1.58%，7次谐波占比为1.03%。逆变器非线性电压前馈补偿方法后，定子电流的THD为3.95%，转矩脉动为±0.2 N·m，5次谐波占比为1.13%，7次谐波占比为0.91%。而采用本文所提6次谐波控制策略后，定子电流的THD降低至3.66%，转矩脉动为±0.15 N·m，5次谐波占比为0.89%，7次谐波占比为0.54%。
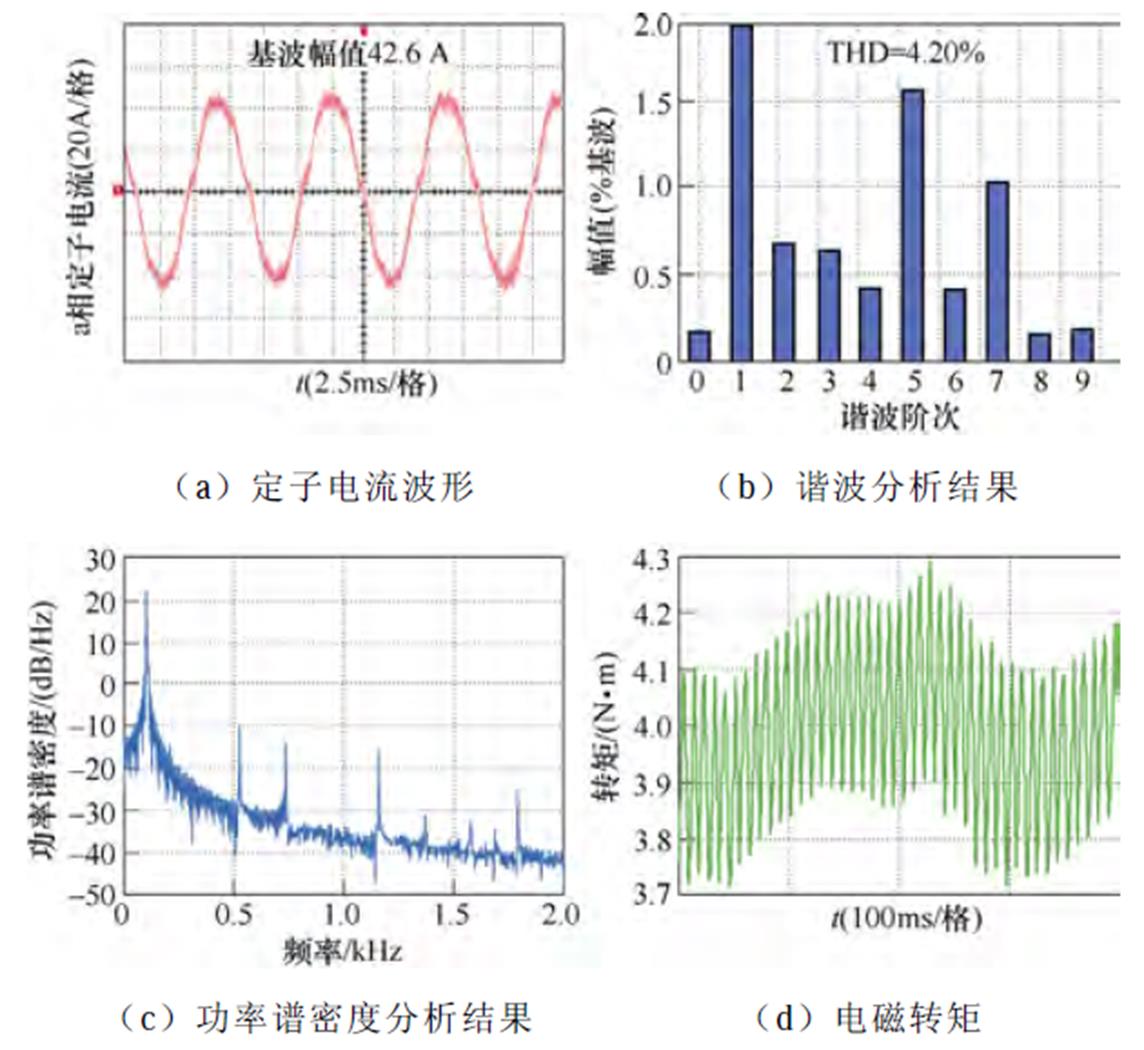
图20 3 000 r/min，4 N·m工况下基于脉冲时间补偿策略的实验波形
Fig.20 Experimental waveforms under compensation of the pulse duration when IM operates at 3 000 r/min and 4 N·m
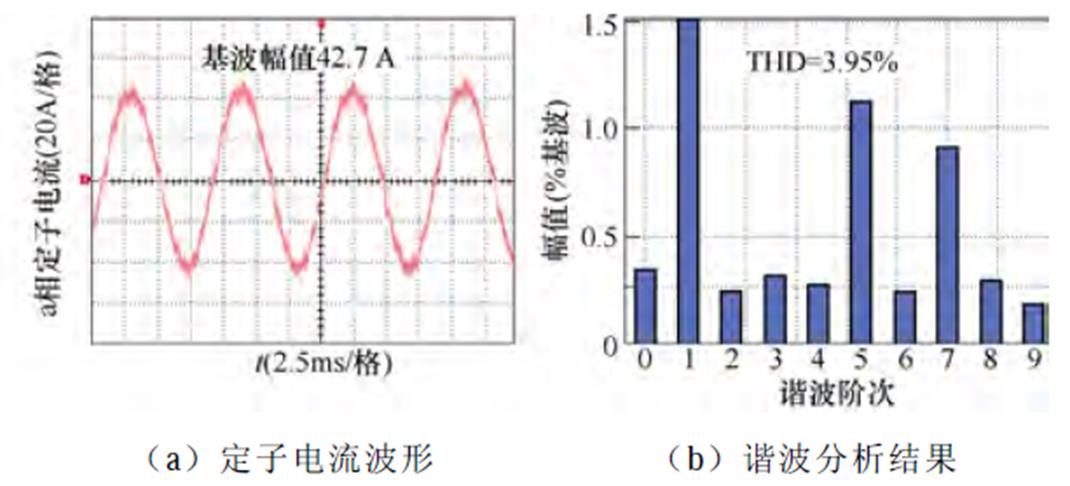
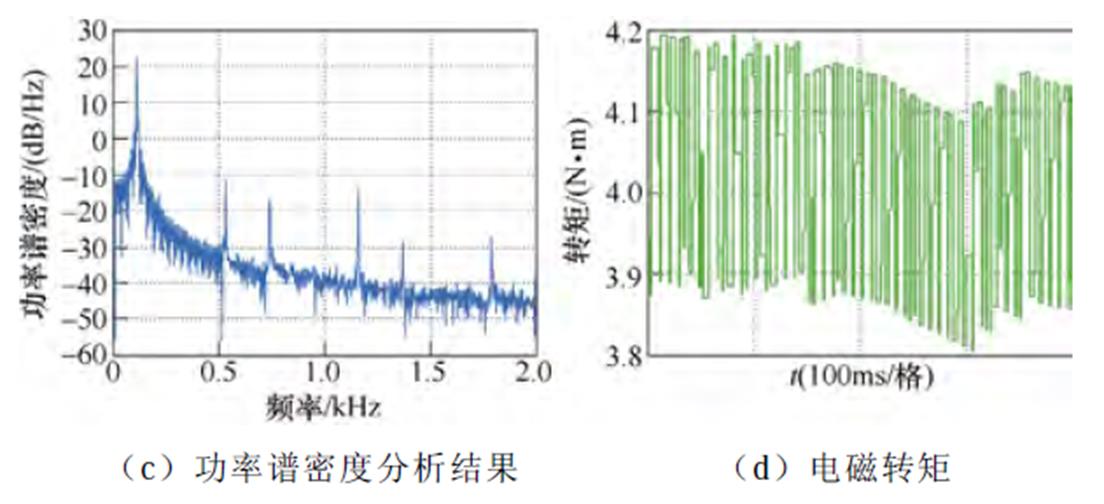
图21 3 000 r/min，4 N·m工况下逆变器非线性前馈补偿策略的实验波形
Fig.21 Experimental waveforms under inverter nonlinearity feedforward compensation when IM operates at 3 000 r/min
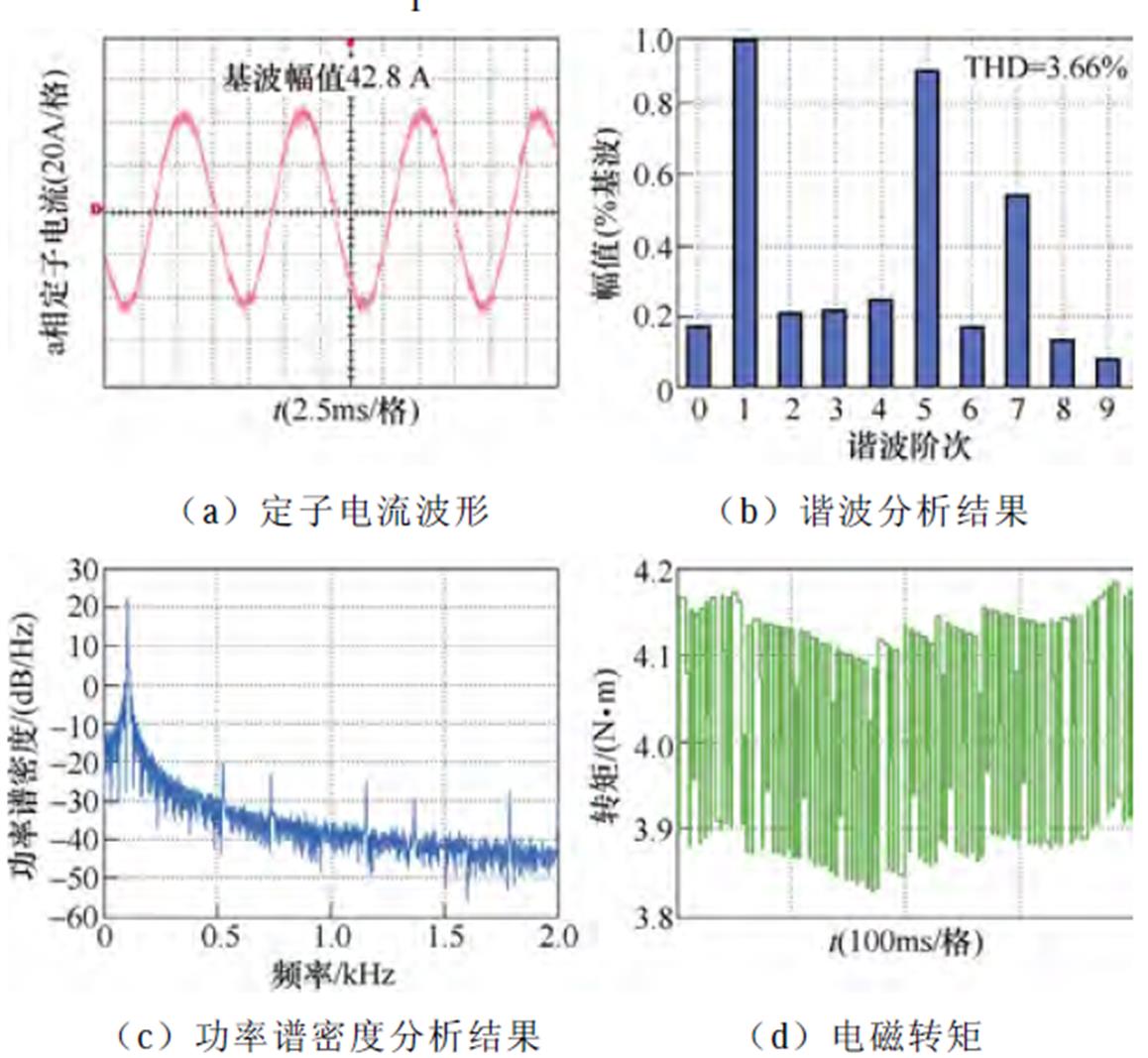
图22 3 000 r/min，4 N·m工况下采用6次谐波控制器的实验波形
Fig.22 Experimental waveforms under control of 6th harmonic when IM operates at 3 000 r/min and 4 N·m
（3）工况3（高速5 000 r/min，额定负载4 N·m）：传统脉冲时间补偿方法、逆变器非线性前馈补偿方法与本文所提6次谐波控制的实验结果依次如图23～图25所示。定子电流基波频率为171.3 Hz，6次谐波控制器中自然频率wn设置为2 240p rad/s。脉冲时间补偿下，定子电流THD为4.77%，转矩脉动为±0.4 N·m，5次谐波占比为1.65%，7次谐波占比为1.5%。采用逆变器非线性电压前馈补偿方法后，定子电流的THD为4.21%，转矩脉动为±0.35 N·m，5次谐波占比为1.3%，7次谐波占比为1.01%。而采用本文所提6次谐波控制策略后，定子电流的THD降低至3.84%，转矩脉动为±0.26 N·m，5次谐波占比为1.04%，7次谐波占比为0.7%，实验结果与仿真结果基本一致。
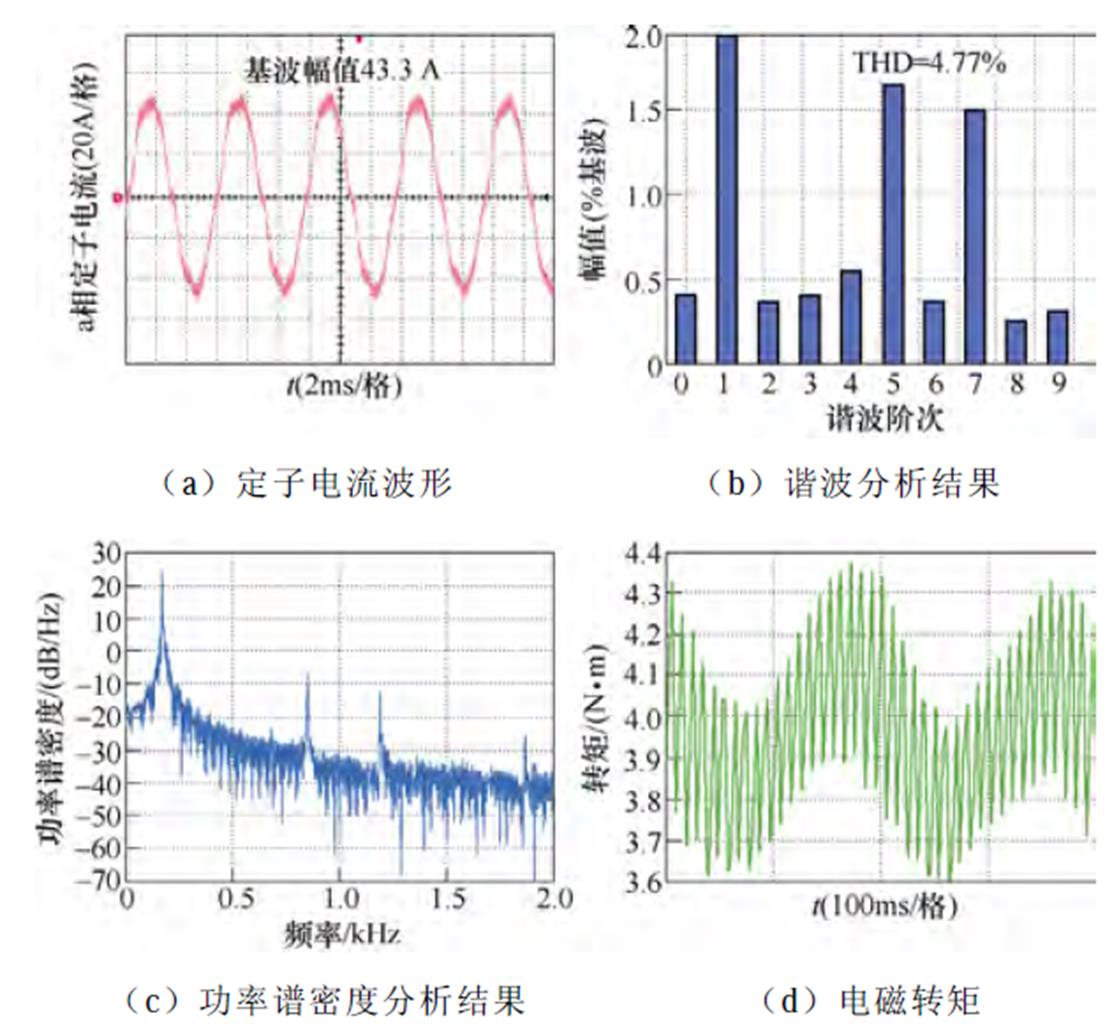
图23 5 000 r/min，4 N·m工况下基于脉冲时间补偿策略的实验波形
Fig.23 Experimental waveforms under compensation of the pulse duration when IM operates at 5 000 r/min and 4 N·m
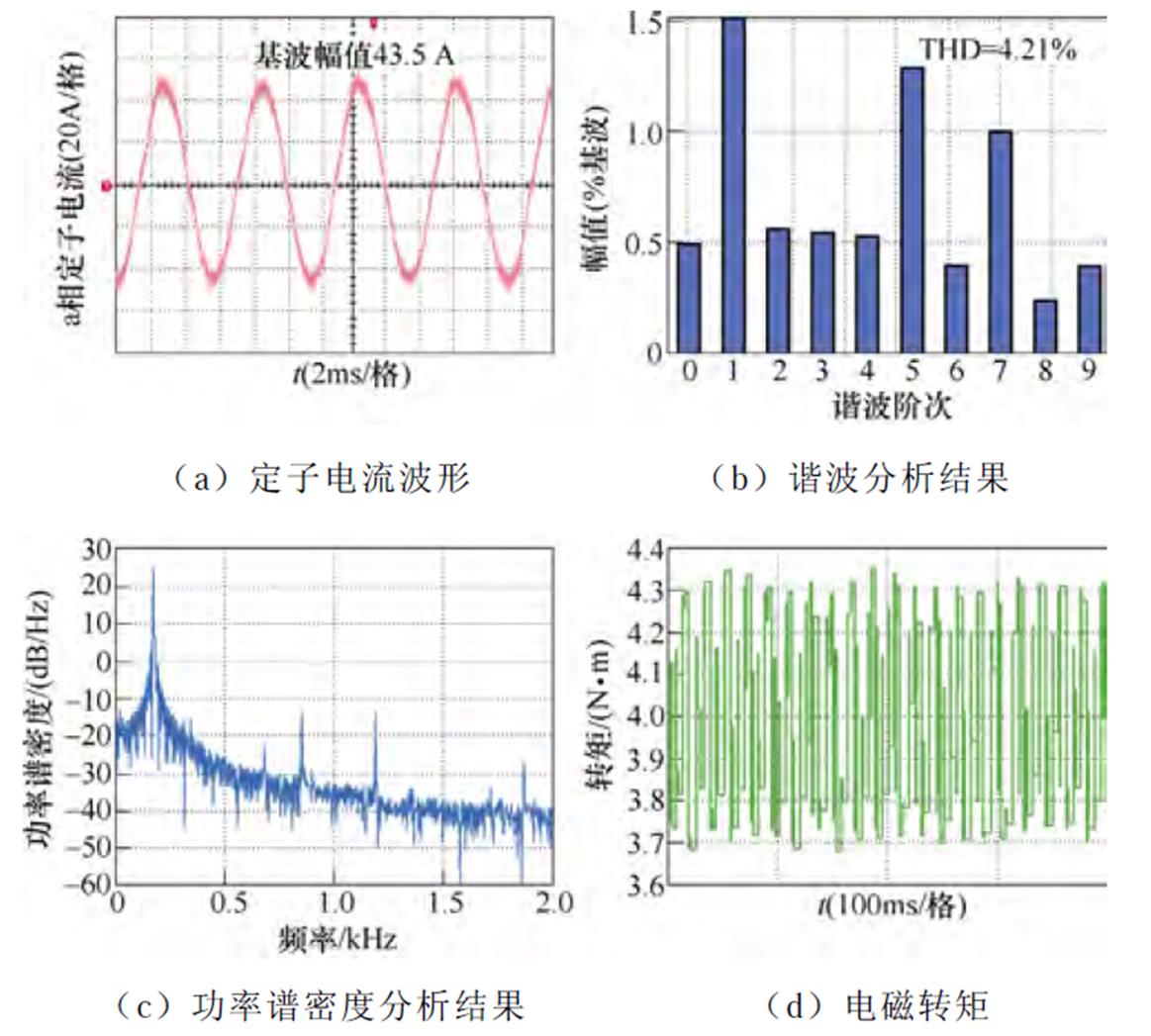
图24 5 000 r/min，4 N·m工况下逆变器非线性前馈补偿策略的实验波形
Fig.24 Experimental waveforms under inverter nonlinearity feedforward compensation when IM operates at 5 000 r/min and 4 N·m
（4）工况4（额定转速3 000 r/min，空载）：传统脉冲时间补偿方法、逆变器非线性前馈补偿方法与本文所提6次谐波控制的实验结果分别如图26～图28所示。定子电流基波频率为100 Hz，6次谐波控制器中自然频率wn设置为1 200p rad/s。脉冲时间补偿下，定子电流THD为6.01%，转矩脉动为±0.4 N·m，5次谐波占比为2.04%，7次谐波占比为1.8%。逆变器非线性电压前馈补偿方法后，定子电流的THD为5.65%，转矩脉动为±0.35 N·m，5次谐波占比为1.88%，7次谐波占比为1.48%。而采用本文所提6次谐波控制策略后，定子电流的THD降低至4.38%，转矩脉动为±0.25 N·m，5次谐波占比为1.55%，7次谐波占比为1.1%。
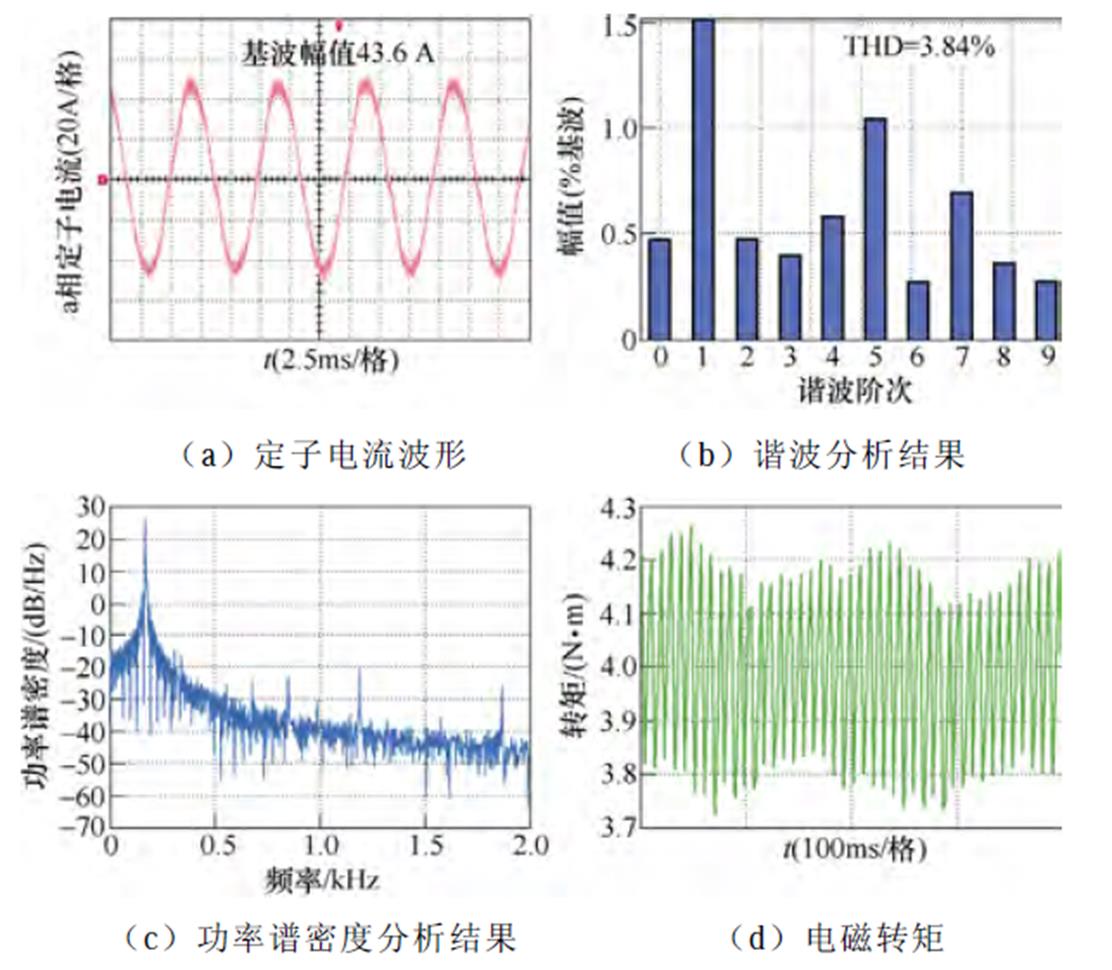
图25 5 000 r/min，4 N·m工况下采用6次谐波控制器的实验波形
Fig.25 Experimental waveforms under control of 6th harmonic when IM operates at 3 000 r/min and 4 N·m
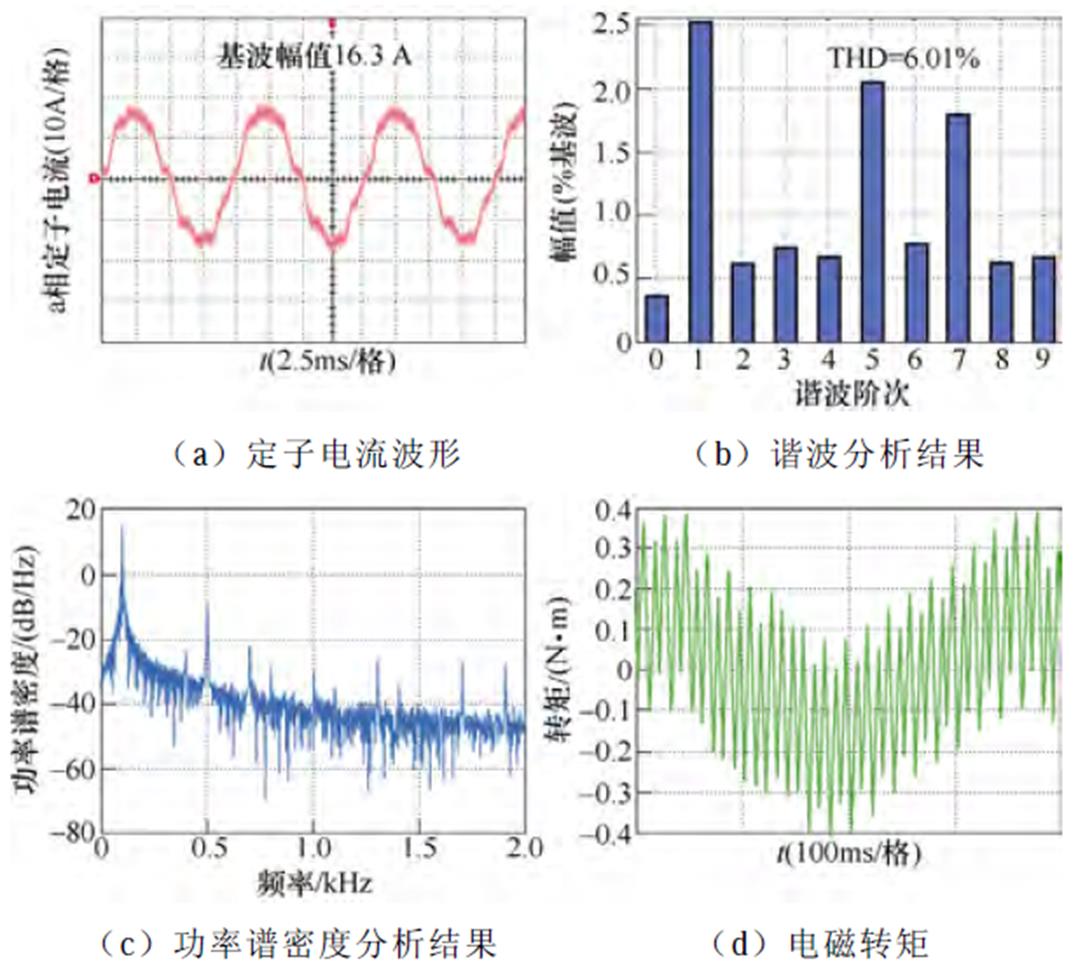
图26 3 000 r/min，空载工况下基于脉冲时间补偿策略的实验波形
Fig.26 Experimental waveforms under compensation of the pulse duration when IM operates at 3 000 r/min and no load
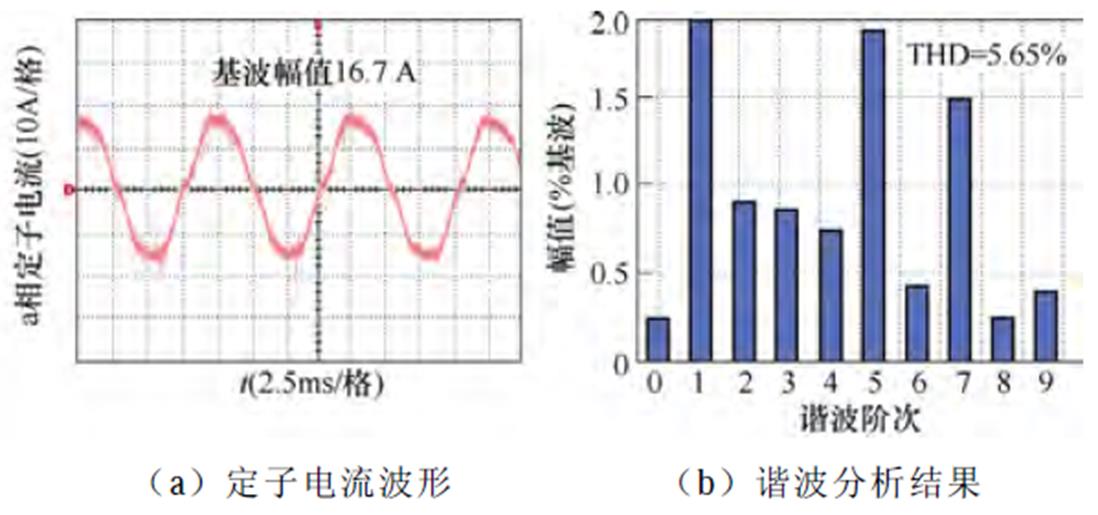
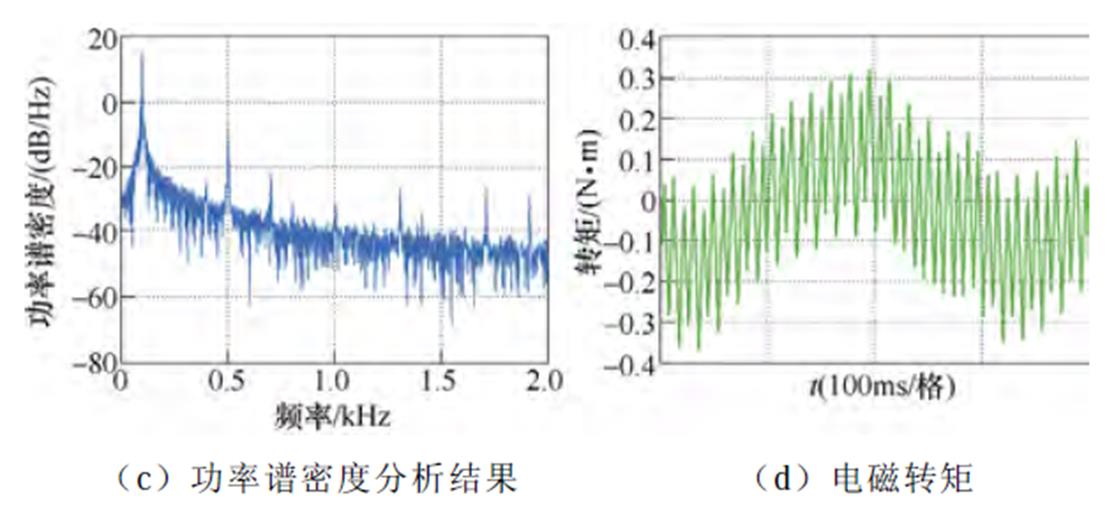
图27 3 000 r/min，空载工况下逆变器非线性前馈补偿策略的实验波形
Fig.27 Experimental waveforms under inverter nonlinearity feedforward compensation when IM operates at 3 000 r/min and no load
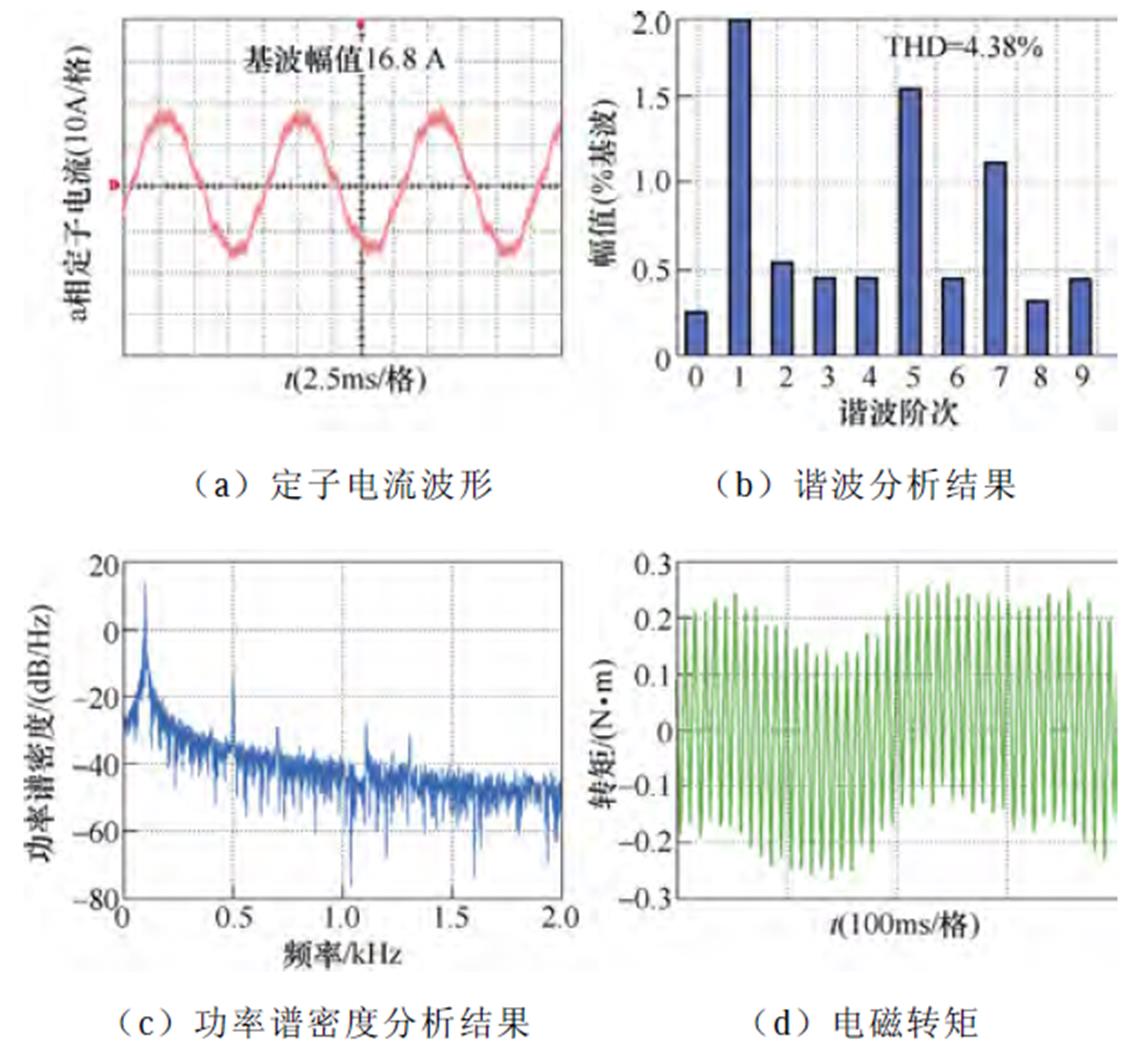
图28 3 000 r/min，空载工况下采用6次谐波控制器的实验波形
Fig.28 Experimental waveforms under control of 6th harmonic when IM operates at 3 000 r/min and no load
以上四组实验结果均表明本文所提6次谐波反馈抑制方法是优于传统基于脉冲时间补偿方法与文献[18]所提出的逆变器非线性前馈补偿方法，也说明配置方法是正确可行的。
为了进一步验证6次谐波控制器对固有频率处共振的抑制效果，让电机在5 000 r/min，4 N·m工况下稳态运行，用振动测量仪对电机的振动频谱进行测试。图29分别给出了未补偿与6次谐波控制下1.8 kHz以内的电机振动的功率谱密度。从图29a可以看出，在未补偿情况下，电机在二阶固有频率附近存在两个振动峰值，分布在850 Hz与1 160 Hz附近。而在dq坐标系下的电流内环控制器中加入6次谐波控制算法后，两个二阶固有频率处的振动得到了明显抑制，实验结果进一步证明了dq坐标系下6次谐波控制器及其参数设计方法对定子电流5次、7次谐波畸变具有良好的抑制作用，在降低转矩脉动的同时，还能够削弱电机的共振，提高电机驱动系统的动力性能。
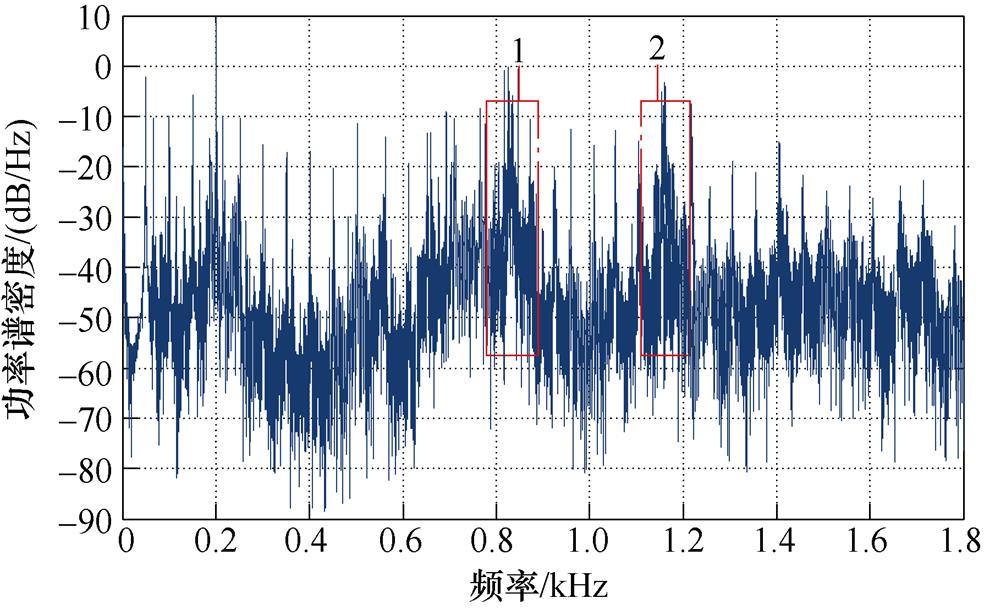
（a）无补偿
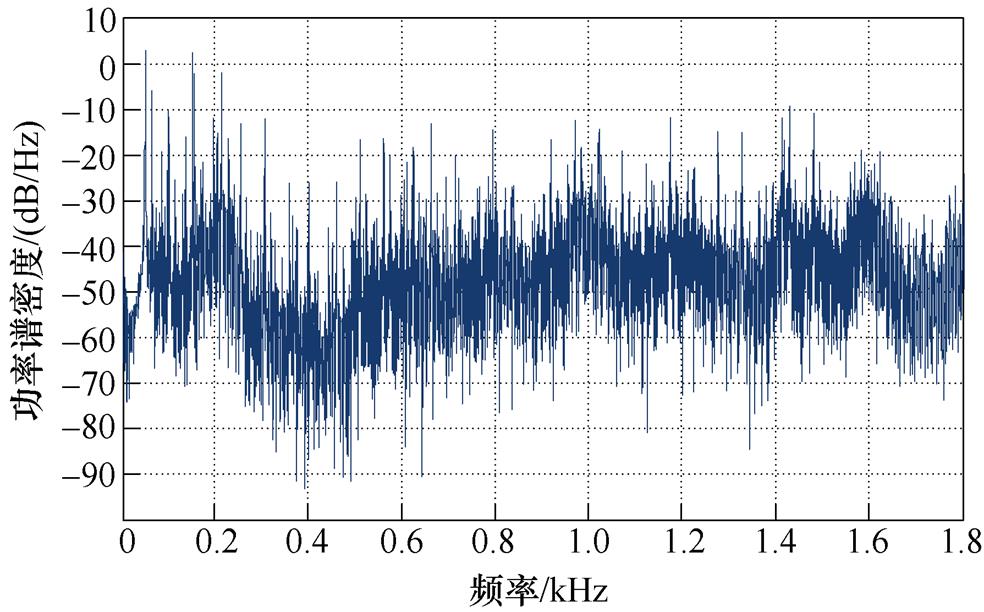
（b）dq坐标系下6次谐波控制
图29 电机振动的功率谱密度测试结果
Fig.29 Power spectral density of the vibration in IM
仿真与实验结果证明了本文所提dq坐标系下6次谐波控制器及其参数设计方法对降低定子电流的5次与7次谐波畸变，削弱电机的低频共振，提高电机驱动系统的动力性能，具有良好的效果，并形成以下结论：
1）死区时间和开关管与二极管压降会在逆变器输出电压中产生非线性误差，基于转子磁链定向的电流内环PI控制器不能抑制由非线性电压引起的定子电流5次与7次谐波畸变。
2）对定子电流中5次与7次谐波进行坐标变换，均转换为dq坐标系的6次谐波，本文所提出的6次谐波控制器能够有效抑制非线性电压的扰动作用，且不产生其他频率的谐波畸变，同时不影响电流内环的控制性能。
3）与离线前馈补偿方法相比，本文所提6次谐波控制器属于特定频率谐波反馈控制方法，谐波控制器能自适应抵消dq轴系下定子电压中的6次谐波分量，具有良好的抗扰动性。
参考文献
[1] 王彦哲, 周胜, 王宇, 等. 中国核电和其他电力技术环境影响综合评价[J]. 清华大学学报 (自然科学版), 2021, 61(4): 377-384.
Wang Yanzhe, Zhou Sheng, Wang Yu, et al. Comprehensive assessment of the environmental impact of China’s nuclear and other power generation technologies[J]. Journal of Tsinghua University (Science and Technology), 2021, 61(4): 377-384.
[2] 郑江, 代颖, 石坚. 车用永磁同步电机的电磁噪声特性[J]. 电工技术学报, 2016, 31(增刊1): 53-59.
Zheng Jiang, Dai Ying, Shi Jian. Electromagnetic noise characteristics of permanent magnet syn- chronous motor applied in electric vehicle[J]. Transa- ctions of China Electrotechnical Society, 2016, 31(S1): 53-59.
[3] 崔纳新, 张承慧, 李珂, 等. 电动汽车异步电机变频驱动系统的自抗扰控制[J]. 电工技术学报, 2007, 22(8): 150-154.
Cui Naxin, Zhang Chenghui, Li Ke, et al. Auto- disturbance-rejection control of induction motor drives for electric vehicles[J]. Transactions of China Electrotechnical Society, 2007, 22(8): 150-154.
[4] Yang Ming, Lü Zekai, Xu Donglin, et al. Resonance suppression and EMI reduction of GaN-based motor drive with sine wave filter[J]. IEEE Transactions on Industry Applications, 2020, 56(3): 2741-2751.
[5] 刘和平, 刘庆, 张威, 等. 电动汽车用感应电机削弱振动和噪声的随机PWM控制策略[J]. 电工技术学报, 2019, 34(7): 1488-1495.
Liu Heping, Liu Qing, Zhang Wei, et al. Random PWM technique for acoustic noise and vibration reduction in induction motors used by electric vehicles[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1488-1495.
[6] Lai Y S, Chang Y T, Chen Boyuan. Novel random- switching PWM technique with constant sampling frequency and constant inductor average current for digitally controlled converter[J]. IEEE Transactions on Industrial Electronics, 2013, 60(8): 3126-3135.
[7] 李国华, 刘春武, 汪玉凤. 单相逆变器随机PWM选择性消谐滞环随机扩频方法[J]. 电工技术学报, 2021, 36(6): 1279-1289.
Li Guohua, Liu Chunwu, Wang Yufeng. A novel hysteresis random spread-spectrum method in random PWM selective harmonic elimination for single-phase inverter[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1279-1289.
[8] 黄鹏, 刘和平, 苗轶如, 等. 基于感应电机电流纹波峰值的可变开关频率脉冲宽度调制[J]. 电工技术学报, 2020, 35(20): 4373-4383.
Huang Peng, Liu Heping, Miao Yiru, et al. Variable switching frequency pulse width modulation for induction motors based on current ripple peak value[J]. Transactions of China Electrotechnical Society, 2020, 35(20): 4373-4383.
[9] 刘和平, 董治平, 邱斌斌, 等. 电压型逆变器分段死区补偿调制策略[J]. 电机与控制学报, 2020, 24(9): 30-38.
Liu Heping, Dong Zhiping, Qiu Binbin, et al. Compensation method for nonlinear factors of inverter for low voltage electric vehicle[J]. Electric Machines and Control, 2020, 24(9): 30-38.
[10] Hwang S H, Kim J M. Dead time compensation method for voltage-fed PWM inverter[J]. IEEE Transactions on Energy Conversion, 2010, 25(1): 1-10.
[11] Kobayashi T, Tajima F, Ito M, et al. Effects of slot combination on acoustic noise from induction motors[J]. IEEE Transactions on Magnetics, 1997, 33(2): 2101-2104.
[12] Zhang Zhendong, Xu Longya. Dead-time com- pensation of inverters considering snubber and parasitic capacitance[J]. IEEE Transactions on Power Electronics, 2014, 29(6): 3179-3187.
[13] 刘和平, 路莹超, 王华斌, 等. 电压型逆变器分段死区补偿调制策略[J]. 电机与控制学报, 2018, 22(3): 25-32.
Liu Heping, Lu Yingchao, Wang Huabin, et al. Dead- time compensation modulation strategy of subsection integrated in voltage source inverter[J]. Electric Machines and Control, 2018, 22(3): 25-32.
[14] Guo Qiang, Dong Zhiping, Liu Heping, et al. Nonlinear characteristics compensation of inverter for low-voltage delta-connected induction motor[J]. Energies, 2020, 13(3): 590.
[15] 廖勇, 甄帅, 刘刃, 等. 用谐波注入抑制永磁同步电机转矩脉动[J]. 中国电机工程学报, 2011, 31(21): 119-127.
Liao Yong, Zhen Shuai, Liu Ren, et al. Torque ripple suppression of permanent magnet synchronous motor by the harmonic injection[J]. Proceedings of the CSEE, 2011, 31(21): 119-127.
[16] Wu Zhaoqian, Ding Kang, Yang Zhijian, et al. Analytical prediction and minimization of deadtime- related harmonics in permanent magnet synchronous motor[J]. IEEE Transactions on Industrial Electronics, 2021, 68(9): 7736-7746.
[17] 罗辞勇, 王英豪, 王卫耀, 等. 单相特定谐波消除脉宽调制高频逆变器的死区补偿策略[J]. 电工技术学报, 2017, 32(14): 155-164.
Luo Ciyong, Wang Yinghao, Wang Weiyao, et al. Study of dead-time compensation strategy in selective harmonic elimination PWM inverter[J]. Transactions of China Electrotechnical Society, 2017, 32(14): 155-164.
[18] Lee J H, Sul S K. Inverter nonlinearity compensation through deadtime effect estimation[J]. IEEE Transa- ctions on Power Electronics, 2021, 36(9): 10684- 10694.
Low Frequency Resonance Reduction Method of Induction Motor Used by Electric Vehicle Based on Sixth Harmonic Suppression in dq Coordinate
Abstract The development of electric vehicles (EVs) is an effective means to solve energy and environmental problems and achieve the goals of “carbon peaking” and “carbon neutrality”. However, the motor drive system in EVs faces severe vibration and noise issues. If the harmonics in the stator current align with the natural frequency of the motor, motor resonance can occur. In an ideal situation, the inverter line voltage and stator current only have sideband harmonics distributed near the fundamental and switching frequencies and their multiples. However, nonlinear factors such as the conduction voltage drop, snubber capacitance, and dead time are added during the modulation process to prevent bridge arm direct connection in the inverter, causing low harmonic distortion of the stator current. In addition, the inherent frequency of induction motors used in EVs is low, and the motor commonly operates over a wide speed range. The low harmonic generated during the modulation process can coincide with the inherent frequency of the motor, resulting in low-frequency resonance.
To suppress the low-order harmonic of the stator current, firstly, the simulation and test method of the natural frequency of the induction motor (IM) is studied, and the natural frequency range of the IM is determined. Then, based on harmonic distortion characteristics caused by dead time and tube voltage drop, a sixth harmonic controller is added to the current inner loop of the vector control system after rotor flux orientation (dq coordinate). Combined with bode plots and pole distribution diagrams, the optimal parameters of the harmonic controller are obtained according to the stability and harmonic suppression characteristics. Finally, the simulation model and experimental platform are established considering current FFT analysis results, power spectral density, and vibration experimental data under four operating conditions (low speed, no load, rated speed, and high speed). Compared with the compensation method of the pulse duration and inverter nonlinearity feedforward, it is proved that suppressing the sixth harmonic in the dq coordinate effectively reduces the fifth and seventh harmonics of the stator current and vibration power of the IM at its natural frequency.
The feasibility and correctness of the proposed method can be certified by the simulation and experimental results, and the conclusions are as follows.
(1) The dead time and voltage drop between the switch and diode can generate nonlinear errors in the output voltage of the inverter. The current inner loop PI controller based on rotor flux orientation cannot suppress the fifth and seventh harmonic distortion of the stator current caused by nonlinear voltage.
(2) The fifth and seventh harmonics in the stator current are transformed into the sixth harmonics in the dq coordinate system. The sixth harmonic controller can effectively suppress the disturbance of nonlinear voltage without generating other harmonic distortion and does not affect the control performance.
(3) Compared with the offline feedforward compensation method, the sixth harmonic controller proposed in this paper belongs to a specific frequency harmonic feedback control method. The harmonic controller can adaptively suppress the sixth harmonic component in the stator voltage under the dq coordinate system and has a good control performance.
keywords：Induction motor (IM), low frequency resonance, low harmonic distortion, control strategy, dead-time
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.220953
国家自然科学基金项目（52077011, 52277034）、湖南省教育厅项目（22A0603）和长沙市重大科技专项项目（kq2105001）资助。
收稿日期 2022-05-30
改稿日期 2023-02-01
冯 婉 女，1984年生，博士，讲师，研究方向为电力电子与电机控制技术。E-mail: fengwan@hnu.edu.cn
张文娟 女，1986年生，博士，教授，研究方向为高性能永磁电机的设计与控制。E-mail: Z20141074@ccsu.edu.cn（通信作者）
（编辑 崔文静）