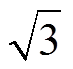 倍。因此,为达到同一最高转速,两种拓扑所使用母线电压等级不同。
倍。因此,为达到同一最高转速,两种拓扑所使用母线电压等级不同。摘要 单级三相全桥驱动拓扑无法保证力矩控制模式的定子无铁心永磁无刷直流电机在全电流指令范围内电枢电流连续。采用增加电枢回路等效电气时间常数的思路,选取Buck+半桥、全桥串联电感、Buck+全桥三种驱动拓扑,对三种驱动拓扑保证电机正常运行的条件以及不同驱动拓扑的固有属性进行理论分析、说明和对比。在基于数字控制器的三种驱动平台上,使用同一台电机进行实验验证。实验结果表明,三种驱动拓扑均能保证电机的正常运行,实测电流波形证明了关于拓扑特点的理论分析的合理性。对三种驱动拓扑实测稳态运行性能进行了详细的数学分析,为小功率无铁心永磁无刷直流电机的工程应用提供了参考依据。
关键词:定子无铁心 永磁无刷直流电机 Buck+半桥 全桥串联电感 Buck+全桥
反作用飞轮或动量轮是一种卫星姿态控制的执行机构。通过控制电机的电能流动方向,使卫星受到沿电机轴向的反作用力矩。多个动量轮组合可实现卫星的三轴姿态稳定[1]。由于电机工作在空间环境,气动阻力可忽略不计;轴承加工及润滑技术的发展保证了动量轮轴承在长寿命中维持极低的摩擦阻力。根据需求,期望动量轮的输出力矩大范围连续可调,但并不需要较大功率的输出,因此电机工作在力矩控制模式下的空载状态。
无刷直流电机(Brushless Direct Current Motor, BLDCM)因其具有结构简单、效率高、功率密度高、寿命长、机械性能好等优点,被广泛地应用于新能源汽车、医疗器械、航空航天、船舶推进、风力发电等多种功率等级的领域[2-6]。近年来出现的定子无铁心设计具有以下优点:①消除了定子铁心损耗和涡流损耗[7],意味着在一定程度上提升了电机的功率密度;②由于定子受力绕组的支撑部件使用非导磁复合材料制成,采用无齿槽设计进一步消除了定子槽引起的磁链谐波[8]及由永磁体和定子铁心作用引起的齿槽转矩[9];③定子绕组不再受到定子齿槽的约束,绕组的设计和安装更加灵活,无铁心电机气隙较大,定子绕组反电动势分布引起的谐波可忽略不计[10],同时大气隙意味着在大的电枢电流激励下难以产生磁饱和情况,在定子绕组散热允许的条件下,电机具有强过载能力;④定子无铁心设计在尺寸和质量上具有优势。因此无铁心电机适用于小功率空载模式的空间应用。
但是,无铁心电机电感值极小,仅有几个到几十个mH。小功率的无铁心电机会产生很大的电流脉动,给电机绕组的相电流带来高次谐波,电机驱动在开关频率较低、输出电流较小的时候会存在电流断续的问题,严重时会导致电机无法正常运行,甚至在起动过程中,电枢绕组发生直通短路,损毁控制器或烧毁电机定子绕组[7]。
根据文献[7],为解决无法正常运行的问题,小电感电机的控制通常有以下四种改进思路:①高开关频率宽禁带功率器件逆变器控制;②电压源型逆变器串联谐波滤波器控制;③电流源型逆变器控制;④多电平逆变器控制。
高开关频率宽禁带功率器件逆变器是指不改变三相全桥驱动拓扑,仅通过大幅提升开关频率来维持电流的连续。文献[11]为将电机电流峰峰值限制在额定电流的10%,将开关频率选取为100 kHz。文献[12]为抑制小电感电机在换相区的转矩脉动,重叠换向控制的开关频率为200 kHz。为保证电枢绕组电流连续,使用的开关频率会大幅增加[13],这导致开关损耗急剧上升,进而减少半导体器件寿命,降低了可靠性[14]。
电压源型逆变器串联谐波滤波器控制是指在三相全桥逆变器的基础上,额外增加一组滤波器,增大系统的电气时间常数。这种方式通常像文献[15-16]一样,使用由电感、电容构成的滤波器对脉冲宽度调制(Pulse Width Modulation, PWM)斩波输出进行滤波。但是,增加一组滤波器后,需要经过计算,以防止造成系统的不稳定。等效相电感增大又会导致换相区续流时间延长,当电机转速提高时,换相区对一拍工作区间占比增大,若不加以控制,电机内部长时间存在不控环流。大电感降低了电流控制响应,传统大电感电机在高速时电流滞后导致的转矩性能下降等问题又将浮现。另外,额外三个功率电感增加了体积和成本。
电流源型逆变器是在三相逆变直流母线侧增加前级DC-DC变换器。前级电流型变换器做电流闭环控制,输出稳定电流,根据电机转速调压,实现后级逆变器的脉冲幅度调制(Pulse Amplitude Modulation, PAM)控制,同时极大地削弱了单级式全桥拓扑PWM斩波引起的转矩脉动。后级电流型逆变器仅起换相的作用。因此,可使用三相全桥或三相半桥等多种拓扑。现如今很多文献都采用双级式驱动拓扑方案来驱动无铁心无刷直流电机。文献[17-19]皆使用Buck变换器作为前级电路,Buck变换器功率电感兼具滤波作用,因此是小电感电机双级式驱动拓扑中最常用的前级电路。文献[20]中使用Boost作为前级电路,用作对直流母线电压进行升压,主要实现高速应用。文献[21]提出使用Sepic变换器作为前级电路,用来调节直流母线电压以解决换相区的脉动问题。文献[22]使用Cuk变换器作为前级电路,并进一步使用三电平中点钳位逆变器来代替两电平逆变器。文献[23-24]针对大功率盘式无铁心电机设计了前级斩波电路,可有效削弱转矩脉动。
多电平逆变器通常适用于大功率电机,多级阶梯电压输出方式可以针对电机转速,给定合适的电压幅值,文献[11]使用二极管钳位三电平逆变器电路拓扑驱动小电感电机。但针对小功率电机,尤其是电压等级低的电机应用较少。
除上述针对基本驱动拓扑的研究外,自文献[25]开始,现有文献对无刷直流电机的研究[22, 25-30]大多针对大电感直流无刷电机换相区的转矩脉动,且出于标准梯形波反电动势的假设。但无铁心电机换相区很短,与普通无刷直流电机性能的优化方法存在一定差别。本文针对使用Halbach[31]方案设计的非理想反电动势无铁心电机电流脉动大的特点,驱动拓扑的改进思路就是增加整个系统的电机时间常数。其中双级式驱动拓扑选择Buck变换器作为前级电路,利用其输出滤波电感为后级逆变器提供稳定电流并根据转速调压,后级电流型逆变器分别选择三相半桥和三相全桥拓扑用以对比。同时研究单级三相全桥级联电感器的拓扑的可行性。
分析三种驱动拓扑的特点。首先,从理论上分析单级全桥拓扑电流断续的问题;然后,根据增加电枢回路等效时间常数的思路,提出不同拓扑的改进方法,并进一步分析三种拓扑的数学模型;最后,使用平均电流控制,分析三种拓扑驱动同一台无铁心直流无刷电机,在稳定工作时的性能并加以对比。
根据开关管数量的不同,在后文中用“B3”表示三相半桥拓扑,用“B6”表示三相全桥拓扑。
与传统单级B6拓扑相比,Buck变换器级联B3拓扑节省了逆变器的三个上桥臂功率开关管及其驱动,但多增加了Buck变换器的一对上下开关管及其驱动。Buck变换器级联B6拓扑则在传统的单级B6拓扑基础上增加前级变换器的两个开关管,体积和成本最高。
B3拓扑和B6拓扑的差别在于,在任一时刻B3逆变器驱动的电机仅有一相导通,B6拓扑有两相反向串联导通。前者使用相反电动势作用输出电磁转矩,而后者使用线反电动势。同一台电机,在同一母线电压等级下,母线电压分别由一相和两相所“占用”,理论上B3拓扑所能达到的最高转速是B6拓扑的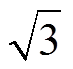 倍。因此,为达到同一最高转速,两种拓扑所使用母线电压等级不同。
倍。因此,为达到同一最高转速,两种拓扑所使用母线电压等级不同。
使用Buck级联B3拓扑需要电机引出中性点,这里设定从电机三相端到中性点为反电动势的正方向。在电动状态下,电能从中性点流入,按照正方向的规定从反电动势最小的一相端流出;B6拓扑中性点悬空,电能从反电动势最大和最小的两相端流入和流出。因此对于同一霍尔信号,B3拓扑开关管的驱动逻辑与B6拓扑的下管驱动逻辑是一致的。三种驱动拓扑电路如图1所示,图中,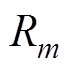 、
、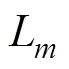 、
、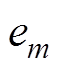 (m= a, b, c)分别为电枢绕组相电阻、相电感和相反电动势,
(m= a, b, c)分别为电枢绕组相电阻、相电感和相反电动势,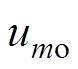 、
、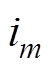 分别为单相端电压及相电流,
分别为单相端电压及相电流,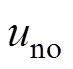 为中性点电压,
为中性点电压,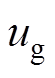 为直流母线电压,
为直流母线电压, 、
、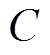 分别为Buck变换器的电感、电容。
分别为Buck变换器的电感、电容。
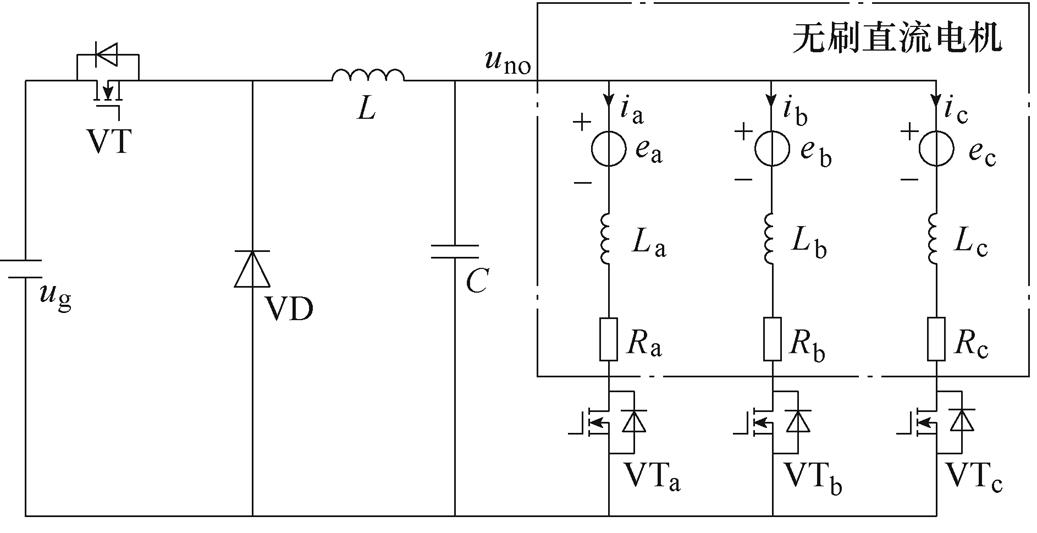
(a)Buck+三相半桥拓扑
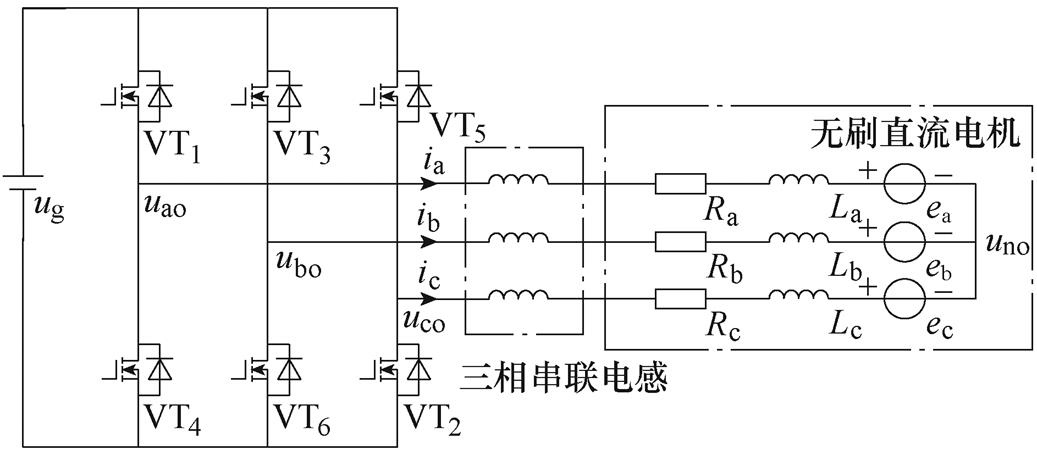
(b)B6串联电感拓扑
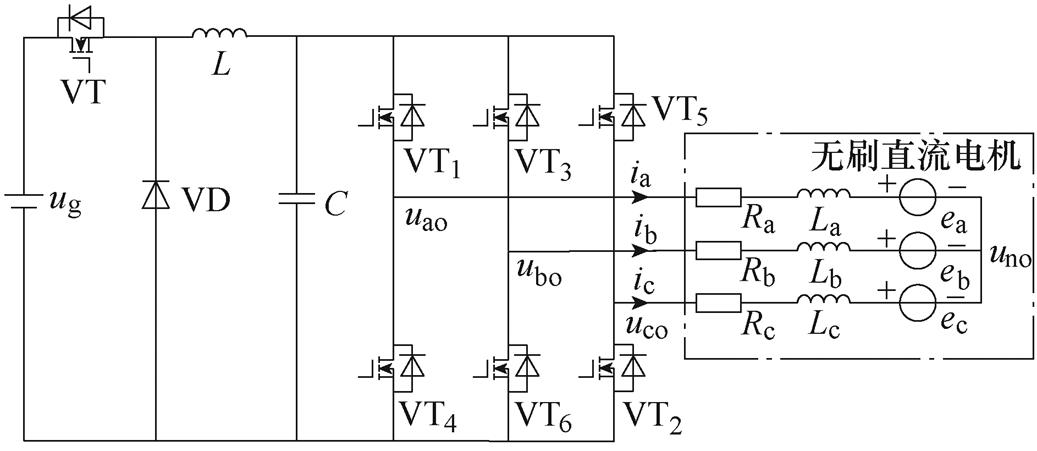
(c)Buck+三相全桥拓扑
图1 三种驱动拓扑电路
Fig.1 Circuits of three drive topologies
1.2.1 H_PWM-L_PWM控制B6拓扑
无铁心电机的电枢时间常数小,具备优异的瞬态响应性能,更适用于高速应用场合,但是,电枢电感值很小导致电枢电流变化率很大。因此,与有铁心电机相比,无铁心电机电枢电流脉动大,甚至在条件恶劣如开关频率较低、输出电流较小的同时,母线电压较大的情况下,电机电枢电流断续,电机无法正常运行。
为继续使用传统B6拓扑来驱动无铁心电机,且保证电枢电流处于电流连续模式,这里分析在使用上下管同一斩波驱动信号,即H_PWM-L_PWM控制方式时,一个开关周期内的电流变化情况。以a、b相导通为例,其等效电路如图2所示。电流通路a、b分别代表开关管导通和关断时期的等效电路。在一个开关周期内,电压方程为
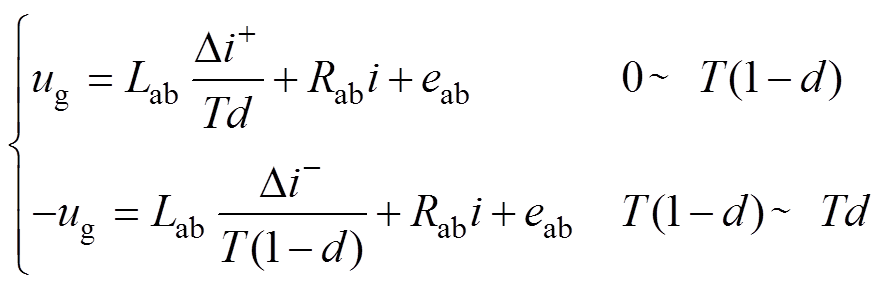 (1)
(1)
式中, 、
、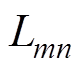 、
、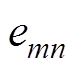 (
(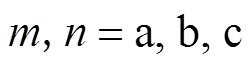 )分别为两相的电阻、电感和线反电动势;
)分别为两相的电阻、电感和线反电动势;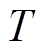 为开关周期;
为开关周期;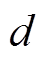 为开关管占空比;
为开关管占空比;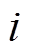 为在理想稳态时电枢绕组的平均电流,也指双级拓扑中前级Buck变换器的稳态输出电流;
为在理想稳态时电枢绕组的平均电流,也指双级拓扑中前级Buck变换器的稳态输出电流;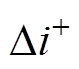 为
为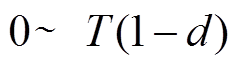 时间内开关管导通时电流上升值;
时间内开关管导通时电流上升值;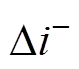 为
为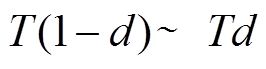 时间内开关管关断时电流下降值。
时间内开关管关断时电流下降值。
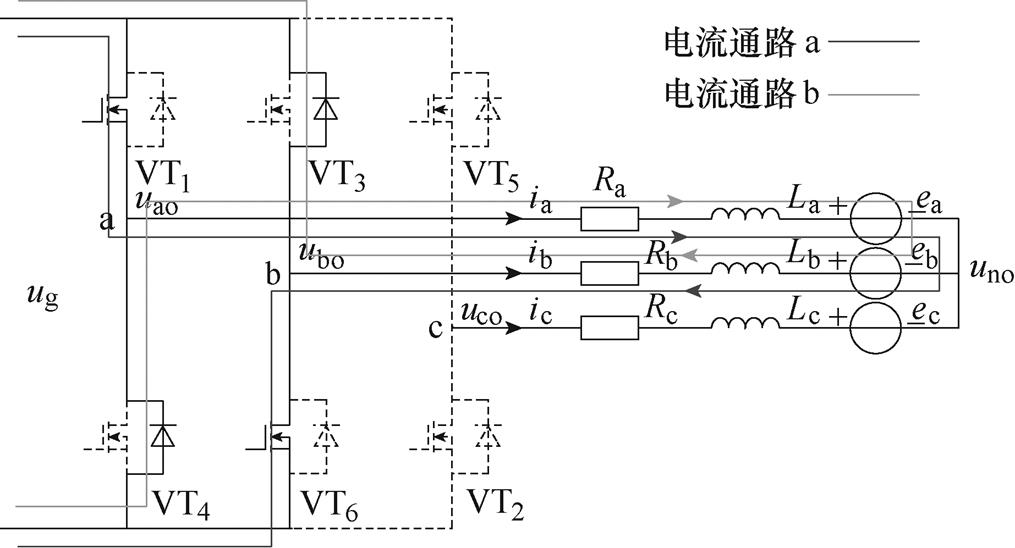
图2 H_PWM-L_PWM控制B6拓扑等效电路
Fig.2 The equivalent circuit of B6 topology controlled in H_PWM-L_PWM mode
在稳态时,根据电流脉动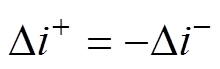 可得开关管的斩波占空比
可得开关管的斩波占空比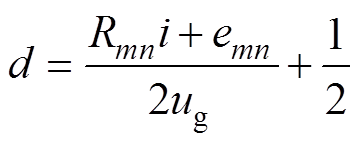 。若电感电流连续,电流脉动的
。若电感电流连续,电流脉动的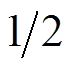 必须小于输出平均电流
必须小于输出平均电流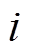 ,将占空比代入式(1),可得要保证电感电流连续的条件为
,将占空比代入式(1),可得要保证电感电流连续的条件为
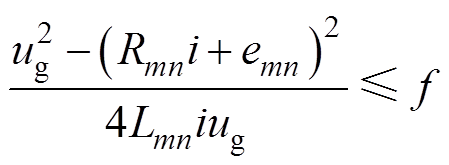 (2)
(2)
式中,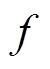 为开关频率。
为开关频率。
根据式(2)可知,不等式左侧对反电动势的导数小于零,则其最大值在反电动势为零,即转速为零时取到。式(2)在反电动势极值点可化简为
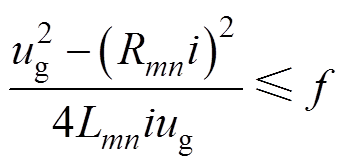 (3)
(3)
研究电机为力矩控制模式,输出电流需要在0~3 A内大范围可调,以实现力矩的调节,将B6拓扑参数代入式(3)进行估算。当输出电流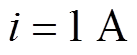 时,可计算得要想满足电机电枢回路处于电流连续模式(Continuous Current Mode, CCM),开关频率至少大于
时,可计算得要想满足电机电枢回路处于电流连续模式(Continuous Current Mode, CCM),开关频率至少大于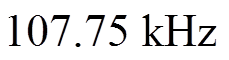 。当电流进一步降低时,所需开关频率将提升至一般开关器件无法承受的程度。图3给出了B6拓扑使用H_PWM-L_PWM控制时,在不同母线电压和电枢平均电流下,处于反电动势为零(转速为零)的最苛刻条件下,保证电枢回路处于CCM的最小开关频率。
。当电流进一步降低时,所需开关频率将提升至一般开关器件无法承受的程度。图3给出了B6拓扑使用H_PWM-L_PWM控制时,在不同母线电压和电枢平均电流下,处于反电动势为零(转速为零)的最苛刻条件下,保证电枢回路处于CCM的最小开关频率。

图3 不同母线电压和输出电流下,保证电流连续的最小开关频率
Fig.3 Minimum switching frequency ensuring continuous current mode under different circumstances of line electromotive force and output current
可以看出,指令电流越小,所需开关频率越高;随着母线电压的升高,所需开关频率越高。对式(2)不等式左侧计算各变量的偏导数可知,母线电压大小的影响要小于指令电流大小的影响。在母线电压很高而电机要以很小的电流起动时,所需开关频率最高可达GHz数量级。小功率无铁心电机,尤其是输出电流较小时,电流断续问题更为严重。大功率无铁心电机,尤其是以较大电流起动的电机不需要处理这个问题,因为在输出电流超过2 A后,即使输入电压超过60 V,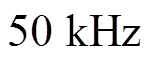 的开关频率足以保证电机电流连续。
的开关频率足以保证电机电流连续。
电流连续条件曲面仅仅保证了电机正常运行,当电机运行点取在曲面上而不留有较大裕量时,斩波引起的电流纹波极大,在电流临界连续时电流纹波等于2倍的输出电流,进一步导致电机性能的恶化。
1.2.2 H_PWM-L_ON控制B6拓扑及双级式驱动拓扑
在方波控制中,还有H_PWM-L_ON、H_ON-L_ PWM、PWM-ON、ON-PWM、PWM-ON-PWM等诸多控制方式,后几种控制方式与H_PWM-L_PWM的不同之处在于开关管关断时,没有母线电压反压加在电枢两端。H_PWM-L_ON控制方式也称为全桥的Buck斩波方式,这里分析使用H_PWM-L_ON控制方式时,在一个开关周期内的电流变化情况。与1.2.1节分析方式一致,电感电流连续条件为
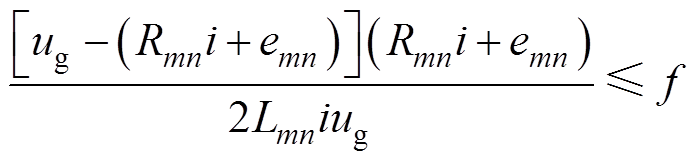 (4)
(4)
分析式(4)可知,与H_PWM-L_PWM控制方式不同,对反电动势求导可知开关频率条件在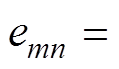
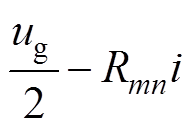 取极大值,即近似最高转速一半的时刻。式(4)在反电动势极值点可化简为
取极大值,即近似最高转速一半的时刻。式(4)在反电动势极值点可化简为
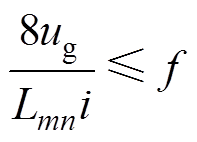 (5)
(5)
将B6拓扑参数代入式(5),可得要想满足电机电枢处于CCM,开关频率至少大于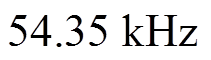 。对比式(3)和式(5)可知,在最苛刻转速时刻而其他所有参数都相同的条件下,后几种控制方式开关频率条件和电流纹波都是H_PWM-L_PWM的1/2。使用后几种控制方式保证电机正常运行所需的要求要低于H_PWM-L_PWM控制方式,且电流性能更加优异。
。对比式(3)和式(5)可知,在最苛刻转速时刻而其他所有参数都相同的条件下,后几种控制方式开关频率条件和电流纹波都是H_PWM-L_PWM的1/2。使用后几种控制方式保证电机正常运行所需的要求要低于H_PWM-L_PWM控制方式,且电流性能更加优异。
1.3.1 H_PWM-L_PWM控制B6拓扑串联电感
根据式(2)可反推B6拓扑在H_PWM-L_PWM控制方式下,维持电枢回路处于CCM,所需的总的回路电感满足
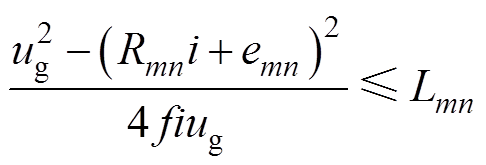 (6)
(6)
根据图4a可以看出,H_PWM-L_PWM控制的最苛刻点在反电动势为零的时候,随转速上升维持CCM所需的电感值变小;过小的电流会导致所需电感值的增大。根据式(6)可得,当电机以电流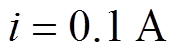 起动时,电枢回路需要
起动时,电枢回路需要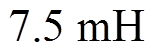 以维持CCM,对于全桥拓扑每一相需要额外串联至少
以维持CCM,对于全桥拓扑每一相需要额外串联至少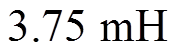 的电感。
的电感。
1.3.2 H_PWM-L_ON控制B6拓扑串联电感与前级Buck变换器电感
同理,根据式(4)可反推得H_PWM-L_ON控制方式下,维持电枢回路处于CCM,所需的总的回路电感满足
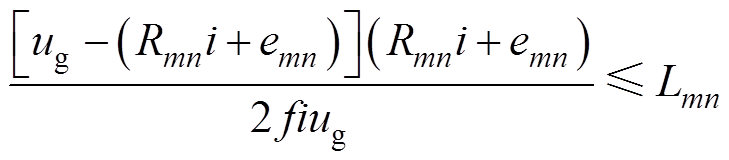 (7)
(7)
B6的H_PWM-L_ON控制也称作Buck斩波方式,其在一个开关周期内等效电路与Buck变换器一致,因此H_PWM-L_ON控制方式计算得到的串联电感值与双级B6拓扑前级Buck变换器的输出电感值是一致的。
根据图4b可知,Buck斩波方式下所需的电感值在转速为最高转速的一半时取到。与H_PWM-L_ PWM控制方式一样,所需电感值与输出电流呈反相关。根据式(7)可得,当电机以电流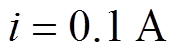 起动至中间转速时,电枢回路需要
起动至中间转速时,电枢回路需要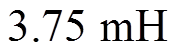 以维持时刻处于CCM,每一相需要串联大于
以维持时刻处于CCM,每一相需要串联大于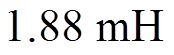 的电感。
的电感。
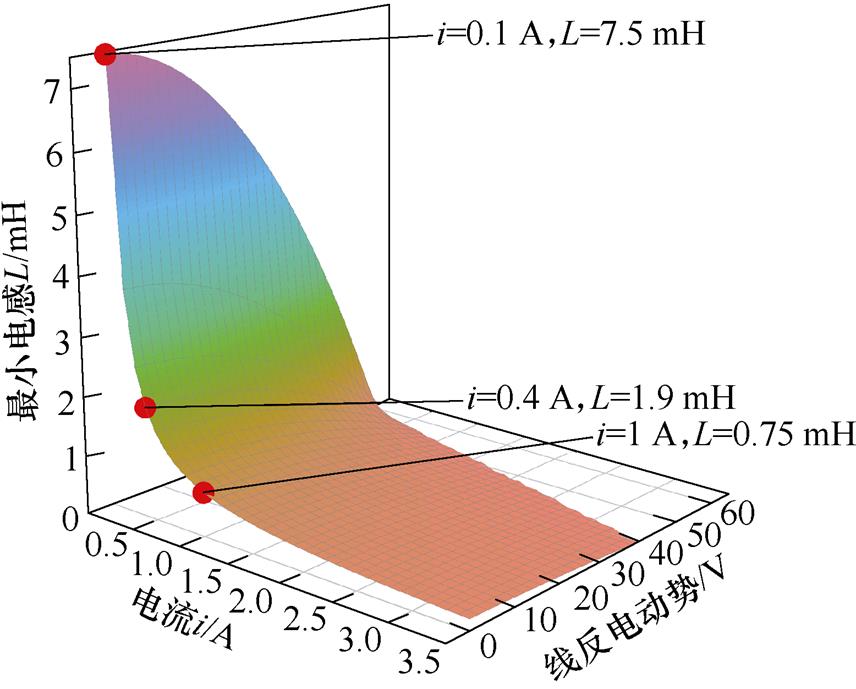
(a)H_PWM-L_PWM控制B6拓扑
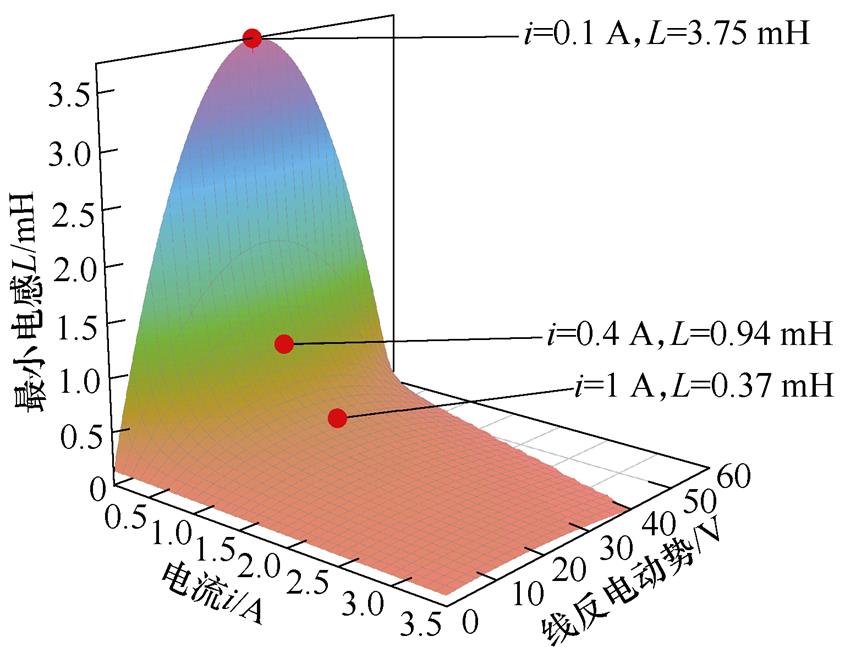
(b)H_PWM-L_ON控制B6拓扑
图4 不同反电动势和输出电流下,保证CCM的最小回路电感值
Fig.4 Minimum inductance value to maintain CCM under different circumstances of line electromotive force and output current
对于同一台电机而言,相同最高转速下,B3拓扑所需母线电压比B6拓扑低。因此,二者计算时考虑的母线电压不一致。当电机以电流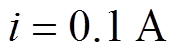 起动至中间转速时,B3拓扑前级Buck电感需要
起动至中间转速时,B3拓扑前级Buck电感需要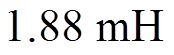 以维持CCM,B6拓扑前级Buck电感需要
以维持CCM,B6拓扑前级Buck电感需要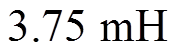 以维持CCM。
以维持CCM。
对于使用Buck变换器作为前级的双级拓扑,由于输出电容引入的零点距离主导极点较远,这里忽略其影响,即认为电容串联寄生电阻为零。但计入功率电感线圈的电阻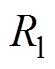 。根据每种拓扑的平均状态空间模型,可得传递函数。式(8)为Buck变换器占空比到电机电枢电流的三阶传递函数,式(9)、式(10)分别为单级B6拓扑分别使用H_PWM-L_ PWM和H_PWM-L_ON控制方式时的一阶传递函数。代入同一电流连续条件下的参数,可得从占空比到电流开环传递函数的伯德图,如图5所示。
。根据每种拓扑的平均状态空间模型,可得传递函数。式(8)为Buck变换器占空比到电机电枢电流的三阶传递函数,式(9)、式(10)分别为单级B6拓扑分别使用H_PWM-L_ PWM和H_PWM-L_ON控制方式时的一阶传递函数。代入同一电流连续条件下的参数,可得从占空比到电流开环传递函数的伯德图,如图5所示。
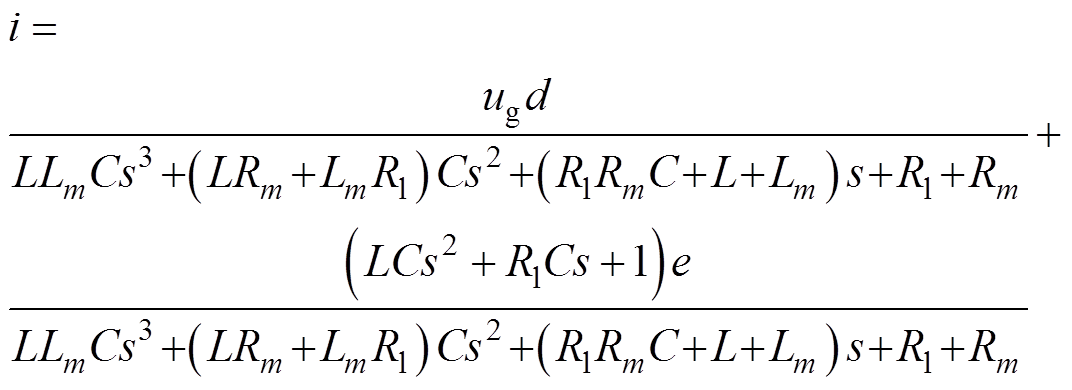 (8)
(8)
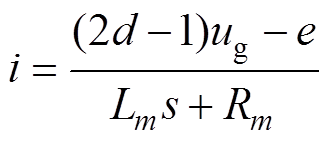 (9)
(9)
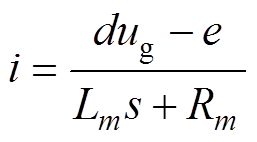 (10)
(10)

图5 不同驱动拓扑开环传递函数伯德图
Fig.5 Bode diagrams of open-loop transfer functions for different drive topologies
驱动拓扑都具有类似低通滤波器的性质,但从伯德图上看,单级B6拓扑的截止频率要高于双级式拓扑,且相位裕度要比后者更大。若采用PI控制等同属于低通性质的控制方式,闭环传递函数的截止频率将进一步降低。在实验中发现,若只为追求双级拓扑的动态性能,根据系统模型配置最优的控制参数,随着转速等状态发生改变,系统很容易不稳定。因此,在实际应用中,对双级式驱动拓扑设计PI控制参数时,为保证系统的稳定性,系统截止频率应设计的比较低。此时系统也无法对瞬时电流进行跟踪,只能实现对平均电流的控制。
不考虑前级电路,假设每一拍内逆变器的输入电压保持uo稳定不变,电机相反电动势为标准的正弦波基波。根据每一拍内电枢等效电路的电压方程及电流初始条件,可得导通区电流的时域方程为
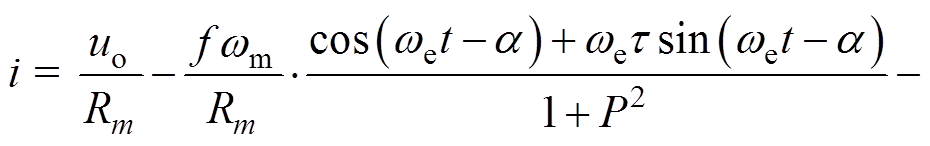
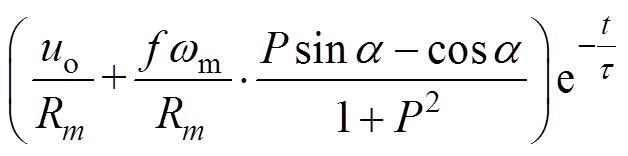 (11)
(11)
式中,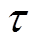 为时间常数,
为时间常数,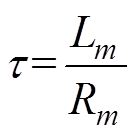 也为电枢总回路的电感与电阻之比;P为等效阻抗比,
也为电枢总回路的电感与电阻之比;P为等效阻抗比,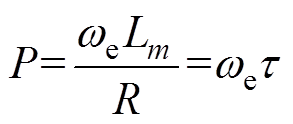 ,
,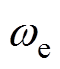 为转子电角速度;
为转子电角速度;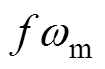 为当前转速下的反电动势最大值,是单位反电动势波形函数的最大值与转子角速度的乘积;定义转子位置
为当前转速下的反电动势最大值,是单位反电动势波形函数的最大值与转子角速度的乘积;定义转子位置 ,
,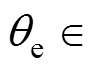
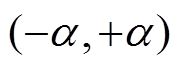 ,
,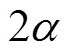 为不同拓扑一拍所持续的电角度,对于B3拓扑三拍式工作方式
为不同拓扑一拍所持续的电角度,对于B3拓扑三拍式工作方式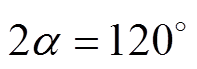 ,对于B6拓扑六拍式工作方式
,对于B6拓扑六拍式工作方式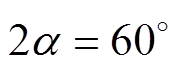 。
。
根据式(11)可知,无论是双级式驱动拓扑输出电流波形,还是单级B6驱动输出的电流波形包络线,在每一拍内为马鞍形波形,具体形状与电机电枢的时间常数有关。单级B6拓扑的电流波形在此基础上叠加斩波的脉动,且斩波脉动会随着转速的上升而减小。
B6拓扑由于续流通路的存在,工作区间分为导通区和换相区。无论是单级还是双级拓扑,B6换相区持续时间与电流脉动和斩波、控制性能、换相角误差等多因素有关,因此这里不做详细理论分析。
本文使用由TI生产的MCU TMS320F28335和ALTERA生产的CPLD EPM1270F256组成的数字控制板来对电机进行控制,采样控制频率设定为20 kHz。对三种驱动拓扑设计环路响应性能相近的PI参数,以平均电流控制方式对无铁心电机进行控制。本文不考虑换相角误差导致非理想二极管续流引起的脉动,且在拓扑对比时使用同一台电机和同一套采样检测软、硬件。图6为5NMS飞轮驱动系统实验平台。驱动硬件采用模块化设计,不同种驱动拓扑可保留相同模块,仅对不同硬件电路替换即可。5NMS飞轮驱动系统的具体参数见表1。

图6 5NMS飞轮驱动系统实验平台
Fig.6 Experimental platform of 5NMS flywheel drive system
表1 5NMS飞轮驱动系统参数
Tab.1 Parameters of 5NMS flywheel drive system
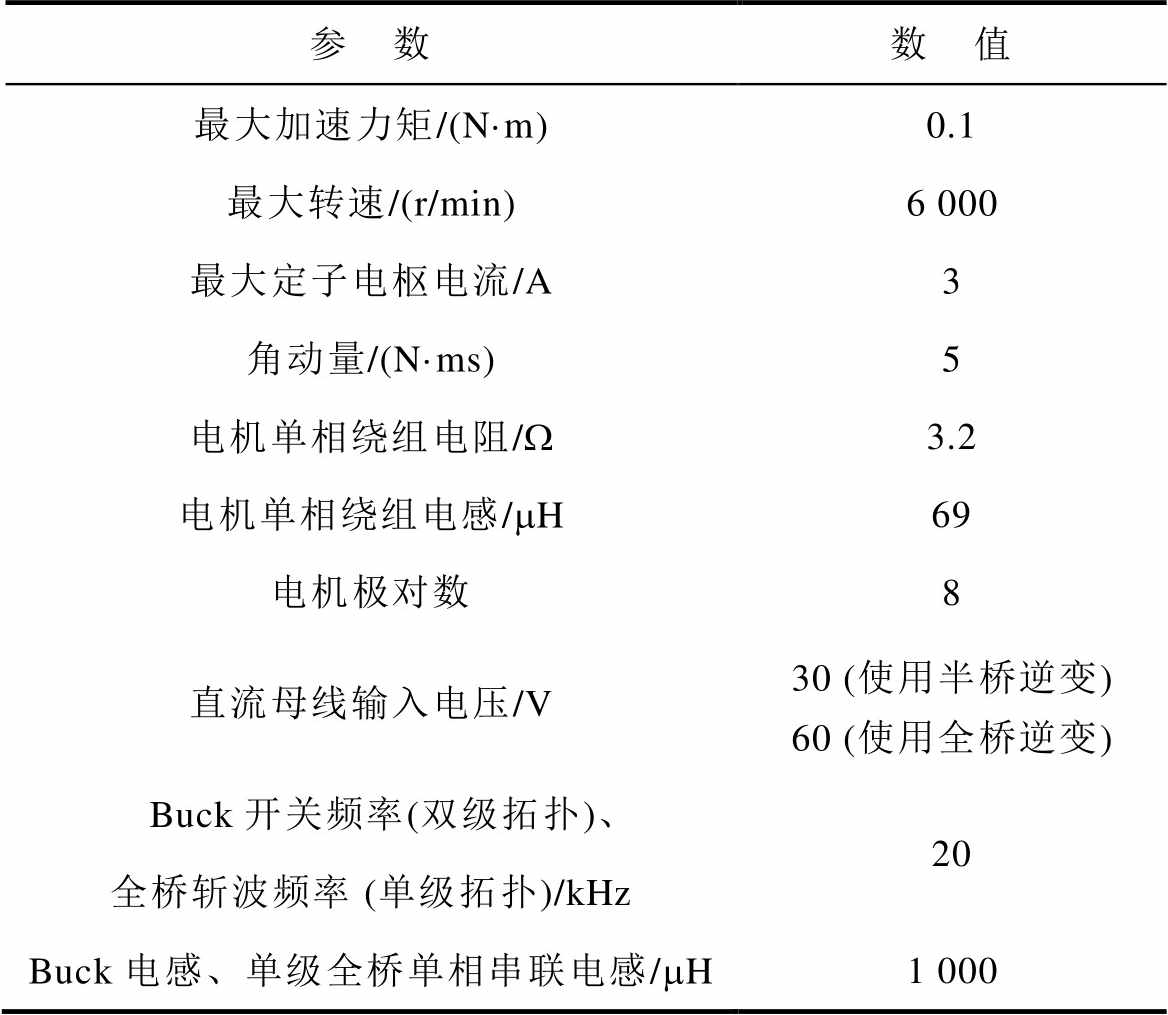
参 数数 值 最大加速力矩/(N·m)0.1 最大转速/(r/min)6 000 最大定子电枢电流/A3 角动量/(N·ms)5 电机单相绕组电阻/W3.2 电机单相绕组电感/mH69 电机极对数8 直流母线输入电压/V30 (使用半桥逆变) 60 (使用全桥逆变) Buck开关频率(双级拓扑)、全桥斩波频率 (单级拓扑)/kHz20 Buck电感、单级全桥单相串联电感/mH1 000
图7为三种驱动拓扑在4 000 r/min时,以400 ns的采样周期获取10 000个采样点的三相电流波形。为保证B3拓扑与全桥拓扑输出力矩大小一致,Buck+B3拓扑输出平均电流控制为1.7 A,后两种拓扑输出平均电流控制为1 A。
通过对比可知,B3拓扑输出电流纹波最大,因其不存在续流通路,在每个导通区结束后,开关管硬关断,在图7a横坐标总时长为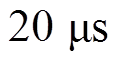 的放大图中,开关管关断一瞬间,母线电压(放大图中绿色曲线)出现54.4 V的短脉冲电压尖峰,持续时间大约
的放大图中,开关管关断一瞬间,母线电压(放大图中绿色曲线)出现54.4 V的短脉冲电压尖峰,持续时间大约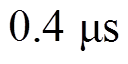 ,且此电压尖峰随转速变化不大,是B3拓扑特有的问题;单级B6串联电感拓扑由于同时进行斩波调节与换相,斩波脉动比较明显,而双级式拓扑由于前级Buck输出电感的电流滤波作用,无明显斩波痕迹。单级B6拓扑斩波引起的脉动会随着转速的上升而降低;Buck+B6拓扑综合前两者的优点,总的换相区电流脉动较小。
,且此电压尖峰随转速变化不大,是B3拓扑特有的问题;单级B6串联电感拓扑由于同时进行斩波调节与换相,斩波脉动比较明显,而双级式拓扑由于前级Buck输出电感的电流滤波作用,无明显斩波痕迹。单级B6拓扑斩波引起的脉动会随着转速的上升而降低;Buck+B6拓扑综合前两者的优点,总的换相区电流脉动较小。
三种拓扑导通区电流脉动和电流纹波率在不同转速下的变化如图8所示,前者用柱状图表示,后者用折线图表示。导通区电流脉动及电流纹波率随转速上升而不断增加,但Buck+B3拓扑的电流脉动上升幅度最大,而Buck+B6拓扑的电流脉动最小。
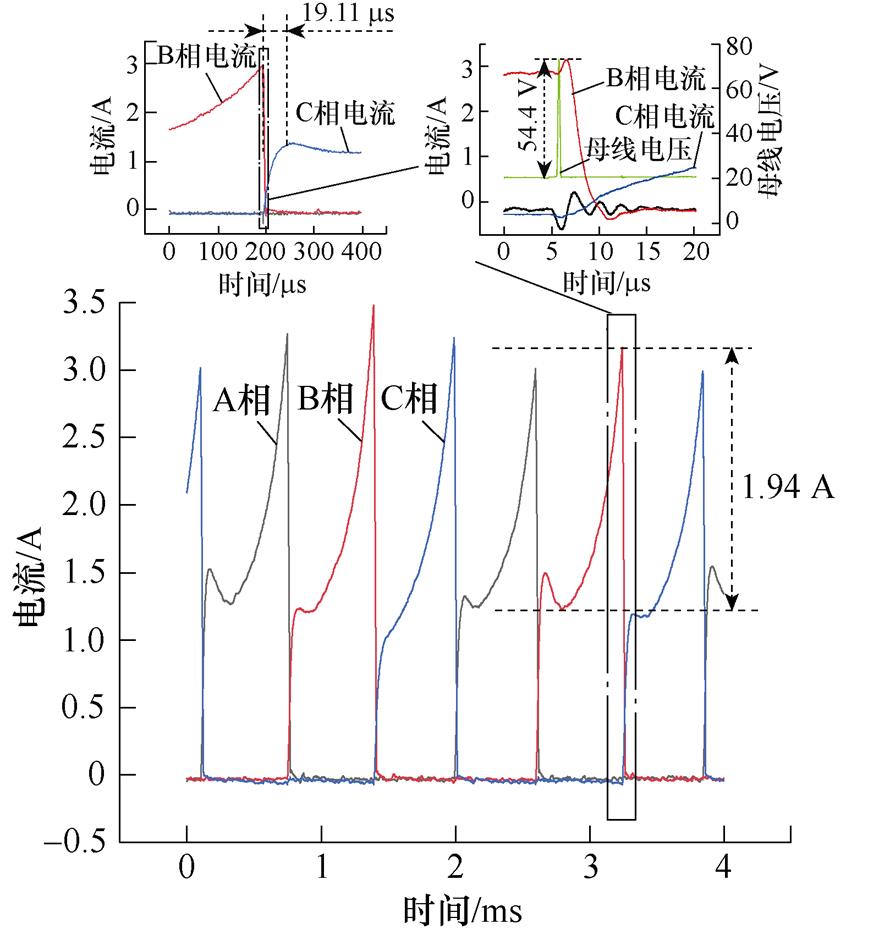
(a)Buck+B3拓扑
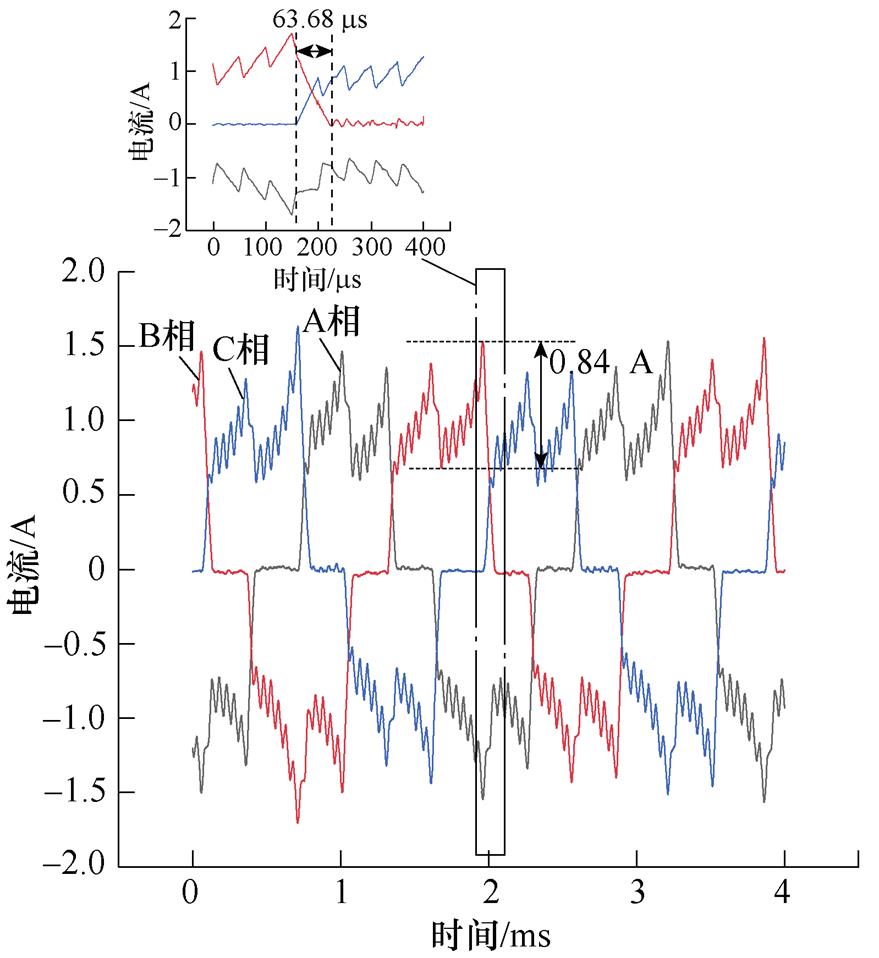
(b)B6级联电感拓扑
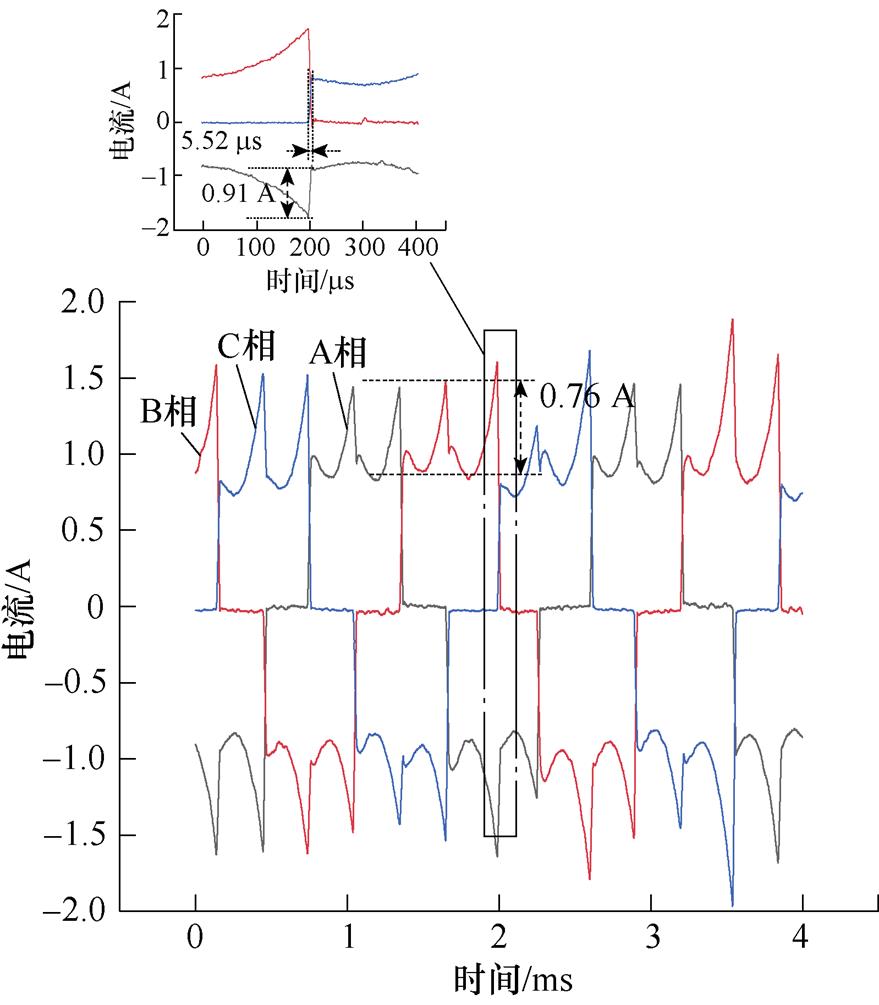
(c)Buck+B6拓扑
图7 不同驱动拓扑在4 000 r/min的电流波形
Fig.7 Current waveforms of different drive topologies when operating at 4 000 r/min
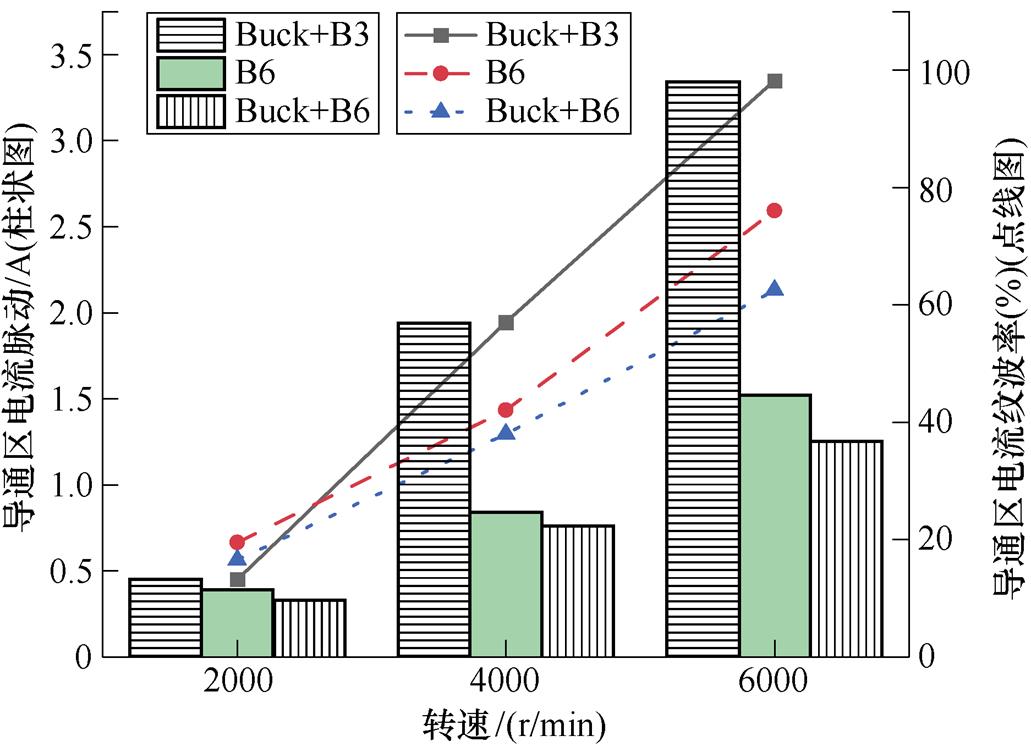
图8 不同驱动拓扑在不同转速下的导通区电流脉动
Fig.8 Conduction current ripple at different speeds for different drive topologies
针对三种驱动拓扑,在不同转速下的电流进行傅里叶分析。图9给出了不同拓扑在2 000 r/min和4 000 r/min工作点,以0 Hz为基频率对电流进行分析,并将直流量认为100%,得出的谐波含量。从图9中可以看出,谐波主要集中在转子电角频率的基波频率和高次倍频。Buck+B3拓扑驱动拓扑输出电流谐波随转速上升幅度较大,总谐波畸变率(Total Harmonic Distortion, THD)在2 000 r/min为16.30%,到了4 000 r/min增加至51.17%,而单级B6拓扑或Buck+B6拓扑电流谐波随转速增加较少,由于其斩波分量随转速降低,从2 000 r/min到4 000 r/min,其THD甚至略有下降,从32.91%降低至31.71%,其高次谐波甚至可以忽略不计,但应当注意的是,单级B6拓扑除了转子电角频率谐波外,还存在大量开关频率基频及其倍频的谐波,其在4 000 r/min时开关频率处的谐波分量占14.79%。
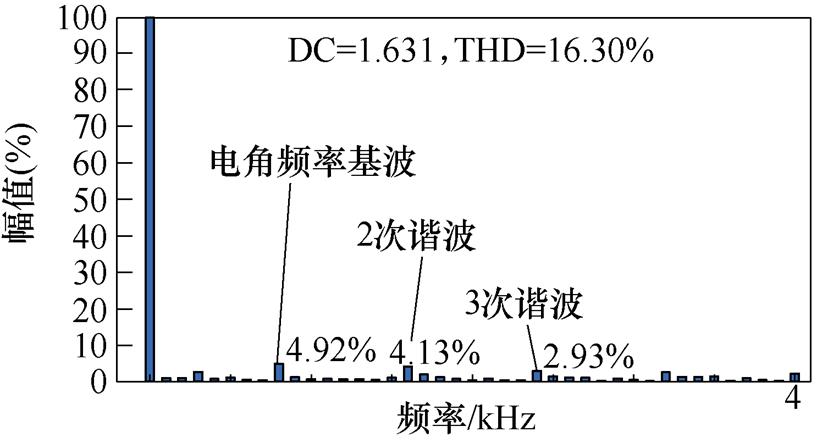
(a)Buck+B3拓扑工作在2 000 r/min
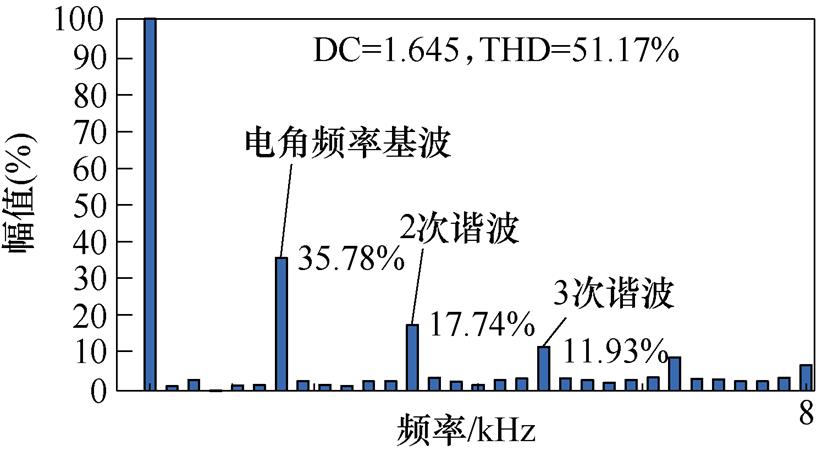
(b)Buck+B3拓扑工作在4 000 r/min
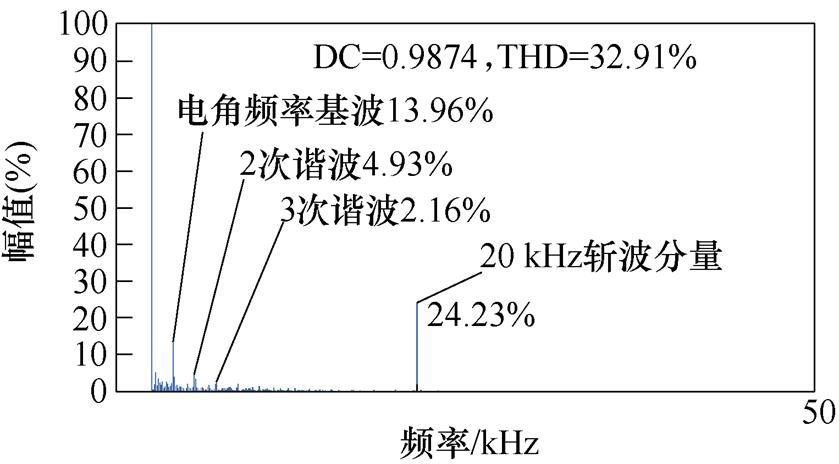
(c)B6级联电感拓扑工作在2 000 r/min
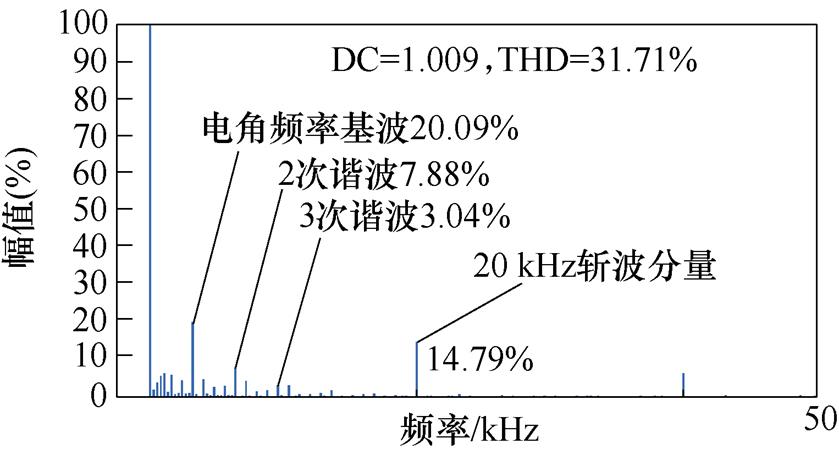
(d)B6级联电感拓扑工作在4 000 r/min

(e)Buck+B6拓扑工作在2 000 r/min
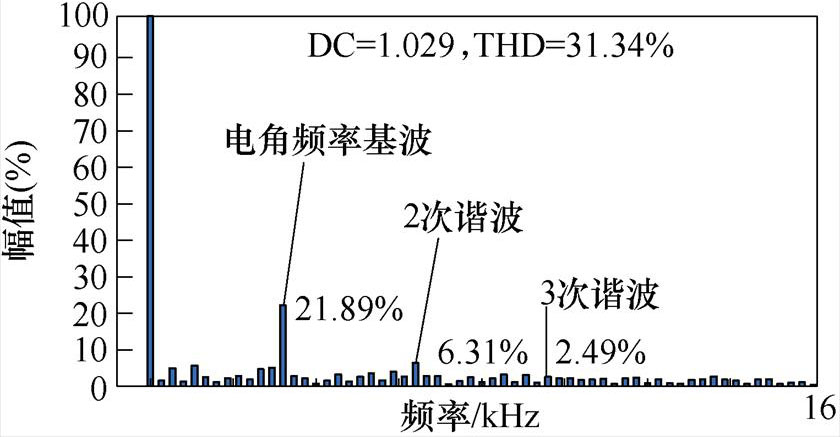
(f)Buck+B6拓扑工作在4 000 r/min
图9 三种拓扑在2 000 r/min和4 000 r/min时电流傅里叶分析结果
Fig.9 Current Fourier analysis results at 2 000 r/min and 4 000 r/min for three drive topologies
B6拓扑存在续流通路,与B3拓扑相比多了换相区。这里比较两种B6拓扑的换相区与B3拓扑换相后电流恢复时间。
由于双级式驱动拓扑提升电路时间常数的思路是在前级预稳压电路中增加电感,而单级B6拓扑将电感串联在每一相电枢回路中,将小电感电机等效为大电感电机。因此,单级B6串联电感的拓扑换相时间要远远高于Buck+B6驱动拓扑。一台8对极的电机使用B6驱动拓扑工作在六拍式方式,在6 000 r/min时,其一拍的电频率为4.8 kHz,以图10中实验数据为例,其换相区对一拍工作区间总时间的占比为54.72%。换相区关断相通过反并联二极管续流的状态是不可控的。这说明单级B6串联电感的方式虽能保证电机的运行,但换相区的延长却会极大恶化电机高速运行的性能。时间常数过大的电机不适合高速运行。
双级式驱动拓扑换相后的稳定时间随转速增加而降低。Buck+B6拓扑驱动下的电机换相时间在全速度范围内只有几个ms,若想在此拓扑基础上,进一步使用重叠换相控制等算法对换相区脉动进行控制,开关频率则至少要达到几百kHz以上。
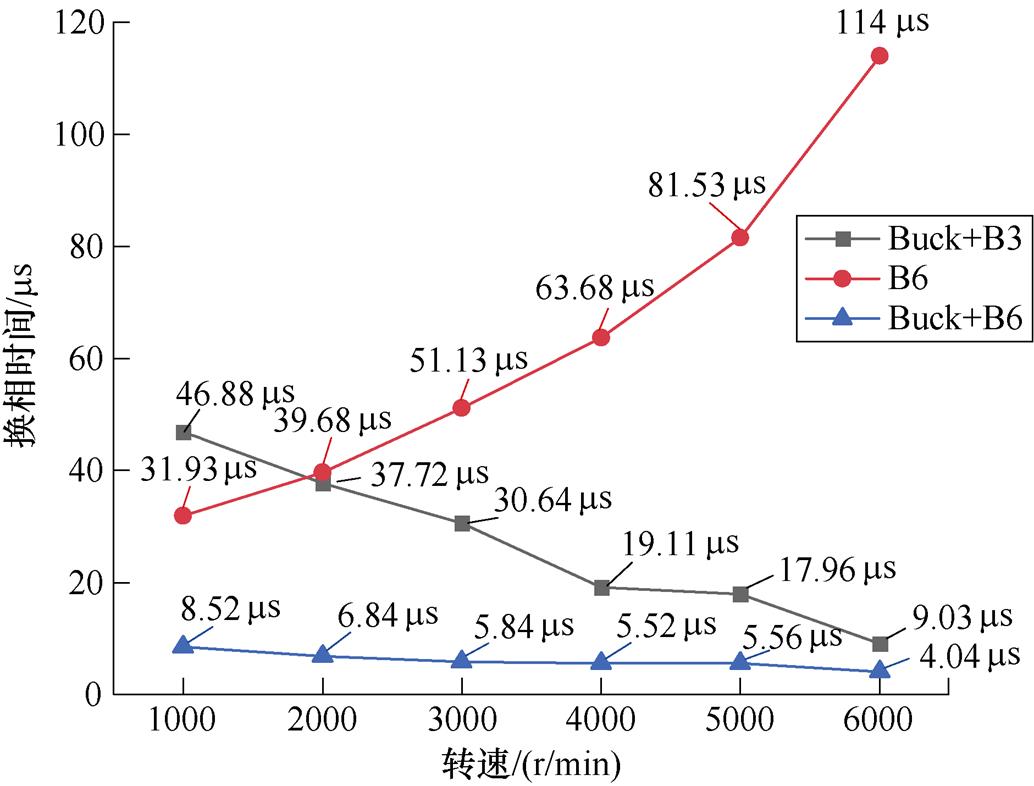
图10 不同驱动拓扑在不同转速下的换相时间
Fig.10 Commutation time at different speeds for different drive topologies
由于单级B6拓扑无法从电机电能输入端测量功率,本文比较两种双级式驱动拓扑的效率。从1 000 r/min到6 000 r/min,Buck+B3拓扑与Buck+ B6拓扑在母线分别为30 V和60 V,并分别输出1.7 A和1 A平均电流的条件下,输出效率如图11所示。随着转速上升,Buck输出电压的增加,其效率也越来越高。但B6拓扑在导通区上下桥臂共两个开关管的损耗必然大于B3拓扑在导通区仅有一个开关管的损耗。三种驱动拓扑对比总结见表2。
本文针对定子无铁心永磁无刷直流电机电枢电感较小导致电流脉动较大,无法使用传统三相全桥直接驱动的问题,根据不同提升时间常数的思路设计并制造了三种驱动拓扑,并使用平均电流控制方法驱动同一台电机,实验结果表明,三种拓扑均能保证无铁心小电感电机在最恶劣情况时的电流连续。但在实际应用中,三种驱动拓扑各有优缺点,结论如下:

图11 双级式拓扑在后级分别为B3和B6时,在不同转速下的效率
Fig.11 The efficiency of the two-stage topologies at different speeds when the rear stages are B3 and B6 respectively
表2 三种驱动拓扑对比总结
Tab.2 Comparison results of three drive topologies
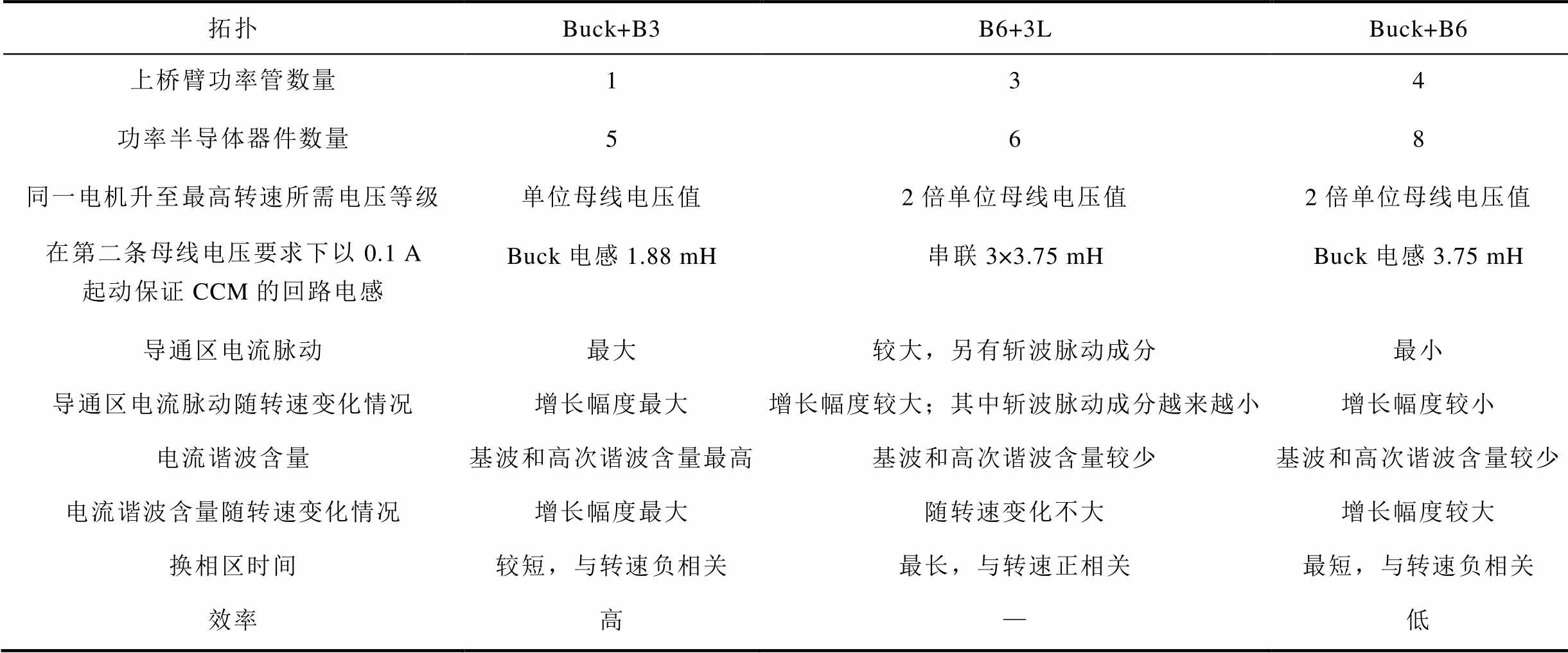
拓扑Buck+B3B6+3LBuck+B6 上桥臂功率管数量134 功率半导体器件数量568 同一电机升至最高转速所需电压等级单位母线电压值2倍单位母线电压值2倍单位母线电压值 在第二条母线电压要求下以0.1 A起动保证CCM的回路电感Buck电感1.88 mH串联3×3.75 mHBuck电感3.75 mH 导通区电流脉动最大较大,另有斩波脉动成分最小 导通区电流脉动随转速变化情况增长幅度最大增长幅度较大;其中斩波脉动成分越来越小增长幅度较小 电流谐波含量基波和高次谐波含量最高基波和高次谐波含量较少基波和高次谐波含量较少 电流谐波含量随转速变化情况增长幅度最大随转速变化不大增长幅度较大 换相区时间较短,与转速负相关最长,与转速正相关最短,与转速负相关 效率高—低
1)Buck+半桥拓扑所需的功率开关管数量最少、驱动难度最小。体积、质量和成本最少。对于同一台电机,升至同一最高转速所需母线电压等级是全桥拓扑的一半。以相同最小电流起动所需的Buck变换器的电感值更小。同时,半桥拓扑单相导通开关管损耗相对更低。但是电流性能较差,无续流通路导致开关管硬关断,母线有较大的电压尖峰,EMC性能较差。电流脉动和谐波会随转速的上升而大幅度地升高。
2)单级半桥串联三电感拓扑的电流谐波成分随转速上升变化不大。等效成大电感电机使其能够使用矢量控制的控制算法。但是将电感增加在电枢回路内的思路使得电机换相时间增加,导致高速可控性能变差。此外,电流脉动成分最多,低速时斩波引起的脉动和谐波成分很高。
3)Buck+全桥拓扑电流脉动及电流谐波最小,换相时间和脉动较少。且导通区和换相区的性能可以进一步优化。但其硬件成本和体积更大,效率较低。
4)普通的单级全桥驱动不能保证无铁心小电感电机在母线输入电压受限情况下,四象限正常可靠运行。Buck+全桥拓扑可以获得最好的电流及转矩性能,在此基础上可通过拓扑及控制算法方面的研究来进一步提升性能,但是在实际工程应用中,由于母线输入电压、体积、质量、成本的限制,可考虑Buck+半桥拓扑来实现无铁心小电感电机四象限正常运行。全桥串联电感拓扑方案仅适合使用在电机中低速区间。
参考文献
[1] Li Haoyan, Xu Haiping, Chen Xi, et al. Comparison of two drive topologies for ironless-stator permanent magnet motor driven by square wave[M]. Singapore: Springer Singapore, 2022.
[2] 李珍国, 王鹏磊, 孙启航, 等. 基于逐相旋转坐标变换的无刷直流电机转子磁场定向瞬时转矩控制技术[J]. 电工技术学报, 2022, 37(22): 5788-5798.
Li Zhenguo, Wang Penglei, Sun Qihang, et al. Instantaneous torque control technology of rotor magnetic field orientation of brushless DC motor based on phase-by-phase rotation coordinate trans- formation[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5788-5798.
[3] 张庆湖, 贾喆武, 王东. 环形绕组无刷直流电机的混合换向方法[J]. 电工技术学报, 2022, 37(17): 4346-4354.
Zhang Qinghu, Jia Zhewu, Wang Dong. Hybrid commutation method of brushless DC motor with ring winding[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4346-4354.
[4] 武洁, 王文磊, 张恒毅, 等. 一种带抽头线圈的无刷直流电机无线驱动与控制方法[J]. 电工技术学报, 2022, 37(23): 6116-6125.
Wu Jie, Wang Wenlei, Zhang Hengyi, et al. Wireless driving and control method of brushless DC motor with tapped coil[J]. Transactions of China Electro- technical Society, 2022, 37(23): 6116-6125.
[5] 边春元, 邢海洋, 李晓霞, 等. 基于速度变化率的无位置传感器无刷直流电机风力发电系统换相误差补偿策略[J]. 电工技术学报, 2021, 36(11): 2374- 2382.
Bian Chunyuan, Xing Haiyang, Li Xiaoxia, et al. Compensation strategy for commutation error of sensorless brushless DC motor wind power generation system based on speed change rate[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2374- 2382.
[6] 李珍国, 孙启航, 王鹏磊, 等. 基于转子永磁体磁场定向的无刷直流电机转矩脉动抑制[J]. 电工技术学报, 2020, 35(14): 2987-2996.
Li Zhenguo, Sun Qihang, Wang Penglei, et al. Torque ripple suppression of brushless DC motor based on rotor permanent magnet magnetic field orientation[J]. Transactions of China Electrotechnical Society, 2020, 35(14): 2987-2996.
[7] 张卓然, 耿伟伟, 陆嘉伟. 定子无铁心永磁电机技术研究现状与发展[J]. 中国电机工程学报, 2018, 38(2): 582-600, 689.
Zhang Zhuoran, Geng Weiwei, Lu Jiawei. Overview of permanent magnet machines with ironless stator[J]. Proceedings of the CSEE, 2018, 38(2): 582-600, 689.
[8] Ooshima M, Kitazawa S, Chiba A, et al. Design and analyses of a coreless-stator type bearingless motor/ generator for clean energy generation and storage systems[C]//2006 IEEE International Magnetics Conference (INTERMAG), San Diego, CA, USA, 2007: 969.
[9] Liu Xiangdong, Hu Hengzai, Zhao Jing, et al. Analytical solution of the magnetic field and EMF calculation in ironless BLDC motor[J]. IEEE Transa- ctions on Magnetics, 2016, 52(2): 1-10.
[10] Fang Jiancheng, Zhou Xinxiu, Liu Gang. Instan- taneous torque control of small inductance brushless DC motor[J]. IEEE Transactions on Power Elec- tronics, 2012, 27(12): 4952-4964.
[11] De S, Rajne M, Poosapati S, et al. Low-inductance axial flux BLDC motor drive for more electric aircraft[J]. IET Power Electronics, 2012, 5(1): 124.
[12] Fang Jiancheng, Zhou Xinxiu, Liu Gang. Precise accelerated torque control for small inductance brushless DC motor[J]. IEEE Transactions on Power Electronics, 2013, 28(3): 1400-1412.
[13] Valle R L, Almeida P M, Ferreira A A, et al. Unipolar PWM predictive current-mode control of a variable- speed low inductance BLDC motor drive[J]. IET Electric Power Applications, 2017, 11(5): 688-696.
[14] Liu Yue, Hu Jianhui, Dong Shili. A torque ripple reduction method of small inductance brushless DC motor based on three-level DC converter[C]//2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi'an, China, 2019: 1669-1674.
[15] Sozer Y, Torrey D A, Reva S. New inverter output filter topology for PWM motor drives[C]//Fifteenth Annual IEEE Applied Power Electronics Conference and Exposition, New Orleans, LA, USA, 2002: 911- 917.
[16] Dzhankhotov V, Pyrhönen J. Passive LC filter design considerations for motor applications[J]. IEEE Transactions on Industrial Electronics, 2013, 60(10): 4253-4259.
[17] Samitha Ransara H K, Madawala U K, Liu Tianhua. Buck converter based model for a brushless DC motor drive without a DC link capacitor[J]. IET Power Electronics, 2015, 8(4): 628-635.
[18] Li Haitao, Zheng Shiqiang, Ren Hongliang. Self- correction of commutation point for high-speed sensorless BLDC motor with low inductance and nonideal back EMF[J]. IEEE Transactions on Power Electronics, 2017, 32(1): 642-651.
[19] 周闯, 秦国辉, 王玉鹏, 等. 基于Buck变换器的无刷直流电机无位置传感器控制[J]. 电工技术学报, 2017, 32(12): 197-204.
Zhou Chuang, Qin Guohui, Wang Yupeng, et al. Sensorless control of brushless DC motor based on Buck converter[J]. Transactions of China Electro- technical Society, 2017, 32(12): 197-204.
[20] Wang Wei, Wang Jingwen. Dynamic response enhan- cement and fault protection of Boost converter-fed brushless DC motor in aerospace applications[J]. Applied Sciences, 2019, 9(10): 2113.
[21] Shi Tingna, Guo Yuntao, Song Peng, et al. A new approach of minimizing commutation torque ripple for brushless DC motor based on DC-DC converter[J]. IEEE Transactions on Industrial Electronics, 2010, 57(10): 3483-3490.
[22] 朱俊杰, 刘浩然, 蒋峰, 等. 无刷直流电机转矩脉动抑制系统的新型拓扑研究[J]. 电工技术学报, 2018, 33(17): 4060-4068.
Zhu Junjie, Liu Haoran, Jiang Feng, et al. A new topology research on torque ripple suppression system of brushless motor[J]. Transactions of China Elec- trotechnical Society, 2018, 33(17): 4060-4068.
[23] 王晓光, 王晓远, 傅涛. 基于电流型斩波控制器的盘式无铁心永磁同步电机控制方法[J]. 中国电机工程学报, 2015, 35(9): 2310-2317.
Wang Xiaoguang, Wang Xiaoyuan, Fu Tao. The control strategy of disc coreless permanent magnet synchronous motor based on the current chopper control[J]. Proceedings of the CSEE, 2015, 35(9): 2310-2317.
[24] 王晓远, 王晓光, 傅涛. 基于电流矢量的盘式无铁心永磁同步电机瞬时转矩控制[J]. 电工技术学报, 2016, 31(16): 43-49.
Wang Xiaoyuan, Wang Xiaoguang, Fu Tao. Instan- taneous torque control for disc coreless permanent magnetic synchronous motor drives based on the current vector[J]. Transactions of China Electro- technical Society, 2016, 31(16): 43-49.
[25] Carlson R, Lajoie-Mazenc M, Fagundes J C D S. Analysis of torque ripple due to phase commutation in brushless DC machines[J]. IEEE Transactions on Industry Applications, 1992, 28(3): 632-638.
[26] Jiang Guokai, Xia Changliang, Chen Wei, et al. Commutation torque ripple suppression strategy for brushless DC motors with a novel noninductive Boost front end[J]. IEEE Transactions on Power Electronics, 2018, 33(5): 4274-4284.
[27] Li Xinmin, Jiang Guokai, Chen Wei, et al. Com- mutation torque ripple suppression strategy of brushless DC motor considering back electromotive force variation[J]. Energies, 2019, 12(10): 1932.
[28] 姚绪梁, 赵继成, 王景芳, 等. 一种基于辅助升压前端的无刷直流电机换相转矩脉动抑制方法研究[J]. 中国电机工程学报, 2020, 40(9): 3021-3031.
Yao Xuliang, Zhao Jicheng, Wang Jingfang, et al. Research on suppressing commutation torque ripple of brushless DC motor based on an auxiliary step-up front end[J]. Proceedings of the CSEE, 2020, 40(9): 3021-3031.
[29] 曹彦飞, 陆海天, 李新旻, 等. 基于无电感升压拓扑的无刷直流电机电流控制策略[J]. 电工技术学报, 2021, 36(6): 1249-1258.
Cao Yanfei, Lu Haitian, Li Xinmin, et al. Current control strategy of brushless DC motor based on non-inductive Boost topology[J]. Transactions of China Electrotechnical Society, 2021, 36(6): 1249- 1258.
[30] 李珍国, 孙启航, 王鹏磊, 等. 无刷直流电机无直轴电枢反应的非正弦转子磁场定向矢量控制技术[J]. 电工技术学报, 2022, 37(16): 4094-4103.
Li Zhenguo, Sun Qihang, Wang Penglei, et al. Non- sinusoidal rotor field oriented vector control tech- nology without d-axis armature reaction in brushless DC motor[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4094-4103.
[31] Zhang Shuangshuang, Zhang Wei, Wang Rui, et al. Optimization design of Halbach permanent magnet motor based on multi-objective sensitivity[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(1): 20-26.
Design and Comparison of Drive Topologies for Stator-Ironless Permanent Magnet Brushless DC Motor
Abstract The ironless permanent magnet brushless DC motor has a very short electrical time constant, and the inductance value of the armature winding is just a few tens of microhenries. When a single-stage, three-phase full-bridge drive topology is used directly to drive an ironless motor in torque control mode, the armature current may be intermittent if the bus input voltage is limited and the average phase current is minimal. The motor may not start correctly in more severe cases. Moreover, the low inductance causes abrupt fluctuations in armature current and torque. The driving characteristics must be examined to improve the motor's performance. Three drive topologies are investigated: Buck cascaded with half-bridge, single-stage full-bridge with inductors in series, and Buck cascaded with full-bridge to ensure normal operation of the ironless motor. Then, the properties of various drive topologies are discussed and contrasted.
Initially, the fundamental distinctions between the three types of drive topologies are discussed. Secondly, while operating an ironless brushless DC motor in current continuous mode, the switching frequency conditions of H_PWM-L_PWM chopping mode for a single-stage full-bridge topology circuit are computed. The calculations show that when the bus voltage rises and the average armature current falls, the needed switching frequency rises to the order of GHz. The switching frequency is half when the H_PWM-L_ON chopping mode is used with all other settings maintained constant. The inductance conditions necessary for the three drives to operate in the current continuous mode can be deduced. The single-stage full-bridge topology requires an additional inductor of at least 3.75 mH per phase if the H_PWM-L_PWM control method is used, or at least 1.88 mH per phase if the H PWM-L ON control method is used when the motor is operated at 0.1 A. The power inductors needed for the Buck converters in dual-stage drives are 1.88 mH and 3.75 mH when the rear stage is a half-bridge and a full-bridge, respectively. Thirdly, the bode diagram is provided together with the transfer functions. Compared with the two-stage design, single-stage topology has a higher cutoff frequency, a bigger phase angle margin, and excellent dynamic performance. Fourthly, the same motor is driven subsequently to evaluate the design and functionality of the three drive topologies based on digital controllers. The experimental results show that all three topologies guarantee the motor's dependable running. The highest current fluctuation and current harmonics content are found in the Buck cascaded with half-bridge topology, exhibiting the quickest rate of change with rotational speed. The current fluctuation is lowest when the Buck is cascaded with a full-bridge topology. While the rate of change with rotational speed is the smallest, the fluctuation brought on by the chopping of the full-bridge cascaded with an extra-inductor is noticeable. The single-stage full-bridge's commutation time is the longest among these three topologies since it uses inductors in series in the armature circuit. At 6 000 r/min in the experiment, the proportion of the commutation region to each operational section is up to 54.72%, indicating that this topology is unsuitable for high-speed operation. Due to the absence of a channel for the energy of the outgoing phase to discharge, the Buck cascaded with half-bridge topology experiences a voltage spike of 54.4 V.
The conclusions are as follows. After the suitable inductor design, all three drive topologies can ensure the normal functioning of the ironless permanent magnet brushless DC motor. Buck cascaded with the three-phase half-bridge topology offers inexpensive cost, simple construction, and control, making it more appropriate for engineering applications of low drive performance. The dynamic response performance of a single-stage full-bridge with inductors in series is superior but unsuitable for high-speed applications.
keywords:Ironless-stator, permanent magnet brushless direct current motor (PMBLDC), Buck+ half-bridge, full-bridge with inductances cascaded, Buck+ full-bridge
中图分类号:TM345; TM359.6; TM921.5
DOI: 10.19595/j.cnki.1000-6753.tces.221742
山东省重点研发计划(重大科技创新工程)(2021CXGC010208)和齐鲁中科电工先进电磁驱动技术研究院科研基金资助项目。
收稿日期 2022-09-14
改稿日期 2022-11-07
李昊岩 男,1994年生,博士研究生,研究方向为电力电子与电力传动。E-mail: lihaoyan19@mail.iee.ac.cn
许海平 男,1967年生,教授,博士生导师,研究方向为电力电子与电力传动。E-mail: hpxu@mail.iee.ac.cn(通信作者)
(编辑 崔文静)