 为直流输入电压,可从前端整流器获得;Q1~Q4为4个开关,构成全桥逆变器;
为直流输入电压,可从前端整流器获得;Q1~Q4为4个开关,构成全桥逆变器;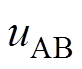 和
和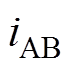 分别为逆变器的瞬时输出电压和电流;补偿元件
分别为逆变器的瞬时输出电压和电流;补偿元件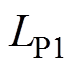 、
、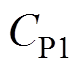 、
、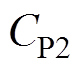 和
和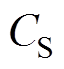 构成LCC/S补偿拓扑;
构成LCC/S补偿拓扑;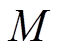 为发射线圈
为发射线圈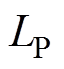 和接收线圈
和接收线圈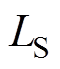 之间的互感;VD1~VD4为4个二极管,构成不可控整流桥;
之间的互感;VD1~VD4为4个二极管,构成不可控整流桥;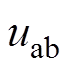 和
和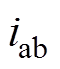 分别为整流器的瞬时输入电压和电流;
分别为整流器的瞬时输入电压和电流;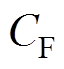 和
和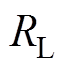 分别为滤波电容和电阻性负载。
分别为滤波电容和电阻性负载。摘要 基于传统完全谐振参数设计方法的感应电能传输(IPT)系统只有在发射线圈和接收线圈完全耦合时才能表现出最佳性能。实际的IPT系统多为变耦合系统,耦合系数变化可能导致输出电压大范围波动和效率降低等问题。该文提出一种基于多目标优化理论的补偿拓扑参数设计方法,在耦合系数和负载变化的情况下仍然可以获得相对恒定的输出电压且能够高效运行。首先,利用基波近似分析法建立LCC/S补偿IPT系统的系统方程。其次,以补偿参数为优化变量,以减小输出电压波动、提升系统效率为优化目标,以电感最大通过电流、电容最大承受电压和零电压开关为约束条件建立多目标优化模型。然后,利用多目标粒子群优化(MOPSO)算法求解所建立的多目标优化模型,并得到Pareto最优解集。最后,根据实际需要,从Pareto最优解集中选择合适的补偿方案,并进行仿真分析和实验验证。实验结果表明,优化方案的电压波动率(VFR)约为传统方案的45%,且优化方案的最低传输效率(87.5%)仍大于传统方案的最高传输效率(86.3%)。该方法可用于优化满足耦合和负载无关恒定输出、高效率、零电压开关等特性的补偿拓扑。
关键词:感应电能传输 多目标优化 耦合无关恒压输出 多目标粒子群优化(MOPSO)算法 Pareto解集
感应电能传输(Inductive Power Transfer, IPT)系统由于具有较高的功率水平和效率特性,已成为无线电能传输(Wireless Power Transfer, WPT)领域的主要研究方向[1-2]。IPT系统具有安全、灵活、可靠、美观等优点,可应用于电动汽车、消费电子、植入式医疗设备、水下电气设备等领域,是替代传统有线充电方式的有效解决方案[3-5]。
基于完全谐振的IPT系统仅在发射和接收线圈完全耦合时才能表现优异的性能[6-7]。然而,线圈之间发生偏移是不可避免的,可能引起系统输出波动较大或效率降低等问题[8-11]。为了在耦合系数变化条件下获得相对恒定的输出并高效运行,专家学者提出了多种解决方案,主要分为控制策略、磁耦合机构设计和补偿拓扑三类[12-13]。其中,控制策略能够得到精确输出,但是当负载和耦合系数在较宽范围内变化时,变换器的调控需求增加,可能会导致控制复杂、效率降低和不稳定等问题[14]。另外,额外增加的变换器也会带来额外的成本、体积和质量。磁耦合机构仅在某个方向偏移时,耦合系数基本保持不变,系统抗偏移范围有限[15]。
补偿拓扑可以降低IPT系统控制复杂度,提升其可靠性和稳定性。基于传统完全谐振补偿参数设计方法的基本补偿拓扑(S/S、S/P、P/S、P/P)不具有抗偏移能力[16],高阶补偿拓扑的抗偏移能力也有限[17-18]。文献[19-20]利用混合型补偿拓扑提升IPT系统的抗偏移能力,一个拓扑的输出增益与耦合系数成正比;另一个拓扑的输出增益与耦合系数成反比。混合型补偿拓扑的增益之和在一定范围内保持相对恒定,但是增加了线圈和补偿元件的数量,系统的成本和复杂性也相应增加。另外,文献[21]提出了重构拓扑方法,以提升系统的抗偏移能力。然而,重构拓扑需要额外的检测电路和控制策略,增加了系统复杂性,降低了运行可靠性。
除了补偿拓扑结构设计,补偿参数优化也能够提升IPT系统的抗偏移能力。文献[22]提出了一种原边感性、副边容性的补偿方法,在宽耦合范围内实现了稳定的输出。文献[23]提出了一种基于枚举法的S/S补偿拓扑参数设计方法,以减小偏移条件下输出电压的波动。文献[24]建立了功率波动的偏微分方程,利用解析法优化了LCC/S补偿参数。然而,以上方法均未考虑IPT系统的传输效率问题。文献[25]提出了一种基于粒子群优化的S/CLC补偿参数设计方法,实现了较高的抗偏移能力和效率。然而,由于采用了加权求和法将多个目标函数合并为一个目标函数,各目标函数的权重需要人为选取,无法精准确定。文献[26]建立了补偿参数多目标优化模型,并利用分支减少优化导航求解器求解所提出非线性优化模型。但该方法仍需建立和求解偏微分方程,建模和求解过程比较复杂。文献[27]提出了一种基于非支配排序遗传算法Ⅲ的拓扑结构和参数同步优化方法。然而,该方法没有进一步分析多目标优化得到的Pareto(帕累托)最优解集,缺乏IPT系统输出电压波动和效率折中方案的分析。
本文突破了传统完全谐振参数设计方法的局限性,将IPT系统补偿参数设计问题转化为多目标优化问题。与单目标优化只能得到唯一解不同,本文建立了多目标优化模型并利用多目标粒子群优化(Multi-Objective Particle Swarm Optimization, MOPSO)算法求解得到了Pareto最优解集。决策者根据实际需要确定各目标权重,从Pareto最优解集中筛选出合适的设计方案,以确保IPT系统在耦合系数和负载变化条件下仍然能够获得相对恒定的输出电压,同时能够高效运行。
LCC/S补偿拓扑的原边补偿电容电压应力较小,轻载时效率较高,副边利于实现手机、可植入设备等紧凑和轻量化要求。因此,本文选用LCC/S补偿拓扑。基于LCC/S补偿拓扑的IPT系统如图1所示,主要由直流电源、逆变器、补偿拓扑、磁耦合机构、整流器、滤波器和负载组成。其中, 为直流输入电压,可从前端整流器获得;Q1~Q4为4个开关,构成全桥逆变器;
为直流输入电压,可从前端整流器获得;Q1~Q4为4个开关,构成全桥逆变器;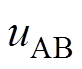 和
和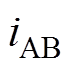 分别为逆变器的瞬时输出电压和电流;补偿元件
分别为逆变器的瞬时输出电压和电流;补偿元件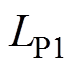 、
、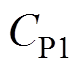 、
、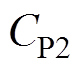 和
和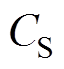 构成LCC/S补偿拓扑;
构成LCC/S补偿拓扑;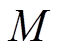 为发射线圈
为发射线圈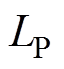 和接收线圈
和接收线圈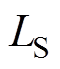 之间的互感;VD1~VD4为4个二极管,构成不可控整流桥;
之间的互感;VD1~VD4为4个二极管,构成不可控整流桥;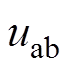 和
和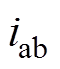 分别为整流器的瞬时输入电压和电流;
分别为整流器的瞬时输入电压和电流;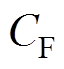 和
和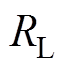 分别为滤波电容和电阻性负载。
分别为滤波电容和电阻性负载。
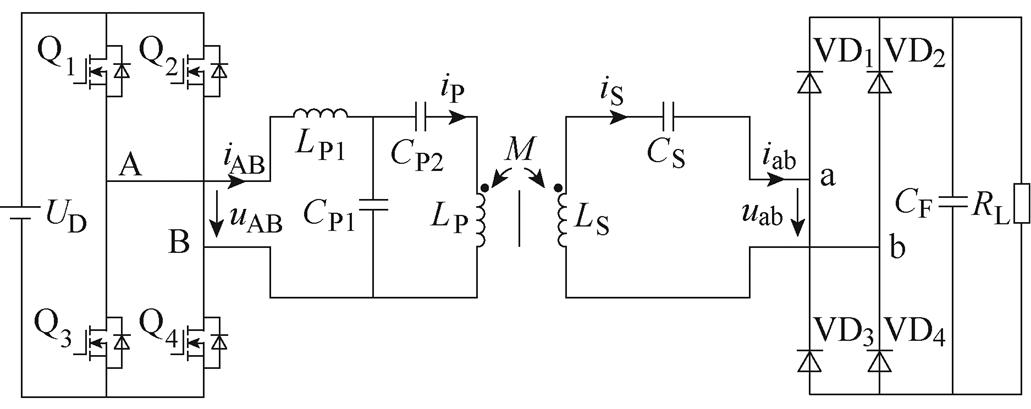
图1 基于LCC/S补偿拓扑的感应电能传输系统
Fig.1 The IPT system with LCC/S compensation topology
利用基波近似分析(Fundamental Harmonic Approximation, FHA)法对图1所示的IPT系统进行分析。设UAB和IAB分别为uAB和iAB的基波有效值,Uab和Iab分别为uab和iab的基波有效值,IP和IS分别为发射线圈和接收线圈的电流的有效值。设逆变器的输出电压的调制占空比为50%,则逆变器的输出电压UAB以及整流桥的输入交流等效电阻Req满足
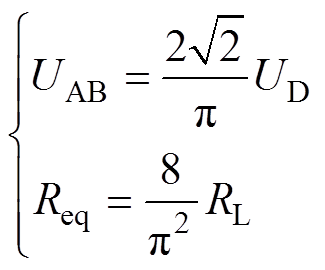 (1)
(1)
根据式(1),可得到基于LCC/S补偿拓扑的IPT系统等效电路如图2所示。基于互感理论建立了该系统的阻抗模型,阻抗定义及其关系可表示为
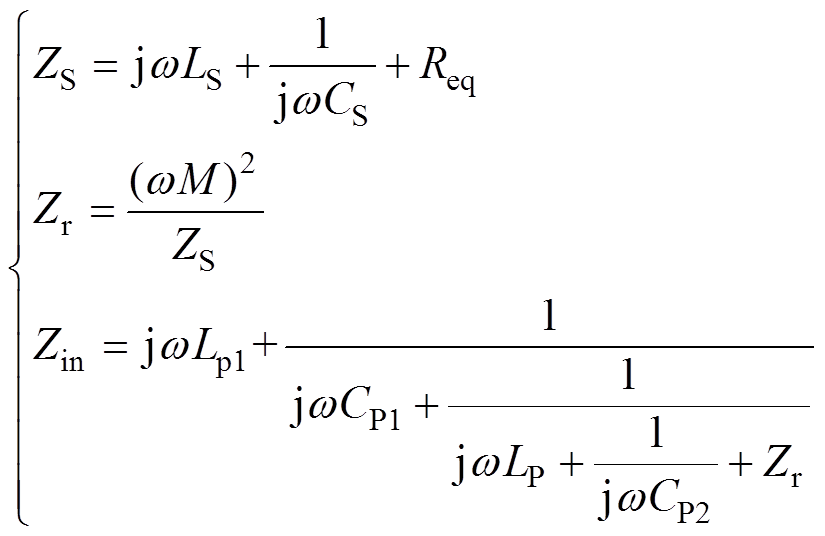 (2)
(2)
式中,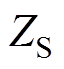 、
、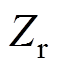 和
和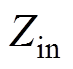 分别为副边阻抗、副边对原边的反射阻抗和系统输入阻抗;
分别为副边阻抗、副边对原边的反射阻抗和系统输入阻抗;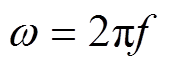 为角频率,
为角频率,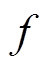 为频率。根据基尔霍夫电压定律和电流定律,可得流过每个补偿元件的电流为
为频率。根据基尔霍夫电压定律和电流定律,可得流过每个补偿元件的电流为
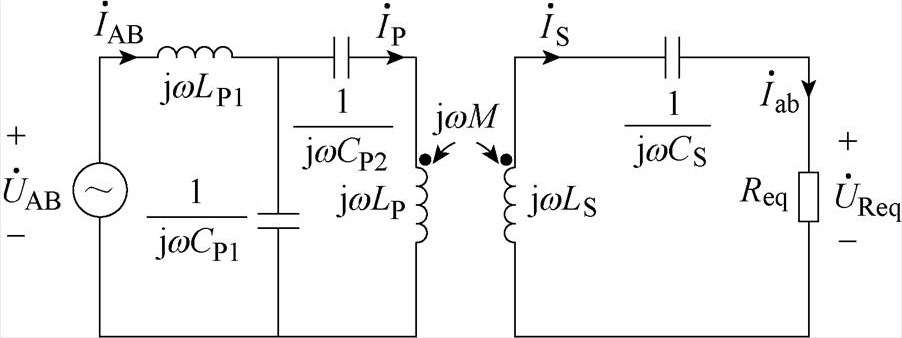
图2 基于LCC/S补偿拓扑的IPT系统等效电路
Fig.2 Equivalent circuit of IPT system based on LCC/S compensation topology
 (3)
(3)
LCC/S补偿拓扑的每个元件的两端电压为
 (4)
(4)
根据等效变换关系,高频整流桥的输入交流电压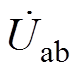 与负载的输出电压
与负载的输出电压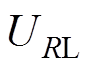 满足关系
满足关系
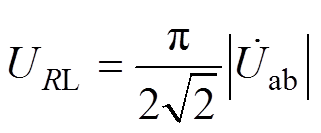 (5)
(5)
根据式(1)~式(5),可得到IPT系统的输出电压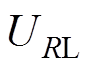 和电压增益
和电压增益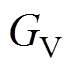 分别为
分别为
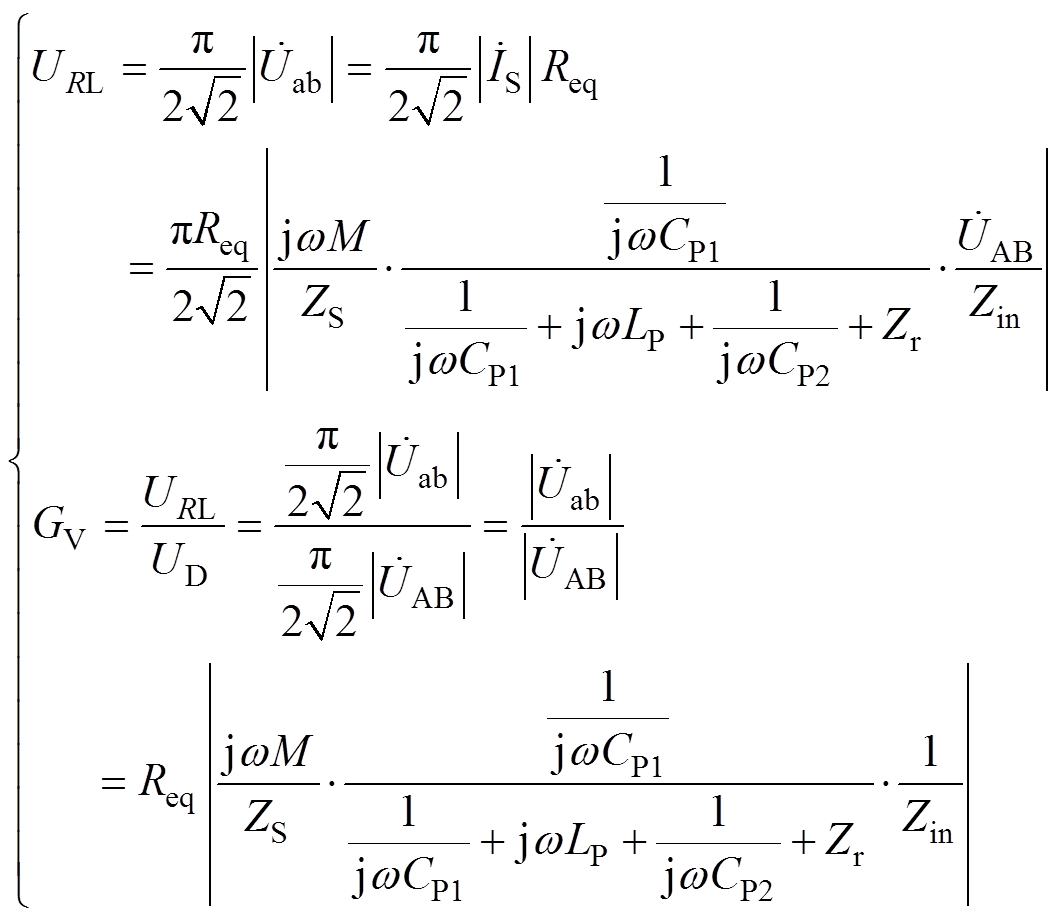 (6)
(6)
传统的补偿参数设计方法采用完全谐振的思想。当系统处于完全谐振状态时,满足
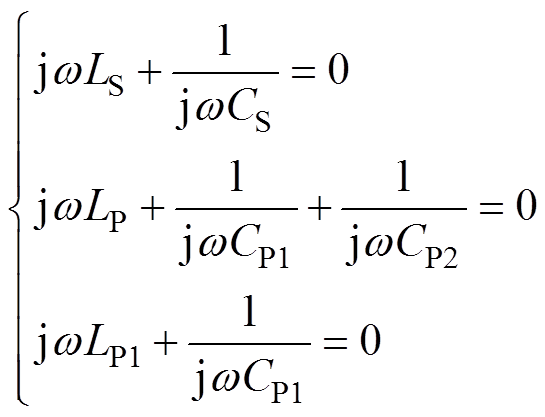 (7)
(7)
将式(7)代入式(6),可得到输出电压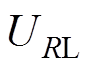 及其增益
及其增益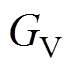 表达式分别为
表达式分别为
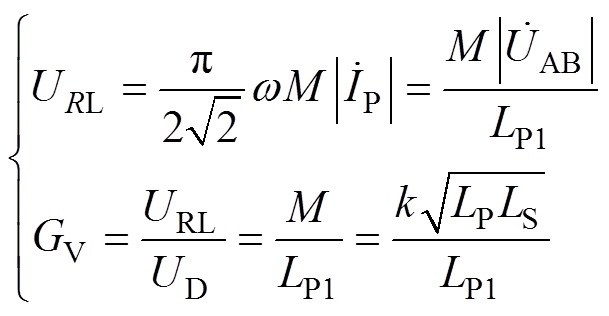 (8)
(8)
式中,k为IPT系统的耦合系数。由式(8)可知,IPT系统的电压增益不受负载影响,但与互感成正比。当IPT系统工作在完全谐振状态时,LCC/S补偿拓扑的4个参数需满足
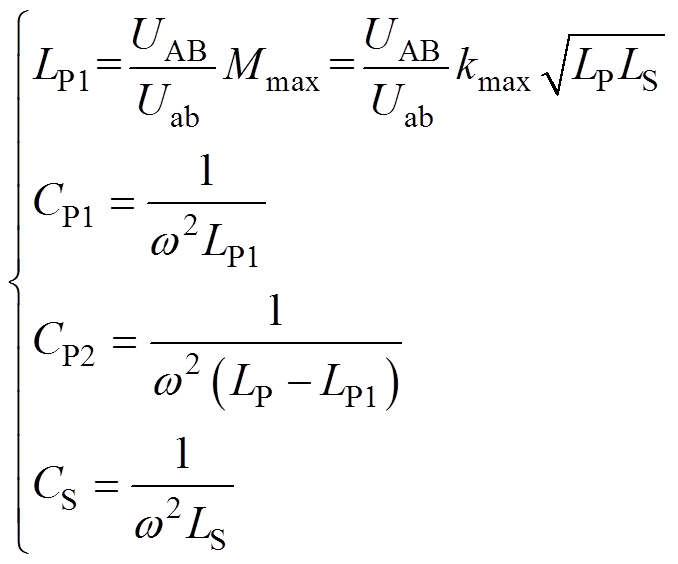 (9)
(9)
由式(8)和式(9)可知,由于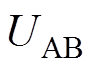 、
、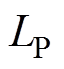 、
、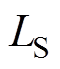 和
和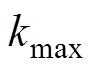 均为定值,可根据输出电压先求出补偿电感
均为定值,可根据输出电压先求出补偿电感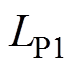 ,再求出另外3个补偿参数
,再求出另外3个补偿参数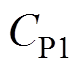 、
、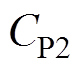 和
和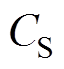 。实际应用中的IPT系统大多是变耦合系统。当耦合系数发生变化时,根据式(9)设计的LCC/S补偿拓扑IPT系统的恒压特性受到破坏。因此,本文提出基于多目标优化理论的补偿参数设计方法,以获得相对恒定的输出,同时确保系统能够高效运行。
。实际应用中的IPT系统大多是变耦合系统。当耦合系数发生变化时,根据式(9)设计的LCC/S补偿拓扑IPT系统的恒压特性受到破坏。因此,本文提出基于多目标优化理论的补偿参数设计方法,以获得相对恒定的输出,同时确保系统能够高效运行。
为了实现耦合无关恒压输出,同时确保系统高效运行,需要建立IPT系统多目标优化模型。多目标优化问题由优化变量、目标函数、系统方程和约束条件组成。通用的多目标优化模型的简要描述为
 (10)
(10)
式中,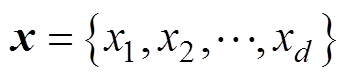 表示d维决策向量,由d个优化变量组成,且
表示d维决策向量,由d个优化变量组成,且 ,
,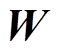 为决策空间。
为决策空间。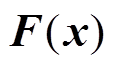 为需要优化的目标函数向量,包含
为需要优化的目标函数向量,包含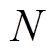 个目标函数。
个目标函数。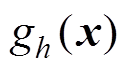 为不等式约束,
为不等式约束,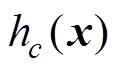 为等式约束。
为等式约束。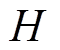 、
、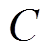 均为正整数。多目标优化算法常用于求解多目标优化问题,得到的解集称为帕累托(Pareto)最优解集。
均为正整数。多目标优化算法常用于求解多目标优化问题,得到的解集称为帕累托(Pareto)最优解集。
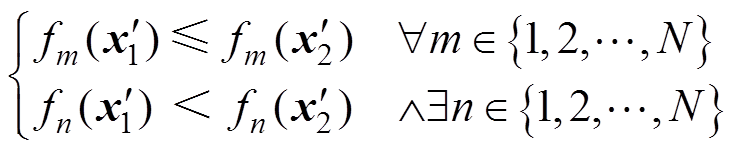 (11)
(11)
若可行解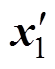 和
和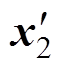 满足关系式(11),则可行解
满足关系式(11),则可行解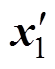 优于可行解
优于可行解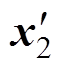 。对于任意一个可行解
。对于任意一个可行解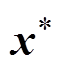 ,如果
,如果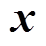 不支配
不支配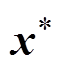 ,则称
,则称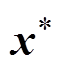 为多目标优化问题的非支配解,即
为多目标优化问题的非支配解,即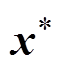 为帕累托最优解或有效解。由所有非劣解组成的集合称为多目标优化问题的Pareto最优解集,这些解集在目标空间的投影称为Pareto前沿。
为帕累托最优解或有效解。由所有非劣解组成的集合称为多目标优化问题的Pareto最优解集,这些解集在目标空间的投影称为Pareto前沿。
优化变量为LCC/S补偿拓扑的4个参数,分别为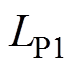 、
、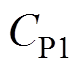 、
、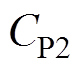 和
和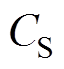 ,可写成决策向量的形式,即
,可写成决策向量的形式,即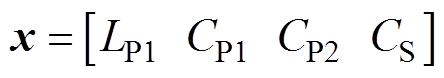 。优化目标为耦合无关恒压输出,效率高,约束条件为元件应力和零电压软开关。
。优化目标为耦合无关恒压输出,效率高,约束条件为元件应力和零电压软开关。
2.2.1 目标函数
1)减小输出电压波动
在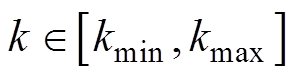 和
和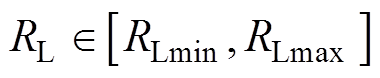 的任何一种状态下,实际输出电压
的任何一种状态下,实际输出电压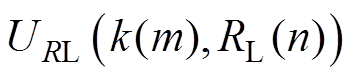 与设定电压
与设定电压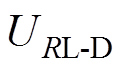 的偏差可用方差来表示,其数学描述为
的偏差可用方差来表示,其数学描述为
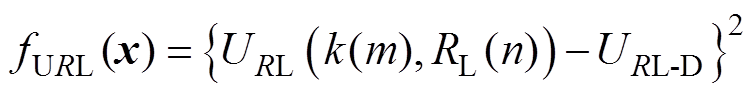 (12)
(12)
根据式(12)可得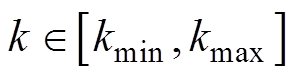 和
和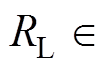
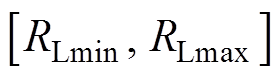 的所有状态下的负载电压方差之和。减小输出电压波动的函数描述为
的所有状态下的负载电压方差之和。减小输出电压波动的函数描述为
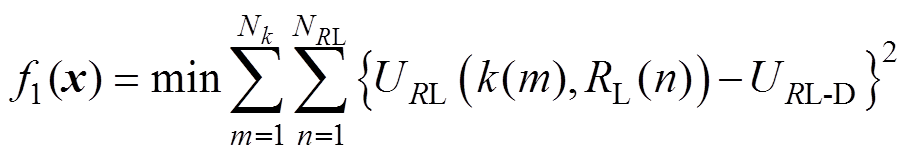 (13)
(13)
式中,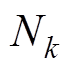 为耦合系数
为耦合系数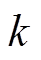 的采样总数,采样间隔为
的采样总数,采样间隔为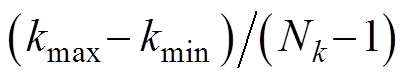 ,其中,
,其中,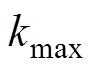 和
和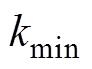 分别为
分别为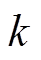 的最大值和最小值;
的最大值和最小值;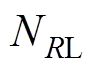 为负载电阻
为负载电阻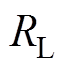 的采样总数,采样间隔为
的采样总数,采样间隔为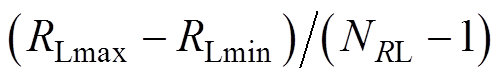 ,其中,
,其中, 和
和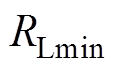 分别为
分别为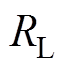 的最大值和最小值;
的最大值和最小值;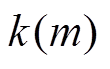 为第
为第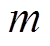 个
个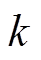 ;
;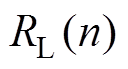 为第
为第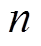 个
个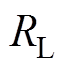 ,
,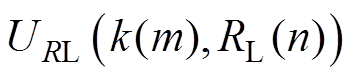 为
为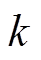 =
=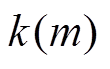 、
、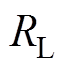 =
=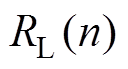 的输出电压;
的输出电压;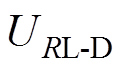 为输出电压的设计值,是一个预定的常数。目标函数
为输出电压的设计值,是一个预定的常数。目标函数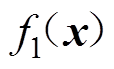 表示系统在所有状态下的输出电压波动之和,其值越小,表示系统的耦合负载无关恒压输出特性越好。
表示系统在所有状态下的输出电压波动之和,其值越小,表示系统的耦合负载无关恒压输出特性越好。
2)减小电感电流应力
基于LCC/S补偿的IPT系统含有3个电感元件,分别表示为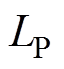 、
、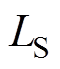 和
和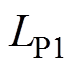 ,寄生等效串联电阻(Equivalent Series Resistance, ESR)分别表示为
,寄生等效串联电阻(Equivalent Series Resistance, ESR)分别表示为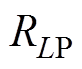 、
、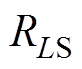 和
和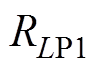 ,流过电感的电流有效值分别为
,流过电感的电流有效值分别为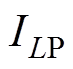 、
、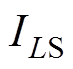 和
和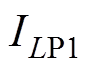 ,则3个电感元件上的总损耗为
,则3个电感元件上的总损耗为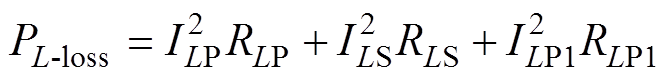 。因此,电感电流应力对IPT系统的效率有很大的影响,实现最小的电感电流应力是一个目标函数。在
。因此,电感电流应力对IPT系统的效率有很大的影响,实现最小的电感电流应力是一个目标函数。在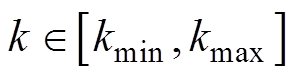 和
和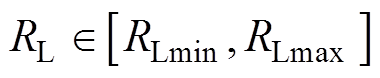 的任何一种状态下,电感电流应力之和定义为
的任何一种状态下,电感电流应力之和定义为
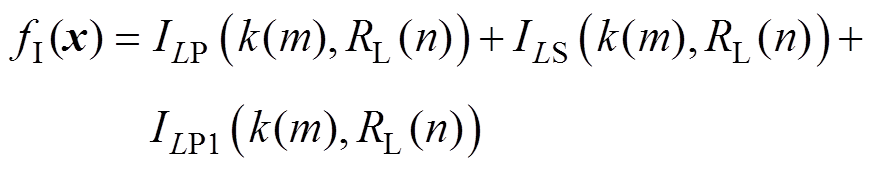 (14)
(14)
根据式(14),可得到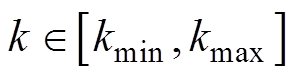 和
和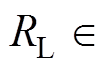
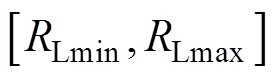 的所有状态下电感电流应力之和。减小电感电流应力的函数可描述为
的所有状态下电感电流应力之和。减小电感电流应力的函数可描述为
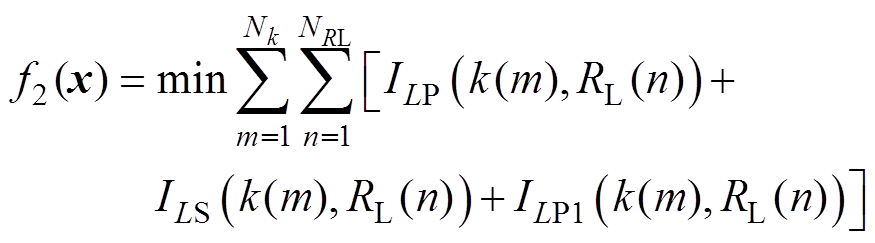 (15)
(15)
式中,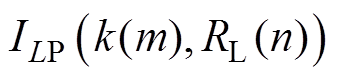 、
、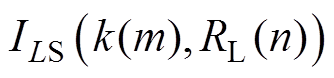 、
、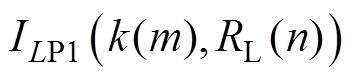 分别为耦合系数为
分别为耦合系数为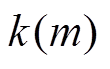 、等效负载电阻为
、等效负载电阻为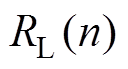 时分别流过
时分别流过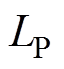 、
、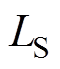 、
、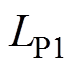 的电流有效值。
的电流有效值。
3)减小输入阻抗角
设逆变器的输入阻抗角为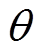 ,则其视在功率满足
,则其视在功率满足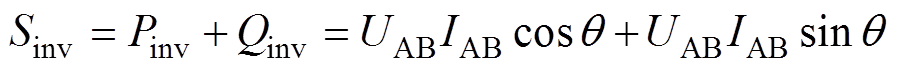 。有功功率
。有功功率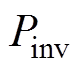 一定的情况下,当输入阻抗角
一定的情况下,当输入阻抗角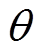 增大时,所需的逆变器容量
增大时,所需的逆变器容量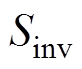 和成本都会增加。同时,无功功率
和成本都会增加。同时,无功功率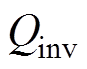 和回路电流增大,损耗必然增大。因此,输入阻抗角是一个优化目标。在
和回路电流增大,损耗必然增大。因此,输入阻抗角是一个优化目标。在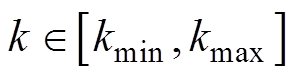 和
和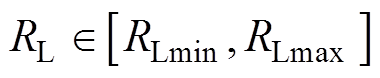 的任何一种状态下,高频逆变器的输入阻抗角定义为
的任何一种状态下,高频逆变器的输入阻抗角定义为
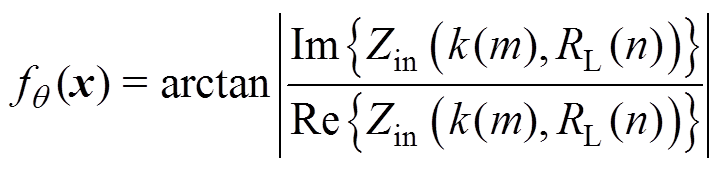 (16)
(16)
根据式(16),可得逆变器在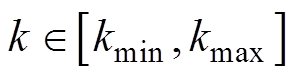 和
和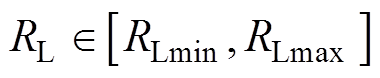 的所有状态下的输入阻抗角之和。
的所有状态下的输入阻抗角之和。
减小输入阻抗角的函数描述为
 (17)
(17)
式中,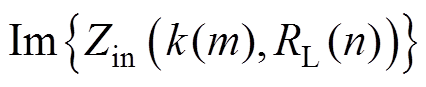 、
、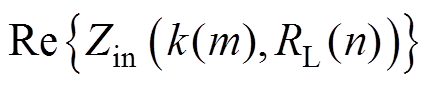 分别表示输入阻抗
分别表示输入阻抗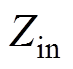 的虚部和实部。因此,耦合无关恒压输出型补偿拓扑优化模型的目标函数可描述为
的虚部和实部。因此,耦合无关恒压输出型补偿拓扑优化模型的目标函数可描述为
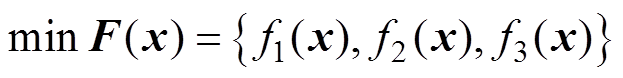 (18)
(18)
2.2.2 约束条件
1)电压约束
每个电容器都有相应的最大耐压值,如果电压超过了极限,电容器就容易击穿。电容器两端的电压受以下条件的限制
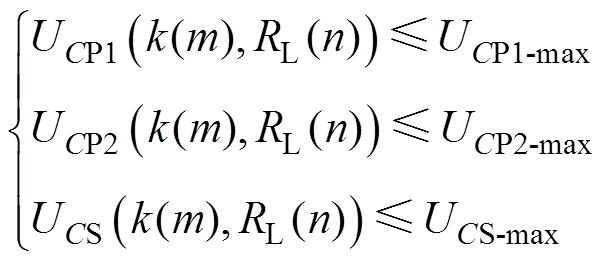 (19)
(19)
式中,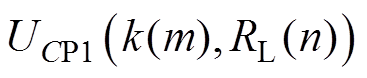 、
、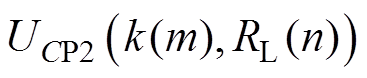 和
和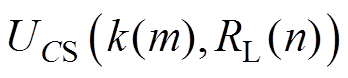 分别为耦合系数为
分别为耦合系数为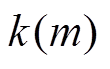 和等效负载电阻为
和等效负载电阻为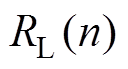 时
时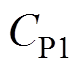 、
、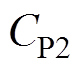 和
和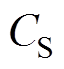 的电压;
的电压;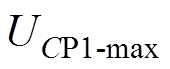 、
、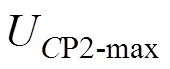 和
和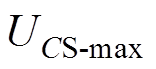 为
为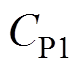 、
、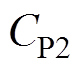 和
和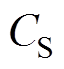 的最大交流耐压值。根据选择的电容器,并设置相应的裕度,可得
的最大交流耐压值。根据选择的电容器,并设置相应的裕度,可得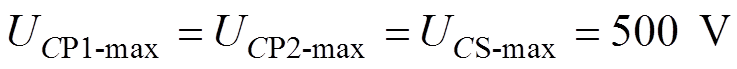 。
。
2)电流约束
每个电感都有相应的最大允许通过电流值,如果电流超过了这个极限,电感就容易发生短路。通过电感器的电流受以下条件的限制
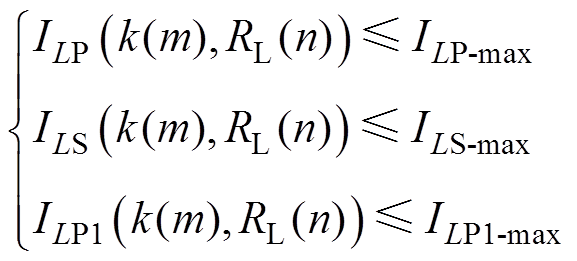 (20)
(20)
式中,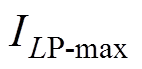 、
、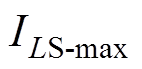 和
和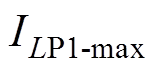 为
为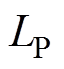 、
、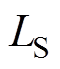 和
和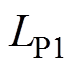 的最大允许通过电流。电感器均由f0.1 mm×180股的利兹(Lize)线绕制而成,最大允许通过电流为
的最大允许通过电流。电感器均由f0.1 mm×180股的利兹(Lize)线绕制而成,最大允许通过电流为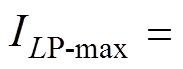
 。
。
3)零电压开关约束
为了减少开关损耗,提高IPT系统效率,系统应工作在零电压软开关(Zero Voltage Switching, ZVS)条件下,即IPT系统的输入阻抗应为感性。输入阻抗角用角度表示,其数学表达式为
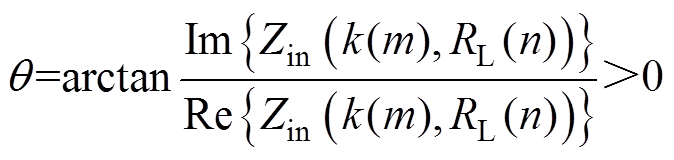 (21)
(21)
有约束优化问题可以转化为无约束优化问题进行求解。无约束优化问题的目标函数为有约束优化问题的目标函数加上相关惩罚项。对于可行域外的解,惩罚项为正,即对该粒子进行惩罚;对于可行域内的解,惩罚项为0,即不做任何惩罚。因此惩罚项促使无约束优化问题的解落在可行域内。对于电容电压应力约束,罚函数定义为
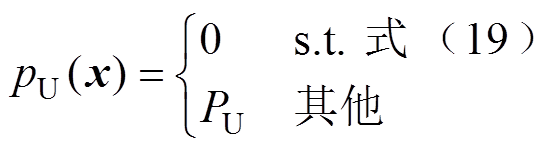 (22)
(22)
同理,对于电感电流应力约束,罚函数定义为
 (23)
(23)
对于零电压开关约束,罚函数定义为
 (24)
(24)
式中,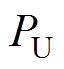 、
、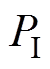 和
和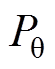 分别为各约束惩罚函数的惩罚常数,一般应足够大。因此,无约束优化问题的目标函数为
分别为各约束惩罚函数的惩罚常数,一般应足够大。因此,无约束优化问题的目标函数为
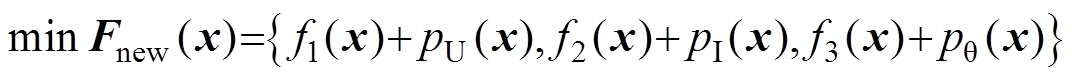 (25)
(25)
2.3.1 MOPSO算法流程
本文选用多目标粒子群优化(MOPSO)算法求解多目标优化问题。粒子群优化(PSO)算法是一种具有较强全局搜索能力的启发式算法,是MOPSO算法的基础。粒子群算法每一个可能的解都表示为种群当中的一个粒子,每一个粒子都有自己的速度向量和位置向量,以及由目标函数确定的适应度。在每次迭代过程中,需要计算目标函数确定当前时刻的个体最优向量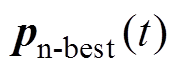 和整个群体的全局最优向量
和整个群体的全局最优向量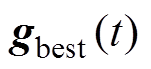 。通过跟踪个体和全局最优向量,由式(26)和式(27)确定下一时刻每个粒子的位置和速度。
。通过跟踪个体和全局最优向量,由式(26)和式(27)确定下一时刻每个粒子的位置和速度。
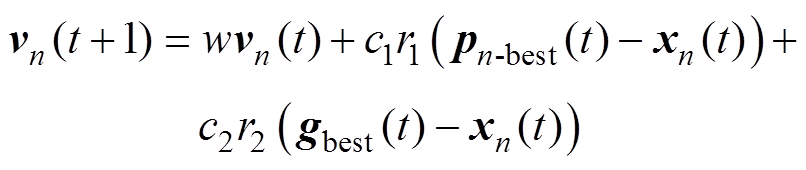 (26)
(26)
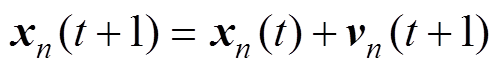 (27)
(27)
式中,w为惯性权值;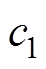 和
和 为学习因子;
为学习因子;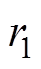 和
和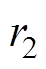 为独立的随机数,在[0, 1]上均匀分布;
为独立的随机数,在[0, 1]上均匀分布;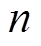 为第
为第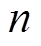 个粒子;
个粒子;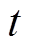 为迭代次数;
为迭代次数;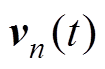 为第
为第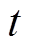 次迭代中第
次迭代中第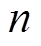 个粒子的速度;
个粒子的速度;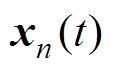 为第
为第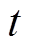 次迭代中第
次迭代中第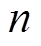 个粒子的位置;
个粒子的位置;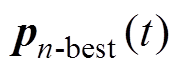 为
为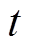 次迭代中第
次迭代中第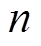 个粒子的个体最优位置;
个粒子的个体最优位置; 为
为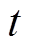 次迭代中群体的全局最优位置。
次迭代中群体的全局最优位置。
C. A. C. Coello等在PSO算法中引入Pareto最优求解多目标优化问题,称为MOPSO算法。MOPSO算法流程如图3所示,步骤如下:①参数初始化;②速度和位置更新;③适应度计算;④个体最优位置更新;⑤档案更新;⑥全局最优向量更新;⑦重复步骤②~步骤⑥,直到满足循环条件结束[28-29]。其中,步骤⑤档案更新共包括三轮:首先,根据支配关系进行第一轮粒子群筛选,可得到Pareto最优解集并存入档案库;然后,根据支配关系对档案库的粒子群进行筛选,去除劣解;最后,若种群数量超过存档阈值,则根据自适应网格法进行清除,网格将被重新划分[28-29]。
2.3.2 求解空间和最大粒子速度
求解空间尤为重要。若求解空间太小,可能不包含最优解;若求解空间太大,求解过程会很长。基于完全谐振的LCC/S补偿IPT系统性能是可以接受的。因此,根据传统的参数配置方法确定MOPSO算法的求解空间。由式(9)可知,当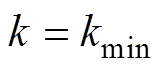 时,由传统参数设计方法得到的参考值为
时,由传统参数设计方法得到的参考值为
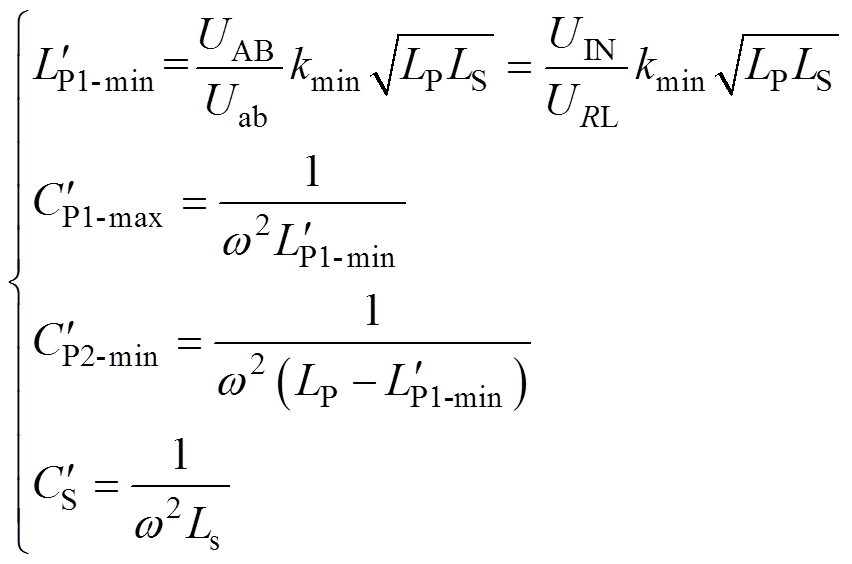 (28)
(28)
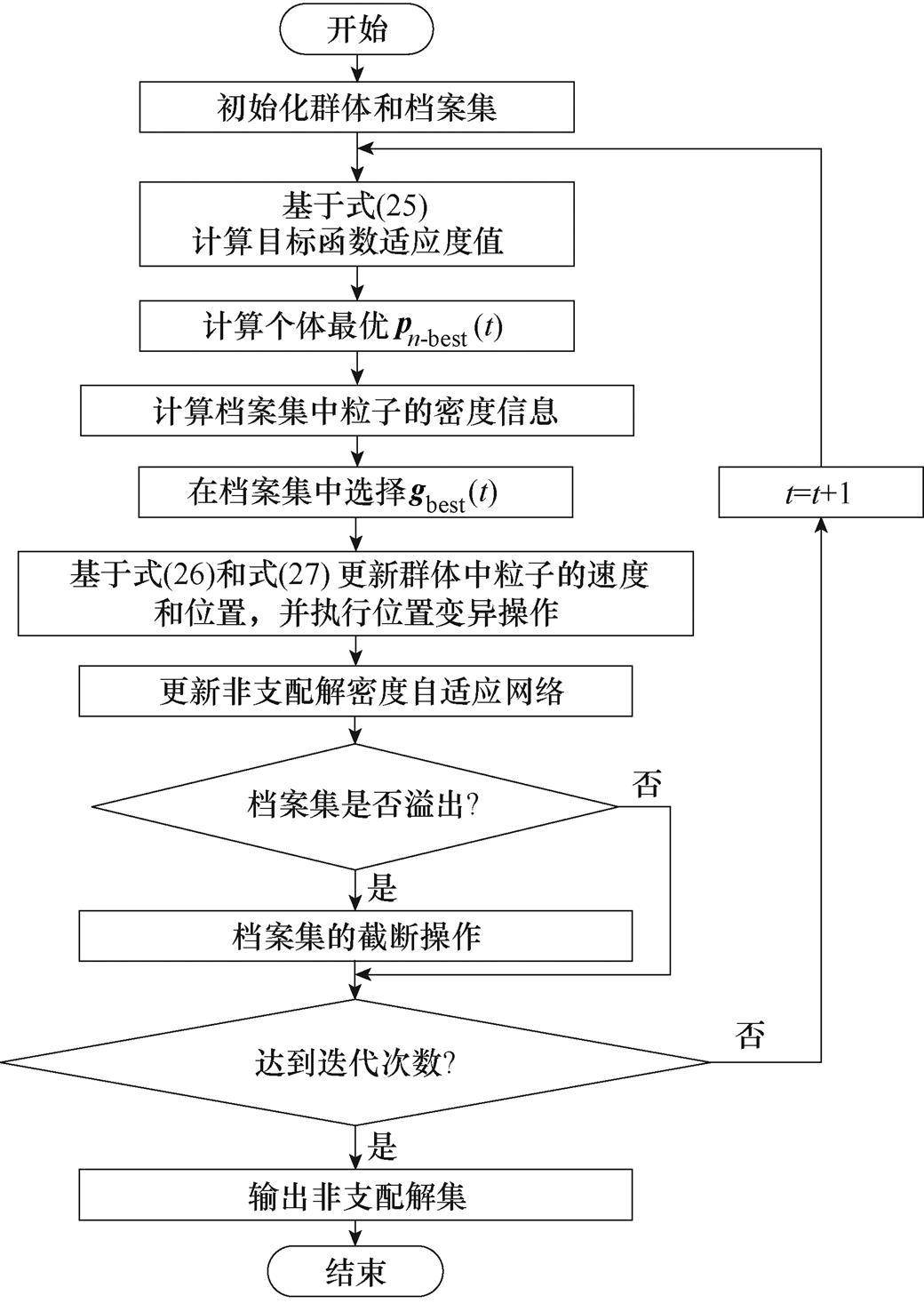
图3 MOPSO算法流程
Fig.3 Flow chart of the MOPSO algorithm
同理,当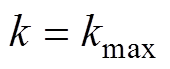 时,根据传统完全谐振参数设计方法得到的求解空间参考值为
时,根据传统完全谐振参数设计方法得到的求解空间参考值为
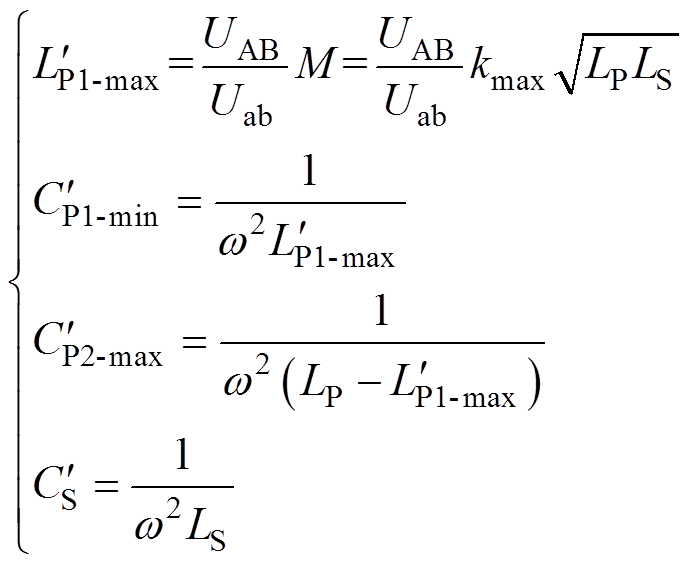 (29)
(29)
根据式(28)和式(29),可得到多目标粒子群优化(MOPSO)算法的补偿参数求解空间为
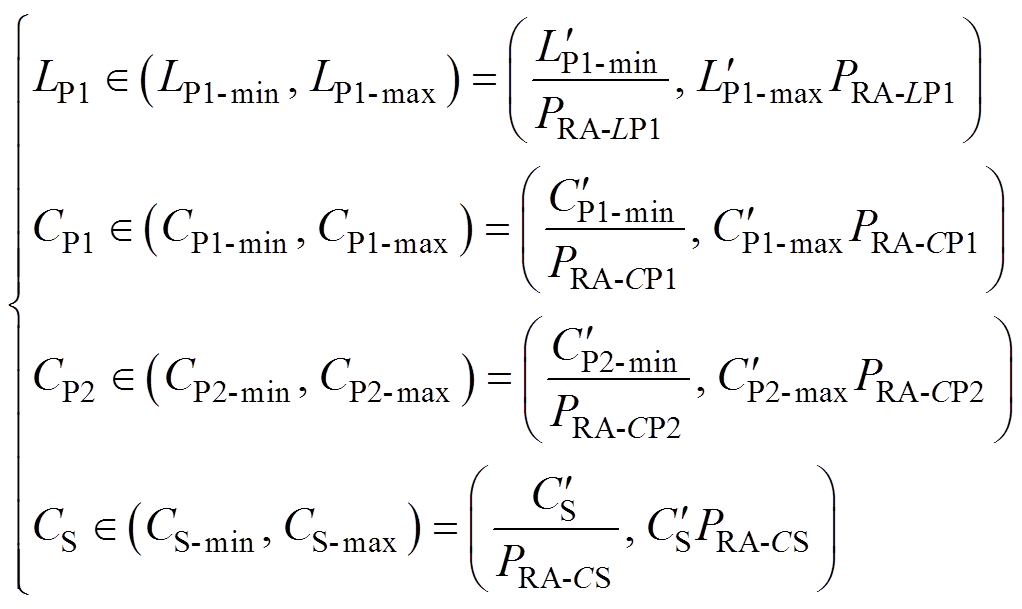 (30)
(30)
式中,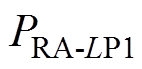 、
、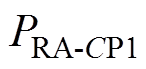 、
、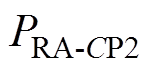 和
和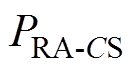 均为定值,决定了相应补偿元件参数的放大系数和缩小系数,主要由IPT系统补偿元件的实际局限性决定。由于补偿元件的实际要求不是很具体,所以要得到
均为定值,决定了相应补偿元件参数的放大系数和缩小系数,主要由IPT系统补偿元件的实际局限性决定。由于补偿元件的实际要求不是很具体,所以要得到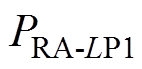 、
、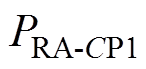 、
、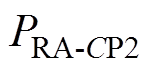 和
和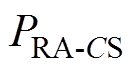 的大致范围,就可以得到系统的最优解。
的大致范围,就可以得到系统的最优解。
MOPSO算法需要确定粒子速度,最大速度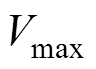 和最小速度
和最小速度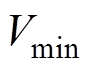 可以在求解空间的基础上得到。一般情况下,最小速度
可以在求解空间的基础上得到。一般情况下,最小速度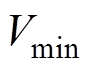 设置为最大速度
设置为最大速度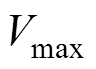 的相反值,即
的相反值,即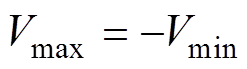 ,
,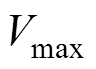 可由式(31)得到。
可由式(31)得到。
 (31)
(31)
式中,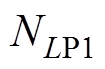 、
、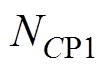 、
、 和
和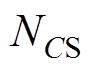 均为正整数。4个整数越大,粒子的最大速度越小,深度搜索能力越强,收敛速度越慢;4个整数越小,粒子最大速度越大,广度搜索能力越强,收敛速度越快。因此,
均为正整数。4个整数越大,粒子的最大速度越小,深度搜索能力越强,收敛速度越慢;4个整数越小,粒子最大速度越大,广度搜索能力越强,收敛速度越快。因此,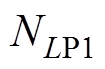 、
、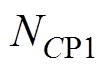 、
、 和
和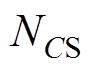 的大小应适中。
的大小应适中。
基于LCC/S补偿拓扑的IPT系统参数见表1,包括发射线圈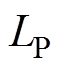 、接收线圈
、接收线圈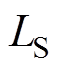 、直流输入电压
、直流输入电压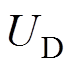 、工作频率
、工作频率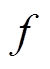 和负载电阻设定值
和负载电阻设定值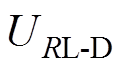 。其中,耦合系数的取值范围在0.18~0.32之间,与大多数实际IPT系统的耦合系数变化范围一致。负载可能是厨房电器、应急照明供电设备等,变化范围较小。因此,负载电阻取值范围在50~60 W 之间。
。其中,耦合系数的取值范围在0.18~0.32之间,与大多数实际IPT系统的耦合系数变化范围一致。负载可能是厨房电器、应急照明供电设备等,变化范围较小。因此,负载电阻取值范围在50~60 W 之间。
表1 IPT系统相关参数
Tab.1 Parameters related to the IPT system
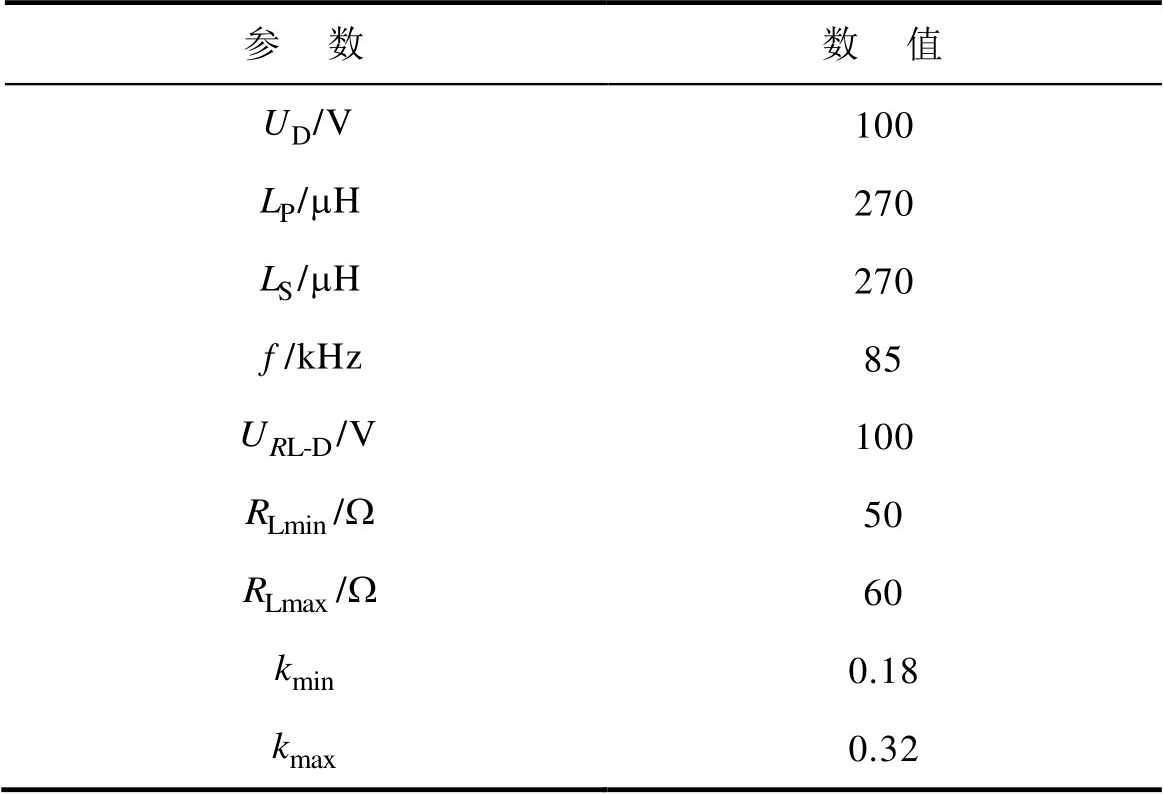
参 数数 值 /V100 /mH270 /mH270 /kHz85 /V100 /W50 /W60 0.18 0.32
将表1的参数代入式(9),可得到基于LCC/S补偿的IPT系统在完全谐振下的补偿拓扑参数,见表2。根据式(28)、式(29)和表1的参数可得到求解空间参考值,见表2。此外,MOPSO算法的相关参数设置值见表3。
表2 传统的参数值和解空间的参考值
Tab.2 Traditional parameter values and the reference values of the solution space
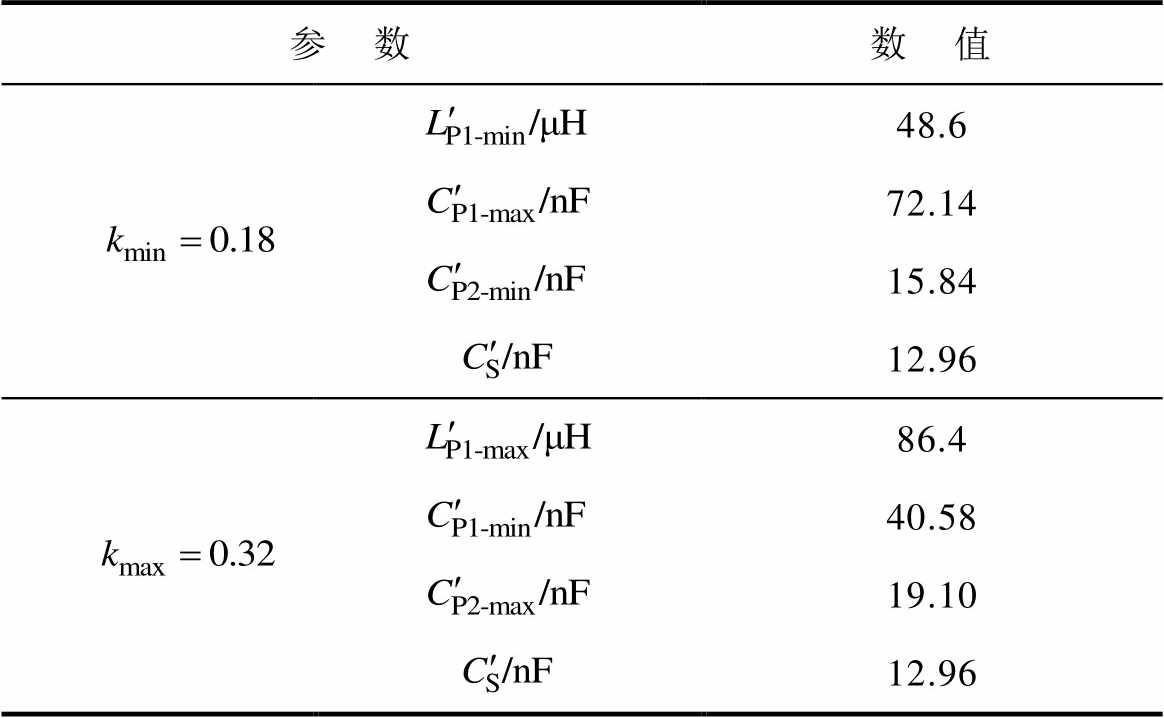
参 数数 值 48.6 72.14 15.84 12.96 86.4 40.58 19.10 12.96
表3 MOPSO算法的相关参数
Tab.3 Parameters related to the MOPSO algorithm

参 数数 值 w0.7 c11.8 c21.8 NP种群200 t200 档案库200 变异率0.01 网格数20 Nk21 NRL21 PRA-LP110 PRA-CP140 PRA-CP240 PRA-CS40 NLP1200 NCP1200 NCP2200 NCS200 PU1 000 PI1 000 1 000
基于MOPSO算法得到的Pareto前沿收敛过程如图4所示,随着迭代次数的增加,Pareto前沿逐渐“减小”,分布逐渐变得光滑均匀,优化结果逐渐收敛。当迭代次数为80时,帕累托前沿基本固定,并与迭代次数为200时的帕累托前沿重叠如图8所示,表明MOPSO算法求解该多目标优化模型的收敛速度较快。
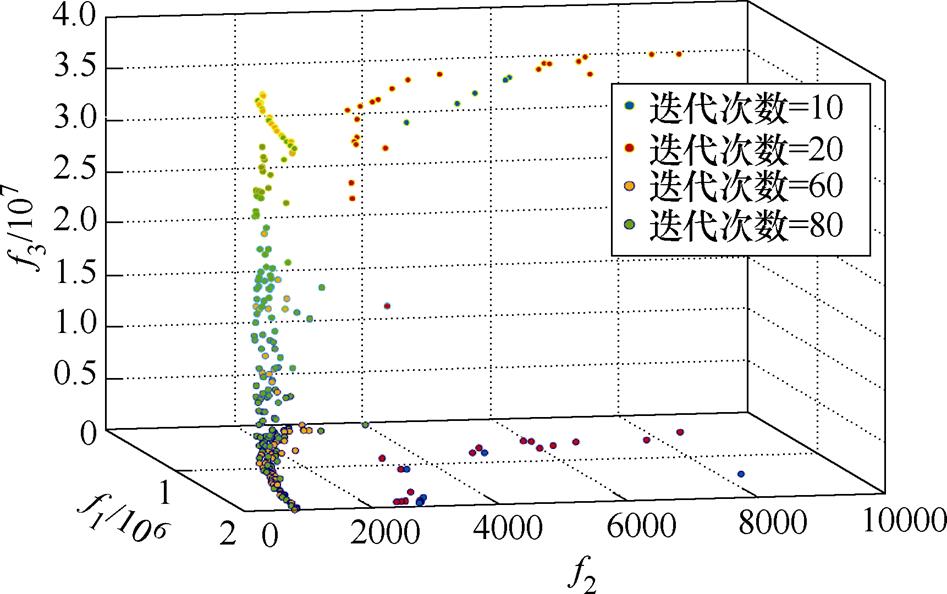
图4 MOPSO算法的收敛性
Fig.4 Convergence of MOPSO algorithm
当输入电压变化时,IPT系统的Pareto前沿对比如图5所示。当输入电压从80 V增大到120 V时,Pareto前沿几乎重合,三种不同输入电压的适应度函数值接近。在不同输出电压要求下,IPT系统的Pareto前沿对比如图6所示。当输出电压在80~120 V范围内变化时,Pareto前沿变化趋势一致,均能够获得较好的适应度函数值。因此,MOPSO算法对输入和输出变量变化不敏感,所建立的多目标优化模型与MOPSO算法具有较好的兼容性。
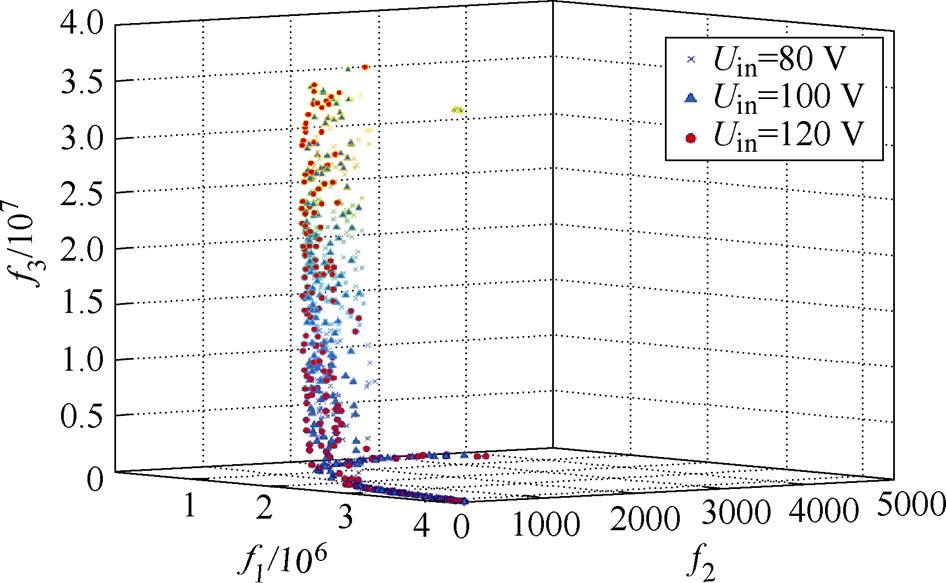
图5 不同输入电压下的Pareto解
Fig.5 Pareto solutions with different input voltages
MOPSO算法经过200次迭代,档案库中先后生成的所有解如图7所示(3D图)。整个算法运行时间约为20 s,最终计算结果收敛到Pareto前沿,如图8所示(2D图)。
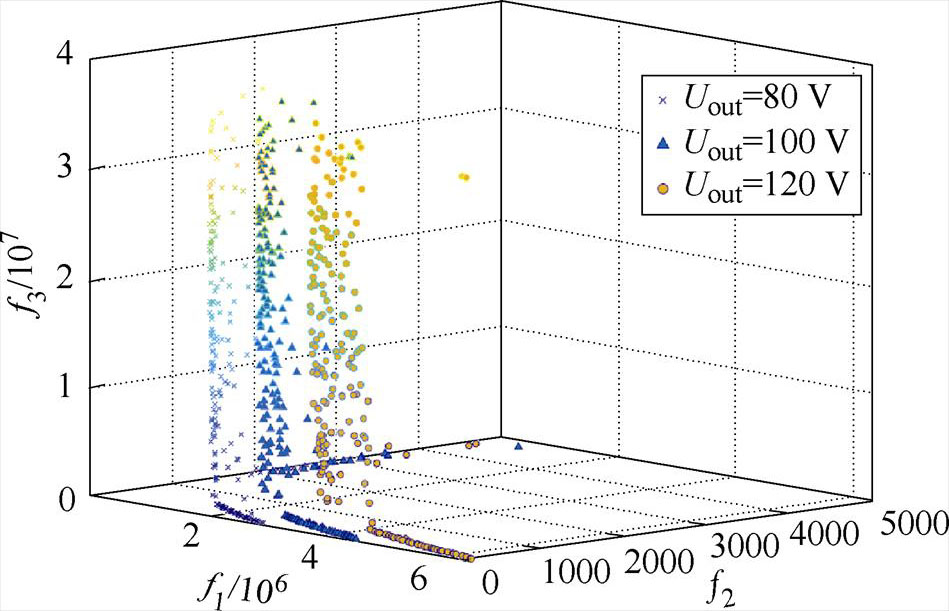
图6 不同输出电压下的Pareto解
Fig.6 Pareto solutions with different output voltages
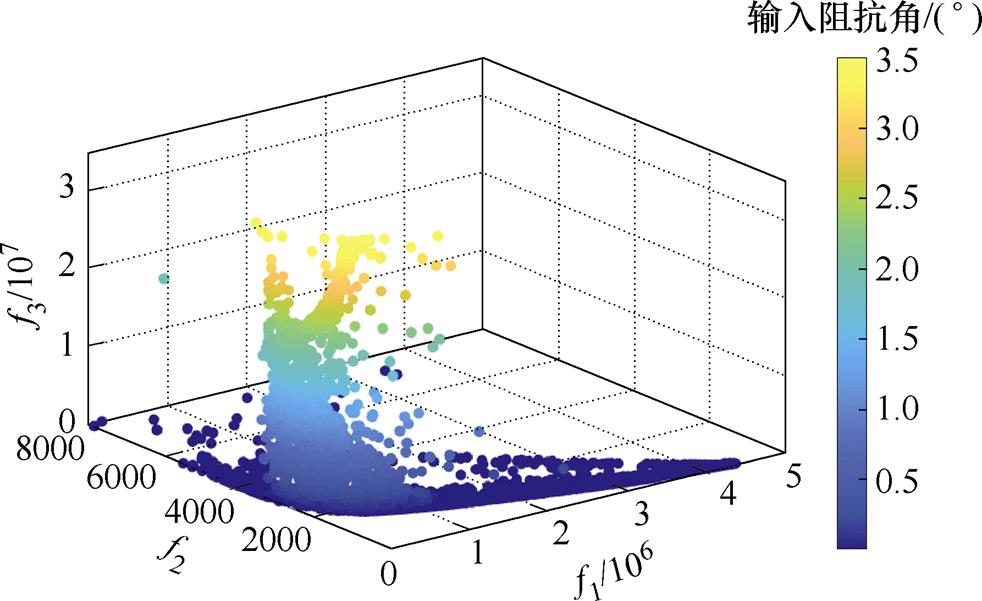
图7 200次迭代的所有解
Fig.7 All the solutions for 200 iterations
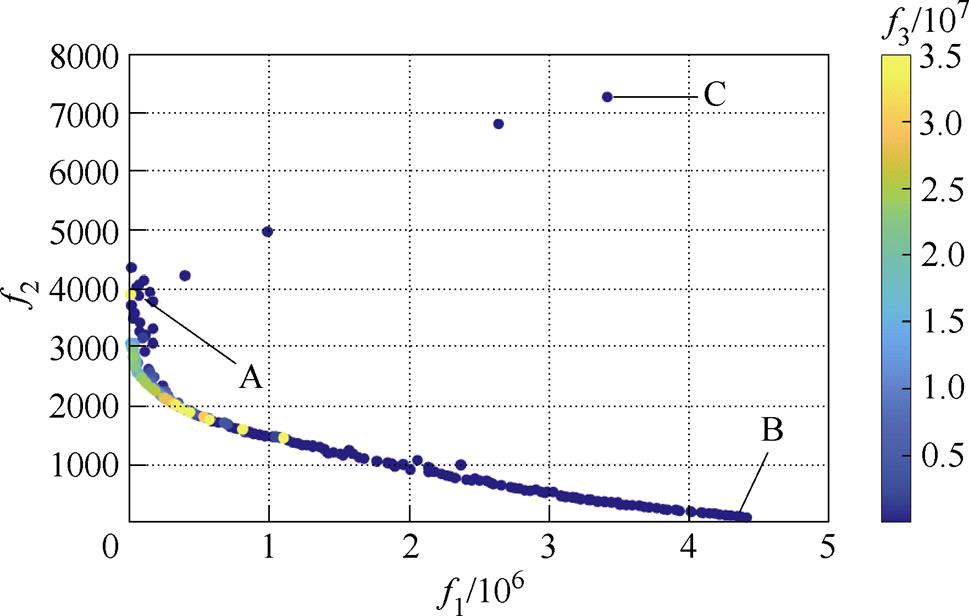
图8 Pareto最优解
Fig.8 Pareto optimal solutions
图8中,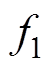 为第一个目标函数,表示输出电压在不同耦合系数和负载下的方差总和;
为第一个目标函数,表示输出电压在不同耦合系数和负载下的方差总和;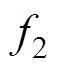 为第二个目标函数,表示不同耦合系数和负载下电流应力总和;图中色条表示第三目标函数
为第二个目标函数,表示不同耦合系数和负载下电流应力总和;图中色条表示第三目标函数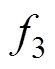 ,
,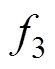 为不同耦合系数和负载下的逆变器输入阻抗角总和。A、B、C 3个特解分别表示最小的输出电压波动、电感的电流应力和输入阻抗角。其中,解A的输出电压波动最小,但输入阻抗角为负;解B的电流应力最小,但输出电压波动最大;解C的输入阻抗角最小,但电压波动和电流应力过大。
为不同耦合系数和负载下的逆变器输入阻抗角总和。A、B、C 3个特解分别表示最小的输出电压波动、电感的电流应力和输入阻抗角。其中,解A的输出电压波动最小,但输入阻抗角为负;解B的电流应力最小,但输出电压波动最大;解C的输入阻抗角最小,但电压波动和电流应力过大。
从图8可以看出,电压波动和电感电流应力不能同时达到最优,而输入阻抗角(Input Impedance Angle, IIA)与两者没有呈正相关或负相关。因此,以电压波动最小为最高优先级,以电感电流应力和输入阻抗角为主要参考因素,在解A附近选择三个相邻解,分别用方案Ⅰ、方案Ⅱ和方案Ⅲ表示,相关参数见表4。不同耦合系数和负载下的输出电压、输入阻抗角、电感电流应力和电容电压应力分别如图9~图12所示。选定方案与传统方案进行的比较和分析结果见表5。
输出电压变化范围、输入阻抗角变化范围、电压波动率、最大电感电流应力、最大电容电压应力等数据列于表5中。其中,IPT系统的输出电压波动率(Voltage Fluctuation Ratio, VFR)定义为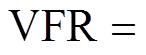
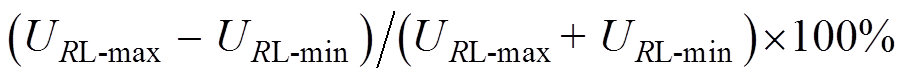 。方案Ⅰ、Ⅱ和Ⅲ的输出电压波动率VFR均优于传统方案,方案Ⅱ和方案Ⅲ的VFR都小于10%。方案Ⅰ与方案Ⅱ的输入阻抗角接近,但略大于方案Ⅲ。优化方案中部分补偿元件的电压应力和电流应力虽然高于传统方案,但均在额定值范围内。由图11可知,传统方案的发射线圈电流是恒定的,而所提方案的发射线圈电流与耦合系数呈负相关,优化方案利用发射线圈电流补偿耦合系数对输出电压的影响。
。方案Ⅰ、Ⅱ和Ⅲ的输出电压波动率VFR均优于传统方案,方案Ⅱ和方案Ⅲ的VFR都小于10%。方案Ⅰ与方案Ⅱ的输入阻抗角接近,但略大于方案Ⅲ。优化方案中部分补偿元件的电压应力和电流应力虽然高于传统方案,但均在额定值范围内。由图11可知,传统方案的发射线圈电流是恒定的,而所提方案的发射线圈电流与耦合系数呈负相关,优化方案利用发射线圈电流补偿耦合系数对输出电压的影响。
表4 基于权衡分析法选择的解决方案
Tab.4 The selected solutions based on trade-off analysis method

方案 I199.1840.5845.7916.4314 879.023 709.8822 032.97 Ⅱ218.2632.46644.6014.508 550.303 761.6924 604.88 Ⅲ37.7725.4513.2812.1410 034.353 219.2713 169.85
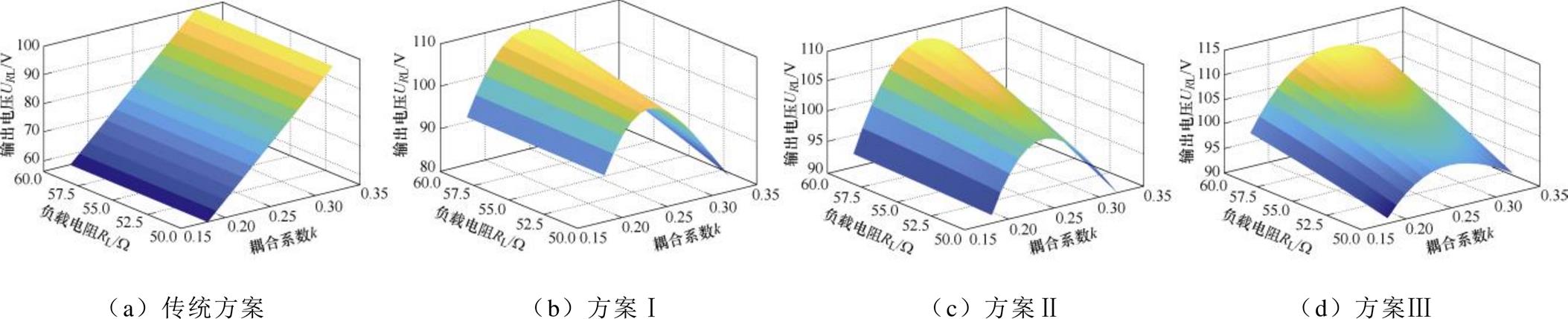
图9 不同方案的输出电压
Fig.9 Output voltages of different schemes

图10 不同方案的输入阻抗角
Fig.10 Input impedance angles of different schemes
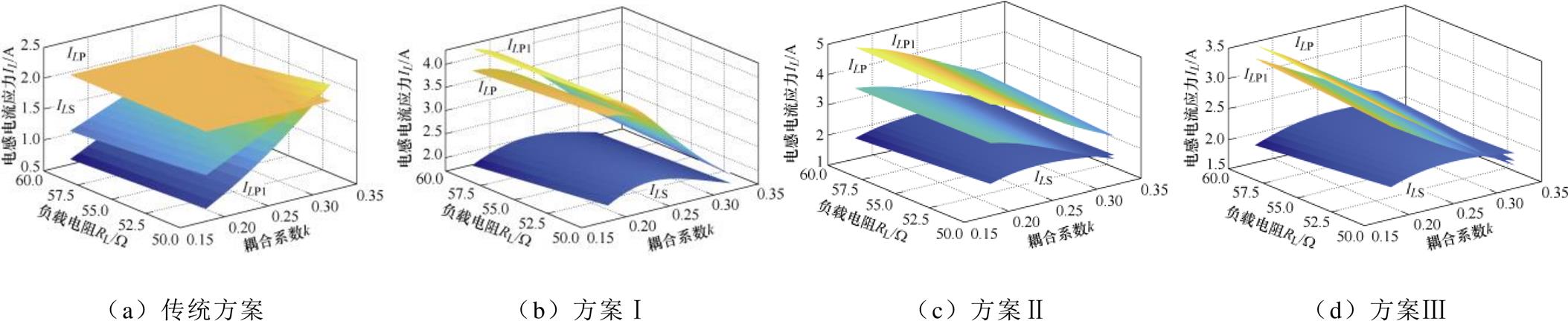
图11 不同方案的电感电流应力
Fig.11 Inductor current stresses of different schemes
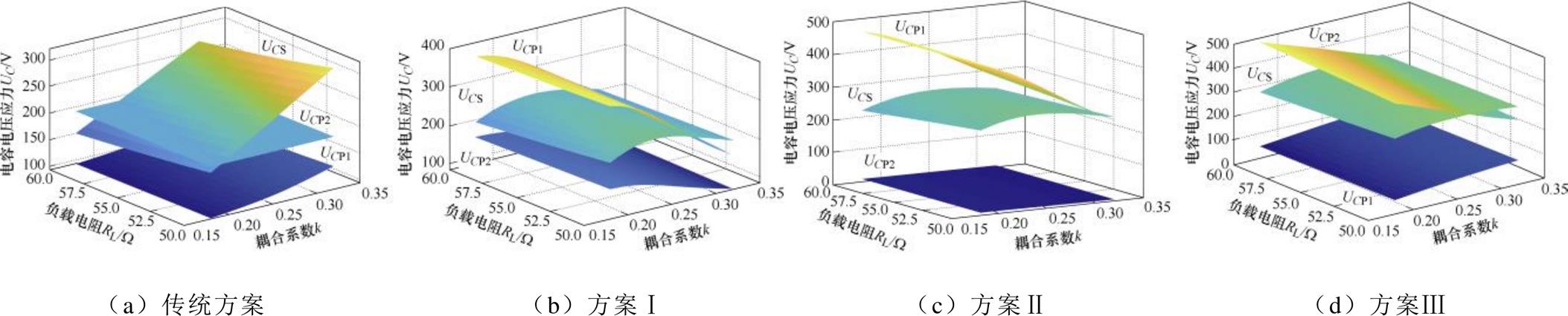
图12 不同方案的电容电压应力
Fig.12 Capacitor voltage stresses of different scheme
表5 传统方案和选定方案对比
Tab.5 Comparison of the traditional scheme and the selected schemes

方案URL范围/VVFR(%)q 范围/(°)ILP-max/AILS-max/AILP1-max/AUCP1-max/VUCP2-max/VUCS-max/V 传统56.25~10028.000~1.241.952.222.22123.9192.08318.76 Ⅰ83.92~108.2312.9840.83~68.433.732.264.19363.6152.2261.2 Ⅱ90.18~108.029.0046.90~70.323.342.234.67460.59.70289.2 Ⅲ91.01~110.269.560.79~57.273.432.183.2197.68483.30334.66
为了验证所提方法有效性,搭建了实验样机并与传统方案进行比较。虽然方案Ⅱ的电压波动率VFR小于方案Ⅲ,但方案Ⅱ的4个补偿参数值都大于方案Ⅲ。受补偿元件尺寸、体积和成本的限制,补偿参数值不能太大,优化方案Ⅲ更加实用。因此,仅对传统方案和方案Ⅲ进行验证和对比分析。
除了4个补偿参数外,传统样机与本文提出的样机基本相同,设计输出电压均为100 V,如图13所示。磁耦合机构选择IPT系统中最常用的平面圆形线圈,控制器采用TMS320F28335 DSP,逆变器开关选用MOSFET IPW90R120C3,功率二极管选用DSE12x101-06A。Chroma 62150H-1000直流电源为系统提供恒定的直流电压。采用泰克MDO3024示波器记录波形,采用HIOKI PW6001功率分析仪记录系统的输出功率和效率等数据。传统方案和方案Ⅲ的补偿参数计算值和测量值见表6。为了平衡理论分析中未包含的各个元件的电压降,实验中将直流输入电压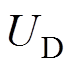 从100 V提高到110 V。其他关键参数,包括
从100 V提高到110 V。其他关键参数,包括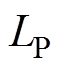 、
、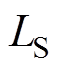 、
、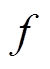 、
、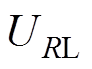 、
、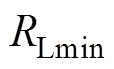 、
、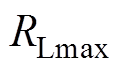 、
、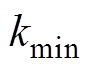 和
和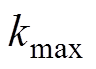 见表1。
见表1。
优化方案Ⅲ的实验波形和DC-DC效率如图14所示。图中,高频逆变器的输出电压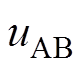 和输出电流
和输出电流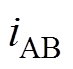 的波形,负载的输出电压
的波形,负载的输出电压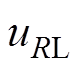 和输出电流
和输出电流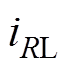 波形由示波器测量。IPT系统的DC-DC效率由功率分析仪记录,
波形由示波器测量。IPT系统的DC-DC效率由功率分析仪记录,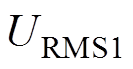 和
和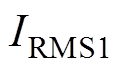 分别为直流输入电压
分别为直流输入电压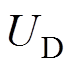 和电流
和电流 ,
,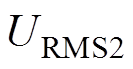 和
和 分别为负载输出电压
分别为负载输出电压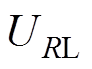 和电流
和电流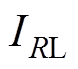 。
。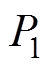 和
和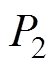 分别为系统的输入功率和输出功率,
分别为系统的输入功率和输出功率,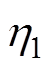 为IPT系统的DC-DC效率。如图14a所示,当
为IPT系统的DC-DC效率。如图14a所示,当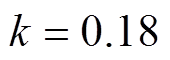 、
、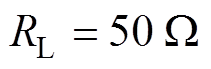 时,输出电压保持在89 V左右,在整个耦合系数和负载变化范围内最低。DC-DC效率保持在88%左右,在整个耦合系数和负载变化范围内也是最低的。如图14b所示,当
时,输出电压保持在89 V左右,在整个耦合系数和负载变化范围内最低。DC-DC效率保持在88%左右,在整个耦合系数和负载变化范围内也是最低的。如图14b所示,当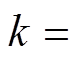
 、
、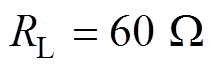 时,输出电压保持在112 V左右。系统DC-DC效率保持在93%左右,在整个耦合系数和负载变化范围内最高。另外,在整个耦合系数和负载变化范围内,IPT系统均能够在ZVS条件下工作。
时,输出电压保持在112 V左右。系统DC-DC效率保持在93%左右,在整个耦合系数和负载变化范围内最高。另外,在整个耦合系数和负载变化范围内,IPT系统均能够在ZVS条件下工作。

图13 IPT系统实验样机
Fig.13 Experimental prototype of the IPT system
表6 传统方案和方案Ⅲ的补偿拓扑参数
Tab.6 Compensation topology parameters of the traditional scheme and scheme Ⅲ

参数传统方案方案Ⅲ 计算值测量值计算值测量值 LP1/mH86.486.637.7737.60 CP1/nF40.5840.3625.4525.14 CP2/nF19.1018.8013.2813.30 CS/nF12.9612.6212.1412.36
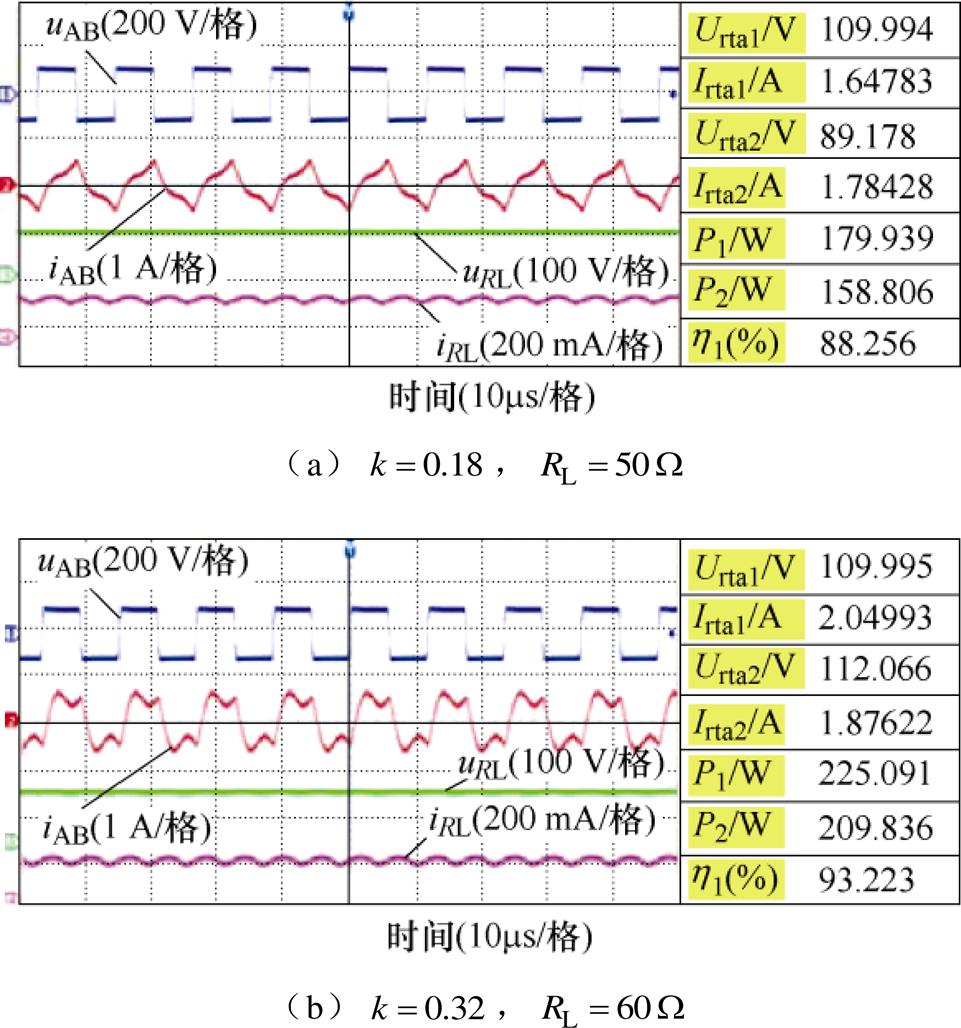
图14 实验波形和DC-DC效率
Fig.14 Experimental waveforms and DC-DC efficiencies
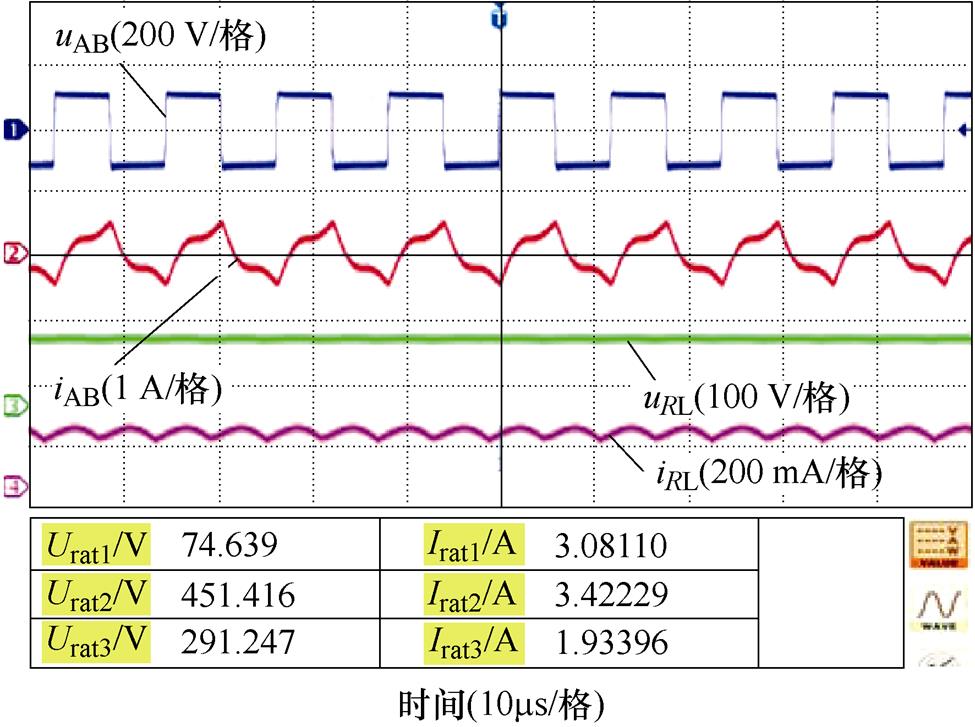
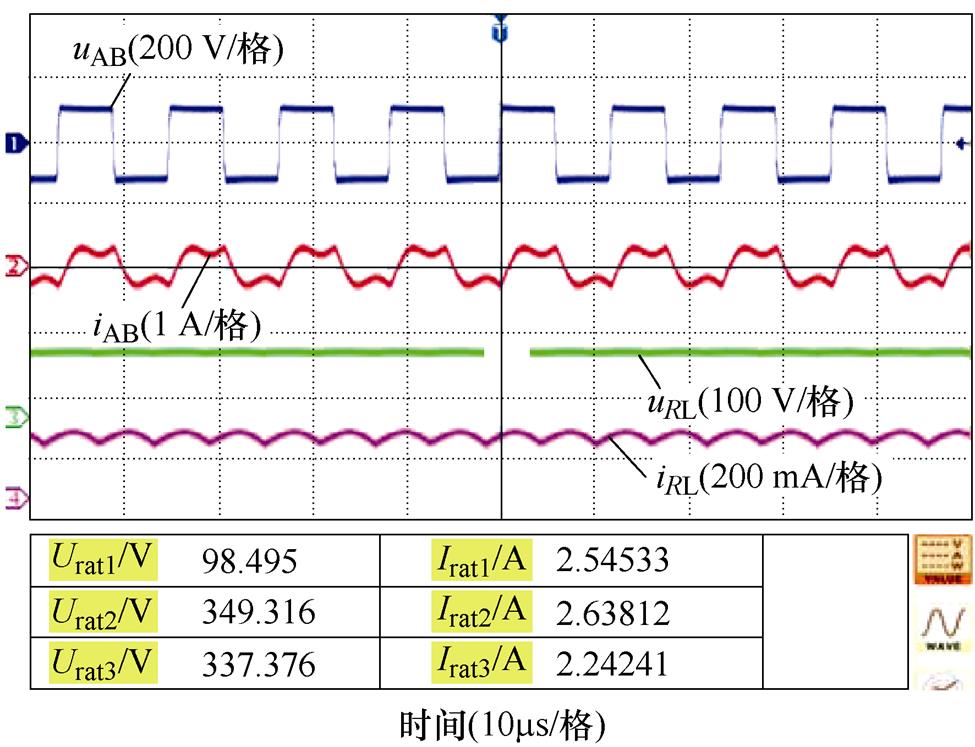
优化方案Ⅲ的补偿元件电压应力和电流应力也进行了实验和测量,图15a、图15b给出了逆变器输出电压和电流波形、负载的输入电压和电流的波形以及补偿元件的应力测量值。其中,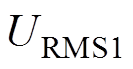 、
、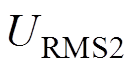 和
和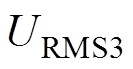 分别为电容
分别为电容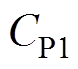 、
、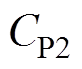 和
和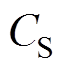 上的电压,
上的电压,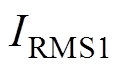 、
、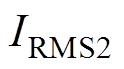 和
和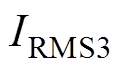 分别为流过电感
分别为流过电感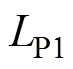 、
、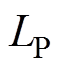 和
和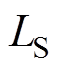 的电流。由图15可得,ZVS也是可以实现的,电感的电流应力和电容的电压应力均在设定的范围内,且与理论分析接近,系统能够安全稳定运行。
的电流。由图15可得,ZVS也是可以实现的,电感的电流应力和电容的电压应力均在设定的范围内,且与理论分析接近,系统能够安全稳定运行。
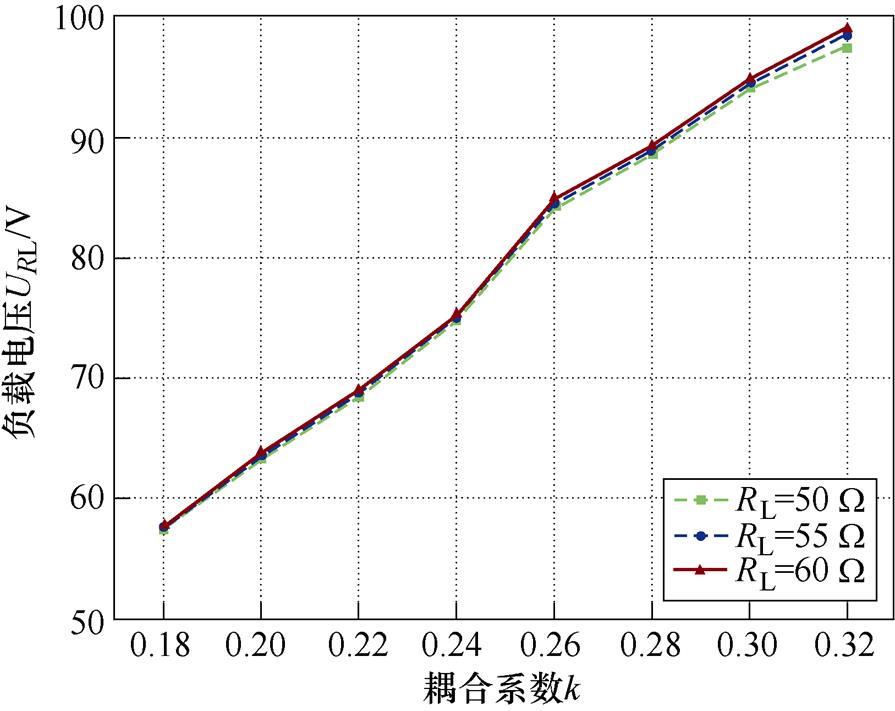
输出电压随耦合系数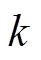 和等效负载电阻
和等效负载电阻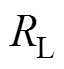 的变化曲线如图16所示。从图16a可以看出,基于传统完全谐振补偿方法的IPT系统输出电压与负载无关,但与耦合系数呈负相关。基于传统完全谐振补偿方法的IPT系统输出电压的最大值为99.11 V(
的变化曲线如图16所示。从图16a可以看出,基于传统完全谐振补偿方法的IPT系统输出电压与负载无关,但与耦合系数呈负相关。基于传统完全谐振补偿方法的IPT系统输出电压的最大值为99.11 V(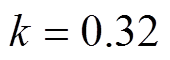 、
、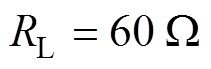 ),最小值为57.13 V(
),最小值为57.13 V(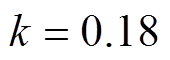 、
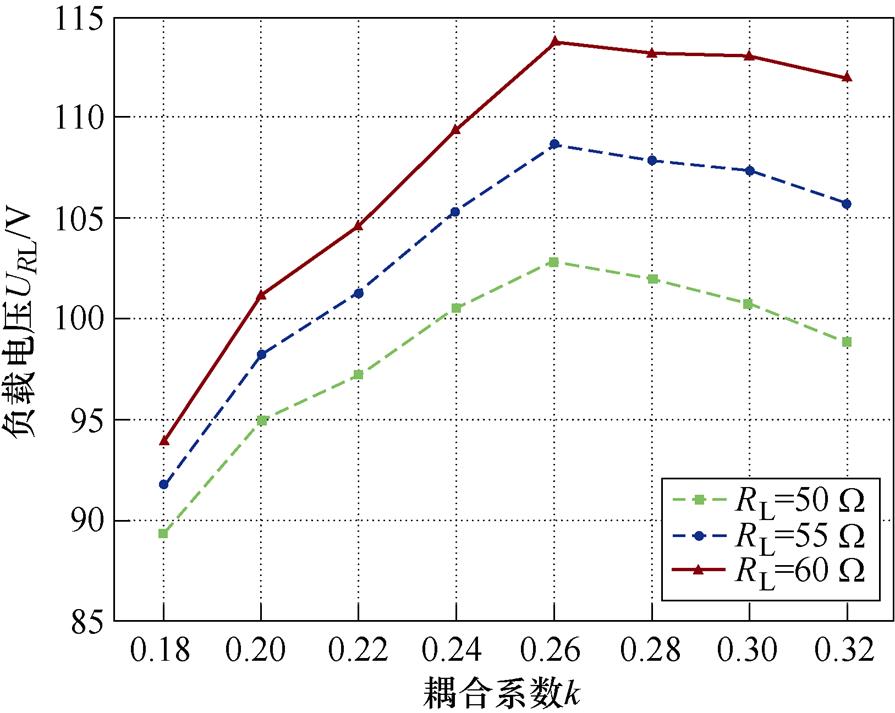
、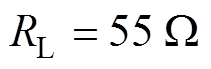 )。根据电压波动率的定义,基于传统补偿方法的IPT系统的电压波动率VFR=26.9%。基于多目标优化补偿方法的IPT系统实验结果如图16b所示。对于特定的电阻性负载,输出电压与耦合系数k不是线性相关的,输出电压随着耦合系数的增大先增大后减小。当耦合系数在0.18~0.32范围内变化时,
)。根据电压波动率的定义,基于传统补偿方法的IPT系统的电压波动率VFR=26.9%。基于多目标优化补偿方法的IPT系统实验结果如图16b所示。对于特定的电阻性负载,输出电压与耦合系数k不是线性相关的,输出电压随着耦合系数的增大先增大后减小。当耦合系数在0.18~0.32范围内变化时,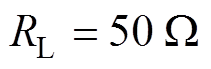 对应的输出电压波动率VFR= 7.0%。当
对应的输出电压波动率VFR= 7.0%。当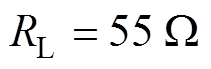 时,电压波动率VFR=8.3%,当
时,电压波动率VFR=8.3%,当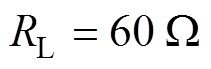 时,电压波动率VFR=9.3%,当负载电阻在50~60 W 范围内变化时,电压波动率VFR<12.0%。特别地,当耦合系数在0.20~0.32范围内变化、负载电阻在50~60 W 范围内变化时,电压波动率VFR<9.0%。此外,当耦合系数不变,负载电阻从50 W 增加60 W 时,最大电压波动率VFR= 6.3%。优化方案的电压波动率VFR约为传统方案的45%。实验测量结果与理论分析值基本一致,较小误差是由测量误差和各元件的寄生参数引起的,均在允许范围内。
时,电压波动率VFR=9.3%,当负载电阻在50~60 W 范围内变化时,电压波动率VFR<12.0%。特别地,当耦合系数在0.20~0.32范围内变化、负载电阻在50~60 W 范围内变化时,电压波动率VFR<9.0%。此外,当耦合系数不变,负载电阻从50 W 增加60 W 时,最大电压波动率VFR= 6.3%。优化方案的电压波动率VFR约为传统方案的45%。实验测量结果与理论分析值基本一致,较小误差是由测量误差和各元件的寄生参数引起的,均在允许范围内。
(a)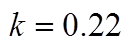 ,
,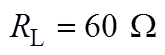
(b)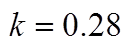 ,
,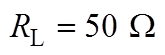
图15 实验波形和元器件应力
Fig.15 Experimental waveforms and component stresses
(a)传统方案
(b)优化方案
图16 输出电压随耦合系数和负载变化曲线
Fig.16 Output voltage versus coupling coefficient and load
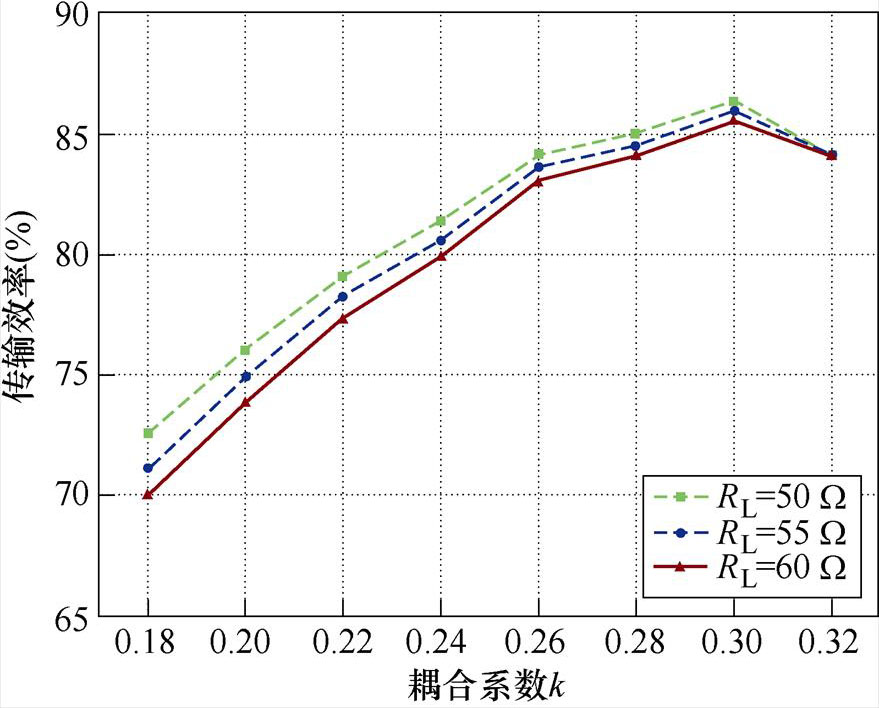
传统方案和优化方案的传输效率随耦合系数和负载的变化曲线如图17所示。基于传统补偿方法的IPT系统传输效率随耦合系数的增大先增大后减小。基于传统补偿方法的IPT系统的最小DC-DC效率和最大DC-DC效率分别为70.0%和86.3%。当耦合系数在0.18~0.32范围内变化、等效负载电阻在50~60 W 范围内变化时,基于多目标优化方法的IPT系统的DC-DC效率随耦合系数的增大而增大。当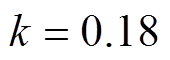 、
、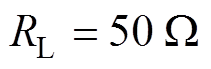 时,DC-DC效率最低,为87.5%。当
时,DC-DC效率最低,为87.5%。当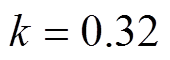 、
、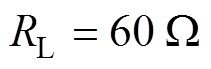 时,DC-DC效率最高,为93.2%。因此,采用多目标优化设计方法的IPT系统比采用传统完全补偿方法的IPT系统具有更高的效率,优化方案的最低效率仍然高于传统补偿方案的最高效率。
时,DC-DC效率最高,为93.2%。因此,采用多目标优化设计方法的IPT系统比采用传统完全补偿方法的IPT系统具有更高的效率,优化方案的最低效率仍然高于传统补偿方案的最高效率。
(a)传统方案
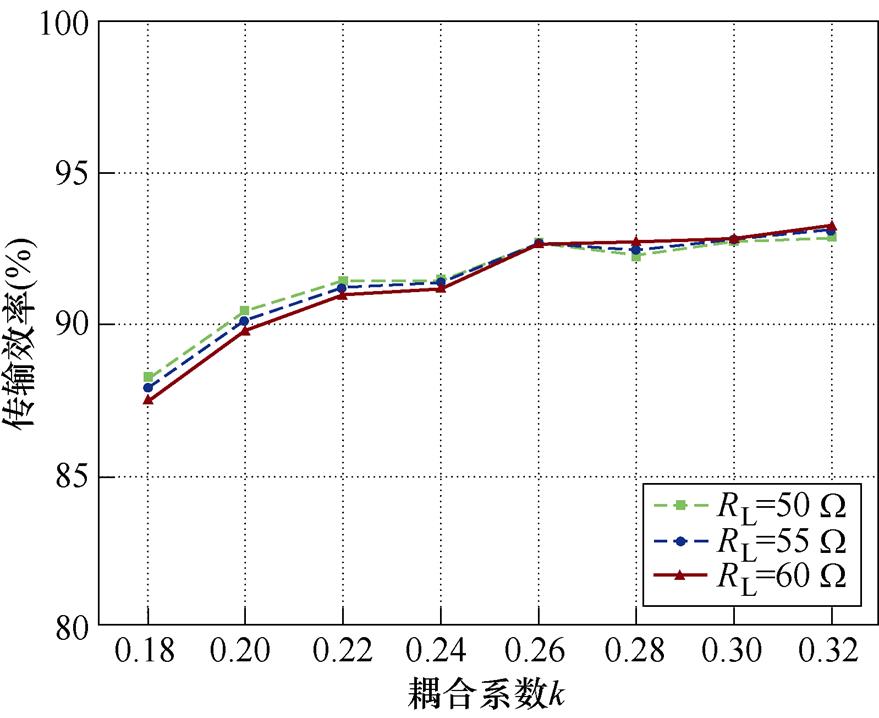
(b)优化方案
图17 效率随耦合系数和负载变化曲线
Fig.17 Efficiency versus coupling coefficient and load
综上所述,优化方案的输出电压波动、DC-DC效率均优于传统方案。实验与理论分析基本一致,从而验证了基于多目标优化理论的补偿拓扑参数设计方法的有效性。基于传统补偿方法的IPT系统发射线圈电流与负载和耦合系数无关,系统的输出电压对耦合系数非常敏感。基于多目标优化方法的IPT系统的发射线圈电流与耦合系数呈负相关,可以跟踪和补偿耦合系数对IPT系统输出电压的影响。优化方案的补偿参数值均小于传统方案的补偿参数值,相应的寄生电阻也小于传统方案。优化方案的发射线圈电流与耦合系数呈负相关,使得接收线圈电流基本不变。因此,优化方案能够在耦合系数和负载变化范围内高效运行。此外,通过合理的开关选择方案可以进一步降低逆变器、整流器等开关元件的损耗,不在本文讨论范围之内。
针对耦合系数变化、负载基本不变的应用场景,提出了一种基于多目标优化理论的耦合无关恒压输出型补偿拓扑设计方法。该方法突破了传统基于完全谐振参数设计方法的局限性,将变耦合IPT系统补偿参数设计问题转化为多目标优化问题。与单目标优化方法只能得到唯一解不同,本文建立的多目标优化模型通过MOPSO算法可以得到Pareto最优解集。研究人员根据应用需求,从Pareto最优解集中选择合适的设计方案。实验结果表明:当耦合系数在0.20~0.32范围内变化、负载在50~60 W 范围内变化时,优化方案的输出电压波动率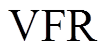 <9.0%;在整个耦合系数和负载变化区间内,优化方案的最低效率为87.5%,最高效率为93.2%;与传统方案的效率(70.0%~86.3%)相比,优化方案效率得到了大幅提升。本文所提方法能够实现耦合无关输出、负载无关输出、ZVS、低器件应力、高效率等传输特性,同样适用于任何其他补偿拓扑。
<9.0%;在整个耦合系数和负载变化区间内,优化方案的最低效率为87.5%,最高效率为93.2%;与传统方案的效率(70.0%~86.3%)相比,优化方案效率得到了大幅提升。本文所提方法能够实现耦合无关输出、负载无关输出、ZVS、低器件应力、高效率等传输特性,同样适用于任何其他补偿拓扑。
参考文献
[1] Zhang Zhen, Pang Hongliang, Georgiadis A, et al. Wireless power transfer-an overview[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 1044-1058.
[2] 薛明, 杨庆新, 章鹏程, 等. 无线电能传输技术应用研究现状与关键问题[J]. 电工技术学报, 2021, 36(8): 1547-1568.
Xue Ming, Yang Qingxin, Zhang Pengcheng, et al. Application status and key issues of wireless power transmission technology[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1547-1568.
[3] Covic G A, Boys J T. Inductive power transfer[J]. Proceedings of the IEEE, 2013, 101(6): 1276-1289.
[4] Li Zhenjie, Zhu Chunbo, Jiang Jinhai, et al. A 3-kW wireless power transfer system for sightseeing car supercapacitor charge[J]. IEEE Transactions on Power Electronics, 2017, 32(5): 3301-3316.
[5] 陈凯楠, 蒋烨, 檀添, 等. 轨道交通350kW大功率无线电能传输系统研究[J]. 电工技术学报, 2022, 37(10): 2411-2421, 2445.
Chen Kainan, Jiang Ye, Tan Tian, et al. Research on 350kW high power wireless power transfer system for rail transit[J]. Transactions of China Electro- technical Society, 2022, 37(10): 2411-2421, 2445.
[6] 谢文燕, 陈为. 基于组合补偿网络的抗偏移恒流输出无线电能传输系统研究[J]. 电工技术学报, 2022, 37(6): 1495-1512.
Xie Wenyan, Chen Wei. Research on anti-offset constant-current output wireless power transfer system based on combined compensation network[J]. Transactions of China Electrotechnical Society, 2022, 37(6): 1495-1512.
[7] 孙淑彬, 张波, 李建国, 等. 多负载磁耦合无线电能传输系统的拓扑发展和分析[J]. 电工技术学报, 2022, 37(8): 1885-1903.
Sun Shubin, Zhang Bo, Li Jianguo, et al. Analysis and development on topologies of multi-load magnetic- coupling wireless power transfer system[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(8): 1885-1903.
[8] Vu V B, Ramezani A, Triviño A, et al. Operation of inductive charging systems under misalignment conditions: a review for electric vehicles[J]. IEEE Transactions on Transportation Electrification, 2022, 9(1): 1857-1887.
[9] 陈阳, 杨斌, 彭云尔, 等. 感应式无线电能传输系统抗偏移技术研究综述[J]. 中国电机工程学报, 2023, 43(14): 5537-5559.
Chen Yang, Yang Bin, Peng Yuner, et al. Review of anti-misalignment technology in inductive wireless power transfer system[J]. Proceedings of the CSEE, 2023, 43(14): 5537-5559.
[10] 陆远方, 黎祎阳, 杨斌, 等. 考虑线圈参数变化的SS型动态无线电能传输系统参数优化设计方法[J].电工技术学报, 2022, 37(18): 4537-4547.
Lu Yuanfang, Li Yiyang, Yang Bin, et al. Parameter design method for SS compensated dynamic wireless power transfer system considering coils’ parameters variations[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4537-4547.
[11] 张献, 韩大稳, 沙琳, 等. 一种共享磁通多耦合模式的无线电能传输系统抗偏移方法[J]. 电工技术学报, 2022, 37(21): 5359-5368.
Zhang Xian, Han Dawen, Sha Lin, et al. An anti- offset method under flux-sharing multi-coupling mode for wireless power transmission system[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5359-5368.
[12] 陈永洪, 黎祎阳, 杨斌, 等. 基于多中继线圈结构的无线电能传输系统恒流/恒压输出方法[J]. 电力系统自动化, 2022, 46(20): 147-154.
Chen Yonghong, Li Yiyang, Yang Bin, et al. Constant-current/constant-voltage output method for wireless power transfer system based on multi-relay coil structure[J]. Automation of Electric Power Systems, 2022, 46(20): 147-154.
[13] 胡秀芳, 王跃, 吕双庆, 等. 基于谐波状态空间的无线电能传输系统建模和稳定性分析[J]. 电力系统自动化, 2022, 46(11): 121-130.
Hu Xiufang, Wang Yue, Lü Shuangqing, et al. Modeling and stability analysis of wireless power transfer system based on harmonic state space[J]. Automation of Electric Power Systems, 2022, 46(11): 121-130.
[14] 王党树, 董振, 古东明, 等. 基于双边LCL变补偿参数谐振式无线充电系统的研究与分析[J]. 电工技术学报, 2022, 37(16): 4019-4028.
Wang Dangshu, Dong Zhen, Gu Dongming, et al. Research and analysis of resonant wireless charging system based on bilateral LCL variable compensation parameters[J]. Transactions of China Electrotechnical Society, 2022, 37(16): 4019-4028.
[15] Dai Zhongyu, Wang Junhua, Zhou Haikuo, et al. A review on the recent development in the design and optimization of magnetic coupling mechanism of wireless power transmission[J]. IEEE Systems Journal, 2020, 14(3): 4368-4381.
[16] Li Weihan, Zhao Han, Deng Junjun, et al. Comparison study on SS and double-sided LCC compensation topologies for EV/PHEV wireless chargers[J]. IEEE Transactions on Vehicular Technology, 2016, 65(6): 4429-4439.
[17] Liu Y C, Zhang Jiantao, Tse C K, et al. General pathways to higher order compensation circuits for IPT converters via sensitivity analysis[J]. IEEE Transactions on Power Electronics, 2021, 36(9): 9897-9906.
[18] Borage M, Tiwari S, Kotaiah S. Analysis and design of an LCL-T resonant converter as a constant-current power supply[J]. IEEE Transactions on Industrial Electronics, 2005, 52(6): 1547-1554.
[19] Zhao Lei, Thrimawithana D J, Madawala U K. Hybrid bidirectional wireless EV charging system tolerant to pad misalignment[J]. IEEE Transactions on Industrial Electronics, 2017, 64(9): 7079-7086.
[20] Villa J L, Sallan J, Sanz Osorio J F, et al. High- misalignment tolerant compensation topology for ICPT systems[J]. IEEE Transactions on Industrial Electronics, 2012, 59(2): 945-951.
[21] Mai Ruikun, Chen Yang, Li Yong, et al. Inductive power transfer for massive electric bicycles charging based on hybrid topology switching with a single inverter[J]. IEEE Transactions on Power Electronics, 2017, 32(8): 5897-5906.
[22] Feng Hao, Cai Tao, Duan Shanxu, et al. A dual-side detuned series-series compensated resonant converter for wide charging region in a wireless power transfer system[J]. IEEE Transactions on Industrial Elec- tronics, 2018, 65(3): 2177-2188.
[23] 任洁, 刘野然, 岳鹏飞, 等. 基于参数优化法的输出抗偏移感应电能传输系统研究[J]. 中国电机工程学报, 2019, 39(5): 1452-1461.
Ren Jie, Liu Yeran, Yue Pengfei, et al. Study on anti-misalignment inductive power transfer system based on parameter optimized method[J]. Proceedings of the CSEE, 2019, 39(5): 1452-1461.
[24] Feng Hao, Cai Tao, Duan Shanxu, et al. An LCC compensated resonant converter optimized for robust reaction to large coupling variation in dynamic wireless power transfer[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10): 6591-6601.
[25] Yao Yousu, Wang Yijie, Liu Xiaosheng, et al. Particle swarm optimization-based parameter design method for S/CLC-compensated IPT systems featuring high tolerance to misalignment and load variation[J]. IEEE Transactions on Power Electronics, 2019, 34(6): 5268-5282.
[26] Ramezani A, Narimani M. Optimized electric vehicle wireless chargers with reduced output voltage sensitivity to misalignment[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(4): 3569-3581.
[27] Chen Weiming, Lu Weiguo, Iu H H C. Compensation network optimal design based on evolutionary algorithm for inductive power transfer system[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2020, 67(12): 5664-5674.
[28] Coello C A C, Lechuga M S. MOPSO: a proposal for multiple objective particle swarm optimization[C]// Proceedings of the 2002 Congress on Evolutionary Computation, Honolulu, HI, USA, 2002: 1051-1056.
[29] Coello C A C, Pulido G T, Lechuga M S. Handling multiple objectives with particle swarm optimi- zation[J]. IEEE Transactions on Evolutionary Com- putation, 2004, 8(3): 256-279.
Coupling-Independent Constant-Voltage Output LCC/S Compensation Inductive Power Transfer System Based on Multi-Objective Optimization Theory
Abstract The inductive power transfer (IPT) system based on the traditional full resonance parameter design method presents the best performance only when the transmitting and receiving coils are fully coupled. Usually, the primary coil is fixed, and the position of the secondary coil is uncertain for human factors, causing lateral and longitudinal misalignment of the magnetic coupling mechanism. This misalignment of the magnetic coupling mechanism directly leads to the variation of the coupling coefficient, which may lead to a wide range of output voltage fluctuation and efficiency reduction. To obtain a relatively constant output voltage and operate efficiently under coupling coefficient and load variations, this paper overcomes the limitations of the traditional full resonance parameter design method, transforming the compensation topology parameter design problem into a multi-objective optimization problem.
Firstly, after analyzing full resonance compensation parameters, the system equations of the IPT system with LCC/S compensation topology are established using the fundamental harmonic approximation (FHA) method. A multi-objective optimization model is established. Herein, compensation topology parameters are used as optimization variables, and output voltage fluctuation reduction and system efficiency improvement are as the optimization objectives. The constraints are maximum inductance passing current, maximum capacitor withstanding voltage, and zero voltage switching (ZVS). Then, a case is designed, and the multi-objective particle swarm optimization (MOPSO) algorithm is used to solve the multi-objective optimization model. Three optimization schemes are selected from the Pareto optimal solution set according to the actual needs, and the simulation analysis is carried out. Finally, based on the multi-objective optimization theory, an experimental platform is built to verify the coupling-independent constant output characteristics and efficient operation characteristics of the compensation parameter design method. The experimental results show that when the coupling coefficient of the IPT system varies in the range of 0.20~0.32, and the equivalent load resistance varies in the range of 50~60 W, the output voltage fluctuation rate (VFR) of the optimized scheme is less than 9.0%. In the whole range of coupling coefficient and load variation, the minimum efficiency is 87.5%, and the maximum efficiency is 93.2%. Compared with the efficiency of the traditional scheme (70.0%~86.3%), the efficiency of the optimized scheme is also greatly improved.
Different from single-objective optimization, which provides only a single solution, the multi-objective optimization model established in this paper can get the Pareto optimal solution set through the MOPSO algorithm. The decision maker determines the weight of each object according to the actual needs and selects the appropriate design scheme from the Pareto optimal solution set. Thus, the IPT system can still obtain a relatively constant output voltage and operate efficiently when the coupling coefficient and load change. This method has high flexibility and wide applicability. It is suitable for optimizing compensation topologies that satisfy features like coupling and load-independent constant output, high efficiency, low device stress, zero voltage switching, and more.
keywords:Inductive power transfer, multi-objective optimization, coupling-independent constant voltage output, multi-objective particle swarm optimization (MOPSO) algorithm, Pareto solutions
中图分类号:TM724
DOI: 10.19595/j.cnki.1000-6753.tces.230325
中央高校基本科研业务费专项资金资助项目(2023JBZX006)。
收稿日期 2023-03-20
改稿日期 2023-06-02
焦超群 男,1976年生,副教授,博士生导师,研究方向为电磁场理论及其应用、大功率IGBT器件、无线电能传输技术等。E-mail: chqjiao@bjtu.edu.cn
杨 旭 男,1987年生,博士研究生,研究方向电力电子变换器、无线电能传输技术等。E-mail: yangxuican@bjtu.edu.cn(通信作者)
(编辑 陈 诚)