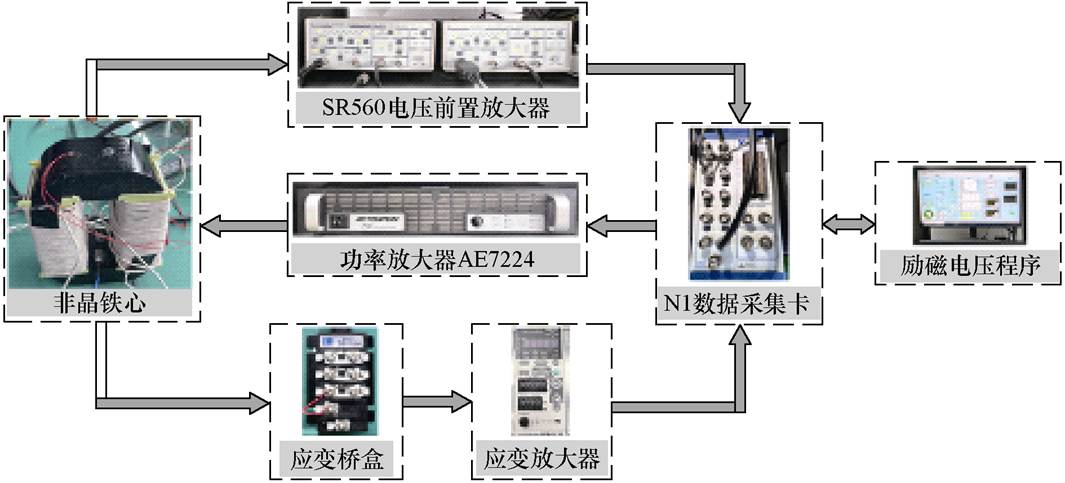
图1 非晶合金磁特性测量系统
Fig.1 Measurement system of magnetic properties of amorphous alloys
摘要 非晶合金用于电抗器铁心可有效降低损耗，但其磁致伸缩系数较大，将引起电抗器剧烈的振动。该文提出一种应用于非晶合金铁心减振结构设计的电磁-机械耦合拓扑优化算法。首先，基于固体各向同性材料惩罚（SIMP）模型，将优化区域材料的相对磁导率和杨氏模量用材料密度的插值函数表示，并采用有限元方法构建电抗器优化模型；其次，以电感值为约束条件，振动最小为优化目标，对非晶合金铁心进行拓扑优化，并采用全局收敛移动渐近线法，将电磁拓扑优化的解作为机械拓扑优化的初始值，缩短电磁-机械耦合拓扑优化的收敛时间；最后，对优化模型进行仿真及实验验证，结果表明：在保证电抗器电感值不变的前提下，优化后铁心气隙区域沿主磁路方向的振动加速度幅值降低24%。证明了提出的电磁-机械耦合拓扑优化算法在减振动结构设计中具备有效性。
关键词：电抗器 拓扑优化 电磁振动 有限元法
由于远距离输电线路的容升效应，线路末端将出现过电压，为了抑制容升效应，常采用并联电抗器补偿线路的无功功率，以保证电网安全、可靠运行。但传统硅钢铁心的并联电抗器，由于硅钢叠片较厚，且材料的剩磁较大，使铁心的涡流和磁滞损耗升高产生局部温升，这种长期的铁心发热将给设备的安全运行带来巨大风险[1]。
新型软磁材料替代传统硅钢应用于电工装备铁心，是降低损耗的重要途径之一，其中非晶合金应用最为广泛[2]。非晶合金不存在晶体结构及阻碍磁畴壁移动的结构缺陷，且带材极薄（20～30 μm），可极大地降低铁心的涡流和磁滞损耗，但其磁致伸缩系数高达27×10-6，是传统硅钢材料的7～8倍，用于电抗器将加剧铁心的振动[3-5]；同时，由于非晶合金带材薄、脆、硬等特性，使非晶合金铁心在剧烈振动时会发生局部变形而产生碎片，造成电抗器绝缘的降低和损耗的增加[6]。
针对电抗器振动的来源，国内外学者进行了广泛的研究。贲彤等结合二次畴转模型与矢量J-A模型提出矢量磁致伸缩模型，通过对电抗器振动特性的仿真，得出磁致伸缩效应会加剧铁心T型区域电磁振动[7]。张鹏宁等采用正交插值法计算并联电抗器铁心的磁致伸缩应变，并对比麦克斯韦力与磁致伸缩力的贡献，得出麦克斯韦力是无气隙垫块的并联电抗器铁心振动的主要原因[8]。因此，电抗器振动噪声的主要来源为铁心的磁致伸缩效应和麦克斯韦电磁应力。
针对电抗器减振方法，闫荣格等于2017年提出在气隙中填充负超磁致伸缩材料，抵消铁心的原始变形，但未给出实验结果来验证所提方法的准确性[9-10]。2020年，提出一种基于谐波注入的减振方法，通过增加反向奇次谐波激励减小输入功率，降低电抗器振动，并利用遗传算法计算出最优的谐波注入量，但遗传算法容易提前收敛，过早陷入局部最值，且注入不适当的谐波量反而会产生更大的振动[11-12]。Gao Yanhui等通过寻找气隙处填充材料的最优杨氏模量来抵消电抗器铁心的振动位移，但未进行实验验证[13]。徐征宇等设计一种多层隔/吸声复合结构的隔声装置来阻隔振动噪声的传播，减小电抗器噪声污染，但该方法会增加额外的设备成本[14]。钟思翀等提出一种有源降噪方法，在铁心正前方放置一个次级声源（扬声器）发射声波来抵消铁心振动产生的声波，但会导致电抗器其他部分路径噪声增大[15]。杜伯学等在电抗器铁心底部加入不同阻尼材料吸收振动能量进行减振，并进行了实验验证，但该方法并未从振动的根源解决问题[16]。祝丽花等提出对电抗器施加夹紧力来抑制铁心的振动，但若对铁心施加不适当的夹紧力则会引起共振，产生更大噪声[17-18]。综上所述，上述减振方法中，文献[9-10, 13]仅从理论的角度证明了方法的可行性，未进行实验验证；文献[14-18]主要集中在隔振/吸振方面，并未从振动的根源解决问题，还增加额外的设备成本。因此，必须从电抗器振动的根源出发，通过优化电抗器铁心的结构参数，即铁心拓扑优化来减小电抗器的振动。
拓扑优化是指对特定的结构区域进行单元划分，在目标函数和一定的约束条件下利用数值分析去决定每个单元材料的添加或者去除，最终得到可以实现优异性能的材料最优分布[19]。目前，该方法已被用于优化电气设备的电磁场分布。基于水平集的拓扑优化方法用于磁致动器的结构设计，可使磁轭与电枢之间的磁力最大化，并且通过在磁阻的定义中引入水平集函数来表示材料边界[20-21]。但是，在优化过程中水平集方程需要用偏微分方程不断更新，这会降低收敛速度或导致无法收敛。为了提高收敛速度，文献[22]将同步电机的铁心划分为非结构化网格，同时采用ON/OFF方法将元素中的材料排列为磁性材料或空气，避免了灰度单元的出现，然而，ON/OFF方法容易陷入局部极值点。
针对以上问题，本文提出一种应用于非晶合金铁心低振动结构设计的电磁-机械耦合拓扑优化算法。为了避免陷入局部极值，采用全局收敛移动渐近线法（Global Convergent Method of Moving Asymptotes, GCMMA），根据目标函数与梯度方向进行迭代搜索来寻找最优解，并将电磁拓扑优化的解作为机械拓扑优化的初始值，提高全局收敛性的同时加快收敛速度。
为了计算电抗器铁心中的磁致伸缩应力及电磁力，须获得非晶合金的磁化特性和磁致伸缩特性。首先对于非晶铁心的磁特性进行测量，搭建非晶铁心磁特性测量系统，如图1所示。
图1 非晶合金磁特性测量系统
Fig.1 Measurement system of magnetic properties of amorphous alloys
首先，励磁电压通过功率放大器加在非晶合金铁心初级绕组上；其次，使用电压传感器和电流传感器分别测量次级绕组的空载电压和初级绕组的电流；最后，依据安培环路定律和电磁感应定律，计算铁心的磁通密度B和磁场强度H，即
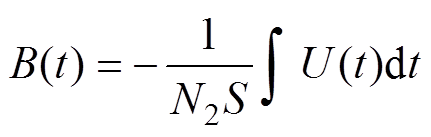（1）
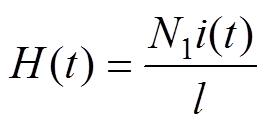（2）
式中，l为铁心磁路长度；i为励磁侧电流；N1为初级线圈匝数；U为感应电压；S为铁心截面积；N2为次级线圈匝数。
采用电阻应变片测量非晶合金铁心的磁致伸缩，将应变片粘贴在铁心表面，为了减小测量误差，应变信号测量过程重复5次并取平均。铁心表面的应变信号通过BNC适配器、数据采集卡采集。最后，利用计算机控制程序对信号进行调制和处理。
50 Hz正弦激励下，非晶铁心基本磁化曲线及相对磁导率测量结果如图2a所示，磁致伸缩量蝴蝶曲线如图2b所示。为了在有限元仿真计算软件中应用测量的磁致伸缩数据，将磁致伸缩蝴蝶曲线峰-峰值和磁场强度峰值通过三次样条插值得到光滑的单值曲线，如图2d所示。
基于测量的非晶合金磁特性，建立电抗器电磁-机械耦合拓扑优化模型。为了加快收敛速度，首先建立电抗器的电磁优化模型并进行首次电磁拓扑优化；然后将电磁拓扑优化结果作为机械拓扑优化的初始值；最后进行电磁-机械耦合拓扑优化。
图2 非晶合金磁特性测量结果
Fig.2 Measurement results of magnetic properties of amorphous alloys
电抗器二维仿真模型如图3所示，由于模型中绕组匝数较少且处于无气隙的旁轭位置，因此绕组所受到的洛伦兹力可以忽略，本文只考虑电磁力和材料的磁致伸缩效应对铁心振动的影响。由于电抗器铁心振动的主要原因是气隙处的电磁力和铁心材料的磁致伸缩效应，因此，优化区域选择为气隙区域周围，如图3所示。由于电磁力主要在气隙与铁心的交界处，因此将优化区域设计在气隙两侧。
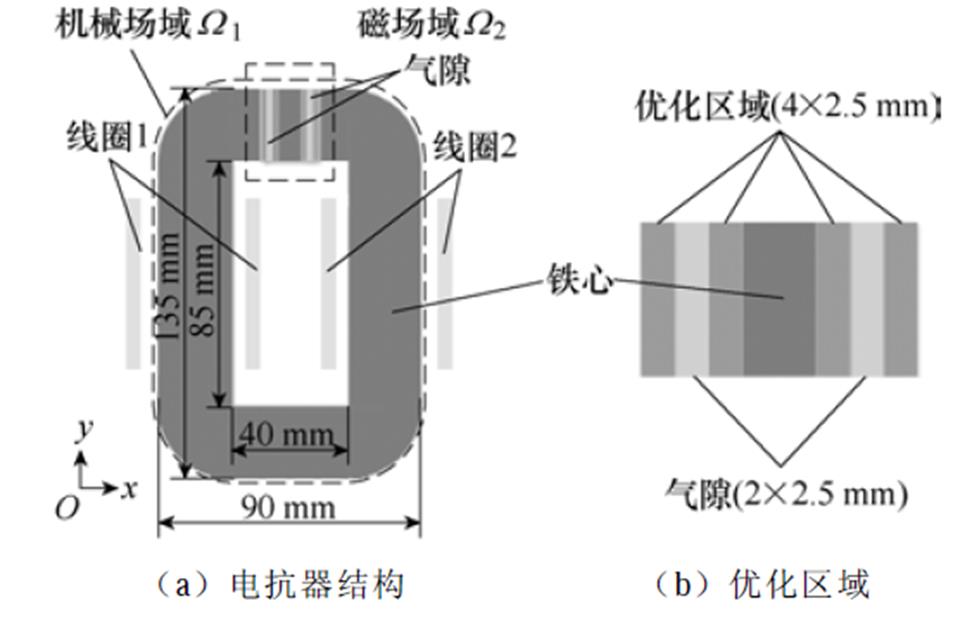
图3 非晶电抗器整体结构
Fig.3 Overall structure of amorphous reactor
为了有效抑制优化过程中出现的中间密度单元，同时提高计算效率，本文采用各向同性材料惩罚（Solid Isotropic Material Penalty, SIMP）模型进行电磁-机械耦合计算。通过假定由0～1连续变化的伪密度理想材料，在伪密度理想材料和真实材料属性之间，建立由连续变量函数描述对应关系；同时，引入惩罚因子对中间密度进行惩罚，迫使中间密度向两端逼近，最终得到收敛于0/1的材料分布。
基于SIMP模型，引入设计变量r，将优化区域内铁心材料的相对磁导率和杨氏模量用设计变量表示为连续函数，同时，设定惩罚因子P对中间密度单元进行惩罚，以此减少优化中的中间密度单元数目，优化区材料的相对磁导率与杨氏模量表示为
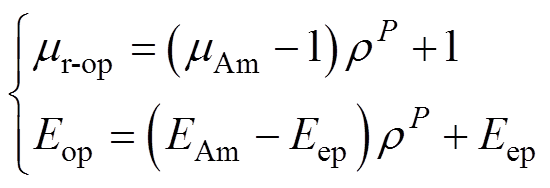0≤r≤1 （3）
式中，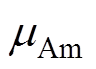
为非晶合金的相对磁导率，其值为图2b所示相对磁导率曲线；EAm为非晶合金的杨氏模量；Eep为气隙区域材料的杨氏模量。不同区域材料的相对磁导率和杨氏模量取值见表1。
表1 电抗器铁心不同区域相对磁导率和杨氏模量取值
Tab.1 Values of relative permeability and Young's modulus in different regions of reactor core
相对磁导率杨氏模量E/(N/m2) 优化区域 铁心1.1×1011 气隙11.7×1010
首先，进行基于SIMP的电抗器电磁计算，电抗器磁场区域满足微分方程
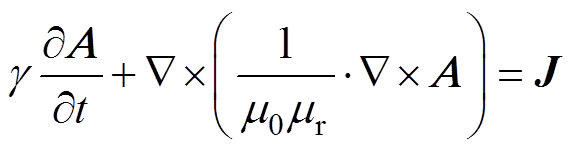（4）
式中，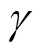
为电导率；J为电流密度；
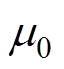为真空磁导率；
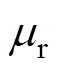为材料的相对磁导率，不同区域取值见表1；A为矢量磁位，存在于整个磁场区域，满足
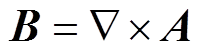（5）
其次，进行基于SIMP的电抗器机械场计算，忽略铁心的阻尼效应，电抗器机械场域的动力学方程描述为
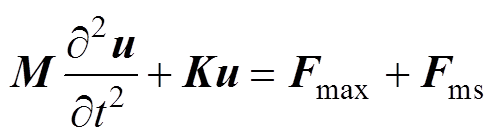（6）
式中，M为质量矩阵；u为振动位移；K为刚度矩阵；Fmax和Fms分别为麦克斯韦力和磁致伸缩力。
采用麦克斯韦应力张量Tmax的面积分计算电抗器铁心中的麦克斯韦力，即
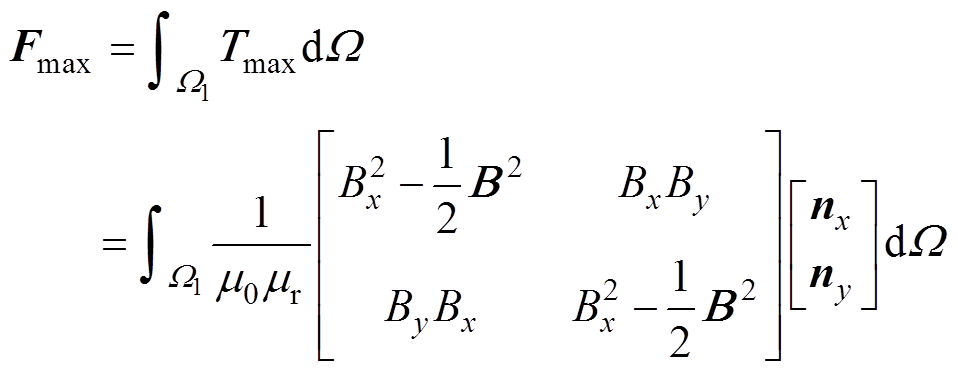（7）
式中，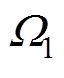
为机械场域，如图3所示；Bx和By分别为x方向和y方向的磁通密度；nx和ny分别为法向量在x方向和y方向的单位向量。
基于弹性力学方法的应力应变关系，磁致伸缩应力Fms用磁致伸缩应变的积分形式表示，即
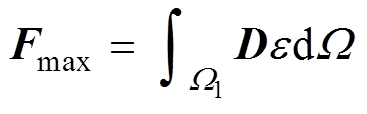（8）
式中，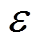
为磁致伸缩应变，其值为图2d所示磁致伸缩单值曲线；D为弹性张量，表示为
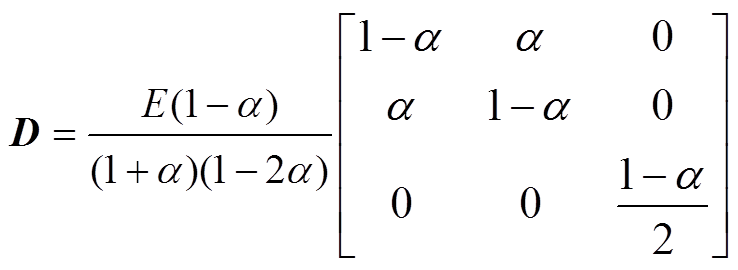（9）
式中，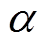
为泊松比，优化区域与铁心区域取0.25，气隙区域取0.3；E为杨氏模量，取值见表1。
最后，采用有限元方法，构建基于SIMP的电抗器电磁-机械耦合模型并进行数值求解，结果作为初值用于电抗器的拓扑优化。
作为电抗器的最重要参数，电感值决定了电抗器能否正常运行，因此，在进行拓扑优化时，首先要保证电抗器的电感值保持不变，即多次迭代后电感误差值小于3%，电感值表示为
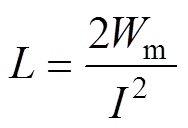（10）
式中，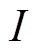
为线圈的激励电流有效值；Wm为磁场域
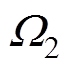（见图3）中的磁场能，表示为
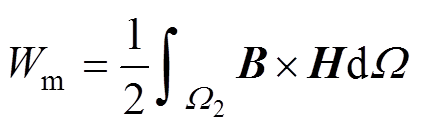（11）
同时，将由于磁致伸缩效应和麦克斯韦应力引起的弹性应变能限制为小于初始值，弹性应变能Ws表示为
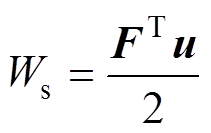（12）
式中，F为机械场域中总载荷，表示为F=Fmax+Fms。
首先，基于电抗器电磁-机械耦合模型的计算初值，进行电磁拓扑优化迭代求解，电磁拓扑优化目标函数fmag及约束条件为
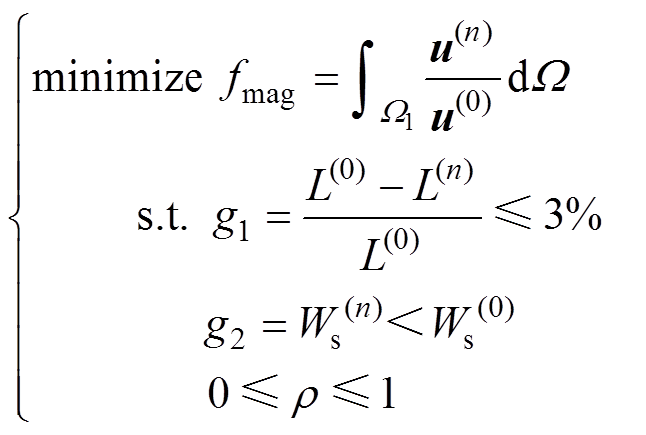（13）
式中，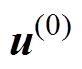
为初始振动位移；
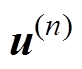为第n次优化迭代时的振动位移；g1和g2为约束函数，其中，对于约束函数g1，
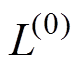为电抗器的初始电感值，
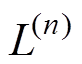为第n次迭代时的电感值；对于约束函数g2，
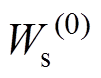为初始弹性应变能，
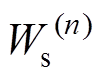为第n次迭代时的弹性应变能。
其次，为了保证电抗器的刚度，进行机械拓扑优化迭代求解，机械拓扑优化目标函数fmec为
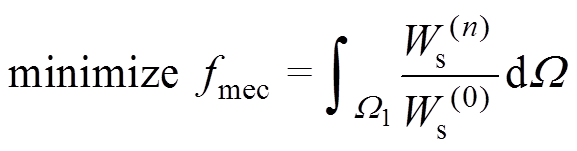（14）
式中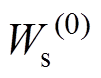，为初始弹性应变能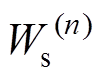；为第n次优化迭代时的弹性应变能。
最后，结合电磁拓扑优化结果以及机械拓扑优化目标，建立电抗器电磁-机械耦合拓扑优化模型，通过引入电磁-机械耦合拓扑优化的目标函数f来进行最小振动和结构刚度之间的权衡，优化目标函数及约束条件表示为
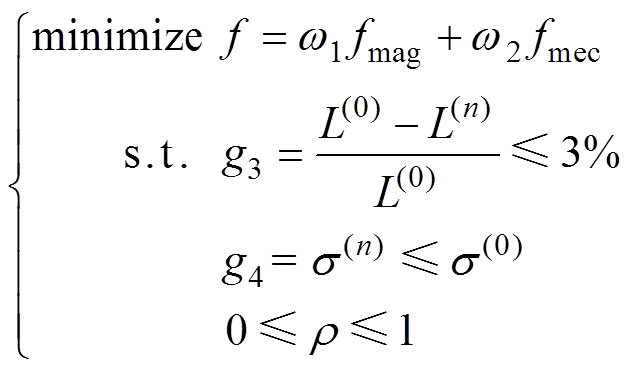（15）
式中，g3和g4为约束函数，其中，对于约束函数g3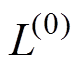，为电抗器的初始电感值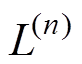，为第n次迭代时的电感值；对于约束函数g4，
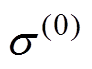为初始应力值，
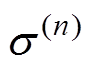为第n次迭代时的应力值；
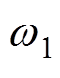和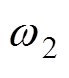
为电磁-机械耦合拓扑优化目标函数f的权重因子，表示为
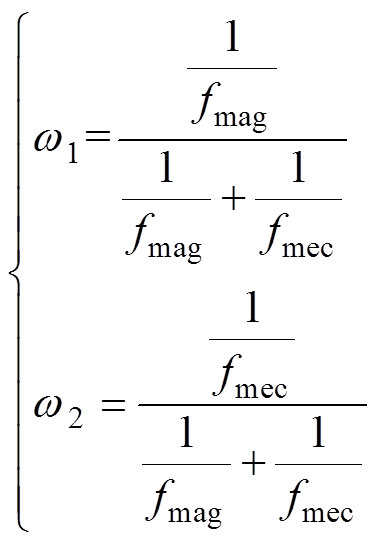（16）
为了分析设计变量的变化对目标函数的影响，需要对电磁拓优化扑和电磁-机械耦合优化拓扑进行灵敏度计算，以得到磁性材料在优化区域中的分布。灵敏度在数值上等于目标函数对设计变量的偏导数，本文采用伴随变量法计算，电磁拓扑优化和电磁-机械耦合拓扑优化的灵敏度分别表示为
（17）
式中，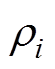
为第i个单元的设计变量；m为单元个数；l1和l2为伴随向量，由伴随函数求得。
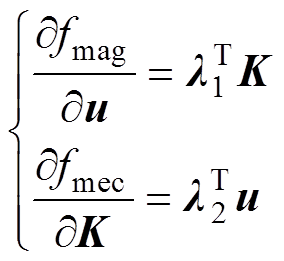（18）
为了增强全局收敛性，结合上述公式计算对应拓扑优化的灵敏度，采用全局收敛移动渐近线法（GCMMA），相比于传统的移动渐近线法，GCMMA具有更强的全局收敛性，根据灵敏度值的正负，更新设计变量，过程如下：首先，计算各个目标函数对初始设计变量r0的偏导数，即目标函数的梯度；其次，沿梯度减小的方向，即梯度下降方向更新设计变量并重新计算目标函数值；最后，重复上述步骤直至求出目标函数极小值（最优解），停止迭代。
为了提高收敛速度，本文将电磁拓扑优化的解作为机械拓扑优化的初始值，以缩短电磁-机械耦合拓扑优化的收敛时间，优化流程如图4所示。首先，进行电磁拓扑优化，在优化区域中初始化设计变量r 的分布后，通过有限元方法计算振动位移和电感值，评估目标函数和灵敏度。然后，根据灵敏度分析和GCMMA方法更新设计变量，若满足电磁拓扑优化的目标函数收敛条件，则得到电磁拓扑优化的最优解。最后，进行电磁-机械耦合拓扑优化，将电磁拓扑优化的解作为初值，重新进行有限元法计算，评估电磁-机械耦合拓扑优化的目标函数和灵敏度，更新设计变量，若满足电磁-机械耦合拓扑优化的目标函数收敛条件，则迭代终止，获得最终拓扑优化方案。
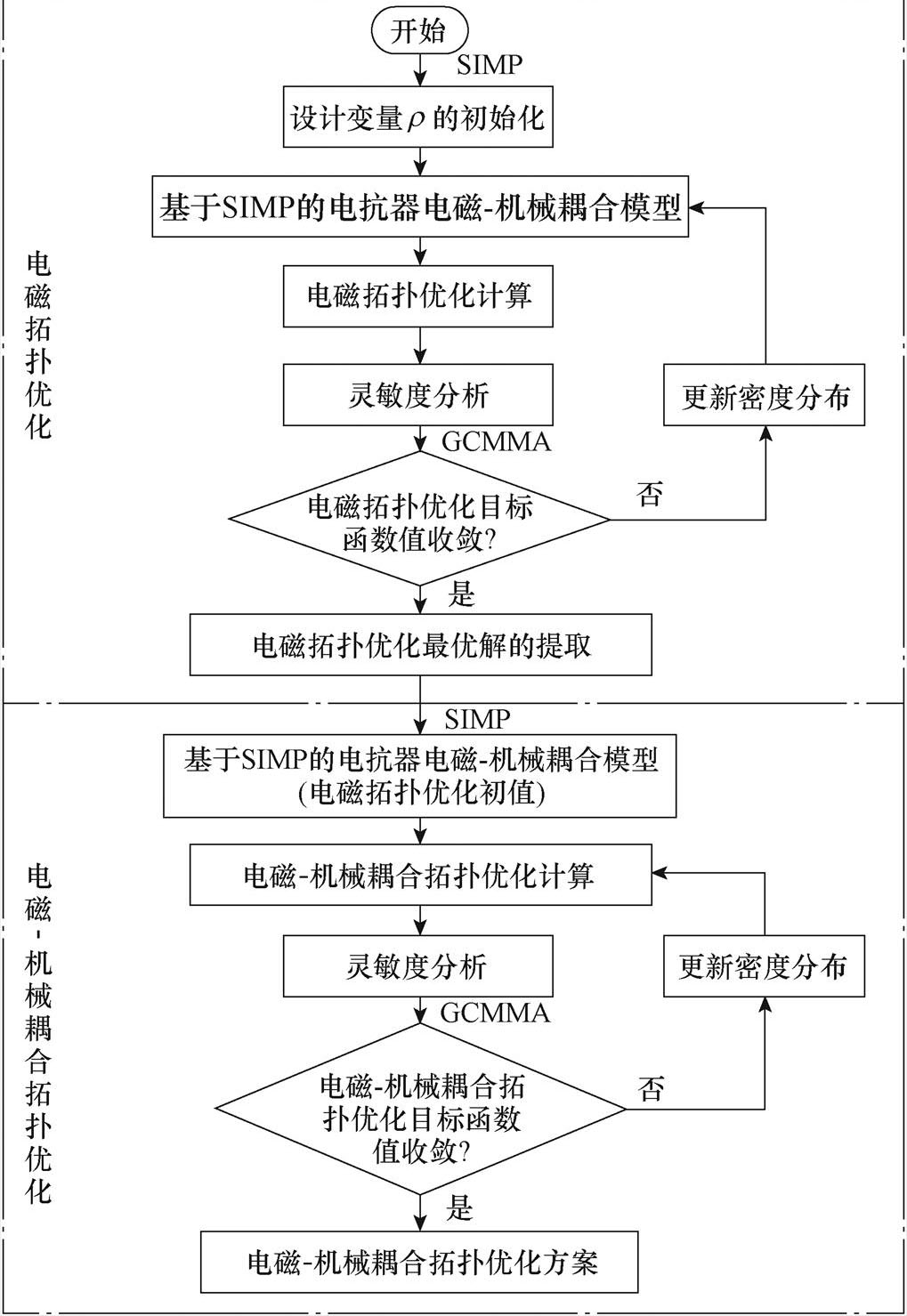
图4 电抗器电磁-机械耦合拓扑优化程序流程
Fig.4 Flow chart of reactor magnetic-mechanical coupling global topology optimization
基于电抗器电磁-机械耦合拓扑优化模型及目标函数与约束条件，进行模型仿真求解，首先，分析采用GCMMA的模型拓扑优化收敛性，对比电磁-机械耦合拓扑优化，电磁-机械耦合拓扑优化模型收敛性分析如图5所示，其中，传统拓扑优化是指以0为初值的电磁-机械耦合拓扑优化，即设计变量r 的初值为0。
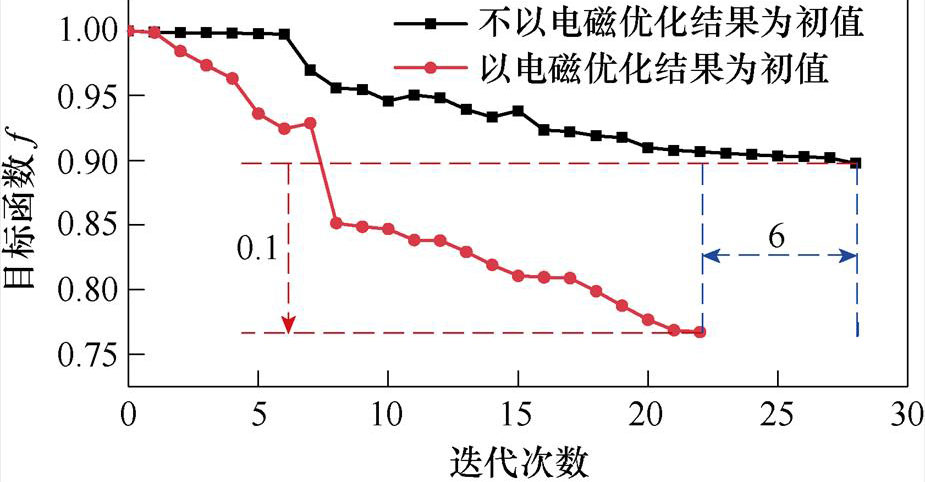
图5 电磁-机械耦合拓扑优化模型收敛性分析
Fig.5 Convergence analysis of magnetic-mechanical coupled global topology optimization model
由图5可知，以电磁拓扑优化结果为初值的电磁-机械耦合拓扑优化的迭代次数减少6次，同时，目标函数值降低0.1，说明电磁-机械耦合拓扑优化具备较高的计算效率与更好的优化效果。
设计变量r 的最优拓扑如图6所示。根据电抗器电磁-机械耦合拓扑优化模型仿真结果，得到优化区域设计变量r 的分布，如图6b所示，可知：设计变量在0～1之间存在中间密度，即图6b中蓝色与红色之间的渐变区域，这将使电抗器铁心的结构不清晰，无法进行样机制作。据此，本文提出阈值函数g(r)来消除中间密度，对设计变量r 的最优拓扑进行过滤，改善材料边界模糊问题，即
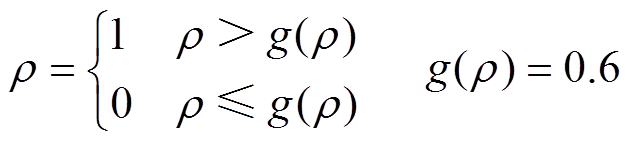（19）
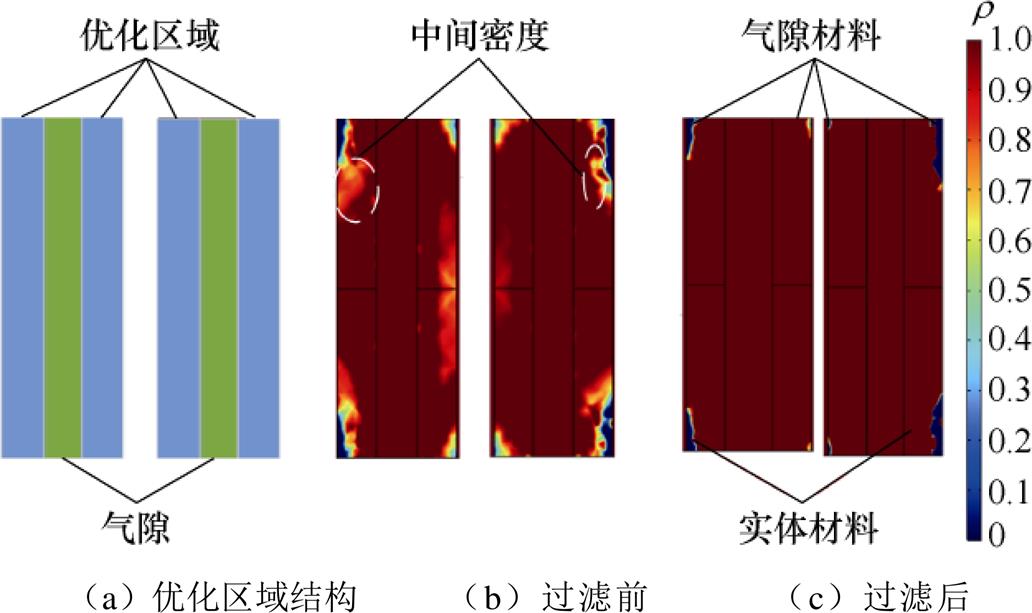
图6 设计变量r 的最优拓扑
Fig.6 Optimal topology of design variables r
当单元的设计变量r 小于阈值函数g(r)，单元材料将被识别为孔洞，即该区域采用气隙材料参数；否则，单元材料被识别为实体材料，即该区域采用铁心材料参数，见表1。
对设计变量r 的最优拓扑进行过滤后，得到最优拓扑如图6c所示，在优化区域中，0即蓝色区域，代表孔洞；1即红色区域，代表实体材料。可知：过滤后材料分布更清晰，有利于优化结构的实物制作；同时，铁心最优拓扑的优化区域的4个拐角为空洞，即填充为气隙的树脂材料，这是由于拐角通常存在旋转磁通，会引起较大的电磁振动，将这些区域填充为非铁心材料，可降低振动，因此，仿真获得的电抗器铁心优化区域的最优拓扑具有合理性。
为了分析仿真模型的减振效果，首先，对比优化前后同一时刻电抗器铁心的磁通密度，如图7所示，可知：优化后电抗器的最大磁通密度为0.591 T，减小约0.84%。电抗器的电感值分别为4.75 mH和4.62 mH，减小约2.7%，几乎保持不变。因此，最优拓扑维持电抗值不变，即保证电抗器的正常运行状态。
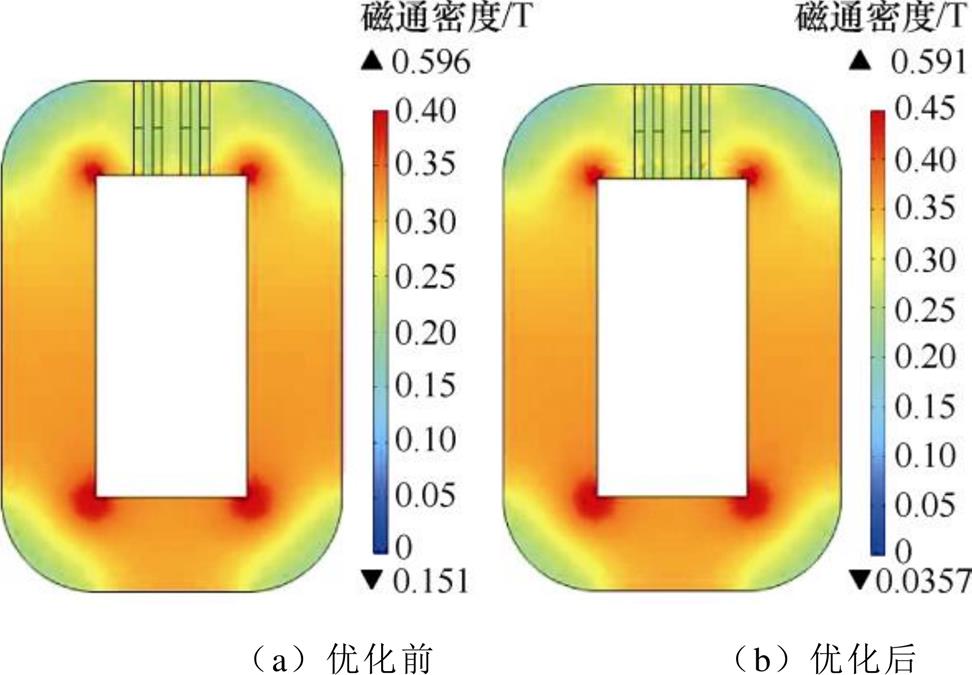
图7 电抗器铁心磁通密度分布
Fig.7 The magnetic flux density of reactor core
其次，对比优化前后同一时刻铁心应力分布，如图8所示，由图8可知，优化后铁心气隙区域应力明显减小。选择铁心上振动位移较大的P点（见图8）分析减振效果，优化前后P点振动位移曲线如图9所示，可知：优化后最大振动位移减少了13%。由此，本文提出的电抗器电磁-机械耦合拓扑优化方法，在保证电抗器的正常运行状态的前提下具有较好的减振效果。
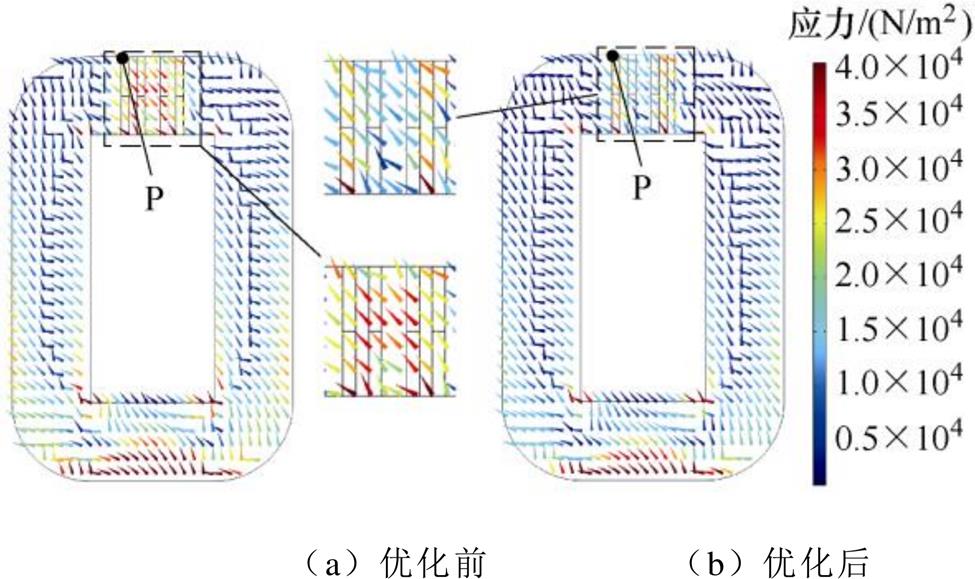
图8 电抗器铁心应力分布
Fig.8 The stress distribution of reactor core
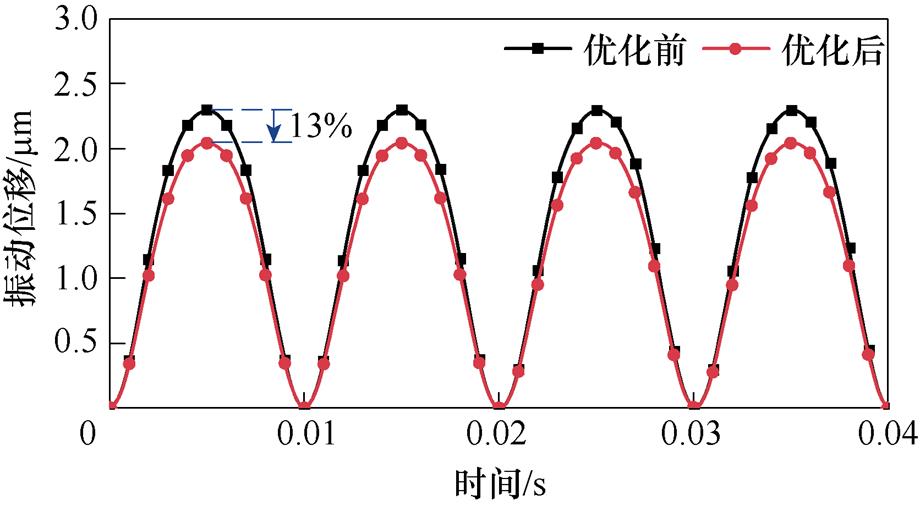
图9 点P处的振动位移曲线
Fig.9 Vibration displacement curves at point P
为了验证本文所提出的电抗器电磁-机械耦合拓扑优化模型的准确性，定制优化前后两种非晶合金铁心模型，其中，铁心为非晶合金带材卷制并固化的开口铁心，开口区域为优化区域，优化区域框架采用3D打印的树脂材料制成，如图10和图11所示，优化拓扑中的孔洞区域为白色树脂板，实体材料区域用铁基非晶合金粉末（化学成分，Fe：80%Si+B：20%）填充。为避免绕组振动对铁心测量产生干扰，将绕组绕制在绝缘套筒骨架上，并使用胶水将绕组固化。
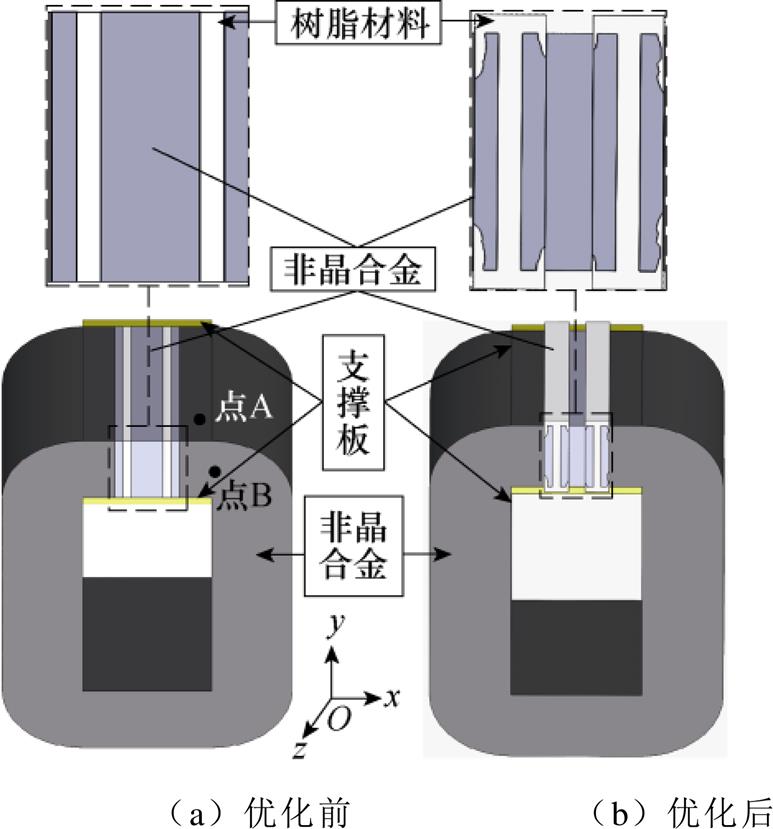
图10 优化前后电抗器铁心结构
Fig.10 The structure diagram of reactor core before and after optimization
图11 优化前后电抗器铁心实物
Fig.11 The physical diagram of reactor core before and after optimization
非晶合金电抗器振动测量系统如图12所示，励磁电压通过功率放大器加在铁心的励磁绕组上，励磁绕组由两个串联的互相增磁的线圈构成；使用电压传感器和电流传感器测量励磁绕组的端口电压和电流，并采用前置放大器进行放大；加速度传感器通过粘合剂粘贴到铁心表面，通过上位机控制数据采集卡采集电抗器的电压、电流和振动信号并保存；为了减小实验误差，使用凸形结构将铁心固定在底板上。
图12 非晶合金电抗器振动测量系统
Fig.12 Vibration measurement system for the reactor
为了验证仿真模型的准确性，对优化前后的非晶合金电抗器进行振动测试，选择电抗器铁心主磁路方向（即x方向）的振动加速度进行对比，励磁绕组的端口电压和电流波形如图13所示，振动加速度波形如图14所示。
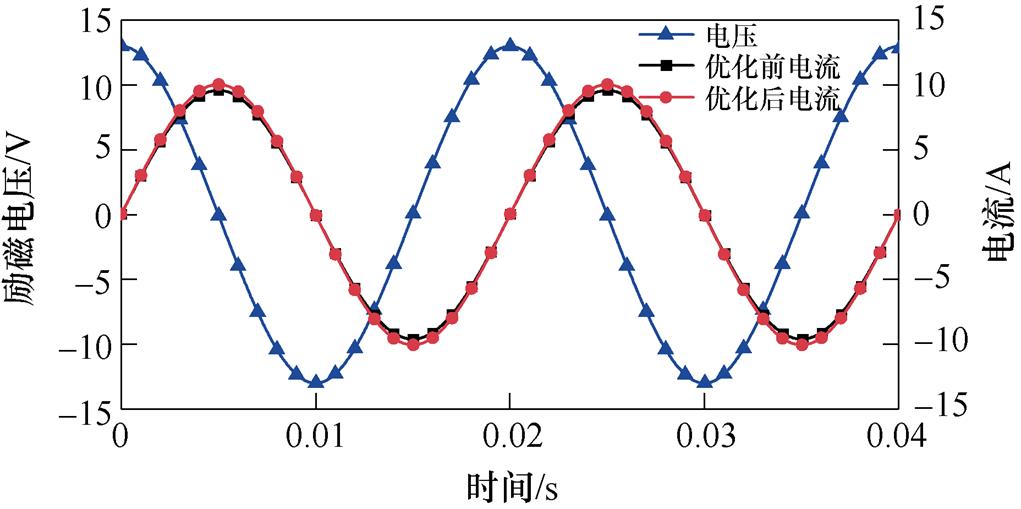
图13 非晶合金电抗器电压与电流波形
Fig.13 The voltage and current waveforms of reactor
由图13可知，在相同励磁电压下，优化前后铁心感应电流幅值分别为9.6 A和10.05 A，波形基本不变；同时，优化前后电抗器的电感值分别为4.31 mH和4.12 mH，优化后电感值减小4.4%。主要原因是由于优化前后铁心气隙区域结构上的差异，使得优化后电抗器的气隙略大（见图10、图11），即优化后电抗器的磁阻更大，导致电感值有所减小。
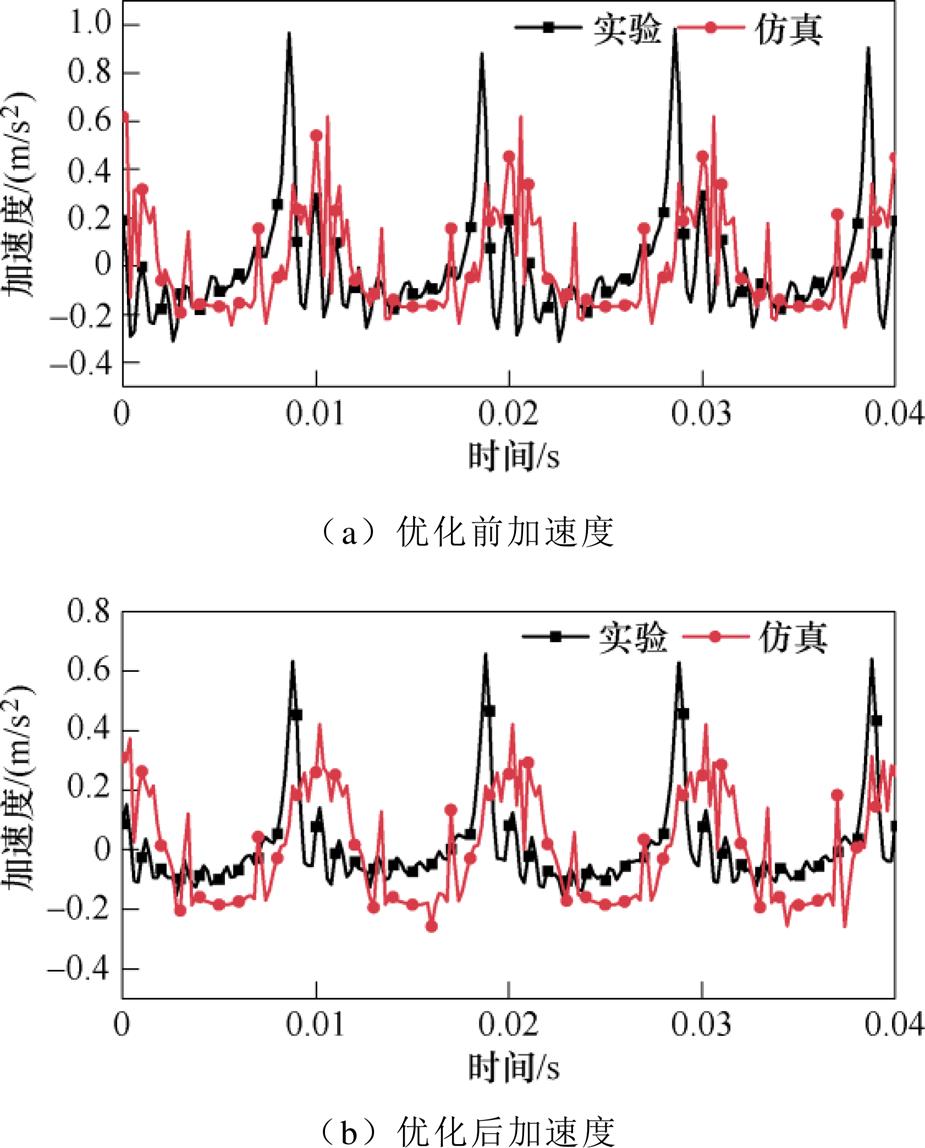
图14 x方向振动加速度仿真与实验对比
Fig.14 The vibration comparison of simulation and experiment in x direction
由图14可知，实验测得的振动加速度幅值要大于仿真的加速度幅值，实验与仿真产生误差的原因主要：实验中所使用的优化结构由3D打印机制成，制作时存在一定误差。但总体来看，测量结果与仿真结果的波形具有相同的变化趋势，同时误差也保持在可接受范围内，可验证仿真模型的正确性。
为了验证实验样机的减振效果，对比优化前后电抗器样机上A点的振动加速度，如图15所示。
由图15可知，优化后减振效果明显，A点三个方向上的振动加速度幅值均有所减小，在x方向、y方向和z方向上的加速度分别减小了33%、33%和42%。同时，x方向为主磁路方向，由于该方向磁通密度较大，因此，在电磁力与磁致伸缩力共同作用下振动加速度最大；z方向为垂直主磁路方向，其磁通密度较小，使得该方向振动加速度最小；y方向为叠片方向，由于叠片之间存在气隙，因此在电磁力的作用下其加速度高于z方向。
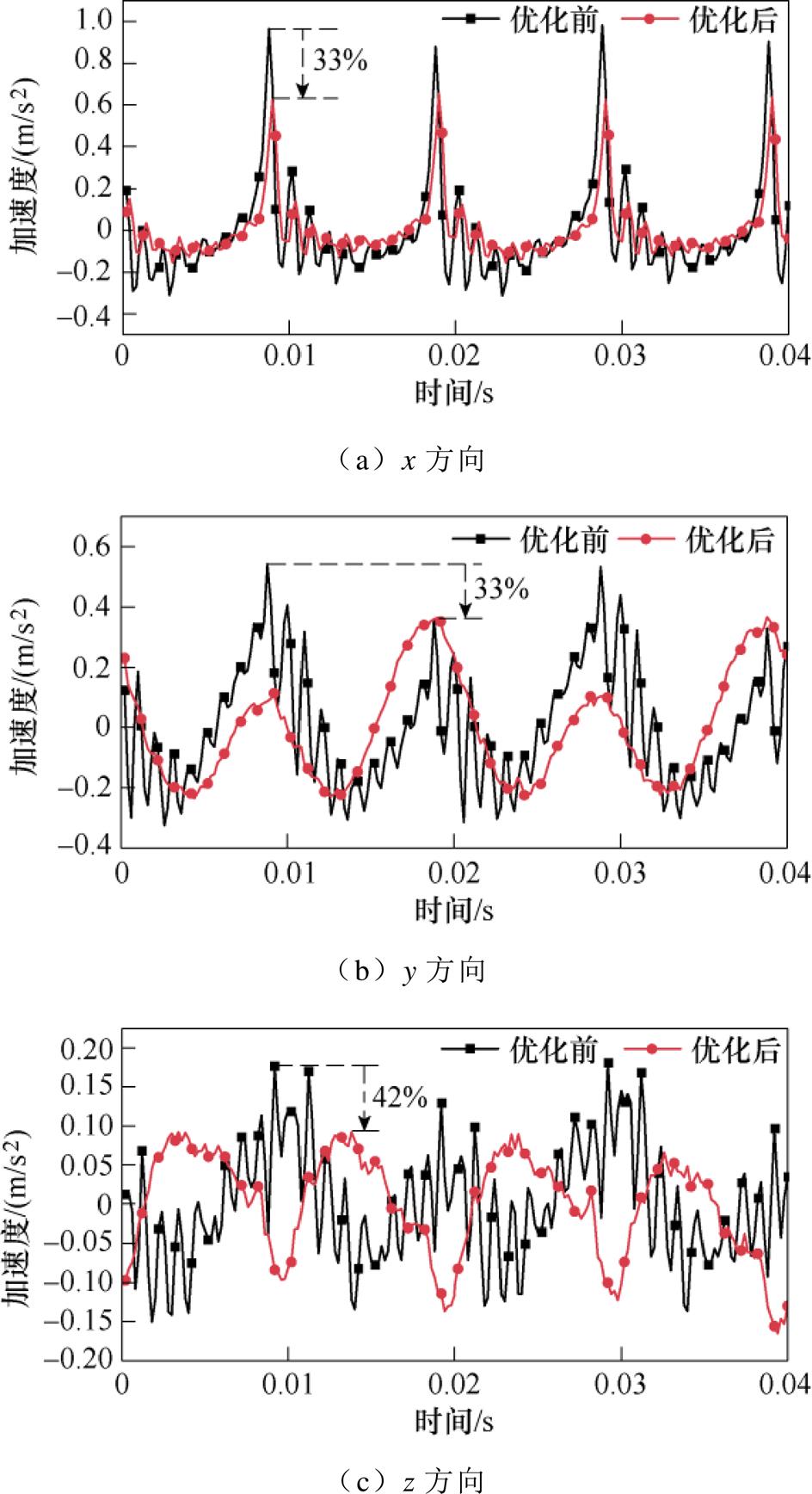
图15 采样点A优化前后振动加速度
Fig.15 The vibration acceleration of sampling point A before and after optimization
对优化前后电抗器铁心上A点的振动加速度波形进行频谱分析，采样点A优化前后振动频谱图如图16所示，由图16可知，在50 Hz激励条件下，优化前后铁心的振动频率主要集中在100 Hz及其倍频上，因此，导致电抗器振动的主要原因为磁致伸缩力和电磁力；除了基频分量外，x方向的加速度中还含有大量高次谐波成分，主要原因为x方向磁通密度较大，由于铁心材料的非线性及饱和特性，导致铁心磁通密度的波形畸变，振动信号的倍频效应导致高次谐波出现。此外，频谱图中出现了直流分量，但占比较小，这主要是由于机械振动、摩擦等因素造成。相较于优化前，优化后A点在x方向、y方向上和z方向上的振动加速度在100 Hz及其倍频上均有所减小，减振效果明显。
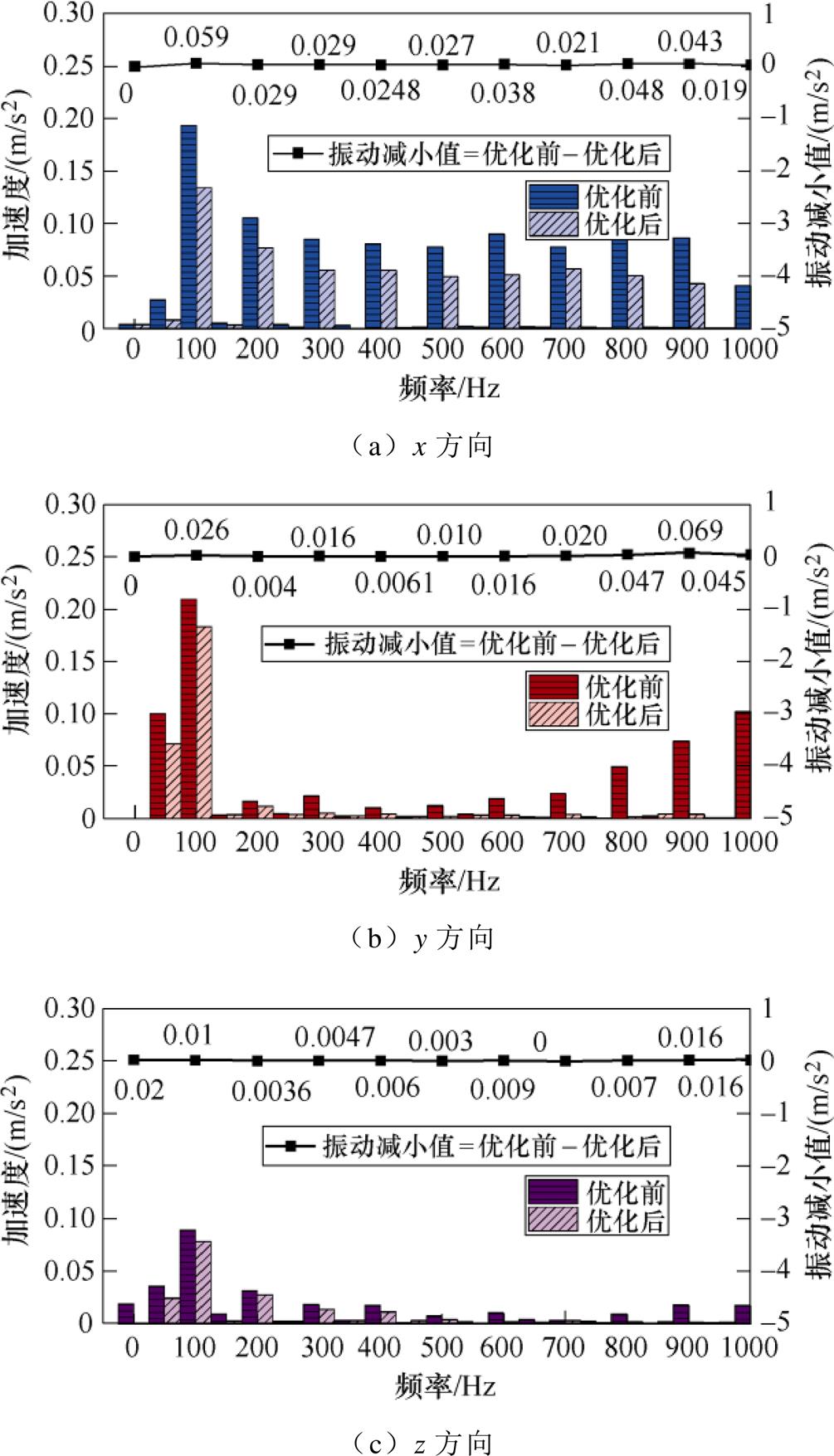
图16 采样点A优化前后振动频谱图
Fig.16 The vibration spectrum of sampling point A before and after optimization
由于优化后电抗器的电感存在负偏差，为了保证电感值不变，即确保其实用性，同时排除电感负偏差对减振效果的影响，本文对优化后的电抗器增加一组补偿线圈并进行振动测试，电抗器及测试结果分别如图17～图19所示。
图17 增加补偿线圈前后的电抗器实物
Fig.17 The reactor before and after adding the compensation coil
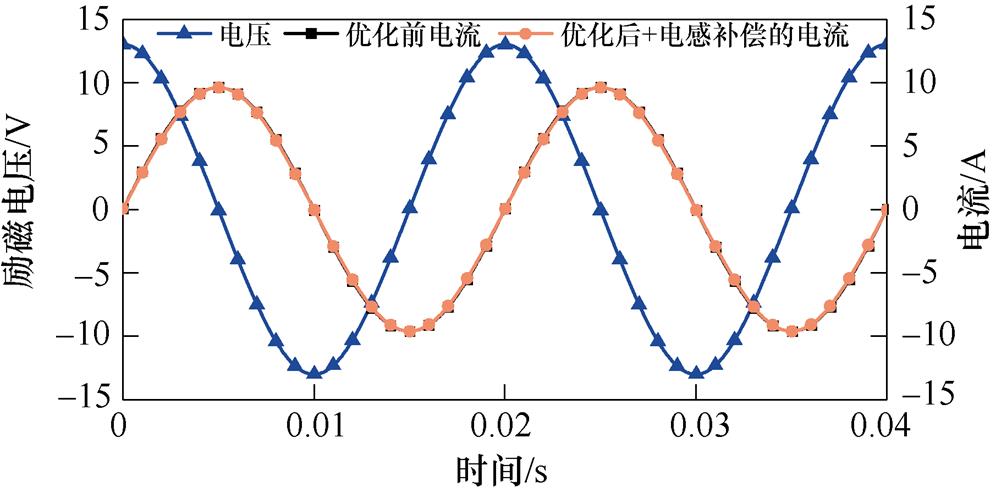
图18 增加补偿线圈前后的电抗器电流波形
Fig.18 The current waveforms of reactor before and after adding the compensation coil
由图18可知，在相同激励电压时，增加补偿线圈后电抗器的电流值为9.6 A，与优化前一致，即电感值不变，这说明增加补偿线圈可抑制优化结构产生的电感负偏差。同时，由图19可知，增加补偿线圈后电抗器的A点上，x方向、y方向和z方向的加速度分别减小24%、25%和13%，且在100 Hz及其倍频上的幅值均减小，这说明使电抗器的振动减小的根本原因为采用铁心拓扑优化结构。
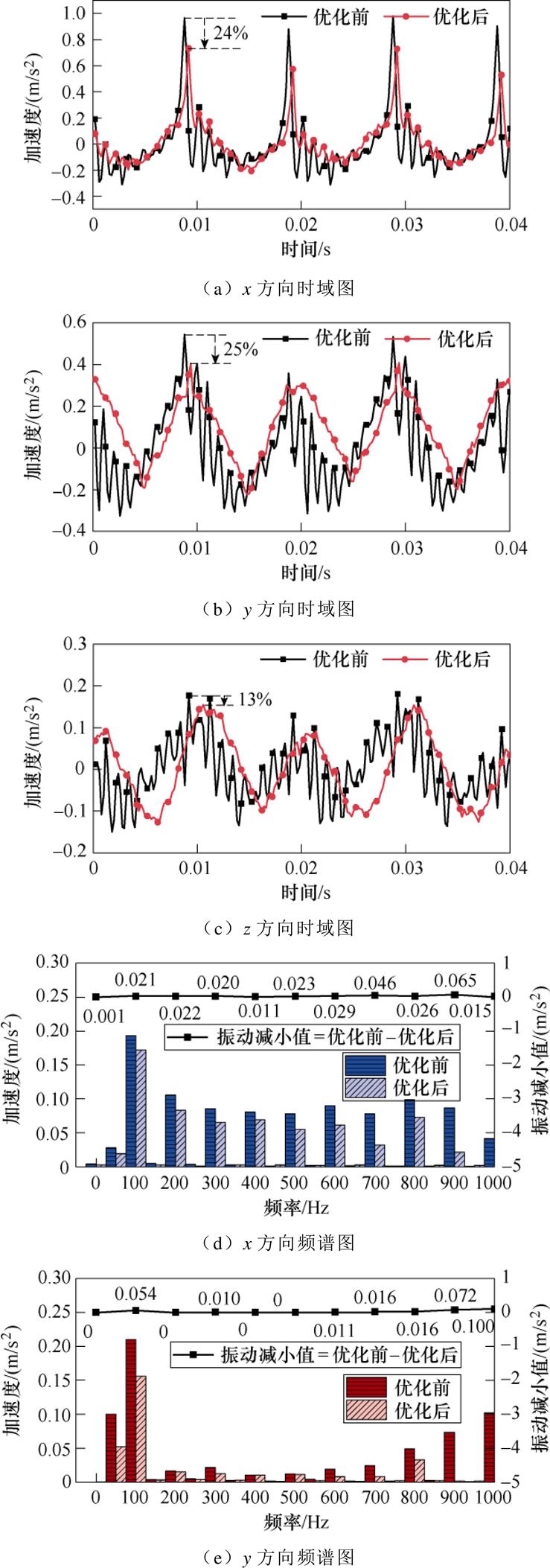
图19 采样点A电感补偿前后振动加速度
Fig.19 The vibration acceleration of sampling point A before and after adding the compensation coil
综上所述，本文提出的电磁-机械耦合拓扑优化方法，可保证电抗器电感稳定的同时降低铁心振动。
本文提出通过电磁-机械耦合拓扑优化的方法减小电抗器铁心振动，仿真及实验表明：
1）优化后铁心气隙区域沿主磁路方向的振动加速度幅值降低33%，且对100 Hz及其倍频上加速度的抑制效果明显，即该铁心的最优拓扑可有效抑制电抗器铁心中的磁致伸缩力和电磁力。
2）由于优化前后铁心气隙区域的结构差异，使优化结构的电感值减小了4.4%；为了排除该电感负偏差对减振效果的影响，增加电抗器的电感补偿线圈，在保证电感稳定后，优化后铁心气隙区域沿主磁路方向的振动加速度幅值仍降低24%。
综上所述，本文提出的电抗器电磁-机械耦合拓扑优化方法，为非晶合金铁心电抗器的减振研究提供了新思路，具有工程应用价值。
参考文献
[1] 王革鹏, 金文德, 曾向阳, 等. 特高压并联电抗器铁心振动的分析与控制研究[J]. 电工技术学报, 2022, 37(9): 2190-2198.
Wang Gepeng, Jin Wende, Zeng Xiangyang, et al. Analysis and control research on core vibration of UHV shunt reactor[J]. Transactions of China Elec- trotechnical Society, 2022, 37(9): 2190-2198.
[2] 吴胜男, 唐任远, 韩雪岩, 等. 磁致伸缩引起的非晶合金永磁电机振动解析计算[J]. 中国电机工程学报, 2016, 36(13): 3635-3641.
Wu Shengnan, Tang Renyuan, Han Xueyan, et al. Analytical calculation of vibration due to mag- netostriction in permanent magnet machines with amorphous metal cores[J]. Proceedings of the CSEE, 2016, 36(13): 3635-3641.
[3] 吴胜男, 唐任远, 韩雪岩, 等. 磁致伸缩引起的非晶合金铁心振动解析计算及影响因素[J]. 电工技术学报, 2016, 31(20): 73-82.
Wu Shengnan, Tang Renyuan, Han Xueyan, et al. Analytical calculation and influence factors of vibration in amorphous metal cores[J]. Transactions of China Electrotechnical Society, 2016, 31(20): 73-82.
[4] Zhang Pengning, Li Lin. Vibration and noise characteristics of high-frequency amorphous trans- former under sinusoidal and non-sinusoidal voltage excitation[J]. International Journal of Electrical Power & Energy Systems, 2020, 123: 106298.
[5] 迟青光, 张艳丽, 陈吉超, 等. 非晶合金铁心损耗与磁致伸缩特性测量与模拟[J]. 电工技术学报, 2021, 36(18): 3876-3883.
Chi Qingguang, Zhang Yanli, Chen Jichao, et al. Measurement and modeling of lossand mag- netostrictive properties for the amorphous alloy core[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3876-3883.
[6] 宋守许, 杜毅, 胡孟成. 定子混合叠压再制造电机空载损耗计算与分析[J]. 中国电机工程学报, 2020, 40(3): 970-980.
Song Shouxu, Du Yi, Hu Mengcheng. Calculation and analysis of no-load iron loss of remanufactured motor with hybrid laminated stator core[J]. Proceedings of the CSEE, 2020, 40(3): 970-980.
[7] Ben Tong, Hou Luqian, Chen Long, et al. The vector electromagnetic vibration of magnetically controlled reactor considering the vector hysteretic magneto- striction effect[J]. IEEE Transactions on Magnetics, 2022, 58(9): 1-5.
[8] 张鹏宁, 李琳, 程志光, 等. 并联电抗器与变压器模型铁心振动仿真与试验对比[J]. 电工技术学报, 2018, 33(22): 5273-5281.
Zhang Pengning, Li Lin, Cheng Zhiguang, et al. Vibration simulation and experiment comparison of shunt reactor and transformer model core[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(22): 5273-5281.
[9] Yan Rongge, Liu Weiying, Wu Yuechao, et al. Reactor vibration reduction based on giant mag- netostrictive materials[J]. AIP Advances, 2017, 7(5): 056677.
[10] 闫荣格, 赵路娜, 贲彤, 等. 70基于负超磁致伸缩效应电抗器减振新方法的研究[J]. 振动与冲击, 2018, 37(19): 254-258.
Yan Rongge, Zhao Luna, Ben Tong, et al. A new vibration reduction method for reactors using NGMM[J]. Journal of Vibration and Shock, 2018, 37(19): 254-258.
[11] 闫荣格, 赵文月, 陈俊杰, 等. 基于谐波注入的串联电抗器的减振研究[J]. 电工技术学报, 2020, 35(16): 3445-3452.
Yan Rongge, Zhao Wenyue, Chen Junjie, et al. Research on vibration reduction of series reactor based on harmonic injection[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3445-3452.
[12] 贲彤, 陈龙, 闫荣格, 等. 考虑磁化及磁致伸缩特性各向异性的感应电机铁心电磁应力分析[J]. 电工技术学报, 2019, 34(1): 66-74.
Ben Tong, Chen Long, Yan Rongge, et al. Stress analysis of induction motor core considering anisotropic magnetic and magnetostrictive pro- perties[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 66-74.
[13] Gao Yanhui, Nagata M, Muramatsu K, et al. Noise reduction of a three-phase reactor by optimization of gaps between cores considering electromagnetism and magnetostriction[J]. IEEE Transactions on Magnetics, 2011, 47(10): 2772-2775.
[14] 徐征宇, 李金忠, 葛栋, 等. 特高压并联电抗器高性能隔声装置研制[J]. 高电压技术, 2018, 44(7): 2276-2283.
Xu Zhengyu, Li Jinzhong, Ge Dong, et al. Development of high performance sound insulation device for UHV shunt reactor[J]. High Voltage Engineering, 2018, 44(7): 2276-2283.
[15] 钟思翀, 祝丽花, 王前超, 等. 电力变压器振动噪声分析及其有源降噪[J]. 电工技术学报, 2022, 37(增刊1): 11-21.
Zhong Sichong, Zhu Lihua, Wang Qianchao, et al. Electromagnetic vibration of power transformer and active noise reduction[J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 11-21.
[16] Du Boxue, Liu D S. Dynamic behavior of magnetostriction-induced vibration and noise of amorphous alloy cores[J]. IEEE Transactions on Magnetics, 2015, 51(4): 1-8.
[17] 祝丽花, 石永恒, 杨庆新. 夹紧力对非晶合金磁特性及铁芯振动的影响研究[J]. 中国电机工程学报, 2020, 40(24): 8155-8164.
Zhu Lihua, Shi Yongheng, Yang Qingxin. Effect of clamping force on magnetic properties and core vibration of amorphous alloys[J]. Proceedings of the CSEE, 2020, 40(24): 8155-8164.
[18] Kitagawa W, Ishihara Y, Todaka T, et al. Analysis of structural deformation and vibration of a transformer core by using magnetic property of magneto- striction[J]. Electrical Engineering in Japan, 2010, 172(1): 19-26.
[19] 王润宇, 李大伟, 范兴纲, 等. 增材制造技术在电机中的应用综述[J]. 中国电机工程学报, 2022, 42(1): 385-406.
Wang Runyu, Li Dawei, Fan Xinggang, et al. A review on application of additive manufacturing technology in electrical machines[J]. Proceedings of the CSEE, 2022, 42(1): 385-406.
[20] Park S I, Min S. Optimal topology design of magnetic devices using level-set method[J]. IEEE Transactions on Magnetics, 2009, 45(3): 1610-1613.
[21] Park S I, Min S, Yamasaki S, et al. Magnetic actuator design using level set based topology optimization[J]. IEEE Transactions on Magnetics, 2008, 44(11): 4037-4040.
[22] Watanabe K, Suga Takao, Kitabatake S. Topology optimization based on the ON/OFF method for synchronous motor[J]. IEEE Transactions on Mag- netics, 2018, 54(3): 1-4.
Optimization of Magnetic-Mechanical Coupling Topology for Vibration Damping Structures of Amorphous Alloy Core Reactor
Abstract Amorphous alloy materials used in reactor cores can reduce the core losses, but their large magnetostrictive coefficient will increase the core vibration. Therefore, this paper proposes a magnetic- mechanical coupling topology optimization algorithm to design amorphous alloy core damping structures. The effectiveness of the proposed method is verified by simulation and experiment.
Firstly, based on the solid isotropic material penalty (SIMP) model, the relative permeability and Young's modulus of the material in the optimization region are expressed as an interpolation function of the material density. The reactor optimization model is then constructed by the finite element method. Secondly, the topology of the amorphous alloy core is optimized with constraints on inductance values and the objective of minimizing vibration. The global convergence moving asymptote method is used to shorten the convergence time of the electromagnetic-mechanical coupled topology optimization by taking the solution of the electromagnetic topology optimization. Meanwhile, a threshold function is introduced to eliminate the intermediate density and address boundary ambiguity. Finally, the optimized model is verified. Due to structural differences in the core air gap region before and after optimization, the inductance value of the optimized reactor is reduced by 4.6%, which falls within an acceptable range, ensuring normal reactor operation. At the same time, the amplitude of vibration acceleration along the main magnetic circuit direction in the core air gap region is reduced by 33% after optimization, and the suppression effect of acceleration on 100 Hz and its octave frequency is noticeable. In addition, to exclude the influence of negative inductance deviation on the vibration-damping effect, a set of compensation coils is added to the optimized reactor, and vibration tests are conducted. The results show a 24% vibration acceleration along the main magnetic circuit direction in the air-gap region with maintaining constant reactor inductance values. Therefore, the proposed electromagnetic-mechanical coupling topology optimization algorithm effectively designs vibration-reducing structures. The following conclusions are drawn from the simulation and experimental analysis: (1) Under the excitation condition of 50 Hz, the vibration frequency of the core before and after optimization is mainly concentrated at 100 Hz and its octave frequency. Thus, the main reasons for the vibration of the reactor are the magnetostrictive force and the electromagnetic force. (2) The optimized structure of the core topology can reduce the vibration of the reactor. (3) The proposed topology optimization method for the reactor with electromagnetic-mechanical coupling has a better vibration reduction effect to ensure the normal operating condition of the reactor, providing a new idea for studying the vibration reduction of amorphous alloy core reactors.
keywords：Reactor, topology optimization, electromagnetic vibration, finite element method (FEM)
中图分类号：TM47
DOI: 10.19595/j.cnki.1000-6753.tces.222350
国家自然科学基金（51977147, 52007102, 52207012）和省部共建电工装备可靠性与智能化国家重点实验室（河北工业大学）开放课题基金（EERI_KF2021015）资助项目。
收稿日期 2022-12-20
改稿日期 2023-05-09
贲 彤 女，1991年生，博士，副教授，博士生导师，研究方向为电工理论及新技术。E-mail: bentong@ctgu.edu.cn
陈 龙 男，1989年生，博士，讲师，硕士生导师，研究方向为磁性材料磁特性模拟、全局优化设计。E-mail: chenlong@ctgu.edu.cn（通信作者）
（编辑 郭丽军）