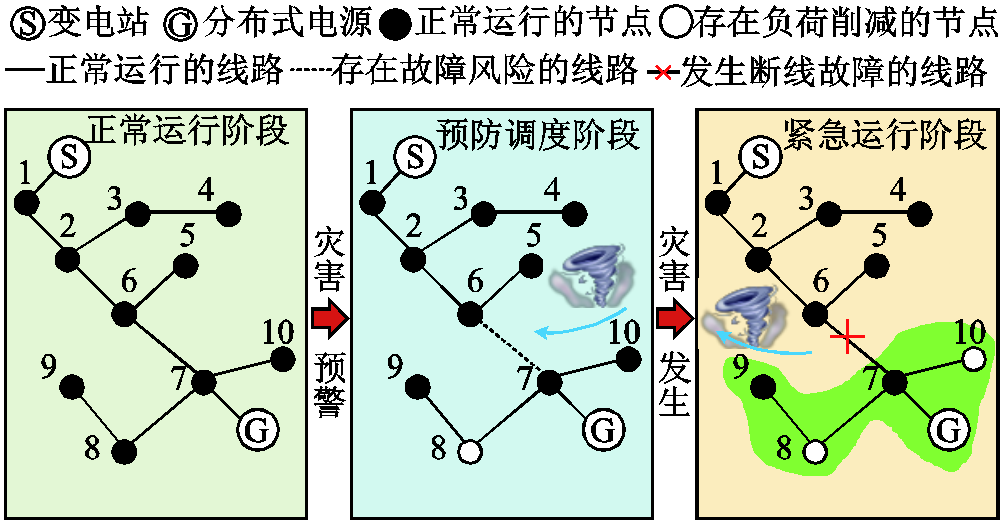
图1 弹性配电网灾前-灾后两阶段调度
Fig.1 Pre- and post- disaster two stage dispatch for resilient distribution systems
摘要 配电网发生紧急故障时,通过构建孤岛微电网对重要负荷进行分区供电,可以缩小停电范围,提升配电网弹性。然而,孤岛微电网建立前线路上流通的功率会对微电网产生阶跃型功率冲击,所造成的频率失稳可能会导致微电网无法安全建立。为此,该文提出一种考虑孤岛微电网建立过程中功率冲击的弹性配电网主动预防调度方法。通过在灾前进行机组组合、网架重构,并限制线路上的流通功率,减少断线故障发生时微电网内的功率冲击,保证灾后孤岛微电网的安全可靠建立。首先,以调度成本和负荷损失量最小为目标,建立考虑功率冲击的配电网灾前-灾后协调调度随机优化模型;然后,对模型进行线性化处理,将其转换为混合整数规划问题进行快速求解;最后,采用IEEE 13节点配电测试系统,对所提预防调度方法的有效性进行验证。
关键词:弹性配电网 孤岛微电网 预防调度 功率冲击 频率稳定
极端自然灾害的频繁发生给配电网的安全运行带来了巨大挑战[1]。以2021年河南省郑州市大停电事故为例,暴雨天气导致800条城市配电线路受损,超过98万人电力供应中断。虽然在灾前对配电线路进行加固能有效减小故障概率[2-3],但仍无法完全避免紧急故障的发生。随着分布式电源(Distributed Generator, DG)大规模接入配电系统,配电网逐渐呈现出多源主动的特性[4-6]。在发生紧急故障时,利用配电网中的DG和未故障线路构建孤岛微电网(Islanded Microgrid, IMG)维持重要负荷持续供电,是缩小停电范围,提升配电网弹性的重要手段[7-8]。
很多基于微电网的弹性提升方法研究聚焦于灾后微电网孤岛划分和运行调度方面。文献[9-10]提出在故障前设计好微电网孤岛运行方案,故障后执行相应的应急控制方案,使配电网以事先划分好的IMG结构继续运行。考虑到各微电网之间可以进行功率交互,文献[11-13]提出以网络化微电网的形式对重要负荷进行供电,通过优化微电网间电能调度策略,以实现负荷损失量最小。然而,当配电网在自然灾害下发生多点故障时,上述基于固定结构的微电网灵活性较差。为了提高灾后微电网拓扑的灵活性,文献[14-17]提出考虑IMG结构优化的配电网弹性恢复策略,通过引入节点分区状态变量,在灾后对配电网进行孤岛划分。各IMG内功率平衡,且至少包含一台具有调频、调压能力的DG以保证微电网稳定运行。考虑到可再生能源出力和负荷需求的波动性,文献[18-21]在文献[16]的基础上提出在孤岛运行过程中考虑IMG分区结构的动态调整,在保证IMG功率平衡的前提下进一步提升重要负荷的供电恢复量。
上述现有研究主要采用紧急控制的方法,即在故障发生后,匹配孤岛微电网运行方案,建立孤岛微电网,对重要负荷进行分区供电。然而,在孤岛微电网建立过程中会存在较大的功率不平衡,当微电网调节能力不足时可能造成机组爬坡等安全约束越限,进而导致无法安全稳定地建立IMG。为此,有学者提出在灾前对配电网进行预防调度,提升IMG建立过程的安全性。文献[22-24]提出在灾前隔离脆弱元件并建立预防性IMG,以减少连锁故障对配电网的影响。但该方法设定灾前微电网对外功率交互为0,存在调度方案较为保守的问题。文献[25-26]对并网运行的微电网进行预防性调度,通过储备充足的备用容量确保离网后负荷的供电需求。文献[27-28]提出在灾前调节电源出力及削减负荷,并在灾后生成一个或多个IMG以提升配电网在自然灾害事件下的弹性。然而,上述预防调度研究主要关注故障前后微电网内静态功率平衡,未考虑孤岛微电网建立过程中的功率冲击。事实上,由于故障发生前输电线路上存在功率流通,故障后线路上功率突变会对孤岛微电网产生较大的阶跃型功率冲击[29],可能导致孤岛微电网内频率越限,进而引发电源切机保护动作及孤岛微电网崩溃。
针对上述问题,本文提出了一种考虑孤岛微电网建立过程中功率冲击的弹性配电网主动预防调度方法。主要创新点包括:①考虑了微电网建立过程中的功率冲击,通过在灾前对配电网进行预防调度,使灾后IMG能够安全建立;②所提方法无需在故障前运行微电网孤岛,减少了预防调度策略的保守性。
以台风灾害为例,对所提自然灾害下考虑IMG建立的配电网弹性运行过程进行说明,如图1所示。台风运动路径如图中蓝色箭头所示。当台风灾害尚未发生时,配电网处于正常运行状态。当台风灾害即将到来时,气象部门发出灾害预警,配电网进入主动预防阶段。其中,配电线路6-7发生断线故障概率较大,因此对该条线路上的流通功率进行限制,避免断线故障发生后对下游电网造成过大的功率冲击。当台风灾害引起配电线路6-7发生断线故障时,配电网进入应急控制阶段。灾害发生后,利用配电网中DG和未故障线路建立IMG,并重新调度DG出力以实现负荷持续供电量最大。在主动预防和应急控制阶段,为了满足供需平衡等约束,可以进行适当的负荷削减。如图1所示,在主动预防阶段对8号节点负荷进行全部削减,在应急控制阶段对10号节点负荷进行部分削减。

图1 弹性配电网灾前-灾后两阶段调度
Fig.1 Pre- and post- disaster two stage dispatch for resilient distribution systems
本文所提的配电网弹性运行操作框架如图2所示。首先,收集需要的数据信息并发送至控制中心,其中包括机组参数、负荷需求参数、配电网拓扑结构、预测的自然灾害强度等;然后,控制中心结合线路脆弱性曲线和自然灾害强度生成可能发生的故障场景及相应的故障概率,并根据所建立的调度模型决策优化的弹性运行策略;最后,控制中心发送调度指令以实施配电网运行方案。其中灾前主动预防调度阶段控制指令包括网架重构指令、DG灾前调度方案、负荷削减指令及线路流通功率控制指令;灾后应急控制阶段指令包括灾后电源再调度指令和负荷削减指令。
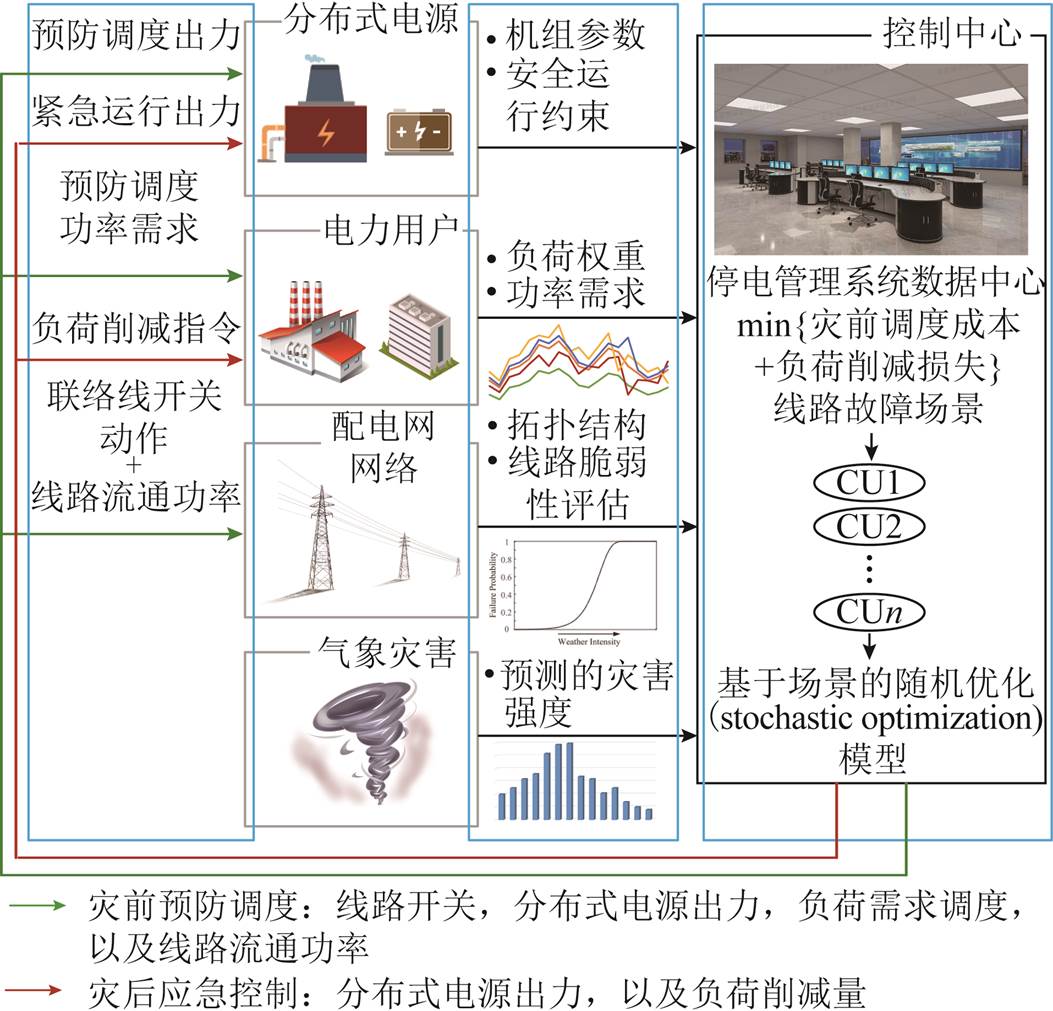
图2 配电网弹性运行框架
Fig.2 Operation framework of distribution systems
在自然灾害下,配电网线路故障具有不确定性。因此,本文以总运行成本和负荷损失量最小为目标,建立配电网弹性运行灾前-灾后两阶段随机优化调度模型。目标函数包含两部分:第一部分为配电网灾前预防调度成本,包括DG出力成本、与主网功率交互成本和灾前负荷削减成本;第二部分为各故障场景下的配电网灾后负荷削减成本。

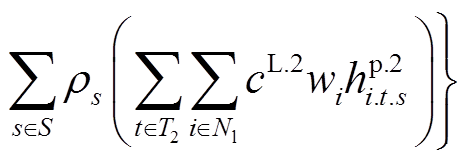 (1)
(1)
式中,上标“1”表示在灾前预防调度阶段的决策变量;上标“2”表示在灾后应急控制阶段的决策变量, s为故障场景;T1和T2分别为预防和应急控制时步集合;Ng为连有DG的节点集合;Nl为负荷节点集合;S为故障场景集合;ρs为故障场景s发生的概率;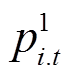 为预防调度阶段连在节点i上DG在第t时步的有功出力;cG为DG出力成本系数;
为预防调度阶段连在节点i上DG在第t时步的有功出力;cG为DG出力成本系数;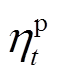 和
和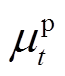 分别为第t时步配电系统中有功功率的不足及盈余;cB和cD分别为配电网向主网购电成本及售电收益系数;wi为节点i的权重系数;
分别为第t时步配电系统中有功功率的不足及盈余;cB和cD分别为配电网向主网购电成本及售电收益系数;wi为节点i的权重系数;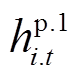 和
和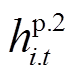 分别为预防调度和应急控制阶段节点i上负荷在第t时步的有功削减量;cL.1和cL.2分别为灾前预防阶段和灾后应急阶段的负荷削减成本系数。
分别为预防调度和应急控制阶段节点i上负荷在第t时步的有功削减量;cL.1和cL.2分别为灾前预防阶段和灾后应急阶段的负荷削减成本系数。
本文与现有研究的区别在于,在极端故障发生前,通过主动控制线路上的流通功率,以避免IMG建立时过大的功率冲击导致系统失稳。因此,本文引入决策变量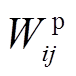 和
和 表示主动防御阶段线路(i,j)上允许流通的功率,并对孤岛微电网建立过程中的功率冲击进行了定量计算。
表示主动防御阶段线路(i,j)上允许流通的功率,并对孤岛微电网建立过程中的功率冲击进行了定量计算。
2.2.1 预防调度阶段模型
在极端自然灾害对配电网造成影响前,可以进行灾前预防调度,以减少故障真实发生时的配电网负荷损失。在进行灾前预防调度时,需要满足配电网辐射状、DG出力、系统潮流等安全约束。
1)电网辐射状约束
假设配电网上线路均配有柔性软开关[30],可以控制线路的开断、闭合状态以实现灾前网架重构。本文参考文献[31],引入虚拟潮流以保证配电网的辐射状运行。为了保证配电网的辐射状结构,虚拟潮流需要满足
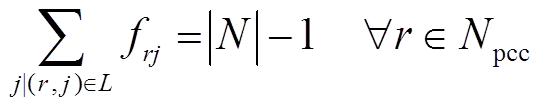 (2)
(2)
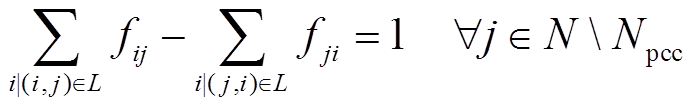 (3)
(3)
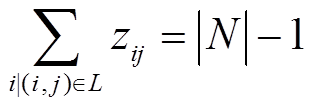 (4)
(4)
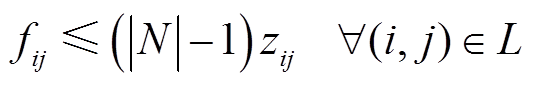 (5)
(5)
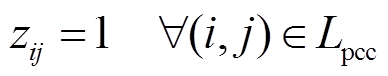 (6)
(6)
式中,整数变量fij为用于表征配电网辐射状的虚拟潮流;0-1变量zij为线路(i, j)上开关的闭合状态节点,zij=1表示开关闭合,线路(i, j)处于连通状态,zij=0表示开关打开,线路(i, j)处于断开状态;N为配电网中节点的集合;Npcc为配电网并网节点的集合;L为配电网中线路的集合;Lpcc为与并网节点相连的线路的集合。式(2)表示有|N|-1个弧离开根节点r以形成一个生成树;式(3)确保生成树的连通性;式(4)保证在所建立的生成树中,连通线路的数量应该比节点数少1;式(5)使得未连接的线路上虚拟潮流为0;式(6)确保与并网节点相连的线路处于连接状态。
2)分布式电源出力约束
配电网在进行灾前预防调度时,DG出力需要满足
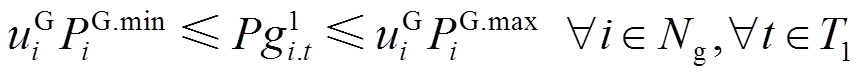 (7)
(7)
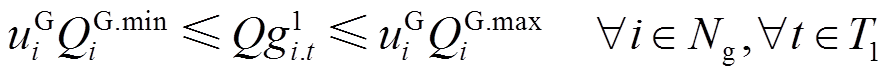 (8)
(8)
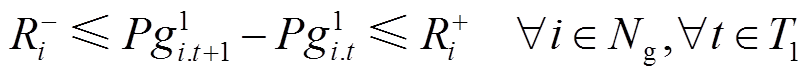 (9)
(9)
式中,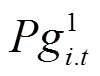 和
和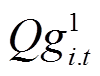 分别为主动防御阶段节点i上DG第t时刻的有功和无功调度出力;
分别为主动防御阶段节点i上DG第t时刻的有功和无功调度出力;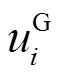 为节点i上DG的启停状态;
为节点i上DG的启停状态;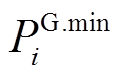 和
和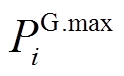 分别为节点i上DG的有功出力下、上限;
分别为节点i上DG的有功出力下、上限;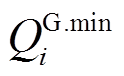 和
和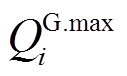 分别为节点i上DG的无功出力下、上限;
分别为节点i上DG的无功出力下、上限;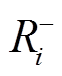 和
和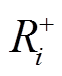 分别为点i上DG的允许下、上调功率限额。式(7)和式(8)对DG的输出功率大小进行了限制;式(9)对相邻时步的DG有功输出功率的变化量进行了限制。
分别为点i上DG的允许下、上调功率限额。式(7)和式(8)对DG的输出功率大小进行了限制;式(9)对相邻时步的DG有功输出功率的变化量进行了限制。
3)负荷削减约束
在灾前预防调度阶段,可以对部分非重要负荷进行功率削减,负荷削减量需满足
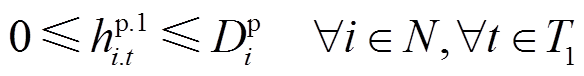 (10)
(10)
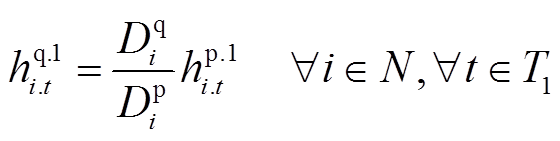 (11)
(11)
式中,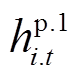 和
和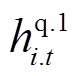 分别为预防调度阶段节点i上负荷在第t时刻的有功、无功功率削减量;
分别为预防调度阶段节点i上负荷在第t时刻的有功、无功功率削减量; 和
和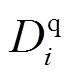 分别为配电网正常运行时节点i上负荷的有功、无功功率需求量。式(10)表示负荷有功功率削减量应小于负荷需求量;式(11)表示负荷无功功率与有功功率成比例削减。
分别为配电网正常运行时节点i上负荷的有功、无功功率需求量。式(10)表示负荷有功功率削减量应小于负荷需求量;式(11)表示负荷无功功率与有功功率成比例削减。
4)配电网操作约束
配电网运行过程中需要满足功率平衡和节点电压等操作约束。现有研究通常采用DistFlow模型[15]对辐射状结构的配电网潮流约束进行建模。进一步,考虑到配电网中线路损耗远小于线路功率[32],有学者提出了DistFlow的线性估计模型[33],并对其有效性进行了证明。在此基础上,本文引入表示线路连通状态的变量zij对线路压降平衡方程进行处理,使得线性DistFlow潮流适用于本文所提的灾前预防调度模型。此外,本文采用恒定的线路阻抗参数,暂不考虑微电网频率变化对系统参数的影响。
灾前主动防御阶段配电网操作约束可表示为

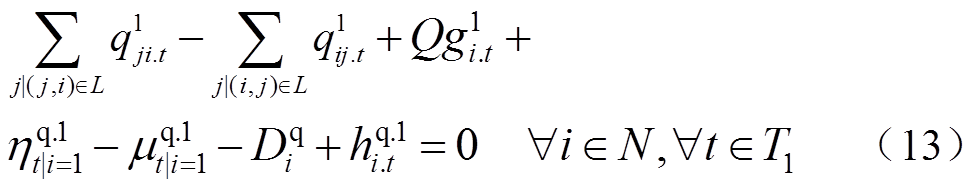
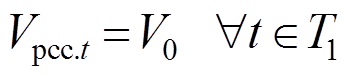 (14)
(14)
 (15)
(15)
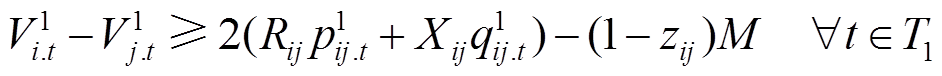 (16)
(16)
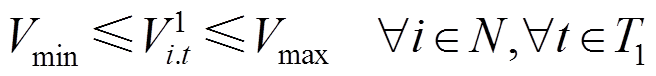 (17)
(17)
式中,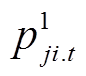 和
和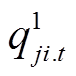 分别为主动预防调度阶段第t时刻从节点j流向节点i的有功、无功功率;Vpcc.t为t时刻配电网并网点电压幅值的二次方;V0为基准电压的二次方;
分别为主动预防调度阶段第t时刻从节点j流向节点i的有功、无功功率;Vpcc.t为t时刻配电网并网点电压幅值的二次方;V0为基准电压的二次方;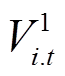 为预防调度阶段节点i在第t时刻电压幅值的二次方;Rij和Xij分别为线路的电阻和电抗;M为一个很大的常数;Vmin和Vmax分别为允许的电压偏移下限和上限。式(12)、式(13)分别表示各节点流入和流出有功/无功功率平衡;式(14)定义了配电网并网点电压为基准值;式(15)、式(16)用以计算节点的电压大小,当zij=1时,Vi和Vj之间为一个等式关系,当zij=0时,Vi和Vj之间关系不受式(15)、式(16)约束;式(17)为配电网节点允许电压偏差约束。
为预防调度阶段节点i在第t时刻电压幅值的二次方;Rij和Xij分别为线路的电阻和电抗;M为一个很大的常数;Vmin和Vmax分别为允许的电压偏移下限和上限。式(12)、式(13)分别表示各节点流入和流出有功/无功功率平衡;式(14)定义了配电网并网点电压为基准值;式(15)、式(16)用以计算节点的电压大小,当zij=1时,Vi和Vj之间为一个等式关系,当zij=0时,Vi和Vj之间关系不受式(15)、式(16)约束;式(17)为配电网节点允许电压偏差约束。
5)线路流通功率约束
在灾前预防调度阶段,线路上功率流通约束可表示为
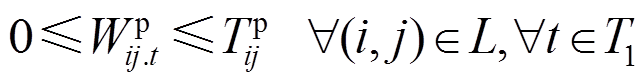 (18)
(18)
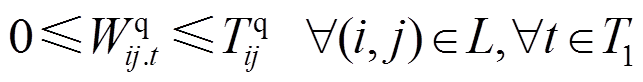 (19)
(19)
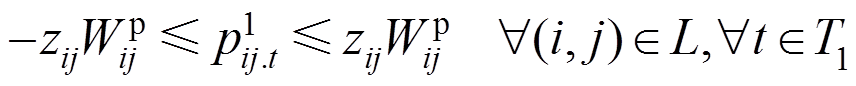 (20)
(20)
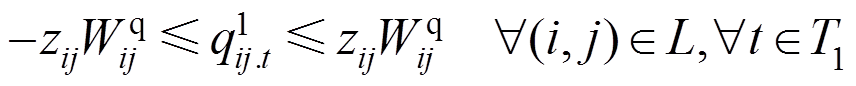 (21)
(21)
式中,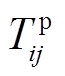 和
和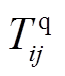 分别为配电网正常运行时线路(i, j)上允许流通的有功、无功功率;
分别为配电网正常运行时线路(i, j)上允许流通的有功、无功功率;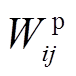 和
和 为决策变量,表示主动防御阶段线路(i, j)上允许流通的有功、无功功率。式(18)、式(19)对配电网线路上允许流通的功率大小进行了限制;式(20)、式(21)表示预防调度阶段线路上实际流通的功率大小应不大于允许的流通功率。
为决策变量,表示主动防御阶段线路(i, j)上允许流通的有功、无功功率。式(18)、式(19)对配电网线路上允许流通的功率大小进行了限制;式(20)、式(21)表示预防调度阶段线路上实际流通的功率大小应不大于允许的流通功率。
2.2.2 微电网建立过程功率冲击约束
本文引入“虚拟运动代理”(Virtual Moving Agent, VMA)对配电网拓扑进行建模,进一步描述故障后配电网中节点在IMG中的归属状态,并在此基础上计算IMG建立过程中的功率冲击。在一个具有n个节点的配电网中,VMA运动路径表被定义为一个n×n的0-1矩阵。矩阵中非对角线元素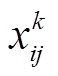 表示在第k个DG所在的IMG中从节点i到节点j之间VMA的运动情况。若节点i和节点j之间存在连通路径,则
表示在第k个DG所在的IMG中从节点i到节点j之间VMA的运动情况。若节点i和节点j之间存在连通路径,则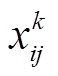 为0-1决策变量,否则
为0-1决策变量,否则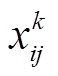 =0且无需决策。运动路径表的行和列分别为VMA的“离开”和“抵达”。
=0且无需决策。运动路径表的行和列分别为VMA的“离开”和“抵达”。
1)VEA运动路径约束
VMA运动路径应满足
 (22)
(22)
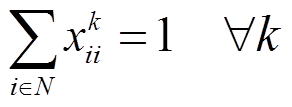 (23)
(23)
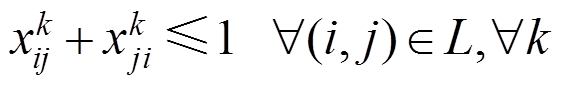 (24)
(24)
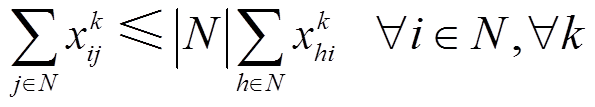 (25)
(25)
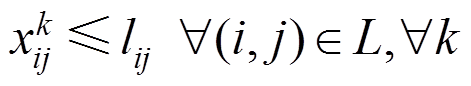 (26)
(26)
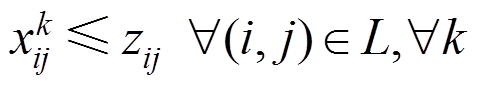 (27)
(27)
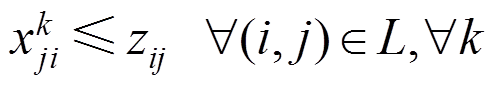 (28)
(28)
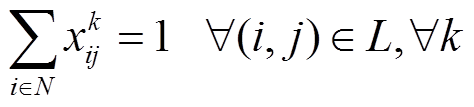 (29)
(29)
式(22)表示VMA运动路径的起点为DG所在节点;式(23)使VMA运动路径表对角线元素之和为1,表示运动路径有且仅有一个起点;式(24)表示VMA不能经过同一个节点超过一次;式(25)表示VMA经过节点j的前提是经过其上游节点i;式(26)~式(28)表示VMA仅能在存在连通路径的线路上运动;式(29)表示VMA能够抵达配电系统中所有节点。
2)故障后配电网状态建模
自然灾害发生后,配电网中线路会发生断线故障,引入矩阵y表征故障后配电网的拓扑状态。各个故障场景下,矩阵y中元素需要满足
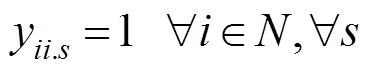 (30)
(30)
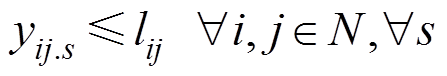 (31)
(31)
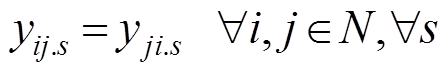 (32)
(32)
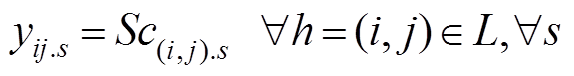 (33)
(33)
式中,lij为节点i和节点j之间是否存在线路连接;Sc(i,j).s为场景s下,线路(i, j)的中断情况。式(30)表示矩阵y中对角线元素为1;式(31)表示只有存在的线路才会发生故障;式(32)保证矩阵y是一个对称矩阵;式(33)表示当线路(i, j)发生故障时,yij=0。
3)功率冲击约束
引入变量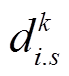 表征配电网发生故障场景s后节点i是否归属于DG k所在IMG。变量
表征配电网发生故障场景s后节点i是否归属于DG k所在IMG。变量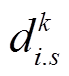 的表达式为
的表达式为
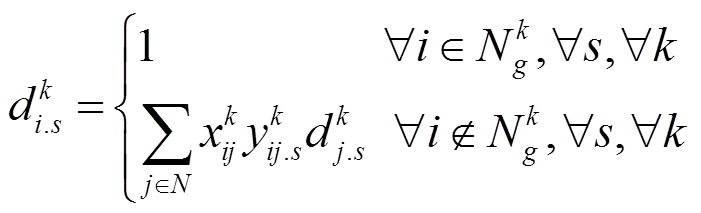 (34)
(34)
节点j归属于DG k所在IMG的前提是其上游节点i归属于该IMG,因此,变量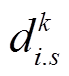 需要满足
需要满足
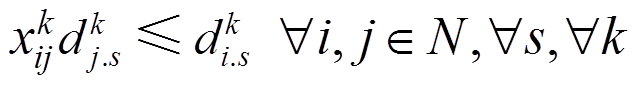 (35)
(35)
由此可以得到当配电网发生故障时,线路(i, j)上流通功率的突变对DG k所在IMG的功率冲击,有
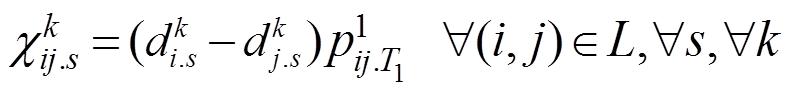 (36)
(36)
微电网建立过程中较大的功率冲击可能会导致微电网内频率失稳。因此,需要对微电网建立瞬间可承受的功率冲击进行限制,以避免较大的频率偏差,有
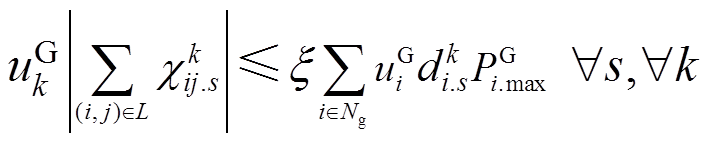 (37)
(37)
式中,ξ为频率响应比例因子,表示允许功率冲击量在DG总容量中的占比。本文参考文献[34],将允许功率冲击量被设为10%的DG总容量,因此式(37)中ξ设为0.1。
2.2.3 应急控制阶段模型
当配电网发生紧急故障后,需要对配电网进行灾后应急控制,以减少负荷停电损失。在进行灾后应急控制时,需要满足如下DG出力调节、负荷削减量、系统潮流、节点电压等安全约束。
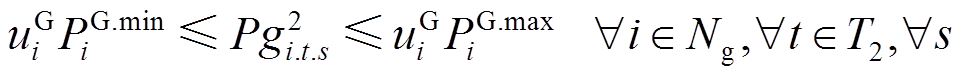 (38)
(38)
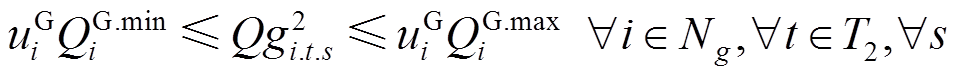 (39)
(39)
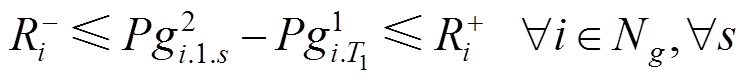 (40)
(40)
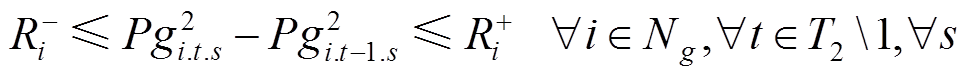 (41)
(41)
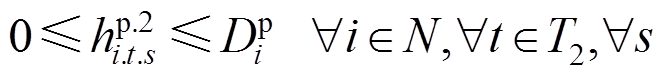 (42)
(42)
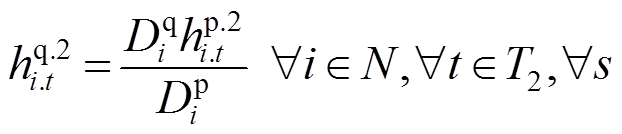 (43)
(43)
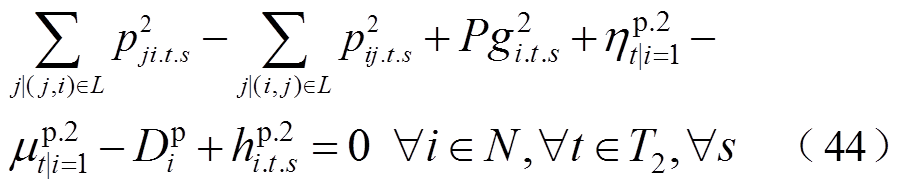
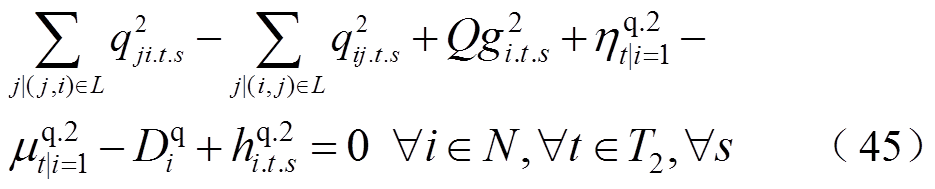
 (46)
(46)
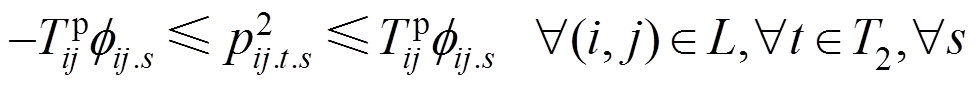 (47)
(47)
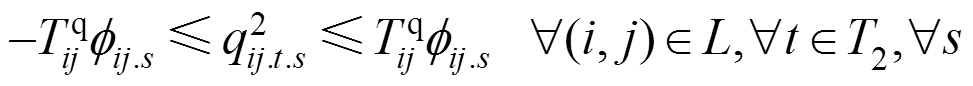 (48)
(48)
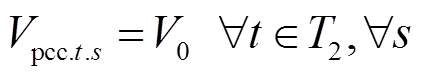 (49)
(49)
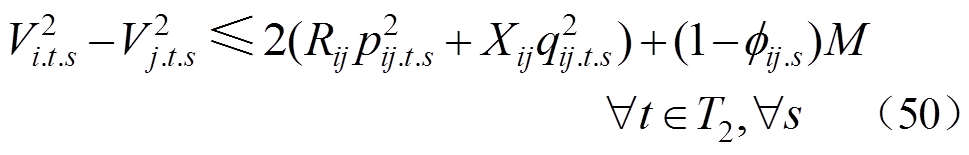
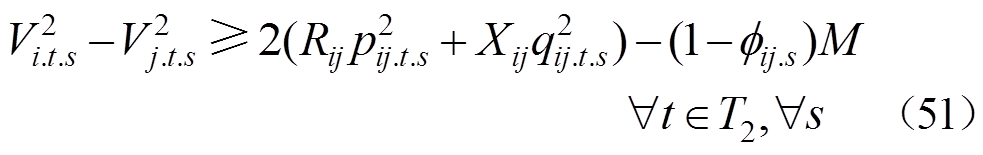
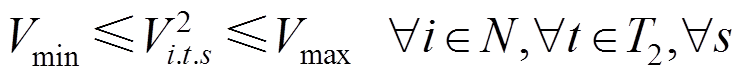 (52)
(52)
式(38)和式(39)对灾后应急控制阶段DG的输出功率大小进行了限制;式(40)和式(41)对相邻时步的DG有功输出功率的变化量进行了限制;式(42)和式(43)限制了灾后应急控制阶段的负荷削减量;式(44)和式(45)表示配电网中各节点流入和流出功率平衡;式(46)表示当节点i和节点j归属于同一个微电网时,线路(i, j)处于连接状态,变量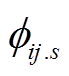 用来表示故障场景s下功率能否在线路(i, j)上流通;式(47)和式(48)对线路上的流通功率大小进行了限制;式(49)~式(51)用于计算配电网中各节点的电压;式(52)对处于供电状态的节点电压大小进行了限制。
用来表示故障场景s下功率能否在线路(i, j)上流通;式(47)和式(48)对线路上的流通功率大小进行了限制;式(49)~式(51)用于计算配电网中各节点的电压;式(52)对处于供电状态的节点电压大小进行了限制。
上述配电网弹性运行模型为混合整数非线性随机规划问题,通常采用启发式算法对其进行求解,存在收敛速度较慢且易出现局部最优化的问题。为了进一步提高求解效率,本节对模型中的非线性项进行线性化处理。
在原模型中,式(46)为条件约束,可以将其线性化为
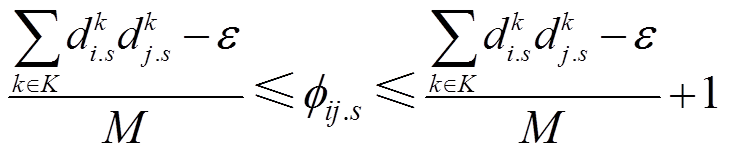 (53)
(53)
式中,ε为一个很小的正数。
式(37)中含有绝对值项,引入变量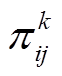 替换式(37)中绝对值项,并引入式(54)。
替换式(37)中绝对值项,并引入式(54)。
 (54)
(54)
式(34)、式(35)和式(37)中存在两个0-1变量相乘的情况,需要对其进行线性化处理。以式(35)中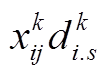 为例,引入一个新的变量
为例,引入一个新的变量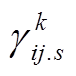 ,并用式(55)对其进行替换。
,并用式(55)对其进行替换。
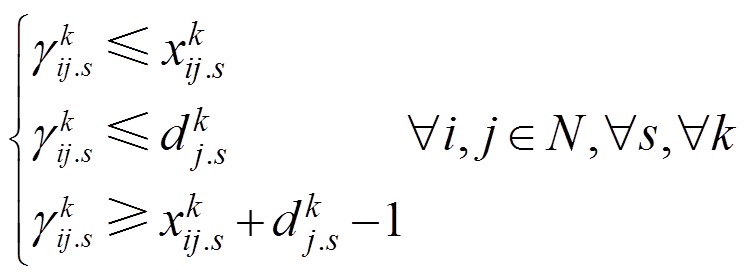 (55)
(55)
此外,灾前主动防御阶段线路容量约束式(20)、式(21)和式(36)、式(37)中还存在0-1变量与连续变量相乘的情况。以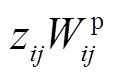 为例,可以利用McCormick envelopes法将其进行线性松弛,引入虚拟变量
为例,可以利用McCormick envelopes法将其进行线性松弛,引入虚拟变量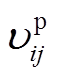 替代
替代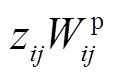 ,且满足
,且满足
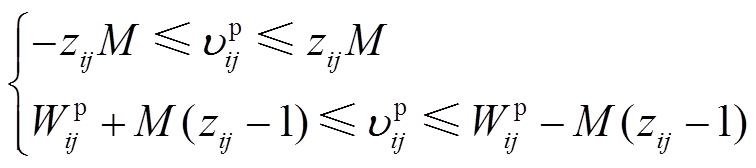 (56)
(56)
利用式(53)替代式(46),式(54)替代式(37),并用式(55)和式(56)中的线性化方法对式(20)、式(21)和式(34)~式(37)进行线性松弛,可以将原模型模型转换为混合整数线性随机(Mixed-Integer Linear Stochastic Programming, MILSP)规划模型。因此,考虑微电网建立过程中功率冲击的配电网弹性运行优化模型可表示如下凸优化问题,该模型可以利用CPLEX等商业求解器进行求解,从而有效地保证优化计算的收敛性和快速性。

本节利用改进的IEEE 13节点配电系统验证所提配电网弹性运行策略的有效性,系统的拓扑结构如图3所示。配电网中包括三条联络线633-692、675-680和646-611,配有两台分布式电源G1和G2。两台分布式电源均具有调频调压能力,操作人员可以对其进行优化调度,以辅助配电网弹性运行。配电网中电源的相关参数详见附表1。

图3 改进的IEEE 13节点系统
Fig.3 Modified IEEE 13-node test system
系统中负荷按重要程度分为三类:Ⅰ类包括关键负荷(如工厂、医院等);Ⅱ类表示重要负荷;Ⅲ类表示普通负荷。负荷参数包括权重、有功功率和无功功率需求量,由电网调度人员提供,本算例中的负荷参数详见附表2。
在台风灾害发生前,可以根据线路脆弱性曲线生成可能发生的系统故障场景及相应的概率。本文重点在于研究配电网弹性运行方法,故障场景及其概率的生成不属于本文研究范围。本算例通过四个故障场景说明所提模型的有效性,各场景中发生断线故障的线路及场景发生概率见表1。假设配电网弹性调度过程中两个连续时步之间的间隔为30 min,预防调度阶段持续时间为三个时步,应急控制阶段持续时间为三个时步。
表1 各场景中故障线路发生概率
Tab.1 Faulted lines in each scenario

故障场景故障线路发生概率 1650-6320.1 2632-645、671-6840.3 3632-671、671-6920.4 4632-671、671-692、680-6750.2
通过求解3.2节中所建立的配电网弹性运行模型,可以得到优化的灾前网架重构方案和主动防御阶段电源调度方案。进行仿真的计算机参数为:3.6 GHz的CPU主频及16 GB内存的酷睿i7处理器。本算例求解时间为16.74 s。
在灾害发生前,通过断开线路671-692和684-611上的开关,闭合联络线633-692和646-611上的开关对配电网进行灾前网架重构,以提升配电网在故障发生时的应对能力。优化的配电网灾前拓扑结构如图4所示。当配电网发生故障后,生成一个或多个IMG,每个IMG中至少含有一台DG。在灾害发生前后,配电网和IMG始终保持辐射状结构。
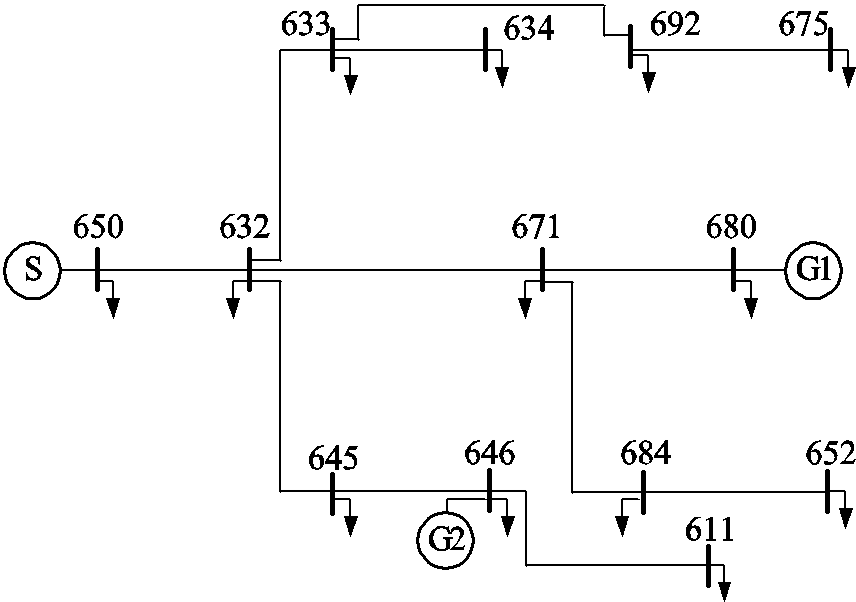
图4 优化的配电网拓扑
Fig.4 Optimized distribution system topology
在灾前预防调度阶段,配电网中各电源设备出力如图5所示。由于分布式电源出力成本小于向主网购电成本,在第1时步G2调度出力较大(出力为1100 kW),配电系统向主网购电量较少。但为了满足后续微电网生成过程中的功率冲击约束,G2逐步减小功率输出至510 kW,且满足发电机爬坡功率约束。同时,配电系统逐步增加向主网购电量以满足负荷功率需求。
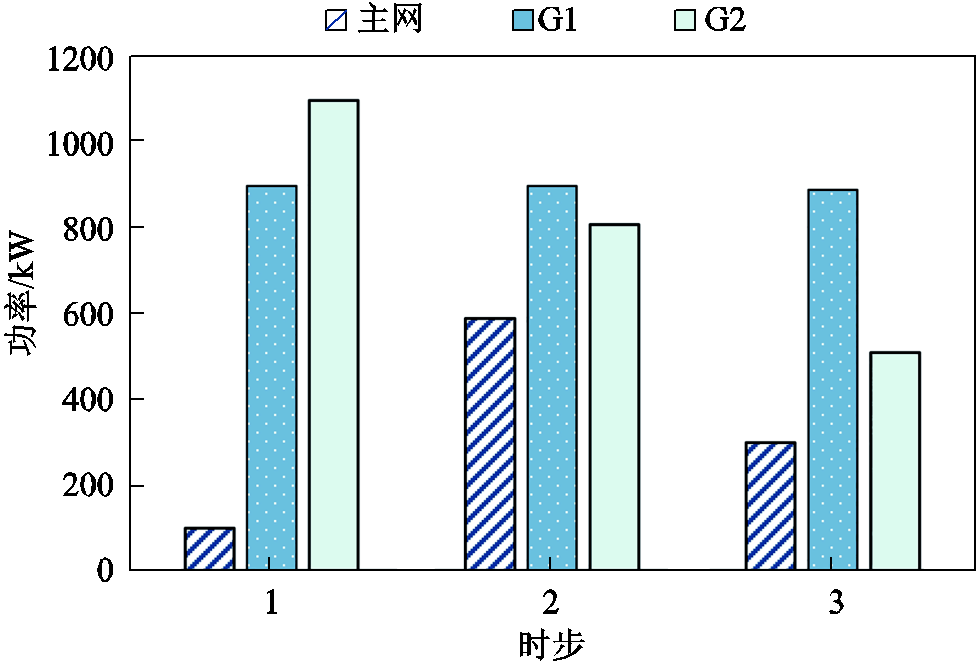
图5 预防调度阶段电源出力
Fig.5 Power source outputs in proactive stage
在主动预防调度阶段的第1时步和第2时步,配电网中不存在负荷削减,在第3时步为了满足后续功率冲击约束,节点633、634和692上分别削减负荷300 kW、200 kW和100 kW。
在第3时步,经过优化的线路流通功率见表2。在故障场景1中线路650-632发生故障,系统建立一个由G1和G2构成的IMG,因此将线路650-632上流通功率控制为200 kW;在故障场景2中线路632-645发生故障,系统建立一个由G2构成的IMG,因此将线路632-645上流通功率控制为110 kW;在故障场景3中线路632-671发生故障,系统建立一个由G1构成的IMG,因此将线路632-671上流通功率控制为90 kW。通过在灾前预防调度阶段控制线路上的流通功率,可以保证IMG建立过程中功率冲击不大于10%的DG总容量。
表2 经过优化的线路流通功率
Tab.2 Optimal power flow through lines

线路/kW线路/kW 650-632200692-675200 632-671-90632-645-110 671-680-690645-646-210 632-633300671-684400 633-6340684-652300 633-692300646-611100
当故障真实发生时,配电网进入应急控制阶段,DG和非故障线路通过构成IMG为重要负荷进行持续供电。图6展示了四个故障场景下各时步的电源出力,各故障场景下不同时步发生负荷削减的节点以及负荷削减量见表3。由于线路675-680在预防调度阶段被主动断开,因此场景4和场景3中故障线路相同,故两场景下电源出力和负荷削减量相同。
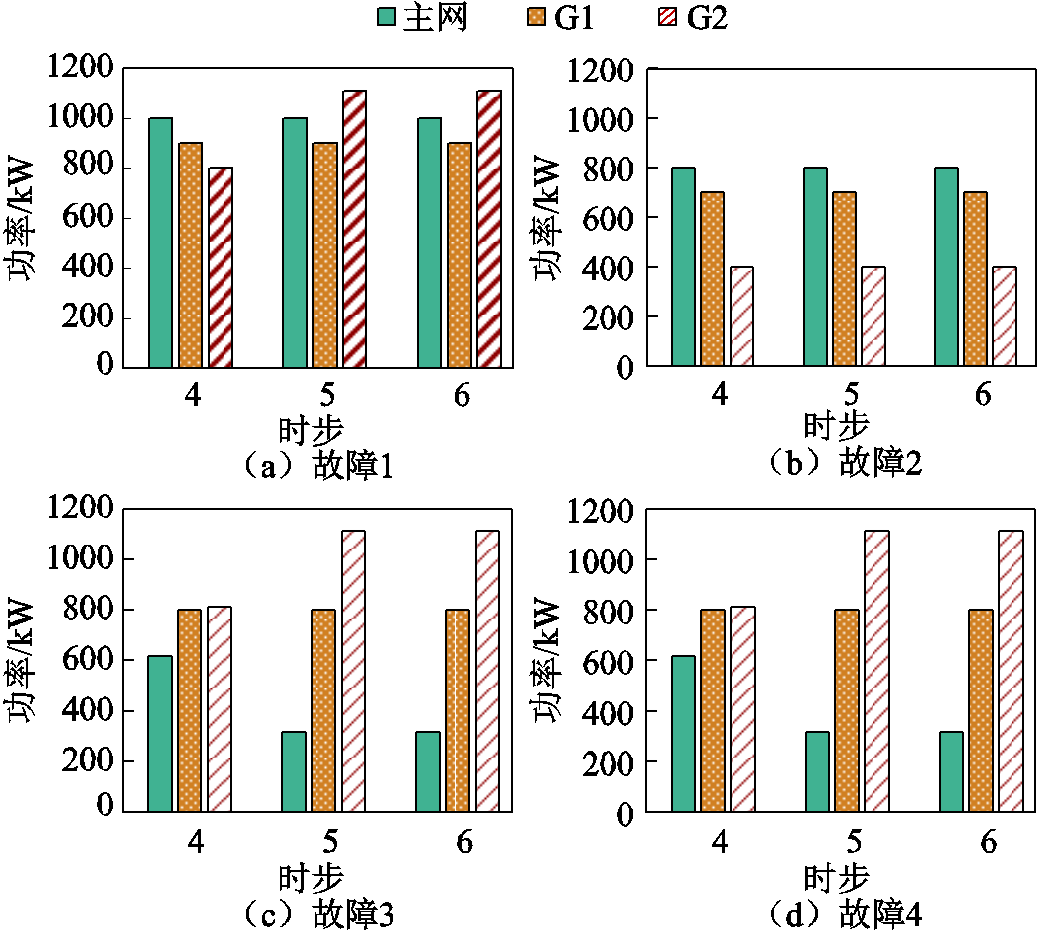
图6 应急控制阶段电源出力
Fig.6 Power source outputs in emergency control stage
从图6和表3中可以看出,微电网内电源设备的出力大小与负荷功率需求量始终保持一致。为了减少功率冲击,在预防调度阶段通常会减小电源出力,在孤岛微电网安全生成之后,电源设备会逐渐增大功率输出以满足应急控制阶段负荷的功率需求。
表3 不同故障场景下负荷削减量
Tab.3 Load shedding in different scenarios

场景负荷削减节点(削减量) 第4时步第5时步第6时步 1633(300 kW)634(190 kW)633(200 kW)633(200 kW) 2684(100 kW)652(300 kW)684(100 kW)652(300 kW)684(100 kW)652(300 kW) 3692(74.85 kW)692(63.28 kW)692(63.28 kW) 4692(74.85 kW)692(63.28 kW)692(63.28 kW)
4.3.1 考虑线路流通功率控制的必要性分析
本节通过两种调度方法说明所提配电网预防调度策略在提升微电网安全建立方面的有效性。方法1采用本文所提弹性调度方法在灾前对线路流通功率进行调节;方法2不考虑灾前主动预防调度,配电网以调度成本最小为目标经济运行,灾后紧急生成孤岛微电网[15]。在确定配电网灾前调度方案后,生成故障线路集以模拟可能发生的故障场景。进一步在Matlab/Simulink中搭建IMG模型对微电网建立过程中的系统频率进行仿真及校验。微电网频率动态模型及参数详见附录。
首先对预测样本内故障场景进行校验。以故障场景2为例,当线路632-645发生断线故障时,建立一个由G2构成的IMG。图7和图8分别展示了方法1和方法2中IMG建立过程中的动态频率。

图7 方法1中IMG建立过程中的动态频率
Fig.7 Frequency dynamic in IMG with Method 1
可以看出,配电网发生紧急故障时,线路上流通的功率会对微电网产生阶跃型功率冲击,导致微电网频率发生波动。由于本文所提方法在灾前对线路流通功率进行调节,IMG建立过程中功率冲击较小。IMG建立瞬间最大频率偏差小于0.4 Hz,且发电机通过调速器动态控制原动机出力可以将系统频率恢复至50 Hz,IMG能够安全建立。而方法2中发生断线故障时,会对G1所在IMG造成极大的功率冲击,导致G1转速快速上升。为防止转速过高引发设备故障,高频切机保护动作切除G1,进一步导致了微电网内频率崩溃。
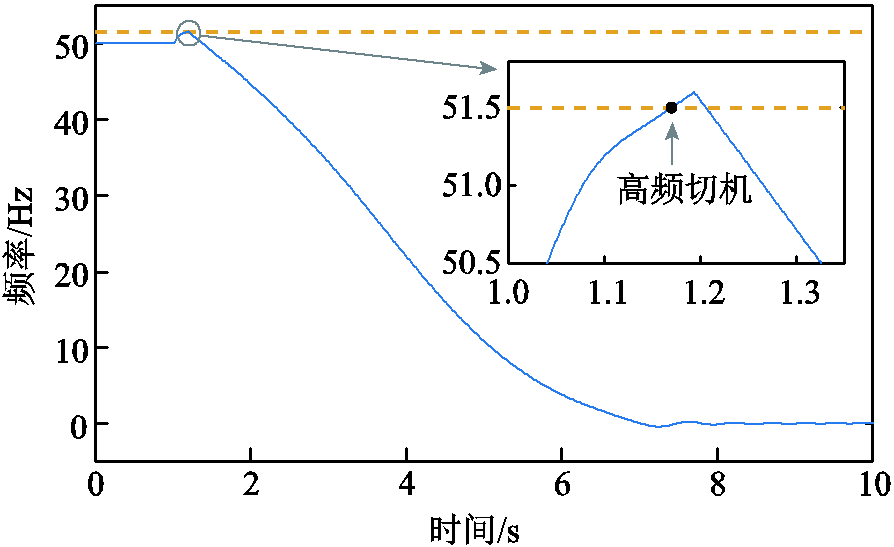
图8 方法2中IMG建立过程中的动态频率
Fig.8 Frequency dynamic in IMG with Method 2
进一步对预测样本外故障场景进行校验,通过蒙特卡洛抽样随机生成30个故障场景。当IMG由于安全约束越线无法顺利生成时,对该IMG内负荷进行切除操作。两种方法下负荷削减量期望值和发生故障后的IMG成功建立占比见表4。配电网弹性运行过程中两种方法下的总负荷电能损失量统计数据如图9所示。
表4 负荷削减量期望值和孤岛微电网成功建立占比
Tab.4 Expected load shedding and successful IMG formation rate

方法负荷削减量期望值/kWIMG成功建立占比(%) 11 169.84683.3 2548.76226.7
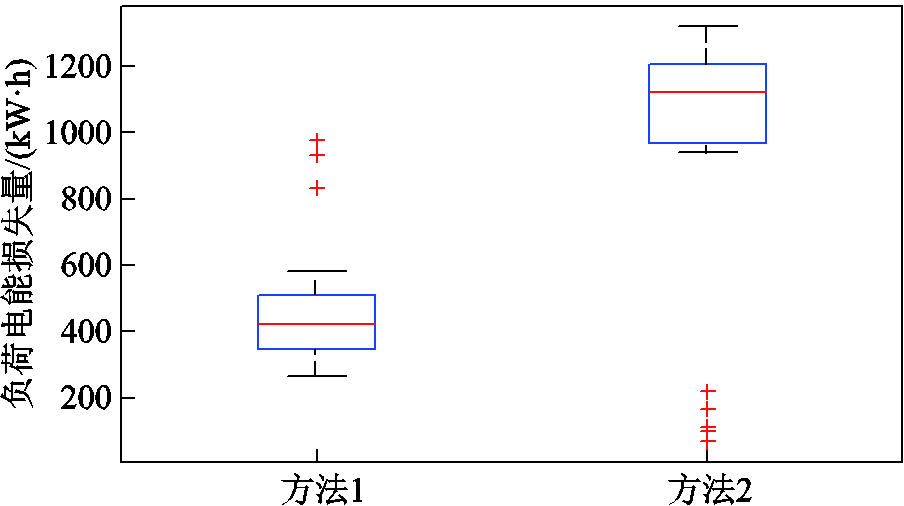
图9 两种方法下总负荷电能损失量统计数据
Fig.9 Statistical power loss of loads with two methods
从表4和图9可以看出:虽然方法2中负荷削减量期望值较低,但当断线故障真实发生时,由于IMG无法安全建立,会造成大量的负荷削减。而本文所提方法虽然在灾前对负荷进行了预防性削减,但在故障发生后能有效提升IMG建立过程中的安全性,因此能够保证更多重要负荷的持续供电。此外,方法1中也存在IMG无法成功建立的情况,这是因为随机规划无法涵盖所有可能发生的故障场景。通过提高对配电网故障场景预测的准确性,可以进一步提升预防调度策略的有效性。
4.3.2 网架重构对弹性运行策略的影响
进一步,通过两组对比算例验证在预防调度阶段考虑优化的网架重构方案对配电网弹性运行效果的影响。算例1:采用本文所提方法在预防调度阶段通过闭合联络线开关优化配电网结构,在此基础上决策预防调度策略;算例2:忽略配电网中联络线,仅根据正常运行时配电网结构对预防调度策略进行决策。两组对比算例中灾前预防调度阶段的负荷削减量,以及应急控制阶段各故障场景下的负荷削减量对比见表5。可以看出,相比于传统忽略网络架构优化的配电网弹性调度方法,在本算例中考虑灾前网架重构的弹性调度方法可以有效减少负荷削减量。这是因为优化的网架结构能有效提升配电网的灵活性,当极端故障真实发生时微电网中DG的利用率更高,能为更多的重要负荷供电。
表5 两组算例中负荷削减量对比
Tab.5 Comparison of load shedding in two cases

场景负荷削减量/kW 算例1算例2 灾前600690 灾后-场景18901 080 灾后-场景21 2001 500 灾后-场景3201.51 260 灾后-场景4201.51 260
4.3.3 所提方法与传统预防性IMG方法对比
进一步,通过对比算例3验证所提方法在减少配电网预防调度策略保守性方面的有效性。算例1采用本文所提方法对配电网进行预防性调度,在灾前对可能发生故障的线路上流通功率进行限制。算例3参考文献[23],在灾害发生前断开故障概率较高的线路上开关,从而将配电网主动划分为多个预防性微电网,各微电网孤岛运行,与外界不存在功率交互。以故障场景1为例,算例1和算例3中各时步的负荷供电量如图10所示。
从图10可以看出,相比于传统在故障前将微电网孤岛运行的预防调度方法,本文所提方法能有效提升负荷供电量。这是由于所提方法考虑IMG建立过程中能够承受一定的功率冲击,允许微电网灾前与外界存在功率交互,减少了预防调度阶段的负荷削减。到第6时步时,两算例中负荷供电量相同,这是由于故障后微电网内负荷完全由分布式电源进行供电。综上所述,本文所提方法可以在保证微电网安全建立的同时,减小弹性配电网预防调度策略的保守性。
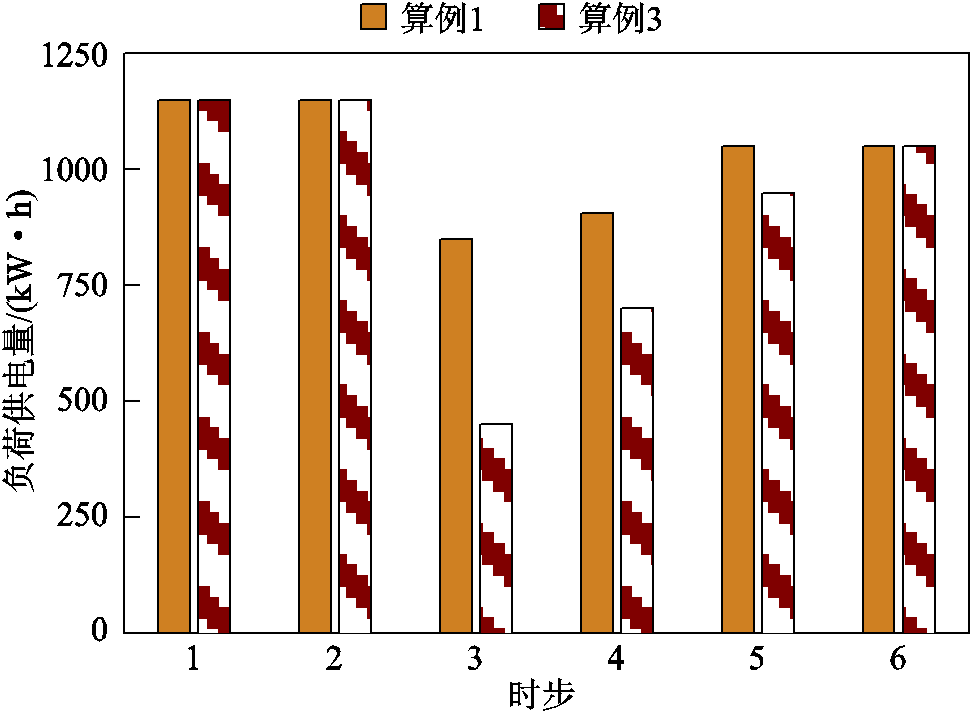
图10 两组对比算例中负荷供电量对比
Fig.10 Comparison of loads supplied in two cases
配电网发生紧急故障时,建立安全稳定孤岛微电网是维持重要负荷持续供电,提升配电网弹性的关键。为了保证孤岛微电网的安全建立,本文提出了一种考虑微电网建立过程中功率冲击的弹性配电网主动预防调度方法。以总运行成本最小为目标,建立配电网弹性运行两阶段随机优化模型,通过灾前网架重构并限制线路上的流通功率,减小断线故障发生时的功率冲击,使孤岛微电网能够安全建立。采用IEEE 13节点配电测试系统及Simulink仿真验证了本文所提主动预防调度方法的有效性。仿真结果表明:
1)相较于传统配网调度策略,在灾害发生前进行预防调度能有效减少IMG建立过程中的功率冲击,提升灾后IMG的安全性。
2)在灾前对配电网进行网架重构,能有效提升DG利用率,为更多重要负荷提供供电。
3)相比于传统在灾前将微电网孤岛运行的预防调度策略,所提方法能够在保证微电网安全生成的同时减少预防调度策略的保守性。
需要指出的是,本文重点在于提出一种考虑微电网建立过程功率冲击的弹性配电网主动预防调度方法,暂未考虑风电、光伏等可再生能源的参与。由于此类可再生能源的出力存在不确定性,会给孤岛微电网内功率平衡带来影响。如何考虑可再生能源出力不确定对电网主动预防调度的影响,将是下一步有待深入研究的工作。此外,本文所采用的潮流模型主要适用于辐射状配电网,但应用于环状配电网时存在收敛性问题。适用于环状配电网的主动预防调度策略是一个重要的研究方向。
附 录
附表1 配电网中电源相关参数
App.Tab.1 Parameters of power sources in the system

电源/kW/kvar/(kW/30min)c S-4 000, 5 000-3 000, 3 000-1 000, 1 0000.40 G10, 9000, 500-200, 2000.25 G20, 11000, 800-300, 3000.28
附表2 配电网中负荷相关参数
App.Tab.2 Parameters of nodes in the system

节点/kW/kvar 6500.855 710040 6324.454 510060 6714.796 5200120 6802.736 120080 6330.693 1300200 6340.746 5200100 6921.287 5200100 6754.203 6200100 6451.271 410080 6464.071 4200120 6841.217 6100100 6524.646 3300200 6111.749 9100100
微电网频率动态模型如附图1所示,IMG中DG的数学模型和频率控制模型参考文献[35]。此外,本文参考文献[36],引入了DG的高频切机保护,以模拟较大功率冲击下系统频率动态过程。在此模型中K=25, T1=0.01 s, T2=0.02 s, T3=0.2 s, T4=0.25 s, T5=0.009 s, T6=0.038 4 s, Td=0.024 s, M=2.14, D=0.2, ωcmax=1.03(pu)。
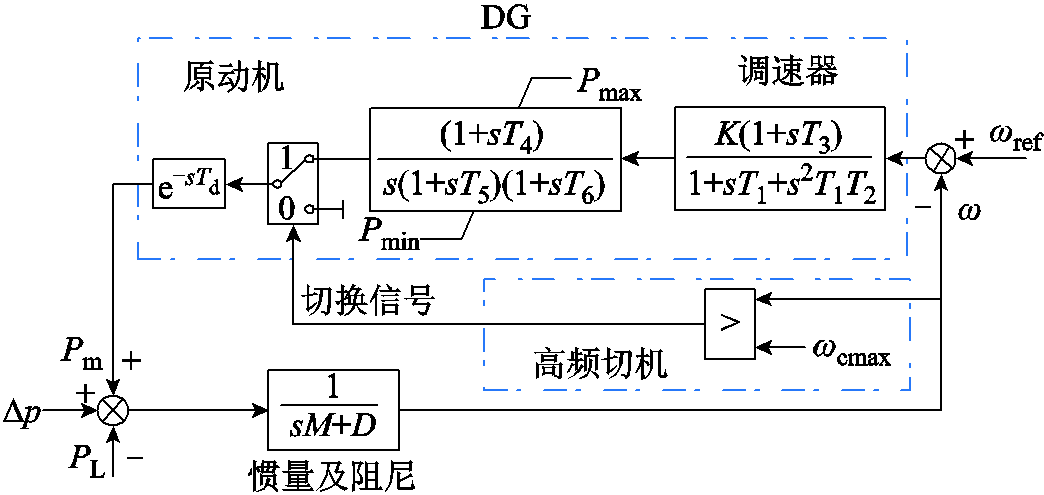
附图1 微电网频率动态模型
App.Fig.1 Frequency dynamic model in microgrids
参考文献
[1] 别朝红, 林雁翎, 邱爱慈. 弹性电网及其恢复力的基本概念与研究展望[J]. 电力系统自动化, 2015, 39(22): 1-9. Bie Zhaohong, Lin Yanling, Qiu Aici. Concept and research prospects of power system resilience[J]. Automation of Electric Power Systems, 2015, 39(22): 1-9.
[2] Tan Yushi, Das A K, Arabshahi P, et al. Distribution systems hardening against natural disasters[J]. IEEE Transactions on Power Systems, 2018, 33(6): 6849-6860.
[3] Wang Xu, Li Zhiyi, Shahidehpour M, et al. Robust line hardening strategies for improving the resilience of distribution systems with variable renewable resources[J]. IEEE Transactions on Sustainable Energy, 2019, 10(1): 386-395.
[4] 尉耀稳, 李跃龙, 陈思超, 等. 多类型源储协调互动的配电网分布鲁棒优化调度[J]. 电力工程技术, 2021, 40(5): 192-199. Yu Yaowen, Li Yuelong, Chen Sichao, et al. Distributionally robust optimal dispatch of distribution network considering multiple source-storage coordinated interaction[J]. Electric Power Engineering Technology, 2021, 40(5): 192-199.
[5] 姜云鹏, 任洲洋, 李秋燕, 等. 考虑多灵活性资源协调调度的配电网新能源消纳策略[J]. 电工技术学报, 2022, 37(7): 1820-1835. Jiang Yunpeng, Ren Zhouyang, Li Qiuyan, et al. An accommodation strategy for renewable energy in distribution network considering coordinated dispatching of multi-flexible resources[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1820-1835.
[6] 倪萌, 王蓓蓓, 朱红, 等. 能源互联背景下面向高弹性的多元融合配电网双层分布式优化调度方法研究[J]. 电工技术学报, 2022, 37(1): 208-219. Ni Meng, Wang Beibei, Zhu Hong, et al. Study of two-layer distributed optimal scheduling strategy for highly elastic multi-resource fusion distribution network in energy interconnection environment[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 208-219.
[7] 许寅, 和敬涵, 王颖, 等. 韧性背景下的配网故障恢复研究综述及展望[J]. 电工技术学报, 2019, 34(16): 3416-3429. Xu Yin, He Jinghan, Wang Ying, et al. A review on distribution system restoration for resilience enhancement[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3416-3429.
[8] 王钰山, 邓晖, 王旭, 等. 考虑台风时空演变的配电网移动储能优化配置与运行策略[J]. 电力系统自动化, 2022, 46(9): 42-51. Wang Yushan, Deng Hui, Wang Xu, et al. Optimal configuration and operation strategy of mobile energy storage in distribution network considering spatial-temporal evolution of typhoon[J]. Automation of Electric Power Systems, 2022, 46(9): 42-51.
[9] Manshadi S D, Khodayar M E. Resilient operation of multiple energy carrier microgrids[J]. IEEE Transactions on Smart Grid, 2015, 6(5): 2283-2292.
[10] Liu Jianzhe, Lu Xiaonan, Wang Jianhui. Resilience analysis of DC microgrids under denial of service threats[J]. IEEE Transactions on Power Systems, 2019, 34(4): 3199-3208.
[11] Wang Zhaoyu, Chen Bokan, Wang Jianhui, et al. Networked microgrids for self-healing power systems[J]. IEEE Transactions on Smart Grid, 2016, 7(1): 310-319.
[12] Ambia M N, Meng Ke, Xiao Weidong, et al. Nested formation approach for networked microgrid self-healing in islanded mode[J]. IEEE Transactions on Power Delivery, 2021, 36(1): 452-464.
[13] Shen Feifan, Wu Qiuwei, Zhao Jin, et al. Distributed risk-limiting load restoration in unbalanced distribution systems with networked microgrids[J]. IEEE Transactions on Smart Grid, 2020, 11(6): 4574-4586.
[14] Kim J, Dvorkin Y. Enhancing distribution system resilience with mobile energy storage and microgrids[J]. IEEE Transactions on Smart Grid, 2019, 10(5): 4996-5006.
[15] Wang Zhaoyu, Wang Jianhui. Self-healing resilient distribution systems based on sectionalization into microgrids[J]. IEEE Transactions on Power Systems, 2015, 30(6): 3139-3149.
[16] Chen Chen, Wang Jianhui, Qiu Feng, et al. Resilient distribution system by microgrids formation after natural disasters[J]. IEEE Transactions on Smart Grid, 2016, 7(2): 958-966.
[17] 陈厚合, 丛前, 姜涛, 等. 多能协同的配电网供电恢复策略[J]. 电工技术学报, 2022, 37(3): 610-622, 685. Chen Houhe, Cong Qian, Jiang Tao, et al. Distribution systems restoration with multi-energy synergy[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 610-622, 685.
[18] 李振坤, 周伟杰, 王坚敏, 等. 基于风光荷功率曲线的有源配电网动态孤岛划分方法[J]. 电力系统自动化, 2016, 40(14): 58-64, 71. Li Zhenkun, Zhou Weijie, Wang Jianmin, et al. Dynamic islanding method of active power distribution network based on wind-photovoltaic-load curve[J]. Automation of Electric Power Systems, 2016, 40(14): 58-64, 71.
[19] 张瑞曦, 徐青山, 程煜, 等. 极端灾害下考虑动态重构的微电网形成策略[J]. 电力工程技术, 2022, 41(1): 56-63. Zhang Ruixi, Xu Qingshan, Cheng Yu, et al. Microgrid formation strategy considering dynamic reconstruction under extreme disasters[J]. Electric Power Engineering Technology, 2022, 41(1): 56-63.
[20] 詹红霞, 肖竣文, 邓小勇, 等. 计及柔性负荷的高比例风光渗透下配电网孤岛划分策略[J]. 电力工程技术, 2022, 41(4): 108-116. Zhan Hongxia, Xiao Junwen, Deng Xiaoyong, et al. Islanding strategy for distribution network with high proportion of wind/photovoltaic penetration considering flexible load[J]. Electric Power Engineering Technology, 2022, 41(4): 108-116.
[21] Cai Sheng, Xie Yunyun, Wu Qiuwei, et al. Active and reactive power coordinated two-stage MG scheduling for resilient distribution systems under uncertainties[J]. IEEE Transactions on Smart Grid, 2022, 13(4): 2986-2998.
[22] Panteli M, Trakas D N, Mancarella P, et al. Boosting the power grid resilience to extreme weather events using defensive islanding[J]. IEEE Transactions on Smart Grid, 2016, 7(6): 2913-2922.
[23] Liu Jiancun, Qin Chao, Yu Yixin. Enhancing distribution system resilience with proactive islanding and RCS-based fast fault isolation and service restoration[J]. IEEE Transactions on Smart Grid, 2020, 11(3): 2381-2395.
[24] Pandey S, Chanda S, Srivastava A K, et al. Resiliency-driven proactive distribution system reconfiguration with synchrophasor data[J]. IEEE Transactions on Power Systems, 2020, 35(4): 2748-2758.
[25] Khodaei A. Resiliency-oriented microgrid optimal scheduling[J]. IEEE Transactions on Smart Grid, 2014, 5(4): 1584-1591.
[26] Lee J, Lee S, Lee K. Multistage stochastic optimization for microgrid operation under islanding uncertainty[J]. IEEE Transactions on Smart Grid, 2021, 12(1): 56-66.
[27] Amirioun M H, Aminifar F, Lesani H. Resilience-oriented proactive management of microgrids against windstorms[J]. IEEE Transactions on Power Systems, 2018, 33(4): 4275-4284.
[28] Gholami A, Shekari T, Grijalva S. Proactive management of microgrids for resiliency enhancement: an adaptive robust approach[J]. IEEE Transactions on Sustainable Energy, 2019, 10(1): 470-480.
[29] Tang Fen, Guerrero J M, Vasquez J C, et al. Distributed active synchronization strategy for microgrid seamless reconnection to the grid under unbalance and harmonic distortion[J]. IEEE Transactions on Smart Grid, 2015, 6(6): 2757-2769.
[30] 贾冠龙, 陈敏, 赵斌, 等. 柔性多状态开关在智能配电网中的应用[J]. 电工技术学报, 2019, 34(8): 1760-1768. Jia Guanlong, Chen Min, Zhao Bin, et al. Application of flexible multi-state switch in intelligent distribution network[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1760-1768.
[31] Babaei S, Jiang Ruiwei, Zhao Chaoyue. Distributionally robust distribution network configuration under random contingency[J]. IEEE Transactions on Power Systems, 2020, 35(5): 3332-3341.
[32] Turitsyn K, Šulc P, Backhaus S, et al. Distributed control of reactive power flow in a radial distribution circuit with high photovoltaic penetration[C]//IEEE PES General Meeting, Minneapolis, MN, USA, 2010: 1-6.
[33] Yeh H G, Gayme D F, Low S H. Adaptive VAR control for distribution circuits with photovoltaic generators[J]. IEEE Transactions on Power Systems, 2012, 27(3): 1656-1663.
[34] Bassey O, Butler-Purry K L, Chen Bo. Dynamic modeling of sequential service restoration in islanded single master microgrids[J]. IEEE Transactions on Power Systems, 2020, 35(1): 202-214.
[35] 郭力, 富晓鹏, 李霞林, 等. 独立交流微电网中电池储能与柴油发电机的协调控制[J]. 中国电机工程学报, 2012, 32(25): 70-78, 12. Guo Li, Fu Xiaopeng, Li Xialin, et al. Coordinated control of battery storage and diesel generators in isolated AC microgrid systems[J]. Proceedings of the CSEE, 2012, 32(25): 70-78, 12.
[36] 张培高, 李兴源, 李政. 孤网频率稳定与控制策略研究[J]. 电力系统保护与控制, 2012, 40(15): 143-149, 155. Zhang Peigao, Li Xingyuan, Li Zheng. Research on frequency stability and control strategy in isolated power grid[J]. Power System Protection and Control, 2012, 40(15): 143-149, 155.
Abstract When an emergency accident occurs in the distribution system under extreme conditions, multiple islanded microgrids (IMGs) are formed to ensure constant power supply to critical loads, which is essential for reducing outage range and enhancing system resilience. However, traditional IMG formation methods focuses on passive MG formation after an emergency and, hence, cannot guarantee the successful IMG formation in the event of significant power imbalance. Recently, proactive approaches were presented to ensure adequate spinning reserve in supplying load demand after the IMG formation, but most of them ignored the non-zero power flow at the moment line disconnects. This was insufficient to ensure a successful MG formation because the significant power impact may lead to the frequency instability in IMGs. To address these issues, this paper proposed a proactive scheduling method that considers the power impact during the IMG formation process. By mitigating the power impact when line outage happens, IMGs can be formed safely and reliably after extreme event happens.
Firstly, a pre- and post-disaster two-stage coordinated stochastic model that considers the power impact was formulated to minimize the operation costs and load shedding. Next, the nonlinear terms in original model were linearized, and thus the nonlinear stochastic model was transformed to a mixed integer linear programming problem to facilitate solution. The main differences between the proposed proactive scheduling model and those in existing literature lie in the line transmission power constraints, in which decision variables 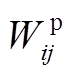 and
and 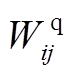 were introduced to restrict the power flow on vulnerable lines prior to the extreme event. In addition, unit commitment and network reconfiguration were also considered in the proposed model to enhance the flexibility of scheduling scheme.
were introduced to restrict the power flow on vulnerable lines prior to the extreme event. In addition, unit commitment and network reconfiguration were also considered in the proposed model to enhance the flexibility of scheduling scheme.
Simulation results on the modified IEEE 13 bus distribution system show that, prior to the event strikes, switches on lines 671-692 and 684-611 are opened and switches on lines 633-692 and 646-611 are closed to optimize the configuration of distribution network. To satisfy the power impact constraint during IMG formation, power flow on lines is restricted and appropriate load shedding (600 kW in this case) is allowed at the pre-disaster stage. When line outage emergencies occur, several IMG are seamless formed to continue supporting critical loads. The total generation of power sources in one MG is equal to the total amount of load consumption for each time step. Comparison of different operation methods shows that, the successful IMG formation rate for operation method with/without considering proactive scheduling is 83.3% and 26.7%, respectively. In other words, the proposed method can improve IMGs’ survivability after disaster but understandably cannot totally avoid the collapse. This is because the stochastic approach cannot be able to cover all the contingency scenarios that may occur. The comparison with proactive scheduling method without network reconfiguration shows that, the optimal network topology can reduce the amount of load shedding by forming more flexible IMGs and improve energy utilization efficiency of power sources. The comparison with traditional preventive defensive islanding method shows that, the proposed method can reduce the amount of load shedding by about 15%. This is because the proposed method reduces power imbalance in MGs through restricting power flow on vulnerable lines rather than totally avoid it. Therefore, less conservative proactive scheduling schemes resulting in less load shedding can be obtained.
The following conclusions can be drawn from the simulation analysis: (1) Compared with traditional distribution system scheduling method, proactive scheduling can reduce the power impact when line outage happens, thereby enhancing the resilience of DSs through forming feasible MGs after extreme events. (2) The proposed model optimizes the network topology prior to the event. Therefore, more flexible MG topology can be obtained to satisfy the supply-and-demand balance and more critical loads can be supplied. (3) The proposed method allows power flow on vulnerable lines before the outage. Compared with the preventive defensive islanding method, a secure and less conservative scheduling strategy can be obtained.
keywords:Resilient distribution system, islanded microgrid, proactive scheduling, power impact, frequency stability
DOI:10.19595/j.cnki.1000-6753.tces.221682
中图分类号:TM73
国家自然科学基金(52177090)和江苏省卓越博士后计划资助项目。
收稿日期 2022-09-02
改稿日期 2022-10-08
蔡 胜 男,1994年生,博士,研究方向极端条件下电力系统运行与控制。E-mail:cs@njust.edu.cn
谢云云 男,1985年生,副教授,研究方向极端条件下电力系统运行与控制、新能源黑启动等。E-mail:xyy_njust@163.com(通信作者)
(编辑 赫蕾)