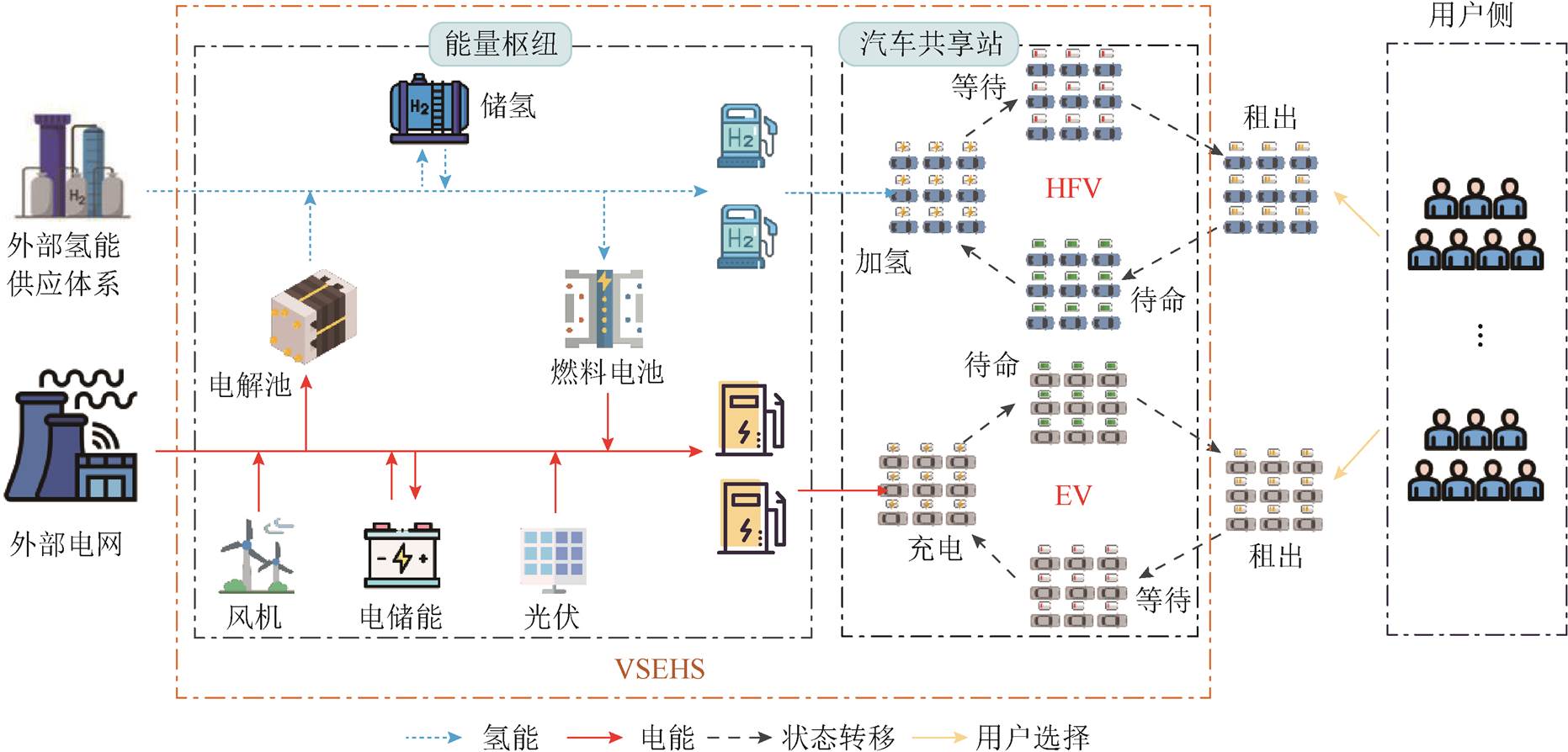
图1 VSEHS系统基本架构
Fig.1 Basic structure of the VSEHS
摘要 在新能源汽车快速发展下,为充分发挥其对交通与能源领域低碳转型目标实现的支撑作用,该文考虑由电动汽车与氢燃料汽车间用车需求可替代性带来的负荷灵活性,采用综合资源规划理念,提出一种含新能源汽车共享站的电-氢微能源网(VSEHS)两阶段规划框架。首先,结合不同参数数据源的异质性,采用区间和概率相结合的混合建模方法处理不确定性,并开展基于演化博弈的用户多车型选择长期偏好及其演化建模,刻画共享汽车服务下用户需求对租赁定价的潜在灵活性;其次,在利用租赁价格引导用户需求的基础上,考虑多种不确定性因素影响下的系统运行模拟,构建基于区间-随机混合规划的VSEHS容量配置与定价决策优化模型;然后,提出区间-随机混合优化方法,将不同类型的不确定性变量归一化,并在同一框架下基于启发式算法实现高效求解;最后,通过相关算例分析,验证所提方法的有效性。
关键词:新能源汽车共享站 电-氢微能源网规划 演化博弈 分时租赁定价 区间-随机混合优化
在“碳达峰、碳中和”目标要求下,为实现交通领域低碳转型,近年来我国大力推动以电动汽车(Electric Vehicle, EV)和氢燃料汽车(Hydrogen Fuel-cell Vehicle, HFV)为主的新能源汽车发展[1-2]。然而,为真正发挥新能源汽车推广对双碳目标的支撑作用,需尽可能保证作为新能源汽车动力的电能与氢能供应来源于可再生能源,否则即是仅仅将车辆行驶过程中的碳排放转移至了能源供应侧[3]。而依托终端停车场和电制氢技术,以电-氢耦合微能源网的形式建立EV充电设施、HFV加氢站与可再生能源发电的直接关联[4-6],则为实现上述目标提供了重要解决方案。
目前,国内外学者已围绕该类基于停车场的微能源网规划开展了一系列的研究。文献[7]提出了同时满足EV充电需求、换电需求及HFV加氢需求的新能源汽车一体化供能站规划模型,实现了可再生能源和多类型新能源汽车充能需求的联合管理;文献[8-10]进一步在规划阶段考虑了可再生能源发电、新能源汽车充电需求及加氢需求的不确定性,分别采用随机优化、鲁棒优化等方法建立了电-氢微能源网容量规划模型;文献[11-13]发掘能源-交通系统之间的互动潜力,建立了基于充电站和加氢站建设的城市综合能源系统规划模型,缓解电力和天然气网络的线路拥堵。为提高新能源汽车动力来源中可再生能源的比例,现有规划研究还进一步考虑利用价格引导用户侧车辆的动力补充行为,使之与可再生能源随机出力匹配,减少因供需不平衡引起的弃风弃光。文献[14]将价格型需求响应纳入共享电动汽车站点规划,结果显示需求响应策略在促进可再生能源消纳的同时,还可减少共享电动汽车的调度时间;文献[15]通过施加外部激励引导EV车主主动参与需求响应计划;文献[16-17]在含EV充电站的配电网扩展规划中,基于动态定价机制引导用户改变EV充放电需求,与可再生能源出力相协调以实现源网荷的利益平衡。
然而,上述研究普遍关注由供应侧电-氢耦合互补,以及需求侧EV或HFV单一动力补充负荷转移所带来的系统灵活性,鲜有研究考虑由EV和HFV间的交通可替代性所带来的能量需求可转化特性。具体而言,用户的出行需求可通过驾驶EV或驾驶HFV满足[18],EV与HFV在用车需求方面的双向可转化特性可带来电-氢负荷间的转化,而若对此加以利用,通过价格引导用户出行用车选择,则可进一步提高系统的灵活性,促进可再生能源消纳。租赁模式下的新能源汽车共享站可认为是实现EV与HFV间用车需求替代及其能量需求转化的典型场景之一[19],鉴于此,本文提出一种基于新能源汽车共享站的电-氢微能源系统(New Energy Vehicle Sharing Station-Based Electro-Hydrogen Micro-Energy System, VSEHS),以同时推进能源-交通领域的低碳转型。
目前,国内外少有关于VSEHS规划的研究,与基于停车场的微能源网规划相比,有效描述用户的车辆选择行为及其动态特性是VSEHS规划面临的重要挑战。由于用户的车辆选择偏好受到租赁价格、服务满意度等因素影响[20-22],且从长期来看,用户的车辆选择行为非一成不变的,可能会随着外部因素的刺激而调整用车策略以最大化自身利益[23],因此在VSEHS规划决策中必须适当考虑需求侧特征的演化性质,通过合理的租赁价格方案引导用户车辆选择偏好,从而提高可再生能源的利用率及VSEHS的投资运营效益。当前虽已有学者基于用户出行选择行为特征分析开展了共享电动汽车定价策略研究[24-25],但现有研究主要通过动态分时租赁价格引导用户改变短时车辆使用行为以缓解交通拥堵,一方面未考虑能源-交通耦合以促进可再生能源消纳,另一方面鲜有文献在规划阶段通过优化价格以引导用户长期车辆选择偏好。
此外,VSEHS规划面临着可再生能源出力和用户出行需求带来的多种不确定性。其中,用户出行需求可通过调查问卷等方法在短时间内获得大量有效数据,便于用基于概率分布的随机变量表示[26]。而可再生能源出力的准确概率分布需要长期的气象监测,在历史数据未知的地点通常难以获得满意的数据,因此有学者认为利用区间数表示可再生能源出力既能保留相应的不确定信息,又便于实现,具有更强的合理性[27]。由此,VSEHS规划将同时含有随机参数和区间参数两类不确定性变量,这使得问题求解具有一定难度,而现有文献中鲜有区间和随机参数联合求解的相关经验。
针对上述研究的不足,本文提出一种容量配置与车辆租赁价格协同优化的VSEHS综合资源规划框架。首先,阐述VSEHS系统架构及考虑多能源-多车型协调互济的低碳运行模式;其次,系统刻画可再生能源及用户需求的不确定性,开展基于演化博弈的用户多车型选择长期偏好及其演化建模;然后,引入基于租赁价格的用户出行引导方案,构建了基于区间-随机混合优化的VSEHS设备配置与定价决策两阶段规划模型;最后,考虑不同形式的不确定变量,提出区间-随机混合求解方法,将其转化为确定性优化问题求解。算例仿真结果验证了本文所提方法的有效性。
本文提出的VSEHS在提供EV和HFV车辆租赁服务的同时,还承担着站内新能源汽车的燃料供应与动力补充任务。一个典型的VSEHS系统主要由新能源汽车共享站和电-氢能量枢纽两部分构成,VSEHS系统的基本架构如图1所示。
VSEHS系统内配置EV和HFV两种不同类型的新能源车辆,通过向用户提供车辆租赁服务获得收入,并配备了相应的充电桩(Charging Pile,CP)和加氢设备(Hydrogenation Equipment, HE),用于为站内多辆可租赁的新能源汽车同时提供能量补充。作为新能源汽车的能量来源,VSEHS中配有小型风机(Wind Turbine, WT)、分布式光伏发电(Photovoltaic Unit, PV)、电解池(Electrolytic Cell, EC)和燃料电池(Fuel Cell, FC)四类能源生产设备,以及电储能(Electrical Energy Storage, ES)和储氢装置(Hydrogen Storage, HS)两类能源储存设备,同时系统还分别与外部电网及氢燃料供应体系相连,从而可以从外部市场购买额外电能和氢能,以补充系统可能出现的供能不足。
此外,在车辆租赁服务方面,本文假设用户可自由选择是否在VSEHS内租赁车辆。若用户选择在VSEHS内租车,则需进一步选择租车车型(EV或HFV),并向VSEHS运营商提供每日出行时间/返回时间、行驶距离等出行习惯数据。而VSEHS在为用户提供所需要的车辆后,将根据车辆租赁价格与时间获得服务收入。若用户拒绝在VSEHS内租车,则认为其通过常规模式出行,与VSEHS无交互。由于用户的租车选择将直接决定VSEHS的能源需求和运行性能,因此为了实现系统盈利最大化,VSEHS运营商有必要设计适当的车辆租赁价格,以激励用户选择最有利于VSEHS的理想出行方式。

图1 VSEHS系统基本架构
Fig.1 Basic structure of the VSEHS
VSEHS规划面临源荷双侧的不确定性,其中源侧主要为可再生能源出力的不确定性,负荷侧主要为车辆充电与加氢负荷的不确定性。其中,车辆动力补充需求与VSEHS内的车辆调度计划紧密相关,由用户的租车行为决定,具体而言,VSEHS需根据车辆租赁时间、返还时间、行驶里程、每一时刻租赁车辆数量、租赁车辆能源形式合理安排站内车辆调度及动力补充,以与电-氢能量枢纽运行相协调,而用户行为同样具有不确定性。因此,本节结合可靠数据概率分布的获取难度,采用区间和随机两种方法,分别对可再生能源出力、用户出行习惯和用户出行方式选择偏好进行不确定性建模,刻画VSEHS源荷双侧不确定性。
此外,需要强调的是,用户租车选择偏好的概率并非恒定,受租赁价格等变量影响而演变。基于此,VSEHS可借助价格方式激发用户车辆使用需求的能源可替代性,引导其选择偏好,以与VSEHS的规划运行相匹配。
在实际工程中,由于气象的复杂性,可再生能源出力的可靠概率分布不仅短期内不易准确得到,而且根据地理位置的不同往往具有较大差异性。考虑到某一地区可再生能源出力的边界值通常可以准确得到,因此本文采用区间方法来表示可再生能源出力,如式(1)~式(3)所示。
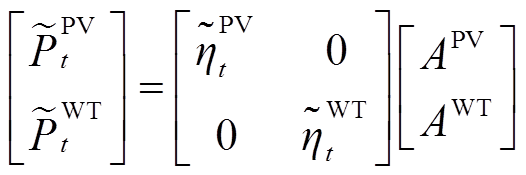 (1)
(1)
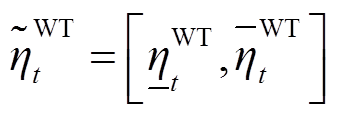 (2)
(2)
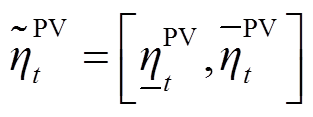 (3)
(3)
式中,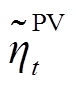 、
、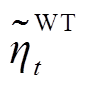 分别为t时刻风机和光伏载荷因数,为区间数;
分别为t时刻风机和光伏载荷因数,为区间数;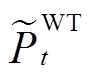 、
、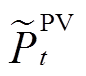 分别为t时刻风机和光伏的发电功率;
分别为t时刻风机和光伏的发电功率;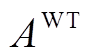 、
、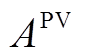 分别为风机和光伏的安装容量。
分别为风机和光伏的安装容量。
第m辆车在i场景下出发时间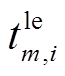 、车辆返回时间
、车辆返回时间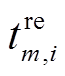 、行驶里程
、行驶里程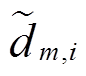 取决于用户的固有出行习惯和驾驶特性[28]。在实际工程中,由于可以在短期内获得大量可靠的用户驾驶行为历史数据以得到其对应的中长期统计特性,因此本文使用概率方法描述VSEHS用户的出行特性。其中,假设车辆返回时间服从正态分布[29],车辆离开时间和行驶里程满足对数正态分布[30-31],其概率密度分布函数如式(4)所示。结合本文模型特点,进一步将分布函数做离散化处理,从而得到基于离散概率的用户日行驶里程分布。
取决于用户的固有出行习惯和驾驶特性[28]。在实际工程中,由于可以在短期内获得大量可靠的用户驾驶行为历史数据以得到其对应的中长期统计特性,因此本文使用概率方法描述VSEHS用户的出行特性。其中,假设车辆返回时间服从正态分布[29],车辆离开时间和行驶里程满足对数正态分布[30-31],其概率密度分布函数如式(4)所示。结合本文模型特点,进一步将分布函数做离散化处理,从而得到基于离散概率的用户日行驶里程分布。
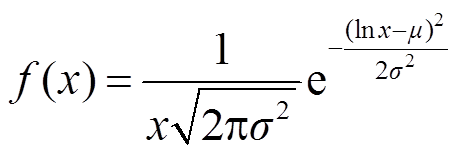 (4)
(4)
式中,μ为该对数正态分布的均值;σ为该对数正态分布的方差。
VSEHS各时刻租赁车辆能源形式与数量由用户租车选择偏好决定,然而在现实生活中,由于外部环境信息的不完全性,租车用户在进行策略选择时往往是有限理性的,其在初始阶段通常无法找到使自己效益最优化的出行方式,但其可以通过不断观察学习自身及其他用户之前采用某种策略所获得的收益,改变自己的租车选择策略以使自己的效用最优。因此,用户对车型的选择并非一成不变,且由于上述学习能力的存在,用户的选择行为遵循行为学中的“反射-反应”(RR)范式[32]:当某种策略在用户群体里被证明有更好的效益时,其他用户会改变自己的固有选择而进行模仿学习;此外,某一种策略越被用户认可,它在用户群体中被学习的可能性越高,被选择的概率也会随之发生改变。
鉴于此,本文选择应用描述有限理性参与者调整自身策略以适应环境的演化博弈理论来刻画RR范式下的用户租车策略选择问题,建立用户选择偏好模型,以准确分析在动态优化的租赁价格引导下用户的车辆选择行为和趋势,求解演化稳定状态下的用户租车策略选择概率,描述租车意愿的相关不确定性。
在演化博弈中,参与者通过类似于遗传机制而非理性选择过程调整策略以适应环境,并由此产生群体行为演化趋势[33]。演化博弈模型主要包括五种元素:参与者集合、策略集、适应度函数、复制者动态方程及演化稳定策略。本文所构建的VSEHS用户选择偏好演化博弈模型如下:
1)博弈参与者:用户群体M。
2)策略集。实际中,每个用户在出行前都会面临选择哪一种租车方式的问题,每一个用户可选择的租车策略集合用J={1,2,3}表示,其中,j=1表示用户拒绝在VSEHS内参与租车服务,可认为是选择在其他租车站进行租车;j=2表示租赁EV;j=3表示租赁HFV。假设xj表示用户选择策略j出行的种群比例,显然满足xj∈[0,1],x1+x2+x3=1。由于用户会根据自己和他人效益进行策略的学习与改变,因此采用不同策略的比例会随之发生变化。
3)适应度函数。本文将每种租车策略j的适应度函数Uj定义为选择该策略的用户群体总效用,如式(5)~式(8)所示,用户个体选择租车策略j的效用函数Um,j为其出行效益与由租车成本及车辆拥挤度所导致的效用折损间的差值。
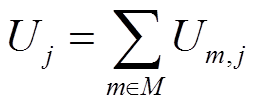 (5)
(5)
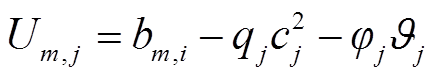 (6)
(6)
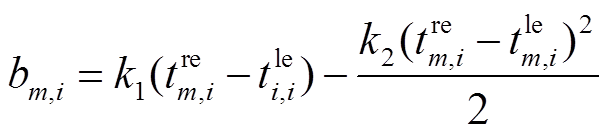 (7)
(7)
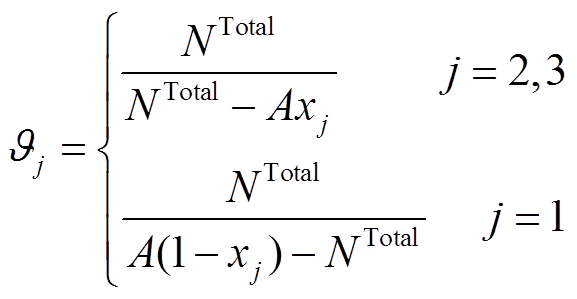 (8)
(8)
式中,m为用户;i为运行场景;j为租赁策略;bm,i为用户m在场景i下租车的出行效益;k1和k2为效益系数;c为车辆租赁价格;q为价格敏感性系数,用于反映租车价格对用户的影响;φ为用户效用折损系数;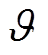 为拥挤系数;A为总用户数;NTotal为规划车辆总数。式(6)中的第二项为由租车成本带来的效用折损项,为同质地比较用户不在VSEHS内租车的效益,本文将拒绝在VSEHS内租车等效于到其他租车站租车,参考租车行业市场平均价格,设定用户拒绝VSEHS租车服务时的等效价格c1[34]。式(6)中第三项表示车辆租赁拥挤所导致的用户服务效用折损。如式(8)所示,对于策略2、3来说,xj越大,表示选择j策略出行的用户越多,但在规划车辆数量一定的情况下,这意味着策略j的车辆调度将更加拥挤,用户的服务满意度将会降低。而拒绝VSEHS租车服务用户的效益折损则通过在VSEHS内租赁车辆的用户服务效益间接反映,具体来说,x1越大,说明租车的人数越少,因此VSEHS车站内的拥挤度较低,由策略1拒绝在该站内租车所带来的便捷度与舒适度的相对优越性便有所降低。
为拥挤系数;A为总用户数;NTotal为规划车辆总数。式(6)中的第二项为由租车成本带来的效用折损项,为同质地比较用户不在VSEHS内租车的效益,本文将拒绝在VSEHS内租车等效于到其他租车站租车,参考租车行业市场平均价格,设定用户拒绝VSEHS租车服务时的等效价格c1[34]。式(6)中第三项表示车辆租赁拥挤所导致的用户服务效用折损。如式(8)所示,对于策略2、3来说,xj越大,表示选择j策略出行的用户越多,但在规划车辆数量一定的情况下,这意味着策略j的车辆调度将更加拥挤,用户的服务满意度将会降低。而拒绝VSEHS租车服务用户的效益折损则通过在VSEHS内租赁车辆的用户服务效益间接反映,具体来说,x1越大,说明租车的人数越少,因此VSEHS车站内的拥挤度较低,由策略1拒绝在该站内租车所带来的便捷度与舒适度的相对优越性便有所降低。
4)复制者动态方程。根据前述模型,可得到所有策略的平均适应度函数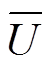 如式(9)所示,它表示了当前策略选择情况下用户群体的平均效益和基准水平,其中M为用户数量集合。
如式(9)所示,它表示了当前策略选择情况下用户群体的平均效益和基准水平,其中M为用户数量集合。
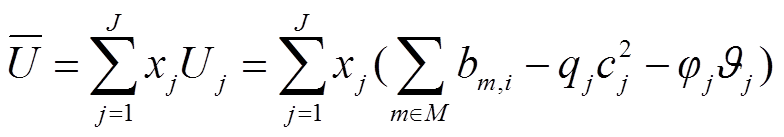 (9)
(9)
在演化博弈过程中,为了保证自身利益最大化,每个VSEHS用户会学习与调整策略。若用户选择策略的收益少于群体平均收益,则说明该策略并不会给用户带来较高的回报,同时该策略在用户群体中也不会受欢迎,因此该策略的增长率为负;反之为正。基于此建立租赁行为中的用户复制者动态方程如式(10)所示,其揭示了选择各个出行策略群体比例的演化规律。
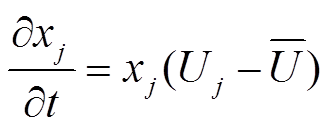 (10)
(10)
5)演化稳定策略。本文采用离散式迭代算法求解演化博弈稳定点。将式(10)所示的基于时间的连续微分方程差分化,可得到离散型复制者动态方程如式(11)所示,并当满足式(12)所示约束时可认为演化博弈达到演化稳定。
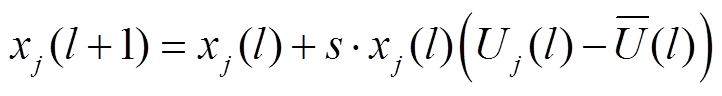 (11)
(11)
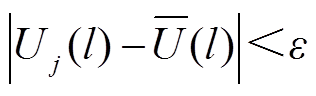 (12)
(12)
式中,l为迭代次数;s为迭代步长;ε为一个极小的正整数。
VSEHS用户租车选择偏好演化稳定点求解首先根据用户的初始策略选择,依次计算所选策略j的适应度和所有其他可用策略下的平均适应度值,然后对策略进行比较、迭代和更新,直到满足收敛条件。
基于上述方法,可以考虑租赁价格引导,得到最终稳定状态下用户群体选择各个租车策略的比例。基于统计学原理,稳定状态下的频率分布与概率分布相同,因此每个独立的用户对不同出行方式的偏好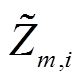 都可以看成是服从事件k的离散型随机变量,其分布律为
都可以看成是服从事件k的离散型随机变量,其分布律为
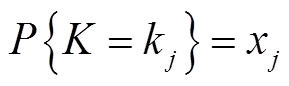 (13)
(13)
由于概率值xj会跟随第一阶段的决策变量而动态变化,因此用户选择偏好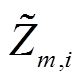 的不确定性是一种内生不确定性。
的不确定性是一种内生不确定性。
本文假设VSEHS的投资与运营均由同一主体承担,其目标是确定VSEHS最优的设备配置与定价策略,以实现自身利润的最大化。然而,由于VSEHS的投资效益与其运行方式是强耦合的,因此在规划阶段必须充分考虑VSEHS运行状态的潜在影响。鉴于此,VSEHS规划是一个典型的两阶段优化问题,需同时考虑投资决策和运行优化及其交互效应,其规划基本框架如图2所示。
在此框架下,第一阶段问题为VSEHS的最优配置设计。具体而言,该问题以系统投资净收益最大化为目标,确定能源生产、转化与储存设备的安装容量,EV、HFV及其动力补充设施的投资数量,以及EV与HFV的租赁定价方案。同时,第一阶段问题受到设备/车辆经济技术参数及租赁价格的约束,而由第一阶段问题产生的决策方案将构成第二阶段问题的参数集。
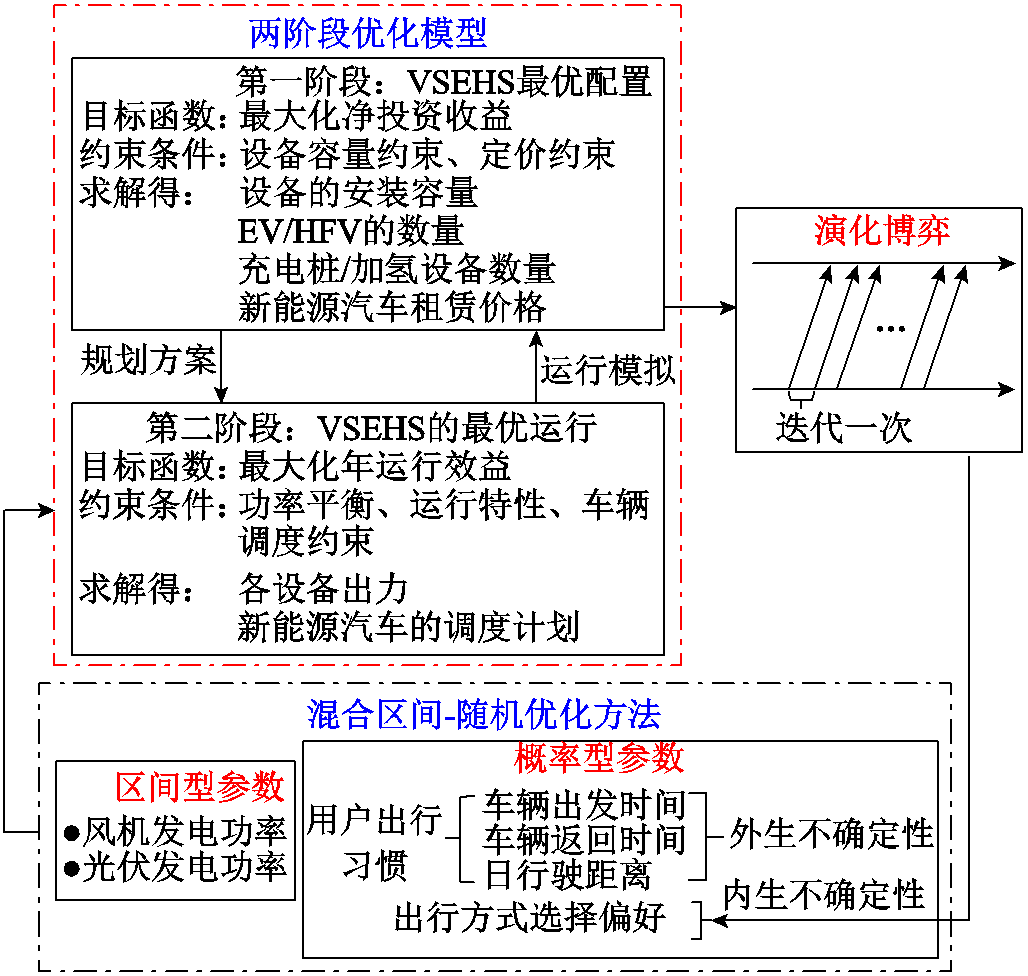
图2 VSEHS规划基本框架
Fig.2 Planning framework of the VSEHS
考虑到运行过程中可能采取的控制策略的影响,第二阶段为系统运行状态模拟。该阶段综合考虑可再生能源出力、用户出行需求和用户选择偏好等不确定性,对拟建VSEHS的实时运行调度进行优化,确定各时间段的能量输入/输出设备出力以及新能源车辆的运行调度安排,进而将给定规划决策和定价方案下的系统运行状态反馈给第一阶段,在一个交互框架下得到VSEHS的最优规划解。
3.2.1 规划-运行两阶段优化目标
VSEHS两阶段规划模型以最大化系统年投资净利润为目标,如式(14)所示,系统年投资净利润等于VSEHS年运行效益减去系统年值化的投资成本。
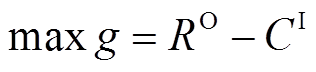 (14)
(14)
式中,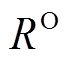 为VSEHS的年运行收益;
为VSEHS的年运行收益;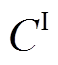 为VSEHS的投资成本年值。
为VSEHS的投资成本年值。
VSEHS投资成本由VSEHS内能源设备配置成本、新能源汽车配置成本和动力补充设备配置成本共同组成,并通过资金回收系数转化为等年值,如式(15)所示。
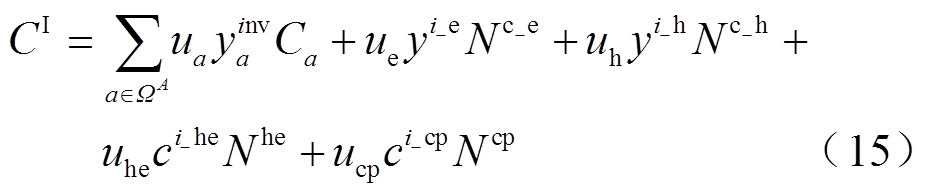
式中,ua、ue、uh、uhe、ucp分别为能源设备、EV、HFV、HE、CP的资本回收因数;为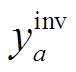 、
、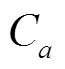 分别为各能源设备的单位投资成本和安装容量;
分别为各能源设备的单位投资成本和安装容量; 、
、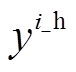 分别分别为单辆EV、HFV的购置成本;
分别分别为单辆EV、HFV的购置成本;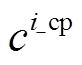 、
、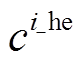 分别为CP和HE的单位投资成本;
分别为CP和HE的单位投资成本;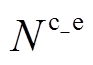 、
、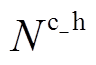 、
、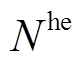 、
、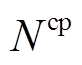 分别为EV、HFV、HE、CP的配置数量;WA为能源设备种类集合。
分别为EV、HFV、HE、CP的配置数量;WA为能源设备种类集合。
VSEHS年运行收入包括车辆租赁收益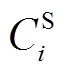 和碳减排收益
和碳减排收益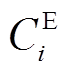 两部分,年运行收入与运行成本
两部分,年运行收入与运行成本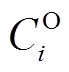 之差即为VSEHS的年运行效益。
之差即为VSEHS的年运行效益。
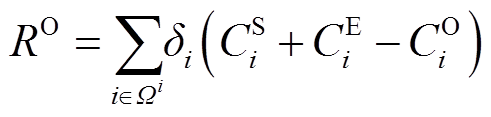 (16)
(16)
式中,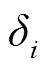 为各运行场景概率。
为各运行场景概率。
VSEHS的车辆租赁收益为EV用户和HFV用户租赁费用的总和,可表示为
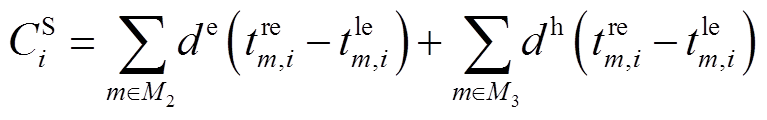 (17)
(17)
式中,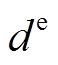 和
和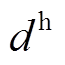 分别为EV和HFV单位时间的租赁价格;M2、M3分别为EV、HFV客户集合。
分别为EV和HFV单位时间的租赁价格;M2、M3分别为EV、HFV客户集合。
同时,VSEHS利用多能互补与多车型联运的灵活性可以促进可再生能源的消纳,系统用电量/耗氢量与外购能源间的差值为VSEHS内的绿电和绿氢供应量,其与外购能源相比无碳排放,其产生的碳减排量可参与碳交易获取碳减排收益。鉴于此,本文将碳减排收益纳入目标函数,将环境指标体系中碳排放量转化为经济指标,以实现环境与经济属性的统一。目标函数为
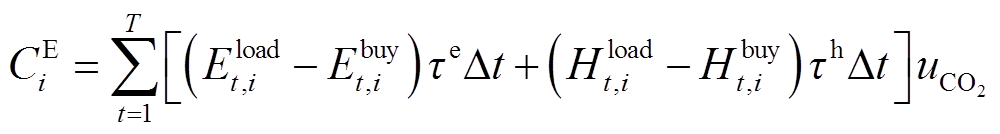 (18)
(18)
式中,i和t分别为场景和时段指标;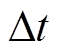 为时间段,这里指1 h;
为时间段,这里指1 h;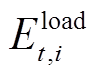 、
、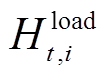 分别为电和氢负荷;
分别为电和氢负荷;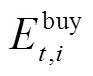 、
、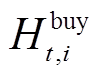 分别为外购电能和氢能量;
分别为外购电能和氢能量;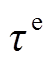 、
、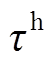 分别为电能和氢能供应的社会平均碳排放系数;
分别为电能和氢能供应的社会平均碳排放系数;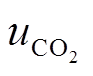 为碳交易市场中的自愿减排量价格。
为碳交易市场中的自愿减排量价格。
此外,VSEHS年运行成本由外购能源成本与运行维护成本共同组成,有
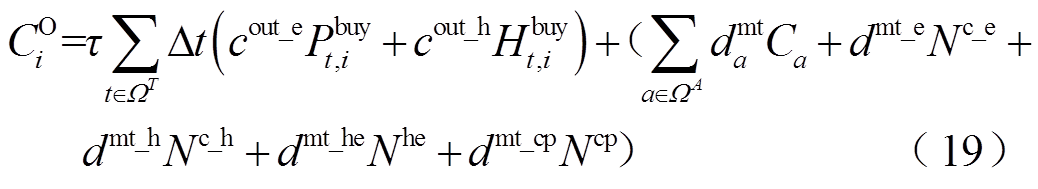
式中,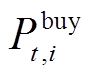 为t时刻i场景下的购电功率;
为t时刻i场景下的购电功率;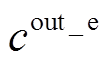 、
、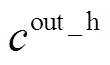 分别为系统外购电价和外购氢价;
分别为系统外购电价和外购氢价;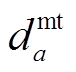 为各能源设备的年单位运维成本;
为各能源设备的年单位运维成本;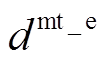 、
、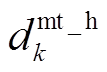 、
、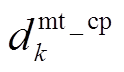 、
、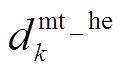 分别为EV、HFV、CP及HE的年单位运维成本;
分别为EV、HFV、CP及HE的年单位运维成本;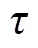 为一年中的天数,即365天。
为一年中的天数,即365天。
3.2.2 规划决策阶段约束条件
规划约束主要包括设备配置容量/数量约束、租赁价格定价约束。
1)设备配置约束
受限于资源可用性、空间等约束限制,VSEHS系统中各类设备的配置容量需满足
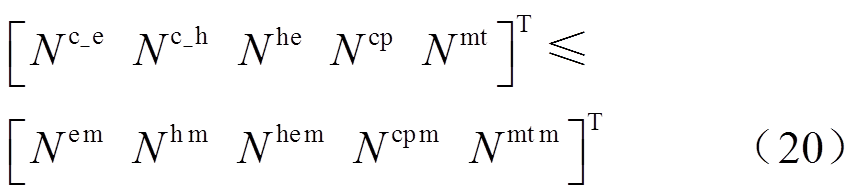
式中,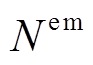 、
、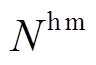 、
、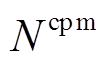 、
、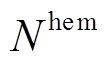 、
、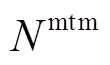 分别为EV、HFV、CP、HE及各类能源设备的最大配置数量或容量。
分别为EV、HFV、CP、HE及各类能源设备的最大配置数量或容量。
2)定价约束
为防止车辆租赁价格波动对民生造成的负面影响,VSEHS内EV、HFV的租赁定价应受到上、下限的限制,即
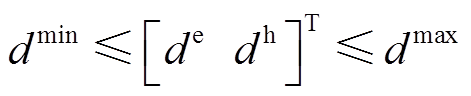 (21)
(21)
式中,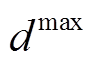 、
、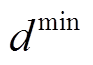 分别为EV和HFV租赁定价的上下限。
分别为EV和HFV租赁定价的上下限。
3.2.3 运行模拟阶段约束条件
运行约束主要包括功率平衡约束、设备运行特性约束和共享站内车辆调度约束。
1)功率平衡约束
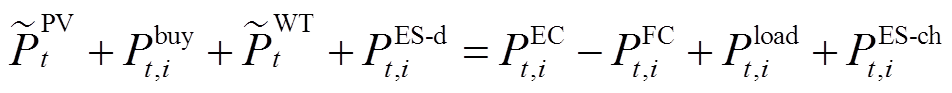 (22)
(22)
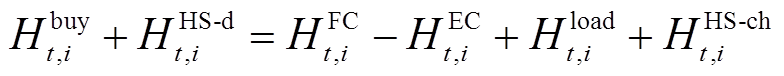 (23)
(23)
式中,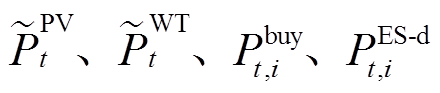 分别为光伏、风机的发电功率、外部电网的购电功率及电储能的放电功率;
分别为光伏、风机的发电功率、外部电网的购电功率及电储能的放电功率;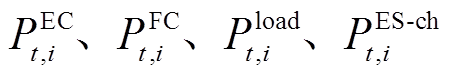 分别为EC、FC的耗电量、负荷功率及电储能的充电功率;
分别为EC、FC的耗电量、负荷功率及电储能的充电功率;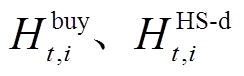 分别为外部购氢量和HS的放氢功率;
分别为外部购氢量和HS的放氢功率;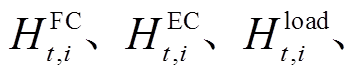
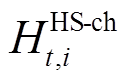 分别为FC的耗氢量、EC的产氢量、负荷的耗氢量及HS的储氢功率。
分别为FC的耗氢量、EC的产氢量、负荷的耗氢量及HS的储氢功率。
电、氢负荷由VSEHS内的新能源汽车充电需求和加氢需求决定,与车辆调度计划紧密相关,具体如式(24)和式(25)所示,而与车辆调度计划相关的用户租车行为不确定性已在前节详细讨论。
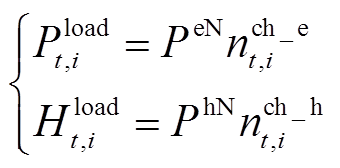 (24)
(24)
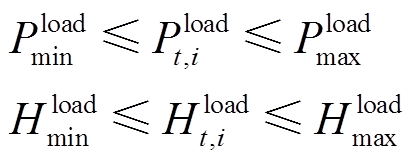 (25)
(25)
式中,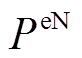 、
、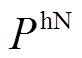 分别为EV的额定充电功率和HFV的额定加氢需求;
分别为EV的额定充电功率和HFV的额定加氢需求;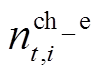 、
、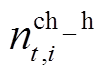 分别为正在充电的EV和正在加氢的HFV数量。
分别为正在充电的EV和正在加氢的HFV数量。
2)设备运行特性约束
(1)电解池
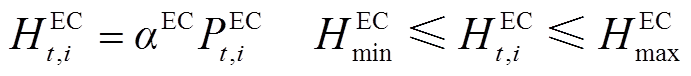 (26)
(26)
式中,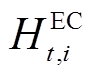 为EC实际产氢量;
为EC实际产氢量;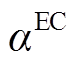 为EC能量转换效率;
为EC能量转换效率;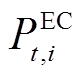 为EC的耗电量;
为EC的耗电量;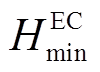 、
、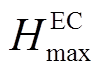 分别为EC的最小、最大产氢量。
分别为EC的最小、最大产氢量。
(2)燃料电池
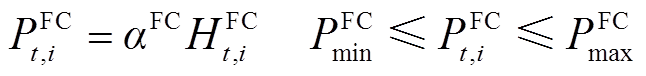 (27)
(27)
式中,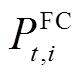 为FC实际功率,
为FC实际功率,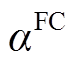 为FC能量转换效率,
为FC能量转换效率,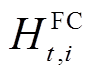 为FC的耗氢量,
为FC的耗氢量,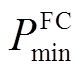 、
、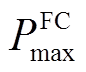 分别为FC的最小、最大功率。
分别为FC的最小、最大功率。
(3)电氢储能设备
 (28)
(28)
式中,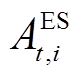 为电储能的储能状态;
为电储能的储能状态;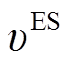 为电储能的自放电率;
为电储能的自放电率;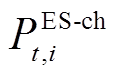 、
、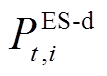 分别为电储能的充、放电功率;
分别为电储能的充、放电功率; 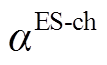 、
、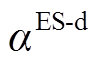 分别为电储能的充、放电效率;
分别为电储能的充、放电效率;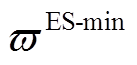 、
、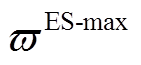 分别为电储能的荷电状态下、上限;
分别为电储能的荷电状态下、上限;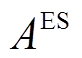 为电储能的配置容量;
为电储能的配置容量;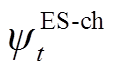 、
、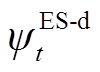 分别为电储能的充、放能状态0-1变量;
分别为电储能的充、放能状态0-1变量;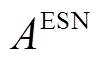 为电储能的最大电功率;氢储能符号含义同理。
为电储能的最大电功率;氢储能符号含义同理。
3)车辆调度约束
本文将VSEHS内的新能源车辆分为三种状态量,分别是充满电/加满氢的车辆、正在充电/正在加氢的车辆、等待充电/等待加氢的车辆,分别用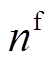 、
、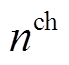 、
、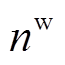 表示。假设新能源汽车租赁需当日归还,且租赁初始时刻车辆均为满电/满氢状态,则系统中各时段不同状态的新能源车辆数量满足
表示。假设新能源汽车租赁需当日归还,且租赁初始时刻车辆均为满电/满氢状态,则系统中各时段不同状态的新能源车辆数量满足
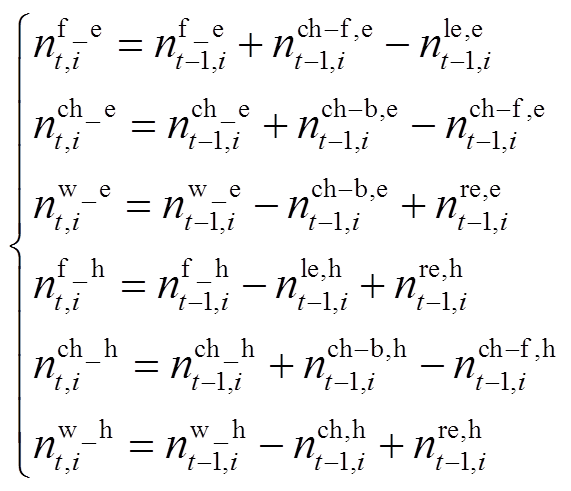 (29)
(29)
式中,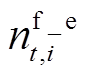 、
、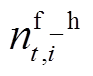 分别为t时刻充满电/加满氢的EV、HFV数量;
分别为t时刻充满电/加满氢的EV、HFV数量;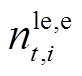 、
、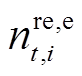 分别为租赁和归还的EV数量;
分别为租赁和归还的EV数量;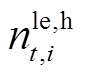 、
、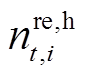 分别为租赁和归还的HFV数量;
分别为租赁和归还的HFV数量;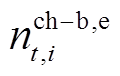 、
、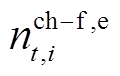 分别为开始充电和完成充电的EV数量;
分别为开始充电和完成充电的EV数量;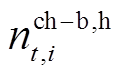 、
、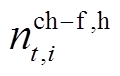 分别为开始加氢和完成加氢的HFV数量。
分别为开始加氢和完成加氢的HFV数量。
此外,针对各时段的车辆调度方案,需满足以下车辆和动力补充设备的数量约束限制。
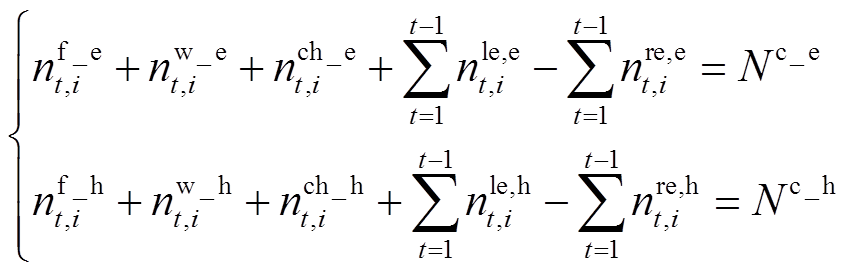 (30)
(30)
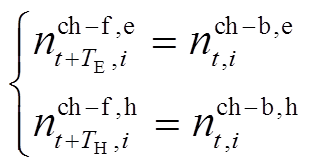 (31)
(31)
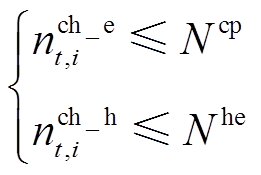 (32)
(32)
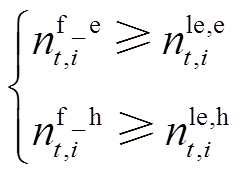 (33)
(33)
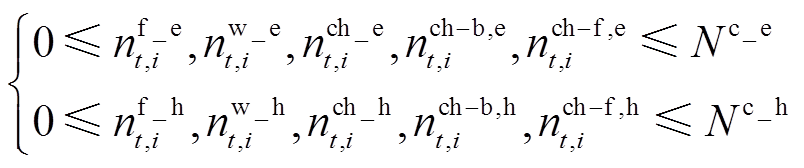 (34)
(34)
式(30)表示任何一个时刻所有状态下的EV/HFV总数应保持恒定。式(31)为EV/HFV的状态转移方程,表示t时刻开始充能的车辆数量等于在t+T时刻完成充能的车辆数量。式(32)表示正在充电/加氢车辆数量应少于加注设施数量。式(33)表示任何一个时刻用户租走的EV/HFV数量应该小于该时刻站内满动力状态的EV/HFV数量,以满足用户出行需求。式(34)表示任何一个时刻下各个状态的EV/HFV数量应少于VSEHS车辆总数量。
由于上述优化模型存在随机与区间两种形式的不确定性参数,此外,相关决策同时涉及规划决策及运行模拟两个阶段,因此,本文所研究的VSEHS规划在数学上属于一个复杂的区间/随机混合二阶段优化问题。本文所提模型的紧凑形式为
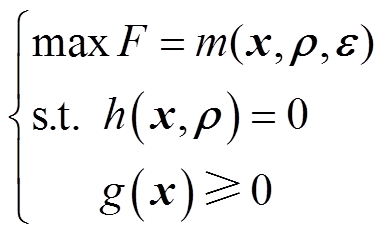 (35)
(35)
式中,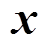 为与规划方案相关的变量矩阵;
为与规划方案相关的变量矩阵;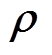 为由区间参数表示的不确定性变量矩阵;
为由区间参数表示的不确定性变量矩阵;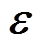 为由随机参数表示的不确定性变量矩阵。
为由随机参数表示的不确定性变量矩阵。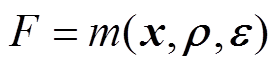 为规划问题的目标函数,对应于式(14)。
为规划问题的目标函数,对应于式(14)。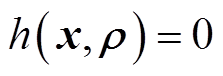 为规划问题中涉及区间变量的等式约束,对应于式(1)、(22)。
为规划问题中涉及区间变量的等式约束,对应于式(1)、(22)。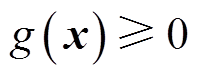 为规划问题中不包含区间变量和随机变量的等式与不等式约束,对应于式(20)、式(21)、(式23)、式(26)~式(34)。
为规划问题中不包含区间变量和随机变量的等式与不等式约束,对应于式(20)、式(21)、(式23)、式(26)~式(34)。
区间变量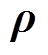 是由上、下界值组成的可再生能源出力的波动区间,即
是由上、下界值组成的可再生能源出力的波动区间,即
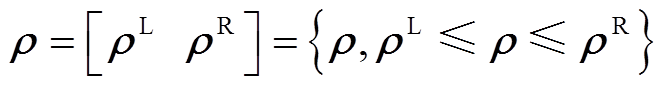 (36)
(36)
式中,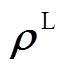 、
、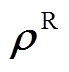 分别为区间变量
分别为区间变量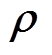 的上、下界。
的上、下界。
为实现对上述模型的有效求解,本文提出一种区间-随机混合优化求解方法:首先,基于蒙特卡罗模拟法生成预想场景集合,以实现对概率型参数的确定化描述,从而将问题转化为一个只含有区间型参数的优化模型;其次,通过引入区间序关系和模糊偏好法,对目标函数和约束条件进行变换,以使含有区间型参数的优化问题最终转化为一个确定性优化问题;最后,利用遗传算法对该确定性优化问题进行求解。
本文模型中的概率型不确定性参数主要包括两类:日常出行习惯(包含车辆出发时间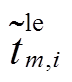 、车辆返回时间
、车辆返回时间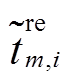 、日行驶距离
、日行驶距离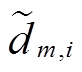 )和租车选择偏好
)和租车选择偏好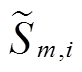 。进一步根据概率分布是否随外部因素发生变化,将概率型不确定性参数归结为内生/外生不确定性,其中
。进一步根据概率分布是否随外部因素发生变化,将概率型不确定性参数归结为内生/外生不确定性,其中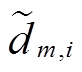 、
、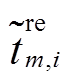 和
和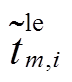 被视为外生不确定性变量,而
被视为外生不确定性变量,而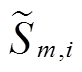 被视为内生不确定性变量。因此,每个VSEHS用户的行为不确定性可以用向量
被视为内生不确定性变量。因此,每个VSEHS用户的行为不确定性可以用向量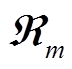 表示为
表示为
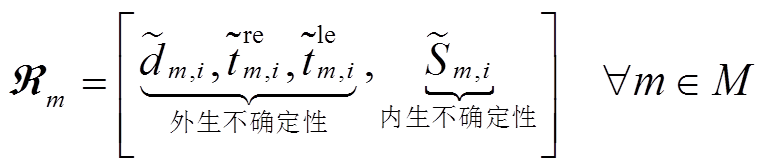 (37)
(37)
综合VSEHS中用户车辆租赁情况,可以得到租车需求场景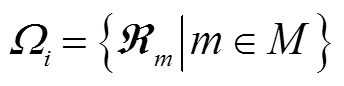 ,它表示了运行过程中可能出现的所有用户租赁信息集合。
,它表示了运行过程中可能出现的所有用户租赁信息集合。
在VSEHS优化规划中,若假设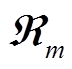 中所有的概率变量之间相互独立,通常可利用蒙特卡罗模拟法生成一组预想场景集合[35],来实现对不确定性影响效果的有效考虑。需要强调的是,与以往研究不同,本文需要考虑内生不确定性变量——用户租车选择偏好
中所有的概率变量之间相互独立,通常可利用蒙特卡罗模拟法生成一组预想场景集合[35],来实现对不确定性影响效果的有效考虑。需要强调的是,与以往研究不同,本文需要考虑内生不确定性变量——用户租车选择偏好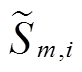 的场景生成。基于此,考虑内外生不确定性随机变量抽样流程如图3所示。
的场景生成。基于此,考虑内外生不确定性随机变量抽样流程如图3所示。
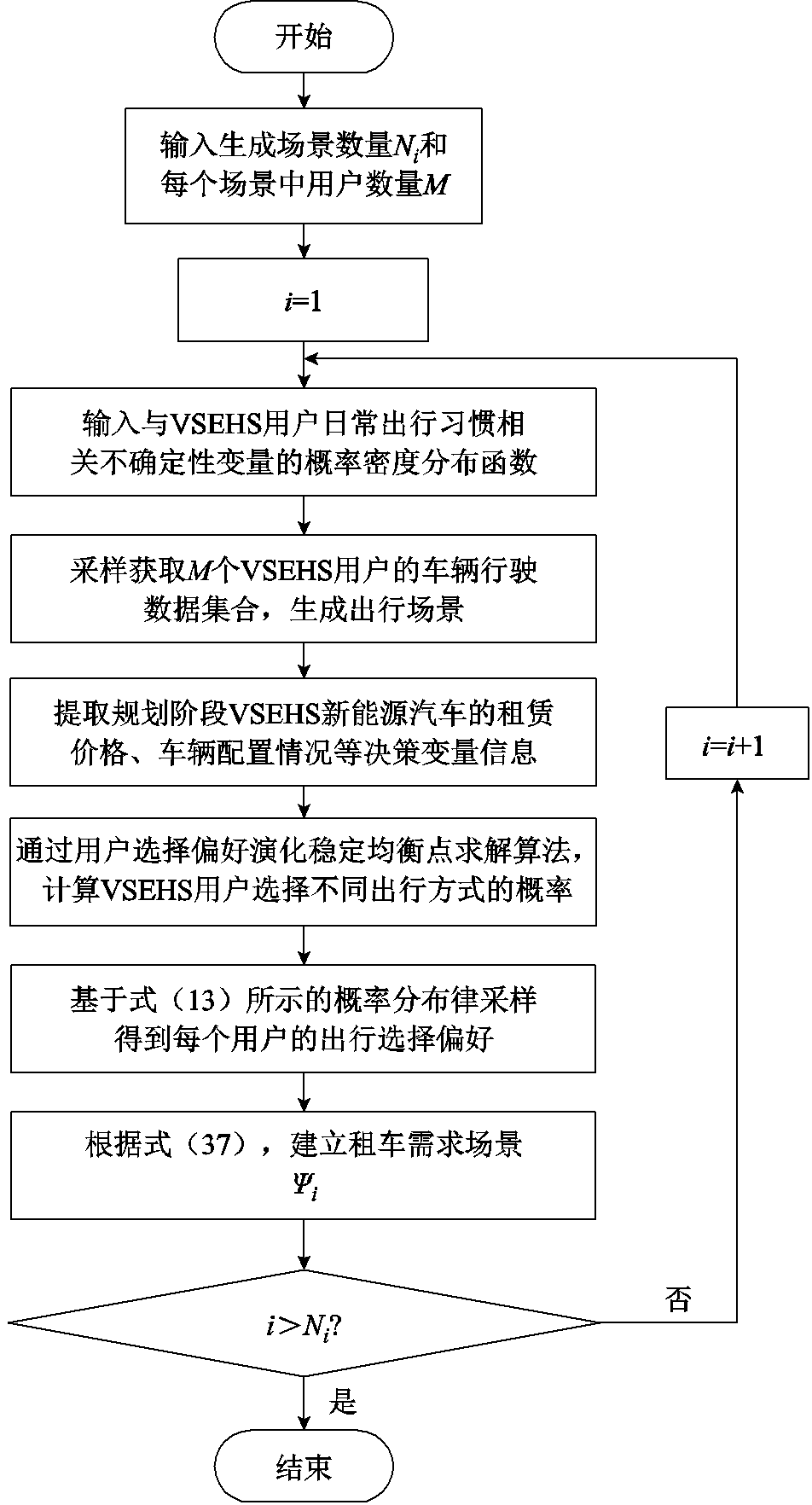
图3 考虑内外生不确定性随机变量抽样流程
Fig.3 The flow chart of sampling process considering endogenous and exogenous uncertain random variables
由于过多的场景会增加优化难度,本文进一步应用基于K-means聚类的场景削减技术来简化上述场景[36]。为减小误差,本文将聚类后的类别数量设置为20个,聚类后各个组别场景的概率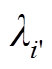 为
为
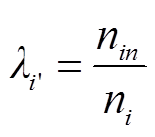 (38)
(38)
式中,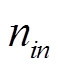 为经约简后落入聚类组n的场景样本数量;
为经约简后落入聚类组n的场景样本数量;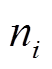 为蒙特卡罗模拟抽样产生的总场景样本数量。
为蒙特卡罗模拟抽样产生的总场景样本数量。
本文所提规划模型中与可再生能源出力相关的不确定性均用区间形式进行描述。本节将对含有区间型参数的目标函数及约束条件的处理方法分别介绍。
1)含区间型参数的目标函数
在区间优化问题中,对于任一区间型参数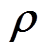 ,由于其存在波动范围,因此系统的目标函数
,由于其存在波动范围,因此系统的目标函数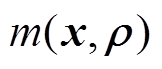 (本文中即指VSEHS投资年利润)也为区间数,如式(39)所示。
(本文中即指VSEHS投资年利润)也为区间数,如式(39)所示。
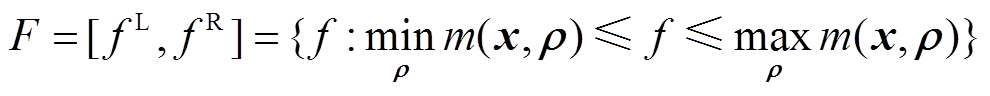 (39)
(39)
本文利用区间序关系对式(14)中的目标函数进行处理[37],使其等效为一个由区间中点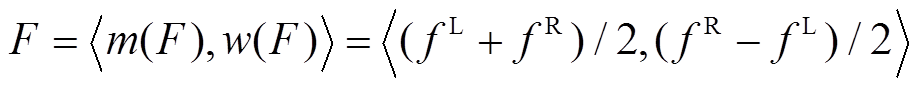 和区间半径值
和区间半径值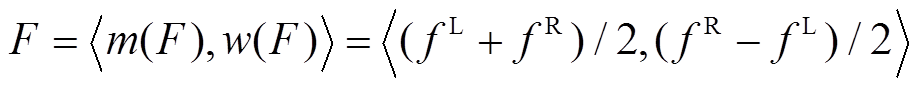 构成的不确定性目标,如式(40)所示。
构成的不确定性目标,如式(40)所示。
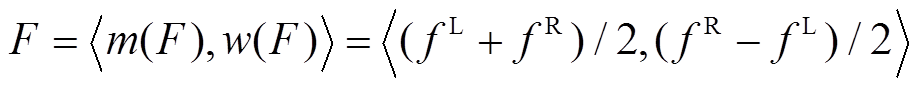 (40)
(40)
式中,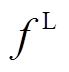 、
、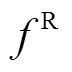 为目标函数F的波动限值。
为目标函数F的波动限值。
根据上述方法,为了确定最优解,本文采用模糊偏好法对区间数进行比较。对于任意两个区间数A和B,通过定义模糊偏好函数,可表示VSEHS投资商对A→B的偏好[38],如式(41)所示。然后,从0到1选取悲观情绪来描述VSEHS投资商的风险承受能力,并将模糊函数值与VSEHS投资商的悲观程度进行比较,以确定优选的区间数。当μ(A)大于ξ值时,VSEHS投资商选择A;否则,选择B。在上述基础上,文献[39]对区间数的比较进行了简化,有
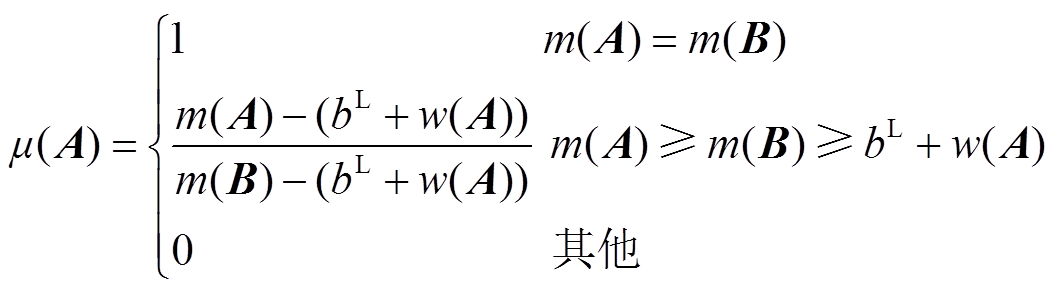 (41)
(41)
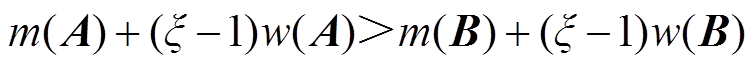 (42)
(42)
式中,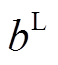 为区间数的下界。
为区间数的下界。
因此通过以上步骤,基于式(14)的VSEHS投资年利润可转换为确定性模型,有
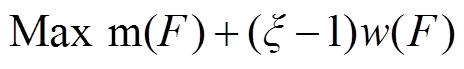 (43)
(43)
2)含区间型参数的约束条件
类似地,针对模型中的约束条件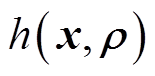 ,其在决策变量x处由不确定变量u造成的取值,可用区间数
,其在决策变量x处由不确定变量u造成的取值,可用区间数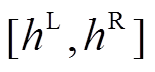 表示。如式(44)、式(45)所示。本文同样采用模糊偏好法对其进行转换处理,根据上述方法,式(35)中的等式约束H可转化为
表示。如式(44)、式(45)所示。本文同样采用模糊偏好法对其进行转换处理,根据上述方法,式(35)中的等式约束H可转化为
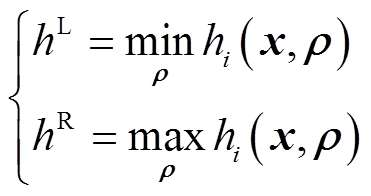 (44)
(44)
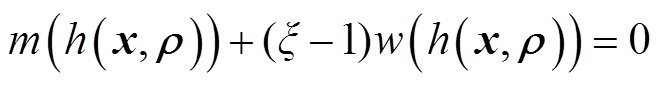 (45)
(45)
式中,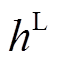 、
、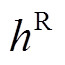 分别表示约束
分别表示约束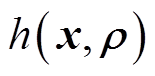 的波动限值;m(h(x,ρ))为约束条件的区间中点;w(h(x,ρ))为约束
的波动限值;m(h(x,ρ))为约束条件的区间中点;w(h(x,ρ))为约束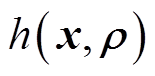 的区间半径。
的区间半径。
通过对目标函数与约束条件的转化,便可以将本文的区间随机优化模型(35)转化为
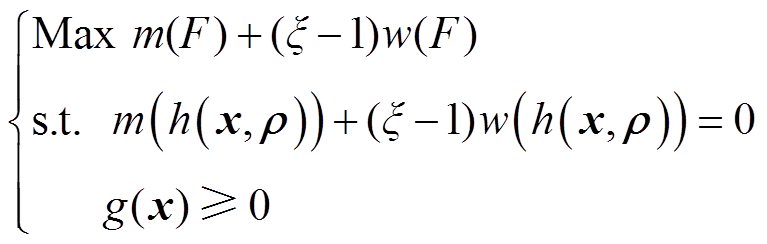 (46)
(46)
由于遗传算法具有适用性强、便于操作、可扩展性的优点,易于与演化博弈迭代算法以及包含内生不确定性变量的场景生成算法结合,因此,本文采用遗传算法作为求解方法,以实现复杂规划问题的高效求解。具体求解流程如图4所示。需要说明的是,本文将最大迭代次数和没有适应性改善的最大迭代时间作为收敛条件,如果达到指定标准里的任意一个,则输出当前最优个体作为最终规划方案。
为了验证本文所提VSEHS区间-随机混合规划方法的有效性,本文以某一城市社区为背景,并考虑该社区内100名用户的出行需求,开展VSEHS规划。该系统的基本结构如图1所示,其可用车型及设备的关键参数见表1和表2。根据该地区历史气象数据,风电和光伏的出力预测曲线及波动区间分别如图5和图6所示。
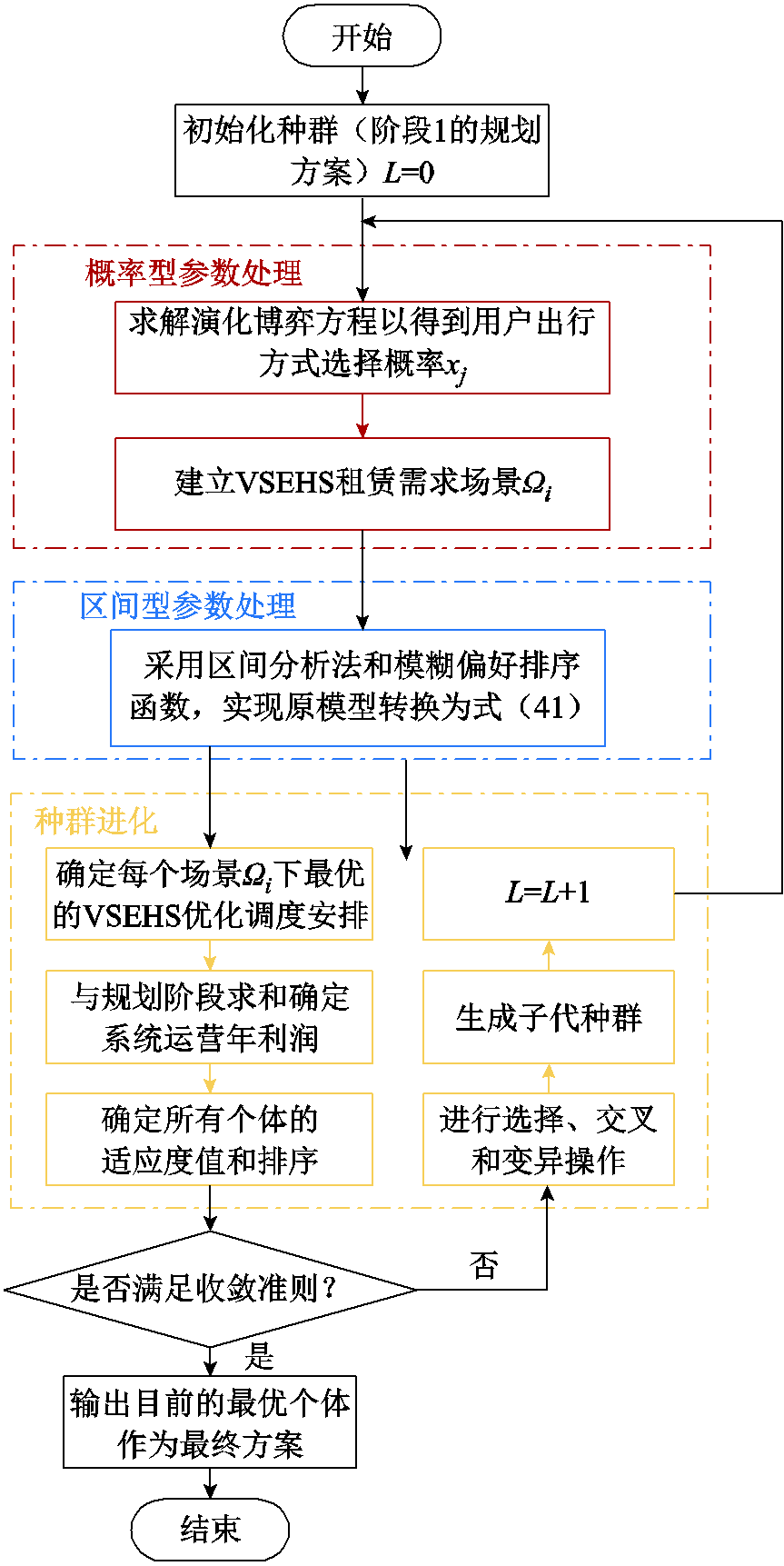
图4 基于遗传算法的区间-随机混合优化求解流程
ig.4 Solution procedure of interval-stochastic hybrid optimization solution flow based on genetic algorithm
表1 车辆参数
Tab.1 Vehicle parameters

车辆类型最大行驶里程/km车辆单价/元单位维修费用/元车辆使用寿命/a BJEV EU7450165 9001 20015 Toyota FCV510240 0001 20015
表2 设备参数[40, 45-48]
Tab.2 Equipment parameters

设备类型投资成本运维成本使用寿命/a其他 WT5 500元/kW120元/kW20— PV8 000元/kW80元/kW20— EC2 210元/kW67元/kW15效率75% FC3 250元/kW40元/kW10效率65% ES1 400元/(kW·h)15元/(kW·h)10充/放电效率98% HS1 500元/(kW·h)5元/(kW·h)15储/放氢效率92%
(续)

设备类型投资成本运维成本使用寿命/a其他 CP800元/台45元/台25— HE1 200元/台45元/台25—
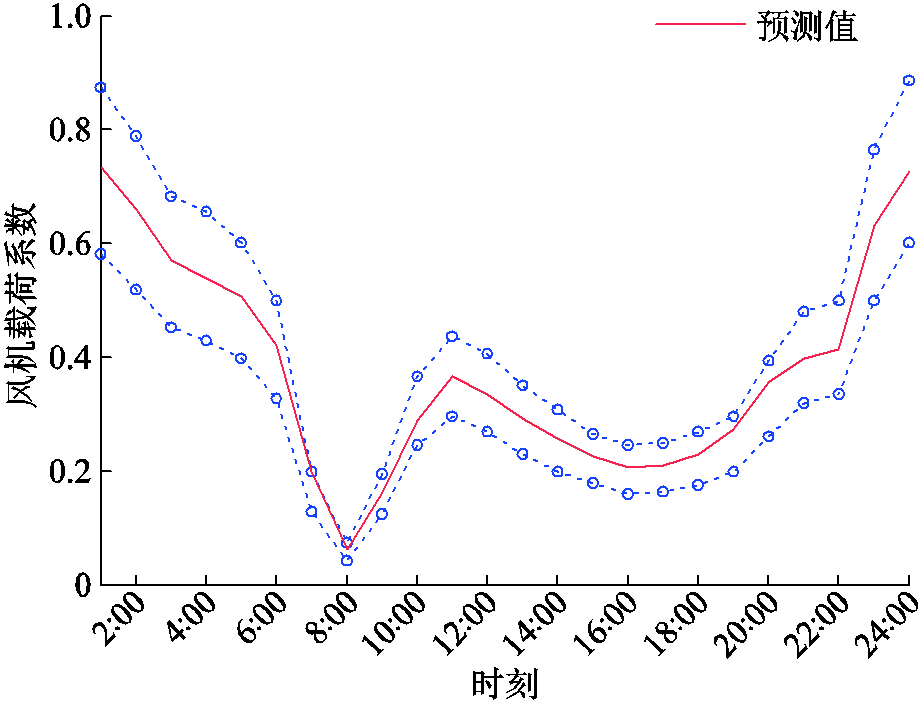
图5 风机出力预测曲线
Fig.5 Forecast curves of wind power output
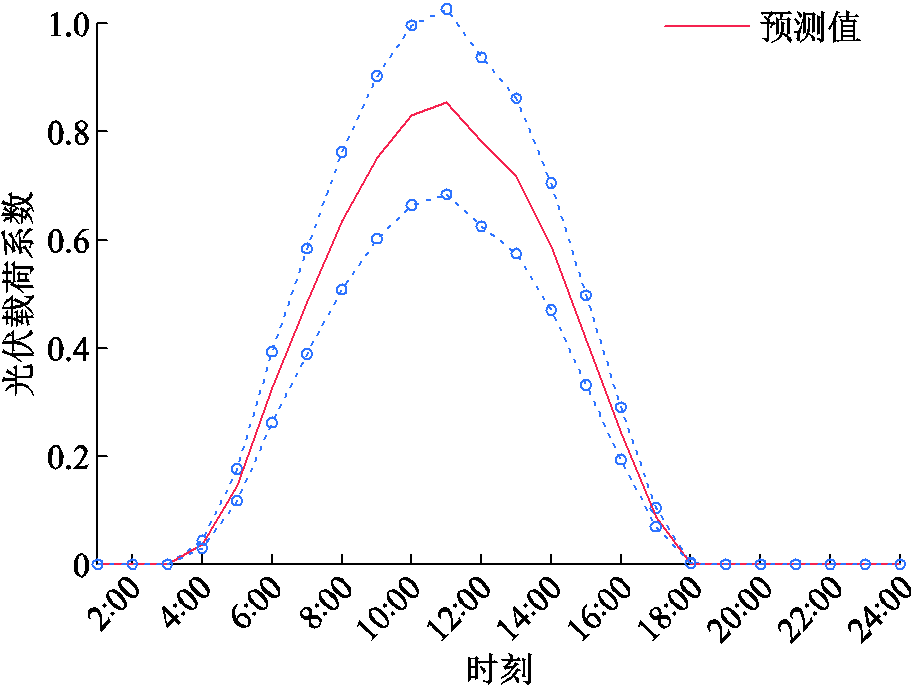
图6 光伏出力预测曲线
Fig.6 Forecast curves of PV output
本文假设系统购电电价为峰谷电价,各时段划分及价格见表3[40],系统从外部能源市场的购氢价格为0.77 元/(kW·h)[41]。此外,碳减排价格为0.16元/kg[42],电力和氢能的碳排放因子分别为0.889 kg/(kW·h)和0.478 3 kg/(kW·h)[43-44]。
表3 分时段电价
Tab.3 Peak-valley electricity price

时段峰时段平时段谷时段 时间10:00—13:0018:00—23:008:00—10:0013:00—18:0023:00—8:00 价格/[元/(kW·h)]1.120.610.32
演化博弈算法相关参数取值情况:k1、k2分别取9.6和0.4;q、φ分别取5.1和3。遗传算法相关参数取值情况:种群规模为100,迭代次数为400,交叉概率为0.9,变异概率为0.2。
通过求解优化模型,得到该VSEHS系统最优规划方案及其经济效益结果见表4和表5。在最优规划方案下,系统年投资净利润为333.99万元,在年运行收入中,车辆租赁收益和碳减排收益分别占比94.35%和8.65%。
表4 最优规划方案
Tab.4 Optimal planning schemes

设备类型配置容量 WT95.63 kW PV343.96 kW EC159.05 kW FC66.54 kW HS380.96 kW·h ES343.65 kW·h EV40辆 HFV17辆 CP11台 HE3台
表5 最优规划效益
Tab.5 Optimal planning results(单位:万元)

经济指标系统净收益租赁收益碳减排收益年投资成本年运行成本 数值333.99524.0149.06220.7618.32
在最优规划方案中,EV的租赁价格为0.483元/ min,HFV的租赁价格为0.717 元/min。在该租赁价格水平下,基于演化博弈的用户出行选择策略演化过程如图7所示。用户策略在迭代到第10次左右逐渐趋于稳定,最终在最大迭代次数为100次的仿真情景下,该问题的演化稳定状态为30%的用户拒绝参与租车服务,49%的用户选择租赁EV,21%的用户选择租赁HFV。这是由于用户在此定价下租赁EV的效益高于HFV,因此,选择租赁EV的用户更多。而得到此定价的原因在于氢-电的运营投资比例会直接影响车站的经济和环境效益,适当的氢需求可以消纳富裕的风光出力,提高可再生能源的消纳率,从而提高碳减排效益。而大量的氢需求则一方面会导致规划成本的大幅增加,另一方面会使站内自备氢来源短缺而导致外购氢量过大,反而增加了系统对高碳排放能量来源的依赖,因此,决策者通过此价格引导用户租赁EV多于HFV。同时,对于决策者来说,定价过高会造成一定数量的用户流失,定价过低可能会影响车站的盈利。因此,本规划结果所显示价格虽然会造成30%的客户流失,但是综合来看营收利润仍为最优值。
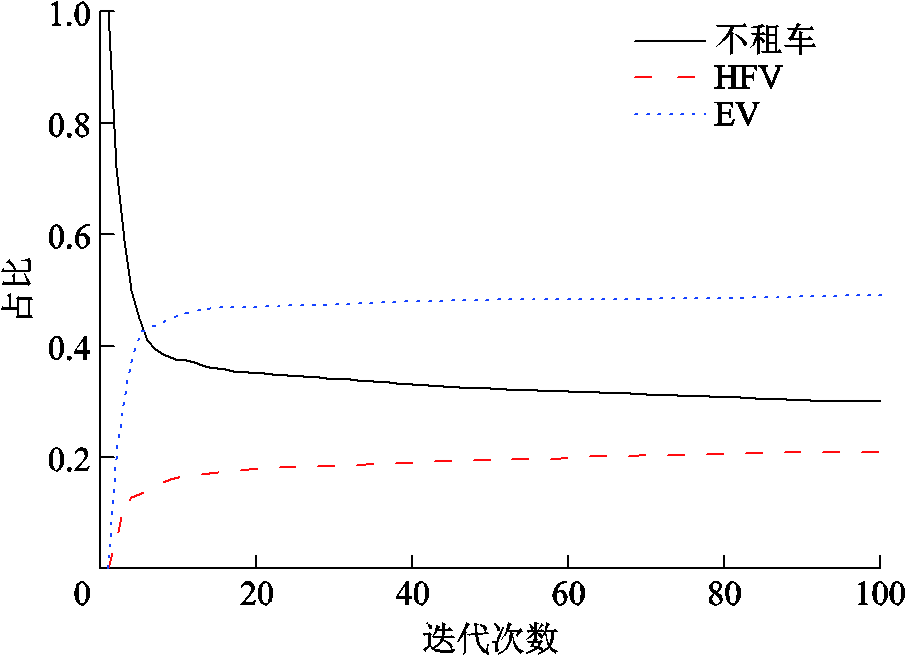
图7 用户租车偏好演化博弈过程
Fig.7 Evolution of users' vehicle rental preferences
该规划方案下24 h内VSEHS各能源设备电功率的运行情况如图8所示。由图8可知,可再生能源出力主要集中在8:00~15:00,为消纳丰富的新能源出力,系统安排EV的充电时间主要集中在白天。但由于该时段电负荷的需求仍小于可再生能源出力,富裕的可再生能源出力大部分通过EC转化为氢能,用于HFV的加氢行为,少量电能通过ES储存。对于傍晚和夜间,可通过FC发电和ES放电为电动汽车充电。
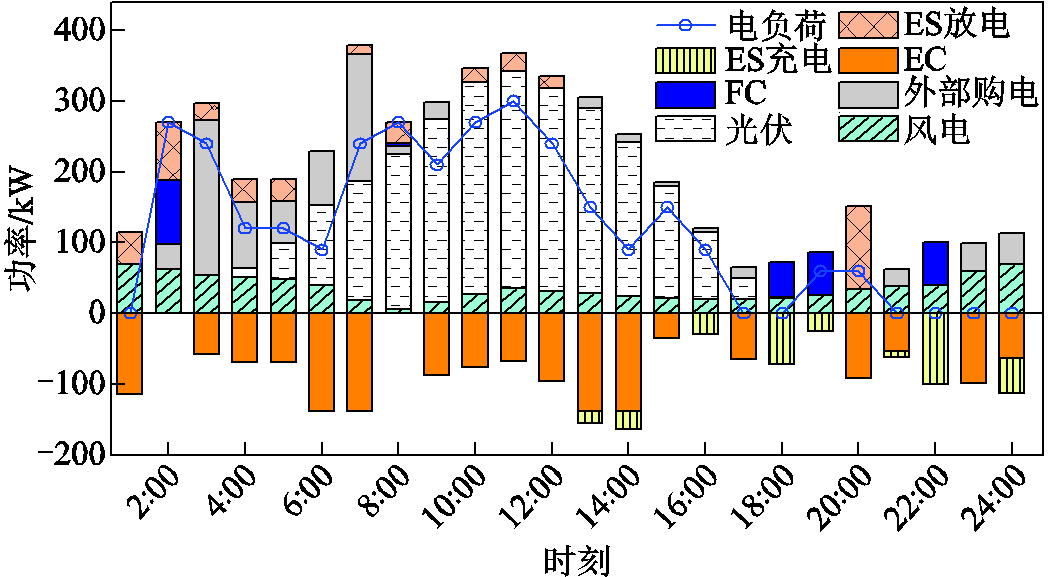
图8 电功率平衡
Fig.8 Electric power balance
图9展示了VSEHS运行过程中的车辆调度情况。由图9可知,充电、加氢车辆数量峰值点均出现在白天,与图8负荷需求相对应,这说明在本文所提出模型下EV/HFV的动力补充和电-氢能量转化调度相协调,在满足用户出行需求的前提下,系统结合新能源实时出力安排车辆调度以提高碳减排效益。对于70人选择站内租车出行的情况,经过能源-车辆协同管理规划只需投资57辆新能源汽车,车辆投资数量减少了18.57%,有效地提高了车辆利用率,从而减少额外的建设投资。
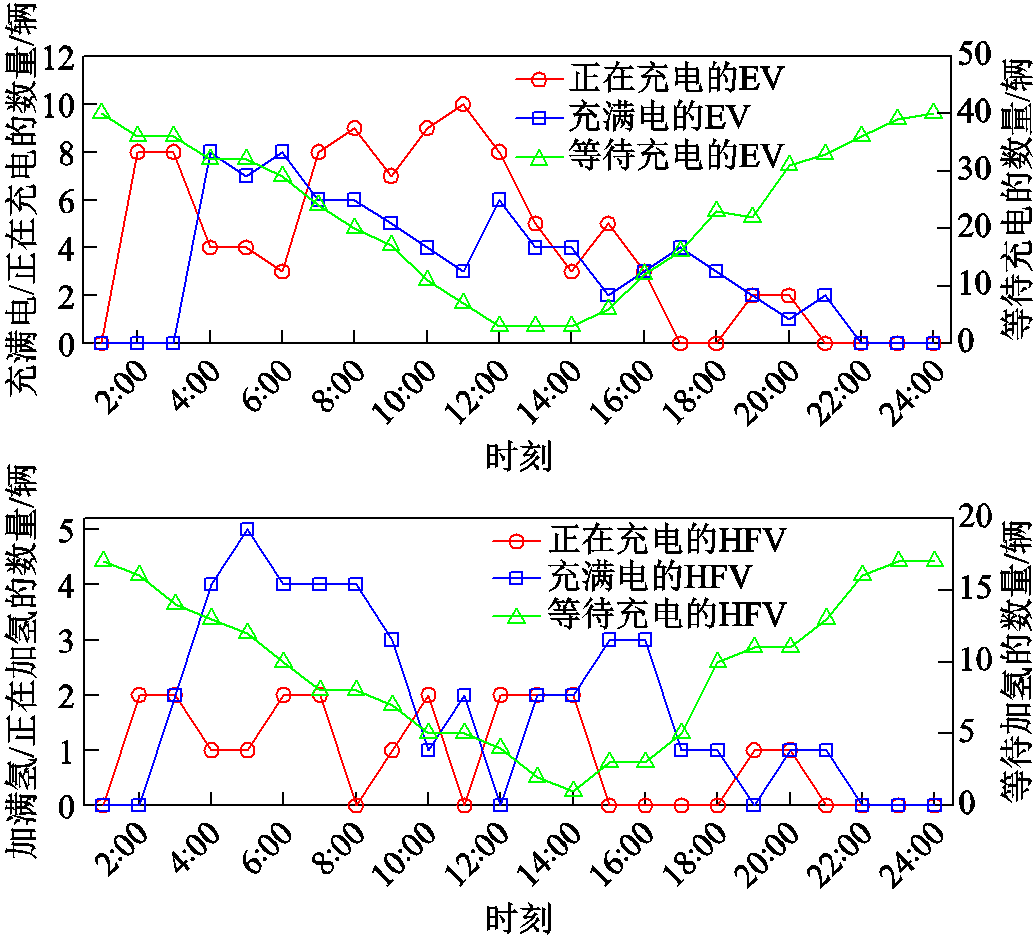
图9 新能源汽车状态
Fig.9 State of the vehicle
该规划方案下氢能相关设备的运行状态由图10所示。一方面大部分HS用于负荷需求,优先供应于HFV的加氢,剩余部分氢能用于电价较高或风光出力较小时的FC出力;另一方面,氢能主要来源于电制氢,少数时刻来源于外部购氢,氢能自给率高达91.3%,可保证HFV的动力来源基本来自于可再生能源。
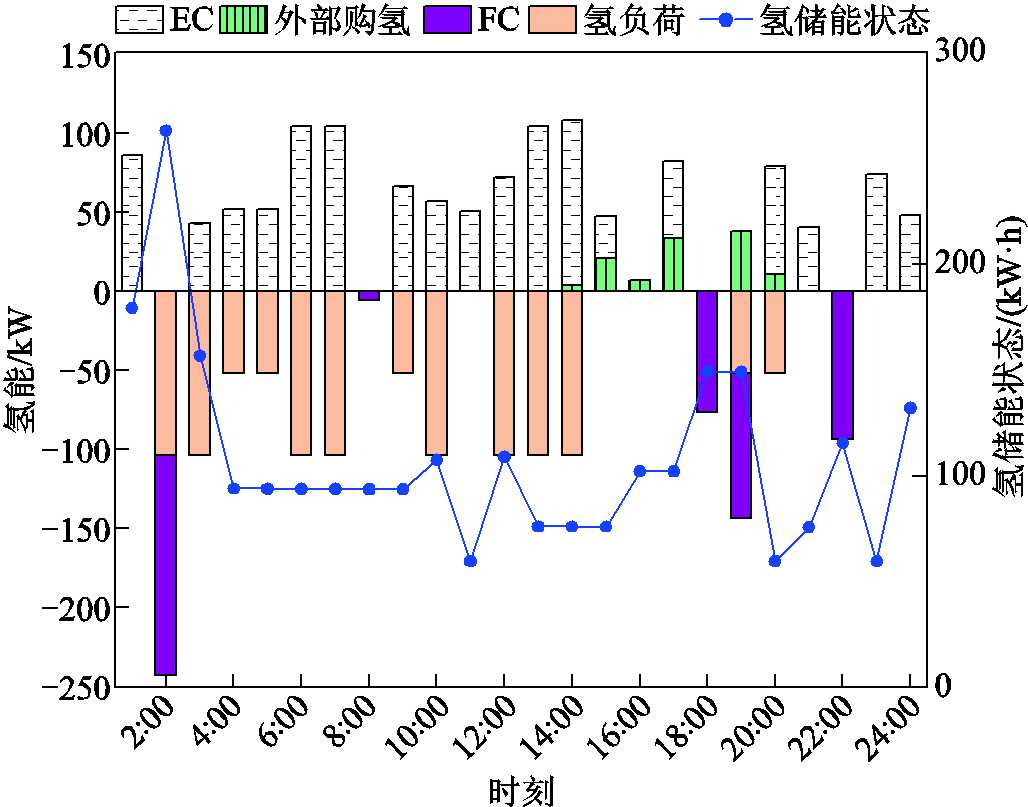
图10 氢能设备运行状态
Fig.10 Operation status of hydrogen energy equipment
5.3.1 情景设置
为揭示VESHS实施电-氢集成规划及优化定价机制带来的效益,本文设置四种情景,对多情景下的最优规划方案、定价方案及其成本效益进行对比分析,各情景下的规划方案及规划效益见表6和表7。
表6 多情景规划方案对比
Tab.6 Comparison of optimization schemes in multiple scenarios
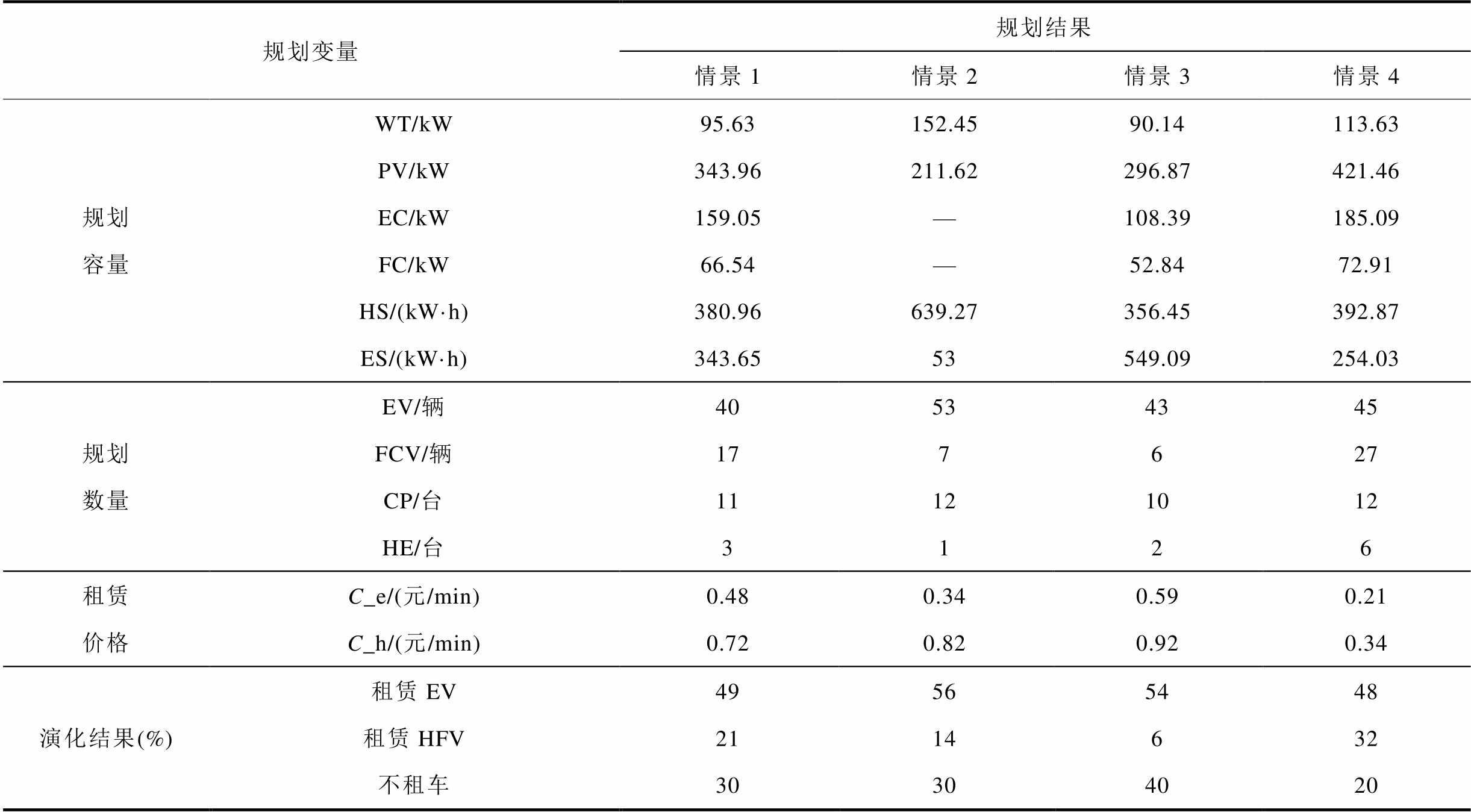
规划变量规划结果 情景1情景2 情景3 情景4 规划容量WT/kW95.63152.4590.14113.63 PV/kW343.96211.62296.87421.46 EC/kW159.05—108.39185.09 FC/kW66.54—52.8472.91 HS/(kW·h)380.96639.27356.45392.87 ES/(kW·h)343.6553549.09254.03 规划数量EV/辆40534345 FCV/辆177627 CP/台11121012 HE/台3126 租赁价格C_e/(元/min)0.480.340.590.21 C_h/(元/min)0.720.820.920.34 演化结果(%)租赁EV49565448 租赁HFV2114632 不租车30304020
情景1:VSEHS电-氢耦合系统,采用优化定价机制。
情景2:电、氢能源系统独立运行,采用优化定价机制,该场景下仅配置可再生能源发电和ES,不使用氢电转换设备与HS,氢能全部外购而不考虑电-氢两种能源形式之间的耦合作用。
情景3:VSEHS电-氢耦合系统,根据当前市场独立共享汽车运营商的EV租车价格定价。参考文献[30],取EV租赁价格为0.59 元/min。由于目前尚无HFV的租赁价格,本文参考EV租赁定价方式,根据氢能源价格、HFV购买维修费用等成本并结合合理收益,取HFV租车价格为0.92 元/min。
情景4:VSEHS电-氢耦合系统,低价格水平的固定价格方案。在本例中,人为地将EV租赁价格设为0.21 元/min,HFV租赁价格设为0.34 元/min。
5.3.2 电氢联合规划效益分析
通过对比情景1和情景2可知,相比于电、氢独立运行的规划方案,电-氢耦合联合规划方案的规划成本大大增加,这主要是因为耦合系统中包含电氢转换设备,其大量使用及可再生能源发电设备的额外投入会直接导致投资成本有明显的增加。但是总体来看,电-氢耦合系统的综合经济效益和环境效益均有较优的结果,情景1的年投资净收益和环境收益较情景2分别提高了11.97%和24.71%。这是由于多能源-多车型的联合优化调度可以利用多余的能量实现电氢转换,增强风光的就地消纳能力,使系统更大程度地利用可再生能源,同时减少对外部市场电能和氢能(即具有高碳排放附加属性的能量来源)的依赖,在双重作用下显著增大环境效益。此外,情景2中由于氢燃料汽车能量直接来源于外部,其环境效益远小于电动汽车,因此,情景2中EV和HFV的租赁定价差价相对更大,以便引导用户使用电动汽车多于氢燃料汽车。
表7 多情景规划效益对比
Tab.7 Comparison of optimization benefits in multiple scenarios(单位:万元)

情景系统净收益租赁收益碳减排收益年投资成本年运行成本 1333.99524.0149.06220.7618.32 2298.29485.3139.33199.9526.40 3296.46471.1442.26202.7814.16 4242.72468.3262.01264.3923.22
为了进一步揭示电-氢耦合系统规划方案的有效性,图11和图12分别展示了情景2下各设备日出力情况和车辆调度情况。
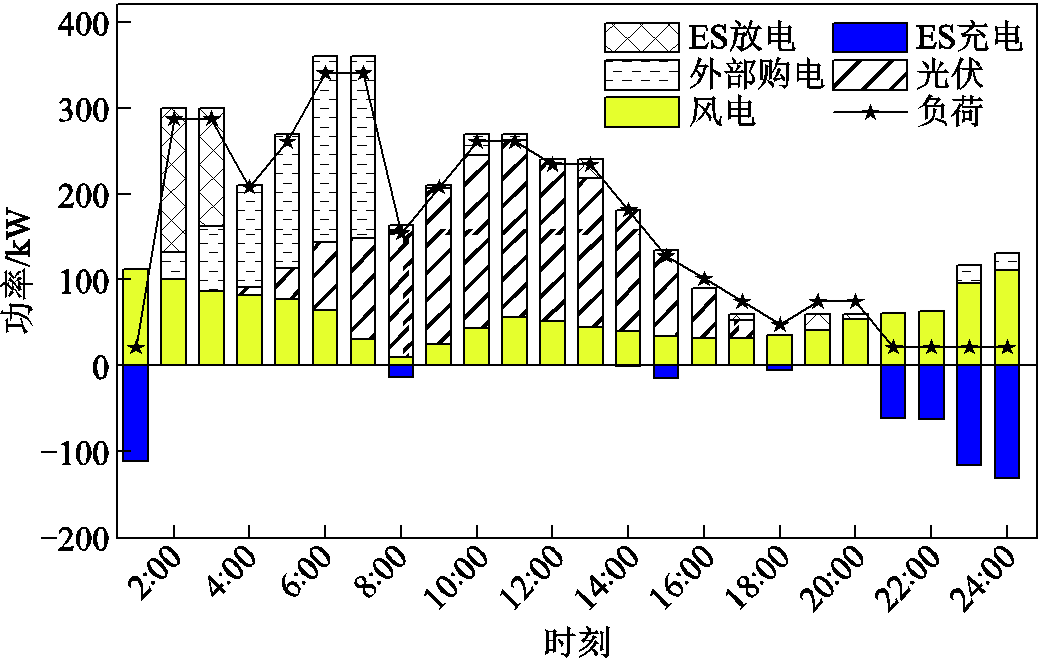
图11 情景2电功率平衡
Fig.11 Electric power balance under Scenario 2
由图11可知,一方面,系统侧在电价低谷时从电网购买较多电量以满足车辆的充电需求;另一方面,在8:00—15:00由于少了EC对新能源的直接消纳,导致白天光伏的利用率大大下降,光伏装机容量下降38.47%,对比图8和图11可以看出光伏最大出力下降30%左右。因此,在非联合规划场景下虽然同样使用新能源汽车,却因不能高效利用“绿氢”和“绿电”而无法实现能源、交通的协同低碳转型。
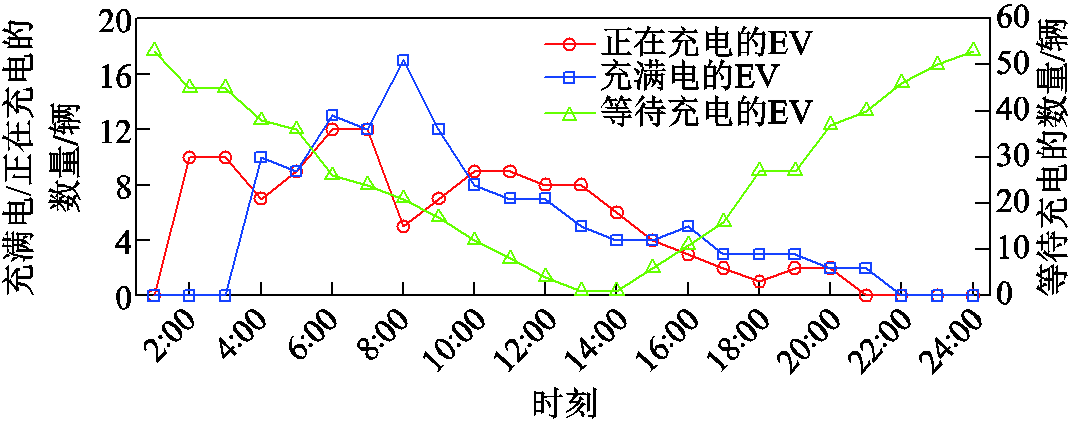
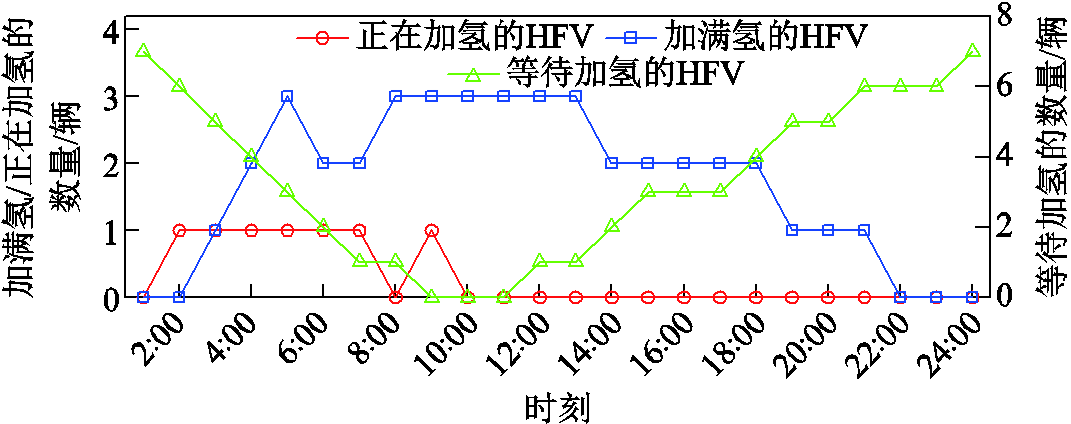
图12 情景2新能源汽车状态
Fig.12 State of the vehicle under Scenario 2
由图12可以看出,充电、加氢车辆数量最高点均出现在早晨,这说明在非联合规划情况下,系统会集中在早上进行大量充电;而联合规划下,可调节的充电和加氢行为使系统更灵活地协调安排各个设备的运行,系统可以根据新能源出力及时调整充电需求,并结合用户出行需求更好地实现车辆的调度安排,进一步提高系统的经济效益和环保效益。
5.3.3 定价机制影响分析
情景3和情景4为固定价格方案,即在给定的车辆租赁价格下进行规划。由表7可知两种固定价格方案下的VSEHS投资收益均低于采用本文优化定价机制的情景1。
由情景3与情景1对比可知,情景3的投资效益和碳减排收益均略逊于情景1,并且情景3的各种设备配置基本都有所减小,这主要是因为综合成本决定了车辆租赁价格,而目前由于充电站和加氢站均独立运营,且能源-车辆之间缺少调度匹配导致其综合成本较高,以至于社会固定租赁价格较VSEHS优化价格整体偏高,因此用户租车意愿明显降低,有40%的用户拒绝参与租车服务。
而VSEHS可以利用富余可再生能源进行电制氢及通过多能互补-车辆协调调度提高资源利用率从而显著降低联合规划运行成本。同时,动态优化定价可间接反映联合规划运行成本,实现价格-成本间的联动以充分发挥联合规划成本低的优势。由规划效益结果显示,优化定价机制可以增加源侧能源系统和用户侧交通出行的交互利润,即租赁收益,表明规划者可以较低的价格获得较大的收益。
对比情景4和情景1可以看出,情景4的投资成本有所增加,但同时其租赁收益大幅下降。这是因为在较低价格水平下,用户租车需求会增加(80%的用户选择在站内租车),设备的装机容量也将随之增加;但同时较低的价格也会使租赁收入不乐观。因此,动态优化定价机制相对于固定价格机制具有明显的优势。
此外,在优化定价机制下,系统可借助用户用车需求所具有的能源可替代性引导其选择偏好,进而根据用户需求调整自身规划运行策略,改变了系统侧的氢电投资比例,从而实现了投资效益的提升。同时,通过基于用户选择偏好的长期需求侧调节还可适度提高地终端负荷需求与可再生能源发电出力的匹配度,提高了系统中可再生能源的消纳率,从而使系统具有更好的运行经济性和低碳效益。
为验证本文所提出的区间-随机混合优化模型的有效性,本节将前述情景1规划方案与传统纯随机优化方法所得规划方案的规划效益进行对比。
在纯随机优化方案中,对于原区间变量,将根据其波动区间及给定概率分布,利用蒙特卡罗模拟生成随机样本序列。需要强调的是,在没有先验信息的条件下,本文采取国内外研究广泛采用的几种分布函数:均匀分布、正态分布、高斯截断分布。假设纯随机优化方法下的模型参数设置均与5.1节相同。
区间-随机混合优化与纯随机的规划效益见表8所示。由表8可知,纯随机优化模型得到的系统规划方案高度依赖所给基准数据的分布信息,在不同分布情况下所得数据具有较强的差异性。因此,基于纯随机的规划方法并不具有普适性,对于不同地区其规划结果相差过大,将给未知数据地区的研究带来巨大的困难。而本文中所提出的区间-随机混合优化模型同时兼顾不同种不确定参数的数据特点,采取最适合的数学处理方法:对于不易于短时间内获得可靠数据的不确定变量采用区间形式以同时兼顾系统在不确定性作用下乐观和悲观两方面情况;对于短时间内易获得大量可靠数据的变量采用随机优化方法,由于其采用确切分布函数描述而有较高的准确性。因此本文所提的区间-随机混合规划方案比传统纯随机方案具有更好的通用可靠性。
表8 混合优化与纯随机优化规划效益对比
Tab.8 Comparison of pure stochastic planning results(单位:万元)
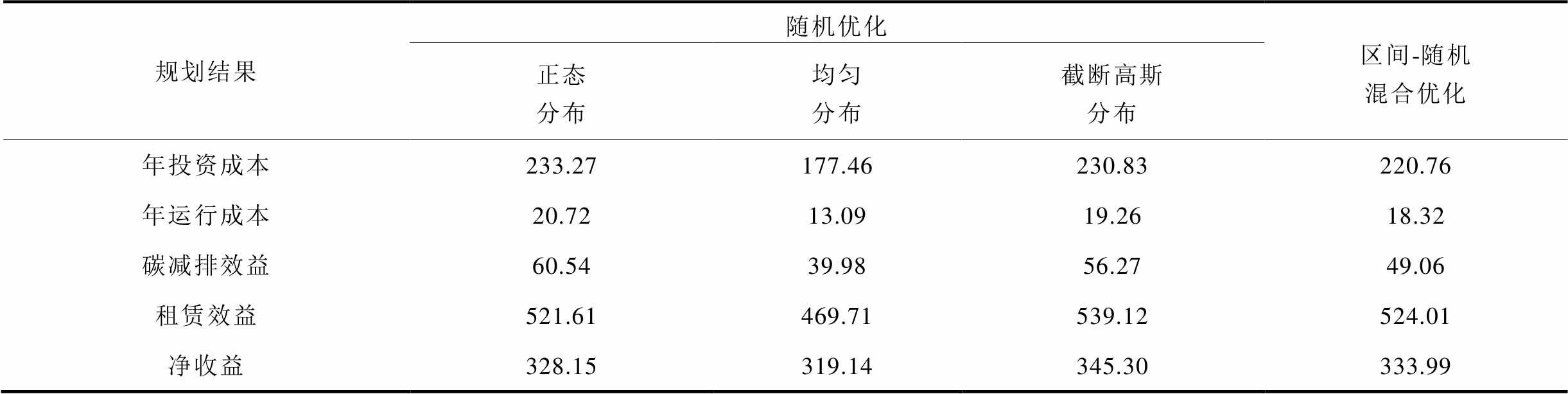
规划结果随机优化区间-随机混合优化 正态分布均匀分布截断高斯分布 年投资成本233.27177.46230.83220.76 年运行成本20.7213.0919.2618.32 碳减排效益60.5439.9856.2749.06 租赁效益521.61469.71539.12524.01 净收益328.15319.14345.30333.99
为充分发挥新能源汽车对能源交通领域低碳转型目标的支撑作用,本文提出一种面向新能源汽车共享站的电-氢微能源系统综合资源规划框架。相比于现有研究,本文重点研究了租赁价格优化引导下用户租车选择偏好对VSEHS长期规划的影响,并考虑到不同参数数据源的异质性,采用区间和随机相结合的混合建模方法来处理规划中的不确定性,进而设计了一种区间-随机混合优化方法进行求解。经过算例仿真分析,可得出以下主要结论:
1)由EV与HFV车辆需求可替代性所引起能量需求转化是VSEHS系统灵活性的来源之一,借助价格引导用户租车选择长期偏好,以与VSEHS的规划运行相匹配,对于制定VSEHS最优规划方案至关重要。
2)考虑电-氢耦合和不同车型联合运行的VSEHS综合资源规划模型能够实现供需平衡,有效地提高VSEHS的经济效益和环境效益。同时,可以实现新能源汽车的动力基本来源于可再生能源,从而有效促进可再生能源消纳和交通领域低碳发展。
3)汽车租赁定价较高或较低都会带来不理想的收益,价格优化机制可以实现价格与系统成本的联动,充分发挥综合资源规划模式下的低成本优势,增加能源系统与用户的互动利润。
4)与传统的纯随机优化方法相比,基于区间-随机混合优化方法的VSEHS规划方案能有效适应某些参数先验信息未知的情况,具有更好的通用性和可靠性。
后续将基于能源-交通耦合视角,进一步考虑VSEHS系统在支撑电网运行及缓解交通堵塞方面的重要作用,开展含多个VSEHS协同运行的区域级综合能源系统规划研究。
参考文献
[1] 国务院. 国务院关于印发2030年前碳达峰行动方案的通知[Z/OL]. (2021-10-24). http://www.gov.cn/ zhengce/content/2021-10/26/content_5644984.htm.
[2] 国务院办公厅. 国务院办公厅关于印发新能源汽车产业发展规划(2021—2035年)的通知[Z/OL]. (2020-10-20). http://www.gov.cn/zhengce/content/ 2020-11/02/content_5556716.htm.
[3] 中国氢能源行业发展前景预测与投资战略规划分析报告[R]. https://bg.qianzhan.com/report/detail/160 7281732570984.html?v=title.
[4] 陈中, 陈妍希, 车松阳. 新能源汽车一体充能站框架及能量优化调度方法[J]. 电力系统自动化, 2019, 43(24): 41-49. Chen Zhong, Chen Yanxi, Che Songyang. Framework of integrated charging station for renewable energy vehicle and energy optimal dispatching method[J]. Automation of Electric Power Systems, 2019, 43(24): 41-49.
[5] 王海鑫, 袁佳慧, 陈哲, 等. 智慧城市车-站-网一体化运行关键技术研究综述及展望[J]. 电工技术学报, 2022, 37(1): 112-132. Wang Haixin, Yuan Jiahui, Chen Zhe, et al. Review and prospect of key techniques for vehicle-station-network integrated operation in smart city[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 112-132.
[6] 毛玲, 张钟浩, 赵晋斌, 等. 车-桩-网交融技术研究现状及展望[J]. 电工技术学报, 2022, 37(24): 6357-6371. Mao Ling, Zhang Zhonghao, Zhao Jinbin, et al. Research status and prospects of fusion technology of vehicle-charging pile-power grid[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6357-6371.
[7] 翁菖宏, 胡志坚, 刘妍, 等. 计及互联调控的新能源汽车一体化供能站规划[J]. 智慧电力, 2021, 49(9): 24-31, 94. Weng Changhong, Hu Zhijian, Liu Yan, et al. Integrated power supply station planning of new energy vehicles with interconnection control[J]. Smart Power, 2021, 49(9): 24-31, 94.
[8] Cao Xiaoyu, Sun Xunhang, Xu Zhanbo, et al. Hydrogen-based networked microgrids planning through two-stage stochastic programming with mixed-integer conic recourse[J]. IEEE Transactions on Automation Science and Engineering, 2022, 19(4): 3672-3685.
[9] 吴孟雪, 房方. 计及风光不确定性的电-热-氢综合能源系统分布鲁棒优化[J]. 电工技术学报, 2023, 38(13): 3473-3485. Wu Mengxue, Fang Fang. Distributionally Robust optimization of electricity-heat-hydrogen integrated energy system with wind and solar uncertainties[J]. Transactions of China Electrotechnical Society, 2023, 38(13): 3473-3485.
[10] Liu Jia, Cao Sunliang, Chen Xi, et al. Energy planning of renewable applications in high-rise residential buildings integrating battery and hydrogen vehicle storage[J]. Applied Energy, 2021, 281: 116038.
[11] 李珂, 邵成成, 王雅楠, 等. 考虑电-气-交通耦合的城市综合能源系统规划[J]. 中国电机工程学报, 2023, 43(6): 2263-2273. Li Ke, Shao Chengcheng, Wang Yanan, et al. Optimal planning of urban integrated energy systems considering electricity-gas-transportation interactions[J]. Proceedings of the CSEE, 2023, 43(6): 2263-2273.
[12] 袁铁江, 计力, 田雪沁, 等. 考虑燃料电池汽车加氢负荷的电-氢系统协同优化运行[J]. 电力系统自动化, 2023, 47(5): 16-25. Yuan Tiejiang, Ji Li, Tian Xueqin, et al. Synergistic optimal operation of electricity-hydrogen systems considering hydrogen refueling loads for fuel cell vehicles[J]. Automation of Electric Power Systems, 2023, 47(5): 16-25.
[13] 闫佳佳, 滕云, 邱实, 等. 计及供能可靠性动态约束与碳减排的充能型微电网互联系统优化模型[J]. 电工技术学报, 2022, 37(23): 5956-5975. Yan Jiajia, Teng Yun, Qiu Shi, et al. Optimization model of charging microgrid interconnection system considering dynamic constraints of energy supply reliability and carbon emission reduction[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 5956-5975.
[14] Ran Cuiling, Zhang Yanzi, Yin Ying. Demand response to improve the shared electric vehicle planning: managerial insights, sustainable benefits[J]. Applied Energy, 2021, 292: 116823.
[15] Aliasghari P, Mohammadi-Ivatloo B, Alipour M, et al. Optimal scheduling of plug-in electric vehicles and renewable micro-grid in energy and reserve markets considering demand response program[J]. Journal of Cleaner Production, 2018, 186: 293-303.
[16] Salyani P, Abapour M, Zare K. Stackelberg based optimal planning of DGs and electric vehicle parking lot by implementing demand response program[J]. Sustainable Cities and Society, 2019, 51: 101743.
[17] Shojaabadi S, Abapour S, Abapour M, et al. Optimal planning of plug-in hybrid electric vehicle charging station in distribution network considering demand response programs and uncertainties[J]. IET Generation, Transmission & Distribution, 2016, 10(13): 3330-3340.
[18] 程妤. 基于心理账户的共享汽车出行选择行为研究[D]. 重庆: 重庆交通大学, 2020.
[19] 程瑜, 邰宇峰, 丁肇豪, 等. 基于网络流的共享电动汽车优化调度[J]. 电工技术学报, 2022, 37(增刊1): 145-152. Cheng Yu, Tai Yufeng, Ding Zhaohao, et al. Optimal scheduling of sharing electric vehicles based on network flow[J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 145-152.
[20] 王亮. 考虑个体异质性的新能源汽车分时租赁出行选择行为研究[D]. 成都: 西南交通大学, 2020.
[21] Fan Jingli, Wang Jiaxing, Zhang Xian. An innovative subsidy model for promoting the sharing of electric vehicles in China: a pricing decisions analysis[J]. Energy, 2020, 201: 117557.
[22] Wang Yue, Yao Enjian, Pan Long. Electric vehicle drivers’ charging behavior analysis considering heterogeneity and satisfaction[J]. Journal of Cleaner Production, 2021, 286: 124982.
[23] Wu Fuzhang, Yang Jun, Zhan Xiangpeng, et al. The online charging and discharging scheduling potential of electric vehicles considering the uncertain responses of users[J]. IEEE Transactions on Power Systems, 2021, 36(3): 1794-1806.
[24] 冰雪. 考虑供需时空特征的共享电动汽车差异化定价研究[D]. 长春: 吉林大学, 2022.
[25] 姬杨蓓蓓, 陈欣萌, 成枫. 考虑排放成本的共享电动汽车和共享停车位最优组合定价研究[J]. 管理工程学报, 2022, 36(1): 134-145. Ji Yangbeibei, Chen Xinmeng, Cheng Feng. Research on optimal pricing of shared vehicles and shared parking considering traffic emission cost[J]. Journal of Industrial Engineering and Engineering Management, 2022, 36(1): 134-145.
[26] Zeynali S, Nasiri N, Marzband M, et al. A hybrid robust-stochastic framework for strategic scheduling of integrated wind farm and plug-in hybrid electric vehicle fleets[J]. Applied Energy, 2021, 300: 117432.
[27] Kou Xiao, Li Fangxing. Interval optimization for available transfer capability evaluation considering wind power uncertainty[J]. IEEE Transactions on Sustainable Energy, 2020, 11(1): 250-259.
[28] Daryabari M K, Keypour R, Golmohamadi H. Robust self-scheduling of parking lot microgrids leveraging responsive electric vehicles[J]. Applied Energy, 2021, 290: 116802.
[29] Tan Jun, Wang Lingfeng. Integration of plug-in hybrid electric vehicles into residential distribution grid based on two-layer intelligent optimization[J]. IEEE Transactions on Smart Grid, 2014, 5(4): 1774-1784.
[30] Lu Xinhui, Zhou Kaile, Yang Shanlin, et al. Multi-objective optimal load dispatch of microgrid with stochastic access of electric vehicles[J]. Journal of Cleaner Production, 2018, 195: 187-199.
[31] Khezri R, Mahmoudi A, Haque M H. Impact of optimal sizing of wind turbine and battery energy storage for a grid-connected household with/without an electric vehicle[J]. IEEE Transactions on Industrial Informatics, 2022, 18(9): 5838-5848.
[32] 陆剑清. 现代消费行为学[M]. 北京: 北京大学出版社, 2013.
[33] 梅生伟, 刘锋, 魏韡. 工程博弈论基础及电力系统应用[M]. 北京: 科学出版社, 2016.
[34] 杨雄. 分时租赁电动汽车运行数据驱动的充/换电设施布局研究[D]. 北京: 北京交通大学, 2020.
[35] Ahn H, Rim D, Pavlak G S, et al. Uncertainty analysis of energy and economic performances of hybrid solar photovoltaic and combined cooling, heating, and power (CCHP + PV) systems using a Monte-Carlo method[J]. Applied Energy, 2019, 255: 113753.
[36] Mei Fei, Zhang Jiatang, Lu Jixiang, et al. Stochastic optimal operation model for a distributed integrated energy system based on multiple-scenario simulations[J]. Energy, 2021, 219: 119629.
[37] Farham H, Mohammadian L, Alipour H, et al. Energy procurement of large industrial consumer via interval optimization approach considering peak demand management[J]. Sustainable Cities and Society, 2019, 46: 101421.
[38] Sengupta A, Pal T K. On comparing interval numbers[J]. European Journal of Operational Research, 2000, 127(1): 28-43.
[39] Liu Yangyang, Jiang Chuanwen, Shen Jingshuang, et al. Coordination of hydro units with wind power generation using interval optimization[J]. IEEE Transactions on Sustainable Energy, 2015, 6(2): 443-453.
[40] Pan Guangsheng, Gu Wei, Qiu Haifeng, et al. Bi-level mixed-integer planning for electricity-hydrogen integrated energy system considering levelized cost of hydrogen[J]. Applied Energy, 2020, 270: 115176.
[41] Dong Xiangxiang, Wu Jiang, Xu Zhanbo, et al. Optimal coordination of hydrogen-based integrated energy systems with combination of hydrogen and water storage[J]. Applied Energy, 2022, 308: 118274.
[42] Zhong Xiaoqing, Zhong Weifeng, Liu Yi, et al. Cooperative operation of battery swapping stations and charging stations with electricity and carbon trading[J]. Energy, 2022, 254: 124208.
[43] Zhang Xizheng, Wang Zeyu, Lu Zhangyu. Multi-objective load dispatch for microgrid with electric vehicles using modified gravitational search and particle swarm optimization algorithm[J]. Applied Energy, 2022, 306: 118018.
[44] Li Junjie, Cheng Wanjing. Comparative life cycle energy consumption, carbon emissions and economic costs of hydrogen production from coke oven gas and coal gasification[J]. International Journal of Hydrogen Energy, 2020, 45(51): 27979-27993.
[45] Jiang Qian, Mu Yunfei, Jia Hongjie, et al. A Stackelberg Game-based planning approach for integrated community energy system considering multiple participants[J]. Energy, 2022, 258: 124802.
[46] Mu Yunfei, Chen Wanqing, Yu Xiaodan, et al. A double-layer planning method for integrated community energy systems with varying energy conversion efficiencies[J]. Applied Energy, 2020, 279: 115700.
[47] Isaac N, Saha A K. Analysis of refueling behavior of hydrogen fuel vehicles through a stochastic model using Markov Chain process[J]. Renewable and Sustainable Energy Reviews, 2021, 141: 110761.
[48] Li Jiale, Liu Zhenbo, Wang Xuefei. Public charging station localization and route planning of electric vehicles considering the operational strategy: a bi-level optimizing approach[J]. Sustainable Cities and Society, 2022, 87: 104153.
Abstract Under the rapid development of electric vehicles (EV) and hydrogen fuel vehicles (HFV), the construction of electric-hydrogen coupling micro-energy networks based on terminal parking lots and renewable energy hydrogen production technology is an important means to effectively promote the low-carbon transformation of the transportation field. The current research on micro-energy grid planning based on parking lot rarely considers the load flexibility brought by the traffic substitutability between EV and HFV, and guides users' long-term vehicle choice preferences by optimizing the price to promotes the consumption of renewable energy source(RES). Considering that the new energy vehicles (NEV) sharing station under the leasing mode is one of the typical scenarios to realize the vehicle demand substitution and energy conversion demand transformation between EV and HFV, this paper takes the new energy vehicle sharing station-based electro-hydrogen micro-energy system (VSEHS) as the research object. In this paper, a two-stage VSEHS planning framework with capacity allocation and vehicle rental price co-optimization is proposed based on the concept of comprehensive resource planning and hybrid interval/stochastic optimization method.
Firstly, the VSEHS architecture and the low-carbon operation mode considering multi-energy and multi-vehicle coordination is described. Secondly, according to the difficulty of obtaining the probabilistic distribution, a hybrid modeling method combining interval and probability is used to deal with the uncertainty of supply side and load side. Secondly, the long-term preference and evolutionary modeling of users' car-rental based on evolutionary game are carried out to describe the potential flexibility of user demand on rental pricing under car-sharing services. And then, on the basis of using rental price to guide user demand, considering the influence of various uncertain factors, the capacity allocation and pricing decision optimization model of VSEHS based on interval-stochastic hybrid programming is constructed. Finally, an interval-stochastic hybrid optimization method is proposed to normalize different types of uncertain variables, and achieve efficient solutions based on heuristic algorithms under the same framework.
The simulation results of VSEHS planning for an urban community show that, under the optimum planning scheme, the rental prices of EV and HFV are 0.483 ¥/min and 0.717 ¥/min respectively. At this price level, 30% of users refuse to participate in the rental service, 49% and 21% of users choose to rent EV and HFV, respectively. Through the coordinated optimization of vehicle scheduling and electric-hydrogen energy conversion scheduling, the hydrogen self-sufficiency rate of the system reaches 91.3%, which can ensure that HFV is basic comes from the RES. The planning schemes under different scenarios show that, compared with the independent operation, the annual net investment and environmental benefits of electric-hydrogen integrated planning can be increased by 11.97% and 24.71%, respectively, and the dynamic optimal pricing mechanism has obvious advantages over the fixed price mechanism. This proves that the electric-hydrogen integrated planning can make greater use of RES and reduce the dependence on external market for electricity and hydrogen energy; for another, it illustrates that under the optimal pricing mechanism, the system can guide the user's choice preferences by energy substitutability in the user's vehicle demand, and then adjust its own planning and operation strategy according to the user's demand. Thus, the improvement of investment efficiency is realized. Finally, the planning schemes of interval/stochastic hybrid optimization and pure stochastic optimization are compared. The results show that, the planning scheme obtained by the pure stochastic optimization is highly dependent on the distribution information of the given data, and the proposed interval/stochastic hybrid planning scheme has better general reliability.
The following conclusions can be drawn from the simulation analysis: (1) the VSEHS planning model considering electron-hydrogen coupling and joint operation of different models can achieve the balance between supply and demand, also realize that NEVs can basically supplied by RES while ensuring the economic benefits. (2) The optimal mechanism of vehicle rental price can not only guide the long-term preferences of users in rental cars to match the planning and operation of VSEHS, but also realize the linkage between price and system cost, which makes full use of the low cost advantage of comprehensive resource planning mode, and increase the interaction profit between supply and demand side. (3) Compared with the traditional pure stochastic optimization method, the VSEHS planning scheme based on interval-random hybrid optimization method can effectively adapt to the situation where the prior information of some parameters is unknown, and has better versatility and reliability.
keywords:New energy vehicle sharing station, electro-hydrogen micro-energy network planning, evolutionary game, pricing for vehicle sharing, interval-stochastic hybrid optimization
DOI:10.19595/j.cnki.1000-6753.tces.L10038
中图分类号:TM715
河北省自然科学基金(G2022502004)、国家自然科学基金(62133015)和中央高校基本科研业务费专项资金(2022JG005)资助项目。
收稿日期 2023-01-13
改稿日期 2023-06-27
王雨晴 女,1994年生,博士,讲师,硕士生导师,研究方向为综合能源系统规划。E-mail:wangyuqingncepu@foxmail.com
王文诗 女,1998年生,硕士,研究方向为电-氢综合能源系统规划。E-mail:qqmavis121@163.com(通信作者)
(编辑 赫蕾)