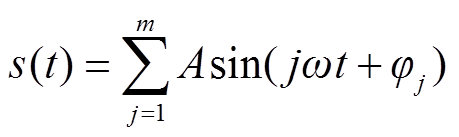（1）
摘要 对于电能质量扰动信号压缩问题，压缩比和重构误差是一对互相矛盾的指标。传统的压缩算法难以同时满足高压缩比和低重构误差的要求。为了同时提高压缩比和减小重构误差，该文提出了一种基于稀疏分解、哈夫曼编码和行程编码的混合压缩算法。首先，使用基于联合字典的稀疏分解算法，将电能质量扰动信号中的暂态分量和稳态分量进行分离；其次，对暂态分量使用小波分析、哈夫曼编码、行程编码算法进行编码压缩，对稳态分量，即基波和谐波分量，则保留其大于设定阈值的部分，进而完成对信号的压缩；最后，仿真信号和实测信号的实验结果表明该算法较对比算法具有更高的压缩比和更低的重构误差，同时证明了其对采样频率和高斯白噪声具有较强的抗干扰能力。
关键词：信号压缩 电能质量扰动 哈夫曼编码 行程编码 小波分析 稀疏分解
电能质量扰动数据对电网是一种十分有用的信息。一般情况下，不同的电能质量扰动波形反映着电网故障或倒闸操作，因此这些数据可用于检测电网扰动类型。例如，负荷投切造成的暂态振荡[1]、电力电子装置换相造成的电压切口[2]、短路故障造成的电压暂降或中断[3]、雷击线路造成的瞬时脉冲等[4]。此外，电能质量扰动波形还可用来对配电网的扰动进行定位[5]。但是随着电网规模的日益扩大，电能质量扰动事件也越来越多。若某个区域的电网监测装置较多，则其对通信带宽的需求会非常高[6]。因此，对电能质量扰动数据的高效压缩算法的需求也更加迫切[7]。
电能质量数据的压缩算法总体上分为两大类：无损压缩和有损压缩。无损压缩是通过编码算法减少数据的冗余度实现压缩，且解压缩后能够完全恢复信号而无任何损失，其中包括哈夫曼编码[8]、Lempel-Ziv-Welch（LZW）编码[9]等算法。复杂电能质量扰动信号的冗余度通常较小，使用编码算法进行压缩一般难以获得较高的压缩比。研究人员对电能质量信号关注的重点在扰动事件本身，而非信号的细节，信号在解压缩后少许细节损失是可接受的，因此当前大多数电能质量信号压缩算法为有损压缩算法。
有损压缩主要可分为直接压缩和间接压缩两类。直接压缩即首先直接利用小波对一维信号进行分解，然后丢弃部分细节系数，进而完成压缩。S. Santoso等提出了基于小波分析的压缩算法[10]。何正友等分析小波基对压缩效果的影响，并提出了一种优化小波的算法[11]。文献[12]指出bior 3.1小波的提升算法计算速度更快，速度上优于其他bior系列的小波，但并未与其他的小波基进行对比。文献[13]将小波包分解应用于信号的压缩，指出小波包可以有效地提高压缩数据中零值的个数，进而提高压缩比，但是小波包对压缩比的提升幅度有限。文献[14]使用提升小波压缩信号，并给出了幅值和相位的重构误差。文献[15]则使用了样条小波和神经网络进行压缩，其压缩比和重构误差结果优于余弦变换和小波变换的压缩效果，在相同的压缩比条件下，重构信号保留了更多原始信号的能量。
一些学者运用图像压缩算法来压缩电能质量扰动数据[16]。文献[17]将一维的电能质量扰动数据转换为二维灰度图，然后用二维小波对图像进行压缩。该算法实现了较高的压缩比，但是丢弃了几乎全部的噪声，导致其重构误差较大。此外，该方法需要较长的数据帧，若扰动持续时间较短，需要采集大量额外的数据才能应用该算法。张明等将基于小波的JPEG2000压缩算法应用于电能质量扰动信号的压缩，实现了有损压缩和无损压缩，且码率可控，该方法的缺点是同样需要很长的数据帧[18]。
除上述压缩算法外,奇异值分解（Singular Value Decomposition, SVD）作为一种重要的有损压缩算法已经被广泛应用于图像压缩[19]。文献[20]将SVD算法用于电能质量扰动数据的压缩，其原理是先将一维数据转换为二维信号，然后对其作SVD分解，丢弃部分较小的值，进而实现压缩。
间接压缩即首先将电能质量扰动信号的暂态和稳态分离开，然后对暂态分量和稳态分量分别使用不同的算法压缩。文献[21-22]使用巴特沃斯滤波器组分离暂态成分和稳态成分，对稳态则使用插值快速傅里叶变换（Fast Fourier Transform, FFT）计算其幅值和相位；对暂态成分则使用一维小波压缩，实现较高的压缩比。文献[23]则提出了基于卡尔曼滤波和提升小波的压缩算法,利用强跟踪卡尔曼滤波器（Strong Tracking Kalman Filter, STKF）进行暂态和稳态的分离，然后对暂态和稳态分别进行压缩，实现了较高的压缩比和较低的重构误差。
文献[24]使用基于单位矩阵（identity matrix）和单位傅里叶变换的联合字典和正交匹配追踪（Orthogonal Matching Pursuit, OMP）算法进行暂稳态的分离，并实现了较高的压缩，但并未考虑信号的噪声。文献[25]将傅里叶字典替换为哈特莱字典，哈特莱变换的本质仍是傅里叶变换，故其分解结果相同。文献[26-27]的频域字典为余弦矩阵+正弦矩阵，该字典的缺点是分解结果的频域部分存在较严重的旁瓣，不利于压缩比的提高。此外，基于OMP的衍生算法可加快求解速度，但计算更为复杂，且压缩算法对实时性要求不高，故而提高稀疏分解的求解速度意义不大[28]。
在现有的研究基础上，本文提出了基于稀疏分解和混合编码的电能质量数据压缩方案。首先，利用稀疏分解对电能质量扰动信号的暂态和稳态成分进行分离；稳态部分可直接压缩，对暂态的成分使用小波作3层分解，得到近似系数和细节系数；对近似系数a3则采用分段近似归置的方法，提高其冗余性，使用LZW编码实现压缩；对细节系数d3、d2、d1设置小波阈值，小于阈值的系数置零，其余的系数保持不变，并使用行程编码对细节系数进行编码，然后用哈夫曼编码对行程编码的结果进行二次编码，以提高压缩比。
电能质量信号s(t)可表示为
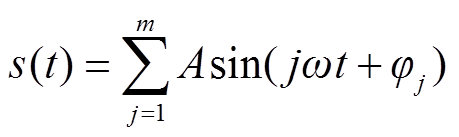（1）
式中，j为第j次谐波；Aj是第j次谐波的幅值；ω为角频率；φj为第
次谐波的初相位。
设第k个状态空间为
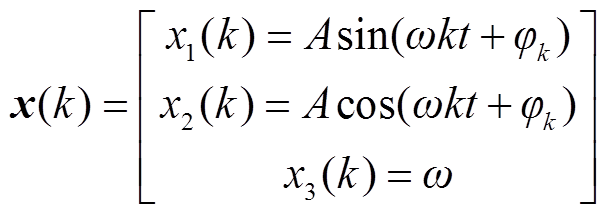（2）
故非线性状态方程中的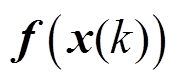
可写为
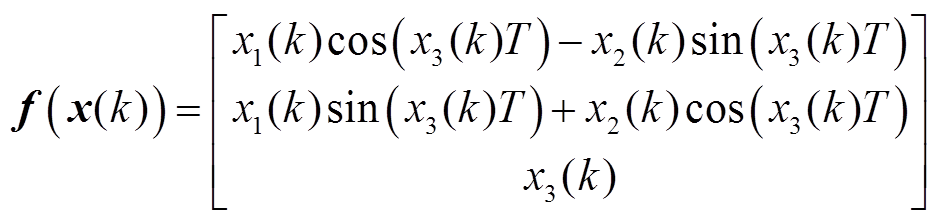（3）
式中，T为信号的采样间隔。
状态观测方程中的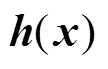
为
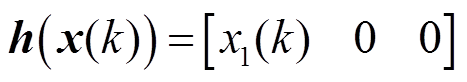（4）
在建立了非线性的状态方程和观测方程，并设置参数矩阵Q和R后，即可计算STKF。STKF总体上可分为两步，即状态一步预测和状态修正。
1）状态一步预测。
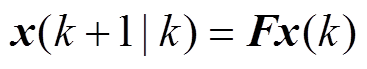（5）
式中，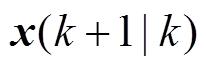
为基于第k个状态
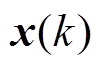的预测值；F为状态转移矩阵。
2）状态修正。状态修正又可以分为4个步骤：
（1）协方差矩阵一步预测。
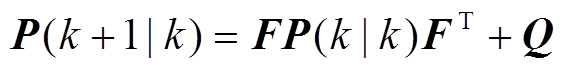（6）
（2）根据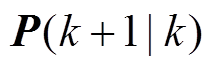
计算滤波增益矩阵
。
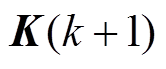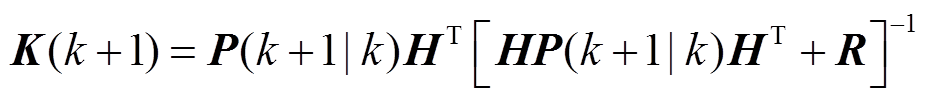（7）
式中，H为状态观测矩阵。
（3）由滤波增益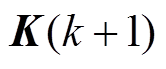修正状态
。
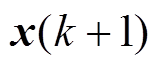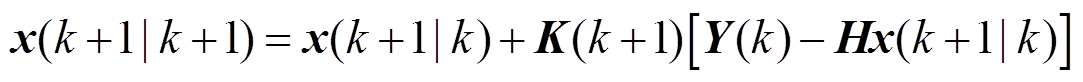（8）
式中，Y为观测量矩阵。
（4）更新状态协方差矩阵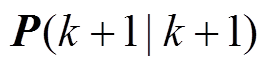
。
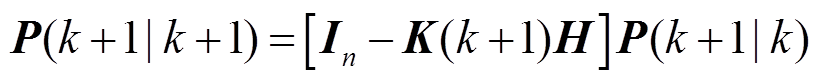（9）
式中，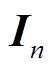
为n阶单位矩阵。
STKF在KF过程中增加了渐消因子（Fading Factor, FF）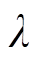
，于是式（6）变为式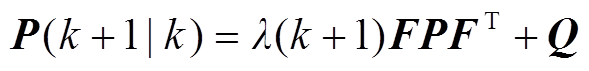（10）。
（10）
其中，渐消因子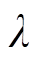的计算步骤为
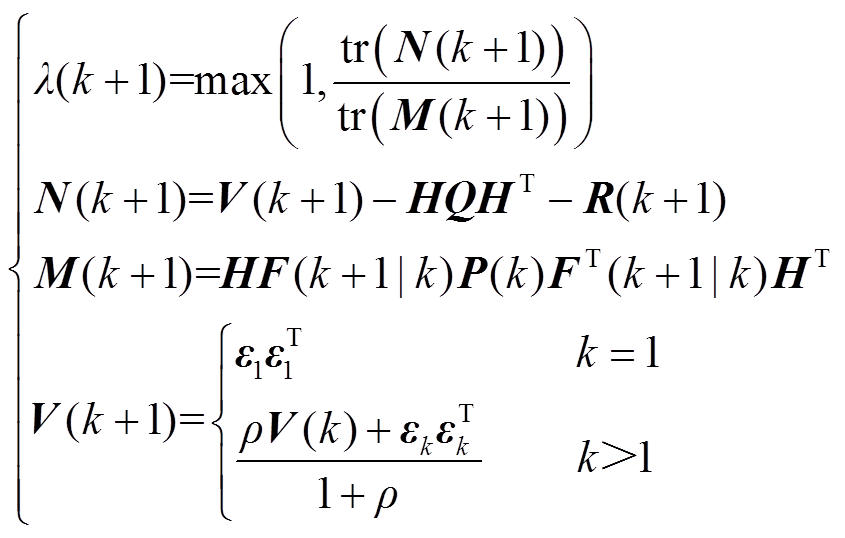（11）
式中，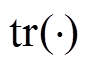
为求矩阵的迹；
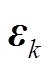为第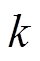
个卡尔曼滤波的计算步骤输出的残差序列；
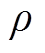为遗忘因子，此处取0.95。
依据STKF的性质可知，若无状态突变，则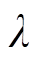恒定为1；否则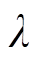，大于1。由此可根据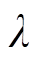是否大于1判断信号的突变情况，并据此设置小波阈值系数[29-34]。
稀疏分解是一种可以将电能质量扰动信号中的暂态成分和稳态成分有效分离的算法。因此，本文选取此方法对电能质量扰动信号进行暂稳态分离，然后分别对其进行压缩处理。
设y为电能质量扰动信号，大小为N×1，则其中对暂态和稳态分量可按式（12）进行分离。
（12）
式中，A为过完备字典，大小为N×M（N＜M）；b为解向量，大小为M×1。适用于电能质量扰动信号的过完备字典通常有三类，分别是：单位矩阵I+单位傅里叶变换矩阵FT即[I FT]；单位矩阵I+单位哈特莱变换矩阵HT，即[I HT]；单位矩阵I+余弦变换矩阵CT+正弦变换矩阵ST，即[I CT ST]。矩阵[I CT ST]所需要的存储空间较大、计算时间长、收敛速度慢；矩阵[I FT]中的傅里叶变换矩阵为复数，需要1.5倍的存储空间；哈特莱变换和傅里叶变换本质是相同的，因此字典[I HT]和[I FT]的计算结果y也相同，故本文选用[I HT]作为过完备字典，HT表达式为
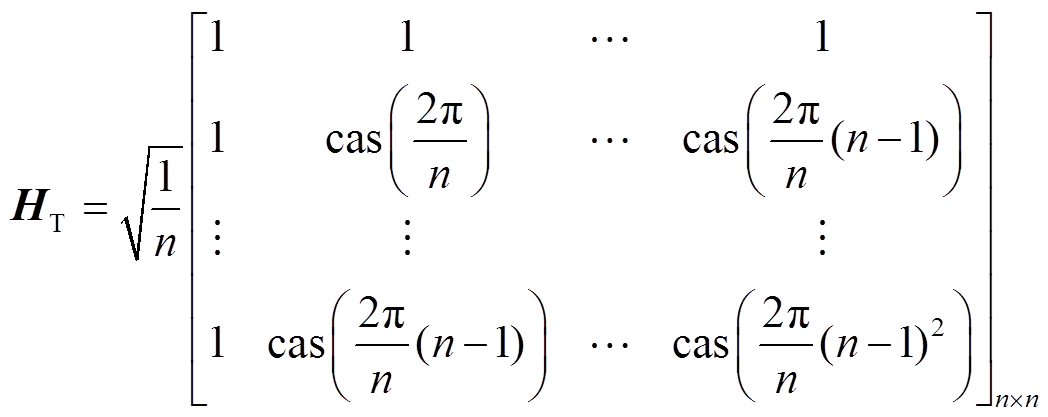（13）
其中，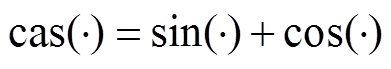
。此时N=n，M=2n。
确定字典A后，需要求解b。本文采用正交匹配追踪（Orthogonal Matching Pursuit, OMP）作为求解方法，其步骤如下：
1）输入A和信号y，初始化残差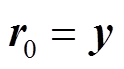
，初始化正交投影矩阵
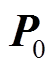为零矩阵；子空间集合初始为空集，即S=
，重构信号b设为零向量，设定迭代次数k。
2）找到第k次残差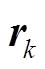
与字典A的内积最大的列向量的索引
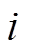，即计算
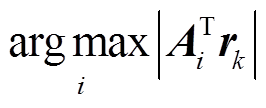，将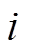保存在子空间集合中，
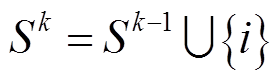，其中
为第k次迭代的最大内积列向量索引的集合。
3）计算第k次迭代的投影矩阵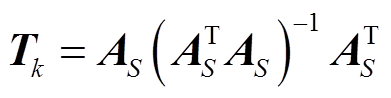
，以及第k次迭代残差
。
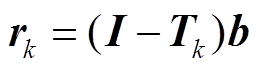4）重复上述过程，直到迭代次数最大时停止迭代。
5）计算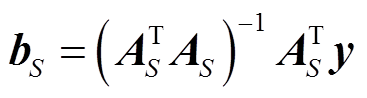
，得到重构信号
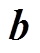中S的元素值，然后返回重构信号。
在信号的暂态和稳态部分分离后，需要对其编码以提高压缩比，暂态部分通常难以压缩，故而高效的编码算法是提高压缩比的关键。本文对暂态部分先使用小波分解出近似系数和细节系数，然后运用LZW编码压缩近似系数，使用哈夫曼编码和行程编码压缩细节系数。
LZW压缩算法通常用于图像和文本压缩，其优势在于压缩后的文件不需要保存编码表也可完成译码，具有良好的自解释性。LZW的压缩步骤如下：
1）设置初始字典，将前缀字符P设为空，当前字符C赋值为第一个字符。
2）继续读取字符，赋值给字符C，令P为上次C的值，然后合并P和C，构成“P+C”。
3）若“P+C”已存在于字典中，则P=“P+C”；否则，将其添加到字典中，令P=C，并输出编码。
4）重复以上过程，直到对字符串完成编码。
LZW译码的关键在于根据压缩结果和初始码表重构出完整码表，其步骤如下：
1）对于首次译码，令前缀字符P为空，给当前值C赋值第一个编码，直接输出译码。
2）然后对当前字符C赋值下一个编码，前缀字符P赋值首次的译码，接下来分两种情况。
3）若字符C的值在码表中有对应值，则合并P和C对应的第一个字符，并构成字符串，将其添加至码表，同时输出译码。
4）若字符C的值在码表中无对应值，则将P对应字符串的首字母赋给C，然后合并“P+C”，并将其添加至码表，同时输出译码。
5）重复以上过程直到完成全部译码。
哈夫曼编码是一种无损压缩编码方案，其编码步骤如下：
1）将序列按从小到大进行排序。
2）选取最小和次小的2个数值，构建一个具有单一根节点和2个叶子节点的2层二叉树，根节点为叶节点数值之和，然后删去叶子节点元素，并将根节点加入序列。
3）递归上述过程，直到构建完整哈夫曼二叉树。对全部叶子节点路径进行编码，左路径为0，右路径为1，即完成整个序列的编码。
哈夫曼编码的译码十分简单，对全部的编码逐次查找哈夫曼表，即可完成全部的译码。
行程编码适用于对含有多个连续零值的稀疏列表进行编码。以列表0、0、0、5、0、0、0、3、0、0、0、2为例，其行程编码为(3, 5)、(3, 3)、(3, 2)，其中括号中的第一个数为连续零值的个数，第二个数值为一串连续零后的非零值。行程编码后仅包含6个整数，而原始列表中有12个整数，故其压缩比为12/6=2。若连续零值的数量越多，则压缩比越高，因为大量的零被单个数值所表示。
行程编码的译码也十分简单：第一个括号(3, 5)的译码为0、0、0、5，依此类推即可完成译码。
综上所述，本文的信号压缩算法流程如图1所示，主要可分为以下步骤：
1）利用基于OMP求解的稀疏分解算法对信号进行暂态和稳态成分的分离。
2）对暂态信号进行小波分解，得到近似系数和细节系数。
3）对近似系数运用LZW编码方案进行压缩。
4）对细节系数，则运用行程编码和哈夫曼编码进行两次压缩，以进一步提高压缩比。
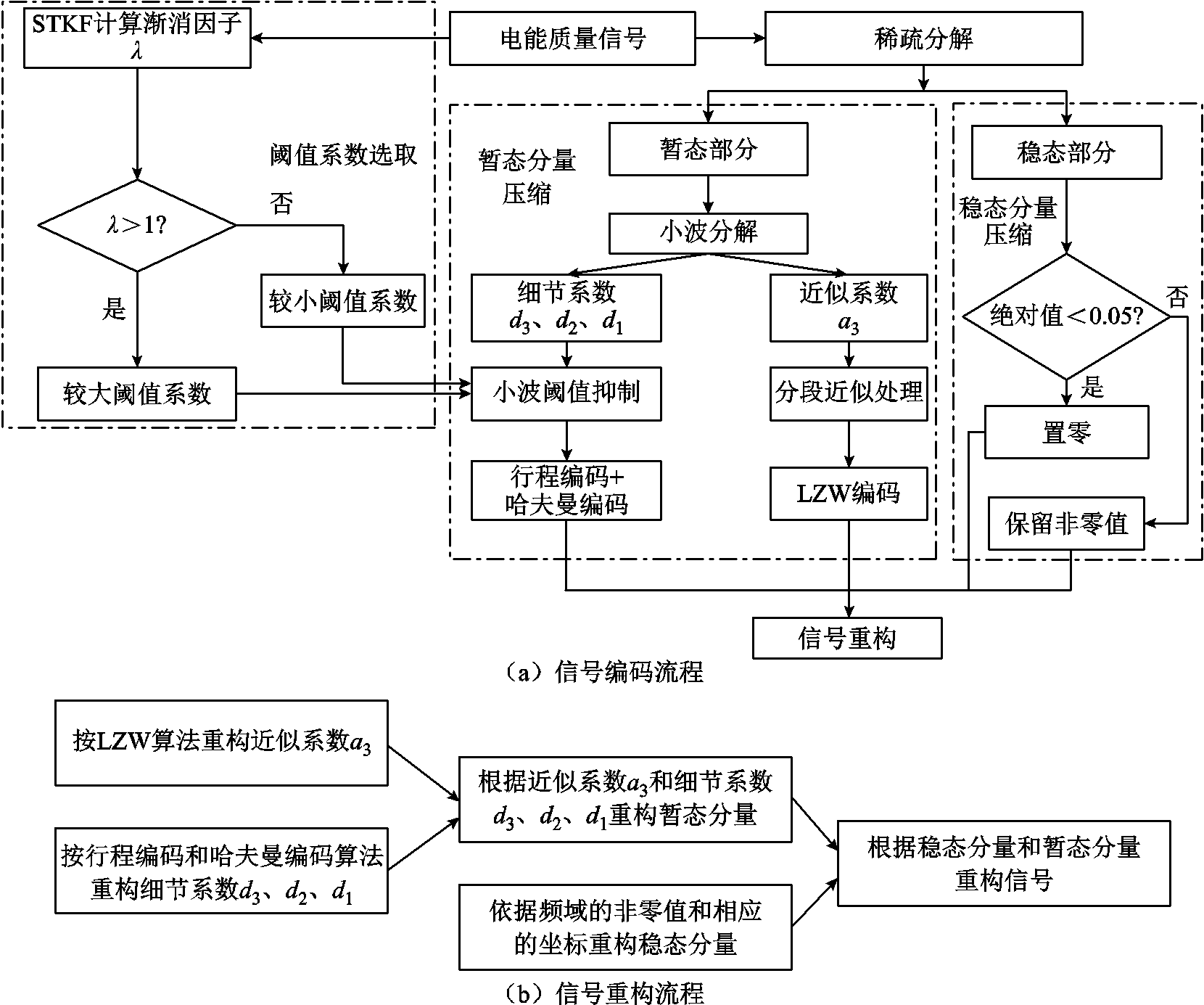
图1 电能质量扰动信号的编码与重构流程
Fig.1 Flow chart of encoding and decoding of power quality disturbances signals
5）对稳态部分，设置阈值抑制其较小的值，仅保留主要的基波和谐波成分。
6）同时，采用STKF中的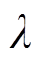
来确定小波细节系数阈值的选取，若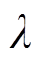＞1则可设置较大值；反之，可选取较小值。
对压缩信号的重构是压缩的逆过程，限于篇幅原因，此处不再赘述。
为了验证本文算法的有效性，在Matlab中生成各类电能质量扰动信号，然后对信号进行压缩和重构。考虑到噪声具有一定的随机性，本文进行10次压缩和重构运算，并取平均值作为结果。信号采样频率为6.4 kHz，时长为0.1 s，共640个采样点。为评价本文算法，采用压缩比（Compress Ratio, CR）和方均根误差百分比（Percentage of Root-mean-square Difference, PRD）两个指标，表达式分别为
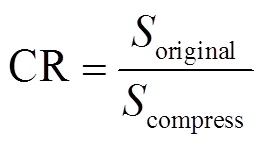（14）
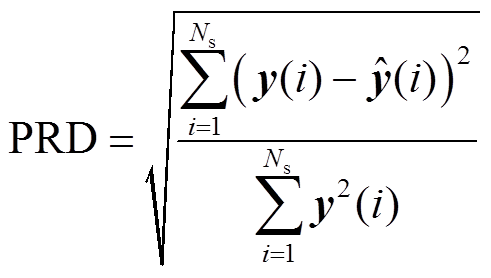（15）
式中，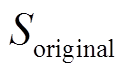
为原始信号所占比特数；
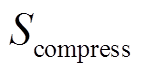为经过压缩后的信号所占比特数；
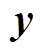为原始信号；
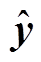为压缩后的重构信号，其物理意义是重构误差与原始信号的能量比值；Ns为采样点数。若原始信号与重构信号的CR越高，同时PRD越小，则说明压缩算法越好。
瞬时脉冲信号通常是雷电击中线路造成的，其波形表现为单极性瞬时脉冲。一般地，脉冲信号的上升时间为5 ns～0.1 ms，而持续时长大于1 ms[24]。故含有高斯白噪声的瞬时脉冲信号模型为
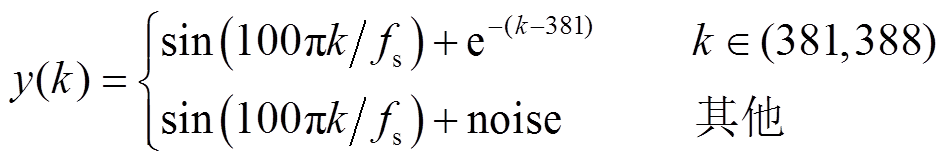（16）
式中，k为采样点；fs为采样频率，fs=6.4 kHz；noise为信噪比（Signal to Noise Ratio, SNR）为40 dB的高斯白噪声。脉冲的发生时间段在第381～388个采样点之间，共计时长约1 ms。
首先，对信号作稀疏分解，其分解结果b分为前后两个部分：前半部分对应着噪声和瞬时脉冲；后半部分为哈特莱变换的结果，如图2所示。
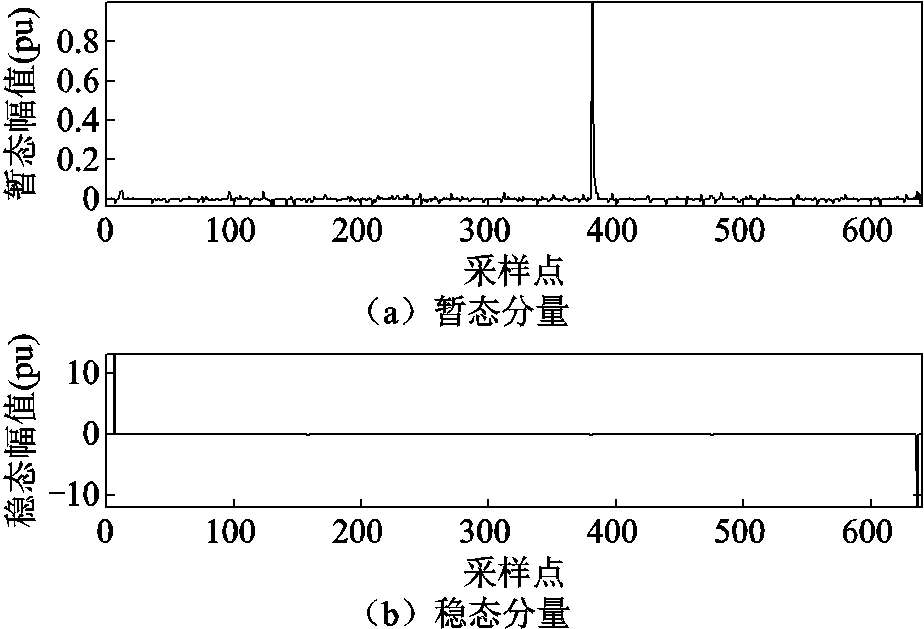
图2 瞬时脉冲信号的暂态分量和稳态分量
Fig.2 Transient and steady-state components of transient impulse signal
由图2可知，经过稀疏分解后，暂态部分被分离出来，包含噪声和瞬时脉冲；稳态部分的波形为稳态分量哈特莱变换结果，其结果为对称且幅值相反的脉冲，故仅需保存幅值和坐标，即可实现对稳态分量的压缩。
然后，对暂态成分进行压缩，对其采用db4小波作3层分解，得到近似系数a3和细节系数d3、d2、d1，如图3所示。
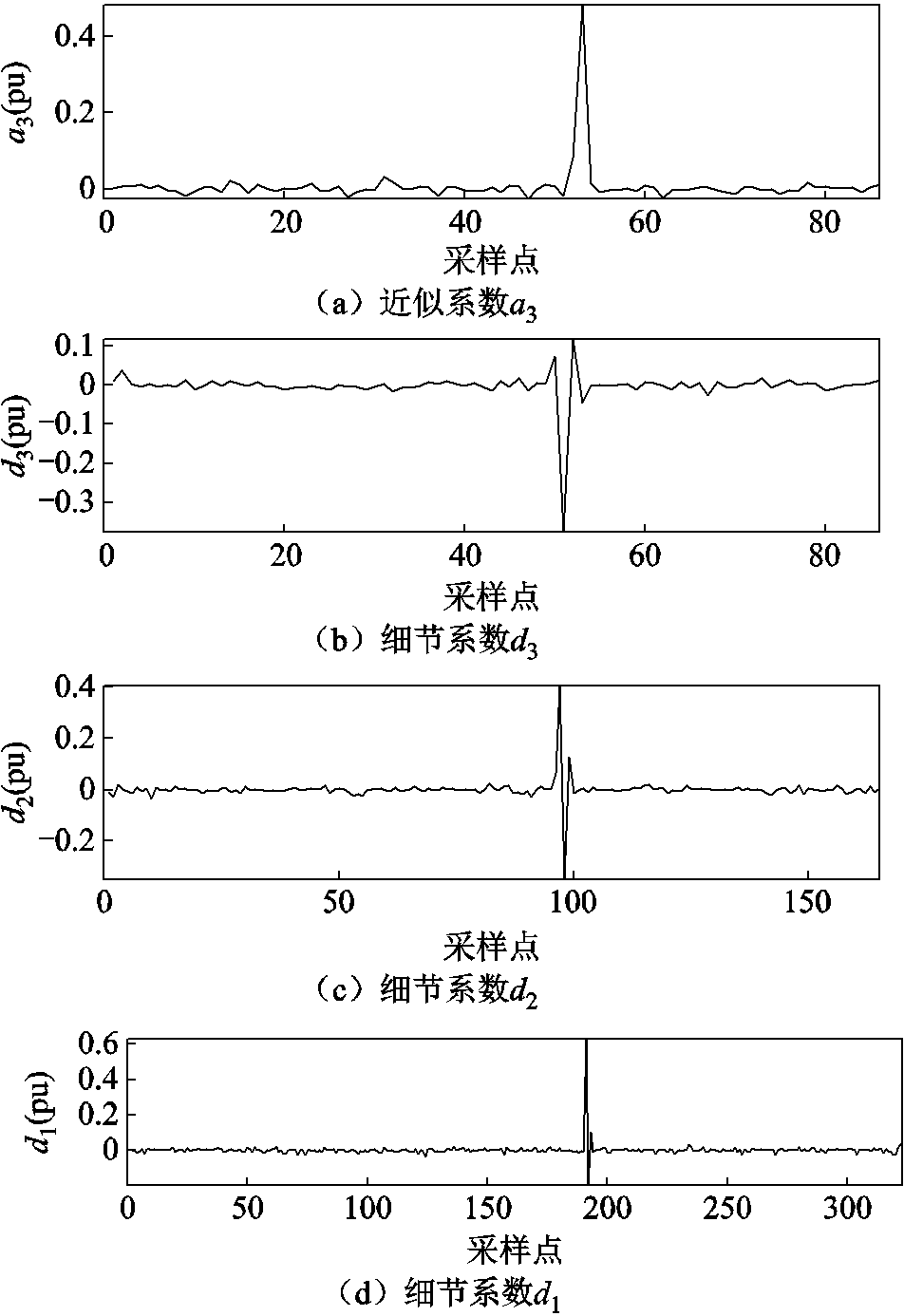
图3 瞬时脉冲信号的暂态部分小波系数
Fig.3 Transient component wavelet coefficients of transient impulse signal
对细节系数和近似系数分别采用不同的策略进行压缩处理。首先，对细节系数采用小波阈值进行压缩，其阈值公式为
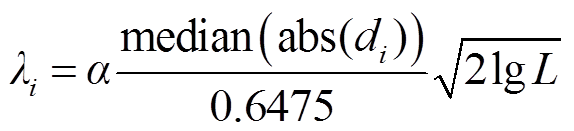（17）
式中，i =1, 2, 3；L为细节系数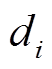
的长度；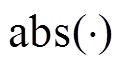
为求绝对值；
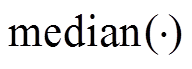为求中间值；0.647 5为经验值；
为阈值调节系数。
注意到强跟踪滤波的渐消因子大于1，如图4所示。
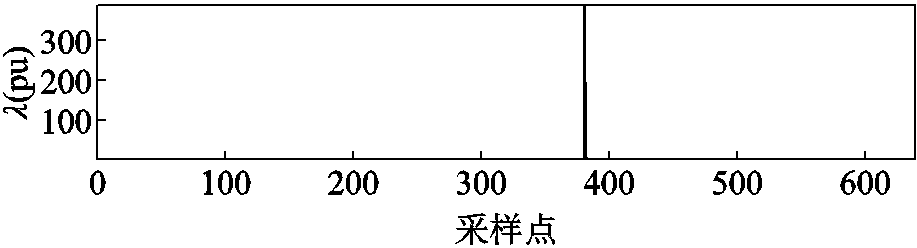
图4 瞬时脉冲信号的渐消因子
Fig.4 Fading factor of transient impulse signal
由图4可知λ＞1，说明信号中有突变发生，对应着信号中有脉冲或振荡出现。若小波阈值调节系数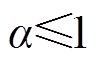
，则阈值调节系数过小，细节系数中大量的“毛刺”将被保留，这对提高CR是不利的。为了提高CR，此处取=2，这样使细节系数中的大部分“毛刺”被置零，压缩比得到提高。经小波阈值系数抑制后的新细节系数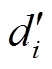
如图5所示。
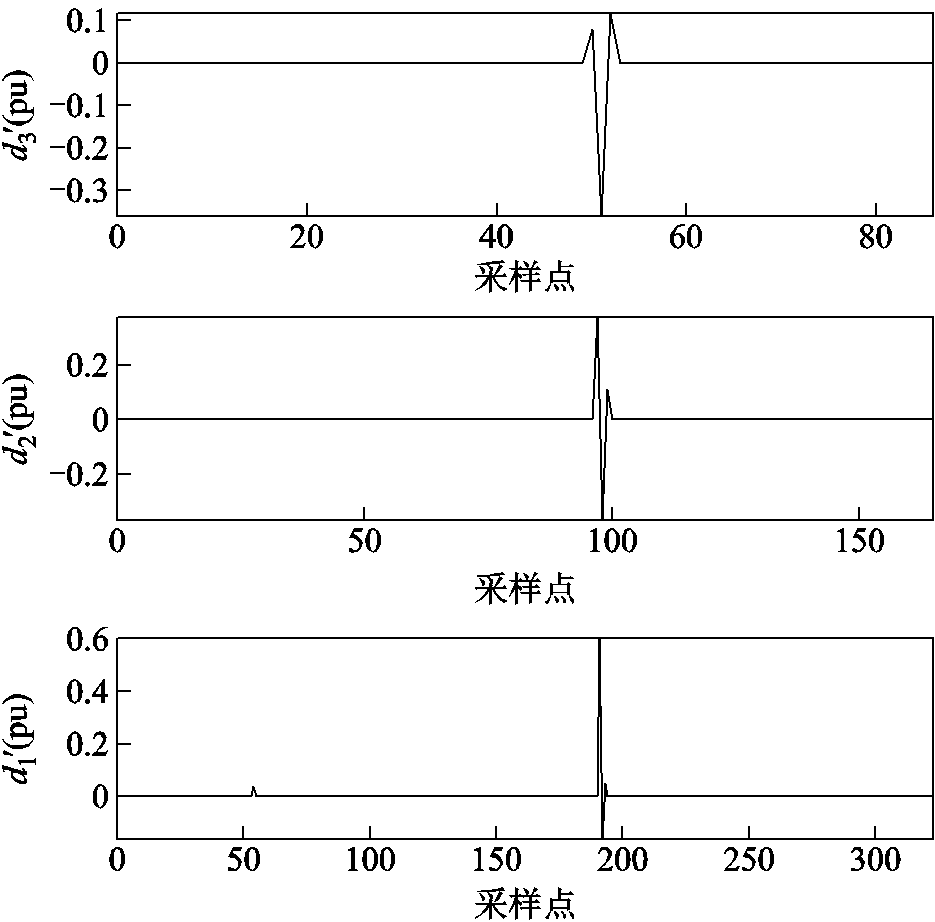
图5 小波阈值抑制后的新细节系数
Fig.5 New detail coefficients after wavelet threshold suppression
对比图3和图5可知，原始细节系数中的较小值被置零，仅保留了主要的脉冲部分，因此细节系数变得十分稀疏，故细节系数可利用行程编码方案进行压缩。
其具体方案如下：首先找出新细节系数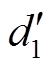
中的非零值和对应坐标。以新细节系数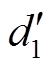为例，其全部的4个非零元素依次为0.040 6、0.603 7、-0.162 0、0.050 8，其对应的位置依次为54、191、192、193。因此，其行程编码为(53, 0.040 6)、(136, 0.603 7)、(0, -0.162 0)、(0, 0.050 8)、129。其中，最后的编码值129代表末尾的129个值全为零。然后，利用哈夫曼编码对其进行二次压缩，其结果见表1。
表1 新细节系数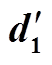
的行程编码值的哈夫曼编码
Tab.1 Huffman encoding of run-length encoded values of new detail coefficients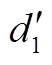
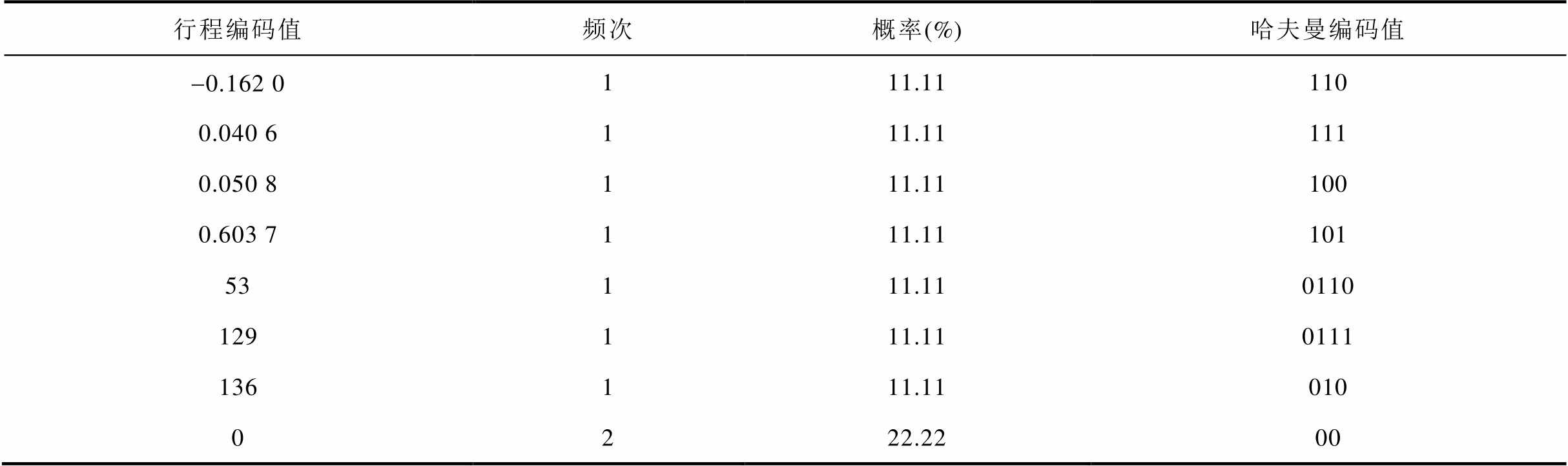
行程编码值频次概率(%)哈夫曼编码值 -0.162 0111.11110 0.040 6111.11111 0.050 8111.11100 0.603 7111.11101 53111.110110 129111.110111 136111.11010 0222.2200
由表1可知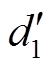，的行程编码经哈夫曼编码后所占的存储空间为表1中第二列与第四列的乘积之和，即5×3+2×4+2×2=27 bits。细节系数d1有323个浮点型数，占用存储空间为323×32=10 336 bits，CR为10 336/27=382.81。因此细节系数d1得到了有效的压缩。
同理，细节系数d3、d2也可按上述行程编码和哈夫曼编码进行两次压缩。限于篇幅，此处不再重复。
近似系数a3的冗余度较低，不利于编码压缩。为提高近似系数冗余度，使其适用于哈夫曼编码，本文对近似系数进行如下处理：①找到近似系数的最大值和最小值；②设置区间段，每段间隔为0.003，一般可得到数十个区间段；③对近似系数的每一个值，将其替换为所属的区间段的中间值，得到新的近似系数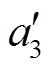
。
经上述处理后，新近似系数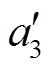仅有19个不同的值，冗余性得到大幅度提高。尽管新近似系数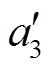和原始近似系数a3存在一定的误差，但其最大误差不超过0.001 5，且冗余度得到提高，有利于进一步压缩。
计算新近似系数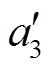中19个不同的值出现的频次和概率，并按概率从小到大排列，对系数分配字母，依次从字母‘a’到字母‘q’，其结果见表2。
表2 新近似系数的哈夫曼编码
Tab.2 Huffman coding of new approximate coefficients
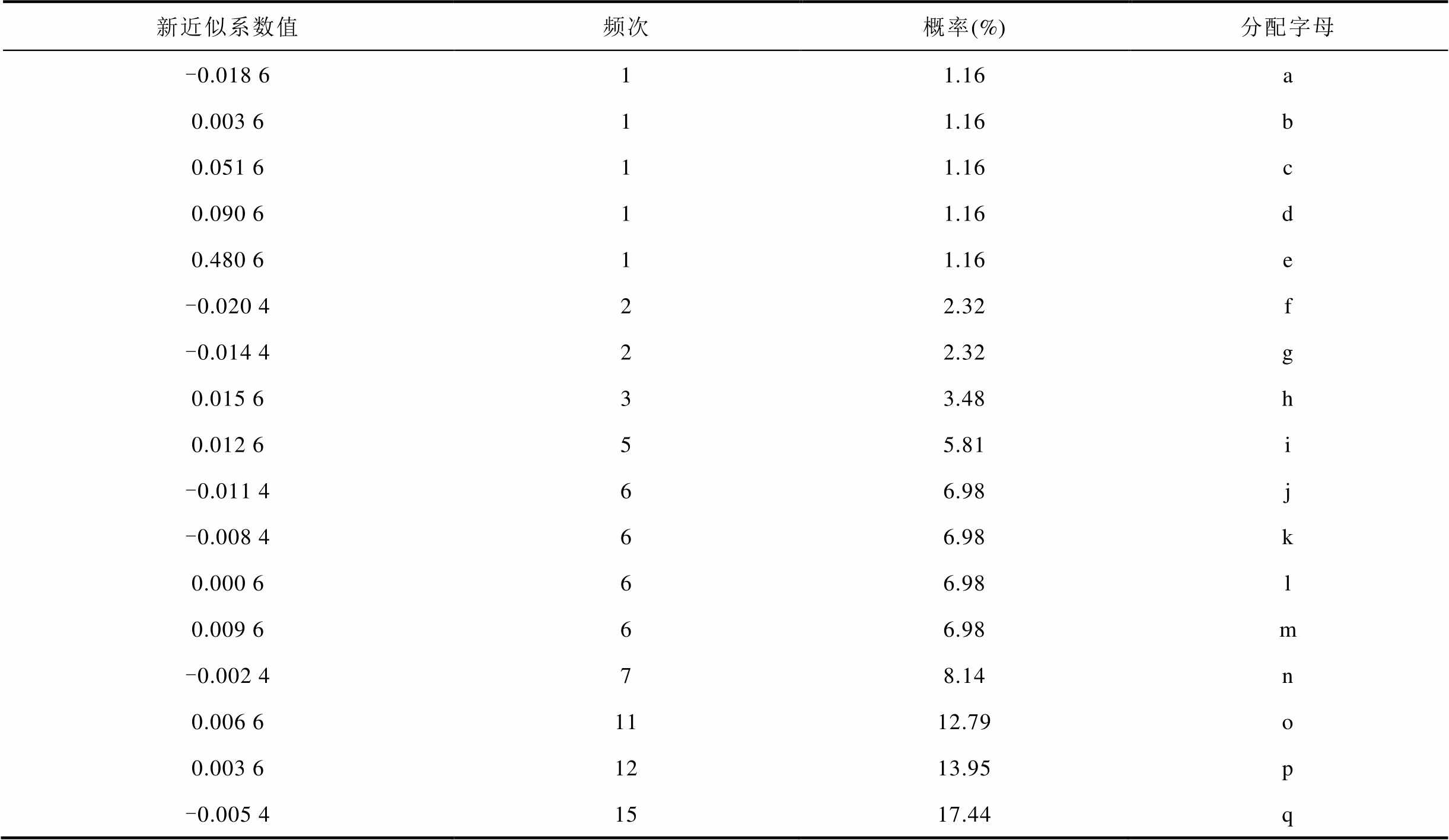
新近似系数值频次概率(%)分配字母 -0.018 611.16a 0.003 611.16b 0.051 611.16c 0.090 611.16d 0.480 611.16e -0.020 422.32f -0.014 422.32g 0.015 633.48h 0.012 655.81i -0.011 466.98j -0.008 466.98k 0.000 666.98l 0.009 666.98m -0.002 478.14n 0.006 61112.79o 0.003 61213.95p -0.005 41517.44q
对新近似系数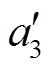全部值分配字母后，则得到对应的字符串“oop…qbc”，共计86个字符。对该字符串运用LZW编码进行压缩，得到72个整型数字，依次为“15、15、16、…、17、2、3”，于是完成了对新近似系数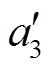的压缩。原始近似系数a3占用86× 32=2 752 bits，而经过LZW压缩后所占用的空间为72×8=576 bits，CR为2 752/576=4.78。因此，近似系数a3经过分段近似处理和LZW编码后，实现了较好的压缩效果。
而对于稳态部分，舍弃绝对值小于0.05的部分，保存2个幅值大于0.05的浮点数和对应的位置，故稳态部分压缩后占32×2+16×2= 96 bits。
综上所述，新近似系数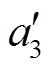的存储空间为576 bits，细节系数
、
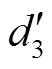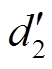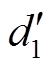、经小波阈值压缩、行程编码和哈夫曼编码压缩后，其所占用的存储空间分别为18 bits、24 bits和27 bits，共计639 bits。原始信号有640个采样点，占用空间为640×32=20 480 bits，故瞬时脉冲信号的压缩比为20 480/(639+96)= 27.86。对压缩信号进行解压缩，得到重构信号和重构误差如图6所示。
图6 瞬时脉冲原始信号、重构信号和误差
Fig.6 Original signal, reconstructed signal and error of impulse signal
依据式（15）计算重构误差PRD，得到信号恢复后的误差为1.24%。考虑到噪声的随机性，本文进行10次蒙特卡罗重复实验，10次实验的CR平均值和标准差为27.64±0.97，PRD的平均值和标准差为1.19%±0.11%。此结果说明本文算法具有很高的压缩比和较低的重构误差，较小的方差证明本文算法具有良好的鲁棒性。
为证明其优越性，与文献[24]中的算法1（稀疏分解）、文献[22]的算法2（快速傅里叶变换+小波分解）和文献[35]算法3（单类支持向量机）的结果进行对比，结果见表3。
表3 瞬时脉冲信号的压缩结果对比
Tab.3 Compression results comparison for impulse signal
算法PRD(%)CR 本文1.1927.64 稀疏分解1.101.59 快速傅里叶变换+小波分解1.205.93 单类支持向量机1.1611.11
从表3中可知，本文算法在CR上优于稀疏分解和快速傅里叶变换+小波分解算法的结果，且PRD无大幅度增加。这是因为本文算法对暂态成分进行压缩，而稀疏分解未压缩暂态成分。快速傅里叶变换+小波分解算法利用小波分解对细节系数进行了压缩，但并未压缩近似系数。此外，单类支持向量机算法的重构误差较小，但其CR小于本文算法。
电压暂降是一种十分常见的电能质量扰动信号，其原因通常是负荷的接入，并且在电压跌落的瞬间伴有强烈的暂态振荡现象。其模型为
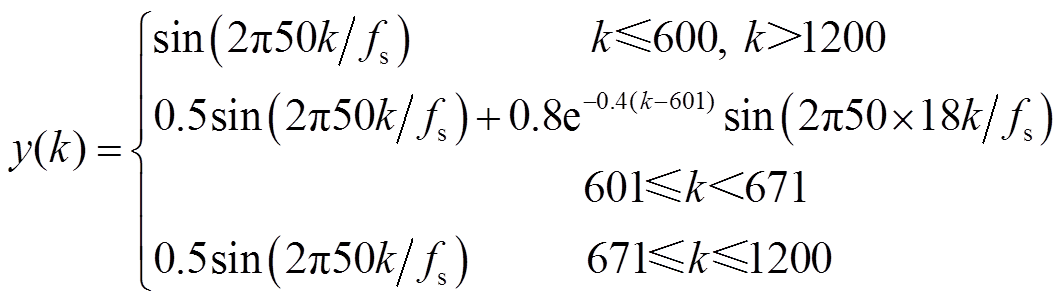（18）
其中，各个变量的含义与式（16）的含义相同，此处不再重复。本节中仍然利用STKF中的λ判断信号的状态突变，其λ如图7所示。
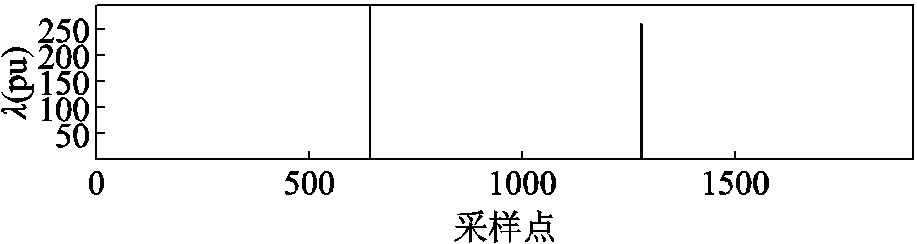
图7 含有暂态振荡的暂降信号的渐消因子
Fig.7 Fading factor of sag signal with transient oscillation
从图7可知，λ两次大于1，故暂降信号可分为三段：暂降发生前、暂降持续段、暂降结束后。将这三段信号进行分割，分别进行压缩和重构，其压缩过程与2.1节中的步骤相同，此处不再赘述。将这三段信号连接起来，得到完整的重构信号和误差，如图8所示。
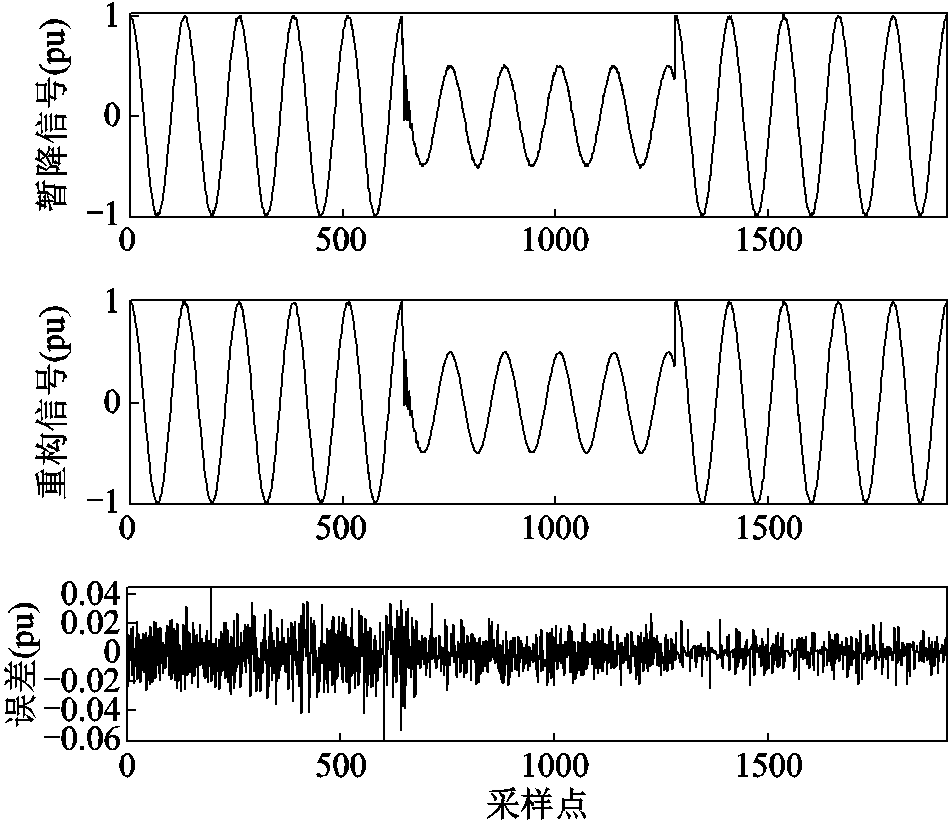
图8 电压暂降信号的原始信号、重构信号和误差
Fig.8 Original signal, reconstructed signal and error of sag with transient oscillation
仍然进行10次重复实验，得到CR平均值为31.12，PRD为1.88%。结果对比见表4。
从表4的结果可知，本文算法的CR大幅度优于对比算法，且PRD基本维持不变，结果证明本文算法具有良好对压缩和重构性能。
表4 含暂态振荡的暂降信号的压缩结果对比
Tab.4 Compression results comparison for sag with transient oscillation
算法PRD(%)CR 本文1.8831.12 稀疏分解1.952.05 快速傅里叶变换+小波分解1.935.79 单类支持向量机2.0310.94
幅值按指数衰减的谐波信号的模型为
其中，各个变量的含义与式（16）的含义相同，此处不再重复。对该信号作稀疏分解，其暂态分量和稳态分量如图9所示。
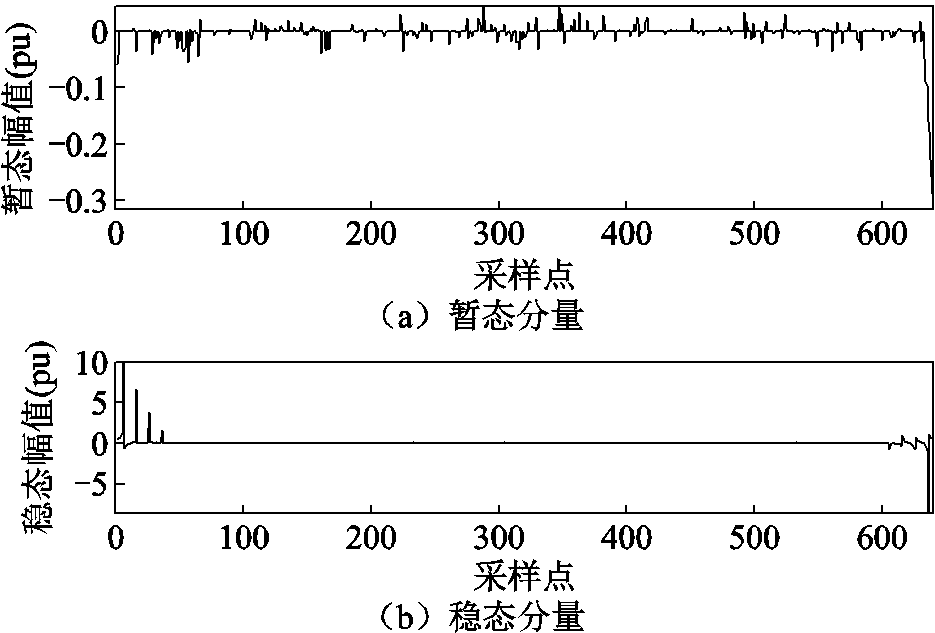
图9 幅值衰减谐波的暂态和稳态分量
Fig.9 Transient and steady-state components of decaying amplitude harmonics
由图9可知，分解后的稳态部分中，非零值达到了316个，但其中大部分值都接近于零。将绝对值较小的非零值直接置零，其阈值设置为0.05。经过抑制后的稳态非零值减少至36个，加上其对应坐标，稳态部分占用空间为36×(32+16)= 1 728 bits。
对于暂态部分，其压缩步骤与2.1节的步骤相同，此处不再赘述。其近似系数a3和细节系数所占空间分别为624、80、10、5 bits。故而其CR为20 480/(1 728+624+80+10+5)=8.37，其PRD为2.07%，此处PRD较高是因为稳态部分的非零值较多。谐波信号、重构信号与重构误差如图10所示。10次重复实验CR和PRD结果与对比算法的结果见表5。
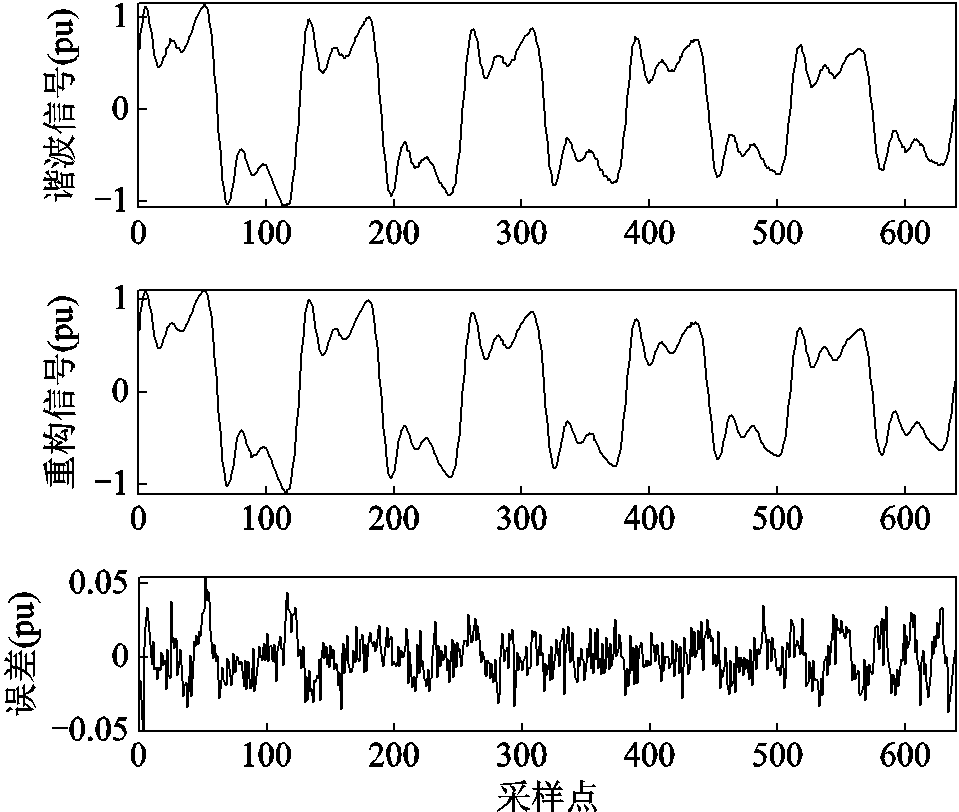
图10 衰减谐波的原始信号、重构信号和误差
Fig.10 Original signal, reconstructed signal and error of decaying attitude harmonics
表5 幅值衰减谐波信号的压缩结果对比
Tab.5 Compression results comparison for decaying amplitude harmonics
算法PRD(%)CR 本文算法2.027.98 稀疏分解2.092.59 快速傅里叶变换+小波分解2.203.74 单类支持向量机01
从表5中可知，对于幅值衰减的谐波信号，本文算法的CR仍然远高于对比算法的CR，说明本文算法有着良好的性能。快速傅里叶变换+小波分解算法的CR好于稀疏分解算法的CR，这是因为快速傅里叶变换+小波分解算法对小波细节系数进行了压缩，而稀疏分解算法未对其进行编码，故其CR较差。此外，单类支持向量机算法的数据在原文中是对闪变进行压缩，CR为1，实际上并未有效压缩闪变信号，而本文则实现了较高的压缩比。
在第2节中，本文对三类复合电能质量扰动信号进行了压缩和重构，其采样频率为6.4 kHz。若系统采样频率为12.8 kHz，且CR保持不变，压缩后的数据所占空间将倍增，这不利于减小数据存储空间。为了考察采样频率对压缩算法的影响，本文使用下列指标对算法进行评估。
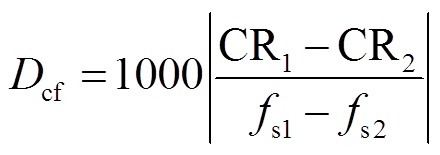（20）
式中，CR1和CR2分别为信号在不同的采样频率下的压缩比；fs1和fs2为两种不同的采样频率，分别为12.8 kHz、6.4 kHz。若Dcf越高，则说明算法受采样率的影响更小，具有良好的鲁棒性。其解释如下：若Dcf=0，说明采样频率倍增时CR不变，对应压缩后的存储空间也增加一倍；反之Dcf越大，则采样频率增加一倍时，CR增长幅度越大，所需的存储空间仅略微增长，因此Dcf越大则算法稳定性越好。
以瞬时脉冲信号为例，采样频率设置为12.8 kHz，然后进行10次重复实验，其波形如图11所示。CR和PRD的平均值分别为29.08，1.20%，Dcf的值为1.6，高于稀疏分解和快速傅里叶变换+小波分解的结果，见表6。
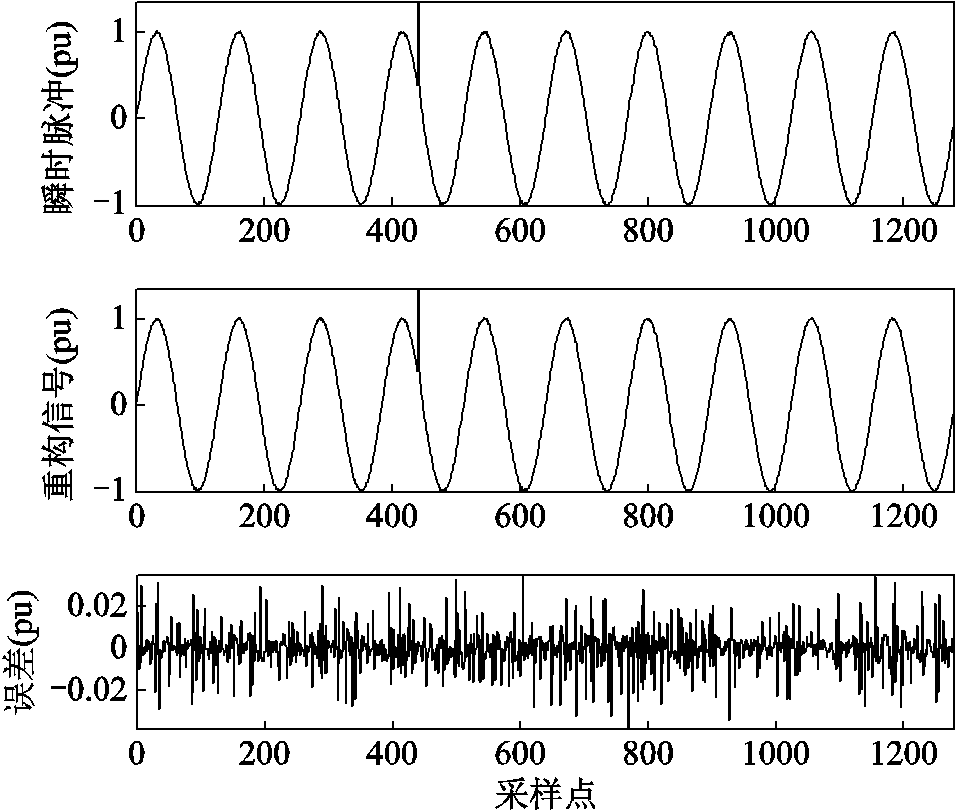
图11 瞬时脉冲对原始信号、重构信号和误差（采样频率12.8 kHz）
Fig.11 Original signal, reconstructed signal and error of impulse signal (fs=12.8 kHz)
表6 采样频率对不同算法的影响结果
Tab.6 The effect of sampling frequency on different algorithms results
指标CR1(fs1=12.8 kHz)CR2(fs2=6.4 kHz)Dcf 本文29.0818.861.60 稀疏分解7.315.050.35 快速傅里叶变换+小波分解9.095.930.49
从表6可知，当
=2.3时，CR提升至29.08，Dcf为1.6，说明即使在fs为12.8 kHz的情况下，仅需要通过略微提升α的值，即可大幅度抵消采样频率增长带来的影响，使得信号压缩后的占用空间保持不变。此外，结果表明本文算法不易受采样频率变化的影响，具有更好对稳定性。
本节分析信号噪声对CR和PRD的影响。以瞬时脉冲信号为例，分别在信噪比为50 dB和30 dB的情况下对其进行压缩和重构，其原始信号、重构信号和误差波形分别如图12和图13所示。
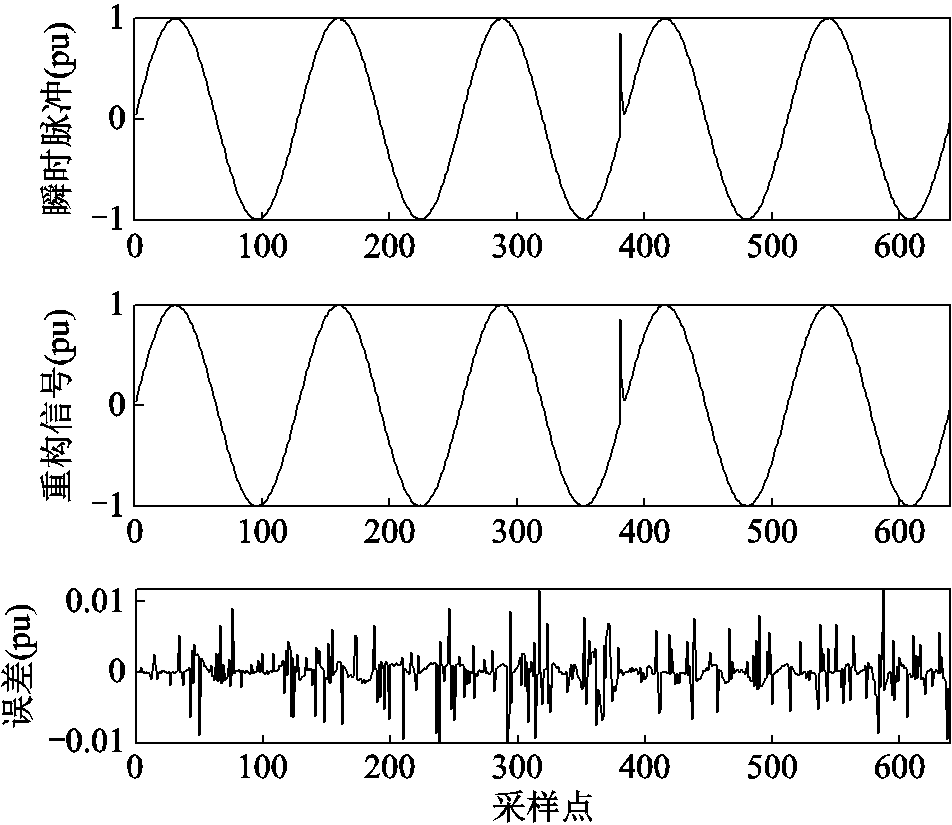
图12 瞬时脉冲信号的原始信号、重构信号和误差（SNR=50 dB）
Fig.12 Original signal, reconstructed signal and error of impulse signal (SNR=50 dB)
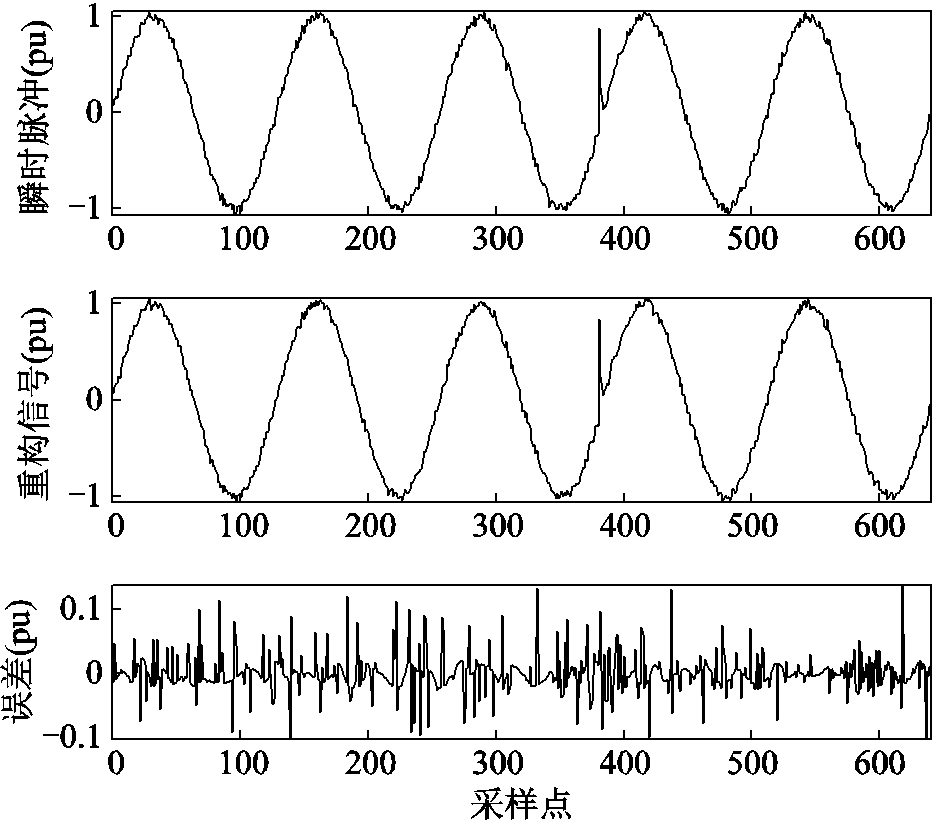
图13 瞬时脉冲信号的原始信号、重构信号和误差（SNR=30 dB）
Fig.13 Original signal, reconstructed signal and error of impulse signal (SNR=30 dB)
比较图12和图13可知，在信噪比为50 dB时，误差的幅值约为0.01；而SNR为30 dB时，误差的幅值约为0.1。这是因为SNR较低时，其噪声幅值较大，大量的噪声成分在压缩过程中被去除，故而其重构误差也相应较大。SNR为50 dB和30 dB时的CR和PRD见表7。这种变化趋势对其他类型的扰动信号显然也是成立的。
表7 不同SNR情况下的CR和PRD
Tab.7 CR and PRD results under different SNR
脉冲信号30 dB40 dB 50 dB CR22.1218.8618.75 PRD(%)3.761.410.36
由表7可知，随着SNR增大，其CR仅小幅度下降，但总体上保持较高的压缩比，PRD 也随之减小。因为SNR较低时，噪声成分的幅值相对较大，在信号压缩过程中有更多的噪声被置零，故PRD较大。
为了验证本文算法在实测信号上的有效性，在华中科技大学电力系统动态模拟实验室搭建了一个简易动态模拟系统，如图14所示，包含模拟发电机、输电线路、模拟变压器、通信装置和故障录波仪。其中，发电机电压为210 V，经模拟变压器降压到100 V。故障信号的采样频率为5 000 Hz，故障波形持续时长为0.12 s，每段信号的采样点为600个，每个采样点为32 bits，共57 600 bits。
图14 动态模拟系统示意图
Fig.14 Schematic diagram of dynamic simulation system
实际的电能质量扰动信号十分复杂，难以对全部扰动类型逐一进行测试。考虑到电压暂降占全部扰动事件总数的80%左右，是十分常见的扰动事件类型，故选取电压暂降信号作为压缩测试对象。故障设置为B相对地短路，得到的实测故障信号由故障录波仪记录并保存，其三相故障波形如图15所示。
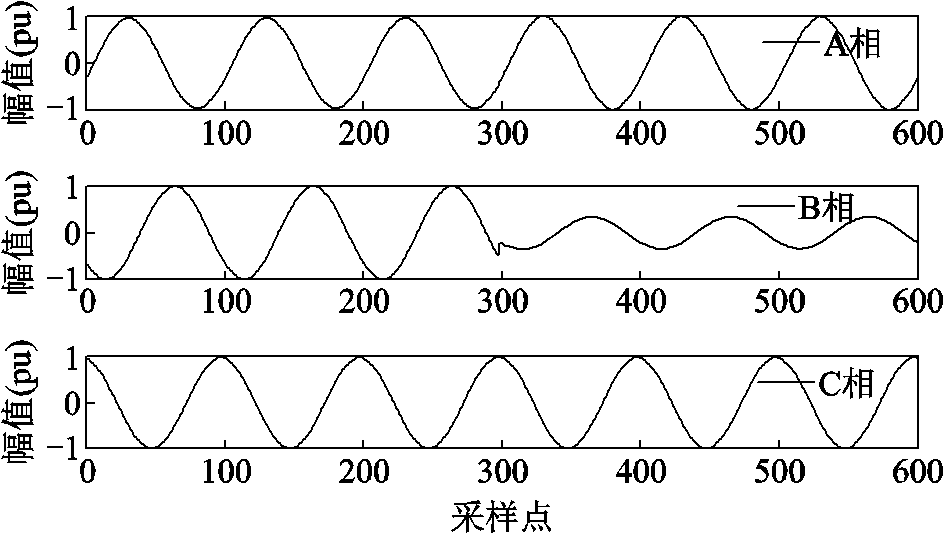
图15 故障录波仪的三相波形
Fig.15 The three-phase waveform of fault recorder
对三相波形的压缩过程与2.1节中的步骤相同，因此不再重复。因为实测信号仅有B相发生暂降，本文仅给出B相原始信号、重构信号和误差的波形，如图16所示。三相波形的CR和PRD见表8。
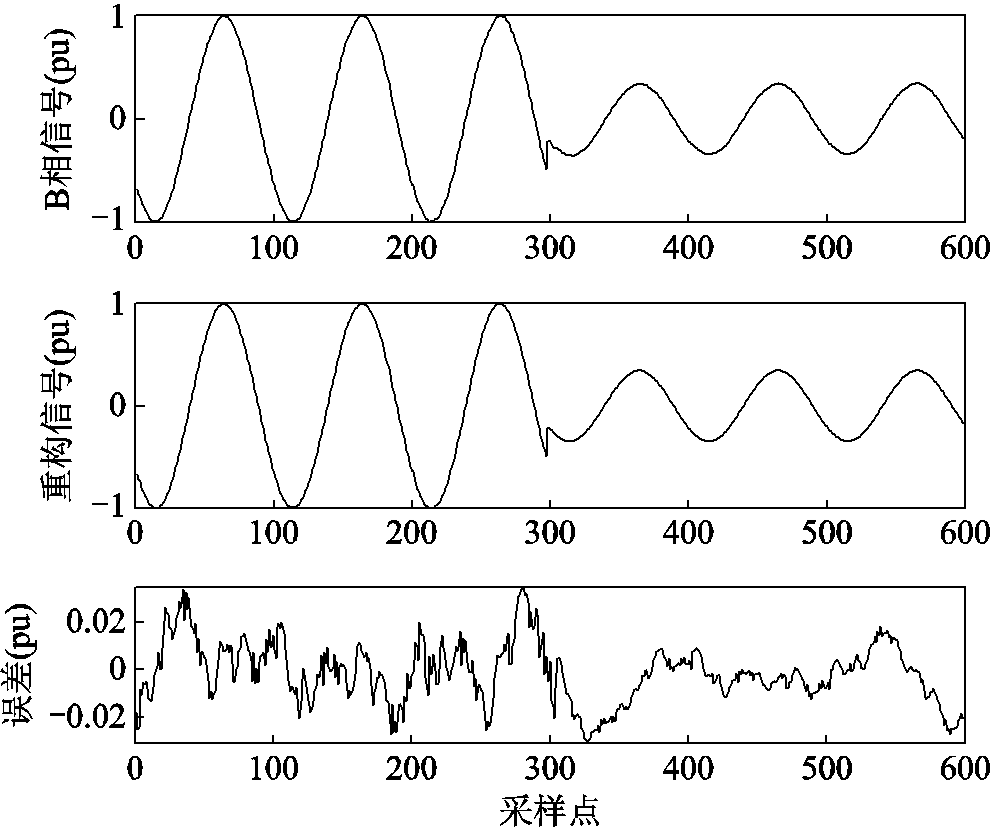
图16 B相实测信号、重构信号和误差
Fig.16 Original signal, reconstructed signal and error of real signal of phase B
表8 实测三相信号的压缩结果对比
Tab.8 Compression results comparison of real three-phase signals
相序本文算法稀疏分解 CRPRD(%)CRPRD(%) A52.741.616.251.84 B46.072.372.041.98 C51.341.834.681.84
从表8中的数据可知，实测信号中A、C相的CR和PRD优于对比算法的CR和PRD，因为本文算法对小波近似系数和细节系数均进行了有效的压缩，而对比算法中未能对噪声进行压缩；对于B相信号而言，其PRD略微大于对比算法的PRD，但是其CR大幅度优于对比算法的CR，其代价仍是值得的。
同时，注意到本节和第3节的暂降信号重构误差曲线有着显著差别，这是因为第3节的暂降信号的噪声是理想高斯白噪声，而实测信号的噪声并非高斯白噪声，因此重构误差有一定区别，属于正常现象。
本文提出了一种基于稀疏分解和混合编码的复合电能质量扰动的高效压缩算法。首先，利用稀疏分解对电能质量扰动信号的暂态部分和稳态部分进行分离：对于暂态部分，利用小波作3层分解得到近似系数和细节系数，然后利用LZW编码、行程编码、哈夫曼编码进行两次压缩；而对于稳态部分，将其中绝对值小于0.05的部分置零。此外，小波阈值系数依据STKF中的渐消系数是否大于1对情况进行设置，防止出现CR和PRD同时过大或过小。仿真信号和实测信号的实验结果说明本文算法具有较高的CR和较低的PRD。本文算法不受采样频率变化的干扰，具有较强的抗噪性能，是一种高效的电能质量扰动信号压缩算法。
参考文献
[1] Pavan P S, Das S. Novel method for location of internal faults in ungrounded double wye shunt capacitor banks[J]. IEEE Transactions on Power Delivery, 2021, 36(2): 899-908.
[2] Li Peng, Xie Lili, Han Jiawei, et al. A new voltage compensation philosophy for dynamic voltage restorer to mitigate voltage sags using three-phase voltage ellipse parameters[J]. IEEE Transactions on Power Electronics, 2018, 33(2): 1154-1166.
[3] Xu Jinming, Hu Yuan, Qian Hao, et al. Delay-based phase-locked loop parameters design based on stability region of grid-connected single-phase inverter under grid voltage sags[J]. IEEE Transactions on Industrial Electronics, 2022, 69(11): 11324-11334.
[4] 陈铿. 基于时频分析与深度学习的交流输电线路雷击波形识别研究[D]. 广州: 华南理工大学, 2020.
[5] Li Dongyu, Ukil A. Fault location estimation in voltage-source-converter-based DC system: the L location[J]. IEEE Transactions on Industrial Electronics, 2022, 69(11): 11198-11209.
[6] Ribeiro M V, Park S H, Romano J M T, et al. A novel MDL-based compression method for power quality applications[J]. IEEE Transactions on Power Delivery, 2007, 22(1): 27-36.
[7] Tcheou M P, Lovisolo L, Ribeiro M V, et al. The compression of electric signal waveforms for smart grids: state of the art and future trends[J]. IEEE Transactions on Smart Grid, 2014, 5(1): 291-302.
[8] Chen Chang, Wang Weikang, Yin He, et al. Real-time lossless compression for ultrahigh-density synchrophasor and point-on-wave data[J]. IEEE Transactions on Industrial Electronics, 2022, 69(2): 2012-2021.
[9] 王刚, 彭华, 唐永旺, 等. Lempel-Ziv-Welch(LZW)压缩数据误码修复技术[J]. 北京理工大学学报, 2020, 40(5): 562-569. Wang Gang, Peng Hua, Tang Yongwang, et al. Error repair technology of lempel-ziv-welch (LZW) compression data[J]. Transactions of Beijing Institute of Technology, 2020, 40(5): 562-569.
[10] Santoso S, Powers E J, Grady W M. Power quality disturbance data compression using wavelet transform methods[J]. IEEE Transactions on Power Delivery, 1997, 12(3): 1250-1257.
[11] 何正友, 钱清泉, 刘志刚. 一种基于优化小波基的电力系统故障暂态数据压缩方法[J]. 中国电机工程学报, 2002, 22(6): 1-5. He Zhengyou, Qian Qingquan, Liu Zhigang. An electric power system fault transient data compression method based on optimal wavelet[J]. Proceedings of the CSEE, 2002, 22(6): 1-5.
[12] 费铭薇, 乐全明, 张沛超, 等. 电力系统故障录波数据压缩与重构小波基选择[J]. 电力系统自动化, 2005, 29(17): 64-67, 97. Fei Mingwei, Yue Quanming, Zhang Peichao, et al. Wavelets selection of compression and reconstruction algorithm based on digital recorded data from a faulted power system[J]. Automation of Electric Power Systems, 2005, 29(17): 64-67, 97.
[13] 成敬周, 张举. 基于小波包分析的录波数据压缩原理[J]. 电力自动化设备, 2004, 24(7): 53-56. Cheng Jingzhou, Zhang Ju. Theory of power system fault data compression based on wavelet packet[J]. Electric Power Automation Equipment, 2004, 24(7): 53-56.
[14] 闫常友, 杨奇逊, 刘万顺. 基于提升格式的实时数据压缩和重构算法[J]. 中国电机工程学报, 2005, 25(9): 6-10. Yan Changyou, Yang Qixun, Liu Wanshun. A real-time data compression & reconstruction method based on lifting scheme[J]. Proceedings of the CSEE, 2005, 25(9): 6-10.
[15] Meher S K, Pradhan A K, Panda G. An integrated data compression scheme for power quality events using spline wavelet and neural network[J]. Electric Power Systems Research, 2004, 69(2/3): 213-220.
[16] Ece D G, Gerek O N. Power quality event detection using joint 2-D-wavelet subspaces[J]. IEEE Transactions on Instrumentation and Measurement, 2004, 53(4): 1040-1046.
[17] 赵艳粉, 杨洪耕. 二维离散小波变换在电能质量检测数据压缩中的应用[J]. 电力系统自动化, 2006, 30(15): 51-55. Zhao Yanfen, Yang Honggeng. Data compression method using 2-dimensional discrete wavelet transform for power quality detection[J]. Automation of Electric Power Systems, 2006, 30(15): 51-55.
[18] 张明, 李开成, 胡益胜. 基于JPEG2000的电能质量扰动数据压缩方法[J]. 电工技术学报, 2011, 26(10): 47-54. Zhang Ming, Li Kaicheng, Hu Yisheng. Power quality disturbance data compression using JPEG2000[J]. Transactions of China Electrotechnical Society, 2011, 26(10): 47-54.
[19] Andrews H, Patterson C. Singular value decomposition (SVD) image coding[J]. IEEE Transactions on Communications, 1976, 24(4): 425-432.
[20] de Souza J C S, Assis T M L, Pal B C. Data compression in smart distribution systems via singular value decomposition[J]. IEEE Transactions on Smart Grid, 2015, 8(1): 275-284.
[21] 张明, 龚建峰, 何顺帆. 基于谐波滤波器组的电能质量扰动数据压缩方法[J]. 电力系统自动化, 2016, 40(15): 93-98. Zhang Ming, Gong Jianfeng, He Shunfan. Data compression method for power quality disturbance based on harmonic filter bank[J]. Automation of Electric Power Systems, 2016, 40(15): 93-98.
[22] Zhang Ming, Li Kaicheng, Hu Yisheng. A high efficient compression method for power quality applications[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(6): 1976-1985.
[23] He Shunfan, Zhang Ming, Tian Wei, et al. A parameterization power data compress using strong trace filter and dynamics[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(10): 2636-2645.
[24] He Shunfan, Tian Wei, Zhang Junmin, et al. A high efficient approach for power disturbance waveform compression in the view of Heisenberg uncertainty[J]. IEEE Transactions on Industrial Informatics, 2019, 15(5): 2580-2591.
[25] Cai Delong, Li Kaicheng, He Shunfan, et al. On the application of joint-domain dictionary mapping for multiple power disturbance assessment[J]. Energies, 2018, 11(2): 347.
[26] Manikandan M S, Samantaray S R, Kamwa I. Detection and classification of power quality disturbances using sparse signal decomposition on hybrid dictionaries[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(1): 27-38.
[27] Manikandan M S, Samantaray S R, Kamwa I. Simultaneous denoising and compression of power system disturbances using sparse representation on overcomplete hybrid dictionaries[J]. IET Generation, Transmission & Distribution, 2015, 9(11): 1077-1088.
[28] Satpathi S, Das R L, Chakraborty M. Improving the bound on the RIP constant in generalized orthogonal matching pursuit[J]. IEEE Signal Processing Letters, 2013, 20(11): 1074-1077.
[29] Ge Quanbo, Shao Teng, Chen Shaodong, et al. Carrier tracking estimation analysis by using the extended strong tracking filtering[J]. IEEE Transactions on Industrial Electronics, 2017, 64(2): 1415-1424.
[30] 肖贤贵, 李开成, 蔡得龙, 等. 一种电能质量扰动信号的联合去噪算法[J]. 电工技术学报, 2021, 36(21): 4418-4428. Xiao Xiangui, Li Kaicheng, Cai Delong, et al. A combined de-noising method for power quality disturbances events[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4418-4428.
[31] 牛胜锁, 王春鑫, 梁志瑞, 等. 基于改进强跟踪无迹卡尔曼滤波的电力信号同步相量跟踪算法[J]. 电工技术学报, 2021, 36(11): 2255-2264. Niu Shengsuo, Wang Chunxin, Liang Zhirui, et al. An algorithm for tracking synchronous phasor of power signals based on improved strong tracking unscented Kalman filter[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2255-2264.
[32] 刘芳, 马杰, 苏卫星, 等. 基于自适应回归扩展卡尔曼滤波的电动汽车动力电池全生命周期的荷电状态估算方法[J]. 电工技术学报, 2020, 35(4): 698-707. Liu Fang, Ma Jie, Su Weixing, et al. State of charge estimation method of electric vehicle power battery life cycle based on auto regression extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 698-707.
[33] 李超然, 肖飞, 樊亚翔, 等. 基于门控循环单元神经网络和Huber-M估计鲁棒卡尔曼滤波融合方法的锂离子电池荷电状态估算方法[J]. 电工技术学报, 2020, 35(9): 2051-2062. Li Chaoran, Xiao Fei, Fan Yaxiang, et al. A hybrid approach to lithium-ion battery SOC estimation based on recurrent neural network with gated recurrent unit and Huber-M robust Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 2051-2062.
[34] 田勇, 冯华逸, 田劲东, 等. 电动汽车动态无线充电系统输出电流模型预测控制[J]. 电工技术学报, 2023, 38(9): 2310-2322, 2447. Tian Yong, Feng Huayi, Tian Jindong, et al. Model predictive control for output current of electric vehicle dynamic wireless charging systems[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2310-2322, 2447.
[35] 黄南天, 彭华, 徐殿国, 等. 主动配电网电能质量信号高效压缩[J]. 电工技术学报, 2015, 30(增刊2): 181-188. Huang Nantian, Peng Hua, Xu Dianguo, et al. High efficiency power quality data compression in active distribution network[J]. Transactions of China Electrotechnical Society, 2015, 30(S2): 181-188.
Abstract The power quality disturbance (PQD) data are useful information for the power grid. Generally, different PQD waveforms correspond to different faults in the power grid, so the data can be used to distinguish the types of PQD signals. For example, the transient oscillation signal is caused by heavy load switching, the voltage notch originates from phase commutation of power electronic devices, voltage sag or interruption occurs because of short circuit faults, and the impulse signal is due to the thunder striking the lines, etc. In addition, the PQD waveforms can be used to locate the disturbance of the distribution network. However, with the scale of the power network increasing, PQD events are inevitably becoming more frequent than ever before. If there are many power grid monitoring devices in a certain distribution grid network, the bandwidth of Ethernet will be tremendous to transmit and receive the uncompressed PQD data, and the disk space for storage will also be huge, which leads to high expense on Ethernet and disk. Therefore, a highly efficient compression algorithm for PQD data calls for much attention and has become more urgent than ever before.
The principle of the algorithm can be described as follow.First, this paper uses joint dictionary based sparse decomposition algorithm to separate the transient and steady-state components in PQD, secondly, the transient components are compressed by wavelet analysis, Huffman coding and run-length coding algorithms, for the steady-state component, i.e. the fundamental and harmonic components, the values that are greater than the threshold is reserved, and the compression is completed. To evaluate the proposed method, two indicators, compression ratio (CR) and percentage of root-mean-square difference (PRD) are utilized. Three kind of PQD signals, including impulse signal, sag with transient oscillation, and harmonic with decaying amplitude are generated in Matlab and compressed. The CR and PRD of impulse signal of the proposed algorithm is 27.64 and 1.19%, which are better than that of the competing methods. Similarly, the CR and PRD of sag with transient oscillation of the proposed algorithm is 31.12 and 1.88%, and the CR and PRD of harmonic with decaying amplitude of the proposed algorithm is 7.98 and 2.02%, showing better compression results. What’s more, a real-life sag signal measured from Power System Dynamic Simulation Laboratory, which is affiliated with Huazhong University of Science and Technology, are compressed and recovered. The CR are as high as 50, while the PRD is less than 2%, which are better than the results of sparse decomposition.
The following conclusions can be drawn from the simulation and experiment results: (1) Compared with the competing methods such as “fast Fourier transform+wavelet transform”, “sparse decomposition”, and one-class support vector machine, the CR in the proposed method is much higher than that of the compared methods without PRD declining significantly. Therefore, it is appropriate to apply the proposed method to the real-life power quality signals. (2) the experiment performed in the Dynamic power system simulation laboratory results show that the CR is higher than the competing methods, which showed better application prospect.
Keywords：Signal compression, power quality disturbance, Huffman coding, run-length coding, wavelet analysis, sparse decomposition
DOI:10.19595/j.cnki.1000-6753.tces.221653
中图分类号：TM71
国家自然科学基金资助项目（52077089）。
收稿日期 2022-08-30
改稿日期 2022-09-14
肖贤贵 男，1988年生，博士研究生，研究方向为电能质量扰动分析及信号处理、机器学习及优化方法在电能质量分析中的应用。E-mail：xiaoxiangui@hust.edu.cn
李开成 男，1962年生，教授，博士生导师，研究方向为电子式互感器、电能质量信号分析。E-mail：likaicheng@hust.edu.cn（通信作者）
（编辑 李冰）