图1 变流器接入弱电网时的系统结构
Fig.1 Structure of the grid-connected converter integrated to the weak grid
摘要 采用有源阻尼抑制弱电网下并网变流器系统失稳振荡的方法近年来受到广泛关注。已有的直接以公共耦合点（PCC）电压为反馈量的有源阻尼方法可有效抑制系统的失稳振荡，但会削弱系统对电网背景谐波电压扰动的抑制能力，进而影响到并网电流质量。为此，该文提出一种基于并网电流谐波微分的有源阻尼策略，通过微分运算将系统失稳振荡引发的谐振电流转换成PCC处的谐振电压，避免了将电网背景谐波电压扰动引入到并网电流参考值，可兼顾弱电网下并网变流器系统稳定控制和高质量并网电流两方面需要。仿真和实验结果验证了该文中理论分析的正确性和所提控制策略的有效性。
关键词：弱电网 并网变流器 失稳振荡 有源阻尼 并网电流谐波微分
在“双碳”战略目标推动下，以风、光等为代表的新能源正加速接入电网，作为新能源并网的关键设备，并网变流器在现代电力系统中的应用越来越广泛。然而，近年来由并网变流器系统与弱电网交互作用引发的失稳振荡现象频发，涉及风电[1]、光伏并网系统[2]和高速铁路牵引供电系统[3]等多个应用领域。这种现象在多机并联时更加突出[4]，已经成为威胁电网安全运行的重要因素。
围绕如何提高弱电网下并网变流器系统稳定性的问题，国内外学者做了大量工作。其中，文献[5]提出有源阻尼器的概念，该方法的基本原理是将公共连接点（Point ofCommon Coupling, PCC）电压的谐波成分除以虚拟电阻值后叠加至并网变流器输出电流参考值上，从而模拟出一个并联至PCC的虚拟阻尼电阻，抑制并网变流器系统接入弱电网可能出现的失稳振荡[6-9]。该方案无需对每个已有设备的控制系统进行改造，可解决许多弱电网下多变流器并网系统中振荡原因不明确、振荡源不能准确定位的失稳振荡问题，具有较好的工程应用前景[10]。
值得注意的是，弱电网不仅表现为较大的等值阻抗，而且PCC电压中通常含有丰富的背景谐波[11-12]，此时直接以PCC电压为反馈量的有源阻尼方法会将电网背景谐波电压扰动引入到并网电流参考值，进而削弱系统对电网背景谐波电压扰动的抑制能力，难以兼顾并网电流质量。
针对该问题，文献[13]指出，当弱电网下并网变流器系统的失稳振荡频率（文中考虑到600 Hz～3 kHz）高于电网背景谐波电压的频率，即系统失稳振荡的频段与背景谐波电压的频段不重叠时，可在有源阻尼控制中的PCC谐波电压提取环节引入高通滤波器来滤除其中频率相对较低的背景谐波电压，使得虚拟阻尼电阻具有“频变电阻”特性，即虚拟阻尼电阻只在系统失稳振荡的频段下表现为适当的电阻值，而在背景谐波电压频段下表现为无穷大阻值。该方案充分利用了系统失稳振荡的频段与背景谐波电压频段不重叠的特点，避免了有源阻尼将电网背景谐波电压扰动引入并网电流参考值，可兼顾弱电网下并网变流器系统稳定控制和高质量并网电流两方面的需要。
然而，越来越多的工程案例和研究表明，弱电网下并网变流器系统失稳振荡时的振荡频率呈现出宽频域的特点[14]，振荡频率可能覆盖10～2 000 Hz[15-17]，这说明弱电网下并网变流器系统失稳振荡的频率段极有可能与背景谐波电压的频段重叠，此时难以通过在PCC谐波电压提取环节引入滤波器来避免有源阻尼对系统电网背景谐波电压扰动抑制能力的不利影响。
可见，在利用有源阻尼提高弱电网下并网变流器系统稳定性方面，目前已取得了一定的研究成果。然而在该过程中如何保证系统对电网背景谐波电压扰动的抑制能力不受影响，即兼顾高质量并网电流，有必要进行深入研究。本文首先建立了弱电网下并网变流器的数学模型，分析了电网等值电感对系统稳定性的影响；其次，提出基于并网电流谐波微分的有源阻尼策略，并分析了其在提高弱电网下并网变流器系统稳定性方面的效果；然后，将该有源阻尼策略与目前以PCC电压为反馈量的有源阻尼策略下系统对电网背景谐波电压扰动的抑制能力进行对比分析，结果表明，基于并网电流谐波微分的有源阻尼策略在实现系统稳定控制的同时不会影响到系统对电网背景谐波电压扰动的抑制能力，可兼顾弱电网下并网变流器系统稳定控制和高质量并网电流两方面需要；最后，通过仿真和实验验证了本文理论分析的正确性和所提控制策略的有效性。
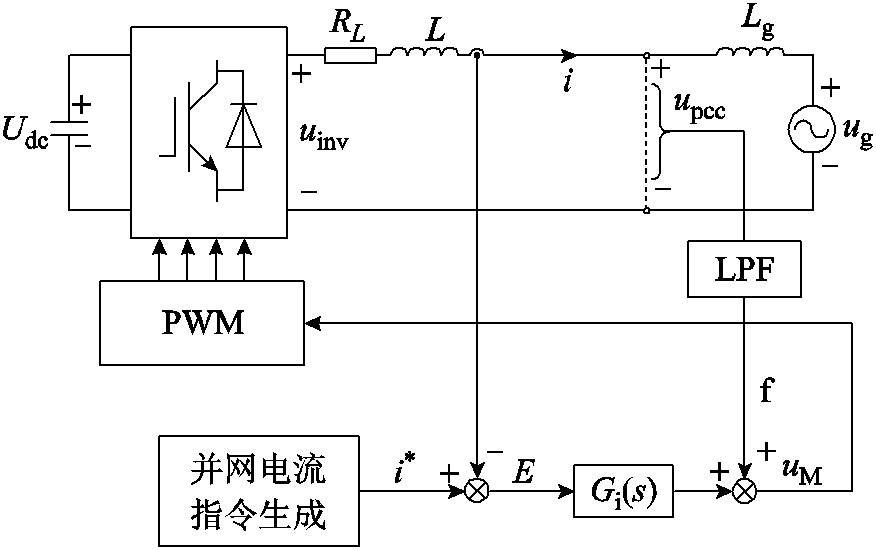
典型的并网变流器接入弱电网时的系统结构如图1所示，其中，Udc、uinv分别为变流器直流侧电压和输出电压；ug、upcc分别为电网电压和PCC电压；L、RL分别为输出滤波电感及其等值电阻；考虑到实际电网阻抗中的阻性分量有利于系统稳定，因此本文仅考虑其中的感性分量Lg从而分析系统稳定性最恶劣的工况[18]；i和i*分别为并网电流及其参考值；f为电压前馈支路，LPF为滤除电压高频分量的二阶低通滤波器；Gi(s)为电流调节器。并网电流参考值i*与实际值i的差值E经过电流调节器后与电压前馈信号相加得到调制信号uM，再经过PWM调制环节控制各开关管的通断。
图1 变流器接入弱电网时的系统结构
Fig.1 Structure of the grid-connected converter integrated to the weak grid
由图1可知，弱电网下电网等值电感的存在使得PCC电压不仅与电网电压有关，还受到并网电流的影响，此时PCC电压可表示为
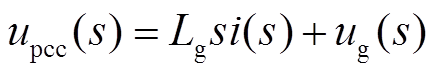（1）
研究表明，锁相环[19]和直流电压控制外环均会对弱电网下并网变流器的稳定性产生一定影响，然而通常在控制参数设计时使得锁相环和直流电压外环的穿越频率远小于电流内环，此时两者与电流内环的耦合较小，因此下文在分析弱电网下系统稳定性问题时忽略了两者的影响[13,20-21]。结合图1可得并网电流的控制框图如图2所示。
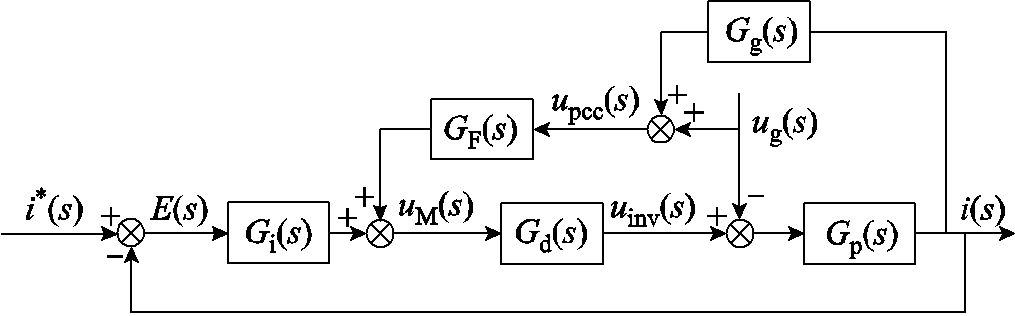
图2 并网电流控制框图
Fig.2 The diagram of grid-injected current control
图2中，Gd(s)为数字控制延时，在滞后一拍装载模式下延时大小约为1.5个采样周期[22]，可表示为
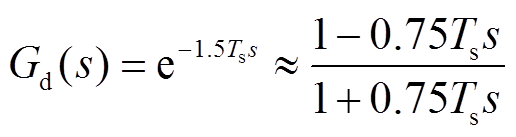（2）
式中，Ts为采样时间。图2中Gp(s)为考虑电网等值电感后系统的等效被控对象，可表示为
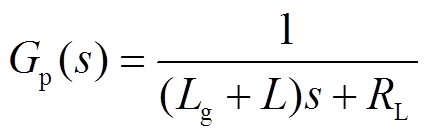（3）
图2中GF(s)为二阶低通滤波器，可表示为
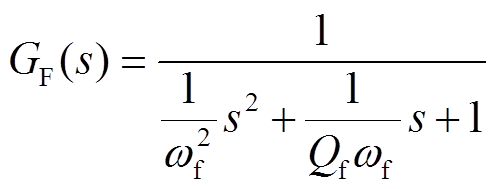（4）
式中，ωf为滤波器的截止频率；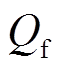
为其品质因数。图2中Gg(s)为电网阻抗，可表示为
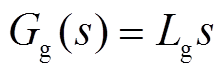（5）
根据图2可得弱电网下并网变流器系统的误差传递函数为
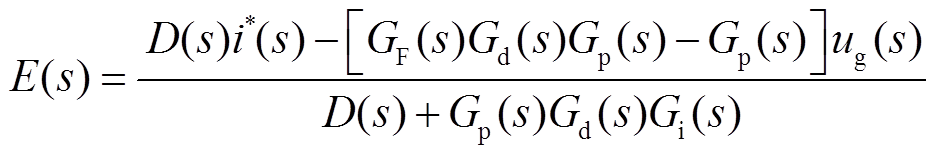（6）
式中，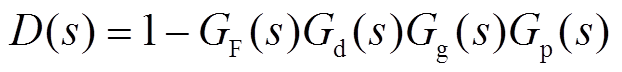
。
电流调节器对系统的性能有着重要影响。为了保证系统对正弦指令电流的跟踪能力和对电网背景谐波电压扰动的抑制能力，即并网电流质量，本文采用对周期性扰动具有较强抑制能力且结构简单的比例重复调节器，其结构如图3所示。
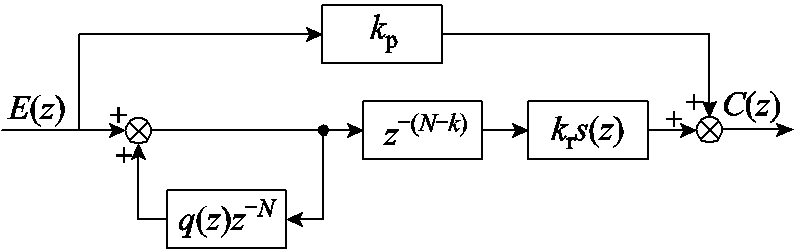
图3 比例重复调节器结构
Fig.3 The structure of proportional-repetitive controller
图3中，kp为比例系数；q(z)为衰减系数，通常取稍小于1的常数；s(z)主要对被控对象的幅频特性进行补偿，一般可设置为二阶低通滤波器；kr为重复调节器的增益；k为超前校正步长，主要补偿被控对象引起的相位滞后；N为控制系统在一个工频周期的采样点数[23]。根据图3可得比例重复调节器的传递函数为
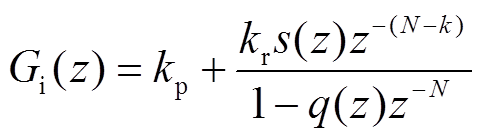（7）
将上述各环节的传递函数代入式（6）并整理可得重复控制下系统的误差传递关系为
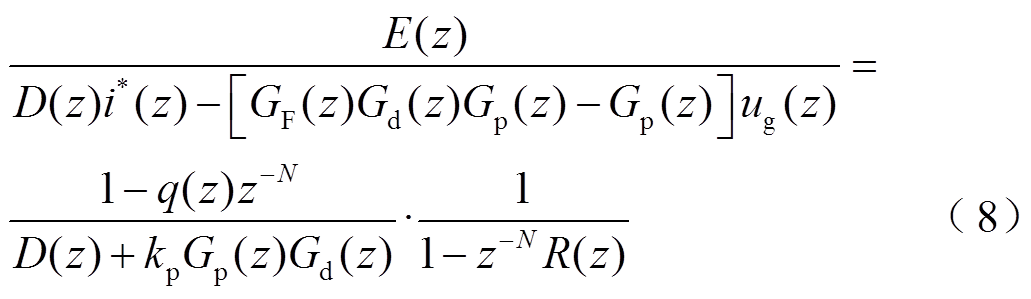
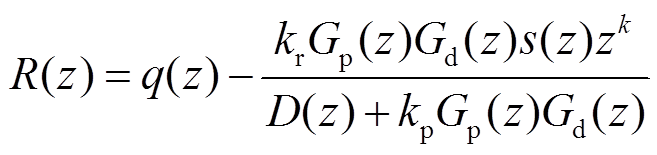（9）
令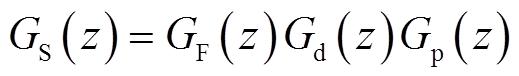
，根据式（8）可得系统的误差传递关系如图4所示。
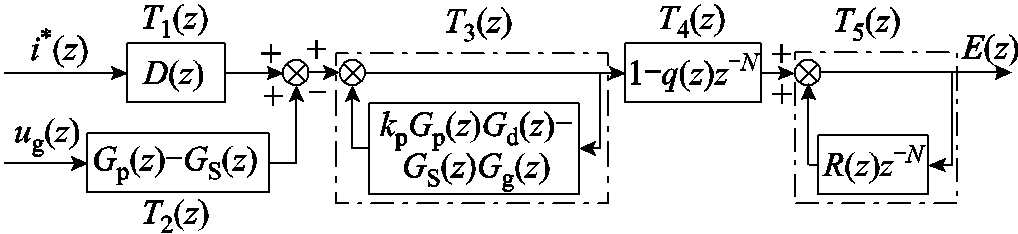
图4 系统的误差传递关系
Fig.4 The transfer relationship of system tracking error
图4表明，系统稳定的条件为图中的T1(z)～T5(z)均稳定[24]。由前文给出的各环节传递函数可知，电网阻抗的变化不会在T1(z)和T2(z)中引入单位圆以外的极点，即T1(z)和T2(z)不会导致系统失稳。由于q(z)通常取稍小于1的常数，因此保证了T4(z)的稳定性。可见，此时系统是否稳定只取决于T3(z)和T5(z)。T3(z)为一负反馈环节，可以利用特征值法分析电网等值电感对其稳定性的影响。T5(z)为高阶正反馈环节，利用特征值法分析其稳定性比较复杂，根据小增益定理，可得使T5(z)稳定的一个充分条件[25]为
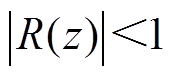（10）
如前文所述，与电流内环相比，通常锁相环的带宽较低，此时变流器可近似为线性系统[26]，并网电流参考值与电网电压之间的相位关系，即功率因数不会影响到系统的稳定性。因此，为了具体分析电网等值电感对并网变流器稳定性的影响，文中以一台额定电流50 A的SVG并网系统为例，其电路参数见表1。
表1 SVG并网系统电路参数
Tab.1 Circuit parameters of SVG gridding system
参数数值 电网电压Ug/V220 采样频率fs/Hz9 600 额定电流Io/A50 滤波电感L/mH0.5 直流侧电容C/mF470×6 滤波电感等效电阻RL/W0.01
由于系统采用单极性调制，等效开关频率为19.2 kHz，为了滤除PCC电压中的开关纹波，GF(s)二阶低通滤波器的截止频率设置在等效开关频率的1/10附近，取2 kHz，品质因数取0.707；根据表1中的电路参数和文献[23]中的调节器参数设计方法，取q(z)=0.97, kr=1.3, k=4, kp=2；s(z)的参数与GF(s)相同。根据系统的采样频率可知N=192。
将上述参数代入具体表达式并整理，可得以电网等值电感为参数时T3(z)的特征方程为
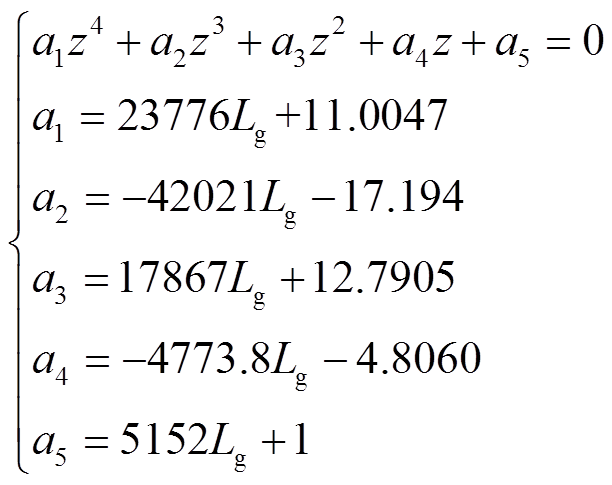（11）
利用Matlab得到当电网等值电感Lg由0 mH增大至1.4 mH时T3(z)的特征根轨迹和R(z)的Nyquist曲线分别如图5和图6所示。图5表明，随着Lg的增大，T3(z)的一对共轭极点逐渐向单位圆移动，但两对极点均位于单位圆内，说明该过程中T3(z)始终是稳定的[27-28]。由图6可知，随着Lg的增大，R(z)的Nyquist曲线迅速向单位圆移动，说明T5(z)的稳定性受Lg的影响较大，当Lg=0.7 mH时R(z)的Nyquist曲线到达单位圆，两者交截处的频率为568 Hz。当Lg=1.4 mH时R(z)的部分Nyquist曲线已超出单位圆，说明此时系统可能进入不稳定状态。可见，此时系统的稳定性对电网等值电感的变化较敏感，根据短路比（Short Circuit Ratio, SCR）的定义[29]，此时变流器所能适应的最小SCR为20（对应Lg=0.7 mH），无法适应弱电网（SCR＜10）工况[29-30]。
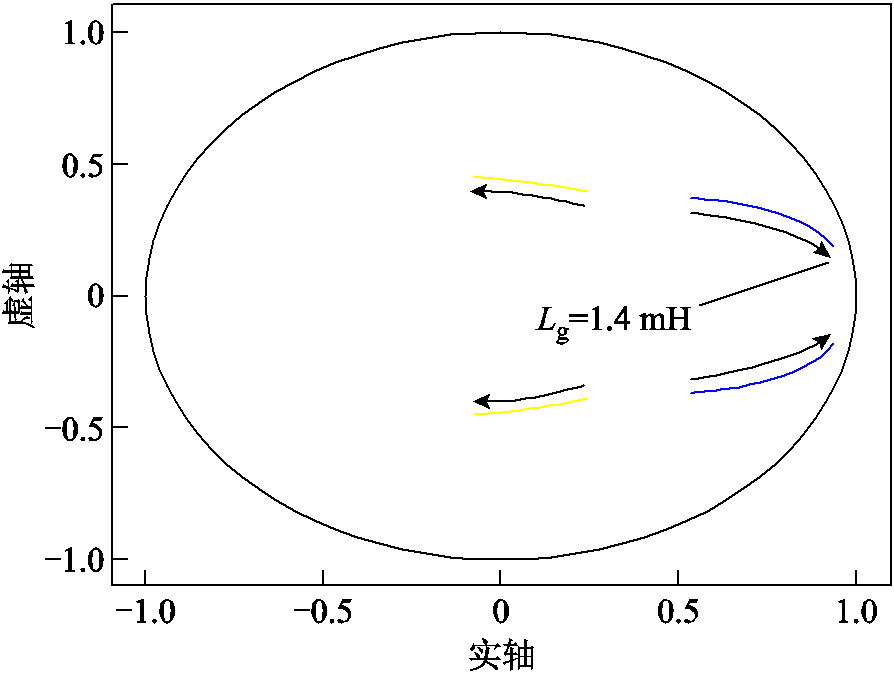
图5 Lg变化时T3(z)的特征根轨迹
Fig.5 Root locus of T3(z) with Lg variation
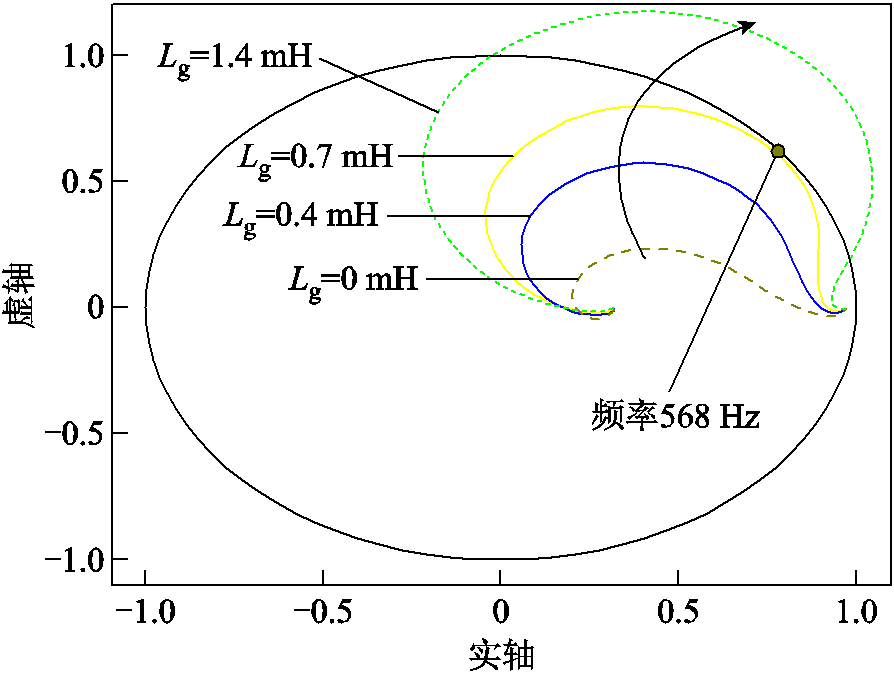
图6 Lg变化时R(z)的Nyquist曲线
Fig.6 Nyquist curve of R(z) with Lg variation
根据第1节的分析可知，若在控制中未考虑电网等值阻抗对系统稳定性的影响，则可能存在变流器对弱电网适应能力较低的问题。为了解决这一问题，文献[31]给出了目前以PCC电压为反馈量的有源阻尼控制的典型框图，如图7所示。由图7可见，其基本思想是将PCC电压的谐波成分除以虚拟电阻值Rv后叠加至变流器输出电流参考值上，从而模拟出一个并联至PCC的虚拟阻尼电阻。该方法物理意义明确，但会将电网背景谐波电压扰动引入并网电流参考值上，而通过提高控制系统性能的方法无法抑制作用于电流参考值上的扰动，因此当电网含有背景谐波电压时，该方法会在并网电流中注入不必要的谐波电流，影响到并网电流质量。
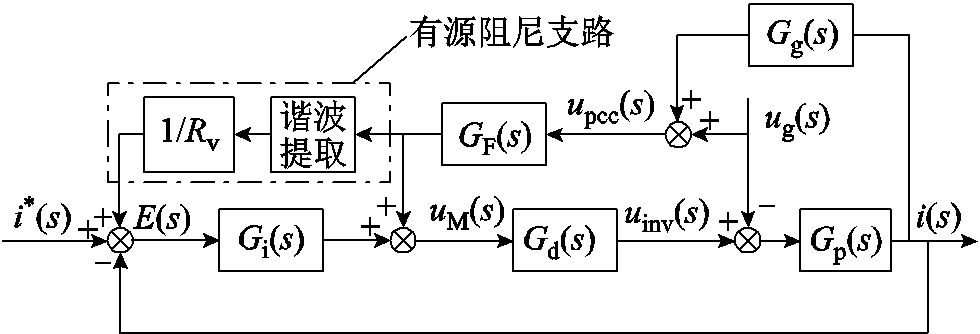
图7 基于PCC电压反馈的有源阻尼控制原理
Fig.7 Schematic of the active damping control based on PCC voltage feedback
针对直接以PCC电压为反馈量的有源阻尼控制会削弱系统对电网背景谐波电压扰动抑制能力的问题，本文提出以并网电流为反馈量的有源阻尼方法，控制原理如图8所示。
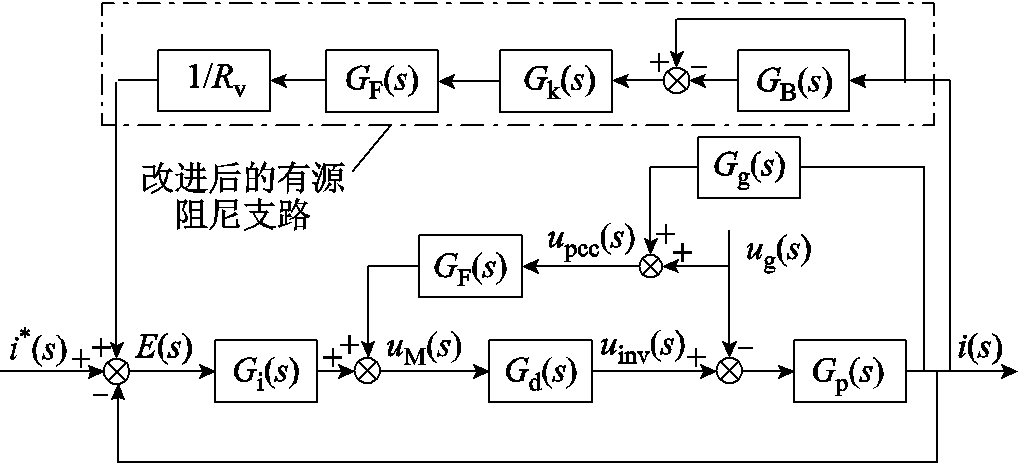
图8 基于并网电流谐波微分的有源阻尼控制原理
Fig.8 Schematic of the active damping control based on the differentiation of injected grid current harmonics
图8中，GB(s)为带通滤波器，传递函数如式（12）所示；Gk(s)为微分运算环节，传递函数如式（13）所示；GF(s)为式（4）所示的二阶低通滤波器。
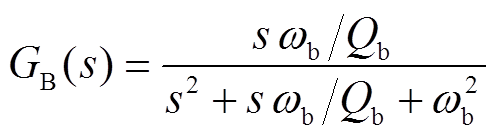（12）
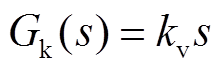（13）
式中，ωb为带通滤波器的中心角频率；Qb为带通滤波器品质因数；kv为微分系数。
其具体流程为：首先将并网电流减去其中的基波分量（基波分量由带通滤波器获得），得到谐波分量；然后对并网电流中的谐波分量进行微分运算，再经过低通滤波，以抑制微分环节可能引入的噪声干扰；最后除以虚拟电阻值叠加至变流器输出电流参考值。该方案中对并网电流中的谐波分量进行微分运算的物理意义是将滤波电感中的谐波电流转换为PCC的谐波电压。如图2所示，未引入有源阻尼控制时，目前已有多种方法可以保证系统对诸如电网背景谐波电压及死区等扰动的抑制能力，比如本文使用的重复控制器，因此稳态情况下可忽略并网电流中除开关纹波以外的谐波。当系统失稳振荡时，并网电流中将出现谐波，此时通过微分将并网电流中由系统失稳振荡产生谐波转换为PCC处的谐振电压再进行有源阻尼控制。可见，与现有的直接利用PCC处的谐波电压进行有源阻尼控制不同，改进后的方案本质上是利用PCC处系统失稳振荡引起的谐波电压进行有源阻尼，不包含电网背景谐波电压，避免了将电网背景谐波电压扰动引入到并网电流参考值上，因此该方案在实现有源阻尼控制的同时不会影响到系统对电网背景谐波电压扰动的抑制能力，可兼顾弱电网下并网变流器系统稳定控制和高质量并网电流两方面的需要。
根据图8可得引入基于并网电流谐波微分的有源阻尼控制后系统的误差传递函数为
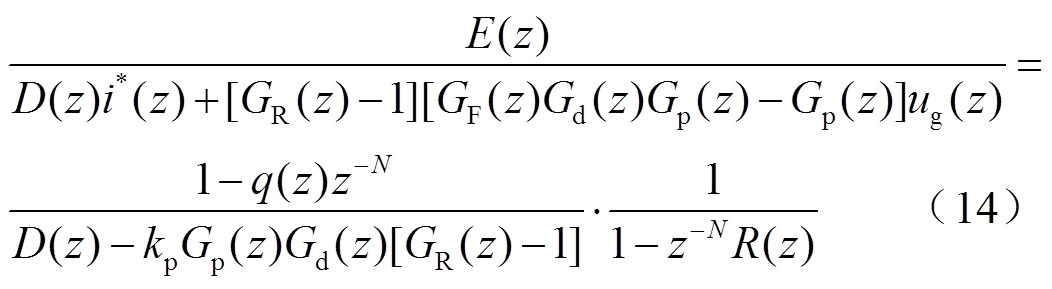
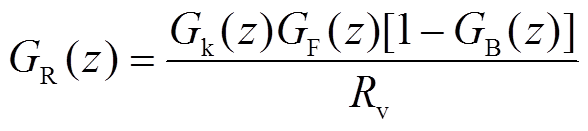（15）
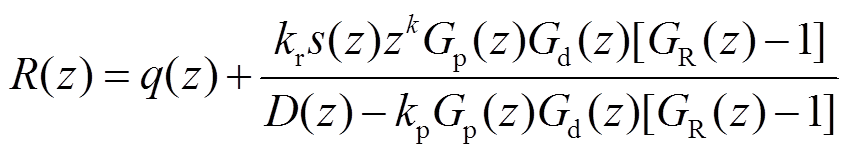（16）
令GY(z)=1-GR(z)，根据式（14）可得此时系统的误差传递关系如图9所示。
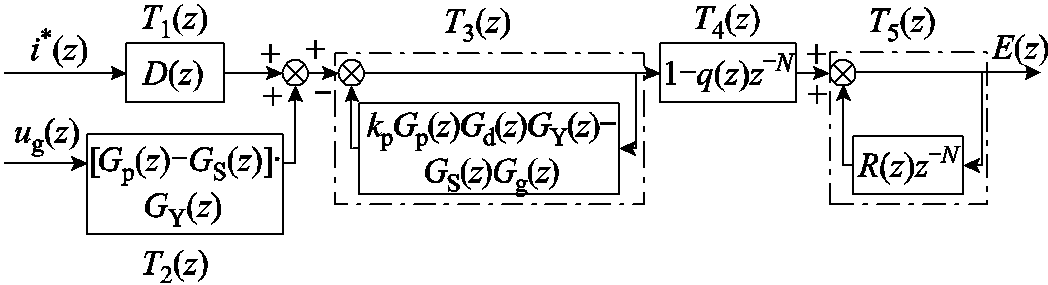
图9 引入并网电流谐波微分有源阻尼控制后系统的误差传递关系
Fig.9 The transfer relationship of system tracking error with the active damping control based on the differentiation of injected grid current harmonics
由各环节传递函数可知，电网阻抗的变化不会导致T1(z)、T2(z)和T4(z)失稳，即系统是否稳定仍只取决于T3(z)和T5(z)。为了具体分析基于并网电流谐波微分有源阻尼的控制效果，取ωb = 100π rad/s、Qb = 0.157、kv = 0.003、Rv = 3 Ω，此时可得Lg增大至6.0 mH时T3(z)的特征根轨迹和R(z)的Nyquist曲线分别如图10和图11所示。图10表明，随着Lg的增大，T3(z)的所有极点始终位于单位圆内，说明该过程中T3(z)始终稳定。由图11可知，与图6所示的未引入有源阻尼控制时相比，随着Lg的增大，R(z)的Nyquist曲线向单位圆移动的速度明显降低，系统所能适应的最大电网阻抗由0.7 mH提高至4.8 mH，对应的SCR=2.9，说明引入基于并网电流谐波微分有源阻尼控制后显著提高了变流器对弱电网的适应能力。
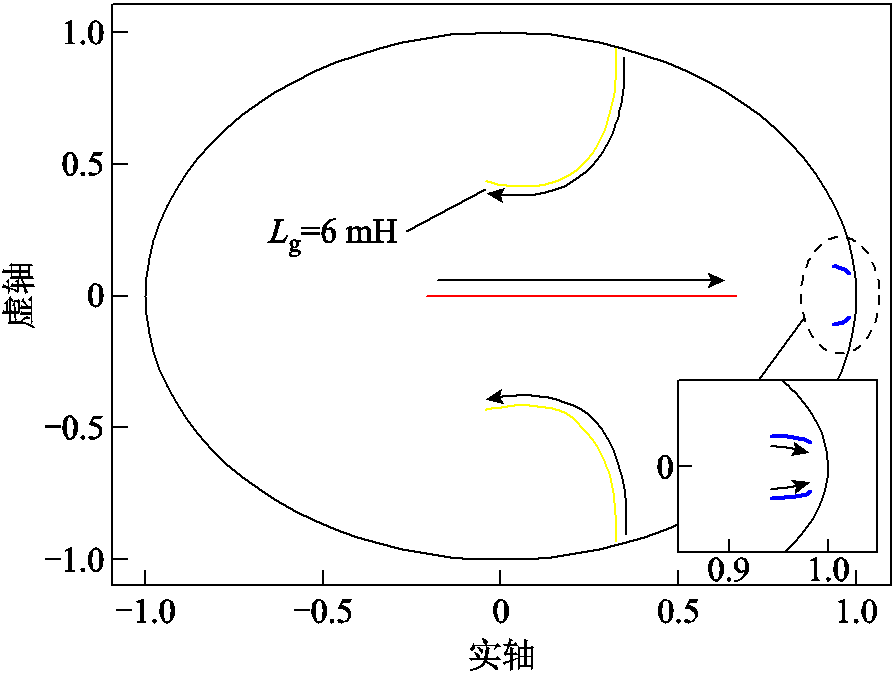
图10 引入并网电流谐波微分有源阻尼控制后Lg变化时T3(z)的特征根轨迹
Fig.10 Root locus of T3(z) with Lg variation with the active damping control based on the differentiation of injected grid current harmonics
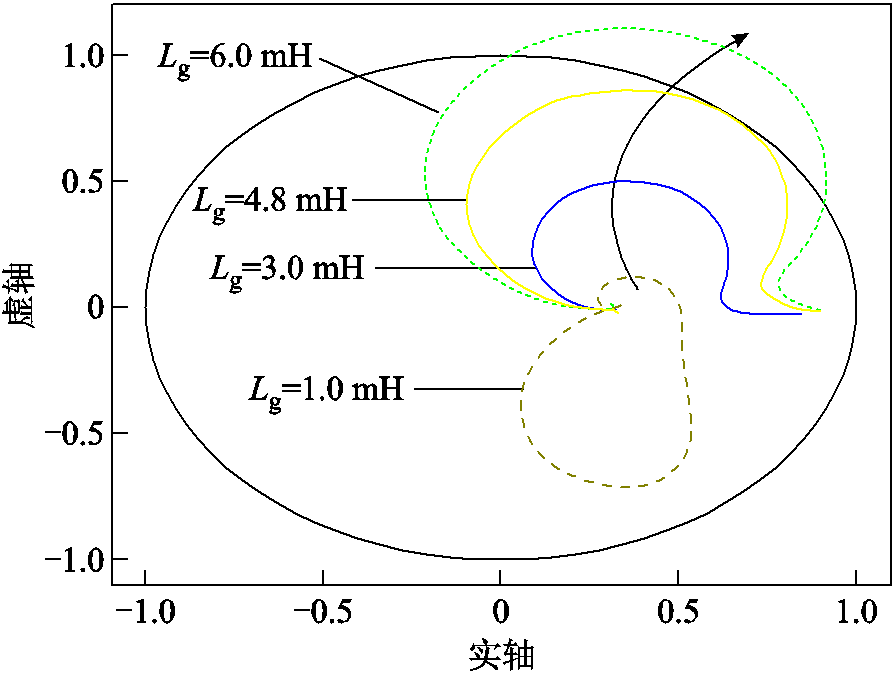
图11 引入并网电流谐波微分有源阻尼控制后Lg变化时R(z)的Nyquist曲线
Fig.11 Nyquist curve of R(z) with Lg variation with the active damping control based on the differentiation of injected grid current harmonics
为了进一步分析基于并网电流谐波微分有源阻尼控制下系统对电网背景谐波电压扰动的抑制能力，在相同的主电路参数、控制参数和虚拟电阻值下分别求取了三种工况下电网电压至并网电流误差的传递函数E(z)/ug(z)。工况1：未引入有源阻尼控制（控制框图如图2所示）；工况2：引入以PCC电压为反馈量的有源阻尼控制（控制框图如图7所示）；工况3：引入基于并网电流谐波微分的有源阻尼控制（控制框图如图8所示）。不同工况下E(z)/ug(z)的幅频特性及其在奇次谐波下的幅值分别如图12和表2所示。可见，与未引入有源阻尼控制相比，引入以PCC电压为反馈量的有源阻尼控制后，E(z)/ug(z)的幅频特性在主要谐波下的幅值会增大，说明系统对电网背景谐波电压扰动的抑制能力降低；而引入基于并网电流谐波微分的有源阻尼控制后，E(z)/ug(z)的幅频特性在主要谐波下的幅值基本不变，说明其不会削弱系统对电网背景谐波电压扰动的抑制能力。
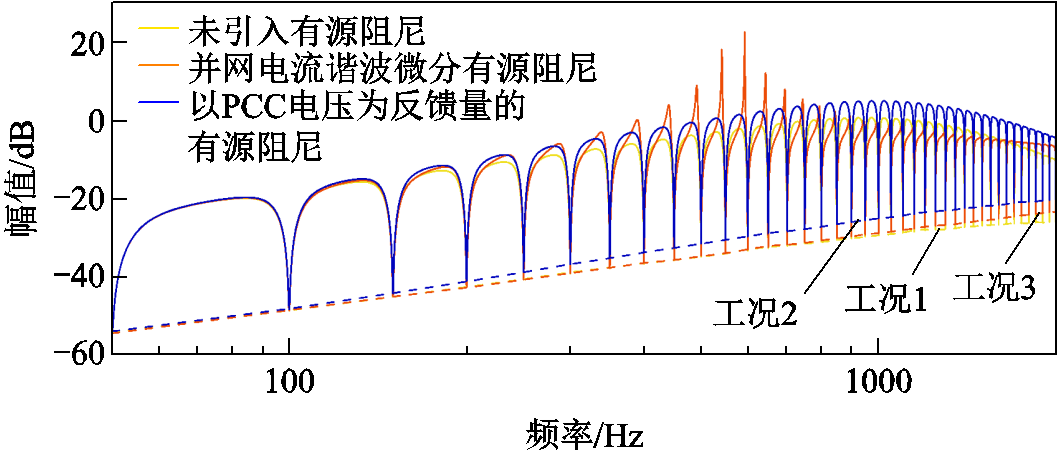
图12 不同控制策略下E(z)/ug(z)的幅频特性曲线
Fig.12 Amplitude-frequency curves of E(z)/ug(z) using different control strategies
表2 不同控制策略下E(z)/ug(z)在奇次谐波处的幅值
Tab.2 Amplitudes of E(z)/ug(z) at odd harmonics using different control strategies
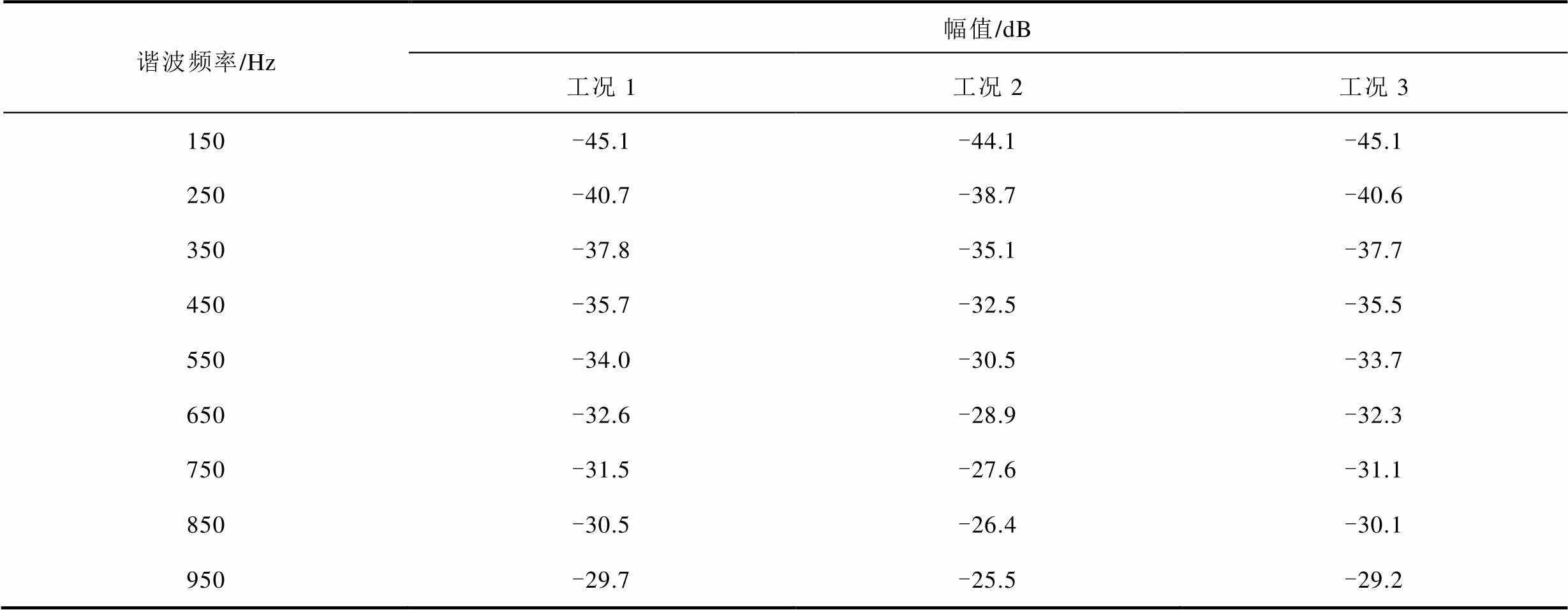
谐波频率/Hz幅值/dB 工况1工况2工况3 150-45.1-44.1-45.1 250-40.7-38.7-40.6 350-37.8-35.1-37.7 450-35.7-32.5-35.5 550-34.0-30.5-33.7 650-32.6-28.9-32.3 750-31.5-27.6-31.1 850-30.5-26.4-30.1 950-29.7-25.5-29.2
本文利用PLECS仿真软件验证理论分析的正确性和基于并网电流谐波微分有源阻尼控制策略的有效性，电路和控制参数如前文所述。为了和下文实验系统一致，通过示波器导出实验系统中的电网电压数据并进行傅里叶分析，根据分析结果构造仿真中的电网电压，如图13所示，可见，电网电压含有一定的背景谐波。图14a表明，未引入有源阻尼控制时，在SCR=20，即电网阻抗较小时变流器输出电流正常；由图14b可知THD为2.78%；然而图14c表明，当电网等值电感增大至Lg=0.75 mH，即SCR=18时变流器输出电流出现振荡，系统进入不稳定状态，相应的频谱分析结果图14d表明，此时的振荡频率在550 Hz附近，这与1.2节的理论分析结果一致。
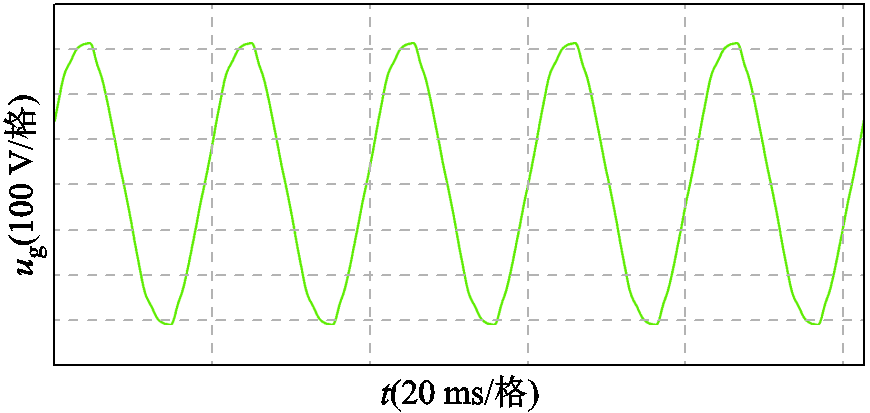
图13 仿真中的电网电压
Fig.13 The grid voltage used for simulation
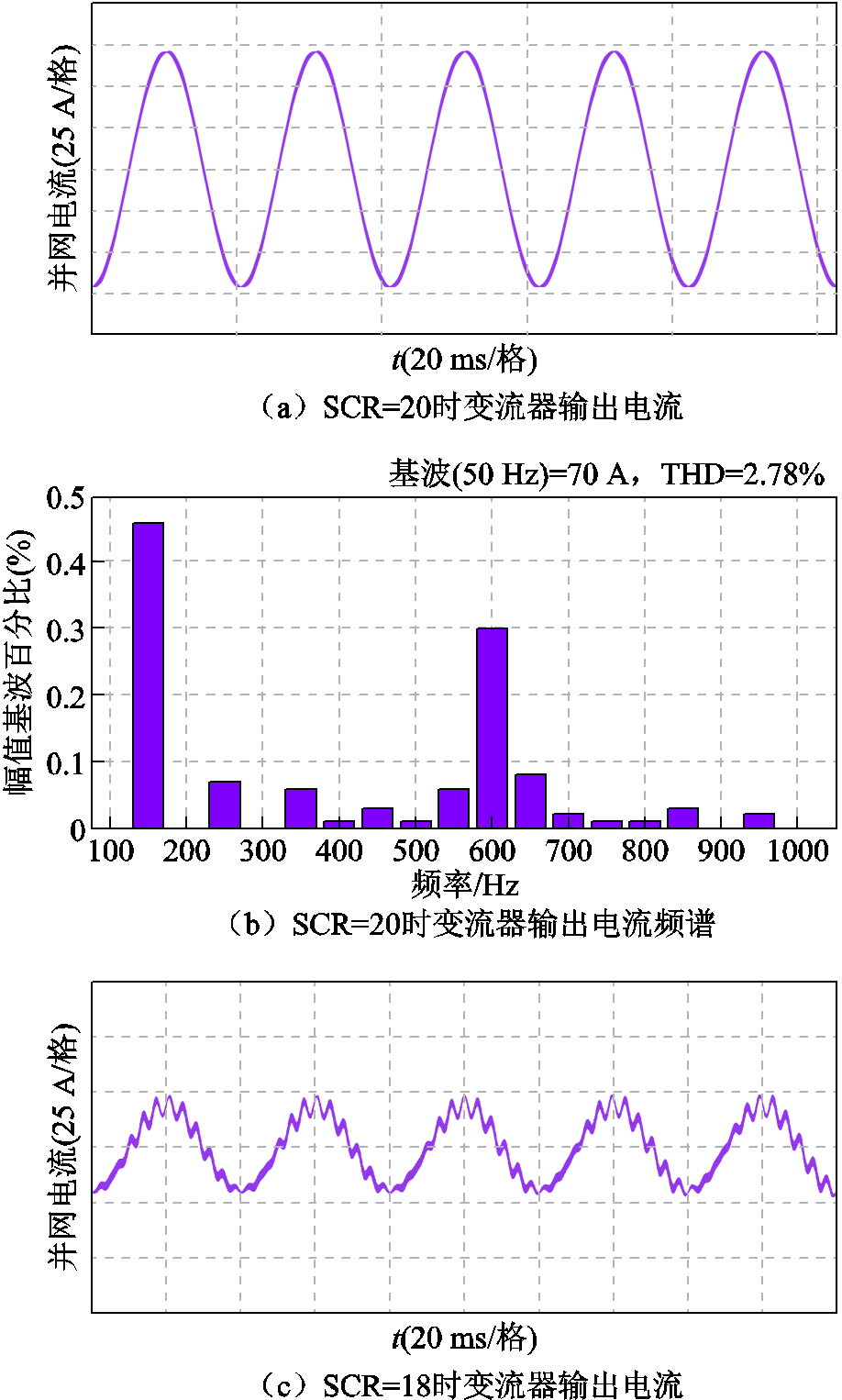
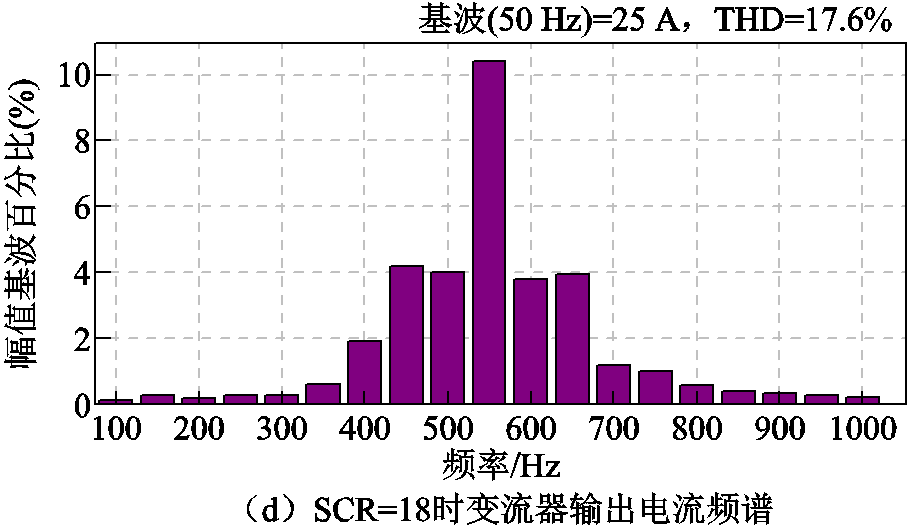
图14 未引入有源阻尼控制时不同SCR下的并网电流
Fig.14 The injected grid current at different SCRs without the active damping control
图15表明，相同调节器参数下，引入基于并网电流谐波微分的有源阻尼后，变流器在SCR为10和4.6（对应Lg=3 mH）两种工况下均能稳定运行，电流的THD分别为2.18%和1.5%，在SCR较低时THD下降的原因在于随着电网等值电感的增大其滤波作用变强，因此电流中的开关纹波减小。可见，引入基于并网电流谐波微分的有源阻尼后变流器对弱电网的适应能力显著增强，这与第2节的理论分析结果一致。
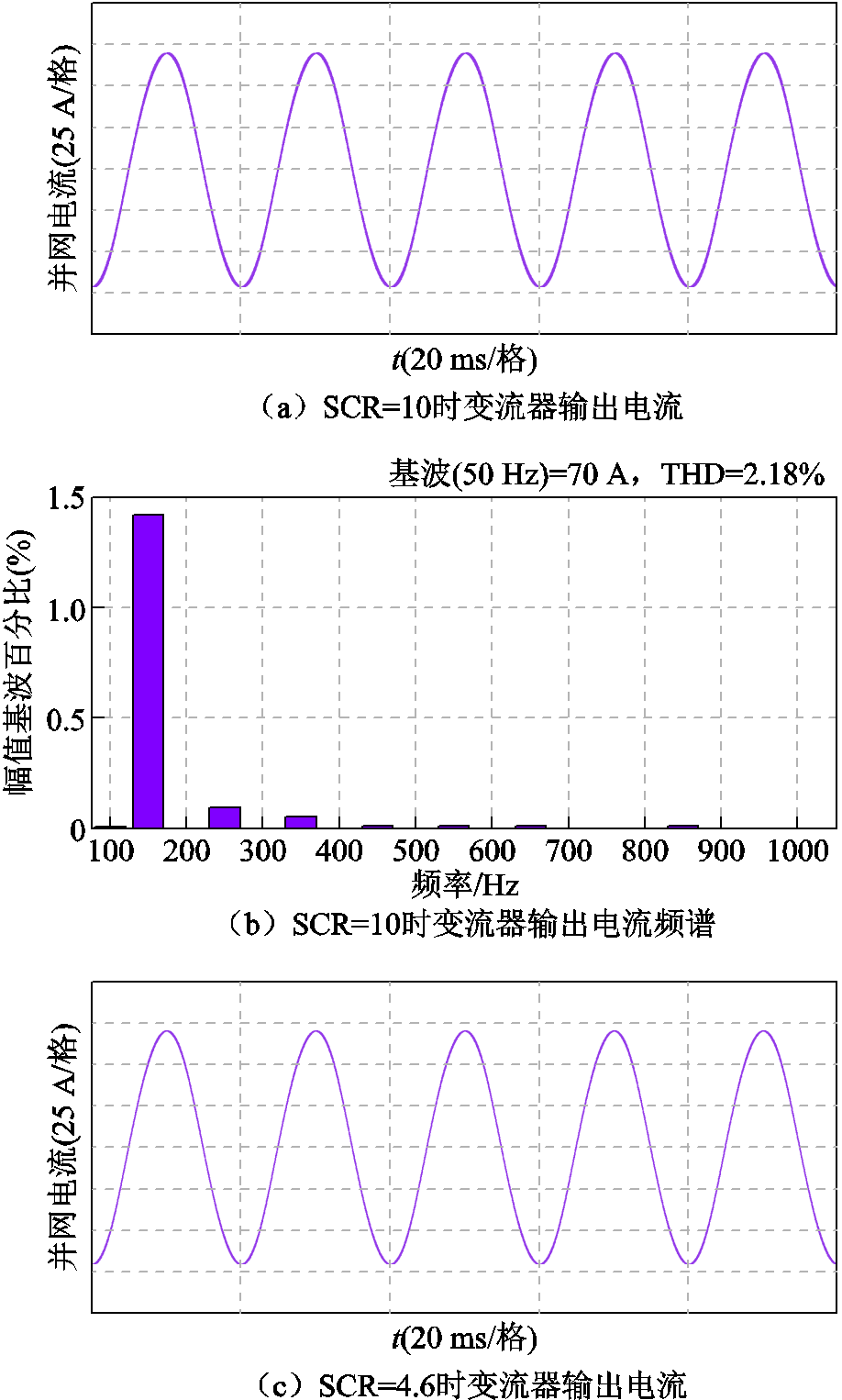
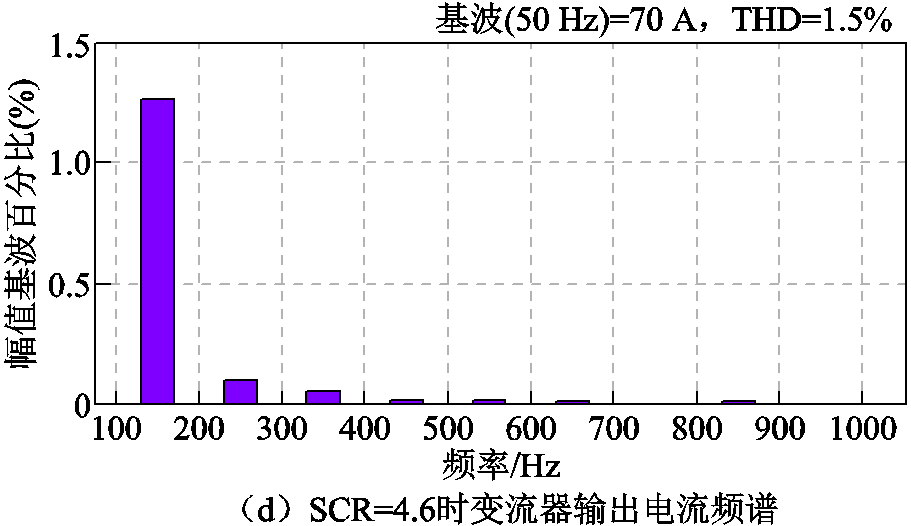
图15 采用基于并网电流谐波微分有源阻尼策略时不同SCR下的并网电流
Fig.15 The injected grid current at different SCRs with the active damping control based on the differentiation of injected grid current harmonics
在相同的调节器参数和虚拟电阻值条件下，图16给出了SCR=10时采用以PCC电压为反馈量的有源阻尼策略时的并网电流。可见，以PCC电压为反馈量的有源阻尼控制能够保证此时系统处于稳定状态。但是比较图16b和图15b可知，受电网背景谐波电压的影响，此时并网电流出现畸变，THD为3.3%，而采用基于并网电流谐波微分的有源阻尼控制时并网电流的THD为2.18%。这说明文中所提出的有源阻尼策略避免了以PCC电压为反馈量的有源阻尼控制对系统电网背景谐波电压扰动抑制能力的不利影响，可兼顾弱电网下并网变流器系统稳定控制和高并网电流质量两方面需求，这与文中第2节的理论分析结果一致。
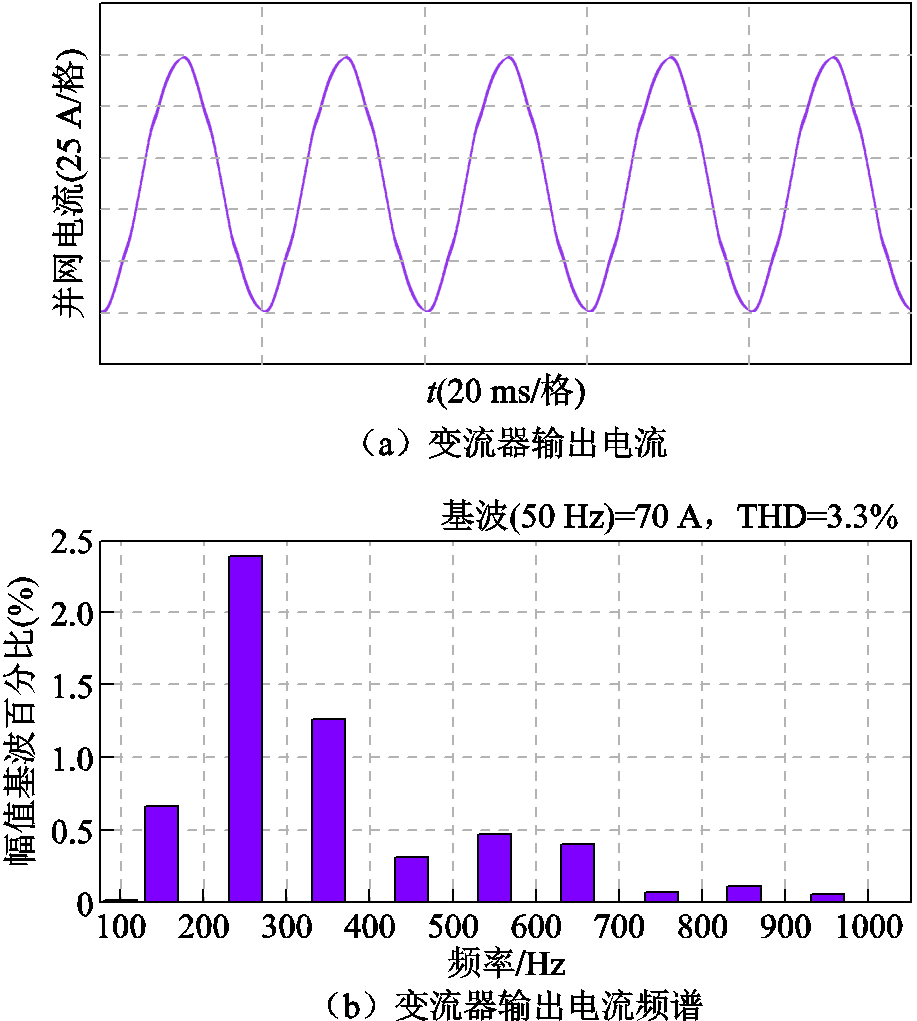
图16 SCR=10时采用以PCC电压为反馈量的有源阻尼策略时的并网电流
Fig.16 The injected grid current at SCR=10 with the active damping control based on PCC voltage feedback
为了进一步验证文中理论分析的正确性和所提控制策略的有效性，搭建了与仿真中参数一致的并网变流器实验系统，实验中的电网电压如图17所示。未引入有源阻尼控制时不同SCR下的并网电流如图18所示。图18a表明，引入有源阻尼控制前，系统稳定时变流器输出电流正常；由图18b可知THD为3.6%；然而图18c表明，当SCR=18时系统进入到不稳定状态，说明变流器对电网等值电感的适应能力较弱；相应的频谱分析结果如图18d所示，实验结果与图14所示的仿真结果基本一致，进一步验证了1.2节理论分析的正确性。
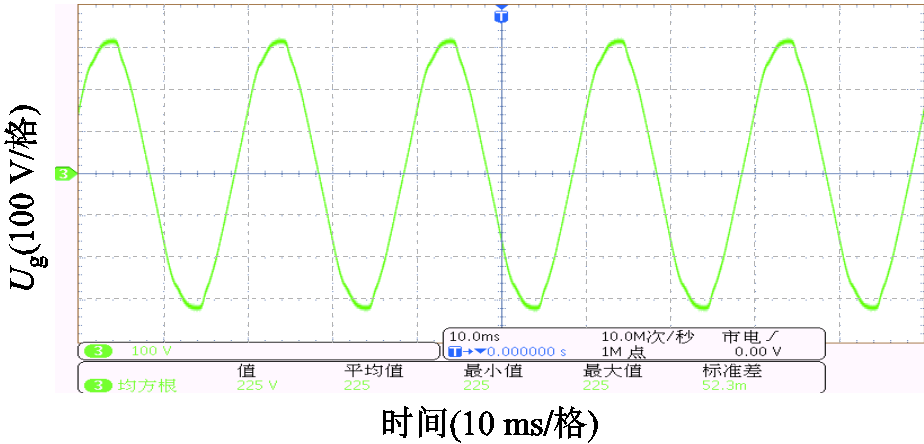
图17 实验中的电网电压
Fig.17 The grid voltage used for experiment
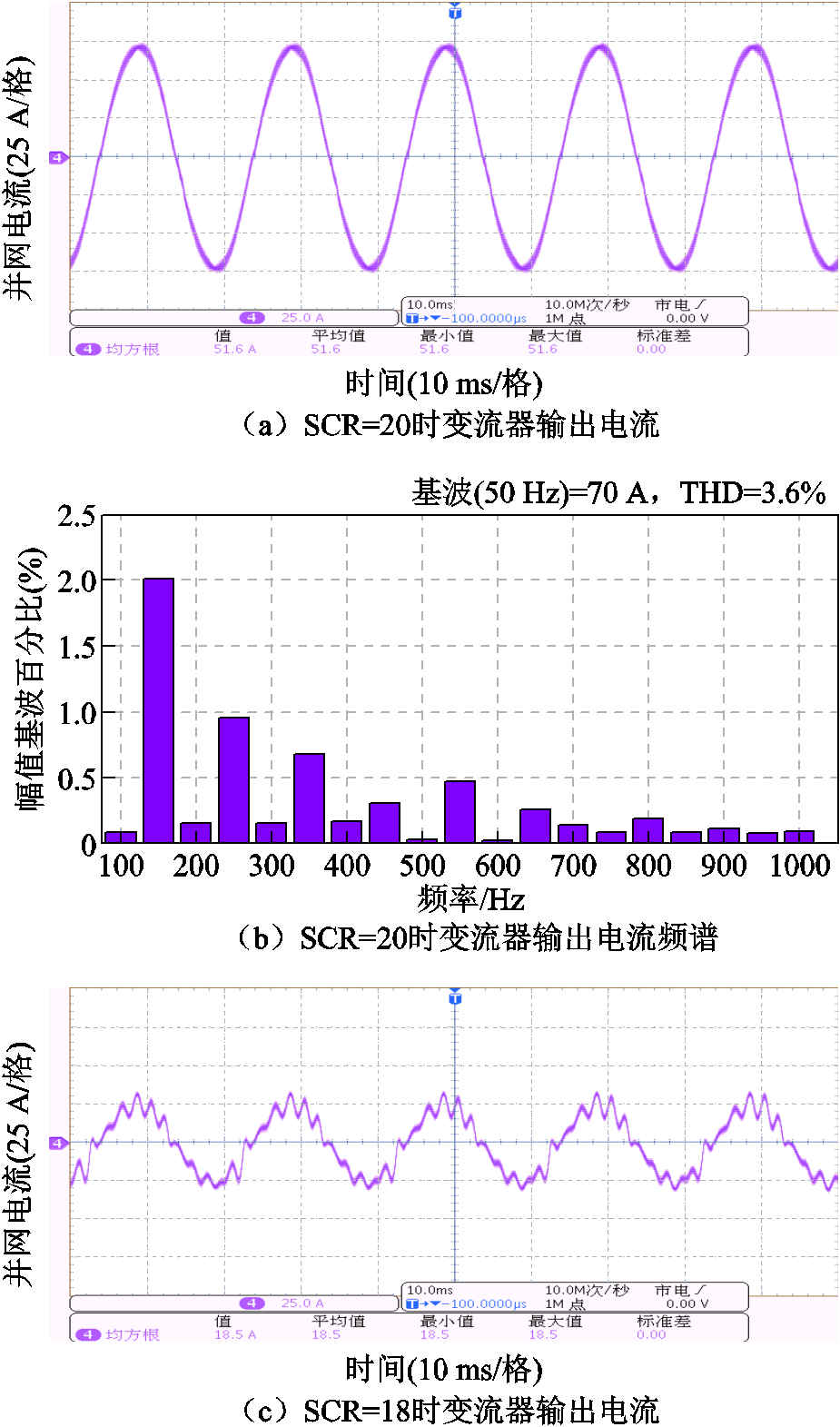
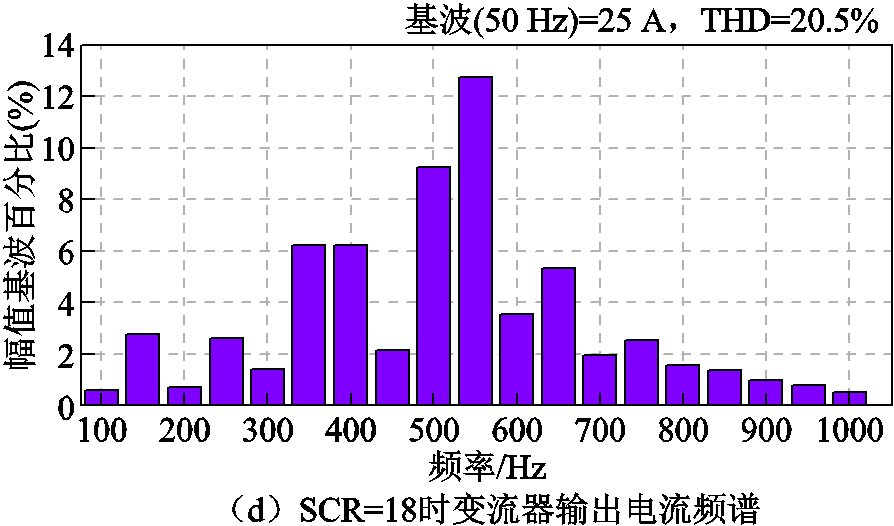
图18 未引入有源阻尼控制时不同SCR下的并网电流
Fig.18 The injected grid current at different SCRs without the active damping control
采用基于并网电流谐波微分有源阻尼策略时不同SCR下的并网电流如图19所示。图19的实验结果表明，引入基于并网电流谐波微分的有源阻尼后，在SCR为10和4.6两种工况下系统均能稳定运行，并网电流的THD分别为2.11%和1.6%，该结果与图15所给出的仿真结果一致，进一步验证了基于并网电流谐波微分的有源阻尼策略在提高弱电网下并网变流器系统稳定性方面的有效性。
SCR=10时采用以PCC电压为反馈量的有源阻尼策略时的并网电流如图20所示。比较图20和图19a、图19b可知，虽然在SCR=10时采用以PCC电压为反馈量和基于并网电流谐波微分的有源阻尼控制均能保证系统稳定运行，但在以PCC电压为反馈量的有源阻尼控制下，由于系统对电网背景谐波电压扰动的抑制能力降低，变流器输出电流出现畸变，THD由基于并网电流谐波微分有源阻尼控制下的2.11%增大至3.0%。这与图16和图15a、图15b所给出的仿真结果一致，进一步验证了基于并网电流谐波微分的有源阻尼控制在实现弱电网下系统稳定控制的同时不会削弱系统对电网背景谐波电压扰动抑制能力的优点。
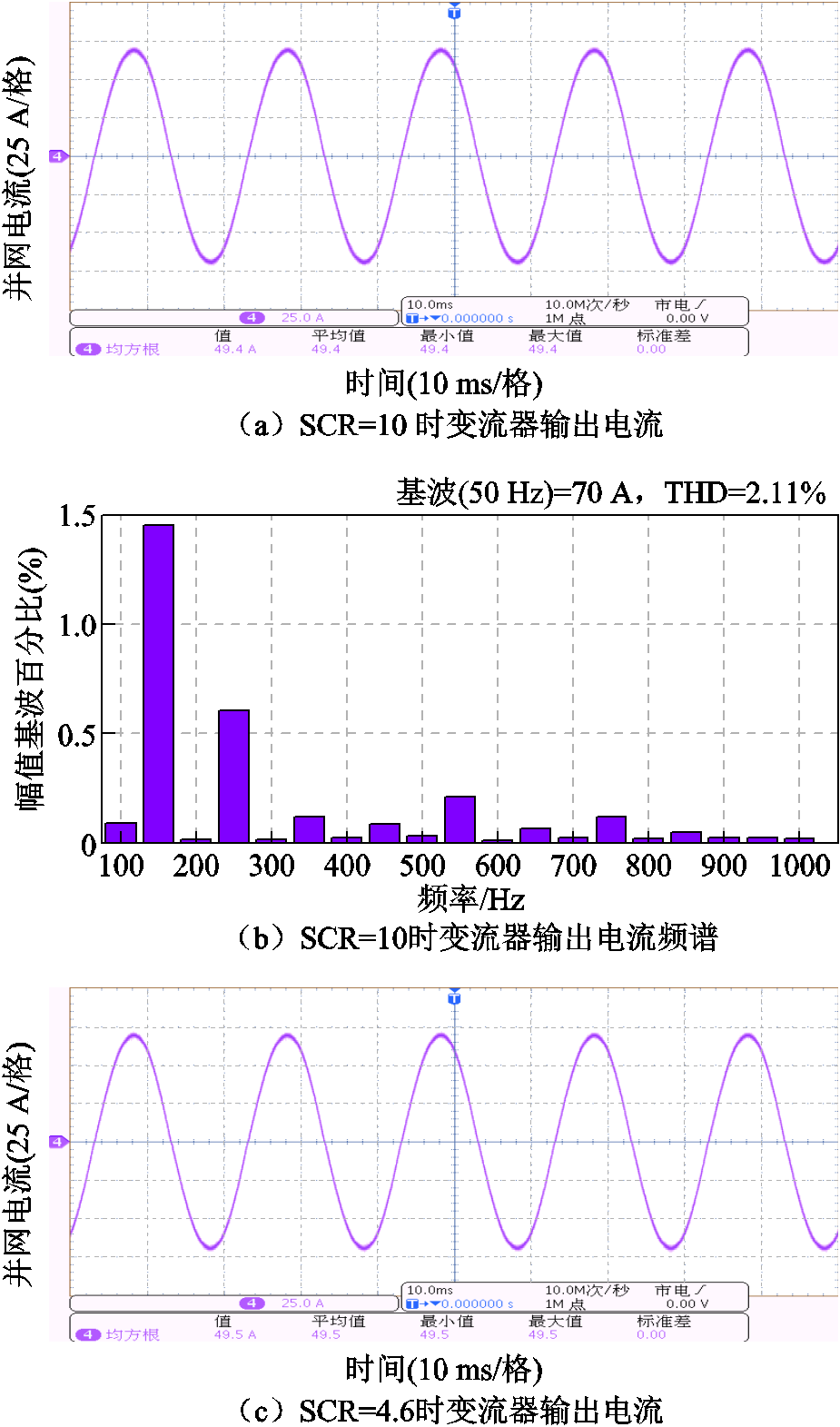
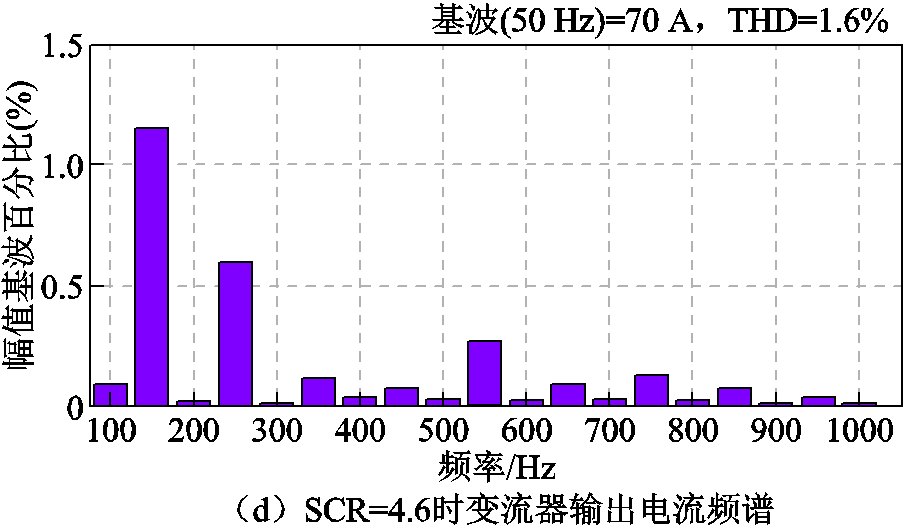
图19 采用基于并网电流谐波微分有源阻尼策略时不同SCR下的并网电流
Fig.19 The injected grid current at different SCRs with the active damping control based on the differentiation of injected grid current harmonics
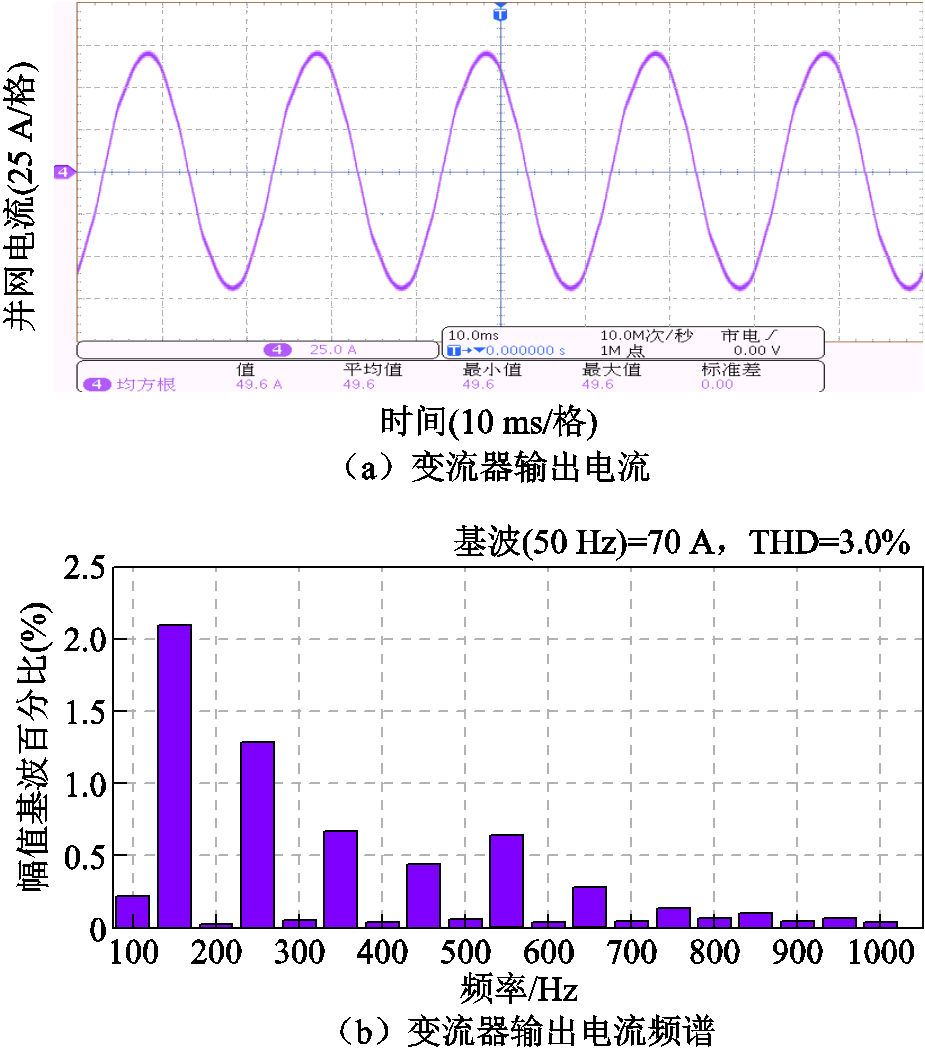
图20 SCR=10时采用以PCC电压为反馈量的有源阻尼策略时的并网电流
Fig.20 The injected grid current at SCR=10 with the active damping control based on PCC voltage feedback
本文针对弱电网下并网变流器系统的稳定性问题进行了研究，为了提高系统的稳定性，提出一种基于并网电流谐波微分的有源阻尼控制策略，最后通过仿真和实验验证了文中理论分析的正确性和所提控制策略的有效性。结果表明：
1）若在并网变流器控制中未考虑电网等值阻抗，弱电网下较大的电网等值电感可能影响到系统的稳定性，甚至导致系统失稳。
2）以PCC电压为反馈量的有源阻尼策略可显著提高弱电网下并网变流器系统的稳定性。然而，该策略可能将电网背景谐波电压扰动引入并网电流参考值上，削弱了系统对电网背景谐波电压扰动的抑制能力，影响并网电流质量。
3）基于并网电流谐波微分的有源阻尼策略，通过微分运算将滤波电感中由系统失稳振荡引发的谐振电流转换为PCC处的谐振电压，可避免将电网背景谐波电压扰动引入并网电流参考值上。该方案在实现有源阻尼控制的同时不会削弱系统对电网背景谐波电压扰动的抑制能力，可兼顾弱电网下并网变流器系统稳定控制和高质量并网电流两方面的需要。
参考文献
[1] 李龙源, 付瑞清, 吕晓琴, 等. 接入弱电网的同型机直驱风电场单机等值建模[J]. 电工技术学报, 2023, 38(3): 712-725. Li Longyuan, Fu Ruiqing, Lü Xiaoqin, et al. Single machine equivalent modeling of weak grid connected wind farm with same type PMSGs[J]. Transactions of China Electrotechnical Society, 2023, 38(3): 712-725.
[2] 徐东坡, 代永恒, 姬成群, 等. 基于RTDS的光伏逆变器接入薄弱电网仿真测试及研究[J]. 电气技术, 2022, 23(3): 82-86. Xu Dongpo, Dai Yongheng, Ji Chengqun, et al. Simulation test and study of photovoltaic inverter connected to weak power grid based on RTDS[J]. Electrical Engineering, 2022, 23(3): 82-86.
[3] 潘鹏宇, 胡海涛, 肖冬华, 等. 高速列车变流器“扫频式”dq阻抗测量中的频率耦合干扰机理及抑制策略[J]. 电工技术学报, 2022, 37(4): 990-999, 1009. Pan Pengyu, Hu Haitao, Xiao Donghua, et al. Frequency coupling interference mechanism and suppression strategy for frequency-sweeping-based dq impedance measurement of high-speed train converter[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 990-999, 1009.
[4] Agorreta J L, Borrega M, López J, et al. Modeling and control of N-paralleled grid-connected inverters with LCL filter coupled due to grid impedance in PV plants[J]. IEEE Transactions on Power Electronics, 2011, 26(3): 770-785.
[5] Wang Xiongfei, Blaabjerg F, Liserre M, et al. An active damper for stabilizing power-electronics-based AC systems[J]. IEEE Transactions on Power Electronics, 2014, 29(7): 3318-3329.
[6] 谢志为, 陈燕东, 伍文华, 等. 弱电网下多逆变器并网系统的全局高频振荡抑制方法[J]. 电工技术学报, 2020, 35(4): 885-895. Xie Zhiwei, Chen Yandong, Wu Wenhua, et al. A global high-frequency oscillation suppression method for multi-inverter grid-connected system in weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 885-895.
[7] 莫必祥, 伍文华, 陈燕东, 等. 抑制直驱风电并网系统次/超同步振荡的储能变流器有源阻尼控制方法[J]. 电网技术, 2023, 47(6): 2380-2390. Mo Bixiang, Wu Wenhua, Chen Yandong, et al. Active damping control method for power conversion system to suppress sub-/super-synchronous oscillation of D-PMSG grid-connected system[J]. Power System Technology, 2023, 47(6): 2380-2390.
[8] Bai Haofeng, Wang Xiongfei, Loh P C, et al. Passivity enhancement of grid-tied converter by series LC-filtered active damper[C]//2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 2015: 5830-5837.
[9] 李云丰, 赵文广, 孔明, 等. 直驱风电场经柔直并网的虚拟并联阻抗次同步振荡抑制策略[J]. 中国电机工程学报, 2022, 42(17): 6326-6338. Li Yunfeng, Zhao Wenguang, Kong Ming, et al. Virtual paralleled-impedance control strategy of flexible HVDC connecting to the PMSG-based wind farm for sub-synchronous oscillation suppression[J]. Proceedings of the CSEE, 2022, 42(17): 6326-6338.
[10] 姜齐荣, 王亮, 谢小荣. 电力电子化电力系统的振荡问题及其抑制措施研究[J]. 高电压技术, 2017, 43(4): 1057-1066. Jiang Qirong, Wang Liang, Xie Xiaorong. Study on oscillations of power-electronized power system and their mitigation schemes[J]. High Voltage Engineering, 2017, 43(4): 1057-1066.
[11] 杨东升, 阮新波, 吴恒. 提高LCL型并网逆变器对弱电网适应能力的虚拟阻抗方法[J]. 中国电机工程学报, 2014, 34(15): 2327-2335. Yang Dongsheng, Ruan Xinbo, Wu Heng. A virtual impedance method to improve the performance of LCL-type grid-connected inverters under weak grid conditions[J]. Proceedings of the CSEE, 2014, 34(15): 2327-2335.
[12] 陈杰, 章新颖, 闫震宇, 等. 基于虚拟阻抗的逆变器死区补偿及谐波电流抑制分析[J]. 电工技术学报, 2021, 36(8): 1671-1680. Chen Jie, Zhang Xinying, Yan Zhenyu, et al. Dead-time effect and background grid-voltage harmonic suppression methods for inverters with virtual impedance control[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1671-1680.
[13] Jia Lei, Ruan Xinbo, Zhao Wenxin, et al. An adaptive active damper for improving the stability of grid-connected inverters under weak grid[J]. IEEE Transactions on Power Electronics, 2018, 33(11): 9561-9574.
[14] 马伟明. 关于电工学科前沿技术发展的若干思考[J]. 电工技术学报, 2021, 36(22): 4627-4636. Ma Weiming. Thoughts on the development of frontier technology in electrical engineering[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4627-4636.
[15] 樊陈, 姚建国, 常乃超, 等. 电网宽频振荡实时监测技术方案[J]. 电力系统自动化, 2021, 45(11): 152-159. Fan Chen, Yao Jianguo, Chang Naichao, et al. Technical scheme for real-time monitoring of wide-frequency oscillation in power grid[J]. Automation of Electric Power Systems, 2021, 45(11): 152-159.
[16] 孙东阳, 孟繁易, 王南, 等. 基于反步自适应准谐振控制的双馈风机次同步振荡抑制策略[J]. 电工技术学报, 2023, 38(9): 2375-2390. Sun Dongyang, Meng Fanyi, Wang Nan, et al. DFIG sub-synchronous oscillation suppression strategy based on backstepping adaptive quasi-resonant control[J]. Transactions of China Electrotechnical Society, 2023, 38(9): 2375-2390.
[17] 杨苓, 陈燕东, 罗安, 等. 多机并网系统的两带阻滤波器高频振荡抑制方法[J]. 中国电机工程学报, 2019, 39(8): 2242-2252, 7. Yang Ling, Chen Yandong, Luo An, et al. High-frequency oscillation suppression method by two notch filters for multi-inverter grid-connected system[J]. Proceedings of the CSEE, 2019, 39(8): 2242-2252, 7.
[18] 沈姝衡, 方天治, 章益凡. 高带宽数字控制LCL型并网逆变器及其提高并网系统鲁棒性的谐振抑制技术研究[J]. 电工技术学报, 2022, 37(21): 5548-5561. Shen Shuheng, Fang Tianzhi, Zhang Yifan. A high-bandwidth digital-control LCL-type grid-tied inverter and resonance-suppressing technique for improving the robustness of grid-connected system[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5548-5561.
[19] 吴恒, 阮新波, 杨东升. 弱电网条件下锁相环对LCL型并网逆变器稳定性的影响研究及锁相环参数设计[J]. 中国电机工程学报, 2014, 34(30): 5259-5268. Wu Heng, Ruan Xinbo, Yang Dongsheng. Research on the stability caused by phase-locked loop for LCL-type grid-connected inverter in weak grid condition[J]. Proceedings of the CSEE, 2014, 34(30): 5259-5268.
[20] Wen Bo, Boroyevich D, Burgos R, et al. Inverse nyquist stability criterion for grid-tied inverters[J]. IEEE Transactions on Power Electronics, 2017, 32(2): 1548-1556.
[21] Tang Yi, Yao Wenli, Loh P C, et al. Design of LCL-filters with LCL resonance frequencies beyond the Nyquist frequency for grid-connected inverters[C]// 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 2015: 5137-5144.
[22] 鲍旭聪, 王晓琳, 顾聪, 等. 超高速永磁电机驱动系统电流环稳定性分析与改进设计[J]. 电工技术学报, 2022, 37(10): 2469-2480. Bao Xucong, Wang Xiaolin, Gu Cong, et al. Stability analysis and improvement design of current loop of ultra-high-speed permanent magnet motor drive system[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2469-2480.
[23] Ji Chao, Zanchetta P, Carastro F, et al. Repetitive control for high-performance resonant pulsed power supply in radio frequency applications[J]. IEEE Transactions on Industry Applications, 2014, 50(4): 2660-2670.
[24] Abusara M, Sharkh S, Zanchetta P. Adaptive repetitive control with feedforward scheme for grid-connected inverters[J]. IET Power Electronics, 2015, 8(8): 1403-1410.
[25] 杨頔, 姚钢, 周荔丹. 功率变化环境下的四线制Vienna整流器优化联合控制方法[J]. 电工技术学报, 2021, 36(2): 305-319. Yang Di, Yao Gang, Zhou Lidan. An improved control method of 4-wire Vienna rectifier considering power fluctuation[J]. Transactions of China Electrotechnical Society, 2021, 36(2): 305-319.
[26] Zhang Xuan, Wang F, Cao Wenchao, et al. Influence of voltage feed-forward control on small-signal stability of grid-tied inverters[C]//2015 IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, NC, USA, 2015: 1216-1221.
[27] 胡寿松. 自动控制原理[M]. 6版. 北京: 科学出版社, 2013.
[28] 赵强松, 陈莎莎, 周晓宇, 等. 用于并网逆变器谐波抑制的重复-比例复合控制器分析与设计[J]. 电工技术学报, 2019, 34(24): 5189-5198. Zhao Qiangsong, Chen Shasha, Zhou Xiaoyu, et al. Analysis and design of combination controller based on repetitive control and proportional control for harmonics suppression of grid-tied inverters[J]. Transactions of China Electrotechnical Society, 2019, 34(24): 5189-5198.
[29] 刘桂花, 曹小娇, 王卫. 弱电网下单相光伏并网逆变器锁频环同步方法[J]. 中国电机工程学报, 2015, 35(19): 5022-5029. Liu Guihua, Cao Xiaojiao, Wang Wei. A frequency locked loop grid synchronization method of single-phase grid-connected PV inverter under weak grid[J]. Proceedings of the CSEE, 2015, 35(19): 5022-5029.
[30] 涂春鸣, 高家元, 赵晋斌, 等. 弱电网下具有定稳定裕度的并网逆变器阻抗重塑分析与设计[J]. 电工技术学报, 2020, 35(6): 1327-1335. Tu Chunming, Gao Jiayuan, Zhao Jinbin, et al. Analysis and design of grid-connected inverter impedance remodeling with fixed stability margin in weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1327-1335.
[31] 杨树德, 李旺, 张新闻, 等. 一种提高变流器弱电网适应能力的虚拟阻抗控制策略[J/OL]. 电源学报, 2021: 1-14. (2021-10-14). https://kns.cnki.net/kcms/ detail/12.1420.TM.20211014.1354.002.html. Yang Shude, Li Wang, Zhang Xinwen, et al. A virtual-impedance based control strategy for improving the adaptability of converter to weak grid[J/OL]. Journal of Power Supply, 2021: 1-14. (2021-10-14). https://kns.cnki.net/kcms/detail/12.1420.TM.20211014.1354.002.html.
Abstract The active damping strategy that simulates a virtual resistor at the point of common coupling (PCC) is effective to improve the converter stability under weak grid. However, in the traditional strategy, the PCC voltage is generally fed to the current reference by multiplying a gain. Naturally, the disturbances of grid background harmonic voltages will be also introduced to the current reference, and the unexpected harmonics will arise in the current. Thus, the traditional strategy will weaken the rejection abilities of the converter on the background harmonic voltages and reduce the current quality. To solve these issues, this paper proposes an active damping strategy based on the differentiation of injected grid current harmonics, which can ensure the system stability and the current quality simultaneously.
First, the control structure of the active damping strategy based on the differentiation of injected grid current harmonics is given, in which the differential operation is used to transfer the harmonic currents to the harmonic voltages. This way, only the harmonic voltages caused by the unstable resonance will be fed to the output current reference, and the grid background harmonic voltages can be excluded. Therefore, the disturbances in the output current reference from grid background harmonic voltages can be eliminated and the output current quality will not be influenced by the active damping control. In addition, the rejection abilities of the converter on the background harmonic voltage disturbances before and after applying the proposed active damping strategy are compared.
Simulation and experimental results show that, with the proposed active damping strategy, the minimum short circuit ratio (SCR) for the grid-connected converter system to operate stably is reduced from 20 to 2.9, which indicates that the proposed method can markedly improve the adaptability of the converter to weak grid condition. Moreover, under a distorted grid voltage condition, the comparison of current total harmonic distortion (THD) with the different active damping methods shows that, the current THDs are 2.18% (simulation result) and 2.11% (experimental result) with the proposed method, while the current THDs are 3.3% (simulation result) and 3.0 (experimental result) with the conventional method. This demonstrates that the proposed active damping method can obtain higher current quality compared to the conventional method. This is because the rejection abilities of the converter on the background harmonic voltage disturbances can remain unchanged when the proposed active damping method is used.
The following conclusions can be drawn from the simulation and experimental analysis: (1) If the grid impedance is not considered, the larger grid inductance of weak grid may affect the converter stability and even to destabilize the system. (2) The active damping strategy based on PCC voltage feedback can improve the stability of the converter under weak grid. However, it will introduce the disturbances of background harmonic voltages to the current reference and weaken the rejection abilities of the converter on these disturbances, thereby reducing the current quality. (3) For the active damping strategy based on the differentiation of injected grid current harmonics, the differential operation is used to transfer the resonant current caused by the instability to the resonant voltage at PCC. Therefore, the disturbances in the current reference from background harmonic voltages can be avoided. The proposed method can realize the active damping performance, and meanwhile, the rejection abilities of the converter on the background harmonic voltages will not be weakened. Both the stability control of the converter system under weak grid and the high quality of grid-injected current can be satisfied.
keywords：Weak grid, grid-connected converter, unstable oscillation, active damping, differentiation of injected grid current harmonics
DOI:10.19595/j.cnki.1000-6753.tces.221559
中图分类号：TM46
江苏省高等学校自然科学基金（19KJB470038）、宁夏自然科学基金（2020AAC03210）和国家自然科学基金（51867001）资助项目。
收稿日期 2022-08-11
改稿日期 2022-09-19
杨树德 男，1986年生，博士，讲师，硕士生导师，研究方向为可再生能源发电系统并网控制及稳定性分析。E-mail：358060069@qq.com（通信作者）
李 旺 男，1996年生，硕士研究生，研究方向为弱电网下并网变流器系统的稳定性分析与增强控制。E-mail：735987495@qq.com
（编辑 赫蕾）