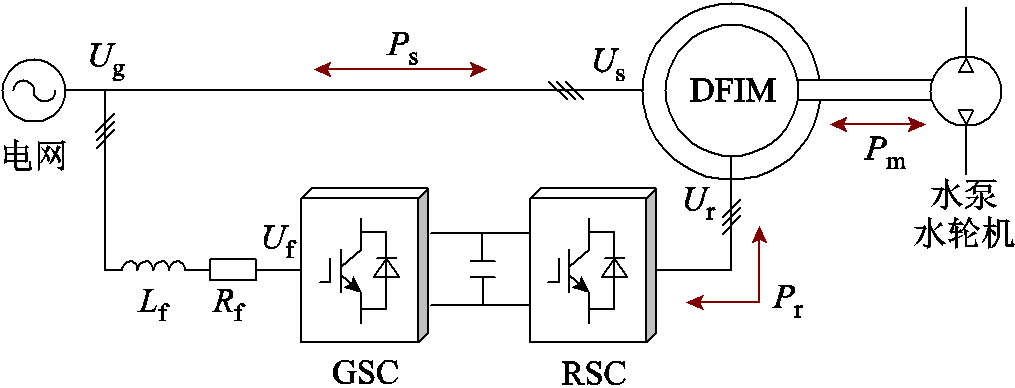
图1 可变速抽水蓄能机组拓扑
Fig.1 Variable speed pumped storage unit topology
摘要 采用双馈电机（DFIM）的可变速抽水蓄能机组具备出色的全工况调速性能和综合效率，是未来电网调峰调频的一种重要手段。然而，传统的频率控制方法通常将电网频率偏差整定为有功功率修正量，导致该环节与电机固有转速控制环节的控制目标相异，进而使得变速抽蓄机组无法充分发挥其动态调频特性。鉴于此，该文提出一种基于附加转速修正量的频率响应特性优化控制策略。首先，采用转速优先控制作为基本控制策略，以发挥机组可快速调速的优势。然后，引入频率响应环节，通过电网频率偏差及其变化率得到转速修正量，并限制机组转速的修正范围。同时，为更加合理地调控转子动能，结合电网频率波动过程中的特点，对频率响应环节的参数进行动态调整。通过与同容量同步电机的对比研究发现，在该文控制策略下，DFIM转子动能具有更大的调整范围。在系统投切负载仿真中，该策略与现有频率-有功控制策略相比，不仅减小了频率的变化幅度及稳态误差，而且抑制了过渡过程中的频率波动。
关键词：双馈电机 可变速抽水蓄能机组 惯量支撑 频率响应 转速控制
高比例新能源接入对电网灵活调节手段的响应特性提出了更高的要求[1]。可变速抽水蓄能电站以转子采用交流励磁的双馈电机（Doubly Fed Induction Machine, DFIM）为核心，配合可变速水泵水轮机，通过转速及导叶开度调节，实现全工况下的功率灵活调控[2]，快速响应新能源发电的出力波动[3]，为解决弃风弃光问题[4-6]提供了有效的解决手段。
目前，DFIM在抽水蓄能应用场景下的频率响应研究仍处于初步阶段，文献[7]以定速抽水蓄能机组参与电网调频为核心，其本质仍是采用同步电机作为调频机组，缺乏变速机组灵活调速的特性，不利于抽水蓄能机组的最高效率运行；文献[8]将频率波动量整定为有功指令的修正量，改变电机转速，释放/吸收转子动能，然而，这与固有转速控制环节存在矛盾，使得调频效果不佳；文献[9]仅针对发电工况下可变速抽水蓄能机组的频率控制策略进行研究，综合调节转速及导叶开度使得机组参与电网一次调频，并未提及抽水工况下的运行特点；文献[10]侧重于系统的整体控制策略研究，建立了可变速抽水蓄能系统的机电暂态模型，并对比采用不同水动态模型时模型的动态响应；文献[11]提出一种功率优先控制下变速抽蓄机组频率响应机理模型，分析其调频稳定性与动态性能两方面的优势。现有文献着重于其本体建模及有功调节特性研究，在频率响应特性研究方面具有以下特点：普遍采用功率优先的控制策略，只能间接控制转子动能；全工况下机组的频率响应特性研究较少；针对可变速抽水蓄能系统所提供的惯量大小方面研究数量有限。
可变速抽水蓄能系统和风力发电系统均采用DFIM作为核心部分，而现有双馈抽水蓄能系统的研究有限，因此围绕双馈风力机组的频率响应特性研究能够为抽水蓄能系统提供思路。双馈风电系统在频率调节方面所采用的核心思想可以总结为降低负载调频[12]、结合直流侧储能设备调频[13]及转子动能释放与吸收进行调频[14]三个方面。降低负载控制将大幅降低风电系统的运行效率，不宜长期使用[15]。在DFIM背靠背变流器的直流母线上增加储能设备共同参与调频可以起到延长频率调节时间的作用，但是电池储能的效果受变流器功率及电池容量限制，难以有效提升其支撑效果[16]。DFIM转子动能调控通过模拟同步发电机的惯量特性主动参与电网调频。诸多研究提出不同的控制算法[14,17]，综合分析风机运行工况、储能容量及设备耐受程度对频率控制器系数的影响[18]，并研究特殊场景下如风电场低电压穿越过程中的虚拟惯量及改进网侧变流器协同控制策略[19]，采用在线辨识方法给定DFIM控制器参数[20]。然而，抽水蓄能系统和风力发电系统仍存在显著的区别：①运行工况不同，风电系统中的DFIM只作为发电机运行，而抽水蓄能系统具有“削峰填谷”的功能，DFIM需按照电网调度指令在不同时刻分别工作于发电及抽水（电动）工况下；②系统的储能形式及惯量大小不同[21]，抽水蓄能系统的惯量由水库、水泵水轮机和DFIM三者提供，惯量远大于风电系统仅依靠DFIM转子所提供的惯量；③基本控制目标不同，风电系统注重其输出功率的最大化控制，常采用最大功率跟踪控制，而抽水蓄能系统的有功指令受调度影响，主要围绕系统的最高效率运行。同时，可变速抽水蓄能机组由于机电耦合性较差，短时的功率/惯量支撑难以通过调节水泵水轮机来实现[22]。
鉴于此，亟须研究在可变速抽水蓄能应用场景下，机组参与电网频率响应的能力及提升手段。本文在转速指令中引入根据电网频率波动情况及控制器参数计算得到的转速修正量，并给出相应控制器参数的整定思路，分析参数对系统惯量的影响，同时对比相同容量同步发电机与DFIM的可调节转子动能及惯量支撑时间。经由仿真分析，模拟抽水蓄能机组稳态情况下的转速、转矩调节过程，以及电网频率发生波动时的频率响应特性，进而验证了所提控制策略的有效性和可行性。
传统抽水蓄能系统中同步电机采用直流励磁，只能通过调节发电机电动势幅值进行无功功率调节，缺乏电机控制上的灵活性；相较之下，可变速抽水蓄能机组中DFIM采用交流励磁，其幅值、频率及相位均可灵活调节，因而具有双向平滑可调、绿色环保、全寿命周期成本低等优越性能，在削峰填谷、调频调相及事故备用方面具有显著的应用前景。
可变速抽水蓄能机组由双馈电机、可变速水泵水轮机、电网侧变流器（Grid-Side Converter, GSC）、转子侧变流器（Rotor-Side Converter, RSC）和滤波器组成，如图1所示。其中电网侧变流器用于维持直流母线电压稳定，实现功率的双向流动，并调节转子绕组并网侧的功率因数；转子侧变流器用于控制电机的转速、转矩和功率。
图1 可变速抽水蓄能机组拓扑
Fig.1 Variable speed pumped storage unit topology
双馈电机的定、转子绕组频率关系为
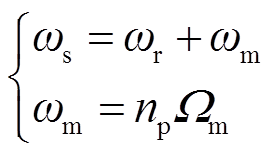（1）
式中，ωs为定子侧电气量的频率；ωr为转子侧电气量的频率；ωm为转子电气旋转角速度；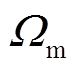
为转子机械角速度；np为电机极对数。通过改变转子励磁电流频率能够实现变速恒频运行。抽水蓄能电站中转子励磁电流适应因水头变化而造成的水泵水轮机转速变化，进而达到维持抽水蓄能机组输出电压频率恒定的目的。
考虑到DFIM定、转子之间的电磁耦合关系相当复杂，下面以同步转速作为旋转坐标系的旋转角速度，得到电机在旋转坐标系下的数学模型，如式（2）～式（5）所示。
磁链方程为
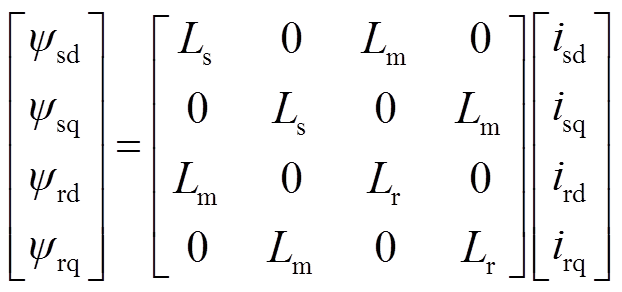（2）
电压方程为
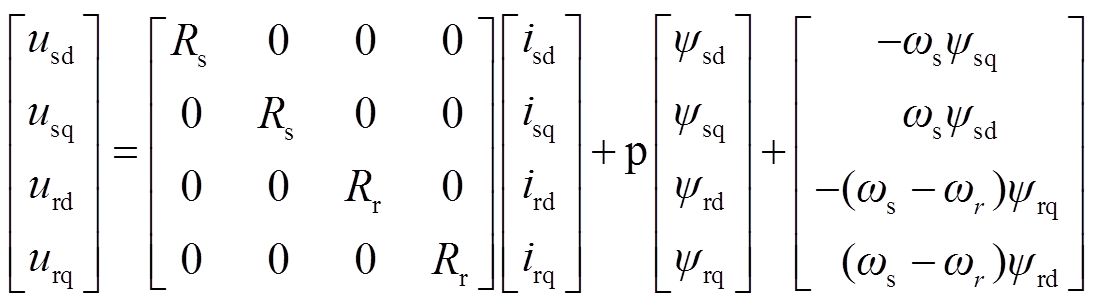（3）
电磁转矩方程为
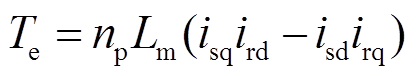（4）
转子运动方程为
（5）
式中，下标s、r分别代表DFIM的定、转子绕组；d、q分别代表旋转坐标系的d轴与q轴；u为绕组电压；i为绕组电流；ψ为绕组磁链；R为绕组电阻；Ls、Lr分别为定、转子自感；Lm为定、转子之间的互感；Te、TL分别为电磁转矩及负载转矩；J为电机转动惯量；p为微分算子。
可变速抽水蓄能系统中DFIM普遍采用转速优先控制或功率优先控制策略，可以实现转速或有功功率、无功功率的调节。然而，电机转速与电网频率解耦的特性导致其对电网缺乏惯量支撑的能力，明显降低了系统抗扰动和主动调频的能力，导致系统调频难度增大。本节所提出的控制策略既要满足日常情况下DFIM转速可调的特性，又要确保DFIM在电网频率发生短时波动时具备有效且快速的响应能力，以此充分发挥抽水蓄能电站在新型电力系统中的优势。
可变速抽水蓄能机组的运行目标主要体现在满足变速恒频运行条件下提升系统的运行效率和通过调节DFIM输出无功功率确保电网的稳定运行。采用转速优先控制策略的可变速抽水蓄能机组，将转速控制器及无功功率控制器作为DFIM的控制外环，内环采用电流控制器对转子电流进行控制。DFIM响应不平衡功率及不同的转速指令快速调节转子电流频率及幅值，实现电机功率和转速控制；同时，结合水头变化和水泵水轮机导叶开度大小对电机转速进行调节，实现最优效率运行，转速优先控制框图如图2所示。此时转速控制器的转速参考值由有功功率参考值经由最优转速计算环节得到，有功功率参考值及电机转速通过最优导叶开度环节得到对应运行状态下的导叶开度。
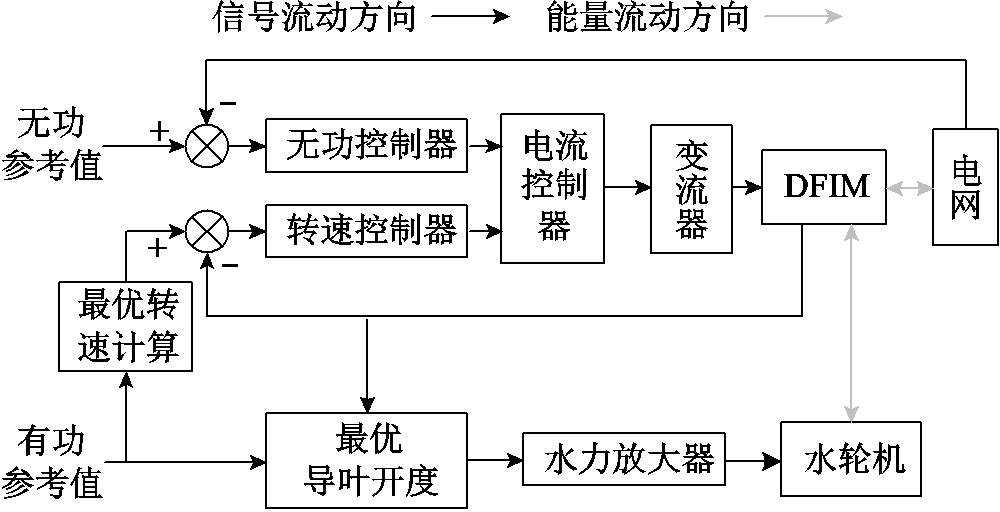
图2 转速优先控制框图
Fig.2 Speed prior control block diagram
基于电网电压定向的dq旋转坐标系下电网侧变流器数学模型为
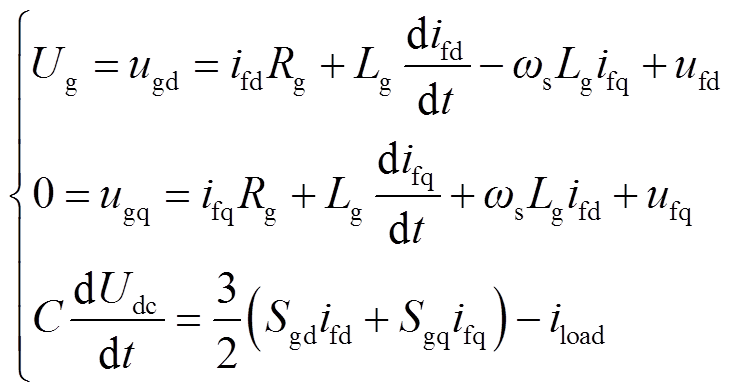（6）
式中，Ug为电网电压；uf和if分别为电网侧变流器交流侧电压和电流；iload为直流侧电流；Rg和Lg分别为电网侧变流器并网电阻和电感；C为直流母线电容；Sgd和Sgq为开关函数。
电网侧变流器控制目标为保持直流侧电容电压稳定，控制输入功率因数。直流母线电压的稳定取决于交流侧和直流侧有功平衡，具体控制框图如图3所示。
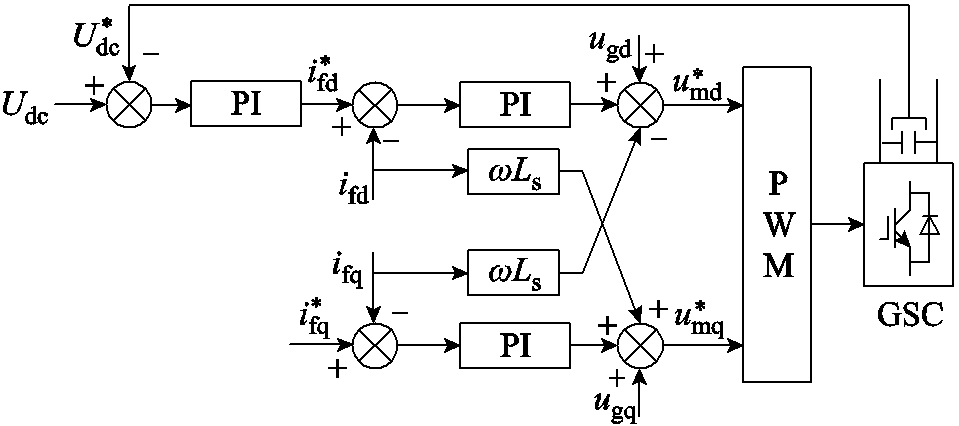
图3 电网侧变流器控制框图
Fig.3 Grid-side converter control block diagram
转子侧变流器数学模型与电网侧变流器一样，当其采用定子绕组磁链定向时，可得
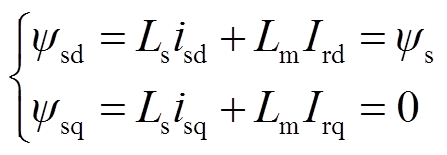（7）
结合式（4）和式（7），推导出电磁转矩及无功功率计算表达式分别为
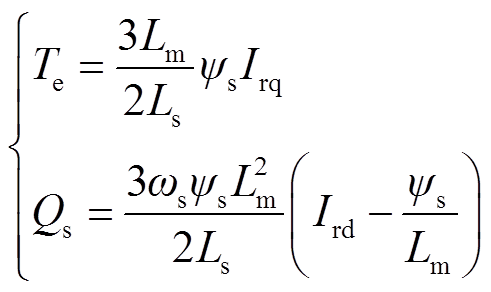（8）
转子电压方程为
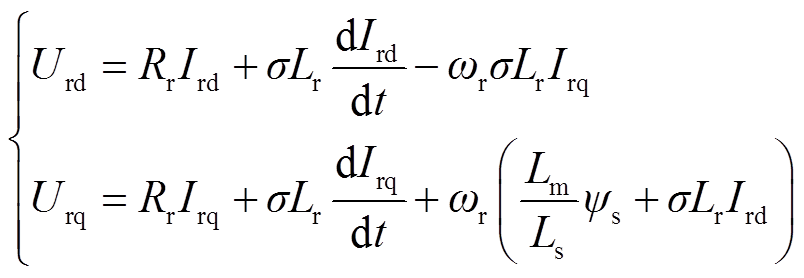（9）
式中，Urd和Urq分别为转子电压d、q轴分量；Ird和Irq分别为转子电流d、q轴分量；σ为漏磁系数，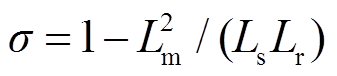
。
考虑到可变速抽水蓄能机组对转速控制的要求较高，在双馈电机转子侧控制中采用转速控制外环取代现有控制策略中广泛采用的有功功率控制外环，以实现电机转速的直接控制，并由转速控制环产生转子q轴电流指令值。同理，根据式（8）可得DFIM无功功率与转子d轴电流分量相关，因此将无功功率偏差得到的电流指令作为转子d轴电流指令。综上所述，转子侧变流器的控制核心在于实现全工况下DFIM转速及无功功率的解耦控制，而转速、转矩及有功功率本质上是一致的，因此q轴上的控制对象可按照不同应用场景及不同控制目标进行选定。转子侧变流器控制策略如图4所示。
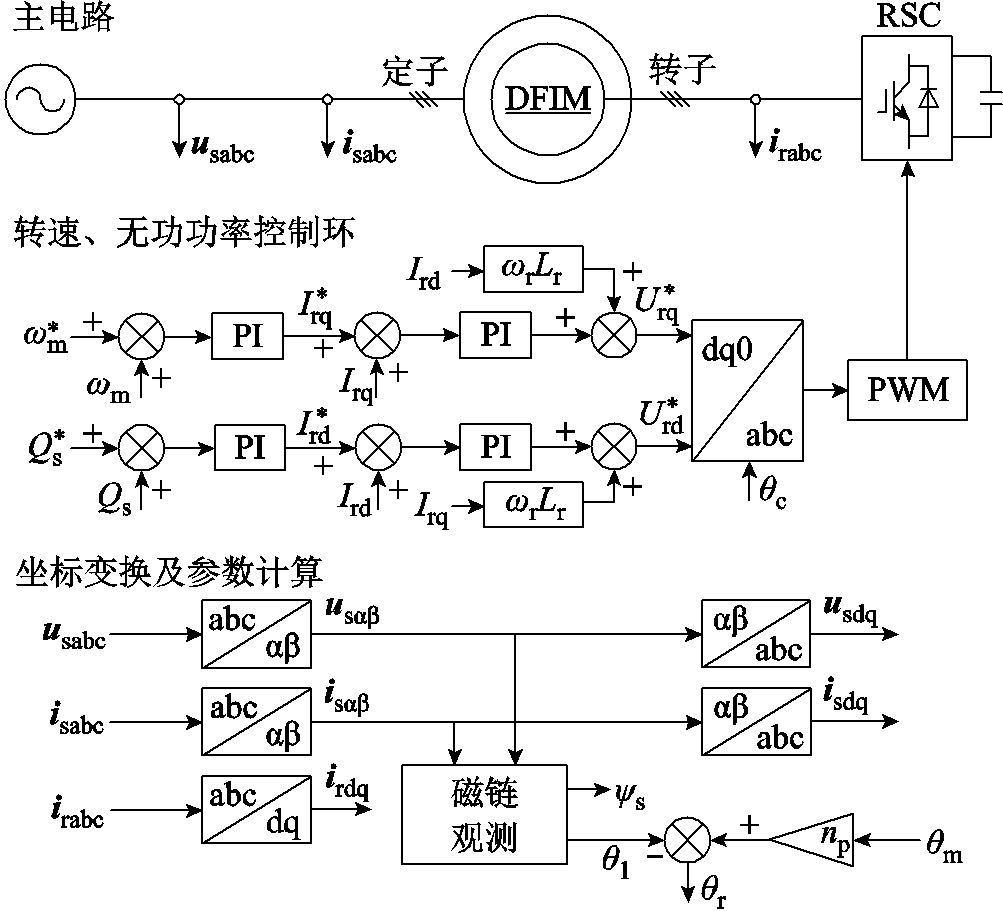
图4 转子侧变流器控制框图
Fig.4 Rotor-side converter control block diagram
电网频率波动本质上是有功潮流的重新分配，电网频率波动时，同步电机凭借其强大的惯量支撑能力，依据同步电机转子运动方程，在频率波动的初始阶段抑制电网功率及频率突变；此后，同步发电机进入频率调节阶段，增加或减少功率输出以达到新的平衡工作点。
鉴于此，提升DFIM频率响应特性的核心在于模拟同步电机的短时惯量支撑能力及频率调节特性，将转子转速与电网频率重新联系起来，释放被“隐藏”的转子动能。在DFIM机侧变流器的转速控制环节处引入频率响应环节，其控制框图如图5所示，转速修正量Δωm根据频率的波动程度对电机的转速进行修正，共同参与电网的频率调节。
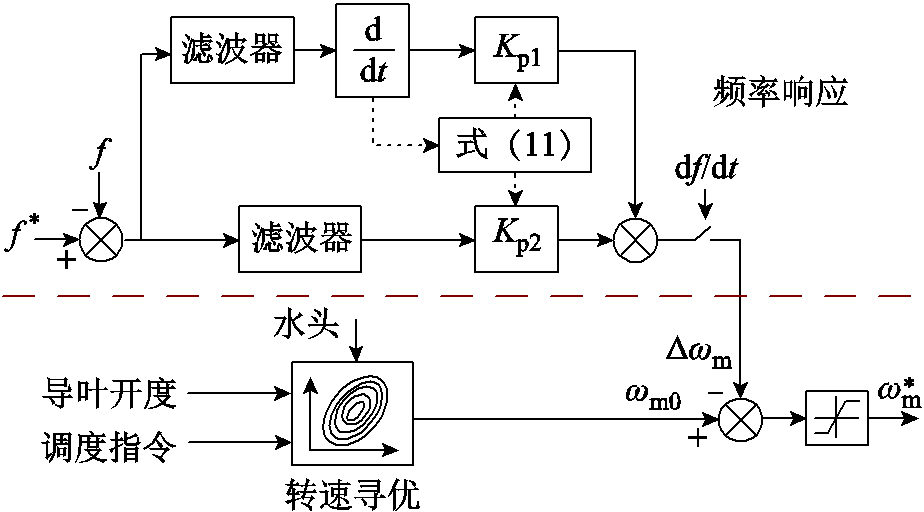
图5 频率响应环节控制框图
Fig.5 Frequency response module block diagram
可变速抽水蓄能机组频率响应流程如图6所示。双馈变速抽水蓄能机组参与电网频率响应的过程为：抽水工况下，随着电网频率f上升超过死区范围，频率响应环节输出正的转速修正量Δωm，将其叠加至转速控制指令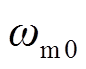
，并对其输出进行限幅，得到修正后的转速指令
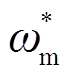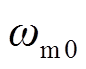。为转速寻优模块的计算结果，其受水头高度、导叶开度和调度指令影响，且调节时间远长于频率响应环节，因此在频率响应过程中视为恒定值。电机转速快速升高，电网多余功率转换为转子动能，缩小电网频率的波动范围。考虑到转子所能利用的动能有限，长时间的频率恢复仍然需要依靠水泵水轮机进行消纳，然而DFIM所提供的短时惯量支撑给予了水泵水轮机进行有功出力调节的时间，在频率波动后的一段时间内起到了至关重要的作用。
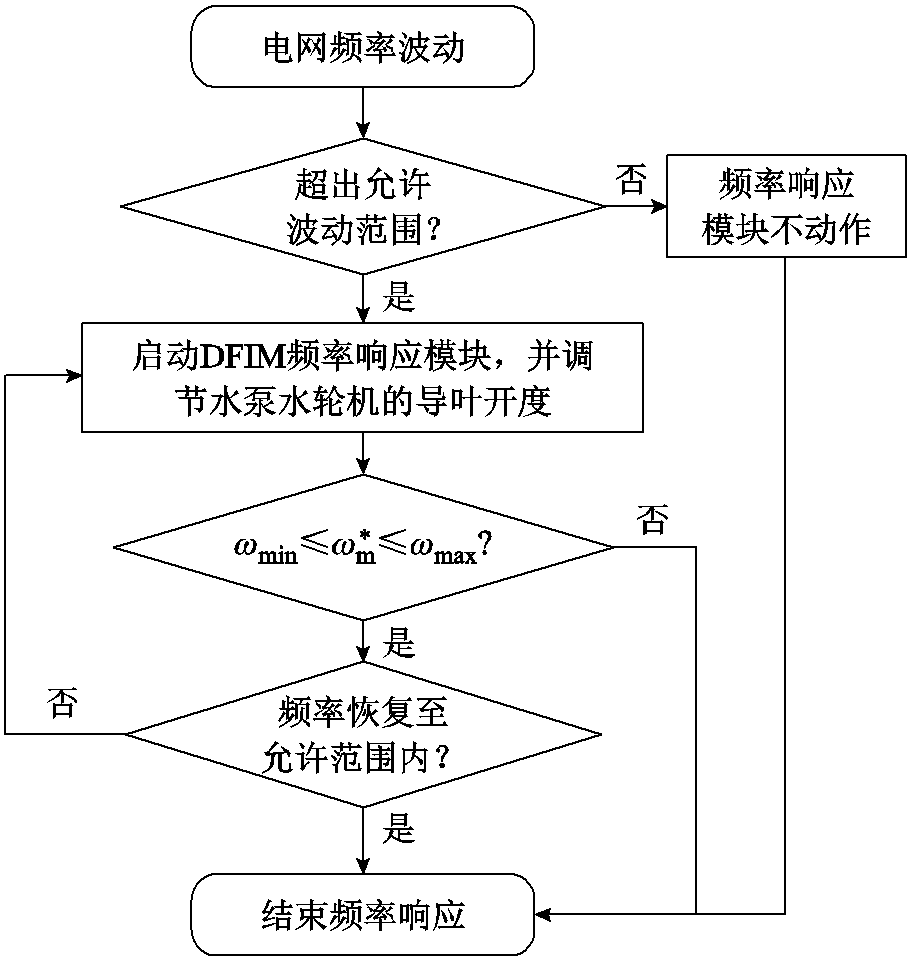
图6 可变速抽水蓄能机组频率响应流程
Fig.6 Frequency response flow diagram of variable speed pumped storage unit
综上所述，所提控制策略通过对机组转速的控制来实现电网频率波动后一段时间内的惯量支撑，若结合水泵水轮机的有功出力控制则可实现长时间电网频率调控。
本文在转速控制环节上引入频率响应环节，转速指令由转速寻优计算结果ωm0和转速修正量Δωm两部分叠加而成。转速修正量反映了频率响应过程中频率变化率及频率偏差量两个部分，前者用于描述频率波动初期电网频率快速跌落或升高的特性，后者则体现频率变化的幅度。转速修正量为
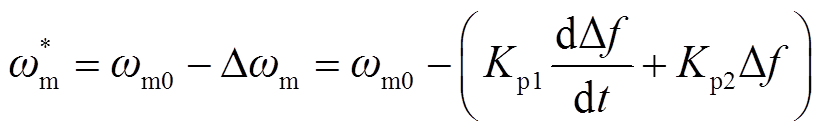（10）
式中，Kp1、Kp2分别为惯量支撑系数与频率调节系数；Δf为电网频差，Δf=f*-f，f*为电网额定频率。
如式（10）所示，转速修正量经由参数动态调整的频率响应环节得到，且在发电及抽水运行工况下符号一致，如频率增加则意味着电网功率过剩，通过将电机转速指令上调，快速吸收部分电网多余功率，实现DFIM的惯量支撑作用；区别在于，发电工况下减少水泵水轮机有功出力，电动工况下增加水泵水轮机的抽水功率。
前述分析得到DFIM在响应电网频率波动的前期和中后期具有不同的特征，前期频率变化速度快，dΔf/dt较大，DFIM以提供惯量为主，着重于减小最大频率波动幅度及抑制频率变化率；中后期Δf较大，DFIM以频率恢复及转速寻优为核心。鉴于此，在频率响应的不同时期，根据电网频率偏差的变化率动态调整频率响应环节的两个控制器参数在频率跌落前期采用较大的惯量支撑系数Kp1，后期增大频率调节系数Kp2并同步减小Kp1，具体整定方法为
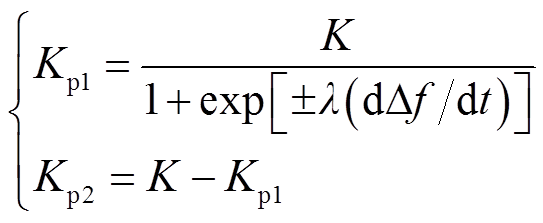（11）
式中，λ为动态整定系数，频率跌落时取正号，升高取负号，其取值将直接影响Kp1和Kp2随dΔf/dt平滑变化的速度；K为比例系数，用于同步改变控制参数的大小。图7给出了频率跌落时参数随dΔf/dt的变化曲线，|λ|随箭头方向增大，依次取5、10、20、40、70，取值越大，参数受dΔf/dt的影响越有限，参数仅在一小段范围内进行动态调整；取值越小，dΔf/dt稍有变动则参数也随之变化。式（11）中，K=Kp1+Kp2，用于同步改变控制参数的大小，在前期反映转速的修正幅度及提供的惯量大小，在后期反映频率的恢复速度及转速寻优的速度。
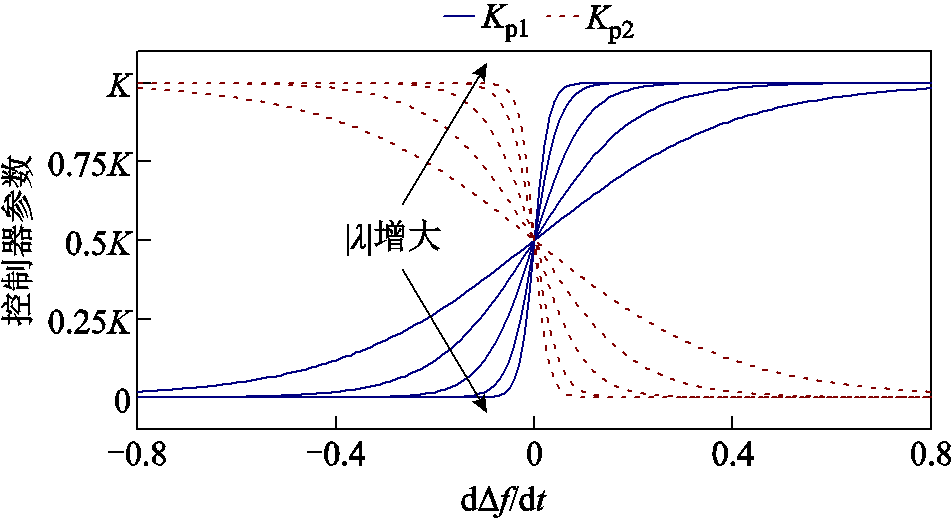
图7 频率跌落时不同λ值对应的控制系数曲线
Fig.7 Control parameter curves corresponding to different λ values when frequency drops
可变速抽水蓄能系统的惯量表现为一个可调节的数值，若将比例系数K取无限大的值，则可实现无限大的虚拟惯量响应。然而，根据能量守恒，该惯量本质上需要有一个物理惯量进行对应。整定出的惯量过大将造成系统失稳，过小则会导致惯量支撑效果不明显，因此，需要对转速修正量加以限制。依据DFIM的运行特性及工程安全规范，转速指令不得超出DFIM的安全工作区，且作为发电机时输出功率不得高于机组允许的最大有功出力，作为电动机时吸收功率不得超出机组所能承受的最大抽水功率，即满足
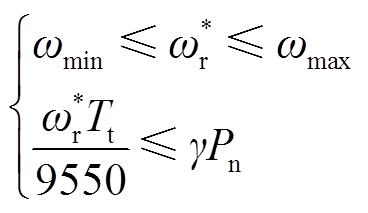（12）
式中，ωmin和ωmax分别为DFIM所允许的最小及最大转速，一般分别为额定转速的70%～120%；γ为比例系数，γPn用于表示机组所能承受的最大功率；Tt为水泵水轮机的机械转矩。
直接改变电网频率，使其突变0.5 Hz，得到如图8所示的不同K值下频率跌落及升高时的转速响应曲线，图8a代表电网频率降低时的响应曲线，图8b代表升高时的响应曲线，K的取值随着箭头的方向依次增大，分别为2、4、6、8、10。由此可知，当电机的初始转速为150 rad/s时，K的取值范围应限制在10以内。考虑到150 rad/s接近于安全运行范围的中间值，其可加速及减速的范围接近，因此对于其他安全运行范围内的转速，K的取值应更小，以确保电机转速不超出范围。
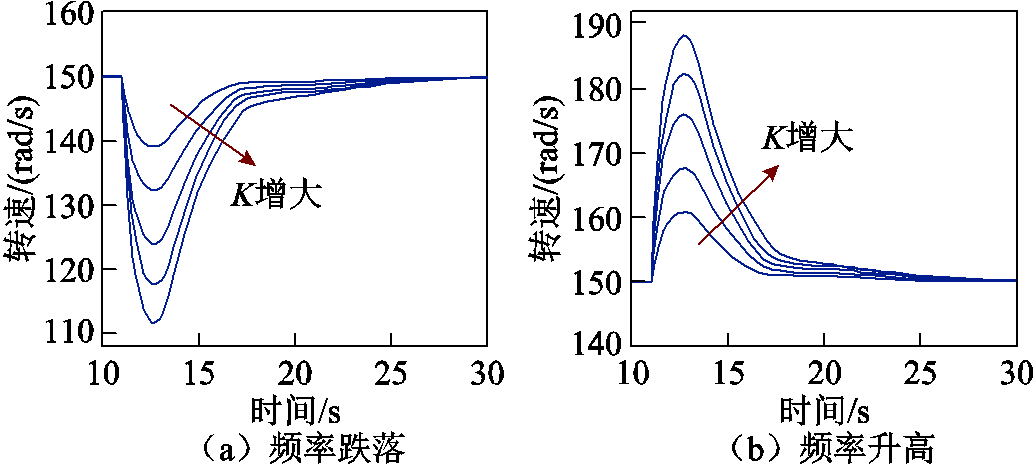
图8 不同K值下转速响应曲线
Fig.8 Rotor speed curves under different K values
当前，以电力电子设备作为并网接口的分布式电源向电网所提供的惯量可分为以下三种类型：①完全通过控制而模拟出惯量特性的系统，如储能电池系统和光伏系统；②具有物理转动惯量，但因控制而与电网完全解耦的系统，如全功率抽水蓄能系统、直驱风电系统等；③具备物理转动惯量，而由于DFIM定子侧与电网直接相连，使得电源与电网不完全解耦，如可变速抽水蓄能系统、双馈风电系统等。后两者通过控制可实现转动惯量与电网之间的重新耦合。本节研究可变速抽水蓄能系统在频率响应过程中所提供的短时惯量特性，并分析控制器参数对系统惯量及频率波动情况所带来的影响。
本文采用释放/储存转子动能的方式响应电网的频率波动，下面以同步电机及DFIM的发电工况为例，在电网频率波动过程中的惯量作用进行简要分析。考虑到电网安全运行的频率下限值为48 Hz，当电网频率波动2 Hz时，对于同步电机而言，转子转速改变幅度为同步转速的4%，过程中同步发电机所释放的能量满足式（13），此时转子释放的最大动能如式（14）所示。
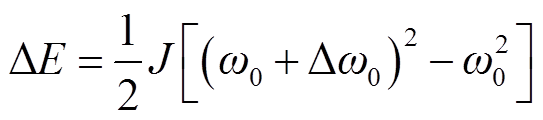（13）
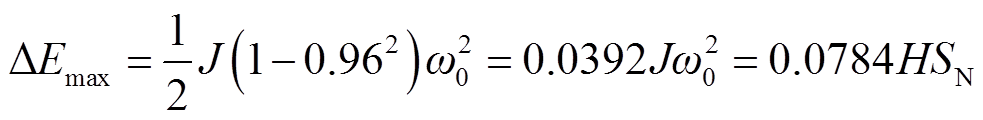（14）
式中，J为同步电机转动惯量；ω0为同步转速；Δω0为转速变化量；SN为电网容量；H为惯性时间常数，用于表征电机转子动能响应电网频率变化的特征，表达式为
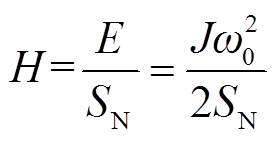（15）
一般运行情况下，DFIM的转子调速范围为70%～120%额定转速，因此其转子所吸收的动能根据不同时刻运行转速的不同而存在差异。这里假设DFIM在电网频率波动后转速由原本的转速降低至70%额定转速。当电网频率从f突变到f-Δf时，在频率响应环节的作用下DFIM角速度从ωm提升到ωm+Δωm，根据式（13），可以列出DFIM动能的变化量为
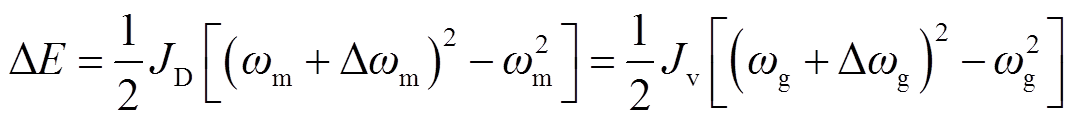（16）
式中，JD为DFIM实际转动惯量；Jv为DFIM等效同步电机虚拟转动惯量；ωg为对应于等效同步电机的旋转角速度，工频稳态下为100π，且Δωg=2πΔf为等效同步电机的旋转角速度增量。
下面围绕DFIM等效同步电机虚拟转动惯量进行分析，对式（16）进行整理，得到其表达式为
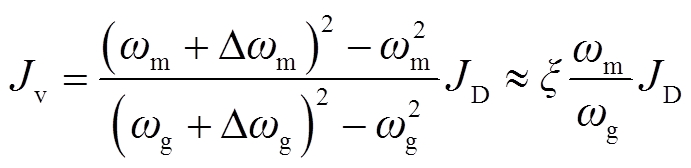（17）
式中，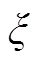
为等效同步电机虚拟转动惯量调节系数，其表达式为
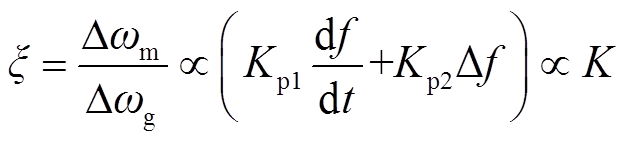（18）
由式（16）～式（18）可以看出，虚拟转动惯量受电机物理转动惯量和控制器参数影响，前者在电机设计时就被确定，后者则可以根据前文所提整定方式在一定范围内灵活地改变虚拟惯量响应。
取相同容量（2 MW为例）的同步电机与DFIM进行对比，同步电机惯性时间常数H=10 s，DFIM转动惯量JD=850 kg·m2，根据式（14）和式（16），得到同步电机转子释放的最大动能为1.57 MJ，DFIM由原本的转速降低至70%额定转速时释放的最大转子动能，后者的结果总结在表1中。由此，即便DFIM处于低速运行状态（1 200 r/min）下，仍然能够提供1.58 MJ的转子能量，较同步电机的最大释放动能大得多。考虑到电网正常运行时频率波动范围根据电网容量大小不同为±0.2～±0.5 Hz，同步电机释放的动能将远小于上面的计算结果。此外，表1中仅考虑了抽水蓄能系统中DFIM自身的惯量大小，由于系统惯量由DFIM与水泵水轮机共同提供，因此，实际上的转动惯量将大于JD，表明双馈变速抽水蓄能机组在惯量支撑方面有着不亚于同步电机的能力。
表1 DFIM在不同转速下转子可释放的动能及惯量支撑时间
Tab.1 The kinetic energy and inertia support time released by DFIM under different rotor speeds
电机转速/(r/min)转子可释放的动能/MJ惯量支撑时间/s 1 8009.978.79 1 5005.358.36 1 3503.367.01 1 2001.586.04
若DFIM采用10%Pn作为调频容量，则根据能量守恒有
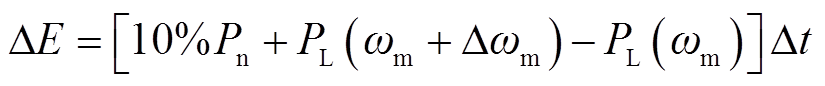（19）
式中，PL(
)和PL(ωm+Δω)分别为DFIM在初始转速和调速后转速下的有功功率。分别计算出不同转速下的惯量支撑时间，并整理在表1中。由此可见，DFIM在电网频率波动后可提供6～9 s不等的短时惯量支撑时间，配合调节可变速水泵水轮机可进一步延长其惯量支撑时间。
综合考虑同步发电机和可变速抽水蓄能机组共同提供的惯量为
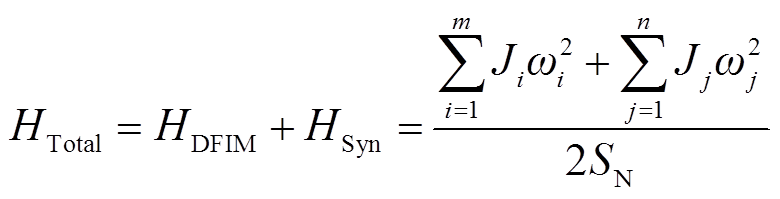（20）
式中，m、n分别为DFIM和同步电机的总台数；i、j分别为第i台DFIM、第j台同步电机；J、ω分别为电机的转动惯量、角速度；HDFIM和HSyn分别为两者等效提供的惯量；HTotal为系统等效惯量。若DFIM采用恒功率/恒转速控制策略，式（20）中第一项为0，系统中DFIM的惯量被隐藏，其惯量远小于全同步电机系统；而当DFIM增加频率响应环节，该项不再为0，则弥补了部分，甚至增大了系统的等效惯量。
在Matlab/Simulink中搭建仿真模型如图9所示，将DFIM并网运行，在母线上接入集中负载，电网频率为50 Hz。双馈电机的主要结构参数为：电机额定容量为2 MV·A，额定电压为690 V，定子绕组电阻为0.026 Ω，定子绕组自感为0.87 mH，转子绕组电阻为0.029 Ω，转子绕组自感为0.87 mH，电机互感为25 mH，极对数为2。
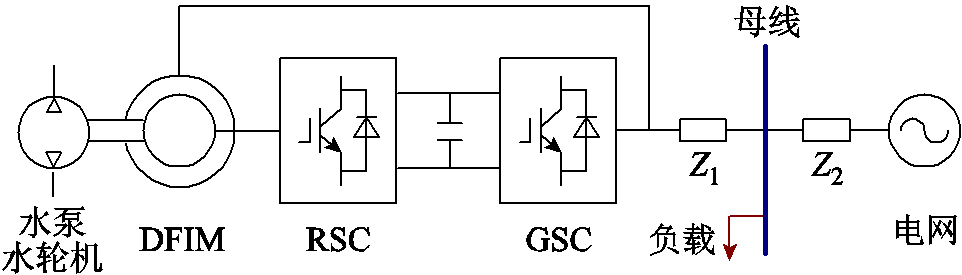
图9 仿真电路结构
Fig.9 Simulation circuit
抽水工况下的双馈电机核心在于综合考虑水头变化及导叶开度对电机转速进行调节。假定双馈电机在初始阶段转速指令为130 rad/s，转矩指令为2 000 N·m，并且在指令改变前保持稳定运行状态。在t=10 s时，转速指令从130 rad/s突增到150 rad/s，在t=20 s时，转矩指令从2 000 N·m突增至5 000 N·m。图10为抽水工况下无功指令恒定，转速、转矩指令分别突增时的仿真波形，依次为转速、转矩、有功功率和无功功率波形。
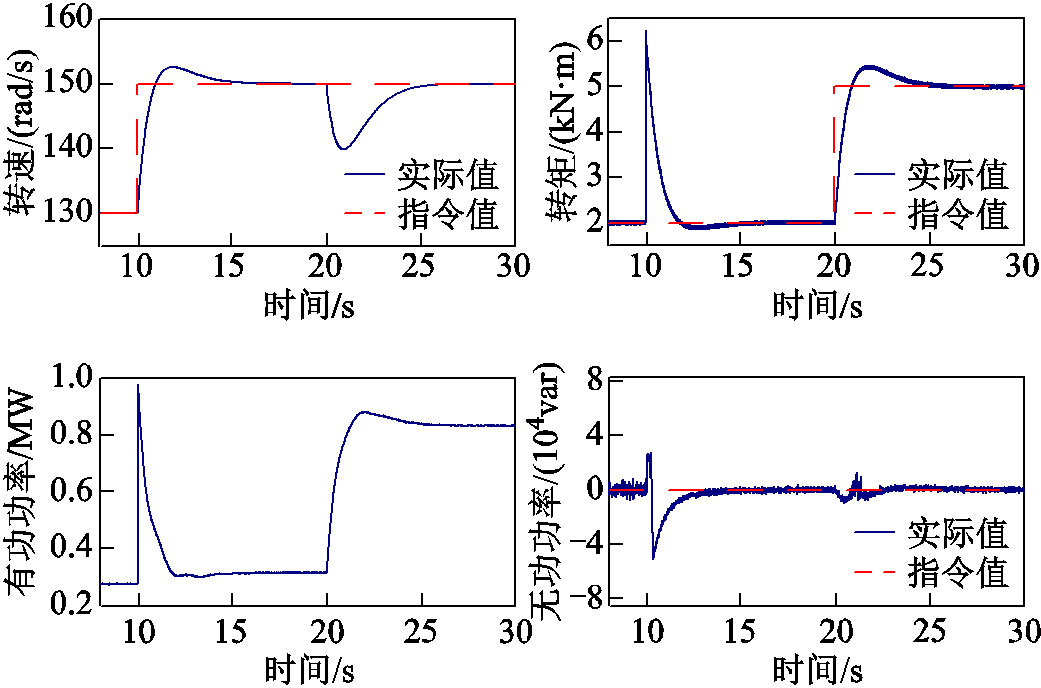
图10 抽水工况下仿真波形
Fig.10 Simulation waveforms under pumping mode
结合图10可以看出，转速指令增加时，双馈电机吸收有功功率及对应的电磁转矩短时增大，转速迅速升高，由于此时转速指令采用阶跃形式突变，因而造成有功及电磁转矩出现明显尖峰；转矩在发生变化时，电机转速降低，随着电机进入稳态，电机转速回升至指令值。在仿真过程中，为了提升电机运行效率，将无功指令设定为零并保持恒定，使电机以单位功率因数运行。由图10可以看出，在稳态期间，电机无功功率维持在零附近。
考虑到发电工况下双馈电机同时应具备无功功率的调相功能，除了改变转速、转矩的指令，同时对电机的无功功率指令进行改变。同样假定双馈电机在初始阶段转速指令为130 rad/s，此时初始转矩指令为-2 000 N·m，电机处于发电运行状态，并且在指令改变前保持稳定运行。在t=10 s时，转速指令从130 rad/s突增到150 rad/s；在t=15 s时，将无功指令设为-100 kvar；在t=20 s时，转矩指令由-2 000 N·m调整为-5 000 N·m。
图11为发电工况下转速、转矩、无功功率指令分别改变时的仿真波形，依次为转速、转矩、有功功率和无功功率波形。与抽水工况相似，电机转速及转矩均能快速响应指令变化，此外，无功功率指令发生变化后，电机无功功率也能迅速发生变化。由此看出，采用矢量解耦控制的电机可以实现转速及无功功率的分别控制，并且其跟踪效果良好，验证了控制方法的正确性及有效性。
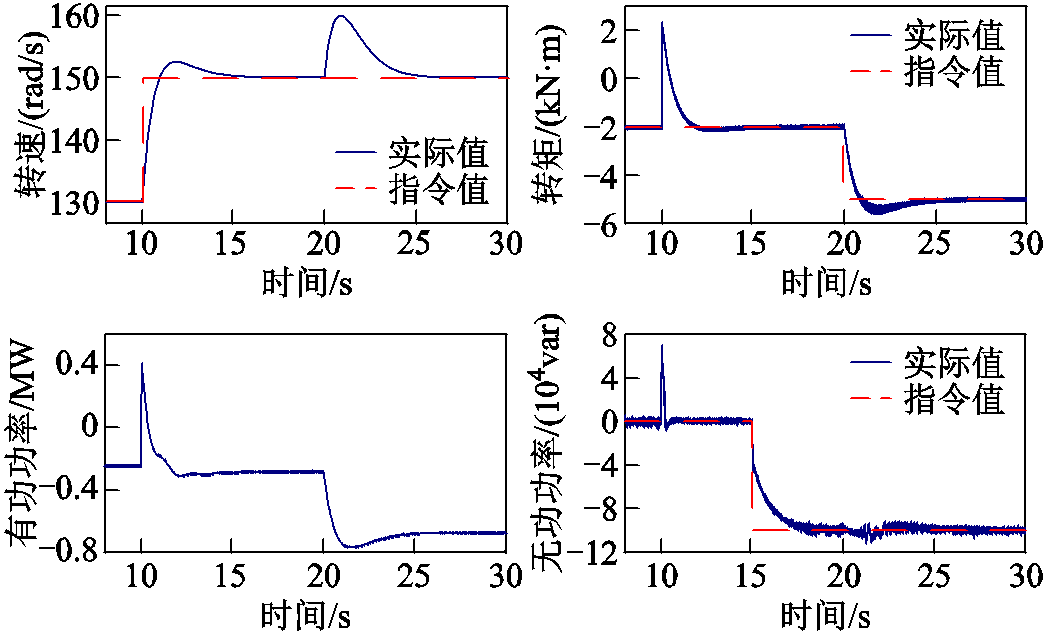
图11 发电工况下仿真波形
Fig.11 Simulation waveforms under generation mode
本节分别在发电工况和抽水工况下进行仿真，通过投切母线上负载模拟系统频率变化事件，以验证所提控制策略在双馈变速抽水蓄能系统中具有提升频率响应特性的效果。分别采用以下三种不同的控制策略：①本文所提策略；②将频率偏差整定为功率修正量的控制策略；③恒转速控制策略。
发电工况下，在图6所示的电网侧采用一台8 MW的传统同步电机，DFIM容量为2 MW并依调度指令输出1.5 MW有功功率，设置负载于11 s时由4 MW增加至5 MW。分别对比三种控制策略下系统频率波动情况，如图12a所示。突增负载使得系统频率在短时间内跌落，采用本文控制策略的最大频率偏差明显小于另外两种控制策略，且频率跌落的速度较另外两者更慢。图12b～图12e依次给出了DFIM频率响应过程的电机转速、输出有功功率、并网点电压及电流波形。电机减速运行，释放转子动能，输出有功功率快速增大，抑制频率跌落。转速降低的幅度受控制参数的影响，不同的控制参数大小将决定不同的转子释放动能。一段时间后，频率降至最低点，转速仍持续降低来参与系统频率恢复。此时随着频率恢复稳态，电机输出的有功功率开始减小，转速也随之提升至频率波动前的转速，电机逐渐恢复稳态运行。并网点电压在频率跌落瞬间存在短时降低，但降低幅度不大，对负载影响小；并网点电流幅值与输出有功功率具有相同变化趋势，在频率跌落初始阶段，电流迅速增大，随着频率恢复，电流逐渐减小至原本的电流大小。
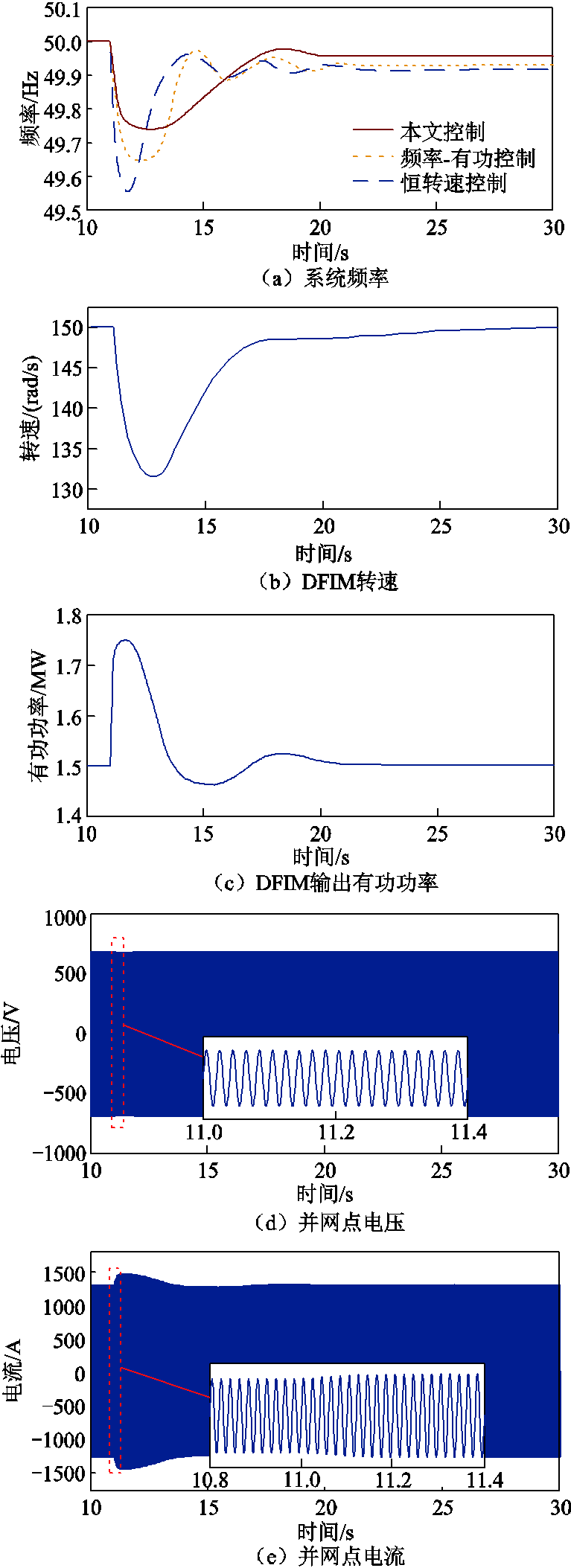
图12 发电工况下投入负载后仿真波形
Fig.12 Simulation waveforms after loading under generation mode
抽水工况下，DFIM根据调度指令吸收1 MW有功功率，负载于11 s时由4 MW突增至5 MW。仿真结果如图13所示。根据两种工况下的仿真波形得到，抽水工况下电机的响应过程与发电工况相似，区别在于有功功率的传递方向不同，抽水工况下的DFIM减少从电网吸收的有功功率，待频率到达稳态后，依照当前调度指令，恢复其吸收的有功功率。仿真结果表明，本文所提控制策略在抽水工况下的频率响应特性同样优于另外两者。
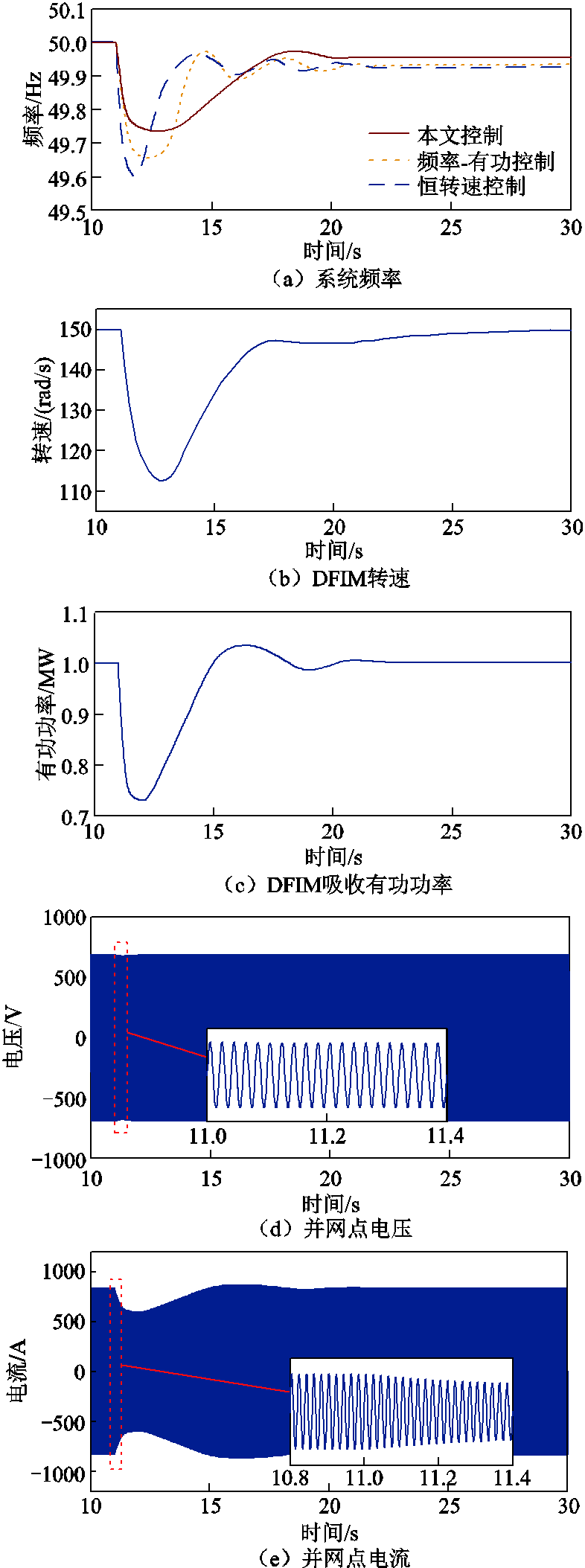
图13 抽水工况下投入负载后仿真波形
Fig.13 Simulation waveforms after loading under pumping mode
图14将不同控制策略下，投入负载时，DFIM分别运行于发电工况和抽水工况的最低跌落频率和恢复稳态时的频率进行对比。相较另外两种控制策略，本文控制策略在发电工况下的最低频率分别提升了0.11 Hz和0.18 Hz，稳态频率分别提升0.02 Hz和0.03 Hz；抽水工况下，最低频率分别提升0.08 Hz和0.13 Hz，稳态频率与发电工况一致。
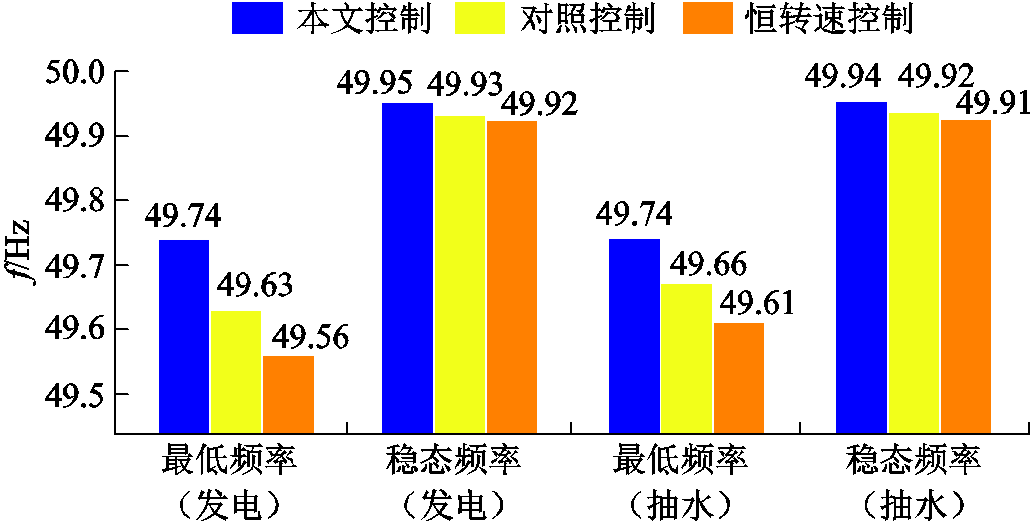
图14 采用三种控制策略的系统最低频率和频率误差
Fig.14 Minimum frequency and frequency error of the system adopting three comtrol startegies
设定发电工况和抽水工况仍采用8 MW的同步电机，负载于11 s时由5 MW切除至4 MW，同样对比三种控制策略的频率响应特性，分别得到如图15所示的两种工况下系统频率波形。切除负载将使得系统频率升高，因此，取动态整定系数为正数。根据系统频率波形，采用本文所提控制策略在发电工况下频率升高至50.21 Hz，电动工况下频率升高至50.20 Hz，在两种工况下均低于另外两种控制策略下的最高频率，且其频率恢复情况及频率恢复过程中的波动程度明显优于另外两种控制策略。仿真结果证明了本文所提控制策略在全工况下系统切除负载时同样具有更优异的频率响应特性。
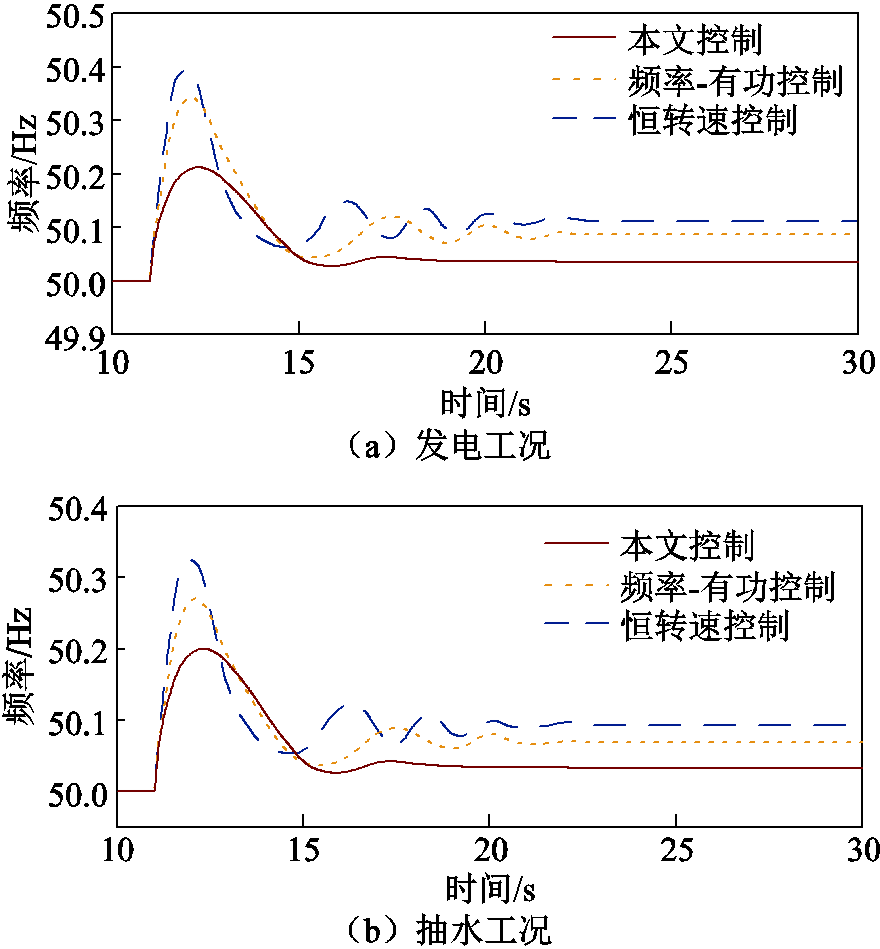
图15 切除负载后系统频率波形
Fig.15 Frequency waveforms after load removal
为提升双馈变速抽水蓄能机组的频率响应特性，本文首先提出了基于转速优先控制及转子动能调控的频率响应策略，在保证DFIM按转速指令运行的基础上，实现频率波动下的转速及有功功率快速灵活调节；其次给定了一种依据电网频率变化率动态整定控制器参数的方法。根据理论研究及仿真分析得到以下结论：
1）在电网频率正常时，本文所提控制策略基于转速优先控制，可以有效实现对电机转速、转矩和无功功率的控制。
2）所引入的频率响应环节将电网频率波动量整定为电机转速指令的修正量，直接对转子动能进行释放或吸收，与现有频率-有功控制策略相比，不仅减小了频率的变化幅度及稳态误差，而且抑制了频率变化过程中的波动。
3）所给定的参数动态整定方法依据不同时刻的电网频率特征，使得控制器参数随电网频率动态调整，在频率波动的全过程中平滑改变，更加合理地分配转子动能的释放/吸收，通过合理给定控制参数，可在安全运行范围内提升DFIM的惯量支撑能力，且该整定方法对控制系统计算能力的要求不高，易于推广到实际工程应用。
参考文献
[1] 李亚楼, 张星, 胡善华, 等. 含高比例电力电子装备电力系统安全稳定分析建模仿真技术[J]. 电力系统自动化, 2022, 46(10): 33-42. Li Yalou, Zhang Xing, Hu Shanhua, et al. Modeling and simulation technology for stability analysis of power system with high proportion of power electronics[J]. Automation of Electric Power Systems, 2022, 46(10): 33-42.
[2] 姜树德, 梁国才, 王纯. 采用双馈电机的抽水蓄能机组技术概述[J]. 水电与抽水蓄能, 2021, 7(4): 20-25. Jiang Shude, Liang Guocai, Wang Chun. Technical overview of pumped storage unit with doubly-fed motor[J]. Hydropower and Pumped Storage, 2021, 7(4): 20-25.
[3] 龚国仙, 李定林, 吕静亮, 等. 双馈式可变速抽水蓄能机组运行控制[J]. 大电机技术, 2022(3): 1-7, 20. Gong Guoxian, Li Dinglin, Lü Jingliang, et al. An overall control of doubly fed variable speed pumped storage unit[J]. Large Electric Machine and Hydraulic Turbine, 2022(3): 1-7, 20.
[4] 赵冬梅, 王浩翔, 陶然. 计及风电-负荷不确定性的风-火-核-碳捕集多源协调优化调度[J]. 电工技术学报, 2022, 37(3): 707-718.Zhao Dongmei, Wang Haoxiang, Tao Ran. A multi-source coordinated optimal scheduling model considering wind-load uncertainty[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 707-718.
[5] 何晨可, 朱继忠, 刘云, 等. 计及碳减排的电动汽车充换储一体站与主动配电网协调规划[J]. 电工技术学报, 2022, 37(1): 92-111. He Chenke, Zhu Jizhong, Liu Yun, et al. Coordinated planning of electric vehicle charging-swapping-storage integrated station and active distribution network considering carbon reduction[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 92-111.
[6] 姜云鹏, 任洲洋, 李秋燕, 等. 考虑多灵活性资源协调调度的配电网新能源消纳策略[J]. 电工技术学报, 2022, 37(7): 1820-1835. Jiang Yunpeng, Ren Zhouyang, Li Qiuyan, et al. An accommodation strategy for renewable energy in distribution network considering coordinated dispatching of multi-flexible resources[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1820-1835.
[7] 孙凯, 舒琼, 薛峰. 定速抽水蓄能机组工况转换及控制流程综述[J]. 水电与抽水蓄能, 2020, 6(6): 49-57. Sun Kai, Shu Qiong, Xue Feng. Summary of working condition conversion and control flow of fixed-speed pumped storage unit[J]. Hydropower and Pumped Storage, 2020, 6(6): 49-57.
[8] 李辉, 刘海涛, 宋二兵, 等. 双馈抽水蓄能机组参与电网调频的改进虚拟惯性控制策略[J]. 电力系统自动化, 2017, 41(10): 58-65. Li Hui, Liu Haitao, Song Erbing, et al. Improved virtual inertia control strategy of doubly fed pumped storage unit for power network frequency modulation[J]. Automation of Electric Power Systems, 2017, 41(10): 58-65.
[9] 龚国仙, 吕静亮, 姜新建, 等. 参与一次调频的双馈式可变速抽水蓄能机组运行控制[J]. 储能科学与技术, 2020, 9(6): 1878-1884. Gong Guoxian, Lü Jingliang, Jiang Xinjian, et al. Operation control of doubly fed adjustable speed pumped storage unit for primary frequency modulation[J]. Energy Storage Science and Technology, 2020, 9(6): 1878-1884.
[10] 刘开培, 朱蜀, 冯欣, 等. 双馈式变速抽水蓄能电厂的机电暂态建模及模型预测控制[J]. 高电压技术, 2020, 46(7): 2407-2418. Liu Kaipei, Zhu Shu, Feng Xin, et al. Electromechanical transient modeling and model predictive control of doubly-fed variable-speed pumped storage power plant[J]. High Voltage Engineering, 2020, 46(7): 2407-2418.
[11] 朱珠, 潘文霞, 刘铜锤, 等. 变速抽蓄机组频率响应机理模型与性能研究[J]. 电网技术, 2023, 47(2): 463-474. Zhu Zhu, Pan Wenxia, Liu Tongchui, et al. Study on frequency response mechanism model and performance of variable speed pumping unit[J]. Power System Technology, 2023, 47(2): 463-474.
[12] 蔡国伟, 钟超, 吴刚, 等. 考虑风电机组超速减载与惯量控制的电力系统机组组合策略[J]. 电力系统自动化, 2021, 45(16): 134-142. Cai Guowei, Zhong Chao, Wu Gang, et al. Unit commitment strategy of power system considering overspeed load reduction and inertia control of wind turbine[J]. Automation of Electric Power Systems, 2021, 45(16): 134-142.
[13] 颜湘武, 崔森, 宋子君, 等. 基于超级电容储能控制的双馈风电机组惯量与一次调频策略[J]. 电力系统自动化, 2020, 44(14): 111-120. Yan Xiangwu, Cui Sen, Song Zijun, et al. Inertia and primary frequency regulation strategy of doubly-fed wind turbine based on super-capacitor energy storage control[J]. Automation of Electric Power Systems, 2020, 44(14): 111-120.
[14] Lao Huanjing, Zhang Li, Zhao Tong, et al. Innovated inertia control of DFIG with dynamic rotor speed recovery[J]. CSEE Journal of Power and Energy Systems, 2020, 8(5): 1417-1427.
[15] Dreidy M, Mokhlis H, Mekhilef S. Inertia response and frequency control techniques for renewable energy sources: a review[J]. Renewable and Sustainable Energy Reviews, 2017, 69: 144-155.
[16] 蔡福霖, 胡泽春, 曹敏健, 等. 提升新能源消纳能力的集中式与分布式电池储能协同规划[J]. 电力系统自动化, 2022, 46(20): 23-32. Cai Fulin, Hu Zechun, Cao Minjian, et al. Collaborative planning of centralized and distributed battery energy storage to improve new energy consumption capacity[J]. Automation of Electric Power Systems, 2022, 46(20): 23-32.
[17] 单煜, 汪震, 周昌平, 等. 基于分段频率变化率的风电机组一次调频控制策略[J]. 电力系统自动化, 2022, 46(11): 19-26. Shan Yu, Wang Zhen, Zhou Changping, et al. Control strategy of primary frequency regulation for wind turbine based on segmented rate of change of frequency[J]. Automation of Electric Power Systems, 2022, 46(11): 19-26.
[18] 李柏慷, 张峰, 丁磊. 双馈风机参与调频的速度控制器模糊协同控制及参数校正策略[J]. 电网技术, 2022, 46(2): 596-605. Li Baikang, Zhang Feng, Ding Lei. Fuzzy cooperative control and parameter correction strategy of speed controller in frequency modulation stage of doubly-fed induction generator[J]. Power System Technology, 2022, 46(2): 596-605.
[19] Verma P, Seethalekshmi K, Dwivedi B. A cooperative approach of frequency regulation through virtual inertia control and enhancement of low voltage ride-through in DFIG-based wind farm[J]. Journal of Modern Power Systems and Clean Energy, 2022, 10(6): 1519-1530.
[20] 王彤, 邢其鹏, 李鸿恩, 等. 计及虚拟惯量控制的DFIG等效惯量在线评估与响应特性分析[J]. 电力系统保护与控制, 2022, 50(11): 52-60. Wang Tong, Xing Qipeng, Li Hongen, et al. Online evaluation and response characteristics analysis of equivalent inertia of a doubly-fed induction generator incorporating virtual inertia control[J]. Power System Protection and Control, 2022, 50(11): 52-60.
[21] Valavi M, Nysveen A. Variable-speed operation of hydropower plants: a look at the past, present, and future[J]. IEEE Industry Applications Magazine, 2018, 24(5): 18-27.
[22] Zhang Xiaoxi, Cheng Yongguang, Yang Zhiyan, et al. Water column separation in pump-turbine after load rejection: 1D-3D coupled simulation of a model pumped-storage system[J]. Renewable Energy, 2021, 163: 685-697.
Abstract With the gradual integration of renewable energy into the power grid, the demand for flexible regulation methods is increasing. To solve this problem, the variable speed pumped storage power station adopts a doubly fed induction machine (DFIM) and a variable speed pump turbine as its main components to achieve adjustable speed and open water diversion gates, thus realizing flexible power regulation under any conditions. However, research on the frequency response characteristics of DFIM in pumped storage is still in the preliminary stage. The commonly used frequency control methods focus on converting grid frequency deviation into active power correction, leading to suboptimal frequency response characteristics. Therefore, this paper proposes a method of frequency response strategy and dynamic adjustment of control parameters, aiming at enhancing the frequency response characteristics of DFIM, and making it more effective in integrating renewable energy into the power grid.
Firstly, atopology of variable speed pumped storage unit is introduced. The speed priority control strategy and its advantages are further discussed to improve overall efficiency. Then, a frequency response module is proposed to convert frequency deviation and its rate of change into speed correction added to the speed controller. Meanwhile, a dynamic adjustment method of controller parameters, determined by the frequency characteristic during deviation, is proposed, resulting in a more reasonable release or obtainment of rotor kinetic energy. Subsequently, DFIM and synchronous machines with the same capacity are compared. The results show that DFIM can release or absorb more kinetic energy than synchronous machines, making it a crucial means to provide short-term power and inertia support to the grid.
This paper conducts two simulations using Matlab/Simulink. The first one is about rotor speed and reactive power regulation, also known as the speed priority control of the DFIM. The second one is to verify the effectiveness of the proposed frequency response strategy. The first simulation results show that the machine can accurately adjust its rotor speed, torque, and reactive power when the reference values change. Due to the reference value being changed in the form of a step function, there is an overshoot in a short period, which must be avoided when used in an actual machine. Then, the proposed frequency response strategy is simulated. This strategy is compared to a commonly used frequency-active power control strategy and a constant-speed control strategy. At the beginning of the simulation, a load was added. The results show that DFIM can lower its speed to release kinetic energy, provide short-term active power, and provide inertia support. When the load is disconnected from the power grid, the power grid frequency increases, and DFIM accelerates, converting the extra active power into rotor kinetic energy. The proposed parameter dynamic adjustment method adjusts the parameters based on the rate of frequency change, shortening the frequency and speed recovery time.
Based on theoretical analysis and simulation results, the following conclusions can be drawn: (1) When there is no frequency disturbance, the speed priority control can effectively control the motor speed, torque, and reactive power of DFIM. (2) The proposed frequency response module converts frequency deviation into speed correction, which can directly release or absorb the rotor kinetic energy. Compared with the frequency-active power control strategy, the strategy reduces frequency variation and steady-state error, and suppresses fluctuations during frequency variation. The frequency response characteristics in both generating and pumping modes are improved. (3) The parameter adjustment method allows the controller parameters to be dynamically adjusted, which can release or absorb the rotor kinetic energy more reasonably during the process. By setting the controller parameters appropriately, the inertia support capability of DFIM can be improved. This method requires little computing capability and can be handily promoted in practical engineering applications.
Keywords：Doubly fed induction machine, variable speed pumped storage unit, inertia support, frequency response, speed regulation
DOI:10.19595/j.cnki.1000-6753.tces.L10036
中图分类号：TM343
国家电网公司总部科技项目资助（SGSCDK00XTJS2200250）。
收稿日期 2023-01-13
改稿日期 2023-05-05
庄凯勋 男，2000年生，硕士研究生，研究方向为电力电子设备接入电力系统。E-mail：rex_zhuang023@163.com
孙建军 男，1975年生，教授，博士生导师，研究方向为大功率电力电子拓扑分析与控制、电机设计与控制、智能电网规划与运行。E-mail：jjsun@whu.edu.cn（通信作者）
（编辑 赫蕾）