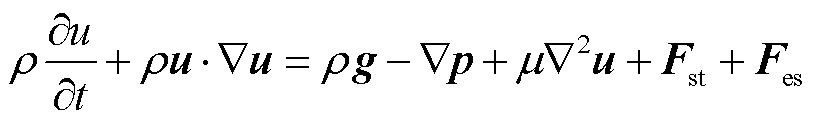（1）
摘要 强暴雨条件下高压导线与杆塔之间的雨柱易发生断裂，降低了导线-杆塔间隙的电气绝缘性能。为了研究强暴雨条件下空气间隙雨柱的断裂特性，该文建立层流-水平集-电场耦合的二维仿真计算模型，提取雨柱断裂过程中的形态特征量及受力情况，分析不同外施电压、雨柱流速下断裂特征参数的变化规律，并开展棒-板间隙雨柱断裂特性试验验证，在此基础上分析直流电压极性对断裂特征参数的影响规律。结果表明：棒-板间隙雨柱断裂过程受电场力、表面张力和粘性力的共同作用，经过射流区、过渡区、断裂区三个阶段，提高外施电压加速了过渡区的螺旋运动，并增加了雨柱断裂的次数和数量。雨柱临界断裂长度、断裂直径均随外施电压的增加而减小，并与雨柱流速呈正相关，且负极性电压下的雨柱临界断裂长度大于正极性的结果。随着外施电压的增加，雨柱最大径向表面张力略有减小，与流速呈负相关；而最大径向电场力随之增加，且流速越大其值越大。断裂直径、临界断裂长度的试验结果与计算值吻合良好，最大偏差均小于10%。
关键词：强暴雨环境 直流放电 空气间隙 雨柱断裂特性 有限元仿真 试验验证
随着全球变暖，极端降雨频次增加，强暴雨天气易引起架空线路、绝缘子串和杆塔形成雨帘，严重时将造成雨柱桥接，显著降低导线-杆塔间隙的电气绝缘性能，致使架空线路发生跳闸并引起停电事故[1-3]。据统计，近三年我国东部某省出现多次因强暴雨天气发生的导线对杆塔间隙的雨柱放电，进而引起500 kV输电线路跳闸事故[4]。分析原因主要是雨柱短接了导线与杆塔之间的绝缘距离，缩短了放电电弧的发展路径，且处于高压电场中的雨柱在表面张力、电场力、重力、粘性力的共同作用下易发生断裂，引起电场畸变[5-6]。因此，研究强暴雨条件下导线-杆塔间隙的雨柱断裂特性具有一定的工程意义和研究价值。
国内外学者针对空间电场中带电流体的形变断裂特性开展了较为深入的研究。文献[7]建立了计及水流断裂时，时空分布规律的Rayleigh模型；据此，文献[8]提出了射流形成的临界速度计算公式；文献[9]基于Weber理论提出了预测射流断裂长度的半经验公式；文献[10]对外加电场作用下带电射流的不稳定性进行了分析，结果表明射流长度和运动形态均发生变化，同时射流断裂后形成的雨滴直径随之减小；文献[11]研究了均匀直流电场作用下，蓖麻油中硅油液滴的电-液动力学行为及其演化过程，认为液滴存在泰勒变形、典型斜旋转、周期振荡和断裂四种行为模式，并且随着电场强度增大，液滴形变程度随之增加。
在此基础上，研究人员对电场作用下的气-液两相流动力学行为进行了研究。文献[12]利用水平集（Level Set, LS）方法，研究了强降雨环境下大直径复合支柱绝缘子伞檐雨滴断裂形态变化，获得了伞檐雨滴初始直径、流速、电导率和外施电压等因素对雨滴动态形变的影响规律；文献[13]基于流动体积法（Volume of Fluid, VOF）提出了流场-电场耦合的计算模型，获得了带电液滴在均匀和非均匀电场作用下的形态特征及运动变化规律；文献[14]采用实验和相场仿真计算相结合的方法，研究了直流/交流电场作用下硅橡胶表面单个水珠的形态及动力学行为，并揭示了其变化机理；文献[15]建立了一种由Navier-Stokes方程、电场计算和描述界面演化的Cahn-Hilliard型方程组成的数学模型，获得了直流电场作用下的水滴聚结机理及液滴体积、液滴距离对绝缘性能的影响规律。
目前学者们针对外施电场条件下雨柱断裂特性的试验研究，主要关注的是绝缘子伞裙边缘或是低电压、小流量的棒-板间隙，而对高压直流、大流量条件下空气间隙中的雨柱断裂特性的研究尚少[16-18]。在强暴雨条件下，高电压等级的输电线路-杆塔易形成雨柱桥接，并在电场作用下发生断裂，导致空气间隙绝缘强度显著降低，但雨柱断裂规律尚未明晰。此外，随着电流体动力学技术的发展，通过将电场和流场耦合，模拟研究外加电场下气-液两相流动力学特性，为探究电场作用下空气间隙中雨柱的断裂行为提供了一种有效途径。因此，有必要开展较高外施电压叠加大流量条件下的棒-板空气间隙雨柱的断裂特性研究。
本文基于层流-水平集-电场耦合的仿真计算方法分析雨柱断裂特性及断裂机理，并开展棒-板间隙雨柱断裂特性试验，获得降雨强度、电压极性效应的影响规律，研究成果将对强降雨特别是特大暴雨环境中输电线路外绝缘的设计与选择提供参考。
为了探究不同外施电压、雨柱流速对空气间隙中雨柱断裂特性的影响规律，本文基于棒-板间隙模拟结构，利用多物理场耦合仿真软件COMSOL Multiphysics，使用层流、水平集和静电物理场建立仿真模型[19]。
仿真模型中假设流体为不可压缩、粘性、低速运动[20]。根据水平集理论，定义一个无量纲的变量ψ（ψ=0～1，0表示空气，1表示水）对水-气两相动力学特性进行计算。根据理论分析，外施电场中的流体受到内力（压力、粘性力、表面张力、重力）和外力（电场力）的共同作用，因此将重力ρg、电场力Fes添加到流体力学Navier-Stokes方程可得
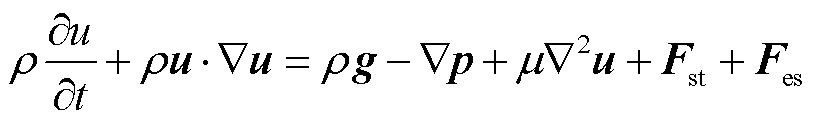（1）
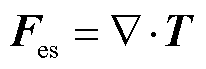（2）
式中，u为流体速度，m/s；ρ为流体密度，kg/m3；p为流体压力，Pa；μ为流体动力粘度，Pa·s；T为麦克斯韦应力张量，N/m3；Fst为表面张力，N/m3；Fes为电场力，N/m3。
在二维平面，麦克斯韦应力张量[21-22]为
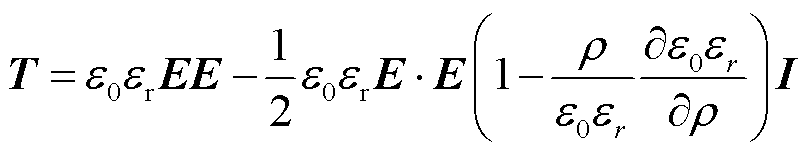（3）
式中，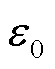
为真空介电常数；
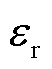为区域相对介电常数；E为电场强度；I为二阶单位张量。
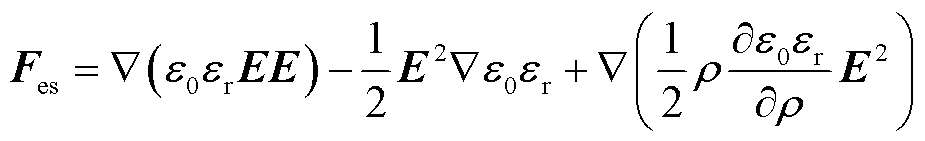（4）
式中，等号右侧第一项为电泳力，是电场施加于流体的表面电荷体积力；第二项为介电电泳力，为外施电场作用下流体因介电常数变化而产生的力，与流体空间位置的电场强度和介电常数的空间变化有关[23]；第三项为电致伸缩力，由于流体不可压缩，外施电场作用下气-液两相的密度和介电常数几乎无变化，可认为对于不可压缩流体的电致收缩力为0，即可忽略。
由于水平集函数ψ是一个平滑的函数，可通过不同的体积分数定义整个区域的相对介电常数，即
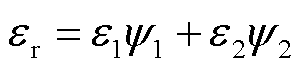（5）
式中，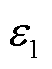
、
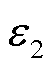分别为空气和水的相对介电常数；ψ1、ψ2分别为空气和水的体积分数。
采用二维非对称模型开展数值计算，仿真模型如图1所示，材料参数设置见表1。高压端几何尺寸为喷嘴电极截面尺寸，边界条件设置如下：入口设定为层流法向流入和水平集水流流入，为提高仿真计算收敛性，入口速度采用阶跃函数，函数step(t= 0.05 s)=1，并进行平滑处理；出口边界条件设定为压力并抑制回流；初始水-气两相区域间设定为初始界面，高压端内壁设定为无滑移壁面，流场中添加电场力和重力。网格划分采用物理场控制网格方式。
暴雨、大暴雨和特大暴雨时的降雨强度瞬时值范围分别为2.68～4.24 mm/min、4.24～6.26 mm/min、6.26～12.38 mm/min[24]，本文选取9、10、11、 12 mm/min作为仿真计算和模拟试验中的降雨强度。雨柱属于Rayleigh断裂模式，此时雨柱向第一类风生断裂过渡的临界速度为2.2 m/s[8]。鉴于此，本文在仿真计算和模拟试验过程中的雨柱流速选取为1.1～2 m/s。
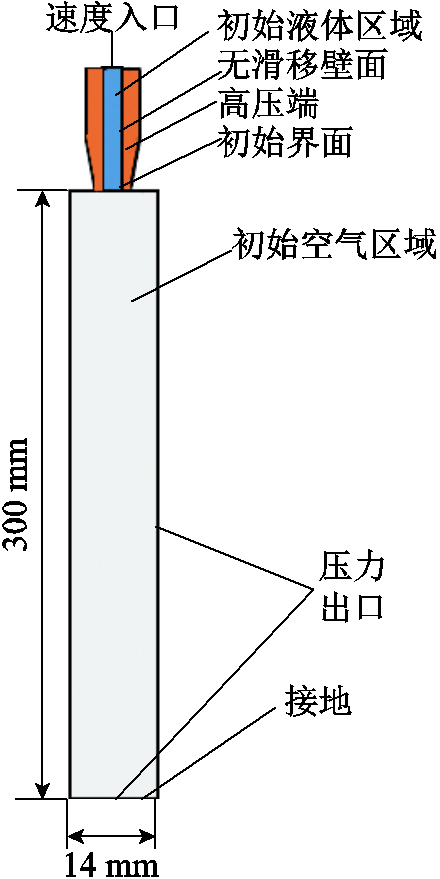
图1 仿真模型
Fig.1 Simulation model
表1 模型材料参数
Tab.1 Material parameters for simulation
材料相对介电常数电导率/(μS/cm)动力粘度/(10-5Pa·s)密度/(kg/cm3) 空气14×10-121.81.3 水811.2×1021001 000 黄铜1 0004×107—8 900
为了能在棒电极末端形成流量可控的雨柱，本文自制了如图2a所示的喷嘴电极。电极由黄铜制成，其中电极中心通孔直径D=3 mm。试验装置如图2b所示，水箱（40 cm×30 cm×40 cm）放置在1.2 m高的平台上，通过内径为12 mm的水管与电极连通。通过调整水箱水位可在电极喷嘴处产生不同流速的水流[25]。测量时，利用单位时间内的雨柱流量Q（单位为mL/min），根据内径D即可求出雨柱平均流速v（单位为m/s）。
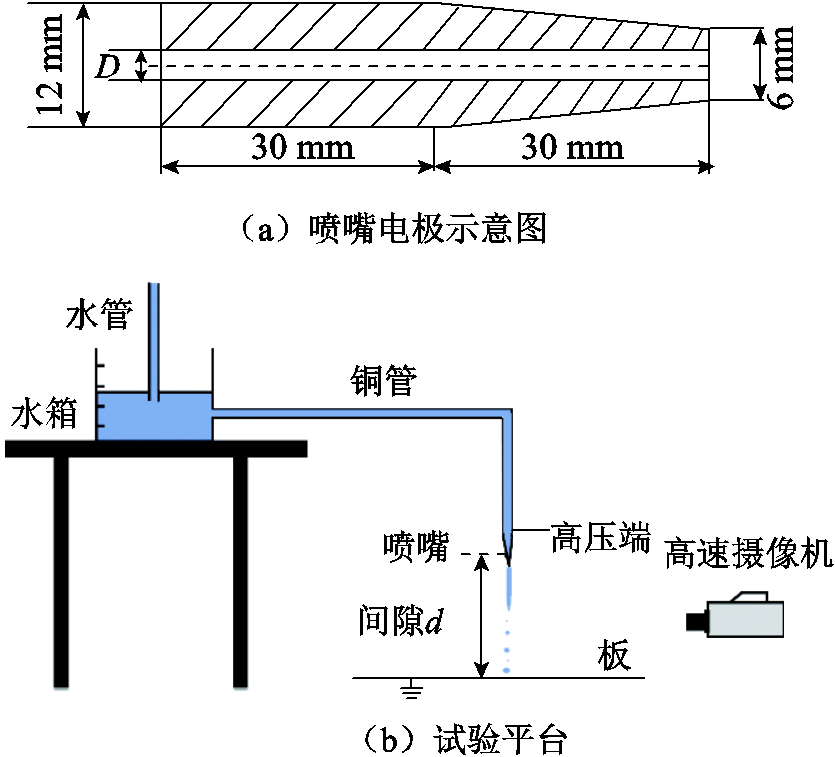
图2 试验装置示意图
Fig.2 Sketch map of test
外施电压U由400 kV/30 mA直流电压发生器提供，分压器测量误差在±1%以内。本文试验采用均匀升压法进行加压，加压速度为4 kV/s，达到预定电压后，采用Photron SAZ型高速相机拍摄雨柱断裂微观过程，试验拍摄速度为1 000 fps，分辨率为1 024×1 024。
本节开展了0～80 kV外施电压、1.45 m/s流速下的棒-板间隙雨柱断裂过程的仿真计算。外施80 kV电压时雨柱断裂过程仿真计算结果如图3所示。
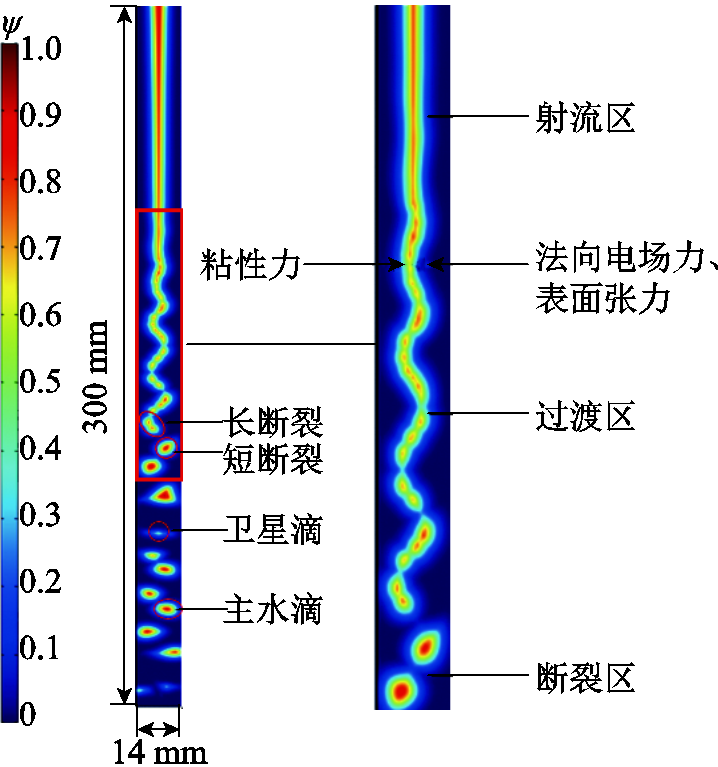
图3 80 kV、1.45 m/s条件下的仿真结果
Fig.3 Simulation results under 80 kV and 1.45 m/s
分析可知，雨柱断裂典型过程依次经过射流区、过渡区、断裂区三个阶段。具有初始速度的雨柱在重力、电场力、表面张力、粘性力的共同作用下形成射流。处于过渡区的雨柱表面电荷发生转移且分布不均，在外施电场作用下，发生螺旋状运动。每个波长的雨柱具有一径向上的速度分量，最大径向速度可达2 m/s，并以1/2螺旋圈的长度进行第1次断裂。进入临界断裂阶段后，雨柱在表面张力及电场力作用下发生第2次断裂，形成多个主雨滴及卫星滴，最终呈现出“主雨滴”“卫星滴”“长断裂”“短断裂”多种形态特征共存的现象[26-27]。带电雨柱断裂过程本质是表面张力、粘性力、电场力共同作用的结果。其中，表面张力向内挤压雨柱，呈收缩趋势；粘性力阻碍雨柱与空气相互错动而变形；电场力与雨柱表面张力方向相同，与粘性力方向相反，促进了雨柱的断裂进程。
80 kV下1.45 m/s流速的雨柱受力计算结果如图4所示。以此为例分析可知，相较于单一表面张力作用，外施电场作用下的雨柱所受最大径向电场力和最大径向表面张力的合力从15 001 N/m3增加至33 247 N/m3，提高了约1.2倍，导致雨柱内外压力差失衡，促进了雨柱形变和断裂。
图4 雨柱在电场中的受力计算结果
Fig.4 Mechanical model of water streams in electrical field
在此基础上研究并获得不同外施电压下雨柱断裂过程的仿真结果如图5所示。分析可知：
1）随着外施电压的增加，雨柱射流区的长度减小，更快地进入到过渡区（从20 kV时的0.065 s降低至80 kV时的0.054 s），并呈螺旋状断裂。这是因为，处于射流区的雨柱在受到外部扰动后，在切向电场力与重力的共同作用下，其运动速度不断地提高。提高外施电压后，电场力对雨柱的扰动作用增强，射流区末端雨柱流速从20 kV时的2.1 m/s增大至80 kV时的2.3 m/s，即降低了射流区的运动时间。同时，过渡区的雨柱表面曲率半径较大、电荷密度较小，且表面张力较大，导致雨柱表面波纹收缩，呈现螺旋状运动，进而断裂为较小的液滴。
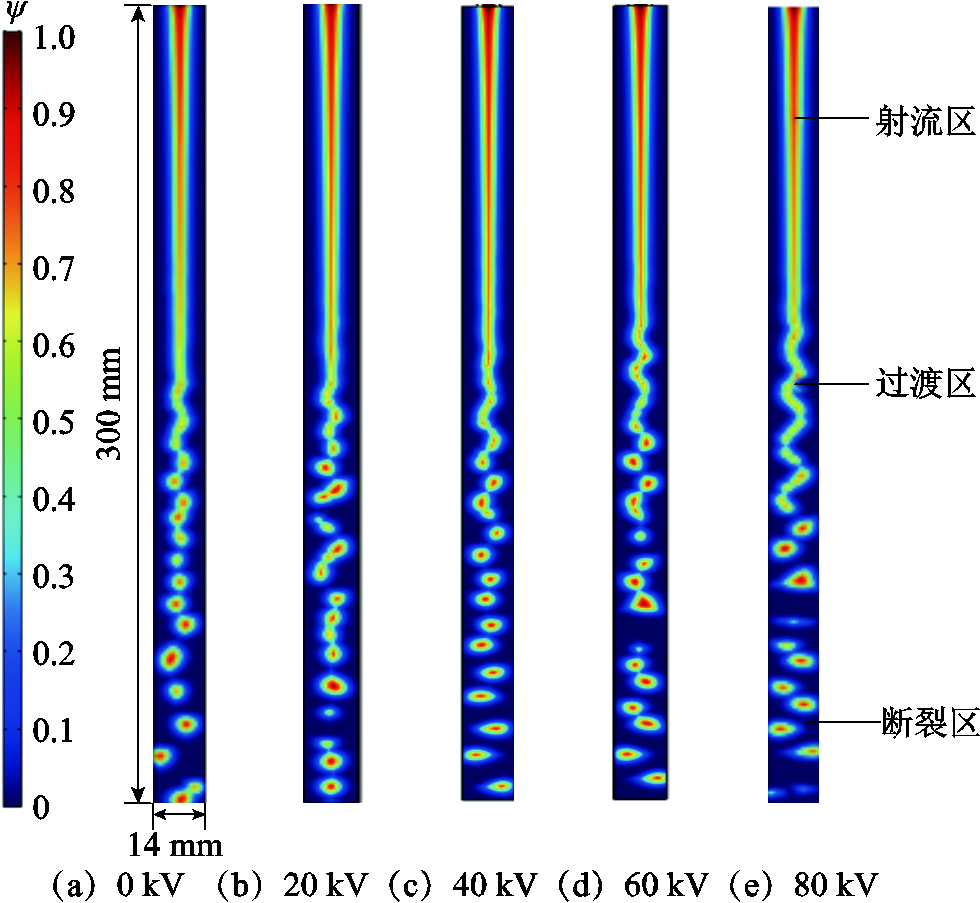
图5 不同外施电压下1.45 m/s时的计算结果
Fig.5 Simulation results with different voltage levels under 1.45 m/s
2）外施电压增大时，过渡区的螺旋运动现象更为明显，表现为雨柱螺旋直径增大、断裂次数增加、螺旋圈及断裂雨滴数量增多。其中，雨柱螺旋直径从20 kV时的4.0 mm增大至80 kV时的7.8 mm，断裂雨滴数量从0 kV时的13个增加至80 kV的18个，螺旋圈断裂次数也增加至80 kV的4次。此外，雨滴的形变程度随之增大，在竖直方向上由于电场力的挤压作用，雨滴变成扁平的椭圆状，当外施电压从20 kV增加至80 kV时，雨滴长短轴之比从0.88增大至2.3。
2.2.1 雨柱断裂形态特征参数
雨柱断裂后形成的雨滴大小不一，且形态随时间发生变化。研究中常取ψ=0.5作为水-气分界面，如图6所示[21-22]。本节选取形状较为规则的雨滴，如球形、椭球形，根据雨滴的长短轴近似计算得到雨滴的断裂直径Dw，并测量雨柱临界断裂长度Lw，二者与外施电压的关系如图7所示。
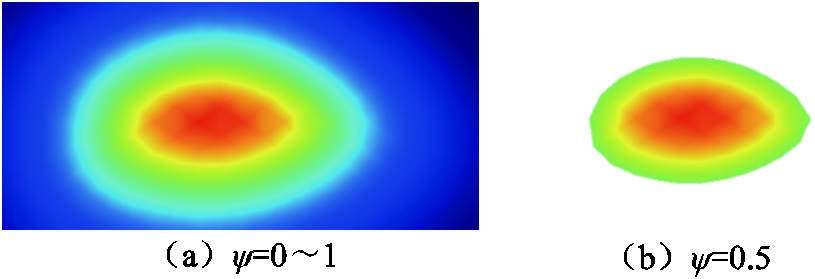
图6 雨滴直径计算
Fig.6 Rain droplet equivalent diameter calculation
分析图7可以得到：
1）不同流速下的雨柱断裂直径Dw均随外施电压的增大而近似线性减小，但降低的趋势减缓；在相同电压作用下，Dw随着雨柱流速的增加而增大。当外施电压为80 kV，雨柱流速从1.25 m/s提高至1.55 m/s时，断裂直径从3.24 mm增大至3.67 mm，但较0 kV时分别降低了13.8%和12.2%。
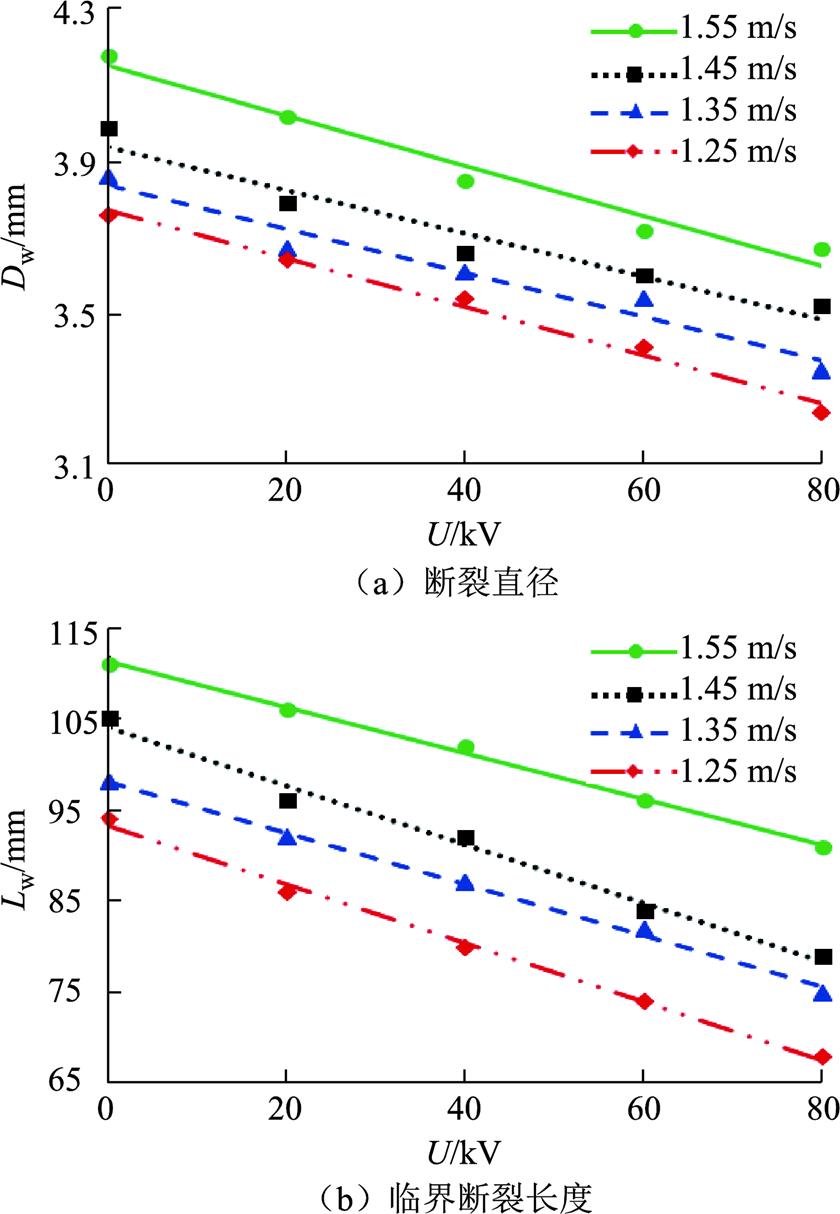
图7 雨柱断裂特性与外施电压关系
Fig.7 Break-up performance of water streams and applied voltage
2）不同流速下的雨柱临界断裂长度Lw均随着外施电压的增大而线性降低，且在相同电压下，Lw与流速呈正相关。80 kV下雨柱流速从1.25 m/s提高至1.55 m/s时，临界断裂长度从68 mm增大至91 mm，但相较于0 kV时的下降幅度分别达到了26%和18%。
2.2.2 雨柱断裂力学特征参数
由于雨柱断裂发生在径向方向，受其表面张力、电场力、粘性力的共同作用；而不同条件下的重力方向保持恒定，仅径向上的作用力对雨柱断裂产生影响。因此，在分析雨柱断裂过程时，忽略了重力的作用。在此基础上，进一步提取了雨柱最大径向表面张力Fstmax和最大径向电场力Fesmax，其变化规律如图8所示。
分析图8可以得到：
1）不同流速下的雨柱最大径向表面张力Fstmax随外施电压的增加而略有减小；且雨柱流速越大，最大径向表面张力越小。流速为1.55 m/s时，雨柱的Fstmax从20 kV的13 978 N/m3下降至80 kV的13 498 N/m3，仅降低了3.4%；外施电压为80 kV时，雨柱的Fstmax从1.25 m/s时的16 584 N/m3下降至1.55 m/s时的13 498 N/m3，降低了18.6%。这是因为，雨柱在高压电场中运动时，其表面吸附能力增强，导致表面电荷增加，表面张力下降，减小了断裂阻力。
2）不同流速下的雨柱最大径向电场力Fesmax均随外施电压增加而增加，且与流速呈正相关。当雨柱流速为1.55 m/s时，Fesmax从20 kV时的3 684 N/m3增加至80 kV时的25 148 N/m3，提高了近6倍。80 kV下，雨柱流速从1.25 m/s增加至1.55 m/s时，其所受最大径向电场力提高了86%。这是由于随着雨柱流速的增大，雨柱的临界断裂长度和断裂直径随之增大，缩短了空气间隙，提高了空间电场强度和畸变率，致使所受最大径向电场力增加。
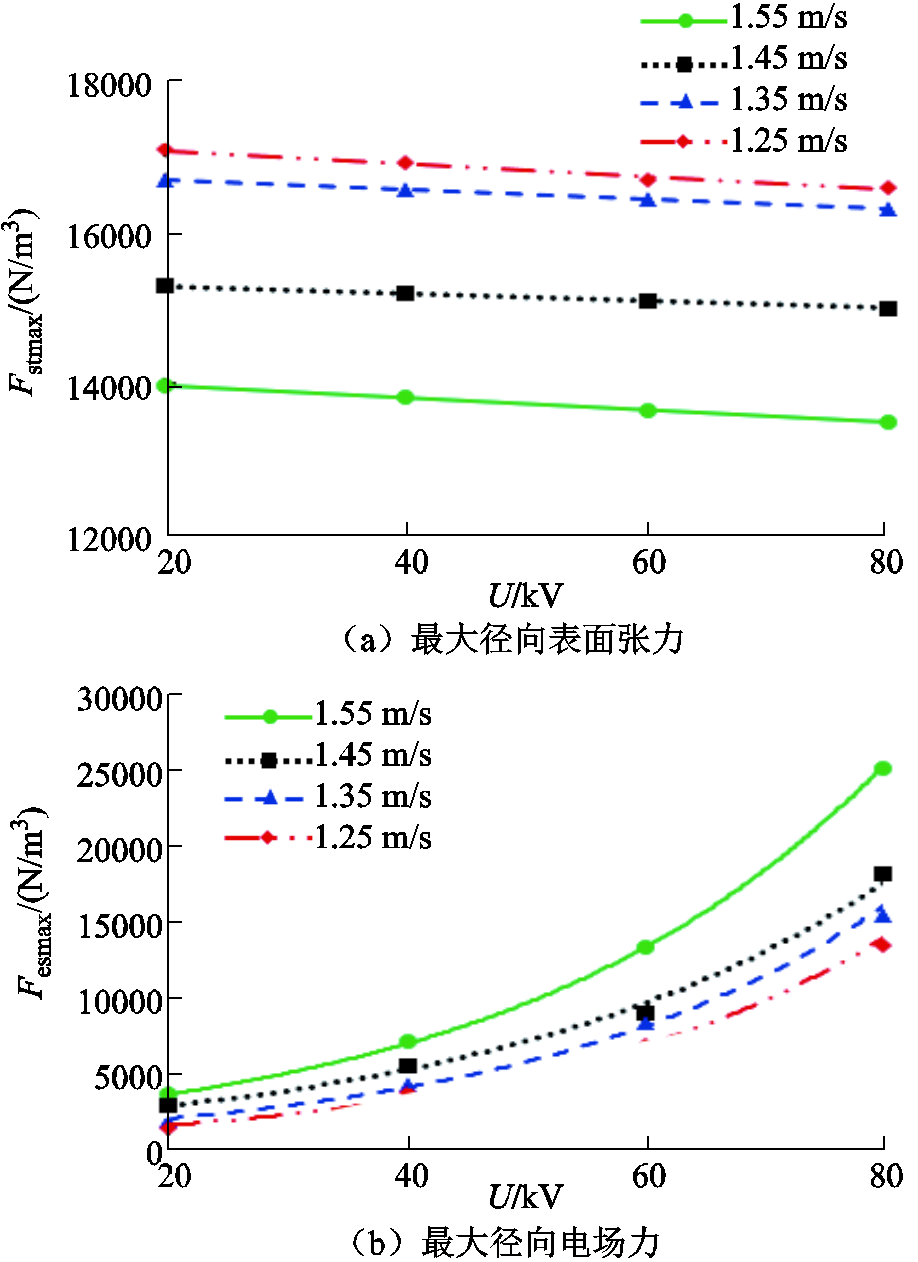
图8 最大径向表面张力、电场力和外施电压关系
Fig.8 Maximum radial surface tension, electric force with applied voltage
因此，在雨柱运动过程中表面张力起重要作用，电场力起到促进作用，使得雨柱抵抗变形的能力减弱，从而更易变形。
为了对第2节仿真计算结果的准确性进行验证，并进一步分析雨柱断裂特性，本节采用喷嘴电极开展雨柱断裂试验。
雨柱流速为1.45 m/s、间隙距离为30 cm、施加0～80 kV直流电压时的棒-板空气间隙雨柱断裂形态如图9所示。分析可知：试验观测的雨柱断裂过程也分为射流区、过渡区、断裂区。随着外施电压的增加，雨柱临界断裂长度显著降低，从0 kV时的112.8 mm减小至80 kV时74.7 mm，减小程度高达33.8%。0 kV时，雨柱及断裂后形成的雨滴沿雨柱中心轴线垂直向下运动；外施电压后，形成的断裂雨滴会偏离中心轴线，并随着外施电压的增加，螺旋运动越加明显；80 kV时，雨柱螺旋运动最大外径可达8.6 mm，最大偏离角高达8°，螺旋圈的断裂次数提高至3次。
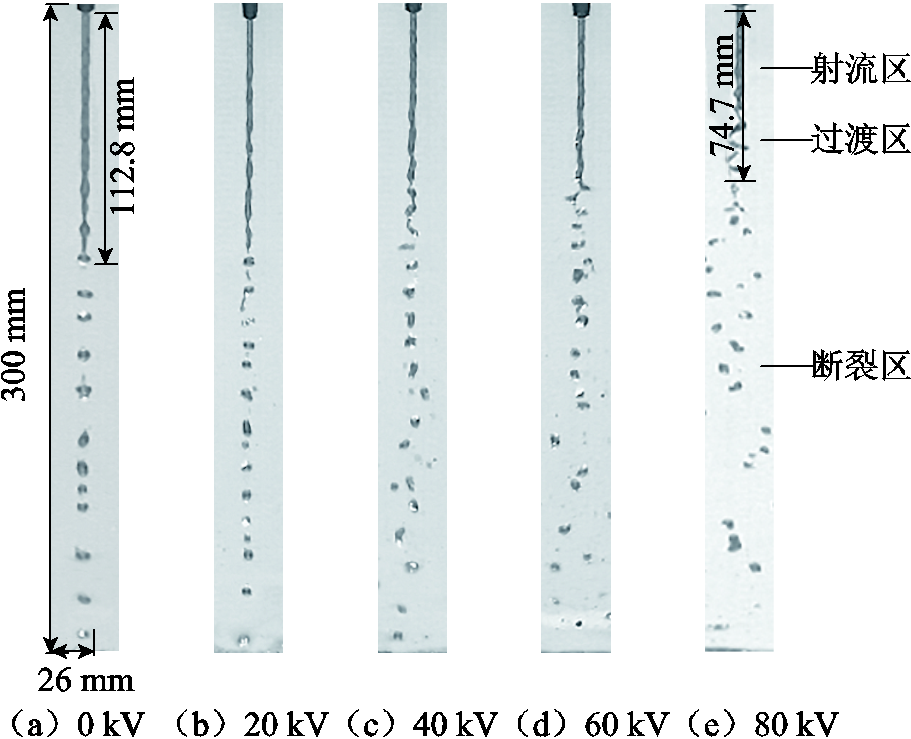
图9 1.45 m/s时不同外施电压条件下雨柱断裂图
Fig.9 Break-up of water streams with different applied voltages under 1.45 m/s
为了进一步解释雨柱螺旋运动，采用微元法将雨柱等效为无数个微元。电场力引发雨柱形变示意图如图10所示，在外施电场作用下，雨柱受到表面张力叠加电场力的综合作用。
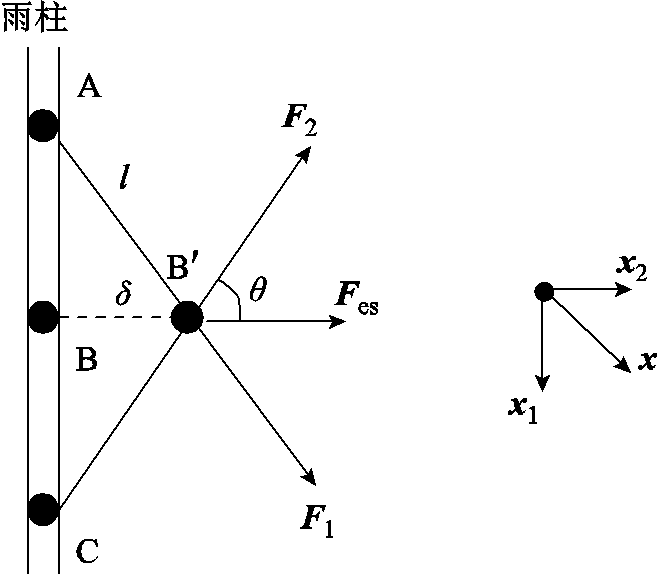
图10 电场力引发雨柱形变示意图
Fig.10 Schematic diagram of water streams deformation induced by electric force
假设雨柱中A、B、C三个微元带电量均为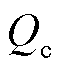
，微元B受到外界扰动时移动δ距离至B′处，则B′处的电场力合力为
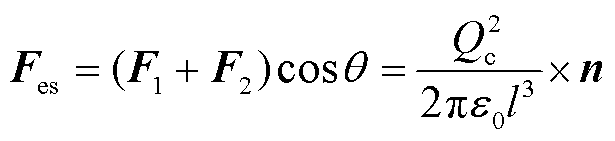（6）
式中，F1、F2分别为微元A、C对B的作用力；θ为微元间的相互作用力与水平方向夹角；l为A、C与B′之间距离；n为雨柱表面的法向量。雨柱在轴向上的速度分量记为x1；B在电场中获得一径向速度分量，记为x2，则B处的合速度x为x1+x2。这会导致雨柱在运动过程中无法保持平衡状态，而产生一个角速度，使得雨柱断裂后的雨滴朝径向方向做螺旋状运动[28]。随着外施电压的增加，微元所受电场力Fes显著增大，由此获得了更大的加速度，提高了微元的运动速度，导致微元的移动距离δ增加，从而表现为雨柱过渡区的半螺旋状断裂次数及螺旋状直径均有所增加。
改变雨柱流速及其外施电压，雨柱临界断裂长度Lw、雨滴断裂直径Dw变化规律如图11所示。
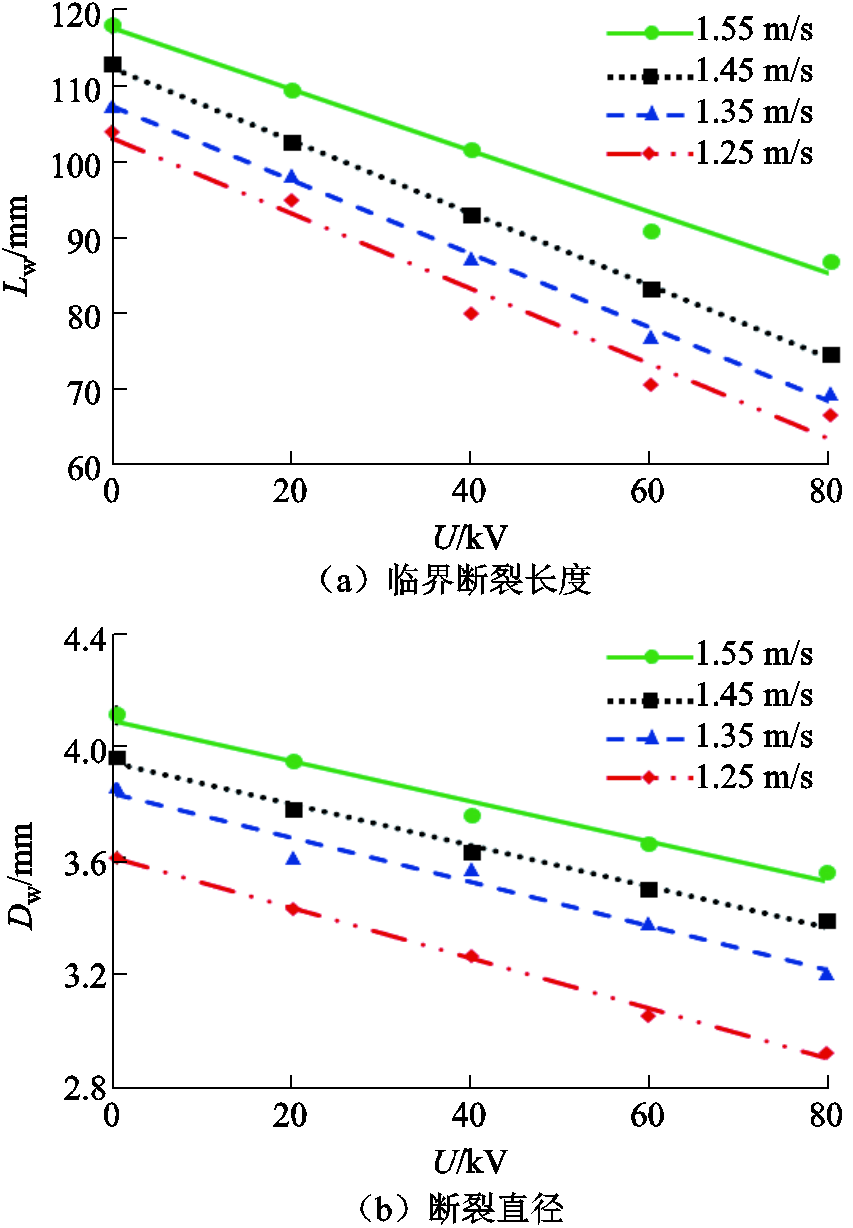
图11 断裂特征参数与外施电压关系
Fig.11 Break-up performance and applied voltage
从图11可以得到，Lw、Dw与外施电压U近似呈线性关系，拟合公式分别为
Lw=aU+b （7）
Dw=cU+d （8）
式中，a、c分别为表征雨柱流速对临界断裂长度Lw、断裂直径Dw的影响特征指数a、c越大，则流速对Lw、Dw的影响越明显。对图11所示数据按照式（7）、式（8）进行拟合，得到D=3 mm时的拟合系数见表2。
分析图11和表2可知：
1）雨柱临界断裂长度Lw与外施电压U呈负相关；且雨柱流速越大，临界断裂长度越大，但变化幅度随之减小。当外施电压从0 kV增长至80 kV时，1.25 m/s雨柱流速下的Lw从104 mm降低至66.8 mm，减小了35.8%；1.55 m/s雨柱流速下的Lw从118 mm降低至87 mm，减小了26.3%。从能量角度分析，雨柱流速越大，其蕴含能量越大，抗外部扰动的能力越强，雨柱越不容易断裂。
表2 断裂特征参数与外施电压关系
Tab.2 The mathematical relationship between break-up performance and the applied voltage
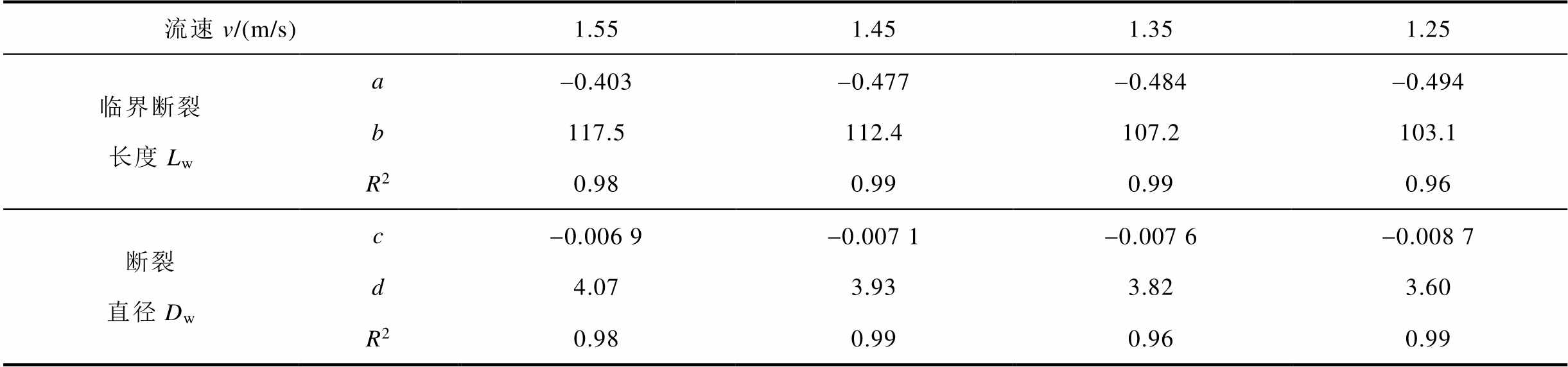
流速v/(m/s)1.551.451.351.25 临界断裂长度Lwa-0.403-0.477-0.484-0.494 b117.5112.4107.2103.1 R20.980.990.990.96 断裂直径Dwc-0.006 9-0.007 1-0.007 6-0.008 7 d4.073.933.823.60 R20.980.990.960.99
2）外施电压越大，断裂直径Dw越小；雨柱的流速越快，Dw越大。当1.25 m/s流速的雨柱承受的外施电压从0 kV增加至80 kV时，断裂直径从3.6 mm降低至2.92 mm，下降了18.9%。
外施电场作用下，雨柱内的电荷随着雨柱运动发生转移，并向雨柱表面移动。电荷转移和重新分布将引起电场力的变化，进一步影响雨柱运动。在此过程中，雨柱所受法向电场力与其表面张力方向相同，处于过渡区的雨柱受到两者的合力而向内收缩，导致临界断裂长度、断裂直径均降低。
对比2.2节与3.2节可知：在流速v=1.25 m/s时，雨滴断裂直径计算结果与试验值的最大偏差小于10%，临界断裂长度最大偏差为9.6%。主要原因是雨柱流速较低时，雨柱总能量较低，易受到外界环境的干扰，但整体试验值与仿真结果的偏差均控制在10%以内，本文建立的仿真模型计算得到的断裂直径、临界断裂长度与试验结果较为吻合，仿真计算可得到较满意的结果。因此，模型计算结果可为强暴雨环境下的雨柱断裂特性提供数据参考。
直流电压极性影响棒电极、雨柱和雨滴对空间电场的畸变程度，导致雨柱所受电场力存在差异[29]。本节对正、负电压极性下30 cm棒-板间隙雨柱断裂特性进行了试验测试；并同步进行了仿真计算，提取了1.25 m/s、1.55 m/s流速下的最大径向电场力Fesmax，结果如图12所示。
分析图12可以得到：
1）雨柱临界断裂长度均随外施电压增大呈线性降低，且负极性电压下的临界断裂长度均大于正极性电压的结果。外施20～80 kV正极性电压时，1.55 m/s流速的雨柱临界断裂长度从109.5 mm降低至 87 mm，所受最大径向电场力从3 684 N/m3增加至25 148 N/m3；而外施负极性电压时，雨柱临界断裂长度从112.9 mm降低至92.5 mm，雨柱所受最大径向电场力从2 321 N/m3增加至19 852 N/m3，故正负极性下的雨柱断裂特征存在明显差异。主要原因是，外施正极性电压时，棒电极处积聚起正电荷，电子崩头部电子到达棒电极后即被中和，削弱了棒电极处的电场，加强了外部空间的电场作用；外施负极性电压时，初始电子崩留下的正电荷（负电荷已向外空间流散）增强了棒电极附近的电场，但削弱了板电极附近的电场。因此，施加正极性电压时的空间电场强度较强，雨柱受到较大的电场力，使得临界断裂长度更低。
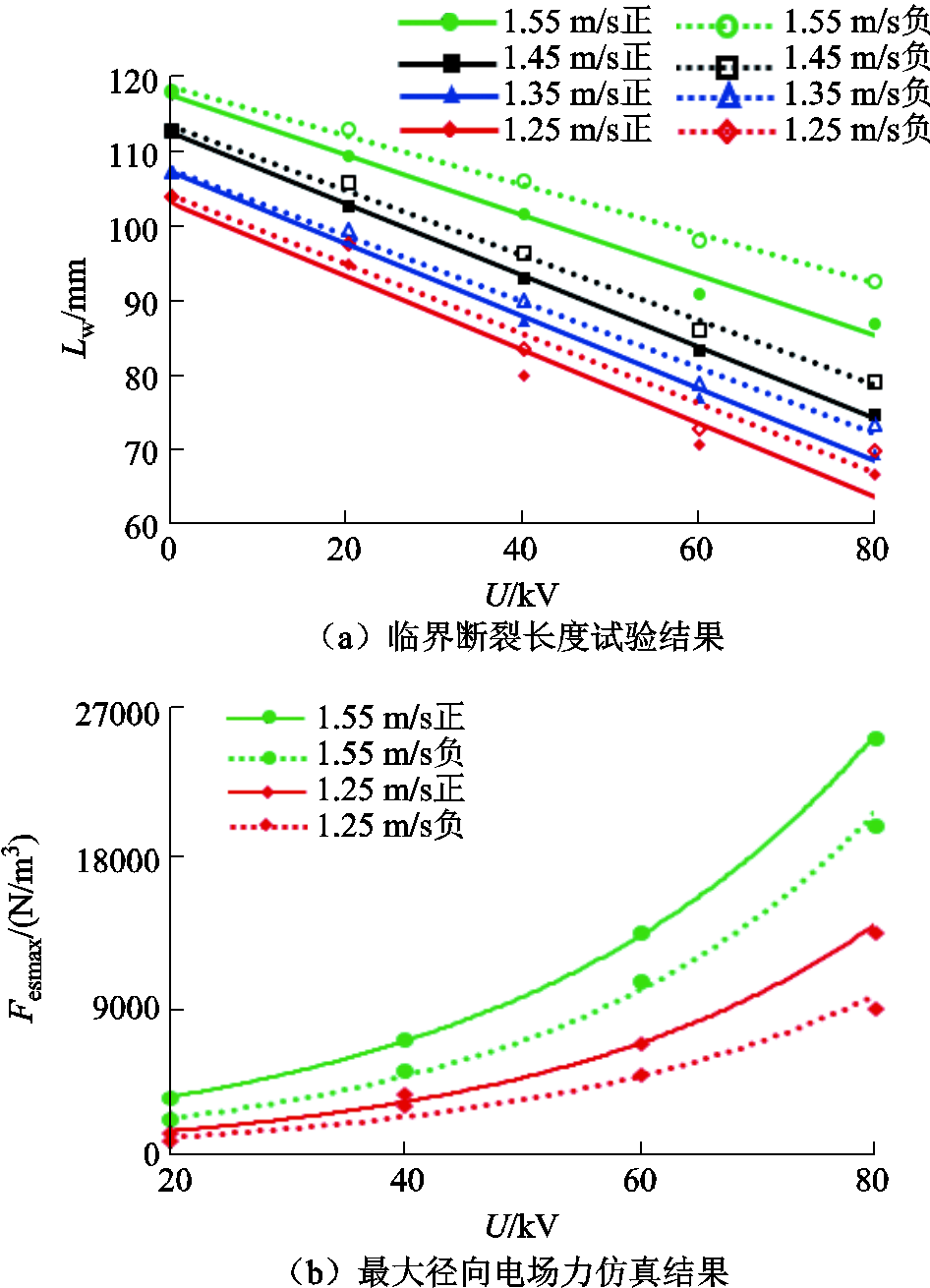
图12 临界断裂长度、最大径向电场力与外施电压关系
Fig.12 Critical break-up length, maximum radial electric force with applied voltage
2）极性效应影响程度与雨柱流速呈正相关；且流速越大，极性效应越明显。1.55 m/s流速下的雨柱临界断裂长度从-80 kV时的92.5 mm降低至80 kV时的87 mm，减小了5.9%；而1.25 m/s下的雨柱临界断裂长度仅减小了4.4%。此外，20～80 kV下，雨柱流速从1.25 m/s增加至1.55 m/s时，最大径向电场力分别提高了11 956 N/m3、21 464 N/m3；而-20～-80 kV下，最大径向电场力则分别提高了7 820 N/m3、17 531 N/m3。这是因为，随着雨柱流速的增加，雨柱的直径、长度增大，断裂雨滴数目增加、直径增大，其表面积聚的带电粒子数量随之增加[30]。由于雨柱、雨滴的内部电场强度较低，外部电场强度较高，加剧了空间电场畸变程度。因此，外施正负极性电压时，雨柱的临界断裂长度差异较大。
1）棒-板间隙雨柱断裂过程实质是表面张力、粘性力和电场力共同作用的结果，表面张力使雨柱表面呈收缩趋势，粘性力阻碍雨柱与空气相互错动而变形，其所受电场力与表面张力的方向相同，而与粘性力方向相反，促进了雨柱断裂进程。雨柱断裂过程经过射流区、过渡区和断裂区，随着外施电压的增加，雨柱更快地进入过渡区，螺旋运动现象越发明显。1.45 m/s流速下，雨柱螺旋运动最大直径从20 kV时的4 mm增至80 kV时的7.8 mm，断裂雨滴数量从0 kV时的13个增至80 kV的18个。
2）雨柱临界断裂长度和断裂直径均随外施电压的增加呈线性降低，降低的趋势随流速增加而变缓，且负极性电压下的雨柱临界断裂长度均大于正极性下的结果。80 kV下1.55 m/s流速雨柱临界断裂长度、断裂直径比0 kV时分别降低了18%、13.8%；相同电压下，临界断裂长度和断裂直径均随流速增大而增加。雨柱最大径向表面张力随外施电压增加而略有减小，且与雨柱流速呈负相关；所受最大径向电场力随外施电压的增加而增大，且增大的趋势与雨柱流速呈正相关。1.55 m/s流速的雨柱所受最大径向电场力从20 kV的3 684 N/m3增加至80 kV的25 148 N/m3，提高了近6倍。
3）棒-板间隙雨柱断裂特性试验结果与仿真值相吻合，即临界断裂长度、断裂直径随外施电压和雨柱流速的变化规律较为一致，且断裂直径、临界断裂长度的试验结果与计算值的最大偏差均小于10%。研究结果可为强暴雨频发地区输电线路-杆塔外绝缘距离设计及选择提供理论参考。
参考文献
[1] Yuan Yao, Jiang Xingliang, Rowland S M, et al. Effect of water streams on the AC breakdown performance of short rod-plane air gaps[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2014, 21(4): 1747-1756.
[2] 刘元庆, 杨晓洪, 姜脉哲, 等. 淋雨后高压直流导线电晕产生的可听噪声特性[J]. 电工技术学报, 2020, 35(增刊2): 371-376.
Liu Yuanqing, Yang Xiaohong, Jiang Maizhe, et al. The characteristics of audible noise produced by corona of HVDC conductors after raining[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 371-376.
[3] 李明哲, 邵仕超, 吴笑寒, 等. 特殊工业粉尘地区绝缘子超疏水涂层应用效果研究[J]. 电力工程技术, 2021, 40(06): 127-133.
Li Mingzhe, Shao Shichao, Wu Xiaohan, et al. Effect of super-hydrophobic coating in special industrial dust area[J]. Electric Power Engineering Technology, 2021, 40(06): 127-133
[4] 周象贤, 刘黎, 王少华, 等. 浙江电网自然灾害特征、趋势与预测技术概况[J]. 浙江电力, 2021, 40(5): 20-29.
Zhou Xiangxian, Liu Li, Wang Shaohua, et al. An overview on characteristics, tendency and prediction technology of natural disasters in Zhejiang power grid[J]. Zhejiang Electric Power, 2021, 40(5): 20-29.
[5] 徐文宝, 周建华. 基于改进模糊层次综合评判法的输电线路舞动预警[J]. 电力工程技术, 2021, 40(5): 107-113.
Yu Wenbao, Zhou Jianhua. Early warning model of transmission line galloping based on improved fuzzy hierarchical comprehensive evaluation[J]. Electric Power Engineering Technology, 2021, 40(5): 107-113.
[6] 夏喻, 李卫国, 陈艳.高空下棒-板间隙直流放电特性及电压校正[J]. 电工技术学报, 2018, 33(9): 2115-2120.
Xia Yu, Li Weiguo, Chen Yan. DC discharge performance and voltage correction of air gaps under high altitude[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 2115-2120.
[7] Lord Rayleigh S R S. XVI. On the instability of a cylinder of viscous liquid under capillary force[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1892, 34(207): 145-154.
[8] Meister B J, Scheele G F. Prediction of jet length in immiscible liquid systems[J]. AIChE Journal, 1969, 15(5): 689-699.
[9] Sterling A M, Sleicher C A. The instability of capillary jets[J]. Journal of Fluid Mechanics, 1975, 68(3): 477-495.
[10] Magarvey R H, Outhouse L E. Note on the break-up of a charged liquid jet[J]. Journal of Fluid Mechanics, 1962, 13(1): 151-157.
[11] Deng Zilong, Sun Meimei, Yu Cheng. Electrohydrodynamic behaviors of droplet under a uniform direct current electric field[J]. Chinese Physics B, 2020, 29(3): 034703.
[12] Yang Lin, Shang Gaofeng, Kuang Zhiqiang, et al. Experimental investigation on flashover charact-eristics of hollow porcelain insulator under extreme rainfall[J]. Electric Power Systems Research, 2022, 203: 107659.
[13] 危卫, 张云伟, 顾兆林. 电场作用下电流变液滴的变形及力学行为[J]. 科学通报, 2013, 58(3): 197-205.
Wei Wei, Zhang Yunwei, Gu Zhaolin. Deformation and mechanical behavior of electrohydrodynamic droplet under external electric field[J]. Chinese Science Bulletin, 2013, 58(3): 197-205.
[14] Cao Wen, Xue Hao, Shen Wei, et al. The effect of dynamic behaviours of the water droplet on DC/AC flashover performance on silicone rubber surface: experiment, simulation and theoretical analysis[J]. High Voltage, 2021, 6(4): 637-646.
[15] Ndoumbe J, Beroual A, Imano A M. Simulation and analysis of coalescence of water droplets on composite insulating surface under DC electric field[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2015, 22(5): 2669-2675.
[16] Schneider J M, Lindblad N R, Hendricks C D, et al. Stability of an electrified liquid jet[J]. Journal of Applied Physics, 1967, 38(6): 2599-2605.
[17] Huebner A L. Disintegration of charged liquid jets[J]. Journal of Fluid Mechanics, 1969, 38(4): 679-688.
[18] Huebner A L, Chu H N. Instability and breakup of charged liquid jets[J]. Journal of Fluid Mechanics, 1971, 49(2): 361-372.
[19] Sun Yijie, Yang Lin, Shang Gaofeng, et al. Effects of dynamic deformation of pendant water drops on the electric field between hollow porcelain insulator sheds under extreme rainfall[J]. High Voltage, 2022, 7(1): 86-97.
[20] 庞乐乐, 杨文勇, 李鹏飞, 等. 基于混合气体热特性的GIL氮气使用配比研究[J]. 电力工程技术, 2022, 41(3): 244-251.
Pang Lele, Yang Wenyong, Li Pengfei, et al. N2 proportion in GIL based on heat characteristics of gas mixture [J]. Electric Power Engineering Technology, 2022, 41(3): 244-251.
[21] Zhu Changsheng, Han Dan, Feng Li, et al. Multi-bubble motion behavior of electric field based on phase field model[J]. Chinese Physics B, 2019, 28(3): 034701.
[22] Zhu Changsheng, Han Dan, Xu Sheng. Phase field simulation of single bubble behavior under an electric field[J]. Chinese Physics B, 2018, 27(9): 094704.
[23] 贺博, 王鹏, 吴锴, 等. 多物理场中染污绝缘油内杂质相动力学行为研究综述[J]. 电工技术学报, 2022, 37(1): 266-282.
He Bo, Wang Peng, Wu Kai, et al. Reviews on impurity phase dynamics in contaminated insulating oil under multi-physical field conditions[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 266-282.
[24] 胡毅, 王力农, 邵瑰玮, 等. 风雨对导线—杆塔空气间隙工频放电特性的影响[J]. 高电压技术, 2008, 34(5): 845-850.
Hu Yi, Wang Linong, Shao Guiwei, et al. Influence of rain and wind on power frequency discharge characteristic of conductor-to-tower air gap[J]. High Voltage Engineering, 2008, 34(5): 845-850.
[25] 袁耀. 短空气间隙暴雨击穿特性与放电模型研究[D]. 重庆: 重庆大学, 2014.
[26] Ashgriz N, Mashayek F. Temporal analysis of capillary jet breakup[J]. Journal of Fluid Mechanics, 1995, 291: 163-190.
[27] Umemura A, Kawanabe S, Suzuki S, et al. Two-valued breakup length of a water jet issuing from a finite-length nozzle under normal gravity[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2011, 84(3 Pt 2): 036309.
[28] 汪朝晖. 高压静电场中液体射流的雾化研究及应用[D]. 重庆: 重庆大学, 2009.
[29] 王胜辉, 邓畅宇, 王新宇, 等. 淋雨对短空气间隙操作冲击放电影响的实验研究[J]. 电网技术, 2019, 43(3): 1092-1098.
Wang Shenghui, Deng Changyu, Wang Xinyu, et al. Experimental study on effects of rain on short air gaps discharge with switching impulse voltage[J]. Power System Technology, 2019, 43(3): 1092-1098.
[30] 申南轩, 苏子寒, 张远航, 等. 湿度对悬浮液滴荷电特性及离子流场特性的影响[J]. 电工技术学报, 2022, 37(13): 3422-3430, 3452.
Shen Nanxuan, Su Zihan, Zhang Yuanhang, et al. Influence of humidity on the charge characteristics of suspension droplets and the characteristics of ion flow field[J]. Transactions of China Electrotechnical Society, 2022, 37(13): 3422-3430, 3452.
Abstract Under heavy rain conditions, the rain streams between the high-voltage wire and the tower is prone to break up, which causes the electric field distortion and reduces the electrical insulation performance of the wire-tower gap. In order to study the break-up characteristics of rain streams in air gap under heavy rain conditions, this paper took rain streams in the short air gap between rod and plane as the research object and established a two-dimensional non-axisymmetric simulation model developed by coupling the continuity equation, Navier-Stokes equation, electric field equation of an incompressible fluid. And then the morphology and stress of the rain streams during the break-up process was analyzed. The changes of break-up characteristic parameters under different external voltages and rain streams flow rates was calculated and studied. Finally, a rod-plane gap rain streams break-up test platform was established with nozzle electrode to carry out break-up characteristic test, and the simulation results were verified. On this basis, the influence law of DC voltage polarity on break-up characteristic parameters was further studied.
The results showed that the break-up process of rain streams in the rod-plane gap is subject to the joint action of the electric force, surface tension and viscous force. The break-up process of rain-streams with rod-plane gap goes through three stages int turn: jet zone, transition zone and break-up zone. Increasing the applied voltage increases the spiral diameter of the rain streams, the number of break-up and the deformation degree of raindrops, and accelerates the spiral motion in the transition zone. Among them, the spiral diameter of the rain streams increases from 4.0 mm at 20 kV to 7.8 mm at 80 kV, the number of raindrops increases from 13 at 0 kV to 18 at 80 kV, and the ratio of the long to short axis of the raindrops increases from 0.88 at 20 kV to 2.3 at 80 kV. The critical break-up length and break-up diameter of the rain streams are linearly reduced with the increase of the applied voltage, and are positively correlated with the flow rates of the rain streams. The critical break-up length and diameter of the rain streams at 1.55 m/s flow rate under 80kV are reduced by 18% and 13% respectively. The critical break-up length of rain streams at negative polarity voltages are greater than those at positive polarity under the same conditions. The maximum radial surface tension of the rain streams decreases slightly with increasing applied voltage and is negatively correlated with the flow rates; the maximum radial electric force increases with the increase of applied voltage, and the larger the flow rates, the larger the force. The maximum radial electric force on the rain streams with a rate of 1.55 m/s increases from 3 684 N/m3 at 20 kV to 25 148 N/m3 at 80 kV, and when the rate of the rain streams increases from 1.25m/s to 1.55m/s at 80 kV, the maximum radial electric force increases by 86%. The experimental results of the break-up diameter and break-up length are in good agreement with the calculated values. At the flow rate v=1.25 m/s, the maximum deviation between the calculated results of the raindrops break-up diameter and the experimental value is less than 10%, the deviation of the critical break-up length is 9.6%, and the overall maximum deviation is less than 10%.
Keywords：Heavy rain conditions, DC discharge, air gap, water streams break-up performance, finite element simulation, experimental verification
董冰冰 男，1987年生，博士（后），副研究员，研究方向为复杂环境下输电线路外绝缘放电理论与试验。E-mail:bndong@126.com
李 特 男，1987年生，高级工程师，研究方向为输电线路外绝缘放电与防护。E-mail:westtoback@163.com（通信作者）
中图分类号：TM852
DOI: 10.19595/j.cnki.1000-6753.tces.221373
国家电网有限公司科技项目（J2022047）和高等学校学科创新引智计划（BP0719039）资助。
收稿日期 2022-07-16
改稿日期 2022-09-05
（编辑 李 冰）