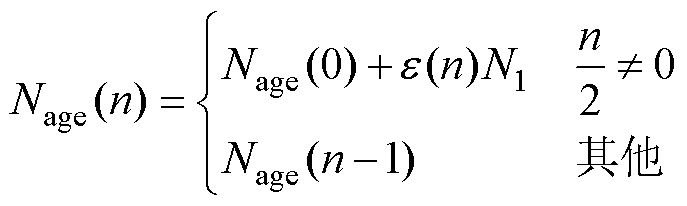 (1)
(1)
摘要 针对储能系统直流侧纹波电流对磷酸铁锂电池寿命影响问题,通过分析磷酸铁锂电池寿命模型的变化机理和规律,发现纹波电流下影响磷酸铁锂电池寿命的关键因素是电池充放电状态期间的电流平均值而非电流有效值,电池充放电状态期间电流的平均值越大,电池老化程度越快,并通过设计仿真以及实验验证了所发现的规律。基于该规律可优化储能系统安全经济运行的控制策略,在电网不平衡时采取抑制交流侧功率波动而放宽直流侧功率波动的控制策略,并在光储系统恒定有功功率并网时,基于电池老化特性曲线和储能系统并网谐波含量符合要求下,提出了一种延长储能电池使用寿命的多储能变流器协调控制策略,与传统控制策略相比,可减缓电池老化速度的19.8%。
关键词:储能系统 磷酸铁锂电池寿命 纹波电流 平均值 协调控制策略
在“双碳”目标的背景下,电化学储能由于可提高清洁能源消纳能力、能源电力供应保障和能源电力系统效率效益而得到快速发展[1-2],但由于储能锂离子电池内部结构和电化学反应比较复杂,使得锂离子电池状态估计技术还不完善[3],同时储能系统与电网之间的交互影响复杂,从而严重制约着“新能源+储能”一体化的快速发展[4]。随着大量的电力电子器件应用到电网,储能系统正常工况下直流侧会存在纹波电流,此外,系统常见的电网电压不平衡现象会造成储能系统直流侧电压电流出现大量谐波分量[5-6]。
针对充放电电流中的谐波分量对锂离子电池寿命影响的问题,相关学者做了大量的研究。在整体影响方面,有的学者称电流中的谐波分量会加速电池的老化[7-10],应对电流中的谐波分量加以限制。而有的学者称电流中的谐波分量不会对电池产生负面影响[11-16],从而可以减小储能系统直流侧的谐波含量要求,降低滤波器成本等。
在许多学者的研究中都体现了电流的有效值是一个重要的老化因素[7, 14-15, 17],文献[7]对LiCoO2电池进行2次老化实验,基于统计方法确定充放电电流的有效值方均根(Root Mean Square, RMS)为重要的老化因素,且电池老化随RMS的增大而增大,而直流分量、电流波形及频率为不重要的老化因素,但其电池循环次数只有300次,且没有涉及同一频率、不同幅值下的谐波对电池老化的影响,此时电流有效值也是不同的。对于同一种频率下的交流分量对电池寿命影响的研究中,文献[12]通过120 Hz的交流电对磷酸铁锂电池进行充放电实验,结果表明,叠加的电流纹波只会在电池温度上产生轻微但明显的差异,电池温度只有0~2℃的区别。文献[13]通过设计双向DC-DC转换器上有无LCL滤波器来产生大电流纹波和小电流纹波并作用在两个锂离子电池组上,实验结果表明,电池的老化与电流纹波无关联。文献[15]通过100 Hz的纹波电流对磷酸铁锂电池进行1 000次循环老化实验,结果表明,100 Hz的纹波电流基本不会对电池容量衰减和阻抗上升有影响,但其中有两组电池电流的RMS一样,两组电流分别为DC(367 mA)和DC(300 mA)+ AC(300 mA),结果却显示仅含DC电流的电池寿命衰减普遍比DC+AC的电池老化多1%~2%。
电流中不同的谐波频率对电池寿命的影响是一个研究热点[8-10, 14, 16-17],文献[8]使用X射线光电子能谱技术研究耦合了DC和AC的电流对LiNiCoAlO2电池老化的影响,其中的AC电流设置了4个频率,实验结果表明,电流中的交流分量会加速SEI膜的增长且增长速度与交流频率有关。文献[9]通过LiNiCoAlO2电池研究电流中不同交流频率对电池性能的影响,结果表明,随着交流频率增加,电池容量衰减和阻抗上升都逐渐增加,同时有交流分量的电池老化速度远大于仅使用直流分量的电池。但有的学者研究结果刚好相反,文献[10]对2A·h- LiCoO2电池进行了交流频率为1~100 kHz的充放电循环实验,结果表明,频率在10 Hz以下的电池容量显著恶化,而在较高频率下电池的容量衰减与相应的日历电池退化相同。文献[17]通过对磷酸铁锂电池进行200天的老化实验,结果也表明,高频交流电不会加速电池的老化,甚至有一些证据表明它可以提高电池寿命,而低频交流电会加速锂库存和活性材料的损失,从而加速了电池的老化。文献[14]通过对2A·h-LiNiMnCoO2电池进行1 500次循环老化实验,结果也表明,高频交流电没有加速电池的老化,而低频交流电使得电池阻抗增加和容量衰减要高1%~2%。此外,文献[16]研究了低中高三种交流频率对28A·h-LiNiMnCoO2电池寿命的影响,实验结果表明,三种交流谐波对电池容量的衰减或功率的衰减都没有影响。
综上所述,关于纹波电流对锂离子电池寿命的影响因素体现了有效值、谐波频率等,但结果上还没有达成一致的共识,故纹波电流对锂离子电池寿命的影响还有待进一步研究。本文先对锂离子电池寿命模型进行分析,发现纹波电流下影响锂离子电池寿命的关键因素是充放电状态期间电流的平均值而不是有效值,且充放电状态期间电流的平均值越大,电池的老化速度越快。接着通过设计仿真以及实验验证了该规律。最后列举了该规律在储能系统安全运行控制策略上的应用,包括在电网不平衡时采取抑制交流侧功率波动而放宽直流侧功率波动的控制策略,以及在光储系统恒定有功功率并网时,基于电池老化特性曲线和储能系统并网谐波含量符合要求下,提出了一种延长储能电池使用寿命的多储能变流器协调控制策略,可有效延长储能电池使用寿命。
目前常见的锂离子电池等效模型有RC等效电路模型、电化学模型、随机模型及分析模型等,其中,Shepherd模型[18]凭借易于搭建、准确度高、便于分析等优势,成为广大学者的研究对象,该电池模型有以下假设:
(1)电池在充电和放电循环期间,电池的内阻恒定不变。
(2)模型的参数由放电特性导出,且假设电池的充电特性和放电特性相同。
(3)电池不存在Peukert效应。
(4)模型未显示电池的自放电,可通过电池端并联一个大电阻来表示。
(5)电池无记忆效应。
但Shepherd模型在描述锂离子电池寿命衰减上还存在不足,文献[19]指出锂离子电池寿命主要与电池工作环境温度、充放电深度及充放电电流大小有关并分别建立了与这些因素相对应的数学模型,Simulink对文献[19]和Shepherd模型进行融合完善得到新的锂离子电池充放电模型[20],并采用松下的锂离子电池进行试验,结果显示,融合后的锂离子电池模型在充电和放电下动态的最大误差为5%(电池的荷电状态(State of Charge, SOC)在10%~100%之间时)),模型中的电池老化循环圈数、最大容量及欧姆内阻的表达式分别为
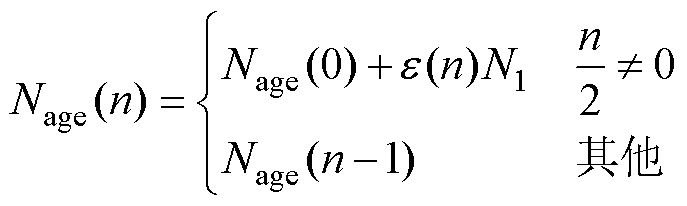 (1)
(1)
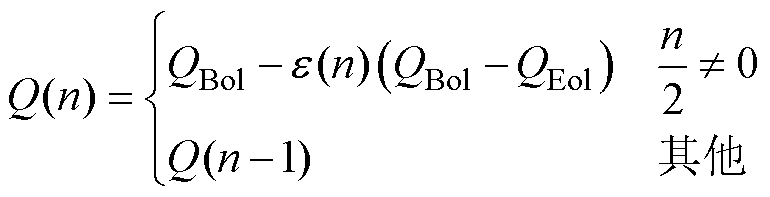 (2)
(2)
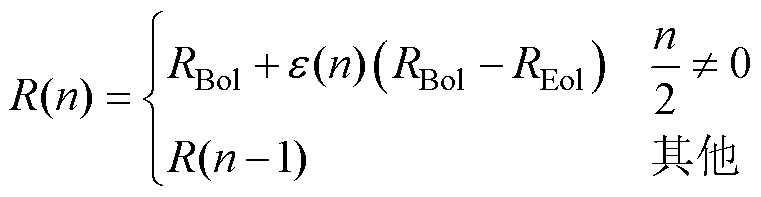 (3)
(3)
其中
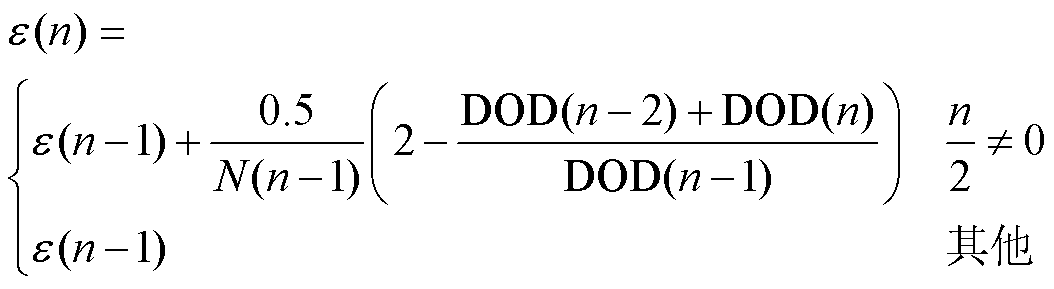 (4)
(4)
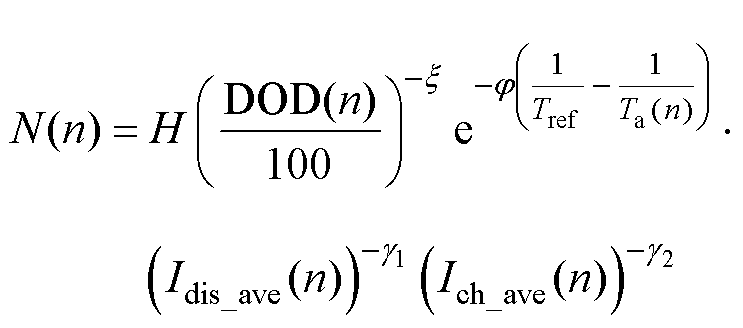 (5)
(5)
式中,n=1, 2, 3,…,充放电过程中,当电池由充电状态变放电状态或由放电状态变充电状态时,n累加1;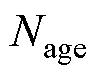 为锂离子电池老化循环圈数;
为锂离子电池老化循环圈数;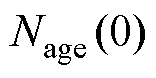 为初始锂离子电池老化循环圈数,新电池
为初始锂离子电池老化循环圈数,新电池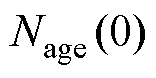 =0;e(n)为电池老化系数;电池放电深度(Depth of Dis-charge, DOD)的表达为DOD=100-SOC;N1为锂离子电池在额定充放电电流且放电深度为100%下的最大循环圈数;Q为锂离子电池的最大容量(A·h);QBol为在标称环境温度下电池开始使用时电池的最大容量(A·h);QEol为在标称环境下电池使用寿命结束时电池的最大容量(A·h);R为锂离子电池的欧姆内阻(W);RBol为在标称环境温度下电池开始使用时的电池欧姆内阻(W);REol为在标称环境下电池使用寿命结束时的电池欧姆内阻(W);N(n)为最大循环次数,不同充放电电流大小及放电深度会使得电池的最大循环次数不同;H为循环常数;x 为DOD的指数因子;j 为循环圈数的Arrhenius速率常数;Tref为设定的环境温度(K);Ta为锂离子电池温度(K);Ich_ave(n)为电池在充电状态期间电流的平均值(A);Idis_ave(n)为电池在放电状态期间电流的平均值(A);g1和g2分别为放电电流和充电电流的指数因子。
=0;e(n)为电池老化系数;电池放电深度(Depth of Dis-charge, DOD)的表达为DOD=100-SOC;N1为锂离子电池在额定充放电电流且放电深度为100%下的最大循环圈数;Q为锂离子电池的最大容量(A·h);QBol为在标称环境温度下电池开始使用时电池的最大容量(A·h);QEol为在标称环境下电池使用寿命结束时电池的最大容量(A·h);R为锂离子电池的欧姆内阻(W);RBol为在标称环境温度下电池开始使用时的电池欧姆内阻(W);REol为在标称环境下电池使用寿命结束时的电池欧姆内阻(W);N(n)为最大循环次数,不同充放电电流大小及放电深度会使得电池的最大循环次数不同;H为循环常数;x 为DOD的指数因子;j 为循环圈数的Arrhenius速率常数;Tref为设定的环境温度(K);Ta为锂离子电池温度(K);Ich_ave(n)为电池在充电状态期间电流的平均值(A);Idis_ave(n)为电池在放电状态期间电流的平均值(A);g1和g2分别为放电电流和充电电流的指数因子。
假设直流侧纹波电流大小一致且为非正弦周期函数,则可将该函数分解成傅里叶级数,即纹波电流可由不同频率下谐波分量Akcos(kwt+fk)构成,即
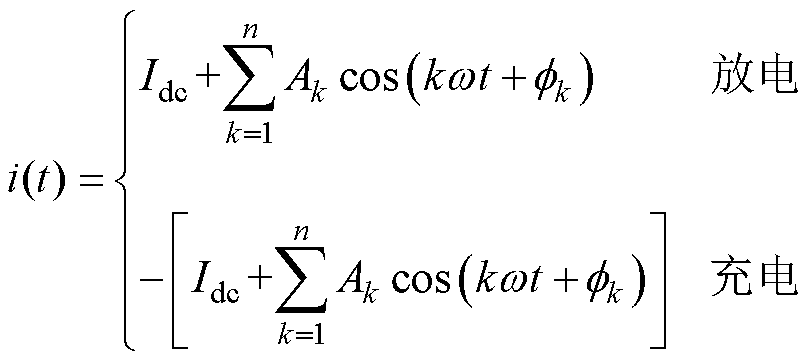 (6)
(6)
式中,Idc为电流中的直流分量;w 为角频率;Ak和fk分别为在频率kw 下余弦分量的幅值和相位。
模型中电池的SOC是采用安时积分法进行估计,电流中的谐波分量经过积分后值为0,故可忽略电流中的谐波分量对DOD的影响。假设环境温度不变,通过化简与谐波分量无关的变量,保留受电流中谐波分量影响的变量,得到
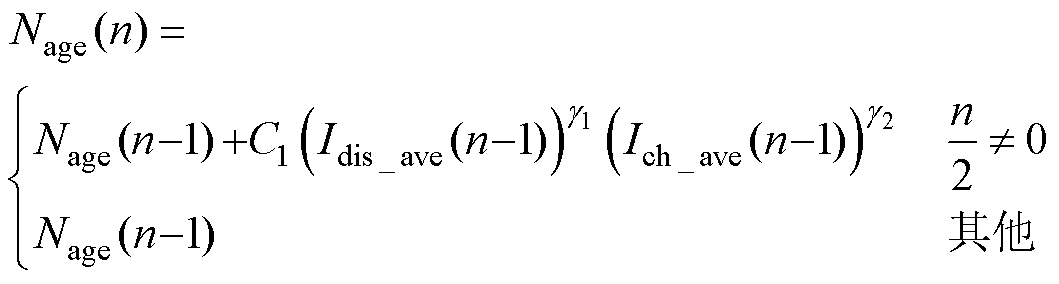 (7)
(7)
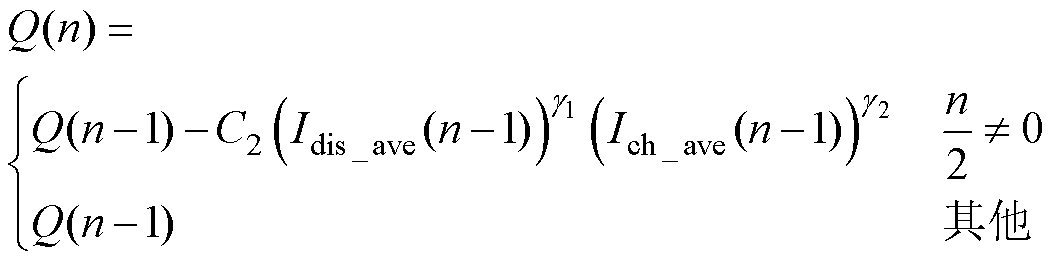 (8)
(8)
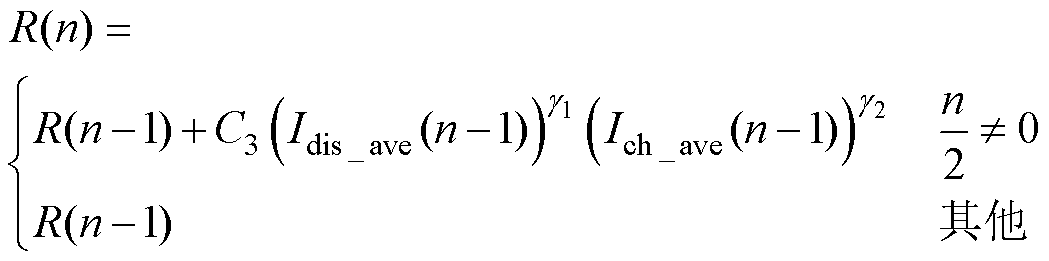 (9)
(9)
式中,C1、C2和C3为不受电流中谐波分量影响的变量。
从式(7)~式(9)可知,纹波电流下对电池寿命影响的关键因素是Ich_ave(n)和Idis_ave(n)而非电流的有效值。当Ich_ave(n)和Idis_ave(n)都增大时,会加速电池寿命的衰减;当Ich_ave(n)和Idis_ave(n)都减小时,会减缓电池寿命的衰减,与实际情况相符。
假设Amin为函数 最小值,在实际工程应用中,储能系统直流侧的纹波电流波动一般都会小于直流分量,故当Amin≤Idc时,电池充放电状态期间电流的平均值为
最小值,在实际工程应用中,储能系统直流侧的纹波电流波动一般都会小于直流分量,故当Amin≤Idc时,电池充放电状态期间电流的平均值为
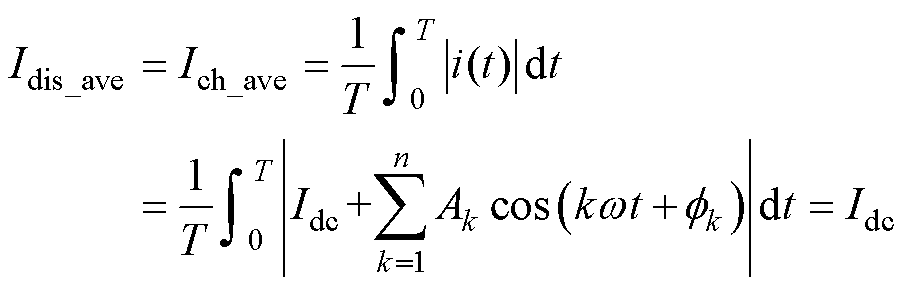 (10)
(10)
而电流的有效值为
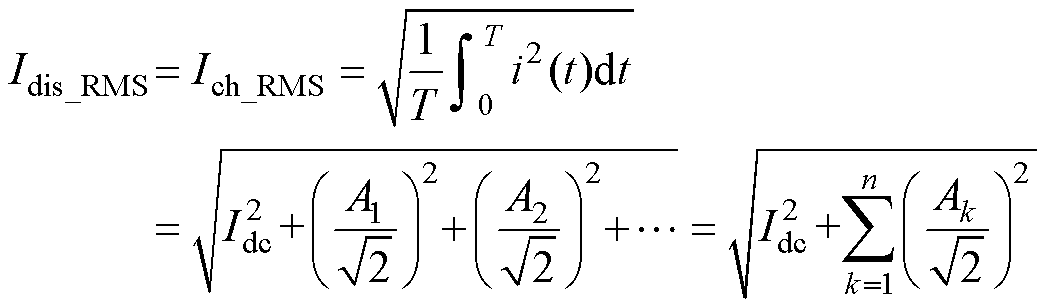 (11)
(11)
从式(10)可知,该区间内电池充放电状态期间电流的平均值都等于直流分量,此时电池寿命的衰减与电流中的谐波分量无关联。结合式(11)可知,直流侧含有纹波电流时,电池充放电状态期间电流的平均值和电池充放电状态期间电流的有效值是不等的。
在Simulink上选择12.8 V/40 A·h的LiFePO4电池作为仿真对象,以电池老化循环圈数为电池寿命的表征量,该电池部分参数见表1。
表1 LiFePO4电池部分参数
Tab.1 Some parameters of LiFePO4 battery

参 数取 值 Nage(0)0 N11 500 H4 729.665 x1.399 9 j1 819.29 Tref/K296.15 g10.280 32 g20.103 019 6
储能系统运行在正常工况时直流侧的纹波较小,但当交流侧发生三相电压不平衡时,直流侧会产生大量的谐波,且其中的谐波以2次谐波分量为主[5]。图1a为储能电站在P/Q控制下交流侧发生单相接地时直流侧电流仿真波形,由于储能电站整体的仿真数据较多,若进行长时间仿真,则会导致软件“崩溃”,为此搭建了可模拟各种谐波分量电流对锂离子电池进行充放电的模型,并设计了充放电电流i1(t)、i2(t)、i3(t)、i4(t)、i5(t)和i6(t),见表2,其中i1(t)和i2(t)分别为故障前0.17~0.19 s的电流和故障后0.23~0.25 s的电流,各电流具体波形如图1所示。
表2 充放电电流设计
Tab.2 Charging and discharging current design(单位: A)

充放电电流平均值有效值 i1(t)48.4549.36 i2(t)49.0753.38 i3(t)49.0749.07 i4(t)=49.07 A+20sin(2wt)49.0751.06 i5(t)=49.07 A+40sin(2wt)49.0756.63 i6(t)56.6356.63
利用上述电流对LiFePO4电池进行充放电,充放电深度如图2中的电池SOC变化曲线所示。
结合图2和表2可知,电流i1(t)和i2(t)的电池老化循环圈数基本一致,这两者的电流平均值基本一致而有效值差别较大;电流为i3(t)、i4(t)和i5(t) 的电池老化循环圈数变换规律一样,这些电流的充放电电流平均值相同而有效值不同;电流为i6(t)的电池比电流为i5(t)的电池老化循环圈数更大,两者有效值相同但电流i6(t)的平均值更大。为此,直流侧纹波电流下锂离子电池的老化循环圈数与电池充放电状态下电流的平均值大小密切相关,而不是电流的有效值。在电池温度变化曲线中,附加的谐波分量会加速电池温度的升高,但温度变化只有0~ 2℃的区别。
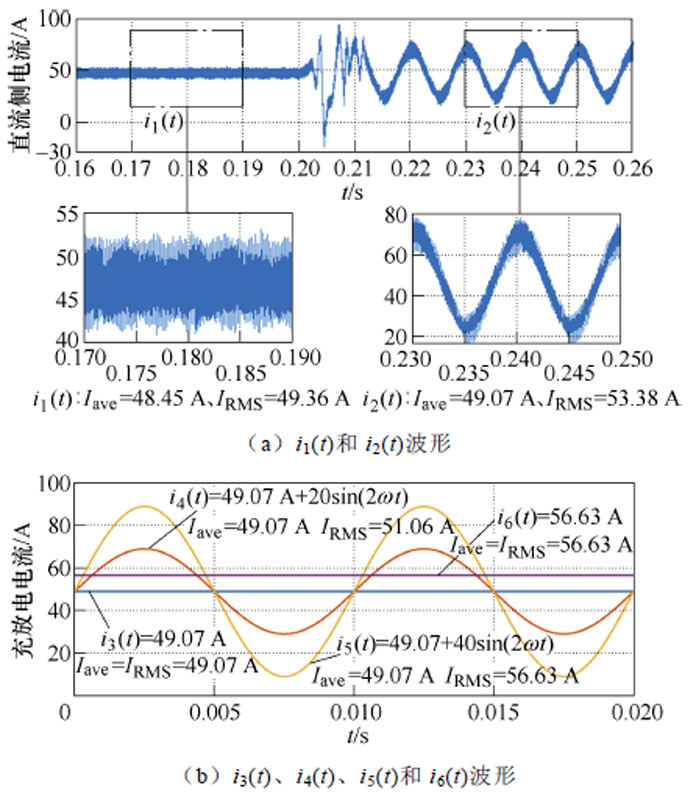
图1 不同充放电电流波形
Fig.1 Waveforms of different charging and discharging currents
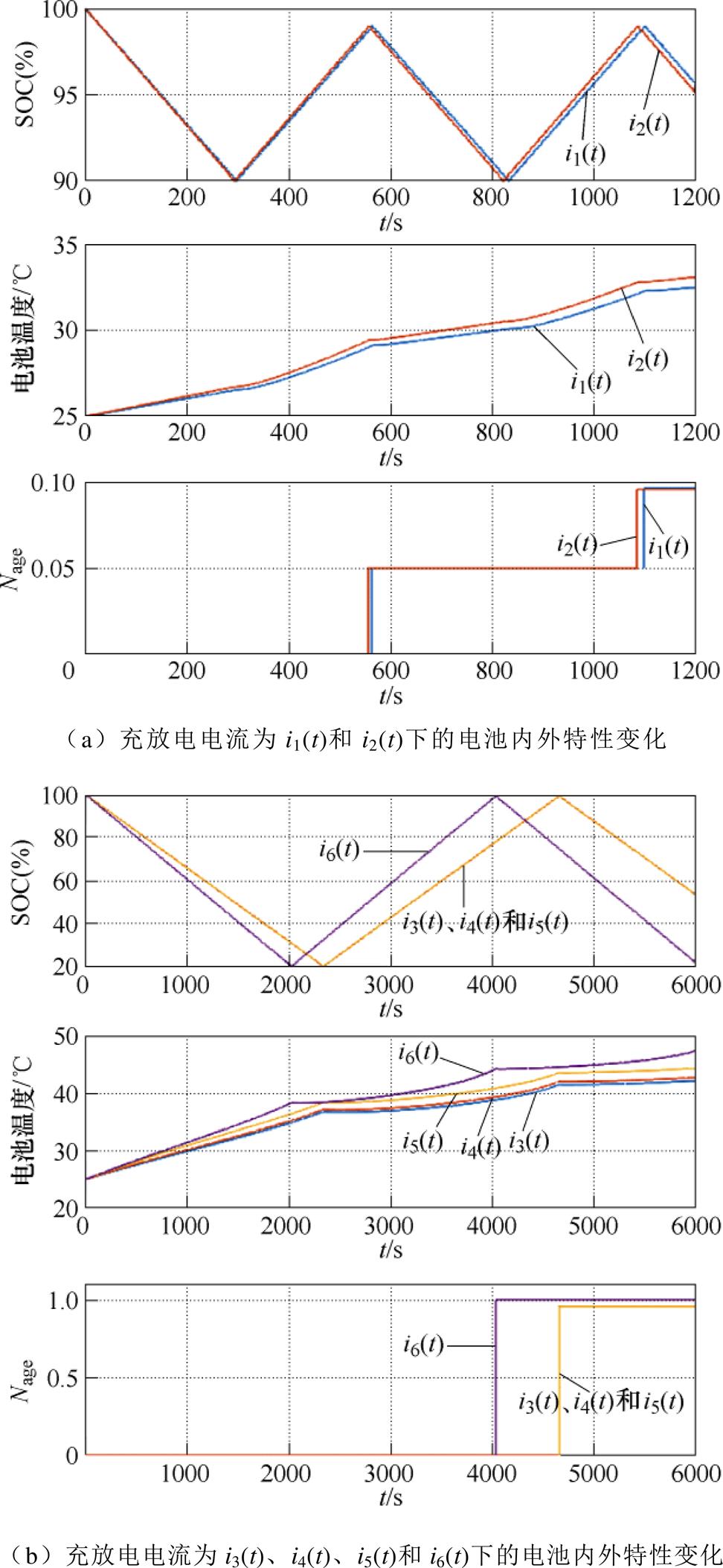
图2 不同充放电电流下电池内外特性变化曲线
Fig.2 Variation curves of internal and external characteristics of the battery under different charging and discharging currents
为了验证纹波电流下对电池寿命影响的主要因素是充放电状态期间电流的平均值还是电流的有效值,选择实验平台如图3a所示,对电池进行充放电的设备为新威的BTS82产品,实验设备的部分参数见表3,图3b为利用不同的脉冲幅值模拟充放电电流中的2次谐波分量。
实验先对新电池进行参考性能测试(Reference Performance Test, RPT),并根据测得的电池最大容量和欧姆内阻的大小筛选出6个差异很小的电池,这些电池的初始阻抗谱如图4a所示。电池最大容量是通过恒流-恒压充电测得的,其中的恒流为C/25倍率下的电流,恒压充电的截止电流设置为0.000 1 mA。电池欧姆电阻是根据交流阻抗谱(Elec- trochemical Impudence Spectroscopy, EIS)技术测量结果得到的Nyquist图中虚部为零的点,EIS技术在SOC为50%时进行,其中交流振幅为10 mV,频率范围从0.01 Hz~100 kHz。
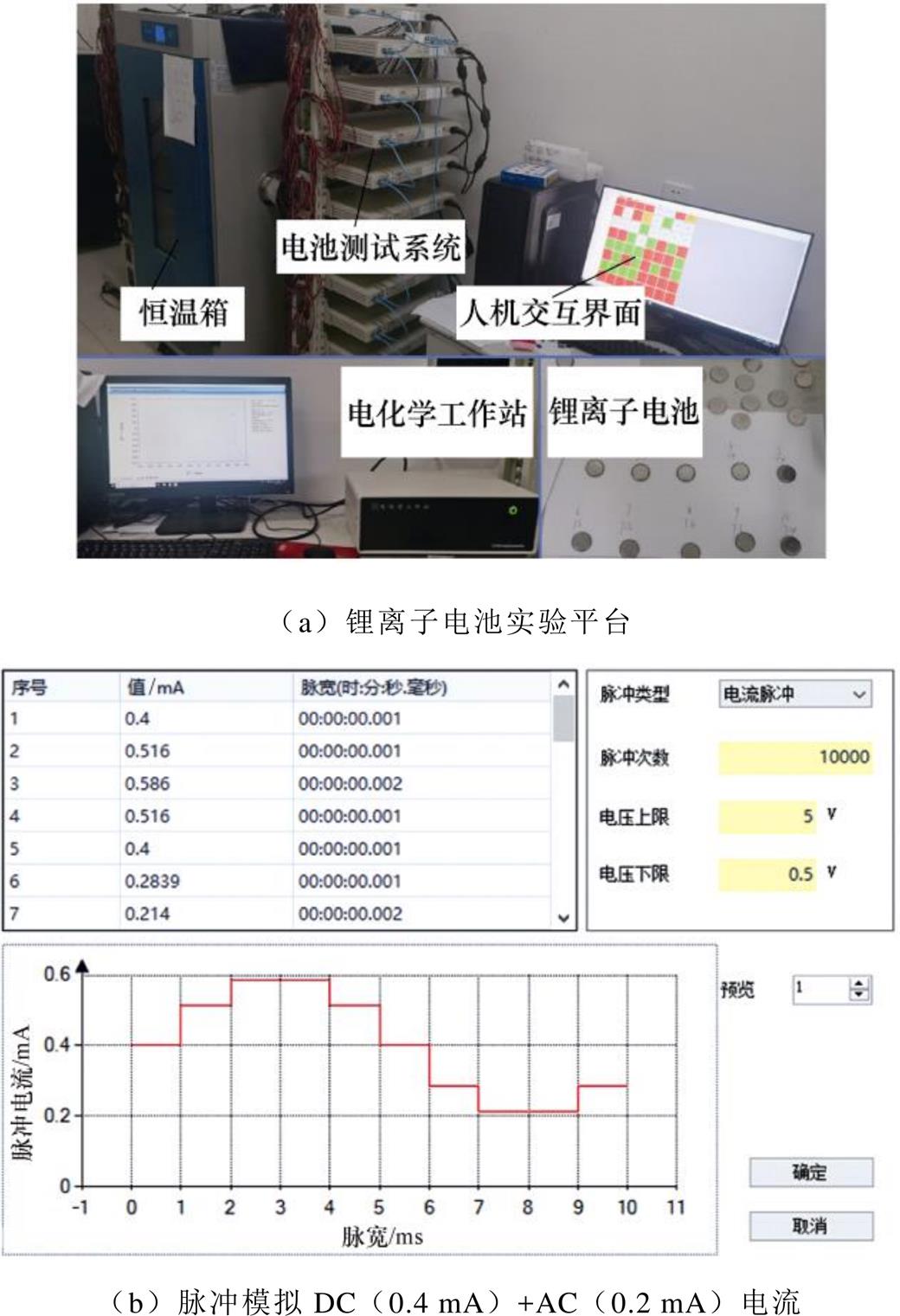
图3 实验平台和测试波形
Fig.3 Experimental platform and test waveforms
表3 实验设备部分参数
Tab.3 Experimental equipment part of the parameters
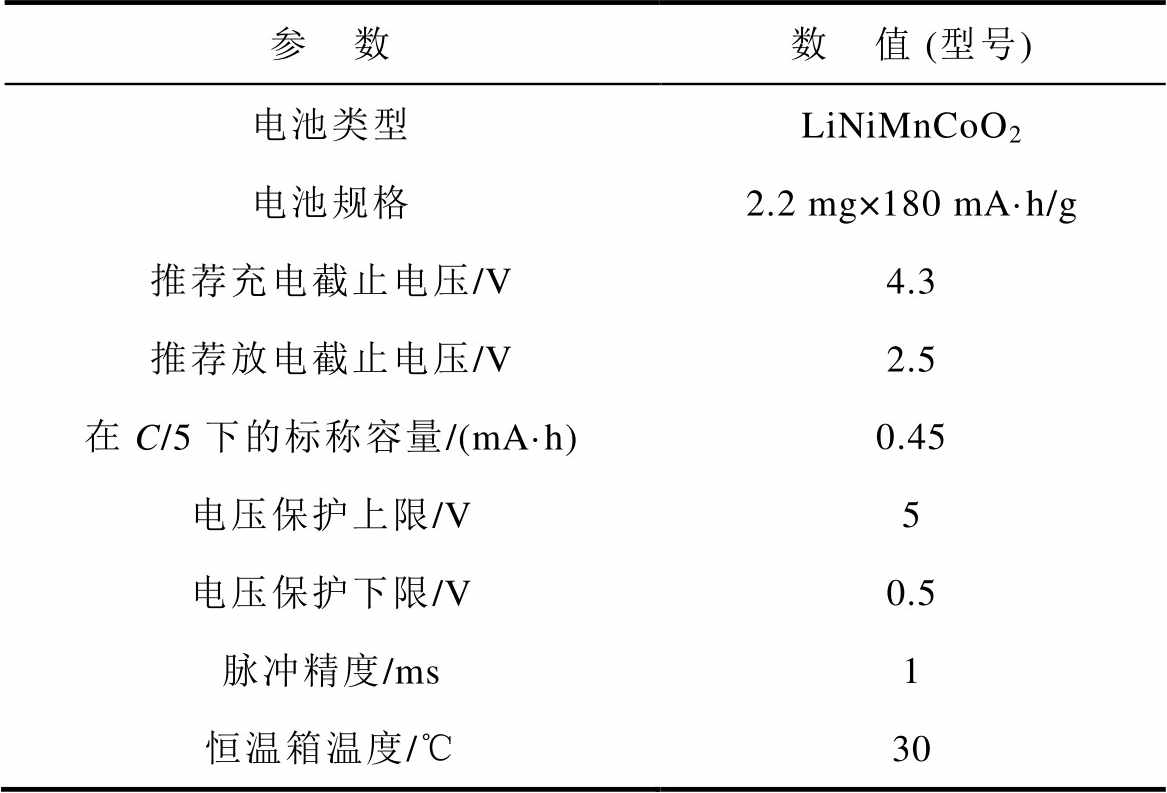
参 数数 值 (型号) 电池类型LiNiMnCoO2 电池规格2.2 mg×180 mA·h/g 推荐充电截止电压/V4.3 推荐放电截止电压/V2.5 在C/5下的标称容量/(mA·h)0.45 电压保护上限/V5 电压保护下限/V0.5 脉冲精度/ms1 恒温箱温度/℃30
本实验把6个电池随机编号成A1~A6,共6组,每个电池充放电电流的设计见表4。由于电流中2次谐波分量越大,电压波动也越大,从而含谐波分量的电池电压更快达到电池截止电压。因此,电池的充放电设置没有按截止电压进行老化循环,而是通过设置电池SOC从90%放电至20%,然后静置5 min,再充电至电池的SOC为90%并静置5 min,这算完成一次老化循环。每完成100个充放电循环后对电池进行RPT,测完后把电池放回恒温箱在30℃里继续进行老化循环实验,整个实验分别对6个电池进行了1 000次老化循环,得到实验结果见表5。
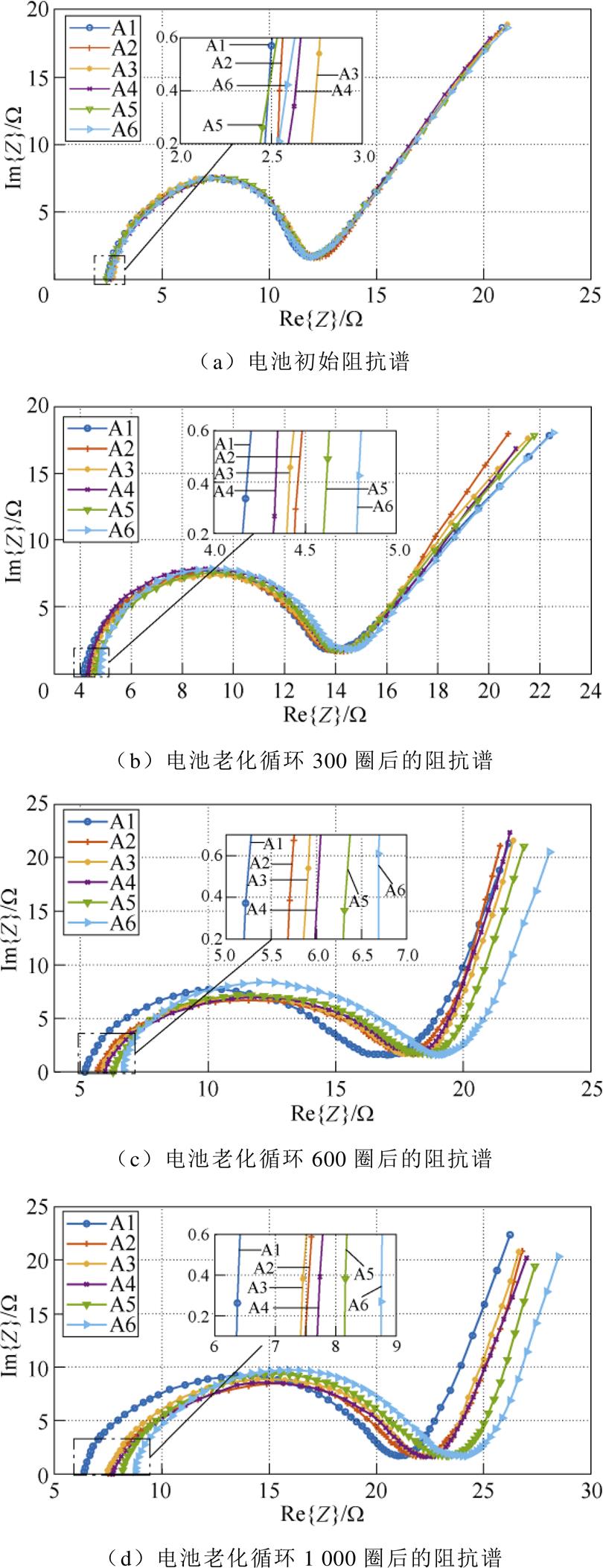
图4 不同老化阶段下电池阻抗谱
Fig.4 Battery impedance spectrum at different aging stages
表4 电池充放电电流设计
Tab.4 Battery charging and discharging current design

电池编号直流/mA交流频率/Hz交流幅值/mA充放电期间电流平均值/mARMS/mA A10.3000.30.3 A20.4000.40.4 A30.41000.20.40.423 A40.41000.30.40.45 A50.423000.4230.423 A60.45000.450.45
表5 电池不同老化圈数下的容量变化
Tab.5 Capacity change of battery with different aging turns

电池编号电池容量容量衰减 (%) 0圈100圈300圈600圈800圈1 000圈 A10.452 70.432 40.425 60.414 50.405 50.399 411.77 A20.452 20.428 90.419 50.404 80.395 40.384 814.91 A30.453 10.428 70.420 80.405 80.396 20.385 414.94 A40.451 40.427 20.420 20.403 90.392 50.384 214.89 A50.452 30.426 30.418 30.399 10.388 40.379 316.14 A60.452 40.423 80.416 10.396 30.385 40.374 117.31
结合表4的充放电电流设计以及上述实验结果可知,电池的老化速度是随着充放电状态下电流的平均值的增大而加速老化(A1、A2、A5和A6),与电流的有效值是无关联的(A2、A3和A4),造成该现象的主要原因是锂离子电池的双层电容滤除了大量纹波电流,进而对电池的寿命影响不显著。
由于纹波电流下影响锂离子电池寿命关键因素是电池充放电状态期间电流的平均值而不是有效值,故可忽略储能系统直流侧纹波电流对锂离子电池寿命的影响,除了在硬件上降低储能系统直流侧滤波器成本外,还可为优化储能安全经济运行的控制策略提供参考。
当电网出现三相不平衡时,交直流侧会出现较大的功率波动,此时变流器常用控制可归纳为三种:①控制输出电流平衡;②抑制电网侧有功功率波动;③抑制电网侧无功功率波动。通过参数k将上述三种控制策略的指令电流统一,可得到一种柔性控制策略[21],柔性控制策略下的电网侧有功功率波动的相对值DPg2w 和直流侧电压波动相对值DU2w 可分别表示[22]为
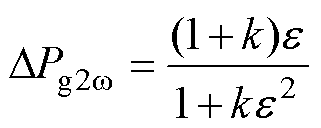 (12)
(12)
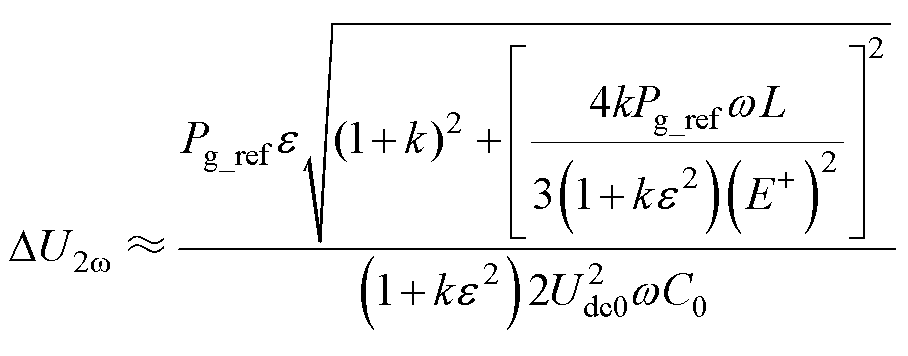 (13)
(13)
式中,e 为电网电压不平衡度,e =E-/E+,E-为负序电压,E+为正序电压;Pg_ref为交流侧功率输出参考指令;Udc0为直流侧额定电压;L和C0分别为交流侧电感和电容。
基于式(12)和式(13)得到图5所示的电网侧有功功率二倍频波动和直流侧电压二倍频波动随不平衡度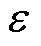 和参数k变化的关系,其中,kÎ[-1, 1],
和参数k变化的关系,其中,kÎ[-1, 1],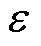 Î[0, 0.7]。
Î[0, 0.7]。
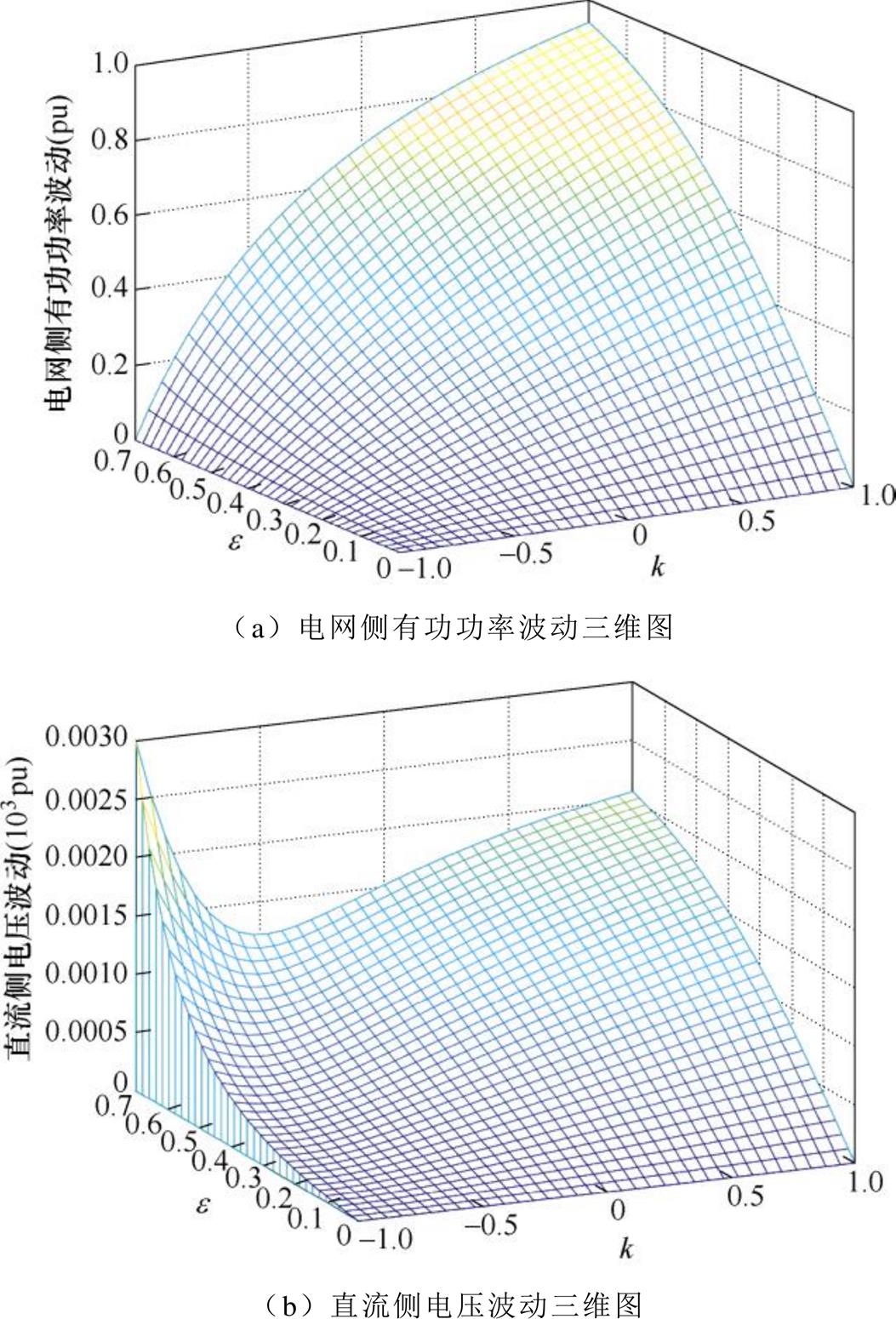
图5 交直流侧功率波动随不平衡度e 和参数k变化关系
Fig.5 AC-DC side power fluctuation with unbalance degree e and parameter k
由图5可知,当柔性控制策略的参数k=-1时,能有效抑制电网侧功率波动,虽然直流侧会产生较大的二倍频功率波动,但该波动不会增大直流侧电流的平均值,进而不会加速锂离子电池寿命的衰减。为此,在电网不平衡时采取抑制交流侧功率波动而放宽直流侧功率波动的控制策略,可实现有效抑制交流侧功率波动并且不会对储能电池产生负面影响。
为明确充放电状态期间不同大小电流平均值对电池寿命的影响,以12.8 V/40 A·h的磷酸铁锂电池为例,设置充电电流和放电电流大小一致,环境温度为25℃,电池SOC从100%放电至20%后又充电至100%,相关参数代入式(1),得到不同充放电电流下电池老化循环圈数变化曲线,如图6所示。
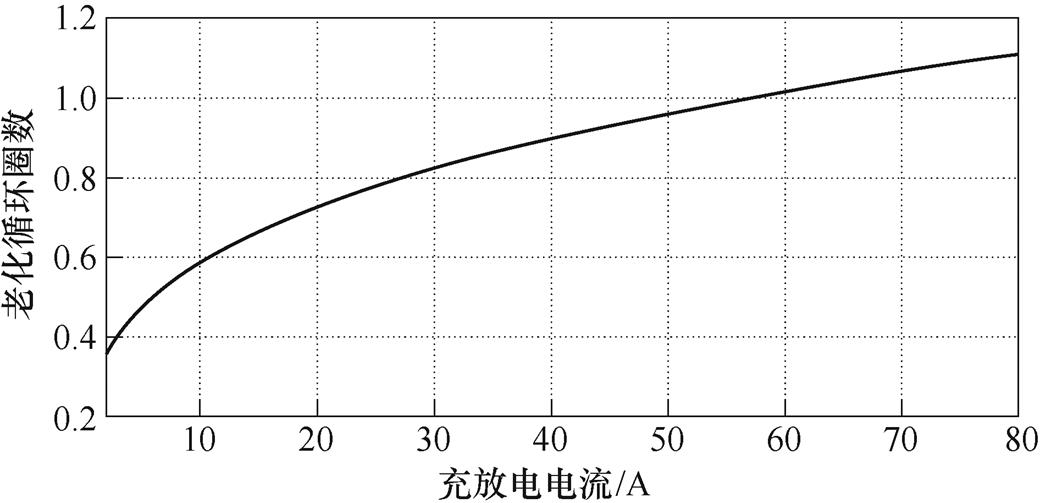
图6 不同充放电电流下电池老化循环圈数变化曲线
Fig.6 Change curve of battery aging cycle number under different charge/discharge current size
从图6可知,在经过一次充放电循环后,随着充放电电流大小的增大,电池的老化循环圈数逐渐增加且呈非线性增长。为此,可以通过减少储能电池电流的大小达到延长储能电池使用寿命。
在光储系统恒定有功功率并网下,光伏系统发电的波动性会造成其输出的功率与设置的并网功率指令之间的差额功率具有波动性,其差额功率将由储能系统承担,为延长储能电池的使用寿命,在对多台储能变流器(Power Conversion System, PCS)进行功率分配时,应尽可能地减小每台PCS的输出功率。但由于交流侧的滤波器参数是基于额定功率下进行的设计,当PCS转换的功率较小时,储能系统交直流侧会出现大量的谐波分量,对直流侧而言,可忽略谐波分量对锂离子电池寿命的影响,对交流侧而言,国内外对并网电流质量有严格限制,国家并网标准GB/T 14549以及IEEE标准IEEE 1547中规定,要求注入电网的电流总谐波畸变率(Total Harmonic Distortion, THD)应小于5%,为保障交流侧THD<5%,需要设置单台PCS的转换功率下限,避免过大的谐波注入电网对其他设备正常运行造成影响。
此外,当光伏发电功率大于并网功率参考值且两者的差额功率小于单台PCS的转换功率下限时,设计储能系统不参与并网;当光伏发电功率小于并网功率参考值且两者的差额功率小于单台PCS的转换功率下限时,设计储能系统用单台PCS参与并网,其输出功率为PCS的转换功率下限,以保证谐波含量和并网功率足够。
综上所述,基于锂离子电池寿命老化特性曲线及并网谐波含量要求,在光储系统恒定有功功率并网时,设计各台PCS功率大小为
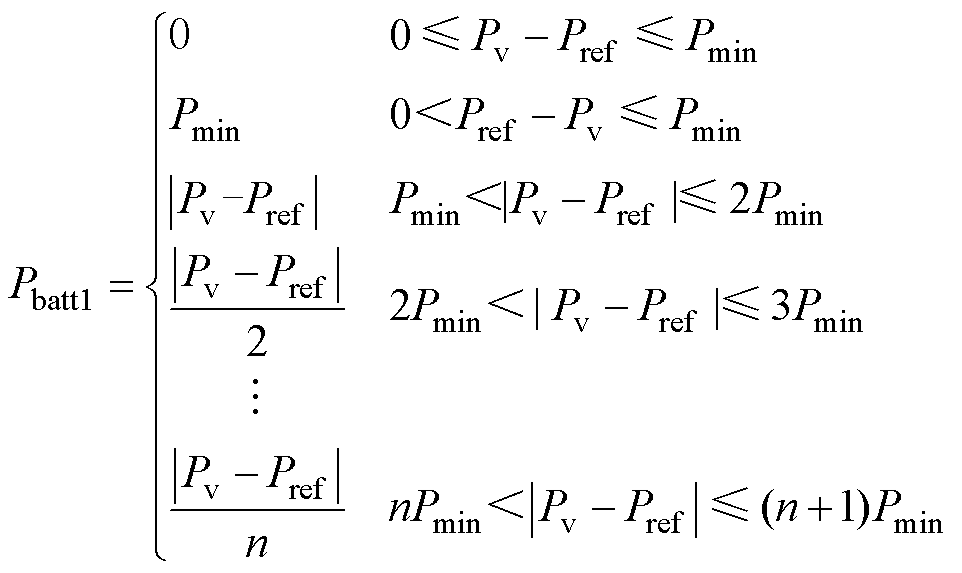 (14)
(14)
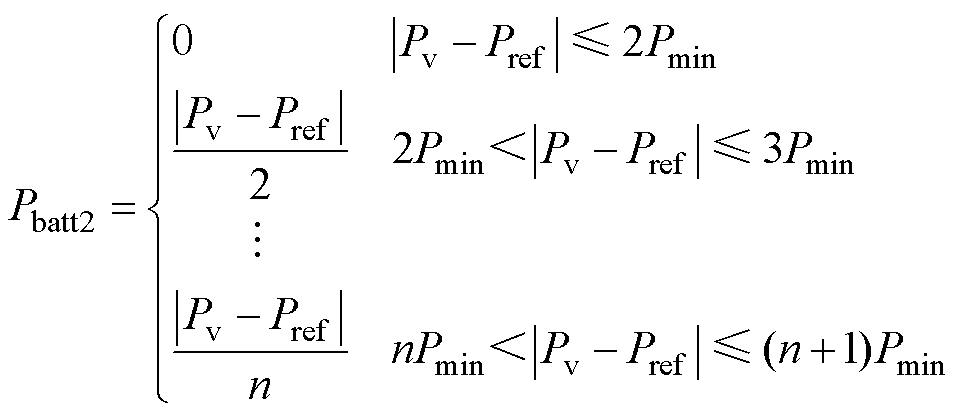 (15)
(15)
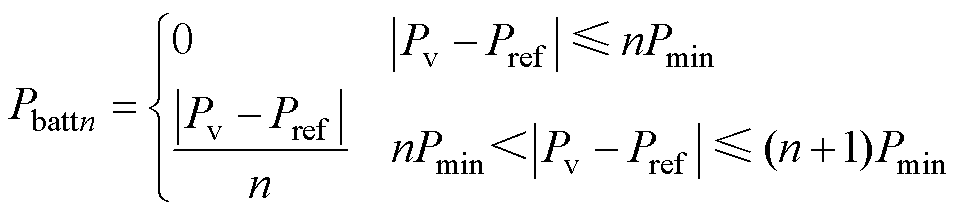 (16)
(16)
式中,Pref为设置的恒定有功功率并网指令;Pv为光伏系统发电的功率;Pmin为单台PCS的转换功率下限;Pbatt1为第1台PCS参与转换的功率;Pbattn为第n台PCS参与转换的功率。
本文选择光储系统并网的拓扑结构如图7a所示,储能电池通过双向DC-DC及PCS后向交流侧进行功率转换。储能系统并网运行时,由于LC滤波器的电容相当于负载,此时的滤波效果等同于单电感L滤波器,而LCL滤波器具有三阶传递函数,会存在谐振问题而导致系统稳定性失衡[23],故本文在光伏和储能交流侧都采用单电感L滤波器。光伏系统采用偏导法跟踪最大功率点,光伏系统并网采用双环控制,其中的外环用电压环,用于定直流侧电压,内环用电流坏,控制交流侧功率。
图7b为储能系统单台PCS并网控制框图,图中Vabc1为和Iabc1分别为PCS交流侧电压和电流,udq1和idq1为其dq轴分量,采集电池簇1的荷电状态SOC1是为了防止储能电池进行过放和过充,分别设置了放电下限为20%,充电上限为90%。协调控制器通过所设计的每台PCS并网功率的大小进行权重分配储能系统并网交流电流dq轴参考值,进而得到每台PCS交流侧电流dq轴的参考值id_ref1和iq_ref1,接着经过电压电流双环控制后生成空间矢量脉宽调制(Space Vector PWM, SVPWM)对PCS进行控制。
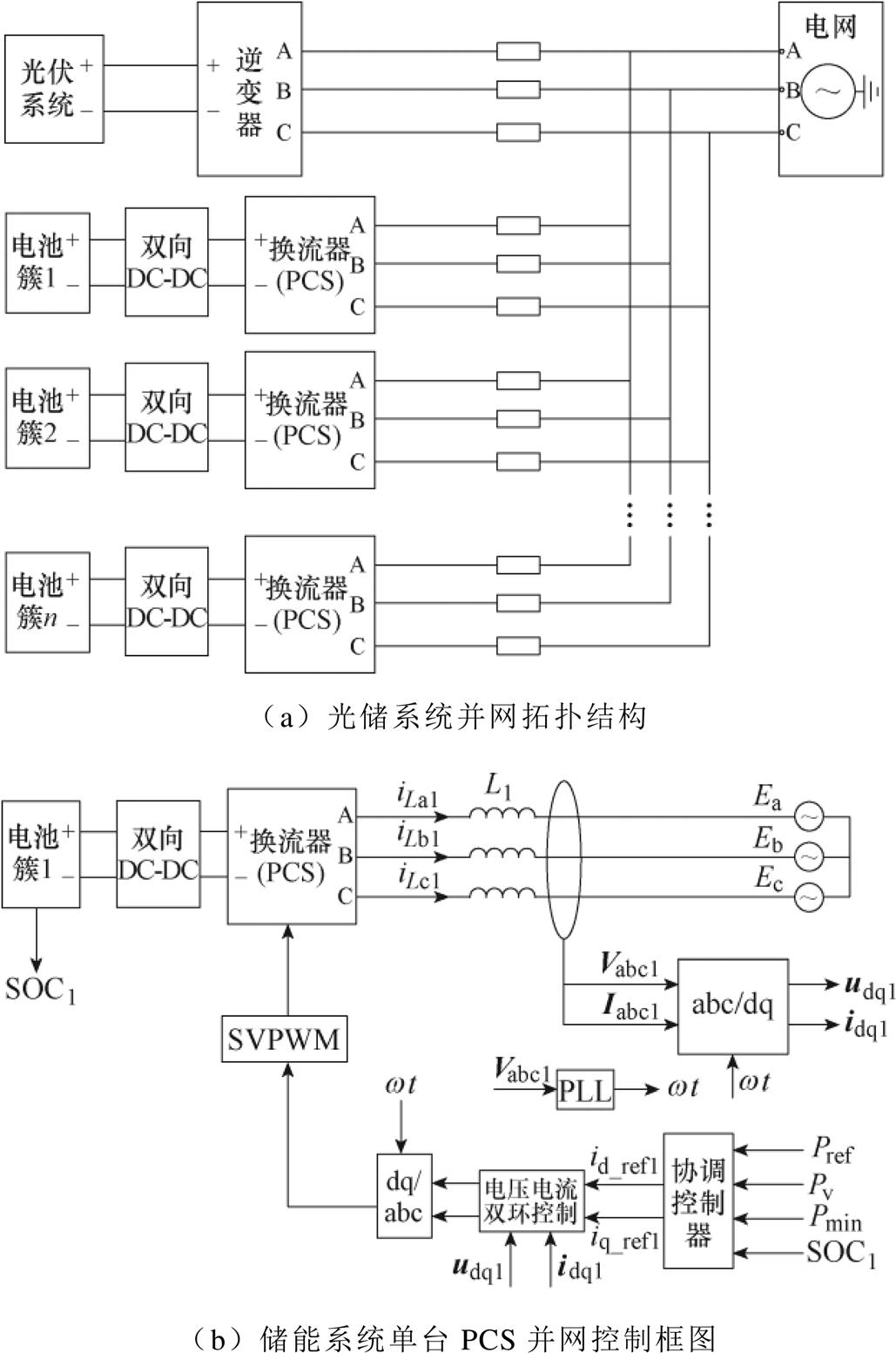
图7 储能系统并网拓扑结构及控制示意图
Fig.7 Schematic diagram of the grid-connected topology and control of the energy storage system
依据图7的光储系统并网拓扑结构及控制示意图在Simulink上搭建仿真模型,本文以3台PCS为例与光伏系统进行恒功率并网仿真,其中为了保证并网谐波含量小于5%,本文参考文献[24-25],设计单台PCS的转换功率下限Pmin为其额定功率的40%,以保证储能系统并网谐波含量符合要求,部分仿真参数的设置见表6。
在恒定有功功率并网过程中,光照强度发生变化会造成光伏系统发出不同大小的有功功率,当光伏系统实际输出有功功率为45 kW时,为保证并网谐波含量在5%以内,储能系统按单台PCS转换功率下限输出6 kW,得到的仿真结果如图8所示。
表6 部分仿真参数
Tab.6 Some simulation parameters

参 数数 值 光伏系统直流侧电压/V800 储能系统直流侧电压/V800 电网电压/V380 光伏系统和储能系统交流侧电感/mH21 光储并网恒定有功功率并网指令/kW50 光伏系统额定输出有功功率/kW60 单台PCS额定运行功率/kW15 单台PCS转换功率下限/kW40%×15
从图8可知,此时储能系统是按一台PCS参与并网,光储系统并网功率为51 kW,储能并网谐波含量为2.99%,在符合要求内。类似地,仿真出光伏系统输出不同有功功率时的情况,并与传统的控制策略进行对比(传统控制策略是指电池簇达到满载后才会投入新的电池簇参与并网运行),得到储能系统参与情况见表7。
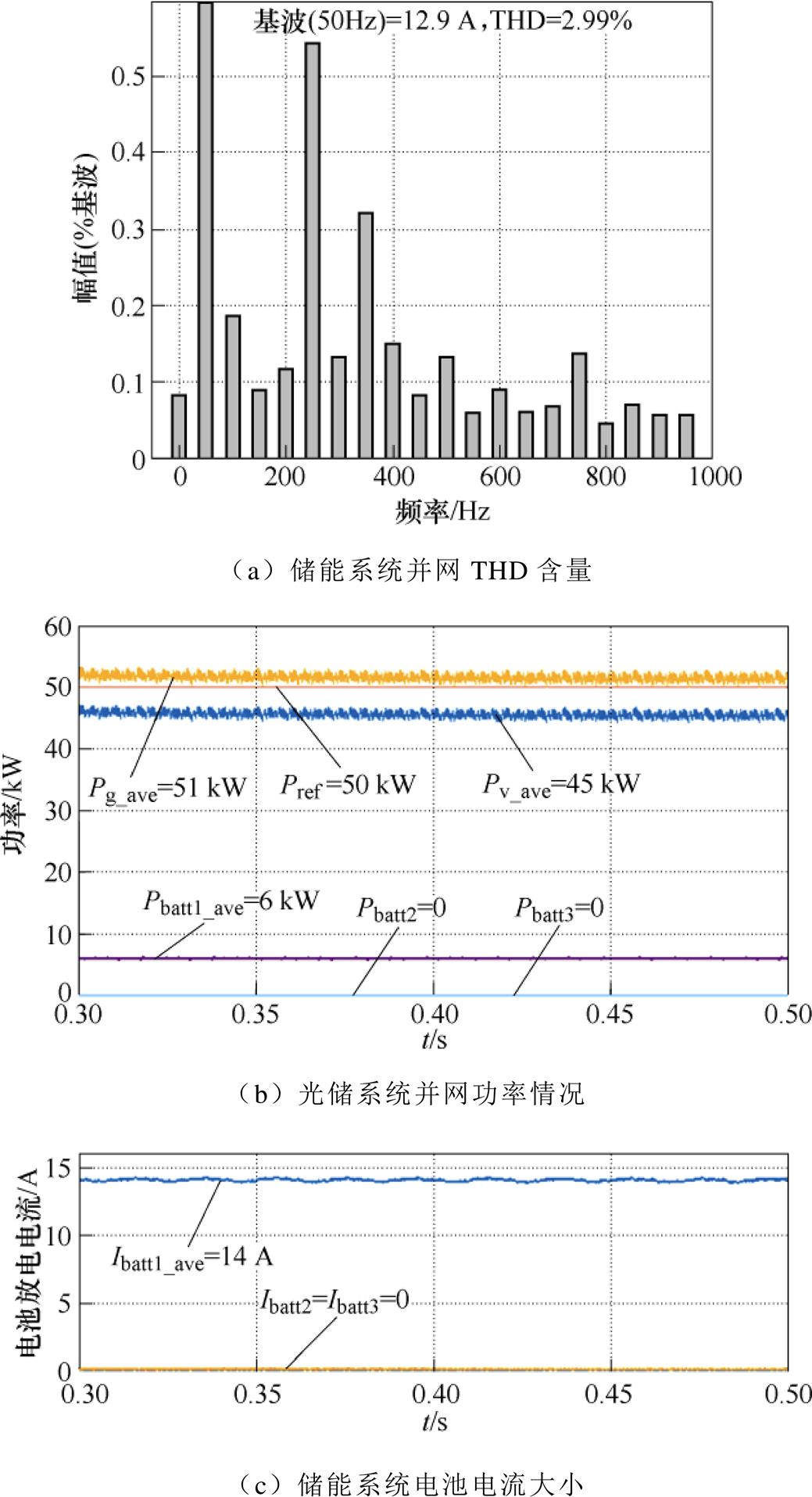
图8 光伏功率为45 kW时系统并网情况
Fig.8 Grid connection of the system at 45 kW PV power
由表7可知,本文设计的协调控制策略能够始终保持储能系统并网的谐波含量在5%以内,而采用传统的控制策略则会出现谐波含量大于5%的情况,如传统控制的序号2。此外,在都消耗电池额定容量的160%(对电池从SOC为100%放电至20%后充电至100%,共160%)下的老化循环圈数对比中,本文所设计的协调控制策略有明显的优势,如表7中的序号都为5时,与传统的控制策略相比,本文的协调控制策略可以减缓电池老化速度19.8%((0.862 5-0.692)/0.862 5≈19.8%)。因此,本文提出的基于锂离子电池老化特性和并网谐波含量要求下协调控制策略可以有效延长储能锂离子电池使用寿命。
表7 光伏不同功率下的光储系统恒定有功功率并网情况
Tab.7 Constant active power grid connection of photovoltaic storage system at different power
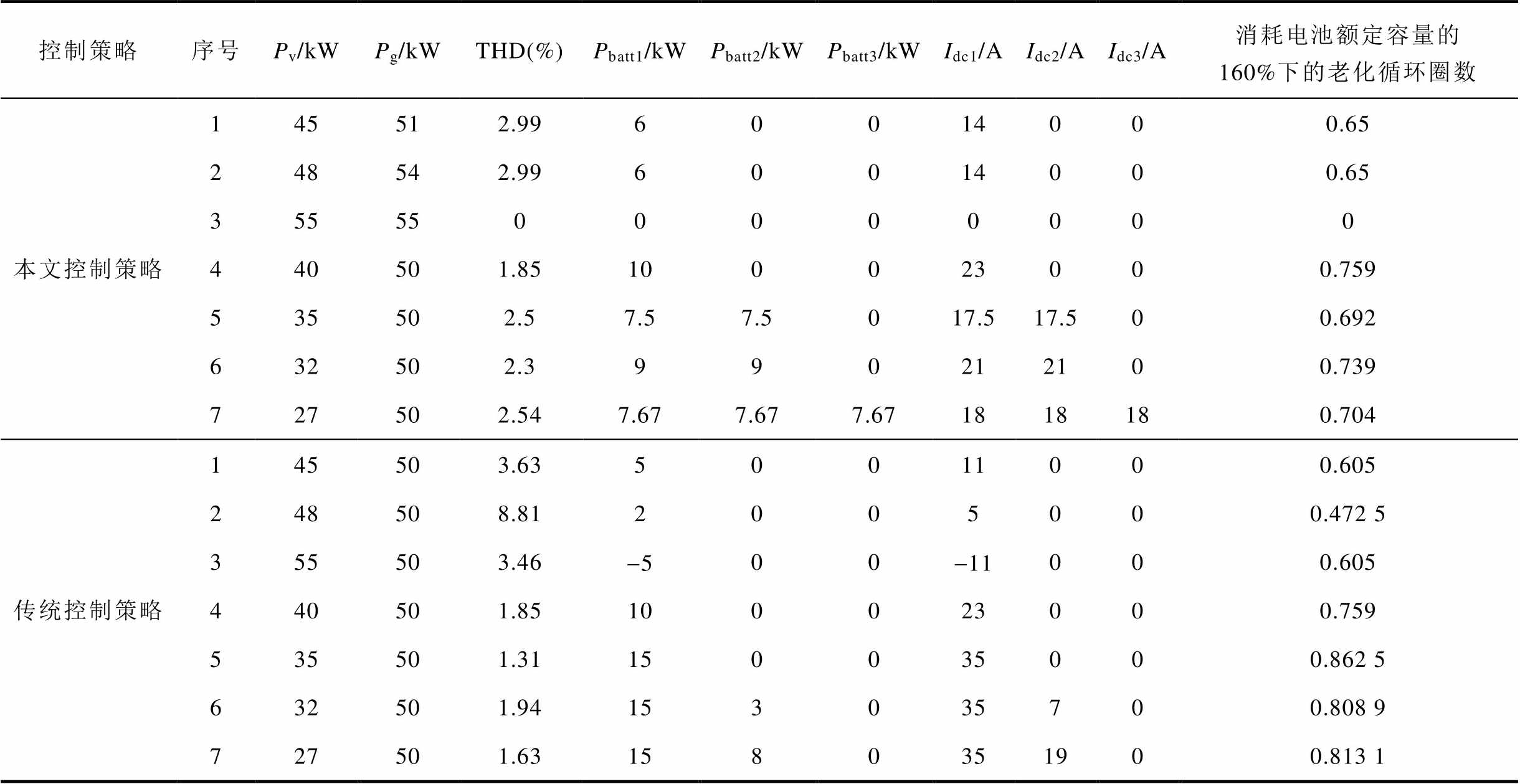
控制策略序号Pv/kWPg/kWTHD(%)Pbatt1/kWPbatt2/kWPbatt3/kWIdc1/AIdc2/AIdc3/A消耗电池额定容量的 160%下的老化循环圈数 本文控制策略145512.9960014000.65 248542.9960014000.65 3555500000000 440501.85100023000.759 535502.57.57.5017.517.500.692 632502.3990212100.739 727502.547.677.677.671818180.704 传统控制策略145503.6350011000.605 248508.812005000.472 5 355503.46-500-11000.605 440501.85100023000.759 535501.31150035000.862 5 632501.94153035700.808 9 727501.631580351900.813 1
针对储能系统直流侧纹波电流对磷酸铁锂电池寿命影响的问题,本文通过理论分析、模型仿真和实验验证研究了纹波电流下磷酸铁锂电池寿命变化规律,并基于所发现的规律优化储能系统安全运行控制策略,研究结果表明:
1)纹波电流下影响磷酸铁锂电池寿命的关键因素是电池充放电状态期间的电流平均值而非电流有效值,电池充放电状态期间的电流平均值越大,电池老化程度越快且呈非线性。
2)纹波电流不会增大电池充放电状态下电流的平均值,可在工程应用中忽略纹波电流对储能磷酸铁锂电池寿命的影响,为优化储能系统安全经济运行的控制策略提供了依据。
3)在电网不平衡时可采取抑制交流侧功率波动而放宽直流侧功率波动的优化控制策略,实现抑制交流侧功率波动而不影响磷酸铁锂电池寿命;在光储系统恒定有功功率并网时,基于电池老化特性曲线和储能系统并网谐波含量符合要求下,提出了一种延长储能电池使用寿命的多储能变流器协调控制策略,与传统控制策略相比,可减缓电池老化速度19.8%。
参考文献
[1] 李建林, 李雅欣, 刘海涛, 等. 计及储能电站安全性的功率分配策略研究[J]. 电工技术学报, 2022, 37(23): 5976-5986.
Li Jianlin, Li Yaxin, Liu Haitao, et al. Research on power distribution strategy considering the safety of energy storage power station[J]. Transactions of China Electrotechnical Society, 2022, 37(23): 5976- 5986.
[2] 夏向阳, 易浩民, 邱欣, 等. 双重功率优化控制的规模化光伏并网电压越限研究[J]. 中国电机工程学报, 2016, 36(19): 5164-5171, 5397.
Xia Xiangyang, Yi Haomin, Qiu Xin, et al. Research on dual power optimal control for scaled photovoltaic grid-connected voltage[J]. Proceedings of the CSEE, 2016, 36(19): 5164-5171, 5397.
[3] 武龙星, 庞辉, 晋佳敏, 等. 基于电化学模型的锂离子电池荷电状态估计方法综述[J]. 电工技术学报, 2022, 37(7): 1703-1725.
Wu Longxing, Pang Hui, Jin Jiamin, et al. A review of SOC estimation methods for lithium-ion batteries based on electrochemical model[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1703- 1725.
[4] 郭慧, 汪飞, 顾永文, 等. 基于电压分层控制的直流微电网及其储能扩容单元功率协调控制策略[J]. 电工技术学报, 2022, 37(12): 3117-3131.
Guo Hui, Wang Fei, Gu Yongwen, et al. Coordinated power control strategy for DC microgrid and storage expansion unit based on voltage hierarchical control[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3117-3131.
[5] 许阔, 王婉君, 贾利虎, 等. 混合微电网交流不对称故障对直流系统的影响[J]. 中国电机工程学报, 2018, 38(15): 4429-4437, 4643.
Xu Kuo, Wang Wanjun, Jia Lihu, et al. Influence of AC unbalanced faults on DC system of hybrid AC/DC microgrid[J]. Proceedings of the CSEE, 2018, 38(15): 4429-4437, 4643.
[6] 朱永强, 刘康, 张泉, 等. 混合微电网交流侧故障传播机理及抑制方法[J]. 电机与控制学报, 2020, 24(4): 1-11.
Zhu Yongqiang, Liu Kang, Zhang Quan, et al. Fault propagation mechanism and suppression method on AC side of hybrid microgrid[J]. Electric Machines and Control, 2020, 24(4): 1-11.
[7] Juang L W, Kollmeyer P J, Anders A E, et al. Investigation of the influence of superimposed AC current on lithium-ion battery aging using statistical design of experiments[J]. Journal of Energy Storage, 2017, 11: 93-103.
[8] Uddin K, Somerville L, Barai A, et al. The impact of high-frequency-high-current perturbations on film formation at the negative electrode-electrolyte inter- face[J]. Electrochimica Acta, 2017, 233: 1-12.
[9] Uddin K, Moore A D, Barai A, et al. The effects of high frequency current ripple on electric vehicle battery performance[J]. Applied Energy, 2016, 178: 142-154.
[10] Uno M, Tanaka K. Influence of high-frequency charge-discharge cycling induced by cell voltage equalizers on the life performance of lithium-ion cells[J]. IEEE Transactions on Vehicular Technology, 2011, 60(4): 1505-1515.
[11] Beh H Z Z, Covic G A, Boys J T. Effects of pulse and DC charging on lithium iron phosphate (LiFePO4) batteries[C]//2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 2013: 315-320.
[12] Bala S, Tengnér T, Rosenfeld P, et al. The effect of low frequency current ripple on the performance of a lithium iron phosphate (LFP) battery energy storage system[C]//2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 2012: 3485-3492.
[13] De Breucker S, Engelen K, D'Hulst R, et al. Impact of current ripple on Li-ion battery ageing[C]//2013 World Electric Vehicle Symposium and Exhibition (EVS27), Barcelona, Spain, 2014: 1-9.
[14] Brand M J, Hofmann M H, Schuster S S, et al. The influence of current ripples on the lifetime of lithium- ion batteries[J]. IEEE Transactions on Vehicular Technology, 2018, 67(11): 10438-10445.
[15] Ghassemi A, Banerjee P C, Zhang Zhe, et al. Aging effects of twice line frequency ripple on lithium iron phosphate (LiFePO4) batteries[C]//2019 21st European Conference on Power Electronics and Applications (EPE'19 ECCE Europe), Genova, Italy, 2019: 1-9.
[16] Bessman A, Soares R, Wallmark O, et al. Aging effects of AC harmonics on lithium-ion cells[J]. Journal of Energy Storage, 2019, 21: 741-749.
[17] Ghassemi A, Chakraborty Banerjee P, Hollenkamp A F, et al. Effects of alternating current on Li-ion battery performance: monitoring degradative pro- cesses with in situ characterization techniques[J]. Applied Energy, 2021, 284: 116192.
[18] Tremblay O, Dessaint L A. Experimental validation of a battery dynamic model for EV applications[J]. World Electric Vehicle Journal, 2009, 3(2): 289-298.
[19] Omar N, Abdel Monem M, Firouz Y, et al. Lithium iron phosphate based battery-assessment of the aging parameters and development of cycle life model[J]. Applied Energy, 2014, 113: 1575-1585.
[20] SIMULINK: Generic battery model[EB/OL]. https:// www.mathworks.com/help/releases/R2020a/physmod/sps/powersys/ref/battery.html.
[21] 李金科, 金新民, 吴学智, 等. 网压不平衡下系统控制目标对MMC运行性能的影响[J]. 电工技术学报, 2016, 31(增刊2): 39-48.
Li Jinke, Jin Xinmin, Wu Xuezhi, et al. The influence of system operation objectives on operation characteristics for MMC under unbalanced grid conditions[J]. Transactions of China Electrotechnical Society, 2016, 31(S2): 39-48.
[22] 欧名勇, 王逸超, 刘文军, 等. 电网电压不平衡下储能变流器的控制策略[J]. 中国电力, 2022, 55(7): 93-101.
Ou Mingyong, Wang Yichao, Liu Wenjun, et al. Control strategy of power conversion system under unbalanced grid voltage[J]. Electric Power, 2022, 55(7): 93-101.
[23] 汤锦慧. 基于虚拟同步机控制的LCL型并网逆变器的研究[D]. 北京: 华北电力大学, 2016.
[24] 张雪. 非隔离型光伏并网逆变器高效MPPT控制方法研究[D]. 广州: 华南理工大学, 2012.
[25] 张思章. 高频隔离型并网逆变器的研制[D]. 广州: 华南理工大学, 2012.
Abstract The rapid development of “new energy + energy storage” integration has introduced numerous power electronic devices into the power system, leading to a large number of ripple currents in the DC side of energy storage systems. Current research reflected in the effective value and harmonic frequency has not reached a consensus. In addition, it is necessary to optimize the energy storage system’s safe operation control strategy while considering the changing characteristics of lithium-ion battery life. Therefore, this paper analyzes the effect of ripple current on the lifetime of Li-ion batteries through theoretical analysis, model simulation, and experimental validation.
The ripple current is first decomposed into Fourier series and introduced into the expression of the lithium-ion battery life model by simplifying the variables unrelated to the harmonic components and retaining the variables in the current affected by the harmonic components. The results show that the key factor affecting the life of Li-ion batteries in the presence of ripple currents is the average current value during charging and discharging. A higher average current value in the charge and discharge states results in accelerated battery ages.
Six sets of charging and discharging currents are designed on the Li-ion battery experimental platform. The results show that the aging rate of the battery is accelerated with the increase of the average current value during the charge/discharge state. The influence of the effective current value is found to be less significant. Since the double-layer capacitor of the Li-ion battery filters out a large amount of ripple current, the effect of the effective current is notably reduced.
The following conclusions are drawn: (1) The key factor affecting the life of Li-ion batteries under ripple current is the average current value during charging and discharging, not the effective current value. Larger average current values lead to faster and more non-linear battery aging. (2) Ripple current does not increase the average current value during the charging and discharging states of the battery. Therefore, the ripple current’s impact on energy storage system life can be ignored in engineering applications. It provides a basis for optimizing control strategies to ensure the safe and economic operation of the energy storage system. (3) When the grid is unbalanced, an optimized control strategy can be adopted to suppress power fluctuations on the AC side and alleviate power fluctuations on the DC side without affecting the life of lithium-ion batteries. When the light storage system is connected to the grid with constant active power, based on the battery aging characteristic curve and the grid connection of the energy storage system, a coordinated control strategy of multiple converters is proposed. This strategy extends the life of energy storage batteries and can reduce the battery aging rate by 19.8% compared with the traditional control strategy.
Keywords:Energy storage systems, Li-ion battery life, ripple current, average value, coordinated control strategy
夏向阳 男,1968年生,教授,博士生导师,研究方向为电网储能安全运行与优化控制。E-mail: xia_xy@126.com
陈贵全 男,1997年生,博士研究生,研究方向为储能安全运行与优化控制。E-mail: 1959248924@qq.com(通信作者)
中图分类号:TM911.3; TM46
DOI: 10.19595/j.cnki.1000-6753.tces.230504
国家自然科学基金项目(51977014)和湖南省研究生科研创新项目(CX20230894)资助。
收稿日期2023-04-20
改稿日期 2023-06-21
(编辑 陈 诚)