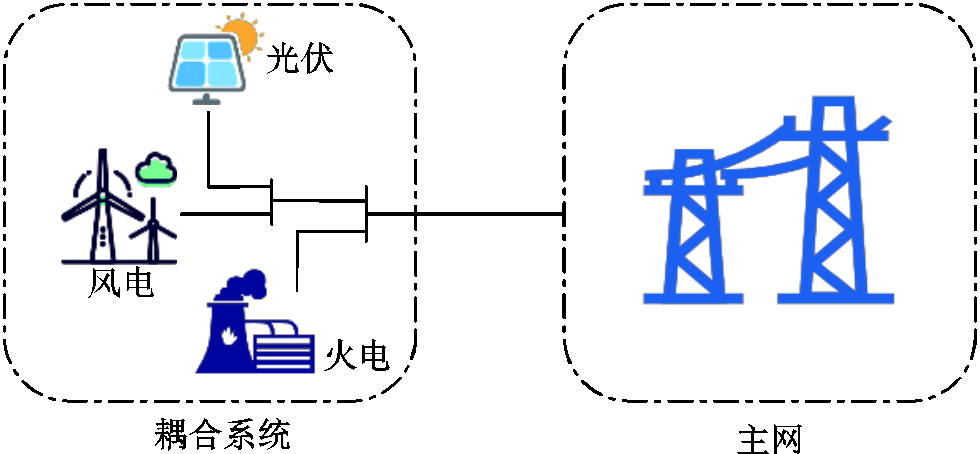
图1 耦合系统示意图
Fig.1 The typical structure of a coupled system
摘要 火电与可再生能源在同一并网点集成为耦合系统能够有效促进可再生能源消纳。传统随机生产模拟方法难以充分考虑外部市场竞争以及内部机组协同对耦合系统运行的影响。为此,提出一种考虑外部博弈和内部协同的耦合系统时序随机生产模拟方法。首先,基于主从博弈,刻画耦合系统与其他发电商及电网之间的电量-电价竞争关系,基于合作博弈,建立了反映耦合系统内火电与可再生能源机组合作竞争关系的内部协同模型;然后,建立考虑外部博弈和内部协同嵌套的耦合系统时序随机生产模拟方法,提出耦合系统的可靠性评估指标以及内部机组经济收益分配方法;最后,采用中国东北某区域电网的实测数据,验证了所提方法的有效性和正确性。仿真结果表明,通过外部博弈和内部协同,耦合系统的经济性和可靠性大幅提升。
关键词:耦合系统 内部协同 外部博弈 随机生产模拟 电力市场
近年来,可再生能源大规模并网导致优质消纳困难[1-3]。国家发展改革委和国家能源局出台了关于“风光火储一体化”的指导意见,强调要充分利用各类能源的互补协调能力,提高可再生能源消纳水平[4]。
我国北方电力系统中普遍存在火电与可再生能源在同一并网点实现物理耦合的耦合系统[5],在提高可再生能源消纳水平的同时又能以更加低廉、可控的出力参与电力市场交易,有利于推进可再生能源规模化发展。如何实现电力市场环境下耦合系统经济性和可靠性的准确评估,对于耦合系统的规划与运行具有重要的理论研究价值和工程应用前景。
随机生产模拟是反映电力系统时序运行状态,评估整体经济性和可靠性的关键基础工具[6-7],可有效支撑多电源耦合系统运行、规划及市场交易等策略制定[8]。近年来,围绕多电源系统的随机生产模拟方法,现有文献开展了大量卓有成效的研究工作[9-15]。其中,文献[9]考虑不同风电消纳策略,建立了风-火联合外送的互联系统随机生产模拟,为互联系统规划、运行提供科学的决策依据;文献[11]结合机组多状态模型提出含风-光-水-火电力系统的多状态随机生产模拟方法,以评估新能源时序特性对常规机组启停的影响;文献[12-13]基于有效容量分布法建立了含风-储多能互补电力系统的时序随机生产模拟方法,量化评估不同调度策略下多能互补系统的可靠性及新能源消纳水平;文献[14]将系统运行调度策略与随机生产模拟中各类型机组的加载顺序相结合,构建了考虑断面约束的多能源电力系统时序随机生产模拟方法,充分保证新能源的优先消纳;文献[15]考虑日前机组组合计划,基于时序负荷曲线,利用随机生产模拟方法建立反映风-火发电系统调节能力的运行备用容量与可靠性之间的量化关系。
然而,上述随机生产模拟方法重点关注系统的时序性和各机组间的相互作用及其对电力系统整体性能的影响。鲜有计及市场竞争环境对多电源耦合系统运行影响的随机生产模拟方法,难以准确评估市场环境下耦合系统的经济性和可靠性水平。
在市场环境下,博弈论作为处理多主体问题的有效方法,被广泛应用于多能源系统耦合的优化运行中。文献[16]基于合作博弈论分析了风火联合外送模式,结果表明相较独立外送,联合外送更有利于提高系统整体经济效益;文献[17]采取合作博弈优化机组运行,并结合Shapley收益分配方法调动虚拟电厂中可再生能源与可控机组协同的积极性;文献[18]为解决供给侧风电消纳问题,提出了风火网三方非合作博弈模型。上述研究往往只考虑多主体耦合系统的外部竞争或内部合作的单一利益关系,而本文研究的可再生能源与火电在同点并网的耦合系统实现了物理耦合,在参与市场竞争时,需计及内部机组运行和外部市场竞争的耦合关系,而现有研究忽略了火电与可再生能源耦合系统内部协同和外部博弈的关联关系,适用性有限,无法充分挖掘耦合系统整体经济性的提升潜力。
针对传统方法无法适应市场环境下耦合系统外部博弈和内部协同的耦合关系,且缺乏有效的耦合系统可靠性和经济性评估方法,本文在深入分析耦合系统内外协同竞争机制的基础上,提出考虑外部博弈和内部协同的耦合系统时序随机生产模拟方法。首先,基于主从博弈,刻画了耦合系统与其他发电商及电网之间的电量-电价竞争关系,建立了反映耦合系统内火电与可再生能源机组协同竞争关系的合作博弈模型;然后,结合时序负荷曲线模拟思想,建立了考虑耦合系统外部博弈和内部协同嵌套的时序随机生产模拟方法,提出了耦合系统可靠性评估指标以及内部机组经济收益分配方法;最后,采用中国东北某区域电网的实测数据,验证了本文方法的有效性。
广义的耦合系统可理解为电力系统中由不同类型电源集成的复合电能生产主体[19],如风火打捆、虚拟电厂等。本文研究的耦合系统特指火电与风电、光伏等可再生能源在同点并网,与空间位置分散的风光火打捆发电系统不同,本文所提耦合系统通过在同点并网,可真正实现火电与可再生能源在物理空间上的耦合。因此,本文的耦合系统可作为整体可控的调控对象和运营主体参与电力系统运行,更具有调度优势。耦合系统示意图如图1所示。
耦合系统利用结构优势可充分发挥火电的灵活调节能力平抑风光出力波动,提高可再生能源消纳水平及电力系统安全、经济运行水平。在电力市场中,耦合系统依靠内部火电与可再生能源的协同配合,可实现低成本、低碳运行,并展现出良好的调节性能,能够大幅提高耦合系统的市场竞争力与经济效益。因此,需综合考虑耦合系统的外部市场竞争环境与内部机组协调配合之间的关联关系,进行耦合系统随机生产模拟,充分挖掘耦合系统灵活运行的潜能。

图1 耦合系统示意图
Fig.1 The typical structure of a coupled system
考虑耦合系统结构特点及运行特点,建立了外部博弈和内部协同机制及随机生产模拟框架,如图2所示。通过外部博弈和内部协同确定耦合系统交易及经济运行策略,利用时序随机生产模拟方法评估耦合系统的经济性和可靠性。
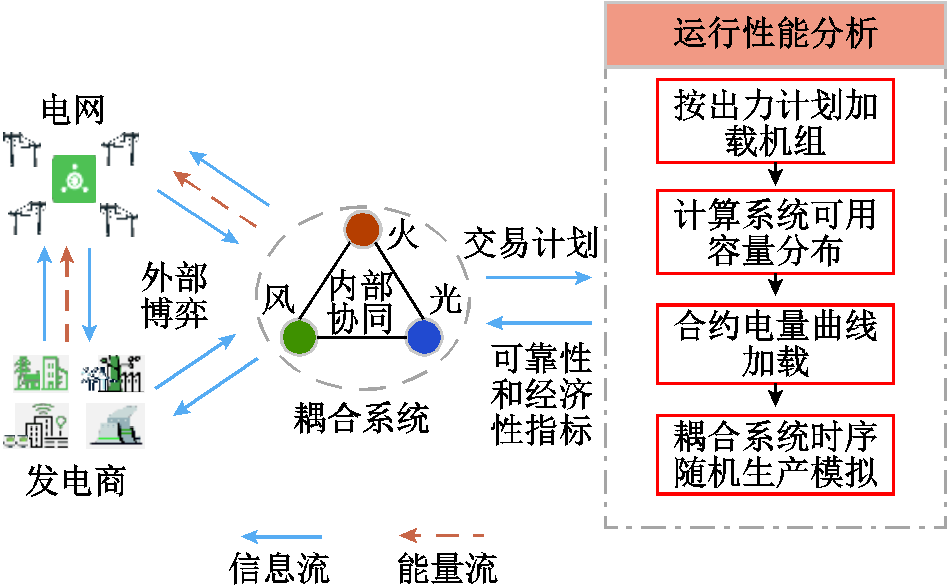
图2 外部博弈和内部协同下耦合系统时序随机生产模拟框架
Fig.2 The framework of sequential probabilistic production simulation for a coupled system considering external game and internal collaboration
在中长期电力市场中,耦合系统与其他发电商、电网之间存在竞争博弈关系。作为售电商,耦合系统与其他发电商都希望通过改变自身报价,获取更高的经济效益,因此两者之间形成非合作博弈关系。而电网在掌握耦合系统与其他发电商的报价信息后,通过优化购电策略,以最小的购电成本满足电网电量需求。电网购电策略会影响各耦合系统与其他发电商的报价策略。因此,电网与耦合系统及其他发电商之间形成主从博弈关系。耦合系统最终的报价决策和交易电量受到电网购电行为和其他发电商报价行为的共同影响[20]。
为降低耦合系统完成合约电量的发电成本,应适当压缩火电的发电空间,提高可再生能源上网电量。然而,火电的利益必将受到损害,其提供灵活调节能力参与耦合系统运行的积极性会降低,从而影响耦合系统整体的安全性和经济性。因此,需要通过合理的利益分配机制,提高火电积极性,促使火电与可再生能源形成合作联盟,保证耦合系统履行合约电量的经济性和可靠性。
耦合系统内外协同配合,可最大程度提高耦合系统售电收益。外部博弈确定的合约电量曲线为耦合系统内部机组协同运行提供边界。内部机组协同优化不仅降低了发电成本,还可提升耦合系统外部博弈竞争能力,进一步提高耦合系统的经济效益,从而形成外部博弈和内部协同的良性循环。
考虑发电商之间的非合作博弈关系以及电网与发电商之间的主从博弈关系,建立耦合系统的外部主从博弈模型,逻辑框图如图3所示。其中,耦合系统和其他发电商作为领导者处于博弈上层,以电价为策略空间;电网作为跟随者处于博弈下层,以交易电量为策略空间。发电商和电网通过改变报价与购电策略达到主从博弈的纳什均衡[21-22]。
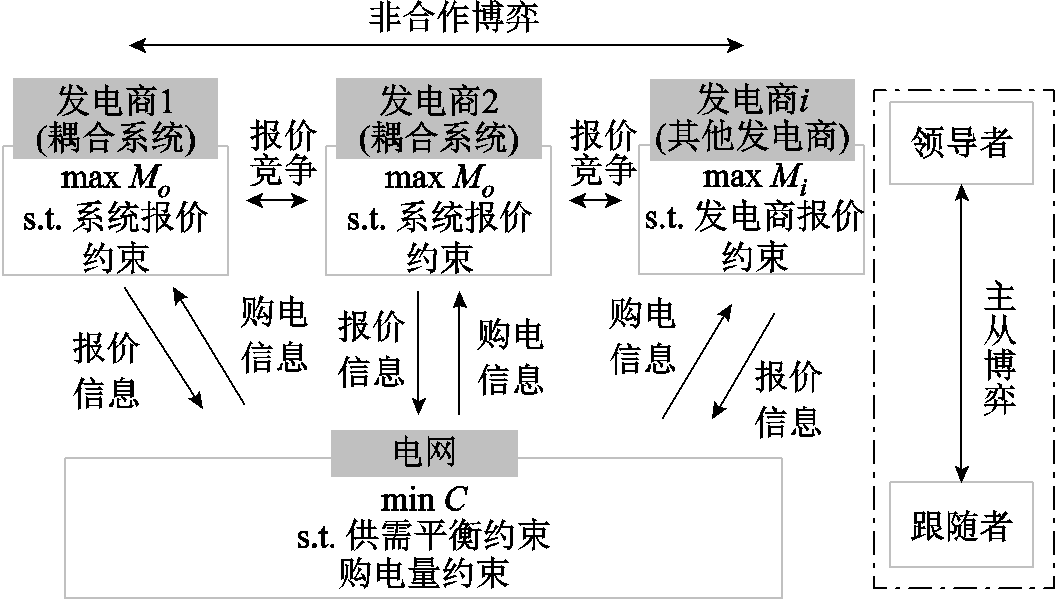
图3 耦合系统外部博弈逻辑框图
Fig.3 The framework of a coupled system considering external game
2.1.1 耦合系统与其他发电商的非合作博弈模型
本文建立了耦合系统与其他发电商的非合作博弈模型,分析其他发电商对耦合系统报价决策的影响。
1)耦合系统博弈模型
考虑售电收益、发电成本、火电机组碳排放惩罚成本、弃能惩罚成本等,以收益最大为目标,建立耦合系统博弈模型,即
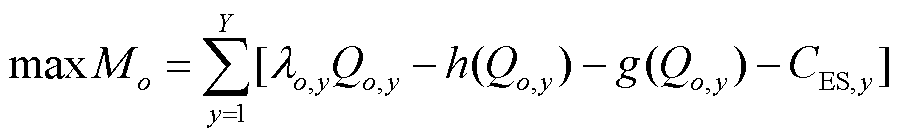 (1)
(1)
其中
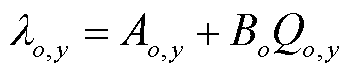 (2)
(2)
式中,Y为交易周期,当进行年度双边交易时,Y=12;λo,y为第y月耦合系统o的报价;Ao,y为第y月耦合系统o初始报价,是耦合系统决策变量;Bo为耦合系统电价增长参数;Qo,y为第y月耦合系统o与电网成交电量,由博弈下层反馈给博弈上层;h(Qo,y)为耦合系统o发电成本;g(Qo,y)为火电机组二氧化碳排放惩罚成本,与火电机组各时刻出力相关;CES,y为弃能惩罚成本,可由2.2节建立的内部协同优化模型确定。
耦合系统的初始报价需要限制在式(3)所示的范围内。
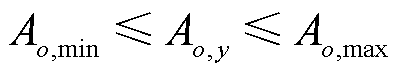 (3)
(3)
式中,Ao,min、Ao,max分别为耦合系统o初始报价的最小、最大值。
2)其他发电商博弈模型
考虑不同类型发电商的经济运行特性,分别建立火电等常规发电商博弈模型及风光等可再生能源发电商博弈模型。
常规发电商博弈模型中主要考虑火电售电收益、发电成本及环境惩罚成本,其目标函数为
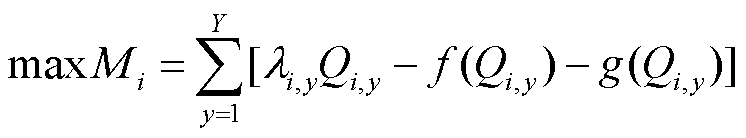 (4)
(4)
其中
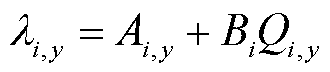 (5)
(5)
式中,Mi为发电商i的收益;λi,y为第y月发电商i的报价;Ai,y为第y月发电商i初始报价,是发电商i的决策变量;Bi为发电商i电价增长参数;Qi,y为第y月发电商与电网成交电量,由博弈下层反馈给博弈上层;f(Qi,y)为发电成本函数;g(Qi,y)为环境惩罚成本函数。
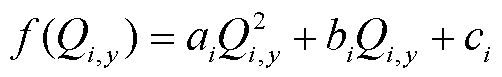 (6)
(6)
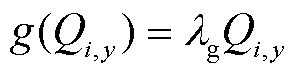 (7)
(7)
式中,lg为火力发电的二氧化碳排放惩罚系数[23];ai、bi、ci为发电商i的发电成本系数。
风光等可再生能源在发电过程中无燃料消耗,在博弈模型中无需考虑发电成本,只需计及售电收益和可再生能源出力偏差惩罚成本,有
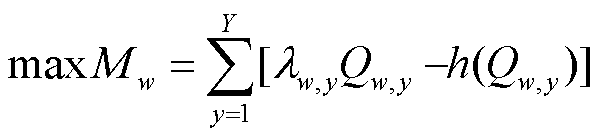 (8)
(8)
式中,λw,y为第y月可再生能源发电商w的报价;Qw,y为第y月可再生能源发电商w与电网成交电量;h(Qw,y)为可再生能源出力偏差惩罚函数。
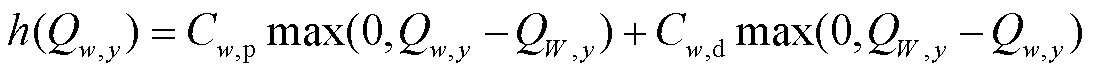 (9)
(9)
式中,Cw,p、Cw,d分别为可再生能源发电商w发电量高估和低估偏差的惩罚系数;QW,y为第y月可再生能源发电商w实际发电量。
为防止恶行竞争,发电商报价的决策变量需限制在式(10)、式(11)所示的范围内。
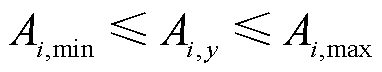 (10)
(10)
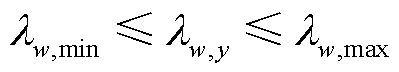 (11)
(11)
式中,Ai,min、Ai,max分别为发电商i初始报价的最小、最大值;λw,min、λw,max分别为可再生能源发电商w报价的最小、最大值。
2.1.2 电网购电策略模型
作为主从博弈中的跟随者,电网根据各发电商的报价和出力预测,以购电成本最小为目标确定购电策略模型,即
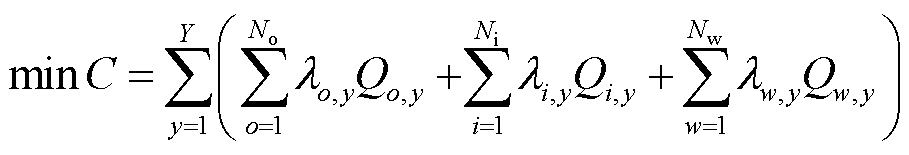 (12)
(12)
式中,No为耦合系统总数;Ni为常规发电商总数;Nw为可再生能源发电商总数。
该模型还需满足供需平衡及购电量约束。
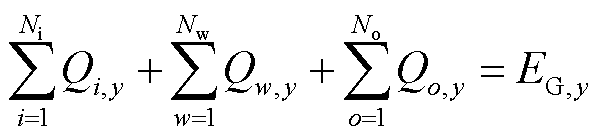 (13)
(13)
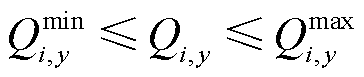 (14)
(14)
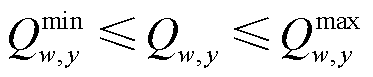 (15)
(15)
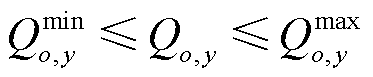 (16)
(16)
式中,EG,y为第y月系统的负荷需求;Qmin i,y、Qmax i,y分别为常规发电商i预测第y月的最小、最大发电量;Qmin w,y、Qmax w,y分别为可再生能源发电商w预测第y月的最小、最大发电量;Qmin o,y、Qmax o,y分别为耦合系统o第y月的最小、最大发电量。式(13)为第y月系统需要满足的供需平衡等式约束;式(14)~式(16)表示电网成交电量需在耦合系统和其他发电商的发电能力范围内。
根据上述模型,当耦合系统和其他发电商的报价给定时,电网可通过优化购电策略以最小成本保证供需平衡;电网购电策略反馈给博弈上层,作用于耦合系统及其他发电商博弈模型,影响其报价策略,直到电网、耦合系统与其他发电商任何一方改变策略都不会使自身效益得到提升,即达到纳什均衡。
当耦合系统外部获得的合约电量一定时,其内部的风光火虽然存在电量竞争,但环保经济而出力可控性低的可再生能源与调节能力较强而发电成本较高的火电存在着一定的互补效益。因此,本文以外部博弈确定的合约电量分解曲线为约束[24-25],基于合作博弈理论,建立耦合系统内部协同运行模型优化机组出力,在保证耦合系统整体电能质量的同时通过提升其内部可再生能源的消纳水平以拉低耦合系统整体发电成本,增强其市场竞争力,使耦合系统这一联盟收益达到最大。该模型示意图如图4所示。
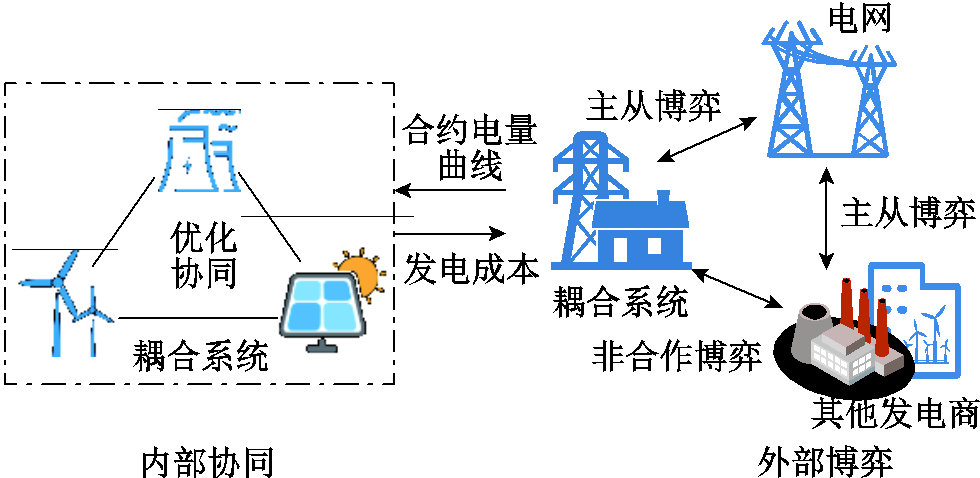
图4 耦合系统内部协同优化模型示意图
Fig.4 The schematic diagram of the internal collaborative optimization model for a coupled system
2.2.1 目标函数
由式(1)可知耦合系统完成合约电量的运行成本越低经济效益越大,因此,考虑耦合系统内部风光火的合作竞争关系,本文基于合作博弈理论,建立以火电机组运行启停成本、环境惩罚成本和可再生能源弃能成本之和最小为目标的风光火统一优化模型,寻求最优发电计划来实现耦合系统市场竞争力的最大化,从而进一步实现发电主体利益的最大化。
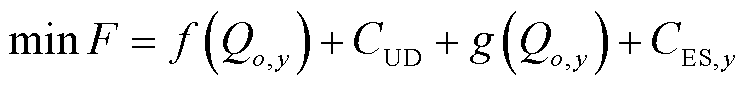 (17)
(17)
其中
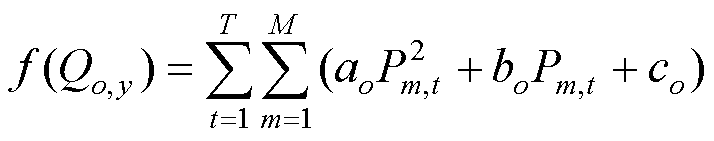 (18)
(18)
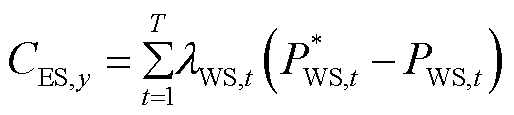 (21)
(21)
式中,CUD为火电机组启停成本;T为优化周期,时间颗粒度为小时级;ao、bo、co为火电机组运行成本系数;Pm,t为t时刻第m台火电机组出力;M为火电机组总台数;um,t为t时刻第m个火电机组的0-1状态变量,1表示启动状态,0表示停机状态;St m为机组m的启停成本;λWS,t为t时刻可再生能源的弃能惩罚系数;P*WS,t为t时刻可再生能源实际出力值;PWS,t为t时刻可再生能源上网功率。
2.2.2 约束条件
耦合系统运行时需满足如下所示的合约电量执行约束和机组出力约束。
1)合约电量执行约束
耦合系统各时段总出力需满足合约执行电量约束,即
式中,Lt为耦合系统t时段合约分解电量。
2)耦合系统内部机组出力约束
耦合系统内各机组的出力上、下限约束为
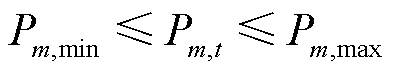 (23)
(23)
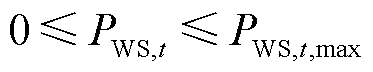 (24)
(24)
式中,Pm,max、Pm,min分别为火电出力上限和下限;PWS,t,max为t时刻可再生能源出力上限。
耦合系统内火电机组的爬坡约束如式(25)所示,启停约束如式(26)和式(27)所示。
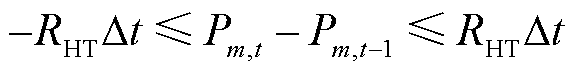 (25)
(25)
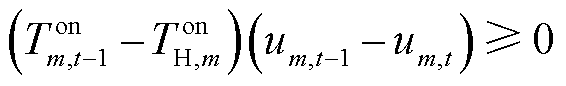 (26)
(26)
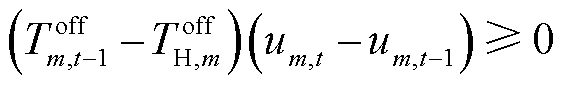 (27)
(27)
式中,RHT为火电机组的爬坡速率;Ton m,t-1为第m个火电机组在t-1时刻的持续运行时间;TonH,m为火电机组最短持续运行时间;Toff H,m为火电机组最短持续停机时间;Toff m,t-1为第m个火电机组在t-1时刻的持续停机时间。
在外部博弈和内部协同博弈模型的基础上,进一步建立耦合系统的时序随机生产模拟,量化评估耦合系统的技术、经济表现。首先,基于第2节确定的耦合系统合约电量曲线和耦合系统内各机组出力,考虑各机组强迫停运率,计算耦合系统各时刻的可用容量,并进一步建立耦合系统可靠性指标及各机组的经济收益分配方法。
耦合系统合约履行的可靠性水平取决于各时刻可用容量与负荷曲线的差值。t时刻耦合系统内机组n的可用容量分布PG,n t为
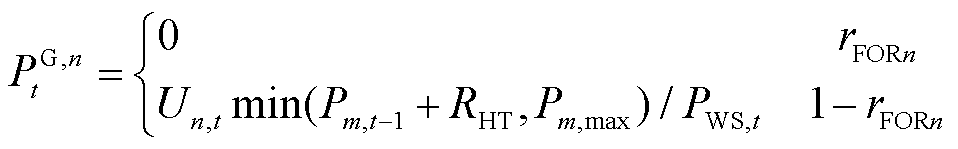 (28)
(28)
式中,Un,t为t时刻博弈模型确定的机组n的0-1状态变量,1表示启动状态,0表示停机状态;rFORn为机组n的强迫停运率。
基于卷积算法,可计算耦合系统t时刻的可用容量Pt为
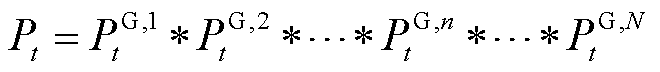 (29)
(29)
式中,N为耦合系统内机组的数量。
在系统可用容量的基础上,本文从合约电力和合约电量完成水平两个角度建立了耦合系统的可靠性评估指标:失合约负荷概率(Loss of Contract Load Probability, LOCLP)和合约电量不足期望值(Expected Contract Energy Not Supplied, ECENS),以评估耦合系统履行合约电量的可靠程度。
1)失合约负荷概率:耦合系统发电可用容量小于合约负荷值的概率,可反映机组故障对耦合系统合约电力履行度的影响。
当耦合系统t时刻可用容量Pt小于该时刻合约负荷Lt时,就会发生失合约负荷。在模拟周期T时段内,耦合系统的失合约负荷概率为
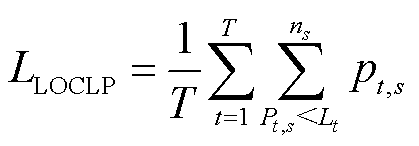 (30)
(30)
式中,ns为耦合系统的可用容量状态数;Pt,s为耦合系统t时刻第s个可用容量大小;pt,s为耦合系统可用容量为Pt,s时的概率。
2)合约电量不足期望:因机组停运导致耦合系统无法完成合约电量的期望值,可量化评估机组故障对耦合系统的影响程度。
在模拟周期T时段内,耦合系统的合约电量不足期望值为
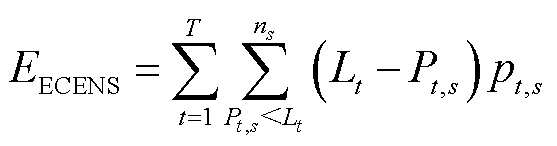 (31)
(31)
耦合系统各机组利益的合理分配是保证耦合系统内部高效协同的关键基础。本节建立了考虑综合贡献的耦合系统内各机组的收益分配模型及其求解方法。
3.2.1 耦合系统机组收益分配模型
耦合系统内部机组的收益分配不仅要考虑机组对耦合系统售电收益的贡献,还需考虑因机组随机故障造成的失合约电量损失。失合约电量损失呈现一定的概率分布特征[26],基于确定性收益的Shapley值[27]和核仁法[28]等传统方法难以适用。为此,本文从确定性售电收益和概率性失合约电量损失两个方面出发,基于个体理性和整体理性,建立了考虑综合贡献的耦合系统机组收益分配机制。
耦合系统收益为确定性售电收益P减去因机组随机故障导致的失合约电量损失Q,其中Q与合约电量不足期望值直接相关,如式(32)所示。考虑耦合系统整体理性和各机组个体理性,建立耦合系统收益分配模型。式(33)表示各机组的最终收益;式(34)~式(36)表示联盟的整体合理性,即大联盟收益与成本实现完全分配;式(37)表示个体合理性,即各机组参与耦合系统协同运行所得收益不小于其不参与耦合系统协同运行时的收益。
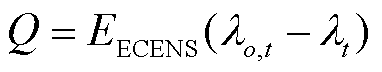 (32)
(32)
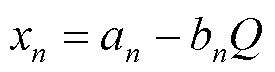 (33)
(33)
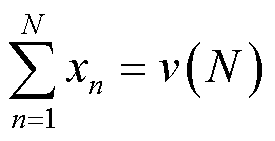 (34)
(34)
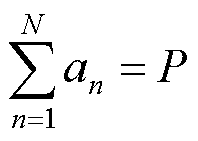 (35)
(35)

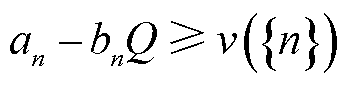 (37)
(37)
式中,λt为t时刻电价;xn为机组n的个体收益函数;an为分配给机组n的确定性收益;bn为失合约电量损失分配系数;v(N)为耦合系统整体收益;v({n})为机组n不参与耦合系统协同运行时的收益。
3.2.2 耦合系统机组收益分配模型的求解方法
基于群智能思想,将收益分配达成共识的过程模拟为:机组提出各自分配方案,根据个体经验学习和群体经验学习不断谈判协商,并调整分配方案,实现方案趋同[29],也即实现对上述收益分配模型的求解。耦合系统N个机组在第k次提出的收益分配方案矩阵Xk可表示为
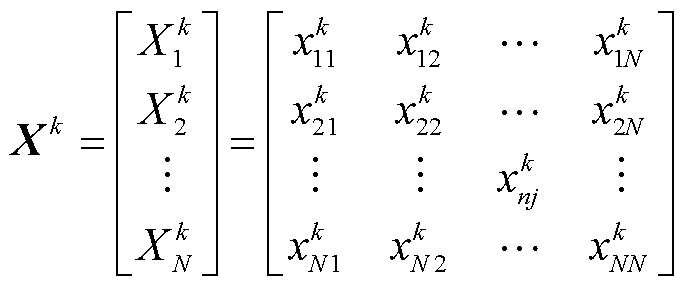 (38)
(38)
式中,Xk n为机组n在第k轮谈判协商提出的利益分配方案,Xk n=[xk n1 xk n2 … xk nN],其中,xnj为机组n对机组j提出的分配方案,xnj=anj-bnjQj。
以差异度函数描述机组个体分配方案与耦合系统群体方案趋同的过程,有
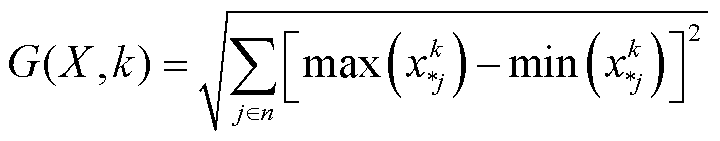 (39)
(39)
式中,max(xk *j)为第k轮谈判协商所有机组对机组j分配的期望收益最大值;min(xk *j)为所有机组对机组j分配的期望收益最小值。差异度函数量化所有机组的最大被分配收益与最小被分配收益间的差距。当机组的分配方案不一致时,机组根据个体信息和群体信息进行谈判协商后,更新各自分配方案,如式(40)、式(41)所示,直到差异度趋近于0,如式(42)所示。此时,耦合系统各机组对确定性售电收益和失合约电量损失分配方案达成一致,即收益分配方案矩阵中每行相同,如式(43)所示。
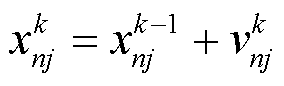 (40)
(40)
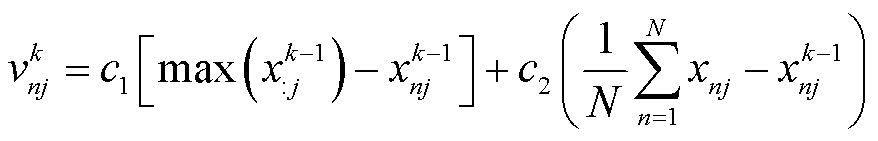 (41)
(41)
式中,vk nj为第k轮谈判收益分配迭代调整值;c1、c2分别为个体和群体学习因子。式(41)的前半部分体现个体偏好,后半部分体现群体偏好。
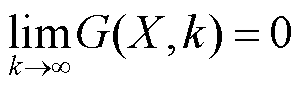 (42)
(42)
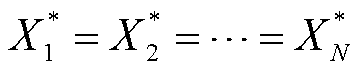 (43)
(43)
式中,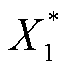 、
、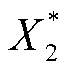 、
、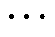 、
、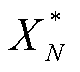 分别为各机组最终确定的收益分配方案。
分别为各机组最终确定的收益分配方案。
所提收益分配方法充分考虑利益分配原则中的个体理性与整体理性原则、综合协商优化原则和满意度原则,通过合作使风光火所得收益不小于其未参与耦合系统协同运行时的收益,并尊重耦合系统内部火电机组和可再生能源的利益诉求,通过协商使各方对收益分配方案的满意度达到平衡,从而增强风光火参与合作协同的积极性。
在本文的随机生产模拟中,依据耦合系统外部博弈和内部协同博弈优化模型确定机组运行加载计划,结合机组强迫停运率,评估耦合系统各时刻以及整个计算周期内的可靠性和经济性。考虑外部博弈和内部协同的耦合系统时序随机生产模拟流程如图5所示。
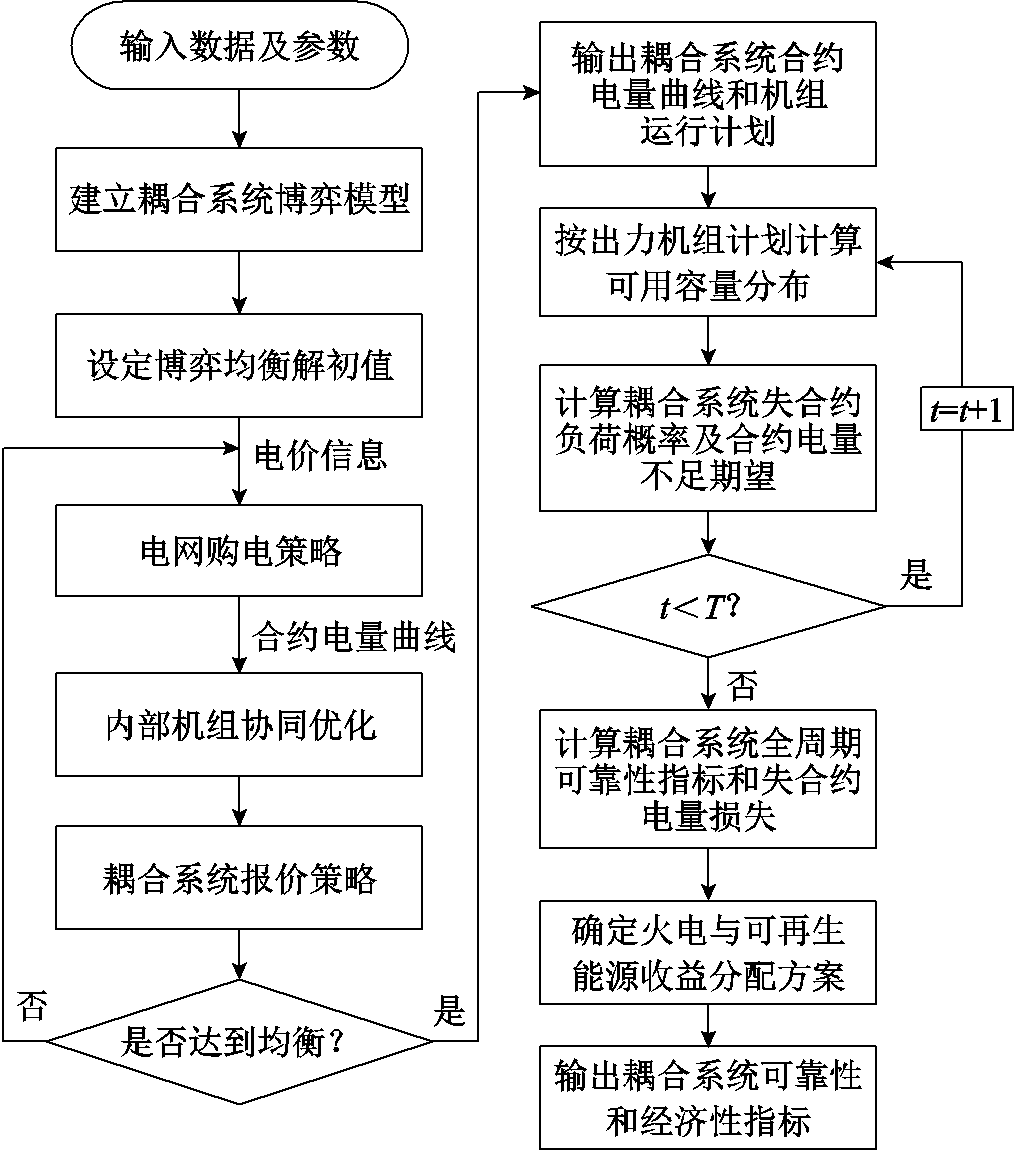
图5 考虑外部博弈和内部协同的耦合系统时序随机生产模拟流程
Fig.5 The flow chart of the proposed sequential probabilistic production simulation method for a coupled system considering external game and internal cooperation
采用中国东北某区域电网的实测数据进行仿真分析,验证本文方法的有效性和正确性。该区域电网最大负荷为2 850 MW,火电总装机容量为 3 600 MW,其中,装机容量为1 200 MW的火电厂、装机容量为100 MW的光伏电站以及装机容量为500 MW的风电场组成耦合系统。耦合系统中火电机组参数见表1,其他参数参考文献[30]。煤炭价格为500元/t[31],弃风、弃光惩罚为176元/MW,月均现货电价为410元/MW。发电商初始报价范围为[300, 400]元/(MW·h)。本文采用8 760 h的年时序曲线模拟负荷、光伏、风电的波动性,如图6~图8所示。
表1 耦合系统中的火电机组参数
Tab.1 Thermal power unit parameters in a coupled system

参数数值参数数值 机组数2ao/[t/(MW2·h)]0.000 064 4 Pmax/MW600bo/[t/(MW·h)]0.274 Pmin/MW180co/(t/h)11.71 RHT/(MW·h)540Sm/万元23.4
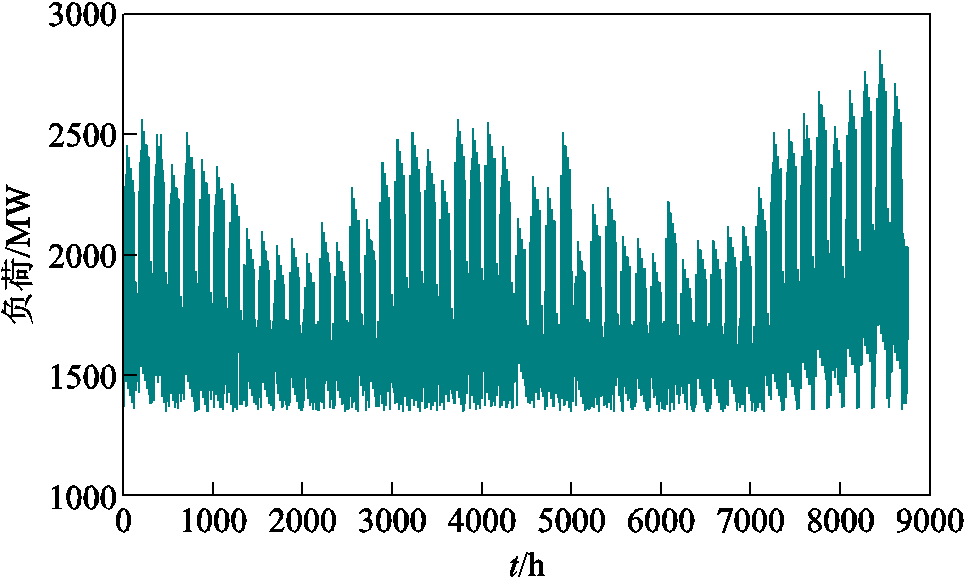
图6 年时序负荷曲线
Fig.6 Annual curve of load
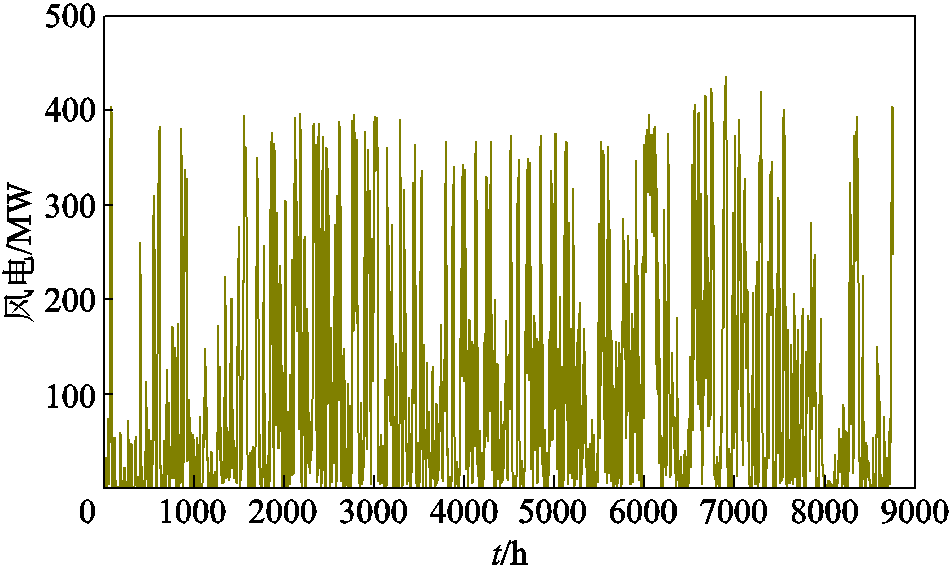
图7 年风电曲线
Fig.7 Annual curve of wind
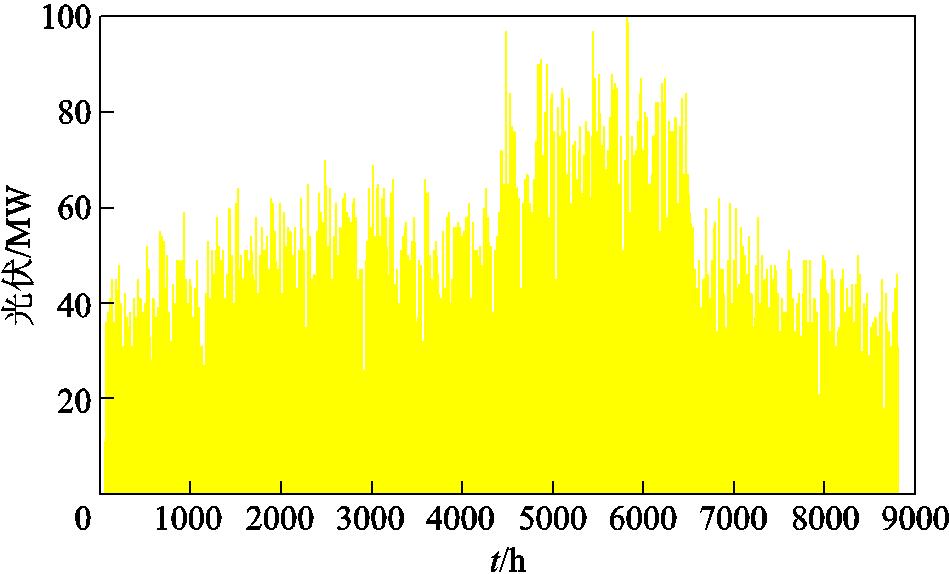
图8 年光伏曲线
Fig.8 Annual curve of PV
为验证耦合考虑外部博弈与内部协同之间相关关系对耦合系统整体运行的影响,以及本文收益分配方案的合理性,本文设置了两种方案进行对比分析,仿真结果见表2,耦合系统收益分配方案如图9所示。表2中的相对增量表示方案2的仿真结果相对方案1仿真结果的增量百分数。不同方案下的平均计算时间约为947 s。
表2 两种方案的仿真结果
Tab.2 The simulation results of cases 1-2

参数数值 方案1方案2相对增量 火电收益/万元6 461.67 282.612.71% 风电收益/万元1 2941 42510.12% 光伏收益/万元256.2266.84.14% Qo/(GW·h)719.15757.655.20% Ao/元386380-1.30% Mo/万元8 011.88 974.412.01% 弃能量/MW5 4043144-41.82% LLOCLP0.038 60.026 5-31.34% EECENS/GW14.9711.35-24.18%
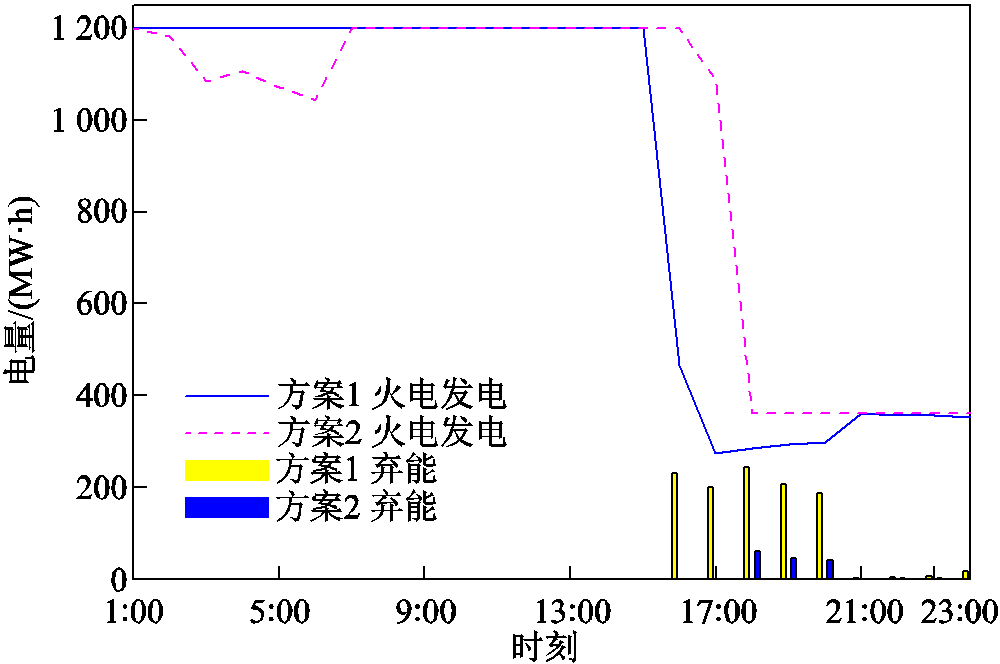
图9 典型日两种方案可再生能源消纳情况
Fig.9 Renewable energy consumption of cases 1-2 on a typical day
方案1:不考虑耦合系统内部协同运行,仅考虑耦合系统参与电力市场的外部博弈关系进行时序生产模拟。
方案2:本文方法,即考虑外部博弈和内部协同进行耦合系统时序生产模拟。
由表2可知,与方案1相比仅考虑耦合系统外部非合作博弈关系,忽略其内外利益协同关系,方案2采用外部博弈和内部协同市场交易策略,耦合系统在市场中的竞争力显著提升,其售电量增加了5.20%,售电收益增加了12.01%,耦合系统内部可再生能源消纳量及其机组的经济收益均大幅增长。其中弃风、弃光量总和减少41.82%,火电、风电和光伏收益提升分别达12.71%、10.12%、4.14%。
本文方法将耦合系统内的火电与风电、光伏形成合作联盟,利用风光发电替代火力发电,有效降低单位发电成本,同时结合火电的灵活调节能力提高风光消纳量。结合图9可知,当风电和光伏较为丰富、耦合系统负荷较低时,火电降低出力让出上网空间,减少弃风弃光情况的发生,不仅提高了可再生能源消纳水平,还降低了耦合系统的环境惩罚成本和燃煤成本。当耦合系统承担的负荷较高且可再生能源出力不足时,火电会提高出力以保证负荷供应。另外,耦合系统售电量的增加又可进一步促进可再生能源消纳,提升风电、光伏及耦合系统收益。而火电机组在可再生能源大发时虽会损失部分上网电量,但因耦合系统合约电量增加,火电售电量及收益也是增加的。由图10所示机组收益分配方案的谈判迭代过程可知,通过多轮谈判协商,各机组的收益分配方案达成共识。火电因可靠性高、调节性能好,因此其承担的失合约电量损失较少,火电机组收益进一步提升。
与方案1相比,本文方法下的耦合系统可靠性水平更高,失合约负荷概率LLOCLP降低了31.34%,合约电量不足期望值EECENS由14.97 GW下降到11.35 GW,降低了24.18%。当有机组发生随机停运时,耦合系统内的火电与风电、光伏作为合作联盟相互支援,未发生故障的机组通过增发功率减少耦合系统失合约负荷电量。
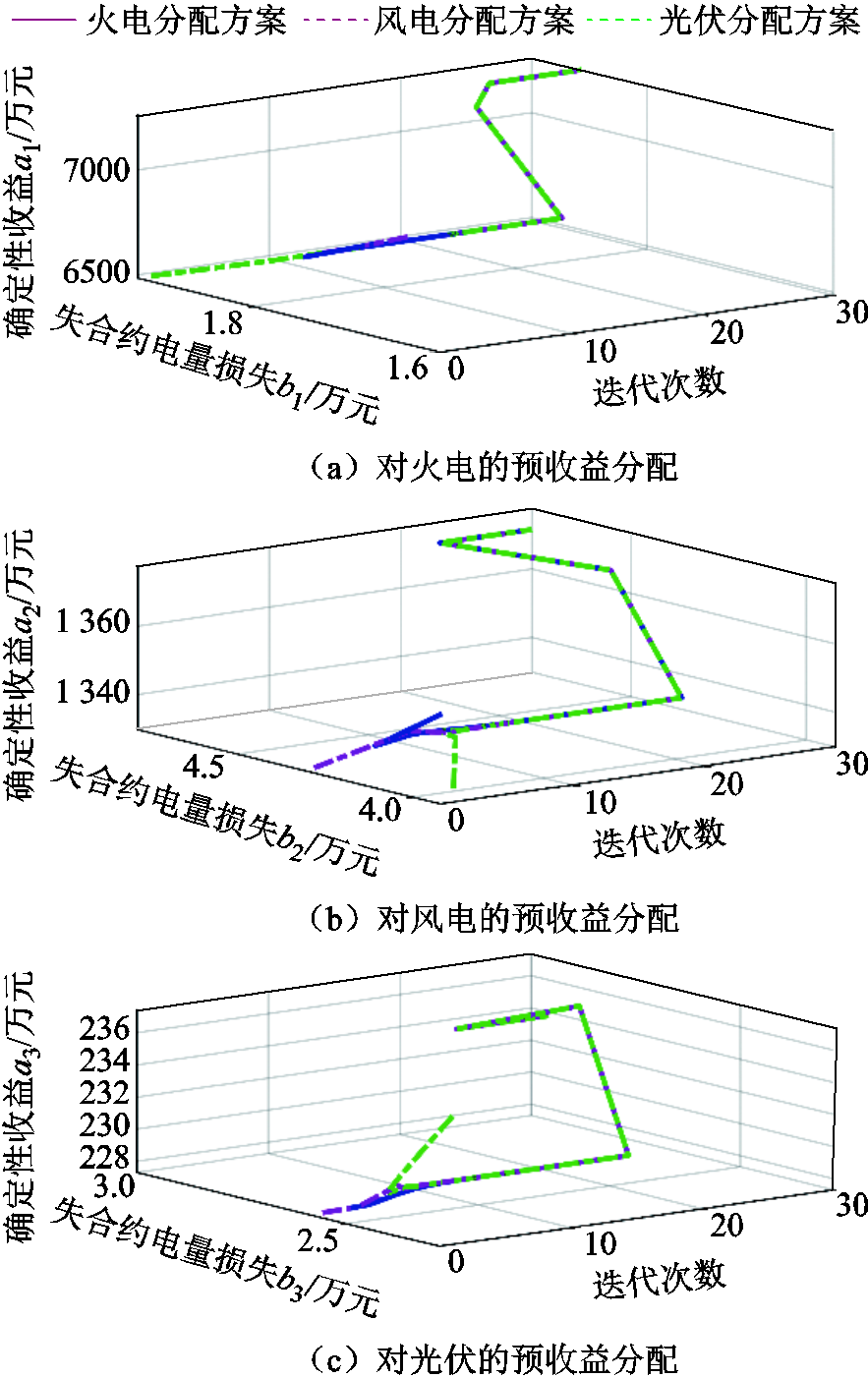
图10 耦合系统收益分配方案
Fig.10 Benefit distribution plan of a coupled system
为进一步分析可再生能源(风电、光伏装机容量之和)与火电装机容量比例对耦合系统运行的影响,在可再生能源容量占比分别为20%、30%、40%和50%的情况下进行仿真分析。仿真结果如表3、图11所示。
表3 不同可再生能源容量占比下的仿真结果
Tab.3 The simulation results of a coupled system with different proportions under different renewable energy capacity

可再生能源(%)Ao/元售电量/(GW·h)售电收益/万元LLOCLPEECENS/GW可再生能源利用率(%) 0385724.236 865.70.023 74.530 20375756.657 957.70.025 410.9988.5 30380757.658 974.40.026 511.3592.7 40384765.719 774.90.026 811.7291.3 50386766.459 872.80.027 112.4877.9
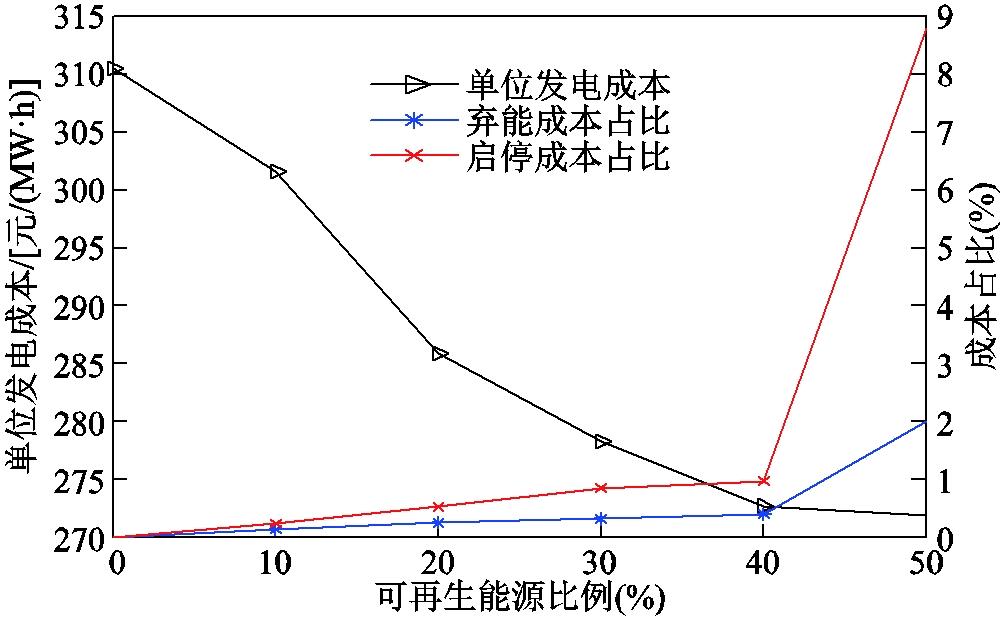
图11 不同可再生能源占比下的经济性指标
Fig.11 The economic indices of a coupled system under different proportions of renewable energy
由表3可知,随着耦合系统中可再生能源装机容量占比的增加,耦合系统的售电量和总体收益逐步增加,但失合约负荷概率LLOCLP和合约电量不足期望值EECENS也随之增加。从图11可知,当可再生能源容量占比增大时,耦合系统的单位发电成本逐渐减小,在电力市场竞争中更具优势,使得耦合系统售电收益增大。但当可再生能源占比超过40%时,因可再生能源出力波动性增大导致火电机组频繁调节,火电机组启停成本及弃能量大幅增加。此时,耦合系统单位发电成本的降低趋势减缓。
随着可再生能源占比的增加,可再生能源利用率呈现出先增大后减小的趋势,主要原因在于,可再生能源装机容量增加后,耦合系统单位发电成本降低,耦合系统在市场竞争中获得售电量增多,可再生能源上网电量随之增加。但当可再生能源占比超过30%后,耦合系统中火电装机容量被压缩,无法满足全额消纳可再生能源的灵活性需求,造成弃能量增加。
本文提出了考虑外部博弈和内部协同的耦合系统时序随机生产模拟方法,采用中国东北某区域电网实测数据验证了本文方法的正确性,并有如下结论:
1)考虑外部博弈和内部协同后,耦合系统的可靠性水平、可再生能源消纳水平和经济收益大幅提升。本文基于群智能思想提出的机组收益分配机制,能够充分考虑各机组实际贡献,充分调动各机组参与耦合系统协同运行的积极性。
2)提高耦合系统内的可再生能源装机容量占比可有效降低单位发电成本,提高经济收益及市场竞争力,但会降低可靠性水平,即会增加失合约负荷概率和合约电量不足期望值。若可再生能源占比过高,则会因火电灵活调节能力不足而导致可再生能源利用率下降,使火电机组启停成本增加。因此,需要合理配置耦合系统内火电与可再生能源装机的容量占比。
随着我国可再生能源渗透率的提高,源荷不确定性将会给耦合系统安全可靠运行带来更加显著的影响,而本文未计及源荷不确定性因素,适用性有待进一步考察。因此,可在进一步的研究中考虑不确定的影响,基于不确定性场景开展考虑不确定性下的耦合系统研究。
附 录
1. 主从博弈收敛性证明
结合文献[32]的研究思路和主从博弈收敛性定理说明本文主从博弈模型的收敛性。
根据主从博弈收敛性定理[33],设领导者决策集合X是Rn上的有界闭集,I是跟随者策略集合,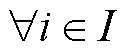 ,Y是Ri中的有界闭凸集。领导者收益函数f在X×Y→R上半连续;
,Y是Ri中的有界闭凸集。领导者收益函数f在X×Y→R上半连续;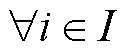 ,跟随者收益函数wi在X×Y→R上连续;且
,跟随者收益函数wi在X×Y→R上连续;且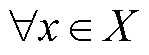 ,
,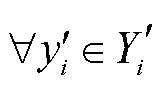 ,
,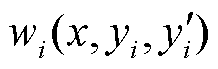 在Yi上是凹的,则主从博弈收敛。
在Yi上是凹的,则主从博弈收敛。
对于本文的主从博弈模型,各发电商和电网采取的策略均属于纯策略,其策略空间均为欧式空间上一个非空、有界的闭凸集。对于各发电商作为领导者收益函数f在策略空间上半连续证明如下:
定理1:设Y 是Rn上的有界闭集,集值映射F:X→P0(Y)是闭的,则F在X上必是上半连续的。
由式(1)可知,耦合系统收益函数Mo由售电收益、发电成本、碳排放惩罚成本和弃能惩罚成本四部分构成,当电网的购电策略确定时,由式(18)、式(20)和式(21)可知耦合系统收益函数为非线性连续函数,由式(3)可知,其报价策略受市场报价约束,其收益函数是报价策略的闭映射,满足定理1,其他发电商同理。由此可知,耦合系统及其他发电商的收益函数是上半连续的。
对于跟随者来说,在本文的主从博弈模型中,跟随者只有电网。且由式(12)和式(13)~式(16)可知,电网购电策略受发电商发电量和电网需求量约束,电网购电优化目标是一个拥有非空可行解集的严格凸二次规划问题。因此,电网的收益函数在其策略空间中是连续凹函数。
综上所述,本文建立的主从博弈模型满足主从博弈收敛性定理,具有收敛性。
2. 主从博弈纳什均衡解的存在性和唯一性证明
根据纳什均衡存在性定理[34]:在n人策略式博弈中,如果每个参与者i的纯策略空间Si是欧式空间上一个非空、闭的、有界的凸集,收益函数fi(s)是连续且在Si拟凹,则该博弈存在唯一纳什均衡策略。本文对于纳什均衡解的存在性证明也是据此展开的。
对耦合系统及其他发电商来说,当以电网最优策略为输入时,发电商之间的博弈为完全信息下的非合作静态博弈。本文中,各发电商报价博弈策略lI受电网售价约束,为欧式空间上的非空有界闭凸集。对于耦合系统及其他发电商的收益函数是相应策略上的连续拟凹函数证明如下。
对于耦合系统发电商,由式(1)可知其收益函数Mo由售电收益、发电成本、碳排放惩罚成本和弃能惩罚成本四部分构成,当电网的购电策略确定时,由式(2)、式(20)和式(21)可知耦合系统收益函数中的售电收益、碳排放惩罚成本和弃能惩罚成本在自身博弈策略lo上均为线性连续函数,线性函数显然为连续拟凹函数;由式(18)可知其发电成本函数为Qo上的非线性函数,但不随lo的变化而改变,可认为是常数,也可认为是策略lo上的线性函数,为连续拟凹函数。由此,可得耦合系统收益函数Mo是其策略lo上的连续拟凹函数。其他类型发电商同理可得,其收益函数为其报价策略上的连续拟凹函数。
而对电网来说,由式(12)可知,电网购电策略受发电商发电量和电网需求量约束,电网购电优化目标是一个拥有非空可行解集的严格凸二次规划问题。由文献[35]中的引理:当lI中的Bi是一恒定的正值,且Aj是一个参数矩阵,其优化问题对任意的Aj来说都是有解的,且最优解唯一。由此可知,电网作为跟随者,当各发电商的策略给定时,电网购电策略具有唯一最优解。
综上所述,在本文的主从博弈模型中,当耦合系统及其他发电商作为领导者的策略给定后,电网作为跟随者存在唯一最优解,而当电网的策略给定后,耦合系统及其他发电商存在唯一最优解,由此可知,本文所建立的主从博弈模型存在唯一均衡解。
参考文献
[1] 伍梦尧. 构建新型电力系统为实现“3060”目标提供重要支撑: 摘自国家电网有限公司总经理张智刚在2021年国际能源变革对话上的主旨演讲[N]. 中国电力报, 2021-06-30(2).
[2] 毛庆汉. 储能联合火电机组参与调频辅助服务市场的工程应用[J]. 电气技术, 2021, 22(7): 103-108.
Mao Qinghan. Engineering application of battery energy storage system coordinated with thermal power unit in regulating ancillary service market[J]. Electrical Engineering, 2021, 22(7): 103-108.
[3] 姜云鹏, 任洲洋, 李秋燕, 等. 考虑多灵活性资源协调调度的配电网新能源消纳策略[J]. 电工技术学报, 2022, 37(7): 1820-1835.
Jiang Yunpeng, Ren Zhouyang, Li Qiuyan, et al. An accommodation strategy for renewable energy in distribution network considering coordinated dispatching of multi-flexible resources[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1820-1835.
[4] 国家能源局. 关于公开征求对《国家发展改革委国家能源局关于开展“风光水火储一体化”“源网荷储一体化”的指导意见(征求意见稿)》意见的公告[EB/OL]. [2020-08-27]. http://www.nea.gov.cn/ 2020-08/27/c_139321964.htm.
[5] 程光, 徐飞, 胡博, 等. 可再生能源与火电集成耦合的协同性能及组合设计研究[J]. 电网技术, 2021, 45(6): 2178-2191.
Cheng Guang, Xu Fei, Hu Bo, et al. Synergistic performance and combination design of coupling of renewable energy and thermal power[J]. Power System Technology, 2021, 45(6): 2178-2191.
[6] 谈天夫, 高山, 李海峰, 等. 基于等效间隔-频率分布的含风电场电力系统随机生产模拟[J]. 电工技术学报, 2014, 29(12): 148-157.
Tan Tianfu, Gao Shan, Li Haifeng, et al. Power system probabilistic production simulation based on equivalent interval frequency distribution including wind farms[J]. Transactions of China Electrotechnical Society, 2014, 29(12): 148-157.
[7] 丁明, 楚明娟, 毕锐, 等. 基于序贯蒙特卡洛随机生产模拟的风电接纳能力评价方法及应用[J]. 电力自动化设备, 2016, 36(9): 67-73.
Ding Ming, Chu Mingjuan, Bi Rui, et al. Wind power accommodation capability evaluation based on sequential Monte Carlo probabilistic production simulation and its application[J]. Electric Power Automation Equipment, 2016, 36(9): 67-73.
[8] 李林川, 王锡凡, 王秀丽. 基于等效电量函数法的互联电力系统随机生产模拟[J]. 中国电机工程学报, 1996, 16(3): 180-184.
Li Linchuan, Wang Xifan, Wang Xiuli. Probabilistic modeling for interconnected power systems based on the equivalent energy function approach[J]. Chinese Society for Electrical Engineering, 1996, 16(3): 180-184.
[9] 姚力, 黄镔, 王秀丽, 等. 考虑风火联合外送的互联系统随机生产模拟[J]. 电网技术, 2015, 39(5): 1219-1225.
Yao Li, Huang Bin, Wang Xiuli, et al. Probabilistic production simulation of interconnected system by considering the joint delivery of wind power and thermal power generation[J]. Power System Technology, 2015, 39(5): 1219-1225.
[10] 孙伟卿, 李恒, 杜习周, 等. 基于有效容量分布的互联系统风电消纳能力评估[J]. 电网技术, 2019, 43(9): 3321-3327.
Sun Weiqing, Li Heng, Du Xizhou, et al. Assessment of wind power accommodation ability based on available capacity distribution in interconnected system[J]. Power System Technology, 2019, 43(9): 3321-3327.
[11] 丁明, 林玉娟, 潘浩. 考虑负荷与新能源时序特性的随机生产模拟[J]. 中国电机工程学报, 2016, 36(23): 6305-6314, 6595.
Ding Ming, Lin Yujuan, Pan Hao. Probabilistic production simulation considering time sequence characteristics of load and new energy[J]. Proceedings of the CSEE, 2016, 36(23): 6305-6314, 6595.
[12] 朱睿, 胡博, 谢开贵, 等. 含风电–光伏–光热–水电–火电–储能的多能源电力系统时序随机生产模拟[J]. 电网技术, 2020, 44(9): 3246-3253.
Zhu Rui, Hu Bo, Xie Kaigui, et al. Sequential probabilistic production simulation of multi-energy power system with wind power, photovoltaics, concentrated solar power, cascading hydro power, thermal power and battery energy storage[J]. Power System Technology, 2020, 44(9): 3246-3253.
[13] 廖庆龙, 谢开贵, 胡博. 含风电和储能电力系统的时序随机生产模拟[J]. 电网技术, 2017, 41(9): 2769-2776.
Liao Qinglong, Xie Kaigui, Hu Bo. Sequential probabilistic production simulation of power systems with wind power and energy storage[J]. Power System Technology, 2017, 41(9): 2769-2776.
[14] 赵书强, 索璕, 许朝阳, 等. 考虑断面约束的多能源电力系统时序性生产模拟[J]. 电力自动化设备, 2021, 41(7): 1-6.
Zhao Shuqiang, Suo Xun, Xu Zhaoyang, et al. Time series production simulation of multi-energy power system considering section constraints[J]. Electric Power Automation Equipment, 2021, 41(7): 1-6.
[15] 周明, 李琰, 李庚银. 基于随机生产模拟的日前发电–备用双层决策模型[J]. 电网技术, 2019, 43(5): 1606-1613.
Zhou Ming, Li Yan, Li Gengyin. A day-ahead power generation-reserve Bi-level decision-making model for power system based on probabilistic production simulation[J]. Power System Technology, 2019, 43(5): 1606-1613.
[16] 谭忠富, 宋艺航, 张会娟, 等. 大规模风电与火电联合外送体系及其利润分配模型[J]. 电力系统自动化, 2013, 37(23): 63-70.
Tan Zhongfu, Song Yihang, Zhang Huijuan, et al. Joint delivery system of large-scale wind power and thermal power generation and its profit distribution model[J]. Automation of Electric Power Systems, 2013, 37(23): 63-70.
[17] 刘思源, 艾芊, 郑建平, 等. 多时间尺度的多虚拟电厂双层协调机制与运行策略[J]. 中国电机工程学报, 2018, 38(3): 753-761.
Liu Siyuan, Ai Qian, Zheng Jianping, et al. Bi-level coordination mechanism and operation strategy of multi-time scale multiple virtual power plants[J]. Proceedings of the CSEE, 2018, 38(3): 753-761.
[18] 赵文会, 闫豪楠, 何威. 基于风火网非合作博弈的电力市场均衡模型[J]. 电网技术, 2018, 42(1): 103-111.
Zhao Wenhui, Yan Haonan, He Wei. Equilibrium model of electricity market based on non-cooperative game of wind farms, thermal power plants and power grid company[J]. Power System Technology, 2018, 42(1): 103-111.
[19] 杨龙杰, 周念成, 胡博, 等. 计及火电阶梯式爬坡率的耦合系统优化调度方法[J]. 中国电机工程学报, 2022, 42(1): 153-164.
Yang Longjie, Zhou Niancheng, Hu Bo, et al. Optimal scheduling method for coupled system based on ladder-type ramp rate of thermal power units[J]. Proceedings of the CSEE, 2022, 42(1): 153-164.
[20] 陈岑, 武传涛, 林湘宁, 等. 计及上下游市场的园区综合能源商购售能策略[J]. 电工技术学报, 2022, 37(1): 220-231.
Chen Cen, Wu Chuantao, Lin Xiangning, et al. Purchase and sale strategies of park integrated energy suppliers in wholesale and retail markets[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 220-231.
[21] 熊宇峰, 司杨, 郑天文, 等. 基于主从博弈的工业园区综合能源系统氢储能优化配置[J]. 电工技术学报, 2021, 36(3): 507-516.
Xiong Yufeng, Si Yang, Zheng Tianwen, et al. Optimal configuration of hydrogen storage in industrial park integrated energy system based on stackelberg game[J]. Transactions of China Electrotechnical Society, 2021, 36(3): 507-516.
[22] 王雪纯, 陈红坤, 陈磊. 提升区域综合能源系统运行灵活性的多主体互动决策模型[J]. 电工技术学报, 2021, 36(11): 2207-2219.
Wang Xuechun, Chen Hongkun, Chen Lei. Multi-player interactive decision-making model for operational flexibility improvement of regional integrated energy system[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2207-2219.
[23] 李军祥, 王宇倩, 何建佳, 等. 基于区块链的微电网电力市场电价与电量动态博弈[J]. 电力系统自动化, 2021, 45(17): 11-19.
Li Junxiang, Wang Yuqian, He Jianjia, et al. Blockchain-based dynamic game of electricity price and power for microgrid electricity market[J]. Automation of Electric Power Systems, 2021, 45(17): 11-19.
[24] 黎灿兵, 胡亚杰, 赵弘俊, 等. 合约电量分解通用模型与算法[J]. 电力系统自动化, 2007, 31(11): 26-30.
Li Canbing, Hu Yajie, Zhao Hongjun, et al. General model and algorithm for contract energy decomposition[J]. Automation of Electric Power Systems, 2007, 31(11): 26-30.
[25] 赵书强, 胡利宁, 田捷夫, 等. 基于中长期风电光伏预测的多能源电力系统合约电量分解模型[J]. 电力自动化设备, 2019, 39(11): 13-19.
Zhao Shuqiang, Hu Lining, Tian Jiefu, et al. Contract power decomposition model of multi-energy power system based on mid-long term wind power and photovoltaic electricity forecasting[J]. Electric Power Automation Equipment, 2019, 39(11): 13-19.
[26] 黄永皓, 尚金成, 康重庆, 等. 电力中长期合约交易市场的运作机制及模型[J]. 电力系统自动化, 2003, 27(4): 24-28.
Huang Yonghao, Shang Jincheng, Kang Chongqing, et al. An operation mechanism and model of long and middle term contract market[J]. Automation of Electric Power Systems, 2003, 27(4): 24-28.
[27] 麻秀范, 余思雨, 朱思嘉, 等. 基于多因素改进Shapley的虚拟电厂利润分配[J]. 电工技术学报, 2020, 35(增刊2): 585-595.
Ma Xiufan, Yu Siyu, Zhu Sijia, et al. Profit allocation to virtual power plant members based on improved multifactor shapley value method[J]. Transactions of China Electrotechnical Society, 2020, 35(S2): 585-595.
[28] 伍栋文, 于艾清. 大规模多源联合外送协调调度中基于核仁理论的利润分配[J]. 电网技术, 2016, 40(10): 2975-2981.
Wu Dongwen, Yu Aiqing. Research on nucleolus theory based profit distribution method for joint delivery system of large-scale hybrid power generation[J]. Power System Technology, 2016, 40(10): 2975-2981.
[29] 李壮阔, 陈水鹏. 联盟收益不确定下合作博弈的多目标粒子群扩展算法求解[J]. 数学的实践与认识, 2020, 50(13): 25-37.
Li Zhuangkuo, Chen Shuipeng. Multi-objective particle swarm optimization algorithm for cooperative game under uncertainty of alliance income[J]. Mathematics in Practice and Theory, 2020, 50(13): 25-37.
[30] Wang Jianxue, Wei Jingdong, Zhu Yuchao, et al. The reliability and operational test system of a power grid with large-scale renewable integration[J]. CSEE Journal of Power and Energy Systems, 2019, 6(3): 704-711.
[31] 黄珊. 风火打捆系统参与大用户直购交易双边定价博弈[D]. 北京: 华北电力大学, 2020.
[32] Chen Yue, Wei Wei, Wang Han, et al. An energy sharing mechanism achieving the same flexibility as centralized dispatch[J]. IEEE Transactions on Smart Grid, 2021, 12(4): 3379-3389.
[33] 俞建. 博弈论选讲[M]. 北京: 科学出版社, 2014.
[34] Luo Zhiquan, Pang J S, Ralph D. Mathematical programs with equilibrium constraints[M]. Cambridge: Cambridge University Press, 1996
[35] 李光久. 博弈论基础教程[M]. 北京: 化学工业出版社, 2005.
Abstract The coupled systems consisting of thermal power plants and renewable energy plants are regarded as an important way to promote renewable energy accommodation. However, the existing probabilistic production simulation methods of multi-energy systems cannot adapt to the coupled systems since the relationship between the external game and internal coordination of the coupled systems in the market environment cannot be accurately simulated. This paper proposes a sequential probabilistic production simulation method for the coupled systems considering external game and internal coordination. The impacts of the internal and external cooperative competition mechanism on the operation of the coupled systems are considered in the probabilistic production simulation. The reliability and economic indices of the coupled systems considering the market trading strategies can also be obtained.
Based on the master-slave game theory, the electricity-price competition relationship between the coupled system and other power suppliers and power grid companies is firstly modeled. A cooperative game model is established for the coupled systems to simulate the collaborative competition relationship between thermal power plants and renewable energy plants in a coupled system. A sequential probabilistic production simulation method for the coupled systems considering external game and internal coordination is developed. By simulating the operating state of the coupled system hour by hour, the reliability evaluation indices and the economic indices of the coupled systems can be obtained by simulating the hourly operation states of the coupled systems with the consideration of the market transaction strategies. An economic benefit allocation method is then proposed for the internal plants of the coupling systems. The comprehensive contribution of each power plant in a coupled system is quantified and considered.
A local power grid in Northeastern China is used to test the proposed method. The simulation results indicate that ignoring the coordinating relationship between the internal interests and external interests of the coupled system will lead to underestimation of the competitiveness of the coupled system in the electricity market. The economic profits of the coupled system and renewable energy accommodation level are significantly increased by considering the external game and internal coordination of the coupled system. The electricity sale is increased by 5.20%, and the electricity sale revenue is increased by 12.01%. The revenues of the internal thermal power plant, wind power plant and photovoltaic power plant are increased by 12.17%, 10.12%, 4.14%, respectively. The reliability of the coupled system is also improved. The probability of losing contract load is reduced by 31.34%. The expected value of contract power shortage is reduced from 14.97 GW to 11.35 GW, which is decreased by 24.18%. Furthermore, the simulation results under different ratios of renewable energy capacity and thermal power capacity indicates that when the penetration rate of renewable energy exceeds 40%, the thermal power units are frequently adjusted to smooth the power outputs of the coupled system and the operation cost of the thermal power units and the renewable energy curtailment are significantly increased.
The following conclusions can be drawn from the simulation analyses in the paper. (1) By considering the external game and internal coordination of the coupled system, the economic profit, the renewable energy accommodation and the reliability level of the coupled system are all greatly improved. (2) Increasing the proportion of renewable energy installed capacity in the coupled system can effectively reduce the unit power generation cost and improve the economic profit and competitiveness in the electricity market, while the reliability level of the coupled system will be decreased. If the proportion of renewable energy in a coupled system is too high, the renewable energy accommodation level will be decreased due to insufficient flexible adjustment capacity of thermal power. Therefore, it is of significant importance to reasonably configure the capacity ratios of thermal power and renewable energy installed capacity in a coupled system.
Keywords:Coupled system, internal collaboration, external game, probabilistic production simulation, electricity market
任洲洋 男,1986年生,副教授,博士生导师,研究方向为电力能源系统低碳运行及规划、人工智能等。E-mail:rzhouyang1108@163.com(通信作者)
程 欢 女,1997年生,硕士研究生,研究方向为新能源发电系统、氢能系统运行等。E-mail:1442215864@qq.com
中图分类号:TM73
DOI:10.19595/j.cnki.1000-6753.tces.221321
国家重点研发计划资助项目(2019YFB1505400)。
收稿日期 2022-07-08
改稿日期 2022-09-23
(编辑 赫 蕾)