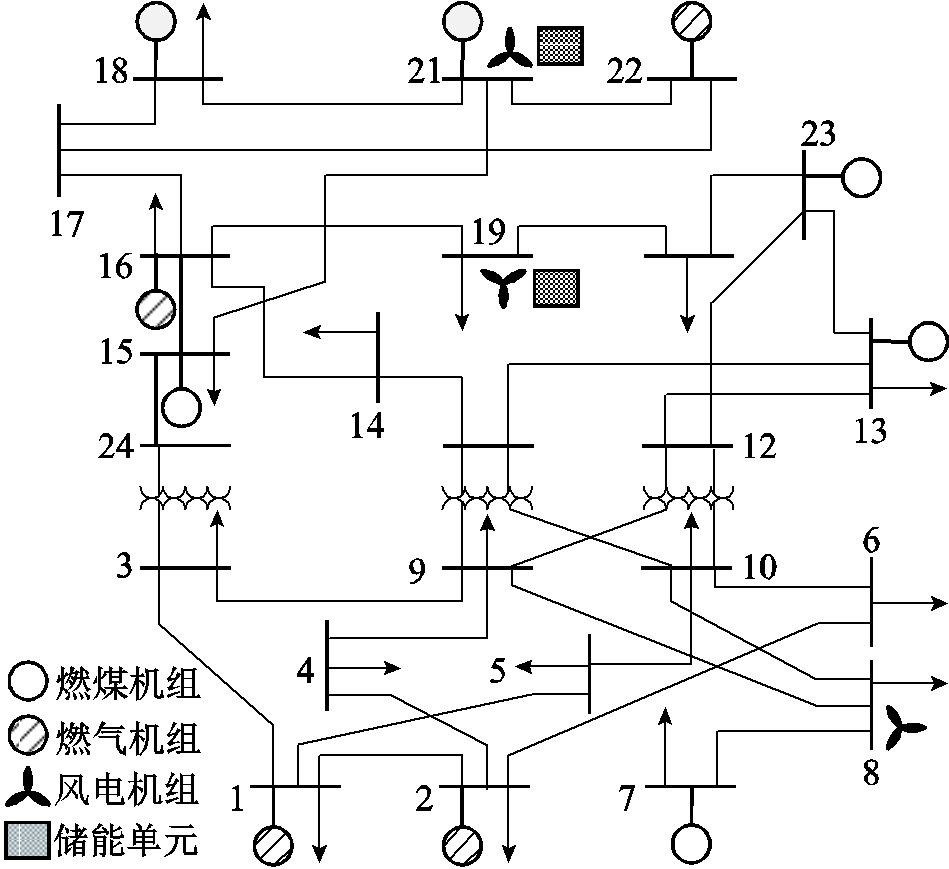
图1 24节点总线系统框图
Fig.1 Diagram of IEEE 24 bus system
摘要 最优传输切换（OTS）是一种应用较为广泛的通过改变网络拓扑结构提高输电网络灵活性的控制机制。然而，输电网络中往往存在不确定风电及负荷需求，这使得常规最优传输切换方案无法达到预期效果。为此，提出将置信间隙决策理论（CGDT）应用于寻求不确定条件下的鲁棒最优传输切换方案。该文分别采用高斯混合模型和正态分布对风电出力及负荷需求预测误差的概率分布函数进行拟合，将不确定性纳入最优传输切换，并以总发电成本最优为目标，建立了基于置信间隙决策理论的输电网络最优传输切换鲁棒优化模型。采用改进的IEEE 24节点系统进行仿真实验，结果表明，使用所提方法求取的最优传输切换方案具有较强的鲁棒性。
关键词：不确定性 风能发电 负荷需求 最优传输切换 置信间隙决策理论
最优传输切换（Optimal Transmission Switching, OTS）是一种为电网增加灵活性的控制机制，在输电网络中的应用较为广泛[1]。其主要思想是通过改变输电线路的状态，进而改变网络拓扑结构，将网络拓扑结构与发电经济调度问题相协调，从而有效地降低系统调度成本，缓解输电网络阻塞，减轻电压和热违规，提高可再生能源发电的集成度[2]。但是，确定OTS方案通常在日前调度阶段进行，输电网络中存在的风电和负荷需求不确定性[3]将会使常规最优传输切换方案难以实现预期优化目标。因此，开发一种能够考虑输电网络多重不确定性的OTS鲁棒优化方法具有重要意义[4]。输电网络中风电出力以及负荷需求的不确定性会导致最优传输切换方案很难达到预期优化结果，因此，开发一种能够考虑输电网络多重不确定性的OTS鲁棒优化方法具有重要意义[5]。
学者们对计及不确定因素求取OTS方案已进行了广泛的研究。M. Peker等提出了一种两阶段随机规划模型，能够在可再生能源削减和减载量受限的条件下，对输电切换操作、输电和存储投资进行协同优化[6]。为提高两阶段随机规划OTS模型的求解效率和精度，S. Dehghan等利用基于线性决策规则（Linear Decision Rules, LDRs）[7]的近似求解方法，将模型重新表述为一个可处理的混合整数线性规划问题，并通过仿真实验对该方法的有效性进行了验证[8]。针对集成了大规模可再生能源的输电网络，R. Ahmed等提出采用Gram-Charlier法[9]求取基于概率负荷潮流的OTS，提高了系统优化结果的准确性[10]。然而，基于常规随机优化求取OTS策略的方法通常遵循样本平均近似[11]和场景缩减[12]，需要依据不确定输入参数的概率密度函数的精确信息进行不确定性建模，计算量大，对算法精度要求高，难以保证OTS结果的鲁棒性，在可扩展性方面难度较大。P. Dehghanian等提出了一种概率拓扑控制方案，该方案通过点估计法[13]来建模不确定性OTS，以减少大规模场景下的计算量[14]。Yuan Yang等构建了一种考虑不确定N-k事故、可再生能源和负荷的最优输电切换模型，利用模糊集和预算不确定性集同时表征电力系统的三种不确定性，所得OTS方案能够保证系统的安全性和经济性[15]。M. Numan等构建了一种新的不确定性风电综合电力系统输电与蓄能联合扩能规划[16]及最优输电切换鲁棒优化模型，并讨论了最小-最大-最小成本优化问题，验证了所提模型的鲁棒性[17]，但是，基于常规鲁棒优化求取OTS方案时，不确定变量是由无分布有界区间定义的，对不确定性变量的粗糙描述通常会使得优化结果较为保守[18]。
针对上述基于常规随机规划和鲁棒优化求取OTS方案所存在的缺陷，本文提出将置信间隙决策理论应用于寻求不确定条件下的鲁棒OTS方案。置信间隙决策理论（Confidence Gap Decision Theory, CGDT）是彭春华等在文献[19]中提出的一种更高效的基于鲁棒驱动的不确定问题处理方法。该方法是基于信息间隙决策理论（Information Gap Decision Theory, IGDT）[20]的改进，旨在满足优化结果不劣于预设目标的前提下，最大限度地提高目标函数对不确定性输入参数的鲁棒性。CGDT不确定性鲁棒优化方法在IGDT鲁棒思想的基础上引入了置信水平，采用概率置信区间描述不确定性[21]，充分反映了不确定参数的随机分布特性，弥补了IGDT对于不确定性描述过于粗糙的缺陷。彭春华等将该方法应用于存在不确定性可再生能源和负载需求的综合能源系统中，实现系统的鲁棒优化调度，提升了综合能源利用的高效性和经济性。文献[22]采用该方法求取机组起动次序鲁棒优化策略，为验证可再生能源机组对加快系统恢复速度[23]的积极作用提供了思路。
本文中为寻求含不确定风电输电网络的鲁棒OTS策略，分别采用高斯混合模型和正态分布拟合风电和负荷需求的不确定性概率分布，将风电及负荷需求不确定性纳入到输电网络OTS模型中。针对其中的不确定性引入了基于鲁棒驱动的置信间隙决策理论（CGDT），提出基于CGDT求取不确定性OTS的鲁棒优化方法，并以总发电成本最小为优化目标，构建基于CGDT的输电网络OTS鲁棒优化混合整数非线性规划模型，引入机会约束，通过最大化置信水平进而最大化规避不确定性参数对OTS优化结果的影响。仿真实验表明，相比于其他常规不确定问题处理方法，采用基于置信间隙决策理论的鲁棒优化方法能够提供具有较强适应性和鲁棒性的OTS方案。
获取OTS方案通常在日前调度阶段进行[24]，依据不确定参数预测值和计及不确定性输电网络最优传输切换模型计算得出。在实时运行阶段，操作员在执行传输切换操作之前根据不确定参数实际值进行一系列可行性检查[25]，在可行的情况下，将新拓扑应用于在线操作。本文将不确定性纳入输电网络OTS模型中，以总发电成本最小为优化目标，建立了计及系统不确定性的OTS模型，对日前阶段鲁棒OTS方案的获取进行了研究。本文所研究的输电网络以改进的IEEE 24节点电力网络为例，其系统框图如图1所示，其中主要包含燃煤发电机组、燃气发电机组、风机、电储能和传输线路等，不确定性参数为风电出力和负荷需求。
图1 24节点总线系统框图
Fig.1 Diagram of IEEE 24 bus system
本文以系统总发电成本最优为目标，系统总发电成本由燃煤机组发电成本、燃气机组发电成本组成，目标函数可描述为
（1）
式中，bg为燃煤机组g的特征参数；
为
时段燃煤机组g的出力；bgas为燃气机组的燃料费用系数；
为时段燃气机组的出力。
1.2.1 功率平衡约束
能量平衡方程为
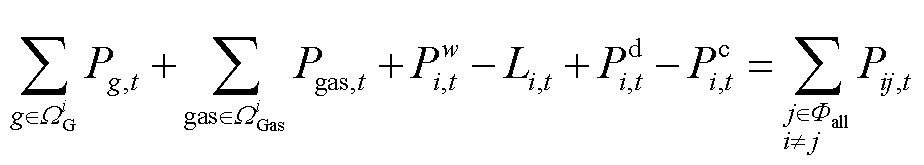（2）
式中，
为与节点
连接的燃煤机组集合；
为与节点连接的燃气机组集合；
，
为网络节点集合；
为时段节点处风电机组w出力；
为节点在时段的负荷值；
、
分别为节点处蓄电池充、放电功率；
为时段支路
的传输功率。
1.2.2 机组调度约束
出力机组包含燃煤机组、燃气机组及风电机组，主要包括机组爬坡约束和机组出力限制，具体表达式为
（3）
（4）
（5）
（6）
（7）
（8）
（9）
式中，
和
为分别燃煤机组g的爬坡和下降速率上限；
和
分别为燃气机组的爬坡和下降速率上限；
、
、分别为时段节点处燃煤机组g、燃气机组gas和风电机组w的发电量；
、
和
、
分别为燃煤机组g和燃气机组gas出力的上、下限；
、
为风电机组w出力的上、下限。式（3）、式（4）分别为燃煤机组出力爬坡和下降速率约束；式（5）、式（6）分别为燃气机组出力爬坡和下降速率约束；式（7）～式（9）分别为燃煤机组、燃气机组和风电机组出力约束。
1.2.3 储能约束
（10）
（11）
（12）
（13）
（14）
（15）
（16）
式中，
和
分别为蓄电池充电和放电效率；
为节点i处蓄电池荷电状态；
为节点处蓄电池的储能量；
为在节点处蓄电池的最大容量；
、
和
、
分别为节点处蓄电池充放电功率上、下限；
和
分别为蓄电池荷电状态最大值和最小值；
、
分别为表示蓄电池的充放电模式的0、1变量，如
表示蓄电池不处于充电状态，
表示蓄电池处于充电状态。式（10）为蓄电池荷电状态平衡方程；式（11）为荷电状态方程；式（12）、式（13）为蓄电池充放电功率约束；式（14）为蓄电池荷电状态约束；式（15）、式（16）为蓄电池充放电状态约束，充放电不可同时进行。
1.2.4 网络约束
（17）
（18）
（19）
（20）
（21）
（22）
（23）
（24）
式中，
为连接节点和
的支路的电纳；为时刻连接节点到的支路的潮流，其正负取决于线路中潮流的流向；
为时刻节点处的电压相角值；
为连接节点和的支路的最大潮流限值；
为二进制变量，表示连接节点和的线路的开/关状态，“0”表示断开，“1”表示闭合；M被称为“大M”值，当二进制变量为1时，M的值无关紧要，当二进制变量为0时，M的值用于确保母线电压角度的差值能同时满足式（17）和式（18）；NSW为网络中允许切换的线路的最大个数；
为与节点相连的节点集合。式（17）～式（20）为电力网络中的线路潮流约束，引入了基尔霍夫定律；式（22）为母线电压相角约束；式（23）为网络中可切换线路数量约束；式（24）为网络连通性约束，用于避免孤岛情况的出现，能够保证各个节点至少连接两条线路，否则一条线路断线故障将无法保证网络的连通性，使得网络解列。
1.2.5 网络阻塞
（25）
式中，
为时刻网络中给定位置节点的节点边际价格，其值由功率平衡约束方程（2）提供；C为输电网络阻塞费用，本文依据输电网络阻塞费用来判断网络的阻塞程度，阻塞费用越少则网络阻塞程度越低，将阻塞程度作为传输切换后产生的新的线路拓扑结构的一项评价指标。
风电出力及负荷需求实际值表达式为
（26）
（27）
式中，
和
分别为时刻节点处风电功率的预测值和预测误差；和
分别为时刻节点处负荷需求的预测值和预测误差。
本文参考文献[16]选用某地区的历史实测风电及负荷数据，采用6个高斯分量线性组合成的高斯混合模型对风电出力预测误差的概率密度函数F(u)进行拟合，高斯混合模型表达式为
（28）
（29）
（30）
式中，
为风电预测误差概率密度函数；
为高斯分量个数；
为第个高斯分量的概率密度函数；
、
和
分别为第n个高斯分量的权重系数、期望和方差。式（29）和式（30）为权重系数约束。
本文采用均值为0且标准差与时刻负荷需求预测值成正比的正态分布拟合负荷需求预测误差的概率密度函数，表达式为
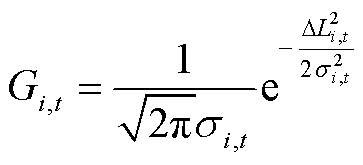（31）
式中，
为负荷预测误差概率密度函数；
为时刻节点处负荷需求预测方差。
风电出力和负荷预测误差概率密度曲线和不同置信水平
对应的置信区间如图2所示，相应的风电出力和负荷预测误差累积分布函数为
和
。
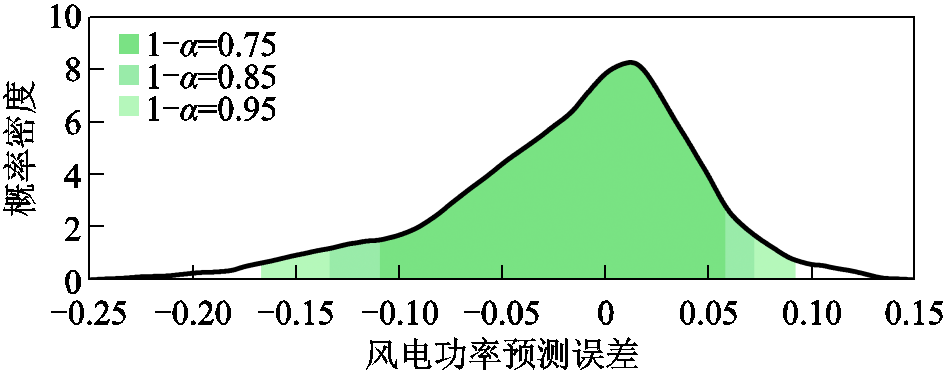
图2 预测误差的概率置信区间
Fig.2 Probability confidence interval of prediction error
置信间隙决策理论（CGDT）是用于高效处理不确定问题的鲁棒优化方法，能够在满足优化结果不差于预设目标的条件下，最大限度地提高目标函数对输入参数不确定性的鲁棒性。它是基于IGDT方法的优化与改进。该方法在IGDT方法的基础上引入了置信水平，采用概率置信区间描述不确定性，可实现对不确定参数的准确描述，弥补了IGDT方法使用对称性波动区间对于不确定性描述过于粗糙的缺陷。此外，引入了机会约束，通过最大化置信水平进而最大程度地规避不确定变量对OTS优化结果的影响，提高OTS优化方案的鲁棒性。
考虑如下优化模型：
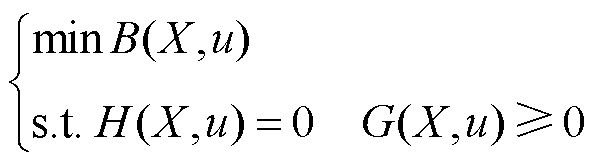（32）
式中，
为决策变量；
为不确定参数；
为目标函数；
和
为等式和不等式约束。
在CGDT中，不确定参数围绕预测值
的波动可描述为
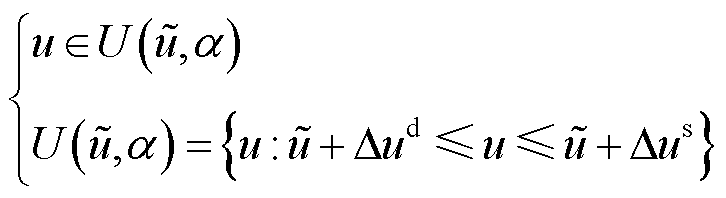（33）
式中，
为置信水平下的不确定参数的波动区间；
为置信水平下不确定参数预测误差置信区间的下界；
为置信水平下不确定参数预测误差置信区间的上界。
在不确定环境中，决策者为保证预设目标的达成，通常会最大化不确定参数的不利扰动，进而最大程度地提高目标函数对不确定性参数影响的规避能力的鲁棒性。对应的CGDT鲁棒优化模型为
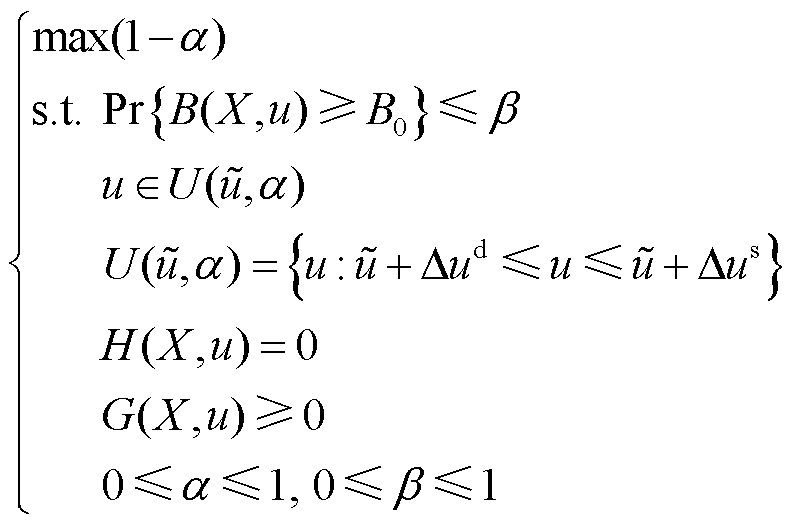（34）
式中，最大化不确定置信水平为目标函数；
为概率；
为目标函数在
的确定性模型的最优解；
为目标显著性水平。
依据第1节所建立的输电网络不确定OTS模型，以及CGDT不确定鲁棒优化方法，建立基于CGDT求解不确定性OTS的鲁棒优化模型为如式（33）所示，其中，决策变量
为系统最优传输切换优化调度方案，即输电网络中的各线路开关状态。
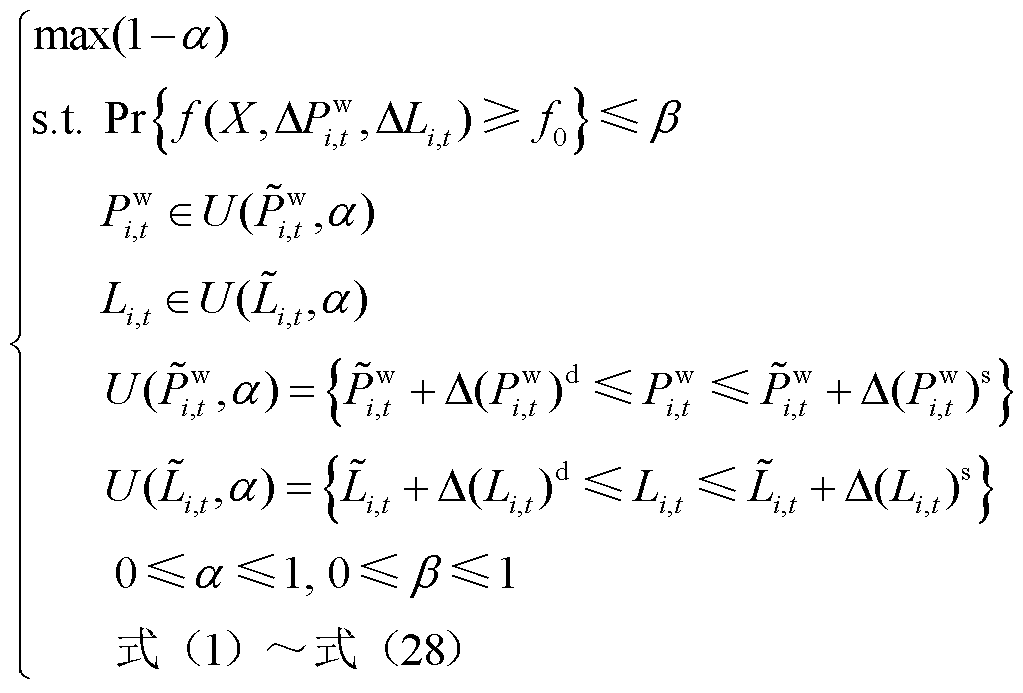（35）
式中，
为目标函数（1）在
、
的确定性模型中的最优解；
、
分别为置信水平下的不确定参数
、的波动区间；
、
和
、
分别为置信水平下不确定参数风电出力、预测误差置信区间的下界和上界。
为降低求解难度，需将所建立的基于CGDT求解不确定性OTS的鲁棒优化模型（33）中存在的不确定机会约束条件
转换为确定性约束条件，过程如下：
设、相互独立，已知、为不确定变量，
为实值可测函数，则
为不确定变量。设
是的不确定分布函数，根据不确定分布的定义则有
（36）
根据第1节所得、分别服从于累积分布函数和，且为实值可测函数，可得
（37）
由不确定变量运算法则可得
（38）
式中，
和
分别为风电出力和负荷需求预测误差的逆累积分布函数。
（39）
综上可得，式（35）中存在的不确定机会约束条件可转换为确定性约束条件
。
综合上述优化方法和优化模型，本文采用GAMS中内置的CONOPT算法进行求解，算法流程如图3所示，给出具体算法步骤如下：
1）将风电出力、负荷需求分别设定为预测值、
，得到目标函数（1）在确定性模型中的最优解
。
2）根据设定的目标显著性水平，将确定性模型最优解代入基于CGDT求解不确定性OTS的鲁棒优化模型（33）进行求解，得到最大化置信水平、最低总发电成本
及鲁棒OTS方案。
3）根据所得置信水平和不确定参数风电出力、负荷需求预测误差概率密度，求解相应的概率置信区间上下界：、和、，进而计算得出风电出力、负荷出力鲁棒波动区间为
、
，结束。
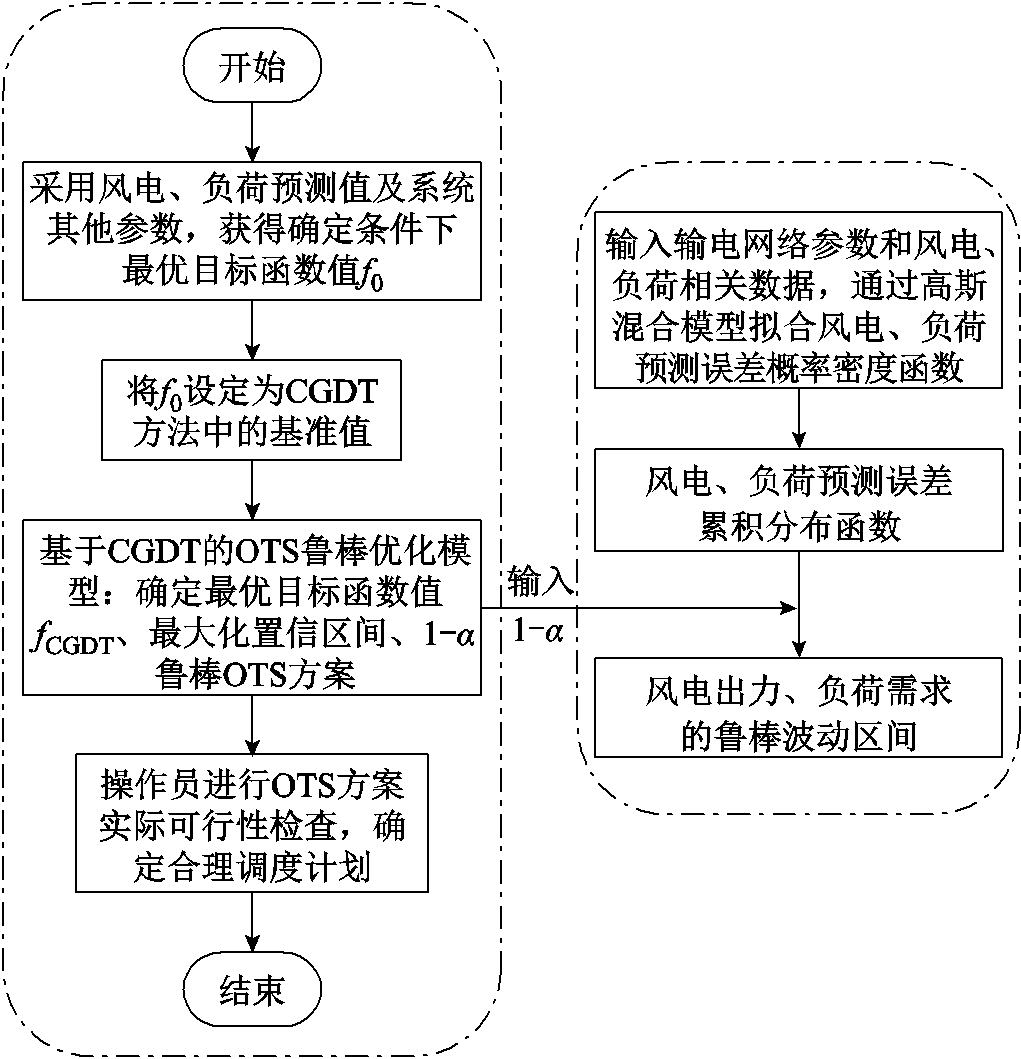
图3 鲁棒OTS方案求解流程
Fig.3 The solving process of robust OTS solution
本文以改进的IEEE 24节点电力网络为例，对所建立的基于CGDT的不确定性OTS鲁棒优化模型进行算例分析，电力网络结构图如图1所示，系统中共有四个燃气发电机组，其余为常规机组；四个燃气发电机组位于1、2、16和22节点；三个风电场分别接于8、19、21节点，容量分别为200 MW、150 MW和100 MW；两个储能单元分别位于19、21节点，最大容量分别为200 MW·h和300 MW·h，最大充放电功率分别为40 MW、60 MW，其充放电效率分别取0.95和0.9；其余参数可参照文献[26]。输电网络中各节点风电出力、负荷需求的预测值分别如图4、图5所示。
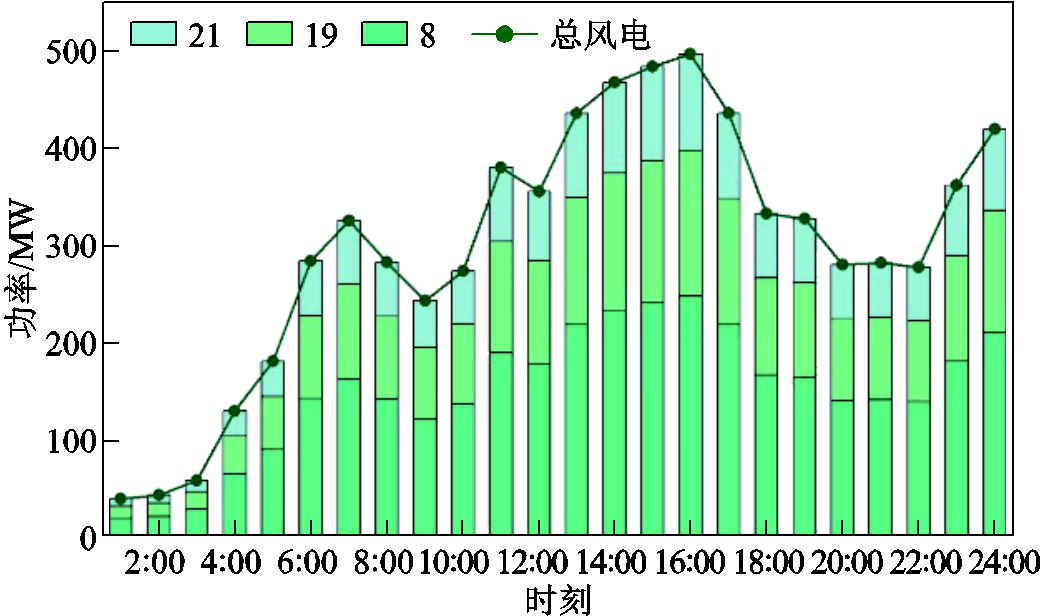
图4 各节点的风电出力预测值
Fig.4 Predicted value of wind power output of each node
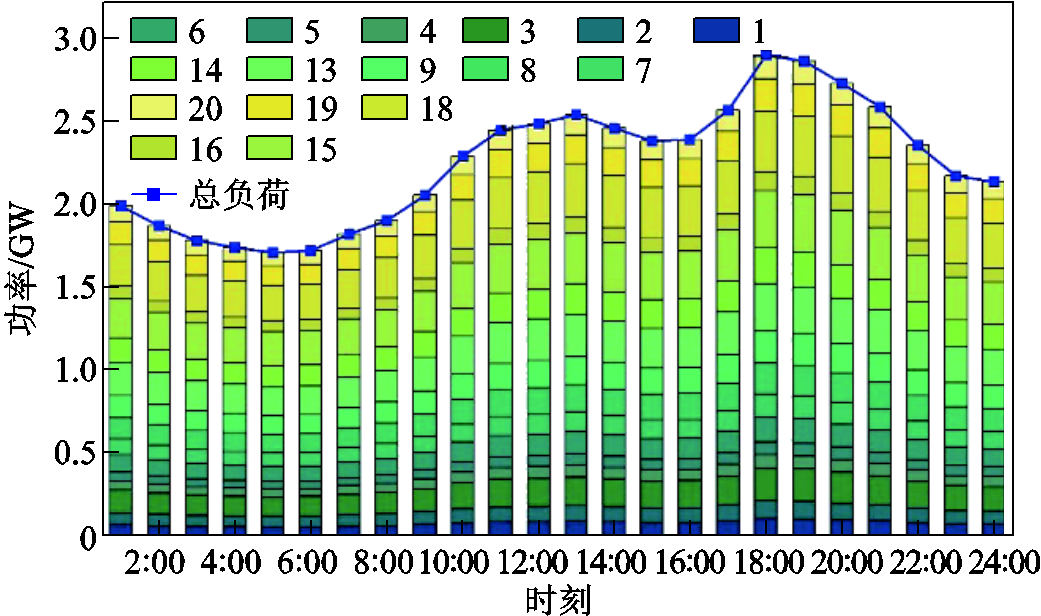
图5 各节点的负荷需求预测值
Fig.5 Load demand forecast value of each node
将风电出力、负荷需求分别设定为预测值、，得到目标函数（1）在确定性模型中的最优解
，此时OTS方案为关闭线路：1-2、1-3、7-8、15-16、16-19。
将确定性模型最优解作为预设值代入式（33），不同目标显著性水平下的最优解以及对应的置信水平、鲁棒OTS方案见表1。由表1可知，不同目标显著性水平会导致鲁棒OTS方案的差异，值设置越小，不确定性置信水平则越小，目标函数值小于预设值的概率越大，但所求解的OTS方案对电力网络中不确定性的规避能力越低，鲁棒性越差。因此，对的选择应根据电力网络处理不确定风险的能力来确定。当设定为0.25时，基于CGDT求解不确定性OTS的鲁棒优化模型最优解为
，最优解对应的OTS方案为关闭线路：1-2、7-8、15-16、16-19、17-18，优化调度结果如图6所示。
表1 不同目标显著性水平下的最优传输切换方案
Tab.1 Three scenarios for system robustness analysis
总发电成本/$最优传输切换方案（关闭线路） 0.15649 819.487 0.1451-2、4-9、7-8、15-16、16-19、17-18 0.2678 748.1720.4711-2、1-3、7-8、15-16、16-19、21-22 0.25708 682.5540.7101-2、7-8、15-16、16-19、17-18
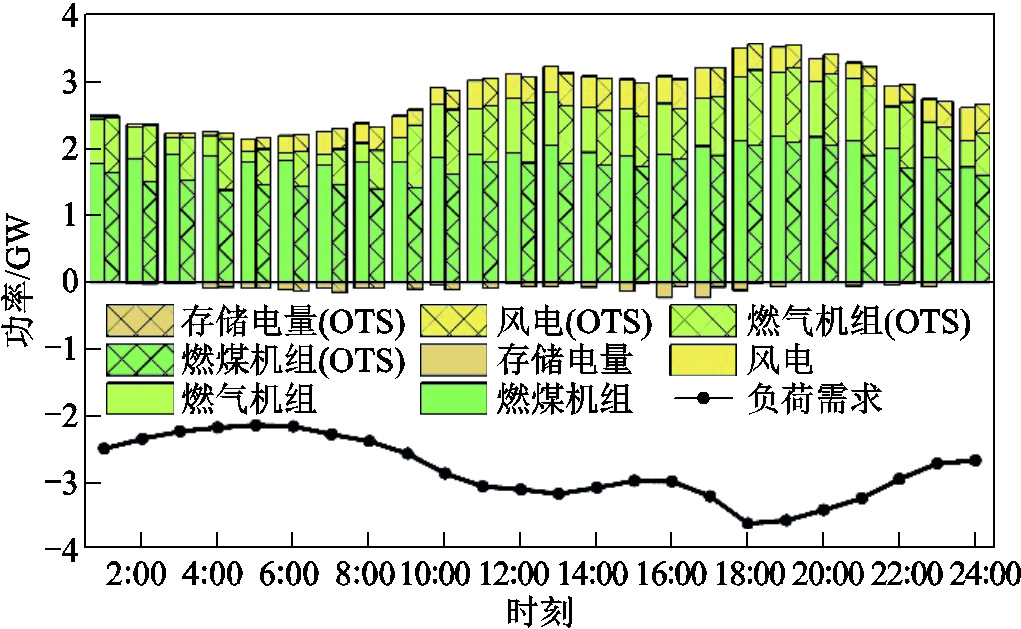
图6 采用OTS方案前后最优出力分布对比
Fig.6 Comparison of optimal output distribution before and after adopting OTS scheme
结合图6，根据OTS方案改变网络拓扑结构后，燃煤机组发电量在电力网络总出力中占比由84.96%降低为60.13%，承担满足负荷需求的发电机组出力由火电机组向发电效率高的燃气机组和发电成本低的风电机组转移，改善了系统发电结构，从而使得总发电成本降低3.9%。此外，系统所需存储容量降低，当负荷需求较低时，蓄电池通过电能的储存和释放，满足系统为消纳风电而产生的削峰填谷需求，提高了电能利用效率。
此时，鲁棒OTS方案对应的最大置信水平
，根据风电出力预测误差概率密度函数可得相应的不确定信概率置信区间上下界分别为
、
；根据负荷需求预测误差概率密度函数可得相应的不确定概率置信区间上下界分别为
、
，进而可知风电出力鲁棒波动区间为，负荷需求的鲁棒波动区间为
，分别对应于图7风电出力区域划分中的S1区域和图8中负荷需求区域划分中的S2区域。
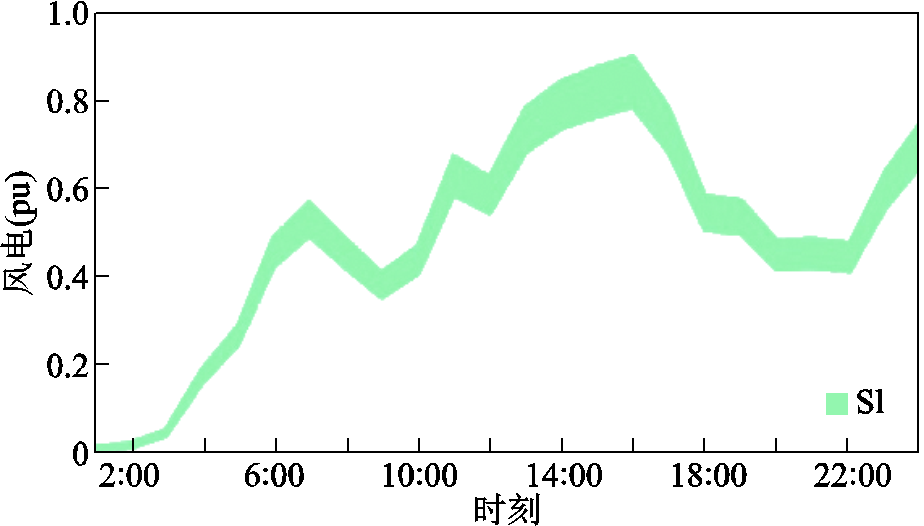
图7 风电出力区域划分
Fig.7 Wind power output regions
图8 负荷需求区域划分
Fig.8 Load demand output area regions
在S1、S2区域采用蒙特卡洛方法抽取1 000组随机风电出力、负荷需求场景，然后固定鲁棒OTS方案对应的输电线路状态，将所抽取的随机场景逐一代入模型式（1）～式（39）中进行求解和检验，得到总发电成本概率分布，概率分布直方图如图9所示。由图可知，概率分布近似服从正态分布，各场景对应的总发电成本均小于
，由此可知基于CGDT求解不确定性OTS的鲁棒优化模型所求解的OTS方案具有良好的适应性。
在相同的运行条件和参数条件下，本文分别采用CGDT鲁棒优化方法、IGDT鲁棒优化方法、基于随机规划的多场景法求取不确定性环境下的OTS方案。设定CGDT方法中目标显著性水平
为0.25，IGDT方法中偏差因子为0.25，IGDT方法参考文献[27]，多场景法参考文献[28]，场景数为10。表2为不同方法下的最优解及OTS方案。此外，在风电出力、负荷需求预测误差波动范围内随机抽取1 000组场景，固定不同优化方法得到的OTS方案对应的输电线路状态，根据式（1）～式（39）求解不同场景对应的系统总发电成本，其统计结果如表3和图10所示。
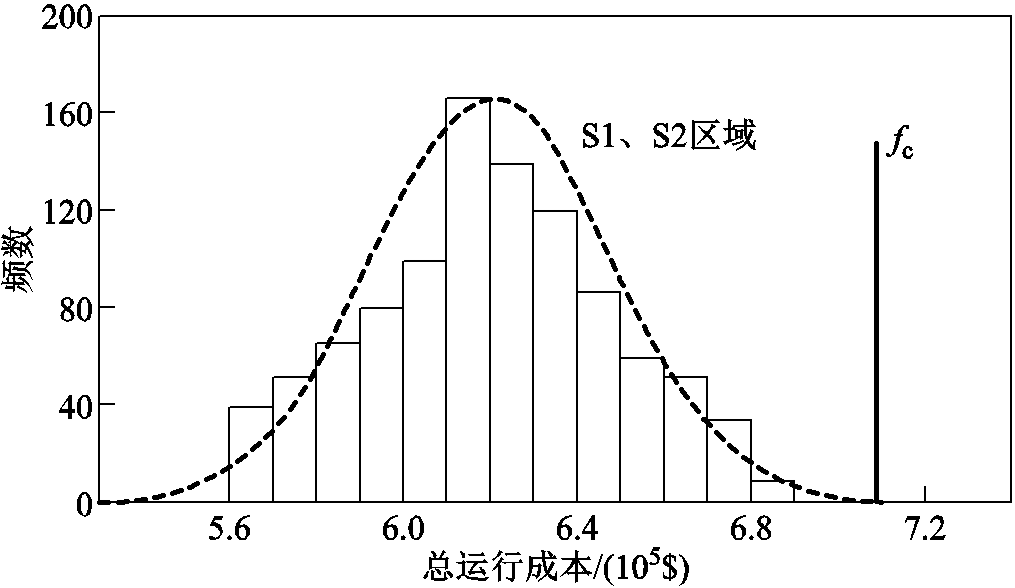
图9 发电成本概率分布
Fig.9 Probability distribution of power generation cost
表2 不同方法下的最优传输切换方案
Tab.2 The optimal transmission switching scheme under different methods analysis
参数IGDT方法CGDT方法多场景法 总发电成本/$708 682.554705 330.784713 711.461 阻塞成本/$000 OTS方案1-2、7-8、 15-16、 17-181-2、4-9、7-8、 15-16、16-19、 17-181-2、1-3、3-9、 7-8、15-16、 16-19 求解时长/s620.063965.4971 640.047
表3 各随机场景总发电成本统计结果
Tab.3 Statistical results of total operating cost of each random scene
方法最大值/$最小值/$平均值/$ 确定性方法1 106 807580 233837 536.540 5 IGDT方法900 377564 041725 635.836 2 CGDT方法788 270563 035688 997.400 6 多场景法1 046 801568 388855 391.854 1
结合表2、表3和图10可知，IGDT、CGDT鲁棒优化方法整体上优于确定性方法和多场景法。这是因为确定性模型是根据日前不确定参数预测值确定OTS方案，未考虑实时运行过程中不确定参数的波动；而采用多场景法获得的OTS方案对场景数量的依赖较高，场景数量越多则对不确定性的描述越准确，所求得的OTS方案适应性也越强，但场景数越多计算时间也就越长，难以保证所求解的OTS 方案的鲁棒性。IGDT、CGDT鲁棒优化方法的计算时间相对较短，能够给出不确定参数的鲁棒波动区间，对决策人员具有重要意义，在实际应用中有良好的可扩展性。
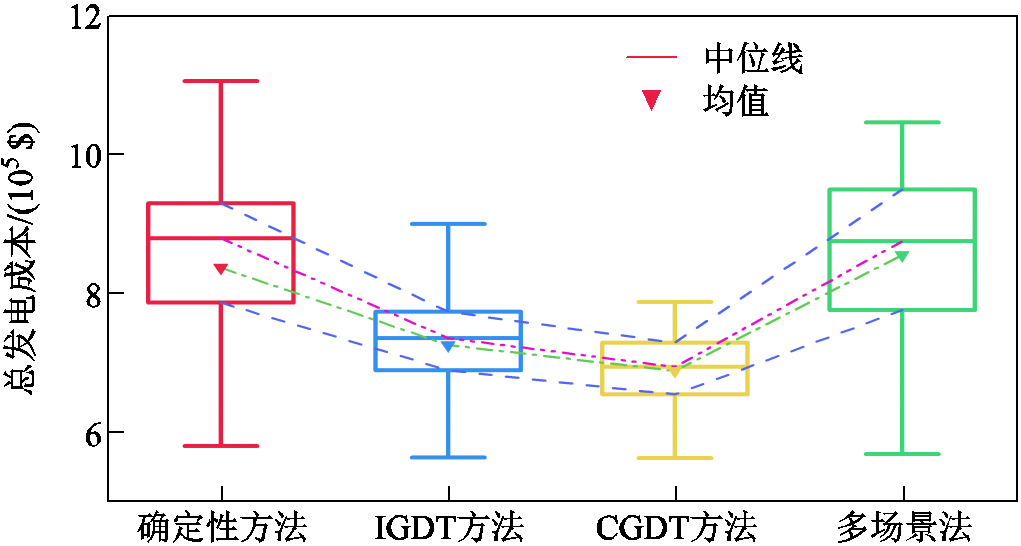
图10 各随机场景总发电成本统计结果
Fig.10 Statistical results of total operating cost of each random scene
此外，相较于IGDT方法，CGDT方法对应的箱体和触须更短，最大值、均值、中位值均优于IGDT，这是因为CGDT方法考虑了不同不确定参数的概率分布的差异性和多态性，并引入了置信水平，采用概率置信区间描述不确定性，弥补了IGDT采用对称波动区间对于不确定性描述过于粗糙的缺陷，通过最大化置信水平从而最大化规避不确定性参数对OTS优化结果的影响，使得所求的OTS方案具有更强的鲁棒性。
为求取含不确定风电输电网络的OTS鲁棒策略，本文将风电及负荷需求不确定性纳入到输电网络OTS模型中，针对其中的不确定性引入了置信间隙决策理论，提出了基于CGDT求解不确定性OTS的鲁棒优化方法。以总发电成本最优为目标，建立了基于置信间隙决策理论的输电网络OTS鲁棒优化混合整数非线性规划模型。
相比于其他求取不确定性OTS的方法，本文所提出的基于CGDT求取不确定性OTS的鲁棒优化方法采用概率置信区间描述不确定性，更充分地反映了不确定参数的实际分布特性，能够避免由于不确定参数描述简陋造成的OTS方案可行性差的缺陷。此外，相较于其他不确定问题处理方法，采用基于CGDT的鲁棒优化方法求取不确定条件下的OTS更具高效性，所获得的OTS方案对于风电出力、负荷需求不确定变量的波动具有良好的鲁棒性和适应性，并且优化了输电网络的拓扑结构，降低了系统总发电成本，提高了含不确定风电输电网络运行的稳定性。
参考文献
[1] 陆明璇, 周明, 黄瀚燕, 等. 含快速线路筛选的电力系统发输电协同优化运行[J]. 中国电机工程学报, 2021, 41(20): 6949-6959.
Lu Mingxuan, Zhou Ming, Huang Hanyan, et al. Synergetic operational optimization of generation and transmission in power systems with rapid line screening[J]. Proceedings of the CSEE, 2021, 41(20): 6949-6959.
[2] He Hongjie, Du Ershun, Zhang Ning, et al. Enhancing the power grid flexibility with battery energy storage transportation and transmission switching[J]. Applied Energy, 2021, 290: 116692.
[3] 赵冬梅, 王浩翔, 陶然. 计及风电-负荷不确定性的风-火-核-碳捕集多源协调优化调度[J]. 电工技术学报, 2022, 37(3): 707-718.
Zhao Dongmei, Wang Haoxiang, Tao Ran. A multi-source coordinated optimal scheduling model considering wind-load uncertainty[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 707-718.
[4] 侯慧, 刘鹏, 黄亮, 等. 考虑不确定性的电-热-氢综合能源系统规划[J]. 电工技术学报, 2021, 36(增刊1): 133-144.
Hou Hui, Liu Peng, Huang Liang, et al. Planning of electricity-heat-hydrogen integrated energy system considering uncertainties[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 133-144.
[5] 王雪纯, 陈红坤, 陈磊. 提升区域综合能源系统运行灵活性的多主体互动决策模型[J]. 电工技术学报, 2021, 36(11): 2207-2219.
Wang Xuechun, Chen Hongkun, Chen Lei. Multi-player interactive decision-making model for operational flexibility improvement of regional integrated energy system[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2207-2219.
[6] Peker M, Kocaman A S, Kara B Y. Benefits of transmission switching and energy storage in power systems with high renewable energy penetration[J]. Applied Energy, 2018, 228: 1182-1197.
[7] Zhou Yuqi, Zhu Hao, Hanasusanto G A. Transmission switching under wind uncertainty using linear decision rules[C]//2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2020: 1-5.
[8] Dehghan S, Amjady N, Conejo A J. Adaptive robust transmission expansion planning using linear decision rules[J]. IEEE Transactions on Power Systems, 2017, 32(5): 4024-4034.
[9] 那广宇, 魏俊红, 王亮, 等. 基于Gram-Charlier级数的含风电电力系统静态电压稳定概率评估[J]. 电力系统保护与控制, 2021, 49(3): 115-122.
Na Guangyu, Wei Junhong, Wang Liang, et al. Probabilistic evaluation of power system static voltage stability with wind power uncertainty based on the Gram-Charlier expansion[J]. Power System Protection and Control, 2021, 49(3): 115-122.
[10] Ahmed R, Nawaz A, Javid Z, et al. Optimal transmission switching based on probabilistic load flow in power system with large-scale renewable energy integration[J]. Electrical Engineering, 2022, 104(2): 883-898.
[11] Pasupathy R, Song Yongjia. Adaptive sequential sample average approximation for solving two-stage stochastic linear programs[J]. SIAM Journal on Optimization, 2021, 31(1): 1017-1048.
[12] 张靠社, 冯培基, 张刚, 等. 考虑机会约束的多能源微电网双层优化配置[J]. 太阳能学报, 2021, 42(8): 41-48.
Zhang Kaoshe, Feng Peiji, Zhang Gang, et al. Bi-level optimization configuration method for multienergy microgrid considering chance constraints[J]. Acta Energiae Solaris Sinica, 2021, 42(8): 41-48.
[13] 曾博, 胡强, 刘裕, 等. 考虑需求响应复杂不确定性的电–气互联系统动态概率能流计算[J]. 中国电机工程学报, 2020, 40(4): 1161-1171, 1408.
Zeng Bo, Hu Qiang, Liu Yu, et al. Dynamic probabilistic energy flow calculation for interconnected electricity-gas system considering complex uncertainties of demand response[J]. Proceedings of the CSEE, 2020, 40(4): 1161-1171, 1408.
[14] Dehghanian P, Kezunovic M. Probabilistic decision making for the bulk power system optimal topology control[J]. IEEE Transactions on Smart Grid, 2016, 7(4): 2071-2081.
[15] Yuan Yang, Cheng Haozhong, Zhang Heng, et al. Transmission expansion planning with optimal transmission switching considering uncertain n-k contingency and renewables[J]. Energy Reports, 2022, 8: 573-583.
[16] Numan M, Feng D, Abbas F, et al. Mobilizing grid flexibility through optimal transmission switching for power systems with large-scale renewable integration[J]. International Transactions on Electrical Energy Systems, 2020, 30(3): e12211.1-e12211.15.
[17] Dehghan S, Amjady N. Robust transmission and energy storage expansion planning in wind farm-integrated power systems considering transmission switching[J]. IEEE Transactions on Sustainable Energy, 2016, 7(2): 765-774.
[18] 夏鹏, 刘文颖, 张尧翔, 等. 考虑风电高阶不确定性的分布式鲁棒优化调度模型[J]. 电工技术学报, 2020, 35(1): 189-200.
Xia Peng, Liu Wenying, Zhang Yaoxiang, et al. A distributionally robust optimization scheduling model considering higher-order uncertainty of wind power[J]. Transactions of China Electrotechnical Society, 2020, 35(1): 189-200.
[19] 彭春华, 郑聪, 陈婧, 等. 基于置信间隙决策的综合能源系统鲁棒优化调度[J]. 中国电机工程学报, 2021, 41(16): 5593-5604.
Peng Chunhua, Zheng Cong, Chen Jing, et al. Robust optimal dispatching of integrated energy system based on confidence gap decision[J]. Proceedings of the CSEE, 2021, 41(16): 5593-5604.
[20] 汪超群, 韦化, 吴思缘. 基于信息间隙决策理论的多源联合优化机组组合[J]. 中国电机工程学报, 2018, 38(12): 3431-3440.
Wang Chaoqun, Wei Hua, Wu Siyuan. Multi-power combined unit commitment based on information gap decision theory[J]. Proceedings of the CSEE, 2018, 38(12): 3431-3440.
[21] 张亚超, 郑峰, 乐健, 等. 考虑风电高阶不确定性的电气综合系统分布鲁棒协同优化调度[J]. 中国电机工程学报, 2020, 40(24): 8012-8026, 8238.
Zhang Yachao, Zheng Feng, Le Jian, et al. A distributionally robust coordinated optimization scheduling of integrated electricity and natural gas systems considering higher-order uncertainty of wind power[J]. Proceedings of the CSEE, 2020, 40(24): 8012-8026, 8238.
[22] 杨智超. 考虑可再生能源接入的电力系统恢复协同优化策略[D]. 合肥: 合肥工业大学, 2021.
[23] 姚琦, 胡阳, 柳玉, 等. 考虑载荷抑制的风电场分布式自动发电控制[J]. 电工技术学报, 2022, 37(3): 697-706.
Yao Qi, Hu Yang, Liu Yu, et al. Distributed automatic generation control of wind farm considering load suppression[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 697-706.
[24] Saavedra R, Street A, Arroyo J M. Day-ahead contingency-constrained unit commitment with Co-optimized post-contingency transmission switching[J]. IEEE Transactions on Power Systems, 2020, 35(6): 4408-4420.
[25] Sheikh M, Aghaei J, Letafat A, et al. Security-constrained unit commitment problem with transmission switching reliability and dynamic thermal line rating[J]. IEEE Systems Journal, 2019, 13(4): 3933-3943.
[26] Soroudi A. Power System Optimization Modeling in GAMS[M]. Cham: Springer International Publishing, 2017
[27] 彭春华, 陈露, 张金克, 等. 基于分类概率机会约束IGDT的配网储能多目标优化配置[J]. 中国电机工程学报, 2020, 40(9): 2809-2819.
Peng Chunhua, Chen Lu, Zhang Jinke, et al. Multi-objective optimal allocation of energy storage in distribution network based on classified probability chance constraint information gap decision theory[J]. Proceedings of the CSEE, 2020, 40(9): 2809-2819.
[28] 谢敏, 罗文豪, 吉祥, 等. 随机风电接入的电力系统动态经济调度多场[J]. 电力自动化设备, 2019, 39(11): 27-33.
Xie Min, Luo Wenhao, Jixiang, et al. Multi-scenario collaborative optimization of dynamic economic dispatching in power system with random wind power access[J]. Electric Power Automation Equipment, 2019, 39(11): 27-33.
Abstract Optimal Transmission Switching (OTS) is a control mechanism that improves the transmission network's flexibility by changing the network's topology. OTS is widely used in transmission networks. OTS schemes are usually determined in the day-ahead scheduling stage. However, there are often uncertain wind power and load demands in the transmission network, which makes OTS schemes unable to achieve the desired effect. In order to solve these problems, this paper proposes to apply the Confidence Gap decision theory (CGDT) to find the OTS scheme under the condition of uncertainty and improve its robustness of OTS scheme.
Firstly, the Gaussian mixture model and normal distribution are used to fit the probability distribution function of wind power output and load demand prediction errors, and the uncertainty is incorporated into the OTS model of the transmission network. Secondly, CGDT based on the robust drive is introduced to solve the uncertainty, and a robust optimization method based on CGDT is proposed to solve the uncertainty OTS scheme. A mixed integer nonlinear programming model based on CGDT for OTS robust optimization of the transmission network is constructed to minimize the total generation cost as the optimization goal. Thirdly, the chance constraints in the model are transformed into equivalent deterministic constraints according to the uncertainty theory. Finally, this paper uses the improved IEEE 24 node power network to analyze the proposed CGDT-based OTS robust optimization model. In the proposed OTS robust optimization method, the influence of uncertainty parameters on OTS optimization results is maximized by maximizing the confidence level to provide a robust OTS scheme.
According to the OTS solution, the transmission network topology is changed. The operation results show that the proportion of the power generation of coal-fired units in the total power output of the power network is reduced from 84.96% to 60.13%. The power output of generating units that meet the load demand is transferred from thermal power units to gas units with high generation efficiency and wind turbines with low generation cost, which improves the power generation structure of the system and reduces the total power generation cost by 3.9%. In wind power and load demand robust range using the Monte Carlo method in extracting 1 000 groups of random wind power and load demand scenario, the total cost by probability distribution results show that the approximate probability distribution is normal, the corresponding scenarios of the total cost is less than the set value. Thus the solving scheme of OTS has good adaptability. Under the same operation condition, CGDT, IGDT, and multi-scene methods are used to obtain the corresponding OTS scheme. One thousand scenarios were randomly selected within the fluctuation range of wind power and load demand prediction errors to solve the total power generation cost corresponding to different scenarios. The statistical results show that the CGDT method has a relatively short computation time, its corresponding maximum, mean, and median values are optimal, and the OTS scheme is more robust. In addition, this method can give a robust fluctuation interval of uncertain parameters, which is of great significance to decision makers and has good scalability in practical applications.
The following conclusions can be drawn from the example analysis: (1) Using the CGDT method to obtain the OTS scheme can optimize the topology structure of the transmission network, reduce the total generation cost of the system, and improve the stability of the operation of the wind power transmission network with uncertainty. (2) Compared with the other methods to calculate the uncertainty OTS, in this paper, based on the proposed CGDT robust optimization method to calculate the uncertainty of OTS using probability and confidence interval to describe uncertainty, more fully reflect the actual distribution of the uncertain parameters, to avoid caused by uncertain parameters to describe humble OTS on defects of poor feasibility. (3) The robust optimization method based on CGDT is more efficient to obtain OTS under uncertain conditions, and the obtained OTS scheme has good robustness and adaptability to fluctuations of uncertain variables of wind power output and load demand.
Keywords：Uncertainty, wind power generation, load demand, optimal transmission switching (OTS), confidence gap decision theory (CGDT)
王东风 男，1971年生，教授，博士生导师，研究方向为先进控制理论及应用。E-mail:wangdongfeng@ncepu.edu.cn
黄 宇 男，1982年生，副教授，研究生导师，研究方向为多类异质综合能源系统分析与优化。E-mail:huangyufish@ncepu.edu.cn（通信作者）
中图分类号：TM734
DOI:10.19595/j.cnki.1000-6753.tces.221375
中央高校基本科研业务费专项资金资助项目（2021MS089）。
收稿日期 2022-07-16
改稿日期 2022-08-29
（编辑 赫 蕾）