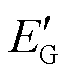 表示;转子电角度用dG表示,假设在负荷突变的初期转子电角度dG不发生突变;发电机暂态阻抗用
表示;转子电角度用dG表示,假设在负荷突变的初期转子电角度dG不发生突变;发电机暂态阻抗用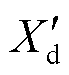 表示;VG和VL分别为发电机机端电压和负荷端口电压;PG为发电机输出电磁功率;为了简化,连接发电机和负荷的线路阻抗用Xl表示。
表示;VG和VL分别为发电机机端电压和负荷端口电压;PG为发电机输出电磁功率;为了简化,连接发电机和负荷的线路阻抗用Xl表示。摘要 该文提出两种适用于孤岛运行的基于永磁同步风机的自动功率平衡控制策略。在控制策略Ⅰ中,风机的网侧换流器保持换流器电压的幅值和频率为恒定,转子侧换流器通过PI控制器调整功率参考值进而维持直流电压;在控制策略Ⅱ中,风机网侧换流器利用直流母线电压的动态特性实现电网同步和惯性响应,机侧换流器根据直流母线电压偏差调整有功功率以模拟一次频率控制。这两种策略都可以有效地保证风机的独立运行,无需锁相环和外部电源。特别地,策略Ⅱ突出了节能特性,将直流电容器中的储备能量用于系统惯性支持和负荷需求响应,以降低风机飞车的风险。为了提高策略Ⅱ在暂态期间并网点的电压质量,该文进一步提出维持并网点电压的改进控制方案。基于PSCAD/EMTDC仿真软件建立了单台风机向若干本地负荷供电的典型孤岛运行模型,在负荷突然降低或升高的情形下分析和对比了所提两种策略的有效性。
关键词:永磁同步风机 孤岛运行模式 自动功率平衡控制 惯量响应 一次调频 节能特性
近年来,新能源在电力系统中的渗透率不断增大,给交流电网的稳定分析、控制和运行带来了一系列新的问题和挑战[1]。传统的并网变速风机利用转子侧换流器(Rotor Side Converter, RSC)实现最大功率追踪(Maximum Power Point Tracking, MPPT)。同时,网侧换流器(Grid Side Converter, GSC)用于维持直流电压恒定[2]。然而,此类经典的控制需要锁相环(Phase Lock Loop, PLL)来获得公共电压点(Point of Common Coupling, PCC)的相位,以此维持风机的正常运行。然而,在高比例新能源的弱交流系统中,PLL的动态行为会恶化系统稳定性[3]。此外,基于传统PLL的风机无法实现自建压,无法适用于孤岛运行方式(Stand-Alone Operation Mode, SAOM)。因此,如何设计新型的并网变速风机的控制策略,以适应高比例新能源渗透的弱交流电网或孤岛运行场景,是未来风力发电大规模应用的重要挑战。
由于优良的控制性能,基于脉冲宽度调制(Pulse Width Modulation, PWM)的电压源转换器(Voltage Source Converter, VSC)在工业领域大范围应用。在功能上,VSC可分为并网模式换流器和离网模式换流器[4-5]。并网换流器控制策略可分为功率相角控制(power-angle control)和矢量电流控制(vector-current control)[6]。功率相角控制通过调整换流器电压和公共点电压之间的相位差来控制输出的有功功率[7];同时,通过调整换流器电压幅值以控制输出的无功功率。然而,该策略无法有效地解耦有功功率和无功功率,且无法抑制交流故障引发的换流器过电流现象。矢量电流控制有效地解决了以上两个问题,并已广泛应用于风力发电[8]和高压直流输电系统[9]中。该控制通过外环(outer loop)即慢环分别控制有功功率和无功功率,内环(inner loop)即快环限制转子电流的交轴分量[10]。但是,以上两个控制策略都需要PLL获取交流系统的同步信息[11],并不适用于离网换流器。
为了提高多换流器系统的稳定性,虚拟同步控制[12-18]成为研究的热点。该控制策略可分为两大类:①通过调整换流器外环控制中的有功功率、无功功率参考值,使VSC具备惯量响应[12]、频率调节[13-15]和区域间阻尼能力[16],这类方案仍然需要PLL获取电网相位,因此只适用于并网模式;②虚拟同步控制方法被称作功率同步控制(Power-Synchronization Control, PSC)[17]。该控制策略利用交流系统自身的同步机制,为弱交流系统提供了充足的电压支撑,实现了无需PLL的同步控制模式。文献[18]研究了功率同步控制策略的频率调制能力。文献[19-20]提出一种利用换流器直流电压传递电网频率信息的电压源型控制策略,同时推导了该控制策略的阻尼表达式。文献[21]提出一种使用虚拟阻抗的虚拟同步机转子角下垂控制策略。文献[22]提出一种基于虚拟电流的虚拟同步控制。以上有关功率同步控制的研究大多集中在单换流器范畴,没有考虑风力发系统中RSC和GSC配合及风力发电机的动态过程。文献[23]考虑了一种基于双馈感应电机的功率同步控制策略。
孤岛运行模式下变速风力发电机控制策略的设计存在两个难点:①风机如何自建压的问题;②如何维持发电机和负荷功率动态平衡的问题。大部分研究[24-25]依赖储能设备建压和平衡当地负荷,该方法并不经济可靠。文献[26]提出一种在孤岛运行模式下,利用风机GSC建立交流电压,RSC维持直流电压稳定的控制策略。但该文献并没有详细地论讨GSC与RSC的协同配合问题,并且该策略并不适用于多机系统。
结合经典基于PLL的控制策略的不足和孤岛运行模式下风机控制策略设计的难点,本文针对PMSG提出了两种适用于孤岛运行模式的自动功率平衡控制策略。控制策略Ⅰ中,风机的GSC侧保持换流器电压幅值和频率恒定,RSC侧通过PI控制器控制有功功率参考值,进而维持直流电压稳定。这种策略的主要缺点是没有考虑负荷电压响应特性,并且可能无法确保SAOM中多风机(Wind Turbine, WT)的功率同步。基于以上缺点,本文进一步提出了控制策略Ⅱ。首先,该策略的GSC根据直流母线电压的偏差改变换流器电压频率以模拟惯性响应,然后RSC根据直流母线电压变化调节来自WT的有功功率以模拟一次调频控制。策略Ⅱ利用直流电容器的储备能量和负荷需求响应平滑系统功率,具有节能特性。两种策略复杂性更低,控制参数易于实现,只需要测量直流母线电压即可。为了维持PCC电压稳定,基于策略Ⅱ提出了一种在GSC控制回路中加入采用PI控制器的电压控制回路的改进策略,称之为策略Ⅱ改进策略。之后,研究了直流电压下垂系数kDC变化对直流电压和调频效果的影响。以PMSG为例,在负荷突然降低或升高场景下,仿真结果验证了两种策略的有效性。最后,研究了风速连续变化情况下两种策略的有效性。
对于任何电网的负荷突变,同步电机通常会依次进行“同步电机电磁功率突变”“同步电机惯量响应”“同步电机一次调频控制”三个连续阶段,以保持发电机和本地负荷之间的平衡。
以图1的单同步机单负荷系统(Single Synchronizing Generator Single Load, SSSL)为例,分析负荷突变引起同步机电磁功率变化的过程。其中同步机为内电动势恒定的经典模型,其内电动势用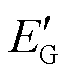 表示;转子电角度用dG表示,假设在负荷突变的初期转子电角度dG不发生突变;发电机暂态阻抗用
表示;转子电角度用dG表示,假设在负荷突变的初期转子电角度dG不发生突变;发电机暂态阻抗用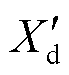 表示;VG和VL分别为发电机机端电压和负荷端口电压;PG为发电机输出电磁功率;为了简化,连接发电机和负荷的线路阻抗用Xl表示。
表示;VG和VL分别为发电机机端电压和负荷端口电压;PG为发电机输出电磁功率;为了简化,连接发电机和负荷的线路阻抗用Xl表示。
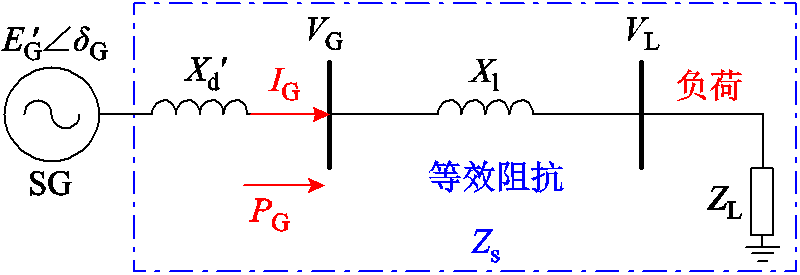
图1 单同步机单负荷系统示意图
Fig.1 The schematic diagram of single SG single load (SSSL) system
图1中本地负荷ZL用恒阻抗模型表示为
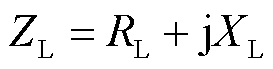 (1)
(1)
式中,RL和XL分别为本地负荷的等效电阻和等效电抗。
根据基尔霍夫电压定理(Kirchhoff′s Voltage Law, KVL),发电机输出电流IG可表示为
 (2)
(2)
因此,发电机输出电磁功率PG可表示为
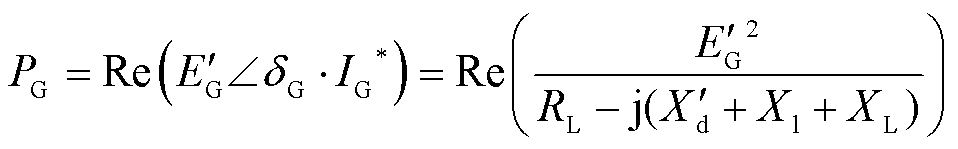 (3)
(3)
式中,Re(·)表示取复数的实部;“*”表示共轭。
为了简化式(3),将图1点画线框中阻抗等效为Zs,其中Zs幅值|Zs|和相角js分别为
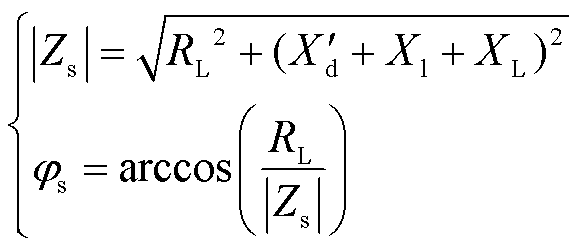 (4)
(4)
合并式(3)和式(4),可得到该SSSL系统中同步发电机输出的有功功率PG为
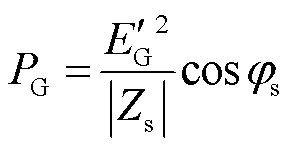 (5)
(5)
在图1的SSSL系统中,假设某一时刻负荷电阻RL和电抗XL分别突变为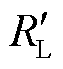 和
和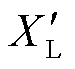 。根据式(4),同样可以求得此时系统的等效阻抗
。根据式(4),同样可以求得此时系统的等效阻抗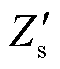 。其中
。其中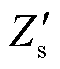 幅值|
幅值|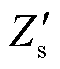 |和相角
|和相角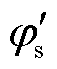 分别为
分别为
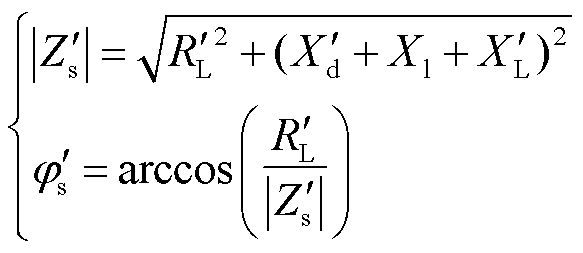 (6)
(6)
因此,可得负荷发生突变后,同步机输出的有功功率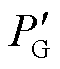 为
为
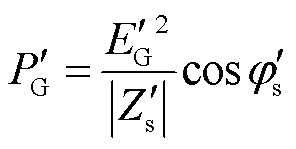 (7)
(7)
由式(5)和式(7)可知,负荷突变前后,同步机输出的有功功率变化量为
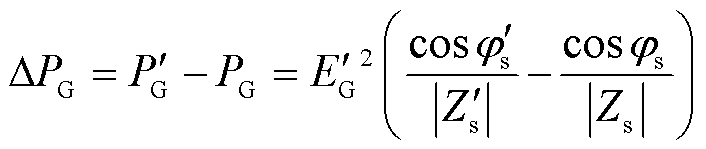 (8)
(8)
从式(8)可以得到以下同步机功率平衡机理:在SSSL系统中,负荷波动引起发电机惯性响应和一次调频控制响应。在该暂态过程中,发电机输出电磁功率的变化只与负荷有关,与发电机转子电角度无关。
在该SSSL系统中,负荷突变后,同步机会经历惯性响应阶段,该阶段可描述为
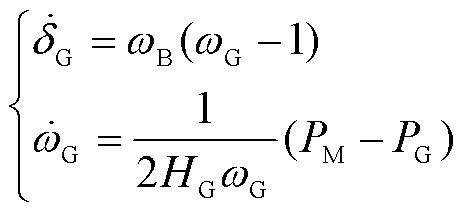 (9)
(9)
式中,wB和wG分别为该SSSL系统的基准转速和发电机转子转速;HG和PM分别为同步机转子惯性时间常数和机械功率。
式(9)表明,负荷突增会引起发电机电磁功率突增,转子转速降低和转子电角度的减小。在SSSL系统中,由于转子电角度的变化并不影响发电机输出功率,因此此处不考虑dG变化对分析的影响。假设该过程中转速偏差非常小(wG≈1),则式(9)可表示为
式中,DPM为发电机机械功率的变化量。
由于调速系统的响应时间较慢,可认为在同步机惯量响应过程中,一次调频未启动。从式(10)中可知,同步机转子利用自身动能平滑系统频率波动,这一过程即为同步发电机的惯性响应。
从式(10)中可知,在负荷突变期间,若不调整原动机机械功率输入,同步机转子角速度将持续增加或减少。因此,当转速偏差超过设定阈值时,系统将激活调速系统用于调整原动机的功率,该过程被称为“一次调频控制”。调速系统的动态行为可以用下垂系数rG和时间常数tg描述,有
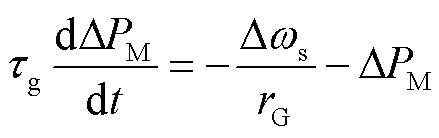 (11)
(11)
由式(11)可得,系统经历一次调频控制之后,同步机转速偏差为
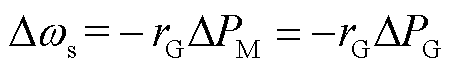 (12)
(12)
综上分析,同步机利用转速来传递发电机和负荷之间的功率不平衡信息。同时,调速系统基于经典的功率-频率下垂特性响应系统频率的变化,以此保证发电机和负荷之间功率的动态平衡。
为了模拟同步机的优良特性,类比第1节交流系统的同步机理,本文提出了两种全新的自动功率平衡控制策略。
图2为PMSG的网侧换流器结构,其中换流器通过换流器等效阻抗XC与本地负荷连接,构成了一个单换流器单负荷系统。
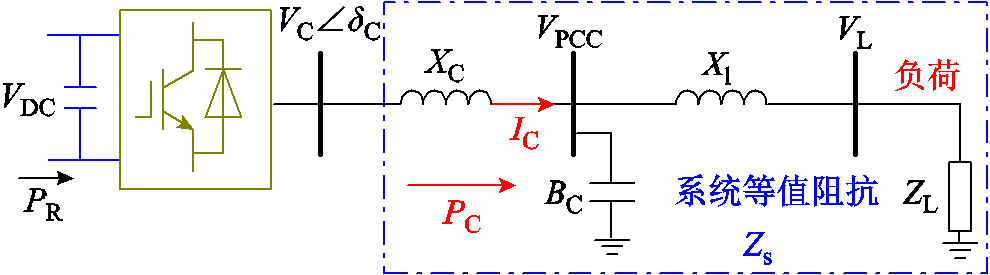
图2 单换流器结构
Fig.2 The schematic diagram of single converter single load system
以图2单换流器单负荷系统为例,同样分析负荷突变造成换流器功率变化的过程和机理。其中,PMSG并网点的电容补偿器等效容抗表示为BC;VDC为直流电压;换流器交流电压用VC∠dC表示,其中VC为换流器电压幅值,dC为换流器电压相角;VPCC和VL分别为换流器PCC电压和负荷端口电压;PC为换流器输出功率;为了简化,连接换流器和负荷的线路阻抗用Xl表示。
根据VSC的基本工作原理,通过控制IGBT的开关动作,换流器交流电压的幅值和频率可被控制在任意可行值。在控制策略Ⅰ中,GSC侧保持换流器交流电压幅值和频率恒定,有效地将换流器交流电压VC和同步机暂态电势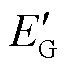 进行类比。VSC直流电压VDC和换流器交流电压VC(线电压)之间的关系为
进行类比。VSC直流电压VDC和换流器交流电压VC(线电压)之间的关系为
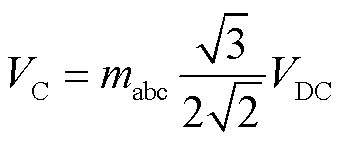 (13)
(13)
式中,mabc为换流器A、B、C三相交流电压的调制比。本文不考虑三相不对称情况,可认为ma=mb=mc=m。
因此,调制比m可表示为
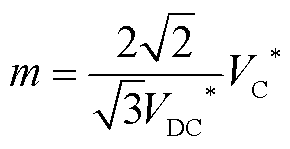 (14)
(14)
式中,VC*和VDC*分别为换流器交流电压和直流电压的参考指令值。
在控制策略Ⅰ中,调制比m、换流器电压的频率f和相角dC被设定成固定值,即
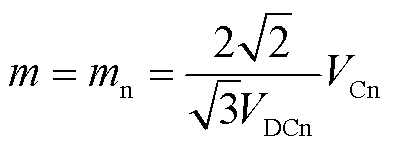 (15)
(15)
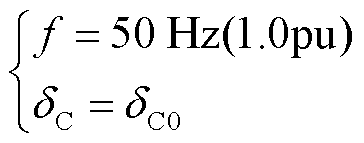 (16)
(16)
式中,dC0为换流器电压相角的初始值;mn为换流器调制比的标称值;VDCn和VCn分别为直流母线电压和换流器电压的标称值。
按照式(15)和式(16),采用正弦脉宽调制法,即可产生固定频率和幅值的电压波形。
仿照1.1节的分析,图2中的单换流器单负荷系统在发生电磁功率变化前后,网络的等效阻抗变化可分别表示为
 (17)
(17)
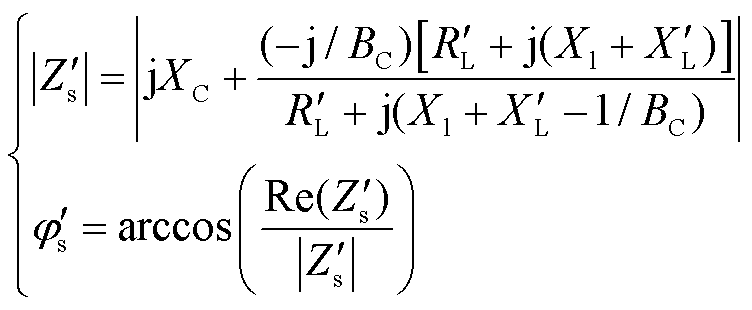 (18)
(18)
因此,同样可以写出PMSG网侧换流器输出功率变化量DPC,I的表达式为
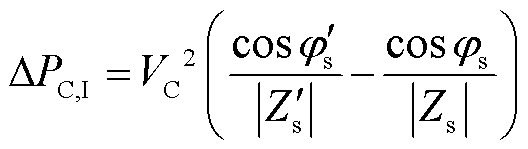 (19)
(19)
式(19)说明在换流器中同样存在类似同步机的功率平衡机理:在单换流器单负荷系统中,换流器在暂态期间输出功率的变化只与负荷有关,与换流器交流电压的相角无关。因此,dC0可在0~2p中任意取值。为了简化,此处dC0可设置为0。
在传统的PMSG控制策略中,RSC侧控制以实现最大功率追踪(MPPT)算法和调整PMSG和RSC之间的无功交换为目标。然而,MPPT算法无法应用于孤岛运行模式或离网运行模式。在该运行模式下,RSC的控制目标应为实时保持风力机和当地负荷之间的功率平衡。图2中,PMSG的直流电容器的动态行为可描述为
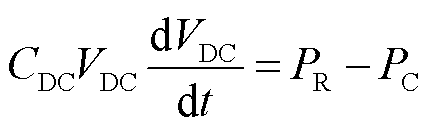 (20)
(20)
式中,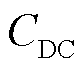 为直流电容容值;PR为来自RSC侧的有功功率。
为直流电容容值;PR为来自RSC侧的有功功率。
在孤岛运行模式下,为了满足风力发电机和当地负荷之间功率的实时平衡,PR由当地负荷或PC决定。由式(20)可知,在两端VSC中,发电机和负荷之间任意有功功率的不平衡会引起直流电压的变化。对比式(20)和式(10),换流器的直流电容动态响应和同步机惯量响应在形式上具有高度的一致性。因此,在暂态过程中直流母线电压可以作为反馈信号跟踪本地负荷波动,以及控制RSC的有功功率,维持功率平衡。以上功率平衡机制和同步机利用系统频率信号进行功率调整的机制是完全类似的。综上所述,在风力发电机孤岛运行模式下,RSC的功率PR*可设置为
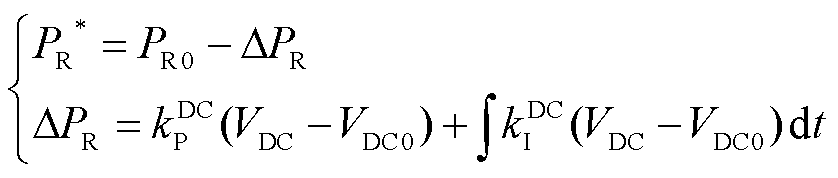 (21)
(21)
式中,DPR为直流电压控制环PI控制器的输出量;kPDC和kIDC分别为直流电压控制环PI控制器的参数;PR0为RSC控制回路中,功率参考值的初始值。
鉴于换流器的快速调制能力,本文分析中认为RSC实际的功率输出能够实时跟踪功率参考值,即PR=PR*。在该策略下,任意负荷波动都会引起直流电压的波动,进而引起RSC有功功率参考值PR*的调整,以确保两端换流器之间的功率平衡。此外,由于换流器功率平衡是通过控制直流电压实现的,PR0可设置为任意可行值。
在负荷波动期间,为了避免DPR的大范围波动,PR0可设置为GSC输出功率PC在某段时间T内的平均值,有
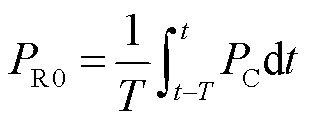 (22)
(22)
在该策略下,风力机捕捉的风能PW和RSC有功功率PR之间的不平衡会引发永磁电机转子加速或减速,该动态过程可描述为
式中,wr和HWT分别为转子转速和惯性时间常数。
在本节分析中,假设风能资源是充足的,因此,在系统暂态期间,通过超速控制或桨距角控制,风轮机捕捉的风能最终会和RSC输出的有功功率达到平衡。综上所述,基于PMSG的自动功率平衡控制策略Ⅰ的整体控制框图如图3所示。
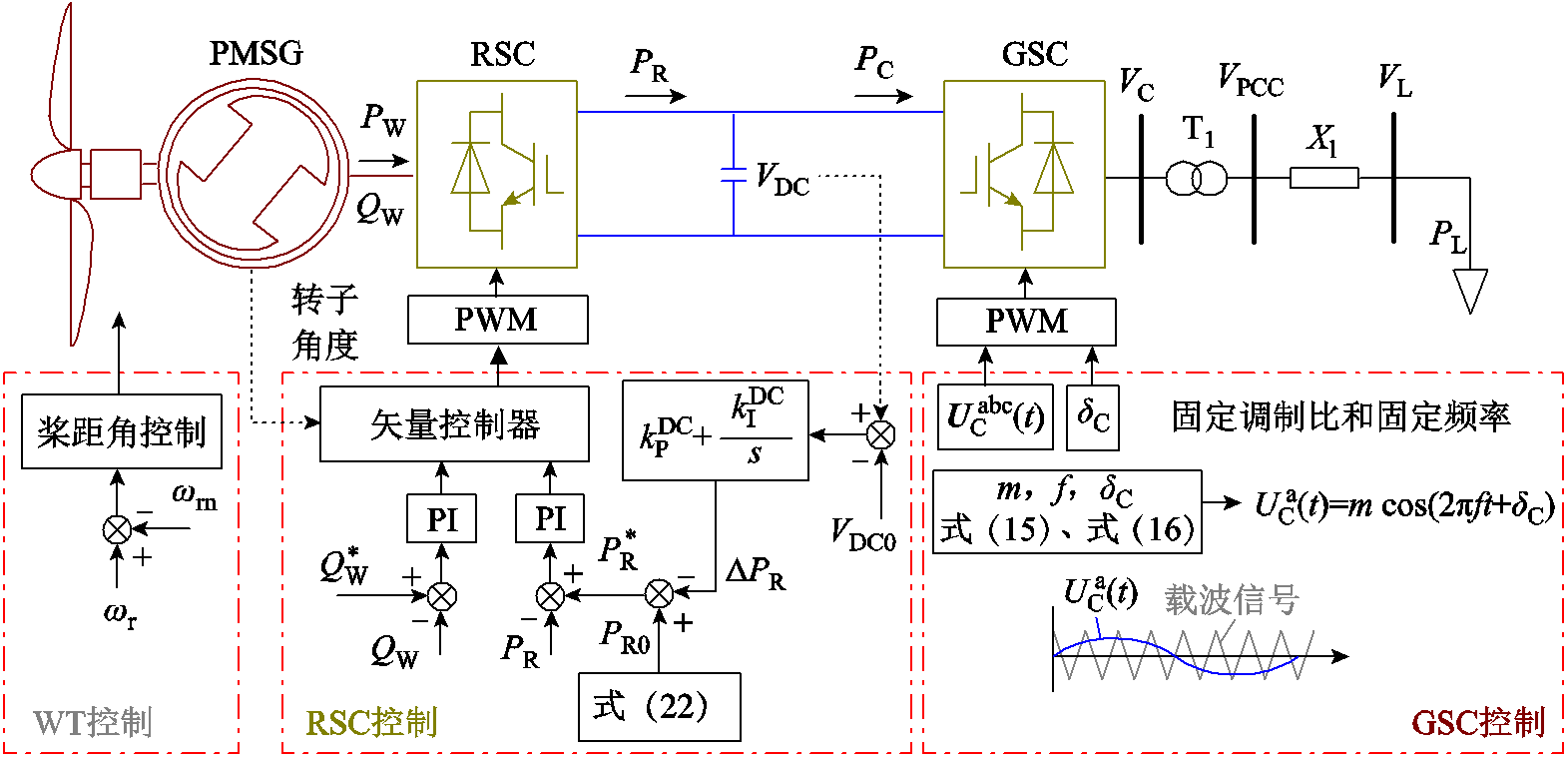
图3 控制策略Ⅰ整体控制框图
Fig.3 Overall control scheme of the proposed Strategy I
在策略Ⅰ中,PMSG的GSC负责产生恒定的交流电压,RSC负责平衡发电机和负荷之间的功率平衡。该策略的功率平衡机理和传统的同步机利用系统频率偏差进行功率调整的机制是完全类似的。但是,该策略存在两个突出的缺点:①策略Ⅰ的控制目标为产生恒定幅值和频率的换流器交流电压,因此在负荷波动期间,它无法利用负荷潜在的电压或频率特性来帮助系统功率恢复平衡,也不适用于多风机系统(这一点将在3.4节说明);②策略Ⅰ仅仅是利用直流电容的动态方程,将直流母线电压作为反馈信号跟踪本地负荷波动,以及控制RSC的有功功率,维持功率平衡,而没有模拟同步机的惯量响应和一次调频控制过程,无法为系统提供有效的惯量支撑。因此,本节提出了基于PMSG的自动功率
平衡控制策略Ⅱ。该策略充分模拟同步机惯量响应和一次调频过程,进而为系统提供有效的惯量支撑,且能有效应用于离网模式和并网模式。
3.1.1 惯量模拟
与第2节中提出的控制策略Ⅰ类似,策略Ⅱ中PMSG的GSC需要具备网络自建压的能力。与控制策略Ⅰ不同的是,控制策略Ⅱ中换流器交流电压频率不被控制为恒定值。第2节分析表明,在负荷变化期间,直流电压可传递系统频率波动信息。为了让GSC模拟同步机惯量响应过程,策略Ⅱ将系统频率和直流电压人为耦合起来。稳态情况下,假设换流器的交流电压频率为f0,幅值为VC,相角为d0,直流电压稳态值为VDC0。在图2中,当负荷发生突变时,由式(19)可知,GSC输出功率也会突变。在此期间,直流电压的动态过程为
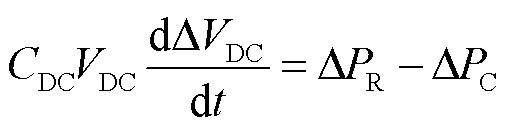 (24)
(24)
式中,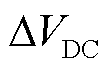 为直流电压的变化量;
为直流电压的变化量;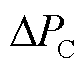 为GSC侧换流器输出功率变化量。
为GSC侧换流器输出功率变化量。
由式(24)可知,两端换流器之间任意的功率不平衡信息会反映到直流电压波动上。对比式(10)和式(24)可知,直流母线电压的动态响应过程和同步机的惯量响应过程十分类似。因此,直流电压通过式(25)准则和系统频率偏差进行人为耦合。
 (25)
(25)
式中,kDC为电压下垂控制的比例系数。
在系统动态期间,假设直流母线电压在标称值VDC0附近小幅度波动,结合式(24)和式(25),GSC的小信号模型为
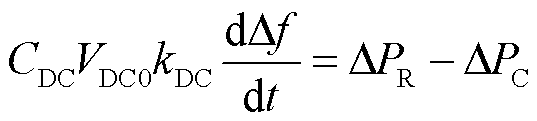 (26)
(26)
由式(26)可得,RSC和GSC之间任意的功率不平衡会导致系统频率的改变,该机制和传统同步机的惯量响应过程类似。不同的是,传统的同步机利用转子质量块动能平衡系统功率的波动,而换流器利用电容储存的能量平滑系统功率的波动。因此,基于式(26),可以得出该控制策略的等效惯性时间常数HC为
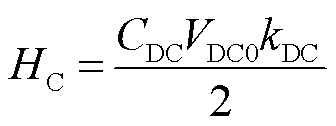 (27)
(27)
式(27)说明,在允许范围内,直流电容越大、直流电压环节下垂系数越大,在负荷波动期间,策略Ⅱ能为系统提供的惯量支撑就越多。综上所述,控制策略Ⅱ中,GSC的控制法则为
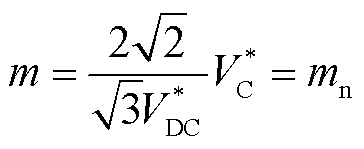 (28)
(28)
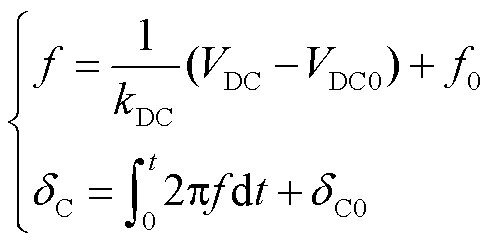 (29)
(29)
式(28)和式(29)中,初相角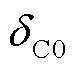 、直流电压的参考值
、直流电压的参考值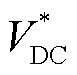 和换流器电压参考值
和换流器电压参考值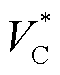 和第2节中控制策略Ⅰ的设计原则类似,在此不再赘述。
和第2节中控制策略Ⅰ的设计原则类似,在此不再赘述。
3.1.2 网侧换流器改进策略
根据3.1.1节的分析,直流电容储存的能量在系统暂态期间可被利用于系统惯量支撑。该过程会引发直流电容电压和换流器交流电压的波动,虽然其利用了负荷的电压响应特性用于快速的功率平衡,但是一定程度上损失了电压稳定性。结合式(13)、式(14)、式(25)及转子侧控制策略(见式(32)~式(34)),在策略Ⅱ中,负荷波动期间,换流器电压偏差为
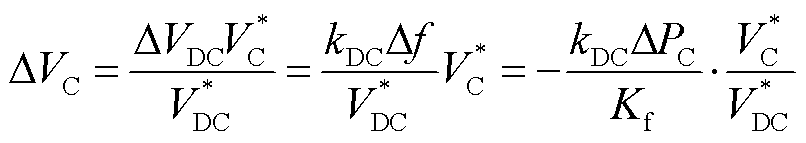 (30)
(30)
式中,Kf为模拟一次调频过程的下垂系数。
式(30)表明,负荷波动期间,换流器交流电压的波动和风机的频率下垂系数、直流电压参考值、负荷功率波动等因素有关。因此,当系统经历大的负荷波动或者控制参数设计不合理时,换流器电压偏差会过大,严重影响负荷的电压质量,这在实际应用中是无法接受的。为了维持PCC电压的稳定,在策略Ⅱ基础上加入PCC电压控制回路,并将此策略称为策略Ⅱ改进策略(注:本文中所涉及的策略Ⅱ均指无PCC电压控制回路的控制策略,即使用3.1.1节所提网侧控制策略,在策略Ⅱ基础上加入PCC电压控制回路的策略称之为策略Ⅱ改进策略)。在系统暂态期间,GSC利用PI控制器,通过改变调制比来维持PCC电压恒定。该控制思路和传统同步机的励磁调节系统非常类似。因此,调制比m的控制法则可描述为
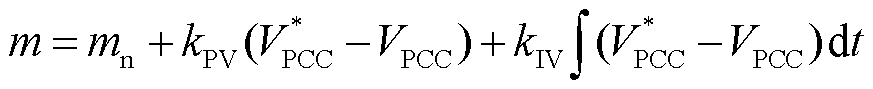 (31)
(31)
式中,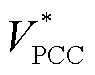 和VPCC分别为PCC参考电压和实际电压;kPV和kIV分别为PI控制器的参数。考虑大扰动工况,为了维持电压稳定性,可能出现调制比过大而超过其合理范围,从而导致系统失稳。此时需要设置调制比上、下限,
和VPCC分别为PCC参考电压和实际电压;kPV和kIV分别为PI控制器的参数。考虑大扰动工况,为了维持电压稳定性,可能出现调制比过大而超过其合理范围,从而导致系统失稳。此时需要设置调制比上、下限,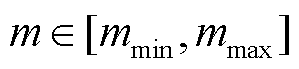 ,防止极端工况下由于调制比饱和引发的稳定性问题。
,防止极端工况下由于调制比饱和引发的稳定性问题。
为了模拟同步机的一次调频过程,RSC通过直流电压传递的频率偏差信息来调整有功功率参考值。因此,RSC功率参考值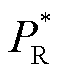 可设置为
可设置为
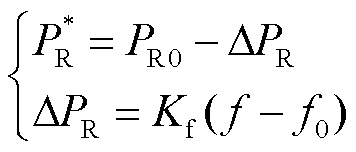 (32)
(32)
PR0的设置原则和控制策略I类似。
结合式(26)和式(32),控制策略Ⅱ中,PMSG的频率响应模型为
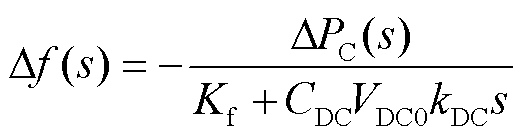 (33)
(33)
稳态时系统频率偏差为
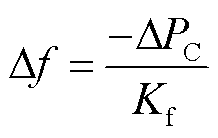 (34)
(34)
在该控制策略下,PMSG的两端换流器之间的功率最终会达到平衡。由式(13)可知
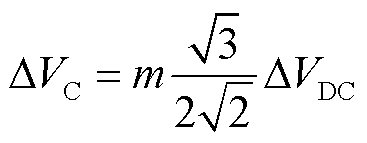 (35)
(35)
则
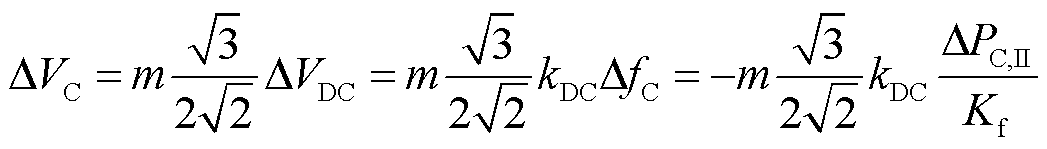 (36)
(36)
暂态期间通过调整式(36)所表示的换流器电压实现负荷需求响应,以系统负荷阻抗突增为例,在策略Ⅱ中,式(24)和式(34)表明,进入新的平衡状态后,直流电容电压和系统频率都会下降。同时,基于式(36),换流器电压会在可接受范围内自发地下降。PMSG网侧换流器输出功率变化量DPC,II为
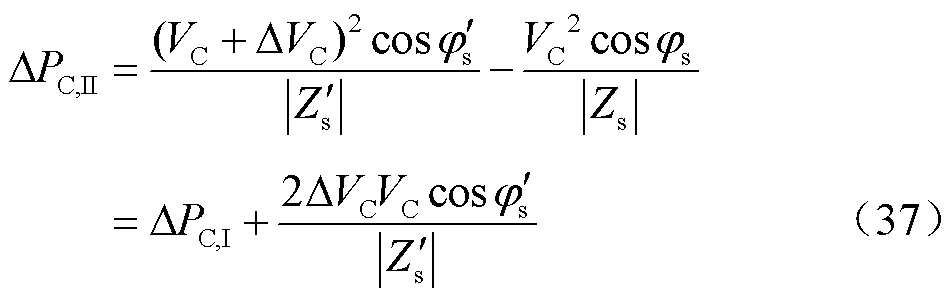
式中,ΔVC<0。
因此,在负荷阻抗变化相同的情况下,策略Ⅱ负荷有功功率的增加相比于策略Ⅰ会更少。
以上分析说明,策略Ⅱ充分利用了负荷的电压响应特性和直流电容储备能量以帮助系统快速恢复功率平衡,降低了风机在负荷变化时飞车的风险。并且在系统动态过程中,每个换流器都会响应负荷变化,同时共同协调实现快速的功率平衡,对孤岛系统来说具有节能效益,也适用于多风机系统。基于PMSG的自动功率平衡控制策略Ⅱ(含改进策略)的整体控制框图如图4所示。
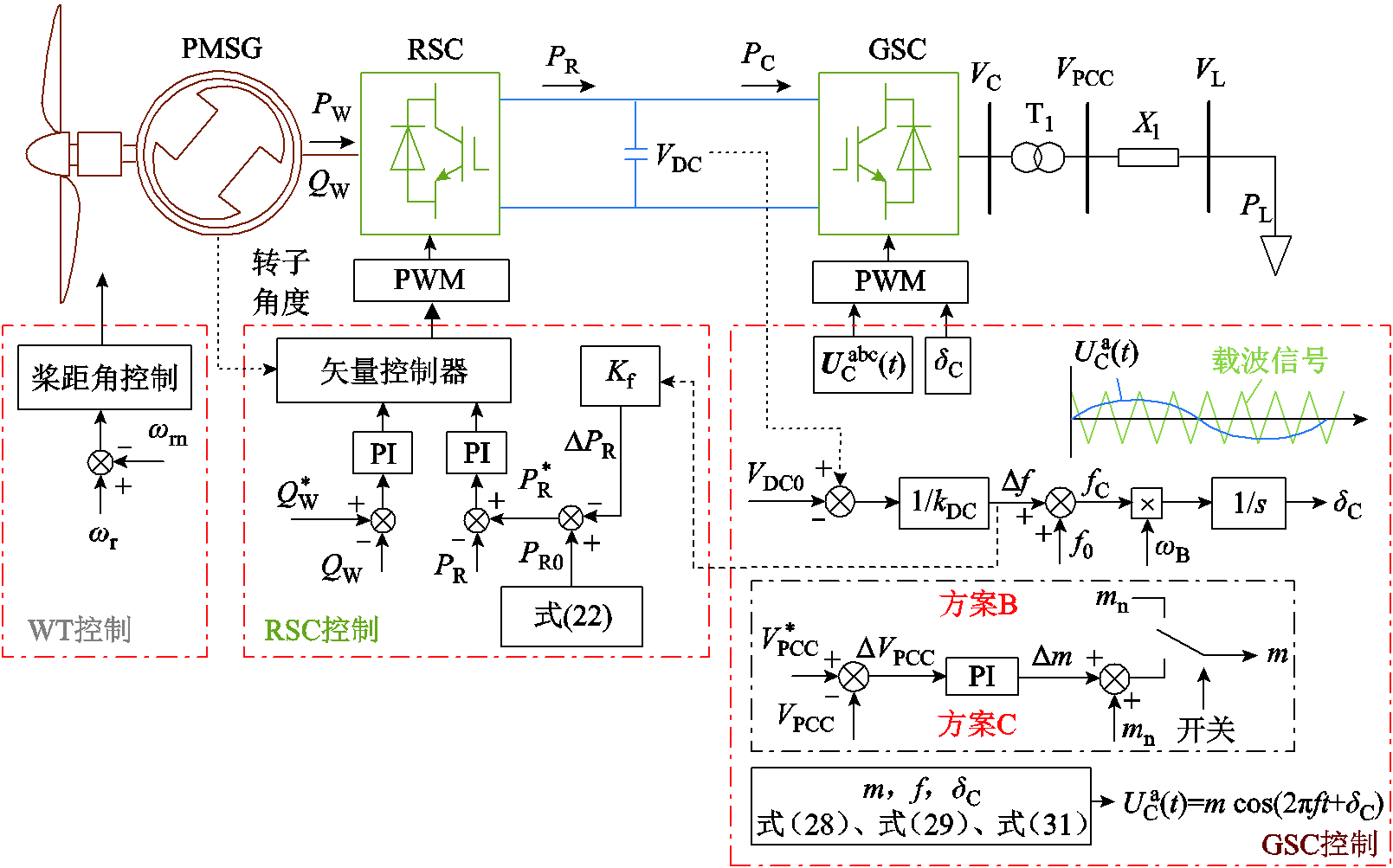
图4 控制策略Ⅱ整体控制框图
Fig.4 Overall control scheme of the proposed StrategyⅡ
在策略Ⅱ中,有两个核心参数需要设计:网侧换流器直流电压环节的下垂系数kDC和转子侧换流器一次调频下垂系数Kf。合理设计这两个参数,有助于提高孤岛运行方式下PMSG的稳定性,同时为系统提供更多的惯量支撑。下面详细介绍这两个参数的设计原则。
在系统动态过程中,直流电压的波动不能超过10%。为了充分利用直流电容的能量为系统提供惯量支撑,直流电容波动能量至少预留一半的裕度以防系统严重的频率偏差。假设系统在经历暂态过程中,直流电压可承受偏差的最大值为ΔVDCmax,系统频率可接受偏差的最大值为Δfmax。在系统频率偏差较大时,直流电容波动的能量至少要释放一半去为系统提供支撑,因此可得出
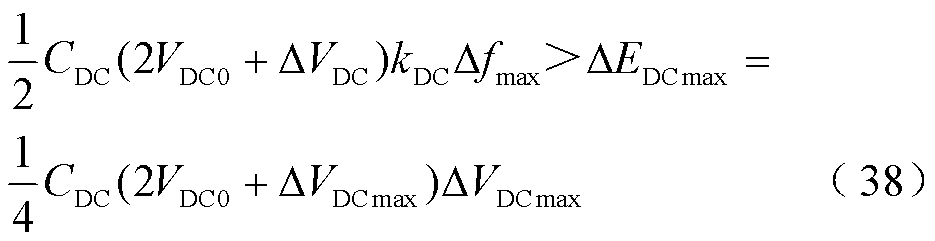
整理可得
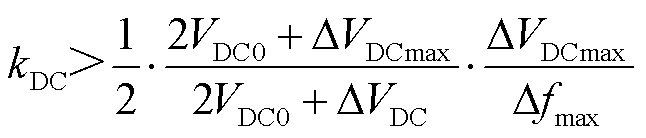 (39)
(39)
将式(39)进行缩放
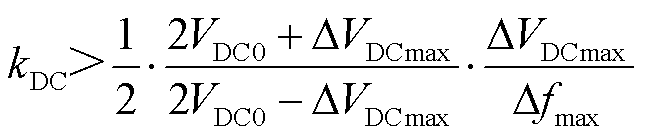 (40)
(40)
实际运行中,直流电容电压需要控制在一个安全范围内以防电容击穿。因此在系统经历最大的频率波动Δfmax时,直流电容电压波动也不能超过ΔVDCmax。容易得出,直流电压下垂系数kDC需控制在式(41)范围内。
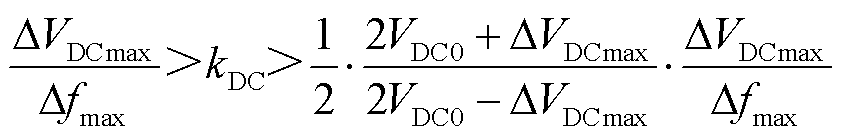 (41)
(41)
转子侧换流器一次调频下垂系数Kf的选择需要同时考虑系统经历的最大负荷波动(将网侧换流器经历的最大有功功率波动记为ΔPCmax),与频率的稳态偏差的最大值Δfsmax。因此一次调频下垂系数Kf可用式(42)确定。
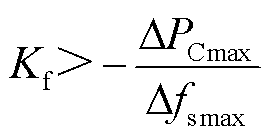 (42)
(42)
另外,直流电容的大小为
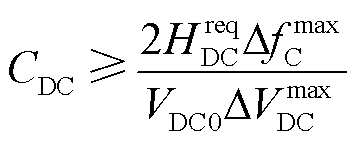 (43)
(43)
式中,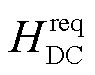 为系统运行所需的虚拟惯性时间常数。一般由风机提供3~10 s等值惯性常数确定。
为系统运行所需的虚拟惯性时间常数。一般由风机提供3~10 s等值惯性常数确定。
在多机系统中,由于换流器电压幅值和频率被控制为恒定值,策略Ⅰ没有考虑功率共享特性。由式(21)可知,在策略Ⅰ下,功率的分配仅与负荷波动有关。由于实际运行中难以确定负荷阻抗的变化量,每台PMSG的RSC侧有功功率参考值难以确定,功率的波动容易导致机组停机。所以策略Ⅰ不适用于多机系统。而由式(25)和式(32)可知,策略Ⅱ通过GSC频率的变化响应负荷变化,每台机组均按照其RSC的一次调频下垂系数的大小分配功率。在系统动态过程中,虽然系统负荷的变化难以确定,但是在控制策略Ⅱ下,每个RSC有功出力的份额是确定的,且与该换流器一次调频下垂系数成正比。在该方案下,通过合理设计控制参数可以很好地实现多机系统的功率协同分配。
本文将不涉及在所提策略下有关换流器动态交互的更多讨论,并将在未来做进一步研究。
为了验证所提两种控制策略的有效性,在电磁暂态仿真软件PSCAD/EMTDC中搭建如图5所示孤岛测试系统。
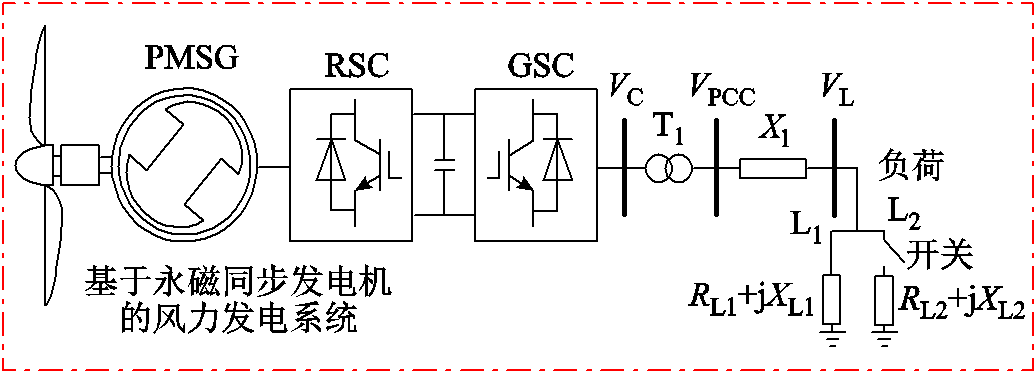
图5 仿真测试系统简化框图
Fig.5 Simple diagram of the studied system
该系统中,PMSG额定功率为2 MW。两个本地负荷L1和L2用恒阻抗模型RL+jXL表示。其中L1为10+j1.63 W,L2为17+j0.93 W。系统中,PMSG的PCC电压被控制在3 kV,换流器电感为0.005 H,变压器阻抗为0.001(pu),PMSG并网点固定电容器为108.3 mF,线路阻抗Xl为0.02+j0.0157 W。其余参数详见附录。为了方便对比不同控制策略,设计了三种控制方案进行对比:
方案A:采用策略Ⅰ,风机的GSC侧保持换流器电压幅值和频率恒定,RSC侧维持直流电压稳定。
方案B:采用策略Ⅱ,风机的GSC侧利用直流母线电压的动态特性实现电网同步和惯性响应,RSC侧换流器根据直流母线电压偏差调整有功功率以模拟一次频率控制。
方案C:采用策略Ⅱ改进策略,调制比不为恒定值。在系统暂态期间,GSC利用PI控制器,通过改变调制比来维持PCC电压恒定。
该场景在稳态运行情况下,系统由一台PMSG向本地负荷L1供电。方案A中直流电压控制环的PI参数分别为1和5;方案B和方案C中直流电压下垂系数和一次调频系数分别为1和2。在t=2 s时,投入本地负荷L2,系统的动态响应结果如图6所示。从仿真结果分析,三种方案都能在没有PLL和外部电源的孤岛运行模式下有效运行,同时保证发电机和负荷之间的功率平衡。
在负荷突增之后,图6a中方案A的PCC电压有效值从3.0 kV跌落到2.93 kV(稳态值),以此适应负荷功率的突增。由于图6e中直流电压的跌落,图6a和图6b中方案B的换流器电压和PCC电压有明显跌落。因为策略Ⅱ的GSC侧能够为系统提供惯量支撑,图6d中方案B和C的PMSG输出有功功率变化速度比方案A更加缓慢。图6e中方案B的直流电压从6 kV跌落至5.8 kV,牺牲的电容能量被用于系统惯量支撑。从图6a中可知,对比三种方案,方案B的PCC电压从3 kV跌落至2.85 kV,是三种方案里跌落率最高的,这在正常运行过程中是无法接受的。为了维持PCC电压,方案C在暂态期间通过自发提高调制比,升高图6b中的换流器电压,将PCC电压稳定在3 kV,能够有效稳定负荷电压。对比图6c和图6d可知,在经历相同负荷阻抗波动下,由于三种方案PCC电压偏差不同,它们的负荷功率变化也不同。方案B充分利用了负荷的电压特性帮助系统快速恢复功率平衡。
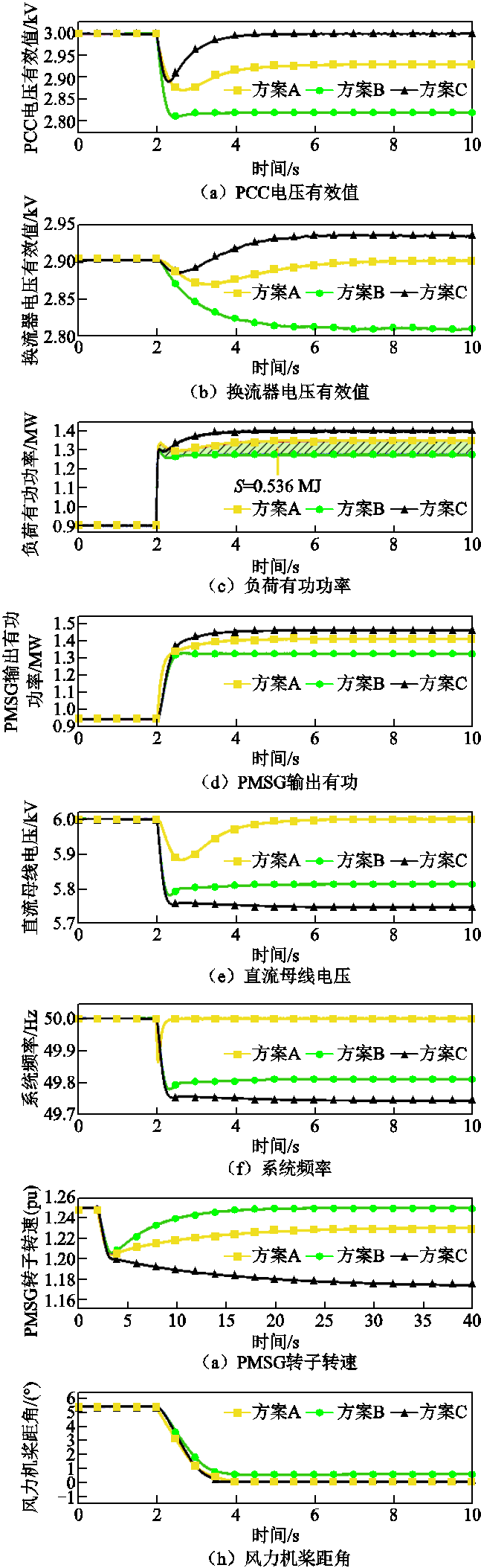
图6 负荷突增场景系统动态响应
Fig.6 Dynamic response of sudden load increase event
图6g和图6h表明,由于RSC的快速功率调制能力,风力机的桨距角和PMSG的转速在系统动态期间会快速响应负荷变化,以维持捕获的风能与PMSG输出功率之间的动态平衡。在方案B中,由于负荷有功功率偏差是最小的,风力机仍然处于桨距角控制模式,同时,PMSG的转速保持在最大转速1.25(pu)。经计算可得,策略Ⅰ在负荷突增后8 s时间内输出电能10.725 MJ,采用策略Ⅱ后会节省电能(阴影面积)0.536 MJ,节省了约5%的电能,减轻了系统负担。因此,方案B利用直流电容器中的储备能量和负荷电压特性稳定系统,这对于孤岛运行的系统而言更加节能。方案A和方案C的GSC侧所需有功功率更大,因此这两个方案的PMSG均处于超速运行模式,风力机桨距角均降为0。
该场景在稳态运行情况下,系统由一台PMSG向两个本地负荷L1和L2供电。系统控制参数与4.2节相同。在t=2 s时,切除本地负荷L2,系统的动态响应结果如图7所示。
在方案A中,从图7f和图7b可知,由于GSC控制交流电压幅值和频率恒定,发电机和负荷之间的任意功率波动都反映在直流电压的波动中。为了维持直流电压恒定,RSC利用PI控制器调整功率参考值,进而维持换流器两端功率平衡。从图7d中可以看出,在负荷突降之后,RSC输出有功功率迅速减小。由于换流器电感的存在,负荷突降后,方案A中PCC电压有效值上升。因此,相比于方案C的恒定PCC电压控制模式,方案A的负荷有功功率会更大。
为了维持系统频率,相比于方案B,在图7g和图7h中方案A需要更大的转速偏差和风能牺牲。为了维持发电机和负荷之间的功率平衡,图7g中PMSG转速迅速升高,图7h中风力机的桨距角控制会随机启动以此减少风轮捕获的风能,从而防止风机飞车。在方案B和方案C中,从图7e和图7f中可以得到,为了使PMSG具备惯量响应和一次调频能力,负荷突降之后,系统频率和直流电压自发地升高。相比于方案A,该过程使得RSC输出的有功功率波动更加平滑。同时,从图7a和图7b中可知,由于方案B中直流电压的升高,PCC电压和换流器电压也显著升高。相比于方案A和C,这一特性使得负荷的功率降低的最少。方案B再一次利用了负荷的电压调节特性帮助系统快速恢复功率平衡。从图7a和图7b中可知,方案C有效地维持了PCC电压恒定,因此也能维持负荷电压稳定。相比于方案A和方案B,负荷突变后,方案C中负荷有功功率最低,且风力机桨距角最大。
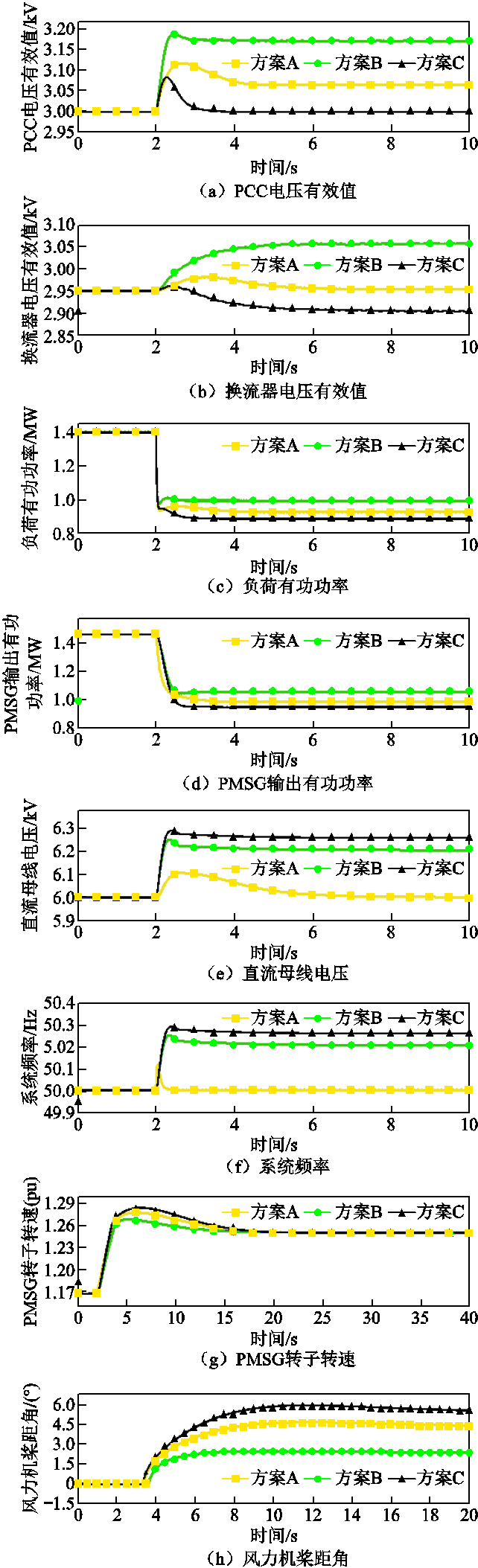
图7 负荷突降场景系统动态响应
Fig.7 Dynamic response of sudden load decrease event
该场景在稳态运行情况下,以负荷突增情况为例,系统由一台PMSG向本地负荷L1供电。选取方案B,一次调频系数设置为2,直流电压下垂系数kDC的倒数分别设置为0.6、0.8、1、1.1。在t=2 s时,投入本地负荷L2。系统的动态响应结果如图8所示。
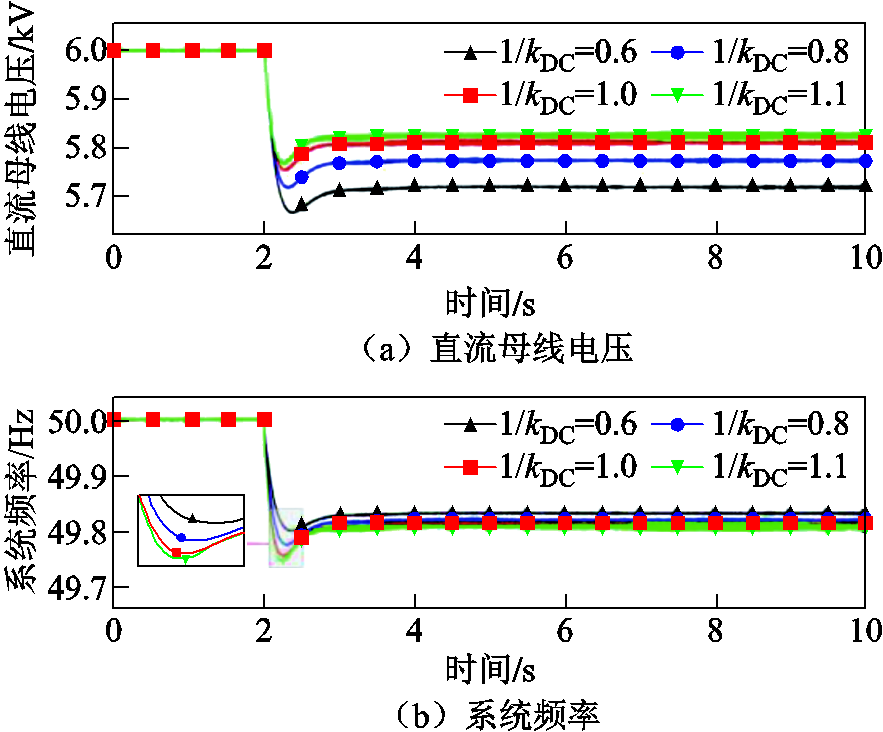
图8 不同kDC下的系统动态响应
Fig.8 Dynamic response under different kDC
在孤岛运行系统中,系统动态过程中直流电压的波动不能超过10%,在系统频率偏差较大时,直流电容波动的能量至少要释放一半去为系统提供支撑。由图8可知,实验所选kDC均能满足此要求。在负荷突增后的暂态过程中,图8a中的直流母线电压波动随kDC的增大而增大,在1/kDC取0.6的时候,直流母线电压最低跌至5.7 kV以下;图8b中的系统频率波动随kDC的增大而减小,在1/kDC取1.1的时候,系统的频率最低跌至49.7 Hz。
这表明在负荷突增之后,kDC越大,直流母线电压波动就越大,从直流电容中释放出用于系统惯性支撑的能量就越多,因此,系统频率的波动就越小。
该场景设置在5 s后风速连续变化情况下,其中风速平均值为11 m/s,标准偏差为1.5 m/s。系统受扰前单独为本地负荷L1供电。方案A中直流电压控制环的PI参数分别为1和5;方案B和方案C中直流电压下垂系数和一次调频系数分别为1和2。系统的动态响应结果如图9所示。
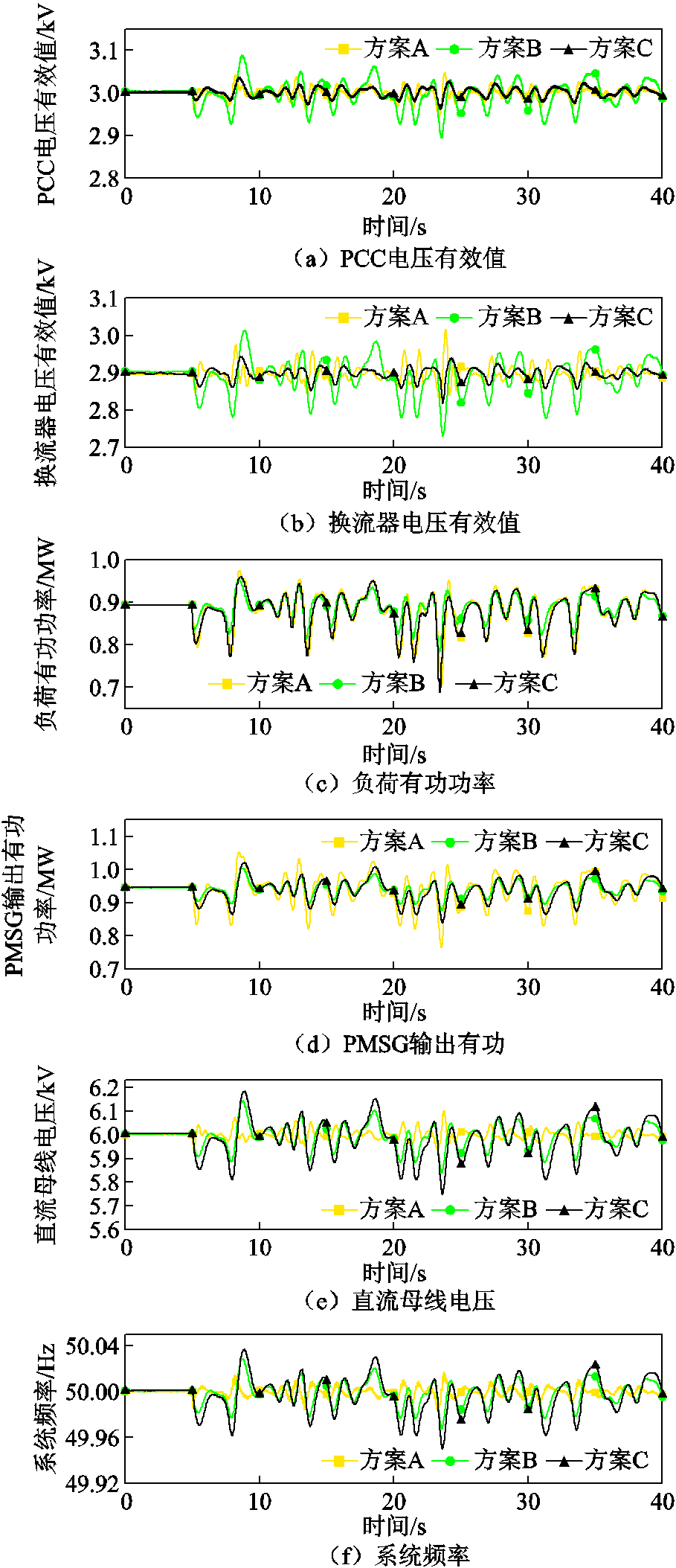
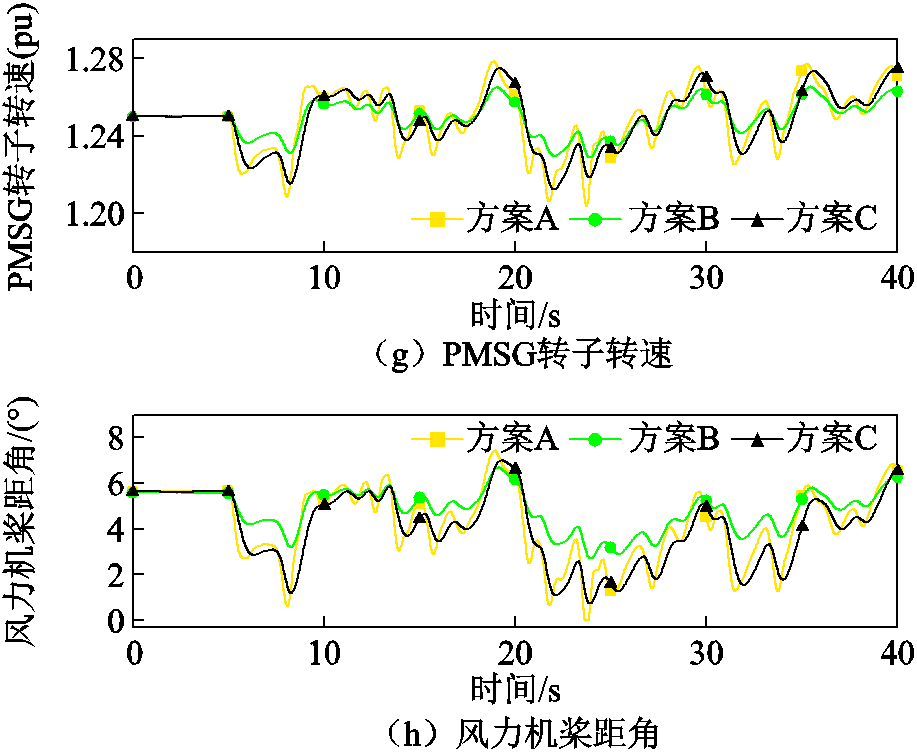
图9 风速连续变化情况下系统动态响应
Fig.9 Dynamic responses under wind speed continual variations
三种方案都能在风速连续变化情况下,保持在孤岛系统下的稳定运行,无需PLL和外部电源。并且所有系统变量的波动都在可接受范围内。如图9a、图9e和图9f所示,与方案B和方案C相比,方案A的PCC电压、直流母线电压和系统频率均保持良好。然而,如图9d、图9g和图9h所示,与其他两种方案相比,方案A需要永磁同步电机提供更多的能量以维持功率平衡和PCC电压稳定,因此方案A的风机转子转速和桨距角产生最大偏差。方案A没有利用负荷需求响应,在系统功率波动期间,风机需要更大的转速偏差和风能牺牲以维持系统频率,这将提高风机运行成本,并可能导致某些情况下风机飞车。
另一方面,方案B和方案C通过利用图9e中的直流母线电压波动使得风机具有惯性响应和一次调频能力。如图9e和图9f所示,方案B和方案C通过控制直流母线电压偏差以响应系统功率波动和频率偏差。在系统动态过程中,直流电容中储存的能量将被利用以维持系统功率平衡,并减轻风机的负担。此外,如图9a所示,方案B充分利用负荷需求响应,在允许范围内自发调整PCC电压。因此,如图9d、图9g和图9h所示,方案B需要永磁同步电机提供用以维持稳定运行的能量最少,因此在风速连续变化期间,方案B风机的转速和桨距角的波动最小。由图9可知,与方案B相比,尽管方案C能有效地维持住PCC电压,但却造成PMSG输出功率、直流母线电压、转子转速和桨距角的更大偏差。
因此可以得出结论:在系统动态过程中,方案A能够很好地维持系统频率,但会提高系统的运行成本;方案B和方案C能够利用直流电容器储备能量维持功率平衡,减轻风机负担,特别地,方案B利用负荷需求响应,降低了风机飞车的可能性;方案C能够有效地维持PCC电压,但也会导致更大的直流母线电压偏差以及风机转速和桨距角偏差。
综上所述,三种控制方案都适用于无PLL和外部电源的PMSG孤岛运行模式。策略Ⅰ将交流电压和频率控制为固定值。策略Ⅱ在暂态过程中,通过自发地改变直流电压进而模拟同步机惯量响应过程,为系统提供有效的惯量支撑。策略Ⅱ同时适用风机的并网模式和离网模式,具有节能效果且能给弱交流系统提供有效的电压支撑。对比方案A,方案B利用了负荷的电压响应特性帮助系统恢复功率平衡,在很大程度上降低了风力机飞车的可能性。基于方案B的PCC电压波动过大可能对负荷电压质量造成影响的问题,进一步提出了方案C,能够有效地稳定PCC电压,维持负荷电压稳定。之后,研究了kDC变化对直流电压和调频效果的影响,负荷增加时,kDC越大,直流母线电压波动就越大,从直流电容中释放出用于系统惯性支撑的能量就越多,系统频率的波动就越小。最后,研究了在风速连续变化情况下三种方案的运行特性。三种方案都能在风速连续变化情况下,保持在孤岛系统下的稳定运行,无需PLL和外部电源。以上三种控制方案对未来风力发电机应用领域有十分显著的指导意义。
1)基于孤岛离网运行模式下的PMSG,本文提出了两种全新的自动功率平衡控制策略。两种控制策略都无需PLL和外部电源。
2)相比于策略Ⅰ,策略Ⅱ利用负荷的电压特性和直流电容器储备能量平滑系统功率,具有节能效应。策略Ⅱ改进策略能够在系统动态期间维持PCC电压稳定性,保证负载电压质量,但相应地会失去节能特性。
3)直流电压下垂系数kDC的变化对直流电压和调频效果有一定的影响。负荷增加时,kDC越大,直流母线电压波动就越大,从直流电容中释放出用于系统惯性支撑的能量就越多,系统频率的波动就越小。
4)通过仿真验证了三种方案在风机孤岛运行模式下的有效性。其中,策略Ⅱ以其惯量响应、一次调频控制、利用负荷的电压调节特性和直流电容器储备能量节能等优良特性,对未来风力发电的大规模运用有重要意义。
附 录
附表1 风机参数
App.Tab.1 Parameters of the wind turbine

参数数值 切入风速vwc/(m/s)4 最低风速vwl/(m/s)7 额定风速vwr/(m/s)12 惯性时间常数Ht/s3.5 阻尼系数Dsh(pu)0.01 转轴刚性系数Ksh(pu)0.5 桨距角控制时间常数Tβ/s0.25
附表2 PMSG参数
App.Tab.2 Parameters of the PMSG

参数数值 额定功率Sp/(MV·A)2 额定电压Up/V690 惯性时间常数Hp/s1.15 转子额定转速ωrn/(rad/s)35.700 定子电阻Rpa/μΩ50 d轴电抗Lpd/H0.00 55 q轴电抗Lpq/H0.003 75 极对数p11
附表3 换流器参数
App.Tab.3 Parameters of the converter

参数数值 网侧电感器电感L/H0.005 直流母线电容CDC/μF10 000 直流母线额定电压VDCn/kV6 方案A的直流母线电压控制中PI控制器增益参数1 方案A的直流母线电压控制中PI控制器积分参数5 方案B和C中直流母线电压控制下垂系数倒数1/kDC1 方案B和C中一次调频控制系数Kf2 PWM载波频率fp/kHz10 初始系统频率fC0/Hz50 基准角频率314.159
参考文献
[1] 马进, 赵大伟, 钱敏慧, 等. 大规模新能源接入弱同步支撑直流送端电网的运行控制技术综述[J]. 电网技术, 2017, 41(10): 3112-3120.
Ma Jin, Zhao Dawei, Qian Minhui, et al. Reviews of control technologies of large-scale renewable energy connected to weakly-synchronized sending-end DC power grid[J]. Power System Technology, 2017, 41(10): 3112-3120.
[2] Chang-Chien L R, Lin Weiting, Yin Y C. Enhancing frequency response control by DFIGs in the high wind penetrated power systems[J]. IEEE Transactions on Power Systems, 2011, 26(2): 710-718.
[3] 吴恒, 阮新波, 杨东升. 弱电网条件下锁相环对LCL型并网逆变器稳定性的影响研究及锁相环参数设计[J]. 中国电机工程学报, 2014, 34(30): 5259-5268.
Wu Heng, Ruan Xinbo, Yang Dongsheng. Research on the stability caused by phase-locked loop for LCL-type grid-connected inverter in weak grid condition[J]. Proceedings of the CSEE, 2014, 34(30): 5259-5268.
[4] Li Yujun, Xu Zhao, Østergaard J, et al. Coordinated control strategies for offshore wind farm integration via VSC-HVDC for system frequency support[J]. IEEE Transactions on Energy Conversion, 2017, 32(3): 843-856.
[5] 王盼宝, 王卫, 孟尼娜, 等. 直流微电网离网与并网运行统一控制策略[J]. 中国电机工程学报, 2015, 35(17): 4388-4396.
Wang Panbao, Wang Wei, Meng Nina, et al. Unified control strategy of islanding and grid-connected operations for DC microgrid[J]. Proceedings of the CSEE, 2015, 35(17): 4388-4396.
[6] Svensson J. Grid-connected voltage source converter[D].Gothenburg: Chalmers University Technol, 1998.
[7] Fischer P. Modelling and control of a line-commutated HVDC transmission system interacting with a VSC STATCOM[D]. Stockholm: Royal Institute of Technology, 2007.
[8] Li Shuhui, Haskew T A, Swatloski R P, et al. Optimal and direct-current vector control of direct-driven PMSG wind turbines[J]. IEEE Transactions on Power Electronics, 2012, 27(5): 2325-2337.
[9] Zhang Lidong, Harnefors L, Nee H P. Modeling and control of VSC-HVDC links connected to island systems[J]. IEEE Transactions on Power Systems, 2011, 26(2): 783-793.
[10] Egea-Alvarez A, Fekriasl S, Hassan F, et al. Advanced vector control for voltage source converters connected to weak grids[J]. IEEE Transactions on Power Systems, 2015, 30(6): 3072-3081.
[11] Wen Bo, Boroyevich D, Burgos R, et al. Analysis of D-Q small-signal impedance of grid-tied inverters[J]. IEEE Transactions on Power Electronics, 2016, 31(1): 675-687.
[12] Kayikci M, Milanovic J V. Dynamic contribution of DFIG-based wind plants to system frequency disturbances[J]. IEEE Transactions on Power Systems, 2009, 24(2): 859-867.
[13] Li Yujun, Xu Zhao, Wong K P. Advanced control strategies of PMSG-based wind turbines for system inertia support[J]. IEEE Transactions on Power Systems, 2017, 32(4): 3027-3037.
[14] 颜湘武, 贾焦心, 王德胜, 等. 基于P/w“导纳”的并联虚拟同步机功频响应建模与分析[J]. 电工技术学报, 2020, 35(15): 3191-3202.
Yan Xiangwu, Jia Jiaoxin, Wang Desheng, et al. Modeling and analysis of active power-frequency response of parallel VSGs using a P/ω “admittance”[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3191-3202.
[15] 于彦雪, 关万琳, 陈晓光, 等. 基于序阻抗的虚拟同步机同步频率谐振现象[J]. 电工技术学报, 2022, 37(10): 2584-2595.
Yu Yanxue, Guan Wanlin, Chen Xiaoguang, et al. Synchronous frequency resonance in virtual sychronous generator based on sequence-impedance[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2584-2595.
[16] Liao Kai, He Zhengyou, Xu Yan, et al. A sliding mode based damping control of DFIG for interarea power oscillations[J]. IEEE Transactions on Sustainable Energy, 2017, 8(1): 258-267.
[17] Zhang Lidong, Harnefors L, Nee H P. Power-synchronization control of grid-connected voltage-source converters[J]. IEEE Transactions on Power Systems, 2010, 25(2): 809-820.
[18] Guan Minyuan, Pan Wulue, Zhang Jing, et al. Synchronous generator emulation control strategy for voltage source converter (VSC) stations[J]. IEEE Transactions on Power Systems, 2015, 30(6): 3093-3101.
[19] 杨仁炘, 张琛, 蔡旭. 具有频率实时镜像和自主电网同步能力的风场–柔直系统控制方法[J]. 中国电机工程学报, 2017, 37(2): 496-506.
Yang Renxin, Zhang Chen, Cai Xu. Control of VSC-HVDC with real-time frequency mirroring and self-synchronizing capability for wind farm integration[J]. Proceedings of the CSEE, 2017, 37(2): 496-506.
[20] 杨仁炘, 施刚, 蔡旭. 海上全直流型风电场的电压源型控制[J]. 电工技术学报, 2018, 33(2): 546-557.
Yang Renxin, Shi Gang, Cai Xu. Voltage source control of offshore all-DC wind farm[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 546-557.
[21] 伍兴煌, 魏强. 使用虚拟阻抗的虚拟同步机转子角下垂控制[J]. 电气技术, 2020, 21(3): 31-36, 58.
Wu Xinghuang, Wei Qiang. Virtual synchronous machine rotor angle droop control using virtual reactance[J]. Electrical Engineering, 2020, 21(3): 31-36, 58.
[22] 兰征, 刁伟业, 曾进辉, 等. 含异构微源孤岛微电网内虚拟同步发电机预同步控制策略[J]. 电力系统自动化, 2022, 46(19): 154-161.
Lan Zheng, Diao Weiye, Zeng Jinhui, et al. Pre-synchronization control strategy of virtual synchronous generator in islanded microgrid with heterogeneous distributed generators[J]. Automation of Electric Power Systems, 2022, 46(19): 154-161.
[23] 颜湘武, 崔森, 常文斐. 考虑储能自适应调节的双馈感应发电机一次调频控制策略[J]. 电工技术学报, 2021, 36(5): 1027-1039.
Yan Xiangwu, Cui Sen, Chang Wenfei. Primary frequency regulation control strategy of doubly-fed induction generator considering supercapacitor SOC feedback adaptive adjustment[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 1027-1039.
[24] Wu Dan, Tang Fen, Dragicevic T, et al. Autonomous active power control for islanded AC microgrids with photovoltaic generation and energy storage system[J]. IEEE Transactions on Energy Conversion, 2014, 29(4): 882-892.
[25] Le H T, Santoso S, Nguyen T Q. Augmenting wind power penetration and grid voltage stability limits using ESS: application design, sizing, and a case study[J]. IEEE Transactions on Power Systems, 2012, 27(1): 161-171.
[26] Kim J, Lee S H, Park J W. Inertia-free stand-alone microgrid—part Ⅱ: inertia control for stabilizing DC-link capacitor voltage of PMSG wind turbine system[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 4060-4068.
Abstract Recently, the permanent magnet synchronous generator-based wind turbine (PMSG-based WT) have gained significant popularity in wind power applications. With the development of microgrids, the PMSG-based WTs are required to be operated in the stand-alone operation mode in some scenarios. The previous studies in stand-alone microgrids mainly focus on the phase-locked loop (PLL)-based controls for WT, which still require the external grid-forming power supplies. The recent studies for the stand-alone operation of PLL-free WTs were relatively complicated and difficult to adjust the parameters. They did not adequately discuss the coordination of grid side converter (GSC) and rotor side converter (RSC) of WT, nor did they consider the demand response in stand-alone operation mode (SAOM). To bridge these gaps, this paper proposed two advanced autonomous power balance control schemes for PMSG-based WT in SAOM.
In the first strategy, the GSC of WT controls the converter voltage as an ideal voltage source with the fixed modulation index and frequency, while the RSC of WT modifies the active power reference by controlling DC-link voltage through one PI controller. The main drawbacks of the first strategy are that the load demand response is not taken into consideration and it may not ensure the power synchronism of multi-WT in SAOM. Therefore, in the second strategy, the GSC of WT achieves grid-synchronization and inertia response utilizing the dynamic of DC-link voltage, while the RSC adjusts active power based on the DC-link voltage deviations to mimic the primary frequency control. Both proposed strategies can effectively ensure the independent operation of WT without PLL and external power supplies. Compared with the typical virtual synchronous generator (VSG) controls and other SAOM controls, the complexity of the proposed strategies is more reduced, and the control parameters are easy to tune, as they only require the measurement of DC-link voltage. Particularly, Strategy Ⅱ stands out by the energy-efficient property by using the reserved energy in DC capacitor for system inertia support and the load demand response to decrease the risks of WT tripping off. In order to improve the voltage profile of the second proposed scheme, an improved GSC control of WT via one simple PI controller for sustaining the point of common coupling (PCC) voltage during system disturbance is further proposed. Nonlinear simulations of one PMSG connected with several local loads considering various power system contingencies have been studied to verify the effectiveness of two proposed strategies.
The following conclusions can be drawn from the simulation analysis: (1) Both strategies can effectively ensure the stable operation of PMSG-based WT in tested stand-alone system. (2) StrategyⅠcan well stabilize the grid frequency and the DC-link voltage. But it requires high operation costs of WT and is not energy-saving in SAOM. (3) Strategy Ⅱ makes the alternation of DC-link voltage proportional to the grid frequency, which reduces the power balance burden of stand-alone WT by temporally absorbing or releasing the energy from DC capacitor during load changes. More importantly, Strategy Ⅱ stands out by fully utilizing the load demand response for fast power balance and decreasing the risk of WT tripping, which is more energy-efficient and is suitable for multi-WTs operation in SAOM.
Keywords:Permanent magnet synchronous generator (PMSG), stand-alone operation, autonomous power balance control, inertia response, primary frequency control, energy-efficient property
陆秋瑜 女,1986年生,高级工程师,博士,研究方向为电力系统调度自动化等。E-mail:luqiuyu22@126.com(通信作者)
戴耀辉 男,1999年生,硕士研究生,研究方向为电力系统运行与控制。E-mail:dyh1499973952@stu.xjtu.edu.cn
中图分类号:TM711
DOI:10.19595/j.cnki.1000-6753.tces.221348
中国南方电网公司科技项目资助(036000KK52210042(GDKJXM20212057))。
收稿日期 2022-07-13
改稿日期 2022-12-30
(编辑 赫 蕾)