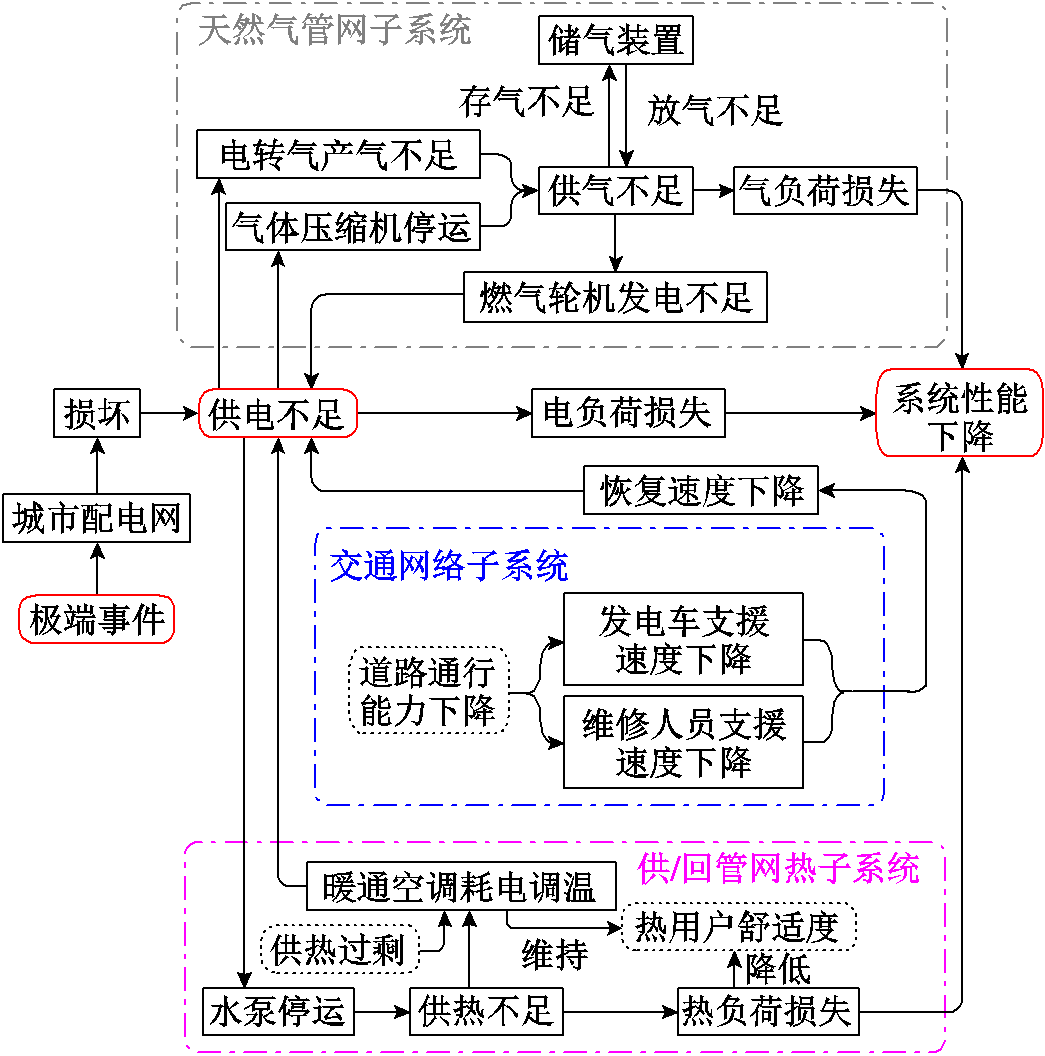
图1 电-气-热-交通系统的相互依存关系
Fig.1 The interdependence of electricity-gas-heat-transport system
摘要 能源转型背景下,城市能源系统得到了快速发展。当高影响、低概率的极端事件发生时,城市能源系统可能因为各子系统间的相互依存关系而承受更大风险。针对此问题,该文提出考虑电-气-热-交通相互依存的城市能源系统韧性评估与提升方法。首先,针对极端事件的发生全过程,提出包含整体性和针对性两个角度的多维韧性评估指标;然后,建立电、气、热、交通各子系统及耦合元件的模型;进而,为实现系统韧性的提升,提出采用发电车紧急供电、维修人员调度、拓扑重构等措施,以及考虑建筑物热惯性的协同优化模型;最后,在一个92节点的电-气-热-交通融合系统中进行算例分析。结果表明,所提的韧性评估指标能全面地反映系统在各个阶段的性能;所提的韧性提升方法可以协调各子系统间的措施与设备,实现系统性能的维持与恢复。
关键词:城市能源系统 韧性 评估 提升 相互依存
在“碳达峰,碳中和”目标的能源转型大环境下,城市能源系统(Urban Energy System, UES)成为未来城市能源网的重要发展方向[1]。UES是指以柔性可控的城市各级配电网为核心,通过能源耦合设备与城市多种形式能源网络灵活互联而形成的城市综合能源供给系统[2]。
随着全球环境的急剧变化,以自然灾害为代表的高影响、低概率(High-Impact and Low-Probability, HILP)极端事件引起了人们的广泛关注[3]。在面对HILP事件时,UES因各能源子系统间复杂的相互依存关系,可能将承受更大的损失。进而,可能会导致终端用户在多个维度对系统性能的损失感知明显增加。为了研究与应对HILP事件带来的不利影响,“UES韧性”的概念应运而生。UES的韧性是指在遭受HILP事件时,维持系统供能并快速恢复到正常状态的能力[2]。
在过去,韧性评估与提升的研究主要针对配电网。在配电网韧性评估方面,文献[4]基于韧性梯形的概念,提出以系统性能缺失面积为指标的配电网韧性评估方法。文献[5]提出用于配电网长期规划设计的预期中断概率指标,以及用于短期运行规划的预期负荷损失指标和预期停电时间指标。文献[6]针对极端冰雪天气,建立了反映配电网恢复力的三类评价指标。在配电网韧性提升方面,根据极端事件的发生过程,韧性提升的研究可以分为事前预防、事中响应和事后恢复三个阶段[7]。文献[8]提出一种利用线路加固和备用分布式机组最优配置的配电网韧性提升方法。文献[9]提出一种通过线路加固和储能配置的配电网韧性提升规划模型。文献[10]针对极端冰暴灾害,提出一种通过调度融冰车的两阶段鲁棒优化韧性提升策略。文献[11]通过可移动电源和维修人员调度,提出一种配电网恢复策略。
与配电网中丰富的韧性研究相比,对UES中的韧性评估与提升的研究还较少。文献[12]针对电-气综合能源系统,提出一种反映网络脆弱性和系统恢复力的综合韧性评估指标。文献[13]针对台风灾害,提出了评估电-气相互依存系统韧性的负荷损失指标、元件损坏成本指标。文献[14]利用配电线路加固、燃气机组最优运行,研究了电-气综合能源系统对极端事件的预防策略。文献[15]考虑电-气-热的能源互补特性,提出一种配电网主动解列的恢复策略。文献[16]考虑电-水-气的相互依存关系,提出一种配电网最优恢复策略。
上述文献涉及的韧性评估方法,部分基于韧性梯形面积计算的扩展,部分沿用了可靠性评估指标,或针对系统响应、恢复能力进行评估,缺乏适配不同阶段、不同系统、不同侧重的更具针对性的评估指标。而对于韧性提升,多数文献主要集中于对特定阶段韧性提升策略的研究,缺乏对各措施在系统层面的综合利用。特别是在UES及其各子系统中,缺乏对不同阶段下韧性提升策略的协调以及对各策略间相互作用的考虑。此外,上述文献大多将韧性评估与提升分别进行研究,忽略了不同阶段韧性评估指标与提升策略间的关联性。
综上所述,本文在现有研究成果的基础上,提出考虑电-气-热-交通相互依存关系的城市能源系统韧性评估与提升方法。在韧性评估方面,计及极端事件的发生全过程,提出整体性和针对性两类,共七个指标,实现对UES全局性能和特别值得关注的系统性能的评估。在韧性提升方面,以最小化加权电、气、热负荷损失之和为目标,建立系统层面的协同优化模型。利用发电车调度、维修人员调度、拓扑重构、建筑物热惯性等,实现UES的韧性提升。由于采取的韧性提升措施中存在对交通网络的依赖,本文考虑交通网络子系统,建立发电车的路径规划和维修人员对线路的最优修复模型。算例分析验证了本文所提韧性评估与提升方法的有效性。
城市配电网作为UES的核心,与其他能源系统耦合紧密,为能源供应提供重要支撑。各系统间的相互依存关系如图1所示。
由于耦合元件接入节点的地理位置不同,极端事件对各子系统的影响可能不是同时或同等程度严重的。因此,极端事件产生的影响在各子系统间可能存在“时间差”和“空间差”。在此特性下,UES中各子系统间的相互依存关系会对系统性能产生“正反”两方面的影响。一方面,供电不足产生的影响会通过耦合元件传播到其他子系统,导致其性能下降,而各子系统的性能下降又会通过耦合元件进一步导致城市配电网的供电不足,加剧UES性能的劣化;另一方面,当某种形式的能源供给遭受损失时,其他形式的能源又可通过能量设备实现能源的替代与互补,对UES的性能产生支撑作用。

图1 电-气-热-交通系统的相互依存关系
Fig.1 The interdependence of electricity-gas-heat-transport system
本文所提的韧性评估与提升框架,主要包括三个部分:
1)极端事件:根据极端事件下配电线路的损坏概率,通过随机采样获取极端事件场景,生成线路损坏状态集。
2)韧性评估:韧性评估从两个方面、七个维度对UES的韧性进行评估。既包含对UES韧性的整体把握(性能维持、抵抗性、响应性、恢复性),又包括对特别值得关注的系统性能的针对性评估(孤岛连通度、孤岛供电覆盖数量、关键负荷维持时间)。
3)韧性提升:韧性提升以最小化加权电、气、热负荷损失之和为优化目标,考虑各子系统间的相互依存和相互影响关系,通过实施多种措施实现系统不同阶段的韧性提升。各场景的目标函数![]() 为
为
其中
式中,![]() 、
、![]() 、
、![]() 分别为城市配电网、天然气管网子系统、供回热管网子系统的加权负荷损失值,kW;
分别为城市配电网、天然气管网子系统、供回热管网子系统的加权负荷损失值,kW;![]() 、
、![]() 、
、![]() 分别为电负荷
分别为电负荷![]() 、气负荷
、气负荷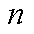 、建筑物
、建筑物![]() 热负荷损失量的权重系数;
热负荷损失量的权重系数;![]() 、
、![]() 、
、![]() 分别为电负荷i、气负荷n、房间r热负荷的损失值,kW;
分别为电负荷i、气负荷n、房间r热负荷的损失值,kW;![]() 为换算系数,其作用是统一量纲,
为换算系数,其作用是统一量纲,![]() 为天然气的高位热值,kBtu/m3,
为天然气的高位热值,kBtu/m3,![]() 为能量转化系数,kBtu/(kW·h);
为能量转化系数,kBtu/(kW·h);![]() 为气负荷n的损失量,m3/h;
为气负荷n的损失量,m3/h;![]() 为调度周期;
为调度周期;![]() 为电网节点的集合;
为电网节点的集合;![]() 为气负荷节点的集合;
为气负荷节点的集合;![]() 为建筑物
为建筑物![]() 中全部房间的集合;
中全部房间的集合;![]() 为建筑物的集合。
为建筑物的集合。
韧性梯形可以较为直观地反映极端事件下系统性能的变化情况[17],系统各阶段性能如图2所示。图中,![]() 为系统的原始性能;
为系统的原始性能;![]() 为极端事件影响下的系统性能。
为极端事件影响下的系统性能。
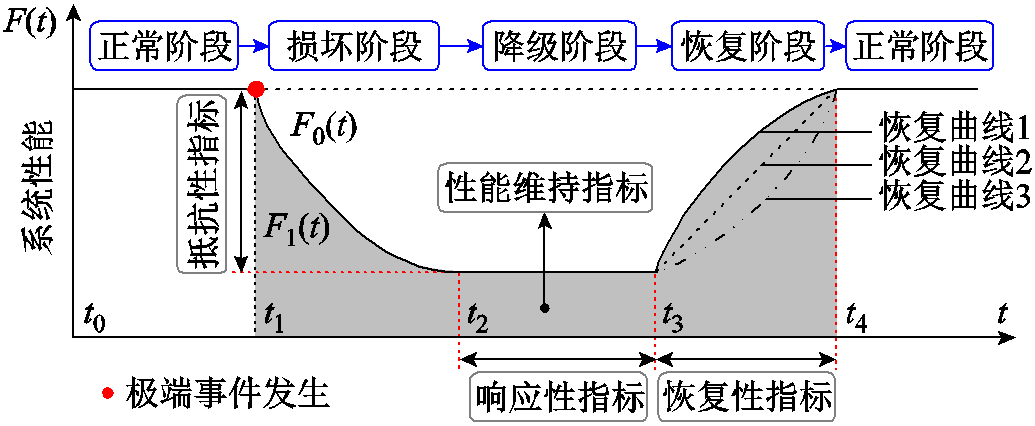
图2 极端事件下系统性能处于的不同阶段
Fig.2 The different stages of system performance under extreme events
图2中列出了所提整体性指标中的性能维持、响应性、抵抗性和恢复性指标与各阶段的对应关系。
1.3.1 性能维持指标
性能维持指标描述了系统受极端事件影响下各个阶段的系统性能的维持情况,相当于图2中阴影部分的面积。考虑电-气-热-交通相互依存的UES包括三个子系统性能的维持,即电负荷维持、气负荷维持、热负荷维持。
其中
 (6)
(6)
式中,![]() 为系统性能维持指标;
为系统性能维持指标;![]() 为城市配电网(urban Distribution System, DS)的性能维持指标;
为城市配电网(urban Distribution System, DS)的性能维持指标;![]() 为天然气管网子系统(natural Gas System, GS)的性能维持指标;
为天然气管网子系统(natural Gas System, GS)的性能维持指标;![]() 为供回热管网子系统(Heating supply and return System, HS)的性能维持指标;系数
为供回热管网子系统(Heating supply and return System, HS)的性能维持指标;系数![]() 的作用是将指标线性映射到区间
的作用是将指标线性映射到区间![]() ,即采用“百分制”进行评估(分数越高韧性越强,下同);
,即采用“百分制”进行评估(分数越高韧性越强,下同);![]() 为极端事件场景
为极端事件场景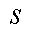 发生的概率;
发生的概率;![]() 为节点
为节点![]() 的电负荷;
的电负荷;![]() 为气负荷
为气负荷 需求天然气的流量;
需求天然气的流量;![]() 为供给建筑物
为供给建筑物![]() 中的房间
中的房间 的热功率;
的热功率;![]() 为抽取的场景总数;
为抽取的场景总数;![]() 、
、![]() 、
、![]() 分别为电、气、热系统损坏阶段的起始时刻。
分别为电、气、热系统损坏阶段的起始时刻。
1.3.2 抵抗性指标
极端事件发生后,DS、GS、HS中负荷的保有量反映了各子系统对极端事件的抵御能力,即
其中
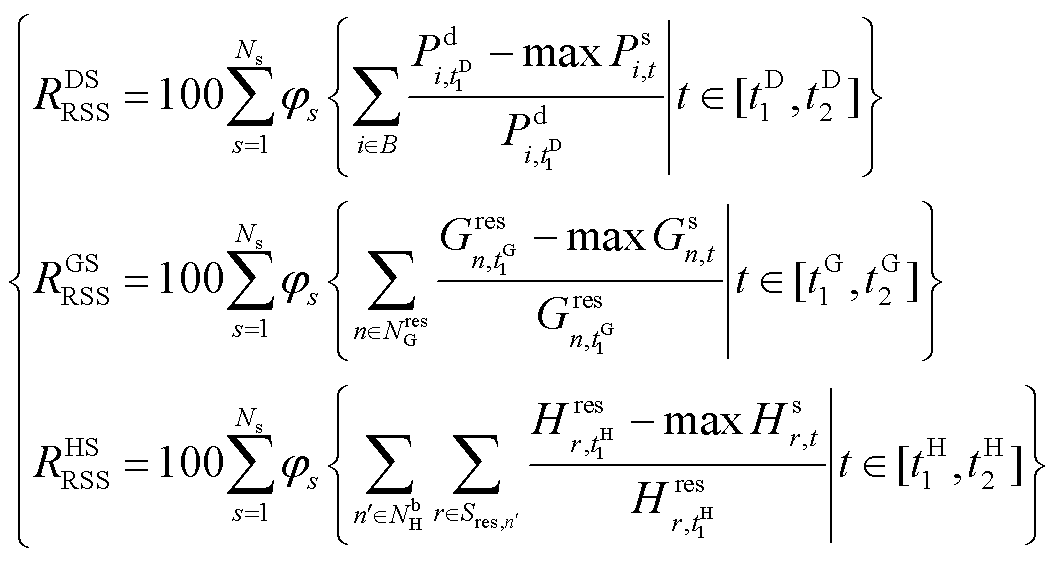 (8)
(8)
式中,![]() 为系统抵抗性指标;
为系统抵抗性指标;![]() 为DS的抵抗性指标;
为DS的抵抗性指标;![]() 为GS的抵抗性指标;
为GS的抵抗性指标;![]() 为HS的抵抗性指标;
为HS的抵抗性指标;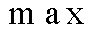 为取最大值;
为取最大值;![]() 、
、![]() 、
、![]() 分别为DS、GS、HS的损坏阶段。
分别为DS、GS、HS的损坏阶段。
1.3.3 响应性指标
响应性指标反映受极端事件影响后,各系统需要经历多长时间才可进入恢复阶段,即
其中
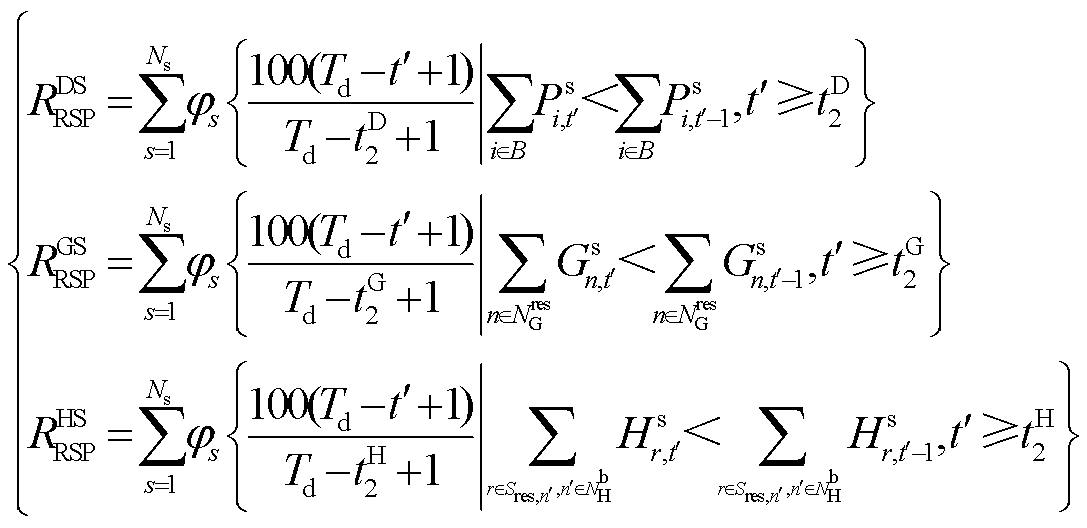 (10)
(10)
式中,![]() 为系统响应性指标;
为系统响应性指标;![]() 、
、![]() 、
、![]() 分别为DS、GS、HS的响应性指标。
分别为DS、GS、HS的响应性指标。
1.3.4 恢复性指标
UES恢复性评估需同时兼顾负荷恢复量和恢复速度。如图2所示,尽管三条恢复曲线代表的最终负荷恢复量相同,但显然恢复曲线1的恢复效果更好。系统的恢复性指标为
其中
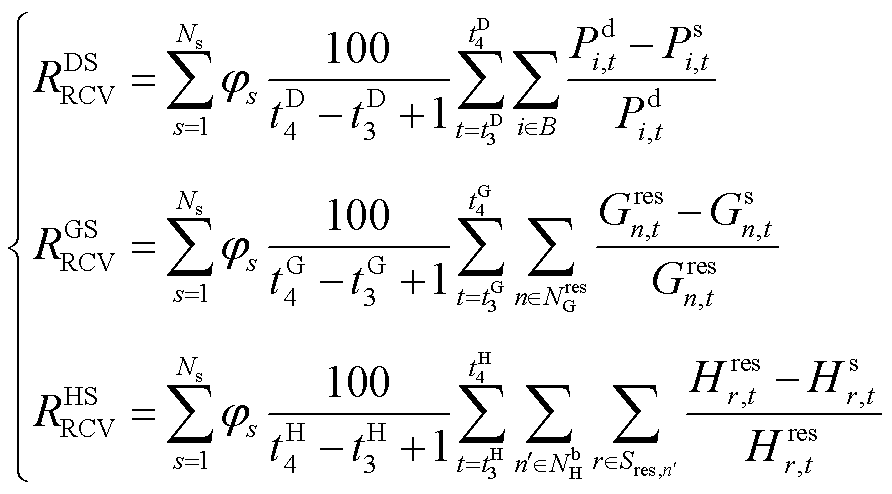 (12)
(12)
式中,![]() 为系统恢复性指标;
为系统恢复性指标;![]() 、
、![]() 、
、![]() 分别为DS、GS、HS的恢复性指标;
分别为DS、GS、HS的恢复性指标;![]() 、
、![]() 、
、![]() 分别为DS、GS、HS的恢复阶段。
分别为DS、GS、HS的恢复阶段。
1.3.5 孤岛连通度指标
孤岛数量反映了DS的撕裂程度,既可表征极端事件后的受破坏程度,又可表征其恢复难度。本节设所有节点均连通情况的孤岛数量为1,并将一个孤立节点视为一个孤岛。孤岛连通度指标为
式中,![]() 为孤岛连通度指标;
为孤岛连通度指标;![]() 为集合
为集合![]() 的势,即节点数量;
的势,即节点数量;![]() 为时刻
为时刻![]() 存在的孤岛数量。
存在的孤岛数量。
1.3.6 孤岛供电覆盖数量指标
孤岛连通度指标![]() 虽然可以反映网络的撕裂程度,但无法反映各孤岛的性能。因此,还需建立孤岛供电覆盖数量指标,进一步对孤岛的性能进行评估,有
虽然可以反映网络的撕裂程度,但无法反映各孤岛的性能。因此,还需建立孤岛供电覆盖数量指标,进一步对孤岛的性能进行评估,有
其中
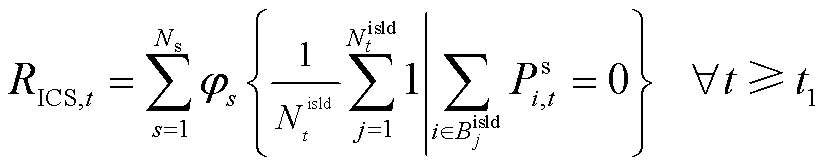 (15)
(15)
式中,![]() 为孤岛供电覆盖数量指标;
为孤岛供电覆盖数量指标;![]() 为时刻
为时刻![]() 的孤岛供电覆盖数量指标;
的孤岛供电覆盖数量指标;![]() 为时刻
为时刻![]() 存在的孤岛数量,
存在的孤岛数量,![]() 为孤岛
为孤岛![]() 中包含的节点的集合。
中包含的节点的集合。
1.3.7 关键负荷维持时间指标
关键负荷在各系统中具有重要地位。为了针对性的评估极端事件下关键负荷的性能,建立关键负荷维持时间指标,即
其中
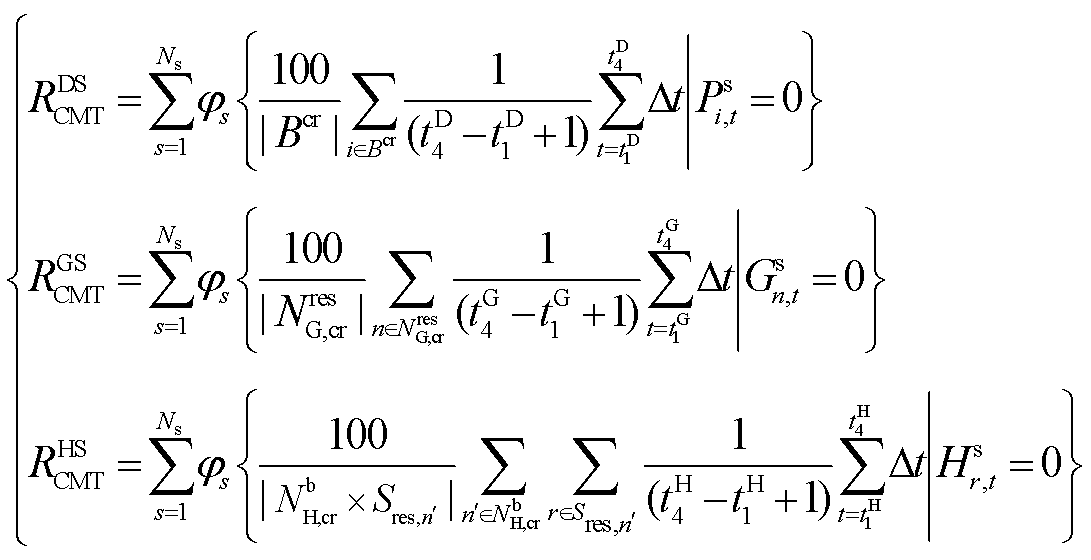 (17)
(17)
式中,![]() 为关键负荷维持时间指标;
为关键负荷维持时间指标;![]() 、
、![]() 、
、![]() 分别为DS、GS、HS的关键负荷维持时间指标;
分别为DS、GS、HS的关键负荷维持时间指标;![]() 、
、![]() 、
、![]() 分别为电、气、热系统中关键负荷节点的集合。
分别为电、气、热系统中关键负荷节点的集合。
管道天然气通过压力驱动,并在节点处满足节点流量平衡方程[18],有
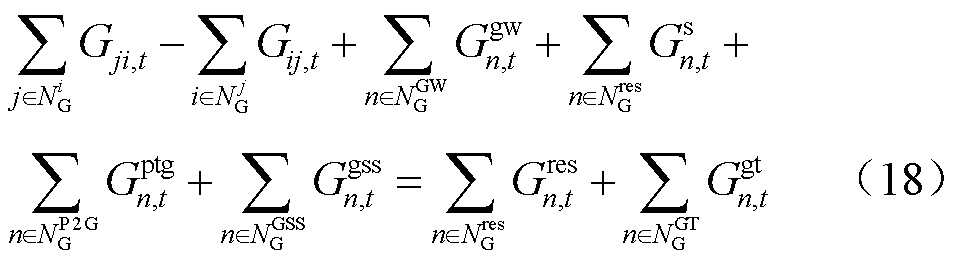
式中,![]() 为管道
为管道![]() 中的天然气流量,m3/h,若管道
中的天然气流量,m3/h,若管道![]() 中天然气流动方向为
中天然气流动方向为![]() ,则
,则![]() ;
;![]() 为气源的产气量,m3/h;
为气源的产气量,m3/h;![]() 为电转气(Power-to-Gas, PtG)的产气量,m3/h;
为电转气(Power-to-Gas, PtG)的产气量,m3/h;![]() 为储气装置的产气量,储气为正,放气为负,m3/h;
为储气装置的产气量,储气为正,放气为负,m3/h;![]() 为气负荷的需求量,m3/h;
为气负荷的需求量,m3/h;![]() 、
、![]() 分别为管道
分别为管道![]() 气流的最大、最小值;
气流的最大、最小值;![]() 、
、![]() 分别为气源产气量的最大、最小值;
分别为气源产气量的最大、最小值;![]() 为燃气轮机(Gas Turbine, GT)的耗气量,m3/h;
为燃气轮机(Gas Turbine, GT)的耗气量,m3/h;![]() 为节点的气压,bar(1 bar=105 Pa);
为节点的气压,bar(1 bar=105 Pa);![]() 为与管道
为与管道![]() 物理特性相关的系数[19];
物理特性相关的系数[19];![]() 、
、![]() 分别为节点
分别为节点![]() 气压的最大、最小值;
气压的最大、最小值;![]() 为与节点
为与节点![]() 连接的节点集合;
连接的节点集合;![]() 为与气源连接的节点集合;
为与气源连接的节点集合;![]() 为与气负荷连接的节点集合;
为与气负荷连接的节点集合;![]() 为与PtG连接的节点集合;
为与PtG连接的节点集合;![]() 为与储气装置连接的节点集合;
为与储气装置连接的节点集合;![]() 为与GT连接的节点集合;
为与GT连接的节点集合;![]() 为天然气管道集合;
为天然气管道集合;![]() 为含气体压缩机的天然气管道集合。
为含气体压缩机的天然气管道集合。
储气装置可在气体压缩机停运而导致下级气网供气不足时提供一定量的天然气供应。气体压缩机(Gas Compressor, GC)、GT和PtG可视为耦合天然气管网子系统与城市配电网的元件。
2.2.1 储气装置
储气装置需要满足的约束条件为
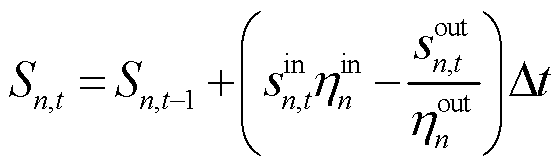 (29)
(29)
式中,![]() 、
、![]() 分别为储气装置
分别为储气装置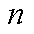 的进、出气量;0-1变量
的进、出气量;0-1变量![]() 、
、![]() 分别为储气装置
分别为储气装置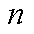 是否进、出气(1为是,0为否);
是否进、出气(1为是,0为否);![]() 、
、![]() 分别为储气装置
分别为储气装置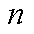 进、出气的最大流量;
进、出气的最大流量;![]() 为储气装置
为储气装置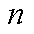 的气体存储量;
的气体存储量;![]() 、
、![]() 分别为储气装置
分别为储气装置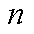 的进、出气效率;
的进、出气效率;![]() 、
、![]() 分别为储气装置
分别为储气装置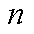 容量的上、下限值。
容量的上、下限值。
2.2.2 气体压缩机
天然气管道中的气体压缩机通过消耗电力来抵抗管道上的气压降落,以维持天然气的流动,其模型为
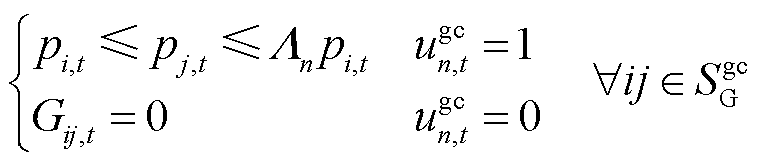 (31)
(31)
式中,![]() 为气体压缩机
为气体压缩机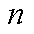 的压缩系数(规定含气体压缩机的管道气体流动方向为
的压缩系数(规定含气体压缩机的管道气体流动方向为![]() );
);![]() 为气体压缩机
为气体压缩机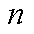 消耗的电功率,kW;0-1变量
消耗的电功率,kW;0-1变量![]() 为气体压缩机
为气体压缩机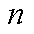 的开关状态(1为开,0为关);
的开关状态(1为开,0为关);![]() 为气体压缩机
为气体压缩机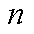 的功率系数,kW/m3。
的功率系数,kW/m3。
2.2.3 燃气轮机
燃气轮机通过消耗天然气来发电,视为城市配电网中的电源、天然气管网子系统中的气负荷,其模型为
式中,![]() 为接入电网节点
为接入电网节点![]() 、接入天然气节点
、接入天然气节点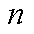 的燃气轮机产生的电功率,kW;
的燃气轮机产生的电功率,kW;![]() 为燃气轮机的效率;
为燃气轮机的效率;![]() 为燃气轮机消耗的气体,m3/h;
为燃气轮机消耗的气体,m3/h;![]() 、
、![]() 分别为产生电功率的上、下限值。
分别为产生电功率的上、下限值。
2.2.4 电转气
与燃气轮机相反,电转气则通过消耗电力来生产天然气,视为城市配电网中的电负荷、天然气管网子系统中的气源,其模型为
式中,![]() 为燃气轮机消耗的气体,m3/h;
为燃气轮机消耗的气体,m3/h;![]() 为燃气轮机产生的电功率,kW;
为燃气轮机产生的电功率,kW;![]() 为燃气轮机的效率;
为燃气轮机的效率;![]() 、
、![]() 分别为产生燃气的上、下限值。
分别为产生燃气的上、下限值。
城市供回热网络的运行通常采用质量调节模式,即通过调节热媒(本节以热水为例)的温度来改变供热功率的大小,而质量流率的数量保持为设计值[20]。
供、回热管道中热媒的流动需要满足
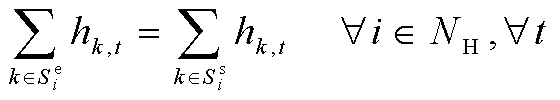 (37)
(37)
式中,![]() 为供/回热管道
为供/回热管道![]() 中热媒的质量流率;
中热媒的质量流率;![]() 、
、![]() 分别为起始、终止于节点
分别为起始、终止于节点![]() 的供/回热管道集合;
的供/回热管道集合;![]() 为供、回热管网的节点集合。
为供、回热管网的节点集合。
供/回热管网中存在普通、分支和交汇三类节点,各节点温度的混合关系如下。
1)普通节点
2)分支节点
3)交汇节点
式中,![]() 、
、![]() 分别为流入、流出供/回热管道
分别为流入、流出供/回热管道![]() 热媒的温度,℃;
热媒的温度,℃;![]() 为供/回热管道集合。
为供/回热管道集合。
同时,供/回热管道中热媒的温度需要限制在合理的范围内,即
式中,![]() 、
、![]() 分别为供/回热管道中热媒温度的上、下限值。通常,回热管道中温度的限值低于供热管道。
分别为供/回热管道中热媒温度的上、下限值。通常,回热管道中温度的限值低于供热管道。
供/回热管道中热媒携带的热功率与管道质量流率、温度成正比,有
式中,![]() 、
、![]() 分别为供/回热管道
分别为供/回热管道![]() 中的流入、流出热功率,kW;
中的流入、流出热功率,kW;![]() 、
、![]() 分别为供/回热管道中的流入、流出的温度,℃;
分别为供/回热管道中的流入、流出的温度,℃;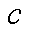 为比热容,kJ/(kg
为比热容,kJ/(kg ℃)。
℃)。
供/回热管道的热功率损失及延迟为
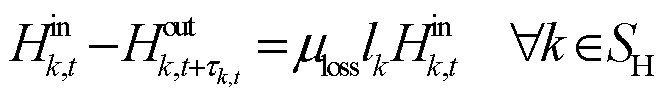 (44)
(44)
式中,![]() 为单位长度的热损失系数;
为单位长度的热损失系数;![]() 为供/回热管道的长度,m;
为供/回热管道的长度,m;![]() 为管道
为管道![]() 在时刻
在时刻![]() 的传输延迟时间。
的传输延迟时间。
热源发出的热功率通过热交换将热能送入供/回热网络中,有
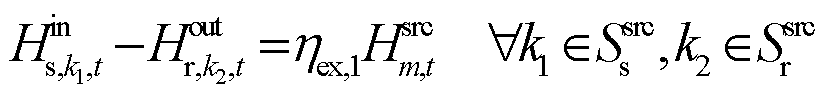 (45)
(45)
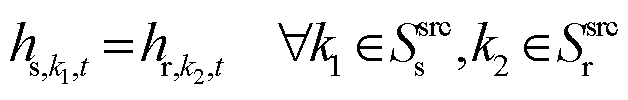 (46)
(46)
式中,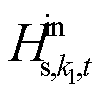 为流入供热管道
为流入供热管道![]() 的热功率;
的热功率;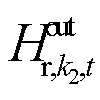 为流出回热管道
为流出回热管道![]() 的热功率;
的热功率;![]() 为热源与供/回热传输管道的热交换效率;
为热源与供/回热传输管道的热交换效率;![]() 为热源
为热源![]() 产生的热功率;
产生的热功率;![]() 、
、![]() 分别为与热源连接的供、回热管道集合。
分别为与热源连接的供、回热管道集合。
热用户(建筑物)通过热交换从供/回热网络中获得热量,有
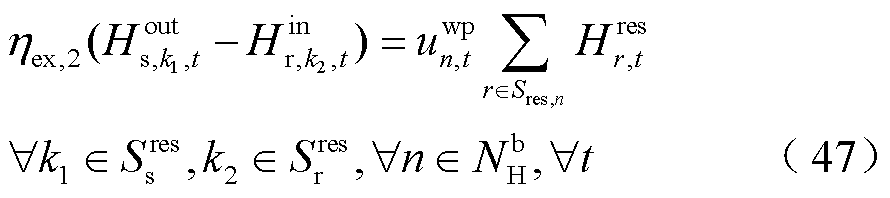
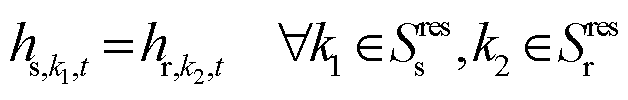 (48)
(48)
式中,![]() 为建筑物与供/回热传输管道的热交换效率;0-1变量
为建筑物与供/回热传输管道的热交换效率;0-1变量![]() 为建筑物
为建筑物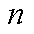 中水泵的运行状态(1为在运,0为停运);
中水泵的运行状态(1为在运,0为停运);![]() 、
、![]() 分别为与建筑物相连的供、回热管道的集合。
分别为与建筑物相连的供、回热管道的集合。
建筑物中房间的室内温度与室外温度、获得的热量等有关,即
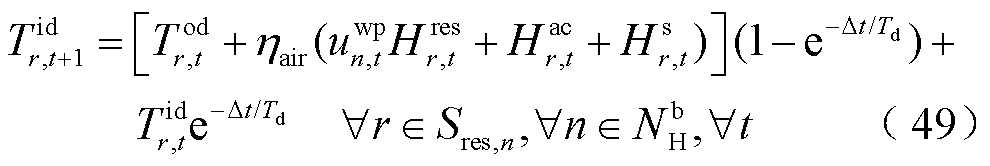
式中,![]() 、
、![]() 分别为房间
分别为房间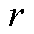 的室内、室外温度,℃;
的室内、室外温度,℃;![]() 为室内空气导热系数的倒数,℃/kW;
为室内空气导热系数的倒数,℃/kW;![]() 为房间
为房间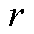 中暖通空调的热功率(制热为正,制冷为负);
中暖通空调的热功率(制热为正,制冷为负);![]() 、
、![]() 分别为室内温度的上、下限值。
分别为室内温度的上、下限值。
水泵(Water Pump, WP)和暖通空调(Heating, Ventilating and Air Conditioning, HVAC)可视为耦合供回热管网子系统与城市配电网的元件。
3.6.1 水泵
向建筑物供热时,需要依靠水泵实现热水的循环。水泵消耗的电功率为
式中,![]() 为接入电网节点
为接入电网节点![]() ,接入建筑物
,接入建筑物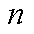 的水泵的电功率,kW;
的水泵的电功率,kW;![]() 为
为![]() 的额定功率,kW。
的额定功率,kW。
3.6.2 暖通空调
暖通空调是建筑物中应用广泛的空气调节设备。可在集中供热系统供热不足或供热过剩时,作为温度调节的补充手段。暖通空调的模型为
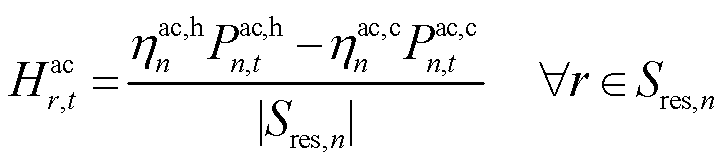 (58)
(58)
式中,![]() 为接入电网节点
为接入电网节点![]() ,安装于建筑物
,安装于建筑物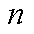 中的暖通空调消耗的电功率,kW;
中的暖通空调消耗的电功率,kW;![]() 、
、![]() 分别为暖通空调消耗的制热、制冷电功率,kW;0-1变量
分别为暖通空调消耗的制热、制冷电功率,kW;0-1变量![]() 、
、![]() 分别为暖通空调是否制热、制冷的状态变量(1为是,0为否);
分别为暖通空调是否制热、制冷的状态变量(1为是,0为否);![]() 、
、![]() 分别为制热、制冷电功率的最大值;
分别为制热、制冷电功率的最大值;![]() 为安装于房间
为安装于房间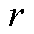 中的暖通空调产生的热功率(制热为正,制冷为负);
中的暖通空调产生的热功率(制热为正,制冷为负);![]() 、
、![]() 分别为制热、制冷效率。
分别为制热、制冷效率。
本节采用半动态的交通流模型对交通网络子系统(Transport System, TS)进行建模。TS可由顶点集合V与边集合![]() 构成的连通图
构成的连通图![]() 表示。起点
表示。起点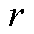 -终点
-终点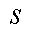 构成的组合
构成的组合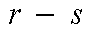 称为“节点对(pair)”。
称为“节点对(pair)”。
由于道路阻塞,道路的通行时间随其通行流量的增加而增加。道路的通行时间可由Bureau of Public Roads(BPR)函数建模[21],即
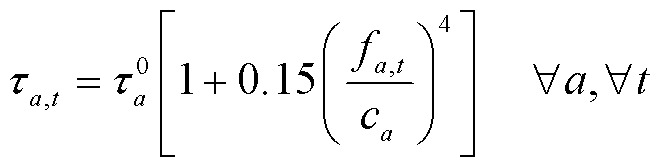 (59)
(59)
其中
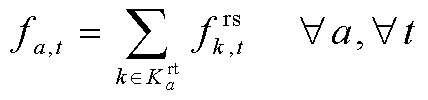 (60)
(60)
式中,![]() 为道路
为道路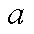 的通行时间;
的通行时间;![]() 为无拥堵情况下道路
为无拥堵情况下道路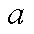 的通行时间;
的通行时间;![]() 为道路
为道路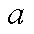 的交通流;
的交通流;![]() 为道路a的通行容量;
为道路a的通行容量;![]() 为路径
为路径![]() 上的交通流;
上的交通流;![]() 为包含道路
为包含道路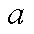 的所有路径的集合。
的所有路径的集合。
路径![]() 的通行时间为其包含的所有道路的通行时间之和,有
的通行时间为其包含的所有道路的通行时间之和,有
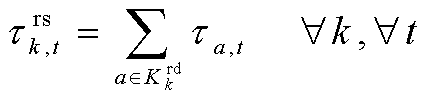 (61)
(61)
式中,![]() 为路径
为路径![]() 的通行时间;
的通行时间;![]() 为路径
为路径![]() 包含的所有道路的集合。
包含的所有道路的集合。
路径![]() 上交通流的分配采用Wardrop用户均衡(User Equilibrium, UE)原则进行建模[22]。
上交通流的分配采用Wardrop用户均衡(User Equilibrium, UE)原则进行建模[22]。
式中,![]() 为路径
为路径![]() 的最小通行时间。式(62)为互补约束,它等价于
的最小通行时间。式(62)为互补约束,它等价于![]() ,
,![]() ,
,![]()
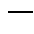
![]()
![]() 。
。
路径![]() 上的交通流需要满足平衡约束[23],即
上的交通流需要满足平衡约束[23],即
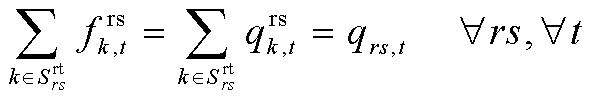 (63)
(63)
式中,![]() 为节点对
为节点对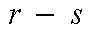 包含的路径
包含的路径![]() 上的交通流量;
上的交通流量;![]() 为节点对
为节点对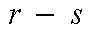 包含的路径上的交通流量之和。
包含的路径上的交通流量之和。
本节将发电车选择某一路径从某一起点移动至其对应的终点称为“发电车的路径规划”。发电车在交通网络中通行时,具有两类状态:①位于节点上;②位于路径上。其通行状态和路径规划约束为
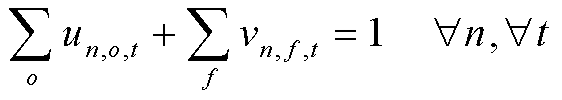 (64)
(64)
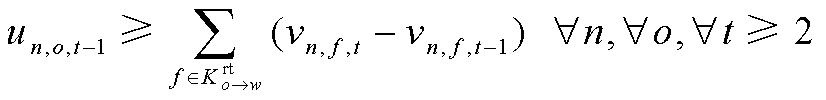 (65)
(65)
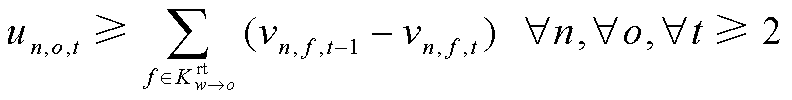 (66)
(66)
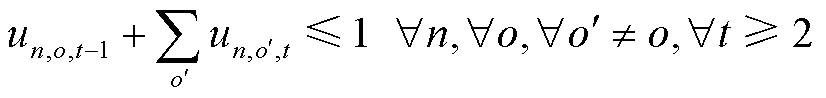 (67)
(67)
式中,0-1变量![]() 为发电车
为发电车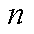 是否位于交通网络中的节点
是否位于交通网络中的节点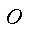 (1为是,0为否);0-1变量
(1为是,0为否);0-1变量![]() 为发电车
为发电车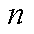 是否位于路径
是否位于路径![]() 上(1为是,0为否);
上(1为是,0为否);![]() 为以节点
为以节点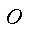 为起点,以节点
为起点,以节点![]() 为终点的所有路径的集合;
为终点的所有路径的集合;![]() 为以节点
为以节点![]() 为起点,以节点
为起点,以节点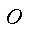 为终点的所有路径的集合。
为终点的所有路径的集合。
节点对 间的路径
间的路径![]() 的通行时间
的通行时间![]() 为
为
发电车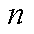 选择路径
选择路径![]() 并在该路径上通行的时间为
并在该路径上通行的时间为
发电车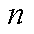 在时刻
在时刻![]() 选择某一路径
选择某一路径![]() 从起点
从起点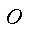 出发需要至少历时
出发需要至少历时![]() 才能抵达终点
才能抵达终点![]() 。为便于建模,首先引入两组0-1变量
。为便于建模,首先引入两组0-1变量![]() 、
、![]() 作为发电车在节点和路径中状态切换的指示变量,有
作为发电车在节点和路径中状态切换的指示变量,有
发电车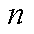 在路径
在路径![]() 上的通行时间需要满足
上的通行时间需要满足
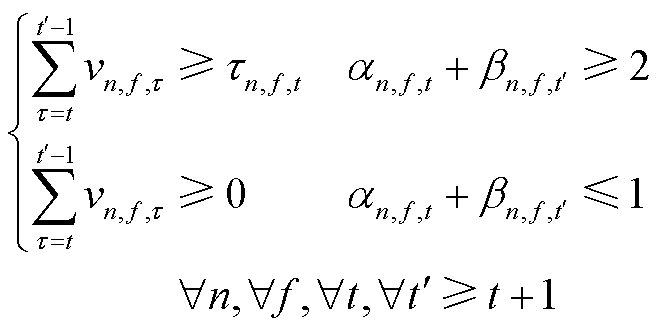 (72)
(72)
本节将维修人员在各损坏的元件间通行,选择某一损坏元件进行修复作业,并使其恢复运行的过程称为“维修人员调度”。在初始时刻,维修人员位于仓库中。维修人员在各个损坏元件间通行,并执行修复作业,需要满足
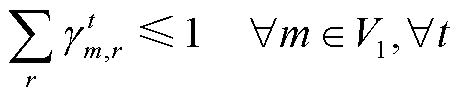 (74)
(74)
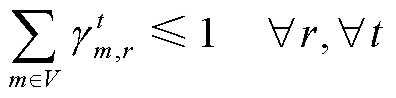 (75)
(75)
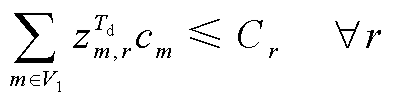 (76)
(76)
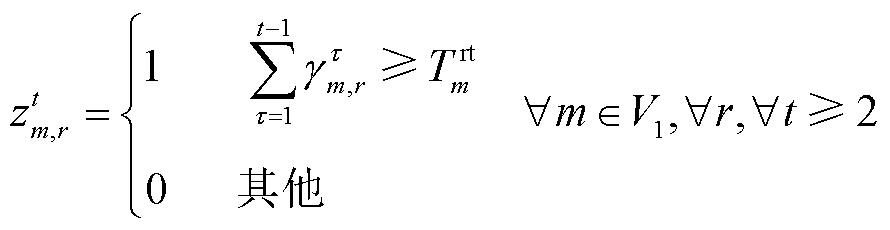 (78)
(78)
式中,0-1变量![]() 为维修人员
为维修人员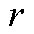 在时刻
在时刻![]() 是否访问元件
是否访问元件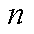 (1为是,0为否);
(1为是,0为否);![]() 为维修人员在元件
为维修人员在元件![]() 、
、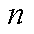 间移动的时间;
间移动的时间;![]() 为所有损坏元件和仓库的集合;
为所有损坏元件和仓库的集合;![]() 为所有损坏元件的集合;0-1变量
为所有损坏元件的集合;0-1变量![]() 为时刻
为时刻![]() 以及在过去时刻
以及在过去时刻![]() ,维修人员
,维修人员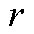 是否已经修复好元件
是否已经修复好元件![]() (1为是,0为否);
(1为是,0为否);![]() 为维修元件
为维修元件![]() 需要消耗的资源数量;
需要消耗的资源数量;![]() 为维修人员
为维修人员 携带的资源总数量;
携带的资源总数量;![]() 为修复元件
为修复元件![]() 需要消耗的时间。
需要消耗的时间。
假设城市配电网和供回热管网子系统通过抽汽凝汽式热电联产机组供能,来考虑供电与供热之间的关系。抽汽凝汽式热电联产机组的电-热特性为
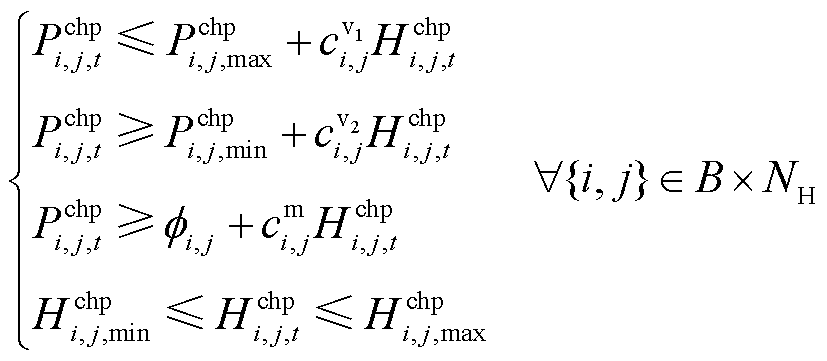 (79)
(79)
式中,![]() 、
、![]() 分别为接入配电网节点
分别为接入配电网节点![]() 、热网节点
、热网节点![]() 的热电联产机组发出的电功率、热功率,kW;
的热电联产机组发出的电功率、热功率,kW;![]() 、
、![]() 、
、![]() 、
、![]() 分别为电功率、热功率的上、下限值,kW;
分别为电功率、热功率的上、下限值,kW;![]() 、
、![]() 分别为最大、最小进汽工况曲线的斜率;
分别为最大、最小进汽工况曲线的斜率;![]() 、
、![]() 分别为最小凝气工况曲线的斜率、截距,kW。
分别为最小凝气工况曲线的斜率、截距,kW。
发电车在交通网络子系统的各节点之间通行,接入某一对应的城市配电网节点,可为配电网提供电力,需满足
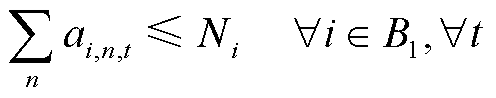 (81)
(81)
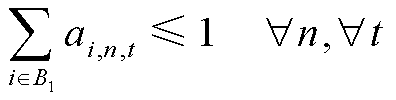 (82)
(82)
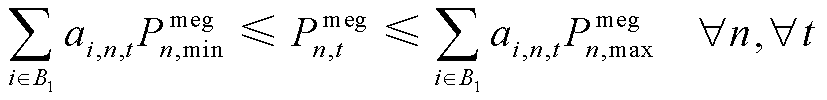 (83)
(83)
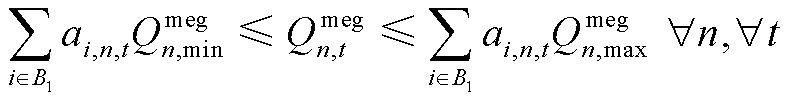 (84)
(84)
式中,![]() 为配电网节点
为配电网节点![]() 允许接入发电车的限值;0-1变量
允许接入发电车的限值;0-1变量![]() 为发电车
为发电车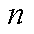 是否接入配电网节点
是否接入配电网节点![]() (1为是,0为否);
(1为是,0为否);![]() 为允许发电车接入的配电网节点的集合;
为允许发电车接入的配电网节点的集合;![]() 为发电车
为发电车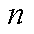 的有功功率;
的有功功率;![]() 、
、![]() 分别为其有功功率的上、下限值;
分别为其有功功率的上、下限值;![]() 为发电车
为发电车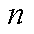 的无功功率;
的无功功率;![]() 、
、![]() 分别为
分别为![]() 的上、下限值;
的上、下限值;![]() 为与配电网节点
为与配电网节点![]() 耦合的交通网络节点的集合。
耦合的交通网络节点的集合。
本节采用在配电网中运用广泛的LinDistFlow模型对配电网潮流进行建模,有
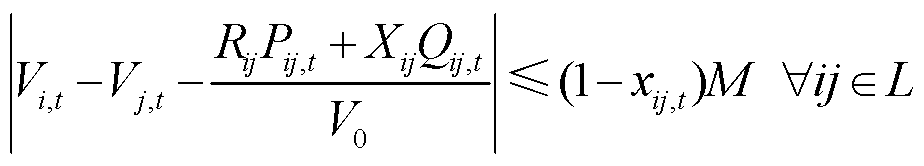 (86)
(86)
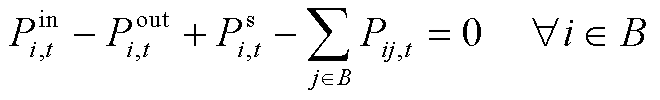 (87)
(87)
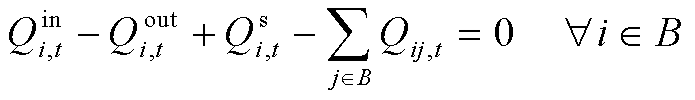 (88)
(88)
式中,![]() 、
、![]() 分别为节点
分别为节点![]() 、
、![]() 的电压幅值;
的电压幅值;![]() 、
、![]() 分别为线路
分别为线路![]() 上的电阻和电抗;
上的电阻和电抗;![]() 、
、![]() 分别为线路
分别为线路![]() 上的有功负荷和无功负荷;
上的有功负荷和无功负荷;![]() 为电压幅值的基准值;0-1变量
为电压幅值的基准值;0-1变量![]() 为线路的连接状态(1为连接,0为断开);
为线路的连接状态(1为连接,0为断开);![]() 、
、![]() 分别为节点
分别为节点![]() 的流入、流出有功功率;
的流入、流出有功功率;![]() 、
、![]() 分别为节点
分别为节点![]() 的流入、流出无功功率;
的流入、流出无功功率;![]() 为节点
为节点![]() 无功功率的损失值;
无功功率的损失值;![]() 为节点
为节点![]() 的无功负荷;
的无功负荷;![]() 为线路
为线路![]() 的有功功率限值;
的有功功率限值;![]() 为线路
为线路![]() 的无功功率限值;
的无功功率限值;![]() 、
、![]() 分别为节点
分别为节点![]() 电压幅值的上、下界。
电压幅值的上、下界。
城市配电网按闭环设计,但通常以辐射状运行,以便于保护装置的配置和其他措施的实施[24]。本节采用单商品流模型[11]来保证在优化过程中配电线路通断操作的辐射状特性,有
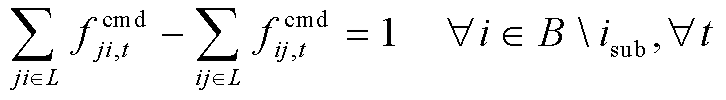 (97)
(97)
 (99)
(99)
式中,![]() 为线路
为线路![]() 上的虚拟商品流;
上的虚拟商品流;![]() 为网络的根节点;0-1变量
为网络的根节点;0-1变量![]() 为线路
为线路![]() 的虚拟连接状态(1为连接,0为断开);
的虚拟连接状态(1为连接,0为断开);![]() 为线路
为线路![]() 上最大的虚拟商品流,取
上最大的虚拟商品流,取![]() 。
。
方便起见,对线路修复状态变量![]() 进行改写,有
进行改写,有
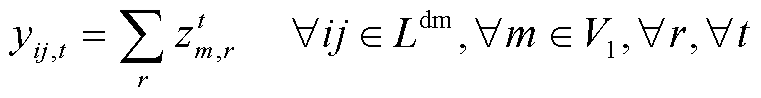 (101)
(101)
式中,0-1变量![]() 为线路
为线路![]() 是否在时刻
是否在时刻![]() 已经处于被修复的状态(1为是,0为否);
已经处于被修复的状态(1为是,0为否);![]() 为损坏线路的集合。
为损坏线路的集合。
线路连接状态![]() 需满足
需满足
式中,0-1变量![]() 为线路
为线路![]() 在时刻
在时刻![]() 是否损坏(过)的标记变量(1为是,0为否);
是否损坏(过)的标记变量(1为是,0为否);![]() 为安装有远程自动联络开关的线路集合。
为安装有远程自动联络开关的线路集合。
本节以如图3所示的电-气-热-交通相互依存的92节点融合系统(以下简称“融合系统”)为例,验证本文所提模型的正确性与有效性。
该融合系统由修改的IEEE 33节点配电系统(DS)、20节点天然气管网子系统(GS)、27节点供回热管网子系统(HS)及12节点交通网络子系统(TS)耦合而成。DS中有7个关键电负荷节点,具体为:5、11、15、19、25、29、30。GS中节点20为关键气负荷节点。HS中节点9为关键热负荷节点。关键电、气、热负荷节点的权重![]() 、
、![]() 、
、![]() 设为3,其他电、气、热负荷权重设为1。算例设置两台发电车和两组维修人员。发电车可接入的DS节点为2、3、8、9、12、14,它们分别与TS中的节点1、3、5、8、10、12对应。
设为3,其他电、气、热负荷权重设为1。算例设置两台发电车和两组维修人员。发电车可接入的DS节点为2、3、8、9、12、14,它们分别与TS中的节点1、3、5、8、10、12对应。
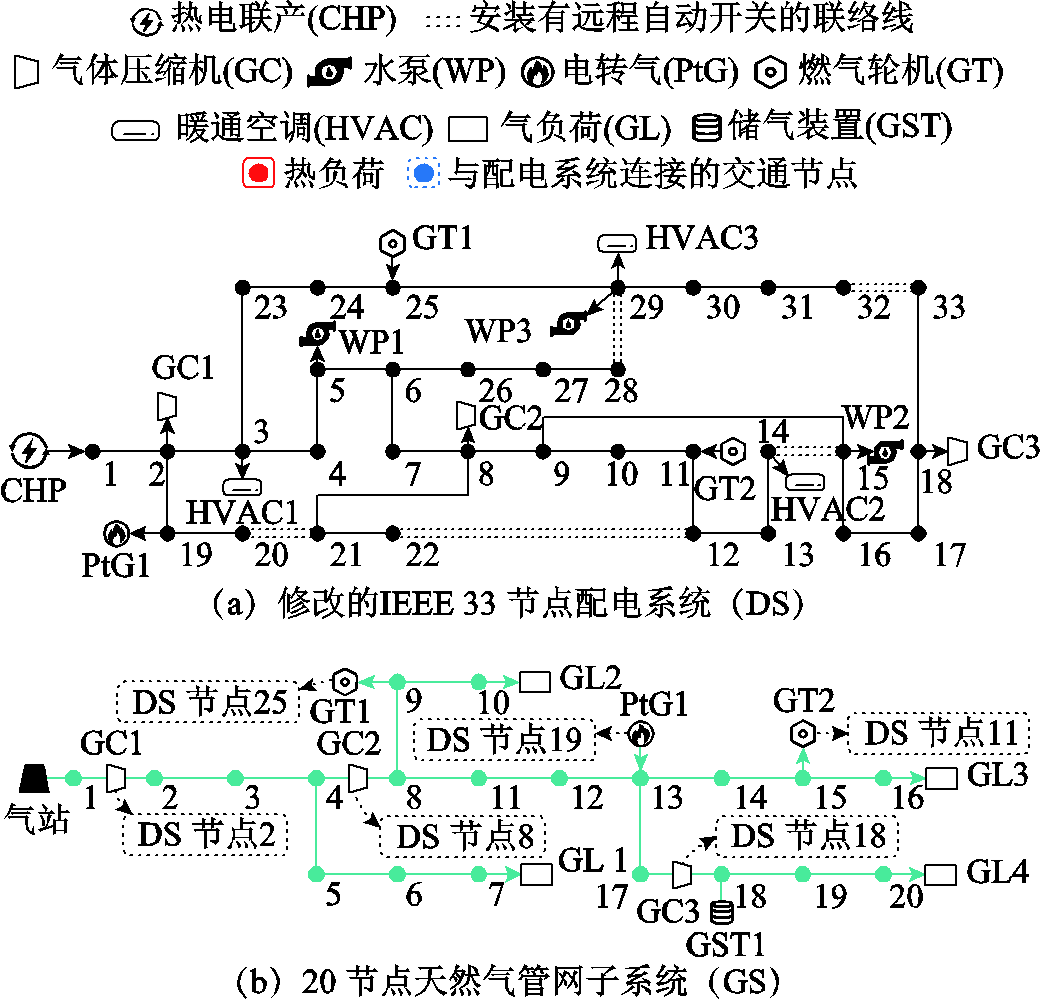
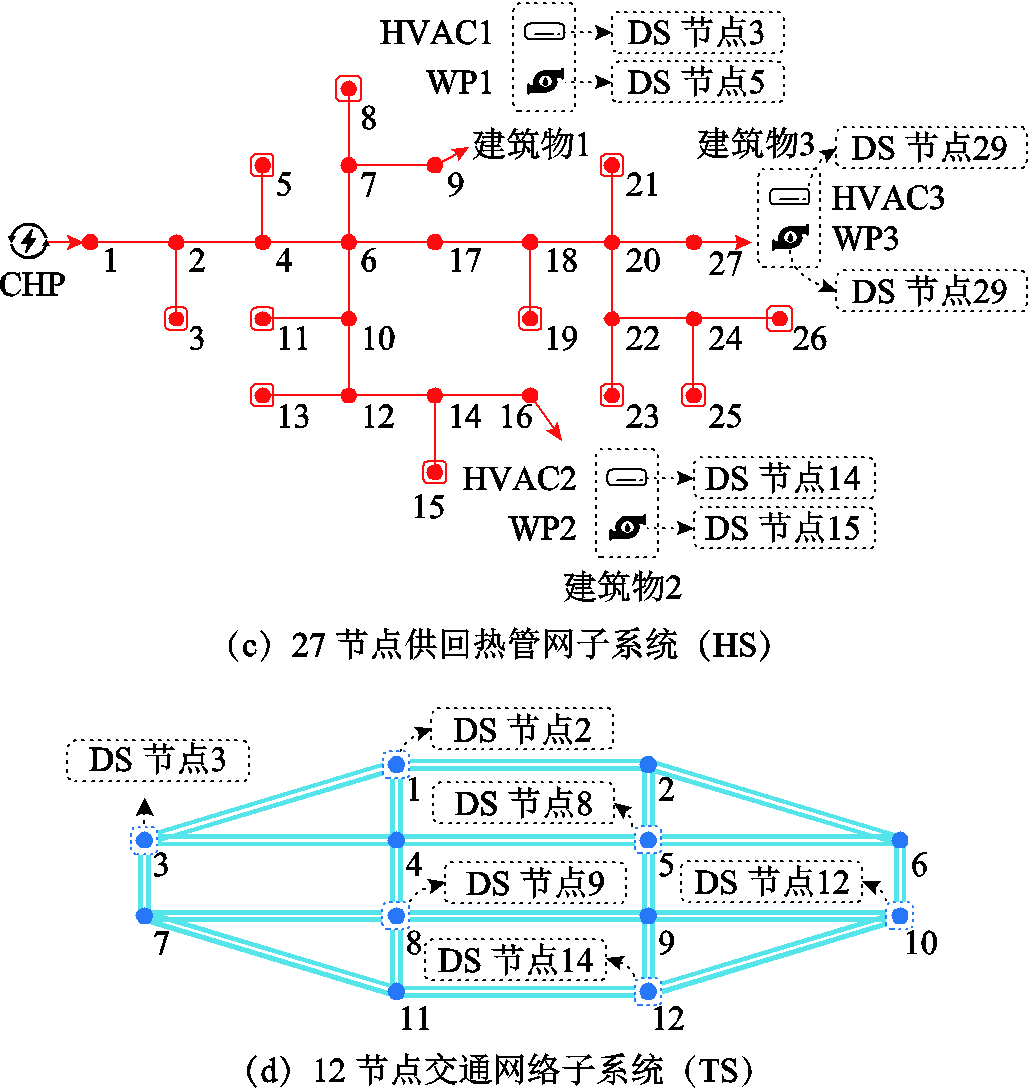
图3 92节点电-气-热-交通融合系统
Fig.3 92-node integrated electricity-gas-heat-transport system
假设受某极端事件的影响,DS每隔50 m架设一座杆塔,其中的导线、杆塔分别有0.007 5,0.005 5的概率发生损坏。假设各杆塔和导线的损坏是独立事件,并将线路等效为导线与杆塔的串联模型[25]。
为评估采取不同措施对各韧性指标的影响,本节算例设置六种情形:①情形A1:本文模型;②情形A2:降低维修人员的支援速度;③情形A3:降低发电车的支援速度;④情形A4:不考虑暖通空调的温度调节;⑤情形A5:不考虑储气装置的存/放气;⑥情形A6:情形A1+A2+A3+A4+A5。
韧性评估的流程为:①根据各线路的损坏概率随机生成并采样1 500个场景,作为情形A1~A6的线路损坏状态集;②在各情形中,对本文所提的韧性提升模型进行求解;③根据求解结果对四个整体性指标和三个针对性指标进行计算与分析。
各情形中,融合系统的性能维持![]() 、抵抗性
、抵抗性![]() 、响应性
、响应性![]() 、恢复性
、恢复性![]() 、孤岛连通度
、孤岛连通度![]() 、孤岛供电覆盖数
、孤岛供电覆盖数![]() 、关键负荷维持时间
、关键负荷维持时间![]() 的指标评估结果见表1。
的指标评估结果见表1。
表1 各情形中融合系统韧性指标的评估结果
Tab.1 Results of resilience assessment metrics for the integrated system in various cases
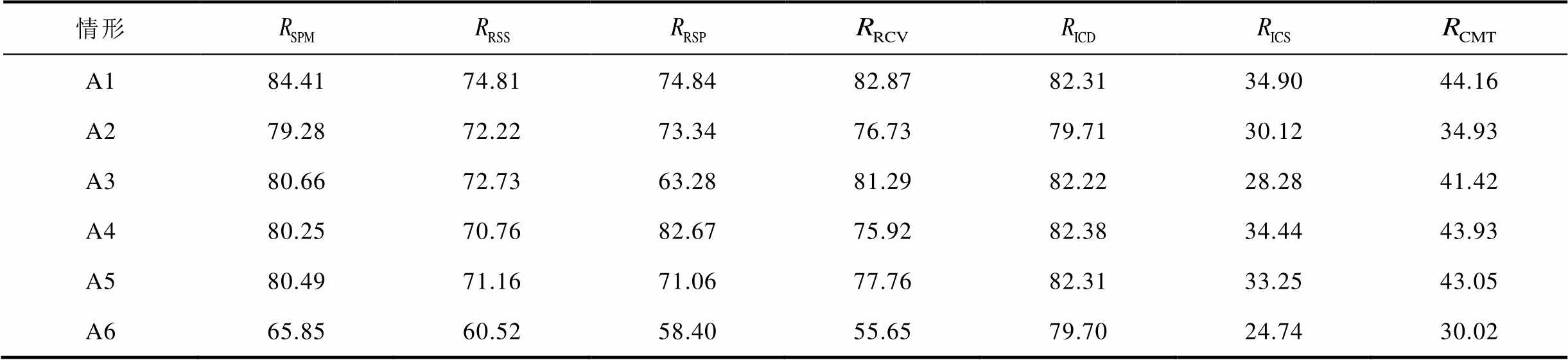
情形 A184.4174.8174.8482.8782.3134.9044.16 A279.2872.2273.3476.7379.7130.1234.93 A380.6672.7363.2881.2982.2228.2841.42 A480.2570.7682.6775.9282.3834.4443.93 A580.4971.1671.0677.7682.3133.2543.05 A665.8560.5258.4055.6579.7024.7430.02
由表1可见,除不考虑暖通空调调温作用的情形A4的响应性指标![]() 外,其他情形的各指标均随不采取措施或采取措施效率的降低而降低。与情形A1相比,情形A6中的各韧性评估指标
外,其他情形的各指标均随不采取措施或采取措施效率的降低而降低。与情形A1相比,情形A6中的各韧性评估指标![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分别下降18.56(21.99%)、14.29(19.10%)、16.44(21.97%)、27.22(32.85%)、2.61(3.17%)、10.16(29.11%)、14.14(32.02%)。
分别下降18.56(21.99%)、14.29(19.10%)、16.44(21.97%)、27.22(32.85%)、2.61(3.17%)、10.16(29.11%)、14.14(32.02%)。
各情形中,电、气、热子系统的性能维持指标(![]() 、
、![]() 、
、![]() )和抵抗性指标(
)和抵抗性指标(![]() 、
、![]() 、
、![]() )见表2。
)见表2。
表2 各情形中电、气、热子系统性能维持和抵抗性指标
Tab.2 Performance maintenance and resistance metrics for electrical, gas and heating systems in various cases

情形 A168.6493.9690.6439.8480.5475.38 A261.0489.6387.1839.8469.8474.14 A363.6290.5987.7839.8479.5074.98 A468.3193.6378.8239.8480.9040.49 A567.8083.4790.1939.8260.9575.26 A655.8173.1568.6039.8261.8240.44
如表2左三列所示,通过降低维修人员和发电车的支援效率的情形A2、A3会同时劣化DS、GS、HS的性能维持指标,其中情形A2的劣化效果更明显;不考虑暖通空调的情形A4主要劣化HS的性能维持指标;不考虑储气装置的情形A5则主要劣化GS的性能维持指标。如表2右三列所示,各情形中,DS的抵抗性指标基本一致,这是由于极端事件直接对DS产生损毁作用,若要提高融合系统整体的抵抗性指标,则只能通过提升其他子系统对极端事件的抵御能力;情形A2、A3中的GS和HS的抵抗性指标也受极端事件影响而下降;情形A4、A5的抵抗性指标的劣化则分别表现在HS、GS中。
各情形中,电、气、热子系统的响应性指标(![]() 、
、![]() 、
、![]() )和恢复性指标(
)和恢复性指标(![]() 、
、![]() 、
、![]() )见表3。
)见表3。
表3 各情形中电、气、热子系统响应性和恢复性指标
Tab.3 Responsiveness and recovery metrics for electrical, gas and heating systems in various cases
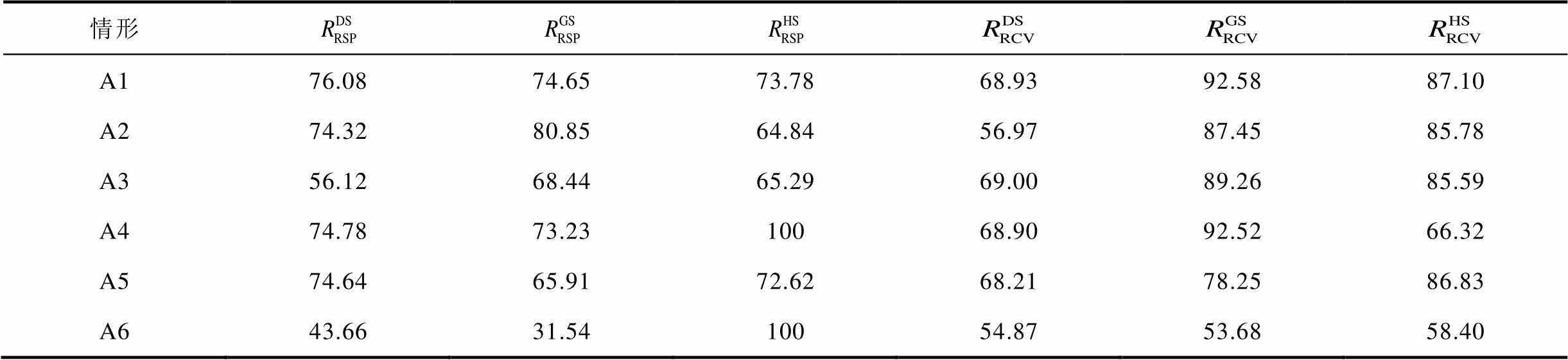
情形 A176.0874.6573.7868.9392.5887.10 A274.3280.8564.8456.9787.4585.78 A356.1268.4465.2969.0089.2685.59 A474.7873.2310068.9092.5266.32 A574.6465.9172.6268.2178.2586.83 A643.6631.5410054.8753.6858.40
如表3的左三列所示,在降低维修人员效率的情形A2中,GS的响应性指标要大于情形A1。这是由于在极端事件发生后,DS的拓扑结构还未得到完全恢复,能源替代效应还未完全发挥出来。因此,在协同优化中,气网负荷首先开始恢复,以提高系统整体的恢复性指标。在不考虑暖通空调的情形A4、A6中,HS的响应性指标均为100,即在HS的性能受损后,立即开始恢复。关于此现象的分析如下。
情形A1、A4的热负荷恢复率如图4所示。在情形A4中,由于不考虑暖通空调的调温作用,在极端事件攻击后,热负荷的损失开始增加,并在![]() h时达到最大值,而在
h时达到最大值,而在![]() h期间,水泵停运,无法从集中供热系统中获得热量,此时的热负荷恢复是因为室外温度的增加,热负荷的需求量减少而导致的。情形A1、A4分别表现出HS的“高性能的维持和响应”和“低性能的立即恢复”。可见,设置多个维度的韧性评估指标对准确掌握系统性能是有益的。
h期间,水泵停运,无法从集中供热系统中获得热量,此时的热负荷恢复是因为室外温度的增加,热负荷的需求量减少而导致的。情形A1、A4分别表现出HS的“高性能的维持和响应”和“低性能的立即恢复”。可见,设置多个维度的韧性评估指标对准确掌握系统性能是有益的。
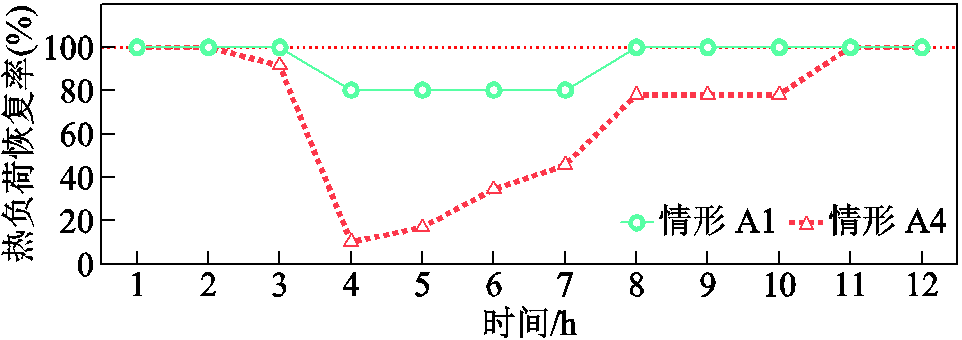
图4 情形A1、A4的热负荷恢复率
Fig.4 Thermal load recovery rate for cases A1 and A4
如表3的右三列所示。各子系统的恢复性指标随着不采取韧性提升措施或采取措施效率的下降而下降。其中,情形A2、A3中各子系统的恢复性指标均低于情形A1,以情形A2尤为明显。情形A4、A5则分别在HS、GS中的恢复性指标劣化更明显。
各情形中,电、气、热子系统的关键负荷维持时间指标(![]() 、
、![]() 、
、![]() )见表4。
)见表4。
表4 各情形中电、气、热子系统关键负荷维持时间指标
Tab.4 Critical load maintenance time metrics for electrical, gas and heating systems in various cases

情形 A163.6434.4299.32 A253.5225.6499.30 A357.9533.1699.13 A463.8233.9961.38 A562.7533.2099.32 A647.5821.2452.32
如表4所示,情形A4、A6中,HS的关键负荷维持时间指标显著低于其他情形。可见,在水泵停运期间,暖通空调对关键热负荷的恢复,提高用户舒适度,具有重要作用。
为便于对比分析实施不同措施对系统性能的影响,本节假设![]() h时,受极端事件影响,配电系统有10条线路损坏,具体为:3-4、6-7、9-10、14-15、20-21、28-29、32-33、25-29、12-22、9-15,并设置六个情形:①情形E1:本文模型;②情形E2:不考虑维修人员对线路的修复;③情形E3:不考虑发电车的移动;④情形E4:不考虑建筑物热惯性;⑤情形E5:不考虑储气罐的存/放气;情形E6:⑥情形E1+E2+E3+E4+E5。
h时,受极端事件影响,配电系统有10条线路损坏,具体为:3-4、6-7、9-10、14-15、20-21、28-29、32-33、25-29、12-22、9-15,并设置六个情形:①情形E1:本文模型;②情形E2:不考虑维修人员对线路的修复;③情形E3:不考虑发电车的移动;④情形E4:不考虑建筑物热惯性;⑤情形E5:不考虑储气罐的存/放气;情形E6:⑥情形E1+E2+E3+E4+E5。
各情形中电、气、热负荷的损失值见表5,各情形中电+气+热负荷的恢复率如图5所示。
表5 各情形中电、气、热负荷损失值
Tab.5 Electricity, gas and heat load shedding values in various scenarios

情形F/kW/kW/kW/kW E122 472.3117 486.544 275.83709.94 E241 522.7227 618.4512 032.511 871.76 E332 141.0522 070.009 356.07714.98 E423 420.3617 486.544 727.951 205.88 E532 915.5717 539.4914 666.13709.94 E671 394.3733 850.0034 489.173 055.20
如表5所示,情形E1中电、气、热的损失值最小。情形E2由于没有考虑维修人员对线路的修复,相比情形E1,各负荷损失值的增加显著,![]() 、
、![]() 、
、![]() 、
、![]() 分别增加了19 050.41 kW(84.77%)、10 131.91 kW(57.94%)、7 756.68 kW(181.41%)、1 161.82 kW(163.65%)。如图5所示,情形E1在
分别增加了19 050.41 kW(84.77%)、10 131.91 kW(57.94%)、7 756.68 kW(181.41%)、1 161.82 kW(163.65%)。如图5所示,情形E1在![]() h时,实现了系统电、气、热负荷的完全恢复。情形E2中,负荷的最终恢复率为82.47%。可见,维修人员的调度是融合系统实现灾后完全恢复的关键。由于情形E3没有考虑发电车的移动,与情形E1相比,情形E3的电、气、热负荷的损失值增加较为明显。
h时,实现了系统电、气、热负荷的完全恢复。情形E2中,负荷的最终恢复率为82.47%。可见,维修人员的调度是融合系统实现灾后完全恢复的关键。由于情形E3没有考虑发电车的移动,与情形E1相比,情形E3的电、气、热负荷的损失值增加较为明显。![]() 、
、![]() 、
、![]() 、
、![]() 的增加值分别为9 668.74 kW(43.03%)、4 583.46 kW(26.21%)、5 080.24 kW(118.81%)、5.04 kW(0.71%)。如图5所示,情形E3尽管采取了线路修复措施,但最终没有实现负荷的完全恢复,恢复率为96.90%。
的增加值分别为9 668.74 kW(43.03%)、4 583.46 kW(26.21%)、5 080.24 kW(118.81%)、5.04 kW(0.71%)。如图5所示,情形E3尽管采取了线路修复措施,但最终没有实现负荷的完全恢复,恢复率为96.90%。
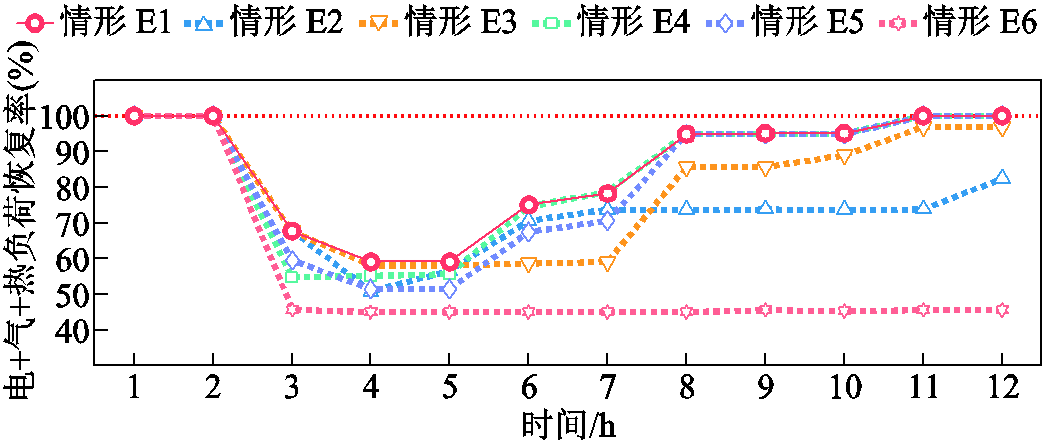
图5 各情形中电+气+热负荷恢复率
Fig.5 Electricity+gas+heat load recovery rates in various cases
各情形中,发电车的出力情况如图6所示。
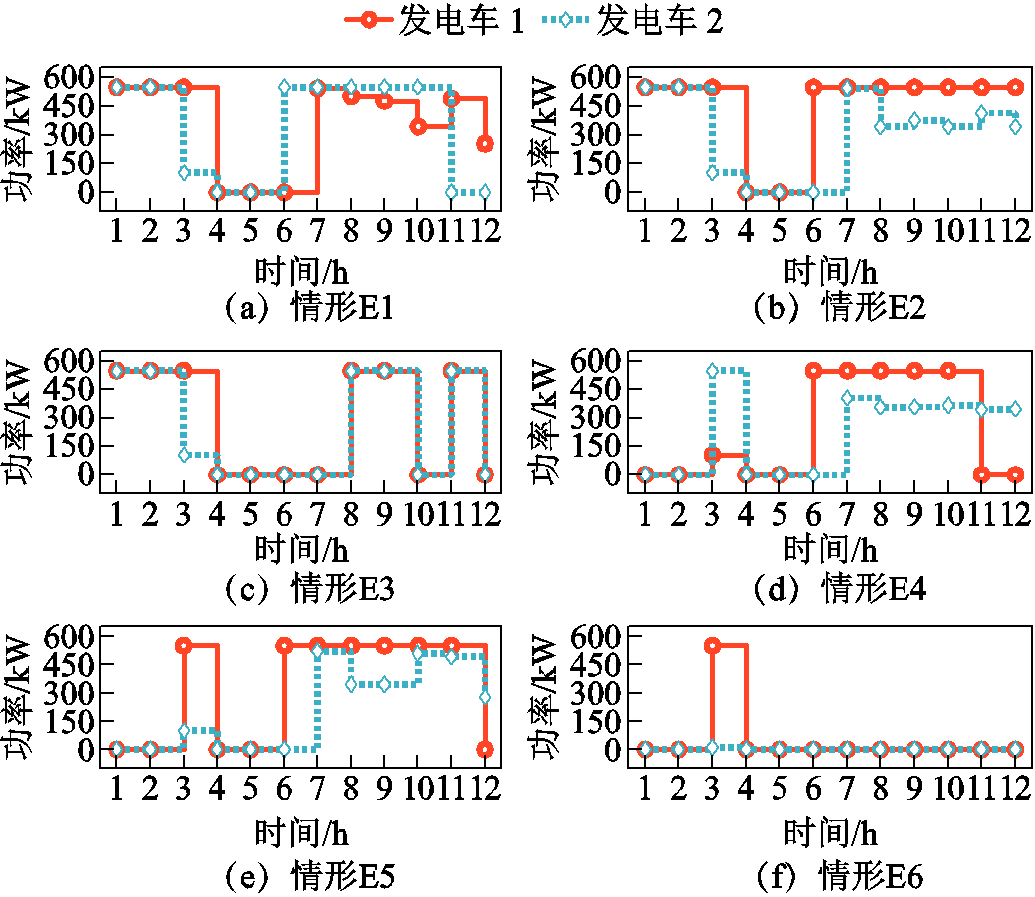
图6 各情形中发电车有功功率
Fig.6 Active power output of MEGs in various cases
受极端事件影响,DS被分割成多个孤岛,由于发电车不可移动,网络的撕裂限制了其出力。如图6所示,情形E3相比情形E2,在负荷恢复阶段发电车的输出更小。在情形E6中,由于维修人员不对线路进行修复,两台不可移动的发电车在调度周期内几乎无法发挥作用。可见,发电车的可移动特性,以及发电车与维修人员的有效配合,为系统维持、恢复性能提供了有效支撑。
如表5所示,与情形E1相比,情形E2、E3、E6气负荷损失的增加更加显著,这主要是由于气体压缩机缺电停运导致的。各情形中气体压缩机的运行状态如图7所示。
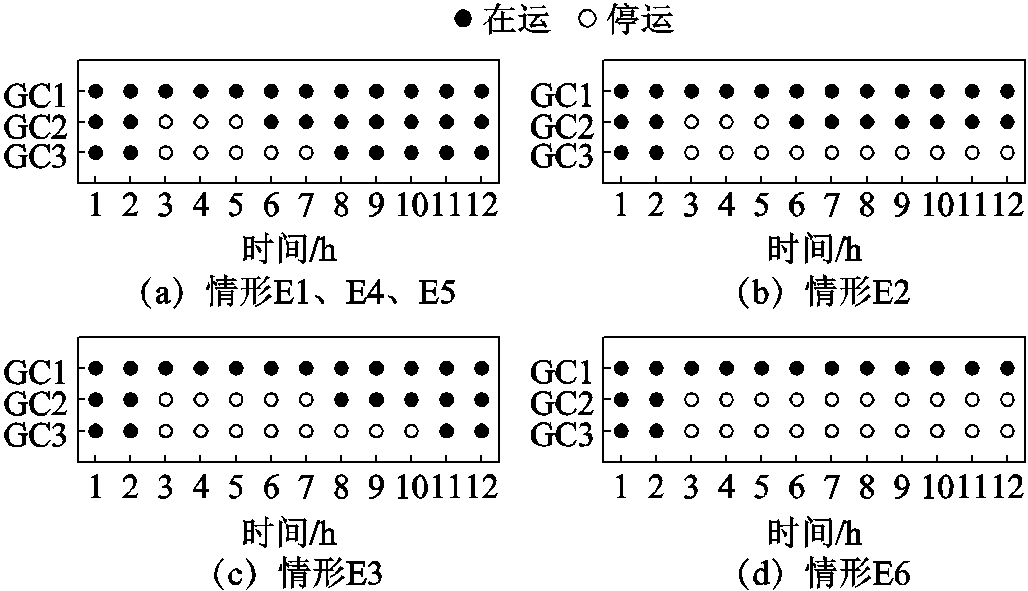
图7 各情形中气体压缩机运行状态
Fig.7 Operating status of the gas compressors in various cases
如表5和图7所示,各情形中,气负荷的损失值与气体压缩机的运行状态具有较强相关性。情形E2与情形E3相比,气体压缩机的运行时间更短,情形E2中气负荷的损失值要比情形E3更大。情形E1和E4的气体压缩机运行状态相同,因此,两者中气负荷的损失差别不大。尽管情形E5中气体压缩机的运行状态与情形E1、E4相同,但与情形E1相比,气负荷损失值的增加十分显著,为10 390.30 kW(243.00%),这是由于情形E5没有考虑储气装置的作用,无法在气体压缩机停运期间为下级气网供气。可见,保证气体压缩机的可靠运行,对减小气负荷的损失具有重要意义。
各情形中燃气轮机、电转气、储气装置的耗/产气量如图8所示。
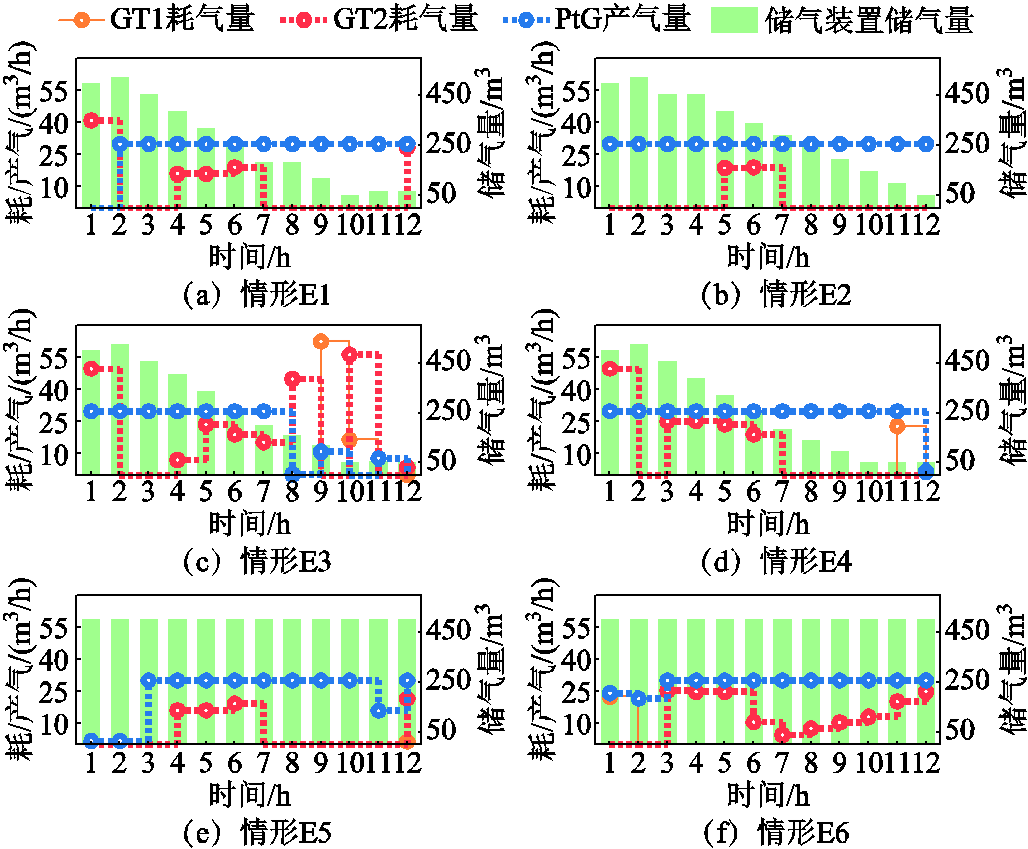
图8 各情形中燃气轮机、电转气、储气装置的耗/产气量
Fig.8 Gas consumption of GTs, gas production of PtG, gas storage of gas storage units in various cases
如图8所示,在考虑了储气装置作用的情形E1~E4中,储气装置在![]() h时,始终处于放气状态,直到气体存储量达到其容量的下限值。在各情形中,电转气在大多数时段中均生产天然气,以在气体压缩机停运期间,提供一定的天然气供应,减少气负荷的损失。情形E3中,燃气轮机在
h时,始终处于放气状态,直到气体存储量达到其容量的下限值。在各情形中,电转气在大多数时段中均生产天然气,以在气体压缩机停运期间,提供一定的天然气供应,减少气负荷的损失。情形E3中,燃气轮机在![]() h期间出力较大。当配电网络的拓扑结构逐渐被维修人员恢复时,由于燃气轮机接入配电网内部的不同节点,因此,可以作为不可移动的发电车的补充。
h期间出力较大。当配电网络的拓扑结构逐渐被维修人员恢复时,由于燃气轮机接入配电网内部的不同节点,因此,可以作为不可移动的发电车的补充。
类似的,热负荷的损失值与水泵的运行状态具有较强相关性。各情形中水泵的运行状态如图9所示。
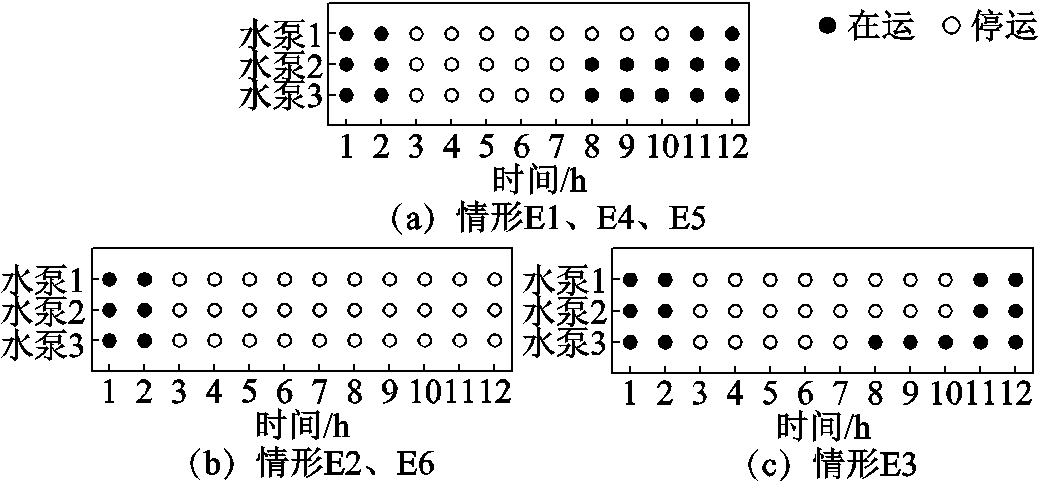
图9 各情形中水泵运行状态
Fig.9 Operating status of the water pumps in various cases
如表5和图9所示,除情形E4外,其他情形中,热负荷的损失值随水泵开启时间的增加而减少。由于情形E4没有考虑建筑物的热惯性,尽管该情形水泵的开启状态与情形E1和E5一致,但其热负荷的损失值显著增加。
由表5可知,不考虑建筑物热惯性的情形E4与情形E1的主要差异体现在热负荷损失值![]() 的增加上,为495.94 kW(69.86%)。
的增加上,为495.94 kW(69.86%)。
各情形中,暖通空调的制热/制冷功率如图10所示。
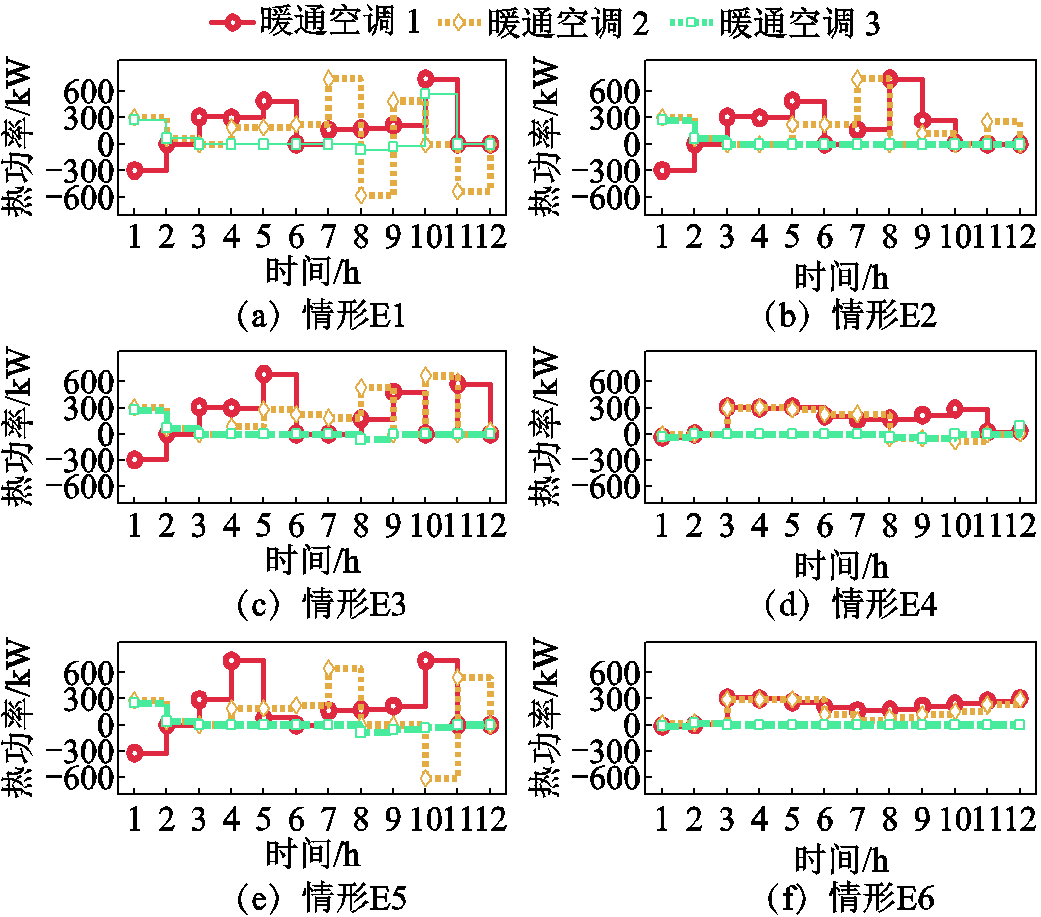
图10 各情形中暖通空调制热/制冷功率
Fig.10 HVAC heating/cooling power in various cases
由如图5所示的恢复曲线可知,情形E1和E4的差异主要体现在![]() h期间。如图10所示,在
h期间。如图10所示,在![]() h期间,尽管情形E1中暖通空调的总制热功率(1 803.15 kW)大于情形E4中的总制热功率(1 478.99 kW),但由于情形E4没有考虑建筑物对热量的存储能力,在
h期间,尽管情形E1中暖通空调的总制热功率(1 803.15 kW)大于情形E4中的总制热功率(1 478.99 kW),但由于情形E4没有考虑建筑物对热量的存储能力,在![]() h期间,情形E4的热负荷损失仍然要大于情形E1的热负荷损失。
h期间,情形E4的热负荷损失仍然要大于情形E1的热负荷损失。
为了更直观地分析维修人员和发电车的调度过程,本节展示情形E1中的DS恢复与拓扑重构结果,如图11所示。
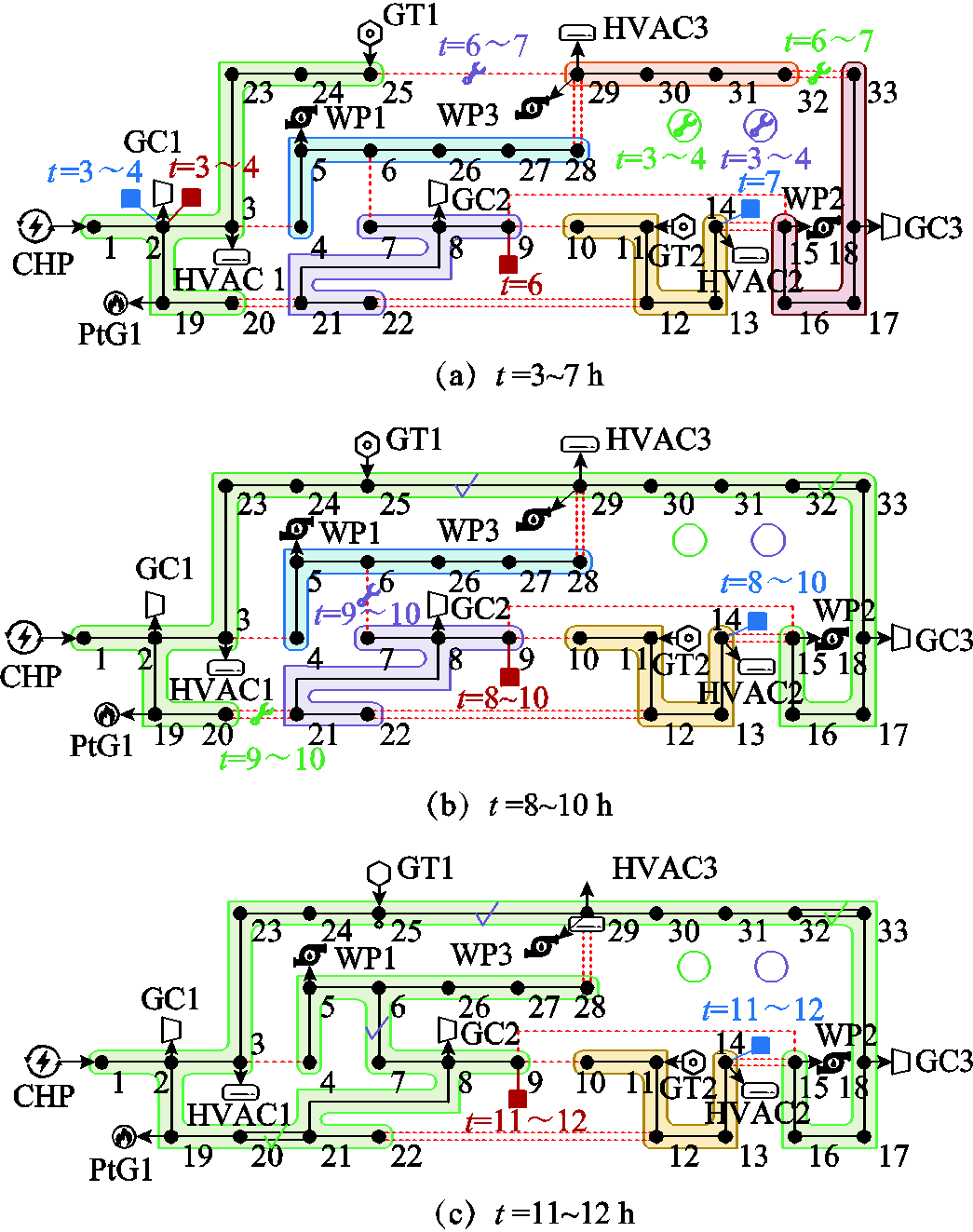
图11 情形E1中系统恢复与拓扑重构

Fig.11 System recovery and topology reconfiguration of case E1
在![]() h期间,DS中的线路没有损坏,所有节点均连通。如图11a所示,当
h期间,DS中的线路没有损坏,所有节点均连通。如图11a所示,当![]() h时,由于线路的损坏,DS被分割成6个独立的供电区域。发电车1、2在
h时,由于线路的损坏,DS被分割成6个独立的供电区域。发电车1、2在![]() h时,均接入DS的节点2(交通网络的节点1)。发电车1、2分别于
h时,均接入DS的节点2(交通网络的节点1)。发电车1、2分别于![]() h、
h、![]() h时抵达DS节点14、9(TS节点12、8)。发电车1的路径规划为:1
h时抵达DS节点14、9(TS节点12、8)。发电车1的路径规划为:1![]() 4
4![]() 8
8![]() 11
11![]() 12,发电车2的路径规划为:1
12,发电车2的路径规划为:1![]() 4
4![]() 8。维修人员1、2在
8。维修人员1、2在![]() 时,均分别闲置在仓库1、2中,并于
时,均分别闲置在仓库1、2中,并于![]() h时,分别开始对线路25-29、32-33进行维修。如图11b所示,当t=8~10 h时,线路25-29、32-33于
h时,分别开始对线路25-29、32-33进行维修。如图11b所示,当t=8~10 h时,线路25-29、32-33于![]() h时,分别被维修人员1、2修复。此时,DS被分割成4个独立的供电区域。维修人员1、2于
h时,分别被维修人员1、2修复。此时,DS被分割成4个独立的供电区域。维修人员1、2于![]() h时分别开始对线路20-21、6-7进行维修。如图11c所示,当t=11~12 h时,线路20-21、6-7于
h时分别开始对线路20-21、6-7进行维修。如图11c所示,当t=11~12 h时,线路20-21、6-7于![]() h时,分别被维修人员1、2修复。此时,DS被分割成2个独立的供电区域,负荷已完全恢复。
h时,分别被维修人员1、2修复。此时,DS被分割成2个独立的供电区域,负荷已完全恢复。
本文提出了考虑电-气-热-交通相互依存的城市能源系统的韧性评估与提升方法,研究表明:
1)对城市能源系统韧性评估与提升的综合研究,可以考虑各韧性提升措施与各韧性评估指标之间的关联性,有利于决策者更好地规避风险并利用多能融合的优势实现系统韧性的提升。
2)所提的韧性评估指标从整体性和针对性两个角度,对系统性能处于的不同阶段进行了评估。多维韧性评估指标可以从系统性能特性和拓扑特征全面的掌握系统性能,由此制定更具针对性的解决方案和应对措施。
3)所提的韧性提升方法实现了各子系统以及各措施间的有效配合与协同优化;增强了UES对极端事件的抵御能力;提高了能源供应的覆盖程度;促进了极端事件后UES的快速恢复。
参考文献
[1] 张儒峰, 李雪, 姜涛, 等. 城市综合能源系统韧性评估与提升综述[J]. 全球能源互联网, 2021, 4(2): 122-132.
Zhang Rufeng, Li Xue, Jiang Tao, et al. Review on resilience assessment and enhancement of urban integrated energy system[J]. Journal of Global Energy Interconnection, 2021, 4(2): 122-132.
[2] 贾宏杰, 穆云飞, 侯恺, 等. 能源转型视角下城市能源系统的形态演化及运行调控[J]. 电力系统自动化, 2021, 45(16): 49-62.
Jia Hongjie, Mu Yunfei, Hou Kai, et al. Morphology evolution and operation regulation of urban energy system from perspective of energy transition[J]. Automation of Electric Power Systems, 2021, 45(16): 49-62.
[3] 阮前途, 谢伟, 许寅, 等. 韧性电网的概念与关键特征[J]. 中国电机工程学报, 2020, 40(21): 6773-6784.
Ruan Qiantu, Xie Wei, Xu Yin, et al. Concept and key features of resilient power grids[J]. Proceedings of the CSEE, 2020, 40(21): 6773-6784.
[4] 周晓敏, 葛少云, 李腾, 等. 极端天气条件下的配电网韧性分析方法及提升措施研究[J]. 中国电机工程学报, 2018, 38(2): 505-513, 681.
Zhou Xiaomin, Ge Shaoyun, Li Teng, et al. Assessing and boosting resilience of distribution system under extreme weather[J]. Proceedings of the CSEE, 2018, 38(2): 505-513, 681.
[5] Gautam P, Piya P, Karki R. Resilience assessment of distribution systems integrated with distributed energy resources[J]. IEEE Transactions on Sustainable Energy, 2021, 12(1): 338-348.
[6] 王守相, 黄仁山, 潘志新, 等. 极端冰雪天气下配电网弹性恢复力指标的构建及评估方法[J]. 高电压技术, 2020, 46(1): 123-132.
Wang Shouxiang, Huang Renshan, Pan Zhixin, et al. Construction and evaluation of resilience restoration capability indices for distribution network under extreme ice and snow weather[J]. High Voltage Engineering, 2020, 46(1): 123-132.
[7] 别朝红, 林超凡, 李更丰, 等. 能源转型下弹性电力系统的发展与展望[J]. 中国电机工程学报, 2020, 40(9): 2735-2745.
Bie Zhaohong, Lin Chaofan, Li Gengfeng, et al. Development and prospect of resilient power system in the context of energy transition[J]. Proceedings of the CSEE, 2020, 40(9): 2735-2745.
[8] Salimi M, Nasr M A, Hosseinian S H, et al. Information gap decision theory-based active distribution system planning for resilience enhancement[J]. IEEE Transactions on Smart Grid, 2020, 11(5): 4390-4402.
[9] 卞艺衡, 别朝红. 面向弹性提升的智能配电网远动开关优化配置模型[J]. 电力系统自动化, 2021, 45(3): 33-39.
Bian Yiheng, Bie Zhaohong. Resilience-enhanced optimal placement model of remote-controlled switch for smart distribution network[J]. Automation of Electric Power Systems, 2021, 45(3): 33-39.
[10] Yan Mingyu, Shahidehpour M, Paaso A, et al. Distribution system resilience in ice storms by optimal routing of mobile devices on congested roads[J]. IEEE Transactions on Smart Grid, 2021, 12(2): 1314-1328.
[11] Lei Shunbo, Chen Chen, Li Yupeng, et al. Resilient disaster recovery logistics of distribution systems: Co-optimize service restoration with repair crew and mobile power source dispatch[J]. IEEE Transactions on Smart Grid, 2019, 10(6): 6187-6202.
[12] 彭寒梅, 李才宝, 刘健锋, 等. 基于异质依存网络的电-气区域综合能源系统弹性评估[J]. 电网技术, 2021, 45(7): 2811-2821.
Peng Hanmei, Li Caibao, Liu Jianfeng, et al. Resilience assessment of electricity-gas regional integrated energy system based on heterogeneous interdependent network[J]. Power System Technology, 2021, 45(7): 2811-2821.
[13] Zhang Huajun, Wang Peng, Yao Shuhan, et al. Resilience assessment of interdependent energy systems under hurricanes[J]. IEEE Transactions on Power Systems, 2020, 35(5): 3682-3694.
[14] 张亚超, 易杨, 胡志鹏, 等. 基于分布鲁棒优化的电-气综合能源系统弹性提升策略[J]. 电力系统自动化, 2021, 45(13): 76-84.
Zhang Yachao, Yi Yang, Hu Zhipeng, et al. Resilience enhancement strategy of electricity-gas integrated energy system based on distributionally robust optimization[J]. Automation of Electric Power Systems, 2021, 45(13): 76-84.
[15] 陈厚合, 丛前, 姜涛, 等. 多能协同的配电网供电恢复策略[J]. 电工技术学报, 2022, 37(3): 610-622, 685.
Chen Houhe, Cong Qian, Jiang Tao, et al. Distribution systems restoration with multi-energy synergy[J]. Transactions of China Electrotechnical Society, 2022, 37(3): 610-622, 685.
[16] Li Jiaxu, Xu Yin, Wang Ying, et al. Resilience-motivated distribution system restoration considering electricity-water-gas interdependency[J]. IEEE Transactions on Smart Grid, 2021, 12(6): 4799-4812.
[17] 许寅, 和敬涵, 王颖, 等. 韧性背景下的配网故障恢复研究综述及展望[J]. 电工技术学报, 2019, 34(16): 3416-3429.
Xu Yin, He Jinghan, Wang Ying, et al. A review on distribution system restoration for resilience enhancement[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3416-3429.
[18] 徐玉琴, 方楠. 基于分段线性化与改进二阶锥松弛的电-气互联系统多目标优化调度[J]. 电工技术学报, 2022, 37(11): 2800-2812.
Xu Yuqin, Fang Nan. Multi objective optimal scheduling of integrated electricity-gas system based on piecewise linearization and improved second order cone relaxation[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2800-2812.
[19] Correa-Posada C M, Sánchez-Martín P. Integrated power and natural gas model for energy adequacy in short-term operation[J]. IEEE Transactions on Power Systems, 2015, 30(6): 3347-3355.
[20] Gu Wei, Wang Jun, Lu Shuai, et al. Optimal operation for integrated energy system considering thermal inertia of district heating network and buildings[J]. Applied Energy, 2017, 199: 234-246.
[21] 张亚超, 郑峰, 舒胜文, 等. 考虑多重不确定性的电-气-交通网络耦合系统数据驱动鲁棒优化调度[J]. 中国电机工程学报, 2021, 41(13): 4450-4462.
Zhang Yachao, Zheng Feng, Shu Shengwen, et al. A data-driven robust optimization scheduling of coupled electricity-gas-transportation systems considering multiple uncertainties[J]. Proceedings of the CSEE, 2021, 41(13): 4450-4462.
[22] 张津珲, 王旭, 蒋传文, 等. 计及交通流量不确定性的多网耦合综合能源系统优化调度方法[J]. 电网技术, 2019, 43(9): 3081-3093.
Zhang Jinhui, Wang Xu, Jiang Chuanwen, et al. Optimal scheduling method of multi-network regional integrated energy system based on traffic flow uncertainty[J]. Power System Technology, 2019, 43(9): 3081-3093.
[23] Wang Xu, Shahidehpour M, Jiang Chuanwen, et al. Resilience enhancement strategies for power distribution network coupled with urban transportation system[J]. IEEE Transactions on Smart Grid, 2019, 10(4): 4068-4079.
[24] 麻秀范, 丁宁, 李龙. 配电网重构中网络辐射形与连通性的判断[J]. 电工技术学报, 2014, 29(8): 289-293.
Ma Xiufan, Ding Ning, Li Long. Judging radial and connectivity of network in distribution networks reconfiguration[J]. Transactions of China Electrotechnical Society, 2014, 29(8): 289-293.
[25] Ma Shanshan, Chen Bokan, Wang Zhaoyu. Resilience enhancement strategy for distribution systems under extreme weather events[J]. IEEE Transactions on Smart Grid, 2018, 9(2): 1442-1451.
Abstract With the rapid changes in the global environment, high-impact and low-probability (HILP) events, represented by natural disasters, have attracted widespread attention. In the face of HILP events, the urban energy system (UES) may suffer more significant losses due to the complex interdependencies between the energy subsystems. Due to the geographical location of the access nodes of the coupling elements, the effects of extreme events on the subsystems may not be simultaneous or of equal severity. As a result, there may be "time differences" and "spatial differences" in the impact of extreme events between subsystems. With this characteristic, the interdependence of the subsystems in the UES can have a “positive” and “negative” impact on system performance. On the one hand, the effects of inadequate power supply propagate through the coupling elements to the other subsystems, resulting in a degradation of their performance. The degradation of the performance of each subsystem will in turn lead to a further undersupply of the urban distribution network through the coupling elements, exacerbating the deterioration of the UES performance. On the other hand, when one form of energy supply is lost, other forms of energy can be substituted and complemented by energy conversion equipment, supporting the performance of the UES.
To address this issue, this paper proposes a resilience assessment and enhancement method for UESs that considers the interdependence of electricity-gas-heat-transport. Firstly, the multidimensional resilience assessment metrics that include both holistic and targeted perspectives are proposed for the whole process of extreme events. Then, the models of electricity, gas, heat and transport subsystems and coupling elements are established. The resilience assessment assesses the resilience of the UES in 2 areas and 7 dimensions. It includes both an overall grasp of UES resilience (performance maintenance, resistance, responsiveness, resilience) and a targeted assessment of system performance of particular concern (island connectivity, number of islands covered by power supply, critical load maintenance time). In terms of resilience enhancement, this paper aims to minimise the sum of weighted electrical, gas and thermal load losses and develop a system-level co-optimisation model. The resilience enhancement of the UES is achieved using power generator scheduling, maintenance staff scheduling, topology reconfiguration, and building thermal inertia. Due to the reliance on the traffic network in the resilience enhancement measures taken, the transport network subsystem is considered in this paper to establish a model for mobile emergency generators routing and repair crews dispatching. Finally, case studies are analysed in a 92-node integrated electricity-gas-heat-transport system.
The following conclusions can be drawn from the simulation analysis: (1) A comprehensive study of UES resilience assessment and enhancement can consider the correlation between each resilience enhancement measure and each resilience assessment metric, which is conducive to decision-makers to avoid risks better and take advantage of multi-energy integration to achieve system resilience enhancement. (2) The proposed resilience assessment index assesses the system performance at different stages from two perspectives: holistic and targeted. The multidimensional resilience assessment metrics provide a comprehensive picture of system performance in terms of its characteristics and topological features, allowing more targeted solutions and countermeasures to be developed. (3) The proposed resilience enhancement method achieves effective coordination and synergistic optimisation of various subsystems and measures; enhances the resilience of the UES to extreme events; improves the coverage of energy supply; and facilitates the rapid recovery of the UES after HILP events.
Keywords:Urban energy system, resilience, assessment, enhancement, interdependency
陶 然 男,1995年生,博士研究生,研究方向为电力系统韧性、电力系统分析与控制、新能源发电与智能电网。E-mail:ta0ran@163.com
赵冬梅 女,1965年生,教授,博士生导师,研究方向为电力系统分析与控制、新能源发电与智能电网。E-mail:zhao-dm@ncepu.edu.cn(通信作者)
中图分类号:TM73
DOI:10.19595/j.cnki.1000-6753.tces.221353
收稿日期2022-08-03
改稿日期2022-10-09
(编辑 赫 蕾)