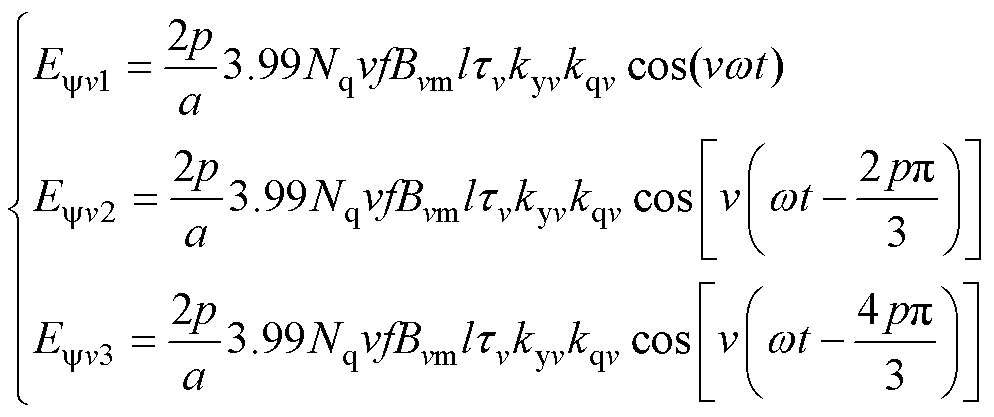（1）
摘要 抽水蓄能机组作为关键电气设备，其运行连续性与可靠性对构建新型电力系统意义重大。针对抽水蓄能机组励磁绕组匝间短路故障的状态监测易受动/静偏心及电枢反应影响，早期故障特征难以有效辨识的问题，该文提出一种基于环流时频图谱的励磁绕组匝间短路故障诊断方法。首先，根据抽水蓄能机组的结构特点及电磁感应关系，推导了动/静偏心及静偏心复合励磁绕组匝间短路状态下的同相多支路环流公式，得到了各状态下的环流特征谐波；其次，搭建了发电容量为334 MV·A的抽水蓄能机组二维有限元仿真模型，计算了动/静偏心及不同匝间短路程度下的同相分支环流大小，绘制了相应的时域、频域及时频图谱，通过对比实验验证了环流时频图谱可从时间、频率角度全面解析故障特征，有效区分偏心、电枢反应干扰与匝间短路故障；最后，基于凸极同步发电机模拟实验平台，模拟了不同故障程度的匝间短路运行状态，采集了同相支路电流数据用于环流时频图谱分析，实验结果证明了该方法可有效排除静偏心及电枢反应干扰，并以包含运行时间、特征频率及信号强度的三维图谱信息直观地展示机组的运行状态。
关键词：抽水蓄能机组 励磁绕组 匝间短路 环流时频图谱
随着水电开发程度的不断扩大，抽水蓄能机组也日趋向高水头、高效率和大容量发展。由于抽水蓄能机组起停迅速、负荷调整快速方便，在电网中承担了大量的调峰、调频、调压和事故备用的任务，因此对设备运行状态切换的要求也愈加频繁，导致机组发生故障的概率大为提高[1-3]。为了有效提升抽水蓄能机组安全运行水平，在线监测技术的研究与应用至关重要，其对实现机组故障的准确分析与及时预测，使机组检修工作从计划性检修转向状态检修具有重大推动作用[4-7]。
统计表明，励磁绕组匝间短路故障是抽水蓄能机组实际运行中出现频率较高的一类电气故障[8-9]，国内山东泰山抽水蓄能电站及福建仙游抽水蓄能电站均发生过不同程度的磁极短路故障。分析故障发生原因，是由于抽水蓄能机组（发电电动机）运行过程中受不平衡电磁力、散热不良、匝间局部放电及外界机械应力等多重因素影响，致使励磁绕组匝间绝缘劣化[10]。严重时会引起机组剧烈振动甚至横差保护动作，致使机组停运[11]。因此，如何快速准确地提取匝间短路早期微弱故障特征，并及时组织状态检修，对预防事故发生、提高机组运行的安全性与可靠性具有重要意义[12-15]。
目前，抽水蓄能机组励磁绕组匝间短路故障诊断主要以离线检测方式为主，常用检测方法主要包括直流电阻比较法[16]、交流阻抗和功率损耗法[17]、交直流分压电压法[18]等。离线检测方法需对各磁极绕组进行逐一测试，检测过程耗时较长，增加了运检人员的工作难度。鉴于离线检测方法存在一定弊端，近年来国内外学者对励磁绕组匝间短路在线诊断方法进行了深入研究。孙宇光团队提出了新型探测线圈检测法，通过将探测线圈进行特殊布置及联接，用于检测气隙磁场故障谐波的感应电压，根据感应电压谐波次数的不同，实现同步发电机励磁绕组匝间短路故障的有效识别[19]。武玉才团队提出了穿心螺杆检测法，并搭建了550 MW水轮发电机仿真模型，计算了匝间短路故障前后穿心螺杆的感应电压，根据感应电压变化规律，诊断水轮发电机励磁绕组匝间短路故障[20]。R. Romary团队提出了漏磁与振动综合检测法，通过采集发电机漏磁信号以及机壳加速度信号，分析漏磁及振动频谱中的敏感分量，实现对水轮发电机组励磁绕组匝间短路的状态监测[21]。A. Nysveen团队提出了杂散磁通检测法，通过在定子铁轭处安装探测线圈，用以采集水轮发电机外部的杂散磁通数据，并结合时频分析法对有限元仿真和实验所得数据进行挖掘提取，实验结果验证了该方法可有效辨识匝间短路故障[22]。郝亮亮团队提出了不平衡电流有效值检测法，基于对水轮发电机励磁绕组匝间短路环流特征的分析，采用移相叠加法最大限度地提取环流分数次谐波有效值，并将其应用于现场故障监测，奠定了环流检测法的研究基础[23]。
以上在线故障诊断方法的提出为励磁绕组匝间短路状态监测提供了新思路，但考虑到现场运行机组受水力、机械、电气及其他因素影响，早期故障特征易被噪声所掩盖，开发一种通用、高灵敏度且抗干扰能力强的励磁绕组匝间短路故障监测方法成为当下研究的热点。本文在综合考虑机组实际运行过程中存在动/静偏心及电枢反应等干扰的基础上，推导了动/静偏心环流公式及静偏心复合励磁绕组匝间短路环流公式，并提出了一种基于环流时频图谱的智能诊断方法。
鉴于动/静偏心程度的变化会引起环流时域幅值的改变，通过设置时域阈值检测匝间短路故障难免会引入动/静偏心干扰；而电枢反应及动偏心也会引起特征分数次谐波的出现，因此通过频谱分析特征谐波的方法难以有效辨识匝间短路故障；环流时频图谱检测法是在综合考虑现场检测实时性与高效性的基础上，将连续小波变换时频分析方法用于计算抽水蓄能机组同相支路环流特征信号，绘制基于运行时间、特征频率及信号强度的三维图谱，并以信号强度以及信号强度差值能量比为判据用于检测匝间短路故障，该方法克服了传统环流检测法[23-26]单一从时域或频域进行分析而无法有效辨识早期微弱故障的缺点，为现场实现微弱匝间短路在线监测提供了可能。本文在有限元仿真模型、动模机组实验平台均模拟了不同程度的匝间短路故障，并采集了各状态下的不平衡电流数据用于时频分析，实验结果证明了环流时频图谱可直观反映设备的运行状态，通过计算时频矩阵的信号强度差值能量比可进一步量化故障程度，防止故障误报警，为现场运检人员开展状态检修工作提供指导。
考虑到实际运行机组往往存在电枢反应、动/静偏心影响，本文对单一励磁绕组匝间短路、动/静偏心、静偏心复合匝间短路状态下的环流特征公式进行了推导。
本文以电枢绕组同相三条支路为例，对支路感应电动势进行分析，三条支路空间机械角相差2p/3，则空间电角度相差2pp/3，由此得各支路感应电动势表达式[24]分别为
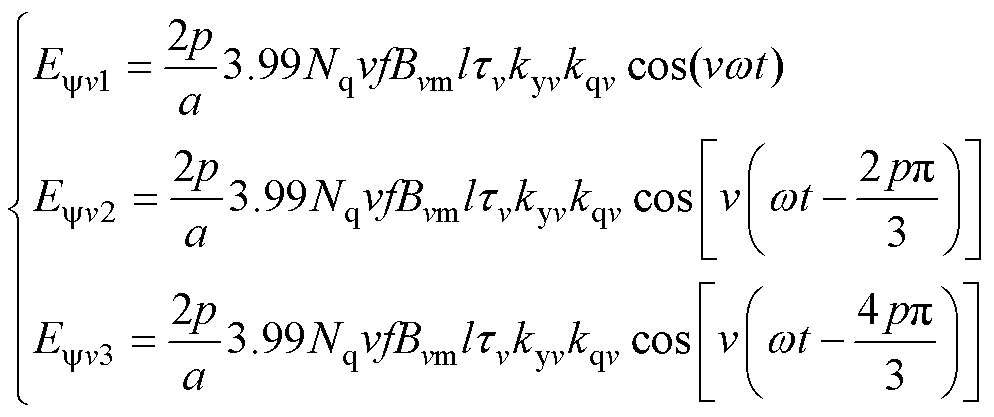（1）
式中，p为极对数；a为同相绕组支路数；Nq为一个线圈组所包含的线圈匝数；f为频率；Bvm为气隙磁通密度v次谐波的最大值；l为定子绕组有效长度；tv为v次谐波对应极距；kyv为短距系数；kqv为绕组分布系数。
当发电电动机发生匝间短路故障时，其磁动势不仅包含基波及奇数次谐波，而且包含分数次谐波，即v=1/p, 2/p,…, n/p，此时定子绕组同相三条支路感应电动势不再相等，即Eyv1≠Eyv2≠Eyv3。
发电电动机电枢绕组某相支路等效电路（支路电阻可忽略不计）如图1所示。
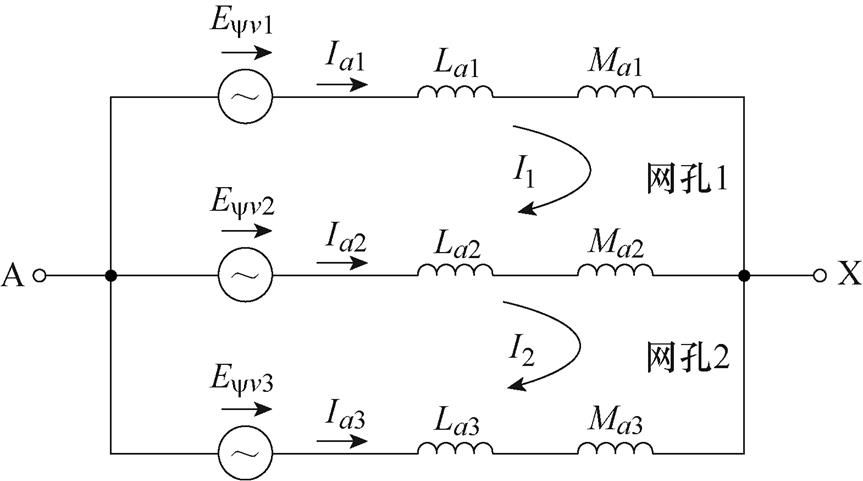
图1 电枢绕组同相支路等效电路
Fig.1 Equivalent circuit diagram of armature winding in-phase branch circuit
采用网孔电流法和基尔霍夫电压定律（Kirchhoff's Voltage Law, KVL）对其进行分析，可得表达式为
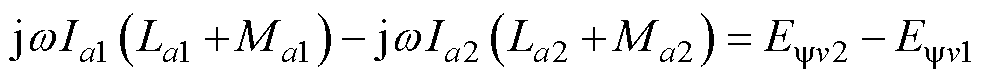（2）
由于同相支路对称，自感La1=La2，支路互感Ma1=Ma2，可将式（2）化简为
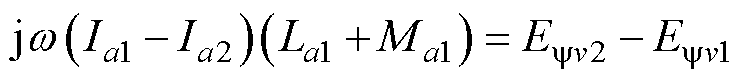（3）
由此可知，当发电电动机处于正常运行状态时（即Eyv1=Eyv2），同相支路电流Ia1=Ia2，即不会出现支路环流现象（负载工况下，受电枢反应影响，使得磁场不对称，由此也会产生支路环流）；当发电电动机处于匝间短路运行状态时（即Eyv1≠Eyv2），同相支路电流Ia1≠Ia2，此时会出现支路环流现象，且只包含k/p（k=1, 2,…, n，且k≠np）分数次谐波。
考虑到实际发电电动机由于制作工艺问题，运行过程中往往存在静偏心影响。同时机组运行过程在受到电磁力、热应力等作用时，发电电动机转子表面易发生变形，致使定转子间径向气隙的最小位置会随着转子旋转而发生改变，机组呈动偏心运行。鉴于上述因素，本文对抽水蓄能机组动/静偏心状态下的环流特征进行分析，以有效滤除其对匝间短路在线监测的影响。
静偏心和动偏心状态下的气隙条件如图2所示，最小气隙沿x轴方向设置。
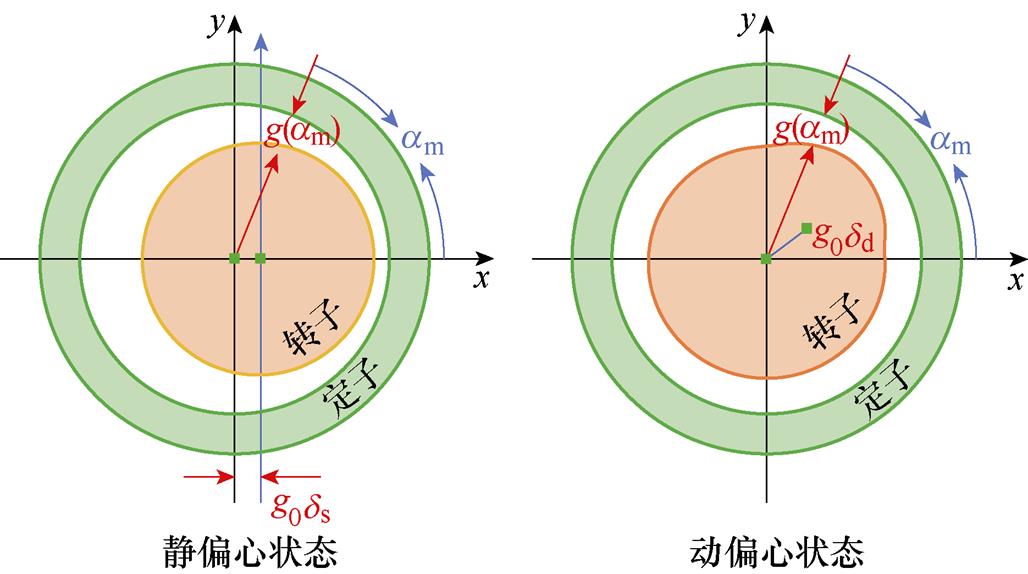
图2 发电电动机动/静偏心状态的气隙示意图
Fig.2 Schematic diagram of the air gap between the static eccentric and dynamic eccentric states of generator-motor
根据图2所示，发电电动机径向气隙长度可以表示[15]为
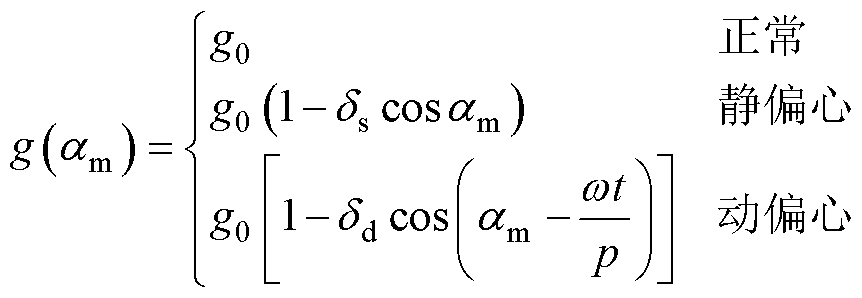（4）
式中，g0为平均气隙长度；am为定子圆周机械角；ds为静态偏心率；dd为动态偏心率。
由于气隙较小，对径向气隙长度的倒数进行幂级数展开，可忽略高阶分量，得到单位磁导率为
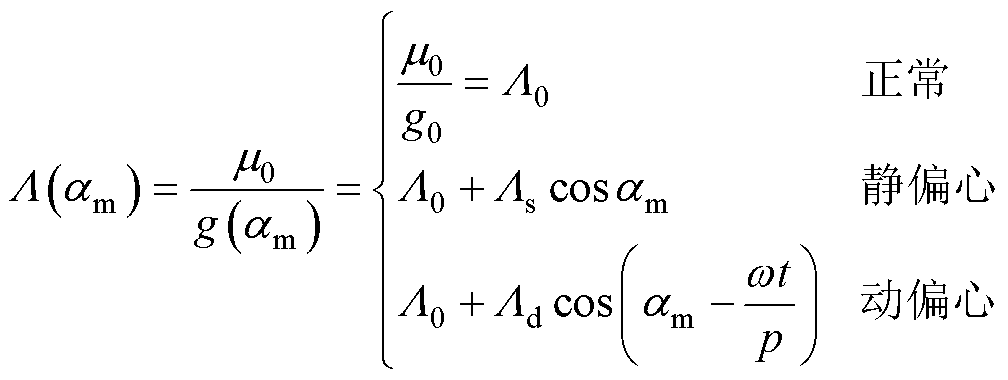（5）
式中，m0为空气磁导率；L0为气隙磁导常数分量；Ls为静偏心磁导分量；Ld为动偏心磁导分量。
综合以上分析，推导静偏心环流公式为
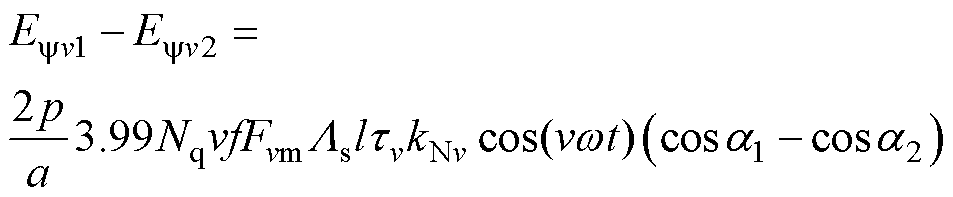（6）
动偏心环流公式为
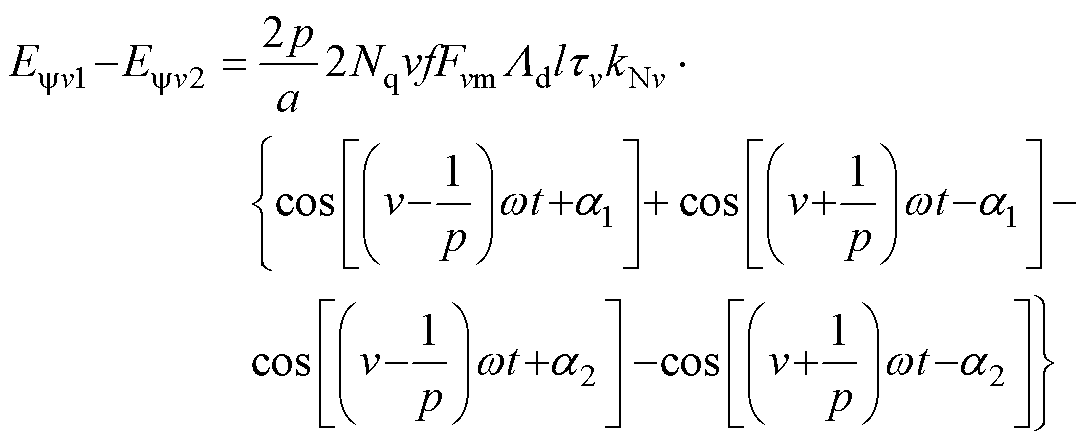（7）
式中，kNv为正常状态下v次谐波磁动势的绕组因数；Fvm（v=1, 3, 5,…, n）为正常状态下磁动势的最大幅值；a1、a2均为电角度。根据环流公式可知，静偏心环流主要包含基波及奇数次谐波，且以基波为主；动偏心环流特征中只包含v-1/p和v+1/p次谐波。
现场抽水蓄能机组运行过程中往往伴有静偏心干扰，因此本文对抽水蓄能机组的静偏心复合匝间短路的环流特征进行了分析，防止由于静偏心问题引起匝间短路的误判，给实际运行造成不良影响。综合1.1节与1.2节分析，推导静偏心复合故障环流公式为
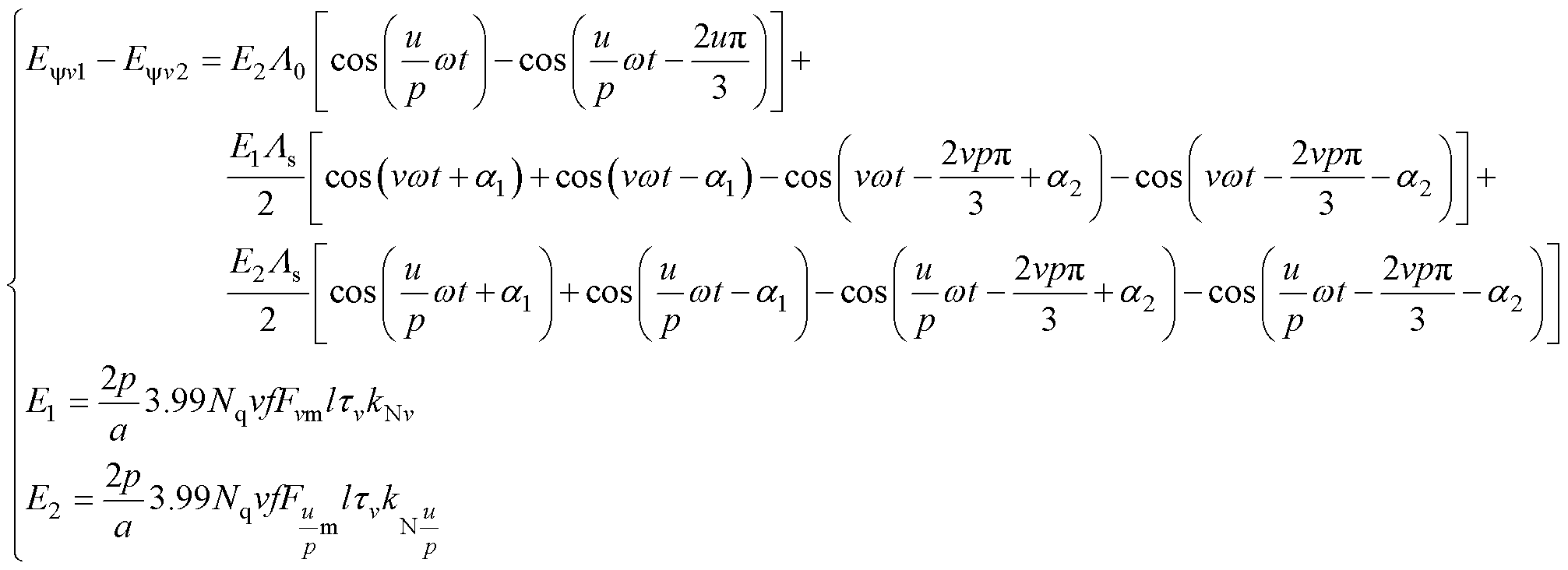（8）
式中，E1、E2分别为支路1、支路2的感应电动势幅值；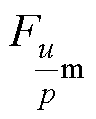
（u=1, 2,…, n且u≠np）为匝间短路状态下磁动势的最大值。根据环流公式可知，静偏心复合故障环流特征主要包含v次及u/p次谐波。
由于现场所采集环流信号易受动/静偏心、电枢反应等因素影响，其中机组动/静偏心程度的变化会引起环流时域幅值的改变，采用环流时域阈值检测法判别匝间短路故障难免会引入动/静偏心干扰；而电枢反应及动偏心会引起分数次特征谐波的出现，因此单一频谱分析方法亦难以有效提取匝间短路故障特征。鉴于所采集环流信号的特殊性，本文在综合考虑现场检测实时性与高效性基础上，提出了适用于在线监测的环流时频图谱检测法，具体实现流程如图3所示。
环流时频图谱检测法通过引入连续小波变 换[27]，可有效实现对待检环流信号的时频局部化分析，完成对分数次环流特征谐波信息的深度挖掘。该方法通过将小波母函数y(t)进行伸缩和平移，并与待检环流信号进行卷积积分运算，进而实现尺度域向频域的准确实时转换，从而有效捕捉不同频率信息在不同时刻的信号强度。对于动/静偏心干扰，时频图谱特征频次处信号强度分布与匝间短路有较大不同；而对于较为微弱的匝间短路，图谱信号强度变化较小，不易直接据此进行判断，因此本文提出信号强度差值能量比R算法，旨在进一步放大故障前后环流时频图谱信号强度变化，从而凸显微弱故障特征，其表达式为
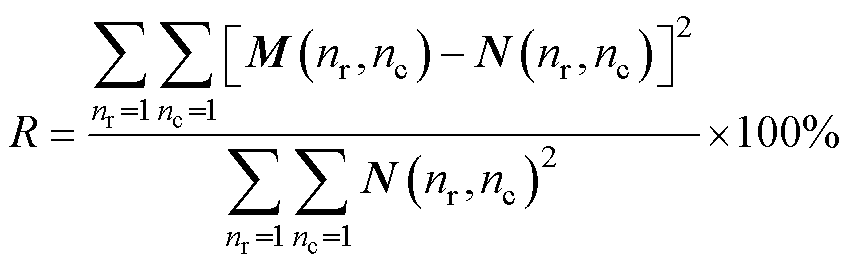（9）
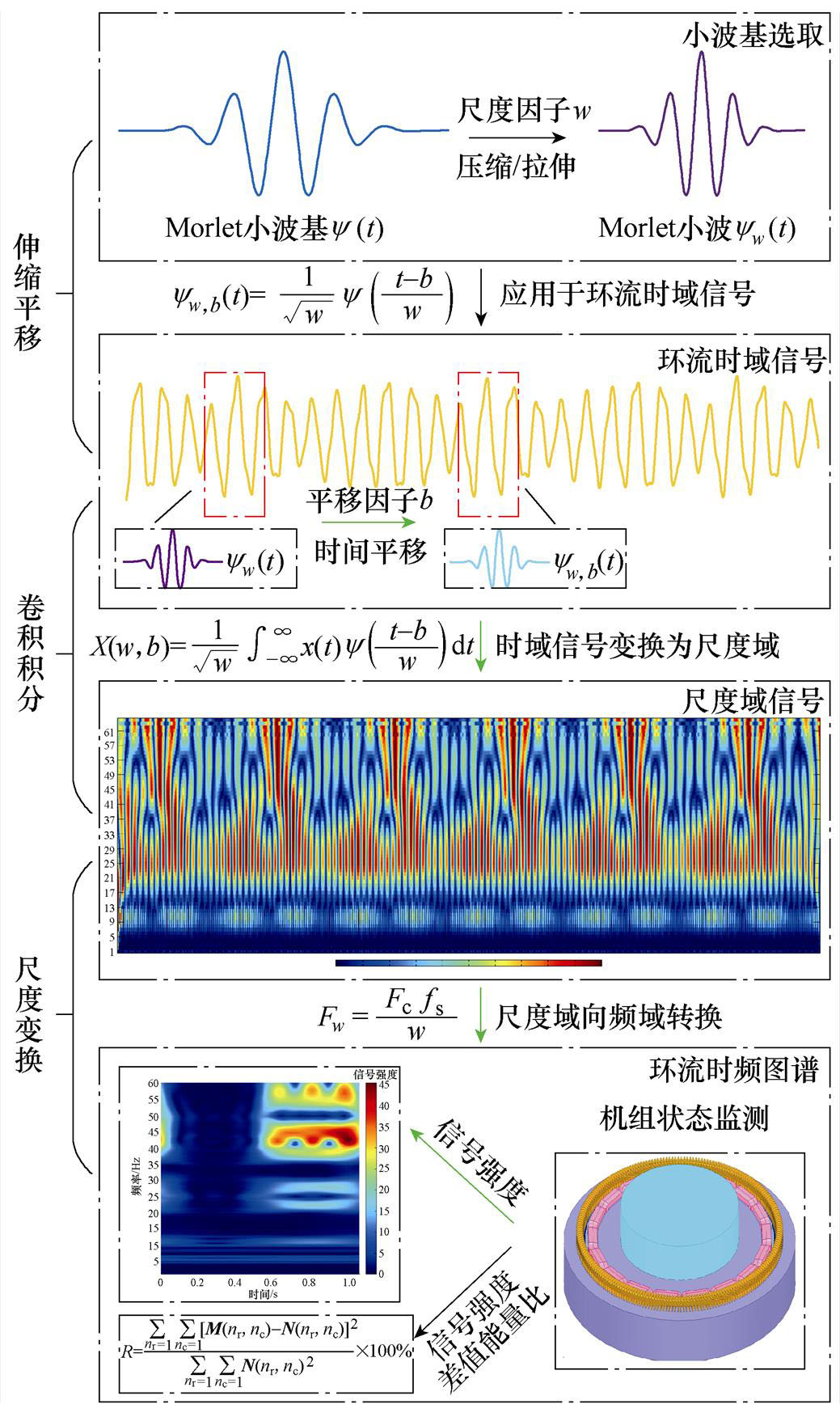
图3 环流时频图谱流程
Fig.3 Flow chart of circulation time-frequency map
式中，nr为时频矩阵行数；nc为时频矩阵列数；M为匝间短路状态下的时频矩阵；N为正常状态下的时频矩阵。由于环流信号采集受外界干扰影响较小，因此机组若运行于正常状态，其差值能量比应无限接近于0，而发生匝间短路后，其差值能量比应大于正常状态值，据此可实现早期微弱匝间短路故障诊断。
本文以国内某电机厂生产的抽水蓄能发电机（运行于国内某抽水蓄能电站）为例，参数见表1。
表1 发电电动机参数
Tab.1 Generator-motor parameters
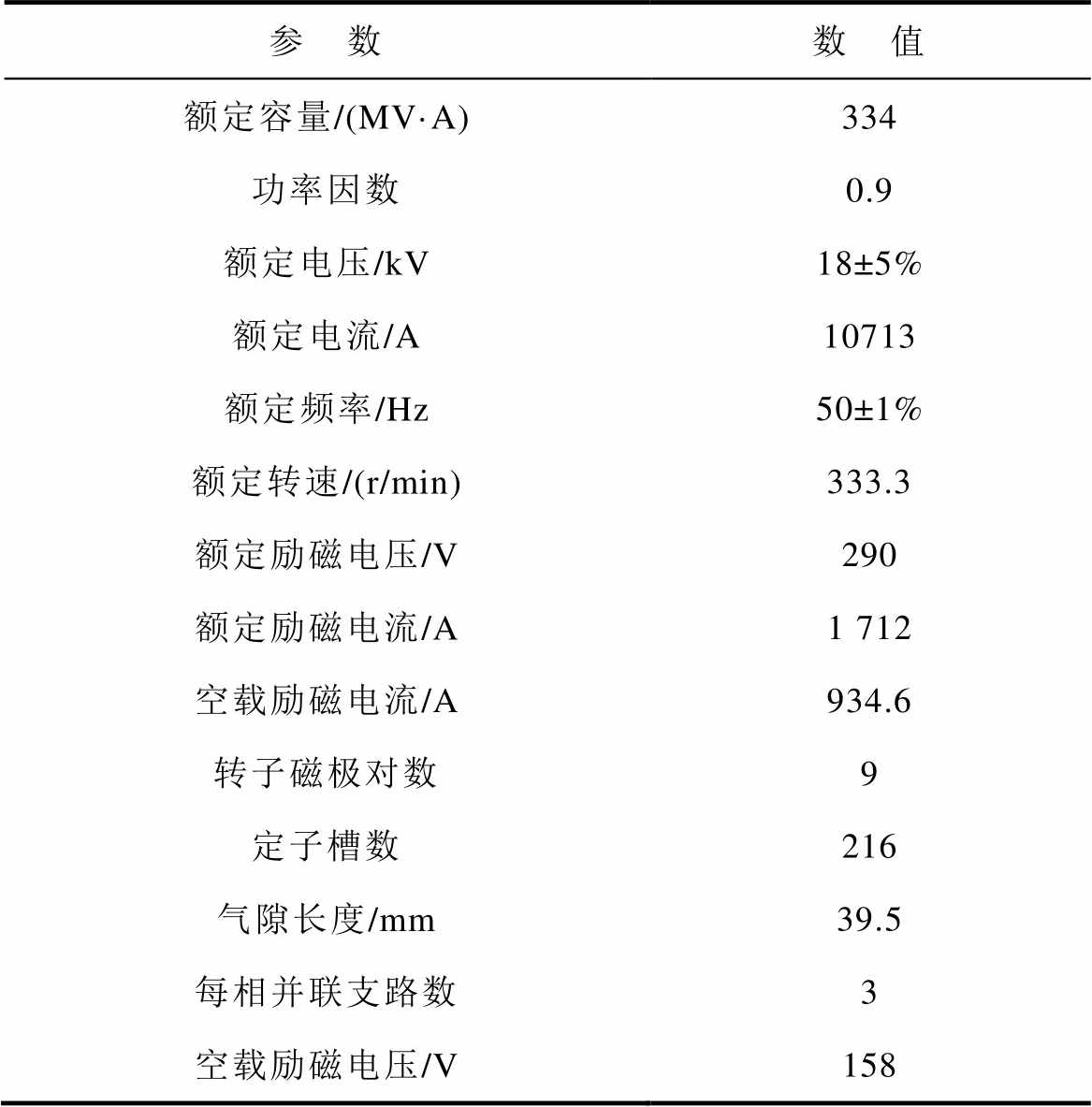
参 数数 值 额定容量/(MV·A)334 功率因数0.9 额定电压/kV18±5% 额定电流/A10713 额定频率/Hz50±1% 额定转速/(r/min)333.3 额定励磁电压/V290 额定励磁电流/A1 712 空载励磁电流/A934.6 转子磁极对数9 定子槽数216 气隙长度/mm39.5 每相并联支路数3 空载励磁电压/V158
采用Ansys Electronics软件搭建发电电动机二维有限元模型，首先，为了模拟现场真实运行，设置某一磁极初始运行于正常状态，在某一时刻发生励磁绕组匝间短路故障，故障程度分别设置为短路1匝、短路2匝（分别对应图4中红色、绿色线匝，且将短路时刻设为0.54 s）；其次，分别模拟机组运行过程中所存在的动、静偏心现象，并设置机组运行所允许的最大偏心程度10%（受仿真条件限制，无法模拟偏心过渡状态）；最后，进行有限元网格剖分设置（剖分网格单元数为38 053），用于二维有限元模型的计算，二维有限元1/9模型剖分如图4所示。将Maxwell 2D与Simplorer进行场路耦合联合仿真，得正常运行和励磁绕组匝间短路状态下的磁力线分布如图5所示（受篇幅限制，仅展示空载工况下的磁力线分布）。
本文对单一励磁绕组匝间短路、单一动/静偏心以及静偏心复合匝间短路状态下所得环流信号进行时域、频域分析，以获取各运行状态下的基本特征。
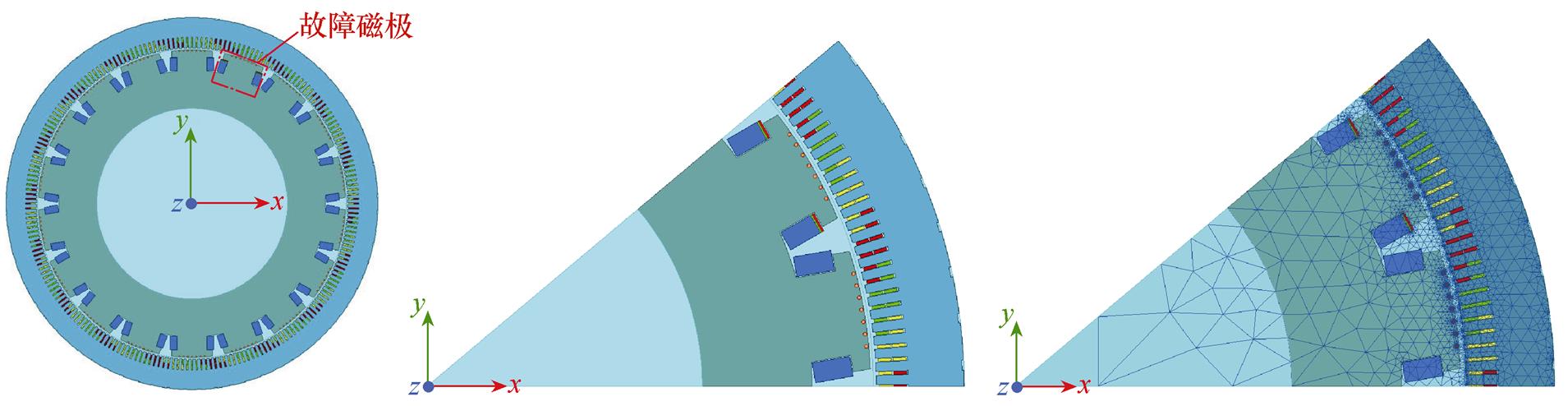
图4 发电电动机二维瞬态电磁场仿真模型
Fig.4 Two-dimensional transient electromagnetic field simulation model for the generator-motor
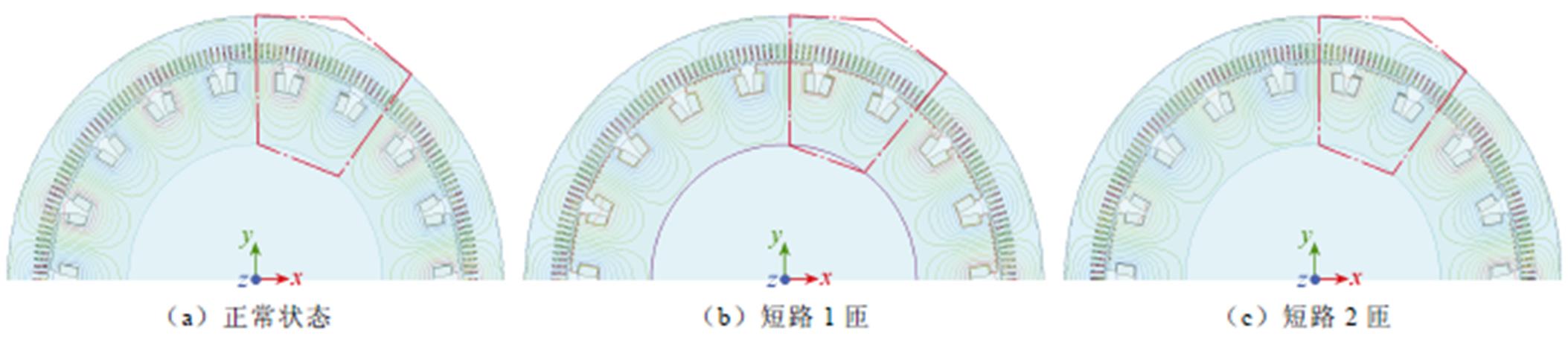
图5 发电电动机空载工况磁力线分布
Fig.5 Distribution of magnet lines in the no-load condition of the generator-motor
3.1.1 单一励磁绕组匝间短路及单一动/静偏心仿真分析
首先，对发电电动机空载运行工况进行仿真分析，分别设置转子某磁极绕组正常、短路1匝、短路2匝、10%动偏心、10%静偏心，其中正常与短路状态下的径向气隙磁通密度分布如图6a所示（动/静偏心状态径向气隙磁通密度见附录），电枢绕组同相支路环流时域谱如图6b所示。对环流时域信号进行傅里叶变换，得环流频谱如图6c所示。
其次，对发电电动机负载运行工况进行仿真分析，设置均与空载工况相同，得径向气隙磁通密度分布如图7a所示（动/静偏心状态径向气隙磁通密度见附录），负载工况环流时域谱如图7b所示，环流频谱如图7c所示。
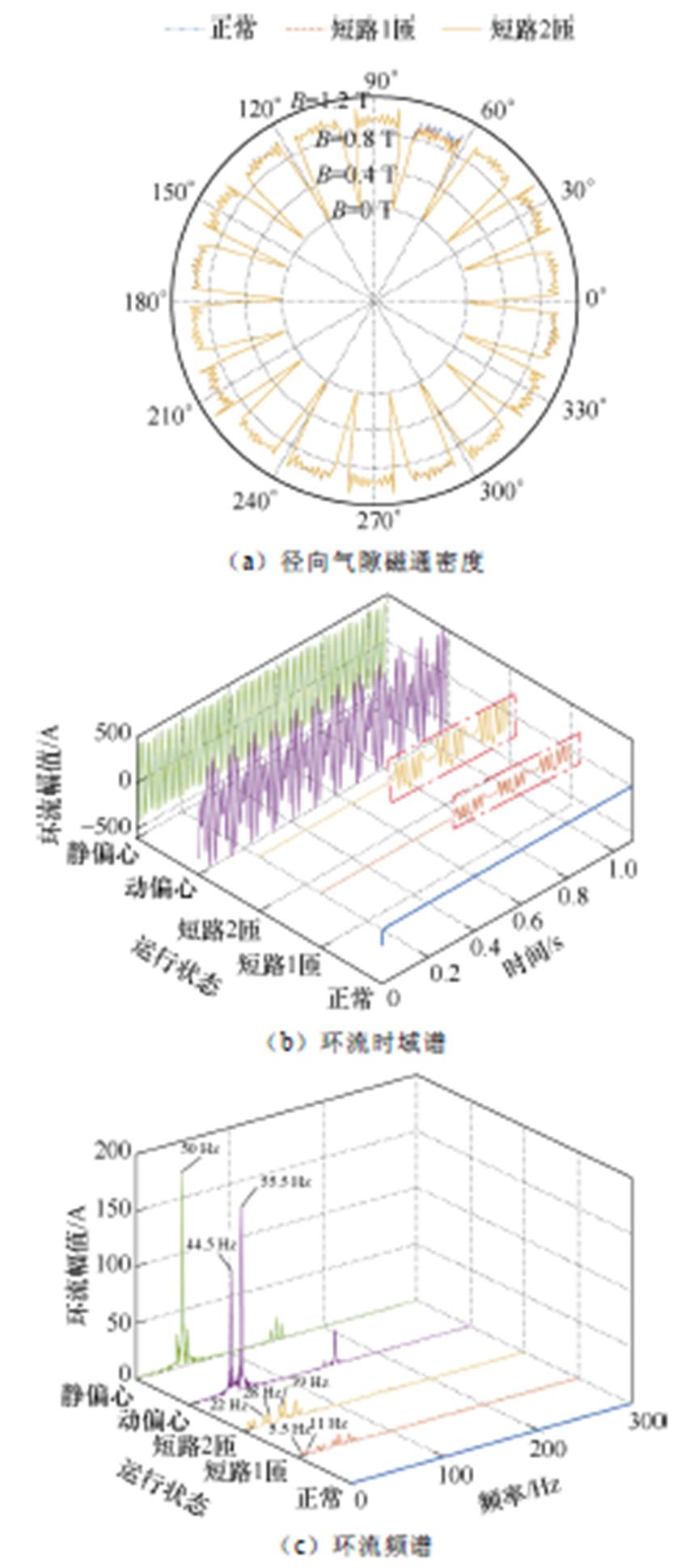
图6 空载工况电磁特征图谱（故障时刻t=0.54 s）
Fig.6 Electromagnetic characteristic spectrum for no-load operation (fault moment t=0.54 s)
由图6a和图7a可以看出，随着故障程度的增大，故障磁极的径向气隙磁通密度呈递减趋势，其中空载工况下的气隙磁通密度变化更为明显，负载工况下由于受电枢反应影响，故障磁极处的气隙磁通密度衰减更为微弱。通过观察气隙磁通密度的变化趋势，验证了所建有限元模型的正确性。
由图6b和图7b可以看出，空载工况下匝间短路故障会使电枢绕组同相支路出现环流，且其时域幅值随故障程度的增加而增大。负载工况下由于受电枢反应影响，正常状态同样会出现环流，且其时域幅值与短路1匝的幅值相差不大，难以判别是否发生匝间短路。同时机组实际运行中偏心程度大小亦会发生改变，动/静偏心程度变大（10%以内）皆会引起环流时域幅值增加，若简单通过设置时域阈值进行故障诊断，难免会引入动/静偏心干扰，造成励磁绕组匝间短路的误判。
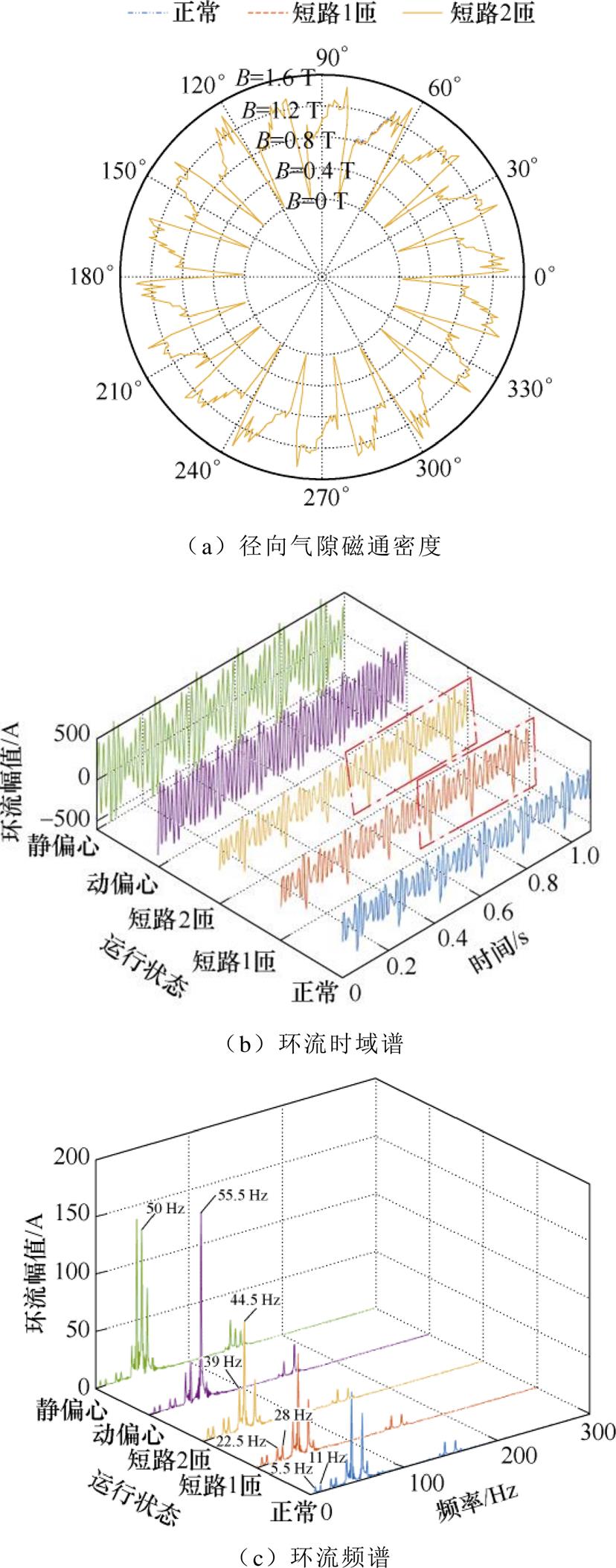
图7 负载工况电磁特征图谱（故障时刻t=0.54 s）
Fig.7 Electromagnetic characteristic spectrum for load operation (fault moment t=0.54 s)
由图6c和图7c可以看出，匝间短路频谱出现了明显的分数次谐波，且其谐波次数为k/9（k= 1, 2,…, n且k≠np）；静偏心频谱出现了基波及3次谐波，动偏心出现了8/9、10/9、17/9及19/9次谐波，由此验证了式（6）、式（7）推导的正确性。负载工况下，受电枢反应影响，正常状态、动偏心状态与匝间短路故障所出现的特征谐波次数均相同，对故障识别造成了干扰。因此，通过频谱图出现的分数次特征谐波进行故障诊断，容易造成故障误判。
3.1.2 静偏心复合励磁绕组匝间短路仿真分析
考虑到实际运行的抽水蓄能机组普遍存在静偏心，本文对静偏心复合励磁绕组匝间短路故障进行仿真分析。
首先，对发电电动机空载运行工况进行仿真分析，静偏心度设为10%，并分别与励磁绕组正常、短路1匝、短路2匝进行复合仿真计算，得径向气隙磁通密度分布如图8a所示，电枢绕组同相支路环流时域谱如图8b所示。对时域信号进行傅里叶分析，得到环流频谱图如图8c所示。
其次，对发电电动机负载运行工况进行仿真分析，偏心度及匝间短路故障程度设置均与空载工况一致，进行复合仿真计算，得静偏心复合匝间短路状态下的径向气隙磁通密度分布如图9a所示，环流时域谱如图9b所示，环流频谱如图9c所示。
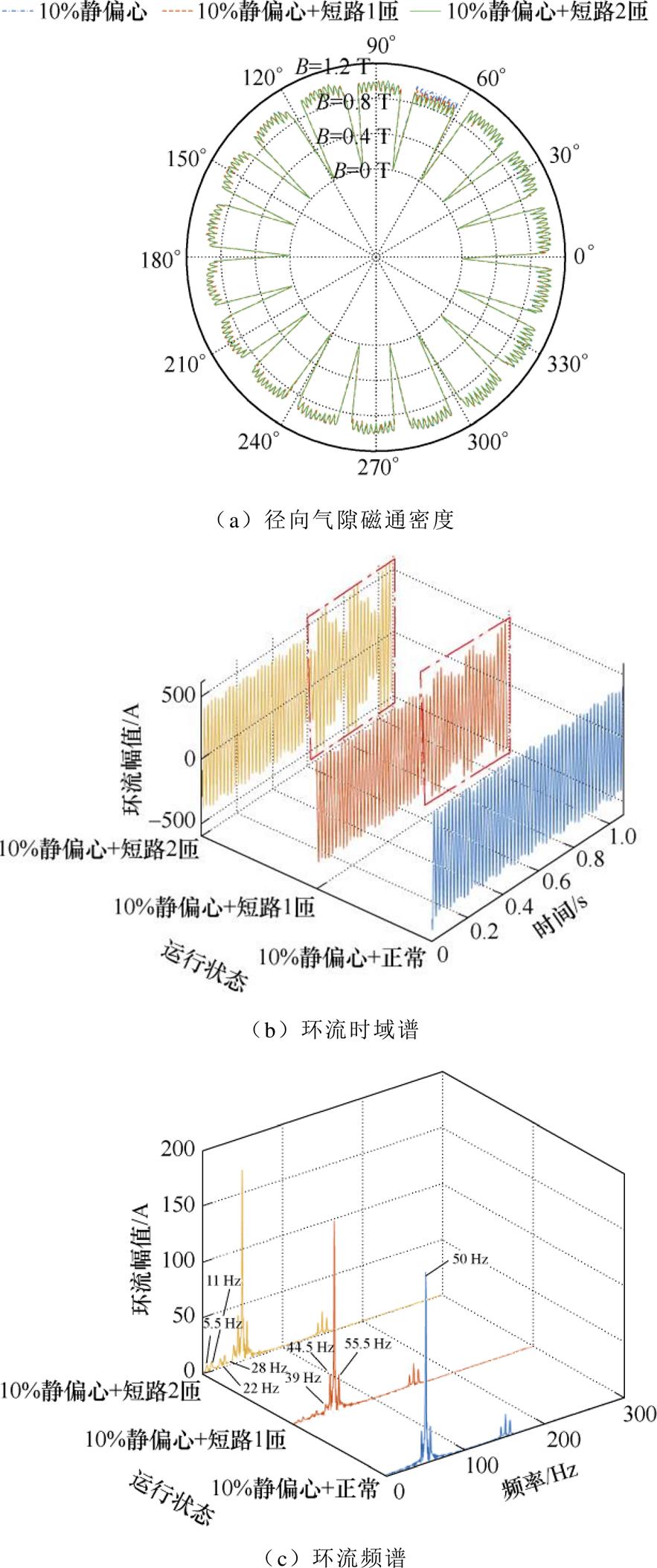
图8 静偏心复合匝间短路-空载工况电磁特征图谱（故障时刻t=0.54 s）
Fig.8 Static eccentricity composite inter-turn short circuit-electromagnetic characteristic spectrum under no load condition (moment of fault t=0.54 s)
由图8、图9可以看出，故障磁极的径向气隙磁通密度随故障程度的增大呈减小趋势，负载工况下由于受电枢反应影响，致使气隙磁通密度减小趋势不易观察。
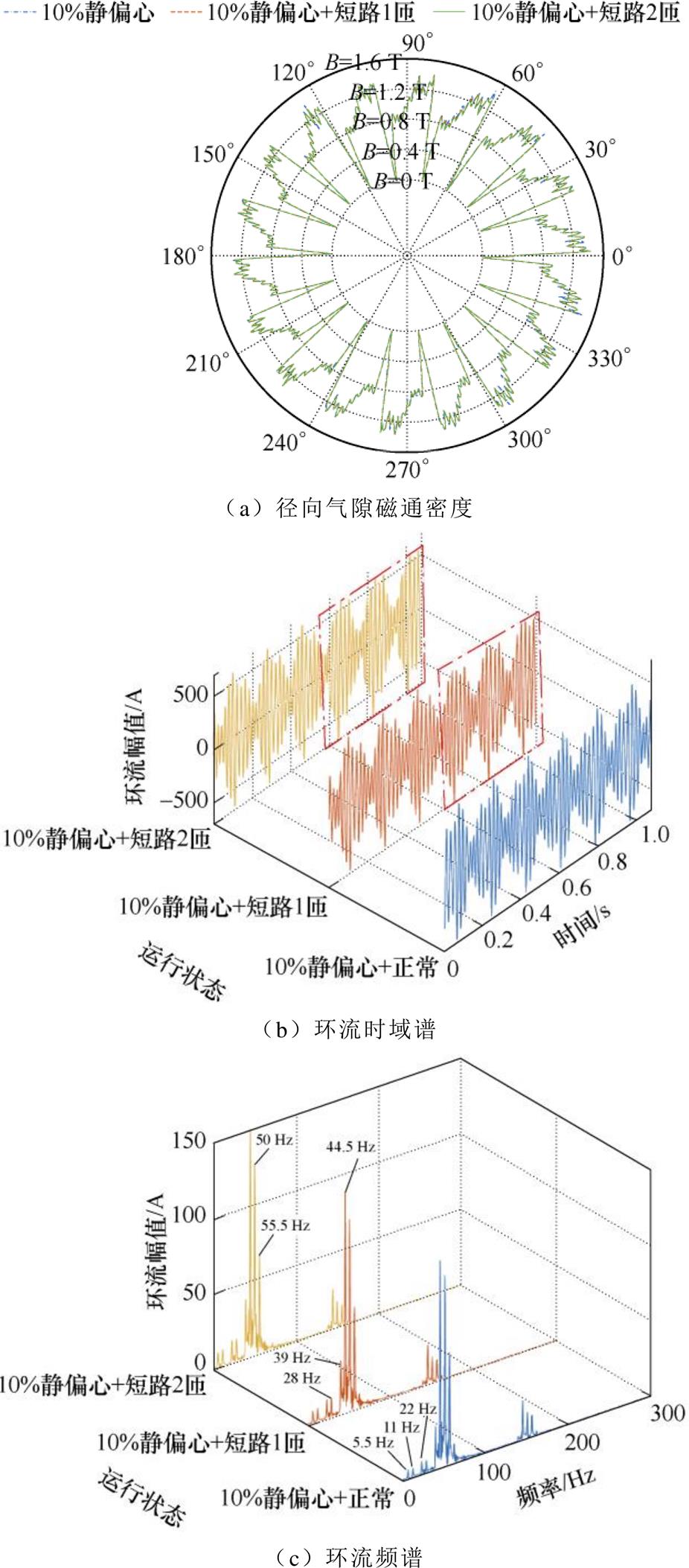
图9 静偏心复合匝间短路-负载工况电磁特征图谱（故障时刻t=0.54 s）
Fig.9 Static eccentricity composite inter-turn short circuit-electromagnetic characteristic spectrum under load condition (fault moment t=0.54 s)
当发电电动机处于静偏心复合正常运行状态时，受静偏心及电枢反应影响，空载/负载工况时域信号均出现了明显的环流，且其时域幅值均与短路1匝的时域幅值较为接近，因此通过时域信号难以准确判别匝间短路故障。
分析空载/负载工况环流频谱信息，均出现了明显的50 Hz基波及k/9（k=1, 2,…, n且k≠np）分数次谐波，验证了静偏心复合匝间短路环流公式推导的正确性。空载工况下，微弱的匝间短路特征谐波易被静偏心基波所掩盖。负载工况下，无论发电电动机处于正常状态还是匝间短路状态，其频谱均出现了分数次特征谐波，对励磁绕组匝间短路故障在线监测造成了干扰，因此通过频谱分析无法有效辨识故障。
为了提高故障诊断精度，实现抽水蓄能机组励磁绕组匝间短路的状态监测，本文将连续小波变换时频方法引入环流特征信号分析。考虑到Morlet小波具有适中的中心频率和窗宽，且其波形与待测环流信号具有较高的相似性，据此对正常与匝间短路状态下的环流信号进行卷积积分计算，并构建三维时频图谱，以期全面反映机组的运行状态。
3.2.1 单一励磁绕组匝间短路及单一动/静偏心-环流时频图谱分析
对发电电动机空载/负载工况下短路1匝、短路2匝、10%静偏心、10%动偏心的环流数据进行时频分析，构建各状态所对应的环流时频图谱。空载工况环流时频图谱如图10所示，负载工况环流时频图谱如图11所示。
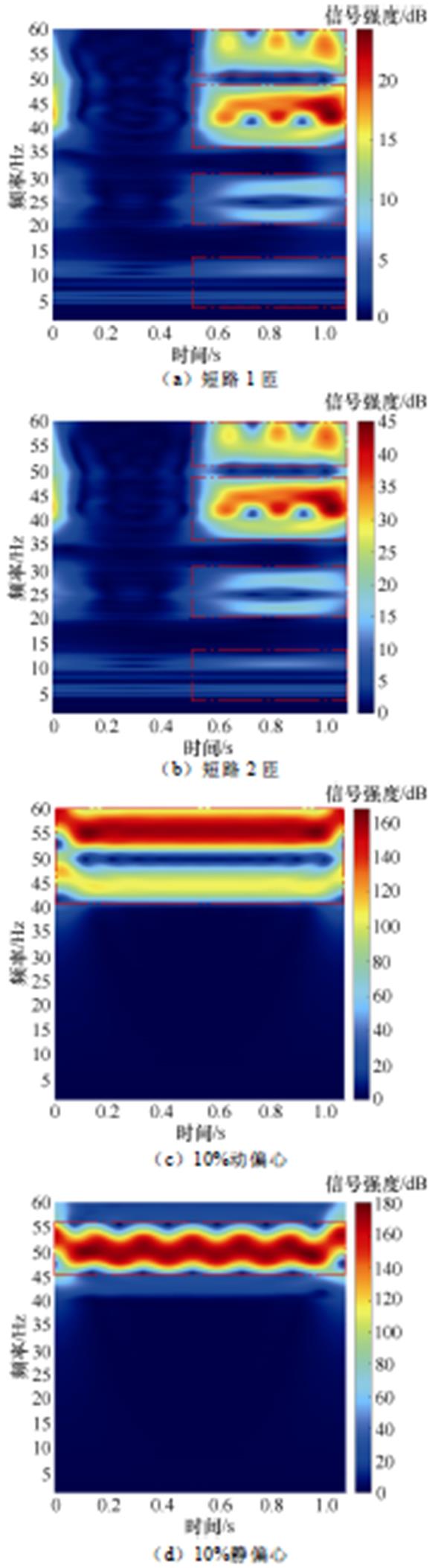
图10 空载工况环流时频图谱（故障时刻t=0.54 s）
Fig.10 Time-frequency maps of circulating current under no-load condition (fault moment t=0.54 s)
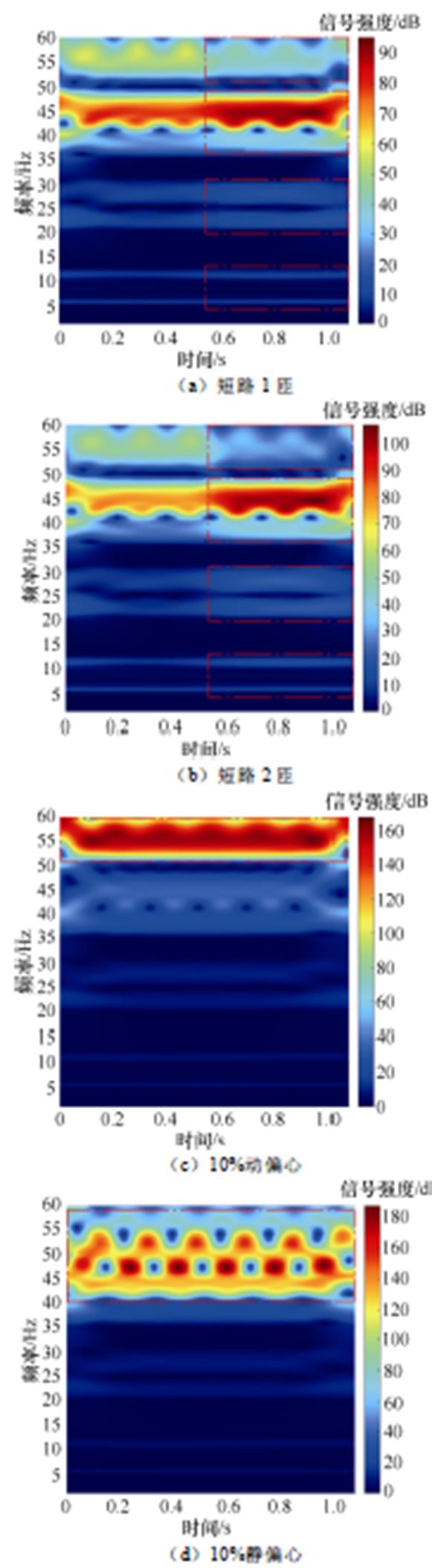
图11 负载工况环流时频图谱（故障时刻t=0.54 s）
Fig.11 Time-frequency maps of circulating current under load condition (fault moment t=0.54 s)
由图10、图11可以看出，当发电电动机发生励磁绕组匝间短路故障，通过环流时频图谱可以清晰定位故障发生的时刻，且故障特征频率处（5.5、11、22、28、39、44.5 Hz）的信号强度相较正常状态明显增强，图中所标记红框可清晰反映机组由正常状态过渡到匝间短路故障状态信号强度的变化。同时，与动/静偏心状态进行比较，可发现动偏心信号强度主要集中于55.5 Hz，静偏心主要集中于50 Hz，与匝间短路故障的特征频率信号强度具有明显区分度。为了防止故障误判，本文对信号强度差值能量比进行计算分析，其中空载匝间短路状态下的计算结果分别为7.13%、13.96%，负载匝间短路状态下的计算结果分别为6.66%、13.44%，均远大于0，可有效判别匝间短路故障。
3.2.2 静偏心复合匝间短路-环流时频图谱分析
对空载/负载工况下静偏心复合匝间短路的环流数据进行时频分析，构建静偏心复合短路1匝、静偏心复合短路2匝所对应的环流时频图谱。其中，空载工况环流时频图谱如图12所示，负载工况环流时频图谱如图13所示。
根据图12、图13所示，环流时频图谱以故障特征频率处信号强度的变化，清晰反映机组发生匝间短路故障后的过渡过程，点画线（红）框标记处可明显观察到发生匝间短路后的信号强度变化，为了防止故障误判，进一步计算信号强度差值能量比，其中空载匝间短路状态为3.94%、6.55%，负载匝间短路状态为8.28%、9.54%，据此可有效辨识匝间短路 故障。
综合以上仿真分析，本文提出的环流时频图谱检测方法可滤除动/静偏心、电枢反应干扰，有效提取励磁绕组匝间短路故障特征，为运行现场匝间短路检测提供了一种新的可实施方案。
图12 静偏心复合匝间短路-空载工况环流时频图谱
Fig.12 Static eccentricity composite inter-turn short circuit-time-frequency maps of circulating current under no-load
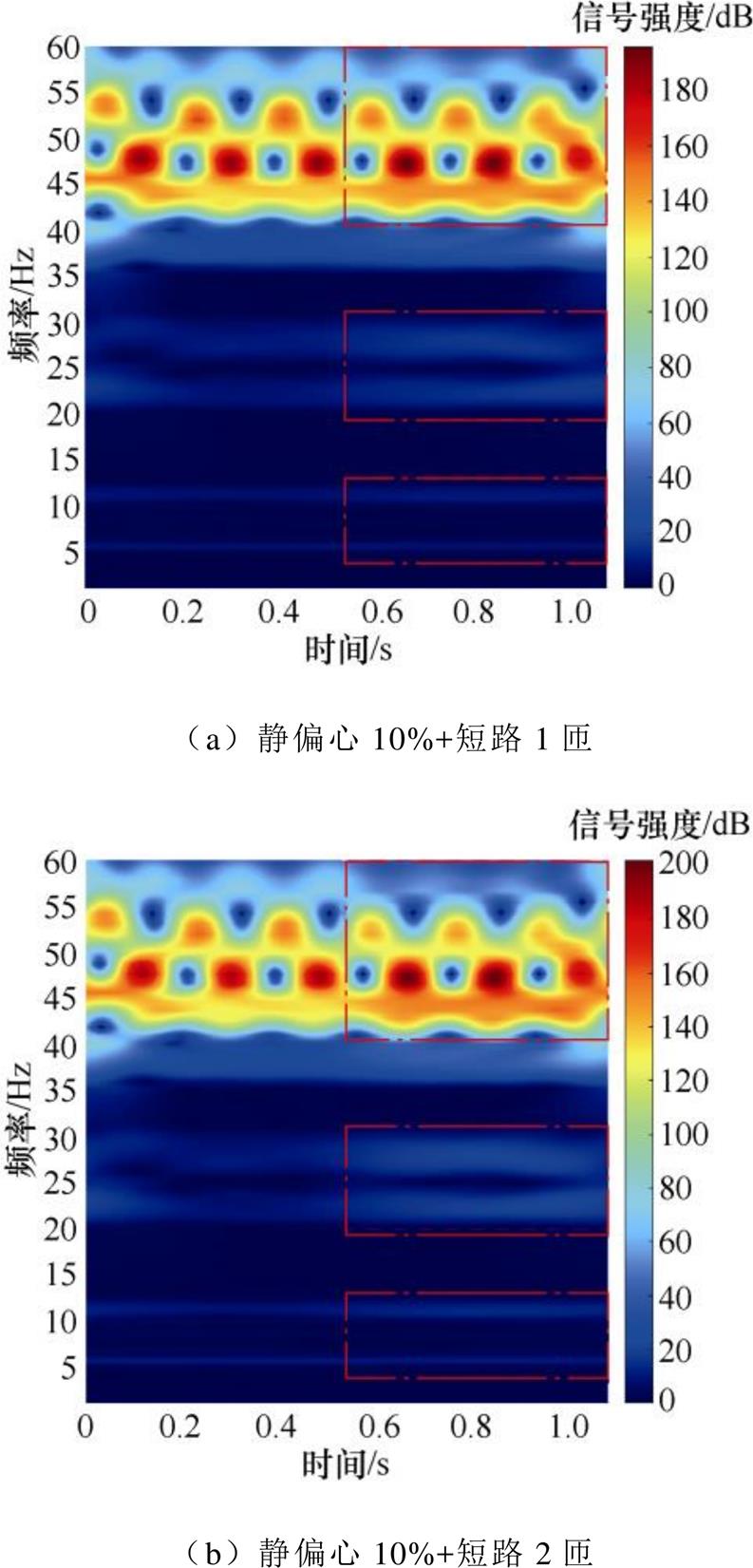
图13 静偏心复合匝间短路-负载工况环流时频图谱
Fig.13 Static eccentricity composite inter-turn short circuit-time-frequency maps of circulating current under load condition
本次实验采用电力系统动态模拟实验室一台型号为TZH-225-TH的凸极同步发电机来模拟抽水蓄能机组发电机状态，其参数见表2。
表2 TZH-225-TH同步发电机参数
Tab.2 TZH-225-TH synchronous generator parameters
参 数数 值 额定容量/(kV·A)12.5 额定电压/V400 径向气隙/mm1 定子内径/mm270 额定转速/(r/min)1 500 定子铁心长度/mm140 每相并联支路数2 节距9 额定励磁电流/A9 极对数2
采用高精度塞尺对转子气隙进行测量，其测量精度可达0.02 mm，测量结果显示，发电机转子气隙最小处为0.96 mm，气隙最大处为1.04 mm，由此可计算出该台机组存在4%的静偏心，具体测量如图14所示。受实验条件限制，未能模拟机组动偏心状态。
为了有效模拟不同故障程度的匝间短路，本次实验选择励磁绕组匝间短路故障程度为50%所对应抽头F1、F13，将两故障抽头间串接滑动变阻器、电流表及刀开关，其中滑动变阻器（48 W/7 A）调至最大阻值位，电流表调至5 A档位，刀开关初始为断开状态。缓慢增大励磁，使发电机端电压上升至额定电压，并记录此时的励磁电流平均值If。
根据故障程度公式计算滑动变阻器分流大小，其表达式为
（10）
式中，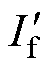
为流过滑动变阻器的电流。缓慢调节滑动变阻器，通过改变其分流的大小，从而模拟发电机发生不同程度的匝间短路故障，实验布置如图14所示。
本次实验对发电机空载工况及负载工况（负载为1.2 kW）下的特征参量进行采集，采用量程为-10～10 A的交流电流探头监测A相支路电流IA1、IA2的变化，采用量程为0～40 A的直流电流探头监测励磁电流If的变化，并采用垂直分辨率为12位、带宽为20 MHz，采样通道数为8的Pico 4824A数字示波器采集同相支路电流、励磁电流及机端电压等数据，采样频率设为2 000 Hz，数字示波器采集、A相分支电流探头布置、实验整体布置如图14所示。
图14 TZH-225-TH凸极同步发电机励磁绕组匝间短路实验平台
Fig.14 TZH-225-TH salient synchronous generator experimental platform for inter-turn short circuit
4.2.1 静偏心复合匝间短路时/频域分析
首先，对空载工况下的励磁电流数据进行分析，得其时域波形如图15a所示。根据滑动变阻器的分流值大小，计算匝间短路程度见表3。进而对同相支路环流数据进行分析，得静偏心复合正常、静偏心复合匝间短路故障的环流时域波形如图15b所示。对时域信号进行傅里叶变换，得不同状态下的频域波形如图15c所示。
由图15a可以看出，随着故障程度的增大，励磁电流也随之增大，直流电流均值由4.811 A增至5.046 A。观察图15b所示环流时域图谱，由于机组存在4%的静偏心，因此在空载正常运行状态下会出现同相支路环流，且正常运行与短路2.5%的时域幅值较为接近，时域法难以完成轻微匝间短路故障的有效辨识。观察图15c所示环流频谱，正常状态下，其频谱出现了静偏心所导致的50 Hz基波及150 Hz谐波，此外凸极效应所产生的特征分数次（25、75、125、175 Hz）谐波亦较为明显。当匝间短路故障程度较小时，其特征分数次谐波幅值与正常状态的幅值亦较为接近，因此通过特征频率及其幅值实现轻微匝间短路故障识别的难度较大。根据以上分析，受静偏心及凸极效应影响，时域、频域分析法均无法有效区分发电机的正常状态与匝间短路状态。
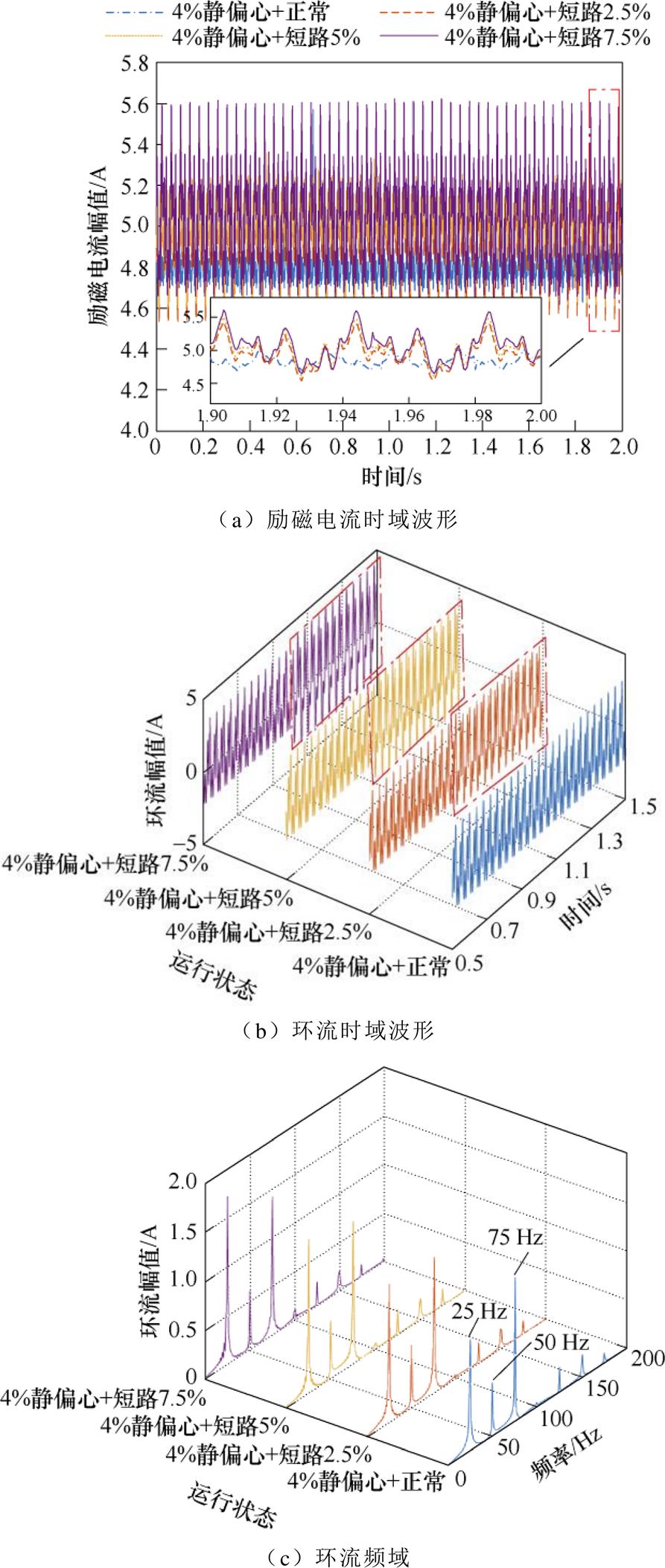
图15 TZH-225-TH空载工况特征参量图谱（故障时刻t=1 s）
Fig.15 TZH-225-TH characteristic parametric spectrum under no-load condition (fault moment t=1 s)
表3 TZH-225-TH空载工况下匝间短路故障程度
Tab.3 TZH-225-TH inter-turn short circuit fault degree under no-load condition
滑动变阻器分流/A励磁电流平均值If/A匝间短路故障程度(%) 04.8110 0.254.9322.5 0.505.0045.0 0.755.0467.5
其次，对负载工况下的励磁电流数据进行分析，得其时域如图16a所示。根据滑动变阻器的分流大小，计算匝间短路程度见表4。进而对同相支路环流数据进行分析，得静偏心复合正常、静偏心复合匝间短路故障的环流时域如图16b所示，不同故障程度下的频域如图16c所示。
由图16a可以看出，随着故障程度的增大，励磁电流也呈上升趋势，其均值由4.932 A增至5.087 A。由于机组存在静偏心及电枢效应影响，因此图16b所示环流时域图谱，其正常状态下的同相支路环流与匝间短路1%的时域幅值较为接近，难以通过时域阈值法进行有效区分。图16c所示环流频谱在正常状态下出现了50 Hz基波、150 Hz谐波及特征分数次（25、75、125、175 Hz）谐波，且其幅值与匝间短路1%状态下的幅值较为接近，对匝间短路故障识别造成了干扰。综上分析，受静偏心及电枢反应影响，时域、频域分析法均无法有效辨识微弱匝间短路故障。
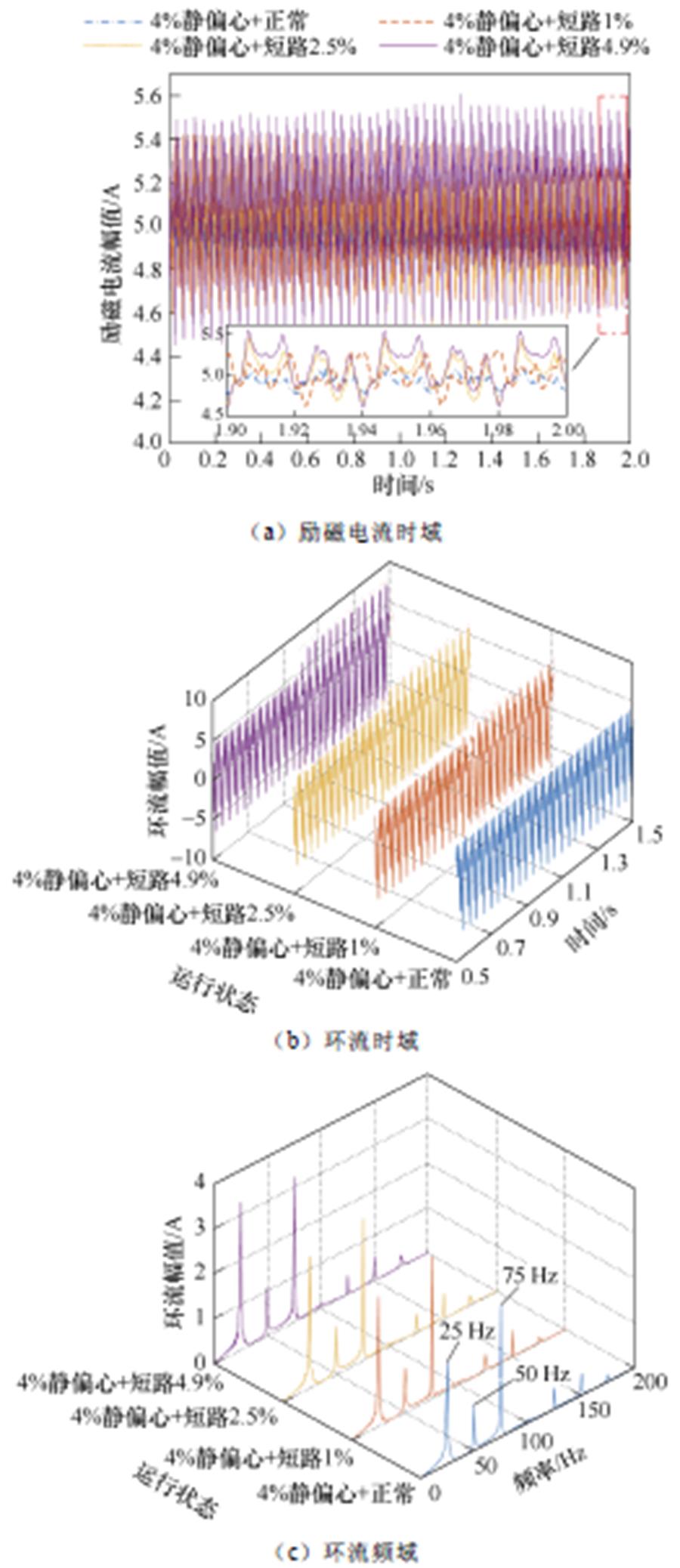
图16 TZH-225-TH负载工况特征参量图谱（故障时刻t=1 s）
Fig.16 TZH-225-TH characteristic parametric spectrum under load condition (fault moment t=1 s)
表4 TZH-225-TH负载工况下匝间短路故障程度
Tab.4 TZH-225-TH inter-turn short circuit fault degree under load condition
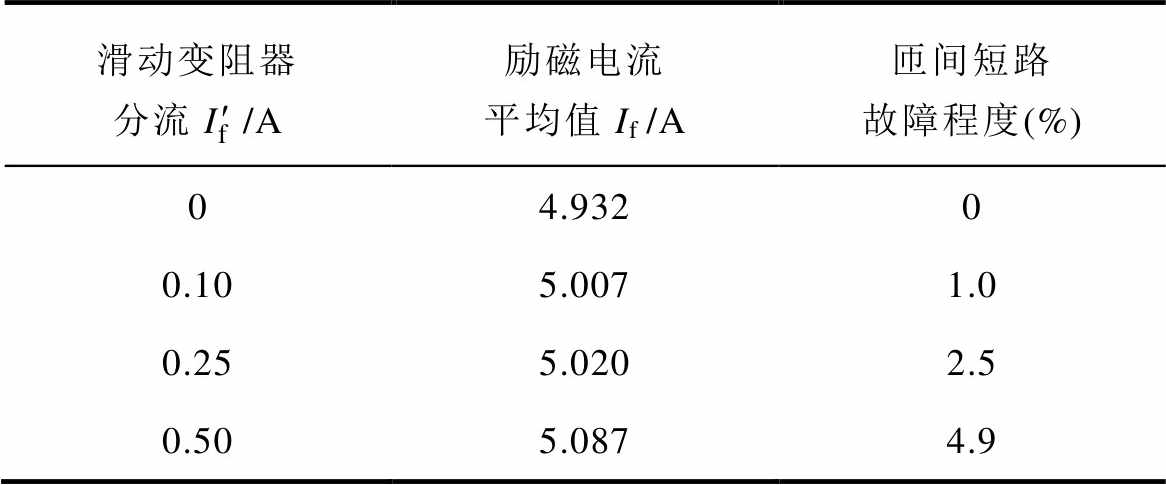
滑动变阻器分流/A励磁电流平均值If /A匝间短路故障程度(%) 04.9320 0.105.0071.0 0.255.0202.5 0.505.0874.9
4.2.2 静偏心复合匝间短路-环流时频图谱分析
首先，对空载工况下的环流数据进行时频分析，构建发电机静偏心复合短路2.5%、静偏心复合短路5.0%、静偏心复合短路7.5%的三维环流时频图谱，如图17所示，由环流时频图谱可以看出，匝间短路故障发生时，其时间与特征频率交叉点的信号强度发生了明显变化，因此可通过信号强度变化（图中25 Hz故障前后的信号强度差值分别为13.05、21.06、29.86 dB）以及信号强度差值能量比（分别为4.16%、5.23%、11.11%，远大于0）检测微弱匝间短路故障并定位故障发生时间。
其次，对负载工况下的环流数据进行时频分析，构建发电机静偏心复合短路1%、静偏心复合短路2.5%、静偏心复合短路4.9%的三维环流时频图谱，如图18所示。根据频率分辨环流图谱中某一时刻与
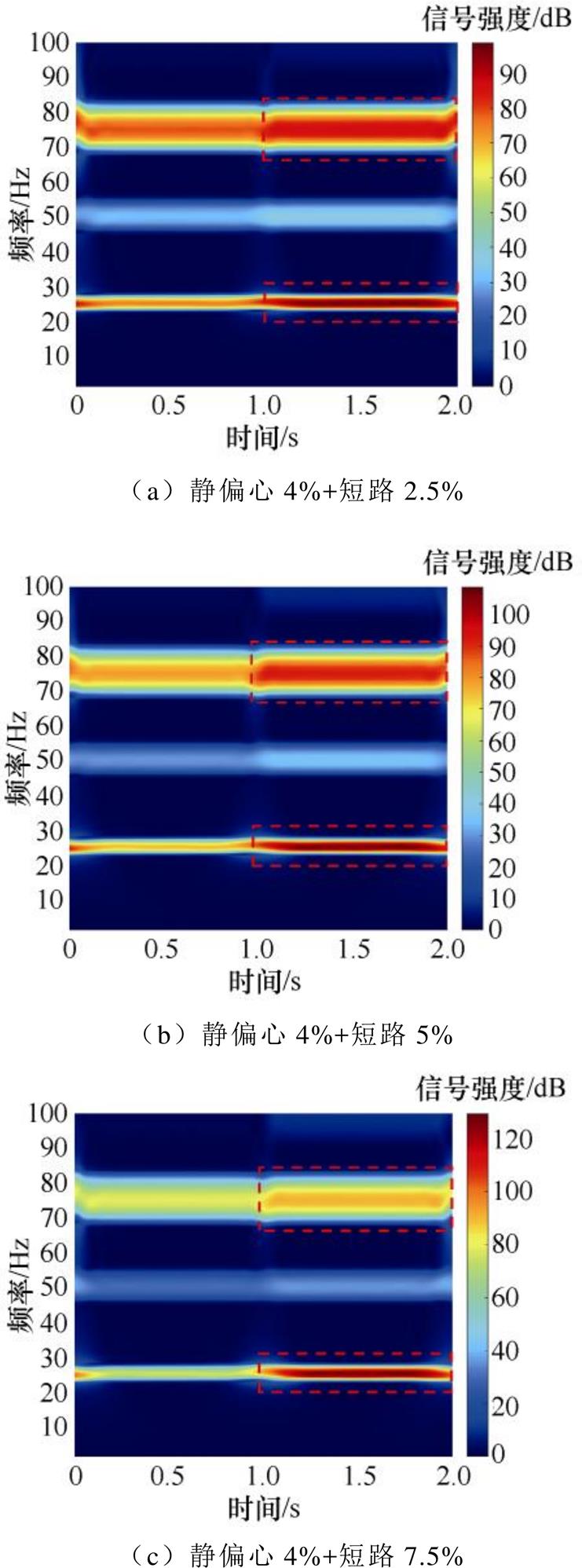
图17 TZH-225-TH空载工况环流时频图谱（故障时刻t=1 s）
Fig.17 TZH-225-TH time-frequency maps of circulating current under no-load condition (fault moment t=1 s)
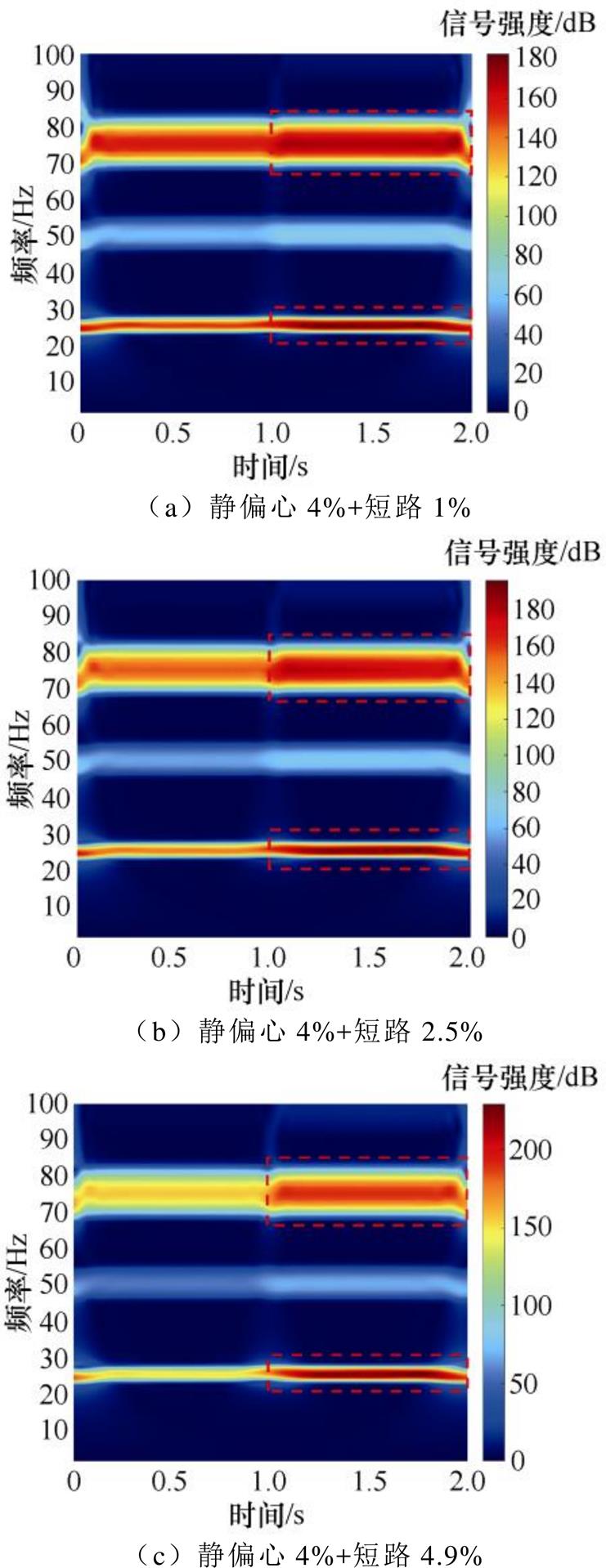
图18 TZH-225-TH负载工况环流时频图谱（故障时刻t=1 s）
Fig.18 TZH-225-TH time-frequency maps of circulating current under load condition (fault moment t=1 s)
特征频率交叉点处信号强度变化（故障前后25 Hz处的信号强度差值分别为29.64、38.56、71.81 dB）及信号强度差值能量比（分别为2.28%、3.13%、15.68%，远大于0），可有效完成微弱匝间短路故障的模式识别。
本文提出了一种基于环流时频图谱的励磁绕组匝间短路智能故障诊断方法，通过有限元仿真和模拟机组实验验证了该方法的有效性，并得出以下结论：
1）抽水蓄能机组发生励磁绕组匝间短路故障，会产生k/p（k=1, 2,…, n且k≠np）分数次环流特征谐波。机组运行于静偏心状态，会产生奇数次环流谐波；机组运行于动偏心状态，则会产生v-1/p和v+1/p次环流谐波（v=1, 3, 5,…, n）。机组若发生静偏心复合励磁绕组匝间短路故障，受静偏心影响，除分数次环流特征谐波外，还会产生奇数次环流谐波（以基波为主）。通过抽水蓄能机组有限元计算及同步发电机组实验所得环流数据，验证了该理论的正确性。
2）抽水蓄能机组运行过程中受动/静偏心及电枢反应影响，匝间短路状态下所得环流时域幅值虽较正常状态有一定增加，但仍具有较高相似度，若以此设置阈值进行故障诊断，极易发生误判。尤其对于机组运行于动偏心状态，其环流时域幅值较正常状态也会出现增加，且负载工况下环流频谱信息与匝间短路状态相同，因此现场运检人员通过单一的时域或频域特征分析法，难以有效辨识机组的运行状态。
3）为了实现抽水蓄能机组运行状态的在线监测，将连续小波变换时频分析方法引入环流特征信息处理流程，并构建基于运行时间、特征频率及信号强度的三维时频图谱，并以图谱信号强度变化以及信号强度差值能量比为判据用于匝间短路在线监测。该方法可有效滤除无关因素影响，提高故障诊断精度，便于应用到工业现场的故障检测，降低了现场运检人员的工作复杂度。
4）环流时频图谱在线检测方法简单易行，抗干扰能力强，且不干扰机组的正常运行。该方法能够发现励磁绕组匝间短路的早期微弱故障，对防止故障恶化、提高新型电力系统的稳定性具有重要意义。
附 录
动/静偏心径向气隙磁通密度如附图1所示。
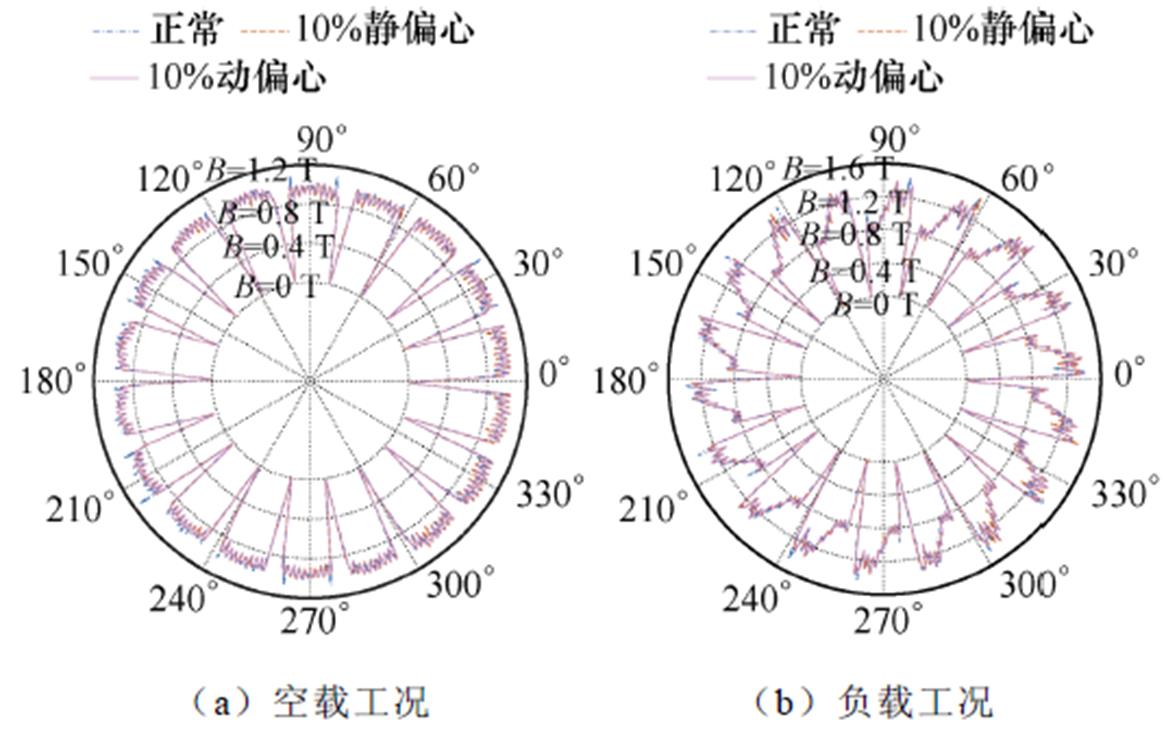
附图1 动/静偏心径向气隙磁通密度
App.Fig.1 Radial air gap flux density with dynamic/static eccentricity
参考文献
[1] 孙宇光, 王炳辉, 徐伟, 等. 发电电动机励磁绕组匝间短路故障在线监测[J]. 电力自动化设备, 2017, 37(3): 211-217.
Sun Yuguang, Wang Binghui, Xu Wei, et al. Online monitoring of excitation winding inter-turn short circuit of generator/motor[J]. Electric Power Auto- mation Equipment, 2017, 37(3): 211-217.
[2] 梁艳萍, 燕秀龙, 于鸿浩. 抽水蓄能电站发电电动机端部磁场及结构件损耗分析计算[J]. 电工技术学报, 2016, 31(6): 21-29.
Liang Yanping, Yan Xiulong, Yu Honghao. Analysis and calculation of magnetic field and structure loss in end region of generator-motor for pumped storage power station[J]. Transactions of China Electro- technical Society, 2016, 31(6): 21-29.
[3] Dirani H C, Merkhouf A, Giroux A M, et al. Impact of real air-gap nonuniformity on the electromagnetic forces of a large hydro-generator[J]. IEEE Transa- ctions on Industrial Electronics, 2018, 65(11): 8464- 8475.
[4] Shaikh M F, Park J, Lee S B. A non-intrusive leakage flux based method for detecting rotor faults in the starting transient of salient pole synchronous motors[J]. IEEE Transactions on Energy Conversion, 2021, 36(2): 1262-1270.
[5] Dirani H C, Merkhouf A, Kedjar B, et al. Rotor interturn short circuit impact on large hydrogenerator magnetic quantities[J]. IEEE Transactions on Industry Applications, 2018, 54(4): 3702-3711.
[6] 李永刚, 王罗, 李俊卿, 等. 基于多源信息融合的同步发电机转子绕组匝间短路故障识别[J]. 电力系统自动化, 2019, 43(16): 162-167, 191.
Li Yonggang, Wang Luo, Li Junqing, et al. Identi- fication of inter-turn short-circuit fault in rotor windings of synchronous generator based on multi- source information fusion[J]. Automation of Electric Power Systems, 2019, 43(16): 162-167, 191.
[7] 桂林, 陈俊, 王凯, 等. 基于柔性光学TA的发电电动机主保护优化设计[J]. 电力系统自动化, 2020, 44(18): 132-138.
Gui Lin, Chen Jun, Wang Kai, et al. Optimal design of main protection for generator-motor based on flexible optical current transformer[J]. Automation of Electric Power Systems, 2020, 44(18): 132-138.
[8] Zamudio-Ramirez I, Osornio-Rios R A, Antonino- Daviu J A, et al. Magnetic flux analysis for the condition monitoring of electric machines: a review[J]. IEEE Transactions on Industrial Infor- matics, 2022, 18(5): 2895-2908.
[9] Ehya H, Nysveen A, Skreien T N. Performance evaluation of signal processing tools used for fault detection of hydrogenerators operating in noisy environments[J]. IEEE Transactions on Industry Applications, 2021, 57(4): 3654-3665.
[10] Ma Minghan, He Pengkang, Li Yonggang, et al. Fault diagnosis method based on multi-source information fusion for weak interturn short circuit in synchronous condensers[J]. IET Electric Power Applications, 2021, 15(9): 1245-1260.
[11] 孙宇光, 杜威, 桂林, 等. 用于多相无刷励磁机开路与短路故障检测的磁极探测线圈设计[J]. 电工技术学报, 2022, 37(14): 3542-3554.
Sun Yuguang, Du Wei, Gui Lin, et al. Design of pole detection coils for open-circuit and short-circuit faults in multiphase brushless exciter[J]. Transactions of China Electrotechnical Society, 2022, 37(14): 3542-3554.
[12] 魏东, 刘侃, 丁荣军, 等. 基于多重同步压缩变换的永磁同步电机初期匝间短路故障检测[J]. 电工技术学报, 2022, 37(18): 4651-4663.
Wei Dong, Liu Kan, Ding Rongjun, et al. A multi-synchrosqueezing transformation based early stage detection of inter-turn short circuit fault in permanent magnet synchronous machine[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(18): 4651-4663.
[13] 谢颖, 胡圣明, 陈鹏, 等. 永磁同步电机匝间短路故障温度场分析[J]. 电工技术学报, 2022, 37(2): 322-331.
Xie Ying, Hu Shengming, Chen Peng, et al. Thermal field analysis on inter-turn short circuit fault of permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(2): 322-331.
[14] 张业成, 刘国海, 陈前. 基于电流波动特征的永磁同步电机匝间短路与局部退磁故障分类诊断研究[J]. 电工技术学报, 2022, 37(7): 1634-1643, 1653.
Zhang Yecheng, Liu Guohai, Chen Qian. Dis- crimination of interturn short-circuit and local demagnetization in permanent magnet synchronous motor based on current fluctuation characteristics[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1634-1643, 1653.
[15] 赵方伟, 王秀和, 赵文良, 等. 内置式永磁同步电机动态偏心故障下的轴电压解析分析和削弱[J]. 电工技术学报, 2022, 37(4): 837-848.
Zhao Fangwei, Wang Xiuhe, Zhao Wenliang, et al. Analysis and reduction of shaft voltage in interior permanent magnet synchronous motors under dynamic eccentricity fault[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 837-848.
[16] 朱洪雷. 水轮发电机磁极线圈匝间短路检查及处理[J]. 防爆电机, 2012, 47(3): 48-50.
Zhu Honglei. Inspection and treatment of interturn short circuit of hydraulic turbine generator magnetic pole coils[J]. Explosion-Proof Electric Machine, 2012, 47(3): 48-50.
[17] 李永刚, 王海蛟, 武玉才, 等. 基于交流阻抗法的发电机励磁绕组短路故障诊断[J]. 大电机技术, 2017(4): 10-14, 22.
Li Yonggang, Wang Haijiao, Wu Yucai, et al. Field winding short circuit fault diagnosis on turbine generators based on the AC impedance test[J]. Large Electric Machine and Hydraulic Turbine, 2017(4): 10-14, 22.
[18] 吕英, 金人文. 水轮发电机磁极线卷匝间短路的寻找和现场处理[J]. 水电站机电技术, 1985, 8(3): 47-51.
Lü Ying, Jin Renwen. Finding and field treatment of turn-to-turn short circuit of magnetic pole wire of hydrogenerator[J]. Mechanical & Electrical Tech- nique of Hydropower Station, 1985, 8(3): 47-51.
[19] 孙宇光, 余锡文, 魏锟, 等. 发电机绕组匝间故障检测的新型探测线圈[J]. 中国电机工程学报, 2014, 34(6): 917-924.
Sun Yuguang, Yu Xiwen, Wei Kun, et al. A new type of search coil for detecting inter-turn faults in synchronous machines[J]. Proceedings of the CSEE, 2014, 34(6): 917-924.
[20] Wu Yucai, Ma Qianqian, Cai Bochong. Fault diag- nosis of rotor winding inter-turn short circuit for sensorless synchronous generator through screw[J]. IET Electric Power Applications, 2017, 11(8): 1475- 1482.
[21] Cuevas M, Romary R, Lecointe J P, et al. Non- invasive detection of winding short-circuit faults in salient pole synchronous machine with squirrel-cage damper[J]. IEEE Transactions on Industry Appli- cations, 2018, 54(6): 5988-5997.
[22] Ehya H, Nysveen A. Pattern recognition of interturn short circuit fault in a synchronous generator using magnetic flux[J]. IEEE Transactions on Industry Applications, 2021, 57(4): 3573-3581.
[23] 郝亮亮, 吴俊勇, 孙宇光, 等. 同步发电机转子匝间短路故障监测方案及其灵敏性分析[J]. 电力系统自动化, 2013, 37(12): 120-127.
Hao Liangliang, Wu Junyong, Sun Yuguang, et al. A monitoring scheme for inter-turn short circuit of field windings in synchronous machines and its sensitivity analysis[J]. Automation of Electric Power Systems, 2013, 37(12): 120-127.
[24] Hao Liangliang, Sun Yuguang, Qiu Arui, et al. Steady-state calculation and online monitoring of interturn short circuit of field windings in syn- chronous machines[J]. IEEE Transactions on Energy Conversion, 2012, 27(1): 128-138.
[25] 郭玉恒, 王思良, 任保瑞, 等. 二滩水轮发电机转子匝间短路故障的电气特征及在线监测[J]. 水电与抽水蓄能, 2018, 4(3): 9-15, 97.
Guo Yuheng, Wang Siliang, Ren Baorui, et al. Electrical characteristics and on-line monitoring of rotor winding inter-turn short circuit fault of Ertan hydrogenerator[J]. Hydropower and Pumped Storage, 2018, 4(3): 9-15, 97.
[26] 辛鹏, 戈宝军, 陶大军, 等. 多极隐极发电机励磁绕组匝间短路时的定子分支环流谐波特性[J]. 电工技术学报, 2017, 32(7): 67-76.
Xin Peng, Ge Baojun, Tao Dajun, et al. Stator branch circulating current harmonic characteristics of multi- pole non-salient-pole generator with field winding inter-turn short circuits[J]. Transactions of China Electrotechnical Society, 2017, 32(7): 67-76.
[27] 钱国超, 赵仲勇, 邹德旭, 等. 基于连续小波变换的变压器绕组变形故障类型检测[J]. 高电压技术, 2017, 43(6): 2016-2023.
Qian Guochao, Zhao Zhongyong, Zou Dexu, et al. Detection of transformer winding deformation fault types based on continuous wavelet transform[J]. High Voltage Engineering, 2017, 43(6): 2016-2023.
Abstract As key electrical equipment, the operational continuity and reliability of pumped storage units are significant to the construction of new power systems. During operation, the inter-turn insulation of the excitation winding is susceptible to deterioration due to multiple factors, such as unbalanced electromagnetic force, thermal stress, and external mechanical stress. It is important to quickly and accurately extract the early weak fault characteristics of inter-turn short circuits (ITSC) and organize timely condition maintenance. The condition monitoring of ITSC faults in the excitation winding is susceptible to dynamic/static eccentricity and armature response, and early fault characteristics are hard to identify. Therefore, this study proposes a fault diagnosis method based on a time-frequency circulating current (TFMCC) map.
Firstly, this study derives the equations for the same phase multi-branch circulating current in the dynamic/static eccentricity and static eccentricity composite ITSC states, and obtains the characteristic harmonics of the circulating current in each state. Secondly, a two-dimensional finite element simulation model of 334 MV·A is constructed, and the magnitude of the same phase branch circulating current under each state is calculated. Comparative experiments have verified that TFMCC can effectively distinguish between eccentricity, armature reaction disturbance, and ITSC faults. Finally, based on the salient synchronous generator simulation platform, the operating conditions of ITSC with different fault levels are simulated.
Simulation results show that changes in the dynamic/static eccentricity degree cause the time domain amplitude of circulating current changes, and the armature response and dynamic eccentricity also cause the appearance of characteristic fractional harmonics. Accordingly, ITSC fault diagnosis by a single-time domain analysis or spectrum analysis can easily lead to fault misclassification. The TFMCC allows the fault to be located at the moment of occurrence. The signal intensity at the characteristic frequencies (5.5, 11, 22, 28, 39, 44.5 Hz) is significantly enhanced compared to the normal state. Meanwhile, a comparison with the dynamic/static eccentricity shows that the signal intensity of the dynamic eccentricity is mainly concentrated at 55.5 Hz, and the static eccentricity is mainly concentrated at 50 Hz. The signal intensity distribution is differentiated from that of ITSC faults. The ratio of the signal intensity difference energy (SIDER) are 7.13% and 13.96% for the no-load ITSC condition, and 6.66% and 13.44% for the load ITSC condition, much greater than zero, which can effectively identify the ITSC faults.
The experiments on salient synchronous generator show that: the TFMCC of static eccentric compound ITSC 2.5%, 5%, and 7.5% under no-load conditions, the signal intensity at the intersection of time and characteristic frequency has changed significantly, and the signal intensity differences at 25 Hz before and after the fault are 13.05, 21.06, and 29.86 dB, respectively. The SIDER are 4.16%, 5.23%, and 11.11%, respectively. Meanwhile, the static eccentricity compound ITSC of 1%, 2.5%, and 4.9% under load conditions, and the signal intensity differences at 25 Hz before and after the fault are 29.64, 38.56, and 71.81 dB, respectively. The SIDER are 2.28%, 3.13%, and 15.68%, respectively, which shows that the method can effectively detect weak ITSC faults and locate the time of fault occurrence.
The experimental results demonstrate that the method eliminates static eccentricity and armature response disturbances, and visualizes the operating conditions of the unit with a three-dimensional map that includes operating time, characteristic frequency, and signal intensity. At the same time, to effectively identify weak ITSC faults, this study also calculates that the SIDER of the time-frequency matrix can further quantify the magnitude of the fault and prevent false alarms, which can provide guidance for field operation and inspection personnel to carry out condition maintenance work.
Keywords：Pumped storage units, excitation winding, inter-turn short circuit, time-frequency map of circulating current
齐 鹏 男，1991年生，博士研究生，研究方向为旋转电力设备运行特性分析及故障诊断。E-mail: qipeng91@foxmail.com
武玉才 男，1982年生，副教授，硕士生导师，研究方向为旋转电力设备运行特性分析及故障诊断、高速磁悬浮及驱动系统设计。E-mail: wuyucaincepu@163.com（通信作者）
中图分类号：TM311
DOI: 10.19595/j.cnki.1000-6753.tces.221466
国家自然科学基金（52277048）和河北省自然科学基金（E2020502064）资助项目。
收稿日期 2022-07-29
改稿日期 2022-08-19
（编辑 崔文静）