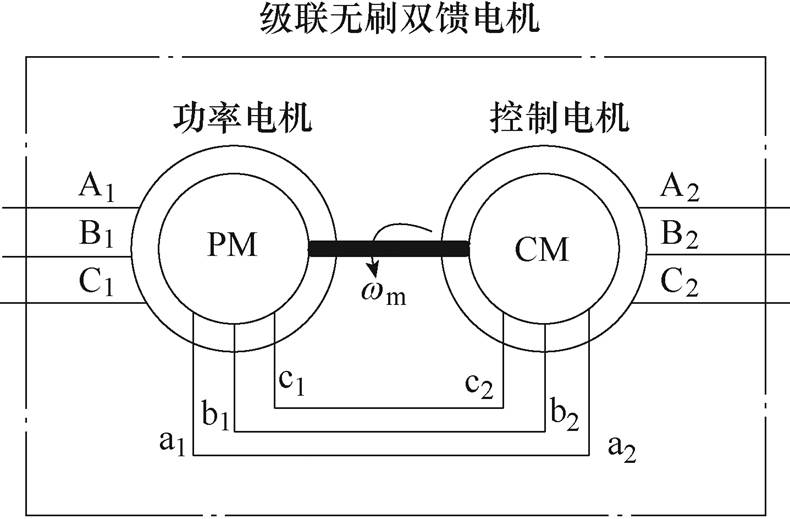
图1 正序连接的级联无刷双馈电机结构
Fig.1 Structure diagram of positive sequence connected cascaded brushless doubly-fed generator
摘要 级联无刷双馈电机无需电刷和集电环,具有电流谐波小、维护成本低等优点,在风力发电等领域具有广阔的应用前景。目前,级联无刷双馈电机常用的控制方法有矢量控制和无差拍控制,当控制器中使用的电机参数由于温度、饱和等因素与实际值不同时,控制效果均有不同程度的恶化。为了克服这一问题,该文提出一种基于扩张状态观测器的级联无刷双馈电机鲁棒预测电流控制方法,同时适用于并网同步和发电过程。该方法基于超局部模型使用扩张状态观测器来估计系统的动态部分和总扰动,并进一步结合无差拍控制,实现控制绕组电流的快速准确控制。与传统的矢量控制和无差拍控制进行了比较,实验结果表明,该方法不仅在电机参数准确时有良好的稳态和动态性能,在电机参数变化时同样能保持较好的控制效果,具有较强的参数鲁棒性。
关键词:级联无刷双馈电机 扩张状态观测器 参数鲁棒性 并网同步和发电
级联无刷双馈电机(Cascaded Brushless Doubly- Fed Generator, CBDFG)由同轴的两台绕线转子异步电机构成,二者的转子绕组直接相连从而无需电刷和集电环,因此具有使用寿命长、可靠性高、维护成本低等优点[1-2]。CBDFG既可用于独立发电,也可用于并网发电,在风力发电和水力发电等领域具有广阔的前景[3]。
目前,国内外学者针对无刷双馈电机的结构原理、数学模型和等效电路进行了深入研究[4-5],为高性能闭环控制提供了良好的基础。在各种闭环控制中,矢量控制(Field-Oriented Control, FOC)较早地在CBDFG控制中得到研究和应用[6]。尽管矢量控制可以获得良好的稳态和动态性能,但由于它本身的多环系统结构和PI等线性控制器的使用,矢量控制严重依赖电机的参数精度并且需要大量的调试整定工作来保证系统的稳定运行[7]。为了消除传统矢量控制中的控制器整定工作,同时提高动态响应和系统对参数变化的鲁棒性,直接转矩控制和直接功率控制被引入CBDFG控制中[8]。该方法根据电机的功率或转矩误差符号以及控制绕组侧磁链所在扇区,从一个预定的矢量表中选择能够减小被控变量误差的电压矢量,具有结构简单、参数鲁棒性强、动态性能好等优点。但是由于控制中采用的是一个启发式矢量表,在某些区域选择的矢量是无效甚至错误的,无法保证功率或转矩的精确控制,导致被控量脉动较大[9]。
近年来,预测控制以其原理简单、动态响应快、多目标控制和易于考虑约束等优点在交流电机控制领域得到了广泛关注[10-12]。预测控制主要包括模型预测控制[13]、无差拍控制[14]等。文献[13]将完整精确的CBDFG模型用于有限状态集模型预测控制,考虑了转子电路的影响,实现了有功和无功的精确解耦控制,由于在每个控制周期施加一个电压矢量,稳态脉动依然较大并且开关频率变化。文献[14]将无差拍预测电流控制(Deadbeat Predictive Current Control, DPCC)用于CBDFG,在固定开关频率的同时减小了稳态脉动。预测控制用于CBDFG控制的主要问题是效果依赖电机精确模型和电机参数,若电机参数发生变化或者参数辨识不准确,被控量在稳态时会出现明显的静差,另外计算量较大。
在实际应用中,如果电机参数发生变化或与控制器中的参数不匹配,传统控制方法的控制性能将会下降。对于无刷双馈电机,由于转子结构封闭,系统各变量之间耦合关系复杂,造成参数辨识困难,控制难度大。因此,鲁棒控制受到了广泛的关注。一般来说,提高控制方法参数鲁棒性的主要方法大致可分为三类:在线参数辨识[15]、扰动观测方法[16-17]和无模型算法[18]。文献[15]利用一种递归最小二乘法在双馈电机运行期间在线估计电机参数,但此类方法容易增加计算负担。扰动观测方法主要是基于扰动观测器或者扩张状态观测器。在文献[16]中,扰动观测器被添加到连续时间预测控制方法的控制回路中。当电机参数变化或者外部扰动出现时,电机仍然可以保持良好的控制效果。文献[17]将基于扩张状态观测器(Extended State Observer, ESO)的无模型预测电流控制应用到双馈电机上,在参数不准确时具有较好的控制性能。文献[18]将无模型控制方法用于无刷双馈电机,其主要思想是存储之前基本电压矢量作用引起的电流变化代替当前对应电压矢量的作用效果。但是当一个电压矢量长时间不作用时,相同电压矢量作用的效果可能有明显变化,这会影响系统的稳态性能。
针对CBDFG参数变化的内扰问题,本文使用ESO来估计系统总扰动[19],提出了一种基于ESO的级联无刷双馈电机鲁棒预测电流控制(Robust Predictive Current Control, RPCC)。所提方法开关频率固定,可以实现无差跟踪,具有良好的参数鲁棒性。大部分无刷双馈电机的控制方法都是针对并网发电过程设计的,虽然现有矢量控制和直接转矩控制也可以用于并网同步过程[20-21],但这方面的研究相对较少。本文则把所提出的控制方法用到了并网同步和并网发电全过程。在相同的实验测试条件下,将其与传统的FOC和DPCC进行了对比,实验结果验证了所提方法的有效性。
本文以正序连接的级联无刷双馈电机为研究对象,其原理结构如图1所示,包括功率电机和控制电机。以功率电机的定子侧为参考,可以得到任意转速同步旋转坐标系下的数学模型。当同步坐标旋转速度等于电网电压角速度wg时,电机的数学模 型为

图1 正序连接的级联无刷双馈电机结构
Fig.1 Structure diagram of positive sequence connected cascaded brushless doubly-fed generator
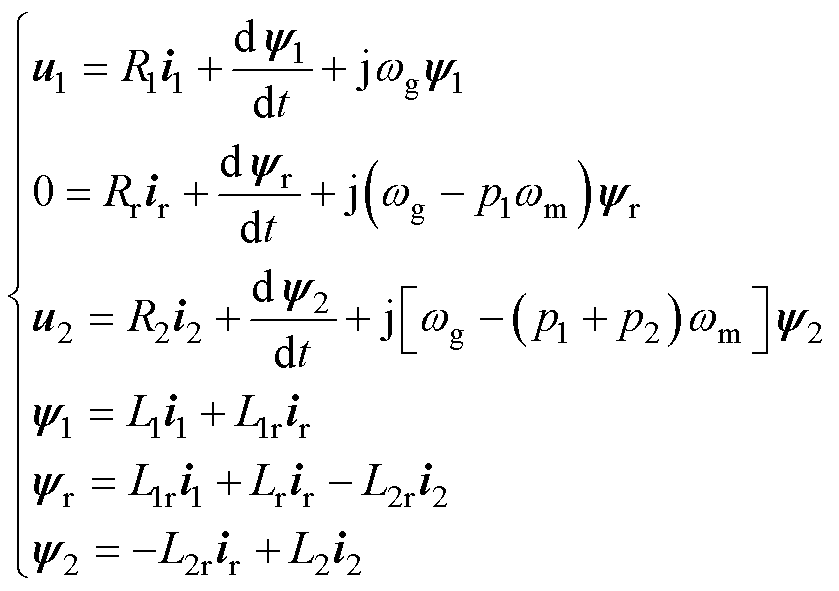 (1)
(1)
式中,u、i和y 分别为电压、电流和磁链矢量;L、R和p分别为绕组电感、绕组电阻和极对数;下标1、2和r分别为功率绕组、控制绕组和转子参数;wm为转子机械角速度。
本文以电网电压作为d轴进行定向,功率电机侧的输出有功功率、无功功率可以分别表示为
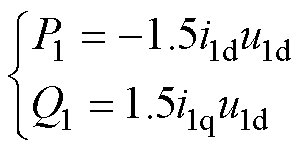 (2)
(2)
同步过程中,显然功率侧不发出功率,功率侧电流i1=0,继而通过式(1)可得
 (3)
(3)
忽略动态过程,功率磁链参考值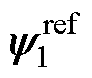 与控制绕组电流参考值
与控制绕组电流参考值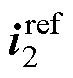 之间的关系为
之间的关系为
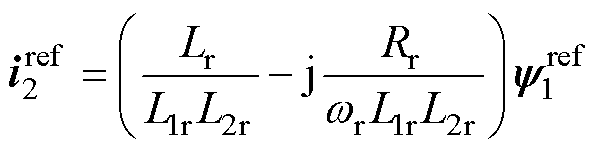 (4)
(4)
式中,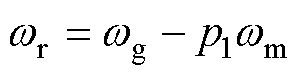 ;功率磁链的参考值可以选择电网的虚拟磁链yv(yv=-jug/wg)来表示,ug为电网电压矢量。
;功率磁链的参考值可以选择电网的虚拟磁链yv(yv=-jug/wg)来表示,ug为电网电压矢量。
根据式(4),设计磁链外环PI为
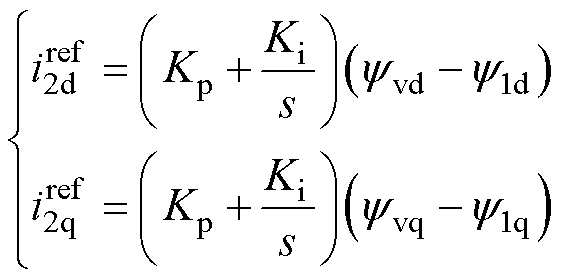 (5)
(5)
式中,下标“d”和“q”代表对应变量的d轴分量和q轴分量;Kp和Ki分别为PI中的比例增益和积分增益。
发电过程中,由式(1)可得
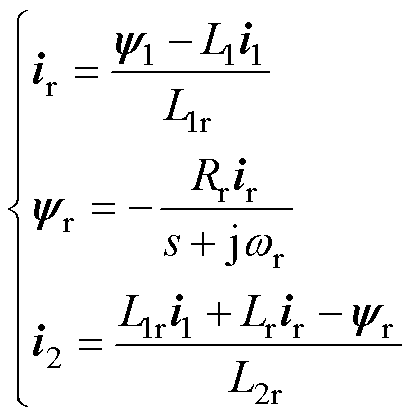 (6)
(6)
求解式(6),可以得到功率电流i1和控制电流i2之间的动态关系为
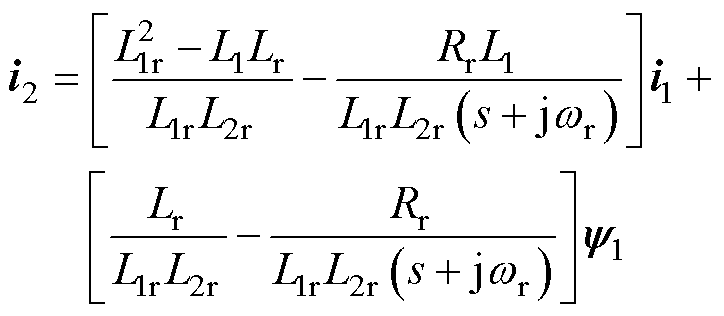 (7)
(7)
由式(2)和式(7)设计功率外环PI为
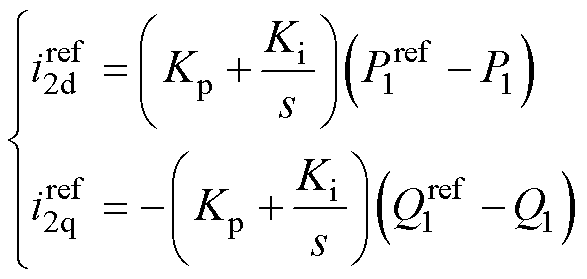 (8)
(8)
式中,上标“ref”为对应变量的参考值。
由式(1)可以得到控制电流与3个磁链之间的关系为
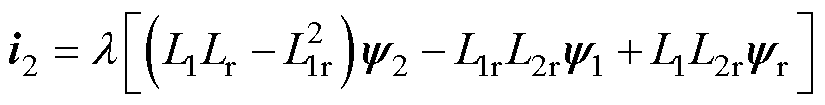 (9)
(9)
其中
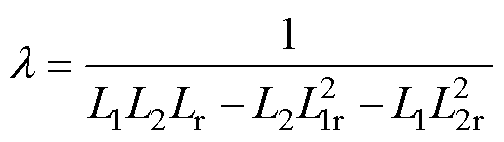
将式(1)与式(9)相结合,可以得到控制电流对时间的微分为
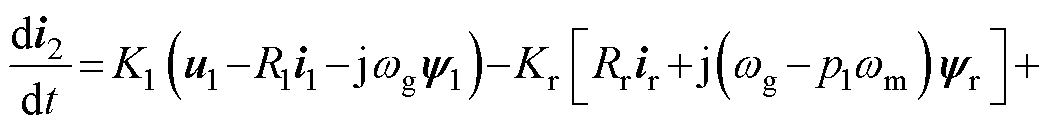
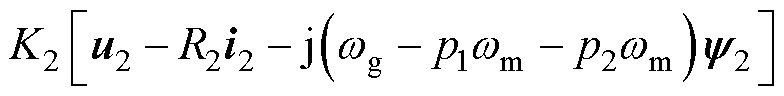 (10)
(10)
其中
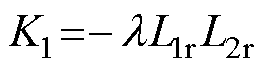
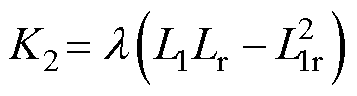
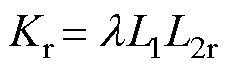
ESO可以将总扰动(包括不确定的系统变量和外部扰动)扩展为一个新扰动,并将这个总扰动反馈给被控制系统,使系统的控制方法既能观察到模型的非线性部分,又能观察到未知的外部扰动。为提高控制方法参数鲁棒性,将式(10)写为超局部模型,有
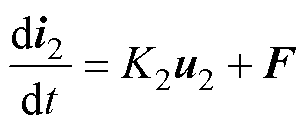 (11)
(11)
式中,F为系统的总扰动。在F中捕捉参数不匹配或参数变化引起的扰动,并由ESO实时观察,以便在控制算法中进行补偿。使用式(11)模型,不需要使用式(1)中CBDFG的完整模型来构建ESO。
在此基础上,采用线性ESO将传统的非线性误差函数替换为线性误差函数[19]。虽然线性ESO的性能可能不如非线性ESO,但设计简单。
根据式(11),系统是一阶单输入单输出系统。因此,在离散域,ESO的状态空间方程可以表示为
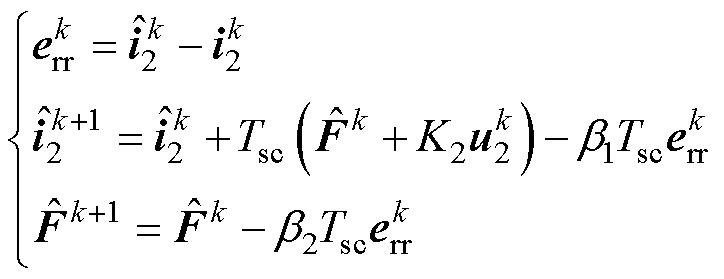 (12)
(12)
式中,k、k+1分别为当前时间和下一个采样时间;Tsc为采样周期;上标“ ”为对应的观测值;b1和b2为观测器的两个需要整定的参数。
”为对应的观测值;b1和b2为观测器的两个需要整定的参数。
根据式(12),通过将采样的控制电流作为输入,估计的控制电流作为输出,控制电压为扰动项,可以得到z域下的ESO结构框图,如图2所示。无刷双馈电机的扩张状态观测器闭环传递函数为
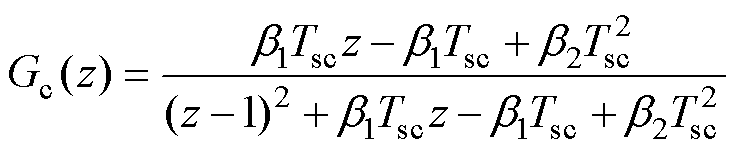 (13)
(13)
则系统的闭环特征方程为
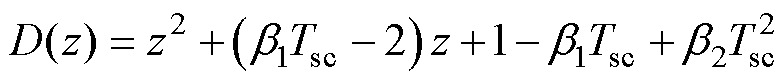 (14)
(14)
当离散系统所有的特征根分布在z域上的单位圆时,系统是稳定的。经过参数整定后,特征方程的极点可以放在同一个点上。因此,扩张状态观测器的参数可以表示为
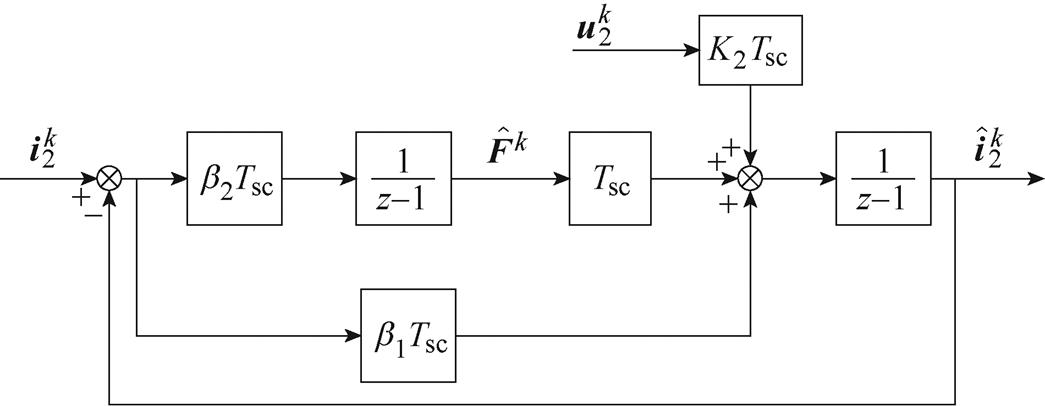
图2 离散域下扩张状态观测器的结构框图
Fig.2 Structural diagram of extended state observer in discrete domain
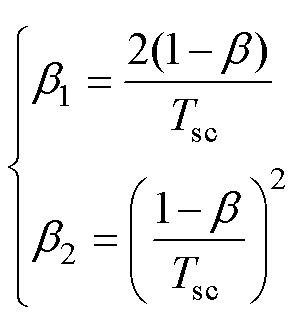 (15)
(15)
由此可见,b 是扩张状态观测器的唯一需要整定的参数。接下来,结合所提RPCC对b 进行设计。
图3为所提RPCC在z域里的控制框图。图中,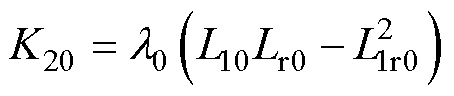 ,下标“0”表示电机参数的标称值,L10为电机功率绕组自感参数L1的标称值,l0为l的标称值,Lr0为转子电感Lr的标称值,L1r0为功率绕组互感L1r的标称值,理想情况下标称值与实际值相同。
,下标“0”表示电机参数的标称值,L10为电机功率绕组自感参数L1的标称值,l0为l的标称值,Lr0为转子电感Lr的标称值,L1r0为功率绕组互感L1r的标称值,理想情况下标称值与实际值相同。 ,B表示为
,B表示为
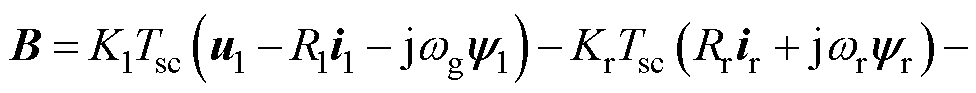
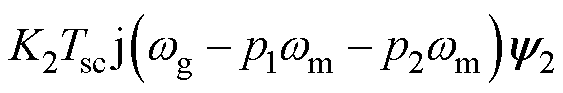 (16)
(16)
根据图3,实际控制电流值与参考值之间的关系为
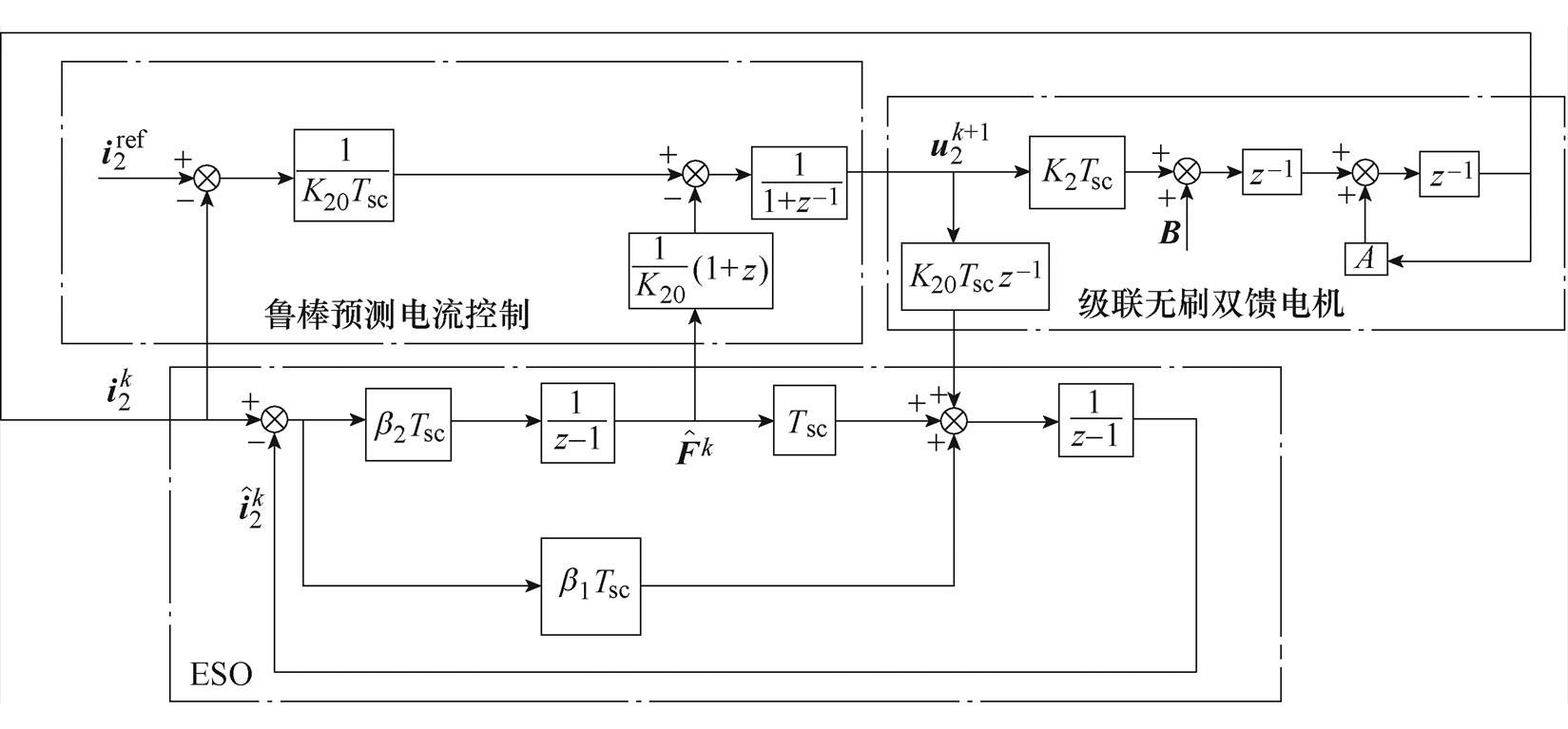
图3 RPCC的结构框图
Fig.3 The structural diagram of the RPCC in the z domain
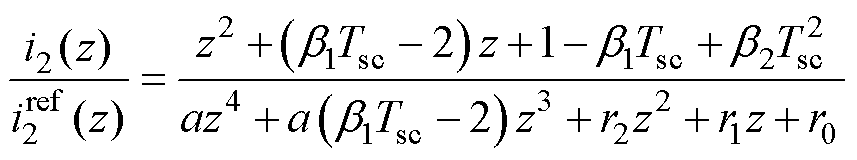 (17)
(17)
其中
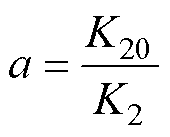
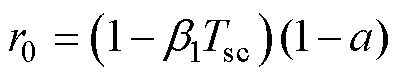
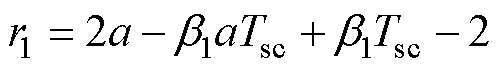
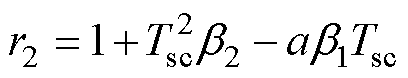
所提RPCC的特征方程为
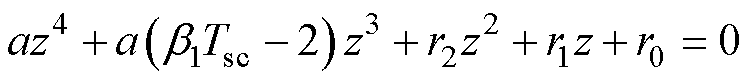 (18)
(18)
为了设计合适的ESO参数b,假设没有电感误差,即a=1。RPCC的特征方程可以简化为
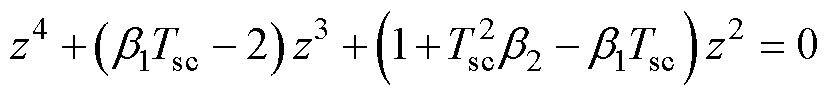 (19)
(19)
考虑式(15),特征方程的根为z1,2=0,z3,4=b。
为了保证稳定性,b 的值应该满足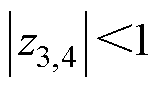 。因此,b 的范围应为
。因此,b 的范围应为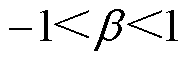 。选择不同的b 值,控制性能也会受到影响。根据文献[19],b 越大,扩张状态观测器的抗扰动能力越强,b 越小,扩张状态观测器的跟踪性能越好。在本文中,b 取0.52。
。选择不同的b 值,控制性能也会受到影响。根据文献[19],b 越大,扩张状态观测器的抗扰动能力越强,b 越小,扩张状态观测器的跟踪性能越好。在本文中,b 取0.52。
上述对参数b 的设计是在忽略电感误差的基础上得到的,接下来对系统能够稳定运行的参数不匹配范围进行分析。通过将式(18)的特征方程转化到w域中,并使用罗斯判据,可得b 取0.52,采样频率Tsc=10 kHz时参数不匹配的稳定范围为a>0.563 4,即
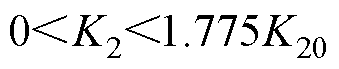 (20)
(20)
在数字控制中,由于当前采样时刻发出的是上一控制周期得到的参考电压矢量,因此需要对各变量进行一拍延迟补偿。将式(11)进行一阶欧拉离散,并认为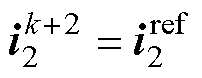 ,可得
,可得
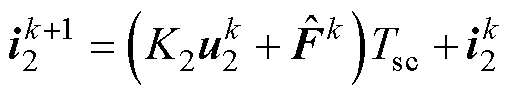 (21)
(21)
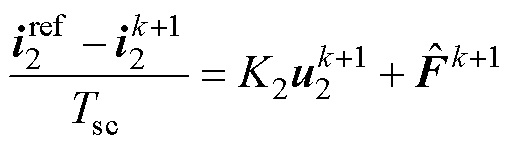 (22)
(22)
式中,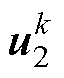 为上一控制周期内计算得到的控制电压参考值,存储在内存中,方便当前控制周期计算使用并用于下一时刻ESO的扰动估计。
为上一控制周期内计算得到的控制电压参考值,存储在内存中,方便当前控制周期计算使用并用于下一时刻ESO的扰动估计。
因此,联立式(21)和式(22),可以得到在同步dq坐标系下的控制电压参考值为
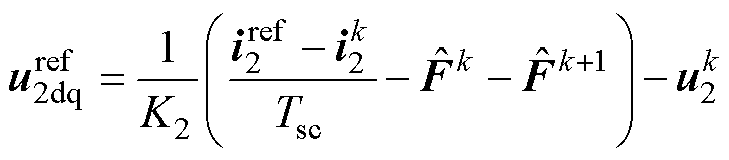 (23)
(23)
最后,将控制电压坐标变换回控制绕组坐标系,并通过空间矢量脉宽调制转换成开关信号作用于机侧逆变器上。本文提出的基于ESO的鲁棒预测电流控制(RPCC-ESO)整体控制框图如图4所示。图4中,上标PW和CW分别表示功率绕组静止坐标系和控制绕组静止坐标系,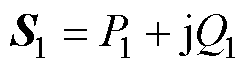 。
。
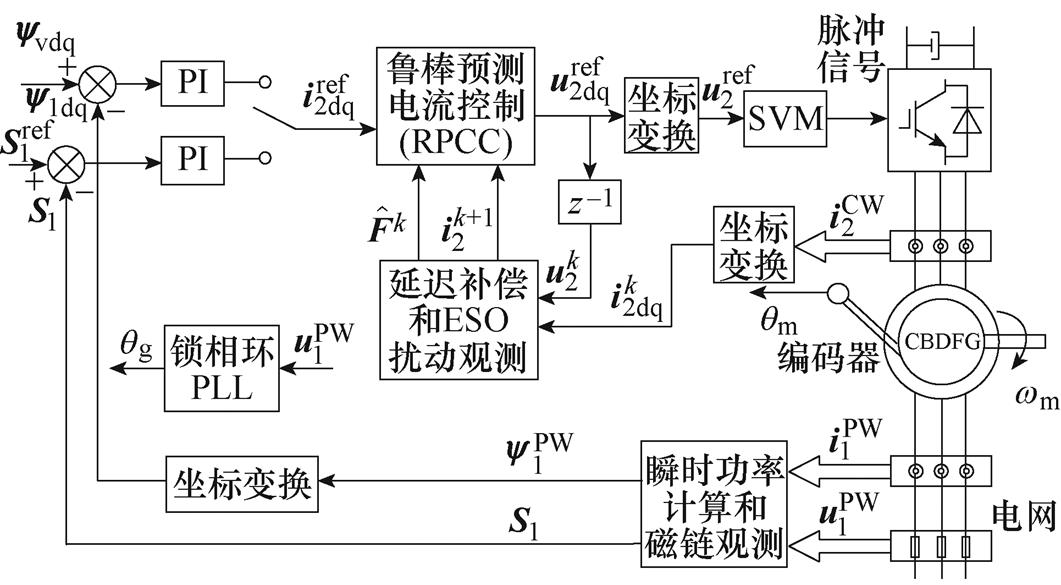
图4 基于ESO的级联无刷双馈电机鲁棒预测电流控制方法结构框图
Fig.4 Structure block diagram of robust predictive current control method for cascaded brushless doubly-fed generator based on ESO
本文为了证明所提方法的有效性,在CBDFG实验平台上进行了测试,实验平台如图5所示。实验所使用的控制电机和功率电机的参数见表1。所有的实验结果都是通过与MicroLabBox和PC接口的ControlDesk进行记录,然后利用Matlab软件对存储的数据进行分析和绘制。实验所使用的电网相电压有效值和母线电压分别为75 V和150 V,采样频率为10 kHz。
图6为所提方法从同步过程切换到发电过程的实验结果。四个通道从上到下分别为功率绕组三相电流、功率绕组磁链、功率绕组感应线电压和控制绕组三相电流。图6中,实线表示采样的实际值,虚线表示对应变量的参考值。可以看出,功率侧的磁链和感应电压基本与参考值重合。在0.08 s左右功率绕组接入电网,切换后功率侧电流无明显冲击,系统可以在不同过程之间平滑切换。

图5 级联无刷双馈电机实验平台
Fig.5 Experimental platform of CBDFG
表1 级联无刷双馈电机参数
Tab.1 The parameters of CBDFG
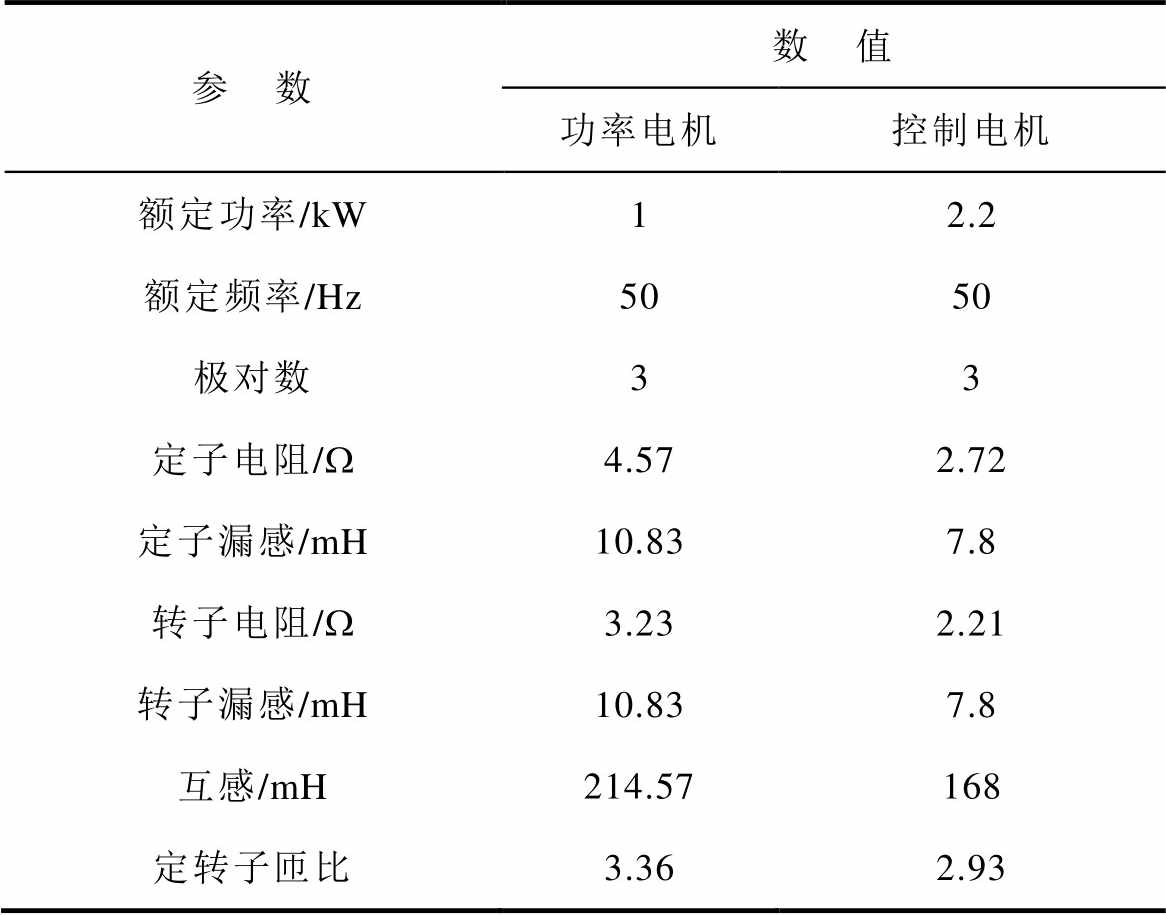
参 数数 值 功率电机控制电机 额定功率/kW12.2 额定频率/Hz5050 极对数33 定子电阻/W4.572.72 定子漏感/mH10.837.8 转子电阻/W3.232.21 转子漏感/mH10.837.8 互感/mH214.57168 定转子匝比3.362.93
图7为所提方法在转速350 r/min下的稳态实验结果。有功功率参考值为-350 W,无功功率参考值为0 var。图7a从上到下依次为:功率绕组有功功率、功率绕组无功功率、功率绕组三相电流、控制绕组三相电流。由图7b可知,功率绕组a相电流总谐波畸变率(Total Harmonic Distortion, THD)为1.116 9%,该方法在稳态下具有良好的控制性能。
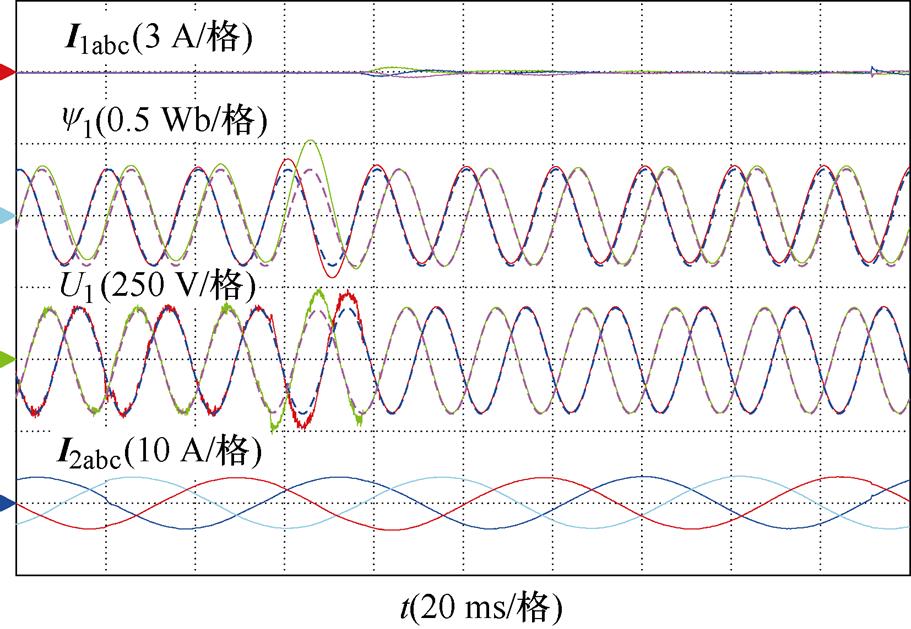
图6 所提控制方法从同步过程切换到发电过程的实验波形
Fig.6 Experimental waveforms of the proposed control method switching from the synchronization process to the power generation process
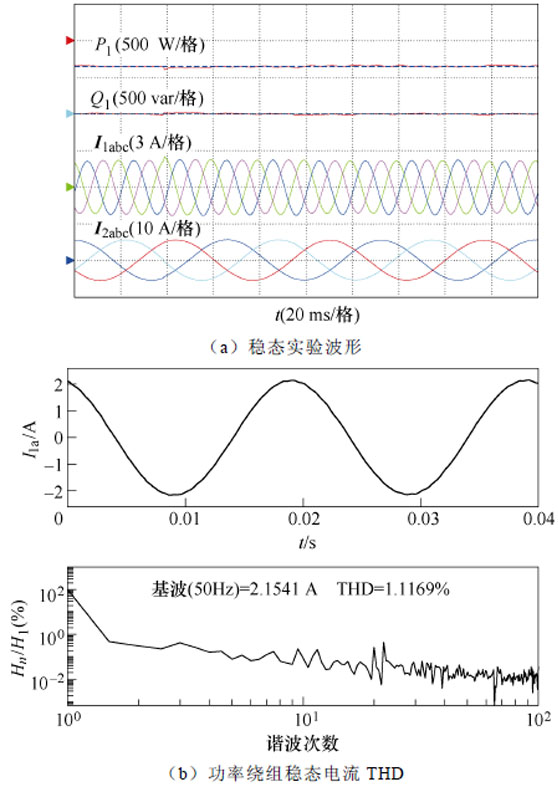
图7 所提控制方法在转速350 r/min下的稳态实验结果
Fig.7 Steady-state experimental results of the proposed control method at 350 r/min
图8为所提控制方法在功率阶跃变化下的实验动态波形。0.06 s时,有功功率参考值从0 W变为-350 W。有功功率较快跟踪参考值,由于所提方法外环PI做了相应的简化,阶跃条件下无功功率和有功功率的控制存在一定的耦合,但是无功功率的波动范围较小并且能迅速稳定。
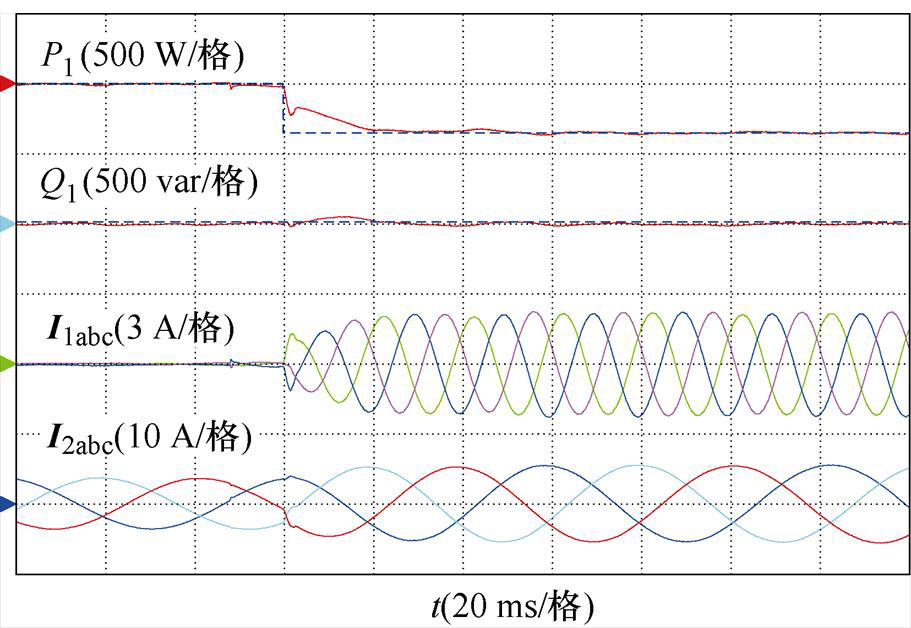
图8 所提控制方法在有功功率阶跃下的实验波形
Fig.8 Experimental waveforms of the proposed control method under active power step
FOC、DPCC和本文所提出的RPCC-ESO方法的实验数据对比见表2。相比于前两种传统的控制方法,所提控制方法在不同转速下稳态功率绕组电流THD都更小。
表2 三种控制方法在不同转速下a相稳态功率电流的THD对比
Tab.2 Comparison of THD of steady-state power current of phase a under three control methods at different speeds(%)

转速/(r/min)电流THD FOCDPCCRPCC-ESO 3501.4881.3741.117 6003.5092.0511.777
图9为所提控制方法在转速由亚同步速变到超同步速的动态波形。转子转速从450 r/min增加到550 r/min,有功功率参考值为-350 W。当转速接近同步转速时,控制绕组电流变为直流,但功率跟踪和功率绕组电流不受影响。
实际风电系统考虑到开关损耗,开关频率往往定在几千赫兹。为了展示本文所提RPCC-ESO方法在低开关频率下的效果,通过仿真,将采样频率为3、5和7 kHz的电流THD与10 kHz的电流THD对比。仿真使用参数与实验完全相同,转速为350 r/min,有功功率参考值为-350 W,无功功率参考值为0 var,对比结果见表3。可以看出,虽然开关频率的下降会使电流THD有所升高,但仍然远小于5%,满足并网要求。
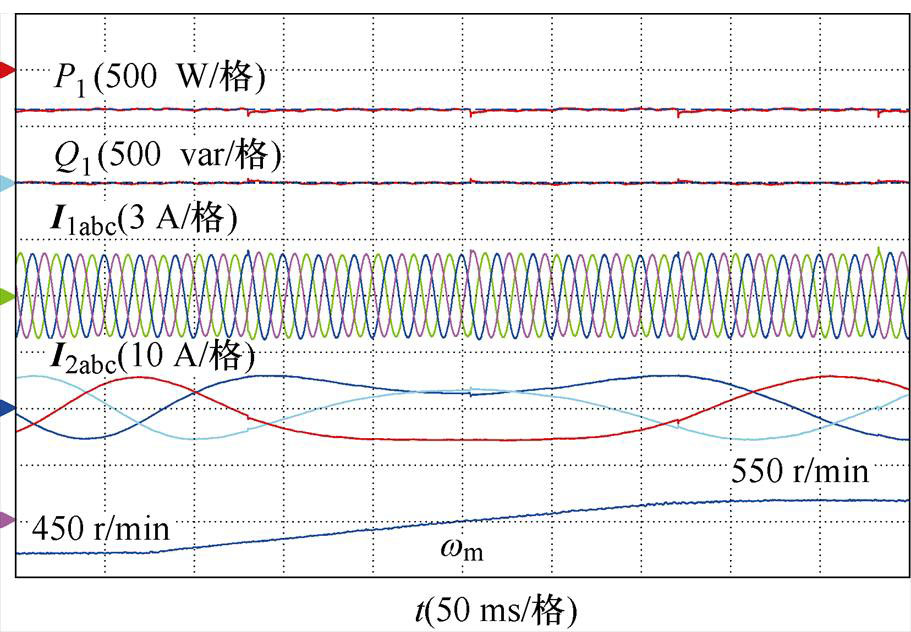
图9 所提控制方法在转速变化下的实验波形
Fig.9 Experimental waveforms of the proposed control method under rotational speed variation
表3 所提控制方法在不同采样频率下a相稳态功率电流和控制电流的THD对比
Tab.3 Comparison of THD of steady-state power current and control current of phase a under proposed control method at different sampling frequencies(%)

电流THD 3 kHz5 kHz7 kHz10 kHz 功率绕组2.0511.5410.9940.782 控制绕组1.1040.7890.5240.411
图10给出了三种控制方法在功率绕组互感参数L1r变化下的实验结果。在实验中人为改变控制器中的电感参数,功率参考值和电机转速维持不变。图10分别给出了矢量控制、无差拍控制和所提控制方法的实验结果。
图10中,最后一个通道表示控制器中使用的功率绕组互感值与实际值的比值。实验中,功率绕组互感参数的实际值L1r始终为214.57 mH,通过改变控制器中功率绕组互感参数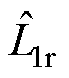 来模拟电感参数失配的工况,
来模拟电感参数失配的工况,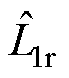 的变化范围为实际值的50%~150%。
的变化范围为实际值的50%~150%。
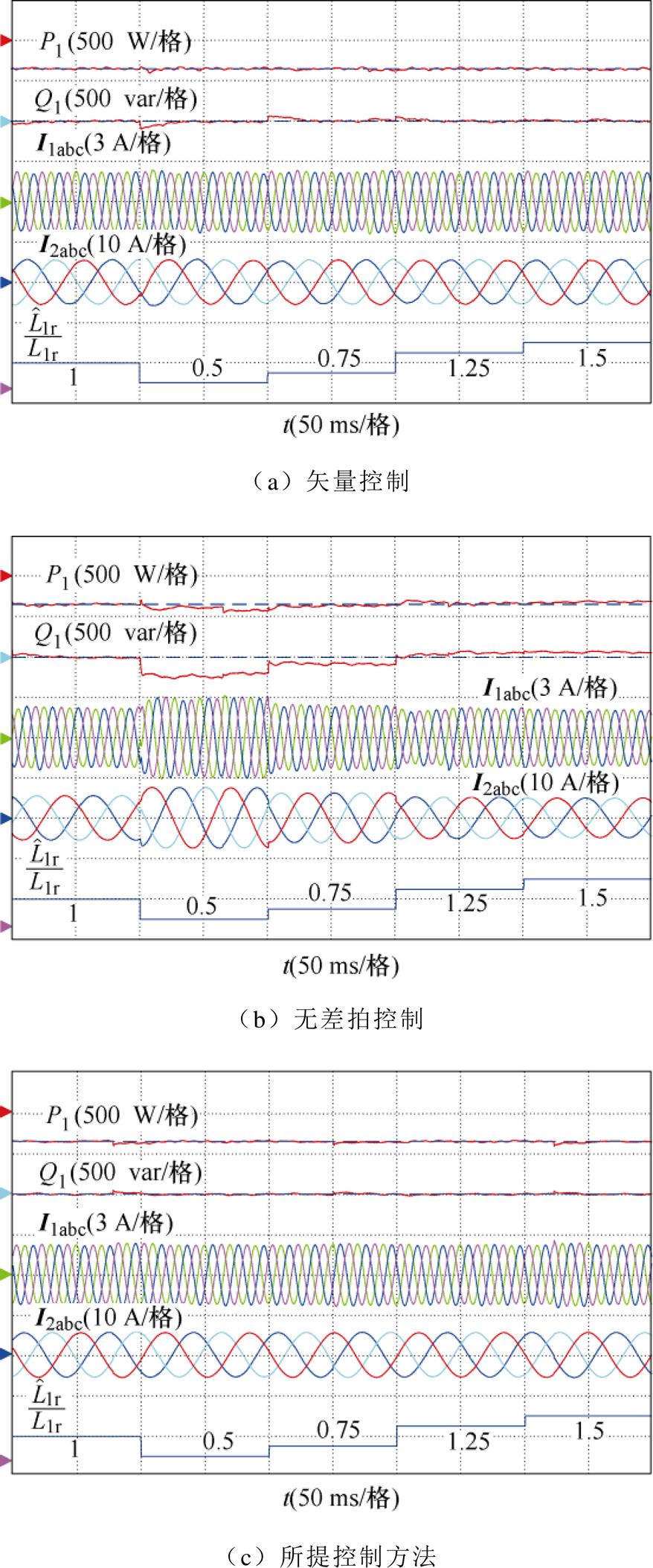
图10 三种控制方法在功率绕组互感L1r变化的实验结果
Fig.10 Experimental results of three control methods under the variation of power winding mutual inductance L1r
可以看出,矢量控制的功率跟踪略有波动,效果虽然不如所提控制方法,但明显好于无差拍控制方法。这是由于矢量控制的补偿项和PI参数的整定虽然与电机参数有关,但改变控制器中的电机参数后,外环PI可以消除功率静差。无差拍控制的功率跟踪会出现静差,相应的功率绕组电流也会发生变化。这是由于无差拍控制本身的公式推导用了完整的电机数学模型,更容易受到参数不匹配的影响。
对于所提方法,不管互感参数如何变化,控制效果基本与参数准确的稳态实验结果一致,具有良好的参数鲁棒性。这是由于该方法的ESO内环不使用电机参数进行控制。
值的一提的是,虽然FOC和所提方法最后均能实现无差跟踪,但是FOC的内环PI参数一般根据截止频率来进行设计,其与控制器中的电机参数有关。因此,当控制器中的电机参数与实际值不匹配时,电流环的控制效果会受到影响,而所提方法的内环参数设计与电机参数无关,具有更强的鲁棒性。
由于功率绕组互感参数L1r对功率跟踪影响较大,受限于篇幅,本文只给出了L1r变化下的实验结果。对于控制绕组互感参数L2r,三种控制方法造成的功率波动范围与L1r接近。对于转子电阻参数Rr,矢量控制基本不受影响,所提控制方法由于不使用电阻参数,故不受影响,无差拍控制的功率跟踪会出现静差。控制绕组电阻参数R2对三种控制方法的影响均可忽略。
本文提出了一种基于ESO的级联无刷双馈电机鲁棒预测电流控制方法。实验结果证明了基于ESO的控制方法不仅在电机参数准确时有较好的稳态和动态波形,在电机参数变化时同样能保持较好的控制效果。相比于传统方法,本文方法具有以下优点:
1)既可以用于并网同步过程,也可以用于并网发电过程。
2)使用线性ESO,经过参数整定后,需要设计的控制器参数只有一个,相比于传统矢量控制显著减少了调试时间。
3)基于超局部模型使用ESO快速估计模型不确定性引起的总扰动,并进一步结合无差拍控制,实现控制绕组电流的快速准确控制。相比传统的矢量控制和无差拍预测控制,该方法有更好的参数鲁棒性。
参考文献
[1] Liang Shuai, Jin Shi, Shi Long. Research on control strategy of grid-connected brushless doubly-fed wind power system based on virtual synchronous generator control[J]. CES Transactions on Electrical Machines and Systems, 2022, 6(4): 404-412.
[2] 阚超豪, 鲍习昌, 王雪帆, 等. 无刷双馈电机的研究现状与最新进展[J]. 中国电机工程学报, 2018, 38(13): 3939-3959, 4036.
Kan Chaohao, Bao Xichang, Wang Xuefan, et al. Overview and recent developments of brushless doubly-fed machines[J]. Proceedings of the CSEE, 2018, 38(13): 3939-3959, 4036.
[3] 程明, 许利通, 曹政, 等. 级联式无刷双馈电机的矢量控制系统和功率流研究[J]. 电工技术学报, 2022, 37(20): 5164-5174.
Cheng Ming, Xu Litong, Cao Zheng, et al. Study on vector control system and power flow of cascaded brushless doubly-fed induction generator[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(20): 5164-5174.
[4] 任泰安, 梁克靖, 王群京, 等. 差调制无刷双馈电机转子绕组设计及性能分析[J]. 电机与控制学报, 2022, 26(4): 57-65.
Ren Taian, Liang Kejing, Wang Qunjing, et al. Rotor winding design and performance analysis of differ- ential modulation brushless doubly-fed machines[J]. Electric Machines and Control, 2022, 26(4): 57-65.
[5] 程明, 韩鹏, 魏新迟. 无刷双馈风力发电机的设计、分析与控制[J]. 电工技术学报, 2016, 31(19): 37- 53.
Cheng Ming, Han Peng, Wei Xinchi. Design, analysis and control of brushless doubly-fed generators for wind power application[J]. Transactions of China Electrotechnical Society, 2016, 31(19): 37-53.
[6] Cheng Ming, Luo Rensong, Wei Xinchi. Design and analysis of current control methods for brushless doubly fed induction machines[J]. IEEE Transactions on Industrial Electronics, 2019, 66(1): 717-727.
[7] Esfandiari G, Ebrahimi M, Tabesh A. Instantaneous torque control method with rated torque-sharing ratio for cascaded DFIMs[J]. IEEE Transactions on Power Electronics, 2017, 32(11): 8671-8680.
[8] Sadeghi R, Madani S M, Ataei M, et al. Super- twisting sliding mode direct power control of a brushless doubly fed induction generator[J]. IEEE Transactions on Industrial Electronics, 2018, 65(11): 9147-9156.
[9] Sadeghi R, Madani S M, Ataei M. A new smooth synchronization of brushless doubly-fed induction generator by applying a proposed machine model[J]. IEEE Transactions on Sustainable Energy, 2018, 9(1): 371-380.
[10] 魏新迟, 许利通, 骆仁松, 等. 考虑饱和效应的无刷双馈发电机功率模型预测控制[J]. 电工技术学报, 2021, 36(17): 3721-3729.
Wei Xinchi, Xu Litong, Luo Rensong, et al. Model predictive power control of brushless doubly-fed induction generator considering saturation effect[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3721-3729.
[11] 卜飞飞, 罗捷, 刘皓喆, 等. 双绕组感应发电机系统无差拍电流预测控制策略[J]. 电工技术学报, 2021, 36(24): 5213-5224.
Bu Feifei, Luo Jie, Liu Haozhe, et al. Deadbeat predictive current control strategy of dual winding induction generator system[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5213-5224.
[12] 章回炫, 范涛, 边元均, 等. 永磁同步电机高性能电流预测控制[J]. 电工技术学报, 2022, 37(17): 4335-4345.
Zhang Huixuan, Fan Tao, Bian Yuanjun, et al. Predictive current control strategy of permanent magnet synchronous motors with high performance[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4335-4345.
[13] Wei Xinchi, Cheng Ming, Zhu Jianguo, et al. Finite- set model predictive power control of brushless doubly fed twin stator induction generator[J]. IEEE Transactions on Power Electronics, 2019, 34(3): 2300-2311.
[14] Li Xuan, Peng Tao, Dan Hanbing, et al. A modulated model predictive control scheme for the brushless doubly fed induction machine[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(4): 1681-1691.
[15] Bhattarai R, Gurung N, Ghosh S, et al. Parametrically robust dynamic speed estimation based control for doubly fed induction generator[J]. IEEE Transactions on Industry Applications, 2018, 54(6): 6529-6542.
[16] Errouissi R, Al-Durra A, Muyeen S M, et al. Offset- free direct power control of DFIG under continuous- time model predictive control[J]. IEEE Transactions on Power Electronics, 2017, 32(3): 2265-2277.
[17] Zhang Yongchang, Jiang Tao, Jiao Jian. Model-free predictive current control of DFIG based on an extended state observer under unbalanced and dis- torted grid[J]. IEEE Transactions on Power Elec- tronics, 2020, 35(8): 8130-8139.
[18] 徐伟, 陈俊杰, 刘毅, 等. 无刷双馈独立发电系统的改进无参数预测电流控制[J]. 电工技术学报, 2021, 36(19): 4002-4015.
Xu Wei, Chen Junjie, Liu Yi, et al. Improved non- parametric predictive current control for standalone brushless doubly-fed induction generators[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(19): 4002-4015.
[19] Liu Feng, Liu Zhangwei, Mei Shengwei, et al. ESO- based inertia emulation and rotor speed recovery control for DFIGs[J]. IEEE Transactions on Energy Conversion, 2017, 32(3): 1209-1219.
[20] Broekhof A, McMahon R, Tatlow M. Vector- controlled grid synchronization for the brushless doubly-fed induction generator[C]//7th IET Inter- national Conference on Power Electronics, Machines and Drives (PEMD 2014), Manchester, UK, 2014: 1-5.
[21] Sadeghi R, Madani S M, Agha Kashkooli M R. Grid synchronization of brushless doubly fed induction generator using direct torque control[C]//2016 7th Power Electronics and Drive Systems Technologies Conference (PEDSTC), Tehran, Iran, 2016: 53-57.
Abstract The cascaded brushless doubly-fed generator (CBDFG) comprises two coaxial wound rotor induction motors, and its rotor windings are directly connected to eliminate the need for brushes and slip rings. Therefore, it has the advantages of long service life, high reliability, and low maintenance cost. CBDFG can be used for independent generation and grid-connected generation, which has broad prospects in wind power and hydroelectric power generation. At present, vector control and deadbeat control are commonly used to control the CBDFG. Because the above two methods use a large number of motor parameters, when the machine parameters in controllers are different from the actual values due to temperature, saturation, and other reasons, the control effects have varying degrees of deterioration. Therefore, this paper proposes an extended state observer (ESO) based robust predictive current control (RPCC) method for CBDFG.
Firstly, the proposed RPCC can be applied to grid synchronization and power generation processes. The only difference between the two processes is the reference value calculation of the control winding current. In the process of grid synchronization, because the power side does not emit power, the virtual flux is needed to calculate the reference value of the control winding current. During the power generation process, the reference value of the control winding current is calculated directly according to the power reference value.
Secondly, the proposed RPCC is based on an ultra-local model and uses an ESO to rapidly estimate the total disturbance caused by model uncertainty. The ESO can extend the total disturbance to a new disturbance and feed this total disturbance back to the controlled system. Based on the state space equation of ESO, the closed-loop transfer function of the ESO for CBDFG is obtained, and the two parameters of ESO are simplified to one. Then, the control block diagram of the proposed RPCC in the z domain is given, and the parameters of ESO are designed according to the characteristic equation of the proposed RPCC. In addition, the parameter stability of the proposed ESO is analyzed.
Finally, according to the designed ESO parameters and the obtained disturbance values, one-step delay compensation is carried out for the current value of the control winding, and deadbeat control is further incorporated to achieve fast and accurate control of the control winding current.
Compared with the traditional field-oriented control and deadbeat control, the experimental results show that this method has good steady-state and dynamic waveforms when the motor parameters are accurate and maintains a good control effect when the CBDFG parameters change. This method has good parameter robustness. The switching frequency is usually set at several kHz to reduce the switching loss in an actual wind power system. The simulation results of the proposed RPCC at low switching frequencies show that although the decrease in switching frequency increases the current THD, it is still far less than 5%, which meets the grid-connection requirements.
Keywords:Cascaded brushless doubly-fed generator, extended state observer, parameter robustness, grid synchronization and power generation
杨长山 男,2000年生,硕士研究生,研究方向为无刷双馈电机模型预测控制。E-mail: yangchangshanyx@163.com
张永昌 男,1982年生,教授,博士生导师,研究方向为电力电子与电机控制等。E-mail: zyc@ncepu.edu.cn(通信作者)
中图分类号:TM346
DOI: 10.19595/j.cnki.1000-6753.tces.L10095
国家自然科学基金(52077002)、国家重点研发计划(2021YFB2400702)和华能集团总部科技项目海上风电与智慧能源系统科技专项(一期)(HNKJ20-H88)资助项目。
收稿日期 2023-01-03
改稿日期 2023-02-21
(编辑 崔文静)