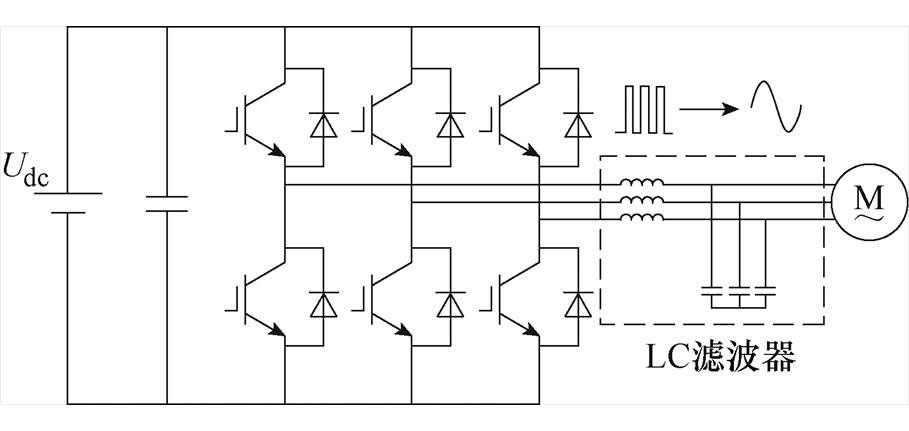
图1 带LC正弦波滤波器的IPMSM驱动系统
Fig.1 Drive system of IPMSM with LC sinusoidal filter
摘要 带有LC正弦波滤波器的内置式永磁同步电机系统形成了一个LCL电路,矢量控制系统的稳定性会受到LCL电路固有谐振现象的影响。通过在电流控制器中引入有源阻尼可从理论上实现谐振抑制,为了获得满意的谐振抑制效果,必须对电流控制器的参数进行合理设计。该文研究带有LC正弦波滤波器的内置式永磁同步电机电流控制器谐振抑制参数设计方法,分析了带有电容电流反馈有源阻尼(CCFAD)的电流控制器的频率特性,通过频域稳定判据分析了电流比例积分调节器参数、有源阻尼系数、LC正弦波滤波器参数与电机参数对系统谐振现象的影响机理,给出了电流控制器谐振抑制参数设计方法。通过实验验证了所提方法的有效性。
关键词:LC正弦波滤波器 内置式永磁同步电机 PI控制器 有源阻尼
内置式永磁同步电机(Interior Permanent Magnet Synchronous Motor, IPMSM)通常是由电压源型逆变器(Voltage-Source Inverter, VSI)供电,功率开关器件快速开关动作引发较大的电压变化率du/dt,带来了一些不可忽视的负面效应,如电机绝缘应力增加[1]、引发轴电压和轴电流[2]、产生突出的电磁干扰[3]。在一些特殊工业应用场景中,如海洋勘测、油田钻井、采矿业等,VSI安装位置与IPMSM距离较远,“长线效应”使得上述负面效应更加突出[4]。在VSI与IPMSM之间安装du/dt滤波器[5-7]能够一定程度上缓解上述负面效应,但只对一定的电缆长度适用[8]。LC正弦波滤波器能够将VSI输出的电压转换成正弦波,适用于任何长度的线缆,能有效解决上述问题[9-19]。带LC正弦波滤波器的IPMSM驱动系统如图1所示。
然而,LC正弦波滤波器的加入使系统模型阶数增加,且会产生固有的谐振现象,对IPMSM的电流控制器设计提出了挑战。在LC正弦波滤波器中增加额外的电阻器是抑制谐振的有效方法[20],此种方法被定义为无源阻尼法,但电阻器的引入不可避免地给系统带来额外有功功率损耗,降低了系统效率。

图1 带LC正弦波滤波器的IPMSM驱动系统
Fig.1 Drive system of IPMSM with LC sinusoidal filter
为了减小功率损耗,有源阻尼法通过在控制器中引入虚拟的电阻,在无需增加额外损耗的情况下即可实现抑制谐振的目的。文献[13-14]针对带有LC正弦波滤波器的感应电机驱动系统,提出了一种电感电流反馈有源阻尼方法,通过在电感上串联虚拟电阻的方式抑制谐振。文献[15]研究了基于电容电压补偿的有源阻尼的谐振抑制方法,将电容电压与有源阻尼系数的乘积叠加在逆变器输出电压指令上,其控制效果相当于在电容支路串联一个虚拟电阻。文献[16]研究了一种电容电流反馈有源阻尼(Capacitor- Current-Feedback-Active-Damping, CCFAD)方法,将电容电流与有源阻尼系数的乘积叠加在逆变器输出电压指令上,相当于在电容支路并联一个虚拟电阻。针对带有LCL正弦波滤波器的永磁同步电机驱动系统,文献[17]在同步旋转坐标系下研究了CCFAD方案,并提出了一种新型的电流解耦策略。此外,还有学者提出了一些新型低损耗谐振抑制方法,如文献[18]研究了模型预测电流控制器中有源阻尼控制器的设计方法。文献[19]通过优化脉宽调制的延时时间来确保带有LC正弦波滤波器的电机驱动系统稳定性,但实现方式较为复杂。
在带有LC正弦波滤波器的IPMSM电流控制器中引入有源阻尼策略时,电流环所采用的比例积分(Proportional Integral, PI)控制参数与有源阻尼系数的设置对系统的稳定性至关重要。然而,现有文献对于带有LC正弦波滤波器的交流电机电流控制器谐振抑制参数设计的研究成果较少。文献[13-15]针对感应电机,给出了在特定PI控制器参数的基础上有源阻尼系数的设计方法,未充分考虑PI控制器参数与有源阻尼系数的耦合影响机理。PI控制器参数、有源阻尼系数与IPMSM参数和LC正弦波滤波器参数之间相互耦合,如果控制器参数设置不合理,系统的谐振现象将无法得到有效抑制[13],这会导致系统产生很高的电压和电流,给系统的运行带来极大的风险。
针对上述问题,本文分析了采用矢量控制时带有LC正弦波滤波器的IPMSM控制系统的电流环谐振产生机理,确定了影响系统稳定性的主要因素。研究了带有LC正弦波滤波器的IPMSM电流控制器谐振抑制参数设计方法,分析了含有CCFAD的电流控制器的频率特性,通过频域稳定判据分析了PI控制器参数、有源阻尼系数、LC正弦波滤波器参数与IPMSM参数对系统谐振现象的影响机理,给出了电流控制器谐振抑制参数设计方法。实验结果验证了所提方法的有效性。
LC正弦波滤波器在同步旋转坐标系中的数学模型如下。
 (1)
(1)
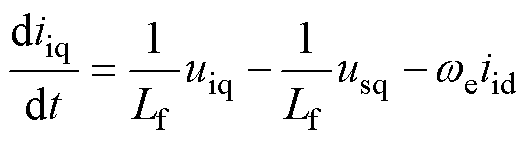 (2)
(2)
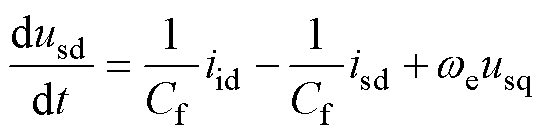 (3)
(3)
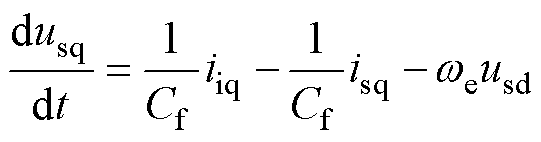 (4)
(4)
式中,Lf和Cf分别为LC正弦波滤波器的电感和电容;uid和uiq为LC正弦波滤波器在d、q轴上的输入电压;usd和usq为IPMSM在d、q轴上的输入电压;iid和iiq为LC滤波器在d、q轴上的电流;isd和isq为IPMSM在d、q轴上的电流;we为IPMSM的转子电角速度。
IPMSM在同步旋转坐标系下的数学模型为
 (5)
(5)
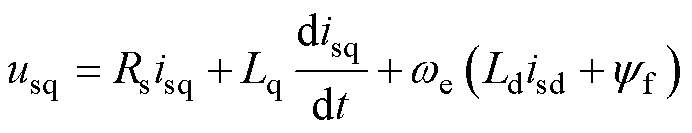 (6)
(6)
式中,Rs为定子绕组电阻;Ld和Lq为IPMSM在d、q轴上的电感;yf为IPMSM的永磁体磁链。
根据式(1)~式(6),将定子绕组电阻产生的压降和交叉耦合项作为控制系统扰动源,可将LC滤波器和IPMSM组成的系统简化为图2所示等效电路。
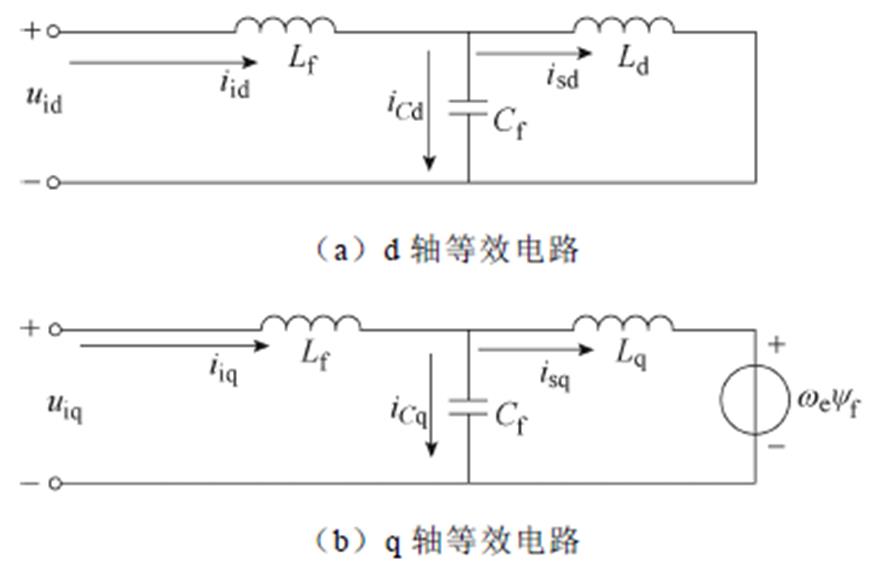
图2 带LC正弦波滤波器的IPMSM控制系统等效电路
Fig.2 Equivalent circuit of IPMSM control system with LC sinusoidal filter
图2b所示的q轴等效电路模型在s域中的传递函数可以描述如下。
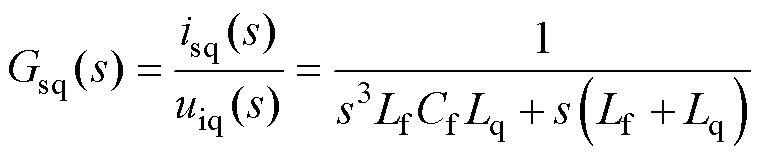 (7)
(7)
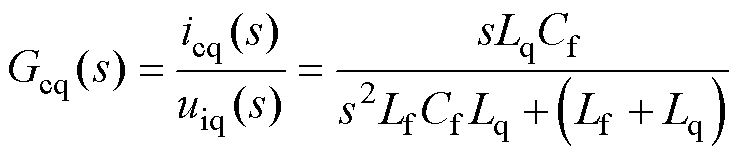 (8)
(8)
 (9)
(9)
控制系统的q轴等效电路谐振频率可表示为
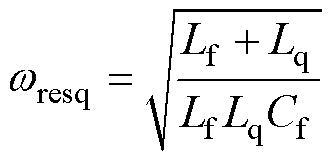 (10)
(10)
图3展示了在未引入有源阻尼情况下带有LC正弦波滤波器的IPMSM的电流环控制架构。三相逆变器侧电流定义为iia、iib与iic,电机侧三相电流定义为isa、isb与isc。控制系统电流环的目标是调节IPMSM的电流,因此电流环的控制目标为电机侧三相电流经过坐标变换转化而来的d、q坐标系下的电流isd与isq,其参考值为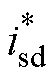 和
和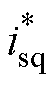 。
。

图3 不采用有源阻尼的电流控制器架构
Fig.3 Current regulator architectures without active damping
当控制系统电流控制器采用如图4所示的架构时,其谐振频率对系统的稳定性会产生影响。图中kp和ki分别为PI控制器的比例和积分系数,对于图4建立的电流控制回路,其开环传递函数为
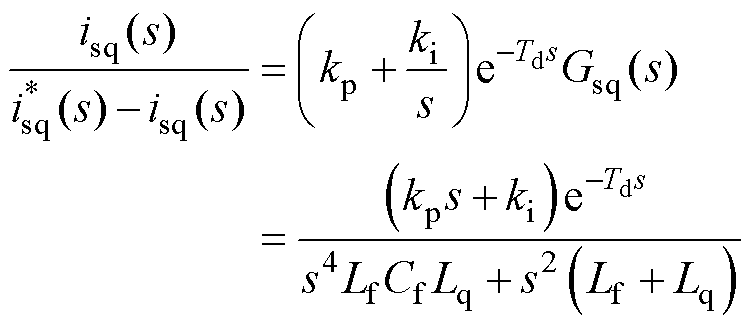 (11)
(11)
式中,Td为系统延迟时间。

图4 q轴电流反馈的控制结构
Fig.4 Current feedback control structure of q axis
根据Nyquist稳定性判据,当系统满足式(12)时,系统可以达到稳定。
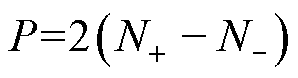 (12)
(12)
式中,P为开环传递函数中具有正实部的极点数;N+表示当幅频特性曲线大于0dB时相频特性曲线正穿越(2k+1)p 线的次数;N-表示当幅频特性曲线大于0 dB时相频特性曲线负穿越(2k+1)p 线的次数。
根据图5所示的q轴电流反馈环路开环传递函数Bode图,相频特性曲线在谐振频率处穿过-p,此时由于系统谐振的影响会产生远高于0 dB的幅频特性曲线,从而使系统无法达到稳定。
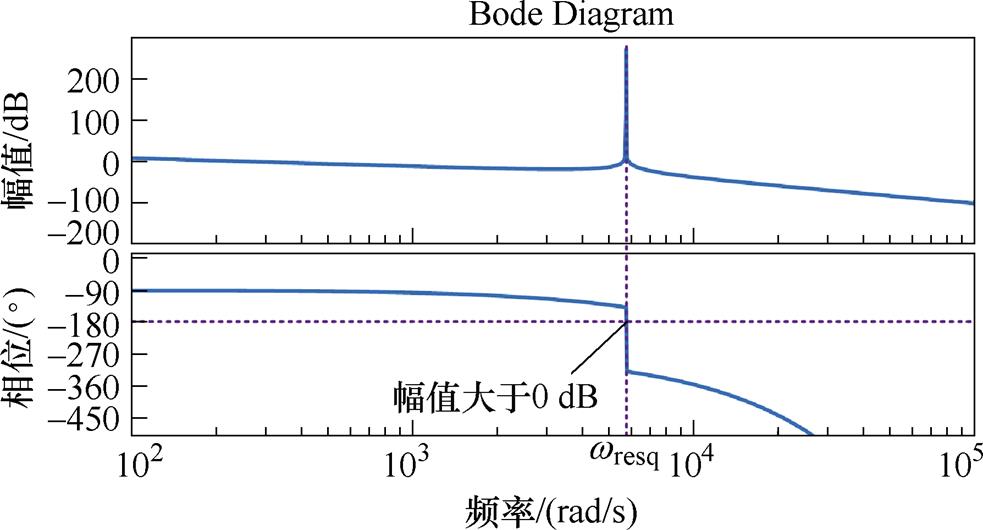
图5 开环传递函数的Bode图(Lq=2.05 mH, Lf =0.5 mH, Cf =75 mF, kp=3.7, ki=92.4)
Fig.5 Bode plot of open loop transfer function(Lq=2.05 mH, Lf =0.5 mH, Cf =75 mF, kp=3.7, ki=92.4)
根据上述分析,为了保证IPMSM在带有LC正弦波滤波器时可以稳定运行,在系统的电流调节器中加入基于电容电流的比例反馈环节作为系统的有源阻尼。所采用方法的总体控制结构如图6所示,其中k为有源阻尼系数。
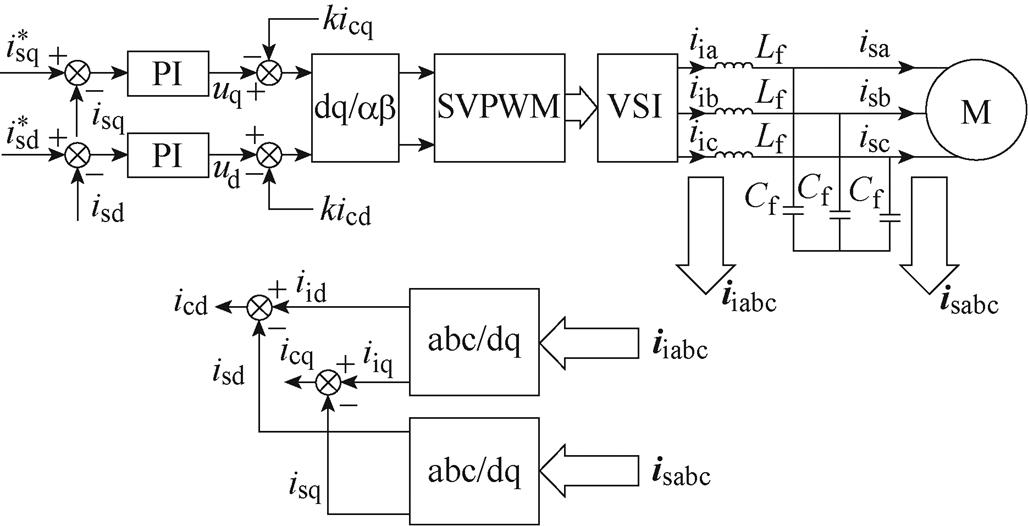
图6 含有CCFAD的电流控制器架构
Fig.6 Current regulator architectures with CCFAD
谐振现象导致系统不稳定的主要原因是开环传递函数在谐振频率处的幅频特性曲线远高于0 dB,可通过引入电容电流比例反馈来抑制。图7展示了基于电容电流有源阻尼的电流调节器结构,相应的开环传递函数为
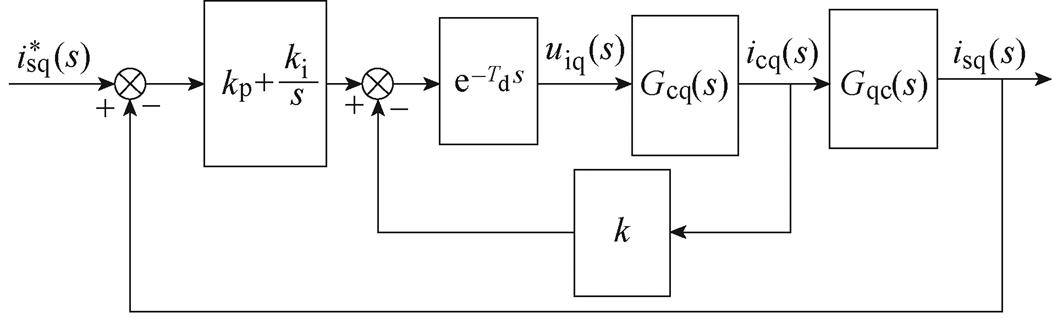
图7 含有CCFAD的q轴电流控制环
Fig.7 Current loop of q axis with CCFAD
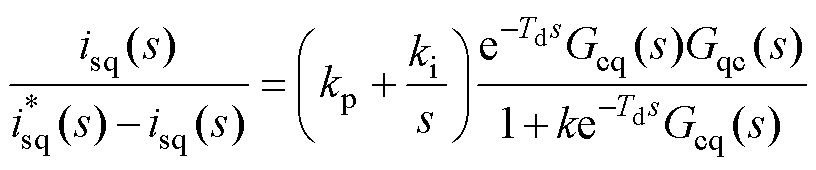
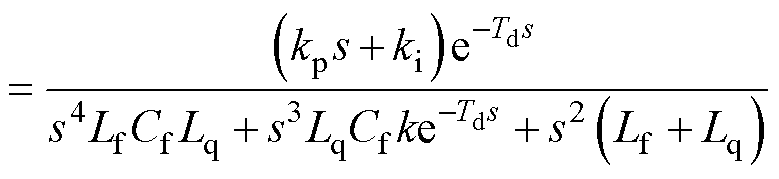 (13)
(13)
通过比较式(11)和式(13)的分母,后者明显多了一个额外的s3项,其可以提供阻尼将不稳定的极点移动到虚轴的左半平面,从而保证系统的稳定性。
图8给出了式(13)中开环传递函数的Bode图,其中所用的参数与图5相同。从图中可以看出,通过有源阻尼法可以很好地抑制谐振频率附近的幅频特性曲线。因此,可以通过选择合适的有源阻尼系数k以使系统避免急剧穿越-p 线,从而保证系统的稳定运行。
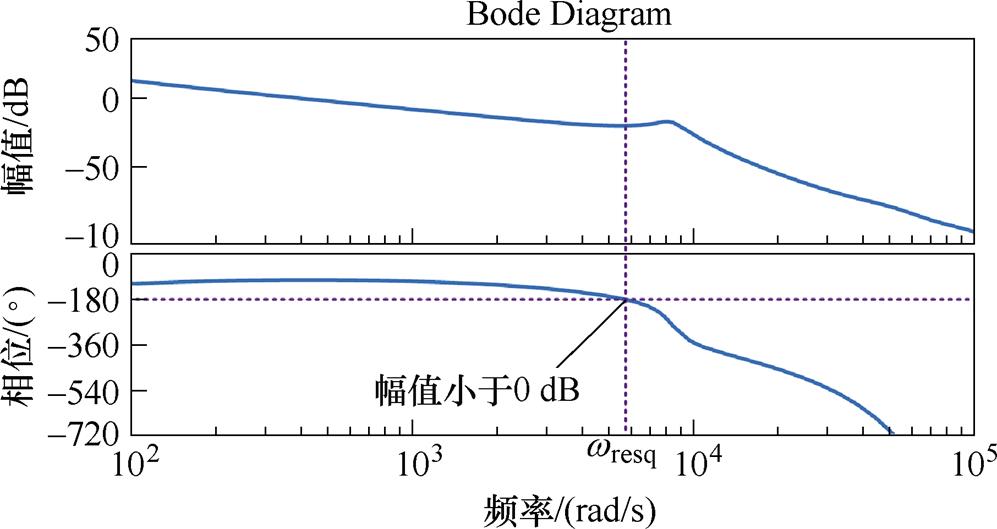
图8 含有CCFAD的q轴电流控制环的开环传递函数Bode图
Fig.8 Bode plot of open looptransferfunction for current controller for q axis with CCFAD
根据上述分析,CCFAD可以有效地抑制系统谐振现象,从而保证系统稳定性。然而,在设计控制系统过程中,当PI控制器参数与有源阻尼系数设置不当时,系统的谐振现象无法得到有效的抑制,控制系统的稳定性也无法得到保证。
根据以上分析,对于含有CCFAD的电流控制器,需要合理设计控制器参数才能起到较好的谐振抑制效果。因此,需要对电流控制器参数设计进行研究。为了更好地评估电流控制器性能与各参数之间的关系,本文进行了一些近似变换来降低系统的复杂程度。
首先,引入Taylor展开式可以进行如下近似变换:
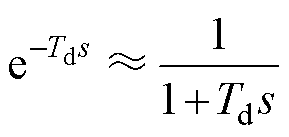 (14)
(14)
当系统频率高于wL=ki/kp时,PI控制器中的积分作用很小,根据图9所示的Bode图,可以将此种情况下的PI控制器简化为kp的形式。

图9 PI控制器Bode图
Fig.9 Bode plot of PI controller
图7所示的控制系统开环传递函数在不同条件下的Bode图如图10所示。图10a表明有源阻尼系数k仅在谐振频率附近对频率响应有显著影响。因此,在研究谐振频率左侧的系统频率响应时参数k对系统的影响可以忽略。由图10b可知,当k值不变,PI控制器kp的增加会导致系统幅频特性曲线上升,从而致使截止频率不断接近谐振频率,最终使系统陷入失稳状态。图10c表明实际系统与电感串联系统在低于谐振频率的频段具有类似的幅频特性曲线。当控制系统带有LC正弦波滤波器后,大于谐振频率的谐波幅值被有效限制,因此dq轴电流主要由直流分量和小于谐振频率的谐波分量组成。根据图10c,对于dq轴电流所在的频率范围,简化后的电感Lf +Lq串联系统与原系统具有相同的幅频特性。
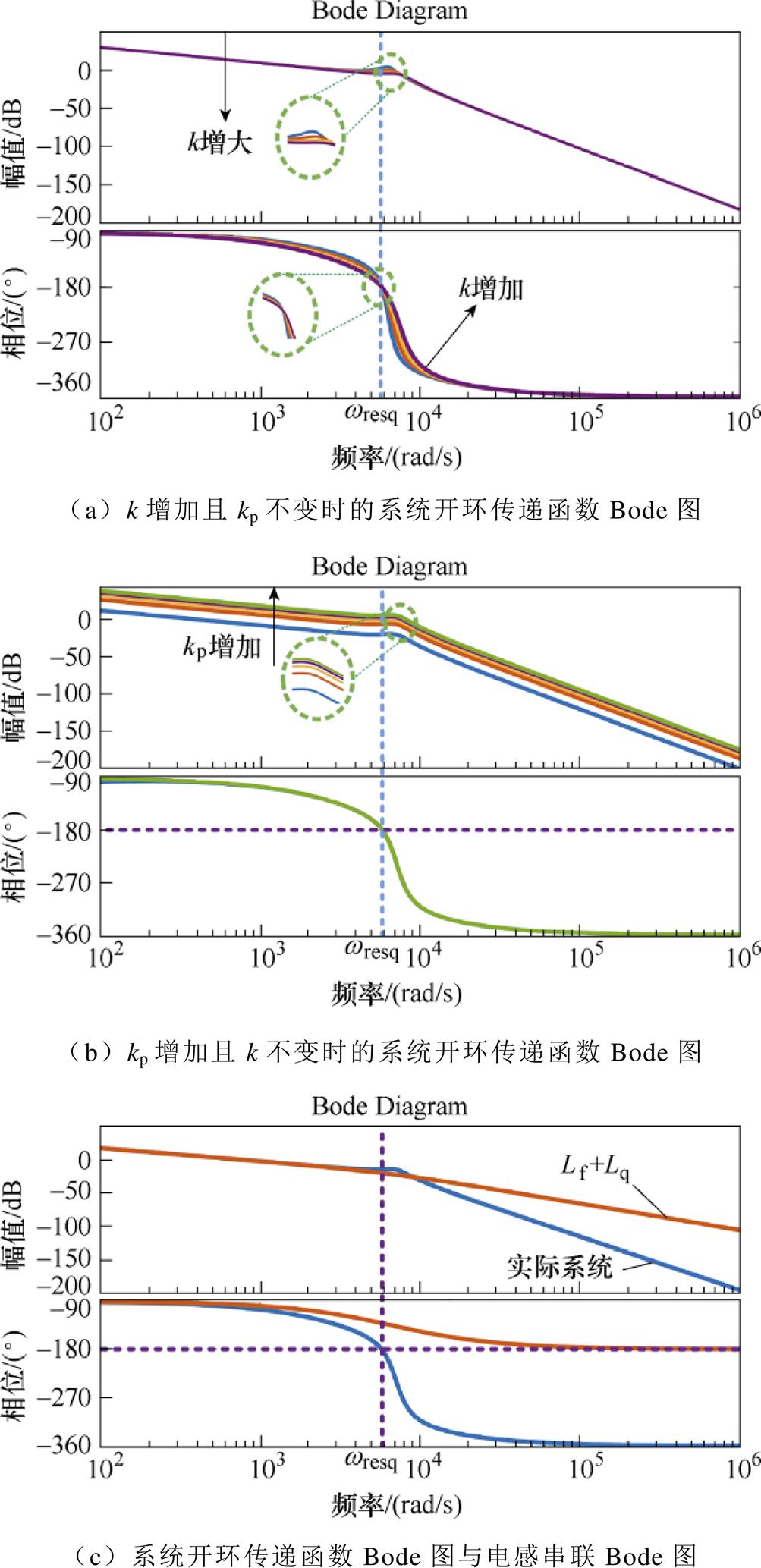
图10 不同条件下系统开环传递函数Bode图
Fig.10 Bode plot of open looptransferfunction under different conditions
因此,可以将原系统简化为电感串联简化分析,控制系统控制结构可简化为图11所示的电感串联模型的电流调节器结构。此种情况下,PI控制器中的积分增益对高于wL频率范围影响较小,为简化系统分析时PI控制器可以简化为kp。此时,系统的截止频率可以表示为
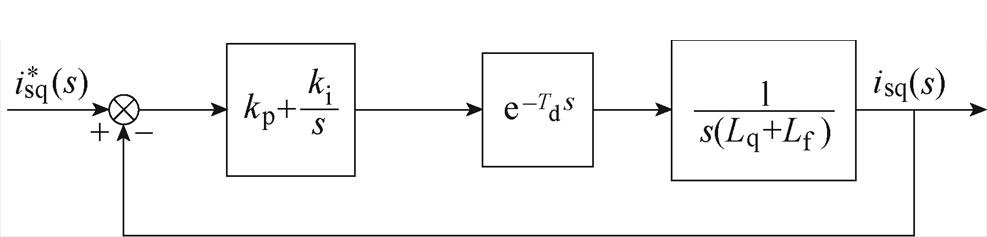
图11 电感串联模型的电流调节器结构
Fig.11 Current regulator architectures with inductance series model
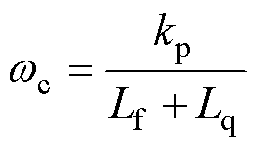 (15)
(15)
在图10c中,当控制系统简化为电感Lf +Lq串联系统时,基于有源阻尼的控制系统与简化后的电感串联系统的幅频特性相同,但是原系统的相频特性较简化的系统,其相位滞后性随着频率的升高而变大,因此需要对两者的相频特性的差异化进行处理。文献[21]在忽略积分对高频段影响的同时将系统的截止频率作为谐振频率wresq的一部分(wc= awresq)并与系统阻尼因子共同建立了控制系统在截止频率处的相位滞后的关系,通过调节kp参数将系统的截止频率设置为wc=0.25wresq可以兼顾电流调节器的响应性能。PI控制器的积分增益ki可以通过系统的相位裕度确定。图11的系统开环传递函数为
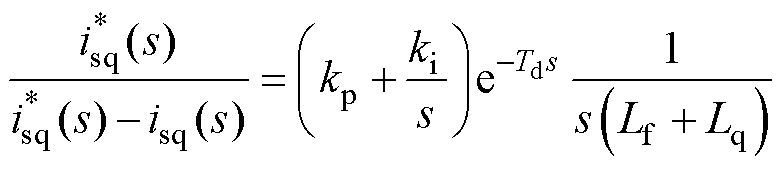 (16)
(16)
当系统设置合适的比例增益kp后,相位裕度g与积分增益ki之间的关系可表示为
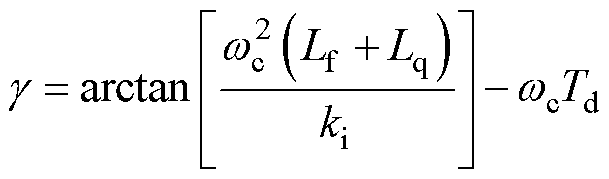 (17)
(17)
进一步,设置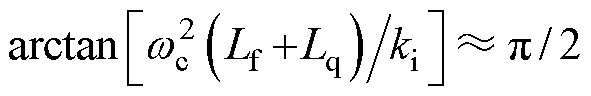 (89°)以使得系统获得最大的相位裕度,因此ki计算式为
(89°)以使得系统获得最大的相位裕度,因此ki计算式为
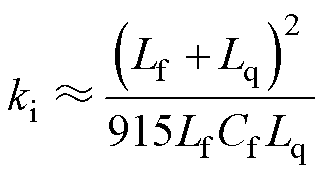 (18)
(18)
电容电流比例反馈增益k与PI控制器的比例增益kp相关,因为二者均影响谐振频率附近的频率响应。控制系统的闭环传递函数可以表示为
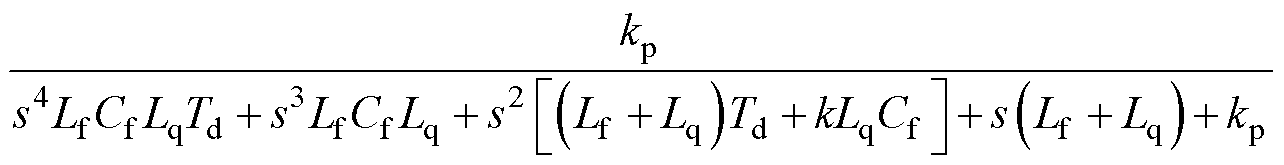 (19)
(19)
根据Routh稳定性判据,可以得出k满足式(20)时系统将保持稳定,其可作为参数k的下限值,即
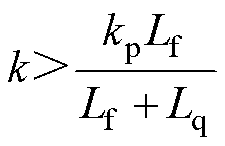 (20)
(20)
在实际应用中存在多种实际问题会影响系统的稳定性与性能。首先,实际系统的运行是基于数字控制系统实现的,这会对系统的稳定性和性能产生一定的影响。采用零阶保持(Zero Order Hold, ZOH)变换将式(8)、式(9)转化为离散域模型,即
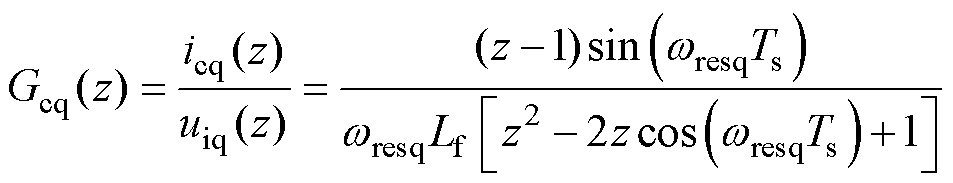 (21)
(21)
式中,Ts为采样周期。
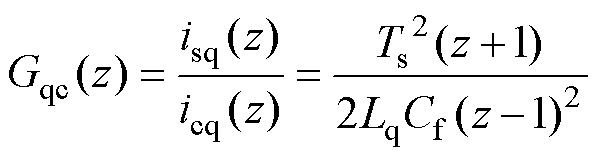 (22)
(22)
在离散域下,含有CCFAD的q轴电流控制器的结构框图如图12所示。

图12 含有CCFAD的q轴电流控制器在z域的框图
Fig.12 The block diagram of the current controller for q axis with CCFAD in z-domain
对于图12中的控制系统,闭环传递函数为
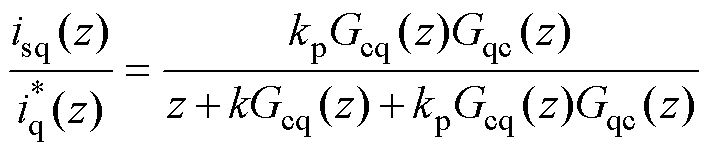 (23)
(23)
为了获得系统关于k参数的根轨迹,将其转化为等效开环传递函数,有
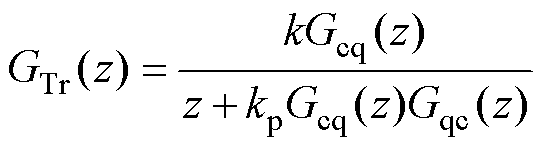 (24)
(24)
图13给出了控制系统在不同kp值下关于参数k的根轨迹图。可以看出,系统根轨迹进入单位圆时的k值近似等于式(20)得出的下限值结果。同时,通过比较图13a、图13b和图13c可以看出,随着kp的增加,系统根轨迹离开单位圆的极点将略微向着Zspecial的左侧移动。其中图13a中的特殊极点Zspecial可以表示为
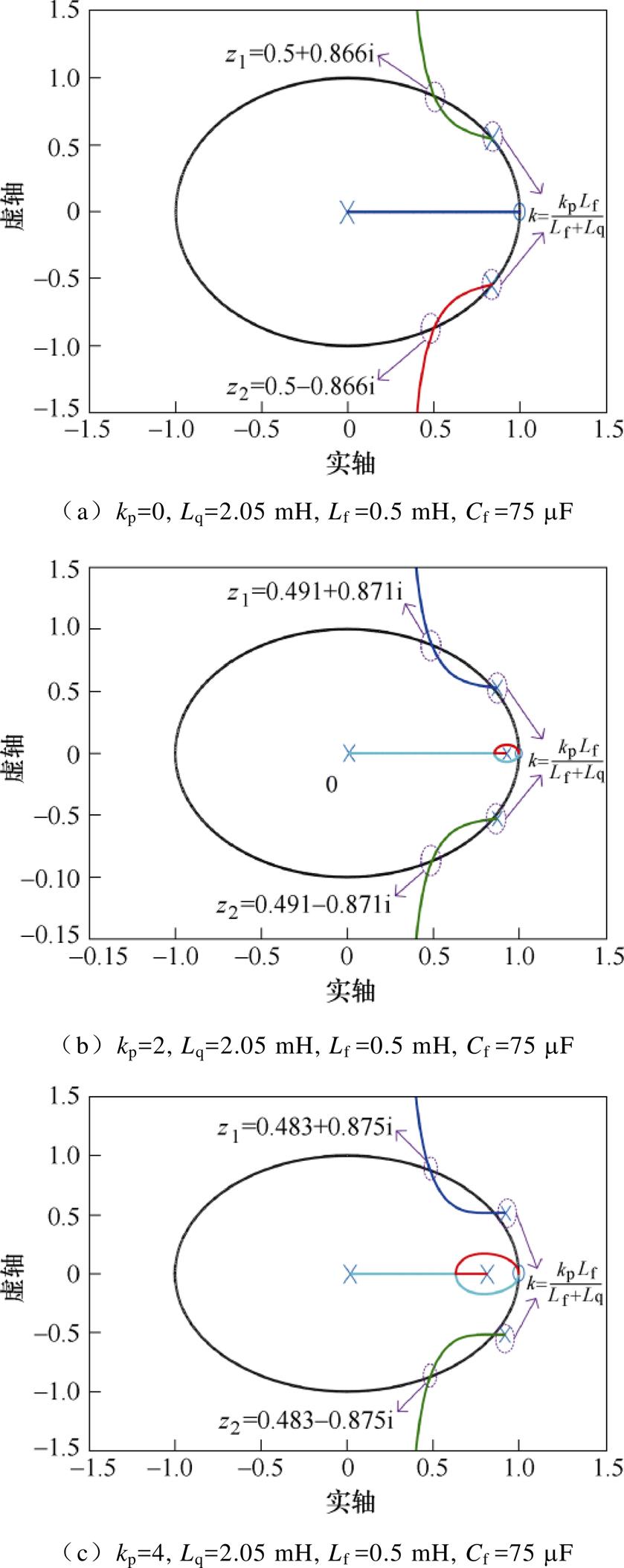
图13 不同kp时有源阻尼系数k的根轨迹图
Fig.13 Root locus of active damping proportional gains with different kp
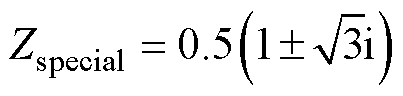 (25)
(25)
图13a中离开单位圆的特殊极点可以代入系统闭环传递函数的特征方程得到k参数的另一个限制条件。因此可以得出结论,对应于系统Zspecial极点的k值将确保控制系统在不同的kp条件的稳定性。同时也表明,当kp=0时,Zspecial点可以近似用来确定有源阻尼系数的另一个约束条件,因为随着kp从0开始增大,离开单位圆的极点会出现在Zspecial的左侧,此时Zspecial点必然出现在单位圆内部。
根据上述分析,k参数的上限值可以通过将极点Zspecial代入系统的特征方程得到,结果为
 (26)
(26)
在实际系统应用中,可以在离线确定电流控制器中PI控制器kp与ki参数后,根据式(20)与式(26)进一步确定有源阻尼增益参数k的上、下限。式(26)形式较为复杂,但当电流环kp确定后,在已知的电机和滤波器参数下,可以采用离线计算的方式确定k的上限值,无需采用数字处理器实时计算,因此,所提出的算法能够实际应用。
按照所提出的设计方法可以保证系统的稳定性。将方法中的Lq用Ld替代,可以同样得到d轴控制系统的参数整定结果。
通过上述分析算法可以构建基于有源阻尼的带有LC滤波器内置式永磁同步电机矢量控制系统框图,如图14所示。其中矢量控制所需要的转子位置角通过编码器获得,iia、iib为测量的逆变器侧电流,isa、isb为测量的电机侧电流,qe为电机转子电角度。同时,在实验中由于谐振所带来的高电压与大电流会对硬件电路产生损害,因此在谐振现象出现的瞬间会立即触发过电压、过电流保护,实验中无法做出谐振效果图。故本文采用仿真辅助实验的手段验证系统谐振现象以及本文所提参数设计对系统谐振抑制的有效性。
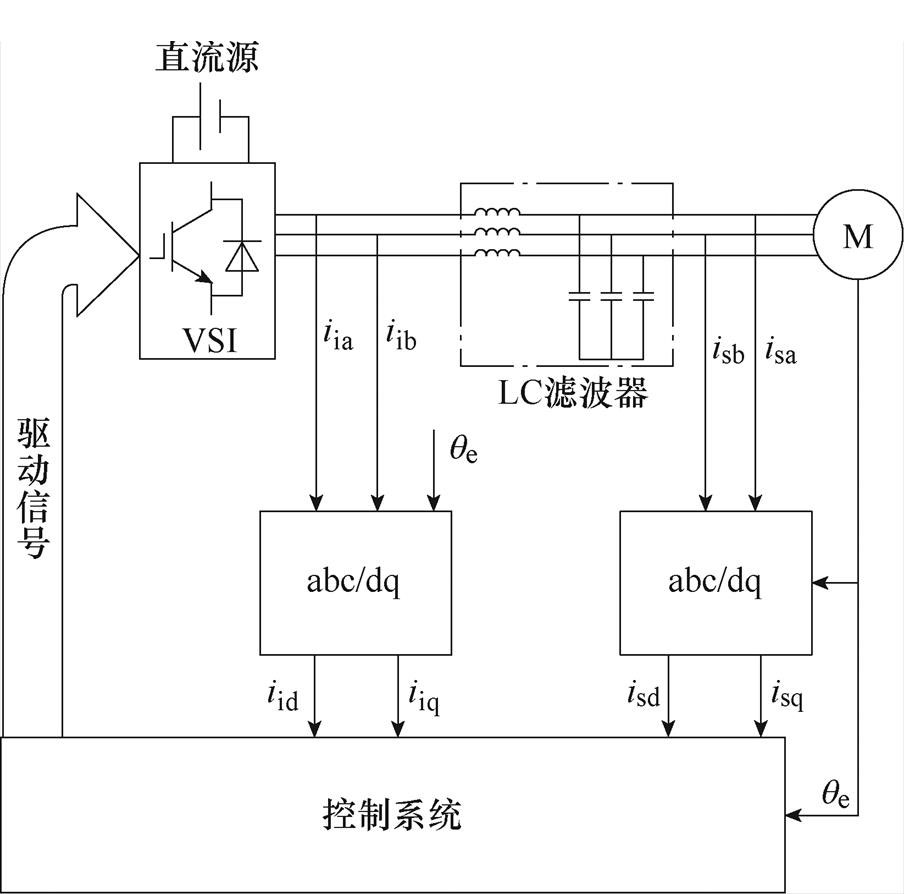
图14 带有LC滤波器的IPMSM控制系统框图
Fig.14 Block diagram of IPMSM control system with LC filter
IPMSM、LC正弦波滤波器和电流控制器参数见表1,其中PI控制器的参数通过式(15)和式(18)推导得到。此外,有源阻尼系数k的取值范围通过式(20)和式(26)得到。
实验是在由VSI供电的带有LC滤波器IPMSM系统中实施,本文所提出的算法通过型号为TMS320F28377D的数字处理器实现,系统主要参数设置见表1。
搭建的实验平台如图15所示,其中包括基于型号为TMS320F28377D的主控电路板、电压源型逆变器、电流传感器、IPMSM和LC滤波器。
表1 控制系统参数
Tab.1 Parameters of control system

参 数数 值 Lf/mH0.5 Cf/mF75 Ld/mH0.95 Lq/mH2.05 Rs/W0.1 yf/Wb0.225 开关频率/kHz10 采样频率/kHz10 d轴PI参数kp, ki2.3, 64.5 q轴PI参数kp, ki3.7, 92.4 d轴k上限、下限3.5、0.8 q轴k上限、下限3.76、0.72

图15 实验平台
Fig.15 Experimental platform
图16和图17给出了基于CCFAD的IPMSM控制系统的稳态性能,其中展示了IPMSM带67.5 N×m负载并且运行于50 Hz和100 Hz时的逆变器侧相电压uia、电机侧相电压usa以及电机电流isa波形。
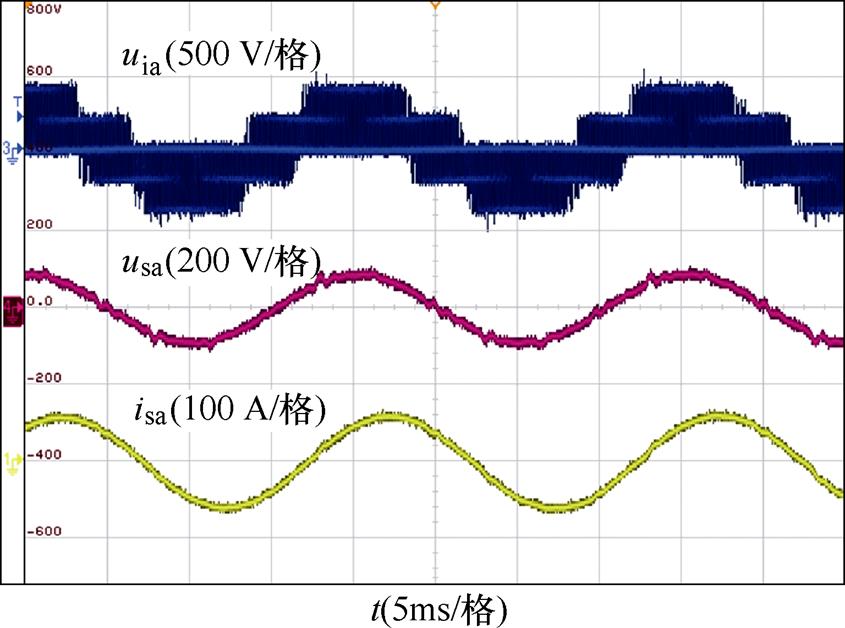
图16 uia、usa和isa在fe=50 Hz时的波形
Fig.16 Waveforms of uia, usa and isa with fe=50 Hz

图17 uia、usa和isa在fe=100 Hz时的波形
Fig.17 Waveforms of uia, usa and isa with fe=100 Hz
从图16和图17中可以看出,逆变器侧电压可以通过LC滤波器在电机端转化为正弦波。PWM算法引起的电压信号中的高du/dt可以在不同的转速下得到很好的抑制。
图18~图20给出了变转速和变负载情况下的动态实验结果。图18和图19展示了在电机运行频率为50 Hz与100 Hz时负载突变条件下的的电机运行频率fe、两相旋转坐标系下的电机定子电流isd、isq以及电机相电压usa波形。图18b、图18c与图19b、图19c展示了波形的局部放大图。
从图18和图19中可以看出,当电机所带负载突变时电机转速可以跟随参考值并且没有振荡现象。对于图18,在负载转矩突增时,IPMSM运行频率跌落仅为7.53 Hz,且在30 ms以内恢复稳态,在负载转矩突减时,IPMSM运行频率上升约6.71 Hz,且同样在30 ms以内恢复稳态。对于图19,在负载转矩突增时,IPMSM运行频率跌落仅为7.97 Hz,且在30 ms以内恢复稳态,在负载转矩突减时,IPMSM运行频率上升约7.86 Hz,且同样在30 ms以内恢复稳态。动态过程中,电机的d、q轴电流响应迅速且平稳,此时电机获得了良好的动态性能。在整个动态过程中,电机相电压可以很好地被转化为正弦波。
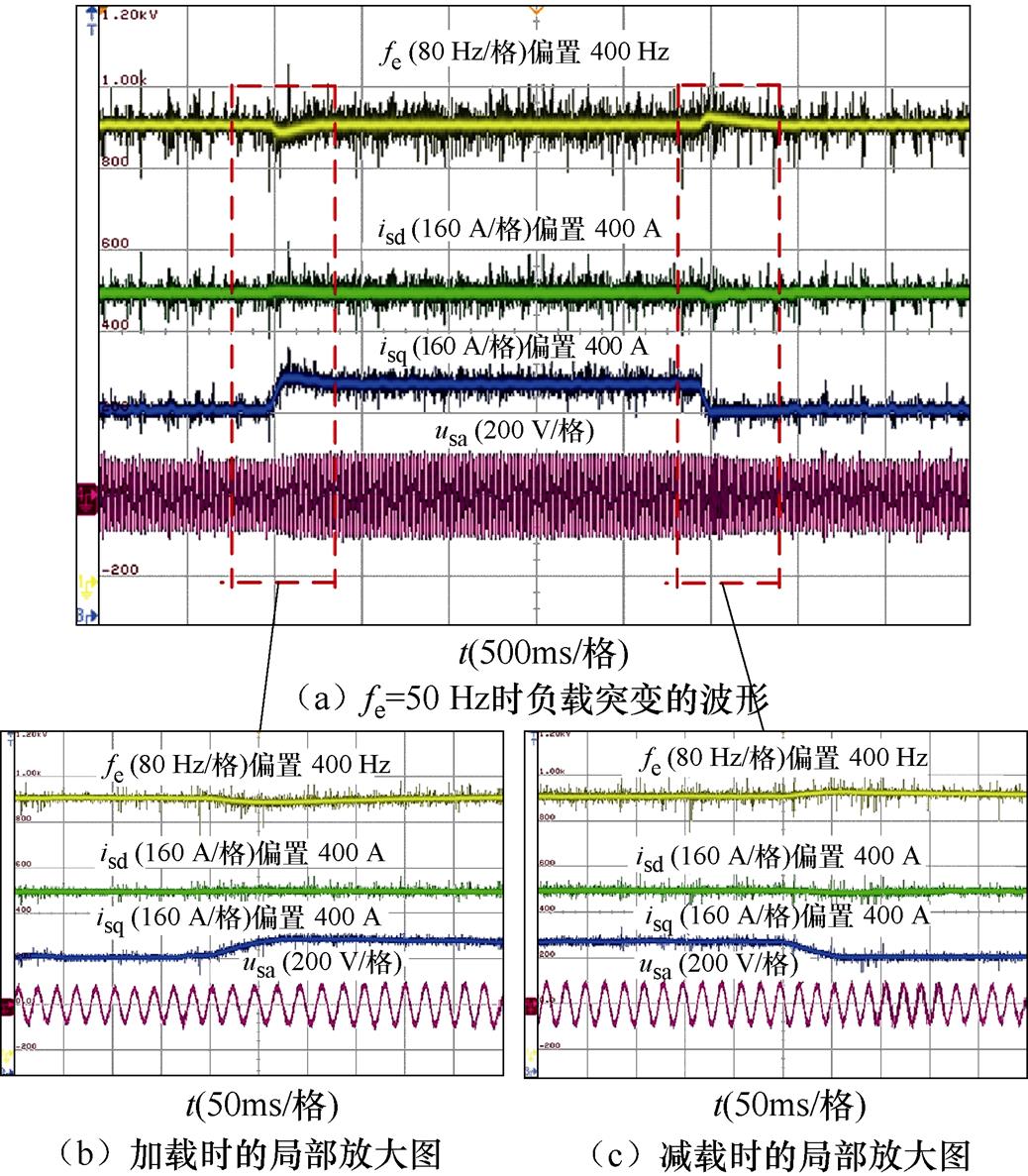
图18 fe、isd、isq和usa在fe=50 Hz时负载突变的波形
Fig.18 Waveforms of fe, isd, isq and usa with fe=50 Hz with sudden change of load

图19 fe、isd、isq和usa在fe=100 Hz时负载突变的波形
Fig.19 Waveforms of fe, isd, isq and usa with fe=100 Hz with sudden change of load
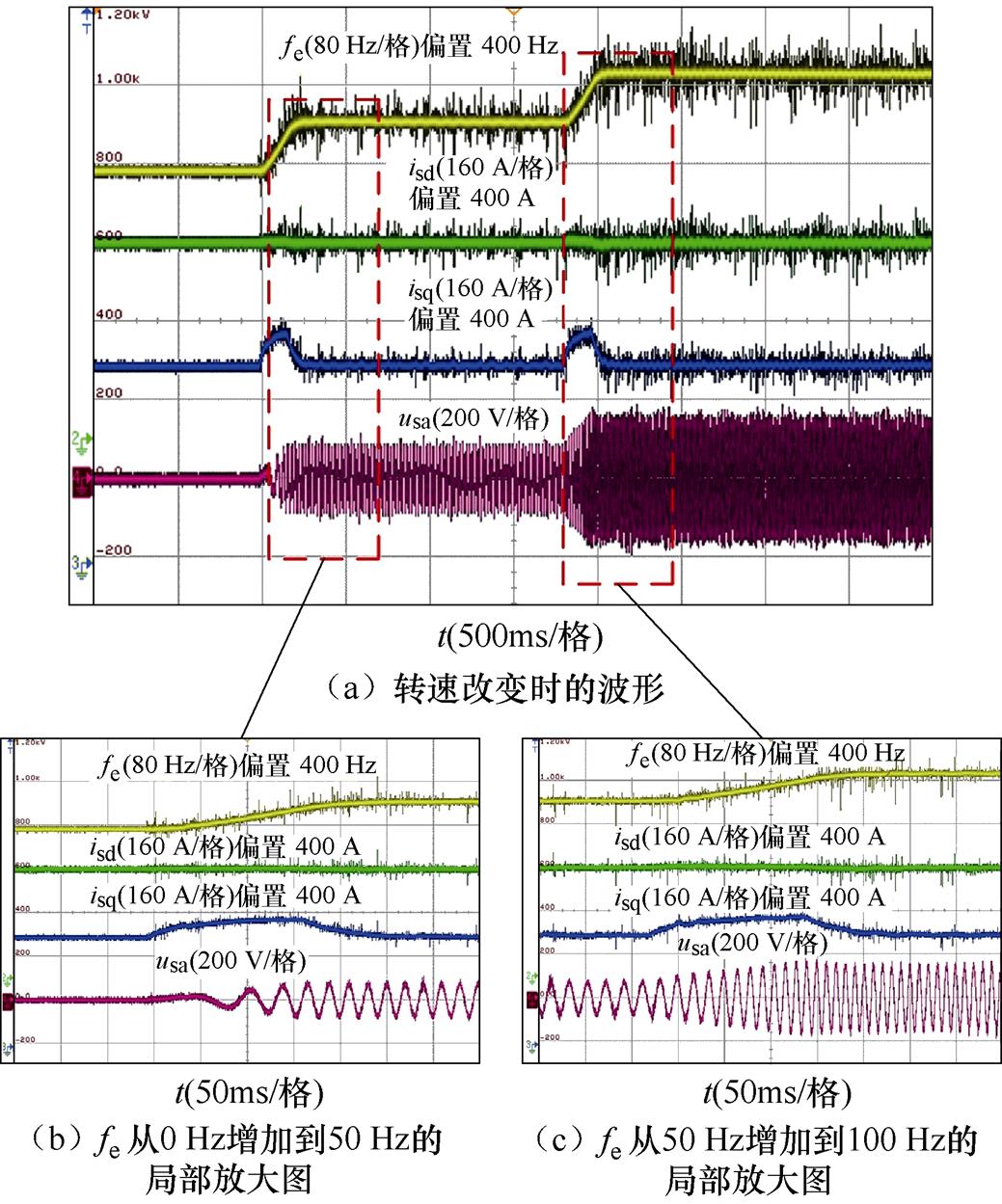
图20 fe、isd、isq和usa在改变转速时的波形
Fig.20 Waveforms of fe, isd, isq and usa at variable rotor speed
图20展示了起动过程中的fe、d、q轴电流以及相电压波形。电机fe从0 Hz加速到50 Hz再加速到100 Hz。图20b与图20c展示了波形的局部放大图。
从图20中可以看出,当电机处于起动过程中时,fe和d、q轴电流可以获得很好的跟随性能,并且此时的电机相电压也保持正弦波形。
图21展示了IPMSM带67.5 N·m负载并且运行于50 Hz时的电机定子dq轴电流isd、isq以及电机定子A相电流isa波形。从图21中可以看出,在保持电流环PI控制器参数不变的情况下,有源阻尼系数k先设置为边界值范围内的合适值,此时电机带载运行状态较好。然而,在正常运行过程中突然将有源阻尼系数k设置为低于下限值时,电机定子电流立即出现振荡现象,且在振荡发生的20 ms内迅速触发系统的过电流保护,电机立即停止运行。
图22展示了电机带载且正常运行时,系统突然将有源阻尼系数k设置为高于上限值时,电机定子电流中同样会出现振荡现象,并且呈现失控运行的状态,此时的电机无法正常运行。

图21 isd、isq和isa在减小k值时的波形
Fig.21 Waveforms of isd, isq and isa when decreasing the value of k
通过图21与图22效果图可以看出,当参数设计不满足论文提出的分析方法时,电机控制系统均会产生明显的振荡现象,影响电机的运行工作,最终使系统失去稳定运行状态。
因此通过在不同条件下的实验结果可以证明所提出电流控制器谐振抑制参数设计的有效性,采用本文所研究的谐振抑制参数设计方法可以使得带有LC正弦波滤波器的IPMSM具备优异的稳、动态调速性能。
本文针对带有LC正弦波滤波器的IPMSM采用矢量控制时的谐振现象进行了分析,并且研究了含有CCFAD的电流控制器参数对系统谐振现象的影响。在此基础上,研究了电流控制器谐振抑制参数设计方法,实验结果表明采用所提出的参数设计方法能使得IPMSM驱动系统能获得优异的稳态与动态性能。
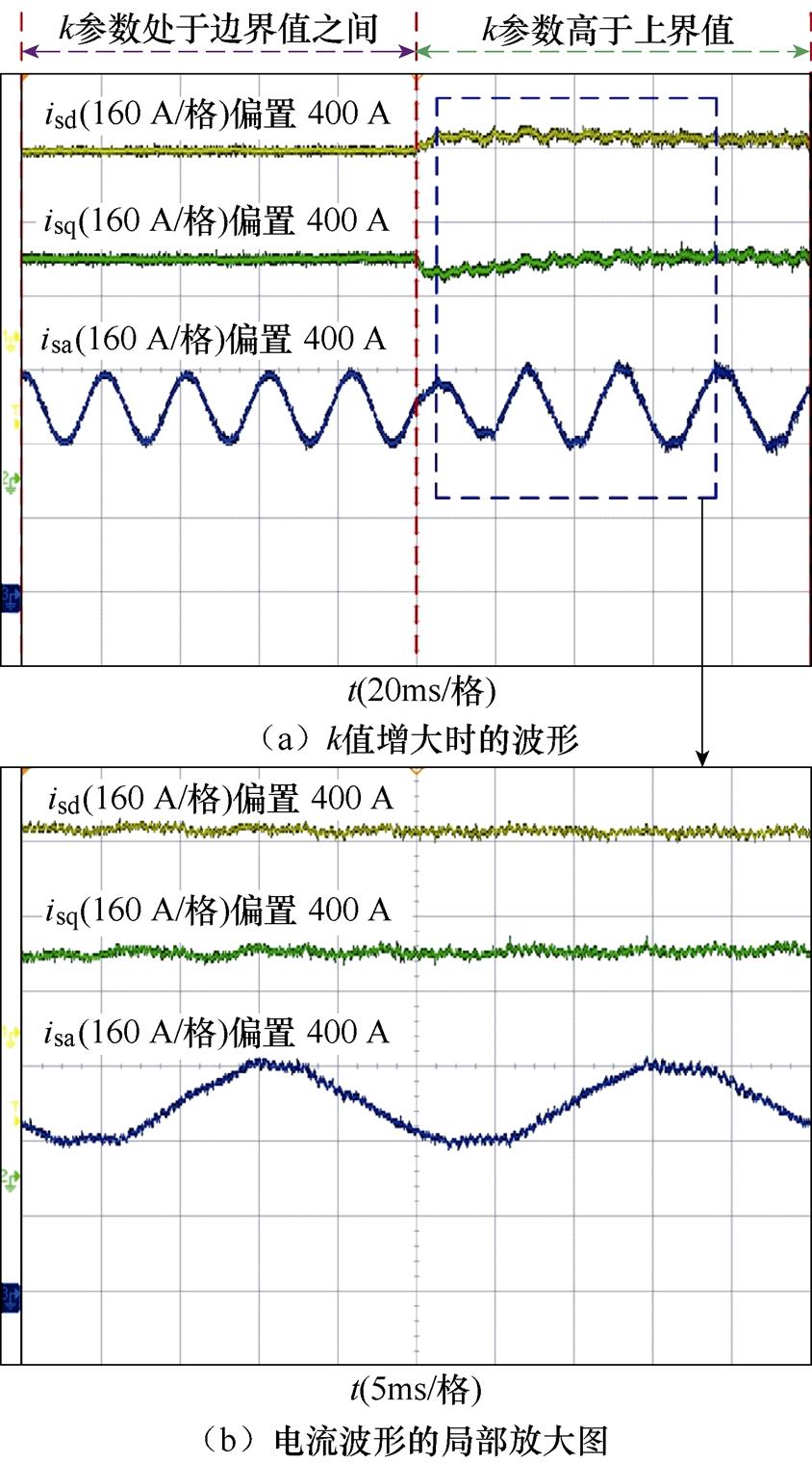
图22 isd、isq和isa在增大k值时的波形
Fig.22 Waveforms of isd, isq and isa when increasing the value of k
参考文献
[1] 鞠孝伟, 程远, 杨明亮, 等. SiC逆变器高频脉冲电压对Hairpin绕组绝缘安全的影响分析[J]. 电工技术学报, 2021, 36(24): 5115-5124.
Ju Xiaowei, Cheng Yuan, Yang Mingliang, et al. Influence analysis of high frequency pulse voltage of SiC inverter on insulation safety of hairpin winding[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5115-5124.
[2] 赵方伟, 王秀和, 赵文良, 等. 内置式永磁同步电机动态偏心故障下的轴电压解析分析和削弱[J]. 电工技术学报, 2022, 37(4): 837-848.
Zhao Fangwei, Wang Xiuhe, Zhao Wenliang, et al. Analysis and reduction of shaft voltage in interior permanent magnet synchronous motors under dynamic eccentricity fault[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 837-848.
[3] 段卓琳, 张栋, 范涛. SiC电机驱动系统传导电磁干扰建模及预测[J]. 电工技术学报, 2020, 35(22): 4726-4738.
Duan Zhuolin, Zhang Dong, Fan Tao. Modeling and prediction of electromagnetic interference in SiC motor drive systems[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4726-4738.
[4] Ganjavi A, Zare F, Kumar D, et al. Mathematical model of common-mode sources in long-cable-fed adjustable speed drives[J]. IEEE Transactions on Industry Applications, 2022, 58(2): 2013-2028.
[5] 姜艳姝, 于晓洋, 齐路路. 基于PWM长线驱动系统模型的变频器输出端RLC滤波器设计[J]. 中国电机工程学报, 2010, 30(36): 93-97.
Jiang Yanshu, Yu Xiaoyang, Qi Lulu. Design of inverter output RLC filter based on the model of PWM long drive system[J]. Proceedings of the CSEE, 2010, 30(36): 93-97.
[6] Velander E, Bohlin G, Sandberg Å, et al. An ultralow loss inductorless dv/dt filter concept for medium- power voltage source motor drive converters with SiC devices[J]. IEEE Transactions on Power Electronics, 2018, 33(7): 6072-6081.
[7] 高强, 徐殿国. PWM逆变器输出端共模与差模电压dv/dt滤波器设计[J]. 电工技术学报, 2007, 22(1): 79-84.
Gao Qiang, Xu Dianguo. Design of common-mode and differential-mode voltage dv/dt filter at PWM inverter output terminals[J]. Transactions of China Electrotechnical Society, 2007, 22(1): 79-84.
[8] 刘学忠, 徐传骧. PWM变频调速电动机端子上过电压的抑制[J]. 中国电机工程学报, 2001, 21(8): 84-88.
Liu Xuezhong, Xu Chuanxiang. Suppression of overvoltage acting on the terminal of PWM inverter- fed motor[J]. Proceedings of the CSEE, 2001, 21(8): 84-88.
[9] 肖烨然, 邵俊波, 邱长青. 基于正弦波滤波器的轮缘推进永磁同步电机无速度传感器控制[J]. 电网技术, 2021, 45(9): 3618-3626.
Xiao Yeran, Shao Junbo, Qiu Changqing. Speed sensorless control of rim driven PMSM based on sine wave filter[J]. Power System Technology, 2021, 45(9): 3618-3626.
[10] 赵仁德, 赵斌, 徐海亮, 等. 带LC滤波器的永磁同步电机控制系统及策略研究[J]. 电工技术学报, 2019, 34(增刊1): 79-86.
Zhao Rende, Zhao Bin, Xu Hailiang, et al. Research on control method of permanent magnet synchronous motor with LC filter[J]. Transactions of China Elec- trotechnical Society, 2019, 34(S1): 79-86.
[11] Xue Cheng, Zhou Dehong, Li Yunwei. Finite-control- set model predictive control for three-level NPC inverter-fed PMSM drives with LC filter[J]. IEEE Transactions on Industrial Electronics, 2021, 68(12): 11980-11991.
[12] Piippo A, Salomaki J, Luomi J. Signal injection in sensorless PMSM drives equipped with inverter output filter[J]. IEEE Transactions on Industry Applications, 2008, 44(5): 1614-1620.
[13] Mishra P, Maheshwari R, Patil D. Stabilization of rotor flux-oriented control of induction motor with filter by active damping[J]. IEEE Transactions on Industrial Electronics, 2019, 66(12): 9173-9183.
[14] Mishra P, Maheshwari R. A simple feedforward approach to stabilize VSI-fed induction motor with filter in RFOC[J]. IEEE Transactions on Industrial Electronics, 2020, 67(12): 10191-10201.
[15] Hatua K, Jain A K, Banerjee D, et al. Active damping of output LC filter resonance for vector-controlled VSI-fed AC motor drives[J]. IEEE Transactions on Industrial Electronics, 2012, 59(1): 334-342.
[16] Geng Weiwei, Zhang Zhuoran, Li Qiang. Analysis and experimental verification of a conventional inverter with output LC filter to drive ironless stator axial-flux PM motor[J]. IEEE Transactions on Transportation Electrification, 2021, 7(4): 2600-2610.
[17] Yao Yu, Huang Yunkai, Peng Fei, et al. Dynamic- decoupled active damping control method for improving current transient behavior of LCL- equipped high-speed PMSMs[J]. IEEE Transactions on Power Electronics, 2022, 37(3): 3259-3271.
[18] Walz S, Liserre M. Hysteresis model predictive current control for PMSM with LC filter considering different error shapes[J]. IEEE Open Journal of Power Electronics, 2020, 1: 190-197.
[19] Yang Ming, Lü Zekai, Xu Donglin, et al. Resonance suppression and EMI reduction of GaN-based motor drive with sine wave filter[J]. IEEE Transactions on Industry Applications, 2020, 56(3): 2741-2751.
[20] 陈希有, 颜斌, 徐殿国, 等. 变频器输出滤波器的模糊优化设计[J]. 中国电机工程学报, 2003, 23(8): 71-75.
Chen Xiyou, Yan Bin, Xu Dianguo, et al. Fuzzy optimization of inverter output filter in motor drive system[J]. Proceedings of the CSEE, 2003, 23(8): 71-75.
[21] Tang Yi, Loh P C, Wang Peng, et al. Exploring inherent damping characteristic of LCL-filters for three-phase grid-connected voltage source inverters[J]. IEEE Transactions on Power Electronics, 2012, 27(3): 1433-1443.
Abstract An interior permanent magnet synchronous motor (IPMSM) is usually powered by a voltage source inverter (VSI). The fast switching action of power switching devices leads to a large voltage change rate (du/dt), which brings about adverse effects that cannot be ignored, such as the increase of insulation stress of the motor, the induction of shaft voltage and shaft current, and the generation of prominent electromagnetic interference. In some particular industrial application scenarios, such as marine surveys, oil field drilling, and mining, the VSI installation location is far away from the IPMSM, and the “long-line effect” makes such adverse effects more prominent. LC sinusoidal filter can convert VSI output voltage into a sine wave, which applies to any cable length and can effectively solve the above problems. However, adding an LC sine wave filter increases the order of the system model. It will produce an inherent resonance phenomenon in the current loop, which poses a challenge to the current controller design of IPMSM.
With the flux-oriented control, resonance suppression can be achieved theoretically by introducing active damping (AD) into the current controller. When the AD is introduced into the IPMSM current controller with an LC sinusoidal filter, the setting of proportional-integral (PI) control parameters and AD coefficient used in the current loop is critical to the stability of the system. However, there are few research results on the resonance suppression parameter design of AC motor current controllers with LC sinusoidal filters. The PI controller parameters, AD coefficient, IPMSM parameters, and LC sinusoidal filter parameters are coupled. If the controller parameters are set unreasonably, the resonance phenomenon of the system will not be effectively suppressed, which will lead to high voltage and current in the drive system and bring great risks to the operation of the system.
In order to obtain a satisfactory resonance suppression effect and guarantee the control performance of the IPMSM with an LC sinusoidal filter, the parameters of the current controller must be reasonably designed. This paper studies the design method of resonance suppression parameters of the current controller for IPMSM with an LC sinusoidal filter and analyzes the frequency characteristics of the current controller with capacitor- current- feedback AD (CCFAD). In addition, the influence mechanism of the current proportional integral regulator, AD coefficient, LC filter parameters, and motor parameters on the system resonance phenomenon is analyzed through the stability criterion in the frequency domain. The design method of resonance suppression parameters of the current controller is accordingly given by the mathematical models in the s and zdomains. The experimental results show that using the proposed parameter design method, the IPMSM drive system can obtain excellent steady-state and dynamic performance.
The paper is organized as follows. The mathematical model of the IPMSM with LC sinusoidal filter is given, the resonance phenomenon and resonance suppression strategy based on CCFAD are analyzed, and the design method of the resonance suppression parameters of the current controller is proposed.
Keywords:LC sinusoidal filter, interior permanent magnet synchronous motor, proportional integral controller, active damping
吴 翔 男,1990年生,博士,讲师,研究方向为电力电子与电力传动。E-mail: wux@cumt.edu.cn(通信作者)
李 超 男,1996年生,硕士研究生,研究方向为永磁同步电机控制。E-mail: ts20130118p31@cumt.edu.cn
中图分类号:TM351
DOI: 10.19595/j.cnki.1000-6753.tces.221734
江苏省自然科学基金(BK20200652)和国家自然科学基金(52007190)资助项目。
收稿日期 2022-09-12
改稿日期 2022-11-23
(编辑 郭丽军)