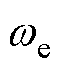为PMSM电磁角速度，S1～S6为逆变器各桥臂开关管。摘要 LC滤波型永磁同步电机（LC-PMSM）驱动系统因具有固有谐振峰而易引起电流环谐振失稳问题，且LC滤波器增大了系统阶数，导致常规线性控制方法结构和参数整定复杂。为解决上述问题，该文提出一种基于虚拟电阻有源阻尼的无差拍预测电流控制策略。考虑到逆变器侧电感电流可由控制器直接控制，首先，设计了一种结构简单的电感电流无差拍预测控制器，其能够实现对定子电流的间接矢量控制；其次，为了抑制系统固有谐振，进一步提出了一种基于滤波电容并联虚拟电阻的有源阻尼控制策略；最后，给出了系统的闭环稳定性分析及参数设计准则，并通过实验验证了所提控制方法的有效性。
关键词：永磁同步电机 LC滤波器 预测控制 虚拟电阻 有源阻尼
永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）驱动系统以其体积小、无需减速机、高功率密度及高可靠性等优点，近年来在煤炭工业广受关注。尤其是在井下刮板运输和深部煤层气开采等领域，PMSM常置于井下用于运输或排采，而逆变器则置于井上，二者通过长动力电缆连接[1]。但过长的动力电缆将引起行波反射效应，加剧电机过电压、轴承损坏和绝缘老化[2]。一种有效的解决方案是在逆变器输出侧安装LC滤波器，构成LC滤波型PMSM（LC-PMSM）[3]驱动系统。然而，LC滤波器与电机定子电感形成了三阶LCL滤波结构，不仅会增大系统模型阶数，其固有谐振峰亦将影响系统运行稳定性。因此，探索LC-PMSM驱动系统的高性能电流控制策略尤为关键。
目前，国内外学者针对LC滤波型交流电机系统的电流环谐振抑制问题展开了广泛研究[4-10]。文献[4]在传统比例积分（Proportional-Integral, PI）双闭环控制基础上额外增加了LC滤波控制环以抑制谐振，但其级联结构复杂、参数多且整定困难；为简化控制实现，文献[5]通过在LC滤波器中增加实体电阻，提出了一种无源阻尼谐振抑制策略，但实体电阻会增大系统有功损耗。为了在不影响系统效率的同时实现与无源阻尼类似的效果，有源阻尼控制方法应运而生[6-9]。文献[6]提出了一种电感电流反馈加基波电容电流补偿的控制策略，通过事先设计谐振点以抑制谐振，但其稳定性易受系统参数的影响；文献[7]提出了一种基于电感电流反馈的有源阻尼方法，对电感电流提取高频分量后生成阻尼项，其等效在电感上串联阻尼电阻；文献[8]提出了一种前馈方法来抑制谐振，即用电流环输出参考电压构造前馈项叠加至定子电流参考中；文献[9]提出了一种基于电容电流反馈的有源阻尼策略；此外，文献[10]通过调整控制延迟以满足系统稳定性要求，但其对采样频率要求高、实现复杂。上述文献均基于双闭环PI框架外加反馈环路设计，其电流内环不仅需要设计多个比例积分参数，且输出存在幅值和相位滞后、易引起超调等问题，因而动态响应欠佳、参数整定工作量大[11-12]。
模型预测控制（Model Predictive Control, MPC）以其实现简单、概念直观和多目标优化等优势在PMSM驱动领域应用广泛[13-14]。目前，国内外学者针对LC-PMSM驱动系统这一特殊应用场合下的MPC研究尚处于起步阶段[15-18]。文献[15]提出了LC-PMSM驱动系统的一种有限集MPC电流控制策略，但其仅考虑对PMSM定子电流的跟踪而未考虑系统的固有谐振抑制，故导致了稳态性能和运行稳定性不佳；文献[16]提出了一种基于滞环的有限集MPC策略以抑制谐振电流，在一定程度上改善了系统稳态精度；文献[17]提出了一种考虑LC滤波器多变量特性的有限集MPC策略，其具有一定的谐振抑制能力，但待设计的权重因子众多且整定复杂；进一步地，文献[18]提出了一种长时域多目标有限集MPC，提升了系统稳态精度，但计算量较大且对硬件要求较高。上述文献所设计的MPC策略均基于有限控制集架构，存在系统稳态性能差、开关频率不固定、谐波谱分布范围广等问题。这不仅不利于输出LC滤波器的设计，也容易激发未知的谐振动态[19]。此外，上述MPC方法亦未从理论的角度分析系统的闭环稳定性。
针对上述问题，本文提出了一种基于虚拟电阻有源阻尼的无差拍预测电流控制方法。首先，设计了一种电感电流无差拍预测控制器，其实现简单、开关频率固定且能够对定子电流进行间接矢量控制；其次，提出了一种基于滤波电容并联虚拟电阻的有源阻尼控制策略以抑制系统谐振；再次，给出了系统闭环稳定性分析及参数设计准则；最后，通过实验验证了所提控制方案的可行性。
LC-PMSM驱动系统结构如图1所示。图中，Vdc为直流母线电压，Lf、Cf分别为滤波电感和电容，vi、if、vs和is分别为逆变器输出电压、电感电流、电容电压和定子电流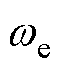，为PMSM电磁角速度，S1～S6为逆变器各桥臂开关管。
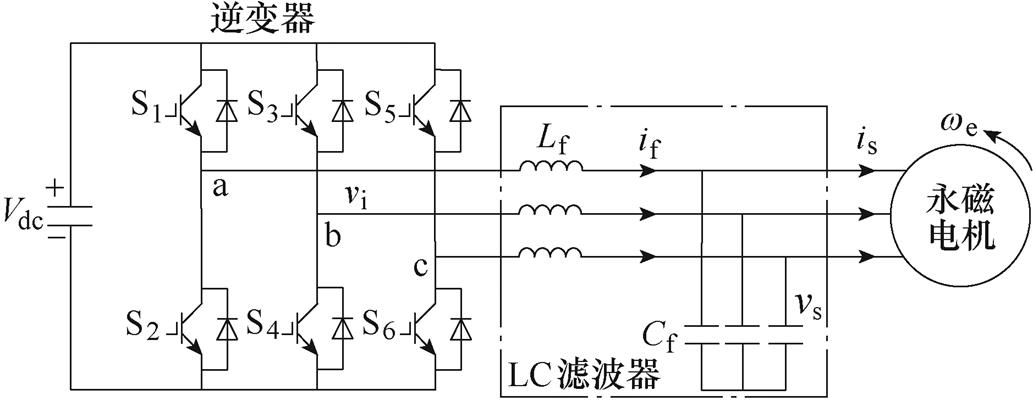
图1 LC-PMSM驱动系统结构
Fig.1 Structure of an LC-PMSM drive system
基于图1，可建立LC滤波型表贴式PMSM驱动系统在连续时间域下的状态空间方程为
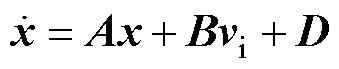（1）
其中
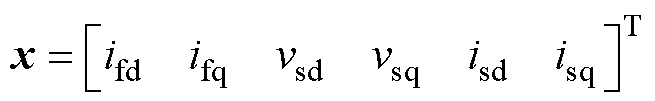
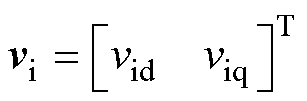
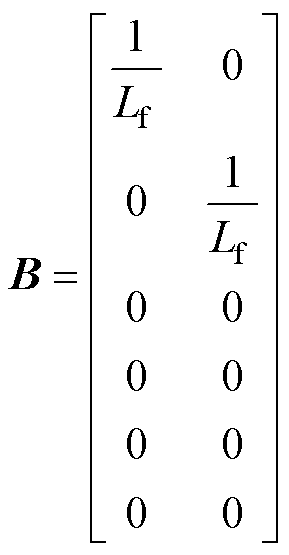
式中，Rf为Lf的寄生电阻；下标d、q分别表示dq旋转坐标系下的状态变量；Rs、Ls和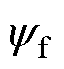
分别为表贴式PMSM的定子电阻、定子电感和转子磁链。
假设系统采样时间为Ts，则可利用零阶保持器对式（1）进行精确离散化，进而得到系统的离散化状态空间模型为
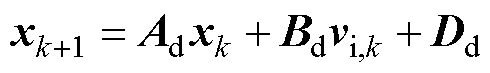（2）
其中
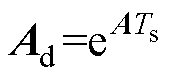
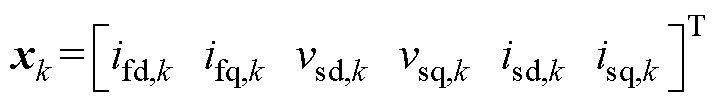
式中，I6为6阶单位矩阵；xk为系统在kTs时刻值；xk+1为系统在(k+1)Ts时刻值；为kTs时刻逆变器输出电压矩阵。
注意到矩阵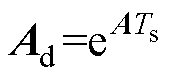包含随电机转速变化的时变矩阵A，故其在每个采样周期内均需在线进行指数运算，因而将引起较大计算负担。为此，本文采用前向欧拉法对式（1）进行离散化，有
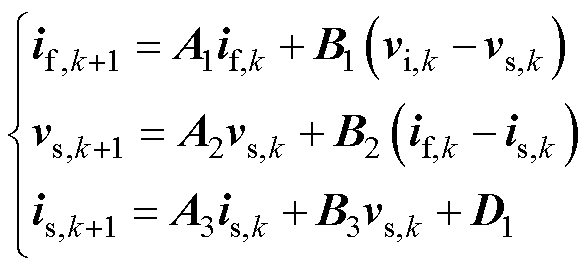（3）
其中
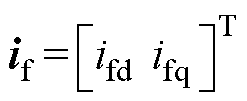
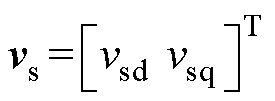
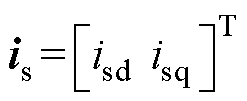
式中，if、vs、is分别为电感电流、电容电压和定子电流矩阵；此外，各系数矩阵分别表示为
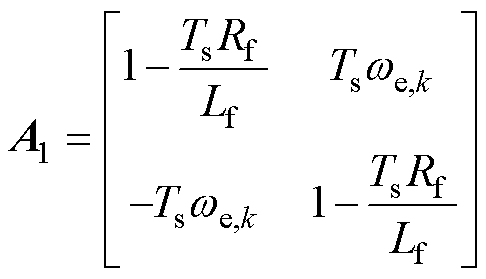
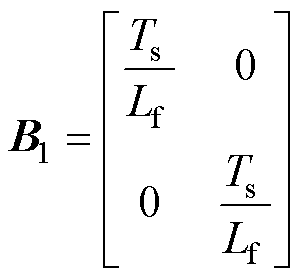
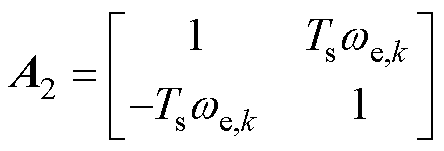
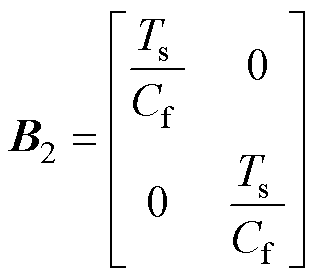
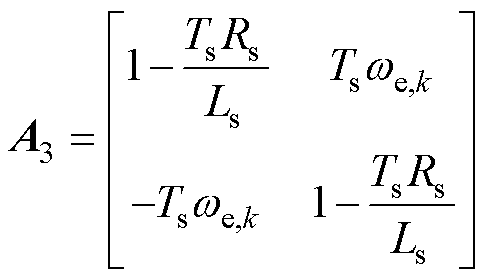
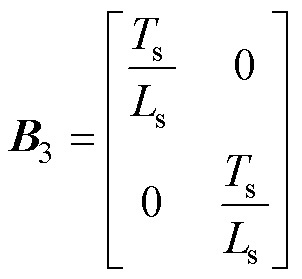
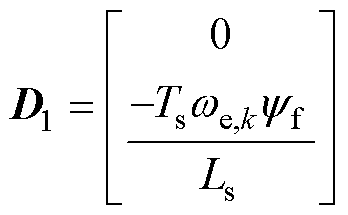
基于式（1）中LC-PMSM的数学模型，忽略其电压电流方程中的交叉耦合项，可得到系统dq轴等效电路，如图2所示。
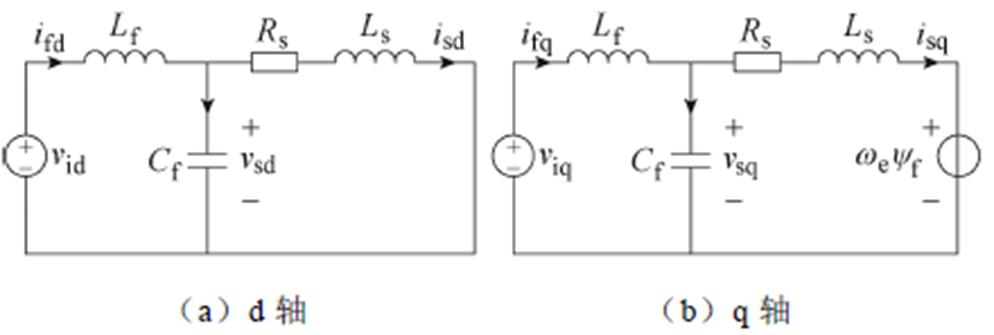
图2 LC-PMSM的dq轴等效电路
Fig.2 dq-axisequivalent circuit of an LC-PMSM
可见，LC滤波器和PMSM定子电感构成了LCL三阶滤波结构。其中，q轴等效电路中反电动势幅值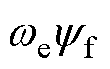
可视为扰动。因此，可推导出从逆变器输出电压到PMSM定子电流的传递函数为
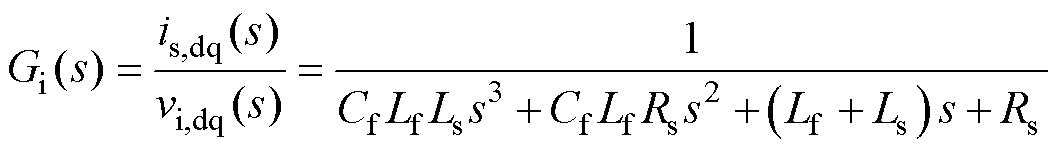（4）
由式（4）可进一步得到系统谐振频率为
（5）
由式（5）可知，LC-PMSM系统具有固有谐振问题，从而影响系统运行稳定性。而且，相较于无输出LC滤波器的常规PMSM驱动系统，加入LC滤波器后，电流环控制阶数由1阶上升为3阶，显著增加了控制难度。因此，亟需设计一种实现简单且具备谐振抑制能力的高性能电流控制器。
为了简化LC-PMSM系统的控制结构，并有效抑制电流环的谐振失稳，本节提出了一种基于虚拟电阻有源阻尼的电感电流无差拍预测控制策略。
由式（3）可看出，电感电流受逆变器输出电压（即控制器输出）控制，故可直接建立其预测模型；而电容电压和定子电流并不直接取决于控制器的输出，故式（3）中的离散模型无法对电容电压和定子电流进行直接预测。鉴于此，本文首先利用电感电流预测值if,k+1替换vs,k+1表达式中的if,k，即可实现对电容电压的预测；同理，利用电容电压预测值vs,k+1替换is,k+1表达式中的vs,k，即可实现对定子电流的预测。因此，系统离散预测模型可构建为
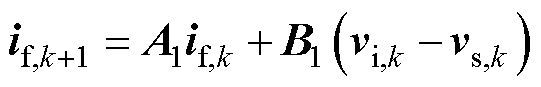（6）
（7）
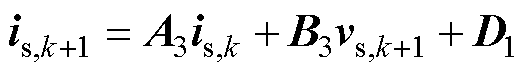（8）
注意到构建逆变器侧电感电流的预测模型最为简单，为降低控制算法复杂度，本文将基于无差拍控制原理设计LC-PMSM驱动系统的一种电感电流预测控制器。
LC-PMSM驱动系统的转速环输出为定子电流参考，而电流环预测控制的目标是实现矢量控制。不同于常规PMSM驱动系统，LC-PMSM系统因LC滤波器电容支路的存在，导致其逆变器侧电感电流和电机侧定子电流之间存在偏差（即电容电流）。为了实施电感电流无差拍预测控制，需首先获取与定子电流矢量控制相对应的电感电流参考值。其可在系统稳态时基于式（1）求得，即令
（9）
其中
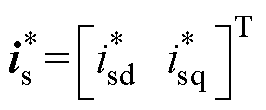
式中，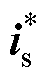
为转速环PI控制器输出的定子电流参考值，且在PMSM矢量控制下有
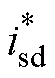=0。
将式（9）代入式（1），即可得到kTs时刻电感电流参考值
，有
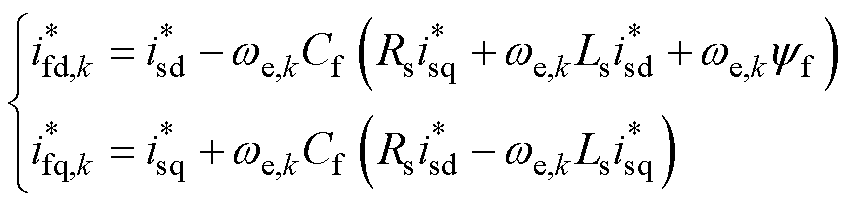（10）
因电感电流无差拍预测控制的最终目标是使电感电流在(k+1)Ts时刻跟随至其参考值，且采样频率较高时电感电流参考值可视为不变，故令式（6）中的
和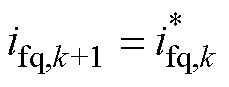
，即可求出电感电流无差拍预测控制电压参考为
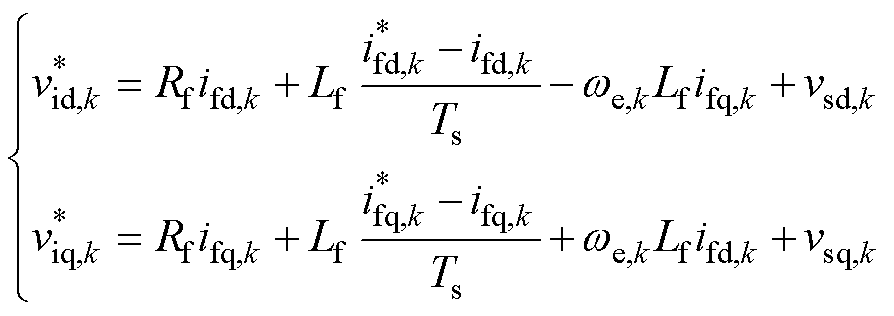（11）
在实际数字实现时，控制器需要耗费一定的时间执行模数转换和控制算法，导致无差拍预测控制电压参考仅能在下一个Ts作用于系统，从而引入一步固有延迟。本文采用“两步向前预测”法对该延迟进行补偿[17]。具体来说，基于式（6），首先利用第k步得到的控制电压参考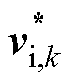
预测出第k+1步的电感电流if,k+1，然后将if,k+1再次代回式（6）去预测第k+2步的电感电流值if,k+2，有
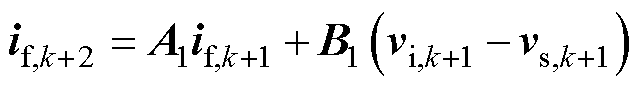（12）
其中
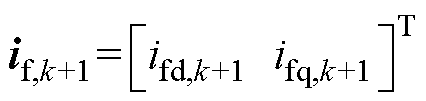
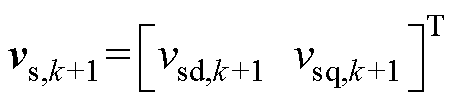
式中，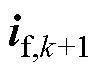
、
分别为上一个采样周期得到的无差拍预测控制电压参考值代入式（6）和式（7）计算而得。
其次，令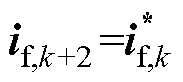
，则式（11）中得到的电感电流无差拍预测控制电压参考值将修正为
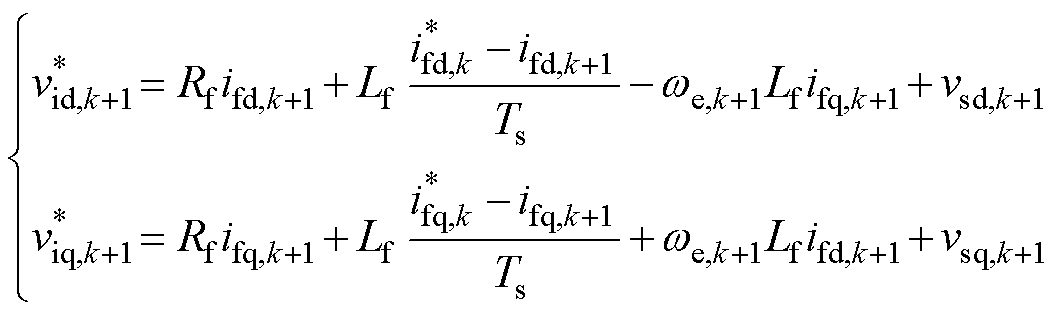（13）
式（13）设计的无差拍预测控制器具有实现简单且无需参数设计的优点。尽管如此，因LC-PMSM系统存在固有谐振问题而将引起电流环失稳。为此，本文在无差拍预测控制基础上，进一步提出了一种基于滤波电容并联虚拟电阻的有源阻尼控制策略。
所设计的基于滤波电容并联虚拟阻尼电阻的系统等效电路如图3所示。由于采用电感电流无差拍预测控制，可近似认为实际电感电流值等于其参考值，即有：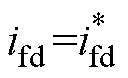
，
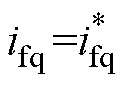。此时，滤波电容并联虚拟电阻Rv后的电感电流方程将变为
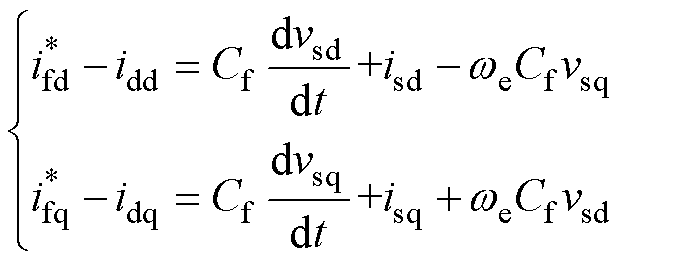（14）
其中
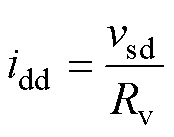
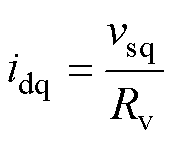
式中，idd、idq为虚拟电阻电流。
因此，在保证硬件电路不变的前提下，从原dq轴电感电流中参考值减去虚拟电阻电流idd和idq，即可等效成在滤波电容上并联一个虚拟阻尼电阻。
注意到式（14）中的电容电压vsd和vsq同时包含基频和谐波分量。实际实现时为避免有源阻尼影响基频，可将电容电压经低通滤波器（Low Pass Filter, LPF）滤除基频分量后，仅使用其谐波分量进行有源阻尼。此时，相应的虚拟电阻电流为
图3 滤波电容并联虚拟电阻的dq轴等效电路
Fig.3 dq-axis equivalent circuit with paralleled virtual resistor and filter capacitor
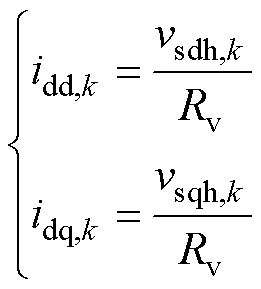（15）
式中，vsdh,k、vsqh,k分别为d、q轴电容电压谐波分量。
进一步地，利用式（10）的电感电流参考值减去式（15）中的虚拟电阻电流，即可得到最终的电感电流参考值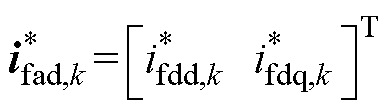
，有
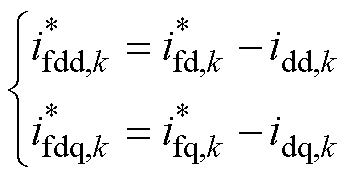（16）
最终，将式（13）中的电感电流参考值替换为式（16），即可得到加入虚拟电阻有源阻尼后的无差拍预测控制电压参考值。将该电压参考值经空间矢量调制（Space Vector Modulation, SVM）生成脉冲信号作用于逆变器。所提基于虚拟电阻有源阻尼的无差拍预测电流控制框图如图4所示。
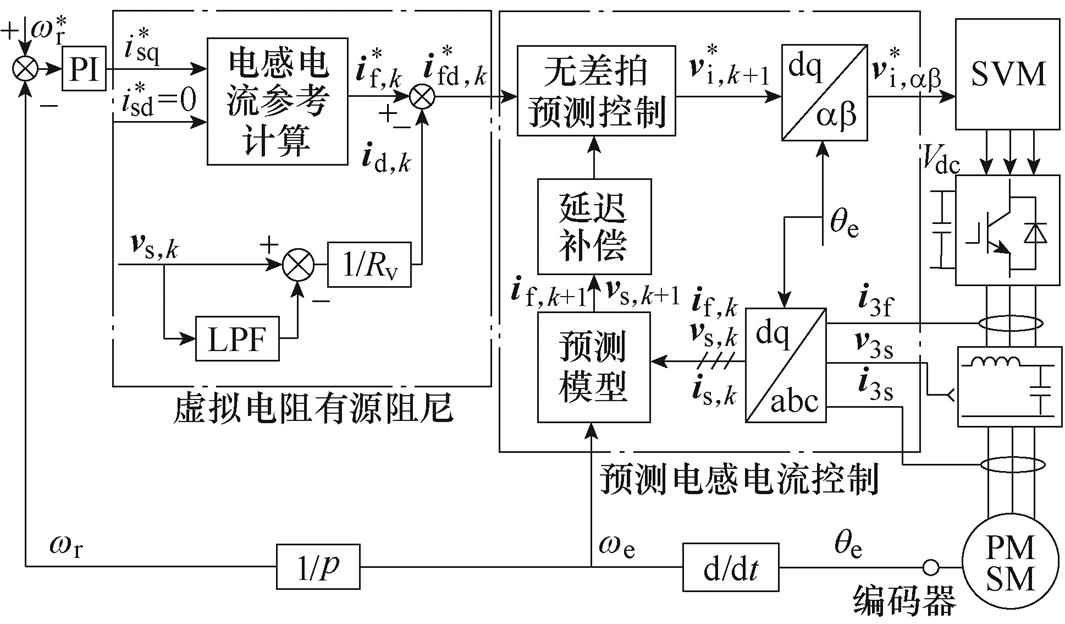
图4 基于虚拟电阻有源阻尼的无差拍预测电流控制框图
Fig.4 Diagram of a virtual resistive active damping based deadbeat predictive current control
从图4可看出，所提控制策略待设计参数少且整定简单。此外，其具有固定开关频率、稳态性能好且输出LC滤波器的设计难度低。
为了便于分析，将式（10）中求得的电感电流参考值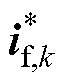
以矩阵形式重写为
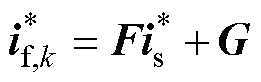（17）
其中
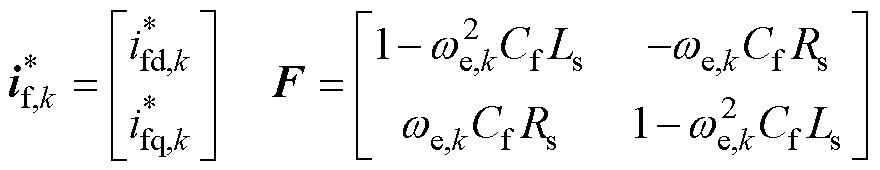
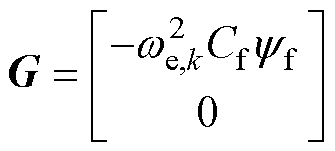
同时，定义式（2）中系统的输出矩阵为
（18）
式中，矩阵C1、C2和C3分别对应于系统的输出变量if,k、vs,k和is,k。
因此，加入虚拟电阻有源阻尼的电感电流参考可写为
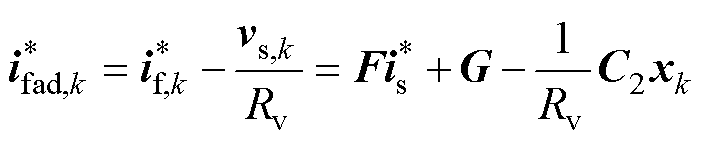（19）
为了更直观地分析，忽略延迟补偿，即令式（6）中的预测模型if,k+1等于式（19）中的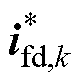
，可得到加入有源阻尼后的无差拍预测控制电压参考的矩阵形式为
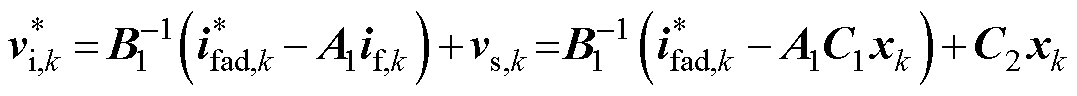（20）
将式（20）作为控制输入回代至系统精确离散状态模型式（2）中，并以定子电流is,k作为系统输出变量yk，可推导出其离散闭环状态方程为
（21）
其中，各系数矩阵表示为
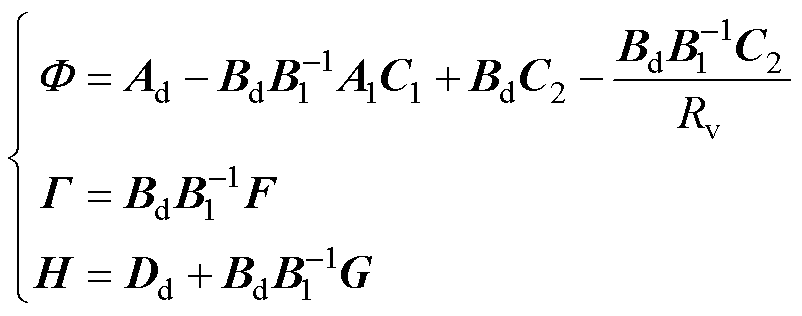（22）
进一步地，对式（21）作离散z变换可得
（23）
由式（23）可知，在离散z域中，由定子电流参考到系统输出定子电流间的闭环传递函数矩阵为
（24）
因此，d、q轴定子电流离散闭环传递函数分别为Gi(z)的第1和第4个对角子元素，有
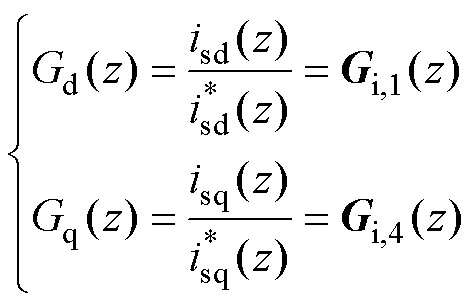（25）
基于式（25），借助Matlab/Simulink数值计算工具，即可获得定子电流闭环传递函数的极点图。若极点全部位于z平面上以原点为中心的单位圆内，则系统稳定；反之，则不稳定。为分析电流环在不加有源阻尼和加入有源阻尼前后的系统稳定性，首先需对系统的参数进行设计。
为了有效滤除系统高次谐波，需合理设计LC滤波器参数[3]。其中，滤波电感Lf的最小值可由逆变器输出电流所允许的最大纹波确定，即
（26）
式中，IN为额定电流；fsw为逆变器开关频率；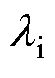
为纹波系数，一般取20%～30%，本文选取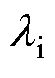=30%。
同时，滤波电感的最大值则可根据其基波压降来确定，有
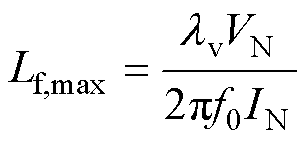（27）
式中，VN为电机相电压的有效值；f0为电机定子基波频率；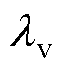
为电感基波压降与电机相电压的比值，本文选取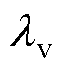=10%。
此外，滤波电容可为高次谐波电流提供低阻抗通路，防止其流入电机侧。但当电容较大时，会引入较大无功功率而降低系统功率因数。故滤波电容的最大值可由其允许产生的最大无功功率确定，有
（28）
式中，PN为逆变器输出单相有功功率；
为滤波电容引入的无功功率与逆变器输出有功功率的比值，一般取5%左右。
为了有效滤除开关次谐波并防止系统谐振峰放大电流谐波，谐振频率应低于开关频率并避开谐波较大的频段；同时，谐振频率也应远高于基波频率，以避免谐振尖峰对基波的影响。因此，系统谐振频率fres通常应满足
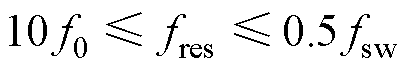（29）
表1给出了本文所用LC-PMSM驱动系统的主要参数。基于上述分析，系统的谐振频率范围为：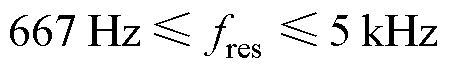
。故本文最终选取的滤波电感Lf=2 mH，滤波电容Cf=9.5 mF，其对应的谐振频率fres=1.57 kHz，满足式（29）的要求。
表1 LC-PMSM驱动系统参数
Tab.1 Parameters of an LC-PMSM drive system
参 数数 值 母线电压Vdc/V150 转子磁链/Wb0.153 额定电流IN/A4.5 开关频率fsw/kHz10 定子电阻Rs/W0.73 定子电感Ls/mH2.35 极对数p4 PMSM基频f0/Hz66.67 额定转矩TN/(N·m)6 转动惯量J/(kg·m2)0.001 5
此外，式（15）中用于有源阻尼的虚拟电阻大小可确定[20]为
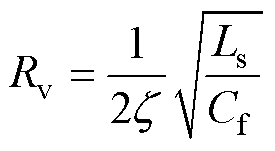（30）
式中，
为阻尼系数。过大时会增大定子电流低次谐波，过小时则无法为系统提供足够的谐振阻尼。因此，本文最终选取=0.5（Rv=15.73 W），以获得较好的阻尼效果和较低的定子电流谐波。
根据所设计的系统参数，即可基于式（25）绘制出转速为1 000 r/min时，不加和加入虚拟电阻有源阻尼控制下的系统闭环极点分布，如图5所示。注意到当虚拟阻尼电阻Rv趋于无穷大时，等效于不加有源阻尼的情形。通过对比图5a和图5b可知，采用单一无差拍控制时（不加阻尼），其z平面单位圆外存在极点，故将引起系统失稳；而加入虚拟电阻有源阻尼（Rv=15.73 W）后，原有不稳定的闭环极点全部移动至单位圆内，故所提控制策略可有效抑制系统谐振而提升系统的稳定裕度。
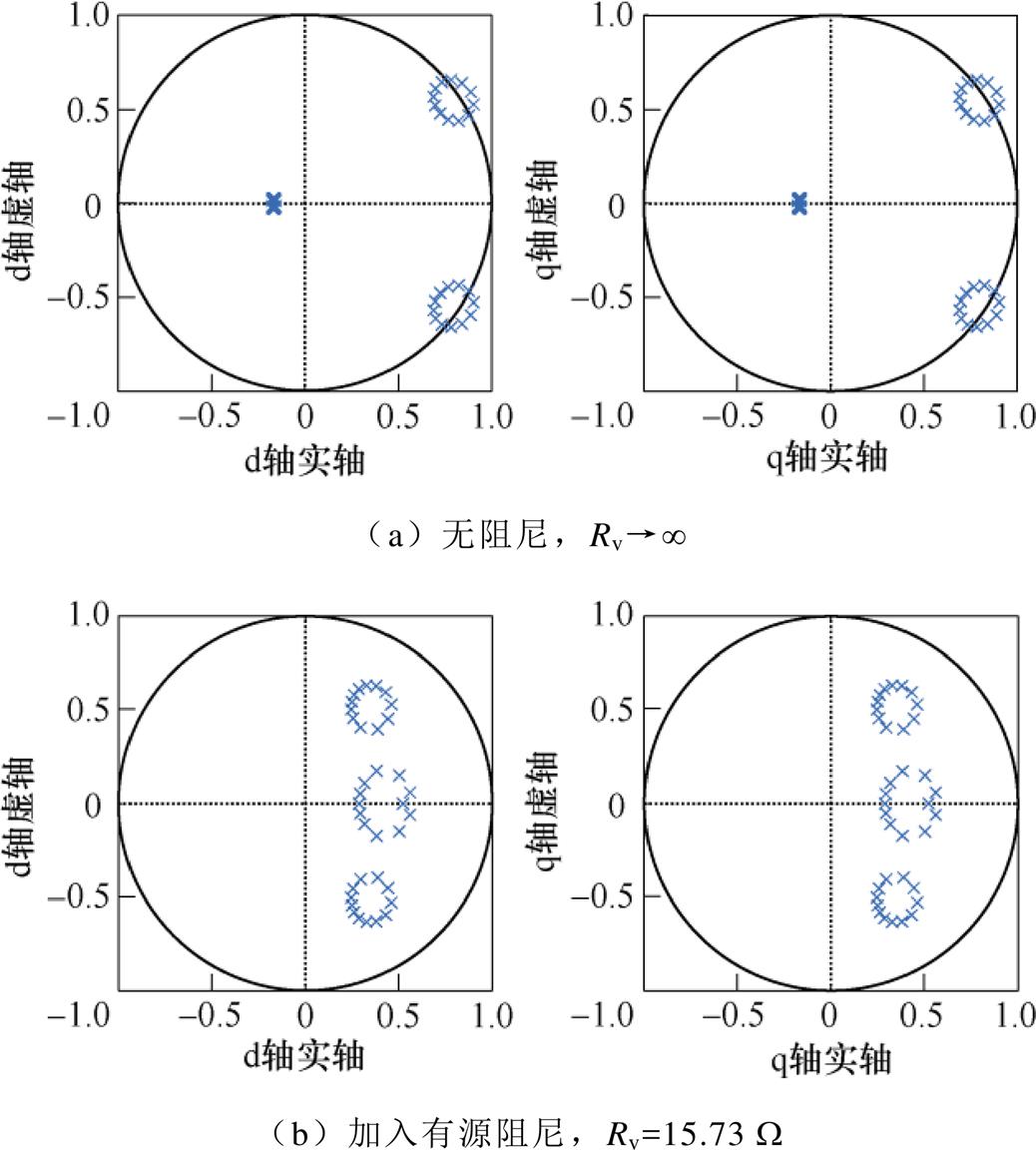
图5 转速1 000 r/min不加和加入有源阻尼的闭环极点图
Fig.5 Closed-loop pole maps without and with active damping under the speed of 1 000 r/min
为验证本文所提基于虚拟电阻有源阻尼的无差拍预测电流控制策略的有效性，搭建了LC滤波型永磁同步电机驱动系统实验平台，如图6所示。平台包含直流电压源、三相电压源逆变器、采样电路、LC滤波器和600 W三相PMSM等。系统主要参数见表1。其中，数字控制器采用DSP TMS320F28335，采样频率fs和开关频率fsw均设置为10 kHz，系统突变负载采用磁滞制动器实现。
图7给出了额定负载条件下，系统转速分别为400 r/min和1 000 r/min时，无有源阻尼的传统无差拍预测电流控制下的稳态实验波形。图中包括电机转速n、q轴定子电流isq、a相定子电流isa及其谐波谱，以及a相电容电压vsa。可以看出，采用单一无差拍预测电流控制时，滤波电容电压与电机定子
图6 LC-PMSM驱动系统实验平台
Fig.6 Experimental platform of LC-PMSM drive system
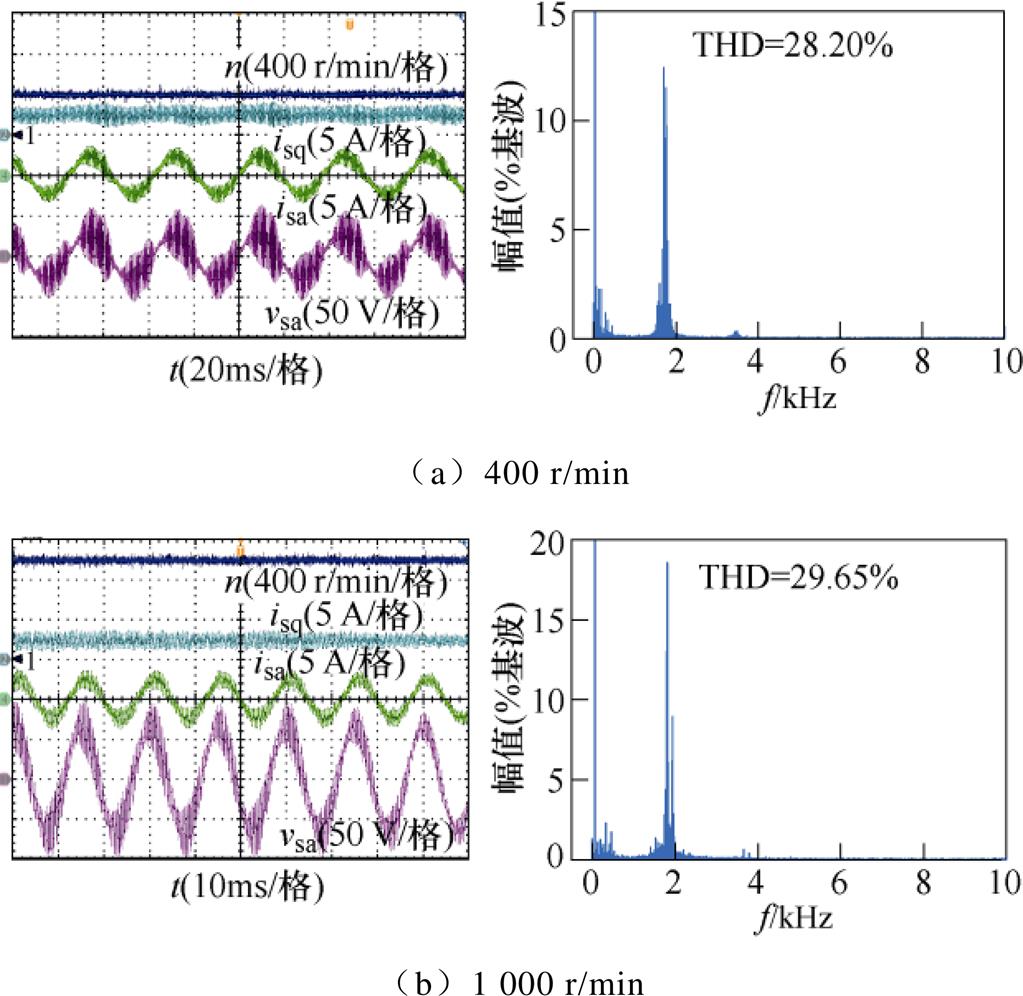
图7 无有源阻尼的传统无差拍预测控制稳态实验波形
Fig.7 Steady-state experimental waveforms of conventional deadbeat predictive control without active damping
电流波形发生了明显的谐振振荡现象，故其无法保证系统的稳定运行。通过分析定子电流的谐波谱可知，其谐振频率在1.6 kHz左右，与理论计算值（1.57 kHz）一致。
图8给出了额定负载条件下、系统转速分别为200 r/min、400 r/min和额定1 000 r/min时，采用所提控制策略下的稳态实验波形。可知，所提控制策略在不同转速下系统均未激发谐振失稳现象，且定子电流总谐波畸变率（Total Harmonic Distortion, THD）维持在期望水平。因此，所提控制策略能够有效抑制系统谐振，保证系统运行稳定性。此外，所提控制策略的定子电流谐波集中分布在开关频率（10 kHz）及其整数倍附近，实现了固定的开关频率，并方便了输出LC滤波器的设计。
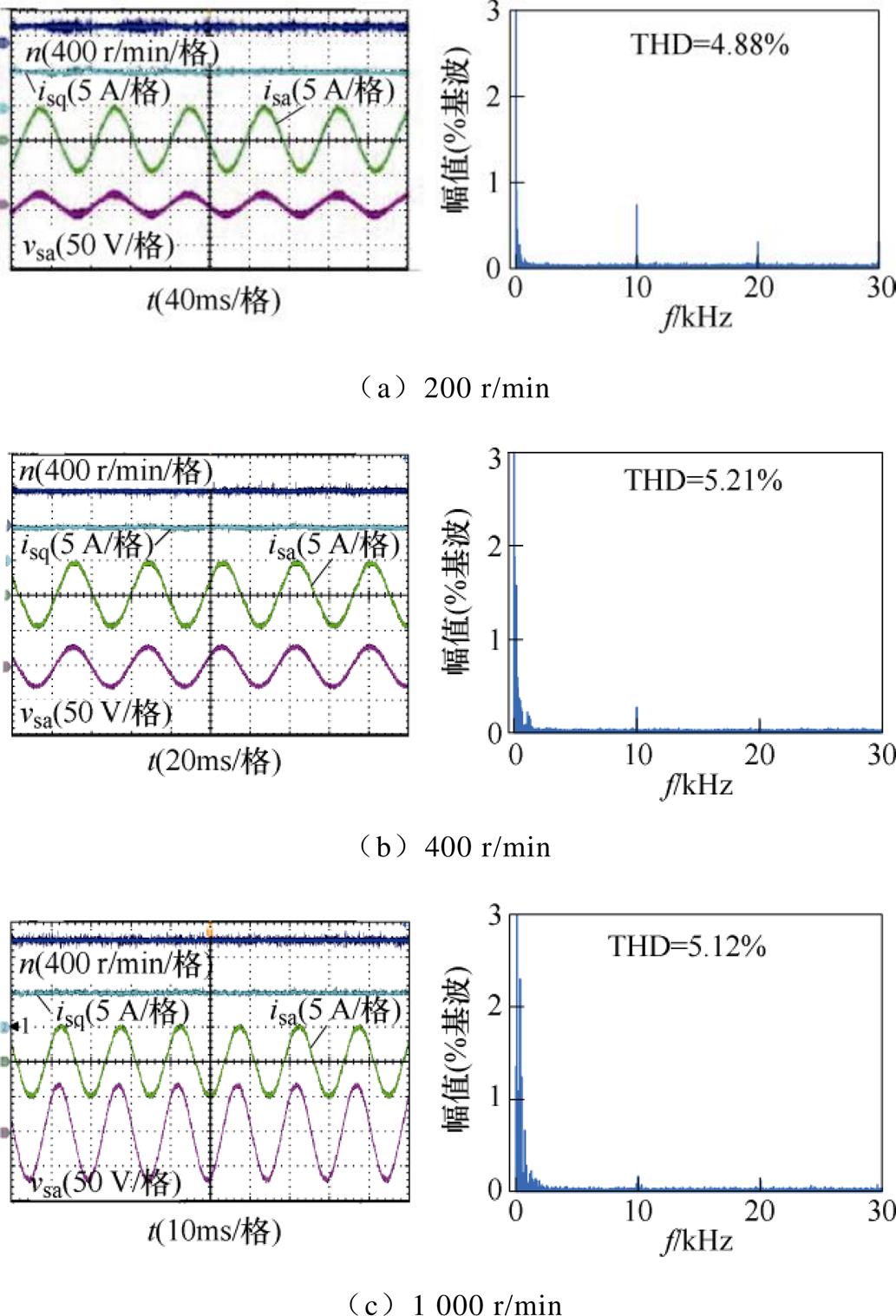
图8 所提虚拟电阻有源阻尼的预测控制稳态实验波形
Fig.8 Steady-state experimental waveforms of the proposed virtual-resistor-active-damping based predictive control
图9给出了系统在额定负载条件转速1 000 r/min时文献[9]中基于有源阻尼PI控制策略的实验波形。通过对比图8c和图9可知，所提控制策略和文献[9]中策略具有相当的定子电流稳态性能，这是因为两种方法最终均采用了SVM。尽管如此，与文献[9]中所采用的带有源阻尼的PI电流内环控制器相比，本文所提的有源阻尼预测电流控制策略可省去两个比例、积分参数的繁杂试凑工作，故能够在保证较优稳态控制性能的同时有效降低参数整定的复杂度。
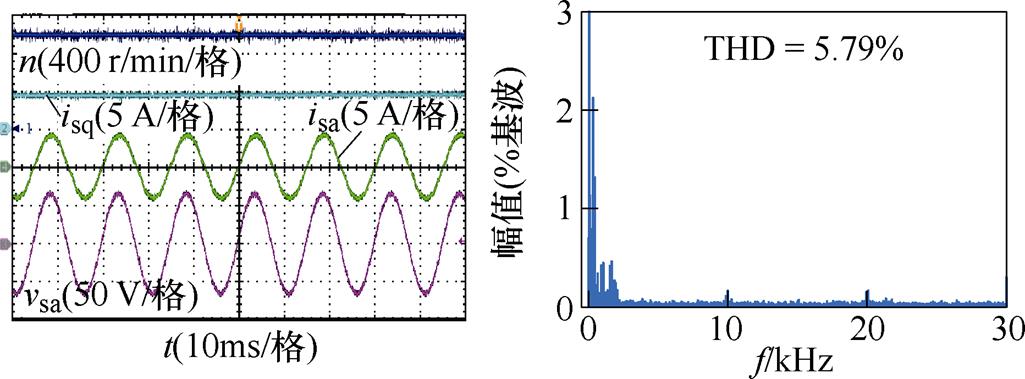
图9 文献[9]中控制策略稳态实验波形
Fig.9 Steady-state experimental waveforms of the control scheme in Ref.[9]
图10为所提基于虚拟电阻有源阻尼的无差拍预测控制策略下系统动态响应实验波形。其中，图10a为系统起动时（0 r/min→1 000 r/min）的动态响应实验波形；而图10b则为系统突变负载（由额定负载→空载）时的动态响应实验波形。从图10a中可看出，PMSM起动过程中定子电流和电容电压均未出现谐振现象，且转速可以很快达到其参考值。实质上，PMSM转速的动态响应主要取决于外环PI控制。此外，从图10b中可看出，系统突卸额定负载至空载情况下，引起的系统转速波动不大且能够很快恢复至参考转速。以上实验结果表明，所提控制策略在跟随参考转速和抗负载扰动等方面亦具有良好的动态性能。
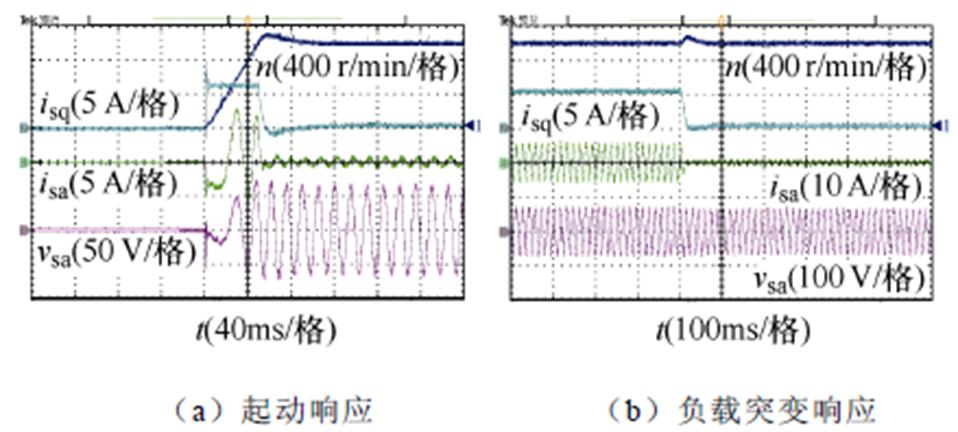
图10 所提控制策略下系统动态实验波形
Fig.10 Dynamic experimental waveforms of the proposed control scheme
一般来说，开关频率提高后控制器带宽亦会提高，故一定程度上可以改善系统稳态性能，反之亦然。为了评估所提控制策略对不同开关频率的适用性，此处给出了在额定转速和负载条件下，开关频率为5 kHz时的实验波形，如图11所示。
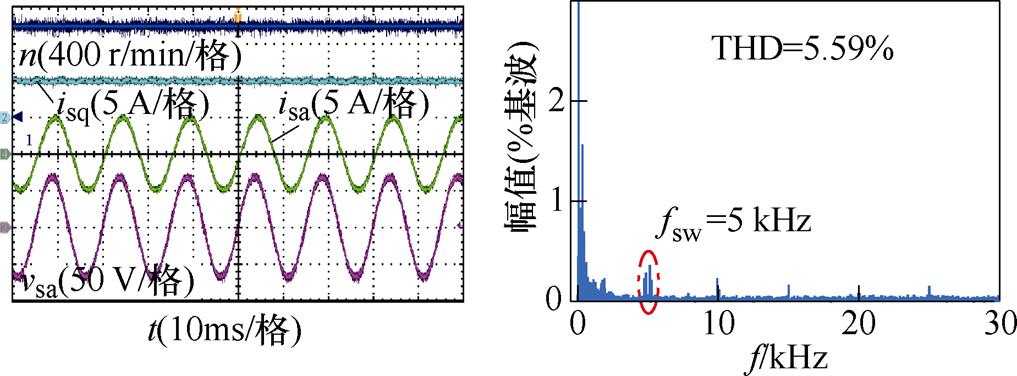
图11 所提控制策略5 kHz开关频率下稳态实验波形
Fig.11 Steady-state experimental waveforms of the proposed control scheme under 5 kHz switching frequency
通过对比图8c和图11可知，所提控制策略在10 kHz开关频率和5 kHz开关频率下的定子电流稳态控制性能相近，均能保持较低的THD且不失稳。
需要额外说明的是，若开关频率过低，则可能造成低载波比等问题。因本文主要针对常规PMSM工作时的控制策略设计，低载波比问题对所设计控制策略的影响将是作者未来研究的重要工作之一。
为了评估所提控制策略对不同滤波器参数的适用性，给出了不同滤波器参数下（满足式（29）中的前提条件）的实验结果，如图12所示。
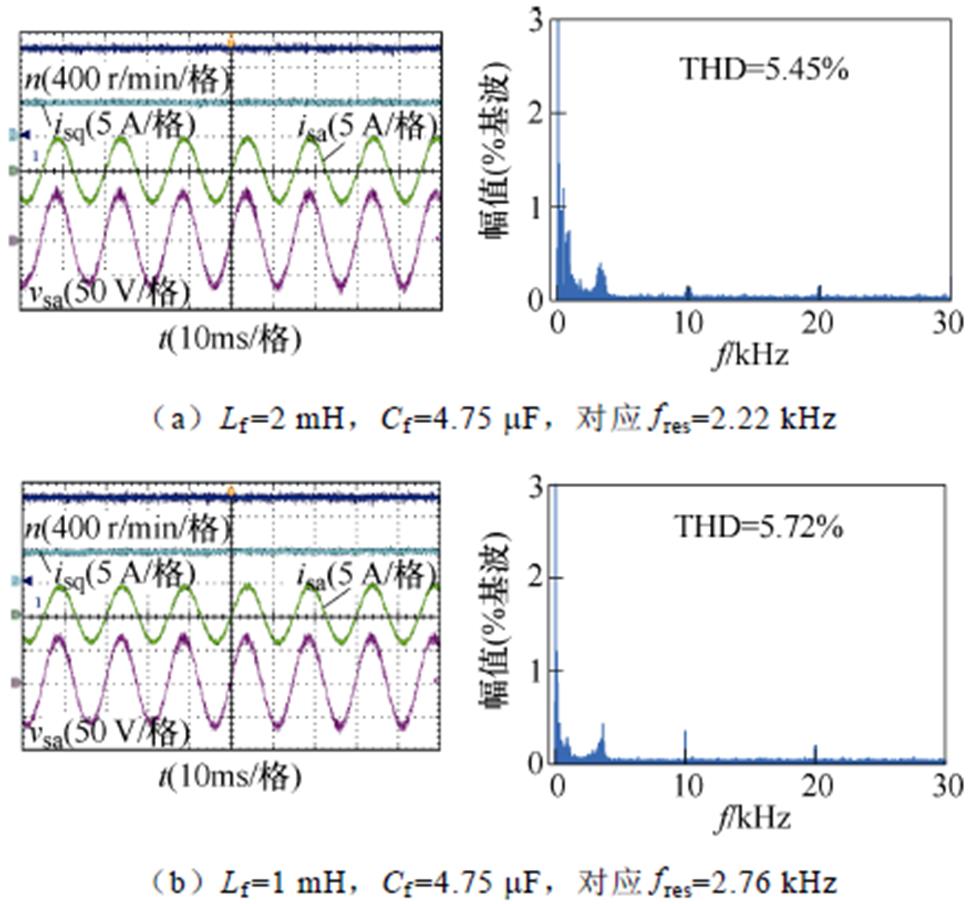
图12 所提控制策略在不同LC滤波参数下实验对比
Fig.12 Experimental comparisons of the proposed control scheme under different LC filter parameters
图12a为实际硬件滤波电感不变，滤波电容降低50%（Cf：9.5 mF→4.75 mF）后的稳态实验波形。而图12b为滤波电感和滤波电容均降低50%（Lf：2 mH→1 mH，Cf：9.5 mF→4.75 mF）后的稳态实验波形。对比图8c和图12可看出，当LC滤波器参数配置在式（29）规定的范围内时，系统稳定性基本不受影响。此外，随着Lf和Cf的减小，LC滤波器的截止频率增大，实验中的电容电压纹波略增大，定子电流THD亦从5.12%上升至5.72%，但仍处于较好的期望水平。因此，所提控制策略能够适应较宽范围变化的LC滤波器参数。
针对LC滤波型PMSM驱动系统，本文提出了一种基于虚拟电阻有源阻尼的无差拍预测电流控制策略。首先，设计了一种电感电流无差拍预测控制器，其结构简单、开关频率固定且能够实现对定子电流的间接控制。其次，提出了一种基于滤波电容并联虚拟电阻的有源阻尼控制策略，有效抑制了系统谐振。最后，给出了系统的闭环稳定性分析及参数整定方法。实验结果表明，所提控制策略能有效提升LC-PMSM驱动系统的运行稳定性。
参考文献
[1] 郑长明, 阳佳峰, 高昂, 等. 永磁同步电机长线变频驱动系统定频滑模预测电流控制[J]. 电工技术学报, 2023, 38(4): 915-924.
Zheng Changming, Yang Jiafeng, Gao Ang, et al. Fixed switching frequency sliding-mode predictive current control of a PMSM variable-frequency drive system with long cables[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 915-924.
[2] 鞠孝伟, 程远, 杨明亮, 等. SiC逆变器高频脉冲电压对Hairpin绕组绝缘安全的影响分析[J]. 电工技术学报, 2021, 36(24): 5115-5124.
Ju Xiaowei, Cheng Yuan, Yang Mingliang, et al. Influence analysis of high frequency pulse voltage of SiC inverter on insulation safety of Hairpin winding[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5115-5124.
[3] 陈东东, 王晋, 李子博, 等. 考虑谐振抑制的永磁同步电机长线缆驱动系统转子初始位置辨识技术[J]. 电工技术学报, 2022, 37(19): 4938-4946.
Chen Dongdong, Wang Jin, Li Zibo, et al. Rotor initial position identification technology for long cable drive system of permanent magnet synchronous motor considering resonance suppression[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(19): 4938-4946.
[4] SalomÄki J, Hinkkanen M, Luomi J. Influence of inverter output filter on maximum torque and speed of PMSM drives[J]. IEEE Transactions on Industry Applications, 2008, 44(1): 153-160.
[5] 刘宝泉, 郭华, 朱一昕, 等. 三相变流器无源阻尼型LCL滤波器的分析与设计[J]. 电工技术学报, 2017, 32(2): 195-205.
Liu Baoquan, Guo Hua, Zhu Yixin, et al. Analysis and design of a passively damping LCL filter in three- phase converters[J]. Transactions of China Electro- technical Society, 2017, 32(2): 195-205.
[6] 赵仁德, 赵斌, 徐海亮, 等. 带LC滤波器的永磁同步电机控制系统及策略研究[J]. 电工技术学报, 2019, 34(增刊1): 79-86.
Zhao Rende, Zhao Bin, Xu Hailiang, et al. Research on control method of permanent magnet synchronous motor with LC filter[J]. Transactions of China Elec- trotechnical Society, 2019, 34(S1): 79-86.
[7] Mishra P, Maheshwari R, Patil D. Stabilization of rotor flux-oriented control of induction motor with filter by active damping[J]. IEEE Transactions on Industrial Electronics, 2019, 66(12): 9173-9183.
[8] Mishra P, Maheshwari R. A simple feedforward approach to stabilize VSI-fed induction motor with filter in RFOC[J]. IEEE Transactions on Industrial Electronics, 2020, 67(12): 10191-10201.
[9] Geng Weiwei, Zhang Zhuoran, Li Qiang. Analysis and experimental verification of a conventional inverter with output LC filter to drive ironless stator axial-flux PM motor[J]. IEEE Transactions on Transportation Electrification, 2021, 7(4): 2600-2610.
[10] Yang Ming, Lü Zekai, Xu Donglin, et al. Resonance suppression and EMI reduction of GaN-based motor drive with sine wave filter[J]. IEEE Transactions on Industry Applications, 2020, 56(3): 2741-2751.
[11] 王宏佳, 徐殿国, 杨明. 永磁同步电机改进无差拍电流预测控制[J]. 电工技术学报, 2011, 26(6): 39-45.
Wang Hongjia, Xu Dianguo, Yang Ming. Improved deadbeat predictive current control strategy of permanent magnet motor drives[J]. Transactions of China Electrotechnical Society, 2011, 26(6): 39-45.
[12] 章回炫, 范涛, 边元均, 等. 永磁同步电机高性能电流预测控制[J]. 电工技术学报, 2022, 37(17): 4335-4345.
Zhang Huixuan, Fan Tao, Bian Yuanjun, et al. Predictive current control strategy of permanent magnet synchronous motors with high performance[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4335-4345.
[13] Rodriguez J, Garcia C, Mora A, et al. Latest advances of model predictive control in electrical drives-part I: basic concepts and advanced strategies[J]. IEEE Transactions on Power Electronics, 2022, 37(4): 3927-3942.
[14] 郭磊磊, 王朋帅, 李琰琰, 等. 不同代价函数下永磁同步电机模型预测控制参数失配可视化分析[J]. 电工技术学报, 2023, 38(4): 903-914.
Guo Leilei, Wang Pengshuai, Li Yanyan, et al. Visual analysis of parameters mismatch in model predictive control for permanent magnet synchronous motor under different cost functions[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 903-914.
[15] Laczynski T, Mertens A. Predictive stator current control for medium voltage drives with LC filters[J]. IEEE Transactions on Power Electronics, 2009, 24(11): 2427-2435.
[16] Walz S, Liserre M. Hysteresis model predictive current control for PMSM with LC filter considering different error shapes[J]. IEEE Open Journal of Power Electronics, 2020, 1: 190-197.
[17] Xue Cheng, Zhou Dehong, Li Yunwei. Finite- control-set model predictive control for three-level NPC inverter-fed PMSM drives with LC filter[J]. IEEE Transactions on Industrial Electronics, 2021, 68(12): 11980-11991.
[18] Geyer T, Karamanakos P, Kennel R. On the benefit of long-horizon direct model predictive control for drives with LC filters[C]//2014 IEEE Energy Con- version Congress and Exposition (ECCE), Pittsburgh, PA, USA, 2014: 3520-3527.
[19] Zheng Changming, Dragicevic T, Zhang Zhenbin, et al. Model predictive control of LC-filtered voltage source inverters with optimal switching sequence[J]. IEEE Transactions on Power Electronics, 2021, 36(3): 3422-3436.
[20] Falkowski P, Sikorski A. Finite control set model predictive control for grid-connected AC-DC con- verters with LCL filter[J]. IEEE Transactions on Industrial Electronics, 2018, 65(4): 2844-2852.
Abstract To achieve efficient and reliable production and transportation for underground coal mine applications, permanent magnet synchronous motors (PMSMs) are usually placed underground, and inverters are deployed above the mine, connected by long power cables. However, long power cables will aggravate motor overvoltage, bearing damage, and insulation aging. Therefore, it is necessary to install LC filters on the output side of the inverter to form an LC-filtered PMSM drive system (LC-PMSM). However, due to the inherent resonance peak of the system, it is easy to cause the resonance instability of the current loop. Moreover, the LC filter increases the system order, complicating the structure and parameter tuning of the conventional linear control method. Therefore, this paper proposes a deadbeat predictive current control strategy based on virtual resistance active damping.
Firstly, a deadbeat predictive controller of inductor current with a simple structure is designed to realize the indirect control of motor stator current. Then, to suppress the instability of the current loop caused by the inherent resonance of the LC-PMSM system, based on the deadbeat predictive control, an active damping control strategy according to the filter capacitor parallel virtual resistance is designed to ensure the system stability. Finally, the discrete closed-loop transfer function of the current loop is constructed, and the LC filter parameters are designed. The stability of the system is also theoretically analyzed.
Experiments were carried out based on the LC-PMSM system. The experimental results show that when conventional deadbeat predictive current control is used under the rated load condition, the stator current has significant resonance oscillations under different speed values. In contrast, the proposed control strategy does not cause significant resonance instability, and the stator current distortion rate is maintained at the desired level. In addition, the stator current harmonics of the proposed control strategy are concentrated near the switching frequency and its integer multiples, which achieves a fixed switching frequency and facilitates the design of the output LC filter. The dynamic response experiment shows that the proposed method causes no resonance phenomenon during the PMSM starting process, and the speed can quickly reach its reference value. Also, when the system suddenly transitions from a rated load to a no-load condition, the speed fluctuation is small and can quickly return to its reference using the proposed method.
The following conclusions can be drawn through the experimental analysis: (1) The proposed deadbeat predictive current control strategy based on virtual resistance active damping can effectively suppress the system resonance and ensure the stability of the system. (2) The proposed control strategy also has good dynamic performance in following the reference speed and resisting load disturbance. (3) The theoretical stability analysis of the system is given and verified.
Keywords：Permanent magnet synchronous motor, LC filter, predictive control, virtual resistance, active damping
郑长明 男，1991年生，讲师，硕士生导师，研究方向为永磁同步电机驱动控制与新能源发电系统。E-mail: jsxzzcm@126.com
公 铮 男，1990年生，副教授，博士生导师，研究方向为大容量功率变换拓扑及控制与柔性直流输配电系统控制及保护。E-mail: zgo@cumt.edu.cn（通信作者）
中图分类号：TM351
DOI: 10.19595/j.cnki.1000-6753.tces.230582
国家自然科学基金面上项目（52277205）和国家自然科学基金青年科学基金项目（51907196, 52107217）资助。
收稿日期 2023-05-01
改稿日期 2023-05-18
（编辑 崔文静）