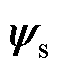 和电磁转矩Te表示,有
和电磁转矩Te表示,有摘要 时间序列数据驱动模型通过采样输入输出数据将被控对象在线拟合为离散传递函数,但在连续控制集(CCS)预测控制中直接应用存在困难。为了解决这个问题,该文结合最小二乘法,提出一种基于时间序列的永磁同步电机(PMSM)连续控制集无模型预测电流控制方法。该方法通过拉格朗日法合理设计回归矢量,在线估算模型待定系数,并建立数据驱动模型预测所需变量。不仅从根本上消除了模型预测控制(MPC)中先验模型对被控对象时变物理参数的依赖,而且所得模型符合电机运动特性,有更高的模型精度和良好控制性能。仿真和实验结果验证了提出方法的有效性,以及在动态性能、电流质量和系统噪声方面的优势。
关键词:无模型预测控制 时间序列模型 最小二乘估计算法 电流预测
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)存在功率密度高、质量体积小、效率高等优势,在电动汽车中得到广泛应用。由于电动汽车需要适应复杂路况,使得电机系统运行环境复杂多变。并且电动汽车对续航里程、可靠性、运行噪声等性能有所需求,对于控制性能要求日益提升,传统的PI控制器无法充分满足要求[1]。模型预测控制(Model Predictive Control, MPC)可提供优良的动态性能,并且上手操作容易,结构贴近被控对象,得到国内外学者的关注[2]。在电机控制领域中,根据首要控制目标的不同,MPC主要分为预测电流控制(Predictive Current Control, PCC)、预测转速控制(Predictive Speed Control, PSC)和预测转矩控制(Predictive Torque Control, PTC)[3-4]。随着PMSM的运行工况不同,其物理参数呈现非线性变化,使先验模型持续处在失配状态,影响控制性能。为了获得良好的控制性能,国内外研究人员从各种角度提高MPC的鲁棒性,如多步预测[5]、变权重系数[6-7]、引入观测器或参数辨识方法等。
在MPC中结合观测器或参数辨识方法,可在线获得电机参数或状态变量,实时调整先验模型,有效提升控制系统鲁棒性[8]。文献[9]结合Lyapunov函数设计扰动观测器(Disturbance Observer, DOB),在保证误差渐近稳定条件下对状态和扰动进行观测。文献[10]采用扩张状态观测器(Extended State Observer, ESO)通过估计参数和抑制干扰降低先验模型参数失配的影响。一些先进观测器同样可用于状态和扰动估计,以获得更高的估计精度和更好的控制性能,如龙伯格观测器[11]、滑模观测器[12]和自适应高增益观测器[13]等。
由于基于观测器的预测控制同样需要依赖先验模型预测状态变量,模型和参数失配的影响无法完全消除。无模型预测控制(Model-Free Predictive Control, MFPC)通过对输入输出数据采样,在线设计训练数据驱动模型,从本质上消除先验模型对物理参数的依赖。该方法需要将数据驱动模型训练为特定结构,主要包括紧格式、偏格式和全格式的动态线性化模型结构[14]、自回归外部输入(Auto- Regressive with eXogenous input, ARX)模型结构[15]、泛模型结构[16]和超局部模型结构[17]等。文献[18]通过第一种结构将非线性系统线性化,实现无模型自适应预测控制,并获得收敛跟踪误差和良好的鲁棒性;文献[15]将被控对象设计为ARX结构,通过估计算法在线拟合结构系数。该方法可很好估计被控对象,但需要强处理器算力实现;文献[19]将被控对象近似为一阶超局部模型,将其中已知和未知部分表示为单一变量,并通过观测器对该部分和状态变量在线估计和预测。该方法仅需较小计算量,即可获得较强鲁棒性和良好动态性能。在此基础上,文献[20]将该方法与线性ESO结合,设计观测器参数和电压成本函数,并结合调制部分有效提升定子电流质量;文献[21]结合滑模观测器提出一种无模型容错预测控制,有效应对永磁体失磁故障。
除了以上结构外,一些人工智能算法也应用至数据驱动模型训练中,如人工神经网络(Artificial Neural Network, ANN)[22]和循环神经网络(Recurrent Neural Network, RNN)算法[23],通过模拟生物神经网络原理在线学习和训练被控对象模型。
由于有限控制集(Finite Control Set type, FCS- type)预测控制谐波含量较高、控制精度有限,连续控制集(Continuous Control Set type, CCS-type)的无模型预测电流控制(Model Free PCC, MF-PCC)更符合电动汽车需求。基于时间序列的MF-PCC策略将电机拟合为离散传递函数形式,更符合电机系统运动特性。但由于在数字计算中无法轻易求得模型的逆,在连续控制集下应用存在困难。本文提出一种基于时间序列连续控制集的MF-PCC策略,通过有合适回归矢量的最小二乘法在线估算模型中待定系数,并结合拉格朗日法设计合适控制律。该方法消除模型中电机时变物理参数及其影响的同时,模型精度更高且控制效果更好。将方法应用至PMSM控制系统中与基于滑模观测器和级-并联ESO的超局部MF-PCC策略比较,仿真和实验结果验证了提出控制策略的有效性,以及在动态性能、定子电流质量和产生噪声方面的优势。
在dq坐标系下,PMSM数学模型可通过定子电压us、定子磁链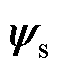 和电磁转矩Te表示,有
和电磁转矩Te表示,有
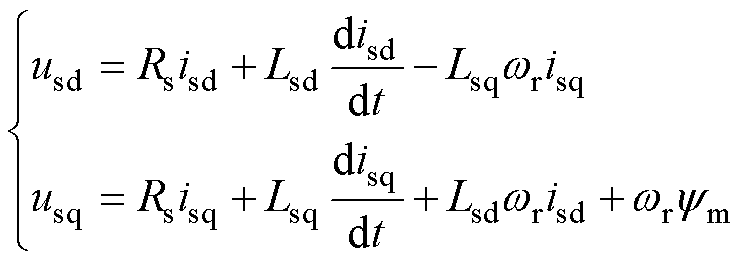 (1)
(1)
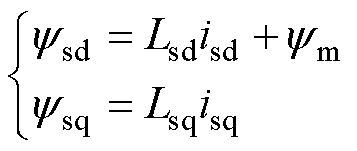 (2)
(2)
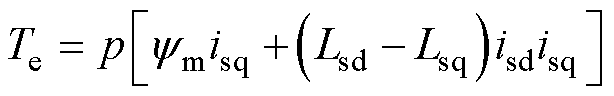 (3)
(3)
式中,下标d和q分别表示变量的d轴和q轴分量;Lsd、Lsq分别为定子电感d轴和q轴分量;Rs为定子电阻;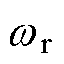 为电机电角速度;
为电机电角速度;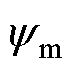 为永磁体磁链;p为极对数。
为永磁体磁链;p为极对数。
基于采样周期Ts,结合前向欧拉法,将状态方程离散化为
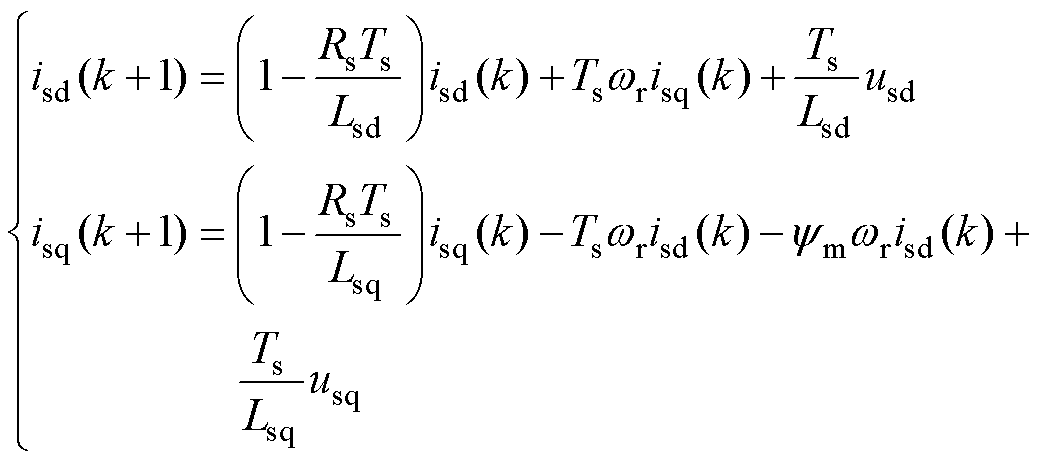 (4)
(4)
式中,isd(k+1)和isq(k+1)为第k+1个采样周期的电流分量预测值。
对于电流控制策略,各个电流分量跟随其参考值工作是首要控制目标。成本函数可设计为
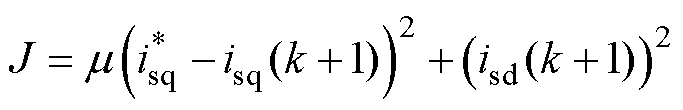 (5)
(5)
式中,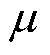 为权重因子;
为权重因子;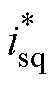 为q轴电流的参考值。成本函数中第一项可使q轴电流跟随其参考值,第二项使d轴电流保持为零。
为q轴电流的参考值。成本函数中第一项可使q轴电流跟随其参考值,第二项使d轴电流保持为零。
分别将成本函数对定子电压分量求偏导,所得结果为零,所得控制律为
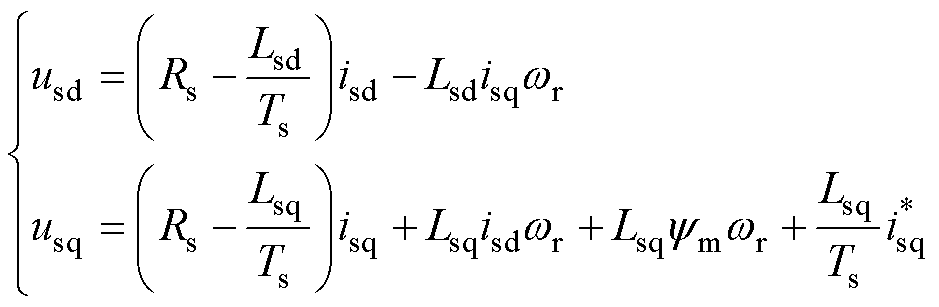 (6)
(6)
超局部模型结构为
 (7)
(7)
其中
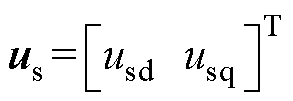
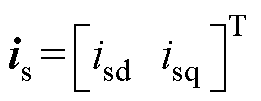
式中,F为变量,将电机系统未知部分统一至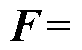
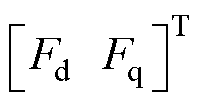 中;
中;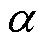 为输入增益系数,通常选择
为输入增益系数,通常选择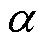 =1/Lsq。
=1/Lsq。
选择滑模观测器估算变量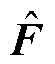 [24]为
[24]为
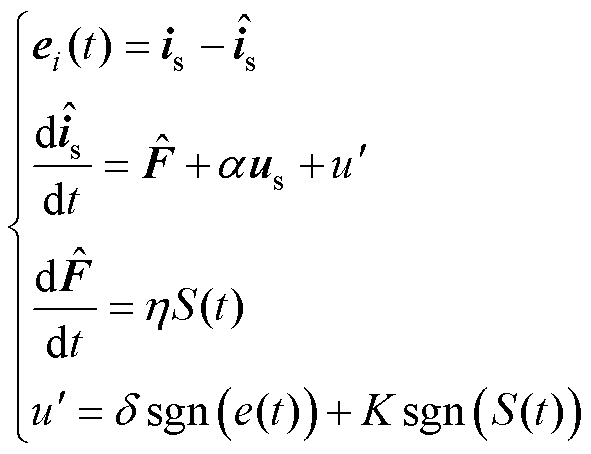 (8)
(8)
其中,比例系数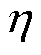 选择为
选择为
 (9)
(9)
式中,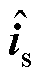 为电流估算值;
为电流估算值;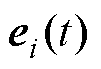 为电流误差;M为F的最大值;isn为归一化电流;
为电流误差;M为F的最大值;isn为归一化电流;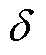 为积分系数;K为观测器增益,均通过控制性能综合选取;S(t)为滑模误差方程;sgn( · )为符号函数。
为积分系数;K为观测器增益,均通过控制性能综合选取;S(t)为滑模误差方程;sgn( · )为符号函数。
在连续控制集下,其控制律设计为
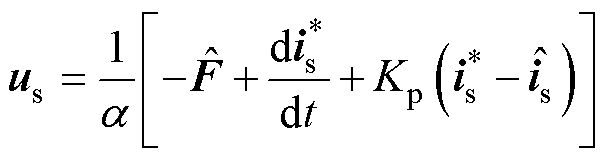 (10)
(10)
式中,Kp为比例增益;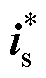 为电流参考值。
为电流参考值。
将基于滑模观测器的超局部MF-PCC命名为传统算法1,并将文献[25]中采用的级-并联ESO超局部MF-PCC方法命名为传统算法2。本文中各传统方法所需参数见表1。
表1 传统算法选取参数
Tab.1 Selected parameters for the conventional strategy
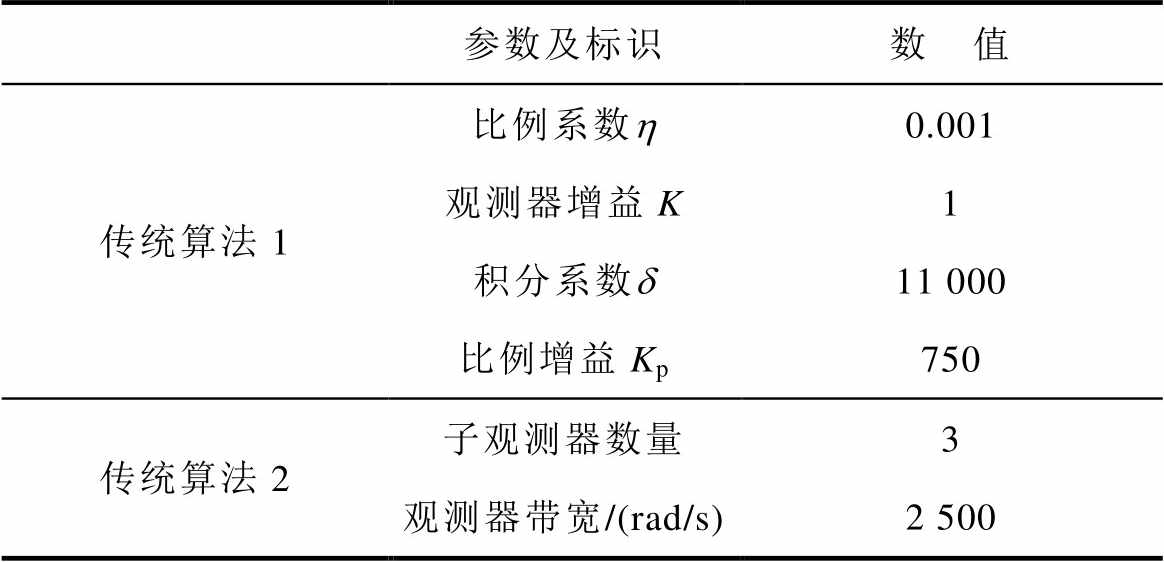
参数及标识数 值 传统算法1比例系数h0.001 观测器增益K1 积分系数d11 000 比例增益Kp750 传统算法2子观测器数量3 观测器带宽/(rad/s)2 500
测试电机主要参数见表2。1.5 s时将负载转矩从4 N·m增加至11.5 N·m;3 s时将转速从500 r/min增加至1 000 r/min。传统算法1和传统算法2的仿真波形分别如图1和图2所示。
表2 主要系统参数
Tab.2 Main system parameters
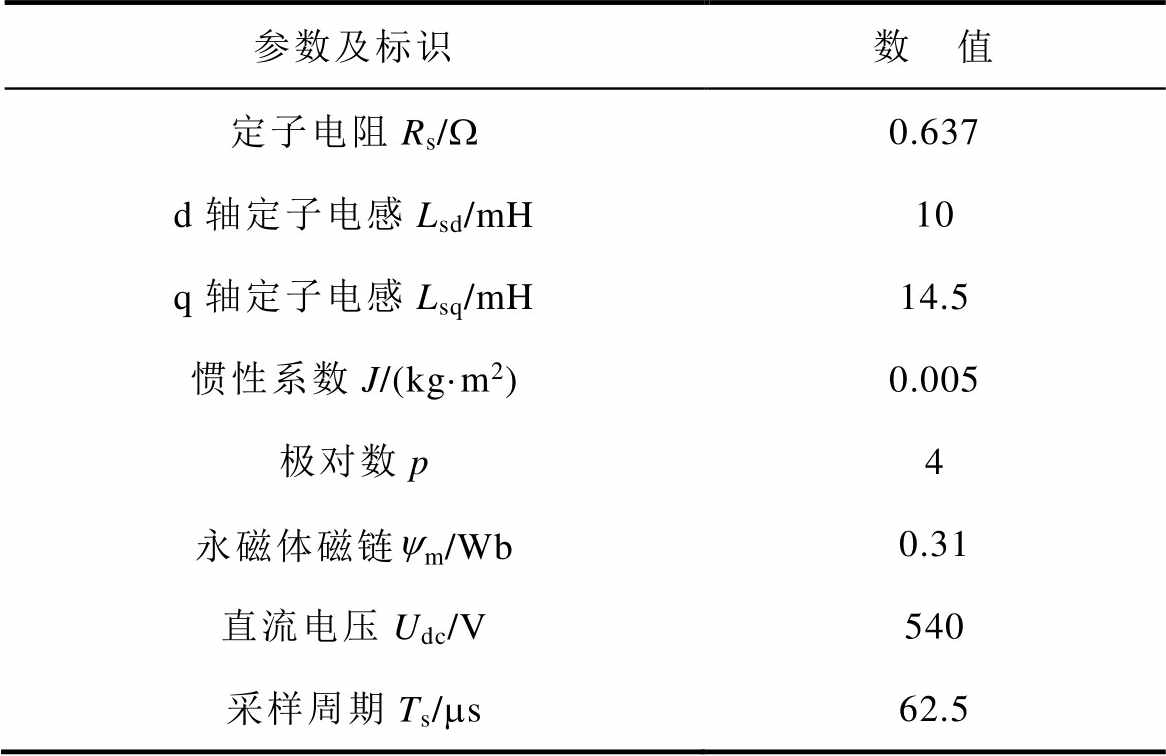
参数及标识数 值 定子电阻Rs/W0.637 d轴定子电感Lsd/mH10 q轴定子电感Lsq/mH14.5 惯性系数J/(kg·m2)0.005 极对数p4 永磁体磁链ym/Wb0.31 直流电压Udc/V540 采样周期Ts/ms62.5
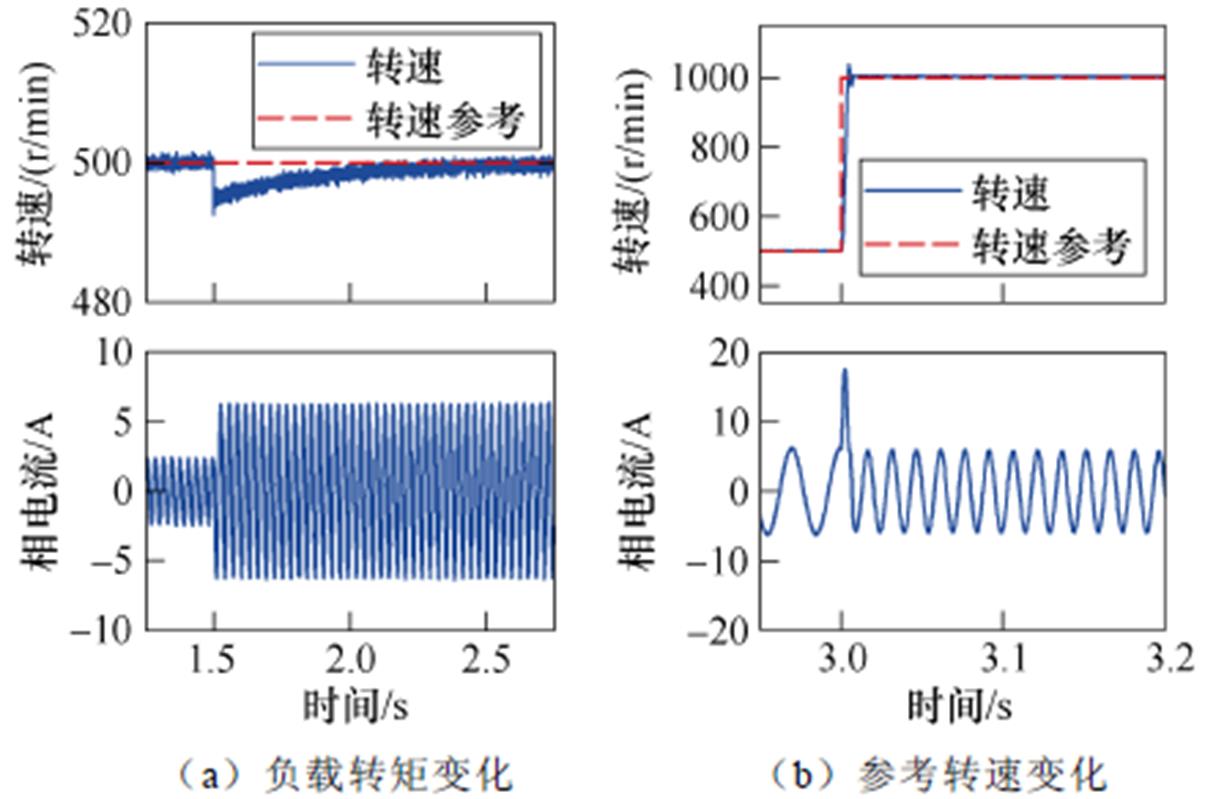
图1 传统算法1仿真波形
Fig.1 Simulation waveforms of the conventional algorithm 1
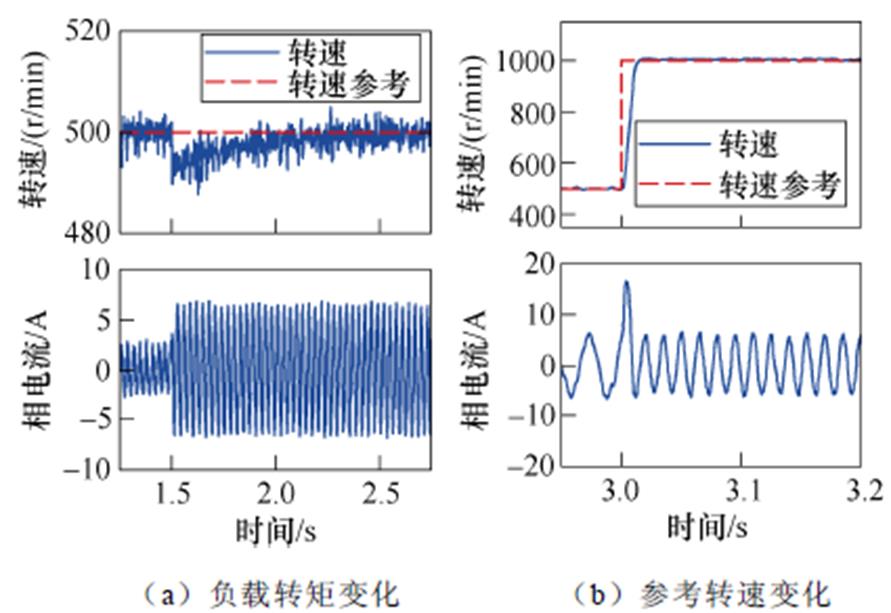
图2 传统算法2仿真波形
Fig.2 Simulation waveforms of the conventional algorithm 2
基于传统算法1的系统抵抗负载转矩扰动过程如图1a所示,超调量约1.64%,调整时间约0.46 s;转速参考跟踪过程如图1b所示,超调量约4.77%,调整时间约7.19 ms。基于传统算法2的系统在抵抗负载转矩扰动过程中超调量约1.49%,调整时间约0.36 s;转速参考跟踪过程中超调量约0.74%,调整时间约15.50 ms。在整个工作过程中,转速综合时间与绝对误差(Integrated Time and Absolute Error, ITAE)值分别为14.54和17.01。
时间序列模型可设计为
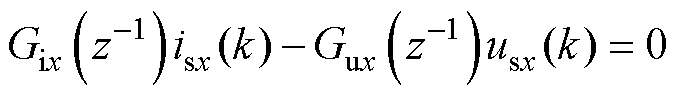 (11)
(11)
其中
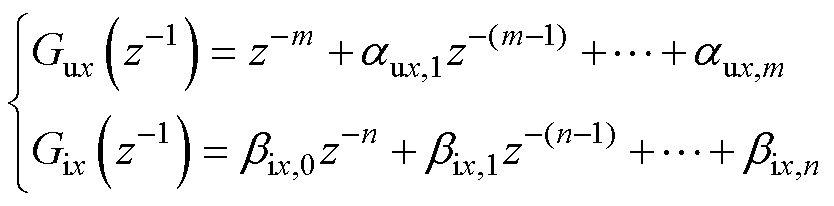 (12)
(12)
式中,aux,m和bix,n为待定系数,下标x表示d轴或q轴分量;n和m为模型维度。该模型将电机拟合为离散传递函数形式。
预先确定模型维度,并将待定系数和输入输出参数分别构成m+n+1维向量,有
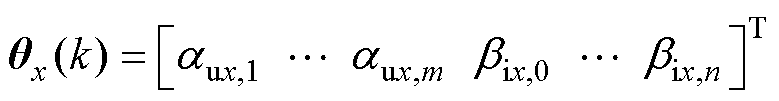 (13)
(13)
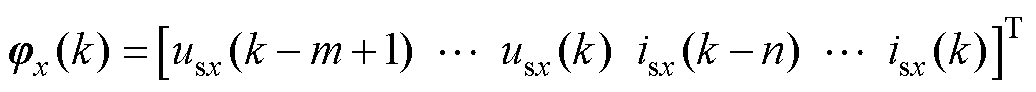 (14)
(14)
通过最小二乘法进行在线估算待定系数,有
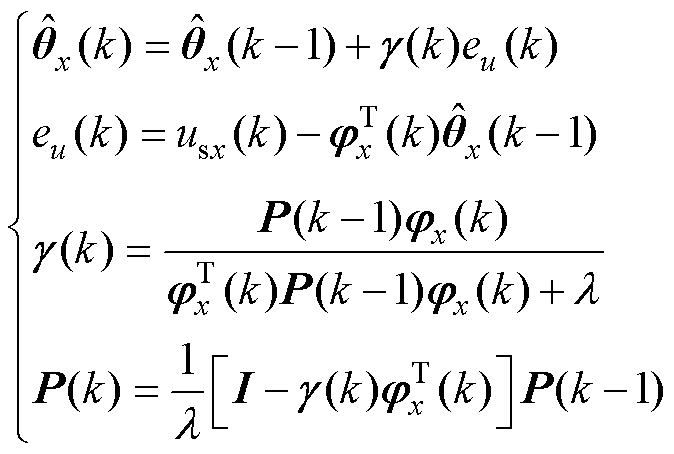 (15)
(15)
式中,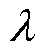 为遗忘因子;eu为电压误差;
为遗忘因子;eu为电压误差;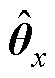 为向量
为向量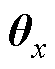 估计值;P为估计参数协方差矩阵,其维度为(m+n+1)×(m+n+1);
估计值;P为估计参数协方差矩阵,其维度为(m+n+1)×(m+n+1);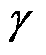 为增益向量,其维度为m+n+1。
为增益向量,其维度为m+n+1。
预计在k+1时刻电流达到其参考值,并且由于采样周期Ts足够小,可将向量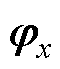 更新为
更新为
 (16)
(16)
控制律设计为
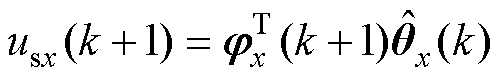 (17)
(17)
式中,k+1时刻的参考电流通过拉格朗日法获得,有
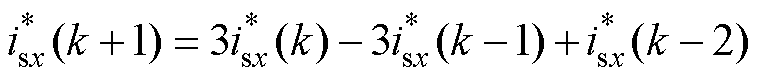 (18)
(18)
综上所述,模型建立和控制律生成过程流程如图3所示,提出方法整体框图如图4所示。
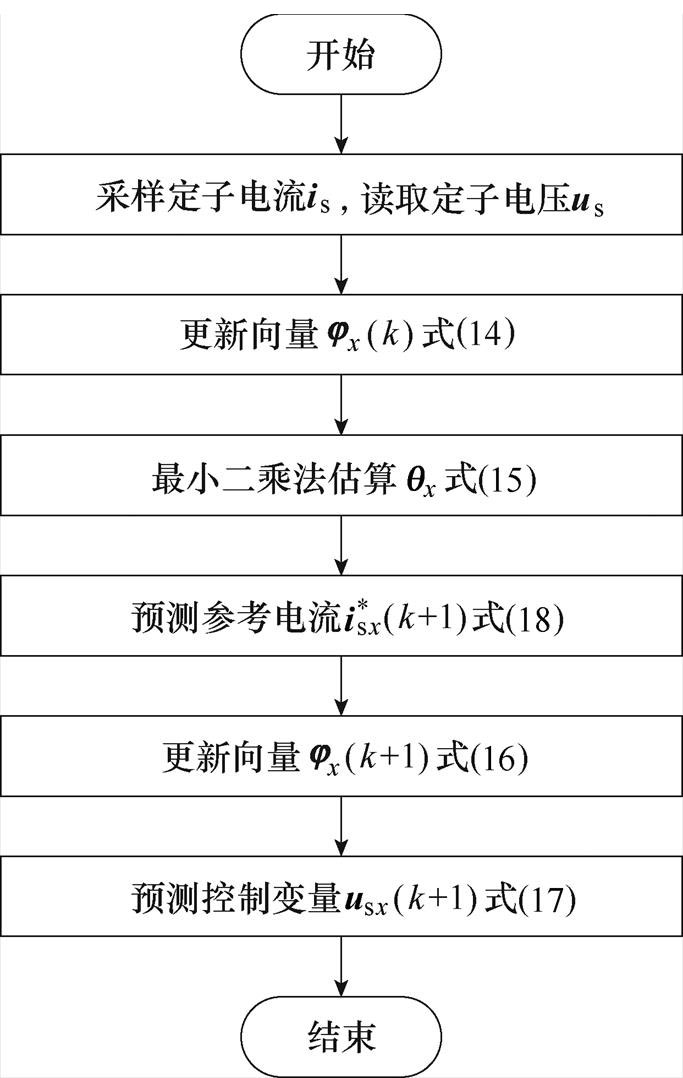
图3 时间序列模型更新过程流程
Fig.3 Time-flow of the updating process of the time-series model

图4 基于时间序列的无模型预测电流控制结构
Fig.4 Structure of the time-series based MF-PCC
根据图4所示结构搭建仿真环境,选择参数见表3。在相同工作条件下,提出方法仿真波形如图5所示。该方法可稳定地追踪转速参考变化,并抵抗负载扰动。抵抗负载转矩扰动过程的超调量约1.50%,调整时间约0.38 s;转速参考跟踪过程的超调量约3.69%,调整时间约5.63 ms。在整个工作过程中,转速ITAE值为12.36。
表3 提出算法选择参数
Tab.3 Selection parameters of the proposed strategy

参数及标识数 值 维度m2 维度n2 遗忘因子l1
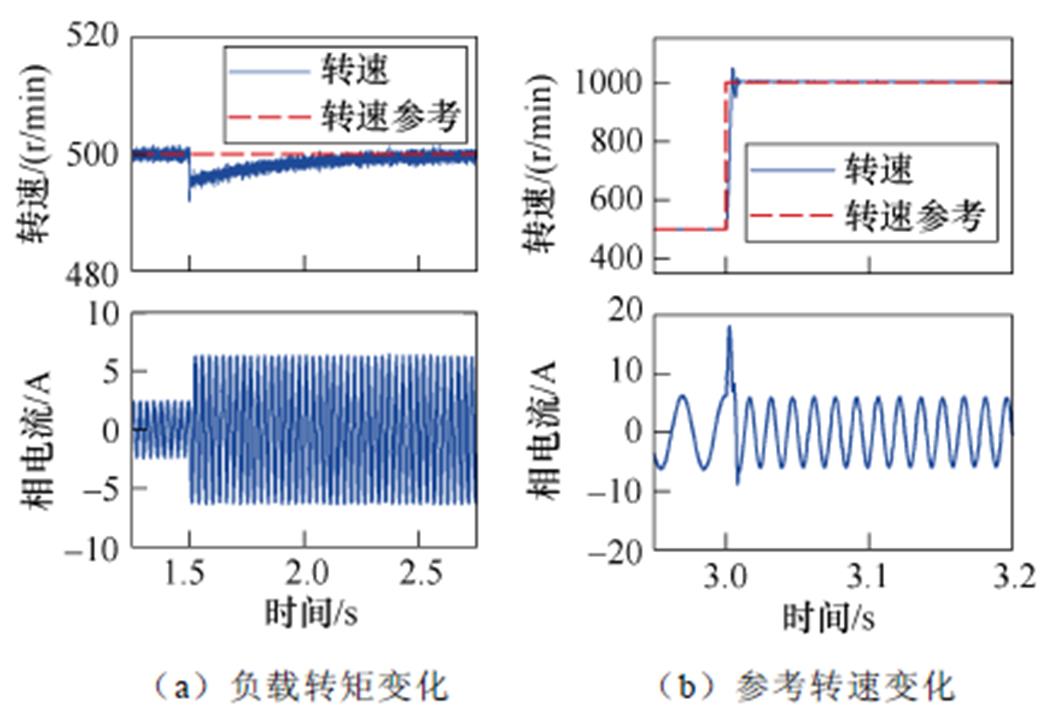
图5 提出算法仿真波形
Fig.5 Simulation waveforms of the proposed strategy
不同维度m和n下,提出方法所得相电流总谐波畸变率(Total Harmonic Distortion, THD)和全工作过程转速ITAE如图6所示。可见,电流THD和转速ITAE均小于传统超局部MF-PCC算法结果,即由于时间序列模型有较高精度,电流和转速质量均有所提升。随着维度m提升,相电流THD有微弱上升趋势,转速ITAE下降;随着维度n提升,电流THD无明显变化趋势,转速ITAE同样下降。
在1 000 r/min转速、11.5 N·m负载转矩稳态运行条件下测定连续5 000个采样周期的提出算法计算时间,并取平均值。不同维度下算法所需运算时间如图7所示。可见,在随着维度上升,计算时间越长;在维度和m+n相同时,运算负担基本相同。由于大维度可能引发系统超时错误,且所得性能不一定满足系统要求,因而可根据所需性能选取维度。
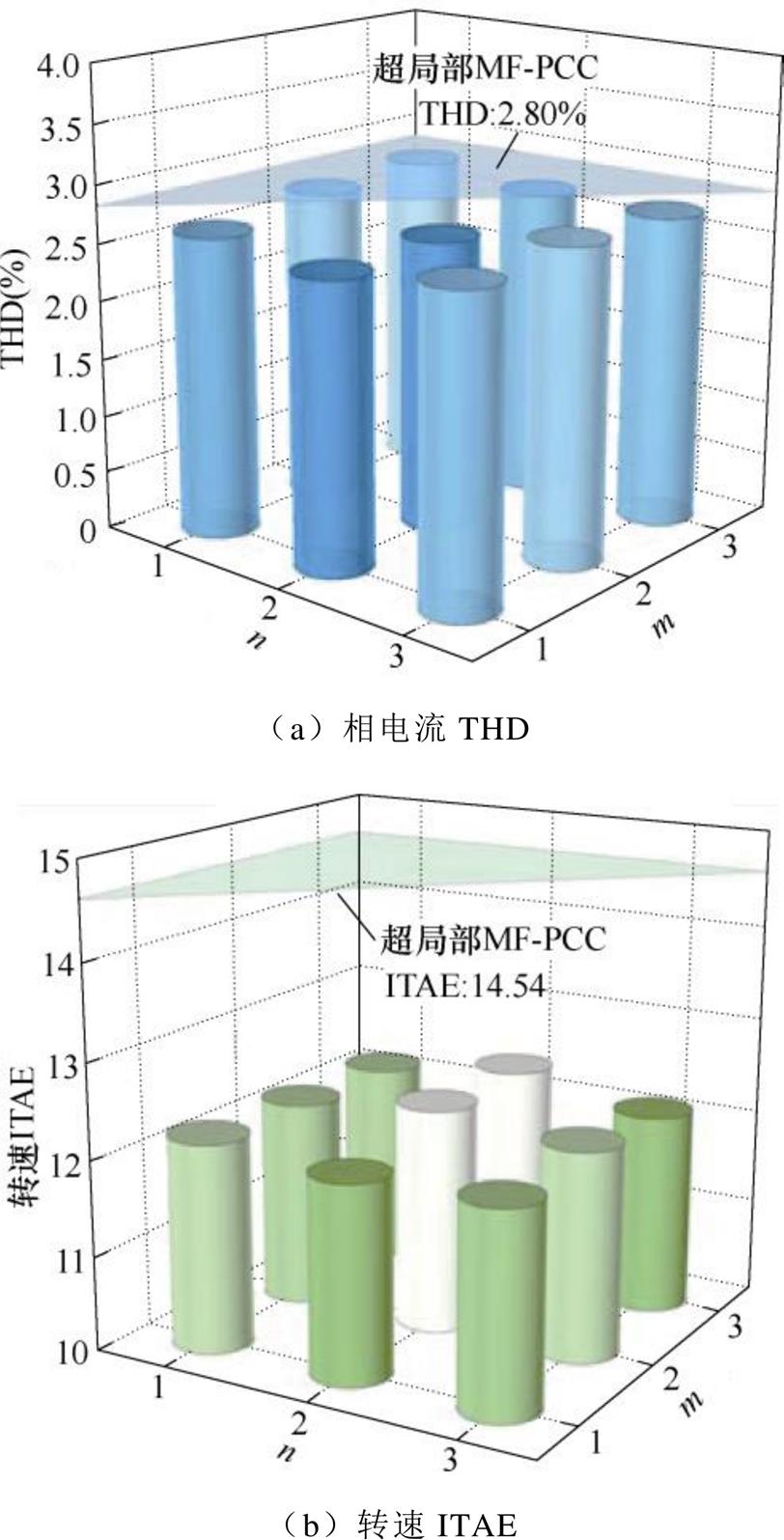
图6 提出算法不同维度下转速和电流性能
Fig.6 Speed and current performances for the proposed strategy with different orders
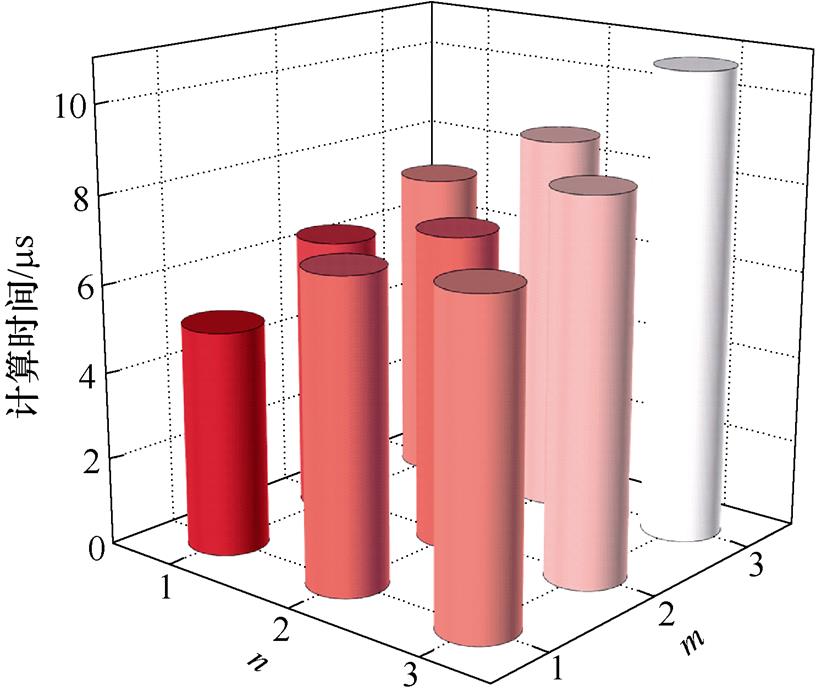
图7 提出算法不同维度运算时间
Fig.7 Calculation times for the proposed strategy with different orders
根据文献[26],遗忘因子通常在[0.9, 1]之间选取,是鲁棒性和快速性的折中。在不同遗忘因子时,相电流THD和转速ITAE结果如图8所示。本文综合考虑控制性能和系统鲁棒性,遗忘因子选取为1。
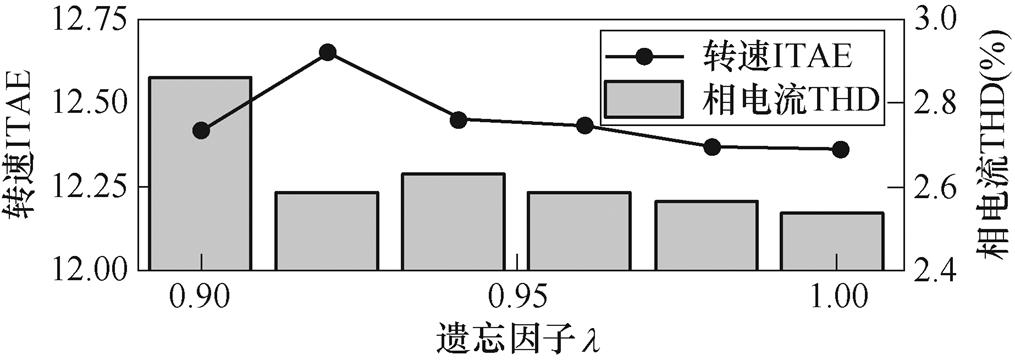
图8 提出算法不同遗忘因子相电流THD和转速ITAE
Fig.8 Stator current THD and speed ITAE for the proposed strategy with different forgetting factors
基于DSP F28379D和4.8kW PMSM搭建实验平台,平台及实验验证系统框图如图9所示,其中,估算算法和数据驱动模型在DSP中实现。电机参数和算法参数分别与表1和表2相同。

图9 实验平台结构
Fig.9 Experimental platform structure
电动汽车运行过程中,加减速和上下坡是最为常见的运行状态。其中,前者反映在电机系统中是增减转子速度,后者是增减负载转矩。将转速参考从500 r/min变化至1 000 r/min,负载转矩从空载变化至11.5 N·m。提出算法和传统算法在连续跟踪参考过程的实验结果如图10所示,抵抗扰动过程的波形如图11所示。可以看出,算法均可追踪参考抵抗扰动。在跟踪参考过程中,提出算法有弱超调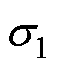 约为1.52%、调整时间ts1为1.86 s,传统算法1产生负超调
约为1.52%、调整时间ts1为1.86 s,传统算法1产生负超调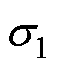 约为1.74%、调整时间ts1为2.24 s,传统算法2同样产生负超调
约为1.74%、调整时间ts1为2.24 s,传统算法2同样产生负超调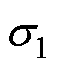 约为1.72%、调整时间ts1为2.34 s;在抵抗负载转矩扰动过程中,提出算法和传统算法1的超调量
约为1.72%、调整时间ts1为2.34 s;在抵抗负载转矩扰动过程中,提出算法和传统算法1的超调量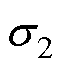 均为17.68%,前者调整时间ts2约为7.28 s,后者调整时间ts2约为7.86 s,传统算法2的超调量
均为17.68%,前者调整时间ts2约为7.28 s,后者调整时间ts2约为7.86 s,传统算法2的超调量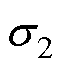 为18.20%,调整时间ts2约为8.94 s。
为18.20%,调整时间ts2约为8.94 s。
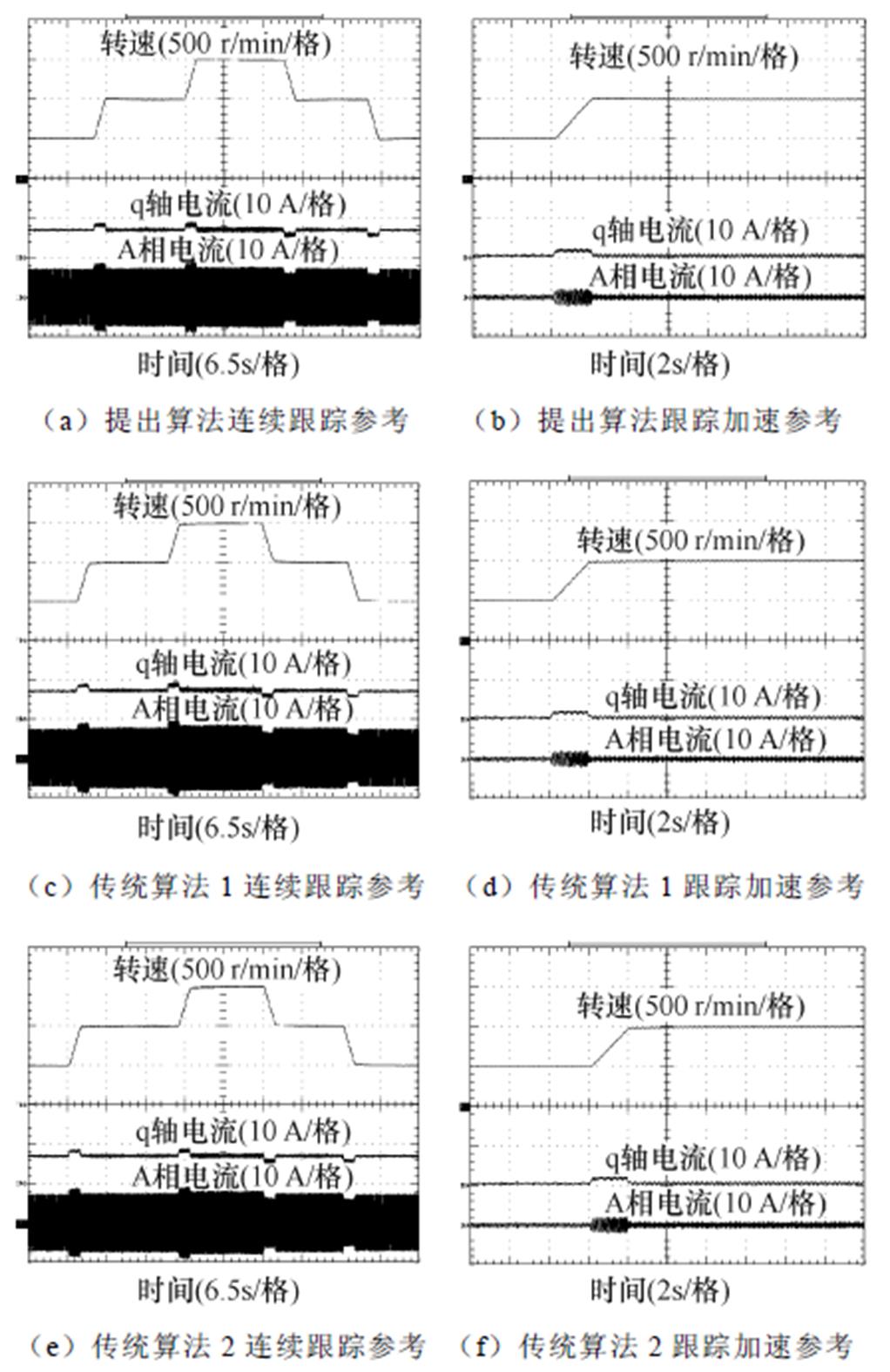
图10 算法跟踪参考过程实验波形
Fig.10 Experimental waveforms of the strategies within the increasing and decreasing processes of speed

图11 算法抵抗扰动过程实验波形
Fig.11 Experimental waveforms of the strategies within the increasing and decreasing processes of load torque
图12为部分放大暂态波形。图中,传统算法1和传统算法2转速性能几乎一致。但根据相电流包络线,提出算法和传统算法2的相电流几乎不存在超调,平滑地进入稳态运行过程。
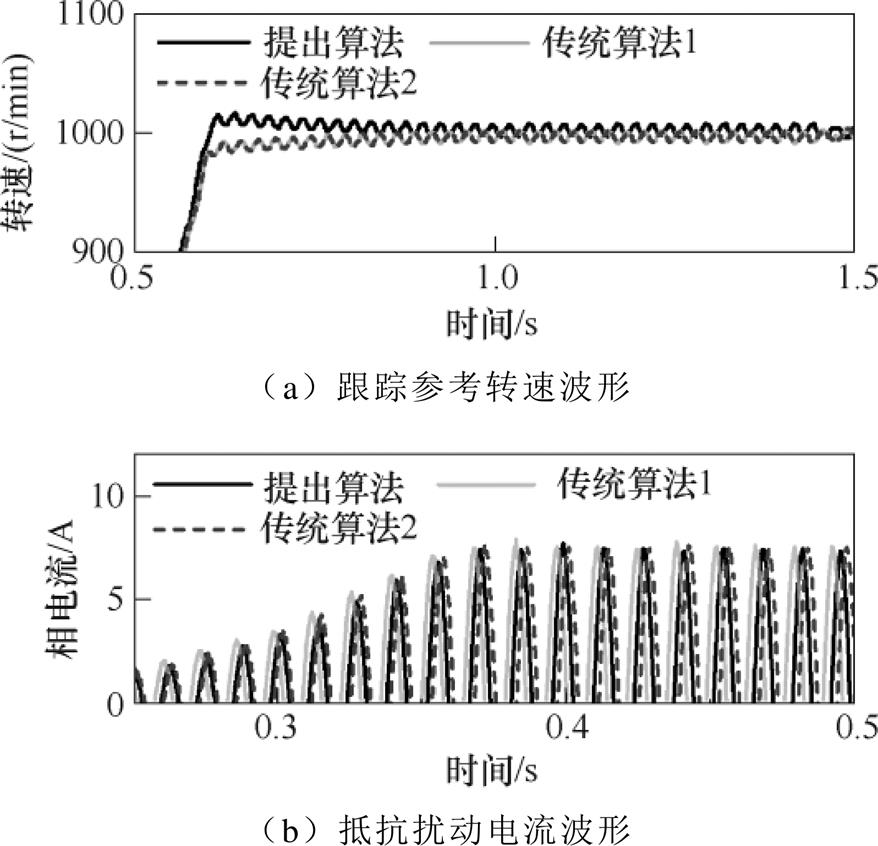
图12 部分放大实验波形比较
Fig.12 Comparisons of enlarged experimental waveforms
为消除傅里叶分析的随机性,在0.8 s内对相电流进行连续采样和分析,统计结果的小提琴图如图13所示。可见,提出算法的相电流THD位于3.3%~3.9%区间,多数THD值集中在3.55%,平均值位于3.53%;传统算法1在3.4%~4.7%区间,多数THD值集中在3.65%和3.8%,平均值位于3.82%;传统算法2在3.8%~4.9%区间,多数THD值集中在4.42%,平均值位于4.34%。
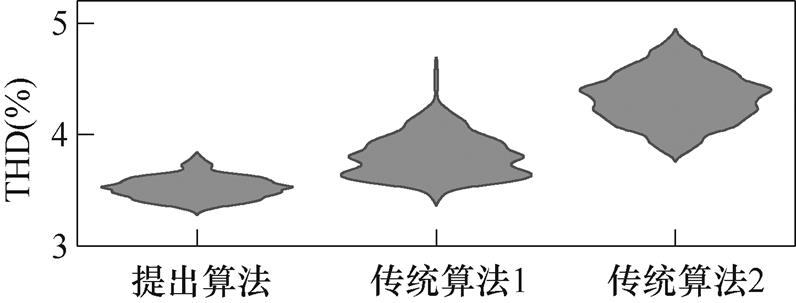
图13 傅里叶分析结果
Fig.13 Fourier analysis results
对预测电流和下一拍实际采样电流进行比较,20 000个采样点内实验结果如图14所示。相较于传统算法,提出算法的q轴电流累积误差分别降低约34.34%和37.47%,d轴电流累计误差分别降低14.99%和19.05%,提出方法模型有更高模型精度。
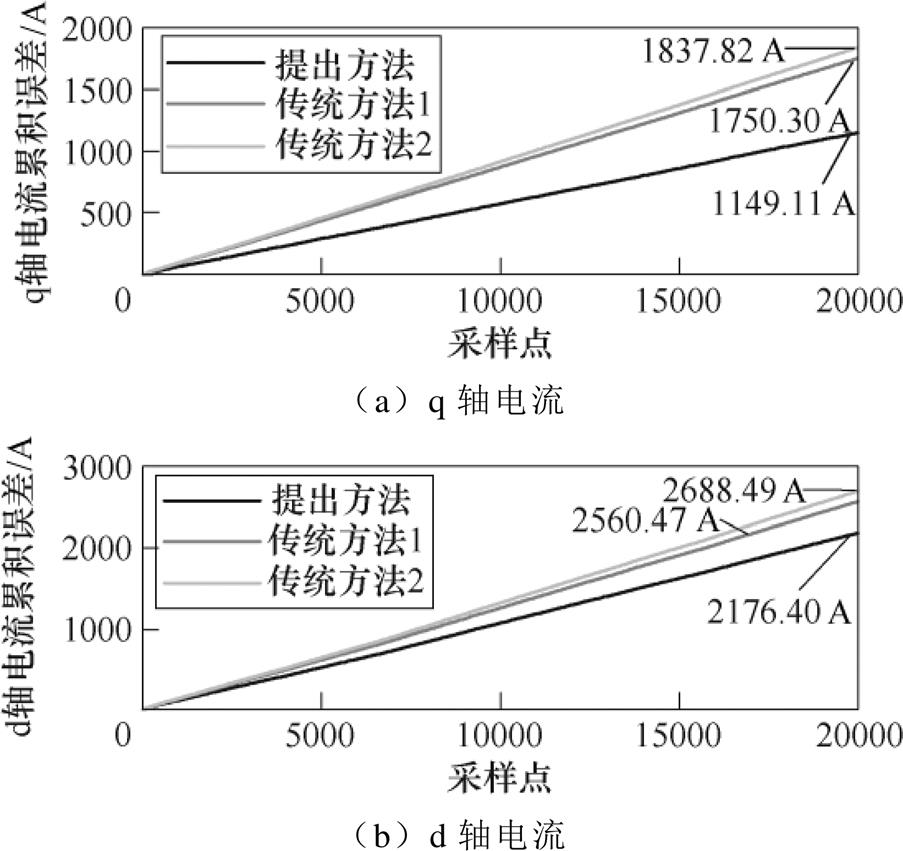
图14 实验电流累积误差
Fig.14 Experimental accumulating current errors
在跟踪加速参考和抵抗扰动阶段,模型主要待定系数anx,1、anx,2、bdx,0、bdx,1变化曲线如图15所示。可以看出,待定系数bdx,0、bdx,1有较大取值,相对变化幅度较为隐晦;待定系数anx,1、anx,2取值较小,相对变化幅度较为明显。在系统出现变化后,待定系数通过在线估算和更新再次收敛,使模型保持对被控对象的高度拟合。
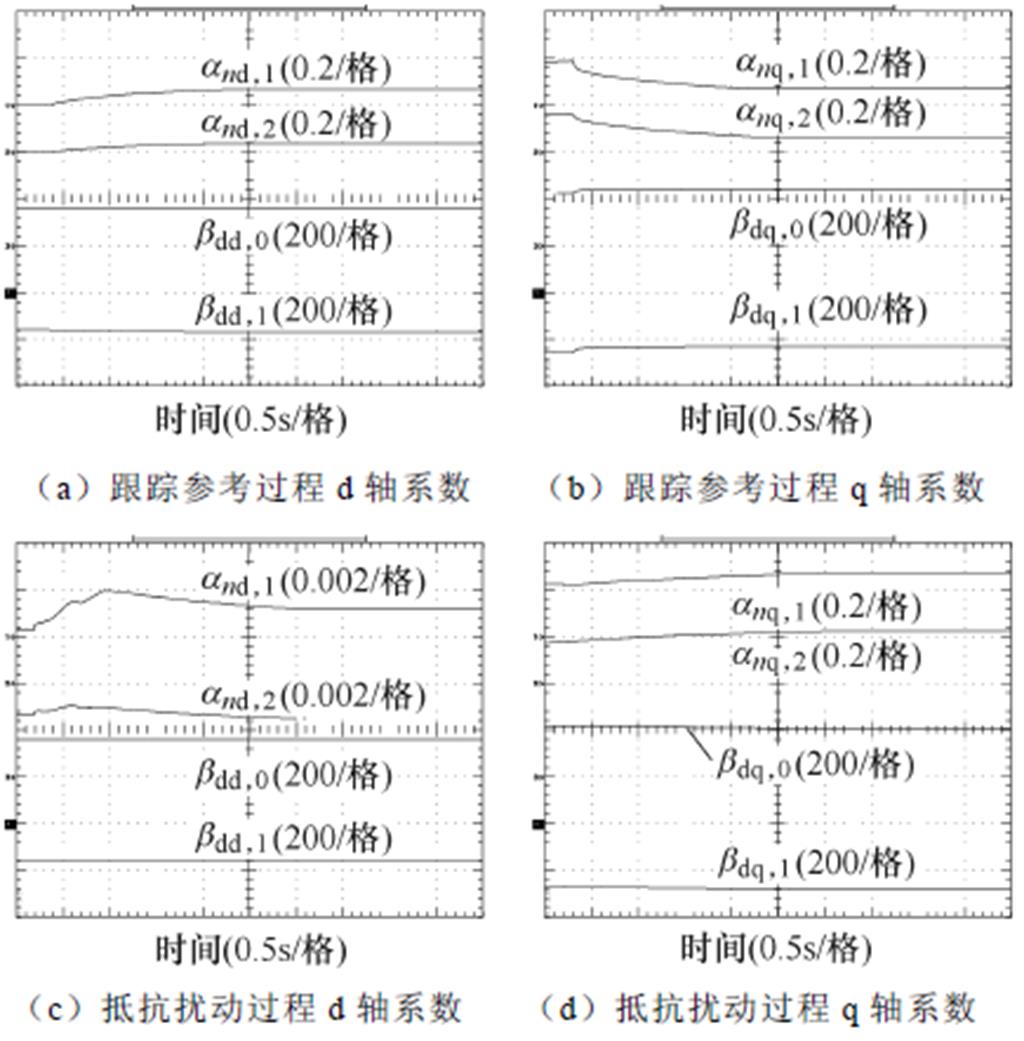
图15 动态过程主要待定系数变化波形
Fig.15 Changing waveforms for the main undetermined coefficients during the transient-state
在DSP中对算法运算时间进行测试。不同维度提出的算法和传统算法比较结果如图16所示,图中提出算法的维度表示为[m, n]。提出算法运算时间随着维度上升而增加,变化趋势与仿真结果基本一致。在提出算法维度为[2, 2]时,运算时间已分别超出传统算法1、传统算法2和基本CCS-PCC算法约48.03%、40.10%和63.11%。实际应用中,提出算法需综合评估处理器资源选取合适的模型维度。

图16 运算时间测试结果
Fig.16 Calculation time testing results
将部分控制指标列写至表4中,其中转速ITAE在稳态连续2 s内求得。可以看出,相较于传统算法1,提出方法所得转速ITAE和电流THD分别提升5.46%和7.59%;相较于传统方法2,转速ITAE和电流THD分别提升2.98%和18.66%,并且超调量和调整时间均有所降低。提出方法由于有更好的模型精度,在电流质量和动态性能方面均有所改善。
表4 系统参数
Tab.4 System parameters

控制性能提出算法传统算法1传统算法2 转速ITAE5.545.865.71 相电流THD (%)3.533.824.34 调整时间ts1/s1.862.242.34 超调量s1 (%)1.52-1.74-1.72 调整时间ts2/s7.287.868.94 超调量s2 (%)17.6817.6818.20
电动汽车在牵引和制动过程中,直流侧电压出现波动。为确保在该过程中系统收敛,根据国家标准[27-28]和平台参数设定直流侧电压浮动范围为440~540 V,并分别在边界条件下对控制策略进行验证。在系统带载稳定运行时,变化直流电源输出电压,提出算法实验波形如图17所示。可以看出,直流侧电压变化前后,相电流基本没有变化,系统保持稳定运行。
电动汽车电机系统噪声直接影响驾驶员体验感。对不同转速下不同控制策略产生的电机系统噪声进行采集,平均噪声幅值如图18所示。可以看出,随着电机转速和负载转矩的上升,噪声幅值同样上升。除传统算法2在2 000 r/min空载运行时有最小的噪声幅值外,在其他工作条件下,相较于传统算法,提出算法产生的噪声得到优化。
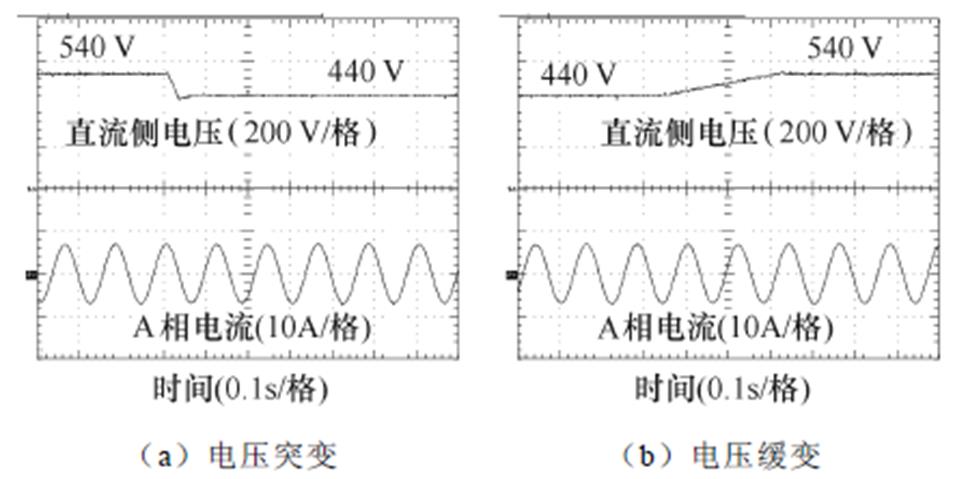
图17 直流侧电压变化实验结果
Fig.17 Experimental results under the conditions of DC voltage changes
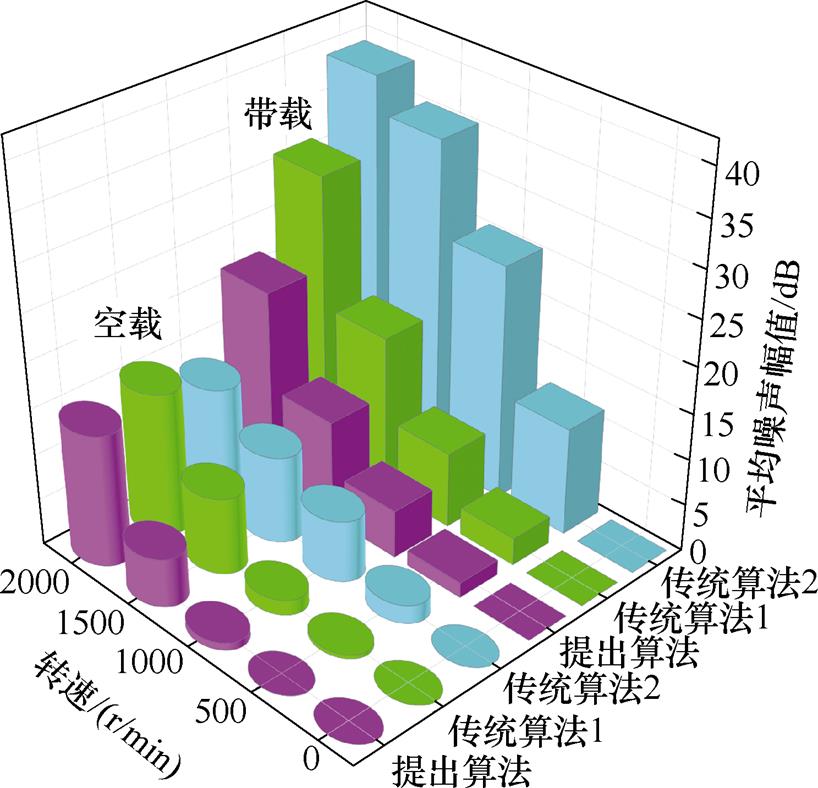
图18 系统噪声测试结果
Fig.18 Test results of system noise
定义Rse、Lse和yme分别为控制算法中定子电阻、定子电感和永磁体磁链选择参数。参数失配条件设定为Rse/Rs=0.2、Lse/Ls=3、yme/ym=0.5和Lse/Ls= 2、yme/ym=2。其中,对于定子电感参数失配同时作用在d轴和q轴分量上。
在不同参数失配条件下,提出算法、传统算法1、传统算法2和基本CCS-PCC算法的实验波形及傅里叶分析结果如图19和图20所示。可以看出,相较于采用先验模型和式(7)控制律的基本CCS-PCC算法中相电流严重谐波含量,提出算法和传统算法由于采用了数据驱动模型,时变物理参数及其影响被完全消除,均可在参数失配条件下稳定运行。在参数失配条件下,提出算法的电流THD较低,波形质量更高。
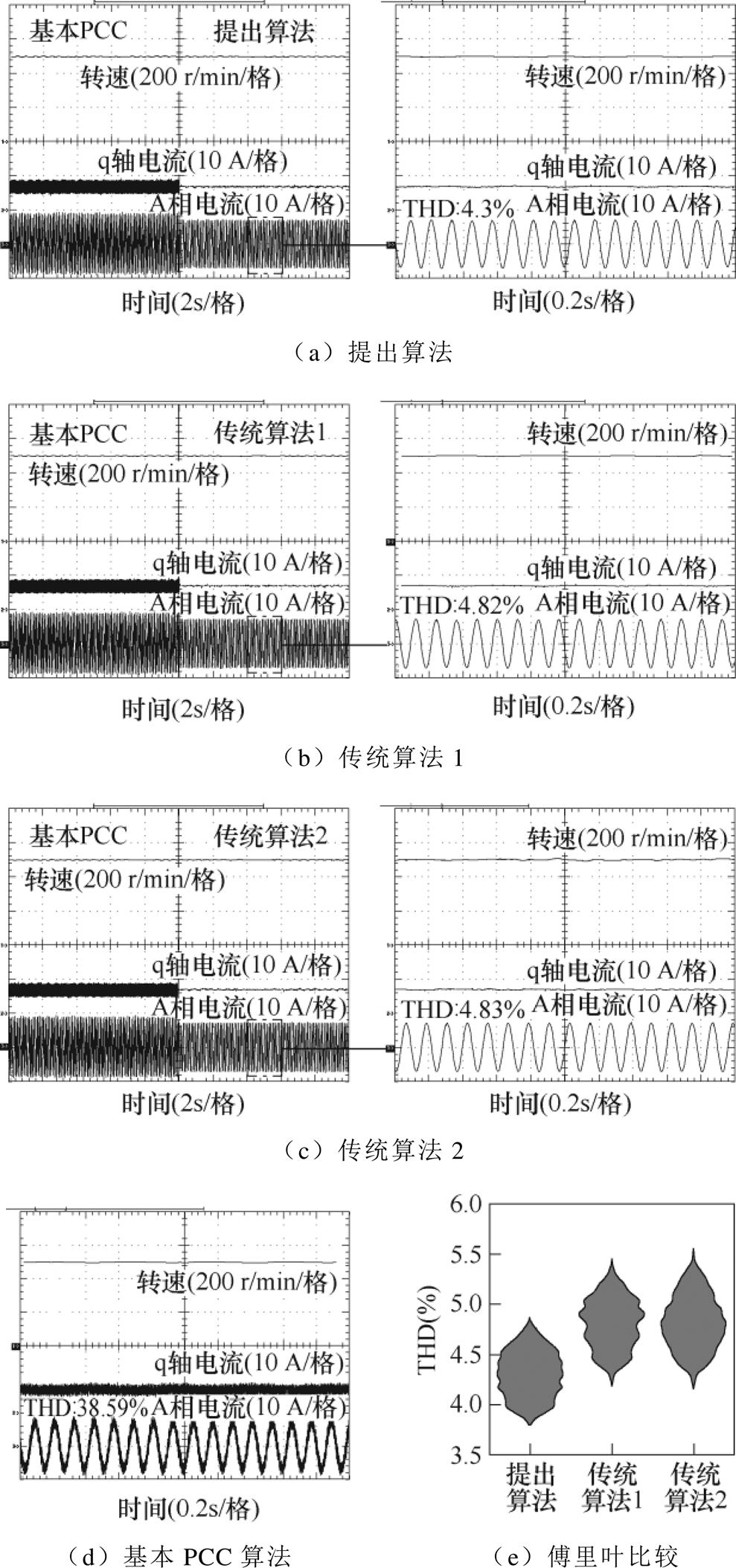
图19 参数失配条件1实验结果
Fig.19 Experimental results under the conditions of parameter mismatches 1

图20 参数失配条件2实验结果
Fig.20 Experimental results under the conditions of parameter mismatches 2
针对时间序列无模型预测控制在连续控制集实现困难问题上,PMSM驱动系统提出一种基于时间序列连续控制集无模型预测控制策略。提出算法通过拉格朗日法设计合适的最小二乘法回归矢量,在线估计模型待定系数并建立被控对象数据驱动模型。建模过程无需被控对象的时变物理参数参与,所得模型完全消除模型失配对控制性能的影响,并且更加符合电机系统运动特性。根据仿真和实验结果,与传统超局部MF-PCC策略相比,提出算法有更好的电流质量、动态性能和系统噪声,以及良好的鲁棒性。
参考文献
[1] 赵剑飞, 花敏琪, 刘廷章. 电动车用多盘式永磁同步电机协同优化与容错控制方法[J]. 中国电机工程学报, 2019, 39(2): 386-394, 636.
Zhao Jianfei, Hua Minqi, Liu Tingzhang. Cooperative optimization and fault-tolerant control method of multi-disk permanent magnet synchronous motor for electric vehicles[J]. Proceedings of the CSEE, 2019, 39(2): 386-394, 636.
[2] 李祥林, 薛志伟, 阎学雨, 等. 基于电压矢量快速筛选的永磁同步电机三矢量模型预测转矩控制[J]. 电工技术学报, 2022, 37(7): 1666-1678.
Li Xianglin, Xue Zhiwei, Yan Xueyu, et al. Voltage vector rapid screening-based three-vector model predictive torque control for permanent magnet synchronous motor[J]. Transactions of China Elec- trotechnical Society, 2022, 37(7): 1666-1678.
[3] 李家祥, 汪凤翔, 柯栋梁, 等. 基于粒子群算法的永磁同步电机模型预测控制权重系数设计[J]. 电工技术学报, 2021, 36(1): 50-59, 76.
Li Jiaxiang, Wang Fengxiang, Ke Dongliang, et al. Weighting factors design of model predictive control for permanent magnet synchronous machine using particle swarm optimization[J]. Transactions of China Electrotechnical Society, 2021, 36(1): 50-59, 76.
[4] 魏尧, 魏艳君, 马云飞, 等. 永磁同步电机转子位置的级联预测控制[J]. 电工技术学报, 2019, 34(1): 41-48.
Wei Yao, Wei Yanjun, Ma Yunfei, et al. Cascade predictive control for rotor position of permanent magnet synchronous machines[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 41- 48.
[5] 王治国, 郑泽东, 李永东, 等. 三相异步电机电流多步预测控制方法[J]. 电工技术学报, 2018, 33(9): 1975-1984.
Wang Zhiguo, Zheng Zedong, Li Yongdong, et al. Predictive current control for three phase induction machine using multi-steps prediction horizon[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 1975-1984.
[6] 王安鹏, 黄旭珍, 李立毅, 等. 永磁直线同步电机的变权重系数多步模型预测电流控制方法[J]. 中国电机工程学报, 2022, 42(22): 8332-8343.
Wang Anpeng, Huang Xuzhen, Li Liyi, et al. Variable weight coefficient multi-step model predictive current control method for permanent magnet linear syn- chronous motor[J]. Proceedings of the CSEE, 2022, 42(22): 8332-8343.
[7] Wei Yao, Wei Yanjun, Gao Yang, et al. A variable prediction horizon self-tuning method for nonlinear model predictive speed control on PMSM rotor position system[J]. IEEE Access, 2021, 9: 78812- 78822.
[8] Wang Fengxiang, Ke Dongliang, Yu Xinhong, et al. Enhanced predictive model based deadbeat control for PMSM drives using exponential extended state observer[J]. IEEE Transactions on Industrial Elec- tronics, 2022, 69(3): 2357-2369.
[9] 贾成禹, 王旭东, 周凯. 基于扰动观测器的PMSM模型预测电流控制[J]. 电力电子技术, 2019, 53(10): 23-25, 95.
Jia Chengyu, Wang Xudong, Zhou Kai. Model predictive current control of PMSM based on dis- turbance observer[J]. Power Electronics, 2019, 53(10): 23-25, 95.
[10] Mousavi M S, Davari S A, Nekoukar V, et al. A robust torque and flux prediction model by a modified disturbance rejection method for finite-set model- predictive control of induction motor[J]. IEEE Transactions on Power Electronics, 2021, 36(8): 9322-9333.
[11] 余晨辉, 汪凤翔, 林贵应. 基于在线扰动补偿的三电平PWM整流器级联式无差拍控制策略[J]. 电工技术学报, 2022, 37(4): 954-963.
Yu Chenhui, Wang Fengxiang, Lin Guiying. Cascaded deadbeat control strategy with online disturbance compensation for three-level PWM rectifier[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 954-963.
[12] 肖雄, 王浩丞, 武玉娟, 等. 基于双滑模估计的主从结构共轴双电机模型预测直接转矩控制无速度传感器控制策略[J]. 电工技术学报, 2021, 36(5): 1014-1026.
Xiao Xiong, Wang Haocheng, Wu Yujuan, et al. Coaxial dual motor with master-slave structure model-predictive direct torque control speed sensor- less control strategy based on double sliding mode estimation[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 1014-1026.
[13] 柯栋梁, 汪凤翔, 李家祥. 基于自适应高增益观测器的永磁同步电机预测电流控制方法[J]. 中国电机工程学报, 2021, 41(2): 728-738.
Ke Dongliang, Wang Fengxiang, Li Jiaxiang. Predictive current control of permanent magnet synchronous motor based on an adaptive high-gain observer[J]. Proceedings of the CSEE, 2021, 41(2): 728-738.
[14] Hou Zhongsheng, Lei Ting. Constrained model free adaptive predictive perimeter control and route guidance for multi-region urban traffic systems[J]. IEEE Transactions on Intelligent Transportation Systems, 2022, 23(2): 912-924.
[15] Heydari R, Young H, Flores-Bahamonde F, et al. Model-free predictive control of grid-forming inverters with LCL filters[J]. IEEE Transactions on Power Electronics, 2022, 37(8): 9200-9211.
[16] 史婷娜, 李聪, 姜国凯, 等. 基于无模型预测控制的无刷直流电机换相转矩波动抑制策略[J]. 电工技术学报, 2016, 31(15): 54-61.
Shi Tingna, Li Cong, Jiang Guokai, et al. Model free predictive control method to suppress commutation torque ripple for brushless DC motor[J]. Transactions of China Electrotechnical Society, 2016, 31(15): 54-61.
[17] 张永昌, 屈祈延, 杨海涛. 基于空间矢量调制的Vienna整流器无模型预测电流控制[J]. 电工技术学报, 2022, 37(21): 5541-5547.
Zhang Yongchang, Qu Qiyan, Yang Haitao. Model free predictive current control of Vienna rectifier based on space vector modulation[J]. Transactions of China Electrotechnical Society, 2022, 37(21): 5541- 5547.
[18] 王誉, 侯忠生. 具有外部扰动的PMSM系统的无模型自适应预测控制[J]. 控制理论与应用, 2022, 39(5): 837-846.
Wang Yu, Hou Zhongsheng. Model-free adaptive predictive control for PMSM systems with external disturbance[J]. Control Theory & Applications, 2022, 39(5): 837-846.
[19] Wang Fengxiang, Wei Yao, Young H, et al. Continuous-control-set model-free predictive funda- mental current control for PMSM system[J]. IEEE Transactions on Power Electronics, 2023, 38(5): 5928-5938.
[20] Zhang Yongchang, Jin Jialin, Huang Lanlan. Model- free predictive current control of PMSM drives based on extended state observer using ultralocal model[J]. IEEE Transactions on Industrial Electronics, 2021, 68(2): 993-1003.
[21] 赵凯辉, 周瑞睿, 冷傲杰, 等. 一种永磁同步电机的有限集无模型容错预测控制算法[J]. 电工技术学报, 2021, 36(1): 27-38.
Zhao Kaihui, Zhou Ruirui, Leng Aojie, et al. Finite control set model-free fault-tolerant predictive control for permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(1): 27-38.
[22] Wang Daming, Shen Z J, Yin Xin, et al. Model predictive control using artificial neural network for power converters[J]. IEEE Transactions on Industrial Electronics, 2022, 69(4): 3689-3699.
[23] Mesai A H, Jlassi I, Marques C A J, et al. Model-free predictive current control of synchronous reluctance motors based on a recurrent neural network[J]. IEEE Transactions on Industrial Electronics, 2022, 69(11): 10984-10992.
[24] Mousavi M S, Davari S A, Nekoukar V, et al. Integral sliding mode observer-based ultralocal model for finite-set model predictive current control of indu- ction motor[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(3): 2912-2922.
[25] Babayomi O, Zhang Zhenbin. Model-free predictive control of power converters with cascade-parallel extended state observers[J]. IEEE Transactions on Industrial Electronics, 2023, 70(10): 10215-10226.
[26] Nelles O. Nonlinear system identification[M]. Kronberg: Springer-Verlag, 2001.
[27] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB/T 18384.1-2015 电动汽车 安全要求 第1部分: 车载可充电储能系统(REESS)[S]. 北京: 中国标准出版社, 2015.
[28] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB/T 18384.2-2015 电动汽车 安全要求 第2部分: 操作安全和故障防护[S]. 北京: 中国标准出版社, 2015.
Abstract The finite-control-set type (FCS-type) predictive control method is not ideal for electric vehicles because of its limited control accuracy and high harmonic content. In contrast, the continuous-control-set type (CCS-type) model-free predictive current control (MF-PCC) is more suitable. The model-free predictive current control (MF-PCC) uses a time-series model as a discrete transfer function, which is more compliant with the motion characteristics of the motor system. However, calculating the inverse of the model in the digital processor makes it challenging to apply in the CCS-type. Therefore, a time-series-based CCS-type MF-PCC strategy is proposed in this paper for a permanent magnet synchronous motor (PMSM) driving system. The plant is accurately expressed, and the control strategy is easily realized in the CCS-type by the online building and updating the time-series model based on the sampled data.
Firstly, this approach establishes a time-series model and updates the regressive vector summarizing input and output signals based on sampled data. Secondly, all undetermined coefficients in the model are estimated through the recursive least square (RLS) algorithm. Herein, the current operating state is described as a discrete- time transfer function within the model. Finally, according to predictive reference by the Lagrange algorithm, the regressive vector is updated to predict the output signal and generate the control law. This time-series model is easily realized in the CCS type with good accuracy, addresses the problem of the complex calculation process, and eliminates all time-varying physical parameters and their influences in the a priori model of the plant.
Simulation and experimental results on a PMSM driving system show that the proposed method resists disturbances and tracks the reference successfully to suit electric vehicle driving operations. The disturbances mainly include changed parameter mismatches, load torque, and DC voltage. Continuous Fourier analysis and accumulated error comparisons between different control strategies demonstrate that the proposed method achieves a range of total harmonic distortion (THD) between 3.3%~3.9%, with an average value of 3.53%. Compared to conventional strategies, the proposed method has the minimum ascending slope of accumulated error of current. Additionally, to analyze the impact of system noise on driver perception, the proposed method is tested under different speed references and load torques. Finally, experimental results are obtained with different parameter mismatches of typical physical parameters, including stator resistance, stator inductance, and magnet flux linkage, and compared using continuous Fourier analysis.
The following conclusions can be drawn. (1) The proposed method represents the current operating state of the motor driving system as a time-series model in the CCS-type. Compared with the conventional MF-PCC strategy using ultra-local, it formulates the system as a group of discrete-time transfer functions. (2) The obtained current quality, dynamics, and system noises are improved due to the good accuracy of the time-series model. (3) Based on the designed estimation algorithm and sampled data, the time-series model includes multiple time-varying physical parameters of the system. (4) The orders of the model should be selected comprehensively, considering the permitted calculation time and performances to prevent overrun error or insufficient accuracy.
Keywords:Model-free predictive control, time series model, least square estimation algorithm, current prediction
魏 尧 男,1993年生,博士,研究方向为新能源汽车电控系统、交流电机伺服系统及其先进控制。E-mail: yao.wei@fjirsm.ac.cn
汪凤翔 男,1982年生,博士,研究员,博士生导师,研究方向为电力电子与电力传动。E-mail: fengxiang.wang@fjirsm.ac.cn(通信作者)
中图分类号:TM341
DOI: 10.19595/j.cnki.1000-6753.tces.230159
国家自然科学基金(52277070)和福建省科技计划(2022T3070)资助项目。
收稿日期 2023-02-14
改稿日期 2023-03-07
(编辑 崔文静)