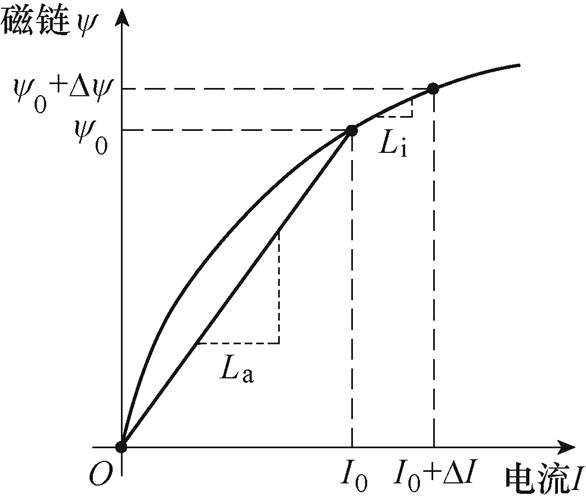
图1 视在电感和增量电感示意图
Fig.1 The diagram of apparent inductance and incremental inductance
摘要 在实际运行过程中，永磁同步电机的电气参数将受到温度、磁饱和等诸多物理因素的影响而发生偏移，进而影响到效率最优控制、电流解耦控制等优化算法的运行效果。因此，为实现高性能电机控制，永磁同步电机的多电气参数在线辨识显得尤为重要。然而，现有参数辨识方法并未考虑铁磁损耗的影响，更未关注铁磁损耗随电流的偏移情况，所以在辨识精度上仍存在提升空间。对此，该文综合考虑铁磁损耗、铜损，将其集总为电磁损耗，并基于串联电磁损耗电阻模型，提出一种考虑等效电磁损耗电阻偏移的永磁同步电机直流信号注入在线参数辨识方法。该方法首先提出等效电磁损耗电阻随电流偏移的电机模型；其次由此设计同时考虑磁饱和、等效电磁损耗电阻偏移的直流信号注入在线参数辨识方法；由于待求解方程组较多，采用最小方均算法进行参数求解；最后通过实验测试所提方法的准确性，测试结果表明，与正弦信号注入法、传统直流信号注入法相比，所提方法的参数精度有所提升。
关键词：永磁同步电机 电磁损耗 参数辨识 直流信号注入
永磁同步电机（Permanent Magnet Synchronous Machine, PMSM）因具有高功率密度、高运行效率等诸多特点，而被广泛应用于电动汽车、家用电器、工业制造等领域[1-2]。在实际运行中，永磁同步电机的电气参数，包括永磁体磁链、定子电阻、铁损电阻、交直轴电感等，由于受到温度、磁路分布与磁饱和等因素影响，会发生偏移[3-4]。电气参数偏移会严重影响电机的控制性能，例如：基于损耗模型的最大效率控制，其优化性能依赖定子电阻、铁损电阻的精度[5]；转矩观测器的估测性能与永磁体磁链、交直轴电感的准确性密切相关[6]；交直轴电流解耦控制也需要精确的电机参数进行配合[7]。因此，多电气参数在线辨识是实现电机高性能控制的关键。
要实现永磁同步电机多电气参数在线辨识，最核心需要解决的是电机特征方程组的欠秩问题，即特征方程数量小于待辨识电气参数，电气参数不能被唯一、准确地确定[8]。目前，解决欠秩问题的技术路线包括：①减少辨识参数数量[9-12]；②增加特征方程数量[13-21]。
其中，减少辨识参数数量的方法可细分为：将部分参数视为固定值[9-11]；分步辨识，即将参数根据变化时间常数分为温度敏感、电气敏感两组，每次仅辨识其中一组参数[12]。然而上述两类方法，前者仍存在部分参数无法在线辨识；后者也面临严苛的初值问题，若初值出错将产生极大误差。
增加特征方程数量的方法包括：考虑电流纹波影响，建立动态电流方程[13-15]；通过信号注入增加特征方程[16-21]。根据信号类型，信号注入法可分为高频正弦信号注入法[16-18]、直流信号注入法[19-21]。其中，电流纹波法并未考虑磁饱和的影响，并且在实际应用中需借助高采样率硬件电路测量电流变化率，应用门槛较高；考虑到电机损耗的频变特性，高频正弦信号注入法求解的高频电阻与目标求解的基频电阻间存在差异[22]，因而无法精确辨识电阻参数。对于传统的直流信号注入法，其通过构建两组不同稳态电流的电机特征方程从而形成满秩矩阵[19-21]。该方法可以计算基频电阻，也考虑了磁饱和影响[19]，并且无需额外的硬件电路支持，便于应用。但是，现有的直流信号注入法均未考虑电机的铁磁损耗。而实际上，铁磁损耗同样是电机损耗中不可忽视的组成部分，在诸多工况下甚至会超过铜损[23]，进而影响电阻、交直轴磁链等与损耗及机械功率相关的参数的辨识精度。所以，为进一步提升直流信号注入法的辨识性能，需对基础理论模型进行修正，并优化相应的参数辨识方法。
现有考虑铁磁损耗的电机模型分为两类：①并联铁损电阻模型[23-25]，提出采用铁损电阻与励磁回路相并联的拓扑结构，以表征铁损的频变特性；②串联电磁电阻模型[26-28]，提出采用等效电磁损耗电阻与励磁回路相串联的拓扑结构，该等效电阻用以表征铁磁损耗与铜损的集总电磁损耗。上述两类模型中，并联铁损电阻模型，因具有较强的物理基础被广泛应用[23-25]。但是，该模型的计算式较为复杂，会对在线参数辨识引入巨大的运算压力[26]。而与之相反，串联电磁电阻模型的拓扑结构简单，计算复杂度低、运算压力小[26-28]，并且，文献[26]也已分析串联电磁电阻模型与并联铁损电阻模型在数学上是等效的。除此之外，串联电磁电阻模型与传统仅考虑铜损的电机模型存在拓扑同一性，相应的理论与控制方法也因此具有较好的通用基础。综上所述，基于串联电磁电阻模型开发相应的在线参数辨识方法，可以降低在线运算负担，并与现有的优化控制算法，如最大效率控制、电流解耦控制等进行适配，具有较大的应用价值。
然而，现有串联电磁电阻模型倘若应用到直流信号注入法中，无法处理不同稳态电流下电磁损耗，亦即等效电磁损耗电阻存在差异的情况。对此，本文基于改进的串联电磁电阻模型，提出考虑等效电磁损耗电阻偏移的永磁同步电机直流信号注入在线参数辨识方法。首先，针对电机电磁损耗与电流的耦合关系，提出等效电磁损耗电阻随电流偏移的串联电磁电阻模型；其次，再基于修正后的模型，提出综合考虑了磁饱和、等效电磁损耗电阻偏移的直流信号注入在线参数辨识方法；由于待求解参数与方程组数较多，为便于计算，采用基于梯度下降的最小方均算法用于参数求解；最后，通过实验验证和比较了所提方法的可行性与准确性。
电机模型是在线参数辨识的关键理论基础，因此，为进一步提高参数辨识性能，本文综合考虑磁饱和、电磁损耗偏移，提出改进串联电磁电阻模型。
磁饱和是铁磁材料的重要特征，它表示在不同强度定子电流激励下磁导率的变化情况，而电机的增量电感也因此随电流矢量的偏移而发生变化[29]。对此，为表征磁饱和的具体影响，通常将电机电感分为视在电感La和增量电感Li，如图1所示[30]。
图1 视在电感和增量电感示意图
Fig.1 The diagram of apparent inductance and incremental inductance
如图1所示，对于任意电流工作点I0，其视在电感La与增量电感Li分别定义为
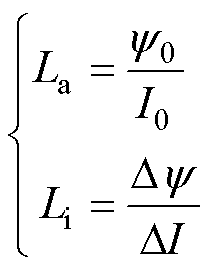（1）
式中，DI与Dy 分别为增量电流与增量磁链；y0为电流工作点I0下的视在磁链。
因此，基于文献[26]讨论的串联永磁同步电机模型，可以推出考虑磁饱和的串联电磁电阻模型，对应的电压电流方程为
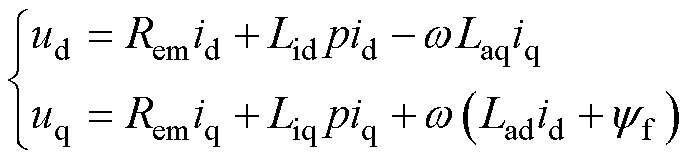（2）
式中，uq、ud为交直轴电机端电压；iq、id为交直轴电流；Liq、Lid为交直轴增量电感；Laq、Lad为交直轴视在电感；p为微分算子；yf为永磁体磁链；w 为电机角速度；Rem为等效电磁损耗电阻，表征铁损与铜损的总损耗。
基于磁路建模理论[31]：永磁体为磁势源，持续提供磁动势Ff；而永磁体实际产生的磁链大小yf，则由磁动势Ff与电机的等效磁路磁导Gf共同决定，满足方程yf =FfGf。换而言之，在不同的电流矢量下，永磁体磁链也会因磁饱和而发生偏移。该偏移效果将与直轴视在电感发生耦合，进而增大参数辨识难度。又考虑到，对于传统的优化控制算法，包括最大效率控制、转矩观测器、电流解耦控制等[5-7]，仅需要交直轴视在磁链、增量电感进行配合，无需细分永磁体磁链yf与直轴视在电感Lad。因此，为便于参数辨识设计，本文采用由视在磁链表示的考虑磁饱和的串联电磁电阻模型，有
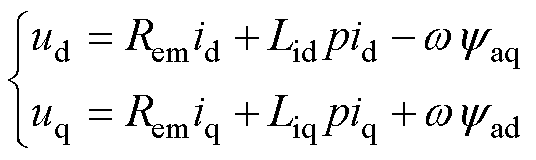（3）
式中，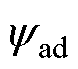
为直轴视在磁链，满足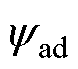=Ladid+
；
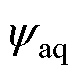为交轴视在磁链，满足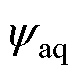=Laqiq。
由式（3）可以推导考虑磁饱和的串联电磁电阻模型，如图2所示。
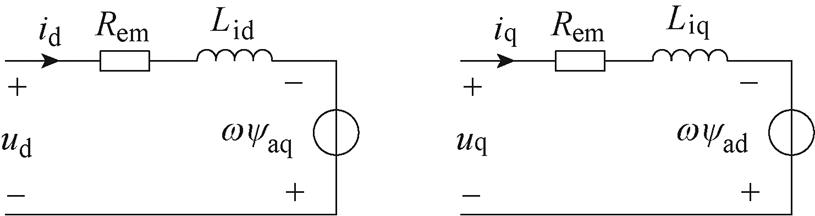
图2 考虑磁饱和的串联电磁电阻模型
Fig.2 The model with equivalent electromagnetic loss resistance considering magnetic saturation
永磁同步电机的电磁损耗可分为铜损、铁磁损耗两部分。其中，当电流矢量发生变化时，电机绕组内电流分布将因邻近效应发生偏移，进而影响定子电阻以及相应铜损大小[32]。对于铁磁损耗而言，其大小与电机内磁场分布密切相关，而磁场分布也同样会受到电流影响[23]。所以，电磁损耗及其等效电阻将随电流而发生偏移。对此，本文将针对一台永磁同步电机样机进行测试，提取在不同电流矢量下的等效电磁损耗电阻Rem，具体样机参数见表1。
表1 被测永磁同步电机参数
Tab.1 Parameters of the PMSM under test
参 数取 值 极对数3 额定电压/V330 额定电流/A6 额定转速/(r/min)800 额定转矩/(N·m)18
基于式（3）的稳态形式，即忽略电流微分项，可推导得到等效电磁损耗电阻Rem的实验计算公式为
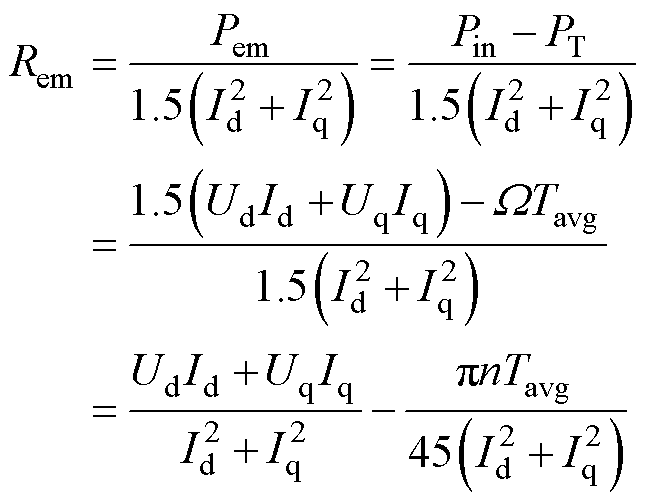（4）
式中，Pem为稳态电磁损耗功率，满足Pem=Pin-PT；Pin为电机稳态输入功率，满足Pin=1.5(UdId+UqIq)；PT为电机稳态输出功率，满足PT=W Tavg；W 为机械角速度，满足W =2pn/60；n为电机转速；Uq、Ud为交直轴端电压的稳态值；Iq、Id为交直轴电流的稳态值；Tavg为转矩传感器所测量的稳态转矩平均值。
基于式（4），测量永磁同步电机样机在200 r/min和800 r/min下、全电流平面内的等效电磁损耗电阻Rem，结果如图3所示。可得，待测电机的等效电磁损耗电阻Rem随转速升高而增大，并且在恒定转速、不同电流下，待测电机的Rem也会发生较大变化，最大Rem可达最小Rem的1.45倍。
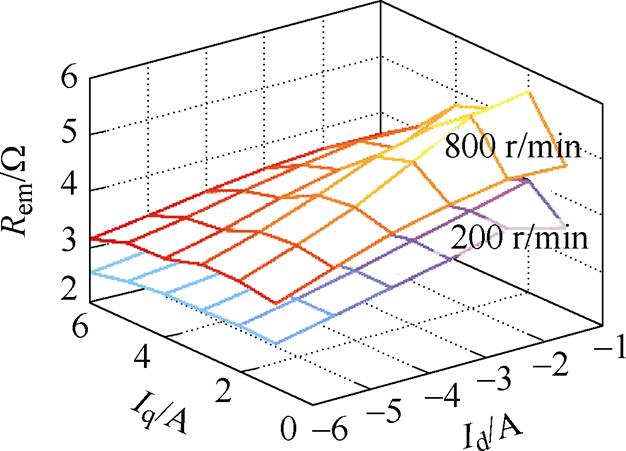
图3 不同转速、电流下的等效电磁损耗电阻Rem
Fig.3 The equivalent electromagnetic loss resistance Rem under different speeds and currents
然而，传统直流信号注入参数辨识方法[21]仅将电磁损耗电阻视为定常参数，忽略损耗电阻的偏移情况，所以在电机损耗建模及其等效电阻辨识上存在缺陷。对此，本文提出采用电阻变化率，对串联电磁电阻模型进行改进。改进后的稳态电压方程为
（5）
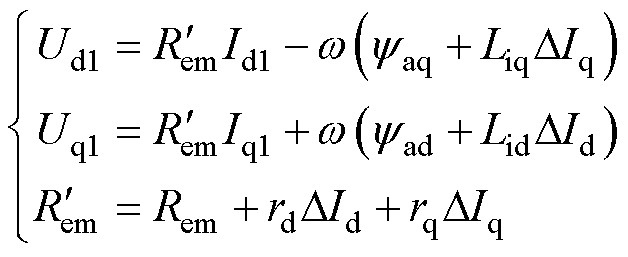（6）
式中，Iq0、Id0为目标求解工作点的交、直轴稳态电流；Uq0、Ud0为电流工作点[Id0, Iq0]的交、直轴稳态端电压；电流[Id1, Iq1]为[Id0, Iq0]附近的交、直轴稳态电流，满足Id1=Id0+DId，Iq1=Iq0+DIq；DIq、DId为交、直轴增量电流；Uq1、Ud1为电流工作点[Id1, Iq1]的交、直轴稳态端电压；rq、rd为交、直轴电磁电阻变化率，用以表征电磁电阻随电流的偏移情况；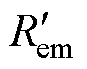
为考虑电流影响的等效电磁损耗电阻。
由式（5）、式（6）可知，本文提出的考虑磁饱和、电磁损耗偏移的改进串联电磁电阻模型总计有7个电气参数，分别为交直轴视在磁链（yaq、yad）、交直轴增量电感（Liq、Lid）、交直轴电磁电阻变化率（rq、rd）、等效电磁损耗电阻Rem。而传统直流信号注入在线辨识方法采用两步稳态电流注入的方式，仅有4个稳态电压方程，仍小于待辨识参数数量，因而本文还需要设计相应的在线参数辨识方法实现上述参数的完全辨识。
为实现上述模型参数的全辨识，需要构建至少7个特征方程，即至少4组线性无关的电流工作点。因此，本文首先将针对注入的直流信号的稳态电流时序进行设计。
为使电磁电阻的增量近似线性，各电流工作点离目标工作点的电流增量不宜过大。因此，本文提出采用交直轴电流交替变化的原则构建电流工作点，如图4所示。该选取规则规定：所注入的电流信号每次仅变化一个轴的电流，从而尽量减小各工作点与目标工作点之间的最大电流偏差。其中，交轴电流Iq变化两次，且每次的变化增量均为DIq；直轴电流Id变化一次，增量为DId。
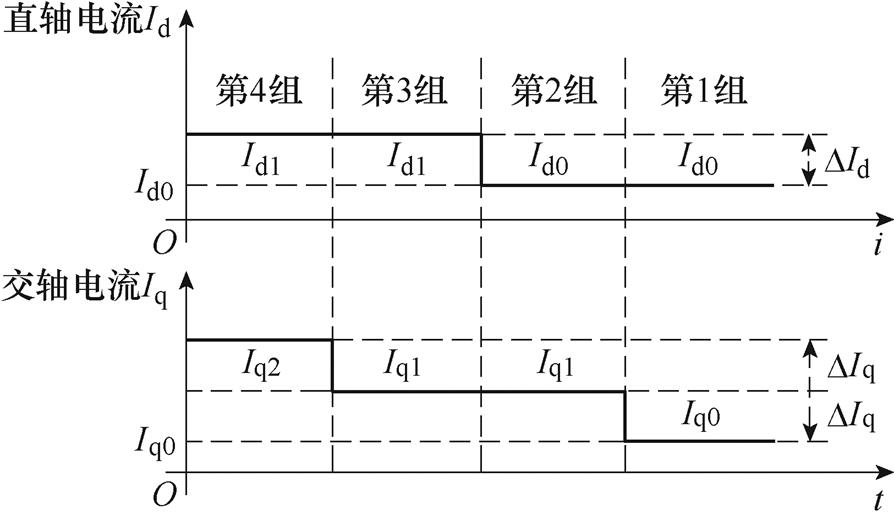
图4 电流工作点示意图
Fig.4 The diagram of current operating points
对于图4中所展示的4组电流工作点，以电流工作点[Id0, Iq0]为基准，定义第j组的交直轴电压为[Ud j, Uq j]、交直轴电流为[Id j, Iq j]、交直轴电流增量为[DId j, DIq j]。进而，可以由式（6）得到对应的电压参数矩阵为
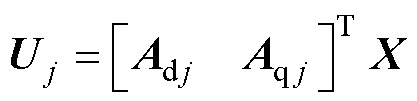（7）
式中，Uj为电压矩阵，Uj=[Udj Uqj]T；X为电机参数矩阵，X=[Rem rd rq Lid Liq yad yaq]T；Adj为直轴系数矩阵，Adj=[Idj IdjDIdj IdjDIqj 0 -wDIqj 0 -w]T；Aqj为交轴系数矩阵，Aq j=[Iq j Iq jDId j Iq jDIq j wDId j 0 w 0]T。
选择第1组的直轴电压方程、第2～4组的交直轴电压方程，可以得到总系数矩阵A为
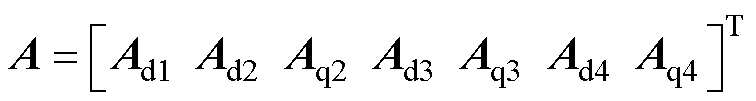（8）
为实现总系数矩阵A满秩，则该矩阵的行列式应当满足不为0[33]，如式（9）所示。其相应推导过程在附录中列出。
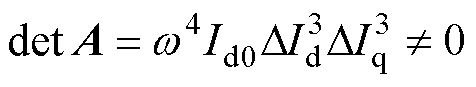（9）
对于常用的内嵌式永磁同步电机而言，为利用磁阻转矩增大转矩密度，直轴电流Id0通常为负。因而由式（9）可知，对于所提直流信号注入参数辨识方法，只需保证每次变化的电流增量DIdq不为0，且转速非0，所构建的总系数矩阵A即满秩，可以实现对目标模型参数的全辨识。
由于本文所提方法的总系数矩阵为7阶矩阵，若进行解析逆运算将面临繁琐的公式推导与巨大的运算压力。因此，本文采用基于梯度下降的最小方均算法，用于求解电机参数。
首先，基于最小方均算法，定义各电压误差的方均和为代价函数fL，有
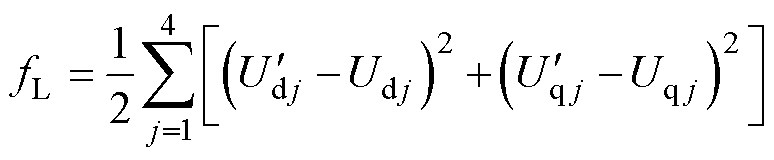（10）
式中，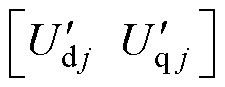
为交直轴电压的估测值，由估测的参数矩阵
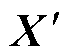、实测电流、实测角速度，经式（7）计算得到；
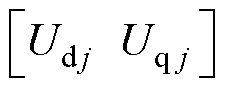为交直轴电压的实测值，在每次工作点达到稳态后，对控制器输出的调制电压进行滑动平均得到。
基于式（7）、式（10），可计算代价函数对各电机参数的梯度为
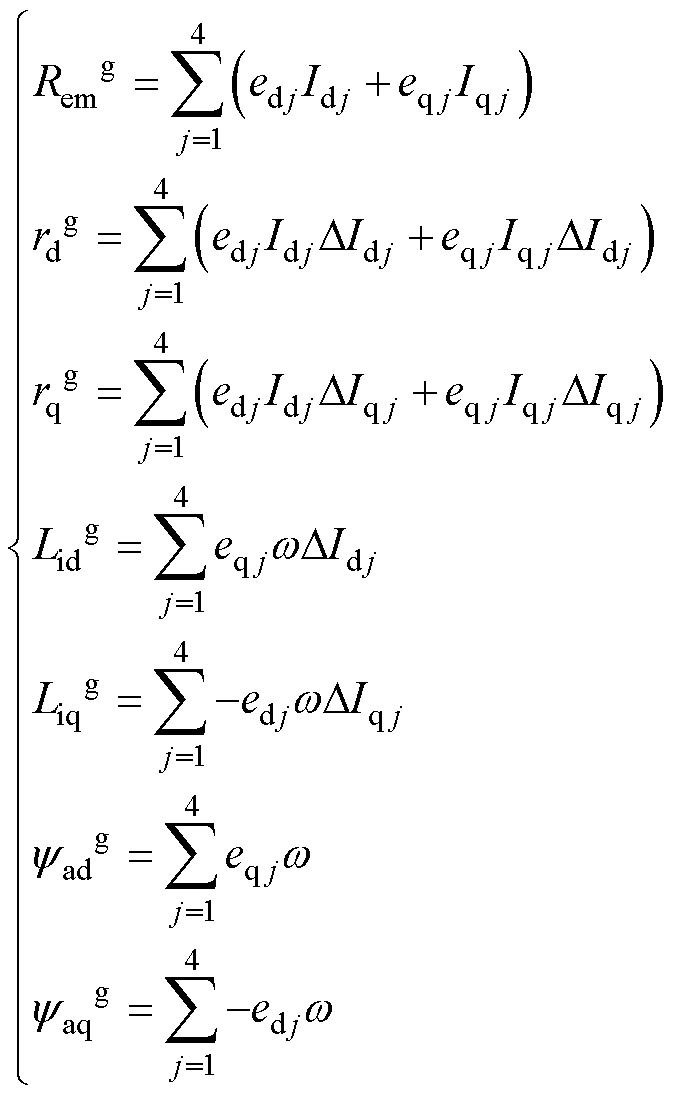（11）
式中，ed j为直轴估测误差，ed j=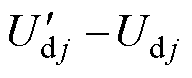
；eq j为交轴估测误差，eq j=
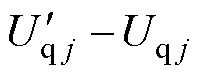；上标g表示各参数的梯度。
综合式（11）中各参数的梯度，构建梯度矩阵G=[Remg rdg rqg Lidg Liqg yadg yaqg]T。进而，为使得代价函数随每次参数迭代而下降，则基于梯度矩阵可得所估测参数矩阵的迭代公式为
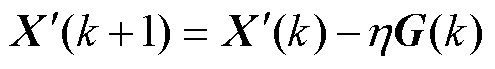（12）
式中，k为迭代次数；
为学习率，通常为正值，用以调节参数迭代的更新步长；G(k)为第k次电压电流计算得到的梯度矩阵；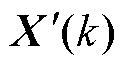
、
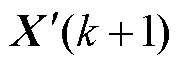分别为第k次、第k+1迭代的所估测参数矩阵。
由此，代价函数，亦即各估测电压的误差方均和，将随迭代而逐步降低，最终得到满足预设估测电压精度的全电机系数矩阵X。本文在实验中所预期的电压精度具体为：代价函数小于1×10-4，即估测电压误差二次方的平均值小于25×10-6，折合平均电压误差约小于0.005。
本文针对所提出的直流信号注入在线参数辨识方法，通过实验的方式验证其辨识精度。所搭建的实验平台如图5所示。待测永磁同步电机的参数见表1；陪测电机用于拖动待测电机到恒定的转速；转矩传感器用于测量待测电机的输出转矩；示波器用于记录待测电机的电流信号、转矩传感器输出的转矩信号。
图5 电机实验平台示意图
Fig.5 The diagram of motor testbench
本文分别对所提参数辨识方法、正弦信号注入法[16]、忽略电阻偏移的传统直流信号注入法[21]进行测试，对比其精度。考虑到各方法所辨识的参数存在差异，所以，本文仅对比通用的基频视在参数，包括电磁损耗电阻Rem、交直轴视在磁链yaqd，分别对应电机的损耗特性与输出转矩特性。
所采用正弦信号注入法，通过对直轴注入频率fh、幅值Imh分别为70 Hz、0.2 A的正弦信号idh，可得相应直轴电压udh；之后，将udh与idh相乘再经过低通滤波，可以得到直流信号Udh；最后，将Udh乘以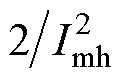
，可以得到损耗电阻Rh。再基于电阻Rh，由式（5）可以计算得到视在磁链yaqd为
（13）
所采用传统直流信号注入法，通过构建两组稳态电流[Id1, Iq1]、[Id0, Iq0]，满足Id1-Id0=DId=0.1 A、Iq1=Iq0，可以获取对应稳态电压差值DUd=Ud1-Ud0；之后，再将DUd除以DId，可以得到损耗电阻Rdc；最后，视在磁链yaqd也同样可由式（13）计算得到。
对于所提改进的直流信号注入法，若所注入的信号幅值过大，将产生较大的转矩与效率波动；若所注入信号幅值过小，将增大信号处理难度、降低辨识精度。因而，本文经不断调整尝试，最终选择了引起波动较小、辨识精度较好的注入信号幅值，即DId和DIq分别为0.1 A和0.05 A。之后，再基于第2节所述的电流工作点时序和最小方均算法迭代计算得到相应的电机参数。
上述三种方法精度对比结果如图6所示。本文选择200 r/min、800 r/min进行测试，分别对应待测电机的低转速、额定转速；在各转速下选择两组电流矢量，分别为：-Id0=Iq0=1、-Id0=Iq0=6，对应待测电机的小转矩、大转矩工况。
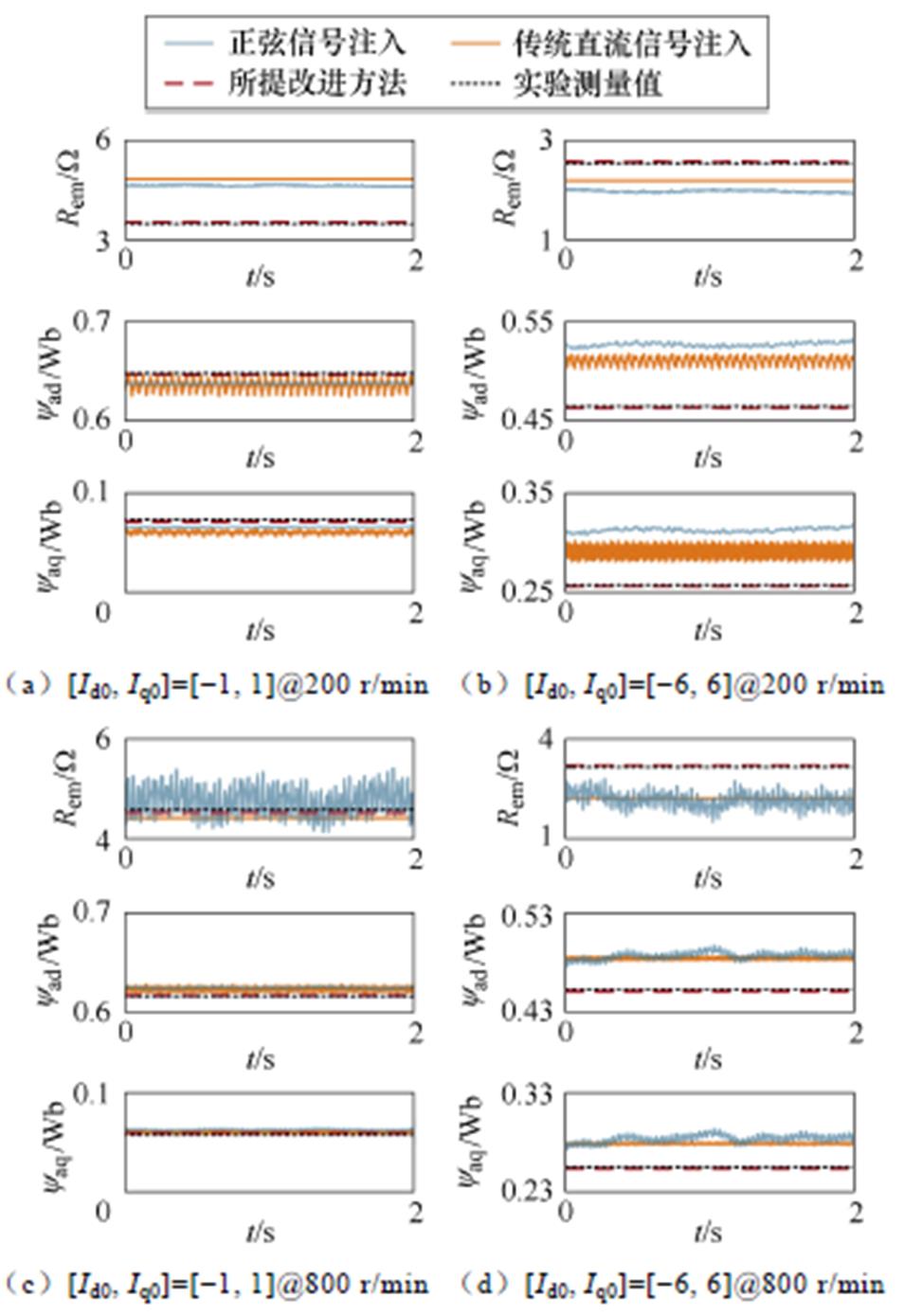
图6 精度对比结果
Fig.6 The accuracy comparison results
基于测试结果，不同运行工况下的模型参数的实测值及不同方法的辨识结果平均值见表2。其中，方法r与方法1～3依次为：实测值、正弦信号注入法、传统直流信号注入法、所提辨识方法。
表2 电机参数实测值及不同方法的辨识结果平均值
Tab.2 The measured results and average identified results of motor parameters using various methods
参数方法Idq0=[-1, 1]@ 200 r/minIdq0=[-6,6]@ 200 r/minIdq0=[-1, 1]@ 800 r/minIdq0=[-6,6]@ 800 r/min Rem/Wr3.4812.5514.5833.113 14.8932.1014.7632.283 25.0212.2954.4042.348 33.5522.5804.4723.142 yad/Wbr0.6480.4720.6180.468 10.6390.5220.6290.501 20.6360.5090.6270.493 30.6460.4700.6200.464 yaq/Wbr0.0740.2620.0610.256 10.0680.3120.0660.292 20.0640.2930.0650.284 30.0720.2590.0630.253
如表2所示，与其他方法相比，所提改进方法在所测试的工况下，对电机外特性相关参数均具有更高辨识精度。其对各参数的相对误差均小于4%。
分别选择200 r/min、800 r/min，对应电机的1/4额定转速、额定转速，对全电流平面下，所提改进方法的参数辨识精度进行详细测试，电流变化步长为1 A。各参数测试结果及其绝对误差（Absolute Error, AE）见附录中的附图1。基于测试结果，可得各参数的平均绝对误差以及平均相对误差（Average Relative Error, ARE），见表3。
表3 电机参数的平均绝对误差与平均相对误差
Tab.3 The average absolute errors and average relative errors of motor parameters
电机参数转速n=200 r/min转速n=800 r/min 平均AEARE(%)平均AEARE(%) Trq/(N·m)0.0770.8310.0660.818 Rem/W0.0561.7640.1451.833 rd/W0.05223.3830.09038.536 rq/W0.09139.4420.19150.190 yad/mWb2.6990.4942.1810.516 yaq/mWb2.4992.2142.5572.204 Lid/mH1.4283.2781.4863.404 Liq/mH1.7833.3891.7883.225
根据表3中的结果可知：所提方法对转矩、视在磁链、等效电磁损耗电阻的辨识均具有较高的精度，平均相对误差均小于2.3%；此外，所提方法对增量电感的辨识精度虽然有所降低，但是平均相对误差仍小于3.5%；然而，所提方法对电阻变化率的平均相对误差较高，大于20%。该差异较大原因：一方面是因为电阻变化率的基值较小（大部分都小于0.2），因而较小的绝对误差也会引起较大的相对误差；另一方面是因为所提方法在电阻变化率估测方面确实存在性能不足，有待进一步提高。
在测试完所提方法的稳态性能之后，将测试该方法的参数迭代动态过程。考虑到过大的迭代步长η将引起迭代振荡，导致无法收敛。因此，本文经过试错尝试，最终得到了一个在样机额定转速内均能有效收敛的数值（0.000 1）作为迭代步长。
本文同样选择200、800 r/min作为转速工况，并且在各转速下选择一组电流阶跃工况进行测试。针对被测电机，选择尽量大的电流阶跃，具体为：在200 r/min下，选择[Id0, Iq0]由[-1 A, 6 A]变为 [-1 A, 1 A]；在800 r/min下，选择[Id0, Iq0]由[-6 A, 1 A]变为[-6 A, 6 A]。并且，针对各稳态电流工作点，选择持续周期为2 s，其中，0.5 s用于等待电压稳定、1.5 s用于采样电压滑动平均值。参数迭代的动态过程测试结果如图7所示。图中，IqRef -Iq0、IdRef -Id0为交直轴电流指令值减去目标稳态电流，即表征电流工作点时序；IqFbk-Iq0、IdFbk-Id0为交直轴电流反馈值减去相应目标稳态电流；iabc为三相电流反馈值；fL为式（10）计算的损失函数；xExp为任意电机参数x的测试值；下标Est表征估测值。
图7 参数迭代动态过程测试
Fig.7 The dynamic test of parameters iteration
由图7可知，为得到满足预设估测电压精度的损失函数与模型系数，即损失函数小于1×10-4、折合平均电压误差约小于0.005，所提方法在200 r/min下需要迭代近80千次（每秒迭代10千次）、在800 r/min下需要迭代近10千次。此时，由于800 r/min的转速与内电动势（电压）更高，所计算的单步梯度更大，因而具有更快的收敛性。
随着所提直流电流信号的注入，电机的转矩与电磁损耗均会受到影响，进而造成转矩与效率波动的不利影响。对此，本文经不断尝试，最终选择了波动较小的信号幅值：DId=0.1 A、DIq=0.05 A。最后，本文也选取了不同的运行工况，以测试采用所选取幅值的直流信号注入下，转矩与效率的波动情况，结果分别如图8、图9所示。此时，同样选择200 r/min和800 r/min进行测试。由于本文所采用电流增量DId、DIq固定，因此转矩波动将随交直轴视在磁链（yaq、yad）增大而增大。对此，本文选择具有尽可能大视在磁链的电流工作点，即[Id0, Iq0]分别为[-1 A, 6 A]、[-6 A, 6 A]，进行测试。
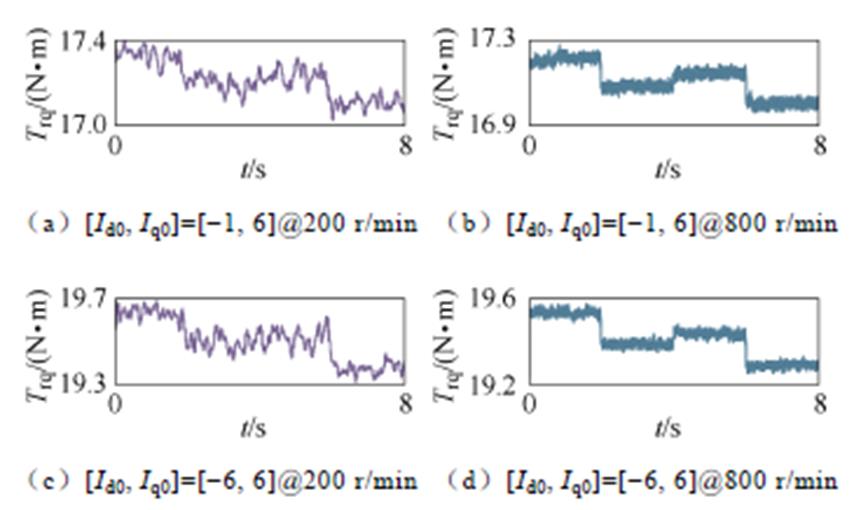
图8 转矩波动测试结果
Fig.8 The test results of torque fluctuation
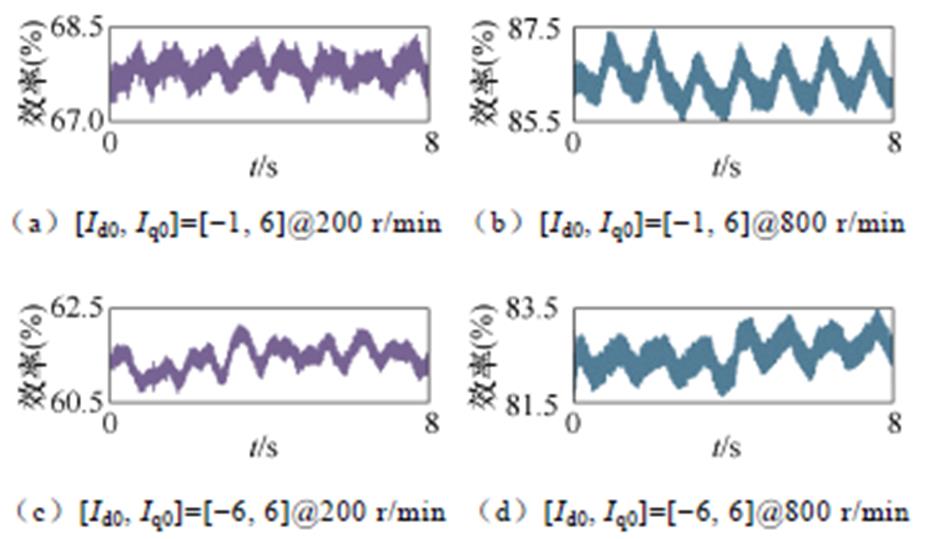
图9 效率波动测试结果
Fig.9 The test results of efficiency fluctuation
根据图8、图9的测试结果可知，所提方法的四步稳态电流工作点之间的转矩波动小于0.4 N·m、效率波动小于2%，波动相对较小。若想进一步减小转矩与效率波动，则需要降低注入信号幅值。然而，随着信号幅值的降低，数据处理难度与测试误差的影响将逐步上升，进而也会影响辨识精度。因此，所提方法尚存在辨识精度与转矩效率波动两者之间的矛盾。
现有永磁同步电机在线参数辨识方法并未考虑铁磁损耗及其随电流的偏移情况。而事实上，铁磁损耗是电机损耗的重要组成部分，在诸多工况下甚至超过铜损，并且，铁磁损耗随电流的偏移量可超过最小值的40%[23]。对此，本文将铁磁损耗、铜损集总为电磁损耗，提出了一种考虑等效电磁损耗电阻偏移的直流信号注入在线参数辨识方法。
首先，提出了一种考虑磁饱和现象与电磁损耗偏移现象的改进串联电磁电阻模型，采用视在磁链、增量电感表征磁饱和现象；并采用电阻变化率表征电磁损耗偏移现象。其次，针对所提模型中的7个待辨识参数，采用交直轴电流交替变化的原则设计了线性无关的4组电流工作点时序，从而构建出满秩的模型参数辨识矩阵。最终，采用基于梯度下降的最小方均算法，根据电压估测误差方均和fL对各电机参数的梯度迭代求解辨识矩阵，最终得到满足预设估测电压精度的模型系数。
本文通过对永磁同步电机样机进行测试，证明该方法的有效性。所提方法与传统正弦信号注入法、传统直流信号注入法相比，对视在磁链、等效电磁损耗电阻等与电机外特性相关的参数，均具有更高的辨识精度，平均相对误差小于2.3%。此外，所提方法对转矩、增量电感也具有较高的辨识精度，平均相对误差分别小于0.9%和3.5%。然而，所提方法对电阻变化率的估测精度尚不理想，有待进一步提高。
本文所提在线参数辨识方法可应用于效率优化在线搜索控制、转矩估测器、电机故障状态检测等应用领域。例如，倘若需要将所提方法与在线搜索控制进行适配，则应当推导满足转矩恒定、有功功率迭代降低、参数辨识矩阵满秩等特征的可变dq电流增量计算式，其中，转矩恒定应依靠所提方法的参数辨识结果计算实现；并且综合设计注入信号（幅值与周期）、参数辨识迭代步长、电流增量计算时序等内容，在确保参数辨识可以在电流增量计算之前完成迭代的同时，尽可能减小转矩与效率波动，并加快参数迭代与在线搜索的速度。
附 录
1. 式（9）推导过程
式（9）的详细推导过程如下：结合所设计的直流信号时序规则，将其代入到总系数矩阵A中，可得其行列式det A为
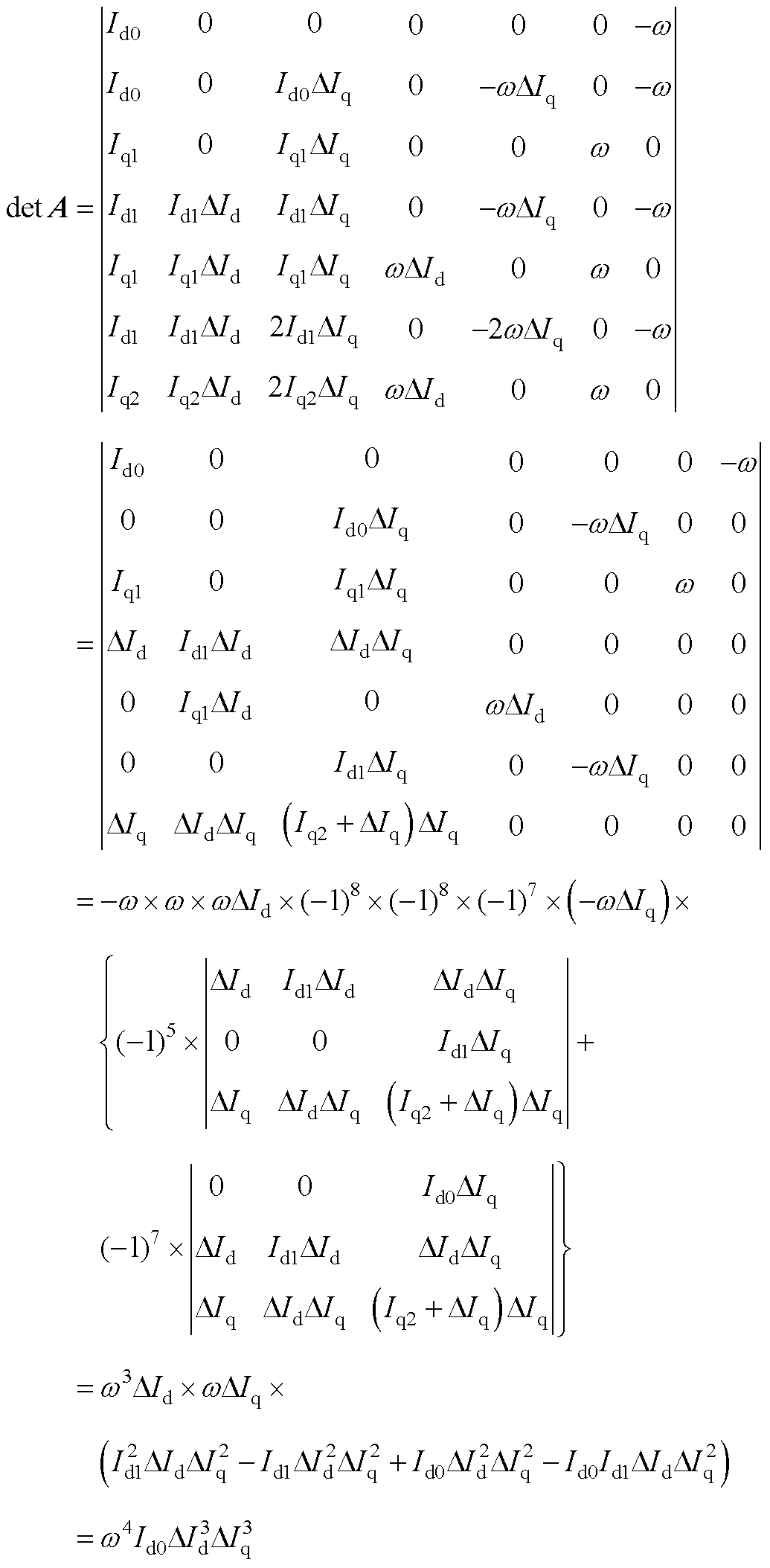
2. 不同转速、电流下的参数辨识精度示意图
各电机参数在不同转速、电流下的辨识结果与辨识精度如附图1所示。对于任意电机参数x，红点为所提方法观测值xEst；三维平面为实验测试值xExp；绝对误差AE=abs(xEst-xExp)。其中，转矩Trq的测试值由转矩传感器测量得到；Rem由式（4）计算得到；rd由两个稳态电流对应的等效电阻差DRem=Rem1-Rem2除以直轴电流差DId=Id1-Id2计算得到，并且两稳态电流的交轴电流恒定，即Iq1=Iq2；rq的测量方式与rd相似，由等效电阻差DRem除以交轴电流差DIq得到；交直轴视在磁链yaq、yad则基于Rem由式（13）计算得到；Lid的测量方式与rd相同，由直轴视在磁链差Dyad=yad1-yad2除以直轴电流差DId计算得到；Liq由交轴视在磁链差Dyaq=yaq1-yaq2除以交轴电流差DIq计算得到。
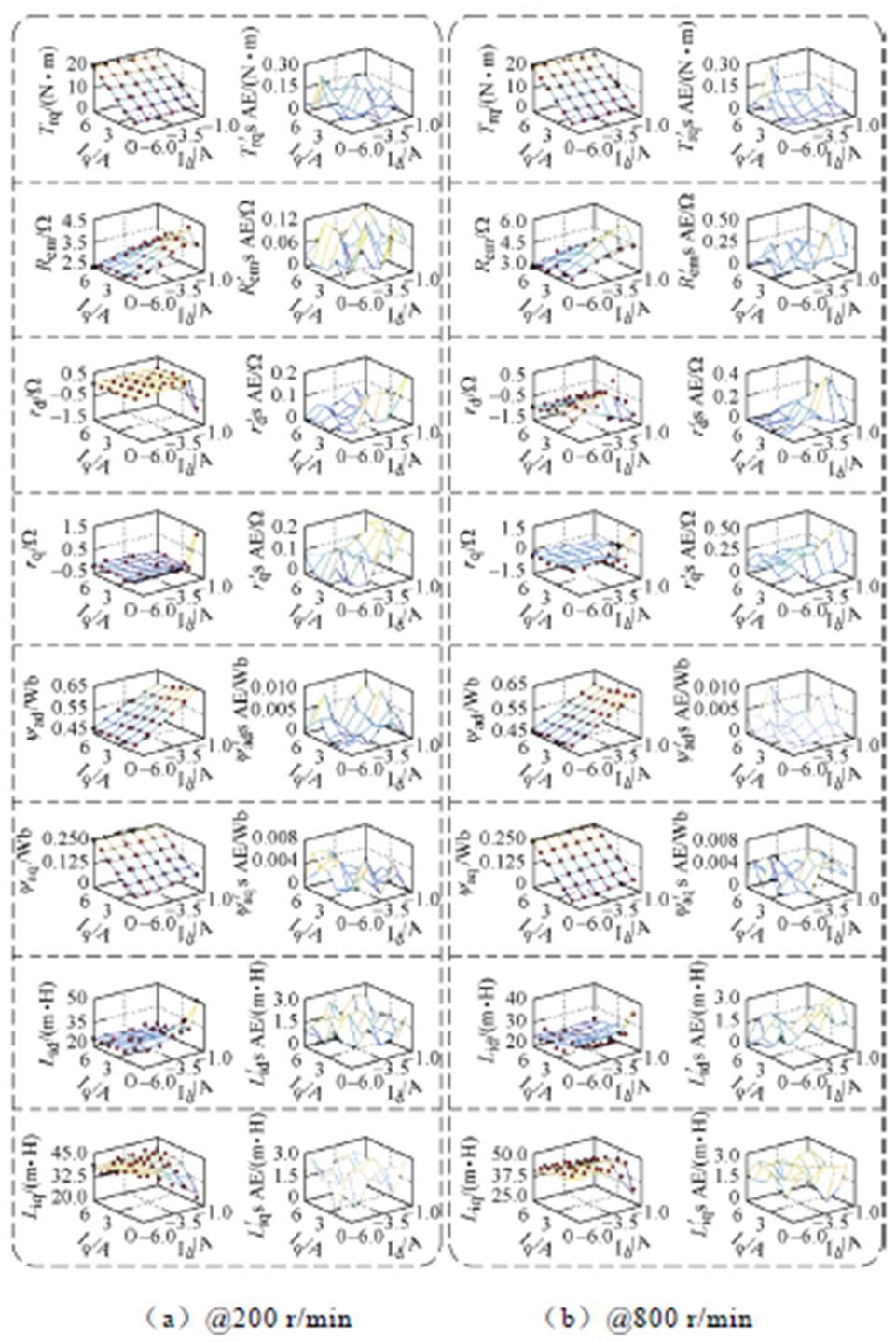
附图1 不同工况下各电机参数的辨识结果与精度对比
App.Fig.1 The identification results and accuracy comparison of motor parameters under various conditions
参考文献
[1] 郭磊磊, 王朋帅, 李琰琰, 等. 不同代价函数下永磁同步电机模型预测控制参数失配可视化分析[J]. 电工技术学报, 2023, 38(4): 903-914.
Guo Leilei, Wang Pengshuai, Li Yanyan, et al. Visual analysis of parameters mismatch in model predictive control for permanent magnet synchronous motor under different cost functions[J]. Transactions of China Electrotechnical Society, 2023, 38(4): 903-914.
[2] Balasubramanian L, Bhuiyan N A, Javied A, et al. Design and optimization of interior permanent magnet (IPM) motor for electric vehicle applications[J]. CES Transactions on Electrical Machines and Systems, 2023, 7(2): 202-209.
[3] 朱洒, 曾峰, 陆剑波, 等. 考虑PWM谐波损耗的车用扁线内嵌式永磁同步电机效率图简化工程计算[J]. 电工技术学报, 2022, 37(22): 5687-5703.
Zhu Sa, Zeng Feng, Lu Jianbo, et al. Simplified engineering calculation of efficiency map of interior permanent magnet synchronous machines with hairpin windings considering PWM-induced harmonic losses[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5687-5703.
[4] 高剑, 李承栩, 黄守道, 等. 高磁路饱和永磁同步电机永磁体负载磁链动态估算[J]. 电工技术学报, 2022, 37(22): 5638-5648.
Gao Jian, Li Chengxu, Huang Shoudao, et al. Dynamic estimation of permanent magnet load flux linkage of permanent magnet synchronous motor with high magnetic circuit saturation[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5638- 5648.
[5] Hang Jun, Wu Han, Ding Shichuan, et al. Improved loss minimization control for IPMSM using equivalent conversion method[J]. IEEE Transactions on Power Electronics, 2021, 36(2): 1931-1940.
[6] Reigosa D, Kang Yegu, Martínez M, et al. SPMSMs sensorless torque estimation using high-frequency signal injection[J]. IEEE Transactions on Industry Applications, 2020, 56(3): 2700-2708.
[7] 吴荒原, 王双红, 辜承林, 等. 内嵌式永磁同步电机改进型解耦控制[J]. 电工技术学报, 2015, 30(1): 30-37.
Wu Huangyuan, Wang Shuanghong, Gu Chenglin, et al. An improved decoupling control strategy for the IPMSMS[J]. Transactions of China Electrotechnical Society, 2015, 30(1): 30-37.
[8] 李婕, 杨淑英, 谢震, 等. 基于有效信息迭代快速粒子群优化算法的永磁同步电机参数在线辨识[J]. 电工技术学报, 2022, 37(18): 4604-4613.
Li Jie, Yang Shuying, Xie Zhen, et al. Online parameter identification of permanent magnet syn- chronous motor based on fast particle swarm optimization algorithm with effective information iterated[J]. Transactions of China Electrotechnical Society, 2022, 37(18): 4604-4613.
[9] 苏有成, 陈志辉. 基于电感扰动的三相横向磁通永磁电机参数辨识与估算位置偏差修正[J]. 电工技术学报, 2023, 38(12): 3165-3175.
Su Youcheng, Chen Zhihui. Parameter identification and estimated position deviation correction of a three- phase transverse flux permanent magnet machine based on inductance perturbation injection[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3165-3175.
[10] Li Xinyue, Kennel R. General formulation of Kalman- filter-based online parameter identification methods for VSI-fed PMSM[J]. IEEE Transactions on Indu- strial Electronics, 2021, 68(4): 2856-2864.
[11] 连传强, 肖飞, 高山, 等. 基于实验标定及双时间尺度随机逼近理论的内置式永磁同步电机参数辨识[J]. 中国电机工程学报, 2019, 39(16): 4892-4898, 4991.
Lian Chuanqiang, Xiao Fei, Gao Shan, et al. Parameter identification for interior permanent magnet synchronous motor based on experimental calibration and stochastic approximation theory with two time scales[J]. Proceedings of the CSEE, 2019, 39(16): 4892-4898, 4991.
[12] Dang D Q, Rafaq M S, Choi H H, et al. Online parameter estimation technique for adaptive control applications of interior PM synchronous motor drives[J]. IEEE Transactions on Industrial Electronics, 2016, 63(3): 1438-1449.
[13] Zhang Jindong, Peng Fei, Huang Yunkai, et al. Online inductance identification using PWM current ripple for position sensorless drive of high-speed surface- mounted permanent magnet synchronous machines[J]. IEEE Transactions on Industrial Electronics, 2022, 69(12): 12426-12436.
[14] Choi K, Kim Y, Kim K S, et al. Using the stator current ripple model for real-time estimation of full parameters of a permanent magnet synchronous motor[J]. IEEE Access, 2019, 7: 33369-33379.
[15] Yu Yelong, Huang Xiaoyan, Li Zhaokai. Overall electrical parameters identification for IPMSMs using current derivative to avoid rank deficiency[J]. IEEE Transactions on Industrial Electronics, 2023, 70(7): 7515-7520.
[16] Liu Zirui, Fan Xinggang, Kong Wubin, et al. Improved small-signal injection-based online multi- parameter identification method for IPM machines considering cross-coupling magnetic saturation[J]. IEEE Transactions on Power Electronics, 2022, 37(12): 14362-14374.
[17] Wang Qiwei, Wang Gaolin, Zhao Nannan, et al. An impedance model-based multiparameter identification method of PMSM for both offline and online con- ditions[J]. IEEE Transactions on Power Electronics, 2021, 36(1): 727-738.
[18] 吴春, 赵宇纬, 孙明轩. 采用测量电压的永磁同步电机多参数在线辨识[J]. 中国电机工程学报, 2020, 40(13): 4329-4340.
Wu Chun, Zhao Yuwei, Sun Mingxuan. Multipara- meter online identification for permanent magnet synchronous machines using voltage measurements[J]. Proceedings of the CSEE, 2020, 40(13): 4329-4340.
[19] Feng Guodong, Lai Chunyan, Mukherjee K, et al. Current injection-based online parameter and VSI nonlinearity estimation for PMSM drives using current and voltage DC components[J]. IEEE Transa- ctions on Transportation Electrification, 2016, 2(2): 119-128.
[20] 谷鑫, 胡升, 史婷娜, 等. 基于神经网络的永磁同步电机多参数解耦在线辨识[J]. 电工技术学报, 2015, 30(6): 114-121.
Gu Xin, Hu Sheng, Shi Tingna, et al. Muti-parameter decoupling online identification of permanent magnet synchronous motor based on neural network[J]. Transactions of China Electrotechnical Society, 2015, 30(6): 114-121.
[21] 刘细平, 胡卫平, 丁卫中, 等. 永磁同步电机多参数辨识方法研究[J]. 电工技术学报, 2020, 35(6): 1198-1207.
Liu Xiping, Hu Weiping, Ding Weizhong, et al. Research on multi-parameter identification method of permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(6): 1198-1207.
[22] Li Chen, Kudra B, Balaraj V, et al. Absolute inductance estimation of PMSM considering high- frequency resistance[J]. IEEE Transactions on Energy Conversion, 2021, 36(1): 81-94.
[23] Balamurali A, Kundu A, Li Ze, et al. Improved harmonic iron loss and stator current vector determination for maximum efficiency control of PMSM in EV applications[J]. IEEE Transactions on Industry Applications, 2021, 57(1): 363-373.
[24] Kumar P, Bhaskar D V, Muduli U R, et al. Iron-loss modeling with sensorless predictive control of PMBLDC motor drive for electric vehicle appli- cation[J]. IEEE Transactions on Transportation Electrification, 2020, 7(3): 1506-1515.
[25] 曹阳, 刘旭. 计及损耗的混合励磁电机建模与硬件在环实时仿真系统[J]. 电工技术学报, 2020, 35(22): 4657-4665.
Cao Yang, Liu Xu. Modeling method for hybrid- excited machine and hardware-in-loop real-time simulation system with accounting for loss calcu- lation[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4657-4665.
[26] Urasaki N, Senjyu T, Uezato K. Relationship of parallel model and series model for permanent magnet synchronous motors taking iron loss into account[J]. IEEE Transactions on Energy Conversion, 2004, 19(2): 265-270.
[27] Senjyu T, Shimabukuro T, Uezato K. Vector control of synchronous permanent magnet motors including stator iron loss[J]. International Journal of Electronics, 1996, 80(2): 181-190.
[28] Kazerooni M, Hamidifar S, Kar N C. Analytical modelling and parametric sensitivity analysis for the PMSM steady-state performance prediction[J]. IET Electric Power Applications, 2013, 7(7): 586-596.
[29] Feng Guodong, Lai Chunyan, Kar N C. A novel current injection-based online parameter estimation method for PMSMs considering magnetic saturation[J]. IEEE Transactions on Magnetics, 2016, 52(7): 1-4.
[30] Zhu Z Q, Liang Dawei, Liu Kan. Online parameter estimation for permanent magnet synchronous machines: an overview[J]. IEEE Access, 2021, 9: 59059-59084.
[31] Kemmetmüller W, Faustner D, Kugi A. Modeling of a permanent magnet synchronous machine with internal magnets using magnetic equivalent circuits[J]. IEEE Transactions on Magnetics, 2014, 50(6): 1-14.
[32] Kim J, Park Y J. Approximate closed-form formula for calculating ohmic resistance in coils of parallel round wires with unequal pitches[J]. IEEE Transa- ctions on Industrial Electronics, 2014, 62(6): 3482- 3489.
[33] Yu Yelong, Huang Xiaoyan, Li Zhaokai, et al. Full parameter estimation for permanent magnet syn- chronous motors[J]. IEEE Transactions on Industrial Electronics, 2022, 69(5): 4376-4386.
Abstract Permanent magnet synchronous machines (PMSMs) are widely used for their high operating efficiency. During the application, the parameters of PMSMs may vary a lot when considering the effect of temperature, magnetic saturation, and so on. In this case, the performance of some optimal control strategies, such as the maximum efficiency control and current decoupling control, may decay. Thus, to achieve high-performance control, online parameter identification is important. However, there are few parameter identification methods considering the ferromagnetic loss and its variation with currents, while the ferromagnetic loss occupies a great proportion of the PMSMs’ loss. Therefore, this paper integrates ferromagnetic loss and copper loss as electromagnetic loss. Then, an improved DC-signal-injection-based online parameters identification is proposed considering equivalent electromagnetic loss resistance variation.
Firstly, the magnetic saturation of PMSMs and the variation of electromagnetic loss with current are discussed. Due to the magnetic saturation characteristic of ferromagnetic materials, the magnetic permanence of PMSMs may be decreased as the current rises, which, in turn, affects the inductance and flux linkage. Besides, when considering the change of current vectors, the copper loss may be variable due to the proximate effect. Meanwhile, the ferromagnetic loss may also vary with the changeable magnetic distribution. An improved series electromagnetic loss resistance model is proposed. Apparent flux linkage and incremental inductance are used to characterize the magnetic saturation, and change rates of the equivalent resistance are used to represent variations in electromagnetic loss.
Secondly, 4 groups of d-/q-axis operating currents are chosen based on the criterion of alternating changes in d-/q-axis currents. According to the analysis, if the current increment of each change is non-zero, the steady-state voltage equations of these 4 groups are linearly independent. That is, the corresponding coefficient matrix is full-rank, allowing for the full parameters identification.
Thirdly, a least mean square (LMS) algorithm is adopted to solve the 4 groups of steady-state voltage equations due to the complexity of analytical computation arising from the high-rank coefficient matrix. The LMS algorithm calculates the gradient of voltage estimation errors’ mean square to each model parameter based on the measured voltages, currents, and speeds. Then, the model parameters are updated iteratively based on the corresponding gradients at each step. After iteration, the model parameters that meet the preset voltage estimation accuracy are obtained.
Finally, the accuracy of the proposed method is validated using a prototype PMSM. Experimental results show that, compared with the sinusoidal-signal-injection-based method and the traditional DC-signal-injection- based method, the proposed method is more precise in identifying electromagnetic resistance and apparent flux linkage, with an average relative error of less than 2.3%. In addition, the proposed method has high identification accuracy for torque and incremental inductance, with average relative errors less than 0.9% and 3.5%, respectively. However, there is room for improving the identification performance of the equivalent resistance change rate.
Keywords：Permanent magnet synchronous machine, electromagnetic loss, parameters identification, DC signal injection
马铱林 男，1996年生，博士研究生，研究方向为高效能电机系统、数字化设计、铁磁材料性能测试等。E-mail: mayilin@zju.edu.cn
杨 欢 男，1981年生，教授，博士生导师，研究方向为分布式发电与微电网、智能配用电、高效能电机系统等。E-mail: yanghuan@zju.edu.cn（通信作者）
中图分类号：TM341
DOI: 10.19595/j.cnki.1000-6753.tces.230176
国家自然科学基金（52177062）和中央高校基本科研业务费专项资金（226-2022-00011）资助项目。
收稿日期 2023-02-16
改稿日期 2023-06-05
（编辑 崔文静）