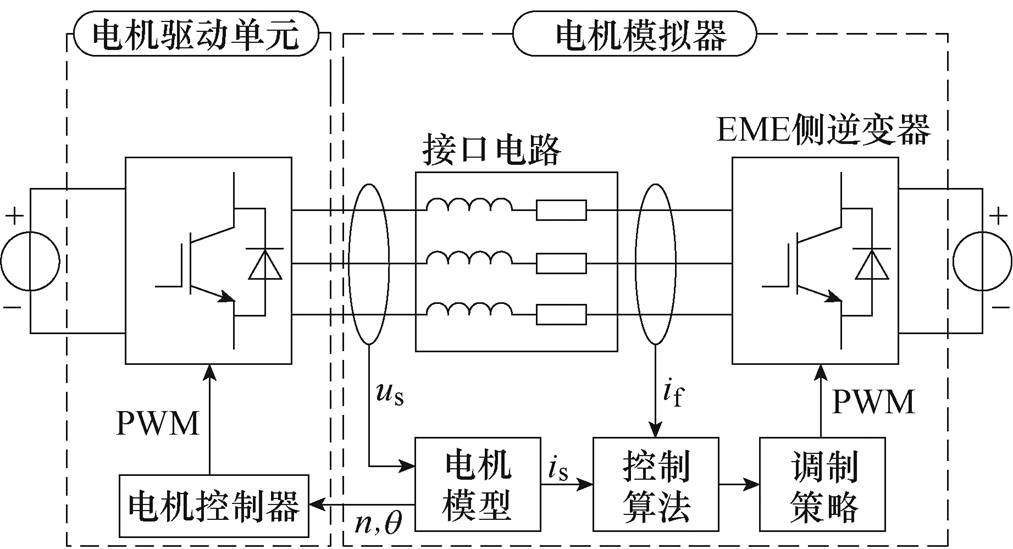
图1 典型电机模拟器结构
Fig.1 Typical structure of the EME
摘要 针对传统PI控制的低通滤波特性对电机模拟器动态控制效果的限制以及传统开环控制策略易受参数扰动影响的问题,该文提出一种基于滑模扰动观测器的开环电流控制策略。首先,根据目标电机数学模型以及接口电路模型推导出不带微分计算的开环控制电压方程;其次,为了解决传统开环控制易受参数扰动影响的问题,设计滑模扰动观测器进行扰动观测;最后,通过实验对比了该文所提控制策略与PI控制和传统开环控制的控制效果。实验结果表明,在存在参数扰动时,该文所提的控制策略无论在瞬态或稳态工况,均比基于传统PI控制和开环控制策略的电机模拟器系统具有更高的模拟精度与准确性。
关键词:电机模拟器 开环控制 PI控制 扰动观测器
电机驱动系统的测试与开发一般采用机械负载测功机系统来实施,然而传统的电机机械负载测试台架存在体积大、成本高、难以实现故障测试等缺陷,已无法满足高效的电驱动系统测试需求。同时,硬件在环(Hardware in the Loop, HIL)测试[1-2]只能进行信号级的验证测试,无法对电机控制器在真实功率流的环境下进行验证测试。基于功率硬件在环(Power Hardware in the Loop, PHIL)的电机模拟器(Electric Motor Emulator, EME),通过电力电子器件和控制算法实现对真实电机端口电流、电压特性的模拟,且能够通过软件实现变负载需求和故障注入,大大提高了电机控制单元的测试效率,缩短电机控制器开发周期,降低研发成本,是用于测试电机控制器性能的新型解决方案。
目前,电机模拟器已应用于永磁同步电机[3-9]、感应电机[10-11]以及开关磁阻电机[12]等。传统的电机模拟器采用基于PI控制的电流闭环控制策略,该策略一方面会与电机驱动单元(Motor Drive Unit, MDU)中的电流环产生冲突,降低系统稳定性;另一方面,PI控制的低通滤波特性会使得电流的高频特性发生畸变[8-9],降低EME电流环的动态响应。文献[3]指出,当EME电流环带宽为MDU电流环带宽5倍时,可忽略电流环的控制冲突,然而被测MDU的控制参数难以准确获取且EME电流环带宽过高会导致系统不稳定;文献[4]在模糊PI控制的基础上引入电压前馈环节,提高了系统的动态响应和鲁棒性,并在一定程度上减少MDU电流环与EME电流环的冲突;文献[5-6]采用LCL型接口滤波电路取代传统的L型结构,电容的存在使得MDU侧电流与EME侧电流解耦,从而避免两侧电流环的冲突,然而LCL型接口滤波电路为三阶系统,存在谐振尖峰,容易产生振荡,控制复杂。
文献[7-9]摒弃了电流闭环策略,采用基于L型接口电路的开环控制(Open Loop Control, OLC)策略以避免电流环冲突。其中,文献[7]基于永磁同步电机数学模型以及接口耦合电路模型直接推导出EME侧所需提供的电压值,但是其引入对采样电流的微分计算,从而引入了高频噪声;文献[8-9]提出了直接阻抗控制策略,实现了更高带宽的特性模拟。然而,在运行过程中电机模拟器接口电路的电感和电阻值会因为饱和或温度而发生变化[13-14]。上述文献的开环控制策略未考虑参数扰动的影响,鲁棒性 较差。
永磁同步电机功率密度高、体积小且结构简单,在电动汽车电驱动系统中得到广泛的应用[15],本文以表贴式永磁同步电机为例,采用L型接口滤波电路进行电机模拟器设计。为了解决电流环的控制冲突,提高系统的动态响应,提出一种基于扰动补偿的开环电流控制策略,该控制方法能在全频率范围内模拟电机的频率特性,同时避免了电流的微分运算,减少了由微分计算引入的高频噪声;为降低参数扰动的影响,基于电机模拟器设计了滑模扰动观测器,将扰动前馈补偿至控制器输入端,提高系统的鲁棒性。
典型的电机模拟器结构如图1所示,硬件部分由接口电路、功率逆变器组成,软件层面包括电机模型、电流控制算法以及调制策略。

图1 典型电机模拟器结构
Fig.1 Typical structure of the EME
接口电路用来连接MDU与EME,同时起到滤波的作用,主要包括LCL型、L型两种结构;电机模型用以产生参考电流,包括线性数学模型,以及考虑电机非线性及磁饱和特性的有限元查找表模型,数学模型因其计算简单、运算速度快常用来进行控制策略的验证。EME侧功率逆变器是电流控制算法的执行原件,受调制后的开关信号控制输出指定的电压。
电机模拟器的工作流程为:传感器将采集到的MDU端电压作为电机模型的输入,经电机模型计算得到电流值is,该电流值作为接口电路实际电流if的期望值。控制算法根据电流期望值与接口电路实际的电流值计算出EME侧逆变器所需输出的电压值,经过调制后输出脉冲宽度调制(Pulse Width Modulation, PWM)信号控制逆变器的开关状态。
永磁同步电机dq坐标系下的电压方程[16-17]为
 (1)
(1)
式中,isd和isq分别为d、q轴电流;usd和usq分别为MDU侧端电压的d、q轴分量;Rs为永磁同步电机相电阻;Lsd和Lsq分别为d、q轴电感;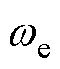 为电角速度;
为电角速度;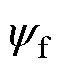 为永磁体磁链。
为永磁体磁链。
基于L型接口电路的电机模拟器等效模型如图2所示。图中,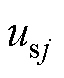 (
(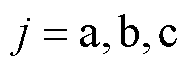 )为MDU侧逆变器输出的三相电压,同时该电压经采样后作为电机模型的输入;
)为MDU侧逆变器输出的三相电压,同时该电压经采样后作为电机模型的输入; 为EME侧逆变器输出的三相电压;
为EME侧逆变器输出的三相电压;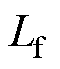 和
和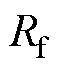 分别为接口电路的实际电感和电阻,其三相坐标系下的电压方程为
分别为接口电路的实际电感和电阻,其三相坐标系下的电压方程为
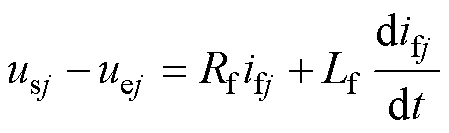 (2)
(2)
式中, 为接口电路三相电流。
为接口电路三相电流。
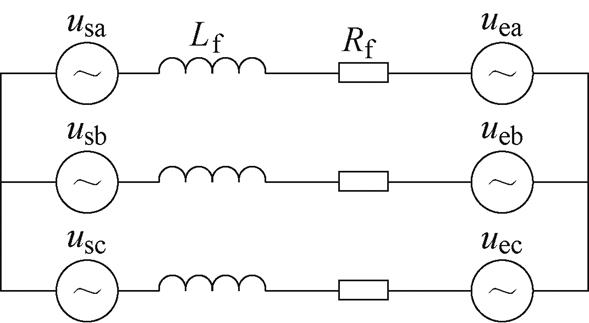
图2 接口电路模型
Fig.2 Model of the interface circuit
经等幅值Clarke、Park变换后可得其dq坐标系下的电压方程[18]为
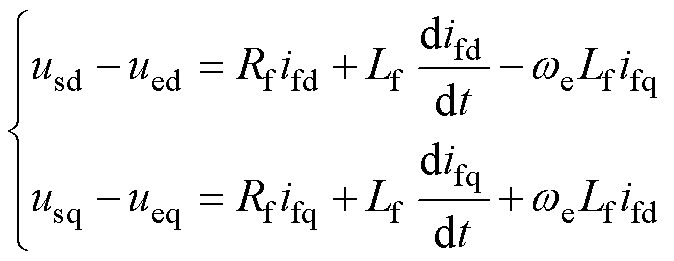 (3)
(3)
式中,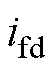 和
和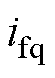 分别为接口电路d、q轴电流;
分别为接口电路d、q轴电流;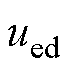 和
和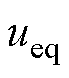 分别为EME侧端电压的d、q轴分量。
分别为EME侧端电压的d、q轴分量。
进行PI控制设计时,常忽略交叉耦合项,将永磁同步电机与接口电路简化为一阶惯性环节进行设计分析,电机以及电机模拟器的q轴电流环控制示意图如图3所示,图中,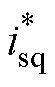 为电机驱动侧q轴参考电流;Kis、Tis为电机驱动侧电流环PI控制参数。由图3可得电机模拟器q轴电流环闭环传递函数为
为电机驱动侧q轴参考电流;Kis、Tis为电机驱动侧电流环PI控制参数。由图3可得电机模拟器q轴电流环闭环传递函数为
 (4)
(4)
式中,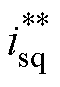 为电机模拟器侧q轴参考电流;
为电机模拟器侧q轴参考电流;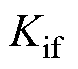 和
和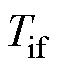 为PI控制参数;
为PI控制参数;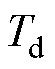 为控制系统集总延时。
为控制系统集总延时。
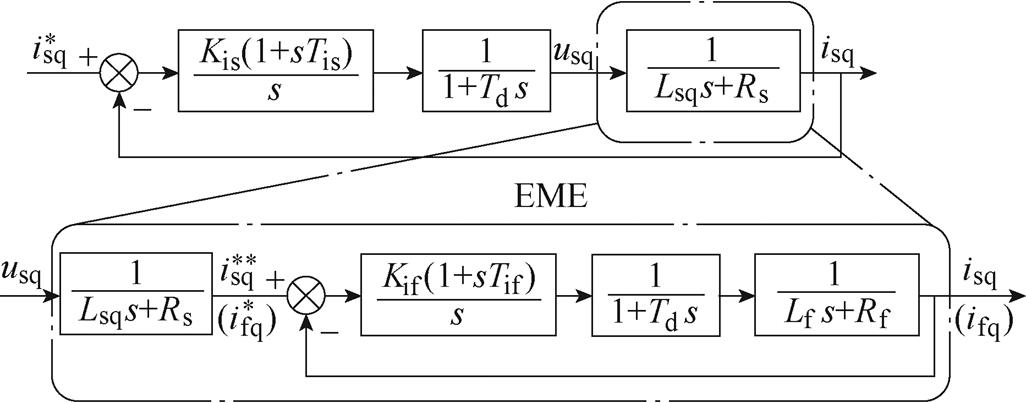
图3 电机模拟器电流环控制框图
Fig.3 Current loop control block diagram of EME
在进行PI参数设计时,采用零极点对消可将式(4)简化为典型二阶系统。为得到综合最优性能,可将二阶系统阻尼比设置为0.707。此时,式(4)中的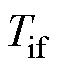 、
、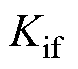 分别为
分别为
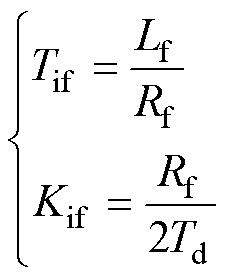 (5)
(5)
用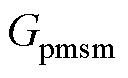 表示永磁同步电机传递函数模型,
表示永磁同步电机传递函数模型,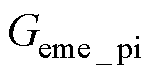 表示电机模拟器传递函数模型,由图3和式(4)可得式(6),代入表1的数据,得到基于PI控制的EME频率特性如图4所示。
表示电机模拟器传递函数模型,由图3和式(4)可得式(6),代入表1的数据,得到基于PI控制的EME频率特性如图4所示。
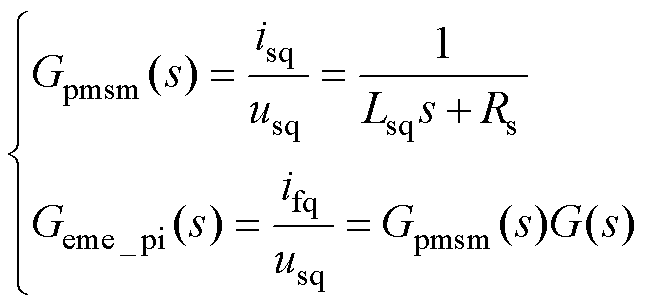 (6)
(6)
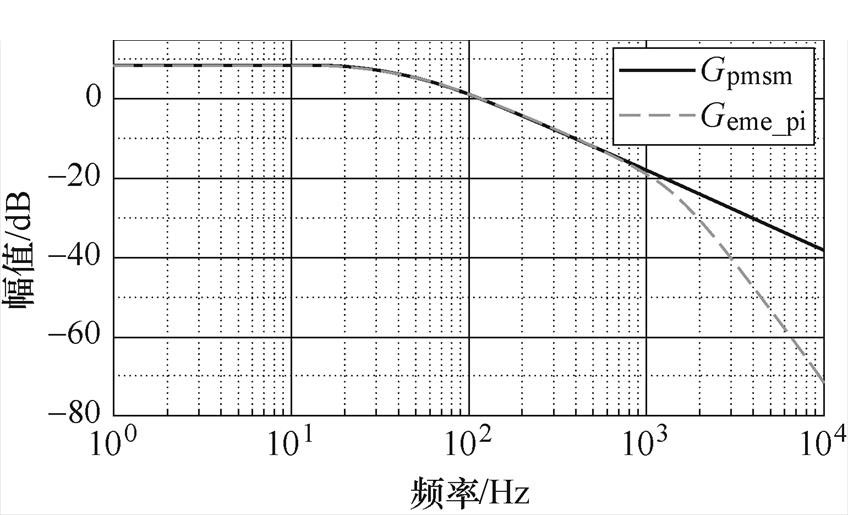
图4 基于PI控制的EME频率特性
Fig.4 Frequency characteristics of EME based on PI control
从频域角度考虑,电机模拟器的设计应具有和目标电机相同的频率特性。然而,由于PI的低通滤波特性,使得基于PI控制的EME电流环频率特性相对于永磁同步电机在高频处产生畸变。
如图4所示,当频率低于所设计电流环的闭环带宽时,电机模拟器可以较好地模拟真实电机的幅频特性;但是,当频率大于所设计电流环的闭环带宽时,电机模拟器有更大的幅频衰减特性。因此,采用PI闭环控制的电机模拟器无法完全模拟真实电机的高频特性,模拟精度受电流环带宽影响,带宽越大,精度越高,动态响应越快。然而,受功率开关器件开关频率的影响,电流环带宽受到限制;另一方面,过高的带宽会造成阻尼系数的减小,引起系统振荡甚至发散。
针对PI电流控制的缺陷,本文提出了基于滑模扰动观测器的开环控制策略,该策略可以在全带宽内实现对电机频率特性的模拟,避免MDU与EME电流环之间的冲突。一方面,本文所提出的方法相较于传统的开环控制策略[6],避免了电流的微分计算,减轻控制器负担的同时减小噪声的引入;另一方面,在电机模拟器实际运行时,电路参数会随之发生变化,从而导致控制效果变差。本文在传统开环控制的基础上设计了滑模扰动观测器,并将扰动前馈补偿,提高了系统的鲁棒性。
考虑实际电路参数的可变性,以名义参数值代替,重写式(3)为
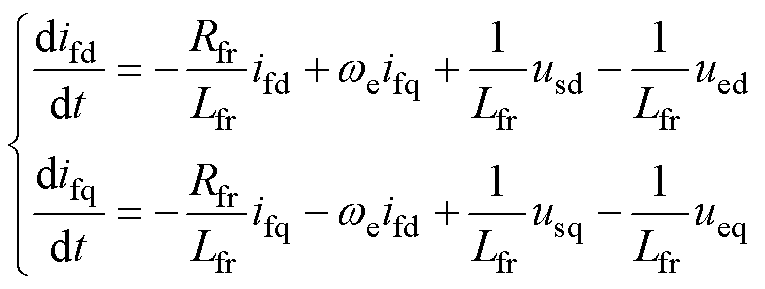 (7)
(7)
式中,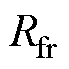 和
和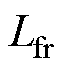 分别为接口电路名义电阻和电感。
分别为接口电路名义电阻和电感。
为了使电机模拟器完全模拟目标电机的端口电流特性,令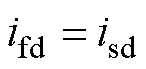 ,
,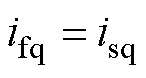 ,并假设其导数也相同,即
,并假设其导数也相同,即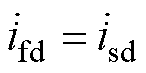 ,
,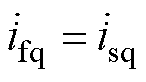 ,联立式(1)和式(7)可反解出控制量为
,联立式(1)和式(7)可反解出控制量为
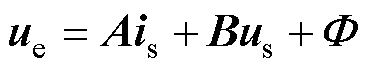 (8)
(8)
其中
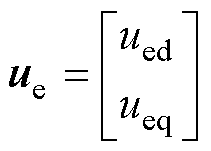
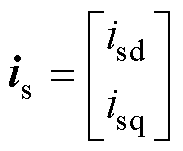

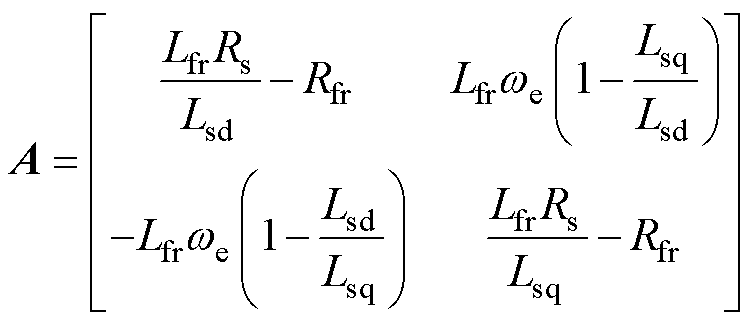
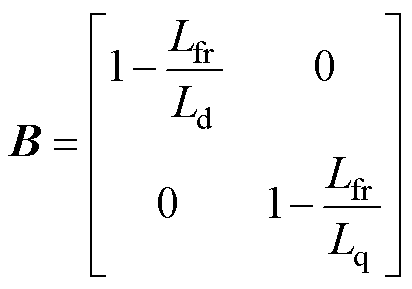
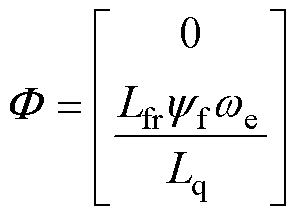
与文献[3]中提出的前馈电压以及文献[6]提出的开环控制策略相比,本文所推导的控制策略避免了对接口电路电流的微分运算,且参与运算的电流值可直接由电机模型的解算值代入,进一步避免了由电流传感器引入的噪声。
将式(8)代回式(3),忽略耦合项,将与反电动势有关项视为扰动。以q轴为例,可得单输入单输出传递函数为
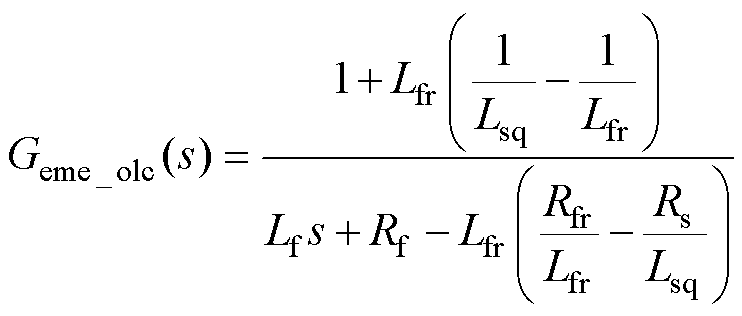 (9)
(9)
当不存在参数扰动,即Lfr=Lf,Rfr=Rf时, ,表明此时电机模拟器与目标永磁同步电机具有相同的频率特性。然而,实际的电感与电阻值会随工作环境变化,电感由于磁心的饱和而减小,电阻则随着线圈的温度升高而增大,导致基于开环控制的电机模拟器产生瞬态以及稳态误差。
,表明此时电机模拟器与目标永磁同步电机具有相同的频率特性。然而,实际的电感与电阻值会随工作环境变化,电感由于磁心的饱和而减小,电阻则随着线圈的温度升高而增大,导致基于开环控制的电机模拟器产生瞬态以及稳态误差。
首先,保持接口电路名义电阻Rfr与实际电阻Rf相同,改变电感值的扰动程度,分析单电感扰动对EME电流环频率特性的影响;同样地,保持接口电路名义电感与实际电感相同,改变电阻值的扰动程度,分析单电阻扰动对EME电流环频率特性的影响。基于同样的参数表所得的两组频率响应曲线如图5所示,当电感与电阻值均未发生扰动时,EME的q轴电流环幅频特性与目标永磁同步电机一致,与前文分析一致。
根据图5可知,电感的扰动主要影响了高频特性,且随着扰动程度的增大,高频特性畸变越大,导致动态响应模拟精度降低;而电阻值的扰动,则主要影响低频特性,随着失配程度的增大,低频特性畸变越大,稳态误差越大。
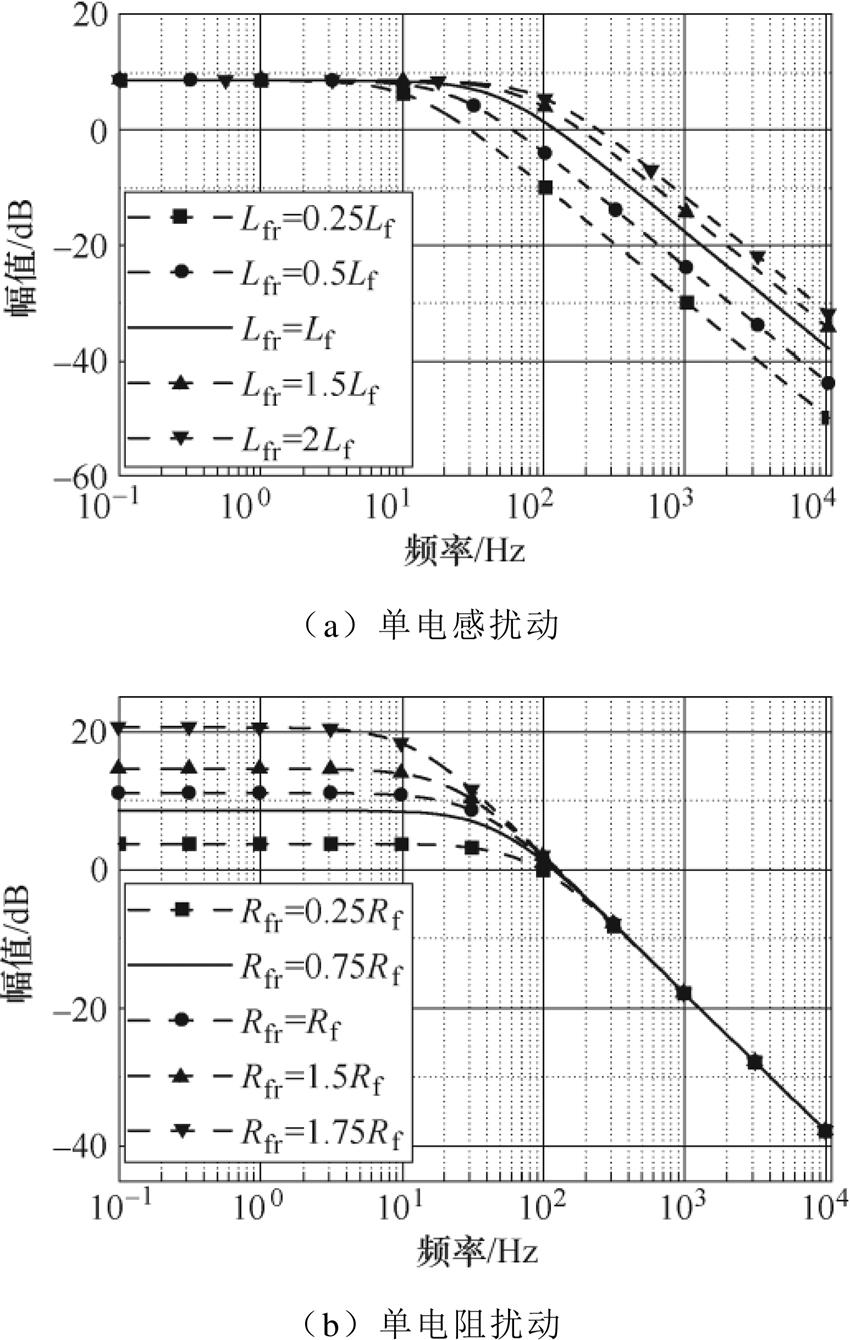
图5 电感与电阻扰动对电机模拟器频率特性的影响
Fig.5 Effect of inductance and resistance perturbation on frequency characteristics of EME
在进行电机驱动系统测试时,包括被测电机控制器在内的电机模拟器系统共存在两个三相逆变器,逆变器的非线性特性也会影响电机模拟器的动态及稳态性能。为了补偿扰动的影响,设计滑模扰动观测器(Sliding Mode Disturbance Observer, SMDO)进行扰动观测[19],并将其等效前馈至输入端。
3.3.1 滑模扰动观测器设计
考虑扰动fd和fq,有
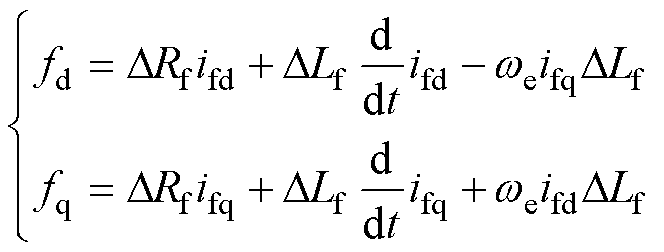 (10)
(10)
其中
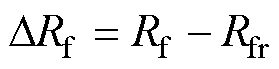
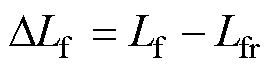
考虑扰动后的式(3)可重写为
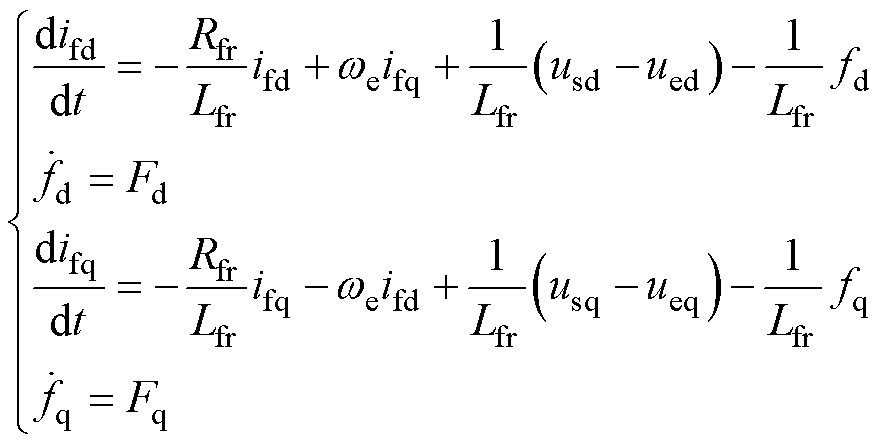 (11)
(11)
设计滑模扰动观测器为
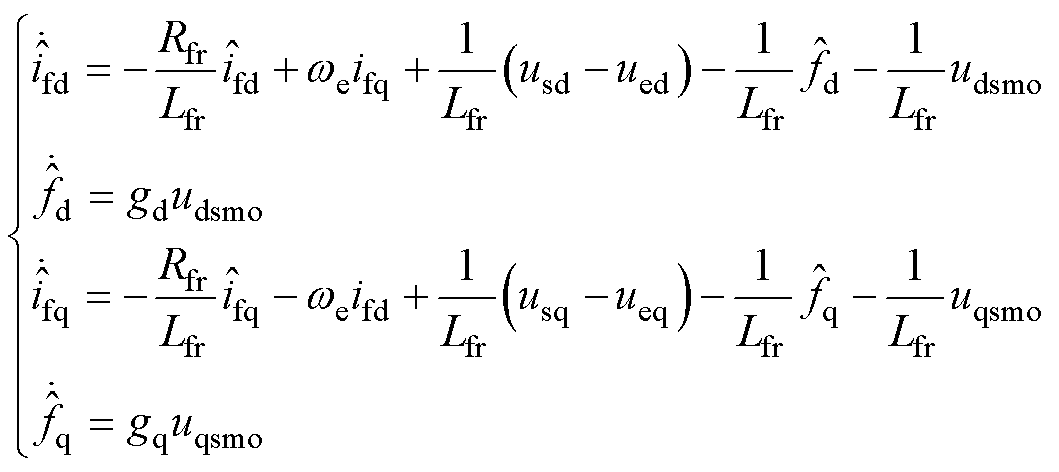 (12)
(12)
式中,udsmo和uqsmo为滑模观测器控制函数;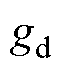 、
、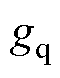 为设计参数。
为设计参数。
根据式(11)和式(12)可得误差方程为
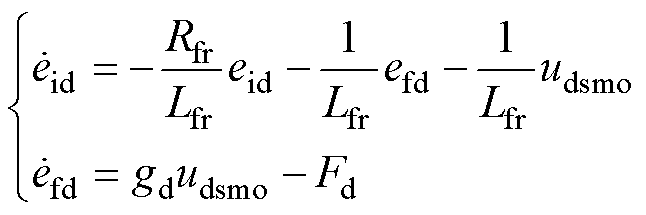 (13)
(13)
 (14)
(14)
其中
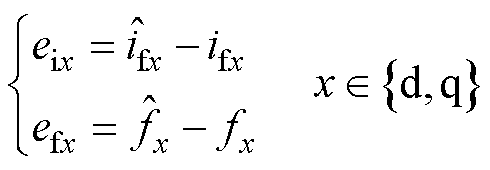
选取滑模面为
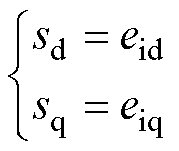 (15)
(15)
为了削减抖振,选取指数趋近率为
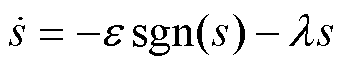 (16)
(16)
式中,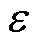 和
和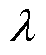 为大于零的设计参数;sgn( · )为符号函数。
为大于零的设计参数;sgn( · )为符号函数。
联立式(13)~式(16),将扰动观测误差efd和efq视为扰动,可推导出滑模观测器控制方程为
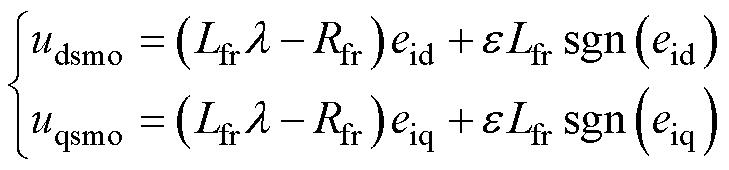 (17)
(17)
所设计滑模扰动观测器框图如图6所示。
3.3.2 稳定性证明
定义李雅普诺夫函数为
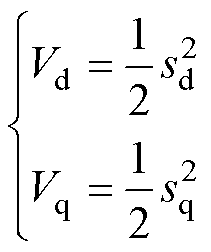 (18)
(18)
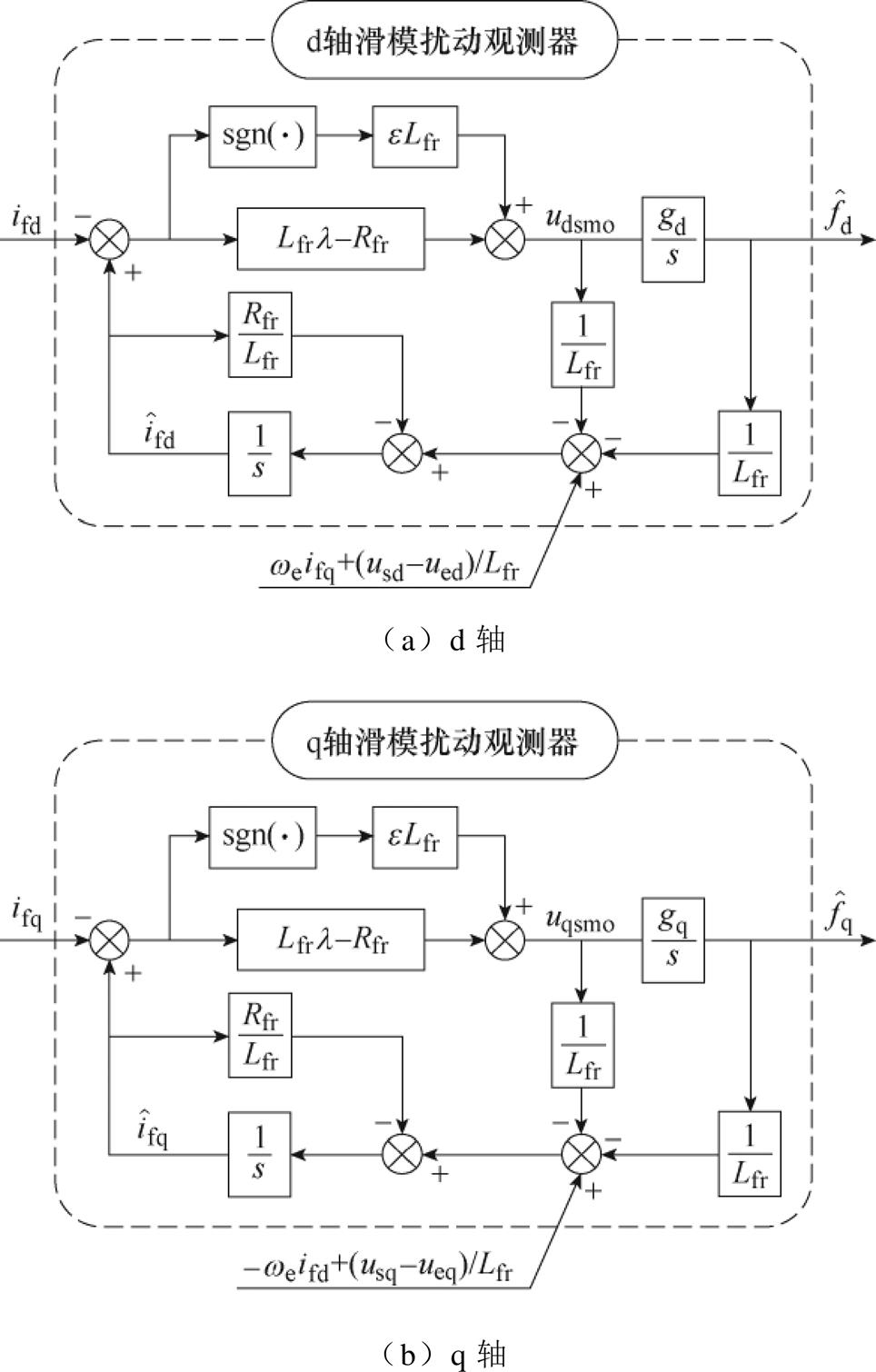
图6 滑模扰动观测器框图
Fig.6 Block diagram of the sliding mode perturbation observer
为保证滑模扰动观测器收敛,需满足条件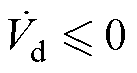 ,
,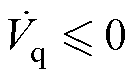 。
。
以d轴为例进行稳定性证明,有
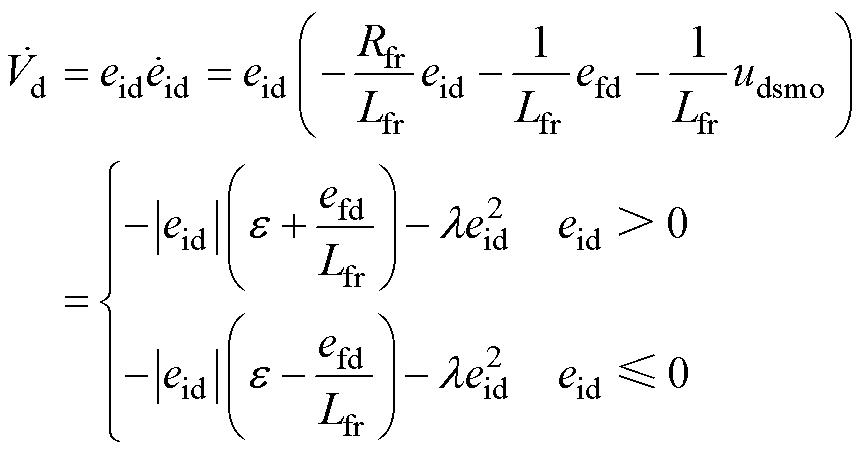 (19)
(19)
由式(19)可知,当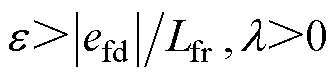 时,
时,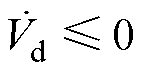 恒成立;同理,当
恒成立;同理,当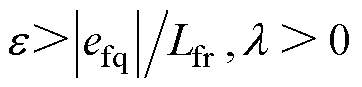 时,
时,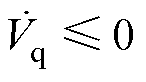 恒成立。综上所述,当滑模趋近率参数满足式(20)时,滑模观测器能够在有限时间内收敛。
恒成立。综上所述,当滑模趋近率参数满足式(20)时,滑模观测器能够在有限时间内收敛。
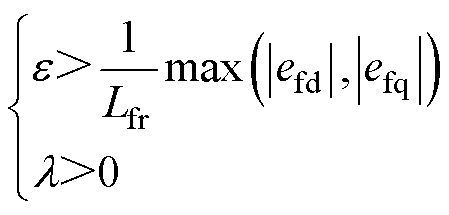 (20)
(20)
滑模观测器收敛后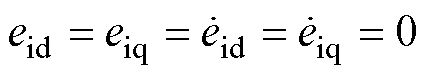 ,代入式(13)和式(14)可解得
,代入式(13)和式(14)可解得
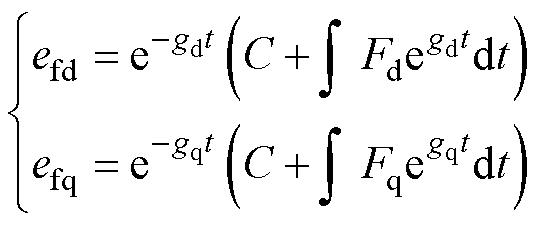 (21)
(21)
因此,为了使扰动观测值与实际值的误差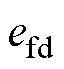 和
和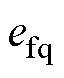 收敛至0,参数
收敛至0,参数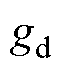 和
和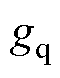 应大于0。
应大于0。
为验证本文所提出的基于滑模扰动观测器的开环电流控制策略的准确性与鲁棒性,分别设计了仿真实验与实物实验进行验证分析,永磁同步电机以及电机模拟器参数见表1。
表1 PMSM与EME参数
Tab.1 Parameters of PMSM and EME

参 数数 值 永磁体极对数np4 电机d轴电感Lsd/mH1.225 电机q轴电感Lsq/mH1.225 定子电阻Rs/W0.365 永磁体磁链/Wb0.166 7 接口电路电感Lf/mH1.6 接口电路电阻Rf/W0.365 开关频率f/kHz10 集总控制延时Td/ms80
被测电机控制器端采用基于id=0的矢量控制策略,转速环与电流环均采用PI控制。电机模拟器中的控制算法分别采用PI控制、传统开环控制和本文所提的基于滑模扰动观测器的开环控制策略进行对比分析与验证。功率逆变器采用电压源型三相逆变器,调制策略采用空间矢量调制策略,接口电路为L型接口电路。
本文首先通过仿真实验验证所提控制算法的有效性,设计仿真条件为转速在0~0.05 s斜坡加速至1 500 r/min,同时在0.1 s施加10 N·m的负载阶跃扰动,并在0.2 s负载扰动阶跃至0。本文所提基于滑模扰动观测器的开环电流控制策略(OLC+SMDO)控制框图如图7所示。为了对比传统PI控制、传统开环控制以及OLC+SMDO的鲁棒性,分别设置25%的电感与35%的电阻参数扰动,即Lfr=0.75Lf,Rfr=1.35Rf,仿真结果如图8~图10所示。
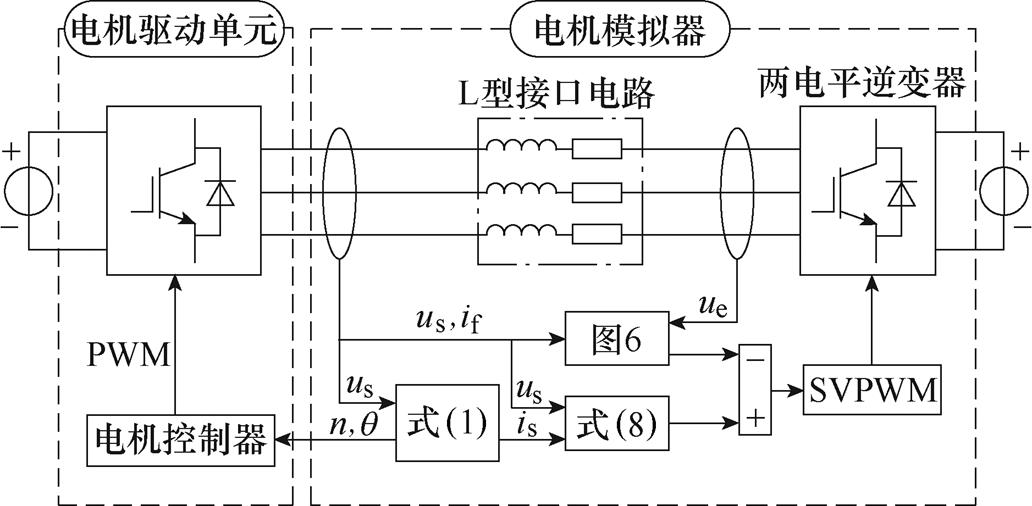
图7 OLC+SMDO控制框图
Fig.7 Block diagram of the OLC+SMDO
由图8可知,当存在参数扰动时,由于传统开环控制策略依赖接口电路参数,使得电机模拟器在瞬态以及稳态时都存在较大的电流模拟误差。其中,在起动加速阶段A相电流模拟误差最大超过3 A,相对误差超过40%。同样地,起动阶段q轴电流存在明显的波动而无法准确跟踪期望值,最大误差超过2 A,相对误差超过40%。突加负载后,A相电流与q轴电流产生了与负载值相关的模拟误差,误差集中在1~2 A之间,相对误差达20%。总的来看,在参数失配的条件下,传统开环控制不论是瞬态或稳态都存在较大的误差,这与3.2节对传统开环控制进行的参数敏感性分析相互验证。
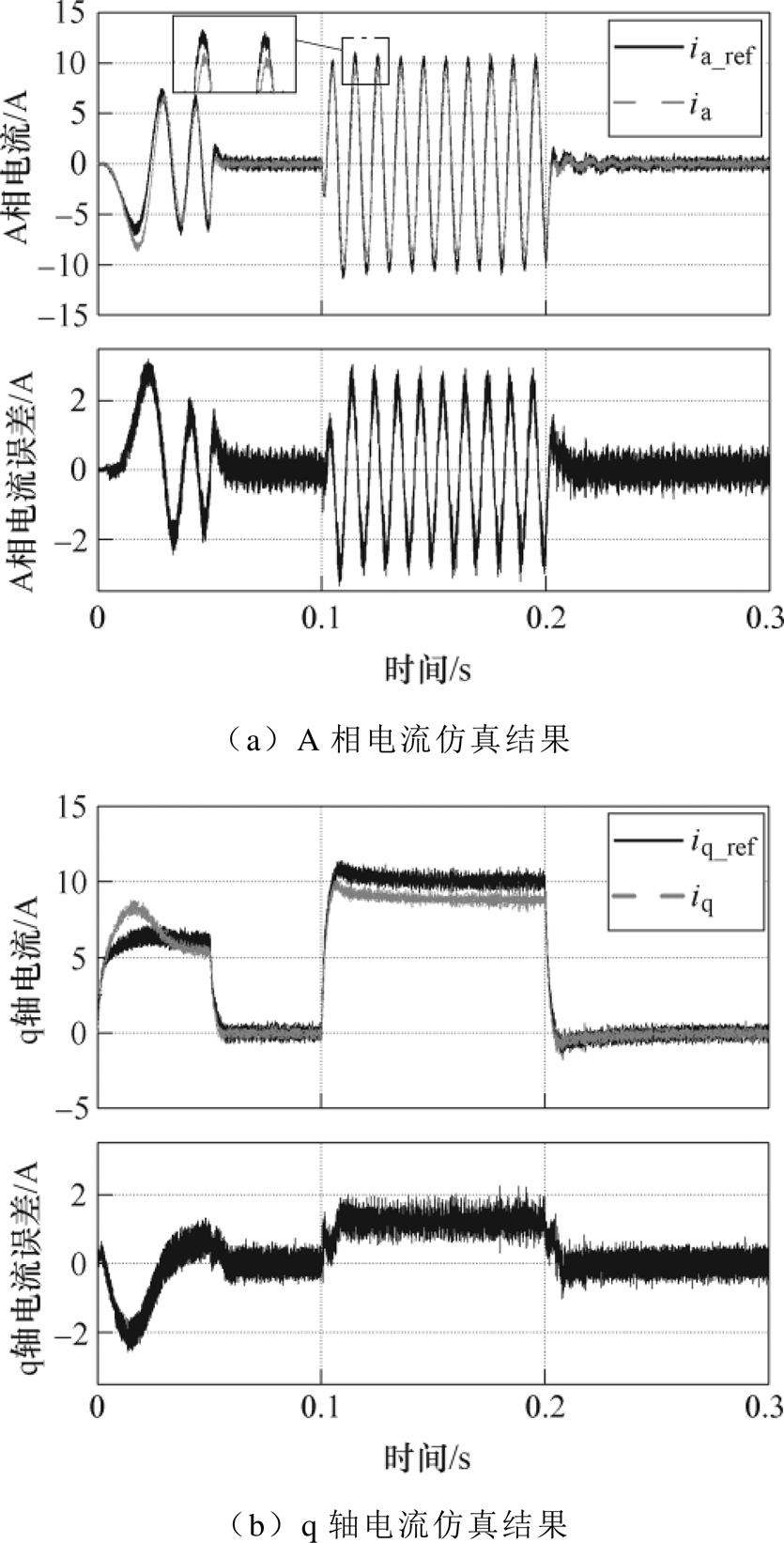
图8 存在参数扰动时传统开环控制仿真结果
Fig.8 Simulation results of traditional open loop control with parameter disturbance
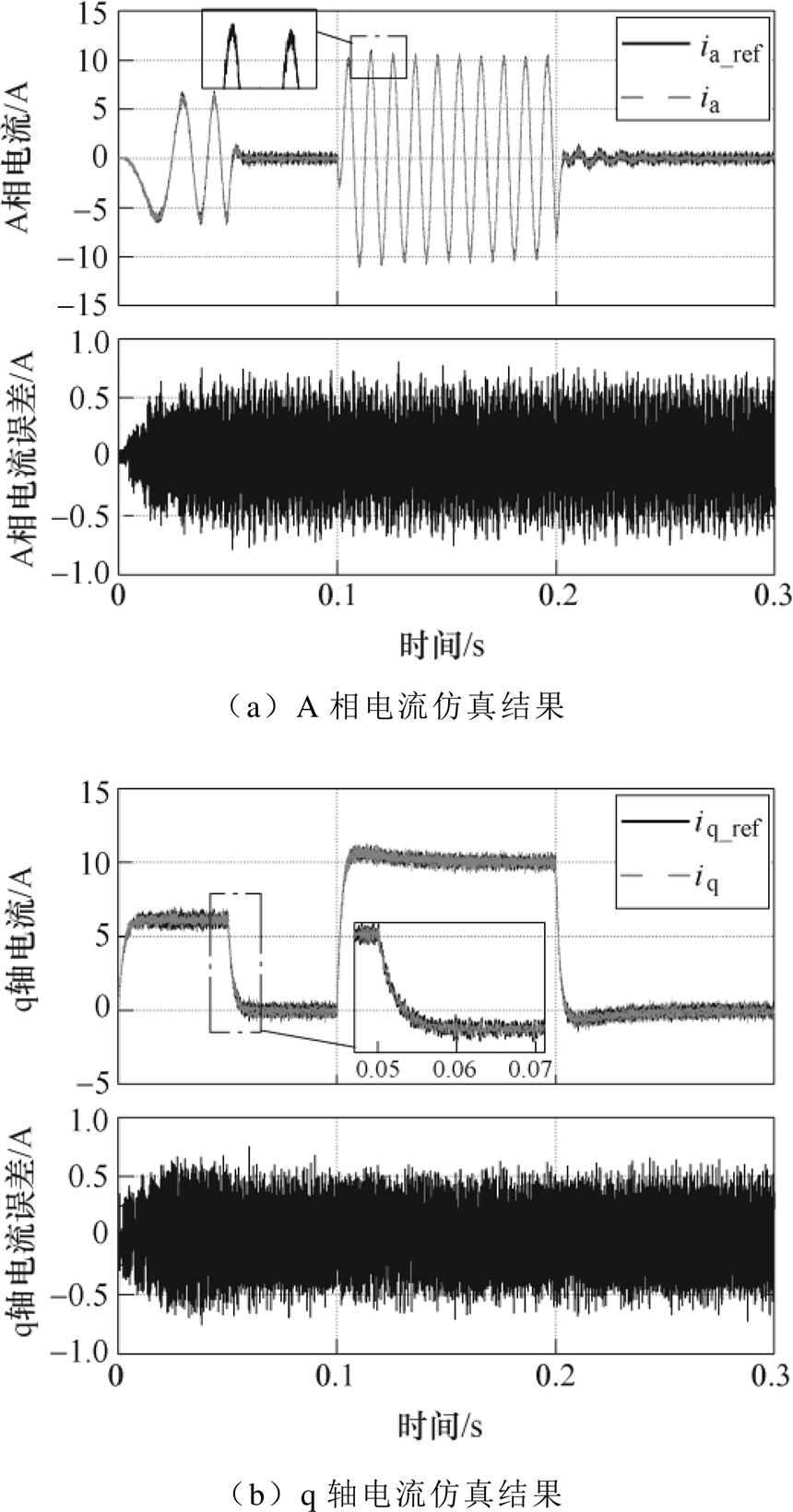
图9 存在参数扰动时OLC+SMDO控制策略仿真结果
Fig.9 Simulation results of OLC+SMDO control strategy with parameter disturbance
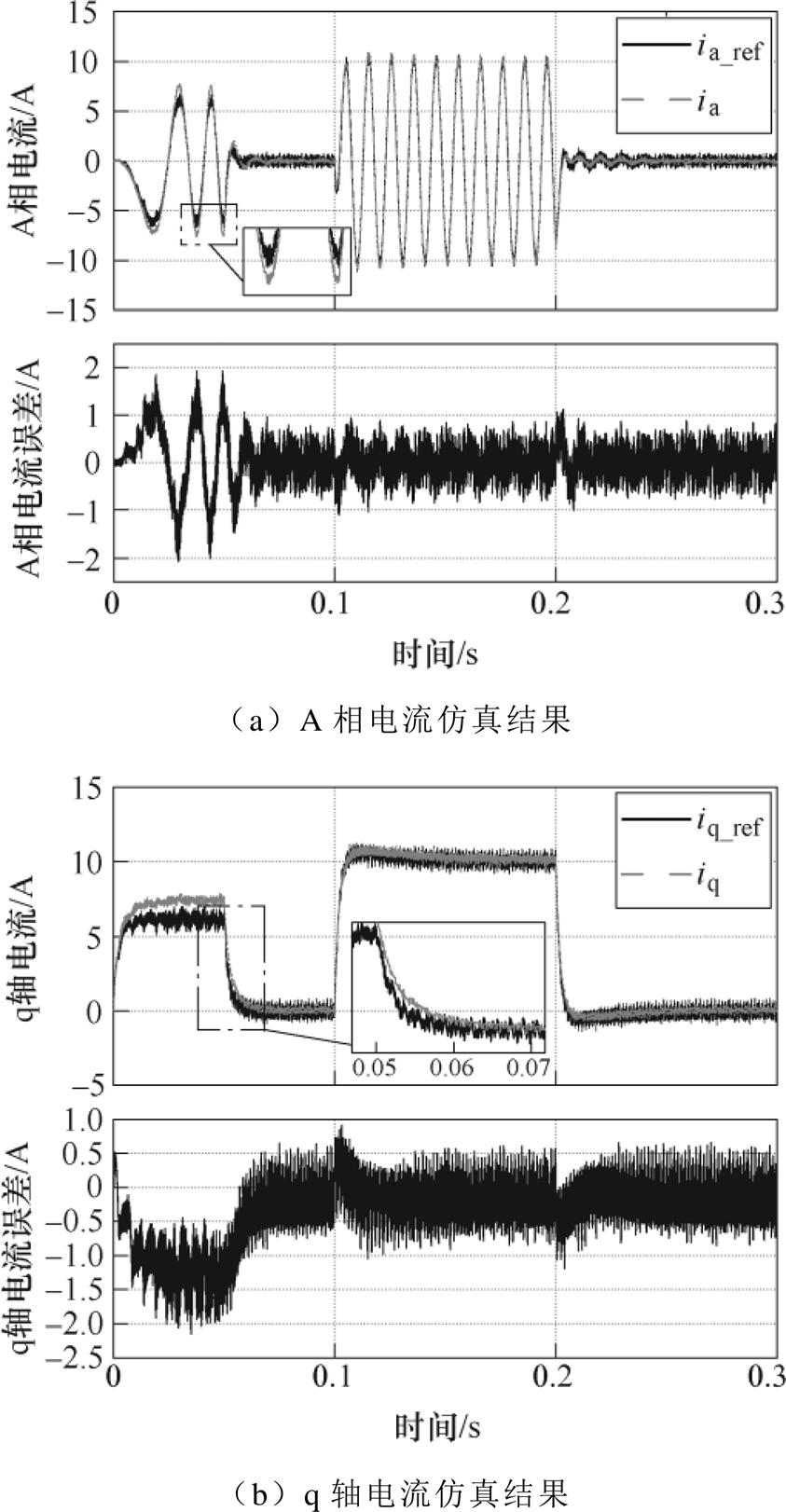
图10 存在参数扰动时传统PI控制仿真结果
Fig.10 Simulation results of traditional PI control with parameter disturbance
从图9可以看出,本文所提出的OLC+SMDO控制策略能够补偿抑制参数扰动的影响。其中,起动加速阶段A相电流与q轴电流的最大模拟误差约为0.7 A,远低于传统开环控制;同时,本文所提的OLC+SMDO的控制策略并没有受到负载突变的影响,在突加负载后总体误差依然控制在0.5 A左右,是传统的开环控制电流模拟误差的25%。总的来看,本文所提的OLC+SMDO控制策略无论是瞬态或稳态的控制效果均优于传统的开环控制策略,受起动加速与负载突变的影响较小。
从图10可以看出,相对于传统的开环控制,基于PI控制策略的EME在一定程度上抑制了参数扰动的影响,在存在参数扰动下的电流模拟精度高于传统开环控制策略,稳态误差较小。但相对于本文所提的OLC+SMDO策略,仍存在以下问题:
(1)在起动加速的0.05 s内,A相电流与q轴电流误差存在较大的波动,峰值模拟误差约为2 A,是本文所提出的OLC+SMDO控制策略的3倍。
(2)在负载阶跃的动态响应过程中,如在0.1 s突加负载与在0.2 s负载突降时,电流模拟误差出现波动,误差值变大,出现超过1 A的误差峰值,是本文所提OLC+SMDO控制策略的2倍。
(3)对比图9b与图10b 0.05 s处的q轴电流局部放大图可以看出,本文所提的控制策略在转速突变时相对于PI控制策略具有更快的响应速度。
以上三点均表明,本文所提OLC+SMDO的控制策略在动态响应上相对于PI控制策略具有更高的模拟精度,与第2节所述PI控制的低通滤波特性对电机模拟器电流环高频特性的限制的理论分析相一致。
实物验证平台如图11所示,选择Typhoon HIL 602+作为实时处理器,目标永磁同步电机模型运行在现场可编程逻辑门阵列(Field-Programmable Gate Array, FPGA)板卡中,电流控制策略以及电压调制策略运行在ARM Cortex A9中。电池模拟器用来给模拟器侧逆变器提供直流电源并吸收电路中的能量。其中,电机驱动单元的控制芯片采用DSP TMSF28335,其逆变器采用IGBT模块,工作频率为10 kHz。接口电路为L型接口电路,用于连接电机驱动单元与模拟器侧功率逆变器。电机与接口电路参数与仿真实验一致,同表1。
为验证本文所提控制策略的有效性,在电阻1.35倍扰动、电感0.75倍扰动的实验条件下进行实验平台验证。设置转速为1 000 r/min,并在0.2~0.3 s内施加2~10 N的斜坡负载扰动,分别对比传统开环控制、PI控制以及本文所提OLC+SMDO控制三种策略的实验效果。图12a所示为目标电机的三相电流波形,图12b~图12d分别为采用传统开环控制、PI控制以及OLC+SMDO三种不同电流控制策略下电机模拟器的三相电流波形,图中每纵格代表的电流大小为5 A。

图11 实验平台
Fig.11 Experimental setups of EME
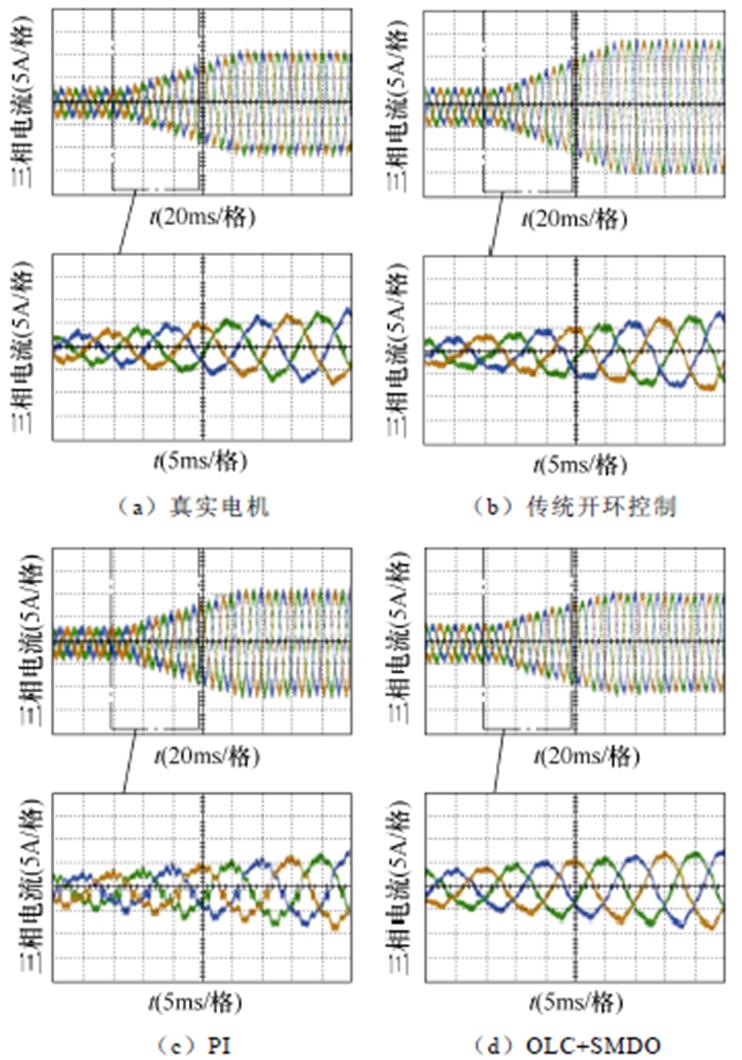
图12 存在参数扰动时不同控制策略下的三相电流
Fig.12 Three-phase current under different control strategies with parameter disturbance
图13所示为不同控制策略在参数扰动条件下,电机模拟器三相电流与真实电机三相电流之差。存在参数扰动时不同控制策略下的dq轴电流及模拟误差如图14所示。从图13a可以看出,发生参数扰动后,传统开环控制产生正弦状误差,且误差幅值与负载扰动的大小呈正相关,最大约为5 A,这说明传统开环控制在参数扰动后不仅存在幅值误差,还会导致相位的扰动。结合图12d与图13c可以看出,发生参数扰动后,由于扰动前馈的补偿作用,本文所提出的OLC+ SMDO策略能够有效解决传统开环控制存在的相位与幅值扰动问题,最大误差不超过1.5 A,相较于传统开环控制缩小了60%,相较于PI控制缩小了10%,验证了所提控制策略的准确性,其中扰动观测值如图15所示,图中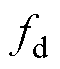 和
和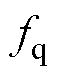 为实际扰动值,
为实际扰动值, 和
和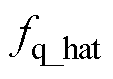 为扰动估计值。
为扰动估计值。
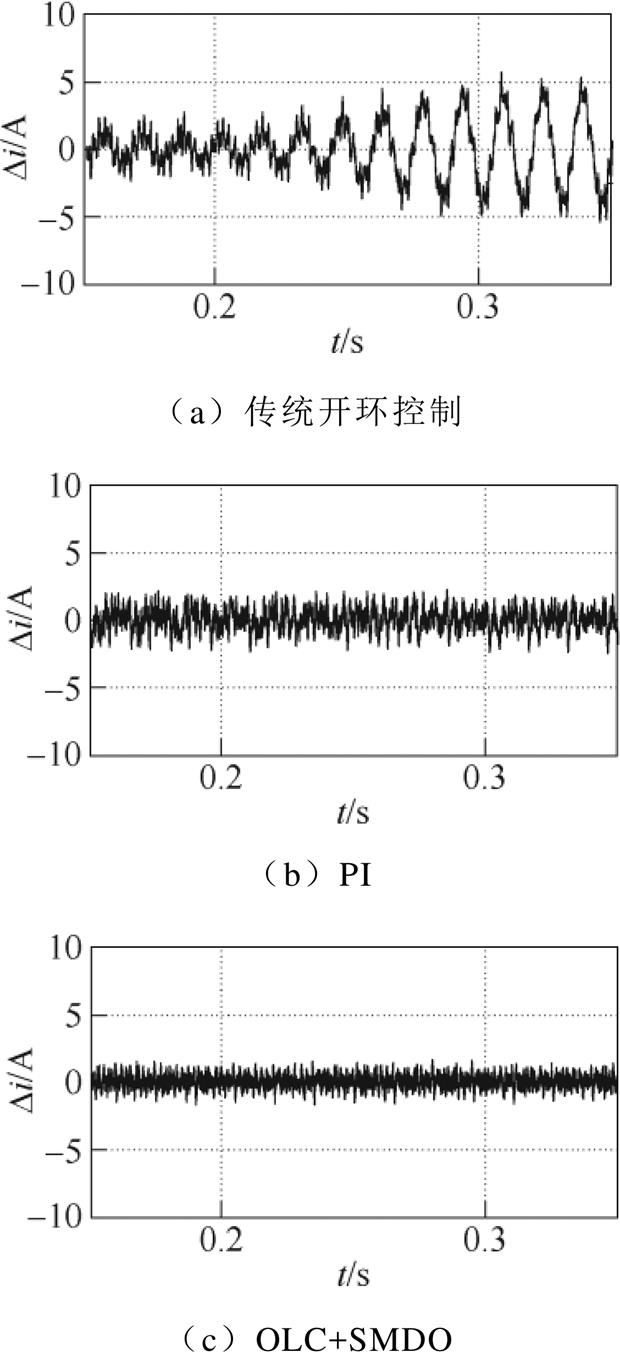
图13 存在参数扰动时不同控制策略下的三相电流模拟误差
Fig.13 Three-phase current errors under different control strategies with parameter disturbance
从图12c可以看出,当发生参数扰动后,基于PI控制的电机模拟器的三相电流发生畸变,相较于OLC+SMDO的控制策略,其谐波含量更高,在误差图中表现为较大的毛刺状误差,最大误差超过2.5 A。

图14 存在参数扰动时不同控制策略下的dq轴电流及模拟误差
Fig.14 dq current errors under different control strategies with parameter disturbance
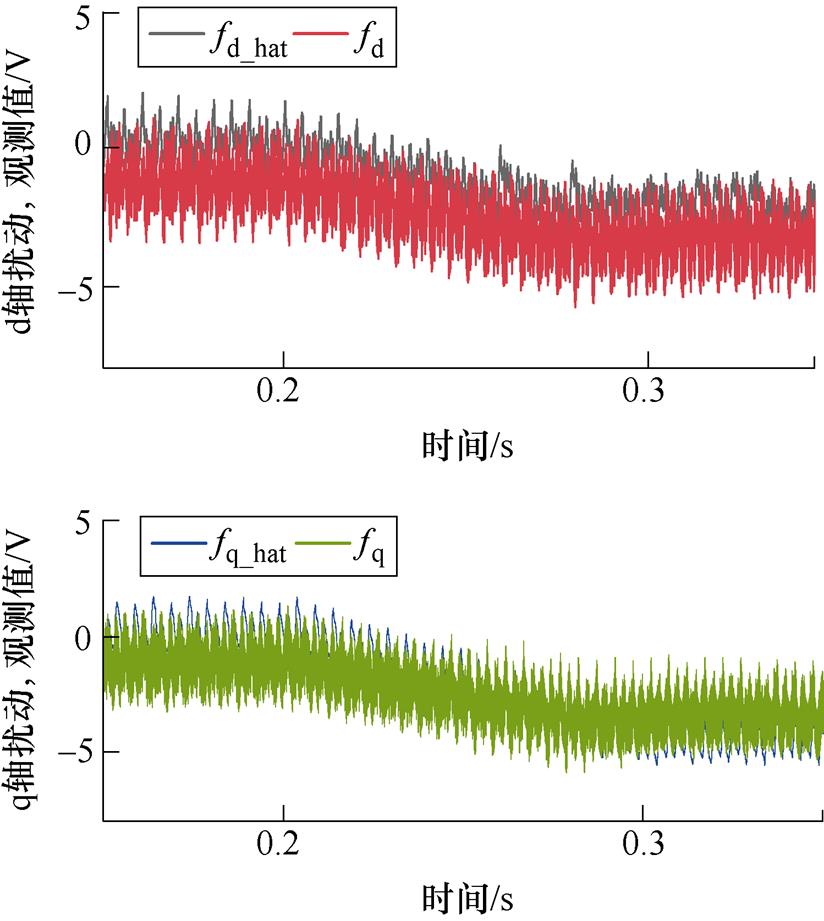
图15 扰动观测值
Fig.15 Perturbation observation
图16所示为基于PI控制和OLC+SMDO两种控制策略下电机模拟器三相电流的谐波分析,可以看出,基于OLC+SMDO控制策略的EME三相电流的总谐波畸变率(Total Harmonic Distortion, THD)相较于PI控制策略减小了2.48%,其中7、11、13、17等高次谐波含量明显减小。一方面是由于参数扰动后,基于PI控制的EME侧电流环动态响应恶化,与MDU侧电流环冲突加剧;另一方面,高鲁棒性滑模扰动观测器的设计可以观测出由逆变器非线性特性产生的扰动并将其前馈补偿,从而使得谐波含量进一步减小。
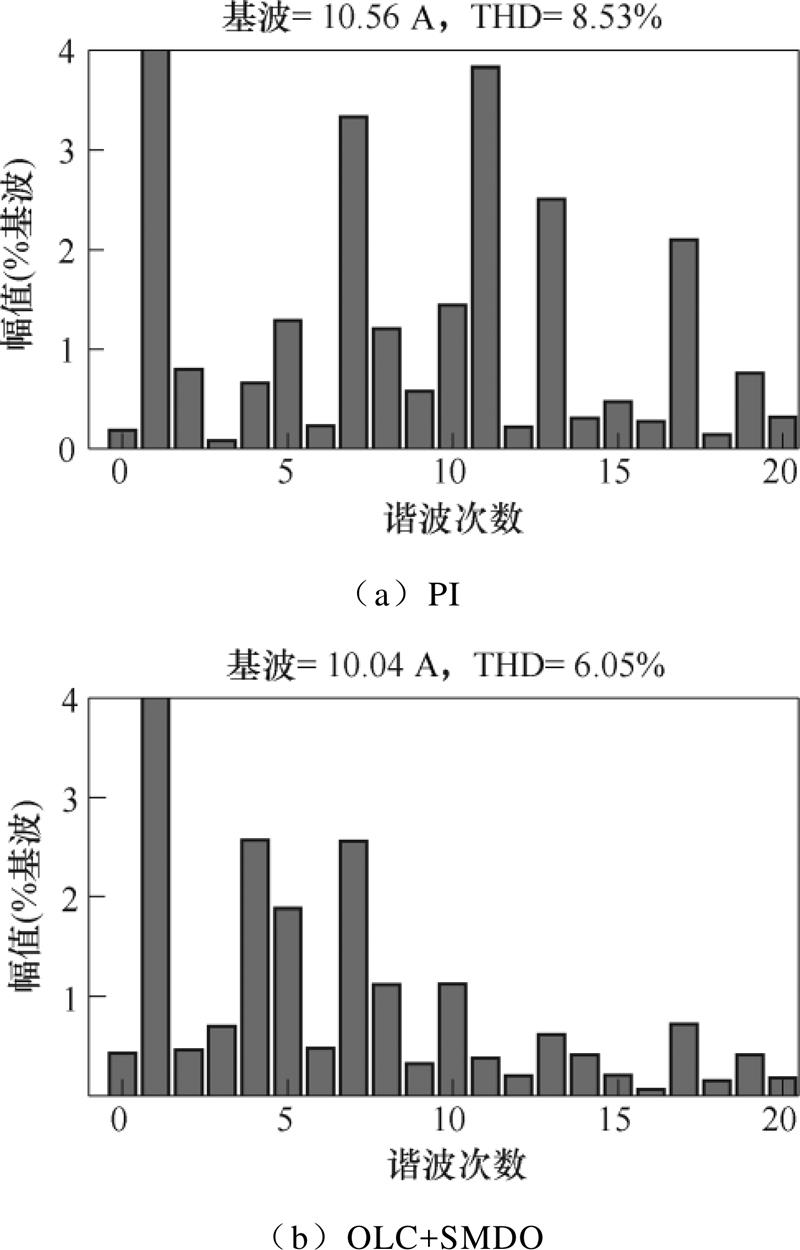
图16 存在参数扰动时不同控制策略下的三相电流谐波分析
Fig.16 Three-phase current harmonic analysis under different control strategies with parameter disturbance
本文针对基于PI控制的电机模拟器的动态响应慢、带宽受限的缺陷,提出了一种基于滑模扰动观测器的开环电流控制策略。该方法一方面避免了电流闭环控制中被测驱动器与电机模拟器两个电流环的控制冲突问题;另一方面解决了传统开环控制易受参数扰动影响的问题,提高了控制系统的鲁棒性。实验验证表明,本文所提出的控制策略无论是动态响应或稳态响应均优于PI控制与传统开环控制。在25%电感扰动与35%电阻扰动的条件下,相电流最大模拟误差相较于传统开环控制缩小60%,相较于PI控制缩小10%。同时,相电流谐波含量相较于PI控制减少了2.48%。
参考文献
[1] 曹阳, 刘旭. 计及损耗的混合励磁电机建模与硬件在环实时仿真系统[J]. 电工技术学报, 2020, 35(22): 4657-4665.
Cao Yang, Liu Xu. Modeling method for hybrid- excited machine and hardware-in-loop real-time simulation system with accounting for loss calcu- lation[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4657-4665.
[2] 高瑾, 黄洋, 宋石阳, 等. 车用电机硬件在环实时仿真与测试平台[J]. 电工技术学报, 2014, 29(11): 99-106.
Gao Jin, Huang Yang, Song Shiyang, et al. Hardware- in-loop real-time simulation and test bench for electrical vehicle[J]. Transactions of China Elec- trotechnical Society, 2014, 29(11): 99-106.
[3] Amitkumar K S, Kaarthik R S, Pillay P. A versatile power-hardware-in-the-loop-based emulator for rapid testing of transportation electric drives[J]. IEEE Transactions on Transportation Electrification, 2018, 4(4): 901-911.
[4] 王志福, 孙庆乐, 李昊龙, 等. 基于有限元分析的永磁同步电机实时模拟器研究[J]. 北京理工大学学报, 2021, 41(9): 918-926.
Wang Zhifu, Sun Qingle, Li Haolong, et al. Research on real-time emulator based on finite element analysis for permanent magnet synchronous motor[J]. Transa- ctions of Beijing Institute of Technology, 2021, 41(9): 918-926.
[5] Sun Qingle, Wang Zhifu, Wang Zeshang, et al. Design and implementation of LCL filter-based electric machine emulator with disturbance com- pensation[J]. IEEE Access, 2022, 10: 82580-82595.
[6] Srinivasa R Y, Chandorkar M C. Real-time electrical load emulator using optimal feedback control tech- nique[J]. IEEE Transactions on Industrial Electronics, 2010, 57(4): 1217-1225.
[7] Zou Xiaomin, Xiao Xi, He Peng, et al. Permanent magnet synchronous machine emulation based on power hardware-in-the-loop simulation[C]//2019 IEEE International Electric Machines & Drives Conference (IEMDC), San Diego, CA, USA, 2019: 248-253.
[8] Ma Ke, Song Yubo. Power-electronic-based electric machine emulator using direct impedance regu- lation[J]. IEEE Transactions on Power Electronics, 2020, 35(10): 10673-10680.
[9] Qi Yuhao, Ma Ke, Tang Weiyu. Full-bandwidth mission profile emulation of the electric machine system with voltage reference signal transmission[J]. IEEE Transactions on Power Electronics, 2022, 37(3): 3473-3483.
[10] Vodyakho O, Steurer M, Edrington C S, et al. An induction machine emulator for high-power appli- cations utilizing advanced simulation tools with graphical user interfaces[J]. IEEE Transactions on Energy Conversion, 2012, 27(1): 160-172.
[11] Masadeh M A, Amitkumar K S, Pillay P. Power electronic converter-based induction motor emulator including main and leakage flux saturation[J]. IEEE Transactions on Transportation Electrification, 2018, 4(2): 483-493.
[12] Fleming F E, Edrington C S. Real-time emulation of switched reluctance machines via magnetic equivalent circuits[J]. IEEE Transactions on Industrial Elec- tronics, 2016, 63(6): 3366-3376.
[13] 黄科元, 周佳新, 刘思美, 等. 考虑逆变器非线性永磁同步电机高频注入电感辨识方法[J]. 电工技术学报, 2021, 36(8): 1607-1616.
Huang Keyuan, Zhou Jiaxin, Liu Simei, et al. Inductance identification method of permanent magnet synchronous motor considering inverter nonlinearity based on high-frequency injection[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1607-1616.
[14] 尹忠刚, 白聪, 杜超, 等. 基于内模干扰观测器的永磁同步直线电机无差拍电流预测控制方法[J]. 电工技术学报, 2018, 33(24): 5741-5750.
Yin Zhonggang, Bai Cong, Du Chao, et al. Deadbeat predictive current control for permanent magnet linear synchronous motor based on internal model dis- turbance observer[J]. Transactions of China Electro- technical Society, 2018, 33(24): 5741-5750.
[15] 郭昕, 黄守道, 彭昱, 等. 基于改进型双幂次趋近律与全局快速终端滑模观测器的IPMSM调速系统滑模控制[J]. 电工技术学报, 2023, 38(1): 190-203.
Guo Xin, Huang Shoudao, Peng Yu, et al. Sliding mode control of IPMSM speed regulation system based on an improved double power reaching law and global fast terminal sliding mode observer[J]. Transa- ctions of China Electrotechnical Society, 2023, 38(1): 190-203.
[16] 章回炫, 范涛, 边元均, 等. 永磁同步电机高性能电流预测控制[J]. 电工技术学报, 2022, 37(17): 4335-4345.
Zhang Huixuan, Fan Tao, Bian Yuanjun, et al. Predictive current control strategy of permanent magnet synchronous motors with high performance[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4335-4345.
[17] 周奇勋, 刘帆, 吴紫辉, 等. 永磁同步电机转矩与定子磁链模型预测控制预测误差补偿方法[J]. 电工技术学报, 2022, 37(22): 5728-5739.
Zhou Qixun, Liu Fan, Wu Zihui, et al. Model predictive torque and stator flux control method for PMSMs with prediction error compensation[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5728-5739.
[18] 吴云亚, 阚加荣, 谢少军. 基于双d-q坐标系的并网逆变器控制策略[J]. 电工技术学报, 2011, 26(8): 106-112.
Wu Yunya, Kan Jiarong, Xie Shaojun. Control strategy for grid-connected inverter based on double d-q coordinates[J]. Transactions of China Electro- technical Society, 2011, 26(8): 106-112.
[19] 武志涛, 李帅, 程万胜. 基于扩展滑模扰动观测器的永磁直线同步电机定结构滑模位置跟踪控制[J]. 电工技术学报, 2022, 37(10): 2503-2512.
Wu Zhitao, Li Shuai, Cheng Wansheng. Fixed structure sliding mode position tracking control for permanent magnet linear synchronous motor based on extended sliding mode disturbance observer[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2503-2512.
Abstract Mechanical load dynamometer systems are commonly used to test and develop motor drive systems. However, traditional mechanical load testbeds for electric motors have several drawbacks, such as large volume, high cost, and difficulties-to-implementing fault testing, which fail to meet the requirements of efficient electric drive system testing. An electric motor emulator (EME) based on power hardware-in-the-loop (PHIL) can simulate the current and voltage characteristics of real motor ports using power electronic devices and control algorithms, making it a novel solution for testing the performance of motor controllers.
The current control strategies are key to affecting the accuracy of EME. However, the low-pass filtering nature of conventional PI control limits the dynamic control effect of EME, and traditional open-loop control strategies are susceptible to parameter perturbations. Therefore, an open-loop current control strategy based on sliding mode perturbing observers is proposed. First, the PI control defect and low-pass filtering properties are analyzed by deriving the transfer function and using the Bode diagram. The theoretical analysis shows that PI control cannot simulate the amplitude-frequency properties of the target motor in the full bandwidth. Second, the open loop control voltage equation without differential calculation is derived based on the mathematical model of the target motor and the interface circuit model. Moreover, the perturbation effects of the resistance and inductance parameters on the control policy are analyzed. The inductance perturbation mainly affects the high-frequency features, which are more distorted as the degree of perturbation increases, leading to a decrease in the accuracy of the simulation of the dynamic response. Resistance perturbations mainly affect the low-frequency features. As the degree of mismatch increases, the distortion of the low-frequency features and the steady-state error become larger. Finally, robust sliding-mode perturbation observers are designed for perturbation observation and feed-forward compensation.
Simulation results show that under 35% resistance disturbance and 25% resistance disturbance, the traditional open-loop control exhibits phase current simulation error as high as 3 A in the dynamic response, and the steady-state error is about 2 A. The PI control has the largest phase current simulation error during the acceleration stage, about 2 A, and the steady-state error is about 0.8 A. The error of the proposed control strategy is within 0.7 A in both dynamic and steady-state responses. Experimental results show that traditional open-loop control experiences amplitude errors and phase perturbations after parameter perturbations. The proposed control strategy has higher precision and accuracy than the motor simulator system based on the traditional PI control and open-loop control strategy, regardless of the transient or steady-state condition when there is parameter disturbance. Under 25% inductance disturbance and 35% resistance disturbance, the maximum phase current simulation error is reduced by 60% compared to the traditional open-loop control and 10% compared to the PI control. Meanwhile, the harmonic content of phase current is reduced by 2.48% compared to PI control.
Keywords:Electric motor emulator, open-loop control, PI control, disturbance observer
王泽尚 男,1999年生,硕士研究生,研究方向为电机控制、电机模拟器系统及其控制。E-mail: wangzeshang@bit.edu.cn
王志福 男,1977年生,教授,硕士生导师,研究方向为电机控制、车辆动力学、电机模拟器等。E-mail: wangzhifu@bit.edu.cn(通信作者)
中图分类号:TM341
DOI: 10.19595/j.cnki.1000-6753.tces.230012
国家自然科学基金资助项目(51775042)。
收稿日期 2023-01-04
改稿日期 2023-04-25
(编辑 崔文静)