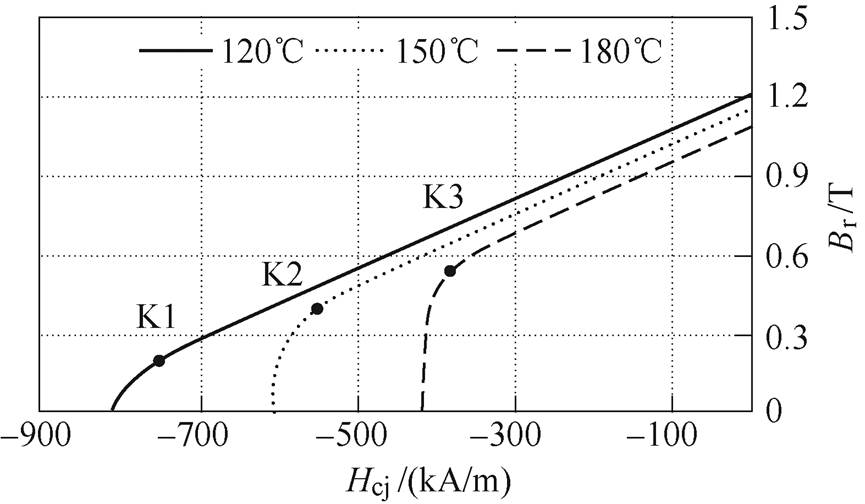
图1 钕铁硼永磁材料磁特性
Fig.1 Magnetic properties of NdFeB permanent magnet materials
摘要 电动汽车用永磁电机普遍使用的高性能钕铁硼永磁材料在高温、强磁场等条件作用下易发生的不可逆失磁故障已成为该类电机高可靠性设计的主要瓶颈。针对电动汽车用永磁电机的失磁问题,该文利用永磁体虚拟分块方法,建立基于永磁体磁特性参数、工作温度、空间位置等变量的永磁体失磁分析模型;利用电磁场和温度场双向耦合的三维多物理场计算方法,研究了永磁电机失磁的空间分布特性及其影响因素。结果表明,永磁电机失磁空间分布存在明显的不均匀性。永磁体失磁分布规律受其工作温度、退磁电流幅值与角度等因素影响。最后,通过一台115 kW的永磁驱动电机样机在永磁体工作温度、转子表磁磁场分布、电机性能方面的测试,验证了该文所提分析方法和结论的准确性。
关键词:永磁同步电机(PMSM) 钕铁硼永磁体 局部失磁 多物理场耦合 失磁影响 空间分布
随着全球能源危机与温室效应的加剧,各国对“碳达峰、碳中和”等工作日益重视,电动汽车作为绿色交通方式替代传统燃油车成为主流出行方式,得到快速发展和应用[1-2]。由于永磁电机具有结构简单、功率密度高、效率高、调速范围宽等优点,已逐步成为当前电动汽车驱动电机的首选型式。电动汽车驱动系统的高集成度、高可靠性等要求对永磁驱动电机的安全稳定运行提出了更高的要求[3-4]。
当前,电动汽车用永磁驱动电机主要使用的是第三代钕铁硼稀土永磁材料。该种材料具有高磁能积、易加工、价格低廉等优势,但其磁性能的稳定性却容易受到外界高温、强磁场、强冲击振动、高辐射和化学腐蚀等因素影响,甚至产生不可逆失磁现象[5-6]。电机中使用的永磁材料作为转子励磁磁场的来源,一旦发生不可逆失磁,将会对驱动电机的稳定运行产生严重影响,甚至可能危及电动汽车驾驶人员的生命安全。因此,对永磁驱动电机的永磁体失磁问题进行准确的计算、分析并开展失磁故障诊断与预防对电动汽车的安全运行具有重要意义。
近年来,国内外学者针对电机永磁体失磁问题开展了大量的研究。对于永磁材料的失磁原因,文献[7-8]从材料学角度研究了高工作温度、强退磁磁场、强冲击振动和强辐射等因素对永磁体磁性能的影响规律;文献[9]结合驱动电机应用场景的特殊性分析,获得了钕铁硼永磁体在电机内部高温与强磁场作用下的磁特性演变规律。
电机用永磁体的失磁特性研究方法主要包括二维与三维有限元法和解析法。文献[10-13]利用二维有限元法,以磁通的下降比例模拟失磁故障,研究了失磁前后电机关键特征参数与动态特性的变化;文献[14-17]利用三维有限元法研究了损耗与永磁体温度及工作点,温度与永磁体失磁特性之间的影响规律;文献[18]利用二维解析磁场模型研究了交错磁极混合励磁发电机的磁场特性。但目前失磁问题的主要研究方法均未能考虑转子永磁体空间温度分布差异对失磁分布特性的影响。
对于电机用永磁体失磁特性影响的研究,文献[12, 19-21]针对自起动永磁电机起动过程,研究了永磁体平均工作点、电枢反应、笼型槽对失磁故障的影响;文献[22-24]研究了永磁电机失磁前后的电磁性能及V字型磁路结构中各永磁体磁性能的变化规律。但相关研究并未分析永磁体失磁空间分布规律的主要影响因素及其作用原理。
由以上永磁电机失磁问题研究现状分析可见,永磁体局部失磁问题是一个涉及电机磁路结构及其建模方法、永磁材料不同工作温度下的物理属性计算方法、失磁环境应力及其作用方式等多维度相关联的复杂问题。针对电动汽车用永磁电机的高功率密度、高可靠性等要求,当前考虑电磁场与温度场相互作用下的永磁体物性分析,对永磁体发生局部失磁的空间分布特性及其影响因素等问题均鲜有深度研究,未能揭示永磁体在电机轴向、周向空间上的磁性能与退磁特性差异。因此,有必要针对以上永磁电机局部失磁的相关问题,开展深入的研究。
本文以一台115 kW、8极的外水套冷却电动汽车用永磁主驱动电机为研究目标,分析了电机局部失磁空间分布特性及其主要影响因素。首先,建立包含永磁体空间位置、工作温度、剩磁与矫顽力温度系数和不可逆退磁率等变量的局部失磁分析模型。其次,利用三维磁热双向耦合计算方法,计算得到电机永磁体稳态工作温度的空间分布特性。再次,分析了工作温度、退磁电流对电机局部失磁空间分布规律的影响,得到失磁故障发生后,电机定转子铁心磁通密度、空载反电动势、输出转矩等特性的变化规律。最后,制造了一台样机,通过对电机转子温度分布、表磁磁场分布、整机工作特性等在失磁故障发生前后的差异进行详细的测试与分析,验证了分析方法的有效性和准确性。本文为进一步开展永磁驱动电机的高可靠性设计、退磁故障的诊断与预防提供了支撑。
钕铁硼稀土永磁材料具有高磁能积、易加工等优势,目前已成为电动汽车永磁驱动电机中应用的主要磁性材料。钕铁硼永磁材料在电机中应用时的磁稳定性易受电机内部的高工作温度、强退磁磁场影响。
图1为一款高性能钕铁硼永磁产品在不同温度下的实测退磁曲线,K1、K2、K3即为该磁体在不同温度下的退磁曲线拐点。可见,随着工作温度提升,钕铁硼永磁材料退磁曲线的拐点向横轴正方向移动,永磁体的抗退磁性能下降,即永磁电机内部高工作温度区域的永磁体更容易发生不可逆失磁。

图1 钕铁硼永磁材料磁特性
Fig.1 Magnetic properties of NdFeB permanent magnet materials
电机内部的退磁磁场主要由定子绕组内所通过的电流产生。随着退磁磁场强度增大,永磁体工作点向拐点靠近,即电机内部承受更大退磁磁场的永磁体更容易发生不可逆失磁。
钕铁硼永磁材料在电机中工作时的磁特性受到其工作温度与作用到其磁化方向上的退磁磁场强度影响。为了准确分析空间不同位置永磁体的磁特性在电机发生失磁故障后的变化规律,以及电机失磁后的运行特性变化规律,需要建立可考虑永磁体空间工作温度差异、永磁体退磁磁场空间分布差异的分析模型。
传统的利用有限元法求解永磁体退磁率的建模方法将每一块永磁体实体建立为一个整体模型。该模型的材料属性唯一。钕铁硼永磁材料磁特性与其工作温度密切相关,在一定条件下,磁体将发生局部失磁[9]。即同一块永磁体不同位置的特性状态并不唯一,使用同一种材料属性无法准确描述工作状态下永磁体复杂的磁特性。为满足失磁问题的分析需求,提升失磁分析准确性,本文基于磁体虚拟分块建模法建立永磁电机失磁分析模型。将永磁体实体模型划分为若干虚拟的分析单元,每个虚拟分析单元简称为单元磁体。由钕铁硼永磁材料物性分析可知,其磁特性随着工作温度的上升而衰减。永磁电机的失磁问题分析中必须考虑工作温度对永磁体磁特性的影响。因此,各单元磁体均使用不同的剩磁、矫顽力、退磁率、工作温度等变量来描述其磁特性。由于在三维电磁场及温度场分析模型中,永磁体空间位置信息已体现,结合永磁体温度空间分布计算结果即可实现对每一个单元磁体在不同工作温度下的磁特性分析。综上所述,建立满足电动汽车用永磁驱动电机失磁空间分布特性研究需求的分析模型。基于单元磁体模型的永磁电机失磁分析方法可以通过对电机全域单元磁体磁特性的描述,准确地模拟任意失磁状态下的永磁体工作状态,进而实现对电机失磁过程及影响的研究。单元磁体模型示意图如图2所示。
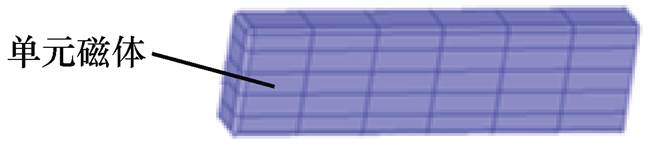
图2 单元磁体模型示意图
Fig.2 Unit magnet model diagram
由于电动汽车用永磁电机调速范围宽,由控制器供电时的电流中带有大量谐波,永磁体表面将感生较大的涡流损耗。永磁电机转子散热条件有限,涡流损耗将成为永磁体实际工作温度的主要影响因素。导电材料的电导率与其工作温度相关,而涡流损耗又会影响导电材料的工作温度。因此,在建立永磁电机失磁空间分布特性研究模型时,需要考虑电磁场分析中永磁体等导电材料的电导率与其工作温度的影响机制,建立各材料电导率与其工作温度的数学关系。
本文在建立电磁场分析模型过程中,首先建立了绕组铜材料、永磁体材料电导率与其工作温度的数学模型[25],如式(1)和式(2)所示,通过电磁场和温度场的双向耦合计算方法实现了材料属性与其工作温度的动态关联。
 (1)
(1)
式中,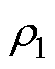 为钕铁硼永磁体的电阻率;T为永磁体的工作温度;y、x为变量,根据本文研究样机所应用的钕铁硼材料中镝含量的实测结果,x和y分别取值为1.258和0.884×10-3。
为钕铁硼永磁体的电阻率;T为永磁体的工作温度;y、x为变量,根据本文研究样机所应用的钕铁硼材料中镝含量的实测结果,x和y分别取值为1.258和0.884×10-3。
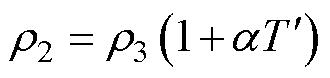 (2)
(2)
式中,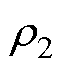 为绕组铜材料在工作温度
为绕组铜材料在工作温度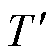 下的电阻率;
下的电阻率;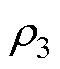 为0℃下铜的电阻率;
为0℃下铜的电阻率;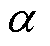 为铜的平均温度系数。
为铜的平均温度系数。
同时,利用式(3)和式(4)[26]建立钕铁硼永磁材料在不同工作温度下的磁特性与其工作温度之间的数学关系为
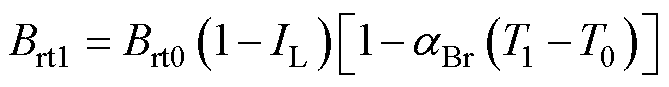 (3)
(3)
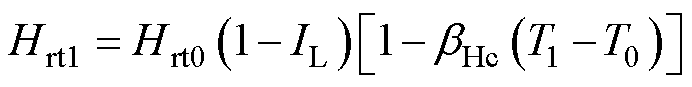 (4)
(4)
式中,Brt0、Brt1分别为参考工作温度T0和工作温度T1时磁体的剩磁;Hrt0、Hrt1分别为参考工作温度T0和工作温度T1时磁体的矫顽力;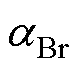 、
、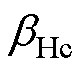 分别为磁体退磁曲线直线段的剩磁和矫顽力温度系数;IL为磁体的不可逆退磁率。
分别为磁体退磁曲线直线段的剩磁和矫顽力温度系数;IL为磁体的不可逆退磁率。
剩磁密度是表征永磁材料磁特性的基本参量,由其计算得到的退磁率可用来准确分析磁体的失磁特性。为准确描述永磁电机内部永磁体的失磁情况,引入磁体退磁率Dem,其计算公式[26]为
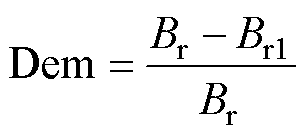 (5)
(5)
式中,Br为永磁体发生退磁前的剩磁密度;Br1为永磁体发生退磁后的剩磁密度。由钕铁硼永磁体的退磁曲线特性分析可知,磁体发生退磁后的新工作曲线直线段近似与初始退磁曲线直线段平行,由原始直线段斜率和退磁后的新工作点即可求得退磁后的永磁体剩磁密度。单元磁体的退磁率由其区域内的永磁体剩磁密度平均值计算得到。
通过各单元磁体退磁率可进一步计算得到每一块永磁体及电机整机的总退磁率。单元磁体退磁率可以用来表征电机永磁体局部位置的退磁严重程度;每一块永磁体及整机的总退磁率则可以用来分析电机反电动势、输出转矩等综合性能的变化。
综上所述,利用三维多物理场耦合方法开展永磁体失磁空间分布特性研究的工作原理及流程为:首先,建立包含永磁体空间位置信息、电阻率及磁特性与温度之间数学关系的三维电磁场、温度场模型。然后,利用电磁场计算初始给定温度下电机各部件损耗,将其传递到温度场计算模型。利用温度场求解电机各部件的工作温度,将其反馈到电磁场模型对应部件的变量中,同步判断永磁体的失磁状态并调整永磁体磁性能。如此迭代反复,直至温度场计算得到的零部件工作温度与电磁场计算损耗使用的温度满足误差控制要求。最后,在达到多场耦合计算稳态基础上,求解该温度分布联合退磁磁场作用下全域单元磁体的磁特性,据此判断单元永磁体的失磁状态并对应调整其不可逆退磁率等特征量,得到该工况下永磁电机的失磁状态,进而可对电机失磁状态下的工作特性、失磁影响因素等问题开展深入研究。利用永磁体虚拟分块建模方法开展电磁场与温度场的双向耦合计算分析时,由于每一个单元磁体均包含多个特性描述变量,大量的数据在两场之间的传递可通过基于Python语言的批处理方法实现,能够较好地满足研究中的计算速度要求。
为使本文的分析方法更具有普适性,本文选用一款电动汽车行业实际开发的主驱动电机产品为研究目标。样机的结构参数、材料选取均与实际电机产品一致。
表1 永磁电机样机参数
Tab.1 The parameters of PMSM prototype
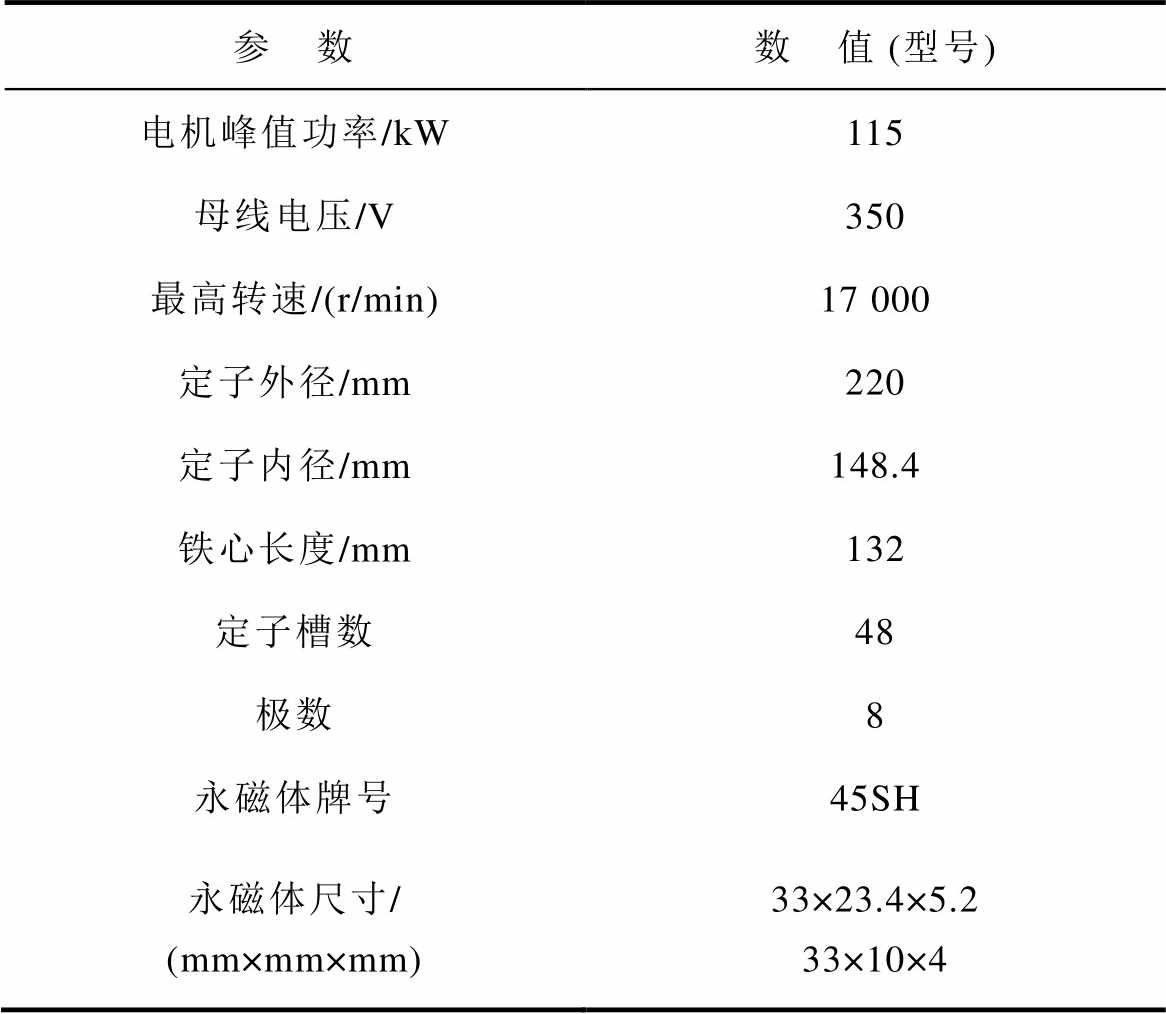
参 数数 值 (型号) 电机峰值功率/kW115 母线电压/V350 最高转速/(r/min)17 000 定子外径/mm220 定子内径/mm148.4 铁心长度/mm132 定子槽数48 极数8 永磁体牌号45SH 永磁体尺寸/ (mm×mm×mm)33×23.4×5.2 33×10×4
采用三维电磁场、温度场的双向耦合方法开展电机失磁问题研究。由于永磁电机在圆周方向上的结构完全相同,电磁场具有周期性分布规律。因此,在圆周方向上建立1/8电磁分析模型。永磁电机驱动端与非驱动端的空间和冷却条件均存在差异,在轴向上建立完整的电磁分析模型。永磁体采用分块的单元磁体模型进行建模。实际电磁场分析模型如图3所示。
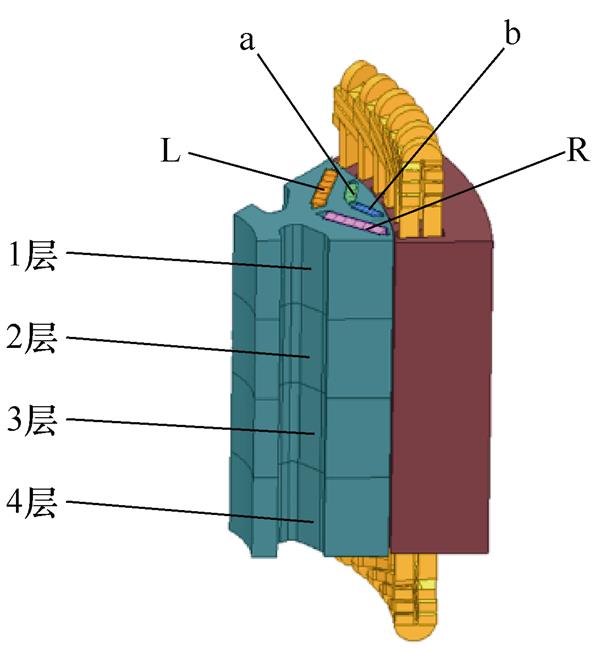
图3 电机电磁场分析模型
Fig.3 Motor electromagnetic field analysis model
如图3所示,为便于分析,定义双V型磁路结构中上层小V型磁体分别为a、b磁体,下层大V型磁体分别为L、R磁体。同时,根据电机的实际设计结构,转子铁心和每一极的各永磁体在轴向上均分为4段并利用虚拟分块法进行磁体建模。为便于详细分析永磁体空间失磁规律,命名近驱动端永磁体为1层磁体,向非驱动端逐渐增加至4层磁体。
考虑到样机永磁体实际体积与计算资源情况,本文中,上层a、b和下层L、R两类磁体的单元磁体尺寸(长×宽×厚)分别划分为5.5 mm×3.9 mm× 5.2 mm和5.5 mm×2 mm×4 mm,即每段磁体划分的单元磁体数量分别为36块和30块,每一极的单元磁体总数量为528个。
考虑到电机驱动端和非驱动端的结构无对称性,圆周方向上进出水口位置对电机冷却效果有一定的影响,建立完整的三维温度场分析模型。电机的温度场分析模型如图4所示。
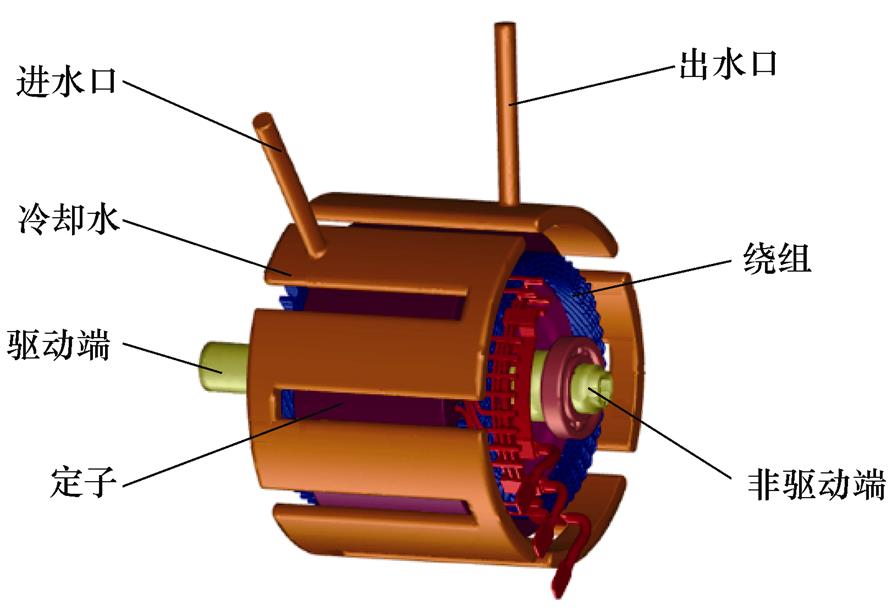
图4 电机温度场分析模型
Fig.4 Motor temperature field analysis model
永磁电机用高性能永磁体热稳态下的磁稳定性主要影响因素是其最高工作温度与作用在其上的退磁磁场强度[9]。已有学者利用二维有限元优化电机转子磁路结构以实现预防失磁的目的。本节着重分析双V型磁路结构下,退磁电流、永磁体工作温度对永磁电机局部失磁空间分布规律的影响机制。
根据永磁电机的电压、磁链等方程,采用功率不变约束的坐标变换,可以得到永磁电机电压、磁链和电磁转矩的表达式,进一步可以建立其空间矢量关系为
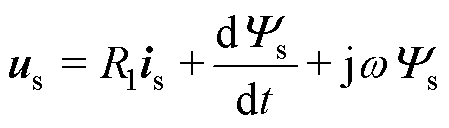 (6)
(6)

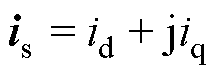 (7)
(7)
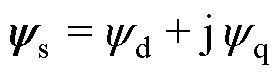 (8)
(8)

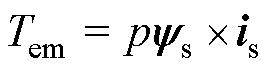 (9)
(9)
式中,R1为电机定子绕组相电阻;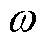 为电机定子电角频率;
为电机定子电角频率;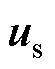 为dq坐标系下的电压;
为dq坐标系下的电压;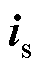 为电机电枢电流;id和iq分别为电机电枢电流的直轴和交轴分量;
为电机电枢电流;id和iq分别为电机电枢电流的直轴和交轴分量;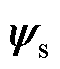 为电机电枢电流产生的磁链;
为电机电枢电流产生的磁链;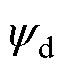 和
和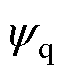 分别为磁链的直轴和交轴分量;p为电机极对数;
分别为磁链的直轴和交轴分量;p为电机极对数;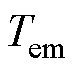 为电机的电磁转矩。
为电机的电磁转矩。
根据式(6)~式(9),建立永磁电机的空间矢量,如图5所示。
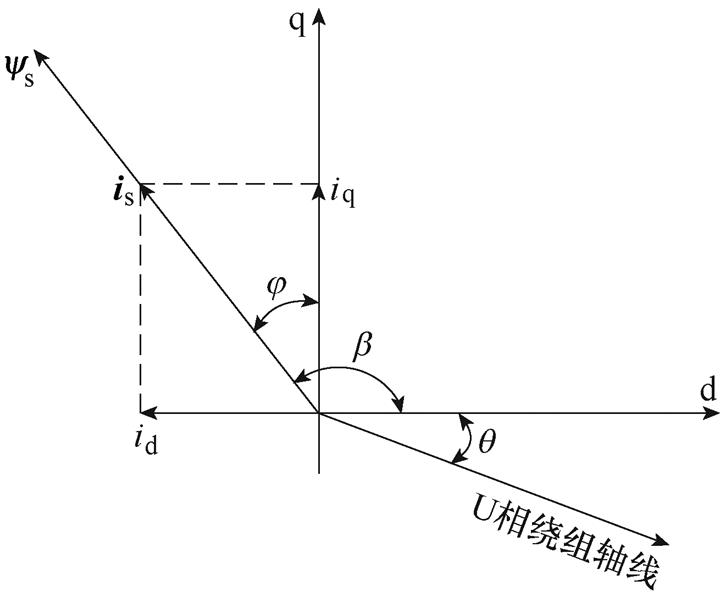
图5 永磁电机空间矢量
Fig.5 Space vector diagram of permanent magnet motor
图5中,is为电机电枢电流;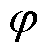 为电枢电流与交轴之间的夹角,即电流角;
为电枢电流与交轴之间的夹角,即电流角;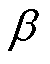 为电枢电流与直轴之间的夹角;id和iq分别为电机电枢电流的直轴和交轴分量;
为电枢电流与直轴之间的夹角;id和iq分别为电机电枢电流的直轴和交轴分量;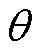 为电机U相绕组轴线与转子磁极直轴之间的夹角。
为电机U相绕组轴线与转子磁极直轴之间的夹角。
由永磁电机空间矢量的分析可知,当电机磁路结构确定后,电枢电流is的幅值及电流角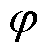 决定了实际作用到电机各永磁体磁化方向上的退磁电流分量大小。当退磁磁场使永磁体工作点超过拐点后,电机即发生失磁故障。
决定了实际作用到电机各永磁体磁化方向上的退磁电流分量大小。当退磁磁场使永磁体工作点超过拐点后,电机即发生失磁故障。
2.1.1 退磁电流幅值的影响
电机电枢电流决定了作用在永磁体上的退磁磁场强度。相同电流角下,电流幅值越大,退磁磁场强度越强,同样工作温度分布下,永磁体也就越容易产生不可逆失磁故障。因此,有必要分析不同退磁电流幅值对永磁体失磁空间分布规律的影响。
综合考虑永磁电机短路故障工况下的冲击电流大小与样机退磁实验台架中控制器最大电流输出能力。为能够体现不同退磁电流幅值下,磁体退磁率分布差异性,经过多轮模拟计算,最终选取600、800和900 A退磁电流在90°电流角的工况下进行研究分析。退磁计算过程中,考虑到永磁体温度分布对失磁的影响,不同电流幅值计算工况均使用了相同工况稳态下存在空间分布差异的永磁体工作温度数据,即模拟在电机永磁体达到稳态工作温度分布后,由于系统突发故障产生不同幅值的故障冲击电流对永磁体磁性能的影响。由于样机永磁体充磁方向厚度与单元磁体长度均较小,可认为每个单元永磁体内部的退磁率是均匀一致的,组合所有的单元磁体退磁率即可得到永磁体整体的退磁率分布。
不同电流幅值下的永磁体退磁率分布如图6~图9所示。图中,横轴为4层永磁体的轴向总长度,纵轴为永磁体宽度。
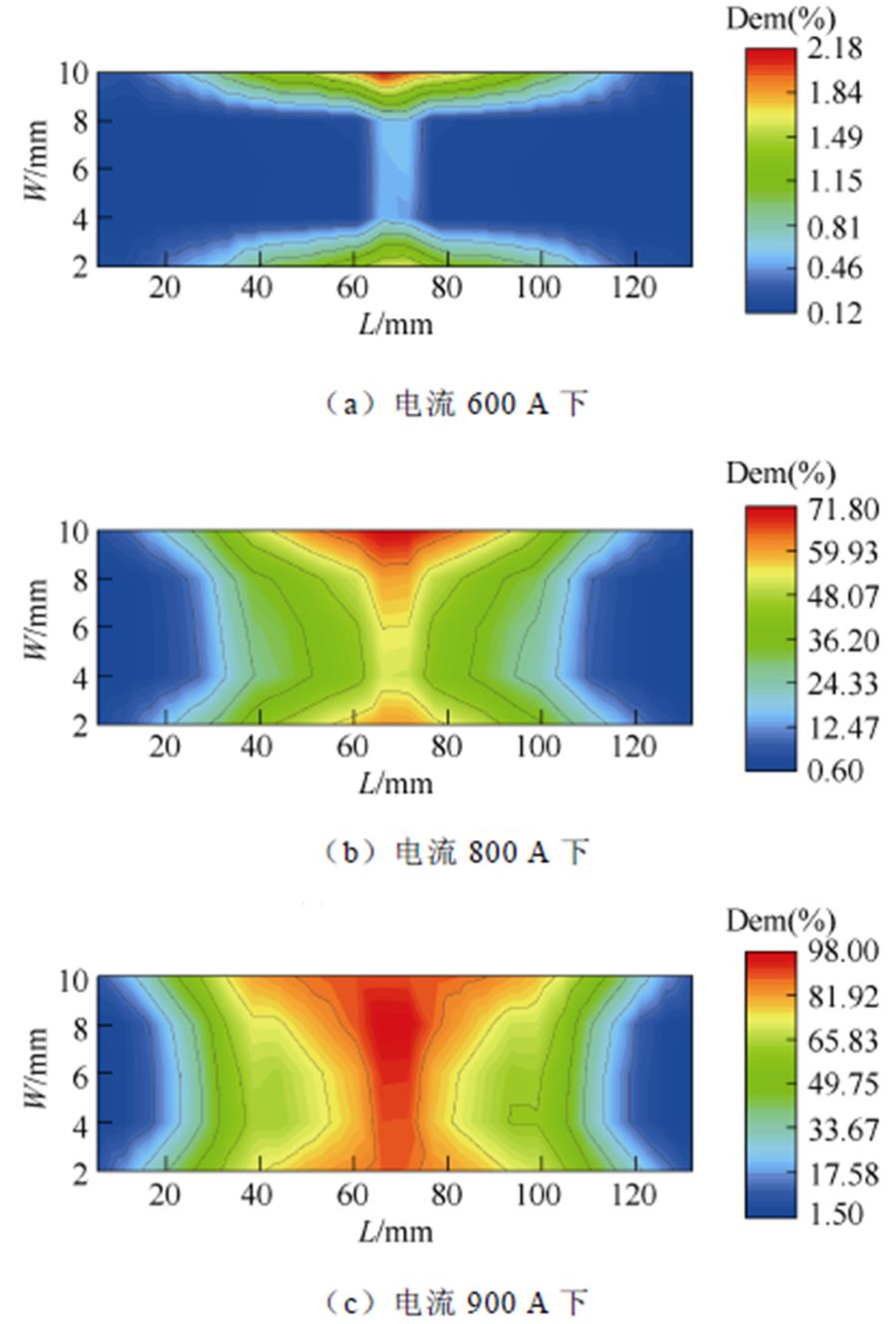
图6 磁体a不同电流下的退磁率分布
Fig.6 Demagnetization ratio distribution of magnet a at different current
不同电流幅值情况下,永磁体的总退磁率及各单元磁体的退磁率详细数据见表2和表3。
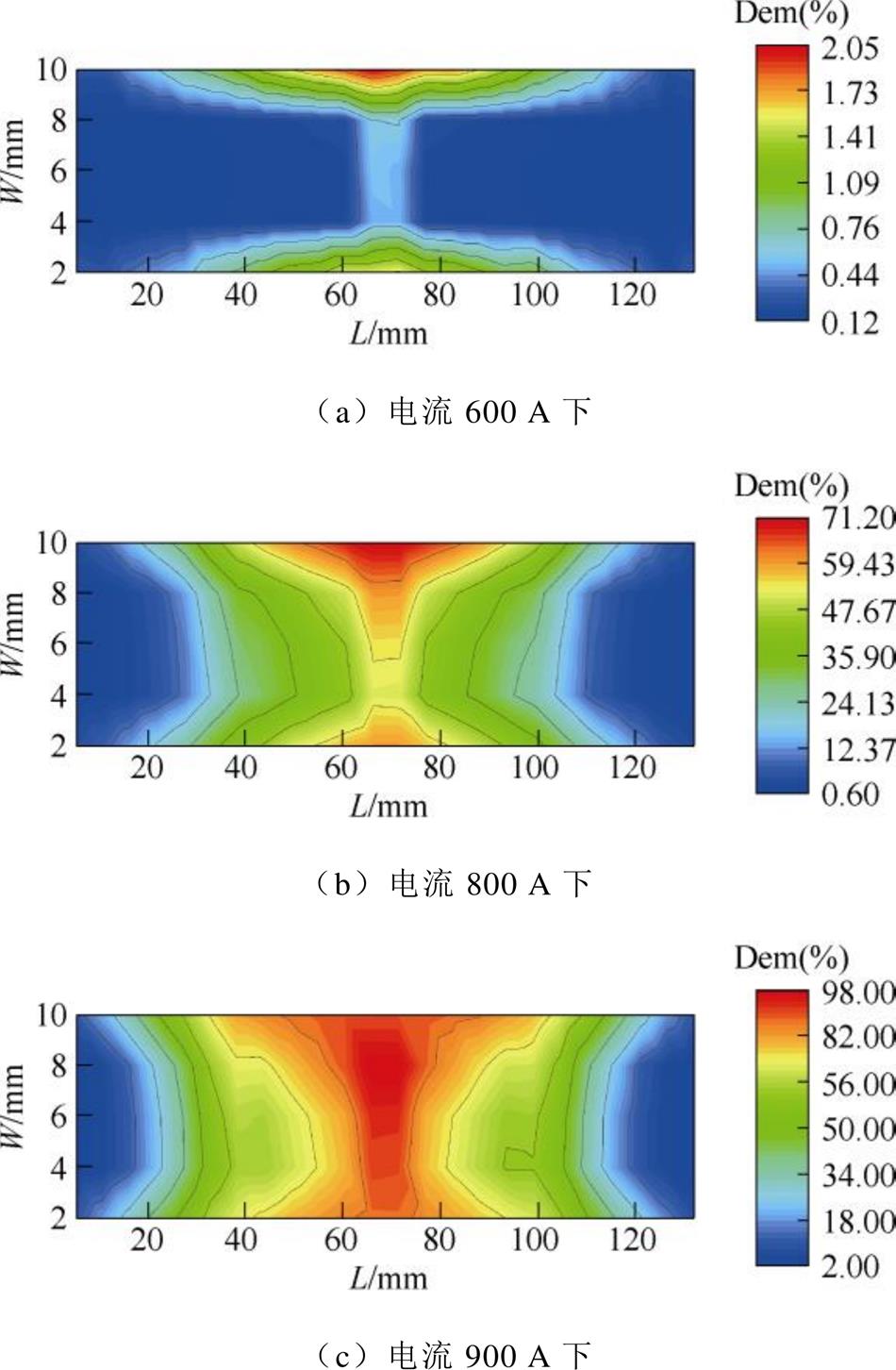
图7 磁体b不同电流下的退磁率分布
Fig.7 Demagnetization ratio distribution of magnet b at different current
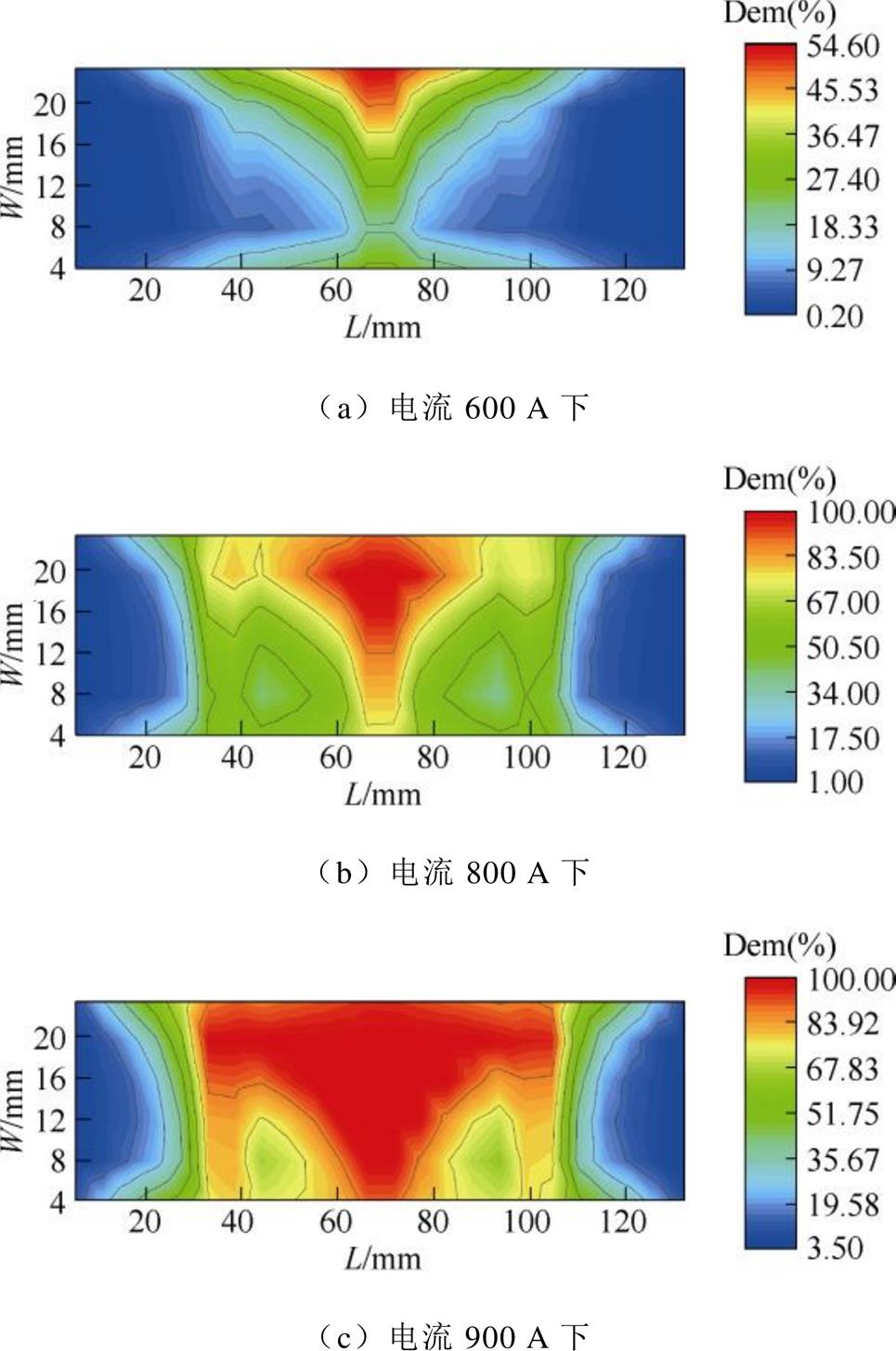
图8 磁体L不同电流下的退磁率分布
Fig.8 Demagnetization ratio distribution of magnet L at different current
由图6~图9及表2、表3可见,各永磁体的总退磁率在不同幅值电流作用下,存在明显的空间分布差异。
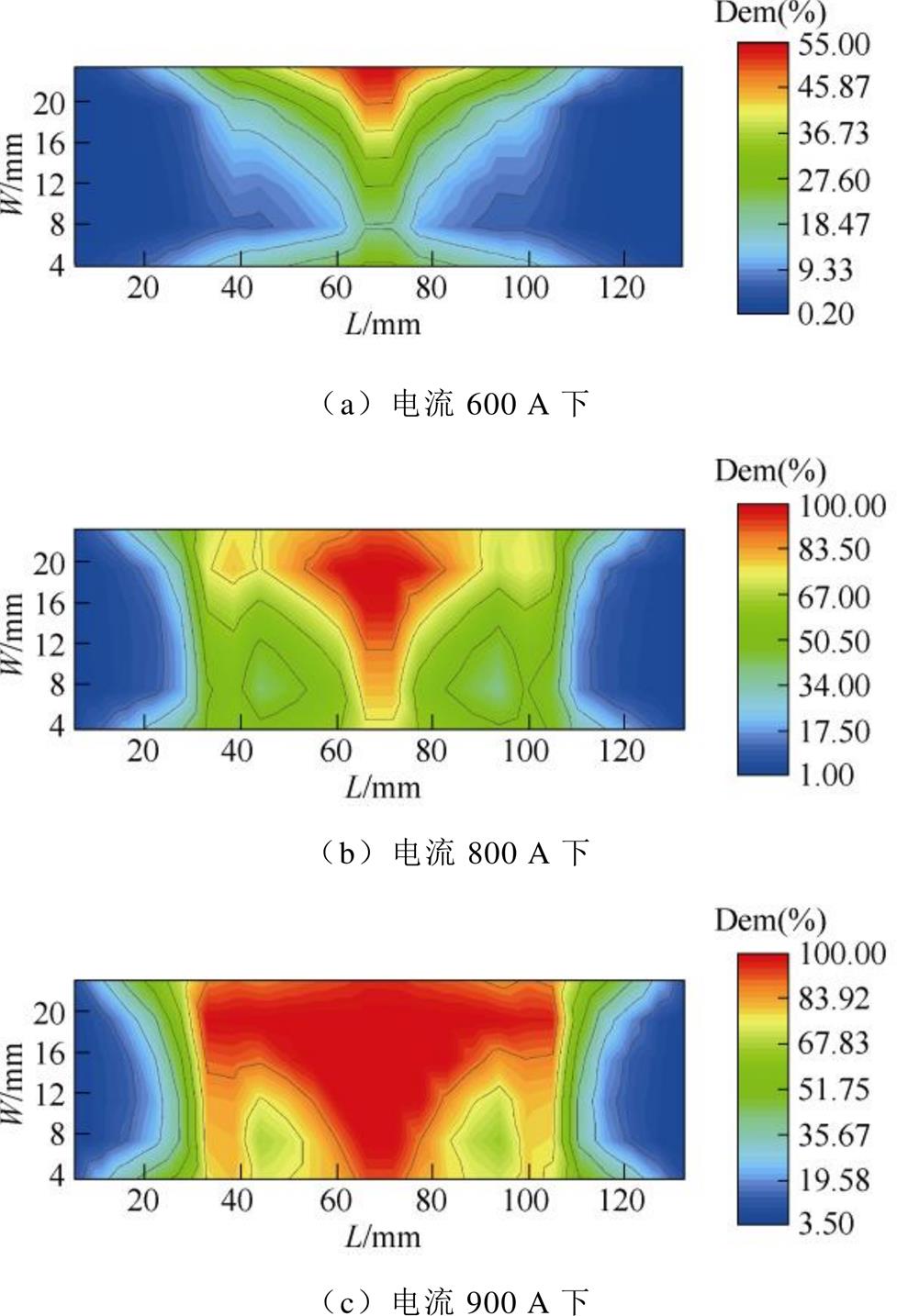
图9 磁体R不同电流下的退磁率分布
Fig.9 Demagnetization ratio distribution of magnet R at different current
表2 不同电流幅值下永磁体的退磁率
Tab.2 Demagnetization ratio of PM at different current amplitude

磁体退磁率(%) 600 A800 A900 A a0.4828.6353.64 b0.5028.8553.80 L13.4245.2561.94 R13.4445.3762.13
表3 不同电流幅值下单元磁体的最大退磁率
Tab.3 Demagnetization ratio of unit magnet at different current amplitude
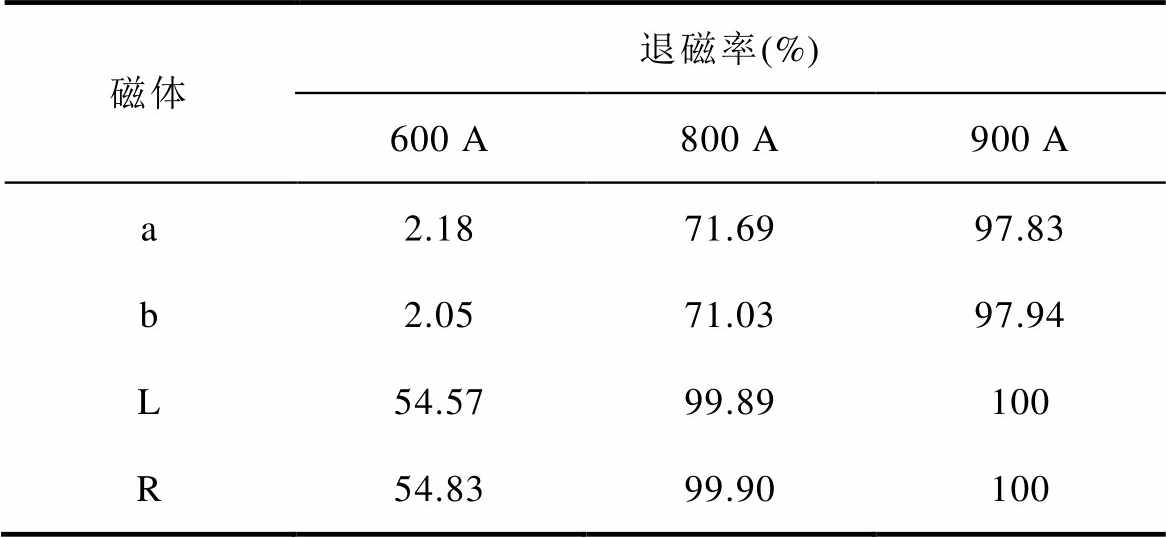
磁体退磁率(%) 600 A800 A900 A a2.1871.6997.83 b2.0571.0397.94 L54.5799.89100 R54.8399.90100
从永磁体总退磁率看,随着电流幅值的增加,各永磁体的整体失磁程度均逐步加剧。当电流幅值较小(600 A)时,磁体a和b基本不发生失磁,磁体L和R位于铁心中心段的高工作温度区域先产生轻微失磁。随着电流幅值增大(800 A、900 A),各磁体的失磁区域均呈现由铁心中心逐渐向两端部扩散的趋势。其中,上层磁体退磁率小于下层磁体的主要原因一方面是上层磁体体积小、损耗较低;另一方面是上层磁体空间位置更靠近气隙,散热条件较好。
从单元永磁体最大退磁率同样可以发现,随着电流幅值的增加,永磁体局部位置的失磁程度逐渐加剧,但磁体a和b的退磁率仍然低于L和R磁体。从800 A开始,L和R磁体的单元磁体退磁率接近100%,即永磁体的部分区域已经完全失磁。由上述分析可知,电机局部位置的失磁严重程度与总体失磁状态并不完全一致。高工作温度的铁心中心区域永磁体的边缘位置最先开始发生局部失磁现象。随着电流幅值的增加,失磁逐渐沿着温度梯度发生 扩散。
2.1.2 退磁电流角度的影响
为研究退磁电流角度对永磁体失磁空间分布的影响,开展在相同退磁电流幅值和永磁体空间温度分布下,不同电流角度的退磁率计算分析。计算过程中,使用的永磁体工作温度空间分布与2.1.1节相同,均为稳态工况下存在空间分布差异的永磁体工作温度数据。结合2.1.1节计算结果,选取退磁电流幅值为800 A工况,分别计算电流角为0°、30°、60°和90°时,永磁体退磁率的空间分布规律。
各永磁体在不同退磁电流角度下的退磁率分布如图10~图13所示。
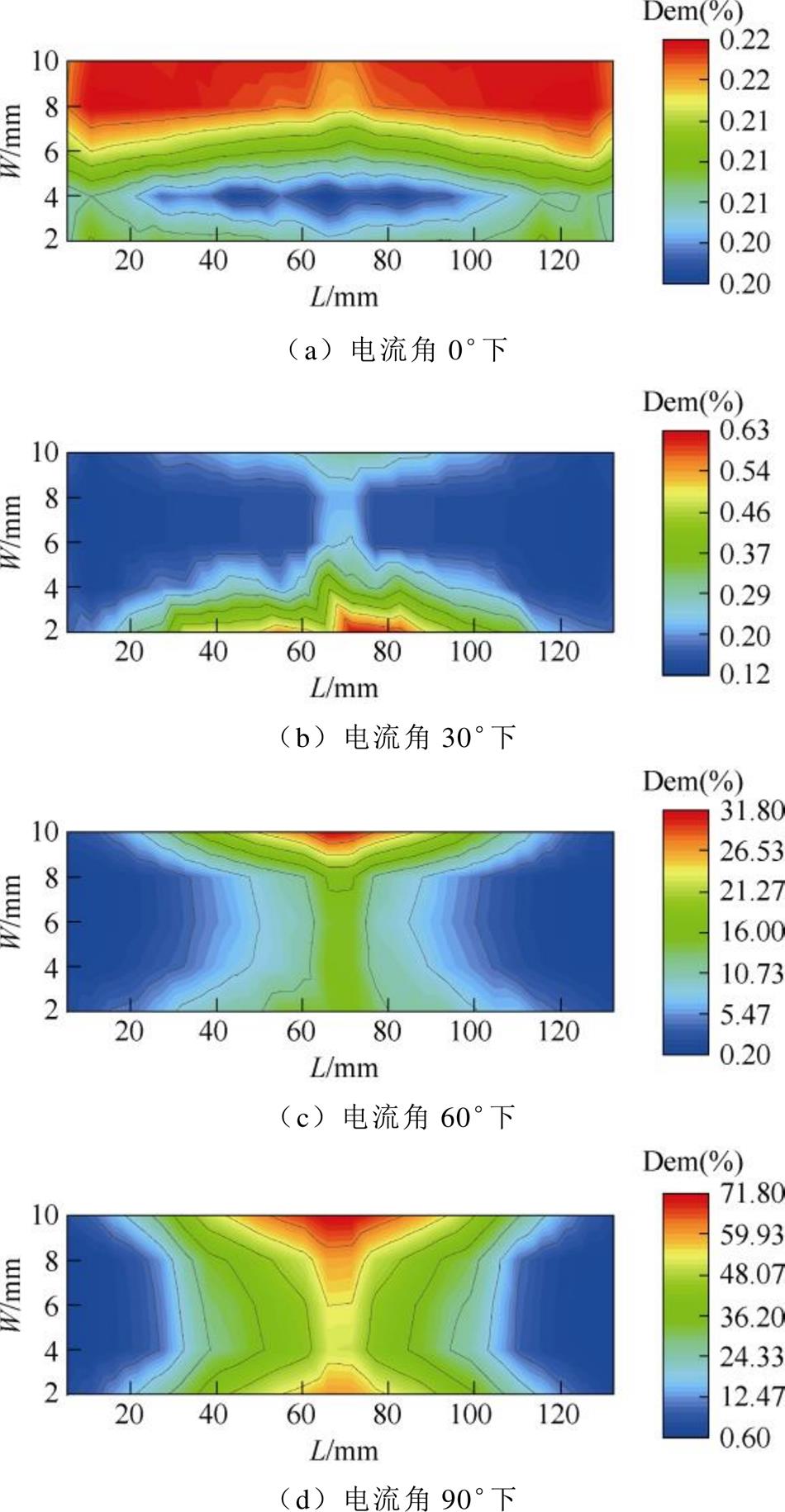
图10 磁体a不同电流角下的退磁率分布
Fig.10 Demagnetization ratio distribution of magnet a at different current angles
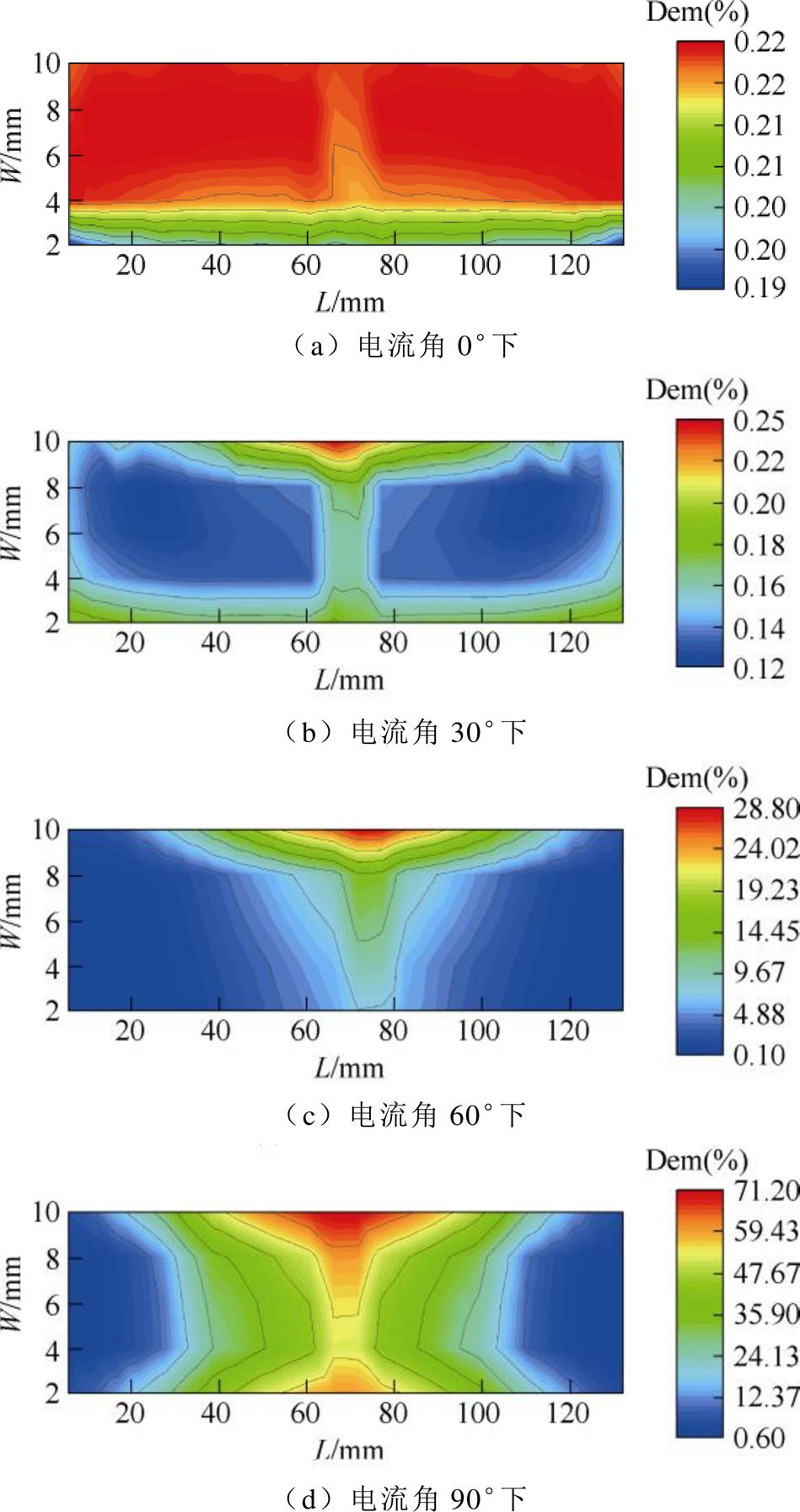
图11 磁体b不同电流角下的退磁率分布
Fig.11 Demagnetization ratio distribution of magnet b at different current angles
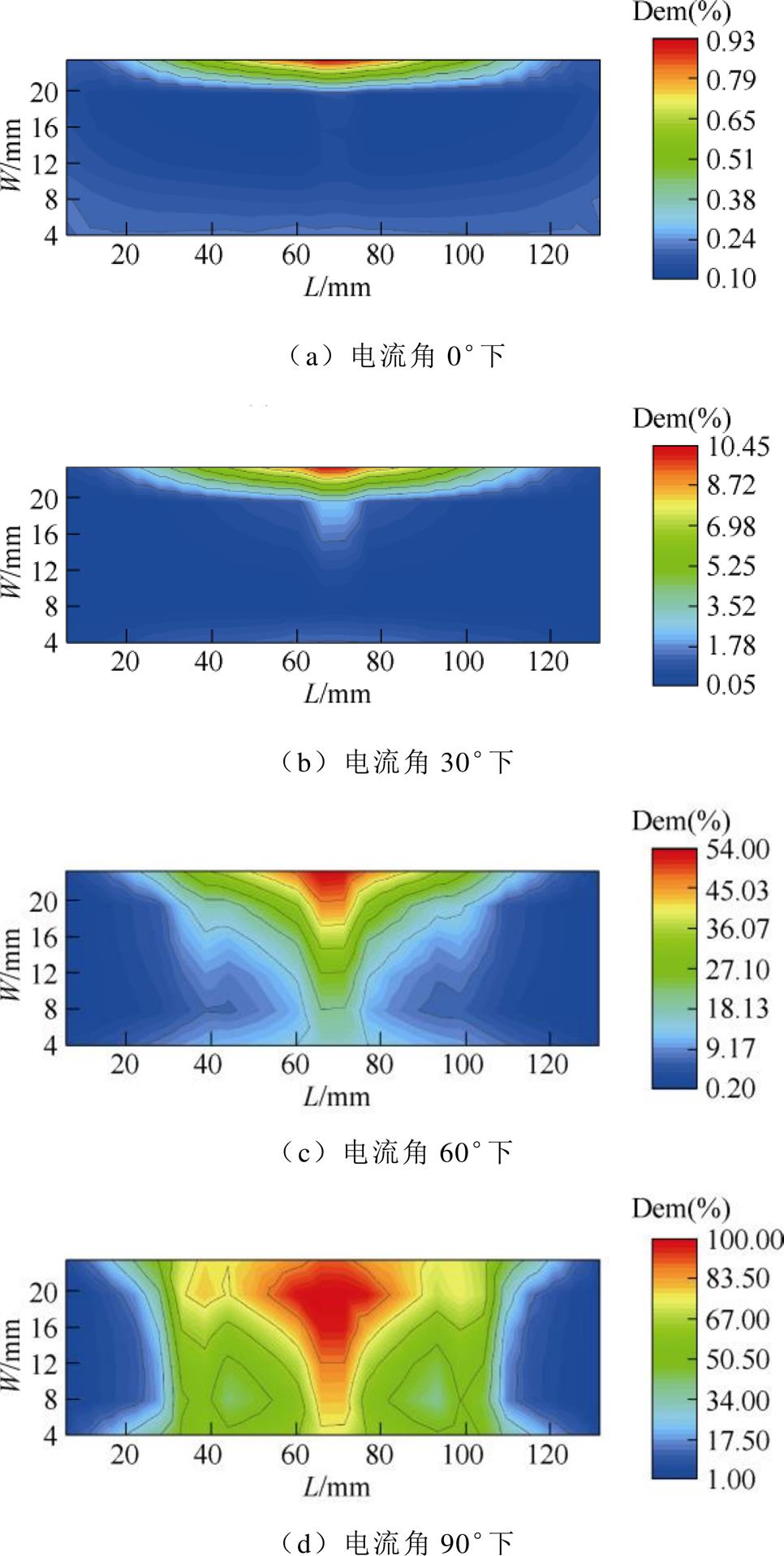
图12 磁体L不同电流角下的退磁率分布
Fig.12 Demagnetization ratio distribution of magnet L at different current angles
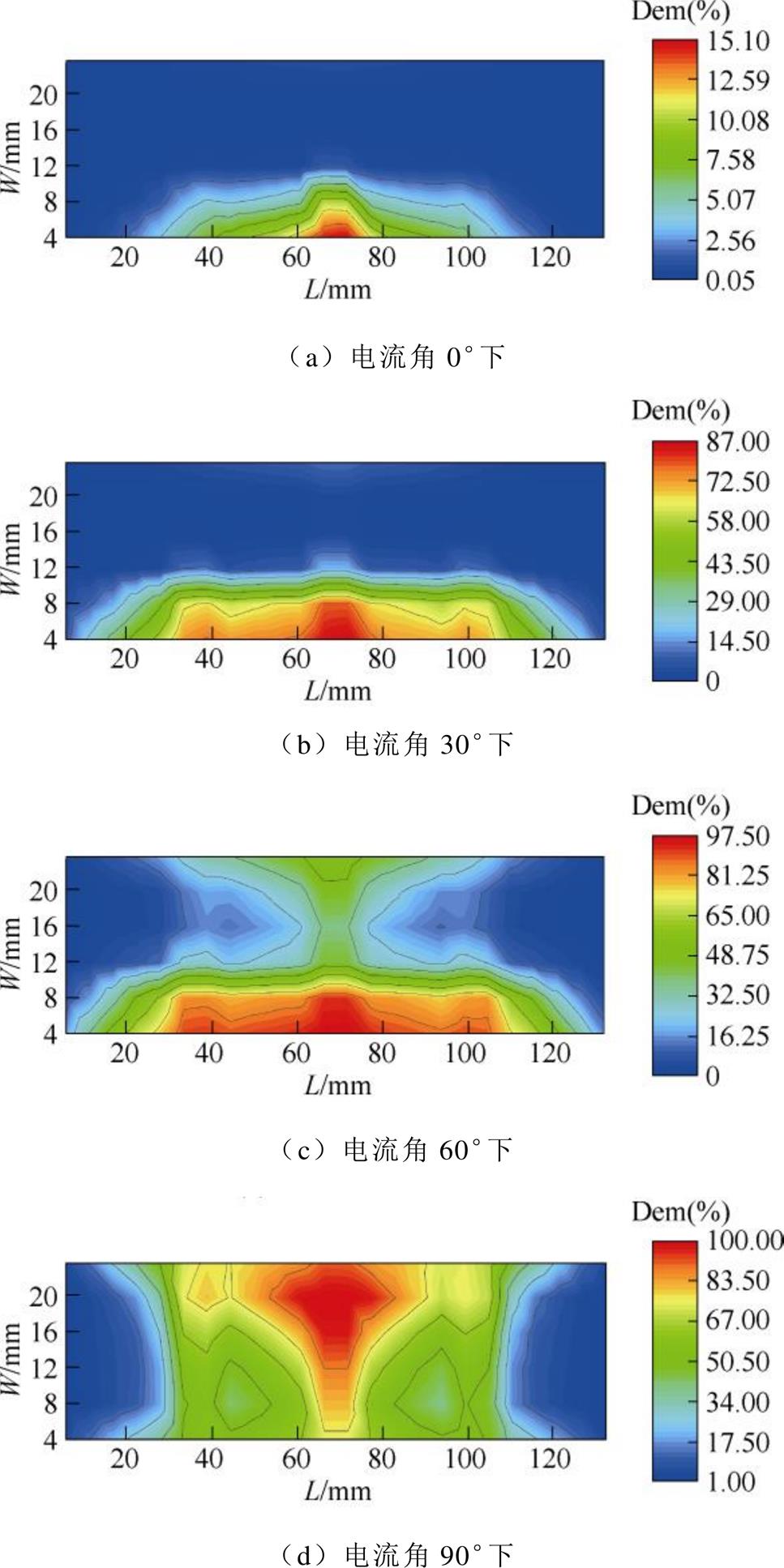
图13 磁体R不同电流角下的退磁率分布
Fig.13 Demagnetization ratio distribution of magnet R at different current angles
表4 不同电流角下永磁体的退磁率
Tab.4 Demagnetization ratio of PM at different current angles

磁体退磁率(%) 0°30°60°90° a0.210.238.0728.63 b0.220.155.4428.85 L0.211.2112.5345.25 R1.7019.4934.7945.37
表5 不同电流角下单元磁体的最大退磁率
Tab.5 Demagnetization ratio of unit magnet at different current angles
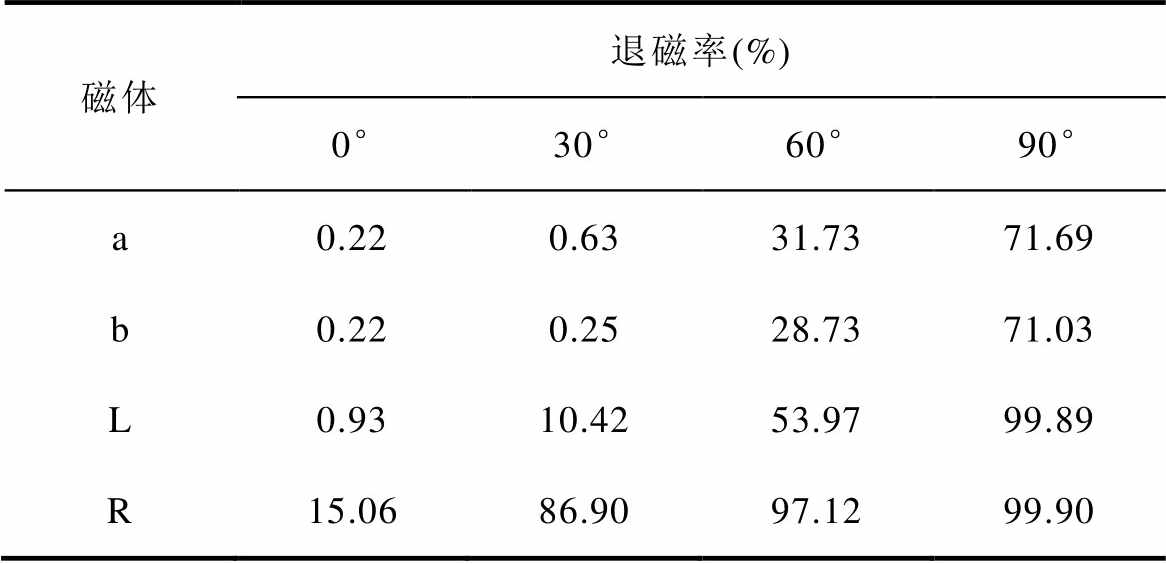
磁体退磁率(%) 0°30°60°90° a0.220.6331.7371.69 b0.220.2528.7371.03 L0.9310.4253.9799.89 R15.0686.9097.1299.90
由图10~图13及表4、表5可见,各永磁体的退磁率在不同电流角度下存在明显的空间分布 差异。
从永磁体总退磁率看,随着电流角度的增加,各永磁体的整体退磁程度均逐步加剧。0°电流角下,各磁体基本不存在退磁。30°~60°电流角下,各磁体逐渐产生退磁,随着角度的增加而呈现退磁加剧趋势。90°电流角下,退磁最为严重。除90°以外的各电流角下,永磁体退磁率均存在不对称性,磁体R的退磁情况最为严重。该现象是由退磁电流与转子磁极中心线的偏移使其在磁体R和L上的退磁分量不同导致。90°电流角时,退磁电流直接施加在直轴,每个磁极中左右永磁体的退磁电流分量一致。同时,圆周方向上,各磁极永磁体的冷却条件均相同,每个磁极左右磁体温度分布一致。因此,90°退磁电流产生的退磁现象呈现对称分布规律。
从单元永磁体最大退磁率看,同样退磁电流角下,磁体L和R的退磁严重程度强于磁体a和b。位于铁心中心段的永磁体高工作温度局部区域先产生退磁,随着电流角度的增加逐渐加剧并向两端部区域扩散。0°电流角时,磁体a和b均基本不发生退磁,但R磁体单元磁体的最大退磁率达到15%,即在该磁体中心段局部位置已出现轻微退磁。30°电流角时,R磁体单元磁体退磁率达到87%,而其总体退磁率仅为约20%,即磁体总体退磁不明显,但其局部位置已发生非常严重的退磁。60°~90°电流角时,各磁体退磁逐渐加剧。电流角90°时退磁最为严重,磁体L和R的退磁率最高值均接近100%,虽然此时永磁体总体只有45%的失磁,但其部分区域已经发生完全退磁。
可见,永磁体局部位置的失磁严重程度与其总的失磁状态并不完全一致。永磁体总失磁不严重的情况下可能存在局部位置的严重失磁现象。
电机轴向上驱动端与非驱动端结构及双V型磁路结构中永磁体空间位置差异均会导致磁体工作温度、工作点的空间分布差异。同样的退磁电流作用下,不同空间位置永磁体的退磁特性会存在区别。因此,根据1.2节所述永磁体局部失磁的空间分布特性分析方法,在电机电磁场和温度场的双向耦合计算分析基础上,研究工作温度对电机失磁空间分布特性的影响规律。
以实测电流为输入,通过电机三维电磁场分析模型计算电机各部件的损耗分布;由电机损耗分布结果计算得到损耗密度代入温度场分析模型;由温度场计算结果进一步计算永磁体、绕组等部件的电导率;由计算得到的电导率重新计算永磁体等部件的损耗分布,以此反复进行多次循环迭代,直至各部件电导率计算温度与温度场计算得到的各部件温度的误差满足分析需求为止。本文的误差控制为5%,即温度场计算得到的物体温度与其电导率计算温度之间的偏差小于5%。电机磁体温度分布如图14所示。
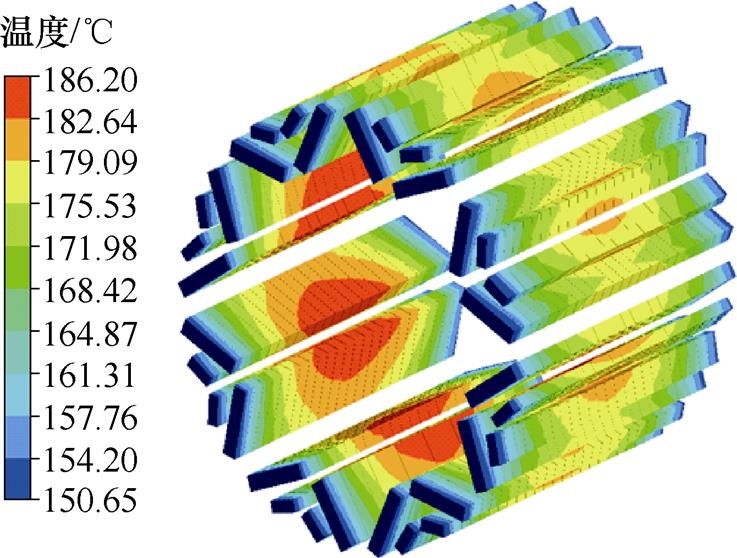
图14 电机磁体温度分布
Fig.14 Temperature distribution of motor magnet
由图14可知,永磁体空间温度分布差异明显,存在约36℃的温差,总体呈现铁心中心位置温度高,端部位置温度低的分布规律。永磁体a和b的温度范围为179.12~149.93℃,略低于L和R的温度范围186.20~150.65℃。该现象产生的原因一方面是a和b体积小,所产生的损耗相应较少;另一方面是a和b的空间位置接近气隙,便于散热。
在该工作温度分布规律下,施加相同的退磁磁场,可分析不同工作温度对永磁体失磁空间分布规律的影响。以800 A产生的退磁磁场为例,分析图6b~图9b可知,永磁体的失磁空间分布规律总体上与其温度分布规律一致,即铁心中心区域的高温位置最先发生失磁现象。随着温度的降低,局部失磁逐渐减弱。从一极磁体的失磁规律看,铁心中心区域永磁体靠近转轴方向的位置失磁最为严重,该现象也与此区域散热困难有关。由上述分析可见,永磁体局部失磁的空间分布规律与其工作温度的分布规律存在明显关联性。
在分析永磁电机失磁空间分布特性影响因素的基础上,采用三维有限元法计算了电机的电磁场,研究永磁电机失磁故障下电机磁场分布、性能等特征量的演变规律。
电机空间磁场分布特性主要受电机磁路结构、定子电流产生的电枢磁场和转子永磁体产生的励磁磁场影响。在电枢磁场不变的情况下,空间磁场的分布状态可反映永磁体局部失磁特性对电机的影响。
选取电机铁心的中心位置、铁心近驱动端位置、铁心近非驱动端位置,计算退磁电流为800 A的失磁工况的电磁场,三个位置的定转子铁心磁通密度分布如图15所示。
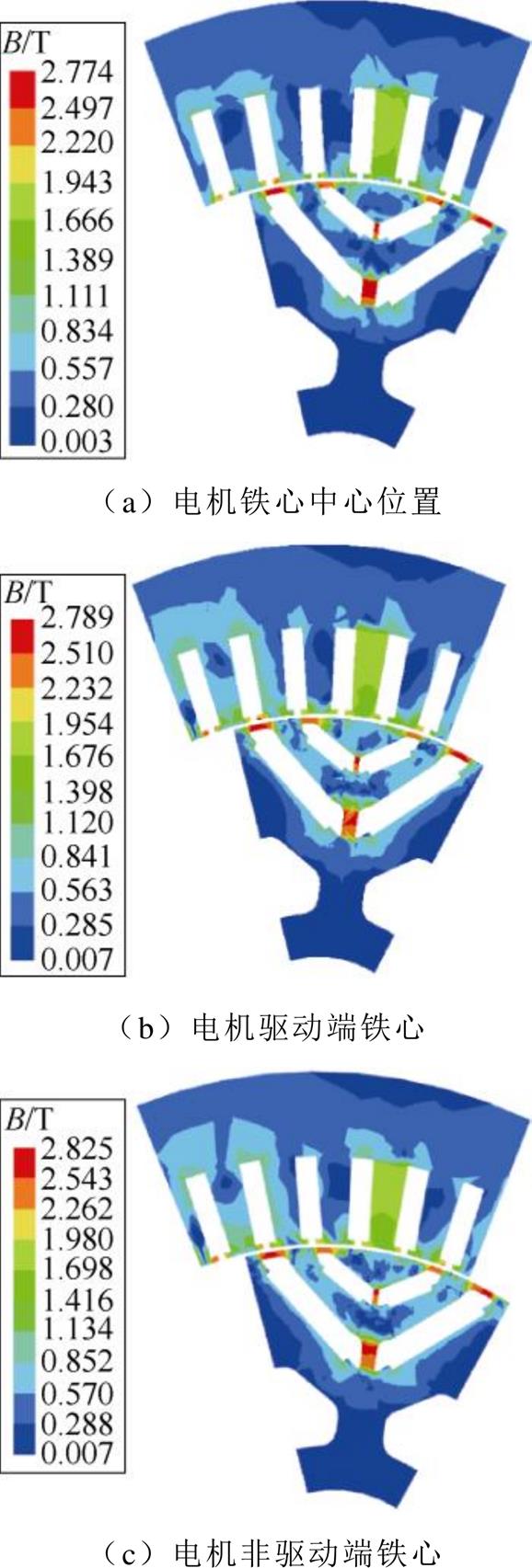
图15 铁心不同位置的磁通密度分布
Fig.15 Distribution of magnetic density at different positions of core
由图15可见,同一时刻下,电机轴向不同位置的定转子铁心磁通密度分布存在一定的差异。由于隔磁桥处磁路的饱和程度高,其附近的磁通密度分布差异更为明显,永磁体在该部位的工作点也将随之改变。其中,下层永磁体L和R之间隔磁桥周围的磁通密度最高。该部位远离气隙,散热条件不良,使之成为易发生退磁故障的重点区域。
空载状态下,电机转子旋转产生的感应电动势完全由永磁体产生。当永磁电机发生失磁故障后,励磁磁场发生的畸变将反映在空载反电动势的特性中。因此,有必要针对电机失磁故障对空载反电动势的影响规律开展深入研究。
以3 000 r/min、20℃工况为例,计算并分析永磁电机发生局部失磁故障前后的空载反电动势波形,以此研究局部失磁故障对电机空载性能的影响。
应用本文建立的电机失磁分析模型,计算得到电机发生失磁故障前后的空载反电动势波形如图16所示。
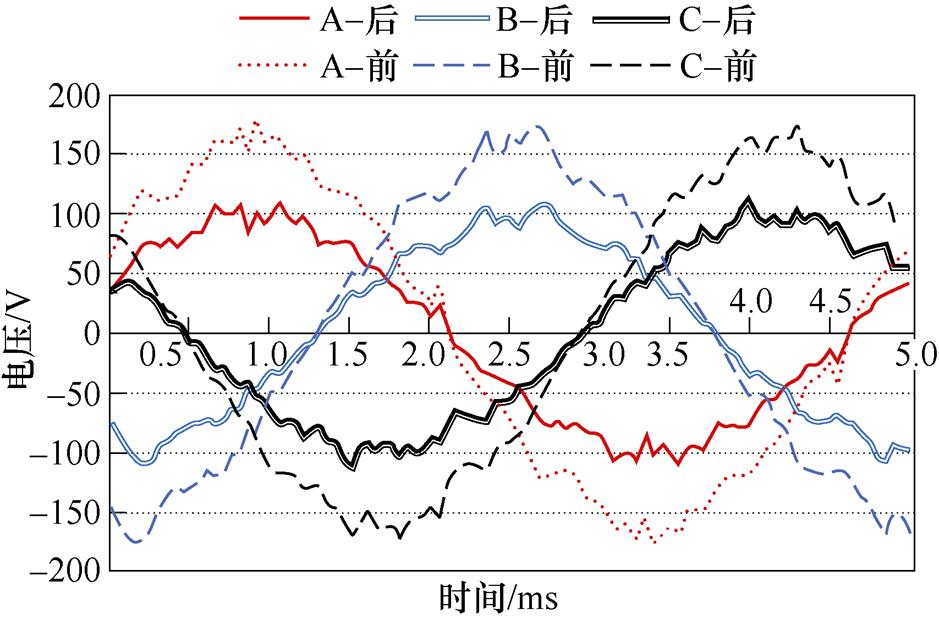
图16 电机失磁前后的空载反电动势波形
Fig.16 Electromotive force waveforms before and after demagnetization
图16中,虚线为失磁前的反电动势波形,实线为失磁后的反电动势波形。分析可见,发生局部失磁前后,电机空载反电动势发生明显的变化。发生退磁故障后,电机空载反电动势幅值明显减小,其最大值由失磁前的175.2 V下降到失磁后的110.16 V,下降比例达到37.1%,即由空载反电动势分析,电机在该工况下发生了37.1%的退磁。
进一步分析失磁故障对电机负载工况下的工作特性的影响。电机输出转矩由电枢磁场和励磁磁场共同作用产生,电枢电流不变情况下,永磁体发生局部失磁将对电机输出转矩产生直接影响。因此,详细分析失磁故障发生前后电机的转矩输出特性变化规律,是局部失磁故障在线检测与预防的基础。
以3 000 r/min,电流有效值为231 A工况为例,电机发生局部失磁故障前后的输出转矩特性如图17所示。
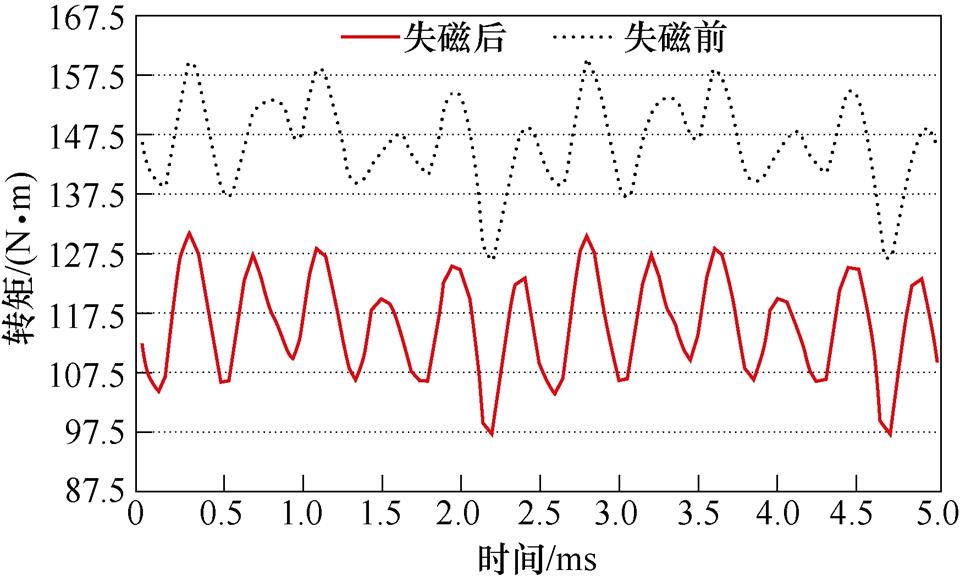
图17 电机失磁前后的转矩波形
Fig.17 Torque waveforms before and after demagnetization
图17中,虚线为失磁前的转矩波形,实线为失磁后的转矩波形。分析可见,局部失磁发生后,电机负载转矩明显减小,转矩平均值由失磁前的146.15 N·m下降到失磁后的115.6 N·m,下降比例达到20.9%,转矩波动由失磁前的11.9%上升到失磁后的14.8%。
为验证本文提出的电机失磁分析方法的准确性,根据表1的电机性能指标制造一台测试样机。对该样机开展包括转子空间温度分布实验、退磁实验、性能实验在内的详细测试。在完成全部实验后,对电机进行拆解,实现转子表磁磁场特性的详细测试。
为实现对电机实际退磁故障的模拟,样机的制造过程中,在其转子不同空间位置的永磁体上布置了多个热电偶测温元件。转子铁心安装测温元件位置需要预先加工出槽位,测温元件的一端安装入槽位并与永磁体测点位置通过胶水固定;另一端经过电机空心转轴与电机转子测温设备连接。该测温设备采用锂电池供电,固定在电机转子端部,随转子同步旋转,可实时记录永磁体各测点的温度数据。
实验台架采用两台同规格电机进行对拖实验。样机为外水套冷却结构,冷却水与仿真分析的输入条件相同,均为8 L/min。电机转子无其他冷却条件。实验台架示意图如图18所示。

图18 实验台架
Fig.18 Test bench
首先开展电机的温度摸底实验。选取图3中的R磁体为测温目标。每个磁体设定上中下3个测点,其中,上部测点为靠近气隙端的永磁体边缘位置,中部测点为磁体几何中心位置,下部测点为靠近转轴的磁体边缘位置。在电机转子非驱动端的转轴端部安装在线测温装置,该装置可每间隔3 s实现一次所有测点的温度记录,并将该数据实时存储到设备存储器中。使用K型热电偶作为测温元件。实验开始时即开启测温设备,该设备可记录电机温升实验全过程的温度变化。实验后提取电机温升稳定状态下的永磁体工作温度即可。测点布置方式及测温元件安装位置如图19所示。
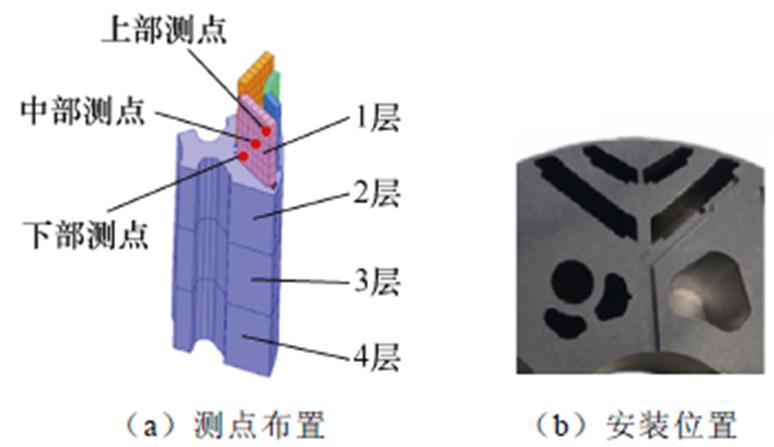
图19 温度测点位置示意图
Fig.19 Temperature test point position schematic
电机热稳态时永磁体的温度分布见表6。
表6 磁体温度测试数据
Tab.6 Magnet temperature test data (单位: ℃)
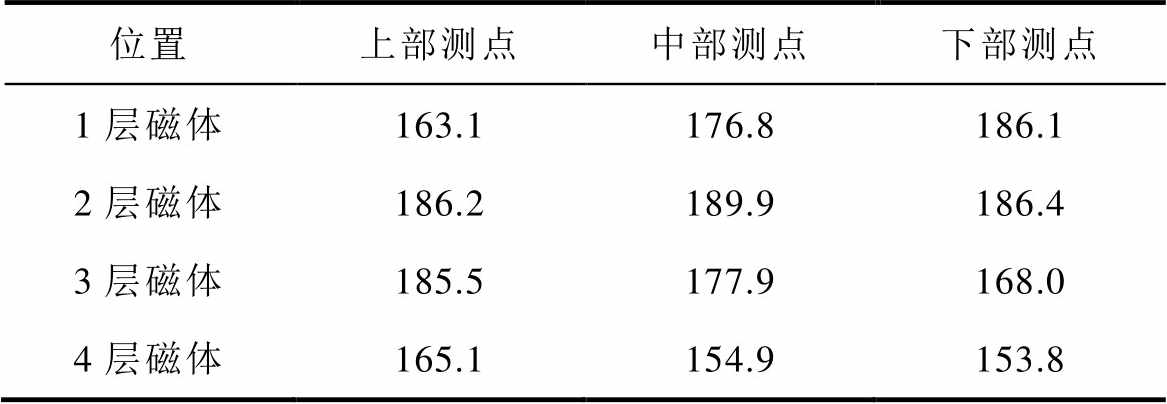
位置上部测点中部测点下部测点 1层磁体163.1176.8186.1 2层磁体186.2189.9186.4 3层磁体185.5177.9168.0 4层磁体165.1154.9153.8
表6中,磁体的位置与图3中所述仿真模型中的磁体位置一致,近驱动端永磁体为1层磁体,向非驱动端逐渐增加至4层磁体。
永磁体温度计算值与实测值对比如图20所示。
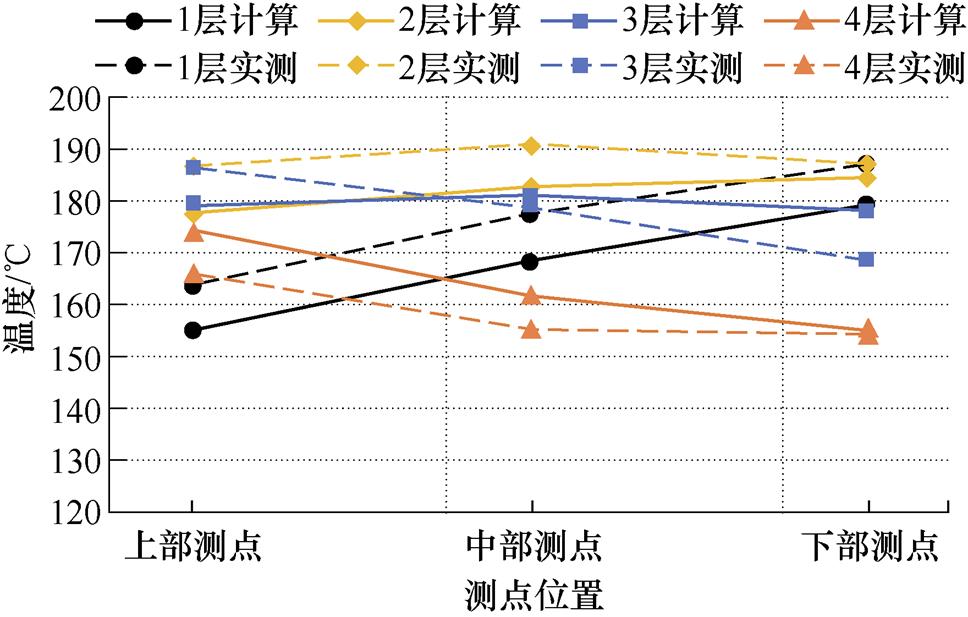
图20 计算与测试数据对比
Fig.20 Comparison of calculation and test data
由图20可见,永磁体实测温度中,同一块永磁体不同位置的工作温度差异达到23℃;同一极永磁体中每一块永磁体相同位置的温度差异达到35℃。永磁体的仿真与实测温度的偏差为5.4%(9.57℃),满足局部失磁问题研究和工程使用需求。温度偏差的产生与测点的仿真与实测位置差异、永磁体不同温度下磁性能估算准确度等原因有关。
为分析永磁体失磁前后的磁特性变化规律,采用表磁测试设备记录电机各段铁心退磁实验前后的表磁数据。在电机转子的4段铁心中各取5个圆周进行测试,5条测试线在每段铁心上均匀分布,测点位置如图21所示。
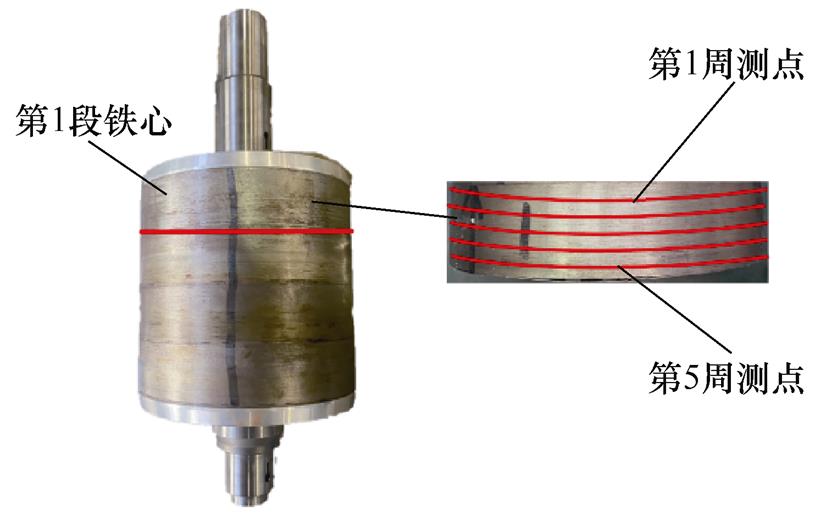
图21 表磁测试位置示意
Fig.21 Surface magnetic test position schematic
每个圆周测点数量为36 000点,取其平均值进行对比分析。具体实验数据见表7、表8。
表7 退磁前铁心表磁测试数据
Tab.7 Core surface magnetic test data before demagnetization(单位: mWb)

位置1段铁心2段铁心3段铁心4段铁心 1周测点228.91228.16228.57237.44 2周测点214.31213.50214.70219.59 3周测点212.02211.44211.31215.97 4周测点214.39212.23213.04218.92 5周测点228.91228.16228.57233.52
表8 退磁后铁心表磁测试数据
Tab.8 Core surface magnetic test data after demagnetization(单位: mWb)

位置1段铁心2段铁心3段铁心4段铁心 1周测点185.9869.28166.73231.44 2周测点175.6864.46152.55215.70 3周测点180.1262.31142.72213.11 4周测点184.0060.97141.00215.95 5周测点196.8262.55147.67231.44
由表7和表8可见,电机发生退磁故障前,不同段铁心的表磁分布规律基本是一致的。退磁故障后,各段铁心的表磁出现明显的差异,第2段铁心表磁大幅度下降,而第4段铁心表磁基本未改变。该现象与仿真结果一致,由于永磁体空间温度分布差异,相同退磁电流作用下,高工作温度区域的磁体先发生了明显的退磁现象。可见,电机局部退磁在空间分布上并非完全一致的。
由表6~表8分析可知,不同永磁体轴向同一位置和同一永磁体不同位置均存在失磁差异性。在电动汽车用永磁电机的大电流运行工况中,铁心中心段等高工作温度区域的失磁明显严重。因此,一方面,在已设计定型的永磁电机运行过程中,可考虑改善电机高发热工况的散热条件,如调节特定工况冷却水流量与温度;另一方面,在永磁电机设计过程中,重点考虑改善永磁体空间温度不均匀性,降低铁心中心段永磁体的工作温度,或考虑提升特定区域永磁体的抗退磁能力,实现永磁电机的失磁预防。
为研究失磁故障对电机性能的影响并验证本文提出的分析方法的准确性,分别测试失磁前后3 000 r/min、20℃工况下的空载反电动势波形和3 000 r/min、231 A、35.4°电流角工况热稳态下的输出转矩。电机退磁实验中实际施加的退磁电流值约为796 A,电流角为90°,即退磁场完全施加到电机直轴。实验数据见表9。
表9 退磁前后空载反电动势比较
Tab.9 Comparison of electromotive force before and after demagnetization(单位: V)

空载反电动势 实测值仿真值 退磁前167.8175.20 退磁后115.8110.16 退磁率(%)31.037.1
由表9可知,退磁实验前,空载反电动势的仿真与实测偏差为4.97%;退磁实验后,二者的偏差为4.87%。由空载反电动势求取的电机退磁率,仿真与实测的偏差为6.1%。均满足局部退磁分析需要。退磁前后输出转矩见表10。
表10 退磁前后输出转矩
Tab.10 Torque before and after demagnetization(单位: N·m)

输出转矩 实测值仿真值 退磁前140146.15 退磁后122115.6
由表10可见,退磁实验前,输出转矩的仿真和实测偏差为3.46%;退磁实验后,二者的偏差为5.25%。退磁实验前后,电机输出转矩下降比例的差异为1.57%,满足局部退磁分析需要。
由以上分析可见,空载反电动势和输出转矩可有效地表征退磁故障对电机整机工作特性的影响。在永磁电机的运行过程中,可分别记录初始工作状态和运行状态下的空载反电动势与输出转矩数值特征量,对比分析各状态下两种数据特征的变化即可实现永磁体失磁故障的监测与预防。
综上所述,通过实验结论可证明本文提出的分析方法有效,其分析准确性可以满足研究需要。
本文针对外水套冷却的电动汽车用内置式磁路结构永磁电机局部失磁问题,通过建立永磁体的虚拟单元磁体分析模型,结合三维电磁场与温度场的双向耦合分析方法,研究了永磁体温度分布、退磁电流幅值及电流角等因素对局部失磁空间分布特性的影响。在此基础上,研究了局部失磁故障与电机空载反电动势、输出转矩等特性的关系。通过样机的测试验证了分析方法和研究结论的正确性。具体研究结论如下:
1)电动汽车用永磁电机的失磁故障在空间分布上存在明显的不均匀性。失磁空间分布呈现铁心轴向中心部位最为严重,向端部区域逐渐减弱的规律。双V型磁路结构中,下层磁体失磁比上层严重。每块永磁体的失磁分布均受其工作温度、退磁电流幅值与角度等因素影响。
2)永磁体局部位置的失磁严重程度与电机整体失磁状态并不完全一致。存在电机整体只发生轻微失磁而永磁体局部位置已经严重失磁的状态。电机轴向中心部位永磁体靠近转轴的边角位置的高工作温度区域最易发生局部失磁。在电机设计过程中,可通过降低铁心中心段永磁体的工作温度或提升其抗退磁能力,实现失磁预防。
3)退磁电流幅值和角度决定了双V型磁路结构左右两个磁体的失磁程度与分布规律。同样温度分布下,退磁电流幅值越大,退磁越严重。退磁电流角为90°时,失磁呈现对称状态;其余电流角下,下层磁体的失磁比上层严重,R磁体失磁比L磁体严重。
4)永磁体局部失磁故障对电机整体特性存在明显影响。空载反电动势和输出转矩可以准确地评估失磁的发生对电机空载和负载特性的影响。
参考文献
[1] 何绍民, 杨欢, 王海兵, 等. 电动汽车功率控制单元软件数字化设计研究综述及展望[J]. 电工技术学报, 2021, 36(24): 5101-5114.
He Shaomin, Yang Huan, Wang Haibing, et al. Review and prospect of software digital design for electric vehicle power control unit[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5101- 5114.
[2] 温传新, 王培欣, 花为. 电动汽车驱动系统的研究现状与发展趋势[J]. 微电机, 2019, 52(10): 103- 109.
Wen Chuanxin, Wang Peixin, Hua Wei. Driving technology of electric vehicles: current developments and future prospects[J]. Micromotors, 2019, 52(10): 103-109.
[3] 孙玉华, 赵文祥, 吉敬华, 等. 高转矩性能多相组永磁电机及其关键技术综述[J]. 电工技术学报, 2023, 38(6): 1403-1420.
Sun Yuhua, Zhao Wenxiang, Ji Jinghua, et al. Overview of multi-star multi-phase permanent magnet machines with high torque performance and its key technologies[J]. Transactions of China Electro- technical Society, 2023, 38(6): 1403-1420.
[4] 曹恒佩, 艾萌萌, 王延波. 永磁辅助同步磁阻电机研究现状及发展趋势[J]. 电工技术学报, 2022, 37(18): 4575-4592.
Cao Hengpei, Ai Mengmeng, Wang Yanbo. Research status and development trend of permanent magnet assisted synchronous reluctance motor[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(18): 4575-4592.
[5] 林迎前, 孙毅, 王云冲, 等. 稀土和铁氧体混用永磁辅助同步磁阻电机[J]. 电工技术学报, 2022, 37(5): 1145-1157.
Lin Yingqian, Sun Yi, Wang Yunchong, et al. A hybrid PM-assisted SynRM with ferrite and rare-earth magnets[J]. Transactions of China Electrotechnical Society, 2022, 37(5): 1145-1157.
[6] You Yongmin, Yoon K Y. Multi-objective optimi- zation of permanent magnet synchronous motor for electric vehicle considering demagnetization[J]. Applied Sciences, 2021, 11(5): 2159.
[7] Peng Peng, Zhang Julia, Li Wanfeng, et al. Time- dependent demagnetization of NdFeB magnets under DC and pulsed magnetic fields[J]. IEEE Transactions on Magnetics, 2020, 56(3): 1-10.
[8] 周头军, 胡贤君, 潘为茂, 等. 工业应用中钕铁硼磁体不可逆磁通损失的影响因素研究[J]. 中国稀土学报, 2019, 37(3): 339-343.
Zhou Toujun, Hu Xianjun, Pan Weimao, et al. Influencing factors on flux irreversible loss of Nd- Fe-B magnet application[J]. Journal of the Chinese Society of Rare Earths, 2019, 37(3): 339-343.
[9] 崔刚, 熊斌, 阮琳, 等. 驱动电机用高性能钕铁硼永磁材料不可逆失磁扩散特性研究[J]. 中国稀土学报, 2023, 41(4): 725-735.
Cui Gang, Xiong Bin, Ruan Lin, et al. Irreversible demagnetization and diffusion characteristics of high performance NdFeB permanent magnet for drive motor[J]. Journal of the Chinese Society of Rare Earths, 2023, 41(4): 725-735.
[10] 李伟力, 程鹏, 吴振兴, 等. 并网永磁同步发电机转子永磁体局部失磁特征量的计算与分析[J]. 中国电机工程学报, 2013, 33(33): 95-105, 12.
Li Weili, Cheng Peng, Wu Zhenxing, et al. Calculation and analysis on the permanent magnet partial demagnetization characteristics of the grid- connected permanent magnet synchronous generator rotor[J]. Proceedings of the CSEE, 2013, 33(33): 95- 105, 12.
[11] Kim H K, Hur J. Dynamic characteristic analysis of irreversible demagnetization in SPM- and IPM-type BLDC motors[J]. IEEE Transactions on Industry Applications, 2017, 53(2): 982-990.
[12] 唐旭, 王秀和, 李莹, 等. 异步起动永磁同步电动机起动过程中永磁体退磁研究[J]. 中国电机工程学报, 2015, 35(4): 961-970.
Tang Xu, Wang Xiuhe, Li Ying, et al. Demagneti- zation study for line-start permanent magnet syn- chronous motor during starting process[J]. Pro- ceedings of the CSEE, 2015, 35(4): 961-970.
[13] 唐旭, 王秀和, 李莹. 三相不对称供电异步起动永磁同步电动机的退磁研究[J]. 中国电机工程学报, 2015, 35(23): 6172-6178.
Tang Xu, Wang Xiuhe, Li Ying. Demagnetization study for line-start permanent magnet synchronous motor fed by three-phase unbalanced voltages[J]. Proceedings of the CSEE, 2015, 35(23): 6172-6178.
[14] Almandoz G, Gómez I, Ugalde G, et al. Study of demagnetization risk in PM machines[J]. IEEE Transactions on Industry Applications, 2019, 55(4): 3490-3500.
[15] Zhang Yue, McLoone S, Cao Wenping. Electro- magnetic loss modeling and demagnetization analysis for high speed permanent magnet machine[J]. IEEE Transactions on Magnetics, 2018, 54(3): 1-5.
[16] Kim B C, Lee J H, Kang D W. A study on the effect of eddy current loss and demagnetization characteri- stics of magnet division[J]. IEEE Transactions on Applied Superconductivity, 2020, 30(4): 1-5.
[17] Guo Baocheng, Huang Yunkai, Peng Fei, et al. General analytical modeling for magnet demag- netization in surface mounted permanent magnet machines[J]. IEEE Transactions on Industrial Elec- tronics, 2019, 66(8): 5830-5838.
[18] 徐敦煌, 王东, 林楠, 等. 失磁故障下交错磁极混合励磁发电机的等效二维解析磁场模型[J]. 电工技术学报, 2017, 32(21): 87-93.
Xu Dunhuang, Wang Dong, Lin Nan, et al. An equivalent two-dimensional analytical model for the consequent-pole hybrid-excitation generator with demagnetization fault[J]. Transactions of China Electrotechnical Society, 2017, 32(21): 87-93.
[19] 唐旭, 王秀和, 徐定旺. 异步起动永磁同步电动机起动过程中永磁体平均工作点的解析计算[J]. 电机与控制学报, 2017, 21(5): 8-14.
Tang Xu, Wang Xiuhe, Xu Dingwang. Analytical calculation of permanent magnets’ average operating point for line-start permanent magnet synchronous motor during starting process[J]. Electric Machines and Control, 2017, 21(5): 8-14.
[20] 卢伟甫, 罗应立, 赵海森. 自起动永磁同步电机起动过程电枢反应退磁分析[J]. 电机与控制学报, 2012, 16(7): 29-33.
Lu Weifu, Luo Yingli, Zhao Haisen. Armature reaction demagnetization analysis for line-start permanent magnet synchronous motor during start process[J]. Electric Machines and Control, 2012, 16(7): 29-33.
[21] 上官璇峰, 周敬乐, 蒋思远. 双转子双鼠笼永磁感应电机起动过程中永磁体退磁研究[J]. 电机与控制学报, 2019, 23(12): 126-134.
Shangguan Xuanfeng, Zhou Jingle, Jiang Siyuan. Demagnetization of dual-rotor permanent magnet induction motor with double squirrel cage during the starting process[J]. Electric Machines and Control, 2019, 23(12): 126-134.
[22] 张志艳, 秦鹏, 徐金涛, 等. 永磁同步电动机失磁故障电磁参数分析[J]. 微特电机, 2018, 46(8): 31- 34, 44.
Zhang Zhiyan, Qin Peng, Xu Jintao, et al. Electro- magnetic parameters analysis of PMSM demagneti- zation[J]. Small & Special Electrical Machines, 2018, 46(8): 31-34, 44.
[23] Nishiyama N, Uemura H, Honda Y. Highly demag- netization performance IPMSM under hot environ- ments[J]. IEEE Transactions on Industry Applications, 2019, 55(1): 265-272.
[24] Lee K D, Kim W H, Jin C S, et al. Local demag- netisation analysis of a permanent magnet motor[J]. IET Electric Power Applications, 2015, 9(3): 280- 286.
[25] Ruoho S, Haavisto M, Takala E, et al. Temperature dependence of resistivity of sintered rare-earth permanent-magnet materials[J]. IEEE Transactions on Magnetics, 2010, 46(1): 15-20.
[26] 唐任远. 现代永磁电机理论与设计[M]. 北京: 机械工业出版社, 2016.
Abstract High-performance Nd-Fe-B permanent magnet materials commonly used in permanent magnet synchronous motors for electric vehicles are prone to irreversible demagnetization under high temperatures and strong magnetic fields. It has become the main bottleneck of the high-reliability design of permanent magnet drive motors. The cavity structure and cooling method of the permanent magnet synchronous motor determine the spatial distribution differences of the working temperature of the permanent magnet. In order to study effective methods for preventing demagnetization faults in permanent magnet synchronous motors, it is necessary to accurately calculate the demagnetization spatial distribution characteristics of permanent magnets and understand their influencing factors.
This paper uses the permanent magnet virtual partitioning method to establish a permanent magnet local demagnetization analysis model based on its magnetic characteristic parameters, working temperature, spatial position, and other variables. The spatial distribution and influencing factors of local demagnetization are studied using the three-dimensional and multi-physical field calculation method with a two-way coupling of the electromagnetic field and temperature field. Finally, the accuracy of the analysis method and results is verified by testing the permanent magnet operating temperature, the magnetic field distribution on the rotor, and the motor performance of a 115 kW-8 pole permanent magnet synchronous motor prototype.
Simulation results show that when the demagnetization current is 600 A, 800 A, and 900 A, and the demagnetization current angle is 90°, the maximum demagnetization rate of the permanent magnet is 13.44%, 45.37%, and 62.13%, respectively. When the demagnetization current is 800 A and the demagnetization current angles are 0°, 30°, 60°, and 90°, the maximum demagnetization rates of the permanent magnet are 1.7%, 19.49%, 34.79%, and 45.37%, respectively. The maximum difference in the spatial distribution of the working temperature of the permanent magnet reaches 36℃. After the demagnetization fault occurred, the value of the no-load back electromotive decreased from 175.2 V to 110.16 V. The torque value decreased from 146.15 N·m to 115.6 N·m. The experimental results show that the working temperature difference at different positions of the same permanent magnet reaches 23℃. The temperature difference at the same position of different permanent magnets in the same pole reaches 35℃. The maximum deviation between the simulation and actual measurement of the no-load back electromotive is 4.97%. The maximum deviation between the simulation and the actual measurement of the output torque is 5.28%. The minimal difference between simulation and actual measurement results indicates that the research method proposed in this paper is accurate and effective.
The following conclusions can be drawn from the simulation analysis and test results. (1) The spatial distribution of demagnetization of the permanent magnet synchronous motor is uneven. (2) When the motor malfunctions, there may be a situation where the entire motor only experiences slight demagnetization, but the local position of the permanent magnet has already experienced severe demagnetization. (3) The demagnetization distribution of the permanent magnet is affected by the working temperature, amplitude, and angle of the demagnetizing current. (4) The no-load back electromotive force and output torque can be used to evaluate the impact of demagnetization faults on the no-load and load characteristics of the motor.
Keywords:Permanent magnet synchronous motor (PMSM), Nd-Fe-B permanent magnet, local demagneti- zation, multi-physical field coupling, demagnetization effect, space distribution
崔 刚 男,1984年生,博士研究生,高级工程师,研究方向为永磁电机设计及故障诊断与分析。E-mail: cuigang@mail.iee.ac.cn
阮 琳 女,1976年生,博士,研究员,博士生导师,研究方向为电气装备与电子信息设备高效热管理。E-mail: rosaline@mail.iee.ac.cn(通信作者)
中图分类号:TM302
DOI: 10.19595/j.cnki.1000-6753.tces.230533
国家自然科学基金资助项目(52177064, U22A20219)。
收稿日期 2023-04-25
改稿日期 2023-05-08
(编辑 崔文静)