0 引言
随着国家“碳达峰、碳中和”目标的提出,适应大规模高比例新能源成为电力系统的未来发展趋势。然而以太阳能和风能为代表的可再生能源具有较强的波动性与间歇性,大规模并网会对电力系统的稳定性构成巨大的挑战,而储能技术有望解决这一难题。在各种储能技术当中,电化学储能能量密度大、能量效率高、响应速度快、配置灵活,是规模储能技术发展的重要方向[1-3]。
在诸多电化学储能技术中,液态金属电池(Liquid Metal Battery, LMB)是一种面向电网规模储能的新型电池储能技术,具有长寿命、低成本等明显应用优势[4-9]。据报道,2020 年12 月,TerraScale公司计划为位于内华达州的Energos Reno 数据中心项目部署可再生能源发电设施和储能系统,将采用规模为250 MW·h 的液态金属电池储能系统。近年来,电化学储能电站的规模呈现集中式、大型化的发展趋势。MW·h 甚至GW·h 级别的储能系统涉及海量的电池成组运行[10-11]。系统性能与电池单体的状态参数密切相关,成组电池间的不一致性不仅会显著降低储能系统性能,还可能会引起安全隐患。为了实现液态金属电池在储能系统中的应用,需要通过电池分选方法筛选出一致性较好的电池进行成组使用。电池分选是指通过容量、内阻等关键分选指标对电池进行筛选、分类并重组,是降低成组电池间不一致性,提升储能系统性能的有效手段。
电池分选方法包括两个重要的组成部分:分选指标的获取与分类重组方法。与分选指标的客观性相比,分类重组方法的标准更具主观性并与应用场景密切相关。此外,分类重组方法结果在很大程度上取决于所获得的分选指标的精度。因此,电池分选指标的获取在电池分选中处于中心位置。传统的通过电池标定获取电池分选指标的方法虽然能实现对分选指标零误差的测量,但是会耗费大量的测试时间与成本,难以适用于规模化储能系统的电池分选。基于机器学习的分选方法具有快速、准确等优点,更适合海量电池的分选。
目前,电池分选的研究主要聚焦于锂离子电池,特别是退役锂离子电池的重组利用,而关于液态金属电池分选的研究极为缺乏。对于分选指标的获取,现有方法一般以获取的电压、电流等关键特征参数作为输入,以容量或内阻等需要预测的分选指标作为输出,通过数据训练构建输入输出的映射,所得到的映射一般也被称为机器学习模型。机器学习模型所需要的输入特征通常需通过额外的电池测试获取。例如,文献[12-15]利用电池充电曲线获取预测用特征,文献[16]通过阻抗谱测试提取特征,文献[17]将电池放电测试中特定时间点的三个电压值作为特征。目前常用的机器学习模型为支持向量机[12]、高斯过程[15]、相关向量机[14]和神经网络[13,16-17]等,其中神经网络是主流的模型。现有的机器学习模型对分选指标的预测误差一般在1%~4%之间。对于电池的分类重组,现有分选方法一般利用电池容量、内阻在内的多维特征对电池间的相似程度进行衡量,通过特定算法对多个电池进行重组与分选[18-23]。目前主要的分类重组算法为各种聚类算法,包括SOM(self-organizing map)聚类[18-20]、K-means 聚类[22]、模糊C 均值聚类[21]和高斯混合模型[23]等。现阶段对于分选重组后电池间不一致性的衡量尚无固定标准,但在分选重组后,电池间放电曲线的差异得到显著减小。
然而,现有的锂离子电池分选方法难以直接运用于液态金属电池的成组分选。一方面,目前的分选方法主要聚焦于退役锂离子电池分选,电池间的不一致性差距显著,而新制备的液态金属电池单体间的不一致性相对较小,对分选指标的估计精度要求更高;另一方面,液态金属电池具有容量大、内阻小的特点[24],要求分选指标的估计有更小的相对误差。此外,现有方法获取输入特征需要额外的电池测试,测试时间与成本还有进一步优化的空间。
针对上述问题,本文提出了一种基于集成机器学习的液态金属电池分选方法。与现有方法相比,在数据来源上,利用活化期的数据作为输入,无需额外的电池测试,分选速度更快;在模型算法上,利用特征选择和集成学习方法,所获得的特征更有效,集成模型对分选指标电池容量的预测误差更小且更可靠。该方法主要分为四个步骤,如图1 所示:首先对电池数据进行整理、选择与划分;然后获得基础模型的最优超参数;接着在训练得到集成模型之后,在测试集上验证得到最优模型;最后基于最优模型进行电池分选。
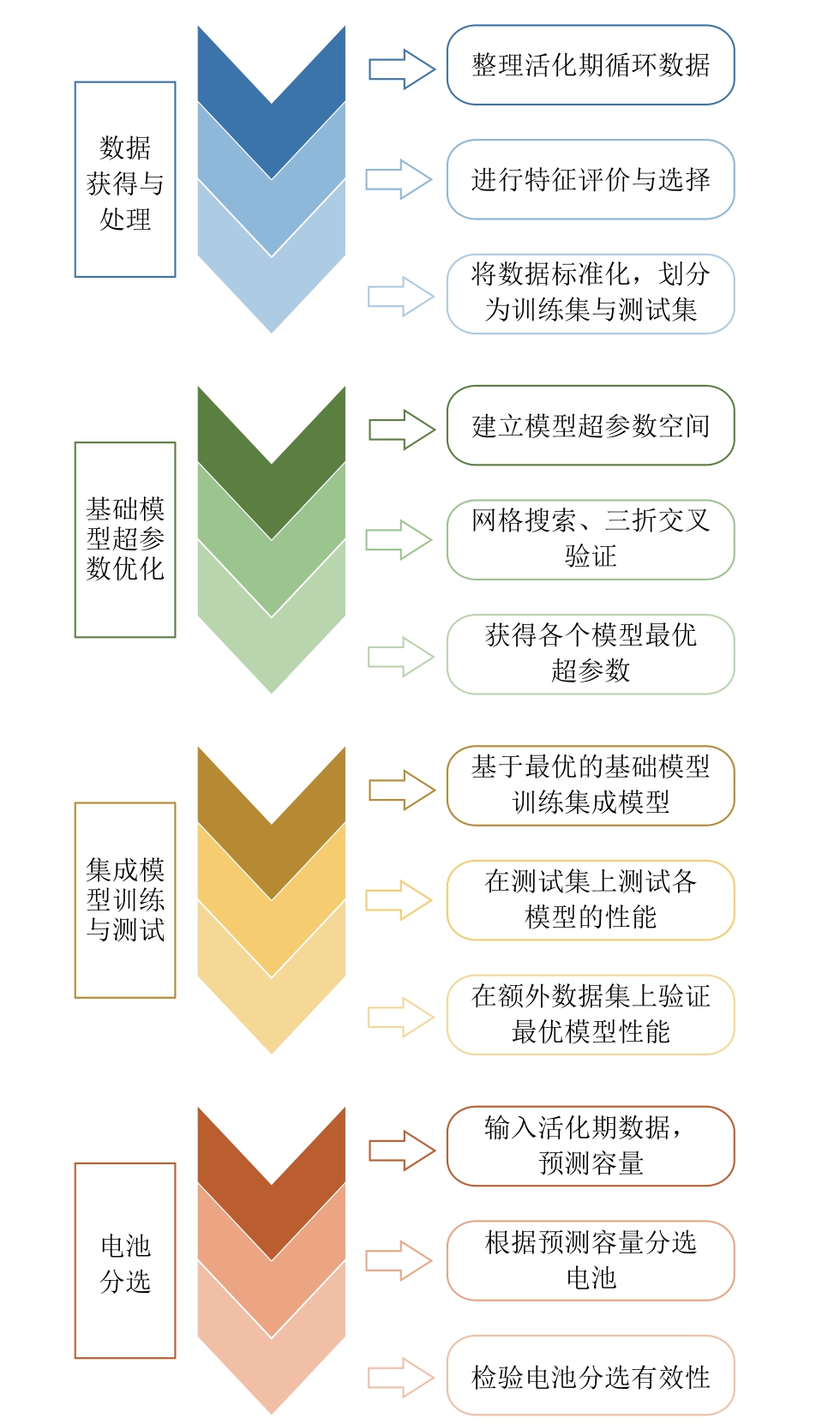
图1 分选方法的主要工作流程
Fig.1 Main workflow of proposed sorting method
本文首先介绍了液态金属电池及其数据集,以及集成模型所用到的基础模型和集成方法;再次,阐述了本文要解决的机器学习问题与评价指标;然后,介绍了主要工作,包括特征选择、模型构建与优化、模型测试与验证、电池分选四个部分;最后,根据模型的测试验证结果和分选结果,对特征选择方法和集成模型的优越性进行了评价与总结。
1 液态金属电池简介与电池数据集
1.1 液态金属电池简介
液态金属电池是一类新型储能电池,在300~700℃的工作温度下,电池正负极和电解质分别为液态金属和熔融态无机盐,三者互不相溶,会根据密度差自动分层[25-26]。全液态设计使该电池在长期运行时不会出现电极形变和枝晶生长等现象,具有长寿命的显著优势。液态金属电池的电极和电解质材料来源广泛、价格低廉、无需隔膜、结构简单、电池成本较低[27-28]。低成本、长寿命的特性让液态金属电池有望满足未来电网大规模储能的应用需求[29]。
本文采用的液态金属电池为理论容量为50 A·h的Li||Sb-Sn 电池,其结构示意图[30]如图2 所示,基本参数见表1。
表1 Li||Sb-Sn 液态金属电池基本参数
Tab.1 Parameters of liquid metal battery
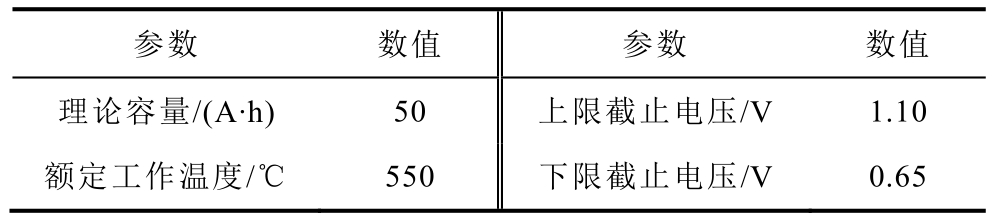
参数 数值 参数 数值理论容量/(A·h) 50 上限截止电压/V 1.10额定工作温度/℃ 550 下限截止电压/V 0.65
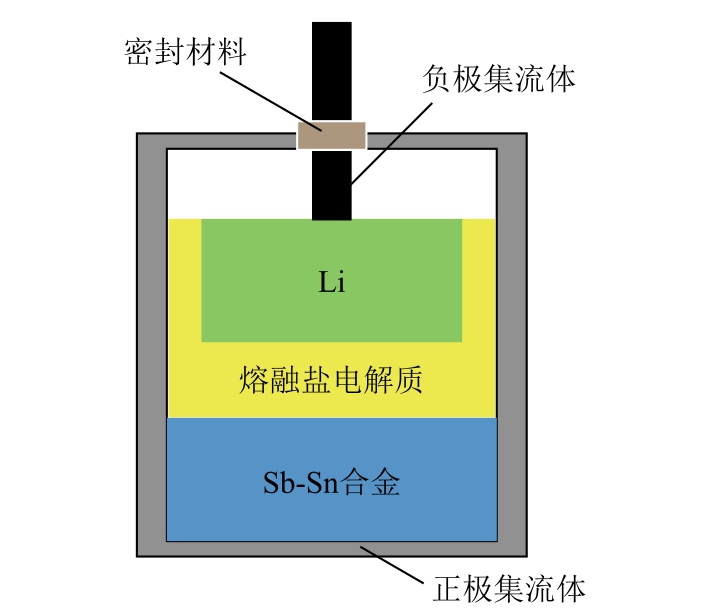
图2 Li||Sb-Sn 液态金属电池结构示意图[30]Fig.2 Structure of Li||Sb-Sn liquid metal battery[30]
1.2 电池数据集与特征
本文所使用的电池数据来自50 A·h Li||Sb-Sn 液态金属电池活化期的循环数据,共包括21 个电池的416 个循环。电池的活化期和稳定状态的定义如下:活化为从新电池到稳定运行的过程,一般在20 个循环内电池即可到达稳定状态,因此本文选取前20 个循环作为活化期;稳定状态为经过活化期后再循环10 圈后的电池状态。在活化期,电池以0.1C 倍率进行充放电循环,放电容量为25 A·h。在活化循环测试中,每10 s 对电池的电压、电流等信息进行一次采样,每一个采样点即为一个时间步。需要指出的是,电池在活化期循环时放电深度(Depth of Discharge, DOD)设定为50%,防止电池出现过充、过放和短路等故障。
本文将电池活化期的各个循环放电过程中的相关特征作为一个样本,其标签为循环所属的电池稳定状态的满放容量。该数据集共有7 个特征:放电起始电压、放电中压、放电终止电压、库伦效率、直流内阻、欧姆内阻和平台到达时间段。其中放电起始电压、放电中压、放电终止电压和库伦效率均可直接测得。欧姆内阻和直流内阻可通过放电结束后瞬间的电压变化和静置后的恢复电压(如图3 所示)计算得到,其计算公式分别为
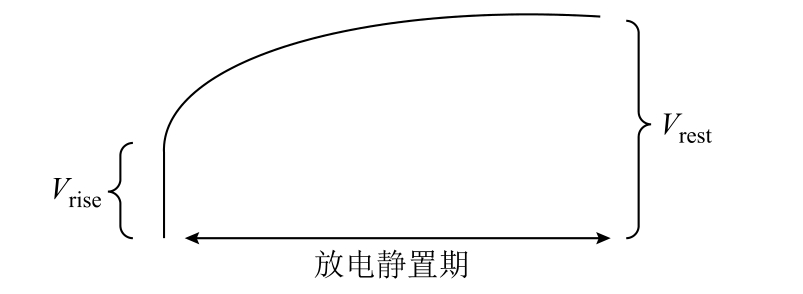
图3 内阻计算示意图
Fig.3 Internal resistance calculation diagram
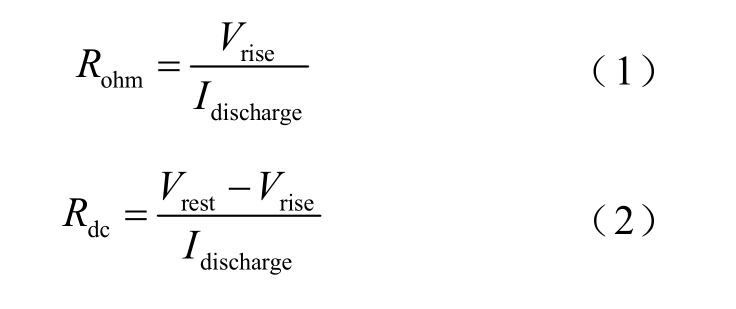
式中,Rohm 为欧姆内阻;Rdc 为直流内阻;Idischarge 为电池放电阶段的电流;Vrise 为放电结束后进入静置阶段电压的瞬时值;Vrest 为静置期电压达到稳定的稳定值。
放电平台的定义来自放电电压曲线各点的切线斜率,当斜率小于某一阈值(接近于0)时可以认为放电进入平台期。平台到达时间示意图如图4 所示,本文认为电池放电电压在10 s 内的变化小于或等于0.002 V 时电池即进入放电平台期,这和液态金属电池的放电特性密切相关。
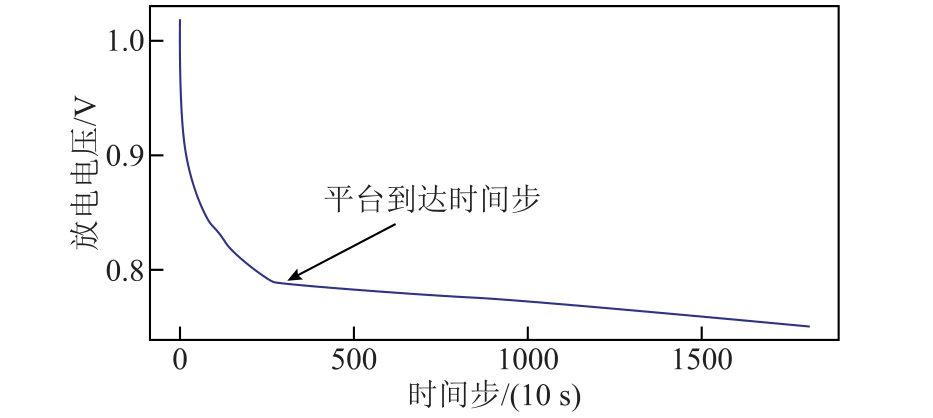
图4 平台到达时间示意图
Fig.4 Plateau arrival time diagram
如图4 所示为液态金属电池放电曲线,箭头指示处的时间步即为平台到达时间步。将时间轴划分为若干个区间并对区间依次编号,平台到达时间步所在的区间即为特征平台到达时间段,其取值即为区间的编号。该特征能够反映电压曲线的部分形貌特征,从而有利于容量预测。
基于分层抽样的方法,数据集被划分为训练集和测试集。其中测试集样本数量为84,训练集样本数量为332。
2 所用模型与集成方法简介
本文集成模型所用的基础模型总共有三个,分别为支持向量回归(Support Vector Regression,SVR) [31-32]、极端梯度提升(Extreme Gradient Boosting, XGBoost)回归[33]和随机森林回归[34];所采用的集成方法有两种,分别为投票法和堆叠法[35]。
2.1 支持向量回归
支持向量回归是一种使用广泛的机器学习模型。对于n 个m 维数据xi,支持向量回归的目标是找到一个函数fsvr(xi),对于所有训练数据的fsvr(xi)与实际目标yi 的最大偏差为ε。其函数表达式为
式中,wsvr 为与x 相乘的权重系数向量;b 为偏置量。
实际应用中,常常允许有一定的误差以提升模型的泛化性能,因此在优化问题中引入了两个松弛变量ξ和ξ*,以及正则化系数C。在此条件下的优化问题为
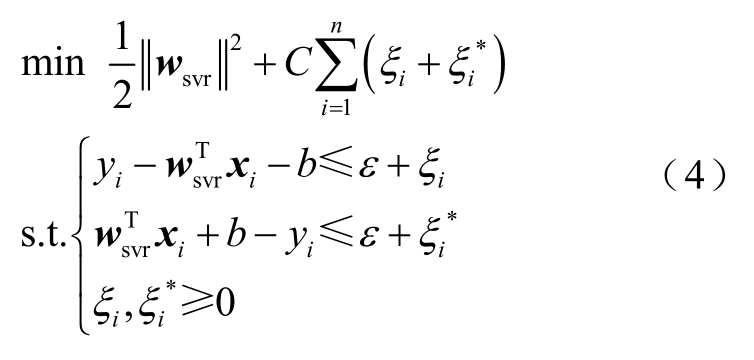
对于非线性的回归问题,支持向量回归存在一种“核技巧”,即通过某种映射Φsvr 将样本映射到一个更高维的特征空间中,将样本空间中的非线性问题转换为高维空间中的线性问题。这种映射通常用核函数来隐式表示为
通过核函数,特征空间内的点积计算就转换为原空间内核函数的计算。常见的核函数有高斯核、多项式核等。本文采用普适性更加广泛的高斯核函数。
2.2 极端梯度提升回归
XGBoost 是一种梯度提升树的变体,其特点是运行速度极快、可扩展与可移植。
对于n 个m 维数据xi,该算法建立K 个回归树来拟合实际目标yi。拟合表达式为
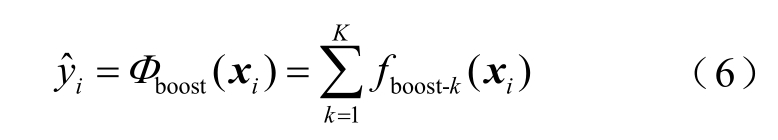
式中,Φboost 为极端梯度提升模型中xi 到yi 的映射;每一个fboost-k 都代表一个独立的树结构。
损失函数为

式中,l 为一个可微的凸损失函数;T 为决策树中叶节点的数量;Ω 为一个惩罚项,以避免过拟合;wboost为每棵树中末端叶上的权重分数;γ 和λ 均为正则化参数。
该算法是一种贪心算法,训练过程中在添加第t-1 棵树后,通过添加最优的第t 棵使得损失最小,即

最后根据最优损失计算得到第t 个树的最优划分和权重。该过程会一直持续下去直到所有的K 个树都建立完毕,最终得到完整的模型。
2.3 随机森林回归
随机森林是最常见的决策树集成模型之一。随机森林回归算法会生成一系列不同的回归决策树形成一个“森林”。具体模型算法如下:
1)利用bagging 采样方法获得d 个训练集子集。
2)在每个子集上分别训练一个回归决策树。
3)训练时,每个决策树分裂时不是采用所有特征,而是用随机的特征子集来划分数据。特征子集的最大数量是固定的,但所含特征是随机选择的。在分裂时从子集中选择一个最优特征,然后找到最优划分点。
4)随机森林回归模型预测的结果是所有d 个决策树模型的预测结果的平均值。
2.4 集成方法
将一组预测模型的预测聚合起来就称为集成。集成方法能够将较弱的模型集合成一个更强的模型,集成得到的模型性能与泛化能力一般强于用于集成的基础模型。在诸多集成方法中,投票法和堆叠法适用于集成多个完全独立的基础模型,所以本文采用这两种方法作为集成的备选方法。
对于回归问题来说,投票法就是将e 个基础模型单独训练,然后将它们的预测结果进行平均。投票法能够提升模型整体性能的原理是,不同的模型所犯的错误的类型不同,将不同模型的预测结果进行平均能够减少整体的误差,其表达式为
式中,Pi 为对样本xi 的最终预测结果;Pe-i 为第e 个基础模型对xi 的预测结果。
堆叠法的思路是将一组基础模型的预测结果作为训练集,对一个简单的顶层模型进行训练,顶层模型输出最终的预测结果,如图5 所示。
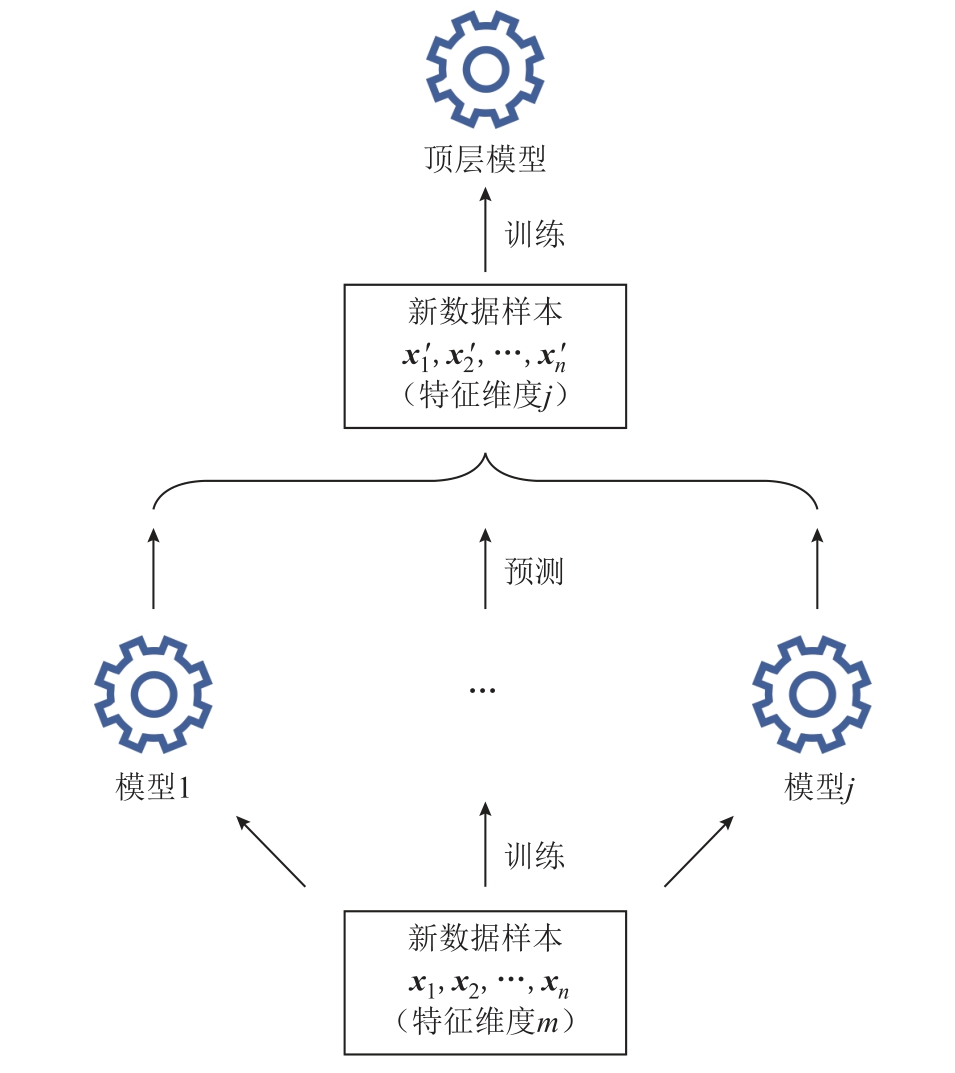
图5 堆叠法示意图
Fig.5 Diagram of stack ensemble method
假设输入样本数为n,特征维度为m,存在j 个底层基础模型,基础模型在整个训练集上进行训练。将它们对训练集的预测结果当作新的训练集传递给上层的一个简单模型,那么这个新的训练集的数目为n,特征维度为j。一般来说j 要远小于m,且底层模型预测的结果与目标输出更加接近,顶层模型能够利用维度更少的、质量更好的数据集进行训练,从而实现整体上更精准的预测。
需要说明的是,集成方法的基础模型应尽量选择相互独立的不同算法,这样有利于提升集成模型的整体性能。本文采用SVR、XGBoost 和随机森林作为基础模型,三个模型采用的算法完全不同且都广泛应用于回归问题。具体而言,XGBoost 采用了梯度提升的算法,因此能够在训练集上实现更小的误差,但相应地模型更容易过拟合;SVR 和随机森林在训练集上的误差相比XGBoost 而言更大,但不易过拟合、泛化能力相对更强。因此,将它们结合起来能够有效平衡模型训练误差和泛化能力之间的矛盾。
3 机器学习问题与评价指标
本文所要解决的机器学习问题是:基于机器学习的方法,构建活化期电池数据与电池容量的非线性映射。数据集包括活化期电池循环放电部分的特征。在获得模型预测的容量后,根据预测容量来对电池进行初分选,按照给定容量阈值将不合格的电池淘汰。
电池容量的预测属于回归问题,回归问题常用的评价指标为平均绝对误差(Mean Absolute Error,MAE)、方均根误差(Root-Mean-Square Error, RMSE)和方均根百分比误差(Root-Mean-Square Percentage Error, RMSPE)等。本文采用RMSE 和RMSPE 作为电池容量预测的评价指标,分别表示为
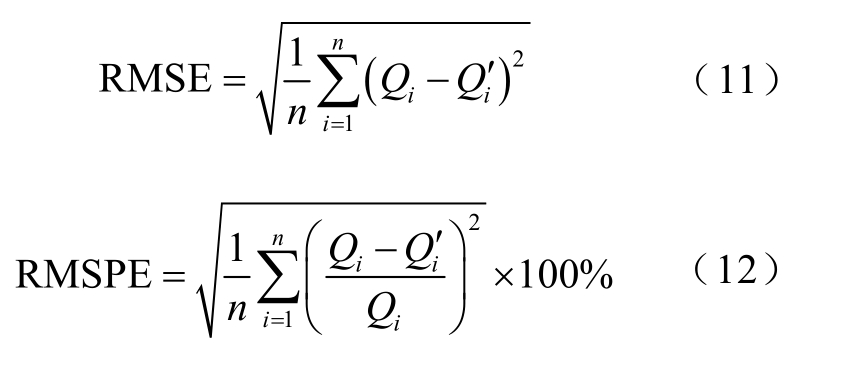
式中,Qi 为容量的真实值; iQ′为容量的预测值。
对于电池分选,采用准确率(Accuracy)和召回率(Recall)作为评价指标,有

式中,TP 表示本身是不合格的电池而被正确预测为不合格;TN 表示本身是合格的电池且被正确预测为合格;FN 表示本身为不合格的电池却被误认为是合格的;ALL 表示所有电池。电池分选方法的准确率和召回率越高,其分选效果越好。
4 主要工作
本文的主要工作包括特征选择、模型构建与优化、模型测试与验证和电池分选四个部分。其中,本文利用Scikit-learn 库[36]对基础模型和集成模型进行训练与超参数优化。对于作为对照组的神经网络模型,采用Keras 框架进行训练与优化。数据处理与其他编程工作均通过Python 编程语言完成。
4.1 特征选择
当数据维度很高时,许多机器学习算法的实现会变得相当困难,这种现象被称为维数灾难(curse of dimension)。本文所使用的数据集样本数量较少(416 个),而特征维数较高(7 个),会导致训练得到的模型泛化能力较差。目前解决这一问题的方法大致有两种:一是增加样本数量,使训练实例达到足够大的密度;二是降低数据维度,即特征的数量。第一种方法在本问题中难以实现,因为所需要的训练实例数量随着维度的增加呈指数上升。因此,本文采用特征选择的方法实现数据降维。
数据降维的目标是尽可能保留有用的、信息量大的特征,剔除冗余的、信息量小的特征。为此采用一种综合性的特征选择方法,通过对特征进行量化评分来选择出最优的特征组合,在对数据降维的同时保留最有用的特征,提升训练得到的模型性能。本方法对特征的量化评价分为四个部分:
1)根据各个特征与目标容量之间的相关系数来评价特征。相关系数主要是衡量特征与目标之间的线性相关程度。
2)根据各个特征与目标容量间的互信息[37]来评价特征。互信息主要是衡量特征与目标之间的非线性相关程度。
3)利用模型选择的方法来评价特征。模型选择方法通过简单的模型对特征进行评价,而这些模型拥有可以定量化的评价指标。
4)利用顺序选择[38]的方法来评价特征。顺序选择方法是一种贪心算法,该方法逐步寻找最优的特征添加到选择的特征集合中,根据特征添加的顺序可以判断特征的有效性。
本文提出的特征选择方法评分准则如下:每个部分中,根据各个部分对应的评价指标对所有特征按照其有效性从高到低进行排序。在第一部分和第二部分,排名第一至第四的特征分别评分为4、3、2、1 分。在第三部分和第四部分各采用两个模型,Lasso 回归模型和极端随机树模型[39]。选择这两个模型的原因为:①这两个模型都有可以量化评价特征的指标,即回归模型的系数和树模型的特征重要性;②这两个模型采用完全不同的算法、相互独立,选择两种模型能增加对特征评价的全面性。针对单个模型,排名第一至第四的特征分别评分为2、1.5、1、0.5 分。最终每个特征的评分总和见表2。
表2 各个特征的评分结果
Tab.2 Scores of all features
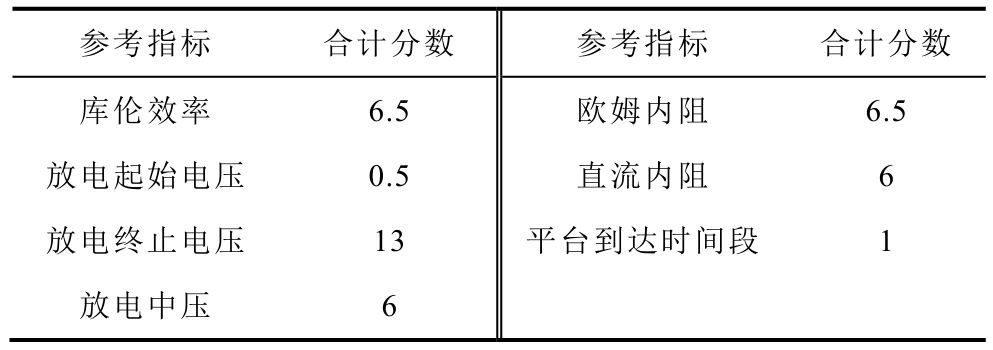
参考指标 合计分数 参考指标 合计分数库伦效率 6.5 欧姆内阻 6.5放电起始电压 0.5 直流内阻 6放电终止电压 13 平台到达时间段 1放电中压 6
从最终合计分数可以看到,放电终止电压是最有效的特征,分数显著超过其他特征分数;库伦效率、放电中压、欧姆内阻及直流内阻四个特征分数基本接近,属于可用特征;而放电起始电压和平台到达时间段这两个特征分数非常低,属于冗余、信息量低的特征。因此,最终选择放电终止电压、库伦效率、放电中压、欧姆内阻及直流内阻5 个特征为最终训练所用特征,数据集的维度从7 维降低到5 维。关于特征选择的有效性,将在本文4.3.2 节进行检验。
4.2 模型构建与优化
4.2.1 基础模型训练与超参数优化
在进行模型的集成与训练之前,需要对三个基础模型SVR、XGBoost 和随机森林进行超参数优化以获取各个模型的最优超参数。更优的超参数能够提升模型性能、提升模型泛化能力并减小其预测的误差。
本文采用网格搜索的方法对模型的超参数进行优化,针对给定的参数搜索空间寻找最优超参数组合。为了评价模型在不同超参数组合下的参数优劣,本文采用三折交叉验证方法。具体为,将训练集划分为等样本数量的三个部分,对模型进行三轮训练与评估。每一轮训练时,选择不同的一折样本作为验证集来评价模型,剩下的两折用来训练模型。由于验证集没有用作模型训练,模型在验证集上的分数能够反映模型的泛化能力与整体性能,是可信的评价指标。
模型的训练与评价流程如图6 所示,本文采用RMSE 作为模型验证分数。将模型在三折交叉验证中三个验证集上的RMSE 分数进行平均即可得到该分数,该分数越小代表该模型的超参数越优。对于超参数空间的每一个组合,都进行一次三折交叉验证得到模型验证分数,直到穷举完模型所有的超参数组合。最优的模型验证分数对应的超参数组合就是最终的模型最优超参数。

图6 模型的超参数优化过程
Fig.6 Process of hyperparameters’ optimization
经过网格搜索优化后,三个基础模型的各自的最优超参数和最优模型验证分数见表3。各个模型所选择的可调整超参数都是模型比较有代表性的关键参数与正则化参数。比如,XGBoost 和随机森林的超参数都是用来控制组成模型的决策树的数量和复杂程度,而SVR 的Gamma 和C 参数则分别控制模型对数据的拟合程度和对误差的容忍程度。因此通过控制这些关键超参数的取值就能有效地控制模型在训练后的复杂程度、误差大小与泛化能力。
表3 各基础模型的最优超参数取值与模型验证分数
Tab.3 Best hyperparameters and model validation scores of each model

模型名称 最优超参数 取值 最优模型验证分数/(A·h)γ 0 XGboost学习率 0.3最大深度 4子模型数量 50 0.280 5 Gamma 1 SVR 0.330 4 C 100子模型数量 20随机森林最大特征数 4最大深度 4叶节点最小样本数 4 0.383 9
三个模型的最优模型验证分数分别为0.280 5、0.330 4 和0.383 9 A·h。从最终的最优模型验证分数来看,具有最优超参数的三个模型的预测效果良好,电池预测的平均误差在0.4 A·h 以内,相对误差小于0.8%。从结果可知XGBoost 模型是性能最佳的基础模型。
4.2.2 集成模型训练与验证
在获取基础模型的最优超参数后,进一步对集成模型进行训练。对于投票集成模型,除基础模型外不需要额外的模型。对于堆叠集成模型,除了基础模型之外,还需要一个模型作为顶层预测器。本文采用L2 正则化的线性模型岭回归模型作为顶层预测器。为了体现集成方法的有效性,同样对两种集成模型进行三折交叉验证。两个集成模型和基础模型的模型验证分数见表4。
表4 基础模型和集成模型的模型验证分数
Tab.4 Model validation scores of base models and ensemble models
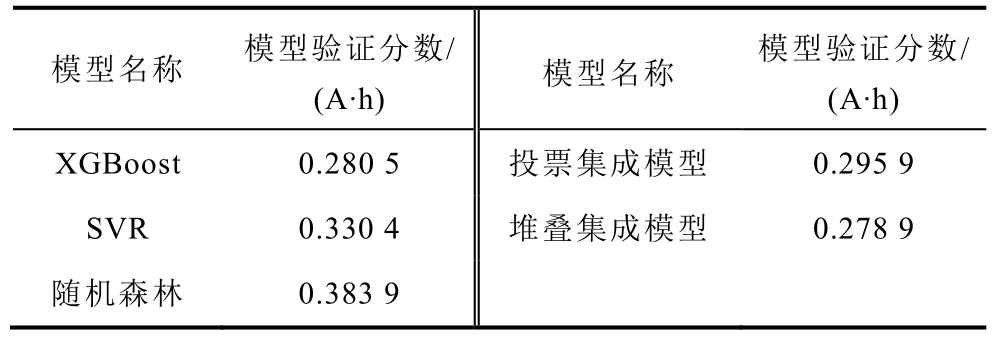
模型名称 模型验证分数/(A·h) 模型名称 模型验证分数/(A·h)XGBoost 0.280 5 投票集成模型 0.295 9 SVR 0.330 4 堆叠集成模型 0.278 9随机森林 0.383 9
从表4 可知,堆叠集成模型的效果最优;投票集成模型的性能虽然也比较好,优于SVR 和随机森林模型,但仍弱于最优的基础模型XGBoost。
4.3 模型测试与验证
4.3.1 测试集上的测试与结论
在获得集成模型的模型验证分数进行初步判断后,将两个集成模型在整个训练集上进行训练得到最终的完整模型。对于基础模型,同样使用最优超参数在整个训练集上进行训练得到最终基础模型,用来检验集成方法是否提升了模型性能。为了进一步体现集成模型的优越性,本文训练了一个额外的神经网络模型作为对照组。该神经网络具有两个隐藏层,每个隐藏层的神经元数目为32 个。此外,该神经网络模型是经过三折交叉验证与网格搜索调整后的最优模型,拥有最优的网络结构与超参数,可以作为衡量集成模型性能的基准。
将所有模型在测试集上进行评估,得到基础模型、集成模型和对照模型(神经网络模型)的测试集分数,以评价模型的泛化能力。测试集分数为RMSE 和RMSPE,用来衡量预测容量同真实容量之间的误差。分数越小,代表模型误差越小、性能越好。最终结果见表5。
表5 所有模型在测试集上的分数
Tab.5 Scores of all models on the test set

模型名称 RMSE/(A·h) RMSPE(%)XGBoost 0.265 4 0.530 8 SVR 0.282 6 0.565 2随机森林 0.392 2 0.784 4投票集成模型 0.250 2 0.500 4堆叠集成模型 0.227 8 0.455 6神经网络模型 0.476 2 0.952 4
由表5 可知,两个集成模型的测试误差均小于基础模型及对照模型,由此可见集成方法确实能有效提高模型的泛化能力、减小预测误差。同时,堆叠集成方法比投票集成方法在本问题上更优,预测误差为0.227 8 A·h 和0.455 6%,实现了对电池容量高精度的预测。
对于电池分选而言,除了关注模型对容量预测的整体误差,也要考察其出现较大误差的概率。如果模型出现较大误差的概率过高,即使整体误差较小也不能有效地进行电池分选。所有模型在测试集84个样本上的预测值与真实值的绝对误差如图7 所示,其中蓝色虚线表示绝对误差为± 0.75 A·h 的边界线。可以看到,即便所有模型的整体预测误差都较小,对于个别样本依然存在误差较大的情况。比如对于第83 个样本,所有模型的绝对误差都超过了0.75 A·h。
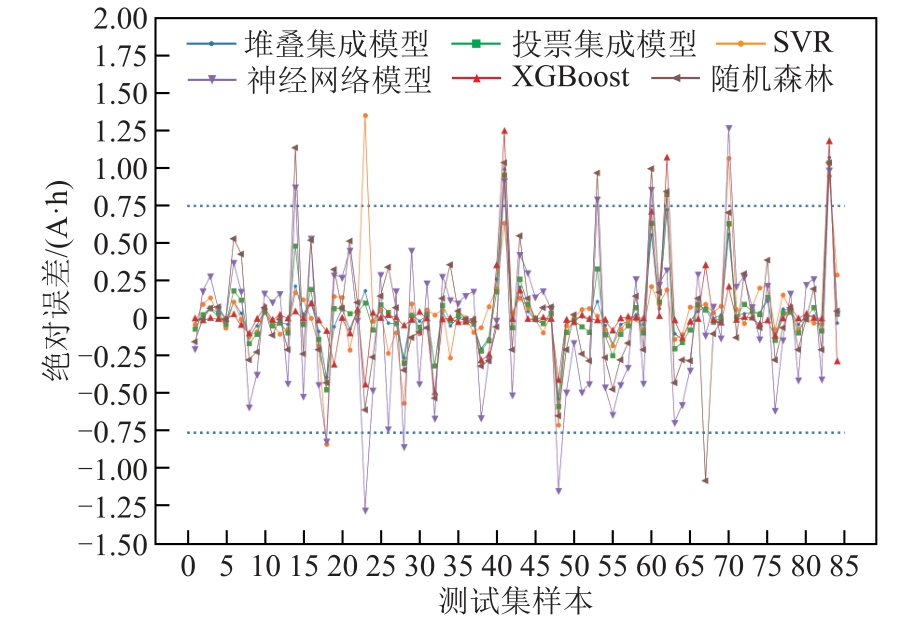
图7 基础模型、集成模型和对照模型在测试集各样本上的绝对误差
Fig.7 Absolute errors of each model on the test set
考虑到神经网络模型在本文中为对照模型,其在测试集上的RMSE 分数为0.476 2 A·h。因此,本文选择采用其RMSE 的1.5 倍左右的数值作为预测失效的阈值,即0.75 A·h,并规定当模型超越误差上限时模型失效。
各个模型在测试集上出现超越误差上限的次数与频率可以用来衡量模型的可靠性。本文利用失效频率来估计失效概率,然后根据失效概率计算模型的可靠性。各个模型的失效次数、失效频率和可靠性见表6。
表6 所有模型在测试集上可靠性评估
Tab.6 Reliability evaluation of all models on the test set

模型名称 失效次数 失效频率(%) 可靠性(%)XGBoost 3 3.57 96.43 SVR 4 4.76 95.24随机森林 7 8.33 91.67投票集成模型 3 3.57 96.43堆叠集成模型 2 2.38 97.42神经网络模型 9 10.71 89.29
从失效次数和频率来看,堆叠集成模型是最优的,仅失效2 次、失效频率为2.38%。从模型的可靠性层面来看,集成方法也能有效地改善模型的可靠性。相较于主流的有监督学习方法(神经网络模型),堆叠集成模型的预测误差显著降低,降低了52.16%;可靠性有了一定的提升,提升了9.10%。因此本文最终选择堆叠集成模型作为分选模型用来预测满放容量。
为了进一步检验根据测试集检验所得到的最优模型堆叠集成模型的泛化能力,本文采用三个50 A·h Li||Sb-Sn 液态金属电池,电池活化期循环数据均未用于训练和测试。电池稳定满放容量分别45.22 A·h、47.28 A·h 和48.97 A·h,总共有57 个活化期循环样本。最终堆叠集成模型在额外电池数据集上的RMSE 和RMSPE 分数分别为0.320 6 A·h 和0.641 2%,失效次数为4 次,可靠性为92.98%。尽管由于额外电池数量比较少,且与训练测试用电池容量分布不同,模型在该数据集上的整体性能比测试集差,但从验证结果来看,堆叠集成模型依然是有效的,在不同于训练与测试的电池上仍拥有较小的预测误差和较好的可靠性。
4.3.2 特征选择方法有效性验证
为了评价在训练模型之前特征选择的有效性,本文设置了一个对照组实验,即在不进行特征选择的情况下,对基础模型进行超参数优化、集成模型训练和测试集测试。对比结果如图7 所示。
由图8 可知,无论是模型验证分数,还是测试集上的分数和失效次数,经过特征选择后的基础模型与集成模型的表现是全方位更优的,在相同类型的模型下误差更低、失效次数更少,表明本文所提出的特征选择方法的有效性与必要性。


图8 经过特征选择与不经过特征选择的模型性能对比
Fig.8 performance comparison between models with feature selection and models without selection
4.4 电池分选结果
本节基于堆叠集成模型进一步预测了电池容量并进行电池分选,将容量大于或等于48 A·h 的电池视作合格,小于48 A·h 的电池视作不合格。本文在选择该阈值时主要考虑了样本数据的分布与电池性能。根据大量正常运行的电池样本数据分布,大部分电池样本集中在48 A·h 附近。将48 A·h 作为阈值,能更加考验模型容量预测的精度与可靠性。同时,电池在容量大于等于48 A·h 时性能更加稳定,因此综合考虑选择48 A·h 作为阈值。
现对训练测试用的24 个电池的所有循环通过堆叠集成模型进行预测,根据预测结果进行电池分选。其分选结果见表7。
表7 整个数据集的分选结果(混淆矩阵)
Tab.7 Sorting results on the whole dataset (confusion matrix)

结果 实际合格 实际不合格预测为合格 293 (TN) 12 (FN)预测为不合格 4 (FP) 164 (TP)
从表7 可知,实际情况与预测结果的重合度非常高,绝大部分样本集中在混淆矩阵的右对角线上(即TN 和TP),表明该方法对绝大多数的电池循环作出了正确的判断。
根据最终的混淆矩阵可知,电池分选的准确率达到了96.62%。且对于不合格电池混入合格电池的情况,即对不合格电池的召回率,堆叠集成模型的预测结果达到了93.18%,满足分选的精度要求。
为了进一步验证该模型在电池分选中的有效性,对4.3.1 节中的额外电池数据通过堆叠集成模型进行预测与分选,在57 个样本上的分选的准确率和召回率均为100%。这充分说明了该集成模型在分选中的应用潜力。
5 结论
针对液态金属电池的快速准确分选问题,本文提出了一种基于集成学习的机器学习模型,通过特征选择和集成学习的方法,实现了电池容量的精确预测和电池的准确分选,研究结果表明:
1)基于集成模型预测容量对电池的分选方法是准确高效的。该方法不仅利用活化期的数据节省了大量的测试时间,也通过高精度的集成模型实现了高准确率和高召回率的电池分选,准确率达到了96.62%,召回率达到了93.18%。
2)本文提出的综合特征选择方法是有效的。与没有进行特征选择所得到的模型相比,选择后训练得到的模型无论是在基础模型上还是在集成模型上都实现了全面的性能提升,拥有更小的误差和更高的可靠性。
3)经过模型验证分数、测试集测试分数和可靠性等指标检验,本文提出的集成模型性能不仅优于用于集成的基础模型,也优于对照组的主流神经网络模型。相较于主流的有监督学习方法(神经网络)模型,所提出的集成模型的预测误差有了显著降低,降低了52.16%;可靠性有了一定的提升,提升了9.10%。这充分说明了集成方法的有效性。最优的堆叠集成模型实现了对电池满放容量的高精度预测,在测试集上的RMSE 和RMSPE 仅有0.227 8 A·h 和0.455 6%,可靠性达到97.42%。
本文提出的方法可用于液态金属电池的快速分选,为电池的分选重组提供高精度与可靠的分选指标。相关的研究方法,比如特征选择方法与集成学习方法,同样可以迁移到其他体系的储能电池的分选研究中。
[1] 任丽彬, 许寒, 宗军, 等.大规模储能技术及应用的研究进展[J].电源技术, 2018, 42(1): 139-142.Ren Libin, Xu Han, Zong Jun, et al.Research progress of large-scale energy storage technologies and applications[J].Chinese Journal of Power Sources,2018, 42(1): 139-142.
[2] 李培平, 姚伟, 高东学, 等.基于电化学储能的多馈入直流系统暂态控制及影响因素分析[J].电工技术学报, 2021, 36(增刊1): 154-167.Li Peiping, Yao Wei, Gao Dongxue, et al.Transient control and influencing factors analysis of multiinfeed HVDC system based on electrochemical energy storage[J].Transactions of China Electrotechnical Society, 2021, 36(S1): 154-167.
[3] 张超, 冯忠楠, 邓少平, 等.考虑电热混合储能的多能互补协同削峰填谷策略[J].电工技术学报,2021, 36(增刊1): 191-199.Zhang Chao, Feng Zhongnan, Deng Shaoping, et al.Multi-energy complementary collaborative peak-load shifting strategy based on electro-thermal hybrid energy storage system[J].Transactions of China Electrotechnical Society, 2021, 36(S1): 191-199.
[4] Wang Kangli, Jiang Kai, Chung B, et al.Lithiumantimony-lead liquid metal battery for grid-level energy storage[J].Nature, 2014, 514(7522): 348-350.
[5] Kim H, Boysen D A, Newhouse J M, et al.Liquid metal batteries: past, present, and future[J].Chemical Reviews, 2013, 113(3): 2075-2099.
[6] Zhang Shilin, Liu Ye, Fan Qining, et al.Liquid metal batteries for future energy storage[J].Energy &Environmental Science, 2021, 14(8): 4177-4202.
[7] Li Haomiao, Yin Huayi, Wang Kangli, et al.Liquid metal electrodes for energy storage batteries[J].Advanced Energy Materials, 2016, 6(14): 1600483.
[8] Li Haomiao, Wang Kangli, Cheng Shijie, et al.High performance liquid metal battery with environmentally friendly antimony-tin positive electrode[J].ACS Applied Materials & Interfaces,2016, 8(20): 12830-12835.
[9] Zhou Hao, Li Haomiao, Gong Qing, et al.A sodium liquid metal battery based on the multi-cationic electrolyte for grid energy storage[J].Energy Storage Materials, 2022, 50: 572-579.
[10] 李建林, 武亦文, 王楠, 等.吉瓦级电化学储能电站研究综述及展望[J].电力系统自动化, 2021,45(19): 2-14.Li Jianlin, Wu Yiwen, Wang Nan, et al.Review and prospect of gigawatt-level electrochemical energy storage power station[J].Automation of Electric Power Systems, 2021, 45(19): 2-14.
[11] 李建林, 武亦文, 王楠, 等.吉瓦级电化学储能电站信息架构与安防体系综述[J].电力系统自动化,2021, 45(23): 179-191.Li Jianlin, Wu Yiwen, Wang Nan, et al.Review of information architecture and security system of gigawatt electrochemical energy storage power station[J].Automation of Electric Power Systems,2021, 45(23): 179-191.
[12] 郑岳久, 李家琦, 朱志伟, 等.基于快速充电曲线的退役锂电池模块快速分选技术[J].电网技术,2020, 44(5): 1664-1673.Zheng Yuejiu, Li Jiaqi, Zhu Zhiwei, et al.Rapid classification based on fast charging curves for reuse of retired lithium-ion battery modules[J].Power System Technology, 2020, 44(5): 1664-1673.
[13] Lai Xin, Qiao Dongdong, Zheng Yuejiu, et al.A rapid screening and regrouping approach based on neural networks for large-scale retired lithium-ion cells in second-use applications[J].Journal of Cleaner Production, 2019, 213: 776-791.
[14] 吕治强, 高仁璟, 黄现国.基于多核相关向量机优化模型的锂离子电池容量在线估算[J].电工技术学报: 2023, 38(7): 1713-1722.Lü Zhiqiang, Gao Renjing, Huang Xianguo.A Li-Ion Battery Capacity Estimation Method Based on Multi-Kernel Relevance Vector Machine Optimized Model[J].Transactions of China Electrotechnical Society, 2023, 38(7): 1713-1722.
[15] 杨胜杰, 罗冰洋, 王菁, 等.基于容量增量曲线峰值区间特征参数的锂离子电池健康状态估算[J].电工技术学报, 2021, 36(11): 2277-2287.Yang Shengjie, Luo Bingyang, Wang Jing, et al.State of health estimation for lithium-ion batteries based on peak region feature parameters of incremental capacity curve[J].Transactions of China Electrotechnical Society, 2021, 36(11): 2277-2287.
[16] Rastegarpanah A, Hathaway J, Ahmeid M, et al.A rapid neural network-based state of health estimation scheme for screening of end of life electric vehicle batteries[J].Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2021, 235(3): 330-346.
[17] Zhou Ping, He Zhonglin, Han Tingting, et al.A rapid classification method of the retired LiCoxNiyMn1-x-yO2 batteries for electric vehicles[J].Energy Reports, 2020,6: 672-683.
[18] Fang Kaizheng, Chen Shi, Mu Daobin, et al.Investigation of nickel-metal hydride battery sorting based on charging thermal behavior[J].Journal of Power Sources, 2013, 224: 120-124.
[19] Garg A, Yun Liu, Gao Liang, et al.Development of recycling strategy for large stacked systems:experimental and machine learning approach to form reuse battery packs for secondary applications[J].Journal of Cleaner Production, 2020, 275: 124152.
[20] He Fengxian, Shen W X, Song Qiang, et al.Clustering LiFePO4 cells for battery pack based on neural network in EVs[C]//2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 2014: 1-5.
[21] Lü Chao, Song Yankong, Wang Lixin, et al.A new method for lithium-ion battery uniformity sorting based on internal criteria[J].Journal of Energy Storage, 2019, 25: 100885.
[22] Ran Aihua, Zhou Zihao, Chen Shuxiao, et al.Datadriven fast clustering of second-life lithium-ion battery: mechanism and algorithm[J].Advanced Theory and Simulations, 2020.3(8): 2000109.
[23] 来鑫, 陈权威, 邓聪, 等.一种基于电化学阻抗谱的大规模退役锂离子电池的软聚类方法[J].电工技术学报, 2022, 37(23): 6054-6064.Lai Xin, Chen Quanwei, Deng Cong, et al.A soft clustering method for the large-scale retired lithiumion batteries based on electrochemical impedance spectroscopy[J].Transactions of China Electrotechnical Society, 2022, 37(23): 6054-6064.
[24] 张娥, 徐成, 王晟, 等.基于模糊逻辑控制器的液态金属电池组两级均衡系统[J].中国电机工程学报,2020, 40(12): 4024-4033.Zhang E, Xu Cheng, Wang Sheng, et al.Two-stage equalizing system of liquid metal batteries based on fuzzy logic controller[J].Proceedings of the CSEE,2020, 40(12): 4024-4033.
[25] 李浩秒, 周浩, 王康丽, 等.液态金属电极的电化学储能应用[J].电化学, 2020, 26(5): 663-682.Li Haomiao, Zhou Hao, Wang Kangli, et al.Liquid metal electrodes for electrochemical energy storage technologies[J].Journal of Electrochemistry, 2020,26(5): 663-682.
[26] 蒋凯, 李浩秒, 李威, 等.几类面向电网的储能电池介绍[J].电力系统自动化, 2013, 37(1): 47-53.Jiang Kai, Li Haomiao, Li Wei, et al.On several battery technologies for power grids[J].Automation of Electric Power Systems, 2013, 37(1): 47-53.
[27] Yan Shuai, Zhou Xianbo, Li Haomiao, et al.Utilizing in situ alloying reaction to achieve the self-healing,high energy density and cost-effective Li||Sb liquid metal battery[J].Journal of Power Sources, 2021, 514:230578.
[28] Zhou Xianbo, Zhou Hao, Yan Shuai, et al.Increasing the actual energy density of Sb-based liquid metal battery[J].Journal of Power Sources, 2022, 534: 231428.
[29] 王大磊, 王康丽, 程时杰, 等.液态金属电池储能特性建模及荷电状态估计[J].中国电机工程学报,2017, 37(8): 2253-2261.Wang Dalei, Wang Kangli, Cheng Shijie, et al.Modeling of energy storage properties and SOC estimation for liquid metal batteries[J].Proceedings of the CSEE, 2017, 37(8): 2253-2261.
[30] Liu Guoan, Xu Cheng, Li Haomiao, et al.State of charge and online model parameters co-estimation for liquid metal batteries[J].Applied Energy, 2019, 250:677-684.
[31] Smola A J, Schölkopf B.A tutorial on support vector regression[J].Statistics and Computing, 2004, 14(3):199-222.
[32] Vapnik V N.The Nature of Statistical Learning Theory[M].New York: Springer, 1995.
[33] Chen Tianqi, Guestrin C.XGBoost: a scalable tree boosting system[C]//Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA,2016: 785-794.
[34] Breiman L.Random forests[J].Machine Learning,2001, 45(1): 5-32.
[35] Wolpert D H.Stacked generalization[J].Neural Networks, 1992, 5(2): 241-259.
[36] Pedregosa F, Varoquaux G, Gramfort A, et al.Scikitlearn: machine learning in python[J].Journal of Machine Learning Research, 2012, 12: 2825-2830.
[37] Cover T M, Thomas J A.Elements of Information Theory[M].2nd ed.New York: Wiley-Interscience,2005.
[38] Ferri F J, Pudil P, Hatef M, et al.Comparative study of techniques for large-scale feature selection[J].Machine Intelligence and Pattern Recognition, 1994,16: 403-413.
[39] Geurts P, Ernst D, Wehenkel L.Extremely randomized trees[J].Machine Learning, 2006, 63(1):3-42.