0 引言
有载分接开关(On-Load Tap Changer, OLTC)是换流变压器实现电压和功率调节功能的重要控制设备,在补偿交流电压波动、稳定直流电压等方面具有不可替代的作用[1]。近年来,部分高压直流换流站内换流变压器OLTC 在运行中突发级间短路故障,进而引起爆炸起火事故,严重威胁电力系统稳定运行[2-3]。由于OLTC 油室狭小、内部心体结构紧密,当发生低阻抗短路时,故障能量急剧释放将剧烈汽化分解绝缘油并导致油压骤升,一旦压力水平超过油室承压极限,OLTC 开裂爆炸将难以避免。
相比于常规电力变压器,换流变压器二次侧连接换流装置,其通断过程会导致网、阀侧端电流波形明显畸变[4-5]。同时,换流变压器OLTC 切换操作更为频繁,并且切换电流变化率大,切换过程恢复电压高,因而具有更高的故障概率和失效风险[6]。换流变压器OLTC 级间短路一般表现为油室中低阻抗电弧短接相邻两级导体,并经引线短接调压绕组两级,因此级间短路故障本质是短接绕组固定小匝数(1.25%或0.86%匝)的短路故障。此外,OLTC狭小油室和紧密机构将进一步加速故障发展,进而对继电保护装置的动作性能提出了更高的要求。
与交流系统中的常规电力变压器类似,换流变压器亦采用纵差动保护作为其电气量主保护[7-8]。作为差动保护动作特性分析的理论基础和重要前提,变压器内部绕组短路故障理论建模与仿真计算长期以来是业界研究的热点问题。文献[9]根据变压器铭牌参数,提出了短路电抗或漏电感矩阵线性拆分的自互感模型。这种方法计算效率高且大大简化绕组短路故障模型,因此被广泛应用于变压器内部短路故障分析与继电保护研究[10-12]。文献[13]通过解析计算建立了电力变压器内部各种短路故障下短路电抗的定量表达式,明确了短路电抗随故障位置变化存在的非线性关系。文献[14]基于时域场路耦合电磁模型分析了变压器绕组匝间短路条件下电流、磁通以及绕组受力的谐响应,并开展动模试验验证了方法的正确性与有效性。
在故障特征研究的基础上,一些学者进一步分析和讨论了不同条件下变压器差动保护的动作特性。文献[15-16]提出了电力变压器内部短路故障电路模型和分析方法,并根据仿真结果分析了现有差动保护的灵敏性问题。文献[17]建立了特高压变压器的动态仿真模型,分析比较了不同故障情况下各类差动保护的灵敏性。文献[18]研究了换流器非线性特征对换流变压器差动保护的影响,并分析了三种典型故障场景下保护的动作特性。文献[19]针对变压器差动保护采用的各种比率制动方式进行了对比分析,研究了区内故障时不同制动方式差动保护的灵敏性和安全性。上述研究成果为分析换流变压器OLTC 级间短路故障下差动保护的动作特性提供了有益借鉴。
目前,换流变压器OLTC 级间短路故障已经引起业界高度关注,现有录波数据表明差动保护在故障过程中存在灵敏性、速动性不足的问题。但是,由于缺少有效的理论模型及仿真手段,级间短路故障特征尚不明晰,针对差动保护动作特性的定量分析亦难以深入。基于此,本文从换流变压器OLTC典型过渡电路拓扑入手,分析OLTC 油中电弧引起级间短路的故障过程,建立含油中电弧时变电导特性的直接场-路耦合模型,仿真分析OLTC 不同分接位置短路故障下常用差动保护方案的动作性能。
1 OLTC 级间短路故障分析
作为换流变压器内部唯一常动部件,OLTC 通常承受着更为复杂的机械和电气应力。随着调压次数的增多,其不良操作和失效概率也相应增加[20-22]。级间短路故障是OLTC 电气故障的主要形式,其故障回路由OLTC 油室内部相邻两级间高能电弧、调压引线以及调压绕组故障段构成,如图1 所示。
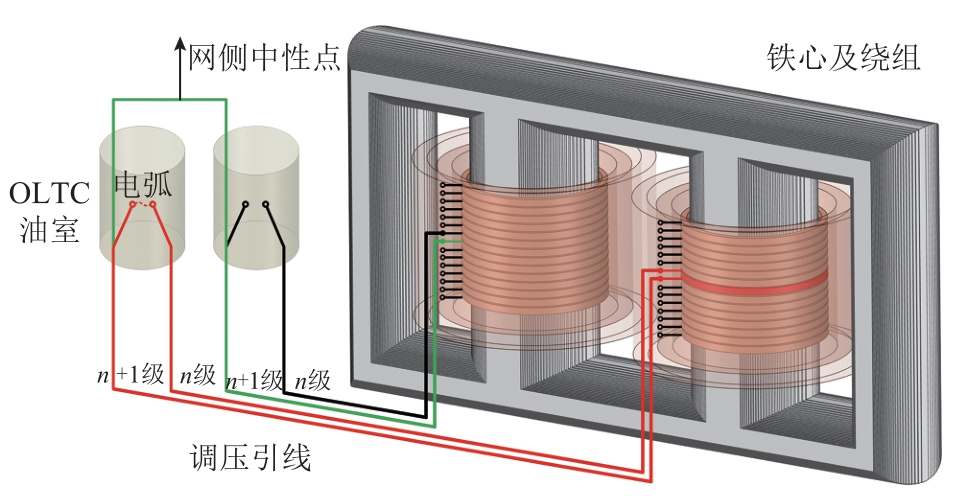
图1 换流变压器OLTC 级间短路故障示意图
Fig.1 Schematic diagram of a converter transformer intertap short-circuit fault inside the OLTC
图2 给出一种典型真空OLTC 过渡电路拓扑[23]和级间短路故障回路。多起换流变压器事故表明,级间短路故障通常发生在OLTC 切换操作完成后。在OLTC 正常切换时,主通断触头与过渡通断触头在真空泡中开断电流,有效地避免了油中拉弧引起的绝缘油碳化[24]。但是,OLTC 长期的带载切换存在触头磨损、机构卡涩、弹簧失能等风险,真空泡亦可能出现真空泄漏、波纹管损坏等问题。这都将导致OLTC 切换过程中转换开关被迫在油中带电拉弧。某次切换操作完成后,主转换开关相邻两级间突发低阻抗电弧放电,从而形成一条不经过过渡电阻的短路故障回路。短路环流isc 产生的巨大焦耳热将造成金属触头严重熔蚀和绝缘油剧烈汽化分解,最终导致切换心体损坏和OLTC 油室破裂爆炸。
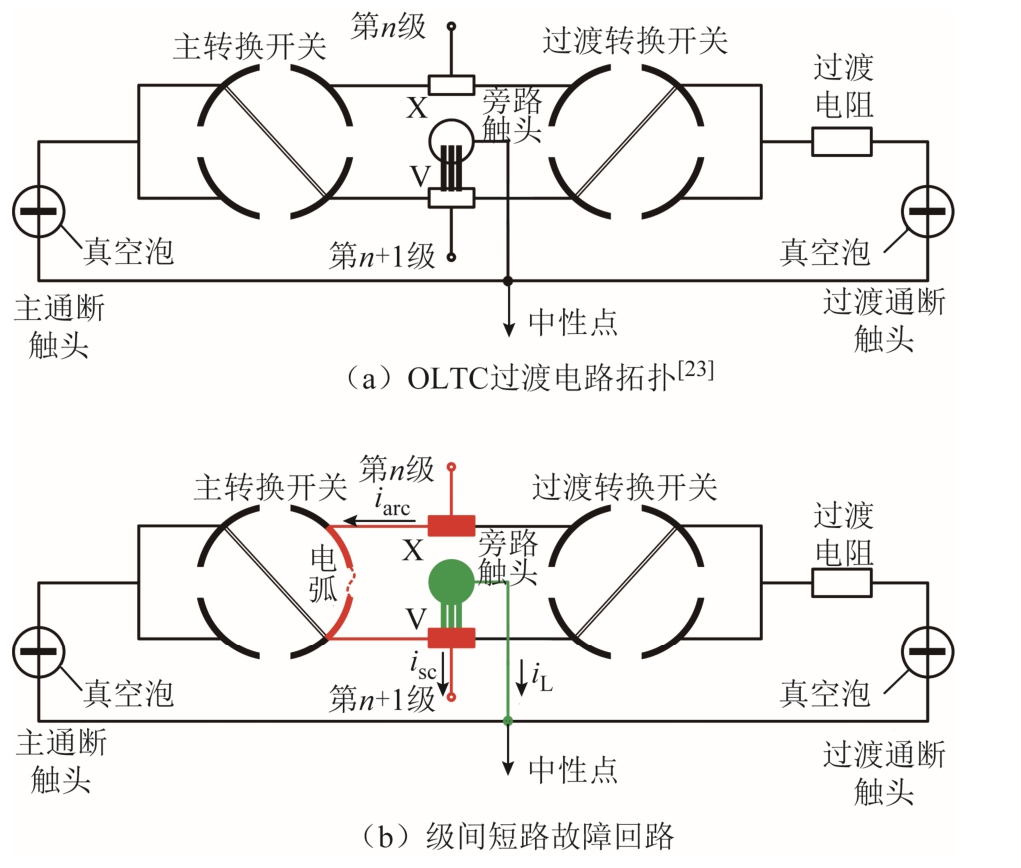
图2 OLTC 过渡电路拓扑和级间短路故障回路
Fig.2 Circuit topology and intertap fault loop of OLTC
2 数学模型
换流变压器发生OLTC 级间短路故障时,巨大短路电流流过调压绕组故障段,引起内部漏磁分布显著畸变,进而造成绕组漏感参数发生变化。在OLTC 油室内部,高能电弧短接相邻两级导体,其时变电导特性将显著影响短路电流。因此,OLTC 级间短路故障是一个复杂的场-路耦合物理问题,涉及绕组漏磁分布、外部电路拓扑以及故障点处油中电弧时变电导的相互作用。基于此,本章依次建立换流变压器内部电磁场方程、外部电路方程以及电弧电导微分方程,进而提出OLTC 级间短路故障直接场-路耦合模型。
2.1 电磁场-电路联合方程
基于Maxwell 方程组,换流变压器内部电磁场可用偏微分方程描述[25]为
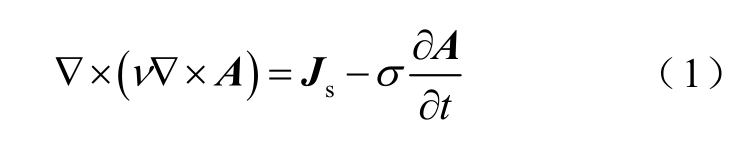
式中,ν为介质的磁阻率;A 为空间磁矢位;Js 为空间电流密度矢量;σ为介质的电导率;t 为时间。
在计算换流变压器内部磁通分布时,一般认为绕组为铰链导体而不考虑其中的涡流场[26]。此时适用于换流变压器绕组的三维电磁场方程可表示为[27]
式中,Js 为电流密度矢量,有

式中,N 为绕组中细导线总数;Is 为流入绕组的总电流;Ssc 为绕组的总截面积。
对于外部电路,模型的输入电压Ui 为绕组感应电压与外部电阻和电感上的总压降之和[26],即

式中,V 为三维电磁场求解域;R 为绕组直流电阻及外部电路总电阻之和;L 为外部电路的总电感。
联合式(2)~式(4),电磁场-电路统一矩阵方程为
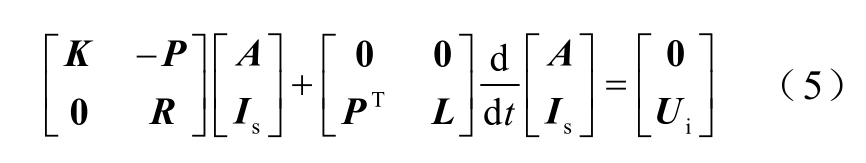
式中,K 和P 均为系数矩阵,由式(2)和式(3)中换流变压器绕组相关几何参数和材料属性决定。
2.2 电弧电导微分方程
不同于常规电力变压器绕组匝间、接地短路故障,换流变压器OLTC 级间短路故障回路不仅包含低阻抗故障电弧,还包含OLTC 内部触头和导体、调压引线以及调压绕组被短路段。因此,OLTC 级间短路故障回路电阻Rsc 可表示为
式中,Rc 为OLTC 内触头和导体电阻,在计算中可忽略不计;Rw 为调压引线电阻;garc 为故障电弧的时变电导,由非线性常微分方程描述。
封闭腔体内油中燃弧试验[28-29]表明,高能电弧剧烈汽化绝缘油并形成脉动增长的气泡,因此油中电弧本质上为气体电弧。目前常用的气体电弧黑盒模型有Cassie 模型[30]、Mayr 模型[31]、控制论模型[32]、Schavemaker 模型[33]等。经典Cassie 和Mayr 模型对于不同时刻下电弧特性的描述准确性不同[34-35],结合两者优势的Schavemaker 模型在电流零区参数的测量和选取方面亦存在局限性。考虑到级间短路环流峰值可达数十千安,且电弧电流过零存在暂态特征,本文选取基于电弧直径的改进电弧模型[36]模拟油中电弧的时变电导特性,通过引入随电流变化的电弧直径参数以实现对于大电流区故障环流的定量求解,以及电流零区暂态特征的准确描述。
基于电弧直径的电弧模型方程一般形式为[36]
式中,τ 为时间常数;uarc 和iarc 分别为电弧电压和电弧电流;Vs 为稳定燃弧区的弧柱压降,近似为常数;a 和c 均为附加校正因子;darc 为随电弧电流iarc变化的电弧直径,可按式(8)估计。
式中,b 和q 为常数参数。
将式(8)代入式(7),并将Vs、a、c、b、q 五个参数整理合并,得到更为简单的电弧微分方程表达形式为
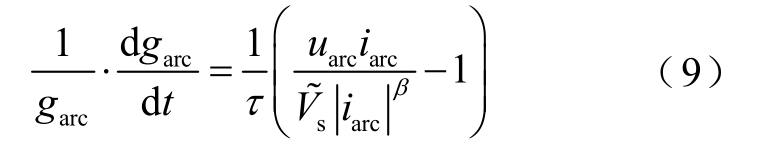
式中, sV˜和β 均为自由参数,其值根据油中电弧故障现场试验[28-29]所得电弧电压波形验证选取。
2.3 直接场-路耦合关系
换流变压器OLTC 级间短路故障直接场-路耦合关系如图3 所示。在每一时间步长下,换流变压器外部电路输入电流为内部铁心和绕组有限元模型提供激励,利用电磁场控制方程计算内部磁通分布并得到耦合接口处的感应电压;同时,电弧电压和短路电流作为变量代入电弧电导常微分方程,求解得到电弧时变电导。随后,将新生成的感应电压与电弧电导带入外部电路方程进行下一步运算。相比于场-路间接耦合法存在计算精度不足的问题,直接场-路耦合法能够实现每一时刻下电磁场与电路之间的双向数据交换,进而保证各部分模型间的瞬态同步求解。
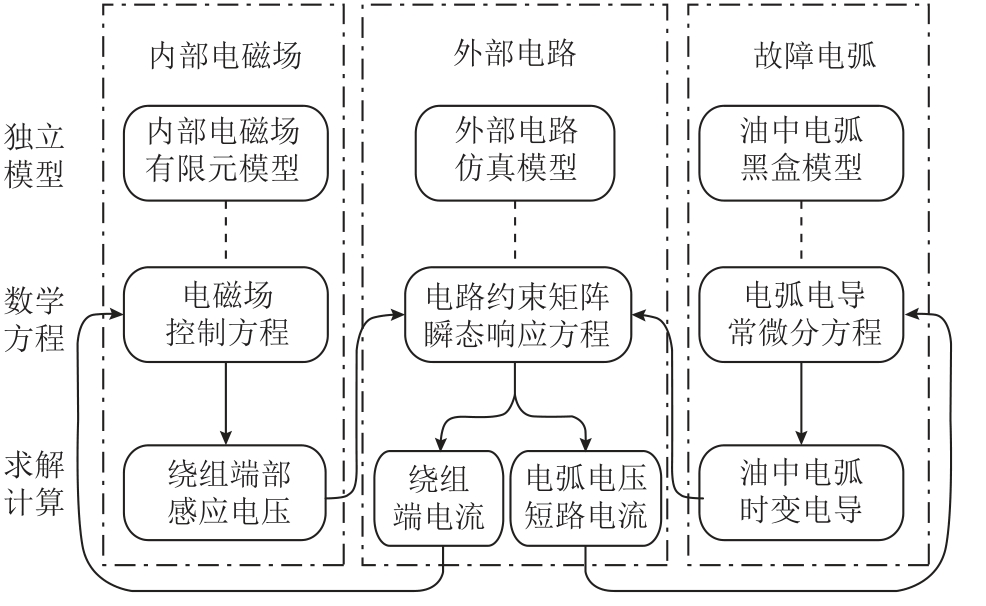
图3 直接场-路耦合关系
Fig.3 Direct field-circuit coupling relationship
3 级间短路故障建模与仿真
3.1 直接场-路耦合建模
以±800 kV 特高压直流换流站典型 ZZDFPZ-509400/500-400 单相两柱旁轭式换流变压器为研究对象,根据表1 中主要铭牌和几何结构参数建立换流变压器铁心和绕组三维模型并进行网格剖分,如图4 所示。模型中心柱和旁轭分别简化为圆柱体和椭圆柱体,心柱周围由内而外依次布置调压绕组、网侧绕组和阀侧绕组。网、阀侧绕组简化为完整同心圆筒结构,而调压绕组简化为14 段相同的同心圆筒结构,根据算例设置部分接入外电路。该型号换流变压器14 段调压绕组通过引线与OLTC 分接选择器相连,每条调压引线均采用长度为10 m、横截面积为240 mm2、电阻率为0.020 97 Ω·mm2/m 的电缆。此外,三维有限元模型包含262 249 个四面体网格单元,按照油箱尺寸设置边界并定义第一类边界条件。
表1 换流变压器主要铭牌和几何参数
Tab.1 Main nameplate and geometric parameters of the simulated converter transformer

参 数 数 值 参 数 数 值换流变压器型号 ZZDFPZ-509400/500 电压组合/kV 306(+23,-5)×1.25% / 99.77额定容量/(MV·A) 509.4 额定频率/Hz 50联结组标号 YNy0 冷却方式 ODAF空载电流(%) 0.15 空载损耗/kW 213短路电压(%) 21 负载损耗/kW 1 317油箱长度/mm 9 550 铁窗高度/mm 2 595油箱宽度/mm 3 165 铁窗宽度/mm 760油箱高度/mm 4 500 铁心柱直径/mm 1 400调压绕组高度/mm 1 315 网侧绕组高度/mm 1 615调压绕组内径/mm 1 474 网侧绕组内径/mm 1 798调压绕组外径/mm 1 602 网侧绕组外径/mm 2 130阀侧绕组高度/mm 1 795 调压绕组匝数 14×7阀侧绕组内径/mm 2 334 网侧绕组匝数 611阀侧绕组外径/mm 2 660 阀侧绕组匝数 179

图4 换流变压器铁心和绕组三维有限元模型
Fig.4 3-D finite-element model of core and windings inside the simulated converter transformer
换流变压器外部电路为等电压双12 脉动双极接线的±800 kV 特高压直流工程送端电网极Ⅰ换流系统,如图5 所示。极Ⅰ系统包含高端组和低端组两个12 脉动换流单元,各单元由Y/Y 和Y/D 两种接线的换流变压器组和换流阀组构成。各换流变压器组包含三台单相换流变压器,网侧出线接入500 kV交流母线,阀侧出线与六脉动换流装置相连。
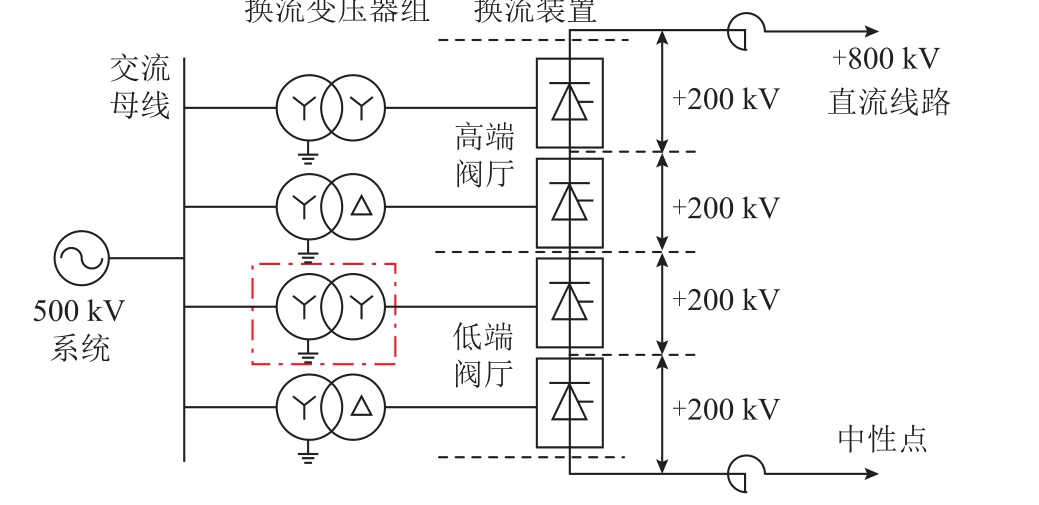
图5 ±800 kV 特高压直流工程送端电网极Ⅰ换流系统
Fig.5 Schematic diagram of the pole Ⅰconverter system in a ±800 kV UHVDC sending-end network
基于铁心和绕组三维有限元模型与外部电路拓扑,通过Ansys Maxwell 瞬态磁求解器与Simplorer瞬态仿真器开展级间短路故障瞬态协同仿真计算,实现耦合接口处的双向数据传输。参数设置如下:三相交流电源电压有效值Us=306 kV,调压引线电阻Rw=0.874 mΩ,电弧时间常数τ =38 μs,电弧自由参数为 sV˜=213 V、β=1.015,换流器触发角α=15°,平波电抗器Ld=75 mH,直流侧等效电阻Rd=140 Ω。
3.2 典型故障算例
本节以A 相换流变压器心柱2 绕组对应OLTC在t=40 ms 时突发+6/+7 级间短路故障为例,利用场-路耦合数值方法计算换流变压器故障前后内部磁场分布、短路电流、电弧电压以及端电流的变化。
换流变压器内部磁感应强度矢量三维分布和二维横截面磁通分布分别如图6 和图7 所示。图6a、图7a 中,正常运行时换流变压器内部漏磁近似为零,磁通线主要被约束在铁心内。t=40 ms 发生OLTC级间短路故障后,巨大短路电流在调压绕组中部感应出峰值达3.77 T 的横向漏磁,导致绕组整体磁通分布发生显著畸变,如图6b、图7b 所示。t=55 ms时,大量磁通线密集环绕于调压绕组故障段,附近漏磁强度峰值可达4.0 T。
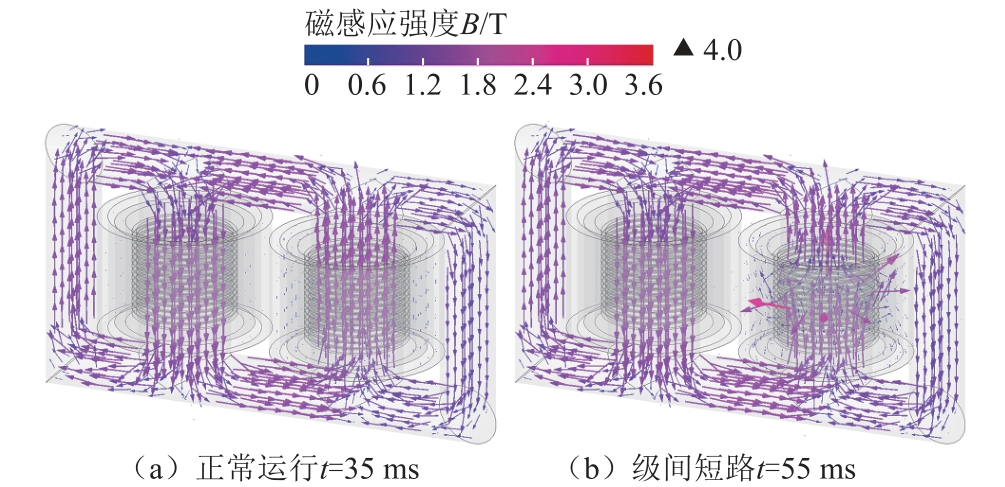
图6 换流变压器内部磁感应强度矢量三维分布
Fig.6 3-D magnetic vector flux distributions inside the simulated converter transformer

图7 换流变压器内部二维横截面磁通分布
Fig.7 2-D cross-sectional magnetic flux distribution inside the simulated converter transformer
短路电流、电弧电压及端电流仿真波形如图8所示。受换流阀通断影响,端电流不再为标准正弦波形,而在每个周波内呈现对称梯形波形。t=40 ms突发级间短路后,换流变压器内部显著的漏磁畸变将在故障段绕组上感应出巨大的反向电动势,并在故障回路中产生峰值达92.87 kA 的短路电流,电弧持续60 ms 内平均电弧电压为250.66 V。此时,A相换流变压器网侧电流由原来的梯形平顶波形变为三角形尖顶波形,其峰值从1.26 kA 上升到2.21 kA。此外,由于级间短路故障引起的电压比改变相对较小,阀侧端电流并未表现出明显变化。

图8 短路电流、电弧电压及端电流仿真波形
Fig.8 Simulation waveforms of the short-circuit current,the arc voltage and the terminal currents
为进一步探究不同级间短路故障下电气量的变化特征,在相同模型参数下对14 组不同分接位置级间短路故障开展仿真计算,得到短路电流峰值和网侧电流峰值增量随分接位置的变化规律,如图9 所示。
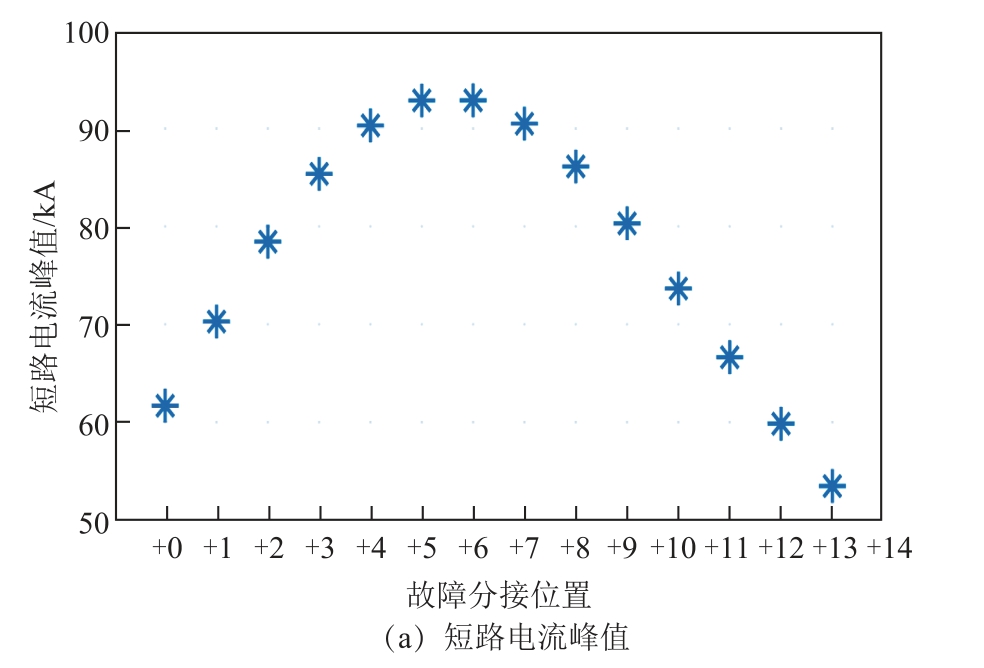

图9 不同分接位置故障下短路电流及端电流变化情况
Fig.9 Variations of short-circuit current and line-side current under faults between different taps
结果表明,OLTC 不同分接位置级间短路故障的严重程度存在显著差异。当故障发生在调压绕组中部对应分接位置+6/+7 时,短路电流峰值达到92.87 kA,同时网侧电流峰值增量也相应达到最大值75.40%。相对地,当下端部对应分接位置+13/+14 故障时,短路电流峰值为53.48 kA,仅为最严重条件下的58%。可以看到,不同分接位置短路故障电流峰值及网侧电流峰值增量呈现非对称分布特征,由于接入电路的调压绕组段数不同,上端部+0/+1 级间短路故障相较于下端部+13/+14 更为严重。
4 差动保护动作特性分析
换流变压器采用差动保护作为主保护,用于甄别绕组接地、匝间短路等内部故障[37]。本节针对主保护中比率差动、工频变化量比率差动及零序差动三种主要配置的保护方案进行动作特性分析。
4.1 比率差动保护
为避免外部故障等引起的误动,微机型变压器保护普遍采用具有比率制动特性的差动保护[38]。具有“三折线”制动特性的保护动作方程一般形式为
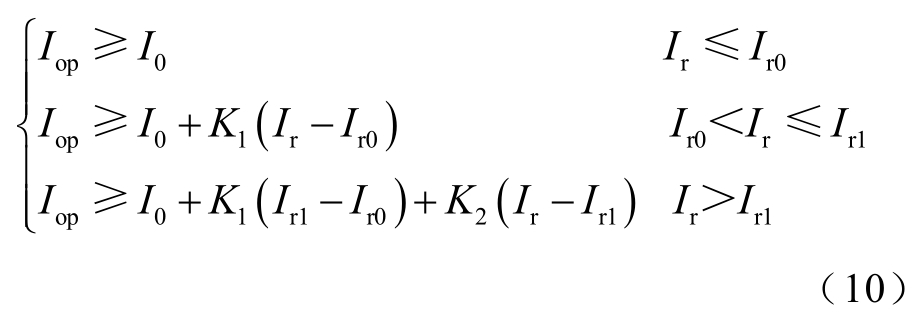
式中,Iop 为动作电流,是端电流相量和的有效值;I0 为启动电流;Ir 为制动电流,为端电流有效值的平均;Ir0、Ir1 为“拐点电流”;K1、K2 为制动系数。
以实际工程中两种常用的保护装置为例,对比率差动保护的动作特性进行分析。装置1 动作特性参数为:I0=0.2IN,Ir0=0.25IN,Ir1=0.5IN,K1=0.2,K2=0.5;装置2 动作特性参数为:I0=0.5IN,Ir0=2.5IN,Ir1=10IN,K1=0.2,K2=1。其中,IN 表示额定电流。
基于故障仿真结果,计算差动电流和制动电流及其对应的保护门槛,如图10 所示。t=40 ms 后,差动电流从零开始增加。由于故障导致的制动电流增长未超过2.5(pu),装置2 动作门槛恒保持在初始制动段。当t=57.6 ms 时,差动电流达到装置1 比率差动保护动作门槛,但全程未达到装置2 门槛,可见在该故障条件下装置2 因灵敏性不足而拒动。需要指出的是,OLTC 级间短路故障瞬时差动电流不具有励磁涌流所含二次谐波、电流间断角等特征,实际装置在闭锁元件开放保护后即可动作于跳闸。

图10 算例中端电流与比率差动电流曲线
Fig.10 Curves of terminal currents and ratio differential currents in the study case
为进一步分析两种装置在不同分接位置级间短路故障条件下比率差动动作特性,将3.2 节中14 组算例对应正常运行和故障条件下的工作点分别绘制于两种装置的比率差动动作平面上,比率差动保护动作特性平面及工作点分布如图11 所示。不同分接位置级间短路故障工作点在比率差动保护的动作特性平面上呈非对称分布。+13/+14 短路故障下差动电流的有效值为0.23(pu),对应于最低的故障工作点。正常运行时的工作点偏离集中分布区域,位于接近Ir 坐标轴的位置。
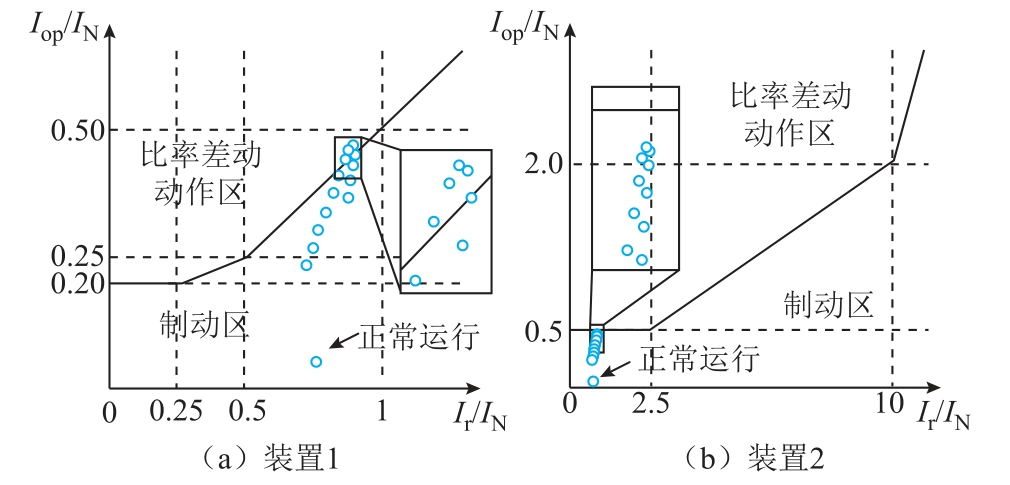
图11 比率差动保护动作特性平面及工作点分布
Fig.11 Operating characteristic plane and operating point distribution of ratio differential protection
通过比较工作点横坐标发现,与外部故障时制动电流不同,级间短路故障制动电流与正常运行时差别较小。对于拐点电流Ir0 大于1(pu)的装置2而言,其能否反映级间短路故障主要取决于初始制动段动作电流I0 的选取。当I0 取为0.5(pu)时,14 组级间短路故障算例下动作电流均未达到整定门槛。相比之下,装置1 在制动电流小于1(pu)部分的动作区域更大,能够反映+3/+4、+4/+5、+5/+6、+6/+7、+7/+8 共五组级间短路故障。但仍有其他9组故障情况落于动作区之外,此时保护将拒动。由此可见,对于换流变压器OLTC 级间短路故障,采用常规比率制动特性的差动保护存在灵敏性不足的问题。
4.2 工频变化量比率差动保护
由于常规比率制动式差动保护的制动电流包含正常运行时的负荷电流,发生绕组小匝数弱故障时制动电流过大将导致保护无法灵敏甄别。针对此问题,部分装置增设工频变化量比率差动保护[37],采用故障增量电流作为动作量和制动量,消除负荷电流影响以提高灵敏度。工频变化量比率差动保护中的动作量Iop 和制动量Ir 为
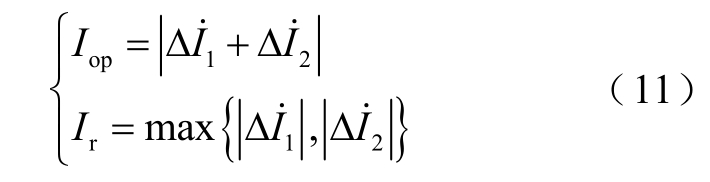
式中,ΔI1˙和ΔI2˙分别为两侧端电流工频变化分量。
工频变化量比率差动保护采用“两折线”或“三折线”制动特性。其中,“三折线”型动作方程满足式(10),其动作特性参数为:I0=0.2IN,Ir0=IN/3,Ir1=3IN,K1=0.6,K2=0.75。同时,常用“两折线”型工频变化量比率差动保护的动作方程为[37]
对于典型故障算例端电流仿真结果,根据式(11)计算得到工频变化量比率差动保护动作电流、制动电流以及其对应的保护门槛,如图12 所示。

图12 算例中端电流与工频变化量比率差动电流曲线
Fig.12 Curves of terminal currents and fault incremental ratio differential current in the study case
图12 中,工频变化量比率差动电流在故障后迅速升高并超过保护门槛。与常规比率差动保护相比,故障增量动作电流明显大于全量动作电流,且对于故障算例表现出更高的灵敏性。此外,动作电流在故障后5.6 ms 达到门槛,相较于比率差动保护缩短12 ms。需要指出的是,实际装置动作还须等待二次谐波制动、间断角闭锁等元件开放保护。
为分析OLTC 不同分接位置级间短路故障条件下工频变化量比率差动保护动作特性,将14 组算例对应工作点绘制于动作平面上。如图13 所示,不同分接位置级间短路故障的工作点在动作特性平面上呈直线分布。其中,最严重的+5/+6 和+6/+7 级间短路故障对应的工作点位于直线最高处,+13/+14 故障对应于直线的最低点,而正常运行时的工作点位于接近坐标原点的位置。对于14 组仿真算例,其故障工作点均落于动作特性平面的动作区内,保护正确动作。因此,采用故障增量电流作为判据的工频变化量比率差动保护的灵敏性与全量比率差动保护相比具有显著优势。
图13 工频变化量比率差动保护动作平面及工作点分布
Fig.13 Operating characteristic plane and operating point distribution of fault incremental ratio differential protection
4.3 零序差动保护
除配置比率制动式差动保护外,换流变压器还装设零序差动保护用于保护中性点接地的网侧绕组,其动作方程通常采用“两折线”制动特性,即
式中,K0 为制动系数,表征不同工况下保护的制动需求,一般取0.5~0.8[7]。
根据动作电流的不同,现有换流变压器零序差动保护方案主要分为两类,其保护判据选取的动作电流Iop 和制动电流Ir 分别可按式(14)和式(15)计算[7,39]。

式中,3 I˙0.s 为换流变压器网侧三相零序电流;3 I˙0.n 为网侧中性点零序电流。
本节针对采用这两类零序差动保护判据的两套装置进行讨论。采用第一类判据的保护装置动作特性参数为:I0=0.3IN,K0=0.5;采用第二类判据的保护装置动作特性参数为:I0=0.1IN,K0=0.8。
基于3.2 节故障仿真结果,计算网侧三相零序电流3 I˙0.s 以及中性点零序电流3I˙0.n ,得到零序差动电流和制动电流及其对应的保护门槛如图14 所示。级间短路故障下,虽然三台单相换流变压器短路电抗的不平衡使得中性点产生零序电流,但网侧绕组两端零序电流相量和恒定为零,即![]() 对于第一类判据,故障零序电流表现为穿越电流,对应动作电流恒定为零,保护拒动。第二类保护判据下动作电流为中性点零序电流,级间短路故障后动作电流快速上升,但全程均未达到保护门槛。
对于第一类判据,故障零序电流表现为穿越电流,对应动作电流恒定为零,保护拒动。第二类保护判据下动作电流为中性点零序电流,级间短路故障后动作电流快速上升,但全程均未达到保护门槛。

图14 算例中端电流与零序差动电流曲线
Fig.14 Curves of terminal currents and zero-sequence differential current in the study case
为分析不同分接位置级间短路故障下零序差动保护动作特性,将14 组仿真算例对应工作点绘制于两类零序差动保护的动作平面上,如图15 所示。
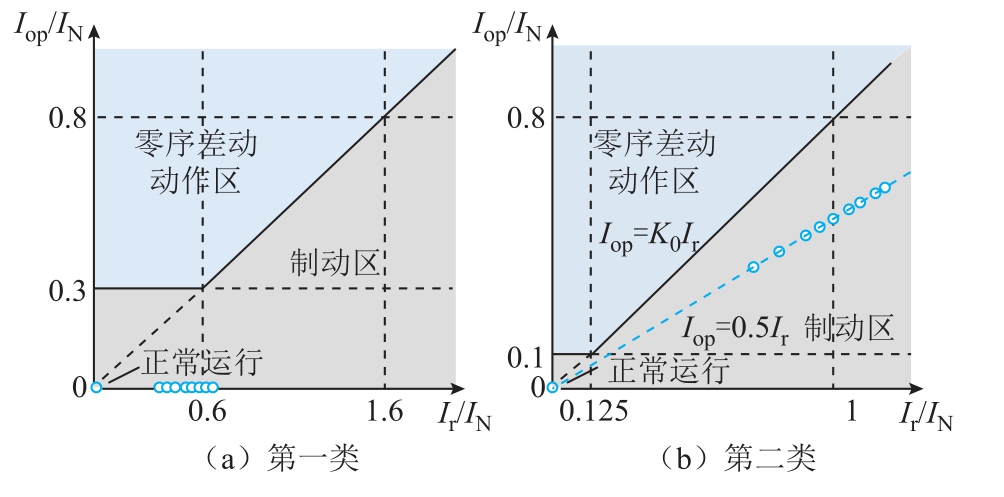
图15 零序差动保护动作特性平面及工作点分布
Fig.15 Operating characteristic plane and operating point distribution of zero-sequence differential protection
图15a 中,不同分接位置级间短路故障下第一类动作电流均为零,其故障工作点位于Ir 轴上,表明此类判据难以有效反映此类故障。对图15b 所示的第二类零序差动保护而言,14 组算例工作点同样均落于制动区。级间短路故障下,3 I˙0.s 与3I˙0.n 幅值相等、相位相反,制动电流在数值上始终等于动作电流的 2 倍,所以动作平面上14 组工作点沿直线Iop=0.5Ir 分布。该方案能否甄别级间短路故障主要取决于制动系数K0 的选取,实际工程中为避免保护误动通常满足K0>0.5,因此现有零序差动保护难以对OLTC 级间短路故障进行有效的判别和切除。
5 结论
近年来,国内相继发生的换流变压器OLTC 级间短路故障受到各方广泛关注,但由于缺少有效的级间短路故障模型和计算方法,目前此类故障下差动保护动作性能研究尚不充分。本文提出含电弧时变电导特性的换流变压器OLTC 级间短路故障直接场-路耦合模型及求解算法,以±800 kV 特高压直流换流站ZZDFPZ-509400/500-400 换流变压器作为研究对象,开展OLTC 级间短路故障建模仿真并定量分析比率差动、工频变化量比率差动及零序差动三种常用保护方案的动作特性。
结果表明,伴随OLTC 级间短路故障发生,换流变压器内部感应出大量横向漏磁并在短路环中产生严重故障环流。故障级位于绕组中部时,横向漏磁和短路环流最大,其峰值分别达到3.77 T 和92.87 kA。OLTC 不同分接位置级间短路故障下,采用端电流全量作为动作量和制动量的比率制动式差动保护存在灵敏性不足的问题,尤其面对故障段靠近绕组端部的情形存在拒动风险。由于故障下零序电流表现为穿越电流,现有零序差动保护亦难以有效反映此类故障。相比之下,采用故障增量电流的工频变化量比率差动保护对于OLTC 级间短路故障具有更高的灵敏度。
[1] 朱英浩, 沈大中.换流变压器用有载分接开关[M].北京: 中国电力出版社, 2016.
[2] 郭贤珊, 李凤祁, 阮思烨, 等.高压直流换流变压器有载分接开关控制优化[J].电力建设, 2021,42(2): 9-19.Guo Xianshan, Li Fengqi, Ruan Siye, et al.Optimization on control strategy of tap changer in HVDC converter transformer[J].Electric Power Construction, 2021, 42(2): 9-19.
[3] 徐海军, 王进, 廖文锋, 等.换流变有载分接开关非电量保护优化配置试验研究[J].变压器, 2021,58(10): 48-52.Xu Haijun, Wang Jin, Liao Wenfeng, et al.Experimental study on optimal configuration of pressure relief device, pressure and oil flow relay of on-load tap-changer[J].Transformer, 2021, 58(10):48-52.
[4] 杨帆, 池骋, 刘刚, 等.计及温度-电场强度非线性的换流变压器瞬态电场影响分析[J].电工技术学报, 2020, 35(23): 4971-4979.Yang Fan, Chi Cheng, Liu Gang, et al.Study on transient insulation condition of converter transformer based on nonlinearity between temperature and electric field[J].Transactions of China Electrotechnical Society, 2020, 35(23): 4971-4979.
[5] 黄天超, 王泽忠.特高压换流变压器拉板损耗的频率特性分析[J].电工技术学报, 2021, 36(19): 4132-4139.Huang Tianchao, Wang Zezhong.Frequency characteristic analysis of flitch plate losses in UHV converter transformer[J].Transactions of China Electrotechnical Society, 2021, 36(19): 4132-4139.
[6] 郑劲.换流变压器及监造技术[M].北京: 中国电力出版社, 2016.
[7] 翁汉琍, 林湘宁.换流站主设备保护关键技术研究[M].北京: 科学出版社, 2021.
[8] 楚皓翔, 宋宇, 李涵.500kV 变压器纵差保护试验方法[J].电气技术, 2022, 23(3): 87-91.Chu Haoxiang, Song Yu, Li Han.Test method of 500kV transformer differential protection[J].Electrical Engineering, 2022, 23(3): 87-91.
[9] Bastard P, Bertrand P, Meunier M.A transformer model for winding fault studies[J].IEEE Transactions on Power Delivery, 1994, 9(2): 690-699.
[10] Kezunovic M, Guo Yong.Modeling and simulation of the power transformer faults and related protective relay behavior[J].IEEE Transactions on Power Delivery, 2000, 15(1): 44-50.
[11] 王雪, 王增平.变压器内部故障仿真模型的设计[J].电网技术, 2004, 28(12): 50-52.Wang Xue, Wang Zengping.Study of simulation of transformer with internal faults[J].Power System Technology, 2004, 28(12): 50-52.
[12] 郝文斌, 李群湛.三相五芯柱变压器内部故障仿真模型研究[J].电力自动化设备, 2007, 27(8): 43-47.Hao Wenbin, Li Qunzhan.Simulation of internal fault of three-phase five-leg transformer[J].Electric Power Automation Equipment, 2007, 27(8): 43-47.
[13] 王赞基, 唐起超, 刘秀成.电力变压器内部短路故障对短路电抗的影响[J].中国电机工程学报, 2006,26(21): 15-21.Wang Zanji, Tang Qichao, Liu Xiucheng.Effects of internal short circuit faults on short circuit reactance of power transformer[J].Proceedings of the CSEE,2006, 26(21): 15-21.
[14] 潘超, 米俭, 王格万, 等.基于场路耦合的变压器绕组匝间短路电磁谐响应分析方法[J].电工技术学报, 2019, 34(4): 673-682.Pan Chao, Mi Jian, Wang Gewan, et al.Electromagnetic harmonic response analysis method of inter-turn short circuit in transformer winding based on field circuit coupling[J].Transactions of China Electrotechnical Society, 2019, 34(4): 673-682.
[15] 唐起超, 王赞基, 王维俭.多绕组电力变压器内部短路稳态分析 (一)建模与仿真[J].电力系统自动化, 2006, 30(10): 44-47, 74.Tang Qichao, Wang Zanji, Wang Weijian.Steadystate analysis of internal short circuits of multiwinding power transformer part I modeling and simulations[J].Automation of Electric Power Systems,2006, 30(10): 44-47, 74.
[16] 唐起超, 王赞基, 王维俭.多绕组电力变压器内部短路稳态分析 (二)实验验证与差动保护灵敏度分析[J].电力系统自动化, 2006, 30(11): 41-43, 66.Tang Qichao, Wang Zanji, Wang Weijian.Steadystate analysis of internal short circuits of multiwinding power transformer part Ⅱ experiment verification and sensitivity analysis of differential relay protection[J].Automation of Electric Power Systems, 2006, 30(11): 41-43, 66.
[17] 柳维衡, 郑涛.基于不同故障情况的特高压变压器差动保护仿真研究[J].现代电力, 2010, 27(1): 12-16.Liu Weiheng, Zheng Tao.Simulation research on UHV transformer DIFP based on different fault conditions[J].Modern Electric Power, 2010, 27(1): 12-16.
[18] 林磊, 陈川, 胡鑫, 等.不同故障下特高压换流变压器差动保护动作特性分析[J].电力系统保护与控制, 2017, 45(21): 123-133.Lin Lei, Chen Chuan, Hu Xin, et al.Research on the characteristics of ultra-high voltage converter transformer differential protection under the internal and external faults[J].Power System Protection and Control, 2017, 45(21): 123-133.
[19] 金瑞, 鲍斌, 时伯年.变压器差动保护的三种比率制动方式及其系数整定的研究[J].电力系统保护与控制, 2018, 46(19): 81-87.Jin Rui, Bao Bin, Shi Bonian.Research on three kinds of percentage restraint methods and their coefficient setting of transformer differential protection[J].Power System Protection and Control, 2018, 46(19): 81-87.
[20] 段若晨, 王丰华, 周荔丹, 等.利用窄带噪声辅助多元经验模态分解算法检测换流变压器用有载分接开关机械状态[J].电工技术学报, 2017, 32(10):182-189.Duan Ruochen, Wang Fenghua, Zhou Lidan, et al.Mechanical condition detection of on-load tapchanger in converter transformer based on narrowband noise assisted multivariate empirical mode decomposition algorithm[J].Transactions of China Electrotechnical Society, 2017, 32(10): 182-189.
[21] 张知先, 陈伟根, 汤思蕊, 等.基于互补集总经验模态分解和局部异常因子的有载分接开关状态特征提取及异常状态诊断[J].电工技术学报, 2019,34(21): 4508-4518.Zhang Zhixian, Chen Weigen, Tang Sirui, et al.State feature extraction and anomaly diagnosis of on-load tap-changer based on complementary ensemble empirical mode decomposition and local outlier factor[J].Transactions of China Electrotechnical Society, 2019, 34(21): 4508-4518.
[22] 马宏忠, 严岩.基于混沌理论和GOA-K-means 算法的有载分接开关状态特征分析计算方法[J].电工技术学报, 2021, 36(7): 1399-1406.Ma Hongzhong, Yan Yan.Analysis and calculation method of on-load tap changers state characteristics based on chaos theory and grasshopper optimization algorithm-K-means algorithm[J].Transactions of China Electrotechnical Society, 2021, 36(7): 1399-1406.
[23] 张德明.变压器真空有载分接开关[M].北京: 中国电力出版社, 2015.
[24] 贺博, 王鹏, 吴锴, 等.多物理场中染污绝缘油内杂质相动力学行为研究综述[J].电工技术学报,2022, 37(1): 266-282.He Bo, Wang Peng, Wu Kai, et al.Reviews on impurity phase dynamics in contaminated insulating oil under multi-physical field conditions[J].Transactions of China Electrotechnical Society, 2022, 37(1): 266-282.
[25] Kulkarni S V, Khaparde S A.Transformer engineering:design, technology, and diagnostics[M].2nd ed.Boca Raton, FL, USA: CRC Press, 2017.
[26] 赵博, 张洪亮.Ansoft 12 在工程电磁场中的应用[M].北京: 中国水利水电出版社, 2013.
[27] 李冰, 王泽忠, 刘恪, 等.特高压变压器直流偏磁对绕组电流的影响[J].电工技术学报, 2020, 35(7):1422-1431.Li Bing, Wang Zezhong, Liu Ke, et al.Research on winding current of UHV transformer under DC-bias[J].Transactions of China Electrotechnical Society, 2020,35(7): 1422-1431.
[28] Yan Chenguang, Zhou Xian, Xu Ya, et al.Experimental study on the gas bubble temperature around an arc under insulation oil[J].IEEE Transactions on Power Delivery, 2021, 36(2): 1245-1248.
[29] Yan Chenguang, Xu Ya, Zhang Peng, et al.Investigation of the gas bubble dynamics induced by an electric arc in insulation oil[J].Plasma Science and Technology, 2022, 24(4): 044003.
[30] Cassie A.Theorie nouvelle des arcs de rupture et de la rigidité des circuits[R].Ohio, USA: CIGRE, 1939.
[31] Mayr O.Beiträge zur theorie des statischen und des dynamischen lichtbogens[J].Archiv Für Elektrotechnik, 1943, 37(12): 588-608.
[32] Hochrainer A, Grütz A.Study of arcs in breakers with the help of a cybernetic model[R].Paris, France:CIGRE, 1972.
[33] Schavemaker P H, van der Slui L.An improved Mayrtype arc model based on current-zero measurements[J].IEEE Transactions on Power Delivery, 2000, 15(2):580-584.
[34] 王钢, 徐子利, 梁远升, 等.基于故障电弧方波曲线相似度的输电线路单端故障测距时域算法[J].电力系统保护与控制, 2012, 40(23): 109-113.Wang Gang, Xu Zili, Liang Yuansheng, et al.Single terminal time domain fault location method based on the similarity of square wave for arc grounding fault[J].Power System Protection and Control, 2012,40(23): 109-113.
[35] 许晔, 郭谋发, 陈彬, 等.配电网单相接地电弧建模及仿真分析研究[J].电力系统保护与控制, 2015,43(7): 57-64.Xu Ye, Guo Moufa, Chen Bin, et al.Modeling and simulation analysis of arc in distribution network[J].Power System Protection and Control, 2015, 43(7):57-64.
[36] Khakpour A, Franke S, Gortschakow S, et al.An improved arc model based on the arc diameter[J].IEEE Transactions on Power Delivery, 2016, 31(3):1335-1341.
[37] 中国南方电网超高压输电公司, 华南理工大学电力学院.高压直流输电系统继电保护原理与技术[M].北京: 中国电力出版社, 2013.
[38] 郑涛, 王增平, 翁汉琍.超/特高压变压器差动保护关键技术与新原理[M].北京: 科学出版社, 2017.
[39] 翁汉琍, 郭祎达, 李昊威, 等.涌流工况下换流变压器零序差动保护误动对策[J].电力系统自动化,2020, 44(23): 143-149.Weng Hanli, Guo Yida, Li Haowei, et al.Countermeasures for mal-operation of zero-sequence differential protection of converter transformer under inrush current condition[J].Automation of Electric Power Systems, 2020, 44(23): 143-149.