0 引言
随着电力系统（Electric Power System, EPS）和区域热力系统（District Heating System, DHS）之间的能量转换和信息交互日益频繁，电-热综合能源系统（Integrated Electricity and Heat System, IEHS）正快速发展[1]。在寒冷的冬季，中国北方地区主要由大型热电联产（Combined Heat and Power Unit, CHP）机组集中给用户供热。目前，大部分CHP 机组采用“以热定电”的模式，即电出力取决于热负荷。在满足热需求的同时，CHP 机组产生了富余电量，限制了风电的消纳空间。2020 年，全国平均弃风率为3%[2]。缓解弃风现象的关键是提高电力系统的灵活性。
松弛CHP 机组电出力和热出力的强耦合关系在一定程度上可以减少弃风。一种直接的方式是安装电锅炉[3]、热泵[4]和储热罐[5]等设备。电锅炉和热泵消耗电能，产生热能。储热罐可以存储热能。然而，这种方式需要新增建设成本。热力系统和电力系统在能量传输时长和动态过程等方面有很大差异。电力系统经济调度一般采用稳态潮流模型。在热力系统中，热源将水或蒸汽通过供热管网传输给用户，该过程具有明显的时间延迟和热量损耗。此特性，合称为“温度半动态特性”。通常采用“分块法”[6]和“节点法”[7]来刻画供热管网的“温度半动态特性”。文献[8]分析了电-热综合能源系统协同运行，但简化了热网模型，这可能导致总体经济效益低下并使优化问题不可行。文献[9]提出一种考虑“温度半动态特性”的热网等值模型，源荷之间形成端口映射。文献[10]进一步证明了热网等值模型的存在性。文献[11]在供热系统建模基础上，提出综合能源系统最优能流计算方法。文献[12]研究了电-热混合储能的多能互补协同削峰填谷策略。实际上，供热管网由许多绝热的管道组成，储能特性显著。
考虑供热管网储能特性的热电联合优化调度可以促进可再生能源消纳，降低电-热综合能源系统运行总成本[13]。热电联合优化调度可以分为集中式优化调度和分布式优化调度两种。集中式优化调度是将电力系统和热力系统合并成一个整体模型，在此基础上集中计算电-热综合能源系统最优调度[14]。集中式优化调度无需迭代，但双方均需要披露各自的拓扑结构、运行状态、网络参数等隐私信息。现实中的电力系统和热力系统隶属于不同管理主体。例如，北京市的供热网络由北京市热力集团有限责任公司独立运营；北京市电网由北京市电力公司管理。因此，集中调度不同的运营主体会存在制度壁垒、技术障碍和隐私泄露等问题。总之，集中式优化调度并非切实可行。
分布式优化调度可以充分保护不同主体隐私。根据迭代原理不同，分布式优化算法大体分为两类：原始问题分解算法和对偶问题分解算法[15]。文献[16]提出基于Bender 分解的热电联合调度。文献[17]介绍了交替方向乘子法（Alternating Direction Multiplier Method, ADMM）电-热综合能源系统分布式优化运行中的应用。最优性条件分解法（Optimality Condition Decomposition, OCD）通过最优化问题的Karush-Kuhn-Tucker 条件，在保证算法收敛性的前提下，双方只交互少量边界耦合信息[18]。文献[19]提出基于异质分解（Heterogeneous Decomposition,HD）的电-热综合能源系统分布式优化调度。文献[20]提出光伏-储能-热电联产综合能源系统分解协调优化运行。然而，上述研究均忽视了不同主体间的激励相容（Incentive Compatibility, IC）[21]。
热电联合优化调度通常基于集体理性（Collective Rationality, CR），即最大化电力系统和热力系统总效用（Total Utility, TU）。相对热电单独优化调度，热电联合优化调度会使电-热综合能源系统总成本减少，但同时会让热力系统的个体利益受损。具体地讲，热电联合优化调度需要热力系统充分利用供热管网储能特性来提高电力系统灵活性，偏离了热力系统独立调度的最优策略。供热管网需要升高温度，造成了更多热损失，进而使热力系统运行总成本增多。基于个体理性（Individual Rationality, IR）假设，热力系统没有动力参与合作。因此，基于整体优化（Holistic Optimization, HO）的热电联合优化调度不是激励相容的。
为了实现激励相容，现有研究分为两大类：市场博弈方法（Market Game Method, MGM）[22-23]和转移支付方法（Transfer Payment Method, TPM）。在市场博弈方法中，将热电联合优化调度作为一个市场博弈，交替计算电力系统优化调度和热力系统优化调度，更新价格信号，直至寻找到平衡点，例如纳什均衡（Nash Equilibrium, NE）点。在转移支付方法中，电力系统分享一些合作剩余（Cooperative Surplus, CS）给热力系统，使双方的运行总成本均减少。文献[24]中，电力系统通过分享部分可再生能源消纳的收益给热力系统来促进合作。然而，合作剩余最优分配比例的计算相对复杂，不易操作。文献[25]提出计及激励型综合需求响应的电-热综合能源系统日前经济调度。在合作博弈中，纳什议价（Nash Bargaining, NB）是一种分配合作剩余的重要方式[26]。文献[27]考虑了不确定性的电-热-氢综合能源系统规划。文献[28]提出计及综合能效的电-气-热综合能源系统多目标优化调度。文献[29]讨论了含多能微网群的区域电热综合能源系统分层自治优化调度。
本文提出一种基于Benders 分解和纳什议价的电-热综合能源系统分布式优化调度方法。首先，热力系统与电力系统依次计算最优热流和最优功率分配，分别得到各自独立调度的运行总成本；然后，利用 Benders 分解计算电-热综合能源系统最优能流，相应得出电-热综合能源系统运行总成本，电力控制中心和热力控制中心只需要交互少量边界耦合信息，充分保护了不同主体的隐私，此外，本文严格证明了相对热电单独优化调度，热电联合优化调度使电力系统运行总成本减少，同时使热力系统运行总成本增多；最后，通过纳什议价分配合作剩余，使电力系统和热力系统运行总成本均减少，即实现激励相容。
1 热力系统模型
热力系统主要由热源（CHP 机组、锅炉等）、供热管网、热负荷组成。
1.1 CHP 机组模型
CHP 机组主要分为背压式机组和抽凝式机组两种。CHP 机组的电出力和热出力的可行域可以近似描述为多边形区域。背压式机组电出力和热出力成正相关，可行域是一条线段。抽汽式机组的可行域是四边形。CHP 机组出力可以通过多边形区域凸组合表示。
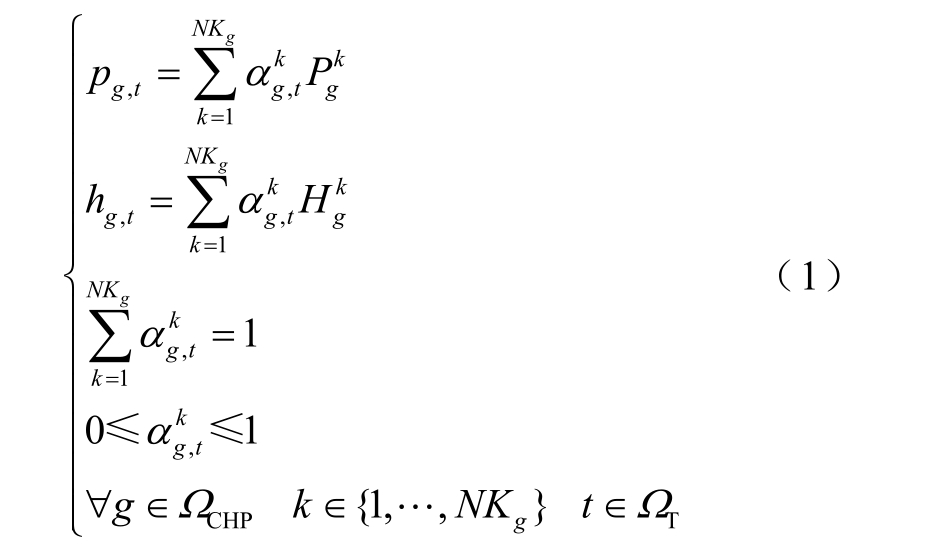
式中，pg,t、hg,t 分别为第g 台CHP 机组在t 时刻的电、热出力；(Pgk, Hgk)为第g 台CHP 机组对应的第k 个极点坐标；αkg,t 为第g 台CHP 机组在t 时刻对应的第k 个极点的凸组合系数；NKg 为第g 台CHP机组运行可行域的极点个数；ΩCHP 为CHP 机组集合；ΩT 为调度时段集合[30]。
1.2 供热管网模型
在供热管网模型中，重点描述供热管网的温度半动态特性[10]。供热管网可以分为一次管网和二次管网。一次管网类似输电网，二次管网类似配电网。热源利用一次管网将高温水或蒸汽传送至换热站，换热站通过二次管网将低温水传送至热用户。供热管网一般有“质调节”（Constant Flow-Variable Temperature, CF-VT）和“量调节”（Variable Flow-Constant Temperature, VF-CT）两种。“质调节”是保持供热管网的流质流量不变，通过改变供热管网的供热水温来满足用户热需求；“量调节”是指保持供热管网的供热水温不变，通过改变网络中的流质流量来满足用户热需求[31]。本文主要研究一次管网和“质调节”。
在本文中，热源包括CHP 机组和锅炉，有
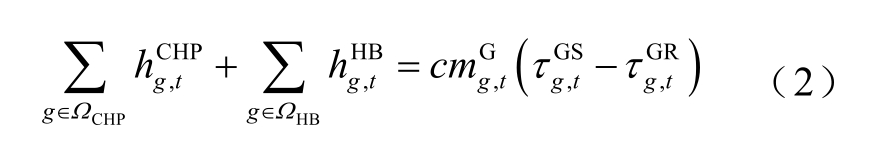
式中，
为第g 台CHP 机组在t 个调度时段的热出力；
为第g 台锅炉在第t 个调度时段的热出力；c 为比热容； 
为第g 个热源在第t 个调度时段的质量流量；
分别为第g 个热源在第t个调度时段的供、回水温度。其次，锅炉热出力须满足上、下限约束，即
式中，
为热出力上限。
热负荷： ∀d ∈ Ω H D， t∈Ω T
式中，
为第d 个热用户在t 个调度时段的热负荷； 
为第d 个热用户在第t 个调度时段的质量流量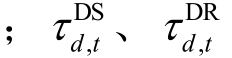
分别为第d 个热用户在第t 个调度时段的供、回水温度；ΩHD 为热负荷集合；ΩHB 为锅炉集合。
本文采用“节点法”刻画供热管网温度半动态特性。“节点法”的基本思想：①在忽略热损耗的条件下，用过去不同调度时段管道入口温度的线性组合表示当前调度时段管道出口温度；②在考虑热损耗的条件下，对当前调度时段管道出口温度进行修正。
在忽略热损耗的条件下，用过去不同调度时段管道入口温度的线性组合表示当前调度时段管道出口温度，即
式中，
分别为忽略热损耗时，第b 条供、回水管道在第t 个调度时段的出口温度；φb, t 为第b 条管道第t 个时段延时时段数；K 为表征传输时延的变量，定义相对复杂，具体内容可以参考文献[32]，不再赘述。
在考虑热损耗的条件下，对当前调度时段管道出口温度进行修正，有
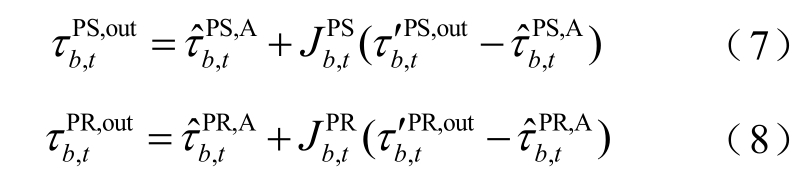
式中，
分别为在考虑热损耗前提下，第b 条供、回水管道在第t 个调度时段的出口温度；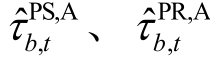
分别为第b 条供、回水管道在第t 个调度时段的环境温度；J 为表征热能损耗的变量，定义相对复杂，具体内容可以参考文献[32]，不再赘述。
根据能量守恒定律，不同管道的流质在同一节点混合后的温度需要满足
式中，
分别为第b 条管道在第t 个调度时段的供、回水温度
分别为第i 个节点在第t 个调度时段的供、回水温度；
分别为以第i 个供热网络节点为终点和起点的供热管道集合；iG 为与第i 个供热网络节点连接的热源集合；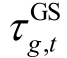
为第g 个热源在第t 个调度时段的供水温度； iD 为第i 个供热网络节点连接的热负荷集合。
从网络节点流出的的流质温度等于该网络节点的温度，即
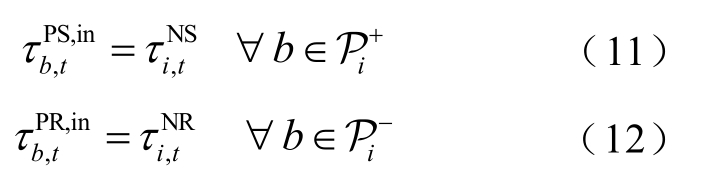
式中，
分别为第b 条供、回水管道在第t 个调度时段的入口温度。
热源和热负荷的温度等于该网络节点的温度，即
节点温度必须满足上、下限约束，即
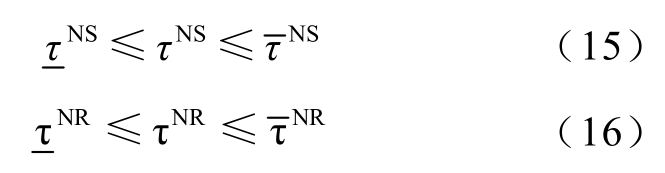
2 热电优化调度模型和求解方法
热电优化调度模型包括热电单独优化调度模型和基于Benders 分解的热电联合优化调度模型。在热电单独优化调度模型中，首先计算热力系统最优热流；然后将求解得到的CHP 机组的热出力传送给电力控制中心；最后计算电力系统最优功率分配。在基于Benders 分解的热电联合优化调度模型中，满足电力系统、热力系统和热电耦合约束下，计算电-热综合能源系统最优出力分配[33]。
2.1 热力系统最优热流计算
热力系统最优热流计算以最小化锅炉运行成本和购热成本为目标，在满足热力系统安全运行约束下，优化锅炉和从CHP 机组购买的热量。
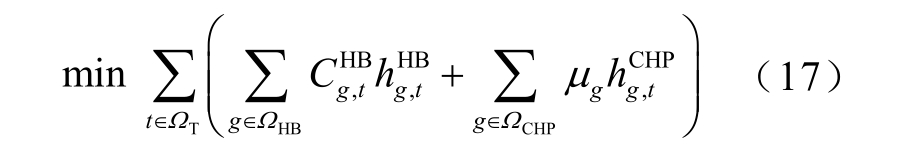
式中， 
为第g 台锅炉在第t 个调度时段的成本系数； 
为第g 台锅炉在第t 个调度时段的热出力；μg 为第g 台CHP 机组出售热量的单价；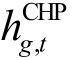
为第g 台CHP 机组在第t 个调度时段的热出力。约束条件：式（1）～式（16）。将热力系统最优热流计算得到的CHP 机组热出力记为
。
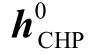2.2 电力系统最优调度计算
热力系统最优热流计算结束后，热力控制中心将CHP 机组热出力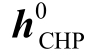
传送给电力控制中心。电力系统最优调度计算[34]以最小化火电机组运行成本、CHP 机组运行成本、弃风成本等为目标。在满足电力系统安全运行约束下，优化火电机组、CHP 机组和风电场的电出力。
式中，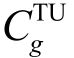 
为第g 台火电机组的运行成本；
为第g 台CHP 机组的运行成本； 
为第g 个风电场的弃风成本。
火电机组运行成本 
是关于电出力pg,t 的二次函数， ∀ g ∈ ΩTU ，有
式中，b0,g、b1,g 和b2,g 分别为常数项系数、一次项系数和二次项系数。
CHP 机组的运行成本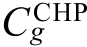
是关于电出力pg,t 和热出力hg,t 的二次函数，有
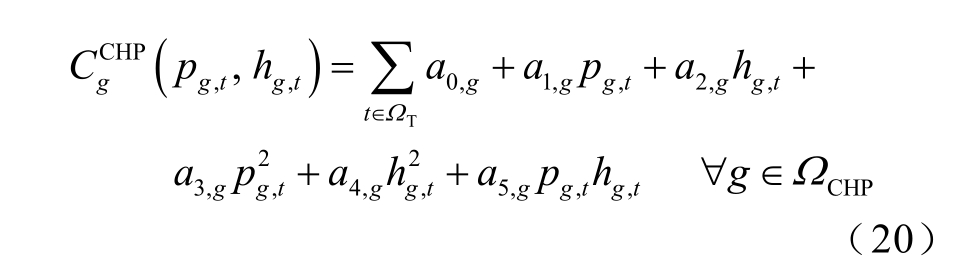
式中，a0,g、a1,g、a2,g、a3,g、a4,g 和a5,g 为CHP 机组的运行成本函数常系数。
弃风成本
， ∀g ∈ Ω wind，有
式中，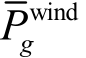
为第g 个风电场在第t 个调度时段的出力预测值； 
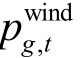第g 个风电场在第t 个调度时段的实际出力；σg 为第g 个风电场的弃风惩罚因子；Ωwind为风电场集合。
电力系统采用直流潮流模型。有功平衡约束为
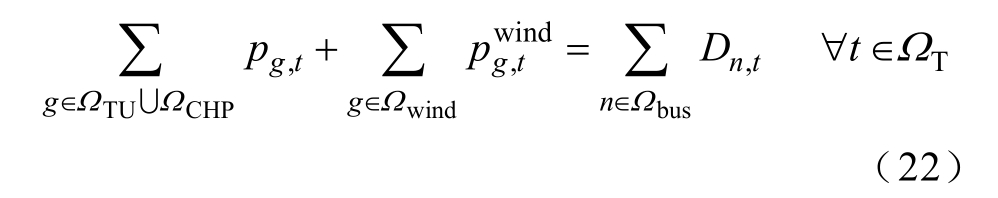
式中， Ωbus 为母线集合。
旋转备用约束为
式中，rug,t 和rdg,t 分别为第g 台火电机组在第t 个调度时段的向上、向下旋转备用容量；SRup 和SRdown分别为电力系统向上、向下旋转备用容量约束。
爬坡约束： ∀g ∈Ω TU ∪Ω C HP ,t ∈Ω T
式中，RUg 和RDg 分别为第g 台机组的向上和向下爬坡速率。
网络约束： ∀l∈Ω li ne ,t∈Ω T
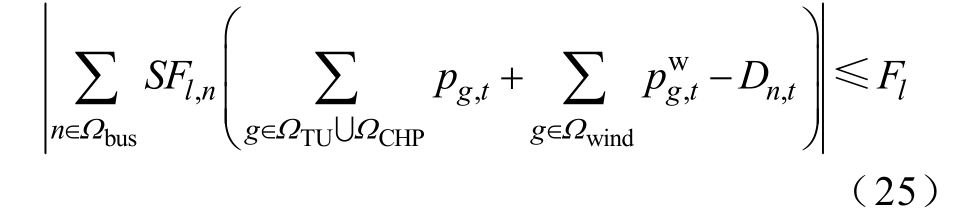
式中，SFl,n 为电力系统第l 条线路潮流对第n 条母线注入功率的转移分布因子；Fl 为电力系统第l 条线路的传输容量；Ωline 为电力系统线路集合。
火电机组和CHP 机组出力限制约束为
风电场出力限制约束为
2.3 基于Benders 分解的热电联合优化调度
基于Benders 分解的热电联合优化调度包括电力系统调度主问题和热力系统调度子问题[16,35-37]。在电力系统、热力系统和热电耦合约束下，优化机组的电出力和热源的热出力，最小化电-热综合能源系统运行总成本。具体形式为
式中， Ex 为电力系统内部变量； xH 为热力系统内部变量； hCHP为CHP 机组热出力。
记目标函数f = [C(xH)+ C(hCHP)]+[C(xE, hCHP)-C(hCHP)]。热力系统运行总成本[C(xH)+ C(hCHP)]对应式（17）。电力系统运行总成本[C(xE, hCHP)-C(hCHP)]对应式（18）。电力系统约束式（29）对应式（1）、式（22）～式（27）。热力系统约束式（30）对应式（3）～式（16）。热电耦合约束式（31）对应式（2）。
1）优化电力系统调度主问题
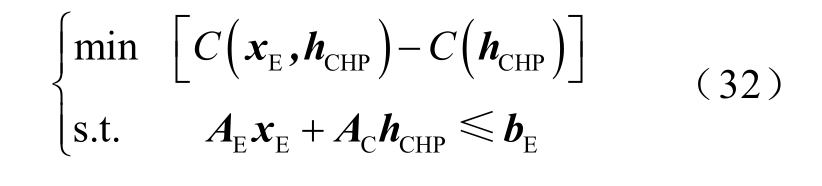
将CHP 机组热出力h'CHP传送给热力控制中心。
2）优化热力系统调度子问题
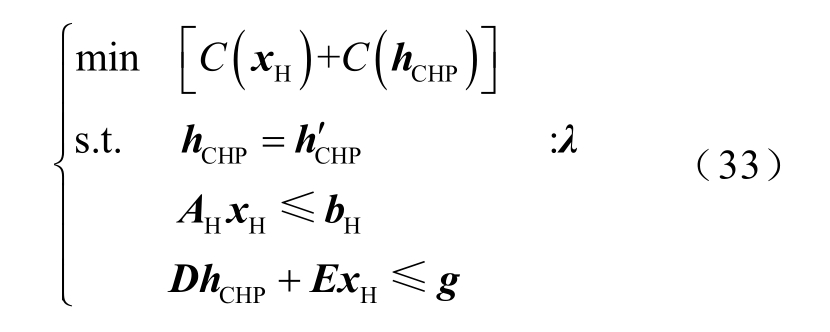
式中，λ 为 hC HP =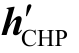
处的对偶乘子。
（1）若子问题可行，则热力控制中心生成一个最优割平面，记为ηH≥AOChCHP + bOC，将其传送给电力控制中心。
若子问题不可行，则构造松弛子问题为
式中，σ 为松弛变量；ω、π 和β 分别为最优解处的对偶乘子。将松弛子问题写成拉格朗日函数，有
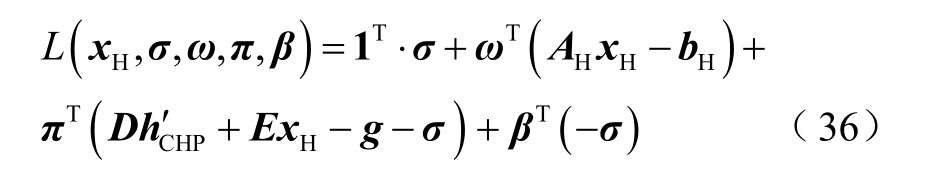
由KKT 条件可知
若子问题不可行，则松弛子问题的最优解大于0。根据强对偶定理，对偶问题的最优解大于0。
（2）若子问题不可行，则生成可行割平面AFChCHP≤bFC，并将其传送给电力控制中心。
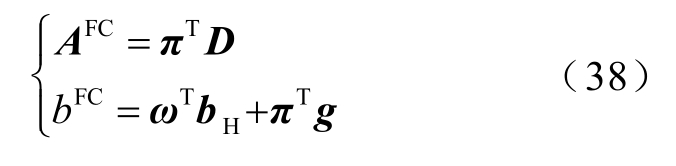
3）电力控制中心接受最优割平面或可行割平面，形成增广电力系统调度主问题。
综上所述，基于Benders 分解的热电联合优化调度可以通过图1 所示算法框图求解。其中，ε 为收敛阈值，k 为迭代次数。
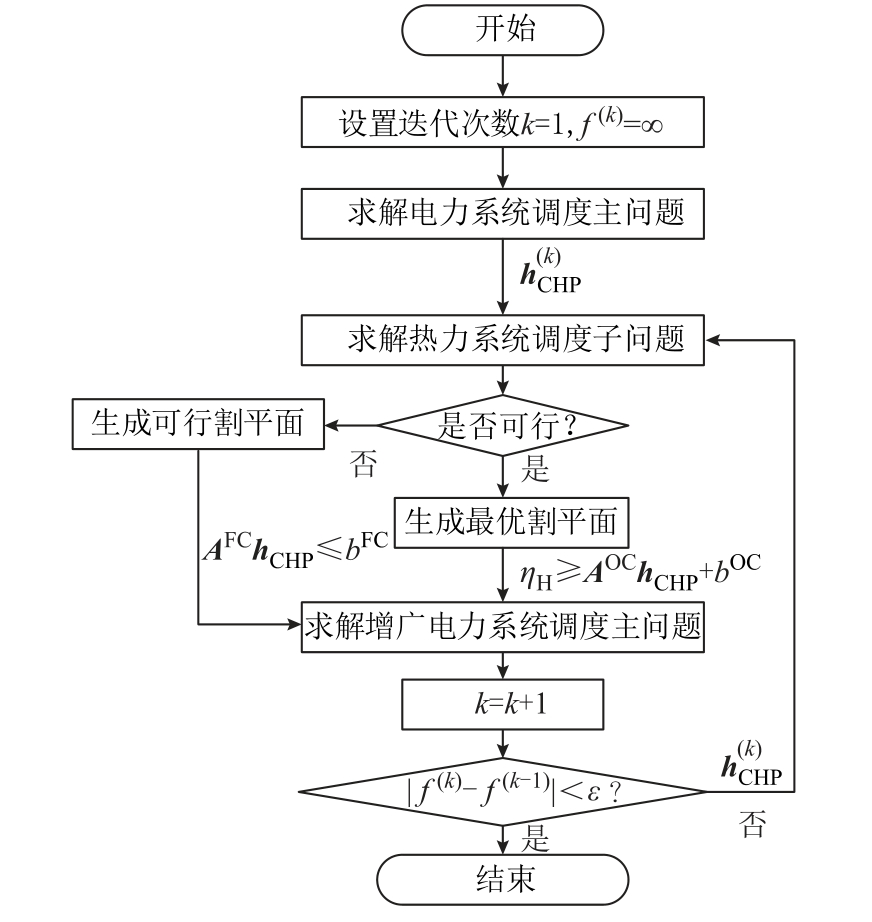
图1 基于Benders 分解的热电联合优化调度框图
Fig.1 Flow chart of combined heat and power optimal scheduling based on Benders decomposition
3 基于纳什议价分配合作剩余
首先，严格证明热电联合优化调度使电力系统运行总成本减少，但使热力系统运行总成本增多。因此，电力系统需要给热力系统合理的转移支付。然后，基于纳什议价按边际贡献分配合作剩余，使得电力系统和热力系统的运行总成本均减小，从而促进电力系统和热力系统合作，实现激励相容。
3.1 转移支付的必要性
在热电单独优化调度中，首先计算热力系统最优热流；然后将CHP 机组的热出力h0CHP 作为边界耦合变量传送给电力控制中心；最后计算电力系统最优出力。在热电联合优化调度中，一次性计算电-热综合能源系统最优功率分配。相对热电单独优化调度，热电联合优化调度会使电-热综合能源系统总成本减少，但是热力系统总成本增多。为了促进合作，电力系统需要和热力系统分享一部分合作剩余。换句话说，电力系统需要给热力系统提供一定的转移支付，使得两者的总成本均减少，实现激励相容。
接下来，证明转移支付的必要性[33]。热力系统最优热流计算为
式中，令CH = C(xH)+ C(hCHP)，C(xH)为热力系统单独优化调度成本，C(hCHP)为热力系统从电力系统的购热成本；CH 为热力系统运行总成本；ΩH 为热力系统最优热流约束条件。记
和
为优化问题式（40）的最优解，热力系统单独优化调度的最小总运行成本为 
。
热力控制中心将热力系统最优热流计算后得到的CHP 机组热出力
作为边界耦合变量传送给电力控制中心，计算电力系统最优功率分配，即
式中，CE=C(xE, hCHP)- C(hCHP)，C(xE, hCHP)为电力系统单独优化调度成本，- C(hCHP)为电力系统的售热利润，CE 为电力系统运行总成本；ΩE 为电力系统最优调度约束条件。记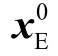
和
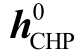为优化问题式（41）的最优解，电力系统单独调度最小总运行成本为 
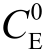。电-热综合能源系统最优调度计算式为
统单独优化调度，热电联合优化调度使电力系统运行总成本减少。综上所述，从个体理性角度考虑，热力系统没有意愿参与热电联合优化调度。电力系统需要给热力系统相应的转移支付，才能激励热力系统和电力系统合作。
3.2 转移支付的计算
经过3.1 节的证明，热电联合优化调度在最大化总体效用时，忽视了个体理性。具体地讲，热电联合优化调度使电力系统运行总成本和热力系统运行总成本之和减少，但热力系统运行总成本反而增多。基于经济学中个体理性的假设，热力系统不愿意与电力系统合作。若要鼓励热力系统参与到热电联合优化调度中，则需要使热力系统运行总成本也相应减少。在热电联合优化调度后，电力系统给热力系统适当的转移支付，可以同时减少双方的运行总成本，实现激励相容。
电力系统和热力系统可视为不同参与者，热电联合优化调度则可视为合作博弈。合作博弈的结果是形成联盟，关键要素是理性和收益[38]。相对热电单独优化调度，热电联合优化调度产生了ΔC 的合作剩余。纳什议价是合作博弈中分配剩余的一种重要方法，其基本思想是根据参与者边际贡献进行利益分配。纳什谈判解建立在以下三个公理化条件之上：①帕累托有效；②线性转换不变性；③对非相关选择的独立性[37]。
热电联合优化调度纳什议价图解如图2 所示，结合图2 描述电力系统和热力系统的纳什谈判过程。
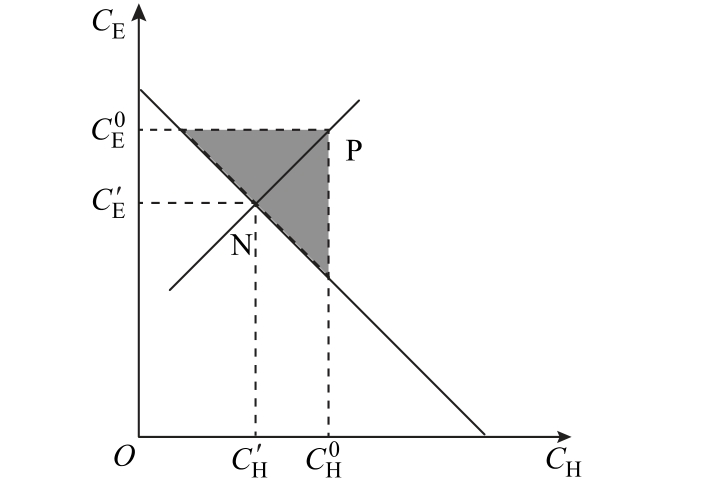
图2 热电联合优化调度纳什议价图解
Fig.2 Schematic diagram of Nash bargaining for combined heat and power optimal scheduling
在图2 中，横坐标CH 代表热力系统成本数额，纵坐标CE 代表电力系统成本数额。若热力系统和电力系统未能达成协议，采取不合作策略，即热力系统和电力系统依次单独调度,则对应谈判破裂点P，此时双方成本记为(
)。实际上，( 
)并不是帕累托最优的，图中阴影部分是帕累托改进空间。因为存在帕累托改进空间，所以热电联合优化调度才有价值。
记热电联合优化调度后的纳什议价谈判点为N，此时双方成本记为( 
)。其中，
分别是热力系统运行总成本和电力系统运行总成本。具体地讲，
α 和1-α分别为热力系统和电力系统的谈判力或边际贡献率。某个参与者边际贡献指他参与合作和不参与合作产生的剩余之差。某个参与者的边际贡献率是指他的边际贡献在总的边际贡献中所占的比例。热力系统和电力系统的边际贡献是一样的，均为ΔC。缺少任何一方合作，电-热综合能源系统运行总成本会增加ΔC。
若纳什议价可以到达一个均衡点，则它是双方均以最小化自身成本为目的进行讨价还价的结果。从直觉上讲，该均衡点应该使双方都离开各自谈判破裂成本最远。因此，基于纳什议价的热电联合优化调度转移支付计算可以转换为以下问题[39]：
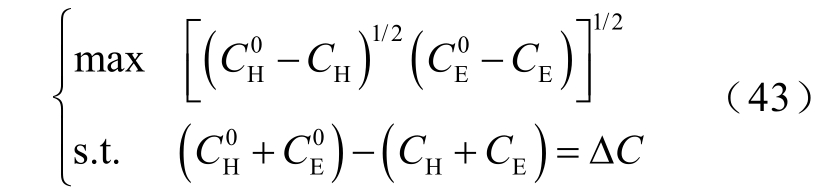
优化问题式（43）旨在合作剩余基础上最大化二者距离乘积，其最优解为
当两个参与者的边际贡献相等时，合作带来剩余收入应该平均分配。( CH′ , CE′)是帕累托最优的，因为电力系统和热力系统都不可以在不损害他人利益的情况下减少自身成本。通过纳什议价，电力系统和热力系统可以组成稳定联盟，即形成热电联合优化调度。
不同调度模式下的经济效益见表1。表1 是对3.1 节和3.2 节的总结：热电联合优化调度会使电-热综合能源系统运行总成本减少，但是造成热力系统运行总成本增多。基于纳什议价分配合作剩余，使得热力系统运行运行成本和电力系统运行总成本均减少，实现激励相容。
表1 不同调度模式下的经济效益
Tab.1 Economic benefits in different dispatch modes
成本 单独调度 联合调度 纳什议价电力成本 0 C *E C ↓ CE′ ↓E热力成本 0 C ↑ CH′ ↓总成本 00 C *H H C +C **H E C +C↓ H E H E C ′C′+ ↓
4 算例分析
为了检验本文中证明、模型和算法的有效性。本节对两个不同规模的电-热综合能源系统进行算例仿真测试。小系统为6 节点电力系统和6 节点热力系统耦合而成的电-热综合能源系统。大系统为319 节点电力系统和40 节点热力系统耦合而成的电-热综合能源系统。在配置Intel i7-10700F 的CPU 和16GB 的RAM 的计算机进行仿真测试。具体数据可以参考数据集[40]。
4.1 小系统算例及分析
小系统为6 节点电力系统和6 节点热力系统合而成的电-热综合能源系统。小体系的拓扑结构如图3 所示。
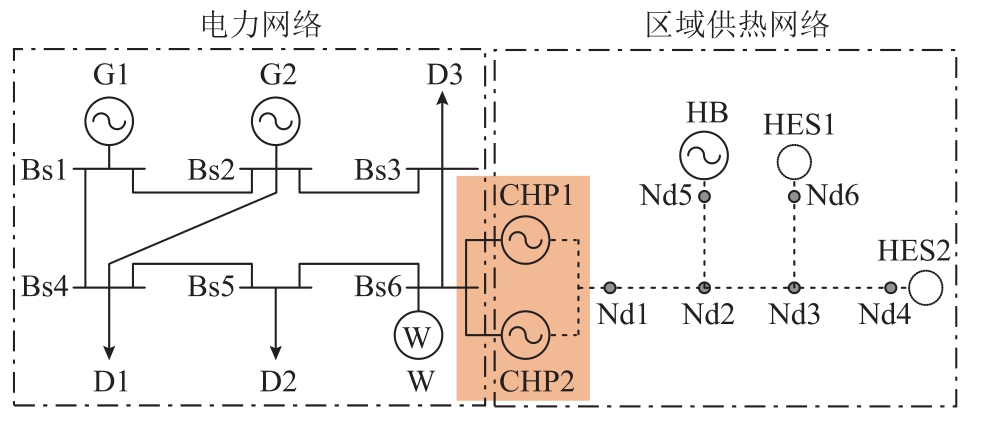
图3 小系统拓扑结构
Fig.3 Topological structure diagram of small-scale system
在图3 中，Bs 表示母线；G 表示发电机；W 表示风电场；D 表示电负荷；CHP 表示热电联产机组；Nd 表示节点；HB 表示锅炉；HES 表示换热站。发电机（G1 和G2）、风机机组（W）和热电联产机组（CHP1 和CHP2）为电网供电。锅炉与热电联产机组为热网供热。
在热电单独优化调度中，先计算热力系统最优热流。热力系统尽可能减少锅炉运行成本和购热成本，在满足热力系统安全运行约束下，优化锅炉和CHP 机组的热出力。在热电联合优化调度中，一次性计算电-热综合能源系统最优调度。不同调度方式下CHP 机组热出力如图4 所示。
图4 CHP 机组热出力
Fig.4 Heat supply of CHP units
图4 是不同调度方式下CHP 机组热出力。在热力系统单独优化调度中，CHP 机组热出力总和为878.94 MW。在热电联合优化调度中，一次性计算电-热综合能源系统最优调度，CHP 机组热出力总和为905.37 MW。相对热力系统单独调度，热电联合优化调度CHP 机组热出力增多26.43 WM，从而产生的购热成本更多。
不同调度方式下弃风量有显著不同，小系统弃风量如图5 所示。
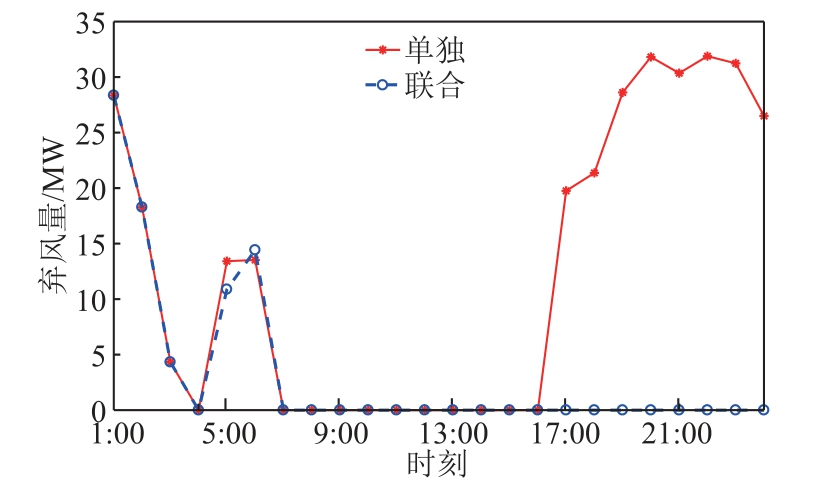
图5 小系统弃风量
Fig.5 Wind curtailment of small-scale system
电力系统单独优化调度时，弃风量为299.41 MW。热电联合优化调度弃风量为76.26 MW。电力系统单独优化调度时，CHP 机组热出力已经由热力系统最优热流计算确定了。CHP 机组热出力不可以调节。热电联合优化调度充分考虑供热管网储能特性，松弛了CHP 机组电出力和热出力的强耦合关系，提高了电力系统灵活性，为风电提供消纳空间，减少弃风223.15 MW，相应弃风成本也减少了。
相对热电单独优化调度，热电联合优化调度使电-热综合能源系统总成本减少，但是热力系统的个体利益受损。因为热电联合优化调度需要热力系统充分利用供热管网储能特性来提高电力系统灵活性，供热管网需要升高温度，造成了更多热损失，进而使得热力系统总成本增多。小系统在不同调度方式下的成本比较见表2。
表2 小系统在不同模式下的成本比较
Tab.2 Cost comparison of small-scale system in different dispatch models
成本 单独调度 联合调度 纳什议价电力成本/$ 82 105 71 296↓ 77 094↓热力成本/$ 26 917 27 704↑ 21 906↓总成本/$ 109 211 99 000↓ 99 000↓
热力系统从电力系统（CHP 机组）购买热量单价μ=30 $/MW。从表2 可以看出，相对热电单独优化调度，热电联合优化调度后电力系统总成本减少了$ 10 809，热力系统总成本增多了$ 787，电-热综合能源系统总成本之和减少了$ 10 022。换句话说，热力系统和电力系统合作产生了$10 022 剩余，但是没有实现激励相容。基于纳什议价分配合作剩余，电力系统总成本变为$ 77 094，相对单独优化调度减少了$ 5 011；热力系统总成本变为$ 21 906，相对单独优化调度减少了$ 5 011。基于纳什议价的热电联合优化调度，电力系统总成本和热力系统总成本都是减少的，实现了激励相容。
基于Benders 分解计算热电联合优化调度，小系统算法收敛曲线如图6 所示。
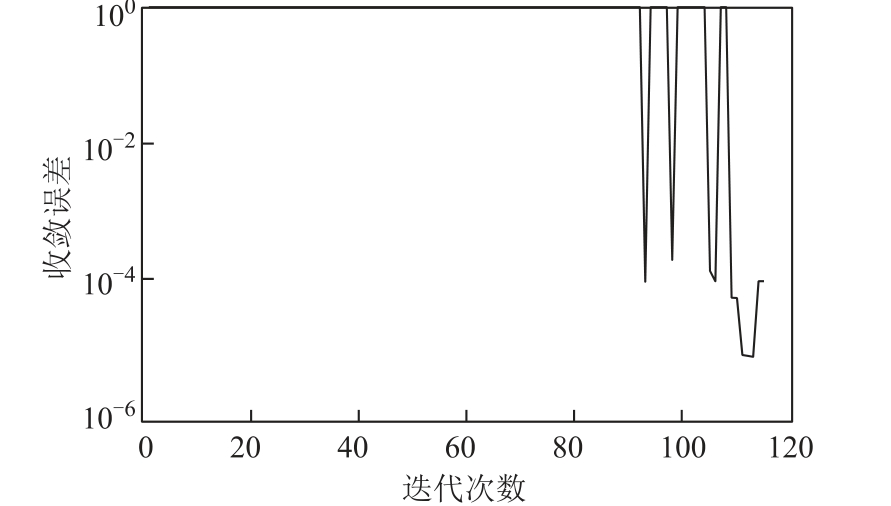
图6 小系统收敛曲线
Fig.6 Convergence curve of small-scale system
图6 是小系统算法收敛曲线。收敛误差定义为Error = |f - f cen|/ f cen，f cen 为集中式热电联合优化调度最优值，f 为基于Benders 分解的热电联合优化调度的目标函数值。当Error = 1 时，可以认为热力系统优化调度子问题不可行。当Error 趋近0 时，说明集中式热电联合优化调度和基于Benders 分解热电联合优化调度的最优值几乎一致，证明了Benders分解算法有效性。当阈值ε=0.02 时，Benders 分解在迭代115 次接近收敛，历时0.59 s。
集中式热电联合优化调度和基于Benders 分解的热电联合优化调度在计算性能上有显著不同，具体见表3。
表3 小系统计算性能比较
Tab.3 Computation performance comparison of small-scale system
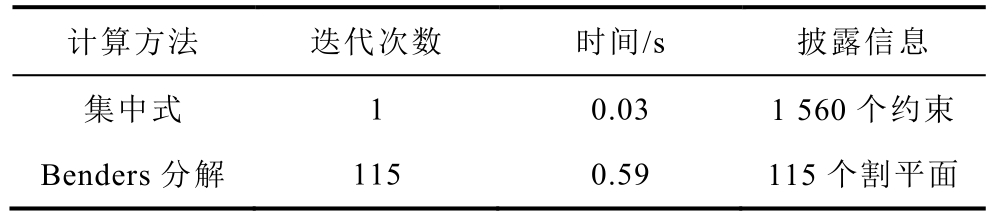
计算方法 迭代次数 时间/s 披露信息集中式 1 0.03 1 560 个约束Benders 分解 115 0.59 115 个割平面
在集中式调度中，热力系统需要披露全部信息，共1 560 个热网约束。集中式调度迭代1 次，历时0.03 s。在基于Benders 分解的热电联合优化调度中，热力控制中心通过传送115 个可行割平面和最优割平面等信息给电力控制中心，不需要披露热力系统的拓扑结构和运行参数等，充分保护了不同主体隐私。
4.2 小系统算例及分析
为了进一步检验证明模型和算法的有效性。采用319 节点电力系统和40 节点热力系统耦合而成电-热综合能源系统（大系统）进一步仿真。大系统在不同调度方式下的成本比较见表4。
表4 大系统在不同模式下的成本比较
Tab.4 Cost comparison of large-scale system in different dispatch models
成本 单独调度 联合调度 纳什议价电力成本/$ 1 208 100 1 106 700↓ 1 166 235↓热力成本/$ 318 320 335 990↑ 276 455↓总成本/$ 1 526 420 1 442 690↓ 1 442 690↓
热力系统从电力系统（CHP 机组）购买热量单价μ=10 $/MW。从表4 可以看出，相对热电单独优化调度，热电联合优化调度后电力系统总成本减少了$ 101 400，热力系统总成本增多了$ 17 670，电-热综合能源系统总成本之和减少了$ 83 730。热力系统和电力系统合作产生了$ 83 730 剩余，但是两者并不是激励相容的。基于纳什议价分配合作剩余，电力系统总成本变为$ 1 166 235，相对单独调度减少了$ 41 865；热力系统总成本变为$ 276 455，相对单独调度减少了$ 41 865。基于纳什议价的热电联合优化调度，电力系统总成本和热力系统总成本都是下降的，实现了激励相容。
基于Benders 分解计算热电联合优化调度，大系统算法收敛曲线如图7 所示。
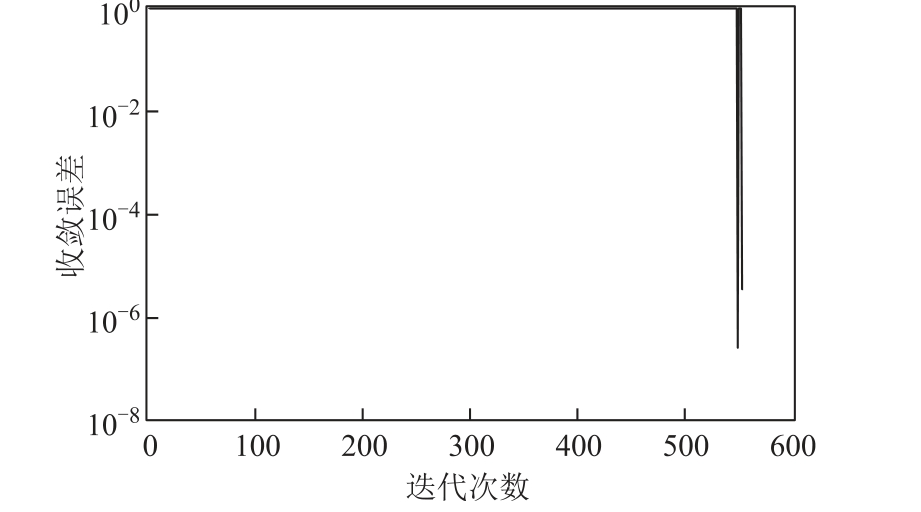
图7 大系统收敛曲线
Fig.7 Convergence curve of large-scale system
收敛误差 Error 定义和小系统一致。当阈值ε=0.02 时，Benders 分解在迭代550 次左右接近收敛，历时308.91 s。
集中式热电联合优化调度和基于Benders 分解的热电联合优化调度在计算性能上有显著不同，具体内容见表5。
表5 大系统计算性能比较
Tab.5 Computation performance comparison of large-scale system
类型 迭代次数 时间/s 披露信息集中式 1 2.26 10 440 个约束Benders 分解 553 308.91 2 765 个割平面
在集中式优化调度中，热力系统需要披露热网全部信息，共10 440 个热网约束。集中式优化调度迭代1 次，历时2.26 s。在基于Benders 分解的热电联合优化调度中，热力控制中心通过传送可2 765个可行割平面和最优割平面等信息给电力控制中心，不需要披露热力系统的拓扑结构和运行参数等，充分保护了不同主体隐私。
5 结论
本文提出一种基于Benders 分解和纳什议价的分布式热电联合优化调度方法。首先，热力系统与电力系统依次计算最优热流和最优功率分配。然后，采用Benders 分解将热电联合优化调度分为电力系统调度主问题和热力系统调度子问题，迭代求解，保护隐私。热电联合优化调度最大化总体效用，不应忽视热力系统个体理性。通过纳什议价分配合作剩余，基本思想是电力系统给予热力系统相应的转移支付，鼓励热力系统充分利用供热管网储能特性。通过两个规模大小不同算例的仿真结果验证了本文所提方法可以保护不同主体隐私，促进可再生能源消纳，实现激励相容。未来拟研究考虑市场信息不对称和可再生能源不确定性的多主体分布式热电联合优化调度。
[1] Kang Chongqing, Chen Xinyu, Xu Qianyao, et al.Balance of power: toward a more environmentally friendly, efficient, and effective integration of energy systems in China[J].IEEE Power and Energy Magazine, 2013, 11(5): 56-64.
[2] 国家能源局2021 年一季度网上新闻发布会文字实录[EB/OL].[2021-01-30].http://www.nea.gov.cn/2021-01/30/c_139708580.htm.
[3] Blarke M B.Towards an intermittency-friendly energy system: comparing electric boilers and heat pumps in distributed cogeneration[J].Applied Energy, 2012,91(1): 349-365.
[4] Papaefthymiou G, Hasche B, Nabe C.Potential of heat pumps for demand side management and wind power integration in the German electricity market[J].IEEE Transactions on Sustainable Energy, 2012, 3(4): 636-642.
[5] Mollenhauer E, Christidis A, Tsatsaronis G.Increasing the flexibility of combined heat and power plants with heat pumps and thermal energy storage[J].Journal of Energy Resources Technology, 2018, 140(2): 020907.
[6] Manson J R, Wallis S G.An accurate numerical algorithm for advective transport[J].Communications in Numerical Methods in Engineering, 1995, 11(12):1039-1045.
[7] Benonysson A, Bøhm B, Ravn H F.Operational optimization in a district heating system[J].Energy Conversion and Management, 1995, 36(5): 297-314.
[8] Liu Xuezhi, Wu Jianzhong, Jenkins N, et al.Combined analysis of electricity and heat networks[J].Applied Energy, 2016, 162: 1238-1250.
[9] Yang Jingwei, Zhang Ning, Botterud A, et al.On an equivalent representation of the dynamics in district heating networks for combined electricity-heat operation[J].IEEE Transactions on Power Systems,2020, 35(1): 560-570.
[10] Zheng Weiye, Hou Yunhe, Li Zhigang.A dynamic equivalent model for district heating networks:formulation, existence and application in distributed electricity-heat operation[J].IEEE Transactions on Smart Grid, 2021, 12(3): 2685-2695.
[11] 张义志, 王小君, 和敬涵, 等.考虑供热系统建模的综合能源系统最优能流计算方法[J].电工技术学报, 2019, 34(3): 562-570.Zhang Yizhi, Wang Xiaojun, He Jinghan, et al.Optimal energy flow calculation method of integrated energy system considering thermal system modeling[J].Transactions of China Electrotechnical Society, 2019, 34(3): 562-570.
[12] 张超, 冯忠楠, 邓少平, 等.考虑电热混合储能的多能互补协同削峰填谷策略[J].电工技术学报,2021, 36(增刊1): 191-199.Zhang Chao, Feng Zhongnan, Deng Shaoping, et al.Multi-energy complementary collaborative peak-load shifting strategy based on electro-thermal hybrid energy storage system[J].Transactions of China Electrotechnical Society, 2021, 36(S1): 191-199.
[13] Li Zhigang, Wu Wenchuan, Shahidehpour M, et al.Combined heat and power dispatch considering pipeline energy storage of district heating network[J].IEEE Transactions on Sustainable Energy, 2016, 7(1):12-22.
[14] Huang Shaojun, Tang Weichu, Wu Qiuwei, et al.Network constrained economic dispatch of integrated heat and electricity systems through mixed integer conic programming[J].Energy, 2019, 179: 464-474.
[15] Conejo A J, Castillo E, Minguez R, et al.Decomposition techniques in mathematical programming:engineering and science applications[M].Berlin:Springer, 2006.
[16] Lin Chenhui, Wu Wenchuan, Zhang Boming, et al.Decentralized solution for combined heat and power dispatch through benders decomposition[J].IEEE Transactions on Sustainable Energy, 2017, 8(4): 1361-1372.
[17] Lu Shuai, Gu Wei, Zhou Suyang, et al.Highresolution modeling and decentralized dispatch of heat and electricity integrated energy system[J].IEEE Transactions on Sustainable Energy, 2020, 11(3):1451-1463.
[18] Huang Jinbo, Li Zhigang, Wu Qinhua.Coordinated dispatch of electric power and district heating networks: a decentralized solution using optimality condition decomposition[J].Applied Energy, 2017,206: 1508-1522.
[19] Xue Yixun, Li Zhengshuo, Lin Chenhui, et al.Coordinated dispatch of integrated electric and district heating systems using heterogeneous decomposition[J].IEEE Transactions on Sustainable Energy, 2020, 11(3):1495-1507.
[20] 张雨曼, 刘学智, 严正, 等.光伏-储能-热电联产综合能源系统分解协调优化运行研究[J].电工技术学报, 2020, 35(11): 2372-2386.Zhang Yuman, Liu Xuezhi, Yan Zheng, et al.Decomposition-coordination based optimization for PV-BESS-CHP integrated energy systems[J].Transactions of China Electrotechnical Society, 2020,35(11): 2372-2386.
[21] Myerson R B.Incentive compatibility and the bargaining problem[J].Econometrica, 1979, 47(1): 61.
[22] Chen Yue, Wei Wei, Liu Feng, et al.Energy trading and market equilibrium in integrated heat-power distribution systems[J].IEEE Transactions on Smart Grid, 2019, 10(4): 4080-4094.
[23] Cao Yang, Wei Wei, Wu Lei, et al.Decentralized operation of interdependent power distribution network and district heating network: a market-driven approach[J].IEEE Transactions on Smart Grid, 2019,10(5): 5374-5385.
[24] Yang Jingwei, Botterud A, Zhang Ning, et al.A costsharing approach for decentralized electricity-heat operation with renewables[J].IEEE Transactions on Sustainable Energy, 2020, 11(3): 1838-1847.
[25] 王昀, 谢海鹏, 孙啸天, 等.计及激励型综合需求响应的电-热综合能源系统日前经济调度[J].电工技术学报, 2021, 36(9): 1926-1934.Wang Yun, Xie Haipeng, Sun Xiaotian, et al.Dayahead economic dispatch for electricity-heating integrated energy system considering incentive integrated demand response[J].Transactions of China Electrotechnical Society, 2021, 36(9): 1926-1934.
[26] Nash J F.The bargaining problem[J].Econometrica,1950, 18(2): 155.
[27] 侯慧, 刘鹏, 黄亮, 等.考虑不确定性的电-热-氢综合能源系统规划[J].电工技术学报, 2021, 36(增刊1): 133-144.Hou Hui, Liu Peng, Huang Liang, et al.Planning of electricity-heat-hydrogen integrated energy system considering uncertainties[J].Transactions of China Electrotechnical Society, 2021, 36(S1): 133-144.
[28] 丁煜蓉, 陈红坤, 吴军, 等.计及综合能效的电-气-热综合能源系统多目标优化调度[J].电力系统自动化, 2021, 45(2): 64-73.Ding Yurong, Chen Hongkun, Wu Jun, et al.Multiobjective optimal dispatch of electricity-gas-heat integrated energy system considering comprehensive energy efficiency[J].Automation of Electric Power Systems, 2021, 45(2): 64-73.
[29] 武梦景, 万灿, 宋永华, 等.含多能微网群的区域电热综合能源系统分层自治优化调度[J].电力系统自动化, 2021, 45(12): 20-29.Wu Mengjing, Wan Can, Song Yonghua, et al.Hierarchical autonomous optimal dispatching of district integrated heating and power system with multi-energy microgrids[J].Automation of Electric Power Systems, 2021, 45(12): 20-29.
[30] 李志刚.消纳大规模风电的互联电网多维协同优化调度方法研究[M].北京: 清华大学出版社, 2021.
[31] 贺平, 孙刚, 王飞, 等.供热工程[M].4 版.北京:中国建筑工业出版社, 2009.
[32] Zhao Hongping.Analysis, modelling, and operational optimization of district heating systems[D].Denmark:Technical University of Denmark, 1995.
[33] Chen Binbin, Wu Wenchuan, Sun Hongbin.Coordinated heat and power dispatch considering mutual benefit and mutual trust: a multi-party perspective[J].IEEE Transactions on Sustainable Energy, 2022, 13(1): 251-264.
[34] Zhu Jizhong.Optimization of power system operation[M].Hoboken: John Wiley & Sons, Inc., 2009.
[35] Sadeghian H R, Ardehali M M.A novel approach for optimal economic dispatch scheduling of integrated combined heat and power systems for maximum economic profit and minimum environmental emissions based on Benders decomposition[J].Energy,2016, 102: 10-23.
[36] Rahmaniani R, Crainic T G, Gendreau M, et al.The Benders decomposition algorithm: a literature review[J].European Journal of Operational Research, 2017,259(3): 801-817.
[37] Abdolmohammadi H R, Kazemi A.A Benders decomposition approach for a combined heat and power economic dispatch[J].Energy Conversion and Management, 2013, 71: 21-31.
[38] 梅生伟, 刘锋, 魏韡.工程博弈论基础及电力系统应用[M].北京: 科学出版社, 2016.
[39] 张维迎.博弈与社会[M].北京: 北京大学出版社,2013.
[40] Supplementary materials for case studies[DB/OL].https://figshare.com/articles/dataset/Test_data_for_combined_heat_and_power_dispatch_xls/2036343.