0 引言
地磁暴是一种威胁电网安全的“低概率、高风险”自然灾害。地磁暴时,地表感生出电场,在其作用下,输电线路、大地、接地的变压器中性点构成的回路中会产生地磁感应电流(Geomagnetically Induced Current, GIC)。由于特高压交流输电线路单位长度电阻小,使特高压交流电网更容易受到地磁暴的侵害。地磁暴时电网感生的GIC 大小与电网规模呈正相关,随着我国特高压电网的进一步建设及联网,其受地磁暴影响也将越来越严重。按照“三华”特高压规划电网的相关参数,将有一半以上的特高压变电站GIC 的“百年一遇”水平超过200 A[1]。
根据北美电力可靠性委员会(North American Electric Reliability Council, NERC)在2012 年发布的地磁暴可靠性评估报告[2],地磁暴时电网感生的GIC 会对电力系统造成两大风险:一是对变压器等电力设备造成潜在损坏的风险;二是系统失去无功功率支持后引发电网电压崩溃的风险。对于整个电网而言,风险二造成的危害远大于风险一。1989 年强地磁暴导致的加拿大魁北克大停电的原因就是GIC 衍生的无功损耗增量(以下简称为GIC-Q)引发连锁反应导致全网电压崩溃,最终魁北克供电中断了9 h,数百万居民生活受到影响[3]。2003 年瑞典马尔默停电也是地磁暴所致[4]。目前,国内关于地磁暴对电网影响的研究多集中在风险一,即GIC 造成变压器偏磁饱和产生的变压器本体谐波增多[5]、热点温升增高[6]、振动和噪声增强[7]、无功损耗增大[8]等方面;在风险二方面的研究较少,文献[9-10]分别计算了我国西北、华东新建特高压电网对地磁暴的响应过程,计算结果表明在地磁暴影响下部分变电站母线电压波动大大达到并超过了相关规程规定。国外对地磁暴较为关注的地区集中在地磁暴频发的北欧、北美等高纬度地区,文献[11]通过建立变压器铁心的非线性模型,可以更精确地模拟地磁暴期间电网的响应,计算不同时刻GIC 通过变压器产生的谐波和无功损耗,求解电网能够耐受的地磁暴幅值与时长。但由于非线性代数方程组求解复杂、迭代时间长、计算量很大,这种方法对CPU 和内存的依赖程度高,计算速度慢,不适应于大规模电网的电压稳定评估。目前应用比较广的是利用连续潮流法对地磁暴造成的电网电压稳定性影响进行研究。文献[12]通过连续潮流法不断增加变压器产生的无功损耗计算出北美中部电网在不同强度地磁暴下的电压波动和电压薄弱点,但这种方法依赖固定电网拓扑的潮流计算,自适应性较差。而且,连续潮流法在计算电压崩溃点时需要从基本工况开始分段增加负荷延拓求解PV 曲线,依靠切线预测与牛顿拉夫逊法校正,存在步长选取困难、求解时间较长、计算复杂等问题。此外,上述方法缺乏能够准确量化地磁暴对电网电压稳定的破坏程度的指标以指导电力生产和电网规划建设。
基于上述原因,本文利用GIC 的准直流特性,运用静态电压方法建立了地磁暴时电压稳定研究模型,并将GIC-Q 代入求解PV 曲线解析式,以获得地磁暴情况下电压崩溃的理论值。此外,通过分析地磁暴期间节点电压波动的机理,提出电网遭受地磁暴侵害时节点电压失稳指标的计算方法,可以综合反映地磁暴对系统电压稳定的影响,为确定地磁暴时电网中电压稳定薄弱点和防治电压崩溃等地磁暴次生灾害提供了参考依据。
1 地磁暴影响下特高压交流电网电压稳定评估的理论基础及研究模型
1.1 电网GIC 计算及变换
GIC 作为一种准直流电流,在输电线路、中性点接地的变压器和大地构成的回路中流通。地磁暴驱动GIC 的等效直流电压U 的大小相当于地面感应电场Eground 沿该线路走向的积分值。
式中,i、j 分别为给定输点线路的两端点。
根据Lehtinen-Pirjola 算法[13]引入系统导纳矩阵Y 和网络接地阻抗矩阵Z,通过诺顿定理可将等效直流电压U 转换为流入变压器的电流,即电网中流通的地磁感应电流IGIC。
式中,IGIC 为n×n 矩阵,表示流经每个变电站的GIC;n 为变电站数量;I 为n×n 单位矩阵;Y、Z 分别为n×n 线路导纳、接地阻抗矩阵;J 为理想条件下的n×1 接地电流矩阵,其中的元素为
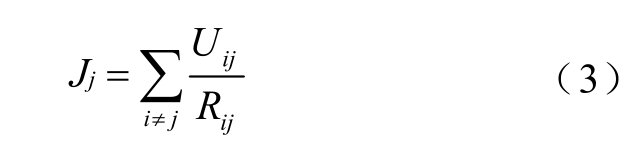
式中,Rij 为节点i 和j 之间的等效电阻。
上述GIC 计算过程涉及自耦变压器等设备的变换可以参考文献[14-15],在此不再赘述。考虑到GIC-Q 对电网电压的扰动呈现慢动作特征,可以用静态电压方法对该问题进行分析。为便于通过数学方法分析GIC-Q 对PV 曲线的影响,需计算通过变压器的GIC 有效值,并建立以变电站母线为中心的单机-单线-变压器-负荷电压稳定分析模型(1.3 节图2)作为研究对象。
如图1a 所示的特高压变电站俯视图,线路L1、L2 为与特高压变电站相连的特高压线路,L3、L4 为与特高压变电站相连的超高压线路,r1、r2 分别为特、超高压线路单位电阻,α、β、γ、ρ 分别为线路L1、L2、L3、L4 与地面感应电场Eground 的夹角。当线路较长时(>100 km),超、特高压变电站的接地电阻相比于线路电阻小得多,从特高压、超高压系统流入变电站的GIC 可以表示为
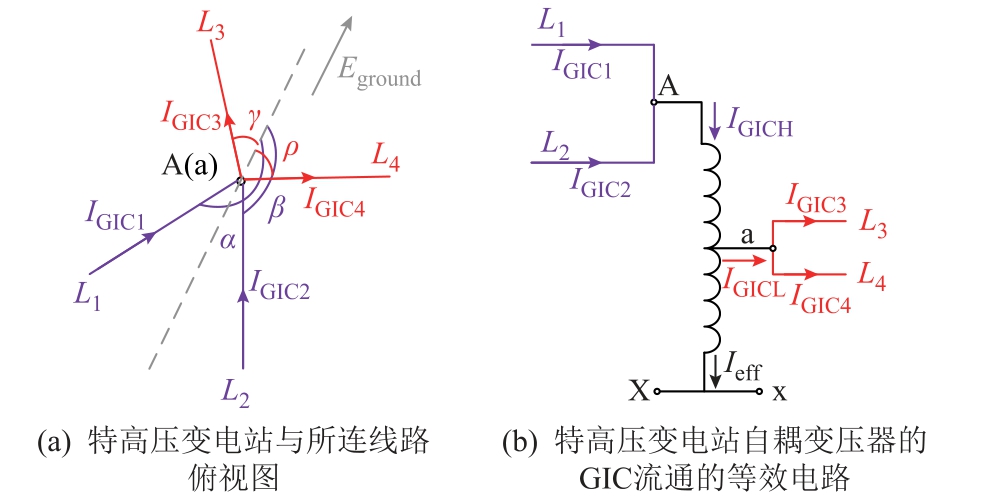
图1 特高压变压器GIC 有效值
Fig.1 Effective value of GIC of UHV transformer

GIC 经输电线路流入接地的变压器。特高压变电站一般采用自耦变压器,自耦变压器的高压侧绕组AX 与中压侧绕组ax 之间有公共绕组Aa,使变压器高、中压侧有电的联系。当GIC 流入变压器中性点时,除了流经高压侧绕组AX 以外,也会通过公共绕组Aa 流入中压侧系统。图1b 所示为特高压变电站自耦变压器的GIC 流通的等效电路,通过自耦变压器GIC 有效值为
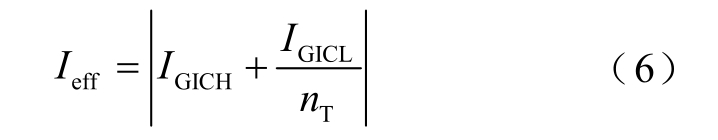
式中, nT 为变压器高压侧与中压侧实际电压比。
由式(4)~式(6)可知,地磁感应电场方向与特高压线路和超高压线路的走向夹角共同决定了通过特高压变压器的GIC 有效值。
1.2 多回进线电气等效参数
多数特高压变电站都有多个进线通道,为了使电压稳定分析模型中线路等效电阻、电抗上所消耗的有功损耗、无功损耗可以综合反映相同功率在不同进线通道之间分配时的无功损耗总水平,需对变电站多回进线的电阻、电抗进行必要的变换。运用文献[16]中的方法求得常用进线回数等效电阻、电抗线路长度见表1。建立电压稳定分析模型时,将等效长度乘以对应线路单位电阻、电抗即可得到模型中的线路电阻、电抗。
表1 进线等效电阻、电抗线路长度
Tab.1 Equivalent resistance and reactance line length of incoming line

进线回数 线路长度 等效线路长度1 L1 L1 2 L1、L2 (L1+L2)/3 3 L1、L2、L3 5(L1+L2+L3)/27 4 L1、L2、L3、L4 (L1+L2+L3+L4)/9
1.3 GIC-Q 电压稳定分析模型
中性点接地的变压器是电网遭受地磁暴侵害时的敏感元件,也是造成地磁暴时系统无功扰动的来源。当GIC 流过变压器时,铁心中便会产生相应的直流磁通,加上原本的交流磁通,总磁通量将超过膝点磁通,造成铁心半波饱和。这不仅使励磁电流发生畸变,同时消耗大量无功功率。由于太阳活动引起的地磁扰动在全球范围内几乎同时发生,使得GIC-Q 扰动具有全网群发性、突发性的特点,这也是地磁暴对于特高压交流电网电压稳定破坏大及防治难的主要原因。GIC-Q 与流过变压器中性点的GIC 呈线性关系[17],目前常用k 值法来计算,对每个特高压变压器组,有
式中,QGIC 为变压器无功损耗(三相),Mvar;Vpu为变压器端电压,为标幺值;k 为变压器无功损耗系数,其量值与变压器铁心结构相关,对于特高压电网所用单相四柱式变压器,参考文献[18]中结论,k值设为2.44 Mvar/A。
建立GIC-Q 电压稳定分析模型如图2 所示,发电厂G 经超高压线路LG 由特高压变压器T1 上网,再由特高压线路L 经特高压变电站负荷母线Bus 至下级变电站或由特高压变压器T2 下网。
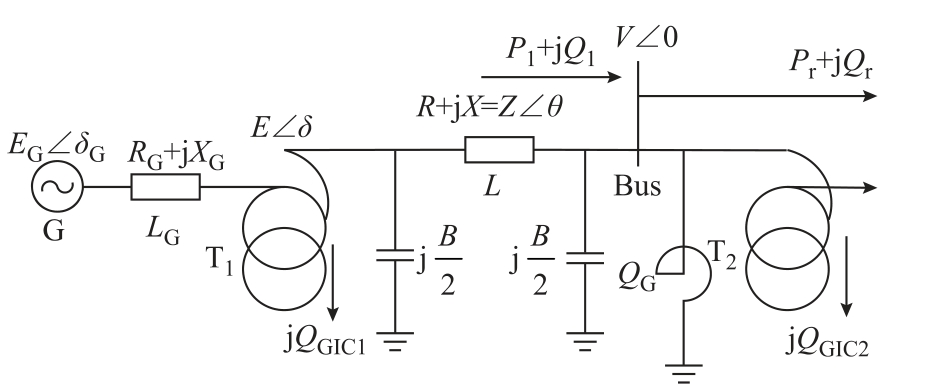
图2 GIC-Q 电压稳定分析模型
Fig.2 GIC-Q voltage stability analysis model
地磁暴影响下,GIC-Q 只影响系统电压幅值,电压相位差可认为保持不变。对某一时刻:EG∠δG 为发电厂电压;RG+jXG 为线路LG 等值阻抗,E∠δ为变压器T1 特高压侧的电压。对于特高压变压器而言,其本体消耗的功率远小于其负荷功率,故本模型不计变压器正常运行时的损耗。设nT1 为自耦变压器T1高压侧与中压侧的实际电压比,若忽略电压下降的横分量,则地磁暴时的T1 特高压侧电压可表示为
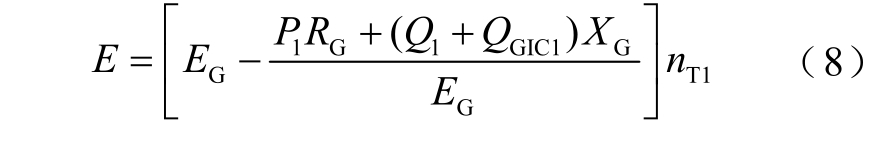
设V∠0 为负荷母线Bus 的电压相量;B 为与母线相连的线路电纳;Z∠θ=R+jX 为特高压线路等值阻抗;QG 为高压电抗器消耗的无功功率;QGIC 为变压器遭受地磁暴侵害时的无功功率增大值;Pr+jQr 为变电站母线输送功率和通过变压器的下网功率总和,则变电站负荷母线侧的供电功率方程式有
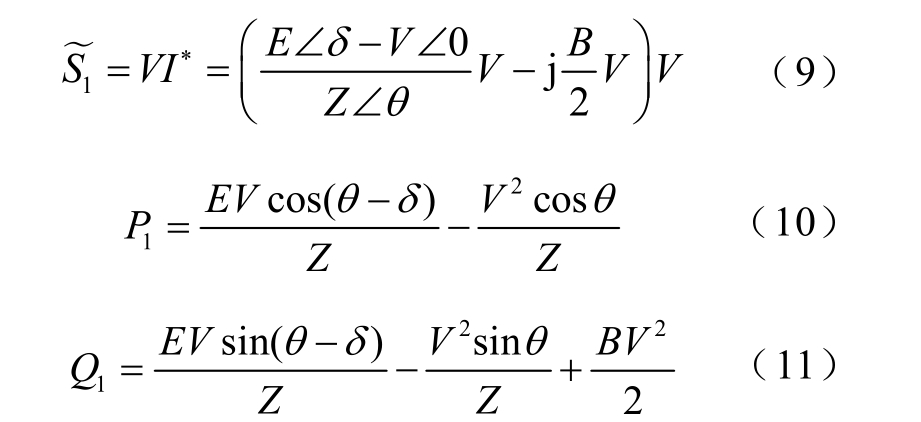
消去δ 得
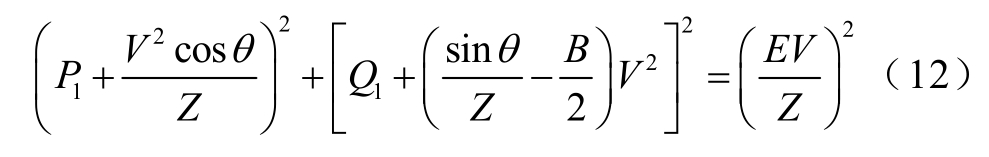
根据变电站母线潮流平衡方程有
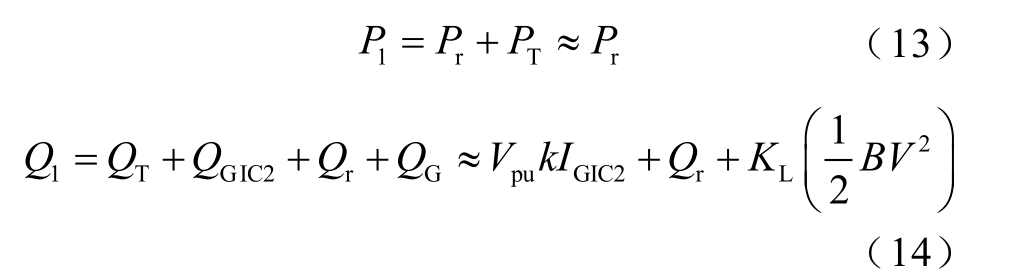
式中, TP 、 TQ 分别为正常运行变压器 2T 消耗的有功功率和无功功率;KL 为电抗器补偿率。
将式(13)、式(14)代入式(12)得
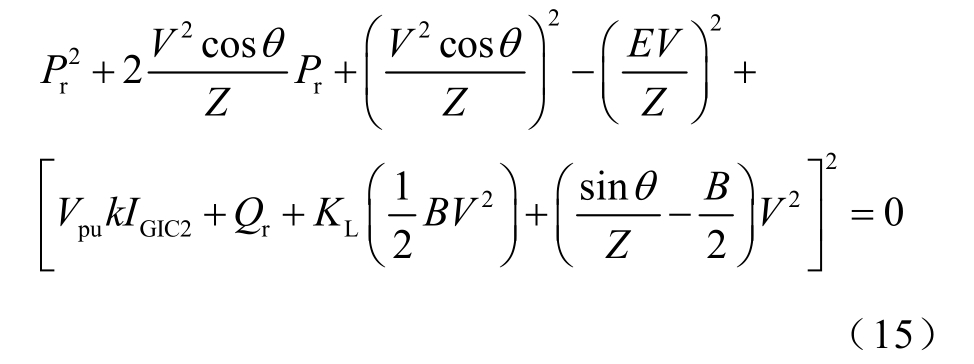
式(15)反映了地磁暴时该负荷母线变电站通过的GIC 与母线电压和负荷功率之间的关系,是后续进行电压稳定分析的基础。
2 地磁暴影响下特高压电网电压稳定的评估方法和指标
2.1 地磁暴作用下特高压电网电压稳定评估流程
对特高压电网电压稳定评估就是量化地磁暴这种自然灾害对特高压电网电压稳定影响的大小,其中最关心的问题是地磁暴对当前电压稳定造成的风险有多大,以及离电压崩溃点还有多远。要回答这个问题,需要确定地磁暴时地面感应电场的幅值有多大。由于地磁暴时的电网电压波动根源于太阳剧烈活动时,太阳风进入地球磁层后引起的地球磁场的强烈扰动,其动态过程受多种因素影响,具有较强的不确定性,目前还难以精准预测,但通过预测地磁暴的强度,已经可以精确计算地磁暴发生过程时地表不同地区的地面感应电场幅值。
量化评估地磁暴对系统电压稳定的影响,首先基于该次地磁暴发生时地面感应电场幅值计算各节点通过的GIC 值,再将算得的GIC 值与电气参数代入该节点GIC-Q 电压稳定分析模型,从系统给定运行状态出发,利用数学方法得出PV 曲线表达式并计算电压崩溃点。对于特高压系统而言,当前运行点到电压崩溃点的有功负荷裕度反映了当前系统承受负荷及故障扰动、维持电压稳定能力的大小,可在一定程度上判断节点电压稳定程度。由于电压崩溃发生在电压稳定性最薄弱的节点上,然后向整个系统扩散,需要制定电压失稳指标衡量各节点对地磁暴的敏感程度,以快速筛选出电压稳定薄弱点,给出告警信号,采取灾前预防措施,避免发生电压崩溃导致大规模停电。
2.2 地磁暴期间电压稳定分析
在特高压变电站空载或轻载时,负荷宜看作恒定功率因数负荷,将Qr=Prtanψ 代入式(15),设图2 模型中E=1.0(pu),不同功率因数负荷对应的PV曲线簇如图3 中实线所示。
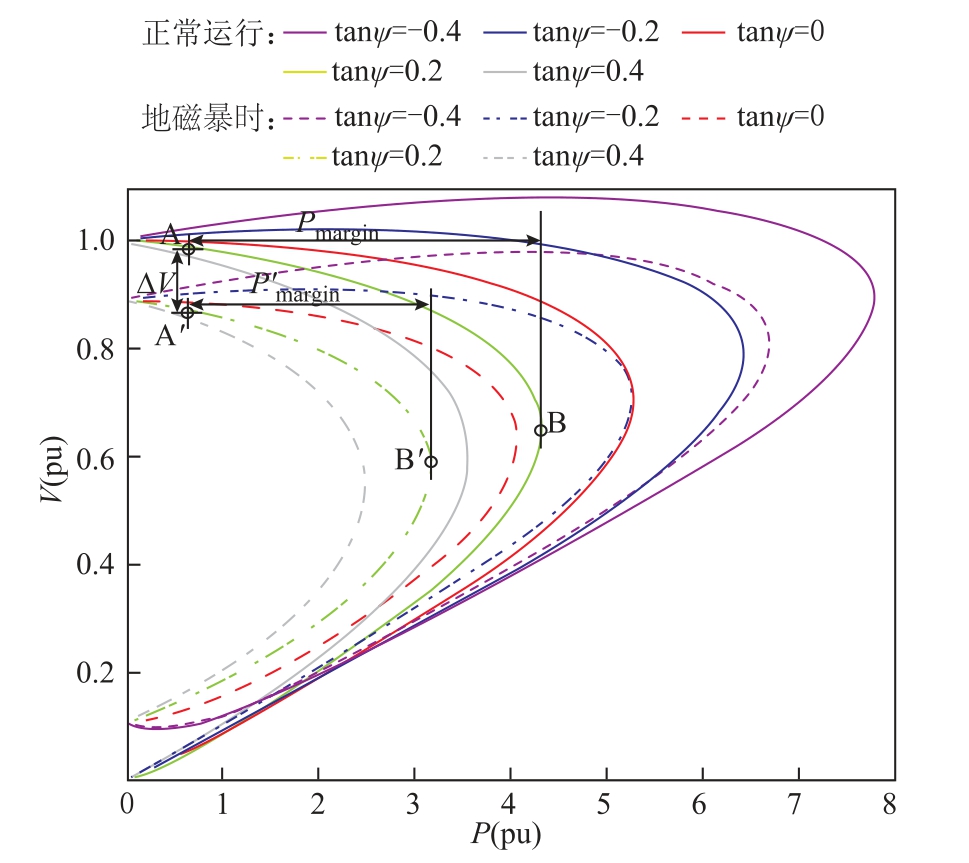
图3 对磁暴期间负荷功率因数PV 曲线的影响
Fig.3 Influence of load power factor on PV curve during geomagnetic storm
PV 曲线的拐点为电压崩溃点,功率因数越超前,达到电压崩溃点前耐受的功率越大,电压崩溃点的电压也越高。负荷母线电压随负荷有功功率增加而降低,直至达到电压崩溃点不能维持稳定导致电压崩溃。考虑GIC-Q 的影响时,利用式(1)~式(7)得到各变电站变压器产生的无功扰动值,再将其代入式(15),对应PV 曲线如图3 虚线所示(设此时QGIC2=1.0(pu))。在不考虑地磁暴影响时,运行点在A 点,B 为电压崩溃点,AB 两点横分量差为有功功率裕度Pmargin;电网受地磁暴侵害时,运行点变为A′点,电压崩溃点变为B′点,有功功率裕度变为A′B′两点的横分量差P′margin;AA′两点的纵分量ΔV 为受地磁暴时的母线电压下降值。
2.3 节点电压失稳指标
随着特高压系统负荷增长,负荷的大部分无功功率由下级变电站提供,特高压变电站负荷无功功率Qr 基本保持不变,将式(15)展开成负荷有功功率P 与母线电压V 的表达式为
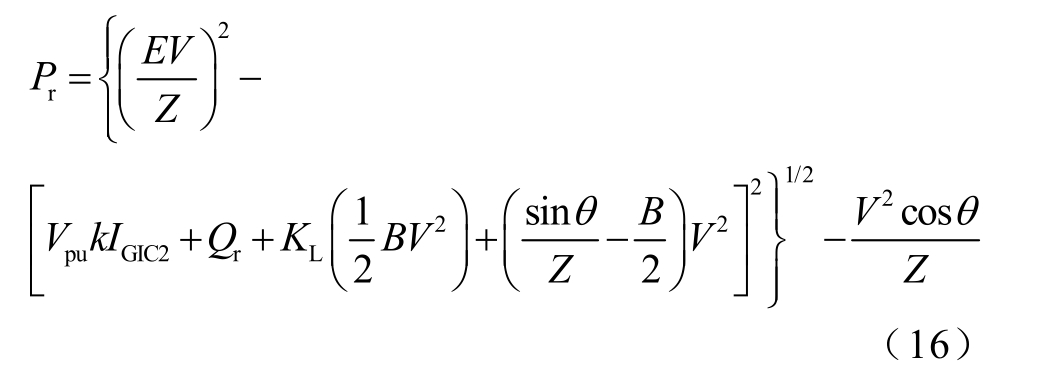
在任一时间节点,基于系统运行方式和通过变压器的GIC 有效值可建立对应的PV 曲线。地面感应电场大小或方向的改变会导致GIC-Q 发生变化,设图2 模型中Z=0.1(pu),θ =85°,B=1.5(pu),KL=0.7,ψ=0°,取变压器的无功损耗QGIC2=0、0.5、1、1.5(pu),并用上标1、2、3 区分不同地磁暴强度下的有功功率裕度变化,分别求解得到PV 曲线如图4 上半部分所示。

图4 地磁暴期间GIC-Q 对PV 曲线及LGIC 影响
Fig.4 Influence of GIC-Q on PV curve and LGIC during geomagnetic storm
分析可知,地磁暴时变压器通过的GIC 越大,母线电压下降幅度越大,负荷有功裕度越小。当负荷有功功率过大或地磁暴引起变压器无功扰动过大导致系统无功无法保持平衡时,就会导致系统电压失稳。因此在制定量化地磁暴对特高压交流电网电压稳定影响的评估指标时,必须综合考虑有功功率、无功功率的作用。由式(16)及图4 可知,在未达到电压崩溃点前,电压对应任一运行点存在不唯一解;在电压崩溃点,电压存在唯一解。由GIC-Q 电压稳定分析模型有
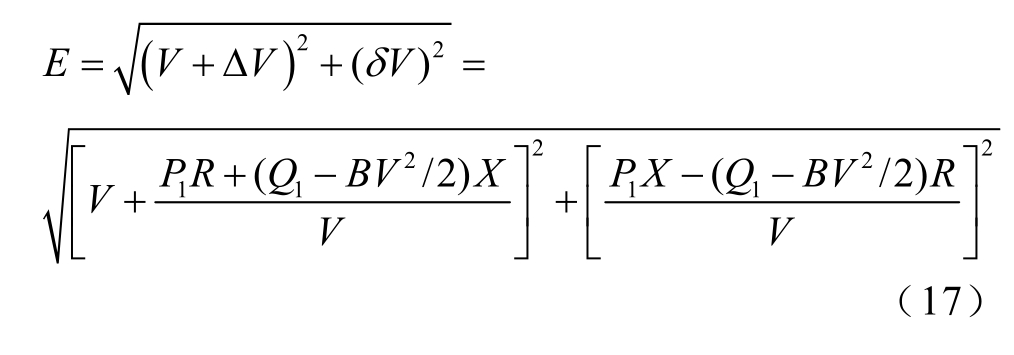
将式(17)展开可得到关于负荷母线电压V2 的一元二次方程为
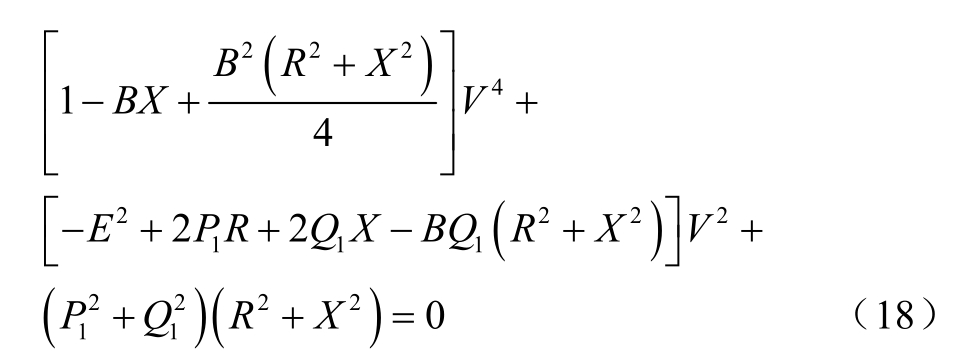
将式(13)、式(14)代入式(18),求解母线电压并定义在该时刻地表感应电场下负荷母线Bus的电压失稳指标LGIC 为
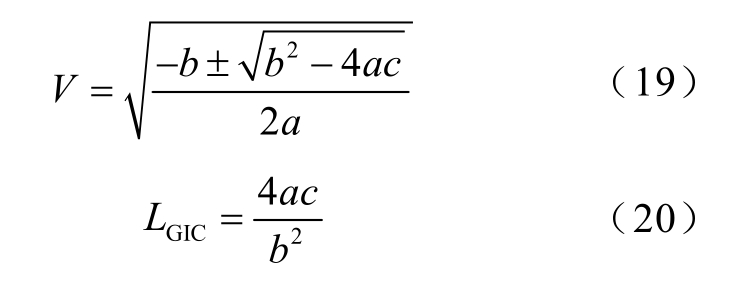
其中
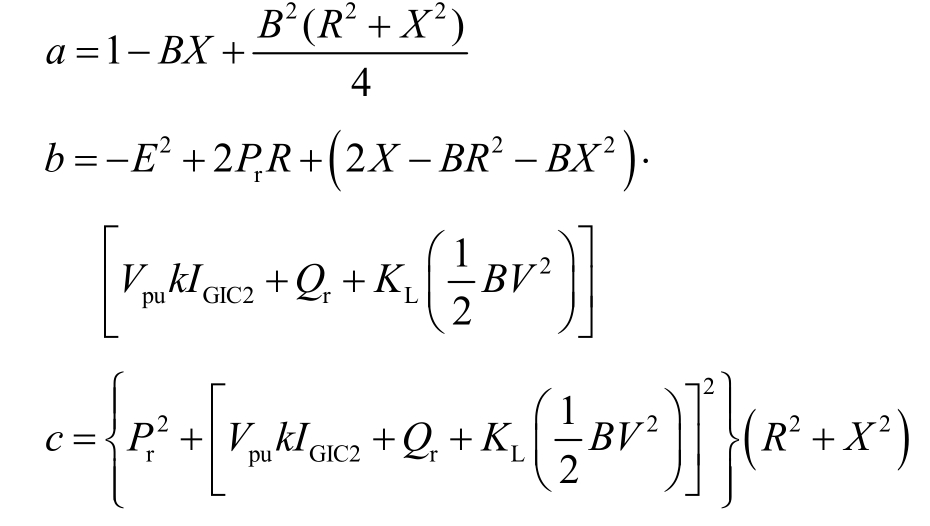
对式(20)进行分析可知,LGIC 可以分成两部分,一部分表示系统未遭受地磁暴侵害时的节点电压失稳程度,即QGIC=0 时的LGIC,这部分由电网拓扑结构、电气参数和运行状态决定,下文称之为LGIC 的基值;另一部分可以表示为系统受地磁暴衍生的GIC-Q 影响节点电压失稳程度的增加值,这部分由地磁暴时通过各节点进入大地的GIC 分布决定,进一步取决于该时刻地面感应电场的大小和方向。在研究强地磁暴对电力系统的影响时,国外学者常基于1 V/km 的地面感应电场幅值讨论电网的响应[19-20],根据我国地磁台的记录数据和相关研究证明这一幅值适用于我国绝大部分地区[1,10,17],在衡量电网抗地磁暴耐受能力时宜选用该幅值。地磁暴发生期间,地面感应电场一般不具备明确的方向性[15]。从保守的角度,要从最严重的情况评估电网的电压稳定性,保证各个方向地面感应电场影响下电压稳定性均能满足要求。因此衡量最强地磁暴期间节点电压稳定性需计算各个方向地面感应电场影响下的LGIC,并以最敏感方向求得的LGIC 作为衡量该节点的电压稳定性指标。
图2 模型中QGIC2=0、0.5、1、1.5(pu)时的PV曲线对应LGIC 变化趋势如图4 下半部分所示。可见,随着GIC-Q 逐渐增大,母线运行电压逐渐减小,LGIC指标逐渐升高。另外需要注意,LGIC 指标是随负荷有功功率增长非线性加速升高的,为防止电压失稳,需设置警戒值以便提前采取转移负荷或调整运行方式等方法降低敏感节点LGIC,本文以LGIC=0.9 作为警戒值,并用Palert 表示达到警戒值时的有功功率裕度。
综上所述,该指标可表征地磁暴时当前运行点距离电压崩溃点的距离,LGIC 越接近1,该节点当前运行点离电压崩溃点越近。该指标具有所需信息量少、计算简单、物理意义明确、易于实现的优点。
3 算例
华东地区是我国经济最发达、电力消费最集中,也是电力供需矛盾最为激烈的地区。华东特高压电力网络目前已基本建成,由淮苏沪、皖电东送、浙福特高压工程一起构成华东特高压交流环网和受端网架,将华东四省一市电网紧密连接。图5 所示为华东特高压规划电网拓扑,规划的华东电网将通过徐州—南京、驻马店—淮南、武汉—皖南特高压线路与华北、华中特高压电网相连,形成结构复杂且规模庞大的特高压交流同步电网——“三华电网”,使华东地区能够接受外来大电源,如西南水电、内蒙古和新疆的火电与可再生能源,甚至蒙古、俄罗斯等国的跨国电力,同时为大容量特高压直流输电提供接入及送出条件。

图5 华东特高压规划电网(丰大运行方式)
Fig.5 East China UHV planned power grid(large operation mode)
设华东特高压规划电网输电线路单位电阻r=0.01 Ω/km,单位电抗 x=0.29 Ω/km,单位电纳b=4.56×10-6 S/km,计算得到无地磁暴影响时华东特高压规划电网丰大运行方式下,各变电站LGIC 的基值见表2。
表2 无地磁暴影响下华东特高压规划电网LGIC 基值
Tab.2 LGIC of East China UHV power grid are planned without geomagnetic storm
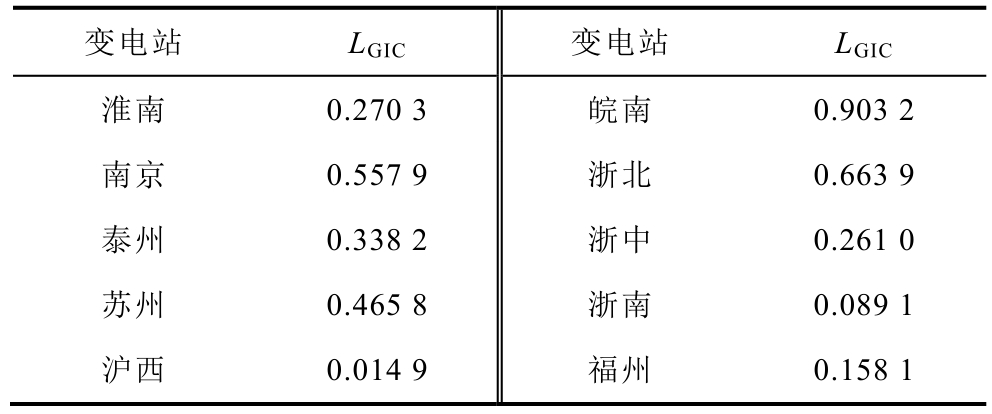
变电站 LGIC 变电站 LGIC淮南 0.270 3 皖南 0.903 2南京 0.557 9 浙北 0.663 9泰州 0.338 2 浙中 0.261 0苏州 0.465 8 浙南 0.089 1沪西 0.014 9 福州 0.158 1
当华东特高压规划电网未遭受地磁暴侵害时,LGIC 基值最高的是皖南站,达到0.903 2,其主要原因是经由皖南站下网和输送至下级变电站的功率很大(达到11 531.4 MW),同时,皖南站的上级线路淮南—皖南、武汉—皖南均很长(334 km、436.19 km),特高压线路电抗消耗的无功功率大大抵消了线路电容产生的无功功率,导致皖南站无功功率严重不足,电压稳定性差。
分别计算方向为正北、东北、正东、东南的1 V/km 地面感应电场情况下华东特高压电网的GIC和LGIC,其结果如图6 所示。由图6 可以看出,GIC在电网中主要沿着与地面电场一致的方向和电阻最小的路径流通;在电网的拓扑末端、拐角、边界节点上GIC 幅值较大,呈现“拐角效应”现象,评估过程中应特别注意这类节点的电压稳定性。

图6 1 V/km 地面感应电场下华东特高压规划电网GIC 与LGIC
Fig.6 GIC and LGIC of East China UHV planned power grid under 1 V/km geoelectric field
表3 列出了LGIC 基值最高的皖南变、浙北变,以及处于拓扑拐弯、末端的泰州变和福州变在1 V/km 地面感应电场下GIC、LGIC、达到电压崩溃点和警戒值时的有功功率裕度。结果表明,皖南站LGIC 计算结果大于1,在强地磁暴作用下将发生电压崩溃,难以满足系统电压稳定的要求,原因在于1 V/km 的地面感应电场作用下,流过皖南站的GIC较大,同时其LGIC 基值过高。对于浙北站,虽然其LGIC 基值较高,但在各方向的1 V/km 地面感应电场作用下,流过的GIC 均不太大,可以满足系统电压稳定的要求。对于处于拓扑拐弯处的泰州站,虽然通过的GIC 很大,但由于其LGIC 基值较低,仍可以满足系统电压稳定的要求。值得注意的是,与变电站的LGIC和其通过的GIC 呈正相关的“直觉”不同,变电站通过的GIC 仅决定了地磁暴时该变电站的无功扰动大小,不能以该变电站通过的GIC 作为该节点电压稳定的判据。比如对于处于拓扑末端的福州站,通过福州站的GIC 在1 V/km 北向地面感应电场影响下比1 V/km 东向地面感应电场影响下大得多,但LGIC 却更小。出现这种情况的原因在于电网在丰大运行方式下,可能会沿供电拓扑出现一连串负荷节点,地磁暴引发的群体GIC-Q 扰动导致各节点电压沿线路拓扑逐级下降,出现电压下降的“累积效应”,东向地面感应电场作用时,拓扑上游产生的“累积效应”使福州站母线电压比北向地面感应电场作用下更接近电压崩溃点。
表3 地磁暴时华东特高压规划电网变电站电压失稳指标及有功功率裕度
Tab.3 GIC, LGIC, Pmargin, Palert of East China UHV power grid are planned during geomagnetic storm

参数正北向地面感应电场(1 V/km) 东北向地面感应电场(1 V/km)皖南 浙北 泰州 福州 皖南 浙北 泰州 福州GIC/A -67.79 27.55 220.53 -104.16 96.17 93.27 251.34 -96.67 LGIC 0.973 5 0.710 5 0.4787 0.360 2 1.005 3 0.779 7 0.476 7 0.521 5 Pmargin/MW 152.37 1 717.44 3 147.01 1 744.07 -3.01 1 227.42 3 185.71 1 022.07 Palert/MW -434.89 1 158.84 2 630.52 1 532.49 -609.48 690.51 2 665.68 841.18参数正东向地面感应电场(1 V/km) 东南向地面感应电场(1 V/km)皖南 浙北 泰州 福州 皖南 浙北 泰州 福州GIC/A 203.83 104.37 134.98 -32.57 192.03 54.31 -60.48 50.61 LGIC 1.140 9 0.839 6 0.410 1 0.870 9 1.124 8 0.784 7 0.39 01 0.718 1 Pmargin/MW -726.71 847.81 3 909.03 182.74 -649.95 1 190.37 4 142.14 463.35 Palert/MW -1 276.87 328.97 3 359.68 42.79 -1 203.28 656.72 35 84.27 310.55
为了预防地磁暴造成的电压崩溃次生灾害,应在电压薄弱点采取相应措施降低该节点LGIC,一方面可以通过转移负荷、增加并行特高压线路条数等方式改变该点负荷有功功率、等效线路长度以降低LGIC 基值;另一方面可以采取变压器中性点电容隔直、电阻隔直等措施调整GIC 流通路径,降低GICQ 带来的电压稳定性影响,但这种方法需考虑GIC流通路径的变化引起其他变电站LGIC 升高。
4 结论
针对地磁暴对特高压电网电压稳定造成的影响,本文通过理论分析和GIC-Q 电压稳定分析模型的搭建,提出了地磁暴时特高压电压稳定的评估方法和指标,可以量化GIC-Q 对电网电压稳定造成的影响,便于分析地磁暴时的电网电压稳定性和判断系统电压稳定薄弱点,具有较大的应用价值。并通过对华东特高压规划电网的算例,计算了各节点电压稳定性,验证了该方法和指标的有效性,并提出了相应的预防和改进措施。
[1] 刘春明, 王红梅, 王璇.多次磁暴下特高压电网GIC 统计规律研究[J].中国电机工程学报, 2019,39(15): 4606-4615.Liu Chunming, Wang Hongmei, Wang Xuan.Statistical analysis of geomagnetically induced currents in UHV power grids under multiple geomagnetic storms[J].Proceedings of the CSEE,2019, 39(15): 4606-4615.
[2] Zanetti L J.Review of North American Electric Reliability Corporation (NERC) interim report:effects of geomagnetic disturbances on the bulk power system february 2012[J].Space Weather the International Journal of Research & Applications,2013, 11(1): 335-336.
[3] Kappenman J G.Geomagnetic storms and their impact on power systems[J].Power Engineering Review,1996, 16(5): 5-10.
[4] Wik M, Viljanen A, Pirjola R, et al.Calculation of geomagnetically induced currents in the 400 kV power grid in southern Sweden[J].Space Weather-the International Journal of Research & Applications,2008, 6(S07005): 1-11.
[5] 李冰, 王泽忠, 刘恪, 等.特高压变压器直流偏磁对绕组电流的影响[J].电工技术学报, 2020, 35(7):1422-1431.Li Bing, Wang Zezhong, Liu Ke, et al.Research on winding current of UHV transformer under DC-bias[J].Transactions of China Electrotechnical Society, 2020,35(7): 1422-1431.
[6] 王泽忠, 李明洋, 宣梦真, 等.单相四柱式变压器直流偏磁下的温升试验及仿真分析[J].电工技术学报, 2021, 36(5): 1006-1013.Wang Zezhong, Li Mingyang, Xuan Mengzhen, et al.Temperature rise test and simulation of single- phase four-column transformer under DC-bias[J].Transactions of China Electrotechnical Society, 2021, 36(5): 1006-1013.
[7] 李冰, 王泽忠, 刘海波, 等.直流偏磁下500 kV 单相变压器振动噪声的试验研究[J].电工技术学报,2021, 36(13): 2801-2811.Li Bing, WangZezhong, Liu Ke, et al.Research on winding current of UHV transformer under DC-bias[J].Transactions of China Electrotechnical Society, 2021,36(13): 2801-2811.
[8] 刘连光, 秦晓培, 葛小宁.基于U-I 曲线的单相自耦变GIC 无功损耗算法[J].电力自动化设备, 2015,35(12):55-59.Liu Lianguang, Qin Xiaopei, Ge Xiaoning.GIC reactive power loss calculation based on U-I curve for single-phase autotransformer[J].Electric Power Automation Equipment, 2015, 35(12): 55-59.
[9] 刘连光, 钱晨, 朱溪, 等.应用K 值算法的甘肃电网 GIC-Q 扰动计算[J].电网技术, 2016, 40(8):2370-2375.Liu Lianguang, Qian Chen, Zhu Xi, et al.Calculation of geomagnetically induced currents reactive power loss disturbance in Gansu grid with parameter K[J].Power System Technology, 2016, 40(8): 2370-2375.
[10] 刘连光, 钱晨, 秦晓培.考虑500 kV 影响的特高压电网 GIC-Q 扰动计算[J].中国科学: 技术科学,2016, 46(11): 1146-1156.Liu Lianguang, Qian Chen, Qin Xiaopei.Calculation of geomagnetically induced currents reactive power loss disturbance in China’s UHV power grid considering the influence of 500 kV power grid[J].Sci Sin Tech, 2016, 46(11): 1146-1156.
[11] Gerin-Lajoie L, Haddadi A, Rezaei-Zare A, et al.Simultaneous DC and AC simulation of GMD impacts in a power systemin[C]//International Conference on Power Systems Transient(IPST), Perpignan, France,2019: 1-6.
[12] Shetye K S, Overbye T J.Parametric steady-state voltage stability assessment of power systems using benchmark scenarios of geomagnetic disturbances[C]//Power and Energy Conference at Illinois (PECI),Champaign, America, 2015: 1-7.
[13] Risto Pirjola.Calculation of geomagnetically induced currents (GIC) in a high-voltage electric power transmission system and estimation of effects of overhead shield wires on GIC modeling[J].Journal of Atmospheric and Solar-Terrestrial Physics, 2007,69(12): 1305-1311.
[14] 郑宽.大电网地磁感应电流影响因素及建模方法研究[D].北京: 华北电力大学, 2014.
[15] 刘春明.中低纬电网地磁感应电流及其评估方法研究[D].北京: 华北电力大学, 2009.
[16] 秦晓辉, 郭强, 周勤勇, 等.一种无功平衡与临界潮流快速分析方法及其在特高压可控高抗需求分析中的应用[J].中国电机工程学报, 2013, 33(19):14, 102-110.Qin Xiaohui, Guo Qiang, Zhou Qinyong, et al.Fast analysis method of reactive power balancing and critical power flow and application to study controllable shunt reactors requirement in UHV grid[J].Proceedings of the CSEE, 2013, 33(19): 14,102-110.
[17] 王泽忠, 黄天超.变压器地磁感应电流-无功功率动态关系分析[J].电工技术学报, 2021, 36(9): 1948-1955.Wang Zezhong, Huang Tianchao.Analysis of geomagnetically induction current-reactive power dynamic relationship of transformer[J].Transactions of China Electrotechnical Society, 2021, 36(9): 1948-1955.
[18] 刘连光, 朱溪, 王泽忠, 等.基于K 值法的单相四柱式特高压主体变的GIC-Q 损耗计算[J].高电压技术, 2017, 43(7): 2340-2348.Liu Lianguang, Zhu Xi, Wang Zezhong, et al.Calculation for reactive power loss of single-phase four limbs UHV main transformer due to geomagnetically induced currents with parameter K[J].High Voltage Engineering, 2017, 43(7): 2340-2348.
[19] Blake S P, Gallagher P T, McCauley J, et al.Geomagnetically induced currents in the Irish power network during geomagnetic storms[J].Space Weather, 2016, 14(12): 1-48.
[20] Viljanen Ari, Pirjola Risto.Influence of spatial variations of the geoelectric field on geomagnetically induced currents[J].Journal of Space Weather and Space Climate, 2017, 7(A22): 1-10.