0 引言
为实现“碳达峰、碳中和”目标，我国正在构建以新能源为主体的新型电力系统[1]。为了充分发挥区域风-光资源禀赋，促进可再生能源消纳，电网出现了新能源汇集后经柔性直流（Voltage Source Converter Based High Voltage Direct Current, VSCHVDC）送出的输电系统（简称送出系统）[2]，常见于海上风电[3]及沙戈荒新能源基地等，是新型电力系统中的典型形态之一。
当新能源汇集距离增加、容量增大，交流系统电压支撑能力相对变弱[4]，可能诱发电压失稳与振荡稳定问题，成为了制约新能源外送水平的主要瓶颈[3]。现有研究多基于简化后的新能源场站与VSCHVDC 互联系统来分析该类稳定问题的主要影响因素。例如，文献[5]与文献[6]基于时域状态空间法分别研究了直驱风电、双馈风电场与VSC-HVDC 互联系统的主导特征值轨迹，结果表明振荡特性与电网运行方式强相关，风电场馈入断面的传输功率与风电并网距离越大，系统振荡风险也越大。此外，送出系统动态特性由新能源变流器与 VSC-HVDC全电力电子控制主导，对送出系统安全稳定运行也构成了全新挑战。例如，文献[7]分析了VSC-HVDC交流电压控制和风机锁相环控制之间相互耦合而引发的振荡风险；文献[8]讨论了优化VSC-HVDC 控制以提升系统稳定性。
在分析包含多新能源场站的大系统时，一般需依据电磁暂态仿真进行详细计算。鉴于主导稳定问题表现出与新能源馈入断面传输极限强相关的特征，电网规划和设计阶段常通过短路比（Short-Circuit Ratio, SCR）评估系统电压支撑强度[9]（后文简称系统强度），从宏观上认知系统动态特性，进而快速获知给定运行方式下的稳定裕度，筛选出失稳风险较高的情形。已有多种短路比指标应用于大规模新能源接入后的系统强度评估。例如，文献[10]基于短路比提出了计及非同步机电源作用的电压刚度指标，从物理上表征稳态运行时的电网强弱；文献[9]提出了新能源多场站短路比指标，并依据潮流方程计算短路比临界值，但该临界值会随电网的变化而剧烈波动，难以确定客观的标准值；文献[11]计及了新能源动态特性对稳定性的影响，从小扰动稳定性的角度提出了广义短路比指标。
然而，现有短路比计算是以同步机提供短路容量或电压支撑为前提，而新能源基地经VSC-HVDC送出场景具有无常规同步电源支撑的特点，现有评估方法在送出系统中的适用性尚不明晰。如何利用系统强度快速获知给定运行方式下系统的稳定裕度缺乏体系化方法，这为电网规划运行与海量新能源的控制协调带来困扰。
为此，本文从小扰动角度聚焦送出系统强度评估问题，首先通过分析送出系统电压动态响应，阐述了系统强度与稳定性之间的关系（若无特殊说明，本文所讨论的稳定性指静态电压稳定性与锁相环带宽内的小扰动同步稳定性）；然后类比了送端VSCHVDC 与同步机的电压源等值阻抗特性，从多端口电流-电压网络灵敏度的角度将广义短路比指标推广到全电力电子送出系统，提出了该系统广义短路比及其临界值计算方法，进而实现了强度量化评估；最后利用多风电场站经柔性直流送出系统的算例验证了方法的有效性。
1 问题描述
1.1 系统强度评估需求
考虑如图1 所示的新能源基地经VSC-HVDC送出系统。图中，送端柔直换流站（简称送端VSCHVDC）工作在整流状态以实现新能源功率经直流外送，同时为交流电网稳定运行提供电压-频率支撑；新能源基地内包含多个风光新能源场站，其中新能源变流器采用锁相环跟网型控制。
图1 新能源基地经VSC-HVDC 换流站送出系统示意图
Fig.1 Diagram of sending-end renewables delivery system with VSC-HVDC
现有研究表明，跟网型新能源并网发电受到与馈入断面强相关的静态电压稳定和小扰动同步稳定制约，必须适应当前系统强度[12]，否则存在振荡等稳定风险。因此，从保障新能源并网安全稳定的需求出发，有必要准确度量当前送出系统强度水平。
另一方面，基于短路比的系统强度评估能快速表征系统运行点的存在性及稳定性，提供工程实用化参考。短路比小于其临界阈值时即表明当前系统强度低、失稳风险高[13]。基于短路比的系统强度评估具有简单直观的优势。因此，从快速获知运行点稳定裕度的工程需求出发，有必要构建送出系统强度评估方法。
1.2 短路比思路的可扩展性问题
目前基于短路比指标的强度评估依赖同步机提供短路电流/容量的假设前提[14]。尽管一些学者还提出了根据电压变化量的短路比算法[9]，但仍基于短路计算中的同步机电网等值模型。例如，新能源单机无穷大系统中，并网母线处的SCR 须通过计算电网中同步机电源提供的短路电流水平，比较交流系统短路容量Sshort 与所接入设备容量SB 得到
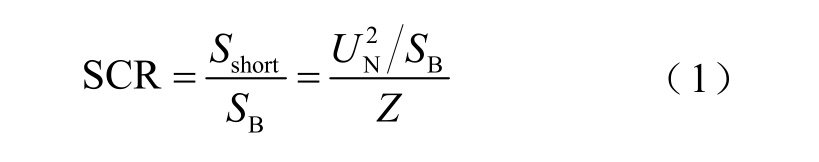
式中，UN 为母线额定电压；Z 为电网等值阻抗。
从短路计算的角度看，图1 所示的新能源基地经VSC-HVDC 送出系统呈现全电力电子特征，不存在同步机电源提供短路电流；而且电力电子设备控制切换、限幅等非线性因素导致送出系统中短路电流的性质复杂[10]，这使得送出系统强度难以通过式（1）的短路比方法简单易行地评估，快速量化稳定裕度也存在挑战。
然而，短路比本质上是由阻抗或导纳反映的一种灵敏度。如式（1）所示，短路比等价于折算到设备容量基准下电网等值阻抗的倒数[11]，描述的是新能源并网母线到电网等效电压源母线之间的相对电气距离：短路比越大，相对电气距离越近，并网点处受电压源的支撑作用越强，母线电压受到馈入电流的影响越不灵敏。传统短路比与同步机短路容量相关联则是因为短路电流恰好反映了该灵敏度[15]。因此，从灵敏度视角看，基于短路比的评估思路可以推广到无同步机支撑的全电力电子系统。由此引出如下问题：如何将短路比的思路推广到送出系统强度评估，并用于快速分析和量化送出系统静态电压稳定与小扰动同步稳定裕度?
2 灵敏度视角下送出系统强度描述
为了回答上述问题，本节首先刻画受扰母线电压对多新能源场站馈入电流的灵敏度关系，阐明受扰后母线电压响应与系统稳定性之间的定性关系。
2.1 送出系统动态建模
图1 所示的新能源基地VSC-HVDC 送出系统在受到小扰动后，其动态可通过系统内各元件的线性化方程来描述。为了便于表示受扰后的母线电压响应，采用频域阻抗/导纳传递函数建模。
送出系统闭环框图如图2 所示。在全局同步旋转xy 坐标系下，可以建立图2 中以扰动电流为输入变量、母线电压为输出变量的闭环系统模型。图2中，ΔIper 表示装备并网母线处并联叠加的小扰动电流向量，ΔVxy 表示装备并网母线电压微增量，ΔIxy 表示装备并网端口馈入电流微增量，YNET(s)表示交流网络导纳传递函数矩阵，YPE(s)表示送端 VSCHVDC、新能源场站等电力电子装备的导纳传递函数矩阵，YCIG(s)为新能源单机设备的2×2 维导纳传递函数矩阵，YVSC-HVDC(s)为端口2×2 维导纳传递函数矩阵，其详细表达式与推导见附录。以下具体介绍各传递函数矩阵的解析表达式。
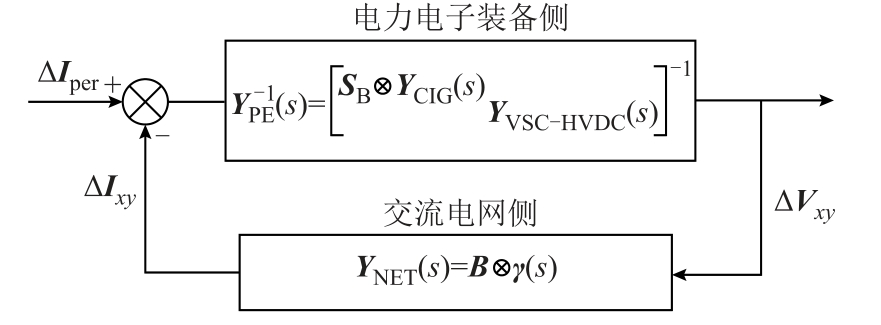
图2 送出系统闭环框图
Fig.2 Closed-loop diagram of a sending-end system
2.1.1 交流电网模型
图2 中网络导纳传递函数矩阵YNET(s)表示了一定假设条件下[11]各装备馈入电流与母线电压之间的多端口灵敏度关系，有
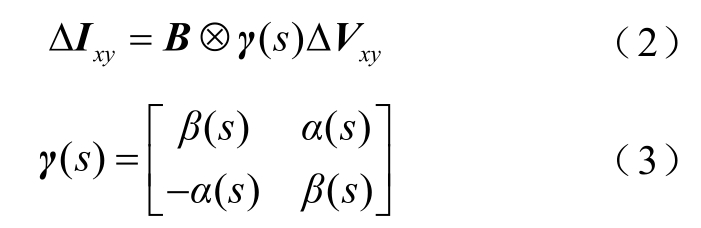
其中
值得一提的是，式（2）中的交流电网模型是通用的，不局限于特定的送出系统拓扑结构，比如链式、干线式等[5]，这使分析结果能适应未来更加多样的新能源送出系统拓扑。
2.1.2 送端VSC-HVDC 及新能源基地导纳模型
图2 中导纳传递函数矩阵YPE(s)包含多新能源场站和送端VSC-HVDC 动态，下面依次介绍。
参考文献[5,16]，送端VSC-HVDC 并网电路及控制结构如图3 所示。系统内新能源发电功率输送到汇流母线后，经升压变压器至送端VSC-HVDC；送端VSC-HVDC 采用定电压-定频率（V-f）控制结构，并由电压-电流双闭环控制维持网侧交流电压为额定值。图3 中，Lac 为换流电感，Cf 为交流滤波器等效电容，LT 为升压变压器漏感。Vabc 和Iabc 分别为送端VSC-HVDC 汇流母线电压与输出电流，Vcabc和Icabc 分别为网侧电压和电流，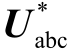 
为换流器期望的输出电压。考虑受端换流站对直流电压控制作用较强，其通过直流环节对送端交流系统稳定性的影响小[5]，故图3 中用直流电压源替代和简化。此外，本文重点关注的是弱系统下送端VSC-HVDC 与新能源的交互作用而非它的内部动态，为简便，采用两电平建模。
图3 VSC-HVDC 送端换流站并网电路及控制结构
Fig.3 Grid-connected circuit and control structure of VSC-HVDC sending-end station
结合图3 推得从汇流母线看进去的送端VSCHVDC 导纳传递函数模型为
为了简洁起见，后续推导过程省略下标n+1。
关于风电、光伏等新能源建模，已有大量文献讨论这些变流器接口发电设备（Converter-Interfaced
Generator, CIG）的动态模型，后文采用文献[17]中导纳传递函数模型。另外，不失一般性，考虑系统内所有新能源发电设备同构，新能源场站与单个设备的动态特性相似[7]，即每个新能源场站按照容量倍乘原则等效为单机设备，进而n 个新能源场站的导纳传递函数矩阵为
式中，SB 为容量比矩阵，SB=diag(SBj)，对角元SBj 记为第 j 个新能源场站额定容量与系统基准容量之比，基准容量取送端VSC-HVDC 的额定容量；Δ IGxy和 ΔVG xy 分别为新能源场站端口电流、电压向量，
2.2 稳定性与送出系统强度的定性关系
系统强度是描述系统电压响应性能的定性概念。根据频域理论[18]，受扰后各装备并网母线电压作为输出变量，能反映图2 所示送出系统的闭环稳定性，即稳定性通过系统强度来定性反映。为了避免母线电压出现大幅跌落或剧烈振荡等系统强度不足的现象[14]，系统的静态电压稳定性与小扰动稳定性应被保证且留有一定裕度。
具体地，小扰动稳定性由式（6）中的主导特征值决定，本文聚焦于跟网型新能源设备锁相环带宽内的次/超同步振荡模式；静态电压稳定性是小扰动稳定性在s=0 处的特例，即关注系统的工频特性[11]。它们都属于结构稳定或特征值问题，故分析模型在数学上可用式（6）统一描述。
式中，det{·}为求矩阵行列式函数。
值得一提的是，关注新能源接入前后母线电压的升降也是一种工程上对系统强度的认识。但电压升降仅影响工频电路求解，由此引申出的系统强度认识仅与静态稳定性相关，难以反映电力电子设备多时间尺度动态环节影响下的小扰动稳定性。
3 基于广义短路比的送出系统强度评估
本节基于上述对系统强度的定性认识，将广义短路比理论推广到送出系统中，进而提出送出系统强度量化方法。
3.1 送出系统广义短路比
3.1.1 送端VSC-HVDC 电压源等值分析
考虑到送端VSC-HVDC 发挥了类似于同步机在传统电力系统中的电压支撑作用[10]，本小节类比同步机经典等效电路，提出适用于静态电压稳定与小扰动同步稳定分析的送端VSC-HVDC 等值方法，以简化系统强度评估。
受扰下送端VSC-HVDC 的电压支撑作用取决于主电路与双闭环控制参数，通过受控电压源与等效阻抗串联的电路方程反映，即
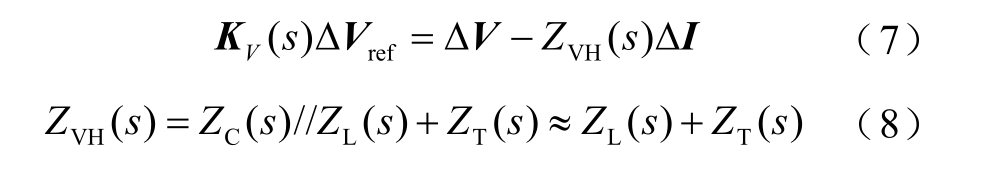
式中，ΔV、ΔI 分别为汇流母线处的正序电压和正序输出电流动态，ΔV=ΔVx +jΔVy，ΔI=ΔIx +jΔIy；KV(s)为电压控制参考相关的传递函数，小扰动下有ΔVref=ΔVdref+jΔVqref=0，故式（7）等式左侧视为受控电压源项；ZVH(s)为送端VSC-HVDC 正序阻抗传递函数，由容性滤波器阻抗传递函数ZC(s)、升压变电抗传递函数ZT(s)及包含双闭环电压控制的阻抗传递函数ZL(s)串并联组成，详细表达式见附录。
上述序阻抗模型建立于同步旋转坐标系[19]，与静止坐标系下的经典序阻抗仅在频率上相差基频，稳定分析结果等价。同时，基于正序阻抗的分析在所关注的频段内一般是有效的[20]，而且送端VSCHVDC 的正、负序阻抗之间对称解耦，依据正序阻抗传递函数ZVH(s)也可知负序阻抗形式，故以下主要讨论正序阻抗。
注意到，在所关注的次/超同步振荡问题对应的频段内，即同步旋转坐标系下0～100 Hz 频段，送端VSC-HVDC 阻抗ZVH(s)具有以下特点：首先，并联容抗项 ZC(s)通常对高频影响大，该频段内可忽略，ZVH(s)由ZT(s)+ZL(s)的串联阻抗主导；其次，ZT(s)+ZL(s)阻抗频域曲线尽管由于控制作用呈现非线性，但整体表现出电感/电抗的特性。不同控制参数集下送端VSC-HVDC 阻抗频域特性如图4 所示，电压-电流环控制参数集及相应的等值电感见表1，其余参数不作变动见附录附表1。
附表1 送端VSC-HVDC 控制参数
App.Tab.1 Parameters of VSC-HVDC in sending-end system
参 数 数 值送端柔直额定有功功率/MW 240额定汇流母线电压/kV 220额定直流母线电压/kV ±320升压变压器漏感LT(pu) 0.107换流电感Lac(pu) 0.05交流滤波器电容Cf(pu) 0.04定电流内环PI 参数 KPI=0.8, KII =12定交流电压外环PI 参数 KPV=6, KIV=10
表1 四种VSC-HVDC 控制PI 参数集及相应的等值电感
Tab.1 Four VSC-HVDC control PI parameter sets and corresponding equivalent inductance values
参数集电压外环PI(KPV, KIV)电流内环PI(KPI, KII)等值电感Leq(pu)1 (6, 10) (0.8, 12) 0.114 2 (3, 10) (0.4, 20) 0.135 3 (3, 50) (0.3, 12) 0.144 4 (2, 50) (0.3, 20) 0.164
图4 不同控制参数集下送端VSC-HVDC 阻抗频域特性
Fig.4 Frequency domain characteristics of impedance of VSC-HVDC under different parameters
根据送端VSC-HVDC 交流侧阻抗的以上特征，可利用等值电感/电抗近似该频段内的阻抗特性。首先，假定等值电抗解析式为
式中，Leq 为待定的等值电感参数。
然后，令s=jω，依据阻抗扫频结果近似获取等值电感的过程，可描述为一个具有不等式约束的最小二乘问题，即
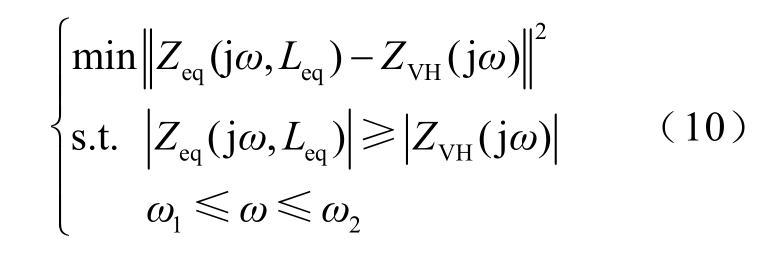
式中，ω1 和ω2 构成的频率区域是潜在振荡频率ωc的邻域，振荡频率满足ωc∈(ω1,ω2)。在振荡频率附近所得的等值结果一般较准确[20]，但如何获取潜在振荡频率并不是本文讨论的重点，故这里取ω1=0 和ω2=2 ω0 来覆盖所关注的0～100 Hz 频段，之后的仿真算例验证了这种扩大分析区间的做法误差较小。此外，约束条件中要求等值电感幅值是实际阻抗幅值的上界，使保证等值结果应用于后续系统强度评估时具备一定鲁棒性[18]。
按照上述等值方法，表1 中各参数集下的等值电感可依次求出。例如，参数集4 对应的等值电抗频域特性如图4 虚线所示，等值电感为Leq=0.164(pu)，其余参数集下的等值结果总结在表1 中。值得一提的是，由于等值电感是线性元件，送端VSC-HVDC交流侧阻抗等值方法在数学上可看作是其分段线性化结果，在一定范围内由低阶的动态环节近似高阶模型以简化分析。
需要说明的是，所提出的等值方法主要关注送端VSC-HVDC 双闭环电压控制的影响，但实际送端柔直内部动态复杂，包含多种控制环节，这使得其阻抗特性更加多变，不一定呈现感性。尽管基于线性化的等值方法仍可以实施，但需要考虑等值结果与实际阻抗之间的误差，此时一种有效的思路是将该误差视作模型不确定性，从鲁棒稳定的角度保证等值结果的可靠性[21]。
从物理意义上看，送端VSC-HVDC 等值模型可类比于考虑励磁控制的同步机经典模型。对于同步机，根据励磁绕组磁链恒定的假设可以导出利用同步电抗或暂态电抗描述的同步机经典模型[22]，在计入自动电压控制（Automatic Voltage Regulator, AVR）动态后，改变励磁磁链以控制机端电压，此时等值电抗随AVR 控制参数而变化；考虑双闭环电压控制的送端VSC-HVDC 等值模型（如图5 所示）也具有这样的特点，每一组电压控制参数对应于一个等值电感值，反映了等效电压源到送端VSC-HVDC 交流侧汇流母线处的电气距离，等值电感值越小表示电气距离越近，送端VSC-HVDC 控制对汇流母线处电压支撑作用越强。
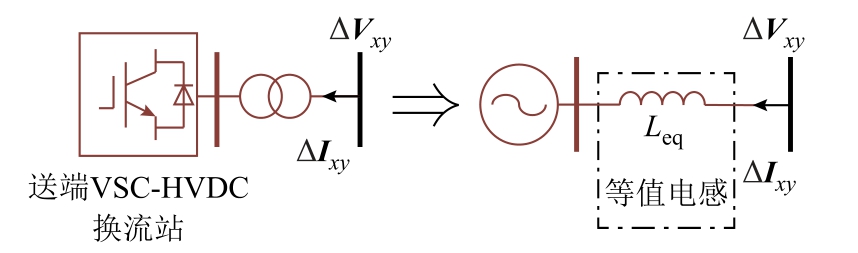
图5 送端VSC-HVDC 换流站等值模型
Fig.5 Equivalent modeling of VSC-HVDC sending-end station
综上所述，等值模型可反映静态/动态过程中送端VSC-HVDC 的外特性，可根据所关注的稳定性问题选择相应的等值模型。
1）小扰动同步稳定性分析。在送出系统振荡频率ωc 附近，利用所提方法计算等值电感Leq 或等值电抗Zeq(s)，其大小与送端VSC-HVDC 双闭环电压控制特性密切相关，反映了受扰后送端VSC-HVDC的动态电压支撑。
2）静态电压稳定性分析。静态时送端 VSCHVDC 控制实现定电压目标，故零频处（ω=0）的等值电抗等于升压变压器漏电抗XT=ω0LT，等值电感Leq=LT。
3.1.2 广义短路比计算
静态或小扰动分析中，系统动态方程经线性化后，电压源母线（电路上等价为无穷大电压母线）动态为零，视为接地[11]，故图5 中的送端VSC-HVDC等值电感作为对地支路可归入电网侧，即电网的节点导纳矩阵B 修正为
式中，Bii 为导纳矩阵B 的第n+1 个对角元素，对应送端VSC-HVDC 所接入的第n+1 个汇流母线；Beq为送端VSC-HVDC 等值电感的电纳，Beq=1/(ω0Leq)，位于对地支路，用于分析静态电压稳定性或小扰动同步稳定性分析等值电感值不同，修正节点导纳矩阵时应按3.1.1 节方法选取； Bii′为修正后节点导纳矩阵 B′∈R( n+1)×( n+1)的对角元素。
基于网络导纳的修正，式（6）中的送出系统可进一步通过特征方程等价变换解耦为n 个新能源单机无穷大系统。
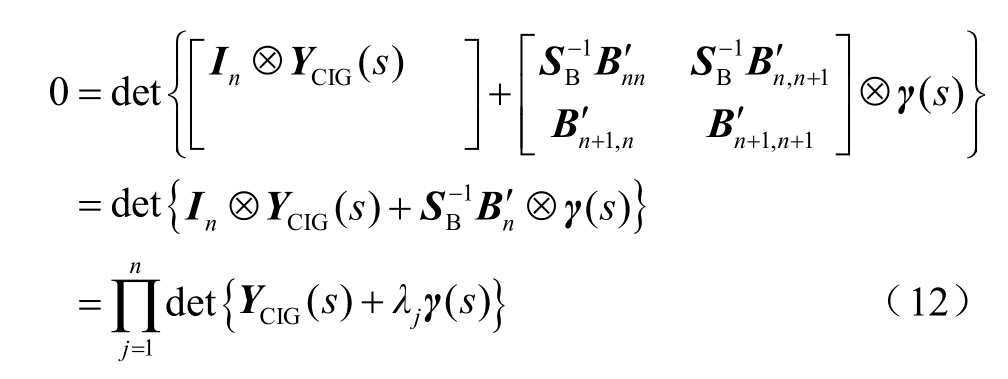
由式（11）、式（12）可知，送出系统中各新能源并网母线到电网中等效电压源母线间的电气距离可以转换为在模态坐标下量化n 个新能源单机到等效电压源的电气距离，如图6 所示。特别地，图6所示的系统稳定性取决于矩阵最小特征值λ1对应的单机子系统[11]，其物理意义是新能源单机经由最低短路比λ1 的电网并入等效电压源母线，该并网设备到电压源母线之间的电气距离最远也最容易失稳。根据文献[15]，该短路比λ1 是量化系统强度的关键参数，是广义短路比（generalized Short-Circuit Ratio,gSCR）在送出系统中的推广。
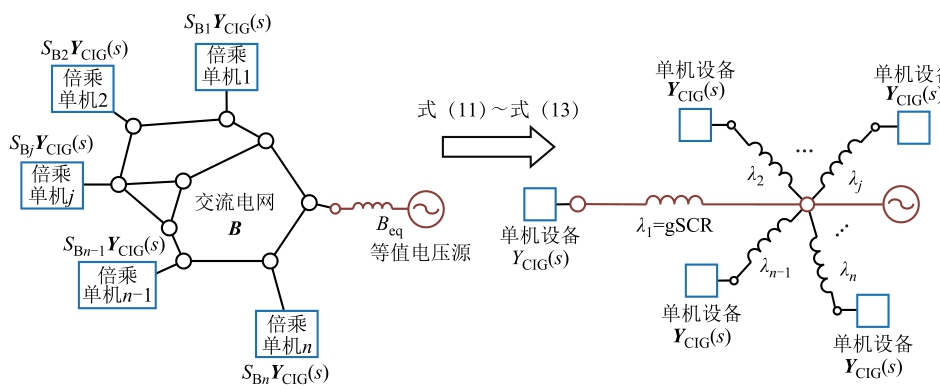
图6 送出系统的广义短路比导出示意图
Fig.6 Derivation of gSCR for sending-end system
广义短路比：矩阵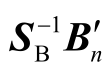
的最小特征值与gSCR[11]具有相同的数学性质和物理意义，表示为
式中，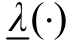
与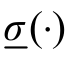
分别为矩阵的最小特征值与奇异值。
与现有短路比方法相比，式（13）中的广义短路比不依赖短路分析计算，而是根据多端口电压对电流的灵敏度与矩阵理论将gSCR 推广应用到送出系统，反映了新能源并网母线到电网等效无穷大母线间的综合电气距离。同时，gSCR 可计及送端VSC-HVDC快速控制响应造成的静态/动态电压支撑特性，为下一步基于gSCR 快速量化系统静态电压稳定与小扰动稳定裕度提供理论基础。
3.2 送出系统强度源-网分离评估方法
为了使基于广义短路比的系统强度评估能够反映系统稳定裕度，如何确定系统临界失稳下的送出系统临界广义短路比（Critical generalized Short-Circuit Ratio, CgSCR）是系统强度评估的关键环节。对于跟网型新能源单机系统，存在最小的电网短路比SCR0 以保证新能源设备接入后恰好适应电网而不失稳，称之为设备临界短路比[15]。设备临界短路比SCR0 反映了新能源设备对弱电网的耐受能力。由3.1 节可知，送出系统与最弱单机系统稳定性等价，物理上对应CgSCR 恰好达到单机设备临界短路比SCR0 时，送出系统发生静态电压失稳或小扰动同步失稳，即CgSCR 满足
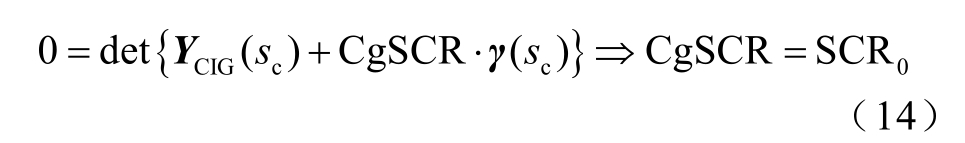
式中，sc 为系统振荡失稳时的主导特征值，sc=jωc，静态电压失稳时sc=0。
因此，系统强度评估可通过源-网分离实现：结合基于电网信息导出的广义短路比（gSCR）与新能源设备临界短路比（CgSCR=SCR0）判别系统稳定性及稳定裕度。若gSCR＜CgSCR 则表明系统存在失稳风险；若gSCR≥CgSCR 则判定系统稳定，且数值越大说明稳定裕度越大。进一步地，考虑工程应用中一般需要留取足够的裕度以远离失稳边界，可定义gSCR 和SCR0 的相对值β%为裕度指标，定量地构建系统强度判据。
系统强度判据：裕度指标β%可量化送出系统强度能否足以保证送出系统的静态电压稳定性或小扰动同步稳定性。例如，需保留至少20%的裕度时，系统强度的β%值应满足
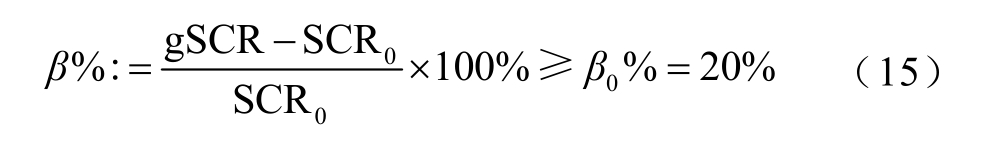
或
上述系统强度评估可从源-网侧分离开展，而后将结果综合，有利于简化系统层面的稳定性分析流程。式（15）或式（16）中的gSCR 和CgSCR 可分别获取：gSCR 取决于交流电网、送端VSC-HVDC等值电感参数与新能源设备容量等参数；CgSCR 等于新能源设备临界短路比SCR0，其大小取决于设备自身控制参数，易通过设备厂家解析计算或仿真测试获得。实现源-网分离的好处还在于明确了系统强度的提升路径，应从增大gSCR 和降低SCR0 的角度提出优化措施[15]，以确保系统强度满足式（15）或式（16）。
需要说明的是，由于新能源场站采用单机倍乘模型简化，设备临界短路比在一定程度上反映了场站层面的动态特性[23]，但尚未考虑场站内部的辅助设备（例如，静止无功补偿器），以及风速等影响下设备运行点的差异等，这些因素使得确定场站层面的临界短路比较为困难，进而考虑上述复杂因素的送出系统强度评估方法还需深入研究。
基于广义短路比的送出系统强度评估方法流程如图7 所示。
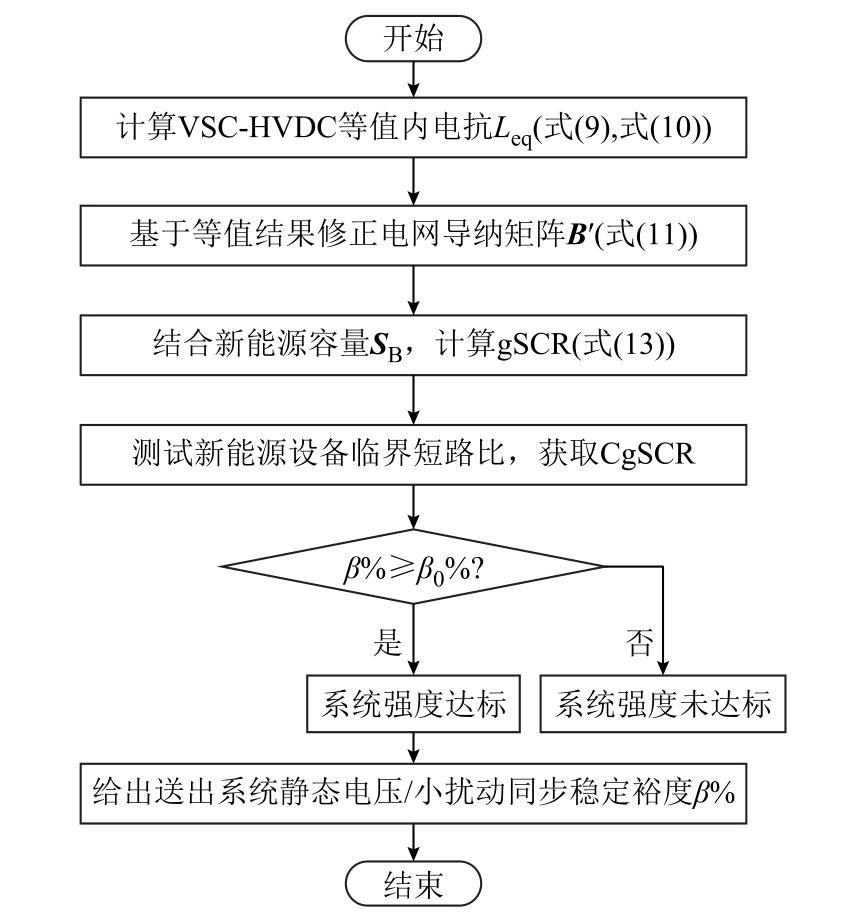
图7 基于广义短路比的送出系统强度评估方法流程
Fig.7 Flow chart of system strength assessment based on gSCR in sending-end system
1）送端VSC-HVDC 电压源等值：根据静态电压稳定性/小扰动同步稳定性分析需求，求解不同送端VSC-HVDC 控制参数下的等值电感Leq（式（9）、式（10））。
2）解析计算广义短路比：利用等值参数修正网络导纳矩阵B 为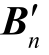 
（式（11））；结合新能源容量矩阵SB，由当前电网信息求取gSCR，即矩阵
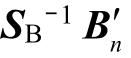的最小特征值λ1（式（13））。
3）获取临界广义短路比：CgSCR 等于新能源设备临界短路比SCR0，由已知模型解析或由新能源厂家单机并网测试得到。
4）根据广义短路比（gSCR）与临界广义短路比（CgSCR）间的相对差值β%判别送出系统强度是否满足工程需要的β0%（式（15）、式（16）），并给出当前系统静态电压稳定/小扰动同步稳定裕度β%。
3.3 方法适用场景讨论
本文所提方法可为多种场景下的系统强度评估提供一种普适思路。例如，新能源基地经弱交流同步电网送出场景中外部电网通过多端口戴维南等值，可看作是送出系统单条汇流母线等值扩展到多条母线/端口，不增加分析的复杂性；该方法也可推广到不含有无穷大母线的微电网场景中评估系统强度，这是因为送出系统可看作是一种特殊的组网型-跟网型混联系统。值得一提的是，基于系统强度评估结果还可以识别系统薄弱线路，指导组网型新能源/储能等设备优化配置[24]，实现系统精准补强。
由于所提出的方法主要关注与馈入断面强相关的小扰动同步稳定和电压稳定模态，其应用场合也有局限性，例如，由串联补偿电容参与的次/超同步振荡，以及并联补偿电容等无源滤波器参与下的谐波谐振和不稳定等与系统强度之间并没有强相关性，尚无法利用短路比分析。
4 算例分析
为了验证送出系统强度评估方法的有效性，本节针对多风电场经VSC-HVDC 送出系统进行案例分析，系统单线图如附图3 所示。该新能源基地内包含4 个等值风电场站（n=4），等值风电场由35 kV/220 kV 变压器升压后接入电网；新能源功率由输电网送至汇流母线，而后经220 kV/330 kV 升压变压器接入送端VSC-HVDC 换流站。送端VSC-HVDC参数和等值风电场参数分别见附表1 和附表2，线路参数见附表3。案例中所有直驱风机具有相同的型号与典型参数，场站模型按单机容量倍乘原则等值得到，涵盖直驱风电机组典型控制结构，直驱风机网侧变流器控制框图如附图4 所示。
附表2 风机网侧变流器控制参数（自身容量基准下）
App.Tab.2 Control parameters of grid-side inverter of wind turbine (under its own base value)
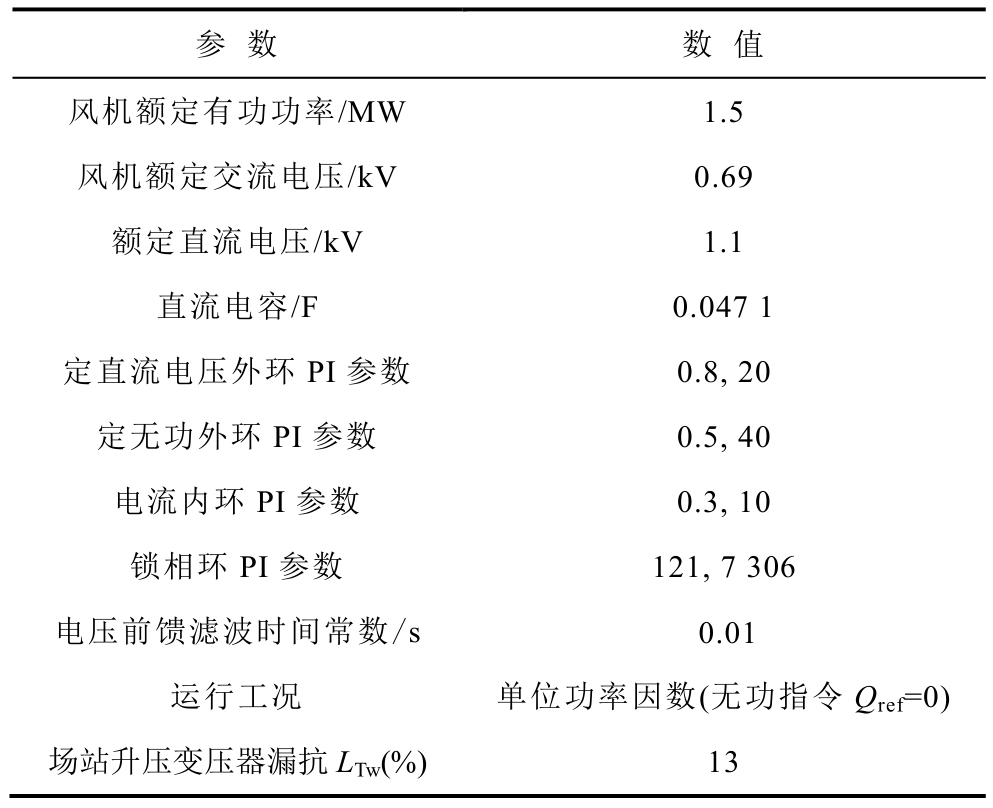
参 数 数 值风机额定有功功率/MW 1.5风机额定交流电压/kV 0.69额定直流电压/kV 1.1直流电容/F 0.047 1定直流电压外环PI 参数 0.8, 20定无功外环PI 参数 0.5, 40电流内环PI 参数 0.3, 10锁相环PI 参数 121, 7 306电压前馈滤波时间常数/s 0.01运行工况 单位功率因数(无功指令Qref=0)场站升压变压器漏抗LTw(%) 13
附表3 风电场柔直送出系统线路参数
App.Tab.3 Network data of wind farms with VSC-HVDC
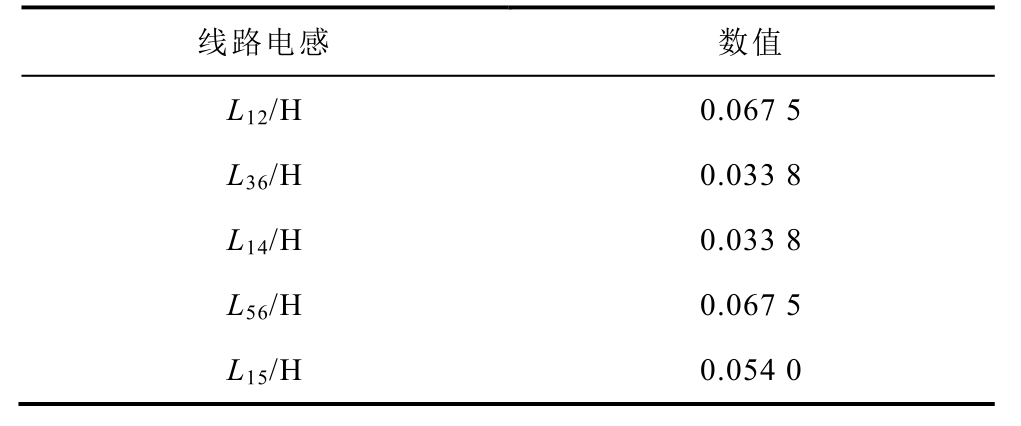
线路电感 数值L12/H 0.067 5 L36/H 0.033 8 L14/H 0.033 8 L56/H 0.067 5 L15/H 0.054 0
表2 四种算例下的系统强度评估结果
Tab.2 Results of system strength assessment in four cases
算例 Leq(pu) gSCR CgSCR=SCR0 系统强度β(%)1 0.114 3.44 3.30 4.18 2 0.135 3.23 3.30 -2.50 3 0.144 3.13 3.30 -5.12 4 0.164 2.95 3.30 -10.5
表3 四种算例下的系统主导特征值分析结果
Tab.3 Results of dominant eigenvalues in four cases
算例 Leq(pu) 主导特征值 稳定性1 0.114 -2.23±j116.7 稳定2 0.135 -0.75±j117.2 稳定3 0.144 ±j117.3 临界失稳4 0.164 1.85±j118.2 失稳
4.1 系统强度理论计算
首先，基于源-网分离的分析思路，在仿真环境中搭建具有附表2 典型参数的直驱风机单机无穷大并网系统，通过修改并网线路距离，测试直驱风机设备临界短路比为SCR0=3.30。
其次，依据第3 节表1 中的VSC-HVDC 控制参数集相应地设置四组仿真算例，其他参数不变（且各风电场站均处于额定运行工况，四组算例中稳态运行点相同）。
按照图7 所示的基于广义短路比的送出系统强度评估流程，分别计算四组算例中gSCR、CgSCR 与系统强度指标β%值，列写于表2 中（为简单起见，本节算例设置阈值β0%=0，β%≥0 表示判定系统稳定）。例如，当送端VSC-HVDC 控制参数取表1 中的参数集1，对应的等值电抗值为0.114(pu)；将其作为边界条件之一，结合网络参数和设备容量信息，计算对应的 gSCR=3.44；又知临界广义短路比CgSCR=SCR0=3.30，故β%=4.18%＞β0%=0，解析地判定当前参数下系统强度可以满足小扰动同步稳定性需求，稳定裕度为β%=4.18%。其余三组算例作类似计算。
4.2 时域仿真对比验证
对比表2 中的系统强度评估结果与后续的时域仿真结果，验证所提评估方法能否较为准确地得到送出系统强度。
表3 列出了基于时域小信号分析计算得到的四组算例中送出系统主导特征值。结果显示，送出系统在0～100 Hz 频率范围内有一对弱阻尼模态，在参数变化过程中可能出现阻尼不足，引发振荡不稳定现象，其中算例3 主导特征值阻尼比为零，系统处于临界失稳。相应地，图8 依次给出了算例1～4的电磁暂态仿真波形。四组算例均在仿真时间T=4.0 s时，在送端VSC-HVDC 接入节点处施加了2%端电压跌落作为小扰动，并且在0.02 s 后清除扰动，观察风电场1～4 的并网母线电压幅值的响应曲线：算例1 和算例2 中的振荡按照不同阻尼比衰减，算例1 的稳定裕度较大；算例3 和算例4 中的母线电压振荡持续，且算例4 中的振荡发散（振荡频率为18.7 Hz 位于锁相环带宽内），系统失稳。
图8 四种算例中风电场并网母线电压幅值时域波形
Fig.8 Voltage amplitude of grid-connected bus of each wind farm in four time-domain simulation cases
通过对比，上述时域仿真趋势与表2 中的系统强度评估结果趋势一致。系统强度指标β%值越小，主导特征值越向复平面右半部分移动，同时时域电压响应波形越容易出现振荡不稳定，系统稳定性越差。特别地，算例3 中观察阻尼比为零的等幅振荡波形，实际系统处于临界失稳状态。在该稳定边界处，系统强度的评估结果β%=-5.12%＜β0%=0，已判定为失稳，说明所提方法在稳定边界处的判定效果略有保守性。分析误差来源于送端VSC-HVDC 电压源的等值过程，但较小的误差说明所提出的系统强度评估方法可以满足工程需求。在实际应用时，有必要考虑其他不确定性因素，在评估结果的基础上增加裕度以作为工程参考。
此外，仿真结果的对比分析还显示了送出系统gSCR 对于送端VSC-HVDC 等值电感大小较为敏感，并呈现单调变化的趋势，即当等值电感大小从0.114(pu)递增为0.164(pu)时，gSCR 值从3.44 下降到2.95。这也说明了送端VSC-HVDC 的双闭环电压控制参数变化对小扰动同步稳定性的影响可从系统强度的角度来分析，应通过提升gSCR 的角度整定送端VSC-HVDC 控制参数，避免由于不合适的某些参数集导致送端VSC-HVDC 对电网支撑弱，引发振荡不稳定的情况。
5 结论
从静态电压稳定和小扰动同步稳定角度，提出了基于广义短路比的新能源基地柔性直流送出系统强度量化分析方法。主要结论如下：全电力电子送出系统仍然存在系统强度概念，与是否存在同步机电源无关，所提出的评估方法可计及受扰后柔性直流的电压支撑效果，是广义短路比在全电力电子送出系统中的推广应用；系统强度由新能源特性和电网特性共同决定，并分别由新能源设备的临界短路比与组网型直流支撑的电网广义短路比量化，其相对值可用于筛选高失稳风险的系统参数和运行方式，满足快速量化当前运行点稳定裕度的工程需求。
从新能源和柔性直流控制参数角度提升新能源基地送出系统的强度，以及评估大扰动下的系统强度将是未来的研究工作。
附 录
1.送端VSC-HVDC 阻抗/导纳推导
根据图3，送端VSC-HVDC 在dq 旋转坐标系下的交流侧线性化方程包括
式中，GI(s)为电流内环PI 控制传递函数，GI(s)=KPI+KII/s；GV(s)为交流电压外环PI 控制传递函数，GV(s)=KPV+KIV/s；Icdref 与Icqref 分别为内环电流dq 轴参考值；ΔVdref=ΔVqref=0；升压变压器电纳为YT(s)=ZT-1(s)。
联立式（A1）～ 式（A4）的动态方程，送端VSCHVDC 中控制部分的导纳传递函数矩阵Yac(s)为
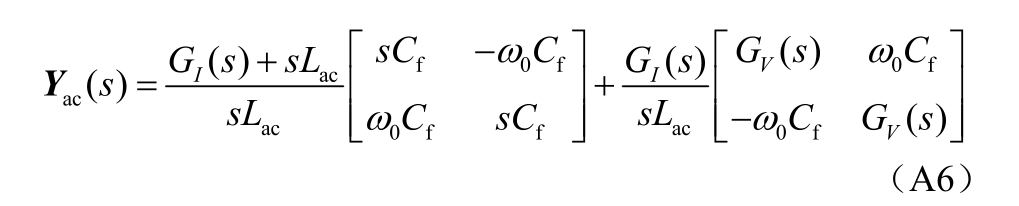
考虑到送端VSC-HVDC 控制器dq 坐标系的旋转角频率即为全局xy 坐标系的同步旋转角频率ω0=100π rad/s，式（4）中从汇流母线看进去的送端VSC-HVDC 导纳传递函数矩阵表示为
进一步地，通过线性变换将同步旋转坐标系中的dq域阻抗转换到序域[19]下，即得到式（7）中送端 VSCHVDC 从汇流母线看进去的序阻抗传递函数矩阵为
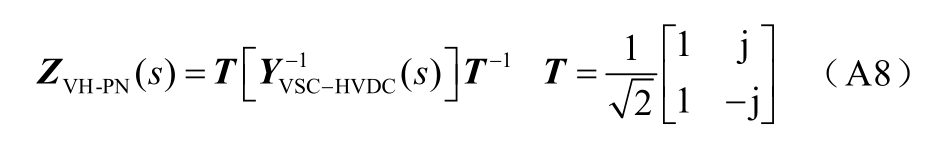
式中，ZVH-PN(s)为送端VSC-HVDC 的2×2 维序阻抗传递函数矩阵；T 为坐标变换矩阵。考虑到送端VSC-HVDC的双闭环电压控制结构是以dq 轴对称的，因此序阻抗矩阵ZVH-PN(s)具有对角形式[19]，即
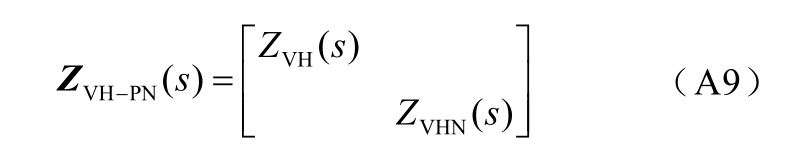
式中， Z VH( s) 与ZVHN( s) 分别为送端VSC-HVDC 正、负序阻抗传递函数。
附图1 与附图2 显示的扫频测量结果验证了式（A7）和式（A8）中导纳/阻抗解析模型的正确性。送端VSCHVDC 采用附表1 参数，其解析模型与仿真测量结果一致，证明了建模的正确性。
此外，式（A6）可写为
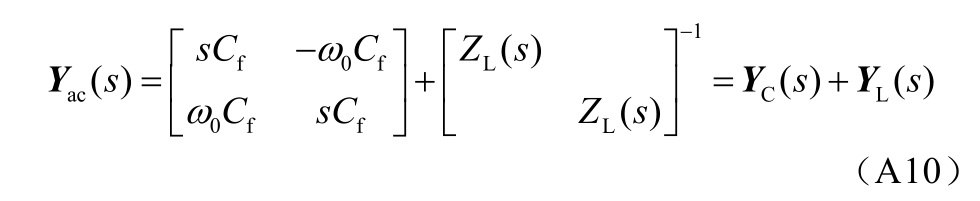
式中，
因此，式（A8）中的正序阻抗具有相应形式，有
式中，Z C ( s )为容性滤波器正序阻抗，Z C ( s ) = C f /( s + jω 0)；Z T ( s )为变压器正序电抗， Z T ( s) = ( s+ jω 0)LT 。
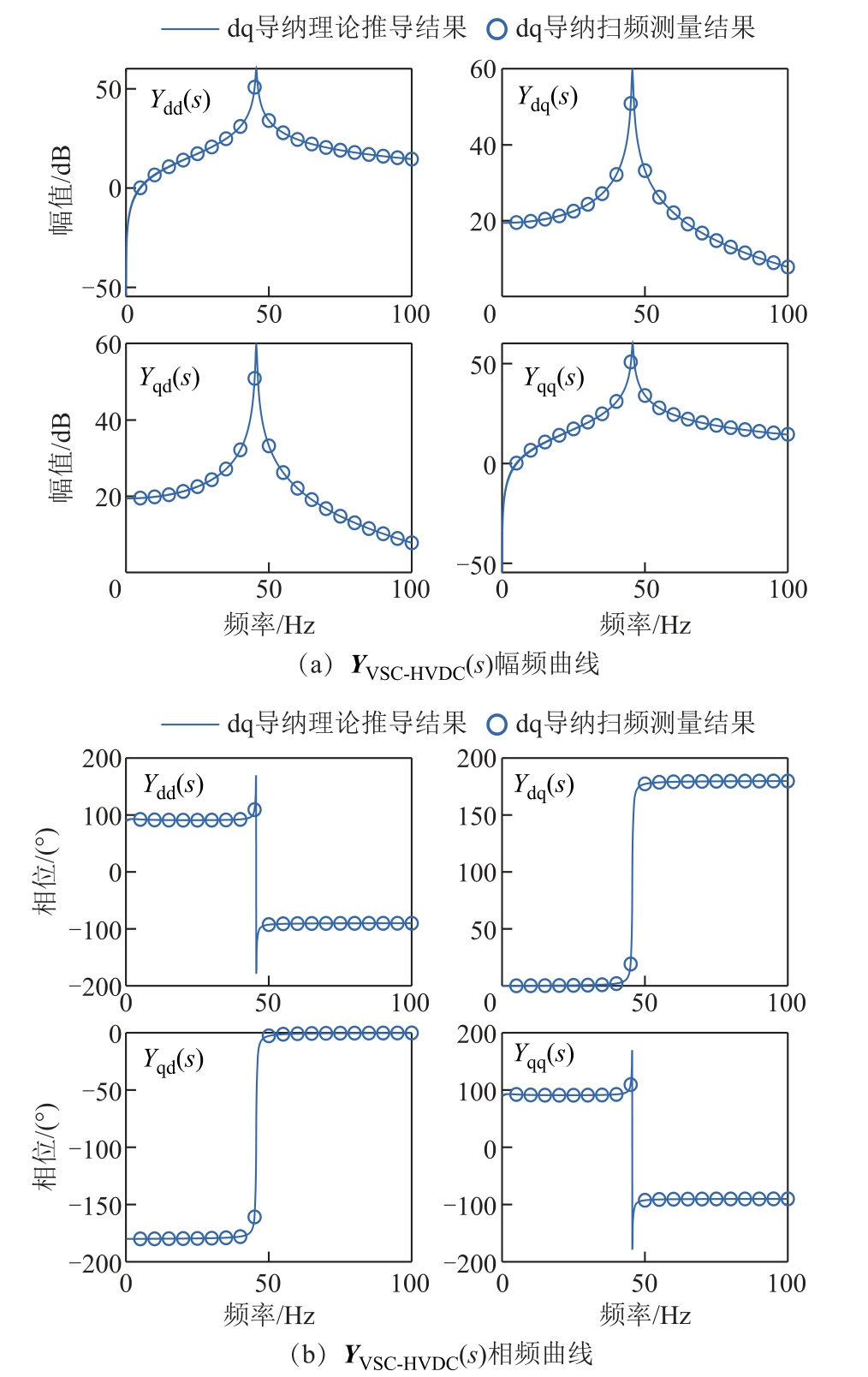
附图1 同步旋转坐标系下送端VSC-HVDC dq 域导纳频率曲线及其测量值
App.Fig.1 Frequency curves and measured values of VSC-HVDC dq-domain admittance in the synchronous rotating frame
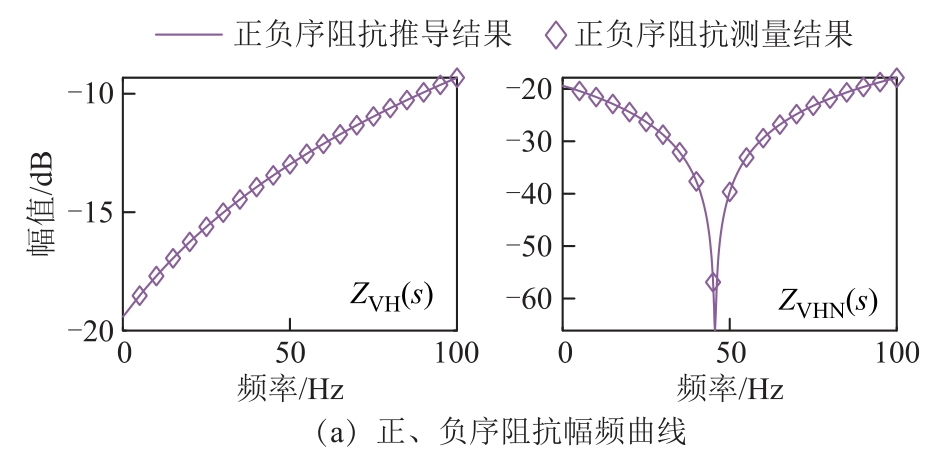
附图2 同步旋转坐标系下送端VSC-HVDC 序域阻抗频率曲线及其测量值
App.Fig.2 Frequency curves and measured values VSCHVDC sequence-domain impedance in the synchronous rotating frame
2.仿真系统参数
附图3 多风电场经柔直送出系统单线图
App.Fig.3 One-line diagram of wind plants with VSC-HVDC
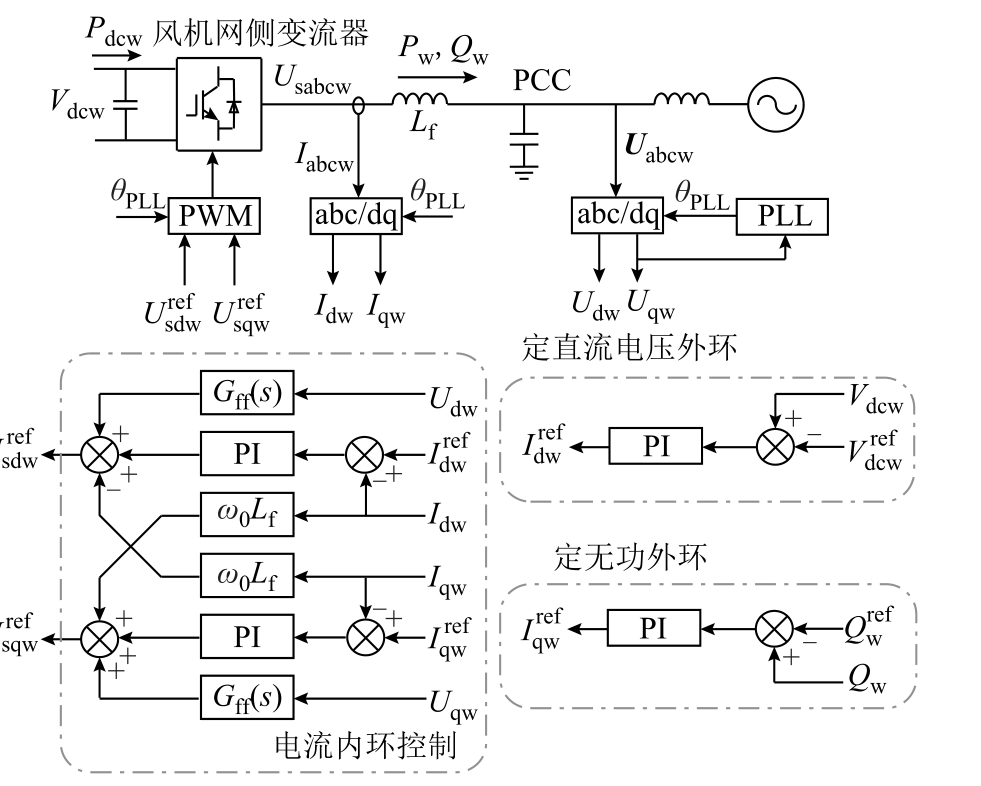
附图4 直驱风机网侧变流器控制框图
App.Fig.4 Control scheme of the grid-side inverter of the direct-drive wind turbine
[1] 舒印彪, 陈国平, 贺静波, 等.构建以新能源为主体的新型电力系统框架研究[J].中国工程科学,2021, 23(6): 61-69.Shu Yinbiao, Chen Guoping, He Jingbo, et al.Building a new electric power system based on new energy sources[J].Strategic Study of CAE, 2021,23(6): 61-69.
[2] 樊肖杰, 迟永宁, 马士聪, 等.大规模海上风电接入电网关键技术与技术标准的研究及应用[J].电网技术, 2022, 46(8): 2859-2870.Fan Xiaojie, Chi Yongning, Ma Shicong, et al.Research and application of key technologies and technical standards for large-scale offshore wind farms connecting to power grid[J].Power System Technology, 2022, 46(8): 2859-2870.
[3] Wang Weisheng, Li Guanghui, Guo Jianbo.Largescale renewable energy transmission by HVDC:challenges and proposals[J].Engineering, 2022, 19:252-267.
[4] 董文凯, 杜文娟, 王海风.弱连接条件下锁相环动态主导的并网直驱风电场小干扰稳定性研究[J].电工技术学报, 2021, 36(3): 609-622.Dong Wenkai, Du Wenjuan, Wang Haifeng.Smallsignal stability of a grid-connected PMSG wind farm dominated by dynamics of PLLs under weak grid connection[J].Transactions of China Electrotechnical Society, 2021, 36(3): 609-622.
[5] 邵冰冰, 赵峥, 肖琪, 等.多直驱风机经柔直并网系统相近次同步振荡模式参与因子的弱鲁棒性分析[J].电工技术学报, 2023, 38(3): 754-769.Shao Bingbing, Zhao Zheng, Xiao Qi, et al.Weak robustness analysis of close subsynchronous oscillation modes’ participation factors in multiple direct-drive wind turbines with the VSC-HVDC system[J].Transactions of China Electrotechnical Society, 2023, 38(3): 754-769.
[6] 王一凡, 赵成勇, 郭春义.双馈风电场孤岛经模块化多电平换流器直流输电并网系统小信号稳定性分析与振荡抑制方法[J].电工技术学报, 2019,34(10): 2116-2129.Wang Yifan, Zhao Chengyong, Guo Chunyi.Small signal stability and oscillation suppression method for islanded double fed induction generator-based wind farm integrated by modular multilevel converter based HVDC system[J].Transactions of China Electrotechnical Society, 2019, 34(10): 2116-2129.
[7] 李光辉, 王伟胜, 郭剑波, 等.风电场经 MMCHVDC 送出系统宽频带振荡机理与分析方法[J].中国电机工程学报, 2019, 39(18): 5281-5297, 5575.Li Guanghui, Wang Weisheng, Guo Jianbo, et al.Broadband oscillation mechanism and analysis for wind farm integration through MMC-HVDC system[J].Proceedings of the CSEE, 2019, 39(18): 5281-5297,5575.
[8] 马秀达, 卢宇, 田杰, 等.柔性直流输电系统的构网型控制关键技术与挑战[J].电力系统自动化,2023, 47(3): 1-11.Ma Xiuda, Lu Yu, Tian Jie, et al.Key technologies and challenges of grid-forming control for flexible DC transmission system[J].Automation of Electric Power Systems, 2023, 47(3): 1-11.
[9] 于琳, 孙华东, 赵兵, 等.新能源并网系统短路比指标分析及临界短路比计算方法[J].中国电机工程学报, 2022, 42(3): 919-929.Yu Lin, Sun Huadong, Zhao Bing, et al.Short circuit ratio index analysis and critical short circuit ratio calculation of renewable energy grid-connected system[J].Proceedings of the CSEE, 2022, 42(3): 919-929.
[10] 徐政.新型电力系统背景下电网强度的合理定义及其计算方法[J].高电压技术, 2022, 48(10): 3805-3819.Xu Zheng.Reasonable definition and calculation method of power grid strength under the background of new type power systems[J].High Voltage Engineering, 2022, 48(10): 3805-3819.
[11] 辛焕海, 董炜, 袁小明, 等.电力电子多馈入电力系统的广义短路比[J].中国电机工程学报, 2016,36(22): 6013-6027.Xin Huanhai, Dong Wei, Yuan Xiaoming, et al.Generalized short circuit ratio for multi power electronic based devices infeed to power systems[J].Proceedings of the CSEE, 2016, 36(22): 6013-6027.
[12] 吴林林, 李蕴红, 于思奇, 等.基于短路比指标的风电汇集系统稳定性分析[J].电力自动化设备,2022, 42(8): 72-78.Wu Linlin, Li Yunhong, Yu Siqi, et al.Stability analysis of dense wind power area based on short circuit ratio index[J].Electric Power Automation Equipment, 2022, 42(8): 72-78.
[13] CIGRE.Connection of wind farms to weak AC networks:CIGRE Working Group B4.62.[S].CIGRE, 2016.
[14] Taylor C W.电力系统电压稳定[M].王伟胜, 译.北京: 中国电力出版社, 2002.
[15] 周瑀涵, 辛焕海, 鞠平.基于广义短路比的多馈入系统强度量化原理与方法：回顾、探讨与展望[J].中国电机工程学报, 2023, 43(10): 3794-3811.Zhou Yuhan, Xin Huanhai, Ju Ping.System strength quantification principle and method of multi-infeed systems based on generalized short-circuit ratio:reviews, discussions and outlooks[J].Proceedings of the CSEE, 2023, 43(10): 3794-3811.
[16] 管敏渊, 徐政.向无源网络供电的MMC 型直流输电系统建模与控制[J].电工技术学报, 2013, 28(2):255-263.Guan Minyuan, Xu Zheng.Modeling and control of modular multilevel converter based VSC-HVDC system connected to passive networks[J].Transactions of China Electrotechnical Society, 2013, 28(2): 255-263.
[17] 杨超然, 宫泽旭, 洪敏, 等.外环动态影响下变流器广义阻抗判据的适用性分析[J].中国电机工程学报, 2021, 41(9): 3012-3024.Yang Chaoran, Gong Zexu, Hong Min, et al.Applicability analysis of the generalized-impedance stability criterion for converters considering the outerloop dynamics[J].Proceedings of the CSEE, 2021,41(9): 3012-3024.
[18] Skogestad S, Postelethwaite I.Multivariable Feedback Control[M].New York: Wiley Publishing, 1996.
[19] Rygg A, Molinas M, Zhang Chen, et al.A modified sequence-domain impedance definition and its equivalence to the dq-domain impedance definition for the stability analysis of AC power electronic systems[J].IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(4): 1383-1396.
[20] 孙焜, 姚伟, 文劲宇.双馈风电场经柔直并网系统次同步振荡机理及特性分析[J].中国电机工程学报, 2018, 38(22): 6520-6533.Sun Kun, Yao Wei, Wen Jinyu.Mechanism and characteristics analysis of subsynchronous oscillation caused by DFIG-based wind farm integrated into grid through VSC-HVDC system[J].Proceedings of the CSEE, 2018, 38(22): 6520-6533.
[21] Rosso R, Engelken S, Liserre M.Robust stability investigation of the interactions among grid-forming and grid-following converters[J].IEEE Journal of Emerging and Selected Topics in Power Electronics,2020, 8(2): 991-1003.
[22] 闵勇, 陈磊, 姜齐荣.电力系统稳定分析[M].北京:清华大学出版社, 2016.
[23] 李龙源, 付瑞清, 吕晓琴, 等.接入弱电网的同型机直驱风电场单机等值建模[J].电工技术学报,2023, 38(3): 712-725.Li Longyuan, Fu Ruiqing, Lü Xiaoqin, et al.Single machine equivalent modeling of weak grid connected wind farm with same type PMSGs[J].Transactions of China Electrotechnical Society, 2023, 38(3): 712-725.
[24] 吴琛, 刘晨曦, 黄伟, 等.提升新能源电力系统稳定性的构网型变流器选址定容方法[J].电力系统自动化, 2023, 47(12): 130-136.Wu Chen, Liu Chenxi, Huang Wei, et al.Siting and sizing method of grid-forming converters for improving stability of power system with renewable energy[J].Automation of Electric Power Systems,2023, 47(12): 130-136.